Frequently, someones says that some indicator variable X “explains” some proportion of some target variable, Y. What does this actually mean? By “mean” I am trying to find some intuition that “clicks” rather than citing the (well-known) formualas.

To start with, let’s load some packages and make up some random data.

library(tidyverse)

n_rows <- 100
set.seed(271828)

df <- data_frame(
  exp_clean = rnorm(n = n_rows, mean = 2, sd = 1),
  cntrl_clean = rnorm(n = n_rows, mean = 0, sd = 1),
  exp_noisy = exp_clean + rnorm(n = n_rows, mean = 0, sd = 3),
  cntrl_noisy = cntrl_clean + rnorm(n = n_rows, mean = 0, sd = 3),
  ID = 1:n_rows)

Here, we drew 100 cases from the population of the “experimental group” (mue = 2) and 100 cases from the control group (mue = 0). We will investigate the effect of noise on our data. So for both groups we make up noisy data: We just add some random noise on the existing data.

To easily plot the data, it is useful to “gather” or “melt” the data from wide to long format.

df_long <-
  df %>%
  gather(key = group, value = value, -ID) %>% 
  separate(col = group, into = c("group", "noise_level"), sep = "_")

Summary data

It is useful to put some summary data in its own dataframe in a structured way:

df_sum <-
  df_long %>%
  group_by(group, noise_level) %>%
  summarise(value_mean = mean(value)) %>% 
  ungroup

knitr::kable(df_sum)

Clean data vs. noisy data

For plotting purposes, it will be handy to have the group means in the main dataframe:

df_sum_noise_level <-
  df_sum %>% 
  select(-group) %>% 
  group_by(noise_level) %>% 
  summarise_all(funs(mean))

knitr::kable(df_sum_noise_level)

df_long_noise_level <- df_long %>%
  left_join(df_sum_noise_level, by = "noise_level")

Joining operations basically merge two dataframes matched by some matchings columns (by argument).

Now, let’s plot the data including the mean value and the within variation.

df_long_noise_level %>% 
  ggplot +
  aes(x = ID, y = value) +
  facet_wrap(~noise_level) + 
  geom_point() + 
  geom_hline(data = df_sum_noise_level, aes(yintercept = mean(value_mean)), color = "firebrick") +
  geom_linerange(aes(ymin = value_mean, ymax = value), color = "grey80") +
  labs(title = "overall mean and variation in clean vs. noisy data") +
  coord_cartesian(ylim = c(-8,8))

We see that the the variation (the grey deviation bars) are larger in the noisy data compared to the clean data.

Now let’s compute the average length (MAD) and the variance of the grey bars.

df_long_noise_level %>% 
  group_by(noise_level) %>% 
  summarise(value_mad = mean(abs(value - mean(.$value))),
            value_var = mean(((value - mean(.$value))^2)))

## # A tibble: 2 × 3
##   noise_level value_mad value_var
##         <chr>     <dbl>     <dbl>
## 1       clean  1.163611  1.963961
## 2       noisy  2.473277  9.985220

Explaining variable

Now let’s investigate the influence of some “explaining” variable. Say, our data stems from two populations, the experimental condition and the control condtion, with differing means. Assume that the experimental condition has a mean 2 sd higher than in the control condition. Hence, the grouping variable will help to reduce the variation.

First, we compute the summary statistics and join them to the main dataframe.

df_sum_group <-
  df_sum %>% 
  select(-noise_level) %>% 
  group_by(group) %>% 
  summarise_all(funs(mean))

knitr::kable(df_sum_group)

df_long_group <- df_long %>%
  left_join(df_sum_group, by = "group")

Now, plot the data conditioned on the explaining variable, ie., the condition (experimental vs. control).

df_long_group %>% 
  ggplot +
  aes(x = ID, y = value) +
  facet_wrap(~group) + 
  geom_point() + 
  geom_hline(data = df_sum_group, aes(yintercept = value_mean), color = "firebrick") +
  geom_linerange(aes(ymin = value_mean, ymax = value), color = "grey80") +
  labs(title = "overall mean and variation in the experimental vs. control group data") +
  coord_cartesian(ylim = c(-8,8))

Practically speaking, if we measure the deviation to the respective group mean, we see that the deviation (aka, variation within each group) has decreased when considering the explaining variable.

In number parlance:

df_long_group %>% 
  group_by(group) %>% 
  summarise(value_mad = mean(abs(value - mean(.$value))),
            value_var = mean(((value - mean(.$value))^2)))

## # A tibble: 2 × 3
##   group value_mad value_var
##   <chr>     <dbl>     <dbl>
## 1 cntrl  1.777131  5.626771
## 2   exp  1.859757  6.322410

Whole picture

Now let’s compare all the four subgroups:

• clean vs. noisy data and
• data from experimental group vs. control group.

Again, we start by adding the group summaries to the main data frame for easier plotting.

df_long_all <- df_long %>%
  left_join(df_sum, by = c("group", "noise_level"))

And now we plot the 4 subgroups.

df_long_all %>% 
  ggplot +
  aes(x = ID, y = value) +
  facet_wrap(noise_level~group) + 
  geom_point() + 
  geom_hline(data = df_sum, aes(yintercept = value_mean), color = "firebrick") +
  geom_linerange(aes(ymin = value_mean, ymax = value), color = "grey80") +
  labs(title = "overall mean and variation ") +
  coord_cartesian(ylim = c(-8,8))

Similarly to the previous steps, we calculate the summary statistics for each of the 4 groups.

df_long_all %>% 
  group_by(noise_level, group) %>% 
  summarise(value_mad = mean(abs(value - mean(.$value))),
            value_var = mean(((value - mean(.$value))^2)))

## Source: local data frame [4 x 4]
## Groups: noise_level [?]
## 
##   noise_level group value_mad value_var
##         <chr> <chr>     <dbl>     <dbl>
## 1       clean cntrl  1.215744  2.090082
## 2       clean   exp  1.111477  1.837840
## 3       noisy cntrl  2.338518  9.163459
## 4       noisy   exp  2.608036 10.806981

Conclusion

Two conclusions can be drawn. First, any explaining variable will reduce the variation within the group (at least it will not increase the within group variation). This effect is what is called “the variable explains the target variable”. To the degree the deviation bars decrease in size (on overage), one can say that “explanation” occurred.

Second, any noise variable will increase the variation within the groups. This effect could be called “the variable blurs the target variable”.

A DOI is useful feature to any electronic document. What the ID number in your passport is to you is the DOI to a document. It simply helps to make sure you address the “object” you want to address.

Similarly, there may exists several “Joachims Zwiwwelkoecks” in this world (well, it may or may not be the case). However, if any of this person gets his (or her) unique ID (could by a simple number), then we would in principle always be certain that we address the right person.

Same idea for DOIs.

Making Github hosted blogs reproducible using DOIs

Blogs may suffer from the problem that they may vanish or change content from one instant to another.

One solution to this problem is using DOIs and Github. On Github, one may make a “release” of a repository, that’s some kind of snapshot of the state of affairs of your project. This snapshot is saved as a zip file and can be downloaded by anybody - thus documenting the state of affairs at the given time. Zenodo offers the feature to provide a DOI to a Github repository.

Learn more about the “howto” here.

DOI of this blog

The DOI of this blog is (timestamp: 2017-05-04).

Datenjudo mit dplyr

Einleitung

Innerhalb der R-Landschaft hat sich das Paket dplyr binnen kurzer Zeit zu einem der verbreitesten Pakete entwickelt; es stellt ein innovatives Konzept der Datenanalyse zur Verfügung. dplyr zeichnet sich durch zwei Ideen aus. Die erste Idee ist, dass nur Tabellen (“dataframes” oder “tibbles”) verarbeitet werden, keine anderen Datenstrukturen. Diese Tabellen werden von Funktion zu Funktion durchgereicht. Der Fokus auf Tabellen vereinfacht die Analyse, da Spalten nicht einzeln oder mittels Schleifen werden müssen. Die zweite Idee ist, typische Tätigkeiten der Datenanalyse anhand einer Taxonomie zu “grammatikalisieren”. Es lassen sich einige Bausteine identifizieren, mit der die typischen Aufgaben der Datenanalyse durchgeführt werden können. Der Workshop stellt beide Ideen von dplyr vor; dabei wird zuerst die Logik von dplyr erläutert ohne Rückgriff auf die R-Syntax. Danach wird die Funktionsweise von dpyr praktisch eingeübt. Der Workshop dauert ca. 90-120 Minuten. Grundkenntnisse in R werden vorausgesetzt.

Organisatorisches

Bitte bringen Sie einen Comptuer zur Veranstaltung mit. Folgende Software nutzen wir im Workshop; bitte vorab installieren:

• R und RStudio
• R-Pakete tidyverse, nycflights13, reshape2

library(tidyverse)  # Datenjudo
library(reshape2)  # Daten klein
library(nycflights13)  # Daten groß
library(okcupiddata)  # Daten groß

Außerdem laden wir noch einen Datensatz herunter; bitte stellen Sie eine Internetverbindung sicher.

Das Paket tidyverse lädt dplyr, ggplot2 und weitere Pakete (für eine Liste s. tidyverse_packages(include_self = TRUE)). Daher ist es komfortabler, tidyverse zu laden, damit spart man sich Tipparbeit. Die eigentliche Funktionalität, die wir in diesem Kapitel nutzen, kommt aus dem Paket dplyr.

Mit Datenjudo ist gemeint, die Daten für die eigentliche Analyse “aufzubereiten”. Unter Aufbereiten ist hier das Umformen, Prüfen, Bereinigen, Gruppieren und Zusammenfassen von Daten gemeint. Die deskriptive Statistik fällt unter die Rubrik Aufbereiten. Kurz gesagt: Alles, wan tut, nachdem die Daten “da” sind und bevor man mit anspruchsvoller(er) Modellierung beginnt.

Ist das Aufbereiten von Daten auch nicht statistisch anspruchsvoll, so ist es trotzdem von großer Bedeutung und häufig recht zeitintensiv. Eine Anekdote zur Relevanz der Datenaufbereitung, die (so will es die Geschichte) mir an einer Bar nach einer einschlägigen Konferenz erzählt wurde (daher keine Quellenangebe, Sie verstehen…). Eine Computerwissenschaftlerin aus den USA (deutschen Ursprungs) hatte einen beeindruckenden “Track Record” an Siegen in Wettkämpfen der Datenanalyse. Tatsächlich hatte sie keine besonderen, raffinierten Modellierungstechniken eingesetzt; klassische Regression war ihre Methode der Wahl. Bei einem Wettkampf, bei dem es darum ging, Krebsfälle aus Krankendaten vorherzusagen (z.B. von Röntgenbildern) fand sie nach langem Datenjudo heraus, dass in die “ID-Variablen” Information gesickert war, die dort nicht hingehörte und die sie nutzen konnte für überraschend (aus Sicht der Mitstreiter) gute Vorhersagen zu Krebsfällen. Wie war das möglich? Die Daten stammten aus mehreren Kliniken, jede Klinik verwendete ein anderes System, um IDs für Patienten zu erstellen. Überall waren die IDs stark genug, um die Anonymität der Patienten sicherzustellen, aber gleich wohl konnte man (nach einigem Judo) unterscheiden, welche ID von welcher Klinik stammte. Was das bringt? Einige Kliniken waren reine Screening-Zentren, die die Normalbevölkerung versorgte. Dort sind wenig Krebsfälle zu erwarten. Andere Kliniken jedoch waren Onkologie-Zentren für bereits bekannte Patienten oder für Patienten mit besonderer Risikolage. Wenig überraschen, dass man dann höhere Krebsraten vorhersagen kann. Eigentlich ganz einfach; besondere Mathe steht hier (zumindest in dieser Geschichte) nicht dahinter. Und, wenn man den Trick kennt, ganz einfach. Aber wie so oft ist es nicht leicht, den Trick zu finden. Sorgfältiges Datenjudo hat hier den Schlüssel zum Erfolg gebracht.

Typische Probleme

Bevor man seine Statistik-Trickkiste so richtig schön aufmachen kann, muss man die Daten häufig erst noch in Form bringen. Das ist nicht schwierig in dem Sinne, dass es um komplizierte Mathe ginge. Allerdings braucht es mitunter recht viel Zeit und ein paar (oder viele) handwerkliche Tricks sind hilfreich. Hier soll das folgende Kapitel helfen.

Einige typische Probleme, die immer wieder auftreten, sind:

• Fehlende Werte: Irgend jemand hat auf eine meiner schönen Fragen in der Umfrage nicht geantwortet!
• Unerwartete Daten: Auf die Frage, wie viele Facebook-Freunde er oder sie habe, schrieb die Person “I like you a lot”. Was tun???
• Daten müssen umgeformt werden: Für jede der beiden Gruppen seiner Studie hat Joachim einen Google-Forms-Fragebogen aufgesetzt. Jetzt hat er zwei Tabellen, die er “verheiraten” möchte. Geht das?
• Neue Variablen (Spalten) berechnen: Ein Student fragt nach der Anzahl der richtigen Aufgaben in der Statistik-Probeklausur. Wir wollen helfen und im entsprechenden Datensatz eine Spalte erzeugen, in der pro Person die Anzahl der richtig beantworteten Fragen steht.

Daten aufbereiten mit dplyr

Es gibt viele Möglichkeiten, Daten mit R aufzubereiten; dplyr ist ein populäres Paket dafür. Eine zentrale Idee von dplyr ist, dass es nur ein paar wenige Grundbausteine geben sollte, die sich gut kombinieren lassen. Sprich: Wenige grundlegende Funktionen mit eng umgrenzter Funktionalität. Der Autor, Hadley Wickham, sprach einmal in einem Forum (citation needed), dass diese Befehle wenig können, das Wenige aber gut. Ein Nachteil dieser Konzeption kann sein, dass man recht viele dieser Bausteine kombinieren muss, um zum gewünschten Ergebnis zu kommen. Außerdem muss man die Logik des Baukastens gut verstanden habe - die Lernkurve ist also erstmal steiler. Dafür ist man dann nicht darauf angewiesen, dass es irgendwo “Mrs Right” gibt, die genau das kann, was ich will. Außerdem braucht man sich auch nicht viele Funktionen merken. Es reicht einen kleinen Satz an Funktionen zu kennen (die praktischerweise konsistent in Syntax und Methodik sind).

Willkommen in der Welt von dyplr! dplyr hat seinen Namen, weil es sich ausschließlich um Dataframes bemüht; es erwartet einen Dataframe als Eingabe und gibt einen Dataframe zurück (zumindest bei den meisten Befehlen).

Die zwei Prinzipien von dplyr

Es gibt viele Möglichkeiten, Daten mit R aufzubereiten; dplyr^[https://cran.r-project.org/web/packages/dplyr/index.html] ist ein populäres Paket dafür. dplyr basiert auf zwei Ideen:

1. Lego-Prinzip Komplexe Datenanalysen in Bausteine zerlegen (
2. Durchpfeifen: Alle Operationen werden nur auf Dataframes angewendet; jede Operation erwartet einen Dataframe als Eingabe und gibt wieder einen Dataframe aus .

Das erste Prinzip von dplyr ist, dass es nur ein paar wenige Grundbausteine geben sollte, die sich gut kombinieren lassen. Sprich: Wenige grundlegende Funktionen mit eng umgrenzter Funktionalität. Der Autor, Hadley Wickham, sprach einmal in einem Forum (citation needed…), dass diese Befehle wenig können, das Wenige aber gut. Ein Nachteil dieser Konzeption kann sein, dass man recht viele dieser Bausteine kombinieren muss, um zum gewünschten Ergebnis zu kommen. Außerdem muss man die Logik des Baukastens gut verstanden habe - die Lernkurve ist also erstmal steiler. Dafür ist man dann nicht darauf angewiesen, dass es irgendwo “Mrs Right” gibt, die genau das kann, was ich will. Außerdem braucht man sich auch nicht viele Funktionen merken. Es reicht einen kleinen Satz an Funktionen zu kennen (die praktischerweise konsistent in Syntax und Methodik sind). Diese Bausteine sind typische Tätigkeiten im Umgang mit Daten; nichts Überraschendes. Wir schauen wir uns diese Bausteine gleich näher an.

Das zweite Prinzip von dplyr ist es, einen Dataframe von Operation zu Operation durchzureichen. dplyr arbeitet also nur mit Dataframes. Jeder Arbeitsschritt bei dplyr erwartet einen Dataframe als Eingabe und gibt im Gegenzug wieder einen Dataframe aus.

Werfen wir einen Blick auf ein paar typische Bausteine von dplyr.

Zentrale Bausteine von dplyr

Zeilen filtern mit filter

Häufig will man bestimmte Zeilen aus einer Tabelle filtern; filter. Zum Beispiel man arbeitet für die Zigarettenindustrie und ist nur an den Rauchern interessiert, nicht an Nicht-Rauchern; es sollen die nur Umsatzzahlen des letzten Quartals untersucht werden, nicht die vorherigen Quartale; es sollen nur die Daten aus Labor X (nicht Labor Y) ausgewertet werden etc.

Ein Sinnbild:

Merke:

Die Funktion filter filtert Zeilen aus einem Dataframe.

Schauen wir uns einige Beispiel an; zuerst die Daten laden nicht vergessen. Achtung: “Wohnen” die Daten in einem Paket, muss dieses Paket installiert sein, damit man auf die Daten zugreifen kann.

data(profiles, package = "okcupiddata")  # Das Paket muss installiert sein

df_frauen <- filter(profiles, sex == "f")  # nur die Frauen
df_alt <- filter(profiles, age > 70)  # nur die alten
df_alte_frauen <- filter(profiles, age > 70, sex == "f")  # nur die alten Frauen, d.h. UND-Verknüpfung
df_nosmoke_nodrinks <- filter(profiles, smokes == "no" | drinks == "not at all") 
# liefert alle Personen, die Nicht-Raucher *oder* Nicht-Trinker sind

Gar nicht so schwer, oder? Allgemeiner gesprochen werden diejenigen Zeilen gefiltert (also behalten bzw. zurückgeliefert), für die das Filterkriterium TRUE ist.

Manche Befehle wie `filter` haben einen Allerweltsnamen; gut möglich, dass ein Befehl mit gleichem Namen in einem anderen (geladenen) Paket existiert. Das kann dann zu Verwirrungen führen - und kryptischen Fehlern. Im Zweifel den Namen des richtigen Pakets ergänzen, und zwar zum Beispiel so: `dplyr::filter(...)`.

Aufgaben F, R, F, F, R

Richtig oder Falsch!?

1. `filter` filtert Spalten.
1. `filter` ist eine Funktion aus dem Paket `dplyr`.
1. `filter` erwartet als ersten Parameter das Filterkriterium.
1. `filter` lässt nur ein Filterkriterium zu.
1. Möchte man aus dem Datensatz `profiles` (`okcupiddata`) die Frauen filtern, so ist folgende Syntax korrekt: `filter(profiles, sex == "f")´.

Lösung: F, R, F, F, R

Vertiefung: Fortgeschrittene Beispiele für filter

Einige fortgeschrittene Beispiele für filter:

Man kann alle Elemente (Zeilen) filtern, die zu einer Menge gehören und zwar mit diesem Operator: %in%:

filter(profiles, body_type %in% c("a little extra", "average"))

Besonders Textdaten laden zu einigen Extra-Überlegungen ein; sagen wir, wir wollen alle Personen filtern, die Katzen bei den Haustieren erwähnen. Es soll reichen, wenn cat ein Teil des Textes ist; also likes dogs and likes cats wäre OK (soll gefiltert werden). Dazu nutzen wir ein Paket zur Bearbeitung von Strings (Textdaten):

filter(profiles, str_detect(pets, "cats"))

Ein häufiger Fall ist, Zeilen ohne fehlende Werte (NAs) zu filtern. Das geht einfach:

profiles_keine_nas <- na.omit(profiles)

Aber was ist, wenn wir nur bei bestimmten Spalten wegen fehlender Werte besorgt sind? Sagen wir bei income und bei sex:

filter(profiles, !is.na(income) | !is.na(sex))

Spalten wählen mit select

Das Gegenstück zu filter ist select; dieser Befehl liefert die gewählten Spalten zurück. Das ist häufig praktisch, wenn der Datensatz sehr “breit” ist, also viele Spalten enthält. Dann kann es übersichtlicher sein, sich nur die relevanten auszuwählen. Das Sinnbild für diesen Befehl:

Merke:

Die Funktion select wählt Spalten aus einem Dataframe aus.

Laden wir als ersten einen Datensatz.

stats_test <- read.csv("https://sebastiansauer.github.io/data/test_inf_short.csv")

Dieser Datensatz beinhaltet Daten zu einer Statistikklausur.

select(stats_test, score)  # Spalte `score` auswählen
select(stats_test, score, study_time)  # Splaten `score` und `study_time` auswählen
select(stats_test, score:study_time) # dito
select(stats_test, 5:6) Spalten 5 bis 6 auswählen

Tatsächlich ist der Befehl select sehr flexibel; es gibt viele Möglichkeiten, Spalten auszuwählen. Im dplyr-Cheatsheet findet sich ein guter Überblick dazu.

Aufgaben

Richtig oder Falsch!?

1. `select` wählt *Zeilen* aus.
1. `select` ist eine Funktion aus dem Paket `knitr`.
1. Möchte man zwei Spalten auswählen, so ist folgende Syntax prinzipiell korrekt: `select(df, spalte1, spalte2)`.
1. Möchte man Spalten 1 bis 10 auswählen, so ist folgende Syntax prinzipiell korrekt: `select(df, spalte1:spalte10)
1. Mit `select` können Spalten nur bei ihrem Namen, aber nicht bei ihrer Nummer aufgerufen werden.

Lösung: F, F, R, R, F

Zeilen sortieren mit arrange

Man kann zwei Arten des Umgangs mit R unterscheiden: Zum einen der “interaktive Gebrauch” und zum anderen “richtiges Programmieren”. Im interaktiven Gebrauch geht es uns darum, die Fragen zum aktuell vorliegenden Datensatz (schnell) zu beantworten. Es geht nicht darum, eine allgemeine Lösung zu entwickeln, die wir in die Welt verschicken können und die dort ein bestimmtes Problem löst, ohne dass der Entwickler (wir) dabei Hilfestellung geben muss. “Richtige” Software, wie ein R-Paket oder Microsoft Powerpoint, muss diese Erwartung erfüllen; “richtiges Programmieren” ist dazu vonnöten. Natürlich sind in diesem Fall die Ansprüche an die Syntax (der “Code”, hört sich cooler an) viel höher. In dem Fall muss man alle Eventualitäten voraussehen und sicherstellen, dass das Programm auch beim merkwürdigsten Nutzer brav seinen Dienst tut. Wir haben hier, beim interaktiven Gebrauch, niedrigere Ansprüche bzw. andere Ziele.

Beim interaktiven Gebrauch von R (oder beliebigen Analyseprogrammen) ist das Sortieren von Zeilen eine recht häufige Tätigkeit. Typisches Beispiel wäre der Lehrer, der eine Tabelle mit Noten hat und wissen will, welche Schüler die schlechtesten oder die besten sind in einem bestimmten Fach. Oder bei der Prüfung der Umsätze nach Filialen möchten wir die umsatzstärksten sowie -schwächsten Niederlassungen kennen.

Ein R-Befehl hierzu ist arrange; einige Beispiele zeigen die Funktionsweise am besten:

arrange(stats_test, score) # liefert die *schlechtesten* Noten zuerst zurück
arrange(stats_test, -score) # liefert die *besten* Noten zuerst zurück
arrange(stats_test, interest, score)

#>     X                 V_1 study_time self_eval interest score
#> 1 234 23.01.2017 18:13:15          3         1        1    17
#> 2   4 06.01.2017 09:58:05          2         3        2    18
#> 3 131 19.01.2017 18:03:45          2         3        4    18
#> 4 142 19.01.2017 19:02:12          3         4        1    18
#> 5  35 12.01.2017 19:04:43          1         2        3    19
#> 6  71 15.01.2017 15:03:29          3         3        3    20
#>    X                 V_1 study_time self_eval interest score
#> 1  3 05.01.2017 23:33:47          5        10        6    40
#> 2  7 06.01.2017 14:25:49         NA        NA       NA    40
#> 3 29 12.01.2017 09:48:16          4        10        3    40
#> 4 41 13.01.2017 12:07:29          4        10        3    40
#> 5 58 14.01.2017 15:43:01          3         8        2    40
#> 6 83 16.01.2017 10:16:52         NA        NA       NA    40
#>     X                 V_1 study_time self_eval interest score
#> 1 234 23.01.2017 18:13:15          3         1        1    17
#> 2 142 19.01.2017 19:02:12          3         4        1    18
#> 3 221 23.01.2017 11:40:30          1         1        1    23
#> 4 230 23.01.2017 16:27:49          1         1        1    23
#> 5  92 17.01.2017 17:18:55          1         1        1    24
#> 6 107 18.01.2017 16:01:36          3         2        1    24

Einige Anmerkungen. Die generelle Syntax lautet arrange(df, Spalte1, ...), wobei df den Dataframe bezeichnet und Spalte1 die erste zu sortierende Spalte; die Punkte ... geben an, dass man weitere Parameter übergeben kann. Man kann sowohl numerische Spalten als auch Textspalten sortieren. Am wichtigsten ist hier, dass man weitere Spalten übergeben kann. Dazu gleich mehr.

Standardmäßig sortiert arrange aufsteigend (weil kleine Zahlen im Zahlenstrahl vor den großen Zahlen kommen). Möchte man diese Reihenfolge umdrehen (große Werte zuert, d.h. absteigend), so kann man ein Minuszeichen vor den Namen der Spalte setzen.

Gibt man zwei oder mehr Spalten an, so werden pro Wert von Spalte1 die Werte von Spalte2 sortiert etc; man betrachte den Output des Beispiels oben dazu.

Merke:

Die Funktion arrange sortiert die Zeilen eines Datafames.

Ein Sinnbild zur Verdeutlichung:

Ein ähnliches Ergebnis erhält mit man top_n(), welches die n größten Ränge widergibt:

top_n(stats_test, 3)
#>      X                 V_1 study_time self_eval interest score
#> 1    3 05.01.2017 23:33:47          5        10        6    40
#> 2    7 06.01.2017 14:25:49         NA        NA       NA    40
#> 3   29 12.01.2017 09:48:16          4        10        3    40
#> 4   41 13.01.2017 12:07:29          4        10        3    40
#> 5   58 14.01.2017 15:43:01          3         8        2    40
#> 6   83 16.01.2017 10:16:52         NA        NA       NA    40
#> 7  116 18.01.2017 23:07:32          4         8        5    40
#> 8  119 19.01.2017 09:05:01         NA        NA       NA    40
#> 9  132 19.01.2017 18:22:32         NA        NA       NA    40
#> 10 175 20.01.2017 23:03:36          5        10        5    40
#> 11 179 21.01.2017 07:40:05          5         9        1    40
#> 12 185 21.01.2017 15:01:26          4        10        5    40
#> 13 196 22.01.2017 13:38:56          4        10        5    40
#> 14 197 22.01.2017 14:55:17          4        10        5    40
#> 15 248 24.01.2017 16:29:45          2        10        2    40
#> 16 249 24.01.2017 17:19:54         NA        NA       NA    40
#> 17 257 25.01.2017 10:44:34          2         9        3    40
#> 18 306 27.01.2017 11:29:48          4         9        3    40
top_n(stats_test, 3, interest)
#>     X                 V_1 study_time self_eval interest score
#> 1   3 05.01.2017 23:33:47          5        10        6    40
#> 2   5 06.01.2017 14:13:08          4         8        6    34
#> 3  43 13.01.2017 14:14:16          4         8        6    36
#> 4  65 15.01.2017 12:41:27          3         6        6    22
#> 5 110 18.01.2017 18:53:02          5         8        6    37
#> 6 136 19.01.2017 18:22:57          3         1        6    39
#> 7 172 20.01.2017 20:42:46          5        10        6    34
#> 8 214 22.01.2017 21:57:36          2         6        6    31
#> 9 301 27.01.2017 08:17:59          4         8        6    33

Gibt man keine Spalte an, so bezieht sich top_n auf die letzte Spalte im Datensatz.

Da sich hier mehrere Personen den größten Rang (Wert 40) teilen, bekommen wir nicht 3 Zeilen zurückgeliefert, sondern entsprechend mehr.

Aufgaben

Richtig oder Falsch!?

1. `arrange` arrangiert Spalten.
1. `arrange` sortiert im Standard absteigend.
1. `arrange` lässt nur ein Sortierkriterium zu.
1. `arrange` kann numerische Werte, aber nicht Zeichenketten sortieren.
1. `top_n(5)` liefert die fünf kleinsten Ränge.

Lösung: F, F, F, F, R

Datensatz gruppieren mit group_by

Einen Datensatz zu gruppieren ist eine häufige Angelegenheit: Was ist der mittlere Umsatz in Region X im Vergleich zu Region Y? Ist die Reaktionszeit in der Experimentalgruppe kleiner als in der Kontrollgruppe? Können Männer schneller ausparken als Frauen? Man sieht, dass das Gruppieren v.a. in Verbindung mit Mittelwerten oder anderen Zusammenfassungen sinnvol ist; dazu im nächsten Abschnitt mehr.

Gruppieren meint, einen Datensatz anhand einer diskreten Variablen (z.B. Geschlecht) so aufzuteilen, dass Teil-Datensätze entstehen - pro Gruppe ein Teil-Datensatz (z.B. Mann vs. Frau).

In der Abbildung wurde der Datensatz anhand der Spalte Fach in mehrere Gruppen geteilt. Wir könnten uns als nächstes z.B. Mittelwerte pro Fach - d.h. pro Gruppe (pro Ausprägung von Fach) - ausgeben lassen; in diesem Fall vier Gruppen (Fach A bis D).

test_gruppiert <- group_by(stats_test, interest)
test_gruppiert
#> Source: local data frame [306 x 6]
#> Groups: interest [7]
#> 
#>        X                 V_1 study_time self_eval interest score
#>    <int>              <fctr>      <int>     <int>    <int> <int>
#> 1      1 05.01.2017 13:57:01          5         8        5    29
#> 2      2 05.01.2017 21:07:56          3         7        3    29
#> 3      3 05.01.2017 23:33:47          5        10        6    40
#> 4      4 06.01.2017 09:58:05          2         3        2    18
#> 5      5 06.01.2017 14:13:08          4         8        6    34
#> 6      6 06.01.2017 14:21:18         NA        NA       NA    39
#> 7      7 06.01.2017 14:25:49         NA        NA       NA    40
#> 8      8 06.01.2017 17:24:53          2         5        3    24
#> 9      9 07.01.2017 10:11:17          2         3        5    25
#> 10    10 07.01.2017 18:10:05          4         5        5    33
#> # ... with 296 more rows

Schaut man sich nun den Datensatz an, sieht man erstmal wenig Effekt der Gruppierung. R teilt uns lediglich mit Groups: interest [7], dass es 7 Gruppen gibt, aber es gibt keine extra Spalte oder sonstige Anzeichen der Gruppierung. Aber keine Sorge, wenn wir gleich einen Mittelwert ausrechnen, bekommen wir den Mittelwert pro Gruppe!

Ein paar Hinweise: Source: local data frame [306 x 6] will sagen, dass die Ausgabe sich auf einen tibble bezieht (siehe Details hier), also eine bestimmte Art von Dataframe. Groups: interest [7] zeigt, dass der Tibble in 7 Gruppen - entsprechend der Werte von interest aufgeteilt ist.

group_by an sich ist nicht wirklich nützlich. Nützlich wird es erst, wenn man weitere Funktionen auf den gruppierten Datensatz anwendet - z.B. Mittelwerte ausrechnet (z.B mit summarise, s. unten). Die nachfolgenden Funktionen (wenn sie aus dplyr kommen), berücksichtigen nämlich die Gruppierung. So kann man einfach Mittelwerte pro Gruppe ausrechnen. dplyr kombiniert dann die Zusammenfassungen (z.B. Mittelwerte) der einzelnen Gruppen in einen Dataframe und gibt diesen dann aus.

Die Idee des “Gruppieren - Zusammenfassen - Kombinieren” ist flexibel; man kann sie häufig brauchen. Es lohnt sich, diese Idee zu lernen (vgl. Abb. \@ref(fig:sac)).

Aufgaben

Richtig oder Falsch!?

1. Mit `group_by` gruppiert man einen Datensatz.
1. `group_by` lässt nur ein Gruppierungskriterium zu.
1. Die Gruppierung durch `group_by` wird nur von Funktionen aus `dplyr` erkannt.
1. `group_by` ist sinnvoll mit `summarise` zu kombinieren.

Lösung: R, F, R, R

Merke:

Mit group_by teilt man einen Datensatz in Gruppen ein, entsprechend der Werte einer mehrerer Spalten.

Eine Spalte zusammenfassen mit summarise

Vielleicht die wichtigste oder häufigte Tätigkeit in der Analyse von Daten ist es, eine Spalte zu einem Wert zusammenzufassen; summarise leistet dies. Anders gesagt: Einen Mittelwert berechnen, den größten (kleinsten) Wert heraussuchen, die Korrelation berechnen oder eine beliebige andere Statistik ausgeben lassen. Die Gemeinsamkeit dieser Operaitonen ist, dass sie eine Spalte zu einem Wert zusammenfassen, “aus Spalte mach Zahl”, sozusagen. Daher ist der Name des Befehls summarise ganz passend. Genauer gesagt fasst dieser Befehl eine Spalte zu einer Zahl zusammen anhand einer Funktion wie mean oder max. Hierbei ist jede Funktion erlaubt, die eine Spalte als Input verlangt und eine Zahl zurückgibt; andere Funktionen sind bei summarise nicht erlaubt.

summarise(stats_test, mean(score))
#>   mean(score)
#> 1        31.1

Man könnte diesen Befehl so ins Deutsche übersetzen: Fasse aus Tabelle stats_test die Spalte score anhand des Mittelwerts zusammen. Nicht vergessen, wenn die Spalte score fehlende Werte hat, wird der Befehl mean standardmäßig dies mit NA quittieren. Ergänzt man den Parameter nr.rm = TRUE, so ignoriert R fehlende Werte und der Befehl mean liefert ein Ergebnis zurück.

Jetzt können wir auch die Gruppierung nutzen:

test_gruppiert <- group_by(stats_test, interest)
summarise(test_gruppiert, mean(score, na.rm = TRUE))
#> # A tibble: 7 × 2
#>   interest `mean(score, na.rm = TRUE)`
#>      <int>                       <dbl>
#> 1        1                        28.3
#> 2        2                        29.7
#> 3        3                        30.8
#> 4        4                        29.9
#> 5        5                        32.5
#> 6        6                        34.0
#> 7       NA                        33.1

Der Befehl summarise erkennt also, wenn eine (mit group_by) gruppierte Tabelle vorliegt. Jegliche Zusammenfassung, die wir anfordern, wird anhand der Gruppierungsinformation aufgeteilt werden. In dem Beispiel bekommen wir einen Mittelwert für jeden Wert von interest. Interessanterweise sehen wir, dass der Mittelwert tendenziell größer wird, je größer interest wird.

Alle diese dplyr-Befehle geben einen Dataframe zurück, was praktisch ist für weitere Verarbeitung. In diesem Fall heißen die Spalten interst und mean(score). Zweiter Name ist nicht so schön, daher ändern wir den wie folgt:

Jetzt können wir auch die Gruppierung nutzen:

test_gruppiert <- group_by(stats_test, interest)
summarise(test_gruppiert, mw_pro_gruppe = mean(score, na.rm = TRUE))
#> # A tibble: 7 × 2
#>   interest mw_pro_gruppe
#>      <int>         <dbl>
#> 1        1          28.3
#> 2        2          29.7
#> 3        3          30.8
#> 4        4          29.9
#> 5        5          32.5
#> 6        6          34.0
#> 7       NA          33.1

Nun heißt die zweite Spalte mw_pro_Gruppe. na.rm = TRUE veranlasst, bei fehlenden Werten trotzdem einen Mittelwert zurückzuliefern (die Zeilen mit fehlenden Werten werden in dem Fall ignoriert).

Grundsätzlich ist die Philosophie der dplyr-Befehle: “Mach nur eine Sache, aber die dafür gut”. Entsprechend kann summarise nur Spalten zusammenfassen, aber keine Zeilen.

Merke:

Mit summarise kann man eine Spalte eines Dataframes zu einem Wert zusammenfassen.

Deskriptive Statistik mit summarise

Die deskriptive Statistik hat zwei Haupt-Bereiche: Lagemaße und Streuungsmaße.

Lagemaße geben den “typischen”, “mittleren” oder “repräsentativen” Vertreter der Verteilung an. Bei den Lagemaßen denkt man sofort an das arithmetische Mittel (synonym: Mittelwert; häufig als \(\bar{X}\) abgekürzt; mean). Ein Nachteil von Mittelwerten ist, dass sie nicht robust gegenüber Extremwerte sind: Schon ein vergleichsweise großer Einzelwert kann den Mittelwert deutlich verändern und damit die Repräsentativität des Mittelwerts für die Gesamtmenge der Daten in Frage stellen. Eine robuste Variante ist der Median (Md; median). Ist die Anzahl der (unterschiedlichen) Ausprägungen nicht zu groß im Verhältnis zur Fallzahl, so ist der Modus eine sinnvolle Statistik; er gibt die häufigste Ausprägung an (Der Modus ist im Standard-R nicht mit einem eigenen Befehl vertreten. Man kann ihn aber leicht von Hand bestimmen; s.u. Es gibt auch einige Pakete, die diese Funktion anbieten: z.B. so).

Streuungsmaße} geben die Unterschiedlichkeit in den Daten wieder; mit anderen Worten: sind die Daten sich ähnlich oder unterscheiden sich die Werte deutlich? Zentrale Statistiken sind der mittlere Absolutabstand (MAA; MAD; Der MAD ist im Standard-R nicht mit einem eigenen Befehl vertreten. Es gibt einige Pakete, die diese Funktion anbieten: z.B. so), die Standardabweichung (sd; sd), die Varianz (Var; var) und der Interquartilsabstand (IQR; IQR). Da nur der IQR nicht auf dem Mittelwert basiert, ist er am robustesten. Beliebige Quantile bekommt man mit dem R-Befehl quantile.

Der Befehl summarise eignet sich, um deskriptive Statistiken auszurechnen.

summarise(stats_test, mean(score))
#>   mean(score)
#> 1        31.1
summarise(stats_test, sd(score))
#>   sd(score)
#> 1      5.74

Natürlich könnte man auch einfacher schreiben:

mean(stats_test$score)
#> [1] 31.1
median(stats_test$score)
#> [1] 31

summarise liefert aber im Unterschied zu mean etc. immer einen Dataframe zurück. Da der Dataframe die typische Datenstruktur ist, ist es häufig praktisch, wenn man einen Dataframe zurückbekommt, mit dem man weiterarbeiten kann. Außerdem lassen mean etc. keine Gruppierungsoperationen zu; über group_by kann man dies aber bei dplyr erreichen.

Aufgaben

Richtig oder Falsch!?

1. Möchte man aus der Tabelle `stats_test` den Mittelwert für die Spalte `score` berechnen, so ist folgende Syntax korrekt: `summarise(stats_test, mean(score))`.
1. `summarise` liefert eine Tabelle, genauer: einen Tibble, zurück.
1. Die Tabelle, die diese Funktion zurückliefert: `summarise(stats_test, mean(score))`, hat eine Spalte mit dem Namen `mean(score)`.
1. `summarise` lässt zu, dass die zu berechnende Spalte einen Namen vom Nutzer zugewiesen bekommt.
1. `summarise` darf nur verwendet werden, wenn eine Spalte zu einem Wert zusammengefasst werden soll.

Lösung: R, R, R, R, R

1. (Fortgeschritten) Bauen Sie einen eigenen Weg, um den mittleren Absolutabstand auszurechnen! Gehen Sie der Einfachheit halber (zuerst) von einem Vektor mit den Werten (1,2,3) aus!

Lösung:

x <- c(1, 2, 3)
x_mw <- mean(x)
x_delta <- x - x_mw
x_delta <- abs(x_delta)
mad <- mean(x_delta)
mad
#> [1] 0.667

Zeilen zählen mit n und count

Ebenfalls nützlich ist es, Zeilen zu zählen. Im Gegensatz zum Standardbefehl nrow (Standardbefehl meint, dass die Funktion zum Standardrepertoire von R gehört, also nicht über ein Paket extra geladen werden muss) versteht der dyplr-Befehl n auch Gruppierungen. n darf nur innerhalb von summarise oder ähnlichen dplyr-Befehlen verwendet werden.

summarise(stats_test, n())
#>   n()
#> 1 306
summarise(test_gruppiert, n())
#> # A tibble: 7 × 2
#>   interest `n()`
#>      <int> <int>
#> 1        1    30
#> 2        2    47
#> 3        3    66
#> 4        4    41
#> 5        5    45
#> 6        6     9
#> 7       NA    68
nrow(stats_test)
#> [1] 306

Außerhalb von gruppierten Datensätzen ist nrow meist praktischer.

Praktischer ist der Befehl count, der nichts anderes ist als die Hintereinanderschaltung von group_by und n. Mit count zählen wir die Häufigkeiten nach Gruppen; Gruppen sind hier zumeist die Werte einer auszuzählenden Variablen (oder mehrerer auszuzählender Variablen). Das macht count zu einem wichtigen Helfer bei der Analyse von Häufigkeitsdaten.

dplyr::count(stats_test, interest)
#> # A tibble: 7 × 2
#>   interest     n
#>      <int> <int>
#> 1        1    30
#> 2        2    47
#> 3        3    66
#> 4        4    41
#> 5        5    45
#> 6        6     9
#> 7       NA    68
dplyr::count(stats_test, study_time)
#> # A tibble: 6 × 2
#>   study_time     n
#>        <int> <int>
#> 1          1    31
#> 2          2    49
#> 3          3    85
#> 4          4    56
#> 5          5    17
#> 6         NA    68
dplyr::count(stats_test, interest, study_time)
#> # A tibble: 29 × 3
#>    interest study_time     n
#>       <int>      <int> <int>
#> 1         1          1    12
#> 2         1          2     7
#> 3         1          3     8
#> 4         1          4     2
#> 5         1          5     1
#> 6         2          1     9
#> 7         2          2    15
#> 8         2          3    16
#> 9         2          4     6
#> 10        2          5     1
#> # ... with 19 more rows

Allgemeiner formuliert lautet die Syntax: count(df, Spalte1, ...), wobei df der Dataframe ist und Spalte1 die erste (es können mehrere sein) auszuzählende Spalte. Gibt man z.B. zwei Spalten an, so wird pro Wert der 1. Spalte die Häufigkeiten der 2. Spalte ausgegeben.

Merke:

n und count zählen die Anzahl der Zeilen, d.h. die Anzahl der Fälle.

Aufgaben

Richtig oder Falsch!?

1. Mit `count` kann man Zeilen zählen.
1. `count` ist ähnlich (oder identisch) zu einer Kombination von `group_by` und `n()`. 
1. Mit `count` kann man nur nur eine Gruppe beim Zählen berücksichtigen.
1. `count` darf nicht bei nominalskalierten Variablen verwendet werden.

Lösung: R, R, F, F

1. Bauen Sie sich einen Weg, um den Modus mithilfe von count und arrange zu bekommen!

stats_count <- count(stats_test, score)
stats_count_sortiert <- arrange(stats_count, -n)
head(stats_count_sortiert,1)
#> # A tibble: 1 × 2
#>   score     n
#>   <int> <int>
#> 1    34    22

Ah! Der Score 34 ist der häufigste!

Die Pfeife

Die zweite Idee kann man salopp als “Durchpfeifen” oder die “Idee der Pfeife” bezeichnen; ikonographisch mit einem Pfeifen ähnlichen Symbol dargestellt ` %>% `. Der Begriff “Durchpfeifen” ist frei vom Englischen “to pipe” übernommen. Das berühmte Bild von René Magritte stand dabei Pate.

Hierbei ist gemeint, einen Datensatz sozusagen auf ein Fließband zu legen und an jedem Arbeitsplatz einen Arbeitsschritt auszuführen. Der springende Punkt ist, dass ein Dataframe als “Rohstoff” eingegeben wird und jeder Arbeitsschritt seinerseits wieder einen Datafram ausgiebt. Damit kann man sehr schön, einen “Flow” an Verarbeitung erreichen, außerdem spart man sich Tipparbeit und die Syntax wird lesbarer. Damit das Durchpfeifen funktioniert, benötigt man Befehle, die als Eingabe einen Dataframe erwarten und wieder einen Dataframe zurückliefern. Das Schaubild verdeutlich beispielhaft eine Abfolge des Durchpfeifens.

Die sog. “Pfeife” (pipe) in Anspielung an das berühmte Bild von René Magritte, verkettet Befehle hintereinander. Das ist praktisch, da es die Syntax vereinfacht. Vergleichen Sie mal diese Syntax

filter(summarise(group_by(filter(stats_test, !is.na(score)), interest), mw = mean(score)), mw > 30)

mit dieser

stats_test %>% 
  filter(!is.na(score)) %>% 
  group_by(interest) %>% 
  summarise(mw = mean(score)) %>% 
  filter(mw > 30)
#> # A tibble: 4 × 2
#>   interest    mw
#>      <int> <dbl>
#> 1        3  30.8
#> 2        5  32.5
#> 3        6  34.0
#> 4       NA  33.1

Es ist hilfreich, diese “Pfeifen-Syntax” in deutschen Pseudo-Code zu übersetzen.

Nimm die Tabelle "stats_test" UND DANN  
filtere alle nicht-fehlenden Werte UND DANN  
gruppiere die verbleibenden Werte nach "interest" UND DANN  
bilde den Mittelwert (pro Gruppe) für "score" UND DANN  
liefere nur die Werte größer als 30 zurück.  

Die zweite Syntax, in “Pfeifenform” ist viel einfacher zu verstehen als die erste! Die erste Syntax ist verschachelt, man muss sie von innen nach außen lesen. Das ist kompliziert. Die Pfeife in der 2. Syntax macht es viel einfacher, die Snytax zu verstehen, da die Befehle “hintereinander” gestellt (sequenziell organisiert) sind.

Die Pfeife zerlegt die “russische Puppe”, also ineinander verschachelteten Code, in sequenzielle Schritte und zwar in der richtigen Reihenfolge (entsprechend der Abarbeitung). Wir müssen den Code nicht mehr von innen nach außen lesen (wie das bei einer mathematischen Formel der Fall ist), sondern können wie bei einem Kochrezept “erstens …, zweitens .., drittens …” lesen. Die Pfeife macht die Syntax einfacher. Natürlich hätten wir die verschachtelte Syntax in viele einzelne Befehle zerlegen können und jeweils eine Zwischenergebnis speichern mit dem Zuweisungspfeil <- und das Zwischenergebnis dann explizit an den nächsten Befehl weitergeben. Eigentlich macht die Pfeife genau das - nur mit weniger Tipparbeit. Und auch einfacher zu lesen. Flow!

Wenn Sie Befehle verketten mit der Pfeife, sind nur Befehle erlaubt, die einen Datensatz als Eingabe verlangen und einen Datensatz ausgeben. Das ist bei den hier vorgestellten Funktionen der Fall. Viele andere Funktionen erfüllen dieses Kriterium aber nicht; in dem Fall liefert `dplyr` eine Fehlermeldung.

Spalten berechnen mit mutate

Wenn man die Pfeife benutzt, ist der Befehl mutate ganz praktisch: Er berechnet eine Spalte. Normalerweise kann man einfach eine Spalte berechnen mit dem Zuweisungsoperator:

Zum Beispiel so:

df$neue_spalte <- df$spalte1 + df$spalte2

Innerhalb einer Pfeifen-Syntax geht das aber nicht (so gut). Da ist man mit der Funtion mutate besser beraten; mutate leistest just dasselbe wie die Pseudo-Syntax oben:

df %>% 
  mutate(neue_spalte = spalte1 + spalte2)

In Worten:

Nimm die Tabelle "df" UND DANN  
bilde eine neue Spalte mit dem Namen `neue_spalte`,  
die sich berechnet als Summe von `spalte1` und `spalte2`.    

Allerdings berücksichtigt mutate auch Gruppierungen, praktischerweise. Der Hauptvorteil ist die bessere Lesbarkeit durch Auflösen der Verschachtelungen.

Ein konkretes Beispiel:

stats_test %>% 
  mutate(bestanden = score > 25) %>% 
  head()
#>   X                 V_1 study_time self_eval interest score bestanden
#> 1 1 05.01.2017 13:57:01          5         8        5    29      TRUE
#> 2 2 05.01.2017 21:07:56          3         7        3    29      TRUE
#> 3 3 05.01.2017 23:33:47          5        10        6    40      TRUE
#> 4 4 06.01.2017 09:58:05          2         3        2    18     FALSE
#> 5 5 06.01.2017 14:13:08          4         8        6    34      TRUE
#> 6 6 06.01.2017 14:21:18         NA        NA       NA    39      TRUE

Diese Syntax erzeugt eine neue Spalte innerhalb von stats_test; diese Spalte prüft pro Persion, ob score > 25 ist. Falls ja (TRUE), dann ist bestanden TRUE, ansonsten ist bestanden FALSE (Pech). head zeigt die ersten 6 Zeilen des resultierenden Dataframes an.

Ein Sinnbild für mutate:

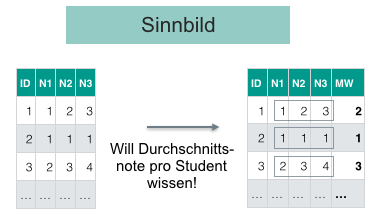
Aufgaben

1. Entschlüsseln Sie dieses Ungetüm! Übersetzen Sie diese Syntax auf Deutsch:

library(nycflights13)
data(flights)

verspaetung <-
  filter(
    summarise(
    group_by(filter(flights, !is.na(dep_delay), month)), delay = mean(dep_delay), n = n()), n > 10)
 

1. Entschlüsseln Sie jetzt diese Syntax bzw. übersetzen Sie sie ins Deutsche:

verspaetung <- flights %>% filter(!is.na(dep_delay)) %>%
group_by(month) %>%
summarise(delay = mean(dep_delay), n = n()) %>% filter(n > 10)

1. (schwierig) Die Pfeife bei arr_delay

• Übersetzen Sie die folgende Pseudo-Syntax ins ERRRische!

Nehme den Datensatz `flights` UND DANN...  
Wähle daraus die Spalte `arr_delay` UND DANN...  
Berechne den Mittelwert der Spalte UND DANN...  
ziehe vom Mittelwert die Spalte ab UND DANN...
quadriere die einzelnen Differenzen UND DANN...
bilde davon den Mittelwert.  

Lösung:

flights %>% 
  select(arr_delay) %>% 
  mutate(arr_delay_delta = arr_delay - mean(flights$arr_delay, na.rm = TRUE)) %>% 
  mutate(arr_delay_delta_quadrat = arr_delay_delta^2) %>% 
  summarise(arr_delay_var = mean(arr_delay_delta_quadrat, na.rm = TRUE)) %>% 
  summarise(sqrt(arr_delay_var))
#> # A tibble: 1 × 1
#>   `sqrt(arr_delay_var)`
#>                   <dbl>
#> 1                  44.6

• Berechnen Sie die sd von arr_delay in flights! Vergleichen Sie sie mit dem Ergebnis der vorherigen Aufgabe!

Lösung: sd(flights$arr_delay, na.rm = TRUE)

• Was hat die Pfeifen-Syntax oben berechnet?

Lösung: die sd von arr_delay

Befehlsübersicht

Verweise

• Die offizielle Dokumentation von dplyr findet sich hier: https://cran.r-project.org/web/packages/dplyr/dplyr.pdf.

• Eine schöne Demonstration der Mächtigkeit von dplyr findet sich hier: http://bit.ly/2kX9lvC.

• Die GUI “exploratory” ist ein “klickbare” Umsetzung von dplyr, mächtig, modern und sieht cool aus: https://exploratory.io.

• R for Data Science bietet umfangreiche Unterstützung zu diesem Thema.

Fallstudie zu dplyr

Lesen Sie diese ausführlichere Fallstudie zu dplyr nach: https://sebastiansauer.github.io/Fallstudie_Flights/.

Many tools exist for academic writing including the notorious W.O.R.D.; but many more are out there. Let’s have a look at those tools, and discuss what’s important (what we expect the tool to deliver, eg., beautiful typesetting).

Typical tools for academic writing

• MS Word: A “classical” choice, relied upon by myriads of white collar workers… I myself have used it extensively for academic writing; the main advantage being its simplicity, that is, well, everybody knows it, and knows more or less how to handle it. It’s widespread use is of course an advantage.

• TeX: The purist’s choice. The learning curve can be steep, but its beauty and elegance of typesetting if unreached.

• Overleaf, Authorea: Web-based apps that make it easy to enjoy modern functionality by making the entry hurdle as low as possible. These riches do not come for free; commercial organizations would like to see some return of investment.

• Full: With the “full” approach I refer to a blended version of several tools, mainly:
  • R
  • RStudio
  • RMarkdown (ie., knitr + markdown + pandoc)
  • Git + Github
  • stylesheets such as papaja (APA6 stylesheet)

• Markdown: Markdown is a simple variant of markup languages such as HTLM or LaTeX. Its marked feature is its simplicity. In fact, it can be learned in 5 minutes (whereas TeX may need 5-50 years, some say…).

• Google Docs: Easy, no (direct) costs, comfortable, but some features are lacking - There’s no easy for citations. In addition, some say intellectual rights are transferred to Google by using G Docs (I have no clue whether that’s true).

Tool comparison table

libs <- c("readr", "tidyverse", "pander", "emo", "htmlTable")
pacman::p_load(char = libs)

tools <- read_csv("academic_writing_tools_competition.csv")

htmlTable(df)

Criterion weight

Let’s assume we have some weights that we assign to the critera:

Scores by tool

So we are able to devise a score or a ranking.

score %>% ggplot + aes(x = reorder(tool_name, score), y = score) + 
    geom_point() + coord_flip() + xlab("tool")

And the winner is…

The full approach. The full approach gets most points (disclaimer: well, I designed this competition, and I like this approach 😄.

Getting started

There are numerous tutorial on “the full approach” out there, .eg.

• RMarkdown materials from RStudio
• Christopher Gandrud’s book Reproducible Research with R and RStudio Second Edition - free pdf full text
• Also by the same author Reproducible Research with R and R Studio
• Find here some case studies on reproducible research.

Correlation is one of the most widely used and a well-known measure of the assocation (linear association, that is) of two variables.

Perhaps less well-known is that the correlation is in principle identical to the covariation.

To see this, consider the a formula of the covariance of two empirical datasets, \(X\) and \(Y\):

In other words, the covariance of $X$ and $Y$ $COV(X,Y)$ is the average of difference of some value to its mean.

This idea is conveyed by this picture:

The covariance is identical to the correlation (?)

What does it mean to say the (coefficient of) correlation is “identical” to the covariation?

If we “feed” z-scaled values to the covariation, we will get back the correlation.

In other words, the correlation equals the covariation if the data are z-scaled.

So, let’s see. We replace \(X\) by \(z_X\) and \(Y\) by \(z_Y\) and see what happens.

However, \(z_{\bar{X}} = 0\), and by analogy, \(z_{\bar{y}} = 0\). So the eqaution simplifies to

Now, \(z_x\) can be expressed as

The same rule applies for \(z_y\), by analogy.

Now, let’s insert the previous equation in the equation of \(Cov(z_X, z_Y)\):

\(sd_X$ and $sd_Y\) can be pulled out of the sum, right at the front of the equation, leaving us with

\(Cov(z_X, z_Y) = \frac{1}{sd_X \cdot sd_Y} \cdot \big( \sum (X_i - \bar{X}) \cdot (Y_i - \bar{Y}) \big)\).

And that’s the definition of the correlation of \(X\) and \(Y\), more frequently put this way:

\(Cov(z_X, z_Y) = \frac {\sum (X_i - \bar{X}) \cdot (Y_i - \bar{Y})}{sd_X \cdot sd_Y}\).

Hence,

\(Cov(z_X, z_Y) = cor(X,Y)\).

Example time

It is helpful to consider an example.

This is a scatterplot of two variables, ie., “raw data” as is “fed in” for the calculation of the (empirical) covariation:

library(tidyverse)
mtcars %>% 
  ggplot +
  aes(x = hp, y = mpg) +
  geom_point()

And now, let’s z-scale the two variables and draw the same diagram again:

mtcars %>% 
  select(hp, mpg) %>% 
  mutate_all(funs(scale)) %>% 
  ggplot +
  aes(x = hp, y = mpg) +
  geom_point()

Now, what’s the difference? Nada, no difference. That’s reassuring, because we just derived that the assocation of the variables is the same - no matter if use the raw data or z-scaled data as input. The diagrams confirms this in an more intuitive way.

Summary

The correlation is a “special case” of the covariance; it is the case when we feed z-scaled data to the covariance.

Happy data analyzing!