Plotting (and more generally, analyzing) survey results is a frequent endeavor in many business environments. Let’s not think about arguments whether and when surveys are useful (for some recent criticism see Briggs’ book).

Typically, respondents circle some option ranging from “don’t agree at all” to “completely agree” for each question (or “item”). Typically, four to six boxes are given where one is expected to tick one.

In this tutorial, I will discuss some barplot type visualizations; the presentation is based on ggplot2 (within the R environment) . Sure, much more can be done than will be presented here, but for the scope of this post, we will stick to the plain barplot (although some variations of it).

Let’s load some needed packages:

library(tidyverse)

EDIT: The preparation part of this post has been excluded and moved to an own post, for clarity.

Loading data

So, first, let’s load some data. That’s a data set of a survey on extraversion. Folks were asked a bunch of questions tapping at their “psychometric extraversion”, and some related behavior, that is, behavior supposed to be related such as “number of Facebook friends”, “how often at a party” etc. Note that college students form the sample.

Data are available only (free as in free and free as in beer).

data <- read.csv("https://osf.io/meyhp/?action=download")


data_backup <- data # backup just in case we screw something up

Here’s the DOI of this piece of data: 10.17605/OSF.IO/4KGZH.

OK, we got ‘em; a dataset of dimension 501, 28. Let’s glimpse at the data:

glimpse(data)

## Observations: 501
## Variables: 28
## $ X                  <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ...
## $ timestamp          <fctr> 11.03.2015 19:17:48, 11.03.2015 19:18:05, ...
## $ code               <fctr> HSC, ERB, ADP, KHB, PTG, ABL, ber, hph, IH...
## $ i01                <int> 3, 2, 3, 3, 4, 3, 4, 3, 4, 4, 3, 3, 4, 4, 3...
## $ i02r               <int> 3, 2, 4, 3, 3, 2, 4, 3, 4, 4, 3, 4, 3, 3, 3...
## $ i03                <int> 3, 1, 1, 2, 1, 1, 1, 2, 1, 2, 1, 1, 1, 4, 1...
## $ i04                <int> 3, 2, 4, 4, 4, 4, 3, 3, 4, 4, 3, 3, 2, 4, 3...
## $ i05                <int> 4, 3, 4, 3, 4, 2, 3, 2, 3, 3, 3, 2, 3, 3, 3...
## $ i06r               <int> 4, 2, 1, 3, 3, 3, 3, 2, 4, 3, 3, 3, 3, 3, 3...
## $ i07                <int> 3, 2, 3, 3, 4, 4, 2, 3, 3, 3, 2, 4, 2, 3, 3...
## $ i08                <int> 2, 3, 2, 3, 2, 3, 3, 2, 3, 3, 3, 2, 3, 3, 4...
## $ i09                <int> 3, 3, 3, 3, 3, 3, 3, 4, 4, 3, 4, 2, 4, 4, 4...
## $ i10                <int> 1, 1, 1, 2, 4, 3, 2, 1, 2, 3, 1, 3, 2, 3, 2...
## $ n_facebook_friends <int> 250, 106, 215, 200, 100, 376, 180, 432, 200...
## $ n_hangover         <int> 1, 0, 0, 15, 0, 1, 1, 2, 5, 0, 1, 2, 20, 2,...
## $ age                <int> 24, 35, 25, 39, 29, 33, 24, 28, 29, 38, 25,...
## $ sex                <fctr> Frau, Frau, Frau, Frau, Frau, Mann, Frau, ...
## $ extra_single_item  <int> 4, 3, 4, 3, 4, 4, 3, 3, 4, 4, 4, 4, 4, 4, 4...
## $ time_conversation  <dbl> 10, 15, 15, 5, 5, 20, 2, 15, 10, 10, 1, 5, ...
## $ presentation       <fctr> nein, nein, nein, nein, nein, ja, ja, ja, ...
## $ n_party            <int> 20, 5, 3, 25, 4, 4, 3, 6, 12, 5, 10, 5, 10,...
## $ clients            <fctr> , , , , , , , , , , , , , , , , , , , , , ...
## $ extra_vignette     <fctr> , , , , , , , , , , , , , , , , , , , , , ...
## $ extra_description  <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,...
## $ prop_na_per_row    <dbl> 0.04347826, 0.04347826, 0.04347826, 0.04347...
## $ extra_mean         <dbl> 2.9, 2.1, 2.6, 2.9, 3.2, 2.8, 2.8, 2.5, 3.2...
## $ extra_median       <dbl> 3.0, 2.0, 3.0, 3.0, 3.5, 3.0, 3.0, 2.5, 3.5...
## $ client_freq        <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,...

Let’s extract only the items, and exclude NAs (there are not many).

data %>% 
  select(i01:i10) %>% nrow

## [1] 501

data %>% 
  select(i01:i10) %>%
  na.omit %>% nrow

## [1] 493

data %>% 
  select(i01:i10) %>%
  na.omit -> data_items

Plotting item distribution

Typical stacked bar plot

The most obvious thing is to plot the distribution of the items (here: 10) of the survey. So let’s do that with ggplot.

On the x-axis we would like to have each item (i1, i2, …), and on the y-axis the frequency of each answer, in some stapled bar fashion. That means, on the x-axis is one variable only. That’s why we need to “melt” the items to one “long” variable.

data_items %>%  
  gather(key = items, value = answer) %>% 
  mutate(answer = factor(answer)) %>% 
  ggplot(aes(x = items)) +
  geom_bar(aes(fill = answer), position = "fill") -> p1
p1

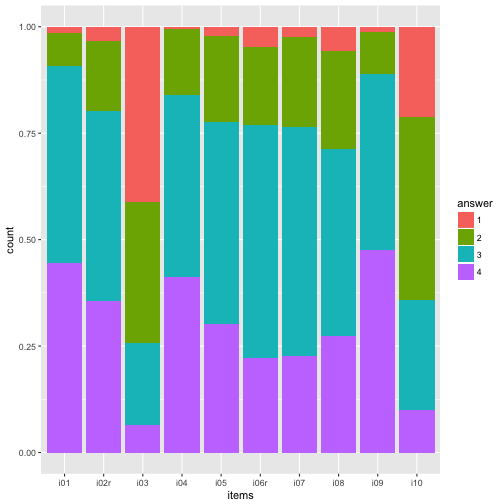
Maybe nicer to turn it 90 degrees:

p1 + coord_flip()

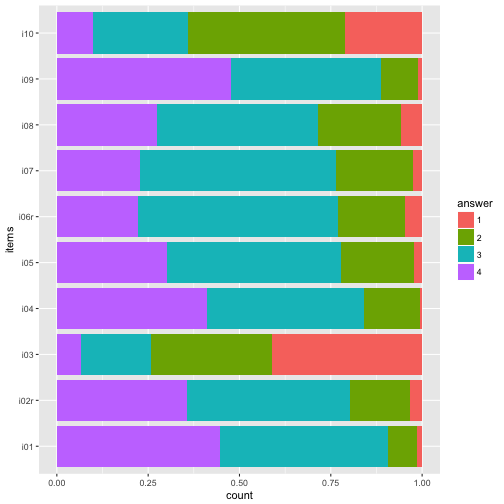
And reverse the order of the items, so that i01 is at the top.

data_items %>% 
  gather(key = items, value = answer) %>% 
  mutate(answer = factor(answer),
         items = factor(items)) -> data2
  
ggplot(data2, aes(x = items)) +
  geom_bar(aes(fill = answer), position = "fill") +
  coord_flip() +
  scale_x_discrete(limits = rev(levels(data2$items))) -> p2
p2

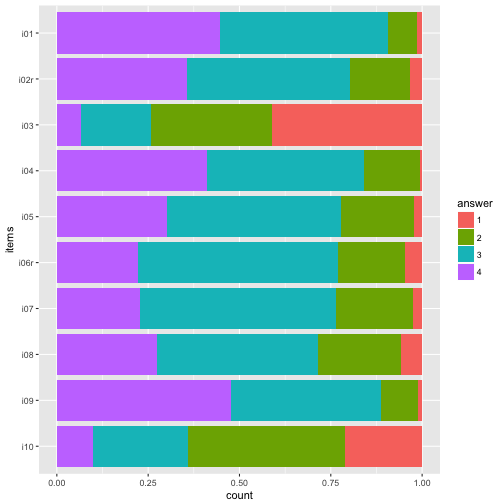
Colors

The beauty of the colors lie in the eye of the beholder… Let’s try a different palette.

Sequential color palettes.

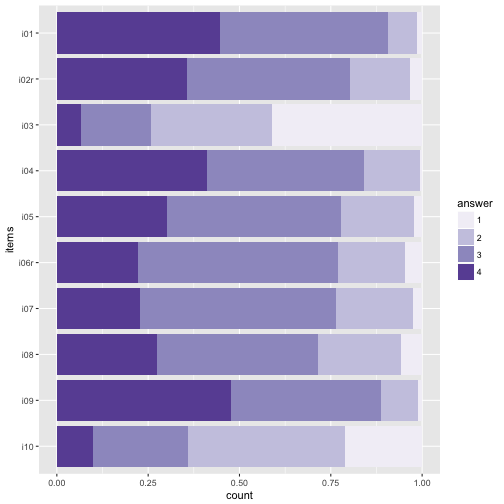
p2 + scale_fill_brewer(palette = "Blues")

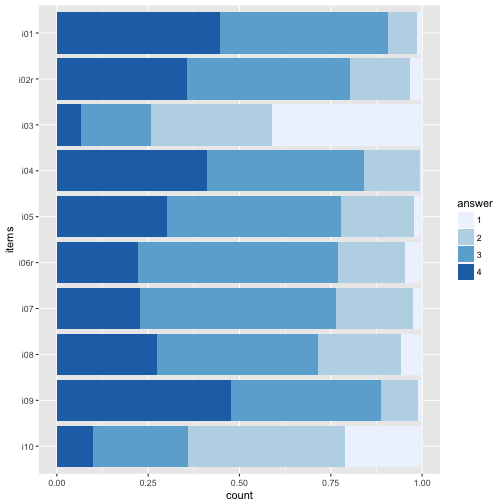
p2 + scale_fill_brewer(palette = "BuGn")

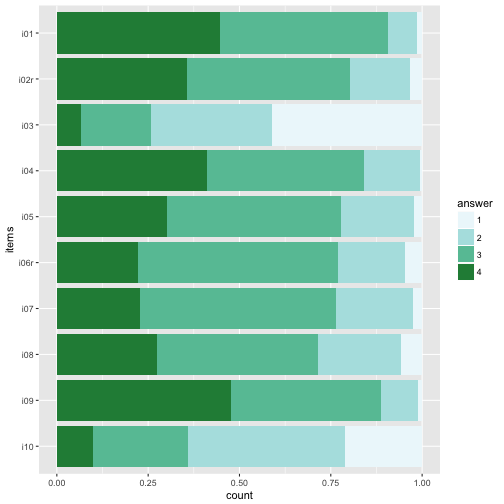
p2 + scale_fill_brewer(palette = 12)

Diverging palettes.

p2 + scale_fill_brewer(palette = "RdYlGn")

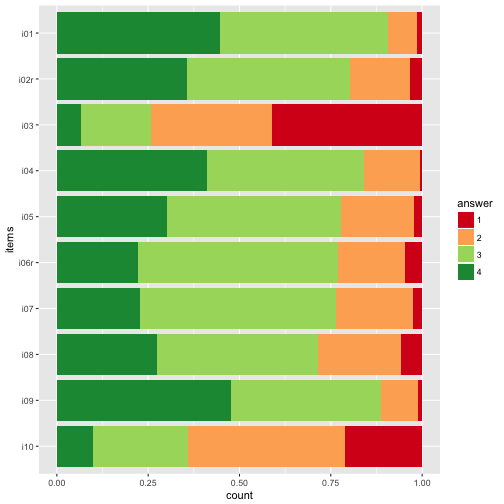
p2 + scale_fill_brewer(palette = "RdYlBu")

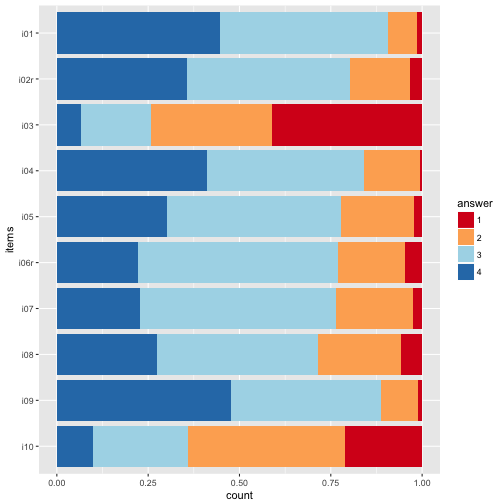
The divering palettes are useful because we have two “poles” - “do not agree” on one side, and “do agree” on the other side.

See here for an overview on Brewer palettes.

Or maybe just grey tones.

p2 + scale_fill_grey()

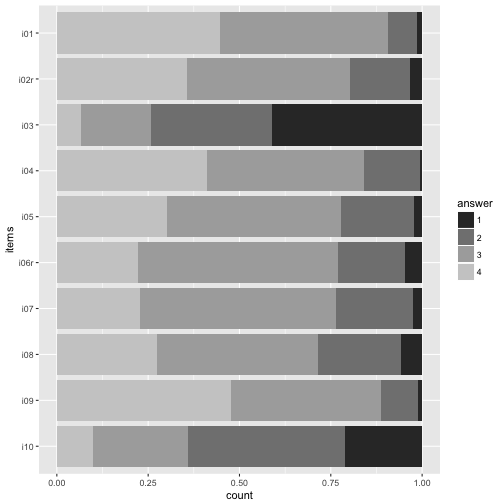
My own favorite-cherished color.

colours <- c("#2121D9", "#9999FF", "#D92121", "#21D921", "#FFFF4D", "#FF9326")
p2 + scale_fill_manual(values=colours)

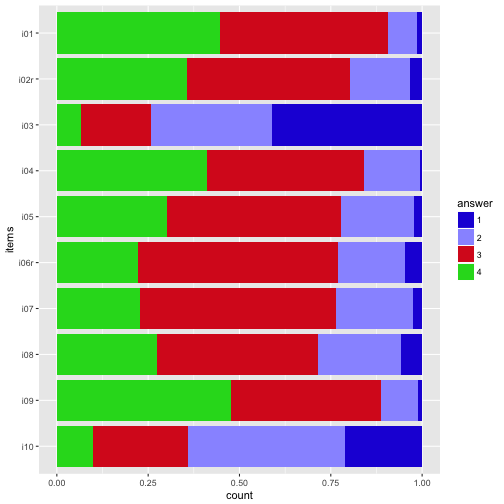
Numbers (count) on bars

It might be helpful to print the exact numbers on the bars.

data2 %>% 
  dplyr::count(items, answer) %>% 
  mutate(y_pos = cumsum(n)/nrow(data_items) - (0.5 * n/nrow(data_items)),
         y_cumsum = cumsum(n)) %>% 
  mutate(items_num = parse_number(items)) -> data3

ggplot(data3, aes(x = items, y = n)) +
  geom_bar(aes(fill = answer), position = "fill", stat = "identity") +
  geom_text(aes(y = y_pos, label = n),  size = 3) -> p3

p3

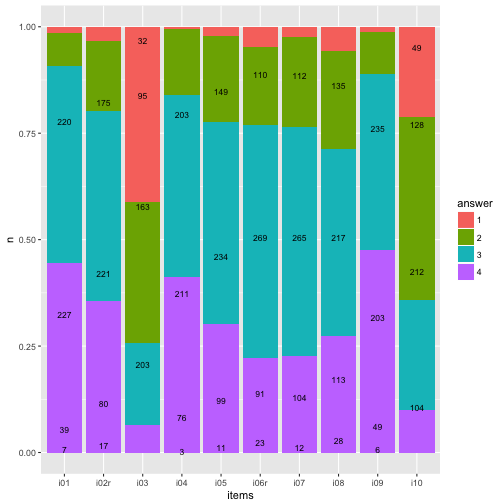
Flip coordinate system, and with “%” labels.

p3 + coord_flip() + 
  scale_y_continuous(labels = scales::percent) +
  ylab("proportion of respondents") -> p4
p4

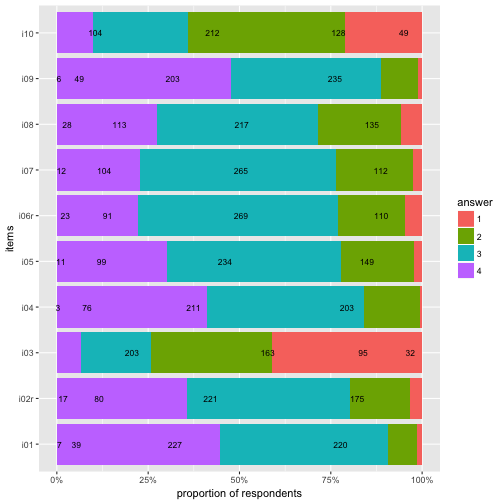
Highlight main category

data3 %>% 
  mutate(answer = as.numeric(answer)) %>% 
  group_by(items) %>% 
  mutate(max_n = max(n)) %>% 
  mutate(max_cat = factor(which(n == max_n))) %>% 
  mutate(fit_cat = (answer == max_cat)) %>% 
  ungroup -> data4


ggplot(data4, aes(x = items, y = n)) +
  geom_bar(aes(fill = factor(answer),
               color = fit_cat), position = "fill", stat = "identity") +
  geom_text(aes(y = y_pos, label = n),  size = 3) +
  scale_color_manual(values = c("NA", "red"), guide = "none") +
  scale_fill_grey()

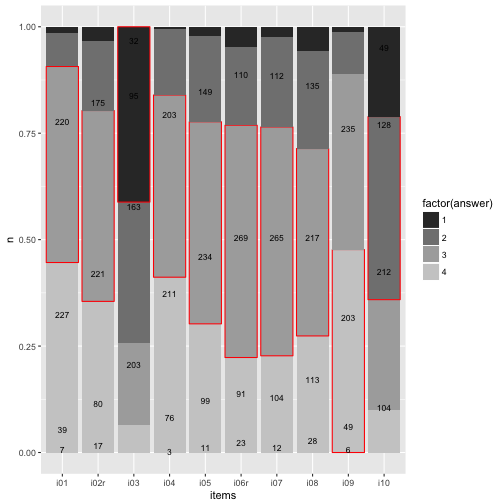
To be honest, does really look nice. Let’s try something different later.

Barplot with geom_rect

This section and code is inspired by this post.

The goal is to produce a more flexible bar plot, such as a “waterfall plot”, where y= 0 is centered at the middle bar height, we need to change the geom. No more geom_bar but the more versatile geom_rect. This geom plots, surprisingly, rectangles. Hence, we need to know the start and the end value (for the y-axis, the width of the bar is just 1).

First, we need to prepare the dataset for that task.

data4 %>% 
  select(items, answer, y_cumsum) %>% 
  group_by(items) %>% 
  spread(key = answer, value = y_cumsum) %>% 
  mutate(zero = 0, end = nrow(data_items)) %>% 
  select(items, zero, `1`, `2`, `3`, `4`, end) %>% 
  ungroup %>% 
  mutate(items_num = 1:10) -> data5



data5 %>% 
  rename(start_1 = zero) %>% 
  mutate(end_1 = `1`) %>% 
  mutate(start_2 = `1`) %>% 
  mutate(end_2 = `2`) %>% 
  mutate(start_3 = `2`) %>% 
  mutate(end_3 = `3`) %>% 
  mutate(start_4 = `3`) %>% 
  mutate(end_4 = end) %>% 
  select(items_num, start_1, end_1, start_2, end_2, start_3, end_3, start_4, end_4) -> data6

head(data6) %>% kable

OK, we have that, pooh, quite a mess.

So, now we need it in long form. Here come a not so elegant, but rather simple, solution for that.

data_cat1 <- select(data6, items_num, start_1, end_1) %>% setNames(c("items", "start", "end")) %>% mutate(answer = 1)
data_cat2 <- select(data6, items_num, start_2, end_2) %>% setNames(c("items","start", "end"))  %>% mutate(answer = 2)
data_cat3 <- select(data6, items_num, start_3, end_3) %>% setNames(c("items","start", "end"))  %>% mutate(answer = 3)
data_cat4 <- select(data6, items_num, start_4, end_4) %>% setNames(c("items","start", "end"))  %>% mutate(answer = 4)

   
data7 <- bind_rows(data_cat1, data_cat2, data_cat3, data_cat4) 

data7 %>% head %>% kable

Now let’s plot the bar graph with the rectangle plot.

data7$answer <- factor(data7$answer)

ggplot(data7) +
  aes() +
  geom_rect(aes(x = items, 
                ymin = start, 
                ymax = end, 
                xmin = items - 0.4, 
                xmax = items + 0.4,
                fill = answer)) +
  scale_x_continuous(breaks = 1:10, name = "items") +
  ylab("n") -> p5

## Warning: Ignoring unknown aesthetics: x

p5 + geom_text(data = data3, aes(x = items_num, y = y_pos*nrow(data), label = n), size = 2) -> p6

p6

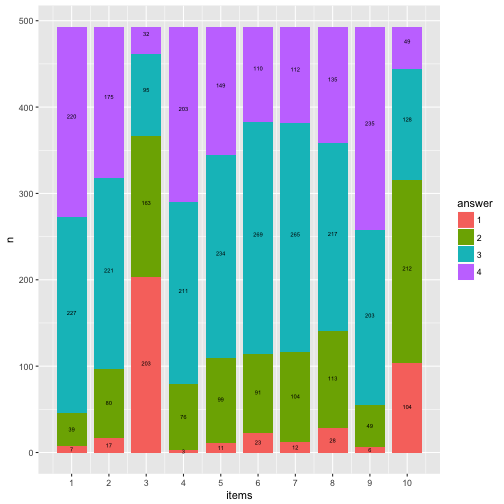
Compare that to the geom_bar solution.

p3

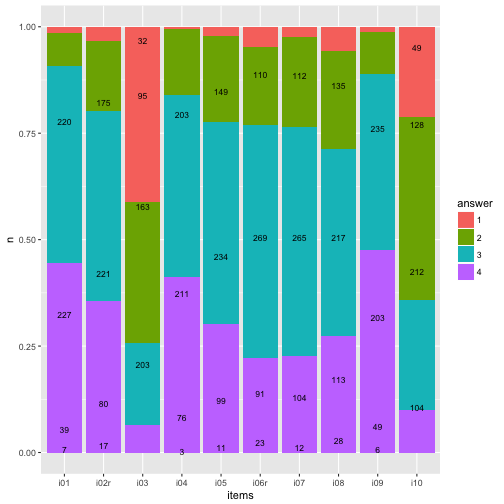
Basically identical (never mind the bar width).

Now flip the coordinates again (and compare to previous solution with geom_bar).

p6 + coord_flip()

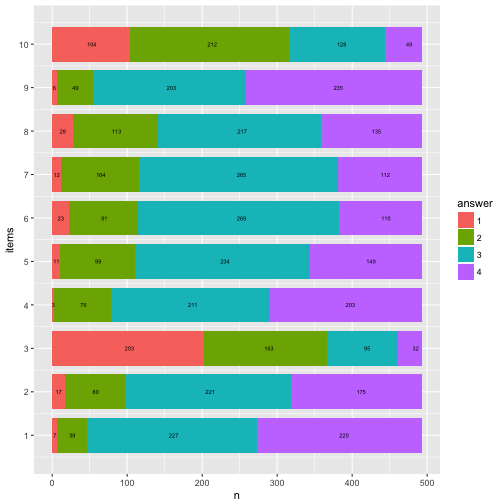
p4

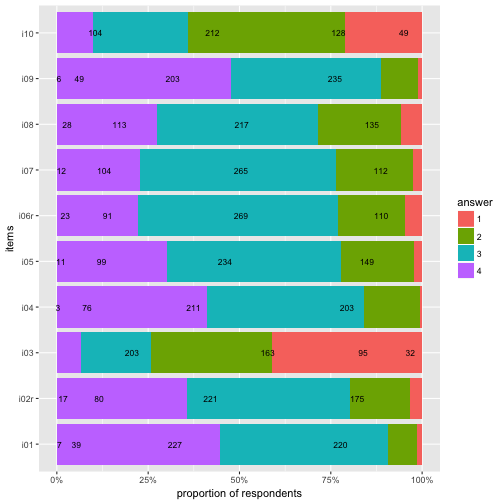
Let’s try to highlight the most frequent answer category for each item.

data7 %>% 
  mutate(n = end - start) %>% 
  group_by(items) %>% 
  mutate(max_n = max(n)) %>% 
  mutate(max_cat = factor(which(n == max_n))) %>% 
  mutate(fit_cat = (answer == max_cat)) %>% 
  ungroup -> data8

data8 %>% 
  filter(fit_cat == TRUE) -> data8a


data7 %>% 
  ggplot() +
  aes() +
  geom_rect(aes(x = items, 
                ymin = start, 
                ymax = end, 
                xmin = items - 0.4, 
                xmax = items + 0.4,
                fill = answer)) +
  scale_x_continuous(breaks = 1:10, name = "items") +
  ylab("n") + 
  scale_fill_grey(start = .4, end = .8) -> p8

## Warning: Ignoring unknown aesthetics: x

p8 + geom_rect(data = data8a, aes(x = items, 
                ymin = start, 
                ymax = end, 
                xmin = items - 0.4, 
                xmax = items + 0.4), fill = "red")  + 
  geom_text(data = data3, aes(x = items_num, y = y_pos*nrow(data), label = n), size = 2) -> p8

## Warning: Ignoring unknown aesthetics: x

p8 + coord_flip()

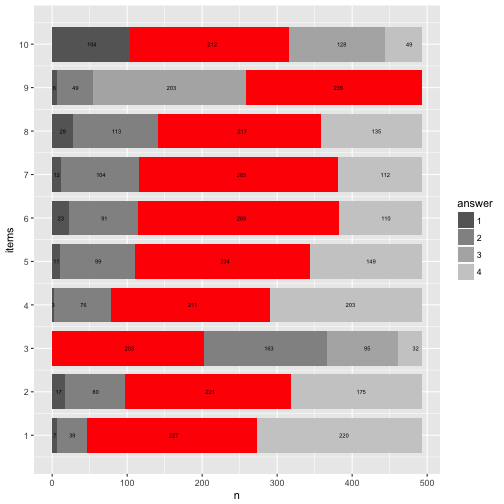
Here’s a cheat sheet on colors and palettes; and here you’ll find an overview on colors (with names and hex codes).

Mrs. Brewer site is a great place to come up with your own palette and learn more about colors.

Rainbow diagram

Let’s try to “move” the bars to our wishes. Precisely, it would be nice if the bars were aligned at the “Rubicon” between “do not agree” and “do agree”. Then we could see better how many persons agree and not.

More practically, if we knew that 104+212 = 316 persons basically disagree, then 316 could be our “zero line” (item 10). Repeat that for each item.

data8 %>% 
  group_by(items) %>% 
  mutate(n_disagree = sum(n[c(1,2)]),
         n_agree = sum(n[c(3,4)]),
         start_adj = start - n_disagree,
         end_adj = end - n_disagree
         ) %>% 
  ungroup -> data9


data9 %>% 
  ggplot() +
  aes() +
  geom_rect(aes(x = items, 
                ymin = start_adj, 
                ymax = end_adj, 
                xmin = items - 0.4, 
                xmax = items + 0.4,
                fill = answer)) +
  scale_x_continuous(breaks = 1:10, name = "items") +
  ylab("n") + 
  scale_fill_grey(start = .4, end = .8) -> p9

## Warning: Ignoring unknown aesthetics: x

p9

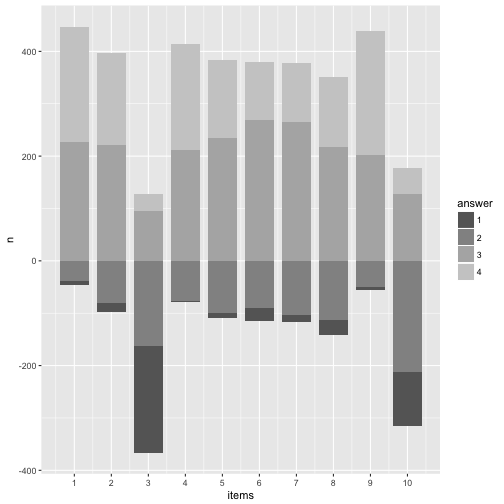
Looks quite cool.

Now let’s add the numbers to that plot.

data4 %>% 
  mutate(items_num = parse_number(items)) %>% 
  dplyr::select(-items) %>% 
  rename(items = items_num) %>% 
  select(items, everything()) %>% 
  arrange(answer, items) %>% 
  ungroup -> data10


data9 %>% 
  mutate(y_pos_adj = data10$y_pos * nrow(data) - n_disagree) -> data11



p9 +  
  geom_text(data = data11, aes(x = items, y = y_pos_adj, label = n), size = 2) -> p11

p11

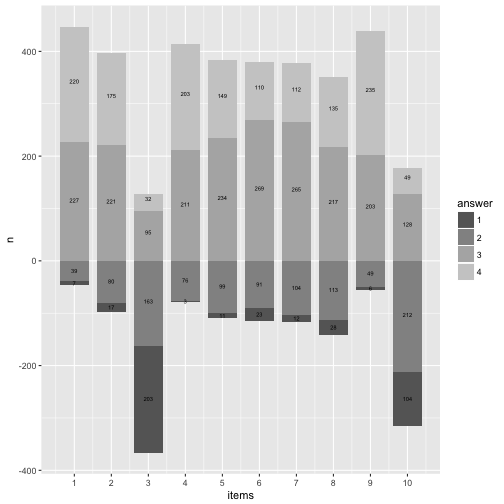
And now let’s highlight the most frequent answer category.

library(ggrepel)

data11 %>% 
  ggplot() +
  aes() +
  geom_rect(aes(x = items,
                ymin = start_adj,
                ymax = end_adj,
                xmin = items - 0.4,
                xmax = items + 0.4,
                fill = answer)) +
  scale_fill_grey(start = .4, end = .8) + 
  geom_rect(data = filter(data11, fit_cat == TRUE), 
            aes(x = items, 
                ymin = start_adj, 
                ymax = end_adj, 
                xmin = items - 0.4, 
                xmax = items + 0.4),
            fill = "red") + 
  geom_text(aes(x = items, y = y_pos_adj, label = n), size = 2) +
  scale_x_continuous(breaks = 1:10) +
  ylab("n") -> p12

## Warning: Ignoring unknown aesthetics: x

## Warning: Ignoring unknown aesthetics: x

p12

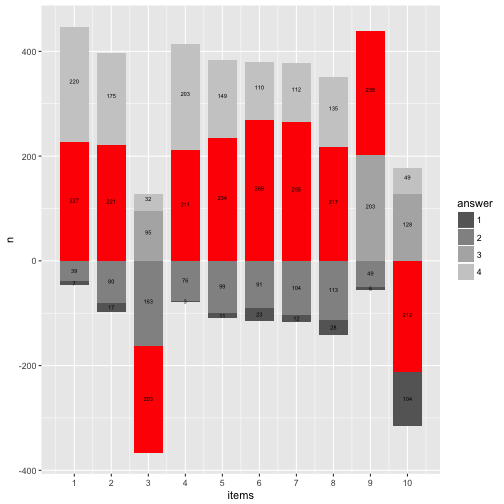
OK, that’s about it for today. May turn the waterfall by 90°.

p12 + coord_flip()

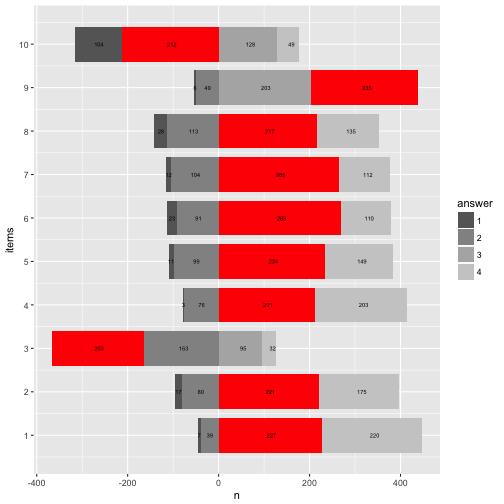
And change the direction of the now numeric items-axis.

p12 + coord_flip() + scale_x_reverse(breaks = 1:10)

## Scale for 'x' is already present. Adding another scale for 'x', which
## will replace the existing scale.

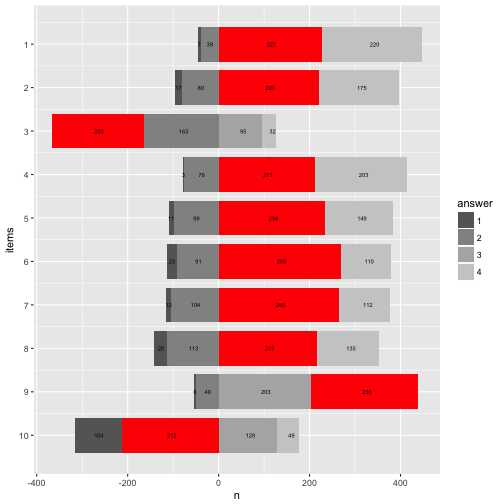
Happy plotting!

Viele Menschen glauben an Horoskope. Doch warum? Ein Grund könnte sein, dass Horoskope einfach gut sind. Was heißt gut: Sie passen auf mich aber nicht auf andere Leute (mit anderen Strernzeichen) und sie sagen Dinge, die nützlich sind.

Ein anderer Grund könnte sein, dass sie uns schmeicheln und Gemeinplätze sind, denen jeder zustimmt: “Sie sind an sich ein Super-Typ, aber manchmal etwas ungeduldig” (oh ja, absolut, passt genau!). “Heute treffen Sie jemanden, der eine große Liebe werden könnte” (Hört sich gut an!). “Wenn Sie nicht aufpassen, könnte Ihnen heute ein Patzer unterlaufen” (Gut, dass ich gewarnt bin, ist nichts passiert heute, was beweisst, dass es richtig war, aufzupassen, Danke, Horoskop!).

Mit anderen Worten: Diese “Null-Hypothese” sagt, dass Horoskop ist so formuliert, dass man gerne zustimmt - unabhängig von den Inhalten. Die Studierenden in meinem Kurs wollten das überprüfen (das ist ein typischer Dozentensatz). Dafür haben wir uns folgende Studie überlegt: Wir legen unbedarften Versuchspersonen entweder ein echtes (vom Urheber des Horoskops als “wahr” erachtet) oder ein von uns gefälschtes Horoskop vor. Dann fragen wir, kurz gesagt: “Wie gut passt das Horoskop auf Dich?”.

Wenn das Horoskop nur Blabla ist, sollte das “Passungsgefühl” (wie gut das Horoskop auf die befragte Person passt) bei echten und gefälschten Horoskopen ungefähr gleich sein. Wenn die Horoskope die Menschen aber gut beschreiben sollten, dann sollten nur die Leute mit echten Horoskopen eine gute Passung berichten, nicht aber die Leute mit den gefälschten Horoskopen. Damit liegt die Hypothesen klar auf den Tisch – für uns, nicht für die Versuchspersonen, denen wir erstmal einen Bären aufbinden (müssen). Das nennt man dann “Coverstory” (klingt freundlicher und cooler).

In der Psychologie ist dieser Effekt als Barnumeffekt bekannt.

Schauen wir uns mal die Daten an.

Daten einlesen

Excel-Datei einlesen.

library(readxl)
data <- read_excel("~/Downloads/horo.xlsx")

Oder online die CSV-Datei einlesen.

data <- read.csv("https://sebastiansauer.github.io/data/horo.csv")

Erster Blick

library(dplyr)
glimpse(data)

## Observations: 54
## Variables: 6
## $ Sternzeichen   <fctr> Zwilling, Skorpion, Skorpion, Steinbock, Waage...
## $ Wahnehmung     <dbl> 0.00, 0.33, 0.33, 0.67, 0.67, 0.00, 0.33, 0.67,...
## $ Geschlecht     <fctr> weiblich, männlich, männlich, weiblich, männli...
## $ Alter          <int> 21, 27, 27, 26, 25, 26, 29, 26, 29, 30, 26, 33,...
## $ Gruppe         <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,...
## $ Richtig_Falsch <fctr> F, F, F, F, F, F, F, F, F, R, R, R, R, R, R, R...

NAs loswerden

data %>% 
  filter(row_number() <= 44) -> data  # ab Zeile 45 kommen nur noch Leerzeilen
# oder in der Excel-Datei die Zeilen (ab Z. 45) löschen

Check

Rechtschreibfehler bei “Wahnehmung”, das korrigieren wir.

rename(data, Wahrnehmung = Wahnehmung) -> data

Die Anzahl der “richtigen” und “falschen” Profilen sollte (etwa) gleich sein.

library(ggplot2)

data %>% 
  count(Richtig_Falsch)

## # A tibble: 2 × 2
##   Richtig_Falsch     n
##           <fctr> <int>
## 1              F    20
## 2              R    24

qplot(x = Richtig_Falsch, data = data)

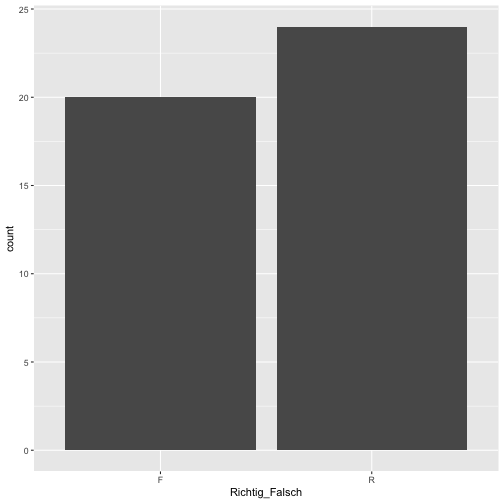Ok, passt in etwa.

Schauen wir uns mal die Verteilung der Horoskope an.

qplot(x = Sternzeichen, data = data) + coord_flip()

qplot(x = Sternzeichen, data = data, fill = Richtig_Falsch) + coord_flip()

Spaßeshalber: Die Altersverteilung.

qplot(x = Geschlecht, data = data)

summary(data$Alter)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   21.00   26.00   27.00   28.56   29.75   38.00      26

qplot(y = Alter, x = Geschlecht, fill = Geschlecht, geom = "boxplot", data = data, alpha = .3)

## Warning: Removed 26 rows containing non-finite values (stat_boxplot).

“Wahrnehmung”

Ist die gefühlte Passgenauigkeit zwischen den beiden Gruppen gleich, so wie es der Barnum-Effekt vorhersagt?

Schauen wir mal…

data %>% 
  filter(!is.na(Wahrnehmung)) %>% 
  group_by(Richtig_Falsch) %>% 
  summarise(wahr_group_mean = mean(Wahrnehmung, na.rm = TRUE),
            wahr_group_md = median(Wahrnehmung, na.rm = TRUE)) -> results1

results1

## # A tibble: 2 × 3
##   Richtig_Falsch wahr_group_mean wahr_group_md
##           <fctr>           <dbl>         <dbl>
## 1              F       0.5835000         0.670
## 2              R       0.4445833         0.415

Das plotten wir mal, ist ja so was wie ein zentrales Ergebnis.

results1 %>% 
  ggplot() +
  aes(y = wahr_group_mean, 
      x = Richtig_Falsch) +
  geom_bar(stat = "identity") +
  xlab("Horoskop-Typ (Richtig vs. Falsch)") +
  ylab("Gefühlte Passung des Horoskops") 

Eigentlich ist dieses Bild recht informationsarm. Schöner ist es (vielleicht) so:

data %>% 
  ggplot(aes(x = Richtig_Falsch, y = Wahrnehmung)) +
  geom_boxplot() +
  geom_jitter()

Hm, sieht etwas komisch aus. Vielleicht lieber ein Histogramm:

data %>% 
  ggplot(aes(x = factor(Wahrnehmung), fill = Richtig_Falsch)) +
  geom_bar(position = "dodge")

Das ist ganz aufschlussreich. Die Balken sind überall in etwa gleich hoch. Nur bei “Null-Passung” finden sich hauptsächlich echte Horoskope. Das spricht nicht für die Glaubhaftigkeit der Horoskope - und damit indirekt Unterstützung für den Barnum-Effekt.

Inferenzstatistik

Schauen wir mal ob sich die beiden Profilgruppen signifikant voneinander unterscheiden:

t.test(Wahrnehmung ~ Richtig_Falsch, data = data)

## 
## 	Welch Two Sample t-test
## 
## data:  Wahrnehmung by Richtig_Falsch
## t = 1.2085, df = 41.436, p-value = 0.2337
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.09315257  0.37098591
## sample estimates:
## mean in group F mean in group R 
##       0.5835000       0.4445833

Der p-Wert ist größer als .05, also nicht signifikant.

Effektstärke und Konfidenzintervall

Wie groß ist die Effektstärke des Unterschieds? Wie groß ist das Konfidenzintervall der Effektstärke?

data %>% 
  count(Richtig_Falsch)

## # A tibble: 2 × 2
##   Richtig_Falsch     n
##           <fctr> <int>
## 1              F    20
## 2              R    24

library(compute.es)
tes(t = 1.21,n.1 = 20, n.2 = 24)

## Mean Differences ES: 
##  
##  d [ 95 %CI] = 0.37 [ -0.25 , 0.98 ] 
##   var(d) = 0.09 
##   p-value(d) = 0.24 
##   U3(d) = 64.29 % 
##   CLES(d) = 60.22 % 
##   Cliff's Delta = 0.2 
##  
##  g [ 95 %CI] = 0.36 [ -0.25 , 0.96 ] 
##   var(g) = 0.09 
##   p-value(g) = 0.24 
##   U3(g) = 64.05 % 
##   CLES(g) = 60.04 % 
##  
##  Correlation ES: 
##  
##  r [ 95 %CI] = 0.18 [ -0.13 , 0.46 ] 
##   var(r) = 0.02 
##   p-value(r) = 0.24 
##  
##  z [ 95 %CI] = 0.19 [ -0.13 , 0.5 ] 
##   var(z) = 0.02 
##   p-value(z) = 0.24 
##  
##  Odds Ratio ES: 
##  
##  OR [ 95 %CI] = 1.94 [ 0.64 , 5.94 ] 
##   p-value(OR) = 0.24 
##  
##  Log OR [ 95 %CI] = 0.66 [ -0.45 , 1.78 ] 
##   var(lOR) = 0.31 
##   p-value(Log OR) = 0.24 
##  
##  Other: 
##  
##  NNT = 8.53 
##  Total N = 44

Wie im Output steht:

d [ 95 %CI] = 0.37 [ -0.25 , 0.98 ]

Fazit

Die Daten sprechen nicht für die Glaubwürdigkeit der Horoskope; in beiden Gruppen (echt vs. gefakt) war die gefühlte Passung ählich. Wir fanden wenig Unterstützung für die Glaubwürdigkeit der Horoskope (bzw. dass die Leute die echten Horoskope glaubhafter einschätzten).

Der Signifikanztest war nicht signifikant; der Unterschied der Mittelwerte reichte nicht aus, um die H0 der Gleichheit zu verwerfen. Dieses Ergebnis kann auf die geringe Stichprobengröße zurückgeführt werden; andererseits kann es auch als Beleg für die Nullhypothese verstanden werden. Natürlich lassen die vorliegenden Daten keine starken Schlüsse zu; aber hey - es war eine schöne Übung :)

Die großen Effektstärkeintervalle sprechen dafür, dass der Effekt nur ungenau geschätzt wurde (aufgrund der geringen Stichprobengröße), was die Aussagekraft der Ergebnisse weiter abschwächt.

Witzigerweise war die mittlere subjektive Passung in der “gefälschten” Gruppe höher als in der “echten” Gruppe; dieser Effekt war von mittlerer Stärke (d = 0.37). Anschaulicher gesprochen: Zieht man eine Person aus jeder Gruppe, so ist die Wahrscheinlichkeit, dass die Person aus der “gefälschten” Gruppe ein größeres Passungsgefühlt hat, ca. 64% (bestenfalls).

Schluss, aus, Feierabend

Ok, für heute reichts :)

We are often interested in the question whether two variables are “associated”, “correlated” (I mean the normal English term) or “dependent”. What exactly, or rather in normal words, does that mean? Let’s look at some easy case.

NOTE: The example has been updated to reflect a more tangible and sensible scenario (find the old one in the previous commit at Github).

Titanic data

For example, let’s look at survival rates of the Titanic disaster, to see whether the probability of survival (event A) depends on the whether you embarked for 1st class (event B).

Let’s load the data and have a look at them.

data(titanic_train, package = "titanic")

library(tidyverse)  # plotting and data mungling
library(pander)  # for markdown tables

data <- titanic_train

glimpse(data)

## Observations: 891
## Variables: 12
## $ PassengerId <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,...
## $ Survived    <int> 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0,...
## $ Pclass      <int> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3,...
## $ Name        <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bra...
## $ Sex         <chr> "male", "female", "female", "female", "male", "mal...
## $ Age         <dbl> 22, 38, 26, 35, 35, NA, 54, 2, 27, 14, 4, 58, 20, ...
## $ SibSp       <int> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4,...
## $ Parch       <int> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1,...
## $ Ticket      <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "1138...
## $ Fare        <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, ...
## $ Cabin       <chr> "", "C85", "", "C123", "", "", "E46", "", "", "", ...
## $ Embarked    <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", ...

Look at the package description for some details on the variables.

Let’s look at the survival rate in general, that is to say to probability of A - irrespective of the the class (1st class or not 1st class).

data %>% 
  count(Survived) %>% 
  ggplot + 
  aes(x = factor(Survived), y = n) +
  geom_bar(stat = "identity") +
  ggtitle("Number of Survivals") +
  theme(plot.title = element_text(hjust = .5))

Maybe that’s a better plot:

data %>% 
  count(Survived) %>% 
  ggplot + 
  aes(x = factor(1), fill = factor(Survived), y = n) +
  geom_bar(stat = "identity") +
  ggtitle("Number of Survivals") +
  theme(plot.title = element_text(hjust = .5)) +
  xlab("")

The exact figures are for the survivals are:

data %>% 
  count(Survived)

## # A tibble: 2 × 2
##   Survived     n
##      <int> <int>
## 1        0   549
## 2        1   342

The exact figures are for the classes (1st vs. other) are:

data %>% 
  mutate(Pclass_bin = ifelse(Pclass == 1, "1st", "not_1st")) %>% 
  count(Pclass_bin)

## # A tibble: 2 × 2
##   Pclass_bin     n
##        <chr> <int>
## 1        1st   216
## 2    not_1st   675

… and the number of passengers per class (1st class vs. other classes) is:

data %>% 
  mutate(Pclass_bin = ifelse(Pclass == 1, "1st", "not_1st")) %>% 
  count(Survived, Pclass_bin)

## Source: local data frame [4 x 3]
## Groups: Survived [?]
## 
##   Survived Pclass_bin     n
##      <int>      <chr> <int>
## 1        0        1st    80
## 2        0    not_1st   469
## 3        1        1st   136
## 4        1    not_1st   206

So, that was warming up. Let’s see what the probability (percentage) of survival is for both 1st class and non-first class.

data %>% 
  mutate(Pclass_bin = ifelse(Pclass == 1, "1st", "not_1st")) %>% 
  count(Pclass_bin, Survived) %>% 
  ggplot + 
  aes(x = factor(Pclass_bin), fill = factor(Survived), y = n, labels = n) +
  geom_bar(stat = "identity") +
  ggtitle("Probability of Survivals given Passenager class") +
  theme(plot.title = element_text(hjust = .5))

We easily conclude that the probability of survival is associated with passenger class. The probability of survival (event A) given 1st class (event B) is considerably higher than the probability of A given non-B (event B is “not 1st class”).

The exact numbers are:

data %>% 
  mutate(Pclass_bin = ifelse(Pclass == 1, "1st", "not_1st")) %>% 
  count(Pclass_bin, Survived) -> data_2

data_2

## Source: local data frame [4 x 3]
## Groups: Pclass_bin [?]
## 
##   Pclass_bin Survived     n
##        <chr>    <int> <int>
## 1        1st        0    80
## 2        1st        1   136
## 3    not_1st        0   469
## 4    not_1st        1   206

pandoc.table(data_2, style = "rmarkdown")

General notion of stochastic independence

A typical definition of stochastic (or statistic) independence is this:

\(p(A|B) = p(A)\) That means in plain English, that the probability of A (survival) given B (1st class) is equal to A irrespective of B, that means irrespective of B is the case or non-B is the case. In short, that would mean the survival probability is equal in both cases (B or non-B).

In math-speak:

Here, the “cup” \(\cup\) means “OR”.

It than follows that if \(p(A|B) = p(A|nonB)\) we deduce

Or more verbose in our Titanic example:

In words, whether someone survives is independent from the question of his or her passenger class: Survival probability is the the same in 1st class and in the other classes (“non 1st class”).

Let’s look at the data of our example:

In R:

p_A <- 342 / (549+342)
p_nonA <- 549 / (549+342)

p_B <- 216 / (216 + 675)
p_nonB <- 549 / (549+342)


p_B <- 216 / (216 + 675)
p_nonB <- 675 / (216 + 675)
p_A_given_B <- 136 / (80+136)
P_nonA_given_B <- 80 / (80+136)

p_A_given_nonB <- 206 / (206+469)
p_nonA_given_nonB <- 469 / (206+469)



p_diff <- p_A_given_B - p_A_given_nonB
p_diff

## [1] 0.3244444

The difference p(A|B) - p(A|nonB) is not zero. Actually it is quite far away: If you are in 1st, your survival rate is 32% higher if you were not in 1st class. Quite strong. However, note that this last step is subjective, no job for statistics.

Finally, let’s look for two variable which are not associated. For example: Shoe size (of adults) and their bank account number.

In our dataset, what about port of Embarkement: Southampton vs. not Southampton and Survival rate.

data %>% 
  mutate(Embarked_bin = ifelse(Embarked == "S", "S", "not_S")) %>% 
  select(Embarked_bin, Survived) %>% 
  count(Embarked_bin, Survived) %>% 
  ggplot +
  aes(x = Embarked_bin, y = n, fill = factor(Survived)) +
  geom_bar(stat = "identity")

Hm, appears to be related/associated/dependent/correlated.

Maybe better plot like this:

data %>% 
  mutate(Embarked_bin = ifelse(Embarked == "S", "S", "not_S")) %>% 
  select(Embarked_bin, Survived) %>% 
  count(Embarked_bin, Survived) %>% 
  ggplot +
  aes(x = Embarked_bin, y = n, fill = factor(Survived)) +
  geom_bar(stat = "identity", position = "fill")

Ah, yes, there is some dependence.

Ok, last try, this is should be a save win: Whether fare is an odd number (eg., 7 Pound) and survival are related.

data %>% 
  mutate(Fare_odd = ifelse(round(Fare) %% 2 == 0, "even", "odd")) %>% 
  select(Fare_odd, Survived) %>% 
  count(Fare_odd, Survived) %>% 
  ggplot +
  aes(x = Fare_odd, y = n, fill = factor(Survived)) +
  geom_bar(stat = "identity", position = "fill")

Well, nearly equal, approximately independent, or independent enough for me (as said, that’s subjective).

Concluding remarks

Of course there are numerous ways to “measure” the strength of assocation. Odds ratios, for example, a popular choice. The reason why I like or presented this version \(p(A|B)-p(A|nonB)\) is that I find it intuitively appealing. In my teaching I found that the Odds Ratio was somewhat more difficult to grasp at first.

Also note that we where looking at discrete events, not continuous.

I found myself doing the following: I had a bunch of predictors, one (numeric) outcome, and wanted to run I simple regression for each of the predictors. Having a bunch of model results, I would like to have them bundled in one data frame.

So, here is one way to do it.

First, load some data.

data(mtcars)
str(mtcars)

## 'data.frame':	32 obs. of  11 variables:
##  $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
##  $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
##  $ disp: num  160 160 108 258 360 ...
##  $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
##  $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
##  $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
##  $ qsec: num  16.5 17 18.6 19.4 17 ...
##  $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
##  $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
##  $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
##  $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Say, mpg is our outcome/ criterion. The rest of the variables are predictors.

Then, some packages.

library(dplyr)
library(purrr)
library(tibble)
library(ggplot2)
library(stringr)
library(tidyr)
library(broom)
library(scales)

For illustration, let’s run a regression with each and all of the predictors as a preliminary step.

lm(mpg ~ ., data = mtcars) %>% glance

##   r.squared adj.r.squared    sigma statistic      p.value df    logLik
## 1 0.8690158     0.8066423 2.650197  13.93246 3.793152e-07 11 -69.85491
##        AIC      BIC deviance df.residual
## 1 163.7098 181.2986 147.4944          21

lm(mpg ~ ., data = mtcars) %>% summary %>% tidy

##           term    estimate   std.error  statistic    p.value
## 1  (Intercept) 12.30337416 18.71788443  0.6573058 0.51812440
## 2          cyl -0.11144048  1.04502336 -0.1066392 0.91608738
## 3         disp  0.01333524  0.01785750  0.7467585 0.46348865
## 4           hp -0.02148212  0.02176858 -0.9868407 0.33495531
## 5         drat  0.78711097  1.63537307  0.4813036 0.63527790
## 6           wt -3.71530393  1.89441430 -1.9611887 0.06325215
## 7         qsec  0.82104075  0.73084480  1.1234133 0.27394127
## 8           vs  0.31776281  2.10450861  0.1509915 0.88142347
## 9           am  2.52022689  2.05665055  1.2254035 0.23398971
## 10        gear  0.65541302  1.49325996  0.4389142 0.66520643
## 11        carb -0.19941925  0.82875250 -0.2406258 0.81217871

Of interest, no p-value is below .05.

Now come the main part, let’s run multiple regression and then combine the results.

mtcars %>% 
  dplyr::select(-mpg) %>% 
  map(~lm(mtcars$mpg ~ .x, data = mtcars)) %>% 
  map(summary) %>% 
  map("coefficients") %>% 
  do.call(rbind.data.frame, .) %>% 
  rownames_to_column %>% 
  as_tibble %>% 
  setNames(c("predictor", "b", "SE", "t", "p")) %>% 
  dplyr::arrange(p) %>% 
  dplyr::filter(!str_detect(predictor, "(Intercept)")) %>% 
  mutate(predictor = str_sub(predictor, start = 1, end = str_length(predictor)-3))

## # A tibble: 10 × 5
##    predictor           b          SE         t            p
##        <chr>       <dbl>       <dbl>     <dbl>        <dbl>
## 1         wt -5.34447157 0.559101045 -9.559044 1.293959e-10
## 2        cyl -2.87579014 0.322408883 -8.919699 6.112687e-10
## 3       disp -0.04121512 0.004711833 -8.747152 9.380327e-10
## 4         hp -0.06822828 0.010119304 -6.742389 1.787835e-07
## 5       drat  7.67823260 1.506705108  5.096042 1.776240e-05
## 6         vs  7.94047619 1.632370025  4.864385 3.415937e-05
## 7         am  7.24493927 1.764421632  4.106127 2.850207e-04
## 8       carb -2.05571870 0.568545640 -3.615750 1.084446e-03
## 9       gear  3.92333333 1.308130699  2.999191 5.400948e-03
## 10      qsec  1.41212484 0.559210130  2.525213 1.708199e-02

Some explanation:

• l2: deselect the outcome variable, so that we can address “all” variables in the next lines
• l3: map each list element to lm; .x is a placeholder for all the list elements (here predictors)
• l4: now get the summary of each lm. More specifically, we have a number of lm models, which are stored as list elements. Now we apply the summary function to each of those list elements (lm results).
• l5: address (extract) the coefficients subelement from each list element
• l6: rownames should be their own column
• l7: tibbles are nic
• l8: make the col names typing-friendly
• l9: filter those lines, where predictor is not equal to “(Intercept)”.
• l10: change the values of predictor such that the strange end part “..x” is removed

Puh, quite some hassle.

Now, for completeness, let’s look at the $R^2$.

mtcars %>% 
  dplyr::select(-mpg) %>% 
  map(~lm(mtcars$mpg ~ .x, data = mtcars)) %>% 
  map(glance) %>% 
  do.call(rbind.data.frame, .) %>% 
  rownames_to_column %>% 
  as_tibble 

## # A tibble: 10 × 12
##    rowname r.squared adj.r.squared    sigma statistic      p.value    df
##      <chr>     <dbl>         <dbl>    <dbl>     <dbl>        <dbl> <int>
## 1      cyl 0.7261800     0.7170527 3.205902 79.561028 6.112687e-10     2
## 2     disp 0.7183433     0.7089548 3.251454 76.512660 9.380327e-10     2
## 3       hp 0.6024373     0.5891853 3.862962 45.459803 1.787835e-07     2
## 4     drat 0.4639952     0.4461283 4.485409 25.969645 1.776240e-05     2
## 5       wt 0.7528328     0.7445939 3.045882 91.375325 1.293959e-10     2
## 6     qsec 0.1752963     0.1478062 5.563738  6.376702 1.708199e-02     2
## 7       vs 0.4409477     0.4223126 4.580827 23.662241 3.415937e-05     2
## 8       am 0.3597989     0.3384589 4.902029 16.860279 2.850207e-04     2
## 9     gear 0.2306734     0.2050292 5.373695  8.995144 5.400948e-03     2
## 10    carb 0.3035184     0.2803024 5.112961 13.073646 1.084446e-03     2
## # ... with 5 more variables: logLik <dbl>, AIC <dbl>, BIC <dbl>,
## #   deviance <dbl>, df.residual <int>

Ok, I admit, I like plotting, particularly with ggplot2.

First, the $R^2$ for all models:

mtcars %>% 
  dplyr::select(-mpg) %>% 
  map(~lm(mtcars$mpg ~ .x, data = mtcars)) %>% 
  map(glance) %>% 
  do.call(rbind.data.frame, .) %>% 
  rownames_to_column %>% 
  as_tibble %>% 
  ggplot(aes(x = reorder(rowname, -adj.r.squared), y = adj.r.squared)) +
  geom_point() +
  coord_flip() + 
  scale_y_continuous(labels = scales::percent)

Last, the p-values of each predictor (OMG).

mtcars %>% 
  dplyr::select(-mpg) %>% 
  map(~lm(mtcars$mpg ~ .x, data = mtcars)) %>% 
  map(summary) %>% 
  map("coefficients") %>% 
  do.call(rbind.data.frame, .) %>% 
  rownames_to_column %>% 
  as_tibble %>% 
  setNames(c("predictor", "b", "SE", "t", "p")) %>% 
  dplyr::arrange(p) %>% 
  dplyr::filter(!str_detect(predictor, "(Intercept)")) %>% 
  mutate(predictor = str_sub(predictor, start = 1, end = str_length(predictor)-3)) %>% 
  ggplot(aes(x = reorder(predictor,p), y = p)) +
  geom_point() +
  geom_hline(yintercept = .05, color = "red")

At times it is convenient to draw a frequency bar plot; at times we prefer not the bare frequencies but the proportions or the percentages per category. There are lots of ways doing so; let’s look at some ggplot2 ways.

First, let’s load some data.

data(tips, package = "reshape2")

And the typical libraries.

library(dplyr)
library(ggplot2)
library(tidyr)
library(scales)  # for percentage scales

Way 1

tips %>% 
  count(day) %>% 
  mutate(perc = n / nrow(tips)) -> tips2

ggplot(tips2, aes(x = day, y = perc)) + geom_bar(stat = "identity")

Way 2

ggplot(tips, aes(x = day)) +  
  geom_bar(aes(y = (..count..)/sum(..count..)))

Way 3

myplot <- ggplot(tips, aes(day)) + 
          geom_bar(aes(y = (..count..)/sum(..count..))) + 
          scale_y_continuous(labels=scales::percent) +
  ylab("relative frequencies")

myplot

Way 4

myplot <- ggplot(tips, aes(day, group = sex)) + 
          geom_bar(aes(y = ..prop.., fill = factor(..x..)), stat="count") + 
          scale_y_continuous(labels=scales::percent) +
          ylab("relative frequencies") +
          facet_grid(~sex)

myplot

Way 5

ggplot(tips, aes(x= day,  group=sex)) + 
    geom_bar(aes(y = ..prop.., fill = factor(..x..)), stat="count") +
    geom_text(aes( label = scales::percent(..prop..),
                   y= ..prop.. ), stat= "count", vjust = -.5) +
    labs(y = "Percent", fill="day") +
    facet_grid(~sex) +
    scale_y_continuous(labels = scales::percent)