10 Schätzen vs. Testen

10.1 Lernsteuerung

10.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

10.1.2 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können…

den Unterschied zwischen dem Schätzen von Modellparametern und dem Testen von Hypothesen erläutern
Vor- und Nachteile des Schätzens und Testens diskutieren
Das ROPE-Konzept erläutern und anwenden
Die Güte von Regressionsmodellen einschätzen und berechnen

10.1.3 Begleitliteratur

Der Stoff dieses Kapitels orientiert sich an (Kruschke, 2018).

10.1.4 Vorbereitung im Eigenstudium

Statistik1, Kap. “Geradenmodelle 2”

10.1.5 R-Pakete

In diesem Kapitel werden folgende R-Pakete benötigt:

library(rstanarm)   # Bayes-Modelle
library(tidyverse)
library(easystats)
library(palmerpenguins)  # Datensatz "penguins"

10.1.6 Benötigte Daten: Pinguine

Abbildung 10.1: Possierlich: Die Pinguine (Horst, 2024)

Übungsaufgabe 10.1 (Machen Sie sich mit den Pinguinen vertraut) Machen Sie sich zunächst mit dem Pinguin-Datensatz vertraut. Sie finden den Datensatz penguins im R-Paket palmerpenguins, das Sie auf gewohnte Art installieren können. im Internet findet man den Datensatz auch als CSV-Datei; s. unten. Importieren Sie den Datensatz und verschaffen Sie sich einen Überblick über die Verteilungen jeder Variablen des Datensatzes.

Sie können den Datensatz penguins entweder via dem Pfad importieren:

penguins_url <- "https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv"

penguins <- read.csv(penguins_url)

Oder via dem zugehörigen R-Paket:

data("penguins", package = "palmerpenguins")

Beide Möglichkeit des Datenimports sind okay. \(\square\)

10.1.7 Einstieg

Betrachten Sie die zwei folgenden Aussagen, die jeweils ein Forschungsziel angeben:

“Lernen für die Klausur bringt etwas!”
“Wie viel bringt Lernen für die Klausur?”

Beispiel 10.1 Diskutieren Sie die epistemologische Ausrichtung sowie mögliches Für und Wider der beiden Ausrichtungen! Einmal Behauptung, einmal Frage – was macht das für einen Unterschied? \(\square\)

10.2 Was ist Testen? Was ist Schätzen?

Forschungsfragen kann man, allgemein gesprochen, auf zwei Arten beantworten:

Hypothesen testen: “Die Daten widerlegen die Hypothese (nicht)”
Parameter schätzen: “Der Effekt von X auf Y liegt zwischen A und B”.

10.2.1 Hypothesen testen

Hypothesen testende Analysen kommen zu einer Ja-Nein-Entscheidung bzgl. einer Hypothese. Genauer muss man sagen: Im besten Fall kommen sie zu einer Ja-Nein-Aussage. Es kann natürlich sein, dass die Datenlage so nebelig oder das Problem so knifflig ist, dass man ehrlicherweise zugeben muss, dass man sich nicht sicher ist oder sogar komplett im Dunkeln tappt.

Beispiel 10.2 (“Lernen erhöht den Prüfungserfolg!”) Die Hypothese Lernen erhöht den Prüfungserfolg kann durch eine Studie und eine entsprechende Analyse grundsätzlich folgende drei Ergebnisse finden. 1) Die Daten widersprechen der Hypothese: Lernen bringt offenbar doch nichts für den Klausurerfolg. 2) Die Daten unterstützen die Hypothese: Lernen erhöht den Prüfungserfolg. 3) Die Daten sind uneindeutig, es ist keine Aussage zum Einfluss von Lernen auf den Prüfungserfolg möglich. \(\square\)

Das Testen einer Hypothese kann zu drei Arten von Ergebnissen führen. Die ersten beiden sind informationsreich, die dritte ist informationsarm.

🟥 Die Daten widersprechen der Hypothese: Auf Basis der Daten (und des Modells) muss man die Hypothese ablehnen (verwerfen, sagt man), also als falsch (falsifziert) betrachten oder zumindest hat die Glaubwürdigkeit der Hypothese gelitten.
🟢 Die Daten unterstützen die Hypothese: Auf Basis der Daten (und des Modells) muss man die Hypothese annehmen (oder kann die Gegenthese zumindest nicht verwerfen). Oder zumindest hat die Hypothese an Glaubwürdigkeit gewonnen.
❓ Die Datenlage ist unklar; zum Teil unterstützen die Daten die Hypothese zum Teil widersprechen sie ihr. Man kann keine oder kaum Schlüsse aus den Daten ziehen. In diesem Fall gibt es keinen (nennenswerten) Erkenntnisgewinn.

Hypothesen prüfen ist binär in dem Sinne, dass sie zu “Schwarz-Weiß-Ergebnissen” führen (sofern die Datenlage stark genug ist).

Wichtig

Eine gängige Variante des Hypothesen testen¹ ist das Testen der Hypothese “Es liegt kein (null) Effekt vor” (Null Effekt). Man geht also davon aus, dass es keinen Zusammenhang zwischen UV und AV gibt und spricht vom Nullhypothesen testen, \(H_0\). \(\square\)

10.2.2 Beispiele für Nullhypothesen

“Lernen bringt nichts”
“Frauen und Männer parken gleich schnell ein”
“Es gibt keinen Zusammenhang von Babies und Störchen”
“Früher war es auch nicht besser (sondern gleich gut)”
“Bei Frauen ist der Anteil, derer, die Statistik mögen gleich hoch wie bei Männern” (Null Unterschied zwischen den Geschlechtern) \(\square\)

Vorteil des Hypothesen testen ist das klare, einfache Ergebnis – die Hypothese ist abgelehnt, angenommen, oder die Datenlage ist unklar. Das unterstützt die Entscheidungsfindung, da es die Komplexität reduziert.

Man kann Hypothesen nicht bestätigen

Karl Poppers These, dass man Hypothesen nicht bestätigen (verifizieren) kann, hatte großen Einfluss auf die Wissenschaftstheorie (und Epistemologie allgemein) ausgeübt (Popper, 2013). Schlagend ist das Beispiel zur Hypothese \(H\) “Alle Schwäne sind weiß”. Auch eine große Stichprobe an weißen Schwänen kann die Wahrheit der Hypothese nicht beweisen. Schließlich ist es möglich, dass wir den schwarzen Schwan einfach noch nicht gefunden haben. ² Umgekehrt reicht die (zuverlässige) Beobachtung eines einzelnen schwarzen Schwans, um die Hypothese \(H\) zu widerlegen (falsifizieren). \(\square\)

Wirklich nicht?

In der Wissenschaftspraxis werden die meisten Hypothesen probabilistisch untersucht. Komplett sichere Belege, wie in Poppers Beispiel mit dem schwarzen Schwan, gibt es nicht. Das bedeutet, dass Evidenz im bestätigenden wie im widerlegenden Sinne tendenziell (d.h.probabilistisch) zu betrachten ist. Auf dieser Basis und der Basis zuverlässiger, repräsentativer Daten erscheint plausibel, dass Hypothesen sowohl bestätigt als auch widerlegt werden können (Kruschke, 2018; Morey & Rouder, 2011). \(\square\)

10.2.3 Parameter schätzen

Beim Schätzen von Parametern untersucht man, wie groß ein Effekt ist, etwa der Zusammenhang zwischen X und Y. Es geht also um eine Skalierung, um ein wieviel und nicht um ein “ja/nein”, was beim Hypothesen testen der Fall ist.

Beim Parameter schätzen gibt es zwei Varianten:

⚫️ Punktschätzung: Das Schätzen eines einzelnen Parameterwerts, sozusagen ein “Best Guess”
📏 Bereichsschätzung: Das Schätzen eines Bereichs plausibler oder wahrscheinlicher Parameterwerte

Allerdings kann man das Parameter schätzen auch wie einen Hypothesentest nutzen: Ist ein bestimmter Wert, etwa die Null, nicht im Schätzbereich enthalten, so kann man die Hypothese verwerfen, dass der Parameter gleich diesem Wert (etwa Null) ist. Das Hypothesen testen ist daher (implizit) im Parameter schätzen enthalten.

Beispiel 10.3 Wie groß ist der Schätzbereich für den Effekt des Parameter “Geschlecht” auf das mittlere Gewicht von Pinguinen? Hat die UV Geschlecht einen großen Einfluss auf das mittlere Gewicht dieser Tiere? Anders gefragt: Um welchen Wert sind männliche Tiere im Schnitt schwerer als weibliche Tiere? Tabelle 10.1 gibt uns die Antwort

data(penguins, package = "palmerpenguins")
penguins_nona <-
  penguins |> drop_na(sex, body_mass_g)  # keine fehlenden Werte

m_penguins_sex <- 
  stan_glm(body_mass_g ~ sex, data = penguins_nona)

Tabelle 10.1: Parameterschätzung des Modells m_penguins; der Gewichtssnterschied zwischen den Mittelwerten der Geschlechter beträgt etwa 700 g.

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	3863.18	(3754.31, 3971.56)	100%	1.000	4069	Normal (4207.06 +- 2013.04)
sexmale	681.11	(528.74, 843.76)	100%	1.000	4053	Normal (0.00 +- 4020.19)

Grob gesagt sind männliche Tiere ca. 500 g bis 800 g schwerer als weibliche Tiere im Schnitt (95%-ETI), laut unserem Modell; der Punktschätzer liegt bei einem Gewichtsunterschied von ca. 681 g. \(\square\)

Beispiel 10.4 (Parameterschätzen als Nullhypothesentest)

Forschungsfrage: Sind männliche Pinguine im Schnitt schwerer als weibliche Tiere?

Gleichung 10.1 formalisiert diese Forschungsfrage als statistische Hypothese \(H\).

\[H: \mu_M \ge \mu_F \rightarrow d = \mu_M - \mu_F \ge 0 \tag{10.1}\]

Theorem 10.1 (Nullhypothesentest) \[H: \mu_M \ge \mu_F \leftrightarrow d = \mu_M - \mu_F \ge 0\quad \square\]

Der Unterschied zwischen den Mittelwerten, \(d\), ist genau dann Null, wenn \(\beta_1 = 0\) in unserem Regressionsmodell m1. Entsprechend gilt \(d \ne 0\) wenn \(\beta_1 \ne 0\).

Um die Forschungsfrage zu beantworten zählen wir wie gewohnt den Anteil der Stichproben in der Post-Verteilung für die UV sexmale, die einen Wert größer Null aufweisen:

m_penguins_sex_post <-
  m_penguins_sex |> 
  as_tibble()

m_penguins_sex_post |> 
  count(sexmale > 0)

100% (4000 von 4000) Stichproben finden einen Wert größer Null für sexmale, dass also weibliche Tiere leichter bzw. männliche Tiere schwerer sind (im Durchschnitt). Entsprechend finden 0% der Stichproben einen Wert, der für das Gegenteil spricht (das weibliche Tiere schwerer wären). Damit resümieren wir, dass unser Modell 100% Wahrscheinlichkeit für die Hypothese einräumt: \(p_H = 1\). Achtung: Die 100%-ige Sicherheit für die Hypothese stammt aus der kleinen Welt, nicht unbedingt aus der großen welt.

Einfach noch zeigt uns parameters(m_penguins_sex), wie groß die Wahrscheinlichkeit für \(\beta_1 > 0\) ist, nämlich anhand des Koeffizienten pd, s. tbl-m-penguins-sex-params.

Aber das Auslesen der Post-Verteilung erlaubt uns auch, andere Hypothesen zu prüfen, etwa die Wahrscheinlichkeit der Hypothese, dass der Gewichtsunterschied zwischen den Geschlechtern mehr als 500 g beträgt.

\(\square\)

Vorteil der Parameterschätzung (gegenüber dem Testen von Hypothesen) ist die Nuanciertheit des Ergebnisses, die der Komplexität echter Systeme besser Rechnung trägt.

Übungsaufgabe 10.2 (Interpretation beim Hypothesen testen) Ein Forschungsteam untersucht die Hypothese, dass hohe Bildschirmzeit mit verringerter Intelligenz bei Kindern einhergeht. Dazu vergleichen Sie Kinder, die sehr viel Zeit am Tag am Bildschirm verbringen, mit Kindern, die sehr wenig Zeit am Tag am Bildschirm verbringen (und die im übrigen vergleichbar sind). Sie finden in ihrer Studie einen Effekt von \(95\% KI[-4;-2]\) IQ-Punkten, zuungunsten der Kinder mit hoher Bildschirmzeit.

Welche Aussage dazu ist korrekt bzw. passt am besten?

Die \(H_0\) ist als sicher falsch zu verwerfen.
Die \(H_0\) ist als sicher richtig anzunehmen.
Die \(H_0\) ist mit 95% Wahrscheinlichkeit richtig.
Die \(H_0\) ist mit 95% Wahrscheinlichkeit falsch.
Die Datenlage ist unklar, es ist keine Entscheidung möglich. \(\square\)

10.3 ROPE: Bereich von “praktisch Null”

📺 Teil 2

Nullhypothesen sind fast immer falsch, s. Abbildung 10.2.

Abbildung 10.2: Du testest EXAKTE Nullhypothesen?

Quelle: Imgflip Meme Generator

We do not generally use null hypothesis significance testing in our own work. In the fields in which we work, we do not generally think null hyptheses can be true: in social science and public health, just about every treatment one might consider will have some effect, and no comparison or regression coefficient of interest will be exactly zero. We do not find it particularly helpful to formulate and test null hypothess that we knowe ahead of time cannot be true. (Gelman et al., 2021)

10.3.1 Alternativen zu Nullhypothesen

Nullhypothesen, \(H_0\), sind z.B.: \(\rho=0\), \(\rho_1 = \rho_2\), \(\mu_1 = \mu_2\), \(\mu=0\), \(\beta_1=0\). Nullhypothesen zu testen, ist sehr verbreitet. Ein Grund ist, dass in der Frequentistischen Statistik keine andere Art von Hypothesentest (einfach) möglich ist.³ Ein anderer Grund ist vermutlich, … wir haben es schon immer so gemacht. 🤷‍♀️ Alternativen zum Testen von Nullhypothesen sind:

Posteriori-Intervalle (ETI oder HDI) berichten
Rope-Konzept (Kruschke, 2018)
Wahrscheinlichkeit von inhaltlich bedeutsamen Hypothesen quantifizieren (z.B. dass \(\beta_1 > 0.42\))
Wahrscheinlichkeit quantifizieren, dass der Effekt ein positives bzw. ein negatives Vorzeichen hat (probability of direction, pd)

10.3.2 “Praktisch kein Unterschied”: Das Rope-Konzept

📺 ROPE-Video

Beispiel 10.5 (Beispiele für ROPE)

Sagen wir, wenn sich zwei Preismittelwerte um höchstens \(d=100\)€ unterscheiden, gilt dieser Unterschied für einen Marketingmanager als “praktisch gleich”, “praktisch kein Unterschied”, “nicht substanziell”, “unbedeutend” bzw. “vernachlässigbar gering”
Bei Pinguinarten definiert eine Biologin nach umfangreichem Studium der Literatur, dass ein Unterschied von max. 100 g Körpergewicht “vernachlässigbar wenig” ist.
Eine findige Geschäftsfrau entscheidet für ihre Firma, dass ein Umsatzunterschied von 100k Euro “praktisch irrelevant” sei. \(\square\)

Definition 10.1 (ROPE) ROPE (Region of Practical Equivalence) ist ein Bereich um den Nullwert, der als praktisch äquivalent zu Null angesehen wird. \(\square\).

Wie legt man den Grenzwert \(d\) fest, bis zu dem ein Unterschied (Differenz) gerade noch bzw. gerade nicht mehr unbedeutend ist? Die Wahl von \(d\) ist subjektiv in dem Sinne als sie von inhaltlichen Überlegungen geleitet sein sollte. Diesen Bereich bezeichnen wir den Indifferenzbereich (Äquivalenzzone, Bereich eines vernachlässigbaren Unterschieds oder Region of practical equivalence, Rope).

Jetzt prüfen wir, ob ein “Großteil” der Posteriori-Stichproben im Rope liegt. Unter “Großteil” wird häufig das 95%-HDI verstanden (das ist auch der Standard der R-Funktion rope(), die wir hier nutzen).

Entscheidungsregel nach Kruschke (2018):

Großteil der Post-Verteilung liegt innerhalb von Rope \(\rightarrow\) Annahme der ROPE-Nullhypothese “praktisch kein Effekt”, \(H_0\)
Großteil der Post-Verteilung liegt außerhalb von Rope \(\rightarrow\) Ablehnung der ROPE-Nullhypothese “praktisch kein Effekt”, \(H_0\)
Ansonsten \(\rightarrow\) keine Entscheidung – die Datenlage ist uneindeutig

Mit “Großteil” meinen wir (per Default) das 95%-KI (der Posteriori-Verteilung).

10.3.3 Vernachlässigbarer Regressionseffekt

Kruschke (2018) schlägt vor, einen Regressionskoeffizienten unter folgenden Umständen als “praktisch Null” zu bezeichnen:

Wenn eine Veränderung über “praktisch den ganzen Wertebereich” von \(X\) (UV) nur einen vernachlässigbaren Effekt auf \(Y\) (AV) hat. Ein vernachlässigbarer Effekt ist dabei \(\hat{y}= \pm 0.1 sd_y\). Das impliziert Rope-Grenzen von \(\beta_x = \pm 0.1\) für z-standardisierte UV und AV. Einfach gesprochen: Eine vernünftige Voreinstellung für die Rope-Grenzen bei Regressionskoeffizienten sind \(\pm 10 \%\) der SD der AV.

ROPE-Defaults

Im der Voreinstellung umfasst die Größe des ROPE ±10% der SD der AV. \(\square\)

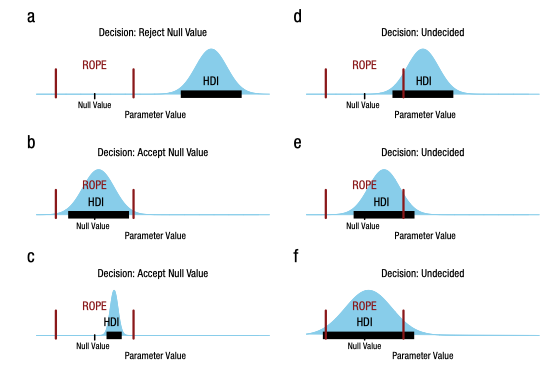
10.3.4 HDI-Rope-Entscheidungsregel visualisiert

Abbildung 10.3: Die Entscheidungsregeln zum ROPE illustiert (Kruschke, 2018); A: Verwerfen der ROPE-Hypothese; B und C: Akzeptieren; D-F: Unklare Datenlage, keine Entscheidung zur ROPE-Hypothese

Abbildung 10.3 illustriert die Entscheidungsregel zum ROPE für die drei Situationen Verwerfen der ROPE-Hypothese, Beibehalten und unklare Datenlage (Kruschke, 2018, Abb. 1, S. 272),

10.3.5 Rope berechnen

Hier ist das Modell, das Gewicht als Funktion der Pinguinart erklärt (m_penguins_species).

m_penguins_species <- stan_glm(body_mass_g ~ species, 
                  data = penguins, 
                  refresh = 0,  # unterdrückt Ausgabe der Posteriori-Stichproben
                  seed = 42  # zur Reproduzierbarkeit
                  )

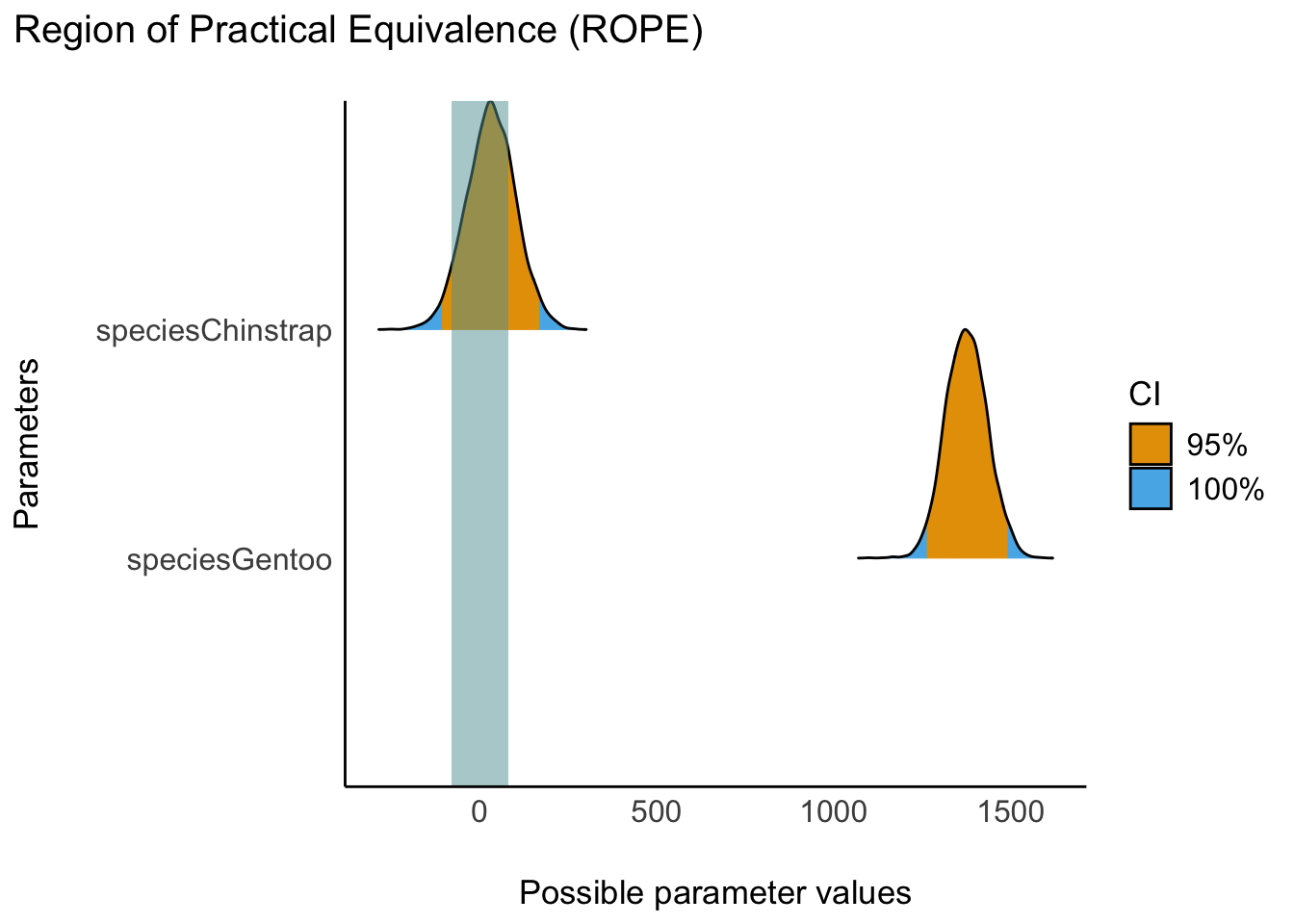
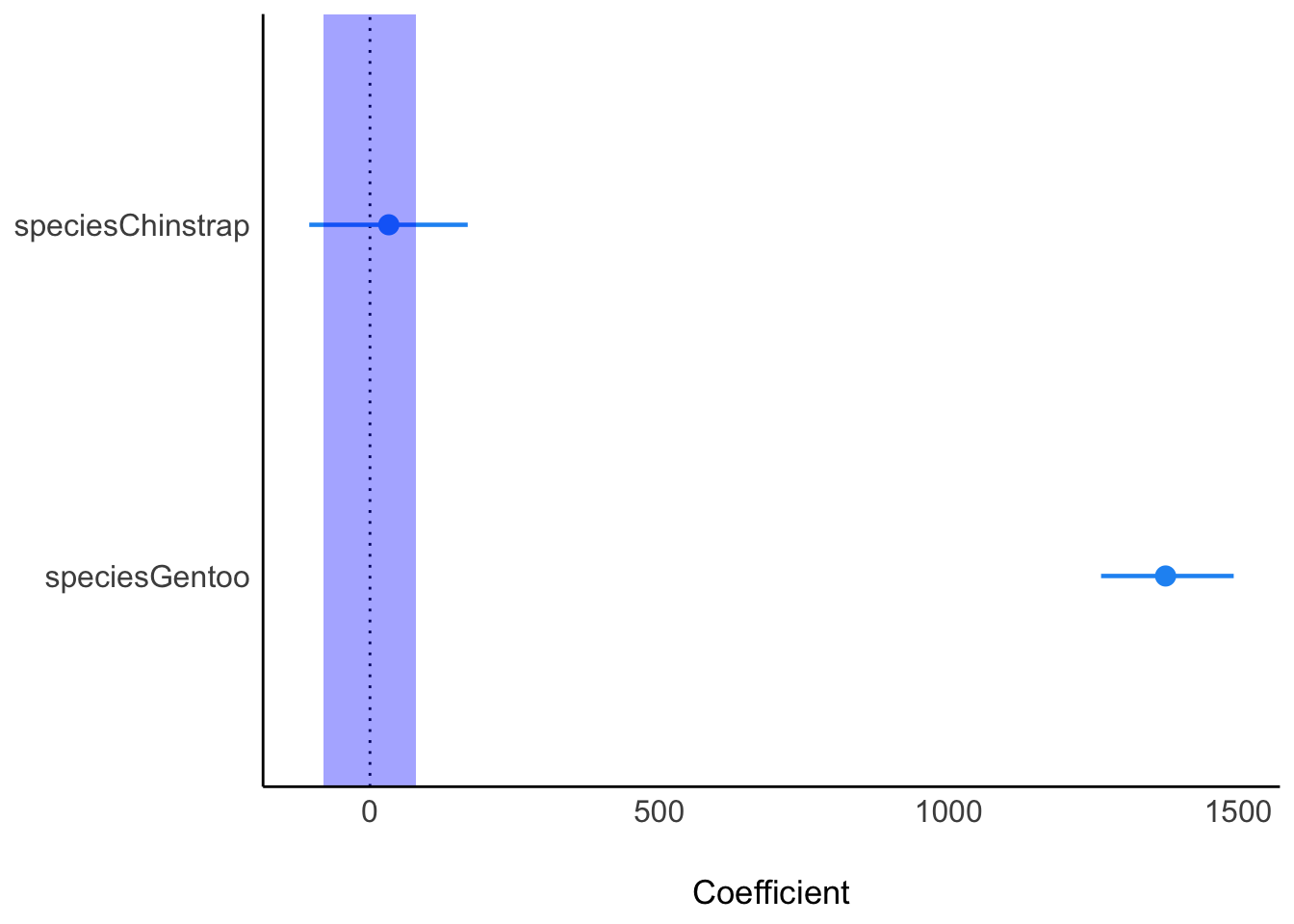
Den Rope berechnet man mit rope(model), s. Tabelle 10.2.

Tabelle 10.2: Der Rope-Bereich für die Stufen der UV (Arten von Pinguinen)

Die Faktorstufe Chinstrap der UV species hat doch einen beträchtlichen Teil ihrer Wahrscheinlichkeitsmasse der Posteriori-Verteilung im ROPE. Wir können daher für diese Gruppe das ROPE nicht verwerfen. Die Datenlage ist unklar. Es ist keine abschließende Entscheidung über die Hypothese möglich.

Aber: Gentoo liegt zu 0% im Rope. Für die Gruppe Gentoo können wir die ROPE-Hypothese verwerfen. Der Effekt von Gentoo ist größer als vernachlässigbar. Anders gesagt: Tiere der Art Gentoo sind im Schnitt substanziell schwerer als Tiere der Referenzgruppe (Adelie). Der ROPE-Grenzwert wurde hier per Voreinstellung auf 80 g Unterschied festgelegt (10% der SD der AV).

Hinweis

Die angegebenen Prozentwerte beziehen sich nicht auf die 100% der Post-Verteilung, sondern (in der Voreinstellung) auf das 95%-ETI. Dabei werden 10% der Streuung der AV als Intervallgrenzen des ROPE angenommen, s. help(rope).

Das hört sich abstrakt an? Dann lassen Sie uns das lieber visualisieren. 🎨

10.3.6 Visualisierung unserer Rope-Werte, m_penguins_species

Ein Großteil der Posteriori-Masse von m_penguins_species liegt nicht innerhalb des Rope. Aber können wir umgekehrt sagen, dass ein Großteil außerhalb liegt? Das erkennt man optisch ganz gut, s. Abbildung 10.4.

(a) Diagramm mit `rope(m_penguins_species) %>% plot()`

Das ROPE druchkreuzt die “Berge” der Posteriori-Verteilung für Chinstrap deutlich. Aber: Das 95%-HDI liegt nicht komplett innerhalb des Rope. Wir können das Nullhypothese für Chinstrap nicht verwerfen, aber auch nicht bestätigen – eine unklare Datenlage.

Gentoo hingegen wird vom vom Rope nicht durchkreuzt, es ist weit entfernt vom “blauen vertikalen Band” des Rope: Gentoo liegt außerhalb des Rope. Es gibt einen “substanziellen” Unterschied zwischen dem Mittelwert der AV in Gruppe Gentoo und in der Referenzgruppe Adelie.

Wir verwerfen die ROPE-Hypothese, die “Praktisch-Null-Hypothese”, in diesem Fall.

10.3.7 Finetuning des Rope

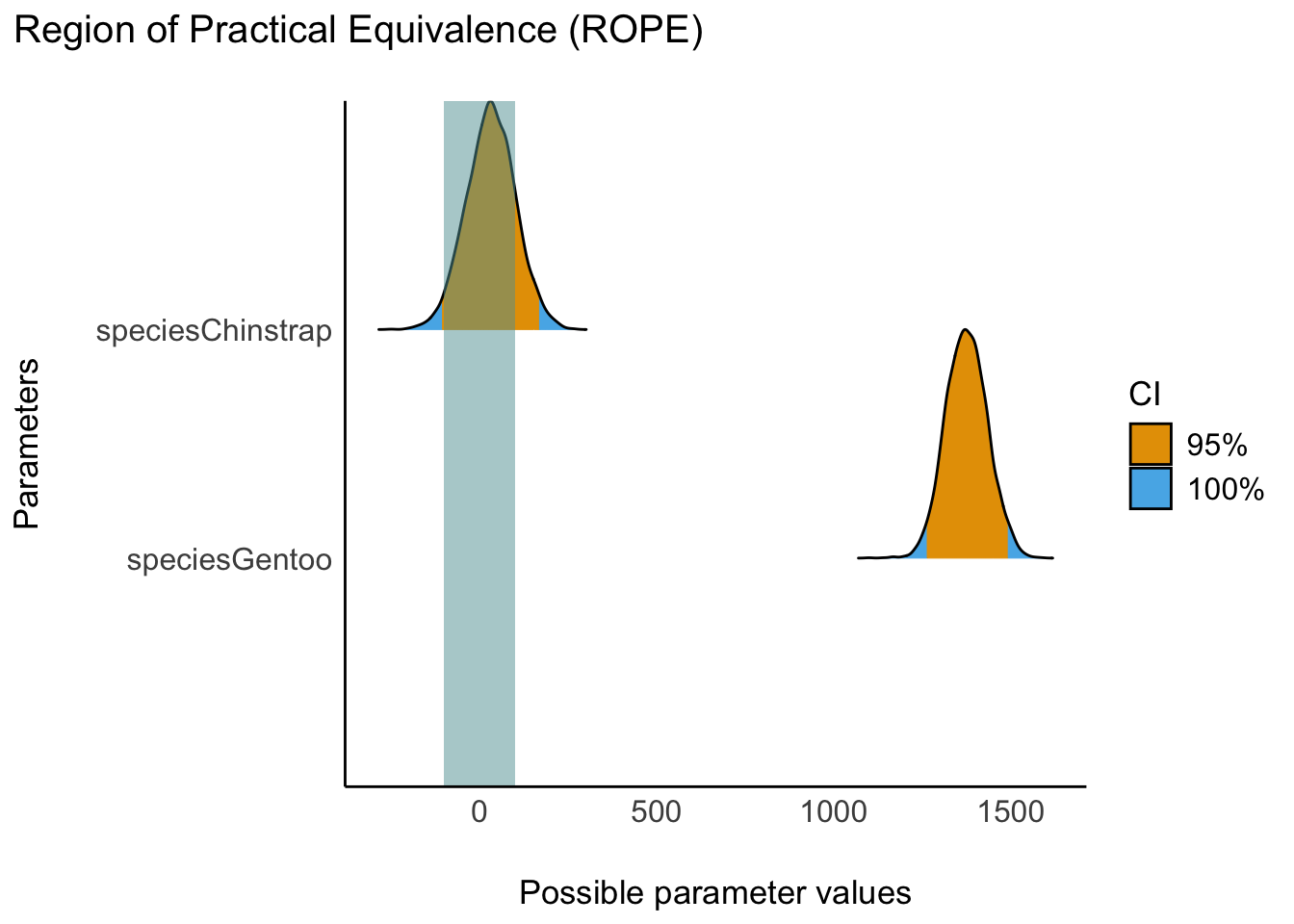
Wir können festlegen, was wir unter “praktischer Äquivalenz” verstehen, also die Grenzen des Ropes verändern. Sagen wir, 200 Gramm sind unsere Grenze für einen vernachlässigbaren Effekt, s. Abbildung 10.5.

plot(rope(m_penguins_species, range = c(-200, 200))) + 
  scale_fill_okabeito()  # schönes Farbschmea

Abbildung 10.5: ROPE mit selber eingestellter Grenze von ±200 (Gramm)

In der Voreinstellung werden 95%-ETI berichtet, das kann man wie folgt ändern, wenn man möchte. Die ROPE-Grenzen sind in @ tbl-rope-species-rope-fine zu sehen.

rope(m_penguins_species, range = c(-500,500), ci = .89, ci_method = "HDI")

Tabelle 10.3: ROPE-Grenzen für das Modell m_penguins_species mit ROPE-Grenzen von 500 g.

Jetzt wird berichtet, welcher Teil eines 89%-CI⁴ sich im Rope befindet.

Übungsaufgabe 10.3 (Peer-Instruction: Interpretation des ROPE-Anteils) In einer Hochschule wird der Effekt eines “Robo-Professors” auf die Lernleistung der Studierenden untersucht, im Fach Statistik. Der “Robo-Professor” ist ein Computerprogramm auf Basis künstlicher Intelligenz, das den Studierenden den Stoff vermittelt. Dazu wird eine Gruppe von Studierenden von einem menschlichen Dozenten unterrichtet, die andere Gruppe von einem “Robo-Professor”. Nach dem Kurs wird die Lernleistung der Studierenden in einer Prüfung gemessen. Das Regressionsmodell m_robo liefert einen Rope-Anteil von 10% für den Koeffizienten robo_professor. Welche Aussage dazu ist korrekt?

Der Robo-Professor hat einen Einfluss von 10% auf die Lernleistung der Studierenden.
Der Einfluss des Robo-Professors auf die Lernleistung der Studierenden ist substanziell.
Es gib keinen Einfluss des Robo-Professors auf die Lernleistung der Studierenden.
Es ist nicht auszuschließen, dass der Robo-Professor keinen substanziellen Einfluss auf die Lernleistung der Studierenden hat.
Der Einfluss des Robo-Professors auf die Lernleistung der Studierenden ist vernachlässigbar. \(\square\)

10.3.8 Beantwortung der Forschungsfrage

Für die Spezeis Gentoo wurde ein substanzieller Gewichtsunterschied zur Referenzgruppe, Adelie, vom Modell entdeckt. Für Chinstrap hingegen ist keine klare inferenzstatistische Aussage hinsichtlich eines Indifferenzbereichs möglich: Es ist plausibel, laut dem Modell, dass es einen praktisch bedeutsamen Unterschied gibt, aber es ist auch plausibel, dass es keinen praktisch bedeutsamen Unterschied gibt.

10.4 Modellgüte

10.4.1 Wozu Modellgüte?

Hat man ein Modell aufgestellt und geprüft und Ergebnisse erhalten, möchte man wissen, wie belastbar diese Ergebnisse sind. Eine Abschätzung zur Belastbarkeit des Modellergebnisse liefern Kennwerte der Modellgüte. Diese Kennwerte zielen z.B. darauf ab, wie präzise die Aussagen des Modells sind. Je präziser die Aussagen eines Modells, desto nützlicher ist es natürlich. Bei einer Parameterschätzung erhält man auch Informationen zur Präzision der Schätzung: Ist der Schätzbereich schmal, so ist die Schätzung präzise (und vice versa). Allerdings könnte ein Modell aus mehreren Parameterschätzungen bestehen, die unterschiedlich präzise sind. Da kann es helfen, eine zusammenfassen Beurteilung zur Präzision, oder allgemeiner zur Güte des Modells, zu erhalten. Im Folgenden ist eine Kennzahl von mehreren gebräuchlichen und sinnvollen vorgestellt, \(R^2\).

10.4.2 Modellgüte mit \(R^2\) bestimmen

\(R^2\) gibt den Anteil der Gesamtvarianz (der AV) an, den das Modell erklärt. - Höhere Wert von \(R^2\) bedeuten, dass das Modell die Daten besser erklärt. \(R^2\) wird normalerweise auf Basis eines Punktschätzers definiert. Solch eine Definition lässt aber viel Information - über die Ungewissheit der Schätzung - außen vor. Daher ist es wünschenswert, diese Information in \(R^2\) einfließen zu lassen: Bayes-R-Quadrat.

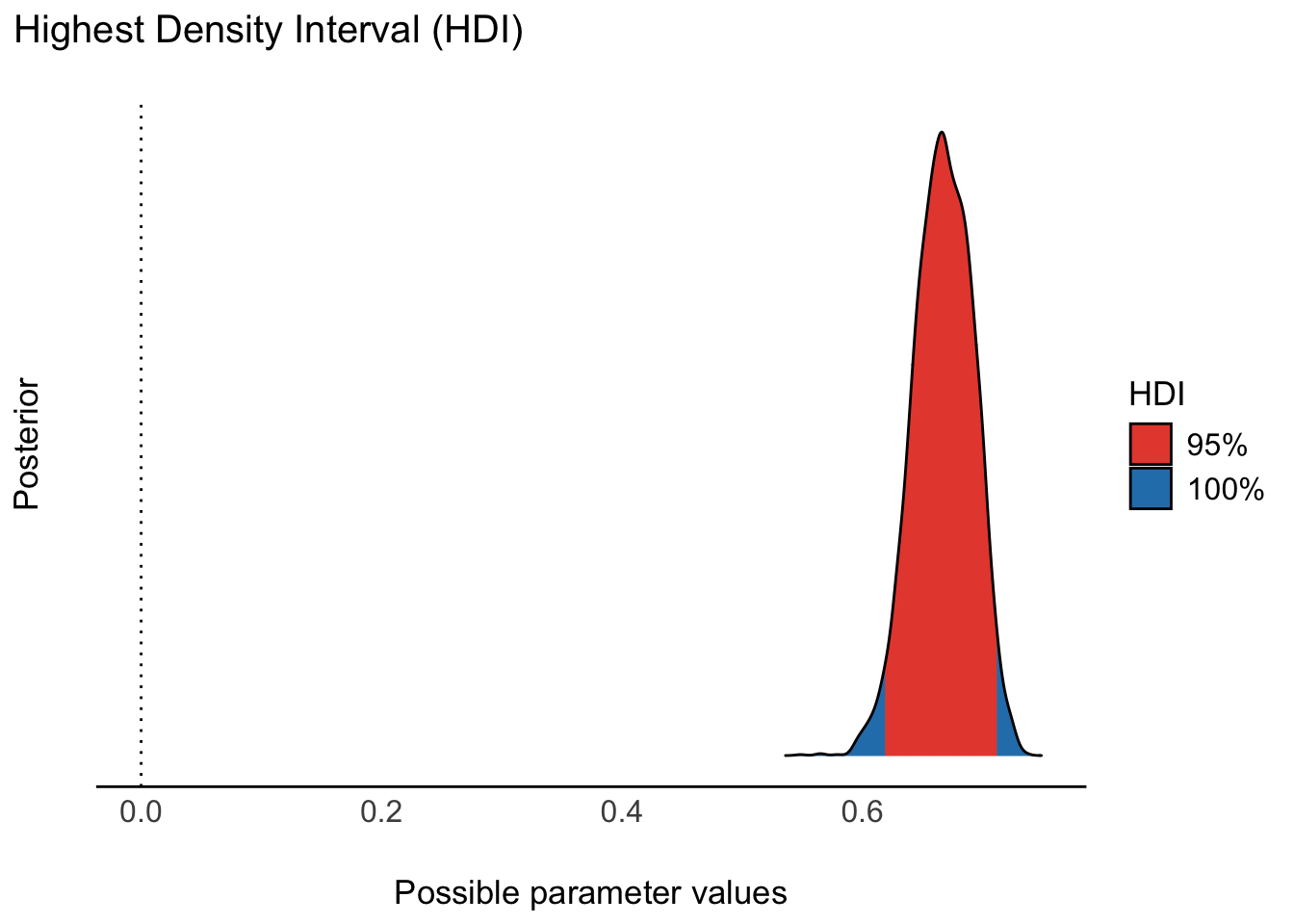
Die Post-Verteilung von \(R^2\) kann man sich wie folgt ausgeben lassen, s. Abbildung 10.6.

m_penguins_species_r2 <-
  m_penguins_species %>% 
  r2_posterior() %>% 
  as_tibble()

hdi(m_penguins_species_r2) %>%  # Intervallgrenzen der Post-Verteilung von R2
  plot()  # visualisieren

Abbildung 10.6: Die Verteilung von R-Quadrat im Modell m_penguins_species

\(R^2\) und \(\sigma\) sind negativ assoziiert: In einem Datensatz mit mit hohem \(R^2\) ist \(\sigma\) gering und umgekehrt. Beide Koeffizienten berechnen sich auf Basis von \(\sigma\) und haben den gleichen Zweck: die Abschätzung der Güte eines Modells. Im Unterschied zum Frequentistischen R-Quadrat erhält man in der Bayes-Statistik nicht nur einen Punktschätzer für \(R^ 2\), sondern wie auch sonst eine Post-Verteilung, so dass man z.B. einen Schätzbereich angeben kann.

Schneller bekommt man den Punkt- und den Intervallschätzer für \(R^2\) mit r2(m_penguins_species).

## # Bayesian R2 with Compatibility Interval
## 
##   Conditional R2: 0.667 (95% CI [0.620, 0.711])

10.5 Fazit

Obwohl das Testen von Hypothesen im Moment verbreiteter ist, spricht einiges zugunsten der Vorzüge der Parameterschätzung. Möchte man aber, um sich bestimmter bestehender Forschung anzunähern, einen Hypothesentest, speziell den Test einer Nullhypothese verwenden, so bietet sich das ROPE-Verfahren an.

Übungsaufgabe 10.4 (Zeit für einen Rückblick: Welche Fragen haben Sie im Moment?) Mittlerweile haben wir einen Großteil des Stoffs absolviert. Welche Punkte sind Ihnen offen geblieben? Wo haben Sie noch Fragen?

Die Lehrkraft stellt Ihnen eine (anonyme) Plattform für Ihre Fragen bereit, so dass Sie in Ruhe Ihre offenen Fragen und diejenigen Ihrer Kommilitonninen und Kommilitonen überdenken können. \(\square\)

10.6 Aufgaben

vor allem in der Frequentistischen Statistik↩︎
Tatsächlich gibt es schwarze Schwäne, aber nicht in Europa: https://en.wikipedia.org/wiki/Black_swan↩︎
Mittlerweile gibt es neue Frequentistische Ansätze für ein Verfahren ähnlich dem ROPE-Ansatz, der weiter unten vorgestellt wird.↩︎
89 ist die nächst kleinste Primzahl unter 95; und 95 wird gemeinhin als Grenzwert für Schätzbereiche verwendet. Damit ist 95 hier eine “magic number”, ein Defacto-Standard ohne hinreichende Begründung. Um darauf hinzuweisen, benutzen einige Forscherinnen und Forscher mit ähem subtilen Humor lieber die 89 als die 95. 🤷‍♂️ ↩︎