11  Fallbeispiele

11.1 Lernsteuerung

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können…

  • typische, deskriptive Forschungsfragen spezifizieren als Regression
  • Forschungsfragen in Regressionsterme übersetzen
  • typische Forschungsfragen auswerten

Der Stoff dieses Kapitels orientiert sich an McElreath (2020), Kap. 4.4 sowie Gelman et al. (2021), Kap. 7 und 10.

Frischen Sie Ihr Wissen in den Grundlagen der einfachen und multiplen Regression (inkl. Interaktionseffekte) auf. Dazu sind z.B. folgende Literaturstellen geeignet.

In diesem Kapitel werden die üblichen R-Pakete benötigt.

library(rstanarm)   # Bayes-Modelle
library(tidyverse)  # Datenjudo
library(easystats)  # Statistik-Komfort

Wir benötigen in diesem Kapitel folgende Datensätze: kidiq, penguins. Den Datensatz kidiq importieren Sie am einfachsten aus dem R-Paket rstanarm, das Sie schon installiert haben. Alternativ können Sie die Daten hier herunterladen.

data("kidiq", package = "rstanarm")

Außerdem benötigen wir den Datensatz penguins. Sie können den Datensatz penguins entweder via dem Pfad importieren oder via dem zugehörigen R-Paket. Beide Möglichkeit sind okay.

penguins_url <- "https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv"

penguins <- read.csv(penguins_url)

data("penguins", package = "palmerpenguins")

11.1.1 Einstieg

Beispiel 11.1 (Was waren noch mal die Skalenniveaus?) Um Forschungsfragen zu klassifizieren, müssen Sie wissen, was die Skalenniveaus der beteiligten AV und der UV(s) sind.1 \(\square\)

Beispiel 11.2 (Was war noch einmal die Interaktion?) Erkären Sie die Grundkonzepte der Interaktion (hier synonym: Moderation) im Rahmen einer Regressionsanalyse!2 \(\square\)

11.1.2 Überblick

Wenn Sie die Skalenniveaus wissen, können Sie die Forschungsfrage korrekt auswerten, also das korrekte (Regressions-)Modell spezifizieren. Wir werden hier viele der typischen Forschungsfragen (aus psychologischen und ähnlichen Fragestellungen) mit Hilfe von Regressionsmodellen beantworten. Das hat den Vorteil, dass sie nicht viele verschiedene Auswertungsmethoden (t-Test, Varianzanalyse, …) lernen müssen. Außerdem ist die Regressionsanalyse (für viele Situationen) die beste Heransgehensweise, da sie viele Möglichkeiten für Erweiterungen bietet. Entsperchend ist das Thema dieses Kapitels gängige Forschungsfragen mit Hilfe der Regressionsanalyse zu untersuchen. Wenn Sie die Grundkonzepte der Regression schon kennen, wird Ihnen vieles sehr bekannt vorkommen. Natürlich würzen wir das Ganze mit einer ordentlichen Portion Post-Verteilungen aus der Bayes-Küche. Allerdings kommt auch dabei nichts Wesentliches mehr hinzu, abgesehen von einer paar Erweiterungen.

11.2 Taxonomie von Forschungsfragen

Wir konzentrieren uns im Folgenden auf Forschungsfragen auf Basis von Regressionsmodellen mit metrischer AV. Andere Skalenniveaus bei der AV klammern wir aus. Im Folgenden sind für die UV(s) nominale sowie metrische Skalenniveaus erlaubt. Modelle mit mehreren UV (und mehreren Stufen an UV) sind ebenfalls erlaubt.

Wir untersuchen in diesem Kapitel häufig verwendete Arten von Forschungsfragen mittels Regressionsanalysen. Für jede Variante ist zumeist ein Beispiel, die Modellformel, der Kausalgraph3, die Forschungsfrage sowie die Grundlagen der Auswertung dargestellt.

Dabei wird folgende Nomenklatur verwendet, um die Skalenniveaus der beteiligten Variablen einer Forschungsfrage zu benennen:

  • y: metrische AV
  • g: Gruppierungsvariable; nominal skalierte UV (querschnittlich)
  • b: binäre UV
  • x: metrische UV
  • u: ungemessene (unbekannte) Variable

11.3 y ~ b

Hintergrund:

Eine Psychologin, die im öffentlichen Dienst als Schulpsychologin arbeitet, versucht herauszufinden, warum einige Kinder intelligenter sind als andere. Dazu wurden in einer aufwändigen Studie die Intelligenz vieler Kinder gemessen. Zusätzliche wurden verschiedene Korrelate der Intelligenz erhoben, in der Hoffnung, “Risikofaktoren” für geringere Intelligenz zu entdecken.

Forschungsfrage:

Ist der mittlere IQ-Wert (kid_score) von Kindern, deren jeweilige Mutter über einen Schlusabschluss (mom_hs, \(x=1\)) verfügt höher, als bei Kinderen, deren jeweilige Mutter nicht über einen Schulabschluss verfügt (\(x=0\))? (ceteris paribus)4.

Die Modellformel zur Forschungsfrage lautet allgemein y ~ b bzw konkret für den vorliegendne Fall kid_iq ~ mom_hs.

Theorem 11.1 drückt die Forschungsfrage formaler und als Hypothese (Behauptung) aus.

Theorem 11.1 (Hypothese für ungleiche Mittelwerte) \[H_A: \mu_{x=1} \gt \mu_{x=0}\quad \square\]

In Worten: “Der mittlere IQ-Wert für Kinder, deren Mütter über einen Schulabschluss verfügen ist höher als in der Gruppe von Kindern, deren Mütter über keinen Schulabschluss verfügen”. Zu beachten ist, dass sich eine Hypothese immer auf Parameterwerte bezieht, also auf die Population, nicht auf die Statistiken der Stichprobe.

Die zugehörige Nullhypothese, \(H_0\) lautet:

\[H_0: \mu_{x=1} = \mu_{x=0}\quad \square\]

Für die Praktisch-Null-Hypothese (ROPE-Hypothese) wählen wir 5 IQ-Punkte als Grenzwert für gerade noch unbedeutend.

\[H_{ROPE}: \mu_{x=1} > \mu_{x=0} + 5\quad \square\]

Die Regressionsformel zur Forschungsfrage lautet: y ~ b bzw. kid_iq ~ mom_hs.

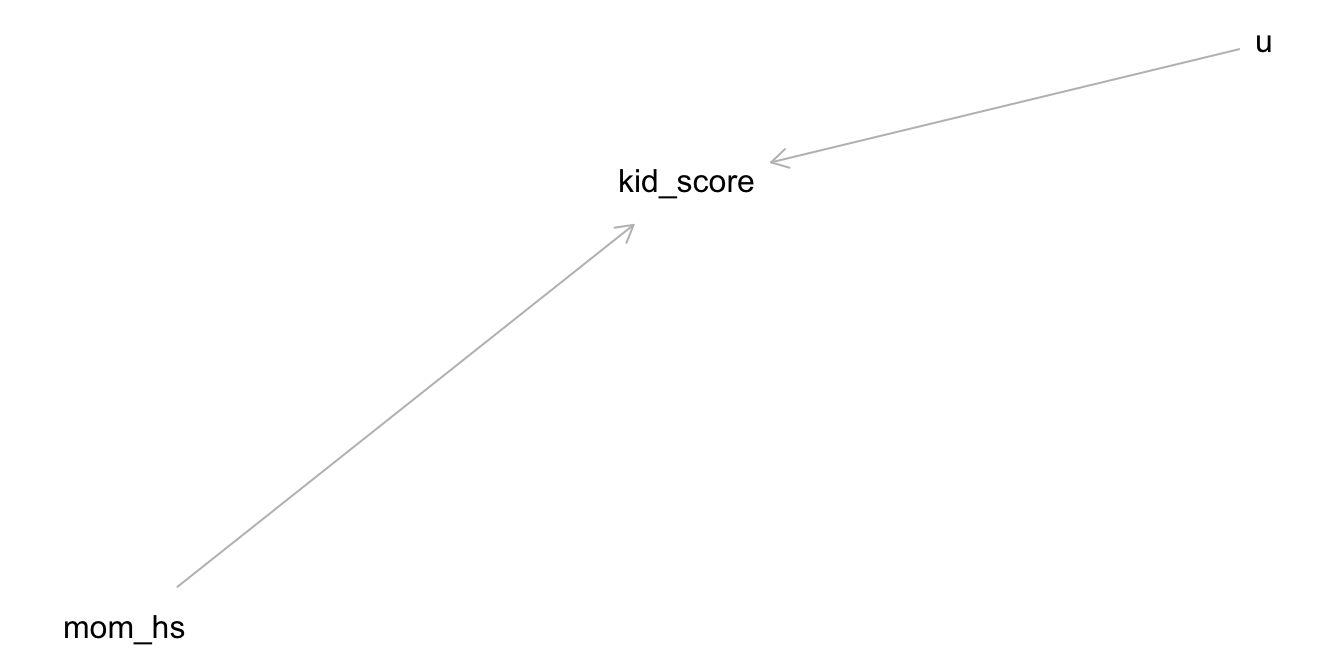
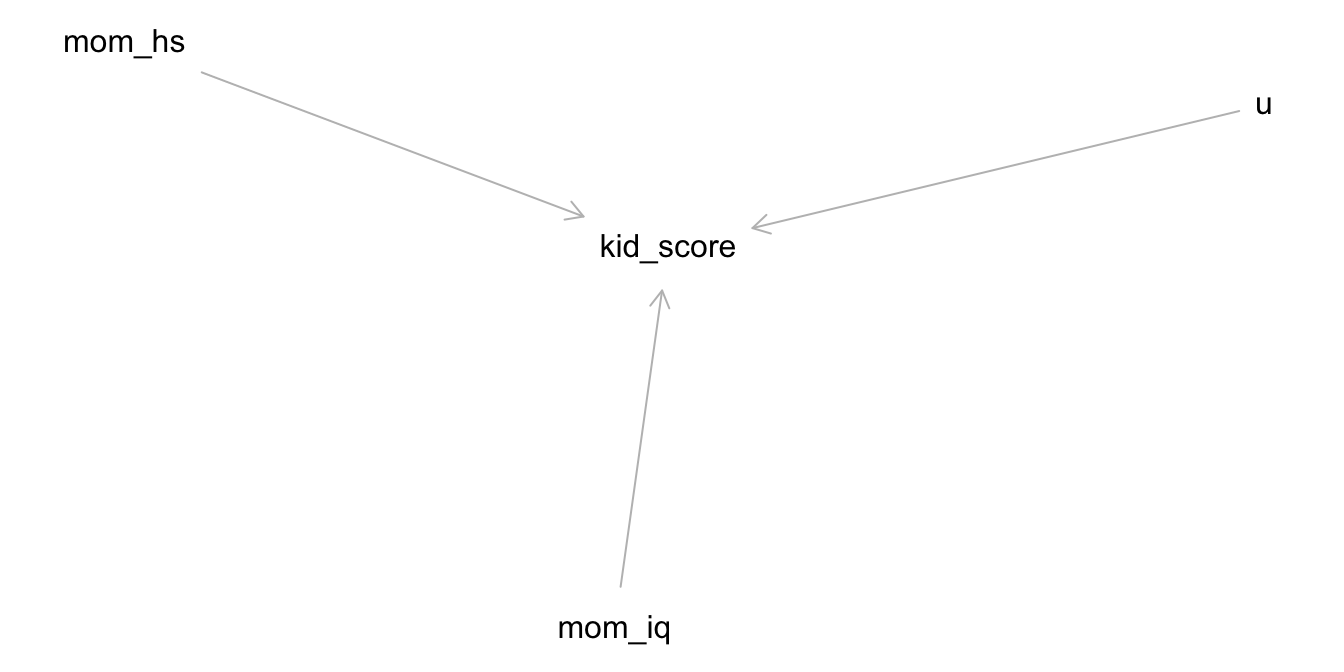
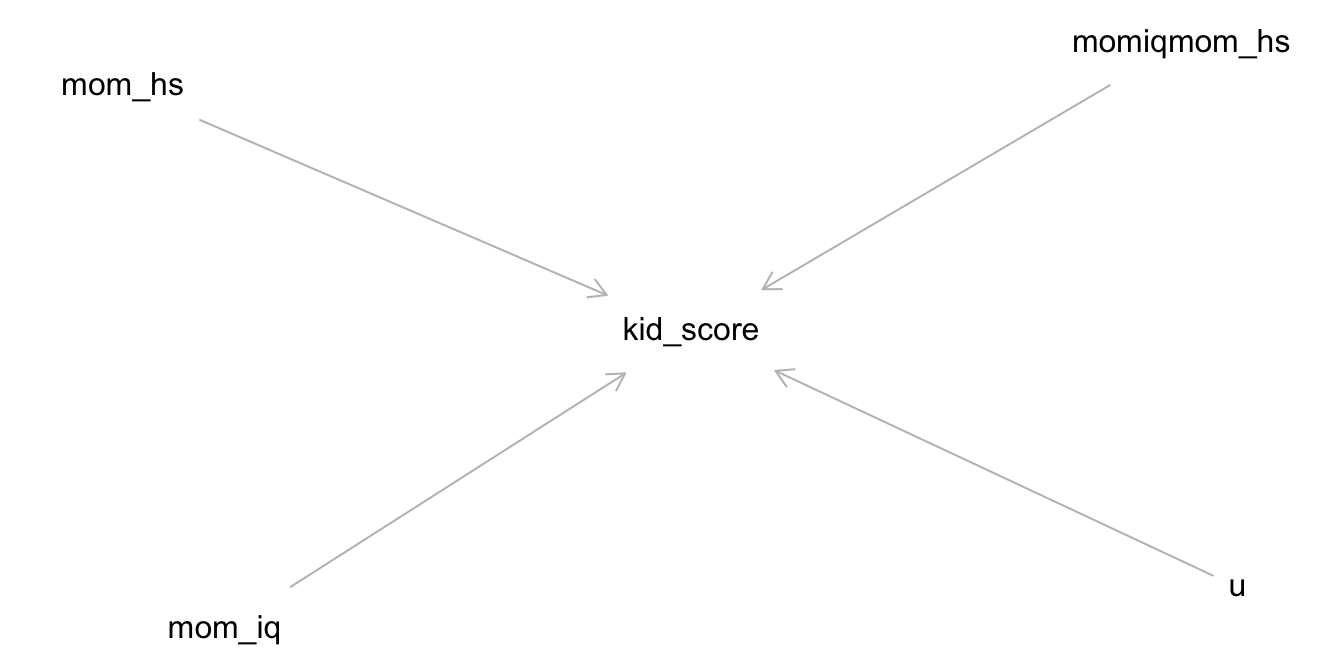
Der Kausalgraph zur Modellformel sieht aus in Abbildung 11.1 dargestellt. Y hat, laut unserem Modell, zwei Ursachen:

  1. mom_hs (b)
  2. u, das steht für “unbekannt”5
Abbildung 11.1: DAG für kid_iq ~ mom_hs

Auf dieser Basis berechnen wir unser Regressionsmodell mit Stan: stan_glm(kid_score ~ mom_hs, data = kidiq)

m10.1 <- stan_glm(
  kid_score ~ mom_hs, 
  data = kidiq)

Der Einfachheit halber übernehmen wir die Prioriwerte von Stan, s. Listing 11.1.

Listing 11.1: Standard-Prioriwerte für m10.1, von Stan vergeben 
prior_summary(m10.1)
## Priors for model 'm10.1' 
## ------
## Intercept (after predictors centered)
##   Specified prior:
##     ~ normal(location = 87, scale = 2.5)
##   Adjusted prior:
##     ~ normal(location = 87, scale = 51)
## 
## Coefficients
##   Specified prior:
##     ~ normal(location = 0, scale = 2.5)
##   Adjusted prior:
##     ~ normal(location = 0, scale = 124)
## 
## Auxiliary (sigma)
##   Specified prior:
##     ~ exponential(rate = 1)
##   Adjusted prior:
##     ~ exponential(rate = 0.049)
## ------
## See help('prior_summary.stanreg') for more details

Die komplette Modellspezifikation ist in Gleichung 11.1 aufgeführt. Wie man sieht, sind die Priori-Verteilungen sehr breit – zu breit vielleicht. Das sollten wir in einem nächsten Mal verbessern.

\[\begin{align*} \text{kid score}_i &\sim \operatorname{Normal}(\mu_i, \sigma) && \text{Likelihood} \\ \mu_i &= \beta_0 + \beta_1 \cdot \text{mom hs}_i && \text{Lineares Modell} \\ \beta_0 &\sim \operatorname{Normal}(87, 51) && \text{Prior Achsenabschnitt} \\ \beta_1 &\sim \operatorname{Normal}(0, 124) && \text{Prior Regressionsgewicht} \\ \sigma &\sim \operatorname{Exp}(0.049) && \text{Prior Vorhersagegüte} \end{align*} \tag{11.1}\]

Mit parameters(m10.1) bekommt man die Parameter des Modells, s. Tabelle 11.1.

Tabelle 11.1: Parameter des Modells m10.1 (sigma ist nicht dargestellt, da meistens nicht von hohem Interesse)
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 77.56 (73.28, 81.64) 100% 1.001 3917 Normal (86.80 +- 51.03)
mom_hs 11.80 (7.18, 16.48) 100% 1.001 3789 Normal (0.00 +- 124.21)

m10.1: kid_score = 78 + 12*mom_hs + error

Der Achsenabschnitt (intercept, \(\beta_0\) oder auch mit \(\alpha\) bezeichnet) ist der mittlere vorhergesagte IQ-Wert von Kindern, deren Mütter über keinen Schulabschluss (mom_hs = 0) verfügen:

kid_score = 78 + 0*12 + error

Das Regressionsgewicht (slope, \(\beta_1\), \(\beta\)) ist der Unterschied im IQ-Wert von Kindern mit Mütter mit Schlulabschluss (im Vergleich zum IQ-Wert von Kindern mit Mütter ohne Schlusabschluss). Dieser Unterschied entspricht der Steigung der Regressionsgeraden.

kid_score = 78 + 1*12 + error = 90 + error

Der Wert von error (\(e\)) zeigt, wie genau die Schätzung (Vorhersage) ist bzw. wie stark UV und AV zusammenhängen. error entspricht dem Vorhersagefehler, also dem Unterschied vom tatsächlichen IQ-Wert des Kindes (\(y\)) zum vom Modell vorhergesagten Wert (\(\hat{y}\)).

Ein lineares Modell der Art y ~ g kann man als Berechnung des Unterschieds im Mittelwert von y zwischen beiden Gruppen (g0 vs. g1) verstehen.

👨‍🏫 Hey Stan! Nimm den Datensatz kidiq, gruppiere nach mom_hs und fasse zusammen anhand des Mittelwerts. Die resultierende Zahl soll heißen kid_score_avg. An die Arbeit!

🤖 Schon mal was von “bitte” gehört?

kidiq %>% 
  group_by(mom_hs) %>% 
  summarise(kid_score_avg = 
              mean(kid_score))
mom_hs kid_score_avg
0 77.55
1 89.32

Der mittlere (average, avg) IQ-Wert unterscheidet sich um ca. 12 Punkte (89.4-77.6), zugunsten der Kinder von Müttern mit Abschluss.

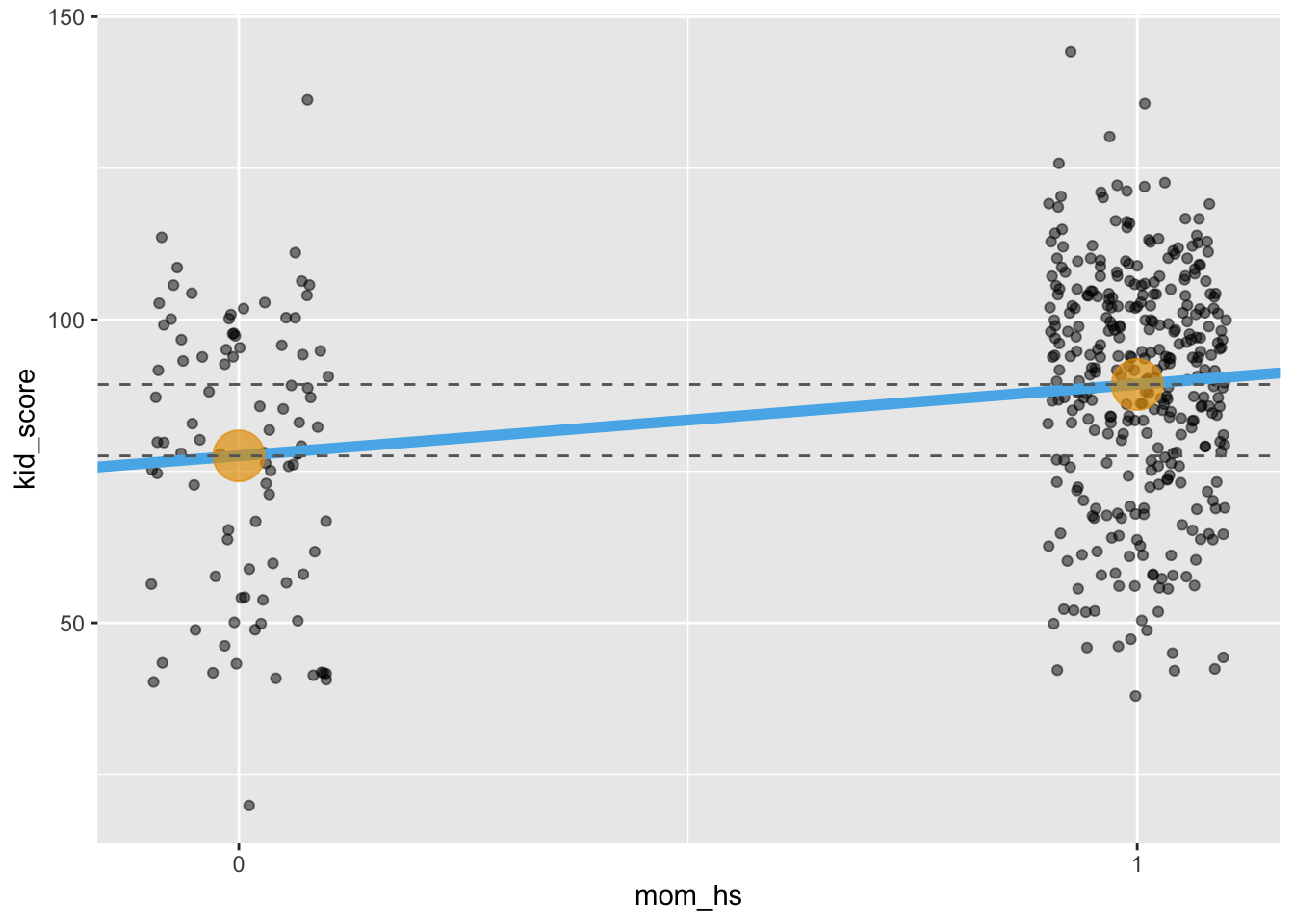
In Abbildung 11.2 ist der Unterschied im IQ der Kinder als Funktion des Schlussabschlusses der Mutter dargestellt, auf Basis des Datensatzes kidiq.

estimate_relation(m10.1) %>% plot()
Abbildung 11.2: Kinder, deren Mütter über einen Schulabschluss verfügen (mom_hs=1), haben im Mittel einen höheren Intelligenztestwert (als Kinder, deren Mütter keinen Schulabschluss haben, mom_hs=0), laut dem vorliegenden Modell. Die Regressionsgerade ist als durchgezogene Linie dargestellt. Die Mittelwerte pro Gruppe als Punkte und als gestrichelte, horizontale Linie.

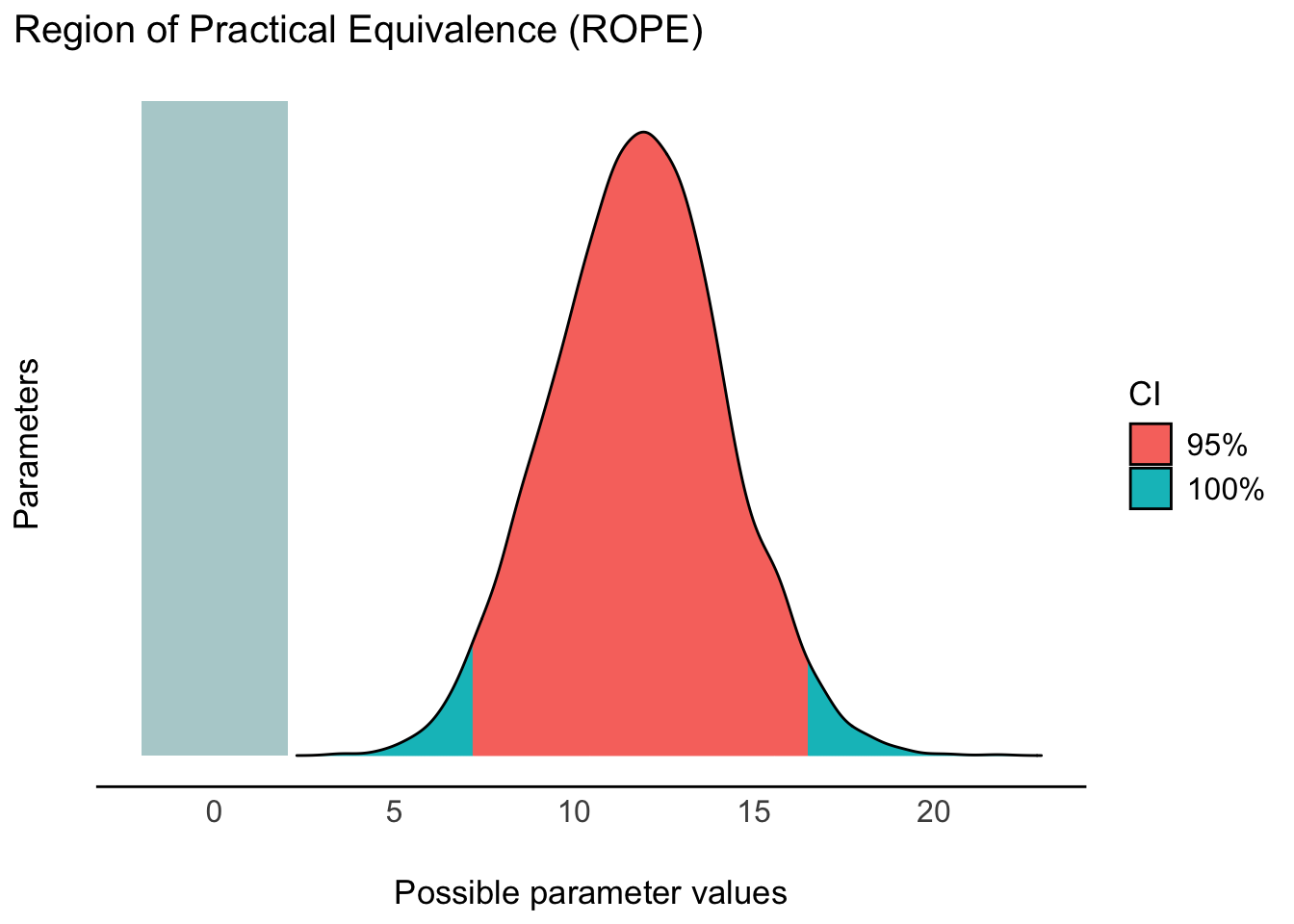
Prüfen wir mit rope(m10.1), ob der Effekt der UV (Unterschied zwischen den Gruppen) “praktisch Null” ist; dazu nutzen wir das ROPE-Verfahren.

rope(m10.1, range = c(-5, 5))

Das Ergebnis zeigt uns, dass es 0% Überlappung vom Rope und dem 95%-HDI (der Posterior-Verteilung) gibt.

Fazit: Wir verwerfen die Praktisch-Null-Hypothese. Adios! Abbildung 11.3 visualisiert die Erstreckung der Posteriori-Verteilung (und des 95%-HDI) sowie des Rope.

(a) Diagramm mit rope(m10.1) %>% plot()
(b) Diagramm mit parameters(m10.1) %>% plot()
Abbildung 11.3: Der Bereich plausibler Werte (der Post-Verteilung von m10.1) liegt komplett außerhalb des Bereichs zu vernachlässigend kleiner Werte (ROPE-Bereich). Wir verwerfen die Praktisch-Null-Hypothese (ROPE-Hypothese).

In der frequentistischen Statistik (die mehrheitlich unterricht wird) untersucht man diese Datensituation – Mittelwertsdifferenz zwischen zwei Gruppen – mit einem sog. t-Test. Der t-Test (für zwei Gruppen) ist ein inferenzstatistisches Verfahren, das prüft, ob die Mittelwertsdifferenz zwischen zwei Gruppen (in der Population) \(\mu_d\) Null ist: \(\mu_d = 0\).6 In der Bayes-Statistik betrachtet man dazu stattdessen die Posteriori-Verteilung (z.B. mit 95%PI).

Alternativ zum t-Test kann man – unabhängig, ob man Frequentistisch oder Bayesianisch unterwegs ist – mit einer Regression vom Typ y ~ b das in etwa gleiche Ergebnis erreichen.7

Zur Beantwortung der Forschungsfrage betrachten wir die Ergebnisse von m10.1.

m10.1_post <-
  m10.1 %>% 
  as_tibble() 

names(m10.1_post) <- c("Achsenabschnitt", "momhs", "sigma")  # schönere Namen

Hier sind die ersten paar Zeilen, s. Tabelle 11.2.

Tabelle 11.2: m10.1, Postverteilung, ersten paar Zeilen
Stichprobe aus der Post-Verteilung
Achsenabschnitt momhs sigma
76.1 12.8 19.7
72.9 17.5 20.5
79.0 11.7 20.5
75.7 13.7 20.6
77.0 12.6 20.0

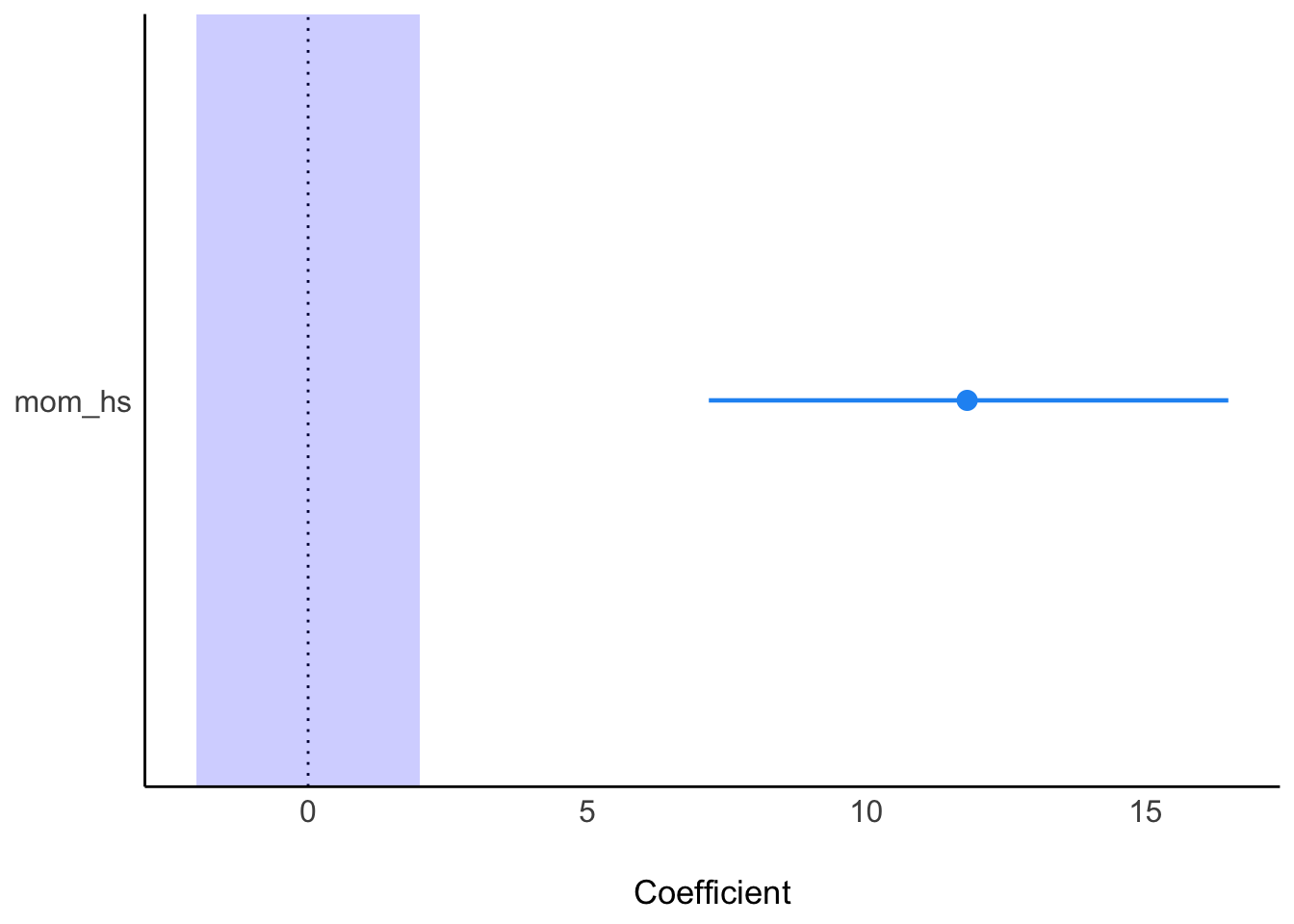
Berechnen wir zur Übung ein 95%-PI von Hand; komfortabler geht es mit eti(m10.1), s. Tabelle 11.1.

pi_mom_hs <-
  m10.1_post %>% 
  summarise(pi_95 = quantile(momhs, c(.025, .975)))

pi_mom_hs

Mit 95% Wahrscheinlichkeit liegt der Unterschied im mittleren IQ-Wert zwischen Kindern von Müttern mit bzw. ohne Schulabschluss im Bereich von 7 bis 14 IQ-Punkten, laut unserem Modell: \(95\%PI: [7,16]\). Die Hypothese, dass es keinen Unterschied oder einen Unterschied in die andere Richtung geben sollte, ist vor diesem Hintergrund als unwahrscheinlich abzulehnen. Mit plot(eti(m10.1)) kann man das 95%-ETI der Post-Verteilung visualisieren.

Wichtig

Zur Erinnerung: Korrelation ungleich Kausation. Von einem “Effekt” zu sprechen, lässt in den meisten Köpfen wohl die Assoziation zu einem kausalen Effekt entstehen. Ein Kausaleffekt ist eine starke (und sehr interessante und wichtige) Behauptung, die mehr Fundierung bedarf als eine einfache Korrelation bzw. ein einfacher Zusammenhang. Für eine Kausalaussage braucht man ein Argument, etwa einen Verweis auf bestehende Studien oder eine Theorie. \(\square\)

11.4 Vertiefung: Toleranzbereich

🏎️VERTIEFUNG, nicht prüfungsrelevant🏎️

Berechnet man ein Regressionsmodell mit stan_glm (🤖😁), dann zieht man dabei Zufallszahlen 🎲. Der Hintergrund ist, dass Stan eine Stichproben-Post-Verteilung erstellt, und das Ziehen der Stichproben erfolgt zufällig. Das erklärt, warum Ihre Ergebnisse einer Regressionsanalyse mittels stan_glm von denen in diesem Buch abweichen können.

Um zu prüfen, ob Ihre Ergebnisse “ähnlich genug” oder “innerhalb eines Toleranzbereichs” sind, kann man die Funktion is_in_tolerance() aus dem R-Paket prada nutzen.

Größe des Toleranzbereichs

Die Größe des relativen Toleranzbereichs ist in is_in_toleranzce() auf 5% festgelegt. Das heißt, ein Unterschied von 5% zwischen einem Referenzwert (dem “wahren” Wert) und Ihrem Wert ist okay, also im Toleranzbereich. Außerdem gibt es noch einen absoluten Toleranzbereich, der auf 10% der SD der AV festgelegt ist (bei Regressionsmodellen). Der größere der beiden Werte gilt. \(\square\)

Wenn Sie diese Funktion nutzen wollen, müssen Sie zunächst das Paket installieren (von Github, nicht vom Standard-R-App-Store CRAN) und dann wie gewohnt starten.

library(remotes)  # dieses Paket können Sie mit `install.packages("remotes") installieren
install_github("sebastiansauer/prada")
library(prada)

Dann testen Sie, ob Ihr Modellparameter, z.B. \(\beta_1\) innerhalb eines Toleranzbereichs liegt.

Sagen wir der “richtige” oder “wahre” Wert (oder schlicht der Wert einer Musterlösung) für \(\beta_0\) ist 77. Unser Wert sei 77.56. Liegt dieser Wert noch innerhalb eines Toleranzbereichs?

is_in_tolerance(asis = 77.56,  # Ihr Wert
                tobe = 77,   # Referenzwert
                tol_rel = .05,   # relative Toleranz
                tol_abs = .10 * sd(kidiq$kid_score)  # absolute Toleranz
                )
## [1] TRUE

Ja, unser Wert ist innerhalb des Toleranzbereichs. ✅

Übungsaufgabe 11.1 (Peer-Instruction: Wählen Sie plausible Priori-Verteilungen für Modell m10.1!) Die Apriori-Verteilungen, die Stan als Voreinstellung gewählt hat, sind recht weit. Das ist nicht unbedingt falsch, aber z.B. weniger Streuung in den Verteilungen wäre wohl plausibler.

Bearbeiten Sie dazu folgende Aufgaben in Kleingruppen:

  1. Welche Parameter gibt es in m10.1?
  2. Geben Sie passende Parameter für diese Apriori-Verteilungen an in mathematischer Notation.
  3. Geben Sie den pasenden R-Befehl für diese Apriori-Werte an.

Bereiten Sie Ihre Lösungen schriftlich elektronisch vor. Die Lehrkraft wird Sie ggf. bitten, Ihre Aufgaben im Plenum zu präsentieren. \(square\)

11.5 y ~ x + b

Forschungsfrage:

Wie stark ist der statistische Effekt von jeweils Schulabschluss der Mutter (mom_hs) und IQ der Mutter (mom_iq) auf den IQ des Kindes (kid_score) ?

Die Modellformel zur Forschungsfrage lautet: y ~ x + b bzw. kid_score ~ mom_iq + mom_hs.

Die Hypothesen lauten:

  1. Der Schulabschluss der Mutter hat einen positiven Effekt auf den IQ des Kindes: \(\beta_{momhs} > 0\).
  2. Der IQ der Mutter hat einen positiven Effekt auf den IQ des Kindes: \(\beta_{momiq} > 0\).

Der Kausalgraph8 zur Modellformel sieht aus in Abbildung 11.4 dargestellt. Laut unserem Modell ist y also eine Funktion zweier (kausaler) Einflüsse, b und u, wobei u für “unbekannt” steht, also für alle sonstigen Einflüsse.9

Abbildung 11.4: DAG für y ~ b

Deskriptive Statistiken zum Datensatz sind in Tabelle Tabelle 11.3 dargestellt.

describe_distribution(kidiq)
Tabelle 11.3: Variablen und ihre Verteilung im Datenatz kidiq
Variable Mean SD IQR Range Skewness Kurtosis n n_Missing
kid_score 86.80 20.41 28.00 (20.00, 144.00) -0.46 -0.16 434 0
mom_hs 0.79 0.41 0.00 (0.00, 1.00) -1.40 -0.05 434 0
mom_iq 100.00 15.00 21.67 (71.04, 138.89) 0.47 -0.57 434 0
mom_age 22.79 2.70 4.00 (17.00, 29.00) 0.18 -0.63 434 0

Berechnen wir als Erstes folgendes einfaches Modell mit nur einer UV: kid_score ~ mom_iq (m10.2), s. Tab. Tabelle 11.4.

m10.2 <-
  stan_glm(kid_score ~ mom_iq, data = kidiq)

m10.2 %>% 
  parameters()
Tabelle 11.4: Parameter des Modells m10.2
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 25.78 (14.04, 36.99) 100% 1.000 3518 Normal (86.80 +- 51.03)
mom_iq 0.61 (0.50, 0.73) 100% 1.000 3486 Normal (0.00 +- 3.40)

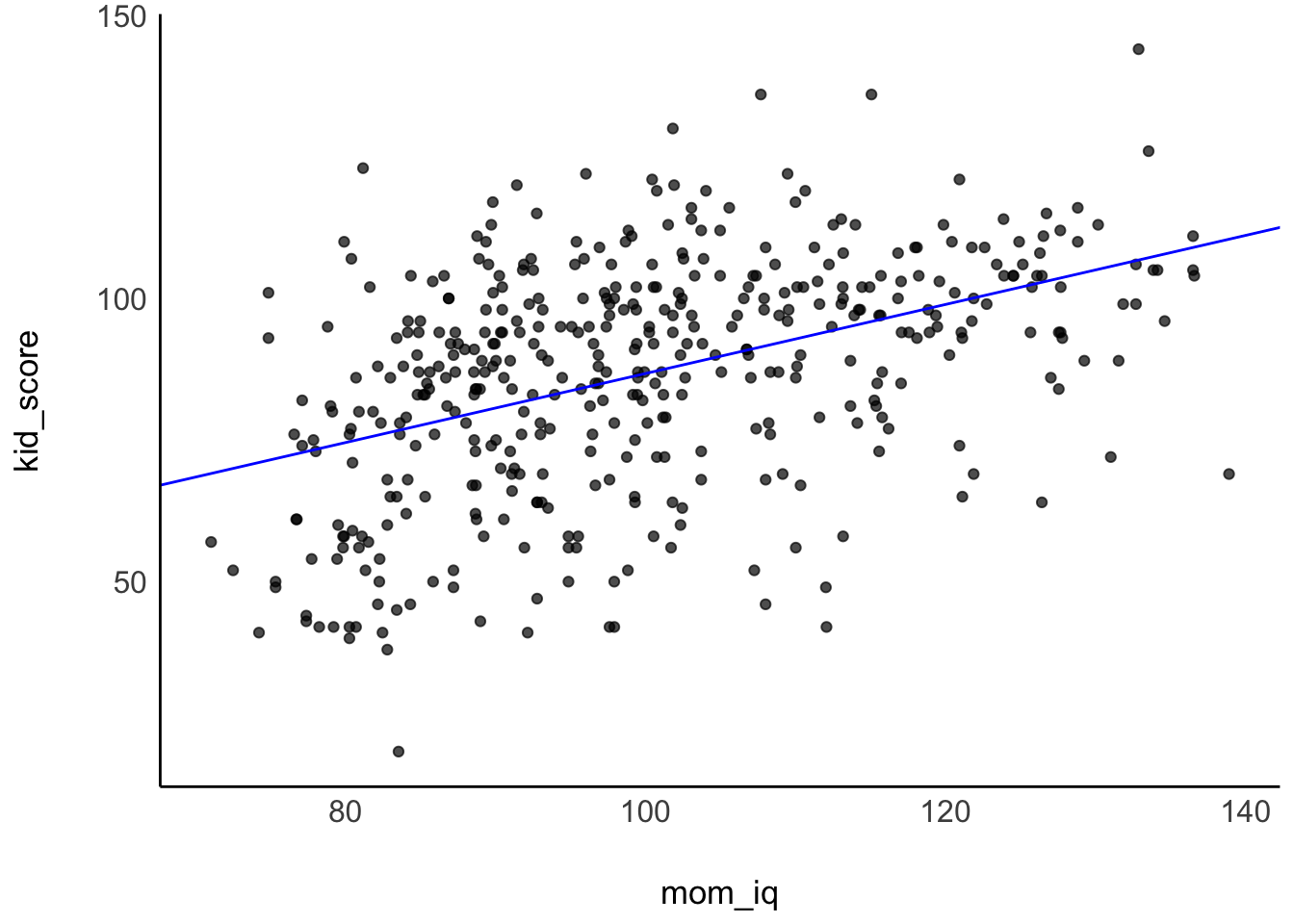
Setzt man die (Punktschätzer der) Parameter in die allgemeine Regressionsgleichung von m10.2 ein, so erhält man: kid_score = 26 + 0.6 * mom_iq + error. Visualisieren wir uns noch das Modell m10.2, s. Abbildung 11.5.

kidiq %>% 
  ggplot(aes(x = mom_iq, y = kid_score)) +
  geom_point(alpha = .7) +
  geom_abline(slope = coef(m10.2)[2],
              intercept = coef(m10.2)[1],
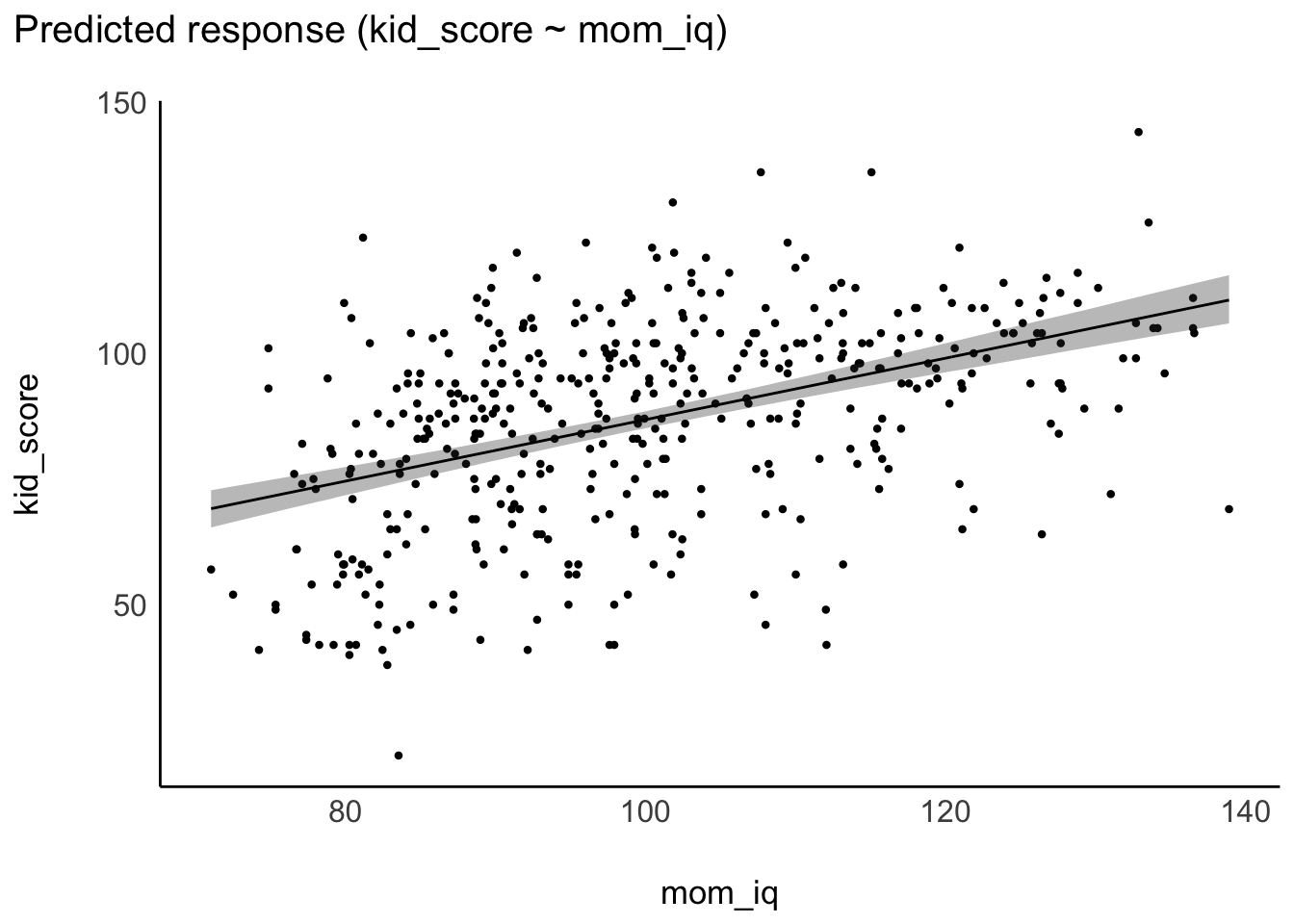
              color = "blue")
Abbildung 11.5: Die Intelligenz eines Kindes als Funktion der Intelligenz der Mutter (m10.2)

Alternativ kann man sich das Modell (m10.2) mit plot(estimate_relation)visualisieren, mit Hilfe des R-Pakets easystats, s. Abbildung 11.6.

plot(estimate_relation(m10.2)) +
  geom_point(data = kidiq, aes(x = mom_iq, y = kid_score))
Abbildung 11.6: Die geschätzten Erwartungswerte von m10.2 visualisiert

Die Linie zeigt die vorhergesagten IQ-Werte der Kinder für verschiedene IQ-Werte der Mütter. Vergleicht man Teilpopulationen von Müttern mit mittleren Unterschied von einem IQ-Punkt, so findet man 0.6 IQ-Punkte Unterschied bei ihren Kindern im Durchschnitt, laut dem Modell m10.2. Der Achsenabschnitt hilft uns nicht weiter, da es keine Menschen mit einem IQ von 0 gibt.

Berechnen wir als nächstes ein Modell mit beiden Prädiktoren: kid_score ~ mom_hs + mom_iq, s. Tabelle 11.5; Modell m10.3.

m10.3 <- 
  stan_glm(
    kid_score ~ mom_iq + mom_hs, 
    refresh = 0,
    data = kidiq)
Tabelle 11.5: Parameter des Modells m10.3 (ohne sigma; ETI-Intervalle)
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 25.74 (13.87, 36.76) 100% 1.001 3961 Normal (86.80 +- 51.03)
mom_iq 0.57 (0.45, 0.69) 100% 1.001 3456 Normal (0.00 +- 3.40)
mom_hs 6.04 (1.62, 10.15) 99.60% 0.999 3616 Normal (0.00 +- 124.21)

Will man nur schnell die Koeffizienten des Modells (d.h. Punktschätzer der Modellparametern, in diesem Fall den Median) wissen, so kann man anstelle von parameters(mein_modell) auch coef(mein_modell) schreiben. Aber natürlich ist es möglich (und einfacher) anstelle von coef den Befehl parameters zu verwenden.

coef(m10.3)
## (Intercept)      mom_iq      mom_hs 
##       25.86        0.56        5.97

m10.3: kid_score = 26 + 0.6*mom_iq + 6*mom_hs + error

Möchte man nur z.B. den 3. Wert aus diesem Vektor, so kann man schreiben:

coef(m10.3)[3]
## mom_hs 
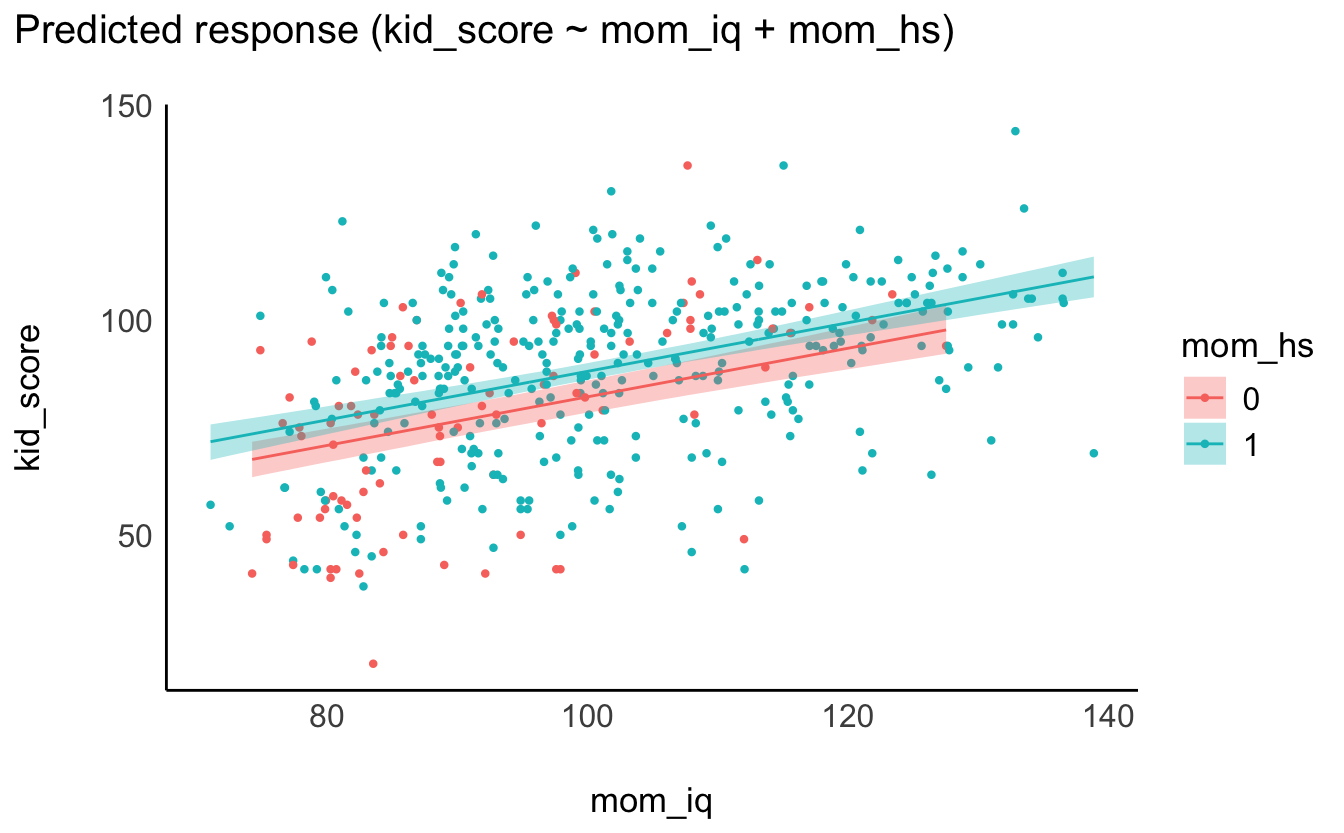
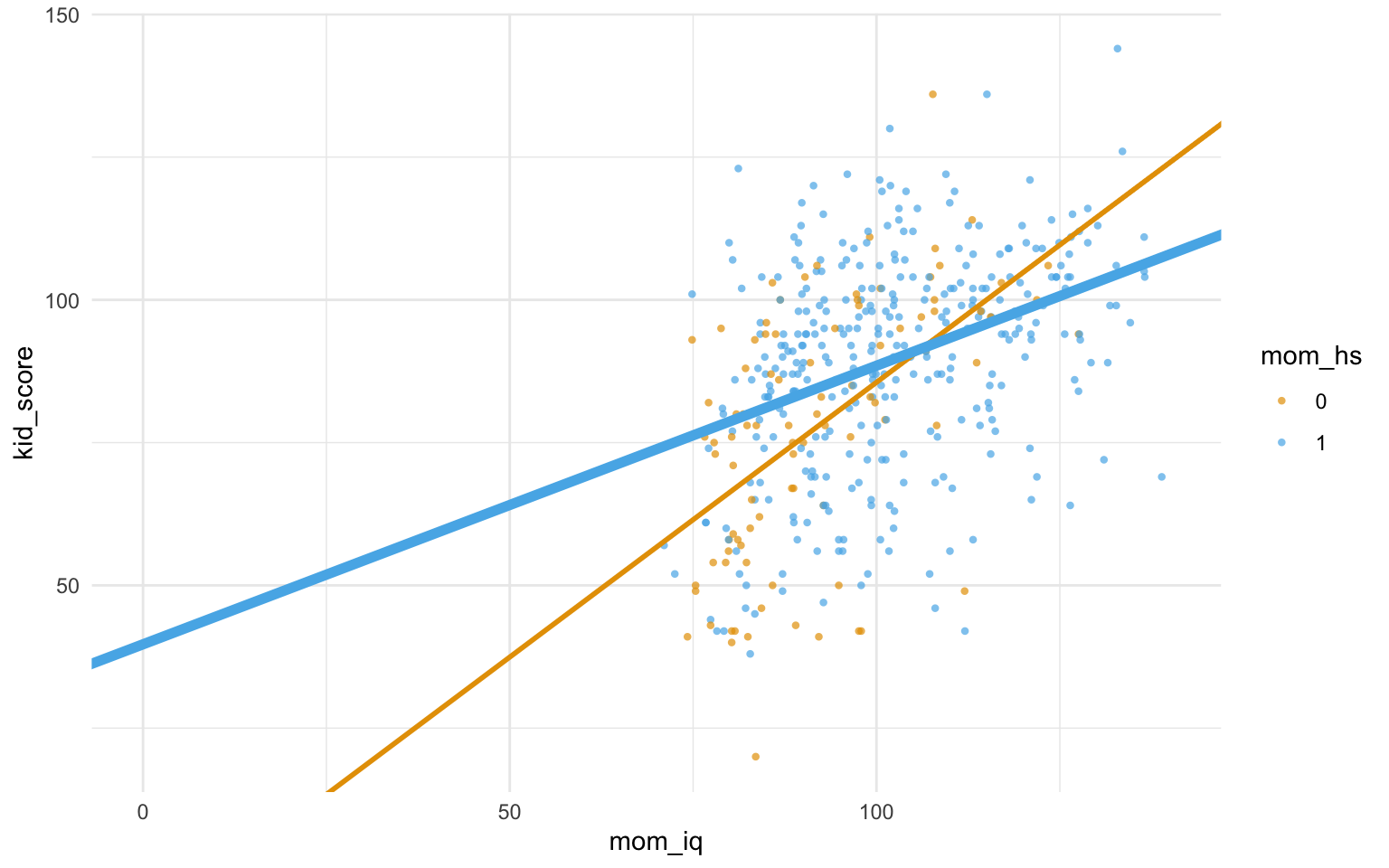
##      6

Abbildung 11.7 visualisiert das Modell m10.3.

kidiq2 <-
  kidiq %>% 
  mutate(mom_hs = as.factor(mom_hs))

m10.3a <- 
  stan_glm(
    kid_score ~ mom_iq + mom_hs, 
    refresh = 0,
    data = kidiq2)

pred <- estimate_relation(m10.3a)

plot(pred) +
  geom_point(data = kidiq2, aes(x = mom_iq, y = kid_score, color = mom_hs))
Abbildung 11.7: Der Effekt von sowohl mütterlicher Intelligenz als auch mütterlichem Schulabschluss.
  • Achsenabschnitt: Hat das Kind eine Mutter mit einem IQ von 0 und ohne Schulabschluss, dann schätzt das Modell den IQ-Wert des Kindes auf 26.
  • Koeffizient zum mütterlichen Schulabschluss: Vergleicht man Kinder von Müttern gleicher Intelligenz, aber mit Unterschied im Schulabschluss, so sagt das Modell einen Unterschied von 6 Punkten im IQ voraus.
  • Koeffizient zur mütterlichen IQ: Vergleicht man Kinder von Müttern mit gleichem Wert im Schulabschluss, aber mit 1 IQ-Punkt Unterschied, so sagt das Modell einen Unterschied von 0.6 IQ-Punkten bei den Kindern voraus.

Mit 95% Wahrscheinlichkeit liegt der Unterschied im mittleren IQ-Wert zwischen Kindern von Müttern mit bzw. ohne Schulabschluss im Bereich von 1.6 bis 10.1 IQ-Punkten, laut unserem Modell. Der Effekt des mütterlichen IQs wird auf 0.5 bis 0.7 geschätzt (95%-ETI). Da für beide UV die Null nicht im Intervall plausibler Werte liegt, kann ein Null-Effekt (die exakte Nullhypothese) abgelehnt werden.

11.6 y ~ x + b + x:b

Forschungsfrage:

Gibt es einen Interaktionseffekt zwischen mütterlichem Schulabschluss und mütterlichem IQ (auf den IQ-Wert des Kindes)?

Außerdem ist man vermutlich auch an den Effekten der beiden UV auf die AV interessiert; diese Fragen haben wir im letzten Abschnitt untersucht (und greifen sie daher nicht noch mal ausführlich auf).

Die Modellformel zur Forschungsfrage lautet: y ~ x + b + x:b. Der Einfachheit halber übernehmen wir wieder die Prioris wie vom R-Paket rstanarm bereitgestellt.

Der DAG zur Modellformel sieht aus in Abbildung 11.8 dargestellt.

Abbildung 11.8: DAG für y ~ x + b + x:b

In m10.3 hat das Modell die Regressionsgeraden gezwungen, parallel zu sein. Betrachtet man das Streudiagramm, so sieht man, das nicht-parallele Geraden besser passen. Sind die Regressionsgeraden nicht parallel, so spricht man von einer Interaktion (synonym: Interaktionseffekt, Moderation). Fügen wir also im nächsten Modell, m10.4 einen Interaktionseffekt hinzu.

Wichtig

Liegt eine Interaktion vor, so unterscheidet sich die Steigung der Geraden in den Gruppen. Liegt keine Interaktion vor, so sind die Geraden parallel.\(\square\)

Wir berechnen mit m10.4 das Modell mit folgender Modellformel: kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq, s. Listing 11.2, Abbildung 11.9 und Tabelle 11.6.

Listing 11.2: Die Modelldefition von m10.4 mit stanglm 
m10.4 <- 
  stan_glm(kid_score ~ mom_iq + mom_hs + mom_hs:mom_iq, 
           data = kidiq, 
           refresh = 0)

In der Regressionsformel sieht man, dass ein zusätzlicher Parametern, eben der Interaktionseffekt, in das Modell aufgenommen wurde.

Tabelle 11.6: Parameter von m10.4
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) -10.33 (-36.72, 16.82) 78.75% 1.001 1463 Normal (86.80 +- 51.03)
mom_iq 0.96 (0.67, 1.24) 100% 1.001 1467 Normal (0.00 +- 3.40)
mom_hs 49.90 (20.08, 78.91) 99.98% 1.002 1415 Normal (0.00 +- 124.21)
mom_iq:mom_hs -0.47 (-0.77, -0.16) 99.88% 1.001 1395 Normal (0.00 +- 1.16)

Mit estimate_relation(m10.4) |> plot() kann man sich das Modell visualisieren, s. Abbildung 11.9.

Abbildung 11.9: m10.4: Wie m10.3, aber mit Interaktionseffekt. Es ist gut zu erkennen, dass der Achsenabschnitt für diese Daten kaum zu interpretieren ist.

Der Achsenabschnitt gibt die IQ-Schätzwerte für Kinder mit Mütter ohne Abschluss und mit einem IQ von 0 an. Kaum zu interpretieren. mom_hs: Dieser Koeffizient zeigt den Unterschied der IQ-Schätzwerte zwischen Kindern mit Mutter ohne bzw. mit Schulabschluss und jeweils mit einem IQ von 0. Puh. mom_iq: Unterschied der IQ-Schätzwerte zwischen Kindern mit Müttern, die sich um einen IQ-Punkt unterscheiden aber jeweils ohne Schulabschluss. Interaktion (mom_hs:mom_iq): Der Unterschied in den Steigungen der Regressiongeraden, also der Unterschied des Koeffizienten für mom_iq zwischen Mütter mit bzw. ohne Schulabschluss. Für beide Gruppen, mom_hs=0 und mom_hs=1 gilt folgende Regressionsformel, s. Gleichung 11.2.

\[\text{kid score} = \beta_0 + \beta_1 \cdot \text{mom hs} + \beta_2 \cdot \text{mom iq} + \beta_3 \cdot \text{mom hs} \cdot \text{mom iq} \tag{11.2}\]

\(\beta_3\) gibt die Stärke des Interaktionseffekts an.

Auf Errisch schreibt mit Gleichung 11.2 so (s. Listing 11.2):

kid_score ~ mom_iq + mom_hs + mom_hs:mom_iq.

Der Doppelpunkt zwischen mom_hs und mom_iq steht für den Interaktionseffekt der beiden Variablen.

Trägt man die Punkteschätzer der Koeffizienten (\(\beta_0, \beta_1, \beta_2, \beta_3\)) ein, so erhält man Gleichung 11.3.

\[\text{kid score} = -10 + 49.1 \cdot \text{mom hs} + 1 \cdot \text{mom iq} + -0.5 \cdot \text{mom hs} \cdot \text{mom iq} \tag{11.3}\]

Teilen wir die Regressionsformel einmal auf die beiden Gruppen (mom_hs=0 bzw. mom_hs=1) auf:

mom_hs=0:

kid_score = -10 + 49.1*0 + 1*mom_iq  - -0.5*0*mom_iq
          = -10 + 1.1*mom_iq

mom_hs=1:

kid_score = -10 + 49.1*mom_hs + 1*mom_iq  - -0.5*mom_hs*mom_iq
          = -10 + 1.1*mom_iq

Nach der Interpretation von 20 unzentrierten Koeffizienten …

via GIPHY

Wir müssen dringend die unzentrierten Prädiktoren loswerden …

Wie in Tabelle 11.6 ersichtlich, kann für alle drei Effekte (mütterliche IQ, mütterlicher Schulabschluss und Interaktion von mütterlichem IQ mit mütterlichem Schulabschluss) ein Nulleffekt ausgeschlossen werden. Ob die Effekte stärker als “praktisch Null” sind, kann mittels des ROPE-Verfahren untersucht werden.

11.7 y ~ x_c + b + x_c:b

Unter Zentrieren (to center) versteht man das Bilden der Differenz eines Messwerts zu seinem Mittelwert.10 Zentrierte Werte geben also an, wie weit ein Messwert vom mittleren (typischen) Messwert entfernt ist. Mit zentrierten Werten ist eine Regression einfacher zu interpretieren. Hier zentrieren wir (nur) mom_iq; die zentrierte Variable kennzeichnen wir durch den Suffix _c, also mom_iq_c. Man könnte auch mom_hs zentrieren, aber für eine einfache Interpretation ist es meist nützlich, nur metrische Prädiktoren zu zentrieren.

kidiq <-
  kidiq %>% 
  mutate(mom_iq_c = mom_iq - mean(mom_iq))

m10.5 <- stan_glm(kid_score ~ mom_hs + mom_iq_c + mom_hs:mom_iq_c, 
                  data = kidiq, 
                  refresh = 0)

coef(m10.5)  # nur die Punktschätzer für die Koeffizienten ausgeben

Tabelle 11.7 zeigt die Punktschätzer der Koeffizienten von m10.5.

Tabelle 11.7: Punktschätzer von m10.5 (zentrierte UV)
Fixed Effects
Parameter Median
(Intercept) 85.34
mom_hs 2.86
mom_iq_c 0.97
mom_hs:mom_iq_c -0.48

Zur Interpretation von m10.5:

  • Der Achsenabschnitt (Intercept) gibt den geschätzten mittleren IQ des Kindes an, wenn man eine Mutter mittlerer Intelligenz und ohne Schulabschluss betrachtet.
  • mom_hs gibt den Unterschied im geschätzten mittleren IQ des Kindes an, wenn man Mütter mittlerer Intelligenz aber mit bzw. ohne Schlusabschluss vergleicht.
  • mom_iq_c gibt den Unterschied im geschätzten mittleren IQ des Kindes an, wenn man Mütter ohne Schlusabschluss aber mit einem IQ-Punkt Unterschied vergleicht.
  • mom_hs:mom_iq_c gibt den mittleren Unterschied in den Koeffizienten für mom_iq_c an zwischen den beiden Grupen von mom_hs.

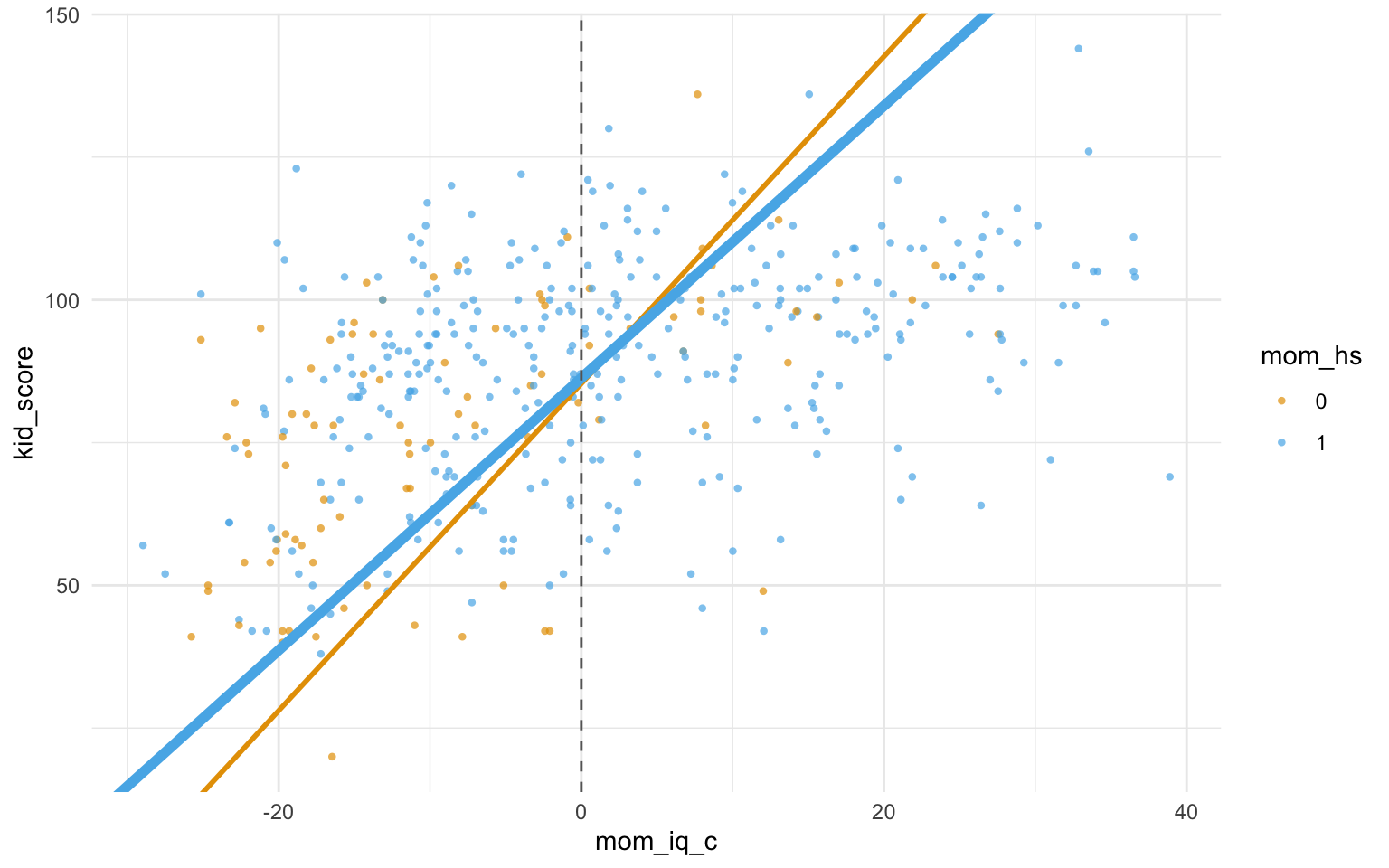
Mit estimate_relation(m10.5) |> plot() kann man sich das Modell visualisieren, s. Abbildung 11.10.

Abbildung 11.10: m10.5: Mit zentrierten Prädiktoren gibt der Achsenabschnitt den Y-Wert für eine Beobachtung mit mittleren X-Wert an; daher ist der Achsenabschnitt besser zu interpretieren als ohne Zentrierung.

Zentrieren ändert nichts an den Vorhersagen. Betrachten wir die Vorhersagen von m10.4. Mit predict kann man sich die Vorhersagen eines Modells ausgeben lassen.

new <- tibble(mom_hs = 0, mom_iq = mean(kidiq$mom_iq))
pred_new <- predict(m10.4, newdata = new)
mean(pred_new)
## [1] 85

Und vergleichen wir Vorhersagen von m10.4 mit denen von m10.5: Wir sehen, die Vorhersagen sind (bis auf Rundungsfehler) identisch.

new <- tibble(mom_hs = 0, mom_iq_c = 0)
pred_new <- predict(m10.5, newdata = new)
mean(pred_new)
## [1] 85

Auch die Streuungen der vorhergesagten Werte unterscheiden sich nicht (wirklich): \(\sigma_{m10.4}= 18\); \(\sigma_{m10.5}= 18\).

Das Zentrieren ändert auch nicht die Regressionskoeffizienten, da die Streuungen dieser Variablen nicht verändert wurden durch das Zentrieren.

Tabelle 11.8 zeigt die Punktschätzer der Parameter für m10.5 sowie ihre ETI. Nutzen Sie dafür parameters(m10.5), s. Tabelle 11.8. Highest Density (Posterior) Intervalle (HDI oder HDPI) kann man sich komfortabel ausgeben lassen mit hdi(m10.5) oder mit parameters(m10.5, ci_method = "hdi"), s. Tabelle 11.9. Im Falle symmetrischer Posteriori-Verteilungen (wie hier) kommen beide Arten von Intervallen zu gleichen Ergebnissen.

Tabelle 11.8: Parameter von m10.5 und ETIs
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 85.34 (81.17, 89.61) 100% 1.003 2348 Normal (86.80 +- 51.03)
mom_hs 2.86 (-1.80, 7.62) 87.98% 1.002 2469 Normal (0.00 +- 124.21)
mom_iq_c 0.97 (0.68, 1.24) 100% 1.004 1833 Normal (0.00 +- 3.40)
mom_hs:mom_iq_c -0.48 (-0.78, -0.16) 99.83% 1.003 1874 Normal (0.00 +- 3.87) 
parameters(m10.5, ci_method = "hdi") %>% 
  display()
Tabelle 11.9: Parameter von m10.5 und HDIs
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 85.34 (80.96, 89.39) 100% 1.003 2348 Normal (86.80 +- 51.03)
mom_hs 2.86 (-1.65, 7.75) 87.98% 1.002 2469 Normal (0.00 +- 124.21)
mom_iq_c 0.97 (0.68, 1.24) 100% 1.004 1833 Normal (0.00 +- 3.40)
mom_hs:mom_iq_c -0.48 (-0.78, -0.17) 99.83% 1.003 1874 Normal (0.00 +- 3.87)

Das Model zeigt keine Belege, dass sich die mittlere Intelligenz von Kindern bei Müttern mit bzw. ohne Schlusabluss unterscheidet (95%PI: [-2.0, 7.8]); die Befundlage ist unklar. Hingegen fand sich ein Effekt der mütterlichen Intelligenz; pro Punkt Unterschied in mütterlichem IQ fand sich ein Unterschied von 0.7 bis 1.3 IQ-Punkte beim Kind (95%PI). Außerdem fand sich ein Beleg, dass der Zusammenhang des IQ zwischen Mutter und Kind durch den Schulabschluss moderiert wird: Bei Mütter mit Schulabschluss war der Regressionskoeffizient zwischen Mutter-IQ und Kind-IQ geringer (95%PI: [-0.80, -0.17]).

Wichtig

Das Modell hat mittels Abbildung 11.11 mutig Kausalaussagen postuliert. Das ist zwar schön, bedarf aber einer Begründung mit Rückgriff auf die Literatur (was hier nicht getan wurde). Ohne eine Begründung ist die Behauptung der Kausalaussage nicht zu verteidigen.

11.8 y ~ g

Hier untersuchen wir ein Modell mit einer nominalen UV mit mehreren Stufen.

Nach Ihrem Studium wurden Sie reich als Unternehmensberaterin; Ihre Kompetenz als Wirtschaftspsychologi war heiß begehrt. Von Statistik wollte niemand etwas wissen… Doch nach einiger Zeit kamen Sie in eine Sinnkrise. Sie warfen Ihre Job hin und beschlossen, in die Wissenschaft zu gehen. Kurz entschlossen bewarben Sie sich auf das erste Stellenangebot als Nachwuchswissenschaftler:in. Ihr Forschungsprojekt führte Sie in die Antarktis… Nun, das war zumindest ein Gegenentwurf zu Ihrem bisherigen Jet-Set-Leben. Ihre Aufgabe bestand nun darin, Pinguine zu untersuchen. Genauer gesagt ging es um Größenunterschiede zwischen drei Pinguinarten. Ja, stimmt, an so ein Forschungsprojekt hatten Sie vorher nie auch nur nur im Traum gedacht.

Forschungsfrage:

Unterscheiden sich die mittleren Körpergewichte der drei Pinguinarten?

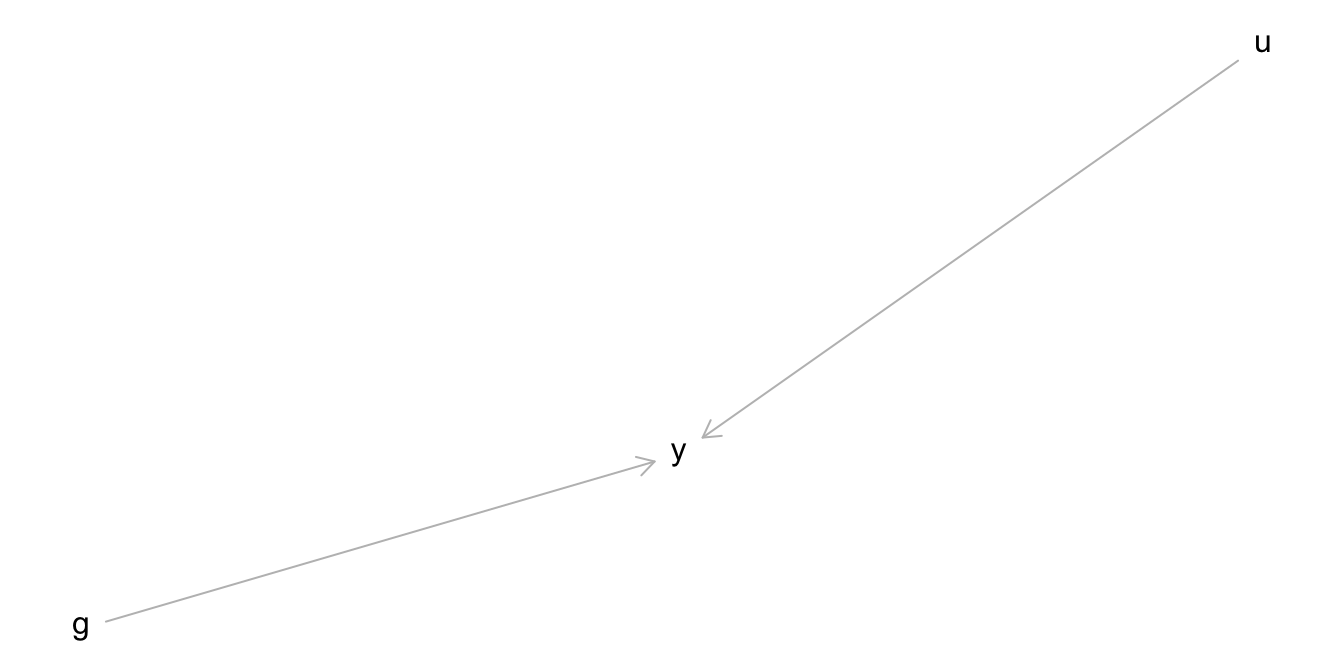
Die allgemeine Modellformel zur Forschungsfrage lautet: y ~ g.

Der DAG zur Modellformel sieht aus in Abbildung 11.11 dargestellt.

Abbildung 11.11: DAG für y ~ g

Prüfen wir die Nullhypothese, \(H_0\), dass alle Mittelwerte gleich sind, exakt gleich (?)

  • Formal: \(\mu_1 = \mu_2 = \ldots = \mu_k\) mit \(k\) verschiedenen Gruppen von Pinguinarten.

  • Hypothesen, die keinen (Null) Unterschied zwischen Gruppen oder keinen Zusammenhang zwischen Variablen postulieren, kann man als Nullhypothesen bezeichnen.

  • Moment. Dass sich alle Mittelwerte um 0,00000000 unterscheiden, ist wohl nicht zu vermuten. Daher ist die bessere Forschungsfrage:

Wie sehr unterscheiden sich mittlere Körpergewichte in Abhängigkeit von der Pinguinart?

Alternativ können wir die Hypothese prüfen, ob die Mittelwerte “praktisch” gleich sind, also sich “kaum” unterscheiden. Der Grenzwert für “praktisch gleich” bzw. “kaum unterschiedlich” ist subjektiv. Dazu in Kapitel 10.3 mehr.

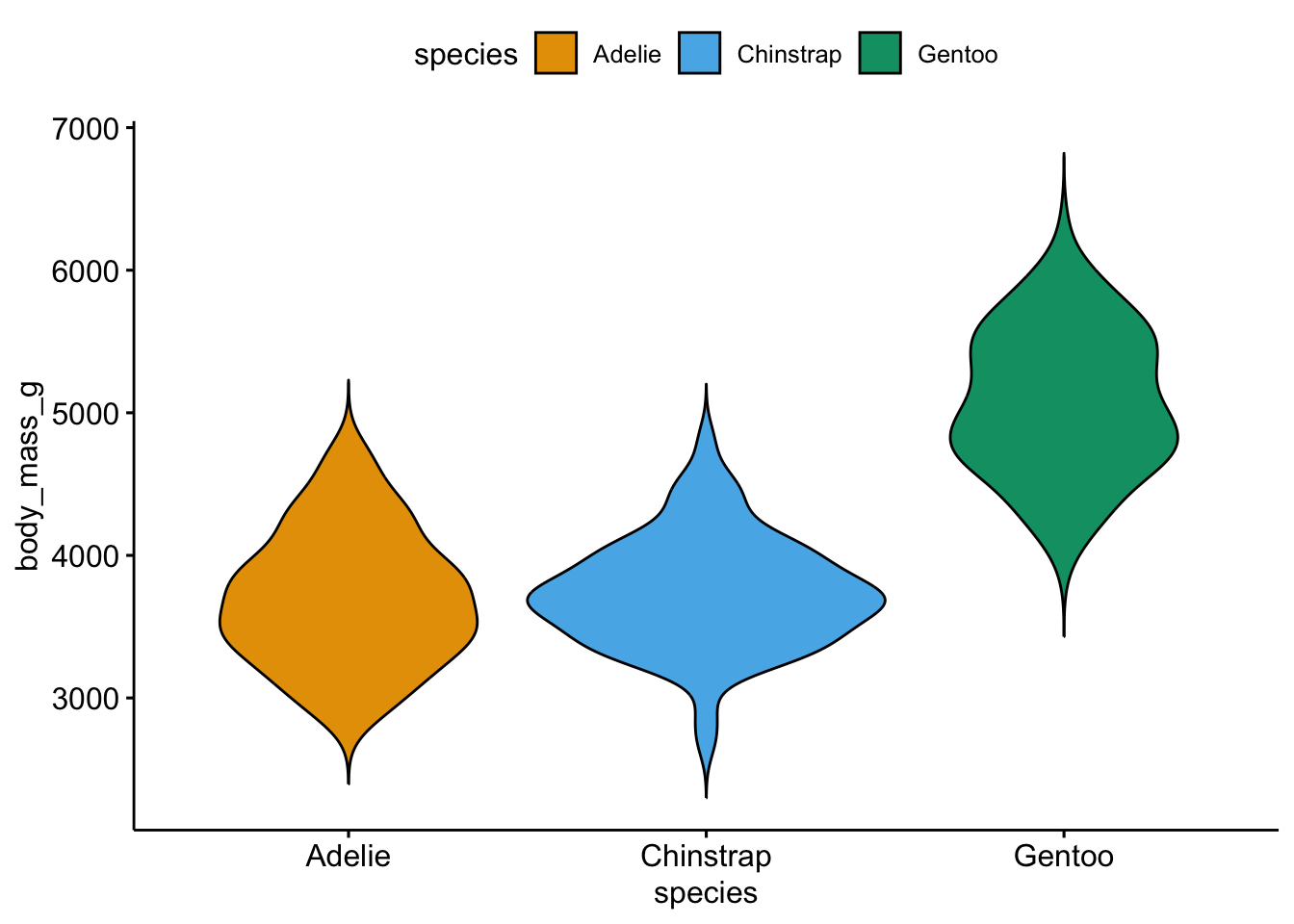
Werfen wir einen Blick in den Datensatz penguins. Hier ist die Verteilung des Gewichts jeder Spezies im Datensatz, Tabelle 11.10.

Palmer Penguins

Palmer Penguins

Datenquelle, Beschreibung des Datensatzes

penguins %>% 
  select(body_mass_g, species) %>% 
  group_by(species) %>% 
  describe_distribution(range = FALSE, iqr = FALSE)
Tabelle 11.10: Die Verteilung des Körpergewichts pro Spezies der Pinguine

Was fällt Ihnen auf? Visualisieren wir als Nächstes die Verteilung der AV, um den Datensatz genauer zu verstehen. Hier kommen die Pinguine! Wie schwer sind die Tiere in unserer Stichprobe, s. Abbildung 11.12?

Abbildung 11.12: Verteilung des Körpergewichts dreier Arten von Pinguinen - Geom Violine

Berechnen wir nun das mittlere Gewicht pro Spezies (Gruppe) der Pinguine, s. m10.6 und Tabelle 11.11. Die Modellformel für m10.6 lautet also body_mass_g ~ species.

options(mc.cores = parallel::detectCores())  # Turbo einschalten

m10.6 <- stan_glm(body_mass_g ~ species, 
                  data = penguins, 
refresh = 0,  # unterdrückt Ausgabe der Posteriori-Stichproben
                  )

m10.6 %>% parameters()
Tabelle 11.11: Parameter des Modells m10.6; neben dem Achsenabschnitt sind die Effekte der Gruppe Adelie und Chinstrap ausgewiesen
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 3700.71 (3629.91, 3775.07) 100% 1.000 4123 Normal (4201.75 +- 2004.89)
speciesChinstrap 33.49 (-103.70, 161.00) 68.47% 1.000 3925 Normal (0.00 +- 5015.92)
speciesGentoo 1373.19 (1260.51, 1484.32) 100% 1.000 4471 Normal (0.00 +- 4171.63)

Zur Interpretation von m10.6:

Die UV hat drei verschiedene Stufen (Werte, Ausprägungen; hier: Spezies), aber es werden in Tabelle 11.11 nur zwei Stufen angezeigt (also eine weniger) zusätzlich zum Achsenabschnitt. Die fehlende Stufe (Adelie, nicht ausgegeben) ist die Vergleichs- oder Referenzkategorie (baseline) und ist im Achsenabschnitt ausgedrückt (Intercept). Die Koeffizienten für species geben jeweils den (vorhergesagten) Unterschied zur Vergleichskategorie wieder. Pinguine der Spezies Adelie haben laut Modell ein mittleres Gewicht von ca. 3700g. Pinguine der Spezies Gentoo sind laut Modell im Mittel gut 1000g schwerer als Pinguine der Spezies Adelie, etc.

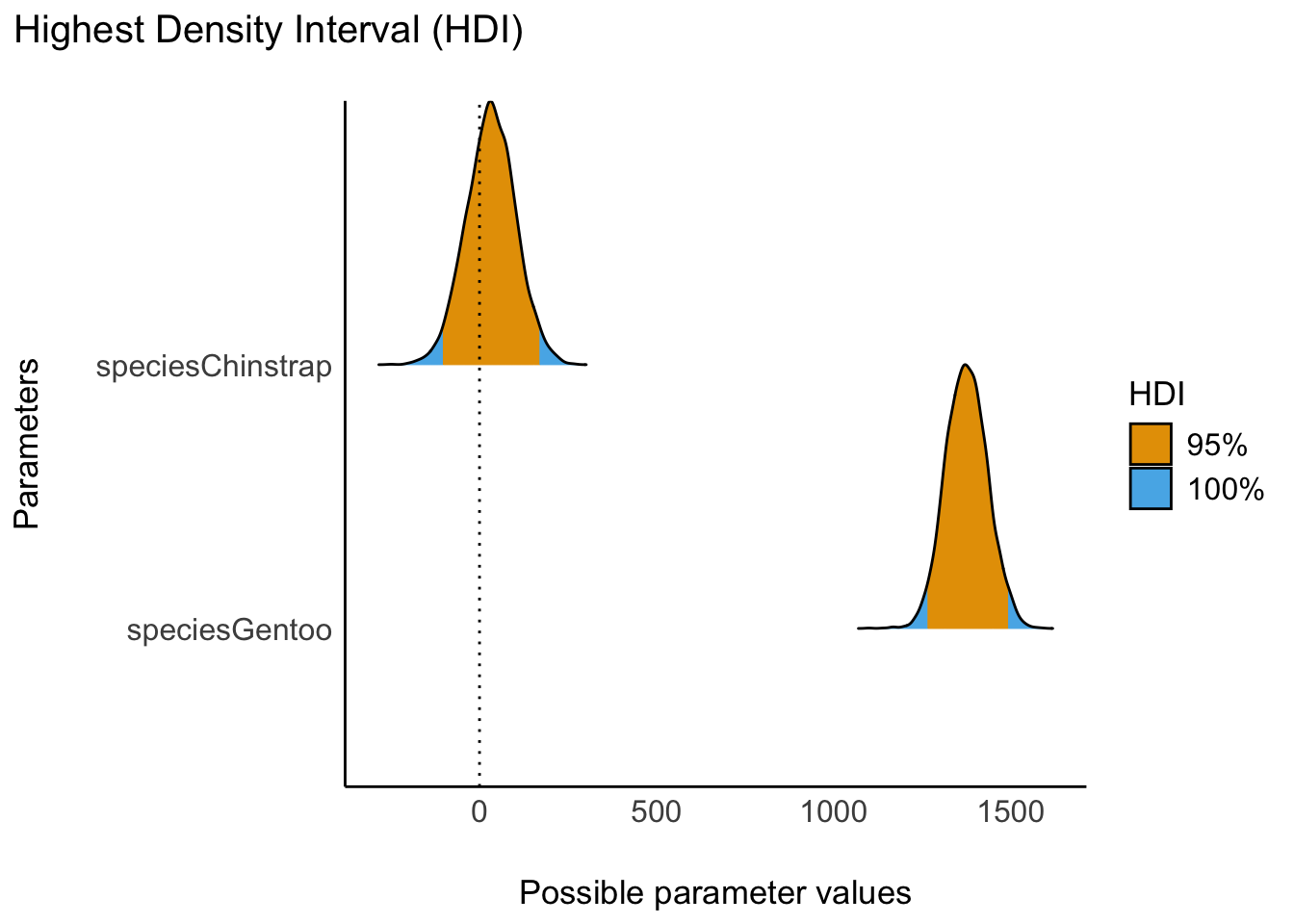
Der Unterschied im mittleren Gewicht von den Gruppen Chinstrap und Gentoo zur Referenzgruppe (Adelie) ist in Abbildung 11.13 verdeutlicht.

plot(hdi(m10.6)) + scale_fill_okabeito()
Abbildung 11.13: Effekt der UV: Unterschiede zur Referenzgruppe (95%-HDI)

Das Farbschema nach Okabe und Ito ist gut geeignet, um nominal skalierte Farben zu kodieren (s. Details hier).

Glauben wir jetzt an Gruppeneffekte?

Glauben wir jetzt, auf Basis der Modellparameter, an Unterschiede (hinsichtlich der AV) zwischen den Gruppen (UV)?

Es scheinen sich nicht alle Gruppen voneinander zu unterscheiden. So ist der Mittelwert der Gruppe Gentoo deutlich höher als der der beiden anderen Gruppen. Umgekehrt sind sich die Pinguinarten Adelie und Chinstrap in ihren Mittelwerten ziemlich ähnlich. Wie in Abbildung 11.13 ersichtlich, überlappt sich der Schätzbereich für den Parameter von Gentoo nicht mit der Null; hingegen überlappt sich der Schätzbereich des Parameters für Chinstrap deutlich mit der Nullinie. Auf Basis unseres Modells verwerfen wir die also (mit hoher Sicherheit) die Hypothese, dass alle Mittelwerte exakt identisch sind. Ehrlicherweise ist sowieso zweifelhaft, dass die exakte Nullhypothese \(\mu_1 = \mu_2 = \ldots = \mu_k\) bis in die letzte Dezimale gilt. Anders gesagt: Die Wahrscheinlichkeit eines bestimmten Wertes einer stetigen Zufallsvariable ist praktisch Null. Aber: Viele Forscherinnen und Forscher prüfen gerne die Nullhypothese, daher diskutieren wir hier den Begriff der (exakten) Nullhypothese. Das Verfahren der Frequentistischen Statistik, um die Nullhypothese \(\mu_1 = \mu_2 = \ldots = \mu_k\) zu testen, nennt man Varianzanalyse (analysis of variance, kurz ANOVA). In der Bayes-Statistik nutzt man – wie immer – primär die Post-Verteilung, um Fragen der Inferenz (z.B. Gruppenunterschiede dieser Art)zu beurteilen.

Unser Modell m10.6 verwendet schwach informierte (weakly informative) Priors. Für Achsenabschnitt und die Regressionskoeffizienten trifft unser Golem Stan folgende Annahmen in der Voreinstellung:

  • Achsenabschnitt und Regressionsgewichte werden als normalverteilt angenommen
  • mit Mittelwert entsprechend den Stichprobendaten
  • und einer Streuung des Mittelwerts, die der 2.5-fachen der Streuung in der Stichprobe entspricht
  • für Sigma wird eine Exponentialverteilung mit Rate \(\lambda=1\) angenommen, skaliert mit der Streuung der AV.

Mehr Infos kann man sich mit prior_summary(modell) ausgeben lassen.

prior_summary(m10.6)
## Priors for model 'm10.6' 
## ------
## Intercept (after predictors centered)
##   Specified prior:
##     ~ normal(location = 4202, scale = 2.5)
##   Adjusted prior:
##     ~ normal(location = 4202, scale = 2005)
## 
## Coefficients
##   Specified prior:
##     ~ normal(location = [0,0], scale = [2.5,2.5])
##   Adjusted prior:
##     ~ normal(location = [0,0], scale = [5015.92,4171.63])
## 
## Auxiliary (sigma)
##   Specified prior:
##     ~ exponential(rate = 1)
##   Adjusted prior:
##     ~ exponential(rate = 0.0012)
## ------
## See help('prior_summary.stanreg') for more details

Wo man man über mehr inhaltliches Wissen verfügt, so wird man die Prioris anpassen wollen. So könnte man z.B. auf Basis von Fachwissen über das Gewicht von Pinguinen postulieren, dass Adelie-Pinguine im Mittel 3000 g wiegen. Und dass die anderen zwei Pinguin-Arten im Mittel sich nicht unterscheiden vom Mittelwert der Adelie-Pinguine.

m10.6b <- stan_glm(
  body_mass_g ~ species, 
  data = penguins, 
  refresh = 0,
  prior = normal(location = c(0, 0),  # betas, Mittelwert
                 scale = c(500, 500)),  # betas, Streuung
  prior_intercept = normal(3000, 500),  # Achsenabschnitt, Mittelwert und Streuung
  prior_aux = exponential(0.001)
)
coef(m10.6b)
##      (Intercept) speciesChinstrap    speciesGentoo 
##             3706               24             1359

Anstelle von Rohwerten (hier Angabe von Gramm Gewicht) kann man die Streuung auch in z-Werten eingeben, das macht es etwas einfacher, s. m10.6c. Dazu gibt man bei dem oder den entsprechenden Parametern den Zusatz autoscale = TRUE an.

m10.6c <- stan_glm(
  body_mass_g ~ species, 
  data = penguins, 
  refresh = 0,
  prior = normal(location = c(0, 0),  # betas, Mittelwert
                 scale = c(2.5, 2.5),  # betas, Streuung
                 autoscale = TRUE),  # in z-Einheiten
  prior_intercept = normal(3000, 2.5,   # Achsenabschnitt, Mittelwert und Streuung
                           autoscale = TRUE), 
  prior_aux = exponential(1, autoscale = TRUE)
)
coef(m10.6c)
##      (Intercept) speciesChinstrap    speciesGentoo 
##             3700               32             1376

Den Parameter für die Streuung des Modells, \(\sigma\), kann man sich mit sigma(modell) ausgeben lassen.

sigma(m10.6b)
## [1] 464

Implizit bekommt man die Informationen zu \(\sigma\) mitgeteilt durch die Größe der Konfidenzintervalle.

Übrigens macht es meistens keinen Sinn, extrem weite Prioris zu definieren.11

11.9 Vertiefung: Wechsel der Referenzkategorie

species ist eine nominale Variable, da passt in R der Typ factor (Faktor) am besten. Aktuell ist der Typ noch character (Text):

penguins <- penguins %>% 
  mutate(species = factor(species))

Im Standard sortiert R die Faktorstufen alphabetisch, aber man kann die Reihenfolge ändern.

levels(penguins$species)
## [1] "Adelie"    "Chinstrap" "Gentoo"

Setzen wir Gentoo als Referenzkategorie und lassen die restliche Reihenfolge, wie sie ist:

library(forcats)
penguins <- penguins %>% 
  mutate(species = factor(species),
    species = fct_relevel(species, "Gentoo"))

Beachten Sie, dass dazu das Paket forcats verfügbar sein muss.

Jetzt haben wir die Referenzkategorie geändert:

levels(penguins$species)
## [1] "Gentoo"    "Adelie"    "Chinstrap"

Der Wechsel der Referenzkategorie ändert nichts Wesentliches am Modell, s. Tabelle 11.12.

m10.6a <- stan_glm(body_mass_g ~ species, data = penguins, refresh = 0)
hdi(m10.6a)
Tabelle 11.12: m10.6a mit geänderter Referenzkategorie; die Effekte der UVs bleiben gleich.
Highest Density Interval
Parameter 95% HDI
(Intercept) [ 4991.94, 5156.32]
speciesAdelie [-1480.16, -1255.85]
speciesChinstrap [-1486.99, -1210.99]

11.10 y ~ x1 + x2

Hier untersuchen wir Forschungsfragen mit zwei metrischen UV (und einer metrischen AV).

Forschungsfrage:

Stehen sowohl der IQ der Mutter als auch, unabhängig davon, das Alter der Mutter im Zusammenhang mit dem IQ des Kindes?

Das ist eine deskriptive Forschungsfrage. Keine Kausalwirkung (etwa “IQ der Mutter ist die Ursache zum IQ des Kindes”) wird impliziert. Es geht in dieser Forschungsfrage rein darum, Zusammenhänge in den Daten - bzw. in der Population - aufzuzeigen. Viele Forschungsfragen gehen allerdings weiter und haben explizit Kausalwirkungen im Fokus. Für solche Fragen ist ein Kausalmodell nötig: Fachlich fundierte Annahmen über Kausalzusammenhänge zwischen UV und AV.

Was heißt, X hängt mit Y zusammen?

Der Begriff “Zusammenhang” ist nicht exakt. Häufig wird er (für metrische Variablen) verstanden als lineare Korrelation \(\rho\) bzw. \(r\) lineare Regression \(\beta\), bzw. \(b\).

Der Regressionskoeffizient misst die Steigung der Regressionsgerade und zeigt, wie groß der vorhergesagte Unterschied in Y ist, wenn man zwei Personen (Beobachtungseinheiten) vergleicht, die sich um eine Einheit in X unterscheiden. Der Regressionskoeffizient wird manchmal mit dem “Effekt von X auf Y” übersetzt. Vorsicht: “Effekt” klingt nach Kausalzusammenhang. Eine Regression ist keine hinreichende Begründung für einen Kausalzusammenhang.

Der Korrelationskoeffizient misst eine Art der Stärke des linearen Zusammenhangs. er zeigt, wie klein die Vorhersagefehler der zugehörigen Regression im Schnitt sind. Korrelation ist nicht (automatisch) Kausation.

Es ist hilfreich, sich die Korrelationen zwischen den (metrischen) Variablen zu betrachten, bevor man ein (Regressions-)Modell aufstellt, s. Tabelle 11.13.

kidiq %>% 
  correlation(bayesian = TRUE)
Tabelle 11.13: Korrelation der Variablen im Datensatz kidiq
Correlation Matrix (pearson-method)
Parameter1 Parameter2 rho 95% CI pd % in ROPE Prior BF
kid_score mom_hs 0.23 (0.14, 0.32) 100%*** 0.35% Beta (3 +- 3) 2.48e+04***
kid_score mom_iq 0.44 (0.37, 0.52) 100%*** 0% Beta (3 +- 3) 6.41e+19***
kid_score mom_age 0.09 (-4.59e-03, 0.18) 97.35%* 57.57% Beta (3 +- 3) 0.686
kid_score mom_iq_c 0.44 (0.36, 0.51) 100%*** 0% Beta (3 +- 3) 6.41e+19***
mom_hs mom_iq 0.28 (0.19, 0.37) 100%*** 0% Beta (3 +- 3) 5.72e+06***
mom_hs mom_age 0.21 (0.13, 0.30) 100%*** 0.92% Beta (3 +- 3) 2.57e+03***
mom_hs mom_iq_c 0.28 (0.19, 0.37) 100%*** 0% Beta (3 +- 3) 5.72e+06***
mom_iq mom_age 0.09 (-2.64e-03, 0.18) 97.42%* 57.03% Beta (3 +- 3) 0.676
mom_iq mom_iq_c 1.00 (1.00, 1.00) 100%*** 0% Beta (3 +- 3)
mom_age mom_iq_c 0.09 (-7.19e-03, 0.18) 96.70% 58.77% Beta (3 +- 3) 0.676

Observations: 434

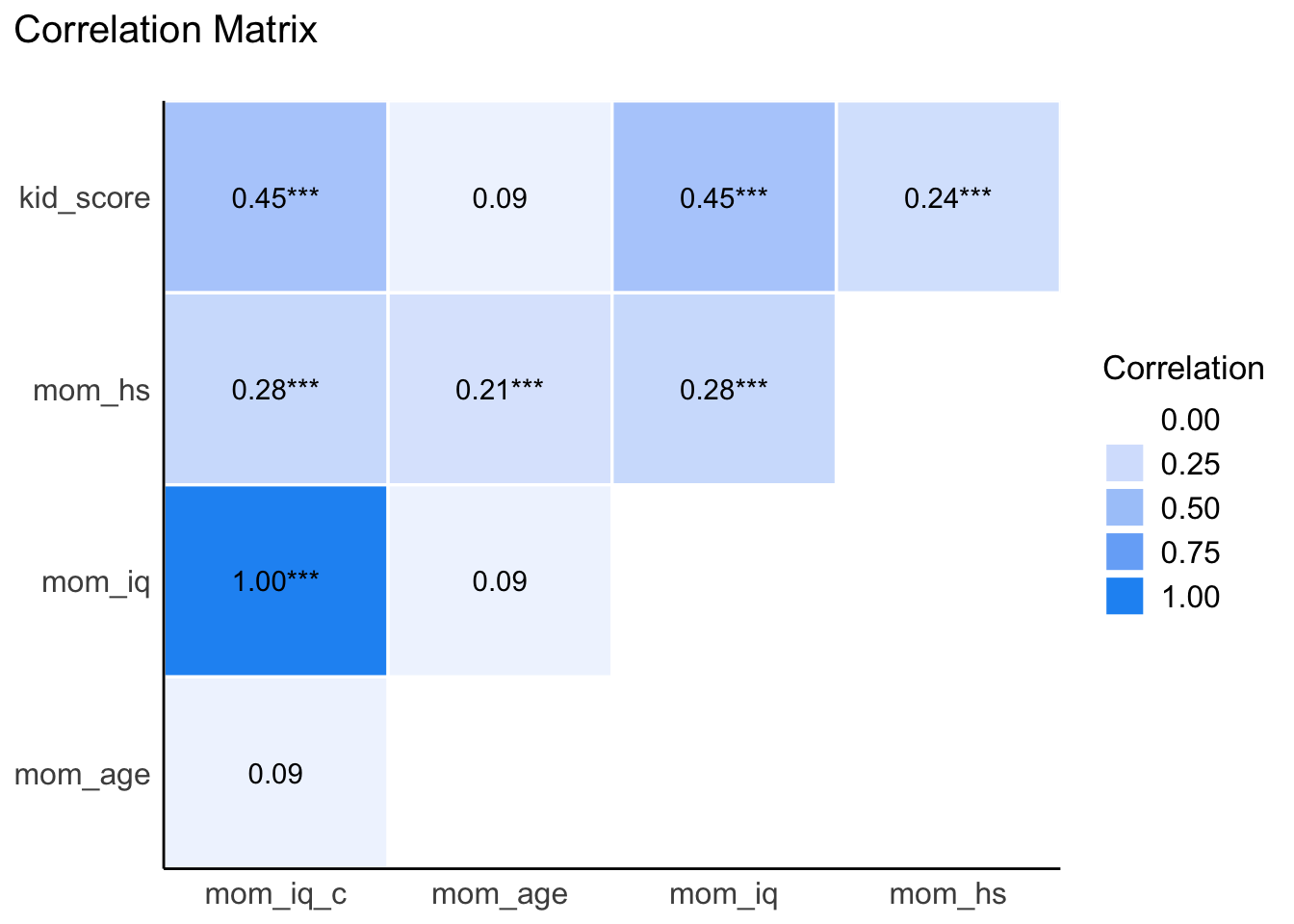
Tabelle 11.14 zeigt die Korrelationsmatrix als Korrelationsmatrix.

kidiq %>% 
  correlation(bayesian = TRUE) %>% 
  summary()
Tabelle 11.14: Die Korrelationen zwischen den Variablen der Tabelle kidiq. Die Sterne geben einen Bereich des p-Werts an (wir ignorieren die Sterne hier).
Correlation Matrix (pearson-method)
Parameter mom_iq_c mom_age mom_iq mom_hs
kid_score 0.45*** 0.09 0.45*** 0.24***
mom_hs 0.28*** 0.21*** 0.28***
mom_iq 1.00*** 0.09
mom_age 0.09

p-value adjustment method: Holm (1979)

Nützlich ist auch die Visualisierung der Korrelationstabelle als Heatmap, Abbildung 11.14.

kidiq %>% 
  correlation() %>% 
  summary() %>% 
  plot()
Abbildung 11.14: Visualisierung der Korrelationsmatrix als Heatmap

Wir berechnen zunächst jeweils eine univariate Regression, pro Prädiktor, also eine für mom_iq und eine für mom_age.

m10.7 <- stan_glm(kid_score ~ mom_iq, data = kidiq, refresh = 0)
m10.8 <- stan_glm(kid_score ~ mom_age, data = kidiq, refresh = 0)

Tabelle 11.15 zeigt die Ergebnisse für mom_iq.

Tabelle 11.15: Parameter für m10.7
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 25.79 (14.59, 37.16) 100% 1.000 4452 Normal (86.80 +- 51.03)
mom_iq 0.61 (0.50, 0.72) 100% 1.000 4436 Normal (0.00 +- 3.40)

Tabelle 11.16 zeigt die Ergebnisse für mom_age.

Tabelle 11.16: Parameter für m10.8
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 71.39 (54.39, 87.44) 100% 0.999 3923 Normal (86.80 +- 51.03)
mom_age 0.68 (-0.02, 1.41) 96.92% 0.999 3917 Normal (0.00 +- 18.89)

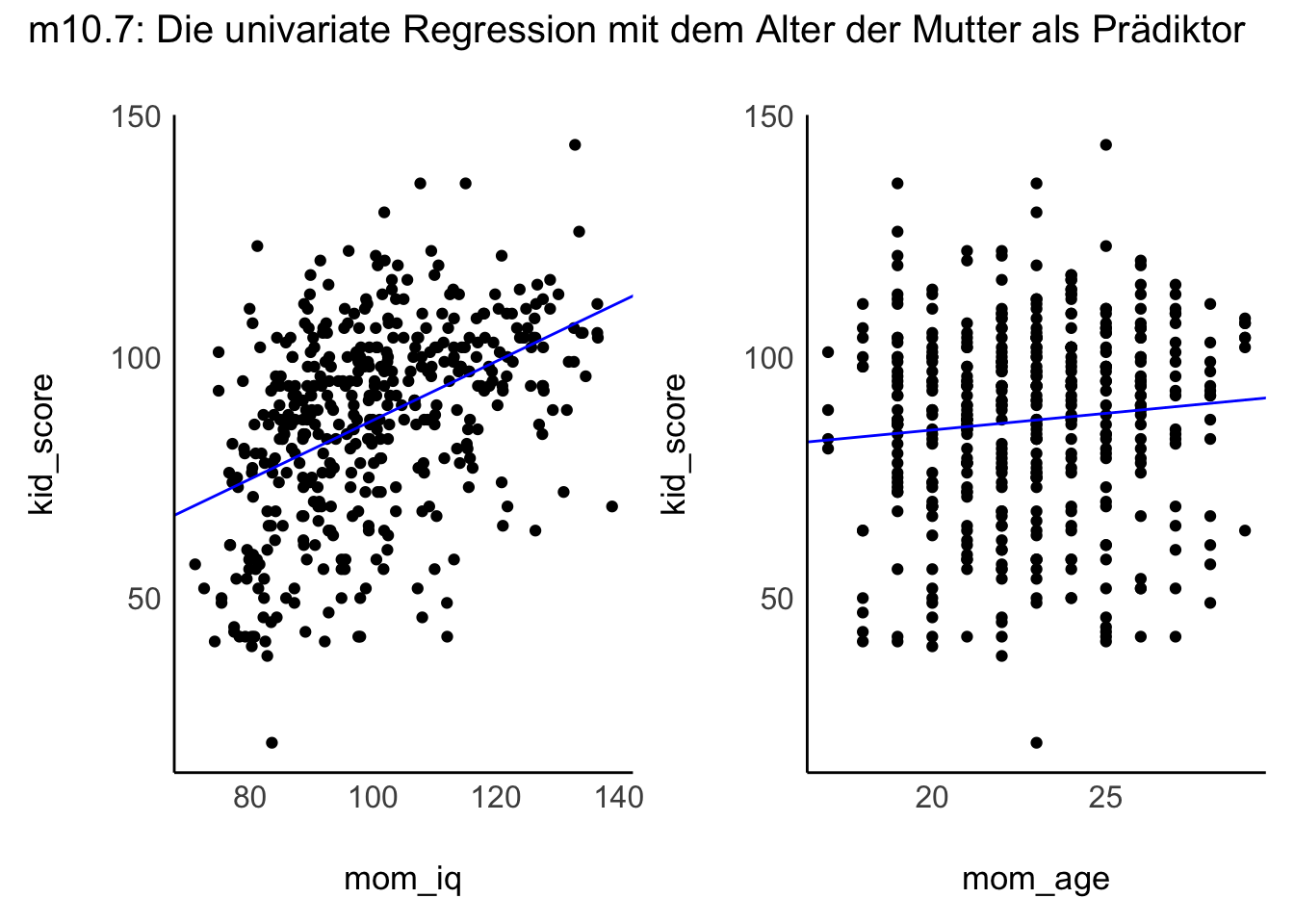
Visualisieren wir nun die univariaten Regressionen. In Abbildung 11.15 ist die univariate Regression mit jeweils einem der beiden Prädiktoren dargestellt.

m10.7: Die Steigung beträgt 0.6. m10.8: Die Steigung beträgt 0.7.

Abbildung 11.15: Zwei univariate Regressionen

Berechnen wir im Foglenden das multiple Modell (beide Prädiktoren), m10.9. m10.9 stellt das multiple Regressionsmodell dar; multipel bedeutet in diesem Fall, dass mehr als ein Prädiktor im Modell aufgenommen ist, s Tabelle 11.17.

m10.9 <- stan_glm(kid_score ~ mom_iq + mom_age, 
                  data = kidiq, 
                  refresh = 0)
parameters(m10.9)
Tabelle 11.17: Parameter für m10.9
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 17.61 (-0.06, 35.67) 97.42% 1.000 6102 Normal (86.80 +- 51.03)
mom_iq 0.60 (0.48, 0.72) 100% 1.000 5162 Normal (0.00 +- 3.40)
mom_age 0.39 (-0.23, 1.02) 88.22% 1.000 4952 Normal (0.00 +- 18.89)
Wichtig

Die Regressionsgewichte unterscheiden sich (potenziell) zu den von den jeweiligen univariaten Regressionen.

Bei einer multiplen Regression ist ein Regressionsgewicht jeweils “bereinigt” vom Zusammenhang mit dem (oder den) anderen Regressionsgewicht. Das bedeutet anschaulich, man betrachtet den den Zusammenhang einee UV mit der AV, wobei man gleichzeitig den anderen Prädiktor konstant hält.

In Abbildung 11.16 ist das Modell m10.9 in 3D dargestellt via Plotly.

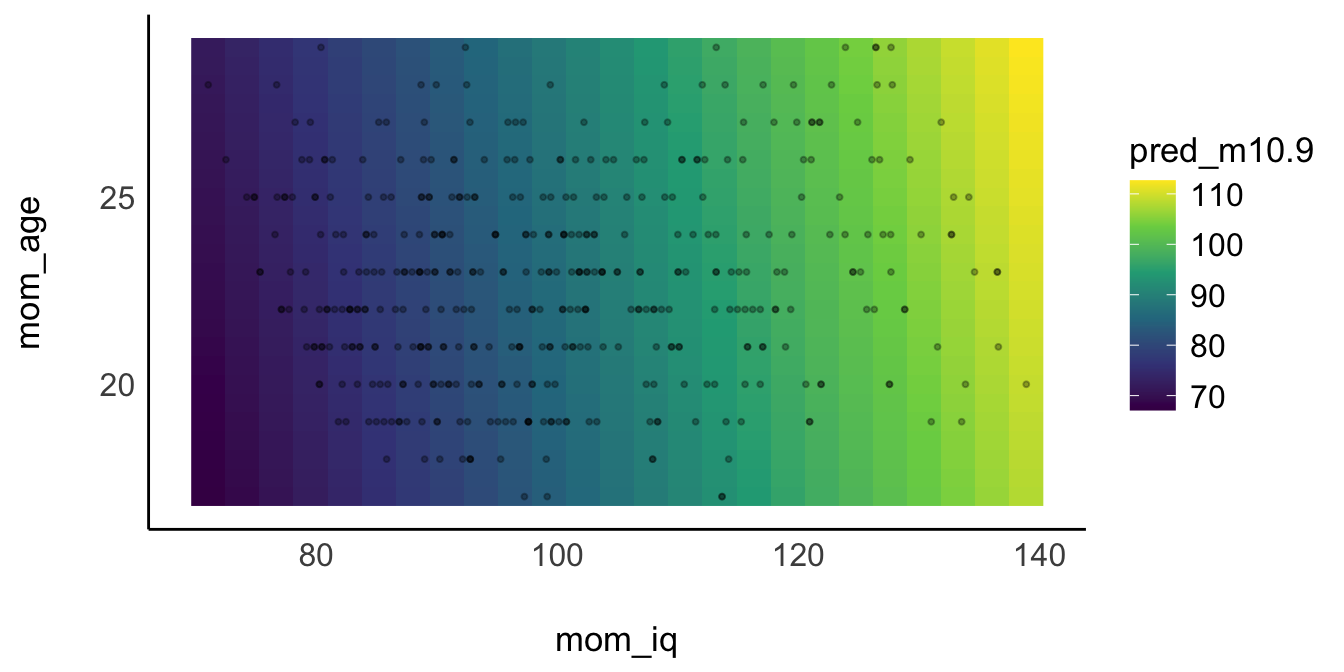
Abbildung 11.16: 3D-Visualisierung von m10.9 (zwei Prädiktoren)

Abbildung 11.17 zeigt eine Visualisierung von m10.9, in der die 3. Dimension durch eine Farbschattierung ersetzt ist.

Abbildung 11.17: Modell m10.9; die Farbverläufe zeigen der Wert der abhängigen Variablen

Auf der Achse von mom_iq erkennt man deutlich (anhand der Farbänderung) die Veränderung für die AV (kid_score). Auf der Achse für mom_age sieht man, dass sich die AV kaum ändert, wenn sich mom_age ändert.

Abbildung 11.18 visualisiert den Zusammenhang von 10 Variablen untereinander.

Abbildung 11.18: So sieht der Zusammenhang im 10-dimensionalen Raum aus

Leider macht mein Hirn hier nicht mit. Unsere Schwächen, eine große Zahl an Dimensionen zu visualisieren, ist der Grund, warum wir mathematische Modelle brauchen. Daher kann man ein Modell verstehen als eine Zusammenfassung eines (ggf. hochdimensionalen) Variablenraums.

11.11 y ~ x1_z + x2_z

In diesem Abschnitt untersuchen wir ein Modell mit zwei z-standardisierten, metrischen Prädiktoren (und einer metrischen, nicht-standardisierten AV).

Zur Relevanz der Prädiktoren: Woher weiß man, welche UV am stärksten mit der AV zusammenhängt? Man könnte auch sagen: Welcher Prädiktor (welche UV) am “wichtigsten” ist oder den “stärksten Einfluss” auf die AV ausübt? Bei solchen kausal konnotierten Ausdrücken muss man vorsichtig sein: Die Regressionsanalyse als solche ist keine Kausalanalyse. Die Regressionsanalyse - wie jede statistische Methoden - kann für sich nur Muster in den Daten, also Zusammenhänge bzw. Unterschiede, entdecken, s. Abbildung 11.19. Möchte man die Relevanz von Prädiktoren vergleichen, so ist ein Kausalmodell empfehlenswert.

Abbildung 11.19: Made at imgflip.com

Welcher Prädiktor ist nun “wichtiger” oder “stärker” in Bezug auf den Zusammenhang mit der AV, mom_iq oder mom_age (Modell m10.9)? Die Antwort hängt auch von der Streuung bzw. Skalierung der Variablen ab. mom_iq hat den größeren Koeffizienten und viel Streuung; mom_age hat weniger Streuung.

Um die Relevanz der Prädiktoren vergleichen zu können, müsste man vielleicht die Veränderung von kid_score betrachten, wenn man von kleinsten zum größten Prädiktorwert geht. Allerdings sind Extremwerte meist instabil (da sie von einer einzigen Beobachtung bestimmt werden). Sinnvoller ist es daher, die Veränderung in der AV zu betrachten, wenn man den Prädiktor von “unterdurchschnittlich” auf “überdurchschnittlich” ändert. Das kann man mit z-Standardisierung erreichen.

kidiq2 <- 
  kidiq %>% 
  mutate(mom_iq_z = ((mom_iq - mean(mom_iq)) / sd(mom_iq)))  %>%  # z-Transformation
  select(mom_iq, mom_iq_z) 

kidiq2 %>% 
  head()

Der Nutzen von Standardisieren (dieser Art) ist die bessere Vergleichbarkeit der Effekte von UV, die (zuvor) verschiedene Mittelwerte und Streuungen hatten12. Die Standardisierung ist ähnlich zur Vergabe von Prozenträngen: “Dieser Messwert gehört zu den Top-3-Prozent”. Diese Aussage ist bedeutsam für Variablen mit verschiedenem Mittelwert und Streuung. So werden vergleichende Aussagen für verschiedene Verteilungen möglich.

Zu den Statistiken zu den z-transformierten Variablen: Tabelle 11.3 zeigt die Verteilung der (metrischen) Variablen im Datensatz kidiq.

Metrische Variablen in z-Werte zu transformieren, hat verschiedenen Vorteile:

  • der Achsenabschnitt ist einfacher zu interpretieren (da er sich dann auf ein Objekt mit mittlerer Ausprägung bezieht)
  • Interaktionen sind einfacher zu interpretieren (aus dem gleichen Grund)
  • Prioriwerte sind einfacher zu definieren (wieder aus dem gleichen Grund)
  • die Effekte verschiedener Prädiktoren sind einfacher in ihrer Größe zu vergleichen, da dann mit gleicher Skalierung/Streuung
  • kleine und ähnlich große Wertebereich erleichtern dem Golem die Rechenarbeit

Man kann die z-Transformation (“Standardisierung”) mit standardize (aus easystats) durchführen, s. Tabelle 11.18.

kidiq_z <- 
  standardize(kidiq, append = TRUE)  # z-transformiert alle numerischen Werte
Tabelle 11.18: z-transformierte Variablen im Datensatz kidiq (erste paar Zeilen)
kid_score mom_hs mom_iq mom_age mom_iq_c pred_m10.9 kid_score_z mom_hs_z mom_iq_z mom_age_z mom_iq_c_z pred_m10.9_z
65 1 121.12 27 21.12 101.14 -1.07 0.52 1.41 1.56 1.41 1.56
98 1 89.36 25 -10.64 81.22 0.55 0.52 -0.71 0.82 -0.71 -0.60
85 1 115.44 27 15.44 97.72 -0.09 0.52 1.03 1.56 1.03 1.19
83 1 99.45 25 -0.55 87.30 -0.19 0.52 -0.04 0.82 -0.04 0.06
115 1 92.75 27 -7.25 84.04 1.38 0.52 -0.48 1.56 -0.48 -0.30
98 0 107.90 18 7.90 89.67 0.55 -1.91 0.53 -1.77 0.53 0.32

Der Schalter append = TRUE sorgt dafür, dass die ursprünglichen Variablen beim z-Standardisieren nicht überschrieben werden, sondern angehängt werden (mit einem Suffix _z).

Man kann auch nur einzelne Variablen mit standardize standardisieren, indem man das Argument select nutzt.

kidiq %>% 
  standardize(select = c("mom_iq", "mom_age", "kid_score"))

Man kann das Standardisieren auch von Hand machen, ohne ein Extra-Paket, s. Tabelle 11.19. Dazu verwendet man den Befehl scale().

kidiq %>% 
  mutate(mom_iq_z2 = scale(mom_iq),
         mom_age_z2 = scale(mom_age),
         kid_score_z2 = scale(kid_score))
Tabelle 11.19: Z-Standardisierung ohne Extrapaket”

Berechnen wir das Modell m10.10: y ~ x1_z + x2_z.

m10.10 <- stan_glm(kid_score ~ mom_iq_z + mom_age_z, 
                   data = kidiq_z, 
                   refresh = 0)
parameters(m10.10)
Tabelle 11.20: Parameter von m10.12
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 86.77 (85.05, 88.48) 100% 1.000 4917 Normal (86.80 +- 51.03)
mom_iq_z 9.04 (7.34, 10.83) 100% 1.000 4719 Normal (0.00 +- 51.03)
mom_age_z 1.04 (-0.73, 2.78) 88.02% 0.999 4786 Normal (0.00 +- 51.03)

11.12 y_z ~ x1_z + x2_z

In diese Abschnitt berechnen wir ein Modell (Modell m10.12), in dem sowohl die Prädiktoren z-transformiert sind (standardisiert) als auch die AV. Das z-Standardisieren der AV, kid_score ist zwar nicht nötig, um den Effekt der Prädiktoren (UV) auf die AV zu untersuchen. Standardisiert man aber die AV, so liefern die Regressionskoeffizienten (Betas) Aussage darüber, um wie viele SD-Einheiten sich die AV verändert, wenn sich ein Prädiktor um eine SD-Einheit verändert. Das kann auch eine interessante(re) Aussage sein.

Berechnen wir das Modell m10.12: y_z ~ x1_z + x2_z.

m10.12 <- stan_glm(kid_score_z ~ mom_iq_z + mom_age_z, 
                   data = kidiq_z, 
                   refresh = 0)
coef(m10.12)
## (Intercept)    mom_iq_z   mom_age_z 
##    -0.00014     0.44384     0.05072
  • Der Achsenabschnitt gibt den Mittelwert der AV (kid_score) an, da kid_score_z = 0 identisch ist zum Mittelwert von kid_score.
  • Der Koeffizient für mom_iq_z gibt an, um wie viele SD-Einheiten sich kid_score (die AV) ändert, wenn sich mom_iq um eine SD-Einheit ändert.
  • Der Koeffizient für mom_age_z gibt an, um wie viele SD-Einheiten sich kid_score (die AV) ändert, wenn sich mom_age um eine SD-Einheit ändert.

Jetzt sind die Prädiktoren in ihrer Relevanz (Zusammenhang mit der AV) vergleichbar. Man sieht, dass die Intelligenz der Mutter deutlich wichtiger ist das Alter der Mutter (im Hinblick auf die Vorhersage bzw. den Zusammenhang mit mit der AV).

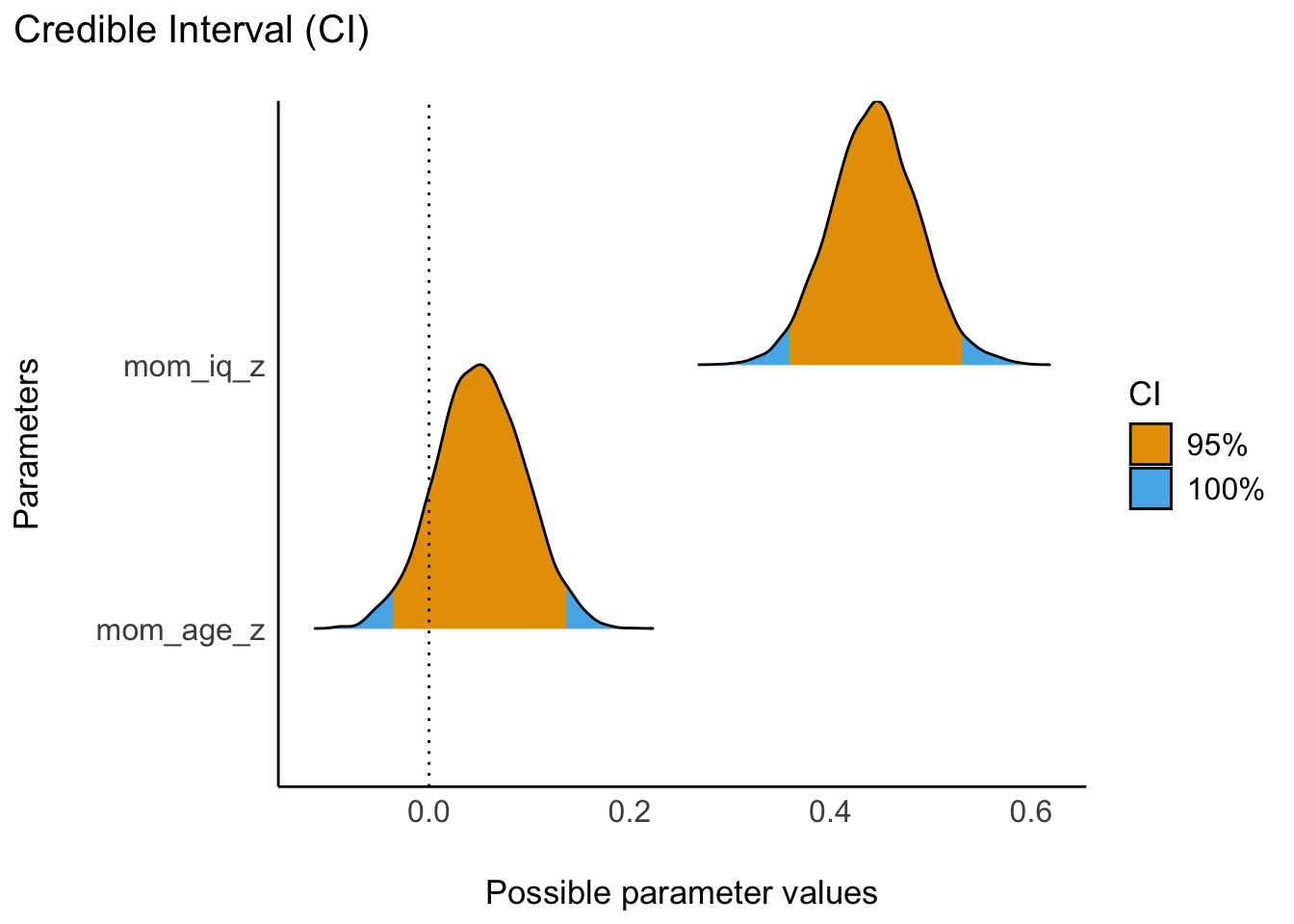
Mit parameters können wir uns ein PI für m10.12 ausgeben lassen, s. Abbildung 11.20; im Standard wird ein 95%-ETI berichtet13.

parameters(m10.12)
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) -1.38e-04 (-0.08, 0.08) 50.20% 1.000 5259 Normal (-2.81e-16 +- 2.50)
mom_iq_z 0.44 (0.36, 0.53) 100% 1.000 4713 Normal (0.00 +- 2.50)
mom_age_z 0.05 (-0.03, 0.14) 87.85% 0.999 4990 Normal (0.00 +- 2.50) 
plot(eti(m10.12)) + scale_fill_okabeito()
Abbildung 11.20: Im Standard wird ein 95%-Intervall gezeigt bzw. berechnet; hier das ETI für m10.12

Wie ist es um die Modellgüte in m10.12 bestellt? Berechnen wir \(R^2\).

r2(m10.12)
## # Bayesian R2 with Compatibility Interval
## 
##   Conditional R2: 0.205 (95% CI [0.144, 0.271])

Ist dieser Wert von \(R2\) “gut”? Diese Frage ist ähnlich zur Frage “Ist das viel Geld?”; man kann die Frage nur im Kontext beantworten.

Eine einfache Lösung ist immer, Modelle zu vergleichen. Dann kann man angeben, welches Modell die Daten am besten erklärt, z.B. auf Basis von \(R^2\).

Zu beachten ist, dass das Modell theoretisch fundiert sein sollte. Vergleicht man viele Modelle aufs Geratewohl, so muss man von zufällig hohen Werten der Modellgüte im Einzelfall ausgehen.

Wenn Sie aber unbedingt eine “objektive” Antwort auf die Frage “wie viel ist viel?” haben wollen, ziehen wir Herrn Cohen zu Rate, der eine Antwort auf die Frage “Wieviel ist viel?” gegeben hat (Cohen, 1992):

interpret_r2(0.2)  # aus `easystats`
## [1] "moderate"
## (Rules: cohen1988)

Danke, Herr Cohen!

Die Prioris für m10.12 kann man sich mit prior_summary(m10.12) ausgeben lassen. Danke, Stan!

prior_summary(m10.12)  # aus rstanarm
## Priors for model 'm10.12' 
## ------
## Intercept (after predictors centered)
##  ~ normal(location = -2.8e-16, scale = 2.5)
## 
## Coefficients
##  ~ normal(location = [0,0], scale = [2.5,2.5])
## 
## Auxiliary (sigma)
##  ~ exponential(rate = 1)
## ------
## See help('prior_summary.stanreg') for more details

🤖 Nix zu danken!

Wie gesagt, Stan nimmt dafür einfach die empirischen Mittelwerte und Streuungen her.14

Stans Ausgabe kann man in Mathe-Sprech so darstellen, s. Gleichung 11.4.

\[ \begin{aligned} \text{kidscore}^z_i &\sim \mathcal{N}(\mu_i,\sigma)\\ \mu_i &= \beta_0 + \beta_1\text{momiq}_i^z + \beta_2\text{momage}_i^z \\ \beta_0 &\sim \mathcal{N}(0,2.5)\\ \beta_1 &\sim \mathcal{N}(0,2.5)\\ \beta_2 &\sim \mathcal{N}(0,2.5)\\ \sigma &\sim \mathcal{E}(1) \end{aligned} \tag{11.4}\]

Man beachte, dass der Achsenabschnitt zur Intelligenz der Kinder auf Null festgelegt wird: Bei mittlerer Intelligenz und mittlerem Alter der Mutter wird mittlere Intelligenz des Kindes erwartet in m10.12. Dadurch, dass nicht nur UV, sondern auch AV z-standardisiert (d.h. zentriert und in der Streuung auf 1 standardisiert) sind, ist der Mittelwert der AV Null. Schreibt man einen Bericht, so bietet es sich an, die Modelldefinition zumindest im Anhang aufzuführen.

Übungsaufgabe 11.2 (Anzahl der Modellparameter) Wie viele Modellparameter hat m10.12?15

Unsere Antwort auf die Forschungsfrage:

Das Modell spricht sich klar für einen statistischen, linearen Effekt von Intelligenz der Mutter auf die Intelligenz des Kindes aus, wenn das Alter der Mutter statistisch kontrolliert wird (95%PI: [0.38, 0.51]). Pro Einheit Standardabweichung in der UV (Intelligenz der Mutter) ändert sich die AV um ca. 0.44 Standardabweichungseinheiten. Hingegen zeigt das Modell, dass das Alter der Mutter statistisch eher keine Rolle spielt (95%PI: [-0.02, 0.12]). Alle Variablen wurden z-transformiert. Insgesamt erkärt das Modell im Median einen Anteil von ca. 0.2 an der Varianz der Kinderintelligenz. Das Modell griff auf die Standard-Priori-Werte aus dem R-Paket rstanarm (Goodrich et al., 2020) zurück (s. Anhang für Details).

Wichtig

Hier wird von einem “statistischen Effekt” gesprochen, um klar zu machen, dass es sich lediglich um assoziative Zusammenhänge, und nicht um kausale Zusammenhänge, handelt. Kausale Zusammenhänge dürfen wir nur verkünden, wenn wir sie a) explizit untersuchen und b) sich in der Literatur Belege dafür finden oder c) wir ein Experiment fachgerecht durchgeführt haben.

11.13 Vertiefung

🏎️VERTIEFUNG, nicht prüfungsrelevant🏎️

Sind X und Y z-standardisiert, so sind Korrelation und Regression identisch, s. Theorem 11.2.

Theorem 11.2 Man kann die Regression als Korrelation verstehen:

\[b = r \frac{sd_x}{sd_y}\quad \square\]

Berechnen wir dazu ein einfaches Modell mit z-standardisierten Variablen und betrachten die Punktschätzer für die Regressionskoeffizienten, s. m10.12.

m10.12 <- 
  stan_glm(kid_score_z ~ mom_iq_z , data = kidiq_z, refresh = 0)
coef(m10.12)
## (Intercept)    mom_iq_z 
##    -0.00033     0.44993

Vergleichen Sie diese Werte mit der Korrelation, s. Tabelle 11.21.16

kidiq_z %>% 
  select(kid_score, mom_iq, kid_score_z, mom_iq_z) %>% 
  correlation() |> 
  display()
Tabelle 11.21: Correlation Matrix (pearson-method)
Correlation Matrix (pearson-method)
Parameter1 Parameter2 r 95% CI t(432) p
kid_score mom_iq 0.45 (0.37, 0.52) 10.42 < .001***
kid_score kid_score_z 1.00 (1.00, 1.00) Inf < .001***
kid_score mom_iq_z 0.45 (0.37, 0.52) 10.42 < .001***
mom_iq kid_score_z 0.45 (0.37, 0.52) 10.42 < .001***
mom_iq mom_iq_z 1.00 (1.00, 1.00) Inf < .001***
kid_score_z mom_iq_z 0.45 (0.37, 0.52) 10.42 < .001***

p-value adjustment method: Holm (1979) Observations: 434

Korrelationen der z-transformierten Variablen im Datensatz kidiq

Zentrale Annahme eines linearen Modells: Die AV ist eine lineare Funktion der einzelnen Prädiktoren, \(y= \beta_0 + \beta_1x_1 + \beta_2 x_2 + \cdots\), vgl. Theorem 2.1.

Hingegen ist es weniger wichtig, dass die AV (y) normalverteilt ist. Zwar nimmt die Regression häufig normalverteilte Residuen an17, aber diese Annahme ist nicht wichtig, wenn es nur darum geht, die Regressionskoeffizienten zu schätzen (Gelman et al., 2021).

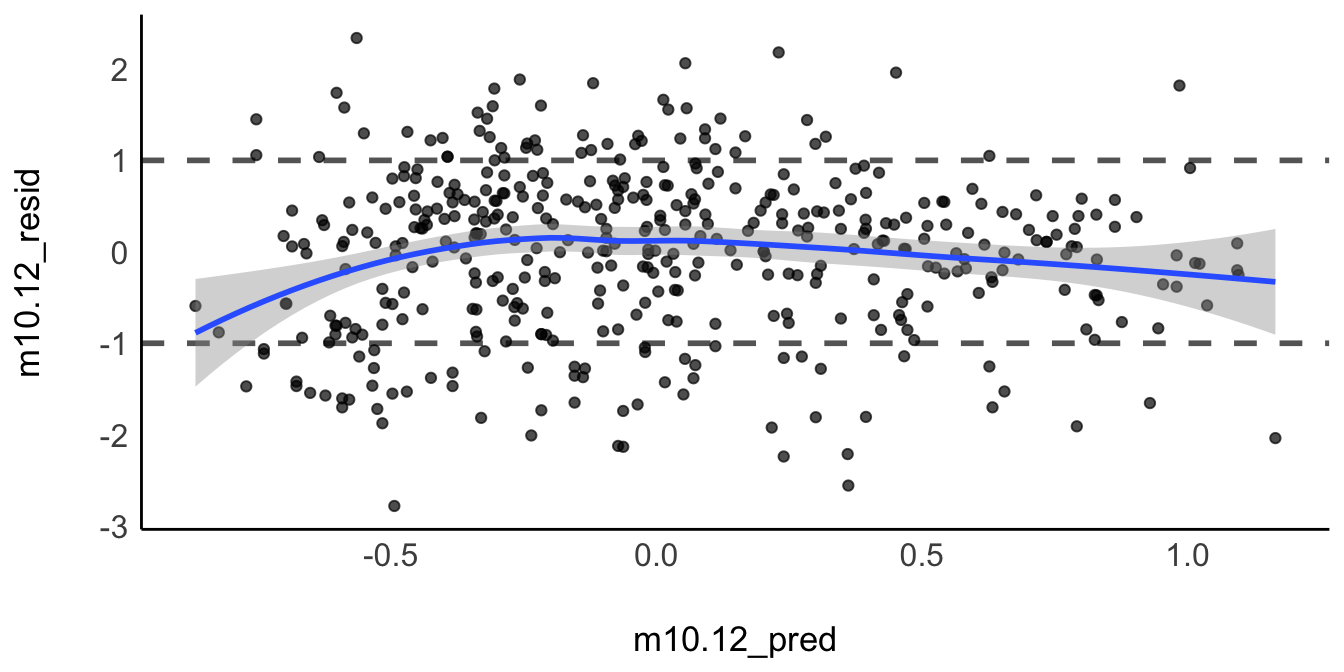
Ist die Linearitätsannahme erfüllt, so sollte der Residualplot nur zufällige Streuung um \(y=0\) herum zeigen, s. Abbildung 11.21.

Ein Residuum \(e\) ist der Vorhersagefehler, also die Differenz zwischen vorhergesagtem und tatsächlichem Wert: \(e_i = y_i - \hat{y}_i\)

kidiq <-
  kidiq %>% 
  mutate(m10.12_pred = predict(m10.12),  # vorhergesagten Werte
         m10.12_resid = resid(m10.12))  # Residuen
kidiq %>% 
  ggplot(aes(x = m10.12_pred, y = m10.12_resid)) +
  geom_hline(color="white", yintercept = 0, size = 2) +
  geom_hline(color = "grey40", 
             yintercept = c(-1,1), 
             size = 1, 
             linetype = "dashed") +
  geom_point(alpha = .7) +
  geom_smooth()
Abbildung 11.21: Die Verteilung der Fehler scheint keinem starken Trend (in Abhängigkeit zum vorhergesagten Wert) zu folgen, was ein gutes Zeichen ist.

Hier erkennt man keine größeren Auffälligkeiten.

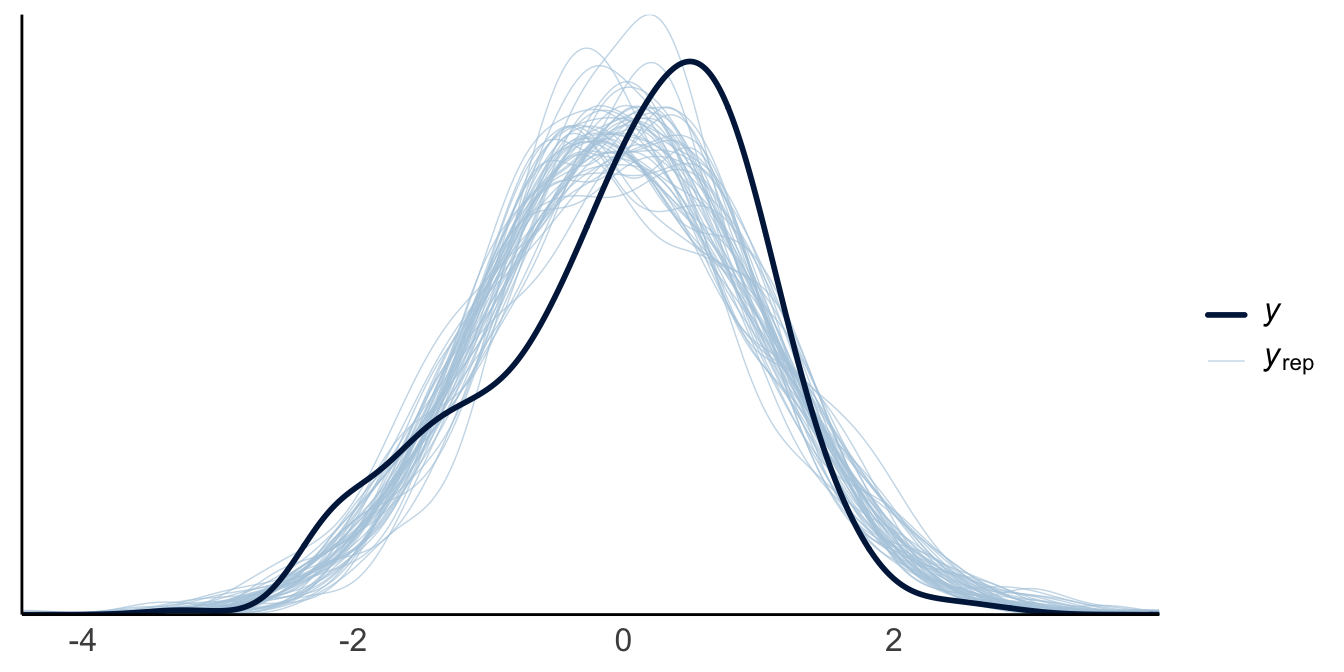
Mit der PPV kann man die Güte des Modells prüfen.

pp_check(m10.12)

Unser Modell - bzw. die Stichproben unserer Posteriori-Verteilung, \(y_{rep}\) verfehlt den Mittelwert von \(y\) leider recht häufig.

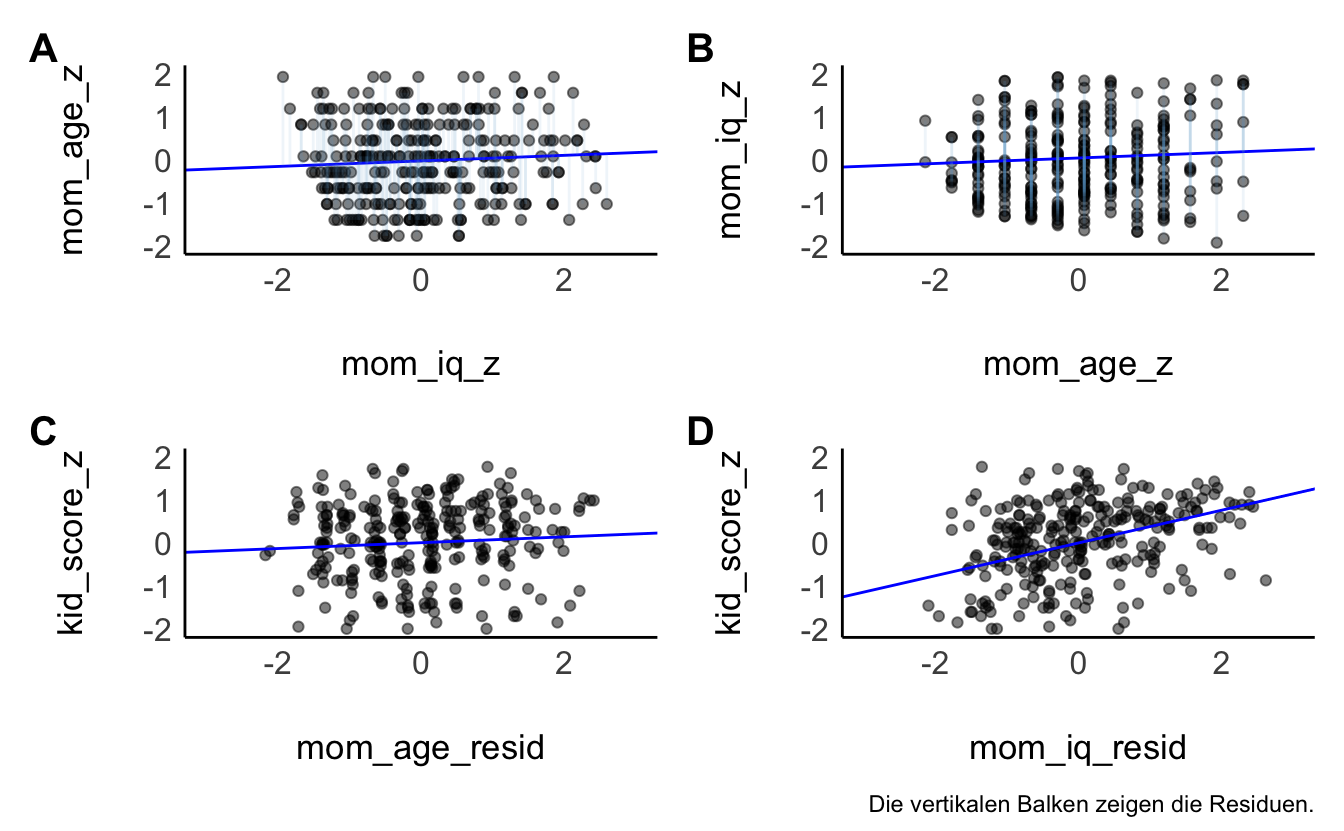
Visualisieren wir noch die bereinigten Regressionskoeffizienten, s. Abbildung 11.22.

Abbildung 11.22: Bereinigte Regressionskoeffizienten

Abbildung 11.22 zeigt in der oberen Reihe die Regression eines Prädiktors auf den anderen Prädiktor. Untere Reihe: Regression der Residuen der oberen Reihe auf die AV, kid-score_z. Unten links (C): Die Residuen von mom_iq_c sind kaum mit der AV assoziiert. Das heißt, nutzt man den Teil von mom_age_z, der nicht mit mom_iq_z zusammenhängt, um kid_score vorher zusagen, findet man keinen (kaum) Zusammenhang. Unten rechts (D): Die Residuen von mom_age_c sind stark mit der AV assoziiert. Das heißt, nutzt man den Teil von mom_iq_z, der nicht mit mom_age_z zusammenhängt, um kid_score vorher zusagen, findet man einen starken Zusammenhang.

Eine multiple Regression liefert die gleichen Regressionskoeffizienten wie die Modelle aus Teildiagrammen (C) und (D).

Was ist eigentlich der numerische Unterschied Bayesianischen vs. Frequentistischen Modellen? Schauen wir es uns an.

Wie man sieht liefern stan_glm() und lm ähnliche Ergebnisse (bei schwach informativen Prioriwerten):

stan_glm(mpg ~ hp + cyl, data = mtcars, refresh = 0) %>% coef()
## (Intercept)          hp         cyl 
##      36.911      -0.019      -2.285

lm(mpg ~ hp + cyl, data = mtcars) %>% coef()
## (Intercept)          hp         cyl 
##      36.908      -0.019      -2.265
Wichtig

Wenn auch die Ergebnisse eines Frequentistischen und Bayes-Modell numerisch ähnlich sein können, so ist doch die Interpretation grundverschieden. Bayesmodelle erlauben Wahrscheinlichkeitsaussagen zu den Parametern, Frequentistische Modelle nicht.

11.14 Fazit

11.14.1 Austieg: Bayes in fünf Minuten

Eine Kurzdarstellung des Bayes-Inferenz findet sich in diesem Post und in diesem.

📺 Musterlösung und Aufgabe im Detail besprochen - Bayes-Modell: mtcars

📺 Musterlösung und Aufgabe im Detail besprochen - Bayes-Modell: CovidIstress

11.14.2 Ausblick: Binäre AV

Forschungsfrage: Kann man anhand des Spritverbrauchs vorhersagen, ob ein Auto eine Automatik- bzw. ein manuelle Schaltung hat? Anders gesagt: Hängen Spritverbrauch und Getriebeart? (Datensatz mtcars)

Dazu nutzen wir den Datensatz mtcars, wobei wir die Variablen z-standardisieren.

data(mtcars)
mtcars2 <-
  mtcars %>% 
  standardize(append = TRUE)

Dann berechnen wir mit Hilfe von Stan ein Regressionsmodell: m14: am ~ mpg_z:

m14 <-
  stan_glm(am ~ mpg_z, 
           data = mtcars2, 
           refresh = 0)
coef(m14)
## (Intercept)       mpg_z 
##         0.4         0.3

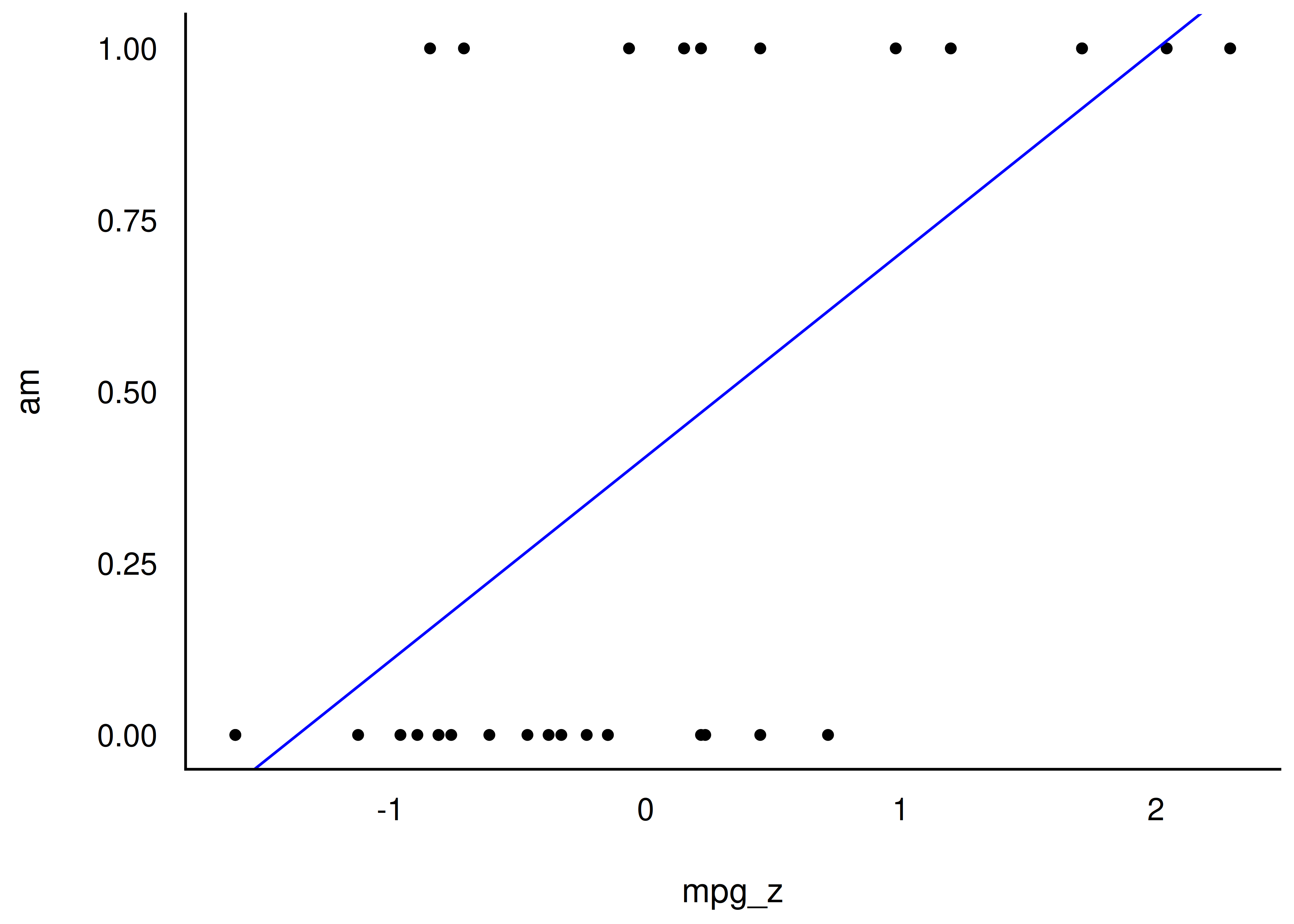
Ab mpg_z = 0.4, 0.3 sagt das Modell am=1 (manuell) vorher. Ganz ok.

mtcars2 %>% 
  ggplot(aes(x = mpg_z, y = am)) +
  geom_hline(yintercept = 0.5, color = "white", size = 2) +
  geom_point() +
  geom_abline(intercept = coef(m14)[1],
              slope = coef(m14)[2],
              color = "blue") 

neg_am <- predict(m14, newdata = tibble(mpg_z = -1.3))

Für kleine Werte von mpg_z (<1.3) sagt unser Modell negative Werte für am voraus. Das macht keinen Sinn: Es gibt keine negative Werte von am, nur 0 und 1. Müssen wir mal bei Gelegenheit besser machen.

11.14.3 Genug für heute

Wir waren fleißig …

Quelle

Wichtig

Kontinuierliches Lernen ist der Schlüssel zum Erfolg.

Genug für heute. 👍

11.14.4 Weiterführende Literatur

Weiter Hinweise zu den Themen dieses Kapitels dazu finden sich bei Gelman et al. (2021), Kap. 10, insbesondere 10.3.

Gelman et al. (2021) bieten einen Zugang mittleren Anspruchs zur Regressionsmodellierung. Das Buch ist von einem weltweit führenden Statistiker geschrieben und vermittelt tiefe Einblicke bei gleichzeitig überschaubarem mathematischen Aufwand.

Für das vorliegende Kapitel sind insbesondere daraus die Kapitel 6,7, und 10 relevant.

11.15 Aufgaben

11.15.1 Papier-und-Bleistift-Aufgaben

  1. anz-params
  2. fofrage-regrformel2
  3. modelldef-regrformel
  4. finde-prior
  5. Nullhyp-Beispiel
  6. Griech-Buchstaben-Inferenz
  7. Interaktionseffekt1
  8. Regression2
  9. Regression3
  10. diamonds-nullhyp-mws
  11. zwert-berechnen
  12. stan_glm_parameterzahl
  13. kausale-verben

11.15.2 Aufgaben, für die man einen Computer benötigt

  1. Regr-Bayes-interpret
  2. Regr-Bayes-interpret03
  3. Regr-Bayes-interpret02
  4. rope4

11.15.3 Vertiefende Aufgaben

  1. Anova-skalenniveau
  2. ttest-skalenniveau
  3. stan_glm_prioriwerte

11.16 —

  1. Hier ist eine kurze Erklärung dazu: https://statistik1.netlify.app/010-rahmen#sec-arten-variablen↩︎

  2. Hier finden Sie eine kurze Erklärung zur Interaktion: https://statistik1.netlify.app/090-regression2#interaktion↩︎

  3. auch DAG genannt, s. ?sec-kausal↩︎

  4. Häufig erlaubt uns unser Vorwissen eine gerichtete Hypothese - “größer als/kleiner als” - zu formulieren, anstelle der “empirisch ärmeren” einfachen, ungerichteten Ungleichheit↩︎

  5. unknown, sozusagen der unbekannte Gott, also für alle sonstigen Einflüsse; man kann das “u” ohne Schaden weglassen, da wir es sowieso nicht modellieren. Hier ist es nur aufgeführt, um zu verdeutlichen, dass wir nicht so verwegen sind, zu behaupten, es gäbe keine anderen Einflüsse als mom_hs auf die IQ des Kindes.↩︎

  6. Genauer gesagt wird geprüft, wie wahrscheinlich es auf Basis des Modell ist, noch extremere Ergebnisse zu beachten unter der Annahme, dass die (exakte) Nullhypothese wahr ist. Es ist etwas kompliziert.↩︎

  7. Genauer gesagt, erlaubt der t-Test in der Form des Welche-Tests auch Abweichungen von der Varianzhomogenität der gestesten Gruppen. Die Regression geht hingegen von Varianzhomogenität (Homoskedastizität) aus. Allerdings ist diese Annahme nicht von besonderer Bedeutung, wenn es um die Regressionskoeffizienten geht.↩︎

  8. DAG, s. ?sec-kausal↩︎

  9. Dabei nehmen wir an, dass x und u nicht voneinander abhängen, was man daran erkennt, dass es keine Pfeile zwischen den beiden Variablen gibt.↩︎

  10. Vgl. Abschnitt “UV zentrieren” im Kursbuch Statistik1.↩︎

  11. s. Details hier.↩︎

  12. am nützlichsten ist diese Standardisierung bei normal verteilten Variablen.↩︎

  13. Zumindest zur Zeit als ich diese Zeilen schreibe. Achtung: Voreinstellungen können sich ändern. Am besten in der Dokumentation nachlesen: ?parameters.↩︎

  14. Nicht unbedingt die feine bayesianische Art, denn die Prioris sollten ja eigentlich apriori, also vor Kenntnis der Daten, bestimmt werden. Auf der anderen Seite behauptet Stan, von uns zur Rede gestellt, dass die empirischen Mittelwerte ja doch gute Schätzer der echten Parameter sein müssten, wenn die Stichprobe, die wir ihm angeschleppt hätten, tatsächlich gut ist…↩︎

  15. 4: \(\beta_0, \beta_1, \beta_2, \sigma\)↩︎

  16. Ignorieren Sie die Zeile mit dem Befehl display(). Dieser Befehl dient nur dazu, die Ausgabe zu verschönern in Markdown-Dokumenten, wie im Quelltext dieses Kapitels.↩︎

  17. was auf normal verteilte AV hinauslaufen kann aber nicht muss↩︎