3 Hallo, Wahrscheinlichkeit

3.1 Lernsteuerung

3.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

3.1.2 Überblick

Dieses Kapitel hat die Wahrscheinlichkeitstheorie (synonym: Wahrscheinlichkeitsrechnung) bzw. das Konzept der Wahrscheinlichkeit zum Thema.¹ Es geht sozusagen um die Mathematik des Zufalls.

3.1.3 Wozu brauche ich dieses Kapitel?

Im wirklichen Leben sind Aussagen (Behauptungen) so gut wie nie sicher.

“Weil sie so schlau ist, ist sie erfolgreich.”
“In Elektroautos liegt die Zukunft.”
“Das klappt sicher, meine Meinung.”
“Der nächste Präsident wird XYZ.”

3.1.4 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

die Grundbegriffe der Wahrscheinlichkeitstheorie erläuternd definieren
die Definitionen von Wahrscheinlichkeit beschreiben
typische Relationen (Operationen) von Ereignissen anhand von Beispielen veranschaulichen
erläutern, was eine Zufallsvariable ist

3.1.5 Begleitliteratur

Lesen Sie zur Begleitung dieses Kapitels Bourier (2011), Kap. 2-4.

3.1.6 Eigenstudium

Wichtig

Dieses Kapitel ist selbständig im Eigenstudium vorzubereiten vor dem Unterricht. Lesen Sie dazu die angegebene Literatur.$\square$

3.1.7 Prüfungsrelevanter Stoff

Der Stoff dieses Kapitels deckt sich (weitgehend) mit Bourier (2011), Kap. 2-4. Weitere Übungsaufgaben finden Sie im dazugehörigen Übungsbuch, Bourier (2022).

Hinweis

In Ihrer Hochschul-Bibliothek kann das Buch als Ebook verfügbar sein. Prüfen Sie, ob Ihr Dozent Ihnen weitere Hilfen im geschützten Bereich (Moodle) eingestellt hat.$\square$

3.1.8 Begleitvideos

Video zum Thema Wahrscheinlichkeit

3.2 Grundbegriffe

3.2.1 Zufallsvorgang

Beispiel 3.1 Klassisches Beispiel für einen Zufallsvorgang ist das (einmalige oder mehrmalige) Werfen einer Münze.$\square$

Werfen Sie eine Münze! Diese hier zum Beispiel:

Quelle: By OpenClipartVectors, CC0

Wiederholen Sie den Versuch 10 Mal.

Das reicht Ihnen nicht? Okay, wiederholen Sie den Versuch 100, nein 1000, nein: $10^6$ Mal.²

Notieren Sie als Ergebnis, wie oft die Seite mit der Zahl oben liegen kommt (“Treffer”).$\square$

Oder probieren Sie die App der Brown University, wenn Sie keine Sehnenscheidenentzündung bekommen wollen.

Definition 3.1 (Zufallsvorgang) Ein Zufallsvorgang oder Zufallsexperiment ist eine einigermaßen klar beschriebene Tätigkeit, deren Ergebnis nicht sicher ist. Allerdings ist die Menge möglicher Ergebnisse bekannt und die Wahrscheinlichkeit für alle Ergebnisse kann quantifiziert werden. $\square$

Beispiel 3.2 (Typische Zufallsvorgänge)

Würfeln: Das Werfen eines fairen Würfels ist ein klassisches Beispiel. Der Ausgang (die Augenzahl) kann 1, 2, 3, 4, 5 oder 6 sein.
Münzwurf: Beim Werfen einer Münze sind die möglichen Ausgänge “Kopf” oder “Zahl”.
Lottoziehung: Die Ziehung von 6 aus 49 Kugeln ist ein komplexeres Zufallsexperiment. Jeder Ausgang ist eine bestimmte Kombination von 6 Zahlen. - Kartenziehen: Das Ziehen einer Karte aus einem gut gemischten Kartendeck ist ein weiteres Beispiel.
Glücksrad: Das Drehen eines Glücksrads mit verschiedenen Feldern (z.B. Farben oder Zahlen). Welches Feld am Ende stehenbleibt, ist zufällig. $\square$

Übungsaufgabe 3.1 Nennen Sie Beispiele für Zufallsvorgänge!³

Vorsicht

Zufall heißt nicht, dass ein Vorgang keine Ursachen hätte. So gehorcht der Fall einer Münze komplett den Gesetzen der Gravitation. Würden wir diese Gesetze und die Ausgangsbedingungen (Luftdruck, Fallhöhe, Oberflächenbeschaffenheit, Gewichtsverteilungen, …) exakt kennen, könnten wir theoretisch sehr genaue Vorhersagen machen. Der “Zufall” würde aus dem Münzwurf verschwinden. Man sollte “Zufall” also besser verstehen als “unbekannt”.$\square$

Übungsaufgabe 3.2 Mit dieser App können Sie Würfelwürfe simulieren und die Ausgänge dieses Zufallsexperiments beobachten.$\square$

3.2.2 Ergebnisraum

Definition 3.2 (Ergebnisraum) Die möglichen Ergebnisse eines Zufallvorgangs fasst man als Menge mit dem Namen Ergebnisraum zusammen. Man verwendet den griechischen Buchstaben $\Omega$ für diese Menge. Die Elemente $\omega$ (kleines Omega) von $\Omega$ nennt man Ergebnisse.$\square$

Beispiel 3.3 Beobachtet man beim Würfelwurf (s. Abbildung 3.10) die oben liegende Augenzahl, so ist

\[\Omega = \{ 1,2,3,4,5,6 \} = \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅\}\]

ein natürlicher Grundraum (Henze, 2019).$\square$

Beispiel 3.4

Münzwurf: $\Omega = \{ \text{Kopf, Zahl} \}$
Lotto: Bei der Ziehung von 6 aus 49 Kugeln ist der Grundraum die Menge aller möglichen Kombinationen von sechs Zahlen, das sind ca. 14 Millionen.
Kartenziehen: Wenn eine einzelne Karte aus einem 52er-Kartendeck gezogen wird, ist der Grundraum die Menge aller 52 Karten.
Glücksrad: Wenn das Glücksrad in vier gleich große, farbige Felder unterteilt ist (Rot, Grün, Blau, Gelb), dann ist der Grundraum die Menge der möglichen Farben: $\Omega = \{ \text{Rot, Grün, Blau, Gelg} \}$ $\square$

Die Wahrscheinlichkeitsrechnung baut auf der Mengenlehre auf, daher wird die Notation der Mengenlehre hier verwendet.

Abbildung 3.1: Ein (sechsseitiger) Würfel, Bildquelle: Peter Steinberg, Wikipedia, CC-BY-SA 3.0

3.2.3 Ereignis

Definition 3.3 (Ereignis) Jede Teilmenge⁴ von $\Omega$ heißt Ereignis; $A \subseteq \Omega$ .$\square$

Beispiel 3.5 Beim Mensch-ärger-dich-nicht Spielen habe ich eine 6 geworfen.⁵ Das Nennen wir das Ereignis $A$: “Augenzahl 6 liegt oben” und schreiben in Kurzform:

$A= \{6\}\square$

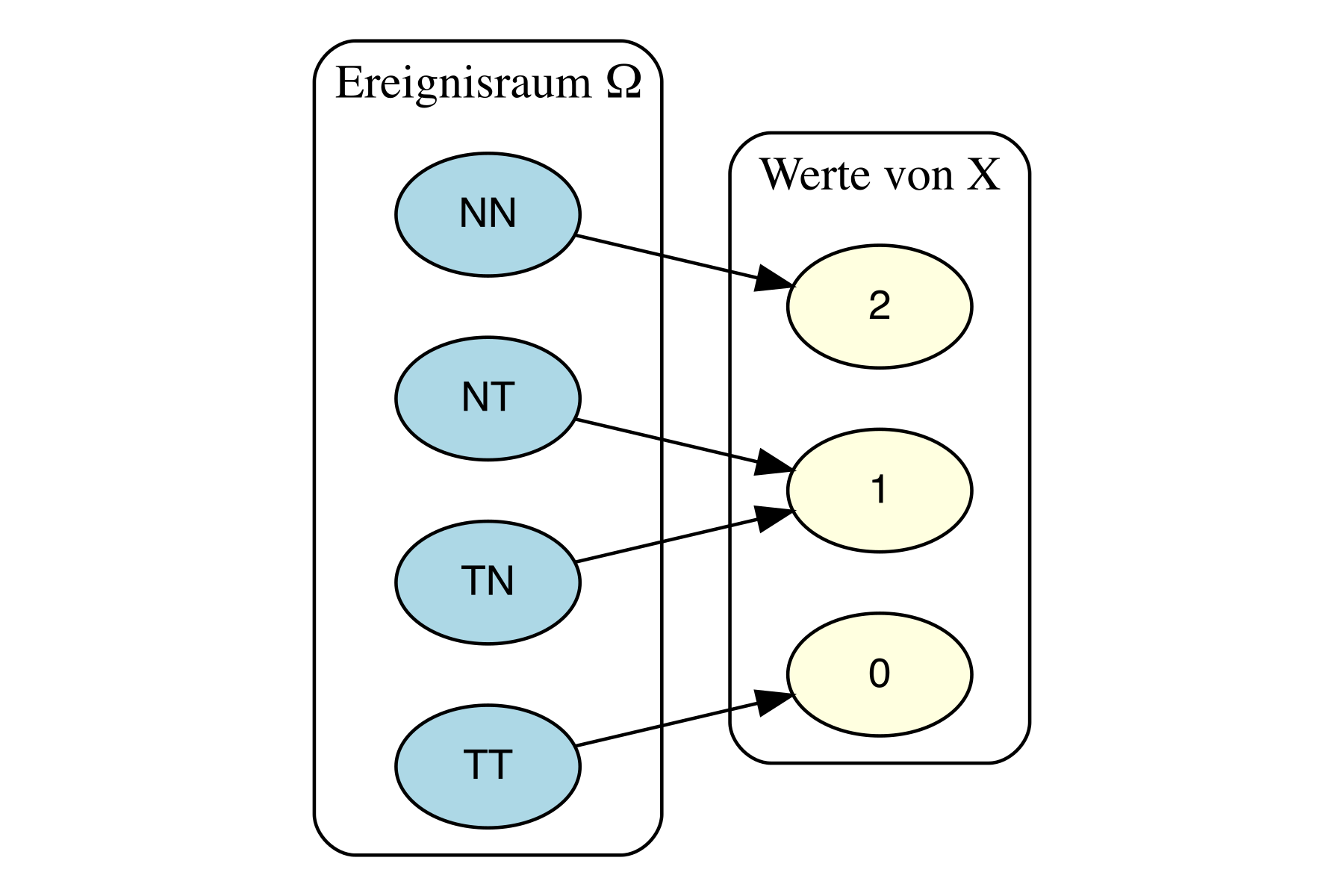
Beispiel 3.6 Sie werfen eine Münze (Sie haben keinen Grund, an ihrer Fairness zu zweifeln). “Soll ich jetzt lernen für die Klausur (Kopf) oder lieber zur Party gehen (Zahl)?”

Abbildung 3.2 zeigt die möglichen Ausgänge (T wie Treffer (Party) und N (Niete, Lernen)) dieses Zufallexperiments.

flowchart LR
 M[Sie werfen die Münze] --> T["T (Treffer) 🥳"]
  M --> N["N (Niete) 📚"]

Abbildung 3.2: Sie werfen eine Münze. Party oder Lernen???

Das Ereignis Zahl ist eingetreten! Treffer! Glück gehabt!⁶$\square$

3.2.4 Unmögliches und sicheres Ereignis

Definition 3.4 (Unmögliches und sicheres Ereignis) Die leere Menge $\varnothing$ heißt das umögliche, der Grundraum $\Omega$ heißt das sichere Ereignis. $\square$

Beispiel 3.7 (Unmögliches Ereignis) Alois behauptet, er habe mit seinem Würfel eine 7 geworfen. Schorsch ergänzt, sein Würfel liege auf einer Ecke, so dass keine Augenzahl oben liegt. Draco hat seinen Würfel runtergeschluckt. Dracos und Alois’ Ereignisse sind unmögliche Ereignisse, zumindest nach unserer Vorstellung des Zufallsexperiments.$\square$

Beispiel 3.8 (Sicheres Ereignis) Nach dem der Würfel geworfen wurde, liegt eine Augenzahl zwischen 1 und 6 oben.$\square$

3.2.5 Elementarereignis

Definition 3.5 (Elementarereignis) Jede einelementige Teilmenge $\{\omega\}$ von $\Omega$ heißt Elementarereignis (häufig mit $A$ bezeichnet). ⁷ $\square$

Beispiel 3.9

Sie spielen Mensch-ärger-dich-nicht. Und brauchen dringend eine 6. Sie würfeln. Das Ereignis $A = \{1\}$ tritt ein.⁸
Sie schreiben eine Statistik-Klausur. Irgendwie haben Sie das Gefühl, das Ergebnis sei ein Zufallsexperiment… Jedenfalls können nach Adam Riese zwei Dinge passieren: $\Omega= \{\text{bestehen, nicht bestehen}\}$. Das erste der beiden Elementarereignisse tritt ein. Yeah!
Sie führen eine Studie durch zur Wirksamkeit einer Lern-App. Es ist nicht klar, ob die App wirklich was bringt für den Lernerfolg. Vereinfacht gesprochen ist der Grundraum dieses Experiments: $\Omega = \{\text{schadet, bringt nichts, nützt}\}$. Die Daten sprechen für das Ereignis $A = \{\text{bringt nichts}\}$.

Übungsaufgabe 3.3 Welche Ereignisse beim Würfelwurf sind keine Elementarereignisse? $\square$

3.2.6 Vollständiges Ereignissystem

Definition 3.6 (Vollständiges Ereignissystem) Wird der Grundraum $\Omega$ vollständig in paarweis disjunkte Ereignisse zerlegt, so bilden diese Ereignisse ein vollständiges Ereignissystem, s. Abbildung 3.3.$\square$

Abbildung 3.3: Zerlegung des Grundraums in ein vollständiges Ereignissystem

Beispiel 3.10 Sei $\Omega$ der typische Ergebnisraum des Würfelwurfs. Wir zerlegen den Grundraum in zwei Ereignisse, $A$ “gerade Zahlen”, und $B$ “ungerade Zahlen”. Damit haben wir ein vollständiges Ereignissystem erstellt, s. Abbildung 3.4.

\[\begin{align} A = \{2,4,6\} \qquad \hfill \boxed{\color{gray}{1}\; \boxed{\color{black}{2}}\; \color{gray}{3}\; \boxed{\color{black}{4}}\; \color{gray}{5}\; \boxed{\color{black}{6}}\;} \\ B = \{1,3,5\} \qquad \hfill \boxed{\boxed{\color{black}{1}}\; \color{gray}{2}\; \boxed{\color{black}{3}}\; \color{gray}{4}\; \boxed{\color{black}{5}}\; \color{gray}{6}\; } \\ \hline \\ \Omega = \{1,2,3,4,5,6\} \qquad \hfill \boxed{1\; 2\; 3\; 4\; 5\; 6 } \end{align}\]

Abbildung 3.4

Ein Beispiel für ein vollständiges Ereignissystem

Beispiel 3.11 Sei $\Omega$ der typische Ergebnisraum des Würfelwurfs. Wir zerlegen den Grundraum in zwei Ereignisse, $A$ “1,2,3”, und $B$ “4,5,6”. Damit haben wir ein vollständiges Ereignissystem erstellt, s. Abbildung 3.4.

\[\begin{align} A = \{1,2,3\} \qquad \qquad \hfill \boxed{\boxed{ \color{black}{1\; 2\; 3}}\; \color{gray}{4\; 5\; 6}} \\ B = \{4,5, 6\} \qquad \qquad \hfill \boxed{\color{gray}{1 \; 2 \; 3}\; \boxed{\color{black}{4\; 5 \; 6}}} \\ \newline \hline \\ \Omega = \{1,2,3,4,5,6\} \qquad \qquad \hfill \boxed{1\; 2\; 3\; 4\; 5\;6} \end{align}\]

Abbildung 3.5: Noch ein Beispiel für ein vollständiges Ereignissystem

3.2.7 Mächtigkeit

Definition 3.7 (Mächtigkeit) Die Anzahl der Elementarereignisse eines Ereignismraums nennt man die Mächtigkeit (des Ergebnisraums).⁹$\square$

Die Mächtigkeit von $\Omega$ bezeichnet man mit dem Symbol $|\Omega|$.

Beispiel 3.12 Beim Wurf eines Würfels mit $\Omega=\{1,2,3,4,5,6\}$ gibt es 6 Elementarereignisse. Die Mächtigkeit ist also 6: $|\Omega|=6$.$\square$

3.2.8 Disjunkte Ereignisse

Seien $A= \{1,2,3\}; B= \{4,5,6\}$.

$A$ und $B$ sind disjunkt¹⁰: ihre Schnittmenge ist leer: $A \cap B = \emptyset$, s. Abbildung 3.6.

Abbildung 3.6: Zwei disjunkte Ereignisse, dargestellt noch überlappungsfreie Kreise

Quelle: rither.de

Beispiel 3.13 Das Ereignis $A$ “Gerade Augenzahl beim Würfelwurf”, $A={2,4,6}$ und das Ereignis $B$ “Ungerade Augenzahl beim Würfelwurf”, $B={1,3,5}$ sind disjunkt, s. Abbildung 3.7.

\[\begin{align} A = \{2,4, 6\} \qquad \hfill \boxed{2\; 4\; 6} \\ B = \{1,3,5\} \qquad \hfill \boxed{1\; 3\; 5} \\ \hline \\ A \cap B = \qquad \hfill \emptyset \end{align}\]

Abbildung 3.7: Beispiel für disjunkte Ereignisse

Die Ereignisse “normaler Wochentag” und “Sonntag” sind disjunkt. $\square$

Übungsaufgabe 3.4 (Peer Instruction: Elementarereignis) Welche der folgenden Ereignisse zeigt ein Elementarereignis des Würfelwurfs (wobei die Augenzahl 1,2,…,6 die Ergebnisse sind).

Gerade Zahl gewürfelt
Ungereade Zahl gewürfelt
Keine 6 gewürfelt
1 gewürfelt
Keine der genannten $\square$

3.3 Was ist Wahrscheinlichkeit?

Die “klassische” Logik der Wissenschaft beruht auf Schlüssen (Syllogismen) wie diesem: “Alle Schwäne sind weiß.” $\rightarrow$ “Dies ist ein Schwan.” $\rightarrow$ “Dieser Schwan ist weiß.”

Mit dem Konzept von Wahrscheinlichkeit können wir jetzt auch folgende Logik anwenden: “Die meisten Schwäne sind weiß.” $\rightarrow$ “Dies ist ein Schwan.” $\rightarrow$ “Dieser Schwan ist wahrscheinlich weiß.” Das ist ein großer Fortschritt, der die Denkweise der Wissenschaft gut widerspiegelt und dafür eine logisch-mathematische Grundlage bereitstellt, s. Abbildung 3.8.

Definition 3.8 (Einfache Definition von Wahrscheinlichkeit) Die Wahrscheinlichkeit ist ein Maß für die Plausibilität einer Aussage $A$, gegeben gewisser Hintergrundinformationen (Daten, $D$): $Pr(A|D)$. Die Wahrscheinlichkeit eines Ereignisses wird (sofern berechenbar) als Zahl zwischen 0 und 1 angegeben, wobei 0 bedeutet, dass das Ereignis als unmöglich angesehen wird, und 1 bedeutet, dass das Ereignis als sicher betrachtet wird. Je näher die Wahrscheinlichkeit bei 1 (0) liegt, desto sicherer ist jemand, dass das Ereignis (nicht) der Fall ist.$\square$

Die Wahrscheinlichkeitsrechnung ist die typische Methode, um Ungewissheit zu präzisieren, d.h. zu quantifizieren.

Wir haben schon mit Definition 3.9 eine erste Definition von Wahrscheinlichkeit versucht. Jetzt gehen wir die Sache noch etwas näher an und vergleichen verschiedene Ideen (Definitionen) von Wahrscheinlichkeit.

3.3.1 Formallogische Definitition

3.3.1.1 Wahrscheinlichkeit als Erweiterung der Logik

Die formallogische Konzeption von Wahrscheinlichkeit sieht Wahrscheinlichkeit als Erweiterung der formalen Logik (Jaynes & Bretthorst, 2003). ¹¹ In der formalen Logik ist ein Ereignis entweder falsch oder wahr. In der formallogischen Konzeption wird der Platz zwischen “falsch” (0) und “richtig” (1) als die Wahrscheinlichkeit $0<p<1$, gesehen (Briggs, 2016), s. Abbildung 3.8. Größere Werte stehen für größere Wahrscheinlichkeit und umgekehrt.

Abbildung 3.8: Wahrscheinlichkeit als Erweiterung der Logik

Nach dieser “Wahrscheinlichkeitslogik” kann man ein Ereignis, von dessen Eintreten man “wenig überzeugt” ist, z.B. mit 0.2 quantifizieren. Hingegen einem Ereignis, von man “recht sicher” ist, mit 0.8 quantifizieren, s. Abbildung 3.9.

Abbildung 3.9: Ein Ereignis von dessen Eintreten man gering bzw. stark überzeugt ist

3.3.1.2 Wahrscheinlichkeit als Ungewissheit

Wahrscheinlichkeit existiert nicht in dem Sinne, wie ein Stein oder ein Mensch existiert. Wahrscheinlichkeit ist stattdessen eine Art von Wissen. Daher ist es (nach Jaynes & Bretthorst (2003)) falsch, zu sagen: “Die Wahrscheinlichkeit für Zahl bei dieser Münze ist 50%.” Richtig wäre für einen unbedarften Spieler: “Ich habe keinen Grund, nicht an der Fairness der Münze zu glauben, also gehe ich von 50% Wahrscheinlichkeit für Zahl aus.” Der Betrüger, der diese Münze in der Hand hat, geht allerdings von einer Wahrscheinlichkeit von 75% für Zahl aus (er kennt die Münze besser als Sie).

Das Beispiel zeigt: Wahrscheinlichkeit ist kein Ding der Welt, sondern ein Wissenszustand.

Formaler ausgedrückt: Sei $Pr$ die Wahrscheinlichkeit des Ereignis $Z$ (Zahl) angibt, gegeben meiner Annahme, dass die Münze fair ist ($F$), also eine Wahrscheinlichkeit von 50% (1/2 = .5) hat für $Z$. Dann kann man kurz schreiben:

\[Pr(Z|F) = 0.5\] Gegeben des Wissens des Betrügers $B$ wäre die Wahrscheinlichkeit für $Z$ anders:

\[Pr(Z|B) = 0.75\]

In Worten: “Die Wahrscheinlichkeit von Zahl ($Z$) gegeben das Wissen des Betrügers über die Münze ($B$) liegt bei 75%.

Das Beispiel zeigt auch, dass die Wahrscheinlichkeit eines Ereignissens (wie $Z$) von Hintergrundinformationen (Annahmen, Daten, Evidenz, …) abhängt. Ohne zu sagen, auf welche Hintergrundinterformationen wir uns beziehen (die des unbedarften Spielers oder die des Betrügers), ist es sinnvoll, eine Wahrscheinlichkeit anzugeben. Daher ist $Pr(Z) = 0.5$ unvollständig. Allerdings wird die Hintergrundinformation oft weggelassen, wenn es klar ist, welche Hintergrundinformation vorliegt. So wird häufig vorausgesetzt, dass eine Münze fair ist.

Beispiel 3.14 (Morgen regnet’s) Es ist daher unvollständig zu sagen: “Morgen wir es mit einer Wahrscheinlichkeit von 70% regnen.”

Man müsste Hintergrundinformation (Evidenz, $E$) ergänzen, z.B. “auf Basis des Wettermodell X”.

Also: Anstelle von $Pr(\text{Regen}) = .7$ besser sagen: $Pr(\text{Regen|Wettermodell X})$. $\square$

Beispiel 3.15 (Wahrscheinlichkeit für Krebs) Jemand beobachtet bei sich Symptome, die für eine eine Hautkrebserkrankung $K$ typisch sind. Die Person sagt sich: “Ach, die Wahrscheinlichkeit für Hautkrebs liegt bei einem Promill. Kein Grund für Sorge.” Formal: $Pr(K) = 0.001$. Aber wenn die Person relevante Symptome $S$ hat, gilt: $Pr(\text{K} \mid \text{S}) \gg 0.001$. $\square$

Hinweis

Sagt jemand: “Die Wahrscheinlichkeit von A ist x%”, frag immer: “gegeben welcher Annahmen, welcher Evidenz?”

Definition 3.9 (Wahrscheinlichkeit unter formallogischer Sichtweise) Die Wahrscheinlichkeit ist ein Maß für unsere Gewissheitt einer Aussage $A$, gegeben gewisser Hintergrundinformationen (Daten, $D$): $Pr(A|D)$. Die Wahrscheinlichkeit eines Ereignisses wird (sofern berechenbar) als Zahl zwischen 0 und 1 angegeben, wobei 0 bedeutet, dass das Ereignis als unmöglich angesehen wird, und 1 bedeutet, dass das Ereignis als sicher betrachtet wird. Je näher die Wahrscheinlichkeit bei 1 (0) liegt, desto sicherer ist jemand, dass das Ereignis (nicht) der Fall ist.$\square$

Definition 3.10 (Indifferenzprinzip) Das Indifferenzprinzip (synonym: Prinzip des unzureichenden Grundes) besagt, dass in Abwesenheit jeglicher Informationen, die bestimmte Ereignisse bevorzugen oder benachteiligen würden, alle möglichen Ereignisse als gleich wahrscheinlich angesehen werden sollten. $\square$

Vor uns liegt ein Würfel. Schlicht, ruhig, unbesonders. Wir haben keinen Grund anzunehmen, dass eine seiner $n=6$ Seiten bevorzugt nach oben zu liegen kommt. Jedes der sechs Elementarereignisse ist uns gleich plausibel; der Würfel erscheint uns fair. In Ermangelung weiteres Wissens zu unserem Würfel gehen wir schlicht davon aus, dass jedes der $n$ Elementarereignis gleich wahrscheinlich ist. Es gibt keinerlei Notwendigkeit, den Würfel in die Hand zu nehmen, um zu einer Wahrscheinlichkeitsaussage auf diesem Weg zu kommen. Natürlich könnten wir unsere Auffassung eines fairen Würfels testen, aber auch ohne das Testen können wir eine stringente Aussage (basierend auf dem Indifferenzprinzip (s. Definition 3.10) der $n$ Elementarereignisse) zur Wahrscheinlichkeit eines bestimmten (Elementar-)Ereignisses $A$ kommen (Briggs, 2016), s. Theorem 3.1.

Theorem 3.1 (Indifferenzprinzip) \[Pr(A) = \frac{1}{n}= \frac{1}{|\Omega|} \quad \square\]

Beispiel 3.16 Sei $A$ = “Der Würfel wird beim nächsten Wurf eine 6 zeigen.” Die Wahrscheinlichkeit für $A$ ist $1/6. \square$

Definition 3.11 (Laplace-Experimt) Ein Zufallsexperiment, bei dem alle Elementarereignisse dieselbe Wahrscheinlichkeit haben, nennt man man ein Laplace-Experiment, s. Theorem 3.2. $\square$

In Erweiterung von Theorem 3.1 können wir für ein Laplace-Experiment schreiben, s. Theorem 3.2.

Theorem 3.2 (Laplace-Experiment) \[Pr(A)=\frac{\text{Anzahl Treffer}}{\text{Anzahl möglicher Ergebnisse}} \quad \square\]

Beispiel 3.17 (Kann Sophia (Einhorn) fliegen?) Sei $A$: “Sophia ist ein Einhorn”. Und sei $B$: “Einhörner mit Flügeln können fliegen und die Hälfte aller Einhörner hat Flügel”. Dann ist $Pr(A|B) = 1/2$. $\square$

Beispiel 3.18 (Ich werfe Zahl beim nächsten Münzwurf) $B$ “Ich habe keinen Grund an der Fairness der Münze zu zweifeln”. $A$: “Es wird Zahl geworfen beim nächsten Wurf dieser Münze”. Es gilt: $Pr(A|B) = 1/2$. $\square$

3.3.2 Frequentistische Definition

In Ermangelung einer Theorie zum Verhalten eines (uns) unbekannten Zufallsvorgangs und unter der Vermutung, dass die Elementarereignisse nicht gleichwahrscheinlich sind, bleibt uns ein einfacher (aber aufwändiger und manchmal unmöglicher) Weg, um die Wahrscheinlichkeit eines Ereignisses zu bestimmen: Ausprobieren.

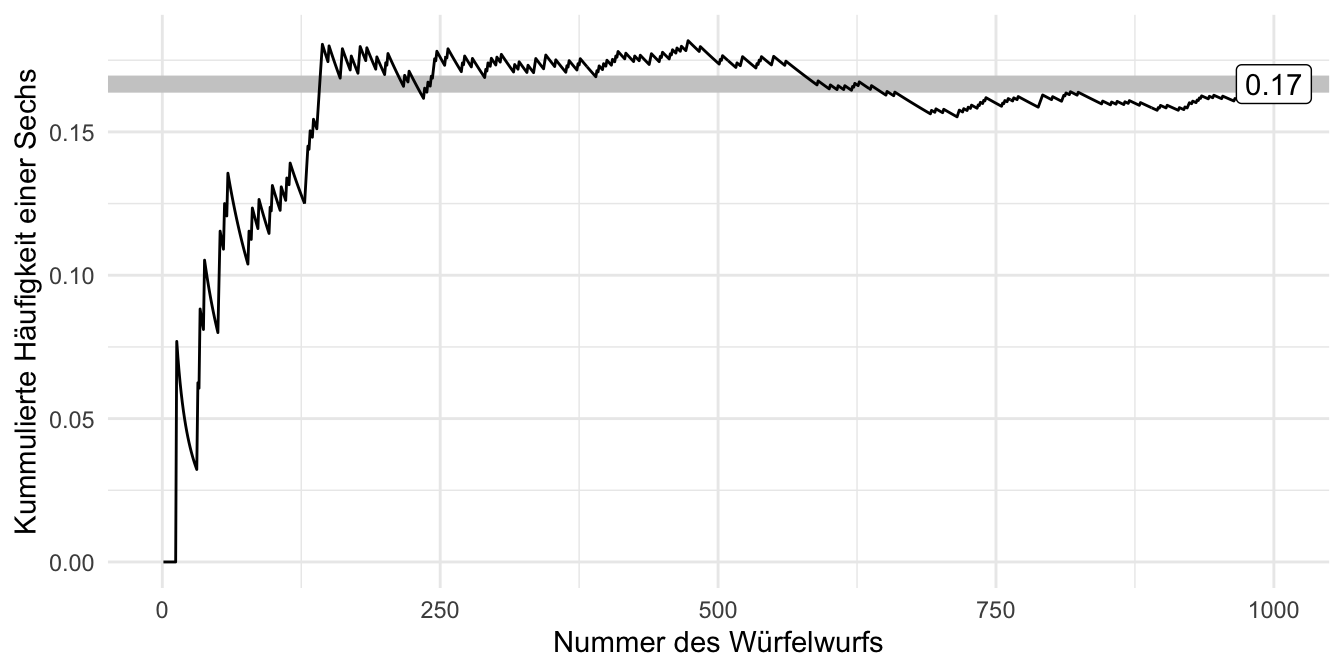
Angenommen, ein Statistik-Dozent, bekannt für seine Vorliebe zum Glücksspiel und mit scheinbar endlosen Glückssträhnen (er wirft andauernd eine 6), hat seinen Lieblingswürfel versehentlich liegen gelassen. Das ist die Gelegenheit! Sie greifen sich den Würfel, und … Ja, was jetzt? Nach kurzer Überlegung kommen Sie zum Entschluss, den Würfel einem “Praxistest” zu unterziehen: Sie werfen ihn 1000 Mal (Puh!) und zählen den Anteil der 6. Falls der Würfel fair ist, müsste gelten $Pr(A=6)=1/6\approx .17$. Schauen wir mal!

Und hier der Anteil von 6 im Verlauf unserer Würfe, s. Abbildung 3.10.

Abbildung 3.10: Das Gesetz der großen Zahl am Beispiel der Stabilisierung des Trefferanteils beim wiederholten Würfelwurf

Hm, auf den ersten Blick ist kein (starkes) Anzeichen für Schummeln bzw. einen gezinkten Würfel zu finden.

3.3.3 Kolmogorovs Definition

Kolmogorov richtet eine Reihe von Forderungen an eine Definition von bzw. an das Rechnen mit Wahrscheinlichkeiten, die direkt plausibel erscheinen:

Nichtnegativität: Die Wahrscheinlichkeit eines Ereignisses kann nicht negativ sein.
Normierung: Das sichere Ereignis hat die Wahrscheinlichkeit 1 bzw. 100%: $Pr(\Omega)=1$; das unmögliche Ereignis hat die Wahrscheinlichkeit 0: $Pr(\emptyset)=0$.
Additivität. Sind $A$ und $B$ disjunkt, dann ist die Wahrscheinlichkeit, dass mindestens eines der beiden Ereignisse eintritt ($A\cup B$) gleich der Summe der beiden Einzelwahrscheinlichkeiten von $A$ und $B$.

Übungsaufgabe 3.5 (Peer Instruction: Ist der Schmockulator im Zustand alpha?) $B$: “Locuratoren und Schmockulatoren kommen in zwei Zuständen vor, alpha und beta. Und zwar gleich häufig”. Leider wissen wir nichts Weiteres über Locuratoren und Schmockulatoren. Vor Ihnen steht ein Schmockulator. Welche möglichst präzise Aussage können wir über den Zustand des Schmockulator treffen?

Der Schmockulator ist sicher im Zustand alpha.
Der Schmockulator ist in einem der beiden Zustände.
Der Schmockulator ist vermutlich im Zustand alpha.
Der Schmockulator ist möglicherweise im Zustand alpha.
Der Schmockulator ist mit einer Wahrscheinlichkeit von 50% im Zustand alpha.
Keine der genannten. $\square$

3.4 Relationen von Ereignissen

Für das Rechnen mit Wahrscheinlichkeiten ist es hilfreich, ein paar Werkzeuge zu kennen, die wir uns im Folgenden anschauen.

Definition 3.12 (Relation) Eine Relation (zweier Ereignisse) bezeichnet die Beziehung, in der die beiden Ereignisse zueinander stehen. $\square$

Typische Relationen sind Gleichheit, Ungleichheit, Vereinigung, Schnitt.

3.4.1 Überblick

Wir gehen von Grundraum $\Omega$ aus, mit dem Ereignis $A$ als Teilmenge von $\Omega$: $A \subset \Omega$.

Da wir Ereignisse als Mengen auffassen, verwenden wir im Folgenden die beiden Begriffe synonym.

Dabei nutzen wir u.a. Venn-Diagramme. Venn-Diagramme eigenen sich, um typische Operationen (Relationen) auf Mengen zu visualisieren. Die folgenden Venn-Diagramme stammen von Wikipedia (En).

Wozu sind die Venn-Diagramme gut? Warum soll ich die lernen?

Venn-Diagramme zeigen Kreise und ihre überlappenden Teile; daraus lassen sich Rückschlüsse auf Rechenregeln für Wahrscheinlichkeiten ableiten. Viele Menschen tun sich leichter, Rechenregeln visuell aufzufassen als mit Formeln und Zahlen alleine. Aber entscheiden Sie selbst!$\square$

Diese App versinnbildlicht das Rechnen mit Relationen von Ereignissen anhand von Venn-Diagrammen.¹²

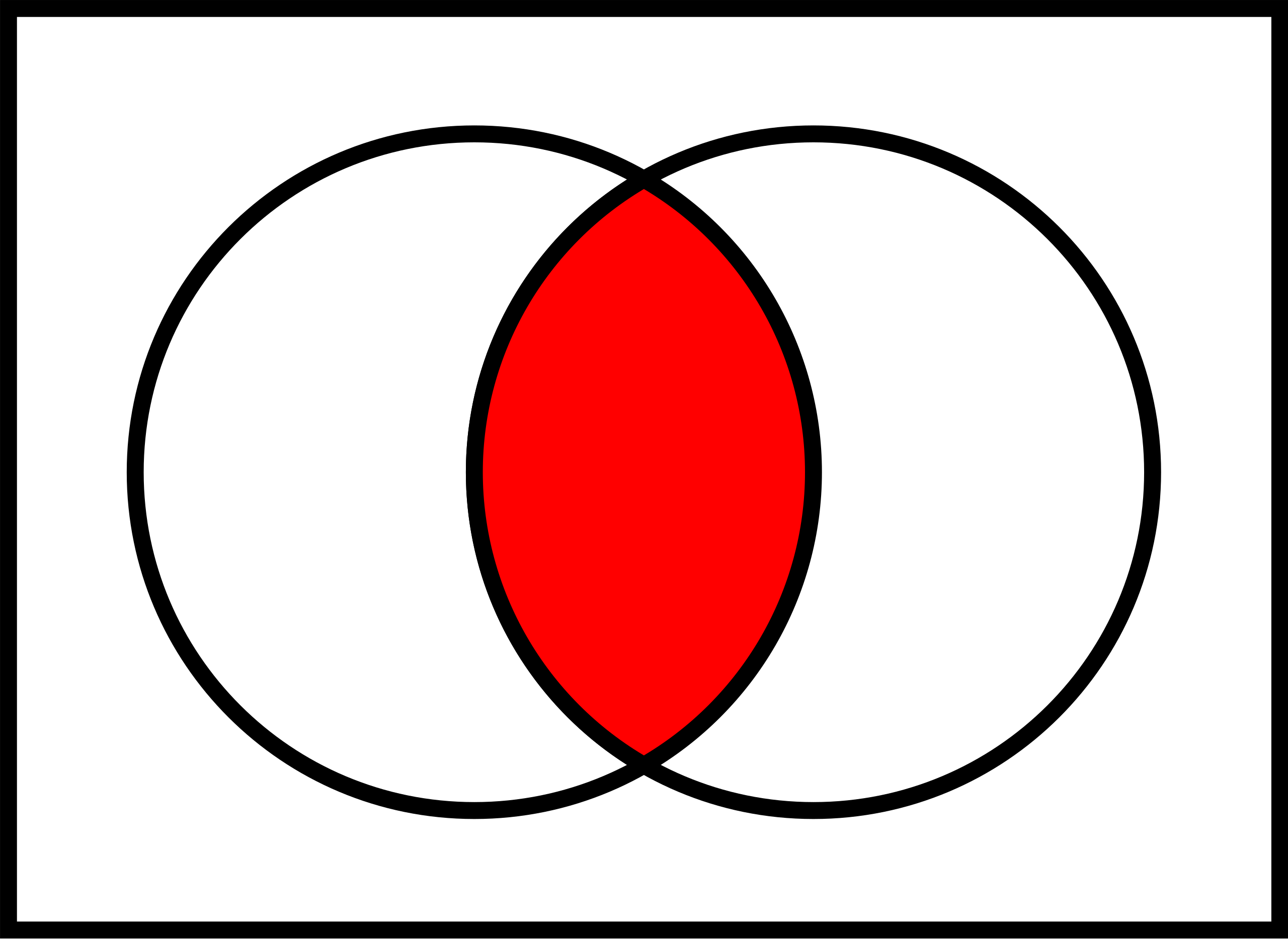
3.4.2 Vereinigung von Ereignissen

Definition 3.13 (Vereinigung von Ereignissen) Vereinigt man zwei Ereignisse $A$ und $B$, dann besteht das neue Ereignis $C$ genau aus den Elementarereignissen der vereinigten Ereignisse. Man schreibt $C = A \cup B$, lies: “C ist A vereinigt mit B”.$\square$

Abbildung 3.11 zeigt ein Venn-Diagramm zur Verdeutlichung der Vereinigung von Ereignissen.

Beispiel 3.19 Um einen (hohen!) Geldpreis zu gewinnen, muss bei ihrem nächsten Wurf mindestens eines der beiden Ereignisse $A= {1,2}$ oder $B={2,3}$ eintreten, s. Abbildung 3.12.

\[\begin{aligned} A = \{1,2\} \qquad \boxed{\boxed{1\; 2}\; \color{gray}{ 3\; 4\; 5\; 6}} \\ B = \{2,3\} \qquad \boxed{1\; \boxed{2\; 3}\; \color{gray}{ 4\; 5\; 6}} \\ \newline \hline \\ A \cup B = \{1,2,3\} \qquad \boxed{\boxed{1\; 2\; 3}\; \color{gray}{4\; 5\; \boxed{6}}} \end{aligned}\]

Abbildung 3.12: Beispiel zur Vereinigung zweier Mengen

Zur besseren Verbildlichung betrachten Sie mal diese Animation zur Vereinigung von Mengen; Quelle.

In R heißt die Vereinigung von Mengen union(). Praktisch zum Ausprobieren:

Code

A <- c(1, 2)
B <- c(2, 3)

union(A, B)
## [1] 1 2 3

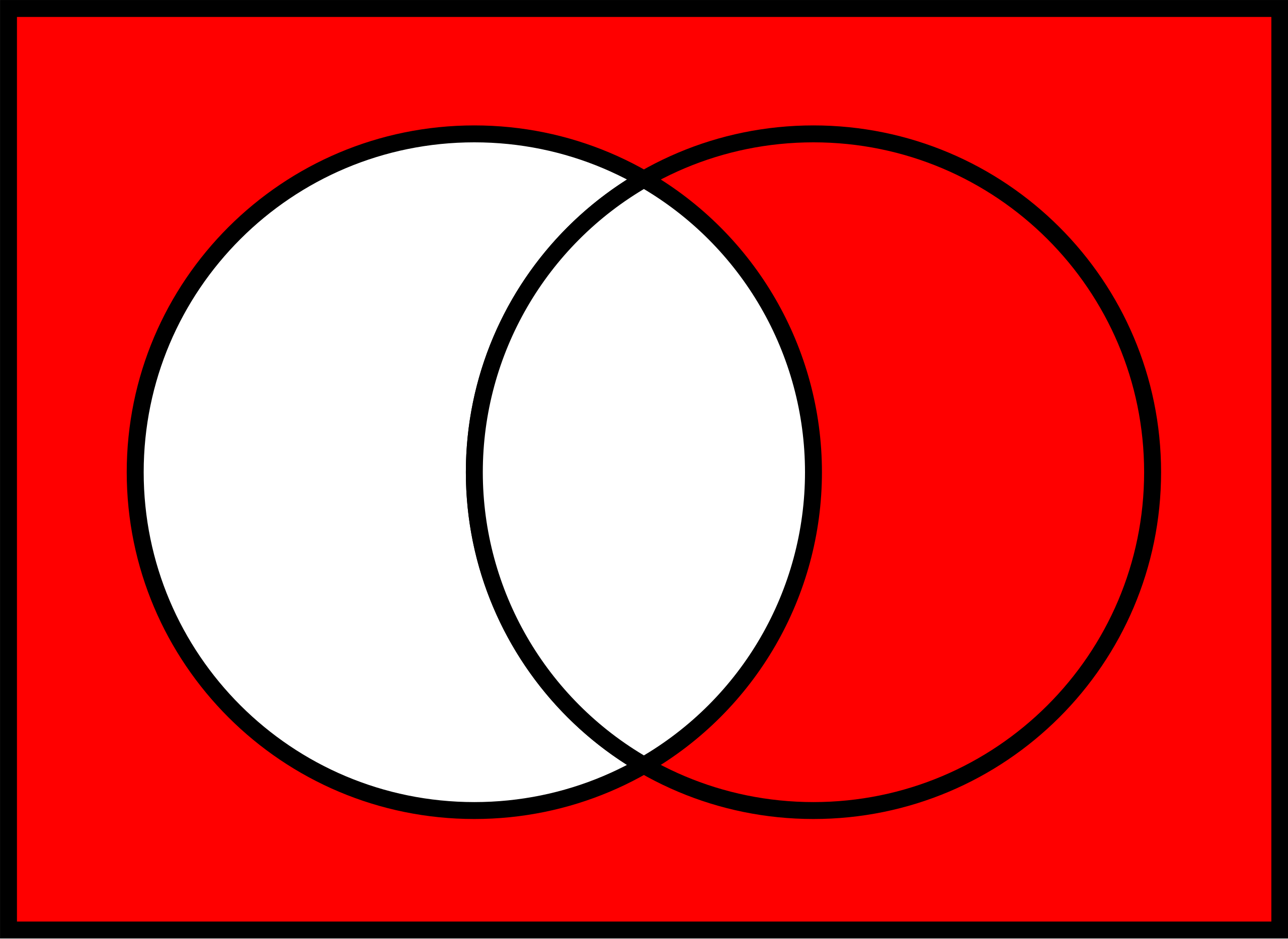
3.4.3 (Durch-)Schnitt von Ereignissen

Definition 3.14 (Schnittmenge von Ereignissen) Die Schnittmenge zweier Ereignisse $A$ und $B$ umfasst genau die Elementarereignisse, die Teil beider Ereignisse sind. Man schreibt: $A \cap B.$¹³ Lies: “A geschnitten B”. $\square$

Abbildung 3.13 zeigt ein Sinnbild zur Schnittmenge zweier Ereignisse.

Abbildung 3.13: $A \cap B$: Schnitt zweier Mengen

Beispiel 3.20 Um einen (hohen!) Geldpreis zu gewinnen, muss bei ihrem nächsten Wurf sowohl das Ereignis $A$ = “gerade Augenzahl” als auch $B$ = “Augenzahl größer 4”, s. Abbildung 3.14.

\[\begin{align} & A = \{2,4,6\} \qquad \hfill \boxed{\color{gray}{1}\; \boxed{\color{black}{2}}\; \color{gray}{3}\; \boxed{\color{black}{4}}\; \color{gray}{5}\; \boxed{\color{black}{6}}\;} \\ & B = \{5,6\} \qquad \qquad \hfill \boxed{ \color{gray}{1\; 2\; 3\; 4\;} \boxed{\color{black}{5\; 6}}} \\ \newline \hline \\ & A \cap B = \{6\} \qquad \qquad \hfill \boxed{\color{gray}{1\; 2\; 3\; 4\; 5\;} \color{black}{6}} \end{align}\]

Abbildung 3.14: Beispiel zum Schnitt zweier Mengen

Code

A <- c(2, 4, 6)
B <- c(5, 6)
intersect(A, B)
## [1] 6

Eselsbrücke zur Vereinigungs- und Schnittmenge

Das Zeichen für eine Vereinigung zweier Mengen kann man leicht mit dem Zeichen für einen Schnitt zweier Mengen leicht verwechseln; daher kommt eine Eselbrücke gelesen, s. Abbildung 3.15.

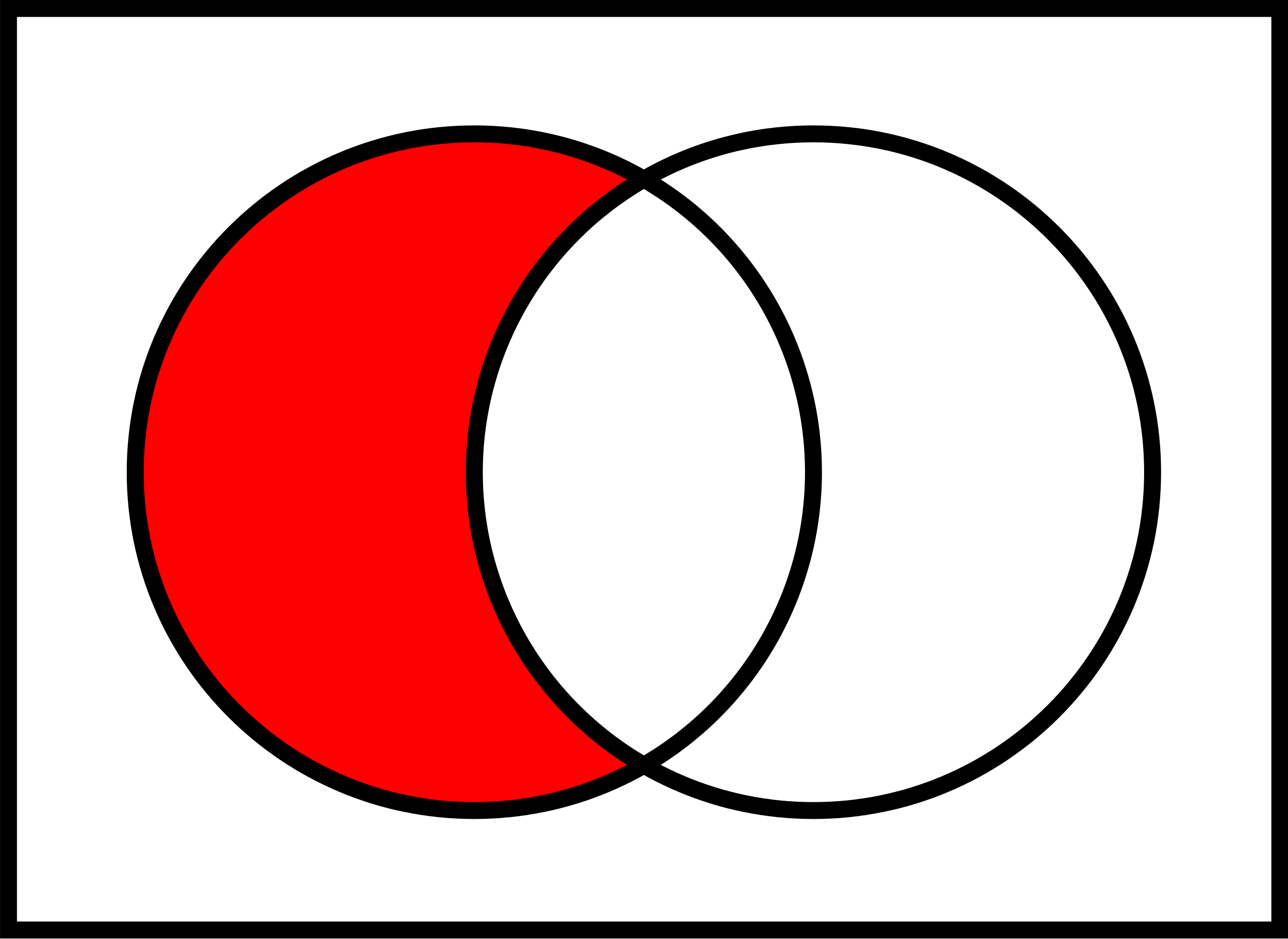
Abbildung 3.15: Eselsbrücke für Vereinigungs- und Schnittmenge

3.4.4 Komplementärereignis

Definition 3.15 (Komplementärereignis) Ein Ereignis $A$ ist genau dann ein Komplementärereignis zu $B$, wenn es genau die Elementarereignisse von $\Omega$ umfasst, die nicht Elementarereignis des anderen Ereignisses sind, s. Abbildung 3.17.$\square$

Man schreibt für das Komplementärereignis¹⁴ von $A$ oft $\bar{A}$ oder $\neg A$¹⁵; lies “Nicht-A” oder “A-quer”.

Beispiel 3.21 Beim normalen Würfelwurf sei $A$ das Ereignis “gerade Augenzahl”; das Komplementärereignis¹⁶ ist dann $\neg A$ “ungerade Augenzahl”, s. Abbildung 3.16.

\[\begin{align} A = \{2,4,6\} \qquad \hfill \boxed{\color{gray}{1}\; \boxed{\color{black}{2}}\; \color{gray}{3}\; \boxed{\color{black}{4}}\; \color{gray}{5}\; \boxed{\color{black}{6}}\;} \\ \hline \\ \neg A = \{1,3,5\} \qquad \hfill \boxed{\boxed{\color{black}{1}}\; \color{gray}{2}\; \boxed{\color{black}{3}}\; \color{gray}{4}\; \boxed{\color{black}{5}}\; \color{gray}{6}\; } \\ \end{align}\]

Abbildung 3.16: Ein Beispiel für ein Komplement

3.4.5 Logische Differenz

Definition 3.16 (Logische Differenz) Die logische Differenz der Ereignisse $A$ und $B$ ist das Ereignis, das genau aus den Elementarereignissen besteht von $A$ besteht, die nicht zugleich Elementarereignis von $B$ sind, s. Abbildung 3.18.$\square$

Die logische Differenz von $A$ zu $B$ schreibt man häufig so: $A \setminus B$; lies “A minus B”.

Beispiel 3.22 Sei $A$ die Menge “große Zahlen” mit $A = \{4,5,6 \}$. Sei $B$ die Menge “gerade Zahlen” mit $B = \{2,4,6\}$. Wir suchen die logische Differenz, $A \setminus B$, s. Abbildung 3.19.

\[\begin{align} A = \{4,5, 6\} \qquad \hfill \boxed{\color{red}{4}\; \color{green}{5}\; \color{red}{6}} \\ B = \{2,4,6\} \qquad \hfill \boxed{\color{grey}{2}\; \color{red}{4}\; \color{red}{6}} \\ \hline \\ A \setminus B \qquad \hfill \boxed{\color{green}{5}} \end{align}\]

Abbildung 3.19: Beispiel für die logische Differenz

In R gibt es die Funktion setdiff(), die eine Mengendifferenz ausgibt.

Code

A <- c(4, 5, 6)
B <- c(2, 4, 6)

setdiff(A, B)
## [1] 5

🤯 Von der Menge $A$ die Menge $B$ abzuziehen, ist etwas anderes, als von $B$ die Menge $A$ abzuziehen.

Vorsicht

$A \setminus B \ne B \setminus A$.

Code

setdiff(B, A)
## [1] 2

3.4.6 Vertiefung

Animation zu Mengenoperationen

Übungsaufgabe 3.6 (Peer Instruction: Das Komplementärereignis von der Bestnote) Sie haben eine Statistikklausur bestanden. Mit Bestnote. Genauer gesagt, haben Sie 100 von 100 Punkten erzielt. Was ist das Komplementärereignis dazu?

99 Punkte
0 Punkte
0-99 Punkte
0-100 Punkte
durchgefallen
keines der genannten $\square$

3.5 Zufallsvariable

3.5.1 Grundlagen

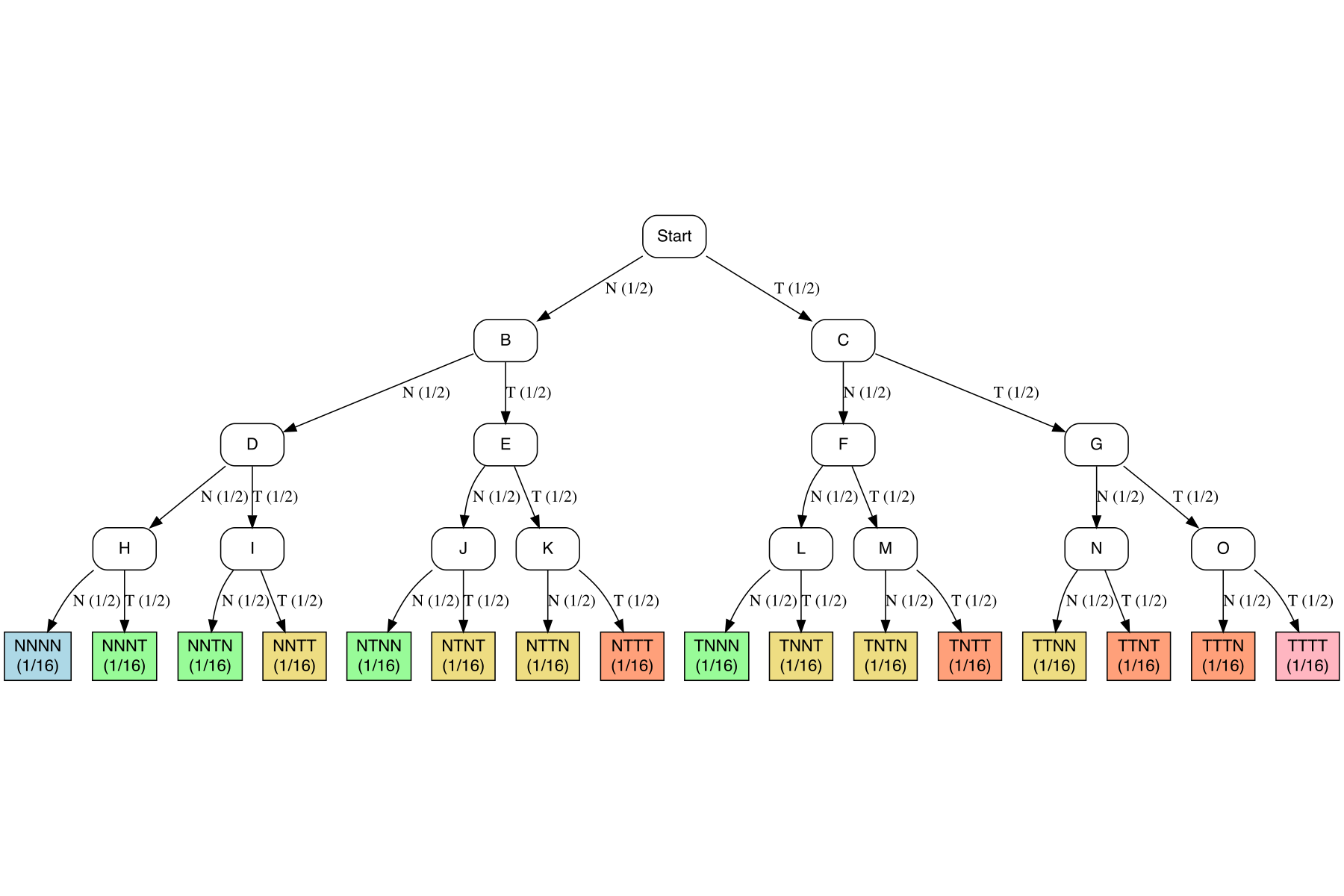
Beispiel 3.23 Schorsch sucht eine Betreuerin für seine Abschlussarbeit. An die ideale Betreuerin setzt er 4 Kriterien an: a) klare, schriftliche fixierte Rahmenbedingungen, b) viel Erfahrung, c) guten Ruf und d) interessante Forschungsinteressen. Je mehr dieser 4 Kriterien erfüllt sind, desto besser. Schorsch geht davon aus, dass die 4 Kriterien voneinander unabhängig sind (ob eines erfüllt ist oder nicht, ändert nichts an der Wahrscheinlichkeit, dass ein anderes Kriterium erfüllt ist). Schorsch interessiert sich also für die Anzahl der erfüllten Kriterien, also eine Zahl von 0 bis 4. Er schätzt die Wahrscheinlichkeit für einen “Treffer” in jedem seiner 4 Kriterien auf 50%. Viel Glück, Schorsch! Sein Zufallsexperiment hat 16 Ausgänge (Knoten 16 bis 31), s. Abbildung 3.20 und Tabelle 3.1. Ganz schön komplex. Eigentlich würden ihm ja eine Darstellung mit 5 Ergebnissen, also der “Gutachter-Score” von 0 bis 4 ja reichen. Wie können wir die Sache übersichtlicher für Schorsch machen? Abbildung 3.20 ist ein Versuch. $\square$

Abbildung 3.20: Ein Baumdiagramm mit 16 Ausgängen, analog zur 4 Münzwürfen. T: Treffer (Kriterium erfüllt). N: Niete (Kriterium nicht erfüllt). NNNT wäre zum Beispiel eine Gutachterin ohne klar fixierte Rahmenbedingungen, ohne viel Erfahrung, mit schlechem Ruf aber mit interessanten Forschungsinteressen.

Tabelle 3.1: Schorschs Zufallsexperiment, Auszug der Elementarereignisse (EE)

i	Elementarereignis	Pr(EE)	Trefferzahl
1	NNNN	1/16	0
2	NNNT	1/16	1
3	NNTN	1/16	1
4	NTNN	1/16	1
5	TNNN	1/16	1
6	NNTT	1/16	2
…	…	…	…

Schorsch braucht also eine übersichtlichere Darstellung; die Zahl der Treffer und ihre Wahrscheinlichkeit würde ihm ganz reichen. In vielen Situationen ist man an der Anzahl der Treffer interessiert. Die Wahrscheinlichkeit für eine bestimmte Trefferanzahl bekommt man einfach durch Addieren der Wahrscheinlichkeiten der zugehörigen Elementarereignisse, s. Tabelle 3.1. Hier kommt die Zufallsvariable ins Spiel. Wir nutzen sie, um die Anzahl der Treffer in einem Zufallsexperiment zu zählen.

Definition 3.17 (Zufallsvariable) Die Zuordnung der Elementarereignisse eines Zufallsexperiments zu genau einer Zahl $\in \mathbb{R}$ nennt man Zufallsvariable.$\square$

Die den Elementarereignissen zugewiesenen Zahlen nennt man Realisationen oder Ausprägungen der Zufallsvariablen.

Beispiel 3.24 (Lotto) Ein Lottospiel hat ca. 14 Millionen Elementarereignisse. Die Zufallsvariable “Anzahl der Treffer” hat nur 7 Realisationen: 0,1,…,6.$\square$

Es hat sich eingebürgert, Zufallszahlen mit $X$ zu bezeichnen (oder anderen Buchstaben weit hinten aus dem Alphabet).

Man schreibt für eine Zufallsvariable kurz: $X: \Omega \rightarrow \mathbb{R}$. “X ist eine Zufallsvariable, die jedem Elementarereignis $\omega$ eine reelle Zahl zuordnet.” Um die Vorschrift der Zuordnung genauer zu bestimmen, kann man folgende Kurzschreibweise nutzen:

${\displaystyle X(\omega )={\begin{cases}1,&{\text{wenn }}\omega ={\text{Kopf}},\\[6pt]0,&{\text{wenn }}\omega ={\text{Zahl}}.\end{cases}}}$

Abbildung 3.21 stellt diese Abbildung dar.

Abbildung 3.21: Eine Zufallsvariable ist eine Zuordnung der Ereignisse zu einer reellen Zahl (nach einer bestimmten Regel

Zufallsverteilungen kann im zwei Arten einteilen:

diskrete Zufallsvariablen
stetige Zufallsvariablen

3.5.2 Diskrete Zufallsvariable

3.5.2.1 Grundlagen

Eine diskrete Zufallsvariable ist dadurch gekennzeichnet, dass nur bestimmte Realisationen möglich sind, zumeist natürliche Zahlen, wie 0, 1, 2,…, . Abbildung 3.22 versinnbildlicht die Zufallsvariable des “Gutachter-Scores”, s. Beispiel 3.23.

Abbildung 3.22: Sinnbild einer diskreten Zufallsvariablen X für Schorschs Suche nach einer Betreuerin seiner Abschlussarbeit. X gibt den Score der Gutachterin wider.

Beispiel 3.25 (Diskrete Zufallsvariablen)

Anzahl der Bewerbungen bis zum ersten Job-Interview
Anzahl Anläufe bis zum Bestehen der Statistik-Klausur
Anzahl der Absolventen an der HS Ansbach pro Jahr
Anzahl Treffer beim Kauf von Losen
Anzahl Betriebsunfälle
Anzahl der Produkte in der Produktpalette$\square$

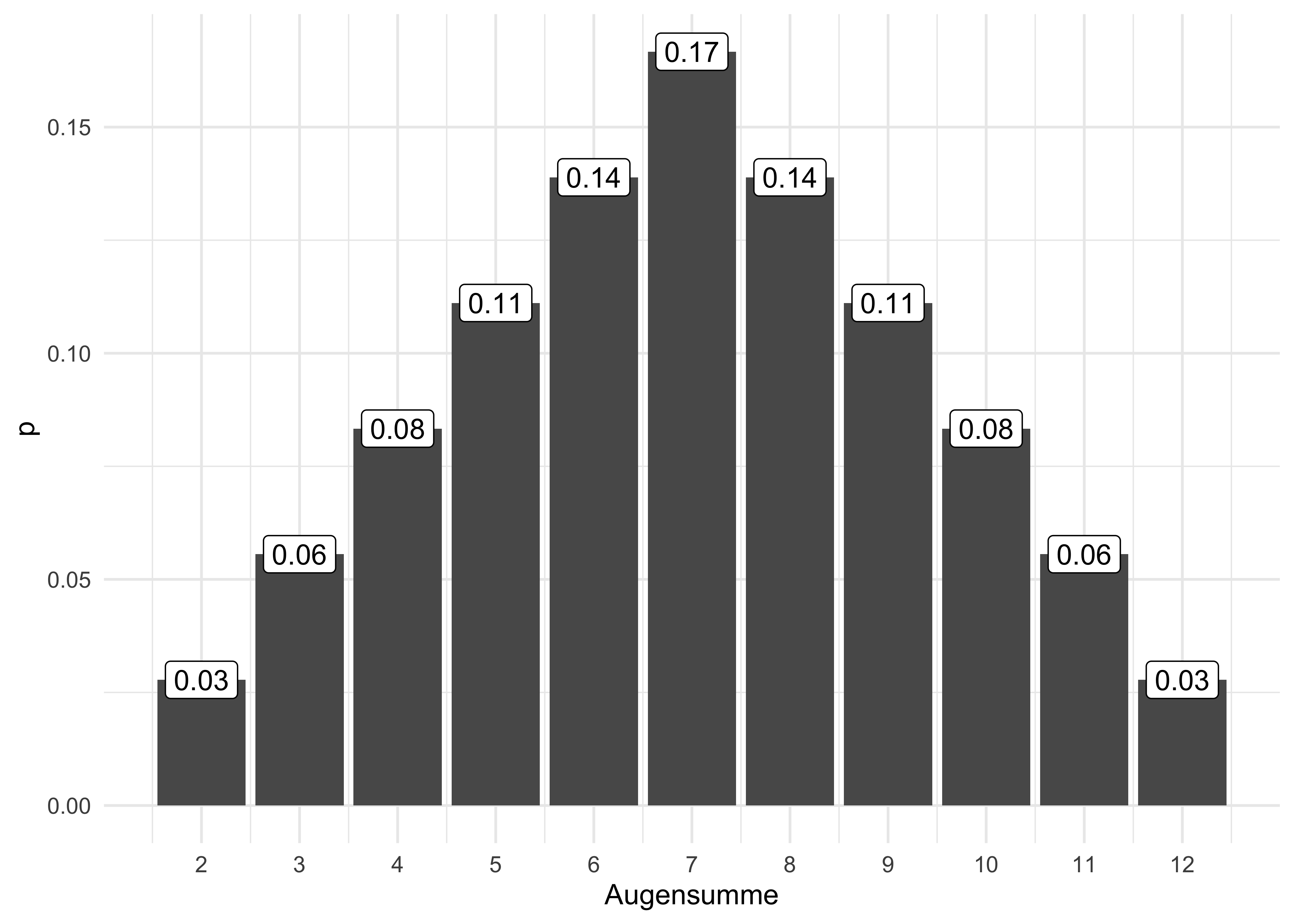
Beispiel 3.26 Der zweifache Würfelwurf ist ein typisches Lehrbuchbeispiel für eine diskrete Zufallsvariable. ¹⁷ Hier ist $S$¹⁸ die Augensumme des zweifachen Würfelwurfs und $S$ ist eine Zahl zwischen 2 und 12. Für jede Realisation $X=x$ kann man die Wahrscheinlichkeit berechnen, Abbildung 3.23 versinnbildlicht die Wahrscheinlichkeit für jede Realisation von $X$.$\square$

Abbildung 3.23: Augensumme des zweifachen Würfelwurfs; für jede Realisation von S ist die zugehörige Wahrscheinlichkeit dargestellt. Bildquelle: Tim Stellmach, Wikipedia, PD

Wahrscheinlichkeitsverteilungen dienen dazu, den Realisationen einer Zufallsvariablen eine Wahrscheinlichkeit zuzuordnen.

Definition 3.18 (Diskrete Wahrscheinlichkeitsverteilung) Eine diskrete Wahrscheinlichkeitsverteilung der (diskreten) Zufallsvariablen $X$ ordnet jeder der $k$ Ausprägungen $X=x$ eine Wahrscheinlichkeit $p$ zu.$\square$

Beispiel 3.27 (Wahrscheinlichkeit des Geschlechts bei der Geburt) So hat die Variable Geschlecht eines Babies die beiden Ausprägungen Mädchen und Junge mit den Wahrscheinlichkeiten $p_M = 51.2\%$ bzw. $p_J = 48.8\%$, laut einer Studie (Gelman et al., 2021).$\square$

Zwischen der deskriptiven Statistik und der Wahrscheinlichkeitstheorie bestehen enge Parallelen, Tabelle 3.2 stellt einige zentrale Konzepte gegenüber. Bei einer guten Stichproben kann man die Kennwerte der deskriptiven Statistik als Schätzwerte für die zugrundeliegende Wahrscheinlichkeit verwenden.

Tabelle 3.2: Gegenüberstellung von Wahrscheinlichkeitstheorie und deskriptiver Statistik

Wahrscheinlichkeitstheorie	Deskriptive Statistik
Zufallsvariable	Merkmal
Wahrscheinlichkeit	relative Häufigkeit, Anteil
Wahrscheinlichkeitsverteilung	einfache relative Häufigkeitsverteilung
Verteilungsfunktion	kumulierte relative Häufigkeitsverteilung
Erwartungswert	Mittelwert
Varianz	Varianz

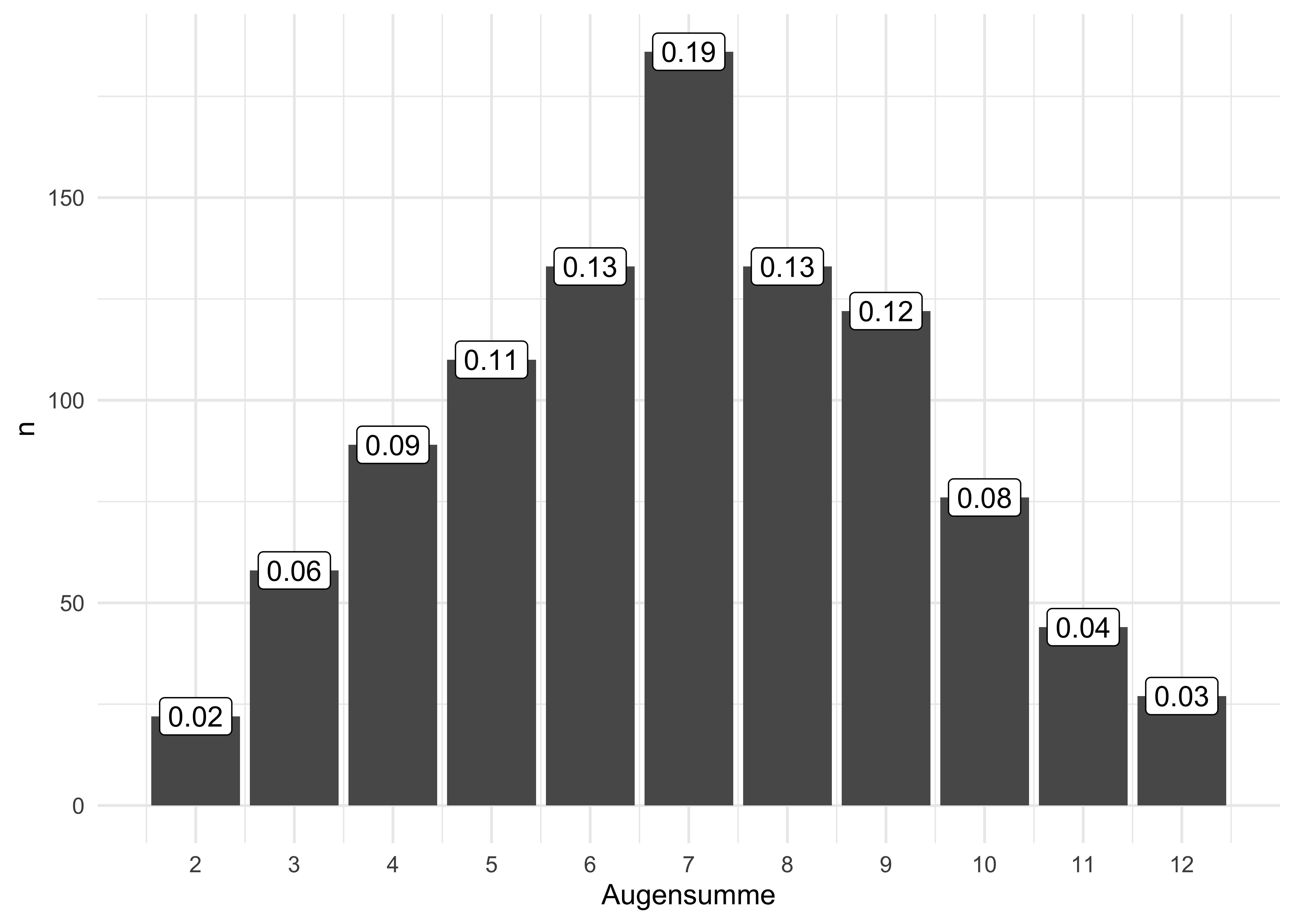
Eine Verteilung zeigt, welche Ausprägungen eine Variable aufweist und wie häufig bzw. wahrscheinlich diese sind. Einfach gesprochen veranschaulicht eine Balken- oder Histogramm eine Verteilung. Man unterscheidet Häufigkeitsverteilungen (s. Abb. Abbildung 3.25) von Wahrscheinlichkeitsverteilungen (Abb. Abbildung 3.24).

Abbildung 3.24: Wahrscheinlichkeitsverteilung der Zufallsvariable “Augenzahl im zweifachen Würfelwurf”

Abbildung 3.25: (relative und absolute) Häufigkeiten des zweifachen Würfelwurfs, 1000 Mal wiederholt

Beispiel 3.28 (Wahrscheinlichkeitsverteilung eines Würfels) Abbildung 3.26 zeigt die Wahrscheinlichkeitsverteilung eines einfachen Würfelwurfs.$\square$

Abbildung 3.26: Wahrscheinlichkeitsverteilung eines einfachen Würfelwurfs, Bildrechte: Olex Alexandrov, Wikipedia, PD

Beispiel 3.29 Die Wahrscheinlichkeitsverteilung für $X$ “Augensumme im zweifachen Würfelwurf” ist in Abbildung 3.24 visualisiert.$\square$

3.5.2.2 Vertiefung: Verteilungsfunktion

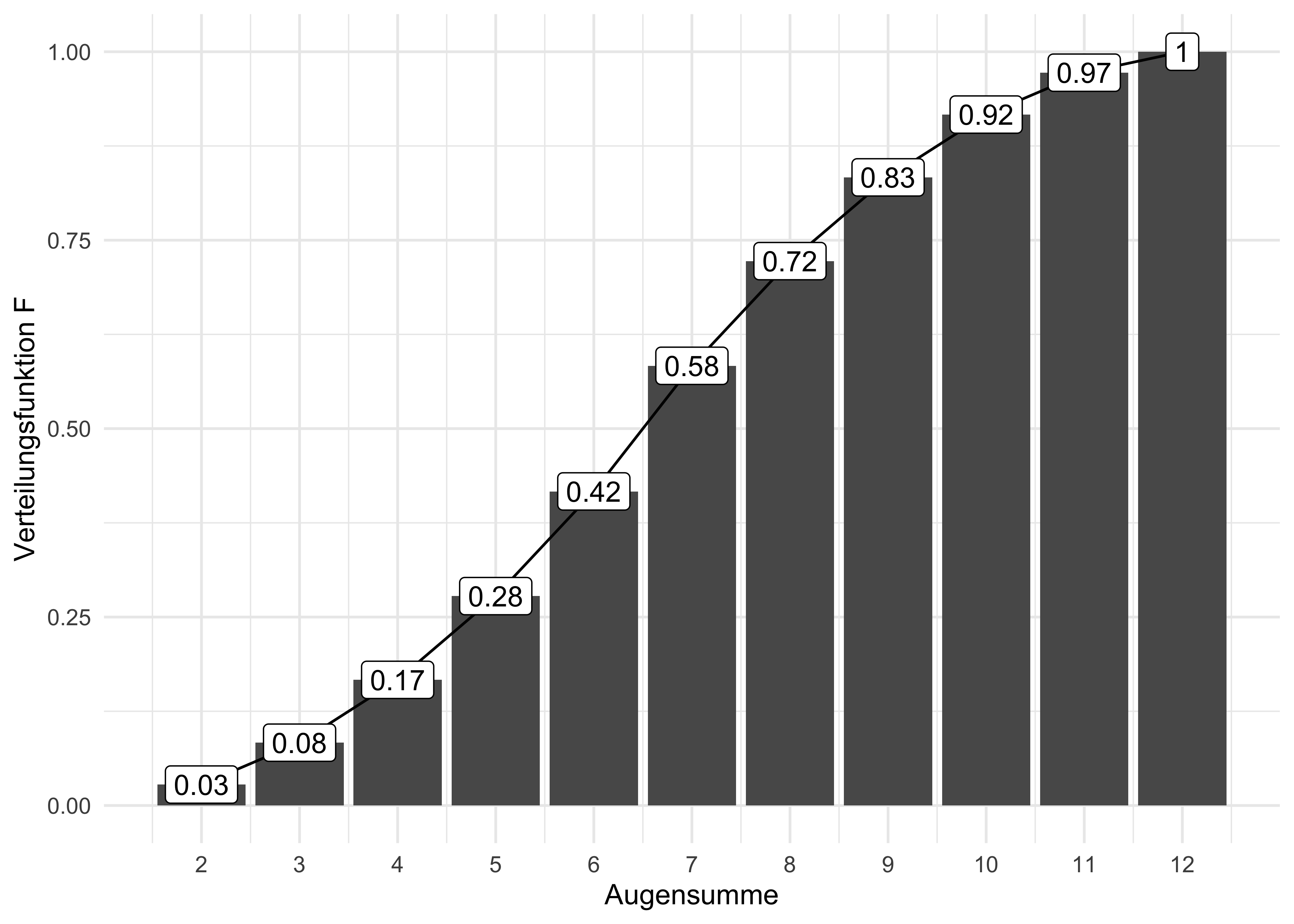
Definition 3.19 (Verteilungsfunktion) Die Verteilungsfunktion $F$ gibt die Wahrscheinlichkeit an, dass die diskrete Zufallsvariable $X$ eine Realisation annimmt, die kleiner oder gleich $x$ ist.$\square$

Die Berechnung von $F(x)$ erfolgt, indem die Wahrscheinlichkeiten aller möglichen Realisationen $x_i$, die kleiner oder gleich dem vorgegebenen Realisationswert $x$ sind, addiert werden:

$F(x) = \sum_{x_ \le x} Pr(X=x_i).$

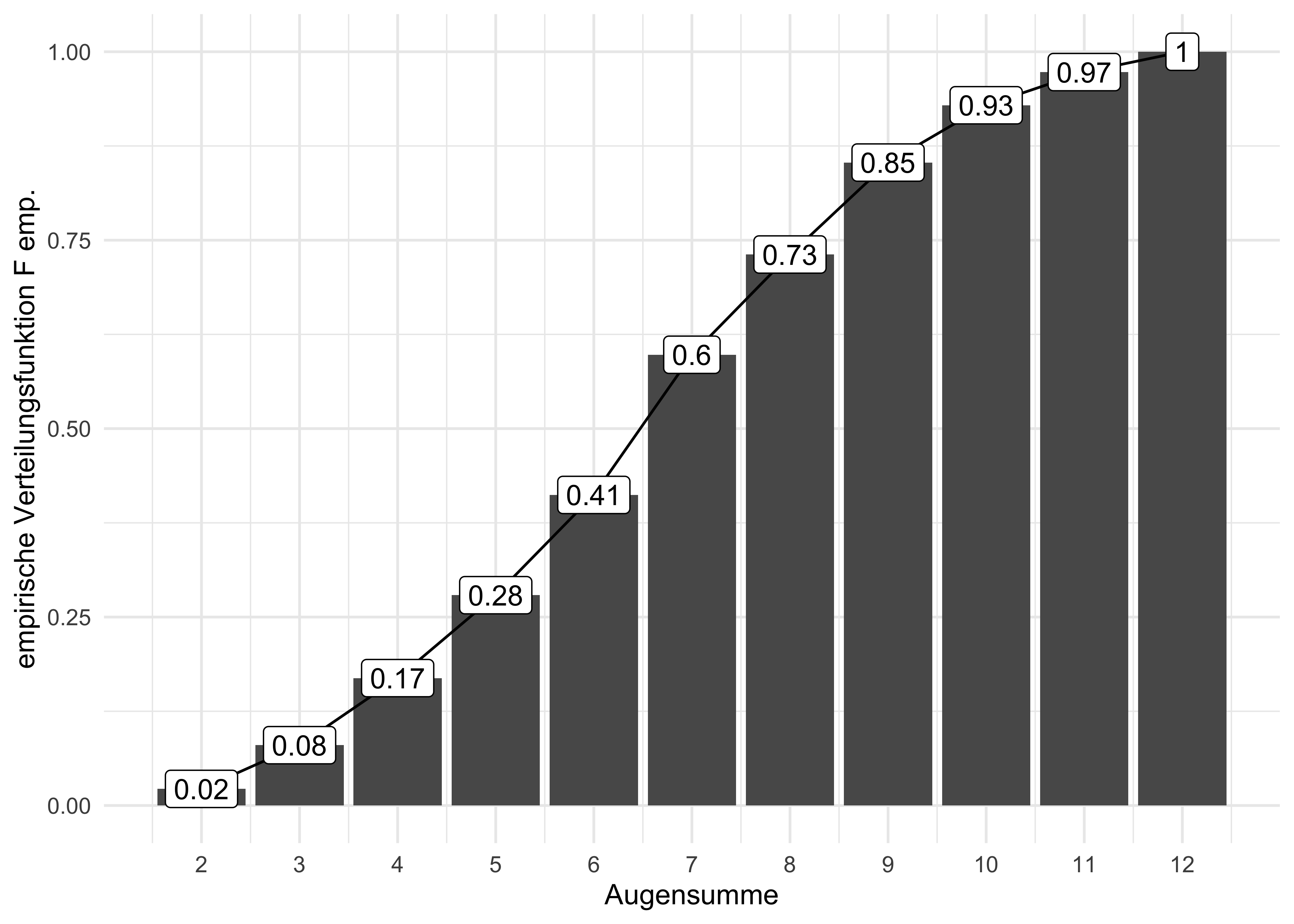
Die Verteilungsfunktion ist das Pendant zur kumulierten Häufigkeitsverteilung, vgl. Abbildung 3.27 und Abbildung 3.28: Was die kumulierte Häufigkeitsverteilung für Häufigkeiten ist, ist die Verteilungsfunktion für Wahrscheinlichkeiten.

Abbildung 3.27: Verteilungsfunktion $F(X \le x_i)$ für die Zufallsvariable “Augenzahl im zweifachen Würfelwurf”

Abbildung 3.28: Empirische Verteilungsfunktion (kumulierte Häufigkeitsverteilung) $F(X \le x_i)$ von 1000 zweifachen Münzwürfen

3.5.3 Stetige Zufallsvariablen

3.5.3.1 Grundlagen

📺 Verteilungen metrischer Zufallsvariablen

Abbildung 3.29 versinnbildlicht die stetige Zufallsvariable “Körpergröße”, die (theoretisch, in Annäherung) jeden beliebigen Wert zwischen 0 und (vielleicht) 2 Meter annehmen kann.

Abbildung 3.29: Sinnbild für eine stetige Zufallsvariable X “Körpergröße”

Definition 3.20 (Stetige Zufallsvariable) Eine stetige Zufallsvariable gleicht einer diskreten, nur dass alle Werte im Intervall erlaubt sind.$\square$

Beispiel 3.30

Spritverbrauch
Körpergewicht von Professoren
Schnabellängen von Pinguinen
Geschwindigkeit beim Geblitztwerden$\square$

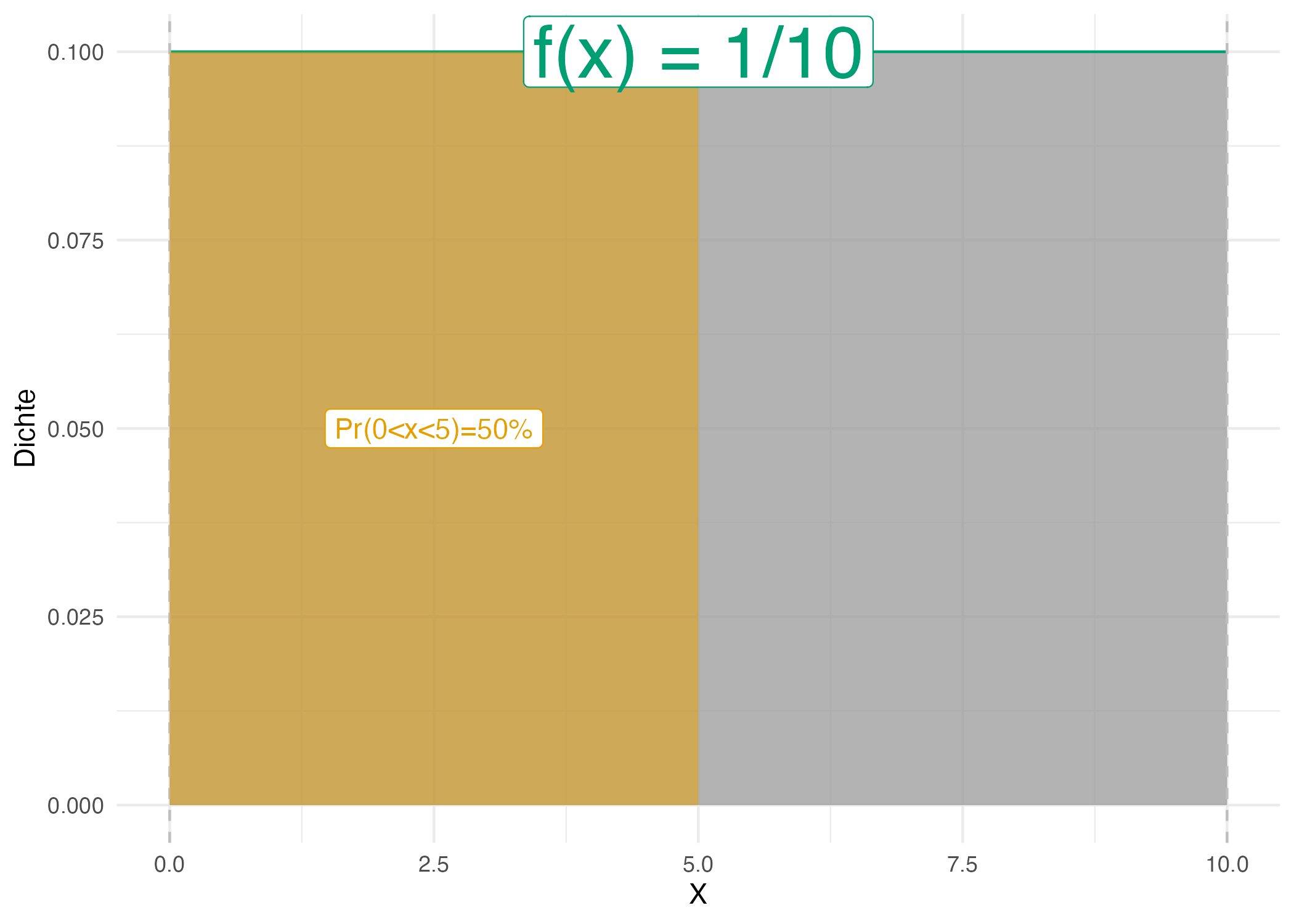
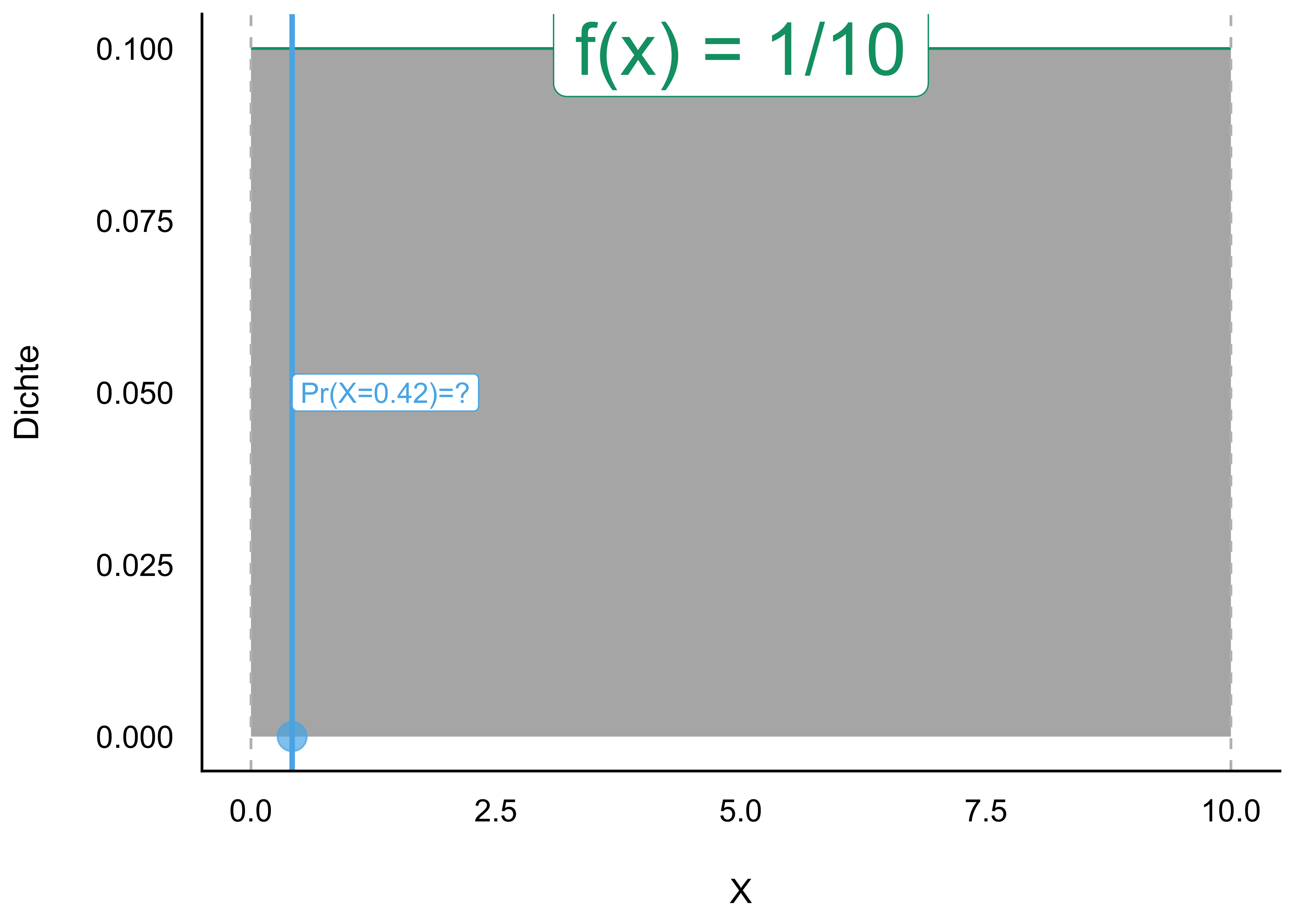
Übungsaufgabe 3.7 (Warten auf den Bus, 42 Sekunden) Sie stehen an der Bushaltestellen und warten auf den Bus. Langweilig. Da kommt Ihnen ein Gedanken in den Sinn: Wie hoch ist wohl die Wahrscheinlichkeit, dass Sie exakt 42 Sekunden auf den Bus warten müssen, s. Abbildung 3.31? Weiterhin überlegen Sie, dass davon auszugehen ist, dass jede Wartezeit zwischen 0 und 10 Minuten gleich wahrscheinlich ist. Spätestens nach 10 Minuten kommt der Bus, so ist die Taktung (extrem zuverlässig). Exakt heißt exakt, also nicht 42.1s, nicht 42.01s, nicht 42.001s, etc. bis zur x-ten Dezimale.$\square$

Nicht so einfach (?). Hingegen ist die Frage, wie hoch die Wahrscheinlichkeit ist, zwischen 0 und 5 Minuten auf den Bus zu warten ($0<x<5$), einfach: Sie beträgt 50%, wie man in Abbildung 3.30 gut sehen kann.

Abbildung 3.30: Wie groß ist die Wahrscheinlichkeit, zwischen 0 und 5 Minuten auf den Bus zu warten? 50 Prozent!

Abbildung 3.31: Wie groß ist die Wahrscheinlichkeit, genau 42 Sekunden auf den Bus zu warten? Hm.

Vergleicht man Abbildung 3.31 und Abbildung 3.30 kommt man (vielleicht) zu dem Schluss, dass die Wahrscheinlichkeit exakt 42s auf den Bus zu warten, praktisch Null ist. Der Grund ist, dass die Fläche des Intervalls gegen Null geht, wenn das Intervall immer schmäler wird. Aus diesem Grund kann man bei stetigen Zufallszahlen nicht von einer Wahrscheinlichkeit eines bestimmten Punktes $X=x$ sprechen. Für einen bestimmten Punkt $X=x$ kann man aber die Dichte der Wahrscheinlichkeit angeben.

Was gleich ist in beiden Situationen ($Pr(X=.42)$ und $Pr(0<x<0.5)$) ist die Wahrscheinlichkeitsdichte, $f$. In Abbildung 3.31 und Abbildung 3.30 ist die Wahrscheinlichkeitsdichte gleich, $f=1/10=0.1$.

Definition 3.21 (Wahrscheinlichkeitsdichte) Die Wahrscheinlichkeitsdichte $f(x)$ gibt an, wie viel Wahrscheinlichkeitsmasse pro Einheit von $X$ an an der Stelle $x$ ist.$\square$

Die Wahrscheinlichkeitsdichte zeigt an, an welchen Stellen $x$ die Wahrscheinlichkeit besonders “geballt” oder “dicht” sind, s. Abbildung 3.32.

Abbildung 3.32: Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert zwischen und annimmt, entspricht dem Inhalt der Fläche unter dem Graph der Wahrscheinlichkeitsdichtefunktion. Bildrechte: 4C, Wikipedia, CC-BY-SA .

Bei stetigen Zufallsvariablen $X$ geht man von unendlich vielen Ausprägungen aus; die Wahrscheinlichkeit einer bestimmten Ausprägung ist Null: $Pr(X=x_j)=0, j=1,…,+

Beispiel 3.31 (Wahrscheinlichkeitsverteilung für die Körpergröße) So ist die Wahrscheinlichkeit, dass eine Person exakt 166,66666666… cm groß ist, ist (praktisch) Null. Man gibt stattdessen die Dichte der Wahrscheinlichkeit an: Das ist die Wahrscheinlichkeit(smasse) pro Einheit von $X$.$\square$

Für praktische Fragen berechnet man zumeist die Wahrscheinlichkeit von Intervallen, s. Abbildung 3.32.

3.5.3.2 Vertiefung: Verteilungsfunktion

Definition 3.22 (Verteilungsfunktion) Die Verteilungsfunktion einer stetigen Zufallsvariablen gibt wie im diskreten Fall an, wie groß die Wahrscheinlichkeit für eine Realisation kleiner oder gleich einem vorgegebenen Realisationswert $x$ ist.$\square$

Die Verteilungsfunktion $F(x)$ ist analog zur kumulierten Häufigkeitsverteilung zu verstehen, vgl. Abbildung 3.33. $\square$

Abbildung 3.33: Verteilungsfunktion F für X=“Wartezeit auf den Bus”

Übungsaufgabe 3.8 (Peer Instruction: Wieder auf den Bus warten) Sie warten wieder auf den Bus, s. Abbildung 3.30. Welche Aussage dazu ist falsch?

Die Wahrscheinlichkeit, genau 5 Minuten zu warten, ist am höchsten.
Die Wahrscheinlichkeit, genau 10 Minuten zu warten, ist Null.
Mit 100% Wahrscheinlichkeit beträgt die Wartezeit zwischen 0 und 10 Minuten.
Die Wahrscheinlichkeit 1 Minute zu warten, beträgt 10%.
Keine der genannten. $\square$

3.6 Aufgaben

Die Webseite datenwerk.netlify.app stellt eine Reihe von einschlägigen Übungsaufgaben bereit. Sie können die Suchfunktion der Webseite nutzen, um die Aufgaben mit den folgenden Namen zu suchen.

3.6.1 Paper-Pencil-Aufgaben

3.6.2 Aufgaben, für die man einen Computer braucht

3.7 Literatur

Die Wahrscheinlichkeitstheorie bildet zusammen mit der Statistik das Fachgebiet der Stochastik.↩︎
$10^6 = 1000000$↩︎
Beispiele für Zufallsexperimente das Messen eines Umweltphänomens wie der Temperatur oder die Anzahl der Kunden, die einen Laden betreten. In jedem dieser Fälle sind die möglichen Ergebnisse nicht im Voraus bekannt und hängen von nicht komplett bekannten Faktoren ab.↩︎
$A$ ist eine Teilmenge von $B$, wenn alle Elemente von $A$ auch Teil von $B$ sind.↩︎
Schon wieder.↩︎
?↩︎
Ein Ergebnis ist ein Element von $\Omega$. Elementarereignisse sind die einelementigen Teilmengen von $\Omega$. Konzeptionell sind die beiden Begriffe sehr ähnlich, vgl. https://de.wikipedia.org/wiki/Ergebnis_(Stochastik). Wir werden uns hier auf den Begriff Elementarereignis konzentrieren und den Begriff Ergebnis nicht weiter verwenden.↩︎
Na toll.↩︎
Die Menge aller Teilmengen einer Menge $A$ nennt man die Potenzmenge $\mathcal{P}(A)$, vgl. hier.↩︎
engl. disjoint↩︎
Manchmal wird diese Art der Wahrscheinlichkeit auch epistemologische Wahrscheinlichkeit genannt.↩︎
https://www.geogebra.org/m/QZvCMSDs ↩︎
Synonym und kürzer: $AB$ anstelle von $A \cap B$.↩︎
synonym: Komplement↩︎
manchmal auch $A^C$; C wie complementary event↩︎
das “Komplement”, nicht zu verwechseln mit “Kompliment”↩︎
da einfach und deutlich↩︎
S wie Summe↩︎