8 Gauss-Modelle

8.1 Lernsteuerung

8.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

8.1.2 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

ein Gaußmodell spezifizieren und in R berechnen
an Beispielen verdeutlichen, wie sich eine vage bzw. eine informationsreiche Priori-Verteilung auf die Posteriori-Verteilung auswirkt

8.1.3 Begleitendes Lehrmaterial

Der Stoff dieses Kapitels orientiert sich an McElreath (2020), Kap. 4.1 bis 4.3. Im YouTube-Kanal des Autors finden sich passende Videos wie 📺 Teil 1 und 📺 Teil 2.

8.1.4 Vorbereitung im Eigenstudium

8.1.5 Benötigte R-Pakete

Für rstanarm wird ggf. weitere Software benötigt.

Hinweis

Software, und das sind R-Pakete, müssen Sie nur einmalig installieren. Aber bei jedem Start von R bzw. RStudio müssen Sie die (benötigten!) Pakete starten.

library(tidyverse)  # Datenjudo
library(rstanarm)  # Bayes-Modelle berechnen
library(easystats)  # Statistik-Komfort
library(DataExplorer)  # Daten verbildlichen
library(ggpubr)  # Daten verbildlichen
library(hexbin)  # stat_bin_hex ggplot2

Wichtig

Ab diesem Kapitel benötigen Sie das R-Paket rstanarm. \(\square\)

8.1.6 Benötigte Daten

Wir benötigen den Datensatz !Kung aus der Datei Howell1a.csv. Quelle der Daten ist McElreath (2020) mit Bezug auf Howell.

Kung_path <-  
  "https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/Howell1a.csv"  

kung <- read.csv(Kung_path) 

head(kung, n = 5)

Datenquelle

8.1.7 Einstieg

Beispiel 8.1 (Was war noch mal eine Normalverteilung?) In diesem Kapitel benötigen Sie ein gutes Verständnis der Normalverteilung (die auch als Gauss-Verteilung bezeichnet wird). Fassen Sie daher die wesentlichen Aspekte der Normalverteilung (soweit im Unterricht behandelt) zusammen! \(\square\)

Beispiel 8.2 (Was war noch mal eine Posteriori-Verteilung?) In diesem Kapitel befragen wir die Post-Verteilung für ein normalverteilte Zufallsvariable, nämlich die Körpergröße der !Kung San. Was war noch mal eine Post-Verteilung und wozu ist sie gut? \(\square\)

8.1.8 Stan stellt sich vor

Hallo, Leute! Ich bin Stan! Ich mache hier die Schwerarbeit.

8.2 Wie groß sind die !Kung San?

Dieser Abschnitt basiert auf McElreath (2020), Kap. 4.3.

8.2.1 !Kung San

In diesem Abschnitt untersuchen wir eine Forschungsfrage in Zusammenhang mit dem Volk der !Kung.

The ǃKung are one of the San peoples who live mostly on the western edge of the Kalahari desert, Ovamboland (northern Namibia and southern Angola), and Botswana.The names ǃKung (ǃXun) and Ju are variant words for ‘people’, preferred by different ǃKung groups. This band level society used traditional methods of hunting and gathering for subsistence up until the 1970s. Today, the great majority of ǃKung people live in the villages of Bantu pastoralists and European ranchers.

Quelle

Wir interessieren uns für die Größe der erwachsenen !Kung, also filtern wir die Daten entsprechend und speichern die neue Tabelle als kung_erwachsen.

kung_erwachsen <- kung %>% 
  filter(age >= 18)

nrow(kung_erwachsen)
## [1] 352

\(N=352\).

Lassen wir uns einige typische deskriptive Statistiken zum Datensatz ausgeben. {easystats} macht das tatsächlich recht easy, s. Tabelle 8.1.

describe_distribution(kung_erwachsen)

Tabelle 8.1: Statistiken der metrischen Variablen im Kung-Datensatz

Variable	Mean	SD	IQR	Min	Max	Skewness	Kurtosis	n
height	154.60	7.74	12.06	136.53	179.07	0.15	−0.48	352.00
weight	44.99	6.46	9.19	31.07	62.99	0.13	−0.51	352.00
age	41.14	15.97	23.00	18.00	88.00	0.67	−0.21	352.00
male	0.47	0.50	1.00	0.00	1.00	0.13	−2.00	352.00

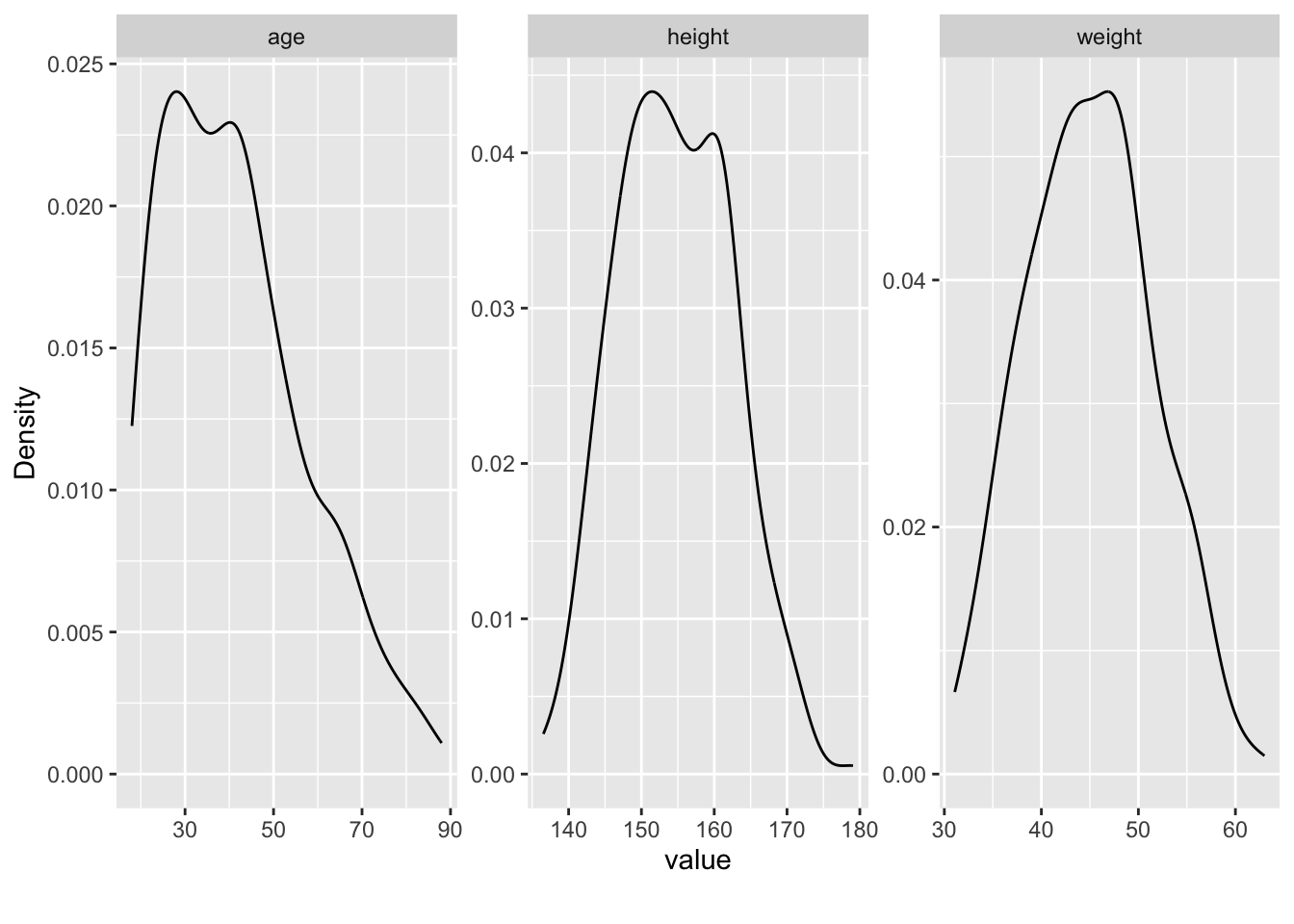
Die Verteilungen lassen sich mit plot_density (aus {DataExplorer}), s. Abbildung 8.1.

plot_density(kung_erwachsen)

Abbildung 8.1: Verteilungen der Variablen im Kung-Datensatz. Größe und Gewicht sind recht symmetrisch bzw. normalverteilt; Alter ist rechtsschief.

8.2.2 Wir gehen apriori von normalverteilter Größe Der !Kung aus

Forschungsfrage: Wie groß sind die erwachsenen !Kung im Durchschnitt?

Wir interessieren uns also für den Mittelwert der Körpergröße einer erwachsenen !Kung-Person, \(\mu\). Der Einfachheit halber gehen wir davon aus, dass Frauen und Männer im Schnitt gleich groß sind.

8.3 Unser Gauss-Modell der !Kung

8.3.1 Normalverteilung als Grundlage des Modells

Hier gehen wir von einer Normalverteilung (synonym: “Gauss-Verteilung”) des Populationsmittelwert, \(\mu\), sowie der tatsächlichen Körpergrößen der einzelnen Personen, \(h_i\) (h wie height) aus.

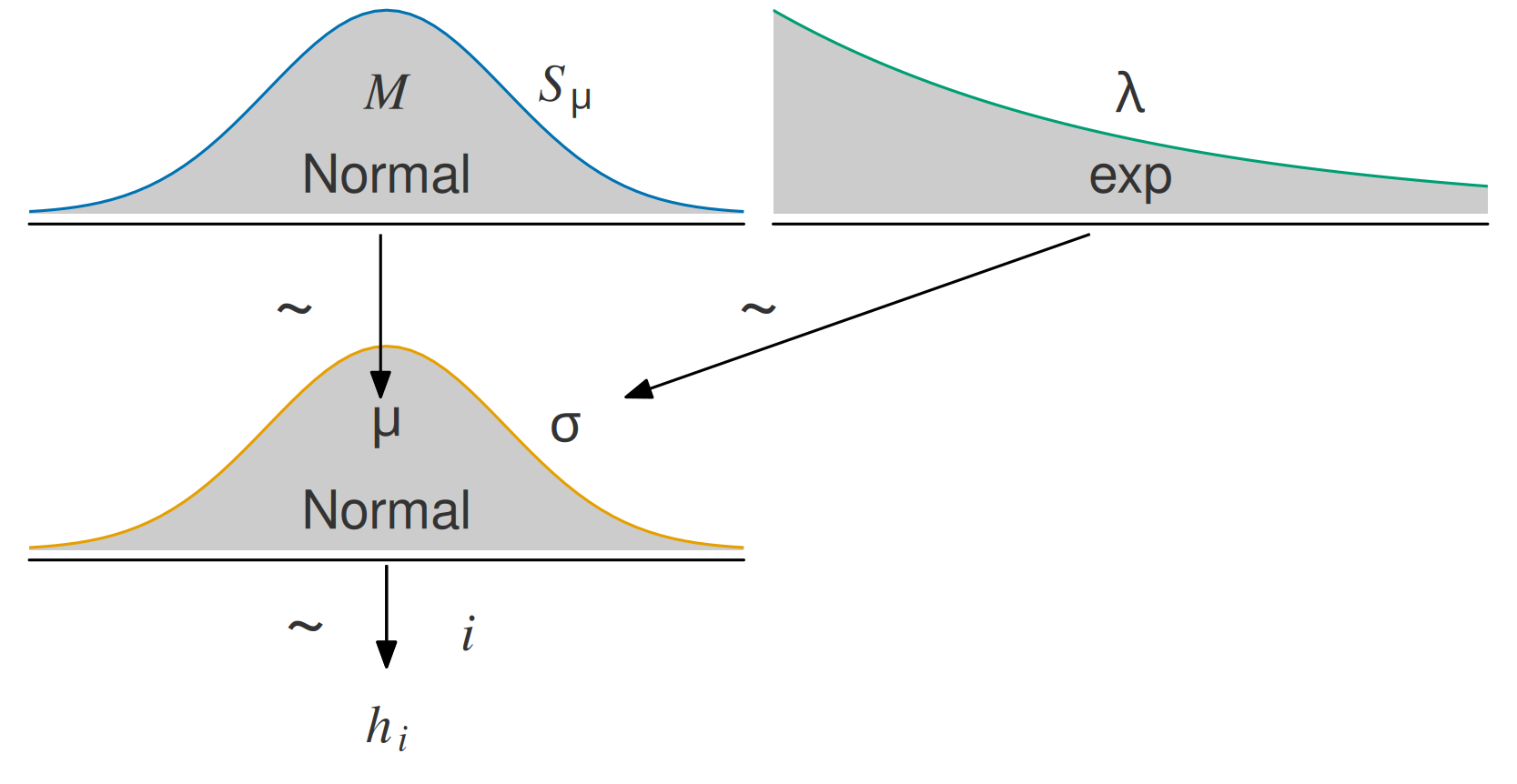
Zur Erinnerung: Die (unstandardisierte) Post-Verteilung ist das Produkt von Apriori und Likelihood, s. Abbildung 8.2. Im Folgenden gehen wir diese Bestimmungsstücke der Reihe nach durch, in gewohnter Manier.

Abbildung 8.2: Apriori mal Likelihood ist gleich der unstandardisierten Post-Verteilung

Nur dass wir dieses Mal die Bayesbox nicht von Hand berechnen, sondern Stan die Arbeit überlassen. Stan liefert uns brav eine Stichproben-Post-Verteilung zurück.

🤖 Ich berechne dir die Stichproben-Postverteilung, ganz ohne Bayesbox!

🧑‍🏫 Toll, dann hab ich ja nix zu tun!

8.3.2 Apriori-Verteilungen

Wir haben zwei Apriori-Größen (Parameter):

Den Mittelwert der Körpergrößen in der Population, \(\mu\). Dieser Parameter beantwortet die Frage: “Wie groß sind die erwachsenen !Kung im Durchschnitt?”
Die Streuung der tatsächlichen Körpergrößen um den Mittelwert der Population herum, \(\sigma\). Dieser Parameter beantwortet die Frage: “Wie unterschiedlich groß sind die erwachsenen !Kung?”

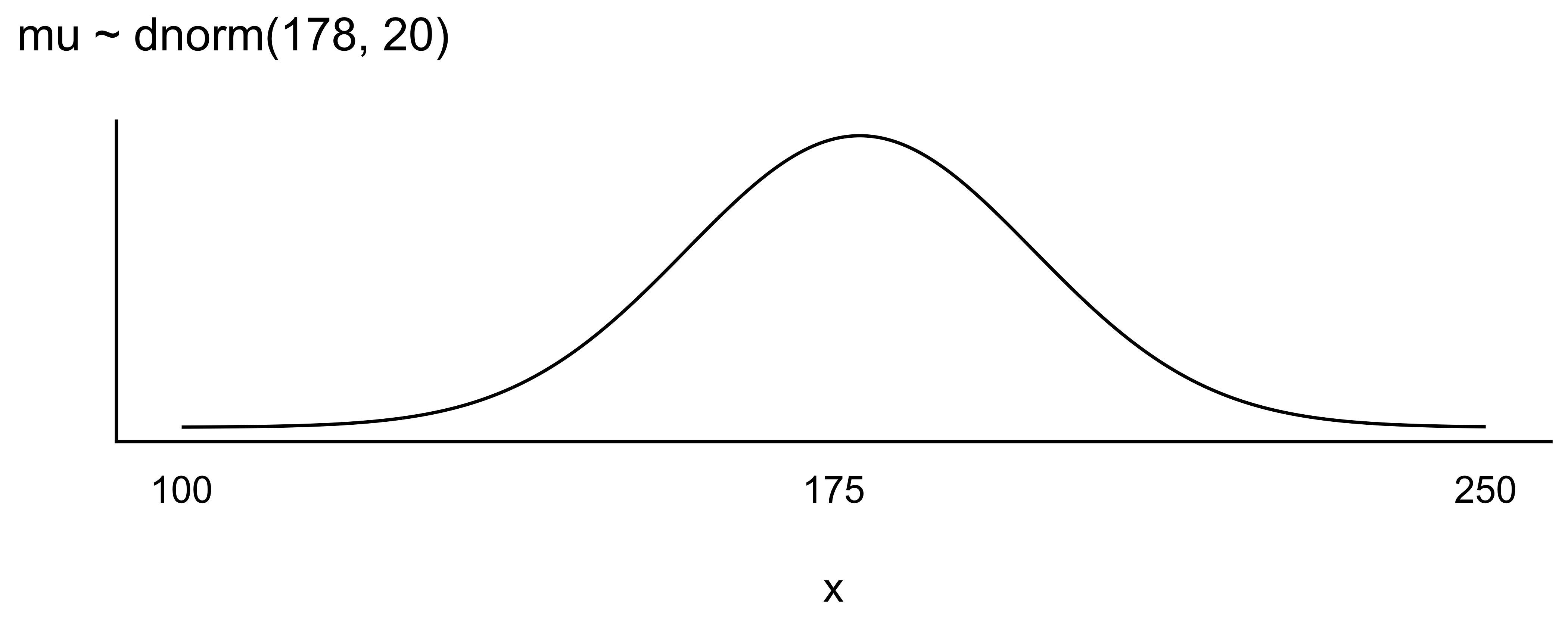
Apriori-Verteilung für \(\mu\): Der Mittelwert der Körpergröße, \(\mu\), sei normalverteilt mit \(\mu=178\) und \(\sigma=20\):

\[\color{blue}{\mu \sim \mathcal{N}(178, 20)} \qquad{\text{Prior}}\]

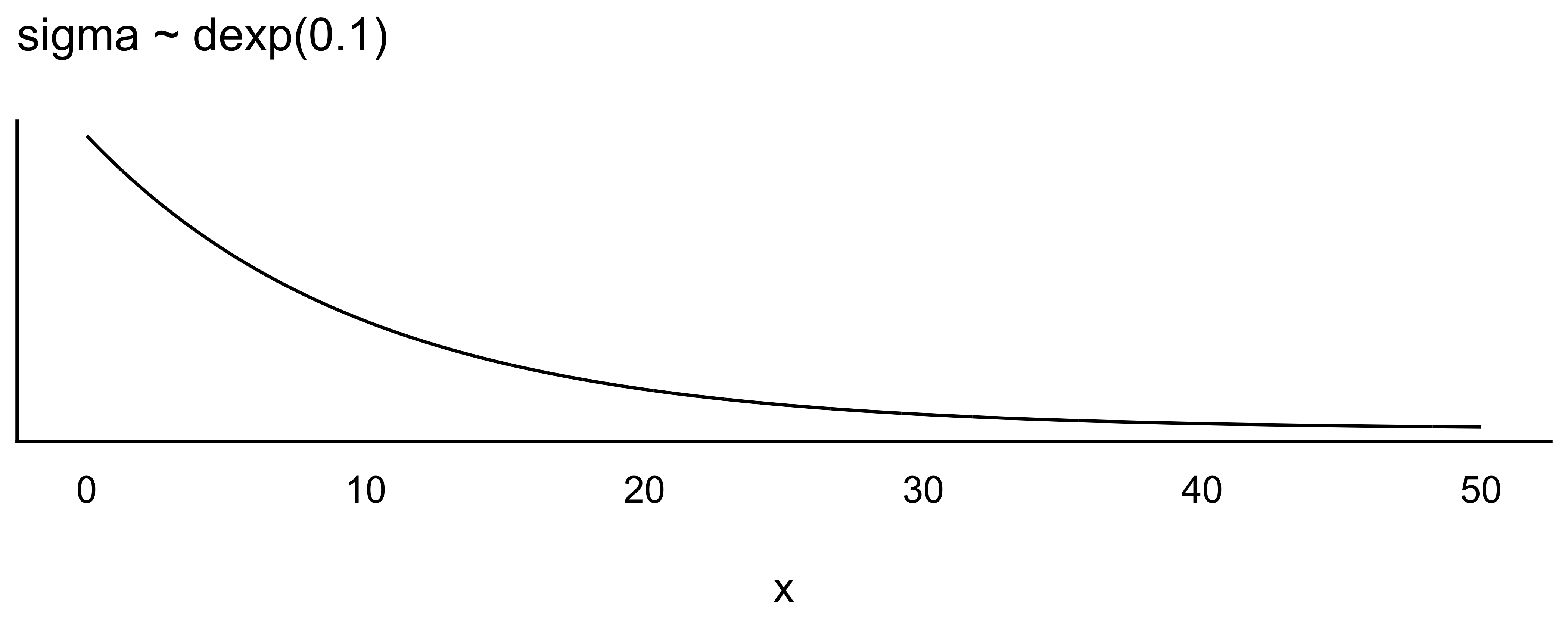
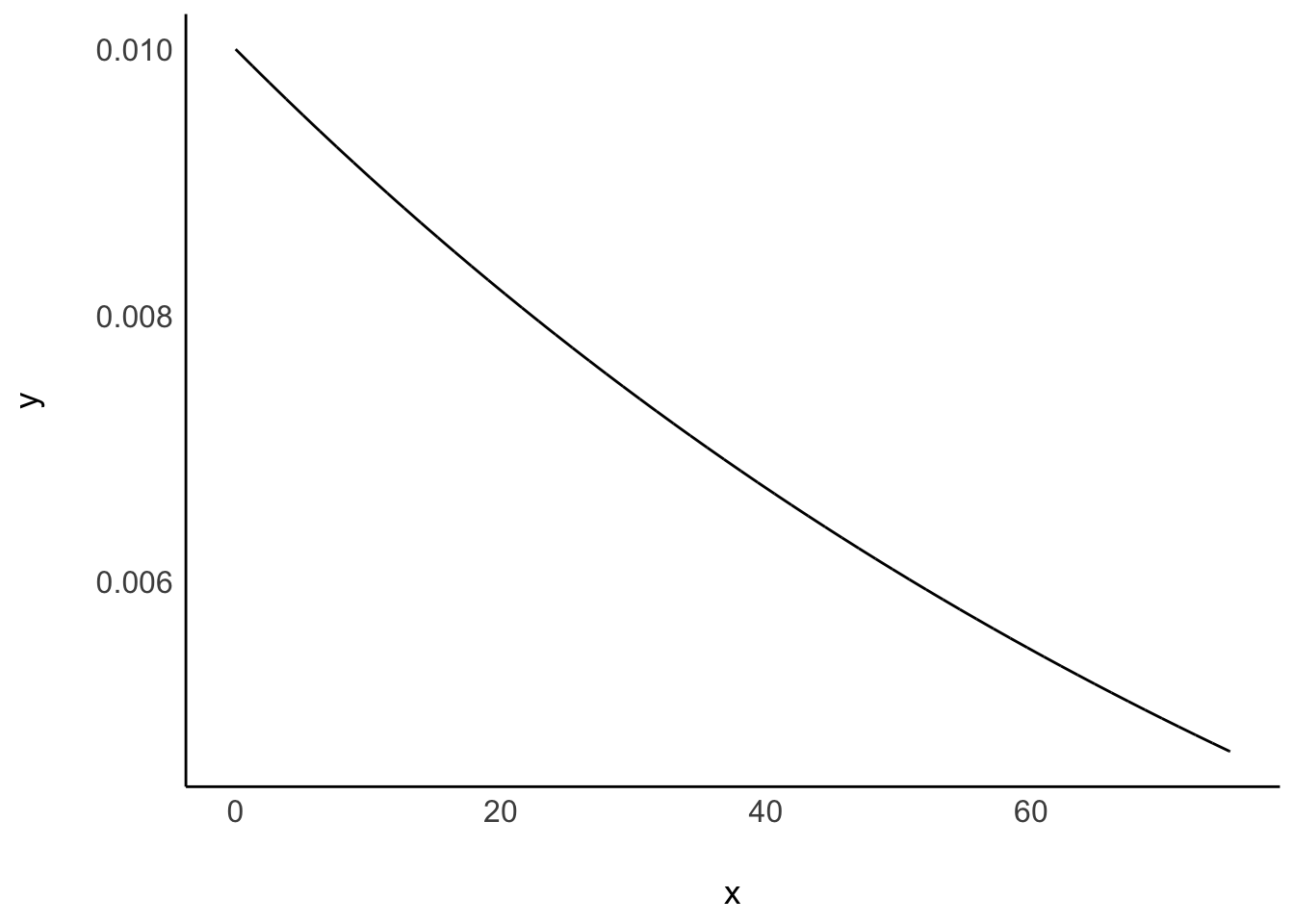
Apriori-Verteilung für \(\sigma\): die Streuung für den \(\sigma\) der Größen sei exponentialverteil (da notwendig positiv) mit \(\lambda = 1/8\).

\[\color{green}{\sigma \sim \mathcal{E}(1/8)} \qquad{\text{Prior}}\] Warum gerade \(\lambda=1/8\)? Das ist einfach ein grobes Abschätzen mit Blick auf Abbildung 5.9: Bei \(\lambda=1/8\) liegt der Median bei ca. 5 cm. Eine Streuung von ca. 5 cm um den Mittelwert herum erscheint nicht ganz falsch. Dann kann man folgern: \(95\%KI( \mu): 178 \pm 40\). In Worten: 95% der erwachsenen !Kung sind zwischen 138 cm und 218 cm groß - laut unserem Modell (unserer Apriori-Verteilung). Das ist ein ausreichend großer Bereich, um Überraschungen zuzulassen, aber eng genug, um biologisch unmögliche Werte auszuschließen.

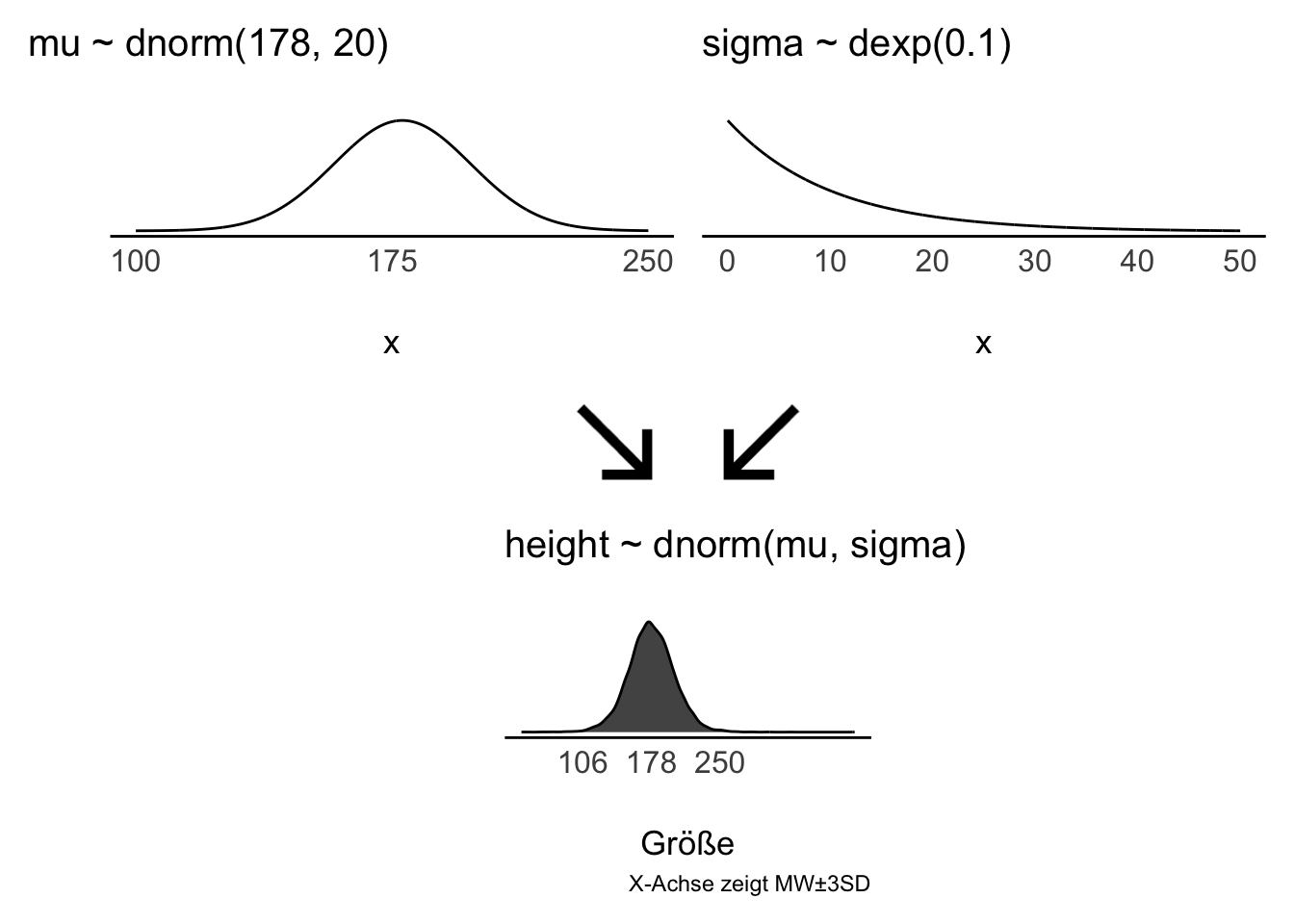
In Abbildung 8.3 sind unsere Priori-Verteilungen visualisiert.

Hinweis

Dieses Modell hat zwei Parameter, \(\mu\) und \(\sigma\). \(\square\)

Warum 178 cm? Kein besonderer Grund. Hier wollen wir den Effekt verschiedener Priori-Werte untersuchen.² In einer echten Untersuchung sollte man einen inhaltlichen Grund für einen Priori-Wert haben. Oder man wählt “schwach informative” Prioris, wie das {rstanarm} im Standard tut: Damit lässt man kaum Vorab-Information in das Modell einfließen, aber man verhindert extreme Prioris, die meistens unsinnig sind (so wie eine SD von 100 Metern bei der Körpergröße).

Hinweis

Wir haben zwar vorab nicht viel Wissen, aber auch nicht gar keines: Eine Gleichverteilung der Körpergrößen kommt nicht in Frage und ein vages Wissen zum Mittelwert haben wir auch. Darüber hinaus ist eine Normalverteilung für Körpergröße biologisch nicht unplausibel und spiegelt sich in den Daten wider, s. Abbildung 8.1.

8.3.3 Likelihood

Für viele Ausprägungen von \(\mu\) und \(\sigma\) müssen wir (bzw. Stan) die jeweilige Likelihood berechnen. Z.B. ist zu fragen, wie groß die Wahrscheinlichkeit ist, dass wir einen !Kung finden mit Körpergröße 190 bis 191 cm (\(h_i = [190,191]\)), gegeben der Hypothesen (Parameterwerte), dass der Populationsmittelwert \(\mu=170\) cm und der Streuung der Körpergrößen \(\sigma = 10\) cm beträgt. Nehmen wir an, dass die Körpergrößen, \(h_i\) normalverteilt sind, dann können wir die Likelihood anhand der Quantile der Normalverteilung berechnen. Etwa so:

\[L = Pr(h_i = [190;191]\quad |\mu=180, \sigma=10)\]

Aber da wir das Rechnen an Stan geben, begnügen wir uns mit einer Kurz-Schreibweise

\[\textcolor{orange}{h_i} \sim \mathcal{\textcolor{orange}{N}}(\textcolor{blue}{\mu}, \textcolor{green}{\sigma}) \qquad \textcolor{black}{\textcolor{orange}{Likelihood}}\]

Lies: “Die Körpergröße ist normalverteilt mit Mittelwert \(\mu\) und Streuung \(\sigma\).” Stan weiß dann, was er zu tun hat. Für die Post-Verteilung muss Stan für alle plausiblen Kombinationen von \(\mu\) und \(\sigma\) die Likelihoods berechnen, s. Abbildung 8.4.

Abbildung 8.4: Die Verteilung der der Körpergrößen, \(h_i\) setzt sich aus zwei Verteilungen zusammen: Dem Mittelwert \(\mu\) und der exponentialverteilten Streuung \(\sigma\)

Jetzt haben wir unser Modell (m_kung) definiert!

Weil es so schön ist, schreiben/zeichnen wir es hier noch einmal auf, Gleichung 8.1.

\[ \begin{aligned} \mu &\sim \mathcal{N}(M=178, S=20) & \text{Prior} \\ \sigma &\sim \mathcal{E}(1/8) & \text{Prior} \\ h_i &\sim \mathcal{N}(\mu, \sigma) & \text{Likelihood} \\ \end{aligned} \tag{8.1}\]

8.3.4 Post-Verteilung berechnen mit Stan

Zur Berechnung von m_kung nutzen wir jetzt dieses Mal aber nicht die Bayesbox, sondern lassen Stan (in R) die Arbeit verrichten.

Okay, Stan, du Golem unseres Vertrauens! An die Arbeit! Berechne uns das Kung-Modell!

# library(rstanarm)  # nicht vergessen, das Paket zu starten
m_kung <- 
  stan_glm(height ~ 1,
  prior_intercept = normal(178, 20),
  prior_aux = exponential(1/8),
  refresh = 0,
  data = kung_erwachsen)  

m_kung_post <- as_tibble(m_kung)
names(m_kung_post) <- c("mu", "sigma")

1: Stan berechnet die Post-Verteilung für die Körpergrößen, \(h_i\), hier height genannt
2: Apriori für \(\mu\)
3: Apriori für \(\sigma\)
4: Stan soll nicht so geschätzig sein und alle seine Stichproben am Bildschirm zeigen, sondern nur das Wichtigste zurückmelden.
5: Modellergebnis in Tabelle umwandeln
6: Schönere Namen für die Spalten geben

Mit stan_glm rufen wir Stan zur Arbeit. stan_glm³ ist eine Funktion, mit der man Regressionsmodelle berechnen kann. Nun haben wir in diesem Fall kein “richtiges” Regressionsmodell. Man könnte sagen, wir haben eine AV (Körpergröße), aber keine UV (keine Prädiktoren). Glücklicherweise können wir auch solche “armen” Regressionsmodelle formulieren: av ~ 1 bzw. in unserem Beispiel height ~ 1 bedeutet, dass man nur die Verteilung der AV berechnen möchte, aber keine Prädiktoren hat (das soll die 1 symbolisieren).

Betrachten wir die Post-Verteilungen von \(\mu\) und von \(\sigma\), fig-kung3.

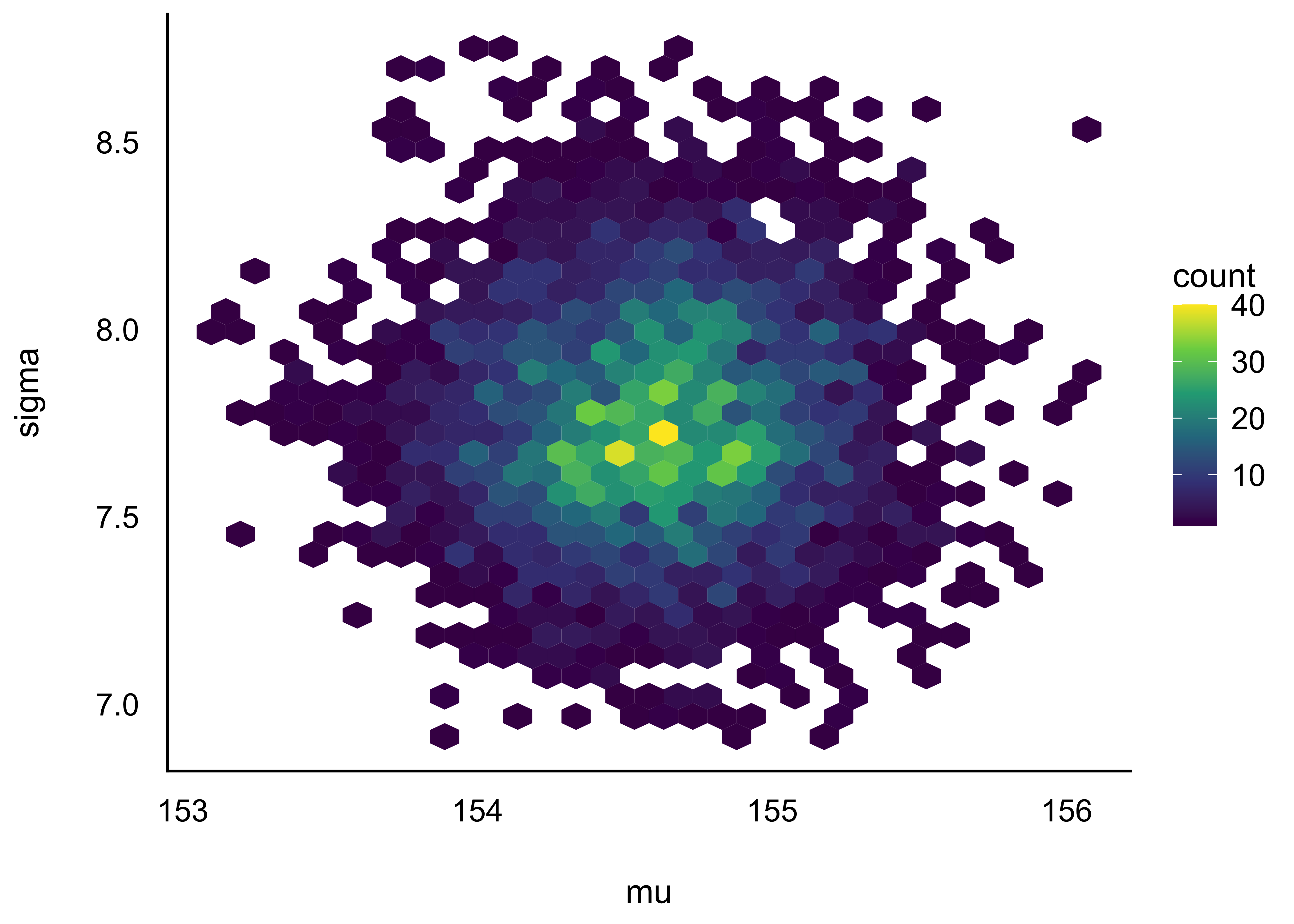
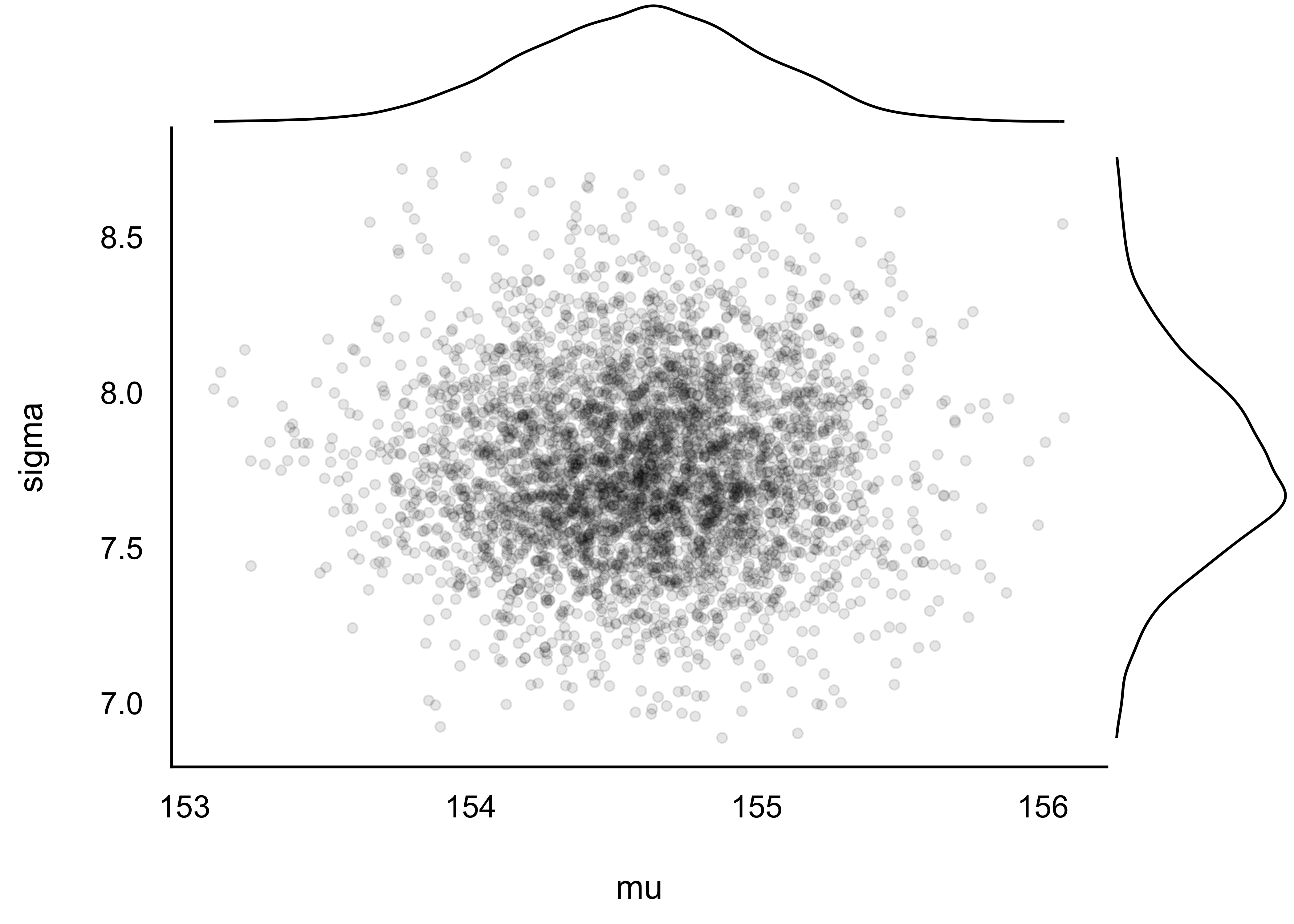
Abbildung 8.5: Die beiden Randverteilungen der Post-Verteilungen, d.h. die Verteilungen für mu und für sigma

Plotten wir mal die gemeinsame Post-Verteilung von m_kung, s. Abbildung 8.6, also die Kombinationen, die “Pärchen” der Werte von Mittelwert und Streuung.

Gemeinsame Post-Verteilung von Mittelwert, \(\mu\) und Streuung, \(\sigma\)

m_kung_post %>% 
  ggplot() +
  aes(x = mu, y = sigma) %>% 
  geom_hex() +
  scale_fill_viridis_c()

Abbildung 8.6: Die gemeinsame Post-Verteilung von Mittelwert und Streuung von m_kung_neue_prioris

Abbildung 8.7: Die Postverteilung in unterschiedlicher Darstellung

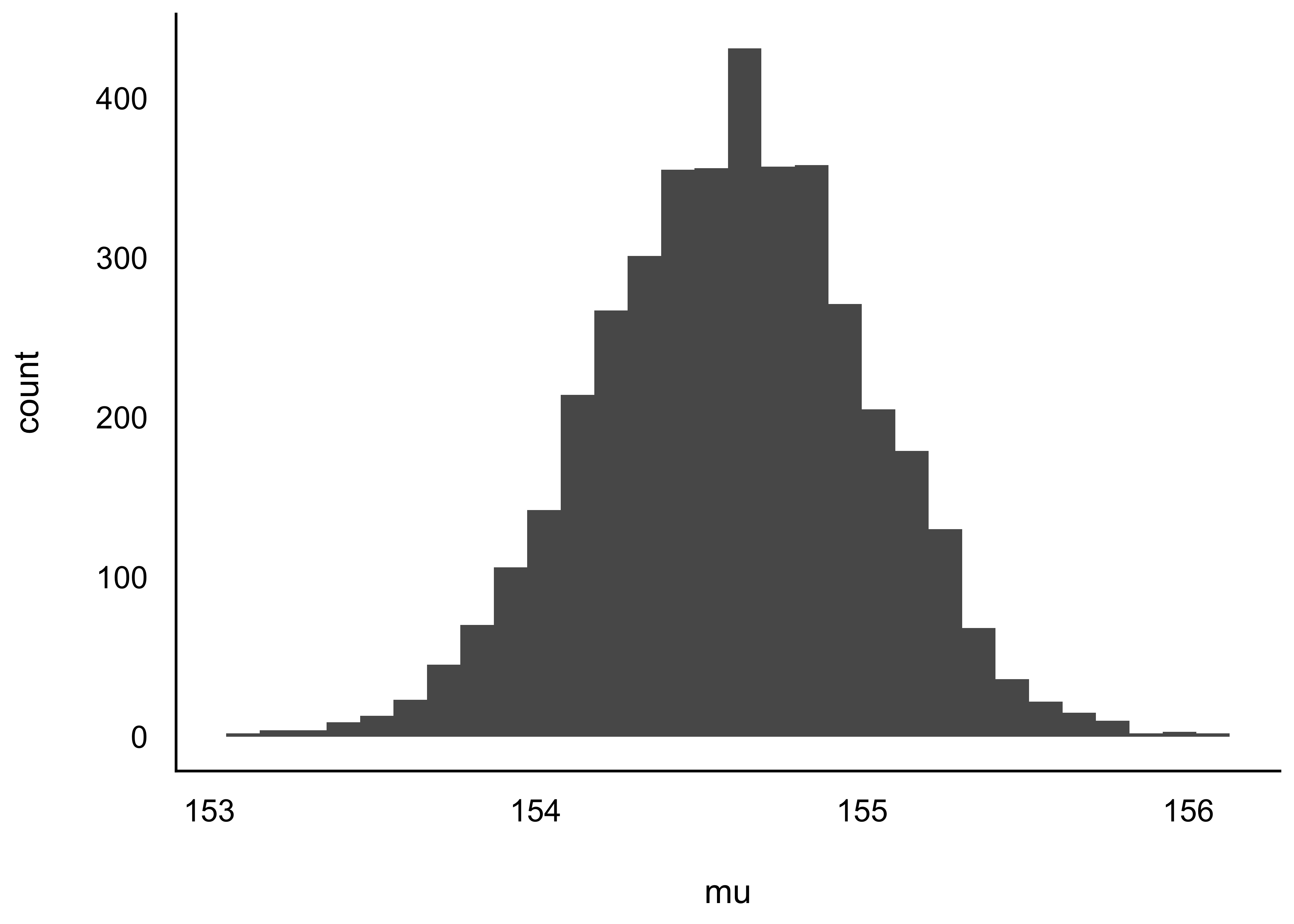
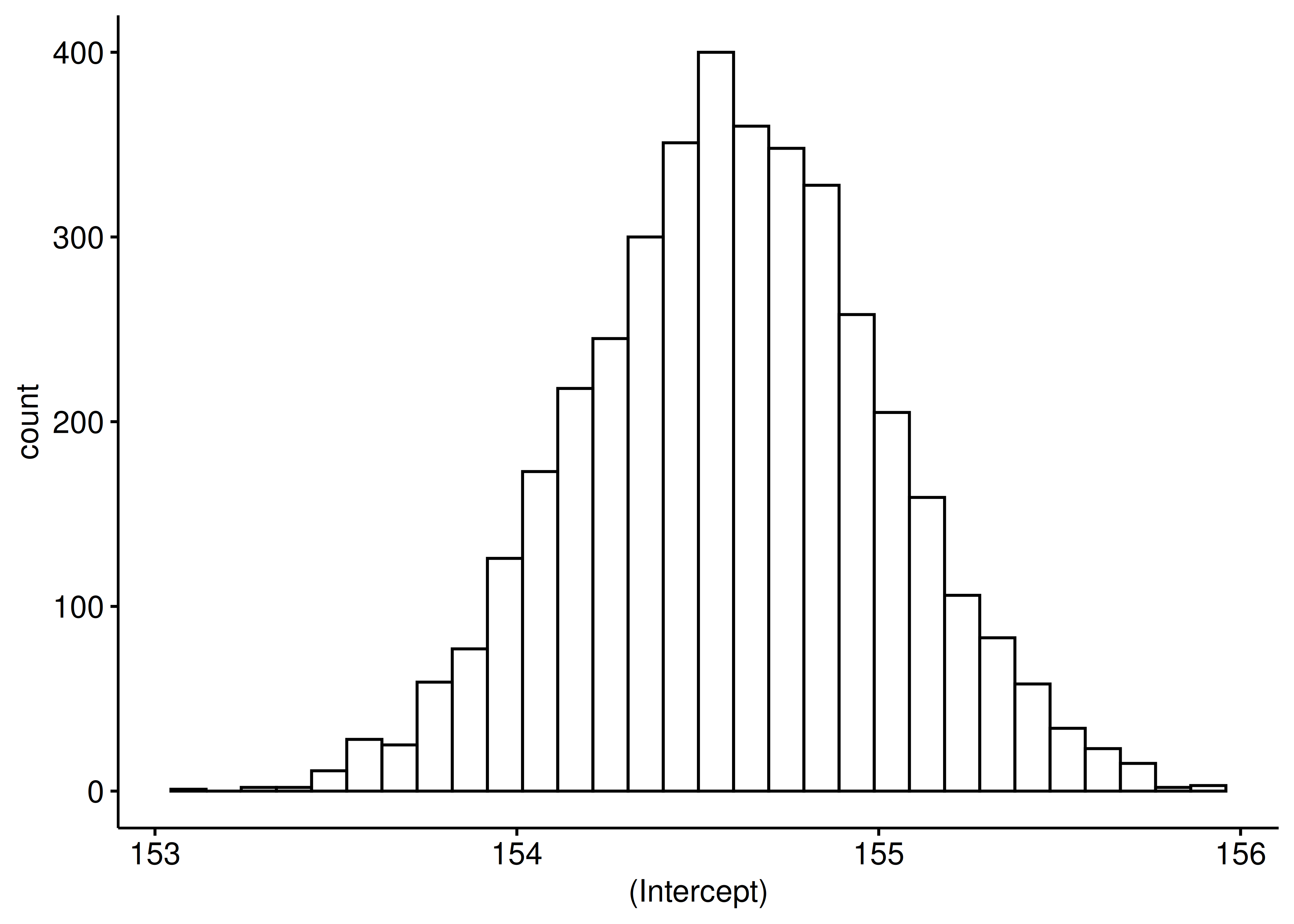
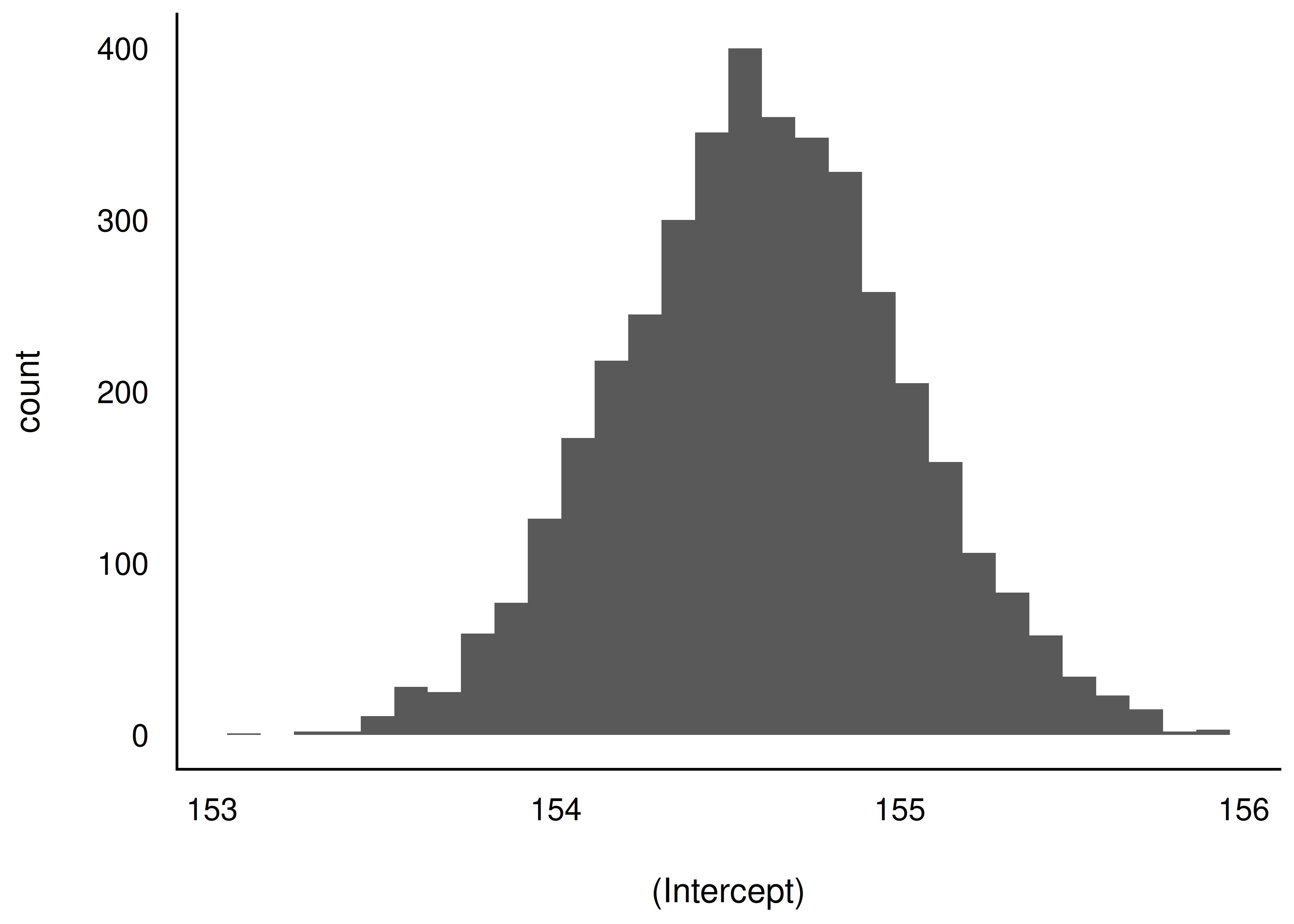
Und hier kommt die Post-Verteilung nur des Mittelwerts.

Natürlich können wir auch nur von einem einzelnen Parameter (z.B. Mittelwert) die Verteilung untersuchen, s. Abbildung 8.8.

Abbildung 8.8: Die Post-Verteilung von mu in m_kung_neue_prioris; ein Balkendiagramm bietet sich an.

Da das Modell zwei Parameter hat, können wir auch beide gleichzeitig plotten. Wie man sieht, sind die beiden Parameter unkorreliert. In anderen Modellen können die Parameter korreliert sein. Abbildung 8.6 erlaubt uns, für jede Kombination von Mittelwert und Streuung zu fragen, wie wahrscheinlich diese bestimmte Kombination ist.

Fassen wir die Ergebnisse dieses Modells zusammen:

Wir bekommen eine Wahrscheinlichkeitsverteilung für \(\mu\) und eine für \(\sigma\) (bzw. eine zweidimensionale Verteilung, für die \(\mu,\sigma\)-Paare).
Trotz des eher vagen Priors ist die Streuung Posteriori-Werte für \(\mu\) und \(\sigma\) klein: Die große Stichprobe hat die Priori-Werte überstimmt.
Ziehen wir Stichproben aus der Posteriori-Verteilung, so können wir interessante Fragen stellen.

8.4 Hallo, Posteriori-Verteilung

… wir hätten da mal ein paar Fragen an Sie. 🕵

Mit welcher Wahrscheinlichkeit ist die mittlere !Kung-Person größer als 1,55m?
Welche mittlere Körpergröße wird mit 95% Wahrscheinlichkeit nicht überschritten, laut dem Modell?
In welchem 90%-PI liegt \(\mu\) vermutlich?
Mit welcher Unsicherheit ist die Schätzung der mittleren Körpergröße behaftet?
Was ist der mediane Schätzwert der mittleren Körpergröße, sozusagen der “Best Guess”?

Antworten folgen etwas weiter unten.

8.4.1 Posteriori-Stichproben von `stan_glm()` berechnen lassen

Mit stan_glm() können wir komfortabel die Posteriori-Verteilung berechnen. Die Gittermethode wird nicht verwendet, aber die Ergebnisse sind - für unsere Fälle - ähnlich. Es werden aber auch viele Stichproben simuliert (sog. MCMC-Methode).

Grob gesagt berechnen wir die Post-Verteilung mit stan_glm so: stan_glm(AV ~ UV, data = meine_daten).

Wir können, wie wir es oben getan haben, uns die Stichproben der Post-Verteilung ausgeben lassen, und diese z.B. plotten.

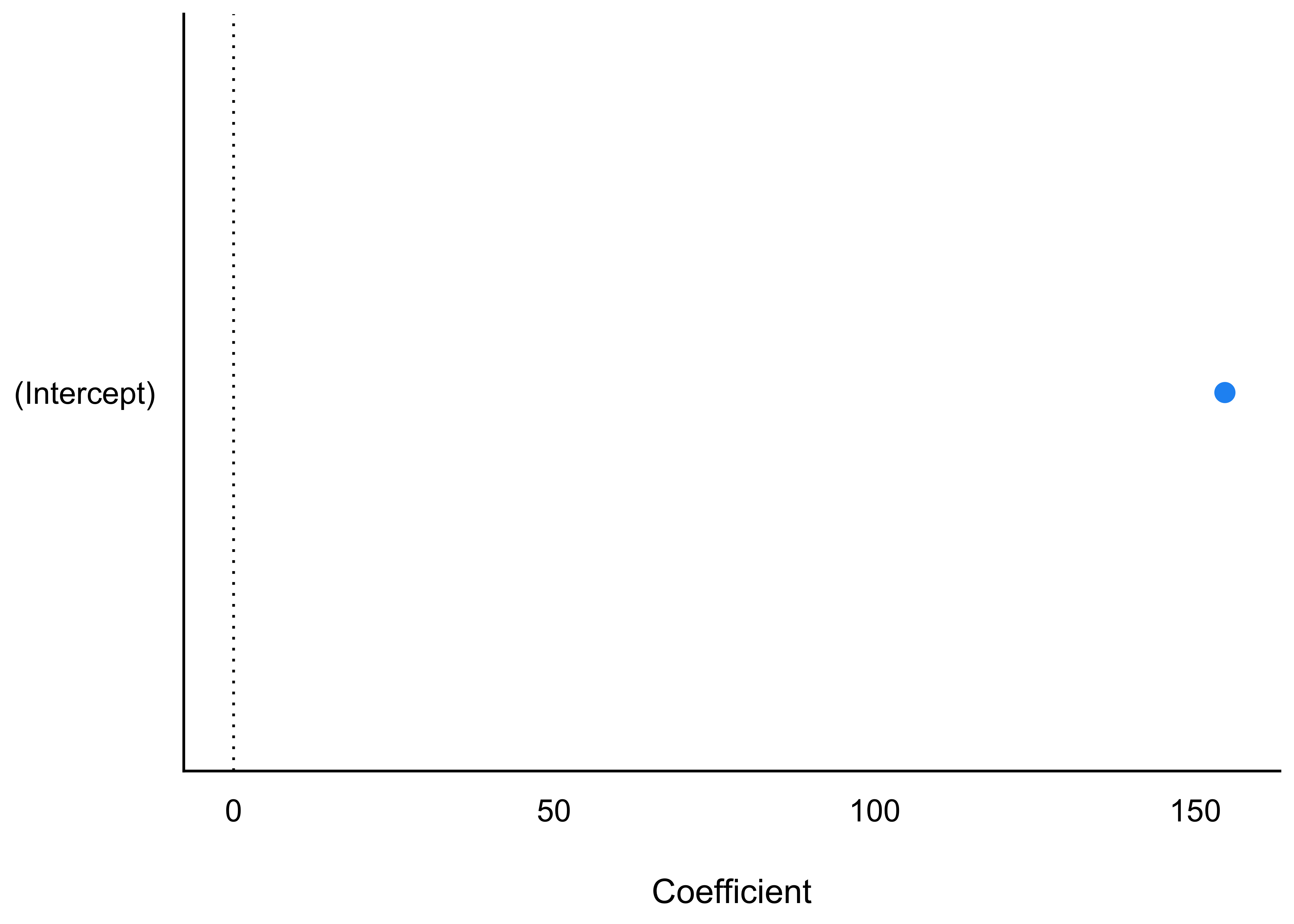
Wir können es aber auch komfortabler haben … Mit dem Befehl parameters kann man sich die geschätzten Parameterwerte einfach ausgeben lassen (s. Abbildung 8.6).

parameters(m_kung)  # aus Paket `easystats`

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	154.61	(153.81, 155.43)	100%	1.000	2404	Normal (178 +- 20)

Das Wesentliche: Unser Golem schätzt den Größenmittelwert der Kung auf ca. 155cm bzw. auf einen Bereich von etwa 153.81 bis 155.43 schätzt (95%-ETI in der Voreinstellung⁴). Informativ ist vielleicht noch, dass wir den Prior erfahren, der im Modell verwendet wurde. Dazu später mehr.

Hinweis

In dieser Ausgabe sind ein paar Angaben, die wir nicht verstehen, wie pd, Rhat und ESS. Kein Problem: Einfach ignorieren 🤓 Wer Näheres wissen will, findet hier einen Anfang. Außerdem sei an McElreath (2020) und Gelman et al. (2021) verwiesen. \(\square\)

8.5 Wie tickt `stan_glm()`?

Quelle

Hier ein paar Kerninfos zu stan_glm:

Stan ist eine Software zur Berechnung von Bayesmodellen; das Paket rstanarm stellt Stan für uns bereit.
stan_glm() ist für die Berechnung von Regressionsmodellen ausgelegt.
Will man nur die Verteilung einer einzelnen Variablen (wie heights) schätzen, so hat man man … eine Regression ohne Prädiktor.
Eine Regression ohne Prädiktor schreibt man auf Errisch so: y ~ 1. Die 1 steht also für die nicht vorhandene UV; y meint die AV (height).
(Intercept) (Achsenabschnitt) gibt den Mittelwert an.

Mehr findet sich in der Dokumentation von RstanArm.

8.5.1 Schätzwerte zu den Modellparameter

Die Parameter eines Modells sind die Größen, für die wir eine Priori-Verteilung annehmen. Außerdem wählen wir die Normalverteilung als Likelihood-Verteilung, so dass wir die Likelihood berechnen können. Auf dieser Basis schätzen wir dann die Post-Verteilung. Ich sage schätzen, um hervorzuheben, dass wir die wahren Werte nicht kennen, sondern nur eine Vermutung haben, unsere Ungewissheit vorab also (wie immer) in der Priori-Verteilung festnageln und unsere Ungewissheit nach Kenntnis der Daten in der Posteriori-Verteilung quantifizieren. Wie gerade gesehen, lassen sich die Modellparameter (bzw. genauer gesagt deren Schätzungen) einfach mit parameters(modellname) auslesen.

8.5.2 Stichproben aus der Posteriori-Verteilung ziehen

Wie wir es vom Globusversuch gewohnt sind, können wir aber auch Stichproben aus der Post-Verteilung ziehen.

Hier die ersten paar Zeilen von m_kung_post:

head(m_kung_post)

In einer Regression ohne Prädiktoren entspricht der Achsenabschnitt dem Mittelwert der AV, daher gibt uns die Spalte (Intercept) Aufschluss über unsere Schätzwerte zu \(\mu\) (der Körpergröße).

Übungsaufgabe 8.1 (Mit welcher Wahrscheinlichkeit ist \(\mu>155\)?)

Lösung


names(m_kung_post) <- 
  c("mu", "sigma")  # den Namen "(Intercept)" durch "mu" ersetzen, ist prägnanter

m_kung_post %>% 
  count(mu > 155) %>% 
  mutate(prop = n/sum(n))

Die Wahrscheinlichkeit ist nicht hoch, aber nicht auszuschließen, dass die Kung im Schnitt größer als 155 cm sind. Wahrscheinlicher ist jedoch, dass sie kleiner als 155 cm sind. \(\square\)

Übungsaufgabe 8.2 (Mit welcher Wahrscheinlichkeit ist \(\mu>165\)?)

Lösung

names(m_kung_post) <- 
  c("mu", "sigma")  # den Namen "(Intercept)" durch "mu" ersetzen, ist prägnanter

m_kung_post %>% 
  count(mu > 165) %>% 
  mutate(prop = n/sum(n))

Oh, diese Hypothese können wir mit an Sicherheit grenzender Wahrscheinlichkeit ausschließen. Aber Achtung: Das war eine Kleine-Welt-Aussage! Die Wahrscheinlichkeit, die Hypothese \(\mu > 165\) auszuschließen ist nur dann hoch, wenn das Modell gilt! Wenn also der Golem keinen Mist gebaut hat. Und sind wir mal ehrlich, der Golem tut, was sein:e Herr:in und Meister:in ihm befiehlt. Letztlich liegt es an uns, den Golem auf Spur zu kriegen.

Beispiel 8.3 (Welche mittlere Körpergröße wird mit 95% Wahrscheinlichkeit nicht überschritten, laut dem Modell m_kung?)

Lösung

m_kung_post %>% 
  summarise(q95 = quantile(mu, .95))

Übungsaufgabe 8.3 (In welchem 90%-PI liegt \(\mu\) vermutlich?)

Lösung

m_kung_post %>% 
  eti()

Ein ETI ist synonym zu PI.

Übungsaufgabe 8.4 (Mit welcher Unsicherheit ist die Schätzung der mittleren Körpergröße behaftet?)

Lösung

m_kung %>% 
  parameters()

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	154.61	(153.81, 155.43)	100%	1.000	2404	Normal (178 +- 20)

Seeing is believing, s. Abbildung 8.9.

m_kung %>% 
  parameters() %>% 
  plot(show_intercept = TRUE)

Abbildung 8.9: Parameter von m_kung, nur einer: der Intercept

Das Modell ist sich recht sicher: die Ungewissheit der mittleren Körpergröße liegt bei nicht viel mehr als einem Zentimeter (95%-CI).

Übungsaufgabe 8.5 (Was ist der mediane Schätzwert der mittleren Körpergröße, sozusagen der “Best Guess”?)

Lösung

parameters(m_kung) hat uns die Antwort schon gegeben: Ca. 155 cm.

🏋️ Ähnliche Fragen bleiben als Übung für die Lesis. 🤓

8.5.3 Standard-Prioriwerte bei `stan_glm()`

Man kann stan_glm() auch ohne Priori-Werte aufrufen. In dem Fall bestimmt Stan die Priori-Werte selber. Welche das sind, kann man sich so anzeigen lassen:

prior_summary(m_kung)
## Priors for model 'm_kung' 
## ------
## Intercept (after predictors centered)
##  ~ normal(location = 178, scale = 20)
## 
## Auxiliary (sigma)
##  ~ exponential(rate = 0.12)
## ------
## See help('prior_summary.stanreg') for more details

Aber welche Priori-Werte verwendet Stan? Ganz einfach: Stan zieht die Stichproben-Daten als Prioris heran. Strenggenommen ist das nicht “pures Bayes”, weil die Priori-Werte ja vorab, also vor Kenntnis der Daten bestimmt werden sollen.

Man sollte diese Standardwerte als (komfortablen) Minimalvorschlag sehen. Kennt man sich im Sachgebiet aus, kann man meist bessere Prioris finden. Die Voreinstellung ist nicht zwingend; andere Werte wären auch denkbar.

Standardwerte von stan_glm

Intercept: \(\mu\), der Mittelwert der Verteilung \(Y\)
- \(\mu \sim \mathcal{N}(\bar{Y}, sd(Y)\cdot 2.5)\)
- als Streuung von \(\mu\) wird die 2.5-fache Streuung der Stichprobe (für \(Y\)) angenommen.
Auxiliary (sigma): \(\sigma\), die Streuung der Verteilung \(Y\)
- \(\sigma \sim \mathcal{E}(\lambda=1/sd(Y))\)
- als “Streuung”, d.h. \(\lambda\) von \(h_i\) wird \(\frac{1}{sd(Y)}\) angenommen. \(\square\)

Eine sinnvolle Strategie ist, einen Prior so zu wählen, dass man nicht übergewiss ist, also nicht zu sicher Dinge behauptet, die dann vielleicht doch passieren (also die Ungewissheit zu gering spezifiziert), andererseits sollte man extreme, unplausible Werte ausschließen.

Wichtig

Bei der Wahl der Prioris gibt es nicht die eine, richtige Wahl. Die beste Entscheidung ist auf transparente Art den Stand der Forschung einfließen zu lassen und eigene Entscheidungen zu begründen. Häufig sind mehrere Entscheidungen möglich. Möchte man lieber vorsichtig sein, weil man wenig über den Gegenstand weiß, dann könnte man z.B. auf die Voreinstellung von rstanarm vertrauen, die “schwachinformativ” ist, also nur wenig Priori-Information in das Modell einfließen lässt.

8.5.4 Wenn es schnell gehen muss

stan_glm() ist deutlich langsamer als z.B. der befreundete Golem lm(). Der Grund für Stans Langsamkeit ist, dass er viele Stichproben zieht, also viel zu zählen hat. Außerdem wiederholt er das Stichprobenziehen (im Standard) 4 Mal, damit sein Meister prüfen kann, ob er (Stan) die Arbeit auch immer richtig gemacht hat. Die Idee dabei ist, wenn alle vier Durchführungen (auch “Ketten” engl., chains) genannt, zum etwa gleichen Ergebnis kommen, dann wird schon alles mit rechten Dingen zugegangen sein. Weichen die Ergebnisse der 4 Ketten voneinander ab, so ist Stan ein Fehler unterlaufen, oder, irgendetwas ist “dumm gelaufen”. An dieser Stelle schauen wir uns die Ketten nicht näher an, aber es sei notiert, dass man die Anzahl der Ketten mit dem Argument chains steuern kann. Möchte man, dass Stan sich beeilt, so kann man chains = 1 setzen, das spart Zeit, s. m_kung_1kette.

m_kung_1kette <- stan_glm(height ~ 1, 
                 data = kung_erwachsen, 
                 chains = 1,  # nur 1 Kette, anstelle von 4 im Default, spart Zeit
                 refresh = 0) 

parameters(m_kung_1kette)

8.6 Modell `m_kung_neue_prioris`: Standard-Priori-Werte

Im Modell m_kung haben wir unsere eigenen Priori-Werte einfließen lassen. Jetzt vertrauen wir die Wahl der Prioris Stand an. Betrachten Sie dazu unser zweites Kung-Modell, m_kung_neue_prioris.

m_kung_neue_prioris <- 
  stan_glm(height ~ 1,
           refresh = FALSE,  # bitte nicht so viel Ausgabe drucken
           data = kung_erwachsen)
parameters(m_kung_neue_prioris)

Tabelle 8.2: Parameter von m_kung_neue_prioris mit Standard-rioriwerten

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	154.60	(153.78, 155.42)	100%	1.001	2189	Normal (154.60 +- 19.36)

Wir haben noch nicht alle Informationen kennengelernt, die in Tabelle 8.2 ausgegeben werden. Im Zweifel: Einfach ignorieren. Wichtige Fähigkeit im Studium. 🤓

Wichtig

Vergleichen Sie die Parameterwerte von m_kung und m_kung_neue_prioris! Was fällt Ihnen auf? Nichts? Gut! Tatsächlich liefern beide Modelle sehr ähnliche Parameterwerte. Die Prioriwerte waren nicht so wichtig, weil wir genug Daten haben. Hat man einigermaßen viele Daten, so fallen Prioriwerte nicht mehr ins Gewicht, zumindest wenn sie moderat gewählt waren.

8.6.1 Posteriori-Verteilung und Parameter plotten

Leider liefert der Stan-Golem leider keinen braven Tibble (Tabelle) zurück.

👨‍🏫 Mensch, Stan, streng dich mal ein bisschen an!

🤖 Mach’s halt selber, wenn du es besser kannst!

Daher müssen wir die Ausgabe des Stan-Golemns erst in eine schöne Tabelle umwandeln:

m_kung_neue_prioris_tibble <-
  as_tibble(m_kung_neue_prioris)

head(m_kung_neue_prioris_tibble)

Außerdem ist der Name der ersten Spalte eigentlich unzulässig, da Spaltennamen in R nicht mit Sonderzeichen anfangen dürfen (sondern mit Buchstaben). Daher müssen wir den Namen mit “Samthandschuhen” anpacken. Auf Errisch sind das die Backticks, die wir um den Namen rumwickeln müssen, s. die folgende Syntax.

Mit {ggpubr}
Mit {ggplot}

m_kung_neue_prioris_tibble |> 
  gghistogram(x = "`(Intercept)`")  # Aus dem Paket "ggpubr"

m_kung_neue_prioris_tibble |> 
  ggplot(aes(x = `(Intercept)`)) +  # Aus dem Paket `ggplot2`
  geom_histogram()

Als Ausblick: Ein Vergleich mehrerer Priori-Werte wäre auch nützlich, um ein skeptisches Publikum von der Wahl (bzw. der Indifferenz) der gewählten Priori-Werte zu überzeugen.

8.6.2 Welche Körpergrößen erwartet unser Modell

Bisher haben wir untersucht, wie die Verteilung der mittleren Körpergrößen, \(\mu\), laut unserem Modell aussehen könnte; wir haben uns also mit der Post-Verteilung von \(\mu\) beschäftigt. Wir könnten aber auch an der Frage der Verteilung der tatsächlichen Körpergrößen, \(h_i\), laut Modell, interessiert sein: Wie groß sind sie denn, die !Kung, laut unserem Modell?

Wie wir wissen, liefert unser Stan-Golem eine Stichproben-Postverteilung. Wenn wir das Ergebnisobjekt unserer Analyse, m_kung in eine Tabelle (Tibble) umwandeln und (die ersten paar Zeilen) betrachen, sehen wir diese Stichproben:

m_kung |> as_tibble() |> head()

Laut unserem Modell sind die Körpergrößen, \(h_i\), normalverteilt mit \(\mu\) und \(\sigma\). \(\mu\) wird von Stan, der in Begriffen der Regressionsanalyse denkt, schnöde als (Intercept) bezeichnet. Wir könnten jetzt also für jede Zeile eine Normalverteilung berechnen. Und daraus zufällig eine Zahl ziehen. Damit hätten wir dann unsere Verteilung von Körpergrößen laut Modell. Diese Verteilung nennt man auch Posterior-Prädiktiv-Verteilung. Prädiktiv daher, weil sie die Werte der Körpergrößen “vorhersagt”.

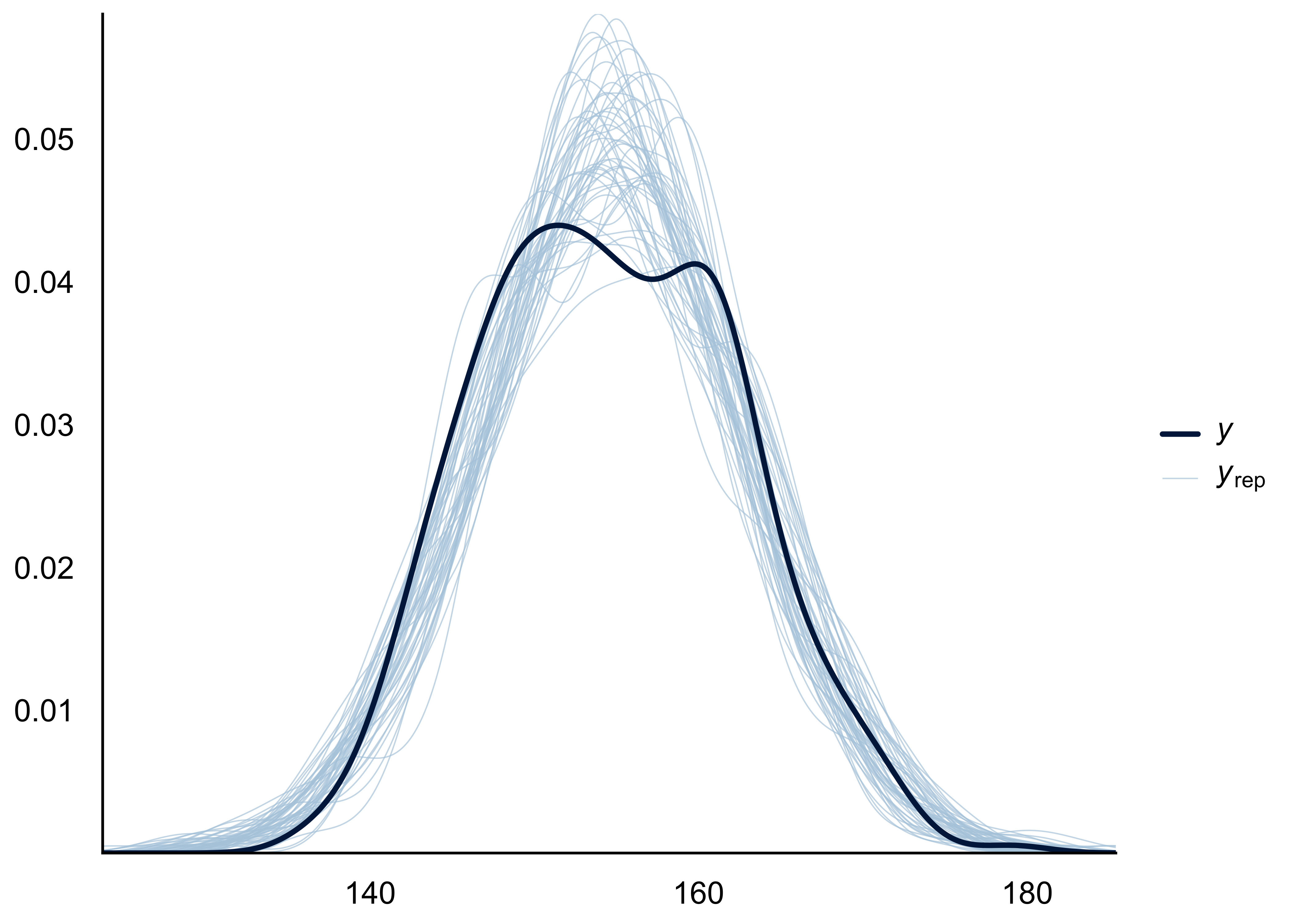
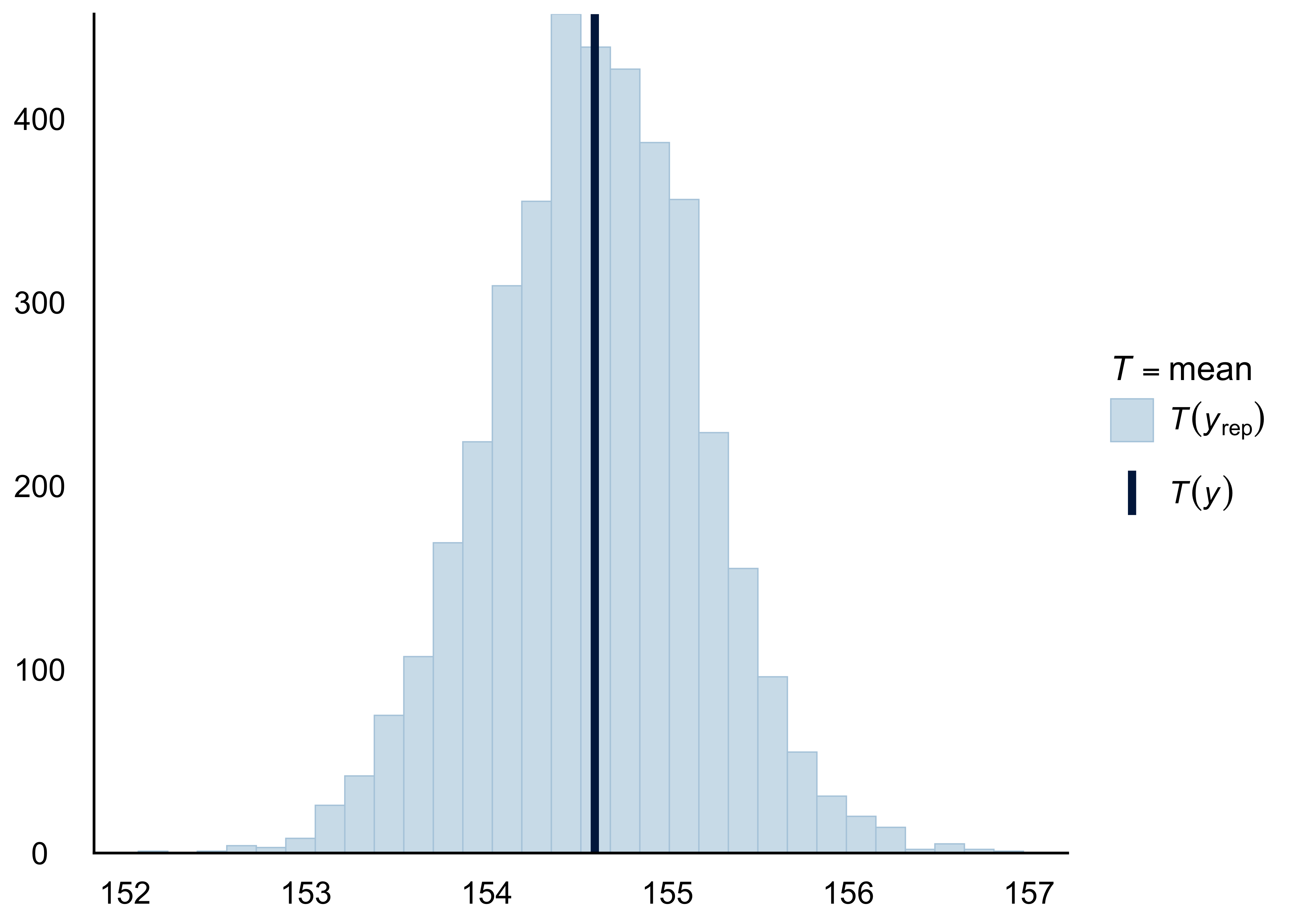
Wir können uns diese Verteilung auch komfortabel von R ausgeben lassen, s. Abbildung 8.10.

pp_check(m_kung)
pp_check(m_kung, "stat")

(a) Die dunkle, dicke Dichtekurve zeigt die tatsächliche Verteilung der Körpergrößen im Datensatz. Die hellen, leichten Dichtekurven zeigen die Verteilungen laut der Post-Verteilung unseres Modells.

8.7 Fazit

8.7.1 Zusammenfassung

Wir haben die Posteriori-Verteilung für ein Gauss-Modell berechnet. Dabei hatten wir ein einfaches Modell mit metrischer Zielvariablen, ohne Prädiktoren, betrachtet. Die Zielvariable, Körpergröße (height), haben wir als normalverteilt mit den Parametern \(\mu\) und \(\sigma\) angenommen. Für \(\mu\) und \(\sigma\) haben wir jeweils keinen einzelnen (fixen) Wert angenommen, sondern eine Wahrscheinlichkeitsverteilung, der mit der Priori-Verteilung für \(\mu\) bzw. \(\sigma\) festgelegt ist.

8.7.2 Botschaft von einem Statistiker

Wichtig

Kontinuierliches Lernen ist der Schlüssel zum Erfolg.

8.8 Vertiefung: Wahl der Priori-Werte

🏎️ Dieser Abschnitt ist eine VERTIEFUNG und nicht prüfungsrelevant. 🏎

8.8.1 Welche Beobachtungen sind auf Basis unseres Modells zu erwarten?

n <- 1e4

sim <- tibble(sample_mu  = 
      rnorm(n, 
            mean = 178, 
            sd   = 20),
    sample_sigma = 
      rexp(n, 
            rate = 0.1)) %>% 
  mutate(height  = 
      rnorm(n, 
            mean = sample_mu, 
            sd   = sample_sigma))

height_sim_sd <- 
  sd(sim$height) %>% round()
height_sim_mean <- 
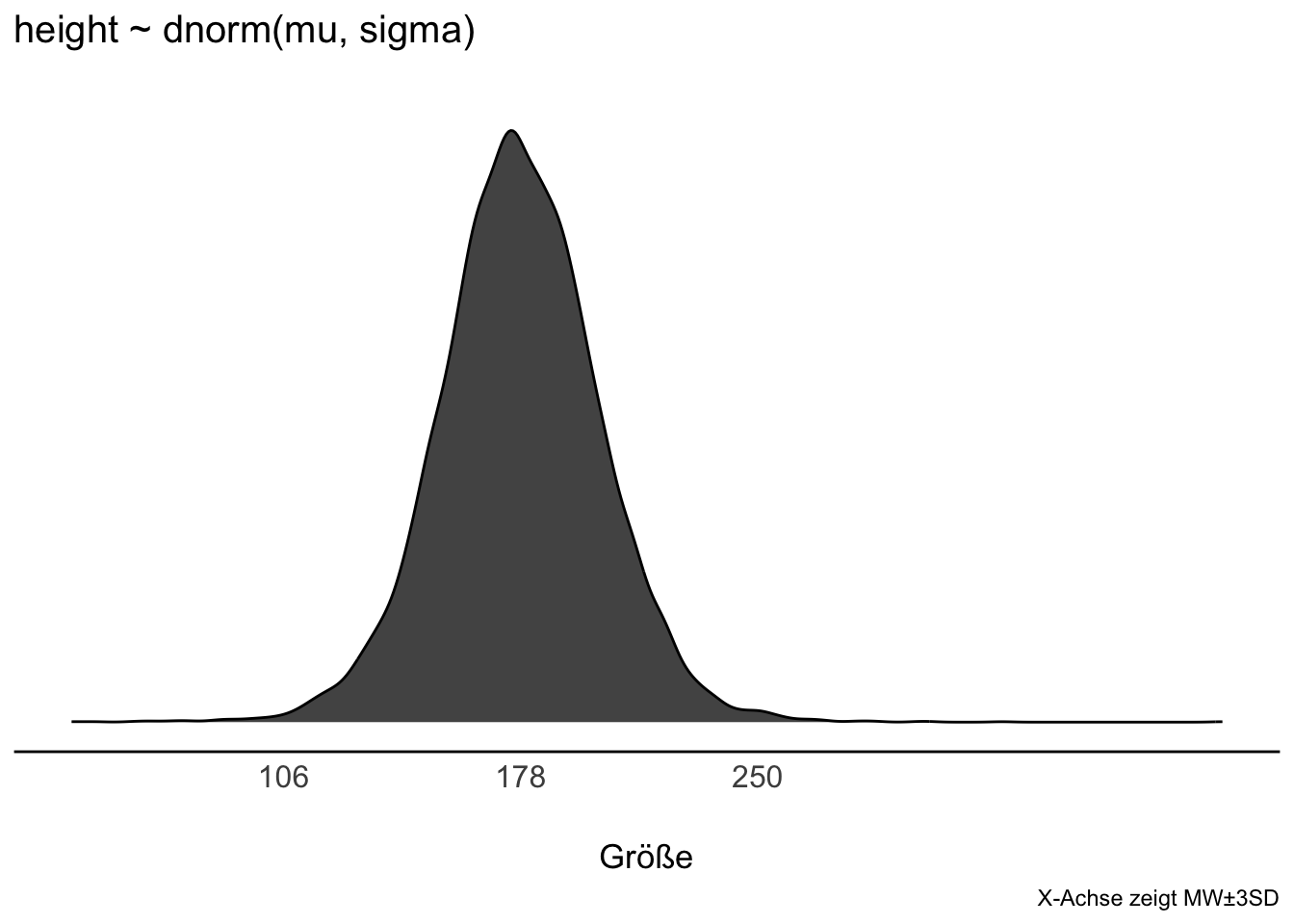
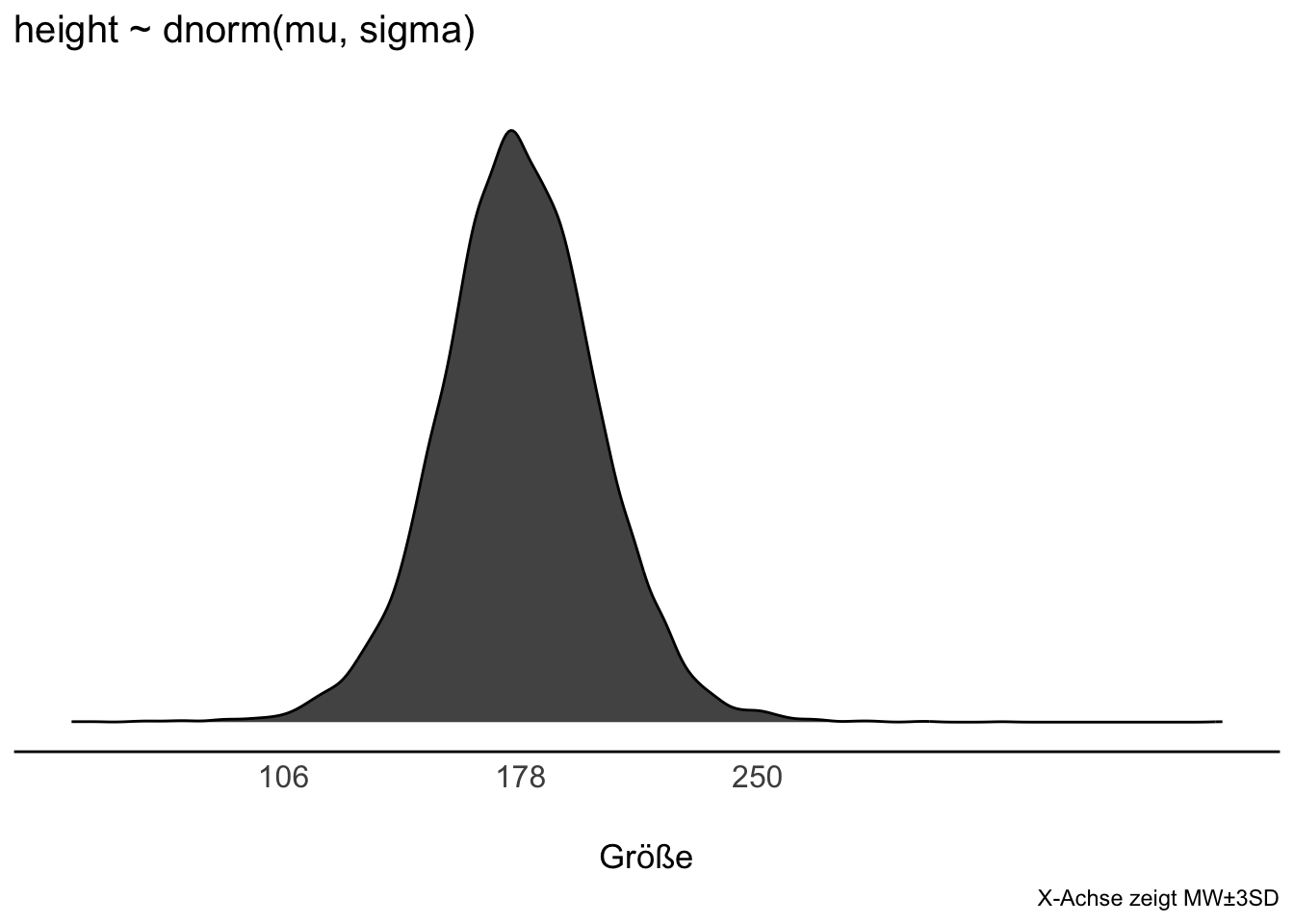
  mean(sim$height) %>% round()

💭 Was denkt der Golem (m_kung) apriori von der Größe der !Kung?

🦾 Ziehen wir mal ein paar Stichproben auf Basis des Modells. Voilà:

p3 <- 
  sim %>% 
  ggplot(aes(x = height)) +
  geom_density(fill = "grey33") +
  scale_x_continuous(breaks = c(0, 178-3*height_sim_sd, 178, 178+3*height_sim_sd)) +
  scale_y_continuous(NULL, breaks = NULL) +
  labs(title = "height ~ dnorm(mu, sigma)",
       caption = "X-Achse zeigt MW±3SD",
       x = "Größe") +
  theme(panel.grid = element_blank()) 

p3

Quellcode

8.8.2 Priori-Werte prüfen mit der Priori-Prädiktiv-Verteilung

Die Priori-Prädiktiv-Verteilung (sim) simuliert Beobachtungen (nur) auf Basis der Priori-Annahmen: \(h_i \sim \mathcal{N}(\mu, \sigma),\) \(\mu \sim \mathcal{N}(178, 20),\) \(\sigma \sim \mathcal{E}(0.1)\)
So können wir prüfen, ob die Priori-Werte vernünftig sind.

Die Priori-Prädiktiv-Verteilung zeigt, dass unsere Priori-Werte ziemlich vage sind, also einen zu breiten Bereich an Größenwerten zulassen:

p3

Anteil \(h_i > 200\):

anteil_großer_kung <- 
sim %>% 
  count( height > 200) %>% 
  mutate(prop = n/sum(n))
anteil_großer_kung

🤔 Sehr große Buschleute? 17 Prozent sind größer als 2 Meter. Das ist diskutabel, muss aber nicht zwangsläufig ein schlechter Prior sein.

8.8.3 Vorhersagen der Priori-Werte

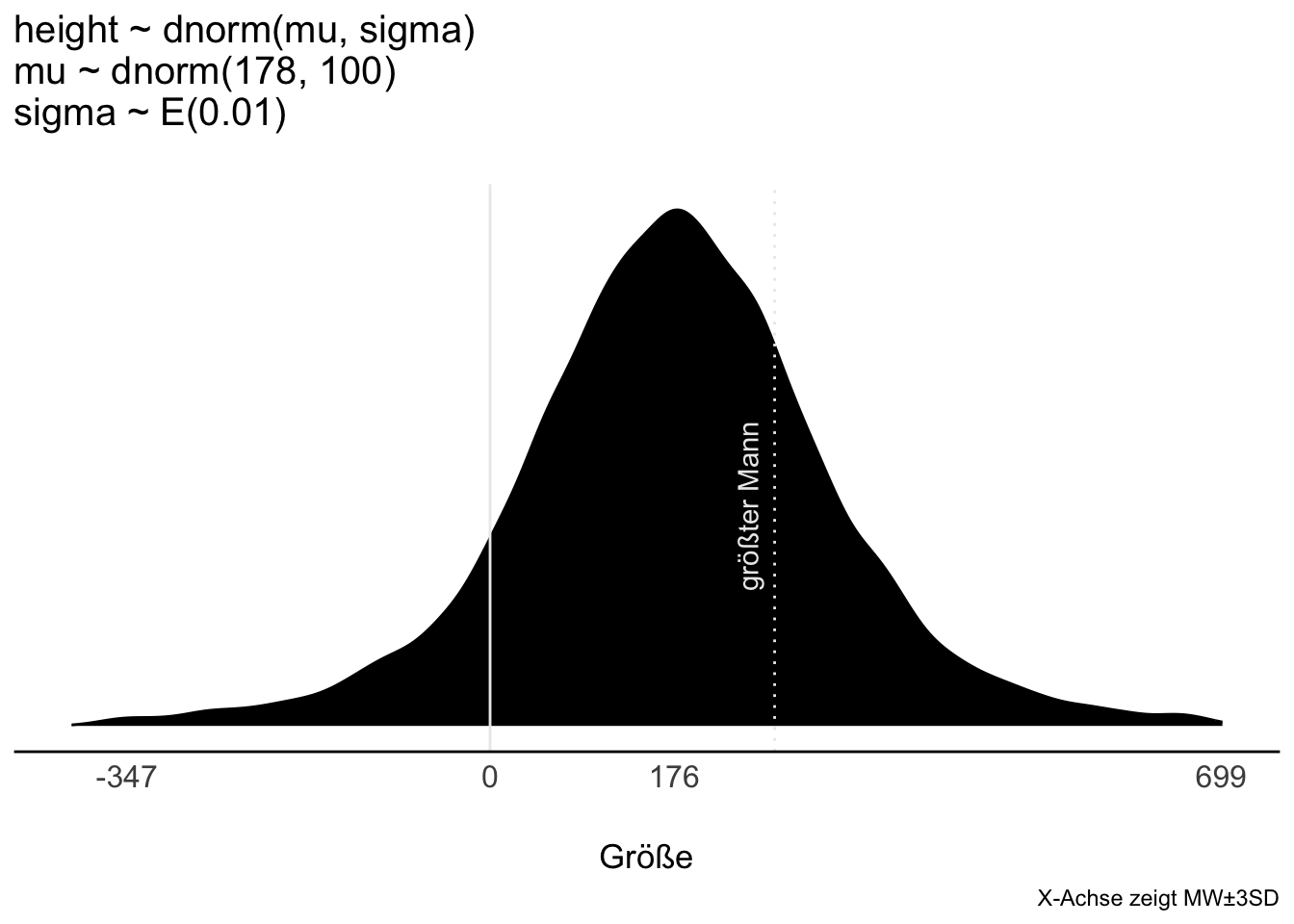
8.8.4 Extrem vage Priori-Verteilung für die Streuung?

\[\sigma \sim \mathcal{E}(\lambda=0.01)\]

Die Streuung der Größen ist weit:

d <- 
  tibble(x = seq(0,75, by =.01),
         y = dexp(x, rate = .01))

d %>% 
  ggplot(aes(x,y)) +
  geom_line()

🤔 Das Modell geht apriori von ein paar Prozent Menschen mit negativer Größe aus. Ein Haufen Riesen 👹 werden bei den !Kung auch erwartet.

🤯 Vage (flache, informationslose, “neutrale”, “objektive”) Priori-Werte machen oft keinen Sinn, weil sie extreme, unplausible Werte zulassen.

8.1 Lernsteuerung

8.1.1 Position im Modulverlauf

8.1.2 Lernziele

8.1.3 Begleitendes Lehrmaterial

8.1.4 Vorbereitung im Eigenstudium

8.1.5 Benötigte R-Pakete

8.1.6 Benötigte Daten

8.1.7 Einstieg

8.1.8 Stan stellt sich vor

8.2 Wie groß sind die !Kung San?

8.2.1 !Kung San

8.2.2 Wir gehen apriori von normalverteilter Größe Der !Kung aus

8.3 Unser Gauss-Modell der !Kung

8.3.1 Normalverteilung als Grundlage des Modells

8.3.2 Apriori-Verteilungen

8.3.3 Likelihood

8.3.4 Post-Verteilung berechnen mit Stan

8.4 Hallo, Posteriori-Verteilung

8.4.1 Posteriori-Stichproben von `stan_glm()` berechnen lassen

8.5 Wie tickt `stan_glm()`?

8.5.1 Schätzwerte zu den Modellparameter

8.5.2 Stichproben aus der Posteriori-Verteilung ziehen

8.5.3 Standard-Prioriwerte bei `stan_glm()`

8.5.4 Wenn es schnell gehen muss

8.6 Modell `m_kung_neue_prioris`: Standard-Priori-Werte

8.6.1 Posteriori-Verteilung und Parameter plotten

8.6.2 Welche Körpergrößen erwartet unser Modell

8.7 Fazit

8.7.1 Zusammenfassung

8.7.2 Botschaft von einem Statistiker

8.8 Vertiefung: Wahl der Priori-Werte

8.8.1 Welche Beobachtungen sind auf Basis unseres Modells zu erwarten?

8.8.2 Priori-Werte prüfen mit der Priori-Prädiktiv-Verteilung

8.8.3 Vorhersagen der Priori-Werte

8.8.4 Extrem vage Priori-Verteilung für die Streuung?

8.9 Aufgaben

8.9.1 Papier-und-Bleistift-Aufgaben

8.9.2 Aufgaben, für die man einen Computer benötigt

8.10 —

8.1 Lernsteuerung

8.1.1 Position im Modulverlauf

8.1.2 Lernziele

8.1.3 Begleitendes Lehrmaterial

8.1.4 Vorbereitung im Eigenstudium

8.1.5 Benötigte R-Pakete

8.1.6 Benötigte Daten

8.1.7 Einstieg

8.1.8 Stan stellt sich vor

8.2 Wie groß sind die !Kung San?

8.2.1 !Kung San

8.2.2 Wir gehen apriori von normalverteilter Größe Der !Kung aus

8.3 Unser Gauss-Modell der !Kung

8.3.1 Normalverteilung als Grundlage des Modells

8.3.2 Apriori-Verteilungen

8.3.3 Likelihood

8.3.4 Post-Verteilung berechnen mit Stan

8.4 Hallo, Posteriori-Verteilung

8.4.1 Posteriori-Stichproben von stan_glm() berechnen lassen

8.5 Wie tickt stan_glm()?

8.5.1 Schätzwerte zu den Modellparameter

8.5.2 Stichproben aus der Posteriori-Verteilung ziehen

8.5.3 Standard-Prioriwerte bei stan_glm()

8.5.4 Wenn es schnell gehen muss

8.6 Modell m_kung_neue_prioris: Standard-Priori-Werte

8.6.1 Posteriori-Verteilung und Parameter plotten

8.6.2 Welche Körpergrößen erwartet unser Modell

8.7 Fazit

8.7.1 Zusammenfassung

8.7.2 Botschaft von einem Statistiker

8.8 Vertiefung: Wahl der Priori-Werte

8.8.1 Welche Beobachtungen sind auf Basis unseres Modells zu erwarten?

8.8.2 Priori-Werte prüfen mit der Priori-Prädiktiv-Verteilung

8.8.3 Vorhersagen der Priori-Werte

8.8.4 Extrem vage Priori-Verteilung für die Streuung?

8.9 Aufgaben

8.9.1 Papier-und-Bleistift-Aufgaben

8.9.2 Aufgaben, für die man einen Computer benötigt

8.10 —

8.4.1 Posteriori-Stichproben von `stan_glm()` berechnen lassen

8.5 Wie tickt `stan_glm()`?

8.5.3 Standard-Prioriwerte bei `stan_glm()`

8.6 Modell `m_kung_neue_prioris`: Standard-Priori-Werte