7 Die Post befragen

7.1 Lernsteuerung

7.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

7.1.2 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

die Post-Verteilung anhand einer Stichprobenverteilung auslesen
Fragen nach Wahrscheinlichkeitsanteilen der Post-Verteilung anhand der Stichprobenverteilung beantworten
Fragen nach Quantilen anhand der Stichprobenverteilung beantworten
Die Post-Verteilung visualisieren mit R
Schätzbereiche (Konfidenzintervalle) aus der Post-Verteilung bestimmen anhand von Perzentilintervallen und Highest Density Intervals (HDI)

7.1.3 Begleitliteratur

Der Stoff dieses Kapitels orientiert sich an McElreath (2020), Kap. 3.1 und 3.2.

7.1.4 Vorbereitung im Eigenstudium

7.1.5 Benötigte R-Pakete

library(tidyverse)
library(easystats)
library(ggpubr)  # optional, Visualisierung
library(prada)    # optional, bayesbox automatisiert

7.1.6 Begleitvideos

Playlist QM2

7.2 Zur Erinnerung: Bayesbox in R berechnen

Berechnen wir mit der Bayesbox (“Gittermethode”) die Postverteilung für den Globusversuch. Die Bayesbox ist ein Weg, die Posteriori-Verteilung zu berechnen. Die Posteriori-Verteilung birgt viele nützliche Informationen. Sie ist das zentrale Ergebnis einer Bayes-Analyse.

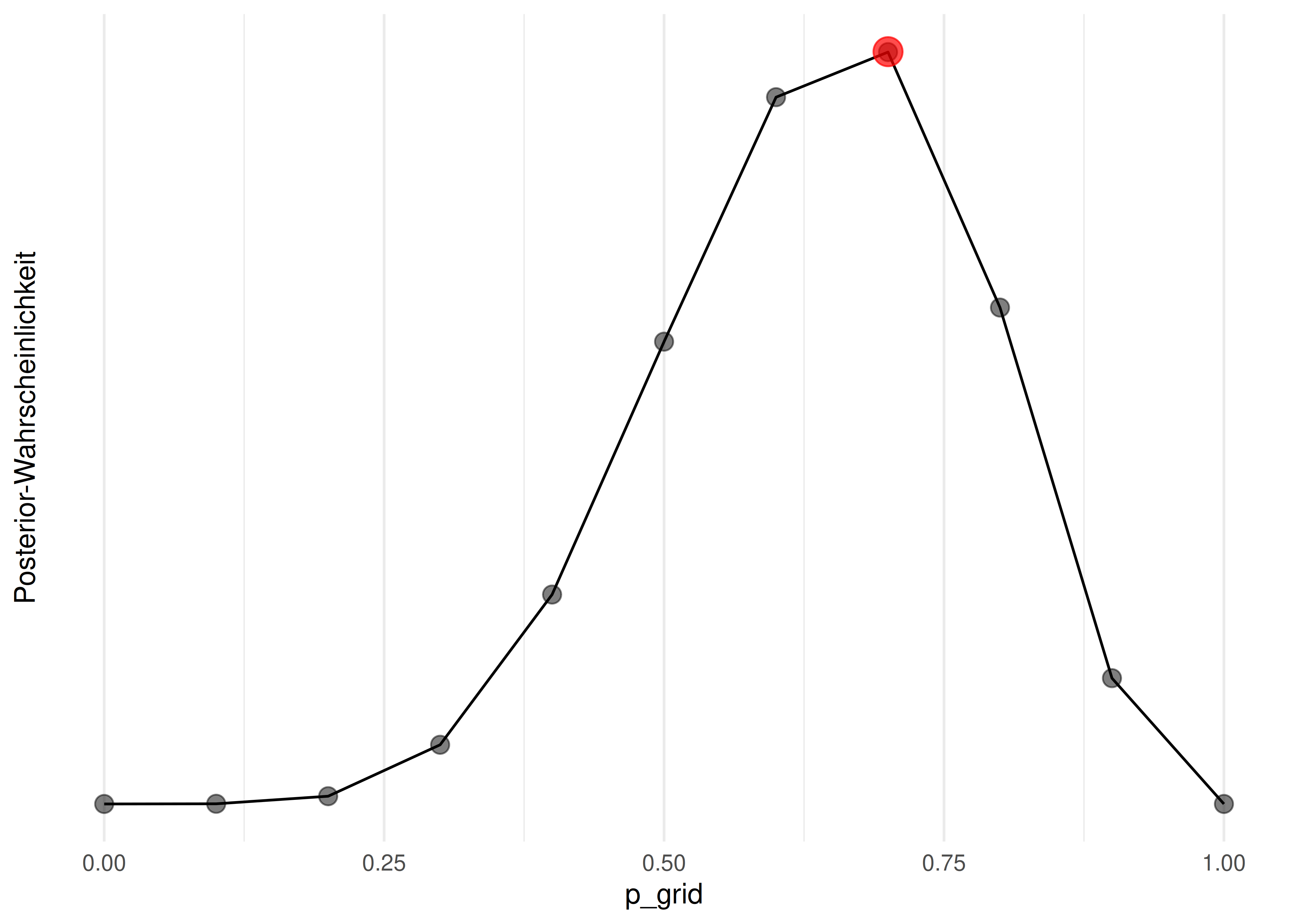
Beispiel 7.1 (Bayesbox für \(W=6\) Wasser bei \(N=9\) Würfen) Betrachten wir wieder das Globusmodell mit folgendem Ergebnis: \(W=6\) Wasser, \(N=9\) Würfen, bei Apriori-Indifferenz gegenüber den Parameterwerten. Und, sagen wir, \(g=11\) Gitterwerten¹ von 0 bis 1, in Schritten von 0.1, \(0.1, 0.2, \ldots, 0.9, 1.0\). \(\square\)

Übungsaufgabe 7.1 (Welcher Paramterwert hat die höchste Posteriori-Wahrscheinlichkeit?)

Lösung

Aufgrund der Apriori-Indifferenz entsprechen die Posteriori-Wahrscheinlichkeiten den Likelihoods. Die höchste Wahrscheinlichkeit (d.h. Likelihood) hat derjenige Parameterwert, zu dem die Daten am besten passen, und das ist 6/9 = 2/3, d. Listing 7.1. \(\square\)

Listing 7.1: Bayesbox mit 6 Wasser bei 9 Versuchen (g=11 Gitterwerte)

n_success <- 6          
n_trials  <- 9
p_grid <- seq(from = 0, to = 1, by = .1)
L <- dbinom(n_success, size = n_trials, prob = p_grid)

bayesbox_6w_9v <-
  tibble(p_grid = p_grid,prior  = 1) %>% 
  mutate(likelihood = L) %>% 
  mutate(unstand_post = (likelihood * prior),
         post = unstand_post / sum(unstand_post))

1: Sequenz von 0 bis 1 mit Schritten der Größe 0.1.
2: Likelihood mit 6 Treffern bei 9 Würfen und das Ganze jeweils für alle 11 Parameterwerte
3: Dann packen wir alles in eine Tabelle.

Abb. Abbildung 7.1 zeigt die resultierende Bayesbox; vor allem ist die Post-Verteilung wichtig.

library(ggpubr)
ggline(bayesbox_6w_9v , x = "p_grid", y = "post")

Abbildung 7.1: Die Postverteilung für W=6, N=9; der wahrscheinlichste Parameterwert ist farblich hervorgehoben

Voilà, die Post-Verteilung zu Beispiel 7.1 als Tabelle, die “Bayesbox”: s. Tabelle 7.1.

Tabelle 7.1: Postverteilung mit der Bayesbox berechnet

p_grid	prior	likelihood	unstand_post	post
0.0	1	0.00	0.00	0.00
0.1	1	0.00	0.00	0.00
0.2	1	0.00	0.00	0.00
0.3	1	0.02	0.02	0.02
0.4	1	0.07	0.07	0.07
0.5	1	0.16	0.16	0.16
0.6	1	0.25	0.25	0.25
0.7	1	0.27	0.27	0.27
0.8	1	0.18	0.18	0.18
0.9	1	0.04	0.04	0.04
1.0	1	0.00	0.00	0.00

7.2.1 Bayesbox automatisiert

Übrigens kann man die Berechnung der Bayesbox auch automatisieren, s. Tabelle 7.2 und Listing 7.2. Entweder importiert (“sourct”) man die Funktion bayesbox direkt von Github:

source("https://raw.githubusercontent.com/sebastiansauer/prada/master/R/NAME_bayesbox.R") 
bayesbox(hyps = p_grid, priors = 1, liks = L)

Mit source importiert man eine R-Skriptdatei. In diesem Fall steht dort der Code für die Funktion bayesbox.

Oder Sie starten das R-Paket prada (mit library(prada)), wo die Funktion wohnt:

Tabelle 7.2: Eine Bayesbox ‘automatisiert’ erstellt, mit Hilfe der Funktion bayesbox

Listing 7.2: Funktion bayesbox, auch im Paket prada erhältlich

library(prada)
bayesbox(hyps = p_grid, priors = 1, liks = L)

1: Das Paket prada steht nicht im Standard-R-App-Store (“CRAN”), sondern auf Github. Sie könnnen es so installieren: devtools::install_github("sebastiansauer/prada").
2: Die Funktion verhält sich wie eine gewöhnliche Bayesbox: Bei hyps schreibt man die Hypothesen (bzw. Parameterwerte) auf. Bei priors die Priori-Werte und bei liks die Likelihoods der jeweiligen Hypothesen.

7.2.2 Bayesbox geht nur für einfache Modelle

Bisher, für einfache Fragestellungen, hat unsere Bayesbox gut funktioniert. Allerdings: Funktioniert sie auch bei komplexeren Modellen? Schließlich wollen wir ja auch irgendwann Regressionsmodelle berechnen. Angenommen, wir haben ein Regressionsmodell mit 1 Prädiktor, dann haben wir folgende drei Parameter zu schätzen: \(\beta_0, \beta_1, \sigma\). Hört sich gar nicht so viel an. Aber Moment, wir müssten dann z.B. die Frage beantworten, wie wahrscheinlich die Daten aposteriori sind, wenn z.B. \(\beta_0 = -3.14\) und \(\beta_1 = 2.71\) und \(\sigma = 0.70\). Wie viele Zeilen brauchen wir dann in der Bayesbox? Wenn wir für die drei Parameter jeweils 10 Ausprägungen annehmen, was wenig ist, kämen wir \(10\cdot10\cdot10= 1000=10^3\) Zeilen in der Bayesbox. Bei 100 Ausprägungen und 3 Parametern wären es schon \(100^3=10^6\) Zeilen. Das wäre doch eine recht lange Tabelle.² Bei einer multiplen Regression mit sagen wir 10 Parametern mit jeweils 100 Ausprägungen rechnet das arme R bis zum jüngsten Tag, denn das sind \(10^{100}\) Variationen, also Zeilen in der Bayesbox.

🤖 Bitte tue mir das nicht an!

👨‍🏫 Schon gut, das können wir R nicht zumuten. Wir brauchen eine andere Lösung!

7.3 Mit Stichproben die Post-Verteilung zusammenfassen

7.3.1 Wir arbeiten jetzt mit Häufigkeit, nicht mit Wahrscheinlichkeit

Kurz gesagt: Komplexere Bayes-Modelle können nicht mehr “einfach mal eben” ausgerechnet werden; die Mathematik wird zu rechenintensiv. Glücklicherweiße gibt es einen Trick, der die Sache nicht nur rechnerisch, sondern auch konzeptionell viel einfacher macht. Dieser Trick lautet: Wir arbeiten nicht mehr mit Wahrscheinlichkeiten, sondern mit Häufigkeiten. Praktischerweise werden wir in Kürze einen R-Golem kennenlernen, der das für uns erledigt (er heißt Stan und kommt aus dem Paket rstanarm). Dieser Golem liefert uns Stichproben aus der Post-Verteilung zurück. Lernen wir jetzt also, wie man mit solchen Stichproben umgeht.

Die Bayesbox-Methode³ ist bei größeren Datensätzen (oder größeren Modellen) zu unpraktisch. In der Praxis werden daher andere, schnellere Verfahren verwendet, sog. Monte-Carlo-Markov-Ketten (MCMC). Wie diese Verfahren funktionieren sind aber nicht mehr Gegenstand dieses Kurses. Wir wenden Sie einfach an, freuen uns und lassen es damit gut sein.⁴

7.3.2 Häufigkeiten sind einfacher als Wahrscheinlichkeiten

Wie gesagt, typische R-Werkzeuge (“R-Golems”, wie Stan) liefern uns die Post-Verteilung in Stichprobenform zurück. Bevor wir uns aber mit diesen R-Werkzeugen beschäftigen, sollten wir uns vertraut machen mit einer Post-Verteilung in Stichprobenform. Erstellen wir uns also einen Tabelle mit Stichprobendaten aus der Posteriori-Verteilung (s. Dataframe bayesbox_6w_9v), s. Listing 7.3.

Listing 7.3: Wir stellen eine Tabelle mit Stichproben aus der Post-Verteilung


samples_6w_9v <-
  bayesbox_6w_9v %>%  # nimm die Tabelle mit Posteriori-Daten,
  slice_sample(  # Ziehe daraus eine Stichprobe,
    n = 1e4,  # mit insgesamt n=10000 Zeilen,
    weight_by = post,  # Gewichte nach Post-Wskt.,
    replace = T)  %>%  # Ziehe mit Zurücklegen
  select(p_grid)

Die Wahrscheinlichkeit, einen bestimmten Parameterwert (d.h. aus der Spalte p_grid) aus Tabelle bayesbox_6w_9v zu ziehen, ist proportional zur Posteriori-Wahrscheinlichkeit (post) dieses Werts. Ziehen mit Zurücklegen hält die Wahrscheinlichkeiten während des Ziehens konstant. Das Argument weight_by legt die Wahrscheinlichkeit fest, mit der eine Zeile gezogen wird. Wir begnügen uns mit der Spalte mit den Wasseranteilswerten (Parameterwerten), p_grid, die anderen Spalten brauchen wir nicht.

Wenn Sie jetzt denken: “Warum machen wir das jetzt? Brauchen wir doch gar nicht!” – Dann haben Sie Recht, für dieses Kapitel. Ab dem nächsten Kapitel werden wir aber, wenn wir mit komplexeren Modellen zu tun haben, nur noch mit Post-Verteilungen auf Stichprobenbasis arbeiten, weil wir Regressionsmodelle nicht mehr mit der Bayesbox berechnen können. Die Anzahl der Zeilen wäre einfach zu groß.

Hier erstmal die ersten 100 gesampelten Parameterwerte (p_grid) aus samples_6w_9v:

##   [1] 0.5 0.9 0.7 0.6 0.9 0.3 0.7 0.6 0.8 0.4 0.7 0.3 0.9 0.7 0.6 0.6 0.4 0.6
##  [19] 0.5 0.5 0.5 0.6 0.8 0.7 0.5 0.7 0.7 0.4 0.8 0.6 0.6 0.7 0.9 0.6 0.9 0.4
##  [37] 0.8 0.9 0.8 0.6 0.6 0.6 0.5 0.7 0.5 0.8 0.7 0.7 0.6 0.8 0.3 0.5 0.8 0.5
##  [55] 0.7 0.6 0.5 0.8 0.7 0.7 0.7 0.7 0.6 0.7 0.5 0.7 0.6 0.6 0.7 0.8 0.7 0.6
##  [73] 0.8 0.5 0.8 0.7 0.7 0.7 0.6 0.8 0.7 0.7 0.9 0.4 0.5 0.6 0.6 0.5 0.8 0.8
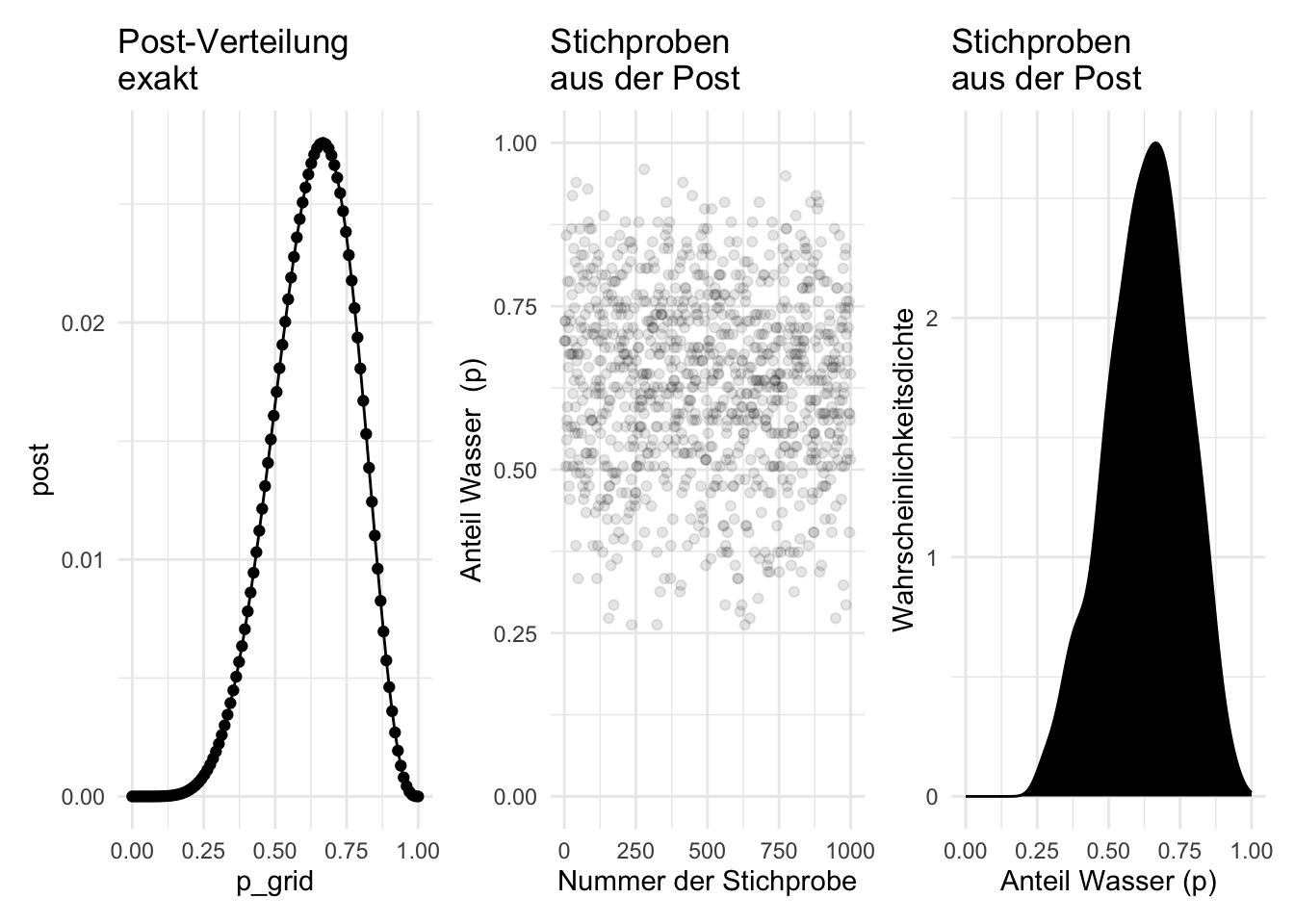
##  [91] 0.7 0.7 0.6 0.9 0.9 0.5 0.5 0.8 0.7 0.8

So sieht unsere “Stichproben-Bayesbox” als Balkendiagramm aus, s. Abbildung 7.2.

Syntax
Output

samples_6w_9v |> 
  count(p_grid) |> 
  ggbarplot(x = "p_grid", y = "n")  # aus ggpubr

Abbildung 7.2: Stichprobenverteilung auf Basis von Stichproben

Aus Abbildung 7.2 können wir einfach auslesen, wie wahrscheinlich gewisse Parameterwerte sind. So sehen wir, dass das Modell Parameterwerte (Wasseranteil, \(\pi\)) zwischen ca. 50% und 70% für am wahrscheinlichsten hält. Aber auch kleine Anteile wie 25% sind nicht auszuschließen (auf Basis der Daten und der Modellannahmen).

Vergleichen Sie Abbildung 7.2 mit Abbildung 6.11: beide sind sehr ähnlich! Das Stichprobenziehen (Abbildung 7.2) nähert sich recht gut an die exakte Berechnung an (Abbildung 6.11).

Es ist hilfreich, sich die Stichproben-Posterior-Verteilung einmal anzuschauen, um ein Gefühl dafür zu bekommen, wie die Post-Verteilung aussieht.

7.3.3 Visualisierung der Stichprobendaten mit \(g=100\) Gitterwerten

\(g=10\) Gitterwerte ist ein grobes Raster. Drehen wir mal die Auflösung auf \(g=100\) Gitterwerte (Ausprägungen) nach oben.

g <- 100
n_success <- 6
n_trials  <- 9

bayesbox_g100 <-
  tibble(p_grid = seq(from = 0, 
                      to = 1, 
                      length.out = g+1),
         prior  = 1) %>%
  mutate(likelihood = dbinom(n_success,
                             size = n_trials, 
                             prob = p_grid)) %>% 
  mutate(unstand_post = (likelihood * prior),
         post = unstand_post / sum(unstand_post))

1: \(g=100\) Gitterwerte
2: \(W=6\) Treffer (Wasser)
3: \(N=9\) Versuche
4: Bayesbox anlegen mit 100 Zeilen, d.h. verschiedenen 100 Parameterwerten
5: Apriori indifferent: Alle Hypothesen haben die gleiche Apriori-Plausibilität
6: Die Likelihood ist binomialverteilt.
7: Post-Verteilung berechnen wie gewohnt

bayesbox_g100 ist eine Bayesbox mit \(W=6, N=9, g=101\); sie ist in Tabelle 7.3 dargestellt.

Tabelle 7.3: Bayesbox mit g=101 Gitterwerten für W=6 Wasser bei N=9 Würfen

Und daraus ziehen wir uns \(n=1000=10^3\) Stichproben:

samples_g100 <-
  bayesbox_g100 %>%  # nimmt die Tabelle mit Posteriori-Daten,
  slice_sample(  # Ziehe daraus eine Stichprobe,
    n = 1000,  # mit insgesamt n=1000 Elementen,
    weight_by = post,  # Gewichte nach Spalte mit Post-Wskt.,
    replace = T)  # Ziehe mit Zurücklegen

Abbildung 7.3 zeigt sowohl die exakte Post-Verteilung (farbige, gepunktete Linie) als auch die Post-Verteilung auf Basis von Stichproben (Histogramm). In beiden Fällen erkennt man gut die zentrale Tendenz: ein Wasseranteil von ca. 70% scheint der “typische” Wert des Modells zu sein. Außerdem erkennt man, dass das Modell durchaus einige Streuung in der Schätzung des Wasseranteils bereithält. Das Modell ist sich nicht sehr sicher, könnte man sagen.

Abbildung 7.3: Post-Verteilung mit 100 Gitterwerten, exakt vs. auf Basis von Stichproben

Die Stichprobendaten nähern sich der “echten” Posteriori-Verteilung an: Die Stichproben-Post-Verteilung ist ähnlich zur echten, exakten Post-Verteilung. Das Stichproben-Verfahren zur Berechnung der Post-Verteilung funktioniert also! Das ist gut, denn wir werden in Zukunft nur noch mit dem Stichproben-Verfahren (zur Erstellung der Post-Verteilung) arbeiten.

Hinweis

Mehr Stichproben und mehr Gitterwerte glätten die Stichproben-Post-Verteilung.

Jetzt die Post-Verteilung noch mal mit mehr Stichproben: \(n=10^6\) Stichproben bei \(g=101\) Gitterwerten aus der Posteriori-Verteilung, s. Abbildung 7.4.

Abbildung 7.4: Post-Verteilung mit einer Million Stichproben und 100 Parameterwerten (Gitterwerten): schön ‘glatt’. Mittelwert (MW), Modus und Median (Md) liegen eng nebeneinander, da die Verteilung recht symmetrisch ist.

Übungsaufgabe 7.2 (Erstellen Sie Ihre eigene Stichproben-Post-Verteilung) Erstellen Sie eine Stichproben-Post-Verteilung auf Basis der Bayesbox bayesbox_6w_9v. Ziehen Sie \(n=100\) Stichproben. Tun Sie das per Hand: Übertragen Sie die Werte Der Spalte p_grid auf kleine Zettel. Dabei soll der Anteil der Zettel pro Wert von p_grid der Posteriori-Wahrscheinlichkeit (post) entsprechen (gerundet auf zwei Dezimalstellen). Beispiel: Wenn der Parameterwert 0.6 eine Posteriori-Wahrscheinlichkeit von 0.27 hat, dann schreiben Sie 27 Zettel (von 100) mit dem Wert 0.6. \(\square\)

7.4 Die Post-Verteilung befragen

So, jetzt befragen wir die Post-Verteilung.

📺 Die Post-Verteilung auslesen

Wichtig

Die Post-Verteilung ist das zentrale Ergebnis einer Bayes-Analyse. Wir können viele nützliche Fragen an sie stellen.

Es gibt zwei Arten von Fragen:

A. nach Wahrscheinlichkeiten (p) B. nach Parameterwerten (Quantilen, q)

Beispiel 7.2 (Beispiele für Fragen an die Post-Verteilung) A. Fragen nach Wahrscheinlichkeiten (p):

Mit welcher Wahrscheinlichkeit liegt der Parameter unter einem bestimmten Wert?
Mit welcher Wahrscheinlichkeit liegt der Parameter über einem bestimmten Wert?
Mit welcher Wahrscheinlichkeit liegt der Parameter zwischen zwei bestimmten Werten?

B. Fragen nach Parameterwerten (Quantilen, q):

Welcher Wert wird mit 95% Wahrscheinlichkeit nicht überschritten?
Mit 5% Wahrscheinlichkeit liegt der Parameterwert nicht unter welchem Wert?
Welcher Parameterwert hat die höchste Wahrscheinlichkeit?
Wie ungewiss ist das Modell über die Parameterwerte?

etc. \(\square\)

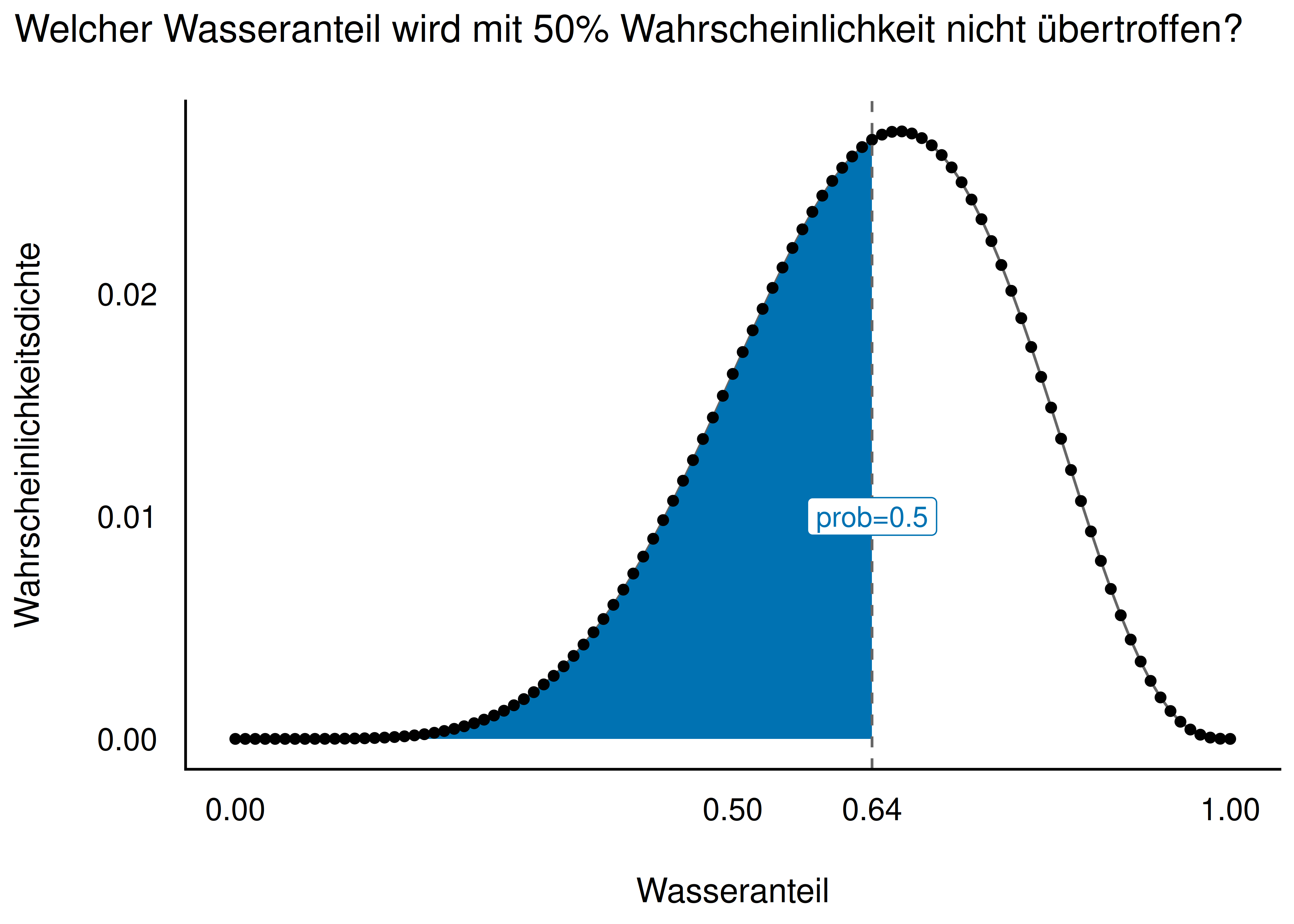
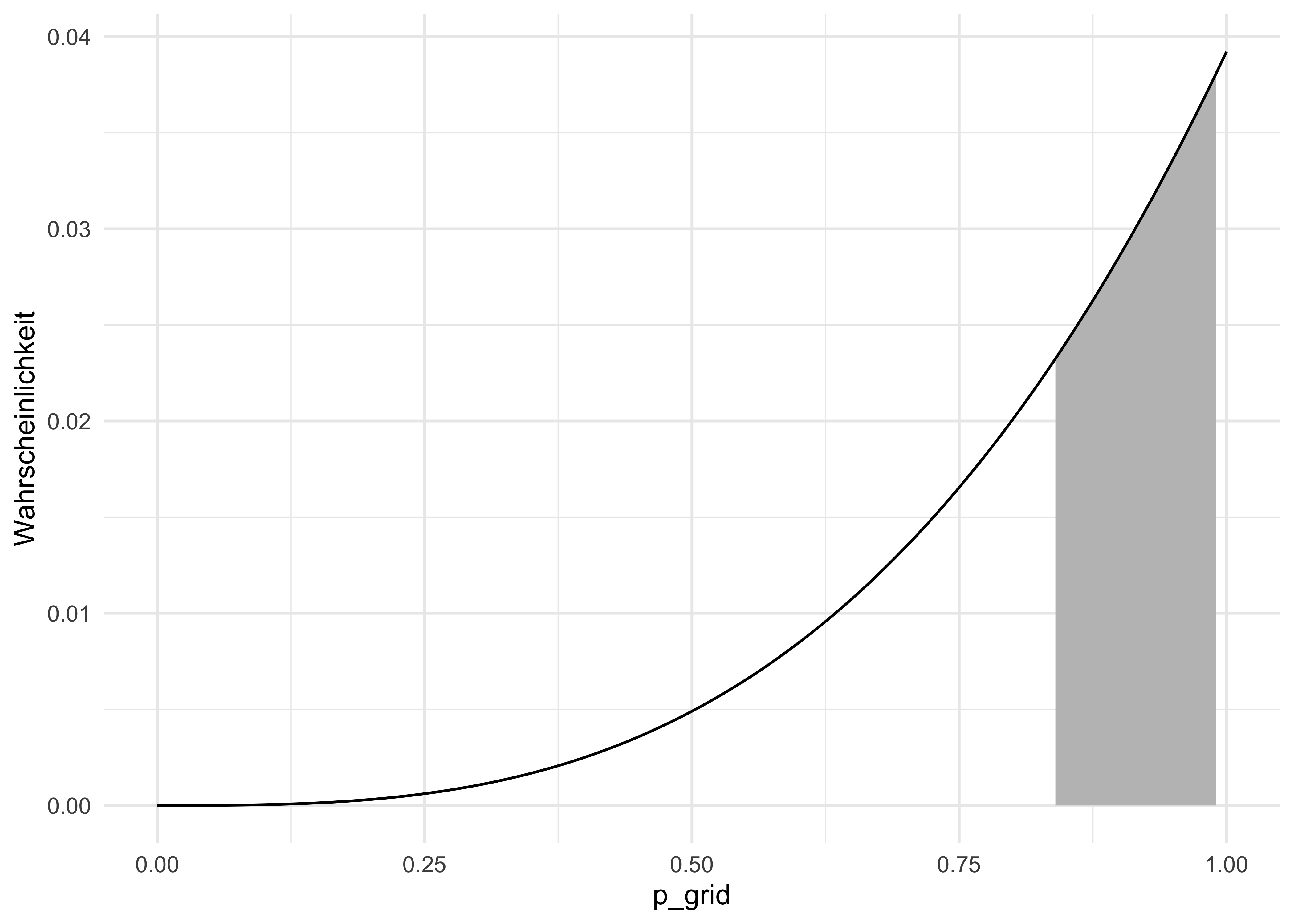
Der Unterschied zwischen beiden Arten von Fragen ist in Abbildung 7.5 schematisch illustriert.

Im linken Teildiagramm von Abbildung 7.5 fragen wir: “Welcher Wasseranteil wird mit einer gegebenen Wahrscheinlichkeit p nicht überschritten?” – Wir suchen also einen Parameterwert (Quantil, q). Im rechten Teildiagramm fragen wir: “Wie wahrscheinlich ist ein Wasseranteil von höchstens q?” – Wir suchen also eine Wahrscheinlichkeit (p).

7.4.1 Fragen nach Wahrscheinlichkeiten (p)

Sagen wir, dass sei unsere Forschungsfrage: Wie groß ist die Wahrscheinlichkeit, dass der Wasseranteil unter 50% liegt? Um diese Frage zu beantworten, zählen wir einfach, wie viele Stichproben die Bedingung erfüllen, und summieren die Wahrscheinlichkeiten dieser Stichproben. Wir zählen (count) also die Stichproben, die sich für einen Wasseranteil (p_grid) von weniger als 50% aussprechen.

samples_6w_9v %>%
  count(p_grid < .5)

Wenn wir insgesamt 10000 (1e4) Stichproben gezogen haben, können wir noch durch diese Zahl teilen, um einen Anteil zu bekommen. Dieser Anteil ist die Antwort auf die Forschungsfrage: Wie Wahrscheinlichkeit (laut Modell) für einen Wasseranteil kleiner als 50%? In unseren Daten ist die Wahrscheinlichkeit ca. 10%.

Übungsaufgabe 7.3 (Was macht die Funktion count?) Zur Erinnerung: Der Befehl count macht Folgendes: Er gruppiert die Stichprobe nach dem Prüfkriterium (hier: p_grid < .5, d.h. Wasseranteil höchstens 50%). Dann zählt er in jeder der beiden Teiltabelle die Zeilen und liefert diese zwei Zahlen dann zurück. \(\square\)

Wir zählen, wie oft der Wasseranteil weniger als 50% beträgt.

samples_6w_9v %>%
  count(p_grid < .5)

Natürlich gibt es verschiedene Wege, die gleiche Frage zu beantworten.

bayesbox_6w_9v %>%
  filter(p_grid < .5) %>%
  summarise(sum = sum(post))

Beispiel 7.3 (Wasseranteil zwischen 50 und 75%?) Noch eine Forschungsfrage: Mit welcher Wahrscheinlichkeit liegt der Parameter (Wasseranteil) zwischen 0.5 und 0.75?

Wir zählen die Stichproben, die diesen Kriterien entsprechen.

samples_6w_9v %>% 
  count(p_grid > .5 & p_grid < .75)

🤖 Ich würde empfehlen, die Anzahl noch in Anteile umzurechnen. Die kann man dann als Wahrscheinlichkeiten auffassen.

👨‍🏫 Das wollte ich auch gerade sagen…

samples_6w_9v %>% 
  count(p_grid > .5 & p_grid < .75) %>% 
  summarise(Anteil = n / 1e4,
            Prozent = 100 * n / 1e4)  # In Prozent

Anstelle von count() könnte man, wenn man möchte, auch filter() verwenden.

samples_6w_9v %>% 
  filter(p_grid > .5 & p_grid < .75) %>% 
  summarise(sum     =       n() / 1e4,
            anteil = 100 * n() / 1e4)  # In Prozent

Fertig 😄 \(\square\)

Beispiel 7.4 (Wasseranteil zwischen 90& und 100%?) Noch ein Beispiel für eine Forschungsfrage: Mit welcher Wahrscheinlichkeit liegt der Parameter zwischen 0.9 und 1?

Syntax
Output

samples_6w_9v %>% 
  count(p_grid >= .9 & p_grid <= 1) %>% 
  summarise(prop = 100 * n() / 1e4)  # prop wie "proportion", Anteil

Laut unserem Modell ist es also sehr unwahrscheinlich, dass der Wasseranteil der Erde mind. 90% beträgt. \(\square\)

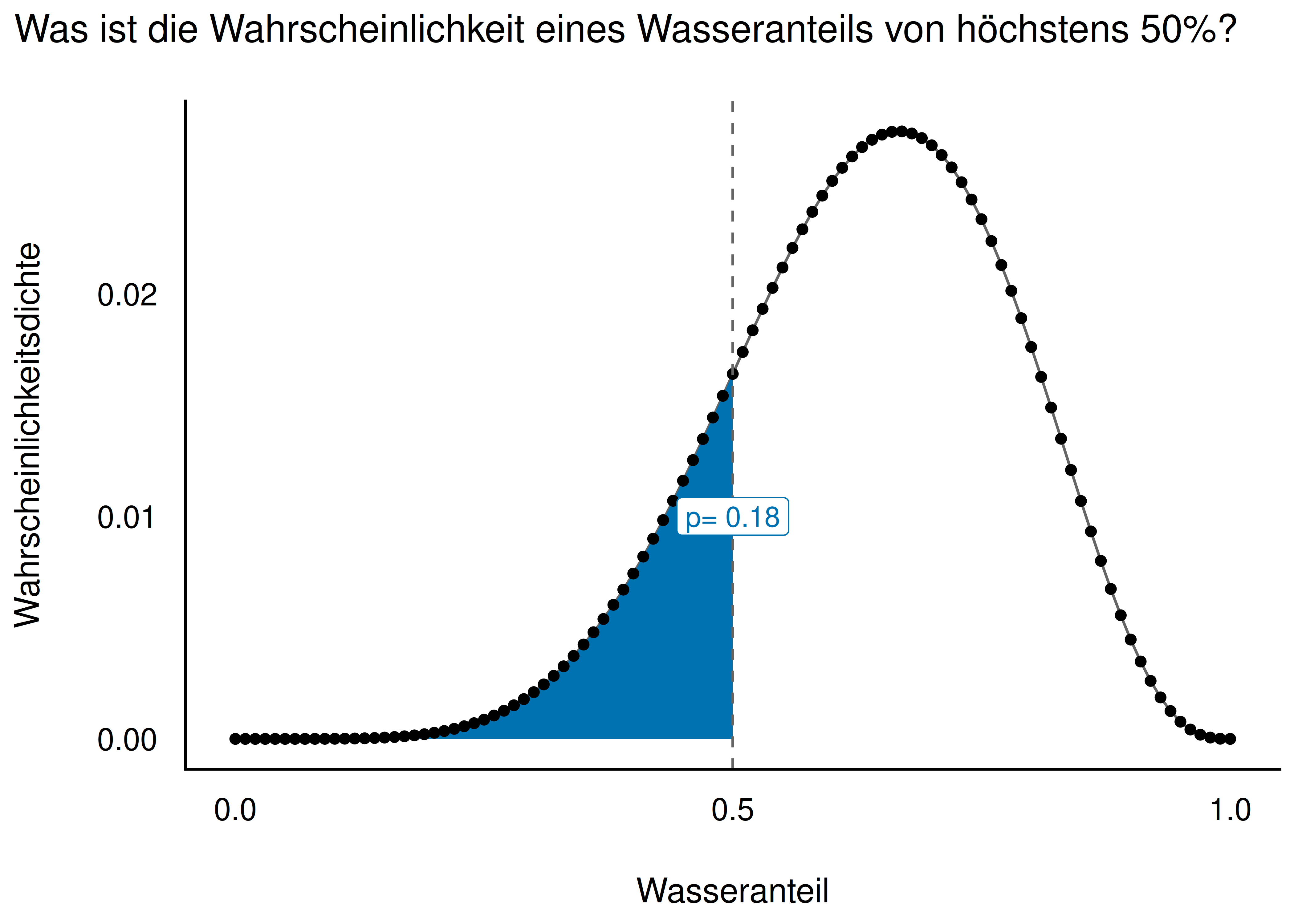
Übungsaufgabe 7.4 (Wasseranteil höchstens 50%?)

👩‍🔬 Mit welcher Wahrscheinlichkeit ist der Planet höchstens zur Hälfte mit Wasser bedeckt?

Lösung

samples_6w_9v %>% count(p_grid <= .5)

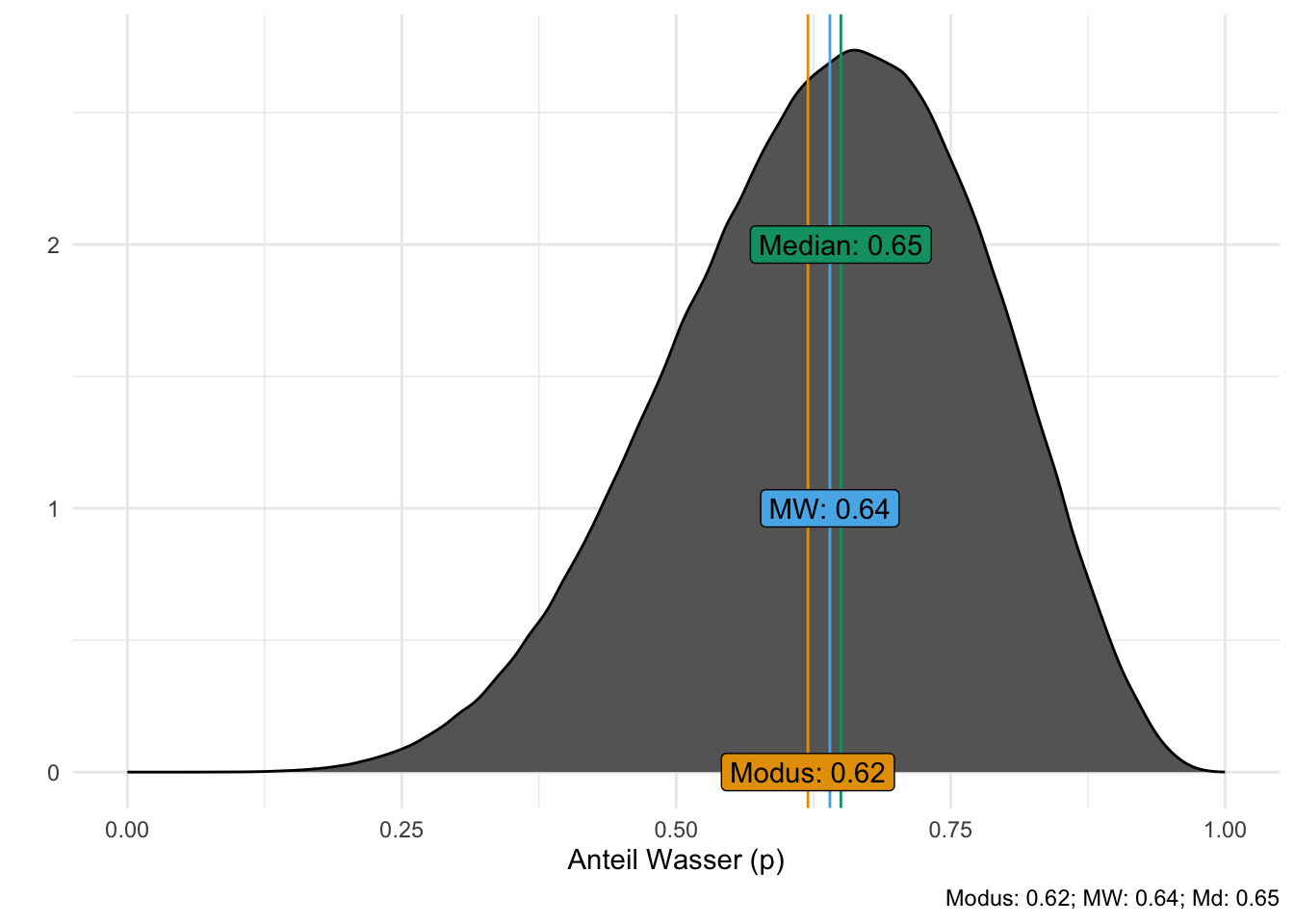
Wir können auch fragen, welcher Parameterwert am wahrscheinlichsten ist; dieser Wert entspricht dem “Gipfel” des Berges, s. Abbildung 7.4.

Für unsere Stichproben-Postverteilung, samples_6w_9v, s. Abbildung 7.2, lässt sich der Modus so berechnen:

map_estimate(samples_6w_9v$p_grid)

Dabei steht map für Maximum Aposteriori, also das Maximum der Post-Verteilung.

Übungsaufgabe 7.5 Bei der Gelegenheit könnten wir folgende, ähnliche Fragen stellen:

Was ist der mittlere Schätzwert (Mittelwert) zum Wasseranteil laut Post-Verteilung?
Was ist der mediane Schätzwert (Median)?

Lösung

samples_6w_9v %>% 
  summarise(mean(p_grid),
            median(p_grid))

7.4.2 Fragen nach Parameterwerten

Wichtig

Schätzbereiche von Parameterwerten nennt man auch Konfidenz- oder Vertrauensintervalle⁵.

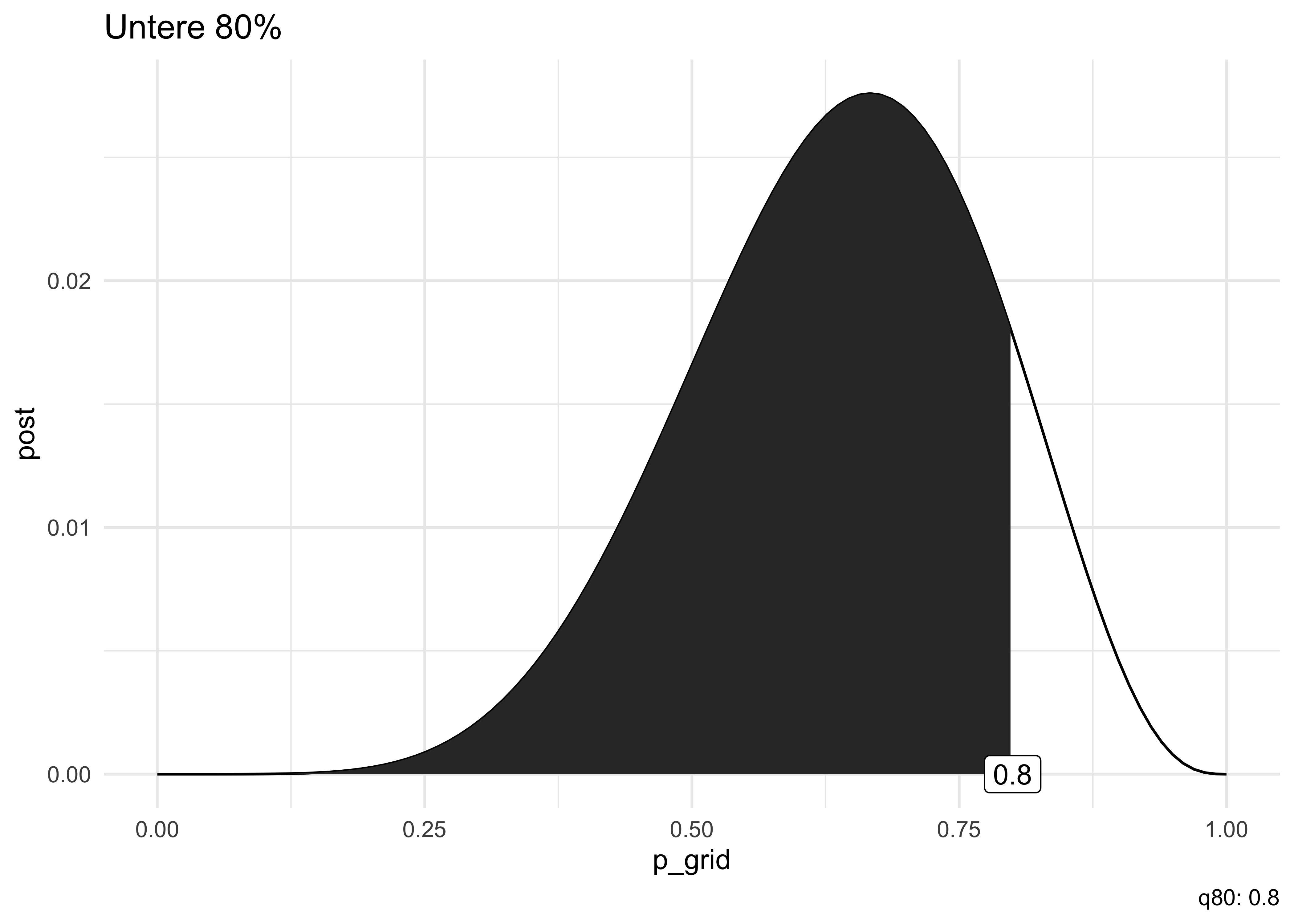
Welcher Parameterwert wird mit 90% Wahrscheinlichkeit nicht überschritten, laut unserem Modell? (Gesucht sind also die unteren 90% der Posteriori-Wahrscheinlichkeit.) Wir möchten also ziemlich sicher, was die Obergrenze an Wasser auf diesem Planeten ist. Diese Frage können wir mit dem Befehl quantile beantworten.

samples_6w_9v %>% 
  summarise(quantil90 = quantile(p_grid, p = .9))

Laut unserem Modell können wir zu 90% sicher sein, dass der Wasseranteil kleiner ist als ca. 78%.

Es hilft vielleicht, sich die Post-Verteilung noch einmal vor Augen zu führen, s. Abbildung 7.4.

Was ist das mittlere Intervall, das mit 90% Wahrscheinlichkeit den Parameterwert enthält, laut dem Modell?

Dafür “schneiden” wir links und rechts die 5% der Stichproben mit den extremsten Werten ab und schauen, bei welchen Parameterwerten wir als Grenzwerte landen:

samples_6w_9v %>% 
  summarise(
    quant_05 = quantile(p_grid, 0.05),
    quant_95 = quantile(p_grid, 0.95))

Solche Fragen lassen sich also mit Hilfe von Quantilen beantworten.

Übungsaufgabe 7.6 (Welcher Parameterwert ist der wahrscheinlich größte?) Übersetzen wir “wahrscheinlich” größte in “mit einer Wahrscheinlichkeit von 99% gibt es keinen größeren”.

Lösung

samples_6w_9v |> 
  summarise(quant99 = quantile(p_grid, p = .99))

Mit einer Wahrscheinlichkeit von 99% ist der höchste zu erwartende Wasseranteil 0.9.

Übungsaufgabe 7.7 (Welcher Parameterwert ist der wahrscheinlich kleinste?) Übersetzen wir “wahrscheinlich” kleinste in “mit einer Wahrscheinlichkeit von 99% gibt es keinen kleineren”.

Lösung

samples_6w_9v |> 
  summarise(wahrscheinlich_kleinste = 
              quantile(p_grid, p = .01))

Mit einer Wahrscheinlichkeit von 99% ist der kleinste zu erwartende Wasseranteil 0.3 – immer auf Basis unserer beobachteten Daten und der Vorannahmen.

Übungsaufgabe 7.8 (Welcher Parameterwert ist der “vermutlich” kleinste?) In der “wirklichen” Welt sind Aussagen nicht immer präzise. Sagen wir, die Chefin der Weltraumbehörde hat in einem Presse-Statement von der “vermutlichen Untergrenze” hinsichtlich des Wasseranteils gesprochen.

Übersetzen wir “vermutlich” kleinste in “mit einer Wahrscheinlichkeit von 90% gibt es keinen kleineren”.

Lösung

samples_6w_9v |> 
  summarise(wahrscheinlich_kleinste = 
              quantile(p_grid, p = .1))

Mit einer Wahrscheinlichkeit von 90% ist der kleinste zu erwartende Wasseranteil 0.5 – immer auf Basis unserer beobachteten Daten und der Vorannahmen.

7.5 Visualisierung der Verteilungen

7.5.1 Perzentilintervalle

Definition 7.1 (Perzentilintervall (PI)) Intervalle (Bereiche), die die “abzuschneidende” Wahrscheinlichkeitsmasse hälftig auf die beiden Ränder aufteilen, nennen wir Perzentilintervalle (PI) oder (synonym) Equal-Tails-Intervalle (ETI), s. Abb. Abbildung 7.6.⁶ \(\square\)

Abbildung 7.6: Perzintilintervalle: Das Intervall umfasst die mittleren 80% der Wahrscheinlichkeit

Das 10%, 20%, … 100%-Quantil⁷ (auf Basis von bayesbox_g100_samples) sind in Abbildung 7.7 illustriert.

Abbildung 7.7: Quantile in 10%-Schriten durch die Verteilung von `bayesbox_g100_samples`

7.5.2 Schiefe Posteriori-Verteilungen sind möglich

Beispiel 7.5 (Globusversuch: 3 Würfe, 3 Treffer) Noch einmal zum Globusversuch: Gehen wir von 3 Würfen mit 3 Mal Wasser (Treffer) aus; auf welche Wasseranteile (Parameterwerte) werden wir jetzt schließen? \(\square\)

Erstellen wir uns dazu mal eine Post-Verteilung (3 Treffer, 3 Würfe), s. Listing 7.4 mit dem Objekt bayesbox_3w_3v.

Listing 7.4: Schiefe Post-Verteilung in einer Bayesbox

bayesbox_3w_3v <- 
  tibble(p_grid = seq(0,1, by = .01),
         prior = 1) %>% 
  mutate(likelihood = dbinom(3, size = 3, prob = p_grid)) %>% 
  mutate(unstand_post = likelihood * prior) %>% 
  mutate(post_33  = unstand_post / sum(unstand_post)) 

samples_3w_3v <- 
  bayesbox_3w_3v %>% 
    slice_sample(n = 1e6, 
                 weight_by = post_33, 
                 replace = T)

So sehen die ersten paar Zeilen der Post-Verteilung, samples_3w_3v, aus.

p_grid	prior	likelihood	unstand_post
0.86	1	0.64	0.64
0.88	1	0.68	0.68
0.62	1	0.24	0.24
0.96	1	0.88	0.88
0.84	1	0.59	0.59
0.88	1	0.68	0.68

Mit dieser “schiefen” Post-Verteilung können wir gut die Auswirkungen auf das Perzentil- und das Höchste-Dichte-Intervall vergleichen.

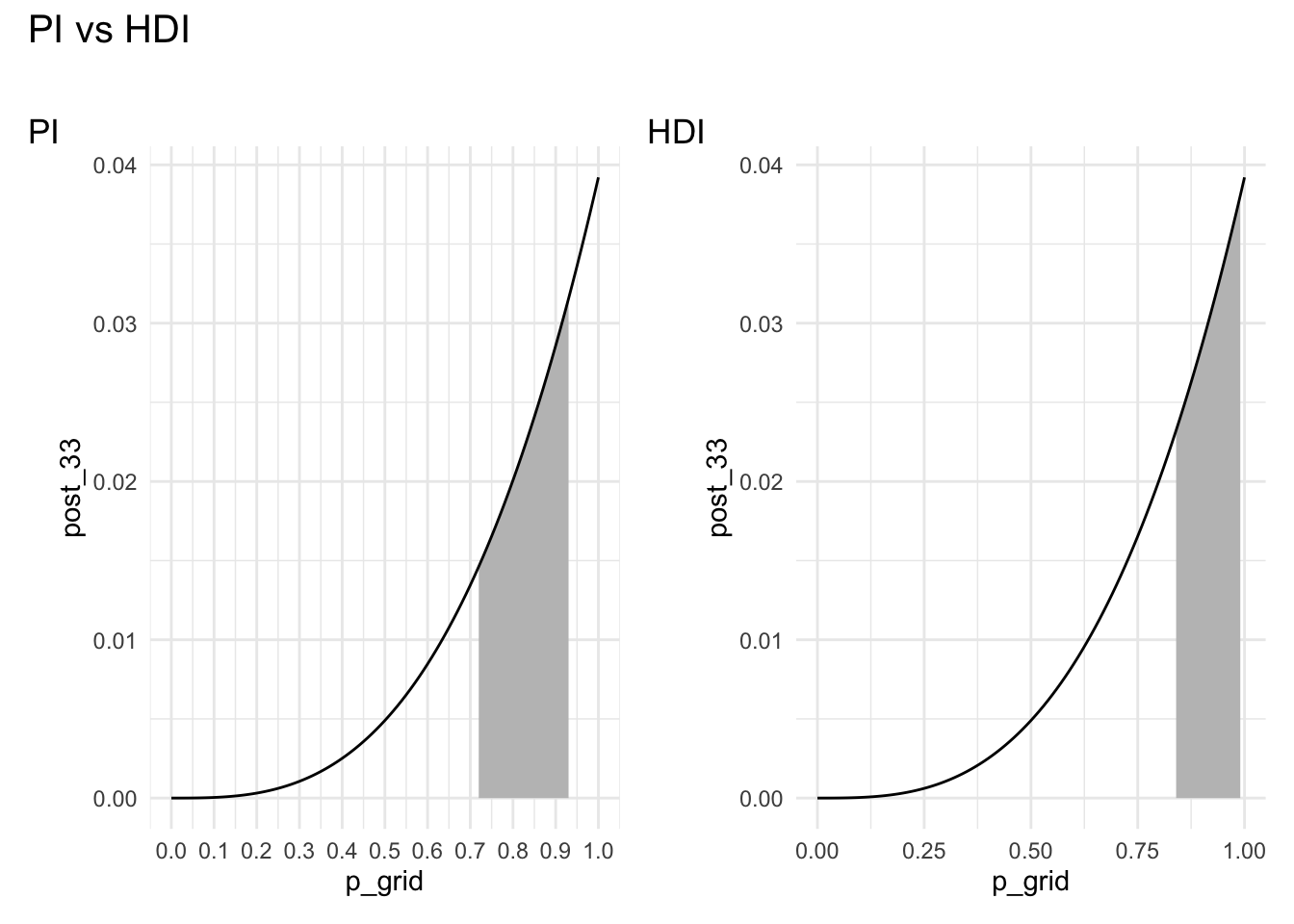
Hier z.B. ein 50%-Perzentilintervall, s. Abb. Abbildung 7.8, (a).

Ein Perzentilintervall kann bei schiefen Verteilungen den wahrscheinlichsten Parameterwert nicht enthalten, diesen plausiblen Wert also zurückweisen. Das macht keinen Sinn.

Ein Highest-Density-Intervall (HDI⁸) ist schmäler als der Perzintilintervall und enthält immer den wahrscheinlichsten Parameterwert.

Die Grenzwerte dieses ETI (oder jedes beliebig breiten) kann man sich z.B. mit dem Befehl eti ausgeben lassen.

samples_3w_3v %>% 
  select(p_grid) %>% 
  eti(ci = .5)  # Paket `easystats`

Der wahrscheinlichste Parameterwert (1) ist nicht im Intervall enthalten. Das ist ein Nachteil der ETI.

7.5.3 Intervalle höchster Dichte

Definition 7.2 (Intervalle höchster Dichte (Highest Density Intervals)) Intervalle höchster Dichte (Highest density Intervals, HDI oder HDPI) sind definiert als das schmälste Intervall, das den gesuchten Parameter enthält (in Bezug auf ein gegebenes Modell). \(\square\)

Der wahrscheinlichste Parameterwert (\(1\)) ist im Intervall enthalten, was Sinn macht, s. Abbildung 7.8. Bei einem HDI sind die abgeschnitten Ränder nicht mehr gleich groß, im Sinne von enthalten nicht (zwangsläufig) die gleiche Wahrscheinlichkeitsmasse. Beim PI ist die Wahrscheinlichkeitsmasse in diesen Rändern hingegen gleich groß.

Je unsymmetrischer die Verteilung, desto weiter liegen die Punktschätzer auseinander (und umgekehrt), s. Abb. Abbildung 7.9.

Abbildung 7.9: Visualisierung der Punktschätzer bei einer schiefen Post-Verteilung (auf Basis von `samples_3w_3v`)

Mit dem Befehl hdi kann man sich die Grenzwerte eines HDI, z.B. eines 50%-HDI, ausgeben lassen, s. Tabelle 7.4.

samples_6w_9v %>% 
  select(p_grid) %>% 
  hdi(ci = .5)  # aus dem Paket `{easystats}`

Tabelle 7.4: 50%-HDI für unser Globusmodell (samples_6w_9v)

Das Modell ist sich also zu 50% sicher, dass der gesuchte Parameter (der Wasseranteil der Erdoberfläche) sich im von ca. .67 bis .78 befindet (auf Basis eines HDI).

7.6 Fazit

Bei symmetrischer Posteriori-Verteilung sind beide Intervalle ähnlich oder identisch
Perzentilintervalle sind verbreiteter
Intervalle höchster Dichte (Highest Density Interval, HDI) sind bei schiefen Post-Verteilungen zu bevorzugen
Intervalle höchster Dichte sind die schmalsten Intervalle für eine gegebene Wahrscheinlichkeitsmasse

Fassen wir zentrale Punkte an einem Beispiel zusammen.

Im Globusversuch, Datensatz samples_6w_9v, s. Listing 7.3. Sagen wir, wir haben 6 Treffer bei 9 Würfen erzielt.

Lageparameter: Welchen mittleren Wasseranteil kann man erwarten?

samples_6w_9v %>% 
  summarise(
    mean   = mean(p_grid),
    median = median(p_grid))

Streuungsparameter: Wie unsicher sind wir in der Schätzung des Wasseranteils?

samples_6w_9v %>% 
  summarise(
    p_sd   = sd(p_grid),
    p_iqr = IQR(p_grid),
    p_mad = mad(p_grid))  # Mean Absolute Deviation, Mittlerer Absolutfehler

Anstelle der Streuungsparameter für den gesuchten Parameter ist es aber üblicher, ein HDI oder PI für den gesuchten Paramenter anzugeben.

Wichtig

Alles Wasser oder was? Im Beispiel dieses Kapitels haben wir unser gefragt, was wohl der Wasseranteil auf dem Planeten Erde ist. Halten Sie sich klar vor Augen: Der Wasseranteil ist ein Beispiel für einen Parameter, einer unbekannten Größes eines Modells.

7.7 Aufgaben

7.7.1 Papier-und-Bleistift-Aufgaben

7.7.2 Aufgaben, bei denen man einen Computer benötigt

7.8 -

Die Anzahl g der Gitterwerte ist nicht Teil des Modells; die Anzahl der Gitterwerte entscheiden nur über die Genauigkeit der Post-Verteilung.↩︎
Vorsicht beim Ausdrucken.↩︎
auch Grid-Methode genannt↩︎
Eine gute Einführung in die Hintergründe findet sich bei McElreath (2020).↩︎
Tatsächlich gibt es eine Vielzahl an Begriffen, die in der Literatur nicht immer konsistent verwendet werden, etwa Kompatibilitätsintervall, Ungewissheitsintervall, Passungsbereich.↩︎
Hier auf Basis der Post-Verteilung samples_6w_9v.↩︎
d.h. die Dezile↩︎
Auch als Highest Hensity Posterior Interval (HDPI) bezeichnet.↩︎