Ok, there are heaps of them on the net. Here comes my YACSDA. Maybe the only thing about it to mention is that it comes in German language.
dplyr, ggplot2Code on Github
Some impression of the tutorial:
One main business for psychologists is to examine questionnaire data. Extraversion, intelligence, attitudes… That’s bread-and-butter job for (research) psychologists.
Similarly, it is common to take the metric level of questionnaire data for granted. Well, not for the item level, it is said. But for the aggregated level, oh yes, that’s OK.
Despite its popularity, the measurement basics of such practice are less clear. On which grounds can this comfortable practice be defended?
In psychology, the classical text book surely is Lord and Novick’s text book (1968) on classical test theory. There, the authors hold some quite lax view on the quantitative attribute of psychological data. Basically, they appear to follow S. S. Stephens theory, that everything can be measured. Stephen’s theory is surely the most liberal definition of measurement (and maybe counter-intuitive for most people). However, his idea makes sense viewed from the broad idea of mapping some empirical domain to a numerical one. The question remaining open is of course: Do the relations of the empirical domain hold in the numerical domain? This is no automatism (probably because in the measurement of length the relations do hold, we assume that they will always hold, which is mistaken).
In measurement theory (particularly for psychology), a authoritative text book is the Foundations of Measurement by Krantz, Luce, Suppes, Tversky. While a definitive resource, it may be more of a resource than one would be happy with for a smooth couch evening :-)
I found this book of Joel Michell to be enlightening; Michell’s criticism on the current practice of measurement is the most pronounced, summarized eg in this paper with the punchy title Normal Science, Pathological Science and Psychometrics. There, Michell argues against the resistance of taking the question of scale level as an empirical one. Surprisingly, psychologists paid little attention and interest to the empirical investigation whether a certain variable possesses metric level; a fact Michell calls a neglect and even a pathology.
One reason of this posited neglect is that methodology is assumed to be missing, that there are no tools for checking whether (or not) a certain variable is metric. However, this view is not quite correct. Psychologist Duncan Luce and statistician John Tukey proposed a theory (conjoint measurement) which can be used for investigating whether a variable is quantitative or not (see 1964 paper).
It is beyond the scope of this article to describe this theory; rather, I would like to demonstrate that metric level cannot be taken for granted. Again, example and intuition based!
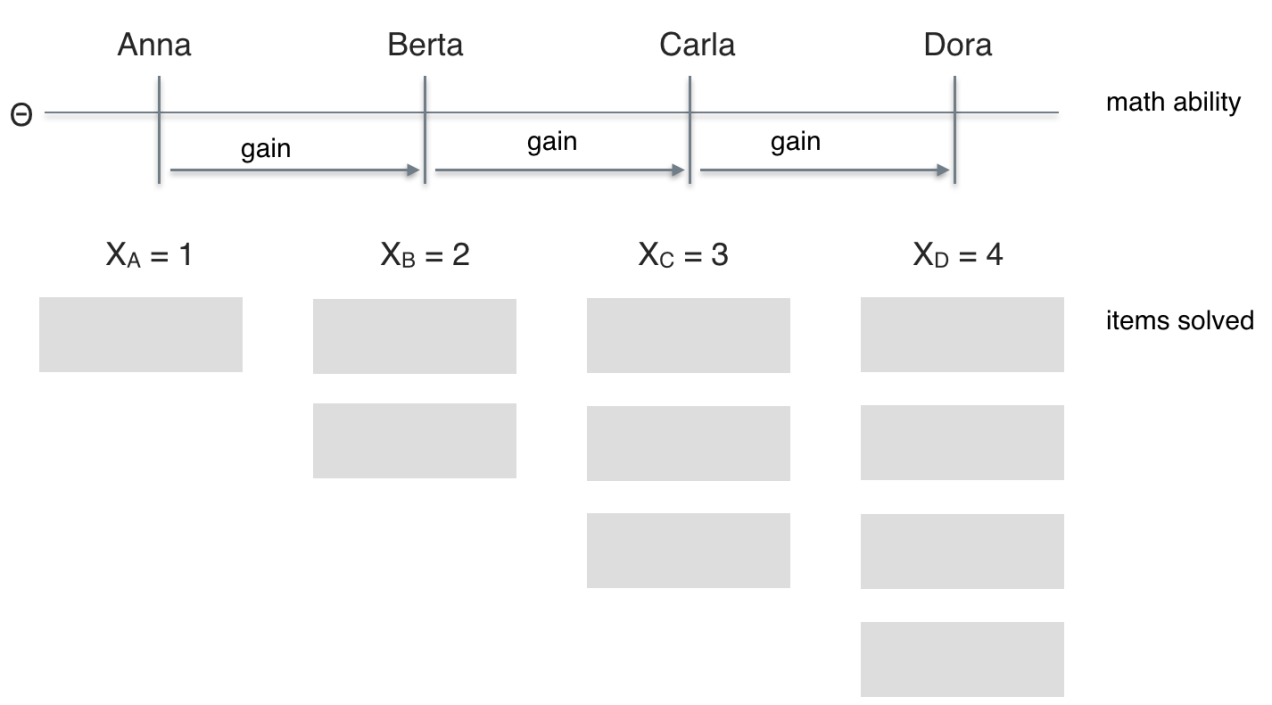
Imagine four students (Anna, Berta, Carla, Dora) probing some math test. Anna solves one item; Berta two; Carla three; Dora four. Thus, the math scores (X) range from 1 (Anna) to 4 (Dora). Let’s assume that higher scores (performance) implies higher math ability (latent psychometric variable, $\theta$. So, the order of ability would be Anna < Berta < Carla < Dora, or, Dora > Carla > Berta > Anna, respectively. Solving one more item translates down to a “gain” in the individual value of the latent variable. In a nutshell, we have established (or assumed) ordinal niveau.
So, let’s look at metric level next. Let’s stick to interval level; ratio level appears out of question for many a psychological variable.
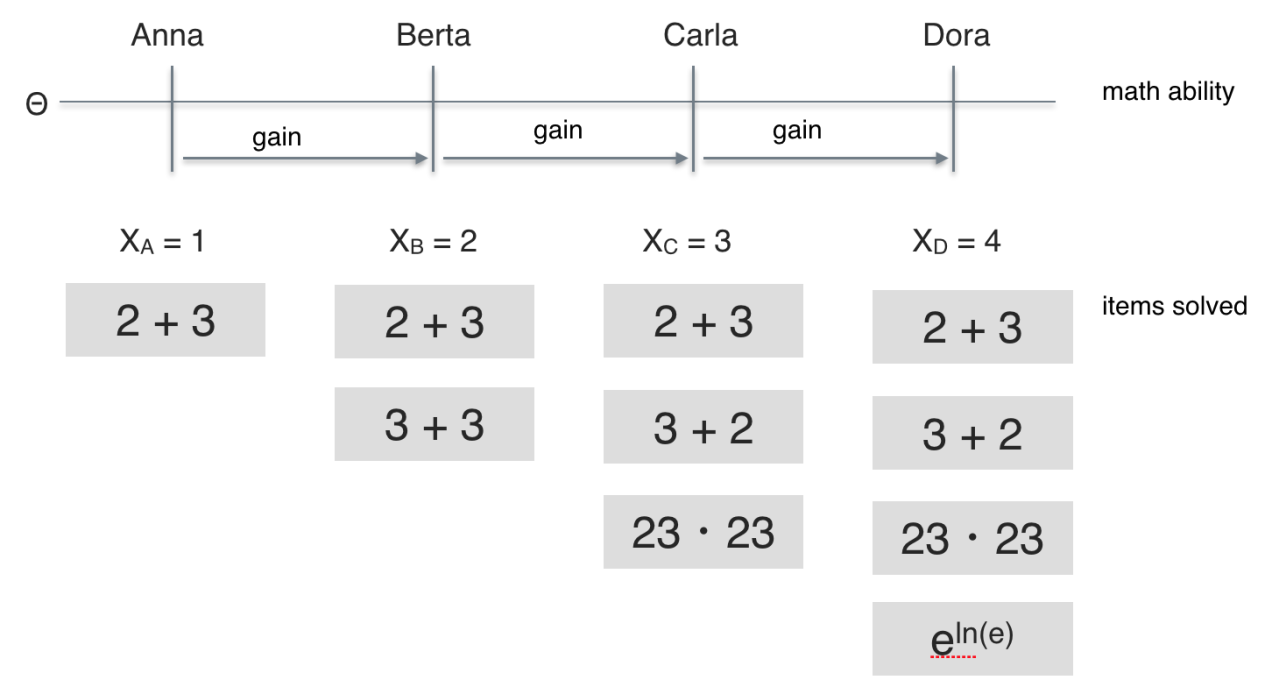
If we look more closely to the items solved we see that they appear to be of different difficulty. Some easier (2+3), some of intermediate difficulty (23*23), and some demanding more advanced knowledge ($e^{lne}$).
So, Berta solved two of the easy items, one easy more item than Anna. But Carla solved a a more difficult item compared to those which were solved by Berta. Thus, the additional ability needed for solving those three items (“gain” in ability) appears greater than the additional ability needed for solving two easy items instead of one. It appears plausible that the ability difference between Anna and Berta is smaller than the ability difference between Berta and Carla. The same reasoning applies for the difference between Carla and Dora.
In sum, equidistance of ability gains appears questionable, at least in this example. More generally, we cannot readily assume equidistance of difficulty/ability differences between adjacent levels. In other words: There are no grounds for assuming metric level just because we have a sum score.
One may argue that the differences could be more or less equal, so that the error should not be too grave. I think a sensible answer would be to test this assertion, and not take it for granted. Given the pivotal of measurement for any empirical science, we should take great care. As a side note, it has been reported that advance in physical science was accompagnied by advance in measurement technology. This alarms us of the importance of measurement theory and practice.
Just as there are optimistic voices about measurement in psychology (“hey no worries, it just works, no need to check”) there are pessimistic voices as well (“there is no quantitative measurement in psychology, just not possible”), see e.g. Guenter Trendler. For example, one could ask whether psychometric variables possess nominal or ordinal level. Consider this example:
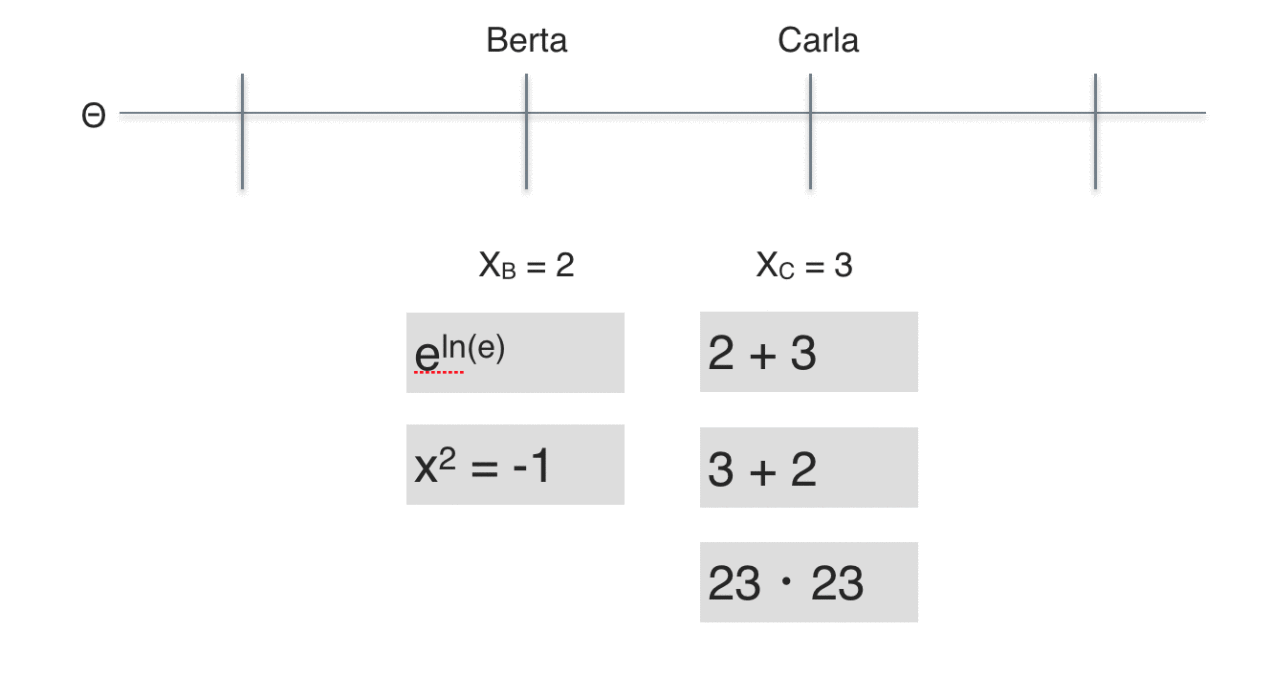
Carla has solved three items ($X_B = 3$) whereas Berta has only solved two ($X_A=2$); one less than Carla. Following the reasoning above, we conclude that Carla exhibits a higher ability compared to Berta.
Looking at the contents of the items, one may doubt whether the ability exhibited by Carla really is greater than Berta’s, because Berta solved more difficult items than Carla did.
Of course there are a number of different aspects that warrant attention, such as whether the items can be seen as of “one type””, so that they are “allowed”” to be summed up. Or whether the Rasch model solves the problem, and guaranties for metric level (it does not).
In sum, the message is that we cannot take metric level for granted. We need to empirically investigate. If we do take metric level for granted, we are prone to a bias of unknown size.
Below some consideration on what to read in summer times. In German language.
Lesezeit/reading time: 10-15 Min.
Literaturempfehlung Sommer 2016
Sommer, Sonne, Sonnenschein — ab in den Süden. Die Zeile “Lesen, lesen, lesen, lesen” würde sich nach meinem Dafürhalten auch ganz gut in den Song einpassen. Dafür hier ein paar Literaturempfehlungen. Von einer anständigen Sommerlektüre erwarte ich zweierlei: Dass die Kunst unterhaltsam sei. Zweitens, wenn als der Dampf sich nach dem Lesen erhebt, dass etwas zurückbleibt, außer dem Dampf. Beides gleichzeitig zu finden ist gar nicht so leicht.
Vielleicht denkt man das zu jeder Zeit, aber gerade aktuell die Welt besonders in Unruhe. Schlimme oder zumindest besorgende Nachrichten häufen sich; Tumult wohin man blickt. Da scheinen Anregungen zu Themen wie
Praktische Ethik, Grenzen, Grenzen der Ethik (Stichwort Flüchtlinge oder besser die Katastrophen, die Menschen zwingen zu fliehen) Demokratie, die offene Gesellschaft, ihr Ursprung und ihre Feinde Das Böse, sein Psychogramm und sein Phänomenologie am Fallbeispiel dem Zeitgeschehen auf den Nabel zu schauen. Manchmal frage ich mich, ob man in Anbetracht der Probleme der heutigen Zeit noch in Ruhe Grundlagenforschung betreiben darf (was ich tue). Jedenfalls heute und diesen Sommer keine Empfehlungen (auch deswegen) zur Grundlagenforschung, sondern drei Literaturempfehlungen zur Psycho-Philosophie des aktuellen Zeitgeschehens.
Zugeben: kein Geheimtipp und schon gar nicht neu. Außerdem gibt es von demselben Autor aktuelle, ganz neue Werke, wie zB. effektiver Altruismus, in welchem der Autor seine Gedanken konsequent und mit praktischer Perspektive fortführt. Sein “Hauptwerk”, die Praktische Ethik ist und bleibt aber (für mich) eines der Bücher, die mich am meisten zum Nachdenken angeregt haben und meine Meinung zu vielen Themen der praktischen Ethik am stärksten beeinflusst haben, weitergebracht haben.
Peter Singer ist ein kontrovers diskutierter Philosoph; er wurde sogar vielfach angefeindet für seine Äußerungen (zB., dass hoch entwickelte Tiere schätzenswerter sind als Babies weil empfindungsfähiger). Wahrscheinlich ist er (trotzdem oder gerade deshalb) der bekannteste zeitgenössische Denker zur praktischen Ethik. Entscheidend ist auch nicht, ob und wie viele seine Thesen man selber unterstützt; seine Argumentationslinie ist einfach lehrreich. Seine Gedankenkette besticht durch Einfachheit, Klarheit und Stringenz. Brilliant! Ein großer Geist; Freude beim Lesen über soviel geistige Klarheit! Und: In Erinnerung geblieben ist mir auch folgender Satz von ihm. Und zwar wurde er bei einem Vortrag in — war es Deutschland oder Österreich? — so laut ausgepfiffen, dass er seinen Vortrag abbrechen musste. In dem Zusammenhang erwähnte er dieses Zitat (in etwa so): “Ihre Meinung mag von meiner diametral abweichen, aber ich werde bis zum Schluss Ihr Recht verteidigen, dass Sie reden dürfen”.
In der Praktischen Ethik diskutiert er auch Fragen im Zusammenhang mit Flüchtlingen; auch ein interessantes Gedankenexperiment ist in dem Kapitel enthalten. Das Buch ist dünn und klein; Reklam. Zumindest lässt das die Ausrede vom Gepäckaufstau nicht gelten:-)
OK, auch ein alter Herr des 20. Jahrhunderts. Aber einer, der es in sich hat. Ein Halb-Österreicher (ähnlich wie Singer, dessen Eltern vor den Nazis aus Österreich geflohen sind in die angelsächsische Welt nach Australien), da er wegen der Nazis nach Neuseeland und dann England ausgewandert ist. Ähnlich wie Singer benutzt er einfache Worte, um klare und tiefe Gedanken auszudrücken. Genuss!
Seine Hauptthese kann man wohl so zusammenfassen: Die Offene Gesellschaft ist die Überwindung der “Urhorde” — der archaischen Gesellschaft und ihre Weiterführung in Staatsformen wie Stammesgesellschaft, Monarchie und totalitären Regimen. Auch der Nationalstaat — die Nation ist wenig mehr als eine modernere Version der Horde — müsse letztlich überwunden werden. Totalitäres Gedankentum findet sich nicht erst in Hitler-Deutschland; vielmehr identifiziert er mit Platon der ersten mächtigen geistigen Vater der totalitären, nicht-offenen Gesellschaft aus. Aristoteles kommt da auch nicht gut weg; aber als neuzeitlicher Hansdampf der Verführer, Dünnbrettbohrer und schaumschlagende Laberbacke wird vor allem Hegel (und Fichte) gebrandmarkt. Marx wird zwar komplett für “falsizifiert” (ein Term von Popper) erklärt, aber vergleichsweise respektabel abgehandelt. Neben Marx ist Popper wohl (einer) der einflussreichste Denker des 20. Jahrhunderts. Sein Buch ist Bildung im besten Sinne; seine Theorie der freien Gesellschaft (vs. Horde bzw. geschlossen-totalitäre Gesellschaft) faszinierend im psychologisch-soziologischem Sinne. Gut, es ist einiges zu lesen (2 Bände, recht beleibt), aber ein Buch, dass für mich prägend im Denken war und ist. Lesen!
Mit einem Buch dieses Titels könnte man in der Ubahn einige Blick ernten, deren Urheber eine andere Lektür vermute. Diesem Anspruch kommt das Buch nicht nach. Die Männerphantasien, die Klaus Theweleit hier analysiert, haben kaum, nichts! mit Erotik zu tun. Im Gegenteil, wahrscheinlich: Er beschreibt die Psyche des nationalsozialistischen Soldaten, die “aggresionsgesättigt” und nicht voll ich-ausgebildet ist, trotzem aber hochfunktional. Gekennzeichnet von Kühle, Beziehungsunfähigkeit, Gefühlskälte, Aggressivitätswalle, Heldenphantasien. Zwar bedient er sich stark einer tiefenpsychologisch-psychoanalytischen Denkschule, aber vor allem besticht (mich) seine Beobachtungs- und Interpretationsfähigkeit. Auf einer einzigen Leseseite findet sich mehr Reichhaltigkeit an gewagten Hypothesen (im besten Sinne) als in dem meisten an modern-wissenschaftlichem Papier, was in “hochgerankten” Fachzeitschriften publiziert ist. Das Psychogramm der Tötungslust oder die Lust am Bösen, könnte man sagen, führt er auf ein patriarchalisches Eltern- besser: Vaterhaus zurück. Eine umfassende (>1000 Seiten…) Analyse der Psyche von “richtig bösen” Menschen, wie Rudolph Höss, der auch besprochen wird neben einer ganzen Reihe weiterer Nazi-Größen. Ob das alles stimmt, was er schreibt? Weiß ich nicht; ich weiß nicht einmal, ob es darauf ankommt. Ob es übertragbar ist auf heute? Nicht sicher. Aber es ist lehrreich, fesselnd, originell, gewagt. Eine Aufarbeitung mit der Psychologie des Bösen in (unserer eigenen) deutschen Vergangenheit — tiefsichtiger als moderne Bücher wie die von Psychologen wie Baumeister oder Zimbardo oder (schon tiefgehender) Welzer. Keine leichte Kost, aber man kann viel Lernen über Bilder der bösen Psyche und ihre (Ab-) Gründe.
Eine große Frage! Tja. Viel Spaß am Strand!
reading time (full): 30 min.
Data Wrangling with dplyr is a popular activity in data science/ statistics. A number of tutorial are available, but not so many in German language.
Data set analyzed in nycflights13::flights (R package). Available on CRAN. Ok, choosing this data set is not very creative, but, hey, quite nice data:)
Thus, here is a case study in German language; code (R)is on Github.
reading time: 5-10 min.
Cohen’s d is a widely known and extensively used measure of effect size. That is, d is used to gauge how strong an effect is (given the fact that the effect exists). For example, one way to estimate d is as follows:
data(tips, package = "reshape2")
library(compute.es)
t1 <- t.test(tip ~ sex, data = tips)
t1$statistic
## t
## -1.489536
table(tips$sex)
##
## Female Male
## 87 157
tes(t1$statistic, 87, 157)
## Mean Differences ES:
##
## d [ 95 %CI] = -0.2 [ -0.46 , 0.06 ]
## var(d) = 0.02
## p-value(d) = 0.14
## U3(d) = 42.11 %
## CLES(d) = 44.4 %
## Cliff's Delta = -0.11
##
## g [ 95 %CI] = -0.2 [ -0.46 , 0.06 ]
## var(g) = 0.02
## p-value(g) = 0.14
## U3(g) = 42.13 %
## CLES(g) = 44.42 %
##
## Correlation ES:
##
## r [ 95 %CI] = 0.1 [ -0.03 , 0.22 ]
## var(r) = 0
## p-value(r) = 0.14
##
## z [ 95 %CI] = 0.1 [ -0.03 , 0.22 ]
## var(z) = 0
## p-value(z) = 0.14
##
## Odds Ratio ES:
##
## OR [ 95 %CI] = 0.7 [ 0.43 , 1.12 ]
## p-value(OR) = 0.14
##
## Log OR [ 95 %CI] = -0.36 [ -0.84 , 0.12 ]
## var(lOR) = 0.06
## p-value(Log OR) = 0.14
##
## Other:
##
## NNT = -19.61
## Total N = 244
However, what does Cohen’s d mean eventually?
Ok, the formula of d is well-known. In essence, d is computed as the difference between two means, normalized by the average variation. So one could say: “Wow, the experimental group was about 0.5 sd above the control! Jippaa!”” Not sure whether “lay persons”” would follow.
How can one get a more intuitive understanding of d?
A first step is to recognize that the two distributions overlap less if d gets larger.
As a sidenote: The size of the overlap can be computed quite easily:
So in total, the overlap area amounts to 0.60 ie. 60%. Ok, good, but what does overlap really means?
A more approachable statistics is CLES. CLES stands for common language effect size. Basically, it answers the question:
“If I draw 100 guys from distribution 1 and 100 from distribution 2, what is the chance that guy from 1 has a higher value than guy from 2?”
Ah! This makes sense! At least to me. We have now an observable, practical description of what this effect size means.
From our example above: The chance is 44% that a woman will tip more willingly than a man. To put it differently: Pick 100 pairs (woman/man). On average, 44 of these women will tip more than their male counterpart.