When plotting a normal curve, it is often helpful to color (or shade) some segments. For example, often we might want to indicate whether an absolute value is greater than 2.

How can we achieve this with ggplot2? Here is one way.

First, load packages and define some constants. Specifically, we define mean, sd, and start/end (z-) value of the area we want to shade. And your favorite color is defined.

library(ggplot2)
library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

mean.1 <-0
sd.1 <- 1
zstart <- 2
zend <- 3
zcritical <- 1.65

my_col <- "#00998a"

Next, we build a sequence from 3sd left to 3sd right to the mean. Along this sequence (for each value) we will compute the density of the normal curve. The data will be used for plotting the curve and the shaded area(s).

x <- seq(from = mean.1 - 3*sd.1, to = mean.1 + 3*sd.1, by = .01)


MyDF <- data.frame(x = x, y = dnorm(x, mean = mean.1, sd = sd.1))

Then, we define a “shading” function which does the shading job.

shade_curve <- function(MyDF, zstart, zend, fill = "red", alpha = .5){
  geom_area(data = subset(MyDF, x >= mean.1 + zstart*sd.1
                          & x < mean.1 + zend*sd.1),
            aes(y=y), fill = fill, color = NA, alpha = alpha)
}

Now we plot it:

p1a <- ggplot(MyDF, aes(x = x, y = y)) + geom_line() +
  shade_curve(MyDF = MyDF, zstart = -1, zend = 1, fill = my_col, alpha = .3) +
  shade_curve(MyDF = MyDF, zstart = 1, zend = 2, fill = my_col, alpha = .5) +
  shade_curve(MyDF = MyDF, zstart = -2, zend = -1, fill = my_col, alpha = .5) +
  shade_curve(MyDF = MyDF, zstart = 2, zend = 6, fill = my_col, alpha = .7) +
  shade_curve(MyDF = MyDF, zstart = -3, zend = -2, fill = my_col, alpha = .7) +
  scale_x_continuous(breaks = -3:3) +
  scale_y_continuous(breaks = NULL) +
  theme_classic() +
  ylab("") + xlab("")

p1a

OK. Another nice feature would be have printed the cumulative percentages for each shaded segment.

For that purpose, let’s add a variable with the cumulative density.

MyDF %>%
  mutate(y_cdf = cumsum(y)) -> MyDF

But we are only interested in some quantiles. So let’s filter these and kick out the rest.

MyDF %>%
  filter(x %in% c(-3, -2.58, -2, -1.65, -1, -.5, 0, .5, 1, 1.65, 2, 2.58, 3)) -> MyDF_filtered

Now, let’s add the cumulative percentages for some quantiles of interest.

p1a + geom_text(data = MyDF_filtered,
                aes(x = x, y = y + .1, label = paste(round(y_cdf, 0),"%")),
                check_overlap = TRUE) +
  geom_segment(data = MyDF_filtered,
               aes(x = x, xend = x, y = 0, yend = y), linetype = "dashed")

Often, both in academic research and more business-driven data analysis, we want to compare some (two in many cases) means. We will not discuss here that friends should not let friends plot barplots. Following the advise of Cleveland’s seminal book we will plot the means using dots, not bars.

However, at times we do not simply want the diagram, but we (or someone) is interested in the bare, plain, naked, exact numbers too. So we would like to put the numbers right into the diagram. One way to achieve this is the following:

First, let’s load some data and some packages (in R):

data(tips, package = "reshape2")  # load some data

library(dplyr)
library(tidyr)
library(ggplot2)

Then, summarize the variables (ie., compute means per group). Note that for ggplot (and many other graphing systems) it is necessary that the the variable depicted at (say) the X-axis conforms to one column in the data set. Thus, we often have to change the structure of the data set (but here not…).

tips %>% 
  group_by(sex, smoker) %>% 
  summarise(mean_group = mean(tip)) -> tips2

OK; now let’s plot it with ggplot2:

tips2 %>% 
    ggplot(aes(x = smoker, y = mean_group, 
             color = sex, shape = smoker,
             group = sex,
             label = round(mean_group, 2))) + 
  geom_point() +
  geom_line() +
  geom_text(aes(x = smoker, y = mean_group + 0.03))

The whole syntax can be accessed at Github.

Plotting a normal distribution is something needed in a variety of situation: Explaining to students (or professors) the basic of statistics; convincing your clients that a t-Test is (not) the right approach to the problem, or pondering on the vicissitudes of life…

If you like ggplot2, you may have wondered what the easiest way is to plot a normal curve with ggplot2?

Here is one:

library(cowplot)

## Loading required package: ggplot2

## 
## Attaching package: 'cowplot'

## The following object is masked from 'package:ggplot2':
## 
##     ggsave

p1 <- ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, args = list(mean = 0, sd = 1)) + ylab("") +
  scale_y_continuous(breaks = NULL)
p1

Note that cowplot here is optional, and gives a more “clean” appearance to the plot. Without cowplot, ie., the standard theme of ggplot2, you will get (better restart your R session before running the next code):

library(ggplot2)


p1 <- ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, args = list(mean = 0, sd = 1)) + ylab("") +
  scale_y_continuous(breaks = NULL)
p1

Pearson’s correlation is a well-known and widely used instrument to gauge the degree of linear association of two variables (see this post for an intuition on correlation).

There a many formulas for correlation, but a short and easy one is this one:

\(r = \varnothing(z_x z_y)\).

In words, \(r\) can be seen as the average product of z-scores.

In “raw values”, r is given by

\(r = \frac{\frac{1}{n}\sum{\Delta X \Delta Y}}{\sqrt{\frac{1}{n}\sum{\Delta X^2}} \sqrt{\frac{1}{n}\sum{\Delta Y^2}}}\).

Here, \(\Delta\) refers to the difference of a value to its mean.

At times it is helpful to write r so that the similarity to the covariance gets clear:

OK. But why is it, that r cannot be larger than 1 (and not smaller than -1)?

That is, why does the following inequality hold: \(-1 \le r \le 1\)?

This is the question we are addressing in this post. I haven’t found much on that on the net, so that’s why I sum up some thoughts in this post.

Cauchy-Schwarz Inequality

One explanation, quite straight forward, is based on the Cauchy-Schwarz Inequality. This inequality can be stated as follows:

\({\langle x,y \rangle}^2 \le \langle x,x \rangle \cdot \langle y,y \rangle\),

where \(\langle x \rangle\) denotes the dot product of a vector, eg. x.

This formula can be rewritten as

But this formula looks very similar to the correlation, if we first take the square root of both sides:

and then cancel out the (1/n) part from the raw values equation of r above:

\(r = \frac{\sum{\Delta X \Delta Y}}{\sqrt{\sum{\Delta X^2}} \sqrt{\sum{\Delta X^2}}}\).

Now rewrite r in this way:

\(\sum{\Delta X \Delta Y} \le \sqrt{\sum{\Delta X^2}} \sqrt{\sum{\Delta Y^2}}\).

The raw formula of r matches now the Cauchy-Schwarz inequality! Thus, the nominator of r raw formula can never be greater than the denominator. In other words, the whole ratio can never exceed an absolute value of 1.

Looking at the regression line

A second line of reasoning why r cannot the greater than 1 (less than -1) is the following.

Suppose X and Y are perfectly correlated, for example like this:

x <- runif(n = 100, min = 0, max = 10)
res <- rnorm(n = 100)
y <- x
library(ggplot2)
library(tibble)
ggplot(tibble(x, y), aes(x = x, y = y)) + geom_point(alpha = .5)

Now, what happens if we z-scale X and Y? Not much:

z_x <- as.numeric(scale(x))
z_y <- as.numeric(scale(y))

df1 <- tibble(z_x, z_y)
ggplot(df1, aes(x = z_x, y = z_y)) + geom_point(alpha = .5)

The difference is that mean X and meany Y is both zero, and SD for both X and Y is 1, so the scaling has changed (the line has a gradient of 1 now).

Note that perfect correlation of z-scaled variables means that for each \(X_i\) there is an \(Y_i\) of same value.

For example:

library(magrittr)
z_x <- x %>%  scale %>% as.numeric %>% sort
z_y <- y %>%  scale %>% as.numeric %>% sort
df2 <- tibble(z_x, z_y)
head(df2)

## # A tibble: 6 x 2
##         z_x       z_y
##       <dbl>     <dbl>
## 1 -1.688960 -1.688960
## 2 -1.688875 -1.688875
## 3 -1.685675 -1.685675
## 4 -1.621873 -1.621873
## 5 -1.554167 -1.554167
## 6 -1.532031 -1.532031

But if \(X_i = Y_i\) for all X and Y it means that the means and variances of X and Y are the same, too. It actually means that X equals Y.

If we look at the formula of the correlation for perfectly correlated z-scaled variables X and Y we find:

In words, when two variables are perfectly correlated (ie., their graph is a line), then r=1.

This article has been published at The Winnower, it is distributed under the terms of the Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and redistribution in any medium, provided that the original author and source are credited.

Data can be accessed here.

Access the paper here.

CITATION: Sebastian Sauer, Alexander Wolff, The effect of a status symbol on success in online dating: an experimental study (data paper), The Winnower 3:e147241.13309 (2016). DOI: 10.15200/winn.147241.13309

ABSTRACT

volutionary psychology suggests that women and men differ in their mating strategies. We operationalized a central claim of evolutionary psychology by manipulating social status of profiles at a dating website: one group of profiles was depicted with a luxury sports car (high status) and second group without car (low status). Six profile were set up (3 female, 3 male) for each of the two groups. Two type of response variables were collected: Whether a “match” occurred (n=3515), and whether a message was sent to the profile (n=1548). Beauty and hip-waist-ratio of straw persons, and age of contacting individuals were recorded. Given strong effect sizes, large sample size, and high interest in human mating, this data set should be of interest for applied researchers in human mating and social psychology.

BACKGROUND

A central claim of evolutionary psychology is that social status has a positive impact on female mating strategy; men exhibiting higher social status are expected to attract more women compared to men with lower social status (Buss 2015). Social status can be defined as the relative social position an individual is perceived to possess; social status refers to the estimation or status attributed to this position (Coie, Dodge, and Coppotelli 1982). The variety of social status indicators includes income, wealth, social power, social esteem of a social role, or educational level. These effects are well known and widely replicated (Buss et al. 2001).

It has been noted that social status, and particularly wealth, is not only for present times and western women a central mating criterion; this preference has been documented in non-western cultures and different times as well. For example, between 1984 and 1989, Buss and colleagues investigated more than 30 cultures around the globe regarding mating preferences. In sum, approx. 10,000 individuals were included in the study, stemming from six continents (Buss et al. 1990; Buss 1989). Results suggest the importance of male financial situation for women’s mating decisions is an intercultural constant.

The theoretical basis for this behavior is theorized as stemming from the different biological fabric of the sexes. In all mammals, males produce much more sperms than female produce ova. Thus, there should be an incentive for females to prefer males with an outlook of secure breeding of the offspring. Social status and in particular financial wealth are widely viewed as predictors of such reproductive success (Buss 2009; Buss 2015). It should be noted that evolution theory suggests that (mating) mechanisms which are active in inter- or intra-sexual selection have developed in extensive time spans, and cannot quickly accommodate to recent environmental changes, e.g. those of modern human culture. This fact may explain why some strategies appear maladaptive for modern life.

Similarly, it has been suggested that women should prefer men who are slightly older then themselves (Buss 2015). This can be explained by the fact than older men normally possess higher social status (e.g. income) compared to younger men. The present data set allows for testing this hypothesis too.

Apart from social status, physical attractiveness has been proposed as an important (positive) predictor for mating success. One explanation for the relevance of beauty is that beauty may be indicative of health (Shackelford and Larsen 1997; Grammer and Thornhill 1994). Thus, more attractive individuals should attract more partners; this is expected for both sexes, but is maybe more pronounced in the selection process of men (Buss 2015; Abramson 1995). One widely used measure for attractiveness and reproductive outlook is the waist-hip-ratio (Streeter and McBurney 2003; Singh and Young 1995). The present data allow for testing the impact of beauty of mating success.

METHODS

SAMPLE

The sample consists of 3515 matches and 1515 messages; in sum, this behavior originated from n = 1920 individuals in total. There are no missings in the data, as all data were collected electronically. Data are anonymized using a hash mechanism (sha256). Mean age was 29.5 years (sd = 5.0 years). Six straw persons were included in the study, each with a profile with luxury car (high status), and without car (low status), yielding a total of 12 profiles on the dating portal. Of all matches, 3205 (91%) were sent to one of the 6 female profiles; of all messages sent, 310 (98%) were sent to a female profile. It should be noted that participants were matched to the experimental factor by chance alone; the allocation was not counterbalanced in any way due to technical/practical constraints of the dating portal. Data was collected between 2015-01-05 and 2016-01-20.

MATERIALS

The main stimulus was the profile picture. Between the two groups of the experimental factor (“car”), the only difference was whether the luxury car (BMW Z4) was present or not (i.e., high vs. low status). To better control for idiosyncrasies of the straw person (eg. attractiveness), 3 different straw persons of each sex were included. Theses six individuals differed in their subjective attractiveness as judged by a rating committee of five persons on a scale from 1 to 10 (M = 5.8; sd = 1.2) and in their waist-hip-ratio (whr; female: M = 0.71; sd = 0.02; male M = 0.91; sd = 0.02). For reasons of personal rights and privacy, pictures of the straw persons are not made public.

For the names of each straw person, typical German names were chosen (female: “Julia”; men: “Christian”). Year of birth was documented as 1987 for each straw person. No family names were shown. As location, “München” (Germany) was specified. In order to make the profiles of the straw persons more realistic, some typical hobbies were filled in: TV series, music, sports, telephoning with friends.

PROCEDURES

The profiles were setup at one of the largest online dating portals (Germany version) with more than 300 million users (as of Aug. 2016).

The dating portal allowed for checking for “matches”, defined were both individuals judge their counterpart as “interesting” thereby communicating principal interest in further interaction. For each of the 12 profiles, we judged the first 600 user profiles that were suggested by the portal as “interesting”. Each of our profiles was online for one week (no overlaps between the two groups). No further contact was undertaken with the individuals contacting our straw persons; in particular, we did not respond to any matching or contact message.

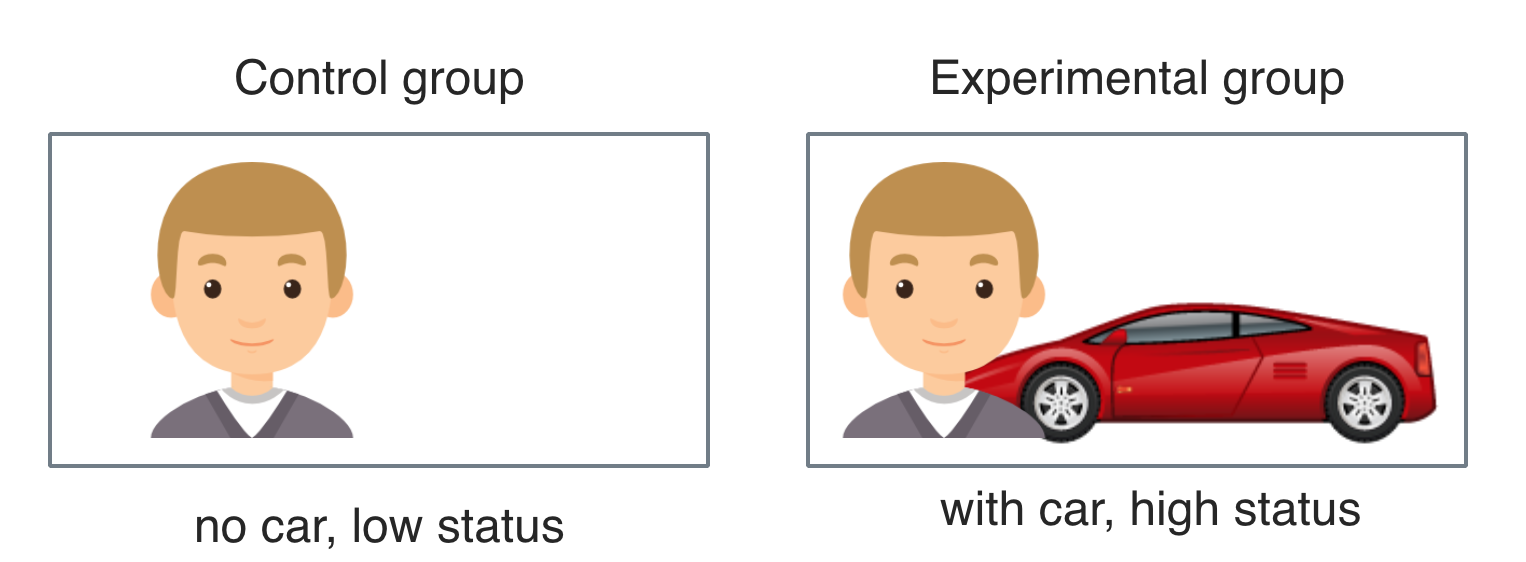
Car icon made by IconShow is licenced for non-commercial use.

Data was collected electronically by the portal, so it can be expected that no typos or similar errors are present in the data. We performed some “sanity checks”, e.g. checked whether all values are plausible. Finally, we checked that the anonymization had worked. No errors or quality restrictions were identified.

ETHICAL ISSUES

This study was part of a MSc thesis, and was approved by the supervising professor (disclaimer: the supervising professor is one of the authors). As we did not engage in any contact with the individuals contacting our straw persons it appears unlikely that strong emotions and strong negative affect occurred. We did not receive any signs of discontent from the participants. No further debriefing took place. We declare that we have no conflicts of interest.

DATASET DESCRIPTION

Object name

data

Data type

primary data (anonymized)

Format names and versions

CSV

Language

English

Licence

CC-BY-4

Embargo

none

Repository location

http://www.osf.io/4hkjm

Publication date at reposository

2016-08-17

Dimensions of data set

5063 observations of 9 variables. See codebook for details.

Reuse potential

The data set allows for testing (replicating) some of the main claims of evolutionary psychology with regard to human mating. The results of the present data have not been published yet; given the strong effects, the large sample size and the high overall interest in evolutionary psychology in general and human mating in particular, this data set can be expected to be of substantial interest. Additional, refined analysis, aggregation to existing bodies of data, and teaching (due to the general “lay” interest) are included in potential reuses of this data set.

ACKNOWLEDGEMENTS

None.

REFERENCES

Abramson, Paul R. 1995. Sexual Nature/sexual Culture. University of Chicago Press.

Buss, David M. 1989. “Sex Differences in Human Mate Preferences: Evolutionary Hypotheses Tested in 37 Cultures.” Behavioral and Brain Sciences 12 (01). Cambridge Univ Press: 1–14.

———. 2009. “The Great Struggles of Life: Darwin and the Emergence of Evolutionary Psychology.” American Psychologist 64 (2). American Psychological Association: 140.

———. 2015. Evolutionary Psychology: The New Science of the Mind. Psychology Press.

Buss, David M, Max Abbott, Alois Angleitner, Armen Asherian, Angela Biaggio, Angel Blanco-Villasenor, M Bruchon-Schweitzer, et al. 1990. “International Preferences in Selecting Mates a Study of 37 Cultures.” Journal of Cross-Cultural Psychology 21 (1). Sage Publications: 5–47.

Buss, David M, Todd K Shackelford, Lee A Kirkpatrick, and Randy J Larsen. 2001. “A Half Century of Mate Preferences: The Cultural Evolution of Values.” Journal of Marriage and Family 63 (2). Wiley Online Library: 491–503.

Coie, John D, Kenneth A Dodge, and Heide Coppotelli. 1982. “Dimensions and Types of Social Status: A Cross-Age Perspective.” Developmental Psychology 18 (4). American Psychological Association: 557.

Grammer, Karl, and Randy Thornhill. 1994. “Human (Homo Sapiens) Facial Attractiveness and Sexual Selection: The Role of Symmetry and Averageness.” Journal of Comparative Psychology 108 (3). American Psychological Association: 233.

Shackelford, Todd K, and Randy J Larsen. 1997. “Facial Asymmetry as an Indicator of Psychological, Emotional, and Physiological Distress.” Journal of Personality and Social Psychology 72 (2). American Psychological Association: 456.

Singh, Devendra, and Robert K Young. 1995. “Body Weight, Waist-to-Hip Ratio, Breasts, and Hips: Role in Judgments of Female Attractiveness and Desirability for Relationships.” Ethology and Sociobiology 16 (6). Elsevier: 483–507.

Streeter, Sybil A, and Donald H McBurney. 2003. “Waist–hip Ratio and Attractiveness: New Evidence and a Critique of a Critical Test.” Evolution and Human Behavior 24 (2). Elsevier: 88–98.