Kapitel 7 Resampling und Tuning

Benötigte R-Pakete für dieses Kapitel:

library(tidyverse)
library(tidymodels)
library(tune)  #  wird nicht autaomtisch mit tidymodels gestartet

7.1 Lernsteuerung

7.1.1 Vorbereitung

• Lesen Sie die Literatur.

7.1.2 Lernziele

• Sie verstehen den Nutzen von Resampling und Tuning im maschinellen Nutzen.
• Sie können Methoden des Resampling und Tunings mit Hilfe von Tidymodels anwenden.

7.1.3 Literatur

• Rhys, Kap. 3
• TMWR, Kap. 10, 12

7.2 Überblick

Der Standardablauf des maschinellen Lernens ist in Abb. 7.1 dargestellt. Eine alternative, hilfreich Abbildung findet sich hier in Kap. 10.2 in Silge and Kuhn (2022).

Abbildung 7.1: Standardablauf des maschinellen Lernens mit Tuning und Resampling

7.3 tidymodels

7.3.1 Datensatz aufteilen

data(ames)

set.seed(4595)
data_split <- initial_split(ames, strata = "Sale_Price")

ames_train <- training(data_split)
ames_test <- testing(data_split)

7.3.2 Rezept, Modell und Workflow definieren

In gewohnter Weise definieren wir den Workflow mit einem kNN-Modell.

ames_rec <-
  recipe(Sale_Price ~ ., data = ames_train) %>%
  step_log(Sale_Price, base = 10) %>%
  step_other(Neighborhood, threshold = .1)  %>%
  step_dummy(all_nominal()) %>%
  step_zv(all_predictors()) 

knn_model <-
  nearest_neighbor(
    mode = "regression",
  ) %>%
  set_engine("kknn")

ames_wflow <-
  workflow() %>%
  add_recipe(ames_rec) %>%
  add_model(knn_model)

Das kNN-Modell ist noch nicht berechnet, es ist nur ein “Rezept” erstellt:

knn_model

## K-Nearest Neighbor Model Specification (regression)
## 
## Computational engine: kknn

ames_wflow

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 4 Recipe Steps
## 
## • step_log()
## • step_other()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## K-Nearest Neighbor Model Specification (regression)
## 
## Computational engine: kknn

7.4 Resampling

Vergleichen Sie die drei Fälle, die sich in der Nutzung von Train- und Test-Sample unterscheiden:

1. Wir fitten ein Klassifikationsmodell in einer Stichprobe, sagen die Y-Werte dieser Stichprobe “vorher”. Wir finden eine Gesamtgenauigkeit von 80%.
2. Wir fitten ein Klassifikationsmodell in einem Teil der ursprünglichen Stichprobe (Train-Sample) und sagen Y-die Werte im verbleibenden Teil der ursprünglichen Stichprobe vorher (Test-Sample). Wir finden eine Gesamtgenauigkeit von 70%.
3. Wir wiederholen Fall 2 noch drei Mal mit jeweils anderer Zuweisung der Fälle zum Train- bzw. zum Test-Sample. Wir finden insgesamt folgende Werte an Gesamtgenauigkeit: 70%, 70%, 65%, 75%.

Welchen der drei Fälle finden Sie am sinnvollsten? Warum?

7.5 Illustration des Resampling

Resampling stellt einen Oberbegriff dar; Kreuzvalidierung ist ein Unterbegriff dazu. Es gibt noch andere Arten des Resampling, etwa Bootstrapping oder Leave-One-Out-Cross-Validation (LOOCV).

Im Folgenden ist nur die Kreuzvalidierung dargestellt, da es eines der wichtigsten und vielleicht das Wichtigste ist. In vielen Quellen finden sich Erläuterungen anderer Verfahren dargestellt, etwa in Silge and Kuhn (2022), James et al. (2021) oder Rhys (2020).

7.5.1 Einfache v-fache Kreuzvalidierung

Abb. 7.2 illustriert die zufällige Aufteilung von \(n=10\) Fällen der Originalstrichprobe auf eine Train- bzw. Test-Stichpobe. Man spricht von Kreuzvalidierung (cross validation, CV).

In diesem Fall wurden 70% der (\(n=10\)) Fälle der Train-Stichprobe zugewiesen (der Rest der Test-Stichprobe); ein willkürlicher, aber nicht unüblicher Anteil. Diese Aufteilung wurde \(v=3\) Mal vorgenommen, es resultieren drei “Resampling-Stichproben”, die manchmal auch als “Faltungen” bezeichnet werden.

Abbildung 7.2: Resampling: Eine Stichprobe wird mehrfach (hier 3 Mal) zu 70% in ein Train- und zu 30% in die Test-Stichprobe aufgeteilt

Sauer (2019) stellt das Resampling so dar (S. 259), s. Abb. 7.3.

Abbildung 7.3: Kreuzvalidierung, Aufteilung in Train- vs. Testsample

Der Gesamtfehler der Vorhersage wird als Mittelwerte der Vorhersagefehler in den einzelnen Faltungen berechnet.

Warum ist die Vorhersage besser, wenn man mehrere Faltungen, mehrere Schätzungen für \(y\) also, vornimmt?

Der Grund ist das Gesetz der großen Zahl, nachdem sich eine Schätzung in Mittelwert und Variabilität stabilisiert mit steigendem Stichprobenumfang, dem wahren Mittelwert also präziser schätzt. Bei Normalverteilungen klappt das gut, bei randlastigen Verteilungen leider nicht mehr (Taleb 2019).

Häufig werden \(v=10\) Faltungen verwendet, was sich empirisch als guter Kompromiss von Rechenaufwand und Fehlerreduktion herausgestellt hat.

7.5.2 Wiederholte Kreuzvalidierung

Die \(r\)-fach wiederholte Kreuzvalidierung wiederholte die einfache Kreuzvalidierung mehrfach (nämlich \(r=4\) mal), Sauer (2019) stellt das Resampling so dar (S. 259), s. Abb. 7.4.

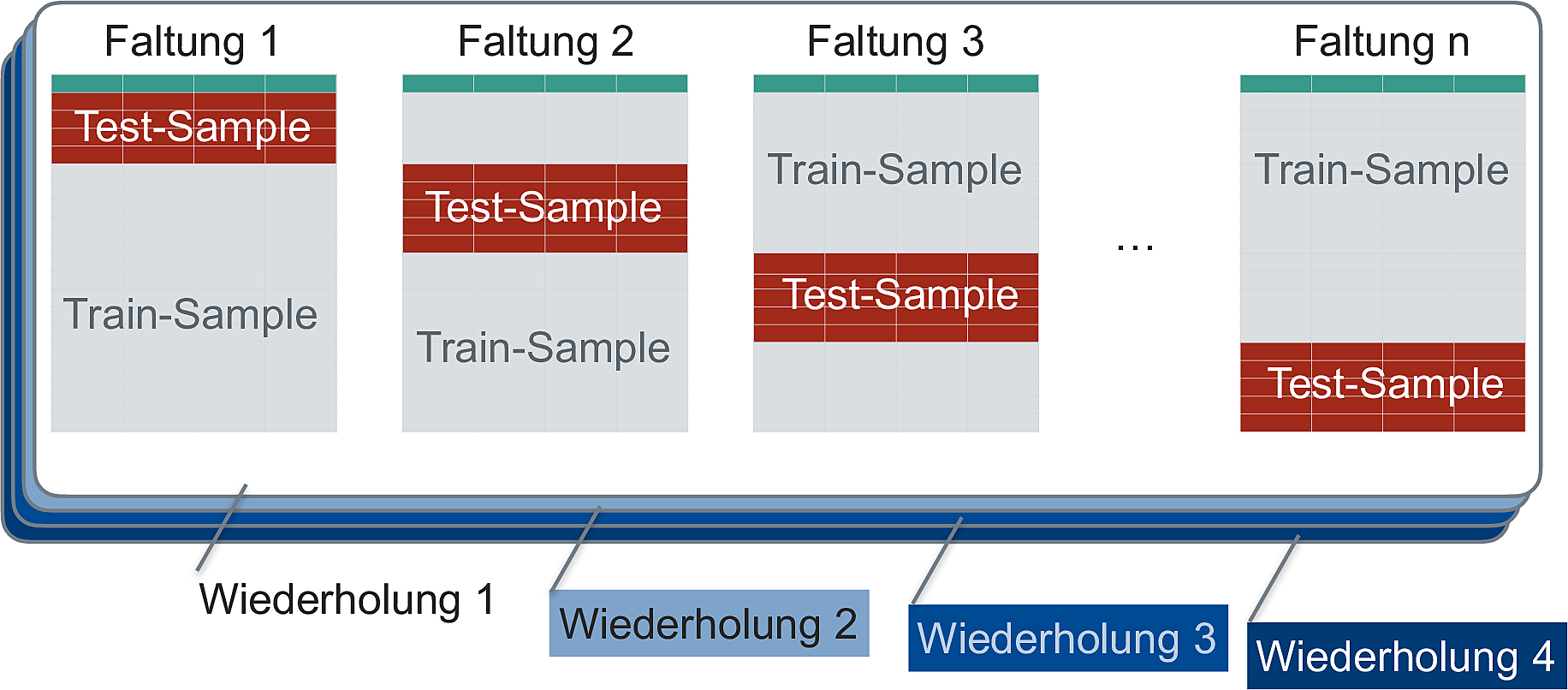
Abbildung 7.4: Wiederholte Kreuzvalidierung

Die wiederholte Kreuzvalidierung reduziert den Standardfehler der Vorhersagen.

Silge and Kuhn (2022) zeigen die Verringerung des Schätzfehlers als Funktion der \(r\) Wiederholungen dar, s. Abb. 7.5.

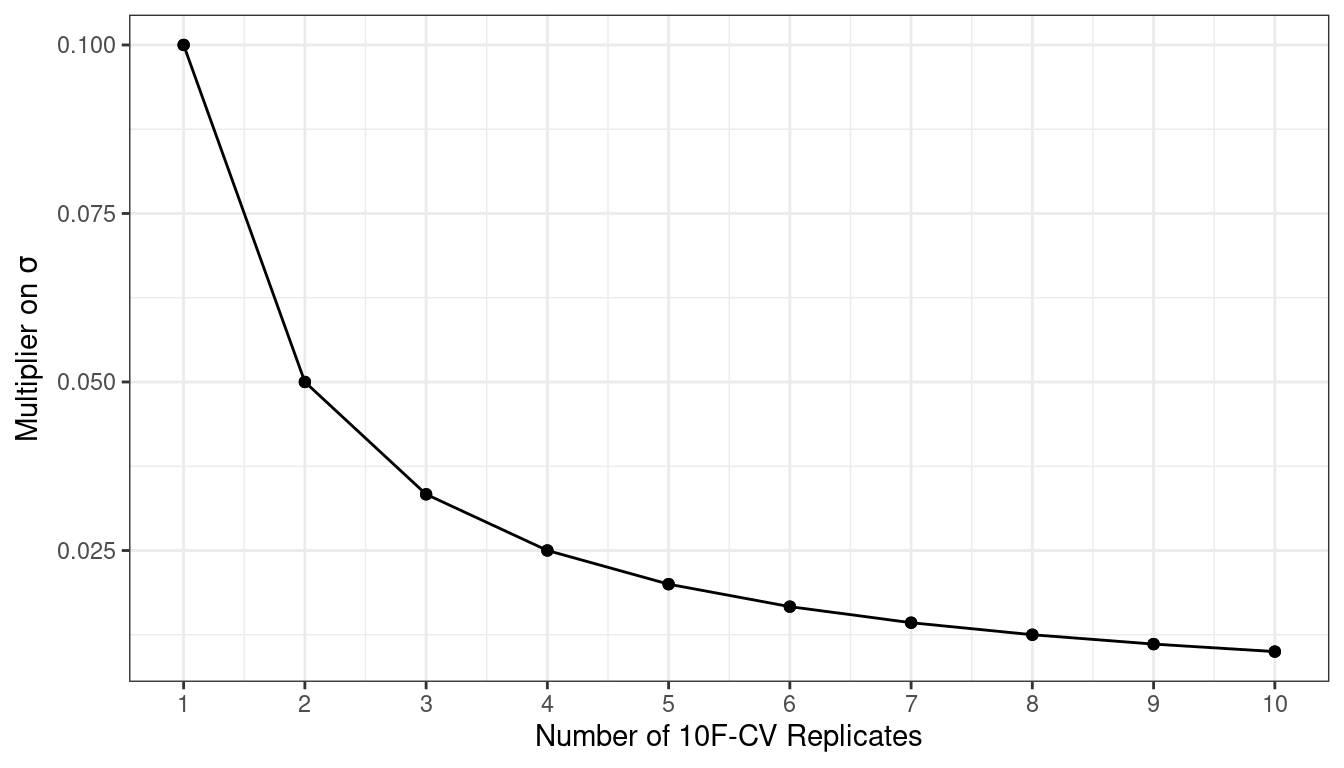
Abbildung 7.5: Reduktion des Schätzfehlers als Funktion der r Wiederhoulugen der Kreuzvalidierung

Warum ist die Wiederholung der Kreuzvalidierung nützlich?

Die Kreuvalidierung liefert einen Schätzwert der Modellparameter, die wahren Modellparameter werden also anhand einer Stichprobe von \(n=1\) geschätzt. Mit höherem Stichprobenumfang kann diese Schätzung natürlich präzisiert werden.

Da jede Stichprobenverteilung bei \(n \rightarrow \infty\) normalverteilt ist - ein zentrales Theorem der Statistik, der Zentrale Grenzwertsatz (Central Limit Theorem) - kann man hoffen, dass sich eine bestimmte Stichprobenverteilung bei kleinerem \(n\) ebenfalls annähernd normalverteilt³. Dann sind die Quantile bekannt und man kann die Streuung der Schätzers, \({\sigma }_{\bar {x}}\), z.B. für den Mittelwert, einfach schätzen:

\[{\displaystyle {\sigma }_{\bar {x}}\ ={\frac {\sigma }{\sqrt {n}}}}\]

7.5.3 Resampling passiert im Train-Sample

Wichtig zu beachten ist, dass die Resampling nur im Train-Sample stattfindet. Das Test-Sample bleibt unangerührt. Dieser Sachverhalt ist in Abb. 7.6, aus Silge and Kuhn (2022), illustriert.

Abbildung 7.6: Resampling im Train-, nicht im Test-Sample

Wie in Abb. 7.6 dargestellt, wird das Modell im Analyse-Sample berechnet (gefittet), und im Assessment-Sample auf Modellgüte hin überprüft.

Die letztliche Modellgüte ist dann die Zusammenfassung (Mittelwert) der einzelnen Resamples.

7.5.4 Andere Illustrationen

Es gibt eine Reihe vergleichbarer Illustrationen in anderen Büchern:

• Timbers, Campbell & Lee, 2022, Kap. 6
• Silge & Kuhn, 2022, Abb. 10.1
• Silge & Kuhn, 2022, Abb. 10.2
• Silge & Kuhn, 2022, Abb. 10.3
• James, Witten, hastie & Tishirani, 2021, Abb. 5.3

7.6 Gesetz der großen Zahl

Nach dem Gesetz der großen Zahl (Law of Large Numbers) sollte sich der Mittelwert einer großen Stichprobe dem theoretischen Mittelwert der zugrundeliegenden Verteilung (Population, datengeneriender Prozess) sehr nahe kommen.

\[\displaystyle \lim _{n\to \infty }\sum _{i=1}^{n}{\frac {X_{i}}{n}}={\overline {X}}\]

David Salazar visualisiert das folgendermaßen in diesem Post seines lesenswerten Blogs, s. Abb. 7.7.

# source: https://david-salazar.github.io/2020/04/17/fat-vs-thin-does-lln-work/
samples <- 1000

thin <- rnorm(samples, sd = 20)

cumulative_mean <- function(numbers) {
    x <- seq(1, length(numbers))
    cum_mean <- cumsum(numbers)/x 
    cum_mean
}

thin_cum_mean <- cumulative_mean(thin)

thin_cum_mean %>%
  tibble(running_mean = .) %>% 
  add_rownames(var = 'number_samples') %>% 
  mutate(number_samples = as.double(number_samples)) %>% 
  arrange(number_samples) %>% 
  ggplot(aes(x = number_samples, y = running_mean)) +
    geom_line(color = 'dodgerblue4') +
    geom_hline(yintercept = 0, linetype = 2, color = 'red') +
  hrbrthemes::theme_ipsum_rc(grid = 'Y') +
  scale_x_continuous(labels = scales::comma) +
  labs(x = "Stichprobengröße",
       title = "Gesetz der großen Zahl", 
       subtitle = "Kumulierter Mittelwert aus einer Normalverteilung mit sd=20")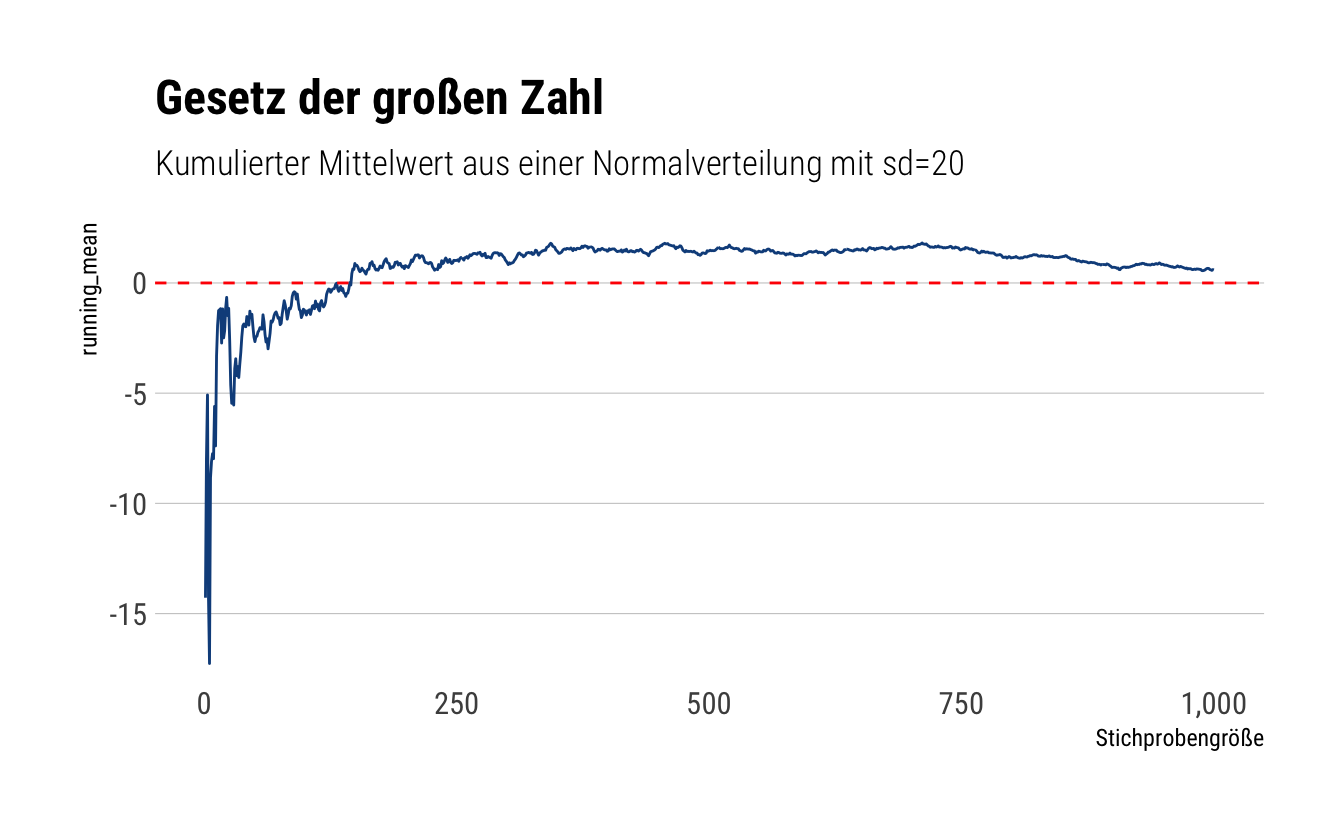

Abbildung 7.7: Gesetz der großen Zahl

Wie man sieht, nähert sich der empirische Mittelwert (also in der Stichprobe) immer mehr dem theoretischen Mittelwert, 0, an.

Achtung: Bei randlastigen Verteilungen darf man dieses schöne, wohlerzogene Verhalten nicht erwarten (Taleb 2019).

7.7 Über- und Unteranpassung an einem Beispiel

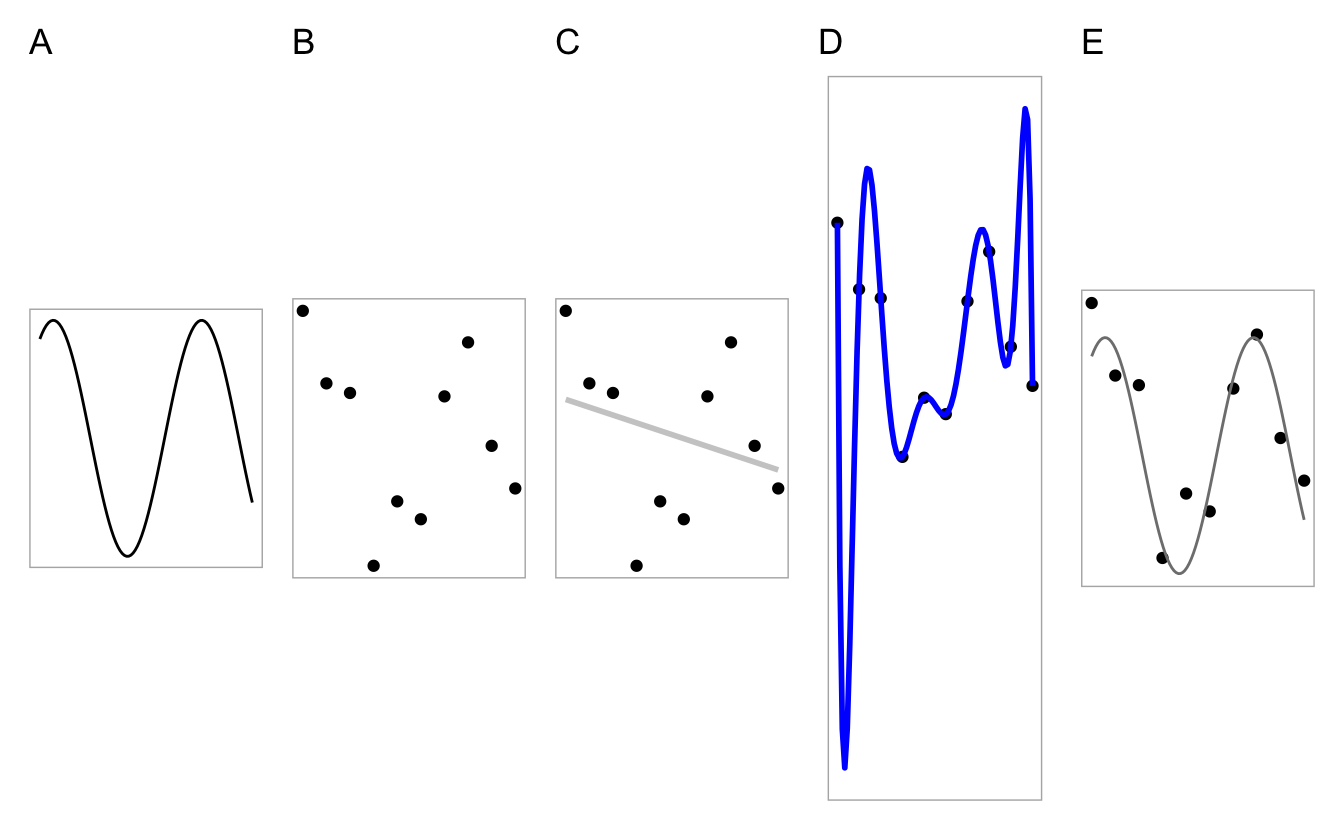
Abbildung 7.8: Welches Modell (Teile C-E) passt am besten zu den Daten (Teil B)? Die ‘wahre Funktion’, der datengenerierende Prozess ist im Teil A dargestellt

Abb. 7.8 zeigt:

• Teil A: Die ‘wahre Funktion’, \(f\), die die Daten erzeugt. Man spricht auch von der “datengenerierenden Funktion”. Wir gehen gemeinhin davon aus, dass es eine wahre Funktion gibt. Das heißt nicht, dass die wahre Funktion die Daten perfekt erklärt, schließlich kann die Funktion zwar wahr, aber unvollständig sein oder unsere Messinstrumente sind nicht perfekt präzise.
• Teil B: Die Daten, erzeugt aus A plus etwas zufälliges Fehler (Rauschen).
• Teil C: Ein zu einfaches Modell: Unteranpassung. Vorhersagen in einer neuen Stichprobe (basierend auf dem datengenerierenden Prozess aus A) werden nicht so gut sein.
• Teil D: Ein zu komplexes Modell: Überanpassung. Vorhersagen in einer neuen Stichprobe (basierend auf dem datengenerierenden Prozess aus A) werden nicht so gut sein.
• Teil E: Ein Modell mittlerer Komplexität. Keine Überanpassung, keine Unteranpassung. Vorhersagen in einer neuen Stichprobe (basierend auf dem datengenerierenden Prozess aus A) werden gut sein.

7.8 CV in tidymodels

7.8.1 CV definieren

So kann man eine einfache v-fache Kreuzvalidierung in Tidymodels auszeichnen:

set.seed(2453)
ames_folds <- vfold_cv(ames_train, strata = "Sale_Price")
ames_folds

## #  10-fold cross-validation using stratification 
## # A tibble: 10 × 2
##    splits             id    
##    <list>             <chr> 
##  1 <split [1976/221]> Fold01
##  2 <split [1976/221]> Fold02
##  3 <split [1976/221]> Fold03
##  4 <split [1976/221]> Fold04
##  5 <split [1977/220]> Fold05
##  6 <split [1977/220]> Fold06
##  7 <split [1978/219]> Fold07
##  8 <split [1978/219]> Fold08
##  9 <split [1979/218]> Fold09
## 10 <split [1980/217]> Fold10

Werfen wir einen Blick in die Spalte splits, erste Zeile:

ames_folds %>% pluck(1, 1)

## <Analysis/Assess/Total>
## <1976/221/2197>

Möchte man die Defaults vpn vfold_cv wissen, schaut man in der Hilfe nach: ?vfold_cv:

vfold_cv(data, v = 10, repeats = 1, strata = NULL, breaks = 4, pool = 0.1, ...)

Probieren wir \(v=5\) und \(r=2\):

ames_folds_rep <- vfold_cv(ames_train, 
                           strata = "Sale_Price", 
                           v = 5,
                           repeats = 2)
ames_folds_rep

## #  5-fold cross-validation repeated 2 times using stratification 
## # A tibble: 10 × 3
##    splits             id      id2  
##    <list>             <chr>   <chr>
##  1 <split [1756/441]> Repeat1 Fold1
##  2 <split [1757/440]> Repeat1 Fold2
##  3 <split [1757/440]> Repeat1 Fold3
##  4 <split [1758/439]> Repeat1 Fold4
##  5 <split [1760/437]> Repeat1 Fold5
##  6 <split [1756/441]> Repeat2 Fold1
##  7 <split [1757/440]> Repeat2 Fold2
##  8 <split [1757/440]> Repeat2 Fold3
##  9 <split [1758/439]> Repeat2 Fold4
## 10 <split [1760/437]> Repeat2 Fold5

7.8.2 Resamples fitten

Hat unser Computer mehrere Rechenkerne, dann können wir diese nutzen und die Berechnungen beschleunigen. Im Standard wird sonst nur ein Kern verwendet.

mycores <- parallel::detectCores(logical = FALSE)
mycores

## [1] 4

Auf Unix/MacOC-Systemen kann man dann die Anzahl der parallen Kerne so einstellen:

library(doMC)
registerDoMC(cores = mycores)

So, und jetzt fitten wir die Resamples und trachten die Modellgüte in den Resamples:

ames_resamples_fit <- 
  ames_wflow %>% 
  fit_resamples(ames_folds)

 ames_resamples_fit %>%
  collect_metrics()

## # A tibble: 2 × 6
##   .metric .estimator   mean     n std_err .config             
##   <chr>   <chr>       <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard   0.0928    10 0.00187 Preprocessor1_Model1
## 2 rsq     standard   0.722     10 0.00864 Preprocessor1_Model1

Natürlich interessiert uns primär die Modellgüte im Test-Sample:

final_ames <-
  last_fit(ames_wflow, data_split)

final_ames %>% 
  collect_metrics()

## # A tibble: 2 × 4
##   .metric .estimator .estimate .config             
##   <chr>   <chr>          <dbl> <chr>               
## 1 rmse    standard       0.103 Preprocessor1_Model1
## 2 rsq     standard       0.678 Preprocessor1_Model1

7.9 Tuning

7.9.1 Tuning auszeichnen

In der Modellspezifikation des Modells können wir mit tune() auszeichnen, welche Parameter wir tunen möchten. Wir könenn

knn_model <-
  nearest_neighbor(
    mode = "regression",
    neighbors = tune()
  ) %>%
  set_engine("kknn")

Wir können dem Tuningparameter auch einen Namen (ID/Laben) geben, z.B. “K”:

knn_model <-
  nearest_neighbor(
    mode = "regression",
    neighbors = tune("K")
  ) %>%
  set_engine("kknn")

7.9.2 Grid Search vs. Iterative Search

Im K-Nächste-Nachbarn-Modell ist der vorhergesagt Wert, \(\hat{y}\) für eine neue Beobachtung \(x_0\) wie folgt definiert:

\[ \hat y = \frac{1}{K}\sum_{\ell = 1}^K x_\ell^*, \]

wobei \(K\) die Anzahl der zu berücksichtigen nächsten Nachbarn darstellt und \(x_\ell^*\) die Werte dieser berücksichtiggten Nachbarn.

Die Wahl von \(K\) hat einen gewaltigen Einfluss auf die Vorhersagen und damit auf die Vorhersagegüte. Allerdings wird \(K\) nicht vom Modell geschätzt. Es liegt an den Nutzi, diesen Wert zu wählen.

Parameter dieser Art (die von den Nutzi zu bestimmen sind, nicht vom Algorithmus), nennt man Tuningparameter.

Abbildung 7.9 aus Silge and Kuhn (2022) stellt exemplarisch dar, welchen großen Einfluss die Wahl des Werts eines Tuningparameters auf die Vorhersagen eines Modells haben.

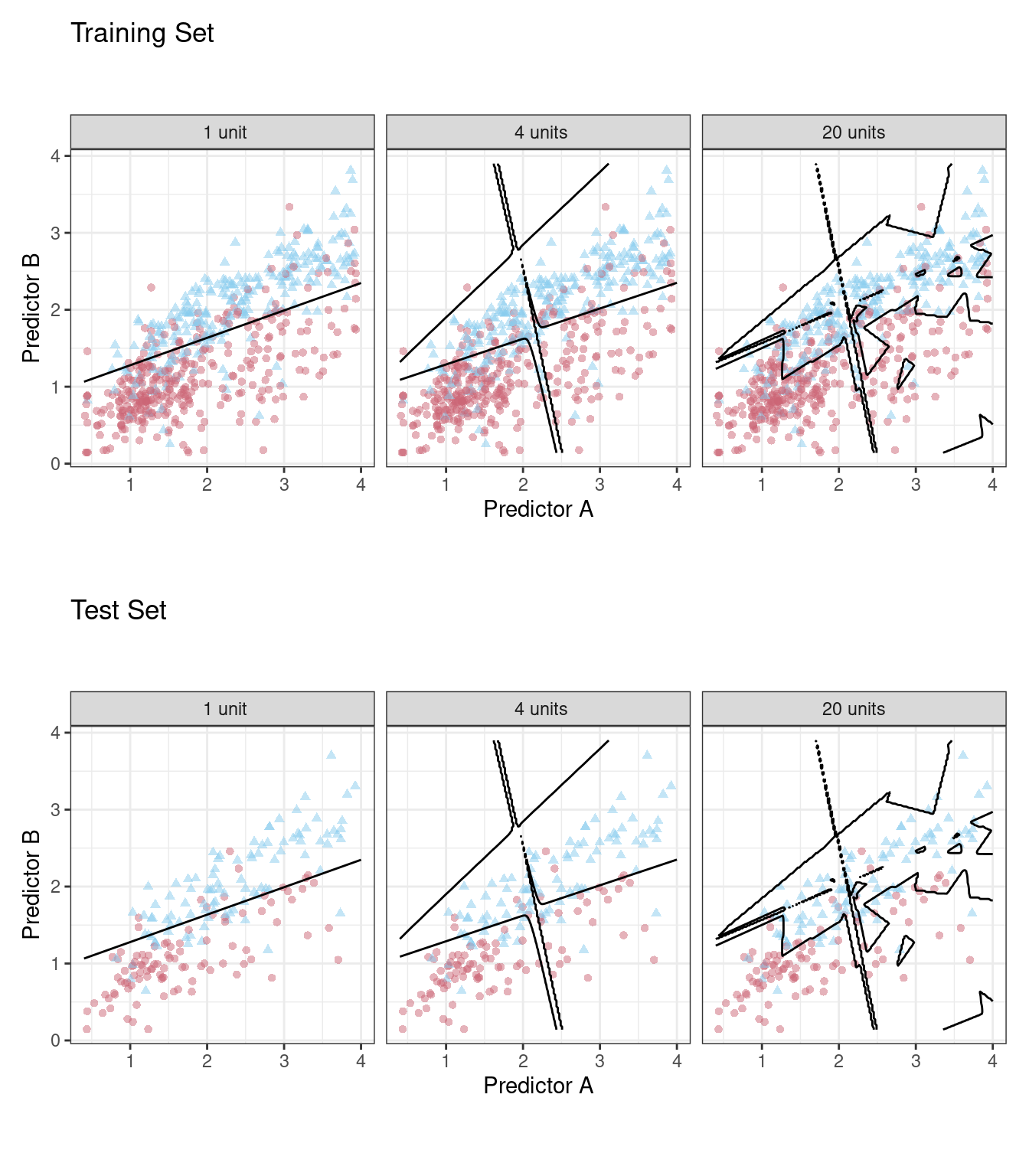
Abbildung 7.9: Overfitting als Funktion der Modellparameter und insofern als Problem de Wahl der Tuningparameter

Aber wie wählt man “gute” Werte der Tuningparater? Zwei Ansätze, grob gesprochen, bieten sich an.

1. Grid Search: Probiere viele Werte aus und schaue, welcher der beste ist. Dabei musst du hoffen, dass du die Werte erwischt, die nicht nur im Train-, sondern auch im Test-Sample gut funktionieren werden.

2. Iterative Search: Wenn du einen Wert eines Tuningparameters hast, nutze diesen, um intelligenter einen neuen Wert eines Tuningparameters zu finden.

Der Unterschied beider Ansätze ist in Silge and Kuhn (2022) wie in Abb. 7.10 dargestellt.

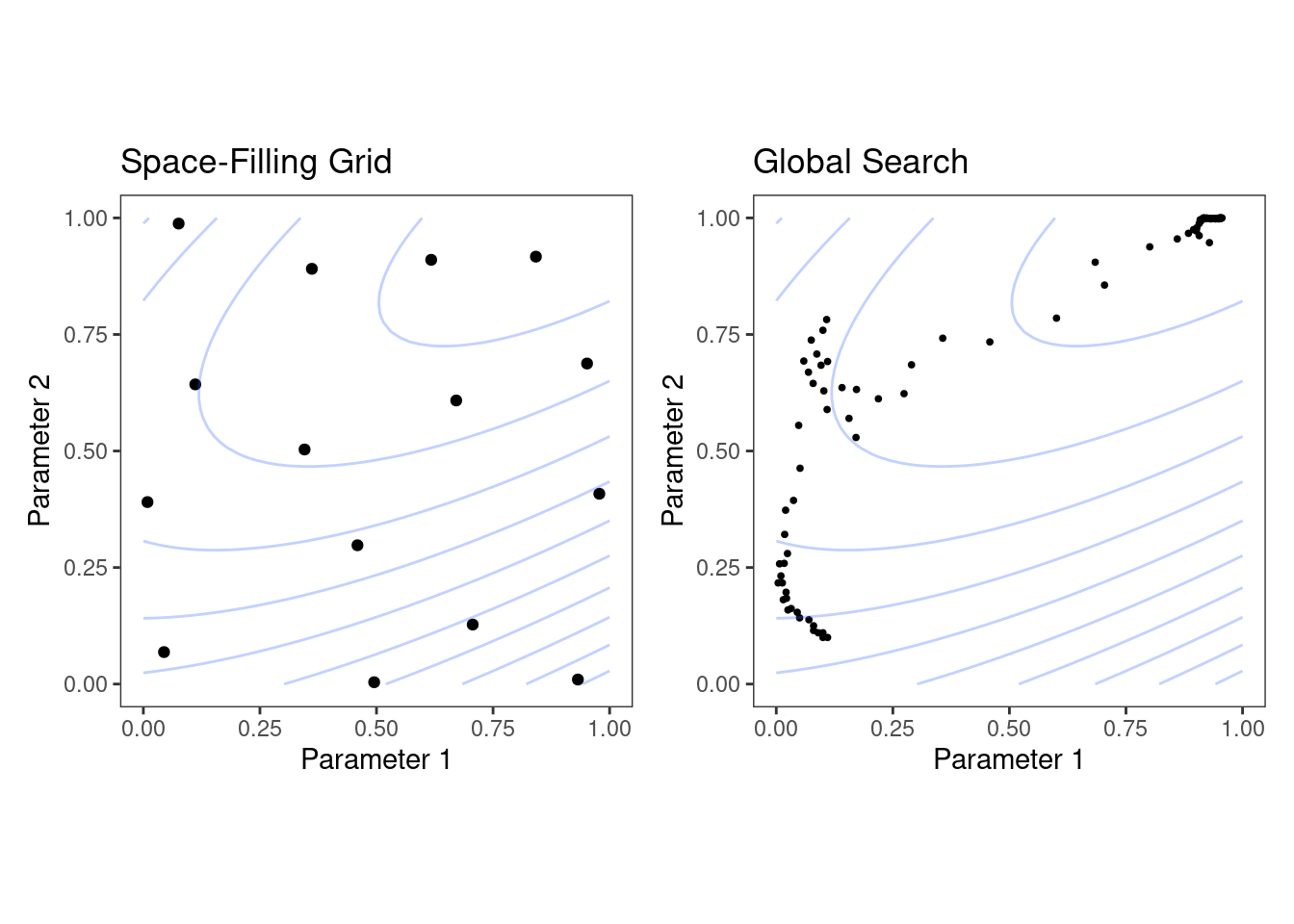
Abbildung 7.10: Links: Grid Search. Rechts: Iterative Search2

In tidymodels kann man mit tune() angeben, dass man einen bestimmten Parameter tunen möchte. tidymodels führt das dann ohne weiteres Federlesens für uns durch.

7.10 Tuning mit Tidymodels

7.10.0.1 Tuningparameter betrachten

Möchte man wissen, welche und wie viele Tuningparameter tidymodels in einem Modell berücksichtigt, kann man extract_parameter_set_dials() aufrufen:

extract_parameter_set_dials(knn_model)

## Collection of 1 parameters for tuning
## 
##  identifier      type    object
##           K neighbors nparam[+]

Die Ausgabe informiert uns, dass es nur einen Tuningparameter gibt in diesem Modell und dass der Name (Label, ID) des Tuningparameters “K” ist. Außerdem sollen die Anzahl der Nachbarn getunt werden. Der Tuningparameter ist numerisch; das sieht man an nparam[+].

Schauen wir uns mal an, auf welchen Wertebereich tidymodels den Parameter \(K\) begrenzt hat:

knn_model %>% 
  extract_parameter_dials("K")

## # Nearest Neighbors (quantitative)
## Range: [1, 15]

Aktualisieren wir mal unseren Workflow entsprechend:

ames_wflow <-
  ames_wflow %>% 
  update_model(knn_model)

Wir können auch Einfluss nehmen und angeben, dass die Grenzen des Wertebereichs zwischen 1 und 50 liegen soll (für den Tuningparameter neighbors):

ames_set <-
  extract_parameter_set_dials(ames_wflow) %>%
  update(K = neighbors(c(1, 50)))

ames_set

## Collection of 1 parameters for tuning
## 
##  identifier      type    object
##           K neighbors nparam[+]

7.10.1 Datenabhängige Tuningparameter

Manche Tuningparameter kann man nur bestimmen, wenn man den Datensatz kennt. So ist die Anzahl der Prädiktoren, mtry in einem Random-Forest-Modell sinnvollerweise als Funktion der Prädiktorenzahl zu wählen. Der Workflow kennt aber den Datensatz nicht. Daher muss der Workflow noch “finalisiert” oder “aktualisiert” werden, um den Wertebereich (Unter- und Obergrenze) eines Tuningparameters zu bestimmen.

Wenn wir im Rezept aber z.B. die Anzahl der Prädiktoren verändert haben, möchten wir die Grenzen des Wertebereichs für mtry (oder andere Tuningparameter) vielleicht nicht händisch, “hartverdrahtet” selber bestimmen, sondern lieber den Computer anweisen, und sinngemäß sagen: “Warte mal mit der Bestimmung der Werte der Tuningparameter, bis du den Datensatz bzw. dessen Dimensionen kennst. Merk dir, dass du, wenn du den Datensatz kennst, die Werte des Tuningparameter noch ändern musst. Und tu das dann auch.” Dazu später mehr.

ames_set <-
  workflow() %>% 
  add_model(knn_model) %>% 
  add_recipe(ames_rec) %>% 
  extract_parameter_set_dials() %>% 
  finalize(ames_train)

7.10.2 Modelle mit Tuning berechnen

Nachdem wir die Tuningwerte bestimmt haben, können wir jetzt das Modell berechnen: Für jeden Wert des Tuningparameters wird ein Modell berechnet:

ames_grid_search <-
  tune_grid(
    ames_wflow,
    resamples = ames_folds
  )
ames_grid_search

## # Tuning results
## # 10-fold cross-validation using stratification 
## # A tibble: 10 × 4
##    splits             id     .metrics          .notes          
##    <list>             <chr>  <list>            <list>          
##  1 <split [1976/221]> Fold01 <tibble [16 × 5]> <tibble [0 × 3]>
##  2 <split [1976/221]> Fold02 <tibble [16 × 5]> <tibble [0 × 3]>
##  3 <split [1976/221]> Fold03 <tibble [16 × 5]> <tibble [0 × 3]>
##  4 <split [1976/221]> Fold04 <tibble [16 × 5]> <tibble [0 × 3]>
##  5 <split [1977/220]> Fold05 <tibble [16 × 5]> <tibble [0 × 3]>
##  6 <split [1977/220]> Fold06 <tibble [16 × 5]> <tibble [0 × 3]>
##  7 <split [1978/219]> Fold07 <tibble [16 × 5]> <tibble [0 × 3]>
##  8 <split [1978/219]> Fold08 <tibble [16 × 5]> <tibble [0 × 3]>
##  9 <split [1979/218]> Fold09 <tibble [16 × 5]> <tibble [0 × 3]>
## 10 <split [1980/217]> Fold10 <tibble [16 × 5]> <tibble [0 × 3]>

Im Default berechnet tiymodels 10 Kandidatenmodelle.

Die Spalte .metrics beinhaltet die Modellgüte für jedes Kandidatenmodell.

ames_grid_search %>% 
  collect_metrics()

## # A tibble: 16 × 7
##        K .metric .estimator   mean     n std_err .config             
##    <int> <chr>   <chr>       <dbl> <int>   <dbl> <chr>               
##  1     2 rmse    standard   0.103     10 0.00213 Preprocessor1_Model1
##  2     2 rsq     standard   0.662     10 0.0112  Preprocessor1_Model1
##  3     4 rmse    standard   0.0950    10 0.00188 Preprocessor1_Model2
##  4     4 rsq     standard   0.708     10 0.00916 Preprocessor1_Model2
##  5     6 rmse    standard   0.0912    10 0.00189 Preprocessor1_Model3
##  6     6 rsq     standard   0.732     10 0.00842 Preprocessor1_Model3
##  7     7 rmse    standard   0.0900    10 0.00192 Preprocessor1_Model4
##  8     7 rsq     standard   0.740     10 0.00829 Preprocessor1_Model4
##  9     9 rmse    standard   0.0883    10 0.00201 Preprocessor1_Model5
## 10     9 rsq     standard   0.752     10 0.00827 Preprocessor1_Model5
## 11    11 rmse    standard   0.0872    10 0.00211 Preprocessor1_Model6
## 12    11 rsq     standard   0.761     10 0.00845 Preprocessor1_Model6
## 13    13 rmse    standard   0.0865    10 0.00217 Preprocessor1_Model7
## 14    13 rsq     standard   0.767     10 0.00848 Preprocessor1_Model7
## 15    15 rmse    standard   0.0861    10 0.00221 Preprocessor1_Model8
## 16    15 rsq     standard   0.772     10 0.00850 Preprocessor1_Model8

Das können wir uns einfach visualisieren lassen:

autoplot(ames_grid_search)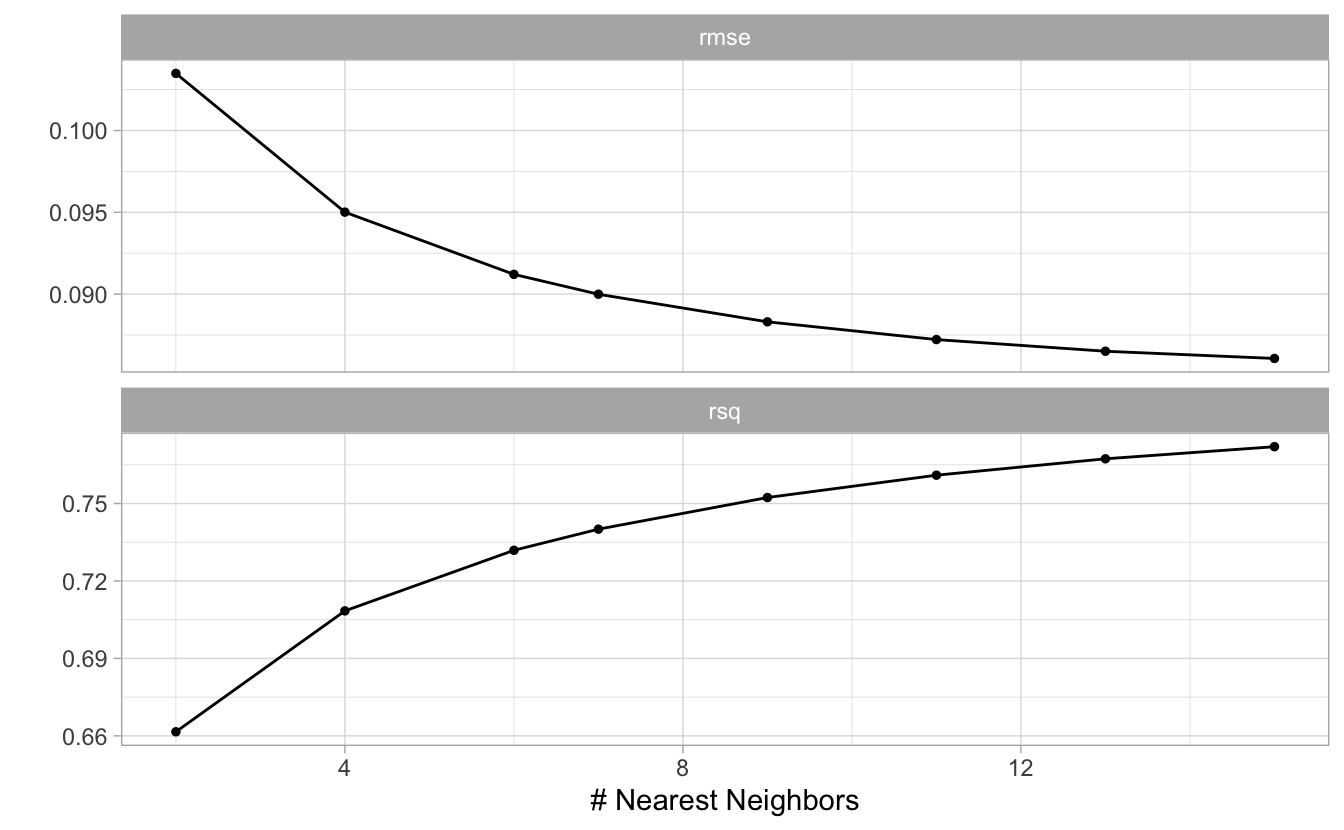

Auf Basis dieser Ergebnisse könnte es Sinn machen, noch größere Werte für \(K\) zu überprüfen.

7.10.3 Vorhersage im Test-Sample

Welches Modellkandidat war jetzt am besten?

show_best(ames_grid_search)

## # A tibble: 5 × 7
##       K .metric .estimator   mean     n std_err .config             
##   <int> <chr>   <chr>       <dbl> <int>   <dbl> <chr>               
## 1    15 rmse    standard   0.0861    10 0.00221 Preprocessor1_Model8
## 2    13 rmse    standard   0.0865    10 0.00217 Preprocessor1_Model7
## 3    11 rmse    standard   0.0872    10 0.00211 Preprocessor1_Model6
## 4     9 rmse    standard   0.0883    10 0.00201 Preprocessor1_Model5
## 5     7 rmse    standard   0.0900    10 0.00192 Preprocessor1_Model4

Wählen wir jetzt mal das beste Modell aus (im Sinne des Optimierungskriteriusms):

select_best(ames_grid_search)

## # A tibble: 1 × 2
##       K .config             
##   <int> <chr>               
## 1    15 Preprocessor1_Model8

Ok, notieren wir uns die Kombination der Tuningparameterwerte im besten Kandiatenmodell. In diesem Fall hat das Modull nur einen Tuningparameter:

ames_knn_best_params <-
  tibble(K = 15)

Unser Workflow weiß noch nicht, welche Tuningparameterwerte am besten sind:

ames_wflow

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 4 Recipe Steps
## 
## • step_log()
## • step_other()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## K-Nearest Neighbor Model Specification (regression)
## 
## Main Arguments:
##   neighbors = tune("K")
## 
## Computational engine: kknn

neighbors = tune("K") sagt uns, dass er diesen Parameter tunen will. Das haben wir jetzt ja erledigt. Wir wollen für das Test-Sample nur noch einen Wert, eben aus dem besten Kandidatenmodell, verwenden:

ames_final_wflow <-
  ames_wflow %>% 
  finalize_workflow(ames_knn_best_params)

ames_final_wflow

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 4 Recipe Steps
## 
## • step_log()
## • step_other()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## K-Nearest Neighbor Model Specification (regression)
## 
## Main Arguments:
##   neighbors = 15
## 
## Computational engine: kknn

Wie man sieht, steht im Workflow nichts mehr von Tuningparameter.

Wir können jetzt das ganze Train-Sample fitten, also das Modell auf das ganze Train-Sample anwenden - nicht nur auf ein Analysis-Sample. Und mit den dann resultierenden Modellkoeffizienten sagen wir das TestSample vorher:

final_ames_knn_fit <-
  last_fit(ames_final_wflow, data_split)

final_ames_knn_fit

## # Resampling results
## # Manual resampling 
## # A tibble: 1 × 6
##   splits             id               .metrics .notes   .predictions .workflow 
##   <list>             <chr>            <list>   <list>   <list>       <list>    
## 1 <split [2197/733]> train/test split <tibble> <tibble> <tibble>     <workflow>

Holen wir uns die Modellgüte:

collect_metrics(final_ames_knn_fit)

## # A tibble: 2 × 4
##   .metric .estimator .estimate .config             
##   <chr>   <chr>          <dbl> <chr>               
## 1 rmse    standard      0.0951 Preprocessor1_Model1
## 2 rsq     standard      0.736  Preprocessor1_Model1

7.11 Aufgaben

• Arbeiten Sie sich so gut als möglich durch diese Analyse zum Verlauf von Covid-Fällen
• Fallstudie zur Modellierung einer logististischen Regression mit tidymodels
• Fallstudie zu Vulkanausbrüchen
• Fallstudie Himalaya

7.12 Vertiefung

• Fields arranged by purity, xkcd 435