Kapitel 6 kNN
6.1 Lernsteuerung
6.1.1 Lernziele
- Sie sind in der Lage, einfache Klassifikationsmodelle zu spezifizieren mit tidymodels
- Sie können den knn-Algorithmus erläutern
- Sie können den knn-Algorithmus in tidymodels anwenden
- Sie können die Gütemetriken von Klassifikationsmodellen einschätzen
6.1.2 Literatur
- Rhys, Kap. 3
- Timbers et al., Kap. 5
6.2 Überblick
In diesem Kapitel geht es um das Verfahren KNN, K-Nächste-Nachbarn.
knitr::opts_chunk$set(echo = TRUE)Benötigte R-Pakete für dieses Kapitel:
6.3 Intuitive Erklärung
K-Nächste-Nachbarn (k nearest neighbors, kNN) ist ein einfacher Algorithmus des maschinellen Lernens, der sowohl für Klassifikation als auch für numerische Vorhersage (Regression) genutzt werden kann. Wir werden kNN als Beispiel für eine Klassifikation betrachten.
Betrachen wir ein einführendes Beispiel von Rhys (2020), für das es eine Online-Quelle gibt. Stellen Sie sich vor, wir laufen durch englische Landschaft, vielleicht die Grafschaft Kent, und sehen ein kleines Tier durch das Gras huschen. Eine Schlange?! In England gibt es (laut Rhys (2020)) nur eine giftige Schlange, die Otter (Adder). Eine andere Schlange, die Grass Snake ist nicht giftig, und dann kommt noch der Slow Worm in Frage, der gar nicht zur Familie der Schlangen gehört. Primär interessiert uns die Frage, haben wir jetzt eine Otter gesehen? Oder was für ein Tier war es?
Zum Glück wissen wir einiges über Schlangen bzw. schlangenähnliche Tiere Englands. Nämlich können wir die betreffenden Tierarten in Größe und Aggressivität einschätzen, das ist in Abbildung 6.1 dargestellt.
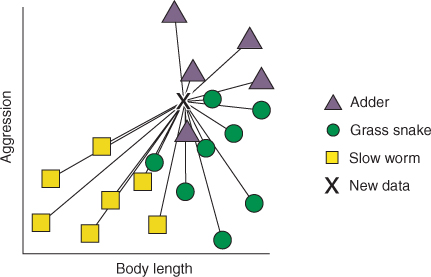
Abbildung 6.1: Haben wir gerade eine Otter gesehen?
Der Algorithmus von kNN sieht einfach gesagt vor, dass wir schauen, welcher Tierarten Tiere mit ähnlicher Aggressivität und Größe angehören. Die Tierart die bei diesen “Nachbarn” hinsichtlich Ähnlichkeit relevanter Merkmale am häufigsten vertreten ist, ordnen wir die bisher unklassifizierte Beobachtung zu.
Etwas zugespitzt:
Wenn es quakt wie eine Ente, läuft wie eine Ente und aussieht wie eine Ente, dann ist es eine Ente.
Die Anzahl \(k\) der nächsten Nachbarn können wir frei wählen; der Wert wird nicht vom Algorithmuss bestimmt. Solche vom Nutzi zu bestimmenden Größen nennt man auch Tuningparameter.
6.4 Krebsdiagnostik
Betrachten wir ein Beispiel von Timbers, Campbell, and Lee (2022), das hier frei eingesehen werden kann.
Die Daten sind so zu beziehen:
data_url <- "https://raw.githubusercontent.com/UBC-DSCI/introduction-to-datascience/master/data/wdbc.csv"
cancer <- read_csv(data_url)In diesem Beispiel versuchen wir Tumore der Brust zu klassifizieren, ob sie einen schweren Verlauf (maligne, engl. malignant) oder einen weniger schweren Verlauf (benigne, engl. benign) erwarten lassen. Der Datensatz ist hier näher erläutert.
Wie in Abb. 6.2 ersichtlich, steht eine Tumordiagnose (malignant vs. benign) in Abhängigkeit von Umfang (engl. perimeter) und Konkavität, die “Gekrümmtheit nach innen”.
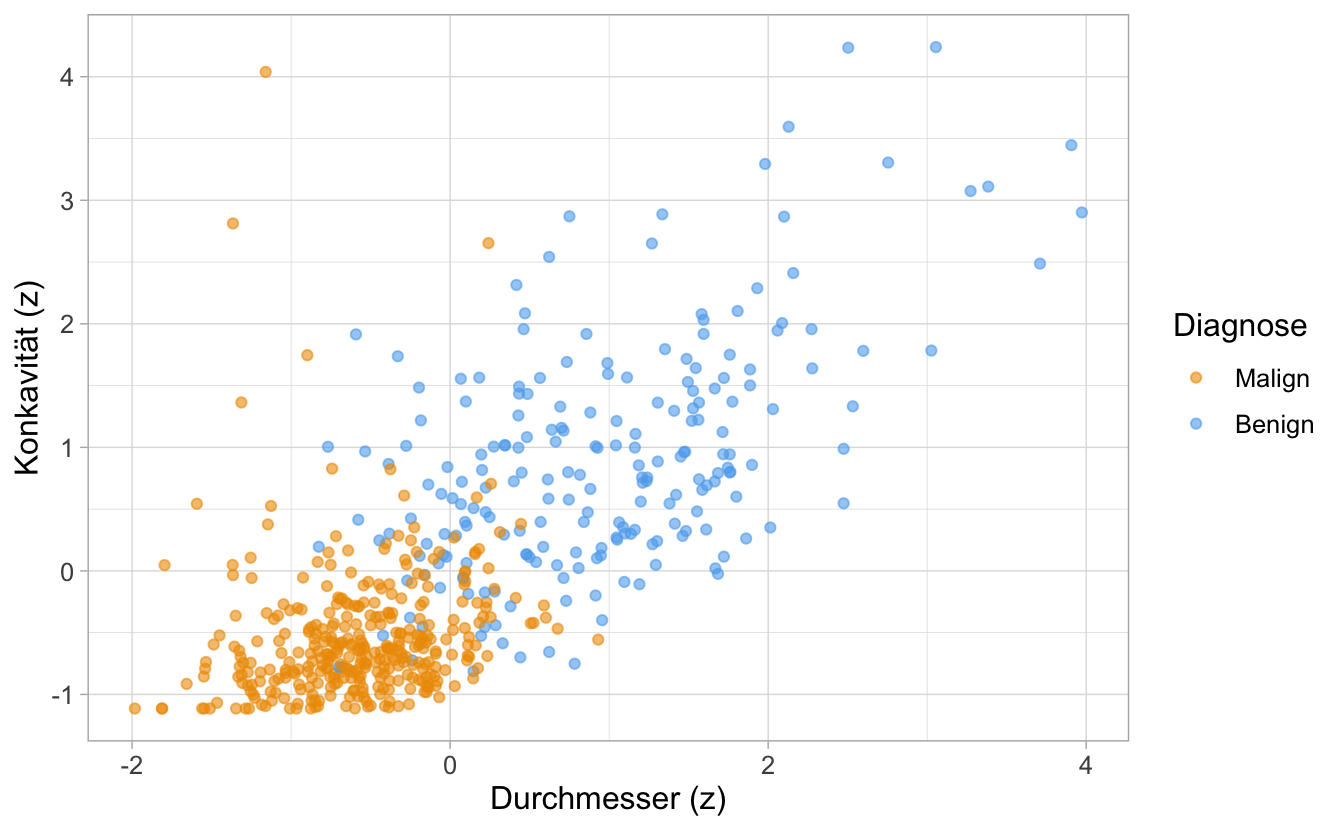
Abbildung 6.2: Streudiagramm zur Einschätzung von Tumordiagnosen
In diesem Code-Beispiel wird die seit R 4.1.0 verfügbare R-native Pfeife verwendet. Wichtig ist vielleicht vor allem, dass diese Funktion nicht läuft auf R-Versionen vor 4.1.0. Einige Unterschiede zur seit längerem bekannten Magrittr-Pfeife sind hier erläutert.
Wichtig ist, dass die Merkmale standardisiert sind, also eine identische Skalierung aufweisen, da sonst das Merkmal mit kleinerer Skala weniger in die Berechnung der Nähe (bzw. Abstand) eingeht.
Für einen neuen, bisher unklassifizierten Fall suchen nur nun nach einer Diagnose, also nach der am besten passenden Diagnose (maligne oder benigne), s. Abb. 6.3, wieder aus Timbers, Campbell, and Lee (2022). Ihr Quellcode für dieses Diagramm (und das ganze Kapitel) findet sich hier.
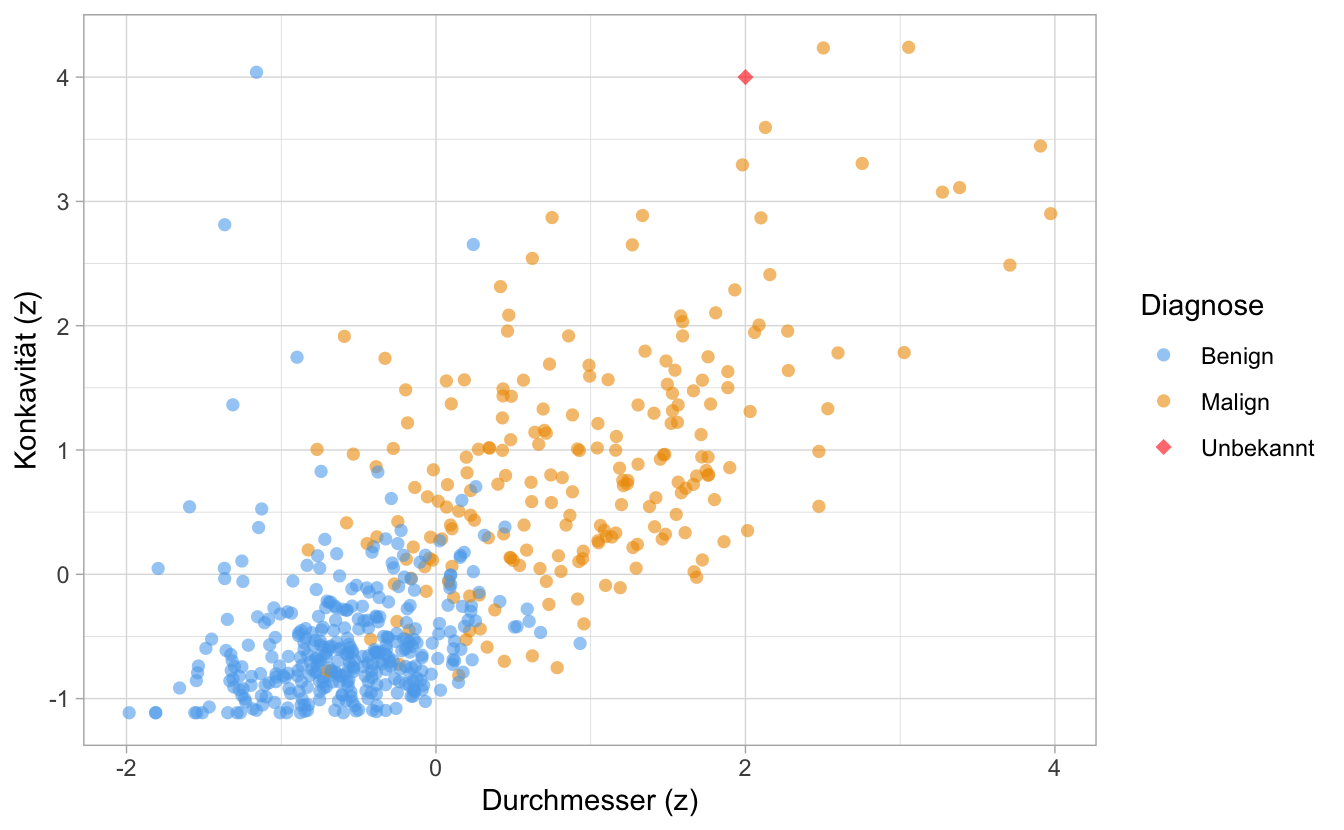
Abbildung 6.3: Ein neuer Fall, bisher unklassifiziert
Wir können zunächst den (im euklidischen Koordinatensystem) nächst gelegenen Fall (der “nächste Nachbar”) betrachten, und vereinbaren, dass wir dessen Klasse als Schätzwert für den unklassiffizierten Fall übernehmen, s. Abb. 6.4.
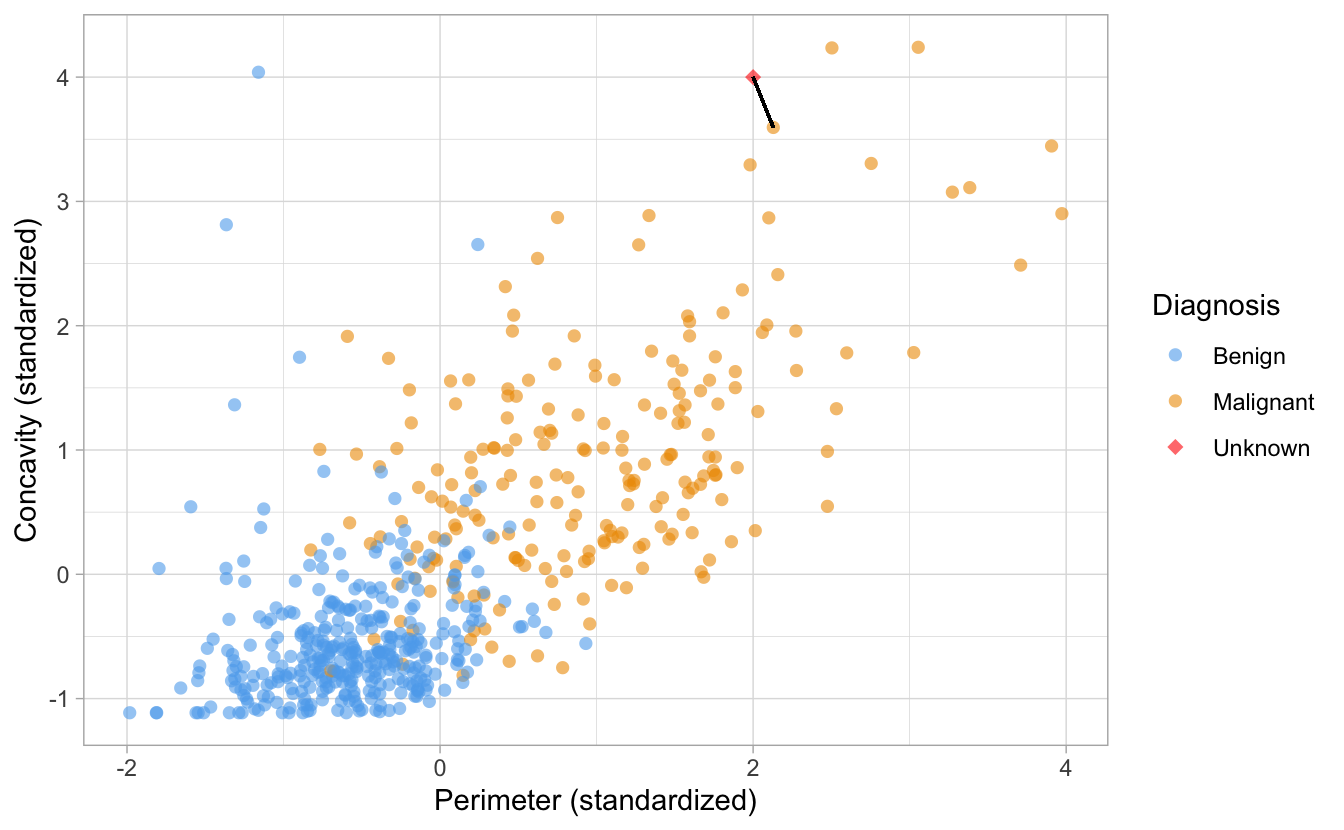
Abbildung 6.4: Ein nächster Nachbar
Betrachten wir einen anderen zu klassifizierenden Fall, s. Abb 6.5. Ob hier die Klassifikation von “benign” korrekt ist? Womöglich nicht, denn viele andere Nachbarn, die etwas weiter weg gelegen sind, gehören zur anderen Diagnose, malign.
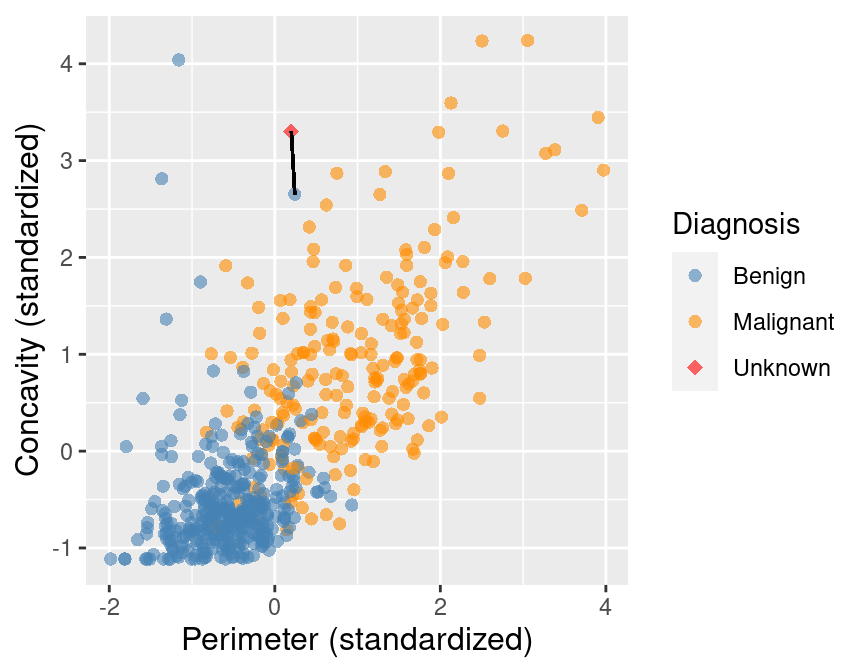
Abbildung 6.5: Trügt der nächste Nachbar?
Um die Vorhersage zu verbessern, können wir nicht nur den nächst gelegenen Nachbarn betrachten, sondern die \(k\) nächst gelegenen, z.B. \(k=3\), s. Abb 6.6.
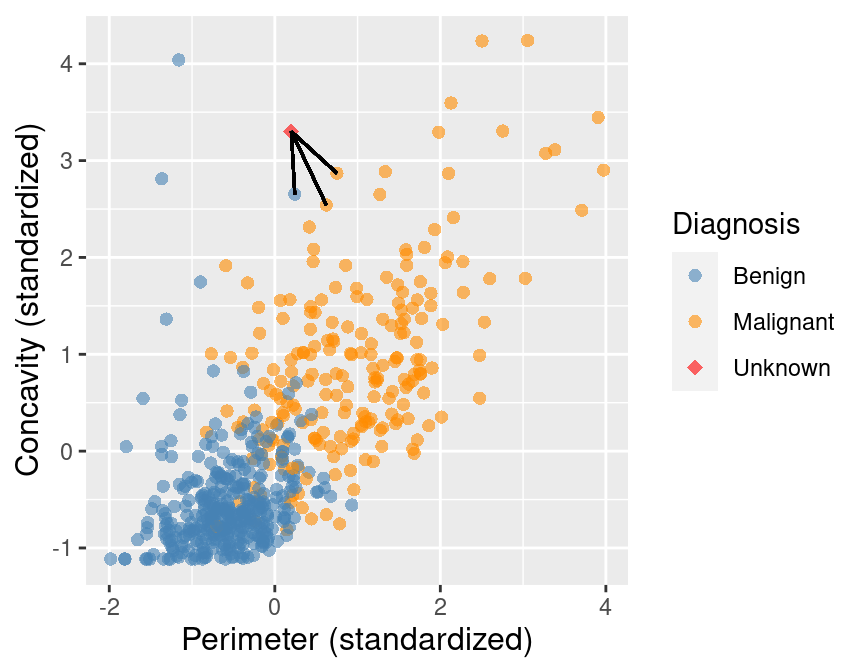
Abbildung 6.6: kNN mit k=3
Die Entscheidungsregel ist dann einfach eine Mehrheitsentscheidung: Wir klassifizieren den neuen Fall entsprechend der Mehrheit in den \(k\) nächst gelegenen Nachbarn.
6.5 Berechnung der Nähe
Es gibt verschiedenen Algorithmen, um die Nähe bzw. Distanz der Nachbarn zum zu klassifizieren Fall zu berechnen.
Eine gebräuchliche Methode ist der euklidische Abstand, der mit Pythagoras berechnet werden kann, s. Abb. 6.7 aus Sauer (2019).
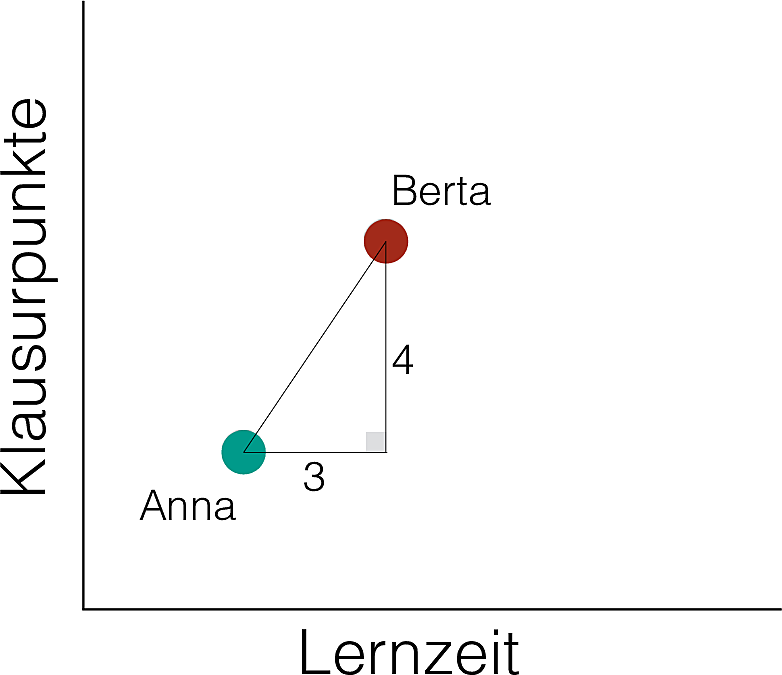
Abbildung 6.7: Euklidischer Abstand wird mit der Regel von Pythagoras berechnet
Wie war das noch mal?
\[c^2 = a^2 + b^2\]
Im Beispiel oben also:
\(c^2 = 3^2 + 4^2 = 5^2\)
Damit gilt: \(c = \sqrt{c^2} = \sqrt{5^2}=5\).
Im 2D-Raum ist das so einfach, dass man das (fat) mit bloßem Augenschein entscheiden kann. In mehr als 2 Dimensionen wird es aber schwierig für das Auge, wie ein Beispiel aus Timbers, Campbell, and Lee (2022) zeigt.
Allerdings kann man den guten alten Pythagoras auch auf Dreiecke mit mehr als zwei Dimensionen anwenden, s. Abb. 6.8 aus Sauer (2019), Kap. 21.1.2.
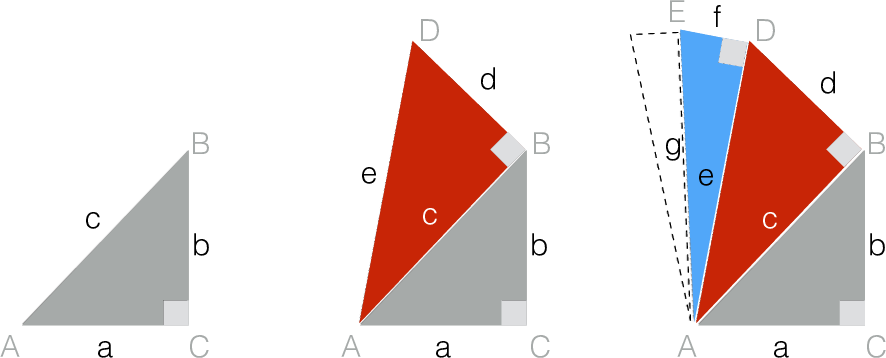
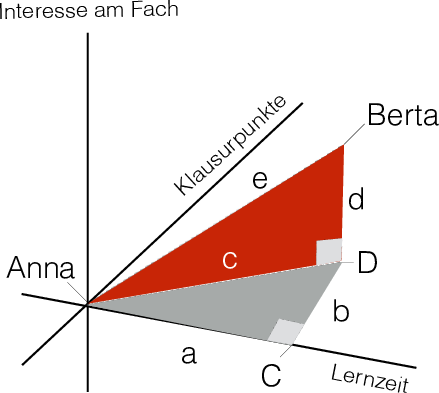
Abbildung 6.8: Pythagoras in der Ebene (links) und in 3D (rechts)
Bleiben wir beim Beispiel von Anna und Berta und nehmen wir eine dritte Variable hinzu (Statistikliebe). Sagen wir, der Unterschied in dieser dritten Variable zwischen Anna und Berta betrage 2.
Es gilt:
\[ \begin{aligned} e^2 &= c^2 + d^2 \\ e^2 &= 5^2 + 2^2 \\ e^2 &= 25 + 4\\ e &= \sqrt{29} \approx 5.4 \end{aligned} \]
6.6 kNN mit Tidymodels
6.6.1 Analog zu Timbers et al.
Eine Anwendung von kNN mit Tidymodels ist in Timbers, Campbell, and Lee (2022), Kap. 5.6, hier beschrieben.
Die Daten aus Timbers, Campbell, and Lee (2022) finden sich in diesem Github-Repo-
Die (z-transformierten) Daten zur Tumorklassifikation können hier bezogen werden.
data_url <- "https://raw.githubusercontent.com/UBC-DSCI/introduction-to-datascience/master/data/wdbc.csv"
cancer <- read_csv(data_url)Timbers, Campbell, and Lee (2022) verwenden in Kap. 5 auch noch nicht standardisierte Daten, unscales_wdbc.csv, die hier als CSV-Datei heruntergeladen werden können.
cancer_unscales_path <- "https://raw.githubusercontent.com/UBC-DSCI/introduction-to-datascience/master/data/unscaled_wdbc.csv"
unscaled_cancer <- read_csv(cancer_unscales_path) |>
mutate(Class = as_factor(Class)) |>
select(Class, Area, Smoothness)
unscaled_cancer## # A tibble: 569 × 3
## Class Area Smoothness
## <fct> <dbl> <dbl>
## 1 M 1001 0.118
## 2 M 1326 0.0847
## 3 M 1203 0.110
## 4 M 386. 0.142
## 5 M 1297 0.100
## 6 M 477. 0.128
## 7 M 1040 0.0946
## 8 M 578. 0.119
## 9 M 520. 0.127
## 10 M 476. 0.119
## # … with 559 more rows6.6.2 Rezept definieren
uc_recipe <- recipe(Class ~ ., data = unscaled_cancer)
print(uc_recipe)## Recipe
##
## Inputs:
##
## role #variables
## outcome 1
## predictor 2Und jetzt die z-Transformation:
uc_recipe <-
uc_recipe |>
step_scale(all_predictors()) |>
step_center(all_predictors())Die Schritte prep() und bake() sparen wir uns, da fit() und predict()
das für uns besorgen.
6.6.3 Modell definieren
knn_spec <- nearest_neighbor(weight_func = "rectangular", neighbors = 5) |>
set_engine("kknn") |>
set_mode("classification")
knn_spec## K-Nearest Neighbor Model Specification (classification)
##
## Main Arguments:
## neighbors = 5
## weight_func = rectangular
##
## Computational engine: kknn6.6.4 Workflow definieren
knn_fit <- workflow() |>
add_recipe(uc_recipe) |>
add_model(knn_spec) |>
fit(data = unscaled_cancer)
knn_fit## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
##
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 2 Recipe Steps
##
## • step_scale()
## • step_center()
##
## ── Model ───────────────────────────────────────────────────────────────────────
##
## Call:
## kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(5, data, 5), kernel = ~"rectangular")
##
## Type of response variable: nominal
## Minimal misclassification: 0.1107206
## Best kernel: rectangular
## Best k: 56.7 Mit Train-Test-Aufteilung
Im Kapitel 5 greifen Timbers, Campbell, and Lee (2022) die Aufteilung in Train- vs. Test-Sample noch nicht auf (aber in Kapitel 6).
Da in diesem Kurs diese Aufteilung aber schon besprochen wurde, soll dies hier auch dargestellt werden.
cancer_split <- initial_split(cancer, prop = 0.75, strata = Class)
cancer_train <- training(cancer_split)
cancer_test <- testing(cancer_split) 6.7.1 Rezept definieren
cancer_recipe <- recipe(Class ~ Smoothness + Concavity, data = cancer_train) |>
step_scale(all_predictors()) |>
step_center(all_predictors())6.7.2 Modell definieren
knn_spec <- nearest_neighbor(weight_func = "rectangular", neighbors = 3) |>
set_engine("kknn") |>
set_mode("classification")6.7.3 Workflow definieren
knn_fit <- workflow() |>
add_recipe(cancer_recipe) |>
add_model(knn_spec) |>
fit(data = cancer_train)
knn_fit## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
##
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 2 Recipe Steps
##
## • step_scale()
## • step_center()
##
## ── Model ───────────────────────────────────────────────────────────────────────
##
## Call:
## kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(3, data, 5), kernel = ~"rectangular")
##
## Type of response variable: nominal
## Minimal misclassification: 0.1244131
## Best kernel: rectangular
## Best k: 36.7.4 Vorhersagen
Im Gegensatz zu Timbers, Campbell, and Lee (2022) verwenden wir hier last_fit() und collect_metrics(),
da wir dies bereits eingeführt haben und künftig darauf aufbauen werden.
cancer_test_fit <- last_fit(knn_fit, cancer_split)
cancer_test_fit## # Resampling results
## # Manual resampling
## # A tibble: 1 × 6
## splits id .metrics .notes .predictions .workflow
## <list> <chr> <list> <list> <list> <list>
## 1 <split [426/143]> train/test split <tibble> <tibble> <tibble> <workflow>6.7.5 Modellgüte
cancer_test_fit %>% collect_metrics()## # A tibble: 2 × 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 accuracy binary 0.909 Preprocessor1_Model1
## 2 roc_auc binary 0.929 Preprocessor1_Model1Die eigentlichen Predictions stecken in der Listenspalte .predictions im Fit-Objekt:
names(cancer_test_fit)## [1] "splits" "id" ".metrics" ".notes" ".predictions"
## [6] ".workflow"Genau genommen ist .predictions eine Spalte, in der in jeder Zeile (und damit Zelle) eine Tabelle (Tibble) steht.
Wir haben nur eine Zeile und wollen das erste Element dieser Spalte herausziehen.
Da hilft pluck():
cancer_test_predictions <-
cancer_test_fit %>%
pluck(".predictions", 1)
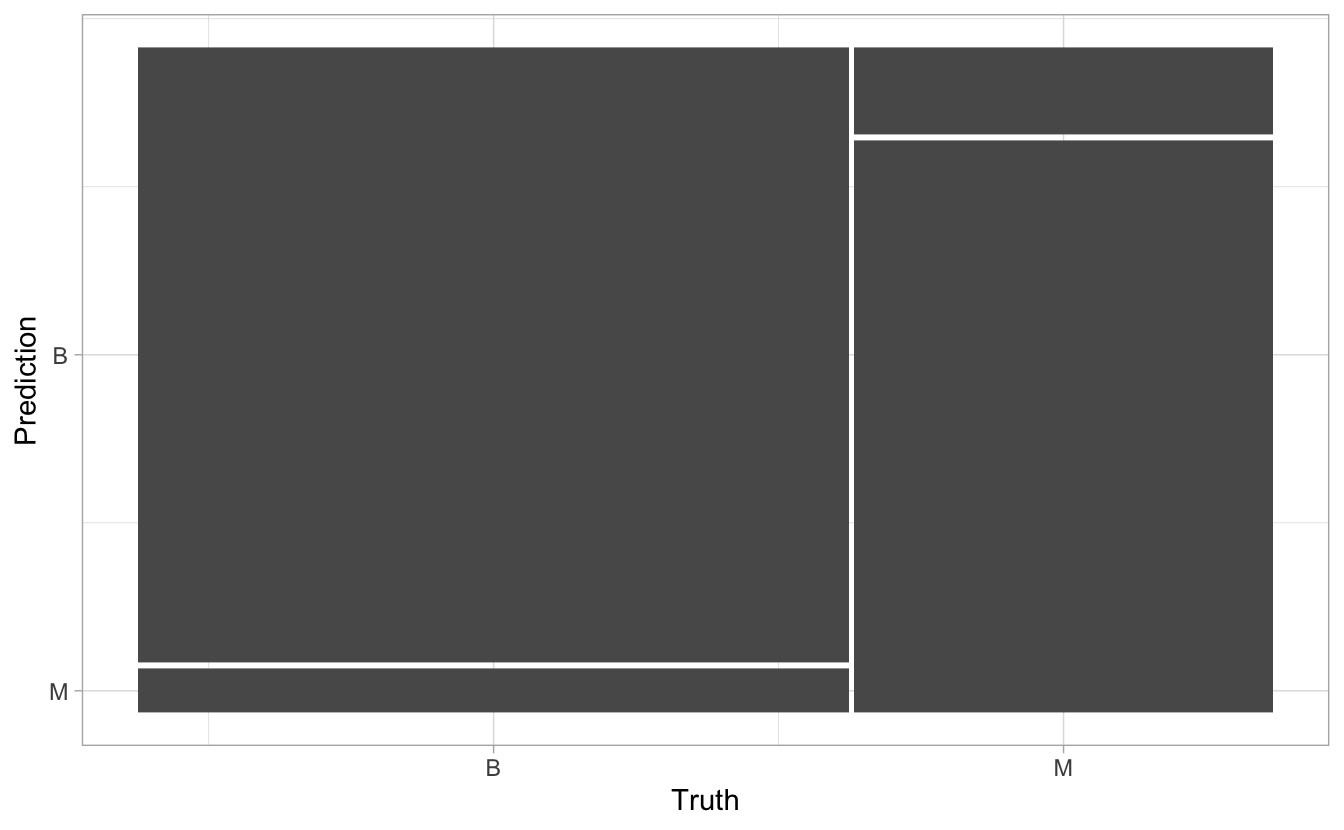
confusion <- cancer_test_predictions |>
conf_mat(truth = Class, estimate = .pred_class)
confusion## Truth
## Prediction B M
## B 84 7
## M 6 466.8 Kennzahlen der Klassifikation
In Sauer (2019), Kap. 19.6, findet sich einige Erklärung zu Kennzahlen der Klassifikationsgüte.
Ein Test kann vier verschiedenen Ergebnisse haben:
| Wahrheit | Als negativ (-) vorhergesagt | Als positiv (+) vorhergesagt | Summe |
|---|---|---|---|
| In Wahrheit negativ (-) | Richtig negativ (RN) | Falsch positiv (FP) | N |
| In Wahrheit positiv (+) | Falsch negativ (FN) | Richtig positiv (RN) | P |
| Summe | N* | P* | N+P |
Es gibt eine verwirrende Vielfalt von Kennzahlen, um die Güte einer Klassifikation einzuschätzen. Hier sind einige davon:
| Geläufige Kennwerte der Klassifikation. | ||
|---|---|---|
| F: Falsch. R: Richtig. P: Positiv. N: Negativ | ||
| Name | Definition | Synonyme |
| FP-Rate | FP/N | Alphafehler, Typ-1-Fehler, 1-Spezifität, Fehlalarm |
| RP-Rate | RP/N | Power, Sensitivität, 1-Betafehler, Recall |
| FN-Rate | FN/N | Fehlender Alarm, Befafehler |
| RN-Rate | RN/N | Spezifität, 1-Alphafehler |
| Pos. Vorhersagewert | RP/P* | Präzision, Relevanz |
| Neg. Vorhersagewert | RN/N* | Segreganz |
| Richtigkeit | (RP+RN)/(N+P) | Korrektklassifikationsrate, Gesamtgenauigkeit |
6.9 Krebstest-Beispiel
Betrachten wir Daten eines fiktiven Krebstest, aber realistischen Daten.
## # A tibble: 1 × 7
## format width height colorspace matte filesize density
## <chr> <int> <int> <chr> <lgl> <int> <chr>
## 1 PNG 500 429 sRGB TRUE 40643 72x72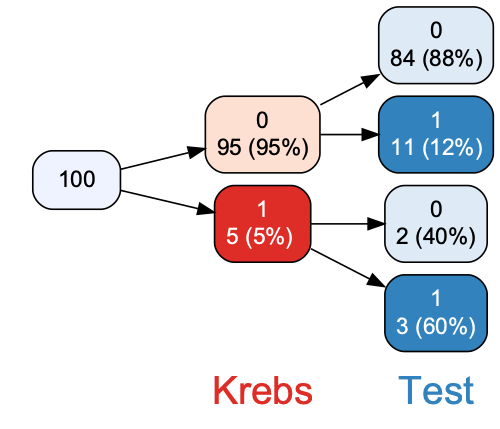
Wie gut ist dieser Test? Berechnen wir einige Kennzahlen.
Da die Funktionen zur Klassifikation stets einen Faktor wollen, wandeln wir die relevanten Spalten zuerst in einen Faktor um (aktuell sind es numerische Spalten).
Gesamtgenauigkeit:
accuracy(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 accuracy binary 0.87Sensitivität:
sens(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 sens binary 0.884Spezifität:
spec(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 spec binary 0.6Kappa:
kap(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 kap binary 0.261Positiver Vorhersagewert:
ppv(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 ppv binary 0.977Negativer Vorhersagewert:
npv(krebstest, truth = Krebs, estimate = Test)## # A tibble: 1 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 npv binary 0.214Während Sensitivität und Spezitivität sehr hoch sind, ist die der negative Vorhersagewert sehr gering:
Wenn man einen positiven Test erhält, ist die Wahrscheinlichkeit, in Wahrheit krank zu sein gering, zum Glück!
6.10 Aufgaben
- Arbeiten Sie sich so gut als möglich durch diese Analyse zum Verlauf von Covid-Fällen
- Fallstudie zur Modellierung einer logististischen Regression mit tidymodels
- Fallstudie zu Vulkanausbrüchen
- Fallstudie Himalaya