Skip to main content

DataScience1: Grundlagen der Prognosemodellierung 🔮🧰

Kapitel 8 Logistische Regression

Benötigte R-Pakete für dieses Kapitel:

datawizard ist, wie Tidymodels und Tidyverse, ein Metapaket, ein R-Paket also, das mehrere Pakete verwaltet und startet. Hier findet sich mehr Info zu Easystats.

Achtung Easystats ist (noch) nicht auf CRAN. Sie können Easystats so installieren:

install.packages("easystats", repos = "https://easystats.r-universe.dev")

Einen flotten Spruch bekommen wir von Easystats gratis dazu:

## [1] "Patience you must have my young padawan."

8.1 Lernsteuerung

8.1.1 Vorbereitung

  • Frischen Sie Ihr Wissen zur logistischen Regression auf bzw. machen Sie sich mit den Grundlagen des Verfahrens vertraut.

8.1.2 Lernziele

  • Sie verstehen den Zusammenhang von linearen und logistischen Modellen
  • Sie können die logistische Regression mit Methoden von tidymodels anwenden

8.1.3 Literatur

  • Rhys, Kap. 4

8.2 Intuitive Erklärung

Die logistische Reression ist ein Spezialfall des linearen Modells (lineare Regression), der für binäre (dichotom) AV eingesetzt wird (es gibt auch eine Variante für multinominale AV). Es können eine oder mehrere UV in eine logistische Regression einfließen, mit beliebigem Skalenniveau.

Beispiele für Forschungsfragen, die mit der logistischen Regression modelliert werden sind:

  • Welche Faktoren sind prädiktiv, um vorherzusagen, ob jemand einen Kredit zurückzahlen kann oder nicht?
  • Haben weibliche Passagiere aus der 1. Klasse eine höhere Überlebenschance als andere Personen auf der Titanic?
  • Welche Faktoren hängen damit zusammen, ob ein Kunde eine Webseite verlässt, bevor er einen Kauf abschließt?

Der Name stammt von der logistischen Funktion, die man in der einfachsten Form so darstellen kann:

\[f(x) = \frac{x}{1+e^{-x}}\]

Da die AV als dichotom modelliert wird, spricht man von einer Klassifikation.

Allerdings ist das Modell reichhaltiger als eine bloße Klassifikation, die (im binären Fall) nur 1 Bit Information liefert: “ja” vs. “nein” bzw. 0 vs. 1.

Das Modell liefert nämlich nicht nur eine Klassifikation zurück, sondern auch eine Indikation der Stärke (epistemologisch) der Klassenzugehörigkeit.

Einfach gesagt heißt das, dass die logistische Regression eine Wahrscheinlichkeit der Klassenzugehörigkeit zurückliefert.

Abbildung 8.1: Definition eines Models in tidymodels

8.3 Profil

Das Profil des Modells kann man wie folgt charakterisieren, vgl. Tab. 8.1.

Tabelle 8.1: Profil der logistischen Regression
Merkmal Logistische Regression
Klassifikation ja
Regression nein
Lerntyp überwacht
parametrisch ja

8.4 Warum nicht die lineare Regression verwenden?

Forschungsfrage: Kann man anhand des Spritverbrauchs vorhersagen, ob ein Auto eine Automatik- bzw. ein manuelle Schaltung hat? Anders gesagt: Hängen Spritverbrauch und Getriebeart? (Datensatz mtcars)

data(mtcars)
d <-
  mtcars %>% 
  mutate(mpg_z = standardize(mpg),
         iv = mpg_z,
         dv = am)

m81 <- lm(dv ~ iv, data = d)
coef(m81)
## (Intercept)          iv 
##   0.4062500   0.2993109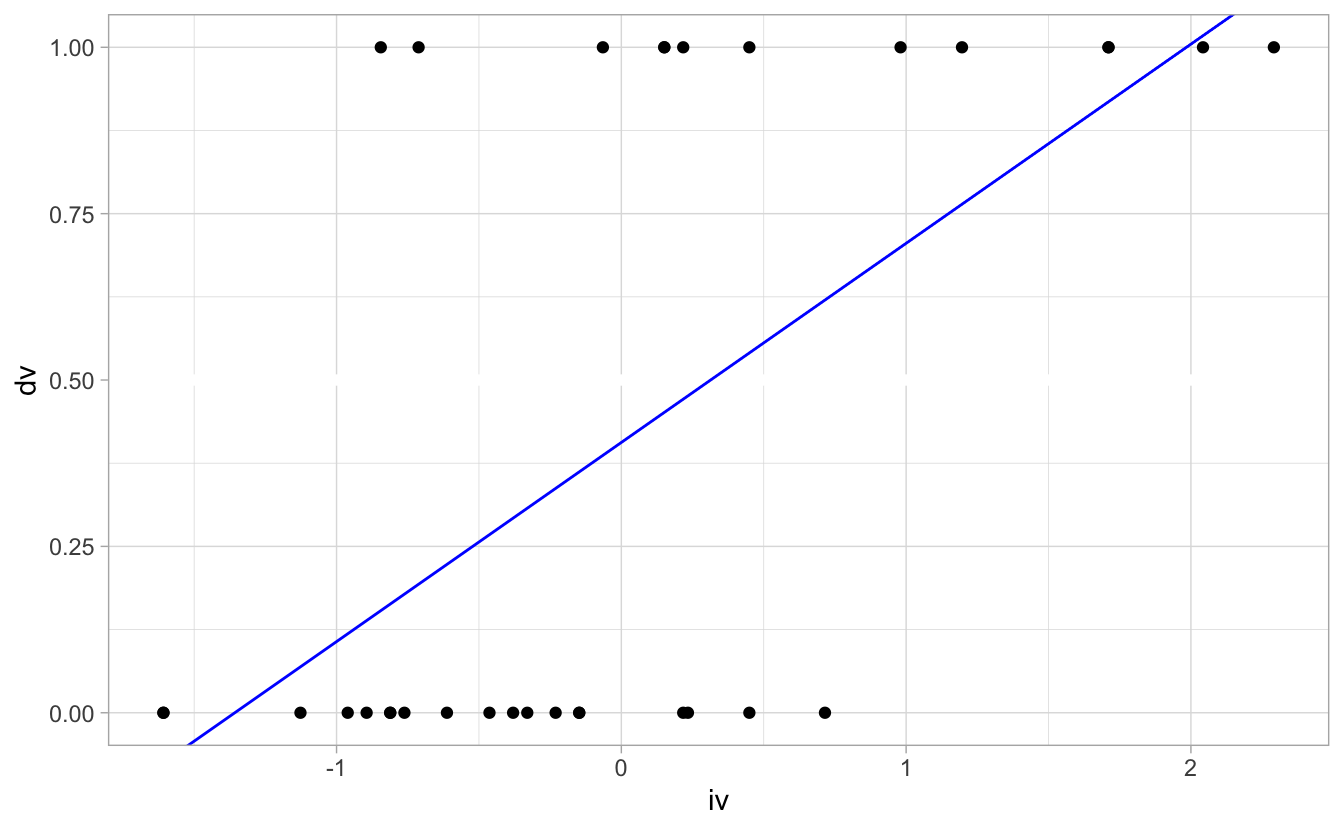

\(Pr(\text{am}=1|m91,\text{mpg_z}=0) = 0.46\): Die Wahrscheinlichkeit einer manuelle Schaltung, gegeben einem durchschnittlichen Verbrauch (und dem Modell m81) liegt bei knapp 50%.

8.4.1 Lineare Modelle running wild

Wie groß ist die Wahrscheinlichkeit für eine manuelle Schaltung …

  • … bei mpg_z = -2?
predict(m81, newdata = data.frame(iv = -2))
##          1 
## -0.1923719

\(Pr(\hat{y})<0\) macht keinen Sinn. ⚡

  • … bei mpg_z = +2?
predict(m81, newdata = data.frame(iv = +2))
##        1 
## 1.004872

\(Pr(\hat{y})>1\) macht keinen Sinn. ⚡

Schauen Sie sich mal die Vorhersage an für mpg_z=5 🤯

8.4.2 Wir müssen die Regressionsgerade umbiegen

… wenn der vorhergesagte Wert eine Wahrscheinlichkeit, \(p_i\), ist.

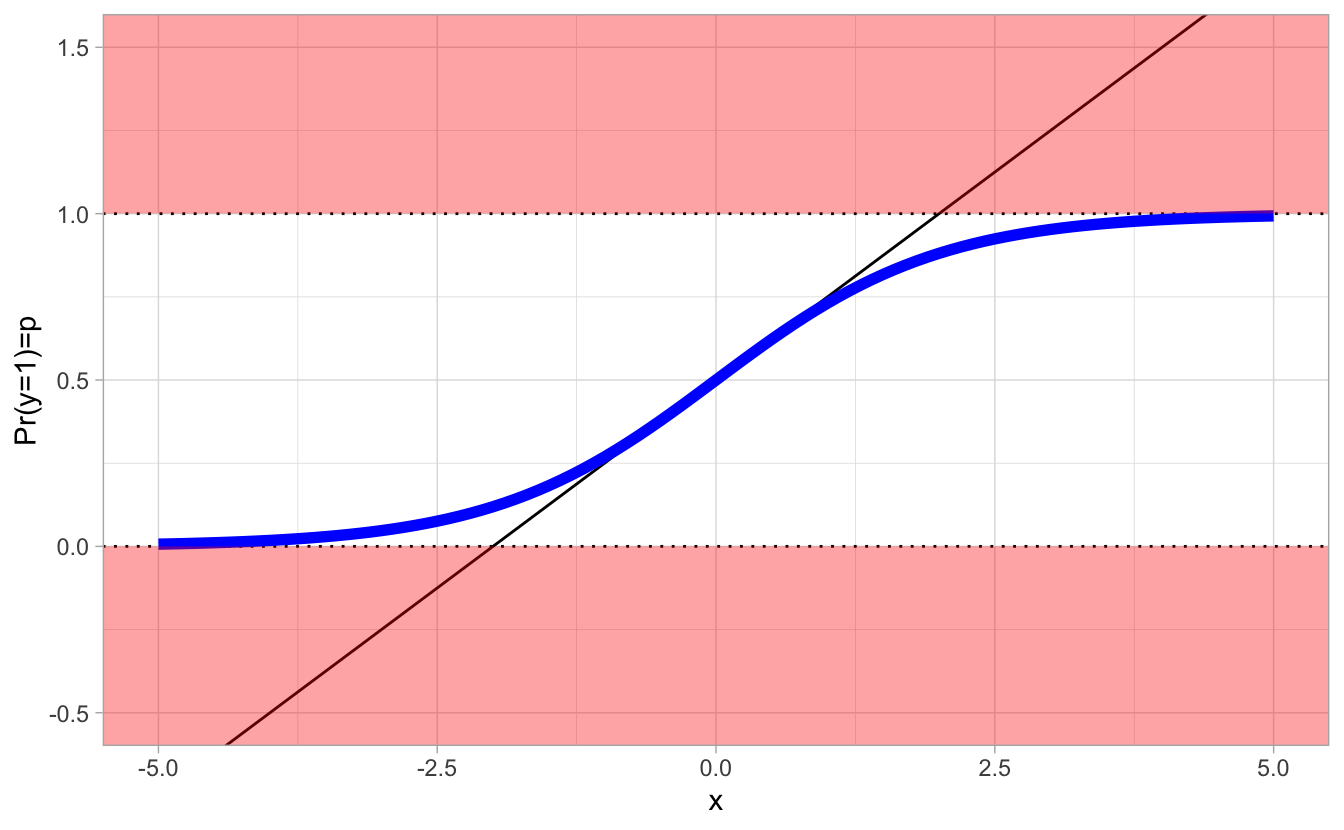
Die schwarze Gerade verlässt den Wertebereich der Wahrscheinlichkeit. Die blaue Kurve, \(\mathcal{f}\), bleibt im erlaubten Bereich, \(Pr(y) \in [0,1]\). Wir müssen also die linke oder die rechte Seite des linearen Modells transformieren: \(p_i = f(\alpha + \beta \cdot x)\) bzw.:

\(f(p) = \alpha + \beta \cdot x\)

\(\mathcal{f}\) nennt man eine Link-Funktion.

8.4.3 Verallgemeinerte lineare Modelle zur Rettung

Für metrische AV mit theoretisch unendlichen Grenzen des Wertebereichs haben wir bisher eine Normalverteilung verwendet:

\[y_i \sim \mathcal{N}(\mu_i, \sigma)\]

Dann ist die Normalverteilung eine voraussetzungsarme Wahl (maximiert die Entropie).

Aber wenn die AV binär ist bzw. Häufigkeiten modelliert, braucht man eine Variable die nur positive Werte zulässt.

Diese Verallgemeinerung des linearen Modells bezeichnet man als verallgemeinertes lineares Modell (generalized linear model, GLM).

Im Falle einer binären (bzw. dichotomen) AV liegt eine bestimmte Form des GLM vor, die man als logistische Regression bezeichnet.

8.6 Aber warum?

Forschungsfrage: Hängt das Überleben (statistisch) auf der Titanic vom Geschlecht ab?

Wie war eigentlich insgesamt, also ohne auf einen (oder mehrere) Prädiktoren zu bedingen, die Überlebenswahrscheinlichkeit?

data(titanic_train, package = "titanic")

m82 <- lm(Survived ~ 1, data = titanic_train)
coef(m82)
## (Intercept) 
##   0.3838384

Die Wahrscheinlichkeit zu Überleben \(Pr(y=1)\) lag bei einem guten Drittel (0.38).

Das hätte man auch so ausrechnen:

titanic_train %>% 
  count(Survived) %>% 
   mutate(prop = n/sum(n))
##   Survived   n      prop
## 1        0 549 0.6161616
## 2        1 342 0.3838384

Anders gesagt: \(p(y=1) = \frac{549}{549+342} \approx 0.38\)

8.6.1 tidymodels, m83

Berechnen wir jetzt ein lineares Modell für die AV Survived mit dem Geschlecht als Pädiktor:

d <-
  titanic_train %>% 
  filter(Fare > 0) %>% 
  mutate(iv = log(Fare),
         dv = factor(Survived))

Die Faktorstufen, genannt levels von Survived sind:

levels(d$dv)
## [1] "0" "1"

Und zwar genau in dieser Reihenfolge.

8.7 lm83, glm

Die klassische Methoden in R, ein logistisches Modell zu berechnen, ist mit der Funktion glm(). Tidymodels greift intern auf diese Funktion zurück. Daher sind die Ergebnisse numerisch identisch.

lm83 <- glm(dv ~ iv, data = d, family = "binomial")
coef(lm83)
## (Intercept)          iv 
##  -2.6827432   0.7479317
  • AV: Überleben (binär/Faktor)
  • UV: Ticketpreis

Mit easystats kann man sich model_parameter() einfach ausgeben lassen:

library(easystats)


model_parameters(lm83)
## Parameter   | Log-Odds |   SE |         95% CI |      z |      p
## ----------------------------------------------------------------
## (Intercept) |    -2.68 | 0.26 | [-3.19, -2.19] | -10.46 | < .001
## iv          |     0.75 | 0.08 | [ 0.59,  0.91] |   9.13 | < .001

Und auch visualisieren lassen:

plot(model_parameters(lm83))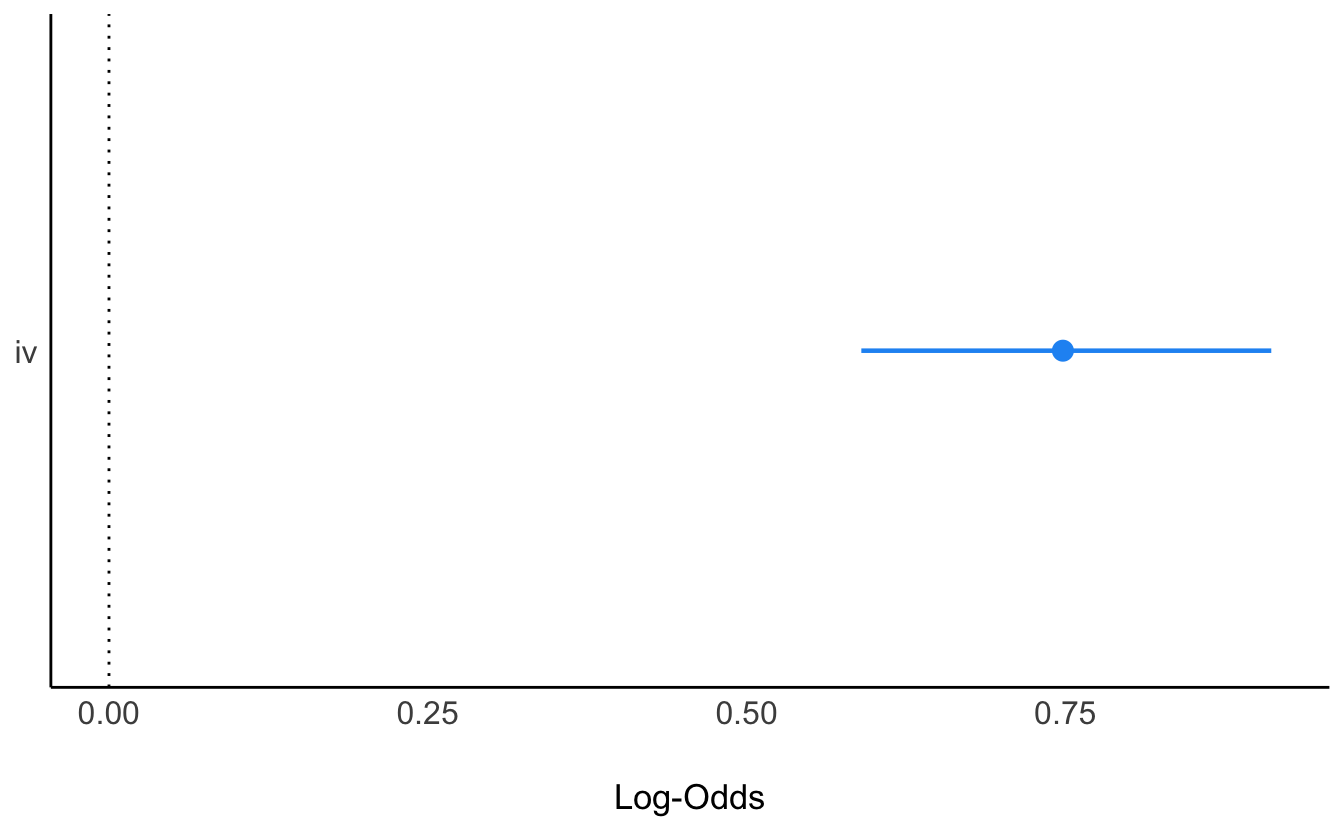

8.8 m83, tidymodels

Achtung! Bei tidymodels muss bei einer Klassifikation die AV vom Type factor sein. Außerdem wird bei tidymodels, im Gegensatz zu (g)lm nicht die zweite, sondern die erste als Ereignis modelliert wird.

Daher wechseln wir die referenzkategorie, wir “re-leveln”, mit relevel():

d2 <-
  d %>% 
  mutate(dv = relevel(dv, ref = "1"))

Check:

levels(d2$dv)
## [1] "1" "0"

Passt.

Die erste Stufe ist jetzt 1, also Überleben.

Jetzt berechnen wir das Modell in gewohnter Weise mit tidymodels.

m83_mod <-
  logistic_reg()

m83_rec <-
  recipe(dv ~ iv, data = d2)

m83_wf <-
  workflow() %>% 
  add_model(m83_mod) %>% 
  add_recipe(m83_rec)

m83_fit <-
  fit(m83_wf, data = d2)

Hier sind die Koeffizienten, die kann man sich aus m83_fit herausziehen:

term estimate std.error statistic p.value
(Intercept) 2.68 0.26 10.46 0.00
iv −0.75 0.08 −9.13 0.00 
## [1]  2.6827432 -0.7479317
## # A tibble: 2 × 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    2.68     0.256      10.5  1.26e-25
## 2 iv            -0.748    0.0819     -9.13 6.87e-20

Die Koeffizienten werden in Logits angegeben.

In Abb. 8.2 ist das Modell und die Daten visualisiert.

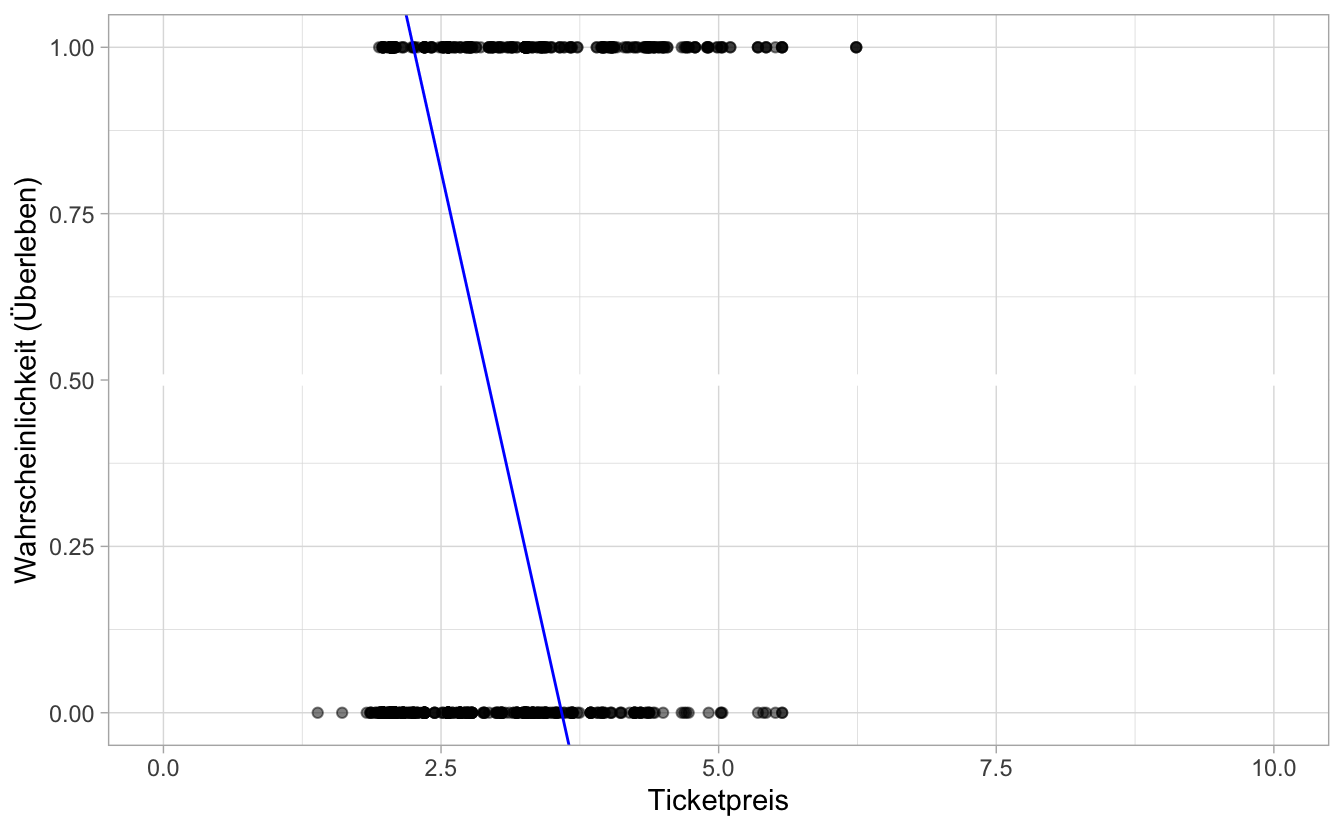
m83 und die Titanic-Daten

Abbildung 8.2: m83 und die Titanic-Daten

Definieren wir als \(y=1\) das zu modellierende Ereignis, hier “Überleben auf der Titanic” (hat also überlebt).

Wie wir oben schon gesehen haben, funktioniert die lineare Regression nicht einwandfrei bei binären (oder dichotomen) AV.

8.8.1 Wahrscheinlichkeit in Odds

Probieren wir Folgendes: Rechnen wir die Wahrscheinlichkeit zu Überlegen für \(y\), kurz \(p\), in Odds (Chancen) um.

\(odds = \frac{p}{1-p}\)

In R:

odds <- 0.38 / 0.62
odds
## [1] 0.6129032

Bildlich gesprochen sagen die Odds: für 38 Menschen, die überlebt haben, kommen (ca.) 62 Menschen, die nicht überlebt haben, s. Abb. 8.3.

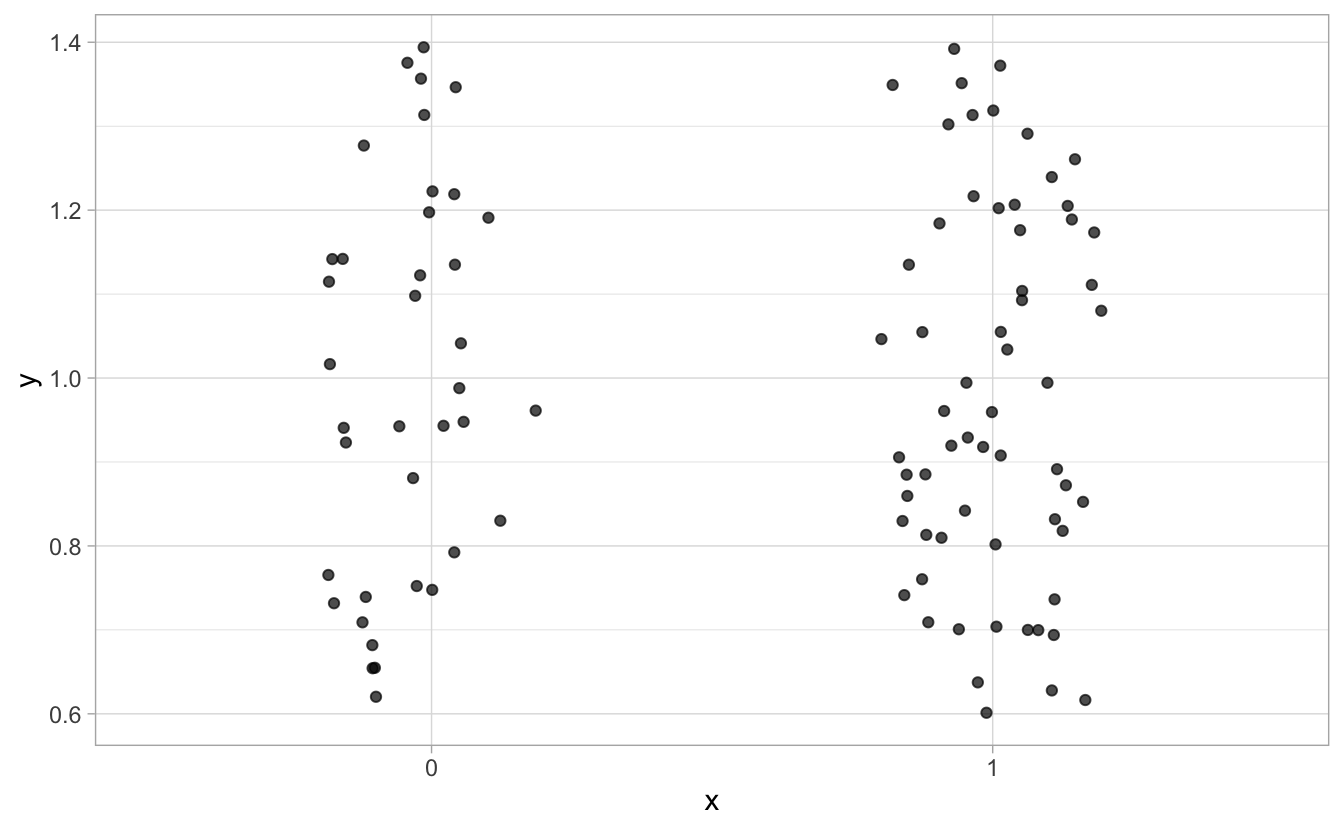
Odds: 38 zu 62

Abbildung 8.3: Odds: 38 zu 62

Plotten wir die Odds als Funktion der UV, s. Abb. 8.4.

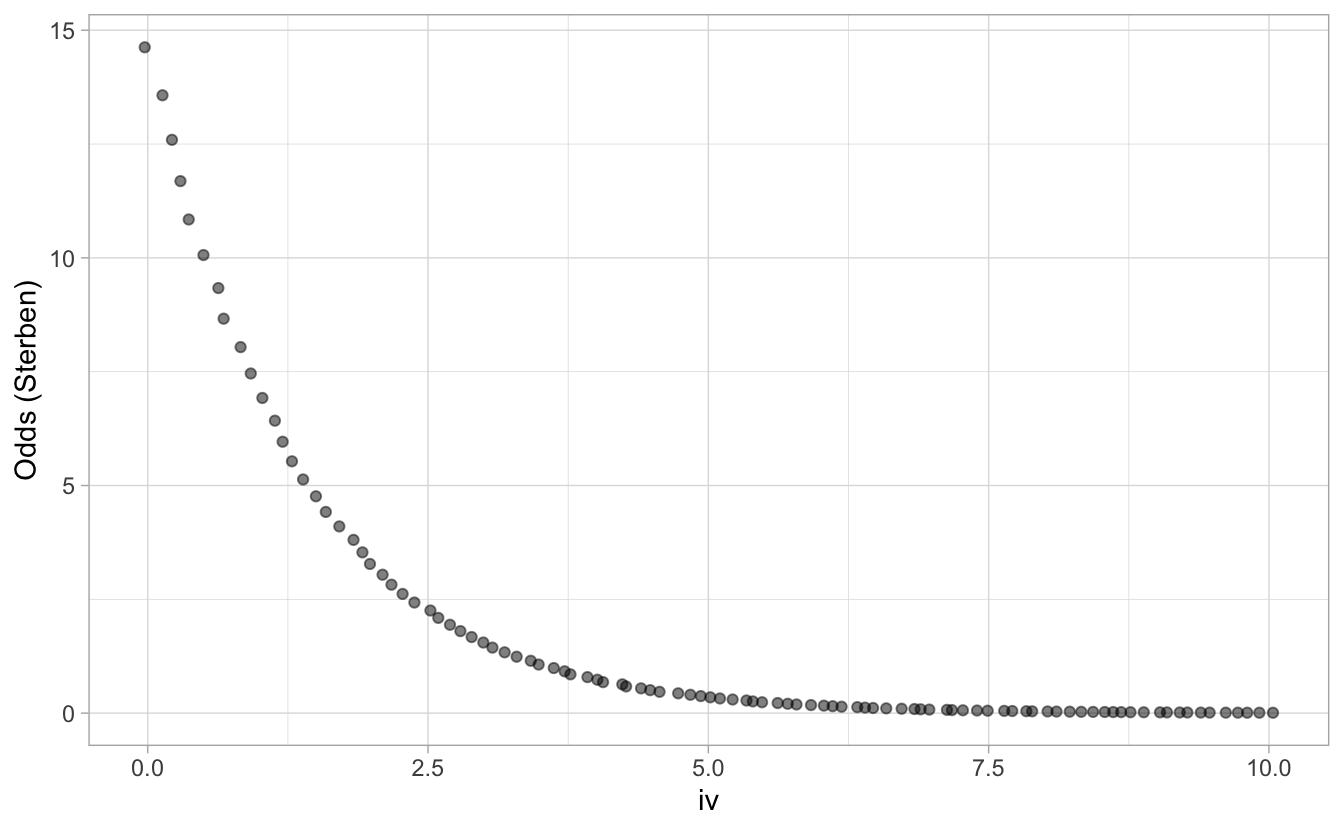
Odds als Funktion der UV

Abbildung 8.4: Odds als Funktion der UV

Wir sind noch nicht am Ziel; die Variable ist noch nicht “richtig gebogen”.

8.8.2 Von Odds zu Log-Odds

Wenn wir jetzt den Logarithmus berechnen der Log-Odds bekommen wir eine “brav gebogenen” Funktion, die Log-Odds, \(\mathcal{L}\), als Funktion der UV, s. Abb. 8.5.

\[\mathcal{L} = log (odds) = log \left(\frac{p}{1-p}\right)\]

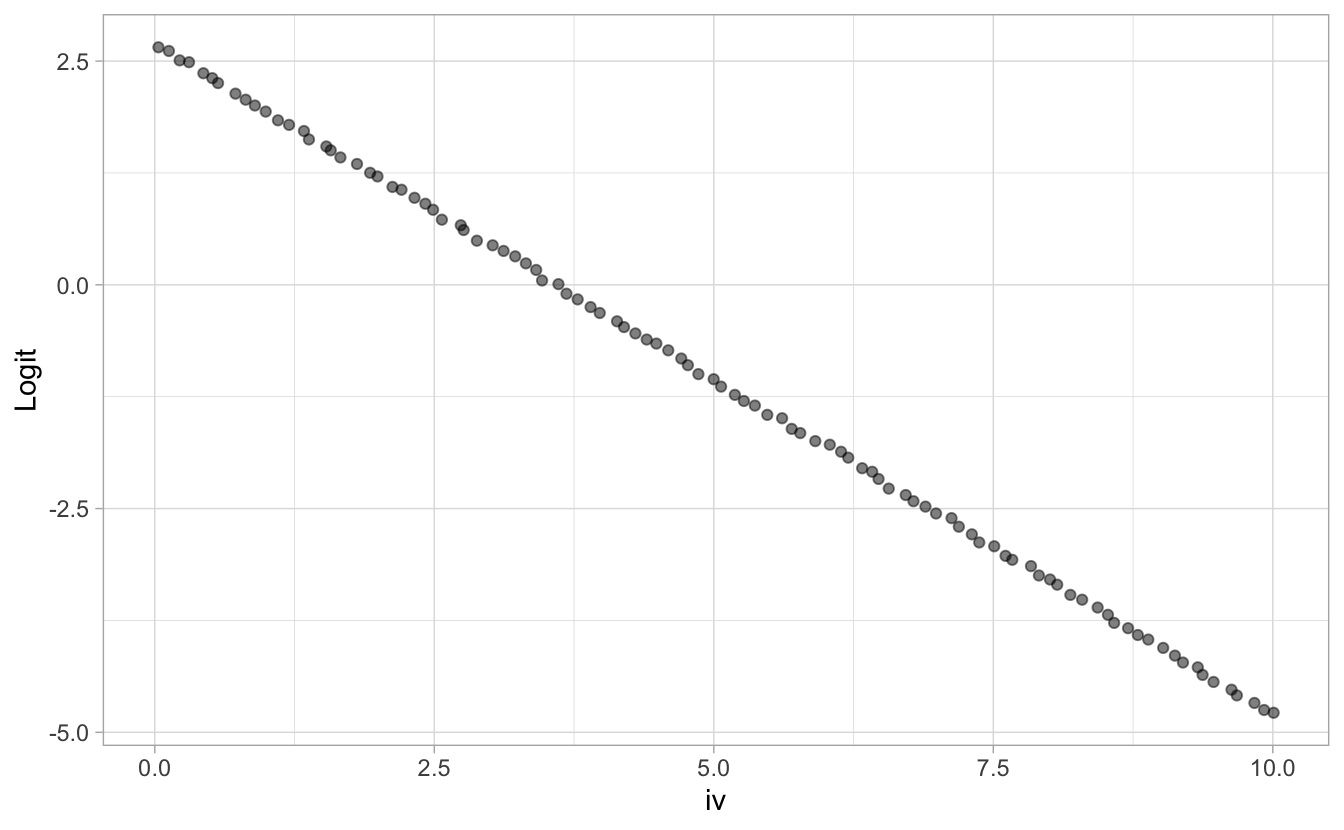
Logit als Funktion der UV

Abbildung 8.5: Logit als Funktion der UV

Linear!

Es gilt also:

\[\text {log-odds} = b_0 + b_1x\]

Log-Odds (Log-Odds) bezeichnet man auch als Logits.

8.9 Inverser Logit

Um nach \(p\) aufzulösen, müssen wir einige Algebra bemühen:

\[ \begin{align} \text{log} \frac{p}{1-p} &= \alpha + \beta x & & \text{Exponentieren}\\ \frac{p}{1-p} &= e^{\alpha + \beta x} \\ p_i &= e^{\alpha + \beta x_i} (1-p) & & \text{Zur Vereinfachung: } x := e^{\alpha + \beta x_i} \\ p_i &= x (1-p) \\ &= x - xp \\ p + px &= x \\ p(1+x) &= x \\ p &= \frac{x} {1+x} & & \text{Lösen wir x wieder auf.} \\ p &= \frac{e^{\alpha + \beta x_i}}{1 + e^{\alpha + \beta x_i}} = \mathcal{L}^{-1} \end{align} \]

Diese Funktion nennt man auch inverser Logit, \(\text{logit}^{-1}, \mathcal{L}^{-1}\).

Zum Glück macht das alles die Rechenmaschine für uns 😄.

8.10 Vom Logit zur Klasse

Praktisch können wir uns die Logits und ihre zugehörige Wahrscheinlichkeit einfach ausgeben lassen mit R. Und die vorhergesagte Klasse (.pred_class) auch:

d3 <-
  d2 %>% 
  bind_cols(predict(m83_fit, new_data = d2, type = "prob")) %>% 
  bind_cols(predict(m83_fit, new_data = d2)) %>%  # Klasse
  bind_cols(logits = predict(m83_fit, new_data = d2, type = "raw"))  # Logits
  
d3 %>% 
  slice_head(n = 3) %>% 
  select(Name, last_col())
##                                                  Name     logits
## 1                             Braund, Mr. Owen Harris  1.2010894
## 2 Cumings, Mrs. John Bradley (Florence Briggs Thayer) -0.5084287
## 3                              Heikkinen, Miss. Laina  1.1345079

8.10.1 Grenzwert wechseln

Im Standard wird 50% als Grenzwert für die vorhergesagte Klasse \(c\) genommen:

  • wenn \(p <= .5 \rightarrow c = 0\)
  • wenn \(p > .5 \rightarrow c = 1\)

Man kann aber den Grenzwert beliebig wählen, um Kosten-Nutzen-Abwägungen zu optimieren; mehr dazu findet sich z.B. hier.

8.11 Logit und Inverser Logit

8.11.1 Logit

\((0,1) \rightarrow (-\infty, +\infty)\)

Praktisch, um Wahrscheinlichkeit zu modellieren.

\[p \rightarrow \fbox{logit} \rightarrow \alpha + \beta x\]

8.11.2 Inv-Logit

\((-\infty, +\infty) \rightarrow (0,1)\)

Praktisch, um in Wahrscheinlichkeiten umzurechnen.

\[p \leftarrow \fbox{inv-logit} \leftarrow \alpha + \beta x\]

8.12 Logistische Regression im Überblick

  • Eine Regression mit binomial verteilter AV und Logit-Link nennt man logistische Regression.

  • Man verwendet die logistische Regression um binomial verteilte AV zu modellieren, z.B.

    • Wie hoch ist die Wahrscheinlichkeit, dass ein Kunde das Produkt kauft?
    • Wie hoch ist die Wahrscheinlichkeit, dass ein Mitarbeiter kündigt?
    • Wie hoch ist die Wahrscheinlichkeit, die Klausur zu bestehen?

  • Die logistische Regression ist eine normale, lineare Regression für den Logit von \(Pr(y=1)\), wobei \(y\) (AV) binomialvereteilt mit \(n=1\) angenommen wird:

\[ \begin{align} y_i &\sim \mathcal{B}(1, p_i) \\ \text{logit}(p_i) &= \alpha + \beta x_i \end{align} \]

  • Da es sich um eine normale, lineare Regression handelt, sind alle bekannten Methoden und Techniken der linearen Regression zulässig.

  • Da Logits nicht einfach zu interpretieren sind, rechnet man nach der Berechnung des Modells den Logit häufig in Wahrscheinlichkeiten um.

8.12.1 Die Koeffizienten sind schwer zu interpretieren

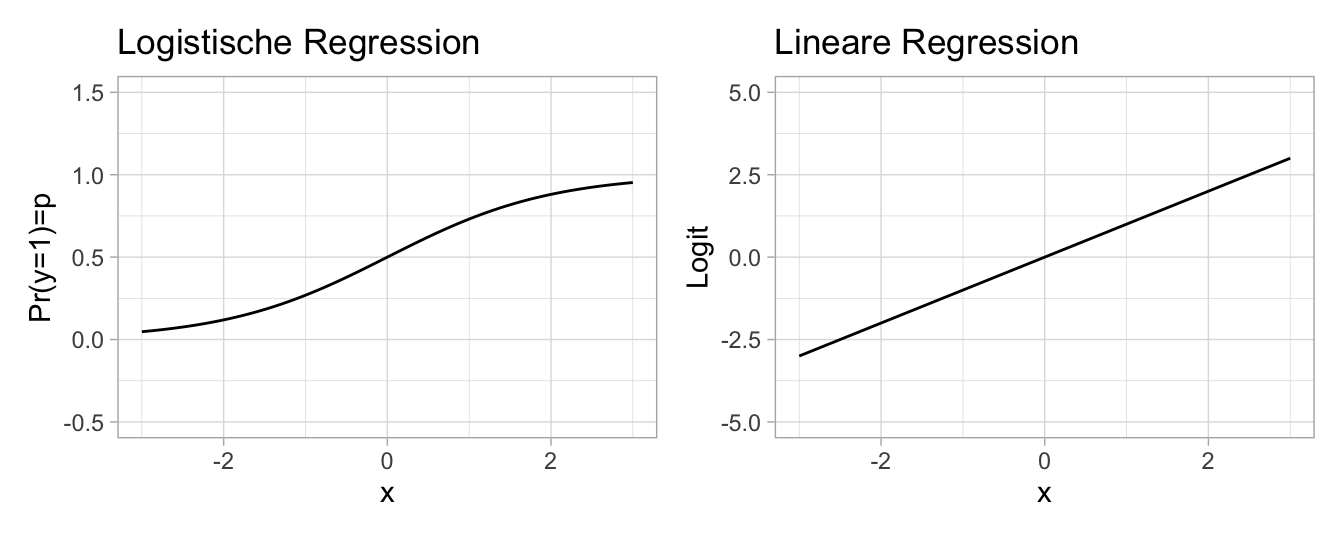
  • In der logistischen Regression gilt nicht mehr, dass eine konstante Veränderung in der UV mit einer konstanten Veränderung in der AV einhergeht.
  • Stattdessen geht eine konstante Veränderung in der UV mit einer konstanten Veränderung im Logit der AV einher.
  • Beim logistischen Modell hier gilt, dass in der Nähe von \(x=0\) die größte Veränderung in \(p\) von statten geht; je weiter weg von \(x=0\), desto geringer ist die Veränderung in \(p\).

8.12.2 Logits vs. Wahrscheinlichkeiten 

konvert_logits <-
  tibble(
    logit = c( -10, -3, 
              -2, -1, -0.5, -.25, 
              0, 
              .25, .5, 1, 2, 
              3, 10),
    p = rstanarm::invlogit(logit)
  )  %>% 
  gt() %>% 
  fmt_number(everything(), decimals = 2)