Case study in data analysis using R package dplyr in German language.

Praktische Datenanalyse mit dplyr

Das R-Paket dplyr von Hadley Wickham ist ein Stargast auf der R-Showbühne; häufig diskutiert in einschlägigen Foren. Mit dyplr kann man Daten “verhackstücken” - umformen und aufbereiten (“to wrangle” auf Englisch); “praktische Datenanalyse” ist vielleicht eine gute Bezeichnung. Es finden sich online viele Einführungen, z.B. hier oder hier.

Dieser Text ist nicht als Einführung oder Erläuterung gedacht, sondern als Übung, um (neu erworbenen Fähigkeiten) in der praktischen Datenanalyse im Rahmen einer Fallstudie auszuprobieren.

Stellen Sie sich folgendes Szenario zur Fallstudie vor: Sie sind Unternehmensberäter bei einer (nach eigenen Angaben) namhaften Gesellschaft. Ihr erster Auftrag führt Sie direkt nach New York City (normal). Ihr Chef hat irgendwie den Eindruck, dass Sie Zahlen- und Computer-affin sind… “Sag mal, schon mal von R gehört?”, fragt er mal eines Abends (22h, noch voll bei der Arbeit). “Eine Programmiersprache zur Datenanalyse und -visualisierung”, antworten Sie wie aus der Pistole geschossen. Das gefällt Ihrem Chef. “Pass mal auf. Bis morgen brauche ich eine Analyse aller Flüge von NYC, Anzahl, nach Origin, nach Destination.. Du weißt schon…”. Natürlich wissen Sie.. “Reicht bis morgen früh um acht”, sagt er noch, bevor er das Büro verlässt.

Ok, also dann sollten wir keine Zeit verlieren…

Aufgaben (und Lösungen)

Laden wir zuerst die nötigen Pakete und Daten; denken Sie daran, dass R-Pakete zuerst installiert werden müssen (einmalig), bevor Sie sie laden können.

# install.packages("nycflights13")
library(dplyr)
library(ggplot2) # Diagramme
data(flights, package = "nycflights13")

Wie viele Flüge starteten in den NYC-Flughäfen in 2013?

flights %>%
  summarise(n_flights = n())

## # A tibble: 1 × 1
##   n_flights
##       <int>
## 1    336776

Ah, eine Menge :-).

Welche Flughäfen gibt es in NYC? Wie viele Flüge starteten von dort jeweils?

flights %>%
  group_by(origin) %>% 
  summarise(Anzahl = n()) 

## # A tibble: 3 × 2
##   origin Anzahl
##    <chr>  <int>
## 1    EWR 120835
## 2    JFK 111279
## 3    LGA 104662

Das könnten wir auch plotten. Allerdings… 3 Zahlen, das kann man auch ohne Diagramm gut erkennen…

Die internationalen Codes von Flughäfen können z.B. hier nachgelesen werden.

Wie viele Flughäfen starteten pro Monat aus NYC?

Das ist praktische die gleiche Frage in grün…

flights %>%
  group_by(month) %>% 
  summarise(Anzahl = n()) 

## # A tibble: 12 × 2
##    month Anzahl
##    <int>  <int>
## 1      1  27004
## 2      2  24951
## 3      3  28834
## 4      4  28330
## 5      5  28796
## 6      6  28243
## 7      7  29425
## 8      8  29327
## 9      9  27574
## 10    10  28889
## 11    11  27268
## 12    12  28135

Das lohnt sich schon eher als Diagramm:

flights %>%
  group_by(month) %>% 
  summarise(Anzahl = n()) %>% 
  ggplot(aes(x = month, y = Anzahl)) + geom_point(color = "firebrick") +
  geom_line()

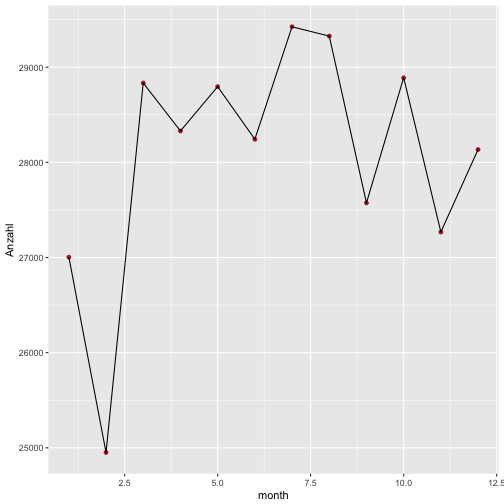
Welche Ziele wurden angeflogen? Wurden MUC und FRA angeflogen?

flights %>%
  group_by(dest) %>% 
  summarise(Anzahl = n()) %>% 
  select(dest) %>% print(n = 200)

## # A tibble: 105 × 1
##      dest
##     <chr>
## 1     ABQ
## 2     ACK
## 3     ALB
## 4     ANC
## 5     ATL
## 6     AUS
## 7     AVL
## 8     BDL
## 9     BGR
## 10    BHM
## 11    BNA
## 12    BOS
## 13    BQN
## 14    BTV
## 15    BUF
## 16    BUR
## 17    BWI
## 18    BZN
## 19    CAE
## 20    CAK
## 21    CHO
## 22    CHS
## 23    CLE
## 24    CLT
## 25    CMH
## 26    CRW
## 27    CVG
## 28    DAY
## 29    DCA
## 30    DEN
## 31    DFW
## 32    DSM
## 33    DTW
## 34    EGE
## 35    EYW
## 36    FLL
## 37    GRR
## 38    GSO
## 39    GSP
## 40    HDN
## 41    HNL
## 42    HOU
## 43    IAD
## 44    IAH
## 45    ILM
## 46    IND
## 47    JAC
## 48    JAX
## 49    LAS
## 50    LAX
## 51    LEX
## 52    LGA
## 53    LGB
## 54    MCI
## 55    MCO
## 56    MDW
## 57    MEM
## 58    MHT
## 59    MIA
## 60    MKE
## 61    MSN
## 62    MSP
## 63    MSY
## 64    MTJ
## 65    MVY
## 66    MYR
## 67    OAK
## 68    OKC
## 69    OMA
## 70    ORD
## 71    ORF
## 72    PBI
## 73    PDX
## 74    PHL
## 75    PHX
## 76    PIT
## 77    PSE
## 78    PSP
## 79    PVD
## 80    PWM
## 81    RDU
## 82    RIC
## 83    ROC
## 84    RSW
## 85    SAN
## 86    SAT
## 87    SAV
## 88    SBN
## 89    SDF
## 90    SEA
## 91    SFO
## 92    SJC
## 93    SJU
## 94    SLC
## 95    SMF
## 96    SNA
## 97    SRQ
## 98    STL
## 99    STT
## 100   SYR
## 101   TPA
## 102   TUL
## 103   TVC
## 104   TYS
## 105   XNA

Eine lange Liste… wäre vielleicht übersichtlicher, die nicht abzubilden ;)

Schauen wir mal, ob MUC (München) oder FRA (Frankfurt) dabei waren.

flights %>%
  filter(dest == "MUC" | dest == "FRA")

## # A tibble: 0 × 19
## # ... with 19 variables: year <int>, month <int>, day <int>,
## #   dep_time <int>, sched_dep_time <int>, dep_delay <dbl>, arr_time <int>,
## #   sched_arr_time <int>, arr_delay <dbl>, carrier <chr>, flight <int>,
## #   tailnum <chr>, origin <chr>, dest <chr>, air_time <dbl>,
## #   distance <dbl>, hour <dbl>, minute <dbl>, time_hour <dttm>

Die resultierende Tabelle (“tibble”) hat 0 Zeilen. Diese Ziele wurden also nicht angeflogen.

Das Zeichen “|” bedeutet “oder” (im logischen Sinne). Demnach kann man die die ganze “Pfeife” so lesen: Nimm flights Filter Zeilen mit Ziel gleich MUC oder Zeilen mit Ziel gleich FRA.

Welche Ziele am häufigsten angeflogen?

flights %>%
  group_by(dest) %>%
  summarise(n_per_dest = n()) %>%
  arrange(desc(n_per_dest))

## # A tibble: 105 × 2
##     dest n_per_dest
##    <chr>      <int>
## 1    ORD      17283
## 2    ATL      17215
## 3    LAX      16174
## 4    BOS      15508
## 5    MCO      14082
## 6    CLT      14064
## 7    SFO      13331
## 8    FLL      12055
## 9    MIA      11728
## 10   DCA       9705
## # ... with 95 more rows

Das könnte man auch wieder “plotten”, aber lieber nur die Top-10.

flights %>%
  group_by(dest) %>%
  summarise(n_per_dest = n()) %>%
  arrange(desc(n_per_dest)) %>% 
  filter(min_rank(n_per_dest) < 11) %>% 
  ggplot(aes(x = dest, y = n_per_dest)) + geom_bar(stat = "identity")

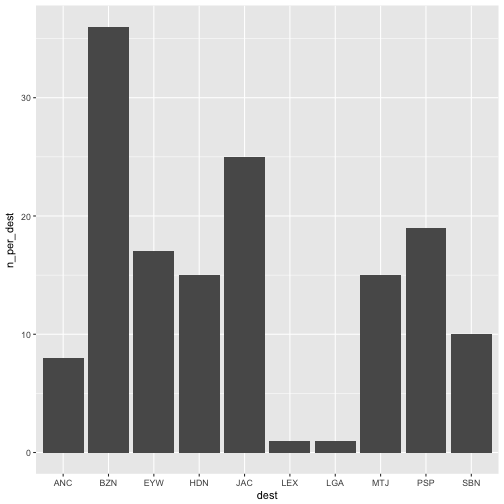
Der Befehl min_rank(n_per_dest) < 11 liefert die 10 kleinsten Rangplätze der Variablen n_per_dest zurück.

Beim Plotten brauchen wir beim Geom bar (Balken) den Zusatz stat = "identity", weil das Geom bar standardgemäß zählen möchte, wie viele Zeilen z.B. “LGA” enthalten. Wir haben aber das Zählen der Zeilen schon vorher mit n() gemacht, so dass der Befehl einfach den Wert, so wie er in unserem Dataframe steht (daher identity) nehmen soll.

Welche Ziele werden mehr als 10000 Mal pro Jahr angeflogen?

flights %>%
  group_by(dest) %>%
  summarise(n_dest = n()) %>%
  filter(n_dest > 10000)

## # A tibble: 9 × 2
##    dest n_dest
##   <chr>  <int>
## 1   ATL  17215
## 2   BOS  15508
## 3   CLT  14064
## 4   FLL  12055
## 5   LAX  16174
## 6   MCO  14082
## 7   MIA  11728
## 8   ORD  17283
## 9   SFO  13331

Welche Flüge gingen von JFK nach PWM (Portland) im Januar zwischen Mitternach und 5 Uhr?

library(knitr)
filter(flights, origin == "JFK" & month == 1, dest == "PWM", dep_time < 500) %>% 
  kable

Der Befehl knitr::kable erstellt eine (einigermaßen) schöne Tabelle (man muss aber das Paket knitr vorher geladen haben.)

Warum Ihr Chef das wissen will, weiß er nur allein…

Welche Flüge starteten von JFK, dieeine Ankunftsverspätung hatten doppelt so groß wie die Abflugverspätung, und die nach Atlanta geflogen sind?

Selten eine Aufgabe gelesen, die aus so einem langen Satz bestand …

filter(flights, origin == "JFK", arr_delay > 2 * dep_delay, month == 1, dest == "ATL") %>% 
  kable

Auch diese Tabelle ist recht lang. Aber sei’s drum :)

Welche Airlines hatten die meiste “Netto-Verspätung”?

f_2 <- group_by(flights, carrier)
f_3 <- mutate(f_2, delay = dep_delay - arr_delay)
f_4 <- filter(f_3, !is.na(delay))
f_5 <- summarise(f_4, delay_mean = mean(delay))
arrange(f_5, delay_mean) 

## # A tibble: 16 × 2
##    carrier delay_mean
##      <chr>      <dbl>
## 1       F9 -1.7195301
## 2       FL -1.5099213
## 3       MQ -0.3293526
## 4       OO  0.6551724
## 5       US  1.6150976
## 6       YV  3.3419118
## 7       B6  3.5095746
## 8       EV  4.0424982
## 9       DL  7.5796089
## 10      WN  8.0125374
## 11      AA  8.2048393
## 12      UA  8.4588972
## 13      9E  9.0599052
## 14      VX 10.9921814
## 15      HA 11.8157895
## 16      AS 15.7616361

Etwas umständlich mit den ganzen Zwischenspeichern… Vielleicht besser so:

flights %>% 
  group_by(carrier) %>% 
  mutate(delay = dep_delay - arr_delay) %>% 
  filter(!is.na(delay)) %>% 
  summarise(delay_mean = mean(delay)) %>% 
  arrange(-delay_mean)

## # A tibble: 16 × 2
##    carrier delay_mean
##      <chr>      <dbl>
## 1       AS 15.7616361
## 2       HA 11.8157895
## 3       VX 10.9921814
## 4       9E  9.0599052
## 5       UA  8.4588972
## 6       AA  8.2048393
## 7       WN  8.0125374
## 8       DL  7.5796089
## 9       EV  4.0424982
## 10      B6  3.5095746
## 11      YV  3.3419118
## 12      US  1.6150976
## 13      OO  0.6551724
## 14      MQ -0.3293526
## 15      FL -1.5099213
## 16      F9 -1.7195301

Das könnten wir mal wieder visualisieren:

flights %>% 
  group_by(carrier) %>% 
  mutate(delay = dep_delay - arr_delay) %>% 
  filter(!is.na(delay)) %>% 
  summarise(delay_mean = mean(delay)) %>% 
  arrange(-delay_mean) -> f_summarised

  ggplot(f_summarised, aes(x = carrier, y = delay_mean)) + geom_point(color = "firebrick") 

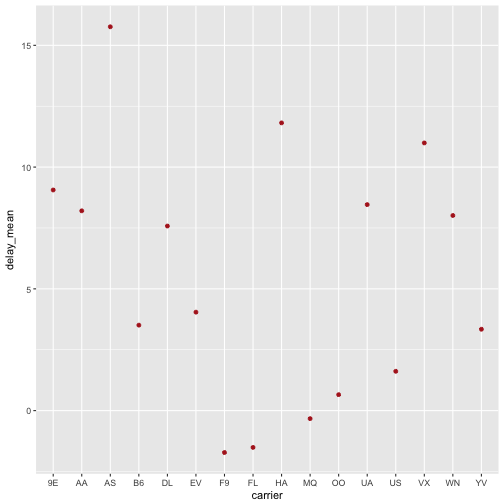
ggplot2 ordnet die X-Achse hier automatisch alphanumerisch. Wenn wir wollen, dass die Achse nach den Werten der Y-Achse (delay_mean) geordnet wird (was sinnvoll ist), können wir das so erreichen:

  ggplot(f_summarised, aes(x = reorder(carrier, delay_mean), y = delay_mean)) + 
    geom_point(color = "firebrick") 

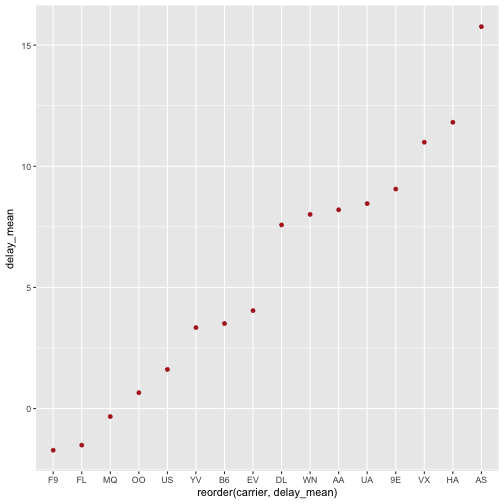
Der Befehl reorder(carrier, delay_mean) ordnet die Werte der Varialbne carrier anhand der Werte der Variablen delay_mean.

Berechnen Sie die mittlere Verspätung aller Flüge mit deutlicher Verspätung (> 1 Stunde)!

flights %>%
  mutate(delay = dep_delay - arr_delay) %>% 
  filter(delay > 60) %>%
  summarise(delay_mean = mean(delay),
            n = n()) %>%  # Anzahl
  arrange(delay_mean)

## # A tibble: 1 × 2
##   delay_mean     n
##        <dbl> <int>
## 1   65.18182   154

Wie sind die Verspätungen verteilt?

ggplot(f_summarised, aes(x = delay_mean)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

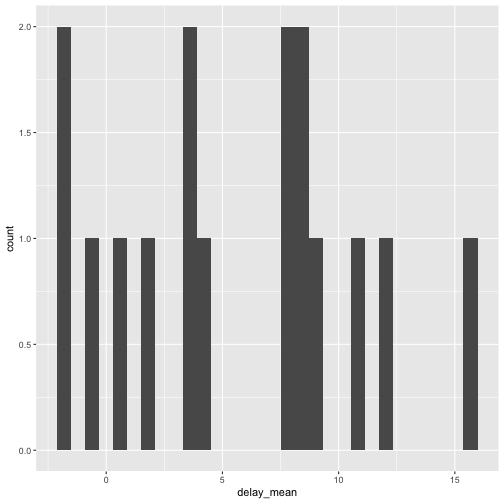
Hängen Flugzeit und Verspätung zusammen?

flights %>%
  mutate(delay = dep_delay - arr_delay) %>% 
  na.omit() %>% 
  ggplot(aes(x = distance, y = delay)) + 
  geom_point(alpha = .1) +
  geom_smooth()

## `geom_smooth()` using method = 'gam'

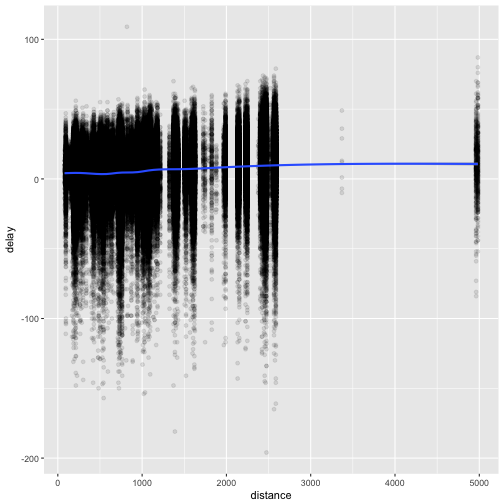
Sag mal, plotten wir gerade wirklich 300.000 Punkte??? Das kann dauern…

Das alpha = .1 macht die Punkte blässlich, fast durchsichtig. Ganz praktisch, wenn viele Punkte aufeinander liegen.

Hängen Verspätung und Jahreszeit zusammen?

Auch eine ganz interessante Frage. Schauen wir mal:

cor(flights$month, flights$dep_delay, use = "complete") 

## [1] -0.02005702

Das use = complete sagt, dass wir Zeilen mit fehlenden Werten ignorieren.

Sieht also nicht nach einem Zusammenhang aus. Das sollte uns ein Diagramm auch bestätigen:

flights %>% 
  group_by(month) %>% 
  na.omit() %>%  # alle Zeilen mit fehlenden Werten löschen
  mutate(delay = dep_delay - arr_delay) %>% 
  ggplot(aes(x = month, y = delay)) + geom_boxplot()

## Warning: Continuous x aesthetic -- did you forget aes(group=...)?

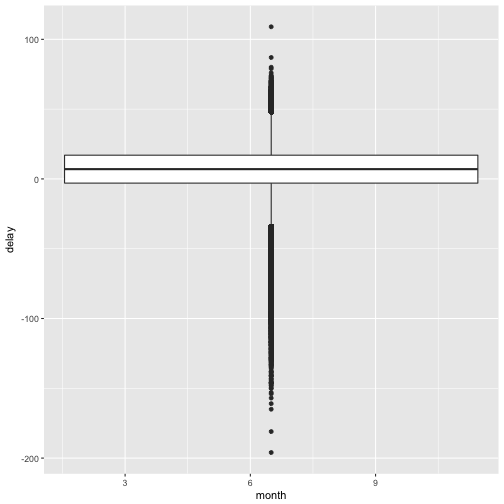
Upps, das sieht ja komisch aus… Hm..ggplot schlägt vor, wir sollen irgendwie group mit reinwursten… Naja, unsere Gruppen könnten die Monate sein. Also probieren wir’s mal…

flights %>% 
  group_by(month) %>% 
  na.omit() %>%  # alle Zeilen mit fehlenden Werten löschen
  mutate(delay = dep_delay - arr_delay) %>% 
  ggplot(aes(x = month, y = delay, group = month)) + geom_boxplot()

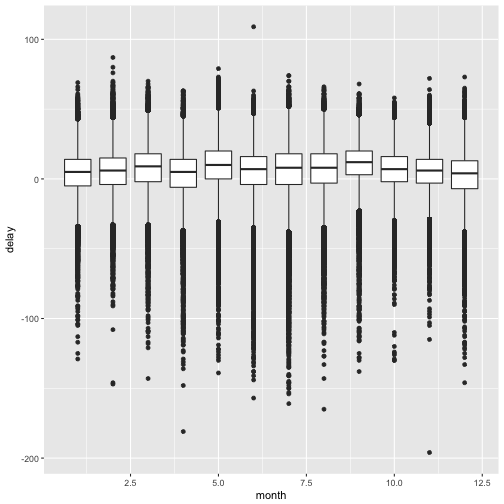
Die X-Achse sieht noch nicht so toll aus (mit den Nachkommastellen), aber das heben wir uns für eine andere Gelegenheit auf :-)

Noch ein kleiner Bonus zum Abschluss: Interaktive Diagramme!

Dazu müssen wir erstmal ein neues Paket laden: plotly (und ggf. vorher installieren).

# install.packages("plotly")
library(plotly)

plotly kann man ein ggplot-Objekt übergeben, welches dann automatisch in ein interaktives Diagramm übersetzt wird. Macht natürlich nur Sinn, wenn man das am Computer anschaut; ausgedruckt ist es dann nicht interaktiv…

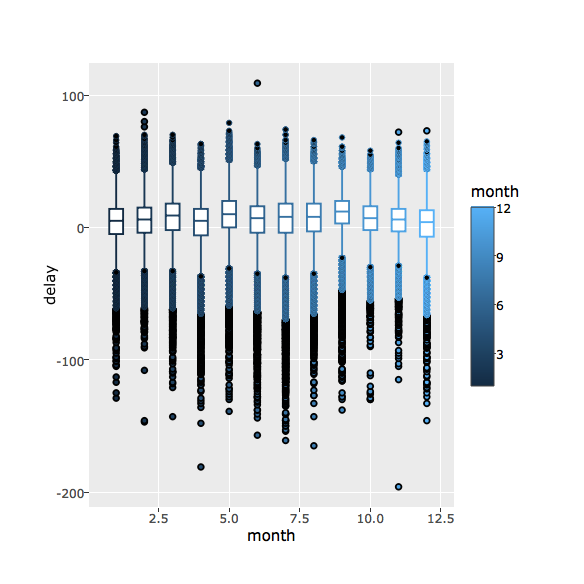
flights %>% 
  group_by(month) %>% 
  na.omit() %>%  # alle Zeilen mit fehlenden Werten löschen
  mutate(delay = dep_delay - arr_delay) %>% 
  ggplot(aes(x = month, y = delay, group = month, color = month)) + geom_boxplot() -> flights_plot

ggplotly(flights_plot)

Für heute reicht’s!

Moderator effects or interaction effect are a frequent topic of scientific endeavor. Put bluntly, such effects respond to the question whether the input variable X (predictor or independent variable IV) has an effect on the output variable (dependent variable DV) Y: “it depends”. More precisely, it depends on a second variable, M (Moderator).

More formally, a moderation effect can be summarized as follows:

If the effect of X on Y depends on M, a moderator effect takes place.

There exist some typical procedures to detect such effects. In this post, however we are concerned only with the visualization of moderation.

To do so, we will distinguish three situations: Where X and M are nominal, where X and M are numeric, and situations where one of them is nominal and the other numeric.

We will look at some visualization methods based on ggplot2 (don’t forget to install upfront if not yet installed). We will use the dataset tips from reshape2. dplyr will be used for data mingling.

library(ggplot2) 
library(dplyr) 
tips <- read.csv("https://sebastiansauer.github.io/data/tips.csv")

IV: numeric, M: nominal

Let’s assume we take total_bill as predictor (X), and sex as moderator; tip is the criterion (outcome).

qplot(x = total_bill, y = tip, facets = ~sex, data = tips) +
  geom_smooth(method = "lm")

The data set is split in two facets; a regression line indicates the strength of association in each level of the moderator.

However, as the two lines are not aligned, they are of limited use for visual comparison. Better place the lines in one, single diagram.

qplot(x = total_bill, y = tip, data = tips, color = sex) +
  geom_smooth(method = "lm") 

Now we see clearly that there are little differences between the groups, if at all.

Some tweaks:

ggplot(tips) +
  aes(x = total_bill, y = tip, color = sex) +
  geom_point(color = "grey") +
  geom_smooth(method = "lm")

Or:

tips_f <- filter(tips, sex == "Female")
tips_m <- filter(tips, sex == "Male")


ggplot(tips) +
  aes(x = total_bill, y = tip, color = sex) +
  geom_point(color = "grey") +
  geom_smooth(method = "lm", data = tips_f) +
   geom_smooth(method = "lm", data = tips_m)

IV: nominal, M: nominal

ggplot(tips) +
  aes(x = sex, y = tip) +
  geom_boxplot() +
  facet_wrap(~smoker)

The moderator effect can be put in this question here “Is the difference between the sexes of equal size in non-smokers the same as in smokers”? It appears that there is little difference in the differences, hence little indication for a moderator effect.

We can also do the statistical summary ourselves:

tips %>% 
  group_by(sex, smoker) %>% 
  summarise(tip_groups = mean(tip)) -> tips2


tips2 %>% 
  ggplot() +
  aes(x = sex, y = tip_groups, color = smoker) +
  geom_line(aes(group = smoker)) +
  geom_point()

This plot argues for some interaction of the two predictors, as the lines are not parallel (in fact they are crossed here).

Similarly, in ggplot2:

tips %>% 
  ggplot() +
  aes(x = sex, color = smoker, group = smoker, y = tip) +
  stat_summary(fun.y = mean, geom = "point") +
  stat_summary(fun.y = mean, geom = "line")

IV: metric, M: metric

As the effect of the metric moderator is not straight-forward to plot, it is convenient to discretize the metric moderator. For example, in two groups (median split) or in three (1 sd below the mean, mean, 1 sd above the mean, or in terciles…). Then we proceed as above.

tips$tip_2tile <- ntile(tips$tip, 2)
head(tips$tip_2tile)

## [1] 1 1 2 2 2 2

tips$tip_3tile <- ntile(tips$tip, 3)
head(tips$tip_3tile)

## [1] 1 1 3 3 3 3

x <- tips$tip

tips$tip_3group <-
  case_when(x > mean(x)+sd(x) ~ "high",
            x < mean(x)+sd(x) & x > mean(x)-sd(x) ~ "average",
            x < mean(x)-sd(x) ~ "low")

count(tips, tip_3group)

## # A tibble: 3 × 2
##   tip_3group     n
##        <chr> <int>
## 1    average   182
## 2       high    32
## 3        low    30

tips %>% 
  ggplot() +
  aes(x = total_bill, y = size, group = tip_3group, color = tip_3group) +
  geom_point(color = "grey", alpha = .7) +
    geom_smooth(method = "lm")

Debrief

In sum, ggplot2 provides some handy functions for visualizing moderator effects. In addition to traditional regression analyses, such plots can help to better grasp what actually is going on.

Dear editorial team,

Thanks for considering me for review. After some thought-meandering I came to the conclusion that traditional publishers - such as the present publisher of this journal - support a business model that I deem unfair and inappropriate for regular science and for the interests of science and scientists alike. That is, the fees are much too high thereby sucking resources out of the science system and out of society which could be used for the better otherwise.

For that reason I will be more likely to conduct unpaid reviews for non- or low-profit organizations but in general less or not for high-margin publishers. Also, I cannot understand why publishers earn heaps of money whereas we are scientists - reviewers, authors, editors alike - are left with empty pockets. Please note that I am in pricinciple prepared to conduct paid reviews.

Please not take my reluctance personally; it is for the improvement of our field that I take this decision.

Regards Sebastian

Hier finden Sie eine Auswahl an wissenschaftlichen Kongressen in 2017 aus der Wirtschaftspsychologie und angrenzender Felder.

Nationale Kongresse 2017 (in Deutschland)

• GWPS, 2.-4. März in Darmstadt
  Fachtagung der Gesellschaft für angewandte Wirtschaftspsychologie (GWPs)
  Submission Deadline: 30. Nov 2016

• TeaP, 26.-29. März in Dresden
  Conference of Experimental Psychologists Submission Deadline: 15. Nov. 2016

• DiffPsy, 4.-6. September in München
  Arbeitstagung der Fachgruppe Differenzielle Psychologie, Persönlichkeitspsychologie und Psychologische Diagnostik
  Submission Deadline: 9. März 2017

• Sozpsy 4.-6. Sept. in Ulm
  Tagung der Fachgruppe Sozialpsychologie
  Submission Deadline: 31. Januar 2017

• MediaPsych2017 6.-8. Sept. in Landau i.d. Pfalz
  Conference of the Media Psychology
  Submission Deadline: 1. März 2017

• AOW, 13.-15. September in Dresden
  Tagung der Fachgruppe Arbeits-, Organisations- und Wirtschaftspsychologie
  Submission Deadline: ~5. März 2017~ verlängert auf 12. März 2017

• GesPsy, 17.-19. Sept., Graz
  Kongress der Fachgruppe Gesundheitspsychologie
  Submission Deadline: ?

• FGME, 17.-20. Sept., Tübingen
  Tagung der Fachgruppe Methoden & Evaluation
  Submission Deadline: 13. April 2017

Internationale Kongresse 2017

• GfA, 15.-17. Februar, Schweiz
  Gesellschaft für Arbeitswissenschaft in der Schweiz
  Submission Deadline: 10. Okt. 2016

• BSAC, 3.-5. May, Brighton
  British Psychological Society Annual Conference
  Submission Deadline: 26. Okt. 2016

• SIOP, 27.-29. April in Orlando, Florida
  32nd Annual Conference of the Society for Industrial and Organizational Psychology
  Submission Deadline: 31. Januar 2017 (Pac. time)

• EAWOP, 17.-20. Mai in Dublin
  European Association of Work and Organizational Psychology
  Submission Deadline: 30. Sept. 2016

• PsySci, 25.-28. Mai in Boston, Maine
  29th Annual Convention of the Association for Psychological Science
  Submission Deadline: 1. Dezember 2016

• ECP2017, 11.-14. Juli in Amsterdam
  European Congress of Psychology
  Submission Deadline: 28. Januar 2017

• IMPS, 17.-21. Juli in Zürich
  International Meeting of the Psychometric Society
  Submission Deadline: 15. Februar 2017

• ECMH, 4.-6. Oktober, Berlin
  6th European Conference on Mental Health
  Submission Deadline: 14. Mai 2017

Links

https://www.dgps.de/index.php?id=2001024

https://www.zpid.de/index.php?wahl=events

https://www.zpid.de/redact/category.php?cat=16

http://www.report-psychologie.de/service/termine/kongresse-tagungen/

https://www.hogrefe.de/veranstaltungen/tagungen-und-kongresse

A typical task in data analysis is to import CSV-formatted data. CSV is nothing more than a text file with data in rectangular form; rows stand for observations (eg., persons), and columns represent variables (such as age). Columns are separed by a “separator”, often a comma. Hence the name “CSV” - “comma separeted values”. Note however that the separator can in principle anything you like (eg., “;” or tabulator or “ “).

An easy example for importing a CSV is this

d <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/MASS/birthwt.csv")
head(d)

##    X low age lwt race smoke ptl ht ui ftv  bwt
## 1 85   0  19 182    2     0   0  0  1   0 2523
## 2 86   0  33 155    3     0   0  0  0   3 2551
## 3 87   0  20 105    1     1   0  0  0   1 2557
## 4 88   0  21 108    1     1   0  0  1   2 2594
## 5 89   0  18 107    1     1   0  0  1   0 2600
## 6 91   0  21 124    3     0   0  0  0   0 2622

It comes in handy that read.csv is able to address websites out of the box!

Now at times it happens that the CSV is somehow strange. Consider this example:

dd <- read.csv("http://www.stat.ufl.edu/~winner/data/slash_survsex.dat")
head(dd)

##         X1.......1.......1
## 1        1       1       1
## 2        1       1       1
## 3        1       1       1
## 4        1       1       1
## 5        1       1       1
## 6        1       1       1

Hm, how many columns do we have?

ncol(dd)

## [1] 1

One only. Something got lost in translation. We would expect three columns. Now what?

To be honest, I am not really sure what the problem exactly consists of. But that does not stop from finding a solution.

The little at X1......1... appear to indicate blanks (spaces). So let’s try to use a blank as the column separator.

dd <- read.csv("http://www.stat.ufl.edu/~winner/data/slash_survsex.dat", 
              sep = " ")
ncol(dd)

## [1] 22

Yosh! 22 columns, that’s too much of something good… Hm, let’s look at the dataframe.

head(dd)

##    X X.1 X.2 X.3 X.4 X.5 X.6 X1 X.7 X.8 X.9 X.10 X.11 X.12 X1.1 X.13 X.14
## 1 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
## 2 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
## 3 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
## 4 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
## 5 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
## 6 NA  NA  NA  NA  NA  NA  NA  1  NA  NA  NA   NA   NA   NA    1   NA   NA
##   X.15 X.16 X.17 X.18 X1.2
## 1   NA   NA   NA   NA    1
## 2   NA   NA   NA   NA    1
## 3   NA   NA   NA   NA    1
## 4   NA   NA   NA   NA    1
## 5   NA   NA   NA   NA    1
## 6   NA   NA   NA   NA    1

It appears that X1, X1.1, and X1.2 are the only columns which are of interest (all others only consist of NAs). So let’s select those columns and discard the rest.

library(dplyr)
dd <- select(dd, X1, X1.1, X1.2)

Worked!

Finally, let’s change the column names to our desire.

dd <- rename(dd, V1 = X1,V2 = X1.1, V3 = X1.2)