reading time: 15-20 min.

Recently, I analyzed some data of a study where the efficacy of online psychotherapy was investigated. The investigator had assessed whether or not a participant suffered from some comorbidities (such as depression, anxiety, eating disorder…).

I wanted to know whether each of these (10 or so) comorbidities was associated with the outcome (treatment success, yes vs. no).

Of course, an easy solution would be to “half-manually” check the association, eg. using table() in R. But I wanted a more reproducible, more automated solution (ok, I confess, I justed wanted it to be cooler, probably…).

As a starter, consider the old question of the Titanic disaster: Did class correlate with survival? Let’s see:

data(titanic, package = "COUNT")  # package need be installed
attach(titanic)  # save some typing
table(class, survived)# tabulate the two variables

##            survived
## class        no yes
##   1st class 122 203
##   2nd class 167 118
##   3rd class 528 178
##   crew        0   0

prop.table(table(class, survived))  # get the percentages/proportions

##            survived
## class               no        yes
##   1st class 0.09270517 0.15425532
##   2nd class 0.12689970 0.08966565
##   3rd class 0.40121581 0.13525836
##   crew      0.00000000 0.00000000

The tabulation results look like this:

Alas! Money can buy you life, it appears…

Note that we are talking about nominal variables with two levels, ie. dichotomous variables. In other words, we are looking at frequencies.

So my idea was:

• take a column of a predictor (say, depression)
• take the column of the outcome variable (treatment success)
• Cross-tabulate the association.
• Repeat those steps for each of the comorbidities
• Make sure it looks (sufficiently) cool…

Have I already told that I like the R-package dplyr? Check it out. Let’s see how to do the job with dplyr. Let’s use the Wages dataset from package ISLR.

This dataset from ISLR shows the wage of some male professionals in the Atlantic US area; along with the wage there are also some “risk factors” for the wage such as health status, education, race. Let’s see if there is an association.

First, load the package and the data:

# don't forget to install the packages upfront.
library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

library(ggplot2)
data(Wage, package = "ISLR")

Now, here comes dplyr:

Wage %>%
  mutate(wage_f = ntile(wage, 2)) %>%  # bin it
  group_by(wage_f, health, race) %>%
  summarise(count = n()) %>%  # summarise by each group
  ggplot(aes(x = factor(wage_f), y = count, fill = race)) +
  geom_bar(stat = "identity") +
  facet_wrap(~health)

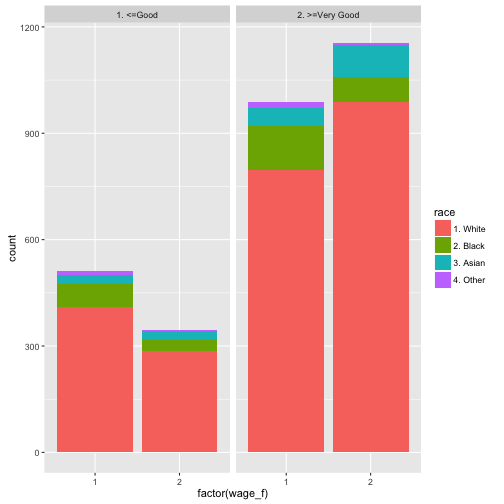
Let’s discuss the code a bit (not every bit), looking briefly the lines:

1. build a column where wage is binned in two groups (low vs. high wage)
2. group by wage group, health status and race (image 222 sub-spreadsheets)
3. count the row number in each group (ie., 8 mini-spreadsheets)
4. plot it, with some parameters

z-transformation is an ubiquitous operation in data analysis. It is often quite practical.

Example: Assume Dr Zack scored 42 points on a test (say, IQ). Average score is 40 in the relevant population, and SD is 1, let’s say. So Zack’s score is 2 points above average. 2 points equals to SDs in this example. We can thus safely infer that Zack is about 2 SDs above average (leaving measurement precision and other issues at side).

If the variable (IQ) is normally distributed, than we are allowed to look up the percentiles of this z-value in a table. Or ask the computer (in R):

pnorm(2)

## [1] 0.9772499

Here, R tells us that approx. 98% of all individuals have an IQ that is smaller than that of Dr. Zack. Lucky guy! Compare the figure.

Here an overview on some frequently used quantiles of the normal distribution:

Now, next step. We have a bunch of guys, and test each of them. Say, 10 guys. Now we can calculate mean and SD of this distribution. To see the differences more clearly, we can z-transform the values.

IQ <- rnorm(10, mean = 40, sd = 1)
IQ

##  [1] 40.91472 38.53260 40.30042 40.87957 40.99679 39.86815 40.14272
##  [8] 39.26335 40.19174 39.85837

IQ_z <- scale(IQ)
IQ_z

##              [,1]
##  [1,]  1.05897590
##  [2,] -2.01783361
##  [3,]  0.26552871
##  [4,]  1.01356631
##  [5,]  1.16497561
##  [6,] -0.29280567
##  [7,]  0.06183789
##  [8,] -1.07397171
##  [9,]  0.12515803
## [10,] -0.30543146
## attr(,"scaled:center")
## [1] 40.09484
## attr(,"scaled:scale")
## [1] 0.7742196

Ok. Let’s compute mean and sd of the z-scaled values:

mean(IQ_z)

## [1] -4.605338e-15

sd(IQ_z)

## [1] 1

So it worked apparently.

But why is it that mean and sd will end up nicely with 0 (mean) and 1 (sd)?

To see this, consider the following. A z-transformation is in step 1 nothing more than subtracting the mean of some value. If I subtract the mean (42 here) from each value, and compute the mean then, I will not be surprised that the mean is now 42 points lower than it was. But 42-42=0. So the new mean (after z-transformation) will be 0.

Ok, but what about sd? Why must it equal 1? A similar reasoning applies. If I divide each value by the SD of the distribution (here 1), the new SD will be exactly by this factor lower. So whatever it used to be before z-transformtion, it will be 1 afterwards, as x / x = 1.