Willkommen zum R-Crashkurs
Nicht jeder liebt Datenanalyse und Statistik… in gleichem Maße! Das ist zumindest meine Erfahrung aus dem Unterricht 🔥. Crashkurse zu R sind vergleichbar zu Tanzkursen vor der Hochzeit: Hat schon vielen das Leben gerettet, aber ersetzt nicht ein Semester in der Pariser Tanzakademie (man beachte den Vergleich zum Unterricht an der Hochschule).
Dieser Crashkurs ist für Studierende oder Anfänger der Datenanalyse gedacht, die in kurzer Zeit einen verzweifelten Versuch … äh … einen grundständigen Überblick über die Datenanalyse erwerben wollen.
Ok, let’s dance 🕺.
Die PDF-Version dieses Kurses finden Sie hier.
Software
Bevor wir uns die Schritte näher anschauen, ein paar Worte zur Software.
Programme
Wir brauchen zwei Programme:
Bitte laden Sie diese herunter und installieren Sie sie. Wenn R installiert ist, dann findet RStudio R auch direkt.
Zur Installation gehen Sie so vor:
- Laden Sie R herunter und öffnen Sie die heruntergeladene Installationsdatei; folgen Sie den Hinweisen, die Sie durch die Installation leiten
- Laden Sie RStudio herunter (Desktop-Version)
- Sie finden eine Version für alle gängigen Betriebssysteme.
Beide Programme sind kostenlos.
Wenn alles läuft, sieht es etwa so aus:
Hilfe
R will nicht so, wie ich wohl will? Hier finden Sie einige Tipps zur Fehlerbehebung. Außerdem hilft erfahrungsgemäß: Googeln Sie nach der Fehlermeldung.
Hier finden sich einige Einführungen in R in unterschiedlichem Niveau; Antworten auf häufige Fragen finden sich hier.
Warum R?
- R ist ein Programm für Statistik und Datenanalyse.
- R ist für Linux, MacOS X und Windows (95 oder höher) Plattformen verfügbar.
- R ist eine elegante und umfassende statistische und grafische Programmiersprache.
- R kann eine steile Lernkurve L haben
(L = Zeiteinheit/Erfolgseinheit). - R ist kostenlos! Wenn Sie Lehrender oder Studierender sind, sind die Vorteile offensichtlich.
- R bietet eine unvergleichliche Plattform für die Programmierung neuer statistischer Methoden in einer einfachen und unkomplizierten Weise.
- R enthält fortgeschrittene statistische Routinen, die noch nicht in anderen Software-Paketen verfügbar sind.
- R verfügt über state-of-the-art Grafiken Fähigkeiten.
Warum RStudio?
RStudio ist eine integrierte Entwicklungsumgebung (IDE), die die Verwendung von R für Anfänger und Experten erleichtert.
Erweiterungen (Pakete, engl. packages)
Pakete installieren
R macht reichlichen Gebrauch von Erweiterungen, also “Zusatz-Software”, welches die Funktionen von R erweitern. Diese Erweiterungen nennt man “Pakete” (engl. packages). Am Anfang kann es verwirren oder verwundern, warum in R so viele Pakete verwendet werden. Tatsächlich ist das eine große Stärke von R: Alle, die sich berufen fühlen, können ein R-Paket entwickeln und alle, die sich berufen fühlen, können ein R-Paket herunterladen. Alles kostenlos und transparent. Und in einem “Appstore” vereint (“CRAN”).
Praktisch bedeutet das, dass Sie ein paar Pakete installieren müssen, um in den Genuss von Zusatz-Funktionen zu kommen. Am einfachsten geht die Installation in RStudio über den Reiter “Packages” und dem Button “Install Packages”:
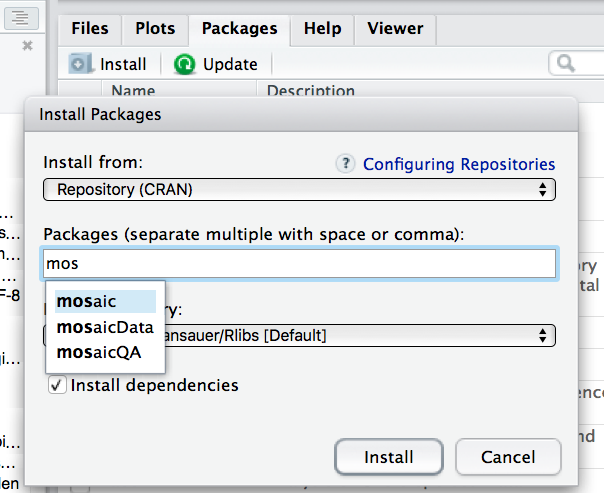
Um einen Befehl zu verwenden, der in einem “Zusatz-Paket wohnt”, müssen Sie zuerst dieses Paket installieren.
Wir werden in diesem Kurs mit folgenden Paketen arbeiten; bitte installieren Sie sie vorab:
mosaic# Zugpferdeffects# Effektplots für ANOVA-Modelleopenxlsx# Excel-Dateien schreibencorrgram# KorrelationsdiagrammeGGally# Korrelationsdiagrammecorrplot# Korrelationsdiagramme
Wie jede Software, müssen Sie ein Paket nur einmal installieren; dann ist es auf Ihrem Computer vorhanden.
Pakete starten
Um einen Befehl zu verwenden, der nicht im Standard-R, sondern in einer Erweiterung von R (“Paket”) wohnt, müssen sie dieses Paket erst starten (laden). Es hört sich trivial an: Sie können nur Pakete laden, die auf Ihrem Computer installiert sind (es ist trivial; aber manchmal vergisst man es). Um ein Paket zu laden, können Sie den Befehl library() verwenden. Wir benötigen die folgenden Pakete; bitte laden:
library(mosaic) # Zugpferd
library(effects) # Effektplots für ANOVA-Modelle
library(openxlsx) # Excel-Dateien schreiben
library(corrgram) # Korrelationsdiagramme
library(GGally) # Korrelationsdiagramme
library(corrplot) # Korrelationsdiagramme
Oder Sie klicken den Namen des Pakets hier an:
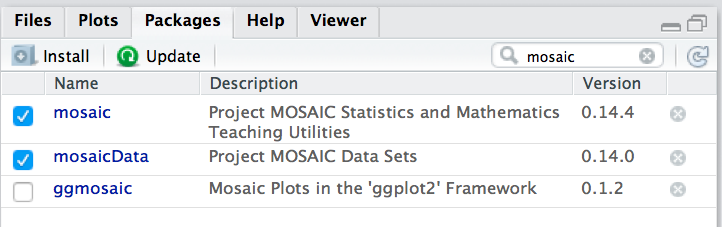
Wir gehen im Folgenden davon aus, dass Sie diese beiden Pakete geladen haben.
Nach jedem Start von R bzw. RStudio müssen Sie die Erweiterung erneut laden (wenn Sie sie benutzen wollen).
⚠️ Um ein Paket zu laden, muss es installiert sein. Klicken Sie zum Installieren auf den Button “Install” unter dem Reiter “Packages” in RStudio:

Sie müssen ein Paket nur einmal installieren, um es verwenden zu können. Sie installieren ja auch nicht Ihren Browser jedes Mal neu, wenn Sie den Computer starten.
Daten
Wir verwenden in diesem Kurs diese Datensätze:
TeachingRatings; Sie können ihn hier herunterladen.mtcars;mtcarsist schon im Standard-R fest eingebaut; Sie müssen also nichts weiter tun.tips; den Datensatztipskönnen Sie hier herunterladen.
⚠️ Bitte stellen Sie sicher, dass Sie auf diese Daten zugreifen können während des Kurs. Laden Sie sie vorab herunter.
🔖 Lesen Sie hier weiter, um Ihr Wissen zu vertiefen zu diesem Thema: R - Software in stallieren.
Über sieben Brücken musst Du gehen - Die Schritte der Datenanalyse

Lizenz: André D Conrad, CC BY SA 3.0 De, https://de.wikipedia.org/wiki/Peter_Maffay#/media/File:Peter_Maffay.jpg
Man kann (wenn man will) die Datenanalyse in sieben fünf Brücken oder Schritte einteilen, angelehnt dem Song von Peter Maffay “Über sieben Brücken musst du gehen”. Wir werden nacheinander alle Schritte bearbeiten: Sieben Mal wirst Du die Asche sein. Aber einmal auch der helle Schein.
Arbeiten mit dem Paket mosaic
Das Paket mosaic wird unser Zugpferd für alle folgenden Analysen ein. Es hat den Charme, über eine einfache, konsistente Syntax zu verfügen. Mit wenig kann man da viel erreichen. Genau das, wovon man als Student träumt… (so denken Dozenten, jedenfalls).
Die folgende Syntax
Zielbefehl(y ~ x \| z, data=...)
wird verwendet für
- graphische Zusammenfassungen,
- numerische Zusammenfassungen und
- inferentstatistische Auswertungen
Für Grafiken gilt:
- y: y-Achse Variable
- x: x-Achse Variable
- z: Bedingungsvariable
Generell gilt:
y ~ x | z
DAs kann in der Regel gelesen werden y wird modelliert von (oder hängt ab von) x gruppiert nach den Stufen von z.
Der Kringel (die Tilde) ~ erzeugt sich beim Mac mit ALT+n und bei Windows steht es auf einer Taste ziemlich rechts auf der Tastatur. Die Verwendung der Tilde wird auch als “Formel-Schreibweise” (engl. “Formula Interface”) bezeichnet.
Literaturempfehlung für den Einstieg in R mit dem Paket mosaic
- Daniel T. Kaplan, Nicholas J. Horton, Randall Pruim, (2013): Project MOSAIC Little Books Start Teaching with R, http://mosaic-web.org/go/Master-Starting.pdf
Brücke 1: Daten einlesen
Der einfachste Weg, Daten einzulesen, ist über den Button “Import Dataset” in RStudio. So lassen sich verschiedene Formate - wie XLS(X) oder CSV - importieren.
⚠️ Beim Importieren von CSV-Dateien ist zu beachten, dass R davon von us-amerikanisch formatierten CSV-Dateien ausgeht. Was heißt das? Das bedeutet, das Spaltentrennzeichen (engl. delimiter) ist ein Komma ,. Deutsch formatierte CSV-Dateien, wie sie ein deutsch-eingestelltes Excel ausgibt, nutzen aber ein Semikolon ; (Strichpunkt) als Spaltentrennzeichen.
Haben Sie also eine “deutsche” CSV-Datei, müssen Sie in der Import-Maske von RStudio als delimiter ein semicolon auswählen.
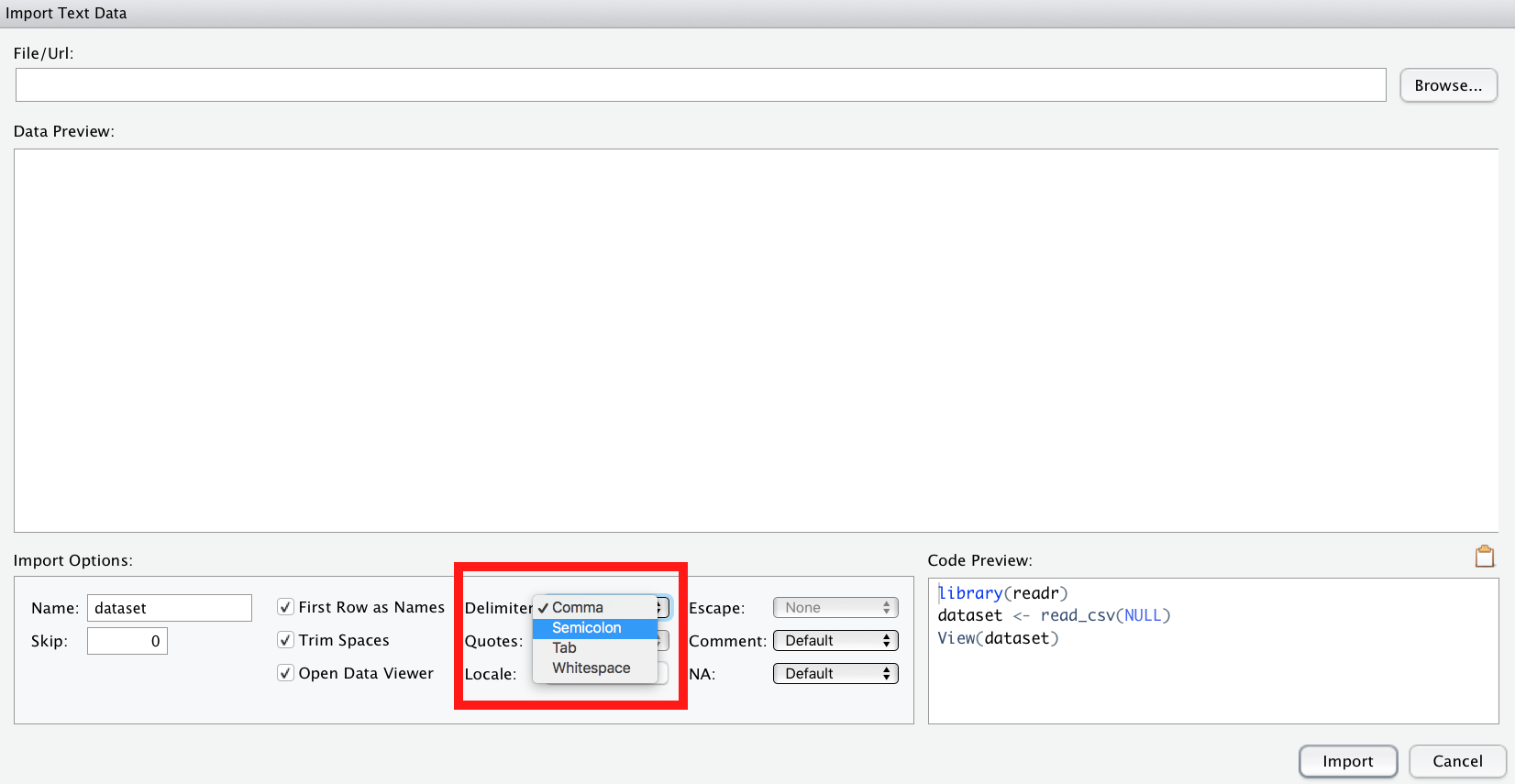
Den TeacherRatings-Datensatz können Sie einfach importieren, indem Sie in der Maske in RStudio den Link https://sebastiansauer.github.io/data/TeachingRatings.csv eingeben (oder den Tips-Datensatz). Oder per Befehl, geht genauso schnell:
TeachingRatings <- read.csv("https://sebastiansauer.github.io/data/TeachingRatings.csv")
Falls die Datei in Ihrem R-Arbeitsverzeichnis liegt, dann brauchen Sie keinen Pfad angeben:
TeachingRatings <- read.csv("TeachingRatings.csv")
Alternativ können Sie natürlich eine XLS- oder XLSX-Datei importieren. Am einfachsten ist es, XLSX-Dateien zu importieren. Da aber CSV-Dateien ein Standard heutzutage sind, sollten Sie sich auch mit diesem Datentyp vertraut machen.
tidy data - Tabellen in Normalform
Damit Sie in R vernünftig mit Ihren Daten arbeiten können, sollten die Daten “tidy” sein, d.h. in Normalform. Was ist Normalform? Betrachten Sie folgende Abbildung - so sieht eine Tabelle in Normalform aus.
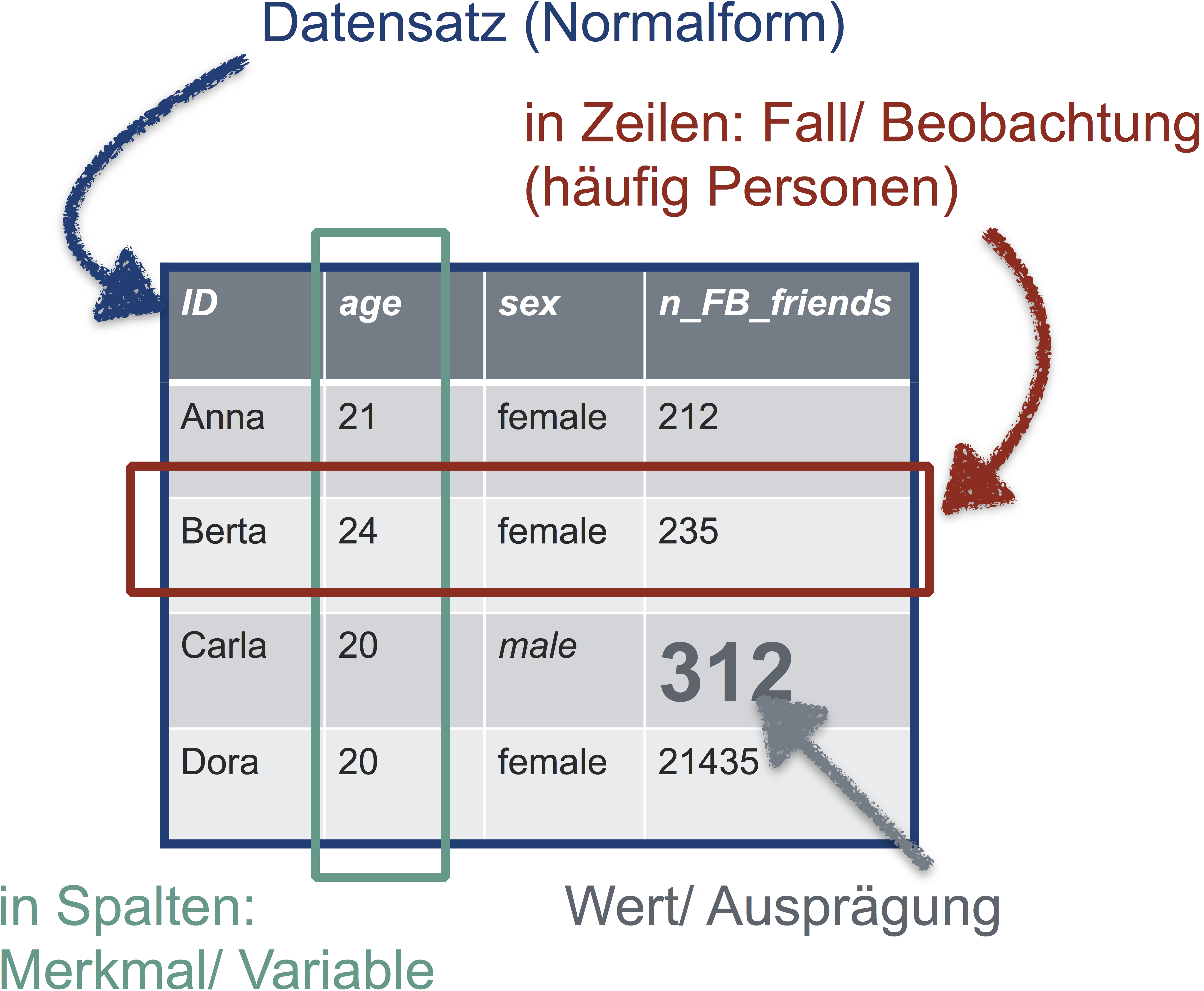
Übrigens heißen Tabellen (mit Spaltennamen) in R Dataframes.
Die goldene Regel der Normalform einer Tabelle lautet also:
In jeder Zeile steht eine Beobachtung (z.B. Person). In jeder Spalte eine Variable (z.B. Geschlecht). In der ersten Zeile stehen die Spaltennamen, danach folgen die Werte. Sonst steht nichts in der Tabelle.
⚠️ Falls Ihre Daten nicht in Normalform sind, sollten Sie diese zunächst in Normalform bringen.
💡 Der einfachste Weg (von der Lernkurve her betrachtet, nicht vom Zeitaufwand), Daten in Normalform zu bringen, ist sie in Excel passend umzubauen.
Beispiel für Daten in Nicht-Normalform
Sie denken, dass Ihre Daten immer/auf jeden Fall in Normalform sind? Dann schauen Sie sich mal dieses Bild an:
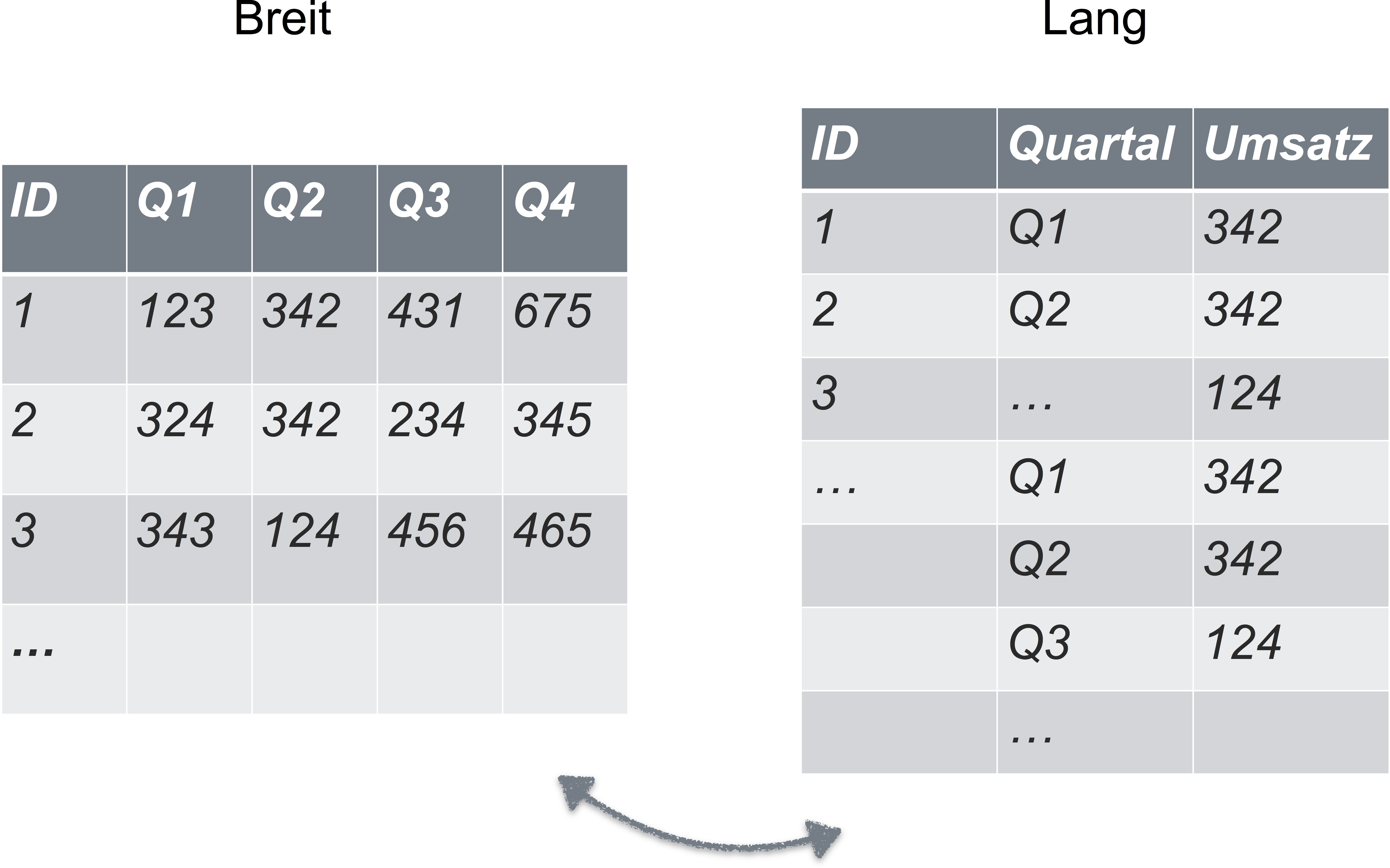
Wir werden in diesem Kurs nicht bearbeiten, wie man Daten von “breit” auf “lang” (=tidy) umformatiert. Aber lesen Sie bei Interesse doch z.B. hier nach.
Daten anschauen
Es empfiehlt sich, zu Beginn einen Blick auf die Daten zu werfen, um zu prüfen, ob alles augenscheinlich seine Richtigkeit hat. Tun Sie das immer, viel Ärger lässt sich so ersparen.
glimpse(TeachingRatings)
#> Observations: 463
#> Variables: 13
#> $ X <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,...
#> $ minority <fctr> yes, no, no, no, no, no, no, no, no, no, yes, no,...
#> $ age <int> 36, 59, 51, 40, 31, 62, 33, 51, 33, 47, 35, 37, 42...
#> $ gender <fctr> female, male, male, female, female, male, female,...
#> $ credits <fctr> more, more, more, more, more, more, more, more, m...
#> $ beauty <dbl> 0.2899157, -0.7377322, -0.5719836, -0.6779634, 1.5...
#> $ eval <dbl> 4.3, 4.5, 3.7, 4.3, 4.4, 4.2, 4.0, 3.4, 4.5, 3.9, ...
#> $ division <fctr> upper, upper, upper, upper, upper, upper, upper, ...
#> $ native <fctr> yes, yes, yes, yes, yes, yes, yes, yes, yes, yes,...
#> $ tenure <fctr> yes, yes, yes, yes, yes, yes, yes, yes, yes, no, ...
#> $ students <int> 24, 17, 55, 40, 42, 182, 33, 25, 48, 16, 18, 30, 2...
#> $ allstudents <int> 43, 20, 55, 46, 48, 282, 41, 41, 60, 19, 25, 34, 4...
#> $ prof <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,...
Selber Daten erzeugen
Normalerweise werden Sie Daten in R einlesen, aber manchmal möchte man selber Daten erzeugen. Dazu sollten Sie wissen: Ein Dataframe besteht aus Spalten, wie Sie wissen. Diese Spalten nennt man auch Vektoren. Ein Vektor ist eine Sammlung von einzelnen Datenstücken, die hintereinander aufgereiht sind, wie Wäsche an der Wäscheleine. Ach ja, Vektoren müssen “sortenrein” sein, also nur Zahlen oder nur Text etc. Um einen Vektor zu erzeugen, benutzt man den Befehle c (wie combine oder concatenate, aneinanderfügen):
meine_freunde <- c("Bibi", "Uschi", "Ulf", "Donald der Große")
Deine_PINs <- c(1234, 7777, 1234567, 0000)
💻 AUFGABE:
- Erzeugen Sie einen Vektor mit einem kreativen Namen.
- Erzeugen Sie einen Vektor, in dem Sie Zahlen und Text mischen. Was passiert?
- Erstellen Sie einen Vektor aus
meine_freundeundDeine_PINs. Was passiert? - Adeln Sie mal Ihren Vektor zu einer waschechten Tabelle (Dataframe) mit dem Befehl
data.frame(vektor); nicht vergessen, der resultierenden Tabelle einen Namen zu geben bzw. eine neue Tabelle zu benennen, die das Ergebnis des Befehledata.framespeichert.
Daten als CSV oder Excel exportieren
Wie kriege ich die Daten aus R wieder raus? Was ist sozusagen mit REXIT-Strategie? Keine Sorge, die Straße fährt in beide Richtungen. Sagen wir, Sie möchten den Dataframe mtcars exportieren, um außerhalb von R damit Kunststücke zu vollbringen:
CSV
write.csv(TeachingRatings, "TeachingRatings.csv")
XLSX
write.xlsx(TeachingRatings, "TeachingRatings.xlsx")
Dieser Befehl (write.xlsx) schreibt eine XLSX-Datei in das aktuelle R-Verzeichnis (das Arbeitsverzeichnis).
Das R-Arbeitsverzeichnis
💡 R schreibt Dateien immer in R R-Arbeitsverzeichnis. Sie wissen nicht, was das R-Arbeitsverzeichnis ist? Lesen Sie hier nach.
💻 AUFGABE:
- Finden Sie Ihr aktuelles Arbeitsverzeichnis heraus.
- Setzen Sie Ihr Arbeitsverzeichnis auf den Ordner, in dem Ihre Lieblings-Skriptdatei liegt.
Textkodierung in UTF-8
Falls Sie RStudio oder ein beliebiger Texteditor irgendwann fragt, wie die Textdatei kodiert sein soll, wählen Sie immer “UTF-8”. UTF-8 ist eine Kodierungstabelle, so dass der Computer weiß, welches Zeichen welcher Taste zugeordnet ist; dabei ist UTF-8 so großzügig geplant, dass alle möglichen Sonderzeichen (Deutsch, Chinesisch, Hebräisch…) dazu passen. UTF-8 ist die Standard-Kodierung für Textdateien im Internet.
💡 In RStudio kann man unter File..Save with Encoding... die Textcodierung einstellen.
🔖 Lesen Sie hier weiter, um Ihr Wissen zu vertiefen zu diesem Thema: Daten Einlesen mit Prada.
💻 AUFGABE:
- Prüfen Sie, in welchem Format Ihr Dokument kodiert ist.
- Setzen Sie das Format ggf. auf UTF-8.
Schritt 2: Aufbereiten
Der Schritt des Aufbereitens ist häufig der zeitintensivste Schritt. In diesem Schritt erledigen Sie alles, bevor Sie zu den “coolen” oder fortgeschrittenen Analysen kommen. Z.B.
- prüfen auf Fehler beim Daten einlesen (und korrigieren)
- Spaltennamen korrigieren
- Daten umkodieren
- Fehlende Werte verarzten
- Komische Werte prüfen
- Daten zusammenfassen
- Zeilenmittelwerte bilden
- Logische Variablen bilden
- …
Auf Fehler prüfen beim Einlesen
⚠️ Ein häufiger Fehler ist, dass die Daten nicht richtig eingelesen werden. Zum Beispiel werden die Spaltentrennzeichen nicht richtig erkannt. Das kann dann so aussehen:
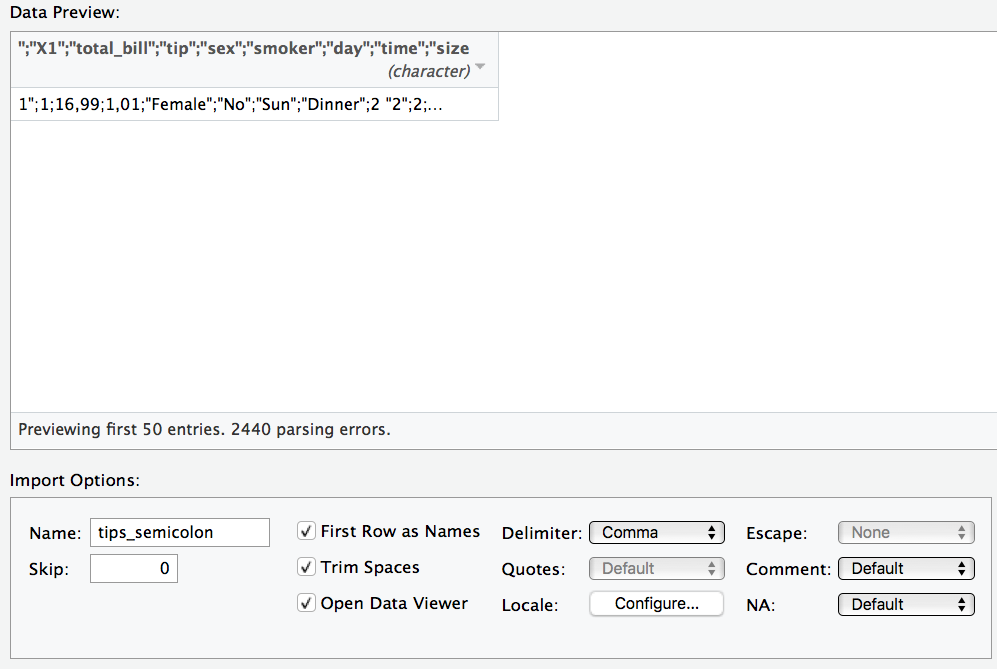
Unter “delimiter” in der Maske können Sie das Trennzeichen anpassen.
⚠️ “Deutsche” CSV-Dateien verwenden als Dezimaltrennzeichen ein Komma; englisch-formatierte CSV-Dateien hingegen einen Punk. R geht per Default von englisch-formatierten CSV-Dateien aus. Importieren Sie eine deutsch-formatierte CSV-Datei, müssen Sie das Dezimaltrennzeichen von Hand ändern; es wird nicht automatisch erkannt.
💡 Unter “locale” können Sie das Dezimaltrennzeichen ggf. anpassen.
Spaltennamen korrigieren
Spaltennamen müssen auch “tidy” sein. Das heißt in diesem Fall:
- keine Leerzeichen
- keine Sonderzeichen (#,ß,ä,…)
- nicht zu lang, aber trotzdem informativ
Spaltennamen sollten nur Buchstaben (ohne Umlaute) und Ziffern enthalten. Für Textdaten in den Spalten sind diese Regeln auch sinnvoll.
💡 Am einfachsten ändern Sie die Spaltennamen in Excel.
In R können Sie Spaltennamen z.B. so ändern:
rename(TeachingRatings, festangestellt = tenure) -> TR2
In Pseudo-R könnte man schreiben:
benenne_spalte_um(meine_tabelle, neuer_name = altername) -> meine_neue_tabelle
Der R-Zuweisungspfeil <- bzw. -> funktioniert in beide Richtungen; er darf nach links oder rechts zeigen. In jedem Fall wird das Objekt, auf das er zeigt, “befüllt” mit den Inhalten die auf der anderen Seite stehen.
💻 AUFGABE:
- Benennen Sie in
TeachingRatingsdie SpaltenativeinMuttersprachlerum; speichern Sie aber das Ergebnis in einem neuen Dataframe. - Suchen Sie sich noch zwei weitere Spalten, und benennen Sie die Spaltennamen nach eigenen Vorstellungen um!
Umkodieren
Gerade bei der Analyse von Fragebogendaten ist es immer wieder nötig, Daten umzukodieren. Klassisches Beispiel: Ein Item ist negativ kodiert. Zum Beispiel das Item “Ich bin ein Couch-Potato” in einem Fragebogen für Extraversion.
Nehmen wir an, das Item “i04” hat die Werte 1 (“stimme überhaupt nicht zu”) bis 4 (“stimme voll und ganz zu”). Kreuzt jemand das Couch-Potato-Item mit 4 an, so sollte er nicht die maximale Extraversion-Punktzahl (4), sondern die minimale Extraversion-Punktzahl (1) erhalten. Also
1 --> 4
2 --> 3
3 --> 2
4 --> 1
Am einfachsten ist dies zu bewerkstelligen mit folgendem R-Befehl:
meine_tabelle$i04_r <- 5 - meine_Tabelle$i04
Rechnet man 5-i04 so kommt der richtige, “neue” Wert heraus (vorausgesetzt, das Item hatte 4 Antwortstufen).
Zur Erinnerung:
$ist das Trennzeichen zwischen Tabellennamen und Spaltenname.<-ist der Zuweisungsbefehl. Wir definieren eine neue Spalte mit dem Nameni04_r. Dasrsoll stehen für “rekodiert”, damit wir wissen, dass in dieser Spalte die umkodierten Werte stehen.
Fehlende Werte
Der einfachste Umgang mit fehlenden Werten ist: nichts machen. Denken Sie nur daran, dass viele R-Befehle von Natur aus nervös sind - beim Anblick von fehlenden Werten werden sie panisch und machen nix mehr. Zum Beispiel der Befehl mean. Haben sie fehlende Werte in ihren Daten, so verwenden Sie den Parameter na.rm = TRUE. na steht für “not available”, also fehlende Werte. rm steht für “remove”. Also mean(meine_tabelle$i04_r, na.rm = TRUE).
💡 Der R-Befehl inspect aus mosaic zeigt Ihnen an, ob es fehlende Werte gibt:
inspect(meine_daten).
💻 AUFGABE:
- Prüfen Sie, ob es in
TeachingRatingsfehlende Werte gibt. - Prüfen Sie, ob es in
mtcarsfehlende Werte gibt.
Komische Werte
Hat ein Spaßvogel beim Alter 999 oder -1 angegeben, kann das Ihre Daten ganz schön verhageln. Prüfen Sie die Daten auf komische Werte. Der einfachste Weg ist, sich die Daten in Excel anzuschauen. Cleverer ist noch, sich Zusammenfassungen auszugeben, wie der kleinste oder der größte Wert, oder der Mittelwert etc., und dann zu schauen, ob einem etwas spanisch vorkommt. Diagramme sind ebenfalls hilfreich. Dann ändern Sie die Werte in Excel und laden die Daten erneut ins R.
Logische Variablen bilden
Sagen wir, uns interessiert welches Auto mehr als 200 PS hat; wir wollen Autos mit mehr als 200 PS vergleichen (“Spass”) mit schwach motorisierten Autos (“Kruecke”). Wie können wir das (einfach) in R erreichen? Logische Variablen sind ein einfacher Weg.
TeachingRatings$Traumdozent <- TeachingRatings$beauty > 1
Dieser Befehl hat eine Spalte (Variable) in der Tabelle TeachingRatings erzeugt, in der TRUE steht, wenn das Auto der jeweiligen Spalte die Bedingung (beauty > 1) erfüllt. Schauen Sie nach.
inspect(TeachingRatings$Traumdozent)
#> # A tibble: 1 x 5
#> class levels n missing
#> <chr> <int> <int> <int>
#> 1 logical 2 463 0
#> # ... with 1 more variables: distribution <chr>
Ok, etwa 15% der Dozenten sind so hübsch. Erzeugen wir einen Teil-Datensatz nur mit diesen Dozentenmodells:
Dozimodels <- filter(TeachingRatings, Traumdozent == TRUE)
glimpse(Dozimodels)
#> Observations: 67
#> Variables: 14
#> $ X <int> 5, 25, 36, 43, 44, 46, 53, 55, 64, 67, 83, 84, 85,...
#> $ minority <fctr> no, no, yes, no, no, no, no, no, no, no, no, yes,...
#> $ age <int> 31, 34, 44, 39, 49, 33, 38, 34, 52, 50, 47, 54, 58...
#> $ gender <fctr> female, female, female, female, male, male, femal...
#> $ credits <fctr> more, more, more, more, more, more, more, more, m...
#> $ beauty <dbl> 1.509794, 1.775517, 1.040902, 1.970023, 1.050950, ...
#> $ eval <dbl> 4.4, 4.6, 3.8, 3.4, 3.9, 4.7, 4.5, 3.1, 3.4, 4.2, ...
#> $ division <fctr> upper, upper, upper, lower, upper, upper, upper, ...
#> $ native <fctr> yes, yes, yes, yes, yes, yes, yes, yes, yes, yes,...
#> $ tenure <fctr> yes, yes, yes, no, yes, yes, yes, yes, yes, yes, ...
#> $ students <int> 42, 20, 30, 22, 28, 30, 46, 24, 31, 15, 16, 18, 16...
#> $ allstudents <int> 48, 26, 55, 24, 45, 31, 65, 36, 44, 16, 21, 18, 17...
#> $ prof <int> 5, 25, 36, 43, 44, 46, 53, 55, 64, 67, 83, 84, 85,...
#> $ Traumdozent <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TR...
inspect(Dozimodels)
#>
#> categorical variables:
#> name class levels n missing
#> 1 minority factor 2 67 0
#> 2 gender factor 2 67 0
#> 3 credits factor 2 67 0
#> 4 division factor 2 67 0
#> 5 native factor 2 67 0
#> 6 tenure factor 2 67 0
#> 7 Traumdozent logical 1 67 0
#> distribution
#> 1 no (82.1%), yes (17.9%)
#> 2 female (58.2%), male (41.8%)
#> 3 more (95.5%), single (4.5%)
#> 4 upper (52.2%), lower (47.8%)
#> 5 yes (100%), no (0%)
#> 6 yes (74.6%), no (25.4%)
#> 7 TRUE (100%)
#>
#> quantitative variables:
#> name class min Q1 median Q3 max
#> 1 X integer 5.000000 108.5000 318.000000 427.500000 460.000000
#> 2 age integer 31.000000 34.0000 39.000000 50.000000 58.000000
#> 3 beauty numeric 1.040902 1.1126 1.232602 1.771301 1.970023
#> 4 eval numeric 3.000000 3.8000 4.200000 4.600000 5.000000
#> 5 students integer 9.000000 16.0000 22.000000 44.500000 111.000000
#> 6 allstudents integer 10.000000 20.0000 31.000000 61.500000 157.000000
#> 7 prof integer 5.000000 44.0000 64.000000 85.000000 93.000000
#> mean sd n missing
#> 1 277.104478 153.6127692 67 0
#> 2 42.507463 9.2529653 67 0
#> 3 1.387867 0.3106707 67 0
#> 4 4.147761 0.5200111 67 0
#> 5 33.298507 24.1271976 67 0
#> 6 44.716418 34.3819041 67 0
#> 7 61.582090 26.8052173 67 0
💻 AUFGABE:
- Erstellen Sie eine Variable
Asbach, definiert alsTRUE, wennage < 70. - Erstellen Sie eine Variable
keiner_mag_mich, definiert als TRUE, wenneval <= 2. - Denken Sie sich noch selber mindestens ein Beispiel aus.
Daten zusammenfassen: Deskriptivstatistik
Deskriptive Statistik ist letztlich nichts anderes, als Daten geschickt zusammenzufassen. Praktisch wird meistens eine Spalte einer Tabelle zu einer Zahl zusammengefasst.

Schauen wir uns das mal mit echten Daten an. Der Datensatz TeachingRatings ist schon in R eingebaut, so dass wir in nicht extra laden müssen. Ganz praktisch. Dazu fragen wir den Inspektor inspect, der würde uns auch noch verraten wie die nominalen Variablen sich so verteilen – wenn wir hier welche hätten.
inspect(TeachingRatings)
#>
#> categorical variables:
#> name class levels n missing
#> 1 minority factor 2 463 0
#> 2 gender factor 2 463 0
#> 3 credits factor 2 463 0
#> 4 division factor 2 463 0
#> 5 native factor 2 463 0
#> 6 tenure factor 2 463 0
#> 7 Traumdozent logical 2 463 0
#> distribution
#> 1 no (86.2%), yes (13.8%)
#> 2 male (57.9%), female (42.1%)
#> 3 more (94.2%), single (5.8%)
#> 4 upper (66.1%), lower (33.9%)
#> 5 yes (94%), no (6%)
#> 6 yes (78%), no (22%)
#> 7 FALSE (85.5%), TRUE (14.5%)
#>
#> quantitative variables:
#> name class min Q1 median Q3
#> 1 X integer 1.000000 116.5000000 232.0000000 347.5000000
#> 2 age integer 29.000000 42.0000000 48.0000000 57.0000000
#> 3 beauty numeric -1.450494 -0.6562689 -0.0680143 0.5456024
#> 4 eval numeric 2.100000 3.6000000 4.0000000 4.4000000
#> 5 students integer 5.000000 15.0000000 23.0000000 40.0000000
#> 6 allstudents integer 8.000000 19.0000000 29.0000000 60.0000000
#> 7 prof integer 1.000000 20.0000000 44.0000000 70.5000000
#> max mean sd n missing
#> 1 463.000000 2.320000e+02 133.8008470 463 0
#> 2 73.000000 4.836501e+01 9.8027420 463 0
#> 3 1.970023 6.263499e-08 0.7886477 463 0
#> 4 5.000000 3.998272e+00 0.5548656 463 0
#> 5 380.000000 3.662419e+01 45.0184813 463 0
#> 6 581.000000 5.517711e+01 75.0727998 463 0
#> 7 94.000000 4.543413e+01 27.5089022 463 0
💡 mit help(Befehl) bekommt man Hilfe zu einem Befehl oder einem sonstigen Objekt (z.B. Datensatz).
Numerische Variablen mit favstats untersuchen
Ein einfacher, um Deskriptivstatistik für eine numerische Variable auf einen Abwasch zu erledigen ist der Befehl favstats aus dem Paket mosaic (vorher laden nicht vergessen):
favstats(TeachingRatings$eval)
#> min Q1 median Q3 max mean sd n missing
#> 2.1 3.6 4 4.4 5 3.998272 0.5548656 463 0
Der Befehl favstats lässt auch Subgruppenanalysen zu, z.B. um Männer und Frauen zu vergleichen:
favstats(eval ~ gender, data = TeachingRatings)
#> gender min Q1 median Q3 max mean sd n missing
#> 1 female 2.3 3.6 3.90 4.3 4.9 3.901026 0.5388026 195 0
#> 2 male 2.1 3.7 4.15 4.5 5.0 4.069030 0.5566518 268 0
Dabei ist mpg die Variable, die sie vergleichen wollen (Spritverbrauch); cyl die Gruppierungsvariable (Anzahl der Zylinder). Gruppierungsvariable bedeutet hier, dass den Spritverbrauch zwischen 4,6 und 8-Zylindern vergleichen wollen.
favstatsist sehr praktisch, weil Sie mit einem Befehl sehr viele Informationen bekommen, sogar Subgruppenanalysen sind möglich. Es lohnt sich für Sie, sich diesen Befehl gut zu merken.
💻 AUFGABE:
- Was sind wichtige Lagemaße für
beauty`? - Was sind wichtige Streuungsmaße für
eval? - Welches Skalenniveau hat
minority? Für den Fall, dassminoritynicht metrisch ist (also kategorial), macht es dann Sinn, Mittelwert oder SD zu berechnen?
Typische Deskriptive Statistiken
Die üblichen Verdächtigen der deskriptiven Statistiken lassen sich leiht aus Ihrem Versteck hervorlocken:
mean(eval~gender, data = TeachingRatings)
#> female male
#> 3.901026 4.069030
median(eval~gender, data = TeachingRatings)
#> female male
#> 3.90 4.15
sd(eval~gender, data = TeachingRatings)
#> female male
#> 0.5388026 0.5566518
var(eval~gender, data = TeachingRatings)
#> female male
#> 0.2903082 0.3098612
IQR(eval~gender, data = TeachingRatings)
#> female male
#> 0.7 0.8
diffmean(eval~gender, data = TeachingRatings)
#> diffmean
#> 0.1680042
min(eval~gender, data = TeachingRatings)
#> female male
#> 2.3 2.1
max(eval~gender, data = TeachingRatings)
#> female male
#> 4.9 5.0
⚠️ Alle diese Befehle sind etwas … nervös. Fehlt in den entsprechenden untersuchten Tabellen nur ein Wert, so legen diese Befehle die Arbeit nieder. Die Begründung lautet, Sie sollen auf das Problem hingewiesen werden. Über diese Logik kann man streiten; möchten Sie die Befehle zum Arbeiten bringen, auch wenn einige Daten fehlen sollten, dann fügen Sie diesen Parameter hinzu: na.rm = TRUE.
Sinngemäß übersetzt: “Hey R, wenn Du NAs triffst (fehlende Werte), dann ‘remove’ (ignoriere) diese. Ja, genauso (TRUE) ist es!”
mean(eval~gender, data = TeachingRatings, na.rm = TRUE)
#> female male
#> 3.901026 4.069030
Korrelationen
Sagen wir, Sie möchten von diesen zwei Variablen hp und mpg die Korrelation berechnen:
cor(eval ~ beauty, data = TeachingRatings)
Falls Sie viele Variablen auf ihre Korrelation untersuchen wollen, können Sie es so auf einen Abwasch tun:
TR2 <- dplyr::select(TeachingRatings, eval, beauty, age)
cor(TR2)
#> eval beauty age
#> eval 1.00000000 0.1890391 -0.05169619
#> beauty 0.18903909 1.0000000 -0.29789253
#> age -0.05169619 -0.2978925 1.00000000
💡 Manchmal gibt’s zwei Häuser, in denen “Herr Maier” wohnt. Um klar zu machen, welchen Maier Sie meinen, empfiehlt es sich, die Adresse mitanzugeben. In R ist es analog: Manchmal gibt es zwei Pakete, in denen ein Befehl mit gleichem Namen (z.B. select) wohnt. Mit dem Operator :: gibt man an, aus welchem Paket man den Befehl ziehen möchte.
Korrelationsplot
Mit Hilfe des Zusatzpakets corrplot lassen sich Korrelationen schön visualisieren.
#Zusatzpaket laden
library(corrplot)
corrplot(cor(TR2))
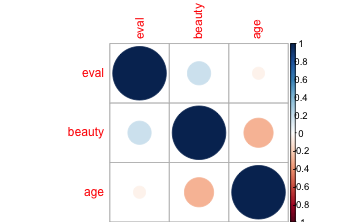
Je intensiver die Farbe, desto höher die Korrelation. Hier gibt es unzählige Einstellmöglichkeiten, siehe ?corrplot bzw. für Beispiele:
vignette("corrplot-intro")
Noch einfacher, aber nicht so schön geht es mit dem Paket corrgram. Hier müssen nicht extra die metrischen Variablen ausgewählt werden. Er nimmt nur alle metrischen Variablen im Datensatz mit.
library(corrgram)
corrgram(TR2)
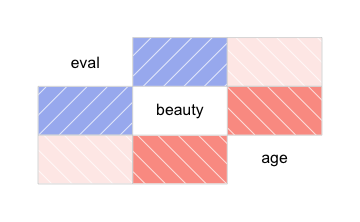
Am schönsten, meiner Meinung nach, sieht es mit dem Paket GGally aus:
library(GGally)
ggcorr(TR2)
ggpairs(TR2)
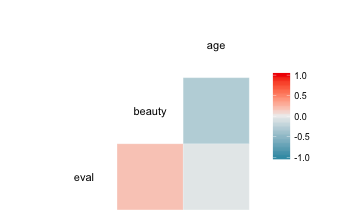
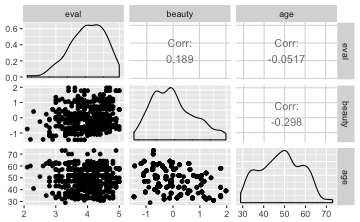
Nominale Variablen
Eine Häufigkeitstabelle für eine nicht-metrische Variable lässt über den Befehl tally erstellen.
Mit dem Befehl summary(meine_tabelle) bekommt man schon eine brauchbare Übersicht für nominale (kategoriale) Variablen. Man kann aber auch den Befehl tally verwenden, um sich Häufigkeit auszählen zu lassen:
tally(~gender, data = TeachingRatings)
#> gender
#> female male
#> 195 268
Ach ja, der inspecter sagt das ja auch:
inspect(TeachingRatings)
#>
#> categorical variables:
#> name class levels n missing
#> 1 minority factor 2 463 0
#> 2 gender factor 2 463 0
#> 3 credits factor 2 463 0
#> 4 division factor 2 463 0
#> 5 native factor 2 463 0
#> 6 tenure factor 2 463 0
#> 7 Traumdozent logical 2 463 0
#> distribution
#> 1 no (86.2%), yes (13.8%)
#> 2 male (57.9%), female (42.1%)
#> 3 more (94.2%), single (5.8%)
#> 4 upper (66.1%), lower (33.9%)
#> 5 yes (94%), no (6%)
#> 6 yes (78%), no (22%)
#> 7 FALSE (85.5%), TRUE (14.5%)
#>
#> quantitative variables:
#> name class min Q1 median Q3
#> 1 X integer 1.000000 116.5000000 232.0000000 347.5000000
#> 2 age integer 29.000000 42.0000000 48.0000000 57.0000000
#> 3 beauty numeric -1.450494 -0.6562689 -0.0680143 0.5456024
#> 4 eval numeric 2.100000 3.6000000 4.0000000 4.4000000
#> 5 students integer 5.000000 15.0000000 23.0000000 40.0000000
#> 6 allstudents integer 8.000000 19.0000000 29.0000000 60.0000000
#> 7 prof integer 1.000000 20.0000000 44.0000000 70.5000000
#> max mean sd n missing
#> 1 463.000000 2.320000e+02 133.8008470 463 0
#> 2 73.000000 4.836501e+01 9.8027420 463 0
#> 3 1.970023 6.263499e-08 0.7886477 463 0
#> 4 5.000000 3.998272e+00 0.5548656 463 0
#> 5 380.000000 3.662419e+01 45.0184813 463 0
#> 6 581.000000 5.517711e+01 75.0727998 463 0
#> 7 94.000000 4.543413e+01 27.5089022 463 0
Allerdings kann tally auch über mehrere Variablen auszählen:
tally(tenure~gender, data = TeachingRatings)
#> gender
#> tenure female male
#> no 50 52
#> yes 145 216
Zeilenmittelwerte bilden
Bei Umfragen kommt es häufig vor, dass man Zeilenmittelwerte bildet. Wieso? Man möchte z.B. in einer Mitarbeiterbefragung den “Engagementwert” jedes Beschäftigten wissen (klingt einfach gut). Dazu addiert man die Werte jedes passenden Items auf. Diese Summe teilen Sie durch die Anzahl der Spalten
💡 Zeilenmittelwerte bilden Sie am einfachsten in Excel.
In R können Sie Zeilen einfach mit dem + Zeichen addieren:
meine_tabelle$zeilenmittelwert <- (meine_tabelle$item1 + meine Tabelle$item2) / 2
Zeilen filtern
Ist man daran interessiert, nur einen Teil der Fälle (=Zeilen) auszuwerten, so hilft der Befehl filter weiter; filter wird über das Paket tidyverse geladen.
filter(TeachingRatings, gender == "male") -> dozi_maenner
💻 AUFGABE:
- Erstellen Sie eine Tabelle mit festangestellten Dozenten !
- Erstellen Sie eine Tabelle nur mit gut aussehenden Dozenten (der genaue Wert bleibt Ihnen überlassen).
Spalten auswählen
Manchmal hat meine “breite” Tabelle, also viele Spalten. Da hilft Abspecken, um die Sachlage übersichtlicher zu machen. Sprich: Nur ein paar wichtige Spalten auswählen, die anderen unter den Tisch fallen lassen.
Das kann man mit dem Befehl select (engl. auswählen) erreichen, der über das Paket tidyverse geladen wird:
select(TeachingRatings, eval, beauty) -> TR2
Der Befehl kann noch ein paar Tricks, die man z.B. hier nachlesen kann.
💻 AUFGABE:
- Erstellen Sie eine Tabelle nur mit
genderundtenure. Dann wenden Sietallydarauf an. - Wenden Sie dann die Befehle
rowSumsundrowMeansauf eine andere von Ihnen erstellten “Mini-Tabelle” an. Speichern Sie das Ergebnis vonrowSumsals neue Spalte vonTeachingRatings.
Spalten einer Tabelle sortieren
Bestimmt haben Sie schon mal in Excel eine Spalte sortiert, z.B. so, dass die großen Eurowerte ganz oben standen. In R kann man das mit dem Befehl arrange (via tidyverse) erreichen:
arrange(TeachingRatings, -eval) %>% head
Der Befehl %>% head bedeutet nur “UND DANN (das ist das %>%) zeige den Kopf (den Beginn) von dem, was Du gerade gemacht (sortiert) hast”.
💻 AUFGABE:
- Sortieren Sie
TeachingRatingsnach Schönheit! - Sortieren Sie
TeachingRatingsnach Bewertungsergebnis! Sortieren SieTeachingRatingsgleichzeitig nach Schönheit und Bewertungsergebnis! (Tipp:arrange(tabelle, spalte1, spalte2)).
Schritt 3: Visualisieren
Ein Bild sagt bekanntlich mehr als 1000 Worte. Betrachten Sie dazu “Anscombes Quartett”:
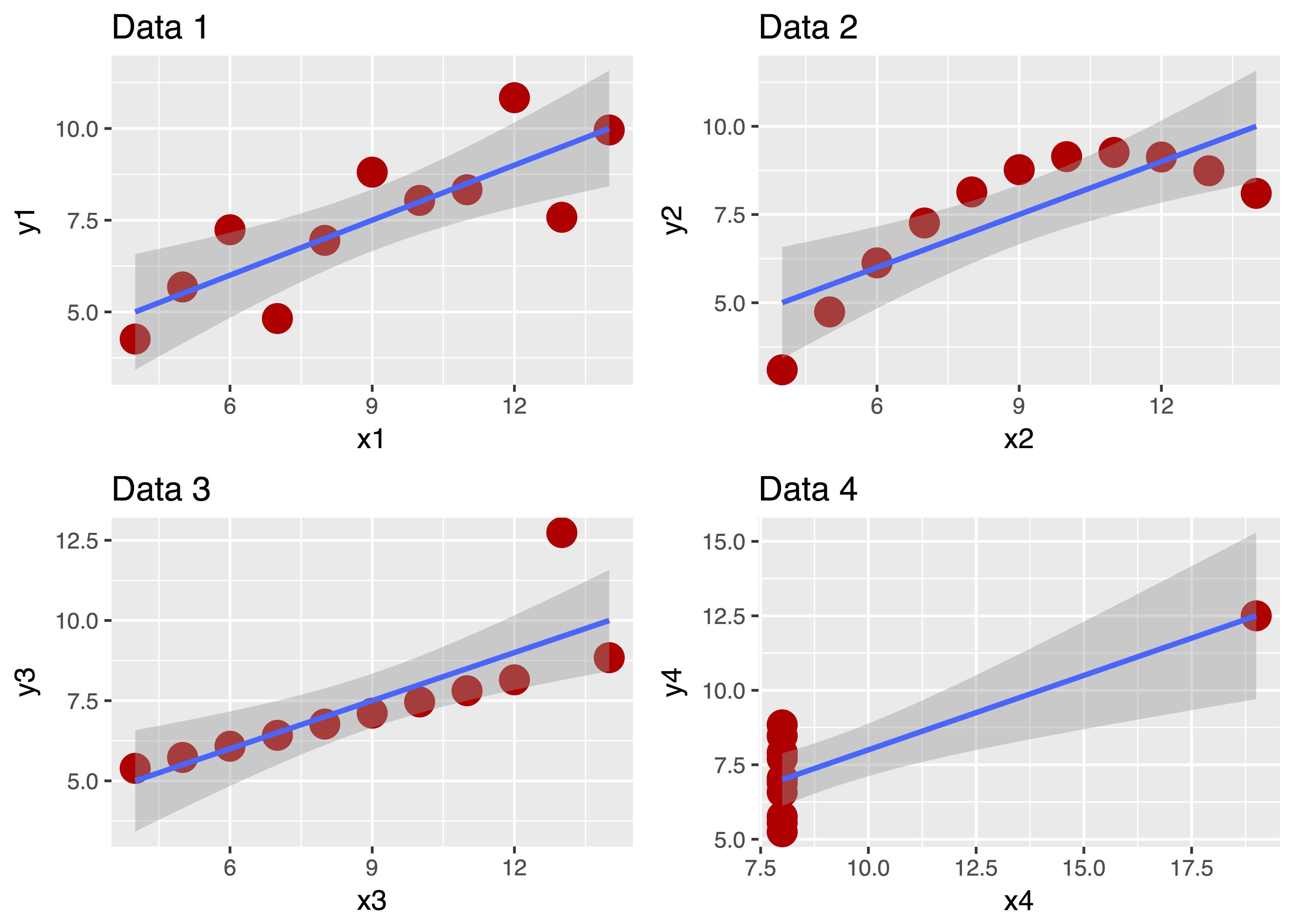
Diese vier Datensätze sehen ganz unterschiedlich aus, nicht wahr? Aber ihre zentralen deskriptiven Statistiken sind praktisch gleich! Ohne Diagramm wäre uns diese Unterschiedlichkeit nicht (so leicht) aufgefallen!
Zur Visualisierung empfehle ich das R-Paket ggforumla. Hinter den Kulissen wir dem verbreiteten Visualiserungspaket ggplot2 die Denkweise von mosaic eingeimpft. Der Hauptbefehl lautet gf_XXX, wobei XXX für eine bestimmte Art (Geom) von Diagramm steht, also z.B. ein Histogramm oder ein Boxplot.
Syntax von gf_XXX
Die normale Denkweise von mosaic wird verwendet:
gf_diagrammtyp(Y_Achse ~ X_Achse, sonstiges, data = meine_daten).
gf_ steht für ggplot und formula.
Darüber hinaus verkraftet der Befehl noch viele andere Schnörkel, die wir uns hier sparen. Interessierte können googeln… Es ist ein sehr mächtiger Befehl, der sehr ansprechende Diagramme erzeugen kann.
Probieren wir’s!
data(mtcars)
gf_point(eval ~ gender, data = TeachingRatings)
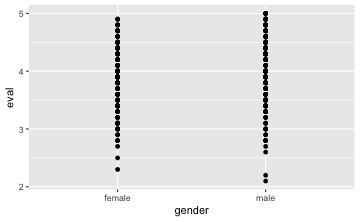
Easy, oder?
Ein anderes Geom:
gf_boxplot(eval ~ gender, data = TeachingRatings)
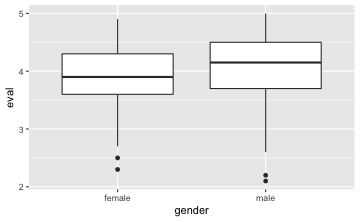
⚠️ Beachten Sie, dass nur dann mehrere Boxplots gezeichnet werden, wenn auf der X-Achse eine nominal skalierte Variable steht.
Oder mal nur eine Variable (ihre Verteilung) malen:
gf_histogram(~eval, data = TeachingRatings)
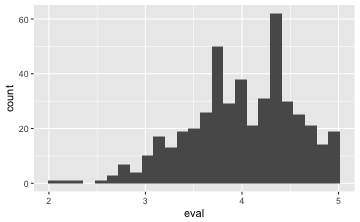
💡 Geben wir keine Y-Variable an, nimmt R eigenständig die Häufigkeit pro X-Wert!
Jittern
Probieren Sie mal diesen Befehl:
gf_point(eval ~ gender, data = TeachingRatings)
Was nicht so schön bei diesem Diagramm ist, ist, dass viele Punkte sich gegenseitig überdecken. Dieses Überdecken bezeichnet man auch als “Overplotting” (hört sich cooler an). Besser wäre es, wenn sich die Punkte nicht überdecken würden, dann würde man besser erkennen, wie viele Punkte wo liegen. Eine einfache Lösung bestünde darin, das Bild etwas zu “schütteln” oder zu “wackeln”, so dass die Punkte etwas verwackelt würden und damit nebeneinander zu liegen kämen. Das kann mit man mit dem Geom jitter (eng. für wackeln) erreichen:
gf_jitter(eval ~ gender, data = TeachingRatings)
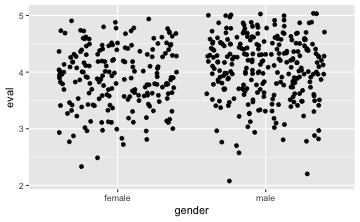
Möchte man die Punkte etwas enger haben, so kann man den Parameter width hinzufügen:
gf_jitter(eval ~ gender, data = TeachingRatings, width = .1)
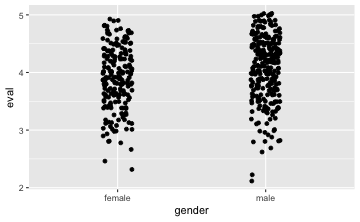
💡 Die Reihenfolge der Parameter in einem R-Befehl ist egal, solange man die Parameter benennt (width, data,…).
💻 AUFGABE:
- Tauschen Sie mal “histogram” mit “density”!
- Erstellen Sie ein Histogramm für
beauty! - Erstellen Sie Boxplots für
beauty, vergleichen Sie dabei Männer und Frauen (Tipp:gendersteht auf der X-Achse). - Erstellen Sie Boxplots für
eval, vergleichen Sie dabei die überdurchschnittlich schöne mit unterdurchschittlichen schönen.
Plot, um Mittelwerte darzustellen
Möchte man nur zwei Mittelwerte darstellen, ist ein Diagramm überflüssig, streng genommen. Schöner ist es, mehr Informationen darzustellen, also z.B. die Rohdaten. Schauen wir uns ein Beispiel aus dem Datensatz tips an:
gf_point(eval ~ gender,
data = TeachingRatings,
stat = "summary",
color = "red",
size = 5)
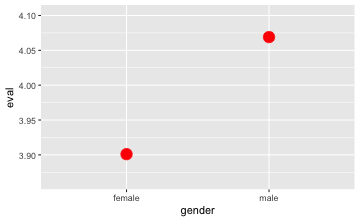
Überprüfen wir mal, ob die Punkte beim Mittelwert liegen:
mean(eval ~ gender, data = TeachingRatings)
#> female male
#> 3.901026 4.069030
😄.
Am besten, wir kombinieren die Rohdaten mit den Mittelerten in einem Plot:
gf_point(eval ~ gender,
data = TeachingRatings) %>%
gf_point(eval ~ gender,
data = TeachingRatings,
stat = "summary",
color = "red", size = 5)
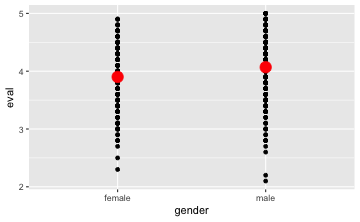
Wir können auch mehrere Gruppen in “Teil-Bildchen” vergleichen, dazu nehmen wir den Operator |; das kann man sich gut merken, wenn man sich vorstellt, dieser vertikale Strich grenzt das linke vom rechten Bild ab:
gf_point(eval ~ gender | minority,
data = TeachingRatings,
stat = "summary",
color = "red", size = 5)
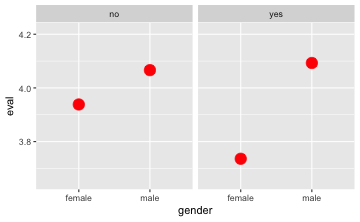
Wann welches Diagramm?
Ein kurze Übersicht, wann sich welches Diagramm anbietet:
- Mittelwerte vergleichen – Mittelwerte (plus Rohdaten) pro Gruppe darstellen
- Mediane vergleiche – Boxplot
- Verteilung verschiedener Gruppen darstellen – Boxplot (evtl. plus Mittelwert)
- Verteilung einer Gruppe – Dichtediagramm und/oder Histogramm bzw. Balkendiagramm
- Zusammenhang zweier Variablen – Streudiagramm
- Zusammenhänge nominaler Variablen (Häufigkeiten) – Fliesendiagramm
Zusammenhänge nominaler Variablen visualisieren
Gibt es bei den Dozenten aus ethnischen Minderheiten mehr Männer als Frauen im Vergleich zu Nicht-Minderheiten?
Erstmal die Häufigkeiten anschauen:
tally(minority ~ gender, data = TeachingRatings)
#> gender
#> minority female male
#> no 159 240
#> yes 36 28
tally(gender ~ minority, data = TeachingRatings, format = "percent")
#> minority
#> gender no yes
#> female 39.84962 56.25000
#> male 60.15038 43.75000
Dann malen; zuerst schauen wir uns die Häufigkeiten pro Variable an, dann die “gemeinsamen” Häufigkeiten:
gf_bar(~ minority, data = TeachingRatings)
gf_bar(~ gender, data = TeachingRatings)
gf_bar(~ gender, data = TeachingRatings, fill = ~minority, position = "fill")
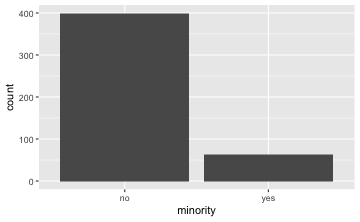
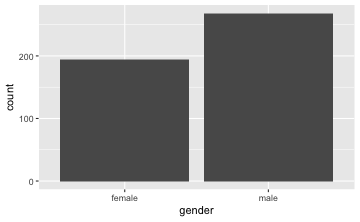
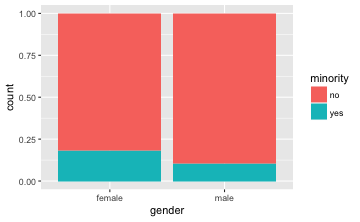
Die “Füllstände” von Minderheiten (in Türkis) bei Frauen und Männer sind unterschiedlich, wie man in der Grafik sieht. Folglich gehen wir davon aus, dass es einen Zusammenhang gibt.
Die Pfeife schlägt zu
Was bedeutet das komische Symbol %>%, welches die beiden Befehle offenbar verkettet? Man nennt es “DIE PFEIFE” (Großbuchstaben machen es erst richtig bedeutsam). Und auf Deutsch heißt dieser Befehl in etwa “UND DANN MACHE…”. Hier verketter die Pfeife die Beiden Diagrammbefehle, so dass beide Diagramme übereinander gezeichent werden - ähnlich wie eine Klarsichtfolie, die über ein Bild gelegt wird.
Der Parameter stat = summary führt dazu, dass als Punkte nicht die Rohdaten, sondern eben eine Zusammenfassung (engl. summary) dargestellt wird. In der Voreinstellung ist das der Mittelwert.
Weitere Geome
Hier finden Sie einen Überblick zu Geomen von ggplot, z.B.:
- Boxplot
gf_boxplot - Punkte
gf_point - Linien
gf_line - Histogramm
gf_histogram - …
🔖 Lesen Sie hier weiter, um Ihr Wissen zu vertiefen zu diesem Thema: Vertiefung zur Datenvisualisierung
Schritt 4: Modellieren
Modellieren hört sich kompliziert an. Für uns hier heißt es vor allem ein (inferenz-)statistisches Verfahren wie die Regression anzuwenden.
Der p-Wert
Ach ja, der p-Wert. Generationen von DozentenStudierenden haben sich wegen ihm oder ob ihm die Haare gerauft. Was war noch mal die Definition des p-Werts? Oder einfacher vielleicht, was will uns der p-Wert sagen?
Der p-Wert gibt an, wie plausibel die Daten unter der getesteten Hypothese sind (der H0).
Etwas präziser ausgedrückt:
Der p-Wert gibt die Häufigkeit an, ein Ergebnis, das mindestens so extrem ist, zu bekommen, wenn man den Versuch unendlich oft unter gleichen Bedingungen wiederholen würde.
Gut am p-Wert ist, dass er ein Entscheidungsmaß bietet. Die Gefahr am p-Wert ist, dass man ihn missversteht: Der p-Wert gibt nicht (Sie haben richtig gelesen: nicht) die Wahrscheinlichkeit an, mit der die H0 gilt. Er gibt auch nicht an, wie wahrscheinlich die H1 ist. Er gibt auch nicht an, ob das Ergebnis praktisch bedeutsam ist.
🔖 Lesen Sie hier weiter, um Ihr Wissen zu vertiefen zu diesem Thema: Vertiefung zum p-Wert.
Wann welchen Test?
Es gibt in vielen Lehrbüchern Übersichten zur Frage, wann man welchen Test rechnen soll. Googeln hilft hier auch weiter. Eine Übersicht findet man hier oder hier.
Wie heißt der jeweilige R-Befehl?
Wenn man diese Befehle nicht häufig verwendet, ist es schwierig, sie auswendig zu wissen. Googeln Sie. Eine gute Übersicht findet sich hier: http://r-statistics.co/Statistical-Tests-in-R.html.
Die Regression als Schweizer Taschenmesser
💡 Das Schweizer Taschenmesser 🔪 und den Modellierungsverfahren ist die Regressionsanalyse. Man kann sie für viele Zwecke einsetzen.
Weil die Regression so praktisch ist, hier ein Beispiel.
lm(eval ~ beauty, data = TeachingRatings)
#>
#> Call:
#> lm(formula = eval ~ beauty, data = TeachingRatings)
#>
#> Coefficients:
#> (Intercept) beauty
#> 3.998 0.133
lm heißt “lineares Modell” - weil man bei der (normalen) Regression eine Gerade in die Punktewolke der Daten legt, um den Trend zu abzuschätzen. Als nächstes gibt man die “Ziel-Variable” (Output) an, hier eval. Dann kommt ein Kringel ~ gefolgt von einer (mehr) Input-Variablen (Prädiktoren, UVs, hier beauty). Schließlich muss noch die Datentabelle erwähnt werden.
Das Ergebnis sagt uns, dass pro Stufe von Beauty die Variable eval um etwa .1 Punkte steigt. Also: Je schöner, desto “besser” sind die Dozenten auch. Immer im Schnitt, versteht sich. (Und wenn die Voraussetzungen erfüllt sind, aber darum kümmern wir uns jetzt nicht.)
Allgemein:
lm(output ~ input, data = meine_daten)
Easy, oder?
Man kann auch mehrere Prädiktoren anführen:
lm(eval ~ beauty + gender, data = TeachingRatings)
#>
#> Call:
#> lm(formula = eval ~ beauty + gender, data = TeachingRatings)
#>
#> Coefficients:
#> (Intercept) beauty gendermale
#> 3.8838 0.1486 0.1978
Möchte man ein ausführliches Ergebnis bekommen, so verlangt man von R eine Zusammenfassung (summary) des lm-Befehl, und zwar mit dem Befehl summary. Den Befehl summary kann man mit dem Und-danach-Befehl (%>%) an den lm-Befehl anschließen:
lm(eval ~ beauty + gender, data = TeachingRatings) %>% summary()
#>
#> Call:
#> lm(formula = eval ~ beauty + gender, data = TeachingRatings)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.87196 -0.36913 0.03493 0.39919 1.03237
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.88377 0.03866 100.47 < 2e-16 ***
#> beauty 0.14859 0.03195 4.65 4.34e-06 ***
#> gendermale 0.19781 0.05098 3.88 0.00012 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5373 on 460 degrees of freedom
#> Multiple R-squared: 0.0663, Adjusted R-squared: 0.06224
#> F-statistic: 16.33 on 2 and 460 DF, p-value: 1.407e-07
Dazu werden die durch + getrennt. Pro Prädiktor wird die Steigung der Regressionsgeraden angegeben. Man kann auch nominale Prädiktoren reinfüttern. Das macht die Regression so praktisch.
In diesem Fall sehen wir, dass Schönheit einen positiven Koeffizienten aufweist, d.h. die Regressionsgerade steigt: Für jeden Punkt Schönheit steigt die (mittlere) Bewertung um etwa 0.15 Punkte. Für Geschlecht gilt, dass genderFemale (die Frauen) um etwa 0.20 schlechter (wegen dem Minuszeichen) in der Beurteilung eingeschätzt werden.
Interaktionseffekte (Moderatoranalysen)
Aber es könnte es nicht sein, dass Schönheit bei Männern wichtiger ist als bei Frauen? Das würde bedeuten, dass jedes bisschen (=jeder Punkt) Schönheit zu mehr Punkten in der Bewertung führt. Es ist also denkbar, dass die Steigung der Regressionsgeraden bei Männern steiler ist als bei Frauen.
Wenn die Geraden also unterschiedlich steil sind (nicht parallel, mit anderen Worten), so liegt ein Interaktionseffekt vor; ansonsten nicht.
Kann man nicht eine Regressionsgerade für Männer und eine für Frauen bekommen. Ja, das geht. Aber schauen wir uns vielleicht erstmal ein Bildchen dazu an, das macht die Sache klarer:
gf_point(eval ~ beauty,
data = TeachingRatings,
color = ~gender) %>%
gf_lm()
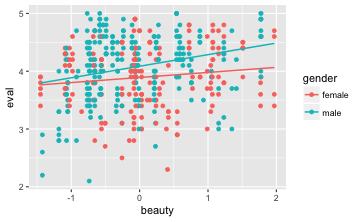
Mit gf_lm bekommen wir eine Anpassungslinie, die mit dem lm-Befehl (also der normalen Regression) im Hintergrund durch erstellt wird, und zwar pro Stufe von Geschlecht (d.h. eine für Frauen und eine für Männer).
Achtung, das ist wichtig: Wenn die beiden Geraden parallel sind, dann gibt es keinen Interaktionseffekt. Hier sind die Geraden augenscheinlich nicht parallel, also liegt ein Interaktionseffekt in den Daten vor.
Um den lm-Befehl zu überzeugen, einen Interaktionseffekt zwischen Geschlecht (gender) und Schönheit (beauty) zu berechnen, schreibt man in den lm-Befehl: + gender:beauty:
lm(eval ~ beauty + gender + + gender:beauty, data = TeachingRatings) %>% summary()
#>
#> Call:
#> lm(formula = eval ~ beauty + gender + +gender:beauty, data = TeachingRatings)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.83820 -0.37387 0.04551 0.39876 1.06764
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.89085 0.03878 100.337 < 2e-16 ***
#> beauty 0.08762 0.04706 1.862 0.063294 .
#> gendermale 0.19510 0.05089 3.834 0.000144 ***
#> beauty:gendermale 0.11266 0.06398 1.761 0.078910 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5361 on 459 degrees of freedom
#> Multiple R-squared: 0.07256, Adjusted R-squared: 0.0665
#> F-statistic: 11.97 on 3 and 459 DF, p-value: 1.47e-07
Das Ergebnis sagt uns, dass der Interaktionseffekt in den Daten zwar da ist (der Koeffizient ist ungleich 0), aber nicht groß genug, um statistische Signifikanz zu erreichen. Genauer gesagt, gibt dieser Koeffizient (~ -0.11) den Unterschied in der Steigung der beiden Geraden an. Für genderfemale ist die Steigung der Gerade um etwa -0.11 Punkte geringer.
Vorhersagen
Man kann die Regression nutzen, um Vorhersagen zu treffen. Sagen wir, der neue Dozent ist umwerfend hübsch (1.5); wie gut wird er wohl (im Schnitt) beurteilt werden?
Als Vorbereitung speichern wir unser Regressionsmodell in einer eigenen Variablen:
mein_lm <- lm(eval ~ beauty, data = TeachingRatings)
Dazu nimmt man am besten den Befehl predict, weil wir wollen eine Vorhersage treffen:
predict(mein_lm, data.frame(beauty = 1.5))
#> 1
#> 4.197774
Aha. Er würde im Schnitt mit 4.2 (auf einer Skala von 1 bis 5) bewertet werden. Tja, Schönheit zahlt sich offenbar vielfältig aus.
Modellgüte
Wie “gut” ist das Modell? Präziser gesagt: Wie genau sagt das Modell die Beurteilung der Dozenten vorher? Eine Antwort darauf gibt $R^2$: Je größer $R^2$, desto besser die Vorhersage. Noch genauer: Wenn man für jeden Dozenten den Mittelwert der Beurteilung als ihr oder seinen Wert vorhersagen würde: Wie groß wäre dann der mittlere Vorhersagefehler? Nennen wir das den Fehler der “Nullmodells” (weil keine/null Prädiktoren). Nun berechnen wir den mittleren Vorhersagefehler in unserem Modell. Dann setzen wir beide Werte in ein Verhältnis: voila, hier steht $R^2$ vor Ihnen.
Eine zweite Möglichkeit bestünde darin, nur den mittleren Vorhersagefehler unseres Modells zu berichten, man spricht dann auch vom Mean Squared Error (MSE) oder dessen Wurzel Root Mean Squeared Error (RMSE). Hier können Sie dazu mehr erfahren. Wir gehen in diesem Kurs aber nicht weiter darauf ein.
Häufige Verfahren der Inferenzstatistik
Chi-Quadarat-Test
Der $\chi^{2}$-Test (sprich: Chi-Quadrat-Test) wird verwendet, um auf Unabhängigkeit zweier Mermale bzw. auf Homogenität der (Häufigkeits-)Verteilungen zweier kategorieller, i.d.R. nominal skalierter Merkmale zu prüfen. Die zugehörige Nullhypothese lautet $H_{0}:$ Die beiden Merkmale sind unabhängig.
Beispiel
Es ist zu prüfen: $H_{0}:$ Das Geschlecht ist unabhängig vom Einstellungsverhältnis}
xchisq.test(tally(gender ~ tenure, data = TeachingRatings))
#>
#> Pearson's Chi-squared test with Yates' continuity correction
#>
#> data: x
#> X-squared = 2.2068, df = 1, p-value = 0.1374
#>
#> 50 145
#> ( 42.96) (152.04)
#> [1.00] [0.28]
#> < 1.07> <-0.57>
#>
#> 52 216
#> ( 59.04) (208.96)
#> [0.72] [0.20]
#> <-0.92> < 0.49>
#>
#> key:
#> observed
#> (expected)
#> [contribution to X-squared]
#> <Pearson residual>
Zusammenhangsmaße wie den Kontingenzkoeffizienten oder Cramérs V erhält man mit nachfolgendem Befehl (das Paket vcd muss aktiviert sein):
library(vcd)
assocstats(tally(gender ~ tenure, data = TeachingRatings))
#> X^2 df P(> X^2)
#> Likelihood Ratio 2.5368 1 0.11122
#> Pearson 2.5571 1 0.10980
#>
#> Phi-Coefficient : 0.074
#> Contingency Coeff.: 0.074
#> Cramer's V : 0.074
Hat man zwei Variablen mit zwei Stufen, dann ist vielleicht einfachste Form, um ein Effektstärkemaß bzw. ein Zusammenhangsmaß zu bekommen, die folgende:
tally(tenure ~ gender, data = TeachingRatings, format = "percent")
#> gender
#> tenure female male
#> no 25.64103 19.40299
#> yes 74.35897 80.59701
Bei den Männern haben ca. 81% eine Festanstellung, bei den Frauen ca. 74%; das sind ca. 7% Unterschied. Diese 7% entspricht dem Phi-Koeffizient.
Noch ein Bildchen dazu:
gf_bar(~gender, fill = ~tenure, data = TeachingRatings) %>%
gf_labs(title = "Zusammenhangsmaße für nominal skalierte Variablen",
x = "Geschlecht",
y = "Anzahl")
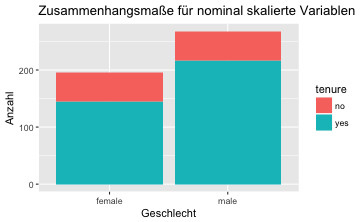
Oder noch schöner mit “gleich hohen” Balken, was man durch den Parameter position = "fill" erreicht:
gf_bar(~gender, fill = ~tenure,
data = TeachingRatings,
position = "fill") %>%
gf_labs(title = "Zusammenhangsmaße für nominal skalierte Variablen",
x = "Geschlecht",
y = "Anzahl")
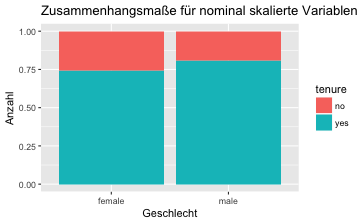
💻 AUFGABE:
Testen Sie die Nullhypothese $H_{0}:$ In den Geschlechtern gibt es gleich viele Individuen aus Minderheiten und bestimmen Sie die Stärke des Zusammenhangs mit dem Kontingenzkoeffizienten.
t-Test
Der t-Test wird verwendet, um Mittelwerte metrisch skalierter Merkmale zu prüfen. Dabei kann entweder der Mittelwert einer Messreihe mit einem vorgegebenen Wert verglichen werden (Beispiel-$H_{0}:$ Das Alter aller FOM-Studierenden ist im Durchschnitt 25 Jahre), oder die Mittelwerte zweier Messreihen werden miteinander verglichen (Beispiel-$H_{0}:$ Studentinnen und Studenten an der FOM sind im Durchschnitt gleich alt). Im Falle zweier Stichproben wird zwischen abhängigen und unabhängigen Stichproben unterschieden.
Zwei Stichproben sind unabhängig, wenn an verschiedenen Subjekten das gleiche Merkmal erhoben wird. Beispiel: Alter (gleiches Merkmal) bei Studentinnen und Studenten (verschiedene Subjekte).
Zwei Stichproben sind abhängig, wenn verschiedene Merkmale an den gleichen Subjekten erhoben werden. Beispiel: Blutdruck vor und nach einer Behandlung (verschiedene Merkmale) an einer Gruppe von Patienten (gleiche Subjekte).
Ein t-Test kann mit einseitiger und zweiseitiger Nullhypothese durchgeführt werden. Bei einer zweiseitigen Nullhypothese wird auf Gleichheit getestet (Beispiel-$H_{0}: \mu=0$), die Nullhypothese wird bei starker Abweichung nach oben und unten verworfen. Bei einer einseitigen Nullhypothese wird auf kleinergleich oder größergleich getestet (Beispiel-$H_{0}: \mu \le 0$ oder $H_{0}: \mu \ge 0$), die Nullhypothese wird bei starker Abweichung nach oben oder unten verworfen.
Einstichproben-t-Test
Beispiel (Trinkgeld-Datensatz)
Es ist zu prüfen $H_{0}:$ Das mittlere Alter der Dozenten beträgt 40 Jahre ($H_{0}: \mu(age) = 40$). Zunächst sollte mit einer grafischen Darstellung und deskriptiven Statistiken begonnen werden.
gf_dens(~age, data = TeachingRatings)
gf_boxplot(age~"alle", data = TeachingRatings)
favstats(~age, data = TeachingRatings)
#> min Q1 median Q3 max mean sd n missing
#> 29 42 48 57 73 48.36501 9.802742 463 0
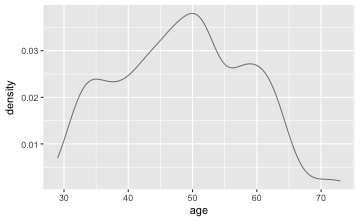
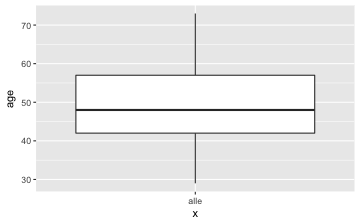
Nun kommt der t-Test; mit dem Parameter mu übergeben wir den zu testenden Wert laut H0:
t.test(~age, data = TeachingRatings, mu = 40)
#> ~age
#>
#> One Sample t-test
#>
#> data: age
#> t = 18.362, df = 462, p-value < 2.2e-16
#> alternative hypothesis: true mean is not equal to 40
#> 95 percent confidence interval:
#> 47.46976 49.26026
#> sample estimates:
#> mean of x
#> 48.36501
Im Output finden sich zunächst der t-Wert (durchschnittliches Trinkgeld dividiert durch den Standardfehler), die Freiheitsgrade (Stichprobenumfang weniger 1) und der p-Wert (Wahrscheinlichkeit für t unter der Nullhypothese). Weiter finden sich ein 95%-Konfidenzintervall für das Alter sowie das mittlere Trinkgeld.
Die Funktion t.test in der Voreinstellung einen zweiseitigen Test durch. Soll ein einseitiger Test durchgeführt werden, so muss dies durch einen zusätzlichen Übergabeparameter kenntlich gemacht werden. Um von diesem die genaue Syntax zu erfahren kann die R-Hilfe zur Funktion aufgerufen werden.
?t.test
Beispiel (Trinkgeld-Datensatz)
Es ist zu prüfen $H_{0}:$ Die Dozenten sind im Mittel gleich oder jünger als 40 Jahre ($H_{0}: \mu(age) \le 40$)
Laut der Beschreibung der Funktionshilfe erwartet R die Spezifikation der Alternativhypothese. Der zugehörige Übergabeparameter lautet alternative="less" und damit lautet der R-Befehl:
t.test(~age, data = TeachingRatings, alternative="less", mu = 40)
#> ~age
#>
#> One Sample t-test
#>
#> data: age
#> t = 18.362, df = 462, p-value = 1
#> alternative hypothesis: true mean is less than 40
#> 95 percent confidence interval:
#> -Inf 49.11587
#> sample estimates:
#> mean of x
#> 48.36501
💻 AUFGABE:
- Testen Sie die Nullhypothese $H_{0}:$ Es wird höchstens zwei Dollar Trinkgeld gegeben ($H_{0}: \mu(tip) \le 2$).
- Bestimmen Sie ein 90%-Konfidenzintervall für das durchschnittliche Trinkgeld.
Zweistichproben-t-Test
Beispiel (Trinkgeld-Datensatz)
Es ist zu prüfen $H_{0}:$ Männer und Frauen geben gleich viel Trinkgeld ($H_{0}: \mu(tip_{Männer})-\mu(tip_{Frauen})= 0$). Es empfiehlt sich, zunächst mit einer grafischen Darstellung sowie deskriptiven Statistiken zu starten. Als grafische Darstellungen bieten sich Boxplots und Mittelwertplots an.
gf_boxplot(eval ~ gender, data = TeachingRatings) # Boxplot
gf_point(eval ~ gender, data = TeachingRatings, stat = "summary") # Mittelwertplot
favstats(eval ~ gender, data = TeachingRatings) # deskriptive Statistiken
#> gender min Q1 median Q3 max mean sd n missing
#> 1 female 2.3 3.6 3.90 4.3 4.9 3.901026 0.5388026 195 0
#> 2 male 2.1 3.7 4.15 4.5 5.0 4.069030 0.5566518 268 0
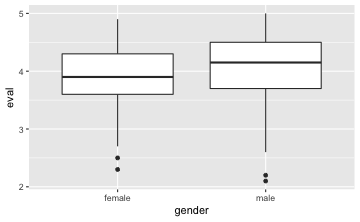
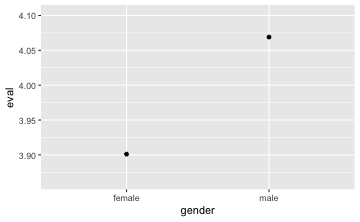
Nun kann der t-Test durchgeführt werden.
t.test(eval ~ gender, data = TeachingRatings)
#> eval ~ gender
#>
#> Welch Two Sample t-test
#>
#> data: eval by gender
#> t = -3.2667, df = 425.76, p-value = 0.001176
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.26909088 -0.06691754
#> sample estimates:
#> mean in group female mean in group male
#> 3.901026 4.069030
💻 AUFGABE:
Testen Sie die Nullhypothese $H_{0}:$ Das durchschnittliche Trinkgeld ist genauso hoch wie die durchschnittliche Restaurantrechnung ($H_{0}: \mu(tip) = \mu(totalbill)$).
Varianzanalyse
Sollen mehr als zwei Mittelwerte miteinander verglichen werden, dann muss anstelle eines t-Tests eine Varianzanalyse durchgeführt werden.
Mit einer Varianzanalyse ist es möglich, sowohl mehr als zwei Mittelwerte miteinander zu vergleichen (einfaktorielle Varianzanalyse) als auch mehr als eine Gruppierungsvariable (mehrfaktorielle Varianzanalyse) zu prüfen. Allgemeiner formuliert prüft die Varianzanalyse, ob ein metrisch skaliertes Merkmal (Zielgröße) von einer oder mehreren kategoriellen Gruppierungsvariablen (Einflussgrößen bzw. Faktoren) abhängt. Dabei lassen sich zum einen für jeden Faktor getrennt die Einflüsse untersuchen (Haupteffekte) als auch die Einflüsse kombinierter Effekte (Wechselwirkungen).
Einfaktorielle Varianzanalyse
Beispiel (Trinkgeld-Datensatz)
⚠️ Bitte nicht vergessen, die Trinkgeld-Daten zu laden.
tips <- read.csv("https://sebastiansauer.github.io/data/tips.csv")
Es ist zu prüfen $H_{0}:$ Die durchschnittlichen Restaurantrechnungen sind an den vier verschiedenen Tagen (Donnerstag bis Sonntag) gleich hoch. Zunächst werden Grafiken und deskriptive Statistiken erstellt.
gf_boxplot(total_bill~day, data = tips) %>%
gf_point(total_bill~day, data = tips, stat = "summary", color = "red") # Mittelwertplot
favstats(total_bill~day, data = tips) # deskriptive Statistiken
#> day min Q1 median Q3 max mean sd n missing
#> 1 Fri 5.75 12.0950 15.38 21.7500 40.17 17.15158 8.302660 19 0
#> 2 Sat 3.07 13.9050 18.24 24.7400 50.81 20.44138 9.480419 87 0
#> 3 Sun 7.25 14.9875 19.63 25.5975 48.17 21.41000 8.832122 76 0
#> 4 Thur 7.51 12.4425 16.20 20.1550 43.11 17.68274 7.886170 62 0
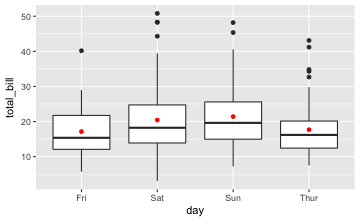
Dann folgt die Varianzanalyse:
anovamodel <- aov(total_bill~day, data = tips)
summary(anovamodel)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> day 3 644 214.65 2.767 0.0425 *
#> Residuals 240 18615 77.56
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Mehrfaktorielle Varianzanalyse
Bei mehrfaktoriellen Varianzanalysen können sowohl die Haupteffekte als auch die Wechselwirkungen zwischen den Haupteffekten untersucht werden.
Beispiel (Trinkgeld-Datensatz)
Folgende drei Hypothesen sind zu prüfen:
$H_{01}:$ Das Geschlecht des Rechnungsbezahlers hat keinen Einfluss auf die Rechnungshöhe.
$H_{02}:$ Das Rauchverhalten des Rechnungsbezahlers hat keinen Einfluss auf die Rechnungshöhe.
$H_{03}:$ Das gibt keine Wechselwirkung zwischen Geschlecht und Rauchverhalten des Rechnungsbezahlers.
anovamodel <- aov(total_bill~sex*smoker, data = tips)
summary(anovamodel)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> sex 1 404 404.2 5.209 0.0233 *
#> smoker 1 140 140.2 1.806 0.1802
#> sex:smoker 1 91 90.6 1.168 0.2810
#> Residuals 240 18623 77.6
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plot(allEffects(anovamodel))
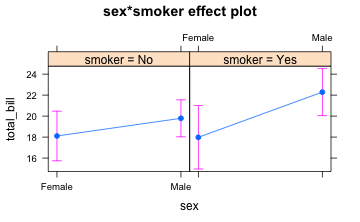
Ein Modell nur für die Haupteffekte funktioniert wie folgt:
anovamodel <- aov(total_bill~sex+smoker, data = tips)
summary(anovamodel)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> sex 1 404 404.2 5.206 0.0234 *
#> smoker 1 140 140.2 1.805 0.1804
#> Residuals 241 18714 77.7
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plot(allEffects(anovamodel))
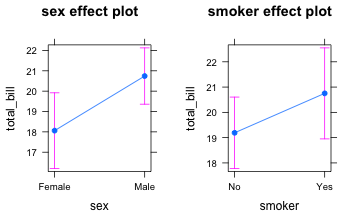
Es folgt das Modell nur für die Wechselwirkungen:
anovamodel <- aov(total_bill~sex:smoker, data = tips)
summary(anovamodel)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> sex:smoker 3 635 211.7 2.728 0.0447 *
#> Residuals 240 18623 77.6
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plot(allEffects(anovamodel))
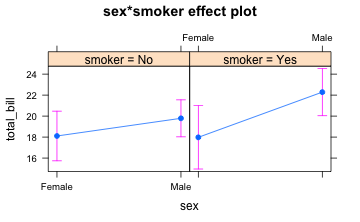
Das hätte man auch so visualisieren können:
gf_jitter(tip ~ sex, color = "grey80", data = tips, width = .1) %>%
gf_point(tip ~ sex, stat = "summary",
data = tips, size = 4, color = ~sex) %>%
gf_facet_wrap(~smoker) %>%
gf_line(tip ~ sex, stat = "summary",
group = ~smoker, data = tips, color = "grey20")
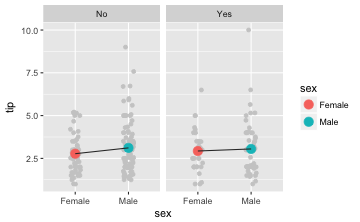
💻 AUFGABE:
Führen Sie eine zweifaktorielle Varianzanalyse für die Zielgröße tip mit den Faktoren time und smoker durch.
Korrelationsanalyse
Die Korrelationsanalyse wird verwendet, um den Zusammenhang von mindestens zwei metrischen oder ordinalen Merkmalen zu beschreiben. Für ordinale Merkmale wird die Spearman-Rangkorrelation verwendet. Da diese auf den Rängen der Ausprägungen basiert, ist sie robust gegen Ausreißer. Für metrische Merkmale wird die Pearson-Korrelation bestimmt, diese ist anfällig gegen Ausreißer. Hier empfiehlt sich zusätzlich die grafische Darstellung mit einem Streudiagramm.
Hinweis: Eine (positive oder negative) Korrelation zwischen zwei Merkmalen bedeutet nicht, dass es auch einen Kausalzusammenhang gibt. Das bekannteste Beispiel hierfür ist die sog. Theorie der Störche. So lässt sich zeigen, dass es eine positive Korrelation zwischen Geburtenraten und Storchpopulationen gibt. Ein Kausalzusammenhang darf bezweifelt werden…
Beispiel
Wie groß ist der (lineare) Zusammenhang von Beurteilung und Schönheit eines Dozenten?
Betrachten wir zuerst ein Streudiagramm, um einen “Einblick” in den Zusammenhang zu bekommen:
gf_point(eval ~ beauty, data = TeachingRatings)
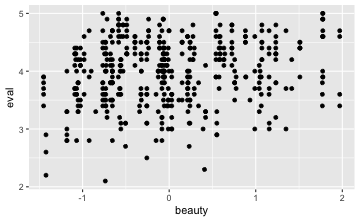
Wir können auch noch für jeden Schönheitswert den mittleren Beurteilungswert anzeigen in einer “Glättungslinien” (smoother):
gf_point(eval ~ beauty, data = TeachingRatings) %>% gf_smooth()
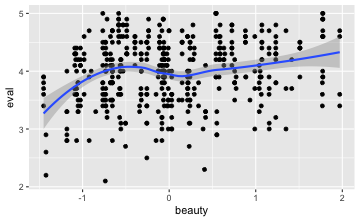
Die aufwärts gerichtete Punktwolke deutet auf eine positive Korrelation hin. Allerdings ist die Punktewolke recht “diffus”, was für eine schwache Korrelation sprichtg. Die Stärke der Korrelation ergibt sich wie folgt:
cor(eval ~ beauty, data = TeachingRatings) # Pearson-Korrelation
#> [1] 0.1890391
cor(eval ~ beauty, data = TeachingRatings, method="spearman") # Spearman-Korrelation
#> [1] 0.1640352
Schritt 5: Kommunizieren
Kommunizieren meint hier, dass Sie Ihre Ergebnisse anderen mitteilen - als Student heißt das häufig in Form einer Seminararbeit an den Dozenten.
Einige Hinweise:
- Die wesentlichen Ergebnisse kommen in den Hauptteil der Arbeit. Interessante Details in den Anhang.
- Der Mensch ist ein Augentier. Ihr Gutachter auch. Achten Sie auf optisch ansprechende Darstellung; schöne Diagramme helfen.
- Dozenten achten gerne auf formale Korrektheit. Das Gute ist, dass dies relativ einfach sicherzustellen ist, da auf starren Regeln basierend.
Tabellen und Diagramme
Daten kommunizieren heißt praktisch zumeist, Tabellen oder Diagramme zu erstellen. Meist gibt es dazu Richtlinien von Seiten irgendeiner (selbsternannten) Autorität wie Dozenten oder Fachgesellschaften. Zum Beispiel hat die APA ein umfangreiches Manual zum Thema Manuskriptgestaltung publiziert; die deutsche Fachgesellschaft der Psychologie entsprechend. Googeln Sie mal, wie in ihren Richtlinien Tabellen und Diagramme zu erstellen sind (oder fragen Sie Ihren Gutachter).
So sieht zum Beispiel eine schöne Tabelle aus:
| rowname | X | age | beauty | eval | students | allstudents | prof |
|---|---|---|---|---|---|---|---|
| X | NA | NA | NA | NA | NA | NA | NA |
| age | 0.09 | NA | NA | NA | NA | NA | NA |
| beauty | -0.02 | -0.30 | NA | NA | NA | NA | NA |
| eval | 0.07 | -0.05 | 0.19 | NA | NA | NA | NA |
| students | 0.01 | -0.03 | 0.13 | 0.04 | NA | NA | NA |
| allstudents | 0.01 | -0.01 | 0.10 | 0.00 | 0.97 | NA | NA |
| prof | 0.65 | 0.08 | 0.05 | 0.02 | 0.02 | 0.03 | NA |
Für Fortgeschrittene: RMarkdown
Wäre das nicht cool: Jegliches Formatieren wird automatisch übernommen und sogar so, das es schick aussieht? Außerdem wird Ihr R-Code und dessen Ergebnisse (Tabellen und Diagramme oder reine Zahlen) automatisch in Ihr Dokument übernommen. Keine Copy-Paste-Fehler mehr. Keine händisches Aktualisieren, weil Sie Daten oder die vorhergehende Analyse geändert haben. Hört sich gut an? Probieren Sie mal RMarkdown aus.
Versionshinweise
- Datum erstellt: 2017-09-24
- R Version: 3.4.0
mosaicVersion: 1.1.0dplyrVersion: 0.7.3