This repo analyzes the probability of finding a agreed time slot for a joint meeting between multiple colleague (“Doodle problem”). Different influence factors are analyzed, including the effect of different assumptions such as independence of colleagues. Monte Carlo methods are used.
Motivation
Have you ever tried to find a time slot for a meeting using a tool such as “Doodle”? If not, consider yourself lucky. Otherwise you will be well aware of the chagrin of finding a time slot that suits all of your colleagues.
Let’s call a time slot where all of your colleagues invited for the meeting have a free time slot a matching time slot, or a match for short. Here’s a sample image for a “doodle” in order to find a a match.
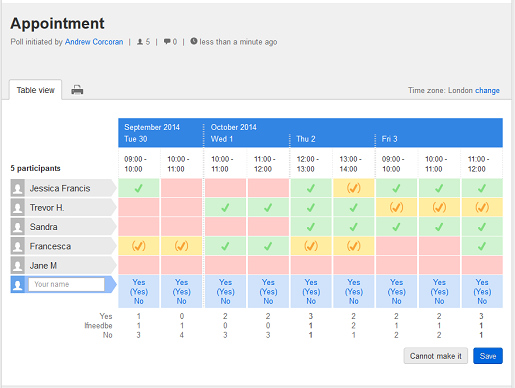
Some persons find that the best way to find a matching time slot is to offer a great number of time slots to your colleagues. Personally I find this approach difficult as I would have to keep track of and block a lot of time slots in my calendar. In addition, I feel it would be difficult to find a matching time slot as most colleagues will not take the hazzle and report many free time slots. Call me pessimistic, but I suspect that most colleagues will choose about 3 time slots, but not more, because it would be too difficult for them to keep their calendars in sync. (A sentiment I share.)
Now, let’s wonder, what ss the probability of finding at least one matching time slot when addressing n colleagues, providing each of them with o options, assuming each colleague will pick p options completely random.
In more stochastic parlance, this problem is a somewhat involved example of the collision problem.
Model
- A number of
n_colleaguescolleagues pick p options from a list of o possible options. - We are interested in the probability that all colleagues pick (at least) one time the same slot.
- There can be an arbitrary degree of (stochastic) dependency between and within the colleagues (parameter:
dep) - p is randomly drawn from a normal distribution with mean p and sd p_sd.
Parameters
In essence, the model is parametrized as follows:
-
n_colleagues: number of colleagues addressed -
p: mean value of picked time slots per colleagues -
o: number of time slots to choose from for each colleague -
dep: proportion of dependency between (and within) reviewers -
p_sd: sd of the number of picked options
In addition, the parameter r states the number of repetitions for drawing Monte Carlo samples.
Example
Three colleagues (n_colleagues=3) - A,B,C - pick exactly p=3 (p_sd=0) slots from o=10 options (with no dependency, ie. dep=0).
For example, colleague A picks options 1, 2, and 3.
| Colleague | Pick1 | Pick2 | Pick3 |
|---|---|---|---|
| A | 1 | 2 | 3 |
| B | 1 | 7 | 9 |
| C | 1 | 7 | 10 |
We have one match: All chose the option 1. (And to choose the option, but that’s not enough for a match, as not all persons chose this number.)