This YACSDA (Yet-another-case-study-on-data-analysis) in composed in German language. Some typical data analytical steps are introduced.
Wovon ist die Häufigkeit von Affären (Seitensprüngen) in Ehen abhängig? Diese Frage soll anhand des Datensates Affair untersucht werden.
Dieser Post stellt beispielhaft eine grundlegende Methoden der praktischen Datenanalyse im Rahmen einer kleinen Fallstudie (YACSDA) vor.
Quelle der Daten: http://statsmodels.sourceforge.net/0.5.0/datasets/generated/fair.html
Der Datensatz findet sich (in ähnlicher Form) auch im R-Paket COUNT (https://cran.r-project.org/web/packages/COUNT/index.html).
Laden wir als erstes den Datensatz in R. Wählen Sie zuerst das Verzeichnis als Arbeitsverzeichnis, in dem die Daten liegen. Dann laden Sie z.B. mit dem R-Commander (s. Skript) oder “per Hand” z.B. bei mir so:
Affair <- read.csv("~/Documents/Literatur/Methoden_Literatur/Datensaetze/Affair.csv")
Schauen wir mal, ob es funktioniert hat (“Datenmatrix betrachten”):
head(Affair)
#> affairs gender age yearsmarried children religiousness education
#> 1 0 male 37 10.00 no 3 18
#> 2 0 female 27 4.00 no 4 14
#> 3 0 female 32 15.00 yes 1 12
#> 4 0 male 57 15.00 yes 5 18
#> 5 0 male 22 0.75 no 2 17
#> 6 0 female 32 1.50 no 2 17
#> occupation rating
#> 1 7 4
#> 2 6 4
#> 3 1 4
#> 4 6 5
#> 5 6 3
#> 6 5 5
Ok scheint zu passen. Was jetzt?
Geben Sie zentrale deskriptive Statistiken an für Affärenhäufigkeit und Ehezufriedenheit!
# nicht robust:
mean(Affair$affairs, na.rm = T)
#> [1] 1.455907
sd(Affair$affairs, na.rm = T)
#> [1] 3.298758
# robust:
median(Affair$affair, na.rm = T)
#> [1] 0
IQR(Affair$affair, na.rm = T)
#> [1] 0
Es scheint, die meisten Leute haben keine Affären:
table(Affair$affairs)
#>
#> 0 1 2 3 7 12
#> 451 34 17 19 42 38
Man kann sich viele Statistiken mit dem Befehl describe aus psych ausgeben lassen, das ist etwas praktischer:
library(psych)
describe(Affair$affairs)
#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 601 1.46 3.3 0 0.55 0 0 12 12 2.34 4.19 0.13
describe(Affair$rating)
#> vars n mean sd median trimmed mad min max range skew kurtosis se
#> X1 1 601 3.93 1.1 4 4.07 1.48 1 5 4 -0.83 -0.22 0.04
Dazu muss das Paket psych natürlich vorher installiert sein. Beachten Sie, dass man ein Paket nur einmal installieren muss, aber jedes Mal, wen Sie R starten, auch starten muss (mit library).
install.packages("psych")
Visualisieren Sie zentrale Variablen!
Sicherlich sind Diagramme auch hilfreich. Dies geht wiederum mit dem R-Commander oder z.B. mit folgenden Befehlen:
library(ggplot2)
qplot(x = affairs, data = Affair)
qplot(x = rating, data = Affair)
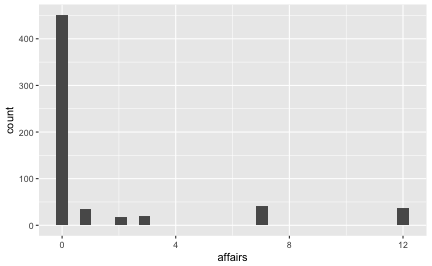
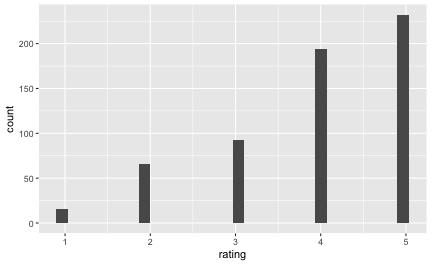
Die meisten Menschen (dieser Stichprobe) scheinen mit Ihrer Beziehung sehr zufrieden zu sein.
Wer ist zufriedener mit der Partnerschaft: Personen mit Kindern oder ohne?
Nehmen wir dazu mal ein paar dplyr-Befehle:
library(dplyr)
Affair %>%
group_by(children) %>%
summarise(rating_children = mean(rating, na.rm = T))
#> # A tibble: 2 × 2
#> children rating_children
#> <fctr> <dbl>
#> 1 no 4.274854
#> 2 yes 3.795349
Ah! Kinder sind also ein Risikofaktor für eine Partnerschaft! Gut, dass wir das geklärt haben.
Wie viele fehlende Werte gibt es? Was machen wir am besten damit?
Diesen Befehl könnten wir für jede Spalte auführen:
sum(is.na(Affair$affairs))
#> [1] 0
Oder lieber alle auf einmal:
Affair %>%
summarise_each(funs(sum(is.na(.))))
#> affairs gender age yearsmarried children religiousness education
#> 1 0 0 0 0 0 0 0
#> occupation rating
#> 1 0 0
Übrigens gibt es ein gutes Cheat Sheet für dplyr.
Ah, gut, keine fehlenden Werte. Das macht uns das Leben leichter.
Wer ist glücklicher: Männer oder Frauen?
Affair %>%
group_by(gender) %>%
summarise(rating_gender = mean(rating))
#> # A tibble: 2 × 2
#> gender rating_gender
#> <fctr> <dbl>
#> 1 female 3.939683
#> 2 male 3.923077
Praktisch kein Unterschied. Heißt das auch, es gibt keinen Unterschied in der Häufigkeit der Affären?
Affair %>%
group_by(gender) %>%
summarise(affairs_gender = mean(affairs))
#> # A tibble: 2 × 2
#> gender affairs_gender
#> <fctr> <dbl>
#> 1 female 1.419048
#> 2 male 1.496503
Scheint auch kein Unterschied zu sein…
Und zum Abschluss noch mal etwas genauer: Teilen wir mal nach Geschlecht und nach Kinderstatus auf, also in 4 Gruppen. Theoretisch dürfte es hier auch keine Unterschiede/Zusammenhänge geben. Zumindest fällt mir kein sinnvoller Grund ein; zumal die vorherige eindimensionale Analyse keine Unterschiede zu Tage gefördert hat.
Affair %>%
group_by(gender, children) %>%
summarise(affairs_mean = mean(affairs),
rating_mean = mean(rating))
#> Source: local data frame [4 x 4]
#> Groups: gender [?]
#>
#> gender children affairs_mean rating_mean
#> <fctr> <fctr> <dbl> <dbl>
#> 1 female no 0.8383838 4.404040
#> 2 female yes 1.6851852 3.726852
#> 3 male no 1.0138889 4.097222
#> 4 male yes 1.6588785 3.864486
Affair %>%
group_by(children, gender) %>%
summarise(affairs_mean = mean(affairs),
rating_mean = mean(rating))
#> Source: local data frame [4 x 4]
#> Groups: children [?]
#>
#> children gender affairs_mean rating_mean
#> <fctr> <fctr> <dbl> <dbl>
#> 1 no female 0.8383838 4.404040
#> 2 no male 1.0138889 4.097222
#> 3 yes female 1.6851852 3.726852
#> 4 yes male 1.6588785 3.864486
Berichten Sie eine relevante Effektstärke!
Hm, auch keine gewaltigen Unterschiede. Höchstens für die Zufriedenheit mit der Partnerschaft bei kinderlosen Personen scheinen sich Männer und Frauen etwas zu unterscheiden. Hier stellt sich die Frage nach der Größe des Effekts, z.B. anhand Cohen’s d. Dafür müssen wir noch die SD pro Gruppe wissen:
Affair %>%
group_by(children, gender) %>%
summarise(rating_mean = mean(rating),
rating_sd = sd(rating))
#> Source: local data frame [4 x 4]
#> Groups: children [?]
#>
#> children gender rating_mean rating_sd
#> <fctr> <fctr> <dbl> <dbl>
#> 1 no female 4.404040 0.9138302
#> 2 no male 4.097222 1.0636070
#> 3 yes female 3.726852 1.1829884
#> 4 yes male 3.864486 1.0460525
d <- (4.4 - 4.1)/(1)
Die Effektstärke beträgt etwa 0.3.
Berechnen und visualisieren Sie zentrale Korrelationen!
Affair %>%
select_if(is.numeric) %>%
cor -> cor_tab
cor_tab
#> affairs age yearsmarried religiousness
#> affairs 1.000000000 0.0952372 0.18684169 -0.14450135
#> age 0.095237204 1.0000000 0.77754585 0.19377693
#> yearsmarried 0.186841686 0.7775458 1.00000000 0.21826067
#> religiousness -0.144501345 0.1937769 0.21826067 1.00000000
#> education -0.002437441 0.1345960 0.04000272 -0.04257108
#> occupation 0.049611758 0.1664125 0.04459201 -0.03972232
#> rating -0.279512403 -0.1989999 -0.24311883 0.02429578
#> education occupation rating
#> affairs -0.002437441 0.04961176 -0.27951240
#> age 0.134596015 0.16641254 -0.19899990
#> yearsmarried 0.040002716 0.04459201 -0.24311883
#> religiousness -0.042571079 -0.03972232 0.02429578
#> education 1.000000000 0.53360524 0.10930347
#> occupation 0.533605242 1.00000000 0.01742227
#> rating 0.109303473 0.01742227 1.00000000
library(corrplot)
corrplot(cor_tab)
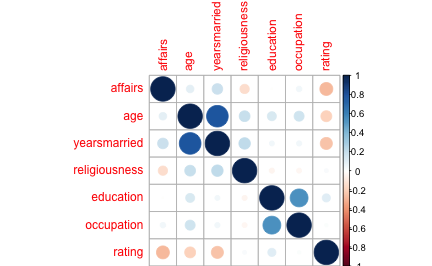
Wie groß ist der Einfluss (das Einflussgewicht) der Ehejahre bzw. Ehezufriedenheit auf die Anzahl der Affären?
Dazu sagen wir R: “Hey R, rechne mal ein lineares Modell”, also eine normale (lineare) Regression. Dazu können wir entweder das entsprechende Menü im R-Commander auswählen, oder folgende R-Befehle ausführen:
lm1 <- lm(affairs ~ yearsmarried, data = Affair)
summary(lm1) # Ergebnisse der Regression zeigen
#>
#> Call:
#> lm(formula = affairs ~ yearsmarried, data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.2106 -1.6575 -0.9937 -0.5974 11.3658
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.55122 0.23511 2.345 0.0194 *
#> yearsmarried 0.11063 0.02377 4.655 4e-06 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.243 on 599 degrees of freedom
#> Multiple R-squared: 0.03491, Adjusted R-squared: 0.0333
#> F-statistic: 21.67 on 1 and 599 DF, p-value: 3.996e-06
lm2 <- lm(affairs ~ rating, data = Affair)
summary(lm2)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.9063 -1.3989 -0.5631 -0.5631 11.4369
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.7421 0.4790 9.900 <2e-16 ***
#> rating -0.8358 0.1173 -7.125 3e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.17 on 599 degrees of freedom
#> Multiple R-squared: 0.07813, Adjusted R-squared: 0.07659
#> F-statistic: 50.76 on 1 and 599 DF, p-value: 3.002e-12
Also: yearsmarried und rating sind beide statistisch signifikante Prädiktoren für die Häufigkeit von Affären. Das adjustierte \(R^2\) ist allerdings in beiden Fällen nicht so groß.
Um wie viel erhöht sich die erklärte Varianz (R-Quadrat) von Affärenhäufigkeit wenn man den Prädiktor Ehezufriedenheit zum Prädiktor Ehejahre hinzufügt? (Wie) verändern sich die Einflussgewichte (b)?
lm3 <- lm(affairs ~ rating + yearsmarried, data = Affair)
lm4 <- lm(affairs ~ yearsmarried + rating, data = Affair)
summary(lm3)
#>
#> Call:
#> lm(formula = affairs ~ rating + yearsmarried, data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1474 -1.6495 -0.8365 -0.1616 11.8945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.76913 0.56715 6.646 6.80e-11 ***
#> rating -0.74395 0.12005 -6.197 1.07e-09 ***
#> yearsmarried 0.07481 0.02377 3.147 0.00173 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.147 on 598 degrees of freedom
#> Multiple R-squared: 0.09315, Adjusted R-squared: 0.09012
#> F-statistic: 30.71 on 2 and 598 DF, p-value: 2.01e-13
summary(lm4)
#>
#> Call:
#> lm(formula = affairs ~ yearsmarried + rating, data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1474 -1.6495 -0.8365 -0.1616 11.8945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.76913 0.56715 6.646 6.80e-11 ***
#> yearsmarried 0.07481 0.02377 3.147 0.00173 **
#> rating -0.74395 0.12005 -6.197 1.07e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.147 on 598 degrees of freedom
#> Multiple R-squared: 0.09315, Adjusted R-squared: 0.09012
#> F-statistic: 30.71 on 2 and 598 DF, p-value: 2.01e-13
Ok. Macht eigentlich die Reihenfolge der Prädiktoren in der Regression einen Unterschied? Der Vergleich von Modell 3 vs. Modell 4 beantwortet diese Frage.
Wir sehen, dass beim 1. Regressionsmodell das R^2 0.03 war; beim 2. Modell 0.08 und beim 3. Modell liegt R^2 bei 0.09. Die Differenz zwischen Modell 1 und 3 liegt bei (gerundet) 0.06; wenig.
Welche Prädiktoren würden Sie noch in die Regressionsanalyse aufnehmen?
Hm, diese Frage klingt nicht so, als ob der Dozent die Antwort selber wüsste… Naja, welche Variablen gibt es denn alles:
#> [1] "affairs" "gender" "age" "yearsmarried"
#> [5] "children" "religiousness" "education" "occupation"
#> [9] "rating"
Z.B. wäre doch interessant, ob Ehen mit Kinder mehr oder weniger Seitensprüngen aufweisen. Und ob die “Kinderfrage” die anderen Zusammenhänge/Einflussgewichte in der Regression verändert. Probieren wir es auch. Wir können wiederum im R-Comamnder ein Regressionsmodell anfordern oder es mit der Syntax probieren:
lm5 <- lm(affairs~ rating + yearsmarried + children, data = Affair)
summary(lm5)
#>
#> Call:
#> lm(formula = affairs ~ rating + yearsmarried + children, data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.3537 -1.7316 -0.8927 -0.1719 12.0162
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.85245 0.58808 6.551 1.24e-10 ***
#> rating -0.74861 0.12043 -6.216 9.57e-10 ***
#> yearsmarried 0.08332 0.02853 2.921 0.00362 **
#> childrenyes -0.18805 0.34817 -0.540 0.58932
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.148 on 597 degrees of freedom
#> Multiple R-squared: 0.09359, Adjusted R-squared: 0.08904
#> F-statistic: 20.55 on 3 and 597 DF, p-value: 1.107e-12
r2_lm5 <- summary(lm5)$r.squared
Das Regressionsgewicht von childrenyes ist negativ. Das bedeutet, dass Ehen mit Kindern weniger Affären verbuchen (aber geringe Zufriedenheit, wie wir oben gesehen haben! Hrks!). Allerdings ist der p-Wert nich signifikant, was wir als Zeichen der Unbedeutsamkeit dieses Prädiktors verstehen können. \(R^2\) lungert immer noch bei mickrigen 0.09 herum. Wir haben bisher kaum verstanden, wie es zu Affären kommt. Oder unsere Daten bergen diese Informationen einfach nicht.
Wir könnten auch einfach mal Prädiktoren, die wir haben, ins Feld schicken. Mal sehen, was dann passiert:
lm6 <- lm(affairs ~ ., data = Affair)
summary(lm6)
#>
#> Call:
#> lm(formula = affairs ~ ., data = Affair)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -5.0503 -1.7226 -0.7947 0.2101 12.7036
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 5.87201 1.13750 5.162 3.34e-07 ***
#> gendermale 0.05409 0.30049 0.180 0.8572
#> age -0.05098 0.02262 -2.254 0.0246 *
#> yearsmarried 0.16947 0.04122 4.111 4.50e-05 ***
#> childrenyes -0.14262 0.35020 -0.407 0.6840
#> religiousness -0.47761 0.11173 -4.275 2.23e-05 ***
#> education -0.01375 0.06414 -0.214 0.8303
#> occupation 0.10492 0.08888 1.180 0.2383
#> rating -0.71188 0.12001 -5.932 5.09e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.095 on 592 degrees of freedom
#> Multiple R-squared: 0.1317, Adjusted R-squared: 0.12
#> F-statistic: 11.23 on 8 and 592 DF, p-value: 7.472e-15
r2_lm6 <- round(summary(lm6)$r.squared, 2)
Der “.” im Befehl affairs ~ . oben soll sagen: nimm “alle Variablen, die noch in der Datenmatrix übrig sind”.
Insgesamt bleibt die erklärte Varian in sehr bescheidenem Rahmen: 0.13. Das zeigt uns, dass es immer noch nur schlecht verstanden ist – im Rahmen dieser Analyse – welche Faktoren die Affärenhäufigkeit erklärt.
Unterscheiden sich die Geschlechter statistisch signifikant? Wie groß ist der Unterschied? Sollte hierlieber das d-Maß oder Rohwerte als Effektmaß angegeben werden?
Hier bietet sich ein t-Test für unabhängige Gruppen an. Die Frage lässt auf eine ungerichtete Hypothese schließen (\(\alpha\) sei .05). Mit dem entsprechenden Menüpunkt im R-Commander oder mit folgender Syntax lässt sich diese Analyse angehen:
t1 <- t.test(affairs ~ gender, data = Affair)
t1
#>
#> Welch Two Sample t-test
#>
#> data: affairs by gender
#> t = -0.28733, df = 594.01, p-value = 0.774
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.6068861 0.4519744
#> sample estimates:
#> mean in group female mean in group male
#> 1.419048 1.496503
Der p-Wert ist mit 0.7739606 > \(\alpha\). Daher wird die \(H_0\) beibehalten. Auf Basis der Stichprobendaten entscheiden wir uns für die \(H_0\). Entsprechend umschließt das 95%-KI die Null.
Da die Differenz nicht signifikant ist, kann argumentiert werden, dass wir d auf 0 schätzen müssen. Man kann sich den d-Wert auch z.B. von {MBESS} schätzen lassen.
Dafür brauchen wir die Anzahl an Männer und Frauen: 315, 286.
library(MBESS)
ci.smd(ncp = t1$statistic,
n.1 = 315,
n.2 = 286)
#> $Lower.Conf.Limit.smd
#> [1] -0.1835475
#>
#> $smd
#> t
#> -0.02346813
#>
#> $Upper.Conf.Limit.smd
#> [1] 0.1366308
Das Konfidenzintervall ist zwar relativ klein (die Schätzung also aufgrund der recht großen Stichprobe relativ präzise), aber der Schätzwert für d smd liegt sehr nahe bei Null. Das stärkt unsere Entscheidung, von einer Gleichheit der Populationen (Männer vs. Frauen) auszugehen.
Rechnen Sie die Regressionsanalyse getrennt für kinderlose Ehe und Ehen mit Kindern!
Hier geht es im ersten Schritt darum, die entsprechenden Teil-Mengen der Datenmatrix zu erstellen. Das kann man natürlich mit Excel o.ä. tun. Alternativ könnte man es in R z.B. so machen:
Affair2 <- Affair[Affair$children == "yes", ]
lm7 <- lm(affairs~ rating, data = Affair2)
summary(lm7)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = Affair2)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1903 -1.4877 -0.5869 -0.4877 11.4131
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 5.0912 0.5701 8.930 < 2e-16 ***
#> rating -0.9009 0.1441 -6.252 9.84e-10 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.336 on 428 degrees of freedom
#> Multiple R-squared: 0.08367, Adjusted R-squared: 0.08153
#> F-statistic: 39.08 on 1 and 428 DF, p-value: 9.845e-10
Affair3 <- Affair[Affair$children == "no", ]
lm8 <- lm(affairs~ rating, data = Affair3)
summary(lm8)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = Affair3)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.5465 -1.0494 -0.5504 -0.5504 11.4496
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.0455 0.9140 3.332 0.00106 **
#> rating -0.4990 0.2083 -2.395 0.01771 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.685 on 169 degrees of freedom
#> Multiple R-squared: 0.03283, Adjusted R-squared: 0.02711
#> F-statistic: 5.737 on 1 and 169 DF, p-value: 0.01771
Übrigens, einfacher geht das “Subsetten” so:
library(dplyr)
Affair4 <- filter(Affair, children == "yes")
head(Affair4)
#> affairs gender age yearsmarried children religiousness education
#> 1 0 female 32 15 yes 1 12
#> 2 0 male 57 15 yes 5 18
#> 3 0 male 57 15 yes 2 14
#> 4 0 female 32 15 yes 4 16
#> 5 0 male 37 15 yes 2 20
#> 6 0 male 27 4 yes 4 18
#> occupation rating
#> 1 1 4
#> 2 6 5
#> 3 4 4
#> 4 1 2
#> 5 7 2
#> 6 6 4
Rechnen Sie die Regression nur für “Halodries”; d.h. für Menschen mit Seitensprüngen. Dafür müssen Sie alle Menschen ohne Affären aus den Datensatz entfernen.
Also, rechnen wir nochmal die Standardregression (lm1). Probieren wir den Befehl filter dazu nochmal aus:
Affair5 <- filter(Affair, affairs != 0)
lm9 <- lm(affairs ~ rating, data = Affair5)
summary(lm9)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = Affair5)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -6.0605 -3.5157 -0.0605 3.6895 7.4843
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.7570 1.0225 8.564 1.3e-14 ***
#> rating -0.8483 0.2800 -3.030 0.00289 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.144 on 148 degrees of freedom
#> Multiple R-squared: 0.05841, Adjusted R-squared: 0.05205
#> F-statistic: 9.181 on 1 and 148 DF, p-value: 0.002887
Berechnen Sie für eine logistische Regression mit “Affäre ja vs. nein” als Kriterium, wie stark der Einfluss von Geschlecht, Kinderstatus, Ehezufriedenheit und Ehedauer ist!
Affair %>%
mutate(affairs_dichotom = if_else(affairs == 0, 0, 1)) %>%
glm(affairs_dichotom ~gender + children + rating + yearsmarried, data = .) -> lm10
summary(lm10)
#>
#> Call:
#> glm(formula = affairs_dichotom ~ gender + children + rating +
#> yearsmarried, data = .)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -0.57662 -0.26766 -0.17186 -0.06459 0.93295
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.515778 0.079344 6.501 1.69e-10 ***
#> gendermale 0.037945 0.034218 1.109 0.268
#> childrenyes 0.054032 0.046307 1.167 0.244
#> rating -0.090337 0.015985 -5.651 2.47e-08 ***
#> yearsmarried 0.003947 0.003787 1.042 0.298
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for gaussian family taken to be 0.1746456)
#>
#> Null deviance: 112.56 on 600 degrees of freedom
#> Residual deviance: 104.09 on 596 degrees of freedom
#> AIC: 663.8
#>
#> Number of Fisher Scoring iterations: 2
Wenn if_else unbekannt ist, lohnt sich ein Blick in die Hilfe mit ?if_else (dplyr muss vorher geladen sein).
Aha, signifikant ist die Ehezufriedenheit: Je größer rating desto geringer die Wahrscheinlickeit für affairs_dichotom. Macht Sinn! Je zufriedener, desto geringer Seitensprung-Gefahr…
Übrigens, die Funktion lm und glm spucken leider keine brave Tabelle in Normalform aus. Aber man leicht eine schöne Tabelle (data.frame) bekommen mit dem Befehl tidy aus broom:
library(broom)
tidy(lm10)
#> term estimate std.error statistic p.value
#> 1 (Intercept) 0.515777667 0.079343849 6.500537 1.693109e-10
#> 2 gendermale 0.037944509 0.034217912 1.108908 2.679172e-01
#> 3 childrenyes 0.054032156 0.046307172 1.166820 2.437495e-01
#> 4 rating -0.090336904 0.015984908 -5.651387 2.468646e-08
#> 5 yearsmarried 0.003946811 0.003786673 1.042290 2.976998e-01
Und Tabellen (d.h. brave Dataframes) kann man sich schön ausgeben lassen z.B. mit dem Befehl knitr::kable:
library(knitr)
tidy(lm10) %>% kable
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.5157777 | 0.0793438 | 6.500538 | 0.0000000 |
| gendermale | 0.0379445 | 0.0342179 | 1.108908 | 0.2679172 |
| childrenyes | 0.0540322 | 0.0463072 | 1.166821 | 0.2437495 |
| rating | -0.0903369 | 0.0159849 | -5.651387 | 0.0000000 |
| yearsmarried | 0.0039468 | 0.0037867 | 1.042290 | 0.2976998 |
Visualisieren wir mal was!
Ok, wie wäre es damit:
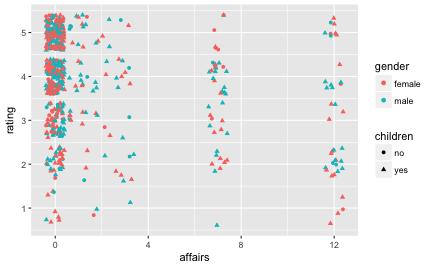
Affair %>%
select(affairs, gender, children, rating) %>%
ggplot(aes(x = affairs, y = rating)) + geom_jitter(aes(color = gender, shape = children))
Affair %>%
mutate(rating_dichotom = ntile(rating, 2)) %>%
ggplot(aes(x = yearsmarried, y = affairs)) + geom_jitter(aes(color = gender)) +
geom_smooth()
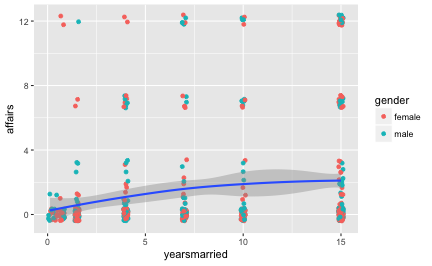
Puh. Geschafft!
Versionshinweise und SessionInfo
- Datum erstellt: 2017-01-06
- R Version: 3.3.2
dplyrVersion: 0.5.0
sessionInfo()
#> R version 3.3.2 (2016-10-31)
#> Platform: x86_64-apple-darwin13.4.0 (64-bit)
#> Running under: macOS Sierra 10.12.2
#>
#> locale:
#> [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] broom_0.4.1 MBESS_4.1.0 corrplot_0.77 ggplot2_2.2.1 psych_1.6.9
#> [6] knitr_1.15.1 dplyr_0.5.0
#>
#> loaded via a namespace (and not attached):
#> [1] Rcpp_0.12.8 magrittr_1.5 munsell_0.4.3
#> [4] mnormt_1.5-5 lattice_0.20-34 colorspace_1.3-2
#> [7] R6_2.2.0 plyr_1.8.4 stringr_1.1.0
#> [10] highr_0.6 tools_3.3.2 parallel_3.3.2
#> [13] grid_3.3.2 nlme_3.1-128 gtable_0.2.0
#> [16] DBI_0.5-1 htmltools_0.3.5 yaml_2.1.14
#> [19] lazyeval_0.2.0.9000 assertthat_0.1 rprojroot_1.1
#> [22] digest_0.6.11 tibble_1.2 tidyr_0.6.0
#> [25] reshape2_1.4.2 codetools_0.2-15 rsconnect_0.7
#> [28] evaluate_0.10 rmarkdown_1.3 labeling_0.3
#> [31] stringi_1.1.2 scales_0.4.1 backports_1.0.4
#> [34] foreign_0.8-67