library(rstanarm)
library(easystats)
library(tidyverse)
library(ggpubr)Wskt-Schluckspecht2a
Aufgabe
Geprüft werden soll folgende Hypothese:
Autos mit wenig PS sind sparsamer als Autos mit viel PS.
Dafür ist folgende Analyse gegeben.
Setup
data(mtcars)Modell und Hypothese
Die Variable mpg (Miles per Gallone) misst die Spritsparsamkeit.
Die Hypothese kann man wie folgt formalisieren:
\[\text{mpg}_{PS=1} < \text{mpg}_{PS=0},\]
“Die mittlere Spritsparsamkeit von Autos mit viel PS ist kleiner als die von Autos mit viel PS”.
Dabei meint \(PS=0\) die Autos mit wenig PS (und \(PS=1\) die Autos mit viel PS).
Man beachte, dass man i.d.R. Hypothesen zum Mittelwert formulieren möchte, nicht allgemein für alle Autos.
Die Prioris übernehmen wir vom Stan-Golem.🤖
🤖 Beep, beep!
👩🏫 An die Arbeit, Stan-Golem!
Vorverarbeitung
Wir definieren PS als eine binäre Variable, die angibt, ob ein Auto mehr oder weniger PS hat als der Median der PS-Werte:
mtcars <-
mtcars |>
mutate(PS_high = case_when(
hp > median(hp) ~ TRUE,
hp <= median(hp) ~ FALSE
)) |>
mutate(PS_high = as.factor(PS_high))Modell berechnen
m <- stan_glm(mpg ~ PS_high, # Regressionsformel
data = mtcars, # Datensatz
refresh = 0, # Nicht so viel Detail-Ausgabe
seed = 42) # ReproduzierbarkeitHier sind die Modellparameter:
parameters(m)| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 24.219612 | 0.95 | 22.07170 | 26.170915 | 1 | 1.0007744 | 3505.490 | normal | 20.09062 | 15.06737 |
| PS_highTRUE | -8.802191 | 0.95 | -11.61645 | -5.804179 | 1 | 0.9995466 | 3526.436 | normal | 0.00000 | 29.71825 |
Der Effekt von PS ist negativ, was bedeutet, dass Autos der Gruppe PS=1 einen um ca. 9 Meilen geringeren MPG-Wert haben als Autos der Gruppe PS=0. Das bedeutet, dass Autos mit wenig PS sparsamer sind (als Autos mit viel PS).
Umgekehrt: Autos mit viel PS einen höheren Spritverbrauch haben als Autos mit wenig PS.
Man beachte, dass in der Zeile PS_highTRUE der Effekt von PS=1 steht, also der Effekt von Autos mit viel PS. Der Effekt besteht im Unterschied zum Mittelwert der Autos mit wenig PS, der in der Zeile des Achsenabschnitts (Intercept) dargestellt ist.
Post-Verteilung auslesen
Hier ist das HDI (95%) zum Effekt von PS:
hdi(m) |> plot()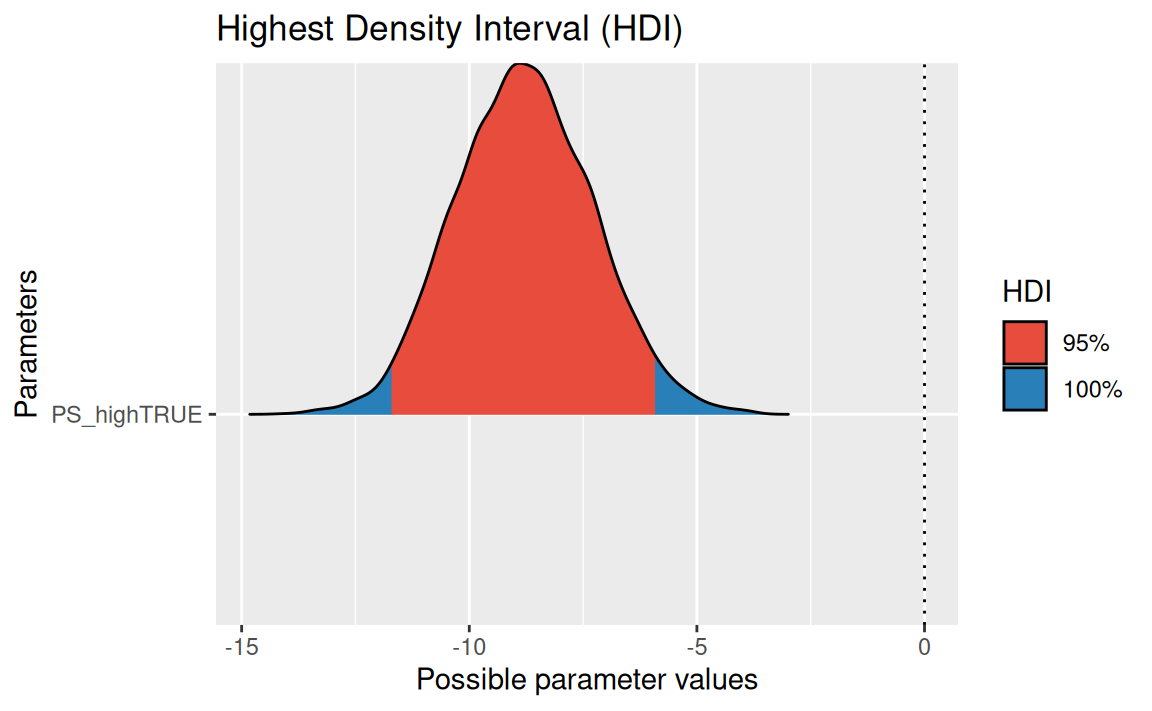
Aufgabe
- Sprechen die Ergebnisse dafür, dass Autos mit wenig PS einen geringen Spritverbrauch haben als Autos mit wenig PS? Begründen Sie.
- Wie hoch ist die Wahrscheinlichkeit, dass die Hypothese wahr ist (laut unserem Modell)?
- Was ist Ihr Punktschätzer für den Unterschied im Spritverbrauch zwischen Autos mit viel und wenig PS?
- Mit einer Wahrscheinlichkeit von 95% liegt der Unterschied im Spritverbrauch zwischen Autos mit viel und wenig PS zwischen welchen Werten (laut unserem Modell)?
- Geben Sie die Skalenniveaus der Variablen in der Regressionsformel an.
Lösung
- Ja, die Ergebnisse sprechen dafür, dass Autos mit wenig PS einen gerinen Spritverbrauch haben als Autos mit wenig PS. Die Posterior-Verteilung zeigt, dass die Wahrscheinlichkeit für die Hypothese sehr hoch ist: Alle Stichproben sind bzw. die gesamte Wahrscheinlichkeitsmasse ist kleiner als Null.
Der Parameter für PS ist negativ, was bedeutet, dass Autos mit viel PS einen höheren Spritverbrauch haben als Autos mit wenig PS. Das sieht man schon in den Stichprobendaten:
ggboxplot(mtcars,
x = "PS_high", y = "mpg",
title = "Spritverbrauch nach PS: Autos mit viel PS brauchen mehr Sprit als Autos mit wenig PS",
subtitle = "rote Punkte: Mittelwert der Gruppe",
add = "mean",
add.params = list(size = 1.5, color = "red"))
- Man sieht in der Visualisierung der Post-Verteilung, dass die komplette Wahrscheinlichkeitsmasse kleiner als Null ist. Das bedeutet, dass die Wahrscheinlichkeit, dass die Hypothese wahr ist, sehr hoch ist, gegen 1 geht.
Ca. -8.8 mpg-Einheiten ist ein guter Punktschätzer für den Unterschied im Spritverbrauch zwischen Autos mit viel und wenig PS. In der Ausgabetabelle (
parameters()) ist der Wert exakt angegeben.Den Unterschied im Spritverbrauch zwischen Autos mit viel und wenig PS liegt mit einer Wahrscheinlichkeit von 95% zwischen -5.8 und -11.62.
Das kann man der Parameter-Tabelle entnehmen. Man sieht es auch im Diagramm recht gut.
- UV: binär, AV: kontinuierlich