within-design-analysis1

regression

within-design

researchdesign

fopro

string

Published

November 8, 2023

Aufgabe

Analysieren Sie die Veränderung in einem längsschnittlichen Experiment (Within-Design).

Im Zuge des Experiments durchliefen alle \(n\) Versuchspersonen 3 Bedingungen. Entsprechend liegen für jede Versuchsperson 3 Messungen vor (y1, y2, y3). Anders gesagt gab es drei Messzeitpunkte (t1, t2, t3), zu denen die abhängige Variable (y) jeweils gemessen wurde Die Messung bestand bei jeder Bedingung aus 10 Items, wobei die Wahrscheinlichkeit, ein Item zu lösen zwischen den Bedingungen unterschiedlich war.

Prüfen Sie die folgende Hypothesen:

\(y_{t2} - y_{t1} > 0\)
\(y_{t3} - y_{t2} > 0\)

Gehen Sie von folgenden (hier einfach simulierten) Daten aus:

n <- 40  # Anzahl Versuchspersonen
n_items <- 10  # Anzahl Items pro Messung von y
prob <- c(.5, .7, .9)  # Lösungswahrscheinlichkeit pro Messzeitpunkt (t1, t2, t3)

library(tidyverse)
set.seed(42)
d <-
  tibble(id = 1:n,
         y1 = rbinom(n = n, size = n_items, prob = prob[1]),
         y2 = rbinom(n = n, size = n_items, prob = prob[2]),
         y3 = rbinom(n = n, size = n_items, prob = prob[3]),
         g = c(rep(times = n/2, x = "A"), rep(times = n/2, x = "B"))
         )
head(d)

id	y1	y2	y3	g
1	7	8	9	A
2	7	7	10	A
3	4	9	9	A
4	7	4	9	A
5	6	7	8	A
6	5	4	9	A

Hinweise:

Orientieren Sie sich im Übrigen an den allgemeinen Hinweisen des Datenwerks.

Lösung

Pakete starten

library(tidyverse)
library(rstanarm)
library(easystats)

Daten aufbereiten

Um die Daten (besser) analysieren zu können, formen wir sie ins “lange Format” um.

d_long <-
  d %>% 
  pivot_longer(cols = c(y1, y2, y3), names_to = "time", values_to = "y")

Daten zusammenfassen

d_long %>% 
  group_by(time) %>% 
  summarise(y_mean = mean(y),
            y_sd = sd(y)) %>% 
  mutate(delta = y_mean - lag(y_mean))

time	y_mean	y_sd	delta
y1	5.450	1.7386998	NA
y2	7.050	1.5516740	1.600
y3	8.975	0.8911963	1.925

Daten visualisieren

d_long %>% 
  ggplot(aes(x = time, y = y)) +
  geom_jitter(width = .1) +
  stat_summary(fun.y = mean, geom = "point", color = "red", size = 3) +
  stat_summary(fun.y = mean, geom = "line", color = "red", linewidth = 1, group = 1)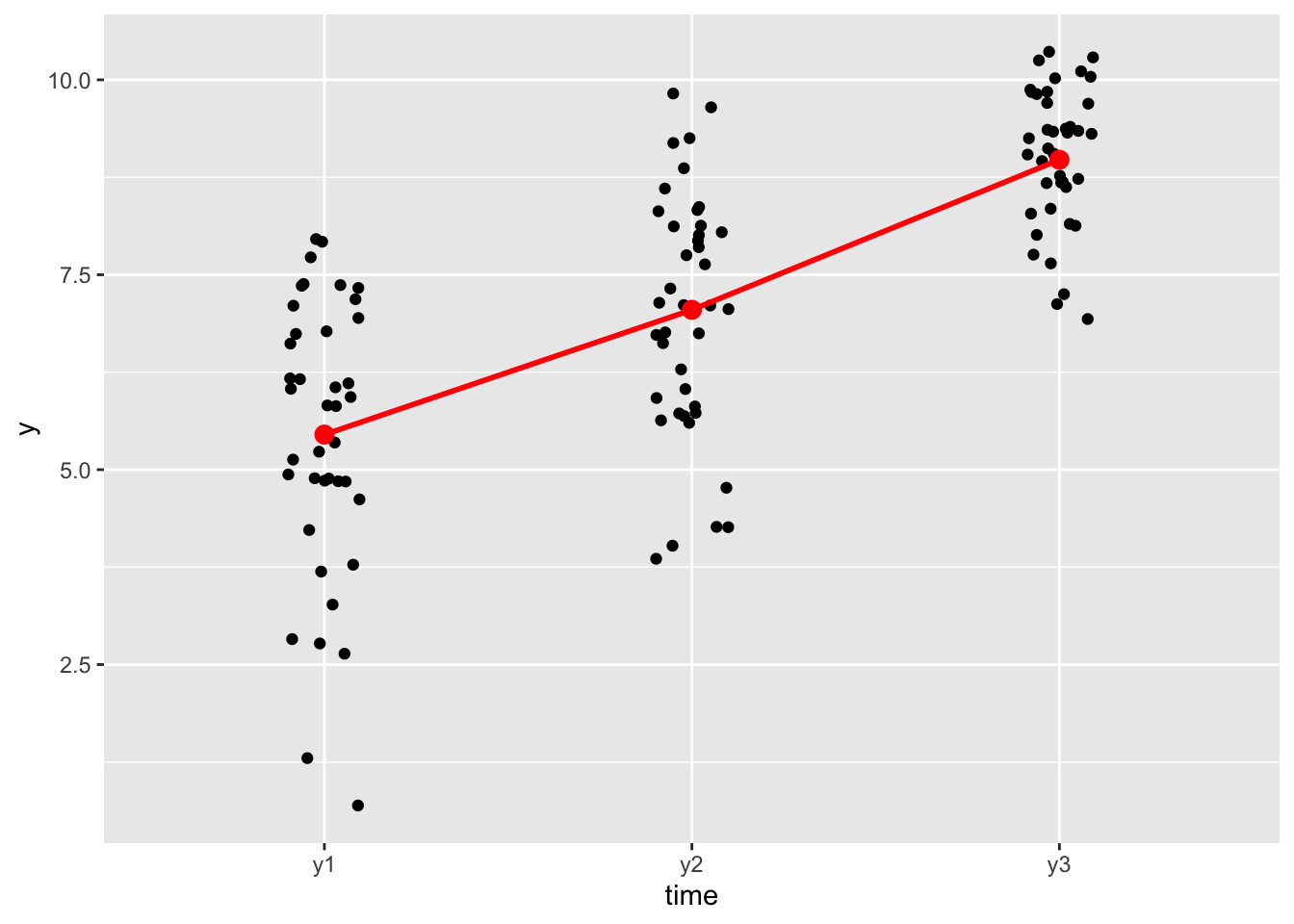

Man sieht, dass der Wert von Y steigt von t1 zu t2 und genauso von t2 zu t3.

Daten transformieren

Man kann auch die Veränderung (das “delta”) zwischen den Messzeitpunkten berechnen, um dann zu prüfen, ob dieses delta dann positiv ist.

d2 <-
  d %>% 
  mutate(t2mt1 = y2 - y1,  # t2 *m*inus t1
         t3mt2 = y3 - y2,  # t3 minus t2
         t3mt1 = y3 - y1)  # t3 mind t1, die Gesamtveränderung von "Anfang" zu "Ende"

d2_long <- 
  d2 %>% 
  pivot_longer(cols = c(t2mt1, t3mt2, t3mt1), names_to = "time", values_to = "delta")

Daten zusammenfassen

d2_long %>% 
  group_by(time) %>% 
  summarise(delta_mean = mean(delta),
            delta_sd = sd(delta)) %>% 
  mutate(delta2 = delta_mean - lag(delta_mean))

time	delta_mean	delta_sd	delta2
t2mt1	1.600	2.629224	NA
t3mt1	3.525	1.782932	1.925
t3mt2	1.925	1.966221	-1.600

Wie man sieht, ist das Delta t2mt1 positiv, im Mittelwert steigt also y. Gleiches gilt für t3mt2 und t3mt1.

d2_long %>% 
  filter(time != "t3mt1") %>% 
  ggplot(aes(x = time, y = delta)) +
  geom_jitter(width = .1) +
  stat_summary(fun.y = mean, geom = "point", color = "red", size = 3) +
  stat_summary(fun.y = mean, geom = "line", color = "red", linewidth = 1, group = 1)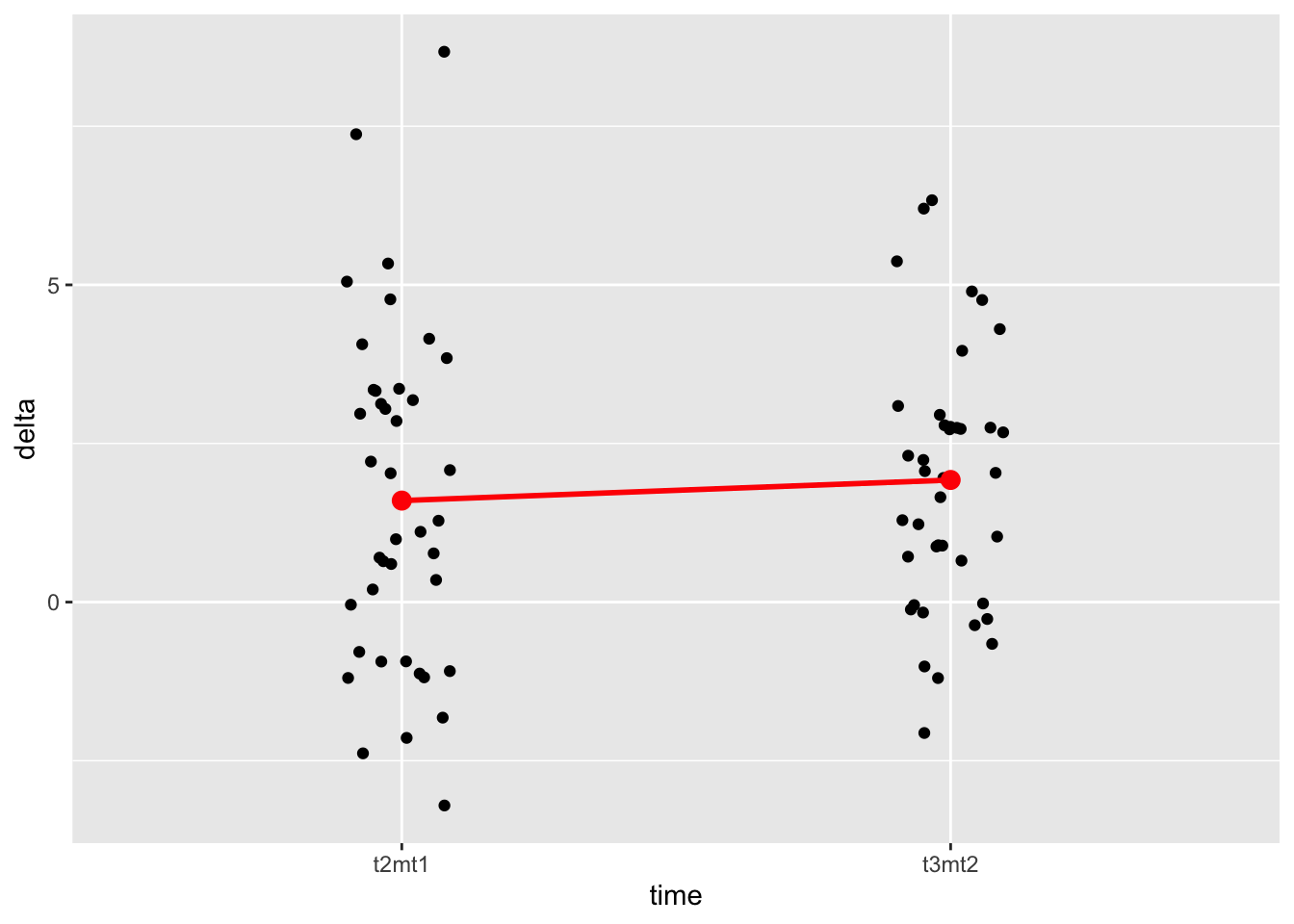

Die Veränderungen von t1 zu t2 (t2mt1) sind ähnlich zu denen von t2 zu t3 (t3mt2).

Modell t2mt1

Das entsprechende Regressionsmodell für t2mt2 liefert einfach den Mittelwert des Deltas.

m1_t2mt1 <- lm(t2mt1 ~ 1, data = d2)
coef(m1_t2mt1)

(Intercept) 
        1.6

Ein Bayes-Modell hat den Vorteil, dass es uns einfach zu interpretierende Inferenzstatistik gibt.

m1_bayes <- stan_glm(t2mt1 ~ 1, data = d2, refresh = 0)
coef(m1_bayes)

(Intercept) 
   1.602565

parameters(m1_bayes)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	1.602565	0.95	0.7677561	2.471188	0.9995	1.000112	2448.837	normal	1.6	6.573061

Mit einer Wahrscheinlichkeit von 100% ist das Delta positiv (laut m1_bayes). Das kann man aus dem Koeffizienten pd ablesen (probability of direction).

m_t3mt2

m_t3mt2_bayes <- stan_glm(t3mt2 ~ 1, data = d2, refresh = 0)
parameters(m_t3mt2_bayes)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	1.928811	0.95	1.32115	2.530593	1	1.000633	2752.526	normal	1.925	4.915553

Auch hier ist das Modell sehr meinungsstark: Mit einer Wahrscheinlichkeit von 100% ist der Koeffizient (Veränderung von t2 zu t3) positiv.

Categories:

regression
within-design
researchdesign
fopro
string