tidymodels-poly02

statlearning

tidymodels

num

Published

May 17, 2023

Aufgabe

Fitten Sie ein Polynomial-Modell für folgende Modellgleichung:

body_mass_g ~ bill_length_mm.

Gesucht ist der RMSE im Test-Set (optimal hinsichtlich minimalem Prognosefehler).

Hinweise:

Datensatz penguins (palmerpenguins)
Verwenden Sie Tidymodels
Fitten Sie Polynome des Grades 1 bis 10.
Definieren Sie die Polynomegrade als Tuningparameter.
Entfernen Sie fehlende Werte in den Prädiktoren.
Wie immer gilt: Verwenden Sie die Standardeinstellungen der Funktionen, soweit nicht anders angegeben.

Lösung

Setup:

library(tidymodels)
data(penguins, package = "palmerpenguins")

Datenaufteilung:

d_split <- initial_split(penguins)
d_train <- training(d_split)
d_test <- testing(d_split)

Rezept:

rec1 <- 
  recipe(body_mass_g ~ bill_length_mm, data = penguins) %>% 
  step_naomit(all_predictors()) %>% 
  step_poly(all_predictors(), degree = tune()) %>% 
  update_role(contains("_poly_"), new_role = "predictor")

Check:

d_baked <- bake(prep(rec1), new_data = NULL)

Rezepte mit Tuningparametern kann man nicht preppen/backen.

Workflow:

wf1 <-
  workflow() %>% 
  add_model(linear_reg()) %>% 
  add_recipe(rec1)

Tuning:

set.seed(42)
tune1 <-
  tune_grid(
    wf1,
    resamples = vfold_cv(data = penguins),
    metrics = metric_set(rmse),
    grid = grid_regular(degree(range = c(1, 10)),
                               levels = 10),
    control = control_grid(save_workflow = TRUE)
  )

autoplot(tune1)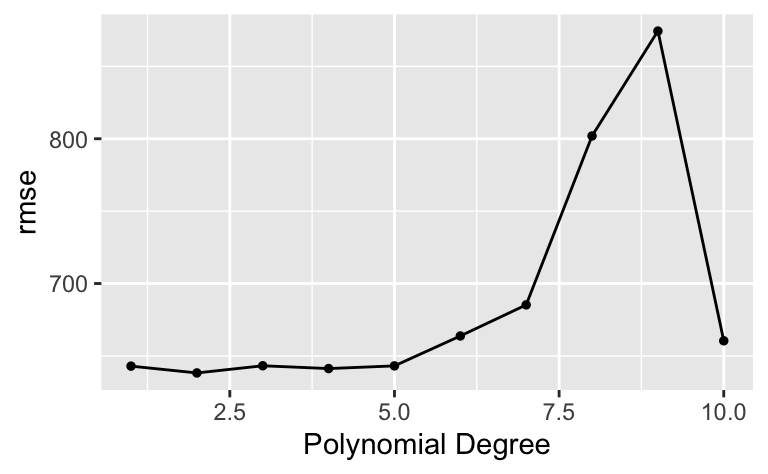

show_best(tune1)

degree	.metric	.estimator	mean	n	std_err	.config
2	rmse	standard	638.2267	10	22.70394	pre02_mod0_post0
4	rmse	standard	641.2418	10	23.69291	pre04_mod0_post0
1	rmse	standard	642.9314	10	21.83462	pre01_mod0_post0
5	rmse	standard	643.0979	10	23.48819	pre05_mod0_post0
3	rmse	standard	643.1772	10	24.16118	pre03_mod0_post0

Finalisieren:

best1 <- fit_best(tune1)
best1

══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: linear_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_naomit()
• step_poly()

── Model ───────────────────────────────────────────────────────────────────────

Call:
stats::lm(formula = ..y ~ ., data = data)

Coefficients:
          (Intercept)  bill_length_mm_poly_1  bill_length_mm_poly_2  
                 4202                   8813                  -1708

Predicten:

final1 <- last_fit(best1, d_split)

Error in `last_fit()`:
! `last_fit()` is not well-defined for a fitted workflow.

collect_metrics(final1)

Error: object 'final1' not found

Oder so:

sol <- 
predict(best1, new_data = d_test) %>% 
  bind_cols(d_test) %>% 
  rmse(truth = body_mass_g, estimate = .pred) %>% 
  pull(.estimate) %>% 
  pluck(1)

sol

[1] 662.8083

Die Antwort lautet: 662.8083105.

Categories:

R
statlearning
tidymodels
num