rope4

rope
bayes
Published

December 15, 2022

Exercise

Einer der (bisher) größten Studien der Untersuchung psychologischer Konsequenzen (oder Korrelate) der Covid-Zeit ist die Studie COVIDiStress.

Im Folgenden sollen Sie folgende Forschungsfrage untersuchen:

Forschungsfrage:

Ist der Unterschied zwischen Männern und Frauen (Dem_gender) im Hinblick zum Zusammenhang von Stress (PSS10_avg, AV) und Neurotizismus (neu, UV) vernachlässigbar klein?

Den Datensatz können Sie so herunterladen (Achtung, groß):

osf_d_path <- "https://osf.io/cjxua/?action=download"

d <- read_csv(osf_d_path)

Hinweise:

  • Sie benötigen einen Computer, um diese Aufgabe zu lösen.
  • Verwenden Sie die statistischen Methoden, die im Unterricht behandelt wurden.
  • Verwenden Sie Ansätze aus der Bayes-Statistik zur Lösung dieser Aufgabe.
  • Bei der Variable für Geschlecht können Sie sich auf Fälle begrenzen, die Männer und Frauen umfassen.
  • Wandeln Sie die die Variable für Geschlecht in eine binäre Variable - also Werte mit 0 und 1 - um.
  • Alle Daten (und weitere Informationen) zum Projekt sind hier abgelegt.
  • Eine Beschreibung der Variablen der Studie finden Sie hier.
  • Fixieren Sie die Zufallszahlen auf den Startwert 42.

Antwortoptionen:

Answerlist

  • Ja
  • Nein
  • Die Daten sind nicht konkludent; es ist keine Entscheidung möglich.
  • Auf Basis der bereitgestellten Informationen ist keine Entscheidung möglich.











Solution

Pakete laden:

library(tidyverse)
library(rstanarm)
library(easystats)

Relevante Spalten auswählen:

d2 <-
  d %>% 
  select(PSS10_avg, neu, Dem_gender)

Das sind die Variablen:

  • Stress
  • Neurotizismus
  • Geschlecht

Deskriptive Statistiken zum Datensatz:

d2 %>% 
  describe_distribution()
Variable Mean SD IQR Min Max Skewness Kurtosis n n_Missing
PSS10_avg 2.631202 0.735594 1.000000 1 5 0.2083341 -0.3101913 116097 9209
neu 3.339708 1.053727 1.333333 1 6 0.0704146 -0.4525880 108367 16939 
d2 %>% 
  count(Dem_gender)
Dem_gender n
Female 90400
Male 33126
Other/would rather not say 1474
NA 306

Datensatz aufbereiten:

d3 <-
  d2 %>% 
  filter(Dem_gender %in% c("Female", "Male")) %>% 
  drop_na() %>% 
  mutate(Female = ifelse(Dem_gender == "Female", 1, 0)) %>% 
  select(-Dem_gender)

Check:

d3 %>% 
  count(Female)
Female n
0 28371
1 78472

Check:

d3 %>% 
  describe_distribution()
Variable Mean SD IQR Min Max Skewness Kurtosis n n_Missing
PSS10_avg 2.6223511 0.7351792 1.000000 1 5 0.2150741 -0.3202387 106843 0
neu 3.3364594 1.0524872 1.333333 1 6 0.0703479 -0.4524212 106843 0
Female 0.7344608 0.4416219 1.000000 0 1 -1.0618369 -0.8725188 106843 0

Modell berechnen:

m1 <-
  stan_glm(PSS10_avg ~ neu + Female + neu:Female, 
           refresh = 0,
           seed = 42,
           data = d3)

Modellkoeffizienten auslesen:

coef(m1)
(Intercept)         neu      Female  neu:Female 
 1.34114221  0.35917641  0.17807121 -0.01910496

Posteriori-Verteilung auslesen:

parameters(m1)
Parameter Median CI CI_low CI_high pd Rhat ESS Prior_Distribution Prior_Location Prior_Scale
(Intercept) 1.3411422 0.95 1.3175222 1.3641160 1 1.001274 1139.6816 normal 2.622351 1.837948
neu 0.3591764 0.95 0.3522757 0.3662896 1 1.001854 1146.7115 normal 0.000000 1.746290
Female 0.1780712 0.95 0.1504310 0.2054727 1 1.002058 984.2769 normal 0.000000 4.161813
neu:Female -0.0191050 0.95 -0.0270895 -0.0109118 1 1.002839 982.9762 normal 0.000000 1.048027

Posteriori-Verteilung plotten:

plot(m1)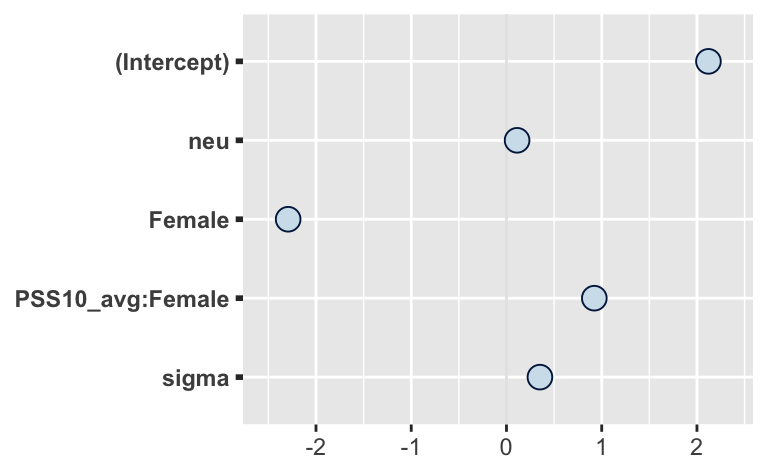

Rope berechnen:

rope(m1)
Parameter CI ROPE_low ROPE_high ROPE_Percentage Effects Component
1 (Intercept) 0.95 -0.0735179 0.0735179 0 fixed conditional
3 neu 0.95 -0.0735179 0.0735179 0 fixed conditional
2 Female 0.95 -0.0735179 0.0735179 0 fixed conditional
4 neu:Female 0.95 -0.0735179 0.0735179 1 fixed conditional

Rope visualisieren:

plot(rope(m1))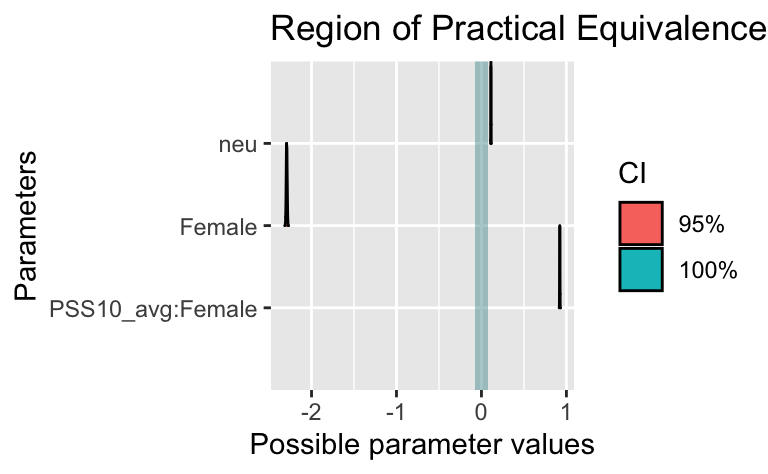

Answerlist

  • Falsch
  • Wahr
  • Falsch
  • Falsch

Categories:

  • rope
  • bayes