osf_d_path <- "https://osf.io/cjxua/?action=download"
d <- read_csv(osf_d_path)rope3
Exercise
Einer der (bisher) größten Studien der Untersuchung psychologischer Konsequenzen (oder Korrelate) der Covid-Zeit ist die Studie COVIDiStress.
Im Folgenden sollen Sie folgende Forschungsfrage untersuchen:
Ist der Zusammenhang von Stress (PSS10_avg, AV) und Neurotizismus (neu, UV) vernachlässigbar klein?
Den Datensatz können Sie so herunterladen (Achtung, groß):
Hinweise:
- Sie benötigen einen Computer, um diese Aufgabe zu lösen.
- Verwenden Sie die statistischen Methoden, die im Unterricht behandelt wurden.
- Verwenden Sie Ansätze aus der Bayes-Statistik zur Lösung dieser Aufgabe.
- Bei der Variable für Geschlecht können Sie sich auf Fälle begrenzen, die Männer und Frauen umfassen.
- Wandeln Sie die die Variable für Geschlecht in eine binäre Variable - also Werte mit 0 und 1 - um.
- Alle Daten (und weitere Informationen) zum Projekt sind hier abgelegt.
- Eine Beschreibung der Variablen der Studie finden Sie hier.
- Das Codebook findet sich hier.
- Der Datensatz ist recht groß (ca. 150 MB).
- Fixieren Sie die Zufallszahlen auf den Startwert 42.
- Berechnen Sie 89%-PIs, wenn Sie Ungewissheit quantifizieren.
Antwortoptionen
Answerlist
- Ja
- Nein
- Die Daten sind nicht konkludent; es ist keine Entscheidung möglich.
- Auf Basis der bereitgestellten Informationen ist keine Entscheidung möglich.
Solution
Pakete laden:
library(tidyverse)
library(rstanarm)
library(easystats)Relevante Spalten auswählen:
d2 <-
d %>%
select(PSS10_avg, neu)Datensatz aufbereiten:
d3 <-
d2 %>%
drop_na()Modell berechnen:
m1 <-
stan_glm(PSS10_avg ~ neu,
refresh = 0,
seed = 42,
data = d3)Modellkoeffizienten auslesen:
coef(m1)(Intercept) neu
1.4533911 0.3509393 Posteriori-Verteilung auslesen:
parameters(m1, ci = .89)| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 1.4533911 | 0.89 | 1.4428916 | 1.463608 | 1 | 0.9999767 | 4301.909 | normal | 2.625455 | 1.841433 |
| neu | 0.3509393 | 0.89 | 0.3480155 | 0.353949 | 1 | 0.9997235 | 4475.252 | normal | 0.000000 | 1.747465 |
Warum 89%? Kein besonderer Grund. Aber ich mag Primzahlen :-)
Posteriori-Verteilung plotten:
plot(parameters(m1, ci = .89), show_intercept = TRUE)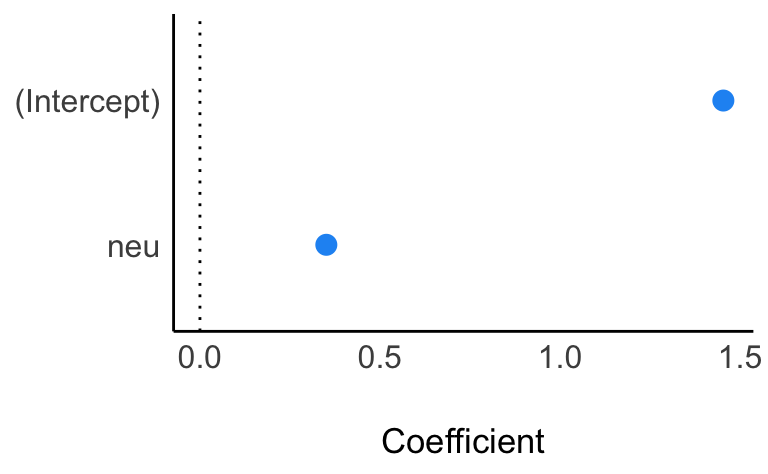
Rope berechnen:
rope_m1 <- rope(m1)Rope visualisieren:
plot(rope_m1)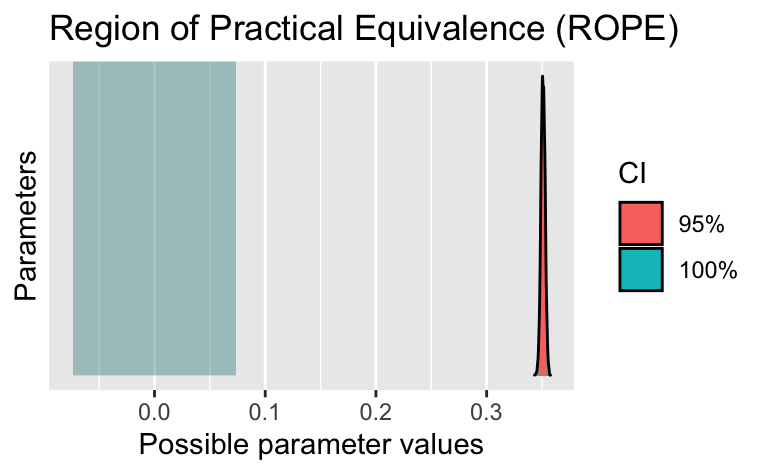
Wie man sieht, kreuzt das “blaue Band” nicht den “roten Berg”. Damit ist die Nullhypothese (ROPE) zu verwerfen.
Answerlist
- Falsch
- Wahr. ROPE ist zu verwerfen, damit sind Werte um die Null herum nicht wahrscheinlich.
- Falsch
- Falsch
Categories:
- rope
- bayes