library(easystats)
library(tidyverse)
library(rstanarm)
data(mtcars)rope2
Aufgabe
Im Datensatz mtcars: Ist der (mittlere) Unterschied im Spritverbrauch (mpg) zwischen den beiden Gruppen Automatik vs. Schaltgetriebe vernachlässigbar?
Wir definieren “vernachlässigbar klein” als “höchstens eine Meile”.
Prüfen Sie rechnerisch, anhand des angegebenen Datensatzes, folgende Behauptung:
Behauptung: “Der Unterschied ist vernachlässigbar klein!”
Nutzen Sie das ROPE-Konzept mit den Standardwerten im Befehl rope aus {easystats}.
Wählen Sie die Antwortoption, die am besten zu der obigen Behauptung passt!
Antwortoptionen:
Answerlist
- Ja, die Behauptung ist korrekt.
- Nein, die Behauptung ist falsch.
- Die Daten sind bzw. das Modell nicht konkludent; es ist keine Entscheidung über die Behauptung möglich.
- Auf Basis der bereitgestellten Informationen ist keine Antwort möglich.
Lösung
Zur ersten Orientierung erstellen wir uns, rein deskriptiv, eine Darstellung des Spritverbrauchs beider Gruppen, z.B. so:
mtcars %>%
mutate(am = factor(am)) %>%
ggplot() +
aes(x = mpg, color = am, fill = am) +
geom_density(alpha = .5)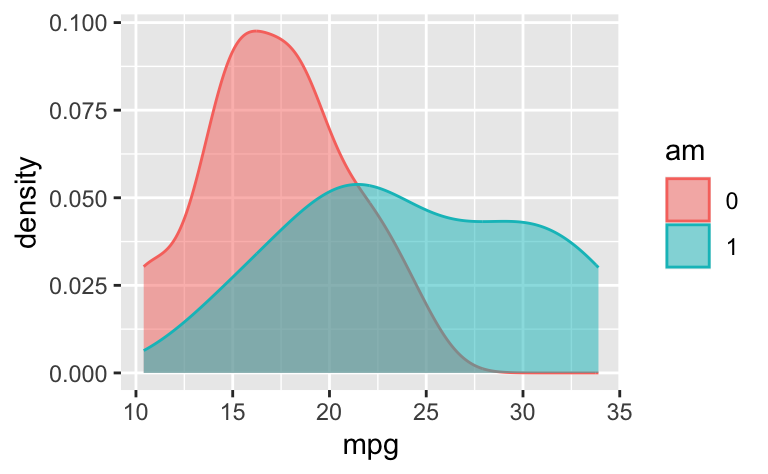
Man sieht direkt, dass es substanzielle Unterschiede zwischen den Mittelwerten beiden Gruppen gibt. Auch wenn sich die Verteilungen überlappen, sind die Mittelwerte doch vermutlich nicht (fast) identisch. Vermutlich wird das Modell, das wir gleich berechnen, uns wenig überraschen, sondern den deskriptiven Befund widerspiegeln.
Modell berechnen:
m1_mtcars <- stan_glm(mpg ~ am,
data = mtcars,
seed = 42,
refresh = 0)Posteriori-Verteilung betrachten:
parameters(m1_mtcars)| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 17.135995 | 0.95 | 14.85310 | 19.50922 | 1.0000 | 0.9992095 | 3739.117 | normal | 20.09062 | 15.06737 |
| am | 7.210857 | 0.95 | 3.72452 | 10.69610 | 0.9995 | 0.9994221 | 3754.841 | normal | 0.00000 | 30.19568 |
Die Funktion spucht im Default ein PI (ETI) aus, kein HDI.
Visualisieren der Posteriori-Verteilung:
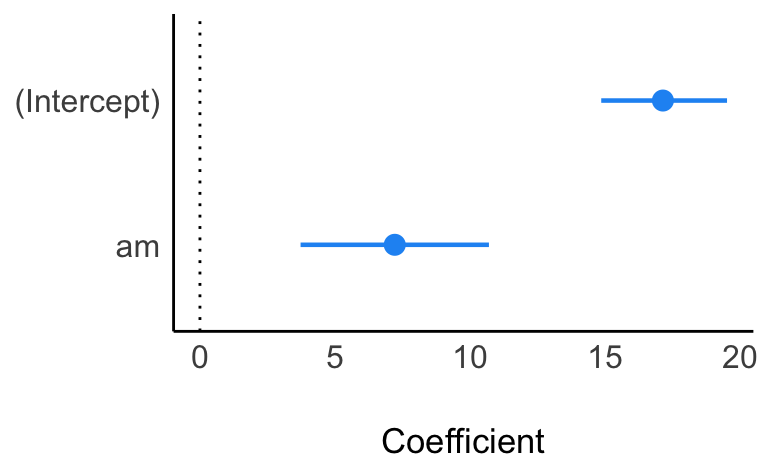
plot(parameters(m1_mtcars), show_intercept = TRUE)Hilfe zum Plot-Befehl von parameters
Rope berechnen:
rope_m1 <- rope(m1_mtcars, range = c(-1, 1)) # ±1 Meile Unterschied
rope_m1| Parameter | CI | ROPE_low | ROPE_high | ROPE_Percentage | Effects | Component |
|---|---|---|---|---|---|---|
| (Intercept) | 0.95 | -1 | 1 | 0 | fixed | conditional |
| am | 0.95 | -1 | 1 | 0 | fixed | conditional |
Rope visualisieren mit plot(rope_m1).
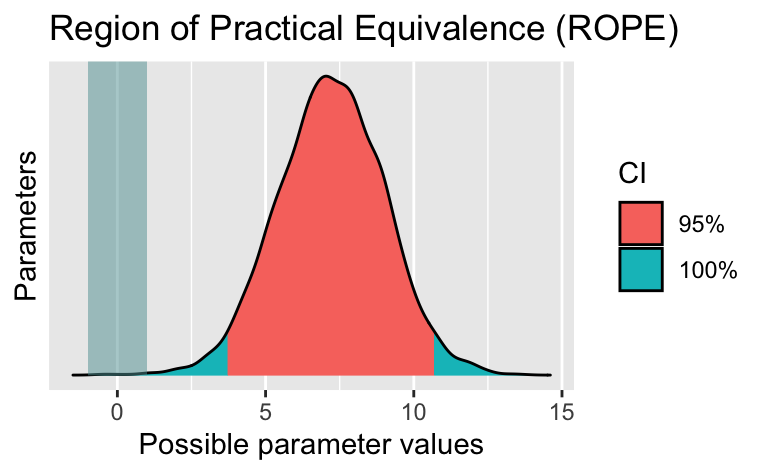
Man sieht, dass der “Berg” - die Posteriori-Verteilung bzw. der Bereich plausibler Werte - außerhalb des Rope-Bereichs liegt.
Wir können also die Hypothese, dass der Unterschied zwischen beiden Gruppen praktisch Null ist, verwerfen.
Natürlich ist das nur ein deskriptiver Befund, wir können nichts dazu sagen, ob der Unterschied auch ein kausaler Effekt ist.
Alternative Rope-Definition: Z-Standardisieren.
Ein kleiner Effekt ist, laut Kruschke 2018, ein Unterschied, der nicht größer ist als ±0.1 SD.
Mit diesen Angaben berechnen wir das ROPE erneut:
m2_mtcars <-
mtcars %>%
mutate(mpg_z = scale(mpg)) %>%
stan_glm(mpg_z ~ am,
seed = 42,
data = ., # Der Punkt bezieht sich auf die Tabelle im vorherigen Pfeifen-Schritt
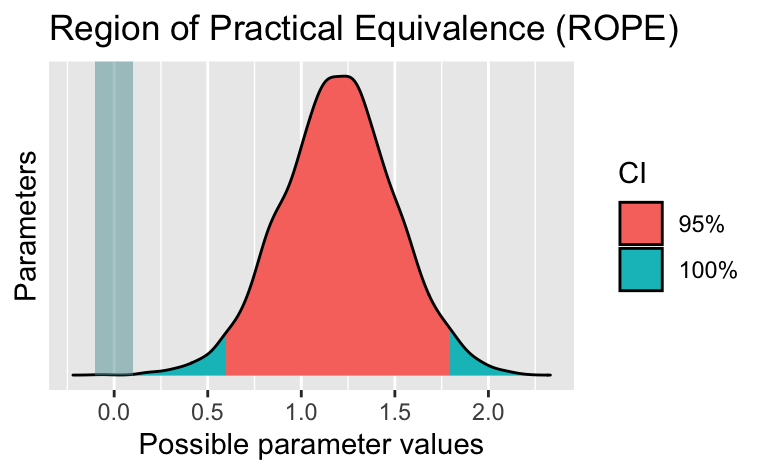
refresh = 0)rope(m2_mtcars)| Parameter | CI | ROPE_low | ROPE_high | ROPE_Percentage | Effects | Component |
|---|---|---|---|---|---|---|
| (Intercept) | 0.95 | -0.1 | 0.1 | 0.0023684 | fixed | conditional |
| am | 0.95 | -0.1 | 0.1 | 0.0000000 | fixed | conditional |
Im Standard bezieht sich rope() auf ein 95%-ETI, wie uns die Hilfe verrät.
Answerlist
- Falsch
- Richtig
- Falsch
- Falsch
Categories:
- rope
- bayes
- regression
- exam-22