priori-streuung

probability

simulation

distributions

bayes

qm2

qm2-pruefung2023

Published

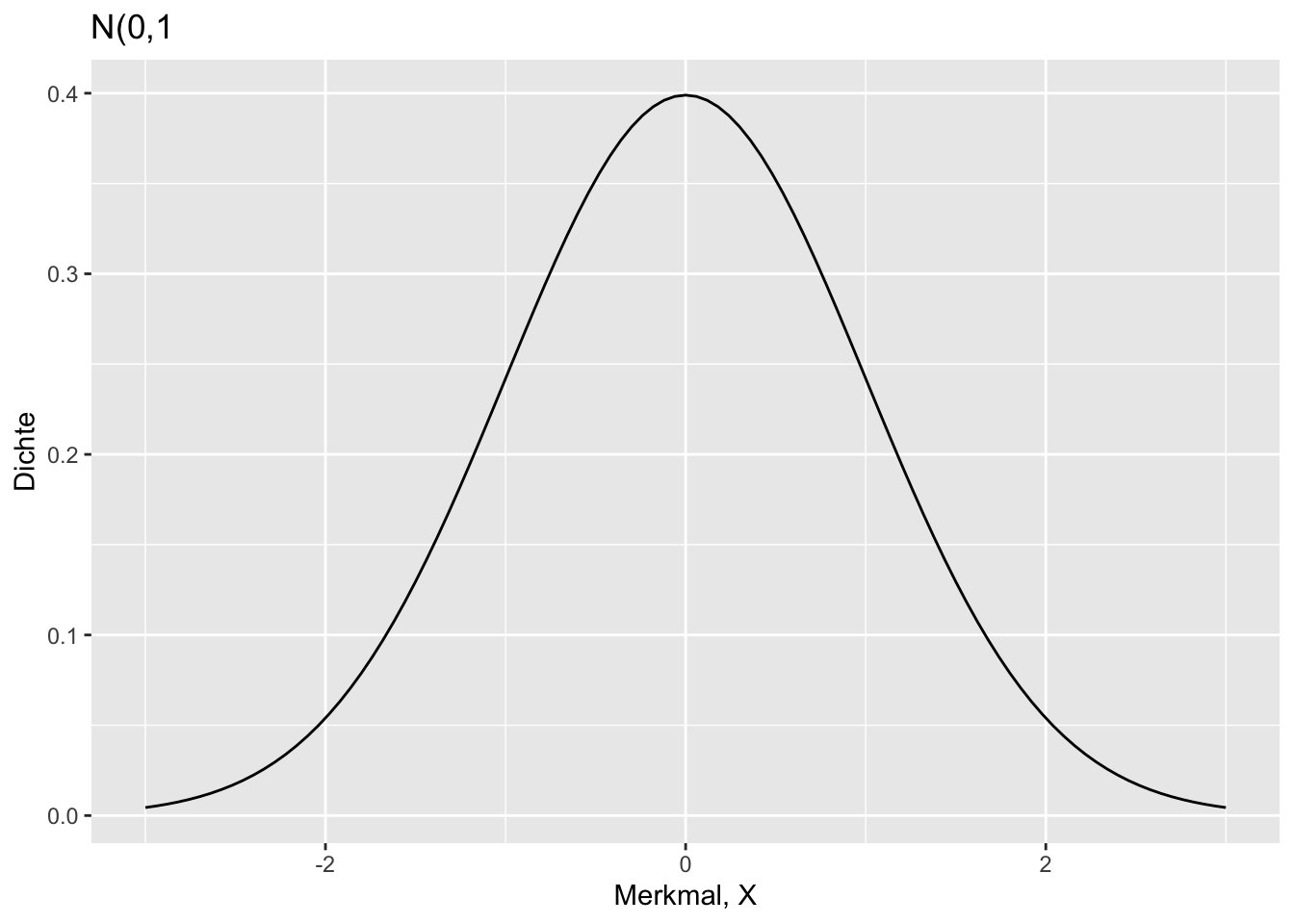
November 5, 2022

Exercise

Welche Verteilung ist (am besten) geeignet, um Streuung (\(\sigma\)) zu modellieren?

Answerlist

N(0,1)
N(1,1)
Exp(1)
Exp(0)
Exp(-1)

Solution

Answerlist

Falsch
Falsch
Wahr
Falsch
Falsch

Da Streuung \(\sigma\) per Definition positiv ist, kommt eine Verteilung, die negative Werte erlaubt, nicht in Frage. Die Normalverteilung scheidet also aus.

Die Rate der Exponentialverteilung regelt gleichzeitig Streuung und Mittelwert. Allerdings hat \(Exp(0)\) eine unendliche Streuung, was nicht wünschenswert ist. Eine negative Rate ist für die Exponentialverteilung nicht definiert.

Normalverteilungen:

\(N(0,1)\):

library(tidyverse)

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "N(0,1")

\(N(1,1)\):

ggplot(data = data.frame(x = c(-2, 4)), aes(x)) +
  stat_function(fun = dnorm, n = 101, args = list(mean = 1, sd = 1)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "N(1,1)")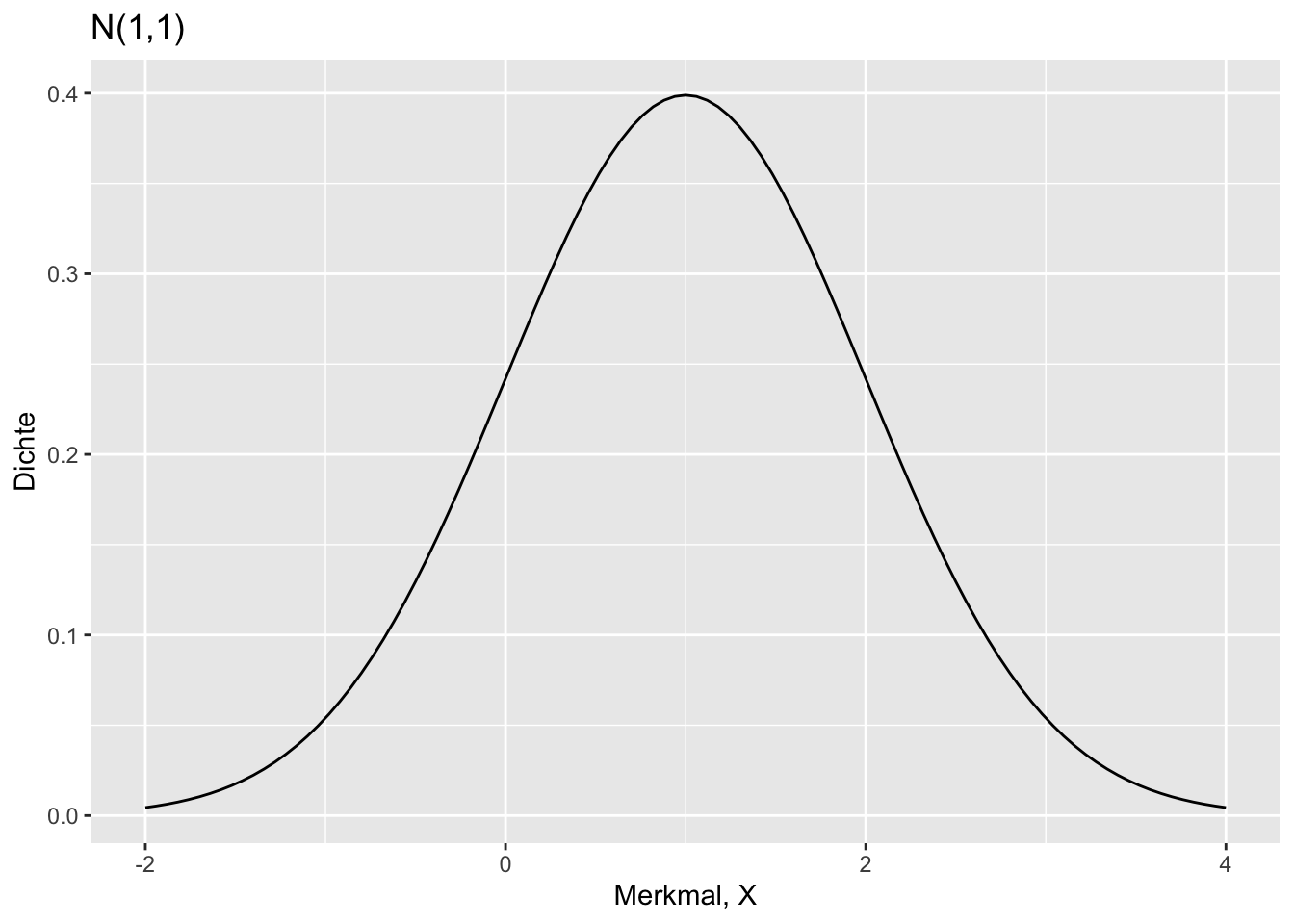

Exponentialverteilungen:

\(Exp(1)\):

ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(1)")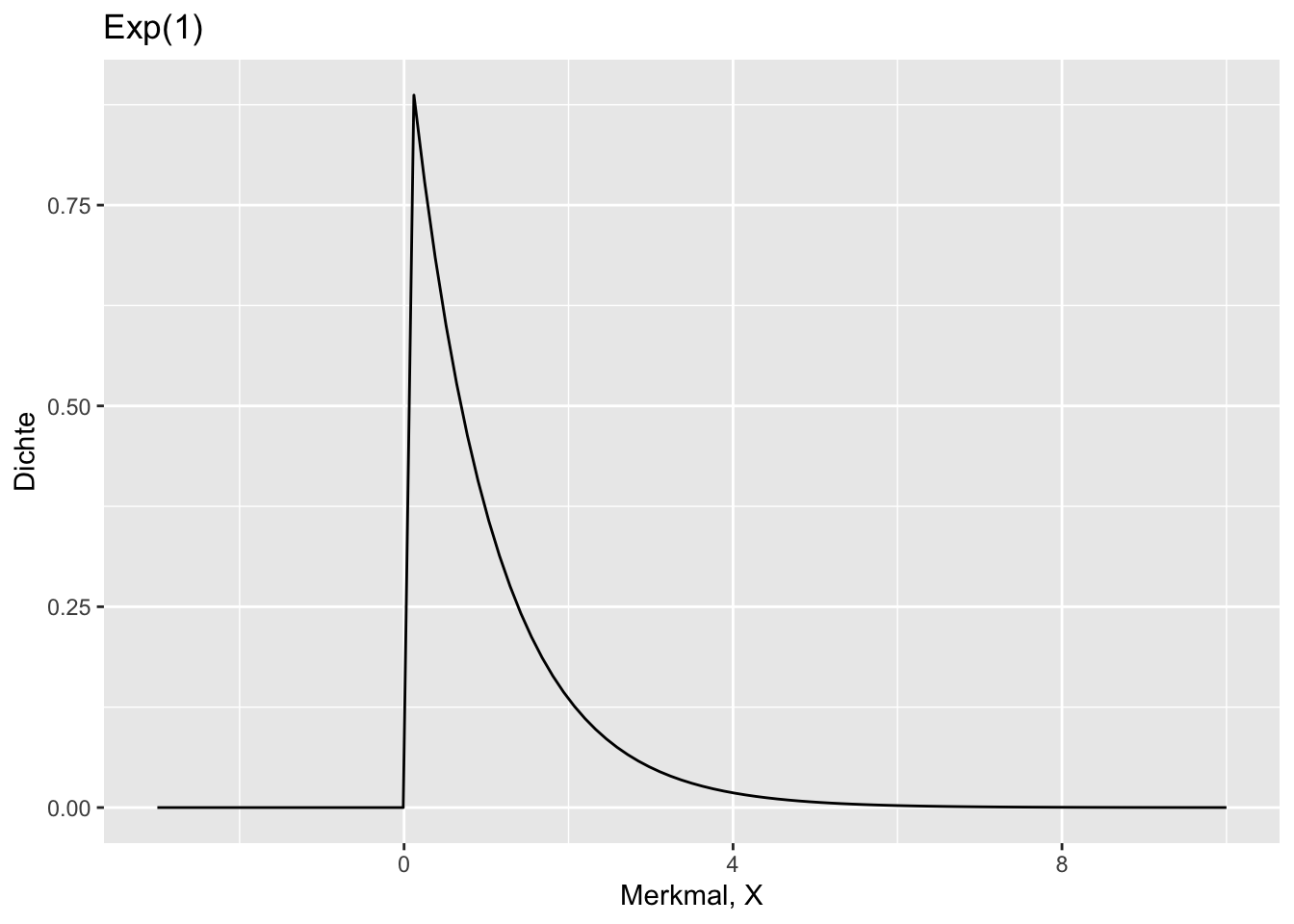

\(Exp(0)\):

ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101, args  = list(rate = 0)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(0)")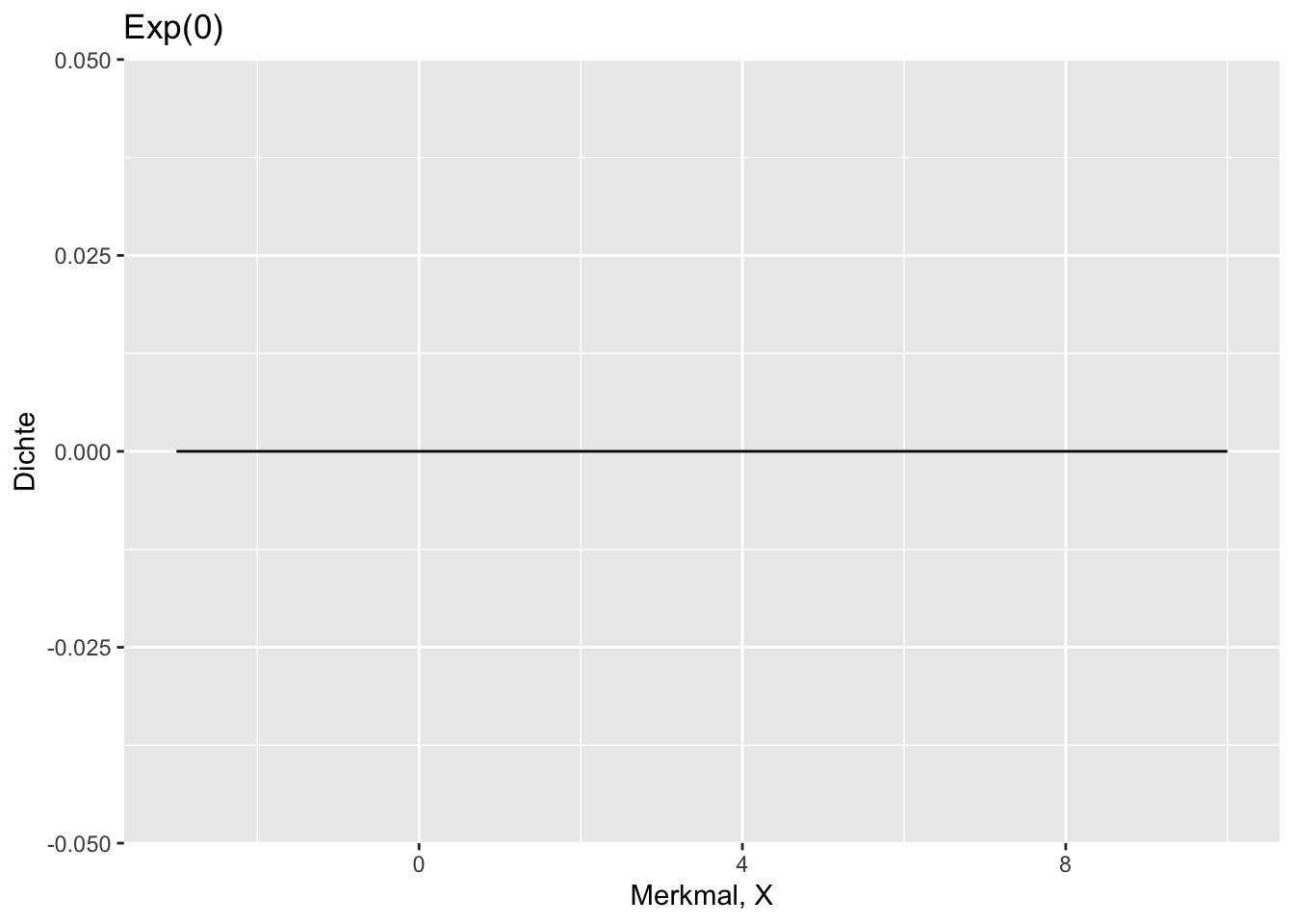

\(Exp(-1)\):

ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101, args  = list(rate = -1)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(-1)")

Categories:

probability
simulation
distributions
bayes

---
exname: geom-point1
extype: schoice
exsolution: 64
exshuffle: no
categories:
- probability
- simulation
- distributions
- bayes
- qm2
- qm2-pruefung2023
date: '2022-11-05'
title: priori-streuung

---




```{r libs, include = FALSE}
library(tidyverse)
```


```{r global-knitr-options, include=FALSE}
knitr::opts_chunk$set(fig.pos = 'H',
                      fig.asp = 0.618,
                      fig.width = 4,
                      fig.cap = "", 
                      fig.path = "",
                      echo = FALSE,
                      message = FALSE,
                      fig.show = "hold")
```






# Exercise

Welche Verteilung ist (am besten) geeignet, um Streuung ($\sigma$) zu modellieren?

Answerlist
----------
* N(0,1)
* N(1,1)
* Exp(1)
* Exp(0)
* Exp(-1)




</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>

# Solution



Answerlist
----------


* Falsch
* Falsch
* Wahr
* Falsch
* Falsch

Da Streuung $\sigma$ per Definition positiv ist, 
kommt eine Verteilung, die negative Werte erlaubt, nicht in Frage. 
Die Normalverteilung scheidet also aus.

Die Rate der Exponentialverteilung regelt gleichzeitig Streuung und Mittelwert.
Allerdings hat $Exp(0)$ eine unendliche Streuung, was nicht wünschenswert ist.
Eine negative Rate ist für die Exponentialverteilung nicht definiert.



Normalverteilungen:

A)

</br>

$N(0,1)$:

```{r}
library(tidyverse)

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "N(0,1")
```


</br>

B)


$N(1,1)$:


```{r}
ggplot(data = data.frame(x = c(-2, 4)), aes(x)) +
  stat_function(fun = dnorm, n = 101, args = list(mean = 1, sd = 1)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "N(1,1)")
```


Exponentialverteilungen:

C)

$Exp(1)$:


```{r}
ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(1)")
```


D)

$Exp(0)$:


```{r}
ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101, args  = list(rate = 0)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(0)")
```



E)

$Exp(-1)$:


```{r}
ggplot(data = data.frame(x = c(-3, 10)), aes(x)) +
  stat_function(fun = dexp, n = 101, args  = list(rate = -1)) +
  labs(y = "Dichte", x = "Merkmal, X",
       title = "Exp(-1)")
```





---

Categories: 

- probability
- simulation
- distributions
- bayes