library(tidyverse) # Datenjudo
library(rstanarm) # Bayes-Inferenz
library(easystats) # Komfortpigs2
Aufgabe
Laden Sie den Datensatz toothgrowth, z.B. von dieser Quelle. In dem Datensatz sind die Daten eines einfaches Experiments berichtet.
In dem Experiment wird der (kausale) Effekt verschiedener Darreichungsformen und Konzentrationen von Vitamin C auf das Zahnwachstum von Meerschweinchen untersucht.
Forschungsfrage:
Hat die Dosis (dose) einen (kausalen) Effekt auf die AV, Zahnlänge (len)?
Wir gehen mal einfach davon aus, dass der Faktor experimentell (also randomisiert und auf Störeffekte hin kontrollliert) veraeicht wurde. Sonst wäre eine Kausalinterpretation nicht (ohne Weiteres) möglich.
Aufgabe: Berechnen Sie die Breite eines 95%-HDI für den Effekt!
Lösung
- Schritt: Modell berechnen
lm2 <- stan_glm(len ~ dose, data = d,
seed = 42,
refresh = 0)Zur Erinnerung: Bei der Regressionsformel gilt immer av ~ uv.
- Schritt: Posteriori-Verteilung betrachten
Mit parameters() kriegt man einen guten Überblick über die Modellparameter:
parameters(lm2)| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS | Prior_Distribution | Prior_Location | Prior_Scale |
|---|---|---|---|---|---|---|---|---|---|---|
| (Intercept) | 7.404367 | 0.95 | 4.841285 | 9.957746 | 1 | 0.9994476 | 3881.400 | normal | 18.81333 | 19.12329 |
| dose | 9.759631 | 0.95 | 7.808405 | 11.758601 | 1 | 0.9994879 | 4144.048 | normal | 0.00000 | 30.40886 |
Das Modell zeigt einen positiven Effekt für dose:
Pro Einheit von dose steigt die Zahnlänge (len) um ca. 8-12 mm im Schnitt (laut unserem Modell).
Null ist nicht im Intervall enthalten; die Nullhypothese ist demnach auszuschließen (falls das jemanden interessiert). Man sagt, man verwirft die Nullhypothese (oder weist sie zurück).
Das können wir auch plotten:
plot(parameters(lm2))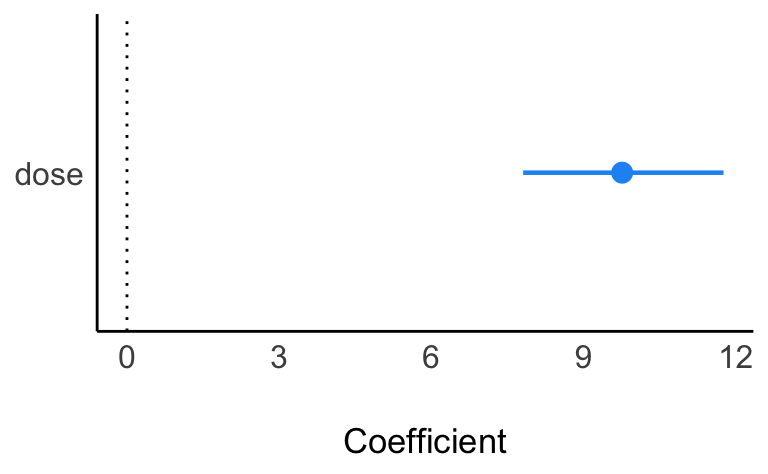
Man kann sich auch ein HDI direkt ausgeben, ohne die sonstigen Informationen, die parameters() ausgibt:
hdi(lm2, ci = .95)| Parameter | CI | CI_low | CI_high | Effects | Component |
|---|---|---|---|---|---|
| (Intercept) | 0.95 | 4.959402 | 10.06051 | fixed | conditional |
| dose | 0.95 | 7.769051 | 11.70019 | fixed | conditional |
Wie wir sehen, wird im Standard ein 95%-Intervall berichtet, wie in der Aufgabenstellung verlangt.
Wieder sehen wir, die Null ist nicht im Intervall enthalten. Null ist also kein plausibler Wert für den gesuchten Effekt (laut unserem Modell).
Schauen wir uns mal zum Vergleich die Stichproben-Daten an:
d %>%
ggplot(aes(y = len, x = dose)) +
geom_point() +
geom_smooth(method = "lm")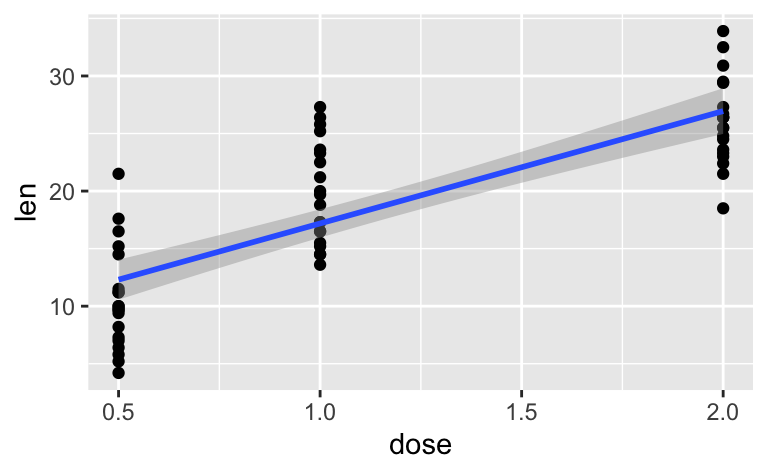
Man sieht deutlich einen positiven Effekt: Die Regressionsgerade steigt.
Die Breite des Schätzintervalls für den Effekt beträgt also:
sol <- 11.70 - 7.77
sol[1] 3.93Categories:
- bayes
- ~
- regression
- exam-22