penguins-stan-06

Aufgabe

Wir untersuchen Einflussfaktoren bzw. Prädiktoren auf das Körpergewicht von Pinguinen. In dieser Aufgabe untersuchen wir in dem Zusammenhang den Zusammenhang des Geschlechts (als UV) und Körpergewicht (als AV).

Aufgabe:

Wie groß ist der statistische Einfluss der UV auf die AV?

1. Geben Sie den Punktschätzer des Effekts an!
2. Geben Sie die Breite eines 90%-HDI an (zum Effekt)!
3. Wie groß ist die Wahrscheinlichkeit, dass der Effekt vorhanden ist (also größer als Null ist), die “Effektwahrscheinlichkeit”?
4. Wie groß ist die Wahrscheinlichkeit, dass der Effekt substanziell vorhanden ist (also größer als 0.5 ist), die “Substantielle Effektwahrscheinlichkeit”?

Hinweise:

• Nutzen Sie die folgende Analyse als Grundlage Ihrer Antworten.
• Beachten Sie die Hinweise des Datenwerks.

Setup:

library(tidyverse)
library(easystats)
library(rstanarm)

data("penguins", package = "palmerpenguins")

Dafür ist folgende Analyse gegeben.

Setup

library(rstanarm)
library(easystats)
library(tidyverse)
library(ggpubr)

Modell und Hypothese

Die Hypothese kann man wie folgt formalisieren:

\[\text{weight}_{m} > \text{weight}_{f},\]

“Der Mittelwert des Gewichts der männliche Tiere ist größer als das der weiblichen (female) Tiere”.

Die Prioris übernehmen wir vom Stan-Golem.🤖

🤖 Beep, beep!

👩‍🏫 An die Arbeit, Stan-Golem!

Alternativ könnten Sie den Datensatz als CSV-Datei importieren:

d_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv"
penguins <- data_read(d_path)  # oder z.B. mit read_csv 

Ein Blick in die Daten zur Kontrolle, ob das Importieren richtig funktioniert hat:

glimpse(penguins)

Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

Wir entfernen noch alle fehlenden Werte:

penguins_nona <- 
  penguins |> 
  filter(sex == "female" | sex == "male")

penguins_nona$sex |> unique()

[1] male   female
Levels: female male

m1 <- stan_glm(body_mass_g ~  sex,  # Regressionsgleichung
               data = penguins_nona, #  Daten
               seed = 42,  # Reproduzierbarkeit
               refresh = 0)  # nicht so viel Output

m1_params <- parameters(m1, ci_method = "hdi", ci = .9)
m1_params

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	3862.7923	0.9	3769.5656	3956.3636	1	1.000089	3572.529	normal	4207.057	2013.040
sexmale	682.2466	0.9	547.2974	816.9999	1	1.000397	3652.939	normal	0.000	4020.192

Lösung

Punktschätzer

Der Punktschätzer ist in der Spalte Median in der Tabelle parameters zu finden. Sein Wert ist:

[1] 682.2466

Hier ist die Post-Verteilung des Effekts:

m1_params |> plot()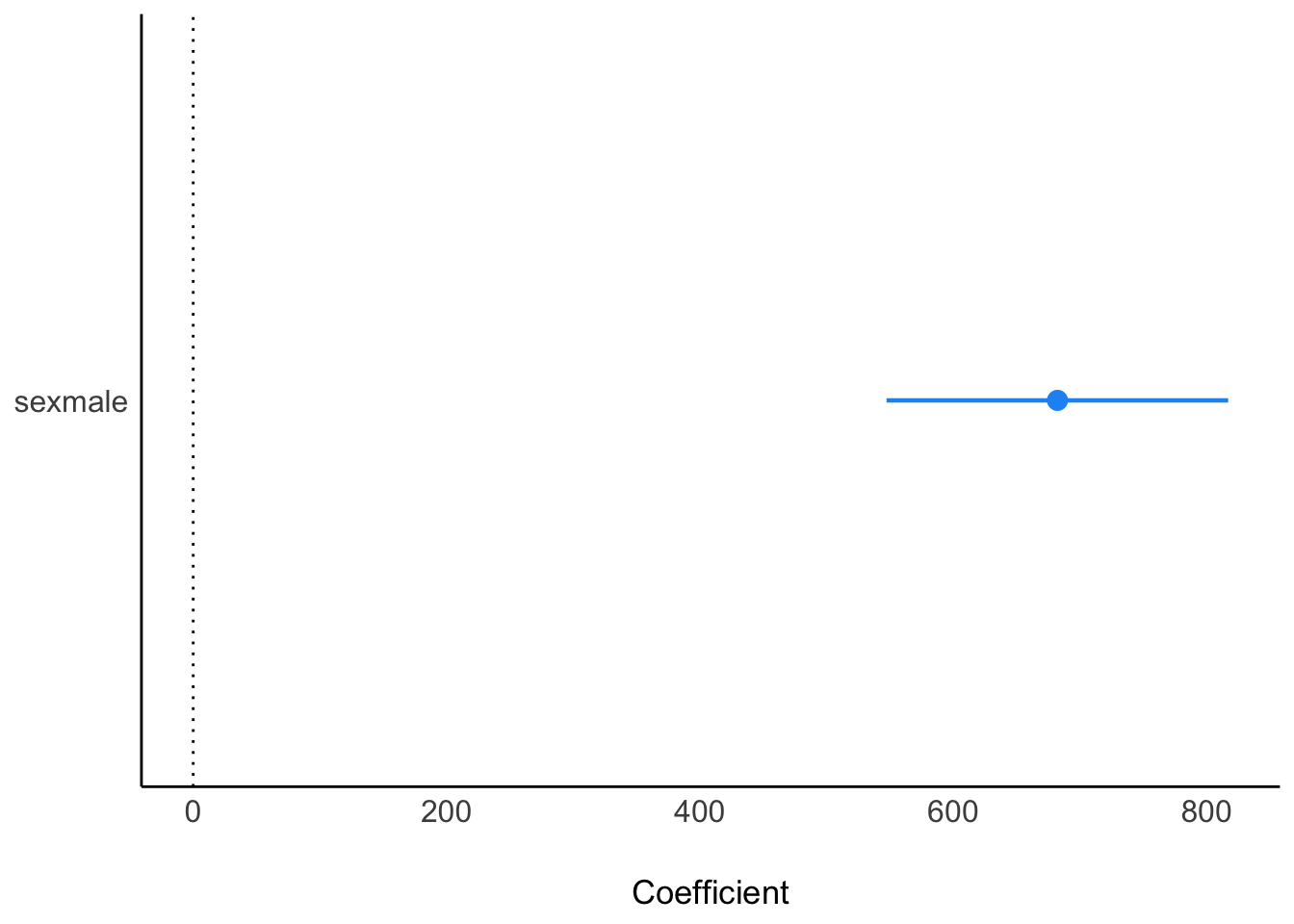

Alternative Visualisierung:

hdi(m1, ci = .9) |> plot()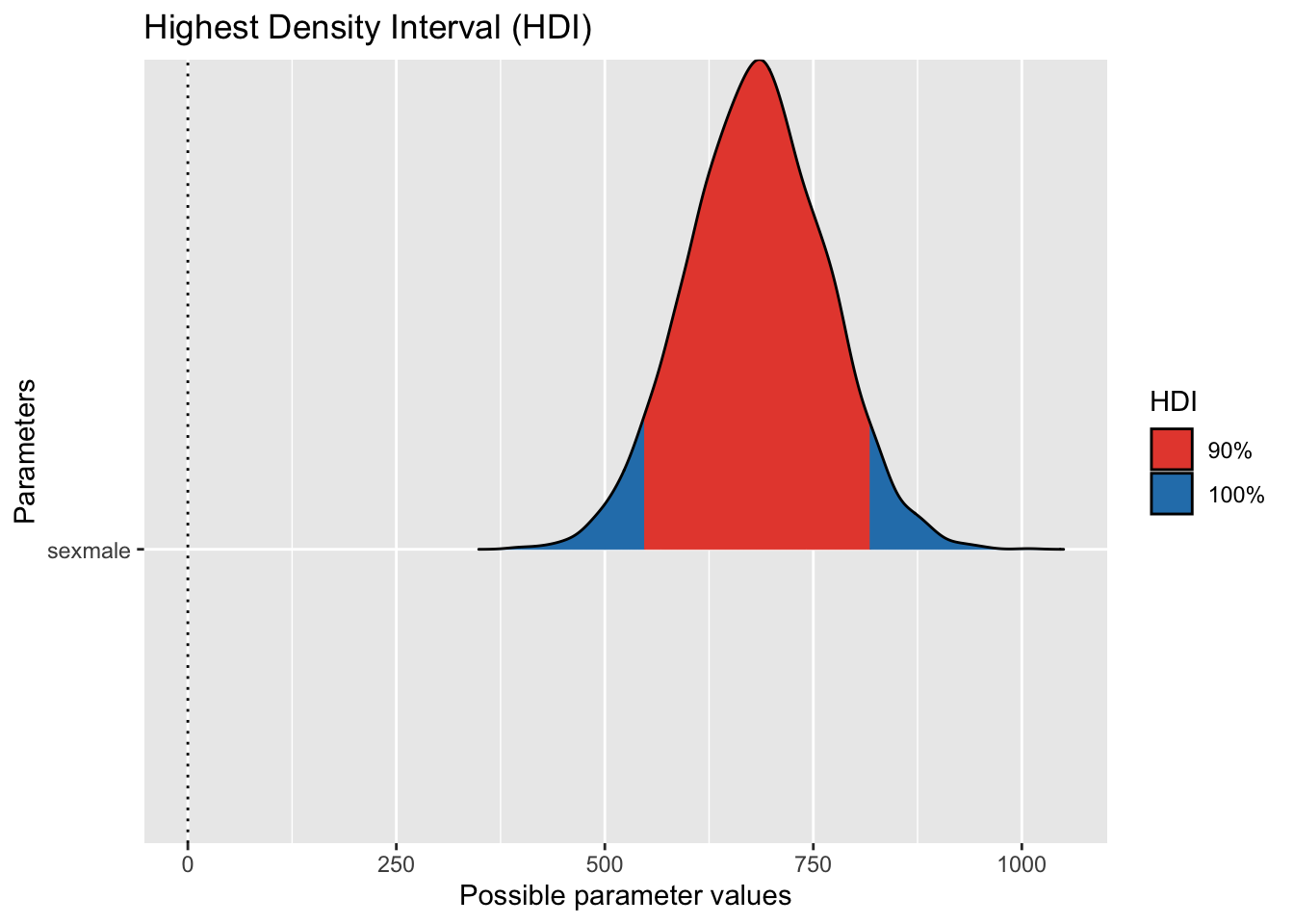

Breite des Intervalls

Dazu liest man die Intervallgrenzen (90% CI) in der richtigen Zeile ab (Tabelle parameters).

Obere Grenze: 816.9999226.

Untere Grenze: 547.2974274.

Differenz = Obere_Grenze - Untere_Grenze:

[1] 269.7025

Einheit: mm

Effektwahrscheinlichkeit

Man erkennt schon im Diagramm zum Konfidenzintervall, dass 100% des Intervalls positiv ist. Daher ist die Effektwahrscheinlichkeit auch positiv.

Man kann diesen Wert aus der Tabelle oben (Ausgabe von parameters()) einfach in der Spalte pd ablesen. pd steht für probability of direction, s. Details hier.

Oder so, ist auch einfach:

pd_m1 <- p_direction(m1) # aus Paket easystats
pd_m1

Parameter	pd	Effects	Component
(Intercept)	1	fixed	conditional
sexmale	1	fixed	conditional

Und plotten ist meist hilfreich: plot(pd_m1).

plot(pd_m1)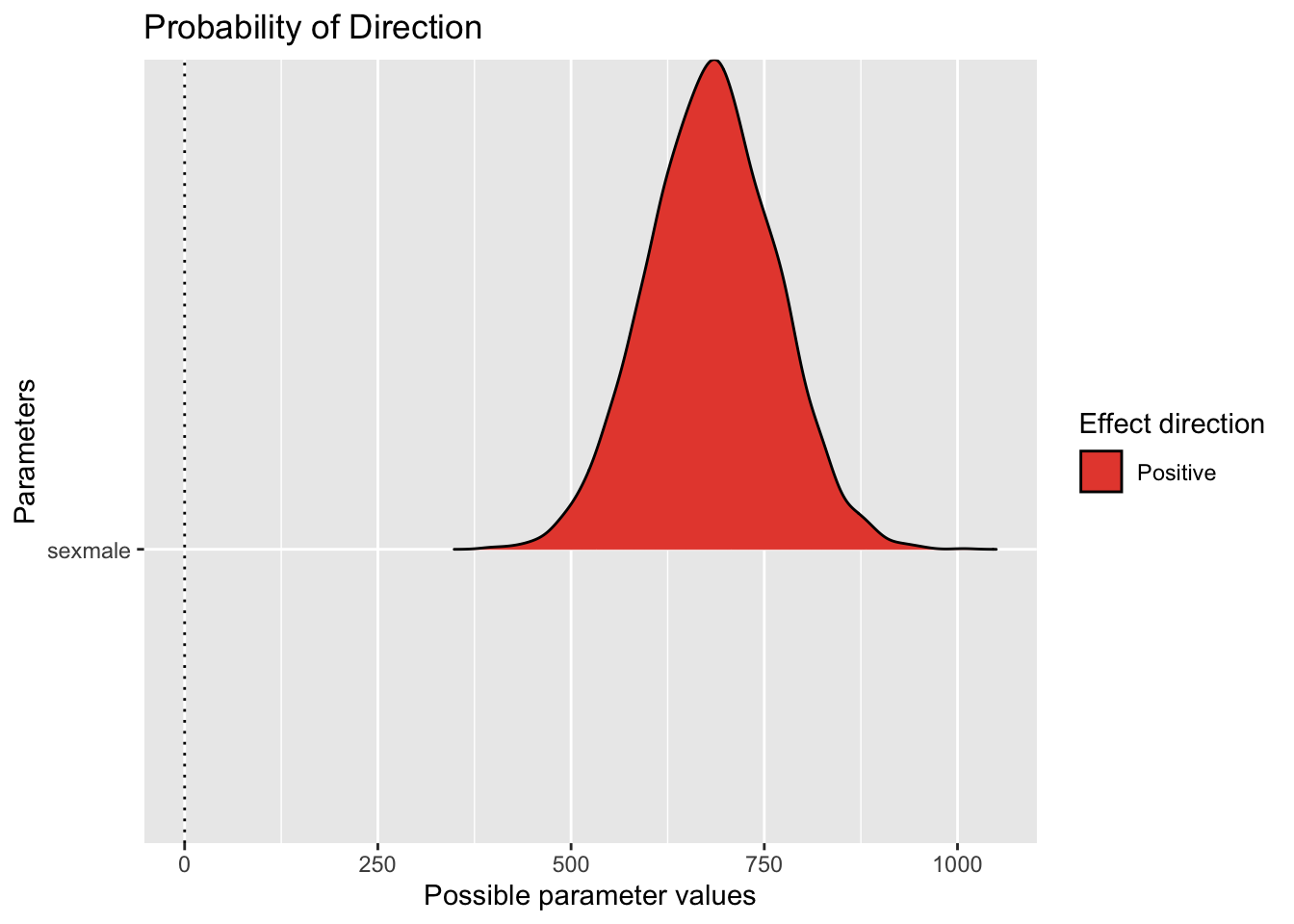

Substanzielle Effektwahrscheinlichkeit

Die Frage ist nichts anderes als nach ROPE zu fragen.

rope_m1 <- rope(m1, range = c(-500,+500))
rope_m1

Parameter	CI	ROPE_low	ROPE_high	ROPE_Percentage	Effects	Component
(Intercept)	0.95	-500	500	0	fixed	conditional
sexmale	0.95	-500	500	0	fixed	conditional

plot(rope_m1)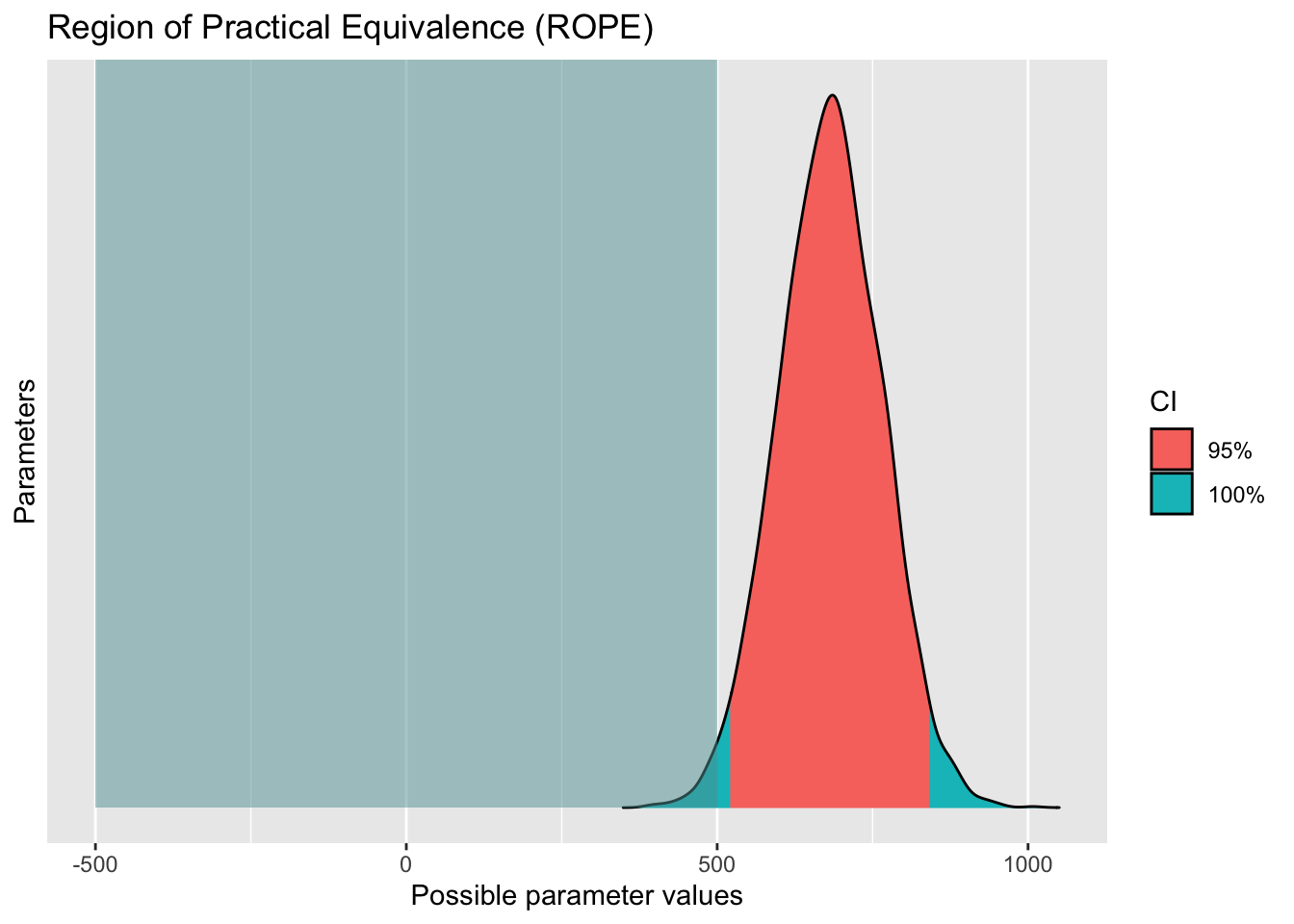

Das 90%-Intervall ist knapp außerhalb des ROPE.

Wir können die ROPE-Hypothese daher zurückweisen.