penguins-interact2

Aufgabe

Eine Forscherin untersucht, ob das Geschlecht eines Pinguins den Einfluss der Flossenlänge (Flipper, mm) auf das Körpergewicht (g) des Tieres moderiert.

Hinweise:

• Nutzen Sie die folgende Analyse als Grundlage Ihrer Antworten.
• Beachten Sie die Hinweise des Datenwerks.
• Unter “substanziell” sei ein Effekt von mind. 100 g verstanden.

Setup

library(tidyverse)
library(easystats)
library(rstanarm)
library(ggpubr)
data("penguins", package = "palmerpenguins")

Dafür ist folgende Analyse gegeben.

Wir entfernen zunächst alle fehlenden Werte:

penguins_nona <- 
  penguins |> 
  filter(sex == "female" | sex == "male")

penguins_nona$sex |> unique()

[1] male   female
Levels: female male

Zur besseren Interpretierbarkeit standardisieren wir die (metrische) UV und AV:

penguins_nona_z <- 
  penguins_nona |> 
  standardise(select = c("flipper_length_mm", "body_mass_g"),
              append = TRUE)

m_interaction <- stan_glm(body_mass_g_z ~  sex + flipper_length_mm_z + sex:flipper_length_mm_z,  # Regressionsgleichung
               data = penguins_nona_z, #  Daten
               seed = 42,  # Reproduzierbarkeit
               refresh = 0)  # nicht so viel Output

m_interaction_params <- parameters(m_interaction, ci_method = "hdi", ci = .9)
m_interaction_params

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	-0.2162622	0.9	-0.2773580	-0.1604693	1.0000	1.000844	3367.317	normal	0	2.500000
sexmale	0.4308790	0.9	0.3469589	0.5114735	1.0000	0.999997	3702.528	normal	0	4.992690
flipper_length_mm_z	0.8210854	0.9	0.7553752	0.8817705	1.0000	1.000643	2564.870	normal	0	2.500000
sexmale:flipper_length_mm_z	-0.0059798	0.9	-0.0873804	0.0805173	0.5385	1.001081	2372.781	normal	0	3.346997

plot(m_interaction_params)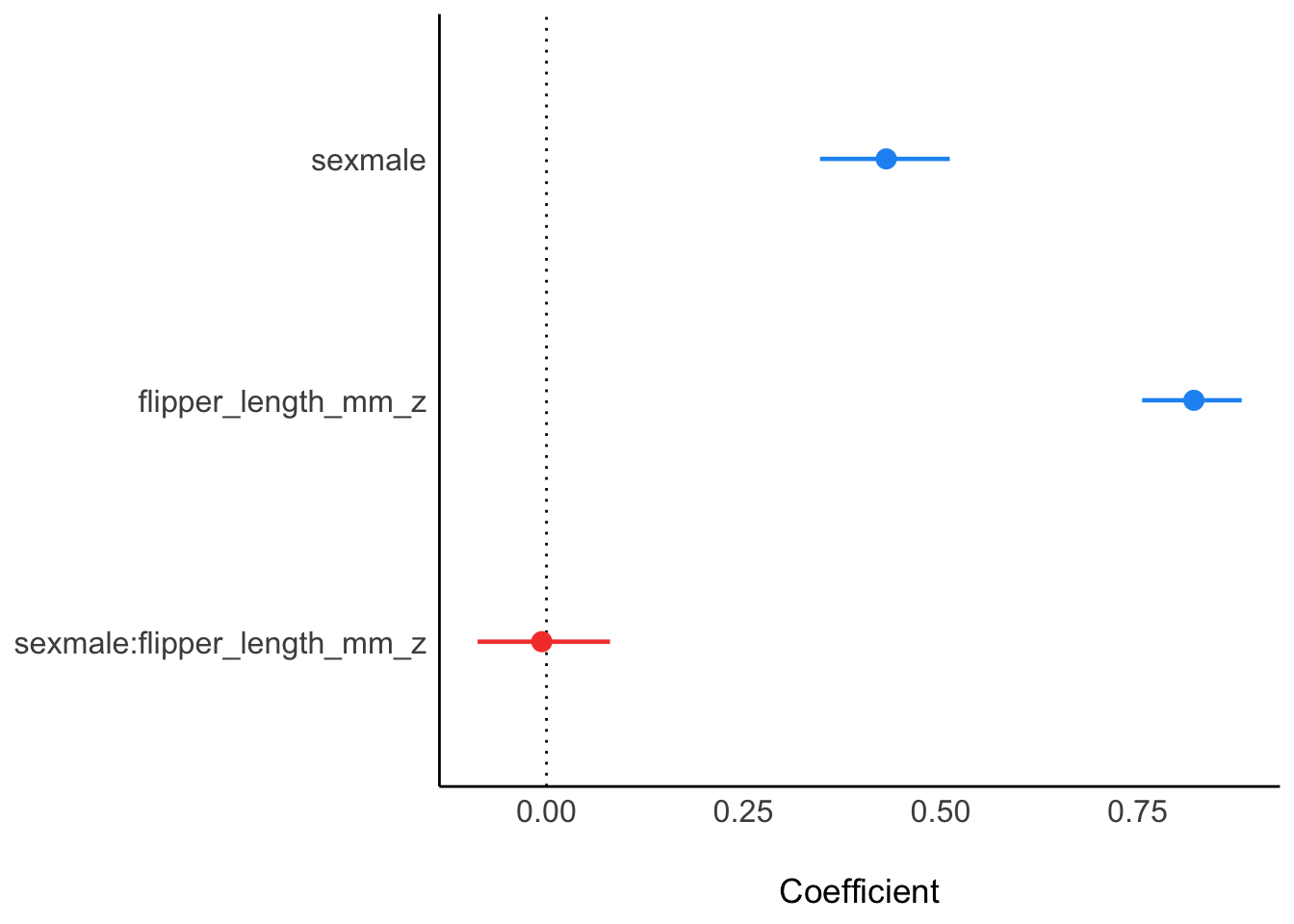

1. Männliche Tiere sind im Schnitt leichter.
2. Es liegt ein Interaktionseffekt vor; die Nullhypothese zum Interaktionseffekt kann verworfen werden.
3. Es liegt kein Interaktionseffekt vor; die Nullhypothese zum Interaktionseffekt kann nicht verworfen werden.
4. Pro Einheit an Flossenlänge (flipper_lengh_mm_z) steigt das Körpergewicht um ca. 0.8 Einheiten bei männlichen Tieren; bei weiblichen Tieren steigt es um ca. 0.4 + 0.8 = 1.2 Einheiten.
5. Pro SD-Einheit an Flossenlänge (flipper_lengh_mm_z) steigt das Körpergewicht um ca. 0.8 SD-Einheiten bei männlichen Tieren; bei weiblichen Tieren steigt es um ca. 0.4 + 0.8 = 1.2 SD-Einheiten.

Lösung

C