nasa06

data

eda

lagemaße

string

Published

May 9, 2023

Aufgabe

Viele Quellen berichten Klimadaten unserer Erde, z.B. auch National Aeronautics and Space Administration - Goddard Institute for Space Studies.

Von dieser Quelle beziehen wir diesen Datensatz.

Die Datensatz sind auf der Webseite wie folgt beschrieben:

Tables of Global and Hemispheric Monthly Means and Zonal Annual Means

Combined Land-Surface Air and Sea-Surface Water Temperature Anomalies (Land-Ocean Temperature Index, L-OTI)

The following are plain-text files in tabular format of temperature anomalies, i.e. deviations from the corresponding 1951-1980 means.

Global-mean monthly, seasonal, and annual means, 1880-present, updated through most recent month: TXT, CSV

Starten Sie zunächst das R-Paket tidyverse falls noch nicht geschehen.

library(tidyverse)

Importieren Sie dann die Daten:

data_path <- "https://data.giss.nasa.gov/gistemp/tabledata_v4/GLB.Ts+dSST.csv"
d <- read_csv(data_path, skip = 1)

Wir lassen die 1. Zeile des Datensatzes aus (Argument skip), da dort Metadaten stehen, also keine Daten, sondern Informationen (Daten) zu den eigentlichen Daten.

Aufgaben

Fassen Sie immer 10 Jahre (eine Dekade) an Jahren zusammen.
Präsentieren Sie gängige Statistiken pro Dekade für alle Monate.

Hinweise:

Sie müssen zuerst die Dekade als neue Spalte berechnen.
Treffen Sie Annahmen, wo nötig.
Beachten Sie die Hinweise.

Lösung

Tabelle in die Lang-Form bringen:

d_long <- 
  d %>% 
  select(Year, Jan:Dec) %>% 
  mutate(across(Jan:Dec, as.numeric)) %>% 
  pivot_longer(cols = Jan:Dec, values_to = "temp", names_to = "month")

Ein Blick in die Tabelle:

head(d_long)

# A tibble: 6 × 3
   Year month  temp
  <dbl> <chr> <dbl>
1  1880 Jan   -0.18
2  1880 Feb   -0.24
3  1880 Mar   -0.09
4  1880 Apr   -0.16
5  1880 May   -0.1 
6  1880 Jun   -0.21

Dekade berechnen:

d_long2 <-
  d_long %>% 
  mutate(decade = round(Year/10) * 10)

tail(d_long2)  # letzten paar Zeilen der Tabelle "d_long2"

# A tibble: 6 × 4
   Year month  temp decade
  <dbl> <chr> <dbl>  <dbl>
1  2024 Jul      NA   2020
2  2024 Aug      NA   2020
3  2024 Sep      NA   2020
4  2024 Oct      NA   2020
5  2024 Nov      NA   2020
6  2024 Dec      NA   2020

d_summarized <-
d_long2 %>% 
  group_by(decade, month) %>% 
  summarise(temp_mean = mean(temp, na.rm = TRUE),
            temp_sd = sd(temp, na.rm = TRUE))

# A tibble: 6 × 4
# Groups:   decade [1]
  decade month temp_mean temp_sd
   <dbl> <chr>     <dbl>   <dbl>
1   1880 Apr      -0.213   0.175
2   1880 Aug      -0.157   0.113
3   1880 Dec      -0.185   0.118
4   1880 Feb      -0.17    0.187
5   1880 Jan      -0.203   0.240
6   1880 Jul      -0.173   0.132

Zum Visualisieren gibt es meist viele Wege. Hier ist ein Weg mit ggplot2:

d_summarized %>% 
  ggplot(aes(x = decade, y = temp_mean)) +
  geom_point(color = "darkblue") +
  geom_errorbar(aes(ymin = temp_mean - temp_sd, ymax = temp_mean + temp_sd)) +
  geom_line(alpha = .7) +
  facet_wrap(~ month) +
  labs(caption = "Fehlerbalken zeigen plus/minus 1 SD")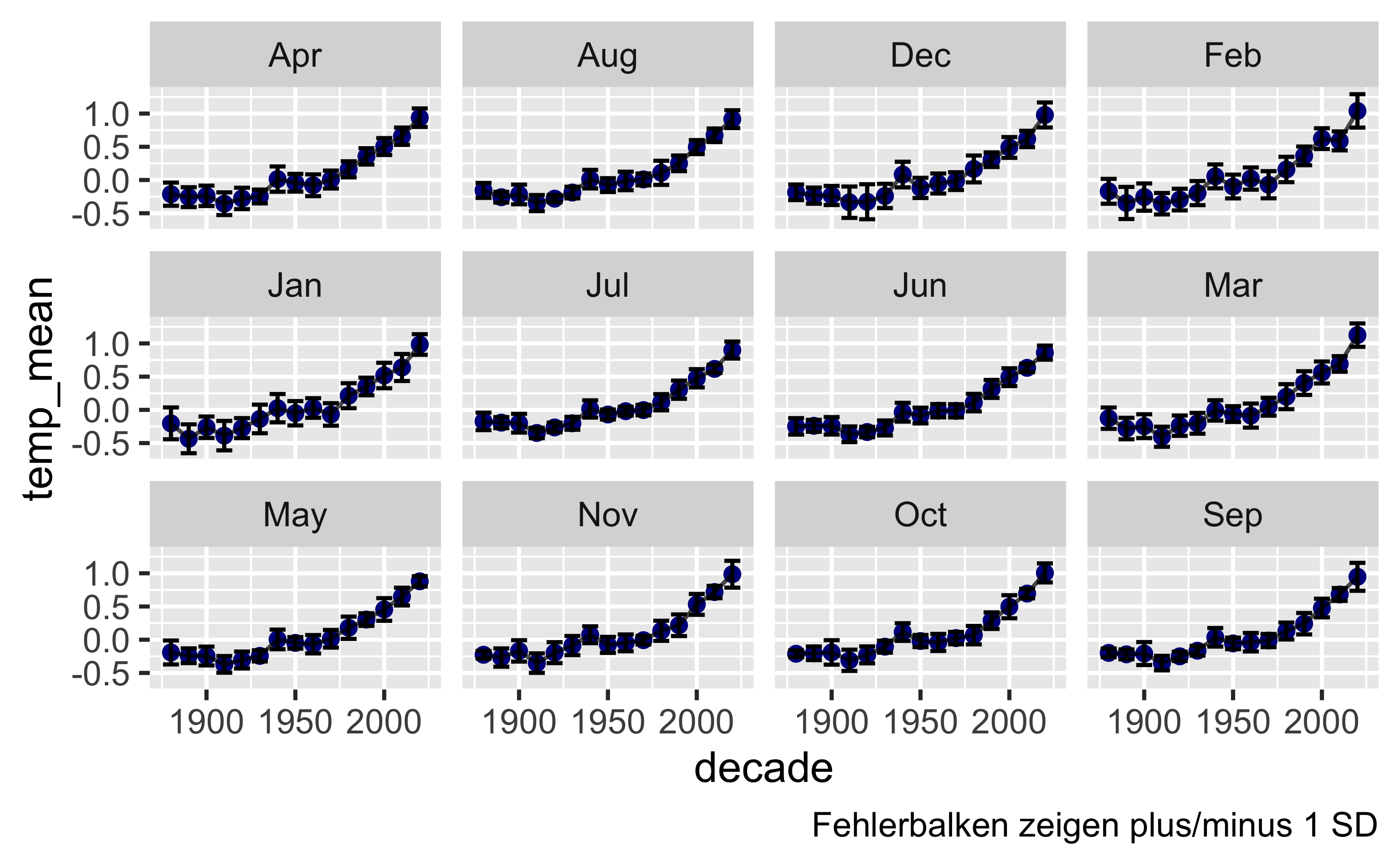

Monate zu einem Jahreswert zusammen:

d_summarized2 <- 
  d_summarized %>% 
  group_by(decade) %>% 
  summarise(temp_mean = mean(temp_mean),
            temp_sd = sd(temp_sd))

d_summarized2

# A tibble: 15 × 3
   decade temp_mean temp_sd
    <dbl>     <dbl>   <dbl>
 1   1880  -0.192    0.0580
 2   1890  -0.265    0.0540
 3   1900  -0.226    0.0216
 4   1910  -0.357    0.0452
 5   1920  -0.272    0.0580
 6   1930  -0.191    0.0470
 7   1940   0.0324   0.0289
 8   1950  -0.0671   0.0357
 9   1960  -0.0341   0.0308
10   1970  -0.00759  0.0401
11   1980   0.145    0.0304
12   1990   0.308    0.0236
13   2000   0.51     0.0235
14   2010   0.655    0.0401
15   2020   0.963    0.0484

Alternativ können Sie zum Visualisieren der Daten z.B. das Paket ggpubr nutzen:

library(ggpubr)
ggscatter(d_summarized2, x = "decade", y = "temp_mean", add = "reg.line")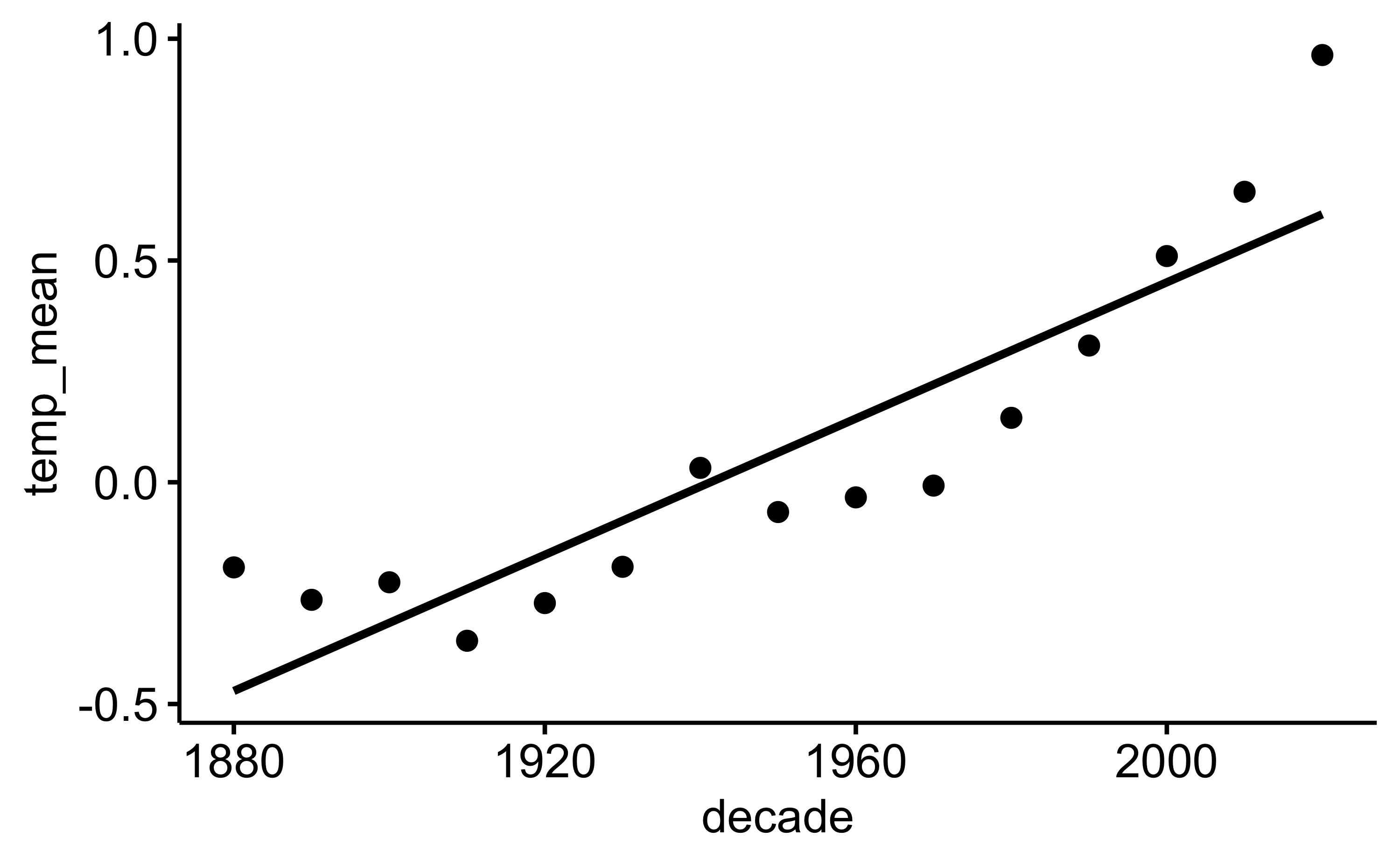

Oder auch mit den Facetten pro Monat:

ggscatter(d_summarized, x = "decade", y = "temp_mean", add = "reg.line",
          facet.by = "month")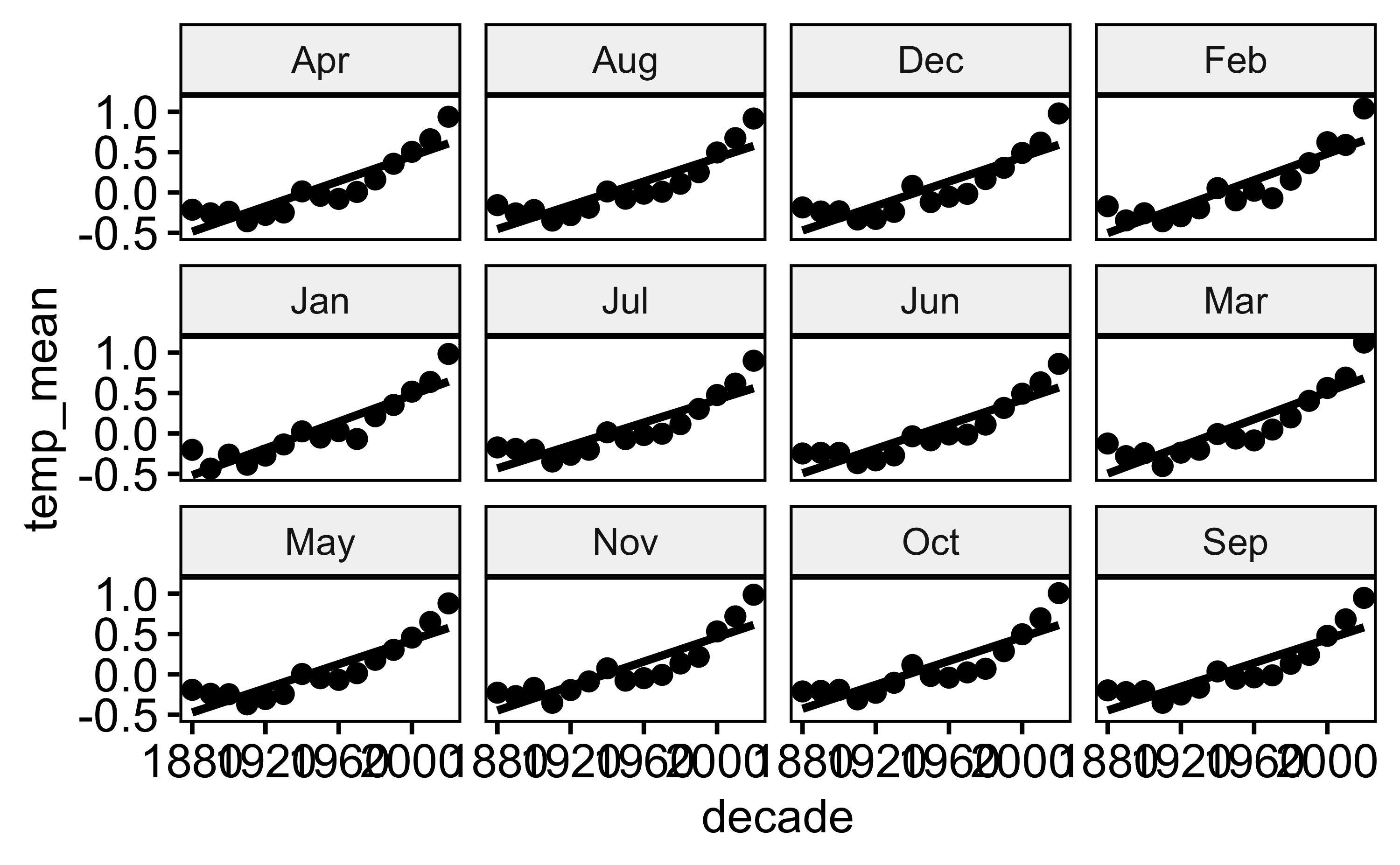

Ähnlich sieht es mit DataExplorer aus:

library(DataExplorer)
d_summarized2 |> 
  select(temp_mean, decade) |> 
  plot_scatterplot(by = "decade")

d_summarized2 |> 
  select(temp_sd, decade) |> 
  plot_scatterplot(by = "decade")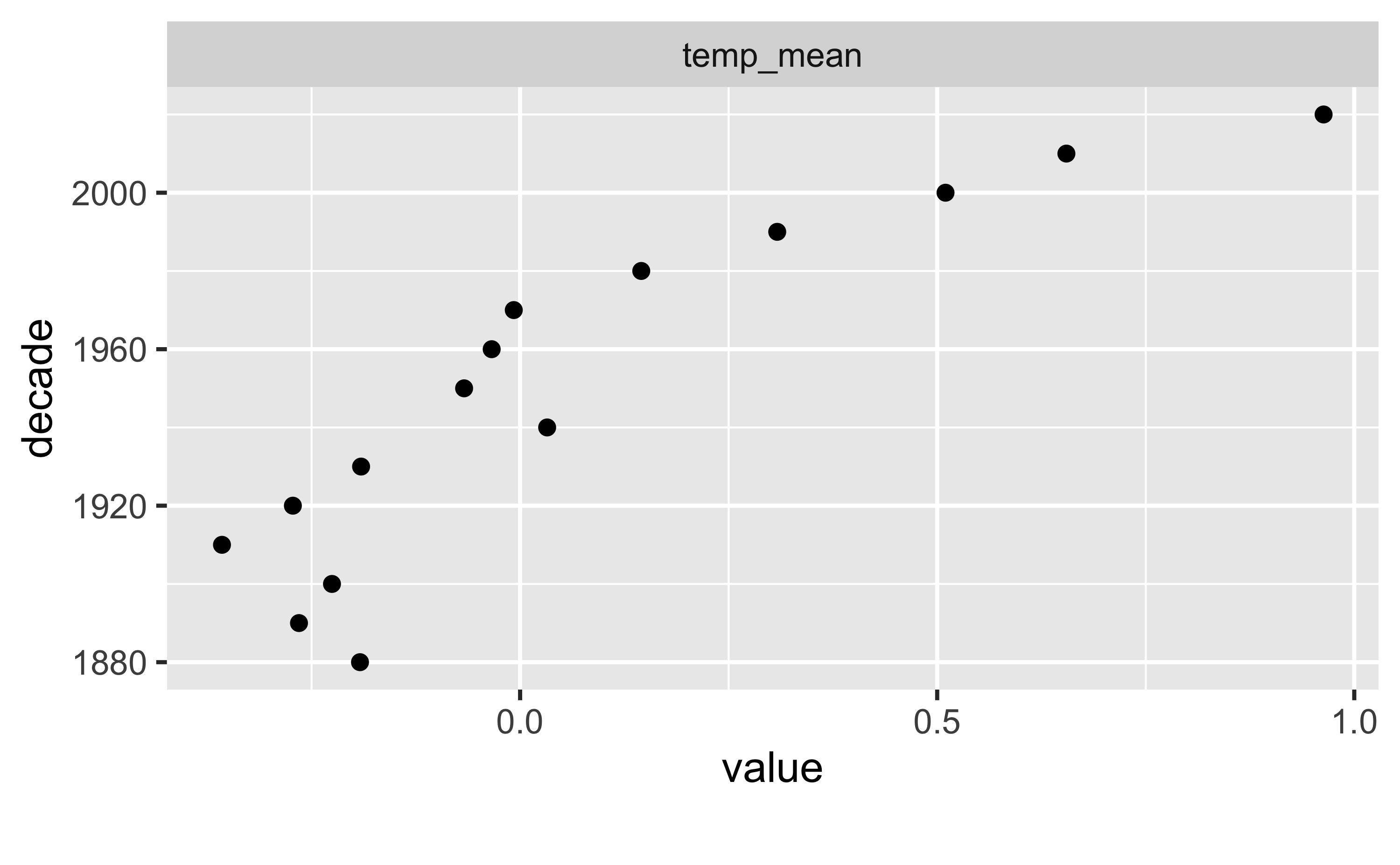

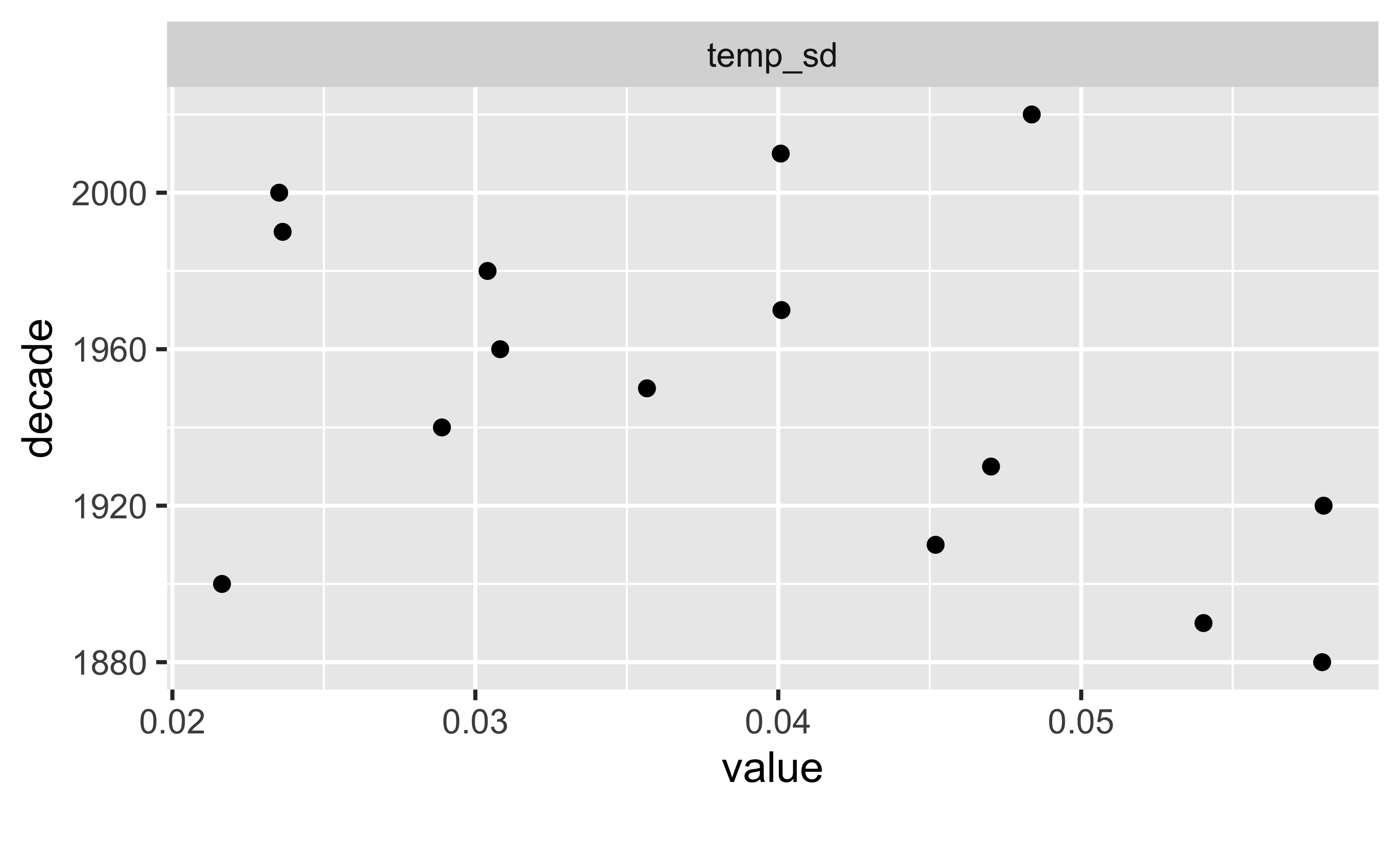
Die weltweilte Temperatur steigt. Bleibt u.a. die Frage, ob eine lineare Funktion angemessen ist, oder ob die Steigung nicht vielleicht prozentual steigt (das wäre eine exponenzielle Steigerung)?

Falls Sie Teile der R-Syntax nicht kennen: Machen Sie sich nichts daraus. 😄

Categories:

data
eda
lagemaße
string