data(mtcars)
library(tidyverse)
library(rstanarm)
library(bayesplot) # Histogramm-Plots für Post-Vert.
library(bayestestR) # ropemtcars-rope1
bayes
regression
post
exam-22
qm2
mtcars
qm2-pruefung2023
Exercise
Im Datensatz mtcars: Ist der (mittlere) Unterschied im Spritverbrauch zwischen den beiden Stufen von vs vernachlässigbar klein?
Definieren Sie “vernachlässigbar klein” mit “höchstens eine Meile”.
- Geben Sie die Breite des 95% PI an (im Bezug zur gesuchten Größe).
- Geben Sie das 95% HDI an (im Bezug zur gesuchten Größe).
- Im Hinblick auf die Rope-Methode: Ist der Unterschied vernachlässigbar klein? (ja/nein/unentschieden)
Hinweise:
- Verwenden Sie ansonsten die Standardwerte (Defaults) der typischen (im Unterricht verwendeten) R-Funktionen.
- Runden Sie auf 2 Dezimalstellen.
- Verwenden Sie Methoden der Bayes-Statistik.
Solution
Setup:
Modell berechnen:
m1 <- stan_glm(mpg ~ vs, data = mtcars,
refresh = 0)coef(m1)(Intercept) vs
16.661120 7.834182 zu a)
95%-PI:
post_m1_vs <- posterior_interval(m1, prob = .95,
pars = "vs")
post_m1_vs[1][1] 4.413905post_m1_vs[2][1] 11.08213Breite des Intervalls:
breite <- post_m1_vs[2] - post_m1_vs[1]
breite <- breite %>% round(2)
breite[1] 6.67Die Antwort für a) lautet also 6.67.
mcmc_areas(m1)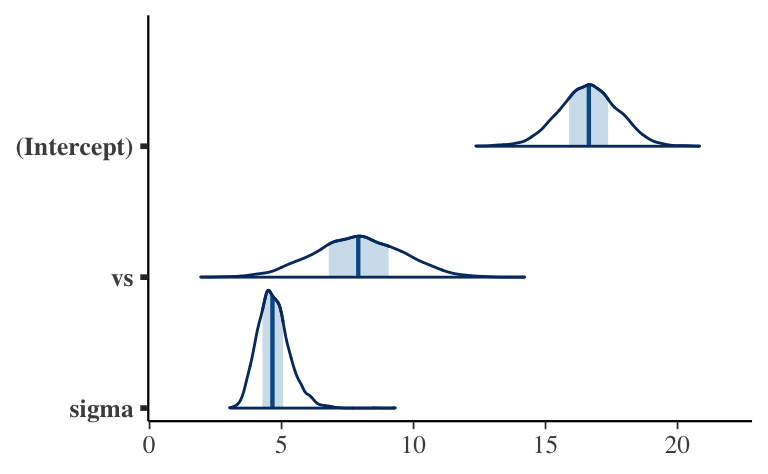
zu b)
Wir nutzen den Befehl hdi() aus {bayestestR}.
hdi(m1)| Parameter | CI | CI_low | CI_high | Effects | Component |
|---|---|---|---|---|---|
| (Intercept) | 0.95 | 14.572981 | 18.95952 | fixed | conditional |
| vs | 0.95 | 4.467643 | 11.12690 | fixed | conditional |
Mit dem Schalter ci = .89 bekäme man bspw. ein 89%-Intervall (s. Hilfe für den Befehl).
“hdi” und “hdpi” und “hpdi” sind synonym.
ggplot(mtcars) +
aes(x = vs, y = mpg) +
geom_point()+
geom_smooth(method = "lm")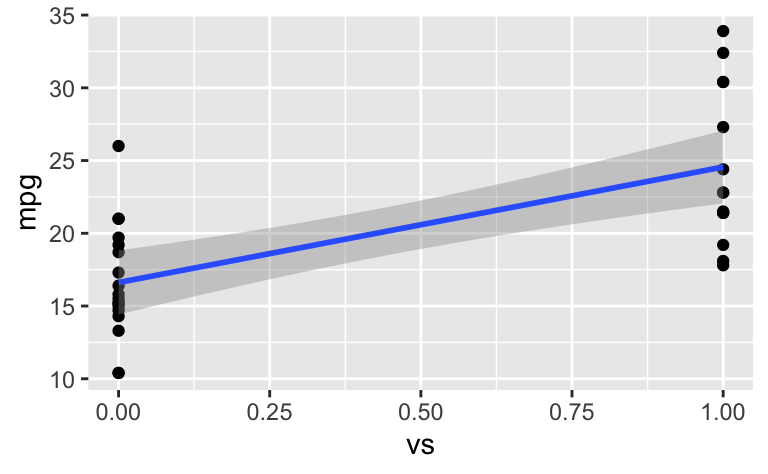
zu c)
rope(m1,range = c(-1,1))| Parameter | CI | ROPE_low | ROPE_high | ROPE_Percentage | Effects | Component |
|---|---|---|---|---|---|---|
| (Intercept) | 0.95 | -1 | 1 | 0 | fixed | conditional |
| vs | 0.95 | -1 | 1 | 0 | fixed | conditional |
plot(rope(m1, range = c(-1,1)))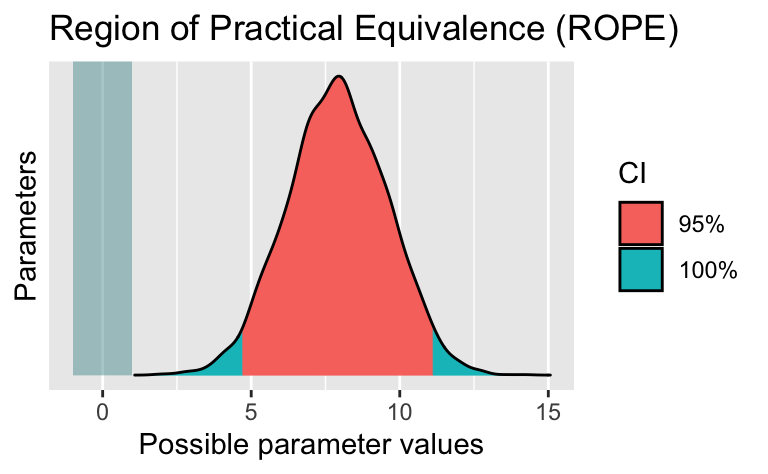
Wir verwerfen also die H0-Rope.
Categories:
- bayes
- lm