mtcars-abhaengig_var3a

probability

bayes

num

Published

November 8, 2023

d_name <- "mtcars"
data(list = d_name)
av <- "mpg"
vars <- names(eval(parse(text = d_name))) 
preds <- setdiff(vars, av)

data("teaching_data")

# all_dfs <- teachertools::teaching_df()
# 
# d_path <- all_dfs |> 
#   dplyr::filter(datasets_names == d_name) |> 
#   dplyr::pull(source)
#  
# pred_chosen_nr <- sample(1:length(preds), 1)
# pred_chosen <- "hp"


# d is the abstracted name of the dataset:
# d <- eval(parse(text = d_name))
# 
# d <- as_tibble(d)

data(mtcars)

Aufgabe

Im Folgenden ist der Datensatz mtcars zu analysieren.

Der Datensatz ist z.B. als CSV-Datei von dieser Webseite abrufbar.

Hilfe zum Datensatz ist via dieser Webseite abrufbar.

Ob die Variable hp (UV) und Spritverbrauch (mpg; AV) wohl voneinander abhängig sind? Was meinen Sie? Was ist Ihre Einschätzung dazu? Vermutlich haben Sie ein (wenn vielleicht auch implizites) Vorab-Wissen zu dieser Frage. Lassen wir dieses Vorab-Wissen aber einmal außen vor und schauen uns rein Daten dazu an. Vereinfachen wir die Frage etwas, indem wir beide Variablen am Mittelwert aufteilen: Wenn eine Beobachtung (d.h. ein Auto) einen Wert in der jeweiligen Variablen höchstens so groß wie der Mittelwert der Variable aufweist, geben wir der Beobachtung der Wert 0, ansonsten den Wert 1. Das Ereignis $A$ sei “hoher Spritverbrauch”, mpg_high == 1. Das Ereignis $B$ sei “hohe PS_Zahl”, hp_high == 1.

mtcars2 <-
  mtcars %>% 
  select(mpg, hp) %>% 
  mutate(mpg_high = case_when(
    mpg <= mean(mpg) ~ 0,
    mpg > mean(mpg) ~ 1
  )) %>% 
  select(-mpg) 

mtcars3 <-  # Jetzt analog für die UV, `hp`:
  mtcars2 |> 
  mutate(hp_high = case_when(
    hp <= mean(hp) ~ 0,
    hp > mean(hp) ~ 1
  )) |> 
  select(-hp)

Berechnen Sie: $Pr(\neg \text{uv high} \, | \, \text{av high})$

Hinweise:

Das “Ellbogen-Zeichen” $\neg$ kennzeichnet eine logische Negierung (das Gegenteil oder Komplement).
Die angegebene Wahrscheinlichkeit ist eine bedingte Wahrscheinlichkeit.
Weitere Hinweise

Lösung

Dieser Prädiktor wurde als UV bestimmt: hp.

Schauen wir zuerst mal in den Datensatz:

data(mtcars)  # mtcars importieren

mtcars %>% 
  select(mpg, hp) %>% 
  slice_head(n = 5)

	mpg	hp
Mazda RX4	21.0	110
Mazda RX4 Wag	21.0	110
Datsun 710	22.8	93
Hornet 4 Drive	21.4	110
Hornet Sportabout	18.7	175

Dann berechnen wir die binären Variablen:

mtcars2 <-
  mtcars %>% 
  select(mpg, hp) %>% 
  mutate(mpg_high = case_when(
    mpg <= mean(mpg) ~ 0,
    mpg > mean(mpg) ~ 1
  )) %>% 
  select(-mpg) 

mtcars3 <-  # Jetzt analog für die UV, `hp`:
  mtcars2 |> 
  mutate(hp_high = case_when(
    hp <= mean(hp) ~ 0,
    hp > mean(hp) ~ 1
  )) |> 
  select(-hp)

Dann filtern wir die gesuchten Wahrscheinlichkeiten bzw. Anteile der AV:

mtcars3_filtered <-
  mtcars3 %>% 
  filter(mpg_high == 1)

mtcars3_filtered

	mpg_high	hp_high
Mazda RX4	1	0
Mazda RX4 Wag	1	0
Datsun 710	1	0
Hornet 4 Drive	1	0
Merc 240D	1	0
Merc 230	1	0
Fiat 128	1	0
Honda Civic	1	0
Toyota Corolla	1	0
Toyota Corona	1	0
Fiat X1-9	1	0
Porsche 914-2	1	0
Lotus Europa	1	0
Volvo 142E	1	0

Die Anzahl der Zeilen in mtcars3_filtered sagt uns, wie viele Autos die gesuchte Bedingung, also den “hinteren Teil” der Wahrscheinlichkeit, erfüllen.

Zur Erinnerung: Bedingte Wahrscheinlichkeit berechnen ist analog zum Filtern einer Tabelle:

Es gibt also 14 Autos, die den oben gesuchten “hinteren Teil” der Bedingung erfüllen (mpg_high = 1).

Filtern wir als nächstes nach dem “vorderen Teil” der gesuchten Wahrscheinlichkeit (was das gleiche ist wie ein Anteil in diesem Fall):

mtcars3_filtered %>% 
  filter(hp_high == 0)

	mpg_high	hp_high
Mazda RX4	1	0
Mazda RX4 Wag	1	0
Datsun 710	1	0
Hornet 4 Drive	1	0
Merc 240D	1	0
Merc 230	1	0
Fiat 128	1	0
Honda Civic	1	0
Toyota Corolla	1	0
Toyota Corona	1	0
Fiat X1-9	1	0
Porsche 914-2	1	0
Lotus Europa	1	0
Volvo 142E	1	0

Es gibt also 14 Autos, für die gilt hp_high == 0.

Mit count kann man sich die Werte zählen lassen:

mtcars3_filtered %>% 
  count(hp_high)

hp_high	n
0	14

Der gesuchte Wert beträgt also 14/14 = 1.

Visualisieren wir noch die bedingten Wahrscheinlichkeiten, so könnte man die gesuchten Anteile einfach abzählen:

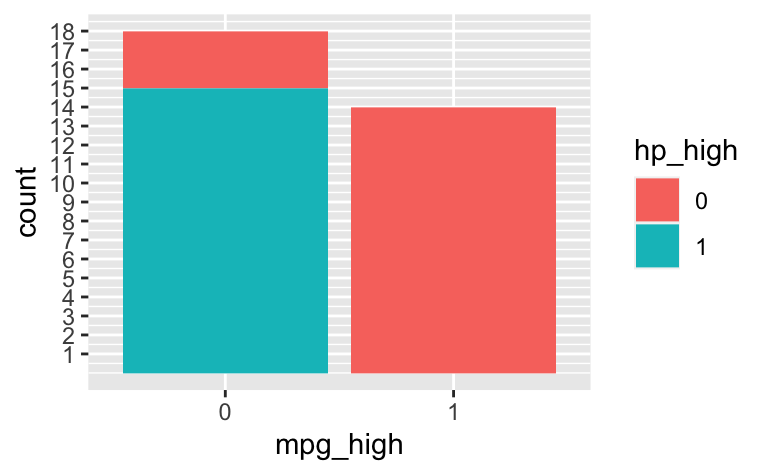
Sieht man in dem Diagramm nur eine Farbe (anstelle von zweien), so heißt das, dass es nur eine Gruppe gibt (und nicht zwei). Die Häufigkeit der nicht vorhandenen Gruppe ist demnach Null.

Categories:

probability
bayes
num

--- extype: num exsolution: 1 exname: mtcars-abhaengig_var3a extol: 0.03 expoints: 1 categories: - probability - bayes - num date: '2023-11-08' title: mtcars-abhaengig_var3a --- ```{r libs, include = FALSE} library(tidyverse) library(gt) library(assertthat) ``` ```{r global-knitr-options, include=FALSE} knitr::opts_chunk$set(fig.pos = 'H', fig.asp = 0.618, fig.width = 4, fig.cap = "", fig.path = "", message = FALSE, echo = FALSE, warning = FALSE, #out.width = "100%", cache = TRUE) ``` ```{r init-data-var} d_name <- "mtcars" data(list = d_name) av <- "mpg" vars <- names(eval(parse(text = d_name))) preds <- setdiff(vars, av) data("teaching_data") # all_dfs <- teachertools::teaching_df() # # d_path <- all_dfs |> # dplyr::filter(datasets_names == d_name) |> # dplyr::pull(source) # # pred_chosen_nr <- sample(1:length(preds), 1) # pred_chosen <- "hp" # d is the abstracted name of the dataset: # d <- eval(parse(text = d_name)) # # d <- as_tibble(d) data(mtcars) ``` # Aufgabe Im Folgenden ist der Datensatz `mtcars` zu analysieren. Der Datensatz ist z.B. als CSV-Datei [von dieser Webseite](https://vincentarelbundock.github.io/Rdatasets/csv/datasetsv) abrufbar. Hilfe zum Datensatz ist via [dieser Webseite](https://vincentarelbundock.github.io/Rdatasets/doc/datasets) abrufbar. Ob die Variable `hp` (UV) und *Spritverbrauch* (`mpg`; AV) wohl voneinander abhängig sind? Was meinen Sie? Was ist Ihre Einschätzung dazu? Vermutlich haben Sie ein (wenn vielleicht auch implizites) Vorab-Wissen zu dieser Frage. Lassen wir dieses Vorab-Wissen aber einmal außen vor und schauen uns rein Daten dazu an. Vereinfachen wir die Frage etwas, indem wir beide Variablen am Mittelwert aufteilen: Wenn eine Beobachtung (d.h. ein Auto) einen Wert in der jeweiligen Variablen höchstens so groß wie der Mittelwert der Variable aufweist, geben wir der Beobachtung der Wert `0`, ansonsten den Wert `1`. Das Ereignis $A$ sei "hoher Spritverbrauch", `mpg_high == 1`. Das Ereignis $B$ sei "hohe PS_Zahl", `hp_high == 1`. ```{r compute-binary-vars} mtcars2 <- mtcars %>% select(mpg, hp) %>% mutate(mpg_high = case_when( mpg <= mean(mpg) ~ 0, mpg > mean(mpg) ~ 1 )) %>% select(-mpg) mtcars3 <- # Jetzt analog für die UV, `hp`: mtcars2 |> mutate(hp_high = case_when( hp <= mean(hp) ~ 0, hp > mean(hp) ~ 1 )) |> select(-hp) ``` *Berechnen Sie:* $Pr(\neg \text{uv high} \, | \, \text{av high})$ *Hinweise*: - Das "Ellbogen-Zeichen" $\neg$ kennzeichnet eine logische Negierung (das Gegenteil oder Komplement). - Die angegebene Wahrscheinlichkeit ist eine bedingte Wahrscheinlichkeit. - [Weitere Hinweise](https://start-bayes.netlify.app/pruefung#bearbeitungshinweise) # Lösung Dieser Prädiktor wurde als UV bestimmt: `hp`. Schauen wir zuerst mal in den Datensatz: ```{r echo = TRUE} data(mtcars) # mtcars importieren mtcars %>% select(mpg, hp) %>% slice_head(n = 5) ``` Dann berechnen wir die binären Variablen: ```{r ref.label="compute-binary-vars", echo = TRUE, eval = FALSE} ``` Dann filtern wir die gesuchten Wahrscheinlichkeiten bzw. Anteile der AV: ```{r echo = TRUE} mtcars3_filtered <- mtcars3 %>% filter(mpg_high == 1) mtcars3_filtered ``` Die Anzahl der Zeilen in `mtcars3_filtered` sagt uns, wie viele Autos die gesuchte Bedingung, also den "hinteren Teil" der Wahrscheinlichkeit, erfüllen. Zur Erinnerung: Bedingte Wahrscheinlichkeit berechnen ist analog zum Filtern einer Tabelle: Es gibt also 14 Autos, die den oben gesuchten "hinteren Teil" der Bedingung erfüllen (`mpg_high = 1)`. Filtern wir als nächstes nach dem "vorderen Teil" der gesuchten Wahrscheinlichkeit (was das gleiche ist wie ein Anteil in diesem Fall): ```{r echo = TRUE} mtcars3_filtered %>% filter(hp_high == 0) ``` Es gibt also 14 Autos, für die gilt `hp_high == 0`. Mit `count` kann man sich die Werte zählen lassen: ```{r} mtcars3_filtered %>% count(hp_high) ``` Der gesuchte Wert beträgt also 14/14 = 1. Visualisieren wir noch die bedingten Wahrscheinlichkeiten, so könnte man die gesuchten Anteile einfach abzählen: ```{r echo = FALSE} mtcars3 %>% mutate(across(everything(), factor)) %>% # factor() brauchen wir nur für die Farbfüllung ggplot() + aes(x = mpg_high, fill = hp_high) + geom_bar() + scale_y_continuous(breaks = 1:100) + scale_x_discrete(drop = FALSE) # zeigt Kategorien ohne Daten in der Legende an. ``` Sieht man in dem Diagramm nur eine Farbe (anstelle von zweien), so heißt das, dass es nur eine Gruppe gibt (und nicht zwei). Die Häufigkeit der nicht vorhandenen Gruppe ist demnach Null. --- Categories: - probability - bayes - num