maschinendesaster

1 Aufgabe

Eine Maschine bestehe aus n=100 Teilen. Jedes Teil habe eine Zuverlässigkeit (für Funktionsfähigkeit) von r=.99 (für ein bestimmtes Zeitintervall t). Nur solange alle Teile arbeiten, arbeitet die Maschine, ansonsten fällt sie aus.

Wie groß ist die Wahrscheinlichkeit, dass die Maschine im Zeitintervall t ausfällt?

Hinweise:

• Gehen Sie von Unabhängigkeit (der Zuverlässigkeit) der Teile aus.
• Beachten Sie die üblichen Hinweise des Datenwerks.

2 Lösung

Nun zur Berechnung der Wahrscheinlichkeit, dass die Maschine im Zeitintervall t ausfällt:

Gegeben sind:

Anzahl der Teile (n): = 100

Zuverlässigkeit jedes Teils (r): = 0,99

n <- 100
r <- 0.99

Die Maschine funktioniert nur, wenn alle 100 Teile funktionieren. D a die Zuverlässigkeiten der Teile unabhängig voneinander sind, ist die Wahrscheinlichkeit, dass die Maschine funktioniert (P(Maschine funktioniert)):

P(Maschine funktioniert) = r^n = (0,99)^100

P_maschine_funzt <- r^n
P_maschine_funzt

[1] 0.3660323

Die Wahrscheinlichkeit, dass die Maschine im Zeitintervall t ausfällt, ist das Komplementärereignis dazu, dass die Maschine funktioniert:

P(Maschine fällt aus) = 1 - P(Maschine funktioniert)

Berechnung:

P_maschine_faellt_aus <- 1 - P_maschine_funzt
P_maschine_faellt_aus

[1] 0.6339677

Die Wahrscheinlichkeit, dass die Maschine im Zeitintervall t ausfällt, beträgt ungefähr 63,40%.

3 Variante

n <- 1000
r <- .99
P_maschine_funzt <- r^n
P_maschine_faellt_aus <- 1 - P_maschine_funzt
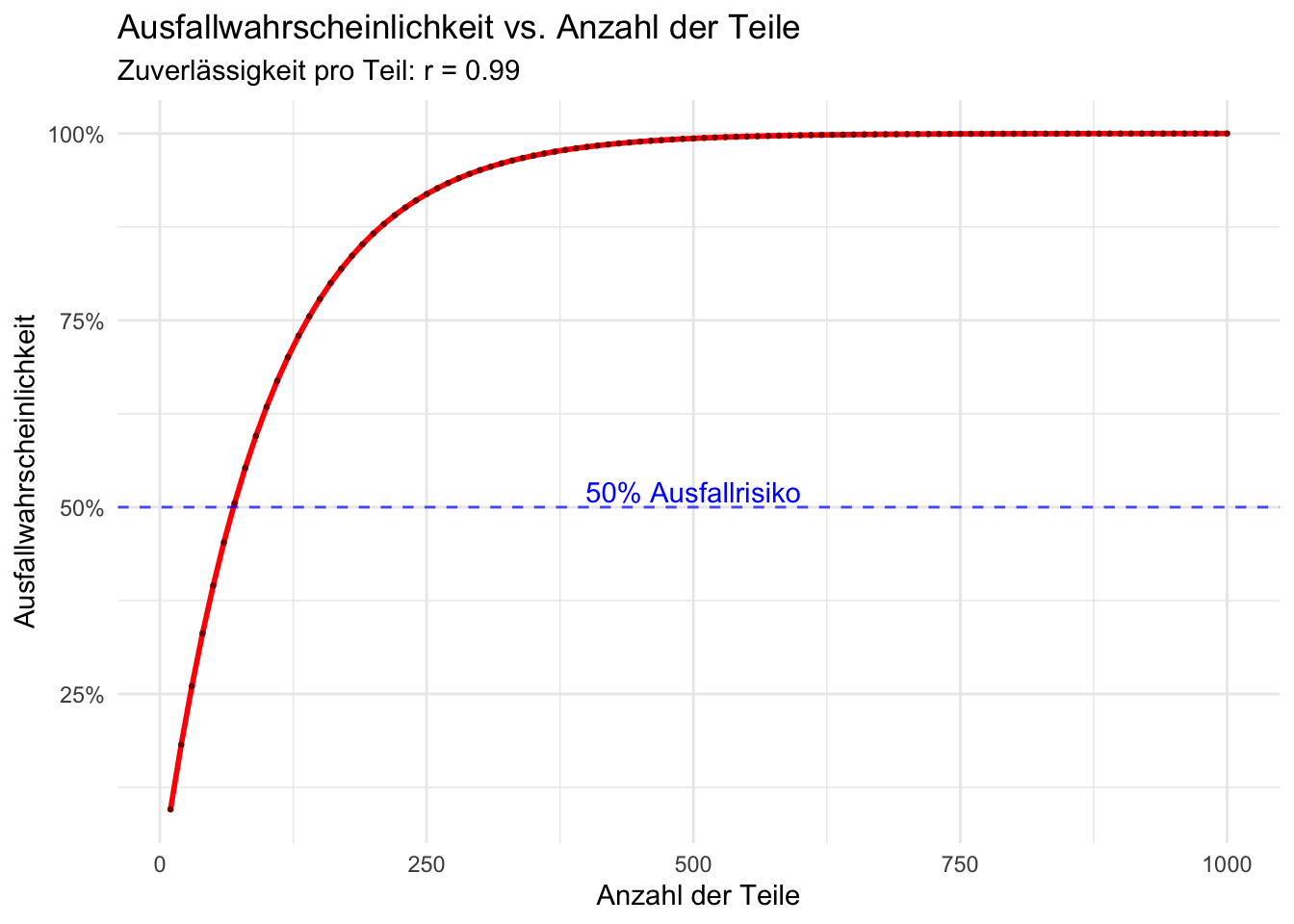
P_maschine_faellt_aus

[1] 0.9999568

4 Ausfallwahrscheinlichkeit in Abhängigkeit der Anzahl der Teile

n_min <- 10
n_max <- 1000
n_teile <- seq(n_min, n_max, by = 10)
P_maschine_faellt_aus <- 1 - r^n_teile

Ergebnisse in einem Data Frame speichern:

 ergebnisse <- data.frame(
  Teile = n_teile,
  Ausfallwahrscheinlichkeit = P_maschine_faellt_aus,
  Ausfallwahrscheinlichkeit_Prozent = P_maschine_faellt_aus * 100
)

 ggplot(ergebnisse, aes(x = Teile, y = Ausfallwahrscheinlichkeit)) +
  geom_line(color = "red", size = 1) +
  geom_point(color = "darkred", size = 0.5) +
  labs(
    title = "Ausfallwahrscheinlichkeit vs. Anzahl der Teile",
    subtitle = paste("Zuverlässigkeit pro Teil: r =", r),
    x = "Anzahl der Teile",
    y = "Ausfallwahrscheinlichkeit"
  ) +
  theme_minimal() +
  scale_y_continuous(labels = scales::percent_format()) +
  geom_hline(yintercept = 0.5, linetype = "dashed", color = "blue", alpha = 0.7) +
  annotate("text", x = 500, y = 0.52, label = "50% Ausfallrisiko", color = "blue")