mariokart_desk-inf-mod

R
bayes
lagemaße
regression
tidyverse
vis
yacsda
Published

February 26, 2025

1 Aufgabe

Untersuchen Sie den Datensatz mariokart. Beantworten Sie dabei die folgende Forschungsfrage:

Erzielen Spiele mit Photo (stock_photo) einen höheren Verkaufspreis (total_pr) im Vergleich zu Spielen ohne Photo?

  1. Prüfen Sie auf fehlende Werte und Extremwerte und führen Sie ggf. entsprechende Schritte aus, um etwaige Probleme in diesem Zusammenhang zu lösen.
  2. Berechnen Sie relevante deskriptive Statistiken.
  3. Visualisieren Sie die die Daten sinnvoll.
  4. Berechnen und interpretieren Sie ein passendes Modell. e.Berechnen und interpretieren Sie Maße der Inferenzstatistik (Bayes oder Frequentistisch).

Hinweise:

  • Beachten Sie die üblichen Hinweise des Datenwerks.













2 Lösung

2.1 Vorbereitung

library(tidyverse)
library(easystats)
library(ggpubr)
library(visdat)
library(rstanarm)
mariokart <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/openintro/mariokart.csv")

2.2 Vorverarbeitung

2.2.1 Extremwerte

gghistogram(mariokart, x = "total_pr")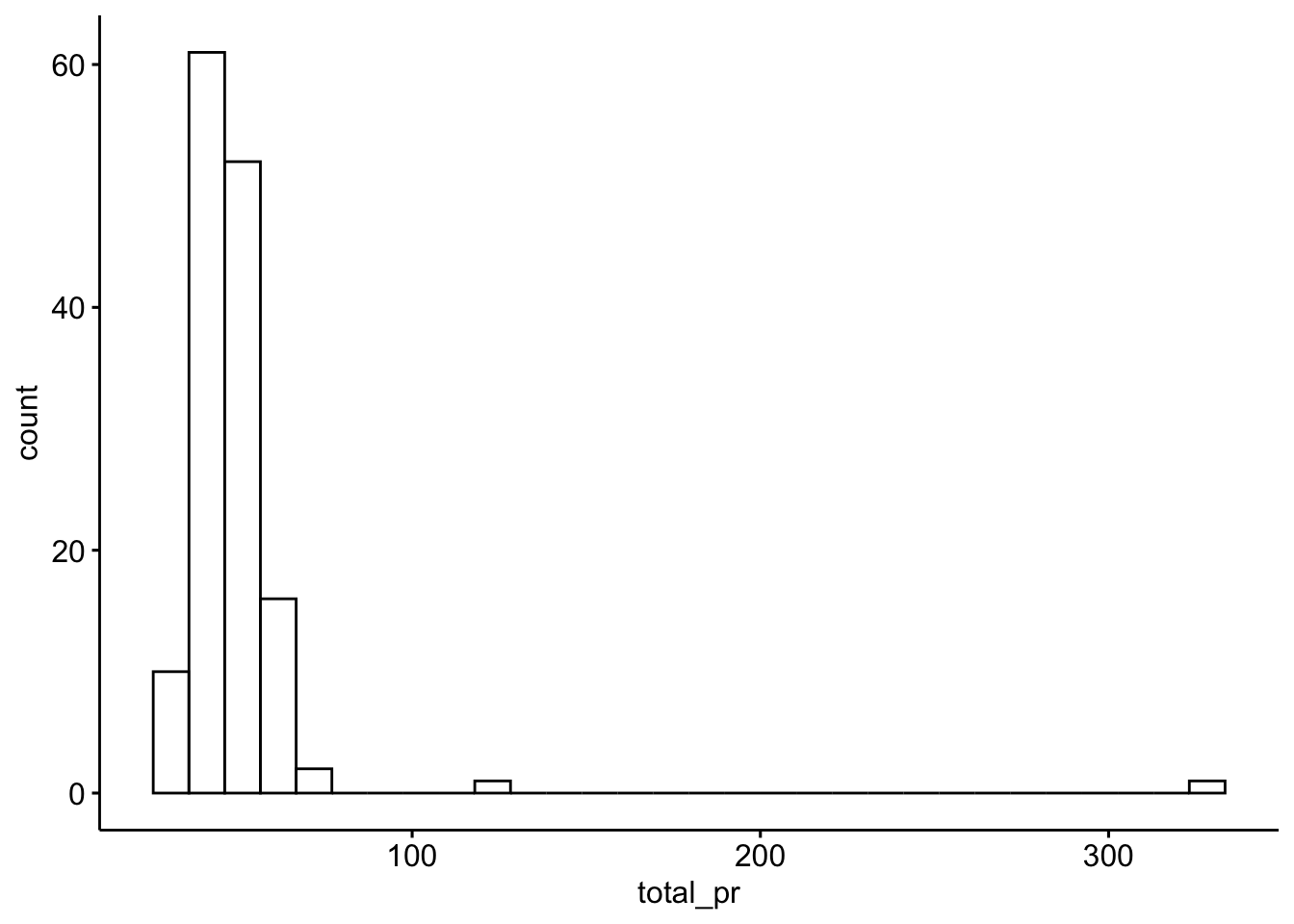

Ja, besser wir entfernen die Extremwerte:

mariokart_no_extreme <- 
  mariokart |> 
  filter(total_pr < 100)

2.2.2 Fehlende Werte

Fehlende Werte visualisieren:

vis_dat(mariokart_no_extreme)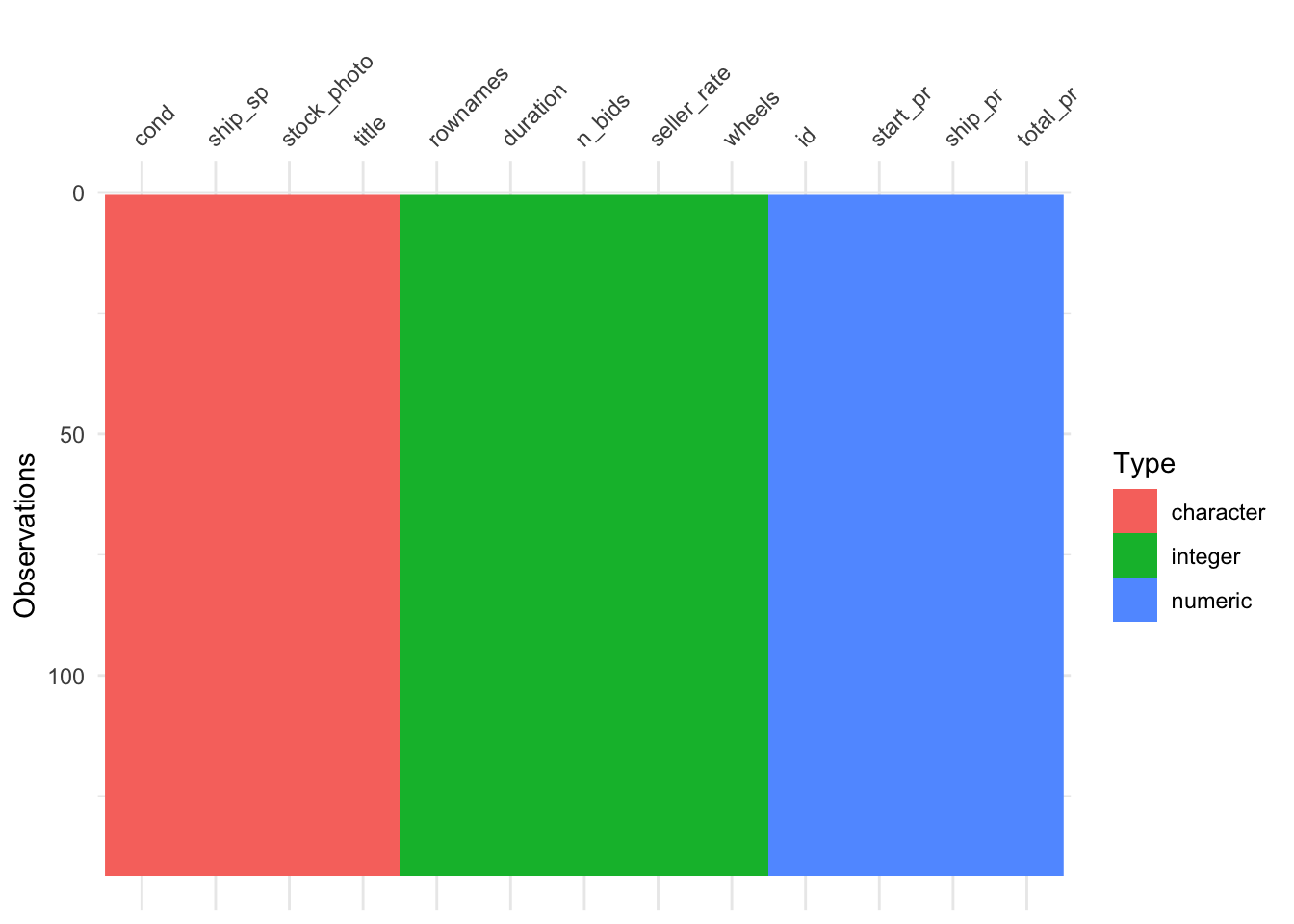

Fehlende Werte zählen:

colSums(is.na(mariokart_no_extreme))
   rownames          id    duration      n_bids        cond    start_pr 
          0           0           0           0           0           0 
    ship_pr    total_pr     ship_sp seller_rate stock_photo      wheels 
          0           0           0           0           0           0 
      title 
          0

Oder so, mit dplyr:

mariokart_no_extreme |> 
  summarise(across(everything(), ~ sum(is.na(.x))))
rownames id duration n_bids cond start_pr ship_pr total_pr ship_sp seller_rate stock_photo wheels title
0 0 0 0 0 0 0 0 0 0 0 0 0

2.3 Deskriptive Statistik

2.3.1 Metrische Variablen

Überblick

describe_distribution(mariokart_no_extreme) |> 
  format_table(digits = 2)
Variable Mean SD IQR Min Max Skewness Kurtosis n n_Missing
rownames 72.42 41.48 72.00 1.00 143.00 -0.02 -1.20 141.00 0
id 2.25e+11 8.78e+10 1.60e+11 1.10e+11 4.00e+11 0.23 -1.24 141.00 0
duration 3.75 2.59 6.00 1.00 10.00 0.35 -1.31 141.00 0
n_bids 13.38 5.76 7.50 1.00 29.00 -0.07 -0.03 141.00 0
start_pr 8.85 15.16 9.01 0.01 69.95 2.35 5.40 141.00 0
ship_pr 2.98 2.62 4.00 0.00 11.45 0.95 1.32 141.00 0
total_pr 47.43 9.11 12.99 28.98 75.00 0.41 -1.75e-03 141.00 0
seller_rate 16122.82 52174.55 4748.50 0.00 2.70e+05 4.06 16.12 141.00 0
wheels 1.15 0.84 2.00 0.00 4.00 0.14 -0.45 141.00 0

Visualisierung:

describe_distribution(mariokart_no_extreme) |> plot()
[[1]]


[[2]]


[[3]]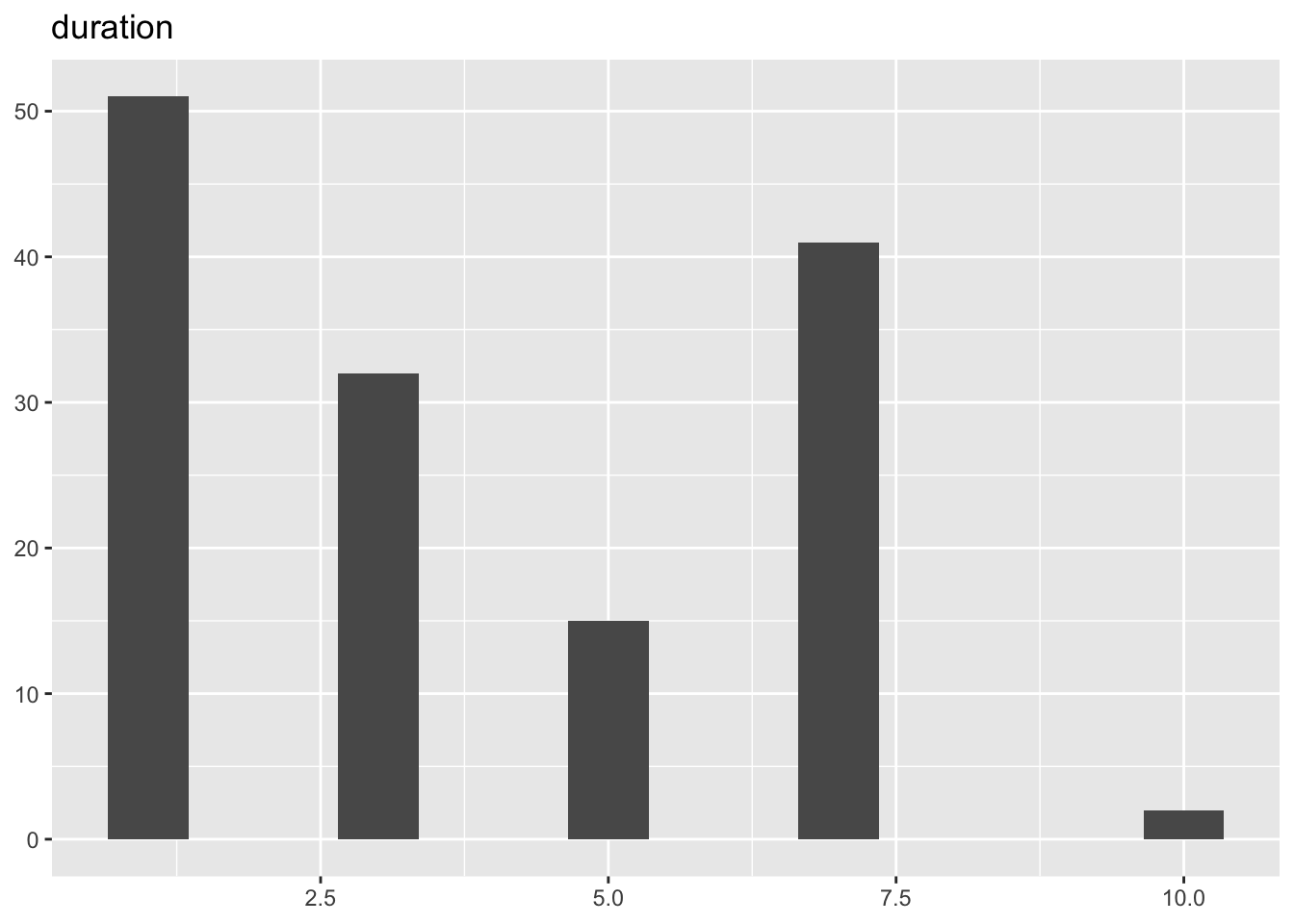


[[4]]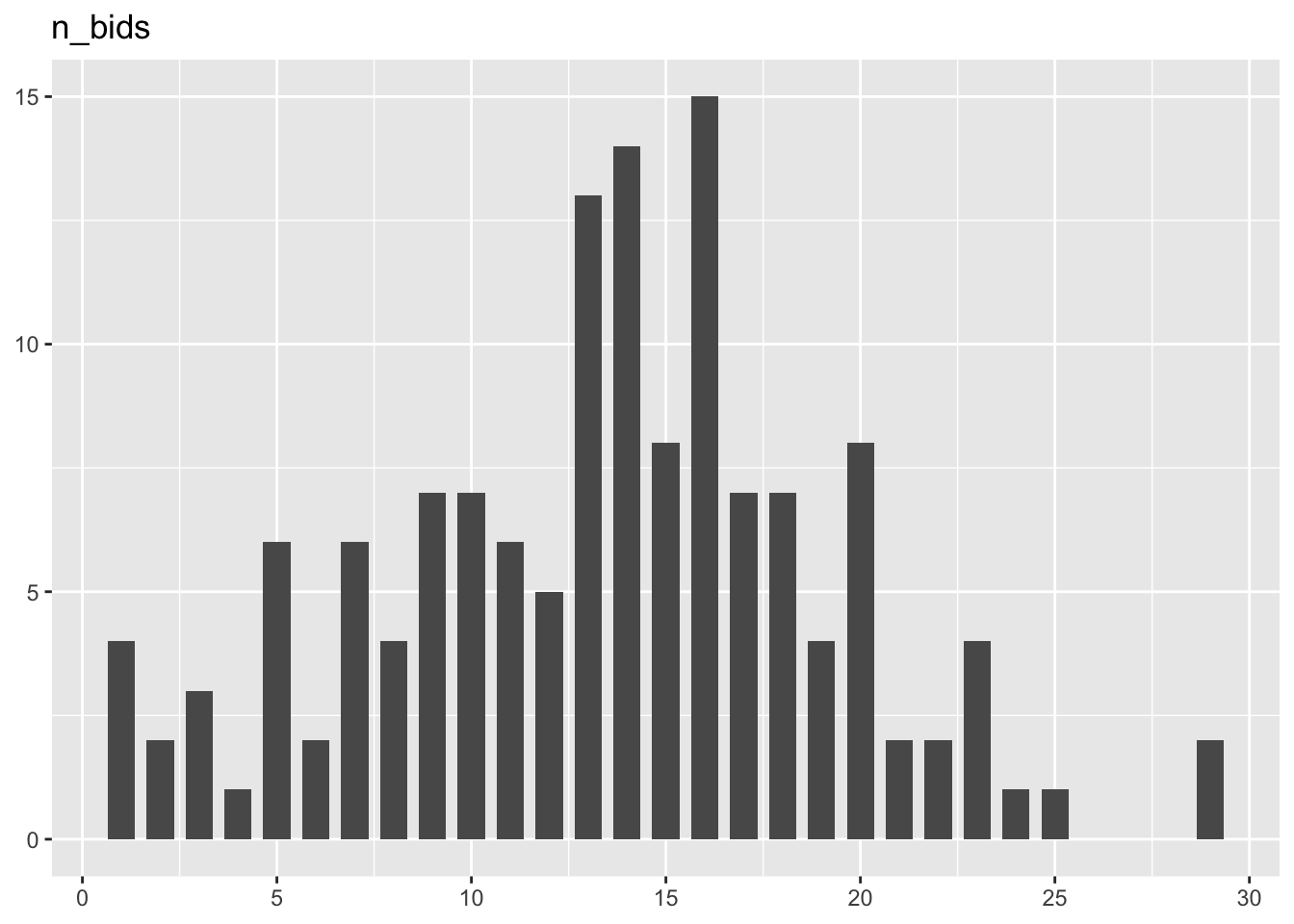


[[5]]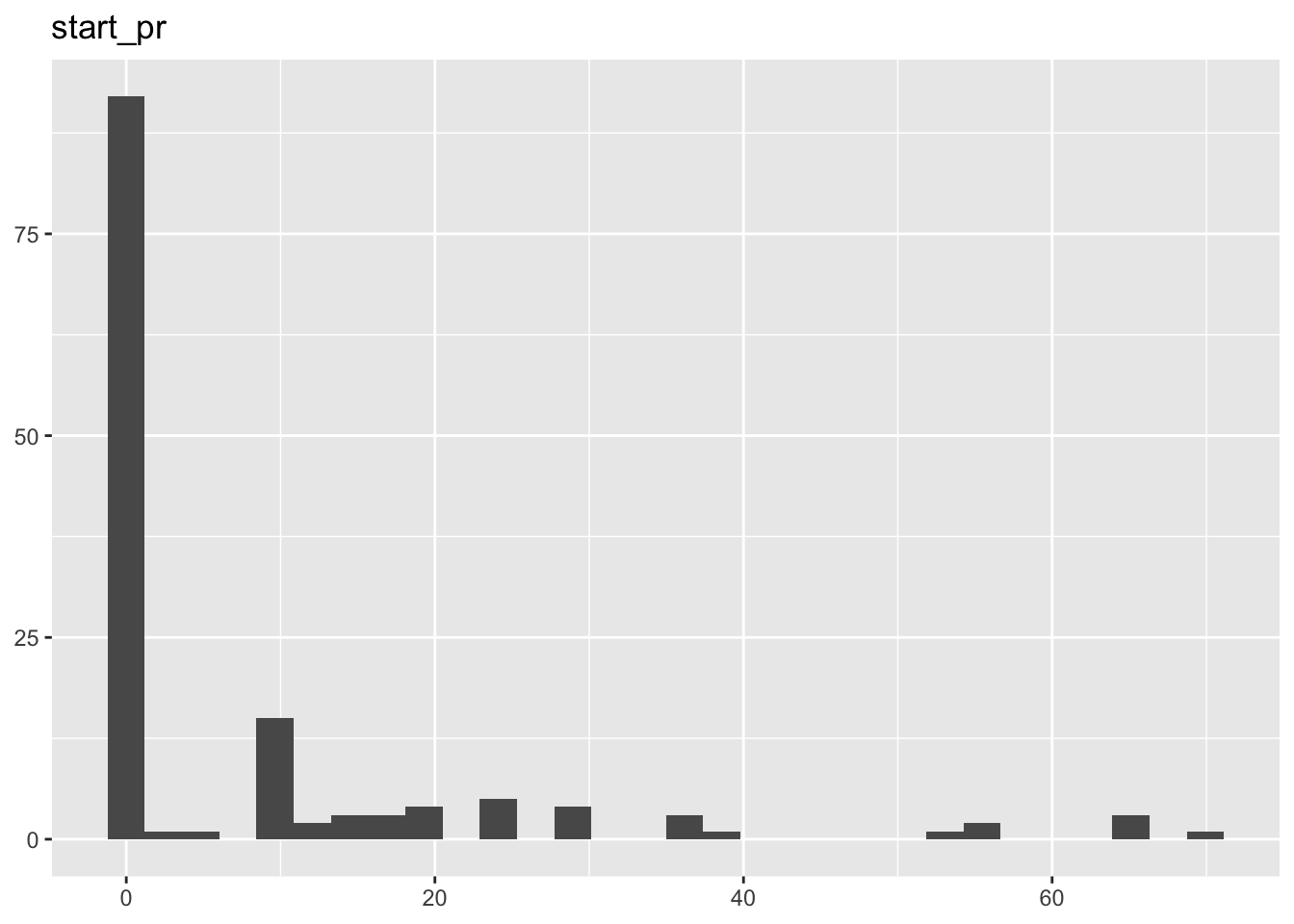


[[6]]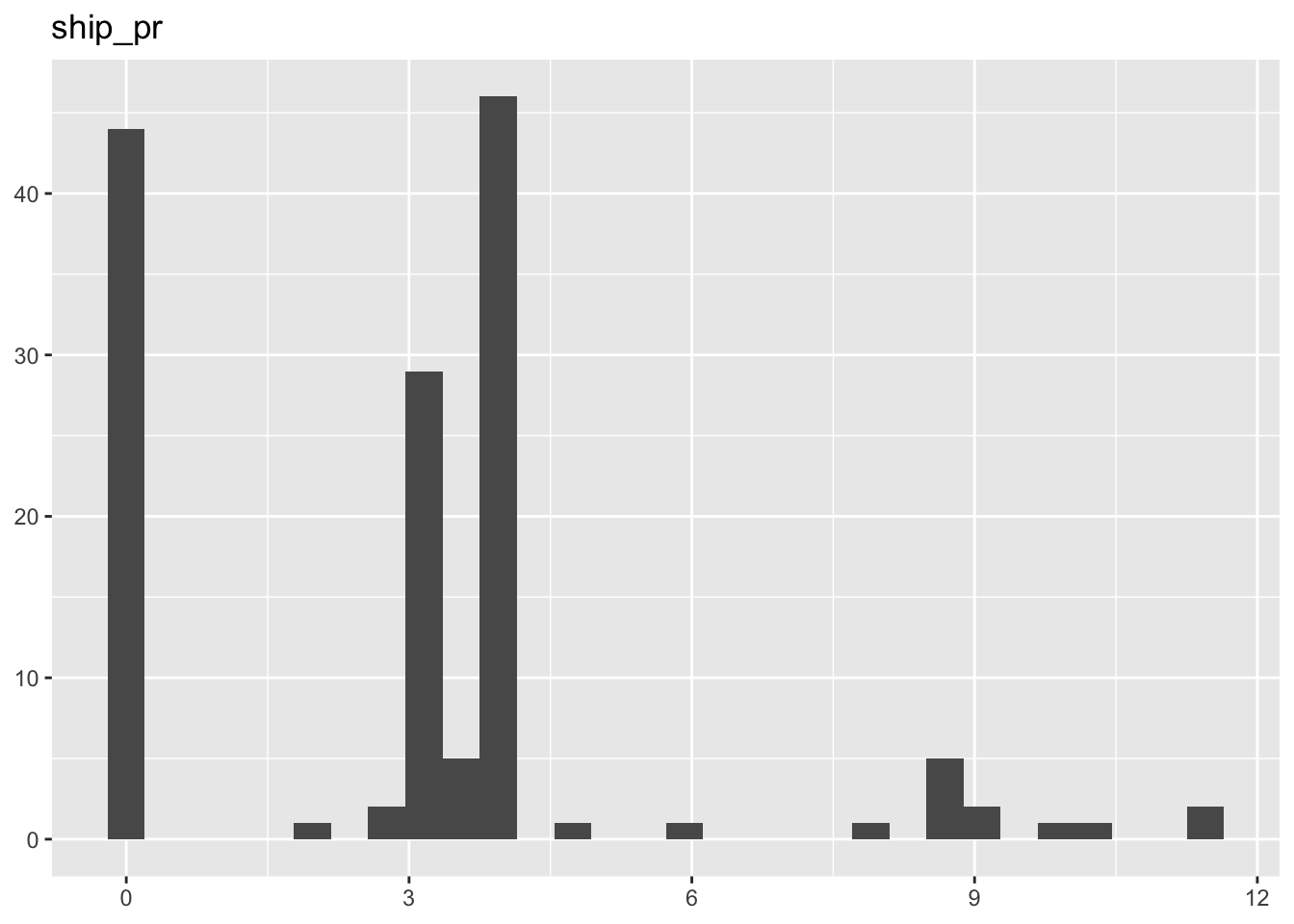


[[7]]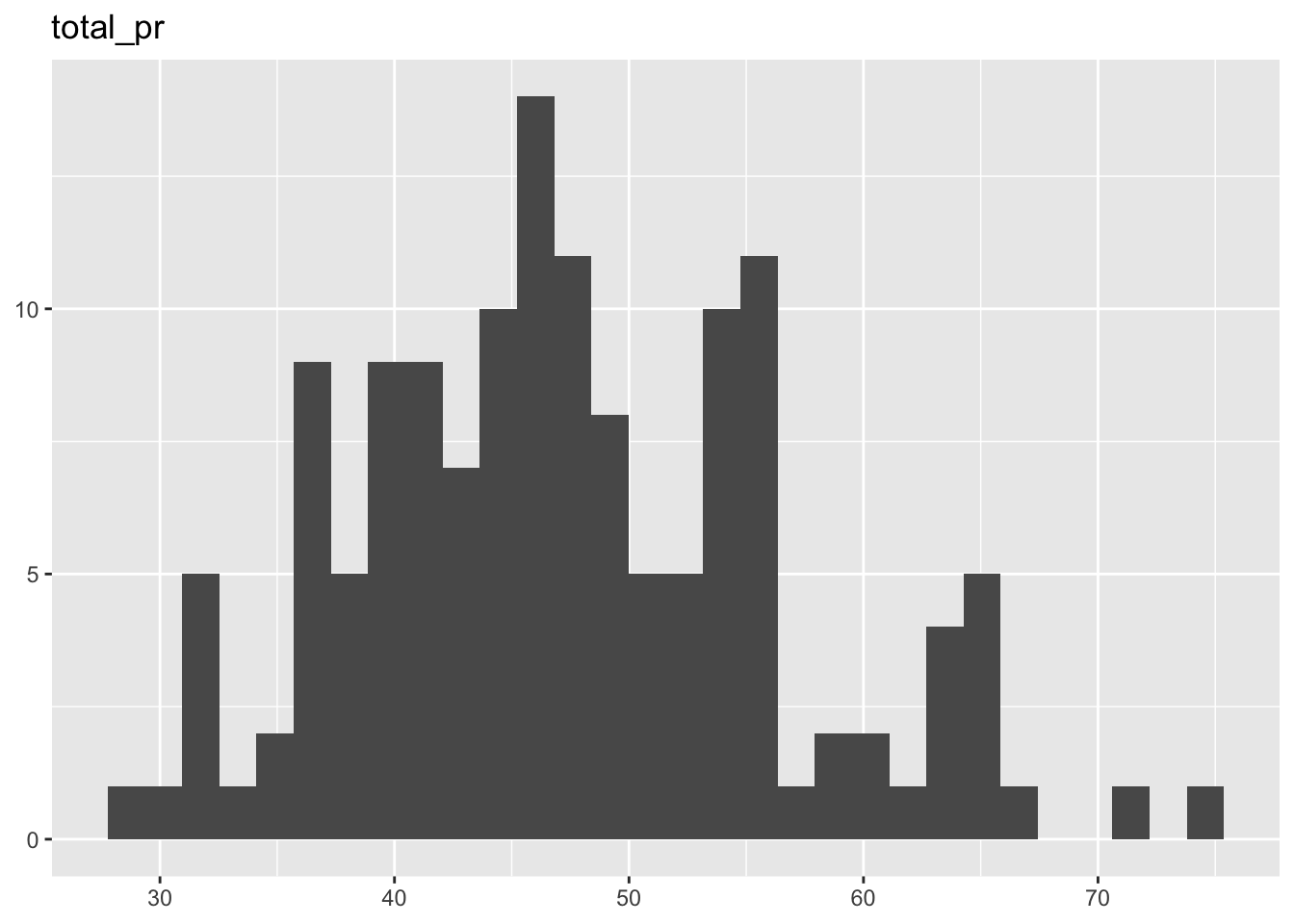


[[8]]


[[9]]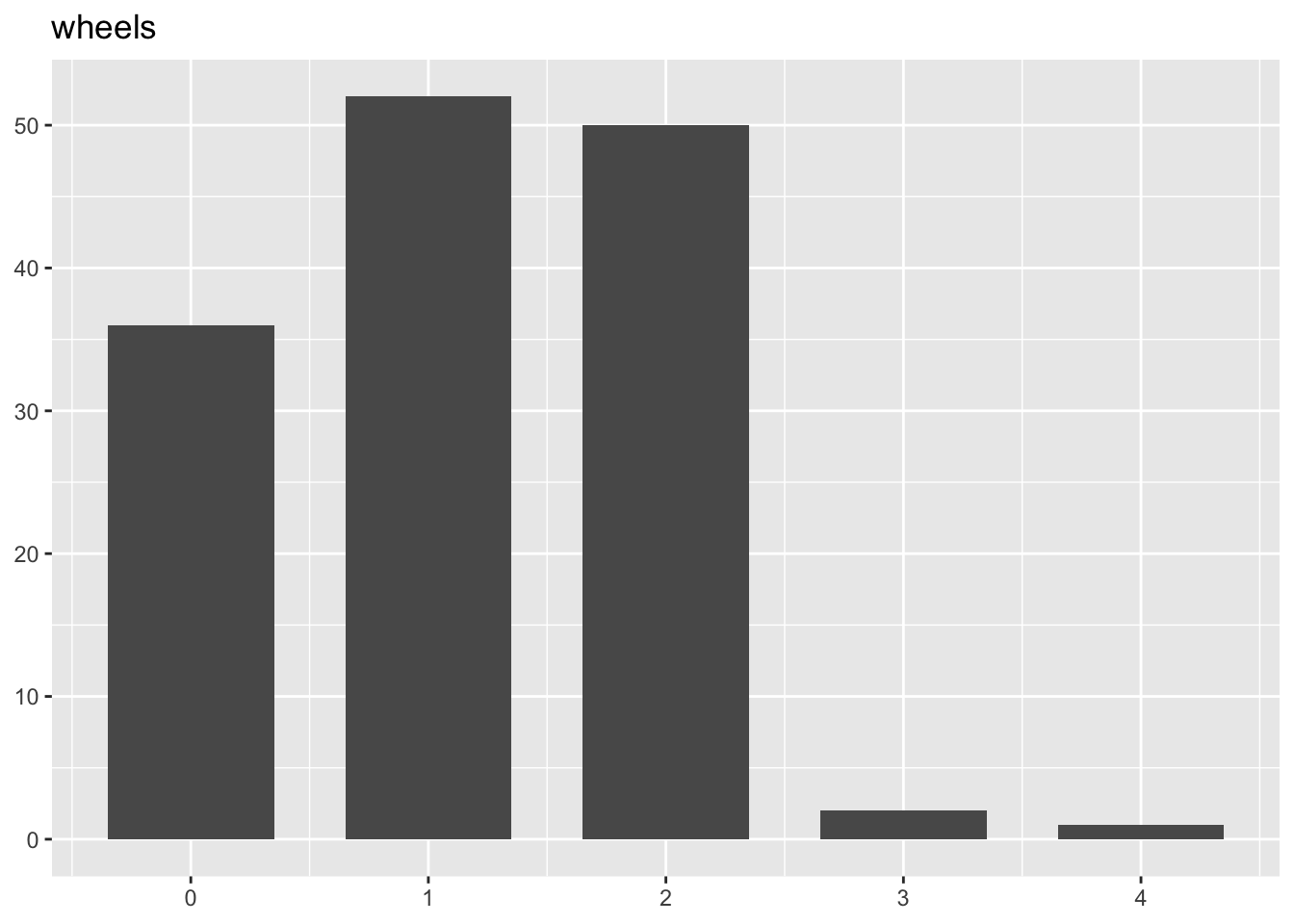

2.3.2 Nominale Variablen

Überblick:

data_tabulate(mariokart_no_extreme, 
              select = c("cond", "ship_sp", "stock_photo")) |> 
  print_md() |> 
  format_table(digits = 2)
x
Table: Frequency Table
|Variable | Value| N|Raw % | Valid %| Cumulative %|
|:———–|———-:|—:|:—–|——-:|————:|
|cond | new| 59|41.84 | 41.84| 41.84|
| | used| 82|58.16 | 58.16| 100.00|
| | (NA)| 0| 0.00 | (NA)| (NA)|
| | | | | | |
|ship_sp | firstClass| 22|15.60 | 15.60| 15.60|
| | media| 14| 9.93 | 9.93| 25.53|
| | other| 3| 2.13 | 2.13| 27.66|
| | parcel| 14| 9.93 | 9.93| 37.59|
| | priority| 23|16.31 | 16.31| 53.90|
| | standard| 33|23.40 | 23.40| 77.30|
| | ups3Day| 1| 0.71 | 0.71| 78.01|
| | upsGround| 31|21.99 | 21.99| 100.00|
| | (NA)| 0| 0.00 | (NA)| (NA)|
| | | | | | |
|stock_photo | no| 36|25.53 | 25.53| 25.53|
| | yes| 105|74.47 | 74.47| 100.00|
| | (NA)| 0| 0.00 | (NA)| (NA)|
| | | | | | |

Visualisierung:

data_tabulate(mariokart_no_extreme, 
              select = c("cond", "ship_sp", "stock_photo")) |> 
  plot()
[[1]]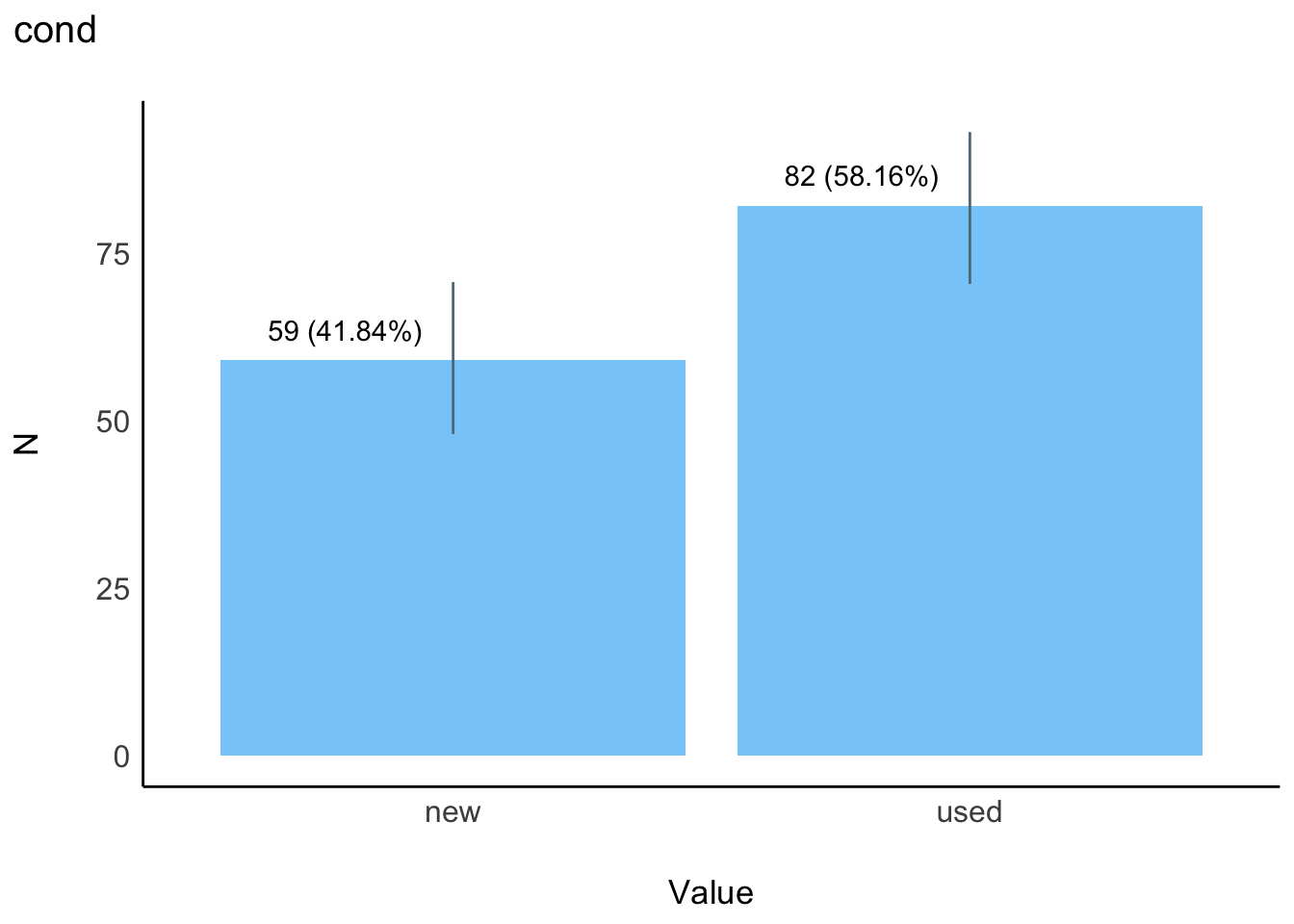


[[2]]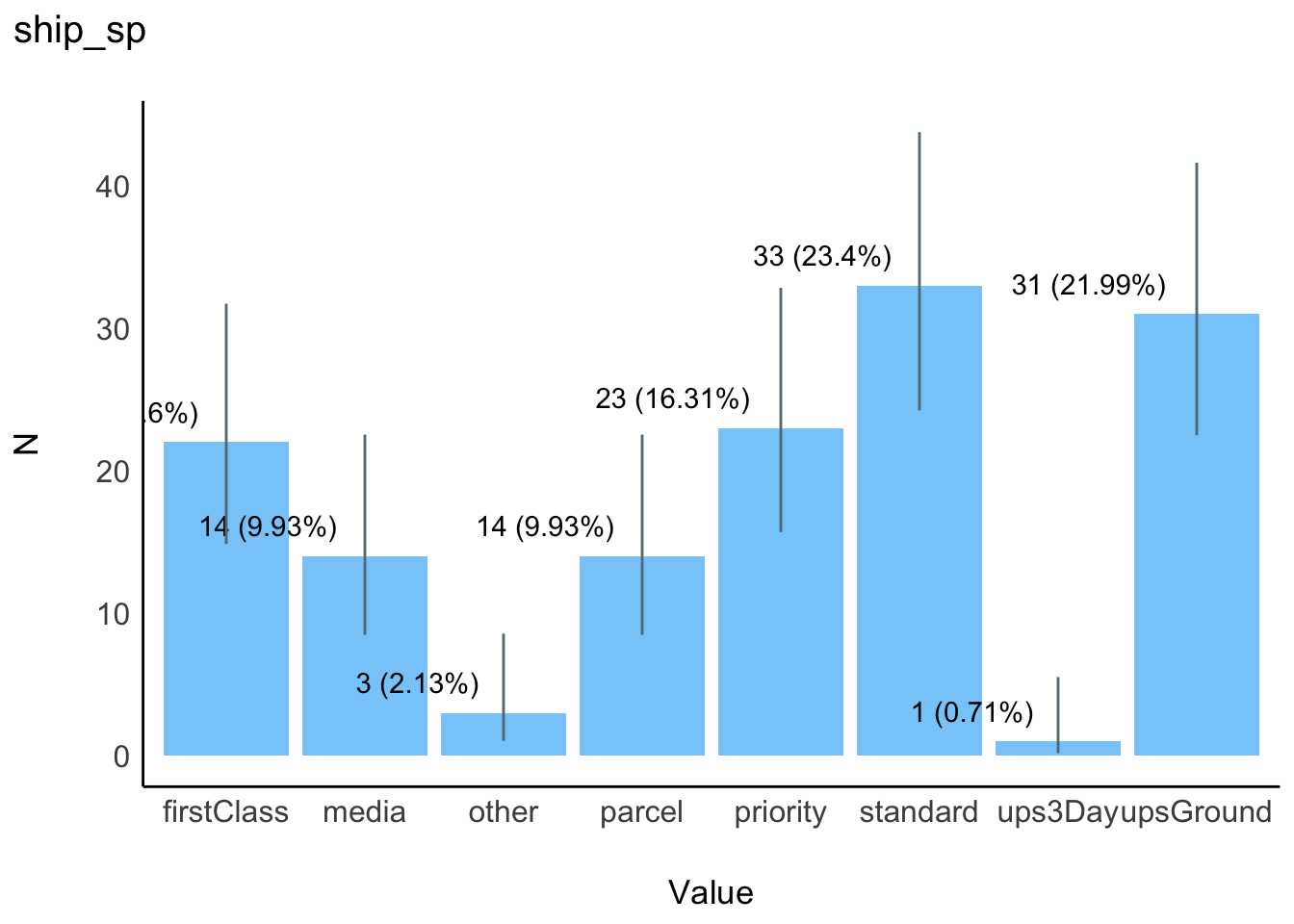


[[3]]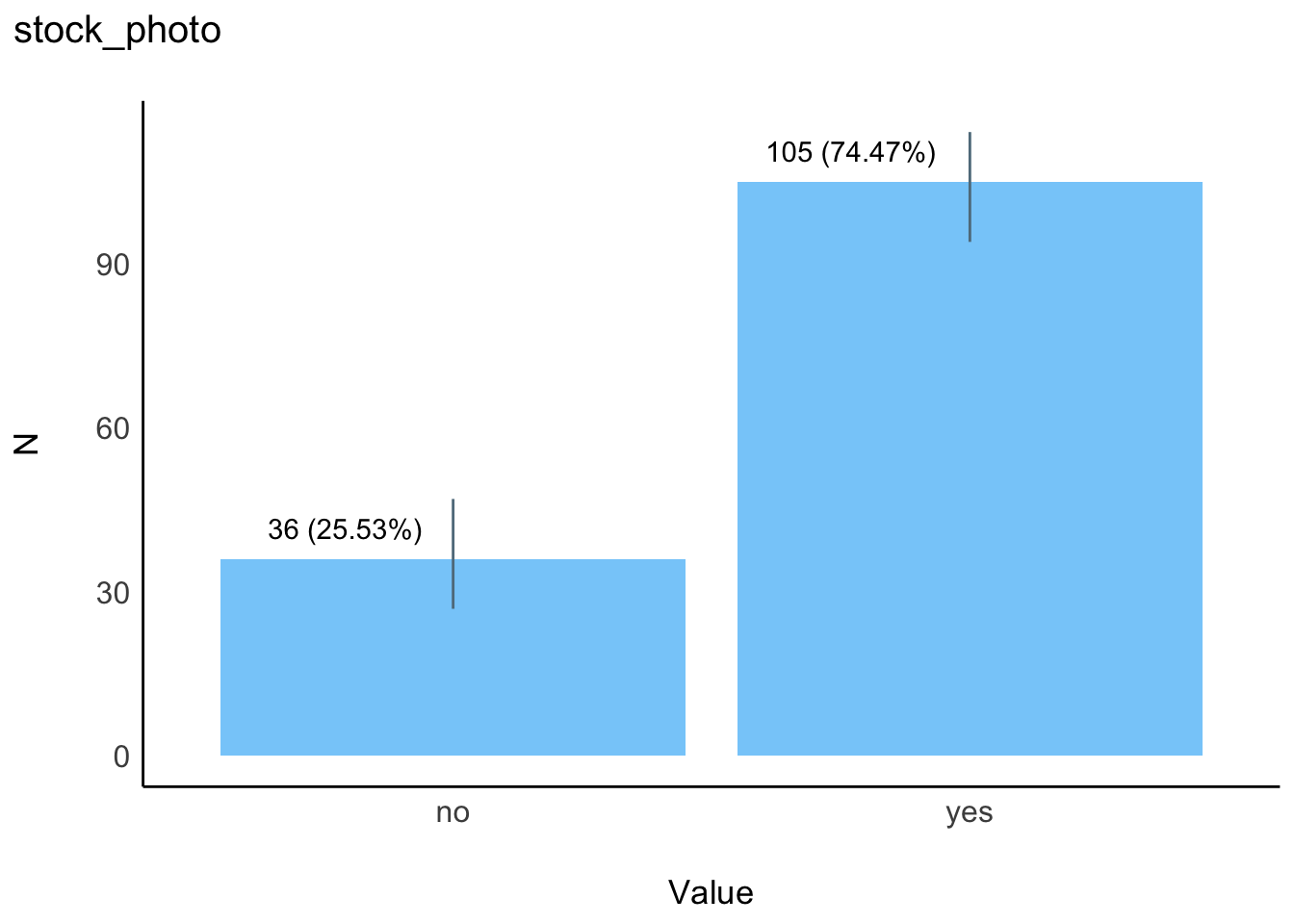

2.3.3 Alternative

skimr::skim(mariokart_no_extreme)
Data summary
Name mariokart_no_extreme
Number of rows 141
Number of columns 13
_______________________
Column type frequency:
character 4
numeric 9
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
cond 0 1 3 4 0 2 0
ship_sp 0 1 5 10 0 8 0
stock_photo 0 1 2 3 0 2 0
title 0 1 0 59 1 79 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
rownames 0 1 7.242000e+01 4.148000e+01 1.000000e+00 3.700000e+01 7.300000e+01 1.080000e+02 1.430000e+02 ▇▇▇▇▇
id 0 1 2.249920e+11 8.784150e+10 1.104395e+11 1.403507e+11 2.303822e+11 3.003523e+11 4.000775e+11 ▇▅▅▅▃
duration 0 1 3.750000e+00 2.590000e+00 1.000000e+00 1.000000e+00 3.000000e+00 7.000000e+00 1.000000e+01 ▇▅▂▆▁
n_bids 0 1 1.338000e+01 5.760000e+00 1.000000e+00 1.000000e+01 1.400000e+01 1.700000e+01 2.900000e+01 ▂▅▇▃▁
start_pr 0 1 8.850000e+00 1.516000e+01 1.000000e-02 9.900000e-01 1.000000e+00 1.000000e+01 6.995000e+01 ▇▁▁▁▁
ship_pr 0 1 2.980000e+00 2.620000e+00 0.000000e+00 0.000000e+00 2.990000e+00 4.000000e+00 1.145000e+01 ▅▇▁▁▁
total_pr 0 1 4.743000e+01 9.110000e+00 2.898000e+01 4.100000e+01 4.603000e+01 5.399000e+01 7.500000e+01 ▃▇▆▂▁
seller_rate 0 1 1.612282e+04 5.217455e+04 0.000000e+00 1.160000e+02 8.200000e+02 4.858000e+03 2.701440e+05 ▇▁▁▁▁
wheels 0 1 1.150000e+00 8.400000e-01 0.000000e+00 0.000000e+00 1.000000e+00 2.000000e+00 4.000000e+00 ▆▇▇▁▁

2.4 Visualisierung

ggboxplot(data = mariokart_no_extreme,
          x = "stock_photo",
          y = "total_pr",
          add = "mean_se",
          add.params = list(color = okabeito_colors()[1]))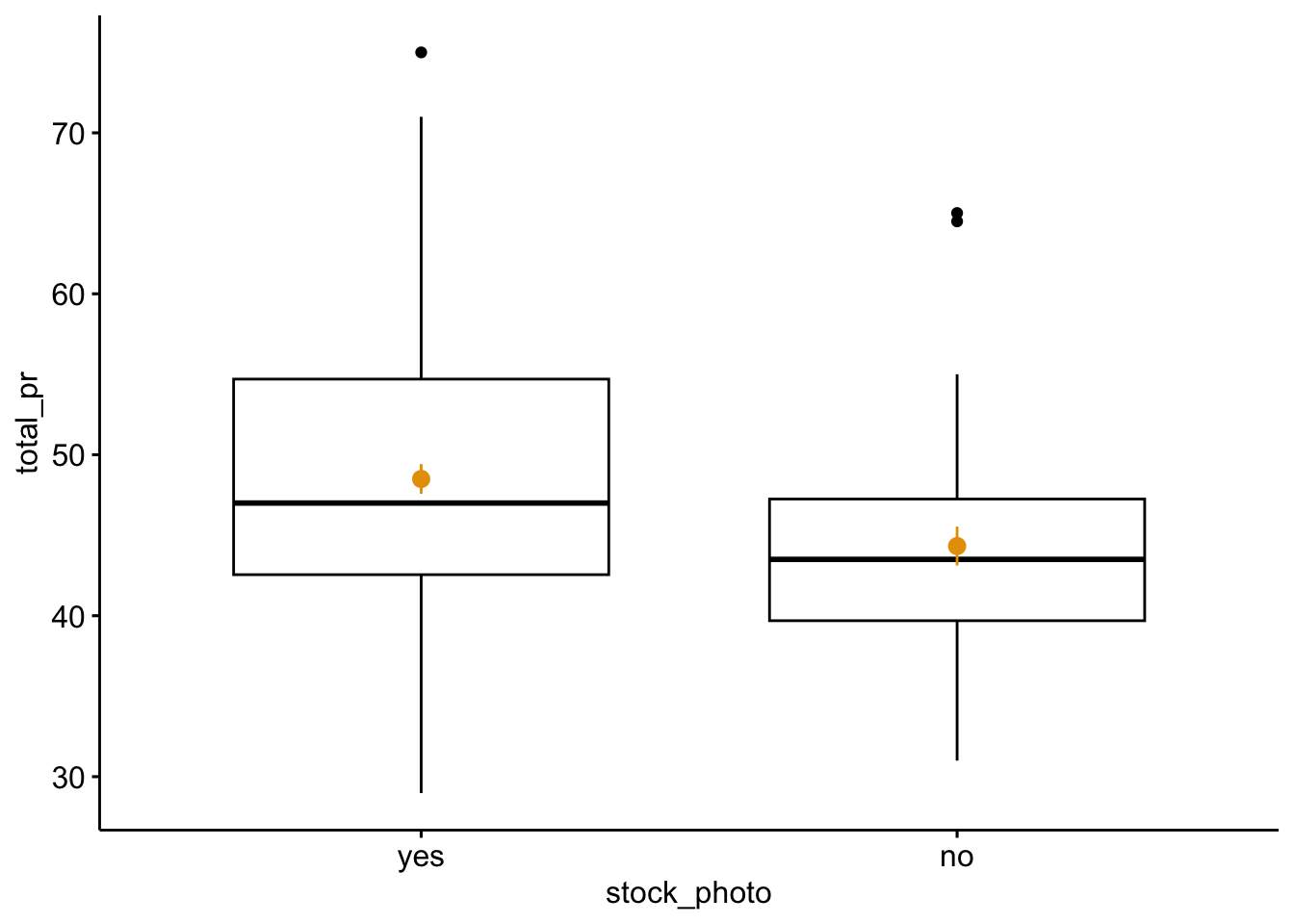

2.5 Modellierung

2.5.1 Kausalmodell

Wir nehmen folgendes Kausalmodell an.

graph LR
  photo --> price
  u --> price

Unter der Annahme dieses Kausalmodells können wir die Modellkoeffizienten als valide betrachten.

2.5.2 Modell - Frequentistisch

Modell berechnen und Parameter prüfen:

lm1 <- lm(total_pr ~ stock_photo, data = mariokart_no_extreme)
parameters(lm1) |> 
  format_table(digits = 2)
Parameter Coefficient SE 95% CI t(139) p
(Intercept) 44.33 1.49 [41.37, 47.28] 29.68 < .001
stock photo [yes] 4.17 1.73 [ 0.75, 7.59] 2.41 0.017

Visualisierung:

parameters(lm1) |> plot()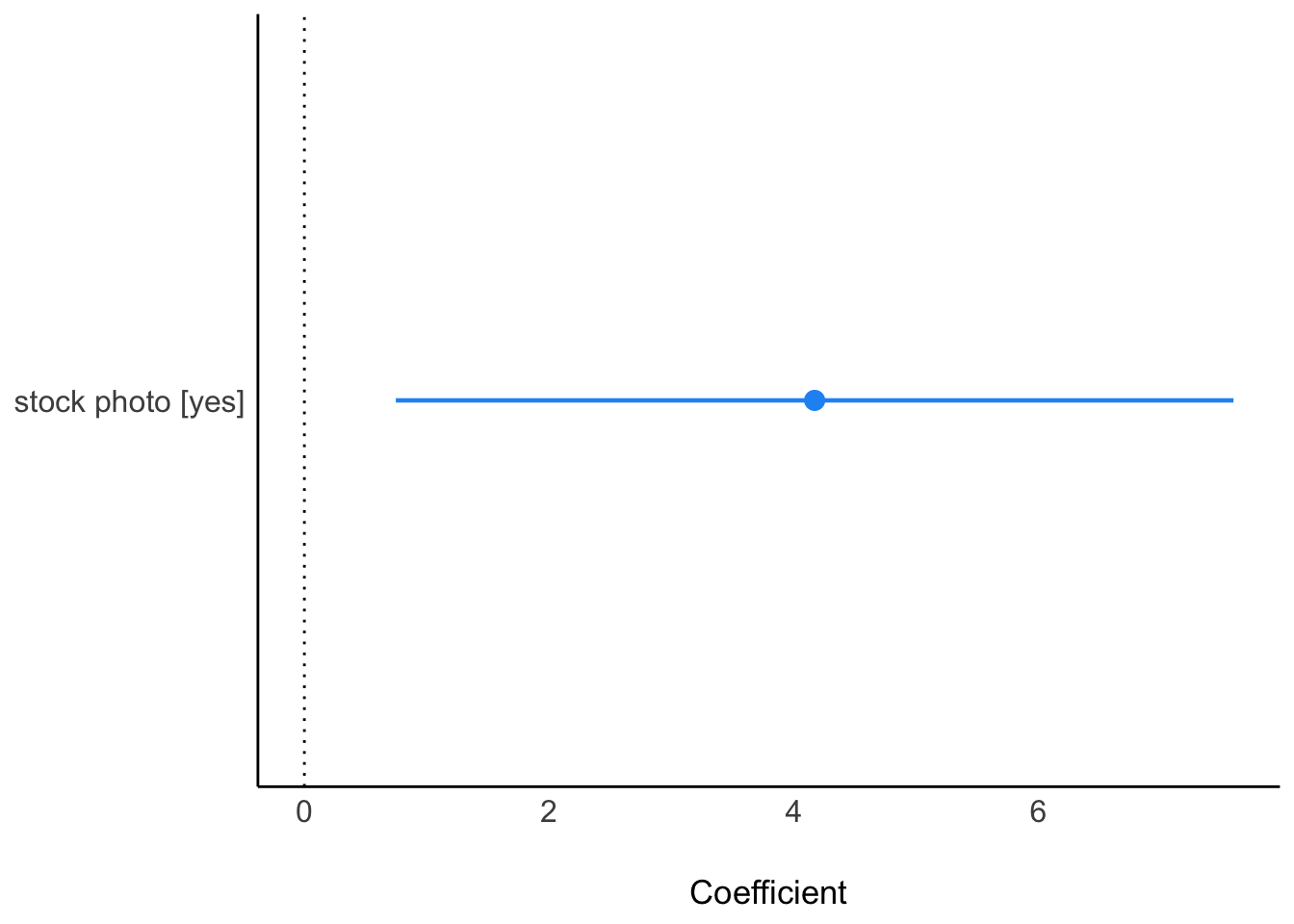

2.5.3 Modell - Bayesianisch

Modell berechnen und Parameter prüfen:

lm1_bayes <- stan_glm(total_pr ~ stock_photo, 
                      data = mariokart_no_extreme,
                      refresh = 0)
parameters(lm1_bayes)
Parameter Median CI CI_low CI_high pd Rhat ESS Prior_Distribution Prior_Location Prior_Scale
(Intercept) 44.357345 0.95 41.4536558 47.380282 1.00000 0.9994405 3895.248 normal 47.43191 22.78413
stock_photoyes 4.141773 0.95 0.6167945 7.738697 0.99075 1.0001186 3964.198 normal 0.00000 52.06671

Visualisierung:

parameters(lm1_bayes) |> plot()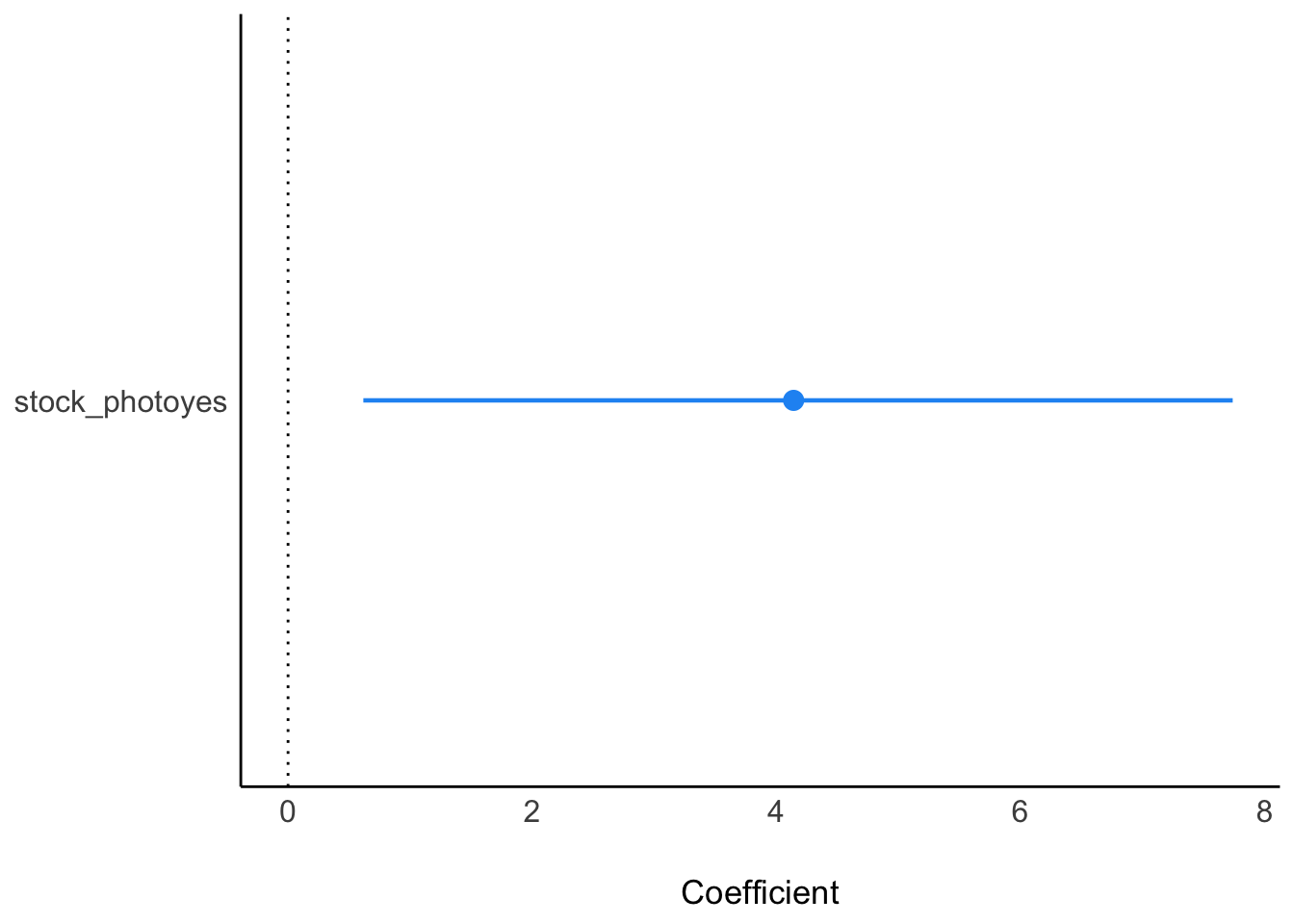

2.6 Inferenzstatistik

2.6.1 Nullhypothese

Wie man sieht, ist die Null nicht im Konfidenzintervall enthalten. Daher können wir die Nullhypothese ausschließen.

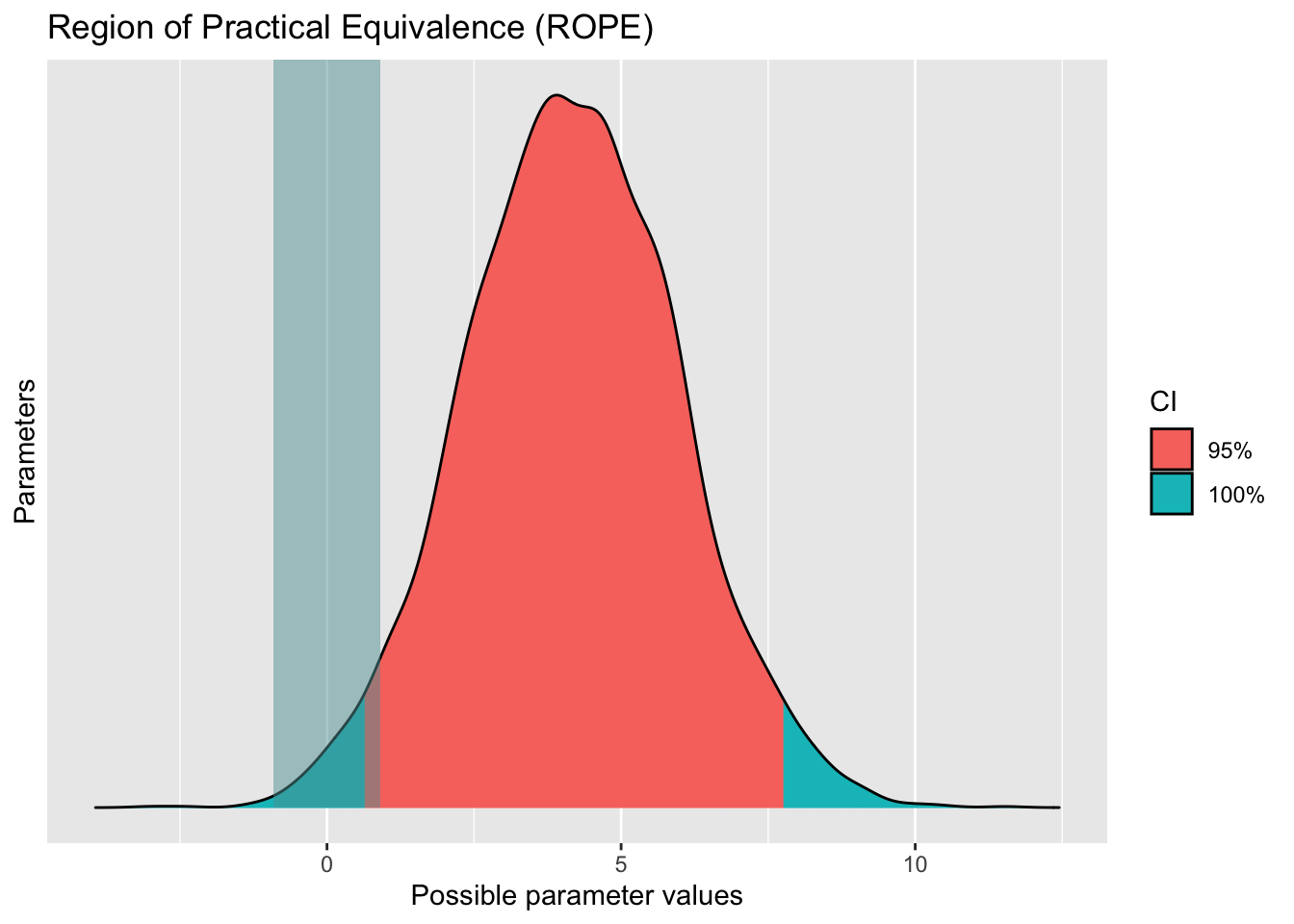
2.6.2 ROPE

Wir können eine ROPE-Nullhypothese nicht komplett ausschließen, aber fast.

rope(lm1_bayes)
Parameter CI ROPE_low ROPE_high ROPE_Percentage Effects Component
(Intercept) 0.95 -0.9113651 0.9113651 0.0000000 fixed conditional
stock_photoyes 0.95 -0.9113651 0.9113651 0.0105263 fixed conditional

Visualisierung:

rope(lm1_bayes) |> plot()