d_a <-
tibble(
k = 0:10,
wskt = dbinom(k, size = 10, prob = .01))
d_a %>%
ggplot() +
aes(x = k, y = wskt) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = 1:10)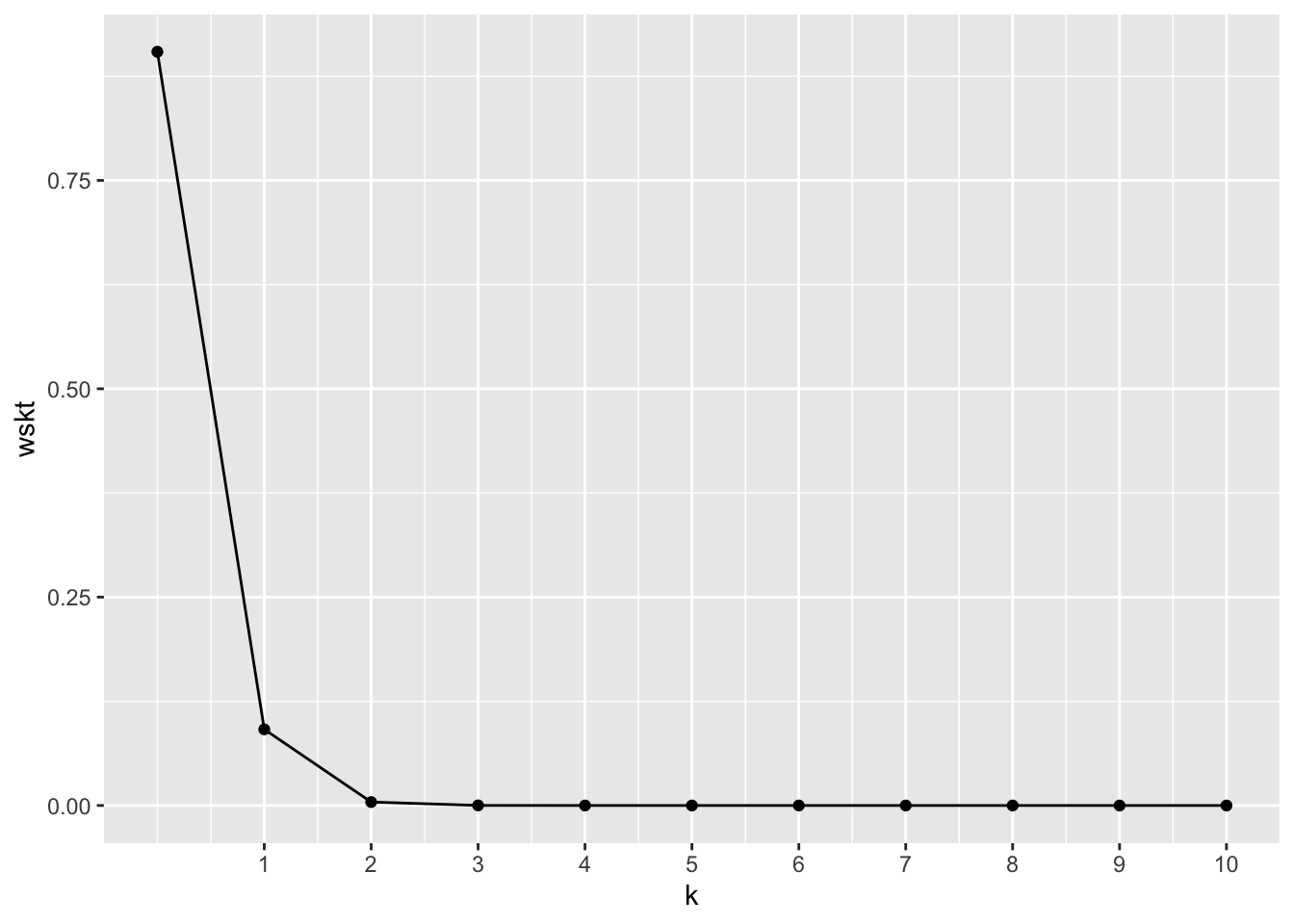
October 28, 2022
In einer Lostrommel befinden sich “sehr viele” Lose, davon ein Anteil \(p\) Treffer (und \(1-p\) Nieten), mit zunächst \(p=0.01\).
Sie kaufen \(n=10\) Lose.
Nutzen Sie die Gittermethode. Treffen Sie Annahmen, wo nötig.
d_a <-
tibble(
k = 0:10,
wskt = dbinom(k, size = 10, prob = .01))
d_a %>%
ggplot() +
aes(x = k, y = wskt) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = 1:10)
| k | wskt |
|---|---|
| 0 | 9.04 × 10−1 |
| 1 | 9.14 × 10−2 |
| 2 | 4.15 × 10−3 |
| 3 | 1.12 × 10−4 |
| 4 | 1.98 × 10−6 |
| 5 | 2.40 × 10−8 |
| 6 | 2.02 × 10−10 |
| 7 | 1.16 × 10−12 |
| 8 | 4.41 × 10−15 |
| 9 | 9.90 × 10−18 |
| 10 | 1.00 × 10−20 |
d2 <-
tibble(
p_grid = seq(0, 1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 3, size = 10, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d2 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line()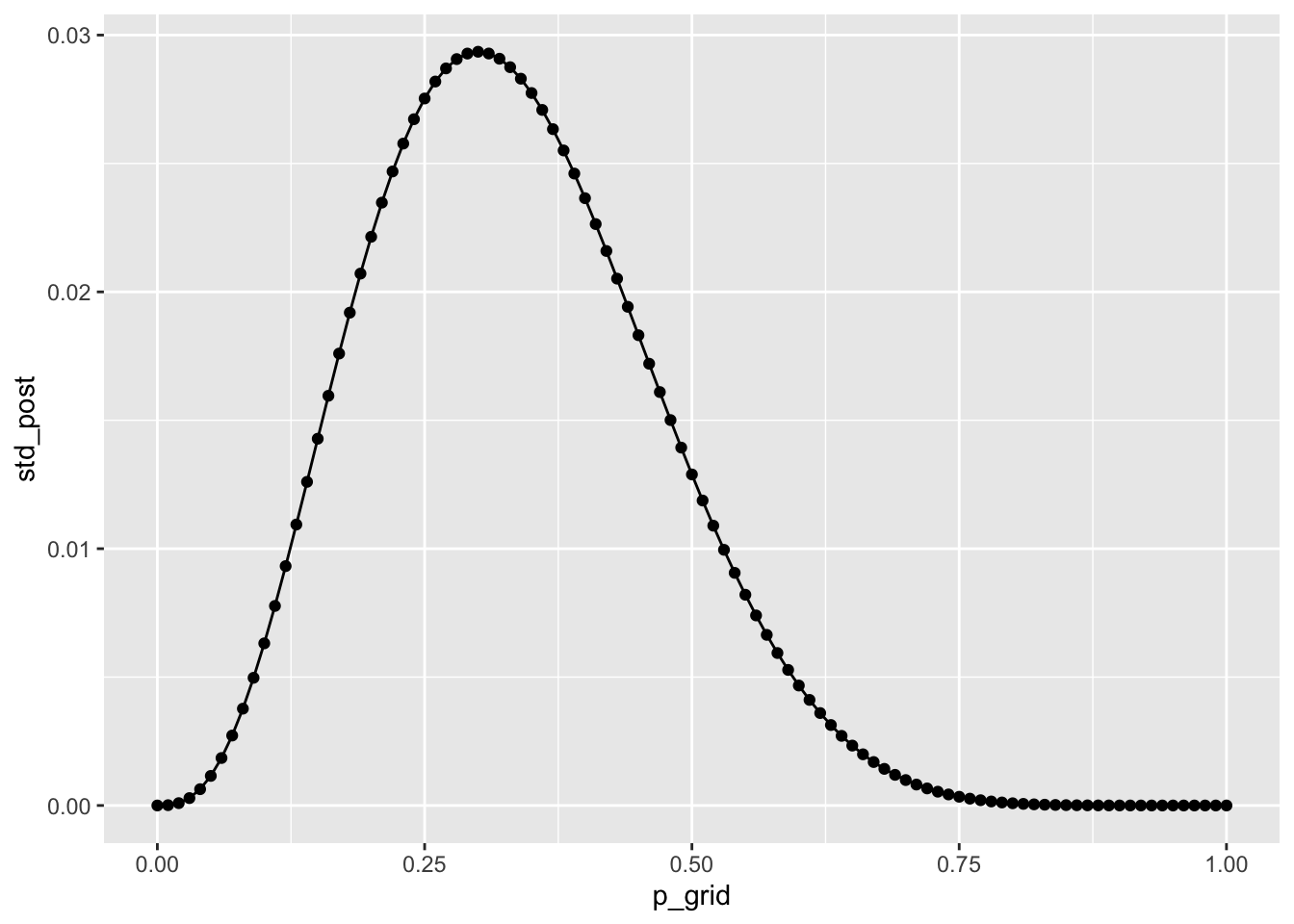
Der Modus liegt bei ca 1/3. Der Bereich plausibler Werte für \(p\) liegt ca. zwischen 0.1 und und 0.7, grob visuell geschätzt. Mehr dazu später.
# n = 2
d3 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 2, size = 6, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d3 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n=20")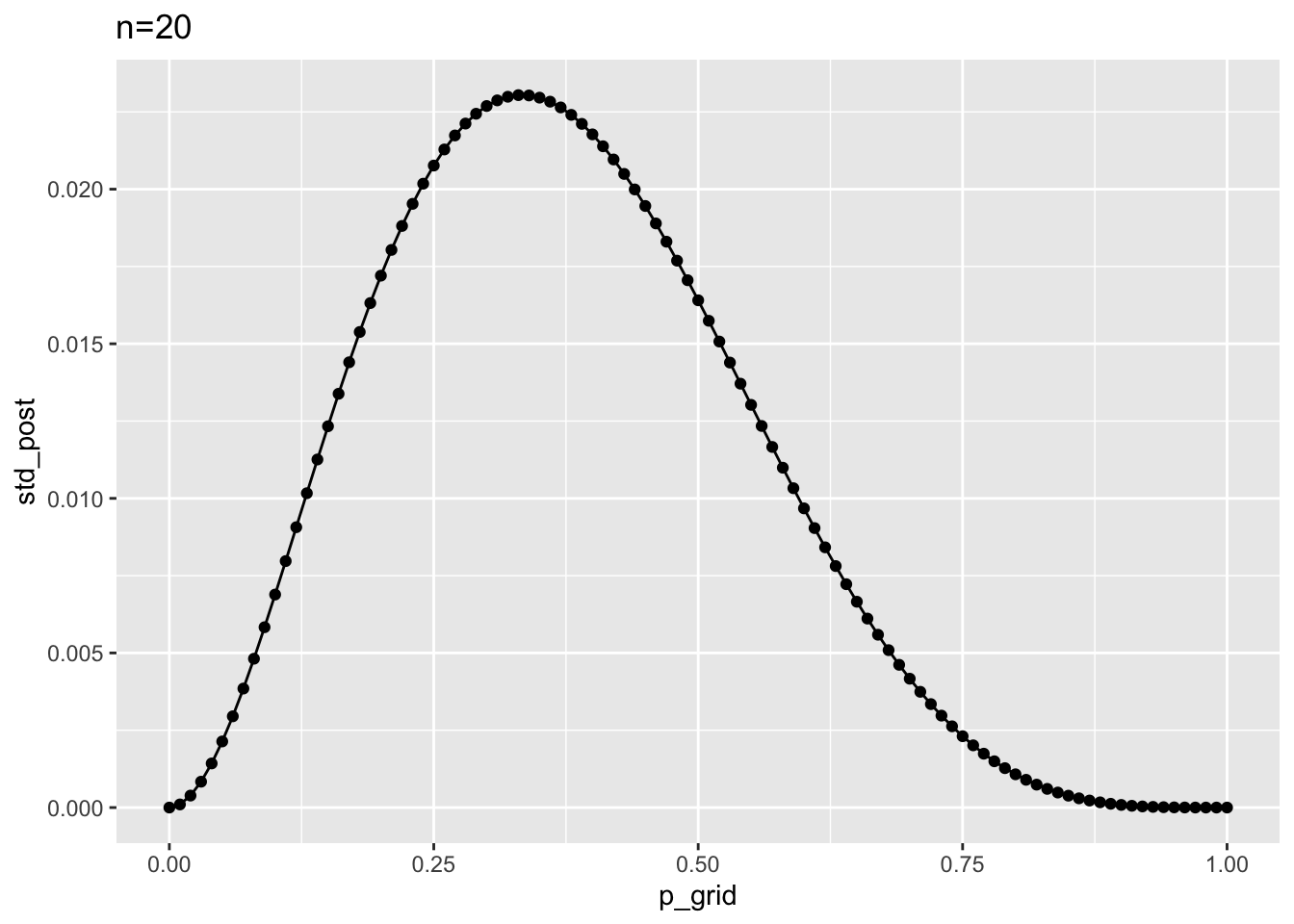
# n = 20
d4 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 20, size = 60, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d4 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n = 20")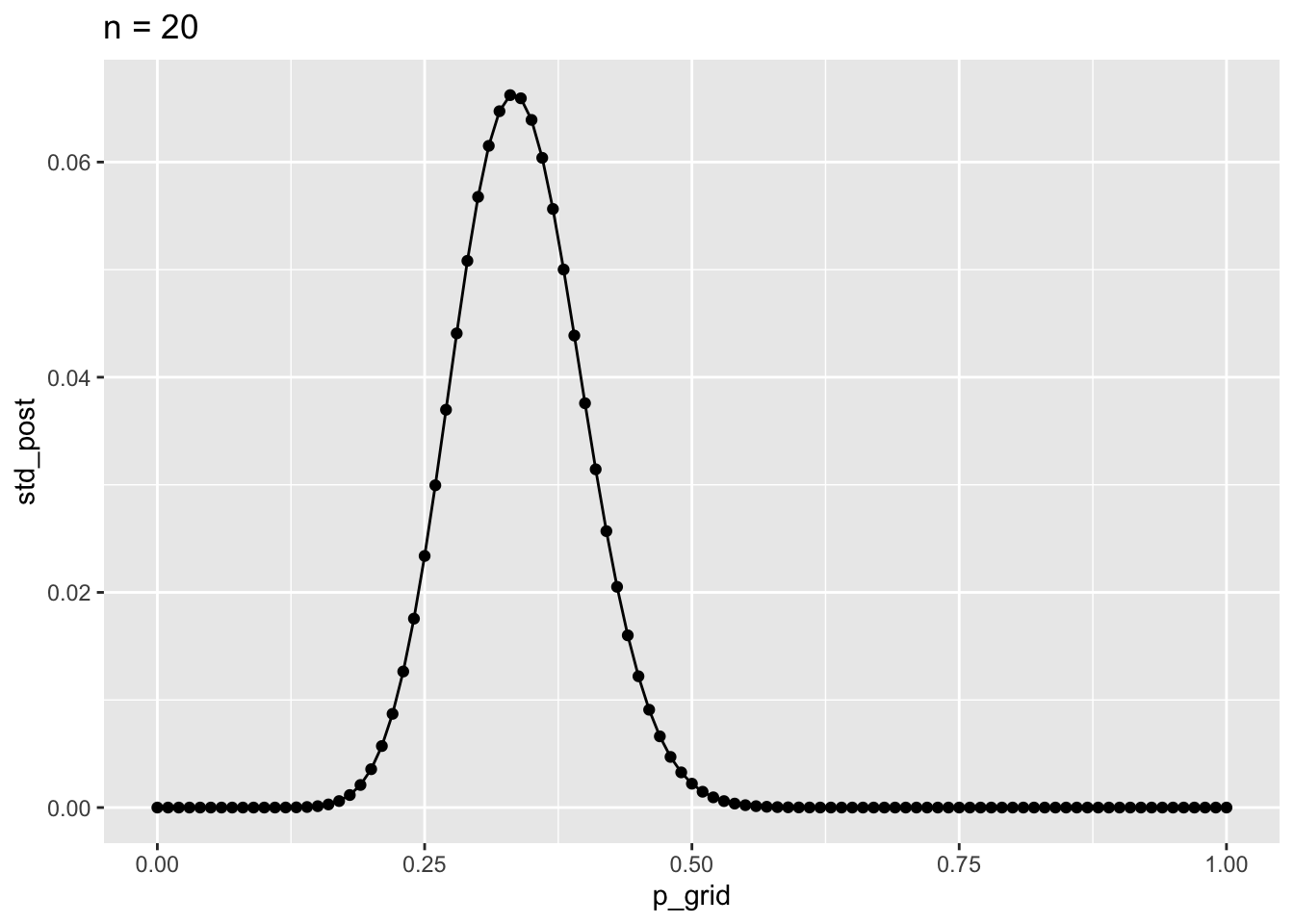
# n = 200
d5 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 200, size = 600, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d5 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n = 20")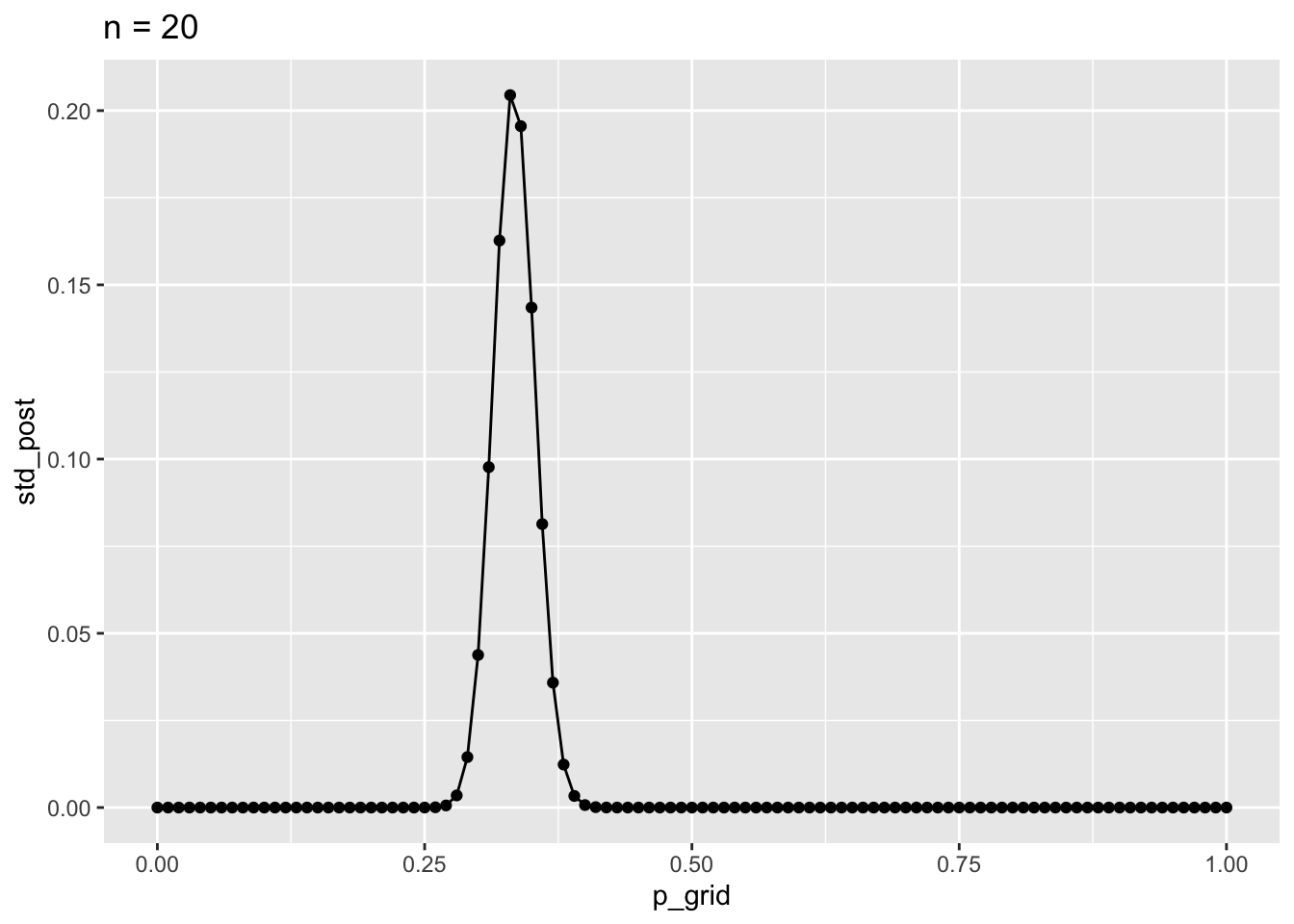
Der Modus und andere Maße der zentralen Tendenz bleiben gleich; die Streuung wird geringer.
Categories:
---
extype: string
exsolution: NA
exname: Lose
expoints: 1
categories:
- probability
- binomial
- distributions
- computer
date: '2022-10-28'
title: lose-nieten-binomial-grid
---
```{r libs, include = FALSE}
library(tidyverse)
library(gt)
```
```{r global-knitr-options, include=FALSE}
knitr::opts_chunk$set(fig.pos = 'H',
fig.asp = 0.618,
fig.width = 4,
fig.cap = "",
fig.path = "",
message = FALSE,
warning = FALSE,
fig.show = "hold",
# out.width = "100%",
cache = TRUE)
```
# Exercise
In einer Lostrommel befinden sich "sehr viele" Lose, davon ein Anteil $p$ Treffer (und $1-p$ Nieten), mit zunächst $p=0.01$.
Sie kaufen $n=10$ Lose.
a) Wie groß ist die Wahrscheinlichkeit für genau $k=0,1,...,10$ Treffer?
b) Sagen wir, Sie haben 3 Treffer in den 10 Losen. Yeah! Jetzt sei $p$ unbekannt und Sie sind indifferent zu den einzelnen Werten von $p$. Visualisieren Sie die Posteriori-Wahrscheinlichkeitsverteilung mit ca. 100 Gridwerten. Was beobachten Sie?
c) Variieren Sie $n$, aber halten Sie die Trefferquote bei 1/3. Was beobachten Sie?
Nutzen Sie die Gittermethode. Treffen Sie Annahmen, wo nötig.
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
# Solution
a) Wie groß ist die Wahrscheinlichkeit für genau $k=0,1,...,10$ Treffer?
```{r}
d_a <-
tibble(
k = 0:10,
wskt = dbinom(k, size = 10, prob = .01))
d_a %>%
ggplot() +
aes(x = k, y = wskt) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = 1:10)
```
```{r echo = FALSE}
d_a %>%
gt() %>%
fmt_scientific(columns = 2)
```
b) Sagen wir, Sie haben 3 Treffer in den 10 Losen. Yeah! Jetzt sei $p$ unbekannt und Sie sind indifferent zu den einzelnen Werten von $p$. Visualisieren Sie die Posteriori-Wahrscheinlichkeitsverteilung mit ca. 100 Gridwerten. Was beobachten Sie?
```{r}
d2 <-
tibble(
p_grid = seq(0, 1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 3, size = 10, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d2 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line()
```
Der Modus liegt bei ca 1/3. Der Bereich plausibler Werte für $p$ liegt ca. zwischen 0.1 und und 0.7, grob visuell geschätzt. Mehr dazu später.
c) Variieren Sie $n$, aber halten Sie die Trefferquote bei 1/3. Was beobachten Sie?
```{r}
# n = 2
d3 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 2, size = 6, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d3 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n=20")
# n = 20
d4 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 20, size = 60, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d4 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n = 20")
# n = 200
d5 <-
tibble(
p_grid = seq(0,1, by = 0.01),
prior = 1,
Likelihood = dbinom(x = 200, size = 600, prob = p_grid),
unstand_post = prior * Likelihood,
std_post = unstand_post / sum(unstand_post)
)
d5 %>%
ggplot() +
aes(x = p_grid, y = std_post) +
geom_point() +
geom_line() +
labs(title = "n = 20")
```
Der Modus und andere Maße der zentralen Tendenz bleiben gleich; die Streuung wird geringer.
---
Categories:
- probability
- binomial