log-y-regression2

regression
lm
qm2
stats-nutshell
Published

September 4, 2022

Exercise

library(tidyverse)
library(easystats)

In dieser Aufgabe modellieren wir den (kausalen) Effekt von Schulbildung auf das Einkommen.

Importieren Sie zunächst den Datensatz und verschaffen Sie sich einen Überblick.

d_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/Ecdat/Treatment.csv"

d <- data_read(d_path)

Dokumentation und Quellenangaben zum Datensatz finden sich hier.

glimpse(d)
Rows: 2,675
Columns: 11
$ rownames <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
$ treat    <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, T…
$ age      <int> 37, 30, 27, 33, 22, 23, 32, 22, 19, 21, 18, 27, 17, 19, 27, 2…
$ educ     <int> 11, 12, 11, 8, 9, 12, 11, 16, 9, 13, 8, 10, 7, 10, 13, 10, 12…
$ ethn     <chr> "black", "black", "black", "black", "black", "black", "black"…
$ married  <lgl> TRUE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE,…
$ re74     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ re75     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ re78     <dbl> 9930.05, 24909.50, 7506.15, 289.79, 4056.49, 0.00, 8472.16, 2…
$ u74      <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, T…
$ u75      <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, T…

Modellieren Sie den Effekt der Bildungsdauer auf das Einkommen! Gehen Sie von einem exponenziellen Zusammenhang der beiden Variablen aus. Wie verändert sich die Verteilung der abhängigen Variablen (Y) durch die Logarithmus-Transformation?

Hinweise:

  • Verwenden Sie lm zur Modellierung.
  • Operationalisieren Sie das Einkommen mit der Variable re74.
  • Fügen Sie keine weiteren Variablen dem Modell hinzu.
  • Gehen Sie von einem kausalen Effekt des Prädiktors aus.











Solution

d2 <-
  d %>% 
  filter(re74 > 0) %>% 
  mutate(re74_log = log(re74))
m <- lm(re74_log ~ educ, data = d2)
ggplot(d2) +
  aes(x = re74) +
  geom_density() +
  labs(title = "Income raw")


ggplot(d2) +
  aes(x = re74_log) +
  geom_density() +
  labs(title = "Income log transformed")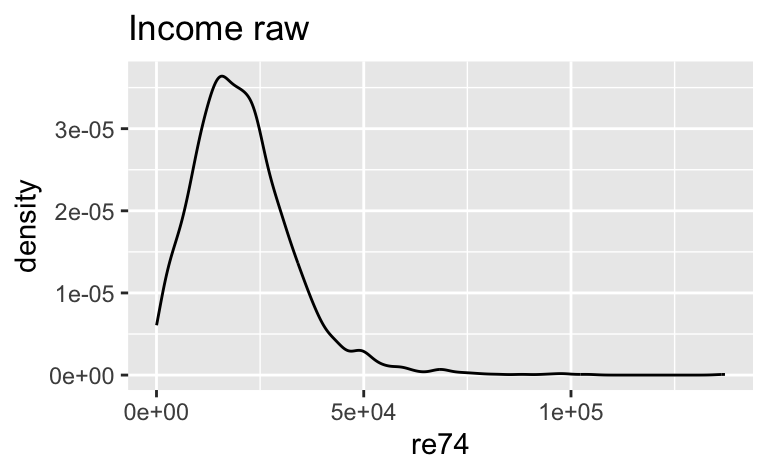

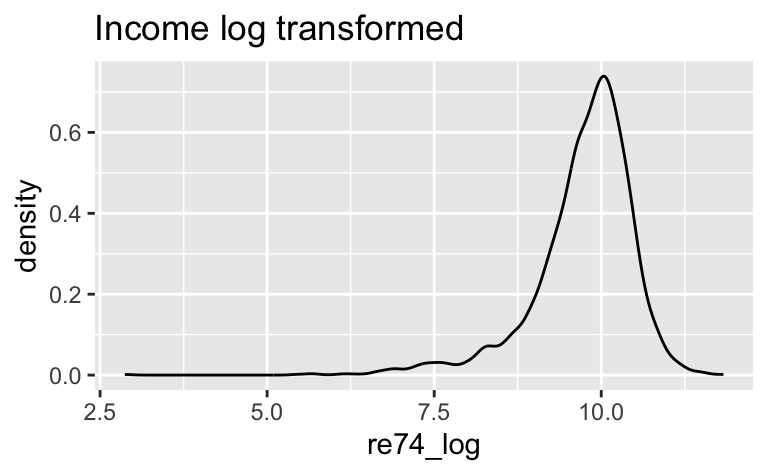
Betrachten wir die deskriptiven Statistiken:

d2 %>% 
  select(re74, re74_log) %>% 
  describe_distribution()
Variable |     Mean |       SD |      IQR |             Range | Skewness | Kurtosis |    n | n_Missing
------------------------------------------------------------------------------------------------------
re74     | 20938.28 | 12631.52 | 15086.30 | [17.63, 1.37e+05] |     1.62 |     6.81 | 2329 |         0
re74_log |     9.73 |     0.76 |     0.80 |     [2.87, 11.83] |    -1.67 |     6.01 | 2329 |         0

Die Log-Transformation hat in diesem Fall nicht wirklich zu einer Normalisierung der Variablen beigetragen. Aber das war auch nicht unser Ziel.

Categories:

  • regression
  • lm
  • qm2
  • stats-nutshell