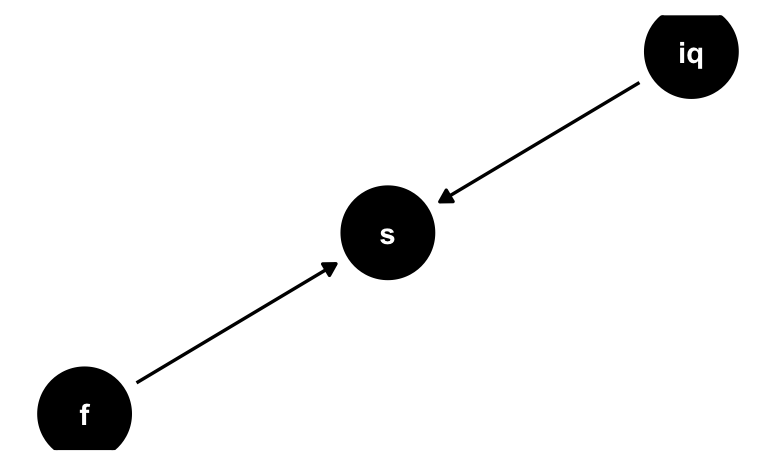
s für Studium, f für fleiss und iq für Intelligenz
December 19, 2023
Sagen wir, über die Eignung, e, für ein Studium würden nur (die individuellen Ausprägungen) von Intelligenz (iq) und Fleiss (fleiss) entscheiden, s. den DAG in Figure 1.

s für Studium, f für fleiss und iq für Intelligenz
Bei positiver Eignung wird ein Studium aufgenommen (studium = 1) ansonsten nicht (studium = 0).
Eignung (fürs Studium) sei definiert als die Summe von iq und fleiss, plus etwas Glück, s. Listing 1.
set.seed(42) # Reproduzierbarkeit
N <- 1e03
d_eignung <-
tibble(
iq = rnorm(N), # normalverteilt mit MW=0, sd=1
fleiss = rnorm(N),
glueck = rnorm(N, mean = 0, sd = .1),
eignung = 1/2 * iq + 1/2 * fleiss + glueck,
# nur wer geeignet ist, studiert (in unserem Modell):
studium = ifelse(eignung > 0, 1, 0)
)Laut unserem Modell setzt sich Eignung zur Hälfte aus Intelligenz und zur Hälfte aus Fleiss zusammen, plus etwas Glück.
Aufgabe: Zeigen Sie, dass eine Scheinkorrelation entsteht zwischen fleiss und iq, wenn man studium kontrolliert. Zeigen Sie außerdem, dass die Scheinkorrelation verschwindet, wenn man studium nicht kontrolliert.
Hinweise:
Hier ist das Modell, in dem wir nur Studenten betrachten, also studium == 1.
m_eignung <-
stan_glm(iq ~ fleiss,
data = d_eignung %>% filter(studium == 1),
refresh = 0)
hdi(m_eignung)| Parameter | CI | CI_low | CI_high | Effects | Component |
|---|---|---|---|---|---|
| (Intercept) | 0.95 | 0.7004608 | 0.8596029 | fixed | conditional |
| fleiss | 0.95 | -0.5266816 | -0.3634545 | fixed | conditional |
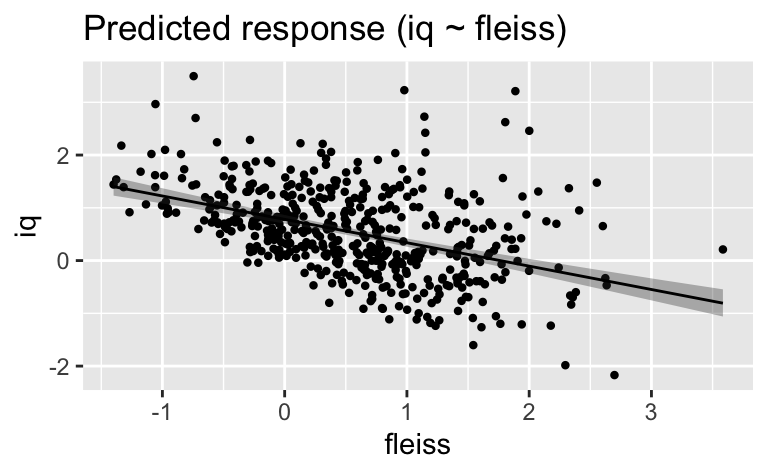
Wie man sieht, gibt es einen Zusammenhang zwischen Fleiss und Intelligenz.
m_eignung_gesamtpop <-
stan_glm(iq ~ fleiss,
data = d_eignung ,
refresh = 0)
plot(estimate_relation(m_eignung_gesamtpop))
hdi(m_eignung_gesamtpop)| Parameter | CI | CI_low | CI_high | Effects | Component |
|---|---|---|---|---|---|
| (Intercept) | 0.95 | -0.0878065 | 0.0344352 | fixed | conditional |
| fleiss | 0.95 | -0.0509851 | 0.0723826 | fixed | conditional |
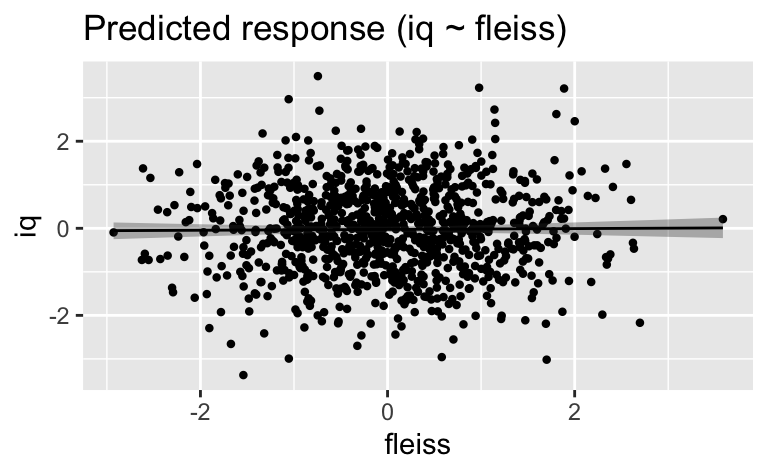
Wie man sieht, löst sich der Zusammenhang zwischen Fleiss und Intelligenz auf, wenn man studium nicht kontrolliert.
---
date: 2023-12-19 # HEUTIGES DATUM EINTRAGEN
draft: false # ACHTUNG DRAFT STEHT AUF TRUE!
title: kollision-eignung # ACHTUNG: HIER NAMEN DER AUFGABE ANGEBEN
execute:
eval: true
highlight-style: arrow
cache: true
extype: string
exsolution: ""
exshuffle: no
categories:
- causal # ENTER CATEGORIES HERE
---
```{r global-knitr-options, include=FALSE}
knitr::opts_chunk$set(fig.pos = 'H',
fig.asp = 0.618,
fig.width = 4,
fig.cap = "",
fig.path = "",
echo = TRUE,
message = FALSE,
fig.show = "hold")
library(dagitty)
library(ggdag)
library(tidyverse)
```
# Aufgabe
Sagen wir, über die *Eignung*, `e`, für ein Studium würden nur (die individuellen Ausprägungen) von Intelligenz (`iq`) und Fleiss (`fleiss`) entscheiden, s. den DAG in @fig-coll3-dag.
```{r coll32-dag}
#| echo: false
#| label: fig-coll3-dag
#| fig-cap: Kollisionsstruktur im Dag zur Studiumseignung, mit `s` für Studium, `f` für fleiss und `iq` für Intelligenz
coll2_dag <- ggdag::dagify(s ~ f + iq,
outcome = "s")
p_coll_dag2 <- ggdag(coll2_dag) + theme_dag_blank()
p_coll_dag2
# coll2_dag <-
# dagify(eignung ~ fleiss + iq)
#
# p_coll_dag2 <-
# coll2_dag %>%
# ggdag() +
# theme_dag()
#
# p_coll_dag2
```
Bei positiver Eignung wird ein Studium aufgenommen (`studium = 1`) ansonsten nicht (`studium = 0)`.
[Quelle](https://data-se.netlify.app/2020/04/16/simulation-berkson-s-paradox/)
Eignung (fürs Studium) sei definiert als die Summe von `iq` und `fleiss`, plus etwas Glück, s. @lst-studium.
```{r d-eignung, echo = TRUE}
#| lst-label: lst-studium
#| lst-cap: Eignung ist die Summe von Fleiss und Intelligenz, plus ein Quentchen Glück
set.seed(42) # Reproduzierbarkeit
N <- 1e03
d_eignung <-
tibble(
iq = rnorm(N), # normalverteilt mit MW=0, sd=1
fleiss = rnorm(N),
glueck = rnorm(N, mean = 0, sd = .1),
eignung = 1/2 * iq + 1/2 * fleiss + glueck,
# nur wer geeignet ist, studiert (in unserem Modell):
studium = ifelse(eignung > 0, 1, 0)
)
```
Laut unserem Modell setzt sich Eignung zur Hälfte aus Intelligenz und zur Hälfte aus Fleiss zusammen, plus etwas Glück.
*Aufgabe*: Zeigen Sie, dass eine Scheinkorrelation entsteht zwischen `fleiss` und `iq`, wenn man `studium` kontrolliert. Zeigen Sie außerdem, dass die Scheinkorrelation verschwindet, wenn man `studium` nicht kontrolliert.
Hinweise:
- Beachten Sie die [Standardhinweise des Datenwerks](https://datenwerk.netlify.app/hinweise).
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
# Lösung
## Setup
```{r libs}
library(rstanarm)
library(easystats)
```
## Modell Nur-Studis
Hier ist das Modell, in dem wir nur Studenten betrachten, also `studium == 1`.
```{r m1}
m_eignung <-
stan_glm(iq ~ fleiss,
data = d_eignung %>% filter(studium == 1),
refresh = 0)
hdi(m_eignung)
plot(estimate_relation(m_eignung))
```
Wie man sieht, gibt es einen Zusammenhang zwischen Fleiss und Intelligenz.
## Modell Alle-Menschen
```{r m2}
m_eignung_gesamtpop <-
stan_glm(iq ~ fleiss,
data = d_eignung ,
refresh = 0)
plot(estimate_relation(m_eignung_gesamtpop))
hdi(m_eignung_gesamtpop)
```
Wie man sieht, löst sich der Zusammenhang zwischen Fleiss und Intelligenz auf, wenn man `studium` *nicht* kontrolliert.