library(tidyverse)
library(ggpubr)kekse03
Exercise
Stellen Sie sich vor, vor Ihnen stehen drei Schalen mit Keksen. Lecker.
Schale 1 enthält 30 Vanillekekse und 10 Schokoladenkekse. Schale 2 ist identisch zu Schale 1. Schale 3 enthält 20 Vanillekekse und 20 Schokoladenkekse. Schalen 1 und 2 sind blau . Schale 3 ist rot .
Sie wählen eine der Schalen zufällig aus und ziehen ohne hinzusehen einen Keks. Der Keks ist Vanille.
Aufgabe Mit welcher Wahrscheinlichkeit stammt der Keks aus einer blauen Schale? Berechnen Sie die Wahrscheinlichkeit!
(Basierend auf einer Aufgabe aus Think Bayes von Allen Downey.)
Hinweise:
- Erstellen Sie eine Bayesbox zur Lösung dieser Aufgabe.
- Gehen Sie davon aus, dass Sie (apriori) indifferent gegenüber der Hypothesen sind.
- Geben Sie Prozentzahlen immer als Anteil an und lassen Sie die führende Null weg (z.B. .42).
- Beachten Sie die üblichen Hinweise des Datenwerks.
Solution
| Hypothesen | Priori | Likelihood | unstd_Post | Post |
|---|---|---|---|---|
| blau | 0.67 | 0.75 | 0.50 | 0.75 |
| rot | 0.33 | 0.50 | 0.17 | 0.25 |
ggbarplot(data = d, x = "Hypothesen", y = "Post",
ylab = "Posteriori-Wahrscheinlichkeit", xlab = "Hypothesen",
title = "Posteriori-Wahrscheinlichkeit für Vanillekeks aus Schale 1",
label = TRUE)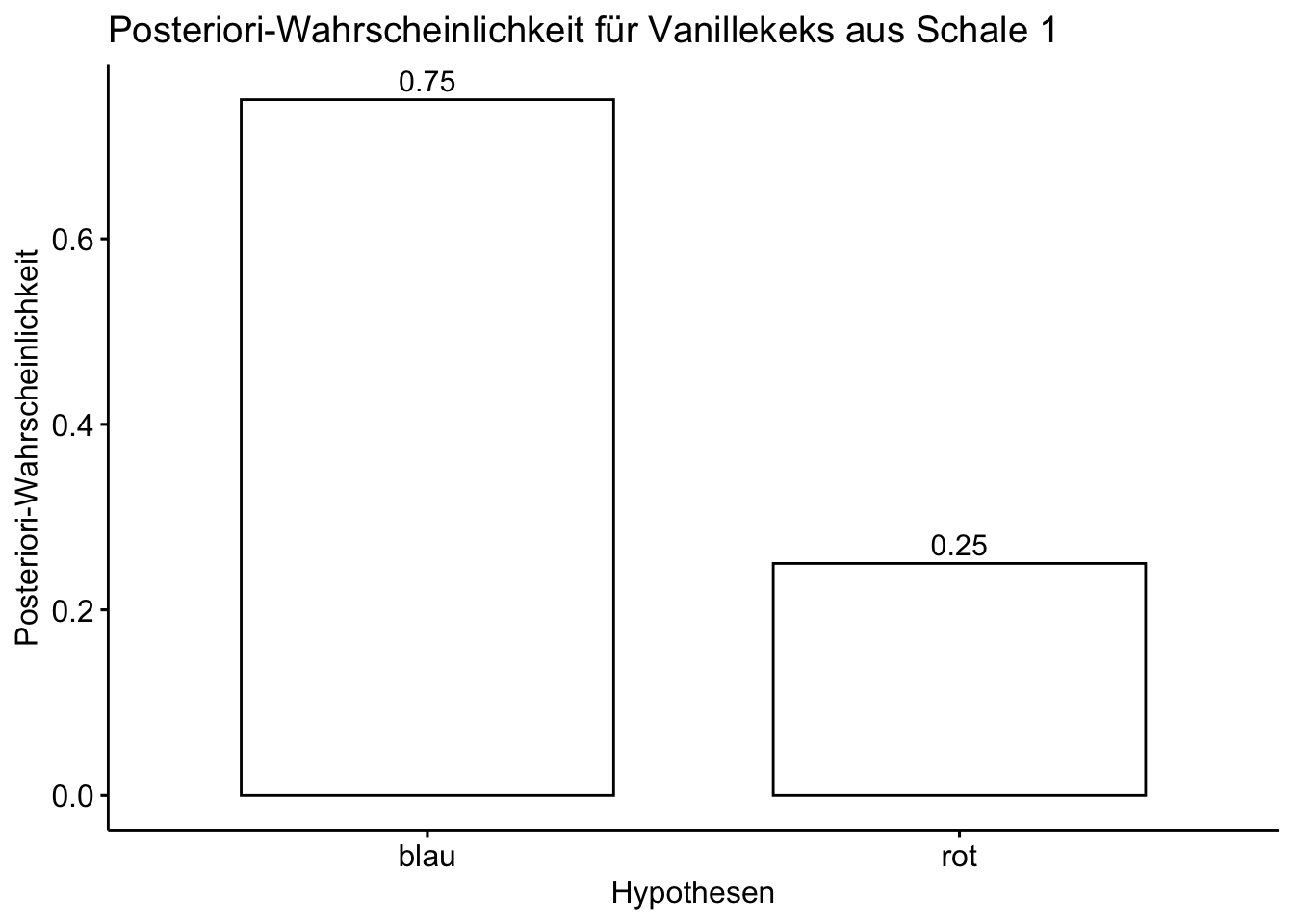
Die Antwort lautet: 0.75.
Es ist übrigens egal, welche konkreten Zahlen Sie für die Priori-Wahrscheinlichkeit wählen. Das Ergebnis bleibt das gleiche. Das Verhältnis der Zahlen muss nur gleich bleiben, also: 2,1 und 2/3, 1/3 stehen jeweils im Verhältnis 3:1. Probieren Sie es aus!
| p_Gitter | Priori | Likelihood | unstd_Post | Post |
|---|---|---|---|---|
| blau | 2 | 0.75 | 1.5 | 0.75 |
| rot | 1 | 0.50 | 0.5 | 0.25 |