kekse02

probability

bayesbox

num

Published

November 8, 2023

Aufgabe

In Think Bayes stellt Allen Downey folgende Aufgabe:

“Next let’s solve a cookie problem with 101 bowls:

Bowl 0 contains 0% vanilla cookies,

Bowl 1 contains 1% vanilla cookies,

Bowl 2 contains 2% vanilla cookies,

and so on, up to

Bowl 99 contains 99% vanilla cookies, and

Bowl 100 contains all vanilla cookies.

As in the previous version, there are only two kinds of cookies, vanilla and chocolate. So Bowl 0 is all chocolate cookies, Bowl 1 is 99% chocolate, and so on.

Suppose we choose a bowl at random, choose a cookie at random, and it turns out to be vanilla. What is the probability that the cookie came from Bowl \(x\), for each value of \(x\)?”

Hinweise:

Untersuchen Sie die Hypothesen \(\pi_0 = 0, \pi_1 = 0.1, \pi_2 = 0.2, ..., \pi_{10} = 1\) für die Trefferwahrscheinlichkeit
Erstellen Sie ein Bayes-Gitter zur Lösung dieser Aufgabe.
Gehen Sie davon aus, dass Sie (apriori) indifferent gegenüber der Hypothesen zu den Parameterwerten sind.
Geben Sie Prozentzahlen immer als Anteil an und lassen Sie die führende Null weg (z.B. .42).

Lösung

d <-
  tibble(
    # definiere die Hypothesen (das "Gitter"): 
    p_Gitter = 0:100 / 101,
    # bestimme den Priori-Wert:       
    Priori  = 1) %>%  
    mutate(
      # berechne Likelihood für jeden Gitterwert:
      Likelihood = p_Gitter,
      # berechen unstand. Posteriori-Werte:
      unstd_Post = Likelihood * Priori,
      # berechne stand. Posteriori-Werte (summiert zu 1):
      Post = unstd_Post / sum(unstd_Post))

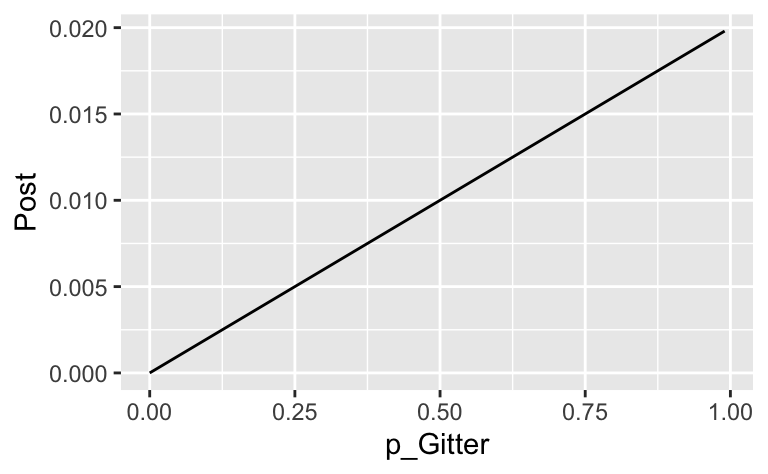
p_Gitter	Priori	Likelihood	unstd_Post	Post
0.00	1	0.00	0.00	0.00
0.01	1	0.01	0.01	0.00
0.02	1	0.02	0.02	0.00
0.03	1	0.03	0.03	0.00
0.04	1	0.04	0.04	0.00
0.05	1	0.05	0.05	0.00
0.06	1	0.06	0.06	0.00
0.07	1	0.07	0.07	0.00
0.08	1	0.08	0.08	0.00
0.09	1	0.09	0.09	0.00
0.10	1	0.10	0.10	0.00
0.11	1	0.11	0.11	0.00
0.12	1	0.12	0.12	0.00
0.13	1	0.13	0.13	0.00
0.14	1	0.14	0.14	0.00
0.15	1	0.15	0.15	0.00
0.16	1	0.16	0.16	0.00
0.17	1	0.17	0.17	0.00
0.18	1	0.18	0.18	0.00
0.19	1	0.19	0.19	0.00
0.20	1	0.20	0.20	0.00
0.21	1	0.21	0.21	0.00
0.22	1	0.22	0.22	0.00
0.23	1	0.23	0.23	0.00
0.24	1	0.24	0.24	0.00
0.25	1	0.25	0.25	0.00
0.26	1	0.26	0.26	0.01
0.27	1	0.27	0.27	0.01
0.28	1	0.28	0.28	0.01
0.29	1	0.29	0.29	0.01
0.30	1	0.30	0.30	0.01
0.31	1	0.31	0.31	0.01
0.32	1	0.32	0.32	0.01
0.33	1	0.33	0.33	0.01
0.34	1	0.34	0.34	0.01
0.35	1	0.35	0.35	0.01
0.36	1	0.36	0.36	0.01
0.37	1	0.37	0.37	0.01
0.38	1	0.38	0.38	0.01
0.39	1	0.39	0.39	0.01
0.40	1	0.40	0.40	0.01
0.41	1	0.41	0.41	0.01
0.42	1	0.42	0.42	0.01
0.43	1	0.43	0.43	0.01
0.44	1	0.44	0.44	0.01
0.45	1	0.45	0.45	0.01
0.46	1	0.46	0.46	0.01
0.47	1	0.47	0.47	0.01
0.48	1	0.48	0.48	0.01
0.49	1	0.49	0.49	0.01
0.50	1	0.50	0.50	0.01
0.50	1	0.50	0.50	0.01
0.51	1	0.51	0.51	0.01
0.52	1	0.52	0.52	0.01
0.53	1	0.53	0.53	0.01
0.54	1	0.54	0.54	0.01
0.55	1	0.55	0.55	0.01
0.56	1	0.56	0.56	0.01
0.57	1	0.57	0.57	0.01
0.58	1	0.58	0.58	0.01
0.59	1	0.59	0.59	0.01
0.60	1	0.60	0.60	0.01
0.61	1	0.61	0.61	0.01
0.62	1	0.62	0.62	0.01
0.63	1	0.63	0.63	0.01
0.64	1	0.64	0.64	0.01
0.65	1	0.65	0.65	0.01
0.66	1	0.66	0.66	0.01
0.67	1	0.67	0.67	0.01
0.68	1	0.68	0.68	0.01
0.69	1	0.69	0.69	0.01
0.70	1	0.70	0.70	0.01
0.71	1	0.71	0.71	0.01
0.72	1	0.72	0.72	0.01
0.73	1	0.73	0.73	0.01
0.74	1	0.74	0.74	0.01
0.75	1	0.75	0.75	0.02
0.76	1	0.76	0.76	0.02
0.77	1	0.77	0.77	0.02
0.78	1	0.78	0.78	0.02
0.79	1	0.79	0.79	0.02
0.80	1	0.80	0.80	0.02
0.81	1	0.81	0.81	0.02
0.82	1	0.82	0.82	0.02
0.83	1	0.83	0.83	0.02
0.84	1	0.84	0.84	0.02
0.85	1	0.85	0.85	0.02
0.86	1	0.86	0.86	0.02
0.87	1	0.87	0.87	0.02
0.88	1	0.88	0.88	0.02
0.89	1	0.89	0.89	0.02
0.90	1	0.90	0.90	0.02
0.91	1	0.91	0.91	0.02
0.92	1	0.92	0.92	0.02
0.93	1	0.93	0.93	0.02
0.94	1	0.94	0.94	0.02
0.95	1	0.95	0.95	0.02
0.96	1	0.96	0.96	0.02
0.97	1	0.97	0.97	0.02
0.98	1	0.98	0.98	0.02
0.99	1	0.99	0.99	0.02

Categories:

probability
bayesbox
num