kausal28

dag

causal

schoice

Published

June 30, 2023

Aufgabe

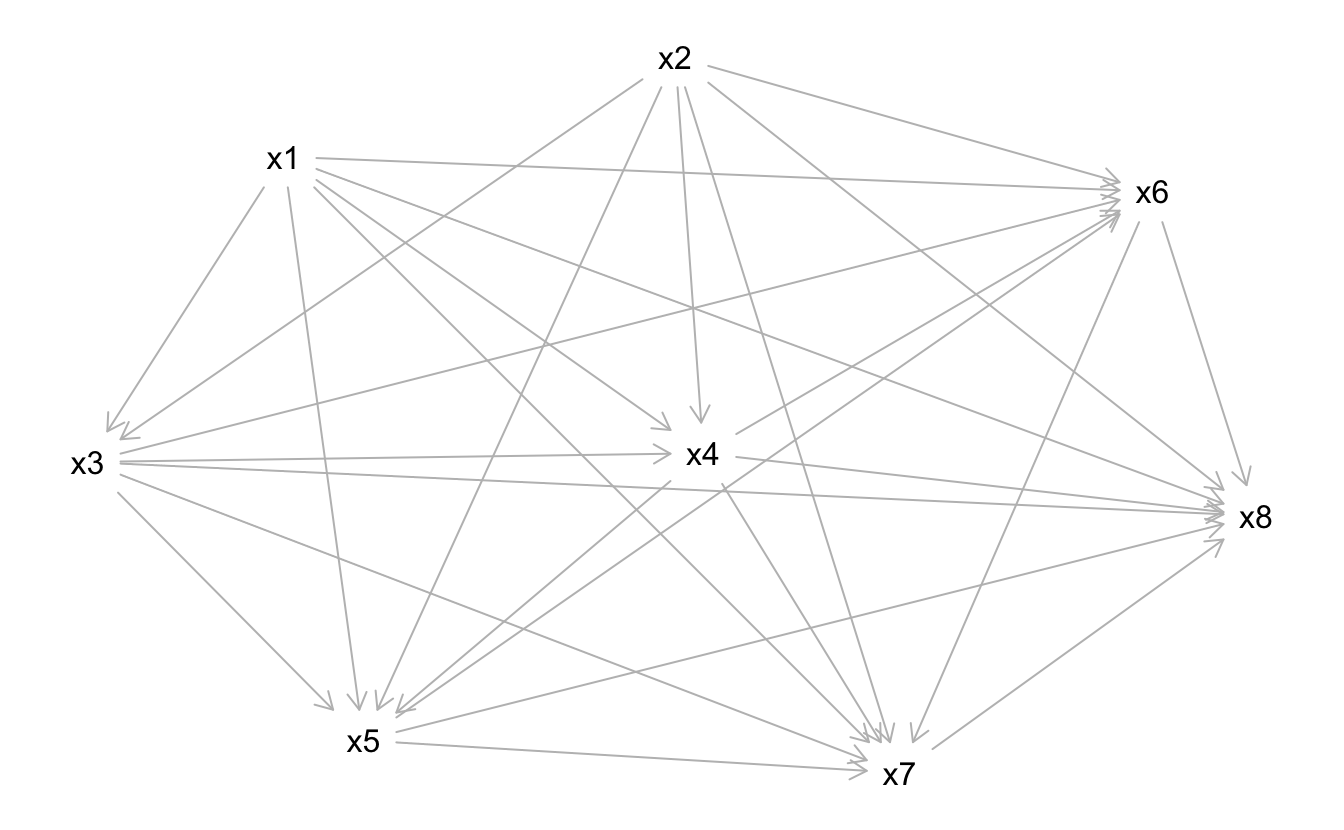
Gegeben sei der DAG g (s. u.). Der DAG verfügt über mehrere Variablen, die als Knoten im Graph dargestellt sind und mit $x_1, x_2, \ldots x_n$ bezeichnet sind.

Welche minimale Variablenmenge muss kontrolliert werden, um den kausalen Effekt von der UV zur AV zu identifizieren?

UV: x7.

AV: x8.

Hinweise:

Mengen sind mittels geschweifter Klammern gekennzeichnet, z.B. {x8, x9} meint die Menge mit den zwei Elementen x8 und x9.
Die leere Menge { } bedeutet, dass keine Variable kontrolliert werden muss, um den kausalen Effekt zu identifizieren.
Alle Variablen werden als gemessen vorausgesetzt.
Es ist möglich, dass es keine Lösung gibt, dass es also keine Adjustierungsmenge gibt, um den kausalen Effekt zu identifizieren. Wenn dies der Fall sein sollte, wählen Sie “keine Lösung”.

Answerlist

{ x1 , x2 , x3 , x4 , x5 , x6 }
{ x3, x4 }
{ x8 }
{ x6, x7 }
{ x2, x5 }

Lösung

Folgende minimale Variablenmenge muss kontrolliert werden, um den kausalen Effekt der UV auf die AV zu identifizieren: { x1 , x2 , x3 , x4 , x5 , x6 }.

Es wird also nach dem minimal adjustment set gefragt. Zu beachten ist, dass es weitere, aber größere Mengen geben kann, die den kausalen Effekt identifizieren, aber gefragt ist nach der minimalen Menge. Außerdem ist es möglich, dass es weitere minimale Adjustierungsmengen gibt, die aber nicht in der Auswahlliste vorkommen.

Erläuterung:

UV und AV sind (durch mindestens einen offenen Pfad) verbunden (“d-connected”).

Folgende Unabhängigkeitsbeziehungen (_||_) werden durch den DAG definiert:

x1 _||_ x2

UV und AV werden durch folgende Pfade verbunden:

$paths
  [1] "x7 -> x8"                                    
  [2] "x7 <- x1 -> x3 -> x4 -> x5 -> x6 -> x8"      
  [3] "x7 <- x1 -> x3 -> x4 -> x5 -> x6 <- x2 -> x8"
  [4] "x7 <- x1 -> x3 -> x4 -> x5 -> x8"            
  [5] "x7 <- x1 -> x3 -> x4 -> x5 <- x2 -> x6 -> x8"
  [6] "x7 <- x1 -> x3 -> x4 -> x5 <- x2 -> x8"      
  [7] "x7 <- x1 -> x3 -> x4 -> x6 -> x8"            
  [8] "x7 <- x1 -> x3 -> x4 -> x6 <- x2 -> x5 -> x8"
  [9] "x7 <- x1 -> x3 -> x4 -> x6 <- x2 -> x8"      
 [10] "x7 <- x1 -> x3 -> x4 -> x6 <- x5 -> x8"      
 [11] "x7 <- x1 -> x3 -> x4 -> x6 <- x5 <- x2 -> x8"
 [12] "x7 <- x1 -> x3 -> x4 -> x8"                  
 [13] "x7 <- x1 -> x3 -> x4 <- x2 -> x5 -> x6 -> x8"
 [14] "x7 <- x1 -> x3 -> x4 <- x2 -> x5 -> x8"      
 [15] "x7 <- x1 -> x3 -> x4 <- x2 -> x6 -> x8"      
 [16] "x7 <- x1 -> x3 -> x4 <- x2 -> x6 <- x5 -> x8"
 [17] "x7 <- x1 -> x3 -> x4 <- x2 -> x8"            
 [18] "x7 <- x1 -> x3 -> x5 -> x6 -> x8"            
 [19] "x7 <- x1 -> x3 -> x5 -> x6 <- x2 -> x4 -> x8"
 [20] "x7 <- x1 -> x3 -> x5 -> x6 <- x2 -> x8"      
 [21] "x7 <- x1 -> x3 -> x5 -> x6 <- x4 -> x8"      
 [22] "x7 <- x1 -> x3 -> x5 -> x6 <- x4 <- x2 -> x8"
 [23] "x7 <- x1 -> x3 -> x5 -> x8"                  
 [24] "x7 <- x1 -> x3 -> x5 <- x2 -> x4 -> x6 -> x8"
 [25] "x7 <- x1 -> x3 -> x5 <- x2 -> x4 -> x8"      
 [26] "x7 <- x1 -> x3 -> x5 <- x2 -> x6 -> x8"      
 [27] "x7 <- x1 -> x3 -> x5 <- x2 -> x6 <- x4 -> x8"
 [28] "x7 <- x1 -> x3 -> x5 <- x2 -> x8"            
 [29] "x7 <- x1 -> x3 -> x5 <- x4 -> x6 -> x8"      
 [30] "x7 <- x1 -> x3 -> x5 <- x4 -> x6 <- x2 -> x8"
 [31] "x7 <- x1 -> x3 -> x5 <- x4 -> x8"            
 [32] "x7 <- x1 -> x3 -> x5 <- x4 <- x2 -> x6 -> x8"
 [33] "x7 <- x1 -> x3 -> x5 <- x4 <- x2 -> x8"      
 [34] "x7 <- x1 -> x3 -> x6 -> x8"                  
 [35] "x7 <- x1 -> x3 -> x6 <- x2 -> x4 -> x5 -> x8"
 [36] "x7 <- x1 -> x3 -> x6 <- x2 -> x4 -> x8"      
 [37] "x7 <- x1 -> x3 -> x6 <- x2 -> x5 -> x8"      
 [38] "x7 <- x1 -> x3 -> x6 <- x2 -> x5 <- x4 -> x8"
 [39] "x7 <- x1 -> x3 -> x6 <- x2 -> x8"            
 [40] "x7 <- x1 -> x3 -> x6 <- x4 -> x5 -> x8"      
 [41] "x7 <- x1 -> x3 -> x6 <- x4 -> x5 <- x2 -> x8"
 [42] "x7 <- x1 -> x3 -> x6 <- x4 -> x8"            
 [43] "x7 <- x1 -> x3 -> x6 <- x4 <- x2 -> x5 -> x8"
 [44] "x7 <- x1 -> x3 -> x6 <- x4 <- x2 -> x8"      
 [45] "x7 <- x1 -> x3 -> x6 <- x5 -> x8"            
 [46] "x7 <- x1 -> x3 -> x6 <- x5 <- x2 -> x4 -> x8"
 [47] "x7 <- x1 -> x3 -> x6 <- x5 <- x2 -> x8"      
 [48] "x7 <- x1 -> x3 -> x6 <- x5 <- x4 -> x8"      
 [49] "x7 <- x1 -> x3 -> x6 <- x5 <- x4 <- x2 -> x8"
 [50] "x7 <- x1 -> x3 -> x8"                        
 [51] "x7 <- x1 -> x3 <- x2 -> x4 -> x5 -> x6 -> x8"
 [52] "x7 <- x1 -> x3 <- x2 -> x4 -> x5 -> x8"      
 [53] "x7 <- x1 -> x3 <- x2 -> x4 -> x6 -> x8"      
 [54] "x7 <- x1 -> x3 <- x2 -> x4 -> x6 <- x5 -> x8"
 [55] "x7 <- x1 -> x3 <- x2 -> x4 -> x8"            
 [56] "x7 <- x1 -> x3 <- x2 -> x5 -> x6 -> x8"      
 [57] "x7 <- x1 -> x3 <- x2 -> x5 -> x6 <- x4 -> x8"
 [58] "x7 <- x1 -> x3 <- x2 -> x5 -> x8"            
 [59] "x7 <- x1 -> x3 <- x2 -> x5 <- x4 -> x6 -> x8"
 [60] "x7 <- x1 -> x3 <- x2 -> x5 <- x4 -> x8"      
 [61] "x7 <- x1 -> x3 <- x2 -> x6 -> x8"            
 [62] "x7 <- x1 -> x3 <- x2 -> x6 <- x4 -> x5 -> x8"
 [63] "x7 <- x1 -> x3 <- x2 -> x6 <- x4 -> x8"      
 [64] "x7 <- x1 -> x3 <- x2 -> x6 <- x5 -> x8"      
 [65] "x7 <- x1 -> x3 <- x2 -> x6 <- x5 <- x4 -> x8"
 [66] "x7 <- x1 -> x3 <- x2 -> x8"                  
 [67] "x7 <- x1 -> x4 -> x5 -> x6 -> x8"            
 [68] "x7 <- x1 -> x4 -> x5 -> x6 <- x2 -> x3 -> x8"
 [69] "x7 <- x1 -> x4 -> x5 -> x6 <- x2 -> x8"      
 [70] "x7 <- x1 -> x4 -> x5 -> x6 <- x3 -> x8"      
 [71] "x7 <- x1 -> x4 -> x5 -> x6 <- x3 <- x2 -> x8"
 [72] "x7 <- x1 -> x4 -> x5 -> x8"                  
 [73] "x7 <- x1 -> x4 -> x5 <- x2 -> x3 -> x6 -> x8"
 [74] "x7 <- x1 -> x4 -> x5 <- x2 -> x3 -> x8"      
 [75] "x7 <- x1 -> x4 -> x5 <- x2 -> x6 -> x8"      
 [76] "x7 <- x1 -> x4 -> x5 <- x2 -> x6 <- x3 -> x8"
 [77] "x7 <- x1 -> x4 -> x5 <- x2 -> x8"            
 [78] "x7 <- x1 -> x4 -> x5 <- x3 -> x6 -> x8"      
 [79] "x7 <- x1 -> x4 -> x5 <- x3 -> x6 <- x2 -> x8"
 [80] "x7 <- x1 -> x4 -> x5 <- x3 -> x8"            
 [81] "x7 <- x1 -> x4 -> x5 <- x3 <- x2 -> x6 -> x8"
 [82] "x7 <- x1 -> x4 -> x5 <- x3 <- x2 -> x8"      
 [83] "x7 <- x1 -> x4 -> x6 -> x8"                  
 [84] "x7 <- x1 -> x4 -> x6 <- x2 -> x3 -> x5 -> x8"
 [85] "x7 <- x1 -> x4 -> x6 <- x2 -> x3 -> x8"      
 [86] "x7 <- x1 -> x4 -> x6 <- x2 -> x5 -> x8"      
 [87] "x7 <- x1 -> x4 -> x6 <- x2 -> x5 <- x3 -> x8"
 [88] "x7 <- x1 -> x4 -> x6 <- x2 -> x8"            
 [89] "x7 <- x1 -> x4 -> x6 <- x3 -> x5 -> x8"      
 [90] "x7 <- x1 -> x4 -> x6 <- x3 -> x5 <- x2 -> x8"
 [91] "x7 <- x1 -> x4 -> x6 <- x3 -> x8"            
 [92] "x7 <- x1 -> x4 -> x6 <- x3 <- x2 -> x5 -> x8"
 [93] "x7 <- x1 -> x4 -> x6 <- x3 <- x2 -> x8"      
 [94] "x7 <- x1 -> x4 -> x6 <- x5 -> x8"            
 [95] "x7 <- x1 -> x4 -> x6 <- x5 <- x2 -> x3 -> x8"
 [96] "x7 <- x1 -> x4 -> x6 <- x5 <- x2 -> x8"      
 [97] "x7 <- x1 -> x4 -> x6 <- x5 <- x3 -> x8"      
 [98] "x7 <- x1 -> x4 -> x6 <- x5 <- x3 <- x2 -> x8"
 [99] "x7 <- x1 -> x4 -> x8"                        
[100] "x7 <- x1 -> x4 <- x2 -> x3 -> x5 -> x6 -> x8"

$open
  [1]  TRUE  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
 [13] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE
 [25] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [49] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [61] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
 [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [85] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [97] FALSE FALSE  TRUE FALSE

Offenen Pfade sind der/die Pfad/e, die in der obigen Ausgabe unter $open mit TRUE gekennzeichnet sind.

Der DAG ist wie folgt definiert:

[1] "\ndag {\nx1\nx2\nx3\nx4\nx5\nx6\nx7\nx8\nx1 -> x3\nx1 -> x4\nx1 -> x5\nx1 -> x6\nx1 -> x7\nx1 -> x8\nx2 -> x3\nx2 -> x4\nx2 -> x5\nx2 -> x6\nx2 -> x7\nx2 -> x8\nx3 -> x4\nx3 -> x5\nx3 -> x6\nx3 -> x7\nx3 -> x8\nx4 -> x5\nx4 -> x6\nx4 -> x7\nx4 -> x8\nx5 -> x6\nx5 -> x7\nx5 -> x8\nx6 -> x7\nx6 -> x8\nx7 -> x8\n}\n\n"

Answerlist

Richtig
Falsch
Falsch
Falsch
Falsch

Categories:

dag
causal
schoice