library(mosaicData)
data("SaratogaHouses")kausal-bedrooms1
Exercise
Betrachten wir den Datensatz SaratogaHouses, den Sie hier herunterladen können. Ein Codebook findet sich hier.
Sie kommen auch so an die Daten ran:
Gegeben sei in diesem Zusammenhang folgender DAG:
dag1 <- "
dag{
a -> p
a -> b -> p
}
"Wobei a für (living) area steht, also der Wohnfläche eines Hauses, b für bedrooms, der Anzahl der Schlafzimmer und p für prize, den Preis, den das Haus beim Verkauf erzielt hat.
So sieht das dann aus:
ggdag(dag1) + theme_dag()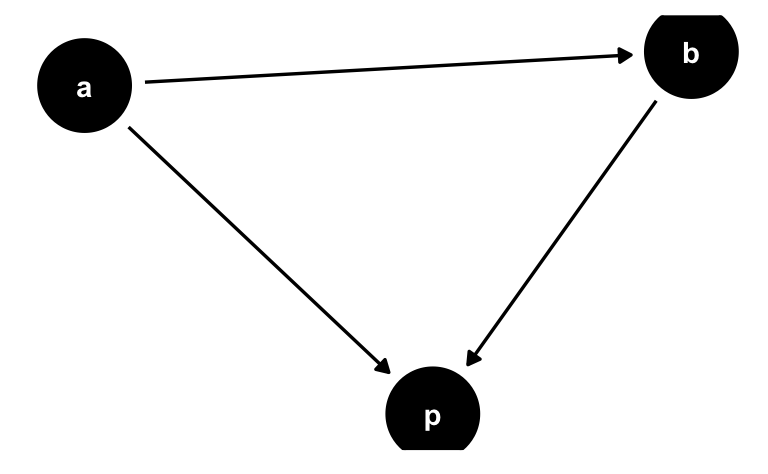
UV sei a; AV sei p.
- Berechnen Sie den direkten Effekt der Wohnfläche auf den Preis!
- Berechnen Sie den totalen Effekt der Wohnfläche auf den Preis!
Mit direkter Effekt ist der kausale Effekt von UV auf AV - ohne Zwischenglieder (Mediatoren) - gemeint. Mit indirekter Effekt ist der kausale Effekt von UV über einen (oder ggf. mehrere) Mediator(en) auf die AV gemeint. Mit totaler Effekt ist die Summe des direkten plus des oder der indirekten Effekte gemeint.
Das folgende Diagramm verdeutlicht diese drei Arten von Kausal-Effekten.
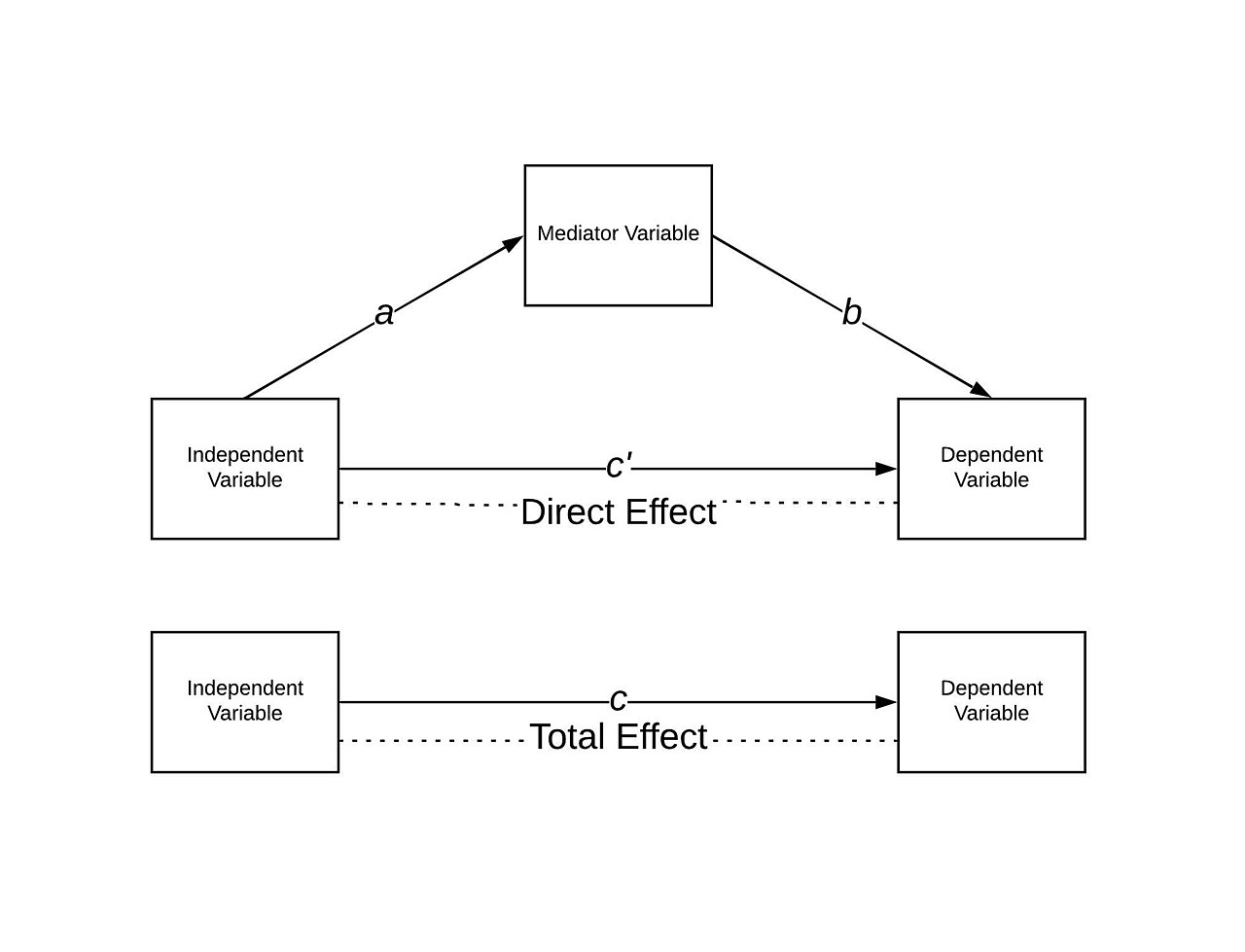
(CC-BY-SA, 3275Sartell, Wikipedia)
Hinweise:
- Geben Sie jeweils den Punktschätzer eines linearen Regressionsmodells an!
- Gehen Sie vom oben genannten DAG aus.
- Runden Sie ohne Dezimalstellen.
Solution
d <-
SaratogaHouses %>%
select(price, bedrooms, livingArea) %>%
drop_na()- direkter Effekt:
direkter_eff_lm <-
stan_glm(price ~ bedrooms + livingArea,
data = d,
refresh = 0)
coef(direkter_eff_lm)(Intercept) bedrooms livingArea
36693.044 -14221.417 125.376 Um einen direkten Effekt zu berechnen, müssen wir den spezifischen, uniquen Effekt der UV berechnen. Das erreichen wir durch eine multiple Regression, in der also die übrigen Prädiktoren aufgenommen sind. Das Resultat ist ein Koeffizient für die Assoziation der UV mit der AV, bereinigt um die Zusammenhänge der übrigen Prädiktoren.
Zur Erinnerung: Die multiple Regression liefert Koeffizienten pro Prädiktor, die bereinigt sind um den (statistischen) Einfluss der anderen Prädiktoren, mit anderne Worten: die Koeffizienten der multiplen Regression zeigen den Effekt von “nur diesem Prädiktor”.
Der Punktschätzer für den direkten Effekt (von Wohnfläche) ist:
direkter_eff <-
coef(direkter_eff_lm)[3] %>%
round(0)
direkter_efflivingArea
125 - totaler Effekt:
(Intercept) livingArea
13594.2277 113.0647 Der totale Effekt lässt sich berechnen, in dem man keine weiteren Prädiktoren neben der UV in die Regression mitaufnimmt. Die einfache (univariate) Regression zeigt den totalen Effekt der UV auf die AV.
Der Punktschätzer für den totalen Effekt beträgt:
livingArea
113 Categories:
- dag
- causal