library(tidyverse)iq07
Aufgabe
Intelligenz wird häufig mittels einem IQ-Test ermittelt.
In einer Population gebe es zwei Subgruppen, für die gilt:
\(IQ_1 \sim N(85, 15)\) \(IQ_2 \sim N(115, 15)\)
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig gezogene Person einen IQ-Wert von mind. 115 Punkten hat?
Hinweise:
- Nutzen Sie Simulationsmethoden.
- Gehen Sie von folgender IQ-Verteilung aus: \(IQ \sim N(100,15)\)
- Geben Sie Anteile oder Wahrscheinlichkeiten stets mit zwei Dezimalstellen an (sofern nicht anders verlangt).
- Simulieren Sie \(n=10^3\) Stichproben pro Subpopulation.
- Nutzen Sie die Zahl 42 als Startwert für Ihre Zufallszahlen (um die Reproduzierbarkeit zu gewährleisten)
Lösung
Wir simulieren die Daten; Subpopulation 1:
set.seed(42)
d1 <- tibble(
id = 1:10^3,
iq = rnorm(n = 10^3, mean = 85, sd = 15))Subpopulation 2:
set.seed(42)
d2 <- tibble(
id = 1:10^3,
iq = rnorm(n = 10^3, mean = 115, sd = 15))Dann kombinieren wir die Daten zu einer Tabelle:
d <-
d1 %>%
bind_rows(d2)Dann filtern wir wie in der Angabe gefragt:
solution_d <-
d %>%
count(iq > 115) %>%
mutate(prop = n / sum(n))
solution_d| iq > 115 | n | prop |
|---|---|---|
| FALSE | 1494 | 0.747 |
| TRUE | 506 | 0.253 |
Die Lösung lautet also 0.253.
Wenn Sie die Zufallszahlen mit set.seed fixiert haben, sollten Sie den exakt gleichen Wert gefunden haben.
Interessant ist es vielleicht, die Gesamtpopulation zu visualisieren:
ggplot(d) +
aes(x = iq) +
geom_density()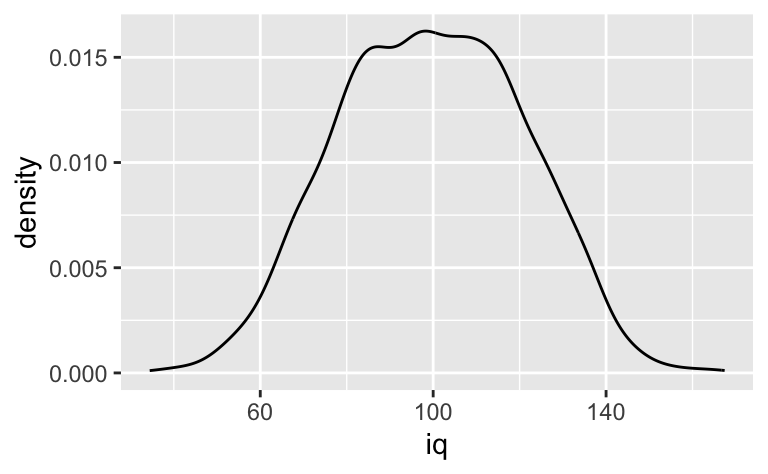
Im Vergleich dazu eine Normalverteilung mit MW=100 und SD=15:
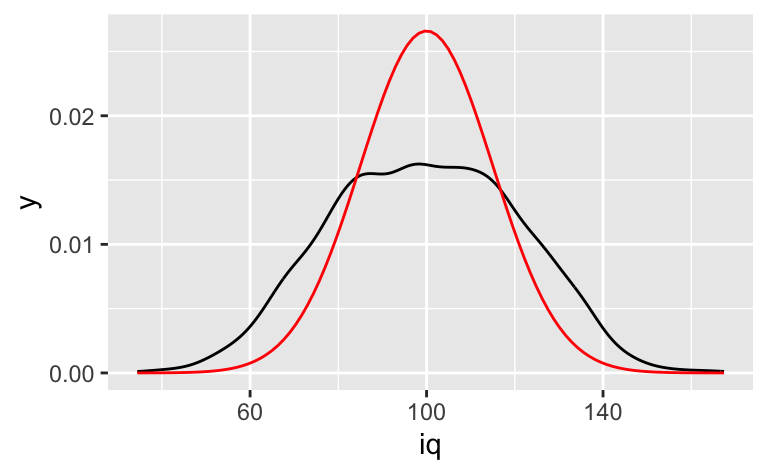
Wir sehen, dass unsere Population über eine (deutlich) höhere Streuung verfügt:
d %>%
summarise(sd(iq))| sd(iq) |
|---|
| 21.23995 |
Categories:
- probability
- simulation
- normal-distribution
- num