globus-bin1

probability

bayes

distributions

Published

November 3, 2024

1 Aufgabe

Sie werfen einen Globus \(n=9\) Mal. (Wenn Sie nach längerem Suchen keinen Globus finden, dann nehmen Sie eine Münze. Das geht genauso, macht aber weniger Spaß.)

Der Versuch läuft so ab: Sie werfen den Globus. Hoch! Und fangen ihn wieder auf. Dann schauen Sie zur Stelle unter Ihrem Zeigefinger. Ist dort Land oder Wasser?

Gehen Sie von einer Trefferwahrscheinlichkeit (für “Wasser”) von \(\pi=.7\) aus.

Aufgabe Berechnen Sie die Wahrscheinlichkeit, dass Sie genau \(0,1,2,\ldots,n\) mal “Wasser” sehen.

2 Lösung

dbinom(x = 0:9, size = 9, prob = .7)

 [1] 0.000019683 0.000413343 0.003857868 0.021003948 0.073513818 0.171532242
 [7] 0.266827932 0.266827932 0.155649627 0.040353607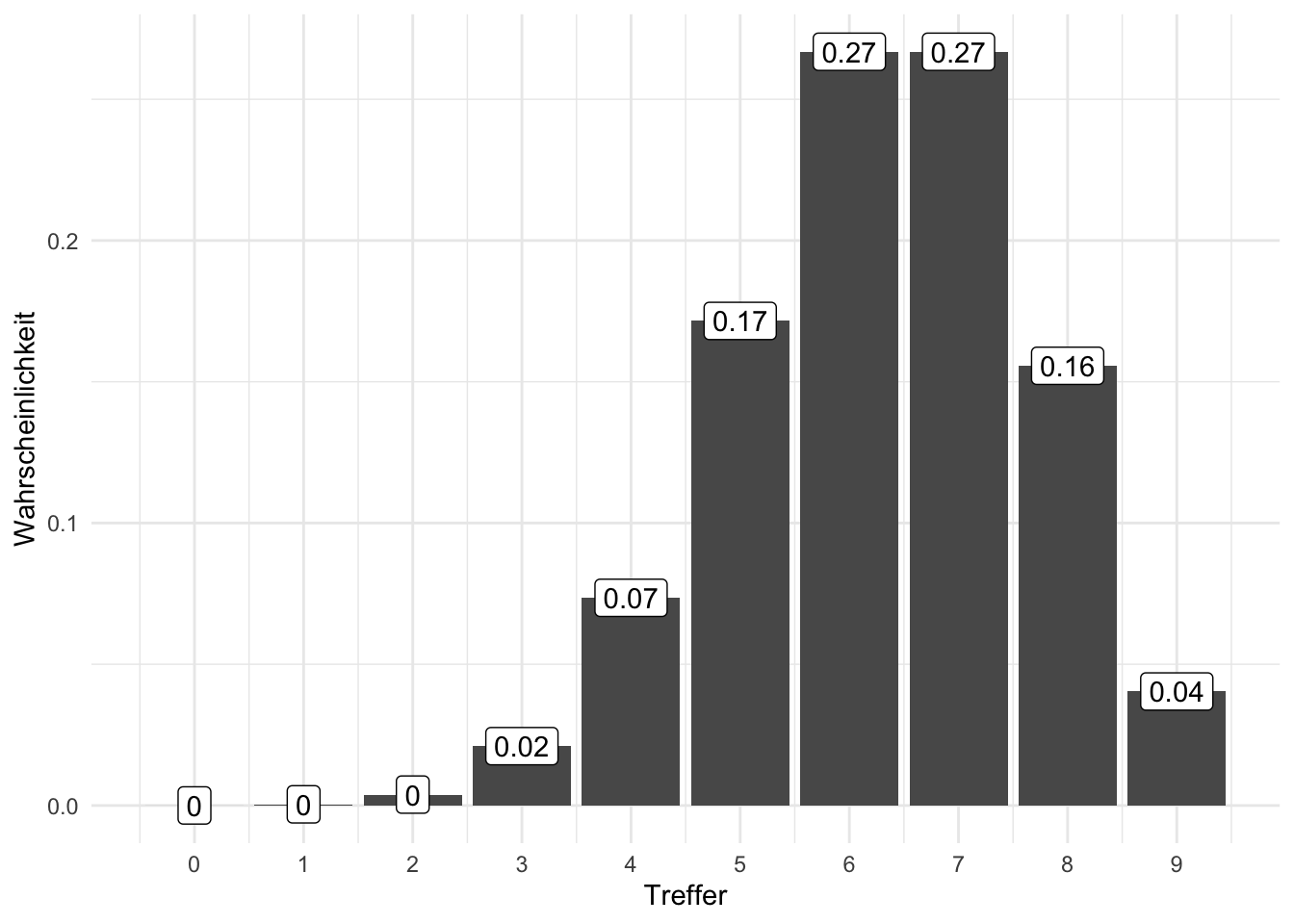

---
# gleich diese Datei in einem Ordner mit Namen der Aufgabe abspeichern!
date: 2024-11-03
draft: FALSE   # ACHTUNG DRAFT STEHT AUF TRUE!
title: globus-bin1  # HIER TITEL DES POSTS EINGEBEN.
execute: 
  
  eval: true 
highlight-style: arrow 
cache: true
toc: true
number-sections: true
extype: string
exsolution: ""
exshuffle: no
categories:
- probability  # ENTER CATEGORIES HERE
- bayes
- distributions

bibliography: "../../library-ses.bib"


---





# Aufgabe 


Sie werfen einen Globus $n=9$ Mal. 
(Wenn Sie nach längerem Suchen keinen Globus finden, dann nehmen Sie eine Münze.
Das geht genauso, macht aber weniger Spaß.)

Der Versuch läuft so ab:
Sie werfen den Globus. Hoch!
Und fangen ihn wieder auf. 
Dann schauen Sie zur Stelle unter Ihrem Zeigefinger.
Ist dort Land oder Wasser?

Gehen Sie von einer Trefferwahrscheinlichkeit (für "Wasser") von $\pi=.7$ aus.


**Aufgabe**
Berechnen Sie die Wahrscheinlichkeit, dass Sie genau $0,1,2,\ldots,n$ mal "Wasser" sehen.

</br>
</br>
</br>

</br>
</br>
</br>

</br>
</br>
</br>

</br>
</br>
</br>











# Lösung 


```{r}
dbinom(x = 0:9, size = 9, prob = .7)
```



```{r}
#| echo: false
#| warning: false

library(tidyverse)


binomial_plot <- function(n, p){
  dbinom(0:n, n, p) %>% 
    tibble(Wahrscheinlichkeit = .,
           Treffer = seq(0,n)) %>% 
    ggplot(aes(x = Treffer, y = Wahrscheinlichkeit)) +
    geom_col() +
    #   geom_segment(aes(xend = Treffer, yend = 0)) + 
    #  geom_point(color = "red", size = 5, alpha = .5) +
    scale_x_continuous(breaks = 0:n) +
    theme_minimal() +
    geom_label(aes(label = round(Wahrscheinlichkeit, 2)))
}

binomial_plot(9, .7)
```