fofrage-regrformel2

1 Aufgabe

Betrachten Sie folgende Forschungsformel:

Gibt es einen Interaktionseffekt zwischen Geschlecht und Schnabellänge auf das Gewicht eines Pinguins? Liegen auch Haupteffekte vor?

Auf Basis der folgenden Analyse ist folgende Frage zu untersuchen. Liegt ein Interaktionseffekt vor?

Hinweise:

• Unter “Haupteffekt” versteht man den Effekt einer UV auf die AV (im Gegensatz zu einem Interaktionseffekt, der ja der gemeinsame Effekt mehrerer UV auf die AV ist).
• Beachten Sie die üblichen Hinweise des Datenwerks.
• Beziehen Sie sich auf den Datensatz penguins.

library(palmerpenguins)
library(tidyverse)
data(penguins)

penguins <-
  penguins |> 
  filter(sex == "female" | sex == "male") |> 
  drop_na()

library(easystats)
library(tidyverse)
library(rstanarm)

glimpse(penguins)

Rows: 333
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, 36.7, 39.3, 38.9, 39.2, 41.1, 38.6…
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, 19.3, 20.6, 17.8, 19.6, 17.6, 21.2…
$ flipper_length_mm <int> 181, 186, 195, 193, 190, 181, 195, 182, 191, 198, 18…
$ body_mass_g       <int> 3750, 3800, 3250, 3450, 3650, 3625, 4675, 3200, 3800…
$ sex               <fct> male, female, female, female, male, female, male, fe…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

Zur besseren Interpretierbarkeit sind die metrischen UV standardisiert:

penguins_z <- standardize(penguins, select = bill_length_mm, append = TRUE)

Es werden verschiedenen Modelle berechnet, die sich in ihrem Regressionsformel unterscheiden:

m1 <- stan_glm(body_mass_g ~ sex, data = penguins_z, 
               refresh = 0)
m2 <- stan_glm(body_mass_g ~ sex + bill_length_mm_z, data = penguins_z, 
               refresh = 0)
m3 <- stan_glm(body_mass_g ~ sex + bill_length_mm_z + sex:bill_length_mm_z, data = penguins_z, 
               refresh = 0)
m4 <- stan_glm(body_mass_g ~ sex:bill_length_mm_z, data = penguins_z, 
               refresh = 0)

Parameter m1:

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	3862.77	(3754.51, 3974.33)	100%	1.001	3757	Normal (4207.06 +- 2013.04)
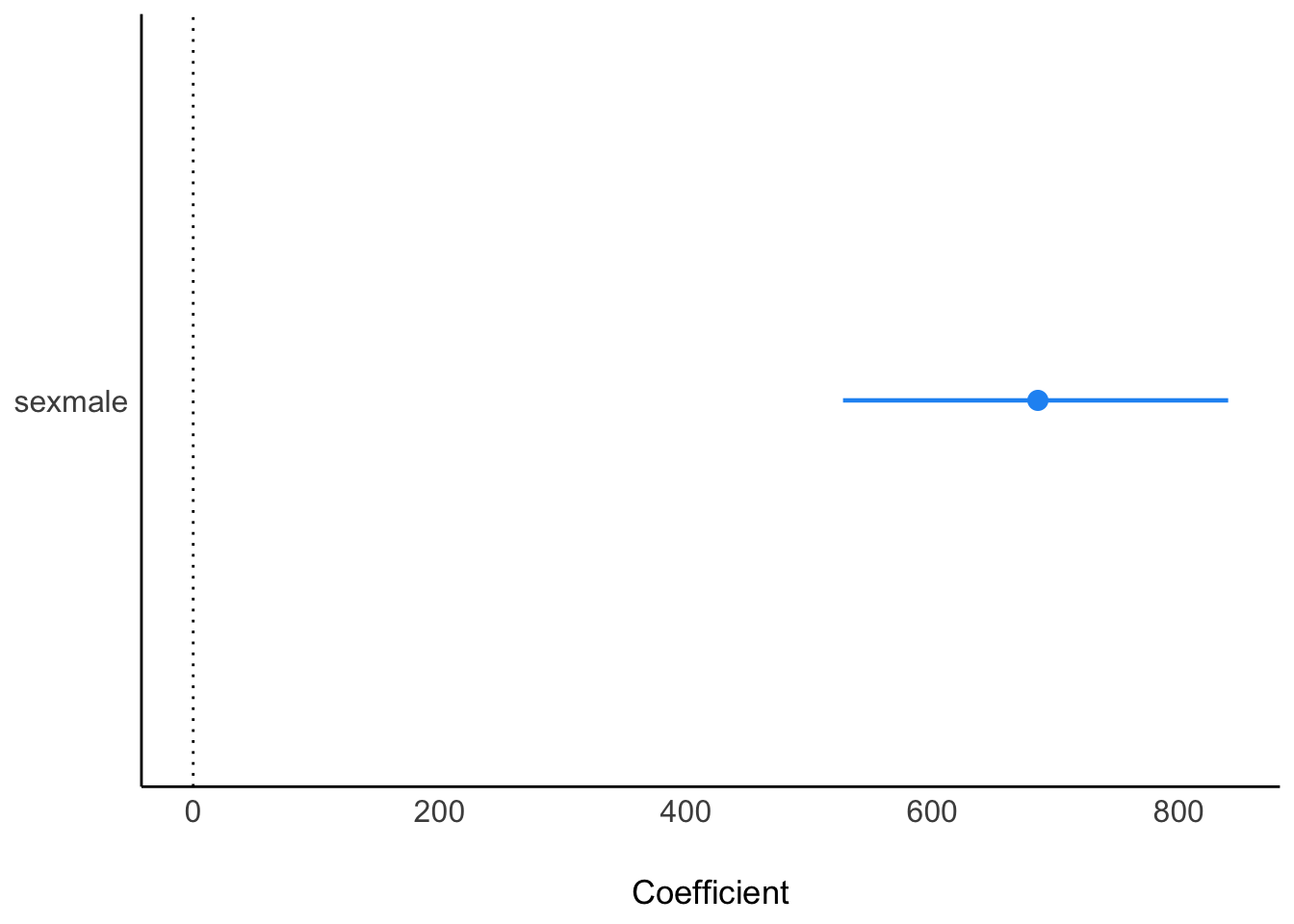
sexmale	682.87	(527.74, 838.00)	100%	1.000	4016	Normal (0.00 +- 4020.19)

Parameter m2:

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	4003.05	(3903.36, 4102.60)	100%	1.000	4240	Normal (4207.06 +- 2013.04)
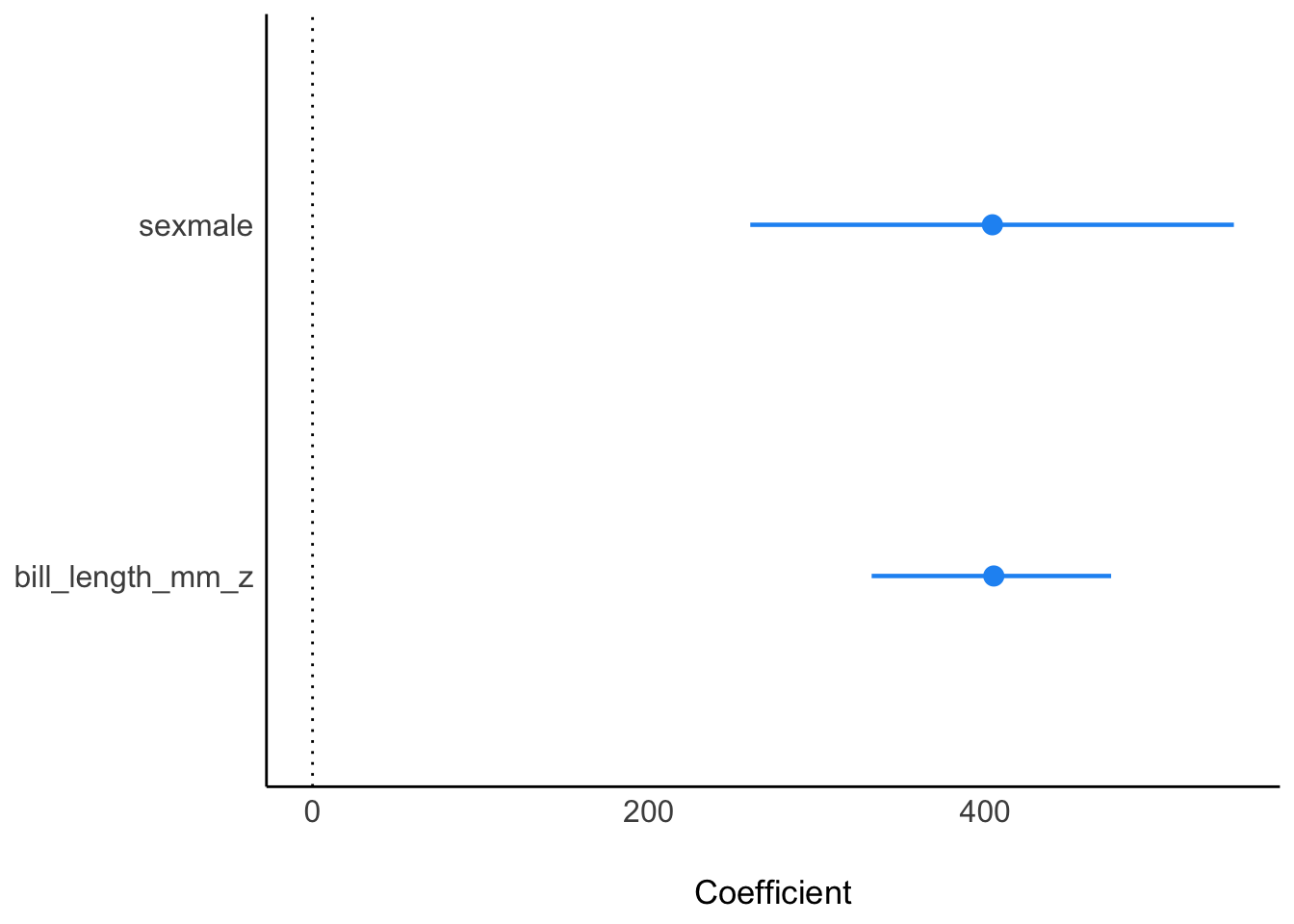
sexmale	404.96	(263.54, 548.73)	100%	1.001	4168	Normal (0.00 +- 4020.19)
bill_length_mm_z	405.98	(335.34, 475.15)	100%	1.000	4183	Normal (0.00 +- 2013.04)

Parameter m3:

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	4011.90	(3909.94, 4111.74)	100%	1.001	2850	Normal (4207.06 +- 2013.04)
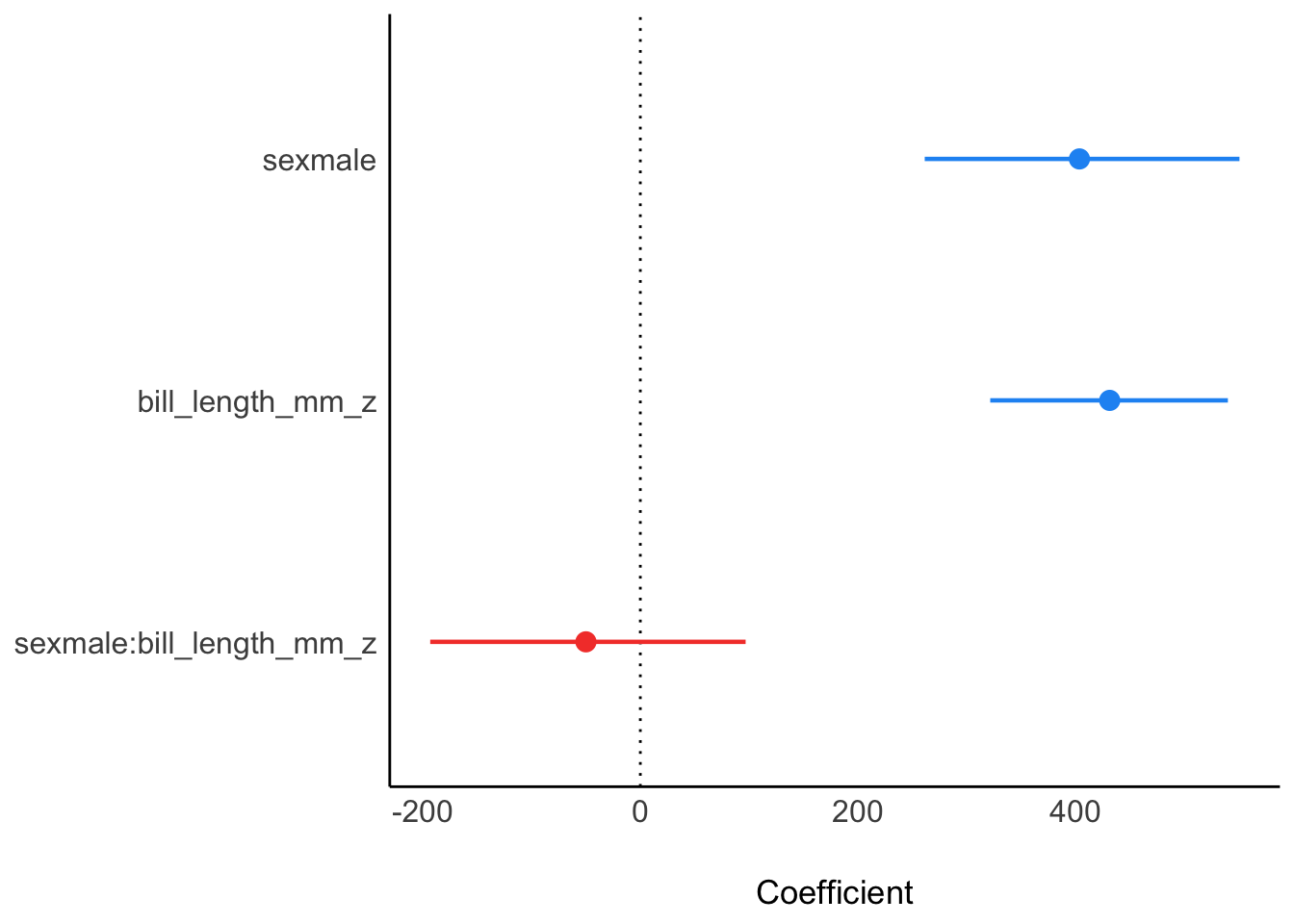
sexmale	402.86	(258.26, 547.62)	100%	1.000	3331	Normal (0.00 +- 4020.19)
bill_length_mm_z	430.91	(323.03, 534.95)	100%	1.000	2268	Normal (0.00 +- 2013.04)
sexmale:bill_length_mm_z	-46.24	(-193.60, 98.95)	74.35%	1.000	2372	Normal (0.00 +- 2809.11)

Parameter m4:

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	4218.11	(4141.49, 4297.53)	100%	1.000	5231	Normal (4207.06 +- 2013.04)
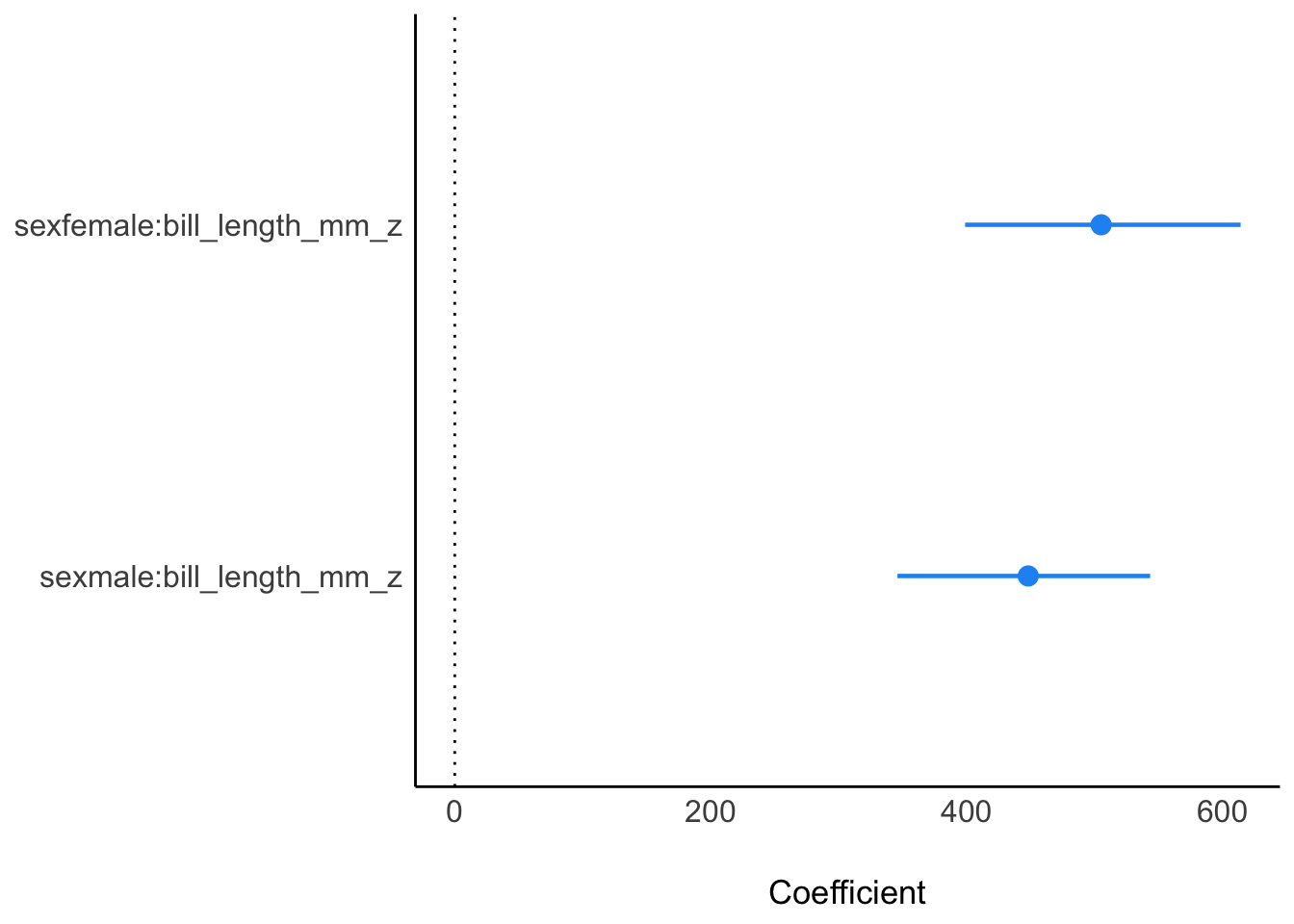
sexfemale:bill_length_mm_z	508.32	(401.67, 616.78)	100%	1.000	4479	Normal (0.00 +- 3079.61)
sexmale:bill_length_mm_z	445.40	(346.36, 546.72)	100%	1.000	5301	Normal (0.00 +- 2809.11)

2 Lösung

Die Regressionsformel lautet: body_mass_g ~ sex + bill_length_mm + sex:bill_length_mm.

Daher ist m3 korrekt.

Die Parameterwerte von m3 zeigen, dass ein Interaktionseffekt nicht bestätigt werden kann, bzw. dass die Null, also keine Interaktion, im Bereich plausibler Werte (d.h. innerhalb des Konfidenzintervalls) liegt.