flights-delay

1 Hintergrund und Forschungsfrage

Wir untersuchen die Forschungsfrage Was sind Prädiktoren von Flugverspätungen. Dazu nutzen wir lineare Modelle als Modellierungsmethoden.

Dieser Post knüpft an den Post zur explorativen Datenanalyse der Flugverspätungen an (es gibt auch hier, Teil 1 und hier, Teil 2 ein Video zu diesem EDA-Post).

2 Setup

2.1 Pakete laden

Wirklich wichtig sind nur tidymodels und tidyverse. Die restlichen Pakete werden nur am Rande benötigt. Man sollte auch nur die Pakete laden, die man für die Analyse benötigt.

library("tidymodels")  # Train- und Test-Sample aufteilen
library("tidyverse")  # data wrangling
library("conflicted")  # Name clashes finden
library("easystats")  # stats made easy

2.2 Daten laden: Flights 2023

Aus Gründen der Datenökonomie nutzen wir eine kleinere Version des Datensatz flights. Wir nutzen nicht mehr die Daten aus dem 2013, sondern die neueren Daten aus dem Jahr 2023.

library(nycflights23)
data(flights)

set.seed(42)  # Reproduzierbarkeit
flights <- 
  flights |> 
  sample_n(size = 3e4)

Achtung: flights ist recht groß; die Regressionsmodelle können leicht ein paar Hundert Megabyte groß werden. Das bringt u.U. auch einen modernen Computer irgendwann ins Straucheln.

3 flights2: Nicht benötigte Variablen entfernen und ID hinzufügen

flights2 <-
  flights %>% 
  select(-c(year, arr_delay)) %>% 
  drop_na(dep_delay) %>% 
  mutate(id = row_number()) %>% 
  select(id, everything())  # id nach vorne ziehen

4 Aufteilung in Train- und Testsample

Der Hintergrund zur Idee der Aufteilung in Train- und Test-Stichprobe kann z.b. hier oder hier, Kapitel 15, nachgelesen werden.

flights_split <- initial_split(flights2, 
                               strata = dep_delay)

5 flights_train2, flights_test2

set.seed(42)  # Reproduzierbarkeit
flights_train2 <- training(flights_split)
flights_test2 <- testing(flights_split)

Die “wirkliche Welt” (was immer das ist) besorgt die Aufteilung von Train- und Test-Sampel für Sie automatisch. Sagen wir, Sie arbeiten für die Flughafen-Aufsicht von New York. Dann haben Sie einen Erfahrungsschatz an Flügen aus der Vergangenheit in Ihrer Datenbank (Train-Sample). Einige Tages kommt Ihr Chef zu Ihnen und sagt: “Rechnen Sie mir mal die zu erwartende Verspätung der Flüge im nächsten Monat aus!”. Da heute nicht klar ist, wie die Verspätung der Flüge in der Zukunft (nächsten Monat) sein wird, stellen die Flüge des nächsten Monats das Test-Sample dar.

Übrigens: In der Prüfung besorgt das Aufteilen von Train- und Test-Sample netterweise Ihr Dozent…

6 lm0: Nullmodell

Eigentlich nicht nötig, das Nullmodell, primär aus didaktischen Gründen berechnet, um zu zeigen, dass in diesem Fall \(R^2\) wirklich gleich Null ist.

lm0 <- lm(dep_delay ~ 1, data = flights_train2)
model_parameters(lm0)  # model_parameters zeit die (geschätzten) Regressionsgewichte (Betas)

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	13.89315	0.3737019	0.95	13.16067	14.62563	37.17709	21918	0

Wir könnten anstatt model_parameters auch parameters nutzen; das ist der gleiche Befehl.

Allerdings gibt es den Befehl parameters in zwei Paketen, es käme also zu einem “Name Clash”. Das umgehen wir, indem wir model_parameter nutzen, und nicht parameters.

7 lm1: origin

lm1 <- lm(dep_delay ~ origin, data = flights_train2)
model_parameters(lm1)  

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	15.106693	0.6574882	0.95	13.8179688	16.395417	22.976372	21916	0.0000000
originJFK	1.370627	0.9408249	0.95	-0.4734579	3.214711	1.456835	21916	0.1451762
originLGA	-4.422138	0.8995398	0.95	-6.1853014	-2.658975	-4.916001	21916	0.0000009

Man vergleiche:

flights_train2 %>% 
  drop_na(dep_delay) %>% 
  group_by(origin) %>% 
  summarise(delay_avg = mean(dep_delay)) %>% 
  mutate(delay_delta = delay_avg - delay_avg[1])

origin	delay_avg	delay_delta
EWR	15.10669	0.000000
JFK	16.47732	1.370627
LGA	10.68455	-4.422138

Der Mittelwertsvergleich und das Modell lm1 sind faktisch informationsgleich.

Aber leider ist es um die Modellgüte nicht so gut bestellt (eigentlich eher “grottenschlecht”):

r2(lm1)

# R2 for Linear Regression
       R2: 0.002
  adj. R2: 0.002

lm1 ist so schlecht, wir löschen es gleich wieder…

rm(lm1)

8 lm2: All in

# NICHT AUSFÜHREN
#lm2_all_in <- lm(dep_delay ~ ., data = flights_train2)

Modell lm2_all_in ist hier keine gute Idee, da nominale Prädiktoren in Indikatorvariablen umgewandelt werden. Hat ein nominaler Prädiktor sehr viele Stufen (wie hier), so resultieren sehr viele Indikatorvariablen, was dem Regressionsmodell Probleme bereiten kann (bei mir hängt sich R auf). Besser ist es in dem Fall, die Anzahl der Stufen von nominalskalierten Variablen vorab zu begrenzen.

Bei kleineren Datensätzen (weniger Variablen, weniger Fälle) lohnt es sich aber oft, das “All-in-Modell” auszuprobieren, als Referenzmaßstab für andere Modelle.

9 flights_train3: Textvariablen in Faktorvariablen umwandeln

Begrenzen wir zunächst die Anzahl der Stufen der nominal skalierten Variablen:

flights_train3 <- 
  flights_train2 %>% 
  mutate(across(
    .cols = where(is.character),
    .fns = as.factor))

Wem das across zu kompliziert ist, der kann auch alternativ (synonym) jede Variable einzeln in einen Faktor umwandeln und zwar so:

flights_train3a <- 
  flights_train2 %>% 
  mutate(tailnum = as.factor(tailnum),
         origin = as.factor(origin),
         dest = as.factor(dest),
         carrier = as.factor(carrier)
      )

Das ist einfacher als mit across, aber dafür mehr Tipperei.

Wir müssen die Transformationen, die wir auf das Train-Sample anwenden, auch auf das Test-Sample anwenden:

10 flights_test3

flights_test3 <- 
  flights_test2 %>% 
  mutate(across(
    .cols = where(is.character),
    .fns = as.factor))

flights_train3 %>% 
  select(where(is.factor)) %>% 
  names()

[1] "carrier" "tailnum" "origin"  "dest"   

Z.B. dest hat viele Stufen:

flights_train3 %>% 
  count(dest, sort = TRUE)

dest	n
ORD	941
BOS	933
ATL	890
MCO	860
LAX	816
MIA	806
FLL	707
CLT	673
SFO	588
DFW	581
RDU	579
DEN	541
DTW	521
DCA	459
BNA	446
TPA	438
PBI	426
PIT	395
IAH	377
CMH	374
CLE	337
BUF	333
IND	331
MSP	311
LAS	299
CVG	295
SJU	293
PHX	270
ORF	269
AUS	258
SEA	252
RSW	251
STL	247
JAX	240
CHS	239
MSY	226
SAN	217
PWM	199
SAV	196
MCI	195
ROC	189
RIC	180
SLC	175
SYR	172
IAD	170
BTV	159
GSO	154
ILM	145
SDF	142
MKE	136
MDW	131
GSP	119
BGR	117
MEM	108
MYR	107
SRQ	101
PDX	97
GRR	91
PVD	86
ALB	80
AVL	77
CHO	74
SNA	74
DAL	65
SAT	59
OMA	58
TYS	54
HOU	52
BQN	50
OKC	49
ITH	46
MSN	46
ACK	45
BHM	43
HNL	43
ORH	42
EYW	41
BWI	40
CAE	40
STT	40
BDL	38
DSM	37
MHT	35
XNA	35
ROA	32
SMF	32
HHH	31
LIT	31
MVY	30
DAY	28
BGM	25
MDT	21
PHL	21
PSE	19
ONT	18
SJC	16
EGE	14
ABQ	12
BUR	12
SCE	12
TVC	12
AVP	11
PSP	11
BZN	10
HYA	10
OAK	10
TUL	10
RNO	8
VPS	7
JAC	6
PNS	5
ANC	4
MTJ	4
AGS	2
HDN	2
SBN	2

flights_train3 %>%
  count(dest) %>%
  ggplot() +
  aes(y = fct_reorder(dest, n), x = n) +
  geom_col()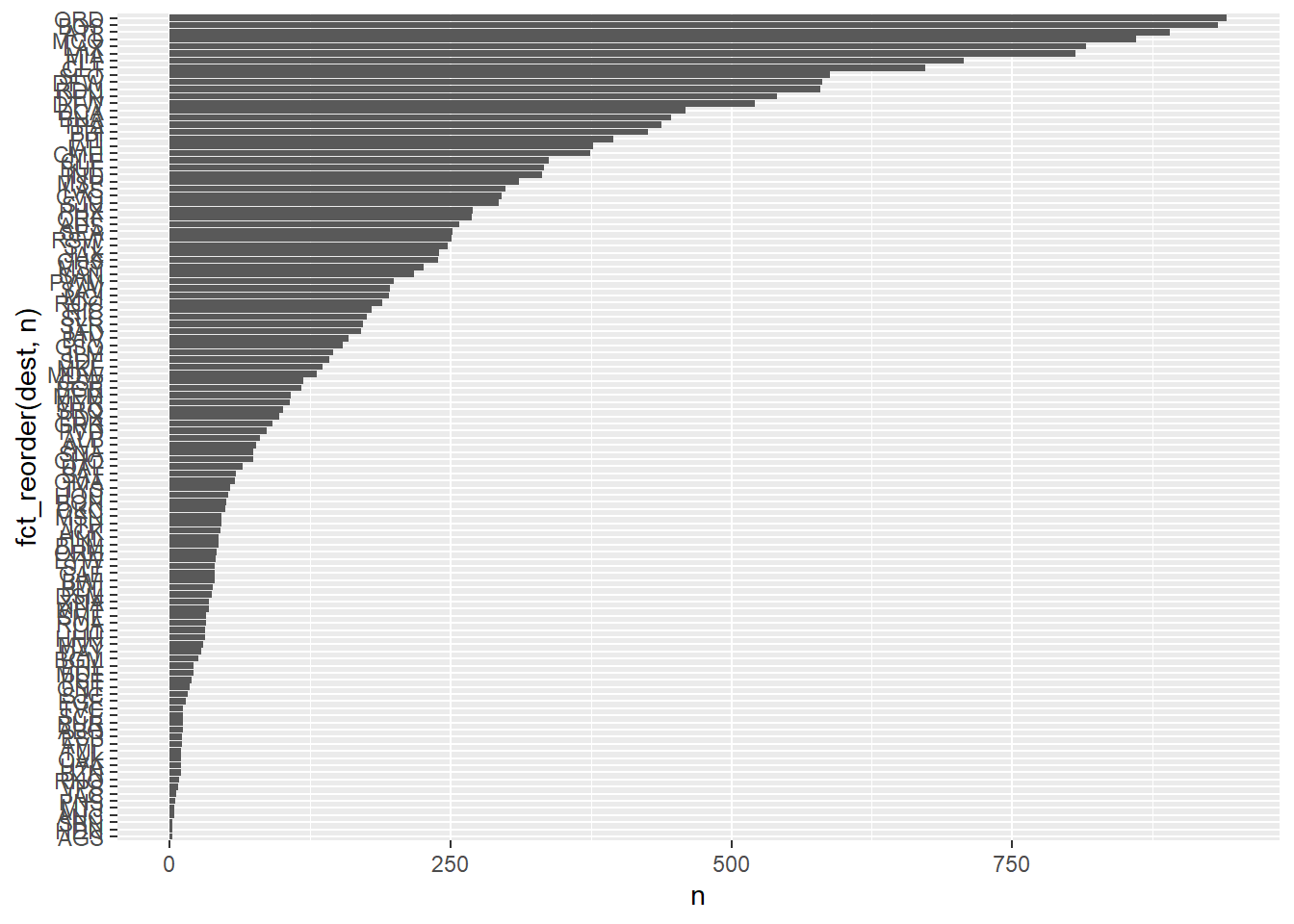

11 flights_train4: Faktorstufen zusammenfassen

flights_train4 <-
  flights_train3 %>% 
  mutate(across(
    .cols = where(is.factor),
    .fns = fct_lump_prop, prop = .025
  ))

12 Variante mit fact_lump_n

Sinngemäß bedeutet das:

“Fasse die Faktorstufen von dest zu 8 Gruppen plus einer ‘Lumpensammler-Kategorie’ zusammen.”

flights_train3 %>% 
  mutate(dest_lump9 = fct_lump_n(dest, n = 8)
  )

id	month	day	dep_time	sched_dep_time	dep_delay	arr_time	sched_arr_time	carrier	flight	tailnum	origin	dest	air_time	distance	hour	minute	time_hour	dest_lump9
11	2	22	622	630	-8	1034	1020	AA	32	N115NN	JFK	SFO	404	2586	6	30	2023-02-22 06:00:00	Other
26	9	27	1137	1147	-10	1255	1317	YX	1066	N726YX	EWR	PIT	56	319	11	47	2023-09-27 11:00:00	Other
28	10	8	1751	1759	-8	2106	2110	B6	944	N935JB	JFK	LAX	316	2475	17	59	2023-10-08 17:00:00	LAX
37	3	30	807	815	-8	917	930	B6	112	N198JB	LGA	BOS	43	184	8	15	2023-03-30 08:00:00	BOS
39	6	14	1019	1025	-6	1127	1151	9E	1757	N695CA	JFK	ROC	47	264	10	25	2023-06-14 10:00:00	Other
47	9	26	1045	1051	-6	1345	1357	DL	373	N318DU	LGA	TPA	149	1010	10	51	2023-09-26 10:00:00	Other
52	5	9	749	759	-10	1009	1014	YX	1358	N122HQ	LGA	CVG	105	585	7	59	2023-05-09 07:00:00	Other
55	2	10	914	920	-6	1044	1115	9E	1289	N480PX	LGA	PIT	63	335	9	20	2023-02-10 09:00:00	Other
59	12	30	1402	1411	-9	1715	1724	UA	473	N65832	EWR	FLL	158	1065	14	11	2023-12-30 14:00:00	FLL
61	11	10	1434	1440	-6	1623	1641	YX	1292	N419YX	LGA	ILM	85	500	14	40	2023-11-10 14:00:00	Other
62	2	15	951	959	-8	1156	1238	B6	848	N184JB	LGA	CHS	99	641	9	59	2023-02-15 09:00:00	Other
66	2	13	819	830	-11	933	1020	B6	399	N354JB	JFK	BNA	111	765	8	30	2023-02-13 08:00:00	Other
69	10	9	740	750	-10	845	927	9E	1484	N604LR	LGA	ROC	45	254	7	50	2023-10-09 07:00:00	Other
72	10	8	1452	1500	-8	1610	1634	9E	1544	N309PQ	LGA	CHO	52	305	15	0	2023-10-08 15:00:00	Other
79	7	23	1622	1629	-7	1822	1908	9E	1104	N337PQ	JFK	CLT	89	541	16	29	2023-07-23 16:00:00	CLT
92	9	26	938	948	-10	1117	1124	UA	441	N76532	EWR	BNA	106	748	9	48	2023-09-26 09:00:00	Other
94	6	19	1653	1659	-6	1908	1933	UA	885	N15712	EWR	LAS	293	2227	16	59	2023-06-19 16:00:00	Other
96	4	25	2038	2050	-12	2153	2227	YX	1517	N212JQ	LGA	RIC	57	292	20	50	2023-04-25 20:00:00	Other
97	2	25	1815	1830	-15	2024	2033	YX	1033	N736YX	EWR	CMH	91	463	18	30	2023-02-25 18:00:00	Other
99	3	18	1553	1600	-7	1900	1921	AA	98	N109NN	JFK	LAX	335	2475	16	0	2023-03-18 16:00:00	LAX
103	6	17	1524	1530	-6	1719	1716	YX	1101	N862RW	EWR	CLE	64	404	15	30	2023-06-17 15:00:00	Other
107	11	11	1719	1729	-10	1954	2020	UA	830	N37556	EWR	LAS	308	2227	17	29	2023-11-11 17:00:00	Other
108	12	24	1507	1515	-8	1720	1756	UA	598	N854UA	LGA	DEN	228	1620	15	15	2023-12-24 15:00:00	Other
113	9	16	1751	1800	-9	1909	1937	AA	192	N744P	LGA	ORD	107	733	18	0	2023-09-16 18:00:00	ORD
119	11	24	1429	1440	-11	1607	1641	YX	1292	N115HQ	LGA	ILM	79	500	14	40	2023-11-24 14:00:00	Other
121	5	25	2124	2130	-6	2247	2250	YX	1696	N214JQ	LGA	PWM	49	269	21	30	2023-05-25 21:00:00	Other
128	2	21	931	940	-9	1432	1444	UA	583	N68801	EWR	SJU	194	1608	9	40	2023-02-21 09:00:00	Other
131	4	16	1713	1720	-7	1831	1849	YX	1520	N824MD	LGA	ROC	45	254	17	20	2023-04-16 17:00:00	Other
133	9	27	1841	1851	-10	2016	2016	UA	584	N76503	EWR	ORF	54	284	18	51	2023-09-27 18:00:00	Other
135	8	19	1146	1152	-6	1257	1309	UA	237	N37516	EWR	BOS	46	200	11	52	2023-08-19 11:00:00	BOS
141	3	13	1056	1105	-9	1230	1258	AA	928	N751UW	LGA	STL	133	888	11	5	2023-03-13 11:00:00	Other
146	4	12	2050	2059	-9	2304	2334	YX	1158	N128HQ	LGA	ATL	103	762	20	59	2023-04-12 20:00:00	ATL
147	2	2	1150	1200	-10	1422	1431	YX	1226	N132HQ	LGA	MEM	186	963	12	0	2023-02-02 12:00:00	Other
150	3	21	840	849	-9	1036	1045	YX	1364	N128HQ	LGA	ILM	81	500	8	49	2023-03-21 08:00:00	Other
156	5	4	1142	1155	-13	1322	1415	G4	164	278NV	EWR	DSM	137	1017	11	55	2023-05-04 11:00:00	Other
163	4	21	2149	2159	-10	2249	2308	DL	445	N144DU	LGA	SYR	40	198	21	59	2023-04-21 21:00:00	Other
164	1	30	1746	1755	-9	1957	2007	DL	626	N338NB	EWR	MSP	166	1008	17	55	2023-01-30 17:00:00	Other
174	9	16	946	959	-13	1111	1158	YX	1181	N736YX	EWR	GSO	65	445	9	59	2023-09-16 09:00:00	Other
179	12	22	1905	1912	-7	2052	2123	AA	618	N712US	LGA	CLT	81	544	19	12	2023-12-22 19:00:00	CLT
187	4	7	1414	1420	-6	1634	1637	9E	1410	N279PQ	LGA	CHS	99	641	14	20	2023-04-07 14:00:00	Other
189	3	17	950	959	-9	1131	1218	9E	1440	N932XJ	LGA	MYR	80	563	9	59	2023-03-17 09:00:00	Other
193	6	13	1223	1229	-6	1514	1517	UA	438	N493UA	LGA	IAH	214	1416	12	29	2023-06-13 12:00:00	Other
196	6	1	1937	1945	-8	2230	2304	DL	815	N365NB	JFK	PBI	130	1028	19	45	2023-06-01 19:00:00	Other
199	8	29	1656	1703	-7	1835	1913	9E	1203	N135EV	JFK	RDU	69	427	17	3	2023-08-29 17:00:00	Other
200	6	4	1129	1135	-6	1256	1311	UA	705	N57286	EWR	CLE	64	404	11	35	2023-06-04 11:00:00	Other
232	2	22	1916	1925	-9	2136	2125	AA	142	N767UW	LGA	RDU	76	431	19	25	2023-02-22 19:00:00	Other
234	5	27	1154	1200	-6	1257	1321	AA	772	N763US	LGA	DCA	43	214	12	0	2023-05-27 12:00:00	Other
235	12	6	942	950	-8	1141	1213	9E	1498	N335PQ	LGA	CVG	87	585	9	50	2023-12-06 09:00:00	Other
238	8	9	652	659	-7	836	857	YX	999	N446YX	LGA	DTW	78	502	6	59	2023-08-09 06:00:00	Other
241	1	13	1241	1250	-9	1537	1559	B6	42	N559JB	JFK	TPA	155	1005	12	50	2023-01-13 12:00:00	Other
244	12	5	708	715	-7	1027	1023	B6	214	N2044J	JFK	FLL	163	1069	7	15	2023-12-05 07:00:00	FLL
251	9	27	2044	2059	-15	2311	2331	YX	1147	N743YX	EWR	SDF	108	642	20	59	2023-09-27 20:00:00	Other
256	8	22	1951	1959	-8	2254	2258	NK	145	N687NK	LGA	MCO	117	950	19	59	2023-08-22 19:00:00	MCO
262	6	28	2152	2200	-8	2318	2321	YX	1365	N126HQ	JFK	BOS	42	187	22	0	2023-06-28 22:00:00	BOS
266	9	13	2039	2050	-11	2156	2227	YX	1965	N882RW	LGA	MSN	113	812	20	50	2023-09-13 20:00:00	Other
282	3	2	552	600	-8	748	801	AA	243	N907AN	LGA	CLT	98	544	6	0	2023-03-02 06:00:00	CLT
286	5	9	1840	1853	-13	2127	2100	UA	539	N37277	EWR	CHS	90	628	18	53	2023-05-09 18:00:00	Other
289	8	25	1753	1759	-6	2001	2008	YX	1035	N441YX	LGA	MCI	153	1107	17	59	2023-08-25 17:00:00	Other
294	11	30	1353	1400	-7	1635	1658	UA	639	N14115	EWR	MCO	142	937	14	0	2023-11-30 14:00:00	MCO
297	5	11	1232	1241	-9	1614	1637	AA	230	N12028	JFK	STT	196	1623	12	41	2023-05-11 12:00:00	Other
302	7	11	1135	1142	-7	1302	1326	YX	1075	N427YX	LGA	ROA	64	405	11	42	2023-07-11 11:00:00	Other
304	7	19	1814	1820	-6	2105	2109	YX	1357	N233JQ	JFK	SAV	107	718	18	20	2023-07-19 18:00:00	Other
308	12	29	524	530	-6	801	912	NK	347	N645NK	EWR	PHX	260	2133	5	30	2023-12-29 05:00:00	Other
311	2	17	1143	1155	-12	1404	1420	G4	924	316NV	EWR	SAV	127	708	11	55	2023-02-17 11:00:00	Other
312	5	17	1646	1653	-7	1836	1901	YX	1012	N747YX	EWR	GSP	91	594	16	53	2023-05-17 16:00:00	Other
316	10	12	1150	1159	-9	1301	1317	UA	419	N414UA	EWR	PWM	50	284	11	59	2023-10-12 11:00:00	Other
323	3	7	820	835	-15	1015	1035	9E	1410	N920XJ	LGA	RDU	71	431	8	35	2023-03-07 08:00:00	Other
325	6	4	553	601	-8	750	759	AA	987	N123NN	EWR	CLT	82	529	6	1	2023-06-04 06:00:00	CLT
326	2	22	1028	1039	-11	1136	1154	B6	56	N198JB	EWR	BOS	38	200	10	39	2023-02-22 10:00:00	BOS
328	10	5	757	805	-8	1106	1135	AA	49	N103NN	JFK	SFO	339	2586	8	5	2023-10-05 08:00:00	Other
342	10	2	1653	1700	-7	1816	1831	YX	1334	N416YX	LGA	RIC	52	292	17	0	2023-10-02 17:00:00	Other
343	5	16	553	600	-7	704	712	B6	795	N317JB	EWR	BOS	38	200	6	0	2023-05-16 06:00:00	BOS
344	6	12	623	630	-7	1014	1023	B6	618	N957JB	JFK	SJU	200	1598	6	30	2023-06-12 06:00:00	Other
345	6	7	1051	1100	-9	1339	1415	B6	298	N564JB	JFK	SAT	207	1587	11	0	2023-06-07 11:00:00	Other
346	2	25	1124	1130	-6	1318	1351	AA	107	N855NN	LGA	CLT	93	544	11	30	2023-02-25 11:00:00	CLT
348	3	15	1521	1529	-8	1712	1733	YX	1395	N430YX	JFK	CLE	78	425	15	29	2023-03-15 15:00:00	Other
353	1	9	2106	2112	-6	2304	2323	UA	938	N412UA	EWR	MSP	148	1008	21	12	2023-01-09 21:00:00	Other
354	10	17	1753	1800	-7	2001	2022	YX	1289	N419YX	LGA	IND	98	660	18	0	2023-10-17 18:00:00	Other
360	5	23	805	811	-6	1012	1026	YX	1094	N641RW	EWR	DTW	78	488	8	11	2023-05-23 08:00:00	Other
364	8	22	1721	1729	-8	1914	1951	YX	857	N744YX	EWR	IND	94	645	17	29	2023-08-22 17:00:00	Other
369	5	27	801	810	-9	922	955	DL	552	N139DU	LGA	ORD	106	733	8	10	2023-05-27 08:00:00	ORD
392	5	29	1021	1030	-9	1115	1140	B6	930	N339JB	JFK	BOS	35	187	10	30	2023-05-29 10:00:00	BOS
398	5	9	934	940	-6	1244	1257	B6	108	N984JB	JFK	LAX	340	2475	9	40	2023-05-09 09:00:00	LAX
399	2	10	2017	2030	-13	2158	2210	YX	1538	N214JQ	LGA	PIT	68	335	20	30	2023-02-10 20:00:00	Other
400	5	19	2153	2200	-7	2317	2347	9E	1447	N297PQ	JFK	ROC	47	264	22	0	2023-05-19 22:00:00	Other
401	2	14	1420	1430	-10	1555	1616	YX	1270	N441YX	JFK	PIT	72	340	14	30	2023-02-14 14:00:00	Other
402	2	7	2057	2108	-11	2244	2319	YX	1289	N413YX	LGA	GSO	84	461	21	8	2023-02-07 21:00:00	Other
404	3	6	1921	1930	-9	2055	2129	YX	1396	N428YX	JFK	DCA	58	213	19	30	2023-03-06 19:00:00	Other
413	10	11	926	933	-7	1140	1158	NK	1186	N645NK	EWR	PHX	282	2133	9	33	2023-10-11 09:00:00	Other
417	2	17	1054	1100	-6	1245	1247	YX	1031	N725YX	EWR	RDU	81	416	11	0	2023-02-17 11:00:00	Other
419	4	20	1550	1559	-9	1747	1814	9E	1327	N337PQ	LGA	CLT	79	544	15	59	2023-04-20 15:00:00	CLT
420	4	18	559	610	-11	731	750	DL	389	N127DU	LGA	ORD	113	733	6	10	2023-04-18 06:00:00	ORD
425	10	9	554	600	-6	843	854	UA	227	N77559	EWR	AUS	201	1504	6	0	2023-10-09 06:00:00	Other
429	12	11	842	848	-6	1053	1110	9E	1398	N926XJ	LGA	CLT	95	544	8	48	2023-12-11 08:00:00	CLT
434	1	6	1921	1929	-8	2106	2137	AA	819	N949AN	JFK	CLT	87	541	19	29	2023-01-06 19:00:00	CLT
435	10	17	1309	1315	-6	1412	1431	B6	252	N267JB	LGA	BOS	35	184	13	15	2023-10-17 13:00:00	BOS
439	2	15	1519	1529	-10	1710	1733	YX	1150	N742YX	EWR	CMH	85	463	15	29	2023-02-15 15:00:00	Other
444	4	19	1749	1800	-11	1933	2025	9E	1375	N490PX	LGA	TYS	88	647	18	0	2023-04-19 18:00:00	Other
446	11	26	845	900	-15	1131	1136	9E	1458	N302PQ	LGA	SAV	125	722	9	0	2023-11-26 09:00:00	Other
452	9	2	553	600	-7	758	820	UA	413	N14735	EWR	ATL	101	746	6	0	2023-09-02 06:00:00	ATL
457	1	5	2207	2216	-9	142	149	B6	1011	N987JT	JFK	SFO	353	2586	22	16	2023-01-05 22:00:00	Other
468	1	27	550	600	-10	712	723	YX	1853	N234JQ	EWR	BOS	41	200	6	0	2023-01-27 06:00:00	BOS
469	6	9	1522	1529	-7	1644	1651	UA	490	N417UA	EWR	BNA	109	748	15	29	2023-06-09 15:00:00	Other
470	7	12	1656	1704	-8	1904	1929	YX	1066	N410YX	JFK	CVG	97	589	17	4	2023-07-12 17:00:00	Other
474	8	17	1039	1050	-11	1345	1408	DL	347	N108DQ	LGA	RSW	162	1080	10	50	2023-08-17 10:00:00	Other
485	3	18	1948	1959	-11	2222	2235	DL	805	N353NB	LGA	MSY	193	1183	19	59	2023-03-18 19:00:00	Other
488	11	24	723	730	-7	1038	1049	AA	966	N9010R	JFK	AUS	223	1521	7	30	2023-11-24 07:00:00	Other
491	1	9	834	843	-9	1001	1023	YX	1176	N729YX	EWR	MKE	111	725	8	43	2023-01-09 08:00:00	Other
492	10	11	1209	1215	-6	1512	1519	YX	1245	N422YX	LGA	OKC	214	1341	12	15	2023-10-11 12:00:00	Other
501	11	18	1020	1030	-10	1322	1356	B6	945	N591JB	JFK	AUS	216	1521	10	30	2023-11-18 10:00:00	Other
509	3	30	1352	1400	-8	1550	1548	OO	1568	N128SY	LGA	ORD	136	733	14	0	2023-03-30 14:00:00	ORD
517	4	14	2208	2214	-6	2323	2359	9E	1322	N320PQ	JFK	BUF	50	301	22	14	2023-04-14 22:00:00	Other
524	12	6	1302	1311	-9	1431	1447	UA	193	N13750	EWR	ORD	119	719	13	11	2023-12-06 13:00:00	ORD
526	7	12	1540	1550	-10	1717	1816	9E	1119	N133EV	LGA	CLT	73	544	15	50	2023-07-12 15:00:00	CLT
531	3	15	652	659	-7	841	846	YX	1074	N863RW	EWR	CLE	65	404	6	59	2023-03-15 06:00:00	Other
536	9	2	704	710	-6	941	1003	UA	665	N27290	EWR	PDX	312	2434	7	10	2023-09-02 07:00:00	Other
537	1	17	659	705	-6	933	1008	DL	425	N362NB	LGA	PBI	137	1035	7	5	2023-01-17 07:00:00	Other
539	10	5	1412	1421	-9	1703	1717	UA	270	N842UA	EWR	AUS	212	1504	14	21	2023-10-05 14:00:00	Other
542	11	27	2151	2159	-8	2324	2321	UA	451	N896UA	EWR	BUF	53	282	21	59	2023-11-27 21:00:00	Other
547	5	4	1916	1925	-9	2022	2053	YX	1331	N435YX	JFK	BOS	38	187	19	25	2023-05-04 19:00:00	BOS
554	3	23	1154	1202	-8	1349	1408	YX	1688	N205JQ	JFK	CLT	85	541	12	2	2023-03-23 12:00:00	CLT
564	1	27	1623	1630	-7	1815	1820	DL	932	N110DU	LGA	BNA	129	764	16	30	2023-01-27 16:00:00	Other
568	5	9	1943	1950	-7	2232	2240	B6	47	N2043J	JFK	PHX	293	2153	19	50	2023-05-09 19:00:00	Other
570	4	27	1651	1700	-9	1927	1925	YX	1280	N867RW	LGA	IND	110	660	17	0	2023-04-27 17:00:00	Other
572	12	27	1722	1729	-7	1950	2047	UA	588	N37319	EWR	SAN	307	2425	17	29	2023-12-27 17:00:00	Other
574	1	30	1929	1935	-6	2352	30	B6	536	N598JB	EWR	SJU	180	1608	19	35	2023-01-30 19:00:00	Other
575	6	9	1124	1135	-11	1330	1341	AA	779	N924NN	LGA	CLT	92	544	11	35	2023-06-09 11:00:00	CLT
577	4	20	822	829	-7	1014	1032	YX	1129	N869RW	LGA	DAY	90	549	8	29	2023-04-20 08:00:00	Other
580	2	7	1621	1630	-9	1823	1840	B6	386	N249JB	JFK	DTW	94	509	16	30	2023-02-07 16:00:00	Other
583	1	18	949	958	-9	1109	1146	9E	1665	N293PQ	LGA	CHO	53	305	9	58	2023-01-18 09:00:00	Other
584	5	11	1438	1444	-6	1721	1740	DL	556	N352NB	LGA	TPA	135	1010	14	44	2023-05-11 14:00:00	Other
590	10	8	954	1000	-6	1151	1219	9E	1571	N326PQ	LGA	CVG	93	585	10	0	2023-10-08 10:00:00	Other
591	7	30	1050	1059	-9	1238	1255	NK	522	N905NK	LGA	DTW	85	502	10	59	2023-07-30 10:00:00	Other
592	9	18	604	610	-6	759	811	DL	430	N369NW	LGA	MSP	141	1020	6	10	2023-09-18 06:00:00	Other
596	5	18	1559	1605	-6	1727	1746	YX	1576	N244JQ	LGA	BNA	116	764	16	5	2023-05-18 16:00:00	Other
602	1	2	1603	1611	-8	1808	1827	YX	1339	N114HQ	LGA	DTW	96	502	16	11	2023-01-02 16:00:00	Other
603	1	15	1055	1106	-11	1208	1242	UA	850	N443UA	EWR	BNA	103	748	11	6	2023-01-15 11:00:00	Other
612	5	17	721	727	-6	925	951	YX	1007	N751YX	EWR	SDF	104	642	7	27	2023-05-17 07:00:00	Other
621	12	31	1916	1930	-14	2214	2239	B6	203	N760JB	LGA	FLL	162	1076	19	30	2023-12-31 19:00:00	FLL
626	12	10	1254	1300	-6	1607	1626	DL	243	N904DN	JFK	SLC	282	1990	13	0	2023-12-10 13:00:00	Other
634	11	4	1601	1609	-8	1810	1842	9E	1613	N691CA	JFK	SAV	107	718	16	9	2023-11-04 16:00:00	Other
637	4	17	1559	1605	-6	1855	1933	B6	302	N983JT	JFK	LAX	334	2475	16	5	2023-04-17 16:00:00	LAX
641	6	7	550	600	-10	828	849	B6	610	N621JB	JFK	TPA	138	1005	6	0	2023-06-07 06:00:00	Other
649	9	14	2035	2045	-10	2312	2248	9E	1466	N228PQ	LGA	MYR	87	563	20	45	2023-09-14 20:00:00	Other
650	6	19	954	1000	-6	1105	1134	YX	1916	N245JQ	LGA	BOS	34	184	10	0	2023-06-19 10:00:00	BOS
652	1	2	1439	1445	-6	1556	1615	YX	1318	N420YX	JFK	ORF	52	290	14	45	2023-01-02 14:00:00	Other
654	2	7	547	600	-13	731	740	AA	948	N813NN	LGA	ORD	134	733	6	0	2023-02-07 06:00:00	ORD
661	11	20	948	959	-11	1153	1220	9E	1523	N131EV	JFK	IND	102	665	9	59	2023-11-20 09:00:00	Other
666	12	5	2049	2059	-10	2215	2240	9E	1353	N910XJ	LGA	ORF	53	296	20	59	2023-12-05 20:00:00	Other
677	11	7	823	830	-7	1421	1438	UA	119	N76055	EWR	HNL	628	4962	8	30	2023-11-07 08:00:00	Other
689	5	9	1512	1519	-7	1806	1842	DL	633	N325DN	JFK	FLL	148	1069	15	19	2023-05-09 15:00:00	FLL
693	4	12	922	929	-7	1054	1120	YX	1164	N413YX	LGA	CLE	68	419	9	29	2023-04-12 09:00:00	Other
695	10	13	1026	1035	-9	1212	1233	UA	473	N27722	EWR	CLT	85	529	10	35	2023-10-13 10:00:00	CLT
700	9	17	1521	1529	-8	1651	1713	YX	1413	N416YX	LGA	STL	125	888	15	29	2023-09-17 15:00:00	Other
701	3	1	1849	1855	-6	2050	2045	WN	638	N963WN	LGA	BNA	125	764	18	55	2023-03-01 18:00:00	Other
713	3	6	1653	1659	-6	1915	1931	UA	600	N829UA	EWR	ATL	113	746	16	59	2023-03-06 16:00:00	ATL
719	3	12	2143	2150	-7	2318	2313	9E	1409	N294PQ	LGA	BGR	58	378	21	50	2023-03-12 21:00:00	Other
726	12	2	1739	1750	-11	1831	1900	9E	1569	N482PX	LGA	PVD	27	143	17	50	2023-12-02 17:00:00	Other
744	3	25	748	755	-7	941	958	AA	608	N951NN	EWR	CLT	88	529	7	55	2023-03-25 07:00:00	CLT
746	9	22	1652	1700	-8	1823	1831	YX	1384	N122HQ	LGA	RIC	59	292	17	0	2023-09-22 17:00:00	Other
747	4	8	1252	1300	-8	1611	1640	AS	4	N971AK	JFK	SFO	352	2586	13	0	2023-04-08 13:00:00	Other
764	4	26	1223	1230	-7	1403	1409	AA	880	N354PT	LGA	ORD	120	733	12	30	2023-04-26 12:00:00	ORD
765	11	29	2120	2129	-9	2251	2325	YX	1068	N745YX	EWR	ILM	71	488	21	29	2023-11-29 21:00:00	Other
772	9	19	1819	1829	-10	2003	2053	9E	1551	N485PX	LGA	TYS	86	647	18	29	2023-09-19 18:00:00	Other
773	9	7	854	900	-6	1008	1026	YX	1404	N871RW	LGA	BUF	49	292	9	0	2023-09-07 09:00:00	Other
774	10	29	1009	1015	-6	1159	1154	UA	672	N417UA	LGA	ORD	134	733	10	15	2023-10-29 10:00:00	ORD
778	12	1	754	800	-6	944	1008	DL	506	N373DX	LGA	DTW	84	502	8	0	2023-12-01 08:00:00	Other
782	8	25	1752	1800	-8	2010	2027	YX	990	N417YX	LGA	TUL	167	1231	18	0	2023-08-25 18:00:00	Other
791	8	7	1052	1100	-8	1236	1254	YX	980	N438YX	JFK	CLE	75	425	11	0	2023-08-07 11:00:00	Other
794	1	15	1838	1845	-7	2132	2147	UA	983	N16009	EWR	LAX	311	2454	18	45	2023-01-15 18:00:00	LAX
800	5	5	624	630	-6	805	819	YX	1575	N203JQ	LGA	CMH	76	479	6	30	2023-05-05 06:00:00	Other
803	1	29	1502	1510	-8	1719	1733	YX	1369	N408YX	JFK	CVG	114	589	15	10	2023-01-29 15:00:00	Other
809	9	13	2056	2110	-14	2254	2309	YX	1322	N104HQ	LGA	MEM	149	963	21	10	2023-09-13 21:00:00	Other
811	9	15	1546	1559	-13	1719	1737	YX	1827	N815MD	LGA	BGR	67	378	15	59	2023-09-15 15:00:00	Other
813	6	6	1824	1833	-9	2159	2116	YX	1329	N409YX	LGA	OKC	190	1341	18	33	2023-06-06 18:00:00	Other
814	12	18	1721	1730	-9	1941	2015	YX	1321	N432YX	LGA	SDF	103	659	17	30	2023-12-18 17:00:00	Other
820	9	10	1955	2005	-10	2159	2212	9E	1576	N538CA	LGA	DAY	96	549	20	5	2023-09-10 20:00:00	Other
828	6	12	1953	2000	-7	2108	2139	OO	1266	N244SY	LGA	MKE	107	738	20	0	2023-06-12 20:00:00	Other
835	5	23	1951	2000	-9	2152	2254	B6	35	N635JB	JFK	DEN	204	1626	20	0	2023-05-23 20:00:00	Other
842	11	6	654	700	-6	939	1020	DL	314	N377DA	JFK	RSW	146	1074	7	0	2023-11-06 07:00:00	Other
845	6	7	723	730	-7	940	1005	9E	1526	N306PQ	LGA	JAX	114	833	7	30	2023-06-07 07:00:00	Other
847	3	9	955	1005	-10	1254	1319	NK	31	N682NK	EWR	MIA	150	1085	10	5	2023-03-09 10:00:00	MIA
855	3	19	1108	1115	-7	1320	1344	YX	1316	N445YX	JFK	IND	109	665	11	15	2023-03-19 11:00:00	Other
858	8	31	2004	2011	-7	2131	2151	YX	1038	N102HQ	LGA	PIT	59	335	20	11	2023-08-31 20:00:00	Other
860	9	15	1059	1110	-11	1229	1243	YX	1311	N110HQ	LGA	PIT	58	335	11	10	2023-09-15 11:00:00	Other
862	7	6	840	850	-10	956	1010	YX	1344	N878RW	EWR	BOS	43	200	8	50	2023-07-06 08:00:00	BOS
863	12	12	648	655	-7	928	950	B6	177	N988JT	JFK	LAS	319	2248	6	55	2023-12-12 06:00:00	Other
864	11	18	927	934	-7	1153	1200	B6	983	N318JB	JFK	CHS	107	636	9	34	2023-11-18 09:00:00	Other
866	10	25	652	700	-8	956	1009	B6	248	N961JT	JFK	LAX	336	2475	7	0	2023-10-25 07:00:00	LAX
868	4	7	1004	1010	-6	1313	1318	DL	893	N126DN	LGA	MCO	143	950	10	10	2023-04-07 10:00:00	MCO
876	5	22	747	759	-12	901	928	UA	225	N484UA	EWR	BOS	39	200	7	59	2023-05-22 07:00:00	BOS
878	2	9	1223	1230	-7	1358	1438	AA	451	N952NN	LGA	ORD	125	733	12	30	2023-02-09 12:00:00	ORD
879	6	14	454	500	-6	732	812	NK	299	N951NK	EWR	OAK	315	2555	5	0	2023-06-14 05:00:00	Other
881	9	18	1119	1129	-10	1339	1333	YX	1334	N112HQ	LGA	AVL	99	599	11	29	2023-09-18 11:00:00	Other
892	2	19	1052	1100	-8	1352	1418	B6	890	N821JB	JFK	MIA	150	1089	11	0	2023-02-19 11:00:00	MIA
896	1	29	1252	1300	-8	1448	1507	AA	935	N874NN	JFK	CLT	88	541	13	0	2023-01-29 13:00:00	CLT
900	12	13	1720	1730	-10	1937	1959	9E	1630	N491PX	LGA	CVG	103	585	17	30	2023-12-13 17:00:00	Other
903	10	4	1717	1725	-8	1915	1934	NK	246	N664NK	EWR	IND	94	645	17	25	2023-10-04 17:00:00	Other
909	11	14	553	600	-7	710	719	UA	420	N27255	EWR	IAD	47	212	6	0	2023-11-14 06:00:00	Other
922	2	7	1446	1455	-9	1624	1630	9E	1440	N272PQ	JFK	RIC	61	288	14	55	2023-02-07 14:00:00	Other
927	1	2	1542	1550	-8	1632	1659	9E	1551	N606LR	LGA	ALB	30	136	15	50	2023-01-02 15:00:00	Other
929	9	5	2157	2210	-13	24	33	NK	253	N954NK	EWR	LAS	295	2227	22	10	2023-09-05 22:00:00	Other
930	11	9	651	700	-9	1035	1024	AS	12	N928AK	JFK	SFO	360	2586	7	0	2023-11-09 07:00:00	Other
934	10	30	930	941	-11	1125	1136	DL	936	N927AT	EWR	DTW	95	488	9	41	2023-10-30 09:00:00	Other
940	3	20	953	959	-6	1230	1221	9E	1481	N187GJ	JFK	SAV	126	718	9	59	2023-03-20 09:00:00	Other
941	6	7	751	800	-9	954	1018	B6	332	N307JB	JFK	SAV	106	718	8	0	2023-06-07 08:00:00	Other
944	9	26	1125	1131	-6	1310	1332	AA	942	N971AN	JFK	CLT	85	541	11	31	2023-09-26 11:00:00	CLT
945	6	20	918	926	-8	1050	1055	YX	1161	N865RW	EWR	PWM	56	284	9	26	2023-06-20 09:00:00	Other
952	6	23	622	630	-8	917	940	B6	5	N992JB	JFK	SFO	338	2586	6	30	2023-06-23 06:00:00	Other
954	10	14	1247	1255	-8	1438	1432	9E	1595	N319PQ	LGA	BNA	127	764	12	55	2023-10-14 12:00:00	Other
958	11	25	1723	1730	-7	2120	2109	DL	292	N704X	JFK	SFO	348	2586	17	30	2023-11-25 17:00:00	Other
973	4	23	1619	1629	-10	1740	1804	YX	1161	N872RW	LGA	CHO	55	305	16	29	2023-04-23 16:00:00	Other
977	6	1	643	650	-7	923	955	AA	951	N867NN	LGA	MIA	141	1096	6	50	2023-06-01 06:00:00	MIA
982	9	16	721	730	-9	925	955	DL	188	N3738B	LGA	DEN	212	1620	7	30	2023-09-16 07:00:00	Other
985	4	9	849	900	-11	1007	1038	B6	701	N274JB	LGA	BNA	115	764	9	0	2023-04-09 09:00:00	Other
992	9	2	1449	1459	-10	1701	1717	9E	1541	N309PQ	JFK	CVG	87	589	14	59	2023-09-02 14:00:00	Other
996	10	17	702	710	-8	1005	1008	UA	782	N47512	EWR	PBI	146	1023	7	10	2023-10-17 07:00:00	Other
1002	1	4	847	855	-8	1128	1143	YX	1797	N212JQ	JFK	JAX	125	828	8	55	2023-01-04 08:00:00	Other
1003	11	6	1220	1230	-10	1358	1403	YX	1785	N239JQ	LGA	MKE	130	738	12	30	2023-11-06 12:00:00	Other
1011	4	25	2124	2130	-6	2300	2309	9E	1199	N181PQ	JFK	RIC	57	288	21	30	2023-04-25 21:00:00	Other
1012	11	11	753	800	-7	849	922	9E	1552	N330PQ	JFK	BWI	36	184	8	0	2023-11-11 08:00:00	Other
1016	12	30	1152	1200	-8	1251	1325	YX	1857	N245JQ	LGA	BOS	39	184	12	0	2023-12-30 12:00:00	BOS
1030	5	3	1153	1159	-6	1446	1510	UA	161	N405UA	EWR	FLL	155	1065	11	59	2023-05-03 11:00:00	FLL
1032	3	25	1820	1830	-10	2005	2003	YX	1325	N439YX	JFK	ORF	66	290	18	30	2023-03-25 18:00:00	Other
1037	1	1	1547	1559	-12	1847	1913	B6	868	N998JE	JFK	PBI	149	1028	15	59	2023-01-01 15:00:00	Other
1038	12	2	719	730	-11	927	947	DL	736	N328NB	LGA	CHS	104	641	7	30	2023-12-02 07:00:00	Other
1039	10	4	554	600	-6	724	751	DL	368	N105DX	LGA	DTW	74	502	6	0	2023-10-04 06:00:00	Other
1049	8	25	1122	1130	-8	1406	1435	AA	94	N109NN	JFK	LAX	310	2475	11	30	2023-08-25 11:00:00	LAX
1054	2	5	909	915	-6	1020	1024	B6	858	N266JB	LGA	BOS	50	184	9	15	2023-02-05 09:00:00	BOS
1058	12	7	1321	1333	-12	1429	1445	UA	383	N493UA	EWR	BOS	42	200	13	33	2023-12-07 13:00:00	BOS
1062	4	7	1404	1410	-6	1647	1656	UA	372	N37277	EWR	MCO	138	937	14	10	2023-04-07 14:00:00	MCO
1064	9	27	554	600	-6	752	751	DL	392	N372DN	LGA	DTW	79	502	6	0	2023-09-27 06:00:00	Other
1069	1	21	1055	1106	-11	1217	1242	UA	850	N444UA	EWR	BNA	126	748	11	6	2023-01-21 11:00:00	Other
1075	6	30	724	730	-6	857	925	9E	1497	N920XJ	LGA	GSO	70	461	7	30	2023-06-30 07:00:00	Other
1080	11	22	1940	1950	-10	2227	2216	9E	1623	N905XJ	LGA	CHS	93	641	19	50	2023-11-22 19:00:00	Other
1081	9	3	1014	1030	-16	1107	1139	B6	972	N318JB	LGA	HYA	35	197	10	30	2023-09-03 10:00:00	Other
1090	7	31	1323	1330	-7	1547	1543	YX	1091	N871RW	LGA	IND	120	660	13	30	2023-07-31 13:00:00	Other
1098	5	6	1538	1546	-8	1725	1729	YX	1252	N132HQ	JFK	DCA	53	213	15	46	2023-05-06 15:00:00	Other
1103	10	4	722	729	-7	946	1024	UA	922	N17752	LGA	IAH	179	1416	7	29	2023-10-04 07:00:00	Other
1106	8	9	1649	1655	-6	2014	2026	AA	46	N103NN	JFK	SFO	349	2586	16	55	2023-08-09 16:00:00	Other
1107	2	21	1704	1712	-8	1903	1908	YX	984	N644RW	EWR	GSO	71	445	17	12	2023-02-21 17:00:00	Other
1130	11	1	1507	1517	-10	1813	1830	NK	588	N673NK	LGA	FLL	153	1076	15	17	2023-11-01 15:00:00	FLL
1133	6	16	913	920	-7	1107	1119	9E	1666	N136EV	LGA	ILM	71	500	9	20	2023-06-16 09:00:00	Other
1134	8	19	833	840	-7	1137	1140	DL	290	N529DT	JFK	SAN	301	2446	8	40	2023-08-19 08:00:00	Other
1139	12	11	1650	1659	-9	1754	1821	YX	1138	N746YX	EWR	BTV	44	266	16	59	2023-12-11 16:00:00	Other
1145	6	16	755	803	-8	1040	1046	B6	355	N591JB	EWR	MCO	130	937	8	3	2023-06-16 08:00:00	MCO
1147	11	15	2153	2159	-6	127	139	B6	923	N962JT	JFK	SFO	372	2586	21	59	2023-11-15 21:00:00	Other
1148	11	1	2050	2059	-9	2300	2255	YX	1244	N447YX	JFK	RDU	76	427	20	59	2023-11-01 20:00:00	Other
1152	10	15	1153	1159	-6	1308	1317	UA	419	N495UA	EWR	PWM	57	284	11	59	2023-10-15 11:00:00	Other
1156	11	26	1022	1030	-8	1234	1253	YX	1326	N413YX	LGA	GSP	105	610	10	30	2023-11-26 10:00:00	Other
1157	7	24	752	759	-7	1001	1013	YX	866	N724YX	EWR	GRR	94	605	7	59	2023-07-24 07:00:00	Other
1164	12	22	1124	1130	-6	1232	1256	YX	1038	N761YX	EWR	ROC	45	246	11	30	2023-12-22 11:00:00	Other
1166	9	15	836	845	-9	1132	1151	YX	1308	N411YX	LGA	IAH	209	1416	8	45	2023-09-15 08:00:00	Other
1167	3	21	1109	1115	-6	1216	1229	B6	245	N281JB	LGA	BOS	44	184	11	15	2023-03-21 11:00:00	BOS
1186	1	10	1119	1130	-11	1311	1352	AA	108	N354PT	LGA	CLT	85	544	11	30	2023-01-10 11:00:00	CLT
1187	7	6	1508	1515	-7	1635	1636	YX	1367	N880RW	LGA	ACK	44	202	15	15	2023-07-06 15:00:00	Other
1194	7	6	958	1005	-7	1311	1305	DL	236	N177DN	JFK	LAX	331	2475	10	5	2023-07-06 10:00:00	LAX
1203	2	1	1518	1530	-12	1701	1712	B6	282	N3118J	JFK	MKE	145	745	15	30	2023-02-01 15:00:00	Other
1205	1	29	954	1000	-6	1616	1605	HA	22	N391HA	JFK	HNL	650	4983	10	0	2023-01-29 10:00:00	Other
1211	8	28	2112	2120	-8	2222	2246	YX	1389	N244JQ	LGA	BUF	49	292	21	20	2023-08-28 21:00:00	Other
1215	1	26	950	1000	-10	1311	1316	UA	779	N474UA	LGA	IAH	234	1416	10	0	2023-01-26 10:00:00	Other
1216	6	3	712	720	-8	907	934	UA	249	N12238	LGA	DEN	207	1620	7	20	2023-06-03 07:00:00	Other
1220	6	9	1729	1735	-6	1930	1938	YX	1824	N240JQ	LGA	CMH	70	479	17	35	2023-06-09 17:00:00	Other
1221	8	29	833	846	-13	1041	1050	UA	319	N38467	EWR	MYR	84	550	8	46	2023-08-29 08:00:00	Other
1223	2	12	1718	1729	-11	1939	2020	UA	820	N67134	EWR	LAS	283	2227	17	29	2023-02-12 17:00:00	Other
1226	5	28	1108	1115	-7	1359	1423	DL	532	N117DX	JFK	FLL	143	1069	11	15	2023-05-28 11:00:00	FLL
1227	4	28	752	800	-8	907	919	AA	683	N768US	LGA	DCA	47	214	8	0	2023-04-28 08:00:00	Other
1230	3	2	1245	1254	-9	1417	1423	YX	1068	N731YX	EWR	PIT	74	319	12	54	2023-03-02 12:00:00	Other
1235	7	21	658	705	-7	1004	1007	DL	310	N330NB	LGA	PBI	140	1035	7	5	2023-07-21 07:00:00	Other
1237	12	29	1722	1730	-8	1845	1916	9E	1552	N298PQ	LGA	MKE	101	738	17	30	2023-12-29 17:00:00	Other
1239	2	26	554	600	-6	817	838	UA	429	N68817	EWR	DEN	246	1605	6	0	2023-02-26 06:00:00	Other
1240	2	10	1533	1543	-10	1738	1754	NK	501	N522NK	LGA	CLT	96	544	15	43	2023-02-10 15:00:00	CLT
1244	11	26	1142	1150	-8	1428	1444	DL	351	N517DN	JFK	LAS	314	2248	11	50	2023-11-26 11:00:00	Other
1245	1	31	1519	1530	-11	1841	1850	B6	604	N564JB	EWR	MIA	158	1085	15	30	2023-01-31 15:00:00	MIA
1246	6	17	1054	1100	-6	1246	1253	YX	1292	N101HQ	JFK	CLE	79	425	11	0	2023-06-17 11:00:00	Other
1250	5	6	952	959	-7	1138	1203	AA	744	N850NN	LGA	CLT	78	544	9	59	2023-05-06 09:00:00	CLT
1252	1	12	758	805	-7	1019	1040	DL	1002	N392DA	EWR	ATL	114	746	8	5	2023-01-12 08:00:00	ATL
1254	7	14	953	1000	-7	1143	1155	YX	936	N647RW	EWR	GSO	90	445	10	0	2023-07-14 10:00:00	Other
1257	9	15	2049	2059	-10	2307	2323	B6	919	N594JB	LGA	MSY	150	1183	20	59	2023-09-15 20:00:00	Other
1264	8	10	959	1005	-6	1107	1142	UA	561	N408UA	LGA	ORD	105	733	10	5	2023-08-10 10:00:00	ORD
1269	5	26	1245	1259	-14	1419	1446	DL	460	N135DQ	LGA	ORD	103	733	12	59	2023-05-26 12:00:00	ORD
1271	10	13	1048	1056	-8	1354	1404	DL	983	N102DU	LGA	SRQ	151	1047	10	56	2023-10-13 10:00:00	Other
1273	10	27	909	915	-6	1200	1228	AA	790	N303RG	LGA	MIA	141	1096	9	15	2023-10-27 09:00:00	MIA
1286	9	1	820	826	-6	952	1008	YX	1365	N435YX	LGA	CLE	66	419	8	26	2023-09-01 08:00:00	Other
1289	8	10	552	600	-8	842	909	AA	635	N328RR	JFK	MIA	143	1089	6	0	2023-08-10 06:00:00	MIA
1291	4	24	1206	1212	-6	1327	1335	9E	1192	N299PQ	LGA	SYR	40	198	12	12	2023-04-24 12:00:00	Other
1297	2	11	618	629	-11	747	805	UA	606	N881UA	LGA	ORD	119	733	6	29	2023-02-11 06:00:00	ORD
1302	6	21	1041	1050	-9	1154	1202	YX	1826	N824MD	JFK	ACK	36	199	10	50	2023-06-21 10:00:00	Other
1309	1	25	720	730	-10	955	1008	B6	528	N273JB	JFK	JAX	130	828	7	30	2023-01-25 07:00:00	Other
1317	3	13	952	1000	-8	1205	1221	UA	508	N873UA	EWR	SAV	115	708	10	0	2023-03-13 10:00:00	Other
1320	10	13	652	700	-8	943	952	UA	391	N875UA	EWR	SRQ	150	1034	7	0	2023-10-13 07:00:00	Other
1322	2	8	1221	1230	-9	1405	1417	YX	1568	N242JQ	LGA	BNA	121	764	12	30	2023-02-08 12:00:00	Other
1327	7	20	938	945	-7	1057	1115	9E	1197	N600LR	JFK	DCA	50	213	9	45	2023-07-20 09:00:00	Other
1341	5	8	2020	2029	-9	2331	2345	AA	749	N865NN	LGA	MIA	151	1096	20	29	2023-05-08 20:00:00	MIA
1342	10	23	1034	1040	-6	1238	1313	YX	1828	N218JQ	LGA	IND	94	660	10	40	2023-10-23 10:00:00	Other
1343	4	23	1011	1020	-9	1154	1221	YX	1205	N414YX	JFK	RDU	73	427	10	20	2023-04-23 10:00:00	Other
1349	7	7	552	600	-8	707	732	UA	323	N37456	EWR	ORD	112	719	6	0	2023-07-07 06:00:00	ORD
1357	3	20	759	810	-11	1005	1028	YX	1397	N129HQ	LGA	CVG	100	585	8	10	2023-03-20 08:00:00	Other
1359	7	5	639	645	-6	935	953	UA	244	N431UA	EWR	FLL	150	1065	6	45	2023-07-05 06:00:00	FLL
1368	3	17	1652	1659	-7	1854	1850	YX	1367	N117HQ	LGA	GSO	86	461	16	59	2023-03-17 16:00:00	Other
1374	9	15	1352	1400	-8	1534	1527	YX	1177	N638RW	EWR	MKE	101	725	14	0	2023-09-15 14:00:00	Other
1386	1	6	1210	1217	-7	1312	1339	YX	1171	N723YX	EWR	PWM	47	284	12	17	2023-01-06 12:00:00	Other
1387	4	27	551	600	-9	751	755	DL	346	N313DN	LGA	DTW	86	502	6	0	2023-04-27 06:00:00	Other
1403	9	7	1345	1354	-9	1618	1612	9E	1636	N307PQ	LGA	TYS	111	647	13	54	2023-09-07 13:00:00	Other
1405	7	24	1340	1347	-7	1449	1453	YX	923	N724YX	EWR	PVD	35	160	13	47	2023-07-24 13:00:00	Other
1406	4	3	852	900	-8	1008	1030	9E	1357	N138EV	LGA	PWM	45	269	9	0	2023-04-03 09:00:00	Other
1408	6	12	738	745	-7	858	917	YX	1404	N409YX	LGA	ORF	55	296	7	45	2023-06-12 07:00:00	Other
1409	11	29	1222	1230	-8	1340	1400	YX	1077	N757YX	EWR	PIT	62	319	12	30	2023-11-29 12:00:00	Other
1414	1	6	622	630	-8	836	907	B6	806	N649JB	JFK	ATL	112	760	6	30	2023-01-06 06:00:00	ATL
1416	3	19	1434	1445	-11	1626	1646	YX	1388	N114HQ	JFK	CMH	81	483	14	45	2023-03-19 14:00:00	Other
1419	9	26	1750	1800	-10	2049	2100	AA	196	N895NN	LGA	DFW	187	1389	18	0	2023-09-26 18:00:00	Other
1427	4	16	749	800	-11	848	920	DL	823	N121DU	LGA	BOS	34	184	8	0	2023-04-16 08:00:00	BOS
1428	2	14	1123	1130	-7	1251	1308	UA	562	N14228	EWR	ORD	119	719	11	30	2023-02-14 11:00:00	ORD
1433	3	4	2055	2105	-10	10	2355	NK	275	N956NK	EWR	LAS	353	2227	21	5	2023-03-04 21:00:00	Other
1434	10	6	2024	2033	-9	2222	2247	9E	1637	N915XJ	LGA	CAE	88	617	20	33	2023-10-06 20:00:00	Other
1449	2	21	1124	1130	-6	1322	1331	YX	1567	N213JQ	LGA	CMH	90	479	11	30	2023-02-21 11:00:00	Other
1454	5	26	558	604	-6	803	812	B6	31	N715JB	JFK	MSY	158	1182	6	4	2023-05-26 06:00:00	Other
1457	12	27	1244	1250	-6	1427	1453	YX	1017	N741YX	EWR	CMH	79	463	12	50	2023-12-27 12:00:00	Other
1462	7	29	1623	1629	-6	1854	1936	AA	91	N103NN	JFK	LAX	313	2475	16	29	2023-07-29 16:00:00	LAX
1470	5	1	854	900	-6	1140	1202	B6	338	N258JB	JFK	PBI	150	1028	9	0	2023-05-01 09:00:00	Other
1473	6	16	726	733	-7	916	926	UA	498	N27276	EWR	CLT	75	529	7	33	2023-06-16 07:00:00	CLT
1475	8	19	1552	1600	-8	1715	1802	9E	1141	N319PQ	LGA	STL	117	888	16	0	2023-08-19 16:00:00	Other
1481	11	11	1514	1525	-11	1722	1741	YX	1140	N752YX	EWR	GSP	99	594	15	25	2023-11-11 15:00:00	Other
1490	12	24	2119	2129	-10	2335	2357	YX	1022	N752YX	EWR	GRR	94	605	21	29	2023-12-24 21:00:00	Other
1497	4	14	1101	1115	-14	1245	1305	YX	1218	N821MD	LGA	ROA	65	405	11	15	2023-04-14 11:00:00	Other
1499	1	27	734	740	-6	1047	1122	B6	6	N988JT	JFK	SFO	350	2586	7	40	2023-01-27 07:00:00	Other
1501	5	15	2122	2130	-8	2333	13	DL	451	N898DN	JFK	ATL	104	760	21	30	2023-05-15 21:00:00	ATL
1503	10	17	1223	1229	-6	1432	1443	9E	1409	N325PQ	LGA	CLT	85	544	12	29	2023-10-17 12:00:00	CLT
1506	2	16	922	929	-7	1020	1044	YX	1043	N726YX	EWR	PVD	36	160	9	29	2023-02-16 09:00:00	Other
1512	3	22	1202	1210	-8	1347	1349	YX	1276	N446YX	LGA	BNA	127	764	12	10	2023-03-22 12:00:00	Other
1515	12	6	1547	1555	-8	1834	1905	B6	735	N964JT	EWR	LAX	323	2454	15	55	2023-12-06 15:00:00	LAX
1516	2	1	716	725	-9	952	924	AA	270	N987NN	LGA	ORD	124	733	7	25	2023-02-01 07:00:00	ORD
1517	9	14	1050	1059	-9	1243	1255	YX	1185	N763YX	EWR	MEM	149	946	10	59	2023-09-14 10:00:00	Other
1519	7	26	1050	1100	-10	1300	1321	YX	1017	N418YX	LGA	XNA	149	1147	11	0	2023-07-26 11:00:00	Other
1528	8	31	2121	2129	-8	2234	2254	YX	988	N119HQ	LGA	RIC	52	292	21	29	2023-08-31 21:00:00	Other
1530	8	2	1022	1030	-8	1147	1215	AA	668	N177XF	LGA	STL	124	888	10	30	2023-08-02 10:00:00	Other
1537	11	1	1443	1453	-10	1635	1653	YX	1398	N430YX	JFK	CMH	80	483	14	53	2023-11-01 14:00:00	Other
1539	5	31	1815	1825	-10	1944	2025	9E	1453	N921XJ	LGA	MEM	125	963	18	25	2023-05-31 18:00:00	Other
1545	1	24	1900	1915	-15	2037	2105	YX	1881	N244JQ	JFK	PIT	69	340	19	15	2023-01-24 19:00:00	Other
1546	3	1	1653	1659	-6	1850	1855	YX	1037	N641RW	EWR	GSO	80	445	16	59	2023-03-01 16:00:00	Other
1549	11	26	2154	2200	-6	32	2318	YX	1255	N104HQ	JFK	BOS	59	187	22	0	2023-11-26 22:00:00	BOS
1560	12	16	920	930	-10	1255	1256	AS	6	N528AS	JFK	SEA	342	2422	9	30	2023-12-16 09:00:00	Other
1564	9	21	620	630	-10	733	801	YX	1329	N418YX	LGA	ORF	47	296	6	30	2023-09-21 06:00:00	Other
1565	5	27	1620	1629	-9	1822	1851	YX	1261	N411YX	JFK	CVG	83	589	16	29	2023-05-27 16:00:00	Other
1567	12	11	1552	1559	-7	1824	1848	YX	1221	N127HQ	LGA	LIT	171	1085	15	59	2023-12-11 15:00:00	Other
1568	10	31	1323	1329	-6	1632	1634	DL	360	N378DA	LGA	IAH	224	1416	13	29	2023-10-31 13:00:00	Other
1569	11	17	1552	1559	-7	1728	1750	AA	131	N922NN	LGA	ORD	115	733	15	59	2023-11-17 15:00:00	ORD
1573	2	2	1320	1329	-9	1501	1503	YX	1574	N217JQ	LGA	IAD	50	229	13	29	2023-02-02 13:00:00	Other
1575	5	30	1152	1159	-7	1431	1455	UA	821	N76288	EWR	TPA	133	997	11	59	2023-05-30 11:00:00	Other
1580	2	8	1254	1300	-6	1541	1619	B6	964	N806JB	JFK	MIA	147	1089	13	0	2023-02-08 13:00:00	MIA
1581	5	31	1451	1500	-9	1813	1807	NK	626	N676NK	LGA	FLL	175	1076	15	0	2023-05-31 15:00:00	FLL
1589	8	16	2150	2159	-9	2237	2304	9E	1190	N324PQ	LGA	BDL	20	101	21	59	2023-08-16 21:00:00	Other
1591	2	8	1020	1029	-9	1227	1254	YX	1527	N879RW	LGA	CLT	92	544	10	29	2023-02-08 10:00:00	CLT
1594	9	27	1158	1210	-12	1345	1359	AA	845	N821AW	LGA	STL	125	888	12	10	2023-09-27 12:00:00	Other
1602	8	5	2240	2250	-10	6	37	9E	1232	N292PQ	JFK	ROC	51	264	22	50	2023-08-05 22:00:00	Other
1612	5	28	2121	2127	-6	2221	2240	9E	1283	N905XJ	LGA	SCE	35	208	21	27	2023-05-28 21:00:00	Other
1613	2	18	749	755	-6	1037	1104	B6	180	N566JB	LGA	PBI	139	1035	7	55	2023-02-18 07:00:00	Other
1615	8	14	723	729	-6	1025	1028	AA	3	N107NN	JFK	LAX	331	2475	7	29	2023-08-14 07:00:00	LAX
1622	8	2	849	855	-6	1046	1049	YX	1044	N127HQ	LGA	GSO	71	461	8	55	2023-08-02 08:00:00	Other
1625	9	25	1004	1011	-7	1235	1215	UA	507	N16701	EWR	CLT	78	529	10	11	2023-09-25 10:00:00	CLT
1628	2	8	1108	1115	-7	1322	1344	YX	1269	N104HQ	JFK	IND	114	665	11	15	2023-02-08 11:00:00	Other
1630	3	23	1857	1905	-8	2107	2124	9E	1569	N325PQ	LGA	CHS	92	641	19	5	2023-03-23 19:00:00	Other
1631	3	29	723	730	-7	1104	1125	B6	621	N913JB	JFK	SJU	196	1598	7	30	2023-03-29 07:00:00	Other
1633	1	26	1440	1449	-9	1752	1750	B6	656	N907JB	EWR	MCO	160	937	14	49	2023-01-26 14:00:00	MCO
1650	9	14	1613	1620	-7	1717	1744	YX	1064	N723YX	EWR	ROC	43	246	16	20	2023-09-14 16:00:00	Other
1659	8	23	922	930	-8	1144	1223	AS	15	N948AK	JFK	SAN	299	2446	9	30	2023-08-23 09:00:00	Other
1676	3	8	2052	2100	-8	2232	2311	YX	1241	N450YX	JFK	CMH	81	483	21	0	2023-03-08 21:00:00	Other
1680	6	30	1103	1110	-7	1223	1240	YX	1403	N116HQ	JFK	ORF	55	290	11	10	2023-06-30 11:00:00	Other
1685	12	2	2006	2012	-6	2319	2320	NK	156	N685NK	LGA	MCO	141	950	20	12	2023-12-02 20:00:00	MCO
1686	12	14	1825	1835	-10	1950	2014	YX	1140	N756YX	EWR	PIT	54	319	18	35	2023-12-14 18:00:00	Other
1687	11	12	653	659	-6	951	1021	AA	536	N849NN	LGA	MIA	158	1096	6	59	2023-11-12 06:00:00	MIA
1708	4	13	1211	1221	-10	1334	1358	YX	1258	N138HQ	LGA	PIT	57	335	12	21	2023-04-13 12:00:00	Other
1712	8	23	1254	1300	-6	1552	1601	UA	87	N439UA	EWR	RSW	142	1068	13	0	2023-08-23 13:00:00	Other
1715	2	20	717	729	-12	841	856	YX	1152	N863RW	EWR	BUF	58	282	7	29	2023-02-20 07:00:00	Other
1717	10	22	1138	1145	-7	1217	1247	YX	1162	N758YX	EWR	PHL	19	80	11	45	2023-10-22 11:00:00	Other
1719	11	10	1650	1659	-9	1926	1949	B6	922	N516JB	LGA	ATL	119	762	16	59	2023-11-10 16:00:00	ATL
1720	5	10	1311	1319	-8	1416	1434	YX	1093	N862RW	EWR	MHT	46	209	13	19	2023-05-10 13:00:00	Other
1722	11	9	1320	1328	-8	1512	1543	YX	1906	N238JQ	LGA	CLT	89	544	13	28	2023-11-09 13:00:00	CLT
1729	12	17	757	803	-6	1140	1113	UA	665	N27520	EWR	FLL	190	1065	8	3	2023-12-17 08:00:00	FLL
1731	5	12	713	720	-7	849	914	YX	1595	N818MD	LGA	GSO	68	461	7	20	2023-05-12 07:00:00	Other
1733	7	27	624	630	-6	813	815	9E	1288	N917XJ	LGA	CLE	74	419	6	30	2023-07-27 06:00:00	Other
1752	5	25	1051	1059	-8	1239	1301	NK	629	N678NK	LGA	DTW	83	502	10	59	2023-05-25 10:00:00	Other
1753	6	14	1653	1659	-6	2016	2030	AA	53	N108NN	JFK	SFO	342	2586	16	59	2023-06-14 16:00:00	Other
1757	9	16	1417	1425	-8	1700	1723	UA	587	N27277	EWR	IAH	190	1400	14	25	2023-09-16 14:00:00	Other
1762	9	1	949	959	-10	1144	1154	YX	1847	N810MD	JFK	CMH	72	483	9	59	2023-09-01 09:00:00	Other
1764	12	8	756	805	-9	915	928	AA	893	N801AW	LGA	DCA	51	214	8	5	2023-12-08 08:00:00	Other
1776	11	18	1550	1600	-10	1807	1841	YX	1375	N121HQ	LGA	SDF	96	659	16	0	2023-11-18 16:00:00	Other
1779	10	10	550	600	-10	841	902	B6	462	N665JB	LGA	FLL	142	1076	6	0	2023-10-10 06:00:00	FLL
1783	3	22	1053	1059	-6	1241	1303	YX	1036	N979RP	EWR	CMH	81	463	10	59	2023-03-22 10:00:00	Other
1789	4	21	1252	1259	-7	1407	1433	9E	1351	N923XJ	JFK	BUF	50	301	12	59	2023-04-21 12:00:00	Other
1795	11	5	1819	1825	-6	2042	2105	YX	1798	N233JQ	LGA	SDF	101	659	18	25	2023-11-05 18:00:00	Other
1797	8	21	2002	2011	-9	2126	2151	YX	1038	N402YX	LGA	PIT	51	335	20	11	2023-08-21 20:00:00	Other
1801	8	3	1453	1500	-7	1655	1707	B6	302	N348JB	JFK	DTW	87	509	15	0	2023-08-03 15:00:00	Other
1803	3	15	752	800	-8	1129	1159	B6	193	N2044J	JFK	SJU	198	1598	8	0	2023-03-15 08:00:00	Other
1812	9	4	804	810	-6	951	951	9E	1568	N296PQ	JFK	RIC	60	288	8	10	2023-09-04 08:00:00	Other
1815	11	27	1749	1759	-10	2109	2115	AA	649	N896NN	LGA	DFW	222	1389	17	59	2023-11-27 17:00:00	Other
1816	12	16	1051	1059	-8	1239	1322	9E	1349	N912XJ	LGA	DSM	147	1031	10	59	2023-12-16 10:00:00	Other
1819	10	25	1730	1740	-10	1917	1940	9E	1458	N146PQ	LGA	MEM	139	963	17	40	2023-10-25 17:00:00	Other
1823	12	3	553	600	-7	831	833	UA	371	N17279	EWR	ATL	129	746	6	0	2023-12-03 06:00:00	ATL
1831	11	25	917	927	-10	1049	1123	9E	1756	N917XJ	LGA	BHM	130	866	9	27	2023-11-25 09:00:00	Other
1853	5	5	554	600	-6	652	715	YX	1622	N231JQ	LGA	BOS	35	184	6	0	2023-05-05 06:00:00	BOS
1855	5	18	1151	1200	-9	1243	1320	YX	1301	N421YX	JFK	ORH	31	150	12	0	2023-05-18 12:00:00	Other
1858	3	28	1135	1145	-10	1502	1504	DL	654	N128DU	LGA	IAH	227	1416	11	45	2023-03-28 11:00:00	Other
1860	6	26	1120	1130	-10	1323	1239	YX	1375	N113HQ	JFK	ORH	31	150	11	30	2023-06-26 11:00:00	Other
1861	11	2	802	810	-8	1034	1049	B6	188	N564JB	JFK	ATL	116	760	8	10	2023-11-02 08:00:00	ATL
1862	1	10	1443	1455	-12	1631	1710	AA	756	N546UW	LGA	CLT	84	544	14	55	2023-01-10 14:00:00	CLT
1864	9	15	1648	1655	-7	1944	2008	B6	298	N961JT	JFK	LAX	321	2475	16	55	2023-09-15 16:00:00	LAX
1869	6	21	1206	1215	-9	1405	1419	YX	1382	N433YX	LGA	DTW	84	502	12	15	2023-06-21 12:00:00	Other
1871	12	23	953	959	-6	1140	1207	9E	1455	N325PQ	JFK	CLE	73	425	9	59	2023-12-23 09:00:00	Other
1872	4	24	1614	1620	-6	1912	1911	UA	123	N19130	EWR	MCO	155	937	16	20	2023-04-24 16:00:00	MCO
1879	11	2	1124	1133	-9	1224	1244	YX	1373	N131HQ	JFK	ORH	32	150	11	33	2023-11-02 11:00:00	Other
1880	1	1	1519	1526	-7	1728	1722	YX	1436	N431YX	JFK	RDU	80	427	15	26	2023-01-01 15:00:00	Other
1882	1	13	1144	1150	-6	1234	1303	YX	1749	N229JQ	LGA	BDL	26	101	11	50	2023-01-13 11:00:00	Other
1887	2	6	1520	1529	-9	1742	1800	YX	1222	N413YX	JFK	IND	101	665	15	29	2023-02-06 15:00:00	Other
1888	9	28	1919	1929	-10	2113	2126	YX	1390	N869RW	LGA	CMH	80	479	19	29	2023-09-28 19:00:00	Other
1894	3	19	739	746	-7	1006	1009	YX	1124	N857RW	EWR	IND	114	645	7	46	2023-03-19 07:00:00	Other
1897	7	15	924	930	-6	1220	1243	B6	72	N640JB	LGA	FLL	147	1076	9	30	2023-07-15 09:00:00	FLL
1898	8	16	1915	1929	-14	2109	2142	YX	1043	N418YX	LGA	CVG	92	585	19	29	2023-08-16 19:00:00	Other
1899	8	31	1649	1657	-8	1837	1922	YX	826	N761YX	EWR	SDF	89	642	16	57	2023-08-31 16:00:00	Other
1901	5	9	1706	1712	-6	1827	1852	UA	771	N14107	EWR	ORD	109	719	17	12	2023-05-09 17:00:00	ORD
1902	11	5	1153	1200	-7	1348	1355	9E	1441	N491PX	LGA	CLE	68	419	12	0	2023-11-05 12:00:00	Other
1910	10	25	2117	2129	-12	2244	2256	YX	1265	N102HQ	LGA	RIC	55	292	21	29	2023-10-25 21:00:00	Other
1925	8	12	605	615	-10	1005	809	UA	382	N414UA	EWR	MSP	NA	1008	6	15	2023-08-12 06:00:00	Other
1938	8	30	1031	1038	-7	1227	1225	B6	71	N807JB	JFK	RDU	71	427	10	38	2023-08-30 10:00:00	Other
1946	9	27	808	815	-7	1121	1138	UA	666	N13113	EWR	SEA	328	2402	8	15	2023-09-27 08:00:00	Other
1947	4	24	814	820	-6	1017	1038	YX	1024	N746YX	EWR	CVG	96	569	8	20	2023-04-24 08:00:00	Other
1948	1	22	1948	2000	-12	2151	2214	B6	609	N247JB	JFK	DTW	96	509	20	0	2023-01-22 20:00:00	Other
1958	8	31	1952	1958	-6	2130	2129	OO	949	N306SY	LGA	MKE	117	738	19	58	2023-08-31 19:00:00	Other
1960	10	25	851	900	-9	1205	1202	AS	13	N956AK	JFK	SAN	346	2446	9	0	2023-10-25 09:00:00	Other
1964	8	29	2058	2110	-12	2234	2303	YX	989	N442YX	LGA	GSO	74	461	21	10	2023-08-29 21:00:00	Other
1982	8	20	621	630	-9	738	757	YX	972	N438YX	JFK	ORF	47	290	6	30	2023-08-20 06:00:00	Other
1986	8	23	1408	1418	-10	1546	1610	B6	223	N216JB	JFK	RDU	65	427	14	18	2023-08-23 14:00:00	Other
1990	8	28	1122	1130	-8	1216	1242	B6	625	N355JB	JFK	ACK	34	199	11	30	2023-08-28 11:00:00	Other
1991	11	11	651	659	-8	906	915	UA	449	N12754	EWR	CHS	106	628	6	59	2023-11-11 06:00:00	Other
1993	1	9	1615	1629	-14	1806	1841	YX	1442	N423YX	LGA	GSO	73	461	16	29	2023-01-09 16:00:00	Other
1996	11	29	1953	1959	-6	2310	2325	DL	598	N313DU	LGA	IAH	211	1416	19	59	2023-11-29 19:00:00	Other
1999	11	2	2107	2115	-8	2303	2314	YX	1260	N106HQ	LGA	MEM	149	963	21	15	2023-11-02 21:00:00	Other
2001	10	2	1548	1554	-6	1910	1924	B6	208	N945JT	JFK	SFO	338	2586	15	54	2023-10-02 15:00:00	Other
2006	2	1	1608	1615	-7	1705	1734	B6	389	N239JB	LGA	BOS	34	184	16	15	2023-02-01 16:00:00	BOS
2008	8	23	1351	1359	-8	1613	1558	YX	825	N726YX	EWR	DTW	104	488	13	59	2023-08-23 13:00:00	Other
2011	12	21	1223	1230	-7	1509	1532	B6	37	N3145J	JFK	TPA	138	1005	12	30	2023-12-21 12:00:00	Other
2025	4	13	1139	1145	-6	1411	1443	DL	189	N919DU	JFK	LAS	287	2248	11	45	2023-04-13 11:00:00	Other
2026	4	19	1417	1425	-8	1621	1633	YX	944	N745YX	EWR	GRR	101	605	14	25	2023-04-19 14:00:00	Other
2034	2	14	1133	1145	-12	1326	1345	YX	1285	N102HQ	JFK	CLE	83	425	11	45	2023-02-14 11:00:00	Other
2035	6	21	617	625	-8	758	809	9E	1632	N349PQ	LGA	RDU	75	431	6	25	2023-06-21 06:00:00	Other
2043	8	11	720	729	-9	955	1015	UA	159	N14249	LGA	IAH	190	1416	7	29	2023-08-11 07:00:00	Other
2044	1	18	2150	2158	-8	2304	2327	UA	891	N76515	EWR	ORF	55	284	21	58	2023-01-18 21:00:00	Other
2045	5	11	1206	1215	-9	1306	1332	B6	199	N249JB	LGA	BOS	39	184	12	15	2023-05-11 12:00:00	BOS
2047	4	28	1411	1419	-8	1618	1637	9E	1410	N479PX	LGA	CHS	98	641	14	19	2023-04-28 14:00:00	Other
2048	5	21	810	817	-7	1008	1030	YX	1094	N863RW	EWR	DTW	78	488	8	17	2023-05-21 08:00:00	Other
2052	8	26	805	815	-10	1025	1029	YX	830	N638RW	EWR	GRR	105	605	8	15	2023-08-26 08:00:00	Other
2068	3	12	614	625	-11	852	925	B6	1011	N324JB	JFK	PBI	140	1028	6	25	2023-03-12 06:00:00	Other
2075	10	15	1848	1856	-8	2138	2155	DL	571	N316DN	LGA	MCO	144	950	18	56	2023-10-15 18:00:00	MCO
2080	9	22	752	800	-8	903	911	B6	39	N203JB	JFK	BOS	38	187	8	0	2023-09-22 08:00:00	BOS
2082	12	2	815	830	-15	1041	1049	9E	1500	N341PQ	JFK	CVG	99	589	8	30	2023-12-02 08:00:00	Other
2095	5	11	1413	1420	-7	1533	1545	WN	74	N8564Z	LGA	MDW	107	725	14	20	2023-05-11 14:00:00	Other
2096	4	18	724	730	-6	845	857	YX	1467	N824MD	LGA	ORF	56	296	7	30	2023-04-18 07:00:00	Other
2097	10	4	1148	1159	-11	1255	1317	UA	419	N426UA	EWR	PWM	48	284	11	59	2023-10-04 11:00:00	Other
2098	9	23	1953	2000	-7	2233	2303	NK	162	N680NK	LGA	MCO	138	950	20	0	2023-09-23 20:00:00	MCO
2099	10	3	901	912	-11	1031	1059	YX	1326	N131HQ	LGA	GSO	66	461	9	12	2023-10-03 09:00:00	Other
2104	6	4	852	900	-8	1112	1117	YX	1232	N653RW	EWR	HHH	105	687	9	0	2023-06-04 09:00:00	Other
2105	3	10	557	605	-8	743	818	DL	887	N337NW	LGA	MSP	146	1020	6	5	2023-03-10 06:00:00	Other
2118	10	2	1522	1531	-9	1617	1643	YX	1083	N728YX	EWR	ALB	31	143	15	31	2023-10-02 15:00:00	Other
2124	1	13	1217	1230	-13	1510	1544	UA	531	N27267	EWR	RSW	160	1068	12	30	2023-01-13 12:00:00	Other
2131	2	10	1624	1630	-6	1738	1756	YX	1597	N222JQ	LGA	ROC	50	254	16	30	2023-02-10 16:00:00	Other
2132	4	14	754	805	-11	958	1010	B6	439	N328JB	JFK	CHS	106	636	8	5	2023-04-14 08:00:00	Other
2140	12	15	1343	1350	-7	1533	1559	9E	1668	N326PQ	LGA	CAE	88	617	13	50	2023-12-15 13:00:00	Other
2143	5	7	1750	1759	-9	2123	2106	F9	951	N364FR	LGA	MIA	162	1096	17	59	2023-05-07 17:00:00	MIA
2144	2	11	810	817	-7	1302	1311	UA	764	N77066	EWR	SJU	200	1608	8	17	2023-02-11 08:00:00	Other
2147	2	19	1654	1701	-7	1834	1904	DL	868	N932AT	EWR	DTW	84	488	17	1	2023-02-19 17:00:00	Other
2148	10	7	920	929	-9	1223	1125	YX	1260	N405YX	JFK	CMH	80	483	9	29	2023-10-07 09:00:00	Other
2151	9	17	1353	1359	-6	1639	1658	AA	991	N306PB	LGA	DFW	192	1389	13	59	2023-09-17 13:00:00	Other
2158	1	29	1835	1844	-9	2131	2120	UA	431	N12109	EWR	DEN	265	1605	18	44	2023-01-29 18:00:00	Other
2163	10	18	623	635	-12	905	946	AA	557	N803NN	LGA	DFW	189	1389	6	35	2023-10-18 06:00:00	Other
2164	4	12	1153	1159	-6	1415	1455	UA	670	N27267	EWR	IAH	176	1400	11	59	2023-04-12 11:00:00	Other
2167	9	23	753	800	-7	1051	1037	B6	138	N980JT	JFK	LAS	309	2248	8	0	2023-09-23 08:00:00	Other
2172	4	28	1339	1345	-6	1547	1602	YX	943	N742YX	EWR	SDF	103	642	13	45	2023-04-28 13:00:00	Other
2180	1	18	1915	1929	-14	2152	2212	YX	1291	N106HQ	LGA	LIT	176	1085	19	29	2023-01-18 19:00:00	Other
2184	1	10	1150	1200	-10	1523	1530	UA	873	N14118	EWR	SFO	365	2565	12	0	2023-01-10 12:00:00	Other
2186	7	28	1948	1959	-11	2204	2208	YX	998	N110HQ	JFK	PIT	64	340	19	59	2023-07-28 19:00:00	Other
2187	12	11	1124	1130	-6	1452	1445	DL	590	N392DA	LGA	MIA	162	1096	11	30	2023-12-11 11:00:00	MIA
2188	6	2	1550	1600	-10	1712	1732	YX	1336	N871RW	LGA	CHO	54	305	16	0	2023-06-02 16:00:00	Other
2191	12	24	1823	1829	-6	2008	2017	UA	423	N37531	EWR	ORD	108	719	18	29	2023-12-24 18:00:00	ORD
2194	5	5	1608	1615	-7	1703	1735	B6	362	N267JB	LGA	BOS	36	184	16	15	2023-05-05 16:00:00	BOS
2196	2	25	2120	2130	-10	2343	2333	UA	146	N76516	EWR	CHS	93	628	21	30	2023-02-25 21:00:00	Other
2201	9	2	1611	1617	-6	1808	1839	9E	1452	N916XJ	LGA	CVG	86	585	16	17	2023-09-02 16:00:00	Other
2202	3	21	1140	1150	-10	1249	1319	YX	1649	N815MD	LGA	PWM	48	269	11	50	2023-03-21 11:00:00	Other
2218	9	18	1526	1535	-9	1636	1704	9E	1526	N176PQ	LGA	ROC	44	254	15	35	2023-09-18 15:00:00	Other
2219	10	17	1653	1700	-7	1801	1826	YX	1716	N216JQ	LGA	BOS	36	184	17	0	2023-10-17 17:00:00	BOS
2223	6	8	655	705	-10	1029	1007	B6	884	N627JB	EWR	MIA	167	1085	7	5	2023-06-08 07:00:00	MIA
2224	8	24	1423	1430	-7	1625	1640	WN	264	N8535S	LGA	MSY	146	1183	14	30	2023-08-24 14:00:00	Other
2226	6	9	2048	2055	-7	2214	2258	YX	1862	N210JQ	JFK	PIT	60	340	20	55	2023-06-09 20:00:00	Other
2228	12	7	1502	1510	-8	1642	1719	YX	1241	N404YX	JFK	CMH	79	483	15	10	2023-12-07 15:00:00	Other
2230	4	7	949	955	-6	1233	1227	AA	714	N418AN	EWR	PHX	302	2133	9	55	2023-04-07 09:00:00	Other
2251	7	11	1949	1955	-6	2149	2249	DL	153	N868DN	JFK	DEN	213	1626	19	55	2023-07-11 19:00:00	Other
2253	9	6	651	659	-8	809	829	YX	1378	N117HQ	LGA	PIT	54	335	6	59	2023-09-06 06:00:00	Other
2254	5	5	720	730	-10	1031	1055	AS	15	N464AS	JFK	SFO	342	2586	7	30	2023-05-05 07:00:00	Other
2259	12	23	1504	1510	-6	1741	1845	DL	151	N509DT	JFK	SEA	316	2422	15	10	2023-12-23 15:00:00	Other
2261	10	13	2115	2124	-9	2301	2325	NK	253	N621NK	LGA	DTW	87	502	21	24	2023-10-13 21:00:00	Other
2262	10	20	1447	1453	-6	1752	1800	NK	837	N620NK	EWR	FLL	163	1065	14	53	2023-10-20 14:00:00	FLL
2277	10	31	952	1000	-8	1116	1128	YX	1146	N657RW	EWR	DCA	49	199	10	0	2023-10-31 10:00:00	Other
2280	3	7	1728	1735	-7	1929	1907	YX	1682	N220JQ	LGA	DCA	55	214	17	35	2023-03-07 17:00:00	Other
2281	3	24	1748	1755	-7	1914	1925	YX	1666	N210JQ	JFK	DCA	52	213	17	55	2023-03-24 17:00:00	Other
2283	12	21	1242	1250	-8	1420	1453	YX	1017	N740YX	EWR	CMH	71	463	12	50	2023-12-21 12:00:00	Other
2288	1	19	652	700	-8	953	1018	UA	916	N27263	EWR	RSW	155	1068	7	0	2023-01-19 07:00:00	Other
2291	12	1	1651	1659	-8	1806	1821	YX	1138	N725YX	EWR	BTV	51	266	16	59	2023-12-01 16:00:00	Other
2301	7	14	721	729	-8	1055	1015	UA	173	N33203	LGA	IAH	195	1416	7	29	2023-07-14 07:00:00	Other
2306	5	31	745	755	-10	931	1010	9E	1363	N293PQ	JFK	CVG	86	589	7	55	2023-05-31 07:00:00	Other
2307	10	11	759	809	-10	915	926	AA	722	N740UW	LGA	DCA	54	214	8	9	2023-10-11 08:00:00	Other
2312	6	8	1128	1135	-7	1255	1319	DL	603	N104DU	LGA	ORD	117	733	11	35	2023-06-08 11:00:00	ORD
2314	3	15	845	851	-6	1149	1203	UA	423	N12238	EWR	MIA	153	1085	8	51	2023-03-15 08:00:00	MIA
2318	9	5	1051	1059	-8	1219	1228	YX	1311	N418YX	LGA	PIT	56	335	10	59	2023-09-05 10:00:00	Other
2323	6	7	1151	1159	-8	1414	1453	UA	763	N78501	EWR	IAH	187	1400	11	59	2023-06-07 11:00:00	Other
2345	4	28	1753	1759	-6	2043	2052	YX	1148	N405YX	LGA	OKC	207	1341	17	59	2023-04-28 17:00:00	Other
2349	1	5	1208	1215	-7	1449	1450	UA	715	N13248	LGA	DEN	220	1620	12	15	2023-01-05 12:00:00	Other
2351	11	10	1237	1245	-8	1501	1519	UA	413	N77525	EWR	ATL	125	746	12	45	2023-11-10 12:00:00	ATL
2352	6	18	1554	1600	-6	1724	1727	YX	1220	N762YX	EWR	PWM	49	284	16	0	2023-06-18 16:00:00	Other
2355	12	17	1423	1430	-7	1716	1752	UA	846	N29124	EWR	LAX	330	2454	14	30	2023-12-17 14:00:00	LAX
2356	9	4	817	827	-10	945	1006	YX	1196	N639RW	EWR	RIC	48	277	8	27	2023-09-04 08:00:00	Other
2360	5	29	1119	1125	-6	1311	1325	YX	1191	N435YX	JFK	CMH	76	483	11	25	2023-05-29 11:00:00	Other
2363	10	19	1023	1030	-7	1125	1159	YX	1074	N750YX	EWR	DCA	39	199	10	30	2023-10-19 10:00:00	Other
2365	1	16	751	800	-9	901	941	YX	1320	N109HQ	LGA	DCA	44	214	8	0	2023-01-16 08:00:00	Other
2367	11	28	717	726	-9	859	911	UA	943	N78438	EWR	RDU	82	416	7	26	2023-11-28 07:00:00	Other
2371	8	15	832	842	-10	948	1024	9E	1267	N907XJ	LGA	CHO	57	305	8	42	2023-08-15 08:00:00	Other
2372	12	19	1448	1455	-7	1544	1622	YX	1828	N208JQ	JFK	BWI	37	184	14	55	2023-12-19 14:00:00	Other
2374	11	7	1342	1350	-8	1509	1540	9E	1473	N315PQ	LGA	BHM	120	866	13	50	2023-11-07 13:00:00	Other
2376	12	9	1217	1223	-6	1444	1457	DL	837	N108DQ	LGA	MSY	183	1183	12	23	2023-12-09 12:00:00	Other
2382	9	5	1153	1159	-6	1440	1517	NK	1028	N685NK	LGA	MIA	142	1096	11	59	2023-09-05 11:00:00	MIA
2385	3	13	943	950	-7	1213	1229	AA	1004	N410AN	EWR	PHX	296	2133	9	50	2023-03-13 09:00:00	Other
2395	4	25	809	820	-11	944	954	9E	1304	N319PQ	LGA	IAD	52	229	8	20	2023-04-25 08:00:00	Other
2396	2	8	919	930	-11	1027	1057	9E	1399	N308PQ	JFK	PWM	47	273	9	30	2023-02-08 09:00:00	Other
2398	9	4	1812	1820	-8	2044	2124	UA	895	N57286	EWR	PDX	306	2434	18	20	2023-09-04 18:00:00	Other
2409	11	4	907	915	-8	1038	1114	B6	374	N239JB	JFK	ORD	122	740	9	15	2023-11-04 09:00:00	ORD
2410	4	24	1153	1159	-6	1517	1445	UA	275	N38257	EWR	MCO	146	937	11	59	2023-04-24 11:00:00	MCO
2412	1	31	546	600	-14	919	926	B6	587	N990JL	EWR	LAX	373	2454	6	0	2023-01-31 06:00:00	LAX
2414	10	20	609	615	-6	732	744	YX	1065	N748YX	EWR	PIT	58	319	6	15	2023-10-20 06:00:00	Other
2415	8	14	853	900	-7	1133	1151	UA	473	N12218	EWR	SAT	198	1569	9	0	2023-08-14 09:00:00	Other
2416	1	18	851	900	-9	1007	1035	YX	1319	N431YX	JFK	BOS	42	187	9	0	2023-01-18 09:00:00	BOS
2418	6	28	821	831	-10	1002	1044	9E	1530	N919XJ	LGA	GSP	87	610	8	31	2023-06-28 08:00:00	Other
2427	11	27	2055	2106	-11	2309	2317	YX	1383	N107HQ	LGA	DTW	92	502	21	6	2023-11-27 21:00:00	Other
2431	10	9	951	1000	-9	1206	1229	YX	1329	N128HQ	LGA	SDF	109	659	10	0	2023-10-09 10:00:00	Other
2433	5	29	658	705	-7	942	1001	DL	658	N343NB	LGA	TPA	138	1010	7	5	2023-05-29 07:00:00	Other
2442	3	8	901	908	-7	1028	1025	B6	965	N236JB	JFK	BOS	40	187	9	8	2023-03-08 09:00:00	BOS
2448	9	15	1949	2000	-11	2138	2123	AA	550	N705UW	LGA	DCA	63	214	20	0	2023-09-15 20:00:00	Other
2449	5	28	1047	1054	-7	1320	1342	B6	330	N640JB	EWR	MCO	127	937	10	54	2023-05-28 10:00:00	MCO
2452	2	19	1906	1915	-9	2341	2258	B6	47	N821JB	JFK	PHX	365	2153	19	15	2023-02-19 19:00:00	Other
2460	3	9	1141	1150	-9	1321	1327	9E	1426	N137EV	LGA	MKE	129	738	11	50	2023-03-09 11:00:00	Other
2466	10	30	949	955	-6	1106	1123	YX	1850	N229JQ	JFK	DCA	49	213	9	55	2023-10-30 09:00:00	Other
2467	8	13	1452	1459	-7	1714	1714	AA	118	N9017P	JFK	CLT	83	541	14	59	2023-08-13 14:00:00	CLT
2469	4	12	1924	1930	-6	2150	2257	AA	42	N108NN	JFK	LAX	297	2475	19	30	2023-04-12 19:00:00	LAX
2470	10	13	1124	1130	-6	1416	1451	AA	610	N343RY	LGA	MIA	143	1096	11	30	2023-10-13 11:00:00	MIA
2472	10	7	1424	1435	-11	1618	1640	UA	332	N486UA	EWR	CLT	86	529	14	35	2023-10-07 14:00:00	CLT
2478	12	18	628	635	-7	921	952	UA	706	N17302	EWR	SNA	324	2434	6	35	2023-12-18 06:00:00	Other
2485	10	18	554	602	-8	736	808	DL	961	N933AT	EWR	MSP	142	1008	6	2	2023-10-18 06:00:00	Other
2488	8	10	1244	1250	-6	1354	1357	9E	1283	N324PQ	JFK	ITH	45	189	12	50	2023-08-10 12:00:00	Other
2490	11	7	1943	1950	-7	2158	2227	YX	1076	N744YX	EWR	MCI	175	1092	19	50	2023-11-07 19:00:00	Other
2493	2	15	2122	2129	-7	2214	2237	YX	993	N863RW	EWR	MDT	33	141	21	29	2023-02-15 21:00:00	Other
2496	10	31	1209	1215	-6	1434	1448	UA	690	N37293	LGA	DEN	231	1620	12	15	2023-10-31 12:00:00	Other
2499	10	26	2121	2128	-7	2254	2309	YX	1061	N751YX	EWR	MSN	123	799	21	28	2023-10-26 21:00:00	Other
2501	3	8	839	849	-10	1024	1045	YX	1364	N403YX	LGA	ILM	74	500	8	49	2023-03-08 08:00:00	Other
2529	10	27	1614	1620	-6	1807	1835	9E	1684	N299PQ	JFK	CLT	83	541	16	20	2023-10-27 16:00:00	CLT
2533	10	18	1519	1525	-6	1806	1849	AS	78	N549AS	EWR	SFO	317	2565	15	25	2023-10-18 15:00:00	Other
2540	10	9	1312	1318	-6	1556	1623	AA	395	N908AN	EWR	DFW	192	1372	13	18	2023-10-09 13:00:00	Other
2547	11	8	1450	1459	-9	1655	1709	DL	750	N365NW	LGA	DTW	89	502	14	59	2023-11-08 14:00:00	Other
2551	11	2	550	600	-10	827	917	B6	37	N968JT	JFK	LAX	315	2475	6	0	2023-11-02 06:00:00	LAX
2557	8	24	947	954	-7	1225	1252	B6	142	N504JB	LGA	PBI	140	1035	9	54	2023-08-24 09:00:00	Other
2559	7	28	948	957	-9	1218	1254	NK	696	N628NK	EWR	AUS	183	1504	9	57	2023-07-28 09:00:00	Other
2569	8	15	1117	1125	-8	1326	1349	YX	1339	N225JQ	LGA	CHS	93	641	11	25	2023-08-15 11:00:00	Other
2573	3	6	1047	1057	-10	1302	1303	YX	1247	N826MD	LGA	AVL	97	599	10	57	2023-03-06 10:00:00	Other
2581	3	13	553	600	-7	818	801	AA	243	N935NN	LGA	CLT	99	544	6	0	2023-03-13 06:00:00	CLT
2585	12	18	1253	1300	-7	1441	1511	YX	1311	N123HQ	LGA	DAY	83	549	13	0	2023-12-18 13:00:00	Other
2590	10	3	2236	2242	-6	2338	2359	YX	1043	N760YX	EWR	MHT	43	209	22	42	2023-10-03 22:00:00	Other
2601	10	18	2138	2154	-16	2225	2255	9E	1667	N902XJ	LGA	BGM	29	147	21	54	2023-10-18 21:00:00	Other
2603	12	21	1151	1200	-9	1252	1303	YX	1257	N102HQ	JFK	ORH	33	150	12	0	2023-12-21 12:00:00	Other
2605	5	29	1244	1252	-8	1345	1402	9E	1320	N482PX	LGA	ALB	29	136	12	52	2023-05-29 12:00:00	Other
2606	4	1	825	835	-10	1134	1145	NK	287	N663NK	LGA	IAH	227	1416	8	35	2023-04-01 08:00:00	Other
2607	6	10	852	900	-8	1125	1159	DL	440	N132DU	LGA	IAH	181	1416	9	0	2023-06-10 09:00:00	Other
2608	5	18	1913	1925	-12	2130	2150	YX	1249	N439YX	LGA	XNA	156	1147	19	25	2023-05-18 19:00:00	Other
2616	2	6	542	550	-8	819	857	AA	598	N965AN	LGA	DFW	197	1389	5	50	2023-02-06 05:00:00	Other
2627	12	13	1250	1258	-8	1412	1409	9E	1394	N336PQ	JFK	ITH	45	189	12	58	2023-12-13 12:00:00	Other
2635	2	15	554	600	-6	743	810	YX	1192	N119HQ	LGA	CMH	94	479	6	0	2023-02-15 06:00:00	Other
2641	9	14	1921	1930	-9	2111	2109	YX	1369	N426YX	LGA	PIT	60	335	19	30	2023-09-14 19:00:00	Other
2642	2	5	1306	1315	-9	1415	1425	B6	803	N348JB	LGA	BOS	36	184	13	15	2023-02-05 13:00:00	BOS
2643	8	4	653	700	-7	800	816	B6	783	N339JB	LGA	BOS	46	184	7	0	2023-08-04 07:00:00	BOS
2656	6	11	1942	1950	-8	2141	2213	9E	1495	N482PX	LGA	CVG	96	585	19	50	2023-06-11 19:00:00	Other
2669	11	22	2054	2100	-6	2209	2241	AA	636	N338PK	EWR	ORD	107	719	21	0	2023-11-22 21:00:00	ORD
2670	6	9	629	635	-6	806	818	9E	1704	N919XJ	LGA	CLE	68	419	6	35	2023-06-09 06:00:00	Other
2682	8	16	939	946	-7	1126	1141	DL	788	N930AT	EWR	DTW	75	488	9	46	2023-08-16 09:00:00	Other
2688	10	26	2116	2125	-9	2216	2248	YX	1785	N860RW	LGA	DCA	44	214	21	25	2023-10-26 21:00:00	Other
2694	10	4	1150	1200	-10	1306	1339	9E	1525	N932XJ	LGA	PIT	58	335	12	0	2023-10-04 12:00:00	Other
2697	12	31	921	930	-9	1211	1257	DL	412	N302DU	LGA	IAH	202	1416	9	30	2023-12-31 09:00:00	Other
2699	2	8	1817	1830	-13	1943	2020	9E	1283	N134EV	LGA	MKE	119	738	18	30	2023-02-08 18:00:00	Other
2701	8	17	1053	1059	-6	1217	1228	YX	979	N407YX	LGA	PIT	59	335	10	59	2023-08-17 10:00:00	Other
2702	10	3	1842	1850	-8	2033	2114	YX	1089	N657RW	EWR	IND	87	645	18	50	2023-10-03 18:00:00	Other
2705	11	28	1124	1130	-6	1428	1434	DL	1011	N127DN	LGA	MCO	160	950	11	30	2023-11-28 11:00:00	MCO
2706	3	28	2022	2030	-8	2206	2214	YX	1639	N201JQ	LGA	BNA	129	764	20	30	2023-03-28 20:00:00	Other
2714	2	19	1953	1959	-6	2151	2219	YX	1204	N117HQ	LGA	CMH	86	479	19	59	2023-02-19 19:00:00	Other
2719	11	20	1643	1650	-7	1901	2011	UA	54	N798UA	EWR	SFO	289	2565	16	50	2023-11-20 16:00:00	Other
2722	10	17	1352	1359	-7	1553	1618	YX	1253	N421YX	JFK	CVG	92	589	13	59	2023-10-17 13:00:00	Other
2728	1	25	924	930	-6	1235	1252	AA	280	N976AN	LGA	DFW	216	1389	9	30	2023-01-25 09:00:00	Other
2729	6	7	620	630	-10	732	752	B6	1011	N368JB	JFK	BUF	53	301	6	30	2023-06-07 06:00:00	Other
2730	4	14	753	800	-7	952	1021	9E	1374	N901XJ	LGA	IND	92	660	8	0	2023-04-14 08:00:00	Other
2735	11	10	1948	1959	-11	2313	2316	AS	83	N586AS	EWR	LAX	346	2454	19	59	2023-11-10 19:00:00	LAX
2754	9	20	2221	2229	-8	114	143	B6	653	N990JL	JFK	LAX	319	2475	22	29	2023-09-20 22:00:00	LAX
2756	10	2	951	959	-8	1201	1201	YX	1306	N101HQ	LGA	GSP	89	610	9	59	2023-10-02 09:00:00	Other
2761	3	24	2006	2015	-9	2142	2219	YX	1331	N426YX	JFK	PIT	71	340	20	15	2023-03-24 20:00:00	Other
2764	10	26	704	710	-6	935	959	B6	183	N579JB	EWR	PBI	131	1023	7	10	2023-10-26 07:00:00	Other
2766	12	27	1341	1349	-8	1715	1645	B6	805	N348JB	EWR	TPA	185	997	13	49	2023-12-27 13:00:00	Other
2768	5	10	917	929	-12	1049	1121	YX	1257	N443YX	LGA	CLE	69	419	9	29	2023-05-10 09:00:00	Other
2770	3	30	1950	1959	-9	2251	2304	NK	181	N683NK	LGA	MCO	132	950	19	59	2023-03-30 19:00:00	MCO
2771	2	11	1928	1945	-17	2206	2235	B6	166	N193JB	LGA	JAX	140	833	19	45	2023-02-11 19:00:00	Other
2787	2	23	1424	1430	-6	1554	1625	AA	846	N802AW	LGA	RDU	74	431	14	30	2023-02-23 14:00:00	Other
2790	10	22	1324	1330	-6	1449	1515	YX	1147	N724YX	EWR	GSO	64	445	13	30	2023-10-22 13:00:00	Other
2813	10	29	728	735	-7	1020	1038	DL	781	N326DN	JFK	FLL	147	1069	7	35	2023-10-29 07:00:00	FLL
2817	1	27	1823	1829	-6	2027	2031	YX	1191	N729YX	EWR	CMH	86	463	18	29	2023-01-27 18:00:00	Other
2827	12	18	1413	1421	-8	1614	1653	UA	78	N483UA	LGA	DEN	215	1620	14	21	2023-12-18 14:00:00	Other
2828	10	26	806	815	-9	925	950	UA	842	N73276	LGA	ORD	112	733	8	15	2023-10-26 08:00:00	ORD
2849	12	21	2023	2030	-7	2258	2305	UA	289	N17306	EWR	JAX	115	820	20	30	2023-12-21 20:00:00	Other
2850	8	19	956	1002	-6	1140	1208	YX	1007	N441YX	LGA	PNS	133	1030	10	2	2023-08-19 10:00:00	Other
2852	1	27	954	1000	-6	1246	1323	UA	811	N2140U	EWR	SFO	321	2565	10	0	2023-01-27 10:00:00	Other
2854	5	25	843	853	-10	1054	1113	9E	1434	N482PX	LGA	TYS	97	647	8	53	2023-05-25 08:00:00	Other
2855	9	29	622	629	-7	903	928	AA	591	N958NN	LGA	DFW	192	1389	6	29	2023-09-29 06:00:00	Other
2859	7	18	2014	2022	-8	2150	2220	DL	823	N894AT	EWR	DTW	77	488	20	22	2023-07-18 20:00:00	Other
2864	9	1	753	759	-6	1003	1001	AA	531	N892NN	JFK	CLT	88	541	7	59	2023-09-01 07:00:00	CLT
2874	8	22	1859	1907	-8	2205	2222	UA	606	N27270	EWR	SEA	333	2402	19	7	2023-08-22 19:00:00	Other
2876	5	3	2044	2050	-6	2213	2253	YX	1620	N246JQ	JFK	CMH	71	483	20	50	2023-05-03 20:00:00	Other
2877	3	24	2038	2045	-7	2224	2243	YX	1653	N229JQ	JFK	CMH	84	483	20	45	2023-03-24 20:00:00	Other
2885	7	12	1326	1335	-9	1442	1452	YX	931	N760YX	EWR	BTV	45	266	13	35	2023-07-12 13:00:00	Other
2886	2	27	649	700	-11	952	1002	UA	776	N17285	EWR	PBI	148	1023	7	0	2023-02-27 07:00:00	Other
2887	12	13	1003	1010	-7	1145	1210	YX	1249	N108HQ	LGA	GSO	85	461	10	10	2023-12-13 10:00:00	Other
2888	10	13	2051	2059	-8	2203	2225	YX	1354	N407YX	JFK	BOS	38	187	20	59	2023-10-13 20:00:00	BOS
2889	7	24	2102	2110	-8	2255	2251	YX	1359	N228JQ	JFK	DCA	52	213	21	10	2023-07-24 21:00:00	Other
2893	1	20	2119	2129	-10	2304	2228	9E	1379	N904XJ	LGA	BGM	82	147	21	29	2023-01-20 21:00:00	Other
2906	10	9	1553	1559	-6	1836	1916	B6	213	N992JB	JFK	LAX	314	2475	15	59	2023-10-09 15:00:00	LAX
2922	8	5	1618	1625	-7	1809	1831	YX	1305	N818MD	LGA	CMH	76	479	16	25	2023-08-05 16:00:00	Other
2932	9	4	1107	1115	-8	1249	1309	YX	1386	N122HQ	LGA	CMH	75	479	11	15	2023-09-04 11:00:00	Other
2940	8	30	1222	1229	-7	1512	1517	OO	1371	N205SY	LGA	IAH	203	1416	12	29	2023-08-30 12:00:00	Other
2941	6	1	1138	1147	-9	1334	1401	YX	1141	N855RW	EWR	IND	90	645	11	47	2023-06-01 11:00:00	Other
2942	10	30	1223	1229	-6	1433	1438	DL	964	N142DU	JFK	MSP	171	1029	12	29	2023-10-30 12:00:00	Other
2943	10	19	812	820	-8	1006	1044	9E	1562	N301PQ	LGA	GRR	93	618	8	20	2023-10-19 08:00:00	Other
2947	5	12	2058	2105	-7	2247	2310	YX	1260	N118HQ	LGA	DTW	75	502	21	5	2023-05-12 21:00:00	Other
2948	8	22	1130	1138	-8	1222	1247	YX	1345	N224JQ	JFK	MVY	36	173	11	38	2023-08-22 11:00:00	Other
2956	11	29	553	600	-7	838	857	B6	90	N607JB	LGA	MCO	137	950	6	0	2023-11-29 06:00:00	MCO
2958	4	4	1138	1145	-7	1441	1504	DL	583	N123DQ	LGA	IAH	203	1416	11	45	2023-04-04 11:00:00	Other
2960	6	4	934	946	-12	1130	1200	UA	916	N78511	LGA	DEN	204	1620	9	46	2023-06-04 09:00:00	Other
2961	8	7	821	829	-8	949	1011	YX	1034	N115HQ	LGA	CLE	67	419	8	29	2023-08-07 08:00:00	Other
2963	9	16	923	930	-7	1027	1102	YX	1814	N201JQ	JFK	DCA	39	213	9	30	2023-09-16 09:00:00	Other
2964	12	11	1421	1430	-9	1712	1721	YX	1805	N239JQ	JFK	JAX	139	828	14	30	2023-12-11 14:00:00	Other
2966	11	21	724	730	-6	918	915	UA	943	N37462	EWR	RDU	80	416	7	30	2023-11-21 07:00:00	Other
2977	9	6	1653	1700	-7	1820	1831	YX	1384	N124HQ	LGA	RIC	53	292	17	0	2023-09-06 17:00:00	Other
2982	12	21	553	600	-7	758	841	UA	359	N854UA	LGA	DEN	224	1620	6	0	2023-12-21 06:00:00	Other
2984	3	19	813	820	-7	1015	1030	YX	1127	N724YX	EWR	DTW	88	488	8	20	2023-03-19 08:00:00	Other
2985	4	4	948	956	-8	1208	1220	YX	1131	N407YX	LGA	AGS	110	678	9	56	2023-04-04 09:00:00	Other
2989	11	15	1214	1220	-6	1357	1408	9E	1738	N147PQ	JFK	RDU	76	427	12	20	2023-11-15 12:00:00	Other
2991	1	17	1745	1755	-10	2046	2127	AA	625	N957AN	LGA	DFW	222	1389	17	55	2023-01-17 17:00:00	Other
2996	9	19	2002	2015	-13	2105	2138	B6	527	N281JB	LGA	BOS	39	184	20	15	2023-09-19 20:00:00	BOS
2997	2	23	844	850	-6	1055	1110	YX	1620	N230JQ	LGA	STL	151	888	8	50	2023-02-23 08:00:00	Other
3019	12	21	854	900	-6	1144	1209	UA	692	N17327	EWR	PBI	136	1023	9	0	2023-12-21 09:00:00	Other
3020	11	4	848	855	-7	1010	1037	YX	1894	N233JQ	LGA	PIT	59	335	8	55	2023-11-04 08:00:00	Other
3023	11	12	1620	1629	-9	1915	1927	UA	792	N66848	EWR	MCO	135	937	16	29	2023-11-12 16:00:00	MCO
3030	3	28	644	650	-6	818	829	YX	1670	N879RW	LGA	PIT	69	335	6	50	2023-03-28 06:00:00	Other
3048	8	2	849	859	-10	1111	1119	YX	1036	N129HQ	LGA	IND	97	660	8	59	2023-08-02 08:00:00	Other
3064	11	6	934	940	-6	1230	1236	NK	1029	N949NK	EWR	MCO	129	937	9	40	2023-11-06 09:00:00	MCO
3069	11	5	949	955	-6	1052	1113	YX	1895	N211JQ	JFK	BOS	33	187	9	55	2023-11-05 09:00:00	BOS
3072	12	26	1028	1035	-7	1232	1251	YX	1289	N417YX	LGA	GSP	100	610	10	35	2023-12-26 10:00:00	Other
3086	11	17	1209	1215	-6	1416	1428	YX	1176	N768YX	EWR	SBN	100	637	12	15	2023-11-17 12:00:00	Other
3092	1	20	659	705	-6	919	936	DL	841	N378DA	EWR	ATL	119	746	7	5	2023-01-20 07:00:00	ATL
3096	4	21	1014	1020	-6	1203	1221	YX	1205	N405YX	JFK	RDU	67	427	10	20	2023-04-21 10:00:00	Other
3100	12	1	1107	1115	-8	1210	1236	B6	227	N266JB	LGA	BOS	40	184	11	15	2023-12-01 11:00:00	BOS
3109	3	6	1022	1029	-7	1132	1152	YX	1103	N746YX	EWR	DCA	40	199	10	29	2023-03-06 10:00:00	Other
3110	7	12	1144	1152	-8	1242	1309	UA	249	N37527	EWR	BOS	36	200	11	52	2023-07-12 11:00:00	BOS
3114	11	25	1115	1124	-9	1247	1306	YX	1298	N406YX	LGA	PIT	59	335	11	24	2023-11-25 11:00:00	Other
3115	9	5	2147	2159	-12	2319	2326	YX	1808	N221JQ	LGA	BGR	61	378	21	59	2023-09-05 21:00:00	Other
3121	4	18	1344	1355	-11	1633	1658	AA	885	N886NN	LGA	DFW	195	1389	13	55	2023-04-18 13:00:00	Other
3124	1	23	644	650	-6	805	816	YX	1757	N209JQ	LGA	ORF	65	296	6	50	2023-01-23 06:00:00	Other
3125	12	1	1543	1553	-10	1741	1757	AA	208	N768US	LGA	DTW	94	502	15	53	2023-12-01 15:00:00	Other
3134	2	9	651	659	-8	832	825	YX	1505	N207JQ	LGA	ORF	54	296	6	59	2023-02-09 06:00:00	Other
3139	10	26	853	900	-7	1111	1139	YX	1759	N236JQ	JFK	JAX	110	828	9	0	2023-10-26 09:00:00	Other
3145	9	6	1552	1559	-7	1746	1817	9E	1635	N307PQ	LGA	GSP	85	610	15	59	2023-09-06 15:00:00	Other
3154	9	19	1428	1435	-7	1615	1647	9E	1698	N313PQ	LGA	CVG	88	585	14	35	2023-09-19 14:00:00	Other
3155	9	6	643	659	-16	813	840	AA	967	N824AW	LGA	RDU	62	431	6	59	2023-09-06 06:00:00	Other
3159	6	30	958	1005	-7	1118	1142	UA	731	N484UA	LGA	ORD	110	733	10	5	2023-06-30 10:00:00	ORD
3168	5	2	1411	1418	-7	1603	1624	YX	1145	N861RW	EWR	CVG	87	569	14	18	2023-05-02 14:00:00	Other
3182	5	14	1801	1810	-9	2028	2030	9E	1390	N915XJ	LGA	GRR	99	618	18	10	2023-05-14 18:00:00	Other
3184	9	20	941	948	-7	1051	1124	UA	441	N33292	EWR	BNA	105	748	9	48	2023-09-20 09:00:00	Other
3191	1	17	954	1000	-6	1159	1229	AA	818	N507AY	LGA	CLT	87	544	10	0	2023-01-17 10:00:00	CLT
3193	1	15	821	829	-8	1111	1208	AA	1060	N931NN	JFK	AUS	206	1521	8	29	2023-01-15 08:00:00	Other
3194	1	31	1443	1450	-7	1606	1619	B6	1082	N306JB	JFK	BUF	64	301	14	50	2023-01-31 14:00:00	Other
3202	2	10	1132	1138	-6	1325	1342	AA	732	N651AW	EWR	CLT	88	529	11	38	2023-02-10 11:00:00	CLT
3204	5	17	1824	1832	-8	2039	2051	YX	990	N649RW	EWR	CVG	88	569	18	32	2023-05-17 18:00:00	Other
3209	8	2	1331	1340	-9	1547	1604	B6	766	N206JB	LGA	SAV	113	722	13	40	2023-08-02 13:00:00	Other
3210	10	10	949	959	-10	1139	1220	9E	1656	N313PQ	LGA	AVL	91	599	9	59	2023-10-10 09:00:00	Other
3217	8	25	1852	1859	-7	2106	2113	9E	1270	N320PQ	LGA	GSP	96	610	18	59	2023-08-25 18:00:00	Other
3220	6	13	1106	1113	-7	1246	1308	YX	1374	N402YX	LGA	CMH	85	479	11	13	2023-06-13 11:00:00	Other
3233	8	23	552	600	-8	759	820	UA	344	N434UA	EWR	ATL	105	746	6	0	2023-08-23 06:00:00	ATL
3239	1	24	855	904	-9	1105	1110	YX	1196	N754YX	EWR	CMH	83	463	9	4	2023-01-24 09:00:00	Other
3241	11	16	720	730	-10	849	917	AA	130	N986NN	LGA	ORD	113	733	7	30	2023-11-16 07:00:00	ORD
3246	4	7	2023	2029	-6	2241	2300	UA	522	N27515	EWR	DEN	228	1605	20	29	2023-04-07 20:00:00	Other
3251	6	2	1602	1608	-6	1711	1718	B6	1004	N281JB	LGA	HYA	37	197	16	8	2023-06-02 16:00:00	Other
3253	8	15	1259	1305	-6	1507	1511	YX	923	N656RW	EWR	CVG	101	569	13	5	2023-08-15 13:00:00	Other
3259	11	14	2047	2055	-8	2220	2254	YX	1768	N206JQ	JFK	PIT	62	340	20	55	2023-11-14 20:00:00	Other
3262	2	24	627	640	-13	919	957	B6	819	N775JB	EWR	MIA	150	1085	6	40	2023-02-24 06:00:00	MIA
3271	2	11	1620	1630	-10	1725	1759	9E	1426	N901XJ	JFK	SYR	47	209	16	30	2023-02-11 16:00:00	Other
3276	3	20	1520	1530	-10	1718	1737	NK	521	N522NK	LGA	CLT	95	544	15	30	2023-03-20 15:00:00	CLT
3278	2	25	1552	1559	-7	2004	1927	B6	338	N945JT	JFK	LAX	390	2475	15	59	2023-02-25 15:00:00	LAX
3279	10	7	823	830	-7	1005	1006	YX	1786	N219YX	JFK	ORF	52	290	8	30	2023-10-07 08:00:00	Other
3280	11	28	1153	1159	-6	1417	1436	OO	1187	N317SY	LGA	SDF	117	659	11	59	2023-11-28 11:00:00	Other
3282	9	2	729	736	-7	920	950	UA	230	N425UA	LGA	DEN	210	1620	7	36	2023-09-02 07:00:00	Other
3285	5	29	938	946	-8	1319	1341	UA	582	N69818	EWR	SJU	198	1608	9	46	2023-05-29 09:00:00	Other
3291	7	18	713	720	-7	822	838	UA	431	N829UA	EWR	BTV	45	266	7	20	2023-07-18 07:00:00	Other
3303	5	7	829	837	-8	1012	1025	B6	823	N329JB	JFK	RDU	65	427	8	37	2023-05-07 08:00:00	Other
3304	3	24	652	700	-8	759	817	AA	789	N775XF	LGA	DCA	47	214	7	0	2023-03-24 07:00:00	Other
3311	9	4	910	926	-16	1033	1107	YX	1193	N741YX	EWR	PIT	50	319	9	26	2023-09-04 09:00:00	Other
3315	8	1	1834	1840	-6	2034	2102	YX	876	N763YX	EWR	IND	91	645	18	40	2023-08-01 18:00:00	Other
3323	5	28	718	730	-12	822	900	B6	376	N317JB	JFK	BNA	98	765	7	30	2023-05-28 07:00:00	Other
3326	6	17	1118	1125	-7	1312	1339	9E	1486	N480PX	LGA	GSP	87	610	11	25	2023-06-17 11:00:00	Other
3327	12	12	1404	1413	-9	1548	1610	9E	1359	N600LR	JFK	RDU	70	427	14	13	2023-12-12 14:00:00	Other
3341	9	6	1427	1440	-13	1546	1612	9E	1500	N480PX	LGA	ORF	50	296	14	40	2023-09-06 14:00:00	Other
3344	9	17	922	929	-7	1129	1116	YX	1312	N425YX	JFK	CLE	75	425	9	29	2023-09-17 09:00:00	Other
3348	2	4	1154	1200	-6	1547	1601	YX	1200	N826MD	LGA	EYW	180	1207	12	0	2023-02-04 12:00:00	Other
3351	2	14	1854	1905	-11	2026	2059	AA	753	N763US	LGA	BNA	127	764	19	5	2023-02-14 19:00:00	Other
3356	2	14	1606	1613	-7	1714	1728	UA	148	N39450	EWR	BOS	45	200	16	13	2023-02-14 16:00:00	BOS
3364	5	31	1154	1200	-6	1433	1446	NK	980	N966NK	EWR	MCO	132	937	12	0	2023-05-31 12:00:00	MCO
3375	1	27	1147	1200	-13	1326	1408	YX	1285	N418YX	JFK	CMH	82	483	12	0	2023-01-27 12:00:00	Other
3378	12	28	554	600	-6	902	908	NK	479	N647NK	LGA	MCO	160	950	6	0	2023-12-28 06:00:00	MCO
3382	9	15	724	730	-6	1011	1015	UA	291	N24736	EWR	MCO	134	937	7	30	2023-09-15 07:00:00	MCO
3393	4	21	719	729	-10	830	857	YX	940	N753YX	EWR	BTV	50	266	7	29	2023-04-21 07:00:00	Other
3394	7	25	1037	1048	-11	1312	1320	F9	423	N388FR	LGA	ATL	118	762	10	48	2023-07-25 10:00:00	ATL
3396	8	14	1928	1937	-9	2324	2249	NK	812	N636NK	EWR	MIA	173	1085	19	37	2023-08-14 19:00:00	MIA
3400	11	7	953	1000	-7	1204	1232	YX	1061	N765YX	EWR	SDF	111	642	10	0	2023-11-07 10:00:00	Other
3411	10	31	908	915	-7	1158	1211	NK	734	N902NK	EWR	MCO	137	937	9	15	2023-10-31 09:00:00	MCO
3414	10	8	920	930	-10	1049	1129	YX	1136	N731YX	EWR	GSO	71	445	9	30	2023-10-08 09:00:00	Other
3418	5	27	554	600	-6	828	849	B6	590	N775JB	JFK	TPA	136	1005	6	0	2023-05-27 06:00:00	Other
3420	2	20	1953	1959	-6	2252	2308	NK	187	N665NK	LGA	MCO	142	950	19	59	2023-02-20 19:00:00	MCO
3421	7	24	858	908	-10	1122	1108	YX	922	N640RW	EWR	CMH	73	463	9	8	2023-07-24 09:00:00	Other
3426	12	6	2121	2130	-9	2351	36	B6	915	N623JB	JFK	MCO	128	944	21	30	2023-12-06 21:00:00	MCO
3449	11	6	1716	1725	-9	1940	2007	B6	849	N805JB	LGA	JAX	120	833	17	25	2023-11-06 17:00:00	Other
3454	10	13	721	730	-9	936	942	YX	1055	N765YX	EWR	GRR	105	605	7	30	2023-10-13 07:00:00	Other
3455	11	17	1646	1655	-9	1949	2000	NK	490	N697NK	EWR	MCO	145	937	16	55	2023-11-17 16:00:00	MCO
3467	8	30	2242	2250	-8	18	36	9E	1232	N147PQ	JFK	ROC	50	264	22	50	2023-08-30 22:00:00	Other
3473	5	31	1542	1552	-10	1659	1725	YX	1294	N826MD	LGA	RIC	54	292	15	52	2023-05-31 15:00:00	Other
3476	5	23	1420	1429	-9	1601	1626	9E	1407	N197PQ	LGA	MEM	133	963	14	29	2023-05-23 14:00:00	Other
3480	4	16	924	930	-6	1226	1305	AS	17	N486AS	JFK	SFO	336	2586	9	30	2023-04-16 09:00:00	Other
3482	5	8	1104	1115	-11	1355	1440	B6	695	N590JB	LGA	RSW	149	1080	11	15	2023-05-08 11:00:00	Other
3486	4	26	2122	2130	-8	2230	2236	YX	1523	N882RW	LGA	PVD	45	143	21	30	2023-04-26 21:00:00	Other
3487	9	28	1103	1110	-7	1235	1243	YX	1311	N408YX	LGA	PIT	64	335	11	10	2023-09-28 11:00:00	Other
3488	12	13	1218	1229	-11	1520	1538	YX	1208	N432YX	LGA	OKC	218	1341	12	29	2023-12-13 12:00:00	Other
3498	9	19	1949	1959	-10	2140	2219	YX	1375	N440YX	LGA	CVG	94	585	19	59	2023-09-19 19:00:00	Other
3499	11	1	624	630	-6	817	818	YX	1820	N235JQ	LGA	RDU	87	431	6	30	2023-11-01 06:00:00	Other
3506	7	27	1338	1347	-9	1451	1453	YX	923	N740YX	EWR	PVD	38	160	13	47	2023-07-27 13:00:00	Other
3509	6	30	1519	1529	-10	1824	1853	AS	92	N963AK	EWR	SFO	334	2565	15	29	2023-06-30 15:00:00	Other
3510	12	12	1729	1738	-9	1923	1941	NK	47	N972NK	LGA	DTW	88	502	17	38	2023-12-12 17:00:00	Other
3511	10	31	1019	1025	-6	1152	1205	UA	73	N16701	EWR	ORD	125	719	10	25	2023-10-31 10:00:00	ORD
3520	11	20	1129	1135	-6	1311	1341	YX	1099	N766YX	EWR	MEM	143	946	11	35	2023-11-20 11:00:00	Other
3523	5	12	1453	1459	-6	1729	1804	AA	371	N827NN	LGA	DFW	181	1389	14	59	2023-05-12 14:00:00	Other
3524	12	23	1632	1641	-9	1937	1947	B6	17	N561JB	JFK	PBI	151	1028	16	41	2023-12-23 16:00:00	Other
3526	10	10	1250	1259	-9	1347	1405	9E	1466	N478PX	LGA	ORH	34	146	12	59	2023-10-10 12:00:00	Other
3527	2	21	1250	1259	-9	1349	1416	YX	1205	N433YX	JFK	BOS	34	187	12	59	2023-02-21 12:00:00	BOS
3531	5	7	1842	1848	-6	2032	2050	AA	652	N306PB	LGA	CLT	83	544	18	48	2023-05-07 18:00:00	CLT
3532	11	11	1357	1405	-8	1645	1632	9E	1449	N931XJ	LGA	SAV	123	722	14	5	2023-11-11 14:00:00	Other
3535	10	18	1053	1100	-7	1314	1308	YX	1284	N427YX	LGA	AVL	87	599	11	0	2023-10-18 11:00:00	Other
3539	9	19	1629	1635	-6	1835	1859	DL	788	N360NB	JFK	MSY	154	1182	16	35	2023-09-19 16:00:00	Other
3546	2	22	1106	1115	-9	1323	1344	YX	1269	N115HQ	JFK	IND	117	665	11	15	2023-02-22 11:00:00	Other
3547	11	29	1413	1420	-7	1630	1704	B6	967	N638JB	LGA	ATL	111	762	14	20	2023-11-29 14:00:00	ATL
3553	3	9	1050	1100	-10	1359	1420	AA	111	N109NN	JFK	LAX	348	2475	11	0	2023-03-09 11:00:00	LAX
3557	1	25	824	830	-6	1002	1020	B6	450	N279JB	JFK	BNA	133	765	8	30	2023-01-25 08:00:00	Other
3560	2	27	621	630	-9	1018	1021	AA	555	N326RP	JFK	PHX	330	2153	6	30	2023-02-27 06:00:00	Other
3561	11	13	1452	1458	-6	1602	1628	YX	1088	N750YX	EWR	ORF	52	284	14	58	2023-11-13 14:00:00	Other
3565	2	11	2149	2157	-8	2338	2359	UA	722	N15751	EWR	DTW	83	488	21	57	2023-02-11 21:00:00	Other
3573	5	29	620	635	-15	734	810	9E	1307	N914XJ	LGA	PIT	56	335	6	35	2023-05-29 06:00:00	Other
3579	8	8	845	859	-14	1045	1102	NK	254	N683NK	LGA	CLT	84	544	8	59	2023-08-08 08:00:00	CLT
3581	10	4	1652	1659	-7	1857	1923	DL	871	N3771K	EWR	ATL	96	746	16	59	2023-10-04 16:00:00	ATL
3587	2	7	1840	1850	-10	2213	2236	UA	314	N12114	EWR	PHX	310	2133	18	50	2023-02-07 18:00:00	Other
3593	5	23	1452	1459	-7	1739	1803	B6	235	N587JB	EWR	PBI	144	1023	14	59	2023-05-23 14:00:00	Other
3595	9	22	1422	1430	-8	1545	1553	YX	1343	N417YX	LGA	BUF	48	292	14	30	2023-09-22 14:00:00	Other
3604	12	23	1632	1641	-9	1748	1814	B6	966	N236JB	JFK	BUF	56	301	16	41	2023-12-23 16:00:00	Other
3606	8	9	1220	1229	-9	1524	1526	DL	430	N377NW	JFK	AUS	207	1521	12	29	2023-08-09 12:00:00	Other
3609	9	15	651	700	-9	903	927	UA	384	N17314	EWR	ATL	104	746	7	0	2023-09-15 07:00:00	ATL
3610	8	23	553	600	-7	703	732	UA	310	N27304	EWR	ORD	108	719	6	0	2023-08-23 06:00:00	ORD
3626	9	12	2053	2059	-6	2217	2239	DL	425	N141DU	LGA	ORD	112	733	20	59	2023-09-12 20:00:00	ORD
3629	9	19	1552	1559	-7	1131	1856	AA	887	N919NN	JFK	DFW	NA	1391	15	59	2023-09-19 15:00:00	Other
3631	8	3	622	630	-8	901	921	UA	549	N78511	EWR	TPA	126	997	6	30	2023-08-03 06:00:00	Other
3632	9	4	1637	1645	-8	1915	1957	UA	626	N2251U	EWR	SFO	314	2565	16	45	2023-09-04 16:00:00	Other
3634	5	21	1654	1700	-6	1758	1832	YX	1668	N217JQ	EWR	BOS	43	200	17	0	2023-05-21 17:00:00	BOS
3635	6	12	1308	1315	-7	1413	1431	B6	294	N337JB	JFK	BOS	39	187	13	15	2023-06-12 13:00:00	BOS
3641	12	6	828	836	-8	1041	1103	9E	1458	N131EV	LGA	TYS	97	647	8	36	2023-12-06 08:00:00	Other
3653	6	5	1949	1959	-10	2135	2148	YX	1421	N133HQ	LGA	ILM	74	500	19	59	2023-06-05 19:00:00	Other
3658	12	10	1451	1500	-9	1658	1624	YX	1145	N739YX	EWR	DCA	48	199	15	0	2023-12-10 15:00:00	Other
3660	2	6	724	730	-6	958	1023	DL	182	N391DA	LGA	DEN	236	1620	7	30	2023-02-06 07:00:00	Other
3661	2	15	1922	1929	-7	2233	2259	DL	306	N125DU	LGA	DFW	225	1389	19	29	2023-02-15 19:00:00	Other
3662	11	2	2050	2100	-10	2240	2254	YX	1403	N117HQ	LGA	ILM	81	500	21	0	2023-11-02 21:00:00	Other
3665	1	7	1028	1035	-7	1203	1157	YX	1155	N643RW	EWR	BOS	41	200	10	35	2023-01-07 10:00:00	BOS
3681	7	12	1049	1055	-6	1154	1212	YX	1371	N221JQ	JFK	ACK	42	199	10	55	2023-07-12 10:00:00	Other
3688	4	24	1453	1500	-7	1659	1720	DL	727	N3732J	EWR	ATL	109	746	15	0	2023-04-24 15:00:00	ATL
3689	3	28	1646	1655	-9	2004	2013	AS	7	N472AS	JFK	SEA	341	2422	16	55	2023-03-28 16:00:00	Other
3690	1	17	1014	1025	-11	1148	1205	YX	1764	N240JQ	LGA	DCA	47	214	10	25	2023-01-17 10:00:00	Other
3695	2	13	2052	2100	-8	2354	18	B6	34	N964JT	JFK	SAN	339	2446	21	0	2023-02-13 21:00:00	Other
3696	11	6	1902	1909	-7	2210	2226	B6	157	N965JT	JFK	ONT	341	2429	19	9	2023-11-06 19:00:00	Other
3698	9	28	1639	1650	-11	1755	1824	YX	1123	N656RW	EWR	BGR	57	393	16	50	2023-09-28 16:00:00	Other
3705	1	25	1809	1816	-7	2154	2128	AA	705	N947NN	EWR	DFW	217	1372	18	16	2023-01-25 18:00:00	Other
3712	5	22	621	630	-9	757	807	B6	384	N509JB	JFK	ORD	120	740	6	30	2023-05-22 06:00:00	ORD
3714	2	22	1052	1100	-8	1211	1243	YX	1180	N418YX	LGA	DCA	50	214	11	0	2023-02-22 11:00:00	Other
3729	11	22	1918	1925	-7	2136	2203	DL	446	N128DU	LGA	MSY	171	1183	19	25	2023-11-22 19:00:00	Other
3738	6	1	923	930	-7	1205	1255	AS	16	N402AS	JFK	SFO	316	2586	9	30	2023-06-01 09:00:00	Other
3741	12	10	1225	1233	-8	1456	1459	UA	225	N27270	EWR	MSY	191	1167	12	33	2023-12-10 12:00:00	Other
3744	2	14	1932	1945	-13	2150	2220	B6	656	N247JB	LGA	SAV	113	722	19	45	2023-02-14 19:00:00	Other
3747	2	26	1337	1345	-8	1614	1619	YX	1336	N406YX	LGA	MCI	198	1107	13	45	2023-02-26 13:00:00	Other
3750	6	14	854	900	-6	1032	1042	UA	706	N24715	EWR	CLE	60	404	9	0	2023-06-14 09:00:00	Other
3751	10	12	756	805	-9	1055	1040	DL	115	N521DT	JFK	PHX	301	2153	8	5	2023-10-12 08:00:00	Other
3755	6	5	958	1005	-7	1139	1142	UA	731	N431UA	LGA	ORD	111	733	10	5	2023-06-05 10:00:00	ORD
3756	5	19	1545	1552	-7	1702	1738	9E	1414	N928XJ	LGA	CHO	52	305	15	52	2023-05-19 15:00:00	Other
3757	1	28	1702	1711	-9	1958	1852	UA	851	N69813	EWR	ORD	137	719	17	11	2023-01-28 17:00:00	ORD
3758	10	12	1056	1103	-7	1349	1404	NK	826	N626NK	EWR	AUS	213	1504	11	3	2023-10-12 11:00:00	Other
3759	5	14	1550	1559	-9	1759	1824	YX	1083	N654RW	EWR	SAV	102	708	15	59	2023-05-14 15:00:00	Other
3760	3	20	933	940	-7	1107	1144	YX	1304	N118HQ	JFK	BNA	122	765	9	40	2023-03-20 09:00:00	Other
3766	11	29	1157	1205	-8	1440	1507	B6	664	N956JT	JFK	PBI	144	1028	12	5	2023-11-29 12:00:00	Other
3790	1	18	854	900	-6	1018	1043	UA	269	N76522	LGA	ORD	120	733	9	0	2023-01-18 09:00:00	ORD
3791	6	9	2239	2250	-11	6	33	9E	1661	N307PQ	JFK	ROC	50	264	22	50	2023-06-09 22:00:00	Other
3793	7	23	1149	1155	-6	1335	1346	9E	1262	N676CA	JFK	RDU	72	427	11	55	2023-07-23 11:00:00	Other
3798	9	7	924	930	-6	1054	1104	YX	1195	N742YX	EWR	PIT	55	319	9	30	2023-09-07 09:00:00	Other
3799	4	9	1220	1229	-9	1304	1325	YX	1028	N740YX	EWR	AVP	29	93	12	29	2023-04-09 12:00:00	Other
3803	4	10	1054	1100	-6	1312	1416	AA	115	N117AN	JFK	LAX	295	2475	11	0	2023-04-10 11:00:00	LAX
3816	12	2	1022	1030	-8	1217	1214	YX	1778	N227JQ	LGA	RIC	56	292	10	30	2023-12-02 10:00:00	Other
3817	9	21	1937	1944	-7	2244	2250	UA	504	N27251	EWR	MIA	146	1085	19	44	2023-09-21 19:00:00	MIA
3821	12	9	1305	1312	-7	1441	1509	YX	1028	N769YX	EWR	CMH	77	463	13	12	2023-12-09 13:00:00	Other
3823	5	28	636	645	-9	815	914	UA	444	N37535	EWR	PHX	262	2133	6	45	2023-05-28 06:00:00	Other
3824	10	25	2004	2010	-6	2300	2332	B6	60	N944JT	JFK	LAX	320	2475	20	10	2023-10-25 20:00:00	LAX
3848	5	23	938	946	-8	1109	1130	9E	1459	N302PQ	LGA	BGR	57	378	9	46	2023-05-23 09:00:00	Other
3849	11	30	1452	1459	-7	1757	1821	B6	230	N987JT	JFK	LAX	347	2475	14	59	2023-11-30 14:00:00	LAX
3855	11	24	2122	2130	-8	22	59	B6	445	N635JB	JFK	AUS	219	1521	21	30	2023-11-24 21:00:00	Other
3861	12	6	1917	1924	-7	2112	2129	UA	513	N69806	EWR	DTW	81	488	19	24	2023-12-06 19:00:00	Other
3864	9	6	1501	1510	-9	1645	1710	DL	625	N119DN	LGA	DTW	77	502	15	10	2023-09-06 15:00:00	Other
3865	6	9	1451	1500	-9	1757	1811	DL	633	N322NB	LGA	TPA	152	1010	15	0	2023-06-09 15:00:00	Other
3867	10	4	905	917	-12	1026	1101	YX	1093	N729YX	EWR	MSN	111	799	9	17	2023-10-04 09:00:00	Other
3873	1	6	1643	1650	-7	1821	1903	NK	52	N619NK	LGA	DTW	76	502	16	50	2023-01-06 16:00:00	Other
3879	9	1	1208	1215	-7	1425	1429	UA	723	N18223	LGA	DEN	214	1620	12	15	2023-09-01 12:00:00	Other
3880	7	18	1200	1210	-10	1431	1410	YX	1332	N879RW	LGA	CMH	75	479	12	10	2023-07-18 12:00:00	Other
3882	4	5	925	935	-10	1046	1108	YX	1519	N207JQ	LGA	DCA	46	214	9	35	2023-04-05 09:00:00	Other
3884	4	12	1230	1240	-10	1351	1419	9E	1212	N132EV	LGA	BGR	59	378	12	40	2023-04-12 12:00:00	Other
3885	1	27	2039	2045	-6	2359	25	UA	771	N19117	EWR	SFO	347	2565	20	45	2023-01-27 20:00:00	Other
3891	7	19	2009	2015	-6	2114	2135	B6	449	N329JB	LGA	BOS	37	184	20	15	2023-07-19 20:00:00	BOS
3892	9	27	947	959	-12	1151	1201	YX	1354	N109HQ	LGA	GSP	100	610	9	59	2023-09-27 09:00:00	Other
3895	12	8	1514	1520	-6	1628	1701	9E	1527	N303PQ	LGA	CHO	55	305	15	20	2023-12-08 15:00:00	Other
3904	4	14	1901	1915	-14	2002	2036	B6	465	N193JB	LGA	BOS	35	184	19	15	2023-04-14 19:00:00	BOS
3907	6	2	1136	1145	-9	1250	1314	NK	291	N626NK	EWR	PIT	51	319	11	45	2023-06-02 11:00:00	Other
3921	6	29	953	1000	-7	1149	1201	YX	1331	N414YX	LGA	GSP	92	610	10	0	2023-06-29 10:00:00	Other
3928	2	12	1252	1300	-8	1438	1510	9E	1380	N901XJ	JFK	DTW	84	509	13	0	2023-02-12 13:00:00	Other
3933	3	12	1447	1455	-8	1716	1744	9E	1412	N136EV	JFK	JAX	120	828	14	55	2023-03-12 14:00:00	Other
3941	1	8	1218	1225	-7	1410	1436	NK	719	N661NK	LGA	DTW	81	502	12	25	2023-01-08 12:00:00	Other
3949	8	1	820	829	-9	954	1014	YX	1034	N419YX	LGA	CLE	67	419	8	29	2023-08-01 08:00:00	Other
3952	9	28	627	641	-14	902	937	NK	485	N912NK	LGA	MCO	134	950	6	41	2023-09-28 06:00:00	MCO
3955	12	10	1214	1223	-9	1403	1420	NK	30	N614NK	EWR	MYR	93	550	12	23	2023-12-10 12:00:00	Other
3957	7	21	958	1006	-8	1154	1219	UA	471	N68817	EWR	DEN	208	1605	10	6	2023-07-21 10:00:00	Other
3958	12	11	1534	1541	-7	1838	1848	UA	527	N78540	EWR	FLL	158	1065	15	41	2023-12-11 15:00:00	FLL
3972	3	1	1222	1229	-7	1453	1506	YX	1756	N212JQ	LGA	SDF	121	659	12	29	2023-03-01 12:00:00	Other
3978	6	13	1653	1700	-7	1805	1820	AA	433	N757UW	LGA	DCA	41	214	17	0	2023-06-13 17:00:00	Other
3986	4	25	911	924	-13	1144	1133	YX	976	N740YX	EWR	AVL	104	583	9	24	2023-04-25 09:00:00	Other
3989	7	16	1939	1945	-6	2218	2251	DL	676	N302NB	LGA	TPA	142	1010	19	45	2023-07-16 19:00:00	Other
3990	7	21	1417	1430	-13	1524	1604	YX	1035	N406YX	LGA	BUF	48	292	14	30	2023-07-21 14:00:00	Other
3991	8	2	921	929	-8	1137	1139	YX	871	N721YX	EWR	AVL	84	583	9	29	2023-08-02 09:00:00	Other
3994	5	3	1751	1759	-8	2054	2117	B6	758	N993JE	EWR	LAX	324	2454	17	59	2023-05-03 17:00:00	LAX
4019	10	23	1007	1015	-8	1209	1239	UA	601	N19136	EWR	DEN	218	1605	10	15	2023-10-23 10:00:00	Other
4022	4	24	901	910	-9	1103	1110	YX	1182	N420YX	LGA	GSO	79	461	9	10	2023-04-24 09:00:00	Other
4023	8	4	1354	1404	-10	1624	1610	YX	838	N862RW	EWR	GRR	101	605	14	4	2023-08-04 14:00:00	Other
4025	3	24	824	830	-6	1220	1232	AA	55	N108NN	JFK	SFO	389	2586	8	30	2023-03-24 08:00:00	Other
4027	6	14	937	945	-8	1228	1242	NK	890	N691NK	EWR	AUS	210	1504	9	45	2023-06-14 09:00:00	Other
4031	8	23	726	736	-10	1007	1029	AA	129	N848NN	LGA	DFW	176	1389	7	36	2023-08-23 07:00:00	Other
4051	10	19	958	1005	-7	1242	1249	UA	78	N426UA	EWR	DFW	180	1372	10	5	2023-10-19 10:00:00	Other
4052	9	21	2037	2044	-7	2328	2344	UA	902	N62884	EWR	TPA	138	997	20	44	2023-09-21 20:00:00	Other
4053	9	20	535	545	-10	721	740	NK	319	N642NK	LGA	MYR	80	563	5	45	2023-09-20 05:00:00	Other
4059	10	25	2121	2129	-8	2324	2332	UA	200	N24729	EWR	CVG	88	569	21	29	2023-10-25 21:00:00	Other
4074	7	7	1634	1640	-6	2051	1837	YX	990	N409YX	LGA	DSM	153	1031	16	40	2023-07-07 16:00:00	Other
4075	11	30	1551	1559	-8	1815	1840	YX	1094	N764YX	EWR	ATL	116	746	15	59	2023-11-30 15:00:00	ATL
4079	4	2	1253	1300	-7	1442	1456	OO	1122	N549CA	EWR	DTW	84	488	13	0	2023-04-02 13:00:00	Other
4080	12	22	1839	1845	-6	2016	2036	DL	903	N143DU	LGA	ORD	117	733	18	45	2023-12-22 18:00:00	ORD
4082	6	19	1822	1829	-7	1954	2012	AA	750	N822AW	LGA	RDU	65	431	18	29	2023-06-19 18:00:00	Other
4088	2	19	2054	2100	-6	2216	2219	YX	1600	N204JQ	LGA	BOS	49	184	21	0	2023-02-19 21:00:00	BOS
4090	9	2	1522	1529	-7	1752	1826	UA	828	N643UA	EWR	IAH	178	1400	15	29	2023-09-02 15:00:00	Other
4091	6	2	1523	1530	-7	1643	1659	YX	1330	N136HQ	LGA	ORF	56	296	15	30	2023-06-02 15:00:00	Other
4096	8	20	1643	1650	-7	1758	1832	YX	1370	N223JQ	LGA	BUF	48	292	16	50	2023-08-20 16:00:00	Other
4097	11	25	1450	1500	-10	1607	1631	9E	1424	N183GJ	JFK	SYR	45	209	15	0	2023-11-25 15:00:00	Other
4098	8	22	635	645	-10	827	847	UA	379	N13248	EWR	CHS	89	628	6	45	2023-08-22 06:00:00	Other
4100	12	13	1412	1419	-7	1629	1653	9E	1506	N337PQ	LGA	MCI	170	1107	14	19	2023-12-13 14:00:00	Other
4102	6	24	723	729	-6	914	932	UA	930	N14735	EWR	MSY	149	1167	7	29	2023-06-24 07:00:00	Other
4104	1	28	1340	1347	-7	1430	1447	YX	1139	N855RW	EWR	PHL	32	80	13	47	2023-01-28 13:00:00	Other
4109	10	2	920	930	-10	1211	1245	AS	7	N291BT	JFK	SEA	314	2422	9	30	2023-10-02 09:00:00	Other
4110	10	9	1917	1929	-12	2213	2234	DL	416	N307DX	LGA	PBI	144	1035	19	29	2023-10-09 19:00:00	Other
4121	10	10	602	610	-8	916	913	DL	410	N303DU	LGA	IAH	217	1416	6	10	2023-10-10 06:00:00	Other
4125	7	14	554	600	-6	836	908	NK	47	N670NK	LGA	FLL	144	1076	6	0	2023-07-14 06:00:00	FLL
4127	6	11	552	600	-8	749	814	UA	639	N38417	EWR	DEN	215	1605	6	0	2023-06-11 06:00:00	Other
4128	8	9	754	800	-6	1016	1038	DL	164	N503DZ	JFK	DEN	231	1626	8	0	2023-08-09 08:00:00	Other
4134	5	18	745	755	-10	927	1010	9E	1363	N293PQ	JFK	CVG	83	589	7	55	2023-05-18 07:00:00	Other
4156	5	31	654	700	-6	816	823	YX	1567	N210JQ	LGA	BOS	46	184	7	0	2023-05-31 07:00:00	BOS
4161	5	6	1619	1627	-8	1738	1757	YX	1091	N732YX	EWR	PIT	59	319	16	27	2023-05-06 16:00:00	Other
4163	10	25	1354	1400	-6	1540	1606	YX	1296	N438YX	LGA	CAE	90	617	14	0	2023-10-25 14:00:00	Other
4174	10	21	2042	2058	-16	2300	2330	YX	1110	N753YX	EWR	SDF	102	642	20	58	2023-10-21 20:00:00	Other
4175	9	21	1136	1145	-9	1406	1443	AS	7	N409AS	JFK	PDX	304	2454	11	45	2023-09-21 11:00:00	Other
4176	4	2	1522	1529	-7	1704	1728	NK	471	N607NK	LGA	MYR	82	563	15	29	2023-04-02 15:00:00	Other
4178	11	1	1859	1905	-6	2303	2257	UA	208	N61881	EWR	BQN	200	1585	19	5	2023-11-01 19:00:00	Other
4179	7	25	754	800	-6	918	937	UA	710	N24702	LGA	ORD	106	733	8	0	2023-07-25 08:00:00	ORD
4189	7	17	1322	1329	-7	1434	1446	UA	443	N47288	EWR	ORF	50	284	13	29	2023-07-17 13:00:00	Other
4192	5	31	1118	1125	-7	1310	1325	YX	1191	N407YX	JFK	CMH	82	483	11	25	2023-05-31 11:00:00	Other
4196	2	20	2029	2035	-6	24	9	AA	57	N116AN	JFK	LAX	363	2475	20	35	2023-02-20 20:00:00	LAX
4199	11	3	721	730	-9	935	1001	DL	188	N3740C	LGA	DEN	229	1620	7	30	2023-11-03 07:00:00	Other
4203	1	28	2022	2030	-8	2156	2229	YX	1396	N133HQ	JFK	PIT	67	340	20	30	2023-01-28 20:00:00	Other
4205	9	21	1511	1519	-8	1741	1731	YX	1804	N232JQ	LGA	OMA	168	1148	15	19	2023-09-21 15:00:00	Other
4206	1	25	1808	1815	-7	1934	1937	B6	510	N267JB	LGA	BOS	44	184	18	15	2023-01-25 18:00:00	BOS
4207	9	28	949	959	-10	1149	1201	YX	1354	N437YX	LGA	GSP	104	610	9	59	2023-09-28 09:00:00	Other
4209	9	19	1052	1100	-8	1200	1225	YX	1932	N243JQ	LGA	BOS	48	184	11	0	2023-09-19 11:00:00	BOS
4212	3	1	559	605	-6	901	913	B6	470	N531JL	LGA	TPA	151	1010	6	5	2023-03-01 06:00:00	Other
4213	1	28	1022	1029	-7	1319	1347	YX	1178	N746YX	EWR	DFW	221	1372	10	29	2023-01-28 10:00:00	Other
4218	5	27	1221	1229	-8	1608	1548	B6	325	N708JB	JFK	SLC	263	1990	12	29	2023-05-27 12:00:00	Other
4219	1	22	2019	2025	-6	2322	2333	B6	443	N590JB	JFK	PBI	158	1028	20	25	2023-01-22 20:00:00	Other
4220	10	24	1221	1229	-8	1406	1443	9E	1409	N910XJ	LGA	CLT	82	544	12	29	2023-10-24 12:00:00	CLT
4229	11	8	1410	1416	-6	1609	1613	YX	1866	N230JQ	LGA	CMH	81	479	14	16	2023-11-08 14:00:00	Other
4231	9	2	2151	2159	-8	2325	2328	B6	170	N328JB	JFK	ROC	54	264	21	59	2023-09-02 21:00:00	Other
4254	9	21	1851	1900	-9	2054	2107	YX	1190	N979RP	EWR	DTW	77	488	19	0	2023-09-21 19:00:00	Other
4257	11	23	1231	1250	-19	1347	1359	9E	1456	N601LR	JFK	ITH	43	189	12	50	2023-11-23 12:00:00	Other
4263	1	16	2116	2122	-6	2327	2327	UA	742	N37434	EWR	CLT	79	529	21	22	2023-01-16 21:00:00	CLT
4265	3	26	801	810	-9	1118	1105	B6	51	N639JB	JFK	SRQ	169	1041	8	10	2023-03-26 08:00:00	Other
4282	11	30	1513	1519	-6	1618	1640	YX	1119	N766YX	EWR	SYR	45	195	15	19	2023-11-30 15:00:00	Other
4285	4	28	620	630	-10	818	818	AA	898	N895NN	LGA	ORD	112	733	6	30	2023-04-28 06:00:00	ORD
4293	10	27	853	900	-7	1011	1032	YX	1180	N754YX	EWR	ORF	49	284	9	0	2023-10-27 09:00:00	Other
4302	7	21	1322	1329	-7	1501	1518	9E	1113	N314PQ	LGA	CLE	73	419	13	29	2023-07-21 13:00:00	Other
4305	1	18	1704	1711	-7	1824	1835	YX	1214	N724YX	EWR	BTV	55	266	17	11	2023-01-18 17:00:00	Other
4307	7	19	1123	1130	-7	1426	1435	DL	811	N128DU	LGA	SRQ	152	1047	11	30	2023-07-19 11:00:00	Other
4320	6	26	854	900	-6	1205	1237	AA	55	N110AN	JFK	SFO	347	2586	9	0	2023-06-26 09:00:00	Other
4328	5	15	2241	2255	-14	2333	2358	B6	250	N279JB	JFK	ORH	32	150	22	55	2023-05-15 22:00:00	Other
4332	12	7	1833	1839	-6	2157	2200	UA	172	N39728	EWR	SNA	342	2434	18	39	2023-12-07 18:00:00	Other
4344	11	24	1050	1059	-9	1256	1337	9E	1751	N341PQ	LGA	SDF	102	659	10	59	2023-11-24 10:00:00	Other
4368	11	29	1106	1115	-9	1408	1349	B6	695	N794JB	LGA	DEN	233	1620	11	15	2023-11-29 11:00:00	Other
4370	2	9	1319	1329	-10	1434	1500	9E	1386	N183GJ	LGA	BGR	52	378	13	29	2023-02-09 13:00:00	Other
4372	2	11	2022	2030	-8	2153	2159	B6	192	N323JB	JFK	ROC	54	264	20	30	2023-02-11 20:00:00	Other
4374	8	26	1648	1655	-7	1842	1909	YX	927	N859RW	EWR	CVG	93	569	16	55	2023-08-26 16:00:00	Other
4379	10	24	1516	1529	-13	1646	1716	YX	1344	N423YX	JFK	BNA	114	765	15	29	2023-10-24 15:00:00	Other
4391	3	28	1017	1025	-8	1235	1228	AA	877	N559UW	EWR	CLT	101	529	10	25	2023-03-28 10:00:00	CLT
4395	11	25	1737	1745	-8	2028	2107	DL	95	N807DN	JFK	FLL	148	1069	17	45	2023-11-25 17:00:00	FLL
4401	12	10	1648	1659	-11	1814	1838	UA	833	N884UA	LGA	ORD	119	733	16	59	2023-12-10 16:00:00	ORD
4402	9	20	2059	2110	-11	12	32	UA	692	N14118	EWR	SFO	339	2565	21	10	2023-09-20 21:00:00	Other
4411	9	20	809	815	-6	1051	1101	UA	255	N648UA	EWR	IAH	189	1400	8	15	2023-09-20 08:00:00	Other
4417	1	17	1607	1615	-8	1722	1734	B6	434	N306JB	LGA	BOS	45	184	16	15	2023-01-17 16:00:00	BOS
4423	12	11	1556	1603	-7	1851	1905	UA	67	N27271	EWR	PBI	155	1023	16	3	2023-12-11 16:00:00	Other
4430	5	6	753	804	-11	1012	1022	YX	994	N755YX	EWR	CVG	90	569	8	4	2023-05-06 08:00:00	Other
4432	5	14	1933	1940	-7	2251	2245	B6	294	N943JT	JFK	LAS	321	2248	19	40	2023-05-14 19:00:00	Other
4435	10	19	2207	2214	-7	19	45	NK	555	N920NK	EWR	ATL	103	746	22	14	2023-10-19 22:00:00	ATL
4440	1	31	1852	1900	-8	2024	2035	YX	1358	N425YX	JFK	ORF	62	290	19	0	2023-01-31 19:00:00	Other
4441	11	9	1207	1215	-8	1431	1444	UA	872	N14115	EWR	DEN	244	1605	12	15	2023-11-09 12:00:00	Other
4443	8	9	1616	1625	-9	1738	1754	9E	1147	N933XJ	LGA	SYR	40	198	16	25	2023-08-09 16:00:00	Other
4444	8	6	2054	2100	-6	2242	2302	YX	978	N407YX	JFK	RDU	72	427	21	0	2023-08-06 21:00:00	Other
4451	4	30	752	800	-8	1113	1115	DL	547	N3764D	JFK	RSW	173	1074	8	0	2023-04-30 08:00:00	Other
4452	7	7	1247	1300	-13	1649	1628	AS	4	N928AK	JFK	SFO	347	2586	13	0	2023-07-07 13:00:00	Other
4461	1	22	1254	1300	-6	1501	1517	AA	710	N542UW	LGA	CLT	102	544	13	0	2023-01-22 13:00:00	CLT
4462	12	2	1820	1829	-9	2128	2134	AA	400	N887NN	JFK	MIA	150	1089	18	29	2023-12-02 18:00:00	MIA
4464	2	28	929	935	-6	1148	1212	9E	1310	N306PQ	LGA	GRR	100	618	9	35	2023-02-28 09:00:00	Other
4467	5	3	651	659	-8	831	908	YX	1242	N409YX	LGA	MSP	141	1020	6	59	2023-05-03 06:00:00	Other
4469	4	24	2151	2159	-8	2236	2305	B6	256	N266JB	JFK	ORH	30	150	21	59	2023-04-24 21:00:00	Other
4470	2	9	1129	1135	-6	1416	1440	DL	450	N392DA	JFK	TPA	145	1005	11	35	2023-02-09 11:00:00	Other
4471	11	1	1818	1828	-10	2042	2026	9E	1602	N932XJ	LGA	STL	140	888	18	28	2023-11-01 18:00:00	Other
4472	1	12	1359	1405	-6	1731	1703	YX	1408	N422YX	LGA	ATL	172	762	14	5	2023-01-12 14:00:00	ATL
4473	1	7	908	915	-7	1005	1024	B6	966	N351JB	LGA	BOS	42	184	9	15	2023-01-07 09:00:00	BOS
4474	10	15	1518	1529	-11	1809	1846	AA	51	N111ZM	JFK	LAX	306	2475	15	29	2023-10-15 15:00:00	LAX
4478	5	2	1321	1335	-14	1620	1637	NK	24	N647NK	EWR	MCO	136	937	13	35	2023-05-02 13:00:00	MCO
4479	9	1	1929	1939	-10	2201	2242	B6	114	N996JL	JFK	ONT	299	2429	19	39	2023-09-01 19:00:00	Other
4484	3	13	1538	1548	-10	1708	1724	YX	1252	N871RW	LGA	RIC	58	292	15	48	2023-03-13 15:00:00	Other
4487	11	16	1801	1810	-9	2017	2042	9E	1490	N906XJ	JFK	SAV	111	718	18	10	2023-11-16 18:00:00	Other
4492	8	27	813	820	-7	932	1004	YX	1026	N403YX	JFK	DCA	42	213	8	20	2023-08-27 08:00:00	Other
4498	9	26	1131	1140	-9	1434	1437	NK	1029	N630NK	EWR	MCO	137	937	11	40	2023-09-26 11:00:00	MCO
4500	8	25	1137	1143	-6	1415	1412	UA	346	N435UA	EWR	ATL	100	746	11	43	2023-08-25 11:00:00	ATL
4506	10	12	1121	1130	-9	1326	1351	YX	1295	N422YX	JFK	IND	102	665	11	30	2023-10-12 11:00:00	Other
4507	9	15	1656	1705	-9	1840	1856	B6	398	N279JB	JFK	RDU	69	427	17	5	2023-09-15 17:00:00	Other
4508	5	25	1946	1959	-13	2130	2132	YX	1334	N871RW	LGA	ORF	55	296	19	59	2023-05-25 19:00:00	Other
4517	6	21	835	843	-8	1117	1134	UA	615	N37293	EWR	SAT	196	1569	8	43	2023-06-21 08:00:00	Other
4523	8	31	1012	1020	-8	1217	1240	9E	1142	N915XJ	LGA	CLT	89	544	10	20	2023-08-31 10:00:00	CLT
4527	12	2	1202	1210	-8	1344	1352	YX	1209	N136HQ	JFK	BNA	139	765	12	10	2023-12-02 12:00:00	Other
4531	11	28	1020	1026	-6	1220	1233	UA	486	N896UA	EWR	CLT	97	529	10	26	2023-11-28 10:00:00	CLT
4536	1	18	1943	1950	-7	2240	2218	YX	1815	N234JQ	LGA	IND	122	660	19	50	2023-01-18 19:00:00	Other
4543	11	14	1552	1559	-7	1807	1820	9E	1624	N147PQ	LGA	CLT	85	544	15	59	2023-11-14 15:00:00	CLT
4544	3	31	2222	2230	-8	2333	2348	UA	593	N13718	EWR	BTV	49	266	22	30	2023-03-31 22:00:00	Other
4558	3	29	955	1003	-8	1205	1214	AA	760	N834NN	LGA	CLT	94	544	10	3	2023-03-29 10:00:00	CLT
4565	6	9	950	959	-9	1209	1235	DL	157	N389DN	LGA	ATL	110	762	9	59	2023-06-09 09:00:00	ATL
4566	12	19	1559	1605	-6	1849	1928	B6	735	N982JB	EWR	LAX	321	2454	16	5	2023-12-19 16:00:00	LAX
4571	4	10	1150	1200	-10	1259	1331	AA	645	N906NN	EWR	ORD	103	719	12	0	2023-04-10 12:00:00	ORD
4578	1	13	1636	1645	-9	1823	1830	YX	1891	N880RW	LGA	PIT	61	335	16	45	2023-01-13 16:00:00	Other
4579	1	26	825	835	-10	1046	1100	9E	1556	N491PX	LGA	TYS	118	647	8	35	2023-01-26 08:00:00	Other
4588	1	12	724	730	-6	1047	1113	AS	15	N935AK	JFK	SFO	354	2586	7	30	2023-01-12 07:00:00	Other
4590	10	27	1353	1400	-7	1520	1546	AA	599	N772XF	LGA	RDU	67	431	14	0	2023-10-27 14:00:00	Other
4594	6	4	553	600	-7	838	845	NK	22	N530NK	EWR	MCO	129	937	6	0	2023-06-04 06:00:00	MCO
4595	12	1	1523	1531	-8	1658	1726	YX	1710	N207JQ	JFK	PIT	68	340	15	31	2023-12-01 15:00:00	Other
4598	4	30	552	600	-8	717	738	UA	855	N818UA	LGA	ORD	113	733	6	0	2023-04-30 06:00:00	ORD
4600	7	15	649	659	-10	835	908	B6	717	N187JB	LGA	CHS	88	641	6	59	2023-07-15 06:00:00	Other
4605	2	2	1338	1345	-7	1505	1522	9E	1474	N931XJ	LGA	BUF	57	292	13	45	2023-02-02 13:00:00	Other
4607	2	17	1052	1059	-7	1407	1348	UA	652	N19130	EWR	MCO	176	937	10	59	2023-02-17 10:00:00	MCO
4609	1	14	1451	1459	-8	1641	1717	DL	487	N318NB	LGA	MSP	141	1020	14	59	2023-01-14 14:00:00	Other
4611	8	4	653	700	-7	944	957	UA	648	N47517	EWR	PBI	143	1023	7	0	2023-08-04 07:00:00	Other
4619	10	5	1647	1653	-6	1845	1913	UA	940	N28457	EWR	DEN	214	1605	16	53	2023-10-05 16:00:00	Other
4624	10	10	1148	1155	-7	1334	1351	YX	1743	N240JQ	LGA	CMH	73	479	11	55	2023-10-10 11:00:00	Other
4631	3	22	2003	2010	-7	10	2340	B6	67	N945JT	JFK	LAX	375	2475	20	10	2023-03-22 20:00:00	LAX
4634	4	18	554	600	-6	716	735	UA	363	N17279	EWR	ORD	114	719	6	0	2023-04-18 06:00:00	ORD
4637	3	21	622	630	-8	1020	1010	AA	33	N107NN	JFK	SFO	391	2586	6	30	2023-03-21 06:00:00	Other
4638	8	29	1521	1529	-8	1825	1839	AS	75	N926AK	EWR	SFO	334	2565	15	29	2023-08-29 15:00:00	Other
4640	5	23	752	759	-7	1000	1002	AA	952	N150UW	LGA	CLT	87	544	7	59	2023-05-23 07:00:00	CLT
4646	11	27	922	930	-8	1239	1256	AS	6	N477AS	JFK	SEA	337	2422	9	30	2023-11-27 09:00:00	Other
4660	4	18	1533	1545	-12	1700	1719	9E	1283	N923XJ	LGA	IAD	50	229	15	45	2023-04-18 15:00:00	Other
4673	3	1	553	600	-7	809	806	AA	949	N339PL	JFK	CLT	92	541	6	0	2023-03-01 06:00:00	CLT
4677	9	17	1123	1129	-6	1327	1331	AA	942	N954NN	JFK	CLT	88	541	11	29	2023-09-17 11:00:00	CLT
4678	3	10	554	600	-6	831	912	B6	581	N564JB	EWR	FLL	141	1065	6	0	2023-03-10 06:00:00	FLL
4679	5	30	1019	1030	-11	1212	1236	YX	1076	N861RW	EWR	DTW	73	488	10	30	2023-05-30 10:00:00	Other
4686	10	1	810	819	-9	1035	1109	DL	234	N111NG	LGA	DFW	176	1389	8	19	2023-10-01 08:00:00	Other
4687	9	4	1053	1100	-7	1336	1408	B6	826	N646JB	JFK	FLL	138	1069	11	0	2023-09-04 11:00:00	FLL
4689	2	16	640	647	-7	754	813	AA	759	N821AW	LGA	DCA	45	214	6	47	2023-02-16 06:00:00	Other
4701	2	28	1052	1100	-8	1302	1327	YX	1190	N806MD	LGA	AVL	101	599	11	0	2023-02-28 11:00:00	Other
4705	12	4	2021	2030	-9	2225	2253	9E	1497	N915XJ	LGA	GRR	95	618	20	30	2023-12-04 20:00:00	Other
4706	12	19	1225	1233	-8	1421	1459	UA	225	N13716	EWR	MSY	158	1167	12	33	2023-12-19 12:00:00	Other
4707	5	8	549	600	-11	826	907	NK	53	N683NK	LGA	FLL	142	1076	6	0	2023-05-08 06:00:00	FLL
4711	11	3	1329	1335	-6	1626	1642	B6	651	N595JB	EWR	RSW	156	1068	13	35	2023-11-03 13:00:00	Other
4715	11	19	603	610	-7	912	945	UA	240	N12116	EWR	SFO	341	2565	6	10	2023-11-19 06:00:00	Other
4716	8	5	939	946	-7	1332	1341	UA	465	N47517	EWR	SJU	193	1608	9	46	2023-08-05 09:00:00	Other
4721	11	12	1653	1700	-7	1859	1919	YX	1227	N438YX	LGA	DSM	157	1031	17	0	2023-11-12 17:00:00	Other
4723	5	17	701	712	-11	902	926	YX	1209	N440YX	LGA	DTW	83	502	7	12	2023-05-17 07:00:00	Other
4726	6	10	1434	1440	-6	1716	1736	UA	920	N14120	EWR	LAX	315	2454	14	40	2023-06-10 14:00:00	LAX
4735	3	1	822	829	-7	1114	1141	AA	676	N8030F	JFK	EGE	253	1746	8	29	2023-03-01 08:00:00	Other
4743	1	9	621	630	-9	852	919	UA	258	N47284	EWR	LAS	309	2227	6	30	2023-01-09 06:00:00	Other
4745	9	23	1018	1030	-12	1316	1341	B6	267	N635JB	JFK	SAT	203	1587	10	30	2023-09-23 10:00:00	Other
4755	9	13	1208	1215	-7	1415	1436	UA	723	N77530	LGA	DEN	216	1620	12	15	2023-09-13 12:00:00	Other
4757	10	9	1138	1145	-7	1405	1459	AS	6	N969AK	JFK	PDX	307	2454	11	45	2023-10-09 11:00:00	Other
4760	5	2	953	1000	-7	1048	1138	UA	700	N448UA	LGA	ORD	103	733	10	0	2023-05-02 10:00:00	ORD
4774	11	29	1053	1059	-6	1426	1419	B6	806	N979JT	JFK	LAX	343	2475	10	59	2023-11-29 10:00:00	LAX
4777	8	22	650	700	-10	751	816	B6	783	N354JB	LGA	BOS	35	184	7	0	2023-08-22 07:00:00	BOS
4778	8	8	823	829	-6	937	957	9E	1118	N490PX	LGA	ROC	51	254	8	29	2023-08-08 08:00:00	Other
4784	4	9	1656	1710	-14	1850	1905	YX	1224	N444YX	LGA	ILM	81	500	17	10	2023-04-09 17:00:00	Other
4785	10	10	610	620	-10	813	841	UA	736	N27269	LGA	DEN	216	1620	6	20	2023-10-10 06:00:00	Other
4787	2	27	620	630	-10	904	925	NK	500	N653NK	LGA	MCO	133	950	6	30	2023-02-27 06:00:00	MCO
4788	3	21	717	725	-8	950	954	UA	452	N853UA	EWR	JAX	124	820	7	25	2023-03-21 07:00:00	Other
4789	8	31	724	730	-6	1041	1038	DL	759	N3773D	LGA	MIA	160	1096	7	30	2023-08-31 07:00:00	MIA
4800	8	30	902	909	-7	1122	1111	UA	197	N12754	EWR	MCI	150	1092	9	9	2023-08-30 09:00:00	Other
4801	8	29	915	929	-14	1038	1100	YX	1050	N409YX	LGA	RIC	54	292	9	29	2023-08-29 09:00:00	Other
4802	8	19	933	940	-7	1236	1238	B6	761	N568JB	JFK	TPA	129	1005	9	40	2023-08-19 09:00:00	Other
4807	9	27	753	800	-7	932	1006	DL	578	N341DN	LGA	MSP	134	1020	8	0	2023-09-27 08:00:00	Other
4810	11	11	2045	2059	-14	2243	2309	UA	777	N77543	EWR	CLT	88	529	20	59	2023-11-11 20:00:00	CLT
4811	4	3	550	600	-10	740	807	YX	1089	N450YX	LGA	CMH	85	479	6	0	2023-04-03 06:00:00	Other
4820	9	21	1052	1059	-7	1419	1430	DL	287	N722TW	JFK	SFO	346	2586	10	59	2023-09-21 10:00:00	Other
4821	1	14	637	645	-8	911	955	NK	926	N696NK	EWR	AUS	192	1504	6	45	2023-01-14 06:00:00	Other
4831	5	8	1702	1710	-8	1855	1907	YX	1306	N826MD	LGA	ILM	75	500	17	10	2023-05-08 17:00:00	Other
4840	1	28	1622	1630	-8	2013	2000	B6	365	N981JT	JFK	LAX	382	2475	16	30	2023-01-28 16:00:00	LAX
4841	6	23	1259	1305	-6	1429	1442	UA	642	N833UA	LGA	ORD	106	733	13	5	2023-06-23 13:00:00	ORD
4845	3	14	753	759	-6	1026	1020	YX	1409	N108HQ	JFK	CVG	96	589	7	59	2023-03-14 07:00:00	Other
4846	9	23	1109	1115	-6	1413	1436	DL	912	N322DN	LGA	FLL	163	1076	11	15	2023-09-23 11:00:00	FLL
4848	1	15	921	930	-9	1127	1210	UA	949	N37290	LGA	DEN	224	1620	9	30	2023-01-15 09:00:00	Other
4868	8	29	624	630	-6	823	833	AA	276	N649AW	JFK	CLT	89	541	6	30	2023-08-29 06:00:00	CLT
4870	6	13	1440	1449	-9	1612	1629	B6	271	N3077J	JFK	MKE	126	745	14	49	2023-06-13 14:00:00	Other
4874	10	31	1947	2000	-13	2226	2240	DL	287	N356DN	LGA	ATL	126	762	20	0	2023-10-31 20:00:00	ATL
4876	8	29	1511	1520	-9	1654	1704	YX	1375	N210JQ	LGA	DCA	48	214	15	20	2023-08-29 15:00:00	Other
4879	11	6	1219	1225	-6	1340	1353	YX	1274	N436YX	LGA	DCA	49	214	12	25	2023-11-06 12:00:00	Other
4881	12	12	1223	1233	-10	1438	1459	UA	225	N17322	EWR	MSY	175	1167	12	33	2023-12-12 12:00:00	Other
4885	10	2	724	730	-6	918	942	YX	1055	N725YX	EWR	GRR	86	605	7	30	2023-10-02 07:00:00	Other
4888	11	12	1017	1025	-8	1316	1323	UA	621	N21108	EWR	MCO	144	937	10	25	2023-11-12 10:00:00	MCO
4890	6	9	1116	1122	-6	1351	1425	DL	462	N855DN	JFK	TPA	139	1005	11	22	2023-06-09 11:00:00	Other
4891	6	7	542	550	-8	801	836	AA	594	N822NN	LGA	DFW	177	1389	5	50	2023-06-07 05:00:00	Other
4897	11	19	854	900	-6	1101	1143	DL	321	N313DN	LGA	ATL	107	762	9	0	2023-11-19 09:00:00	ATL
4903	10	27	634	645	-11	935	948	UA	243	N33209	EWR	FLL	154	1065	6	45	2023-10-27 06:00:00	FLL
4912	9	2	1523	1530	-7	1644	1702	YX	1131	N750YX	EWR	BNA	99	748	15	30	2023-09-02 15:00:00	Other
4922	1	31	1157	1205	-8	1456	1520	B6	689	N2027J	JFK	FLL	160	1069	12	5	2023-01-31 12:00:00	FLL
4928	10	31	1204	1210	-6	1517	1515	UA	445	N27734	EWR	DFW	222	1372	12	10	2023-10-31 12:00:00	Other
4929	5	27	2106	2115	-9	2226	2256	DL	853	N127DU	JFK	BUF	48	301	21	15	2023-05-27 21:00:00	Other
4930	3	23	749	759	-10	1013	1017	YX	1288	N426YX	LGA	MSP	184	1020	7	59	2023-03-23 07:00:00	Other
4949	2	28	1525	1532	-7	1731	1757	YX	1224	N112HQ	LGA	DTW	85	502	15	32	2023-02-28 15:00:00	Other
4956	3	28	932	940	-8	1203	1220	B6	577	N607JB	JFK	DEN	241	1626	9	40	2023-03-28 09:00:00	Other
4957	2	1	620	630	-10	814	818	YX	1274	N870RW	LGA	PIT	65	335	6	30	2023-02-01 06:00:00	Other
4961	5	3	2034	2045	-11	2240	2326	YX	1255	N127HQ	JFK	IND	99	665	20	45	2023-05-03 20:00:00	Other
4964	10	28	1832	1840	-8	2127	2152	AA	613	N868NN	EWR	MIA	142	1085	18	40	2023-10-28 18:00:00	MIA
4971	11	24	830	840	-10	1004	1034	9E	1756	N904XJ	LGA	BHM	129	866	8	40	2023-11-24 08:00:00	Other
4973	10	19	1031	1039	-8	1240	1314	YX	1269	N402YX	LGA	XNA	167	1147	10	39	2023-10-19 10:00:00	Other
4977	1	21	1420	1430	-10	1652	1716	YX	1338	N867RW	LGA	SDF	123	659	14	30	2023-01-21 14:00:00	Other
4978	5	9	723	730	-7	857	907	9E	1431	N310PQ	LGA	ORF	51	296	7	30	2023-05-09 07:00:00	Other
4983	10	23	1852	1900	-8	2109	2124	YX	1270	N419YX	LGA	IND	98	660	19	0	2023-10-23 19:00:00	Other
4986	2	22	1022	1029	-7	1239	1254	YX	1527	N878RW	LGA	CLT	98	544	10	29	2023-02-22 10:00:00	CLT
4987	2	13	1623	1630	-7	1759	1823	DL	734	N140DU	LGA	RDU	70	431	16	30	2023-02-13 16:00:00	Other
4993	2	8	1822	1830	-8	1933	1949	UA	388	N27270	EWR	BOS	45	200	18	30	2023-02-08 18:00:00	BOS
4996	11	29	815	825	-10	926	952	YX	1864	N211JQ	EWR	BOS	44	200	8	25	2023-11-29 08:00:00	BOS
4998	6	13	651	700	-9	908	933	B6	269	N583JB	JFK	JAX	121	828	7	0	2023-06-13 07:00:00	Other
5004	8	9	920	930	-10	1129	1147	YX	924	N755YX	EWR	HHH	101	687	9	30	2023-08-09 09:00:00	Other
5009	5	21	1507	1513	-6	1904	1907	B6	746	N588JB	JFK	BQN	209	1576	15	13	2023-05-21 15:00:00	Other
5022	3	22	1052	1100	-8	1229	1233	YX	1244	N444YX	LGA	DCA	44	214	11	0	2023-03-22 11:00:00	Other
5027	5	10	1224	1231	-7	1313	1336	YX	1658	N880RW	LGA	BDL	23	101	12	31	2023-05-10 12:00:00	Other
5036	8	16	1202	1209	-7	1307	1329	YX	995	N112HQ	JFK	BOS	32	187	12	9	2023-08-16 12:00:00	BOS
5050	1	30	855	904	-9	1120	1140	B6	1046	N317JB	LGA	SAV	122	722	9	4	2023-01-30 09:00:00	Other
5056	2	15	832	840	-8	956	1014	YX	1213	N106HQ	JFK	BOS	42	187	8	40	2023-02-15 08:00:00	BOS
5059	12	13	1054	1100	-6	1354	1419	AA	742	N902NN	LGA	DFW	215	1389	11	0	2023-12-13 11:00:00	Other
5062	4	8	653	659	-6	943	1011	AA	819	N935NN	LGA	MIA	149	1096	6	59	2023-04-08 06:00:00	MIA
5065	2	22	954	1000	-6	1151	1151	B6	83	N355JB	JFK	RDU	74	427	10	0	2023-02-22 10:00:00	Other
5075	11	30	1153	1159	-6	1337	1400	9E	1498	N137EV	LGA	ILM	80	500	11	59	2023-11-30 11:00:00	Other
5077	5	22	1805	1815	-10	1905	1937	B6	441	N284JB	LGA	BOS	34	184	18	15	2023-05-22 18:00:00	BOS
5091	9	26	2137	2145	-8	2326	2336	YX	1301	N405YX	JFK	RDU	71	427	21	45	2023-09-26 21:00:00	Other
5098	6	5	553	600	-7	731	814	AA	246	N920US	LGA	CLT	77	544	6	0	2023-06-05 06:00:00	CLT
5102	1	26	820	830	-10	1006	1016	AA	134	N915NN	LGA	ORD	113	733	8	30	2023-01-26 08:00:00	ORD
5103	3	9	853	900	-7	1049	1103	YX	1358	N826MD	LGA	CMH	83	479	9	0	2023-03-09 09:00:00	Other
5105	5	18	1811	1820	-9	2016	2038	YX	1193	N429YX	LGA	LIT	151	1085	18	20	2023-05-18 18:00:00	Other
5113	3	29	1643	1650	-7	1846	1900	9E	1383	N918XJ	LGA	DSM	164	1031	16	50	2023-03-29 16:00:00	Other
5114	8	29	921	930	-9	1226	1243	B6	66	N568JB	LGA	FLL	148	1076	9	30	2023-08-29 09:00:00	FLL
5115	12	13	1504	1511	-7	1714	1717	YX	1237	N131HQ	LGA	CLE	85	419	15	11	2023-12-13 15:00:00	Other
5127	9	18	646	654	-8	759	811	AA	547	N803AW	LGA	DCA	51	214	6	54	2023-09-18 06:00:00	Other
5131	12	6	952	959	-7	1214	1245	DL	141	N370DN	LGA	ATL	99	762	9	59	2023-12-06 09:00:00	ATL
5141	12	14	1924	1930	-6	2045	2109	UA	425	N53441	EWR	ORD	103	719	19	30	2023-12-14 19:00:00	ORD
5153	3	21	921	930	-9	1144	1212	UA	876	N413UA	LGA	DEN	232	1620	9	30	2023-03-21 09:00:00	Other
5156	12	15	2152	2159	-7	2306	2330	9E	1640	N923XJ	LGA	BUF	50	292	21	59	2023-12-15 21:00:00	Other
5159	8	1	1421	1429	-8	1532	1604	9E	1179	N676CA	JFK	SYR	42	209	14	29	2023-08-01 14:00:00	Other
5160	11	5	836	843	-7	1129	1217	UA	564	N24706	EWR	SAT	211	1569	8	43	2023-11-05 08:00:00	Other
5168	10	18	1651	1705	-14	1844	1915	YX	1243	N427YX	LGA	DSM	146	1031	17	5	2023-10-18 17:00:00	Other
5172	5	8	1040	1047	-7	1221	1248	YX	995	N732YX	EWR	CMH	75	463	10	47	2023-05-08 10:00:00	Other
5174	3	28	654	705	-11	1005	1011	DL	681	N347NB	LGA	TPA	163	1010	7	5	2023-03-28 07:00:00	Other
5179	6	8	1452	1459	-7	1623	1651	YX	1781	N233JQ	LGA	MEM	129	963	14	59	2023-06-08 14:00:00	Other
5181	11	28	813	820	-7	1114	1135	DL	258	N114DU	LGA	DFW	215	1389	8	20	2023-11-28 08:00:00	Other
5182	3	6	2000	2010	-10	2255	2249	B6	36	N507JT	JFK	DEN	270	1626	20	10	2023-03-06 20:00:00	Other
5184	2	1	722	730	-8	1110	1054	AA	1	N105NN	JFK	LAX	354	2475	7	30	2023-02-01 07:00:00	LAX
5185	11	15	805	816	-11	1132	1142	UA	783	N77552	EWR	SEA	349	2402	8	16	2023-11-15 08:00:00	Other
5187	10	3	1617	1630	-13	1912	1935	B6	739	N947JB	EWR	LAX	330	2454	16	30	2023-10-03 16:00:00	LAX
5196	5	24	552	604	-12	757	812	B6	31	N571JB	JFK	MSY	158	1182	6	4	2023-05-24 06:00:00	Other
5202	11	16	1614	1620	-6	1729	1751	YX	1071	N751YX	EWR	BUF	50	282	16	20	2023-11-16 16:00:00	Other
5203	7	18	1219	1229	-10	1517	1400	YX	991	N420YX	JFK	ORF	53	290	12	29	2023-07-18 12:00:00	Other
5205	7	17	1620	1629	-9	1945	1936	AA	91	N106NN	JFK	LAX	325	2475	16	29	2023-07-17 16:00:00	LAX
5214	11	5	1348	1355	-7	1624	1659	B6	533	N504JB	EWR	MCO	126	937	13	55	2023-11-05 13:00:00	MCO
5216	9	14	621	630	-9	858	904	B6	213	N970JB	JFK	MCO	132	944	6	30	2023-09-14 06:00:00	MCO
5224	9	19	839	848	-9	1001	1028	9E	1447	N924XJ	LGA	BHM	125	866	8	48	2023-09-19 08:00:00	Other
5225	12	30	1530	1538	-8	1737	1809	YX	1252	N421YX	JFK	IND	93	665	15	38	2023-12-30 15:00:00	Other
5235	8	9	953	959	-6	1125	1154	YX	1328	N213JQ	JFK	CMH	72	483	9	59	2023-08-09 09:00:00	Other
5239	10	19	950	1000	-10	1430	1455	HA	18	N360HA	JFK	HNL	614	4983	10	0	2023-10-19 10:00:00	Other
5240	12	4	1200	1210	-10	1510	1515	UA	202	N497UA	EWR	DFW	212	1372	12	10	2023-12-04 12:00:00	Other
5242	6	13	809	815	-6	906	930	B6	114	N273JB	LGA	BOS	32	184	8	15	2023-06-13 08:00:00	BOS
5255	3	7	819	827	-8	1112	1104	B6	923	N794JB	LGA	MSY	174	1183	8	27	2023-03-07 08:00:00	Other
5263	8	25	1327	1335	-8	1446	1452	YX	905	N740YX	EWR	BTV	49	266	13	35	2023-08-25 13:00:00	Other
5270	10	10	1353	1359	-6	1453	1520	YX	1705	N212JQ	LGA	BOS	41	184	13	59	2023-10-10 13:00:00	BOS
5280	4	14	2204	2211	-7	2324	2334	UA	452	N38467	EWR	BUF	47	282	22	11	2023-04-14 22:00:00	Other
5288	3	29	720	730	-10	932	945	DL	1005	N342NB	LGA	MSP	153	1020	7	30	2023-03-29 07:00:00	Other
5292	4	3	1223	1229	-6	1520	1533	UA	566	N443UA	LGA	IAH	211	1416	12	29	2023-04-03 12:00:00	Other
5301	3	10	724	730	-6	1035	1025	B6	149	N929JB	JFK	LAS	327	2248	7	30	2023-03-10 07:00:00	Other
5307	2	13	1851	1859	-8	2017	2032	YX	978	N641RW	EWR	BGR	57	393	18	59	2023-02-13 18:00:00	Other
5313	6	20	554	600	-6	833	844	B6	96	N516JB	LGA	MCO	135	950	6	0	2023-06-20 06:00:00	MCO
5315	10	19	753	800	-7	1047	1105	B6	764	N967JT	JFK	LAX	293	2475	8	0	2023-10-19 08:00:00	LAX
5324	12	12	2119	2129	-10	2215	2241	YX	1039	N770YX	EWR	MHT	39	209	21	29	2023-12-12 21:00:00	Other
5326	10	29	1354	1400	-6	1705	1623	9E	1559	N336PQ	LGA	OMA	195	1148	14	0	2023-10-29 14:00:00	Other
5330	9	8	943	950	-7	1110	1113	YX	1912	N234JQ	JFK	BOS	50	187	9	50	2023-09-08 09:00:00	BOS
5338	9	7	827	835	-8	1025	1050	9E	1725	N349PQ	LGA	MCI	154	1107	8	35	2023-09-07 08:00:00	Other
5341	9	27	1754	1800	-6	2033	2100	AA	196	N901AN	LGA	DFW	187	1389	18	0	2023-09-27 18:00:00	Other
5346	4	9	1638	1650	-12	1822	1900	9E	1260	N918XJ	LGA	DSM	143	1031	16	50	2023-04-09 16:00:00	Other
5356	4	1	623	630	-7	915	924	AA	514	N315RJ	JFK	PHX	313	2153	6	30	2023-04-01 06:00:00	Other
5357	3	9	1403	1409	-6	1646	1701	YX	1339	N104HQ	LGA	ATL	117	762	14	9	2023-03-09 14:00:00	ATL
5360	8	2	1135	1142	-7	1259	1326	YX	1056	N869RW	LGA	ROA	61	405	11	42	2023-08-02 11:00:00	Other
5368	12	15	1430	1440	-10	1619	1644	YX	1251	N425YX	LGA	ILM	75	500	14	40	2023-12-15 14:00:00	Other
5372	10	3	553	600	-7	841	854	UA	227	N27292	EWR	AUS	195	1504	6	0	2023-10-03 06:00:00	Other
5373	2	21	1527	1535	-8	1717	1740	YX	1333	N416YX	JFK	CLE	87	425	15	35	2023-02-21 15:00:00	Other
5383	4	3	2040	2050	-10	2222	2248	9E	1441	N301PQ	LGA	GSO	71	461	20	50	2023-04-03 20:00:00	Other
5385	8	23	1209	1215	-6	1456	1511	B6	225	N637JB	JFK	AUS	194	1521	12	15	2023-08-23 12:00:00	Other
5388	10	9	748	759	-11	853	919	YX	1741	N201JQ	LGA	BOS	40	184	7	59	2023-10-09 07:00:00	BOS
5390	12	19	1743	1750	-7	1942	2029	9E	1392	N319PQ	JFK	MCI	148	1113	17	50	2023-12-19 17:00:00	Other
5393	12	1	2147	2153	-6	2243	2259	YX	1829	N246JQ	LGA	ALB	31	136	21	53	2023-12-01 21:00:00	Other
5402	6	2	1601	1610	-9	1738	1739	9E	1390	N479PX	LGA	PWM	54	269	16	10	2023-06-02 16:00:00	Other
5403	2	14	2106	2120	-14	2205	2226	9E	1367	N919XJ	LGA	ALB	31	136	21	20	2023-02-14 21:00:00	Other
5407	11	6	1523	1530	-7	1702	1740	YX	1283	N425YX	JFK	CMH	81	483	15	30	2023-11-06 15:00:00	Other
5411	3	20	2047	2100	-13	2342	14	B6	220	N531JL	LGA	FLL	151	1076	21	0	2023-03-20 21:00:00	FLL
5426	8	24	554	600	-6	812	859	AA	1	N111ZM	JFK	LAX	298	2475	6	0	2023-08-24 06:00:00	LAX
5429	11	15	2223	2229	-6	2343	2356	B6	28	N198JB	JFK	BUF	59	301	22	29	2023-11-15 22:00:00	Other
5433	12	5	2220	2230	-10	2341	2358	9E	1383	N131EV	JFK	PWM	44	273	22	30	2023-12-05 22:00:00	Other
5434	8	15	1723	1730	-7	1918	1923	YX	1008	N406YX	LGA	CMH	78	479	17	30	2023-08-15 17:00:00	Other
5435	5	24	1345	1355	-10	1535	1615	YX	1036	N740YX	EWR	SDF	92	642	13	55	2023-05-24 13:00:00	Other
5438	2	9	1050	1100	-10	1159	1228	YX	1612	N228JQ	LGA	BOS	40	184	11	0	2023-02-09 11:00:00	BOS
5448	8	7	1328	1335	-7	1511	1452	YX	905	N730YX	EWR	BTV	47	266	13	35	2023-08-07 13:00:00	Other
5465	11	10	1002	1008	-6	1241	1238	UA	529	N461UA	EWR	DEN	243	1605	10	8	2023-11-10 10:00:00	Other
5479	10	18	1424	1430	-6	1534	1552	YX	1086	N764YX	EWR	PWM	53	284	14	30	2023-10-18 14:00:00	Other
5484	3	5	1223	1230	-7	1324	1353	9E	1352	N922XJ	LGA	SCE	44	208	12	30	2023-03-05 12:00:00	Other
5485	12	30	624	630	-6	901	954	UA	537	N17279	EWR	SNA	312	2434	6	30	2023-12-30 06:00:00	Other
5487	8	4	953	1000	-7	1222	1242	UA	75	N27263	EWR	DFW	182	1372	10	0	2023-08-04 10:00:00	Other
5490	6	19	1831	1840	-9	2053	2102	YX	1139	N638RW	EWR	IND	103	645	18	40	2023-06-19 18:00:00	Other
5492	7	13	1153	1159	-6	1351	1351	YX	852	N640RW	EWR	CMH	84	463	11	59	2023-07-13 11:00:00	Other
5497	1	25	2028	2034	-6	20	2359	UA	978	N25201	EWR	SMF	321	2500	20	34	2023-01-25 20:00:00	Other
5503	8	22	1949	2000	-11	2131	2207	9E	1092	N131EV	LGA	DAY	82	549	20	0	2023-08-22 20:00:00	Other
5504	3	17	1840	1850	-10	2059	2105	9E	1433	N916XJ	LGA	GRR	107	618	18	50	2023-03-17 18:00:00	Other
5529	1	29	846	859	-13	957	1034	YX	1809	N211JQ	EWR	BOS	46	200	8	59	2023-01-29 08:00:00	BOS
5533	6	3	904	915	-11	1208	1237	AA	844	N313SB	LGA	MIA	157	1096	9	15	2023-06-03 09:00:00	MIA
5537	5	8	944	950	-6	1100	1115	9E	1295	N932XJ	JFK	IAD	49	228	9	50	2023-05-08 09:00:00	Other
5538	9	18	1248	1255	-7	1610	1600	B6	17	N537JT	LGA	TPA	151	1010	12	55	2023-09-18 12:00:00	Other
5539	5	28	1751	1800	-9	1906	1920	AA	422	N820AW	LGA	DCA	52	214	18	0	2023-05-28 18:00:00	Other
5546	11	10	1402	1410	-8	1709	1705	NK	76	N957NK	EWR	DFW	211	1372	14	10	2023-11-10 14:00:00	Other
5547	4	8	2044	2054	-10	2227	2247	YX	958	N726YX	EWR	GSO	82	445	20	54	2023-04-08 20:00:00	Other
5549	4	11	1351	1400	-9	1458	1520	YX	1478	N216JQ	LGA	BOS	37	184	14	0	2023-04-11 14:00:00	BOS
5551	6	20	1453	1500	-7	1737	1742	B6	676	N323JB	JFK	ATL	125	760	15	0	2023-06-20 15:00:00	ATL
5555	10	24	1452	1500	-8	1602	1630	YX	1159	N739YX	EWR	PIT	52	319	15	0	2023-10-24 15:00:00	Other
5560	8	31	753	800	-7	1053	1112	AA	410	N935NN	EWR	MIA	156	1085	8	0	2023-08-31 08:00:00	MIA
5563	3	15	747	755	-8	1051	1104	B6	174	N623JB	LGA	PBI	144	1035	7	55	2023-03-15 07:00:00	Other
5582	1	28	1539	1545	-6	1928	1922	DL	278	N171DN	JFK	LAX	369	2475	15	45	2023-01-28 15:00:00	LAX
5584	1	25	618	630	-12	757	818	YX	1391	N867RW	LGA	PIT	71	335	6	30	2023-01-25 06:00:00	Other
5586	5	27	1150	1200	-10	1445	1446	NK	980	N614NK	EWR	MCO	145	937	12	0	2023-05-27 12:00:00	MCO
5587	3	21	741	750	-9	846	917	9E	1543	N937XJ	JFK	BTV	47	266	7	50	2023-03-21 07:00:00	Other
5591	12	20	922	929	-7	1125	1147	YX	1063	N751YX	EWR	AVL	88	583	9	29	2023-12-20 09:00:00	Other
5594	10	19	802	815	-13	903	933	B6	98	N284JB	LGA	BOS	38	184	8	15	2023-10-19 08:00:00	BOS
5595	4	23	2047	2059	-12	2306	2334	YX	1158	N447YX	LGA	ATL	112	762	20	59	2023-04-23 20:00:00	ATL
5599	8	30	1349	1400	-11	1522	1554	YX	1059	N867RW	LGA	ILM	75	500	14	0	2023-08-30 14:00:00	Other
5606	5	7	551	600	-9	727	801	AA	231	N534UW	LGA	CLT	76	544	6	0	2023-05-07 06:00:00	CLT
5607	4	8	727	735	-8	1008	1032	NK	432	N679NK	EWR	MCO	131	937	7	35	2023-04-08 07:00:00	MCO
5611	3	7	1156	1203	-7	1442	1428	YX	1287	N409YX	LGA	MSP	188	1020	12	3	2023-03-07 12:00:00	Other
5612	3	2	818	825	-7	1002	1039	9E	1544	N313PQ	LGA	ILM	77	500	8	25	2023-03-02 08:00:00	Other
5621	8	4	1322	1328	-6	1427	1440	YX	860	N732YX	EWR	SYR	37	195	13	28	2023-08-04 13:00:00	Other
5632	4	19	1713	1720	-7	2034	2059	B6	252	N648JB	JFK	SJC	364	2569	17	20	2023-04-19 17:00:00	Other
5639	7	22	1709	1715	-6	1812	1855	YX	1388	N231JQ	LGA	DCA	41	214	17	15	2023-07-22 17:00:00	Other
5645	7	17	1134	1140	-6	1244	1308	NK	246	N654NK	EWR	PIT	50	319	11	40	2023-07-17 11:00:00	Other
5648	3	5	1853	1859	-6	2040	2044	UA	209	N459UA	EWR	RDU	70	416	18	59	2023-03-05 18:00:00	Other
5649	6	20	922	930	-8	1153	1247	AS	9	N967AK	JFK	SEA	304	2422	9	30	2023-06-20 09:00:00	Other
5659	2	9	1032	1040	-8	1254	1327	DL	122	N316DN	LGA	ATL	122	762	10	40	2023-02-09 10:00:00	ATL
5662	11	2	816	829	-13	958	1014	YX	1345	N101HQ	LGA	CLE	75	419	8	29	2023-11-02 08:00:00	Other
5667	10	28	2111	2124	-13	2256	2326	UA	75	N66893	EWR	CLT	80	529	21	24	2023-10-28 21:00:00	CLT
5671	3	24	1401	1407	-6	1633	1629	UA	311	N845UA	EWR	MSY	177	1167	14	7	2023-03-24 14:00:00	Other
5682	10	28	1400	1410	-10	1528	1608	YX	1341	N434YX	LGA	ILM	73	500	14	10	2023-10-28 14:00:00	Other
5691	12	4	754	800	-6	1044	1034	DL	886	N355NB	JFK	MSY	192	1182	8	0	2023-12-04 08:00:00	Other
5694	11	1	1450	1500	-10	1646	1713	9E	1536	N134EV	EWR	CVG	97	569	15	0	2023-11-01 15:00:00	Other
5696	5	5	1220	1227	-7	1330	1345	YX	1051	N855RW	EWR	PWM	52	284	12	27	2023-05-05 12:00:00	Other
5697	10	20	1340	1348	-8	1459	1529	MQ	1023	N282NN	EWR	ORD	103	719	13	48	2023-10-20 13:00:00	ORD
5703	3	16	1842	1855	-13	2217	2209	AS	12	N481AS	JFK	SAN	341	2446	18	55	2023-03-16 18:00:00	Other
5705	8	16	1314	1320	-6	1429	1454	YX	1360	N875RW	LGA	DCA	48	214	13	20	2023-08-16 13:00:00	Other
5716	8	26	624	630	-6	916	918	UA	348	N410UA	EWR	SRQ	136	1034	6	30	2023-08-26 06:00:00	Other
5719	10	12	1753	1800	-7	1914	1931	YX	1033	N753YX	EWR	BUF	50	282	18	0	2023-10-12 18:00:00	Other
5721	2	13	2132	2139	-7	2302	2325	B6	515	N238JB	JFK	RDU	68	427	21	39	2023-02-13 21:00:00	Other
5725	3	3	1614	1629	-15	1828	1827	YX	1372	N434YX	LGA	ILM	88	500	16	29	2023-03-03 16:00:00	Other
5726	10	4	906	914	-8	1106	1125	UA	652	N16732	EWR	MCI	143	1092	9	14	2023-10-04 09:00:00	Other
5744	5	18	1523	1529	-6	1757	1835	AS	85	N928VA	EWR	LAX	307	2454	15	29	2023-05-18 15:00:00	LAX
5745	10	24	1152	1200	-8	1501	1508	B6	799	N2105J	JFK	LAX	339	2475	12	0	2023-10-24 12:00:00	LAX
5748	2	3	1101	1115	-14	1227	1244	B6	891	N266JB	JFK	BUF	64	301	11	15	2023-02-03 11:00:00	Other
5757	2	14	1606	1615	-9	1749	1814	YX	1308	N128HQ	JFK	RDU	71	427	16	15	2023-02-14 16:00:00	Other
5763	8	3	717	730	-13	917	945	B6	265	N608JB	JFK	SAV	99	718	7	30	2023-08-03 07:00:00	Other
5764	4	7	1124	1130	-6	1344	1402	DL	782	N363NB	LGA	MSY	177	1183	11	30	2023-04-07 11:00:00	Other
5769	8	15	1254	1300	-6	1545	1601	UA	87	N416UA	EWR	RSW	152	1068	13	0	2023-08-15 13:00:00	Other
5780	4	30	1520	1529	-9	1734	1727	YX	1073	N446YX	JFK	CLE	72	425	15	29	2023-04-30 15:00:00	Other
5781	10	25	1850	1906	-16	2026	2109	YX	1340	N427YX	LGA	CMH	73	479	19	6	2023-10-25 19:00:00	Other
5782	2	13	558	605	-7	708	729	YX	1579	N207JQ	EWR	BOS	39	200	6	5	2023-02-13 06:00:00	BOS
5783	11	14	1150	1200	-10	1448	1502	B6	664	N903JB	JFK	PBI	142	1028	12	0	2023-11-14 12:00:00	Other
5785	12	6	1842	1850	-8	2051	2127	YX	1725	N245JQ	LGA	OMA	161	1148	18	50	2023-12-06 18:00:00	Other
5789	2	1	1921	1935	-14	2200	2239	B6	288	N806JB	LGA	MCO	139	950	19	35	2023-02-01 19:00:00	MCO
5799	1	9	553	600	-7	708	722	YX	1245	N727YX	EWR	IAD	46	212	6	0	2023-01-09 06:00:00	Other
5807	8	1	720	729	-9	841	915	AA	778	N829NN	LGA	ORD	108	733	7	29	2023-08-01 07:00:00	ORD
5808	12	26	941	950	-9	1135	1243	UA	160	N37413	EWR	LAS	272	2227	9	50	2023-12-26 09:00:00	Other
5809	11	27	2150	2200	-10	2345	2335	YX	1329	N121HQ	JFK	DCA	50	213	22	0	2023-11-27 22:00:00	Other
5818	8	11	619	625	-6	900	913	UA	216	N839UA	EWR	AUS	203	1504	6	25	2023-08-11 06:00:00	Other
5819	2	14	923	930	-7	1043	1059	YX	1518	N219YX	JFK	DCA	59	213	9	30	2023-02-14 09:00:00	Other
5826	8	6	1011	1020	-9	1137	1157	9E	1296	N921XJ	JFK	ROC	48	264	10	20	2023-08-06 10:00:00	Other
5830	9	28	849	855	-6	1007	1033	9E	1483	N916XJ	LGA	ORF	55	296	8	55	2023-09-28 08:00:00	Other
5845	3	22	1918	1929	-11	2248	2318	AA	93	N106NN	JFK	LAX	355	2475	19	29	2023-03-22 19:00:00	LAX
5846	10	29	1153	1159	-6	1450	1431	OO	1237	N313SY	LGA	SDF	118	659	11	59	2023-10-29 11:00:00	Other
5849	5	1	1919	1930	-11	2109	2148	YX	1193	N124HQ	LGA	LIT	150	1085	19	30	2023-05-01 19:00:00	Other
5852	2	27	551	600	-9	842	908	B6	452	N599JB	LGA	TPA	151	1010	6	0	2023-02-27 06:00:00	Other
5855	3	18	954	1000	-6	1114	1143	UA	726	N475UA	LGA	ORD	117	733	10	0	2023-03-18 10:00:00	ORD
5856	8	30	2029	2040	-11	2204	2217	9E	1216	N136EV	LGA	CHO	55	305	20	40	2023-08-30 20:00:00	Other
5861	9	4	936	945	-9	1101	1123	YX	1936	N245JQ	LGA	PWM	51	269	9	45	2023-09-04 09:00:00	Other
5865	8	31	1944	1950	-6	2232	2246	DL	208	N129DU	LGA	DFW	187	1389	19	50	2023-08-31 19:00:00	Other
5867	5	16	703	715	-12	809	827	B6	947	N281JB	LGA	BOS	40	184	7	15	2023-05-16 07:00:00	BOS
5870	4	26	1750	1759	-9	1918	1940	UA	724	N893UA	LGA	ORD	121	733	17	59	2023-04-26 17:00:00	ORD
5872	6	21	858	907	-9	1008	1030	B6	631	N236JB	JFK	BTV	44	266	9	7	2023-06-21 09:00:00	Other
5890	5	21	2051	2100	-9	2204	2247	YX	1186	N403YX	JFK	ORF	51	290	21	0	2023-05-21 21:00:00	Other
5892	3	24	1554	1600	-6	1930	1934	AS	89	N477AS	EWR	SFO	367	2565	16	0	2023-03-24 16:00:00	Other
5893	5	25	846	855	-9	1228	1222	AA	342	N108NN	JFK	SNA	336	2454	8	55	2023-05-25 08:00:00	Other
5894	2	9	839	900	-21	1021	1044	9E	1427	N131EV	JFK	RIC	58	288	9	0	2023-02-09 09:00:00	Other
5903	10	4	950	959	-9	1236	1307	UA	585	N38257	EWR	RSW	139	1068	9	59	2023-10-04 09:00:00	Other
5904	10	20	2149	2159	-10	2308	2327	9E	1380	N131EV	LGA	BGR	55	378	21	59	2023-10-20 21:00:00	Other
5907	4	10	2049	2059	-10	2302	2334	YX	1158	N106HQ	LGA	ATL	111	762	20	59	2023-04-10 20:00:00	ATL
5908	6	9	2237	2250	-13	2355	21	9E	1735	N138EV	JFK	SYR	46	209	22	50	2023-06-09 22:00:00	Other
5910	5	31	1602	1615	-13	1724	1800	9E	1483	N605LR	JFK	ORF	52	290	16	15	2023-05-31 16:00:00	Other
5913	12	8	1855	1905	-10	2159	2223	YX	1339	N119HQ	LGA	OKC	207	1341	19	5	2023-12-08 19:00:00	Other
5920	2	20	858	904	-6	1123	1147	B6	442	N618JB	JFK	ATL	124	760	9	4	2023-02-20 09:00:00	ATL
5928	6	17	555	601	-6	729	759	AA	987	N151UW	EWR	CLT	75	529	6	1	2023-06-17 06:00:00	CLT
5929	6	27	1125	1133	-8	1250	1244	B6	808	N239JB	JFK	ACK	39	199	11	33	2023-06-27 11:00:00	Other
5934	1	8	1750	1800	-10	1905	1912	9E	1399	N601LR	LGA	PVD	33	143	18	0	2023-01-08 18:00:00	Other
5941	10	3	1723	1729	-6	1840	1916	AA	987	N826AW	LGA	STL	122	888	17	29	2023-10-03 17:00:00	Other
5951	1	20	1549	1555	-6	1748	1817	9E	1720	N197PQ	LGA	CLT	92	544	15	55	2023-01-20 15:00:00	CLT
5959	2	1	1702	1709	-7	1904	1915	UA	502	N68802	EWR	DTW	94	488	17	9	2023-02-01 17:00:00	Other
5969	5	16	1916	1925	-9	2142	2158	YX	1198	N826MD	LGA	TUL	181	1231	19	25	2023-05-16 19:00:00	Other
5974	4	29	621	630	-9	823	900	UA	192	N466UA	LGA	DEN	219	1620	6	30	2023-04-29 06:00:00	Other
5977	10	30	1913	1925	-12	2149	2155	9E	1675	N921XJ	LGA	IND	118	660	19	25	2023-10-30 19:00:00	Other
5979	11	3	1552	1600	-8	1920	1933	AA	49	N107NN	JFK	SFO	365	2586	16	0	2023-11-03 16:00:00	Other
5980	4	13	2124	2130	-6	2219	2236	YX	1523	N879RW	LGA	PVD	33	143	21	30	2023-04-13 21:00:00	Other
5981	5	10	953	1000	-7	1225	1303	AA	606	N903AN	LGA	DFW	184	1389	10	0	2023-05-10 10:00:00	Other
5984	9	30	919	929	-10	1136	1154	YX	1063	N745YX	EWR	HHH	101	687	9	29	2023-09-30 09:00:00	Other
5992	12	13	1748	1759	-11	1950	2011	YX	1207	N136HQ	LGA	DSM	160	1031	17	59	2023-12-13 17:00:00	Other
5995	6	8	1100	1110	-10	1229	1240	YX	1403	N434YX	JFK	ORF	59	290	11	10	2023-06-08 11:00:00	Other
5998	3	15	1520	1529	-9	1733	1758	YX	1270	N417YX	JFK	IND	96	665	15	29	2023-03-15 15:00:00	Other
6000	12	2	1124	1130	-6	1424	1433	B6	672	N2060J	JFK	PBI	156	1028	11	30	2023-12-02 11:00:00	Other
6001	10	4	651	700	-9	753	815	UA	468	N37536	EWR	BOS	39	200	7	0	2023-10-04 07:00:00	BOS
6004	1	30	921	930	-9	1044	1059	YX	1773	N232JQ	JFK	DCA	64	213	9	30	2023-01-30 09:00:00	Other
6013	8	22	1049	1100	-11	1311	1343	UA	253	N883UA	EWR	DFW	169	1372	11	0	2023-08-22 11:00:00	Other
6014	6	14	853	900	-7	1105	1117	YX	1232	N856RW	EWR	HHH	102	687	9	0	2023-06-14 09:00:00	Other
6019	3	27	954	1000	-6	1115	1126	AA	799	N838AW	LGA	DCA	50	214	10	0	2023-03-27 10:00:00	Other
6020	12	6	2054	2100	-6	2346	28	AA	50	N104NN	JFK	LAX	326	2475	21	0	2023-12-06 21:00:00	LAX
6029	1	20	852	900	-8	1035	1113	AA	1062	N338ST	JFK	ORD	116	740	9	0	2023-01-20 09:00:00	ORD
6038	2	13	1200	1210	-10	1324	1342	YX	1233	N453YX	JFK	ORF	54	290	12	10	2023-02-13 12:00:00	Other
6046	11	16	1819	1825	-6	2043	2105	YX	1798	N232JQ	LGA	SDF	100	659	18	25	2023-11-16 18:00:00	Other
6053	1	3	1647	1654	-7	1832	1853	DL	898	N717JL	EWR	DTW	88	488	16	54	2023-01-03 16:00:00	Other
6056	10	2	818	830	-12	1045	1123	UA	124	N12021	EWR	LAX	293	2454	8	30	2023-10-02 08:00:00	LAX
6060	11	11	1402	1410	-8	1712	1713	OO	1200	N307SY	LGA	OKC	226	1341	14	10	2023-11-11 14:00:00	Other
6062	6	14	847	859	-12	1116	1123	YX	1340	N403YX	LGA	IND	102	660	8	59	2023-06-14 08:00:00	Other
6064	7	12	1714	1720	-6	1907	1902	YX	1423	N233JQ	LGA	BNA	116	764	17	20	2023-07-12 17:00:00	Other
6082	1	29	753	800	-7	1147	1146	B6	16	N612JB	JFK	PHX	324	2153	8	0	2023-01-29 08:00:00	Other
6083	1	1	1042	1050	-8	1156	1224	YX	1118	N746YX	EWR	ORF	52	284	10	50	2023-01-01 10:00:00	Other
6085	7	23	1948	1958	-10	2119	2130	OO	975	N253SY	LGA	MKE	109	738	19	58	2023-07-23 19:00:00	Other
6087	11	13	654	700	-6	1006	1008	UA	807	N14102	EWR	IAH	210	1400	7	0	2023-11-13 07:00:00	Other
6090	9	4	1231	1240	-9	1417	1417	AA	987	N881NN	LGA	ORD	104	733	12	40	2023-09-04 12:00:00	ORD
6111	8	15	2016	2029	-13	1	2357	AS	17	N423AS	JFK	SFO	323	2586	20	29	2023-08-15 20:00:00	Other
6117	11	14	2011	2021	-10	2331	2338	B6	550	N929JB	EWR	LAX	338	2454	20	21	2023-11-14 20:00:00	LAX
6119	2	6	1323	1330	-7	1437	1502	YX	1588	N216JQ	LGA	RIC	53	292	13	30	2023-02-06 13:00:00	Other
6130	2	5	1423	1429	-6	1510	1529	B6	319	N323JB	JFK	ORH	29	150	14	29	2023-02-05 14:00:00	Other
6139	8	18	554	600	-6	756	800	AA	751	N554UW	EWR	CLT	90	529	6	0	2023-08-18 06:00:00	CLT
6142	12	5	629	635	-6	1016	1021	AA	832	N321RL	JFK	PHX	304	2153	6	35	2023-12-05 06:00:00	Other
6153	5	13	1059	1105	-6	1239	1259	DL	950	N891AT	EWR	DTW	80	488	11	5	2023-05-13 11:00:00	Other
6166	9	28	1952	2000	-8	2200	2222	YX	1957	N212JQ	JFK	CLT	89	541	20	0	2023-09-28 20:00:00	CLT
6174	2	2	1752	1800	-8	1907	1927	YX	1565	N216JQ	JFK	PWM	47	273	18	0	2023-02-02 18:00:00	Other
6180	11	21	1220	1229	-9	1325	1333	9E	1418	N479PX	LGA	ORH	33	146	12	29	2023-11-21 12:00:00	Other
6186	11	25	2015	2030	-15	2136	2201	NK	1038	N617NK	LGA	ORD	118	733	20	30	2023-11-25 20:00:00	ORD
6191	10	31	1700	1710	-10	1832	1844	9E	1465	N928XJ	LGA	ROC	52	254	17	10	2023-10-31 17:00:00	Other
6195	5	31	1427	1435	-8	1604	1633	YX	1351	N872RW	LGA	STL	124	888	14	35	2023-05-31 14:00:00	Other
6196	10	8	1021	1030	-9	1326	1343	B6	668	N584JB	LGA	RSW	165	1080	10	30	2023-10-08 10:00:00	Other
6198	12	31	655	708	-13	915	1010	UA	230	N17254	EWR	BZN	238	1882	7	8	2023-12-31 07:00:00	Other
6203	11	14	2152	2159	-7	2303	2318	YX	1255	N408YX	JFK	BOS	37	187	21	59	2023-11-14 21:00:00	BOS
6212	4	8	720	729	-9	940	946	B6	308	N206JB	JFK	SAV	118	718	7	29	2023-04-08 07:00:00	Other
6213	8	19	1742	1750	-8	1931	2013	9E	1222	N931XJ	LGA	CLT	80	544	17	50	2023-08-19 17:00:00	CLT
6214	4	28	1214	1221	-7	1353	1358	YX	1258	N104HQ	LGA	PIT	66	335	12	21	2023-04-28 12:00:00	Other
6215	1	27	1917	1925	-8	2021	2040	YX	1307	N422YX	JFK	BOS	43	187	19	25	2023-01-27 19:00:00	BOS
6219	8	3	1320	1329	-9	1449	1508	9E	1116	N931XJ	JFK	RIC	57	288	13	29	2023-08-03 13:00:00	Other
6223	11	25	1217	1225	-8	1315	1353	YX	1274	N122HQ	LGA	DCA	43	214	12	25	2023-11-25 12:00:00	Other
6226	3	6	624	635	-11	818	827	YX	1611	N220JQ	LGA	CMH	90	479	6	35	2023-03-06 06:00:00	Other
6235	11	25	1854	1900	-6	2202	2206	DL	862	N326US	JFK	AUS	229	1521	19	0	2023-11-25 19:00:00	Other
6252	4	11	623	630	-7	732	746	B6	872	N328JB	JFK	BUF	56	301	6	30	2023-04-11 06:00:00	Other
6255	3	5	608	615	-7	834	825	B6	42	N317JB	JFK	MSP	183	1029	6	15	2023-03-05 06:00:00	Other
6257	2	1	1022	1029	-7	1236	1244	YX	1084	N649RW	EWR	GSP	105	594	10	29	2023-02-01 10:00:00	Other
6258	11	5	846	854	-8	1015	1055	9E	1442	N922XJ	LGA	CLE	67	419	8	54	2023-11-05 08:00:00	Other
6262	8	9	731	737	-6	1033	1029	AA	129	N867NN	LGA	DFW	193	1389	7	37	2023-08-09 07:00:00	Other
6266	11	20	1201	1210	-9	1311	1320	9E	1748	N485PX	LGA	BGM	34	147	12	10	2023-11-20 12:00:00	Other
6275	5	4	548	600	-12	644	719	AA	729	N730US	LGA	DCA	41	214	6	0	2023-05-04 06:00:00	Other
6278	11	10	1143	1149	-6	1254	1325	YX	1767	N879RW	LGA	BGR	54	378	11	49	2023-11-10 11:00:00	Other
6281	5	16	1620	1629	-9	1821	1844	YX	1211	N401YX	LGA	GSP	97	610	16	29	2023-05-16 16:00:00	Other
6282	8	20	1522	1529	-7	1635	1658	YX	1024	N121HQ	LGA	ORF	54	296	15	29	2023-08-20 15:00:00	Other
6285	12	1	650	659	-9	848	914	AA	180	N908NN	LGA	CLT	91	544	6	59	2023-12-01 06:00:00	CLT
6291	12	2	1435	1445	-10	1554	1615	YX	1276	N138HQ	LGA	BUF	58	292	14	45	2023-12-02 14:00:00	Other
6295	5	17	1817	1825	-8	2117	2131	AS	171	N260AK	EWR	SEA	320	2402	18	25	2023-05-17 18:00:00	Other
6298	9	14	723	730	-7	910	930	UA	461	N17565	EWR	CLT	83	529	7	30	2023-09-14 07:00:00	CLT
6303	1	10	820	830	-10	935	1011	YX	1398	N871RW	LGA	RIC	55	292	8	30	2023-01-10 08:00:00	Other
6306	3	31	1910	1918	-8	2223	2229	UA	566	N27268	EWR	RSW	156	1068	19	18	2023-03-31 19:00:00	Other
6308	8	16	853	900	-7	1144	1222	AS	16	N964AK	JFK	SFO	319	2586	9	0	2023-08-16 09:00:00	Other
6309	11	4	1417	1425	-8	1631	1652	9E	1464	N303PQ	LGA	SAV	105	722	14	25	2023-11-04 14:00:00	Other
6317	10	8	1402	1408	-6	1555	1617	9E	1575	N348PQ	JFK	CVG	92	589	14	8	2023-10-08 14:00:00	Other
6321	10	26	824	830	-6	1039	1057	B6	943	N517JB	LGA	ATL	105	762	8	30	2023-10-26 08:00:00	ATL
6340	12	4	1624	1637	-13	1742	1824	9E	1388	N904XJ	LGA	PIT	58	335	16	37	2023-12-04 16:00:00	Other
6348	2	9	1459	1505	-6	1749	1815	DL	751	N339NW	LGA	TPA	148	1010	15	5	2023-02-09 15:00:00	Other
6358	9	22	723	729	-6	1008	1031	DL	790	N3759	JFK	PBI	137	1028	7	29	2023-09-22 07:00:00	Other
6360	10	3	1050	1057	-7	1224	1244	YX	1072	N749YX	EWR	RDU	68	416	10	57	2023-10-03 10:00:00	Other
6366	11	17	1219	1226	-7	1522	1540	DL	510	N331NB	JFK	AUS	212	1521	12	26	2023-11-17 12:00:00	Other
6368	6	2	1151	1200	-9	1252	1306	B6	761	N348JB	JFK	HYA	36	196	12	0	2023-06-02 12:00:00	Other
6369	10	16	822	830	-8	1030	1123	UA	124	N12020	EWR	LAX	282	2454	8	30	2023-10-16 08:00:00	LAX
6382	3	28	1930	1945	-15	2314	2241	B6	687	N307JB	LGA	PBI	179	1035	19	45	2023-03-28 19:00:00	Other
6383	11	1	913	923	-10	1214	1226	AA	229	N927AN	EWR	DFW	200	1372	9	23	2023-11-01 09:00:00	Other
6386	11	5	1018	1025	-7	1151	1216	YX	1351	N414YX	LGA	ROA	69	405	10	25	2023-11-05 10:00:00	Other
6400	12	1	1704	1710	-6	2013	1950	YX	1031	N768YX	EWR	JAX	132	820	17	10	2023-12-01 17:00:00	Other
6404	3	28	953	1000	-7	1305	1236	B6	16	N958JB	JFK	PHX	328	2153	10	0	2023-03-28 10:00:00	Other
6405	10	15	2148	2155	-7	35	119	B6	912	N943JT	JFK	SFO	323	2586	21	55	2023-10-15 21:00:00	Other
6407	4	22	1353	1359	-6	1601	1633	DL	170	N398DA	JFK	DEN	217	1626	13	59	2023-04-22 13:00:00	Other
6409	9	18	1253	1300	-7	1546	1618	AS	5	N435AS	JFK	SFO	324	2586	13	0	2023-09-18 13:00:00	Other
6410	11	8	1140	1150	-10	1314	1337	9E	1446	N303PQ	LGA	PIT	67	335	11	50	2023-11-08 11:00:00	Other
6412	1	19	1725	1735	-10	2101	2105	B6	1037	N935JB	JFK	LAX	335	2475	17	35	2023-01-19 17:00:00	LAX
6420	7	13	653	700	-7	947	1001	UA	734	N17302	EWR	MIA	141	1085	7	0	2023-07-13 07:00:00	MIA
6421	4	24	2024	2030	-6	2206	2212	YX	1071	N401YX	EWR	ORD	116	719	20	30	2023-04-24 20:00:00	ORD
6436	1	30	1751	1800	-9	1915	1936	AA	398	N724UW	LGA	DCA	53	214	18	0	2023-01-30 18:00:00	Other
6442	10	6	2051	2100	-9	2210	2226	B6	62	N231JB	JFK	BTV	46	266	21	0	2023-10-06 21:00:00	Other
6446	11	4	1511	1520	-9	1631	1659	YX	1853	N206JQ	LGA	BNA	117	764	15	20	2023-11-04 15:00:00	Other
6457	5	12	1022	1029	-7	1132	1220	9E	1397	N296PQ	LGA	ORF	48	296	10	29	2023-05-12 10:00:00	Other
6458	11	13	1150	1200	-10	1323	1355	9E	1441	N491PX	LGA	CLE	76	419	12	0	2023-11-13 12:00:00	Other
6466	4	10	1020	1030	-10	1129	1153	YX	929	N653RW	EWR	DCA	43	199	10	30	2023-04-10 10:00:00	Other
6469	6	13	1952	2000	-8	2246	2256	B6	86	N2039J	JFK	MCO	137	944	20	0	2023-06-13 20:00:00	MCO
6470	1	12	1159	1210	-11	1508	1443	B6	642	N794JB	JFK	DEN	242	1626	12	10	2023-01-12 12:00:00	Other
6471	10	26	1254	1304	-10	1405	1420	YX	1165	N859RW	EWR	SYR	40	195	13	4	2023-10-26 13:00:00	Other
6476	8	29	1751	1759	-8	2001	2027	UA	700	N809UA	LGA	DEN	217	1620	17	59	2023-08-29 17:00:00	Other
6477	3	20	1553	1600	-7	1917	1921	AA	98	N116AN	JFK	LAX	363	2475	16	0	2023-03-20 16:00:00	LAX
6478	7	25	1449	1455	-6	1828	1710	DL	520	N315NB	LGA	DTW	80	502	14	55	2023-07-25 14:00:00	Other
6484	8	26	1615	1625	-10	1806	1830	YX	1305	N233JQ	LGA	CMH	80	479	16	25	2023-08-26 16:00:00	Other
6490	11	27	1525	1531	-6	1702	1726	YX	1769	N246JQ	JFK	PIT	69	340	15	31	2023-11-27 15:00:00	Other
6505	2	8	1533	1543	-10	1743	1754	NK	501	N522NK	LGA	CLT	82	544	15	43	2023-02-08 15:00:00	CLT
6511	10	2	642	650	-8	933	956	B6	766	N637JB	JFK	RSW	148	1074	6	50	2023-10-02 06:00:00	Other
6512	9	21	840	848	-8	1114	1131	YX	1846	N225JQ	JFK	JAX	120	828	8	48	2023-09-21 08:00:00	Other
6520	8	22	826	840	-14	1118	1142	B6	536	N980JT	EWR	LAX	312	2454	8	40	2023-08-22 08:00:00	LAX
6526	12	9	1553	1600	-7	1731	1800	WN	796	N8727M	LGA	STL	140	888	16	0	2023-12-09 16:00:00	Other
6527	10	26	1316	1325	-9	1441	1504	YX	1351	N107HQ	JFK	PIT	65	340	13	25	2023-10-26 13:00:00	Other
6533	11	17	2104	2110	-6	2220	2232	9E	1584	N901XJ	JFK	BWI	37	184	21	10	2023-11-17 21:00:00	Other
6538	12	19	2024	2030	-6	2141	2159	YX	1100	N758YX	EWR	DCA	49	199	20	30	2023-12-19 20:00:00	Other
6541	10	9	620	630	-10	752	808	UA	254	N27263	EWR	CLE	65	404	6	30	2023-10-09 06:00:00	Other
6546	3	16	550	600	-10	829	912	B6	581	N587JB	EWR	FLL	127	1065	6	0	2023-03-16 06:00:00	FLL
6549	11	7	2016	2025	-9	2150	2200	YX	1776	N860RW	LGA	DCA	54	214	20	25	2023-11-07 20:00:00	Other
6551	8	19	1733	1743	-10	1917	1954	YX	1018	N425YX	LGA	OMA	147	1148	17	43	2023-08-19 17:00:00	Other
6552	10	24	633	640	-7	804	822	9E	1658	N915XJ	LGA	CLE	67	419	6	40	2023-10-24 06:00:00	Other
6561	9	22	1753	1800	-7	2125	2103	DL	339	N179DN	JFK	LAX	333	2475	18	0	2023-09-22 18:00:00	LAX
6569	11	16	1509	1515	-6	1625	1654	UA	918	N882UA	LGA	ORD	115	733	15	15	2023-11-16 15:00:00	ORD
6571	4	20	954	1000	-6	1246	1300	UA	365	N14001	EWR	LAX	317	2454	10	0	2023-04-20 10:00:00	LAX
6572	8	11	1641	1649	-8	1800	1822	YX	878	N749YX	EWR	BGR	60	393	16	49	2023-08-11 16:00:00	Other
6574	2	17	1138	1145	-7	1328	1345	YX	1285	N450YX	JFK	CLE	89	425	11	45	2023-02-17 11:00:00	Other
6576	10	25	2008	2015	-7	2226	2246	B6	893	N506JB	LGA	ATL	107	762	20	15	2023-10-25 20:00:00	ATL
6584	11	6	623	630	-7	908	926	NK	471	N629NK	LGA	MCO	126	950	6	30	2023-11-06 06:00:00	MCO
6593	11	30	1136	1142	-6	1343	1354	YX	1313	N102HQ	JFK	IND	104	665	11	42	2023-11-30 11:00:00	Other
6597	8	31	2111	2119	-8	2214	2228	YX	839	N753YX	EWR	MDT	26	141	21	19	2023-08-31 21:00:00	Other
6606	11	6	1050	1059	-9	1401	1359	NK	260	N655NK	LGA	MCO	130	950	10	59	2023-11-06 10:00:00	MCO
6608	3	6	824	830	-6	938	958	YX	1651	N227JQ	LGA	SYR	43	198	8	30	2023-03-06 08:00:00	Other
6613	3	2	550	600	-10	829	902	B6	110	N975JT	EWR	MCO	142	937	6	0	2023-03-02 06:00:00	MCO
6615	10	14	1650	1700	-10	1759	1826	YX	1716	N204JQ	LGA	BOS	35	184	17	0	2023-10-14 17:00:00	BOS
6622	2	24	630	639	-9	851	901	UA	821	N24706	EWR	MSY	182	1167	6	39	2023-02-24 06:00:00	Other
6623	6	29	903	915	-12	1012	1035	B6	927	N266JB	LGA	BOS	38	184	9	15	2023-06-29 09:00:00	BOS
6625	3	2	1749	1755	-6	2021	2007	DL	561	N351NB	EWR	MSP	174	1008	17	55	2023-03-02 17:00:00	Other
6634	12	11	851	901	-10	1114	1128	YX	1244	N421YX	LGA	CVG	105	585	9	1	2023-12-11 09:00:00	Other
6635	8	18	2054	2100	-6	2224	2253	9E	1175	N491PX	LGA	RDU	67	431	21	0	2023-08-18 21:00:00	Other
6639	9	13	846	855	-9	1051	1118	YX	1831	N228JQ	LGA	SDF	107	659	8	55	2023-09-13 08:00:00	Other
6652	12	2	2219	2230	-11	2325	2358	9E	1383	N676CA	JFK	PWM	44	273	22	30	2023-12-02 22:00:00	Other
6656	3	8	1213	1220	-7	1404	1427	9E	1458	N930XJ	LGA	STL	145	888	12	20	2023-03-08 12:00:00	Other
6658	2	23	1124	1130	-6	1316	1320	DL	584	N145DQ	LGA	ORD	133	733	11	30	2023-02-23 11:00:00	ORD
6659	3	8	1132	1138	-6	1332	1345	DL	287	N113DQ	EWR	MSP	159	1008	11	38	2023-03-08 11:00:00	Other
6662	11	24	1923	1929	-6	2121	2139	AA	472	N9010R	JFK	CLT	89	541	19	29	2023-11-24 19:00:00	CLT
6672	11	3	2050	2100	-10	2221	2254	YX	1403	N122HQ	LGA	ILM	76	500	21	0	2023-11-03 21:00:00	Other
6675	10	20	1223	1232	-9	1324	1351	YX	1272	N447YX	JFK	BOS	33	187	12	32	2023-10-20 12:00:00	BOS
6679	4	1	1254	1304	-10	1425	1424	YX	1113	N412YX	JFK	BOS	39	187	13	4	2023-04-01 13:00:00	BOS
6682	3	24	1359	1405	-6	1559	1618	YX	1073	N723YX	EWR	CHS	92	628	14	5	2023-03-24 14:00:00	Other
6685	8	18	1243	1250	-7	1349	1357	9E	1283	N153PQ	JFK	ITH	40	189	12	50	2023-08-18 12:00:00	Other
6686	12	10	719	730	-11	1022	1105	AS	10	N963AK	JFK	SEA	328	2422	7	30	2023-12-10 07:00:00	Other
6687	9	21	2151	2159	-8	2303	2323	YX	1381	N419YX	JFK	BOS	37	187	21	59	2023-09-21 21:00:00	BOS
6691	10	7	1041	1047	-6	1144	1155	YX	1127	N741YX	EWR	AVP	27	93	10	47	2023-10-07 10:00:00	Other
6694	4	4	2004	2012	-8	2214	2221	YX	941	N721YX	EWR	DTW	83	488	20	12	2023-04-04 20:00:00	Other
6696	12	12	1821	1830	-9	2013	2056	9E	1633	N316PQ	LGA	GSP	93	610	18	30	2023-12-12 18:00:00	Other
6697	10	22	1931	1940	-9	2225	2216	DL	883	N107DU	LGA	JAX	112	833	19	40	2023-10-22 19:00:00	Other
6703	6	4	639	645	-6	932	950	UA	288	N460UA	EWR	FLL	158	1065	6	45	2023-06-04 06:00:00	FLL
6711	9	20	1049	1059	-10	1157	1237	9E	1629	N935XJ	LGA	BNA	103	764	10	59	2023-09-20 10:00:00	Other
6712	8	1	1549	1559	-10	1712	1749	9E	1198	N933XJ	LGA	BGR	54	378	15	59	2023-08-01 15:00:00	Other
6716	4	27	2149	2159	-10	119	158	B6	654	N965JT	JFK	SJU	178	1598	21	59	2023-04-27 21:00:00	Other
6722	9	28	2131	2140	-9	2250	2303	UA	261	N449UA	EWR	MKE	102	725	21	40	2023-09-28 21:00:00	Other
6724	3	14	745	754	-9	1051	1030	YX	1114	N727YX	EWR	SDF	116	642	7	54	2023-03-14 07:00:00	Other
6736	12	23	851	859	-8	1117	1137	B6	22	N3065J	JFK	MSY	164	1182	8	59	2023-12-23 08:00:00	Other
6737	1	22	2051	2100	-9	2326	2323	YX	1368	N124HQ	LGA	DTW	92	502	21	0	2023-01-22 21:00:00	Other
6739	5	11	832	841	-9	1019	1035	NK	296	N686NK	LGA	MYR	81	563	8	41	2023-05-11 08:00:00	Other
6740	1	17	2053	2100	-7	2209	2252	YX	1263	N639RW	LGA	ORD	111	733	21	0	2023-01-17 21:00:00	ORD
6747	5	16	2138	2147	-9	2253	2312	9E	1435	N319PQ	LGA	BUF	51	292	21	47	2023-05-16 21:00:00	Other
6749	1	15	1407	1415	-8	1525	1527	B6	368	N266JB	LGA	BOS	48	184	14	15	2023-01-15 14:00:00	BOS
6752	5	15	1859	1908	-9	2153	2155	YX	1243	N436YX	LGA	OKC	194	1341	19	8	2023-05-15 19:00:00	Other
6759	12	22	1309	1318	-9	1424	1450	YX	1051	N727YX	EWR	PIT	56	319	13	18	2023-12-22 13:00:00	Other
6760	4	26	652	659	-7	1007	1020	B6	644	N570JB	LGA	RSW	164	1080	6	59	2023-04-26 06:00:00	Other
6773	4	20	1152	1200	-8	1252	1308	YX	1217	N137HQ	JFK	ORH	33	150	12	0	2023-04-20 12:00:00	Other
6783	1	7	833	841	-8	1035	1113	YX	1793	N880RW	LGA	CHS	98	641	8	41	2023-01-07 08:00:00	Other
6784	12	20	1823	1829	-6	1930	2001	YX	1723	N206JQ	LGA	BOS	44	184	18	29	2023-12-20 18:00:00	BOS
6787	11	17	1738	1745	-7	1931	1938	YX	1070	N763YX	EWR	GSO	78	445	17	45	2023-11-17 17:00:00	Other
6788	4	14	946	1000	-14	1102	1127	AA	433	N827AW	LGA	DCA	49	214	10	0	2023-04-14 10:00:00	Other
6790	2	26	1548	1555	-7	1709	1710	9E	1476	N326PQ	LGA	ALB	35	136	15	55	2023-02-26 15:00:00	Other
6801	5	30	1858	1908	-10	2141	2155	YX	1243	N442YX	LGA	OKC	182	1341	19	8	2023-05-30 19:00:00	Other
6810	9	4	2123	2130	-7	2302	2335	YX	1961	N219YX	JFK	CMH	70	483	21	30	2023-09-04 21:00:00	Other
6815	7	28	1644	1650	-6	2008	2018	AS	11	N215AK	JFK	SFO	340	2586	16	50	2023-07-28 16:00:00	Other
6817	1	11	551	600	-9	732	755	DL	834	N989AT	EWR	DTW	83	488	6	0	2023-01-11 06:00:00	Other
6822	3	20	1148	1155	-7	1359	1420	G4	975	316NV	EWR	SAV	117	708	11	55	2023-03-20 11:00:00	Other
6831	4	26	1453	1459	-6	1625	1643	UA	554	N818UA	EWR	RDU	69	416	14	59	2023-04-26 14:00:00	Other
6833	4	27	2119	2129	-10	2237	2249	YX	1470	N219YX	LGA	BTV	49	258	21	29	2023-04-27 21:00:00	Other
6839	12	30	753	800	-7	907	943	UA	847	N895UA	LGA	ORD	104	733	8	0	2023-12-30 08:00:00	ORD
6840	9	3	1032	1040	-8	1136	1210	YX	1394	N417YX	JFK	BNA	100	765	10	40	2023-09-03 10:00:00	Other
6848	4	11	830	838	-8	957	1037	YX	959	N754YX	EWR	GSO	62	445	8	38	2023-04-11 08:00:00	Other
6850	8	31	1731	1740	-9	1920	1943	9E	1269	N907XJ	LGA	DSM	139	1031	17	40	2023-08-31 17:00:00	Other
6855	6	9	1335	1344	-9	1651	1658	B6	94	N599JB	JFK	AUS	193	1521	13	44	2023-06-09 13:00:00	Other
6857	2	19	523	530	-7	824	835	UA	195	N68843	EWR	IAH	213	1400	5	30	2023-02-19 05:00:00	Other
6858	5	28	1908	1915	-7	2139	2215	UA	779	N443UA	EWR	DFW	177	1372	19	15	2023-05-28 19:00:00	Other
6860	9	7	621	630	-9	754	801	UA	955	N17730	LGA	ORD	118	733	6	30	2023-09-07 06:00:00	ORD
6872	2	5	1658	1707	-9	1840	1917	AA	423	N807AW	LGA	STL	134	888	17	7	2023-02-05 17:00:00	Other
6878	2	5	1246	1255	-9	1501	1530	YX	1572	N203JQ	LGA	SDF	115	659	12	55	2023-02-05 12:00:00	Other
6889	10	5	1853	1900	-7	2300	2304	DL	666	N857DZ	JFK	SJU	214	1598	19	0	2023-10-05 19:00:00	Other
6890	8	5	1023	1029	-6	1208	1227	9E	1185	N324PQ	LGA	MYR	86	563	10	29	2023-08-05 10:00:00	Other
6892	11	24	1054	1100	-6	1456	1405	AA	218	N902AN	JFK	MIA	173	1089	11	0	2023-11-24 11:00:00	MIA
6896	5	10	701	710	-9	949	1012	DL	600	N308DN	LGA	FLL	141	1076	7	10	2023-05-10 07:00:00	FLL
6910	10	10	1710	1720	-10	1913	1940	9E	1481	N491PX	LGA	CVG	97	585	17	20	2023-10-10 17:00:00	Other
6911	1	5	637	645	-8	940	954	B6	517	N638JB	LGA	TPA	159	1010	6	45	2023-01-05 06:00:00	Other
6920	1	25	916	923	-7	1039	1053	B6	690	N183JB	JFK	BUF	59	301	9	23	2023-01-25 09:00:00	Other
6924	5	19	1243	1250	-7	1349	1359	9E	1269	N310PQ	JFK	ITH	42	189	12	50	2023-05-19 12:00:00	Other
6928	5	2	1913	1920	-7	2157	2229	DL	329	N3745B	LGA	PBI	143	1035	19	20	2023-05-02 19:00:00	Other
6929	8	15	922	929	-7	1159	1153	YX	907	N640RW	EWR	TVC	99	644	9	29	2023-08-15 09:00:00	Other
6930	6	23	554	600	-6	740	732	UA	394	N37553	EWR	ORD	106	719	6	0	2023-06-23 06:00:00	ORD
6933	10	28	654	700	-6	812	815	UA	468	N39418	EWR	BOS	46	200	7	0	2023-10-28 07:00:00	BOS
6938	9	3	1723	1729	-6	2000	2031	AA	973	N341RW	JFK	AUS	189	1521	17	29	2023-09-03 17:00:00	Other
6941	8	29	758	805	-7	1001	1014	DL	447	N339NB	JFK	MSP	154	1029	8	5	2023-08-29 08:00:00	Other
6943	10	24	752	800	-8	1010	1015	B6	289	N561JB	JFK	SAV	100	718	8	0	2023-10-24 08:00:00	Other
6950	1	23	1022	1029	-7	1233	1244	YX	1206	N654RW	EWR	GSP	100	594	10	29	2023-01-23 10:00:00	Other
6955	3	24	516	525	-9	652	700	AA	913	N856NN	EWR	ORD	129	719	5	25	2023-03-24 05:00:00	ORD
6961	10	15	945	954	-9	1101	1133	9E	1579	N932XJ	JFK	RIC	55	288	9	54	2023-10-15 09:00:00	Other
6964	11	10	2129	2135	-6	150	231	B6	648	N950JT	JFK	SJU	187	1598	21	35	2023-11-10 21:00:00	Other
6967	8	10	1618	1625	-7	2011	1935	AA	84	N117AN	JFK	LAX	366	2475	16	25	2023-08-10 16:00:00	LAX
6976	1	30	2121	2129	-8	2303	2336	YX	1438	N136HQ	LGA	CLE	82	419	21	29	2023-01-30 21:00:00	Other
6978	11	29	1248	1259	-11	1510	1537	DL	280	N119DN	LGA	ATL	110	762	12	59	2023-11-29 12:00:00	ATL
6989	3	5	1923	1929	-6	2225	2259	DL	293	N127DU	LGA	DFW	205	1389	19	29	2023-03-05 19:00:00	Other
6990	9	3	1901	1910	-9	2050	2127	YX	1340	N871RW	LGA	IND	90	660	19	10	2023-09-03 19:00:00	Other
6994	10	14	851	900	-9	1146	1218	AA	1	N108NN	JFK	LAX	328	2475	9	0	2023-10-14 09:00:00	LAX
6998	12	4	1428	1435	-7	1551	1616	9E	1425	N200PQ	JFK	RIC	59	288	14	35	2023-12-04 14:00:00	Other
7004	5	26	2049	2059	-10	2211	2222	YX	1708	N216JQ	LGA	BOS	44	184	20	59	2023-05-26 20:00:00	BOS
7006	8	13	1622	1629	-7	1756	1822	AA	763	N760US	LGA	RDU	65	431	16	29	2023-08-13 16:00:00	Other
7008	11	14	1023	1029	-6	1214	1226	9E	1513	N181GJ	LGA	RDU	71	431	10	29	2023-11-14 10:00:00	Other
7025	11	10	1920	1929	-9	2132	2151	9E	1593	N915XJ	LGA	CVG	105	585	19	29	2023-11-10 19:00:00	Other
7026	9	4	854	900	-6	953	1025	UA	671	N471UA	EWR	ORF	44	284	9	0	2023-09-04 09:00:00	Other
7027	9	28	830	840	-10	1037	1051	YX	1362	N401YX	LGA	MCI	152	1107	8	40	2023-09-28 08:00:00	Other
7046	2	15	1504	1510	-6	1723	1737	NK	847	N637NK	EWR	MSY	181	1167	15	10	2023-02-15 15:00:00	Other
7051	5	13	1105	1115	-10	1333	1414	B6	204	N589JB	EWR	PBI	130	1023	11	15	2023-05-13 11:00:00	Other
7058	3	8	1221	1231	-10	1534	1551	UA	796	N35236	EWR	SAT	233	1569	12	31	2023-03-08 12:00:00	Other
7064	2	20	1327	1335	-8	1504	1526	AA	156	N940AN	LGA	ORD	120	733	13	35	2023-02-20 13:00:00	ORD
7074	11	17	2150	2156	-6	2303	2316	UA	873	N66808	EWR	ORF	47	284	21	56	2023-11-17 21:00:00	Other
7075	9	1	1818	1824	-6	2005	2044	DL	383	N387DN	LGA	MSP	141	1020	18	24	2023-09-01 18:00:00	Other
7084	11	13	1521	1527	-6	1719	1724	YX	1279	N136HQ	LGA	CLE	79	419	15	27	2023-11-13 15:00:00	Other
7093	7	24	1816	1825	-9	2136	2020	YX	1008	N105HQ	JFK	CMH	76	483	18	25	2023-07-24 18:00:00	Other
7097	4	3	1924	1930	-6	2305	2319	AA	94	N110AN	JFK	LAX	357	2475	19	30	2023-04-03 19:00:00	LAX
7098	9	18	1253	1304	-11	1347	1415	YX	1045	N749YX	EWR	MDT	30	141	13	4	2023-09-18 13:00:00	Other
7100	11	2	851	858	-7	1049	1059	YX	1778	N244JQ	LGA	CMH	82	479	8	58	2023-11-02 08:00:00	Other
7103	5	17	747	754	-7	1015	1110	UA	661	N27277	EWR	PDX	311	2434	7	54	2023-05-17 07:00:00	Other
7111	10	7	2134	2144	-10	2304	2322	YX	1025	N758YX	EWR	BGR	67	393	21	44	2023-10-07 21:00:00	Other
7114	10	16	2053	2059	-6	2212	2225	YX	1354	N403YX	JFK	BOS	40	187	20	59	2023-10-16 20:00:00	BOS
7116	2	1	545	600	-15	958	926	B6	510	N993JE	EWR	LAX	353	2454	6	0	2023-02-01 06:00:00	LAX
7118	4	7	1918	1925	-7	2227	2242	UA	813	N14120	EWR	LAX	327	2454	19	25	2023-04-07 19:00:00	LAX
7120	12	3	1652	1700	-8	1835	1843	9E	1478	N479PX	LGA	RIC	60	292	17	0	2023-12-03 17:00:00	Other
7134	12	30	805	815	-10	1002	1112	UA	216	N12109	EWR	EGE	219	1725	8	15	2023-12-30 08:00:00	Other
7137	11	12	1019	1027	-8	1319	1336	DL	378	N339DN	LGA	TPA	151	1010	10	27	2023-11-12 10:00:00	Other
7139	12	13	1007	1015	-8	1315	1340	DL	412	N130DU	LGA	IAH	220	1416	10	15	2023-12-13 10:00:00	Other
7144	3	3	917	923	-6	1129	1143	UA	783	N441UA	EWR	MCI	164	1092	9	23	2023-03-03 09:00:00	Other
7145	3	23	1731	1740	-9	1941	1958	9E	1380	N902XJ	LGA	CVG	105	585	17	40	2023-03-23 17:00:00	Other
7149	3	9	1124	1130	-6	1411	1434	DL	1010	N371DN	LGA	MCO	133	950	11	30	2023-03-09 11:00:00	MCO
7152	11	1	1354	1400	-6	1457	1521	YX	1822	N234JQ	LGA	BOS	34	184	14	0	2023-11-01 14:00:00	BOS
7157	12	12	1926	1935	-9	2115	2137	OO	1193	N323SY	JFK	ORD	139	740	19	35	2023-12-12 19:00:00	ORD
7178	6	13	1616	1627	-11	1822	1852	YX	1187	N859RW	EWR	SDF	102	642	16	27	2023-06-13 16:00:00	Other
7179	11	12	806	816	-10	1135	1143	UA	783	N444UA	EWR	SEA	357	2402	8	16	2023-11-12 08:00:00	Other
7182	12	3	1133	1140	-7	1225	1243	YX	1257	N406YX	JFK	ORH	29	150	11	40	2023-12-03 11:00:00	Other
7186	2	1	550	600	-10	739	724	AA	445	N834AW	LGA	DCA	52	214	6	0	2023-02-01 06:00:00	Other
7190	8	14	2124	2130	-6	2231	2256	YX	1049	N131HQ	JFK	BOS	42	187	21	30	2023-08-14 21:00:00	BOS
7191	2	16	1324	1330	-6	1424	1443	B6	41	N355JB	JFK	SYR	44	209	13	30	2023-02-16 13:00:00	Other
7199	7	24	923	930	-7	1252	1249	B6	35	N964JT	JFK	SFO	329	2586	9	30	2023-07-24 09:00:00	Other
7203	2	8	2048	2100	-12	2207	2255	YX	1187	N447YX	LGA	RIC	55	292	21	0	2023-02-08 21:00:00	Other
7205	5	26	1107	1115	-8	1357	1414	B6	204	N806JB	EWR	PBI	152	1023	11	15	2023-05-26 11:00:00	Other
7211	10	31	1004	1015	-11	1317	1321	B6	636	N980JT	EWR	LAX	338	2454	10	15	2023-10-31 10:00:00	LAX
7212	9	19	723	730	-7	1030	1040	AS	12	N946AK	JFK	SEA	324	2422	7	30	2023-09-19 07:00:00	Other
7214	2	16	1619	1628	-9	1745	1818	YX	1250	N871RW	LGA	CHO	60	305	16	28	2023-02-16 16:00:00	Other
7218	12	20	1343	1350	-7	1546	1614	9E	1547	N324PQ	LGA	TYS	99	647	13	50	2023-12-20 13:00:00	Other
7219	10	11	949	955	-6	1235	1245	DL	399	N358DN	JFK	MCO	142	944	9	55	2023-10-11 09:00:00	MCO
7222	6	29	552	559	-7	726	733	AA	1039	N961AN	EWR	ORD	110	719	5	59	2023-06-29 05:00:00	ORD
7223	11	27	1622	1629	-7	1917	1927	UA	792	N37419	EWR	MCO	145	937	16	29	2023-11-27 16:00:00	MCO
7224	4	28	1243	1250	-7	1341	1357	YX	1456	N236JQ	LGA	PVD	32	143	12	50	2023-04-28 12:00:00	Other
7225	2	28	1344	1352	-8	1657	1708	AA	174	N824NN	LGA	DFW	214	1389	13	52	2023-02-28 13:00:00	Other
7235	2	3	609	615	-6	854	853	DL	732	N707TW	JFK	ATL	137	760	6	15	2023-02-03 06:00:00	ATL
7240	10	25	905	917	-12	1058	1101	YX	1093	N749YX	EWR	MSN	128	799	9	17	2023-10-25 09:00:00	Other
7250	10	31	657	705	-8	1002	1010	DL	943	N3740C	LGA	MIA	154	1096	7	5	2023-10-31 07:00:00	MIA
7256	3	6	1107	1115	-8	1337	1411	UA	255	N17105	EWR	TPA	134	997	11	15	2023-03-06 11:00:00	Other
7259	1	5	1059	1110	-11	1333	1342	YX	1384	N432YX	JFK	IND	111	665	11	10	2023-01-05 11:00:00	Other
7261	2	11	2052	2100	-8	2206	2243	UA	781	N872UA	LGA	ORD	116	733	21	0	2023-02-11 21:00:00	ORD
7269	5	8	1013	1019	-6	1156	1228	9E	1403	N600LR	LGA	MYR	79	563	10	19	2023-05-08 10:00:00	Other
7272	5	28	2148	2159	-11	147	205	B6	285	N768JB	JFK	PSE	206	1617	21	59	2023-05-28 21:00:00	Other
7275	5	30	1705	1717	-12	2142	2029	B6	212	N606JB	LGA	FLL	144	1076	17	17	2023-05-30 17:00:00	FLL
7276	3	30	716	722	-6	957	1017	UA	708	N497UA	EWR	TPA	142	997	7	22	2023-03-30 07:00:00	Other
7279	8	23	706	715	-9	925	935	WN	577	N455WN	LGA	ATL	105	762	7	15	2023-08-23 07:00:00	ATL
7283	3	26	2049	2055	-6	2310	2301	YX	1242	N118HQ	LGA	MEM	162	963	20	55	2023-03-26 20:00:00	Other
7291	4	19	1640	1647	-7	2244	1954	YX	1554	N213JQ	LGA	OKC	NA	1341	16	47	2023-04-19 16:00:00	Other
7299	2	1	1632	1640	-8	1958	2010	AS	7	N955AK	JFK	SEA	362	2422	16	40	2023-02-01 16:00:00	Other
7309	1	22	1354	1400	-6	1506	1530	YX	1321	N132HQ	LGA	DCA	56	214	14	0	2023-01-22 14:00:00	Other
7314	5	9	1534	1546	-12	1701	1729	YX	1252	N119HQ	JFK	DCA	59	213	15	46	2023-05-09 15:00:00	Other
7315	4	3	1150	1159	-9	1341	1405	YX	1075	N414YX	JFK	CMH	79	483	11	59	2023-04-03 11:00:00	Other
7316	12	14	1059	1110	-11	1341	1416	B6	38	N706JB	EWR	MCO	131	937	11	10	2023-12-14 11:00:00	MCO
7318	6	23	1438	1445	-7	1600	1615	9E	1763	N936XJ	LGA	ROC	41	254	14	45	2023-06-23 14:00:00	Other
7321	12	5	1411	1421	-10	1722	1732	B6	658	N570JB	EWR	RSW	170	1068	14	21	2023-12-05 14:00:00	Other
7331	12	5	2045	2058	-13	2211	2239	9E	1662	N176PQ	LGA	MSN	116	812	20	58	2023-12-05 20:00:00	Other
7333	10	3	1644	1653	-9	1840	1918	YX	1078	N727YX	EWR	SDF	90	642	16	53	2023-10-03 16:00:00	Other
7334	10	19	833	842	-9	1036	1049	YX	1124	N747YX	EWR	DTW	77	488	8	42	2023-10-19 08:00:00	Other
7338	5	10	1319	1325	-6	1441	1457	YX	1200	N440YX	JFK	ORF	52	290	13	25	2023-05-10 13:00:00	Other
7340	12	2	1608	1620	-12	2008	1944	B6	82	N775JB	JFK	AUS	256	1521	16	20	2023-12-02 16:00:00	Other
7342	10	31	1002	1010	-8	1131	1142	YX	1357	N106HQ	JFK	ORF	60	290	10	10	2023-10-31 10:00:00	Other
7347	6	10	929	940	-11	1128	1201	DL	880	N106DU	LGA	CHS	89	641	9	40	2023-06-10 09:00:00	Other
7348	10	15	1953	2000	-7	2213	2220	YX	1815	N222JQ	JFK	CLT	87	541	20	0	2023-10-15 20:00:00	CLT
7349	11	16	1843	1850	-7	2102	2127	YX	1786	N227JQ	LGA	OMA	165	1148	18	50	2023-11-16 18:00:00	Other
7353	2	8	621	630	-9	744	818	YX	1274	N112HQ	LGA	PIT	62	335	6	30	2023-02-08 06:00:00	Other
7355	2	26	823	830	-7	1017	1030	9E	1417	N937XJ	JFK	RDU	76	427	8	30	2023-02-26 08:00:00	Other
7362	2	26	2007	2015	-8	2146	2216	YX	1278	N410YX	JFK	PIT	67	340	20	15	2023-02-26 20:00:00	Other
7366	4	13	1701	1708	-7	1859	1940	AA	852	N170US	EWR	PHX	270	2133	17	8	2023-04-13 17:00:00	Other
7372	7	13	647	654	-7	930	952	UA	664	N27519	EWR	PBI	146	1023	6	54	2023-07-13 06:00:00	Other
7396	2	10	1346	1352	-6	1650	1708	AA	174	N947AN	LGA	DFW	219	1389	13	52	2023-02-10 13:00:00	Other
7407	11	25	1105	1116	-11	1342	1350	B6	695	N508JL	LGA	DEN	238	1620	11	16	2023-11-25 11:00:00	Other
7408	3	7	943	950	-7	1144	1145	YX	1758	N818MD	LGA	BNA	126	764	9	50	2023-03-07 09:00:00	Other
7413	4	12	2123	2130	-7	2318	2341	UA	585	N832UA	EWR	MCI	143	1092	21	30	2023-04-12 21:00:00	Other
7416	6	23	851	859	-8	1037	1110	9E	1739	N137EV	LGA	TVC	86	655	8	59	2023-06-23 08:00:00	Other
7420	5	26	623	630	-7	905	955	UA	380	N34131	EWR	SFO	320	2565	6	30	2023-05-26 06:00:00	Other
7427	6	19	1452	1458	-6	1641	1709	9E	1695	N272PQ	EWR	CVG	89	569	14	58	2023-06-19 14:00:00	Other
7431	12	11	908	915	-7	1029	1033	B6	855	N358JB	LGA	BOS	36	184	9	15	2023-12-11 09:00:00	BOS
7435	2	27	1533	1540	-7	1738	1806	B6	865	N583JB	JFK	CHS	97	636	15	40	2023-02-27 15:00:00	Other
7438	6	14	938	948	-10	1147	1156	YX	1167	N979RP	EWR	CVG	97	569	9	48	2023-06-14 09:00:00	Other
7449	9	29	852	900	-8	1019	1029	YX	1075	N750YX	EWR	DCA	43	199	9	0	2023-09-29 09:00:00	Other
7450	6	5	1423	1429	-6	1636	1644	9E	1518	N914XJ	LGA	MCI	160	1107	14	29	2023-06-05 14:00:00	Other
7453	3	6	1518	1527	-9	1729	1731	YX	1213	N740YX	EWR	CMH	86	463	15	27	2023-03-06 15:00:00	Other
7459	4	26	620	630	-10	944	1004	AA	32	N110AN	JFK	SFO	350	2586	6	30	2023-04-26 06:00:00	Other
7462	12	7	1857	1905	-8	2106	2150	YX	1341	N106HQ	LGA	XNA	165	1147	19	5	2023-12-07 19:00:00	Other
7463	6	7	1143	1154	-11	1348	1408	YX	1083	N757YX	EWR	SDF	102	642	11	54	2023-06-07 11:00:00	Other
7464	2	18	1530	1540	-10	1729	1754	9E	1441	N920XJ	EWR	CVG	96	569	15	40	2023-02-18 15:00:00	Other
7466	4	2	1022	1030	-8	1332	1354	AA	3	N115NN	JFK	LAX	342	2475	10	30	2023-04-02 10:00:00	LAX
7472	5	2	1222	1235	-13	1507	1542	AA	191	N867NN	LGA	DFW	192	1389	12	35	2023-05-02 12:00:00	Other
7479	5	19	647	659	-12	811	827	AA	558	N821AW	LGA	DCA	46	214	6	59	2023-05-19 06:00:00	Other
7483	3	21	954	1001	-7	1417	1328	YX	1291	N806MD	LGA	EYW	180	1207	10	1	2023-03-21 10:00:00	Other
7491	1	19	1625	1635	-10	1750	1808	YX	1772	N218JQ	LGA	DCA	55	214	16	35	2023-01-19 16:00:00	Other
7492	9	10	1924	1930	-6	2124	2151	YX	1196	N762YX	EWR	MCI	148	1092	19	30	2023-09-10 19:00:00	Other
7493	2	7	1822	1829	-7	1945	2014	UA	445	N61882	EWR	ORD	119	719	18	29	2023-02-07 18:00:00	ORD
7500	10	25	2053	2100	-7	2216	2236	UA	650	N881UA	LGA	ORD	111	733	21	0	2023-10-25 21:00:00	ORD
7508	9	6	1840	1850	-10	2029	2114	YX	1119	N743YX	EWR	IND	87	645	18	50	2023-09-06 18:00:00	Other
7511	3	19	1334	1340	-6	1457	1516	AA	150	N892NN	LGA	ORD	115	733	13	40	2023-03-19 13:00:00	ORD
7516	9	5	705	715	-10	946	1011	B6	431	N568JB	LGA	TPA	131	1010	7	15	2023-09-05 07:00:00	Other
7517	4	4	918	924	-6	1111	1133	YX	976	N748YX	EWR	AVL	92	583	9	24	2023-04-04 09:00:00	Other
7518	1	8	721	729	-8	1021	1052	AA	169	N898NN	LGA	DFW	215	1389	7	29	2023-01-08 07:00:00	Other
7519	4	26	1720	1729	-9	1935	1928	B6	403	N375JB	JFK	RDU	71	427	17	29	2023-04-26 17:00:00	Other
7524	10	7	552	600	-8	847	927	AA	26	N117AN	JFK	SFO	330	2586	6	0	2023-10-07 06:00:00	Other
7526	5	5	1222	1228	-6	1448	1525	DL	528	N121DZ	JFK	MCO	127	944	12	28	2023-05-05 12:00:00	MCO
7528	1	18	1437	1445	-8	1724	1717	B6	791	N375JB	LGA	MSY	186	1183	14	45	2023-01-18 14:00:00	Other
7542	1	13	1908	1915	-7	2024	2031	B6	563	N198JB	LGA	BOS	40	184	19	15	2023-01-13 19:00:00	BOS
7547	3	29	1743	1750	-7	2201	2131	AA	953	N105NN	JFK	SFO	396	2586	17	50	2023-03-29 17:00:00	Other
7549	11	22	854	900	-6	1208	1236	AS	15	N535AS	JFK	SFO	341	2586	9	0	2023-11-22 09:00:00	Other
7558	1	18	1457	1508	-11	1615	1646	YX	1170	N649RW	EWR	RIC	54	277	15	8	2023-01-18 15:00:00	Other
7562	11	11	2242	2250	-8	115	124	F9	823	N344FR	LGA	ATL	125	762	22	50	2023-11-11 22:00:00	ATL
7565	1	20	821	830	-9	1031	1056	YX	1798	N229JQ	LGA	CLT	105	544	8	30	2023-01-20 08:00:00	CLT
7567	12	21	1205	1215	-10	1329	1339	YX	1029	N744YX	EWR	PWM	56	284	12	15	2023-12-21 12:00:00	Other
7575	11	5	1809	1815	-6	1935	1954	UA	949	N883UA	LGA	ORD	117	733	18	15	2023-11-05 18:00:00	ORD
7576	3	4	1519	1525	-6	1816	1850	B6	304	N807JB	LGA	PBI	150	1035	15	25	2023-03-04 15:00:00	Other
7581	1	26	1604	1610	-6	1920	1919	DL	505	N385DZ	JFK	MCO	159	944	16	10	2023-01-26 16:00:00	MCO
7596	3	27	1139	1147	-8	1344	1401	YX	1062	N856RW	EWR	IND	106	645	11	47	2023-03-27 11:00:00	Other
7602	5	11	659	705	-6	941	1005	DL	655	N124DU	LGA	IAH	185	1416	7	5	2023-05-11 07:00:00	Other
7604	11	14	1548	1559	-11	1730	1730	9E	1565	N348PQ	LGA	BUF	53	292	15	59	2023-11-14 15:00:00	Other
7611	4	21	556	605	-9	835	901	UA	780	N75428	EWR	TPA	135	997	6	5	2023-04-21 06:00:00	Other
7617	6	18	923	930	-7	1214	1220	AS	15	N268AK	JFK	SAN	324	2446	9	30	2023-06-18 09:00:00	Other
7625	5	22	1524	1538	-14	1729	1800	9E	1323	N313PQ	LGA	TYS	100	647	15	38	2023-05-22 15:00:00	Other
7632	5	9	548	600	-12	827	849	B6	590	N712JB	JFK	TPA	141	1005	6	0	2023-05-09 06:00:00	Other
7637	11	12	1722	1729	-7	1936	1948	9E	1704	N918XJ	LGA	CVG	93	585	17	29	2023-11-12 17:00:00	Other
7641	9	21	1509	1515	-6	1706	1650	UA	606	N73259	LGA	ORD	115	733	15	15	2023-09-21 15:00:00	ORD
7657	10	3	1522	1530	-8	1757	1829	UA	796	N644UA	EWR	IAH	186	1400	15	30	2023-10-03 15:00:00	Other
7659	9	13	1651	1659	-8	1813	1838	UA	218	N17719	EWR	CLE	62	404	16	59	2023-09-13 16:00:00	Other
7660	9	19	621	630	-9	907	919	B6	41	N531JL	JFK	TPA	147	1005	6	30	2023-09-19 06:00:00	Other
7662	12	16	1138	1145	-7	1447	1508	AS	5	N946AK	JFK	PDX	338	2454	11	45	2023-12-16 11:00:00	Other
7674	10	24	1734	1740	-6	1912	1940	9E	1458	N601LR	LGA	MEM	133	963	17	40	2023-10-24 17:00:00	Other
7677	7	26	2007	2015	-8	2125	2135	B6	449	N193JB	LGA	BOS	43	184	20	15	2023-07-26 20:00:00	BOS
7680	9	19	1659	1706	-7	1909	1902	9E	1459	N295PQ	JFK	RDU	76	427	17	6	2023-09-19 17:00:00	Other
7683	4	29	1119	1125	-6	1350	1312	OO	1031	N252SY	JFK	ORD	124	740	11	25	2023-04-29 11:00:00	ORD
7691	1	30	2110	2119	-9	2241	2304	YX	1313	N431YX	LGA	RIC	60	292	21	19	2023-01-30 21:00:00	Other
7692	8	3	2014	2022	-8	2218	2220	DL	802	N943AT	EWR	DTW	76	488	20	22	2023-08-03 20:00:00	Other
7694	10	12	1321	1330	-9	1539	1550	9E	1565	N903XJ	JFK	CHS	100	636	13	30	2023-10-12 13:00:00	Other
7713	8	28	1202	1209	-7	1324	1329	YX	995	N413YX	JFK	BOS	33	187	12	9	2023-08-28 12:00:00	BOS
7717	8	24	754	800	-6	949	944	OO	941	N316SY	JFK	ORD	115	740	8	0	2023-08-24 08:00:00	ORD
7718	12	29	1752	1800	-8	2051	2056	UA	766	N75428	EWR	MCO	156	937	18	0	2023-12-29 18:00:00	MCO
7731	5	24	1055	1105	-10	1226	1245	UA	721	N480UA	LGA	ORD	116	733	11	5	2023-05-24 11:00:00	ORD
7733	6	21	1354	1400	-6	1609	1624	DL	841	N874DN	EWR	ATL	104	746	14	0	2023-06-21 14:00:00	ATL
7735	12	28	918	924	-6	1229	1232	DL	396	N303DN	LGA	MCO	165	950	9	24	2023-12-28 09:00:00	MCO
7736	11	7	1920	1935	-15	2058	2115	UA	794	N17753	EWR	CLE	74	404	19	35	2023-11-07 19:00:00	Other
7738	5	18	1521	1530	-9	1705	1658	B6	567	N317JB	JFK	BOS	49	187	15	30	2023-05-18 15:00:00	BOS
7747	9	28	919	929	-10	1101	1116	YX	1312	N443YX	JFK	CLE	69	425	9	29	2023-09-28 09:00:00	Other
7750	10	17	1751	1800	-9	1950	2011	NK	246	N669NK	EWR	IND	92	645	18	0	2023-10-17 18:00:00	Other
7758	8	20	1557	1605	-8	1825	1903	AA	798	N972AN	LGA	DFW	168	1389	16	5	2023-08-20 16:00:00	Other
7762	5	9	1350	1400	-10	1620	1619	NK	36	N624NK	EWR	ATL	108	746	14	0	2023-05-09 14:00:00	ATL
7763	3	4	922	929	-7	1243	1249	YX	1123	N653RW	EWR	DFW	225	1372	9	29	2023-03-04 09:00:00	Other
7768	11	30	1519	1525	-6	1649	1700	YX	1843	N878RW	LGA	DCA	46	214	15	25	2023-11-30 15:00:00	Other
7769	9	28	702	710	-8	1047	1107	B6	586	N520JB	EWR	SJU	200	1608	7	10	2023-09-28 07:00:00	Other
7773	12	14	2144	2150	-6	2259	2315	9E	1373	N335PQ	LGA	ROC	51	254	21	50	2023-12-14 21:00:00	Other
7775	7	3	1151	1158	-7	1433	1414	YX	858	N740YX	EWR	SDF	100	642	11	58	2023-07-03 11:00:00	Other
7778	11	25	811	820	-9	953	1024	9E	1689	N918XJ	LGA	GSO	76	461	8	20	2023-11-25 08:00:00	Other
7788	6	9	1450	1458	-8	1639	1709	9E	1695	N232PQ	EWR	CVG	86	569	14	58	2023-06-09 14:00:00	Other
7802	10	17	1203	1212	-9	1317	1339	NK	369	N523NK	EWR	BNA	111	748	12	12	2023-10-17 12:00:00	Other
7804	6	17	1039	1045	-6	1229	1255	9E	1690	N294PQ	LGA	CAE	88	617	10	45	2023-06-17 10:00:00	Other
7805	11	14	821	829	-8	1001	1027	9E	1731	N903XJ	LGA	RDU	72	431	8	29	2023-11-14 08:00:00	Other
7812	8	14	712	719	-7	1023	1020	DL	589	N126DN	EWR	SLC	287	1969	7	19	2023-08-14 07:00:00	Other
7825	8	12	557	604	-7	842	850	B6	188	N640JB	EWR	TPA	134	997	6	4	2023-08-12 06:00:00	Other
7827	5	11	703	712	-9	939	1013	DL	350	N370NB	LGA	PBI	135	1035	7	12	2023-05-11 07:00:00	Other
7832	5	14	1306	1314	-8	1618	1621	UA	497	N27251	EWR	FLL	139	1065	13	14	2023-05-14 13:00:00	FLL
7836	3	24	915	929	-14	1242	1314	YX	1186	N657RW	EWR	EYW	176	1196	9	29	2023-03-24 09:00:00	Other
7837	1	11	1923	1929	-6	2056	2103	YX	1766	N216JQ	LGA	DCA	53	214	19	29	2023-01-11 19:00:00	Other
7846	12	21	1604	1610	-6	1728	1751	UA	755	N12754	EWR	CLE	63	404	16	10	2023-12-21 16:00:00	Other
7850	1	25	1146	1159	-13	1437	1517	B6	896	N983JT	JFK	LAX	323	2475	11	59	2023-01-25 11:00:00	LAX
7852	9	19	1619	1629	-10	1826	1857	UA	694	N464UA	LGA	DEN	222	1620	16	29	2023-09-19 16:00:00	Other
7853	2	15	2150	2159	-9	2325	2339	UA	516	N37474	EWR	CLE	70	404	21	59	2023-02-15 21:00:00	Other
7860	5	29	803	815	-12	855	930	B6	113	N183JB	LGA	BOS	36	184	8	15	2023-05-29 08:00:00	BOS
7863	11	25	753	800	-7	1101	1112	UA	890	N26226	EWR	IAH	214	1400	8	0	2023-11-25 08:00:00	Other
7865	2	11	551	600	-9	806	850	UA	184	N27251	EWR	LAS	289	2227	6	0	2023-02-11 06:00:00	Other
7882	10	29	1116	1122	-6	1401	1428	UA	139	N17279	EWR	FLL	146	1065	11	22	2023-10-29 11:00:00	FLL
7888	9	5	1016	1022	-6	1151	1220	YX	1059	N726YX	EWR	ILM	68	488	10	22	2023-09-05 10:00:00	Other
7894	3	18	554	600	-6	919	919	B6	849	N625JB	JFK	MIA	165	1089	6	0	2023-03-18 06:00:00	MIA
7895	5	8	1405	1412	-7	1637	1700	UA	384	N37252	EWR	MCO	125	937	14	12	2023-05-08 14:00:00	MCO
7896	3	21	1829	1840	-11	1957	2017	AA	973	N956NN	LGA	ORD	111	733	18	40	2023-03-21 18:00:00	ORD
7904	10	3	723	729	-6	1017	1042	AA	565	N319TE	JFK	MIA	146	1089	7	29	2023-10-03 07:00:00	MIA
7907	6	14	746	755	-9	918	941	UA	991	N18220	EWR	RDU	67	416	7	55	2023-06-14 07:00:00	Other
7909	12	9	654	700	-6	909	946	UA	211	N19141	EWR	LAS	293	2227	7	0	2023-12-09 07:00:00	Other
7927	11	10	653	659	-6	806	830	AA	955	N766US	LGA	DCA	52	214	6	59	2023-11-10 06:00:00	Other
7929	3	26	1722	1729	-7	2007	2008	YX	1273	N107HQ	LGA	ATL	130	762	17	29	2023-03-26 17:00:00	ATL
7932	12	3	1141	1152	-11	1426	1419	YX	1019	N755YX	EWR	SAV	138	708	11	52	2023-12-03 11:00:00	Other
7933	1	27	1923	1929	-6	2055	2109	YX	1469	N427YX	JFK	DCA	62	213	19	29	2023-01-27 19:00:00	Other
7952	5	29	654	705	-11	959	1007	B6	829	N593JB	EWR	MIA	151	1085	7	5	2023-05-29 07:00:00	MIA
7957	8	30	704	710	-6	900	921	9E	1202	N131EV	LGA	CHS	94	641	7	10	2023-08-30 07:00:00	Other
7959	7	3	652	659	-7	811	834	AA	509	N921NN	EWR	ORD	102	719	6	59	2023-07-03 06:00:00	ORD
7973	2	7	904	918	-14	1210	1234	UA	608	N14107	EWR	FLL	142	1065	9	18	2023-02-07 09:00:00	FLL
7981	8	27	942	950	-8	1141	1145	9E	1281	N916XJ	LGA	CLE	71	419	9	50	2023-08-27 09:00:00	Other
7988	9	4	644	654	-10	756	831	AA	301	N926AN	EWR	ORD	105	719	6	54	2023-09-04 06:00:00	ORD
7990	6	1	845	855	-10	1002	1040	YX	1846	N246JQ	LGA	PIT	58	335	8	55	2023-06-01 08:00:00	Other
7994	5	25	622	629	-7	801	815	AA	959	N990AN	LGA	ORD	121	733	6	29	2023-05-25 06:00:00	ORD
7998	5	1	2005	2015	-10	2135	2151	YX	1334	N869RW	LGA	ORF	52	296	20	15	2023-05-01 20:00:00	Other
8000	9	7	1127	1135	-8	1329	1355	DL	877	N311DU	LGA	MSY	157	1183	11	35	2023-09-07 11:00:00	Other
8002	4	27	801	810	-9	919	943	9E	1194	N300PQ	LGA	MKE	116	738	8	10	2023-04-27 08:00:00	Other
8003	2	13	652	700	-8	951	1008	UA	813	N69847	EWR	RSW	152	1068	7	0	2023-02-13 07:00:00	Other
8008	2	19	1803	1810	-7	2021	2031	YX	1007	N724YX	EWR	CVG	109	569	18	10	2023-02-19 18:00:00	Other
8010	10	3	1403	1415	-12	1515	1550	UA	923	N17244	LGA	ORD	103	733	14	15	2023-10-03 14:00:00	ORD
8019	11	28	750	800	-10	1059	1112	UA	890	N17262	EWR	IAH	217	1400	8	0	2023-11-28 08:00:00	Other
8025	10	24	752	759	-7	1046	1108	AA	118	N926NN	LGA	MIA	138	1096	7	59	2023-10-24 07:00:00	MIA
8027	11	29	1905	1913	-8	2204	2225	UA	718	N14237	EWR	RSW	154	1068	19	13	2023-11-29 19:00:00	Other
8032	5	10	1847	1900	-13	2027	2057	YX	1303	N430YX	LGA	CMH	78	479	19	0	2023-05-10 19:00:00	Other
8042	2	21	1649	1657	-8	1911	1931	UA	581	N839UA	EWR	ATL	113	746	16	57	2023-02-21 16:00:00	ATL
8045	11	9	1121	1129	-8	1318	1347	9E	1566	N308PQ	LGA	GSP	92	610	11	29	2023-11-09 11:00:00	Other
8056	1	10	1940	1950	-10	2124	2159	YX	1312	N124HQ	JFK	RDU	70	427	19	50	2023-01-10 19:00:00	Other
8059	1	14	2115	2124	-9	2316	2350	YX	1195	N749YX	EWR	IND	95	645	21	24	2023-01-14 21:00:00	Other
8061	10	3	1519	1529	-10	1648	1713	YX	1361	N124HQ	LGA	STL	128	888	15	29	2023-10-03 15:00:00	Other
8068	10	8	905	915	-10	1009	1035	B6	870	N216JB	LGA	BOS	46	184	9	15	2023-10-08 09:00:00	BOS
8074	11	3	1416	1423	-7	1638	1652	9E	1613	N601LR	JFK	SAV	112	718	14	23	2023-11-03 14:00:00	Other
8081	9	21	1923	1930	-7	2059	2101	YX	1228	N748YX	EWR	PWM	54	284	19	30	2023-09-21 19:00:00	Other
8083	2	8	1904	1912	-8	2019	2022	YX	1018	N746YX	EWR	ALB	32	143	19	12	2023-02-08 19:00:00	Other
8085	1	18	833	840	-7	1033	1057	YX	1747	N880RW	LGA	STL	148	888	8	40	2023-01-18 08:00:00	Other
8088	11	1	2153	2159	-6	2330	2332	9E	1519	N272PQ	JFK	BTV	48	266	21	59	2023-11-01 21:00:00	Other
8103	5	31	707	715	-8	958	1011	UA	680	N77259	EWR	TPA	138	997	7	15	2023-05-31 07:00:00	Other
8107	1	24	551	600	-9	840	904	NK	51	N678NK	LGA	FLL	147	1076	6	0	2023-01-24 06:00:00	FLL
8115	4	23	1754	1800	-6	2119	2136	AA	847	N109NN	JFK	SFO	345	2586	18	0	2023-04-23 18:00:00	Other
8127	6	7	652	659	-7	837	858	YX	1310	N128HQ	LGA	DTW	84	502	6	59	2023-06-07 06:00:00	Other
8128	1	5	1912	1924	-12	2229	2248	B6	674	N985JT	EWR	LAX	343	2454	19	24	2023-01-05 19:00:00	LAX
8135	6	18	1622	1630	-8	1748	1817	DL	637	N127DU	LGA	ORD	112	733	16	30	2023-06-18 16:00:00	ORD
8167	11	20	555	605	-10	728	729	YX	1828	N245JQ	LGA	DCA	53	214	6	5	2023-11-20 06:00:00	Other
8172	6	16	620	626	-6	757	753	UA	992	N24202	LGA	ORD	122	733	6	26	2023-06-16 06:00:00	ORD
8179	2	10	1523	1530	-7	1831	1855	AA	120	N108NN	JFK	LAX	338	2475	15	30	2023-02-10 15:00:00	LAX
8194	10	28	1008	1017	-9	1127	1148	9E	1501	N319PQ	JFK	ROC	52	264	10	17	2023-10-28 10:00:00	Other
8195	11	29	2006	2015	-9	2132	2154	UA	423	N37560	EWR	ORD	116	719	20	15	2023-11-29 20:00:00	ORD
8199	1	28	1541	1555	-14	1743	1816	9E	1459	N931XJ	JFK	CHS	98	636	15	55	2023-01-28 15:00:00	Other
8203	10	20	659	705	-6	932	957	UA	383	N17314	EWR	IAH	184	1400	7	5	2023-10-20 07:00:00	Other
8206	12	22	2214	2220	-6	2336	11	OO	1206	N256SY	JFK	BUF	55	301	22	20	2023-12-22 22:00:00	Other
8212	6	12	919	930	-11	1214	1255	AS	16	N285AK	JFK	SFO	314	2586	9	30	2023-06-12 09:00:00	Other
8213	5	28	1313	1323	-10	1511	1537	YX	1619	N220JQ	LGA	CLT	87	544	13	23	2023-05-28 13:00:00	CLT
8224	5	14	1859	1906	-7	2052	2047	YX	1667	N878RW	LGA	PIT	54	335	19	6	2023-05-14 19:00:00	Other
8232	1	12	1148	1155	-7	1342	1359	G4	1103	320NV	EWR	VPS	152	988	11	55	2023-01-12 11:00:00	Other
8242	12	4	2152	2200	-8	2316	2346	9E	1579	N294PQ	JFK	BUF	57	301	22	0	2023-12-04 22:00:00	Other
8243	10	23	1333	1343	-10	1514	1518	9E	1681	N134EV	JFK	BGR	62	382	13	43	2023-10-23 13:00:00	Other
8251	6	2	622	632	-10	849	924	AA	1000	N925AN	EWR	DFW	176	1372	6	32	2023-06-02 06:00:00	Other
8258	11	29	906	913	-7	1050	1111	B6	374	N229JB	JFK	ORD	124	740	9	13	2023-11-29 09:00:00	ORD
8272	8	4	1428	1435	-7	1630	1609	YX	895	N729YX	EWR	IAD	40	212	14	35	2023-08-04 14:00:00	Other
8274	11	29	1844	1850	-6	2059	2127	YX	1786	N210JQ	LGA	OMA	173	1148	18	50	2023-11-29 18:00:00	Other
8283	9	25	552	600	-8	651	705	B6	963	N249JB	JFK	BOS	33	187	6	0	2023-09-25 06:00:00	BOS
8284	3	18	1808	1815	-7	2010	2040	NK	283	N658NK	EWR	IND	107	645	18	15	2023-03-18 18:00:00	Other
8285	4	5	1251	1300	-9	1446	1505	AA	426	N553UW	LGA	CLT	83	544	13	0	2023-04-05 13:00:00	CLT
8287	9	7	1123	1132	-9	1335	1337	AA	754	N834NN	LGA	CLT	80	544	11	32	2023-09-07 11:00:00	CLT
8296	2	24	1050	1059	-9	1407	1423	B6	90	N569JB	JFK	AUS	233	1521	10	59	2023-02-24 10:00:00	Other
8298	10	22	1322	1329	-7	1438	1445	YX	1249	N407YX	JFK	BOS	40	187	13	29	2023-10-22 13:00:00	BOS
8316	5	18	1030	1039	-9	1222	1313	YX	1114	N729YX	EWR	SDF	90	642	10	39	2023-05-18 10:00:00	Other
8318	5	24	1814	1820	-6	2006	2038	YX	1193	N108HQ	LGA	LIT	150	1085	18	20	2023-05-24 18:00:00	Other
8321	11	13	1543	1553	-10	1732	1757	AA	217	N762US	LGA	DTW	89	502	15	53	2023-11-13 15:00:00	Other
8333	3	23	1405	1413	-8	1538	1550	YX	1627	N224JQ	LGA	PIT	65	335	14	13	2023-03-23 14:00:00	Other
8337	9	1	1359	1405	-6	1640	1646	UA	489	N403UA	EWR	DFW	180	1372	14	5	2023-09-01 14:00:00	Other
8339	5	11	752	800	-8	920	938	UA	848	N14731	LGA	ORD	113	733	8	0	2023-05-11 08:00:00	ORD
8340	1	31	1107	1114	-7	1317	1320	YX	1325	N427YX	LGA	ROA	76	405	11	14	2023-01-31 11:00:00	Other
8345	6	28	731	740	-9	845	906	NK	291	N516NK	EWR	PIT	54	319	7	40	2023-06-28 07:00:00	Other
8346	4	24	603	610	-7	744	810	DL	398	N353NB	LGA	MSP	136	1020	6	10	2023-04-24 06:00:00	Other
8350	12	28	1119	1130	-11	1228	1256	YX	1038	N743YX	EWR	ROC	46	246	11	30	2023-12-28 11:00:00	Other
8354	3	12	1024	1030	-6	1407	1407	YX	1186	N979RP	EWR	EYW	175	1196	10	30	2023-03-12 10:00:00	Other
8356	5	19	1754	1800	-6	1900	1920	AA	422	N748UW	LGA	DCA	51	214	18	0	2023-05-19 18:00:00	Other
8365	1	29	1959	2015	-16	2120	2213	YX	1451	N826MD	LGA	ORF	56	296	20	15	2023-01-29 20:00:00	Other
8371	9	16	1722	1729	-7	2010	2030	B6	678	N634JB	LGA	MCO	133	950	17	29	2023-09-16 17:00:00	MCO
8375	11	15	1633	1642	-9	1844	1916	UA	934	N14115	EWR	DEN	227	1605	16	42	2023-11-15 16:00:00	Other
8378	5	16	853	901	-8	1104	1126	UA	492	N25705	EWR	SAV	101	708	9	1	2023-05-16 09:00:00	Other
8382	7	22	958	1005	-7	1109	1142	UA	581	N407UA	LGA	ORD	107	733	10	5	2023-07-22 10:00:00	ORD
8398	4	22	629	636	-7	925	942	UA	267	N480UA	EWR	FLL	158	1065	6	36	2023-04-22 06:00:00	FLL
8407	5	21	1742	1751	-9	2041	2101	UA	557	N37295	EWR	SAN	320	2425	17	51	2023-05-21 17:00:00	Other
8416	4	26	2153	2159	-6	2253	2308	DL	445	N140DU	LGA	SYR	40	198	21	59	2023-04-26 21:00:00	Other
8425	4	12	856	905	-9	1023	1031	B6	556	N339JB	JFK	BUF	59	301	9	5	2023-04-12 09:00:00	Other
8426	10	12	951	1000	-9	1207	1229	YX	1329	N434YX	LGA	SDF	105	659	10	0	2023-10-12 10:00:00	Other
8429	10	3	1143	1152	-9	1338	1347	YX	1059	N858RW	EWR	CMH	67	463	11	52	2023-10-03 11:00:00	Other
8447	2	24	858	904	-6	1143	1147	B6	442	N561JB	JFK	ATL	123	760	9	4	2023-02-24 09:00:00	ATL
8448	5	8	1709	1715	-6	1842	1842	B6	396	N273JB	LGA	BOS	43	184	17	15	2023-05-08 17:00:00	BOS
8452	4	26	1737	1745	-8	2040	2052	B6	21	N608JB	LGA	TPA	156	1010	17	45	2023-04-26 17:00:00	Other
8460	4	22	1230	1240	-10	1537	1552	AA	595	N440AN	JFK	MIA	160	1089	12	40	2023-04-22 12:00:00	MIA
8464	3	8	809	815	-6	1134	1153	AA	982	N903AN	JFK	AUS	225	1521	8	15	2023-03-08 08:00:00	Other
8466	1	26	1754	1800	-6	1938	2021	DL	478	N352NW	LGA	MSP	146	1020	18	0	2023-01-26 18:00:00	Other
8473	2	22	1439	1445	-6	1650	1708	9E	1296	N491PX	LGA	CVG	105	585	14	45	2023-02-22 14:00:00	Other
8476	3	29	1138	1150	-12	1328	1354	YX	1714	N239JQ	LGA	CMH	80	479	11	50	2023-03-29 11:00:00	Other
8479	7	30	639	645	-6	914	929	UA	267	N37464	EWR	SAN	312	2425	6	45	2023-07-30 06:00:00	Other
8483	8	31	854	900	-6	1037	1050	YX	903	N646RW	EWR	STL	125	872	9	0	2023-08-31 09:00:00	Other
8488	5	30	1738	1744	-6	2009	2039	UA	814	N26226	EWR	MCO	130	937	17	44	2023-05-30 17:00:00	MCO
8501	6	3	1343	1350	-7	1511	1522	YX	1908	N236JQ	JFK	BOS	51	187	13	50	2023-06-03 13:00:00	BOS
8510	7	12	1719	1730	-11	1920	1958	YX	1407	N208JQ	LGA	SDF	97	659	17	30	2023-07-12 17:00:00	Other
8511	2	3	719	729	-10	844	905	9E	1462	N901XJ	LGA	BUF	57	292	7	29	2023-02-03 07:00:00	Other
8513	3	14	549	600	-11	740	806	AA	949	N338RS	JFK	CLT	87	541	6	0	2023-03-14 06:00:00	CLT
8514	11	21	716	730	-14	1024	1055	AS	11	N296AK	JFK	SEA	338	2422	7	30	2023-11-21 07:00:00	Other
8522	1	30	1918	1928	-10	2051	2107	AA	277	N936AN	EWR	ORD	121	719	19	28	2023-01-30 19:00:00	ORD
8523	8	4	621	629	-8	820	836	YX	1022	N413YX	LGA	MSP	153	1020	6	29	2023-08-04 06:00:00	Other
8525	4	19	1738	1755	-17	2018	2054	B6	633	N324JB	EWR	MCO	126	937	17	55	2023-04-19 17:00:00	MCO
8526	5	8	2053	2100	-7	12	54	AA	55	N117AN	JFK	SFO	353	2586	21	0	2023-05-08 21:00:00	Other
8534	11	12	1817	1825	-8	2108	2126	DL	752	N307DX	LGA	MCO	138	950	18	25	2023-11-12 18:00:00	MCO
8536	7	20	1253	1300	-7	1602	1628	AS	4	N435AS	JFK	SFO	346	2586	13	0	2023-07-20 13:00:00	Other
8539	1	21	1406	1415	-9	1603	1626	YX	1402	N821MD	LGA	ILM	80	500	14	15	2023-01-21 14:00:00	Other
8541	5	27	1509	1515	-6	1614	1651	YX	1232	N428YX	LGA	BUF	44	292	15	15	2023-05-27 15:00:00	Other
8542	2	6	1619	1630	-11	1914	1946	NK	347	N679NK	LGA	FLL	140	1076	16	30	2023-02-06 16:00:00	FLL
8553	6	23	1301	1307	-6	1424	1433	9E	1585	N479PX	LGA	BTV	44	258	13	7	2023-06-23 13:00:00	Other
8563	8	28	554	600	-6	808	820	UA	344	N413UA	EWR	ATL	109	746	6	0	2023-08-28 06:00:00	ATL
8567	3	19	1822	1830	-8	2003	2028	9E	1427	N915XJ	LGA	RDU	81	431	18	30	2023-03-19 18:00:00	Other
8574	6	14	945	953	-8	1121	1145	DL	1027	N935AT	EWR	DTW	78	488	9	53	2023-06-14 09:00:00	Other
8576	2	27	607	620	-13	904	927	B6	51	N729JB	JFK	SRQ	150	1041	6	20	2023-02-27 06:00:00	Other
8577	12	11	654	700	-6	803	846	UA	822	N33209	EWR	ORD	105	719	7	0	2023-12-11 07:00:00	ORD
8585	3	19	1508	1514	-6	1625	1637	YX	1165	N746YX	EWR	BTV	47	266	15	14	2023-03-19 15:00:00	Other
8590	5	16	1003	1009	-6	1146	1222	DL	646	N384DN	LGA	DTW	78	502	10	9	2023-05-16 10:00:00	Other
8594	7	19	1353	1400	-7	1519	1521	AA	392	N701UW	LGA	DCA	48	214	14	0	2023-07-19 14:00:00	Other
8600	1	27	1617	1630	-13	1815	1840	B6	430	N274JB	JFK	DTW	94	509	16	30	2023-01-27 16:00:00	Other
8612	5	31	1923	1929	-6	2032	2108	YX	1672	N225JQ	LGA	BNA	103	764	19	29	2023-05-31 19:00:00	Other
8614	4	29	1535	1545	-10	1656	1724	YX	1178	N426YX	LGA	PIT	60	335	15	45	2023-04-29 15:00:00	Other
8620	8	23	1919	1930	-11	2218	2242	B6	614	N503JB	LGA	RSW	138	1080	19	30	2023-08-23 19:00:00	Other
8625	10	26	752	804	-12	921	941	9E	1415	N906XJ	LGA	PIT	56	335	8	4	2023-10-26 08:00:00	Other
8627	5	30	921	929	-8	1028	1046	B6	611	N247JB	JFK	BTV	44	266	9	29	2023-05-30 09:00:00	Other
8634	5	29	1236	1245	-9	1447	1542	NK	81	N643NK	EWR	DFW	168	1372	12	45	2023-05-29 12:00:00	Other
8645	4	16	2123	2130	-7	2304	2327	YX	1128	N432YX	JFK	RDU	70	427	21	30	2023-04-16 21:00:00	Other
8646	8	27	754	800	-6	1044	1115	AA	478	N891NN	JFK	MIA	144	1089	8	0	2023-08-27 08:00:00	MIA
8647	6	2	812	820	-8	1210	1219	DL	730	N890DN	JFK	SJU	199	1598	8	20	2023-06-02 08:00:00	Other
8648	12	29	701	709	-8	914	929	9E	1669	N676CA	JFK	DTW	79	509	7	9	2023-12-29 07:00:00	Other
8653	2	2	1229	1240	-11	1359	1428	YX	1287	N821MD	LGA	ORF	62	296	12	40	2023-02-02 12:00:00	Other
8658	12	5	1719	1729	-10	2026	2032	UA	732	N62883	EWR	SRQ	162	1034	17	29	2023-12-05 17:00:00	Other
8664	12	1	922	929	-7	1228	1259	B6	675	N646JB	LGA	RSW	163	1080	9	29	2023-12-01 09:00:00	Other
8665	2	27	2142	2151	-9	1	2338	UA	421	N480UA	EWR	MEM	141	946	21	51	2023-02-27 21:00:00	Other
8667	11	10	648	655	-7	952	957	B6	428	N521JB	LGA	TPA	150	1010	6	55	2023-11-10 06:00:00	Other
8669	4	8	1052	1059	-7	1347	1359	UA	249	N63899	EWR	TPA	148	997	10	59	2023-04-08 10:00:00	Other
8670	9	21	846	855	-9	1010	1033	9E	1722	N337PQ	LGA	CHO	54	305	8	55	2023-09-21 08:00:00	Other
8677	4	22	756	805	-9	1004	1010	B6	439	N198JB	JFK	CHS	102	636	8	5	2023-04-22 08:00:00	Other
8679	8	1	709	715	-6	950	1011	B6	361	N665JB	LGA	TPA	134	1010	7	15	2023-08-01 07:00:00	Other
8683	3	8	1450	1459	-9	1629	1644	B6	650	N306JB	JFK	BNA	125	765	14	59	2023-03-08 14:00:00	Other
8685	10	5	1524	1530	-6	1757	1829	UA	796	N655UA	EWR	IAH	184	1400	15	30	2023-10-05 15:00:00	Other
8688	2	3	831	840	-9	943	1014	YX	1213	N452YX	JFK	BOS	37	187	8	40	2023-02-03 08:00:00	BOS
8691	11	18	823	830	-7	1013	1058	AA	508	N825NN	JFK	CLT	90	541	8	30	2023-11-18 08:00:00	CLT
8702	8	6	1517	1525	-8	1709	1737	9E	1133	N349PQ	LGA	ILM	78	500	15	25	2023-08-06 15:00:00	Other
8704	10	24	1823	1830	-7	2047	2103	B6	130	N307JB	JFK	ATL	104	760	18	30	2023-10-24 18:00:00	ATL
8708	1	28	1353	1400	-7	1600	1631	DL	879	N928AT	EWR	ATL	115	746	14	0	2023-01-28 14:00:00	ATL
8709	8	7	1721	1730	-9	2011	1957	YX	1363	N244JQ	LGA	SDF	123	659	17	30	2023-08-07 17:00:00	Other
8714	8	5	1519	1525	-6	1703	1737	9E	1133	N348PQ	LGA	ILM	73	500	15	25	2023-08-05 15:00:00	Other
8719	6	22	1452	1458	-6	1614	1625	YX	1136	N642RW	EWR	BUF	53	282	14	58	2023-06-22 14:00:00	Other
8720	11	27	1859	1905	-6	2130	2134	YX	1294	N401YX	LGA	IND	117	660	19	5	2023-11-27 19:00:00	Other
8721	8	24	1739	1746	-7	2026	1945	YX	1332	N810MD	LGA	CMH	78	479	17	46	2023-08-24 17:00:00	Other
8722	8	22	923	929	-6	1155	1153	YX	907	N654RW	EWR	TVC	109	644	9	29	2023-08-22 09:00:00	Other
8726	8	20	1638	1647	-9	1828	1901	YX	927	N748YX	EWR	CVG	87	569	16	47	2023-08-20 16:00:00	Other
8729	1	19	1352	1359	-7	1655	1712	B6	154	N905JB	LGA	MCO	139	950	13	59	2023-01-19 13:00:00	MCO
8736	11	15	2137	2150	-13	2302	2316	9E	1715	N153PQ	LGA	BUF	56	292	21	50	2023-11-15 21:00:00	Other
8737	11	15	1031	1041	-10	1313	1344	UA	247	N37319	EWR	TPA	144	997	10	41	2023-11-15 10:00:00	Other
8746	4	18	1813	1820	-7	1959	2019	YX	1504	N213JQ	LGA	STL	131	888	18	20	2023-04-18 18:00:00	Other
8749	6	1	554	600	-6	900	925	AA	29	N112AN	JFK	SFO	344	2586	6	0	2023-06-01 06:00:00	Other
8750	12	11	1623	1630	-7	1925	1954	AA	88	N107NN	JFK	LAX	341	2475	16	30	2023-12-11 16:00:00	LAX
8762	10	25	2115	2123	-8	2208	2230	YX	1073	N758YX	EWR	PHL	19	80	21	23	2023-10-25 21:00:00	Other
8763	6	9	1040	1050	-10	1145	1202	YX	1826	N879RW	JFK	ACK	44	199	10	50	2023-06-09 10:00:00	Other
8764	1	22	1357	1405	-8	1659	1703	YX	1408	N433YX	LGA	ATL	148	762	14	5	2023-01-22 14:00:00	ATL
8765	11	12	652	659	-7	936	1019	UA	80	N76526	EWR	SNA	322	2434	6	59	2023-11-12 06:00:00	Other
8769	2	26	621	630	-9	930	948	B6	817	N592JB	JFK	MIA	149	1089	6	30	2023-02-26 06:00:00	MIA
8783	4	8	947	1000	-13	1309	1304	UA	638	N884UA	LGA	IAH	208	1416	10	0	2023-04-08 10:00:00	Other
8791	11	14	1154	1200	-6	1505	1531	UA	387	N67134	EWR	SFO	341	2565	12	0	2023-11-14 12:00:00	Other
8792	1	13	701	707	-6	838	854	YX	1234	N733YX	EWR	CLE	70	404	7	7	2023-01-13 07:00:00	Other
8802	1	25	1208	1215	-7	1425	1450	UA	715	N26215	LGA	DEN	226	1620	12	15	2023-01-25 12:00:00	Other
8806	11	23	920	929	-9	1027	1049	YX	1079	N655RW	EWR	SYR	45	195	9	29	2023-11-23 09:00:00	Other
8809	1	9	1848	1855	-7	2015	2046	DL	341	N119DU	LGA	BNA	112	764	18	55	2023-01-09 18:00:00	Other
8824	10	20	924	930	-6	1228	1228	B6	45	N566JB	JFK	SRQ	151	1041	9	30	2023-10-20 09:00:00	Other
8827	10	13	2150	2159	-9	2252	2319	UA	442	N24702	EWR	PWM	46	284	21	59	2023-10-13 21:00:00	Other
8830	9	28	1753	1759	-6	1929	1955	YX	1387	N126HQ	JFK	CMH	76	483	17	59	2023-09-28 17:00:00	Other
8836	1	17	906	915	-9	1132	1123	AA	1068	N915NN	EWR	CLT	89	529	9	15	2023-01-17 09:00:00	CLT
8841	10	20	1751	1800	-9	2023	2105	AA	182	N891NN	LGA	DFW	187	1389	18	0	2023-10-20 18:00:00	Other
8842	2	6	1854	1902	-8	2206	2235	AA	406	N956AN	LGA	DFW	197	1389	19	2	2023-02-06 19:00:00	Other
8843	7	12	1336	1345	-9	1532	1547	YX	1038	N440YX	LGA	CAE	86	617	13	45	2023-07-12 13:00:00	Other
8850	9	25	923	930	-7	1253	1243	AA	822	N930AN	LGA	MIA	155	1096	9	30	2023-09-25 09:00:00	MIA
8855	4	20	1943	1950	-7	2234	2256	B6	176	N571JB	LGA	FLL	143	1076	19	50	2023-04-20 19:00:00	FLL
8856	9	16	1113	1120	-7	1232	1301	9E	1447	N927XJ	LGA	BHM	120	866	11	20	2023-09-16 11:00:00	Other
8871	2	9	918	930	-12	1049	1059	YX	1518	N245JQ	JFK	DCA	65	213	9	30	2023-02-09 09:00:00	Other
8881	10	10	651	700	-9	757	810	B6	973	N206JB	LGA	BOS	43	184	7	0	2023-10-10 07:00:00	BOS
8883	11	6	954	1000	-6	1612	1605	HA	18	N389HA	JFK	HNL	650	4983	10	0	2023-11-06 10:00:00	Other
8887	8	31	1223	1229	-6	1423	1457	OO	945	N256SY	LGA	SDF	100	659	12	29	2023-08-31 12:00:00	Other
8893	7	25	1116	1123	-7	1304	1319	YX	905	N858RW	EWR	ILM	73	488	11	23	2023-07-25 11:00:00	Other
8900	10	11	1620	1630	-10	1728	1752	9E	1414	N910XJ	LGA	PWM	41	269	16	30	2023-10-11 16:00:00	Other
8901	6	14	754	800	-6	1019	1030	DL	341	N116DN	LGA	ATL	117	762	8	0	2023-06-14 08:00:00	ATL
8902	1	22	1521	1530	-9	1643	1649	B6	468	N307JB	JFK	BOS	47	187	15	30	2023-01-22 15:00:00	BOS
8910	12	1	825	835	-10	1042	1043	NK	295	N678NK	LGA	CLT	96	544	8	35	2023-12-01 08:00:00	CLT
8913	3	8	1600	1610	-10	1741	1812	YX	1330	N429YX	JFK	RDU	68	427	16	10	2023-03-08 16:00:00	Other
8924	12	20	1453	1500	-7	1640	1650	YX	1237	N410YX	LGA	CLE	69	419	15	0	2023-12-20 15:00:00	Other
8928	6	19	956	1003	-7	1147	1159	OO	1271	N607CZ	LGA	MEM	140	963	10	3	2023-06-19 10:00:00	Other
8929	2	21	1039	1045	-6	1359	1407	DL	565	N351NB	LGA	RSW	160	1080	10	45	2023-02-21 10:00:00	Other
8934	10	29	1624	1630	-6	1736	1806	9E	1374	N301PQ	JFK	PWM	47	273	16	30	2023-10-29 16:00:00	Other
8936	9	16	1651	1659	-8	1849	1852	YX	1301	N422YX	JFK	RDU	71	427	16	59	2023-09-16 16:00:00	Other
8937	2	13	904	914	-10	1109	1128	YX	1301	N110HQ	LGA	CMH	77	479	9	14	2023-02-13 09:00:00	Other
8939	6	9	1217	1225	-8	1411	1424	YX	1319	N430YX	LGA	DAY	86	549	12	25	2023-06-09 12:00:00	Other
8942	11	4	1751	1759	-8	2055	2112	B6	125	N999JQ	JFK	MCO	135	944	17	59	2023-11-04 17:00:00	MCO
8943	2	5	1123	1130	-7	1330	1353	YX	1056	N755YX	EWR	IND	105	645	11	30	2023-02-05 11:00:00	Other
8950	8	25	1617	1624	-7	1752	1750	UA	581	N77543	EWR	IAD	37	212	16	24	2023-08-25 16:00:00	Other
8959	2	21	1355	1405	-10	1526	1537	UA	605	N871UA	EWR	BNA	126	748	14	5	2023-02-21 14:00:00	Other
8970	11	16	1924	1931	-7	2131	2155	9E	1465	N297PQ	JFK	DTW	87	509	19	31	2023-11-16 19:00:00	Other
8971	7	4	1659	1705	-6	2002	2002	B6	632	N991JT	EWR	LAX	309	2454	17	5	2023-07-04 17:00:00	LAX
8973	1	10	749	800	-11	956	1013	AA	1075	N971NN	LGA	CLT	86	544	8	0	2023-01-10 08:00:00	CLT
8978	1	6	1556	1605	-9	1805	1850	DL	845	N398DA	LGA	DEN	224	1620	16	5	2023-01-06 16:00:00	Other
8981	1	11	653	705	-12	1131	936	DL	841	N3762Y	EWR	ATL	NA	746	7	5	2023-01-11 07:00:00	ATL
8983	10	31	1512	1520	-8	1747	1745	YX	1845	N235JQ	LGA	MCI	181	1107	15	20	2023-10-31 15:00:00	Other
8994	1	23	1522	1529	-7	1853	1848	AA	120	N873NN	JFK	MIA	168	1089	15	29	2023-01-23 15:00:00	MIA
9000	1	28	1253	1259	-6	1446	1458	9E	1458	N325PQ	EWR	DTW	90	488	12	59	2023-01-28 12:00:00	Other
9004	9	4	1323	1329	-6	1502	1505	YX	1402	N425YX	JFK	PIT	62	340	13	29	2023-09-04 13:00:00	Other
9007	5	28	1252	1259	-7	1413	1429	YX	1676	N223JQ	LGA	BOS	47	184	12	59	2023-05-28 12:00:00	BOS
9010	2	20	1504	1510	-6	1715	1724	YX	992	N739YX	EWR	GRR	107	605	15	10	2023-02-20 15:00:00	Other
9013	11	15	711	720	-9	828	900	WN	345	N272WN	LGA	BNA	114	764	7	20	2023-11-15 07:00:00	Other
9017	7	2	2017	2025	-8	2144	2208	AA	628	N751UW	LGA	ORD	112	733	20	25	2023-07-02 20:00:00	ORD
9024	12	14	1134	1140	-6	1249	1309	YX	1862	N233JQ	LGA	DCA	43	214	11	40	2023-12-14 11:00:00	Other
9027	12	2	1946	1955	-9	2212	2241	DL	871	N126DU	LGA	JAX	127	833	19	55	2023-12-02 19:00:00	Other
9028	9	6	1344	1354	-10	1544	1612	9E	1636	N924XJ	LGA	TYS	90	647	13	54	2023-09-06 13:00:00	Other
9030	10	16	1720	1727	-7	1923	1946	YX	1067	N764YX	EWR	IND	97	645	17	27	2023-10-16 17:00:00	Other
9040	10	17	1211	1219	-8	1332	1355	9E	1534	N181PQ	LGA	BUF	47	292	12	19	2023-10-17 12:00:00	Other
9042	12	12	1647	1655	-8	1915	1945	B6	900	N524JB	LGA	ATL	121	762	16	55	2023-12-12 16:00:00	ATL
9051	1	7	753	759	-6	931	949	YX	1256	N726YX	EWR	RDU	76	416	7	59	2023-01-07 07:00:00	Other
9052	3	2	1650	1659	-9	2037	2020	AA	95	N103NN	JFK	LAX	384	2475	16	59	2023-03-02 16:00:00	LAX
9057	5	12	653	700	-7	830	847	9E	1336	N478PX	LGA	STL	128	888	7	0	2023-05-12 07:00:00	Other
9063	5	7	2019	2030	-11	2220	2243	YX	1192	N421YX	JFK	CMH	78	483	20	30	2023-05-07 20:00:00	Other
9066	2	15	2139	2150	-11	2252	2310	YX	1541	N241JQ	LGA	BTV	46	258	21	50	2023-02-15 21:00:00	Other
9067	2	2	1722	1729	-7	1908	1915	UA	597	N13718	EWR	CLE	83	404	17	29	2023-02-02 17:00:00	Other
9077	7	13	559	605	-6	756	817	DL	684	N998AT	EWR	ATL	102	746	6	5	2023-07-13 06:00:00	ATL
9078	4	28	1824	1830	-6	2000	2005	YX	1057	N747YX	EWR	PIT	57	319	18	30	2023-04-28 18:00:00	Other
9083	12	7	938	945	-7	1122	1147	9E	1423	N906XJ	EWR	RDU	80	416	9	45	2023-12-07 09:00:00	Other
9085	1	24	2008	2019	-11	2205	2220	DL	1090	N993AT	EWR	DTW	98	488	20	19	2023-01-24 20:00:00	Other
9089	9	17	1355	1405	-10	1548	1631	DL	112	N3761R	LGA	DEN	209	1620	14	5	2023-09-17 14:00:00	Other
9093	5	20	1314	1320	-6	1554	1541	B6	651	N613JB	JFK	MSY	173	1182	13	20	2023-05-20 13:00:00	Other
9097	2	7	2013	2020	-7	2113	2134	9E	1428	N309PQ	LGA	PVD	34	143	20	20	2023-02-07 20:00:00	Other
9103	11	23	1212	1220	-8	1342	1408	9E	1738	N921XJ	JFK	RDU	70	427	12	20	2023-11-23 12:00:00	Other
9108	8	3	1352	1359	-7	1640	1632	DL	551	N3772H	LGA	DEN	217	1620	13	59	2023-08-03 13:00:00	Other
9118	1	31	1349	1359	-10	1517	1536	AA	184	N4005X	EWR	ORD	124	719	13	59	2023-01-31 13:00:00	ORD
9119	10	15	940	950	-10	1102	1138	YX	1800	N882RW	LGA	MSN	119	812	9	50	2023-10-15 09:00:00	Other
9121	11	24	2216	2223	-7	241	313	NK	361	N625NK	EWR	SJU	188	1608	22	23	2023-11-24 22:00:00	Other
9122	6	2	1122	1132	-10	1417	1434	DL	417	N365NB	JFK	PBI	141	1028	11	32	2023-06-02 11:00:00	Other
9123	9	5	1435	1445	-10	1623	1635	YX	1413	N409YX	LGA	STL	122	888	14	45	2023-09-05 14:00:00	Other
9127	7	26	858	905	-7	1115	1208	YX	1001	N408YX	LGA	IAH	178	1416	9	5	2023-07-26 09:00:00	Other
9129	7	25	852	900	-8	1204	1124	YX	1011	N406YX	JFK	CVG	100	589	9	0	2023-07-25 09:00:00	Other
9131	1	7	1204	1210	-6	1257	1318	YX	1333	N109HQ	JFK	ORH	32	150	12	10	2023-01-07 12:00:00	Other
9135	11	27	1422	1430	-8	1524	1542	UA	565	N27520	EWR	BOS	41	200	14	30	2023-11-27 14:00:00	BOS
9136	6	24	1151	1201	-10	1317	1339	9E	1557	N135EV	JFK	BUF	52	301	12	1	2023-06-24 12:00:00	Other
9144	1	16	1122	1130	-8	1358	1456	AS	8	N248AK	JFK	PDX	310	2454	11	30	2023-01-16 11:00:00	Other
9154	5	25	516	523	-7	729	820	UA	177	N27251	EWR	IAH	176	1400	5	23	2023-05-25 05:00:00	Other
9157	9	18	723	730	-7	1016	1008	YX	1838	N243JQ	LGA	JAX	132	833	7	30	2023-09-18 07:00:00	Other
9163	6	18	1537	1545	-8	1722	1753	YX	1316	N444YX	LGA	DTW	77	502	15	45	2023-06-18 15:00:00	Other
9169	5	26	1545	1552	-7	1723	1725	YX	1294	N806MD	LGA	RIC	55	292	15	52	2023-05-26 15:00:00	Other
9180	9	30	1409	1415	-6	1555	1533	B6	300	N274JB	LGA	BOS	40	184	14	15	2023-09-30 14:00:00	BOS
9190	9	4	659	710	-11	931	1008	DL	530	N349NB	LGA	TPA	133	1010	7	10	2023-09-04 07:00:00	Other
9193	5	4	1319	1329	-10	1447	1515	YX	1203	N402YX	LGA	CLE	67	419	13	29	2023-05-04 13:00:00	Other
9194	11	8	625	635	-10	803	819	YX	1124	N761YX	EWR	CLE	77	404	6	35	2023-11-08 06:00:00	Other
9196	11	13	1947	1959	-12	2203	2239	B6	683	N517JB	LGA	MSY	172	1183	19	59	2023-11-13 19:00:00	Other
9198	9	18	1752	1759	-7	1942	1955	YX	1387	N422YX	JFK	CMH	72	483	17	59	2023-09-18 17:00:00	Other
9203	6	21	1122	1129	-7	1254	1320	UA	722	N460UA	EWR	DTW	71	488	11	29	2023-06-21 11:00:00	Other
9204	5	8	1057	1105	-8	1225	1245	UA	721	N452UA	LGA	ORD	126	733	11	5	2023-05-08 11:00:00	ORD
9207	11	20	1954	2000	-6	2115	2120	AA	703	N773XF	LGA	DCA	52	214	20	0	2023-11-20 20:00:00	Other
9210	3	28	624	630	-6	855	854	UA	192	N831UA	LGA	DEN	241	1620	6	30	2023-03-28 06:00:00	Other
9211	4	19	1657	1705	-8	2004	2010	NK	582	N683NK	EWR	FLL	143	1065	17	5	2023-04-19 17:00:00	FLL
9214	1	5	1222	1230	-8	1418	1422	YX	1344	N108HQ	JFK	RDU	89	427	12	30	2023-01-05 12:00:00	Other
9219	8	14	1254	1300	-6	1554	1628	AS	4	N535AS	JFK	SFO	337	2586	13	0	2023-08-14 13:00:00	Other
9225	2	15	651	659	-8	852	910	YX	1332	N403YX	LGA	DTW	99	502	6	59	2023-02-15 06:00:00	Other
9229	10	9	1949	2000	-11	2114	2149	YX	1323	N434YX	JFK	PIT	63	340	20	0	2023-10-09 20:00:00	Other
9240	4	21	1721	1730	-9	2041	2056	DL	569	N359NW	JFK	AUS	226	1521	17	30	2023-04-21 17:00:00	Other
9241	10	31	752	800	-8	944	952	YX	1347	N411YX	LGA	ILM	84	500	8	0	2023-10-31 08:00:00	Other
9246	11	7	1551	1559	-8	1735	1744	YX	1132	N729YX	EWR	CLE	77	404	15	59	2023-11-07 15:00:00	Other
9253	8	23	719	730	-11	905	908	B6	314	N583JB	JFK	ORD	120	740	7	30	2023-08-23 07:00:00	ORD
9264	6	17	1039	1045	-6	1320	1411	DL	947	N922DZ	JFK	SLC	255	1990	10	45	2023-06-17 10:00:00	Other
9268	6	22	2110	2119	-9	2221	2219	9E	1741	N478PX	LGA	ALB	29	136	21	19	2023-06-22 21:00:00	Other
9287	12	17	1024	1030	-6	1232	1248	YX	1289	N132HQ	LGA	GSP	101	610	10	30	2023-12-17 10:00:00	Other
9289	12	27	621	630	-9	850	954	UA	537	N37318	EWR	SNA	310	2434	6	30	2023-12-27 06:00:00	Other
9293	11	16	1646	1653	-7	1839	1907	9E	1457	N325PQ	JFK	DTW	88	509	16	53	2023-11-16 16:00:00	Other
9294	9	19	2106	2113	-7	2302	2317	UA	437	N77536	EWR	CHS	86	628	21	13	2023-09-19 21:00:00	Other
9299	4	20	649	655	-6	908	928	B6	120	N179JB	LGA	JAX	109	833	6	55	2023-04-20 06:00:00	Other
9309	7	24	848	855	-7	1150	1114	9E	1123	N307PQ	LGA	GRR	96	618	8	55	2023-07-24 08:00:00	Other
9319	10	13	651	700	-9	753	815	UA	468	N37536	EWR	BOS	42	200	7	0	2023-10-13 07:00:00	BOS
9321	7	26	638	645	-7	829	847	UA	397	N24212	EWR	CHS	84	628	6	45	2023-07-26 06:00:00	Other
9325	10	3	2141	2147	-6	2226	2258	YX	1137	N654RW	EWR	MDT	27	141	21	47	2023-10-03 21:00:00	Other
9328	4	2	1221	1229	-8	1335	1402	YX	1578	N823MD	LGA	IAD	50	229	12	29	2023-04-02 12:00:00	Other
9329	1	22	1209	1215	-6	1415	1426	YX	1285	N446YX	JFK	CMH	96	483	12	15	2023-01-22 12:00:00	Other
9338	1	17	1046	1055	-9	1211	1233	YX	1904	N233JQ	LGA	ORF	55	296	10	55	2023-01-17 10:00:00	Other
9340	6	21	1922	1930	-8	2112	2116	YX	1810	N860RW	LGA	PIT	56	335	19	30	2023-06-21 19:00:00	Other
9346	7	17	1655	1705	-10	1900	1921	9E	1322	N485PX	LGA	LIT	153	1085	17	5	2023-07-17 17:00:00	Other
9350	12	2	1840	1855	-15	2018	2037	AA	720	N835AW	LGA	ORD	133	733	18	55	2023-12-02 18:00:00	ORD
9351	5	12	829	835	-6	1033	1109	DL	537	N690DL	JFK	ATL	100	760	8	35	2023-05-12 08:00:00	ATL
9352	10	13	1920	1930	-10	2233	2239	UA	470	N17312	EWR	SEA	315	2402	19	30	2023-10-13 19:00:00	Other
9356	10	18	653	700	-7	1058	1057	B6	552	N506JB	EWR	SJU	215	1608	7	0	2023-10-18 07:00:00	Other
9357	9	18	1123	1130	-7	1337	1353	YX	1865	N818MD	LGA	MCI	153	1107	11	30	2023-09-18 11:00:00	Other
9358	11	5	2033	2040	-7	132	146	NK	361	N654NK	EWR	SJU	208	1608	20	40	2023-11-05 20:00:00	Other
9375	10	9	1542	1550	-8	1822	1856	DL	194	N313DU	LGA	DFW	195	1389	15	50	2023-10-09 15:00:00	Other
9376	5	31	1054	1100	-6	1418	1416	B6	195	N2105J	JFK	LAX	306	2475	11	0	2023-05-31 11:00:00	LAX
9383	6	20	451	500	-9	634	658	AA	950	N195UW	EWR	CLT	77	529	5	0	2023-06-20 05:00:00	CLT
9384	6	24	1853	1859	-6	2247	2151	AS	95	N551AS	EWR	SAN	322	2425	18	59	2023-06-24 18:00:00	Other
9393	5	29	1023	1029	-6	1331	1239	YX	1246	N430YX	LGA	GSP	84	610	10	29	2023-05-29 10:00:00	Other
9399	9	5	1751	1800	-9	1920	1930	YX	1907	N230JQ	LGA	BOS	38	184	18	0	2023-09-05 18:00:00	BOS
9400	5	24	1449	1459	-10	1607	1627	YX	1232	N438YX	LGA	BUF	52	292	14	59	2023-05-24 14:00:00	Other
9402	11	14	1122	1129	-7	1352	1424	DL	426	N858DZ	JFK	TPA	139	1005	11	29	2023-11-14 11:00:00	Other
9403	4	15	1437	1450	-13	NA	1633	NK	24	N526NK	EWR	MYR	NA	550	14	50	2023-04-15 14:00:00	Other
9405	5	18	626	635	-9	936	1012	AA	32	N103NN	JFK	SFO	343	2586	6	35	2023-05-18 06:00:00	Other
9406	4	1	1751	1759	-8	2117	2117	B6	697	N935JB	EWR	LAX	345	2454	17	59	2023-04-01 17:00:00	LAX
9412	2	10	1702	1709	-7	2041	2020	NK	631	N670NK	EWR	FLL	149	1065	17	9	2023-02-10 17:00:00	FLL
9418	11	3	2033	2040	-7	2257	2300	UA	617	N39416	EWR	SAV	101	708	20	40	2023-11-03 20:00:00	Other
9419	4	26	2116	2129	-13	2329	2339	YX	1078	N418YX	JFK	CMH	78	483	21	29	2023-04-26 21:00:00	Other
9428	2	13	2020	2029	-9	2308	2354	B6	787	N615JB	JFK	MIA	139	1089	20	29	2023-02-13 20:00:00	MIA
9429	10	13	1824	1830	-6	2135	2137	UA	638	N28987	EWR	SFO	326	2565	18	30	2023-10-13 18:00:00	Other
9436	3	18	1205	1215	-10	1326	1348	9E	1402	N331PQ	LGA	ORF	64	296	12	15	2023-03-18 12:00:00	Other
9438	9	4	1050	1059	-9	1221	1255	YX	1089	N858RW	EWR	ILM	68	488	10	59	2023-09-04 10:00:00	Other
9446	1	30	1121	1130	-9	1257	1326	AA	119	N819AW	LGA	ORD	128	733	11	30	2023-01-30 11:00:00	ORD
9450	2	9	1524	1535	-11	1722	1740	YX	1333	N132HQ	JFK	CLE	80	425	15	35	2023-02-09 15:00:00	Other
9451	4	8	1749	1759	-10	1910	1940	UA	724	N809UA	LGA	ORD	122	733	17	59	2023-04-08 17:00:00	ORD
9455	9	17	852	900	-8	1025	1038	B6	782	N306JB	LGA	BNA	119	764	9	0	2023-09-17 09:00:00	Other
9461	1	27	720	730	-10	912	923	9E	1568	N349PQ	LGA	CLE	71	419	7	30	2023-01-27 07:00:00	Other
9467	4	25	621	631	-10	839	851	UA	415	N17753	EWR	ATL	112	746	6	31	2023-04-25 06:00:00	ATL
9468	2	8	1235	1245	-10	1354	1414	9E	1309	N182GJ	LGA	BTV	49	258	12	45	2023-02-08 12:00:00	Other
9475	12	30	2019	2030	-11	2118	2143	AA	841	N770UW	LGA	BOS	40	184	20	30	2023-12-30 20:00:00	BOS
9478	10	3	1148	1200	-12	1409	1353	YX	1350	N122HQ	LGA	MEM	131	963	12	0	2023-10-03 12:00:00	Other
9479	2	13	1324	1330	-6	1436	1459	YX	1534	N214JQ	JFK	DCA	52	213	13	30	2023-02-13 13:00:00	Other
9481	6	2	749	800	-11	904	924	AA	782	N801AW	LGA	DCA	43	214	8	0	2023-06-02 08:00:00	Other
9488	10	11	616	629	-13	752	822	AA	950	N755US	LGA	RDU	71	431	6	29	2023-10-11 06:00:00	Other
9490	12	1	1835	1844	-9	2017	2047	9E	1381	N912XJ	LGA	GSO	75	461	18	44	2023-12-01 18:00:00	Other
9492	12	9	1400	1408	-8	1601	1633	UA	195	N68801	EWR	DEN	221	1605	14	8	2023-12-09 14:00:00	Other
9505	5	28	2053	2100	-7	2231	2256	YX	1183	N429YX	LGA	MEM	131	963	21	0	2023-05-28 21:00:00	Other
9507	10	17	1949	2000	-11	2056	2149	YX	1323	N437YX	JFK	PIT	51	340	20	0	2023-10-17 20:00:00	Other
9511	2	26	1222	1230	-8	1336	1359	9E	1309	N678CA	LGA	BTV	49	258	12	30	2023-02-26 12:00:00	Other
9512	11	3	1547	1555	-8	1706	1715	WN	788	N8562Z	LGA	MDW	115	725	15	55	2023-11-03 15:00:00	Other
9513	1	12	830	837	-7	1020	1042	YX	1143	N721YX	EWR	GSO	78	445	8	37	2023-01-12 08:00:00	Other
9528	4	14	1214	1221	-7	1335	1358	YX	1258	N443YX	LGA	PIT	56	335	12	21	2023-04-14 12:00:00	Other
9532	3	17	652	700	-8	1019	1015	B6	145	N775JB	EWR	FLL	139	1065	7	0	2023-03-17 07:00:00	FLL
9533	4	26	832	838	-6	1029	1035	9E	1399	N491PX	LGA	GSO	81	461	8	38	2023-04-26 08:00:00	Other
9536	10	24	944	950	-6	1044	1115	YX	1308	N104HQ	LGA	DCA	43	214	9	50	2023-10-24 09:00:00	Other
9537	2	14	1354	1400	-6	1508	1520	YX	1516	N205JQ	LGA	BOS	42	184	14	0	2023-02-14 14:00:00	BOS
9539	1	27	923	930	-7	1040	1057	9E	1577	N303PQ	JFK	PWM	47	273	9	30	2023-01-27 09:00:00	Other
9543	10	14	1748	1754	-6	1908	1928	9E	1429	N272PQ	LGA	BGR	56	378	17	54	2023-10-14 17:00:00	Other
9544	1	30	1221	1229	-8	1335	1357	YX	1348	N409YX	JFK	ORF	54	290	12	29	2023-01-30 12:00:00	Other
9546	3	16	815	829	-14	1029	1056	YX	1072	N865RW	EWR	CVG	93	569	8	29	2023-03-16 08:00:00	Other
9548	2	6	1509	1515	-6	1711	1727	YX	1532	N220JQ	LGA	STL	141	888	15	15	2023-02-06 15:00:00	Other
9555	3	24	554	600	-6	840	855	UA	872	N14107	EWR	TPA	142	997	6	0	2023-03-24 06:00:00	Other
9561	10	25	852	858	-6	1106	1133	YX	1742	N201JQ	LGA	SDF	108	659	8	58	2023-10-25 08:00:00	Other
9571	2	7	657	705	-8	945	1015	DL	533	N351DN	LGA	MIA	141	1096	7	5	2023-02-07 07:00:00	MIA
9573	2	17	1038	1055	-17	1245	1320	G4	522	193NV	EWR	TYS	100	631	10	55	2023-02-17 10:00:00	Other
9574	8	4	617	625	-8	951	913	UA	216	N884UA	EWR	AUS	204	1504	6	25	2023-08-04 06:00:00	Other
9586	9	26	647	659	-12	829	835	AA	1009	N909NN	EWR	ORD	133	719	6	59	2023-09-26 06:00:00	ORD
9587	8	16	1249	1300	-11	1502	1509	UA	715	N829UA	EWR	MSY	168	1167	13	0	2023-08-16 13:00:00	Other
9596	12	3	2005	2015	-10	2115	2134	B6	514	N317JB	LGA	BOS	31	184	20	15	2023-12-03 20:00:00	BOS
9599	1	19	850	900	-10	958	1030	YX	1730	N211JQ	JFK	IAD	50	228	9	0	2023-01-19 09:00:00	Other
9600	8	18	710	717	-7	1006	1010	UA	718	N86534	EWR	SNA	309	2434	7	17	2023-08-18 07:00:00	Other
9605	2	7	951	1000	-9	1101	1124	UA	691	N435UA	EWR	IAD	44	212	10	0	2023-02-07 10:00:00	Other
9609	10	23	1706	1715	-9	1821	1849	9E	1473	N490PX	LGA	RIC	48	292	17	15	2023-10-23 17:00:00	Other
9611	12	13	1302	1310	-8	1416	1445	YX	1326	N410YX	LGA	RIC	59	292	13	10	2023-12-13 13:00:00	Other
9612	6	28	918	926	-8	1050	1107	YX	1217	N723YX	EWR	PIT	55	319	9	26	2023-06-28 09:00:00	Other
9615	5	8	1046	1052	-6	1257	1316	YX	1102	N655RW	EWR	HHH	107	687	10	52	2023-05-08 10:00:00	Other
9634	2	8	654	701	-7	845	915	AA	331	N949AN	LGA	CLT	85	544	7	1	2023-02-08 07:00:00	CLT
9638	6	20	1621	1627	-6	1740	1800	YX	1370	N114HQ	LGA	RIC	59	292	16	27	2023-06-20 16:00:00	Other
9640	11	25	1937	1945	-8	2224	2252	DL	877	N806DN	JFK	TPA	149	1005	19	45	2023-11-25 19:00:00	Other
9649	12	8	1021	1030	-9	1116	1148	B6	56	N657JB	JFK	BOS	34	187	10	30	2023-12-08 10:00:00	BOS
9652	9	5	1753	1759	-6	1949	2024	UA	422	N37422	EWR	DEN	204	1605	17	59	2023-09-05 17:00:00	Other
9656	5	16	902	910	-8	1145	1236	AA	707	N316RK	JFK	MIA	142	1089	9	10	2023-05-16 09:00:00	MIA
9665	7	18	1211	1217	-6	1425	1341	AA	806	N810AW	LGA	BNA	126	764	12	17	2023-07-18 12:00:00	Other
9666	6	2	1552	1559	-7	1654	1712	9E	1734	N902XJ	LGA	ALB	29	136	15	59	2023-06-02 15:00:00	Other
9672	10	23	822	830	-8	1003	1010	B6	349	N279JB	JFK	ORD	124	740	8	30	2023-10-23 08:00:00	ORD
9673	8	21	700	710	-10	819	845	9E	1176	N485PX	LGA	RIC	52	292	7	10	2023-08-21 07:00:00	Other
9680	5	6	906	920	-14	1057	1120	NK	543	N606NK	EWR	CHS	86	628	9	20	2023-05-06 09:00:00	Other
9685	4	5	1411	1418	-7	2045	1624	YX	1047	N752YX	EWR	CVG	NA	569	14	18	2023-04-05 14:00:00	Other
9691	11	4	959	1010	-11	1156	1208	YX	1246	N408YX	JFK	CLE	82	425	10	10	2023-11-04 10:00:00	Other
9693	9	14	1143	1159	-16	1341	1423	YX	1055	N649RW	EWR	SDF	98	642	11	59	2023-09-14 11:00:00	Other
9698	7	24	741	747	-6	950	950	UA	728	N848UA	EWR	MSY	158	1167	7	47	2023-07-24 07:00:00	Other
9706	8	4	1418	1430	-12	1538	1604	YX	1013	N413YX	LGA	BUF	52	292	14	30	2023-08-04 14:00:00	Other
9718	1	27	1318	1326	-8	1458	1538	YX	1316	N129HQ	LGA	CMH	83	479	13	26	2023-01-27 13:00:00	Other
9719	10	30	1237	1245	-8	1452	1519	UA	389	N498UA	EWR	ATL	118	746	12	45	2023-10-30 12:00:00	ATL
9721	3	29	1017	1029	-12	1138	1209	9E	1558	N186PQ	LGA	ORF	51	296	10	29	2023-03-29 10:00:00	Other
9725	3	30	1911	1920	-9	2141	2202	9E	1461	N337PQ	LGA	JAX	119	833	19	20	2023-03-30 19:00:00	Other
9727	2	21	1557	1610	-13	1745	1759	DL	457	N136DQ	LGA	ORD	136	733	16	10	2023-02-21 16:00:00	ORD
9731	11	6	1807	1815	-8	2037	2109	9E	1540	N926XJ	JFK	MCI	177	1113	18	15	2023-11-06 18:00:00	Other
9733	8	24	827	835	-8	1045	1057	9E	1247	N329PQ	JFK	CHS	88	636	8	35	2023-08-24 08:00:00	Other
9735	1	7	2152	2159	-7	2315	2331	B6	35	N247JB	JFK	BUF	56	301	21	59	2023-01-07 21:00:00	Other
9736	1	10	2053	2100	-7	2259	2309	YX	1413	N450YX	LGA	GSO	71	461	21	0	2023-01-10 21:00:00	Other
9737	2	20	818	825	-7	1149	1158	DL	227	N133DU	LGA	DFW	247	1389	8	25	2023-02-20 08:00:00	Other
9740	8	26	2251	2259	-8	253	252	B6	122	N996JL	JFK	SJU	220	1598	22	59	2023-08-26 22:00:00	Other
9741	11	29	1150	1159	-9	1335	1354	9E	1441	N919XJ	LGA	CLE	73	419	11	59	2023-11-29 11:00:00	Other
9744	5	3	2123	2129	-6	2251	2316	YX	1319	N402YX	LGA	CLE	65	419	21	29	2023-05-03 21:00:00	Other
9746	1	8	2023	2029	-6	2332	2327	YX	1297	N124HQ	LGA	ATL	128	762	20	29	2023-01-08 20:00:00	ATL
9748	12	13	1821	1829	-8	2108	2152	AS	158	N215AK	EWR	SEA	307	2402	18	29	2023-12-13 18:00:00	Other
9753	8	22	749	759	-10	938	1010	YX	1082	N131HQ	LGA	CVG	83	585	7	59	2023-08-22 07:00:00	Other
9774	11	27	621	630	-9	754	819	9E	1759	N182GJ	LGA	RDU	73	431	6	30	2023-11-27 06:00:00	Other
9781	6	7	1059	1112	-13	1353	1406	UA	259	N27255	EWR	TPA	150	997	11	12	2023-06-07 11:00:00	Other
9792	12	28	1704	1710	-6	1838	1853	UA	833	N489UA	LGA	ORD	113	733	17	10	2023-12-28 17:00:00	ORD
9796	11	24	830	837	-7	1117	1159	UA	783	N17529	EWR	SEA	316	2402	8	37	2023-11-24 08:00:00	Other
9806	12	14	2148	2157	-9	2243	2334	YX	1292	N409YX	JFK	DCA	38	213	21	57	2023-12-14 21:00:00	Other
9816	11	25	652	659	-7	817	830	AA	955	N751UW	LGA	DCA	44	214	6	59	2023-11-25 06:00:00	Other
9817	5	16	2115	2126	-11	2315	2328	NK	283	N691NK	LGA	DTW	87	502	21	26	2023-05-16 21:00:00	Other
9819	12	20	732	740	-8	913	935	YX	1264	N138HQ	LGA	STL	132	888	7	40	2023-12-20 07:00:00	Other
9822	3	12	1650	1659	-9	1850	1920	YX	1125	N639RW	EWR	IND	101	645	16	59	2023-03-12 16:00:00	Other
9834	8	21	2010	2020	-10	2143	2223	9E	1154	N478PX	LGA	GSO	65	461	20	20	2023-08-21 20:00:00	Other
9838	12	4	948	955	-7	1306	1255	B6	664	N328JB	EWR	MCO	159	937	9	55	2023-12-04 09:00:00	MCO
9845	9	1	726	733	-7	956	954	UA	472	N27263	EWR	SAV	109	708	7	33	2023-09-01 07:00:00	Other
9850	9	14	848	857	-9	1025	1035	9E	1483	N912XJ	LGA	ORF	53	296	8	57	2023-09-14 08:00:00	Other
9852	1	18	2014	2030	-16	2255	2328	B6	399	N510JB	EWR	MCO	135	937	20	30	2023-01-18 20:00:00	MCO
9860	4	14	552	600	-8	720	749	DL	699	N982AT	EWR	DTW	72	488	6	0	2023-04-14 06:00:00	Other
9866	9	7	1041	1047	-6	1325	1353	NK	511	N665NK	EWR	FLL	141	1065	10	47	2023-09-07 10:00:00	FLL
9872	11	26	2054	2100	-6	2321	2217	YX	1271	N445YX	JFK	BOS	47	187	21	0	2023-11-26 21:00:00	BOS
9885	1	9	1051	1059	-8	1201	1216	YX	1731	N240JQ	JFK	BOS	42	187	10	59	2023-01-09 10:00:00	BOS
9890	11	23	1013	1025	-12	1252	1323	UA	621	N13138	EWR	MCO	135	937	10	25	2023-11-23 10:00:00	MCO
9905	11	18	1423	1434	-11	1542	1546	UA	565	N479UA	EWR	BOS	36	200	14	34	2023-11-18 14:00:00	BOS
9910	9	30	1809	1815	-6	1941	1944	UA	396	N61886	EWR	BNA	104	748	18	15	2023-09-30 18:00:00	Other
9916	1	27	550	600	-10	742	754	YX	1857	N823MD	LGA	STL	145	888	6	0	2023-01-27 06:00:00	Other
9918	2	14	650	700	-10	1006	1024	B6	301	N976JT	JFK	LAX	350	2475	7	0	2023-02-14 07:00:00	LAX
9923	2	6	804	815	-11	1107	1134	AA	557	N829NN	LGA	DFW	199	1389	8	15	2023-02-06 08:00:00	Other
9929	9	7	1619	1630	-11	NA	1922	UA	469	N793UA	EWR	LAX	NA	2454	16	30	2023-09-07 16:00:00	LAX
9930	10	18	1316	1323	-7	1432	1455	UA	93	N12218	EWR	ORD	110	719	13	23	2023-10-18 13:00:00	ORD
9931	3	3	656	705	-9	938	949	DL	186	N344NW	LGA	ATL	130	762	7	5	2023-03-03 07:00:00	ATL
9933	8	4	2018	2029	-11	42	2357	AS	17	N215AK	JFK	SFO	370	2586	20	29	2023-08-04 20:00:00	Other
9939	9	14	1453	1502	-9	1631	1657	DL	757	N944AT	EWR	MSP	141	1008	15	2	2023-09-14 15:00:00	Other
9941	7	25	1148	1156	-8	1353	1400	AA	765	N942AN	JFK	CLT	95	541	11	56	2023-07-25 11:00:00	CLT
9947	4	8	853	900	-7	1045	1105	YX	1215	N806MD	LGA	CMH	92	479	9	0	2023-04-08 09:00:00	Other
9954	3	18	609	615	-6	800	817	DL	980	N993AT	EWR	MSP	148	1008	6	15	2023-03-18 06:00:00	Other
9966	9	1	1528	1534	-6	1709	1739	9E	1507	N136EV	LGA	STL	125	888	15	34	2023-09-01 15:00:00	Other
9969	2	20	1650	1700	-10	1754	1828	YX	1596	N246JQ	LGA	BOS	34	184	17	0	2023-02-20 17:00:00	BOS
9974	5	22	1239	1259	-20	1425	1456	NK	502	N692NK	LGA	MYR	78	563	12	59	2023-05-22 12:00:00	Other
9988	9	3	707	715	-8	941	1011	B6	431	N535JB	LGA	TPA	134	1010	7	15	2023-09-03 07:00:00	Other
9992	4	14	623	630	-7	825	818	AA	898	N821NN	LGA	ORD	113	733	6	30	2023-04-14 06:00:00	ORD
10001	8	22	2101	2107	-6	2259	2312	UA	193	N69885	EWR	CVG	85	569	21	7	2023-08-22 21:00:00	Other
10002	10	26	2033	2040	-7	2148	2220	9E	1515	N937XJ	LGA	RIC	53	292	20	40	2023-10-26 20:00:00	Other
10004	1	1	1304	1310	-6	1419	1445	WN	550	N903WN	LGA	BNA	116	764	13	10	2023-01-01 13:00:00	Other
10008	11	18	1615	1625	-10	1731	1806	YX	1865	N217JQ	LGA	RIC	50	292	16	25	2023-11-18 16:00:00	Other
10011	11	8	752	759	-7	950	1000	YX	1052	N732YX	EWR	CMH	84	463	7	59	2023-11-08 07:00:00	Other
10020	2	28	2148	2156	-8	2328	2338	UA	811	N38424	EWR	RDU	67	416	21	56	2023-02-28 21:00:00	Other
10027	2	5	2041	2050	-9	2226	2253	YX	1528	N204JQ	JFK	CMH	79	483	20	50	2023-02-05 20:00:00	Other
10030	4	23	1911	1917	-6	2113	2145	YX	1550	N218JQ	LGA	MCI	161	1107	19	17	2023-04-23 19:00:00	Other
10031	2	16	1523	1530	-7	1836	1855	AA	120	N102NN	JFK	LAX	347	2475	15	30	2023-02-16 15:00:00	LAX
10045	5	24	613	623	-10	800	821	YX	1194	N118HQ	LGA	CMH	78	479	6	23	2023-05-24 06:00:00	Other
10048	9	25	552	600	-8	749	802	AA	228	N509AY	LGA	CLT	84	544	6	0	2023-09-25 06:00:00	CLT
10049	3	3	1706	1715	-9	1809	1833	B6	420	N265JB	LGA	BOS	32	184	17	15	2023-03-03 17:00:00	BOS
10050	5	31	1812	1820	-8	2012	2049	YX	1677	N231JQ	LGA	SDF	98	659	18	20	2023-05-31 18:00:00	Other
10052	12	30	1823	1829	-6	1953	2017	UA	423	N14731	EWR	ORD	110	719	18	29	2023-12-30 18:00:00	ORD
10056	5	8	942	950	-8	1137	1145	9E	1391	N916XJ	JFK	CMH	76	483	9	50	2023-05-08 09:00:00	Other
10064	1	10	1028	1035	-7	1152	1235	WN	1003	N7842A	LGA	STL	126	888	10	35	2023-01-10 10:00:00	Other
10080	1	13	1214	1225	-11	1329	1348	NK	314	N626NK	EWR	PIT	55	319	12	25	2023-01-13 12:00:00	Other
10083	8	3	2047	2056	-9	2225	2302	YX	932	N724YX	EWR	CMH	71	463	20	56	2023-08-03 20:00:00	Other
10086	6	7	922	930	-8	1208	1255	AS	16	N435AS	JFK	SFO	325	2586	9	30	2023-06-07 09:00:00	Other
10087	3	28	1308	1315	-7	1411	1431	B6	833	N354JB	LGA	BOS	38	184	13	15	2023-03-28 13:00:00	BOS
10088	5	29	1310	1316	-6	1517	1540	YX	1655	N213JQ	LGA	SDF	93	659	13	16	2023-05-29 13:00:00	Other
10098	10	18	2109	2115	-6	2234	2257	AA	1001	N834AW	LGA	RDU	65	431	21	15	2023-10-18 21:00:00	Other
10104	5	31	700	712	-12	954	1013	DL	350	N366NB	LGA	PBI	140	1035	7	12	2023-05-31 07:00:00	Other
10110	4	3	954	1000	-6	1118	1131	YX	968	N748YX	EWR	BUF	58	282	10	0	2023-04-03 10:00:00	Other
10111	4	8	1652	1659	-7	1827	1840	UA	717	N853UA	LGA	ORD	125	733	16	59	2023-04-08 16:00:00	ORD
10112	2	9	1001	1015	-14	1110	1130	B6	218	N183JB	LGA	BOS	43	184	10	15	2023-02-09 10:00:00	BOS
10118	10	31	918	930	-12	1228	1245	AS	7	N253AK	JFK	SEA	329	2422	9	30	2023-10-31 09:00:00	Other
10127	10	26	1150	1159	-9	1431	1431	OO	1195	N310SY	LGA	SDF	120	659	11	59	2023-10-26 11:00:00	Other
10130	7	7	1345	1355	-10	1552	1503	9E	1254	N918XJ	LGA	BGM	35	147	13	55	2023-07-07 13:00:00	Other
10134	11	29	2022	2029	-7	2137	2209	YX	1086	N758YX	EWR	PIT	57	319	20	29	2023-11-29 20:00:00	Other
10144	6	13	2102	2110	-8	2216	2243	YX	1401	N408YX	LGA	ORF	52	296	21	10	2023-06-13 21:00:00	Other
10146	8	29	1049	1100	-11	1235	1251	UA	671	N841UA	EWR	MEM	141	946	11	0	2023-08-29 11:00:00	Other
10147	7	5	955	1005	-10	1110	1142	UA	581	N414UA	LGA	ORD	100	733	10	5	2023-07-05 10:00:00	ORD
10153	12	31	1411	1420	-9	1519	1600	9E	1552	N919XJ	LGA	MKE	107	738	14	20	2023-12-31 14:00:00	Other
10155	5	19	609	616	-7	905	916	UA	365	N17301	EWR	SAN	332	2425	6	16	2023-05-19 06:00:00	Other
10158	1	30	1206	1212	-6	1432	1455	YX	1354	N404YX	LGA	MSP	182	1020	12	12	2023-01-30 12:00:00	Other
10165	1	17	524	530	-6	648	710	AA	981	N909NN	EWR	ORD	111	719	5	30	2023-01-17 05:00:00	ORD
10172	1	24	1923	1935	-12	2227	2257	NK	1105	N698NK	EWR	MIA	160	1085	19	35	2023-01-24 19:00:00	MIA
10177	9	12	1352	1401	-9	1501	1523	YX	1116	N753YX	EWR	PWM	49	284	14	1	2023-09-12 14:00:00	Other
10180	6	20	919	929	-10	1038	1101	AA	742	N177XF	LGA	PIT	59	335	9	29	2023-06-20 09:00:00	Other
10183	1	27	2228	2235	-7	17	2359	9E	1693	N604LR	JFK	BTV	45	266	22	35	2023-01-27 22:00:00	Other
10188	11	11	1123	1129	-6	1355	1405	DL	859	N101DU	LGA	MSY	191	1183	11	29	2023-11-11 11:00:00	Other
10196	3	16	2141	2150	-9	2300	2313	9E	1409	N184GJ	LGA	BGR	62	378	21	50	2023-03-16 21:00:00	Other
10203	2	6	904	915	-11	1101	1125	YX	1569	N213JQ	LGA	CMH	71	479	9	15	2023-02-06 09:00:00	Other
10205	10	20	1057	1106	-9	1221	1236	YX	1335	N102HQ	LGA	CHO	58	305	11	6	2023-10-20 11:00:00	Other
10206	1	18	1748	1800	-12	1914	1936	AA	398	N822AW	LGA	DCA	57	214	18	0	2023-01-18 18:00:00	Other
10215	1	28	1152	1200	-8	1518	1530	UA	873	N29124	EWR	SFO	366	2565	12	0	2023-01-28 12:00:00	Other
10221	10	17	1952	2000	-8	2221	2317	AA	83	N109NN	JFK	LAX	308	2475	20	0	2023-10-17 20:00:00	LAX
10229	11	20	1553	1559	-6	1722	1744	YX	1132	N733YX	EWR	CLE	68	404	15	59	2023-11-20 15:00:00	Other
10235	8	12	2006	2015	-9	2213	2222	NK	73	N695NK	LGA	DTW	106	502	20	15	2023-08-12 20:00:00	Other
10241	11	4	1739	1755	-16	1850	1931	9E	1680	N919XJ	LGA	BUF	50	292	17	55	2023-11-04 17:00:00	Other
10244	11	27	1251	1259	-8	1443	1441	YX	1299	N108HQ	JFK	PIT	80	340	12	59	2023-11-27 12:00:00	Other
10253	1	15	742	750	-8	954	1026	UA	789	N853UA	LGA	DEN	227	1620	7	50	2023-01-15 07:00:00	Other
10258	11	10	810	819	-9	937	938	AA	916	N770UW	LGA	DCA	66	214	8	19	2023-11-10 08:00:00	Other
10265	11	10	736	745	-9	1059	1053	UA	576	N27290	EWR	SAN	347	2425	7	45	2023-11-10 07:00:00	Other
10276	12	4	1440	1449	-9	1605	1620	9E	1527	N153PQ	LGA	CHO	55	305	14	49	2023-12-04 14:00:00	Other
10279	3	17	1828	1835	-7	2059	2123	9E	1460	N232PQ	JFK	JAX	125	828	18	35	2023-03-17 18:00:00	Other
10285	8	27	622	630	-8	745	757	YX	972	N412YX	JFK	ORF	56	290	6	30	2023-08-27 06:00:00	Other
10289	8	28	651	700	-9	935	912	UA	116	N45440	EWR	DEN	213	1605	7	0	2023-08-28 07:00:00	Other
10291	12	16	1533	1539	-6	1839	1850	UA	716	N76508	EWR	RSW	167	1068	15	39	2023-12-16 15:00:00	Other
10292	5	7	1652	1659	-7	1824	1850	YX	1014	N727YX	EWR	GSO	68	445	16	59	2023-05-07 16:00:00	Other
10294	8	29	823	830	-7	1103	1128	AA	476	N983AN	EWR	DFW	186	1372	8	30	2023-08-29 08:00:00	Other
10295	6	11	1347	1355	-8	1501	1523	9E	1625	N292PQ	LGA	BUF	52	292	13	55	2023-06-11 13:00:00	Other
10301	8	2	2054	2100	-6	2236	2314	OO	961	N293SY	JFK	CLE	76	425	21	0	2023-08-02 21:00:00	Other
10312	1	17	1305	1311	-6	1627	1626	UA	199	N836UA	EWR	AUS	229	1504	13	11	2023-01-17 13:00:00	Other
10313	8	30	1448	1455	-7	1642	1725	YX	1322	N878RW	JFK	CLT	90	541	14	55	2023-08-30 14:00:00	CLT
10334	9	3	954	1005	-11	1108	1142	UA	706	N410UA	LGA	ORD	108	733	10	5	2023-09-03 10:00:00	ORD
10336	7	3	852	900	-8	1157	1237	AA	52	N110AN	JFK	SFO	333	2586	9	0	2023-07-03 09:00:00	Other
10350	1	28	1723	1729	-6	1841	1854	B6	494	N274JB	JFK	ROC	56	264	17	29	2023-01-28 17:00:00	Other
10353	11	6	754	805	-11	1035	1130	B6	46	N279JB	JFK	SRQ	143	1041	8	5	2023-11-06 08:00:00	Other
10356	9	22	1346	1355	-9	1514	1538	AA	761	N804AW	LGA	RDU	69	431	13	55	2023-09-22 13:00:00	Other
10359	2	27	1230	1241	-11	1705	1729	AA	258	N9004F	JFK	STT	184	1623	12	41	2023-02-27 12:00:00	Other
10360	3	2	1517	1527	-10	1710	1712	UA	685	N21723	EWR	CLE	84	404	15	27	2023-03-02 15:00:00	Other
10362	4	28	1120	1129	-9	1434	1432	B6	20	N583JB	LGA	TPA	155	1010	11	29	2023-04-28 11:00:00	Other
10369	2	9	1720	1730	-10	2012	2050	AS	88	N535AS	EWR	PDX	325	2434	17	30	2023-02-09 17:00:00	Other
10380	5	19	2221	2230	-9	2345	9	9E	1381	N292PQ	JFK	BGR	55	382	22	30	2023-05-19 22:00:00	Other
10381	2	10	1201	1207	-6	1259	1316	UA	154	N75436	EWR	BOS	38	200	12	7	2023-02-10 12:00:00	BOS
10383	12	17	2123	2129	-6	2313	2325	YX	1042	N748YX	EWR	ILM	87	488	21	29	2023-12-17 21:00:00	Other
10389	5	15	752	759	-7	956	1002	AA	952	N152UW	LGA	CLT	81	544	7	59	2023-05-15 07:00:00	CLT
10391	12	29	928	935	-7	1249	1239	B6	38	N584JB	EWR	MCO	154	937	9	35	2023-12-29 09:00:00	MCO
10398	9	5	552	600	-8	720	759	YX	1317	N872RW	LGA	CMH	69	479	6	0	2023-09-05 06:00:00	Other
10405	2	22	2221	2230	-9	2342	4	9E	1353	N926XJ	JFK	BGR	52	382	22	30	2023-02-22 22:00:00	Other
10411	4	18	1909	1917	-8	2106	2145	YX	1550	N238JQ	LGA	MCI	156	1107	19	17	2023-04-18 19:00:00	Other
10420	10	14	1722	1730	-8	1845	1904	9E	1473	N914XJ	LGA	RIC	55	292	17	30	2023-10-14 17:00:00	Other
10428	11	10	654	702	-8	902	918	UA	449	N23721	EWR	CHS	105	628	7	2	2023-11-10 07:00:00	Other
10430	8	29	1622	1630	-8	1829	1903	B6	97	N323JB	JFK	SAV	108	718	16	30	2023-08-29 16:00:00	Other
10444	5	6	1400	1410	-10	1536	1558	9E	1273	N298PQ	LGA	CLE	67	419	14	10	2023-05-06 14:00:00	Other
10449	1	30	2054	2100	-6	29	38	B6	362	N988JT	JFK	SFO	371	2586	21	0	2023-01-30 21:00:00	Other
10453	9	18	1154	1200	-6	1349	1324	YX	1953	N210JQ	LGA	BOS	34	184	12	0	2023-09-18 12:00:00	BOS
10457	2	15	1206	1213	-7	1425	1452	YX	1238	N409YX	LGA	MSP	172	1020	12	13	2023-02-15 12:00:00	Other
10472	1	4	822	830	-8	944	1019	AA	134	N972NN	LGA	ORD	116	733	8	30	2023-01-04 08:00:00	ORD
10473	9	2	1657	1705	-8	1947	2012	NK	865	N624NK	EWR	FLL	142	1065	17	5	2023-09-02 17:00:00	FLL
10481	12	4	1911	1920	-9	2027	2107	YX	1736	N879RW	LGA	PIT	60	335	19	20	2023-12-04 19:00:00	Other
10483	10	3	550	600	-10	822	856	AA	948	N919NN	EWR	DFW	179	1372	6	0	2023-10-03 06:00:00	Other
10487	11	23	1154	1200	-6	1434	1510	DL	787	N345DN	LGA	PBI	136	1035	12	0	2023-11-23 12:00:00	Other
10497	4	25	539	550	-11	829	852	AA	553	N992NN	LGA	DFW	203	1389	5	50	2023-04-25 05:00:00	Other
10498	8	31	1349	1359	-10	1545	1611	YX	975	N136HQ	JFK	CVG	91	589	13	59	2023-08-31 13:00:00	Other
10506	2	18	1110	1117	-7	1319	1330	YX	1037	N756YX	EWR	DTW	91	488	11	17	2023-02-18 11:00:00	Other
10507	11	4	1028	1034	-6	1233	1254	YX	1112	N722YX	EWR	CHS	95	628	10	34	2023-11-04 10:00:00	Other
10510	1	8	720	729	-9	836	927	AA	285	N354PT	LGA	ORD	103	733	7	29	2023-01-08 07:00:00	ORD
10517	3	2	1211	1218	-7	1338	1350	YX	1063	N639RW	EWR	BUF	61	282	12	18	2023-03-02 12:00:00	Other
10518	11	15	2110	2120	-10	2222	2239	9E	1550	N901XJ	JFK	ITH	44	189	21	20	2023-11-15 21:00:00	Other
10519	10	27	838	844	-6	1008	1040	9E	1397	N917XJ	LGA	BHM	121	866	8	44	2023-10-27 08:00:00	Other
10521	12	18	1500	1510	-10	1754	1822	B6	130	N273JB	EWR	RSW	151	1068	15	10	2023-12-18 15:00:00	Other
10530	12	1	951	959	-8	1102	1115	YX	1777	N211JQ	LGA	BOS	42	184	9	59	2023-12-01 09:00:00	BOS
10532	10	8	2022	2030	-8	2146	2159	YX	1050	N747YX	EWR	DCA	40	199	20	30	2023-10-08 20:00:00	Other
10550	2	16	817	825	-8	1146	1158	DL	227	N144DU	LGA	DFW	226	1389	8	25	2023-02-16 08:00:00	Other
10553	12	1	2045	2058	-13	2234	2239	9E	1662	N302PQ	LGA	MSN	134	812	20	58	2023-12-01 20:00:00	Other
10556	9	4	1324	1330	-6	1433	1447	UA	521	N38268	EWR	ORF	45	284	13	30	2023-09-04 13:00:00	Other
10572	4	17	623	630	-7	839	848	UA	415	N15712	EWR	ATL	111	746	6	30	2023-04-17 06:00:00	ATL
10576	11	29	1519	1529	-10	1651	1731	9E	1472	N482PX	LGA	GSO	75	461	15	29	2023-11-29 15:00:00	Other
10591	4	29	1023	1030	-7	1144	1209	AA	150	N358PW	LGA	ORD	113	733	10	30	2023-04-29 10:00:00	ORD
10610	4	11	934	950	-16	1116	1211	9E	1264	N479PX	LGA	GRR	83	618	9	50	2023-04-11 09:00:00	Other
10618	5	22	1722	1730	-8	1927	1944	YX	1654	N212JQ	LGA	LIT	153	1085	17	30	2023-05-22 17:00:00	Other
10622	5	28	1107	1117	-10	1258	1342	YX	1201	N126HQ	LGA	XNA	145	1147	11	17	2023-05-28 11:00:00	Other
10623	10	8	1137	1146	-9	1302	1327	YX	1343	N430YX	JFK	BNA	112	765	11	46	2023-10-08 11:00:00	Other
10626	6	22	623	630	-7	837	837	AA	348	N829NN	JFK	CLT	107	541	6	30	2023-06-22 06:00:00	CLT
10627	9	22	1123	1129	-6	1359	1418	UA	590	N803UA	EWR	DFW	191	1372	11	29	2023-09-22 11:00:00	Other
10631	6	18	629	635	-6	803	828	YX	1414	N134HQ	JFK	RDU	70	427	6	35	2023-06-18 06:00:00	Other
10634	11	14	824	835	-11	1126	1138	B6	222	N643JB	LGA	MCO	136	950	8	35	2023-11-14 08:00:00	MCO
10636	12	12	1106	1117	-11	1254	1314	NK	18	N664NK	EWR	MYR	86	550	11	17	2023-12-12 11:00:00	Other
10641	8	10	1150	1200	-10	1337	1356	YX	1068	N407YX	LGA	MEM	141	963	12	0	2023-08-10 12:00:00	Other
10642	3	3	652	659	-7	858	909	YX	1280	N445YX	LGA	DTW	104	502	6	59	2023-03-03 06:00:00	Other
10643	2	6	607	615	-8	921	931	UA	825	N17133	EWR	LAX	334	2454	6	15	2023-02-06 06:00:00	LAX
10645	3	1	853	900	-7	1254	1230	AS	86	N930VA	EWR	LAX	383	2454	9	0	2023-03-01 09:00:00	LAX
10648	11	26	1921	1929	-8	2154	2133	9E	1557	N138EV	JFK	RDU	82	427	19	29	2023-11-26 19:00:00	Other
10652	6	19	944	950	-6	1125	1147	YX	1817	N238JQ	JFK	CMH	78	483	9	50	2023-06-19 09:00:00	Other
10660	8	28	1332	1338	-6	1623	1545	AA	118	N9006	JFK	CLT	110	541	13	38	2023-08-28 13:00:00	CLT
10661	9	20	1315	1325	-10	1534	1550	NK	32	N690NK	EWR	ATL	106	746	13	25	2023-09-20 13:00:00	ATL
10665	4	12	1252	1300	-8	1356	1421	YX	1539	N201JQ	LGA	BOS	36	184	13	0	2023-04-12 13:00:00	BOS
10679	2	7	1346	1352	-6	1653	1708	AA	174	N992AN	LGA	DFW	216	1389	13	52	2023-02-07 13:00:00	Other
10680	1	17	920	930	-10	1255	1252	AA	280	N809NN	LGA	DFW	229	1389	9	30	2023-01-17 09:00:00	Other
10682	2	11	823	830	-7	1127	1119	9E	1300	N907XJ	JFK	JAX	143	828	8	30	2023-02-11 08:00:00	Other
10684	5	31	923	939	-16	1032	1055	B6	833	N283JB	LGA	ACK	39	202	9	39	2023-05-31 09:00:00	Other
10687	8	9	1120	1130	-10	1252	1315	YX	1056	N870RW	LGA	ROA	70	405	11	30	2023-08-09 11:00:00	Other
10689	11	17	1223	1233	-10	1331	1345	UA	448	N69806	EWR	BOS	46	200	12	33	2023-11-17 12:00:00	BOS
10703	12	15	1339	1350	-11	1542	1614	9E	1457	N912XJ	LGA	TYS	98	647	13	50	2023-12-15 13:00:00	Other
10712	10	10	606	615	-9	900	909	UA	656	N37267	EWR	TPA	144	997	6	15	2023-10-10 06:00:00	Other
10714	4	10	1948	1959	-11	2200	2220	9E	1407	N335PQ	LGA	CVG	92	585	19	59	2023-04-10 19:00:00	Other
10728	4	13	844	850	-6	948	1042	DL	763	N115DU	LGA	ORD	106	733	8	50	2023-04-13 08:00:00	ORD
10729	5	17	1123	1132	-9	1440	1439	DL	389	N351NB	LGA	TPA	144	1010	11	32	2023-05-17 11:00:00	Other
10750	6	19	2100	2110	-10	2216	2243	YX	1401	N431YX	LGA	ORF	49	296	21	10	2023-06-19 21:00:00	Other
10753	5	9	2021	2027	-6	2316	2335	UA	703	N411UA	EWR	RSW	149	1068	20	27	2023-05-09 20:00:00	Other
10758	5	9	906	915	-9	1037	1047	YX	1715	N207JQ	LGA	BTV	46	258	9	15	2023-05-09 09:00:00	Other
10763	4	26	1747	1755	-8	2129	2107	AA	678	N303RE	LGA	MIA	184	1096	17	55	2023-04-26 17:00:00	MIA
10765	11	14	931	945	-14	1233	1256	B6	645	N521JB	LGA	MCO	137	950	9	45	2023-11-14 09:00:00	MCO
10766	1	28	653	700	-7	959	1012	UA	772	N894UA	LGA	IAH	224	1416	7	0	2023-01-28 07:00:00	Other
10779	10	29	1348	1355	-7	1509	1525	YX	1093	N727YX	EWR	PIT	59	319	13	55	2023-10-29 13:00:00	Other
10782	3	5	1553	1559	-6	1957	1949	AA	612	N306SP	JFK	PHX	326	2153	15	59	2023-03-05 15:00:00	Other
10792	6	9	1918	1925	-7	2132	2149	9E	1498	N930XJ	LGA	IND	99	660	19	25	2023-06-09 19:00:00	Other
10794	6	11	753	759	-6	1047	1110	AA	620	N304RB	JFK	MIA	151	1089	7	59	2023-06-11 07:00:00	MIA
10799	9	27	1021	1030	-9	1323	1341	B6	267	N559JB	JFK	SAT	221	1587	10	30	2023-09-27 10:00:00	Other
10801	6	21	1052	1100	-8	1230	1253	YX	1292	N428YX	JFK	CLE	72	425	11	0	2023-06-21 11:00:00	Other
10802	1	24	1444	1453	-9	1626	1640	UA	185	N69824	EWR	RDU	73	416	14	53	2023-01-24 14:00:00	Other
10815	10	24	1818	1825	-7	1943	2001	UA	681	N26226	LGA	ORD	117	733	18	25	2023-10-24 18:00:00	ORD
10826	4	9	1858	1905	-7	2025	2101	9E	1305	N134EV	LGA	CLE	62	419	19	5	2023-04-09 19:00:00	Other
10837	4	20	1129	1137	-8	1245	1304	YX	1033	N649RW	EWR	PIT	55	319	11	37	2023-04-20 11:00:00	Other
10841	10	16	2022	2030	-8	2316	4	AA	925	N116AN	JFK	SFO	326	2586	20	30	2023-10-16 20:00:00	Other
10843	10	10	942	950	-8	1049	1115	YX	1308	N119HQ	LGA	DCA	46	214	9	50	2023-10-10 09:00:00	Other
10847	8	27	939	945	-6	1138	1145	WN	104	N8878L	LGA	MCI	156	1107	9	45	2023-08-27 09:00:00	Other
10852	11	16	2051	2059	-8	2213	2217	YX	1271	N422YX	JFK	BOS	47	187	20	59	2023-11-16 20:00:00	BOS
10856	11	24	1122	1130	-8	1330	1402	DL	981	N834DN	JFK	ATL	107	760	11	30	2023-11-24 11:00:00	ATL
10859	9	1	922	929	-7	1145	1153	YX	1184	N650RW	EWR	TVC	94	644	9	29	2023-09-01 09:00:00	Other
10871	4	4	1021	1029	-8	1149	1209	9E	1415	N197PQ	LGA	ORF	53	296	10	29	2023-04-04 10:00:00	Other
10875	9	4	1348	1355	-7	1624	1656	DL	284	N183DN	JFK	LAX	300	2475	13	55	2023-09-04 13:00:00	LAX
10877	11	3	749	755	-6	918	939	UA	652	N18243	EWR	CLE	68	404	7	55	2023-11-03 07:00:00	Other
10880	5	24	1822	1829	-7	2025	2052	YX	1225	N422YX	LGA	IND	97	660	18	29	2023-05-24 18:00:00	Other
10884	11	13	827	836	-9	1141	1210	UA	564	N445UA	EWR	SAT	233	1569	8	36	2023-11-13 08:00:00	Other
10898	12	9	1523	1530	-7	1642	1704	NK	572	N956NK	EWR	BNA	119	748	15	30	2023-12-09 15:00:00	Other
10900	12	9	723	730	-7	1004	1030	UA	616	N36247	EWR	MCO	131	937	7	30	2023-12-09 07:00:00	MCO
10907	1	24	742	755	-13	1107	1115	AS	88	N930VA	EWR	LAX	335	2454	7	55	2023-01-24 07:00:00	LAX
10911	9	18	1026	1037	-11	1130	1158	9E	1591	N928XJ	JFK	BTV	43	266	10	37	2023-09-18 10:00:00	Other
10912	11	8	1154	1200	-6	1422	1439	YX	1305	N404YX	LGA	XNA	170	1147	12	0	2023-11-08 12:00:00	Other
10916	12	16	1218	1225	-7	1335	1353	YX	1234	N423YX	LGA	DCA	52	214	12	25	2023-12-16 12:00:00	Other
10925	1	29	2123	2130	-7	2325	2340	NK	325	N975NK	LGA	DTW	99	502	21	30	2023-01-29 21:00:00	Other
10933	3	22	717	730	-13	1040	1025	B6	149	N944JT	JFK	LAS	354	2248	7	30	2023-03-22 07:00:00	Other
10941	5	24	2023	2029	-6	2133	2201	YX	1325	N806MD	LGA	BUF	48	292	20	29	2023-05-24 20:00:00	Other
10948	8	14	922	930	-8	1134	1159	YX	1351	N875RW	LGA	HHH	104	701	9	30	2023-08-14 09:00:00	Other
10949	5	19	853	900	-7	1207	1210	AS	131	N517AS	EWR	SFO	341	2565	9	0	2023-05-19 09:00:00	Other
10957	10	13	1850	1859	-9	2035	2104	9E	1537	N904XJ	LGA	GSO	77	461	18	59	2023-10-13 18:00:00	Other
10962	12	12	850	900	-10	1105	1133	9E	1396	N187GJ	LGA	SAV	113	722	9	0	2023-12-12 09:00:00	Other
10972	1	12	1221	1229	-8	1348	1357	YX	1348	N441YX	JFK	ORF	55	290	12	29	2023-01-12 12:00:00	Other
10977	11	16	1553	1600	-7	1903	1910	AS	78	N537AS	EWR	SEA	332	2402	16	0	2023-11-16 16:00:00	Other
10979	11	23	1203	1210	-7	1327	1355	YX	1237	N137HQ	LGA	BHM	126	866	12	10	2023-11-23 12:00:00	Other
10987	10	29	1227	1237	-10	1408	1346	9E	1548	N482PX	LGA	BGM	31	147	12	37	2023-10-29 12:00:00	Other
10996	8	23	2102	2110	-8	2237	2303	YX	989	N123HQ	LGA	GSO	70	461	21	10	2023-08-23 21:00:00	Other
11003	9	21	600	610	-10	801	818	YX	1330	N127HQ	LGA	DTW	81	502	6	10	2023-09-21 06:00:00	Other
11005	6	23	1407	1420	-13	1627	1630	9E	1548	N482PX	LGA	TYS	105	647	14	20	2023-06-23 14:00:00	Other
11007	4	12	1452	1459	-7	1800	1806	DL	457	N319NB	LGA	RSW	157	1080	14	59	2023-04-12 14:00:00	Other
11015	10	10	654	700	-6	808	842	UA	831	N14231	EWR	ORD	108	719	7	0	2023-10-10 07:00:00	ORD
11020	1	27	1556	1602	-6	1712	1736	UA	952	N879UA	EWR	PIT	56	319	16	2	2023-01-27 16:00:00	Other
11023	2	9	721	730	-9	850	910	YX	1593	N818MD	LGA	PIT	65	335	7	30	2023-02-09 07:00:00	Other
11029	10	17	624	630	-6	747	808	UA	254	N27273	EWR	CLE	62	404	6	30	2023-10-17 06:00:00	Other
11035	1	30	2020	2030	-10	2158	2229	9E	1417	N678CA	LGA	ROA	68	405	20	30	2023-01-30 20:00:00	Other
11036	3	4	1123	1130	-7	1420	1426	UA	255	N67134	EWR	TPA	147	997	11	30	2023-03-04 11:00:00	Other
11039	12	4	1324	1333	-9	1419	1445	UA	383	N427UA	EWR	BOS	35	200	13	33	2023-12-04 13:00:00	BOS
11041	3	29	1923	1929	-6	2149	2200	YX	1724	N241JQ	LGA	OMA	185	1148	19	29	2023-03-29 19:00:00	Other
11042	10	31	1246	1257	-11	1458	1515	9E	1431	N308PQ	LGA	GRR	107	618	12	57	2023-10-31 12:00:00	Other
11046	12	26	1151	1200	-9	1506	1456	DL	601	N378DN	JFK	MCO	154	944	12	0	2023-12-26 12:00:00	MCO
11057	8	17	2101	2110	-9	2238	2303	YX	989	N428YX	LGA	GSO	74	461	21	10	2023-08-17 21:00:00	Other
11064	7	20	944	950	-6	1040	1102	9E	1236	N341PQ	LGA	ALB	29	136	9	50	2023-07-20 09:00:00	Other
11065	4	21	1023	1029	-6	1145	1209	9E	1287	N920XJ	LGA	BUF	51	292	10	29	2023-04-21 10:00:00	Other
11066	3	27	1658	1705	-7	2000	2014	B6	698	N806JB	LGA	MCO	147	950	17	5	2023-03-27 17:00:00	MCO
11087	7	12	1104	1111	-7	1354	1434	DL	511	N3759	LGA	MIA	146	1096	11	11	2023-07-12 11:00:00	MIA
11091	11	17	1124	1130	-6	1248	1306	YX	1330	N419YX	LGA	CHO	59	305	11	30	2023-11-17 11:00:00	Other
11096	2	5	1704	1710	-6	1944	2011	NK	522	N626NK	EWR	MCO	146	937	17	10	2023-02-05 17:00:00	MCO
11097	9	3	850	859	-9	1022	1048	YX	1314	N124HQ	JFK	CMH	73	483	8	59	2023-09-03 08:00:00	Other
11099	2	7	1517	1530	-13	1718	1742	NK	501	N516NK	LGA	CLT	92	544	15	30	2023-02-07 15:00:00	CLT
11108	12	9	1839	1845	-6	2037	2047	YX	1125	N757YX	EWR	CMH	80	463	18	45	2023-12-09 18:00:00	Other
11124	5	18	1013	1019	-6	1215	1228	9E	1403	N309PQ	LGA	MYR	102	563	10	19	2023-05-18 10:00:00	Other
11127	2	22	1538	1545	-7	1731	1720	YX	1247	N103HQ	JFK	DCA	55	213	15	45	2023-02-22 15:00:00	Other
11129	10	13	1624	1630	-6	1813	1811	DL	522	N141DU	LGA	ORD	129	733	16	30	2023-10-13 16:00:00	ORD
11130	9	24	921	930	-9	1236	1241	B6	99	N923JB	JFK	LAX	323	2475	9	30	2023-09-24 09:00:00	LAX
11133	4	26	2004	2010	-6	2137	2153	YX	1485	N230JQ	LGA	MSN	132	812	20	10	2023-04-26 20:00:00	Other
11144	3	5	2247	2255	-8	2	3	YX	1634	N206JQ	JFK	BWI	35	184	22	55	2023-03-05 22:00:00	Other
11146	2	13	653	700	-7	940	1006	UA	291	N47284	EWR	FLL	140	1065	7	0	2023-02-13 07:00:00	FLL
11152	3	12	1053	1100	-7	1410	1420	AA	111	N106NN	JFK	LAX	349	2475	11	0	2023-03-12 11:00:00	LAX
11158	11	6	840	849	-9	1101	1112	YX	1285	N412YX	LGA	CVG	102	585	8	49	2023-11-06 08:00:00	Other
11160	7	13	757	805	-8	941	1003	AA	492	N940AN	EWR	CLT	78	529	8	5	2023-07-13 08:00:00	CLT
11164	11	2	1820	1831	-11	2130	2130	DL	475	N302DU	EWR	SLC	276	1969	18	31	2023-11-02 18:00:00	Other
11176	4	20	1323	1330	-7	1430	1442	B6	41	N197JB	JFK	SYR	45	209	13	30	2023-04-20 13:00:00	Other
11181	11	14	2119	2129	-10	2246	2300	YX	1841	N216JQ	LGA	DCA	42	214	21	29	2023-11-14 21:00:00	Other
11184	1	31	1556	1602	-6	1716	1736	UA	952	N445UA	EWR	PIT	63	319	16	2	2023-01-31 16:00:00	Other
11186	11	30	1454	1502	-8	1642	1706	DL	914	N967AT	EWR	MSP	148	1008	15	2	2023-11-30 15:00:00	Other
11196	8	1	1839	1845	-6	2123	2127	YX	1023	N439YX	LGA	OKC	178	1341	18	45	2023-08-01 18:00:00	Other
11199	2	16	1431	1440	-9	1614	1641	YX	1329	N422YX	JFK	CMH	80	483	14	40	2023-02-16 14:00:00	Other
11205	9	28	1654	1700	-6	1839	1852	9E	1590	N137EV	LGA	CLE	66	419	17	0	2023-09-28 17:00:00	Other
11214	11	2	1743	1750	-7	1925	1936	YX	1237	N137HQ	LGA	BHM	140	866	17	50	2023-11-02 17:00:00	Other
11220	11	14	2114	2125	-11	2253	2328	YX	1092	N762YX	EWR	MEM	131	946	21	25	2023-11-14 21:00:00	Other
11228	11	4	2127	2135	-8	2325	2340	UA	440	N33284	EWR	CHS	94	628	21	35	2023-11-04 21:00:00	Other
11233	2	26	1953	1959	-6	2300	2318	DL	866	N320NB	LGA	RSW	152	1080	19	59	2023-02-26 19:00:00	Other
11250	3	23	1135	1145	-10	1323	1331	YX	1348	N806MD	LGA	ROA	71	405	11	45	2023-03-23 11:00:00	Other
11253	10	21	1744	1750	-6	2046	2058	UA	615	N24736	EWR	PDX	327	2434	17	50	2023-10-21 17:00:00	Other
11254	3	6	1823	1830	-7	2017	2042	YX	1646	N860RW	LGA	STL	148	888	18	30	2023-03-06 18:00:00	Other
11260	5	6	849	900	-11	1209	1214	AS	131	N524AS	EWR	SFO	349	2565	9	0	2023-05-06 09:00:00	Other
11263	2	15	653	700	-7	947	954	UA	328	N37437	EWR	MCO	141	937	7	0	2023-02-15 07:00:00	MCO
11267	11	22	1512	1519	-7	1646	1723	NK	1035	N629NK	LGA	DTW	74	502	15	19	2023-11-22 15:00:00	Other
11271	4	17	1918	1925	-7	2229	2257	AS	91	N978AK	EWR	SFO	351	2565	19	25	2023-04-17 19:00:00	Other
11278	10	10	545	600	-15	842	905	NK	46	N678NK	LGA	FLL	144	1076	6	0	2023-10-10 06:00:00	FLL
11279	1	10	550	600	-10	653	723	YX	1853	N211JQ	EWR	BOS	42	200	6	0	2023-01-10 06:00:00	BOS
11287	3	6	2022	2029	-7	2314	2354	B6	818	N625JB	JFK	MIA	142	1089	20	29	2023-03-06 20:00:00	MIA
11289	5	10	1301	1309	-8	1455	1510	UA	295	N68836	EWR	MSP	148	1008	13	9	2023-05-10 13:00:00	Other
11299	4	6	1835	1841	-6	2021	2018	AA	690	N930NN	LGA	ORD	126	733	18	41	2023-04-06 18:00:00	ORD
11301	2	11	1135	1145	-10	1322	1345	YX	1285	N425YX	JFK	CLE	80	425	11	45	2023-02-11 11:00:00	Other
11303	5	30	2221	2230	-9	12	9	9E	1381	N303PQ	JFK	BGR	57	382	22	30	2023-05-30 22:00:00	Other
11304	11	14	552	600	-8	711	726	AA	237	N836AW	LGA	DCA	39	214	6	0	2023-11-14 06:00:00	Other
11310	10	6	954	1000	-6	1424	1455	HA	18	N361HA	JFK	HNL	597	4983	10	0	2023-10-06 10:00:00	Other
11313	1	3	1351	1359	-8	1524	1607	YX	1308	N438YX	LGA	CLE	73	419	13	59	2023-01-03 13:00:00	Other
11317	1	20	1119	1130	-11	1244	1326	AA	119	N767UW	LGA	ORD	112	733	11	30	2023-01-20 11:00:00	ORD
11323	9	22	1428	1437	-9	1536	1601	UA	598	N880UA	EWR	BNA	105	748	14	37	2023-09-22 14:00:00	Other
11326	5	4	1850	1900	-10	2006	2102	YX	1265	N121HQ	JFK	PIT	58	340	19	0	2023-05-04 19:00:00	Other
11329	5	5	723	730	-7	849	900	B6	376	N307JB	JFK	BNA	107	765	7	30	2023-05-05 07:00:00	Other
11333	3	4	638	645	-7	932	1002	B6	851	N775JB	EWR	MIA	155	1085	6	45	2023-03-04 06:00:00	MIA
11335	10	3	924	930	-6	1201	1228	B6	45	N510JB	JFK	SRQ	137	1041	9	30	2023-10-03 09:00:00	Other
11336	8	3	1950	1958	-8	2140	2130	OO	949	N246SY	LGA	MKE	135	738	19	58	2023-08-03 19:00:00	Other
11346	5	8	1023	1030	-7	1154	1153	YX	1066	N725YX	EWR	DCA	42	199	10	30	2023-05-08 10:00:00	Other
11347	7	26	1058	1109	-11	1245	1302	YX	1073	N419YX	LGA	CMH	72	479	11	9	2023-07-26 11:00:00	Other
11353	8	28	1213	1224	-11	1404	1421	YX	1012	N441YX	LGA	DAY	89	549	12	24	2023-08-28 12:00:00	Other
11363	1	22	621	630	-9	738	752	B6	1056	N238JB	JFK	BUF	59	301	6	30	2023-01-22 06:00:00	Other
11365	11	26	924	930	-6	1120	1133	YX	1280	N112HQ	JFK	CLE	79	425	9	30	2023-11-26 09:00:00	Other
11377	2	23	1703	1709	-6	1906	1932	AA	592	N169UW	LGA	CLT	93	544	17	9	2023-02-23 17:00:00	CLT
11381	1	5	622	630	-8	903	907	B6	806	N828JB	JFK	ATL	131	760	6	30	2023-01-05 06:00:00	ATL
11385	4	26	1347	1355	-8	1512	1525	B6	835	N283JB	JFK	BUF	57	301	13	55	2023-04-26 13:00:00	Other
11394	5	28	1219	1229	-10	1442	1533	UA	609	N820UA	LGA	IAH	187	1416	12	29	2023-05-28 12:00:00	Other
11399	4	4	1048	1100	-12	1255	1320	YX	1198	N426YX	LGA	SDF	110	659	11	0	2023-04-04 11:00:00	Other
11400	7	30	1121	1130	-9	1428	1437	AA	101	N108NN	JFK	LAX	320	2475	11	30	2023-07-30 11:00:00	LAX
11425	2	9	1429	1435	-6	1714	1735	DL	465	N331DN	LGA	MCO	136	950	14	35	2023-02-09 14:00:00	MCO
11455	7	1	1615	1625	-10	1857	1936	AA	91	N111ZM	JFK	LAX	310	2475	16	25	2023-07-01 16:00:00	LAX
11475	9	28	936	942	-6	1154	1152	B6	976	N526JL	JFK	CHS	107	636	9	42	2023-09-28 09:00:00	Other
11480	10	4	820	829	-9	946	1011	YX	1756	N818MD	LGA	PIT	61	335	8	29	2023-10-04 08:00:00	Other
11482	11	4	653	700	-7	1002	1015	AA	301	N9023N	JFK	AUS	220	1521	7	0	2023-11-04 07:00:00	Other
11488	8	11	835	846	-11	958	1028	YX	1396	N231JQ	LGA	PIT	56	335	8	46	2023-08-11 08:00:00	Other
11490	6	20	741	751	-10	856	912	UA	813	N812UA	EWR	BTV	49	266	7	51	2023-06-20 07:00:00	Other
11492	6	1	549	600	-11	643	721	AA	765	N771XF	LGA	DCA	39	214	6	0	2023-06-01 06:00:00	Other
11504	3	2	651	659	-8	917	909	YX	1280	N421YX	LGA	DTW	97	502	6	59	2023-03-02 06:00:00	Other
11508	8	3	1508	1515	-7	1621	1634	YX	1331	N878RW	LGA	ACK	39	202	15	15	2023-08-03 15:00:00	Other
11517	9	15	1617	1625	-8	1807	1805	9E	1524	N478PX	LGA	PIT	55	335	16	25	2023-09-15 16:00:00	Other
11518	6	10	1154	1201	-7	1330	1339	9E	1557	N601LR	JFK	BUF	64	301	12	1	2023-06-10 12:00:00	Other
11520	7	3	908	915	-7	1011	1035	B6	725	N304JB	LGA	BOS	35	184	9	15	2023-07-03 09:00:00	BOS
11522	12	13	2045	2055	-10	2237	2300	9E	1486	N922XJ	LGA	ILM	82	500	20	55	2023-12-13 20:00:00	Other
11528	6	4	1422	1430	-8	1548	1559	YX	1320	N422YX	LGA	BUF	50	292	14	30	2023-06-04 14:00:00	Other
11534	3	16	1917	1925	-8	2129	2158	YX	1142	N635RW	EWR	SDF	101	642	19	25	2023-03-16 19:00:00	Other
11536	1	20	550	600	-10	712	723	YX	1853	N212JQ	EWR	BOS	39	200	6	0	2023-01-20 06:00:00	BOS
11541	4	9	1124	1130	-6	1456	1445	AA	748	N934AN	LGA	MIA	154	1096	11	30	2023-04-09 11:00:00	MIA
11546	1	24	705	715	-10	800	827	B6	1066	N323JB	LGA	BOS	37	184	7	15	2023-01-24 07:00:00	BOS
11553	7	2	1008	1016	-8	1208	1240	AA	654	N150UW	EWR	PHX	267	2133	10	16	2023-07-02 10:00:00	Other
11558	5	22	1217	1225	-8	1353	1359	YX	1231	N414YX	LGA	BNA	112	764	12	25	2023-05-22 12:00:00	Other
11560	1	27	931	938	-7	1253	1301	B6	586	N534JB	LGA	FLL	179	1076	9	38	2023-01-27 09:00:00	FLL
11561	6	1	1220	1229	-9	1509	1521	DL	544	N379DN	JFK	MCO	131	944	12	29	2023-06-01 12:00:00	MCO
11568	9	3	1425	1435	-10	1538	1609	YX	1152	N757YX	EWR	IAD	44	212	14	35	2023-09-03 14:00:00	Other
11571	10	5	910	921	-11	1137	1213	UA	447	N14249	EWR	MCO	118	937	9	21	2023-10-05 09:00:00	MCO
11574	6	9	1052	1100	-8	1317	1416	B6	203	N2105J	JFK	LAX	302	2475	11	0	2023-06-09 11:00:00	LAX
11576	2	13	1652	1659	-7	1834	1848	B6	430	N328JB	JFK	RDU	71	427	16	59	2023-02-13 16:00:00	Other
11579	11	7	942	950	-8	1150	1213	9E	1571	N348PQ	LGA	CVG	101	585	9	50	2023-11-07 09:00:00	Other
11582	11	7	654	700	-6	955	1008	UA	807	N29124	EWR	IAH	195	1400	7	0	2023-11-07 07:00:00	Other
11587	1	16	1423	1430	-7	1631	1711	YX	1305	N422YX	LGA	IND	95	660	14	30	2023-01-16 14:00:00	Other
11588	9	20	644	651	-7	801	814	YX	1051	N726YX	EWR	BTV	46	266	6	51	2023-09-20 06:00:00	Other
11589	1	20	1041	1055	-14	1209	1233	YX	1904	N878RW	LGA	ORF	57	296	10	55	2023-01-20 10:00:00	Other
11590	8	20	820	830	-10	1115	1140	UA	530	N18112	EWR	SEA	322	2402	8	30	2023-08-20 08:00:00	Other
11591	11	25	849	900	-11	1113	1110	NK	509	N517NK	EWR	CHS	97	628	9	0	2023-11-25 09:00:00	Other
11592	6	12	1220	1229	-9	1325	1341	B6	891	N328JB	LGA	ACK	42	202	12	29	2023-06-12 12:00:00	Other
11597	4	25	735	743	-8	1103	1113	YX	1059	N862RW	EWR	EYW	178	1196	7	43	2023-04-25 07:00:00	Other
11599	10	30	1823	1829	-6	2112	2129	DL	227	N524DE	JFK	LAS	314	2248	18	29	2023-10-30 18:00:00	Other
11600	5	21	857	905	-8	1044	1115	9E	1537	N348PQ	LGA	ILM	82	500	9	5	2023-05-21 09:00:00	Other
11606	7	18	653	659	-6	828	834	YX	1067	N869RW	LGA	PIT	61	335	6	59	2023-07-18 06:00:00	Other
11607	10	31	2022	2029	-7	2330	2259	UA	229	N17752	EWR	ATL	127	746	20	29	2023-10-31 20:00:00	ATL
11609	10	16	2050	2059	-9	2231	2255	9E	1476	N917XJ	LGA	RDU	65	431	20	59	2023-10-16 20:00:00	Other
11616	10	16	2115	2124	-9	2243	2259	YX	1088	N862RW	EWR	MKE	100	725	21	24	2023-10-16 21:00:00	Other
11618	7	17	913	920	-7	1033	1053	AA	589	N711UW	LGA	PIT	54	335	9	20	2023-07-17 09:00:00	Other
11625	7	20	1506	1513	-7	1707	1732	9E	1181	N314PQ	JFK	CVG	90	589	15	13	2023-07-20 15:00:00	Other
11628	3	16	941	950	-9	1235	1318	B6	205	N2142J	JFK	LAX	327	2475	9	50	2023-03-16 09:00:00	LAX
11634	4	5	645	655	-10	1007	1023	B6	5	N944JT	JFK	SFO	361	2586	6	55	2023-04-05 06:00:00	Other
11639	12	7	1836	1845	-9	2124	2147	UA	482	N37318	EWR	PBI	134	1023	18	45	2023-12-07 18:00:00	Other
11642	6	18	1654	1700	-6	1812	1836	YX	1825	N201JQ	LGA	BOS	33	184	17	0	2023-06-18 17:00:00	BOS
11655	5	15	1450	1459	-9	1749	1705	YX	1190	N418YX	JFK	CLE	74	425	14	59	2023-05-15 14:00:00	Other
11661	4	20	923	929	-6	1105	1120	YX	1164	N410YX	LGA	CLE	68	419	9	29	2023-04-20 09:00:00	Other
11665	12	22	1653	1700	-7	1926	1915	YX	1207	N138HQ	LGA	DSM	150	1031	17	0	2023-12-22 17:00:00	Other
11684	12	18	2144	2150	-6	2250	2254	9E	1642	N912XJ	LGA	BGM	34	147	21	50	2023-12-18 21:00:00	Other
11686	9	21	918	929	-11	1039	1057	AA	716	N715UW	LGA	PIT	56	335	9	29	2023-09-21 09:00:00	Other
11687	5	15	2132	2147	-15	2246	2312	9E	1435	N337PQ	LGA	BUF	46	292	21	47	2023-05-15 21:00:00	Other
11689	10	17	605	615	-10	841	909	UA	656	N36247	EWR	TPA	136	997	6	15	2023-10-17 06:00:00	Other
11694	1	31	746	755	-9	945	1004	AA	1075	N825NN	LGA	CLT	99	544	7	55	2023-01-31 07:00:00	CLT
11695	5	8	749	800	-11	953	1017	B6	317	N192JB	JFK	SAV	101	718	8	0	2023-05-08 08:00:00	Other
11701	9	3	1326	1338	-12	1515	1545	AA	132	N90024	JFK	CLT	77	541	13	38	2023-09-03 13:00:00	CLT
11705	9	27	2150	2159	-9	2256	2310	DL	946	N103DU	LGA	BOS	35	184	21	59	2023-09-27 21:00:00	BOS
11706	8	7	1544	1555	-11	1847	1729	YX	1032	N122HQ	LGA	CHO	84	305	15	55	2023-08-07 15:00:00	Other
11712	10	6	1644	1650	-6	1802	1824	YX	1039	N754YX	EWR	BGR	60	393	16	50	2023-10-06 16:00:00	Other
11726	8	29	922	930	-8	1221	1230	AS	8	N946AK	JFK	SEA	317	2422	9	30	2023-08-29 09:00:00	Other
11733	7	21	1223	1229	-6	1506	1526	DL	447	N340NW	JFK	AUS	200	1521	12	29	2023-07-21 12:00:00	Other
11741	10	30	1535	1541	-6	1657	1709	YX	1313	N438YX	LGA	CHO	57	305	15	41	2023-10-30 15:00:00	Other
11744	1	18	1154	1205	-11	1344	1348	AA	504	N859NN	EWR	ORD	130	719	12	5	2023-01-18 12:00:00	ORD
11755	11	7	1126	1139	-13	1357	1441	B6	824	N639JB	EWR	TPA	134	997	11	39	2023-11-07 11:00:00	Other
11758	11	15	1919	1929	-10	2124	2151	9E	1593	N136EV	LGA	CVG	94	585	19	29	2023-11-15 19:00:00	Other
11763	1	30	1551	1559	-8	1642	1711	9E	1705	N915XJ	LGA	ALB	29	136	15	59	2023-01-30 15:00:00	Other
11766	2	19	959	1015	-16	1105	1130	B6	218	N306JB	LGA	BOS	40	184	10	15	2023-02-19 10:00:00	BOS
11770	2	23	942	950	-8	1208	1220	WN	193	N415WN	LGA	MCI	179	1107	9	50	2023-02-23 09:00:00	Other
11777	3	27	1537	1548	-11	1719	1724	YX	1252	N872RW	LGA	RIC	65	292	15	48	2023-03-27 15:00:00	Other
11780	10	18	1342	1350	-8	1544	1547	9E	1552	N147PQ	LGA	ILM	73	500	13	50	2023-10-18 13:00:00	Other
11788	3	14	2037	2043	-6	2346	2353	UA	659	N28478	EWR	MIA	149	1085	20	43	2023-03-14 20:00:00	MIA
11791	8	5	526	535	-9	744	807	B6	93	N524JB	EWR	MCO	117	937	5	35	2023-08-05 05:00:00	MCO
11797	10	5	1607	1615	-8	1720	1741	B6	333	N355JB	LGA	BOS	47	184	16	15	2023-10-05 16:00:00	BOS
11798	5	8	623	630	-7	732	741	B6	190	N197JB	JFK	BOS	38	187	6	30	2023-05-08 06:00:00	BOS
11807	2	28	1813	1820	-7	1952	2011	DL	378	N114DU	LGA	ORD	123	733	18	20	2023-02-28 18:00:00	ORD
11811	2	9	659	705	-6	928	936	DL	747	N374DA	EWR	ATL	111	746	7	5	2023-02-09 07:00:00	ATL
11814	1	26	1550	1557	-7	1818	1815	YX	1159	N731YX	EWR	CHS	126	628	15	57	2023-01-26 15:00:00	Other
11815	5	12	653	700	-7	934	953	UA	792	N76502	EWR	PBI	135	1023	7	0	2023-05-12 07:00:00	Other
11816	5	22	1834	1840	-6	2047	2108	9E	1308	N676CA	JFK	CLT	83	541	18	40	2023-05-22 18:00:00	CLT
11820	1	14	2040	2051	-11	2147	2226	YX	1250	N863RW	EWR	PIT	48	319	20	51	2023-01-14 20:00:00	Other
11823	1	16	554	600	-6	703	724	AA	510	N766US	LGA	DCA	41	214	6	0	2023-01-16 06:00:00	Other
11824	1	10	2149	2159	-10	2308	2314	YX	1283	N424YX	JFK	BOS	40	187	21	59	2023-01-10 21:00:00	BOS
11825	8	4	952	1000	-8	1151	1206	YX	1025	N432YX	LGA	GSP	99	610	10	0	2023-08-04 10:00:00	Other
11826	2	16	723	730	-7	951	1025	B6	155	N945JT	JFK	LAS	307	2248	7	30	2023-02-16 07:00:00	Other
11828	7	26	1522	1530	-8	1647	1659	YX	1045	N435YX	LGA	ORF	55	296	15	30	2023-07-26 15:00:00	Other
11830	8	28	1952	2000	-8	2323	2324	AA	81	N102NN	JFK	LAX	326	2475	20	0	2023-08-28 20:00:00	LAX
11832	4	9	950	959	-9	1248	1252	NK	261	N695NK	LGA	MCO	141	950	9	59	2023-04-09 09:00:00	MCO
11841	9	5	917	930	-13	1156	1223	AS	14	N978AK	JFK	SAN	311	2446	9	30	2023-09-05 09:00:00	Other
11855	3	7	743	755	-12	924	927	YX	1350	N109HQ	LGA	CHO	59	305	7	55	2023-03-07 07:00:00	Other
11856	3	8	2049	2059	-10	2214	2234	YX	1670	N235JQ	LGA	RIC	50	292	20	59	2023-03-08 20:00:00	Other
11857	9	3	1603	1610	-7	1729	1805	YX	1396	N106HQ	LGA	GSO	68	461	16	10	2023-09-03 16:00:00	Other
11868	8	24	1833	1840	-7	2150	2144	B6	735	N652JB	JFK	MCO	124	944	18	40	2023-08-24 18:00:00	MCO
11872	11	21	1323	1330	-7	1504	1511	YX	1299	N434YX	JFK	PIT	75	340	13	30	2023-11-21 13:00:00	Other
11875	11	11	1349	1400	-11	1550	1617	YX	1154	N757YX	EWR	CVG	98	569	14	0	2023-11-11 14:00:00	Other
11881	2	8	1708	1715	-7	1818	1833	B6	414	N307JB	LGA	BOS	37	184	17	15	2023-02-08 17:00:00	BOS
11884	4	16	1435	1445	-10	1546	1612	9E	1312	N314PQ	LGA	ROC	42	254	14	45	2023-04-16 14:00:00	Other
11885	1	30	651	700	-9	1001	1009	B6	409	N558JB	JFK	PBI	157	1028	7	0	2023-01-30 07:00:00	Other
11906	11	21	925	932	-7	1145	1158	YX	1378	N416YX	LGA	IND	109	660	9	32	2023-11-21 09:00:00	Other
11913	7	27	821	830	-9	1049	1055	NK	147	N929NK	EWR	LAS	293	2227	8	30	2023-07-27 08:00:00	Other
11916	9	12	1152	1158	-6	1450	1513	NK	1028	N670NK	LGA	MIA	153	1096	11	58	2023-09-12 11:00:00	MIA
11920	1	30	1156	1205	-9	1447	1520	B6	689	N2044J	JFK	FLL	150	1069	12	5	2023-01-30 12:00:00	FLL
11921	1	27	2202	2210	-8	243	317	NK	436	N651NK	EWR	SJU	204	1608	22	10	2023-01-27 22:00:00	Other
11930	3	12	1922	1929	-7	2147	2153	YX	1243	N115HQ	LGA	LIT	181	1085	19	29	2023-03-12 19:00:00	Other
11931	1	16	2242	2250	-8	2358	2358	YX	1761	N214JQ	JFK	BWI	35	184	22	50	2023-01-16 22:00:00	Other
11933	5	29	559	606	-7	739	836	UA	619	N36447	EWR	DEN	202	1605	6	6	2023-05-29 06:00:00	Other
11937	2	27	1120	1129	-9	1423	1445	B6	20	N630JB	LGA	TPA	147	1010	11	29	2023-02-27 11:00:00	Other
11939	1	21	1050	1100	-10	1346	1418	B6	63	N615JB	EWR	FLL	149	1065	11	0	2023-01-21 11:00:00	FLL
11949	7	7	1352	1359	-7	1507	1523	9E	1199	N319PQ	JFK	SYR	42	209	13	59	2023-07-07 13:00:00	Other
11954	2	6	1623	1630	-7	1923	1953	UA	730	N12116	EWR	LAX	334	2454	16	30	2023-02-06 16:00:00	LAX
11958	4	26	830	836	-6	1156	1151	UA	564	N16703	EWR	SAT	229	1569	8	36	2023-04-26 08:00:00	Other
11963	8	20	1449	1457	-8	1722	1758	UA	63	N27267	EWR	PBI	132	1023	14	57	2023-08-20 14:00:00	Other
11966	8	22	920	928	-8	1232	1228	AA	291	N104NN	JFK	SNA	303	2454	9	28	2023-08-22 09:00:00	Other
11968	3	8	652	700	-8	803	817	AA	789	N821AW	LGA	DCA	43	214	7	0	2023-03-08 07:00:00	Other
11970	1	21	1529	1535	-6	1712	1744	YX	1467	N428YX	JFK	CLE	78	425	15	35	2023-01-21 15:00:00	Other
11971	3	18	737	745	-8	1114	1125	YX	1044	N646RW	EWR	EYW	187	1196	7	45	2023-03-18 07:00:00	Other
11980	6	28	1654	1700	-6	1754	1820	AA	433	N757UW	LGA	DCA	43	214	17	0	2023-06-28 17:00:00	Other
11982	5	5	2029	2035	-6	2242	2256	YX	1028	N741YX	EWR	GRR	97	605	20	35	2023-05-05 20:00:00	Other
11983	6	13	807	817	-10	951	956	YX	1127	N655RW	EWR	PIT	58	319	8	17	2023-06-13 08:00:00	Other
11992	11	26	1820	1829	-9	2033	2011	YX	1237	N444YX	LGA	BHM	159	866	18	29	2023-11-26 18:00:00	Other
11994	11	17	923	930	-7	1246	1235	AS	13	N938AK	JFK	SAN	353	2446	9	30	2023-11-17 09:00:00	Other
11998	10	28	1625	1632	-7	1819	1858	DL	751	N368NB	JFK	MSY	157	1182	16	32	2023-10-28 16:00:00	Other
11999	6	6	840	850	-10	953	1039	9E	1450	N303PQ	LGA	BHM	112	866	8	50	2023-06-06 08:00:00	Other
12003	10	22	2140	2150	-10	2253	2304	9E	1648	N134EV	LGA	SYR	41	198	21	50	2023-10-22 21:00:00	Other
12010	8	14	1534	1540	-6	1743	1804	B6	717	N267JB	JFK	CHS	89	636	15	40	2023-08-14 15:00:00	Other
12011	9	16	1521	1530	-9	1656	1716	YX	1418	N439YX	LGA	RDU	66	431	15	30	2023-09-16 15:00:00	Other
12023	6	14	553	559	-6	723	733	AA	1039	N978NN	EWR	ORD	109	719	5	59	2023-06-14 05:00:00	ORD
12030	3	9	1154	1200	-6	1350	1403	YX	1240	N429YX	JFK	CMH	89	483	12	0	2023-03-09 12:00:00	Other
12032	10	10	908	915	-7	1208	1228	AA	790	N321TG	LGA	MIA	156	1096	9	15	2023-10-10 09:00:00	MIA
12036	6	2	1423	1430	-7	1620	1559	YX	1320	N424YX	LGA	BUF	55	292	14	30	2023-06-02 14:00:00	Other
12041	1	23	2133	2139	-6	2303	2325	B6	592	N306JB	JFK	RDU	66	427	21	39	2023-01-23 21:00:00	Other
12045	8	30	1912	1918	-6	2039	2055	YX	856	N730YX	EWR	PWM	53	284	19	18	2023-08-30 19:00:00	Other
12050	8	23	742	750	-8	920	945	9E	1167	N133EV	JFK	RDU	65	427	7	50	2023-08-23 07:00:00	Other
12051	11	4	753	759	-6	946	1011	YX	1168	N863RW	EWR	GSP	92	594	7	59	2023-11-04 07:00:00	Other
12064	8	22	1619	1629	-10	1757	1813	AA	577	N837AW	LGA	RDU	70	431	16	29	2023-08-22 16:00:00	Other
12080	10	30	1125	1135	-10	1248	1301	YX	1051	N754YX	EWR	BUF	54	282	11	35	2023-10-30 11:00:00	Other
12081	12	30	2051	2100	-9	2228	2308	UA	280	N24715	EWR	DTW	75	488	21	0	2023-12-30 21:00:00	Other
12093	12	10	2021	2030	-9	2218	2256	9E	1497	N302PQ	LGA	GRR	94	618	20	30	2023-12-10 20:00:00	Other
12094	12	4	853	900	-7	1147	1233	AA	68	N116AN	JFK	LAX	332	2475	9	0	2023-12-04 09:00:00	LAX
12095	8	1	651	657	-6	942	950	B6	238	N981JT	JFK	LAX	309	2475	6	57	2023-08-01 06:00:00	LAX
12096	4	27	1319	1329	-10	1512	1539	9E	1413	N937XJ	LGA	CVG	96	585	13	29	2023-04-27 13:00:00	Other
12103	2	9	1037	1045	-8	1331	1354	B6	412	N355JB	EWR	MCO	139	937	10	45	2023-02-09 10:00:00	MCO
12120	5	10	1939	1945	-6	2353	2337	DL	89	N172DN	JFK	SFO	360	2586	19	45	2023-05-10 19:00:00	Other
12126	9	6	2048	2059	-11	2151	2231	YX	1899	N226JQ	LGA	PWM	42	269	20	59	2023-09-06 20:00:00	Other
12128	7	8	922	929	-7	1200	1153	YX	935	N747YX	EWR	TVC	96	644	9	29	2023-07-08 09:00:00	Other
12130	7	31	933	945	-12	1052	1135	9E	1106	N917XJ	LGA	BGR	55	378	9	45	2023-07-31 09:00:00	Other
12147	9	4	652	700	-8	956	1022	DL	171	N177DN	JFK	SFO	336	2586	7	0	2023-09-04 07:00:00	Other
12148	3	28	1722	1730	-8	1949	1959	YX	1712	N229JQ	LGA	SDF	118	659	17	30	2023-03-28 17:00:00	Other
12152	10	4	1145	1159	-14	1248	1307	B6	827	N274JB	LGA	ACK	39	202	11	59	2023-10-04 11:00:00	Other
12155	8	28	1008	1015	-7	1145	1202	AA	179	N822AW	LGA	STL	129	888	10	15	2023-08-28 10:00:00	Other
12157	9	17	953	959	-6	1157	1201	YX	1354	N416YX	LGA	GSP	106	610	9	59	2023-09-17 09:00:00	Other
12159	3	24	1921	1929	-8	2146	2200	YX	1724	N201JQ	LGA	OMA	178	1148	19	29	2023-03-24 19:00:00	Other
12167	10	11	752	804	-12	1001	1037	YX	1264	N131HQ	JFK	CVG	100	589	8	4	2023-10-11 08:00:00	Other
12171	5	31	2045	2056	-11	2211	2250	9E	1557	N294PQ	LGA	RDU	64	431	20	56	2023-05-31 20:00:00	Other
12181	7	7	953	959	-6	1155	1230	9E	1172	N330PQ	JFK	SAV	98	718	9	59	2023-07-07 09:00:00	Other
12185	5	31	706	715	-9	852	918	UA	480	N845UA	EWR	CLT	78	529	7	15	2023-05-31 07:00:00	CLT
12187	12	12	829	838	-9	1051	1118	YX	1818	N244JQ	LGA	SDF	112	659	8	38	2023-12-12 08:00:00	Other
12198	11	15	1205	1215	-10	1416	1448	UA	688	N33284	LGA	DEN	229	1620	12	15	2023-11-15 12:00:00	Other
12207	4	13	1010	1016	-6	1301	1337	DL	450	N131DU	LGA	SRQ	154	1047	10	16	2023-04-13 10:00:00	Other
12211	12	2	552	601	-9	910	913	UA	62	N62896	EWR	AUS	242	1504	6	1	2023-12-02 06:00:00	Other
12212	1	31	1853	1910	-17	2027	2105	YX	1370	N123HQ	LGA	PIT	66	335	19	10	2023-01-31 19:00:00	Other
12216	9	16	1149	1159	-10	1308	1339	YX	1857	N882RW	LGA	RIC	50	292	11	59	2023-09-16 11:00:00	Other
12227	8	17	908	915	-7	1241	1237	AA	652	N324RA	LGA	MIA	158	1096	9	15	2023-08-17 09:00:00	MIA
12232	12	2	939	949	-10	1245	1209	9E	1535	N922XJ	LGA	AVL	103	599	9	49	2023-12-02 09:00:00	Other
12240	5	16	1254	1300	-6	1448	1502	AA	358	N585UW	LGA	CLT	81	544	13	0	2023-05-16 13:00:00	CLT
12242	5	16	1105	1115	-10	1218	1225	B6	57	N231JB	EWR	BOS	48	200	11	15	2023-05-16 11:00:00	BOS
12262	4	12	1907	1915	-8	2034	2113	9E	1305	N538CA	LGA	CLE	64	419	19	15	2023-04-12 19:00:00	Other
12264	10	4	2056	2104	-8	2339	2339	UA	574	N17301	EWR	LAS	293	2227	21	4	2023-10-04 21:00:00	Other
12268	10	13	1608	1615	-7	1804	1823	YX	1274	N135HQ	LGA	GSP	95	610	16	15	2023-10-13 16:00:00	Other
12269	8	10	1120	1130	-10	1239	1300	YX	1367	N882RW	LGA	DCA	50	214	11	30	2023-08-10 11:00:00	Other
12270	8	28	1818	1824	-6	2009	2044	DL	323	N111DC	LGA	MSP	138	1020	18	24	2023-08-28 18:00:00	Other
12273	9	28	1552	1559	-7	1741	1750	AA	937	N766US	LGA	RDU	72	431	15	59	2023-09-28 15:00:00	Other
12276	5	16	2051	2100	-9	2308	2320	B6	889	N828JB	LGA	MSY	176	1183	21	0	2023-05-16 21:00:00	Other
12280	2	8	1255	1305	-10	1516	1537	NK	36	N632NK	EWR	ATL	119	746	13	5	2023-02-08 13:00:00	ATL
12288	11	9	554	604	-10	749	817	9E	1589	N303PQ	LGA	CLT	89	544	6	4	2023-11-09 06:00:00	CLT
12291	10	20	2024	2030	-6	2	4	AA	925	N117AN	JFK	SFO	355	2586	20	30	2023-10-20 20:00:00	Other
12293	1	4	1221	1230	-9	1406	1422	YX	1344	N117HQ	JFK	RDU	80	427	12	30	2023-01-04 12:00:00	Other
12294	7	5	1822	1830	-8	2203	2136	NK	705	N608NK	EWR	FLL	169	1065	18	30	2023-07-05 18:00:00	FLL
12301	9	5	2243	2250	-7	100	144	F9	932	N354FR	LGA	DFW	170	1389	22	50	2023-09-05 22:00:00	Other
12302	2	13	850	900	-10	1051	1052	9E	1289	N925XJ	LGA	PIT	70	335	9	0	2023-02-13 09:00:00	Other
12304	4	15	817	829	-12	1047	1114	YX	1083	N123HQ	JFK	CVG	94	589	8	29	2023-04-15 08:00:00	Other
12312	8	3	758	805	-7	1002	1003	AA	468	N909NN	EWR	CLT	81	529	8	5	2023-08-03 08:00:00	CLT
12317	1	20	1324	1330	-6	1430	1456	YX	1127	N736YX	EWR	ORF	51	284	13	30	2023-01-20 13:00:00	Other
12319	5	30	1407	1415	-8	1511	1532	B6	312	N249JB	LGA	BOS	36	184	14	15	2023-05-30 14:00:00	BOS
12320	5	17	2021	2030	-9	2239	2238	9E	1423	N298PQ	LGA	ILM	75	500	20	30	2023-05-17 20:00:00	Other
12323	5	29	2113	2126	-13	2254	2328	NK	283	N611NK	LGA	DTW	71	502	21	26	2023-05-29 21:00:00	Other
12333	12	13	656	705	-9	1006	1014	DL	517	N369NW	LGA	TPA	160	1010	7	5	2023-12-13 07:00:00	Other
12338	2	4	1203	1210	-7	1316	1342	YX	1233	N439YX	JFK	ORF	54	290	12	10	2023-02-04 12:00:00	Other
12343	1	9	1224	1230	-6	1521	1544	UA	531	N47275	EWR	RSW	151	1068	12	30	2023-01-09 12:00:00	Other
12347	12	6	2050	2100	-10	2208	2212	AA	841	N806AW	LGA	BOS	38	184	21	0	2023-12-06 21:00:00	BOS
12349	9	18	1949	1959	-10	2237	2219	YX	1375	N405YX	LGA	CVG	92	585	19	59	2023-09-18 19:00:00	Other
12352	9	27	1518	1528	-10	1652	1709	YX	1349	N432YX	LGA	CLE	70	419	15	28	2023-09-27 15:00:00	Other
12355	10	1	1703	1710	-7	1856	1926	9E	1481	N904XJ	LGA	CVG	81	585	17	10	2023-10-01 17:00:00	Other
12357	10	27	1704	1715	-11	1828	1848	YX	1334	N419YX	LGA	RIC	55	292	17	15	2023-10-27 17:00:00	Other
12358	12	6	1809	1815	-6	2010	2109	9E	1469	N331PQ	JFK	MCI	155	1113	18	15	2023-12-06 18:00:00	Other
12360	5	2	2153	2159	-6	2257	2308	DL	939	N138DU	LGA	BOS	41	184	21	59	2023-05-02 21:00:00	BOS
12370	7	22	1323	1330	-7	1511	1522	YX	1085	N123HQ	LGA	MEM	145	963	13	30	2023-07-22 13:00:00	Other
12373	12	16	1623	1630	-7	1849	1858	9E	1582	N335PQ	LGA	SAV	112	722	16	30	2023-12-16 16:00:00	Other
12376	9	22	632	640	-8	807	826	YX	1879	N226JQ	LGA	CMH	75	479	6	40	2023-09-22 06:00:00	Other
12377	12	6	1622	1629	-7	1805	1826	9E	1524	N605LR	LGA	CLE	67	419	16	29	2023-12-06 16:00:00	Other
12385	12	17	1428	1436	-8	1544	1607	YX	1276	N131HQ	LGA	BUF	49	292	14	36	2023-12-17 14:00:00	Other
12386	6	1	1917	1925	-8	2055	2131	YX	1773	N206JQ	JFK	PIT	55	340	19	25	2023-06-01 19:00:00	Other
12388	9	5	1254	1300	-6	1547	1612	AA	221	N320TF	LGA	MIA	141	1096	13	0	2023-09-05 13:00:00	MIA
12392	3	18	1428	1434	-6	1534	1550	YX	1107	N727YX	EWR	BOS	33	200	14	34	2023-03-18 14:00:00	BOS
12393	5	25	1302	1309	-7	1441	1510	UA	295	N68880	EWR	MSP	137	1008	13	9	2023-05-25 13:00:00	Other
12399	5	24	1539	1552	-13	1648	1725	YX	1294	N821MD	LGA	RIC	50	292	15	52	2023-05-24 15:00:00	Other
12400	2	21	1719	1729	-10	1903	1923	YX	1277	N429YX	JFK	RDU	75	427	17	29	2023-02-21 17:00:00	Other
12405	8	11	1913	1919	-6	2046	2135	DL	200	N349NB	LGA	DTW	73	502	19	19	2023-08-11 19:00:00	Other
12411	5	31	608	615	-7	848	930	AA	15	N111ZM	JFK	LAX	318	2475	6	15	2023-05-31 06:00:00	LAX
12413	9	2	1613	1629	-16	1818	1904	DL	854	N368NW	JFK	MSP	150	1029	16	29	2023-09-02 16:00:00	Other
12414	12	31	1621	1630	-9	1908	1935	UA	483	N217UA	EWR	LAX	294	2454	16	30	2023-12-31 16:00:00	LAX
12416	5	13	1454	1505	-11	1620	1643	UA	606	N812UA	LGA	ORD	116	733	15	5	2023-05-13 15:00:00	ORD
12422	7	5	1019	1025	-6	1223	1230	AA	537	N199UW	EWR	CLT	83	529	10	25	2023-07-05 10:00:00	CLT
12430	9	6	904	914	-10	1040	1038	UA	616	N874UA	EWR	PWM	48	284	9	14	2023-09-06 09:00:00	Other
12436	3	6	908	915	-7	1108	1125	YX	1704	N221JQ	LGA	CMH	87	479	9	15	2023-03-06 09:00:00	Other
12444	10	6	2121	2130	-9	1107	33	B6	28	N937JB	JFK	SAN	NA	2446	21	30	2023-10-06 21:00:00	Other
12454	4	10	613	619	-6	754	822	AA	322	N924US	JFK	CLT	81	541	6	19	2023-04-10 06:00:00	CLT
12458	4	25	1322	1339	-17	1651	1654	AA	402	N960AN	JFK	MIA	173	1089	13	39	2023-04-25 13:00:00	MIA
12459	2	8	1754	1800	-6	1943	1952	UA	282	N23707	EWR	STL	136	872	18	0	2023-02-08 18:00:00	Other
12464	11	28	1552	1559	-7	1900	1919	B6	308	N969JT	JFK	LAX	319	2475	15	59	2023-11-28 15:00:00	LAX
12474	6	11	2147	2156	-9	152	208	B6	302	N775JB	JFK	PSE	206	1617	21	56	2023-06-11 21:00:00	Other
12478	7	5	1010	1016	-6	1205	1236	AA	654	N509AY	EWR	PHX	265	2133	10	16	2023-07-05 10:00:00	Other
12479	4	20	554	600	-6	840	902	B6	698	N526JL	LGA	FLL	137	1076	6	0	2023-04-20 06:00:00	FLL
12485	3	28	1533	1541	-8	1644	1648	YX	1106	N753YX	EWR	PVD	33	160	15	41	2023-03-28 15:00:00	Other
12486	4	3	1051	1100	-9	1425	1420	AA	115	N116AN	JFK	LAX	370	2475	11	0	2023-04-03 11:00:00	LAX
12488	10	30	1859	1905	-6	2105	2118	AA	617	N970AN	LGA	CLT	95	544	19	5	2023-10-30 19:00:00	CLT
12489	11	1	2019	2029	-10	2317	2257	YX	1342	N419YX	JFK	IND	104	665	20	29	2023-11-01 20:00:00	Other
12492	5	30	1012	1018	-6	1259	1320	NK	27	N678NK	EWR	MIA	145	1085	10	18	2023-05-30 10:00:00	MIA
12493	4	15	652	700	-8	927	1002	B6	616	N991JT	JFK	PSP	305	2378	7	0	2023-04-15 07:00:00	Other
12495	3	26	1134	1142	-8	1238	1245	YX	1250	N115HQ	JFK	ORH	32	150	11	42	2023-03-26 11:00:00	Other
12498	12	26	1523	1529	-6	1704	1733	NK	1003	N607NK	LGA	DTW	80	502	15	29	2023-12-26 15:00:00	Other
12499	2	15	1523	1532	-9	1738	1757	YX	1224	N414YX	LGA	DTW	97	502	15	32	2023-02-15 15:00:00	Other
12503	8	7	1131	1142	-11	1343	1406	YX	974	N105HQ	JFK	IND	94	665	11	42	2023-08-07 11:00:00	Other
12510	8	23	2159	2205	-6	2329	2354	9E	1250	N906XJ	JFK	BTV	52	266	22	5	2023-08-23 22:00:00	Other
12511	5	30	1143	1150	-7	1317	1346	DL	611	N966AT	EWR	MSP	132	1008	11	50	2023-05-30 11:00:00	Other
12516	11	14	801	809	-8	1006	1020	AA	551	N301PA	EWR	CLT	91	529	8	9	2023-11-14 08:00:00	CLT
12517	7	26	1732	1740	-8	1950	2007	9E	1116	N914XJ	LGA	CVG	88	585	17	40	2023-07-26 17:00:00	Other
12519	1	5	2115	2125	-10	2222	2300	WN	381	N7881A	LGA	MDW	108	725	21	25	2023-01-05 21:00:00	Other
12525	12	7	1212	1219	-7	1407	1424	DL	463	N966AT	EWR	MSP	157	1008	12	19	2023-12-07 12:00:00	Other
12529	5	27	743	750	-7	855	929	9E	1493	N691CA	JFK	ROC	48	264	7	50	2023-05-27 07:00:00	Other
12530	12	2	1813	1820	-7	2112	2120	UA	783	N78506	EWR	TPA	150	997	18	20	2023-12-02 18:00:00	Other
12531	11	17	635	645	-10	751	820	UA	818	N15751	EWR	BNA	110	748	6	45	2023-11-17 06:00:00	Other
12535	5	31	1556	1605	-9	1706	1743	YX	1254	N867RW	LGA	CHO	53	305	16	5	2023-05-31 16:00:00	Other
12536	12	18	1909	1916	-7	2224	2257	UA	287	N27267	EWR	PHX	281	2133	19	16	2023-12-18 19:00:00	Other
12543	5	4	1258	1305	-7	1419	1454	DL	460	N132DU	LGA	ORD	104	733	13	5	2023-05-04 13:00:00	ORD
12545	5	15	554	600	-6	736	808	YX	1624	N235JQ	LGA	CLT	85	544	6	0	2023-05-15 06:00:00	CLT
12551	10	21	654	700	-6	919	934	UA	202	N77572	EWR	LAS	299	2227	7	0	2023-10-21 07:00:00	Other
12553	7	12	1152	1200	-8	1306	1347	YX	1409	N202JQ	LGA	PIT	54	335	12	0	2023-07-12 12:00:00	Other
12555	2	25	2019	2025	-6	2143	2201	YX	1560	N209JQ	JFK	DCA	59	213	20	25	2023-02-25 20:00:00	Other
12561	9	20	1529	1545	-16	1840	1845	B6	541	N595JB	JFK	MCO	143	944	15	45	2023-09-20 15:00:00	MCO
12562	10	9	1753	1759	-6	2111	2105	F9	443	N347FR	LGA	MCO	148	950	17	59	2023-10-09 17:00:00	MCO
12569	5	31	1159	1209	-10	1327	1347	9E	1429	N324PQ	LGA	BGR	57	378	12	9	2023-05-31 12:00:00	Other
12574	6	17	707	715	-8	936	931	DL	810	N3763D	EWR	ATL	95	746	7	15	2023-06-17 07:00:00	ATL
12576	8	15	909	915	-6	1036	1048	YX	828	N758YX	EWR	BUF	47	282	9	15	2023-08-15 09:00:00	Other
12579	11	5	722	730	-8	1031	1045	AS	11	N920AK	JFK	SEA	336	2422	7	30	2023-11-05 07:00:00	Other
12582	3	26	2103	2109	-6	19	4	UA	474	N27251	EWR	SRQ	158	1034	21	9	2023-03-26 21:00:00	Other
12591	12	5	1150	1159	-9	1448	1543	NK	1158	N638NK	EWR	PHX	282	2133	11	59	2023-12-05 11:00:00	Other
12592	6	22	822	829	-7	943	1009	9E	1717	N325PQ	LGA	CHO	55	305	8	29	2023-06-22 08:00:00	Other
12593	11	1	2021	2030	-9	2246	2302	UA	876	N14735	EWR	MSY	173	1167	20	30	2023-11-01 20:00:00	Other
12595	10	17	1952	1959	-7	2229	2301	NK	152	N671NK	LGA	MCO	128	950	19	59	2023-10-17 19:00:00	MCO
12597	4	2	2114	2120	-6	2202	2222	YX	1565	N215JQ	LGA	BDL	20	101	21	20	2023-04-02 21:00:00	Other
12601	11	9	654	700	-6	946	1020	DL	314	N387DA	JFK	RSW	156	1074	7	0	2023-11-09 07:00:00	Other
12605	4	25	715	730	-15	846	910	B6	756	N603JB	JFK	RDU	72	427	7	30	2023-04-25 07:00:00	Other
12612	1	10	1839	1845	-6	2052	2119	DL	897	N991AT	EWR	ATL	103	746	18	45	2023-01-10 18:00:00	ATL
12615	9	10	951	959	-8	1156	1156	YX	1806	N234JQ	JFK	CMH	84	483	9	59	2023-09-10 09:00:00	Other
12618	7	2	634	640	-6	757	815	UA	255	N17279	EWR	CLE	59	404	6	40	2023-07-02 06:00:00	Other
12641	8	22	930	940	-10	1135	1207	9E	1242	N348PQ	JFK	IND	95	665	9	40	2023-08-22 09:00:00	Other
12642	3	20	1708	1714	-6	1856	1905	AA	432	N766US	LGA	STL	134	888	17	14	2023-03-20 17:00:00	Other
12651	1	19	1651	1659	-8	1821	1827	9E	1502	N480PX	LGA	PWM	41	269	16	59	2023-01-19 16:00:00	Other
12653	9	5	939	945	-6	1121	1156	9E	1446	N604LR	EWR	CVG	80	569	9	45	2023-09-05 09:00:00	Other
12662	1	8	1119	1129	-10	1234	1259	YX	1785	N241JQ	LGA	DCA	45	214	11	29	2023-01-08 11:00:00	Other
12669	10	11	1109	1117	-8	1255	1310	NK	20	N668NK	EWR	MYR	89	550	11	17	2023-10-11 11:00:00	Other
12675	10	8	1732	1744	-12	1933	2004	YX	1851	N208JQ	LGA	IND	96	660	17	44	2023-10-08 17:00:00	Other
12676	7	25	621	629	-8	829	833	YX	1043	N429YX	LGA	MSP	149	1020	6	29	2023-07-25 06:00:00	Other
12680	1	12	749	755	-6	909	920	YX	1193	N744YX	EWR	PWM	52	284	7	55	2023-01-12 07:00:00	Other
12689	3	7	553	600	-7	937	920	AA	52	N101NN	JFK	LAX	373	2475	6	0	2023-03-07 06:00:00	LAX
12691	3	8	928	935	-7	1238	1243	B6	403	N337JB	JFK	MCO	135	944	9	35	2023-03-08 09:00:00	MCO
12698	8	21	1947	1955	-8	2146	2214	9E	1126	N912XJ	LGA	CVG	81	585	19	55	2023-08-21 19:00:00	Other
12709	4	14	636	644	-8	753	836	AA	305	N995NN	EWR	ORD	112	719	6	44	2023-04-14 06:00:00	ORD
12710	12	6	818	825	-7	1125	1140	NK	571	N951NK	EWR	MIA	163	1085	8	25	2023-12-06 08:00:00	MIA
12712	10	10	1850	1859	-9	2056	2123	9E	1482	N298PQ	LGA	CLT	90	544	18	59	2023-10-10 18:00:00	CLT
12717	12	31	1502	1510	-8	1743	1837	DL	349	N869DN	JFK	SLC	255	1990	15	10	2023-12-31 15:00:00	Other
12721	8	27	1112	1118	-6	1405	1414	DL	359	N814DN	JFK	TPA	141	1005	11	18	2023-08-27 11:00:00	Other
12725	3	25	654	700	-6	912	942	DL	176	N394DA	LGA	DEN	229	1620	7	0	2023-03-25 07:00:00	Other
12727	9	26	1717	1725	-8	1919	1931	YX	1326	N116HQ	LGA	GSP	93	610	17	25	2023-09-26 17:00:00	Other
12730	5	23	1918	1929	-11	2038	2114	YX	1199	N421YX	LGA	BHM	125	866	19	29	2023-05-23 19:00:00	Other
12736	9	19	1948	1955	-7	2200	2216	9E	1775	N228PQ	LGA	IND	103	660	19	55	2023-09-19 19:00:00	Other
12739	8	15	1258	1305	-7	1459	1442	UA	494	N465UA	LGA	ORD	110	733	13	5	2023-08-15 13:00:00	ORD
12741	3	3	1842	1850	-8	2034	2024	YX	1208	N644RW	EWR	PIT	70	319	18	50	2023-03-03 18:00:00	Other
12742	5	1	2121	2129	-8	2233	2249	YX	1597	N222JQ	LGA	BTV	47	258	21	29	2023-05-01 21:00:00	Other
12744	7	13	1640	1650	-10	2011	2018	AS	11	N933AK	JFK	SFO	352	2586	16	50	2023-07-13 16:00:00	Other
12745	8	22	851	900	-9	1153	1210	AS	109	N552AS	EWR	SFO	324	2565	9	0	2023-08-22 09:00:00	Other
12750	5	23	654	700	-6	941	1005	DL	533	N866DN	JFK	TPA	140	1005	7	0	2023-05-23 07:00:00	Other
12753	11	6	1841	1850	-9	2119	2127	YX	1786	N238JQ	LGA	OMA	183	1148	18	50	2023-11-06 18:00:00	Other
12756	5	28	513	523	-10	735	820	UA	177	N17296	EWR	IAH	176	1400	5	23	2023-05-28 05:00:00	Other
12759	8	24	1820	1829	-9	2113	2109	YX	1023	N417YX	LGA	OKC	180	1341	18	29	2023-08-24 18:00:00	Other
12763	11	19	1336	1346	-10	1457	1512	9E	1462	N138EV	JFK	PWM	53	273	13	46	2023-11-19 13:00:00	Other
12766	1	1	1051	1059	-8	1443	1421	B6	226	N981JT	JFK	LAX	370	2475	10	59	2023-01-01 10:00:00	LAX
12768	2	15	558	605	-7	911	935	B6	692	N615JB	LGA	RSW	162	1080	6	5	2023-02-15 06:00:00	Other
12774	8	25	2144	2150	-6	46	2353	B6	426	N184JB	JFK	DTW	88	509	21	50	2023-08-25 21:00:00	Other
12775	10	13	853	900	-7	1107	1139	YX	1759	N231JQ	JFK	JAX	117	828	9	0	2023-10-13 09:00:00	Other
12778	12	10	1314	1320	-6	1500	1503	9E	1435	N905XJ	LGA	BNA	138	764	13	20	2023-12-10 13:00:00	Other
12779	9	19	2015	2025	-10	2121	2153	YX	1403	N871RW	LGA	BUF	48	292	20	25	2023-09-19 20:00:00	Other
12783	4	24	619	629	-10	739	812	YX	1197	N871RW	LGA	PIT	62	335	6	29	2023-04-24 06:00:00	Other
12785	8	10	1453	1500	-7	1637	1636	UA	483	N27258	LGA	ORD	124	733	15	0	2023-08-10 15:00:00	ORD
12803	9	28	1421	1430	-9	1543	1553	YX	1343	N445YX	LGA	BUF	46	292	14	30	2023-09-28 14:00:00	Other
12812	9	1	2030	2038	-8	2313	2324	UA	465	N27283	EWR	IAH	186	1400	20	38	2023-09-01 20:00:00	Other
12817	12	27	704	710	-6	1010	1015	DL	517	N369NW	LGA	TPA	163	1010	7	10	2023-12-27 07:00:00	Other
12825	6	9	835	845	-10	1053	1105	9E	1554	N135EV	LGA	SAV	112	722	8	45	2023-06-09 08:00:00	Other
12831	5	18	852	859	-7	1016	1044	UA	671	N37516	EWR	ORD	109	719	8	59	2023-05-18 08:00:00	ORD
12837	11	27	2130	2140	-10	2327	2336	YX	1244	N102HQ	JFK	RDU	82	427	21	40	2023-11-27 21:00:00	Other
12841	8	27	1144	1150	-6	1319	1336	9E	1129	N232PQ	LGA	PIT	64	335	11	50	2023-08-27 11:00:00	Other
12843	2	9	2113	2120	-7	2219	2226	9E	1367	N904XJ	LGA	ALB	32	136	21	20	2023-02-09 21:00:00	Other
12846	9	7	653	700	-7	939	952	UA	417	N841UA	EWR	SRQ	141	1034	7	0	2023-09-07 07:00:00	Other
12847	12	5	1150	1200	-10	1340	1358	9E	1390	N605LR	JFK	CLT	93	541	12	0	2023-12-05 12:00:00	CLT
12850	9	19	1733	1740	-7	1903	1933	9E	1669	N292PQ	LGA	MEM	129	963	17	40	2023-09-19 17:00:00	Other
12858	11	29	1619	1628	-9	1735	1803	YX	1135	N726YX	EWR	PIT	58	319	16	28	2023-11-29 16:00:00	Other
12865	5	27	1607	1615	-8	1757	1832	9E	1562	N337PQ	LGA	CLT	88	544	16	15	2023-05-27 16:00:00	CLT
12879	4	24	1704	1710	-6	1841	1849	YX	1526	N879RW	LGA	BNA	124	764	17	10	2023-04-24 17:00:00	Other
12881	9	8	1323	1330	-7	1447	1509	UA	664	N17566	EWR	CLE	63	404	13	30	2023-09-08 13:00:00	Other
12884	9	20	1804	1810	-6	1959	2021	DL	383	N302DN	LGA	MSP	139	1020	18	10	2023-09-20 18:00:00	Other
12891	8	22	1051	1059	-8	1231	1255	YX	859	N749YX	EWR	ILM	69	488	10	59	2023-08-22 10:00:00	Other
12896	3	24	1157	1203	-6	1439	1445	UA	901	N439UA	LGA	DEN	244	1620	12	3	2023-03-24 12:00:00	Other
12922	5	25	605	615	-10	853	906	DL	286	N133DU	LGA	DFW	175	1389	6	15	2023-05-25 06:00:00	Other
12925	2	19	1654	1700	-6	1847	1857	YX	1618	N220JQ	LGA	CLE	76	419	17	0	2023-02-19 17:00:00	Other
12926	8	30	2244	2250	-6	9	25	9E	1279	N341PQ	JFK	SYR	42	209	22	50	2023-08-30 22:00:00	Other
12936	2	15	1114	1120	-6	1443	1448	B6	351	N568JB	JFK	SLC	298	1990	11	20	2023-02-15 11:00:00	Other
12938	8	12	953	1000	-7	1155	1206	YX	1025	N132HQ	LGA	GSP	89	610	10	0	2023-08-12 10:00:00	Other
12944	12	5	736	745	-9	904	927	B6	373	N3115J	JFK	BNA	122	765	7	45	2023-12-05 07:00:00	Other
12950	3	9	1408	1415	-7	1523	1543	YX	1113	N729YX	EWR	PIT	54	319	14	15	2023-03-09 14:00:00	Other
12953	2	28	1113	1120	-7	1336	1325	YX	1294	N425YX	LGA	ROA	82	405	11	20	2023-02-28 11:00:00	Other
12954	10	22	1021	1030	-9	1123	1159	YX	1074	N739YX	EWR	DCA	43	199	10	30	2023-10-22 10:00:00	Other
12964	5	18	654	700	-6	955	1031	B6	565	N945JT	JFK	SFO	337	2586	7	0	2023-05-18 07:00:00	Other
12967	7	19	1135	1142	-7	1336	1326	YX	1075	N826MD	LGA	ROA	71	405	11	42	2023-07-19 11:00:00	Other
12970	10	17	1945	1952	-7	2200	2216	YX	1143	N765YX	EWR	SAV	107	708	19	52	2023-10-17 19:00:00	Other
12971	6	22	1334	1340	-6	1508	1511	YX	1765	N208JQ	JFK	BOS	44	187	13	40	2023-06-22 13:00:00	BOS
12976	7	9	922	930	-8	1209	1220	AS	15	N291BT	JFK	SAN	318	2446	9	30	2023-07-09 09:00:00	Other
12982	11	27	1453	1459	-6	1635	1709	DL	750	N348NW	LGA	DTW	83	502	14	59	2023-11-27 14:00:00	Other
12986	2	27	1243	1250	-7	1401	1430	9E	1284	N908XJ	LGA	MKE	116	738	12	50	2023-02-27 12:00:00	Other
12988	6	20	1410	1420	-10	1611	1630	9E	1548	N479PX	LGA	TYS	97	647	14	20	2023-06-20 14:00:00	Other
12990	10	24	1934	1942	-8	2157	2215	UA	263	N878UA	EWR	JAX	110	820	19	42	2023-10-24 19:00:00	Other
12992	8	28	821	830	-9	945	954	YX	881	N650RW	EWR	ROC	45	246	8	30	2023-08-28 08:00:00	Other
13000	11	15	2151	2200	-9	2257	2335	YX	1329	N124HQ	JFK	DCA	44	213	22	0	2023-11-15 22:00:00	Other
13005	12	1	1151	1200	-9	1455	1519	UA	765	N18112	EWR	LAX	341	2454	12	0	2023-12-01 12:00:00	LAX
13009	4	10	752	800	-8	903	917	B6	59	N187JB	JFK	ROC	47	264	8	0	2023-04-10 08:00:00	Other
13016	4	23	1351	1400	-9	1513	1523	YX	1242	N134HQ	LGA	DCA	48	214	14	0	2023-04-23 14:00:00	Other
13022	11	17	2041	2050	-9	2237	2313	9E	1568	N330PQ	LGA	GRR	97	618	20	50	2023-11-17 20:00:00	Other
13024	9	22	1624	1630	-6	1922	1937	AA	91	N105NN	JFK	LAX	324	2475	16	30	2023-09-22 16:00:00	LAX
13025	3	16	1446	1455	-9	1627	1719	YX	1695	N211JQ	JFK	CLT	78	541	14	55	2023-03-16 14:00:00	CLT
13036	10	28	646	700	-14	1026	1024	AS	12	N474AS	JFK	SFO	374	2586	7	0	2023-10-28 07:00:00	Other
13038	3	29	1514	1520	-6	1812	1823	B6	195	N613JB	EWR	FLL	150	1065	15	20	2023-03-29 15:00:00	FLL
13040	9	19	822	832	-10	1033	1041	YX	1332	N404YX	LGA	OMA	172	1148	8	32	2023-09-19 08:00:00	Other
13042	12	13	1717	1730	-13	1959	2015	YX	1321	N122HQ	LGA	SDF	120	659	17	30	2023-12-13 17:00:00	Other
13043	10	29	1326	1333	-7	1433	1445	UA	640	N470UA	EWR	BOS	43	200	13	33	2023-10-29 13:00:00	BOS
13044	2	16	857	905	-8	1207	1150	DL	364	N386DA	JFK	DEN	245	1626	9	5	2023-02-16 09:00:00	Other
13048	10	31	1551	1559	-8	1753	1750	YX	1300	N104HQ	LGA	STL	152	888	15	59	2023-10-31 15:00:00	Other
13059	4	17	638	646	-8	1055	954	UA	755	N13716	EWR	RSW	165	1068	6	46	2023-04-17 06:00:00	Other
13063	3	23	1417	1430	-13	1605	1614	YX	1318	N430YX	JFK	PIT	77	340	14	30	2023-03-23 14:00:00	Other
13070	12	16	953	1000	-7	1249	1302	UA	246	N33262	EWR	PBI	154	1023	10	0	2023-12-16 10:00:00	Other
13088	9	12	1923	1930	-7	2224	2236	UA	697	N17311	EWR	SLC	260	1969	19	30	2023-09-12 19:00:00	Other
13089	11	9	923	929	-6	1229	1259	B6	666	N766JB	LGA	RSW	157	1080	9	29	2023-11-09 09:00:00	Other
13090	12	8	1126	1135	-9	1253	1301	YX	1046	N758YX	EWR	BUF	52	282	11	35	2023-12-08 11:00:00	Other
13093	1	9	2044	2055	-11	2242	2308	YX	1330	N407YX	LGA	MEM	141	963	20	55	2023-01-09 20:00:00	Other
13094	12	22	1550	1559	-9	1817	1846	DL	244	N915DU	JFK	DEN	226	1626	15	59	2023-12-22 15:00:00	Other
13097	11	30	1129	1135	-6	1332	1341	YX	1099	N769YX	EWR	MEM	150	946	11	35	2023-11-30 11:00:00	Other
13122	10	15	1840	1850	-10	2144	2158	AS	9	N431AS	JFK	SAN	298	2446	18	50	2023-10-15 18:00:00	Other
13123	8	25	1150	1158	-8	1412	1414	YX	844	N722YX	EWR	SDF	95	642	11	58	2023-08-25 11:00:00	Other
13127	4	11	1327	1335	-8	1507	1525	UA	190	N37290	EWR	MSP	135	1008	13	35	2023-04-11 13:00:00	Other
13128	10	27	1255	1302	-7	1549	1605	B6	651	N662JB	EWR	RSW	151	1068	13	2	2023-10-27 13:00:00	Other
13130	2	27	1713	1721	-8	2038	2055	YX	1039	N649RW	EWR	EYW	173	1196	17	21	2023-02-27 17:00:00	Other
13131	11	27	1527	1537	-10	1800	1744	YX	1343	N102HQ	JFK	CLE	82	425	15	37	2023-11-27 15:00:00	Other
13137	11	29	1747	1755	-8	1925	1954	YX	1817	N222JQ	LGA	CMH	78	479	17	55	2023-11-29 17:00:00	Other
13147	3	14	1447	1455	-8	1651	1631	OO	1108	N243SY	JFK	BNA	117	765	14	55	2023-03-14 14:00:00	Other
13150	11	16	1318	1330	-12	1559	1634	NK	329	N955NK	LGA	DFW	188	1389	13	30	2023-11-16 13:00:00	Other
13151	4	24	717	725	-8	940	1010	B6	153	N947JB	JFK	LAS	299	2248	7	25	2023-04-24 07:00:00	Other
13152	5	31	2248	2255	-7	2351	2358	B6	250	N284JB	JFK	ORH	31	150	22	55	2023-05-31 22:00:00	Other
13163	3	19	825	835	-10	1145	1145	NK	308	N672NK	LGA	IAH	235	1416	8	35	2023-03-19 08:00:00	Other
13166	4	18	1644	1654	-10	1928	1920	B6	121	N179JB	JFK	SAV	111	718	16	54	2023-04-18 16:00:00	Other
13167	5	24	959	1005	-6	1120	1114	B6	762	N337JB	JFK	ACK	53	199	10	5	2023-05-24 10:00:00	Other
13174	11	30	1048	1055	-7	1333	1402	NK	260	N690NK	LGA	MCO	139	950	10	55	2023-11-30 10:00:00	MCO
13175	2	5	722	730	-8	940	1023	DL	182	N378DA	LGA	DEN	238	1620	7	30	2023-02-05 07:00:00	Other
13176	8	20	1010	1017	-7	1248	1311	UA	313	N17312	EWR	TPA	124	997	10	17	2023-08-20 10:00:00	Other
13188	12	1	1013	1020	-7	1145	1205	9E	1363	N301PQ	LGA	RIC	60	292	10	20	2023-12-01 10:00:00	Other
13194	12	25	1711	1720	-9	1810	1847	YX	1751	N219YX	LGA	SYR	39	198	17	20	2023-12-25 17:00:00	Other
13197	1	15	1154	1200	-6	1256	1300	9E	1466	N479PX	LGA	BGM	34	147	12	0	2023-01-15 12:00:00	Other
13200	2	28	919	929	-10	1326	1307	YX	1118	N861RW	EWR	EYW	169	1196	9	29	2023-02-28 09:00:00	Other
13201	6	4	1128	1134	-6	1316	1325	DL	603	N118DU	LGA	ORD	108	733	11	34	2023-06-04 11:00:00	ORD
13205	10	30	1953	1959	-6	2303	2236	DL	112	N873DN	JFK	DEN	249	1626	19	59	2023-10-30 19:00:00	Other
13208	8	2	1344	1350	-6	1537	1610	YX	1355	N245JQ	LGA	CLT	83	544	13	50	2023-08-02 13:00:00	CLT
13211	3	13	1758	1804	-6	1955	2023	DL	425	N360NB	LGA	MSP	136	1020	18	4	2023-03-13 18:00:00	Other
13212	10	18	1623	1629	-6	2038	1943	B6	193	N618JB	LGA	FLL	NA	1076	16	29	2023-10-18 16:00:00	FLL
13215	9	18	1733	1740	-7	1938	1933	9E	1669	N937XJ	LGA	MEM	137	963	17	40	2023-09-18 17:00:00	Other
13220	10	24	2053	2100	-7	2317	2339	DL	319	N396DN	LGA	ATL	107	762	21	0	2023-10-24 21:00:00	ATL
13229	3	9	506	515	-9	653	652	NK	437	N938NK	EWR	BNA	112	748	5	15	2023-03-09 05:00:00	Other
13231	12	22	744	750	-6	929	930	9E	1691	N182GJ	LGA	RIC	60	292	7	50	2023-12-22 07:00:00	Other
13233	4	5	619	625	-6	1000	923	UA	217	N57439	EWR	SAN	382	2425	6	25	2023-04-05 06:00:00	Other
13234	8	28	1224	1240	-16	1514	1533	NK	280	N624NK	LGA	DFW	207	1389	12	40	2023-08-28 12:00:00	Other
13236	10	14	2001	2010	-9	2159	2230	UA	854	N838UA	EWR	DEN	215	1605	20	10	2023-10-14 20:00:00	Other
13239	9	5	1219	1228	-9	1319	1348	NK	394	N525NK	EWR	BNA	99	748	12	28	2023-09-05 12:00:00	Other
13242	5	16	1021	1029	-8	1138	1206	YX	1600	N222JQ	LGA	DCA	41	214	10	29	2023-05-16 10:00:00	Other
13246	8	22	856	905	-9	1121	1212	YX	976	N434YX	LGA	IAH	175	1416	9	5	2023-08-22 09:00:00	Other
13250	3	8	1319	1329	-10	1446	1500	9E	1463	N604LR	LGA	BGR	60	378	13	29	2023-03-08 13:00:00	Other
13259	6	11	935	945	-10	1050	1133	9E	1451	N904XJ	LGA	BGR	56	378	9	45	2023-06-11 09:00:00	Other
13260	2	23	1450	1459	-9	1728	1759	UA	590	N17262	EWR	TPA	140	997	14	59	2023-02-23 14:00:00	Other
13282	4	18	1941	1955	-14	2159	2152	YX	1219	N425YX	LGA	CMH	77	479	19	55	2023-04-18 19:00:00	Other
13289	1	24	657	705	-8	1142	1204	UA	657	N24736	EWR	STT	206	1634	7	5	2023-01-24 07:00:00	Other
13293	11	10	2151	2159	-8	109	139	DL	324	N721TW	JFK	SFO	347	2586	21	59	2023-11-10 21:00:00	Other
13295	10	29	1533	1540	-7	1800	1750	9E	1629	N182GJ	LGA	CHS	93	641	15	40	2023-10-29 15:00:00	Other
13304	1	24	1251	1259	-8	1424	1452	9E	1572	N303PQ	LGA	CLE	73	419	12	59	2023-01-24 12:00:00	Other
13319	3	10	719	725	-6	944	954	UA	452	N839UA	EWR	JAX	113	820	7	25	2023-03-10 07:00:00	Other
13339	6	15	553	600	-7	918	837	B6	530	N977JE	EWR	LAX	326	2454	6	0	2023-06-15 06:00:00	LAX
13340	3	28	1417	1430	-13	1508	1535	9E	1559	N331PQ	LGA	ORH	32	146	14	30	2023-03-28 14:00:00	Other
13345	8	12	656	705	-9	926	932	B6	125	N982JB	JFK	LAS	305	2248	7	5	2023-08-12 07:00:00	Other
13346	12	14	1340	1350	-10	1529	1614	9E	1457	N485PX	LGA	TYS	90	647	13	50	2023-12-14 13:00:00	Other
13353	3	1	1541	1550	-9	1744	1812	9E	1602	N294PQ	LGA	CLT	89	544	15	50	2023-03-01 15:00:00	CLT
13358	3	29	1350	1400	-10	1612	1624	YX	1254	N413YX	LGA	IND	113	660	14	0	2023-03-29 14:00:00	Other
13360	5	5	1847	1855	-8	2142	2158	DL	487	N145DQ	LGA	IAH	196	1416	18	55	2023-05-05 18:00:00	Other
13364	4	19	2017	2025	-8	2124	2139	YX	965	N731YX	EWR	ALB	36	143	20	25	2023-04-19 20:00:00	Other
13366	5	17	838	848	-10	1038	1049	9E	1396	N490PX	LGA	MEM	146	963	8	48	2023-05-17 08:00:00	Other
13371	8	30	622	630	-8	913	929	B6	757	N651JB	JFK	FLL	147	1069	6	30	2023-08-30 06:00:00	FLL
13374	6	23	722	729	-7	848	919	AA	1016	N963AN	LGA	ORD	104	733	7	29	2023-06-23 07:00:00	ORD
13376	8	30	1918	1930	-12	2105	2127	YX	1057	N867RW	LGA	CMH	78	479	19	30	2023-08-30 19:00:00	Other
13378	10	18	1821	1830	-9	2023	2054	YX	1298	N437YX	LGA	OMA	159	1148	18	30	2023-10-18 18:00:00	Other
13385	4	23	649	655	-6	923	928	B6	120	N258JB	LGA	JAX	131	833	6	55	2023-04-23 06:00:00	Other
13388	4	18	1308	1315	-7	1649	1647	UA	675	N41140	EWR	SFO	370	2565	13	15	2023-04-18 13:00:00	Other
13389	5	17	1124	1135	-11	1245	1259	YX	1678	N218JQ	LGA	SYR	44	198	11	35	2023-05-17 11:00:00	Other
13392	3	20	1623	1629	-6	1928	2008	DL	216	N896DN	JFK	SLC	277	1990	16	29	2023-03-20 16:00:00	Other
13401	4	5	949	959	-10	1118	1137	9E	1370	N926XJ	LGA	BGR	58	378	9	59	2023-04-05 09:00:00	Other
13405	1	28	723	730	-7	1002	1008	B6	528	N265JB	JFK	JAX	134	828	7	30	2023-01-28 07:00:00	Other
13409	12	7	1917	1930	-13	2029	2059	B6	890	N206JB	JFK	DCA	39	213	19	30	2023-12-07 19:00:00	Other
13411	1	15	1753	1800	-7	1928	2000	YX	1743	N875RW	LGA	CMH	70	479	18	0	2023-01-15 18:00:00	Other
13413	2	1	1702	1709	-7	1854	1850	UA	754	N14219	EWR	ORD	135	719	17	9	2023-02-01 17:00:00	ORD
13414	3	10	753	800	-7	857	916	B6	285	N283JB	JFK	BOS	39	187	8	0	2023-03-10 08:00:00	BOS
13421	9	11	1122	1129	-7	1442	1439	DL	495	N3747D	JFK	MIA	171	1089	11	29	2023-09-11 11:00:00	MIA
13423	8	26	1524	1530	-6	1755	1847	AA	48	N105NN	JFK	LAX	298	2475	15	30	2023-08-26 15:00:00	LAX
13424	4	27	1651	1659	-8	1839	1835	YX	1502	N880RW	LGA	RIC	58	292	16	59	2023-04-27 16:00:00	Other
13427	12	15	1824	1830	-6	2110	2132	B6	117	N965JT	JFK	MCO	131	944	18	30	2023-12-15 18:00:00	MCO
13430	9	26	752	800	-8	1048	1134	DL	293	N712TW	JFK	SFO	324	2586	8	0	2023-09-26 08:00:00	Other
13433	9	2	2123	2130	-7	2320	2326	YX	1310	N437YX	JFK	RDU	65	427	21	30	2023-09-02 21:00:00	Other
13442	8	31	1206	1215	-9	1501	1511	B6	225	N584JB	JFK	AUS	198	1521	12	15	2023-08-31 12:00:00	Other
13443	3	1	554	600	-6	848	919	B6	849	N537JT	JFK	MIA	147	1089	6	0	2023-03-01 06:00:00	MIA
13444	10	11	2020	2030	-10	2151	2159	YX	1050	N758YX	EWR	DCA	39	199	20	30	2023-10-11 20:00:00	Other
13460	12	10	1232	1242	-10	1627	1545	UA	814	N66831	EWR	TPA	167	997	12	42	2023-12-10 12:00:00	Other
13467	10	29	1923	1929	-6	2313	2333	DL	666	N838DN	JFK	SJU	206	1598	19	29	2023-10-29 19:00:00	Other
13471	3	20	1759	1805	-6	1955	2026	YX	1201	N754YX	EWR	CVG	93	569	18	5	2023-03-20 18:00:00	Other
13475	11	23	750	800	-10	1042	1125	B6	46	N216JB	JFK	SRQ	148	1041	8	0	2023-11-23 08:00:00	Other
13479	12	23	2005	2015	-10	2117	2155	UA	52	N27290	EWR	BNA	104	748	20	15	2023-12-23 20:00:00	Other
13480	5	24	1650	1700	-10	2008	2020	B6	776	N249JB	JFK	RSW	159	1074	17	0	2023-05-24 17:00:00	Other
13484	5	31	646	655	-9	932	956	B6	450	N779JB	LGA	TPA	145	1010	6	55	2023-05-31 06:00:00	Other
13485	9	14	729	735	-6	1026	1037	DL	790	N389DA	JFK	PBI	150	1028	7	35	2023-09-14 07:00:00	Other
13488	12	8	848	859	-11	1132	1204	B6	213	N834JB	LGA	MCO	135	950	8	59	2023-12-08 08:00:00	MCO
13491	7	11	1054	1100	-6	1337	1348	AA	615	N979AN	LGA	DFW	197	1389	11	0	2023-07-11 11:00:00	Other
13501	9	14	1223	1229	-6	1336	1344	DL	577	N115DU	JFK	BOS	34	187	12	29	2023-09-14 12:00:00	BOS
13503	9	27	1449	1459	-10	1655	1713	9E	1632	N490PX	LGA	GSP	96	610	14	59	2023-09-27 14:00:00	Other
13505	10	22	1429	1435	-6	1619	1640	UA	332	N899UA	EWR	CLT	83	529	14	35	2023-10-22 14:00:00	CLT
13512	10	24	2033	2040	-7	2146	2220	9E	1515	N306PQ	LGA	RIC	52	292	20	40	2023-10-24 20:00:00	Other
13516	5	10	814	820	-6	1036	1041	9E	1466	N605LR	LGA	MCI	176	1107	8	20	2023-05-10 08:00:00	Other
13521	2	20	1604	1610	-6	1733	1759	DL	457	N132DU	LGA	ORD	123	733	16	10	2023-02-20 16:00:00	ORD
13523	10	18	1955	2005	-10	2117	2144	9E	1449	N919XJ	LGA	ORF	48	296	20	5	2023-10-18 20:00:00	Other
13525	11	3	1953	2000	-7	2242	2317	AA	92	N102NN	JFK	LAX	329	2475	20	0	2023-11-03 20:00:00	LAX
13533	1	23	1628	1635	-7	1923	2007	AS	90	N486AS	EWR	SFO	332	2565	16	35	2023-01-23 16:00:00	Other
13534	2	7	1535	1545	-10	1713	1736	YX	1571	N211JQ	LGA	PIT	64	335	15	45	2023-02-07 15:00:00	Other
13535	2	17	1624	1630	-6	1953	2008	B6	253	N992JB	JFK	SFO	365	2586	16	30	2023-02-17 16:00:00	Other
13542	11	9	1634	1640	-6	2122	2137	B6	443	N579JB	EWR	SJU	204	1608	16	40	2023-11-09 16:00:00	Other
13550	11	26	652	659	-7	916	914	AA	188	N935AN	LGA	CLT	91	544	6	59	2023-11-26 06:00:00	CLT
13552	10	3	1624	1630	-6	1923	1937	AA	87	N104NN	JFK	LAX	332	2475	16	30	2023-10-03 16:00:00	LAX
13554	5	31	810	820	-10	919	945	AA	743	N804AW	LGA	DCA	50	214	8	20	2023-05-31 08:00:00	Other
13555	8	17	2041	2050	-9	2209	2240	9E	1144	N915XJ	LGA	ROA	62	405	20	50	2023-08-17 20:00:00	Other
13557	12	31	752	759	-7	900	937	YX	1314	N114HQ	JFK	DCA	42	213	7	59	2023-12-31 07:00:00	Other
13560	8	5	1050	1059	-9	1230	1255	NK	500	N615NK	LGA	DTW	78	502	10	59	2023-08-05 10:00:00	Other
13562	5	30	2024	2030	-6	2226	2243	YX	1192	N118HQ	JFK	CMH	70	483	20	30	2023-05-30 20:00:00	Other
13575	3	22	1717	1723	-6	1818	1831	YX	1033	N736YX	EWR	MDT	31	141	17	23	2023-03-22 17:00:00	Other
13578	2	5	651	700	-9	1005	1005	UA	564	N47281	EWR	TPA	152	997	7	0	2023-02-05 07:00:00	Other
13582	11	20	554	600	-6	741	740	UA	866	N13138	EWR	ORD	120	719	6	0	2023-11-20 06:00:00	ORD
13584	1	24	1719	1730	-11	1847	1904	YX	1803	N209JQ	JFK	DCA	58	213	17	30	2023-01-24 17:00:00	Other
13590	3	7	607	615	-8	1005	940	UA	896	N17128	EWR	LAX	362	2454	6	15	2023-03-07 06:00:00	LAX
13600	8	26	1839	1845	-6	2247	2248	B6	569	N994JL	JFK	SJU	203	1598	18	45	2023-08-26 18:00:00	Other
13601	1	22	552	600	-8	917	859	B6	48	N834JB	EWR	PBI	150	1023	6	0	2023-01-22 06:00:00	Other
13602	3	6	1456	1505	-9	1635	1623	9E	1559	N490PX	LGA	ORH	31	146	15	5	2023-03-06 15:00:00	Other
13604	4	22	1504	1510	-6	1616	1647	UA	637	N39475	EWR	ORD	105	719	15	10	2023-04-22 15:00:00	ORD
13611	7	19	1917	1925	-8	2221	2240	DL	389	N302NB	LGA	PBI	144	1035	19	25	2023-07-19 19:00:00	Other
13613	5	17	1314	1320	-6	1524	1541	B6	651	N638JB	JFK	MSY	167	1182	13	20	2023-05-17 13:00:00	Other
13629	10	13	1600	1606	-6	1753	1810	YX	1161	N657RW	EWR	MYR	85	550	16	6	2023-10-13 16:00:00	Other
13630	11	27	1537	1545	-8	1836	1917	AA	91	N116AN	JFK	LAX	331	2475	15	45	2023-11-27 15:00:00	LAX
13631	3	1	922	930	-8	1303	1308	YX	1186	N636RW	EWR	EYW	174	1196	9	30	2023-03-01 09:00:00	Other
13632	10	2	1556	1604	-8	1858	1820	YX	1358	N405YX	LGA	TYS	93	647	16	4	2023-10-02 16:00:00	Other
13633	5	18	901	912	-11	1023	1044	YX	1043	N736YX	EWR	BOS	41	200	9	12	2023-05-18 09:00:00	BOS
13642	4	20	1154	1200	-6	1311	1325	YX	1548	N879RW	LGA	BTV	48	258	12	0	2023-04-20 12:00:00	Other
13645	6	28	759	805	-6	1240	1206	DL	730	N839DN	JFK	SJU	208	1598	8	5	2023-06-28 08:00:00	Other
13648	8	8	1849	1859	-10	2138	2158	NK	400	N687NK	LGA	IAH	196	1416	18	59	2023-08-08 18:00:00	Other
13655	2	21	1142	1150	-8	1323	1347	YX	1322	N108HQ	LGA	PIT	69	335	11	50	2023-02-21 11:00:00	Other
13657	10	10	1923	1930	-7	2149	2212	B6	838	N657JB	LGA	JAX	124	833	19	30	2023-10-10 19:00:00	Other
13662	2	20	2050	2059	-9	2206	2229	OO	1167	N308SY	JFK	IAD	51	228	20	59	2023-02-20 20:00:00	Other
13675	7	22	1123	1130	-7	1401	1339	YX	1025	N407YX	LGA	AVL	96	599	11	30	2023-07-22 11:00:00	Other
13677	7	13	1928	1935	-7	2140	2122	OO	989	N306SY	JFK	BNA	124	765	19	35	2023-07-13 19:00:00	Other
13682	10	11	821	829	-8	954	1013	YX	1800	N860RW	LGA	MSN	135	812	8	29	2023-10-11 08:00:00	Other
13686	12	5	1720	1728	-8	1904	1930	YX	1082	N741YX	EWR	CMH	78	463	17	28	2023-12-05 17:00:00	Other
13689	1	24	1542	1559	-17	1926	1920	B6	140	N537JT	LGA	FLL	175	1076	15	59	2023-01-24 15:00:00	FLL
13693	1	28	957	1005	-8	1251	1319	NK	26	N686NK	EWR	MIA	154	1085	10	5	2023-01-28 10:00:00	MIA
13701	9	26	2052	2100	-8	2228	2252	YX	1862	N212JQ	JFK	PIT	66	340	21	0	2023-09-26 21:00:00	Other
13715	3	30	817	823	-6	1041	1104	YX	1302	N118HQ	LGA	ATL	112	762	8	23	2023-03-30 08:00:00	ATL
13720	12	3	705	715	-10	1022	1016	UA	417	N17264	EWR	SRQ	175	1034	7	15	2023-12-03 07:00:00	Other
13724	2	25	1448	1459	-11	1642	1715	AA	665	N851NN	LGA	CLT	94	544	14	59	2023-02-25 14:00:00	CLT
13730	3	27	1047	1057	-10	1256	1303	YX	1247	N821MD	LGA	AVL	108	599	10	57	2023-03-27 10:00:00	Other
13741	9	17	714	723	-9	953	1015	B6	209	N644JB	EWR	TPA	139	997	7	23	2023-09-17 07:00:00	Other
13746	5	1	1534	1541	-7	1627	1648	YX	1144	N753YX	EWR	PVD	30	160	15	41	2023-05-01 15:00:00	Other
13752	12	1	2044	2059	-15	2210	2240	9E	1353	N331PQ	LGA	ORF	56	296	20	59	2023-12-01 20:00:00	Other
13754	2	15	912	920	-8	1100	1125	9E	1420	N676CA	LGA	CLE	80	419	9	20	2023-02-15 09:00:00	Other
13756	12	13	720	730	-10	829	907	9E	1676	N912XJ	LGA	ORF	52	296	7	30	2023-12-13 07:00:00	Other
13757	12	26	1004	1010	-6	1205	1233	9E	1566	N316PQ	JFK	CHS	96	636	10	10	2023-12-26 10:00:00	Other
13759	5	30	1836	1845	-9	1946	2019	B6	2	N317JB	JFK	BUF	48	301	18	45	2023-05-30 18:00:00	Other
13766	4	21	804	810	-6	1202	1139	AA	559	N326SJ	JFK	MIA	150	1089	8	10	2023-04-21 08:00:00	MIA
13770	12	10	1359	1411	-12	1533	1544	UA	132	N446UA	EWR	BNA	128	748	14	11	2023-12-10 14:00:00	Other
13775	6	14	950	956	-6	1157	1222	UA	586	N27267	EWR	LAS	281	2227	9	56	2023-06-14 09:00:00	Other
13776	10	30	1723	1730	-7	1911	1909	9E	1593	N292PQ	LGA	BNA	132	764	17	30	2023-10-30 17:00:00	Other
13778	4	6	820	830	-10	1005	1025	NK	287	N664NK	LGA	MYR	83	563	8	30	2023-04-06 08:00:00	Other
13781	7	29	718	729	-11	930	1015	UA	173	N26226	LGA	IAH	178	1416	7	29	2023-07-29 07:00:00	Other
13784	5	10	653	700	-7	925	953	UA	792	N17289	EWR	PBI	130	1023	7	0	2023-05-10 07:00:00	Other
13786	2	23	1439	1448	-9	1625	1648	YX	1140	N748YX	EWR	MYR	85	550	14	48	2023-02-23 14:00:00	Other
13792	1	9	1407	1415	-8	1533	1527	B6	368	N279JB	LGA	BOS	39	184	14	15	2023-01-09 14:00:00	BOS
13796	2	6	617	630	-13	917	935	B6	92	N958JB	LGA	MCO	135	950	6	30	2023-02-06 06:00:00	MCO
13804	3	20	936	945	-9	1159	1224	B6	884	N659JB	LGA	CHS	115	641	9	45	2023-03-20 09:00:00	Other
13805	9	19	1933	1940	-7	2225	2243	B6	114	N971JT	JFK	ONT	324	2429	19	40	2023-09-19 19:00:00	Other
13813	12	8	1550	1559	-9	1700	1721	B6	363	N354JB	LGA	BOS	34	184	15	59	2023-12-08 15:00:00	BOS
13815	1	25	1508	1515	-7	1840	1832	UA	747	N27251	EWR	RSW	167	1068	15	15	2023-01-25 15:00:00	Other
13816	4	25	1100	1107	-7	1405	1418	DL	478	N344DN	JFK	MIA	159	1089	11	7	2023-04-25 11:00:00	MIA
13817	2	5	752	800	-8	922	943	UA	837	N25705	LGA	ORD	124	733	8	0	2023-02-05 08:00:00	ORD
13820	9	24	1151	1159	-8	1254	1317	UA	633	N449UA	EWR	PWM	46	284	11	59	2023-09-24 11:00:00	Other
13823	11	14	622	630	-8	745	805	B6	256	N3102J	JFK	MKE	127	745	6	30	2023-11-14 06:00:00	Other
13828	6	5	616	622	-6	902	926	NK	202	N976NK	EWR	FLL	142	1065	6	22	2023-06-05 06:00:00	FLL
13829	5	6	754	800	-6	916	924	AA	743	N773XF	LGA	DCA	46	214	8	0	2023-05-06 08:00:00	Other
13843	1	31	1239	1245	-6	1336	1358	YX	1311	N119HQ	JFK	BOS	31	187	12	45	2023-01-31 12:00:00	BOS
13844	11	19	1850	1856	-6	2141	2203	DL	811	N380DN	LGA	TPA	139	1010	18	56	2023-11-19 18:00:00	Other
13850	12	5	1508	1515	-7	1718	1714	9E	1607	N695CA	LGA	RDU	72	431	15	15	2023-12-05 15:00:00	Other
13853	7	10	1909	1920	-11	2134	2054	YX	996	N445YX	LGA	BHM	153	866	19	20	2023-07-10 19:00:00	Other
13858	12	14	844	900	-16	1213	1238	AS	375	N976AK	JFK	PSP	314	2378	9	0	2023-12-14 09:00:00	Other
13864	11	16	2033	2043	-10	2321	2359	UA	548	N47284	EWR	AUS	202	1504	20	43	2023-11-16 20:00:00	Other
13871	2	2	934	940	-6	1042	1057	9E	1406	N601LR	LGA	ALB	30	136	9	40	2023-02-02 09:00:00	Other
13880	4	28	1044	1050	-6	1307	1235	NK	393	N964NK	EWR	MYR	98	550	10	50	2023-04-28 10:00:00	Other
13886	5	25	1421	1430	-9	1635	1657	YX	1335	N404YX	LGA	IND	110	660	14	30	2023-05-25 14:00:00	Other
13889	2	21	925	934	-9	1241	1250	B6	81	N615JB	JFK	IAH	223	1417	9	34	2023-02-21 09:00:00	Other
13899	4	30	1043	1054	-11	1224	1306	DL	391	N365NW	LGA	MSP	132	1020	10	54	2023-04-30 10:00:00	Other
13901	10	17	553	600	-7	737	802	AA	928	N836NN	EWR	CLT	76	529	6	0	2023-10-17 06:00:00	CLT
13902	9	15	654	700	-6	959	1012	AS	85	N280AK	EWR	SEA	313	2402	7	0	2023-09-15 07:00:00	Other
13910	7	20	1023	1030	-7	1213	1215	AA	685	N741UW	LGA	STL	140	888	10	30	2023-07-20 10:00:00	Other
13919	8	11	2046	2100	-14	2218	2253	YX	991	N428YX	LGA	MEM	130	963	21	0	2023-08-11 21:00:00	Other
13921	5	2	754	800	-6	951	1014	YX	1586	N214JQ	JFK	CLT	85	541	8	0	2023-05-02 08:00:00	CLT
13937	10	9	825	832	-7	1108	1139	DL	221	N127DU	JFK	DFW	196	1391	8	32	2023-10-09 08:00:00	Other
13942	11	22	931	937	-6	1207	1155	9E	1610	N919XJ	LGA	AVL	106	599	9	37	2023-11-22 09:00:00	Other
13953	10	27	1918	1925	-7	2138	2159	YX	1780	N246JQ	LGA	SDF	100	659	19	25	2023-10-27 19:00:00	Other
13970	3	27	1122	1130	-8	1331	1342	YX	1363	N430YX	LGA	DTW	102	502	11	30	2023-03-27 11:00:00	Other
13971	9	7	1650	1659	-9	2045	2028	AA	49	N102NN	JFK	SFO	367	2586	16	59	2023-09-07 16:00:00	Other
13975	3	22	2147	2158	-11	2244	2306	YX	1049	N743YX	EWR	MDT	33	141	21	58	2023-03-22 21:00:00	Other
13980	5	12	1846	1859	-13	2048	2141	YX	1284	N435YX	JFK	CVG	91	589	18	59	2023-05-12 18:00:00	Other
13984	11	2	1823	1835	-12	1934	2005	9E	1734	N491PX	LGA	PWM	48	269	18	35	2023-11-02 18:00:00	Other
13987	2	3	553	600	-7	739	740	AA	948	N943NN	LGA	ORD	125	733	6	0	2023-02-03 06:00:00	ORD
13988	10	18	1319	1330	-11	1418	1449	YX	1249	N424YX	JFK	BOS	39	187	13	30	2023-10-18 13:00:00	BOS
13989	2	11	2249	2259	-10	5	23	YX	1506	N202JQ	JFK	PWM	50	273	22	59	2023-02-11 22:00:00	Other
13993	10	2	1947	1955	-8	2136	2155	YX	1166	N736YX	EWR	CMH	69	463	19	55	2023-10-02 19:00:00	Other
14002	8	25	654	700	-6	817	816	B6	783	N339JB	LGA	BOS	46	184	7	0	2023-08-25 07:00:00	BOS
14003	2	6	2123	2130	-7	2229	2234	YX	1495	N815MD	LGA	BDL	25	101	21	30	2023-02-06 21:00:00	Other
14006	1	7	1152	1200	-8	1450	1505	DL	1036	N106DU	LGA	SRQ	155	1047	12	0	2023-01-07 12:00:00	Other
14015	4	12	1917	1925	-8	2016	2053	YX	1252	N432YX	JFK	BOS	36	187	19	25	2023-04-12 19:00:00	BOS
14023	5	30	739	750	-11	1038	1045	NK	833	N647NK	EWR	AUS	188	1504	7	50	2023-05-30 07:00:00	Other
14026	3	5	1500	1510	-10	1624	1647	YX	1264	N424YX	JFK	ORF	53	290	15	10	2023-03-05 15:00:00	Other
14027	8	26	1020	1029	-9	1209	1226	9E	1185	N181PQ	LGA	MYR	80	563	10	29	2023-08-26 10:00:00	Other
14029	12	13	837	849	-12	1137	1127	YX	1720	N220JQ	LGA	OMA	184	1148	8	49	2023-12-13 08:00:00	Other
14031	8	11	1748	1759	-11	2046	2107	F9	395	N387FR	LGA	MCO	138	950	17	59	2023-08-11 17:00:00	MCO
14032	1	11	2213	2220	-7	2338	2343	B6	202	N184JB	JFK	ROC	50	264	22	20	2023-01-11 22:00:00	Other
14033	1	7	1353	1359	-6	1520	1553	9E	1507	N602LR	LGA	CLE	65	419	13	59	2023-01-07 13:00:00	Other
14034	9	22	921	930	-9	1202	1240	AS	8	N563AS	JFK	SEA	305	2422	9	30	2023-09-22 09:00:00	Other
14038	1	20	1203	1215	-12	1406	1450	YX	1295	N134HQ	LGA	DAY	91	549	12	15	2023-01-20 12:00:00	Other
14042	3	30	1550	1559	-9	1838	1907	B6	347	N328JB	JFK	MCO	129	944	15	59	2023-03-30 15:00:00	MCO
14046	3	17	2143	2153	-10	2259	2315	9E	1391	N932XJ	LGA	BUF	53	292	21	53	2023-03-17 21:00:00	Other
14058	9	16	940	946	-6	1131	1207	UA	880	N37290	LGA	DEN	214	1620	9	46	2023-09-16 09:00:00	Other
14059	1	21	936	945	-9	1151	1222	YX	1810	N202JQ	LGA	IND	113	660	9	45	2023-01-21 09:00:00	Other
14060	12	12	1659	1705	-6	1851	1908	YX	1860	N810MD	LGA	RDU	77	431	17	5	2023-12-12 17:00:00	Other
14065	9	13	651	659	-8	951	1005	DL	657	N345NW	JFK	AUS	211	1521	6	59	2023-09-13 06:00:00	Other
14066	3	9	1533	1542	-9	1750	1750	YX	1272	N433YX	LGA	DTW	91	502	15	42	2023-03-09 15:00:00	Other
14070	9	1	1723	1729	-6	1924	1957	AA	585	N336SR	JFK	PHX	272	2153	17	29	2023-09-01 17:00:00	Other
14073	2	17	1342	1348	-6	1607	1617	YX	990	N724YX	EWR	SDF	121	642	13	48	2023-02-17 13:00:00	Other
14075	12	1	1848	1857	-9	2010	2035	B6	580	N284JB	JFK	BUF	61	301	18	57	2023-12-01 18:00:00	Other
14078	8	29	1903	1910	-7	2113	2144	UA	326	N17262	EWR	LAS	282	2227	19	10	2023-08-29 19:00:00	Other
14080	10	24	1522	1531	-9	1619	1643	YX	1083	N655RW	EWR	ALB	37	143	15	31	2023-10-24 15:00:00	Other
14082	7	30	940	946	-6	1125	1141	DL	808	N923AT	EWR	DTW	84	488	9	46	2023-07-30 09:00:00	Other
14086	4	11	758	805	-7	1031	1112	AA	557	N163US	EWR	DFW	159	1372	8	5	2023-04-11 08:00:00	Other
14095	3	6	2216	2225	-9	2333	2348	B6	185	N284JB	JFK	ROC	59	264	22	25	2023-03-06 22:00:00	Other
14096	7	6	2017	2030	-13	2219	2244	9E	1281	N295PQ	EWR	CVG	88	569	20	30	2023-07-06 20:00:00	Other
14098	3	19	1454	1500	-6	1619	1635	YX	1261	N417YX	LGA	DCA	57	214	15	0	2023-03-19 15:00:00	Other
14099	10	18	1301	1315	-14	1413	1438	B6	882	N304JB	JFK	DCA	52	213	13	15	2023-10-18 13:00:00	Other
14100	10	10	1532	1540	-8	1745	1804	UA	845	N77572	EWR	DEN	221	1605	15	40	2023-10-10 15:00:00	Other
14101	1	19	1319	1330	-11	1448	1459	YX	1796	N224JQ	JFK	DCA	54	213	13	30	2023-01-19 13:00:00	Other
14105	5	15	1938	1945	-7	2132	2205	DL	790	N337NB	LGA	MSY	150	1183	19	45	2023-05-15 19:00:00	Other
14113	9	7	747	759	-12	1140	1126	AA	50	N103NN	JFK	SFO	368	2586	7	59	2023-09-07 07:00:00	Other
14119	2	15	1209	1215	-6	1311	1325	B6	304	N279JB	LGA	BOS	39	184	12	15	2023-02-15 12:00:00	BOS
14122	8	28	2153	2159	-6	2337	2352	UA	327	N851UA	EWR	MEM	142	946	21	59	2023-08-28 21:00:00	Other
14123	11	19	1652	1700	-8	1800	1823	AA	398	N733UW	LGA	DCA	46	214	17	0	2023-11-19 17:00:00	Other
14128	6	9	554	600	-6	829	837	UA	184	N17254	EWR	IAH	181	1400	6	0	2023-06-09 06:00:00	Other
14145	12	8	1504	1510	-6	1635	1719	YX	1241	N406YX	JFK	CMH	73	483	15	10	2023-12-08 15:00:00	Other
14147	8	25	803	810	-7	1031	1055	DL	166	N145DQ	LGA	DFW	177	1389	8	10	2023-08-25 08:00:00	Other
14151	5	1	1626	1632	-6	1728	1752	YX	1715	N823MD	LGA	BTV	41	258	16	32	2023-05-01 16:00:00	Other
14153	6	20	1924	1930	-6	2030	2045	B6	533	N306JB	LGA	PWM	43	269	19	30	2023-06-20 19:00:00	Other
14162	3	25	1020	1030	-10	1213	1229	YX	1283	N441YX	JFK	RDU	80	427	10	30	2023-03-25 10:00:00	Other
14163	8	25	850	900	-10	959	1037	UA	204	N14231	LGA	ORD	110	733	9	0	2023-08-25 09:00:00	ORD
14167	4	11	905	915	-10	1014	1034	B6	798	N203JB	LGA	BOS	44	184	9	15	2023-04-11 09:00:00	BOS
14168	5	24	1713	1720	-7	1821	1848	YX	1022	N639RW	EWR	ROC	47	246	17	20	2023-05-24 17:00:00	Other
14175	1	26	1059	1114	-15	1248	1320	YX	1325	N432YX	LGA	ROA	79	405	11	14	2023-01-26 11:00:00	Other
14176	11	3	2119	2129	-10	2227	2250	9E	1673	N325PQ	LGA	BTV	45	258	21	29	2023-11-03 21:00:00	Other
14187	10	22	757	804	-7	1004	1037	YX	1264	N429YX	JFK	CVG	95	589	8	4	2023-10-22 08:00:00	Other
14208	3	16	1720	1729	-9	1947	2008	YX	1273	N135HQ	LGA	ATL	113	762	17	29	2023-03-16 17:00:00	ATL
14209	8	21	1138	1145	-7	1420	1445	AS	9	N952AK	JFK	SEA	308	2422	11	45	2023-08-21 11:00:00	Other
14211	10	22	1753	1800	-7	1922	1931	YX	1033	N764YX	EWR	BUF	49	282	18	0	2023-10-22 18:00:00	Other
14213	6	9	1504	1511	-7	1814	1820	DL	380	N314NB	LGA	PBI	152	1035	15	11	2023-06-09 15:00:00	Other
14220	11	12	1023	1030	-7	1241	1253	YX	1326	N405YX	LGA	GSP	108	610	10	30	2023-11-12 10:00:00	Other
14224	3	17	752	800	-8	909	922	YX	1749	N242JQ	LGA	BOS	45	184	8	0	2023-03-17 08:00:00	BOS
14233	3	22	2037	2050	-13	2206	2220	9E	1315	N301PQ	LGA	IAD	51	229	20	50	2023-03-22 20:00:00	Other
14237	1	31	550	600	-10	806	812	YX	1298	N439YX	LGA	CMH	94	479	6	0	2023-01-31 06:00:00	Other
14240	12	30	808	815	-7	859	927	AA	514	N770UW	LGA	BOS	35	184	8	15	2023-12-30 08:00:00	BOS
14242	2	13	1024	1030	-6	1248	1314	YX	1275	N115HQ	LGA	SDF	106	659	10	30	2023-02-13 10:00:00	Other
14243	8	20	2018	2025	-7	2139	2156	YX	901	N740YX	EWR	DCA	38	199	20	25	2023-08-20 20:00:00	Other
14244	5	5	938	945	-7	1235	1301	B6	60	N2039J	JFK	SAN	335	2446	9	45	2023-05-05 09:00:00	Other
14246	4	22	1345	1355	-10	1547	1624	B6	665	N712JB	LGA	DEN	217	1620	13	55	2023-04-22 13:00:00	Other
14250	11	30	844	853	-9	949	1029	9E	1578	N933XJ	LGA	CHO	50	305	8	53	2023-11-30 08:00:00	Other
14256	2	10	1442	1455	-13	1655	1711	AA	665	N961NN	LGA	CLT	98	544	14	55	2023-02-10 14:00:00	CLT
14269	1	17	1338	1345	-7	1639	1710	DL	300	N183DN	JFK	LAX	333	2475	13	45	2023-01-17 13:00:00	LAX
14271	2	3	1003	1010	-7	1205	1219	AA	100	N167US	JFK	CLT	99	541	10	10	2023-02-03 10:00:00	CLT
14272	11	14	558	607	-9	918	918	AA	429	N853NN	LGA	MIA	152	1096	6	7	2023-11-14 06:00:00	MIA
14273	8	23	1253	1300	-7	1446	1507	AA	599	N975AN	LGA	CLT	80	544	13	0	2023-08-23 13:00:00	CLT
14274	10	25	752	800	-8	926	944	UA	644	N56859	EWR	ORD	117	719	8	0	2023-10-25 08:00:00	ORD
14278	8	3	1152	1159	-7	1336	1351	YX	832	N642RW	EWR	CMH	78	463	11	59	2023-08-03 11:00:00	Other
14279	11	8	1752	1759	-7	2021	2026	YX	1404	N440YX	LGA	IND	113	660	17	59	2023-11-08 17:00:00	Other
14285	5	4	1453	1502	-9	1742	1810	DL	556	N335NB	LGA	TPA	134	1010	15	2	2023-05-04 15:00:00	Other
14296	2	9	853	900	-7	1409	1053	9E	1473	N479PX	LGA	MSN	NA	812	9	0	2023-02-09 09:00:00	Other
14301	3	5	1018	1030	-12	1239	1313	DL	320	N127DU	LGA	MCI	184	1107	10	30	2023-03-05 10:00:00	Other
14304	12	18	1728	1737	-9	1945	1959	AA	733	N973UY	LGA	CLT	100	544	17	37	2023-12-18 17:00:00	CLT
14306	5	3	813	820	-7	1013	1038	YX	1695	N204JQ	LGA	CLT	95	544	8	20	2023-05-03 08:00:00	CLT
14313	8	20	1451	1459	-8	1704	1752	YX	1354	N215JQ	JFK	JAX	113	828	14	59	2023-08-20 14:00:00	Other
14320	5	12	1132	1140	-8	1317	1342	YX	1189	N434YX	JFK	CLE	78	425	11	40	2023-05-12 11:00:00	Other
14330	10	25	1250	1259	-9	1423	1453	9E	1499	N316PQ	LGA	RDU	66	431	12	59	2023-10-25 12:00:00	Other
14337	11	14	1621	1629	-8	1823	1859	YX	1129	N742YX	EWR	SDF	99	642	16	29	2023-11-14 16:00:00	Other
14340	9	12	1313	1330	-17	1515	1527	YX	1342	N419YX	LGA	DAY	86	549	13	30	2023-09-12 13:00:00	Other
14342	4	27	641	647	-6	830	853	UA	451	N16703	EWR	CHS	90	628	6	47	2023-04-27 06:00:00	Other
14348	9	30	1822	1830	-8	2012	2026	YX	1420	N418YX	JFK	RDU	66	427	18	30	2023-09-30 18:00:00	Other
14350	6	14	1253	1259	-6	1441	1458	NK	517	N629NK	LGA	MYR	88	563	12	59	2023-06-14 12:00:00	Other
14355	7	25	659	705	-6	915	919	DL	243	N896DN	JFK	PHX	268	2153	7	5	2023-07-25 07:00:00	Other
14362	1	30	920	930	-10	1136	1217	YX	1820	N210JQ	LGA	SDF	117	659	9	30	2023-01-30 09:00:00	Other
14363	6	3	1342	1350	-8	1533	1612	YX	1334	N109HQ	LGA	XNA	150	1147	13	50	2023-06-03 13:00:00	Other
14364	9	3	2146	2200	-14	2308	2341	YX	1335	N403YX	LGA	RDU	62	431	22	0	2023-09-03 22:00:00	Other
14374	1	29	952	959	-7	1250	1309	B6	1041	N608JB	JFK	TPA	151	1005	9	59	2023-01-29 09:00:00	Other
14376	1	18	1446	1455	-9	1552	1607	YX	1812	N810MD	LGA	BDL	22	101	14	55	2023-01-18 14:00:00	Other
14379	3	9	2005	2011	-6	2130	2152	YX	1378	N872RW	LGA	ORF	52	296	20	11	2023-03-09 20:00:00	Other
14386	4	13	1554	1600	-6	1658	1730	YX	1468	N241JQ	LGA	BOS	32	184	16	0	2023-04-13 16:00:00	BOS
14391	8	26	1353	1402	-9	1515	1535	UA	640	N410UA	EWR	STL	127	872	14	2	2023-08-26 14:00:00	Other
14392	10	29	2051	2059	-8	2330	2330	UA	643	N61881	EWR	DEN	240	1605	20	59	2023-10-29 20:00:00	Other
14394	9	21	554	600	-6	903	915	AA	432	N341SV	LGA	MIA	150	1096	6	0	2023-09-21 06:00:00	MIA
14408	7	26	1452	1458	-6	1627	1624	YX	913	N746YX	EWR	BUF	53	282	14	58	2023-07-26 14:00:00	Other
14409	9	3	1720	1730	-10	1932	1952	YX	1084	N755YX	EWR	IND	88	645	17	30	2023-09-03 17:00:00	Other
14416	7	14	1105	1111	-6	1433	1434	DL	511	N3768	LGA	MIA	162	1096	11	11	2023-07-14 11:00:00	MIA
14418	1	30	821	830	-9	1002	1020	B6	450	N279JB	JFK	BNA	141	765	8	30	2023-01-30 08:00:00	Other
14422	11	22	819	825	-6	1117	1136	AA	200	N844NN	LGA	DFW	191	1389	8	25	2023-11-22 08:00:00	Other
14428	12	4	1510	1519	-9	1624	1640	YX	1073	N751YX	EWR	SYR	42	195	15	19	2023-12-04 15:00:00	Other
14429	1	10	2044	2055	-11	2304	2321	YX	1290	N105HQ	LGA	MEM	146	963	20	55	2023-01-10 20:00:00	Other
14431	2	19	821	829	-8	1019	1035	YX	1006	N753YX	EWR	GSO	81	445	8	29	2023-02-19 08:00:00	Other
14432	3	14	902	908	-6	1019	1025	B6	965	N249JB	JFK	BOS	39	187	9	8	2023-03-14 09:00:00	BOS
14441	10	11	921	929	-8	1130	1153	YX	1848	N815MD	LGA	HHH	107	701	9	29	2023-10-11 09:00:00	Other
14442	4	12	937	945	-8	1214	1235	B6	366	N307JB	JFK	MCO	129	944	9	45	2023-04-12 09:00:00	MCO
14451	1	9	1134	1140	-6	1321	1347	YX	1406	N135HQ	JFK	CLE	78	425	11	40	2023-01-09 11:00:00	Other
14456	10	13	701	710	-9	1003	959	B6	183	N531JL	EWR	PBI	144	1023	7	10	2023-10-13 07:00:00	Other
14462	2	27	652	700	-8	1004	1008	UA	813	N14235	EWR	RSW	153	1068	7	0	2023-02-27 07:00:00	Other
14463	11	6	855	902	-7	1247	1237	AA	883	N101NN	JFK	SNA	346	2454	9	2	2023-11-06 09:00:00	Other
14475	10	27	2024	2030	-6	2	2342	UA	377	N58101	EWR	LAX	344	2454	20	30	2023-10-27 20:00:00	LAX
14493	11	23	853	900	-7	1145	1206	UA	101	N47293	EWR	TPA	146	997	9	0	2023-11-23 09:00:00	Other
14496	9	6	637	645	-8	828	855	UA	456	N418UA	EWR	CHS	88	628	6	45	2023-09-06 06:00:00	Other
14499	12	12	1147	1157	-10	1330	1353	YX	1118	N756YX	EWR	ILM	84	488	11	57	2023-12-12 11:00:00	Other
14500	6	7	1324	1330	-6	1621	1603	B6	1014	N588JB	LGA	ATL	108	762	13	30	2023-06-07 13:00:00	ATL
14504	6	10	1054	1100	-6	1239	1253	YX	1292	N438YX	JFK	CLE	77	425	11	0	2023-06-10 11:00:00	Other
14506	10	18	837	845	-8	1043	1115	YX	1280	N442YX	LGA	OMA	167	1148	8	45	2023-10-18 08:00:00	Other
14508	1	21	1321	1330	-9	1513	1536	YX	1807	N815MD	LGA	STL	149	888	13	30	2023-01-21 13:00:00	Other
14512	11	27	720	730	-10	1020	1030	UA	611	N76288	EWR	MCO	149	937	7	30	2023-11-27 07:00:00	MCO
14515	2	22	622	630	-8	913	948	B6	817	N527JL	JFK	MIA	150	1089	6	30	2023-02-22 06:00:00	MIA
14526	9	26	1752	1759	-7	1933	1955	YX	1387	N114HQ	JFK	CMH	79	483	17	59	2023-09-26 17:00:00	Other
14530	12	12	1631	1640	-9	1907	1908	9E	1393	N326PQ	LGA	CHS	103	641	16	40	2023-12-12 16:00:00	Other
14531	12	13	1409	1415	-6	1503	1531	B6	310	N337JB	LGA	BOS	35	184	14	15	2023-12-13 14:00:00	BOS
14532	11	18	2123	2129	-6	2310	2339	YX	1085	N647RW	EWR	MSP	150	1008	21	29	2023-11-18 21:00:00	Other
14540	2	21	624	630	-6	850	858	UA	437	N16217	EWR	JAX	123	820	6	30	2023-02-21 06:00:00	Other
14541	10	14	1305	1313	-8	1418	1433	YX	1060	N723YX	EWR	BTV	50	266	13	13	2023-10-14 13:00:00	Other
14543	9	26	819	829	-10	1137	1150	AA	712	N342RX	JFK	MIA	164	1089	8	29	2023-09-26 08:00:00	MIA
14548	11	10	1251	1300	-9	1613	1627	YX	1045	N655RW	EWR	EYW	176	1196	13	0	2023-11-10 13:00:00	Other
14556	1	26	1137	1144	-7	1619	1648	NK	1110	N603NK	EWR	SJU	200	1608	11	44	2023-01-26 11:00:00	Other
14557	6	23	1456	1502	-6	1816	1809	NK	645	N686NK	LGA	FLL	163	1076	15	2	2023-06-23 15:00:00	FLL
14560	9	22	1320	1330	-10	1434	1439	B6	37	N249JB	JFK	SYR	41	209	13	30	2023-09-22 13:00:00	Other
14564	10	1	2123	2129	-6	2250	2300	9E	1646	N605LR	LGA	BUF	47	292	21	29	2023-10-01 21:00:00	Other
14566	2	7	1813	1820	-7	1948	2011	DL	378	N140DU	LGA	ORD	121	733	18	20	2023-02-07 18:00:00	ORD
14569	10	26	1025	1035	-10	1211	1233	UA	473	N27722	EWR	CLT	76	529	10	35	2023-10-26 10:00:00	CLT
14574	12	10	1821	1829	-8	2216	2205	DL	96	N886DN	JFK	SLC	274	1990	18	29	2023-12-10 18:00:00	Other
14582	3	22	1805	1812	-7	2025	2040	9E	1343	N296PQ	JFK	SAV	106	718	18	12	2023-03-22 18:00:00	Other
14585	8	19	1421	1430	-9	1544	1600	YX	928	N724YX	EWR	DCA	38	199	14	30	2023-08-19 14:00:00	Other
14592	10	7	749	755	-6	1009	1014	DL	899	N360NB	JFK	MSY	171	1182	7	55	2023-10-07 07:00:00	Other
14595	1	18	2148	2200	-12	2245	2322	AA	855	N832AW	LGA	DCA	44	214	22	0	2023-01-18 22:00:00	Other
14604	4	21	1324	1330	-6	1612	1630	UA	442	N405UA	EWR	RSW	149	1068	13	30	2023-04-21 13:00:00	Other
14610	3	18	1722	1729	-7	2104	2110	YX	1122	N635RW	EWR	EYW	183	1196	17	29	2023-03-18 17:00:00	Other
14617	12	31	624	630	-6	907	929	UA	303	N47505	EWR	MCO	134	937	6	30	2023-12-31 06:00:00	MCO
14622	1	21	1032	1045	-13	1258	1320	YX	1296	N438YX	LGA	AVL	111	599	10	45	2023-01-21 10:00:00	Other
14626	3	30	921	930	-9	1224	1257	AA	814	N326RP	LGA	MIA	142	1096	9	30	2023-03-30 09:00:00	MIA
14638	5	12	706	715	-9	1038	1035	AA	1	N111ZM	JFK	LAX	350	2475	7	15	2023-05-12 07:00:00	LAX
14645	12	22	1119	1127	-8	1303	1329	YX	1277	N413YX	LGA	STL	136	888	11	27	2023-12-22 11:00:00	Other
14653	10	22	624	630	-6	916	935	UA	871	N17139	EWR	LAX	320	2454	6	30	2023-10-22 06:00:00	LAX
14656	2	20	649	659	-10	905	909	YX	1029	N979RP	EWR	GSP	109	594	6	59	2023-02-20 06:00:00	Other
14666	12	9	821	830	-9	1123	1133	UA	124	N12003	EWR	LAX	301	2454	8	30	2023-12-09 08:00:00	LAX
14673	11	19	1549	1559	-10	1741	1835	YX	1250	N419YX	LGA	LIT	152	1085	15	59	2023-11-19 15:00:00	Other
14678	4	26	1721	1729	-8	2009	2038	B6	640	N559JB	JFK	PSP	308	2378	17	29	2023-04-26 17:00:00	Other
14686	10	10	824	830	-6	1022	1049	9E	1527	N295PQ	LGA	CLT	84	544	8	30	2023-10-10 08:00:00	CLT
14689	2	9	1213	1220	-7	1516	1549	DL	323	N110DU	LGA	DFW	211	1389	12	20	2023-02-09 12:00:00	Other
14694	9	20	1053	1100	-7	1150	1209	B6	59	N368JB	JFK	BOS	38	187	11	0	2023-09-20 11:00:00	BOS
14697	9	28	900	908	-8	1112	1128	YX	1086	N855RW	EWR	MCI	150	1092	9	8	2023-09-28 09:00:00	Other
14704	5	9	1724	1730	-6	1918	1915	OO	1151	N260SY	JFK	MKE	128	745	17	30	2023-05-09 17:00:00	Other
14706	10	31	1924	1930	-6	2127	2109	UA	400	N27724	EWR	ORD	114	719	19	30	2023-10-31 19:00:00	ORD
14713	7	5	1609	1615	-6	1724	1741	B6	318	N306JB	LGA	BOS	36	184	16	15	2023-07-05 16:00:00	BOS
14719	10	8	2003	2010	-7	2214	2223	9E	1630	N306PQ	EWR	CVG	87	569	20	10	2023-10-08 20:00:00	Other
14720	6	8	748	755	-7	1055	1100	AA	320	N754UW	JFK	AUS	198	1521	7	55	2023-06-08 07:00:00	Other
14721	9	27	921	930	-9	1025	1102	YX	1814	N223JQ	JFK	DCA	44	213	9	30	2023-09-27 09:00:00	Other
14723	10	15	853	900	-7	1104	1107	AA	543	N970UY	EWR	CLT	84	529	9	0	2023-10-15 09:00:00	CLT
14724	11	30	650	700	-10	918	935	UA	503	N17264	EWR	ATL	115	746	7	0	2023-11-30 07:00:00	ATL
14725	11	29	1620	1628	-8	1730	1744	AA	860	N824AW	LGA	BOS	44	184	16	28	2023-11-29 16:00:00	BOS
14727	11	2	637	645	-8	942	953	UA	886	N37504	EWR	MIA	158	1085	6	45	2023-11-02 06:00:00	MIA
14729	10	27	654	700	-6	1014	1010	AS	81	N964AK	EWR	SEA	343	2402	7	0	2023-10-27 07:00:00	Other
14733	10	28	1923	1938	-15	2139	2200	UA	866	N456UA	EWR	MSY	161	1167	19	38	2023-10-28 19:00:00	Other
14748	7	20	1540	1550	-10	1758	1816	9E	1119	N326PQ	LGA	CLT	80	544	15	50	2023-07-20 15:00:00	CLT
14749	11	16	2033	2043	-10	2315	2330	UA	767	N37318	EWR	LAS	314	2227	20	43	2023-11-16 20:00:00	Other
14752	11	21	816	829	-13	1052	1057	YX	1277	N442YX	LGA	OMA	176	1148	8	29	2023-11-21 08:00:00	Other
14753	9	29	646	654	-8	758	811	AA	547	N765US	LGA	DCA	52	214	6	54	2023-09-29 06:00:00	Other
14765	1	18	640	650	-10	746	816	9E	1546	N908XJ	LGA	ORF	48	296	6	50	2023-01-18 06:00:00	Other
14773	8	28	622	630	-8	858	924	UA	708	N13113	EWR	LAX	311	2454	6	30	2023-08-28 06:00:00	LAX
14774	12	5	1921	1929	-8	2056	2131	YX	1081	N764YX	EWR	STL	136	872	19	29	2023-12-05 19:00:00	Other
14777	1	24	2153	2159	-6	120	126	B6	768	N947JB	JFK	LAX	345	2475	21	59	2023-01-24 21:00:00	LAX
14781	9	22	1159	1205	-6	1313	1333	AA	794	N756US	LGA	DCA	42	214	12	5	2023-09-22 12:00:00	Other
14782	7	20	1137	1146	-9	1337	1346	YX	1033	N871RW	LGA	DAY	86	549	11	46	2023-07-20 11:00:00	Other
14789	2	15	2153	2210	-17	2319	2349	B6	357	N591JB	LGA	BNA	125	764	22	10	2023-02-15 22:00:00	Other
14790	8	2	1336	1347	-11	1451	1521	AA	507	N807NN	EWR	ORD	105	719	13	47	2023-08-02 13:00:00	ORD
14793	11	12	1923	1929	-6	2137	2151	9E	1593	N921XJ	LGA	CVG	97	585	19	29	2023-11-12 19:00:00	Other
14804	1	16	943	949	-6	1108	1141	YX	1160	N653RW	EWR	CLE	63	404	9	49	2023-01-16 09:00:00	Other
14806	10	24	2050	2058	-8	2249	2316	YX	1062	N727YX	EWR	GRR	94	605	20	58	2023-10-24 20:00:00	Other
14809	3	1	921	930	-9	1041	1059	YX	1642	N217JQ	JFK	DCA	57	213	9	30	2023-03-01 09:00:00	Other
14812	6	1	1123	1130	-7	1355	1435	DL	462	N3767	JFK	TPA	134	1005	11	30	2023-06-01 11:00:00	Other
14815	1	29	1220	1230	-10	1353	1413	9E	1405	N320PQ	LGA	MKE	135	738	12	30	2023-01-29 12:00:00	Other
14818	2	25	1629	1635	-6	2002	2011	AS	7	N943AK	JFK	SEA	362	2422	16	35	2023-02-25 16:00:00	Other
14822	1	22	830	840	-10	1132	1120	B6	28	N712JB	JFK	MSY	207	1182	8	40	2023-01-22 08:00:00	Other
14823	10	5	1924	1930	-6	2114	2142	AA	725	N3014R	JFK	CLT	80	541	19	30	2023-10-05 19:00:00	CLT
14824	2	2	554	600	-6	855	859	B6	48	N615JB	EWR	PBI	150	1023	6	0	2023-02-02 06:00:00	Other
14825	3	22	1651	1700	-9	2019	2022	UA	139	N2749U	EWR	SFO	342	2565	17	0	2023-03-22 17:00:00	Other
14827	2	26	2053	2100	-7	2319	2329	YX	1288	N428YX	JFK	IND	109	665	21	0	2023-02-26 21:00:00	Other
14835	2	26	2055	2105	-10	7	2355	NK	287	N938NK	EWR	LAS	327	2227	21	5	2023-02-26 21:00:00	Other
14838	1	6	1508	1515	-7	1612	1633	UA	156	N47282	EWR	BOS	37	200	15	15	2023-01-06 15:00:00	BOS
14844	12	16	1708	1715	-7	1942	1955	YX	1031	N767YX	EWR	JAX	125	820	17	15	2023-12-16 17:00:00	Other
14853	9	28	559	605	-6	713	725	YX	1795	N882RW	LGA	DCA	49	214	6	5	2023-09-28 06:00:00	Other
14854	1	16	1615	1622	-7	1753	1809	YX	1363	N867RW	LGA	CHO	50	305	16	22	2023-01-16 16:00:00	Other
14855	11	1	724	730	-6	954	959	B6	313	N3113J	JFK	SAV	131	718	7	30	2023-11-01 07:00:00	Other
14866	1	26	623	635	-12	918	955	UA	906	N67501	EWR	SEA	320	2402	6	35	2023-01-26 06:00:00	Other
14870	5	29	854	900	-6	1136	1205	AS	16	N586AS	JFK	SAN	306	2446	9	0	2023-05-29 09:00:00	Other
14879	9	13	2145	2157	-12	2307	2334	YX	1356	N441YX	JFK	DCA	43	213	21	57	2023-09-13 21:00:00	Other
14883	4	3	948	959	-11	1314	1330	YX	1038	N654RW	EWR	EYW	177	1196	9	59	2023-04-03 09:00:00	Other
14894	11	20	602	610	-8	904	934	DL	432	N142DU	LGA	IAH	215	1416	6	10	2023-11-20 06:00:00	Other
14900	4	16	2059	2105	-6	2243	2253	YX	1102	N134HQ	LGA	GSO	75	461	21	5	2023-04-16 21:00:00	Other
14903	10	3	622	630	-8	913	942	B6	4	N990JL	JFK	SFO	332	2586	6	30	2023-10-03 06:00:00	Other
14917	7	24	803	810	-7	1042	1055	DL	180	N118DU	LGA	DFW	185	1389	8	10	2023-07-24 08:00:00	Other
14929	9	15	1819	1828	-9	2031	2041	YX	1366	N870RW	LGA	MCI	159	1107	18	28	2023-09-15 18:00:00	Other
14931	5	23	809	820	-11	930	945	AA	743	N756US	LGA	DCA	58	214	8	20	2023-05-23 08:00:00	Other
14932	4	7	608	615	-7	812	817	DL	873	N996AT	EWR	MSP	169	1008	6	15	2023-04-07 06:00:00	Other
14933	1	10	1051	1100	-9	1236	1311	YX	1115	N728YX	EWR	DTW	80	488	11	0	2023-01-10 11:00:00	Other
14940	11	15	601	608	-7	810	817	AA	233	N971UY	LGA	CLT	95	544	6	8	2023-11-15 06:00:00	CLT
14943	4	18	1544	1550	-6	1713	1729	9E	1314	N309PQ	LGA	BGR	54	378	15	50	2023-04-18 15:00:00	Other
14949	8	12	1054	1103	-9	1418	1419	B6	452	N984JB	JFK	SFO	347	2586	11	3	2023-08-12 11:00:00	Other
14956	2	9	1747	1754	-7	2101	2141	AA	904	N107NN	JFK	SFO	337	2586	17	54	2023-02-09 17:00:00	Other
14957	2	19	1621	1629	-8	1818	1844	YX	999	N743YX	EWR	GSP	96	594	16	29	2023-02-19 16:00:00	Other
14964	3	2	1751	1800	-9	2019	2017	9E	1573	N905XJ	LGA	MEM	174	963	18	0	2023-03-02 18:00:00	Other
14965	6	2	550	600	-10	811	820	UA	446	N481UA	EWR	ATL	104	746	6	0	2023-06-02 06:00:00	ATL
14968	2	20	1617	1630	-13	1934	2008	B6	253	N961JT	JFK	SFO	351	2586	16	30	2023-02-20 16:00:00	Other
14974	12	16	849	855	-6	1011	1057	OO	1182	N244SY	LGA	ORD	115	733	8	55	2023-12-16 08:00:00	ORD
14976	12	13	1821	1830	-9	2126	2205	B6	59	N923JB	JFK	LAX	333	2475	18	30	2023-12-13 18:00:00	LAX
14977	9	28	1351	1400	-9	1454	1510	YX	1223	N642RW	EWR	PVD	31	160	14	0	2023-09-28 14:00:00	Other
14979	12	25	1522	1530	-8	1833	1836	B6	324	N216JB	JFK	MCO	141	944	15	30	2023-12-25 15:00:00	MCO
14987	3	10	820	830	-10	1139	1155	B6	60	N991JT	JFK	SAN	352	2446	8	30	2023-03-10 08:00:00	Other
14990	12	18	1935	1942	-7	2121	2153	YX	1324	N447YX	LGA	DTW	73	502	19	42	2023-12-18 19:00:00	Other
14998	6	5	1459	1505	-6	1653	1708	AA	791	N867NN	LGA	CLT	79	544	15	5	2023-06-05 15:00:00	CLT
15002	2	22	1031	1045	-14	1248	1251	AA	884	N756US	LGA	STL	162	888	10	45	2023-02-22 10:00:00	Other
15004	9	18	2149	2200	-11	2344	2359	NK	1027	N656NK	EWR	DTW	74	488	22	0	2023-09-18 22:00:00	Other
15021	9	4	1007	1015	-8	1231	1254	UA	711	N25982	EWR	IAH	172	1400	10	15	2023-09-04 10:00:00	Other
15030	7	20	928	935	-7	1122	1143	YX	1006	N427YX	JFK	CMH	79	483	9	35	2023-07-20 09:00:00	Other
15040	1	28	1352	1400	-8	1523	1557	AA	781	N732US	LGA	RDU	76	431	14	0	2023-01-28 14:00:00	Other
15041	8	23	919	929	-10	1032	1100	YX	1050	N412YX	LGA	RIC	48	292	9	29	2023-08-23 09:00:00	Other
15047	10	30	1112	1120	-8	1408	1429	UA	821	N66808	EWR	MIA	156	1085	11	20	2023-10-30 11:00:00	MIA
15054	10	23	941	950	-9	1121	1158	9E	1561	N482PX	LGA	GSO	69	461	9	50	2023-10-23 09:00:00	Other
15056	6	30	1357	1405	-8	1529	1558	YX	1378	N442YX	LGA	ILM	71	500	14	5	2023-06-30 14:00:00	Other
15057	10	10	1429	1435	-6	1553	1602	UA	564	N872UA	EWR	BNA	114	748	14	35	2023-10-10 14:00:00	Other
15060	5	16	1528	1538	-10	1724	1800	9E	1323	N319PQ	LGA	TYS	93	647	15	38	2023-05-16 15:00:00	Other
15063	2	15	749	755	-6	1057	1110	AA	958	N930AN	EWR	MIA	161	1085	7	55	2023-02-15 07:00:00	MIA
15077	8	2	1809	1815	-6	2101	2128	AA	595	N308RD	LGA	MIA	136	1096	18	15	2023-08-02 18:00:00	MIA
15080	8	20	1748	1755	-7	2031	2057	B6	540	N504JB	LGA	MCO	122	950	17	55	2023-08-20 17:00:00	MCO
15086	3	2	924	930	-6	1201	1212	UA	876	N847UA	LGA	DEN	248	1620	9	30	2023-03-02 09:00:00	Other
15097	5	19	936	946	-10	1058	1130	9E	1459	N324PQ	LGA	BGR	53	378	9	46	2023-05-19 09:00:00	Other
15098	9	27	1430	1440	-10	1555	1612	9E	1500	N678CA	LGA	ORF	55	296	14	40	2023-09-27 14:00:00	Other
15103	8	30	824	830	-6	1203	1121	DL	174	N122DU	JFK	DFW	197	1391	8	30	2023-08-30 08:00:00	Other
15105	4	18	926	932	-6	1127	1140	UA	441	N16732	EWR	MCI	150	1092	9	32	2023-04-18 09:00:00	Other
15107	8	23	1957	2005	-8	2153	2215	YX	870	N639RW	EWR	GSP	88	594	20	5	2023-08-23 20:00:00	Other
15113	9	5	2114	2120	-6	3	28	NK	628	N945NK	EWR	FLL	139	1065	21	20	2023-09-05 21:00:00	FLL
15116	3	20	2147	2155	-8	2253	2313	YX	1733	N879RW	LGA	PWM	51	269	21	55	2023-03-20 21:00:00	Other
15117	10	27	1509	1520	-11	1642	1658	B6	792	N307JB	LGA	BNA	119	764	15	20	2023-10-27 15:00:00	Other
15120	9	17	553	600	-7	838	905	NK	47	N682NK	LGA	FLL	145	1076	6	0	2023-09-17 06:00:00	FLL
15124	5	2	1650	1700	-10	1916	1833	YX	1659	N215JQ	LGA	BOS	58	184	17	0	2023-05-02 17:00:00	BOS
15134	2	20	952	1000	-8	1100	1134	YX	1536	N211JQ	LGA	BOS	39	184	10	0	2023-02-20 10:00:00	BOS
15142	5	26	1122	1129	-7	1419	1443	DL	969	N351NB	LGA	PBI	155	1035	11	29	2023-05-26 11:00:00	Other
15144	10	21	637	645	-8	938	1003	DL	85	N309DU	LGA	SLC	281	1983	6	45	2023-10-21 06:00:00	Other
15148	9	13	1310	1316	-6	1612	1621	YX	1397	N122HQ	LGA	IAH	219	1416	13	16	2023-09-13 13:00:00	Other
15149	5	10	813	820	-7	1019	1056	B6	437	N339JB	JFK	ATL	104	760	8	20	2023-05-10 08:00:00	ATL
15161	1	29	1840	1850	-10	2004	2024	YX	1358	N401YX	JFK	ORF	53	290	18	50	2023-01-29 18:00:00	Other
15162	3	31	1652	1700	-8	1841	1902	9E	1446	N330PQ	JFK	RDU	73	427	17	0	2023-03-31 17:00:00	Other
15165	12	7	829	841	-12	1029	1046	YX	1018	N859RW	EWR	DTW	90	488	8	41	2023-12-07 08:00:00	Other
15168	11	16	1920	1929	-9	2042	2108	YX	1237	N440YX	LGA	BHM	122	866	19	29	2023-11-16 19:00:00	Other
15170	7	24	1258	1305	-7	1404	1440	UA	99	N78511	EWR	ORD	106	719	13	5	2023-07-24 13:00:00	ORD
15180	7	1	709	715	-6	827	831	B6	803	N239JB	LGA	BOS	60	184	7	15	2023-07-01 07:00:00	BOS
15182	4	26	1558	1605	-7	1855	1933	B6	302	N946JL	JFK	LAX	328	2475	16	5	2023-04-26 16:00:00	LAX
15186	3	4	757	803	-6	946	952	B6	399	N198JB	JFK	BNA	131	765	8	3	2023-03-04 08:00:00	Other
15198	11	15	554	600	-6	711	715	B6	102	N203JB	JFK	BOS	45	187	6	0	2023-11-15 06:00:00	BOS
15203	6	28	1422	1429	-7	1630	1657	UA	990	N409UA	LGA	DEN	229	1620	14	29	2023-06-28 14:00:00	Other
15210	3	12	1339	1345	-6	1515	1534	YX	1256	N447YX	LGA	CLE	75	419	13	45	2023-03-12 13:00:00	Other
15213	2	8	2059	2105	-6	2341	2355	NK	287	N927NK	EWR	LAS	308	2227	21	5	2023-02-08 21:00:00	Other
15217	11	27	833	841	-8	1023	1040	YX	1789	N233JQ	LGA	CMH	83	479	8	41	2023-11-27 08:00:00	Other
15225	2	21	602	610	-8	719	728	DL	403	N130DU	JFK	BOS	31	187	6	10	2023-02-21 06:00:00	BOS
15226	12	7	554	600	-6	839	906	B6	535	N640JB	EWR	FLL	132	1065	6	0	2023-12-07 06:00:00	FLL
15231	4	17	553	600	-7	832	830	DL	313	N385DZ	LGA	ATL	123	762	6	0	2023-04-17 06:00:00	ATL
15236	9	26	649	700	-11	934	952	UA	417	N840UA	EWR	SRQ	147	1034	7	0	2023-09-26 07:00:00	Other
15242	2	12	1449	1455	-6	1639	1700	YX	1529	N215JQ	JFK	CMH	77	483	14	55	2023-02-12 14:00:00	Other
15255	3	16	1356	1405	-9	1602	1618	YX	1073	N750YX	EWR	CHS	86	628	14	5	2023-03-16 14:00:00	Other
15260	9	14	1230	1236	-6	1349	1345	9E	1736	N918XJ	LGA	BGM	30	147	12	36	2023-09-14 12:00:00	Other
15264	8	31	1523	1530	-7	1840	1839	UA	607	N78001	EWR	SFO	322	2565	15	30	2023-08-31 15:00:00	Other
15267	10	26	1441	1450	-9	1631	1703	9E	1570	N325PQ	LGA	GSP	89	610	14	50	2023-10-26 14:00:00	Other
15277	10	3	2151	2200	-9	2311	2336	DL	348	N344NB	JFK	BUF	52	301	22	0	2023-10-03 22:00:00	Other
15280	8	1	1509	1518	-9	1703	1722	YX	1011	N442YX	JFK	RDU	76	427	15	18	2023-08-01 15:00:00	Other
15287	8	31	1254	1300	-6	1451	1509	UA	715	N844UA	EWR	MSY	161	1167	13	0	2023-08-31 13:00:00	Other
15293	6	4	2004	2016	-12	2209	2229	9E	1437	N133EV	LGA	CAE	89	617	20	16	2023-06-04 20:00:00	Other
15295	1	27	658	705	-7	1002	1014	DL	741	N349NW	LGA	TPA	165	1010	7	5	2023-01-27 07:00:00	Other
15313	8	30	823	829	-6	1215	1208	AA	47	N101NN	JFK	SFO	357	2586	8	29	2023-08-30 08:00:00	Other
15327	9	2	1707	1715	-8	1808	1854	YX	1882	N202JQ	LGA	DCA	40	214	17	15	2023-09-02 17:00:00	Other
15328	5	3	705	715	-10	910	920	9E	1467	N138EV	LGA	CVG	98	585	7	15	2023-05-03 07:00:00	Other
15343	4	18	603	615	-12	709	727	B6	70	N306JB	LGA	BOS	40	184	6	15	2023-04-18 06:00:00	BOS
15347	5	31	919	925	-6	1151	1222	DL	205	N126DU	LGA	DFW	178	1389	9	25	2023-05-31 09:00:00	Other
15348	5	16	1141	1148	-7	1322	1345	YX	1673	N204JQ	LGA	CMH	78	479	11	48	2023-05-16 11:00:00	Other
15353	6	8	819	829	-10	936	1009	9E	1717	N304PQ	LGA	CHO	55	305	8	29	2023-06-08 08:00:00	Other
15354	9	20	653	659	-6	949	1013	DL	345	N317DU	LGA	PBI	149	1035	6	59	2023-09-20 06:00:00	Other
15355	8	1	921	929	-8	1141	1159	YX	1351	N824MD	LGA	HHH	101	701	9	29	2023-08-01 09:00:00	Other
15358	2	9	943	955	-12	1115	1145	B6	744	N203JB	LGA	BNA	127	764	9	55	2023-02-09 09:00:00	Other
15362	10	21	1150	1159	-9	1449	1458	B6	409	N641JB	LGA	PBI	133	1035	11	59	2023-10-21 11:00:00	Other
15363	9	4	1447	1455	-8	1617	1621	9E	1667	N336PQ	JFK	BWI	45	184	14	55	2023-09-04 14:00:00	Other
15364	3	24	1850	1900	-10	2023	2034	YX	1301	N108HQ	LGA	PIT	71	335	19	0	2023-03-24 19:00:00	Other
15368	7	17	1851	1900	-9	2024	2051	YX	1358	N220JQ	LGA	PIT	62	335	19	0	2023-07-17 19:00:00	Other
15371	11	20	2111	2117	-6	2326	2330	UA	217	N37577	EWR	CVG	98	569	21	17	2023-11-20 21:00:00	Other
15372	3	1	1048	1054	-6	1246	1300	UA	564	N27252	EWR	CHS	91	628	10	54	2023-03-01 10:00:00	Other
15385	2	25	2208	2215	-7	220	141	B6	680	N976JT	JFK	LAX	404	2475	22	15	2023-02-25 22:00:00	LAX
15386	2	8	2016	2027	-11	2140	2214	UA	146	N17752	EWR	RDU	63	416	20	27	2023-02-08 20:00:00	Other
15387	10	4	1400	1409	-9	1549	1604	9E	1494	N135EV	JFK	RDU	68	427	14	9	2023-10-04 14:00:00	Other
15393	11	5	1950	1959	-9	2133	2200	YX	1169	N744YX	EWR	CMH	74	463	19	59	2023-11-05 19:00:00	Other
15406	3	30	822	830	-8	1044	1052	YX	1397	N431YX	LGA	CVG	108	585	8	30	2023-03-30 08:00:00	Other
15408	5	13	738	745	-7	906	921	UA	839	N448UA	EWR	ORD	113	719	7	45	2023-05-13 07:00:00	ORD
15409	10	24	1255	1303	-8	1444	1508	AA	721	N948NN	LGA	CLT	81	544	13	3	2023-10-24 13:00:00	CLT
15411	5	17	745	755	-10	923	924	YX	1297	N821MD	LGA	CHO	61	305	7	55	2023-05-17 07:00:00	Other
15413	6	7	554	600	-6	816	838	UA	944	N855UA	LGA	IAH	185	1416	6	0	2023-06-07 06:00:00	Other
15414	10	13	851	900	-9	1049	1105	9E	1623	N676CA	JFK	CVG	93	589	9	0	2023-10-13 09:00:00	Other
15416	4	28	1720	1727	-7	2104	2104	YX	951	N863RW	EWR	EYW	183	1196	17	27	2023-04-28 17:00:00	Other
15417	9	18	611	620	-9	812	841	UA	379	N831UA	LGA	DEN	215	1620	6	20	2023-09-18 06:00:00	Other
15422	4	16	1346	1355	-9	1512	1525	B6	835	N358JB	JFK	BUF	54	301	13	55	2023-04-16 13:00:00	Other
15429	8	21	1453	1459	-6	1755	1806	UA	194	N895UA	EWR	MIA	146	1085	14	59	2023-08-21 14:00:00	MIA
15430	10	19	833	840	-7	1008	1030	B6	880	N266JB	JFK	RDU	67	427	8	40	2023-10-19 08:00:00	Other
15431	1	18	2123	2129	-6	2243	2303	YX	1202	N647RW	EWR	BGR	59	393	21	29	2023-01-18 21:00:00	Other
15432	1	6	724	730	-6	1419	1035	UA	815	N21723	EWR	BZN	NA	1882	7	30	2023-01-06 07:00:00	Other
15444	10	9	1447	1459	-12	1602	1632	9E	1544	N176PQ	LGA	CHO	54	305	14	59	2023-10-09 14:00:00	Other
15449	5	15	830	837	-7	1017	1025	B6	823	N324JB	JFK	RDU	70	427	8	37	2023-05-15 08:00:00	Other
15456	9	2	1158	1205	-7	1314	1333	9E	1553	N678CA	JFK	BUF	56	301	12	5	2023-09-02 12:00:00	Other
15459	8	10	1008	1015	-7	1247	1254	UA	566	N27957	EWR	IAH	180	1400	10	15	2023-08-10 10:00:00	Other
15461	5	10	1952	2000	-8	2328	2335	B6	69	N944JT	JFK	LAX	334	2475	20	0	2023-05-10 20:00:00	LAX
15464	8	28	923	930	-7	1049	1059	YX	885	N761YX	EWR	PWM	49	284	9	30	2023-08-28 09:00:00	Other
15473	8	17	832	840	-8	1102	1142	B6	536	N962JT	EWR	LAX	296	2454	8	40	2023-08-17 08:00:00	LAX
15474	4	25	851	859	-8	1119	1102	9E	1188	N922XJ	LGA	MEM	146	963	8	59	2023-04-25 08:00:00	Other
15479	8	9	852	900	-8	1222	1228	AA	47	N102NN	JFK	SFO	357	2586	9	0	2023-08-09 09:00:00	Other
15480	7	31	922	930	-8	1209	1154	YX	935	N728YX	EWR	TVC	101	644	9	30	2023-07-31 09:00:00	Other
15483	6	23	2052	2100	-8	2204	2231	YX	1395	N821MD	LGA	BUF	46	292	21	0	2023-06-23 21:00:00	Other
15495	1	27	1207	1215	-8	1423	1450	UA	715	N14240	LGA	DEN	230	1620	12	15	2023-01-27 12:00:00	Other
15496	5	8	1347	1355	-8	1543	1550	YX	1226	N434YX	JFK	RDU	69	427	13	55	2023-05-08 13:00:00	Other
15499	11	19	1110	1120	-10	1258	1319	9E	1750	N491PX	LGA	CMH	77	479	11	20	2023-11-19 11:00:00	Other
15500	12	17	1253	1259	-6	1417	1410	9E	1356	N349PQ	JFK	ITH	39	189	12	59	2023-12-17 12:00:00	Other
15501	6	15	1249	1305	-16	1421	1442	UA	642	N14235	LGA	ORD	116	733	13	5	2023-06-15 13:00:00	ORD
15503	9	13	723	730	-7	845	906	DL	629	N317DU	LGA	ORD	113	733	7	30	2023-09-13 07:00:00	ORD
15504	3	5	854	904	-10	1107	1140	B6	971	N228JB	LGA	SAV	114	722	9	4	2023-03-05 09:00:00	Other
15506	5	9	1123	1130	-7	1421	1435	DL	447	N3763D	JFK	TPA	141	1005	11	30	2023-05-09 11:00:00	Other
15510	6	6	823	829	-6	945	954	YX	1152	N723YX	EWR	ROC	46	246	8	29	2023-06-06 08:00:00	Other
15511	10	25	1023	1030	-7	1317	1333	UA	628	N12125	EWR	LAX	315	2454	10	30	2023-10-25 10:00:00	LAX
15518	11	14	1610	1620	-10	1743	1751	YX	1071	N762YX	EWR	BUF	57	282	16	20	2023-11-14 16:00:00	Other
15531	6	13	1448	1455	-7	1655	1710	YX	1423	N102HQ	LGA	CVG	104	585	14	55	2023-06-13 14:00:00	Other
15533	9	1	2050	2058	-8	2217	2302	YX	1115	N757YX	EWR	GSO	65	445	20	58	2023-09-01 20:00:00	Other
15537	12	12	1550	1559	-9	1842	1848	YX	1221	N439YX	LGA	LIT	163	1085	15	59	2023-12-12 15:00:00	Other
15543	1	31	823	829	-6	1023	1014	UA	238	N826UA	EWR	BNA	136	748	8	29	2023-01-31 08:00:00	Other
15545	11	12	1513	1520	-7	1634	1647	9E	1488	N326PQ	LGA	PWM	51	269	15	20	2023-11-12 15:00:00	Other
15547	9	3	1815	1825	-10	2136	2052	UA	422	N29124	EWR	DEN	281	1605	18	25	2023-09-03 18:00:00	Other
15558	1	28	1443	1453	-10	1648	1705	YX	1228	N729YX	EWR	DTW	94	488	14	53	2023-01-28 14:00:00	Other
15561	9	28	653	700	-7	934	954	DL	189	N177DZ	JFK	LAX	307	2475	7	0	2023-09-28 07:00:00	LAX
15564	2	12	1823	1830	-7	2131	2146	NK	972	N601NK	LGA	FLL	149	1076	18	30	2023-02-12 18:00:00	FLL
15567	8	9	1224	1230	-6	1521	1525	DL	119	N106DU	LGA	DFW	203	1389	12	30	2023-08-09 12:00:00	Other
15577	4	12	1753	1800	-7	2009	2110	DL	338	N318NB	JFK	DFW	172	1391	18	0	2023-04-12 18:00:00	Other
15579	5	16	1121	1130	-9	1418	1457	AA	112	N108NN	JFK	LAX	329	2475	11	30	2023-05-16 11:00:00	LAX
15581	4	18	750	800	-10	1005	1021	9E	1374	N335PQ	LGA	IND	107	660	8	0	2023-04-18 08:00:00	Other
15584	10	22	620	630	-10	843	852	B6	231	N579JB	JFK	JAX	116	828	6	30	2023-10-22 06:00:00	Other
15593	11	14	723	730	-7	928	915	UA	943	N38459	EWR	RDU	74	416	7	30	2023-11-14 07:00:00	Other
15594	12	11	1309	1315	-6	1624	1638	DL	123	N123DQ	LGA	DFW	203	1389	13	15	2023-12-11 13:00:00	Other
15595	2	27	936	945	-9	1051	1116	YX	1153	N855RW	EWR	PWM	53	284	9	45	2023-02-27 09:00:00	Other
15597	11	16	847	900	-13	1210	1210	AS	85	N947AK	EWR	LAX	321	2454	9	0	2023-11-16 09:00:00	LAX
15607	4	10	638	644	-6	823	854	YX	1134	N129HQ	LGA	DTW	80	502	6	44	2023-04-10 06:00:00	Other
15608	4	25	618	630	-12	804	818	AA	898	N981NN	LGA	ORD	120	733	6	30	2023-04-25 06:00:00	ORD
15610	11	29	1241	1251	-10	1528	1555	YX	1229	N410YX	LGA	OKC	210	1341	12	51	2023-11-29 12:00:00	Other
15611	9	19	2212	2227	-15	2324	2344	YX	1067	N762YX	EWR	MHT	40	209	22	27	2023-09-19 22:00:00	Other
15623	12	9	1356	1402	-6	1537	1545	UA	764	N39726	EWR	STL	138	872	14	2	2023-12-09 14:00:00	Other
15631	10	29	923	930	-7	1110	1131	YX	1258	N421YX	JFK	CLE	86	425	9	30	2023-10-29 09:00:00	Other
15636	1	20	518	530	-12	805	836	B6	250	N834JB	EWR	TPA	145	997	5	30	2023-01-20 05:00:00	Other
15651	2	1	1525	1534	-9	1648	1714	YX	1592	N216JQ	JFK	DCA	61	213	15	34	2023-02-01 15:00:00	Other
15656	12	12	921	930	-9	1037	1044	YX	1067	N760YX	EWR	PVD	35	160	9	30	2023-12-12 09:00:00	Other
15657	1	16	2045	2052	-7	2335	2359	UA	628	N17272	EWR	PBI	133	1023	20	52	2023-01-16 20:00:00	Other
15658	5	31	1652	1659	-7	1905	1922	UA	520	N481UA	EWR	ATL	105	746	16	59	2023-05-31 16:00:00	ATL
15659	6	16	933	941	-8	1217	1232	AA	243	N964NN	EWR	DFW	200	1372	9	41	2023-06-16 09:00:00	Other
15666	2	4	1253	1300	-7	1445	1447	YX	1012	N753YX	EWR	GSO	70	445	13	0	2023-02-04 13:00:00	Other
15671	9	14	1259	1307	-8	1436	1454	YX	1219	N748YX	EWR	RDU	75	416	13	7	2023-09-14 13:00:00	Other
15676	10	17	709	715	-6	932	1020	UA	147	N78511	EWR	SNA	302	2434	7	15	2023-10-17 07:00:00	Other
15678	6	8	651	659	-8	806	830	YX	1361	N422YX	LGA	PIT	56	335	6	59	2023-06-08 06:00:00	Other
15679	1	28	1751	1800	-9	2114	2121	UA	983	N67134	EWR	LAX	361	2454	18	0	2023-01-28 18:00:00	LAX
15683	1	21	1751	1759	-8	2057	2116	AA	137	N803NN	JFK	MIA	159	1089	17	59	2023-01-21 17:00:00	MIA
15694	11	30	553	600	-7	837	857	B6	90	N636JB	LGA	MCO	132	950	6	0	2023-11-30 06:00:00	MCO
15698	2	5	1921	1929	-8	2054	2116	YX	1591	N237JQ	LGA	PIT	63	335	19	29	2023-02-05 19:00:00	Other
15700	6	2	707	715	-8	958	1025	DL	329	N329NB	LGA	RSW	147	1080	7	15	2023-06-02 07:00:00	Other
15702	1	30	956	1006	-10	1128	1151	UA	784	N804UA	LGA	ORD	122	733	10	6	2023-01-30 10:00:00	ORD
15705	8	24	1020	1027	-7	1140	1211	9E	1123	N919XJ	LGA	RIC	53	292	10	27	2023-08-24 10:00:00	Other
15710	3	17	1452	1459	-7	1636	1706	DL	527	N301NB	LGA	DTW	84	502	14	59	2023-03-17 14:00:00	Other
15713	3	16	2149	2156	-7	2345	2358	UA	752	N69847	EWR	DTW	81	488	21	56	2023-03-16 21:00:00	Other
15714	2	7	1303	1310	-7	1606	1625	UA	190	N881UA	EWR	AUS	219	1504	13	10	2023-02-07 13:00:00	Other
15721	3	4	850	900	-10	1309	1250	AS	17	N462AS	JFK	SFO	395	2586	9	0	2023-03-04 09:00:00	Other
15724	9	15	2011	2017	-6	12	23	NK	355	N611NK	EWR	SJU	216	1608	20	17	2023-09-15 20:00:00	Other
15728	12	15	952	1000	-8	1119	1127	YX	1022	N766YX	EWR	BTV	52	266	10	0	2023-12-15 10:00:00	Other
15733	9	28	1553	1559	-6	1837	1904	AA	362	N977NN	LGA	DFW	186	1389	15	59	2023-09-28 15:00:00	Other
15736	3	20	1857	1905	-8	2100	2124	9E	1569	N313PQ	LGA	CHS	100	641	19	5	2023-03-20 19:00:00	Other
15741	12	27	820	832	-12	1153	1150	DL	542	N395DN	LGA	RSW	185	1080	8	32	2023-12-27 08:00:00	Other
15743	7	25	1125	1132	-7	1321	1339	AA	616	N947NN	LGA	CLT	90	544	11	32	2023-07-25 11:00:00	CLT
15748	1	29	1354	1400	-6	1508	1530	YX	1321	N102HQ	LGA	DCA	53	214	14	0	2023-01-29 14:00:00	Other
15749	8	28	1248	1255	-7	1411	1430	WN	279	N426WN	LGA	STL	129	888	12	55	2023-08-28 12:00:00	Other
15750	12	9	647	653	-6	933	955	B6	432	N506JB	LGA	TPA	145	1010	6	53	2023-12-09 06:00:00	Other
15758	8	20	906	915	-9	1157	1237	AA	652	N816NN	LGA	MIA	152	1096	9	15	2023-08-20 09:00:00	MIA
15759	7	10	1352	1359	-7	1539	1536	9E	1282	N937XJ	LGA	BHM	128	866	13	59	2023-07-10 13:00:00	Other
15760	12	26	749	800	-11	917	953	YX	1290	N405YX	LGA	CLE	66	419	8	0	2023-12-26 08:00:00	Other
15761	3	5	724	730	-6	950	1012	UA	513	N821UA	LGA	DEN	248	1620	7	30	2023-03-05 07:00:00	Other
15767	1	27	2110	2119	-9	2244	2304	YX	1313	N108HQ	LGA	RIC	57	292	21	19	2023-01-27 21:00:00	Other
15777	9	28	2149	2155	-6	2305	2325	B6	33	N266JB	JFK	BUF	52	301	21	55	2023-09-28 21:00:00	Other
15782	5	17	915	921	-6	1131	1210	B6	480	N593JB	JFK	LAS	286	2248	9	21	2023-05-17 09:00:00	Other
15788	3	14	1833	1840	-7	1959	2017	AA	973	N863NN	LGA	ORD	108	733	18	40	2023-03-14 18:00:00	ORD
15796	3	29	1301	1310	-9	1525	1541	NK	37	N692NK	EWR	ATL	118	746	13	10	2023-03-29 13:00:00	ATL
15806	9	20	1908	1915	-7	2026	2051	UA	750	N489UA	LGA	ORD	108	733	19	15	2023-09-20 19:00:00	ORD
15813	8	28	2004	2010	-6	2144	2207	9E	1286	N279PQ	LGA	MYR	80	563	20	10	2023-08-28 20:00:00	Other
15817	10	3	1551	1559	-8	1651	1723	YX	1250	N442YX	JFK	BOS	38	187	15	59	2023-10-03 15:00:00	BOS
15823	10	24	1850	1900	-10	2048	2124	YX	1270	N412YX	LGA	IND	98	660	19	0	2023-10-24 19:00:00	Other
15831	4	25	707	715	-8	814	827	B6	884	N307JB	LGA	BOS	32	184	7	15	2023-04-25 07:00:00	BOS
15841	11	13	1151	1200	-9	1330	1346	AA	722	N774XF	LGA	RDU	71	431	12	0	2023-11-13 12:00:00	Other
15853	11	1	1334	1345	-11	1501	1518	9E	1740	N928XJ	JFK	BGR	56	382	13	45	2023-11-01 13:00:00	Other
15854	2	28	1130	1138	-8	1334	1345	DL	299	N110DU	EWR	MSP	153	1008	11	38	2023-02-28 11:00:00	Other
15858	11	23	1005	1014	-9	1244	1320	B6	633	N991JT	EWR	LAX	319	2454	10	14	2023-11-23 10:00:00	LAX
15863	12	8	1318	1325	-7	1442	1502	9E	1350	N349PQ	JFK	ORF	48	290	13	25	2023-12-08 13:00:00	Other
15873	11	24	1933	1944	-11	2129	2147	AA	637	N954AN	EWR	CLT	88	529	19	44	2023-11-24 19:00:00	CLT
15874	1	26	1339	1347	-8	1439	1447	YX	1139	N861RW	EWR	PHL	33	80	13	47	2023-01-26 13:00:00	Other
15875	10	13	1914	1920	-6	2202	2231	DL	836	N509DT	JFK	MCO	133	944	19	20	2023-10-13 19:00:00	MCO
15878	8	19	1749	1755	-6	1933	2000	NK	44	N693NK	LGA	DTW	76	502	17	55	2023-08-19 17:00:00	Other
15887	5	8	619	629	-10	740	807	YX	1285	N867RW	LGA	PIT	59	335	6	29	2023-05-08 06:00:00	Other
15891	10	5	2153	2159	-6	2247	2303	9E	1586	N905XJ	LGA	PVD	37	143	21	59	2023-10-05 21:00:00	Other
15893	3	6	843	849	-6	1043	1045	YX	1364	N450YX	LGA	ILM	77	500	8	49	2023-03-06 08:00:00	Other
15894	11	27	1838	1844	-6	2030	2047	9E	1445	N917XJ	LGA	GSO	81	461	18	44	2023-11-27 18:00:00	Other
15900	10	24	1445	1459	-14	1607	1632	9E	1612	N482PX	LGA	ORF	51	296	14	59	2023-10-24 14:00:00	Other
15901	1	23	1145	1151	-6	1322	1359	YX	1175	N727YX	EWR	MEM	141	946	11	51	2023-01-23 11:00:00	Other
15904	5	9	1231	1240	-9	1541	1602	AA	644	N324RN	JFK	MIA	166	1089	12	40	2023-05-09 12:00:00	MIA
15911	5	13	1853	1900	-7	2124	2212	B6	124	N965JT	JFK	ONT	310	2429	19	0	2023-05-13 19:00:00	Other
15912	3	29	1539	1548	-9	1653	1724	YX	1252	N138HQ	LGA	RIC	57	292	15	48	2023-03-29 15:00:00	Other
15913	6	19	1830	1837	-7	2010	2045	DL	1010	N301DU	EWR	MSP	140	1008	18	37	2023-06-19 18:00:00	Other
15915	12	5	1303	1310	-7	1431	1445	YX	1326	N419YX	LGA	RIC	59	292	13	10	2023-12-05 13:00:00	Other
15917	5	8	553	600	-7	749	801	AA	231	N189UW	LGA	CLT	89	544	6	0	2023-05-08 06:00:00	CLT
15922	4	12	1149	1159	-10	1338	1423	UA	355	N37434	EWR	DEN	208	1605	11	59	2023-04-12 11:00:00	Other
15924	9	3	1022	1030	-8	1307	1334	DL	648	N140DU	JFK	SAT	202	1587	10	30	2023-09-03 10:00:00	Other
15926	8	27	1258	1306	-8	1532	1545	YX	965	N126HQ	LGA	OKC	193	1341	13	6	2023-08-27 13:00:00	Other
15927	12	27	722	730	-8	1019	1053	B6	273	N964JT	JFK	LAX	314	2475	7	30	2023-12-27 07:00:00	LAX
15929	12	13	722	730	-8	1008	1030	UA	753	N57299	EWR	PBI	144	1023	7	30	2023-12-13 07:00:00	Other
15932	4	21	1551	1559	-8	1747	1814	9E	1327	N147PQ	LGA	CLT	81	544	15	59	2023-04-21 15:00:00	CLT
15938	10	25	1220	1229	-9	1414	1443	9E	1409	N349PQ	LGA	CLT	83	544	12	29	2023-10-25 12:00:00	CLT
15939	11	14	839	849	-10	1047	1112	YX	1285	N438YX	LGA	CVG	94	585	8	49	2023-11-14 08:00:00	Other
15940	11	17	557	604	-7	759	817	9E	1589	N337PQ	LGA	CLT	89	544	6	4	2023-11-17 06:00:00	CLT
15941	8	26	553	600	-7	816	838	UA	720	N465UA	LGA	IAH	175	1416	6	0	2023-08-26 06:00:00	Other
15942	2	16	653	659	-6	847	905	UA	518	N894UA	EWR	CLT	88	529	6	59	2023-02-16 06:00:00	CLT
15952	9	29	807	815	-8	1011	1025	9E	1573	N183GJ	LGA	GRR	89	618	8	15	2023-09-29 08:00:00	Other
15954	1	12	1748	1759	-11	2039	2023	YX	1335	N102HQ	LGA	CMH	85	479	17	59	2023-01-12 17:00:00	Other
15956	3	9	1123	1133	-10	1244	1309	UA	383	N73256	EWR	ORD	121	719	11	33	2023-03-09 11:00:00	ORD
15962	5	18	1545	1555	-10	1735	1759	YX	1223	N433YX	LGA	DTW	80	502	15	55	2023-05-18 15:00:00	Other
15965	10	31	2118	2125	-7	2251	2303	YX	1772	N217JQ	LGA	PIT	69	335	21	25	2023-10-31 21:00:00	Other
15973	5	2	1123	1130	-7	1414	1445	AA	812	N806NN	LGA	MIA	149	1096	11	30	2023-05-02 11:00:00	MIA
15978	1	28	823	829	-6	949	1019	B6	450	N238JB	JFK	BNA	124	765	8	29	2023-01-28 08:00:00	Other
15992	6	8	735	744	-9	924	956	9E	1746	N601LR	JFK	CLT	88	541	7	44	2023-06-08 07:00:00	CLT
15993	5	10	1106	1115	-9	1258	1319	YX	1217	N867RW	LGA	AVL	92	599	11	15	2023-05-10 11:00:00	Other
15996	10	13	2208	2215	-7	2326	2331	YX	1331	N446YX	JFK	BOS	43	187	22	15	2023-10-13 22:00:00	BOS
16000	11	4	556	605	-9	817	830	WN	785	N202WN	LGA	DEN	227	1620	6	5	2023-11-04 06:00:00	Other
16008	9	12	724	730	-6	913	932	UA	461	N26226	EWR	CLT	81	529	7	30	2023-09-12 07:00:00	CLT
16012	3	29	1940	1950	-10	2151	2218	9E	1368	N601LR	LGA	MCI	168	1107	19	50	2023-03-29 19:00:00	Other
16016	2	11	1301	1310	-9	1439	1455	B6	38	N323JB	JFK	ORD	127	740	13	10	2023-02-11 13:00:00	ORD
16017	7	3	1119	1125	-6	1342	1335	YX	1025	N118HQ	LGA	AVL	100	599	11	25	2023-07-03 11:00:00	Other
16021	7	16	1422	1428	-6	1646	1620	B6	236	N273JB	JFK	RDU	68	427	14	28	2023-07-16 14:00:00	Other
16023	5	6	1237	1245	-8	1459	1542	NK	81	N635NK	EWR	DFW	182	1372	12	45	2023-05-06 12:00:00	Other
16028	8	29	1041	1057	-16	1317	1330	F9	318	N343FR	LGA	ATL	120	762	10	57	2023-08-29 10:00:00	ATL
16033	9	19	1314	1322	-8	1420	1438	YX	1090	N724YX	EWR	SYR	40	195	13	22	2023-09-19 13:00:00	Other
16037	5	19	2122	2130	-8	2304	2335	YX	1188	N116HQ	JFK	RDU	70	427	21	30	2023-05-19 21:00:00	Other
16046	2	27	550	600	-10	700	724	AA	445	N802AW	LGA	DCA	43	214	6	0	2023-02-27 06:00:00	Other
16047	2	13	944	950	-6	1121	1135	YX	976	N742YX	EWR	MKE	111	725	9	50	2023-02-13 09:00:00	Other
16050	11	12	2151	2159	-8	2247	2315	UA	171	N66897	EWR	BOS	35	200	21	59	2023-11-12 21:00:00	BOS
16055	10	10	817	830	-13	941	1008	YX	1149	N764YX	EWR	MKE	111	725	8	30	2023-10-10 08:00:00	Other
16060	12	16	1223	1229	-6	1440	1456	YX	1279	N137HQ	JFK	IND	103	665	12	29	2023-12-16 12:00:00	Other
16065	10	2	2121	2130	-9	2311	2335	YX	1767	N217JQ	JFK	CMH	66	483	21	30	2023-10-02 21:00:00	Other
16071	7	5	1746	1753	-7	2119	2131	DL	228	N113DX	JFK	SLC	286	1990	17	53	2023-07-05 17:00:00	Other
16076	8	23	529	538	-9	909	931	B6	476	N994JL	JFK	SJU	195	1598	5	38	2023-08-23 05:00:00	Other
16080	3	12	1102	1108	-6	1407	1431	DL	636	N377DN	LGA	MIA	149	1096	11	8	2023-03-12 11:00:00	MIA
16082	6	21	1619	1627	-8	1834	1852	YX	1187	N861RW	EWR	SDF	93	642	16	27	2023-06-21 16:00:00	Other
16091	11	19	1320	1329	-9	1521	1557	DL	251	N3763D	LGA	DEN	218	1620	13	29	2023-11-19 13:00:00	Other
16092	7	13	841	849	-8	1043	1110	9E	1252	N337PQ	LGA	TYS	95	647	8	49	2023-07-13 08:00:00	Other
16096	11	19	654	700	-6	939	1006	B6	1009	N506JB	EWR	TPA	138	997	7	0	2023-11-19 07:00:00	Other
16100	10	2	910	917	-7	1037	1050	9E	1415	N917XJ	LGA	PWM	50	269	9	17	2023-10-02 09:00:00	Other
16104	7	4	1719	1725	-6	2043	2007	B6	706	N656JB	LGA	JAX	137	833	17	25	2023-07-04 17:00:00	Other
16109	5	3	1339	1345	-6	1459	1510	YX	1072	N729YX	EWR	PIT	56	319	13	45	2023-05-03 13:00:00	Other
16114	3	20	2039	2045	-6	2223	2257	YX	1241	N438YX	JFK	CMH	80	483	20	45	2023-03-20 20:00:00	Other
16119	9	19	1255	1302	-7	1556	1605	B6	684	N789JB	EWR	RSW	158	1068	13	2	2023-09-19 13:00:00	Other
16121	1	15	1650	1659	-9	1814	1827	9E	1502	N914XJ	LGA	PWM	49	269	16	59	2023-01-15 16:00:00	Other
16132	2	28	2120	2129	-9	2312	2321	YX	1281	N129HQ	JFK	RDU	80	427	21	29	2023-02-28 21:00:00	Other
16133	11	25	921	930	-9	1041	1116	AA	748	N760US	LGA	ORD	112	733	9	30	2023-11-25 09:00:00	ORD
16137	2	28	1353	1400	-7	1533	1555	YX	1113	N728YX	EWR	ILM	75	488	14	0	2023-02-28 14:00:00	Other
16138	7	28	836	845	-9	1111	1027	DL	312	N115DU	LGA	ORD	107	733	8	45	2023-07-28 08:00:00	ORD
16139	9	13	2221	2230	-9	2325	2347	YX	1067	N742YX	EWR	MHT	35	209	22	30	2023-09-13 22:00:00	Other
16141	5	25	1927	1934	-7	2051	2113	9E	1286	N924XJ	LGA	MKE	106	738	19	34	2023-05-25 19:00:00	Other
16144	5	14	1003	1009	-6	1220	1241	UA	257	N25705	EWR	JAX	109	820	10	9	2023-05-14 10:00:00	Other
16145	11	11	1748	1800	-12	2029	2109	UA	657	N17105	EWR	SAN	324	2425	18	0	2023-11-11 18:00:00	Other
16148	2	13	2143	2150	-7	2252	2310	YX	1541	N216JQ	LGA	BTV	45	258	21	50	2023-02-13 21:00:00	Other
16151	8	23	1738	1745	-7	2018	2050	B6	590	N3065J	JFK	MCO	120	944	17	45	2023-08-23 17:00:00	MCO
16157	9	20	1420	1428	-8	1554	1548	UA	821	N21723	EWR	MKE	105	725	14	28	2023-09-20 14:00:00	Other
16158	4	11	736	744	-8	911	1009	UA	758	N62895	EWR	DEN	195	1605	7	44	2023-04-11 07:00:00	Other
16161	10	25	1704	1715	-11	1845	1915	DL	690	N341NW	LGA	DTW	80	502	17	15	2023-10-25 17:00:00	Other
16162	8	31	1753	1759	-6	2033	2050	UA	328	N27733	EWR	JAC	250	1874	17	59	2023-08-31 17:00:00	Other
16167	10	27	1823	1830	-7	2114	2137	UA	638	N14019	EWR	SFO	325	2565	18	30	2023-10-27 18:00:00	Other
16168	1	20	1921	1929	-8	2029	2109	YX	1469	N121HQ	JFK	DCA	45	213	19	29	2023-01-20 19:00:00	Other
16171	1	9	1353	1359	-6	1550	1551	9E	1691	N485PX	LGA	RDU	70	431	13	59	2023-01-09 13:00:00	Other
16173	8	4	950	957	-7	1251	1249	UA	387	N27734	EWR	AUS	201	1504	9	57	2023-08-04 09:00:00	Other
16180	3	9	1619	1629	-10	1744	1752	YX	1112	N864RW	EWR	DCA	43	199	16	29	2023-03-09 16:00:00	Other
16183	5	2	1051	1059	-8	1235	1236	UA	566	N39728	EWR	RDU	68	416	10	59	2023-05-02 10:00:00	Other
16187	8	22	2217	2229	-12	2331	2356	YX	922	N749YX	EWR	PWM	51	284	22	29	2023-08-22 22:00:00	Other
16194	6	18	850	900	-10	1215	1237	AA	55	N110AN	JFK	SFO	354	2586	9	0	2023-06-18 09:00:00	Other
16198	6	1	620	635	-15	740	810	9E	1379	N931XJ	LGA	PIT	56	335	6	35	2023-06-01 06:00:00	Other
16205	6	10	1318	1325	-7	1421	1437	YX	1833	N238JQ	EWR	BOS	40	200	13	25	2023-06-10 13:00:00	BOS
16208	10	20	921	929	-8	1119	1121	YX	1258	N437YX	JFK	CLE	73	425	9	29	2023-10-20 09:00:00	Other
16209	2	8	1048	1100	-12	1253	1327	YX	1190	N431YX	LGA	AVL	98	599	11	0	2023-02-08 11:00:00	Other
16213	12	6	1718	1727	-9	1829	1849	UA	128	N436UA	EWR	IAD	47	212	17	27	2023-12-06 17:00:00	Other
16214	9	16	1738	1745	-7	2006	2025	UA	849	N27271	EWR	LAS	298	2227	17	45	2023-09-16 17:00:00	Other
16217	11	2	745	755	-10	1008	1004	YX	1312	N117HQ	LGA	GRR	102	618	7	55	2023-11-02 07:00:00	Other
16224	6	15	1205	1212	-7	1347	1405	YX	1393	N432YX	LGA	MEM	140	963	12	12	2023-06-15 12:00:00	Other
16236	11	20	2102	2117	-15	2227	2259	UA	638	N37434	EWR	CLE	66	404	21	17	2023-11-20 21:00:00	Other
16241	1	14	1754	1800	-6	2059	2121	UA	983	N14118	EWR	LAX	341	2454	18	0	2023-01-14 18:00:00	LAX
16248	7	12	1953	2000	-7	2129	2138	B6	756	N304JB	JFK	BUF	57	301	20	0	2023-07-12 20:00:00	Other
16254	3	4	1924	1930	-6	2300	2315	AA	93	N112AN	JFK	LAX	363	2475	19	30	2023-03-04 19:00:00	LAX
16258	10	9	1409	1415	-6	1511	1533	B6	286	N318JB	LGA	BOS	39	184	14	15	2023-10-09 14:00:00	BOS
16264	5	26	1220	1229	-9	1330	1341	B6	834	N355JB	LGA	ACK	36	202	12	29	2023-05-26 12:00:00	Other
16266	1	7	657	705	-8	939	1014	B6	187	N564JB	LGA	PBI	136	1035	7	5	2023-01-07 07:00:00	Other
16267	1	18	821	827	-6	1040	1115	YX	1133	N722YX	EWR	SDF	114	642	8	27	2023-01-18 08:00:00	Other
16268	2	9	2045	2055	-10	2226	2249	9E	1453	N478PX	LGA	RDU	74	431	20	55	2023-02-09 20:00:00	Other
16273	6	12	1415	1425	-10	1536	1559	B6	1033	N236JB	JFK	BUF	56	301	14	25	2023-06-12 14:00:00	Other
16274	8	4	652	700	-8	920	942	UA	257	N38417	EWR	MCO	131	937	7	0	2023-08-04 07:00:00	MCO
16277	10	29	748	800	-12	1042	1112	UA	879	N37305	EWR	IAH	207	1400	8	0	2023-10-29 08:00:00	Other
16280	12	17	1552	1559	-7	1741	1723	YX	1145	N766YX	EWR	DCA	46	199	15	59	2023-12-17 15:00:00	Other
16282	10	14	1509	1515	-6	1631	1650	UA	573	N830UA	LGA	ORD	113	733	15	15	2023-10-14 15:00:00	ORD
16285	9	6	1249	1259	-10	1352	1422	YX	1893	N241JQ	LGA	BOS	34	184	12	59	2023-09-06 12:00:00	BOS
16288	7	29	1116	1123	-7	1306	1301	YX	873	N721YX	EWR	CLE	64	404	11	23	2023-07-29 11:00:00	Other
16298	3	12	1450	1500	-10	1625	1635	YX	1261	N121HQ	LGA	DCA	49	214	15	0	2023-03-12 15:00:00	Other
16319	5	3	618	625	-7	908	923	UA	210	N68805	EWR	SAN	323	2425	6	25	2023-05-03 06:00:00	Other
16321	9	20	2136	2142	-6	2235	2253	YX	1183	N727YX	EWR	MDT	30	141	21	42	2023-09-20 21:00:00	Other
16324	7	11	912	920	-8	1031	1053	AA	589	N772XF	LGA	PIT	62	335	9	20	2023-07-11 09:00:00	Other
16331	4	9	1052	1100	-8	1217	1228	YX	1100	N117HQ	LGA	DCA	43	214	11	0	2023-04-09 11:00:00	Other
16340	12	12	623	630	-7	926	944	AA	620	N308TB	JFK	MIA	163	1089	6	30	2023-12-12 06:00:00	MIA
16341	5	3	1254	1300	-6	1626	1611	AA	224	N401AN	LGA	MIA	161	1096	13	0	2023-05-03 13:00:00	MIA
16342	8	14	2241	2250	-9	16	36	9E	1232	N181PQ	JFK	ROC	47	264	22	50	2023-08-14 22:00:00	Other
16343	9	21	1258	1304	-6	1354	1415	YX	1045	N755YX	EWR	MDT	29	141	13	4	2023-09-21 13:00:00	Other
16344	12	13	654	700	-6	1009	1018	DL	769	N387DA	JFK	FLL	166	1069	7	0	2023-12-13 07:00:00	FLL
16345	7	6	825	831	-6	1010	1044	9E	1170	N491PX	LGA	GSP	84	610	8	31	2023-07-06 08:00:00	Other
16346	6	7	934	940	-6	1218	1245	B6	998	N635JB	JFK	TPA	139	1005	9	40	2023-06-07 09:00:00	Other
16348	4	11	2152	2159	-7	2258	2316	YX	1561	N217JQ	LGA	PWM	50	269	21	59	2023-04-11 21:00:00	Other
16352	10	12	953	959	-6	1219	1244	DL	136	N358DN	LGA	ATL	117	762	9	59	2023-10-12 09:00:00	ATL
16353	5	8	800	810	-10	1049	1128	AA	601	N836NN	JFK	MIA	141	1089	8	10	2023-05-08 08:00:00	MIA
16354	8	13	1143	1150	-7	1312	1336	9E	1129	N903XJ	LGA	PIT	60	335	11	50	2023-08-13 11:00:00	Other
16356	1	16	2110	2120	-10	2323	2346	9E	1414	N309PQ	JFK	SAV	106	718	21	20	2023-01-16 21:00:00	Other
16359	9	26	845	855	-10	1023	1033	9E	1722	N305PQ	LGA	CHO	58	305	8	55	2023-09-26 08:00:00	Other
16360	11	15	906	915	-9	1037	1113	B6	374	N274JB	JFK	ORD	123	740	9	15	2023-11-15 09:00:00	ORD
16361	12	7	1309	1316	-7	1501	1506	DL	973	N961AT	EWR	DTW	87	488	13	16	2023-12-07 13:00:00	Other
16369	10	10	1200	1211	-11	1333	1345	YX	1795	N226JQ	JFK	BUF	64	301	12	11	2023-10-10 12:00:00	Other
16371	2	19	756	804	-8	1114	1121	B6	698	N633JB	JFK	IAH	224	1417	8	4	2023-02-19 08:00:00	Other
16377	8	27	1249	1300	-11	1449	1506	YX	923	N640RW	EWR	CVG	90	569	13	0	2023-08-27 13:00:00	Other
16378	9	7	550	600	-10	846	902	B6	497	N508JL	LGA	FLL	139	1076	6	0	2023-09-07 06:00:00	FLL
16382	12	13	823	830	-7	952	1015	9E	1421	N915XJ	LGA	MKE	124	738	8	30	2023-12-13 08:00:00	Other
16401	10	5	808	819	-11	1107	1109	DL	234	N123DQ	LGA	DFW	202	1389	8	19	2023-10-05 08:00:00	Other
16408	2	11	1551	1600	-9	1720	1749	DL	378	N145DQ	LGA	ORD	122	733	16	0	2023-02-11 16:00:00	ORD
16414	9	27	1428	1434	-6	1537	1556	B6	931	N266JB	JFK	BUF	51	301	14	34	2023-09-27 14:00:00	Other
16416	1	9	944	955	-11	1109	1128	9E	1654	N187GJ	LGA	ROC	50	254	9	55	2023-01-09 09:00:00	Other
16417	2	6	952	1000	-8	1415	1359	YX	1245	N869RW	LGA	EYW	171	1207	10	0	2023-02-06 10:00:00	Other
16419	2	8	752	800	-8	1022	1058	UA	395	N12114	EWR	EGE	248	1725	8	0	2023-02-08 08:00:00	Other
16424	10	12	1047	1057	-10	1346	1335	F9	521	N331FR	LGA	ATL	120	762	10	57	2023-10-12 10:00:00	ATL
16428	12	3	940	950	-10	1214	1213	9E	1498	N908XJ	LGA	CVG	122	585	9	50	2023-12-03 09:00:00	Other
16434	1	24	648	659	-11	900	943	B6	871	N806JB	LGA	DEN	228	1620	6	59	2023-01-24 06:00:00	Other
16436	10	18	559	610	-11	745	811	UA	558	N36469	EWR	MSP	144	1008	6	10	2023-10-18 06:00:00	Other
16438	11	29	1908	1916	-8	2224	2257	UA	289	N27263	EWR	PHX	292	2133	19	16	2023-11-29 19:00:00	Other
16439	7	18	950	1000	-10	1240	1317	AA	70	N116AN	JFK	LAX	317	2475	10	0	2023-07-18 10:00:00	LAX
16441	10	6	822	829	-7	1007	1000	YX	1748	N223JQ	LGA	DCA	48	214	8	29	2023-10-06 08:00:00	Other
16442	11	25	1419	1429	-10	1709	1745	B6	846	N504JB	LGA	SRQ	150	1047	14	29	2023-11-25 14:00:00	Other
16444	8	23	622	630	-8	901	922	B6	42	N625JB	JFK	SRQ	134	1041	6	30	2023-08-23 06:00:00	Other
16446	7	8	1426	1435	-9	1604	1609	YX	920	N647RW	EWR	IAD	52	212	14	35	2023-07-08 14:00:00	Other
16449	10	20	1053	1059	-6	1322	1343	UA	78	N27276	EWR	DFW	177	1372	10	59	2023-10-20 10:00:00	Other
16451	9	24	1018	1025	-7	1206	1220	NK	21	N673NK	EWR	MYR	85	550	10	25	2023-09-24 10:00:00	Other
16453	11	7	2044	2100	-16	2338	2359	B6	179	N534JB	LGA	MCO	125	950	21	0	2023-11-07 21:00:00	MCO
16460	3	28	814	825	-11	1006	1024	9E	1523	N676CA	LGA	ILM	85	500	8	25	2023-03-28 08:00:00	Other
16463	11	15	1153	1200	-7	1245	1304	YX	1297	N427YX	JFK	ORH	32	150	12	0	2023-11-15 12:00:00	Other
16464	2	2	948	955	-7	1136	1145	B6	744	N229JB	LGA	BNA	141	764	9	55	2023-02-02 09:00:00	Other
16467	12	27	707	715	-8	1017	1037	UA	53	N823UA	EWR	AUS	225	1504	7	15	2023-12-27 07:00:00	Other
16471	8	26	853	900	-7	1041	1036	OO	959	N240SY	JFK	BNA	113	765	9	0	2023-08-26 09:00:00	Other
16472	8	30	554	600	-6	848	859	AA	1	N115NN	JFK	LAX	311	2475	6	0	2023-08-30 06:00:00	LAX
16474	1	30	1648	1656	-8	1907	1927	YX	1219	N979RP	EWR	SAV	119	708	16	56	2023-01-30 16:00:00	Other
16490	10	11	1421	1430	-9	1552	1552	YX	1086	N736YX	EWR	PWM	47	284	14	30	2023-10-11 14:00:00	Other
16493	12	17	1444	1450	-6	1607	1629	9E	1403	N183GJ	LGA	RIC	54	292	14	50	2023-12-17 14:00:00	Other
16499	9	19	845	856	-11	1043	1119	9E	1621	N293PQ	LGA	TYS	96	647	8	56	2023-09-19 08:00:00	Other
16511	11	29	951	959	-8	1204	1245	DL	150	N118DY	LGA	ATL	108	762	9	59	2023-11-29 09:00:00	ATL
16512	1	23	922	930	-8	1201	1210	UA	949	N14219	LGA	DEN	227	1620	9	30	2023-01-23 09:00:00	Other
16514	5	23	640	653	-13	839	910	YX	1071	N863RW	EWR	IND	94	645	6	53	2023-05-23 06:00:00	Other
16517	8	4	920	930	-10	1148	1147	YX	924	N754YX	EWR	HHH	99	687	9	30	2023-08-04 09:00:00	Other
16518	6	13	2149	2159	-10	2325	2337	YX	1068	N646RW	EWR	BGR	55	393	21	59	2023-06-13 21:00:00	Other
16519	12	22	1341	1347	-6	1514	1530	MQ	1001	N637RW	EWR	ORD	119	719	13	47	2023-12-22 13:00:00	ORD
16521	11	6	2008	2024	-16	2139	2201	9E	1618	N301PQ	LGA	CHO	53	305	20	24	2023-11-06 20:00:00	Other
16529	11	5	2048	2055	-7	2216	2257	9E	1555	N902XJ	LGA	ILM	68	500	20	55	2023-11-05 20:00:00	Other
16530	5	13	1032	1040	-8	1248	1317	YX	1604	N240JQ	LGA	OMA	167	1148	10	40	2023-05-13 10:00:00	Other
16531	1	27	2051	2100	-9	2247	2309	YX	1413	N411YX	LGA	GSO	81	461	21	0	2023-01-27 21:00:00	Other
16546	10	22	602	610	-8	749	811	UA	558	N27266	EWR	MSP	144	1008	6	10	2023-10-22 06:00:00	Other
16551	1	21	953	1000	-7	1255	1348	DL	318	N176DN	JFK	SFO	328	2586	10	0	2023-01-21 10:00:00	Other
16563	2	20	1658	1707	-9	1839	1917	AA	423	N772XF	LGA	STL	144	888	17	7	2023-02-20 17:00:00	Other
16567	2	22	1242	1250	-8	1347	1416	9E	1309	N918XJ	LGA	BTV	44	258	12	50	2023-02-22 12:00:00	Other
16575	12	1	2133	2140	-7	2321	2336	YX	1218	N115HQ	JFK	RDU	74	427	21	40	2023-12-01 21:00:00	Other
16580	2	1	2218	2230	-12	2337	2359	9E	1353	N936XJ	JFK	BGR	58	382	22	30	2023-02-01 22:00:00	Other
16586	11	17	640	649	-9	835	851	YX	1296	N136HQ	LGA	MSP	159	1020	6	49	2023-11-17 06:00:00	Other
16587	2	4	1808	1814	-6	2018	2040	YX	1049	N732YX	EWR	IND	101	645	18	14	2023-02-04 18:00:00	Other
16592	8	27	621	630	-9	901	918	UA	348	N488UA	EWR	SRQ	142	1034	6	30	2023-08-27 06:00:00	Other
16594	5	31	1128	1135	-7	1236	1259	YX	1678	N880RW	LGA	SYR	38	198	11	35	2023-05-31 11:00:00	Other
16595	2	6	728	738	-10	833	903	UA	613	N414UA	EWR	ORF	48	284	7	38	2023-02-06 07:00:00	Other
16597	12	17	1820	1829	-9	2014	2036	9E	1492	N923XJ	LGA	STL	132	888	18	29	2023-12-17 18:00:00	Other
16598	4	24	2141	2155	-14	28	40	B6	728	N655JB	JFK	MCO	145	944	21	55	2023-04-24 21:00:00	MCO
16601	5	8	1953	1959	-6	2231	2226	B6	887	N624JB	LGA	ATL	106	762	19	59	2023-05-08 19:00:00	ATL
16603	5	16	1749	1756	-7	2053	2108	AA	736	N306SW	LGA	MIA	149	1096	17	56	2023-05-16 17:00:00	MIA
16608	10	22	1708	1715	-7	1956	2014	NK	476	N624NK	EWR	MCO	130	937	17	15	2023-10-22 17:00:00	MCO
16609	3	31	1546	1555	-9	1711	1727	9E	1519	N329PQ	LGA	BGR	54	378	15	55	2023-03-31 15:00:00	Other
16612	7	24	1646	1652	-6	1911	1917	YX	878	N728YX	EWR	SDF	97	642	16	52	2023-07-24 16:00:00	Other
16615	10	30	753	800	-7	1112	1115	UA	814	N33289	EWR	RSW	162	1068	8	0	2023-10-30 08:00:00	Other
16616	10	20	652	659	-7	853	906	9E	1379	N292PQ	JFK	DTW	80	509	6	59	2023-10-20 06:00:00	Other
16623	11	27	1408	1415	-7	1548	1608	AA	391	N712US	LGA	RDU	76	431	14	15	2023-11-27 14:00:00	Other
16630	12	1	751	800	-9	947	939	UA	631	N47293	LGA	ORD	126	733	8	0	2023-12-01 08:00:00	ORD
16637	9	14	1049	1059	-10	1149	1159	YX	1075	N739YX	EWR	AVP	29	93	10	59	2023-09-14 10:00:00	Other
16640	8	24	454	501	-7	832	843	B6	730	N913JB	JFK	BQN	192	1576	5	1	2023-08-24 05:00:00	Other
16644	5	5	820	829	-9	942	1011	AA	126	N872NN	LGA	ORD	109	733	8	29	2023-05-05 08:00:00	ORD
16649	5	8	1844	1855	-11	2146	2206	AS	12	N942AK	JFK	SAN	329	2446	18	55	2023-05-08 18:00:00	Other
16654	11	5	1358	1405	-7	1558	1639	UA	885	N16709	EWR	ATL	101	746	14	5	2023-11-05 14:00:00	ATL
16664	3	17	1402	1410	-8	1652	1727	B6	336	N566JB	EWR	PBI	151	1023	14	10	2023-03-17 14:00:00	Other
16670	3	17	2152	2158	-6	2324	2322	UA	495	N81449	EWR	BUF	55	282	21	58	2023-03-17 21:00:00	Other
16672	1	21	1759	1807	-8	1948	1945	YX	1249	N722YX	EWR	PIT	58	319	18	7	2023-01-21 18:00:00	Other
16678	2	20	1947	1955	-8	2148	2148	9E	1269	N325PQ	JFK	PIT	71	340	19	55	2023-02-20 19:00:00	Other
16685	11	15	503	509	-6	806	823	AA	405	N319TE	EWR	MIA	155	1085	5	9	2023-11-15 05:00:00	MIA
16688	12	25	1202	1210	-8	1440	1513	UA	240	N17321	EWR	PBI	140	1023	12	10	2023-12-25 12:00:00	Other
16691	6	19	1101	1110	-9	1235	1240	YX	1403	N432YX	JFK	ORF	58	290	11	10	2023-06-19 11:00:00	Other
16693	8	1	749	755	-6	1029	1055	AA	256	N836AW	JFK	AUS	196	1521	7	55	2023-08-01 07:00:00	Other
16697	8	3	852	900	-8	1219	1235	AA	47	N105NN	JFK	SFO	357	2586	9	0	2023-08-03 09:00:00	Other
16698	6	7	1052	1059	-7	1226	1250	UA	877	N882UA	EWR	MEM	131	946	10	59	2023-06-07 10:00:00	Other
16703	4	18	1454	1505	-11	1614	1643	UA	563	N817UA	LGA	ORD	117	733	15	5	2023-04-18 15:00:00	ORD
16706	10	8	1141	1152	-11	1309	1347	YX	1059	N748YX	EWR	CMH	71	463	11	52	2023-10-08 11:00:00	Other
16707	11	26	1651	1700	-9	1842	1825	YX	1139	N743YX	EWR	PWM	50	284	17	0	2023-11-26 17:00:00	Other
16711	12	3	950	1000	-10	1042	1116	9E	1548	N482PX	LGA	ALB	26	136	10	0	2023-12-03 10:00:00	Other
16716	2	9	1750	1759	-9	1954	1927	YX	1009	N654RW	EWR	ROC	47	246	17	59	2023-02-09 17:00:00	Other
16720	3	9	1421	1427	-6	1600	1627	YX	1207	N859RW	EWR	MYR	81	550	14	27	2023-03-09 14:00:00	Other
16729	11	1	1524	1530	-6	1706	1724	B6	29	N354JB	JFK	ORD	119	740	15	30	2023-11-01 15:00:00	ORD
16732	5	14	1750	1759	-9	1911	1924	B6	421	N323JB	JFK	ROC	52	264	17	59	2023-05-14 17:00:00	Other
16734	12	13	747	800	-13	906	933	9E	1369	N279PQ	LGA	ROC	55	254	8	0	2023-12-13 08:00:00	Other
16737	3	28	1646	1655	-9	1808	1822	YX	1684	N875RW	LGA	ROC	49	254	16	55	2023-03-28 16:00:00	Other
16741	11	12	944	950	-6	1304	1332	B6	13	N526JL	JFK	PHX	284	2153	9	50	2023-11-12 09:00:00	Other
16750	8	18	1052	1100	-8	1247	1320	B6	102	N821JB	LGA	DEN	211	1620	11	0	2023-08-18 11:00:00	Other
16754	11	3	1919	1929	-10	2059	2137	9E	1468	N908XJ	JFK	RDU	69	427	19	29	2023-11-03 19:00:00	Other
16757	12	5	1914	1920	-6	2042	2107	YX	1736	N860RW	LGA	PIT	61	335	19	20	2023-12-05 19:00:00	Other
16766	7	22	2151	2159	-8	2255	2327	YX	1069	N410YX	JFK	BOS	35	187	21	59	2023-07-22 21:00:00	BOS
16767	10	24	1711	1720	-9	1904	1940	9E	1481	N479PX	LGA	CVG	92	585	17	20	2023-10-24 17:00:00	Other
16769	3	27	748	755	-7	1107	1113	AS	86	N924VA	EWR	LAX	347	2454	7	55	2023-03-27 07:00:00	LAX
16778	9	28	1046	1059	-13	1250	1316	YX	1121	N741YX	EWR	IND	99	645	10	59	2023-09-28 10:00:00	Other
16780	5	3	2050	2059	-9	2257	2334	YX	1251	N439YX	LGA	ATL	106	762	20	59	2023-05-03 20:00:00	ATL
16782	5	31	950	958	-8	1135	1211	AA	914	N568UW	JFK	CLT	82	541	9	58	2023-05-31 09:00:00	CLT
16792	9	27	1822	1828	-6	2040	2041	YX	1366	N871RW	LGA	MCI	167	1107	18	28	2023-09-27 18:00:00	Other
16793	9	13	2221	2229	-8	111	143	B6	653	N944JT	JFK	LAX	321	2475	22	29	2023-09-13 22:00:00	LAX
16795	4	12	636	645	-9	907	936	UA	725	N37263	EWR	PBI	131	1023	6	45	2023-04-12 06:00:00	Other
16796	5	9	1412	1421	-9	1553	1603	9E	1386	N298PQ	LGA	ORF	55	296	14	21	2023-05-09 14:00:00	Other
16812	8	9	1253	1300	-7	1540	1628	AS	4	N270AK	JFK	SFO	323	2586	13	0	2023-08-09 13:00:00	Other
16816	10	15	1858	1906	-8	2050	2109	YX	1340	N108HQ	LGA	CMH	82	479	19	6	2023-10-15 19:00:00	Other
16822	10	24	941	950	-9	1141	1212	9E	1395	N324PQ	EWR	CVG	88	569	9	50	2023-10-24 09:00:00	Other
16831	11	14	1719	1728	-9	1918	1930	YX	1117	N754YX	EWR	CMH	71	463	17	28	2023-11-14 17:00:00	Other
16834	4	18	1520	1529	-9	1802	1802	YX	1139	N441YX	JFK	IND	102	665	15	29	2023-04-18 15:00:00	Other
16838	4	9	1307	1315	-8	1409	1431	B6	743	N265JB	LGA	BOS	38	184	13	15	2023-04-09 13:00:00	BOS
16839	8	9	1750	1759	-9	1952	2030	9E	1220	N326PQ	JFK	CHS	88	636	17	59	2023-08-09 17:00:00	Other
16843	4	7	1821	1829	-8	2029	2048	YX	1125	N438YX	LGA	IND	109	660	18	29	2023-04-07 18:00:00	Other
16853	4	23	838	845	-7	1022	1046	YX	1054	N736YX	EWR	CMH	71	463	8	45	2023-04-23 08:00:00	Other
16858	11	28	618	630	-12	758	824	9E	1712	N186PQ	LGA	STL	140	888	6	30	2023-11-28 06:00:00	Other
16859	7	2	625	635	-10	830	828	YX	1096	N105HQ	JFK	RDU	90	427	6	35	2023-07-02 06:00:00	Other
16860	3	25	1740	1750	-10	1912	1915	9E	1566	N478PX	LGA	PWM	45	269	17	50	2023-03-25 17:00:00	Other
16861	5	25	618	630	-12	730	749	B6	937	N265JB	JFK	BUF	54	301	6	30	2023-05-25 06:00:00	Other
16870	11	7	2022	2030	-8	2242	2253	9E	1568	N912XJ	LGA	GRR	104	618	20	30	2023-11-07 20:00:00	Other
16871	2	26	1945	1952	-7	2235	2302	UA	455	N47280	EWR	MIA	142	1085	19	52	2023-02-26 19:00:00	MIA
16877	10	5	804	813	-9	941	1005	YX	1347	N119HQ	LGA	ILM	75	500	8	13	2023-10-05 08:00:00	Other
16880	1	10	1123	1130	-7	1235	1247	YX	1147	N863RW	EWR	BTV	48	266	11	30	2023-01-10 11:00:00	Other
16884	6	5	952	959	-7	1103	1129	YX	1816	N218JQ	JFK	BOS	41	187	9	59	2023-06-05 09:00:00	BOS
16901	8	7	654	700	-6	1046	1058	B6	161	N633JB	JFK	SJU	196	1598	7	0	2023-08-07 07:00:00	Other
16903	4	8	1333	1339	-6	1634	1654	AA	402	N844NN	JFK	MIA	154	1089	13	39	2023-04-08 13:00:00	MIA
16909	6	9	900	910	-10	1111	1116	NK	559	N639NK	EWR	CHS	97	628	9	10	2023-06-09 09:00:00	Other
16912	2	20	652	700	-8	827	901	YX	1235	N434YX	LGA	RDU	78	431	7	0	2023-02-20 07:00:00	Other
16916	11	30	1913	1920	-7	2036	2107	YX	1797	N860RW	LGA	PIT	55	335	19	20	2023-11-30 19:00:00	Other
16920	5	6	651	700	-9	930	1011	AS	14	N435AS	JFK	SEA	314	2422	7	0	2023-05-06 07:00:00	Other
16931	8	29	649	659	-10	809	830	YX	1046	N435YX	LGA	PIT	58	335	6	59	2023-08-29 06:00:00	Other
16934	5	10	842	850	-8	1034	1044	YX	1057	N733YX	EWR	CLE	67	404	8	50	2023-05-10 08:00:00	Other
16936	4	10	913	920	-7	1058	1120	NK	504	N653NK	EWR	CHS	85	628	9	20	2023-04-10 09:00:00	Other
16938	1	31	1523	1530	-7	1627	1649	B6	468	N318JB	JFK	BOS	32	187	15	30	2023-01-31 15:00:00	BOS
16942	7	10	920	930	-10	1029	1100	YX	1338	N211JQ	LGA	DCA	45	214	9	30	2023-07-10 09:00:00	Other
16945	9	6	1359	1407	-8	1656	1707	UA	450	N14240	EWR	AUS	195	1504	14	7	2023-09-06 14:00:00	Other
16947	4	18	1225	1235	-10	1525	1542	AA	201	N960NN	LGA	DFW	200	1389	12	35	2023-04-18 12:00:00	Other
16952	4	26	1822	1830	-8	2105	2136	UA	801	N79521	EWR	PBI	136	1023	18	30	2023-04-26 18:00:00	Other
16959	2	9	754	800	-6	911	927	YX	1556	N246JQ	LGA	BOS	42	184	8	0	2023-02-09 08:00:00	BOS
16964	1	31	1148	1155	-7	1322	1327	YX	1795	N213JQ	LGA	DCA	51	214	11	55	2023-01-31 11:00:00	Other
16969	3	1	1622	1629	-7	1759	1812	UA	99	N824UA	EWR	RDU	73	416	16	29	2023-03-01 16:00:00	Other
16974	9	20	1147	1200	-13	1317	1339	9E	1585	N320PQ	LGA	PIT	57	335	12	0	2023-09-20 12:00:00	Other
16985	10	30	1513	1526	-13	1654	1658	9E	1554	N602LR	JFK	SYR	52	209	15	26	2023-10-30 15:00:00	Other
16990	4	17	943	950	-7	1056	1113	9E	1246	N936XJ	JFK	PWM	44	273	9	50	2023-04-17 09:00:00	Other
16992	1	12	1323	1329	-6	1434	1452	YX	1908	N223JQ	JFK	PWM	49	273	13	29	2023-01-12 13:00:00	Other
16996	4	11	1831	1841	-10	1946	2018	AA	690	N931NN	LGA	ORD	110	733	18	41	2023-04-11 18:00:00	ORD
16997	2	28	1624	1635	-11	1811	1808	YX	1517	N824MD	LGA	DCA	67	214	16	35	2023-02-28 16:00:00	Other
17001	5	8	1220	1229	-9	1506	1538	UA	783	N492UA	EWR	SAT	212	1569	12	29	2023-05-08 12:00:00	Other
17004	2	22	2050	2100	-10	2326	2329	YX	1288	N104HQ	JFK	IND	110	665	21	0	2023-02-22 21:00:00	Other
17005	3	25	2143	2149	-6	29	17	UA	641	N836UA	EWR	ATL	124	746	21	49	2023-03-25 21:00:00	ATL
17007	2	7	1732	1740	-8	2036	2110	B6	914	N969JT	JFK	LAX	338	2475	17	40	2023-02-07 17:00:00	LAX
17018	12	9	2020	2030	-10	2158	2222	YX	1347	N121HQ	JFK	PIT	67	340	20	30	2023-12-09 20:00:00	Other
17019	10	10	1246	1259	-13	1417	1453	9E	1499	N937XJ	LGA	RDU	69	431	12	59	2023-10-10 12:00:00	Other
17030	12	6	1153	1200	-7	1339	1358	9E	1390	N153PQ	JFK	CLT	80	541	12	0	2023-12-06 12:00:00	CLT
17031	11	14	819	825	-6	1113	1136	AA	200	N818NN	LGA	DFW	199	1389	8	25	2023-11-14 08:00:00	Other
17035	3	24	1813	1820	-7	1926	1950	9E	1566	N482PX	LGA	PWM	50	269	18	20	2023-03-24 18:00:00	Other
17038	3	16	759	805	-6	922	939	9E	1532	N901XJ	JFK	ROC	55	264	8	5	2023-03-16 08:00:00	Other
17050	10	13	1039	1047	-8	1133	1155	YX	1127	N740YX	EWR	AVP	29	93	10	47	2023-10-13 10:00:00	Other
17059	8	25	1722	1729	-7	2017	2031	AA	770	N307TA	JFK	AUS	189	1521	17	29	2023-08-25 17:00:00	Other
17063	12	2	1220	1226	-6	1543	1540	DL	521	N341NB	JFK	AUS	239	1521	12	26	2023-12-02 12:00:00	Other
17066	3	7	954	1000	-6	1146	1202	9E	1527	N184GJ	EWR	RDU	77	416	10	0	2023-03-07 10:00:00	Other
17072	12	28	1552	1600	-8	1821	1920	AS	74	N953AK	EWR	SEA	299	2402	16	0	2023-12-28 16:00:00	Other
17076	1	3	635	645	-10	917	954	B6	517	N603JB	LGA	TPA	146	1010	6	45	2023-01-03 06:00:00	Other
17080	6	8	753	802	-9	904	927	B6	60	N337JB	JFK	ROC	49	264	8	2	2023-06-08 08:00:00	Other
17082	12	12	1500	1510	-10	1701	1719	YX	1241	N420YX	JFK	CMH	86	483	15	10	2023-12-12 15:00:00	Other
17088	11	13	2023	2030	-7	2237	2255	YX	1322	N428YX	JFK	IND	112	665	20	30	2023-11-13 20:00:00	Other
17094	1	19	1124	1130	-6	1314	1332	YX	1377	N124HQ	JFK	CLE	85	425	11	30	2023-01-19 11:00:00	Other
17101	8	17	1509	1515	-6	1610	1633	YX	1331	N882RW	LGA	ACK	35	202	15	15	2023-08-17 15:00:00	Other
17106	6	13	620	630	-10	759	846	UA	189	N848UA	LGA	DEN	198	1620	6	30	2023-06-13 06:00:00	Other
17107	10	10	642	650	-8	939	1016	DL	103	N102DN	JFK	SLC	269	1990	6	50	2023-10-10 06:00:00	Other
17111	1	23	1421	1430	-9	1556	1615	YX	1385	N118HQ	JFK	PIT	65	340	14	30	2023-01-23 14:00:00	Other
17113	2	21	2240	2259	-19	2356	23	YX	1506	N240JQ	JFK	PWM	47	273	22	59	2023-02-21 22:00:00	Other
17121	8	21	1549	1559	-10	1821	1901	B6	260	N976JT	JFK	LAX	303	2475	15	59	2023-08-21 15:00:00	LAX
17122	12	20	1249	1303	-14	1408	1433	YX	1256	N115HQ	JFK	ORF	53	290	13	3	2023-12-20 13:00:00	Other
17129	10	22	932	940	-8	1020	1055	9E	1456	N480PX	LGA	PVD	32	143	9	40	2023-10-22 09:00:00	Other
17130	10	1	1620	1630	-10	1829	1846	9E	1550	N310PQ	LGA	CLT	79	544	16	30	2023-10-01 16:00:00	CLT
17139	10	17	1558	1605	-7	1729	1807	OO	1150	N244SY	JFK	ORD	116	740	16	5	2023-10-17 16:00:00	ORD
17142	10	13	1654	1700	-6	1837	1844	AA	987	N815AW	LGA	STL	144	888	17	0	2023-10-13 17:00:00	Other
17147	4	27	1253	1300	-7	1430	1448	DL	614	N980AT	EWR	DTW	83	488	13	0	2023-04-27 13:00:00	Other
17148	3	27	1202	1210	-8	1420	1432	YX	1287	N408YX	LGA	MSP	164	1020	12	10	2023-03-27 12:00:00	Other
17151	12	21	651	700	-9	910	915	DL	736	N123DQ	LGA	CHS	90	641	7	0	2023-12-21 07:00:00	Other
17164	2	9	730	740	-10	1026	1059	UA	289	N36247	EWR	IAH	213	1400	7	40	2023-02-09 07:00:00	Other
17167	9	29	1310	1317	-7	1549	1615	NK	1029	N621NK	EWR	MCO	134	937	13	17	2023-09-29 13:00:00	MCO
17175	10	15	1443	1450	-7	1647	1703	9E	1570	N272PQ	LGA	GSP	99	610	14	50	2023-10-15 14:00:00	Other
17181	5	24	1321	1330	-9	1428	1442	B6	40	N358JB	JFK	SYR	43	209	13	30	2023-05-24 13:00:00	Other
17186	4	18	1255	1303	-8	1602	1559	UA	775	N17300	EWR	PBI	154	1023	13	3	2023-04-18 13:00:00	Other
17189	11	1	942	951	-9	1206	1224	YX	1364	N121HQ	LGA	SDF	113	659	9	51	2023-11-01 09:00:00	Other
17192	12	6	1651	1659	-8	1825	1857	9E	1698	N133EV	LGA	RDU	65	431	16	59	2023-12-06 16:00:00	Other
17193	8	10	1553	1559	-6	1725	1734	YX	899	N762YX	EWR	PIT	55	319	15	59	2023-08-10 15:00:00	Other
17195	10	3	550	600	-10	808	844	DL	233	N107DU	LGA	DFW	177	1389	6	0	2023-10-03 06:00:00	Other
17197	6	7	654	700	-6	908	927	DL	192	N348DN	LGA	ATL	107	762	7	0	2023-06-07 07:00:00	ATL
17198	6	24	806	815	-9	1036	1029	YX	1094	N645RW	EWR	GRR	89	605	8	15	2023-06-24 08:00:00	Other
17199	10	10	2015	2030	-15	2135	2213	9E	1631	N919XJ	LGA	MSN	115	812	20	30	2023-10-10 20:00:00	Other
17207	12	12	1354	1400	-6	1648	1717	UA	393	N792UA	EWR	SFO	334	2565	14	0	2023-12-12 14:00:00	Other
17213	11	23	1024	1030	-6	1316	1335	UA	675	N25201	EWR	IAH	210	1400	10	30	2023-11-23 10:00:00	Other
17219	10	28	704	710	-6	932	1005	DL	505	N326DN	LGA	MCO	128	950	7	10	2023-10-28 07:00:00	MCO
17220	12	15	620	630	-10	855	926	UA	303	N77530	EWR	MCO	129	937	6	30	2023-12-15 06:00:00	MCO
17223	11	8	1547	1555	-8	1848	1915	DL	874	N324NB	JFK	AUS	205	1521	15	55	2023-11-08 15:00:00	Other
17225	10	24	753	800	-7	1002	1020	DL	899	N301NB	JFK	MSY	156	1182	8	0	2023-10-24 08:00:00	Other
17226	9	25	923	929	-6	1046	1040	9E	1503	N299PQ	LGA	PVD	31	143	9	29	2023-09-25 09:00:00	Other
17238	3	30	639	645	-6	939	934	B6	1011	N283JB	JFK	PBI	145	1028	6	45	2023-03-30 06:00:00	Other
17239	4	28	554	600	-6	717	715	YX	1556	N203JQ	LGA	DCA	45	214	6	0	2023-04-28 06:00:00	Other
17244	4	9	1516	1529	-13	1705	1738	YX	1119	N405YX	LGA	DTW	77	502	15	29	2023-04-09 15:00:00	Other
17254	11	13	2206	2214	-8	29	45	NK	559	N947NK	EWR	ATL	121	746	22	14	2023-11-13 22:00:00	ATL
17266	12	12	1323	1329	-6	1427	1451	YX	1739	N212JQ	LGA	SYR	38	198	13	29	2023-12-12 13:00:00	Other
17268	11	30	829	839	-10	1029	1044	YX	1063	N638RW	EWR	DTW	86	488	8	39	2023-11-30 08:00:00	Other
17271	9	21	818	825	-7	1058	1118	AA	332	N305NX	LGA	DFW	184	1389	8	25	2023-09-21 08:00:00	Other
17272	7	3	1451	1500	-9	1706	1718	YX	1343	N216JQ	LGA	CHS	93	641	15	0	2023-07-03 15:00:00	Other
17274	10	17	1311	1325	-14	1424	1504	YX	1351	N416YX	JFK	PIT	52	340	13	25	2023-10-17 13:00:00	Other
17275	6	5	928	939	-11	1047	1055	B6	890	N323JB	LGA	ACK	35	202	9	39	2023-06-05 09:00:00	Other
17281	10	18	946	954	-8	1103	1133	9E	1579	N325PQ	JFK	RIC	56	288	9	54	2023-10-18 09:00:00	Other
17285	9	21	1642	1649	-7	1847	1914	YX	1226	N864RW	EWR	SDF	93	642	16	49	2023-09-21 16:00:00	Other
17298	12	3	1318	1330	-12	1646	1634	NK	331	N622NK	LGA	DFW	235	1389	13	30	2023-12-03 13:00:00	Other
17301	10	22	1854	1900	-6	2005	2030	WN	677	N7726A	LGA	MDW	109	725	19	0	2023-10-22 19:00:00	Other
17311	3	18	1752	1800	-8	1905	1922	AA	487	N772XF	LGA	DCA	56	214	18	0	2023-03-18 18:00:00	Other
17313	8	9	620	630	-10	916	926	NK	402	N933NK	LGA	MCO	130	950	6	30	2023-08-09 06:00:00	MCO
17320	3	21	915	925	-10	1019	1050	9E	1339	N906XJ	JFK	IAD	44	228	9	25	2023-03-21 09:00:00	Other
17321	12	22	953	959	-6	1115	1130	YX	1833	N244JQ	LGA	BOS	37	184	9	59	2023-12-22 09:00:00	BOS
17331	12	5	727	735	-8	1045	1048	DL	750	N3743H	JFK	PBI	157	1028	7	35	2023-12-05 07:00:00	Other
17332	9	22	2019	2027	-8	2239	2238	YX	1140	N654RW	EWR	GSP	90	594	20	27	2023-09-22 20:00:00	Other
17334	6	21	1217	1229	-12	1351	1400	YX	1279	N426YX	JFK	ORF	56	290	12	29	2023-06-21 12:00:00	Other
17335	1	11	2021	2029	-8	2319	2338	B6	748	N760JB	LGA	PBI	142	1035	20	29	2023-01-11 20:00:00	Other
17341	1	21	1702	1711	-9	1907	1935	AA	680	N192UW	LGA	CLT	98	544	17	11	2023-01-21 17:00:00	CLT
17346	2	14	650	658	-8	837	847	YX	1090	N732YX	EWR	CLE	70	404	6	58	2023-02-14 06:00:00	Other
17347	8	22	2039	2048	-9	2336	2357	UA	553	N78501	EWR	SLC	268	1969	20	48	2023-08-22 20:00:00	Other
17349	10	26	2050	2059	-9	2244	2257	UA	579	N37255	EWR	MSP	140	1008	20	59	2023-10-26 20:00:00	Other
17350	12	17	1053	1100	-7	1357	1423	AA	2	N117AN	JFK	LAX	338	2475	11	0	2023-12-17 11:00:00	LAX
17354	5	17	1424	1430	-6	1547	1602	B6	956	N324JB	JFK	BUF	56	301	14	30	2023-05-17 14:00:00	Other
17355	10	2	721	729	-8	907	929	AA	498	N929AN	JFK	CLT	82	541	7	29	2023-10-02 07:00:00	CLT
17356	11	23	554	600	-6	851	910	B6	831	N556JB	EWR	MIA	144	1085	6	0	2023-11-23 06:00:00	MIA
17364	2	6	1513	1520	-7	1815	1845	DL	114	N129DU	LGA	DFW	199	1389	15	20	2023-02-06 15:00:00	Other
17373	3	28	716	725	-9	1046	1047	AA	1	N110AN	JFK	LAX	360	2475	7	25	2023-03-28 07:00:00	LAX
17384	2	5	1722	1729	-7	1918	1923	YX	1277	N129HQ	JFK	RDU	85	427	17	29	2023-02-05 17:00:00	Other
17388	1	12	937	955	-18	1140	1151	9E	1535	N153PQ	JFK	CLE	79	425	9	55	2023-01-12 09:00:00	Other
17394	5	17	1723	1729	-6	2028	1955	9E	1458	N319PQ	LGA	SAV	113	722	17	29	2023-05-17 17:00:00	Other
17395	10	31	1152	1200	-8	1337	1353	YX	1333	N437YX	JFK	RDU	86	427	12	0	2023-10-31 12:00:00	Other
17397	5	13	853	900	-7	1103	1133	DL	196	N3765	JFK	DEN	228	1626	9	0	2023-05-13 09:00:00	Other
17400	12	13	809	816	-7	1107	1143	UA	770	N458UA	EWR	SEA	326	2402	8	16	2023-12-13 08:00:00	Other
17401	12	21	1449	1455	-6	1546	1622	YX	1828	N202JQ	JFK	BWI	37	184	14	55	2023-12-21 14:00:00	Other
17402	5	23	1352	1400	-8	1539	1526	YX	1321	N407YX	LGA	DCA	44	214	14	0	2023-05-23 14:00:00	Other
17403	3	17	1948	1954	-6	2249	2320	B6	607	N946JL	EWR	LAX	330	2454	19	54	2023-03-17 19:00:00	LAX
17405	11	24	2127	2135	-8	2317	2340	UA	440	N37253	EWR	CHS	92	628	21	35	2023-11-24 21:00:00	Other
17406	4	28	1320	1329	-9	1536	1548	YX	1160	N135HQ	LGA	MCI	160	1107	13	29	2023-04-28 13:00:00	Other
17412	8	24	1650	1659	-9	1810	1831	B6	317	N348JB	JFK	BOS	44	187	16	59	2023-08-24 16:00:00	BOS
17416	5	25	1152	1200	-8	1244	1311	B6	762	N368JB	JFK	ACK	35	199	12	0	2023-05-25 12:00:00	Other
17420	1	29	1953	1959	-6	2140	2221	YX	1301	N411YX	LGA	CMH	83	479	19	59	2023-01-29 19:00:00	Other
17425	9	28	647	700	-13	958	1025	AS	13	N947AK	JFK	SFO	335	2586	7	0	2023-09-28 07:00:00	Other
17428	10	6	1451	1500	-9	1646	1710	YX	1153	N728YX	EWR	CVG	89	569	15	0	2023-10-06 15:00:00	Other
17433	8	30	853	900	-7	1057	1043	YX	1314	N234JQ	JFK	PIT	60	340	9	0	2023-08-30 09:00:00	Other
17440	5	10	2020	2030	-10	2211	2243	YX	1192	N413YX	JFK	CMH	73	483	20	30	2023-05-10 20:00:00	Other
17441	4	30	1641	1647	-6	1924	1954	YX	1554	N210JQ	LGA	OKC	198	1341	16	47	2023-04-30 16:00:00	Other
17447	10	25	1123	1130	-7	1240	1253	YX	1853	N240JQ	LGA	BOS	40	184	11	30	2023-10-25 11:00:00	BOS
17448	11	20	847	854	-7	1037	1055	9E	1442	N920XJ	LGA	CLE	69	419	8	54	2023-11-20 08:00:00	Other
17453	5	15	1629	1635	-6	1857	1921	UA	830	N17300	EWR	LAS	294	2227	16	35	2023-05-15 16:00:00	Other
17456	6	22	1133	1145	-12	1407	1445	AS	7	N294AK	JFK	PDX	306	2454	11	45	2023-06-22 11:00:00	Other
17459	5	1	749	755	-6	921	924	YX	1297	N806MD	LGA	CHO	57	305	7	55	2023-05-01 07:00:00	Other
17461	3	3	1217	1225	-8	1428	1436	NK	652	N668NK	LGA	DTW	89	502	12	25	2023-03-03 12:00:00	Other
17463	4	28	1926	1935	-9	2225	2231	B6	220	N607JB	EWR	TPA	147	997	19	35	2023-04-28 19:00:00	Other
17468	4	3	1342	1355	-13	1643	1624	B6	665	N559JB	LGA	DEN	260	1620	13	55	2023-04-03 13:00:00	Other
17474	12	6	1047	1100	-13	1300	1334	B6	694	N571JB	LGA	DEN	218	1620	11	0	2023-12-06 11:00:00	Other
17486	1	25	1418	1429	-11	1534	1602	9E	1625	N914XJ	LGA	BGR	50	378	14	29	2023-01-25 14:00:00	Other
17487	5	28	849	855	-6	1043	1111	YX	1017	N862RW	EWR	AVL	85	583	8	55	2023-05-28 08:00:00	Other
17491	8	24	841	850	-9	1018	1043	YX	1044	N433YX	LGA	GSO	68	461	8	50	2023-08-24 08:00:00	Other
17506	6	11	958	1005	-7	1247	1308	DL	440	N143DU	LGA	IAH	204	1416	10	5	2023-06-11 10:00:00	Other
17516	8	21	1614	1620	-6	1801	1821	UA	247	N15710	EWR	CLT	80	529	16	20	2023-08-21 16:00:00	CLT
17531	1	6	1515	1522	-7	1621	1639	YX	1204	N748YX	EWR	MHT	41	209	15	22	2023-01-06 15:00:00	Other
17533	11	11	1321	1329	-8	1536	1557	DL	251	N3747D	LGA	DEN	233	1620	13	29	2023-11-11 13:00:00	Other
17535	11	8	1550	1559	-9	1706	1730	B6	992	N258JB	JFK	BUF	61	301	15	59	2023-11-08 15:00:00	Other
17539	4	22	1516	1525	-9	1629	1637	9E	1189	N924XJ	LGA	BGM	30	147	15	25	2023-04-22 15:00:00	Other
17543	1	15	1549	1555	-6	1757	1841	DL	375	N391DN	LGA	ATL	105	762	15	55	2023-01-15 15:00:00	ATL
17544	3	5	737	744	-7	1024	1039	UA	227	N37295	EWR	LAS	323	2227	7	44	2023-03-05 07:00:00	Other
17549	2	9	657	710	-13	935	1021	UA	778	N27256	EWR	DFW	194	1372	7	10	2023-02-09 07:00:00	Other
17551	12	4	752	800	-8	1122	1115	UA	133	N86534	EWR	RSW	171	1068	8	0	2023-12-04 08:00:00	Other
17557	11	5	602	608	-6	801	817	AA	233	N191UW	LGA	CLT	91	544	6	8	2023-11-05 06:00:00	CLT
17560	8	3	1626	1632	-6	1730	1812	9E	1160	N676CA	LGA	PWM	43	269	16	32	2023-08-03 16:00:00	Other
17562	3	6	1627	1635	-8	1950	2011	AS	7	N487AS	JFK	SEA	347	2422	16	35	2023-03-06 16:00:00	Other
17567	4	10	1902	1915	-13	2022	2036	B6	465	N193JB	LGA	BOS	49	184	19	15	2023-04-10 19:00:00	BOS
17569	12	7	1639	1648	-9	1825	1839	AA	212	N775XF	LGA	STL	140	888	16	48	2023-12-07 16:00:00	Other
17580	10	10	2112	2122	-10	2241	2259	YX	1715	N201JQ	LGA	BNA	125	764	21	22	2023-10-10 21:00:00	Other
17587	7	18	619	627	-8	804	816	YX	1010	N127HQ	LGA	CMH	80	479	6	27	2023-07-18 06:00:00	Other
17593	8	16	758	805	-7	1145	1209	DL	560	N872DN	JFK	SJU	203	1598	8	5	2023-08-16 08:00:00	Other
17594	12	26	1553	1559	-6	1731	1802	YX	1023	N724YX	EWR	CMH	74	463	15	59	2023-12-26 15:00:00	Other
17598	9	23	927	938	-11	1105	1132	DL	996	N978AT	EWR	DTW	75	488	9	38	2023-09-23 09:00:00	Other
17605	4	6	1423	1430	-7	1517	1535	9E	1416	N136EV	LGA	ORH	28	146	14	30	2023-04-06 14:00:00	Other
17608	2	9	1441	1447	-6	1721	1747	UA	406	N18112	EWR	MCO	137	937	14	47	2023-02-09 14:00:00	MCO
17610	11	11	1412	1420	-8	1726	1723	UA	557	N73256	EWR	IAH	218	1400	14	20	2023-11-11 14:00:00	Other
17611	5	19	1441	1450	-9	1609	1626	B6	253	N3115J	JFK	MKE	122	745	14	50	2023-05-19 14:00:00	Other
17614	7	12	527	535	-8	757	807	B6	100	N520JB	EWR	MCO	120	937	5	35	2023-07-12 05:00:00	MCO
17615	10	24	1950	1959	-9	2258	2316	AS	76	N562AS	EWR	LAX	337	2454	19	59	2023-10-24 19:00:00	LAX
17618	1	2	1131	1142	-11	1335	1408	YX	1362	N102HQ	LGA	DAY	97	549	11	42	2023-01-02 11:00:00	Other
17623	10	29	852	859	-7	1056	1109	DL	484	N111DC	LGA	DTW	91	502	8	59	2023-10-29 08:00:00	Other
17627	5	29	620	630	-10	915	931	B6	925	N589JB	JFK	FLL	145	1069	6	30	2023-05-29 06:00:00	FLL
17631	11	11	649	655	-6	943	952	B6	186	N942JB	JFK	LAS	314	2248	6	55	2023-11-11 06:00:00	Other
17634	3	21	1804	1811	-7	2106	2130	UA	440	N38727	EWR	PDX	338	2434	18	11	2023-03-21 18:00:00	Other
17636	6	5	839	853	-14	1045	1115	9E	1471	N480PX	LGA	GRR	91	618	8	53	2023-06-05 08:00:00	Other
17662	11	13	1833	1843	-10	2135	2144	DL	250	N524DE	JFK	LAS	320	2248	18	43	2023-11-13 18:00:00	Other
17663	7	29	659	705	-6	912	932	B6	136	N986JB	JFK	LAS	288	2248	7	5	2023-07-29 07:00:00	Other
17668	1	20	2147	2155	-8	2254	2314	YX	1806	N203JQ	LGA	DCA	42	214	21	55	2023-01-20 21:00:00	Other
17677	2	11	1842	1850	-8	2157	2202	B6	932	N594JB	JFK	TPA	175	1005	18	50	2023-02-11 18:00:00	Other
17687	2	24	1151	1159	-8	1311	1316	YX	1011	N732YX	EWR	SYR	52	195	11	59	2023-02-24 11:00:00	Other
17689	1	18	1023	1030	-7	1229	1251	9E	1592	N298PQ	JFK	SAV	107	718	10	30	2023-01-18 10:00:00	Other
17702	7	13	1919	1928	-9	2232	2130	YX	1435	N226JQ	LGA	CMH	79	479	19	28	2023-07-13 19:00:00	Other
17704	2	20	1219	1225	-6	1412	1454	YX	1242	N427YX	LGA	DAY	99	549	12	25	2023-02-20 12:00:00	Other
17705	12	4	1205	1215	-10	1415	1444	UA	848	N14115	EWR	DEN	226	1605	12	15	2023-12-04 12:00:00	Other
17712	2	13	652	701	-9	834	915	AA	331	N966NN	LGA	CLT	84	544	7	1	2023-02-13 07:00:00	CLT
17714	10	22	906	915	-9	1008	1050	UA	213	N408UA	LGA	ORD	105	733	9	15	2023-10-22 09:00:00	ORD
17716	9	19	1449	1456	-7	1708	1719	OO	1254	N242SY	JFK	IND	102	665	14	56	2023-09-19 14:00:00	Other
17718	2	7	1710	1718	-8	1901	1932	YX	999	N656RW	EWR	GSP	93	594	17	18	2023-02-07 17:00:00	Other
17722	4	22	1322	1329	-7	1522	1548	YX	1160	N821MD	LGA	MCI	162	1107	13	29	2023-04-22 13:00:00	Other
17723	8	6	1950	2000	-10	2105	2131	YX	1383	N882RW	LGA	BOS	45	184	20	0	2023-08-06 20:00:00	BOS
17732	2	12	1754	1800	-6	1910	1927	YX	1565	N214JQ	JFK	PWM	45	273	18	0	2023-02-12 18:00:00	Other
17737	10	26	807	813	-6	1004	1032	9E	1562	N272PQ	LGA	GRR	95	618	8	13	2023-10-26 08:00:00	Other
17739	4	21	1659	1708	-9	1928	1940	AA	852	N447AN	EWR	PHX	287	2133	17	8	2023-04-21 17:00:00	Other
17741	10	31	552	600	-8	900	910	B6	821	N516JB	EWR	MIA	156	1085	6	0	2023-10-31 06:00:00	MIA
17746	8	28	922	930	-8	1115	1142	DL	175	N318DX	LGA	DTW	88	502	9	30	2023-08-28 09:00:00	Other
17749	12	12	1822	1829	-7	2014	2015	AA	720	N831AW	LGA	ORD	124	733	18	29	2023-12-12 18:00:00	ORD
17750	9	20	723	730	-7	1011	1027	AA	140	N992AN	LGA	DFW	194	1389	7	30	2023-09-20 07:00:00	Other
17751	12	26	1509	1515	-6	1638	1715	WN	700	N266WN	LGA	STL	131	888	15	15	2023-12-26 15:00:00	Other
17753	5	29	750	759	-9	941	1002	AA	952	N549UW	LGA	CLT	87	544	7	59	2023-05-29 07:00:00	CLT
17755	10	24	748	800	-12	1033	1052	B6	50	N807JB	JFK	MCO	128	944	8	0	2023-10-24 08:00:00	MCO
17760	5	22	1921	1929	-8	2048	2055	AA	905	N762US	LGA	BNA	118	764	19	29	2023-05-22 19:00:00	Other
17774	7	30	1311	1318	-7	1411	1434	B6	689	N339JB	JFK	ACK	36	199	13	18	2023-07-30 13:00:00	Other
17777	4	22	1130	1145	-15	1404	1454	AS	11	N955AK	JFK	SEA	307	2422	11	45	2023-04-22 11:00:00	Other
17780	12	26	1252	1300	-8	1535	1640	AS	3	N912AK	JFK	SFO	321	2586	13	0	2023-12-26 13:00:00	Other
17783	6	1	1552	1558	-6	1755	1808	YX	1408	N435YX	LGA	TYS	93	647	15	58	2023-06-01 15:00:00	Other
17785	9	14	1153	1200	-7	1359	1400	YX	1389	N104HQ	LGA	ROA	72	405	12	0	2023-09-14 12:00:00	Other
17787	1	21	2051	2059	-8	2244	2248	B6	263	N346JB	JFK	ORD	132	740	20	59	2023-01-21 20:00:00	ORD
17788	11	16	1302	1310	-8	1417	1443	YX	1387	N131HQ	LGA	RIC	53	292	13	10	2023-11-16 13:00:00	Other
17791	10	29	1452	1459	-7	1814	1805	DL	969	N364NW	LGA	TPA	146	1010	14	59	2023-10-29 14:00:00	Other
17798	7	25	1254	1300	-6	1653	1555	B6	561	N505JB	EWR	RSW	161	1068	13	0	2023-07-25 13:00:00	Other
17806	8	14	633	640	-7	815	829	9E	1254	N183GJ	LGA	CMH	77	479	6	40	2023-08-14 06:00:00	Other
17810	10	24	624	630	-6	1003	1027	B6	563	N966JT	JFK	SJU	187	1598	6	30	2023-10-24 06:00:00	Other
17816	10	16	1844	1855	-11	2145	2210	NK	1016	N664NK	LGA	MIA	156	1096	18	55	2023-10-16 18:00:00	MIA
17823	2	8	938	945	-7	1051	1135	WN	91	N965WN	LGA	BNA	117	764	9	45	2023-02-08 09:00:00	Other
17828	4	7	754	800	-6	1100	1130	DL	547	N3760C	JFK	RSW	166	1074	8	0	2023-04-07 08:00:00	Other
17830	4	26	1939	1945	-6	2201	2207	B6	612	N206JB	LGA	SAV	113	722	19	45	2023-04-26 19:00:00	Other
17839	1	20	2043	2053	-10	2219	2304	YX	1474	N821MD	LGA	ILM	77	500	20	53	2023-01-20 20:00:00	Other
17850	3	21	1337	1345	-8	1508	1511	YX	1741	N860RW	LGA	DCA	43	214	13	45	2023-03-21 13:00:00	Other
17853	4	27	705	713	-8	1000	1031	B6	276	N946JL	JFK	LAX	312	2475	7	13	2023-04-27 07:00:00	LAX
17855	7	30	2123	2129	-6	2312	2325	NK	254	N916NK	LGA	DTW	82	502	21	29	2023-07-30 21:00:00	Other
17856	3	26	1021	1029	-8	1210	1202	UA	696	N76517	EWR	ORD	123	719	10	29	2023-03-26 10:00:00	ORD
17858	9	11	621	630	-9	746	808	UA	272	N17262	EWR	CLE	58	404	6	30	2023-09-11 06:00:00	Other
17859	9	18	601	608	-7	858	852	B6	325	N606JB	EWR	MCO	143	937	6	8	2023-09-18 06:00:00	MCO
17860	7	17	1323	1329	-6	1452	1508	9E	1131	N297PQ	JFK	RIC	54	288	13	29	2023-07-17 13:00:00	Other
17872	6	15	1450	1459	-9	1642	1713	9E	1521	N490PX	LGA	GSP	89	610	14	59	2023-06-15 14:00:00	Other
17873	4	27	917	930	-13	1221	1239	AS	10	N293AK	JFK	SEA	327	2422	9	30	2023-04-27 09:00:00	Other
17876	9	27	2137	2148	-11	2315	2341	YX	1115	N653RW	EWR	GSO	76	445	21	48	2023-09-27 21:00:00	Other
17883	2	14	1339	1348	-9	1559	1617	YX	990	N742YX	EWR	SDF	118	642	13	48	2023-02-14 13:00:00	Other
17891	5	9	1621	1629	-8	1731	1810	YX	1691	N240JQ	JFK	BOS	37	187	16	29	2023-05-09 16:00:00	BOS
17895	3	18	1252	1259	-7	1553	1559	UA	866	N493UA	EWR	PBI	160	1023	12	59	2023-03-18 12:00:00	Other
17897	5	17	551	600	-9	758	808	YX	1624	N229JQ	LGA	CLT	98	544	6	0	2023-05-17 06:00:00	CLT
17899	2	17	1106	1115	-9	1209	1229	B6	261	N375JB	LGA	BOS	37	184	11	15	2023-02-17 11:00:00	BOS
17907	4	28	1645	1651	-6	1824	1834	YX	994	N721YX	EWR	CLE	67	404	16	51	2023-04-28 16:00:00	Other
17914	6	7	812	820	-8	912	950	9E	1487	N134EV	LGA	ROC	43	254	8	20	2023-06-07 08:00:00	Other
17915	11	12	1654	1700	-6	2000	2005	B6	400	N2102J	JFK	SAN	334	2446	17	0	2023-11-12 17:00:00	Other
17916	3	22	603	610	-7	739	750	UA	757	N489UA	LGA	ORD	121	733	6	10	2023-03-22 06:00:00	ORD
17920	10	26	1414	1420	-6	1546	1610	YX	1788	N205JQ	LGA	CMH	78	479	14	20	2023-10-26 14:00:00	Other
17921	12	13	909	915	-6	1101	1108	OO	1183	N607CZ	JFK	PIT	82	340	9	15	2023-12-13 09:00:00	Other
17923	1	12	752	800	-8	900	927	YX	1884	N203JQ	LGA	BOS	33	184	8	0	2023-01-12 08:00:00	BOS
17934	7	12	1523	1529	-6	1831	1853	AS	82	N956AK	EWR	SFO	334	2565	15	29	2023-07-12 15:00:00	Other
17938	10	9	634	645	-11	840	855	UA	428	N37313	EWR	CHS	98	628	6	45	2023-10-09 06:00:00	Other
17941	3	6	1339	1345	-6	1646	1717	B6	290	N763JB	JFK	SAT	226	1587	13	45	2023-03-06 13:00:00	Other
17942	11	24	556	602	-6	747	817	AA	936	N183UW	EWR	CLT	89	529	6	2	2023-11-24 06:00:00	CLT
17944	2	11	930	938	-8	1224	1231	AA	662	N8030F	LGA	EGE	232	1739	9	38	2023-02-11 09:00:00	Other
17946	5	11	1203	1209	-6	1321	1347	9E	1429	N913XJ	LGA	BGR	58	378	12	9	2023-05-11 12:00:00	Other
17948	11	24	1451	1500	-9	1714	1742	DL	332	N348DN	LGA	ATL	113	762	15	0	2023-11-24 15:00:00	ATL
17952	10	31	724	730	-6	921	945	DL	515	N301NB	JFK	MSP	159	1029	7	30	2023-10-31 07:00:00	Other
17958	11	4	1719	1730	-11	1913	1904	OO	1215	N246SY	JFK	MKE	124	745	17	30	2023-11-04 17:00:00	Other
17961	1	10	1322	1330	-8	1446	1459	YX	1796	N228JQ	JFK	DCA	57	213	13	30	2023-01-10 13:00:00	Other
17963	3	22	1359	1405	-6	1607	1618	YX	1073	N744YX	EWR	CHS	101	628	14	5	2023-03-22 14:00:00	Other
17964	4	29	852	900	-8	1148	1217	AA	728	N323SG	LGA	MIA	152	1096	9	0	2023-04-29 09:00:00	MIA
17970	2	16	624	630	-6	839	858	UA	437	N37263	EWR	JAX	118	820	6	30	2023-02-16 06:00:00	Other
17977	8	3	1030	1038	-8	1206	1206	9E	1191	N936XJ	JFK	BTV	52	266	10	38	2023-08-03 10:00:00	Other
17984	10	26	1224	1232	-8	1341	1351	YX	1272	N137HQ	JFK	BOS	44	187	12	32	2023-10-26 12:00:00	BOS
17985	2	13	1121	1130	-9	1426	1449	DL	471	N341NW	LGA	SRQ	147	1047	11	30	2023-02-13 11:00:00	Other
17989	9	4	1039	1055	-16	1227	1300	G4	117	327NV	EWR	CVG	82	569	10	55	2023-09-04 10:00:00	Other
17996	2	15	1553	1600	-7	1731	1729	YX	1155	N855RW	EWR	PIT	62	319	16	0	2023-02-15 16:00:00	Other
18002	11	6	1752	1800	-8	1955	2028	9E	1410	N917XJ	LGA	TYS	106	647	18	0	2023-11-06 18:00:00	Other
18004	5	2	1947	1955	-8	2140	2152	YX	1303	N419YX	LGA	CMH	77	479	19	55	2023-05-02 19:00:00	Other
18006	8	30	1006	1013	-7	1157	1148	YX	861	N728YX	EWR	BGR	58	393	10	13	2023-08-30 10:00:00	Other
18013	2	10	624	630	-6	1009	945	B6	740	N535JB	LGA	FLL	185	1076	6	30	2023-02-10 06:00:00	FLL
18014	5	8	1254	1300	-6	1555	1610	UA	808	N17128	EWR	LAX	333	2454	13	0	2023-05-08 13:00:00	LAX
18015	5	5	1749	1759	-10	2040	2106	F9	951	N307FR	LGA	MIA	145	1096	17	59	2023-05-05 17:00:00	MIA
18020	10	28	2150	2159	-9	2318	2332	YX	1254	N402YX	JFK	ORF	55	290	21	59	2023-10-28 21:00:00	Other
18030	11	14	1404	1415	-11	1541	1601	YX	1095	N766YX	LGA	ORD	117	733	14	15	2023-11-14 14:00:00	ORD
18034	3	1	1014	1025	-11	1210	1228	AA	877	N976UY	EWR	CLT	94	529	10	25	2023-03-01 10:00:00	CLT
18039	11	20	812	820	-8	1114	1135	DL	258	N145DQ	LGA	DFW	215	1389	8	20	2023-11-20 08:00:00	Other
18041	7	12	1451	1500	-9	1639	1707	B6	315	N229JB	JFK	DTW	86	509	15	0	2023-07-12 15:00:00	Other
18044	9	27	1934	1945	-11	2116	2145	YX	1222	N751YX	EWR	CMH	73	463	19	45	2023-09-27 19:00:00	Other
18050	2	8	755	805	-10	1045	1125	B6	246	N2044J	JFK	FLL	144	1069	8	5	2023-02-08 08:00:00	FLL
18057	4	9	819	829	-10	1015	1032	YX	1129	N869RW	LGA	DAY	93	549	8	29	2023-04-09 08:00:00	Other
18060	1	6	1054	1100	-6	1346	1410	DL	1036	N105DU	LGA	SRQ	154	1047	11	0	2023-01-06 11:00:00	Other
18061	9	2	651	659	-8	1033	1057	B6	586	N637JB	EWR	SJU	203	1608	6	59	2023-09-02 06:00:00	Other
18063	5	30	1137	1145	-8	1410	1450	AS	11	N972AK	JFK	SEA	302	2422	11	45	2023-05-30 11:00:00	Other
18066	9	18	1953	1959	-6	2242	2311	UA	630	N37545	EWR	SMF	318	2500	19	59	2023-09-18 19:00:00	Other
18067	9	14	823	829	-6	1036	1046	YX	1870	N204JQ	LGA	IND	107	660	8	29	2023-09-14 08:00:00	Other
18074	5	19	2224	2230	-6	119	203	B6	907	N946JL	JFK	SFO	329	2586	22	30	2023-05-19 22:00:00	Other
18082	11	11	752	800	-8	1014	1049	DL	183	N509DT	JFK	DEN	238	1626	8	0	2023-11-11 08:00:00	Other
18085	5	31	1919	1925	-6	2110	2158	YX	1198	N428YX	LGA	TUL	161	1231	19	25	2023-05-31 19:00:00	Other
18088	1	30	2048	2055	-7	2145	2203	9E	1526	N901XJ	LGA	ALB	29	136	20	55	2023-01-30 20:00:00	Other
18092	11	1	1818	1825	-7	2056	2049	YX	1315	N433YX	LGA	OMA	177	1148	18	25	2023-11-01 18:00:00	Other
18100	5	22	930	939	-9	1028	1055	B6	833	N284JB	LGA	ACK	35	202	9	39	2023-05-22 09:00:00	Other
18106	2	23	1132	1140	-8	1432	1450	WN	274	N8741L	LGA	DAL	215	1381	11	40	2023-02-23 11:00:00	Other
18107	10	19	722	730	-8	920	1001	DL	173	N3756	LGA	DEN	210	1620	7	30	2023-10-19 07:00:00	Other
18110	2	24	1229	1241	-12	1656	1729	AA	258	N9018E	JFK	STT	186	1623	12	41	2023-02-24 12:00:00	Other
18114	2	13	1659	1708	-9	1854	1915	DL	876	N365NW	LGA	DTW	80	502	17	8	2023-02-13 17:00:00	Other
18116	11	29	1343	1350	-7	1634	1705	UA	939	N4888U	LGA	IAH	215	1416	13	50	2023-11-29 13:00:00	Other
18120	3	26	916	930	-14	1139	1159	B6	971	N334JB	LGA	SAV	120	722	9	30	2023-03-26 09:00:00	Other
18121	5	2	1638	1647	-9	1903	1954	YX	1687	N239JQ	LGA	OKC	186	1341	16	47	2023-05-02 16:00:00	Other
18138	7	19	924	930	-6	1156	1154	YX	935	N747YX	EWR	TVC	99	644	9	30	2023-07-19 09:00:00	Other
18141	5	2	2020	2030	-10	2141	2211	9E	1547	N197PQ	LGA	CHO	53	305	20	30	2023-05-02 20:00:00	Other
18143	6	14	753	759	-6	944	958	AA	558	N103US	JFK	CLT	86	541	7	59	2023-06-14 07:00:00	CLT
18146	10	25	1510	1517	-7	1754	1830	NK	587	N659NK	LGA	FLL	136	1076	15	17	2023-10-25 15:00:00	FLL
18155	6	3	721	729	-8	949	1031	AA	3	N107NN	JFK	LAX	303	2475	7	29	2023-06-03 07:00:00	LAX
18156	12	14	1950	1959	-9	2146	2218	YX	1108	N770YX	EWR	GSP	83	594	19	59	2023-12-14 19:00:00	Other
18157	4	3	621	630	-9	932	951	B6	644	N796JB	LGA	RSW	161	1080	6	30	2023-04-03 06:00:00	Other
18162	6	30	954	1000	-6	1059	1134	YX	1916	N228JQ	LGA	BOS	33	184	10	0	2023-06-30 10:00:00	BOS
18170	12	2	721	732	-11	1103	1049	AA	531	N829NN	LGA	DFW	250	1389	7	32	2023-12-02 07:00:00	Other
18172	10	27	1945	1959	-14	2102	2137	9E	1686	N924XJ	LGA	CHO	55	305	19	59	2023-10-27 19:00:00	Other
18178	1	14	1045	1055	-10	1408	1420	NK	1106	N515NK	LGA	MIA	149	1096	10	55	2023-01-14 10:00:00	MIA
18179	8	6	1011	1020	-9	1203	1241	9E	1142	N308PQ	LGA	CLT	81	544	10	20	2023-08-06 10:00:00	CLT
18188	1	26	1252	1300	-8	1441	1447	YX	1149	N748YX	EWR	GSO	85	445	13	0	2023-01-26 13:00:00	Other
18199	1	25	751	759	-8	853	900	YX	1183	N733YX	EWR	PHL	34	80	7	59	2023-01-25 07:00:00	Other
18213	8	26	2110	2119	-9	2217	2228	YX	839	N762YX	EWR	MDT	30	141	21	19	2023-08-26 21:00:00	Other
18214	1	15	818	830	-12	940	1016	AA	134	N847NN	LGA	ORD	113	733	8	30	2023-01-15 08:00:00	ORD
18216	11	27	832	839	-7	1023	1039	UA	94	N16701	EWR	DTW	85	488	8	39	2023-11-27 08:00:00	Other
18219	11	18	900	906	-6	1205	1211	UA	694	N47284	EWR	PBI	152	1023	9	6	2023-11-18 09:00:00	Other
18225	1	28	2048	2100	-12	2254	2336	YX	1412	N421YX	JFK	IND	107	665	21	0	2023-01-28 21:00:00	Other
18226	1	28	753	800	-7	1003	1020	DL	1089	N331NB	LGA	MSP	162	1020	8	0	2023-01-28 08:00:00	Other
18227	2	10	1302	1310	-8	1446	1517	YX	1202	N105HQ	LGA	CLE	78	419	13	10	2023-02-10 13:00:00	Other
18229	2	12	832	840	-8	1136	1206	AA	783	N359PX	LGA	MIA	160	1096	8	40	2023-02-12 08:00:00	MIA
18230	4	9	1617	1625	-8	1752	1807	AA	662	N708UW	LGA	RDU	68	431	16	25	2023-04-09 16:00:00	Other
18235	11	12	604	615	-11	856	920	UA	701	N36444	EWR	FLL	154	1065	6	15	2023-11-12 06:00:00	FLL
18239	11	12	936	945	-9	1228	1256	B6	645	N504JB	LGA	MCO	142	950	9	45	2023-11-12 09:00:00	MCO
18244	8	29	622	629	-7	743	756	UA	756	N897UA	LGA	ORD	115	733	6	29	2023-08-29 06:00:00	ORD
18253	7	16	1339	1345	-6	1603	1547	YX	1038	N408YX	LGA	CAE	112	617	13	45	2023-07-16 13:00:00	Other
18256	9	22	1253	1300	-7	1556	1609	AA	221	N342SX	LGA	MIA	157	1096	13	0	2023-09-22 13:00:00	MIA
18260	2	16	1323	1329	-6	1620	1643	UA	664	N855UA	LGA	IAH	219	1416	13	29	2023-02-16 13:00:00	Other
18262	11	16	1622	1629	-7	1917	1927	UA	792	N75425	EWR	MCO	138	937	16	29	2023-11-16 16:00:00	MCO
18263	5	25	1253	1259	-6	1446	1452	9E	1355	N337PQ	LGA	STL	131	888	12	59	2023-05-25 12:00:00	Other
18264	11	22	842	854	-12	1040	1055	9E	1442	N490PX	LGA	CLE	69	419	8	54	2023-11-22 08:00:00	Other
18270	8	26	1737	1745	-8	1930	1946	YX	884	N646RW	EWR	CMH	79	463	17	45	2023-08-26 17:00:00	Other
18273	3	28	924	930	-6	1159	1200	UA	876	N806UA	LGA	DEN	236	1620	9	30	2023-03-28 09:00:00	Other
18275	12	14	636	645	-9	815	854	YX	1255	N128HQ	LGA	MSP	144	1020	6	45	2023-12-14 06:00:00	Other
18280	8	17	1054	1100	-6	1357	1412	AA	224	N991NN	JFK	MIA	162	1089	11	0	2023-08-17 11:00:00	MIA
18287	3	29	658	710	-12	850	853	B6	408	N334JB	JFK	ORD	133	740	7	10	2023-03-29 07:00:00	ORD
18289	8	13	1222	1229	-7	1348	1400	YX	964	N115HQ	JFK	ORF	62	290	12	29	2023-08-13 12:00:00	Other
18293	4	8	1935	1945	-10	2156	2207	B6	612	N184JB	LGA	SAV	119	722	19	45	2023-04-08 19:00:00	Other
18301	3	28	1015	1029	-14	1136	1209	9E	1408	N485PX	LGA	BUF	52	292	10	29	2023-03-28 10:00:00	Other
18302	3	9	718	730	-12	1116	1120	AS	15	N298AK	JFK	SFO	388	2586	7	30	2023-03-09 07:00:00	Other
18304	1	10	1550	1600	-10	1822	1916	YX	1897	N878RW	LGA	OKC	196	1341	16	0	2023-01-10 16:00:00	Other
18306	9	19	645	700	-15	835	900	AA	321	N955AN	LGA	CLT	81	544	7	0	2023-09-19 07:00:00	CLT
18317	3	31	1204	1210	-6	1306	1326	YX	1259	N428YX	JFK	BOS	34	187	12	10	2023-03-31 12:00:00	BOS
18318	9	29	724	730	-6	853	906	DL	629	N101DU	LGA	ORD	109	733	7	30	2023-09-29 07:00:00	ORD
18319	8	1	923	929	-6	1051	1101	YX	1050	N440YX	LGA	RIC	57	292	9	29	2023-08-01 09:00:00	Other
18321	11	6	1620	1629	-9	1816	1830	NK	1035	N904NK	LGA	DTW	91	502	16	29	2023-11-06 16:00:00	Other
18322	5	31	2039	2050	-11	2217	2301	YX	1620	N203JQ	JFK	CMH	69	483	20	50	2023-05-31 20:00:00	Other
18333	4	15	602	610	-8	737	810	DL	398	N319NB	LGA	MSP	136	1020	6	10	2023-04-15 06:00:00	Other
18335	8	24	1519	1528	-9	1744	1759	YX	1004	N427YX	JFK	IND	105	665	15	28	2023-08-24 15:00:00	Other
18337	8	27	1746	1755	-9	1938	2000	NK	44	N931NK	LGA	DTW	83	502	17	55	2023-08-27 17:00:00	Other
18339	2	24	1613	1625	-12	1815	1820	AA	405	N723UW	LGA	RDU	83	431	16	25	2023-02-24 16:00:00	Other
18340	10	17	950	1000	-10	1208	1229	YX	1329	N122HQ	LGA	SDF	96	659	10	0	2023-10-17 10:00:00	Other
18343	2	28	1650	1700	-10	2033	2025	AA	600	N852NN	LGA	DFW	214	1389	17	0	2023-02-28 17:00:00	Other
18351	5	24	757	805	-8	947	954	OO	1097	N310SY	JFK	ORD	123	740	8	5	2023-05-24 08:00:00	ORD
18352	4	26	1104	1110	-6	1355	1340	YX	1092	N134HQ	LGA	XNA	173	1147	11	10	2023-04-26 11:00:00	Other
18353	8	3	1053	1059	-6	1245	1313	UA	362	N37434	EWR	PHX	267	2133	10	59	2023-08-03 10:00:00	Other
18364	5	19	1237	1245	-8	2034	1542	NK	81	N640NK	EWR	DFW	NA	1372	12	45	2023-05-19 12:00:00	Other
18372	10	16	959	1008	-9	1216	1231	YX	1151	N731YX	EWR	SAV	115	708	10	8	2023-10-16 10:00:00	Other
18382	7	21	1048	1055	-7	1215	1212	YX	1371	N880RW	JFK	ACK	40	199	10	55	2023-07-21 10:00:00	Other
18383	5	31	1135	1145	-10	1416	1450	AS	11	N491AS	JFK	SEA	302	2422	11	45	2023-05-31 11:00:00	Other
18385	12	2	1449	1458	-9	1600	1628	YX	1078	N728YX	EWR	ORF	54	284	14	58	2023-12-02 14:00:00	Other
18386	7	26	2019	2025	-6	2215	2247	B6	649	N608JB	LGA	MSY	148	1183	20	25	2023-07-26 20:00:00	Other
18390	9	26	922	929	-7	1059	1116	YX	1312	N410YX	JFK	CLE	74	425	9	29	2023-09-26 09:00:00	Other
18392	9	4	803	810	-7	1037	1055	DL	185	N139DU	LGA	DFW	179	1389	8	10	2023-09-04 08:00:00	Other
18393	1	21	1547	1559	-12	1851	1920	B6	140	N636JB	LGA	FLL	157	1076	15	59	2023-01-21 15:00:00	FLL
18401	11	24	1240	1250	-10	1338	1359	9E	1456	N187GJ	JFK	ITH	41	189	12	50	2023-11-24 12:00:00	Other
18405	12	12	704	710	-6	831	902	DL	607	N132DU	LGA	ORD	120	733	7	10	2023-12-12 07:00:00	ORD
18408	9	21	2205	2214	-9	35	45	NK	590	N920NK	EWR	ATL	114	746	22	14	2023-09-21 22:00:00	ATL
18411	11	30	550	600	-10	806	833	UA	366	N27260	EWR	ATL	114	746	6	0	2023-11-30 06:00:00	ATL
18412	11	10	624	630	-6	917	931	UA	931	N17309	EWR	TPA	141	997	6	30	2023-11-10 06:00:00	Other
18415	7	27	642	650	-8	933	957	AA	745	N804NN	LGA	MIA	149	1096	6	50	2023-07-27 06:00:00	MIA
18417	4	7	1322	1329	-7	1556	1548	YX	1160	N108HQ	LGA	MCI	179	1107	13	29	2023-04-07 13:00:00	Other
18419	8	16	1521	1529	-8	1748	1839	AS	75	N508AS	EWR	SFO	312	2565	15	29	2023-08-16 15:00:00	Other
18421	3	14	609	615	-6	921	940	UA	896	N34137	EWR	LAX	328	2454	6	15	2023-03-14 06:00:00	LAX
18424	9	20	824	840	-16	928	956	B6	51	N281JB	EWR	BOS	42	200	8	40	2023-09-20 08:00:00	BOS
18434	12	5	1936	1942	-6	2154	2153	YX	1324	N122HQ	LGA	DTW	89	502	19	42	2023-12-05 19:00:00	Other
18435	10	27	1100	1106	-6	1216	1236	YX	1335	N412YX	LGA	CHO	57	305	11	6	2023-10-27 11:00:00	Other
18440	7	23	1708	1715	-7	1836	1855	YX	1388	N875RW	LGA	DCA	43	214	17	15	2023-07-23 17:00:00	Other
18446	10	19	1053	1059	-6	1302	1342	DL	267	N110DX	LGA	ATL	110	762	10	59	2023-10-19 10:00:00	ATL
18448	12	2	1659	1706	-7	1852	1906	9E	1524	N902XJ	LGA	CLE	78	419	17	6	2023-12-02 17:00:00	Other
18452	10	14	1724	1730	-6	1910	1930	NK	47	N691NK	LGA	DTW	83	502	17	30	2023-10-14 17:00:00	Other
18458	1	10	1622	1629	-7	1723	1738	9E	1640	N482PX	LGA	PVD	32	143	16	29	2023-01-10 16:00:00	Other
18462	11	6	756	805	-9	1029	1034	UA	828	N14118	EWR	DEN	240	1605	8	5	2023-11-06 08:00:00	Other
18464	7	22	1654	1700	-6	1802	1828	9E	1165	N676CA	LGA	SYR	40	198	17	0	2023-07-22 17:00:00	Other
18467	3	6	649	659	-10	900	909	YX	1280	N136HQ	LGA	DTW	99	502	6	59	2023-03-06 06:00:00	Other
18469	6	29	834	840	-6	1051	1114	DL	163	N532DN	JFK	ATL	97	760	8	40	2023-06-29 08:00:00	ATL
18476	12	16	504	510	-6	757	825	AA	411	N989AN	EWR	MIA	155	1085	5	10	2023-12-16 05:00:00	MIA
18485	8	31	1049	1055	-6	1155	1211	YX	1334	N878RW	JFK	ACK	36	199	10	55	2023-08-31 10:00:00	Other
18488	5	16	1812	1820	-8	2028	2038	YX	1193	N134HQ	LGA	LIT	156	1085	18	20	2023-05-16 18:00:00	Other
18490	1	10	1120	1129	-9	1307	1326	9E	1681	N301PQ	LGA	RDU	76	431	11	29	2023-01-10 11:00:00	Other
18492	11	16	601	607	-6	911	918	AA	429	N964NN	LGA	MIA	151	1096	6	7	2023-11-16 06:00:00	MIA
18500	2	22	1420	1430	-10	1634	1625	AA	846	N802AW	LGA	RDU	76	431	14	30	2023-02-22 14:00:00	Other
18508	6	11	1416	1422	-6	1548	1559	B6	1033	N304JB	JFK	BUF	53	301	14	22	2023-06-11 14:00:00	Other
18510	12	4	743	750	-7	943	1009	YX	1036	N769YX	EWR	GRR	103	605	7	50	2023-12-04 07:00:00	Other
18518	4	19	553	600	-7	801	830	UA	371	N67827	EWR	DEN	228	1605	6	0	2023-04-19 06:00:00	Other
18524	5	9	1519	1525	-6	1721	1735	AA	910	N933NN	JFK	CLT	89	541	15	25	2023-05-09 15:00:00	CLT
18529	8	21	1903	1910	-7	2100	2144	UA	326	N37278	EWR	LAS	269	2227	19	10	2023-08-21 19:00:00	Other
18534	3	30	1051	1100	-9	1406	1427	B6	27	N593JB	JFK	SEA	353	2422	11	0	2023-03-30 11:00:00	Other
18542	3	2	1752	1800	-8	2034	2041	UA	885	N853UA	LGA	DEN	248	1620	18	0	2023-03-02 18:00:00	Other
18543	12	31	937	944	-7	1219	1251	B6	213	N709JB	LGA	MCO	132	950	9	44	2023-12-31 09:00:00	MCO
18545	9	26	2120	2128	-8	2241	2309	YX	1103	N651RW	EWR	MSN	110	799	21	28	2023-09-26 21:00:00	Other
18549	11	16	1057	1103	-6	1247	1242	9E	1629	N912XJ	LGA	ORF	53	296	11	3	2023-11-16 11:00:00	Other
18551	10	24	950	1000	-10	1200	1201	YX	1306	N431YX	LGA	GSP	92	610	10	0	2023-10-24 10:00:00	Other
18554	2	11	1829	1835	-6	2140	2150	AS	12	N942AK	JFK	SAN	336	2446	18	35	2023-02-11 18:00:00	Other
18560	5	10	1752	1800	-8	1914	1946	9E	1364	N914XJ	LGA	ORF	53	296	18	0	2023-05-10 18:00:00	Other
18565	9	28	1220	1230	-10	1504	1526	NK	482	N652NK	LGA	IAH	191	1416	12	30	2023-09-28 12:00:00	Other
18575	1	18	1322	1330	-8	1430	1453	YX	1908	N246JQ	JFK	PWM	52	273	13	30	2023-01-18 13:00:00	Other
18587	12	3	732	740	-8	956	1008	UA	790	N16703	EWR	SAV	115	708	7	40	2023-12-03 07:00:00	Other
18598	10	19	854	900	-6	1117	1218	AA	1	N111ZM	JFK	LAX	294	2475	9	0	2023-10-19 09:00:00	LAX
18599	4	5	554	600	-6	919	904	B6	481	N986JB	EWR	LAX	353	2454	6	0	2023-04-05 06:00:00	LAX
18602	4	13	620	630	-10	731	745	UA	477	N23707	EWR	BOS	45	200	6	30	2023-04-13 06:00:00	BOS
18603	10	18	2051	2059	-8	2226	2255	YX	1256	N426YX	JFK	RDU	67	427	20	59	2023-10-18 20:00:00	Other
18604	4	6	854	900	-6	1020	1030	9E	1357	N491PX	LGA	PWM	48	269	9	0	2023-04-06 09:00:00	Other
18605	4	7	841	847	-6	1143	1204	UA	457	N27261	EWR	AUS	222	1504	8	47	2023-04-07 08:00:00	Other
18608	6	10	1312	1320	-8	1508	1529	YX	1408	N134HQ	LGA	TYS	95	647	13	20	2023-06-10 13:00:00	Other
18609	11	11	1051	1059	-8	1145	1217	UA	274	N17104	EWR	BOS	34	200	10	59	2023-11-11 10:00:00	BOS
18612	5	28	1139	1145	-6	1356	1448	AS	8	N272AK	JFK	PDX	292	2454	11	45	2023-05-28 11:00:00	Other
18614	4	25	1249	1300	-11	1552	1611	B6	630	N510JB	EWR	RSW	160	1068	13	0	2023-04-25 13:00:00	Other
18620	6	16	1253	1300	-7	1353	1421	YX	1282	N108HQ	JFK	BOS	35	187	13	0	2023-06-16 13:00:00	BOS
18621	1	9	1112	1120	-8	1309	1334	YX	1418	N869RW	LGA	ROA	67	405	11	20	2023-01-09 11:00:00	Other
18623	12	25	1809	1815	-6	1943	2004	UA	480	N66803	EWR	RDU	70	416	18	15	2023-12-25 18:00:00	Other
18628	9	14	552	600	-8	735	802	AA	947	N172US	EWR	CLT	84	529	6	0	2023-09-14 06:00:00	CLT
18631	1	27	850	900	-10	1004	1030	YX	1126	N746YX	EWR	DCA	47	199	9	0	2023-01-27 09:00:00	Other
18634	10	15	928	935	-7	1030	1050	B6	575	N273JB	JFK	BTV	43	266	9	35	2023-10-15 09:00:00	Other
18651	7	3	1553	1600	-7	1930	1803	YX	1020	N407YX	LGA	GSP	102	610	16	0	2023-07-03 16:00:00	Other
18655	4	22	907	915	-8	1038	1034	B6	798	N228JB	LGA	BOS	32	184	9	15	2023-04-22 09:00:00	BOS
18661	8	8	1752	1800	-8	1903	1931	YX	1364	N210JQ	LGA	BOS	40	184	18	0	2023-08-08 18:00:00	BOS
18662	8	15	553	600	-7	857	905	NK	43	N658NK	LGA	FLL	155	1076	6	0	2023-08-15 06:00:00	FLL
18675	10	30	1750	1800	-10	2052	2106	F9	443	N367FR	LGA	MCO	139	950	18	0	2023-10-30 18:00:00	MCO
18676	1	21	1445	1455	-10	1636	1710	AA	756	N195UW	LGA	CLT	89	544	14	55	2023-01-21 14:00:00	CLT
18687	11	20	1402	1408	-6	1603	1633	UA	382	N66897	EWR	DEN	215	1605	14	8	2023-11-20 14:00:00	Other
18695	10	3	554	600	-6	759	818	DL	730	N6712B	JFK	ATL	103	760	6	0	2023-10-03 06:00:00	ATL
18696	12	21	2151	2200	-9	2312	2350	YX	1212	N438YX	LGA	RDU	65	431	22	0	2023-12-21 22:00:00	Other
18701	6	4	852	900	-8	1011	1051	YX	1332	N432YX	JFK	DCA	50	213	9	0	2023-06-04 09:00:00	Other
18713	10	3	1235	1242	-7	1358	1408	9E	1560	N920XJ	LGA	BTV	44	258	12	42	2023-10-03 12:00:00	Other
18716	9	9	736	745	-9	1017	959	B6	882	N523JB	LGA	CHS	129	641	7	45	2023-09-09 07:00:00	Other
18720	5	28	554	600	-6	709	738	UA	768	N18243	LGA	ORD	108	733	6	0	2023-05-28 06:00:00	ORD
18727	2	9	1753	1759	-6	2043	2124	B6	50	N806JB	JFK	SMF	326	2521	17	59	2023-02-09 17:00:00	Other
18728	1	2	1608	1615	-7	1749	1820	AA	112	N982NN	JFK	CLT	83	541	16	15	2023-01-02 16:00:00	CLT
18731	11	24	652	700	-8	1007	1020	DL	314	N391DA	JFK	RSW	173	1074	7	0	2023-11-24 07:00:00	Other
18734	6	6	945	951	-6	1257	1253	UA	643	N57299	EWR	RSW	147	1068	9	51	2023-06-06 09:00:00	Other
18740	9	12	1118	1125	-7	1326	1349	B6	22	N656JB	LGA	DEN	219	1620	11	25	2023-09-12 11:00:00	Other
18742	6	23	653	700	-7	818	830	YX	1780	N226JQ	JFK	BOS	36	187	7	0	2023-06-23 07:00:00	BOS
18746	6	1	1019	1029	-10	1218	1248	YX	1305	N133HQ	LGA	XNA	148	1147	10	29	2023-06-01 10:00:00	Other
18751	8	4	1305	1315	-10	1514	1529	9E	1114	N134EV	JFK	CHS	94	636	13	15	2023-08-04 13:00:00	Other
18753	5	23	940	949	-9	1046	1056	YX	1675	N220JQ	LGA	BDL	26	101	9	49	2023-05-23 09:00:00	Other
18758	8	24	620	629	-9	742	756	UA	756	N845UA	LGA	ORD	113	733	6	29	2023-08-24 06:00:00	ORD
18765	9	4	1457	1505	-8	1746	1821	DL	347	N328NB	LGA	PBI	132	1035	15	5	2023-09-04 15:00:00	Other
18776	6	7	1126	1135	-9	1417	1434	B6	30	N267JB	JFK	MCO	141	944	11	35	2023-06-07 11:00:00	MCO
18783	8	6	1611	1620	-9	1733	1804	9E	1168	N914XJ	LGA	RIC	54	292	16	20	2023-08-06 16:00:00	Other
18787	5	5	1650	1659	-9	1805	1835	YX	1631	N228JQ	LGA	RIC	56	292	16	59	2023-05-05 16:00:00	Other
18794	9	7	1551	1559	-8	NA	1803	YX	1217	N748YX	EWR	MYR	NA	550	15	59	2023-09-07 15:00:00	Other
18798	8	31	1801	1808	-7	2044	2058	UA	510	N33209	EWR	MCO	131	937	18	8	2023-08-31 18:00:00	MCO
18801	9	25	1523	1529	-6	1816	1844	AS	82	N287AK	EWR	SFO	320	2565	15	29	2023-09-25 15:00:00	Other
18804	4	20	2229	2235	-6	19	6	YX	1452	N212JQ	JFK	PWM	48	273	22	35	2023-04-20 22:00:00	Other
18814	1	10	1829	1845	-16	2021	2107	9E	1550	N183GJ	LGA	CLT	80	544	18	45	2023-01-10 18:00:00	CLT
18824	1	9	1923	1937	-14	2114	2150	YX	1301	N433YX	LGA	CMH	72	479	19	37	2023-01-09 19:00:00	Other
18829	3	8	620	635	-15	804	827	YX	1611	N209JQ	LGA	CMH	83	479	6	35	2023-03-08 06:00:00	Other
18832	6	18	837	845	-8	1037	1105	9E	1554	N303PQ	LGA	SAV	107	722	8	45	2023-06-18 08:00:00	Other
18833	10	10	1852	1900	-8	2109	2124	YX	1270	N420YX	LGA	IND	103	660	19	0	2023-10-10 19:00:00	Other
18834	3	29	1009	1015	-6	1330	1314	UA	417	N23707	EWR	SRQ	157	1034	10	15	2023-03-29 10:00:00	Other
18842	10	2	922	932	-10	1039	1043	9E	1456	N293PQ	LGA	PVD	32	143	9	32	2023-10-02 09:00:00	Other
18848	6	16	1252	1303	-11	1447	1448	DL	889	N977AT	EWR	DTW	100	488	13	3	2023-06-16 13:00:00	Other
18849	7	7	804	810	-6	1009	1036	B6	777	N569JB	LGA	ATL	101	762	8	10	2023-07-07 08:00:00	ATL
18850	7	30	653	659	-6	808	831	AA	509	N942NN	EWR	ORD	116	719	6	59	2023-07-30 06:00:00	ORD
18851	4	10	1222	1229	-7	1305	1325	YX	1028	N730YX	EWR	AVP	27	93	12	29	2023-04-10 12:00:00	Other
18852	5	12	722	730	-8	953	1026	B6	319	N583JB	JFK	PBI	132	1028	7	30	2023-05-12 07:00:00	Other
18856	10	18	1139	1145	-6	1232	1247	YX	1162	N754YX	EWR	PHL	31	80	11	45	2023-10-18 11:00:00	Other
18857	9	5	1516	1522	-6	1746	1801	YX	1851	N210JQ	LGA	JAX	112	833	15	22	2023-09-05 15:00:00	Other
18861	10	18	1221	1229	-8	1340	1349	DL	538	N126DU	JFK	BOS	41	187	12	29	2023-10-18 12:00:00	BOS
18874	9	9	1521	1530	-9	NA	1748	B6	831	N589JB	JFK	MCI	NA	1113	15	30	2023-09-09 15:00:00	Other
18875	12	8	2050	2059	-9	2239	2306	NK	994	N710NK	EWR	DTW	79	488	20	59	2023-12-08 20:00:00	Other
18876	10	17	943	950	-7	1054	1115	YX	1308	N407YX	LGA	DCA	51	214	9	50	2023-10-17 09:00:00	Other
18877	10	29	2120	2129	-9	2316	2311	YX	1348	N413YX	LGA	CLE	76	419	21	29	2023-10-29 21:00:00	Other
18881	4	6	709	715	-6	947	953	9E	1341	N132EV	LGA	JAX	117	833	7	15	2023-04-06 07:00:00	Other
18890	12	13	747	755	-8	939	939	UA	66	N36247	EWR	CLE	75	404	7	55	2023-12-13 07:00:00	Other
18902	11	28	1622	1630	-8	1752	1819	DL	563	N111NG	LGA	ORD	117	733	16	30	2023-11-28 16:00:00	ORD
18903	4	1	851	900	-9	1215	1225	AS	135	N596AS	EWR	SFO	348	2565	9	0	2023-04-01 09:00:00	Other
18909	3	24	1625	1635	-10	1800	1811	YX	1295	N870RW	LGA	CHO	66	305	16	35	2023-03-24 16:00:00	Other
18913	12	31	1309	1319	-10	1451	1515	9E	1400	N480PX	LGA	RDU	72	431	13	19	2023-12-31 13:00:00	Other
18928	4	20	810	816	-6	1031	1040	YX	1563	N206JQ	LGA	MCI	172	1107	8	16	2023-04-20 08:00:00	Other
18929	4	4	621	630	-9	1009	1004	AA	32	N103NN	JFK	SFO	365	2586	6	30	2023-04-04 06:00:00	Other
18931	5	2	931	940	-9	1039	1110	YX	1651	N224JQ	LGA	DCA	45	214	9	40	2023-05-02 09:00:00	Other
18933	10	17	831	840	-9	955	1007	YX	1849	N238JQ	EWR	BOS	38	200	8	40	2023-10-17 08:00:00	BOS
18935	10	4	848	859	-11	1139	1210	UA	560	N16234	EWR	SAT	203	1569	8	59	2023-10-04 08:00:00	Other
18944	3	9	651	700	-9	855	926	B6	335	N558JB	JFK	SAV	104	718	7	0	2023-03-09 07:00:00	Other
18946	3	5	1234	1241	-7	1747	1729	AA	242	N9017P	JFK	STT	196	1623	12	41	2023-03-05 12:00:00	Other
18947	2	11	904	915	-11	1048	1125	YX	1569	N233JQ	LGA	CMH	79	479	9	15	2023-02-11 09:00:00	Other
18948	5	10	1532	1542	-10	1715	1739	YX	1570	N243JQ	LGA	STL	132	888	15	42	2023-05-10 15:00:00	Other
18950	10	19	1349	1355	-6	1614	1659	DL	268	N171DN	JFK	LAX	294	2475	13	55	2023-10-19 13:00:00	LAX
18951	10	17	2018	2026	-8	2210	2238	YX	1119	N726YX	EWR	AVL	87	583	20	26	2023-10-17 20:00:00	Other
18955	9	20	1037	1043	-6	1336	1353	DL	1000	N123DQ	LGA	SRQ	150	1047	10	43	2023-09-20 10:00:00	Other
18963	6	7	654	705	-11	958	1010	B6	703	N593JB	EWR	RSW	159	1068	7	5	2023-06-07 07:00:00	Other
18964	11	10	824	830	-6	1130	1133	UA	134	N13018	EWR	LAX	321	2454	8	30	2023-11-10 08:00:00	LAX
18966	12	1	1443	1450	-7	1717	1716	9E	1506	N925XJ	LGA	MCI	187	1107	14	50	2023-12-01 14:00:00	Other
18968	12	17	700	709	-9	857	929	9E	1669	N301PQ	JFK	DTW	87	509	7	9	2023-12-17 07:00:00	Other
18970	1	17	2149	2200	-11	2325	2355	YX	1449	N131HQ	LGA	RDU	79	431	22	0	2023-01-17 22:00:00	Other
18974	1	24	1657	1705	-8	1831	1836	YX	1742	N215JQ	LGA	BTV	45	258	17	5	2023-01-24 17:00:00	Other
18984	4	20	1051	1100	-9	1340	1413	B6	191	N779JB	JFK	FLL	139	1069	11	0	2023-04-20 11:00:00	FLL
18990	9	1	1322	1330	-8	1433	1447	UA	521	N17302	EWR	ORF	51	284	13	30	2023-09-01 13:00:00	Other
18998	9	2	2123	2135	-12	2307	2302	9E	1634	N134EV	JFK	ITH	48	189	21	35	2023-09-02 21:00:00	Other
19002	1	24	1620	1627	-7	2014	1947	UA	730	N854UA	EWR	AUS	259	1504	16	27	2023-01-24 16:00:00	Other
19005	3	15	518	525	-7	640	700	AA	913	N895NN	EWR	ORD	109	719	5	25	2023-03-15 05:00:00	ORD
19006	11	22	1148	1157	-9	1408	1353	YX	1104	N722YX	EWR	ILM	99	488	11	57	2023-11-22 11:00:00	Other
19017	3	16	1918	1925	-7	2136	2149	9E	1550	N582CA	JFK	DTW	93	509	19	25	2023-03-16 19:00:00	Other
19026	1	18	550	600	-10	752	810	AA	273	N922US	LGA	CLT	99	544	6	0	2023-01-18 06:00:00	CLT
19039	10	10	2154	2200	-6	2310	2333	9E	1539	N305PQ	JFK	BTV	47	266	22	0	2023-10-10 22:00:00	Other
19040	6	10	858	910	-12	1047	1116	NK	559	N609NK	EWR	CHS	86	628	9	10	2023-06-10 09:00:00	Other
19044	11	18	917	925	-8	1208	1229	DL	581	N109DN	LGA	MCO	134	950	9	25	2023-11-18 09:00:00	MCO
19056	2	26	850	900	-10	1100	1136	B6	920	N193JB	LGA	SAV	107	722	9	0	2023-02-26 09:00:00	Other
19061	3	4	1721	1729	-8	2021	2040	UA	475	N17262	EWR	IAH	202	1400	17	29	2023-03-04 17:00:00	Other
19063	4	17	645	655	-10	922	928	B6	120	N307JB	LGA	JAX	132	833	6	55	2023-04-17 06:00:00	Other
19065	7	7	542	550	-8	811	831	AA	482	N866NN	LGA	DFW	183	1389	5	50	2023-07-07 05:00:00	Other
19067	5	25	1518	1525	-7	1658	1735	DL	570	N322NB	LGA	MSP	135	1020	15	25	2023-05-25 15:00:00	Other
19069	3	6	1503	1510	-7	1817	1835	B6	865	N307JB	LGA	SRQ	149	1047	15	10	2023-03-06 15:00:00	Other
19071	1	24	1722	1730	-8	1957	1952	9E	1453	N183GJ	LGA	CVG	101	585	17	30	2023-01-24 17:00:00	Other
19072	10	4	1128	1135	-7	1323	1355	DL	847	N316DU	LGA	MSY	151	1183	11	35	2023-10-04 11:00:00	Other
19081	11	2	1407	1415	-8	1657	1713	UA	639	N33132	EWR	MCO	142	937	14	15	2023-11-02 14:00:00	MCO
19088	12	15	502	510	-8	743	825	B6	488	N961JT	EWR	LAX	319	2454	5	10	2023-12-15 05:00:00	LAX
19094	12	22	1144	1154	-10	1329	1405	YX	1345	N419YX	LGA	MEM	137	963	11	54	2023-12-22 11:00:00	Other
19098	12	10	921	930	-9	1209	1310	AS	12	N472AS	JFK	SAN	329	2446	9	30	2023-12-10 09:00:00	Other
19100	2	11	852	900	-8	1027	1119	AA	931	N907AN	JFK	ORD	126	740	9	0	2023-02-11 09:00:00	ORD
19109	3	1	1235	1250	-15	1405	1423	YX	1340	N870RW	LGA	ORF	60	296	12	50	2023-03-01 12:00:00	Other
19118	4	24	2207	2214	-7	2345	2359	9E	1322	N319PQ	JFK	BUF	57	301	22	14	2023-04-24 22:00:00	Other
19121	10	17	1655	1701	-6	1826	1840	UA	757	N17139	EWR	ORD	107	719	17	1	2023-10-17 17:00:00	ORD
19122	5	25	1918	1925	-7	2130	2150	YX	1249	N416YX	LGA	XNA	157	1147	19	25	2023-05-25 19:00:00	Other
19123	11	15	903	910	-7	1027	1053	DL	907	N129DU	LGA	ORD	118	733	9	10	2023-11-15 09:00:00	ORD
19126	8	17	1222	1229	-7	1507	1529	UA	642	N410UA	EWR	SAT	203	1569	12	29	2023-08-17 12:00:00	Other
19128	3	31	2127	2135	-8	2240	2258	YX	1661	N202JQ	LGA	ROC	49	254	21	35	2023-03-31 21:00:00	Other
19129	8	19	1413	1420	-7	1542	1608	AA	172	N717UW	LGA	ORD	114	733	14	20	2023-08-19 14:00:00	ORD
19130	9	20	1334	1346	-12	1458	1519	YX	1866	N224JQ	JFK	ORF	56	290	13	46	2023-09-20 13:00:00	Other
19133	12	27	553	603	-10	703	728	YX	1046	N859RW	LGA	IAD	48	229	6	3	2023-12-27 06:00:00	Other
19136	12	30	1553	1559	-6	1728	1802	YX	1023	N721YX	EWR	CMH	68	463	15	59	2023-12-30 15:00:00	Other
19138	10	31	2149	2159	-10	2246	2320	YX	1331	N413YX	JFK	BOS	32	187	21	59	2023-10-31 21:00:00	BOS
19142	12	21	1837	1850	-13	2039	2119	9E	1438	N929XJ	JFK	IND	95	665	18	50	2023-12-21 18:00:00	Other
19148	10	21	1926	1933	-7	2138	2209	DL	335	N106DU	LGA	JAX	114	833	19	33	2023-10-21 19:00:00	Other
19151	11	15	1641	1650	-9	1825	1840	AA	221	N760US	LGA	STL	138	888	16	50	2023-11-15 16:00:00	Other
19154	2	20	1039	1045	-6	1227	1251	AA	884	N814AW	LGA	STL	148	888	10	45	2023-02-20 10:00:00	Other
19155	3	11	2223	2230	-7	2353	8	9E	1423	N300PQ	JFK	BGR	62	382	22	30	2023-03-11 22:00:00	Other
19161	10	25	2125	2135	-10	2316	2341	OO	1206	N324SY	JFK	CLE	77	425	21	35	2023-10-25 21:00:00	Other
19163	5	23	1731	1741	-10	1916	1945	9E	1404	N297PQ	LGA	MYR	82	563	17	41	2023-05-23 17:00:00	Other
19167	9	30	822	829	-7	1048	1129	UA	289	N47284	EWR	SAN	310	2425	8	29	2023-09-30 08:00:00	Other
19172	6	15	748	755	-7	854	919	AA	782	N770UW	LGA	DCA	41	214	7	55	2023-06-15 07:00:00	Other
19174	6	1	1051	1101	-10	1231	1234	YX	1403	N420YX	JFK	ORF	56	290	11	1	2023-06-01 11:00:00	Other
19180	9	17	802	810	-8	1146	1207	UA	806	N59053	EWR	SJU	191	1608	8	10	2023-09-17 08:00:00	Other
19183	6	21	933	939	-6	1126	1145	YX	1294	N129HQ	JFK	CMH	80	483	9	39	2023-06-21 09:00:00	Other
19185	7	26	2042	2050	-8	2213	2229	YX	1413	N242JQ	LGA	ORF	63	296	20	50	2023-07-26 20:00:00	Other
19187	5	2	823	829	-6	1010	1032	YX	1229	N867RW	LGA	DAY	85	549	8	29	2023-05-02 08:00:00	Other
19199	3	25	842	848	-6	1102	1112	DL	613	N117DU	LGA	CHS	101	641	8	48	2023-03-25 08:00:00	Other
19202	12	22	653	659	-6	755	828	YX	1272	N101HQ	LGA	DCA	43	214	6	59	2023-12-22 06:00:00	Other
19203	12	14	1034	1041	-7	1320	1344	UA	242	N47280	EWR	TPA	143	997	10	41	2023-12-14 10:00:00	Other
19204	10	5	1825	1831	-6	2027	2037	DL	896	N983AT	EWR	MSP	160	1008	18	31	2023-10-05 18:00:00	Other
19205	7	11	1227	1235	-8	1452	1534	DL	129	N118DU	LGA	DFW	182	1389	12	35	2023-07-11 12:00:00	Other
19212	2	13	951	1000	-9	1130	1143	UA	697	N454UA	LGA	ORD	114	733	10	0	2023-02-13 10:00:00	ORD
19219	10	22	2151	2159	-8	2318	2327	9E	1380	N305PQ	LGA	BGR	64	378	21	59	2023-10-22 21:00:00	Other
19228	2	22	818	825	-7	950	1039	9E	1438	N908XJ	LGA	ILM	74	500	8	25	2023-02-22 08:00:00	Other
19234	2	14	2052	2100	-8	2221	2239	AA	264	N765US	EWR	ORD	115	719	21	0	2023-02-14 21:00:00	ORD
19241	10	5	2049	2059	-10	2154	2231	YX	1804	N810MD	LGA	PWM	46	269	20	59	2023-10-05 20:00:00	Other
19251	8	27	917	924	-7	1351	1326	UA	457	N21723	EWR	STT	243	1634	9	24	2023-08-27 09:00:00	Other
19253	3	17	1321	1330	-9	1444	1443	B6	41	N982JB	JFK	SYR	47	209	13	30	2023-03-17 13:00:00	Other
19258	9	6	1059	1113	-14	1238	1310	9E	1612	N197PQ	LGA	RDU	62	431	11	13	2023-09-06 11:00:00	Other
19267	10	11	1243	1250	-7	1343	1359	9E	1381	N928XJ	JFK	ITH	42	189	12	50	2023-10-11 12:00:00	Other
19270	10	24	1024	1030	-6	1312	1343	B6	668	N579JB	LGA	RSW	147	1080	10	30	2023-10-24 10:00:00	Other
19277	12	30	1722	1729	-7	2024	2042	UA	549	N17316	EWR	FLL	156	1065	17	29	2023-12-30 17:00:00	FLL
19280	12	1	658	704	-6	943	1009	DL	517	N366NW	LGA	TPA	147	1010	7	4	2023-12-01 07:00:00	Other
19283	4	13	837	847	-10	1108	1204	UA	457	N17285	EWR	AUS	188	1504	8	47	2023-04-13 08:00:00	Other
19293	1	9	1943	1950	-7	2156	2229	YX	1877	N810MD	LGA	MCI	158	1107	19	50	2023-01-09 19:00:00	Other
19307	6	7	1237	1245	-8	1427	1415	9E	1460	N134EV	LGA	MKE	107	738	12	45	2023-06-07 12:00:00	Other
19313	12	1	918	929	-11	1125	1147	YX	1063	N754YX	EWR	AVL	101	583	9	29	2023-12-01 09:00:00	Other
19314	1	1	1322	1329	-7	1513	1544	YX	1299	N826MD	LGA	CMH	86	479	13	29	2023-01-01 13:00:00	Other
19317	3	17	824	830	-6	1002	1007	AA	126	N949NN	LGA	ORD	118	733	8	30	2023-03-17 08:00:00	ORD
19319	10	3	1948	1955	-7	2126	2145	9E	1403	N316PQ	EWR	RDU	67	416	19	55	2023-10-03 19:00:00	Other
19320	8	5	1053	1100	-7	1215	1234	YX	1061	N429YX	JFK	BNA	108	765	11	0	2023-08-05 11:00:00	Other
19328	9	28	2123	2130	-7	2347	33	B6	30	N981JT	JFK	SAN	307	2446	21	30	2023-09-28 21:00:00	Other
19332	12	4	552	600	-8	815	833	UA	371	N17264	EWR	ATL	125	746	6	0	2023-12-04 06:00:00	ATL
19333	9	23	620	629	-9	800	807	UA	272	N17262	EWR	CLE	61	404	6	29	2023-09-23 06:00:00	Other
19342	8	10	752	759	-7	1018	1012	UA	673	N66808	EWR	DEN	224	1605	7	59	2023-08-10 07:00:00	Other
19347	9	6	2153	2159	-6	2252	2303	9E	1650	N490PX	LGA	PVD	35	143	21	59	2023-09-06 21:00:00	Other
19359	2	10	1729	1735	-6	2101	2101	DL	447	N370NW	JFK	AUS	240	1521	17	35	2023-02-10 17:00:00	Other
19362	11	11	951	1000	-9	1203	1232	YX	1061	N760YX	EWR	SDF	107	642	10	0	2023-11-11 10:00:00	Other
19364	1	19	449	500	-11	759	811	AA	237	N899NN	EWR	DFW	223	1372	5	0	2023-01-19 05:00:00	Other
19371	3	28	2044	2050	-6	2234	2250	OO	1194	N297SY	JFK	CLE	81	425	20	50	2023-03-28 20:00:00	Other
19373	5	23	554	600	-6	707	722	AA	729	N778XF	LGA	DCA	45	214	6	0	2023-05-23 06:00:00	Other
19377	12	9	1723	1729	-6	2023	2050	UA	749	N17265	EWR	PDX	340	2434	17	29	2023-12-09 17:00:00	Other
19379	7	30	1453	1459	-6	1657	1719	YX	1037	N104HQ	JFK	IND	101	665	14	59	2023-07-30 14:00:00	Other
19384	8	1	1326	1335	-9	1454	1452	YX	905	N763YX	EWR	BTV	45	266	13	35	2023-08-01 13:00:00	Other
19387	8	23	2052	2100	-8	2227	2238	UA	571	N874UA	LGA	ORD	112	733	21	0	2023-08-23 21:00:00	ORD
19389	7	3	1054	1100	-6	1312	1322	YX	1017	N443YX	LGA	XNA	170	1147	11	0	2023-07-03 11:00:00	Other
19391	9	5	620	630	-10	836	850	B6	245	N559JB	JFK	JAX	106	828	6	30	2023-09-05 06:00:00	Other
19393	9	7	1320	1330	-10	1456	1533	YX	1350	N412YX	LGA	MSP	144	1020	13	30	2023-09-07 13:00:00	Other
19394	7	3	856	907	-11	1003	1030	B6	510	N190JB	JFK	BTV	42	266	9	7	2023-07-03 09:00:00	Other
19395	8	22	620	630	-10	807	830	YX	1080	N421YX	JFK	RDU	66	427	6	30	2023-08-22 06:00:00	Other
19403	5	17	1318	1329	-11	1454	1515	YX	1323	N426YX	JFK	PIT	67	340	13	29	2023-05-17 13:00:00	Other
19422	4	20	1003	1010	-7	1301	1313	NK	30	N665NK	EWR	MIA	145	1085	10	10	2023-04-20 10:00:00	MIA
19429	4	9	924	930	-6	1131	1200	UA	784	N845UA	LGA	DEN	221	1620	9	30	2023-04-09 09:00:00	Other
19430	10	18	823	830	-7	1000	1012	UA	586	N38467	EWR	CLE	61	404	8	30	2023-10-18 08:00:00	Other
19432	3	24	2221	2232	-11	2337	2359	9E	1560	N308PQ	JFK	SYR	41	209	22	32	2023-03-24 22:00:00	Other
19436	1	30	1923	1929	-6	2038	2103	YX	1766	N223JQ	LGA	DCA	49	214	19	29	2023-01-30 19:00:00	Other
19443	11	25	926	933	-7	1211	1201	B6	977	N3132J	JFK	SAV	114	718	9	33	2023-11-25 09:00:00	Other
19450	6	1	1050	1100	-10	1337	1412	AA	275	N861NN	JFK	MIA	147	1089	11	0	2023-06-01 11:00:00	MIA
19453	3	29	1150	1200	-10	1258	1316	AA	775	N776XF	LGA	DCA	46	214	12	0	2023-03-29 12:00:00	Other
19460	10	10	851	900	-9	1012	1044	UA	667	N37549	EWR	ORD	111	719	9	0	2023-10-10 09:00:00	ORD
19471	1	24	1721	1729	-8	2053	2048	B6	192	N534JB	LGA	FLL	171	1076	17	29	2023-01-24 17:00:00	FLL
19487	3	16	1448	1500	-12	1606	1635	YX	1261	N138HQ	LGA	DCA	48	214	15	0	2023-03-16 15:00:00	Other
19488	12	2	1434	1440	-6	1632	1644	UA	362	N847UA	EWR	CLT	93	529	14	40	2023-12-02 14:00:00	CLT
19492	3	13	722	730	-8	948	1025	B6	149	N978JB	JFK	LAS	297	2248	7	30	2023-03-13 07:00:00	Other
19497	11	14	641	650	-9	803	832	YX	1793	N882RW	LGA	PIT	62	335	6	50	2023-11-14 06:00:00	Other
19503	8	21	1047	1053	-6	1315	1350	B6	277	N505JB	EWR	MCO	118	937	10	53	2023-08-21 10:00:00	MCO
19504	4	7	1452	1459	-7	1709	1729	YX	1168	N442YX	JFK	CVG	100	589	14	59	2023-04-07 14:00:00	Other
19508	3	12	923	930	-7	1215	1258	AS	9	N943AK	JFK	SEA	320	2422	9	30	2023-03-12 09:00:00	Other
19523	4	25	1158	1205	-7	1354	1422	YX	1145	N105HQ	LGA	MSP	147	1020	12	5	2023-04-25 12:00:00	Other
19524	4	18	1118	1130	-12	1412	1448	AA	261	N901NN	JFK	MIA	160	1089	11	30	2023-04-18 11:00:00	MIA
19528	4	12	1852	1859	-7	2032	2058	YX	1040	N859RW	EWR	CMH	67	463	18	59	2023-04-12 18:00:00	Other
19539	5	30	2050	2100	-10	2218	2247	YX	1186	N406YX	JFK	ORF	51	290	21	0	2023-05-30 21:00:00	Other
19543	11	26	835	843	-8	1206	1217	UA	564	N469UA	EWR	SAT	247	1569	8	43	2023-11-26 08:00:00	Other
19544	2	2	731	738	-7	849	903	UA	613	N442UA	EWR	ORF	58	284	7	38	2023-02-02 07:00:00	Other
19552	3	8	624	630	-6	921	943	B6	963	N657JB	JFK	FLL	138	1069	6	30	2023-03-08 06:00:00	FLL
19556	8	31	1153	1200	-7	1428	1443	UA	660	N215UA	EWR	LAX	299	2454	12	0	2023-08-31 12:00:00	LAX
19558	1	18	653	700	-7	936	1005	UA	647	N27255	EWR	TPA	144	997	7	0	2023-01-18 07:00:00	Other
19561	1	24	1844	1850	-6	2134	2200	B6	84	N2043J	JFK	MCO	137	944	18	50	2023-01-24 18:00:00	MCO
19564	12	24	826	835	-9	1405	1451	UA	110	N66051	EWR	HNL	618	4962	8	35	2023-12-24 08:00:00	Other
19581	2	8	1442	1449	-7	1713	1750	B6	573	N998JE	EWR	MCO	128	937	14	49	2023-02-08 14:00:00	MCO
19584	10	11	924	933	-9	1304	1330	B6	990	N974JT	JFK	SJU	189	1598	9	33	2023-10-11 09:00:00	Other
19588	1	27	1104	1114	-10	1246	1320	YX	1325	N434YX	LGA	ROA	74	405	11	14	2023-01-27 11:00:00	Other
19589	11	24	1534	1540	-6	1656	1725	9E	1603	N931XJ	LGA	BNA	118	764	15	40	2023-11-24 15:00:00	Other
19601	3	21	1541	1548	-7	1706	1726	YX	1293	N428YX	JFK	DCA	58	213	15	48	2023-03-21 15:00:00	Other
19603	11	16	2122	2129	-7	2329	14	DL	825	N505DZ	JFK	ATL	101	760	21	29	2023-11-16 21:00:00	ATL
19609	6	2	821	829	-8	951	1014	DL	886	N116DU	LGA	ORD	108	733	8	29	2023-06-02 08:00:00	ORD
19615	9	23	953	959	-6	1228	1258	NK	250	N695NK	LGA	MCO	129	950	9	59	2023-09-23 09:00:00	MCO
19617	9	22	734	745	-11	925	957	YX	1208	N638RW	EWR	GRR	88	605	7	45	2023-09-22 07:00:00	Other
19619	3	28	1057	1109	-12	1152	1218	YX	1729	N210JQ	LGA	BDL	22	101	11	9	2023-03-28 11:00:00	Other
19620	8	4	553	600	-7	840	839	DL	222	N108DQ	LGA	DFW	204	1389	6	0	2023-08-04 06:00:00	Other
19621	5	9	1322	1330	-8	1558	1548	YX	1253	N129HQ	LGA	MCI	178	1107	13	30	2023-05-09 13:00:00	Other
19623	10	14	2021	2027	-6	2114	2146	YX	1173	N728YX	EWR	ITH	35	172	20	27	2023-10-14 20:00:00	Other
19625	11	30	2019	2025	-6	2227	2245	UA	617	N38454	EWR	SAV	106	708	20	25	2023-11-30 20:00:00	Other
19629	7	12	1451	1500	-9	1634	1655	YX	1097	N418YX	LGA	STL	128	888	15	0	2023-07-12 15:00:00	Other
19632	7	12	724	730	-6	904	927	9E	1142	N479PX	LGA	GSO	64	461	7	30	2023-07-12 07:00:00	Other
19657	9	5	2150	2200	-10	2308	2323	B6	918	N206JB	JFK	SYR	39	209	22	0	2023-09-05 22:00:00	Other
19669	4	23	1254	1300	-6	1417	1448	YX	1027	N858RW	LGA	ORD	104	733	13	0	2023-04-23 13:00:00	ORD
19674	10	26	1049	1055	-6	1216	1255	G4	1012	307NV	EWR	VPS	127	988	10	55	2023-10-26 10:00:00	Other
19682	4	27	1249	1300	-11	1546	1611	B6	630	N708JB	EWR	RSW	145	1068	13	0	2023-04-27 13:00:00	Other
19686	10	6	1030	1039	-9	1247	1314	YX	1269	N417YX	LGA	XNA	170	1147	10	39	2023-10-06 10:00:00	Other
19687	11	12	853	900	-7	1215	1233	AA	70	N108NN	JFK	LAX	333	2475	9	0	2023-11-12 09:00:00	LAX
19691	10	24	1321	1327	-6	1620	1639	NK	1013	N632NK	EWR	MIA	132	1085	13	27	2023-10-24 13:00:00	MIA
19701	11	9	2047	2059	-12	2212	2233	9E	1438	N314PQ	LGA	ROC	57	254	20	59	2023-11-09 20:00:00	Other
19702	3	28	1755	1805	-10	2127	2134	DL	637	N357NW	JFK	AUS	237	1521	18	5	2023-03-28 18:00:00	Other
19704	2	5	1423	1430	-7	1539	1558	YX	1212	N103HQ	JFK	ORF	59	290	14	30	2023-02-05 14:00:00	Other
19705	1	23	654	700	-6	824	843	YX	1871	N810MD	LGA	PIT	66	335	7	0	2023-01-23 07:00:00	Other
19707	10	3	2054	2100	-6	2238	2252	YX	1775	N222JQ	JFK	PIT	62	340	21	0	2023-10-03 21:00:00	Other
19711	10	8	909	917	-8	1030	1101	YX	1093	N750YX	EWR	MSN	116	799	9	17	2023-10-08 09:00:00	Other
19712	9	5	1005	1015	-10	1131	1202	AA	200	N773XF	LGA	STL	118	888	10	15	2023-09-05 10:00:00	Other
19713	11	30	1621	1629	-8	1801	1826	9E	1599	N932XJ	LGA	CLE	69	419	16	29	2023-11-30 16:00:00	Other
19717	4	25	751	800	-9	1021	1021	9E	1374	N329PQ	LGA	IND	105	660	8	0	2023-04-25 08:00:00	Other
19724	4	28	1409	1415	-6	1533	1516	B6	286	N193JB	JFK	ORH	30	150	14	15	2023-04-28 14:00:00	Other
19733	11	12	2019	2025	-6	2153	2200	YX	1776	N860RW	LGA	DCA	56	214	20	25	2023-11-12 20:00:00	Other
19735	12	24	2047	2055	-8	2	50	B6	307	N989JT	JFK	SFO	334	2586	20	55	2023-12-24 20:00:00	Other
19736	8	22	827	837	-10	1019	1059	9E	1293	N478PX	LGA	CLT	83	544	8	37	2023-08-22 08:00:00	CLT
19738	2	20	2050	2100	-10	2207	2255	YX	1187	N123HQ	LGA	RIC	57	292	21	0	2023-02-20 21:00:00	Other
19741	11	2	2035	2045	-10	2157	2224	B6	264	N328JB	JFK	BUF	59	301	20	45	2023-11-02 20:00:00	Other
19746	1	6	554	600	-6	811	830	UA	491	N57111	EWR	DEN	224	1605	6	0	2023-01-06 06:00:00	Other
19747	9	27	1605	1613	-8	1817	1814	AA	418	N893NN	EWR	CLT	87	529	16	13	2023-09-27 16:00:00	CLT
19748	11	5	1814	1820	-6	2107	2132	UA	718	N68880	EWR	RSW	144	1068	18	20	2023-11-05 18:00:00	Other
19757	4	12	1646	1655	-9	1938	2013	AS	7	N440AS	JFK	SEA	322	2422	16	55	2023-04-12 16:00:00	Other
19758	9	3	1958	2011	-13	2155	2247	YX	1364	N420YX	JFK	IND	90	665	20	11	2023-09-03 20:00:00	Other
19765	1	29	2252	2259	-7	2	23	YX	1865	N221JQ	JFK	PWM	47	273	22	59	2023-01-29 22:00:00	Other
19766	6	1	1046	1054	-8	1341	1342	B6	349	N587JB	EWR	MCO	133	937	10	54	2023-06-01 10:00:00	MCO
19770	8	15	621	630	-9	822	846	UA	160	N73251	LGA	DEN	218	1620	6	30	2023-08-15 06:00:00	Other
19780	2	24	1706	1712	-6	1859	1908	YX	984	N979RP	EWR	GSO	88	445	17	12	2023-02-24 17:00:00	Other
19785	5	31	1651	1700	-9	1919	2005	AA	942	N941AN	LGA	DFW	180	1389	17	0	2023-05-31 17:00:00	Other
19786	2	25	1645	1700	-15	1821	1845	YX	1615	N242JQ	LGA	PIT	66	335	17	0	2023-02-25 17:00:00	Other
19793	10	19	1724	1730	-6	2033	2125	DL	265	N717TW	JFK	SFO	343	2586	17	30	2023-10-19 17:00:00	Other
19811	11	7	1048	1103	-15	1209	1242	9E	1629	N131EV	LGA	ORF	51	296	11	3	2023-11-07 11:00:00	Other
19815	11	25	1650	1659	-9	1940	2024	AS	4	N283AK	JFK	SEA	324	2422	16	59	2023-11-25 16:00:00	Other
19816	4	18	1916	1925	-9	2115	2156	YX	1152	N451YX	LGA	XNA	163	1147	19	25	2023-04-18 19:00:00	Other
19818	12	13	738	745	-7	1103	1050	B6	79	N986JB	JFK	SAN	346	2446	7	45	2023-12-13 07:00:00	Other
19828	5	10	1853	1859	-6	2001	2029	YX	1710	N204JQ	LGA	BOS	33	184	18	59	2023-05-10 18:00:00	BOS
19830	8	27	1352	1359	-7	1536	1558	YX	825	N858RW	EWR	DTW	83	488	13	59	2023-08-27 13:00:00	Other
19837	5	12	1812	1820	-8	2035	2033	NK	274	N671NK	EWR	IND	93	645	18	20	2023-05-12 18:00:00	Other
19844	5	10	708	715	-7	948	947	DL	167	N3750D	LGA	DEN	239	1620	7	15	2023-05-10 07:00:00	Other
19846	11	20	1816	1829	-13	2102	2137	YX	1401	N108HQ	LGA	OKC	200	1341	18	29	2023-11-20 18:00:00	Other
19849	5	23	649	655	-6	816	830	AA	313	N951AA	EWR	ORD	109	719	6	55	2023-05-23 06:00:00	ORD
19860	1	15	954	1000	-6	1131	1229	AA	818	N575UW	LGA	CLT	78	544	10	0	2023-01-15 10:00:00	CLT
19871	1	7	1112	1118	-6	1408	1441	B6	79	N658JB	LGA	FLL	146	1076	11	18	2023-01-07 11:00:00	FLL
19873	7	26	1720	1729	-9	1950	1951	YX	1063	N419YX	LGA	SDF	98	659	17	29	2023-07-26 17:00:00	Other
19880	4	26	1543	1549	-6	1848	1849	UA	714	N401UA	EWR	RSW	156	1068	15	49	2023-04-26 15:00:00	Other
19887	5	18	1850	1900	-10	2018	2057	YX	1303	N407YX	LGA	CMH	71	479	19	0	2023-05-18 19:00:00	Other
19892	1	19	1459	1510	-11	1736	1733	YX	1369	N138HQ	JFK	CVG	116	589	15	10	2023-01-19 15:00:00	Other
19893	7	14	1704	1710	-6	2018	2009	DL	230	N523DE	JFK	LAS	312	2248	17	10	2023-07-14 17:00:00	Other
19898	1	27	1944	1955	-11	2127	2135	9E	1679	N311PQ	EWR	RDU	77	416	19	55	2023-01-27 19:00:00	Other
19902	11	12	1210	1220	-10	1354	1408	9E	1738	N232PQ	JFK	RDU	81	427	12	20	2023-11-12 12:00:00	Other
19909	6	15	920	929	-9	1039	1110	YX	1192	N725YX	EWR	STL	121	872	9	29	2023-06-15 09:00:00	Other
19911	11	17	1806	1815	-9	1935	1954	UA	949	N809UA	LGA	ORD	118	733	18	15	2023-11-17 18:00:00	ORD
19925	10	24	1007	1015	-8	1109	1136	B6	179	N228JB	LGA	BOS	35	184	10	15	2023-10-24 10:00:00	BOS
19933	3	27	1051	1100	-9	1232	1236	YX	1380	N427YX	LGA	PIT	70	335	11	0	2023-03-27 11:00:00	Other
19935	5	29	1949	1959	-10	2131	2219	9E	1457	N479PX	LGA	MCI	136	1107	19	59	2023-05-29 19:00:00	Other
19936	2	9	554	600	-6	738	809	AA	901	N902NN	JFK	CLT	83	541	6	0	2023-02-09 06:00:00	CLT
19940	12	10	1819	1830	-11	1956	2021	DL	613	N102DU	LGA	ORD	115	733	18	30	2023-12-10 18:00:00	ORD
19945	3	24	801	815	-14	902	925	B6	112	N231JB	LGA	BOS	33	184	8	15	2023-03-24 08:00:00	BOS
19954	1	19	746	757	-11	847	910	9E	1586	N932XJ	LGA	BDL	22	101	7	57	2023-01-19 07:00:00	Other
19959	2	28	1829	1840	-11	2233	2210	AS	11	N274AK	JFK	SAN	389	2446	18	40	2023-02-28 18:00:00	Other
19960	4	10	1621	1630	-9	1857	1929	UA	434	N17752	EWR	SNA	309	2434	16	30	2023-04-10 16:00:00	Other
19962	11	5	652	700	-8	901	935	UA	503	N37535	EWR	ATL	109	746	7	0	2023-11-05 07:00:00	ATL
19964	12	13	1650	1659	-9	1952	2016	OO	1181	N259SY	LGA	OKC	211	1341	16	59	2023-12-13 16:00:00	Other
19965	7	4	953	959	-6	1145	1201	AA	537	N560UW	EWR	CLT	78	529	9	59	2023-07-04 09:00:00	CLT
19971	7	11	552	600	-8	649	722	AA	608	N711UW	LGA	DCA	40	214	6	0	2023-07-11 06:00:00	Other
19974	2	12	919	930	-11	1059	1059	YX	1518	N212JQ	JFK	DCA	52	213	9	30	2023-02-12 09:00:00	Other
19984	2	23	2126	2135	-9	2245	2247	B6	6	N193JB	JFK	SYR	47	209	21	35	2023-02-23 21:00:00	Other
19985	6	4	1028	1035	-7	1222	1309	B6	405	N554JB	LGA	DEN	205	1620	10	35	2023-06-04 10:00:00	Other
19988	11	30	1247	1255	-8	1401	1414	DL	548	N134DU	JFK	BOS	52	187	12	55	2023-11-30 12:00:00	BOS
20004	1	21	1455	1509	-14	1804	1834	B6	933	N216JB	LGA	SRQ	167	1047	15	9	2023-01-21 15:00:00	Other
20005	8	19	1329	1335	-6	1427	1451	YX	1357	N213JQ	LGA	MVY	35	175	13	35	2023-08-19 13:00:00	Other
20032	3	22	658	705	-7	1044	1104	UA	591	N17730	EWR	STT	207	1634	7	5	2023-03-22 07:00:00	Other
20035	5	14	1239	1245	-6	1350	1415	WN	875	N566WN	LGA	BNA	109	764	12	45	2023-05-14 12:00:00	Other
20036	6	25	1653	1659	-6	1915	1835	YX	1345	N113HQ	JFK	ORF	52	290	16	59	2023-06-25 16:00:00	Other
20039	10	10	1230	1237	-7	1324	1346	9E	1548	N904XJ	LGA	BGM	33	147	12	37	2023-10-10 12:00:00	Other
20040	4	24	1820	1829	-9	2202	2141	AA	183	N834NN	JFK	MIA	178	1089	18	29	2023-04-24 18:00:00	MIA
20042	2	8	2023	2030	-7	2143	2210	YX	1538	N236JQ	LGA	PIT	61	335	20	30	2023-02-08 20:00:00	Other
20044	7	21	1640	1650	-10	1958	2018	AS	11	N282AK	JFK	SFO	346	2586	16	50	2023-07-21 16:00:00	Other
20046	2	3	642	650	-8	800	816	9E	1382	N336PQ	LGA	ORF	55	296	6	50	2023-02-03 06:00:00	Other
20054	11	5	1345	1355	-10	1539	1633	B6	905	N605JB	LGA	MSY	146	1183	13	55	2023-11-05 13:00:00	Other
20061	1	24	621	635	-14	909	945	B6	517	N580JB	LGA	TPA	150	1010	6	35	2023-01-24 06:00:00	Other
20062	12	9	1332	1340	-8	1631	1648	B6	17	N779JB	JFK	PBI	144	1028	13	40	2023-12-09 13:00:00	Other
20079	8	11	1038	1045	-7	1210	1216	YX	1061	N424YX	JFK	BNA	120	765	10	45	2023-08-11 10:00:00	Other
20091	10	19	1723	1730	-7	1857	1920	YX	1251	N427YX	LGA	BHM	132	866	17	30	2023-10-19 17:00:00	Other
20093	2	28	636	645	-9	902	902	YX	1131	N754YX	EWR	CHS	97	628	6	45	2023-02-28 06:00:00	Other
20094	8	9	1933	1941	-8	2047	2113	UA	721	N38727	EWR	IAD	39	212	19	41	2023-08-09 19:00:00	Other
20098	5	17	1818	1825	-7	2054	2051	YX	1238	N439YX	LGA	OMA	160	1148	18	25	2023-05-17 18:00:00	Other
20101	4	18	851	900	-9	1049	1112	9E	1268	N133EV	LGA	GSP	98	610	9	0	2023-04-18 09:00:00	Other
20106	2	8	943	949	-6	1310	1329	AA	952	N412UW	EWR	PHX	298	2133	9	49	2023-02-08 09:00:00	Other
20109	9	27	918	927	-9	1051	1101	YX	1114	N855RW	EWR	PIT	59	319	9	27	2023-09-27 09:00:00	Other
20113	4	29	1651	1659	-8	2002	2040	AS	13	N277AK	JFK	SFO	334	2586	16	59	2023-04-29 16:00:00	Other
20117	7	31	853	900	-7	1003	1019	B6	510	N206JB	JFK	BTV	44	266	9	0	2023-07-31 09:00:00	Other
20121	9	23	1804	1810	-6	1949	2021	DL	427	N302DN	LGA	MSP	139	1020	18	10	2023-09-23 18:00:00	Other
20125	10	4	1425	1435	-10	1533	1602	UA	564	N847UA	EWR	BNA	104	748	14	35	2023-10-04 14:00:00	Other
20126	3	24	2050	2100	-10	2300	2306	YX	1299	N411YX	LGA	DTW	99	502	21	0	2023-03-24 21:00:00	Other
20127	10	8	2117	2129	-12	2254	2335	9E	1568	N138EV	LGA	ILM	79	500	21	29	2023-10-08 21:00:00	Other
20129	7	24	654	700	-6	1000	1020	NK	835	N964NK	EWR	SLC	273	1969	7	0	2023-07-24 07:00:00	Other
20139	6	9	654	700	-6	937	1003	DL	548	N848DN	JFK	TPA	138	1005	7	0	2023-06-09 07:00:00	Other
20147	3	26	1607	1615	-8	1946	1943	B6	328	N962JT	JFK	LAX	372	2475	16	15	2023-03-26 16:00:00	LAX
20149	5	8	1550	1600	-10	1703	1713	9E	1555	N479PX	LGA	ALB	30	136	16	0	2023-05-08 16:00:00	Other
20150	9	3	1217	1224	-7	1341	1412	YX	1415	N409YX	JFK	RDU	61	427	12	24	2023-09-03 12:00:00	Other
20165	1	30	2042	2050	-8	2241	2302	9E	1708	N915XJ	LGA	GSP	102	610	20	50	2023-01-30 20:00:00	Other
20170	10	1	1112	1120	-8	1250	1315	YX	1743	N217JQ	LGA	CMH	70	479	11	20	2023-10-01 11:00:00	Other
20179	5	29	1021	1029	-8	1324	1333	UA	393	N17233	EWR	SRQ	147	1034	10	29	2023-05-29 10:00:00	Other
20183	3	28	2011	2020	-9	2317	2300	UA	177	N26226	EWR	LAS	314	2227	20	20	2023-03-28 20:00:00	Other
20187	7	28	1134	1142	-8	1257	1326	YX	1075	N826MD	LGA	ROA	61	405	11	42	2023-07-28 11:00:00	Other
20189	11	27	553	600	-7	807	836	UA	742	N455UA	LGA	DEN	234	1620	6	0	2023-11-27 06:00:00	Other
20191	11	9	1549	1557	-8	1747	1759	YX	1155	N747YX	EWR	CMH	84	463	15	57	2023-11-09 15:00:00	Other
20194	12	19	1819	1829	-10	1925	2001	YX	1723	N214JQ	LGA	BOS	35	184	18	29	2023-12-19 18:00:00	BOS
20214	10	12	1022	1030	-8	1330	1333	UA	628	N17104	EWR	LAX	337	2454	10	30	2023-10-12 10:00:00	LAX
20216	7	13	1118	1130	-12	1237	1300	YX	1411	N875RW	LGA	DCA	50	214	11	30	2023-07-13 11:00:00	Other
20217	4	25	1246	1259	-13	1359	1422	9E	1326	N600LR	JFK	ORF	55	290	12	59	2023-04-25 12:00:00	Other
20218	11	6	952	1000	-8	1304	1318	UA	263	N206UA	EWR	SFO	349	2565	10	0	2023-11-06 10:00:00	Other
20226	9	16	820	830	-10	1043	1057	B6	961	N521JB	LGA	ATL	109	762	8	30	2023-09-16 08:00:00	ATL
20230	3	24	1834	1840	-6	2032	2020	UA	461	N54241	EWR	ORD	125	719	18	40	2023-03-24 18:00:00	ORD
20241	9	7	1107	1114	-7	1357	1416	UA	149	N17566	EWR	FLL	140	1065	11	14	2023-09-07 11:00:00	FLL
20244	12	10	905	915	-10	1029	1053	UA	222	N38257	LGA	ORD	119	733	9	15	2023-12-10 09:00:00	ORD
20257	11	5	918	930	-12	1055	1101	B6	397	N239JB	JFK	ROC	57	264	9	30	2023-11-05 09:00:00	Other
20270	11	19	2119	2129	-10	2222	2300	YX	1841	N211JQ	LGA	DCA	41	214	21	29	2023-11-19 21:00:00	Other
20286	4	22	1450	1459	-9	1644	1635	YX	1570	N201JQ	LGA	BNA	134	764	14	59	2023-04-22 14:00:00	Other
20287	9	22	903	912	-9	1054	1059	YX	1376	N432YX	LGA	GSO	77	461	9	12	2023-09-22 09:00:00	Other
20292	5	13	1507	1515	-8	1636	1725	9E	1423	N187GJ	LGA	ILM	72	500	15	15	2023-05-13 15:00:00	Other
20294	11	27	1451	1459	-8	1744	1814	DL	356	N340NW	LGA	PBI	154	1035	14	59	2023-11-27 14:00:00	Other
20298	3	3	1439	1445	-6	1538	1545	B6	307	N273JB	JFK	ORH	32	150	14	45	2023-03-03 14:00:00	Other
20306	12	12	2139	2150	-11	2222	2258	YX	1829	N235JQ	LGA	ALB	29	136	21	50	2023-12-12 21:00:00	Other
20311	9	15	1248	1255	-7	1355	1417	YX	1303	N407YX	JFK	BOS	40	187	12	55	2023-09-15 12:00:00	BOS
20314	4	21	2055	2105	-10	2231	2253	YX	1102	N421YX	LGA	GSO	72	461	21	5	2023-04-21 21:00:00	Other
20315	8	15	1722	1730	-8	1949	2034	AS	74	N525AS	EWR	PDX	306	2434	17	30	2023-08-15 17:00:00	Other
20328	6	9	2153	2200	-7	2307	2323	9E	1626	N349PQ	JFK	ITH	41	189	22	0	2023-06-09 22:00:00	Other
20330	2	20	820	826	-6	1054	1045	UA	861	N815UA	EWR	ATL	123	746	8	26	2023-02-20 08:00:00	ATL
20332	8	18	730	740	-10	948	1000	UA	393	N27256	EWR	SAV	98	708	7	40	2023-08-18 07:00:00	Other
20335	8	7	949	955	-6	1109	1147	9E	1262	N182GJ	EWR	RDU	65	416	9	55	2023-08-07 09:00:00	Other
20336	8	18	1109	1115	-6	1246	1309	YX	1053	N401YX	LGA	CMH	80	479	11	15	2023-08-18 11:00:00	Other
20340	12	24	1651	1700	-9	1950	2033	DL	840	N314NB	JFK	AUS	210	1521	17	0	2023-12-24 17:00:00	Other
20348	10	21	1856	1906	-10	2032	2109	YX	1340	N136HQ	LGA	CMH	83	479	19	6	2023-10-21 19:00:00	Other
20351	2	9	1850	1859	-9	2159	2211	UA	240	N17265	EWR	DFW	211	1372	18	59	2023-02-09 18:00:00	Other
20355	10	24	1000	1010	-10	1244	1306	UA	370	N846UA	LGA	IAH	191	1416	10	10	2023-10-24 10:00:00	Other
20368	4	30	837	846	-9	1023	1043	9E	1381	N308PQ	LGA	CLE	72	419	8	46	2023-04-30 08:00:00	Other
20370	8	29	1650	1701	-11	1946	1952	AA	779	N975AN	LGA	DFW	202	1389	17	1	2023-08-29 17:00:00	Other
20372	4	3	2143	2153	-10	2259	2315	9E	1267	N311PQ	LGA	BUF	52	292	21	53	2023-04-03 21:00:00	Other
20376	11	10	2052	2100	-8	2156	2217	YX	1271	N424YX	JFK	BOS	42	187	21	0	2023-11-10 21:00:00	BOS
20380	6	10	1252	1300	-8	1444	1507	AA	781	N578UW	LGA	CLT	78	544	13	0	2023-06-10 13:00:00	CLT
20383	10	7	1653	1659	-6	1932	2015	AS	75	N966AK	EWR	LAX	306	2454	16	59	2023-10-07 16:00:00	LAX
20385	4	15	1153	1159	-6	1402	1353	YX	1237	N436YX	LGA	ILM	81	500	11	59	2023-04-15 11:00:00	Other
20386	5	29	1935	1945	-10	2129	2152	9E	1475	N301PQ	EWR	CVG	82	569	19	45	2023-05-29 19:00:00	Other
20387	4	11	1124	1130	-6	1305	1336	YX	1229	N427YX	LGA	DTW	76	502	11	30	2023-04-11 11:00:00	Other
20388	5	24	813	820	-7	944	1004	YX	1237	N423YX	LGA	RDU	73	431	8	20	2023-05-24 08:00:00	Other
20389	8	18	1523	1529	-6	1640	1654	UA	376	N895UA	EWR	BNA	108	748	15	29	2023-08-18 15:00:00	Other
20393	4	22	1539	1550	-11	1712	1735	YX	1465	N210JQ	LGA	PIT	60	335	15	50	2023-04-22 15:00:00	Other
20396	10	11	1020	1030	-10	1134	1159	YX	1074	N761YX	EWR	DCA	42	199	10	30	2023-10-11 10:00:00	Other
20397	12	4	706	715	-9	1036	1023	B6	214	N994JL	JFK	FLL	171	1069	7	15	2023-12-04 07:00:00	FLL
20398	2	2	1951	1959	-8	2329	2336	AS	90	N292AK	EWR	SFO	369	2565	19	59	2023-02-02 19:00:00	Other
20408	12	10	1002	1010	-8	1309	1320	DL	386	N374DX	LGA	MCO	160	950	10	10	2023-12-10 10:00:00	MCO
20410	4	21	1558	1605	-7	1852	1933	B6	302	N988JT	JFK	LAX	318	2475	16	5	2023-04-21 16:00:00	LAX
20411	10	3	651	700	-9	815	831	YX	1328	N112HQ	LGA	PIT	61	335	7	0	2023-10-03 07:00:00	Other
20415	6	23	753	800	-7	1143	1111	AA	528	N810NN	EWR	MIA	190	1085	8	0	2023-06-23 08:00:00	MIA
20421	10	2	952	1000	-8	1136	1202	B6	59	N266JB	JFK	DTW	78	509	10	0	2023-10-02 10:00:00	Other
20422	1	28	1130	1140	-10	1344	1403	YX	1433	N107HQ	LGA	DTW	100	502	11	40	2023-01-28 11:00:00	Other
20424	1	10	957	1005	-8	1438	1516	B6	682	N651JB	EWR	SJU	196	1608	10	5	2023-01-10 10:00:00	Other
20432	12	14	1350	1359	-9	1507	1538	9E	1380	N478PX	LGA	RIC	51	292	13	59	2023-12-14 13:00:00	Other
20435	3	22	734	744	-10	1035	1039	UA	227	N27276	EWR	LAS	336	2227	7	44	2023-03-22 07:00:00	Other
20436	5	23	1618	1629	-11	1813	1844	YX	1211	N403YX	LGA	GSP	97	610	16	29	2023-05-23 16:00:00	Other
20440	1	24	951	1000	-9	1157	1229	AA	818	N192UW	LGA	CLT	90	544	10	0	2023-01-24 10:00:00	CLT
20441	4	5	1118	1125	-7	1357	1425	DL	427	N334NW	JFK	TPA	137	1005	11	25	2023-04-05 11:00:00	Other
20449	10	11	1052	1100	-8	1223	1258	YX	1139	N741YX	EWR	ILM	76	488	11	0	2023-10-11 11:00:00	Other
20450	10	2	941	950	-9	1121	1154	9E	1561	N600LR	LGA	GSO	70	461	9	50	2023-10-02 09:00:00	Other
20454	4	4	1252	1300	-8	1615	1640	AS	4	N961AK	JFK	SFO	355	2586	13	0	2023-04-04 13:00:00	Other
20455	6	3	1119	1130	-11	1334	1338	YX	1312	N409YX	LGA	AVL	84	599	11	30	2023-06-03 11:00:00	Other
20463	5	25	1921	1930	-9	2043	2127	YX	1248	N131HQ	JFK	DCA	52	213	19	30	2023-05-25 19:00:00	Other
20464	5	31	2021	2029	-8	2340	2345	AA	749	N357PV	LGA	MIA	151	1096	20	29	2023-05-31 20:00:00	MIA
20467	12	21	819	825	-6	1114	1146	DL	254	N142DU	LGA	DFW	208	1389	8	25	2023-12-21 08:00:00	Other
20474	9	24	553	600	-7	733	802	AA	228	N171US	LGA	CLT	81	544	6	0	2023-09-24 06:00:00	CLT
20475	8	2	2110	2119	-9	2159	2228	YX	839	N641RW	EWR	MDT	31	141	21	19	2023-08-02 21:00:00	Other
20481	8	5	753	800	-7	920	938	YX	854	N750YX	EWR	MKE	114	725	8	0	2023-08-05 08:00:00	Other
20486	1	4	1019	1030	-11	1216	1251	9E	1544	N491PX	LGA	ILM	77	500	10	30	2023-01-04 10:00:00	Other
20488	3	6	1352	1400	-8	1618	1624	YX	1254	N414YX	LGA	IND	113	660	14	0	2023-03-06 14:00:00	Other
20493	11	16	1154	1200	-6	1516	1519	UA	835	N19136	EWR	LAX	359	2454	12	0	2023-11-16 12:00:00	LAX
20501	11	7	1921	1930	-9	2128	2128	OO	1210	N306SY	JFK	ORD	144	740	19	30	2023-11-07 19:00:00	ORD
20508	1	26	1601	1610	-9	1813	1807	YX	1344	N102HQ	JFK	RDU	92	427	16	10	2023-01-26 16:00:00	Other
20510	1	9	1101	1110	-9	1235	1256	YX	1373	N134HQ	JFK	BNA	116	765	11	10	2023-01-09 11:00:00	Other
20514	12	19	1734	1743	-9	1924	1946	NK	47	N703NK	LGA	DTW	79	502	17	43	2023-12-19 17:00:00	Other
20517	7	20	1241	1250	-9	1526	1527	YX	1041	N119HQ	LGA	OKC	203	1341	12	50	2023-07-20 12:00:00	Other
20518	1	21	1509	1515	-6	1759	1840	UA	726	N2645U	EWR	SFO	319	2565	15	15	2023-01-21 15:00:00	Other
20520	5	9	740	750	-10	857	929	9E	1493	N335PQ	JFK	ROC	50	264	7	50	2023-05-09 07:00:00	Other
20521	10	28	2123	2130	-7	2321	2330	YX	1829	N206JQ	JFK	CMH	82	483	21	30	2023-10-28 21:00:00	Other
20526	5	27	1613	1625	-12	1736	1803	YX	1312	N424YX	JFK	BNA	107	765	16	25	2023-05-27 16:00:00	Other
20537	12	25	1723	1730	-7	1824	1907	YX	1806	N215JQ	LGA	DCA	41	214	17	30	2023-12-25 17:00:00	Other
20544	2	17	1223	1229	-6	1511	1506	YX	1614	N240JQ	LGA	SDF	124	659	12	29	2023-02-17 12:00:00	Other
20554	10	31	2121	2129	-8	2223	2250	9E	1613	N903XJ	LGA	BTV	41	258	21	29	2023-10-31 21:00:00	Other
20578	10	7	622	630	-8	904	926	NK	451	N646NK	LGA	MCO	134	950	6	30	2023-10-07 06:00:00	MCO
20579	4	8	1337	1345	-8	1502	1510	YX	997	N739YX	EWR	PIT	65	319	13	45	2023-04-08 13:00:00	Other
20581	3	22	2147	2159	-12	2248	2301	YX	1689	N223JQ	LGA	PVD	32	143	21	59	2023-03-22 21:00:00	Other
20584	11	22	1908	1915	-7	2146	2234	AA	753	N970NN	LGA	DFW	179	1389	19	15	2023-11-22 19:00:00	Other
20586	3	11	1107	1115	-8	1321	1344	YX	1316	N412YX	JFK	IND	108	665	11	15	2023-03-11 11:00:00	Other
20587	10	16	2240	2250	-10	2354	27	9E	1421	N341PQ	JFK	ROC	46	264	22	50	2023-10-16 22:00:00	Other
20593	4	13	1254	1301	-7	1442	1507	YX	1086	N870RW	LGA	AVL	92	599	13	1	2023-04-13 13:00:00	Other
20603	10	25	1909	1915	-6	2038	2051	UA	938	N488UA	LGA	ORD	118	733	19	15	2023-10-25 19:00:00	ORD
20605	10	3	1402	1408	-6	1602	1617	9E	1575	N910XJ	JFK	CVG	91	589	14	8	2023-10-03 14:00:00	Other
20610	5	9	1847	1855	-8	2201	2206	AS	12	N956AK	JFK	SAN	332	2446	18	55	2023-05-09 18:00:00	Other
20614	3	11	945	959	-14	1111	1120	YX	1104	N725YX	EWR	BOS	39	200	9	59	2023-03-11 09:00:00	BOS
20616	3	22	952	1005	-13	1134	1156	B6	84	N334JB	JFK	RDU	70	427	10	5	2023-03-22 10:00:00	Other
20617	12	20	1105	1111	-6	1249	1312	YX	1261	N440YX	LGA	RDU	65	431	11	11	2023-12-20 11:00:00	Other
20618	6	9	1447	1455	-8	1731	1710	YX	1423	N445YX	LGA	CVG	95	585	14	55	2023-06-09 14:00:00	Other
20630	10	26	1818	1829	-11	1946	2000	OO	1241	N315SY	JFK	BNA	112	765	18	29	2023-10-26 18:00:00	Other
20646	1	16	706	715	-9	949	1040	AS	14	N975AK	JFK	SEA	306	2422	7	15	2023-01-16 07:00:00	Other
20647	4	18	2036	2044	-8	2351	2359	UA	587	N27271	EWR	MIA	152	1085	20	44	2023-04-18 20:00:00	MIA
20648	2	13	1941	1955	-14	2055	2148	9E	1445	N335PQ	LGA	BHM	117	866	19	55	2023-02-13 19:00:00	Other
20656	4	3	822	829	-7	1035	1101	9E	1374	N186PQ	LGA	IND	107	660	8	29	2023-04-03 08:00:00	Other
20671	11	16	2110	2117	-7	2310	2330	UA	217	N37554	EWR	CVG	87	569	21	17	2023-11-16 21:00:00	Other
20672	11	29	1704	1711	-7	1957	2019	UA	537	N27266	EWR	FLL	147	1065	17	11	2023-11-29 17:00:00	FLL
20679	4	29	1232	1240	-8	1618	1552	AA	595	N428AA	JFK	MIA	152	1089	12	40	2023-04-29 12:00:00	MIA
20680	5	13	903	910	-7	1153	1236	AA	707	N313SB	JFK	MIA	146	1089	9	10	2023-05-13 09:00:00	MIA
20686	2	24	909	915	-6	1232	1226	UA	593	N27270	EWR	RSW	163	1068	9	15	2023-02-24 09:00:00	Other
20687	9	7	554	600	-6	723	800	DL	830	N134DU	LGA	RDU	67	431	6	0	2023-09-07 06:00:00	Other
20694	5	13	722	730	-8	957	1036	AA	152	N305NX	LGA	DFW	183	1389	7	30	2023-05-13 07:00:00	Other
20703	5	28	1920	1929	-9	2104	2114	YX	1199	N421YX	LGA	BHM	111	866	19	29	2023-05-28 19:00:00	Other
20705	6	12	810	820	-10	939	959	YX	1224	N862RW	EWR	RIC	54	277	8	20	2023-06-12 08:00:00	Other
20709	12	29	1840	1850	-10	2006	2053	YX	1795	N224JQ	LGA	CMH	71	479	18	50	2023-12-29 18:00:00	Other
20714	8	26	1441	1450	-9	1706	1720	9E	1223	N183GJ	LGA	SAV	104	722	14	50	2023-08-26 14:00:00	Other
20720	5	17	1053	1102	-9	1240	1229	UA	491	N57286	EWR	BNA	114	748	11	2	2023-05-17 11:00:00	Other
20721	11	10	2224	2230	-6	2352	2358	9E	1447	N600LR	JFK	PWM	49	273	22	30	2023-11-10 22:00:00	Other
20723	12	4	1846	1857	-11	2017	2035	B6	580	N236JB	JFK	BUF	57	301	18	57	2023-12-04 18:00:00	Other
20728	5	10	1253	1300	-7	1534	1614	AA	224	N415AN	LGA	MIA	137	1096	13	0	2023-05-10 13:00:00	MIA
20733	8	26	2150	2159	-9	2250	2342	YX	1027	N131HQ	JFK	DCA	38	213	21	59	2023-08-26 21:00:00	Other
20736	10	9	1722	1729	-7	1952	2037	AA	36	N108NN	JFK	LAX	310	2475	17	29	2023-10-09 17:00:00	LAX
20743	5	23	1043	1050	-7	1231	1308	9E	1514	N605LR	LGA	CLT	84	544	10	50	2023-05-23 10:00:00	CLT
20745	10	4	833	840	-7	941	1001	YX	1849	N223JQ	EWR	BOS	37	200	8	40	2023-10-04 08:00:00	BOS
20751	4	19	954	1000	-6	1111	1138	UA	647	N474UA	LGA	ORD	116	733	10	0	2023-04-19 10:00:00	ORD
20765	5	19	754	800	-6	1018	1017	B6	317	N329JB	JFK	SAV	115	718	8	0	2023-05-19 08:00:00	Other
20766	11	14	547	600	-13	832	900	B6	47	N715JB	LGA	FLL	145	1076	6	0	2023-11-14 06:00:00	FLL
20767	12	7	1441	1449	-8	1540	1615	9E	1492	N913XJ	JFK	BWI	36	184	14	49	2023-12-07 14:00:00	Other
20772	10	4	624	630	-6	737	801	YX	1277	N114HQ	LGA	ORF	52	296	6	30	2023-10-04 06:00:00	Other
20778	11	5	1212	1220	-8	1417	1435	DL	1005	N132DU	JFK	MSP	161	1029	12	20	2023-11-05 12:00:00	Other
20785	10	11	834	846	-12	1033	1110	9E	1558	N182GJ	LGA	TYS	95	647	8	46	2023-10-11 08:00:00	Other
20787	7	6	1656	1704	-8	1943	1929	YX	1066	N432YX	JFK	CVG	94	589	17	4	2023-07-06 17:00:00	Other
20788	4	13	758	805	-7	1004	1025	DL	831	N3744F	EWR	ATL	102	746	8	5	2023-04-13 08:00:00	ATL
20791	5	20	952	1000	-8	1332	1356	B6	957	N958JB	JFK	SJU	196	1598	10	0	2023-05-20 10:00:00	Other
20808	3	21	648	700	-12	939	1009	AS	92	N472AS	EWR	SEA	322	2402	7	0	2023-03-21 07:00:00	Other
20821	12	16	1152	1200	-8	1435	1519	UA	765	N14120	EWR	LAX	320	2454	12	0	2023-12-16 12:00:00	LAX
20827	8	12	1104	1110	-6	1429	1338	YX	976	N870RW	LGA	HHH	102	701	11	10	2023-08-12 11:00:00	Other
20834	5	10	1411	1418	-7	1531	1551	9E	1437	N329PQ	LGA	MKE	117	738	14	18	2023-05-10 14:00:00	Other
20835	12	15	1520	1529	-9	1830	1841	DL	587	N386DA	JFK	PBI	147	1028	15	29	2023-12-15 15:00:00	Other
20836	3	17	1850	1900	-10	2020	2034	YX	1301	N441YX	LGA	PIT	65	335	19	0	2023-03-17 19:00:00	Other
20837	10	24	1623	1630	-7	1800	1836	UA	119	N37295	EWR	CLT	73	529	16	30	2023-10-24 16:00:00	CLT
20840	10	3	1428	1435	-7	1540	1602	YX	1094	N762YX	EWR	MKE	101	725	14	35	2023-10-03 14:00:00	Other
20844	3	18	1021	1030	-9	1229	1229	YX	1283	N421YX	JFK	RDU	90	427	10	30	2023-03-18 10:00:00	Other
20846	1	7	1750	1800	-10	2012	2053	UA	964	N27277	EWR	LAS	300	2227	18	0	2023-01-07 18:00:00	Other
20854	12	7	2020	2030	-10	2146	2226	YX	1211	N131HQ	LGA	BHM	121	866	20	30	2023-12-07 20:00:00	Other
20857	10	17	550	600	-10	843	927	AA	26	N117AN	JFK	SFO	328	2586	6	0	2023-10-17 06:00:00	Other
20862	7	15	701	710	-9	946	1004	UA	549	N892UA	EWR	PDX	324	2434	7	10	2023-07-15 07:00:00	Other
20864	8	23	1520	1529	-9	1707	1737	YX	981	N406YX	JFK	CLE	68	425	15	29	2023-08-23 15:00:00	Other
20868	1	10	1459	1510	-11	1720	1733	YX	1369	N423YX	JFK	CVG	96	589	15	10	2023-01-10 15:00:00	Other
20869	4	22	1452	1500	-8	1712	1704	YX	1491	N245JQ	JFK	CMH	85	483	15	0	2023-04-22 15:00:00	Other
20870	12	2	703	710	-7	1039	1035	DL	309	N538DN	JFK	SEA	336	2422	7	10	2023-12-02 07:00:00	Other
20874	4	5	815	825	-10	938	959	9E	1194	N928XJ	LGA	MKE	122	738	8	25	2023-04-05 08:00:00	Other
20878	8	6	1244	1250	-6	1411	1358	9E	1283	N299PQ	JFK	ITH	39	189	12	50	2023-08-06 12:00:00	Other
20883	9	28	1750	1757	-7	1933	1954	YX	1807	N236JQ	LGA	CMH	76	479	17	57	2023-09-28 17:00:00	Other
20890	10	24	1553	1600	-7	1745	1818	YX	1262	N425YX	LGA	LIT	156	1085	16	0	2023-10-24 16:00:00	Other
20893	5	22	1021	1029	-8	1312	1333	UA	393	N459UA	EWR	SRQ	154	1034	10	29	2023-05-22 10:00:00	Other
20896	8	24	1130	1140	-10	1246	1312	YX	964	N404YX	JFK	ORF	46	290	11	40	2023-08-24 11:00:00	Other
20897	9	25	1103	1110	-7	1352	1420	DL	414	N396DN	JFK	FLL	144	1069	11	10	2023-09-25 11:00:00	FLL
20914	10	18	1752	1800	-8	1947	2022	YX	1289	N444YX	LGA	IND	97	660	18	0	2023-10-18 18:00:00	Other
20928	3	15	2123	2130	-7	100	59	B6	672	N989JT	JFK	LAX	342	2475	21	30	2023-03-15 21:00:00	LAX
20929	1	28	1630	1640	-10	1810	1850	YX	1442	N102HQ	LGA	GSO	76	461	16	40	2023-01-28 16:00:00	Other
20936	8	31	1045	1100	-15	1248	1320	B6	102	N563JB	LGA	DEN	210	1620	11	0	2023-08-31 11:00:00	Other
20938	11	9	1144	1150	-6	1312	1337	9E	1446	N301PQ	LGA	PIT	61	335	11	50	2023-11-09 11:00:00	Other
20939	6	20	1749	1755	-6	1953	2008	YX	1422	N428YX	LGA	IND	100	660	17	55	2023-06-20 17:00:00	Other
20946	12	3	812	819	-7	1130	1143	UA	113	N14735	EWR	EYW	172	1196	8	19	2023-12-03 08:00:00	Other
20948	6	19	1751	1757	-6	2010	2046	B6	289	N996JL	JFK	LAS	289	2248	17	57	2023-06-19 17:00:00	Other
20949	10	25	705	720	-15	933	1008	UA	276	N37560	EWR	MCO	119	937	7	20	2023-10-25 07:00:00	MCO
20950	3	4	1710	1717	-7	2010	2012	UA	852	N27255	EWR	LAS	332	2227	17	17	2023-03-04 17:00:00	Other
20955	5	2	924	930	-6	1218	1239	AS	10	N483AS	JFK	SEA	315	2422	9	30	2023-05-02 09:00:00	Other
20959	8	13	1947	2000	-13	2140	2216	YX	827	N736YX	EWR	AVL	88	583	20	0	2023-08-13 20:00:00	Other
20960	3	1	1749	1755	-6	2107	2104	AA	560	N950NN	LGA	DFW	227	1389	17	55	2023-03-01 17:00:00	Other
20961	2	24	636	647	-11	744	813	AA	759	N831AW	LGA	DCA	47	214	6	47	2023-02-24 06:00:00	Other
20967	1	13	1118	1130	-12	1307	1332	YX	1377	N451YX	JFK	CLE	81	425	11	30	2023-01-13 11:00:00	Other
20968	10	20	2122	2128	-6	2259	2309	YX	1061	N762YX	EWR	MSN	114	799	21	28	2023-10-20 21:00:00	Other
20974	4	15	1138	1145	-7	1428	1500	AS	11	N292AK	JFK	SEA	321	2422	11	45	2023-04-15 11:00:00	Other
20976	11	6	1553	1559	-6	1805	1839	DL	174	N128DN	LGA	ATL	111	762	15	59	2023-11-06 15:00:00	ATL
20981	10	12	816	830	-14	919	942	9E	1456	N915XJ	LGA	PVD	34	143	8	30	2023-10-12 08:00:00	Other
20988	8	22	1926	1933	-7	2223	2237	UA	502	N17303	EWR	SMF	325	2500	19	33	2023-08-22 19:00:00	Other
20989	10	11	724	730	-6	849	915	AA	223	N824NN	LGA	ORD	114	733	7	30	2023-10-11 07:00:00	ORD
20990	11	3	1213	1219	-6	1513	1525	B6	978	N506JB	LGA	TPA	147	1010	12	19	2023-11-03 12:00:00	Other
20991	6	14	945	955	-10	1157	1214	YX	1362	N826MD	LGA	SDF	103	659	9	55	2023-06-14 09:00:00	Other
20994	9	18	1152	1200	-8	1409	1358	YX	1393	N135HQ	LGA	DTW	86	502	12	0	2023-09-18 12:00:00	Other
20997	8	17	613	620	-7	834	815	DL	775	N929AT	EWR	MSP	177	1008	6	20	2023-08-17 06:00:00	Other
20998	10	11	1949	1959	-10	2104	2137	9E	1686	N678CA	LGA	CHO	52	305	19	59	2023-10-11 19:00:00	Other
21004	1	28	1727	1735	-8	2042	2101	DL	512	N353NW	JFK	AUS	233	1521	17	35	2023-01-28 17:00:00	Other
21005	9	20	637	645	-8	926	948	UA	260	N34455	EWR	FLL	150	1065	6	45	2023-09-20 06:00:00	FLL
21008	12	5	617	625	-8	750	801	UA	603	N1902U	LGA	ORD	122	733	6	25	2023-12-05 06:00:00	ORD
21012	9	6	949	959	-10	1113	1126	YX	1408	N420YX	JFK	ORF	47	290	9	59	2023-09-06 09:00:00	Other
21015	12	3	553	600	-7	837	857	B6	84	N569JB	LGA	MCO	139	950	6	0	2023-12-03 06:00:00	MCO
21019	3	6	1623	1630	-7	1754	1756	YX	1743	N240JQ	LGA	ROC	47	254	16	30	2023-03-06 16:00:00	Other
21027	3	16	1322	1329	-7	1605	1643	UA	778	N893UA	LGA	IAH	201	1416	13	29	2023-03-16 13:00:00	Other
21030	5	26	1752	1800	-8	1925	1946	9E	1364	N904XJ	LGA	ORF	56	296	18	0	2023-05-26 18:00:00	Other
21035	11	30	652	700	-8	806	825	AA	696	N764US	LGA	BOS	45	184	7	0	2023-11-30 07:00:00	BOS
21039	1	18	1349	1359	-10	1642	1633	YX	1855	N214JQ	LGA	MCI	193	1107	13	59	2023-01-18 13:00:00	Other
21041	1	18	2010	2020	-10	2132	2131	9E	1632	N316PQ	LGA	PVD	31	143	20	20	2023-01-18 20:00:00	Other
21051	9	21	1122	1129	-7	1243	1301	UA	352	N78448	EWR	ORD	109	719	11	29	2023-09-21 11:00:00	ORD
21052	1	20	2115	2121	-6	2336	2359	UA	557	N69840	EWR	JAX	115	820	21	21	2023-01-20 21:00:00	Other
21054	2	7	902	914	-12	1113	1128	YX	1301	N443YX	LGA	CMH	89	479	9	14	2023-02-07 09:00:00	Other
21055	2	16	2120	2129	-9	2307	2321	YX	1281	N429YX	JFK	RDU	78	427	21	29	2023-02-16 21:00:00	Other
21059	1	19	920	930	-10	1150	1217	YX	1820	N218JQ	LGA	SDF	121	659	9	30	2023-01-19 09:00:00	Other
21060	5	23	1952	1959	-7	2240	2250	NK	170	N682NK	LGA	MCO	134	950	19	59	2023-05-23 19:00:00	MCO
21061	1	7	1329	1336	-7	1636	1707	YX	1235	N858RW	EWR	EYW	169	1196	13	36	2023-01-07 13:00:00	Other
21066	5	15	1030	1039	-9	1236	1313	YX	1114	N742YX	EWR	SDF	96	642	10	39	2023-05-15 10:00:00	Other
21068	6	7	1429	1435	-6	1916	1737	YX	1388	N136HQ	LGA	IAH	NA	1416	14	35	2023-06-07 14:00:00	Other
21072	12	15	759	805	-6	922	948	B6	373	N229JB	JFK	BNA	105	765	8	5	2023-12-15 08:00:00	Other
21073	11	8	2235	2255	-20	2348	15	B6	62	N249JB	JFK	BTV	47	266	22	55	2023-11-08 22:00:00	Other
21079	7	6	1659	1705	-6	1856	1859	DL	792	N928AT	EWR	DTW	84	488	17	5	2023-07-06 17:00:00	Other
21081	8	29	642	650	-8	947	1001	AA	726	N889NN	LGA	MIA	164	1096	6	50	2023-08-29 06:00:00	MIA
21082	11	5	2043	2057	-14	2215	2253	9E	1436	N917XJ	LGA	ROA	61	405	20	57	2023-11-05 20:00:00	Other
21083	3	7	1915	1925	-10	2141	2158	YX	1142	N653RW	EWR	SDF	107	642	19	25	2023-03-07 19:00:00	Other
21086	3	27	1524	1530	-6	1833	1850	AA	118	N103NN	JFK	LAX	341	2475	15	30	2023-03-27 15:00:00	LAX
21091	7	27	623	630	-7	731	806	YX	997	N423YX	JFK	ORF	49	290	6	30	2023-07-27 06:00:00	Other
21092	9	6	1923	1930	-7	2214	2236	UA	697	N47288	EWR	SLC	260	1969	19	30	2023-09-06 19:00:00	Other
21096	3	7	1811	1820	-9	2040	2008	YX	1747	N245JQ	LGA	BNA	122	764	18	20	2023-03-07 18:00:00	Other
21105	10	4	818	830	-12	943	1012	UA	586	N67846	EWR	CLE	56	404	8	30	2023-10-04 08:00:00	Other
21110	7	5	1917	1925	-8	2212	2154	9E	1239	N279PQ	JFK	MSP	146	1029	19	25	2023-07-05 19:00:00	Other
21114	9	6	1604	1615	-11	1754	1819	9E	1615	N326PQ	LGA	ILM	72	500	16	15	2023-09-06 16:00:00	Other
21116	12	23	1023	1030	-7	1345	1343	UA	584	N17317	EWR	FLL	146	1065	10	30	2023-12-23 10:00:00	FLL
21142	3	21	1823	1829	-6	1939	2000	YX	1325	N439YX	JFK	ORF	56	290	18	29	2023-03-21 18:00:00	Other
21143	1	13	1025	1035	-10	1234	1320	B6	796	N552JB	LGA	DEN	213	1620	10	35	2023-01-13 10:00:00	Other
21144	5	19	2210	2220	-10	2334	2355	9E	1548	N272PQ	JFK	BTV	45	266	22	20	2023-05-19 22:00:00	Other
21146	1	11	553	600	-7	737	755	DL	429	N368DN	LGA	DTW	80	502	6	0	2023-01-11 06:00:00	Other
21154	2	28	2155	2204	-9	2312	2327	YX	1178	N422YX	JFK	BOS	34	187	22	4	2023-02-28 22:00:00	BOS
21163	12	4	823	829	-6	1104	1120	UA	615	N37305	EWR	LAS	306	2227	8	29	2023-12-04 08:00:00	Other
21166	10	26	907	915	-8	1149	1225	AA	573	N814NN	LGA	DFW	196	1389	9	15	2023-10-26 09:00:00	Other
21187	6	12	1653	1659	-6	1828	1835	YX	1345	N119HQ	JFK	ORF	62	290	16	59	2023-06-12 16:00:00	Other
21190	8	3	745	755	-10	911	937	9E	1184	N915XJ	LGA	ORF	51	296	7	55	2023-08-03 07:00:00	Other
21194	3	12	824	830	-6	923	949	AA	770	N833AW	LGA	DCA	42	214	8	30	2023-03-12 08:00:00	Other
21197	4	10	552	559	-7	736	759	AA	237	N982VJ	LGA	CLT	80	544	5	59	2023-04-10 05:00:00	CLT
21201	7	13	1010	1020	-10	1204	1241	9E	1158	N307PQ	LGA	CLT	84	544	10	20	2023-07-13 10:00:00	CLT
21202	8	2	851	900	-9	1139	1201	B6	92	N942JB	JFK	LAX	318	2475	9	0	2023-08-02 09:00:00	LAX
21206	2	13	1449	1457	-8	1548	1614	UA	724	N401UA	EWR	IAD	41	212	14	57	2023-02-13 14:00:00	Other
21207	10	4	712	719	-7	959	1023	DL	304	N301DU	EWR	SLC	261	1969	7	19	2023-10-04 07:00:00	Other
21210	1	4	1201	1210	-9	1500	1500	NK	1269	N509NK	LGA	IAH	214	1416	12	10	2023-01-04 12:00:00	Other
21211	7	5	952	959	-7	1239	1302	NK	237	N618NK	LGA	MCO	129	950	9	59	2023-07-05 09:00:00	MCO
21219	2	23	909	915	-6	1131	1158	DL	591	N107DU	JFK	MSY	179	1182	9	15	2023-02-23 09:00:00	Other
21223	11	27	938	945	-7	1247	1256	B6	645	N504JB	LGA	MCO	148	950	9	45	2023-11-27 09:00:00	MCO
21224	5	29	720	730	-10	940	1036	AA	152	N891NN	LGA	DFW	173	1389	7	30	2023-05-29 07:00:00	Other
21225	3	10	652	700	-8	802	817	AA	789	N765US	LGA	DCA	44	214	7	0	2023-03-10 07:00:00	Other
21228	1	19	734	740	-6	1018	1041	UA	861	N62895	EWR	MCO	135	937	7	40	2023-01-19 07:00:00	MCO
21235	11	6	2121	2129	-8	2217	2241	YX	1065	N758YX	EWR	MHT	42	209	21	29	2023-11-06 21:00:00	Other
21239	10	21	1720	1730	-10	1840	1904	9E	1473	N479PX	LGA	RIC	54	292	17	30	2023-10-21 17:00:00	Other
21240	8	26	1248	1255	-7	1441	1513	9E	1212	N480PX	LGA	CLT	84	544	12	55	2023-08-26 12:00:00	CLT
21242	5	3	929	935	-6	1211	1229	B6	222	N635JB	LGA	MCO	137	950	9	35	2023-05-03 09:00:00	MCO
21243	4	13	614	620	-6	853	905	B6	224	N659JB	JFK	MCO	129	944	6	20	2023-04-13 06:00:00	MCO
21249	5	26	835	845	-10	1109	1050	9E	1560	N491PX	LGA	AVL	89	599	8	45	2023-05-26 08:00:00	Other
21258	6	18	752	759	-7	1034	1109	UA	621	N410UA	EWR	FLL	143	1065	7	59	2023-06-18 07:00:00	FLL
21268	1	10	1729	1735	-6	2026	2101	DL	512	N366NW	JFK	AUS	205	1521	17	35	2023-01-10 17:00:00	Other
21280	1	26	1809	1815	-6	2005	2027	9E	1565	N902XJ	LGA	DSM	156	1031	18	15	2023-01-26 18:00:00	Other
21286	7	18	2053	2100	-7	21	24	AA	87	N112AN	JFK	LAX	310	2475	21	0	2023-07-18 21:00:00	LAX
21288	9	20	1313	1320	-7	1503	1523	YX	1350	N440YX	LGA	MSP	147	1020	13	20	2023-09-20 13:00:00	Other
21304	3	7	1150	1200	-10	1252	1314	9E	1414	N901XJ	LGA	ALB	32	136	12	0	2023-03-07 12:00:00	Other
21309	7	26	1115	1121	-6	1252	1312	UA	574	N415UA	EWR	DTW	72	488	11	21	2023-07-26 11:00:00	Other
21310	4	19	1138	1146	-8	1338	1350	DL	274	N964AT	EWR	MSP	161	1008	11	46	2023-04-19 11:00:00	Other
21311	2	8	1523	1530	-7	1636	1649	B6	409	N273JB	JFK	BOS	47	187	15	30	2023-02-08 15:00:00	BOS
21313	8	22	823	830	-7	950	957	UA	236	N434UA	EWR	BNA	104	748	8	30	2023-08-22 08:00:00	Other
21314	4	12	1120	1130	-10	1318	1336	YX	1229	N867RW	LGA	DTW	79	502	11	30	2023-04-12 11:00:00	Other
21316	9	19	1009	1015	-6	1303	1313	UA	711	N17309	EWR	IAH	197	1400	10	15	2023-09-19 10:00:00	Other
21331	8	10	1737	1745	-8	1931	1955	YX	1035	N870RW	LGA	MCI	153	1107	17	45	2023-08-10 17:00:00	Other
21333	2	14	1150	1200	-10	1252	1314	9E	1345	N176PQ	LGA	ALB	31	136	12	0	2023-02-14 12:00:00	Other
21339	4	26	1650	1700	-10	1828	1847	AA	617	N716UW	LGA	STL	136	888	17	0	2023-04-26 17:00:00	Other
21347	4	19	2051	2057	-6	2225	2250	YX	958	N749YX	EWR	GSO	63	445	20	57	2023-04-19 20:00:00	Other
21357	11	7	1601	1608	-7	1811	1842	UA	692	N24715	EWR	ATL	106	746	16	8	2023-11-07 16:00:00	ATL
21367	8	15	1149	1155	-6	1431	1455	DL	477	N327DN	LGA	MCO	132	950	11	55	2023-08-15 11:00:00	MCO
21369	12	14	1108	1115	-7	1400	1419	B6	127	N559JB	EWR	FLL	143	1065	11	15	2023-12-14 11:00:00	FLL
21371	10	5	1324	1330	-6	1413	1441	YX	1060	N742YX	EWR	MDT	33	141	13	30	2023-10-05 13:00:00	Other
21375	8	10	1654	1700	-6	1840	1857	DL	772	N940AT	EWR	DTW	78	488	17	0	2023-08-10 17:00:00	Other
21376	4	11	514	520	-6	626	636	NK	270	N506NK	EWR	PIT	50	319	5	20	2023-04-11 05:00:00	Other
21378	10	17	849	859	-10	1016	1059	9E	1639	N906XJ	LGA	STL	114	888	8	59	2023-10-17 08:00:00	Other
21381	7	8	1052	1059	-7	1227	1255	NK	522	N903NK	LGA	DTW	75	502	10	59	2023-07-08 10:00:00	Other
21382	11	20	1013	1025	-12	1250	1323	UA	621	N19141	EWR	MCO	131	937	10	25	2023-11-20 10:00:00	MCO
21392	8	19	2053	2059	-6	2240	2239	YX	848	N743YX	EWR	PIT	51	319	20	59	2023-08-19 20:00:00	Other
21395	8	17	1102	1108	-6	1351	1407	UA	211	N47281	EWR	PBI	150	1023	11	8	2023-08-17 11:00:00	Other
21398	7	27	623	630	-7	911	938	B6	5	N969JT	JFK	SFO	327	2586	6	30	2023-07-27 06:00:00	Other
21399	5	18	953	1000	-7	1204	1222	YX	1259	N821MD	LGA	IND	96	660	10	0	2023-05-18 10:00:00	Other
21404	5	5	1534	1540	-6	1815	1804	UA	378	N66825	EWR	DEN	233	1605	15	40	2023-05-05 15:00:00	Other
21409	4	14	1250	1259	-9	1428	1505	DL	704	N328NB	LGA	DTW	73	502	12	59	2023-04-14 12:00:00	Other
21413	1	17	2120	2130	-10	2305	2340	NK	325	N616NK	LGA	DTW	79	502	21	30	2023-01-17 21:00:00	Other
21420	2	28	1247	1255	-8	1510	1525	YX	1342	N110HQ	LGA	CVG	102	585	12	55	2023-02-28 12:00:00	Other
21426	2	22	1043	1053	-10	1218	1224	YX	1000	N650RW	EWR	PIT	71	319	10	53	2023-02-22 10:00:00	Other
21437	12	8	1405	1413	-8	1553	1610	9E	1359	N906XJ	JFK	RDU	68	427	14	13	2023-12-08 14:00:00	Other
21439	3	20	1816	1825	-9	2020	2051	YX	1278	N103HQ	LGA	IND	102	660	18	25	2023-03-20 18:00:00	Other
21441	1	30	1944	1950	-6	2226	2229	YX	1877	N860RW	LGA	MCI	192	1107	19	50	2023-01-30 19:00:00	Other
21445	4	28	618	625	-7	910	910	B6	93	N524JB	LGA	MCO	147	950	6	25	2023-04-28 06:00:00	MCO
21460	8	13	1148	1155	-7	1311	1344	YX	1056	N417YX	LGA	ROA	63	405	11	55	2023-08-13 11:00:00	Other
21461	2	11	1728	1735	-7	2023	2101	DL	447	N334NW	JFK	AUS	221	1521	17	35	2023-02-11 17:00:00	Other
21464	8	25	1740	1759	-19	2013	2110	F9	395	N363FR	LGA	MCO	127	950	17	59	2023-08-25 17:00:00	MCO
21470	10	24	1146	1153	-7	1340	1403	YX	1108	N760YX	EWR	CVG	94	569	11	53	2023-10-24 11:00:00	Other
21472	8	31	1152	1158	-6	1401	1414	YX	844	N731YX	EWR	SDF	99	642	11	58	2023-08-31 11:00:00	Other
21476	5	31	1252	1300	-8	1421	1447	DL	965	N943AT	EWR	DTW	73	488	13	0	2023-05-31 13:00:00	Other
21495	9	25	942	950	-8	1125	1130	9E	1743	N915XJ	LGA	BGR	54	378	9	50	2023-09-25 09:00:00	Other
21499	3	19	1521	1529	-8	1812	1754	UA	837	N492UA	EWR	MSY	198	1167	15	29	2023-03-19 15:00:00	Other
21501	1	17	1808	1815	-7	1917	1937	B6	510	N192JB	LGA	BOS	43	184	18	15	2023-01-17 18:00:00	BOS
21511	3	22	953	1000	-7	1202	1207	B6	65	N228JB	JFK	DTW	88	509	10	0	2023-03-22 10:00:00	Other
21516	2	6	1701	1707	-6	1944	2007	UA	187	N27268	EWR	MCO	127	937	17	7	2023-02-06 17:00:00	MCO
21517	3	29	1830	1837	-7	2053	2100	YX	1034	N636RW	EWR	IND	112	645	18	37	2023-03-29 18:00:00	Other
21519	6	29	1145	1158	-13	1434	1414	YX	1083	N726YX	EWR	SDF	99	642	11	58	2023-06-29 11:00:00	Other
21540	6	5	1138	1145	-7	1410	1448	AS	7	N926AK	JFK	PDX	300	2454	11	45	2023-06-05 11:00:00	Other
21541	11	7	1020	1029	-9	1237	1304	YX	1855	N235JQ	LGA	MCI	176	1107	10	29	2023-11-07 10:00:00	Other
21549	2	28	2004	2015	-11	2152	2216	YX	1278	N427YX	JFK	PIT	68	340	20	15	2023-02-28 20:00:00	Other
21555	12	22	1251	1300	-9	1449	1514	9E	1412	N182GJ	LGA	MEM	136	963	13	0	2023-12-22 13:00:00	Other
21559	2	1	907	920	-13	1107	1054	YX	1589	N209JQ	LGA	PWM	44	269	9	20	2023-02-01 09:00:00	Other
21560	5	28	1858	1905	-7	2150	2236	B6	28	N796JB	JFK	SLC	258	1990	19	5	2023-05-28 19:00:00	Other
21578	10	17	1248	1300	-12	1348	1416	UA	427	N38479	EWR	BOS	41	200	13	0	2023-10-17 13:00:00	BOS
21584	10	2	921	927	-6	1202	1219	AA	573	N916NN	LGA	DFW	175	1389	9	27	2023-10-02 09:00:00	Other
21590	12	24	1125	1131	-6	1335	1404	UA	655	N66837	EWR	JAX	113	820	11	31	2023-12-24 11:00:00	Other
21591	8	26	1554	1600	-6	1725	1725	YX	1013	N871RW	LGA	BUF	50	292	16	0	2023-08-26 16:00:00	Other
21595	9	3	2151	2159	-8	133	101	B6	653	N944JT	JFK	LAX	321	2475	21	59	2023-09-03 21:00:00	LAX
21596	9	19	1600	1610	-10	1730	1743	YX	1363	N872RW	LGA	CHO	55	305	16	10	2023-09-19 16:00:00	Other
21598	10	30	718	730	-12	1031	1031	UA	391	N481UA	EWR	SRQ	148	1034	7	30	2023-10-30 07:00:00	Other
21601	10	3	914	922	-8	1007	1046	YX	1803	N222JQ	LGA	SYR	40	198	9	22	2023-10-03 09:00:00	Other
21603	11	23	1543	1549	-6	1826	1850	DL	785	N899DN	JFK	MCO	133	944	15	49	2023-11-23 15:00:00	MCO
21605	5	27	1310	1320	-10	1531	1541	B6	651	N606JB	JFK	MSY	155	1182	13	20	2023-05-27 13:00:00	Other
21613	12	16	722	730	-8	901	915	UA	914	N78438	EWR	RDU	69	416	7	30	2023-12-16 07:00:00	Other
21614	9	17	1120	1130	-10	1211	1233	9E	1636	N308PQ	LGA	BDL	25	101	11	30	2023-09-17 11:00:00	Other
21636	6	14	728	735	-7	1012	1034	DL	815	N354NB	JFK	PBI	142	1028	7	35	2023-06-14 07:00:00	Other
21638	3	29	852	900	-8	1007	1030	9E	1585	N138EV	JFK	ORF	50	290	9	0	2023-03-29 09:00:00	Other
21639	12	29	1422	1430	-8	1745	1741	UA	374	N27269	EWR	MIA	170	1085	14	30	2023-12-29 14:00:00	MIA
21648	3	19	1148	1156	-8	1501	1507	DL	413	N343NW	LGA	TPA	169	1010	11	56	2023-03-19 11:00:00	Other
21654	4	27	726	735	-9	1009	1032	NK	432	N667NK	EWR	MCO	134	937	7	35	2023-04-27 07:00:00	MCO
21656	9	5	1623	1630	-7	1907	1941	NK	308	N660NK	LGA	FLL	139	1076	16	30	2023-09-05 16:00:00	FLL
21659	11	14	2122	2130	-8	13	28	B6	121	N618JB	LGA	FLL	146	1076	21	30	2023-11-14 21:00:00	FLL
21661	3	19	1723	1729	-6	2030	2040	UA	475	N37295	EWR	IAH	211	1400	17	29	2023-03-19 17:00:00	Other
21663	12	31	1719	1725	-6	1914	1946	YX	1792	N238JQ	LGA	CLT	89	544	17	25	2023-12-31 17:00:00	CLT
21666	6	1	636	645	-9	847	908	AA	571	N316SE	JFK	PHX	276	2153	6	45	2023-06-01 06:00:00	Other
21679	7	20	704	715	-11	953	1011	B6	376	N597JB	LGA	TPA	140	1010	7	15	2023-07-20 07:00:00	Other
21684	10	2	1234	1240	-6	1403	1425	WN	602	N939WN	LGA	STL	119	888	12	40	2023-10-02 12:00:00	Other
21687	8	10	1814	1820	-6	1942	2003	AA	577	N808AW	LGA	RDU	67	431	18	20	2023-08-10 18:00:00	Other
21696	2	24	722	730	-8	1026	1010	UA	779	N33286	LGA	DEN	265	1620	7	30	2023-02-24 07:00:00	Other
21697	1	3	1153	1200	-7	1358	1432	YX	1341	N114HQ	LGA	MEM	156	963	12	0	2023-01-03 12:00:00	Other
21700	5	2	1054	1100	-6	1335	1416	AA	112	N106NN	JFK	LAX	319	2475	11	0	2023-05-02 11:00:00	LAX
21701	12	11	1951	2000	-9	2059	2120	UA	874	N17105	EWR	IAD	46	212	20	0	2023-12-11 20:00:00	Other
21702	9	14	1430	1436	-6	1643	1629	YX	1875	N232JQ	LGA	MEM	138	963	14	36	2023-09-14 14:00:00	Other
21704	7	1	945	955	-10	1138	1155	G4	830	239NV	EWR	TYS	86	631	9	55	2023-07-01 09:00:00	Other
21705	2	26	954	1000	-6	1205	1151	B6	83	N228JB	JFK	RDU	74	427	10	0	2023-02-26 10:00:00	Other
21710	10	15	1754	1800	-6	2107	2105	AA	182	N985NN	LGA	DFW	187	1389	18	0	2023-10-15 18:00:00	Other
21712	3	31	1044	1057	-13	1307	1303	YX	1247	N821MD	LGA	AVL	105	599	10	57	2023-03-31 10:00:00	Other
21713	1	8	802	810	-8	1007	1041	YX	1317	N105HQ	LGA	CVG	105	585	8	10	2023-01-08 08:00:00	Other
21727	5	18	1615	1625	-10	1805	1803	YX	1312	N418YX	JFK	BNA	111	765	16	25	2023-05-18 16:00:00	Other
21728	3	9	1722	1729	-7	1854	1913	UA	228	N23721	EWR	CLE	68	404	17	29	2023-03-09 17:00:00	Other
21744	11	28	1720	1729	-9	1931	1948	9E	1704	N480PX	LGA	CVG	97	585	17	29	2023-11-28 17:00:00	Other
21745	5	30	954	1000	-6	1115	1138	UA	723	N486UA	LGA	ORD	105	733	10	0	2023-05-30 10:00:00	ORD
21752	11	29	2047	2055	-8	2207	2254	YX	1768	N233JQ	JFK	PIT	62	340	20	55	2023-11-29 20:00:00	Other
21757	3	22	1848	1855	-7	2231	2209	AS	12	N434AS	JFK	SAN	373	2446	18	55	2023-03-22 18:00:00	Other
21760	1	18	1659	1710	-11	1858	1919	AA	484	N767UW	LGA	STL	157	888	17	10	2023-01-18 17:00:00	Other
21764	10	31	1454	1500	-6	1612	1623	9E	1503	N914XJ	LGA	BTV	42	258	15	0	2023-10-31 15:00:00	Other
21786	12	21	1741	1750	-9	1936	2029	9E	1392	N336PQ	JFK	MCI	156	1113	17	50	2023-12-21 17:00:00	Other
21789	9	8	857	905	-8	1058	1113	NK	533	N621NK	EWR	CHS	88	628	9	5	2023-09-08 09:00:00	Other
21792	4	4	846	856	-10	1037	1103	YX	1535	N815MD	LGA	CMH	77	479	8	56	2023-04-04 08:00:00	Other
21793	11	14	1340	1346	-6	1504	1512	9E	1462	N131EV	JFK	PWM	56	273	13	46	2023-11-14 13:00:00	Other
21798	10	3	1903	1910	-7	2133	2152	YX	1304	N419YX	LGA	OKC	182	1341	19	10	2023-10-03 19:00:00	Other
21803	10	13	1322	1329	-7	1540	1558	DL	102	N3749D	LGA	DEN	238	1620	13	29	2023-10-13 13:00:00	Other
21805	1	17	649	659	-10	857	943	B6	871	N705JB	LGA	DEN	225	1620	6	59	2023-01-17 06:00:00	Other
21806	3	1	1807	1815	-8	2116	2137	UA	453	N2250U	EWR	SFO	341	2565	18	15	2023-03-01 18:00:00	Other
21807	10	17	1744	1750	-6	2034	2058	UA	615	N12754	EWR	PDX	331	2434	17	50	2023-10-17 17:00:00	Other
21811	2	7	941	950	-9	1209	1220	WN	193	N935WN	LGA	MCI	176	1107	9	50	2023-02-07 09:00:00	Other
21814	1	10	1223	1235	-12	1500	1607	AA	223	N829NN	LGA	DFW	192	1389	12	35	2023-01-10 12:00:00	Other
21815	8	22	1451	1459	-8	1628	1651	YX	1079	N439YX	JFK	CMH	74	483	14	59	2023-08-22 14:00:00	Other
21818	3	17	2046	2059	-13	2300	2300	YX	1210	N726YX	EWR	CMH	84	463	20	59	2023-03-17 20:00:00	Other
21829	2	27	1827	1840	-13	2043	2136	YX	1236	N446YX	LGA	OMA	172	1148	18	40	2023-02-27 18:00:00	Other
21836	10	17	2151	2159	-8	2256	2312	UA	445	N27258	EWR	SYR	35	195	21	59	2023-10-17 21:00:00	Other
21840	5	26	554	601	-7	728	747	DL	760	N979AT	EWR	DTW	77	488	6	1	2023-05-26 06:00:00	Other
21842	6	13	551	600	-9	852	908	NK	51	N663NK	LGA	FLL	162	1076	6	0	2023-06-13 06:00:00	FLL
21846	1	4	1624	1630	-6	1752	1830	AA	146	N869NN	LGA	ORD	119	733	16	30	2023-01-04 16:00:00	ORD
21851	2	3	623	630	-7	810	837	YX	1199	N132HQ	LGA	STL	146	888	6	30	2023-02-03 06:00:00	Other
21852	1	4	1043	1050	-7	1222	1236	YX	1373	N408YX	JFK	BNA	129	765	10	50	2023-01-04 10:00:00	Other
21857	12	6	1535	1545	-10	1814	1849	B6	805	N517JB	EWR	TPA	132	997	15	45	2023-12-06 15:00:00	Other
21862	8	4	1253	1259	-6	1357	1429	9E	1163	N316PQ	LGA	PWM	42	269	12	59	2023-08-04 12:00:00	Other
21863	5	9	1850	1856	-6	2056	2101	UA	704	N28478	EWR	CLT	90	529	18	56	2023-05-09 18:00:00	CLT
21865	1	26	1702	1710	-8	1853	1907	YX	1905	N823MD	LGA	CLE	88	419	17	10	2023-01-26 17:00:00	Other
21874	1	18	2050	2105	-15	2319	2329	B6	422	N337JB	LGA	CHS	97	641	21	5	2023-01-18 21:00:00	Other
21881	9	28	737	745	-8	948	959	B6	882	N506JB	LGA	CHS	99	641	7	45	2023-09-28 07:00:00	Other
21884	1	30	740	749	-9	918	926	YX	1349	N407YX	JFK	DCA	67	213	7	49	2023-01-30 07:00:00	Other
21889	4	10	1522	1529	-7	1708	1727	YX	1073	N118HQ	JFK	CLE	74	425	15	29	2023-04-10 15:00:00	Other
21891	10	16	626	632	-6	734	750	B6	960	N197JB	JFK	BUF	53	301	6	32	2023-10-16 06:00:00	Other
21898	5	27	1749	1755	-6	2106	2121	B6	310	N964JT	JFK	LAX	302	2475	17	55	2023-05-27 17:00:00	LAX
21904	2	1	752	800	-8	1206	1128	B6	758	N964JT	JFK	LAX	360	2475	8	0	2023-02-01 08:00:00	LAX
21905	9	18	2050	2100	-10	2233	2236	UA	681	N883UA	LGA	ORD	108	733	21	0	2023-09-18 21:00:00	ORD
21908	2	6	1250	1300	-10	1611	1637	B6	567	N977JE	JFK	SFO	354	2586	13	0	2023-02-06 13:00:00	Other
21915	3	22	1438	1450	-12	1551	1623	9E	1473	N197PQ	LGA	CHO	54	305	14	50	2023-03-22 14:00:00	Other
21916	1	16	621	630	-9	745	752	B6	1056	N355JB	JFK	BUF	58	301	6	30	2023-01-16 06:00:00	Other
21917	9	4	2002	2011	-9	2135	2151	YX	1369	N432YX	LGA	PIT	53	335	20	11	2023-09-04 20:00:00	Other
21920	12	5	1852	1859	-7	2012	2028	YX	1053	N730YX	EWR	PWM	51	284	18	59	2023-12-05 18:00:00	Other
21921	1	6	720	730	-10	938	1007	B6	992	N746JB	LGA	MSY	168	1183	7	30	2023-01-06 07:00:00	Other
21922	9	5	952	1000	-8	1119	1159	YX	1181	N656RW	EWR	GSO	69	445	10	0	2023-09-05 10:00:00	Other
21934	5	27	1940	1950	-10	2250	2307	YX	1099	N732YX	EWR	RSW	160	1068	19	50	2023-05-27 19:00:00	Other
21942	6	12	936	946	-10	1315	1341	UA	602	N37420	EWR	SJU	202	1608	9	46	2023-06-12 09:00:00	Other
21945	8	9	920	926	-6	1039	1107	YX	913	N733YX	EWR	PIT	54	319	9	26	2023-08-09 09:00:00	Other
21947	12	1	604	610	-6	905	934	DL	438	N104DU	LGA	IAH	220	1416	6	10	2023-12-01 06:00:00	Other
21948	7	5	1209	1215	-6	1400	1408	YX	1059	N443YX	LGA	CMH	73	479	12	15	2023-07-05 12:00:00	Other
21950	11	7	1851	1859	-8	2036	2102	YX	1361	N438YX	LGA	CMH	81	479	18	59	2023-11-07 18:00:00	Other
21951	5	17	1423	1430	-7	1650	1657	YX	1335	N413YX	LGA	IND	104	660	14	30	2023-05-17 14:00:00	Other
21953	4	25	2008	2020	-12	2202	2234	9E	1355	N482PX	LGA	GSP	90	610	20	20	2023-04-25 20:00:00	Other
21958	6	22	652	659	-7	821	830	YX	1361	N107HQ	LGA	PIT	58	335	6	59	2023-06-22 06:00:00	Other
21960	5	18	1008	1015	-7	1107	1132	B6	155	N283JB	LGA	BOS	36	184	10	15	2023-05-18 10:00:00	BOS
21961	1	16	1826	1833	-7	2117	2017	UA	259	N15712	EWR	CLE	63	404	18	33	2023-01-16 18:00:00	Other
21963	5	9	1352	1402	-10	1600	1618	YX	1236	N867RW	LGA	CAE	98	617	14	2	2023-05-09 14:00:00	Other
21972	8	3	1253	1300	-7	1554	1628	AS	4	N956AK	JFK	SFO	338	2586	13	0	2023-08-03 13:00:00	Other
21974	7	25	1046	1052	-6	1335	1350	B6	289	N516JB	EWR	MCO	131	937	10	52	2023-07-25 10:00:00	MCO
21982	3	2	1501	1507	-6	1701	1648	UA	650	N39297	EWR	ORD	141	719	15	7	2023-03-02 15:00:00	ORD
21984	6	5	1522	1529	-7	1842	1827	UA	411	N37466	EWR	AUS	212	1504	15	29	2023-06-05 15:00:00	Other
21993	1	15	725	734	-9	936	1006	UA	714	N77259	EWR	MSY	158	1167	7	34	2023-01-15 07:00:00	Other
21998	2	5	1653	1700	-7	1806	1828	YX	1596	N232JQ	LGA	BOS	46	184	17	0	2023-02-05 17:00:00	BOS
21999	8	17	1409	1420	-11	1531	1552	YX	852	N747YX	EWR	MKE	112	725	14	20	2023-08-17 14:00:00	Other
22000	12	1	745	752	-7	904	926	YX	1139	N979RP	EWR	PIT	60	319	7	52	2023-12-01 07:00:00	Other
22003	4	16	2119	2129	-10	2249	2316	YX	1238	N410YX	LGA	CLE	66	419	21	29	2023-04-16 21:00:00	Other
22008	8	24	1653	1659	-6	1919	1951	UA	414	N17300	EWR	SAN	299	2425	16	59	2023-08-24 16:00:00	Other
22009	2	20	723	730	-7	901	924	AA	270	N853NN	LGA	ORD	123	733	7	30	2023-02-20 07:00:00	ORD
22010	12	12	1005	1011	-6	1216	1236	OO	1167	N307SY	LGA	MEM	159	963	10	11	2023-12-12 10:00:00	Other
22014	12	2	1310	1317	-7	1503	1530	AA	724	N966NN	LGA	CLT	92	544	13	17	2023-12-02 13:00:00	CLT
22015	9	25	626	634	-8	825	850	AA	1013	N420AN	EWR	PHX	277	2133	6	34	2023-09-25 06:00:00	Other
22018	11	10	1722	1729	-7	1935	1958	YX	1850	N243JQ	LGA	IND	111	660	17	29	2023-11-10 17:00:00	Other
22025	2	6	1001	1010	-9	1220	1235	9E	1364	N309PQ	LGA	MYR	83	563	10	10	2023-02-06 10:00:00	Other
22026	3	21	2005	2015	-10	2154	2219	YX	1331	N106HQ	JFK	PIT	71	340	20	15	2023-03-21 20:00:00	Other
22038	5	2	1915	1929	-14	2124	2157	YX	1618	N232JQ	LGA	OMA	159	1148	19	29	2023-05-02 19:00:00	Other
22044	1	18	1113	1130	-17	1426	1456	AS	8	N471AS	JFK	PDX	341	2454	11	30	2023-01-18 11:00:00	Other
22049	5	18	1451	1457	-6	1628	1641	UA	572	N834UA	EWR	RDU	68	416	14	57	2023-05-18 14:00:00	Other
22056	1	19	1317	1326	-9	1513	1538	YX	1316	N134HQ	LGA	CMH	88	479	13	26	2023-01-19 13:00:00	Other
22057	8	3	2120	2129	-9	2247	2255	YX	988	N412YX	LGA	RIC	55	292	21	29	2023-08-03 21:00:00	Other
22060	2	14	1723	1730	-7	2007	2050	AS	88	N564AS	EWR	PDX	314	2434	17	30	2023-02-14 17:00:00	Other
22061	11	1	2014	2020	-6	2316	2255	WN	178	N467WN	LGA	DEN	228	1620	20	20	2023-11-01 20:00:00	Other
22065	1	20	2034	2043	-9	2221	2240	9E	1667	N918XJ	LGA	RDU	75	431	20	43	2023-01-20 20:00:00	Other
22070	4	20	517	525	-8	752	800	B6	114	N955JB	EWR	MCO	127	937	5	25	2023-04-20 05:00:00	MCO
22073	12	20	2149	2159	-10	2248	2317	YX	1848	N227JQ	LGA	SYR	39	198	21	59	2023-12-20 21:00:00	Other
22074	2	23	921	930	-9	1105	1120	B6	744	N304JB	LGA	BNA	126	764	9	30	2023-02-23 09:00:00	Other
22084	1	18	1202	1210	-8	1259	1319	YX	1300	N115HQ	JFK	ORH	33	150	12	10	2023-01-18 12:00:00	Other
22089	3	24	654	700	-6	946	1000	UA	948	N27292	EWR	PBI	146	1023	7	0	2023-03-24 07:00:00	Other
22092	1	24	1253	1300	-7	1429	1447	YX	1149	N745YX	EWR	GSO	74	445	13	0	2023-01-24 13:00:00	Other
22094	6	1	1922	1930	-8	2228	2244	AA	98	N102NN	JFK	LAX	316	2475	19	30	2023-06-01 19:00:00	LAX
22097	6	10	2221	2233	-12	2340	10	9E	1671	N319PQ	JFK	PWM	42	273	22	33	2023-06-10 22:00:00	Other
22103	4	1	926	932	-6	1151	1149	YX	1012	N752YX	EWR	MCI	170	1092	9	32	2023-04-01 09:00:00	Other
22104	3	19	708	714	-6	934	934	UA	846	N17285	EWR	MSY	184	1167	7	14	2023-03-19 07:00:00	Other
22108	5	9	554	600	-6	752	808	YX	1624	N222JQ	LGA	CLT	90	544	6	0	2023-05-09 06:00:00	CLT
22110	2	5	1346	1352	-6	1625	1708	AA	174	N987AN	LGA	DFW	200	1389	13	52	2023-02-05 13:00:00	Other
22116	1	28	1658	1708	-10	1901	1915	DL	988	N339NW	LGA	DTW	97	502	17	8	2023-01-28 17:00:00	Other
22117	5	2	1319	1329	-10	1519	1548	YX	1253	N432YX	LGA	MCI	161	1107	13	29	2023-05-02 13:00:00	Other
22118	6	6	1445	1455	-10	1719	1710	YX	1423	N133HQ	LGA	CVG	97	585	14	55	2023-06-06 14:00:00	Other
22120	12	12	1048	1054	-6	1344	1417	DL	875	N124DX	LGA	FLL	150	1076	10	54	2023-12-12 10:00:00	FLL
22123	6	7	839	845	-6	1003	1028	UA	808	N76508	EWR	ORD	106	719	8	45	2023-06-07 08:00:00	ORD
22124	8	27	1711	1717	-6	1913	1933	AA	753	N456AN	EWR	PHX	272	2133	17	17	2023-08-27 17:00:00	Other
22129	8	30	551	600	-9	858	922	AA	28	N113AN	JFK	SFO	335	2586	6	0	2023-08-30 06:00:00	Other
22133	3	6	746	800	-14	919	918	AA	770	N747UW	LGA	DCA	54	214	8	0	2023-03-06 08:00:00	Other
22135	4	18	1402	1415	-13	1500	1532	B6	304	N334JB	LGA	BOS	33	184	14	15	2023-04-18 14:00:00	BOS
22141	9	12	1808	1817	-9	1946	1950	YX	1184	N979RP	EWR	BNA	114	748	18	17	2023-09-12 18:00:00	Other
22151	5	19	853	900	-7	1028	1027	YX	1164	N736YX	EWR	DCA	48	199	9	0	2023-05-19 09:00:00	Other
22152	5	31	753	759	-6	915	928	UA	225	N459UA	EWR	BOS	46	200	7	59	2023-05-31 07:00:00	BOS
22153	1	29	2149	2200	-11	2307	2309	9E	1381	N176PQ	JFK	ITH	43	189	22	0	2023-01-29 22:00:00	Other
22156	6	10	1043	1050	-7	1237	1310	9E	1756	N299PQ	LGA	CVG	92	585	10	50	2023-06-10 10:00:00	Other
22157	11	3	626	632	-6	836	902	AA	519	N302SA	JFK	PHX	288	2153	6	32	2023-11-03 06:00:00	Other
22160	1	27	1647	1655	-8	1837	1853	9E	1530	N133EV	LGA	RDU	77	431	16	55	2023-01-27 16:00:00	Other
22162	12	23	1606	1615	-9	1832	1846	YX	1340	N119HQ	LGA	IND	99	660	16	15	2023-12-23 16:00:00	Other
22166	8	1	2054	2100	-6	2242	2256	YX	887	N640RW	EWR	ILM	76	488	21	0	2023-08-01 21:00:00	Other
22170	12	1	552	600	-8	738	737	AA	227	N817NN	LGA	ORD	129	733	6	0	2023-12-01 06:00:00	ORD
22173	12	31	1010	1020	-10	1136	1209	YX	1308	N135HQ	LGA	ROA	68	405	10	20	2023-12-31 10:00:00	Other
22181	8	27	918	929	-11	1155	1153	YX	907	N647RW	EWR	TVC	97	644	9	29	2023-08-27 09:00:00	Other
22183	7	11	859	905	-6	1132	1208	YX	1001	N440YX	LGA	IAH	187	1416	9	5	2023-07-11 09:00:00	Other
22184	7	19	1252	1300	-8	1502	1534	DL	395	N814DN	JFK	ATL	100	760	13	0	2023-07-19 13:00:00	ATL
22187	9	1	854	900	-6	1040	1036	OO	1290	N258SY	JFK	BNA	103	765	9	0	2023-09-01 09:00:00	Other
22196	5	29	748	800	-12	854	928	YX	1712	N209JQ	LGA	BOS	41	184	8	0	2023-05-29 08:00:00	BOS
22201	10	26	1238	1251	-13	1355	1413	9E	1503	N919XJ	LGA	BTV	51	258	12	51	2023-10-26 12:00:00	Other
22204	3	22	2153	2159	-6	214	133	B6	943	N929JB	JFK	SFO	390	2586	21	59	2023-03-22 21:00:00	Other
22205	4	25	1813	1820	-7	2020	2053	9E	1371	N600LR	JFK	IND	103	665	18	20	2023-04-25 18:00:00	Other
22207	10	13	2141	2151	-10	2326	2334	YX	1348	N410YX	LGA	CLE	73	419	21	51	2023-10-13 21:00:00	Other
22211	10	20	723	730	-7	851	913	DL	646	N123DQ	LGA	ORD	106	733	7	30	2023-10-20 07:00:00	ORD
22213	10	3	824	830	-6	943	1005	OO	1193	N254SY	JFK	BNA	114	765	8	30	2023-10-03 08:00:00	Other
22217	3	21	819	826	-7	939	1003	UA	506	N17730	EWR	BNA	108	748	8	26	2023-03-21 08:00:00	Other
22219	2	7	1427	1435	-8	1526	1553	UA	473	N76502	EWR	BOS	37	200	14	35	2023-02-07 14:00:00	BOS
22221	2	10	758	810	-12	1018	1034	YX	1335	N109HQ	LGA	CVG	114	585	8	10	2023-02-10 08:00:00	Other
22229	10	18	551	600	-9	834	854	UA	227	N37313	EWR	AUS	198	1504	6	0	2023-10-18 06:00:00	Other
22232	4	3	1324	1330	-6	1441	1442	B6	41	N258JB	JFK	SYR	47	209	13	30	2023-04-03 13:00:00	Other
22237	10	3	1123	1129	-6	1412	1447	AA	610	N959NN	LGA	MIA	149	1096	11	29	2023-10-03 11:00:00	MIA
22240	10	20	1938	1946	-8	2102	2112	YX	1832	N242JQ	EWR	BOS	35	200	19	46	2023-10-20 19:00:00	BOS
22241	9	2	1652	1700	-8	1807	1827	9E	1519	N314PQ	LGA	SYR	41	198	17	0	2023-09-02 17:00:00	Other
22243	6	29	924	930	-6	1210	1247	AS	9	N477AS	JFK	SEA	316	2422	9	30	2023-06-29 09:00:00	Other
22247	6	11	927	935	-8	1044	1103	B6	617	N197JB	JFK	BUF	54	301	9	35	2023-06-11 09:00:00	Other
22258	8	22	620	630	-10	905	932	B6	5	N961JT	JFK	SFO	326	2586	6	30	2023-08-22 06:00:00	Other
22263	9	12	746	757	-11	1033	1104	UA	601	N12225	EWR	FLL	144	1065	7	57	2023-09-12 07:00:00	FLL
22279	10	18	1840	1850	-10	2053	2123	9E	1416	N297PQ	JFK	SAV	105	718	18	50	2023-10-18 18:00:00	Other
22284	5	10	600	610	-10	747	809	DL	415	N349NB	LGA	MSP	141	1020	6	10	2023-05-10 06:00:00	Other
22287	12	31	1009	1015	-6	1244	1326	B6	639	N968JT	EWR	LAX	309	2454	10	15	2023-12-31 10:00:00	LAX
22303	12	30	1249	1259	-10	1418	1502	DL	748	N336NB	LGA	DTW	74	502	12	59	2023-12-30 12:00:00	Other
22307	2	12	1452	1500	-8	1722	1755	B6	831	N571JB	LGA	JAX	122	833	15	0	2023-02-12 15:00:00	Other
22312	6	1	1153	1200	-7	1355	1422	YX	1287	N118HQ	JFK	IND	95	665	12	0	2023-06-01 12:00:00	Other
22314	2	25	1717	1725	-8	1832	1904	YX	1558	N232JQ	LGA	IAD	54	229	17	25	2023-02-25 17:00:00	Other
22329	2	1	716	730	-14	1002	954	B6	865	N637JB	JFK	CHS	106	636	7	30	2023-02-01 07:00:00	Other
22330	2	24	1053	1059	-6	1306	1246	YX	1031	N746YX	EWR	RDU	80	416	10	59	2023-02-24 10:00:00	Other
22337	12	28	900	906	-6	1111	1116	9E	1499	N921XJ	LGA	ILM	81	500	9	6	2023-12-28 09:00:00	Other
22340	1	31	2021	2034	-13	1	2359	UA	978	N37267	EWR	SMF	357	2500	20	34	2023-01-31 20:00:00	Other
22344	2	8	1344	1350	-6	1615	1631	DL	145	N361NW	LGA	ATL	115	762	13	50	2023-02-08 13:00:00	ATL
22345	9	2	923	930	-7	1214	1223	AS	14	N917AK	JFK	SAN	312	2446	9	30	2023-09-02 09:00:00	Other
22356	3	9	1111	1118	-7	1407	1425	DL	469	N372DA	LGA	PBI	142	1035	11	18	2023-03-09 11:00:00	Other
22366	7	2	1252	1259	-7	1600	1606	AA	531	N973AN	EWR	MIA	165	1085	12	59	2023-07-02 12:00:00	MIA
22372	1	29	1138	1144	-6	1425	1440	UA	320	N27269	EWR	MCO	135	937	11	44	2023-01-29 11:00:00	MCO
22373	7	21	1853	1900	-7	2018	2051	YX	1358	N824MD	LGA	PIT	58	335	19	0	2023-07-21 19:00:00	Other
22383	8	23	611	629	-18	743	814	AA	764	N833AW	LGA	RDU	68	431	6	29	2023-08-23 06:00:00	Other
22386	11	12	1753	1759	-6	1958	2007	9E	1443	N311PQ	LGA	MEM	145	963	17	59	2023-11-12 17:00:00	Other
22387	6	12	819	825	-6	1123	1115	AA	618	N177US	EWR	DFW	204	1372	8	25	2023-06-12 08:00:00	Other
22389	8	20	1501	1510	-9	1621	1646	UA	528	N47281	EWR	CLE	59	404	15	10	2023-08-20 15:00:00	Other
22392	3	18	1452	1500	-8	1902	1657	YX	1762	N233JQ	LGA	STL	NA	888	15	0	2023-03-18 15:00:00	Other
22395	11	1	1022	1030	-8	1323	1336	B6	951	N586JB	JFK	TPA	161	1005	10	30	2023-11-01 10:00:00	Other
22408	2	6	1919	1929	-10	2052	2116	YX	1591	N221JQ	LGA	PIT	55	335	19	29	2023-02-06 19:00:00	Other
22420	2	5	920	929	-9	1251	1314	B6	40	N947JB	JFK	SFO	371	2586	9	29	2023-02-05 09:00:00	Other
22421	6	1	652	659	-7	828	849	YX	1414	N417YX	JFK	RDU	70	427	6	59	2023-06-01 06:00:00	Other
22427	10	29	948	955	-7	1124	1143	YX	1079	N760YX	EWR	CLE	75	404	9	55	2023-10-29 09:00:00	Other
22432	2	10	624	630	-6	749	752	B6	925	N334JB	JFK	BUF	64	301	6	30	2023-02-10 06:00:00	Other
22433	9	1	953	1000	-7	1248	1304	UA	816	N37018	EWR	SFO	321	2565	10	0	2023-09-01 10:00:00	Other
22436	9	7	723	730	-7	1002	1030	AS	80	N922VA	EWR	LAX	307	2454	7	30	2023-09-07 07:00:00	LAX
22439	3	20	1937	1945	-8	2225	2259	B6	813	N649JB	JFK	RNO	328	2411	19	45	2023-03-20 19:00:00	Other
22443	8	20	852	900	-8	1133	1222	AS	16	N929AK	JFK	SFO	314	2586	9	0	2023-08-20 09:00:00	Other
22447	12	5	650	700	-10	1019	1020	DL	282	N3759	JFK	RSW	175	1074	7	0	2023-12-05 07:00:00	Other
22448	2	4	552	600	-8	738	755	DL	741	N994AT	EWR	DTW	89	488	6	0	2023-02-04 06:00:00	Other
22450	7	19	1120	1128	-8	1433	1445	AA	534	N886NN	LGA	MIA	159	1096	11	28	2023-07-19 11:00:00	MIA
22455	4	7	1213	1220	-7	1334	1344	9E	1401	N302PQ	LGA	BTV	42	258	12	20	2023-04-07 12:00:00	Other
22458	12	13	653	700	-7	922	928	DL	746	N915DU	EWR	ATL	116	746	7	0	2023-12-13 07:00:00	ATL
22459	7	20	808	820	-12	1013	1047	YX	1364	N214JQ	LGA	IND	100	660	8	20	2023-07-20 08:00:00	Other
22466	1	13	817	825	-8	945	1024	DL	700	N110DU	LGA	ORD	109	733	8	25	2023-01-13 08:00:00	ORD
22491	10	19	918	929	-11	1057	1114	AA	604	N772XF	LGA	STL	139	888	9	29	2023-10-19 09:00:00	Other
22493	7	20	750	759	-9	943	1005	AA	812	N178US	LGA	CLT	83	544	7	59	2023-07-20 07:00:00	CLT
22496	10	7	1259	1305	-6	1515	1541	UA	109	N17302	EWR	LAS	287	2227	13	5	2023-10-07 13:00:00	Other
22504	1	12	835	845	-10	1158	1232	YX	1231	N638RW	EWR	EYW	177	1196	8	45	2023-01-12 08:00:00	Other
22513	12	5	1138	1145	-7	1448	1510	UA	377	N39418	EWR	SAT	230	1569	11	45	2023-12-05 11:00:00	Other
22517	11	6	2120	2128	-8	2315	2329	NK	279	N648NK	LGA	DTW	90	502	21	28	2023-11-06 21:00:00	Other
22526	3	31	1622	1630	-8	1816	1811	YX	1286	N436YX	JFK	BNA	123	765	16	30	2023-03-31 16:00:00	Other
22527	7	12	1054	1100	-6	1204	1231	YX	1447	N226JQ	LGA	BOS	41	184	11	0	2023-07-12 11:00:00	BOS
22530	8	16	1010	1020	-10	1123	1156	9E	1296	N232PQ	JFK	ROC	48	264	10	20	2023-08-16 10:00:00	Other
22536	11	12	1254	1305	-11	1423	1434	B6	894	N206JB	JFK	DCA	66	213	13	5	2023-11-12 13:00:00	Other
22537	4	3	1644	1650	-6	1848	1900	9E	1260	N918XJ	LGA	DSM	153	1031	16	50	2023-04-03 16:00:00	Other
22542	1	28	1845	1855	-10	2104	2119	9E	1596	N606LR	JFK	IND	114	665	18	55	2023-01-28 18:00:00	Other
22550	12	6	1409	1416	-7	1553	1613	YX	1822	N209JQ	LGA	CMH	74	479	14	16	2023-12-06 14:00:00	Other
22556	7	22	529	535	-6	805	807	B6	100	N505JB	EWR	MCO	128	937	5	35	2023-07-22 05:00:00	MCO
22562	9	20	1434	1440	-6	1607	1612	9E	1500	N917XJ	LGA	ORF	51	296	14	40	2023-09-20 14:00:00	Other
22567	4	20	854	900	-6	1038	1100	YX	1455	N216JQ	LGA	STL	123	888	9	0	2023-04-20 09:00:00	Other
22571	8	11	2211	2217	-6	2313	2326	UA	707	N491UA	EWR	SYR	34	195	22	17	2023-08-11 22:00:00	Other
22575	10	29	1554	1600	-6	1936	1933	AA	48	N116AN	JFK	SFO	378	2586	16	0	2023-10-29 16:00:00	Other
22580	11	7	1322	1328	-6	1503	1543	YX	1906	N211JQ	LGA	CLT	81	544	13	28	2023-11-07 13:00:00	CLT
22590	9	4	1227	1237	-10	1406	1430	DL	784	N948AT	EWR	MSP	136	1008	12	37	2023-09-04 12:00:00	Other
22591	12	27	1602	1610	-8	1726	1751	UA	755	N24736	EWR	CLE	61	404	16	10	2023-12-27 16:00:00	Other
22596	12	26	1905	1915	-10	2023	2050	YX	1306	N404YX	LGA	PIT	58	335	19	15	2023-12-26 19:00:00	Other
22601	5	17	834	840	-6	1014	1028	YX	1047	N745YX	EWR	PIT	54	319	8	40	2023-05-17 08:00:00	Other
22609	1	10	2152	2200	-8	2306	2322	AA	855	N771XF	LGA	DCA	47	214	22	0	2023-01-10 22:00:00	Other
22615	10	24	1039	1047	-8	1127	1155	YX	1127	N655RW	EWR	AVP	28	93	10	47	2023-10-24 10:00:00	Other
22617	10	21	1256	1308	-12	1535	1557	UA	688	N19136	EWR	MCO	130	937	13	8	2023-10-21 13:00:00	MCO
22618	8	2	1733	1741	-8	2049	2141	DL	214	N532DN	JFK	SLC	271	1990	17	41	2023-08-02 17:00:00	Other
22638	3	28	1833	1840	-7	1959	2017	AA	973	N301NW	LGA	ORD	116	733	18	40	2023-03-28 18:00:00	ORD
22643	10	23	1819	1825	-6	2123	2135	AA	716	N305NX	LGA	MIA	142	1096	18	25	2023-10-23 18:00:00	MIA
22653	6	5	1847	1855	-8	2001	2018	AA	903	N814AW	LGA	BNA	110	764	18	55	2023-06-05 18:00:00	Other
22654	10	16	2113	2120	-7	2240	2320	YX	1767	N243JQ	JFK	CMH	69	483	21	20	2023-10-16 21:00:00	Other
22657	5	16	2017	2029	-12	2317	2326	B6	180	N505JB	LGA	MCO	137	950	20	29	2023-05-16 20:00:00	MCO
22659	3	9	1408	1415	-7	1524	1527	B6	330	N307JB	LGA	BOS	38	184	14	15	2023-03-09 14:00:00	BOS
22661	3	29	949	955	-6	1217	1215	WN	977	N472WN	LGA	MCI	173	1107	9	55	2023-03-29 09:00:00	Other
22663	7	22	1052	1100	-8	1249	1252	YX	1004	N444YX	JFK	CLE	79	425	11	0	2023-07-22 11:00:00	Other
22664	3	10	624	630	-6	1016	1010	AA	33	N117AN	JFK	SFO	392	2586	6	30	2023-03-10 06:00:00	Other
22678	6	5	551	600	-9	819	925	B6	5	N964JT	JFK	SFO	311	2586	6	0	2023-06-05 06:00:00	Other
22681	12	28	924	930	-6	1045	1120	B6	380	N284JB	JFK	ORD	105	740	9	30	2023-12-28 09:00:00	ORD
22682	2	15	1802	1815	-13	1914	1937	B6	445	N279JB	LGA	BOS	37	184	18	15	2023-02-15 18:00:00	BOS
22687	10	13	834	845	-11	1107	1115	YX	1280	N106HQ	LGA	OMA	182	1148	8	45	2023-10-13 08:00:00	Other
22691	7	11	1337	1345	-8	1611	1547	YX	1038	N418YX	LGA	CAE	106	617	13	45	2023-07-11 13:00:00	Other
22692	6	11	1222	1229	-7	1340	1400	YX	1279	N424YX	JFK	ORF	48	290	12	29	2023-06-11 12:00:00	Other
22694	3	21	1850	1900	-10	2010	2034	YX	1301	N104HQ	LGA	PIT	60	335	19	0	2023-03-21 19:00:00	Other
22696	4	9	1052	1100	-8	1332	1416	AA	115	N106NN	JFK	LAX	317	2475	11	0	2023-04-09 11:00:00	LAX
22706	4	9	652	659	-7	956	1011	AA	819	N880NN	LGA	MIA	162	1096	6	59	2023-04-09 06:00:00	MIA
22709	10	5	1828	1835	-7	2154	2152	B6	227	N651JB	JFK	SJC	351	2569	18	35	2023-10-05 18:00:00	Other
22711	10	3	1059	1105	-6	1355	1418	DL	576	N3756	LGA	MIA	145	1096	11	5	2023-10-03 11:00:00	MIA
22714	6	8	652	659	-7	843	901	AA	350	N965AN	LGA	CLT	91	544	6	59	2023-06-08 06:00:00	CLT
22727	2	25	1323	1330	-7	1448	1455	YX	1582	N246JQ	JFK	ORF	67	290	13	30	2023-02-25 13:00:00	Other
22731	4	21	1854	1900	-6	2147	2207	DL	279	N133DU	LGA	DFW	205	1389	19	0	2023-04-21 19:00:00	Other
22740	9	24	1812	1820	-8	2056	2104	DL	240	N539DN	JFK	LAS	294	2248	18	20	2023-09-24 18:00:00	Other
22741	6	23	752	759	-7	902	937	YX	1107	N731YX	EWR	MKE	104	725	7	59	2023-06-23 07:00:00	Other
22754	9	27	553	600	-7	904	925	AA	28	N115NN	JFK	SFO	329	2586	6	0	2023-09-27 06:00:00	Other
22755	1	14	718	725	-7	848	901	YX	1830	N208JQ	LGA	BUF	51	292	7	25	2023-01-14 07:00:00	Other
22764	4	18	1714	1720	-6	2010	2038	AA	868	N335RT	JFK	AUS	199	1521	17	20	2023-04-18 17:00:00	Other
22766	2	6	923	935	-12	1200	1212	9E	1310	N600LR	LGA	GRR	96	618	9	35	2023-02-06 09:00:00	Other
22768	10	8	654	700	-6	1043	1057	B6	552	N519JB	EWR	SJU	202	1608	7	0	2023-10-08 07:00:00	Other
22770	9	27	915	922	-7	1021	1046	YX	1898	N243JQ	LGA	SYR	40	198	9	22	2023-09-27 09:00:00	Other
22778	10	17	720	729	-9	959	1024	UA	922	N17752	LGA	IAH	182	1416	7	29	2023-10-17 07:00:00	Other
22790	11	29	753	800	-7	949	954	B6	827	N3104J	JFK	RDU	71	427	8	0	2023-11-29 08:00:00	Other
22793	1	21	653	700	-7	1007	1024	DL	739	N125DU	LGA	IAH	227	1416	7	0	2023-01-21 07:00:00	Other
22804	1	17	2156	2211	-15	2313	2349	UA	763	N79541	EWR	BNA	118	748	22	11	2023-01-17 22:00:00	Other
22809	5	2	1642	1650	-8	1946	2008	B6	764	N613JB	JFK	MIA	155	1089	16	50	2023-05-02 16:00:00	MIA
22812	9	29	906	915	-9	1015	1035	B6	891	N231JB	LGA	BOS	34	184	9	15	2023-09-29 09:00:00	BOS
22821	8	9	1420	1430	-10	1602	1626	AA	603	N765US	LGA	RDU	71	431	14	30	2023-08-09 14:00:00	Other
22827	2	13	1710	1720	-10	1923	2005	YX	1339	N434YX	LGA	IND	103	660	17	20	2023-02-13 17:00:00	Other
22842	3	6	1250	1300	-10	1434	1502	AA	639	N172US	LGA	CLT	82	544	13	0	2023-03-06 13:00:00	CLT
22860	9	3	555	610	-15	833	850	B6	498	N993JE	EWR	LAX	304	2454	6	10	2023-09-03 06:00:00	LAX
22866	10	10	2136	2147	-11	2247	2258	YX	1137	N865RW	EWR	MDT	31	141	21	47	2023-10-10 21:00:00	Other
22869	12	4	1852	1859	-7	2035	2102	YX	1316	N124HQ	LGA	CMH	77	479	18	59	2023-12-04 18:00:00	Other
22872	7	3	1356	1405	-9	1528	1558	YX	1077	N869RW	LGA	ILM	80	500	14	5	2023-07-03 14:00:00	Other
22874	8	14	1159	1205	-6	1347	1411	YX	1060	N113HQ	LGA	DTW	86	502	12	5	2023-08-14 12:00:00	Other
22875	7	21	853	900	-7	1020	1034	B6	639	N187JB	LGA	BNA	108	764	9	0	2023-07-21 09:00:00	Other
22891	10	28	2006	2015	-9	2259	2246	B6	893	N526JL	LGA	ATL	110	762	20	15	2023-10-28 20:00:00	ATL
22896	5	14	2220	2230	-10	2341	4	9E	1526	N929XJ	JFK	SYR	41	209	22	30	2023-05-14 22:00:00	Other
22897	9	11	923	929	-6	1202	1246	DL	295	N891DN	JFK	SLC	265	1990	9	29	2023-09-11 09:00:00	Other
22903	10	27	1850	1859	-9	2036	2059	YX	1366	N411YX	JFK	RDU	67	427	18	59	2023-10-27 18:00:00	Other
22906	10	9	2132	2140	-8	2233	2259	9E	1633	N187GJ	JFK	ITH	41	189	21	40	2023-10-09 21:00:00	Other
22908	7	28	914	920	-6	1026	1053	AA	589	N757UW	LGA	PIT	55	335	9	20	2023-07-28 09:00:00	Other
22920	11	4	753	800	-7	1100	1115	UA	825	N37535	EWR	RSW	153	1068	8	0	2023-11-04 08:00:00	Other
22928	1	26	817	825	-8	948	1024	DL	700	N113DQ	LGA	ORD	110	733	8	25	2023-01-26 08:00:00	ORD
22949	10	11	1510	1517	-7	1639	1647	9E	1446	N602LR	LGA	MKE	122	738	15	17	2023-10-11 15:00:00	Other
22964	2	8	745	751	-6	1006	1027	UA	816	N58101	EWR	DEN	232	1605	7	51	2023-02-08 07:00:00	Other
22970	12	5	2019	2029	-10	2306	2337	UA	375	N14228	EWR	IAH	201	1400	20	29	2023-12-05 20:00:00	Other
22971	12	14	2005	2015	-10	2110	2134	B6	514	N206JB	LGA	BOS	44	184	20	15	2023-12-14 20:00:00	BOS
22972	9	2	624	630	-6	800	830	YX	1412	N114HQ	JFK	RDU	72	427	6	30	2023-09-02 06:00:00	Other
22974	11	2	722	730	-8	957	1034	B6	85	N981JT	JFK	SAN	312	2446	7	30	2023-11-02 07:00:00	Other
22977	1	9	815	825	-10	938	1024	DL	700	N108DQ	LGA	ORD	114	733	8	25	2023-01-09 08:00:00	ORD
22979	11	1	620	629	-9	810	841	YX	1321	N437YX	LGA	MSP	150	1020	6	29	2023-11-01 06:00:00	Other
22981	2	18	826	835	-9	1049	1121	YX	1257	N409YX	LGA	ATL	113	762	8	35	2023-02-18 08:00:00	ATL
22985	4	13	1849	1855	-6	2106	2158	AA	372	N316PF	LGA	DFW	177	1389	18	55	2023-04-13 18:00:00	Other
22994	8	28	824	830	-6	1028	1038	YX	869	N743YX	EWR	GSP	96	594	8	30	2023-08-28 08:00:00	Other
23002	2	7	2039	2045	-6	2347	2355	NK	290	N648NK	EWR	IAH	210	1400	20	45	2023-02-07 20:00:00	Other
23004	5	8	838	845	-7	1024	1040	YX	1270	N119HQ	LGA	GSO	70	461	8	45	2023-05-08 08:00:00	Other
23005	6	5	911	919	-8	1119	1120	YX	1814	N216JQ	LGA	CMH	78	479	9	19	2023-06-05 09:00:00	Other
23007	10	10	1823	1829	-6	2034	2055	9E	1627	N602LR	JFK	CHS	93	636	18	29	2023-10-10 18:00:00	Other
23009	5	30	551	600	-9	844	907	NK	53	N685NK	LGA	FLL	156	1076	6	0	2023-05-30 06:00:00	FLL
23013	3	1	605	615	-10	706	728	B6	72	N179JB	LGA	BOS	39	184	6	15	2023-03-01 06:00:00	BOS
23025	1	12	820	830	-10	1045	1056	YX	1798	N227JQ	LGA	CLT	93	544	8	30	2023-01-12 08:00:00	CLT
23027	8	29	1603	1610	-7	1711	1802	9E	1197	N232PQ	JFK	ROC	43	264	16	10	2023-08-29 16:00:00	Other
23032	5	10	936	945	-9	1251	1317	YX	1133	N863RW	EWR	EYW	159	1196	9	45	2023-05-10 09:00:00	Other
23035	11	11	1738	1745	-7	2048	2050	B6	263	N658JB	LGA	MCO	141	950	17	45	2023-11-11 17:00:00	MCO
23037	10	3	822	829	-7	1107	1140	AA	320	N110AN	JFK	SNA	321	2454	8	29	2023-10-03 08:00:00	Other
23044	10	13	1023	1029	-6	1208	1210	9E	1617	N301PQ	LGA	BUF	53	292	10	29	2023-10-13 10:00:00	Other
23046	8	8	753	800	-7	923	944	OO	941	N243SY	JFK	ORD	114	740	8	0	2023-08-08 08:00:00	ORD
23050	9	19	853	900	-7	1011	1029	YX	1101	N749YX	EWR	DCA	43	199	9	0	2023-09-19 09:00:00	Other
23058	12	19	749	755	-6	1249	1247	UA	763	N76062	EWR	SJU	204	1608	7	55	2023-12-19 07:00:00	Other
23060	3	28	1114	1120	-6	1228	1250	YX	1700	N231JQ	LGA	ROC	50	254	11	20	2023-03-28 11:00:00	Other
23066	9	22	1007	1015	-8	1248	1313	UA	711	N17296	EWR	IAH	189	1400	10	15	2023-09-22 10:00:00	Other
23083	12	7	1456	1505	-9	1636	1710	YX	1803	N879RW	LGA	STL	132	888	15	5	2023-12-07 15:00:00	Other
23088	2	14	902	914	-12	1105	1128	YX	1301	N410YX	LGA	CMH	78	479	9	14	2023-02-14 09:00:00	Other
23093	5	8	1020	1030	-10	1117	1140	B6	930	N197JB	JFK	BOS	38	187	10	30	2023-05-08 10:00:00	BOS
23096	11	1	844	852	-8	1011	1033	9E	1428	N915XJ	LGA	ORF	60	296	8	52	2023-11-01 08:00:00	Other
23098	1	4	1154	1200	-6	1514	1530	UA	873	N19130	EWR	SFO	355	2565	12	0	2023-01-04 12:00:00	Other
23100	9	14	1314	1321	-7	1612	1636	AA	638	N887NN	EWR	MIA	156	1085	13	21	2023-09-14 13:00:00	MIA
23104	10	25	1252	1259	-7	1539	1602	DL	123	N136DQ	LGA	DFW	200	1389	12	59	2023-10-25 12:00:00	Other
23115	9	14	1451	1500	-9	1633	1634	9E	1607	N905XJ	LGA	CHO	55	305	15	0	2023-09-14 15:00:00	Other
23116	5	16	1246	1259	-13	1452	1459	DL	766	N328NB	LGA	DTW	81	502	12	59	2023-05-16 12:00:00	Other
23122	12	8	744	750	-6	949	1009	YX	1036	N754YX	EWR	GRR	98	605	7	50	2023-12-08 07:00:00	Other
23123	3	16	603	610	-7	723	750	UA	757	N874UA	LGA	ORD	116	733	6	10	2023-03-16 06:00:00	ORD
23124	8	31	1613	1620	-7	1805	1821	UA	247	N16703	EWR	CLT	80	529	16	20	2023-08-31 16:00:00	CLT
23132	2	6	2119	2130	-11	2320	2340	NK	305	N613NK	LGA	DTW	84	502	21	30	2023-02-06 21:00:00	Other
23135	9	1	1853	1900	-7	2054	2121	YX	1357	N435YX	LGA	XNA	160	1147	19	0	2023-09-01 19:00:00	Other
23138	5	3	1831	1837	-6	2035	2100	YX	993	N729YX	EWR	IND	97	645	18	37	2023-05-03 18:00:00	Other
23143	5	4	2052	2100	-8	2206	2251	YX	1098	N655RW	LGA	ORD	109	733	21	0	2023-05-04 21:00:00	ORD
23146	8	24	1853	1900	-7	2114	2119	UA	56	N12238	EWR	SAV	100	708	19	0	2023-08-24 19:00:00	Other
23157	2	4	551	600	-9	923	945	AA	463	N188US	EWR	PHX	308	2133	6	0	2023-02-04 06:00:00	Other
23160	9	1	709	717	-8	949	1010	UA	904	N78501	EWR	SNA	310	2434	7	17	2023-09-01 07:00:00	Other
23166	1	17	1020	1030	-10	1154	1235	YX	1302	N446YX	LGA	ORD	122	733	10	30	2023-01-17 10:00:00	ORD
23187	12	8	551	600	-9	703	732	YX	1853	N882RW	LGA	DCA	45	214	6	0	2023-12-08 06:00:00	Other
23189	5	23	1747	1755	-8	2034	2121	B6	310	N937JB	JFK	LAX	312	2475	17	55	2023-05-23 17:00:00	LAX
23196	4	24	537	545	-8	831	832	B6	357	N556JB	JFK	PBI	155	1028	5	45	2023-04-24 05:00:00	Other
23198	9	5	1610	1620	-10	1716	1744	YX	1064	N726YX	EWR	ROC	41	246	16	20	2023-09-05 16:00:00	Other
23203	12	7	1032	1040	-8	1232	1305	9E	1366	N153PQ	LGA	DSM	150	1031	10	40	2023-12-07 10:00:00	Other
23208	5	18	1815	1825	-10	2026	2051	YX	1238	N440YX	LGA	OMA	166	1148	18	25	2023-05-18 18:00:00	Other
23234	10	3	554	600	-6	716	720	YX	1836	N226JQ	LGA	BOS	42	184	6	0	2023-10-03 06:00:00	BOS
23235	8	24	1252	1300	-8	1539	1612	AA	198	N304RB	LGA	MIA	139	1096	13	0	2023-08-24 13:00:00	MIA
23247	9	25	653	700	-7	835	900	AA	321	N805NN	LGA	CLT	81	544	7	0	2023-09-25 07:00:00	CLT
23252	11	26	650	700	-10	1016	1033	AS	12	N968AK	JFK	SFO	355	2586	7	0	2023-11-26 07:00:00	Other
23260	9	5	950	959	-9	1154	1232	YX	1947	N810MD	LGA	HHH	92	701	9	59	2023-09-05 09:00:00	Other
23262	1	17	553	600	-7	835	930	B6	779	N804JB	LGA	RSW	147	1080	6	0	2023-01-17 06:00:00	Other
23265	10	28	709	715	-6	1023	1020	UA	147	N77530	EWR	SNA	348	2434	7	15	2023-10-28 07:00:00	Other
23269	6	14	810	821	-11	1013	1048	YX	1818	N234JQ	LGA	IND	101	660	8	21	2023-06-14 08:00:00	Other
23273	9	23	1947	1959	-12	2055	2115	B6	501	N192JB	LGA	PWM	46	269	19	59	2023-09-23 19:00:00	Other
23274	5	2	1657	1705	-8	1830	1850	9E	1334	N348PQ	JFK	BUF	61	301	17	5	2023-05-02 17:00:00	Other
23277	8	17	843	850	-7	1033	1043	YX	1044	N418YX	LGA	GSO	82	461	8	50	2023-08-17 08:00:00	Other
23282	4	12	2117	2126	-9	2258	2329	NK	278	N919NK	LGA	DTW	76	502	21	26	2023-04-12 21:00:00	Other
23288	2	14	1938	1955	-17	2128	2138	9E	1458	N319PQ	EWR	RDU	68	416	19	55	2023-02-14 19:00:00	Other
23290	8	16	1008	1015	-7	1128	1205	AA	585	N808AW	LGA	ORD	108	733	10	15	2023-08-16 10:00:00	ORD
23299	11	10	1546	1554	-8	1709	1720	YX	1899	N205JQ	JFK	BOS	46	187	15	54	2023-11-10 15:00:00	BOS
23307	10	5	1604	1610	-6	1734	1806	YX	1345	N427YX	LGA	GSO	77	461	16	10	2023-10-05 16:00:00	Other
23312	4	29	1135	1145	-10	1320	1331	9E	1204	N491PX	LGA	BHM	140	866	11	45	2023-04-29 11:00:00	Other
23319	4	30	1534	1541	-7	1712	1648	YX	1046	N739YX	EWR	PVD	35	160	15	41	2023-04-30 15:00:00	Other
23320	7	3	829	835	-6	946	1010	9E	1295	N924XJ	JFK	ORF	50	290	8	35	2023-07-03 08:00:00	Other
23327	10	1	1352	1359	-7	1536	1625	DL	102	N3738B	LGA	DEN	203	1620	13	59	2023-10-01 13:00:00	Other
23332	3	3	1622	1629	-7	1741	1752	YX	1112	N655RW	EWR	DCA	49	199	16	29	2023-03-03 16:00:00	Other
23336	8	21	752	800	-8	937	1007	AA	793	N586UW	LGA	CLT	78	544	8	0	2023-08-21 08:00:00	CLT
23350	3	31	754	800	-6	937	938	UA	874	N829UA	LGA	ORD	124	733	8	0	2023-03-31 08:00:00	ORD
23357	9	13	1902	1910	-8	2141	2152	YX	1352	N132HQ	LGA	OKC	203	1341	19	10	2023-09-13 19:00:00	Other
23358	5	2	654	700	-6	956	1049	DL	175	N712TW	JFK	SFO	335	2586	7	0	2023-05-02 07:00:00	Other
23366	7	5	924	930	-6	1128	1152	YX	1352	N208JQ	LGA	OMA	153	1148	9	30	2023-07-05 09:00:00	Other
23373	2	6	2152	2159	-7	2304	2330	UA	497	N850UA	EWR	PIT	53	319	21	59	2023-02-06 21:00:00	Other
23378	9	14	654	700	-6	944	1010	DL	305	N3773D	JFK	RSW	153	1074	7	0	2023-09-14 07:00:00	Other
23379	1	24	2029	2037	-8	2147	2212	YX	1250	N753YX	EWR	PIT	56	319	20	37	2023-01-24 20:00:00	Other
23380	5	23	1055	1102	-7	1216	1229	UA	491	N47280	EWR	BNA	104	748	11	2	2023-05-23 11:00:00	Other
23385	11	24	2023	2029	-6	2202	2209	YX	1086	N745YX	EWR	PIT	54	319	20	29	2023-11-24 20:00:00	Other
23388	3	1	2022	2029	-7	2309	2353	AA	1012	N833NN	LGA	MIA	148	1096	20	29	2023-03-01 20:00:00	MIA
23392	9	26	1343	1350	-7	1605	1600	YX	1800	N810MD	LGA	CLT	102	544	13	50	2023-09-26 13:00:00	CLT
23394	12	13	843	849	-6	1027	1057	9E	1472	N485PX	LGA	GSO	81	461	8	49	2023-12-13 08:00:00	Other
23396	5	27	553	600	-7	711	735	UA	375	N452UA	EWR	ORD	104	719	6	0	2023-05-27 06:00:00	ORD
23398	1	19	620	630	-10	726	743	B6	222	N236JB	JFK	BOS	40	187	6	30	2023-01-19 06:00:00	BOS
23417	12	13	850	900	-10	1124	1129	YX	1038	N766YX	EWR	IND	109	645	9	0	2023-12-13 09:00:00	Other
23422	1	24	715	726	-11	1039	1051	AA	169	N836NN	LGA	DFW	233	1389	7	26	2023-01-24 07:00:00	Other
23423	1	27	2013	2020	-7	2316	2339	UA	436	N17254	EWR	SLC	285	1969	20	20	2023-01-27 20:00:00	Other
23444	8	26	1420	1430	-10	1535	1600	YX	928	N739YX	EWR	DCA	41	199	14	30	2023-08-26 14:00:00	Other
23445	11	29	1115	1123	-8	1347	1425	NK	1029	N605NK	EWR	MCO	132	937	11	23	2023-11-29 11:00:00	MCO
23446	9	5	944	953	-9	1056	1129	UA	441	N15751	EWR	BNA	94	748	9	53	2023-09-05 09:00:00	Other
23447	10	11	947	954	-7	1109	1133	9E	1579	N931XJ	JFK	RIC	56	288	9	54	2023-10-11 09:00:00	Other
23454	8	13	1222	1230	-8	1446	1525	NK	400	N647NK	LGA	IAH	183	1416	12	30	2023-08-13 12:00:00	Other
23461	5	19	1217	1225	-8	1342	1359	YX	1231	N410YX	LGA	BNA	111	764	12	25	2023-05-19 12:00:00	Other
23466	1	25	724	730	-6	919	923	9E	1568	N182GJ	LGA	CLE	78	419	7	30	2023-01-25 07:00:00	Other
23470	11	24	1138	1147	-9	1437	1457	NK	349	N974NK	EWR	FLL	159	1065	11	47	2023-11-24 11:00:00	FLL
23471	2	18	1719	1730	-11	1936	2018	YX	1223	N872RW	LGA	SDF	106	659	17	30	2023-02-18 17:00:00	Other
23472	7	22	1724	1731	-7	2009	2025	AA	193	N426AN	EWR	DFW	190	1372	17	31	2023-07-22 17:00:00	Other
23479	12	1	1240	1250	-10	1340	1359	9E	1394	N136EV	JFK	ITH	43	189	12	50	2023-12-01 12:00:00	Other
23485	6	17	1019	1025	-6	1337	1353	YX	1218	N757YX	EWR	EYW	159	1196	10	25	2023-06-17 10:00:00	Other
23488	5	28	1154	1200	-6	1331	1336	AA	697	N906AN	EWR	ORD	104	719	12	0	2023-05-28 12:00:00	ORD
23491	6	28	722	730	-8	919	946	B6	332	N821JB	JFK	SAV	93	718	7	30	2023-06-28 07:00:00	Other
23495	11	17	1358	1408	-10	1609	1622	YX	1314	N136HQ	LGA	CAE	100	617	14	8	2023-11-17 14:00:00	Other
23497	6	15	1617	1623	-6	1811	1826	YX	1308	N447YX	LGA	GSP	91	610	16	23	2023-06-15 16:00:00	Other
23499	5	27	608	615	-7	842	925	UA	864	N17104	EWR	LAX	307	2454	6	15	2023-05-27 06:00:00	LAX
23503	12	9	1153	1159	-6	1241	1255	YX	1084	N747YX	EWR	AVP	29	93	11	59	2023-12-09 11:00:00	Other
23504	3	31	1619	1630	-11	1727	1730	9E	1592	N480PX	LGA	ALB	34	136	16	30	2023-03-31 16:00:00	Other
23509	2	8	713	730	-17	1043	1113	AS	15	N921AK	JFK	SFO	361	2586	7	30	2023-02-08 07:00:00	Other
23510	4	13	1622	1630	-8	1733	1758	YX	945	N863RW	EWR	DCA	37	199	16	30	2023-04-13 16:00:00	Other
23512	8	23	754	800	-6	1018	1047	B6	633	N988JT	JFK	LAX	303	2475	8	0	2023-08-23 08:00:00	LAX
23523	3	2	824	830	-6	1203	1155	B6	60	N968JT	JFK	SAN	339	2446	8	30	2023-03-02 08:00:00	Other
23526	10	11	850	900	-10	1121	1139	YX	1759	N233JQ	JFK	JAX	132	828	9	0	2023-10-11 09:00:00	Other
23534	12	29	643	649	-6	820	858	YX	1255	N134HQ	LGA	MSP	139	1020	6	49	2023-12-29 06:00:00	Other
23538	1	19	718	730	-12	914	920	DL	634	N130DU	LGA	ORD	117	733	7	30	2023-01-19 07:00:00	ORD
23542	3	26	1543	1554	-11	1731	1719	YX	1171	N644RW	EWR	DCA	44	199	15	54	2023-03-26 15:00:00	Other
23546	1	27	754	805	-11	907	928	YX	1784	N204JQ	LGA	SYR	43	198	8	5	2023-01-27 08:00:00	Other
23548	12	6	1319	1329	-10	1436	1506	YX	1831	N242JQ	JFK	DCA	48	213	13	29	2023-12-06 13:00:00	Other
23552	6	20	1815	1825	-10	2008	2045	YX	1875	N214JQ	LGA	OMA	143	1148	18	25	2023-06-20 18:00:00	Other
23565	10	18	1727	1735	-8	1929	1945	9E	1628	N907XJ	LGA	DSM	145	1031	17	35	2023-10-18 17:00:00	Other
23569	10	18	720	730	-10	1017	1039	AA	132	N956NN	LGA	DFW	185	1389	7	30	2023-10-18 07:00:00	Other
23570	8	13	459	505	-6	839	855	B6	476	N973JT	JFK	SJU	194	1598	5	5	2023-08-13 05:00:00	Other
23574	11	7	621	629	-8	728	741	UA	281	N39475	EWR	BOS	42	200	6	29	2023-11-07 06:00:00	BOS
23578	10	31	859	905	-6	1023	1032	B6	960	N318JB	JFK	BUF	60	301	9	5	2023-10-31 09:00:00	Other
23583	6	9	1026	1035	-9	1230	1309	B6	405	N656JB	LGA	DEN	208	1620	10	35	2023-06-09 10:00:00	Other
23593	5	7	1924	1930	-6	2102	2127	YX	1248	N401YX	JFK	DCA	61	213	19	30	2023-05-07 19:00:00	Other
23595	12	13	736	745	-9	1030	1053	UA	588	N47284	EWR	SAN	336	2425	7	45	2023-12-13 07:00:00	Other
23601	4	22	720	730	-10	1022	1055	AS	15	N514AS	JFK	SFO	341	2586	7	30	2023-04-22 07:00:00	Other
23603	4	9	1443	1450	-7	1639	1640	YX	1126	N118HQ	JFK	RDU	80	427	14	50	2023-04-09 14:00:00	Other
23611	12	27	1430	1440	-10	1618	1643	9E	1487	N305PQ	LGA	STL	137	888	14	40	2023-12-27 14:00:00	Other
23617	8	5	1011	1020	-9	1123	1157	9E	1296	N134EV	JFK	ROC	51	264	10	20	2023-08-05 10:00:00	Other
23622	8	23	1923	1929	-6	2038	2105	YX	1378	N220JQ	LGA	DCA	45	214	19	29	2023-08-23 19:00:00	Other
23627	5	24	800	809	-9	958	1037	YX	1195	N131HQ	JFK	CVG	91	589	8	9	2023-05-24 08:00:00	Other
23632	1	17	1624	1630	-6	1801	1820	DL	932	N123DQ	LGA	BNA	128	764	16	30	2023-01-17 16:00:00	Other
23636	2	16	1152	1200	-8	1337	1330	AA	743	N832AW	LGA	DCA	80	214	12	0	2023-02-16 12:00:00	Other
23637	9	11	755	805	-10	933	955	YX	1398	N403YX	LGA	ILM	77	500	8	5	2023-09-11 08:00:00	Other
23639	1	30	2059	2105	-6	2310	2329	B6	422	N318JB	LGA	CHS	102	641	21	5	2023-01-30 21:00:00	Other
23646	5	10	1453	1500	-7	1750	1807	NK	626	N659NK	LGA	FLL	138	1076	15	0	2023-05-10 15:00:00	FLL
23653	1	20	1159	1209	-10	1308	1317	YX	1300	N447YX	JFK	ORH	35	150	12	9	2023-01-20 12:00:00	Other
23656	1	6	1405	1415	-10	1504	1527	B6	368	N193JB	LGA	BOS	38	184	14	15	2023-01-06 14:00:00	BOS
23657	3	25	1522	1530	-8	1738	1808	UA	906	N54241	LGA	DEN	226	1620	15	30	2023-03-25 15:00:00	Other
23673	8	30	1341	1350	-9	1542	1609	YX	1355	N238JQ	LGA	CLT	96	544	13	50	2023-08-30 13:00:00	CLT
23688	7	13	620	627	-7	806	816	YX	1010	N406YX	LGA	CMH	83	479	6	27	2023-07-13 06:00:00	Other
23691	10	29	1152	1200	-8	1416	1402	YX	1350	N430YX	LGA	MEM	155	963	12	0	2023-10-29 12:00:00	Other
23695	4	7	2122	2129	-7	2304	2339	YX	1078	N413YX	JFK	CMH	80	483	21	29	2023-04-07 21:00:00	Other
23700	8	31	820	830	-10	937	954	YX	881	N727YX	EWR	ROC	48	246	8	30	2023-08-31 08:00:00	Other
23701	9	14	552	600	-8	739	734	AA	542	N843NN	LGA	ORD	111	733	6	0	2023-09-14 06:00:00	ORD
23703	7	9	754	800	-6	935	937	UA	710	N27722	LGA	ORD	126	733	8	0	2023-07-09 08:00:00	ORD
23705	2	10	748	759	-11	938	1019	DL	953	N367NW	LGA	MSP	144	1020	7	59	2023-02-10 07:00:00	Other
23707	11	15	944	950	-6	1308	1306	NK	1041	N945NK	LGA	MIA	164	1096	9	50	2023-11-15 09:00:00	MIA
23721	1	17	824	835	-11	1040	1058	9E	1395	N313PQ	LGA	CVG	106	585	8	35	2023-01-17 08:00:00	Other
23725	6	9	1412	1420	-8	1617	1639	9E	1472	N937XJ	LGA	CVG	88	585	14	20	2023-06-09 14:00:00	Other
23733	3	11	2058	2105	-7	38	50	AA	54	N111ZM	JFK	SFO	360	2586	21	5	2023-03-11 21:00:00	Other
23736	12	31	1506	1515	-9	1653	1756	UA	598	N874UA	LGA	DEN	207	1620	15	15	2023-12-31 15:00:00	Other
23737	6	2	1348	1358	-10	1533	1604	YX	1085	N726YX	EWR	GRR	84	605	13	58	2023-06-02 13:00:00	Other
23746	4	30	1231	1241	-10	1624	1635	AA	236	N9025B	JFK	STT	200	1623	12	41	2023-04-30 12:00:00	Other
23759	1	16	1823	1829	-6	2036	2050	9E	1416	N695CA	LGA	CHS	91	641	18	29	2023-01-16 18:00:00	Other
23766	10	30	551	559	-8	858	907	AA	767	N336TM	JFK	MIA	151	1089	5	59	2023-10-30 05:00:00	MIA
23772	2	15	1320	1326	-6	1511	1536	YX	1211	N403YX	LGA	CMH	95	479	13	26	2023-02-15 13:00:00	Other
23773	2	12	551	600	-9	751	809	AA	260	N915US	LGA	CLT	96	544	6	0	2023-02-12 06:00:00	CLT
23777	7	9	801	810	-9	1124	1059	DL	180	N112DU	LGA	DFW	207	1389	8	10	2023-07-09 08:00:00	Other
23788	4	2	1853	1900	-7	2005	2022	YX	1573	N228JQ	LGA	BOS	34	184	19	0	2023-04-02 19:00:00	BOS
23790	2	6	1153	1159	-6	1507	1517	B6	798	N981JT	JFK	LAX	342	2475	11	59	2023-02-06 11:00:00	LAX
23792	10	4	601	608	-7	835	852	B6	306	N658JB	EWR	MCO	121	937	6	8	2023-10-04 06:00:00	MCO
23808	9	16	1449	1459	-10	1650	1655	YX	1411	N420YX	JFK	CMH	71	483	14	59	2023-09-16 14:00:00	Other
23810	12	1	954	1000	-6	1251	1312	DL	255	N176DN	JFK	LAX	326	2475	10	0	2023-12-01 10:00:00	LAX
23816	4	11	759	805	-6	1002	1030	DL	828	N133DU	JFK	MSY	148	1182	8	5	2023-04-11 08:00:00	Other
23819	7	13	644	650	-6	940	934	AA	781	N943NN	EWR	DFW	199	1372	6	50	2023-07-13 06:00:00	Other
23820	10	17	1205	1215	-10	1432	1519	YX	1245	N136HQ	LGA	OKC	180	1341	12	15	2023-10-17 12:00:00	Other
23827	3	16	1124	1132	-8	1251	1259	YX	1676	N236JQ	JFK	DCA	54	213	11	32	2023-03-16 11:00:00	Other
23831	9	28	1422	1430	-8	1630	1646	9E	1448	N336PQ	JFK	CLT	88	541	14	30	2023-09-28 14:00:00	CLT
23832	5	9	1345	1355	-10	1501	1513	B6	46	N203JB	JFK	BTV	51	266	13	55	2023-05-09 13:00:00	Other
23834	6	19	1914	1925	-11	2047	2100	AA	978	N931AN	EWR	ORD	103	719	19	25	2023-06-19 19:00:00	ORD
23838	8	13	1653	1700	-7	1808	1842	B6	2	N368JB	JFK	BUF	54	301	17	0	2023-08-13 17:00:00	Other
23844	4	12	1524	1530	-6	1744	1846	AA	58	N101NN	JFK	LAX	301	2475	15	30	2023-04-12 15:00:00	LAX
23846	12	23	1213	1220	-7	1323	1347	YX	1798	N203JQ	LGA	SYR	42	198	12	20	2023-12-23 12:00:00	Other
23848	12	19	1341	1350	-9	1629	1705	UA	912	N440UA	LGA	IAH	197	1416	13	50	2023-12-19 13:00:00	Other
23853	12	7	835	844	-9	1017	1046	YX	1728	N239JQ	LGA	CMH	80	479	8	44	2023-12-07 08:00:00	Other
23855	5	3	850	900	-10	1140	1153	UA	501	N17262	EWR	MCO	130	937	9	0	2023-05-03 09:00:00	MCO
23856	1	8	624	630	-6	932	952	AA	426	N963NN	LGA	DFW	222	1389	6	30	2023-01-08 06:00:00	Other
23862	1	20	1153	1200	-7	1357	1431	YX	1341	N413YX	LGA	MEM	162	963	12	0	2023-01-20 12:00:00	Other
23870	11	5	853	859	-6	1153	1257	AA	519	N778AN	JFK	PHX	274	2153	8	59	2023-11-05 08:00:00	Other
23876	1	20	1316	1325	-9	1430	1445	YX	1890	N219YX	JFK	IAD	48	228	13	25	2023-01-20 13:00:00	Other
23886	10	1	1947	1955	-8	2152	2216	9E	1698	N134EV	LGA	IND	91	660	19	55	2023-10-01 19:00:00	Other
23891	1	29	2014	2030	-16	2300	2328	B6	399	N203JB	EWR	MCO	137	937	20	30	2023-01-29 20:00:00	MCO
23897	7	3	1624	1630	-6	1820	1810	9E	1240	N176PQ	LGA	RIC	74	292	16	30	2023-07-03 16:00:00	Other
23901	2	6	651	659	-8	815	839	AA	949	N895NN	EWR	ORD	112	719	6	59	2023-02-06 06:00:00	ORD
23903	6	4	2119	2129	-10	2238	2255	YX	1300	N104HQ	LGA	RIC	48	292	21	29	2023-06-04 21:00:00	Other
23909	12	7	1826	1835	-9	2031	2049	DL	595	N952AT	EWR	MSP	156	1008	18	35	2023-12-07 18:00:00	Other
23910	5	1	635	645	-10	900	951	UA	730	N37518	EWR	SEA	287	2402	6	45	2023-05-01 06:00:00	Other
23913	10	28	1052	1059	-7	1351	1359	NK	236	N603NK	LGA	MCO	126	950	10	59	2023-10-28 10:00:00	MCO
23914	2	15	1636	1650	-14	1804	1835	YX	1554	N824MD	LGA	PIT	69	335	16	50	2023-02-15 16:00:00	Other
23924	11	28	1354	1400	-6	1548	1617	YX	1154	N753YX	EWR	CVG	97	569	14	0	2023-11-28 14:00:00	Other
23925	4	1	1422	1430	-8	1717	1741	YX	1148	N867RW	LGA	OKC	217	1341	14	30	2023-04-01 14:00:00	Other
23935	9	4	1749	1759	-10	2003	2008	YX	1366	N127HQ	LGA	MCI	146	1107	17	59	2023-09-04 17:00:00	Other
23941	6	14	1149	1159	-10	1448	1508	NK	1059	N677NK	LGA	MIA	156	1096	11	59	2023-06-14 11:00:00	MIA
23946	11	12	1447	1455	-8	1552	1609	YX	1128	N744YX	EWR	MHT	43	209	14	55	2023-11-12 14:00:00	Other
23948	5	19	1343	1349	-6	1531	1533	YX	1095	N656RW	EWR	RDU	73	416	13	49	2023-05-19 13:00:00	Other
23950	1	16	1219	1230	-11	1342	1402	YX	1145	N646RW	EWR	PIT	55	319	12	30	2023-01-16 12:00:00	Other
23957	3	9	1153	1201	-8	1326	1335	AA	455	N816AW	EWR	ORD	121	719	12	1	2023-03-09 12:00:00	ORD
23963	1	30	2150	2159	-9	2254	2309	9E	1443	N482PX	LGA	SCE	45	208	21	59	2023-01-30 21:00:00	Other
23964	10	16	1758	1805	-7	1914	1957	9E	1390	N316PQ	LGA	BHM	112	866	18	5	2023-10-16 18:00:00	Other
23968	8	28	2132	2140	-8	2313	2303	B6	729	N328JB	JFK	SYR	40	209	21	40	2023-08-28 21:00:00	Other
23971	3	10	617	625	-8	924	925	B6	1011	N375JB	JFK	PBI	145	1028	6	25	2023-03-10 06:00:00	Other
23972	3	21	1244	1250	-6	1409	1414	9E	1477	N147PQ	JFK	BUF	61	301	12	50	2023-03-21 12:00:00	Other
23974	1	18	1056	1114	-18	1233	1320	YX	1325	N123HQ	LGA	ROA	71	405	11	14	2023-01-18 11:00:00	Other
23977	5	17	1309	1315	-6	1513	1517	AA	640	N150UW	EWR	CLT	82	529	13	15	2023-05-17 13:00:00	CLT
23987	10	9	1609	1615	-6	1802	1823	YX	1274	N128HQ	LGA	GSP	95	610	16	15	2023-10-09 16:00:00	Other
24001	2	23	1951	1959	-8	2204	2229	DL	900	N3754A	EWR	ATL	110	746	19	59	2023-02-23 19:00:00	ATL
24007	2	10	1421	1430	-9	1612	1626	AA	215	N971NN	LGA	ORD	125	733	14	30	2023-02-10 14:00:00	ORD
24013	8	3	938	946	-8	1121	1141	DL	788	N974AT	EWR	DTW	78	488	9	46	2023-08-03 09:00:00	Other
24022	11	25	1456	1505	-9	1629	1706	YX	1279	N112HQ	LGA	CLE	76	419	15	5	2023-11-25 15:00:00	Other
24024	12	25	721	730	-9	1005	1029	UA	379	N17564	EWR	MCO	142	937	7	30	2023-12-25 07:00:00	MCO
24029	10	16	724	730	-6	929	942	YX	1055	N724YX	EWR	GRR	85	605	7	30	2023-10-16 07:00:00	Other
24034	11	10	819	825	-6	1000	1004	YX	1327	N425YX	LGA	CLE	76	419	8	25	2023-11-10 08:00:00	Other
24041	12	5	2053	2100	-7	2159	2212	AA	841	N717UW	LGA	BOS	34	184	21	0	2023-12-05 21:00:00	BOS
24043	2	3	553	600	-7	859	859	B6	48	N564JB	EWR	PBI	162	1023	6	0	2023-02-03 06:00:00	Other
24053	2	2	752	800	-8	948	1020	DL	953	N352NW	LGA	MSP	159	1020	8	0	2023-02-02 08:00:00	Other
24062	10	30	1220	1229	-9	1437	1427	YX	1320	N443YX	LGA	CMH	94	479	12	29	2023-10-30 12:00:00	Other
24063	3	26	2020	2030	-10	2252	2249	YX	1089	N861RW	EWR	GRR	111	605	20	30	2023-03-26 20:00:00	Other
24065	11	30	826	835	-9	1024	1043	NK	296	N672NK	LGA	CLT	97	544	8	35	2023-11-30 08:00:00	CLT
24066	5	28	854	900	-6	1225	1212	UA	399	N27283	EWR	MIA	149	1085	9	0	2023-05-28 09:00:00	MIA
24074	4	19	1722	1730	-8	1930	2004	B6	157	N339JB	JFK	ATL	105	760	17	30	2023-04-19 17:00:00	ATL
24079	2	17	907	916	-9	1111	1103	YX	997	N746YX	EWR	CLE	73	404	9	16	2023-02-17 09:00:00	Other
24086	1	27	1819	1835	-16	2146	2150	AS	11	N274AK	JFK	SAN	355	2446	18	35	2023-01-27 18:00:00	Other
24088	1	10	2043	2053	-10	2254	2304	YX	1474	N821MD	LGA	ILM	68	500	20	53	2023-01-10 20:00:00	Other
24094	9	6	1315	1322	-7	1440	1509	YX	1219	N750YX	EWR	RDU	63	416	13	22	2023-09-06 13:00:00	Other
24099	8	11	1452	1459	-7	1658	1722	YX	1015	N416YX	JFK	IND	94	665	14	59	2023-08-11 14:00:00	Other
24100	12	5	1827	1834	-7	2142	2149	AA	972	N844NN	EWR	MIA	167	1085	18	34	2023-12-05 18:00:00	MIA
24103	4	19	638	645	-7	937	934	B6	913	N239JB	JFK	PBI	151	1028	6	45	2023-04-19 06:00:00	Other
24104	5	14	1220	1227	-7	1334	1345	YX	1051	N746YX	EWR	PWM	50	284	12	27	2023-05-14 12:00:00	Other
24106	11	5	1449	1459	-10	1739	1814	DL	356	N374NW	LGA	PBI	138	1035	14	59	2023-11-05 14:00:00	Other
24118	4	7	2043	2050	-7	2306	2259	9E	1301	N491PX	LGA	CAE	99	617	20	50	2023-04-07 20:00:00	Other
24119	7	7	1153	1159	-6	1447	1453	UA	454	N34222	EWR	TPA	139	997	11	59	2023-07-07 11:00:00	Other
24123	4	19	720	730	-10	1133	1125	B6	557	N950JT	JFK	SJU	217	1598	7	30	2023-04-19 07:00:00	Other
24141	9	7	722	729	-7	909	929	AA	531	N909NN	JFK	CLT	79	541	7	29	2023-09-07 07:00:00	CLT
24143	10	31	1019	1029	-10	1313	1306	YX	1269	N417YX	LGA	XNA	196	1147	10	29	2023-10-31 10:00:00	Other
24144	11	10	744	752	-8	908	926	YX	1097	N655RW	EWR	PIT	64	319	7	52	2023-11-10 07:00:00	Other
24147	5	19	702	709	-7	1044	1110	B6	593	N547JB	EWR	SJU	194	1608	7	9	2023-05-19 07:00:00	Other
24148	1	18	1349	1359	-10	1547	1554	9E	1648	N304PQ	LGA	GSO	76	461	13	59	2023-01-18 13:00:00	Other
24151	6	28	2102	2110	-8	2237	2306	YX	1301	N867RW	LGA	GSO	73	461	21	10	2023-06-28 21:00:00	Other
24155	7	23	1723	1729	-6	2003	2041	AA	788	N303RG	JFK	AUS	196	1521	17	29	2023-07-23 17:00:00	Other
24161	3	8	551	600	-9	950	920	AA	52	N113AN	JFK	LAX	392	2475	6	0	2023-03-08 06:00:00	LAX
24162	2	26	551	600	-9	924	902	B6	110	N966JT	EWR	MCO	133	937	6	0	2023-02-26 06:00:00	MCO
24175	7	12	1053	1100	-7	1241	1312	YX	1394	N242JQ	JFK	CLT	76	541	11	0	2023-07-12 11:00:00	CLT
24178	9	7	1003	1015	-12	1223	1313	UA	711	N78511	EWR	IAH	175	1400	10	15	2023-09-07 10:00:00	Other
24180	12	6	650	700	-10	818	846	UA	822	N78506	EWR	ORD	111	719	7	0	2023-12-06 07:00:00	ORD
24181	4	12	900	912	-12	1040	1102	YX	979	N755YX	EWR	CLE	63	404	9	12	2023-04-12 09:00:00	Other
24182	11	30	1931	1940	-9	2053	2104	YX	1164	N769YX	EWR	BOS	47	200	19	40	2023-11-30 19:00:00	BOS
24184	5	29	1954	2000	-6	2103	2123	AA	560	N820AW	LGA	DCA	48	214	20	0	2023-05-29 20:00:00	Other
24191	3	1	1820	1830	-10	2026	2047	9E	1461	N931XJ	LGA	CLT	90	544	18	30	2023-03-01 18:00:00	CLT
24194	1	24	805	815	-10	1104	1135	B6	262	N966JT	JFK	FLL	151	1069	8	15	2023-01-24 08:00:00	FLL
24197	5	14	623	630	-7	848	916	NK	503	N970NK	LGA	MCO	120	950	6	30	2023-05-14 06:00:00	MCO
24201	3	8	1723	1730	-7	2026	2045	AS	87	N487AS	EWR	PDX	344	2434	17	30	2023-03-08 17:00:00	Other
24205	10	11	1918	1929	-11	2228	2246	DL	402	N116DU	LGA	RSW	161	1080	19	29	2023-10-11 19:00:00	Other
24207	5	11	750	800	-10	1000	1017	B6	317	N266JB	JFK	SAV	103	718	8	0	2023-05-11 08:00:00	Other
24209	1	25	1122	1130	-8	1241	1247	YX	1147	N636RW	EWR	BTV	53	266	11	30	2023-01-25 11:00:00	Other
24211	6	20	1058	1110	-12	1227	1240	YX	1403	N437YX	JFK	ORF	57	290	11	10	2023-06-20 11:00:00	Other
24213	10	24	1400	1406	-6	1530	1542	UA	771	N804UA	EWR	STL	129	872	14	6	2023-10-24 14:00:00	Other
24216	12	26	1125	1131	-6	1358	1404	UA	655	N68452	EWR	JAX	126	820	11	31	2023-12-26 11:00:00	Other
24217	11	19	948	956	-8	1107	1137	9E	1421	N176PQ	JFK	RIC	55	288	9	56	2023-11-19 09:00:00	Other
24218	1	1	2037	2050	-13	2332	2354	B6	915	N637JB	EWR	TPA	140	997	20	50	2023-01-01 20:00:00	Other
24219	3	30	1550	1600	-10	1734	1733	9E	1421	N324PQ	LGA	BUF	57	292	16	0	2023-03-30 16:00:00	Other
24220	3	3	751	800	-9	911	918	AA	770	N755US	LGA	DCA	51	214	8	0	2023-03-03 08:00:00	Other
24225	4	7	853	900	-7	1216	1219	UA	721	N785UA	EWR	SFO	345	2565	9	0	2023-04-07 09:00:00	Other
24228	6	9	1811	1820	-9	2036	2106	9E	1607	N319PQ	JFK	SAV	109	718	18	20	2023-06-09 18:00:00	Other
24231	4	26	1841	1849	-8	2051	2111	YX	1466	N222JQ	LGA	CLT	95	544	18	49	2023-04-26 18:00:00	CLT
24236	11	1	2134	2140	-6	2311	2320	B6	172	N354JB	JFK	ROC	53	264	21	40	2023-11-01 21:00:00	Other
24246	12	30	1435	1447	-12	1550	1623	UA	195	N37325	EWR	BNA	112	748	14	47	2023-12-30 14:00:00	Other
24251	9	7	1315	1329	-14	1510	1534	9E	1535	N914XJ	LGA	CAE	92	617	13	29	2023-09-07 13:00:00	Other
24257	3	30	651	700	-9	915	934	DL	186	N369NW	LGA	ATL	112	762	7	0	2023-03-30 07:00:00	ATL
24258	12	11	1809	1815	-6	1957	1954	UA	454	N831UA	LGA	ORD	112	733	18	15	2023-12-11 18:00:00	ORD
24263	6	5	1505	1515	-10	1622	1636	YX	1822	N880RW	LGA	ACK	36	202	15	15	2023-06-05 15:00:00	Other
24264	6	5	1551	1559	-8	1718	1757	B6	35	N279JB	JFK	ORD	117	740	15	59	2023-06-05 15:00:00	ORD
24267	5	9	554	600	-6	707	738	UA	768	N851UA	LGA	ORD	115	733	6	0	2023-05-09 06:00:00	ORD
24275	2	21	1424	1430	-6	1718	1713	DL	120	N3736C	JFK	DEN	250	1626	14	30	2023-02-21 14:00:00	Other
24276	6	19	1131	1140	-9	1304	1326	YX	1376	N867RW	LGA	ROA	70	405	11	40	2023-06-19 11:00:00	Other
24277	4	24	723	729	-6	1038	1034	AA	159	N996NN	LGA	DFW	199	1389	7	29	2023-04-24 07:00:00	Other
24279	4	6	554	600	-6	851	902	B6	148	N641JB	EWR	FLL	143	1065	6	0	2023-04-06 06:00:00	FLL
24281	6	14	1251	1300	-9	1359	1421	YX	1282	N404YX	JFK	BOS	33	187	13	0	2023-06-14 13:00:00	BOS
24285	9	9	842	850	-8	1033	1058	NK	287	N677NK	LGA	CLT	82	544	8	50	2023-09-09 08:00:00	CLT
24288	10	12	953	959	-6	1321	1302	B6	204	N521JB	LGA	MCO	180	950	9	59	2023-10-12 09:00:00	MCO
24289	4	12	1904	1914	-10	2014	2051	UA	581	N808UA	EWR	BNA	97	748	19	14	2023-04-12 19:00:00	Other
24290	9	6	1748	1759	-11	2031	2053	UA	829	N17245	EWR	TPA	132	997	17	59	2023-09-06 17:00:00	Other
24291	12	1	1739	1745	-6	1915	1923	AA	954	N177XF	LGA	BNA	128	764	17	45	2023-12-01 17:00:00	Other
24295	12	14	851	900	-9	1046	1107	YX	1740	N226JQ	JFK	CMH	73	483	9	0	2023-12-14 09:00:00	Other
24297	7	3	653	659	-6	903	901	AA	290	N867NN	LGA	CLT	82	544	6	59	2023-07-03 06:00:00	CLT
24308	2	7	821	830	-9	1201	1239	AA	55	N112AN	JFK	SFO	370	2586	8	30	2023-02-07 08:00:00	Other
24312	6	20	1128	1135	-7	1305	1319	DL	603	N112DU	LGA	ORD	110	733	11	35	2023-06-20 11:00:00	ORD
24313	4	23	1618	1625	-7	1757	1802	YX	1231	N413YX	JFK	BNA	127	765	16	25	2023-04-23 16:00:00	Other
24317	4	26	513	525	-12	801	800	B6	114	N959JB	EWR	MCO	135	937	5	25	2023-04-26 05:00:00	MCO
24318	7	18	820	827	-7	955	1006	YX	850	N863RW	EWR	RIC	57	277	8	27	2023-07-18 08:00:00	Other
24321	10	9	1943	1959	-16	2042	2115	B6	468	N274JB	LGA	PWM	42	269	19	59	2023-10-09 19:00:00	Other
24333	9	20	1343	1350	-7	1545	1600	YX	1800	N823MD	LGA	CLT	80	544	13	50	2023-09-20 13:00:00	CLT
24335	6	30	923	930	-7	1156	1228	B6	168	N520JB	LGA	PBI	129	1035	9	30	2023-06-30 09:00:00	Other
24347	7	19	2054	2100	-6	1	2359	B6	29	N967JT	JFK	SAN	328	2446	21	0	2023-07-19 21:00:00	Other
24349	6	2	733	740	-7	843	908	YX	1794	N880RW	LGA	DCA	44	214	7	40	2023-06-02 07:00:00	Other
24350	8	24	1549	1559	-10	1746	1757	YX	849	N638RW	EWR	GSO	72	445	15	59	2023-08-24 15:00:00	Other
24357	3	14	1504	1510	-6	1655	1715	DL	935	N934AT	EWR	MSP	142	1008	15	10	2023-03-14 15:00:00	Other
24365	10	19	1129	1136	-7	1250	1308	UA	331	N67845	EWR	ORD	110	719	11	36	2023-10-19 11:00:00	ORD
24367	7	19	1119	1125	-6	1341	1334	YX	1025	N405YX	LGA	AVL	96	599	11	25	2023-07-19 11:00:00	Other
24368	5	27	2150	2159	-9	2301	2319	B6	888	N228JB	JFK	SYR	42	209	21	59	2023-05-27 21:00:00	Other
24371	3	25	921	930	-9	1318	1305	AS	17	N409AS	JFK	SFO	353	2586	9	30	2023-03-25 09:00:00	Other
24380	9	4	1812	1820	-8	2012	2016	OO	1215	N312SY	JFK	MKE	112	745	18	20	2023-09-04 18:00:00	Other
24384	11	6	1520	1526	-6	1747	1814	YX	1795	N221JQ	LGA	JAX	120	833	15	26	2023-11-06 15:00:00	Other
24385	3	19	1537	1545	-8	1655	1704	B6	413	N239JB	JFK	BOS	48	187	15	45	2023-03-19 15:00:00	BOS
24387	10	12	1652	1659	-7	1835	1848	9E	1528	N316PQ	LGA	CLE	72	419	16	59	2023-10-12 16:00:00	Other
24388	11	29	1832	1845	-13	2020	2047	YX	1147	N768YX	EWR	CMH	76	463	18	45	2023-11-29 18:00:00	Other
24391	9	3	2020	2030	-10	2248	2329	UA	486	N12218	EWR	PBI	121	1023	20	30	2023-09-03 20:00:00	Other
24392	8	31	2151	2158	-7	2239	2300	9E	1239	N927XJ	LGA	PVD	29	143	21	58	2023-08-31 21:00:00	Other
24396	12	5	647	700	-13	1131	1204	UA	546	N13750	EWR	STT	203	1634	7	0	2023-12-05 07:00:00	Other
24398	5	8	1921	1930	-9	2229	2254	B6	755	N590JB	LGA	RSW	146	1080	19	30	2023-05-08 19:00:00	Other
24402	8	27	554	600	-6	858	916	AA	362	N837NN	LGA	MIA	151	1096	6	0	2023-08-27 06:00:00	MIA
24403	5	25	1849	1900	-11	2023	2057	YX	1265	N128HQ	JFK	PIT	72	340	19	0	2023-05-25 19:00:00	Other
24423	10	25	652	659	-7	851	906	9E	1379	N186PQ	JFK	DTW	87	509	6	59	2023-10-25 06:00:00	Other
24439	7	10	553	600	-7	844	859	AA	1	N115NN	JFK	LAX	317	2475	6	0	2023-07-10 06:00:00	LAX
24448	4	25	1315	1323	-8	1623	1632	B6	916	N644JB	JFK	MIA	168	1089	13	23	2023-04-25 13:00:00	MIA
24457	7	13	558	604	-6	851	850	B6	201	N580JB	EWR	TPA	132	997	6	4	2023-07-13 06:00:00	Other
24465	5	1	2040	2055	-15	2220	2227	YX	1635	N823MD	LGA	DCA	50	214	20	55	2023-05-01 20:00:00	Other
24472	10	31	751	759	-8	1107	1116	UA	687	N37513	EWR	MIA	154	1085	7	59	2023-10-31 07:00:00	MIA
24473	7	10	1353	1359	-6	1620	1646	AA	533	N849NN	EWR	DFW	178	1372	13	59	2023-07-10 13:00:00	Other
24474	11	14	1321	1330	-9	1556	1610	NK	1040	N614NK	LGA	ATL	114	762	13	30	2023-11-14 13:00:00	ATL
24477	10	17	1700	1706	-6	1902	1907	9E	1412	N305PQ	JFK	RDU	73	427	17	6	2023-10-17 17:00:00	Other
24482	10	25	639	645	-6	834	855	UA	428	N37295	EWR	CHS	86	628	6	45	2023-10-25 06:00:00	Other
24484	9	2	2049	2100	-11	2215	2228	YX	1405	N439YX	JFK	BOS	44	187	21	0	2023-09-02 21:00:00	BOS
24490	4	18	552	600	-8	751	830	UA	371	N75429	EWR	DEN	222	1605	6	0	2023-04-18 06:00:00	Other
24494	2	11	1717	1725	-8	1836	1904	YX	1558	N203JQ	LGA	IAD	53	229	17	25	2023-02-11 17:00:00	Other
24511	1	24	1428	1435	-7	1648	1651	9E	1421	N915XJ	LGA	CVG	104	585	14	35	2023-01-24 14:00:00	Other
24521	3	21	1034	1040	-6	1246	1309	UA	456	N27256	EWR	ATL	105	746	10	40	2023-03-21 10:00:00	ATL
24528	9	27	849	900	-11	1204	1206	B6	73	N821JB	LGA	FLL	163	1076	9	0	2023-09-27 09:00:00	FLL
24529	10	24	652	700	-8	1040	1057	B6	552	N504JB	EWR	SJU	190	1608	7	0	2023-10-24 07:00:00	Other
24530	11	5	1358	1408	-10	1601	1622	YX	1314	N439YX	LGA	CAE	88	617	14	8	2023-11-05 14:00:00	Other
24532	1	24	953	1000	-7	1147	1211	AA	100	N126UW	JFK	CLT	88	541	10	0	2023-01-24 10:00:00	CLT
24536	3	1	1946	1955	-9	2118	2138	9E	1572	N296PQ	EWR	RDU	69	416	19	55	2023-03-01 19:00:00	Other
24537	4	12	553	600	-7	833	906	UA	158	N26210	EWR	FLL	143	1065	6	0	2023-04-12 06:00:00	FLL
24539	11	19	854	902	-8	1247	1237	AA	883	N101NN	JFK	SNA	339	2454	9	2	2023-11-19 09:00:00	Other
24540	9	11	913	922	-9	1029	1046	YX	1898	N229JQ	LGA	SYR	45	198	9	22	2023-09-11 09:00:00	Other
24555	12	27	857	905	-8	1022	1056	YX	1040	N769YX	EWR	MKE	111	725	9	5	2023-12-27 09:00:00	Other
24561	1	1	1253	1300	-7	1503	1537	B6	791	N775JB	LGA	MSY	169	1183	13	0	2023-01-01 13:00:00	Other
24566	2	27	1421	1429	-8	1618	1631	NK	498	N617NK	LGA	MYR	88	563	14	29	2023-02-27 14:00:00	Other
24568	3	31	1143	1150	-7	1306	1254	9E	1366	N329PQ	LGA	ALB	34	136	11	50	2023-03-31 11:00:00	Other
24575	11	17	1511	1519	-8	1613	1640	YX	1119	N748YX	EWR	SYR	40	195	15	19	2023-11-17 15:00:00	Other
24583	5	1	1812	1820	-8	1952	2019	YX	1633	N215JQ	LGA	STL	125	888	18	20	2023-05-01 18:00:00	Other
24585	3	30	933	942	-9	1045	1109	UA	489	N881UA	EWR	BOS	38	200	9	42	2023-03-30 09:00:00	BOS
24587	8	26	1553	1559	-6	1712	1734	YX	970	N104HQ	JFK	BOS	36	187	15	59	2023-08-26 15:00:00	BOS
24588	4	8	1720	1735	-15	1944	2007	YX	1152	N447YX	LGA	XNA	187	1147	17	35	2023-04-08 17:00:00	Other
24590	7	6	652	700	-8	1011	1020	NK	835	N957NK	EWR	SLC	283	1969	7	0	2023-07-06 07:00:00	Other
24601	8	23	1136	1145	-9	1302	1326	YX	1056	N123HQ	LGA	ROA	64	405	11	45	2023-08-23 11:00:00	Other
24607	2	8	1139	1150	-11	1308	1347	YX	1322	N426YX	LGA	PIT	57	335	11	50	2023-02-08 11:00:00	Other
24608	5	20	623	630	-7	746	749	B6	937	N203JB	JFK	BUF	57	301	6	30	2023-05-20 06:00:00	Other
24616	11	3	847	855	-8	1009	1038	YX	1073	N731YX	EWR	PIT	60	319	8	55	2023-11-03 08:00:00	Other
24620	8	25	1736	1745	-9	1900	1918	B6	86	N216JB	JFK	PWM	49	273	17	45	2023-08-25 17:00:00	Other
24622	10	13	624	630	-6	806	801	UA	935	N24702	LGA	ORD	126	733	6	30	2023-10-13 06:00:00	ORD
24624	12	27	1953	1959	-6	2308	2255	UA	612	N37532	EWR	MCO	151	937	19	59	2023-12-27 19:00:00	MCO
24625	1	22	1652	1659	-7	1929	1933	YX	1130	N979RP	EWR	SDF	125	642	16	59	2023-01-22 16:00:00	Other
24642	1	3	1236	1245	-9	1402	1400	YX	1286	N113HQ	JFK	BOS	32	187	12	45	2023-01-03 12:00:00	BOS
24644	10	3	1912	1922	-10	2103	2140	YX	1276	N131HQ	LGA	IND	89	660	19	22	2023-10-03 19:00:00	Other
24649	11	12	1253	1259	-6	1601	1641	AA	974	N323RM	JFK	PHX	288	2153	12	59	2023-11-12 12:00:00	Other
24651	4	26	1822	1829	-7	1942	2004	YX	1169	N439YX	LGA	PIT	62	335	18	29	2023-04-26 18:00:00	Other
24653	12	19	1023	1030	-7	1310	1400	B6	274	N2060J	JFK	SAT	207	1587	10	30	2023-12-19 10:00:00	Other
24658	9	19	1000	1009	-9	1149	1219	AA	758	N183UW	LGA	CLT	84	544	10	9	2023-09-19 10:00:00	CLT
24661	7	7	624	630	-6	858	921	UA	566	N33289	EWR	TPA	129	997	6	30	2023-07-07 06:00:00	Other
24670	6	27	1252	1300	-8	1415	1421	YX	1282	N406YX	JFK	BOS	53	187	13	0	2023-06-27 13:00:00	BOS
24671	12	21	2009	2020	-11	2328	2359	AS	13	N483AS	JFK	SFO	342	2586	20	20	2023-12-21 20:00:00	Other
24674	10	10	1500	1507	-7	1636	1700	YX	1299	N405YX	LGA	CLE	72	419	15	7	2023-10-10 15:00:00	Other
24676	1	28	1521	1530	-9	1847	1858	B6	269	N715JB	JFK	LAX	365	2475	15	30	2023-01-28 15:00:00	LAX
24678	1	9	751	759	-8	930	945	UA	1030	N890UA	EWR	RDU	73	416	7	59	2023-01-09 07:00:00	Other
24679	2	24	1312	1318	-6	1542	1554	UA	560	N23708	EWR	JAX	128	820	13	18	2023-02-24 13:00:00	Other
24683	6	6	2021	2029	-8	2249	2247	YX	1112	N744YX	EWR	GRR	101	605	20	29	2023-06-06 20:00:00	Other
24685	11	24	553	600	-7	743	752	DL	747	N992AT	EWR	DTW	93	488	6	0	2023-11-24 06:00:00	Other
24690	9	9	854	900	-6	1154	1206	B6	73	N507JT	LGA	FLL	146	1076	9	0	2023-09-09 09:00:00	FLL
24691	9	27	2106	2113	-7	2256	2317	UA	437	N78509	EWR	CHS	85	628	21	13	2023-09-27 21:00:00	Other
24697	2	5	1452	1501	-9	1611	1645	UA	815	N824UA	LGA	ORD	114	733	15	1	2023-02-05 15:00:00	ORD
24702	8	1	723	730	-7	1003	1035	AA	3	N102NN	JFK	LAX	315	2475	7	30	2023-08-01 07:00:00	LAX
24714	11	29	2119	2126	-7	2315	2329	YX	1092	N769YX	EWR	MEM	141	946	21	26	2023-11-29 21:00:00	Other
24715	2	12	853	900	-7	1054	1044	9E	1427	N907XJ	JFK	RIC	60	288	9	0	2023-02-12 09:00:00	Other
24716	5	16	1721	1730	-9	1939	1944	YX	1654	N212JQ	LGA	LIT	163	1085	17	30	2023-05-16 17:00:00	Other
24725	7	6	1119	1129	-10	1222	1237	YX	1074	N413YX	JFK	ORH	37	150	11	29	2023-07-06 11:00:00	Other
24729	6	4	918	925	-7	1023	1101	YX	1854	N246JQ	LGA	DCA	41	214	9	25	2023-06-04 09:00:00	Other
24750	10	27	1750	1800	-10	1945	2022	YX	1289	N124HQ	LGA	IND	95	660	18	0	2023-10-27 18:00:00	Other
24753	1	26	951	959	-8	1314	1317	B6	43	N796JB	EWR	MCO	157	937	9	59	2023-01-26 09:00:00	MCO
24765	9	5	1251	1259	-8	1406	1415	YX	1303	N439YX	JFK	BOS	46	187	12	59	2023-09-05 12:00:00	BOS
24769	4	9	1215	1229	-14	1329	1351	9E	1192	N918XJ	LGA	SYR	42	198	12	29	2023-04-09 12:00:00	Other
24775	6	13	1514	1520	-6	1720	1752	YX	1322	N421YX	JFK	IND	105	665	15	20	2023-06-13 15:00:00	Other
24781	9	25	650	659	-9	941	1009	DL	305	N3751B	JFK	RSW	152	1074	6	59	2023-09-25 06:00:00	Other
24786	3	14	823	830	-7	1004	1007	AA	126	N979AN	LGA	ORD	101	733	8	30	2023-03-14 08:00:00	ORD
24787	11	20	1402	1408	-6	1606	1622	YX	1314	N404YX	LGA	CAE	95	617	14	8	2023-11-20 14:00:00	Other
24788	10	7	1132	1142	-10	1421	1438	UA	600	N73251	EWR	PBI	143	1023	11	42	2023-10-07 11:00:00	Other
24793	5	10	1321	1330	-9	1457	1527	YX	1264	N438YX	LGA	CMH	75	479	13	30	2023-05-10 13:00:00	Other
24796	1	4	1645	1655	-10	1825	1847	OO	1682	N106SY	LGA	ORD	119	733	16	55	2023-01-04 16:00:00	ORD
24802	4	24	848	854	-6	1022	1040	YX	1460	N823MD	LGA	PIT	62	335	8	54	2023-04-24 08:00:00	Other
24804	2	26	1301	1310	-9	1444	1517	YX	1202	N419YX	LGA	CLE	79	419	13	10	2023-02-26 13:00:00	Other
24807	11	24	753	800	-7	943	954	B6	827	N3085J	JFK	RDU	71	427	8	0	2023-11-24 08:00:00	Other
24808	1	12	1244	1250	-6	1515	1531	DL	220	N365NW	LGA	ATL	123	762	12	50	2023-01-12 12:00:00	ATL
24809	2	26	1050	1059	-9	1236	1303	YX	983	N979RP	EWR	CMH	84	463	10	59	2023-02-26 10:00:00	Other
24813	11	14	2205	2215	-10	37	42	UA	111	N37307	EWR	ATL	117	746	22	15	2023-11-14 22:00:00	ATL
24815	6	29	1253	1259	-6	1559	1615	AA	668	N884NN	JFK	MIA	162	1089	12	59	2023-06-29 12:00:00	MIA
24818	3	9	554	600	-6	723	730	WN	992	N8614M	LGA	MDW	116	725	6	0	2023-03-09 06:00:00	Other
24819	5	16	950	959	-9	1129	1203	AA	744	N863NN	LGA	CLT	76	544	9	59	2023-05-16 09:00:00	CLT
24824	10	8	2052	2059	-7	2237	2225	YX	1354	N402YX	JFK	BOS	49	187	20	59	2023-10-08 20:00:00	BOS
24828	12	16	1953	1959	-6	2134	2201	YX	1081	N765YX	EWR	STL	131	872	19	59	2023-12-16 19:00:00	Other
24829	5	25	853	900	-7	1017	1016	DL	891	N129DU	LGA	BOS	33	184	9	0	2023-05-25 09:00:00	BOS
24836	8	17	1106	1115	-9	1257	1309	YX	1053	N423YX	LGA	CMH	79	479	11	15	2023-08-17 11:00:00	Other
24845	5	10	1720	1730	-10	1920	1944	YX	1654	N227JQ	LGA	LIT	149	1085	17	30	2023-05-10 17:00:00	Other
24850	3	9	1824	1830	-6	2234	2210	B6	326	N967JT	JFK	SFO	392	2586	18	30	2023-03-09 18:00:00	Other
24854	3	8	657	705	-8	930	1008	DL	372	N319NB	LGA	PBI	127	1035	7	5	2023-03-08 07:00:00	Other
24858	11	22	1009	1015	-6	1309	1349	AA	783	N556UW	EWR	PHX	269	2133	10	15	2023-11-22 10:00:00	Other
24868	1	6	742	750	-8	931	1006	DL	331	N356DN	LGA	MSP	142	1020	7	50	2023-01-06 07:00:00	Other
24869	8	19	857	903	-6	1054	1103	YX	896	N751YX	EWR	CMH	71	463	9	3	2023-08-19 09:00:00	Other
24871	9	28	750	759	-9	1058	1126	AA	50	N106NN	JFK	SFO	337	2586	7	59	2023-09-28 07:00:00	Other
24886	12	28	1242	1250	-8	1423	1453	YX	1017	N725YX	EWR	CMH	73	463	12	50	2023-12-28 12:00:00	Other
24896	3	28	1357	1404	-7	1508	1523	YX	1050	N730YX	EWR	ROC	49	246	14	4	2023-03-28 14:00:00	Other
24906	3	11	1045	1053	-8	1313	1332	F9	583	N395FR	LGA	ATL	108	762	10	53	2023-03-11 10:00:00	ATL
24908	6	8	656	705	-9	1003	1010	B6	703	N651JB	EWR	RSW	156	1068	7	5	2023-06-08 07:00:00	Other
24917	11	10	2047	2054	-7	2210	2243	AA	738	N924AN	LGA	ORD	123	733	20	54	2023-11-10 20:00:00	ORD
24926	4	25	1732	1744	-12	1916	1918	YX	960	N640RW	EWR	PIT	62	319	17	44	2023-04-25 17:00:00	Other
24930	10	29	1945	1955	-10	2248	2300	B6	86	N703JB	EWR	FLL	157	1065	19	55	2023-10-29 19:00:00	FLL
24931	11	28	754	800	-6	1035	1026	9E	1671	N907XJ	JFK	CHS	115	636	8	0	2023-11-28 08:00:00	Other
24932	9	15	1049	1056	-7	1217	1243	YX	1159	N639RW	EWR	RDU	69	416	10	56	2023-09-15 10:00:00	Other
24933	7	24	1708	1715	-7	1813	1842	B6	332	N375JB	LGA	BOS	44	184	17	15	2023-07-24 17:00:00	BOS
24934	4	18	2150	2159	-9	2303	2305	B6	256	N190JB	JFK	ORH	31	150	21	59	2023-04-18 21:00:00	Other
24936	1	30	1858	1905	-7	2155	2224	DL	977	N374DA	LGA	RSW	156	1080	19	5	2023-01-30 19:00:00	Other
24940	8	7	733	740	-7	1009	1000	UA	393	N17719	EWR	SAV	102	708	7	40	2023-08-07 07:00:00	Other
24949	11	12	1040	1050	-10	1211	1217	9E	1567	N906XJ	JFK	ROC	55	264	10	50	2023-11-12 10:00:00	Other
24951	7	24	831	840	-9	1055	1034	YX	1083	N119HQ	LGA	ILM	101	500	8	40	2023-07-24 08:00:00	Other
24963	1	25	1642	1655	-13	1901	1858	YX	1402	N404YX	LGA	ILM	97	500	16	55	2023-01-25 16:00:00	Other
24969	4	18	1429	1437	-8	1635	1645	NK	786	N633NK	EWR	MSY	165	1167	14	37	2023-04-18 14:00:00	Other
24979	8	24	1911	1918	-7	2048	2055	YX	856	N729YX	EWR	PWM	48	284	19	18	2023-08-24 19:00:00	Other
24994	1	30	906	915	-9	1051	1125	YX	1840	N220JQ	LGA	CMH	85	479	9	15	2023-01-30 09:00:00	Other
24996	1	10	1345	1355	-10	1635	1707	AA	995	N898NN	LGA	DFW	192	1389	13	55	2023-01-10 13:00:00	Other
24997	6	10	621	630	-9	913	921	NK	518	N974NK	LGA	MCO	127	950	6	30	2023-06-10 06:00:00	MCO
25011	11	24	815	821	-6	1011	1026	AA	751	N841NN	LGA	CLT	96	544	8	21	2023-11-24 08:00:00	CLT
25012	4	13	1148	1200	-12	1249	1308	YX	1217	N441YX	JFK	ORH	33	150	12	0	2023-04-13 12:00:00	Other
25020	6	10	1951	2000	-9	2241	2256	B6	86	N2060J	JFK	MCO	129	944	20	0	2023-06-10 20:00:00	MCO
25022	5	20	1849	1855	-6	2057	2121	DL	808	N982AT	EWR	ATL	106	746	18	55	2023-05-20 18:00:00	ATL
25031	12	6	1021	1030	-9	1137	1158	YX	1243	N430YX	JFK	ORF	54	290	10	30	2023-12-06 10:00:00	Other
25038	9	2	1744	1750	-6	2027	2049	NK	27	N964NK	EWR	LAX	317	2454	17	50	2023-09-02 17:00:00	LAX
25040	11	16	1245	1251	-6	1514	1555	YX	1229	N438YX	LGA	OKC	189	1341	12	51	2023-11-16 12:00:00	Other
25044	1	31	747	800	-13	1014	1028	B6	122	N258JB	JFK	SAV	118	718	8	0	2023-01-31 08:00:00	Other
25046	2	26	1423	1430	-7	1644	1721	YX	1606	N815MD	LGA	JAX	118	833	14	30	2023-02-26 14:00:00	Other
25050	2	2	1728	1735	-7	2048	2105	B6	914	N993JE	JFK	LAX	353	2475	17	35	2023-02-02 17:00:00	LAX
25051	10	27	653	700	-7	930	952	UA	391	N810UA	EWR	SRQ	140	1034	7	0	2023-10-27 07:00:00	Other
25057	9	23	925	935	-10	1131	1155	9E	1746	N914XJ	LGA	MCI	151	1107	9	35	2023-09-23 09:00:00	Other
25068	9	18	708	715	-7	814	840	B6	709	N281JB	JFK	DCA	45	213	7	15	2023-09-18 07:00:00	Other
25070	8	29	1826	1834	-8	2015	2040	NK	497	N514NK	LGA	MYR	86	563	18	34	2023-08-29 18:00:00	Other
25078	4	23	1122	1131	-9	1232	1309	AA	693	N949NN	LGA	ORD	103	733	11	31	2023-04-23 11:00:00	ORD
25081	10	14	1421	1430	-9	1515	1540	YX	1118	N733YX	EWR	PVD	38	160	14	30	2023-10-14 14:00:00	Other
25082	2	7	1706	1715	-9	2007	2037	DL	283	N402DX	JFK	LAX	332	2475	17	15	2023-02-07 17:00:00	LAX
25083	3	1	1513	1525	-12	1801	1827	B6	710	N318JB	EWR	MCO	137	937	15	25	2023-03-01 15:00:00	MCO
25085	8	23	1047	1055	-8	1206	1211	YX	1334	N209JQ	JFK	ACK	39	199	10	55	2023-08-23 10:00:00	Other
25101	2	26	1424	1430	-6	1631	1646	YX	1261	N870RW	LGA	STL	158	888	14	30	2023-02-26 14:00:00	Other
25107	1	26	1023	1030	-7	1304	1357	AA	3	N107NN	JFK	LAX	306	2475	10	30	2023-01-26 10:00:00	LAX
25112	5	13	1731	1740	-9	1909	1931	YX	1306	N869RW	LGA	ILM	78	500	17	40	2023-05-13 17:00:00	Other
25123	1	22	1421	1429	-8	1612	1631	NK	575	N694NK	LGA	MYR	94	563	14	29	2023-01-22 14:00:00	Other
25132	2	7	851	900	-9	1044	1053	9E	1473	N904XJ	LGA	MSN	135	812	9	0	2023-02-07 09:00:00	Other
25135	5	8	854	900	-6	1239	1214	AS	131	N563AS	EWR	SFO	378	2565	9	0	2023-05-08 09:00:00	Other
25138	1	8	822	835	-13	1010	1040	YX	1435	N412YX	LGA	ILM	85	500	8	35	2023-01-08 08:00:00	Other
25142	4	26	616	625	-9	901	923	UA	217	N69813	EWR	SAN	324	2425	6	25	2023-04-26 06:00:00	Other
25147	2	8	754	800	-6	921	943	UA	837	N25705	LGA	ORD	120	733	8	0	2023-02-08 08:00:00	ORD
25149	1	22	1151	1200	-9	1323	1344	9E	1697	N931XJ	LGA	PIT	66	335	12	0	2023-01-22 12:00:00	Other
25156	8	15	1219	1230	-11	1502	1525	NK	400	N624NK	LGA	IAH	191	1416	12	30	2023-08-15 12:00:00	Other
25166	3	12	1916	1925	-9	2043	2055	AA	783	N772XF	LGA	BNA	124	764	19	25	2023-03-12 19:00:00	Other
25172	12	21	523	530	-7	656	721	NK	326	N649NK	LGA	MYR	77	563	5	30	2023-12-21 05:00:00	Other
25173	11	8	753	800	-7	1040	1054	NK	430	N687NK	EWR	MCO	131	937	8	0	2023-11-08 08:00:00	MCO
25181	5	9	2046	2055	-9	6	2357	B6	98	N537JT	EWR	FLL	167	1065	20	55	2023-05-09 20:00:00	FLL
25182	5	28	857	908	-11	1151	1206	B6	165	N503JB	LGA	PBI	139	1035	9	8	2023-05-28 09:00:00	Other
25184	12	22	552	600	-8	857	916	AA	433	N833NN	LGA	MIA	147	1096	6	0	2023-12-22 06:00:00	MIA
25187	1	21	1716	1729	-13	2026	2048	B6	192	N618JB	LGA	FLL	161	1076	17	29	2023-01-21 17:00:00	FLL
25190	1	10	1155	1203	-8	1254	1311	YX	1300	N453YX	JFK	ORH	33	150	12	3	2023-01-10 12:00:00	Other
25193	7	5	1153	1200	-7	1410	1435	DL	277	N121DZ	LGA	ATL	106	762	12	0	2023-07-05 12:00:00	ATL
25200	3	1	1452	1458	-6	1755	1755	B6	868	N768JB	LGA	JAX	123	833	14	58	2023-03-01 14:00:00	Other
25201	1	10	1702	1710	-8	1837	1907	YX	1905	N818MD	LGA	CLE	65	419	17	10	2023-01-10 17:00:00	Other
25202	5	30	1558	1605	-7	1910	1916	B6	764	N595JB	JFK	PBI	136	1028	16	5	2023-05-30 16:00:00	Other
25207	3	7	1019	1025	-6	1256	1307	DL	875	N123DQ	LGA	MSY	178	1183	10	25	2023-03-07 10:00:00	Other
25208	2	7	1715	1725	-10	2027	2047	B6	75	N983JT	JFK	SEA	342	2422	17	25	2023-02-07 17:00:00	Other
25209	2	6	1018	1025	-7	1251	1307	DL	840	N113DQ	LGA	MSY	160	1183	10	25	2023-02-06 10:00:00	Other
25211	2	10	1819	1830	-11	2136	2146	NK	972	N622NK	LGA	FLL	161	1076	18	30	2023-02-10 18:00:00	FLL
25214	4	22	1031	1039	-8	1406	1354	B6	78	N635JB	LGA	FLL	179	1076	10	39	2023-04-22 10:00:00	FLL
25216	4	8	1919	1929	-10	2138	2215	UA	390	N63899	EWR	LAS	293	2227	19	29	2023-04-08 19:00:00	Other
25226	1	23	1024	1030	-6	1255	1235	YX	1302	N414YX	LGA	ORD	113	733	10	30	2023-01-23 10:00:00	ORD
25229	8	23	924	930	-6	1134	1159	YX	1351	N882RW	LGA	HHH	96	701	9	30	2023-08-23 09:00:00	Other
25239	3	28	651	700	-9	1013	1009	AS	92	N926AK	EWR	SEA	342	2402	7	0	2023-03-28 07:00:00	Other
25241	10	28	1119	1125	-6	1357	1349	B6	21	N590JB	LGA	DEN	247	1620	11	25	2023-10-28 11:00:00	Other
25257	9	5	1340	1347	-7	1611	1641	AA	991	N979NN	LGA	DFW	180	1389	13	47	2023-09-05 13:00:00	Other
25261	10	7	2104	2110	-6	2348	32	UA	889	N17105	EWR	SFO	319	2565	21	10	2023-10-07 21:00:00	Other
25263	11	30	1237	1245	-8	1500	1519	UA	83	N449UA	EWR	ATL	115	746	12	45	2023-11-30 12:00:00	ATL
25268	11	20	853	900	-7	1048	1129	YX	1064	N733YX	EWR	IND	99	645	9	0	2023-11-20 09:00:00	Other
25271	9	6	1318	1330	-12	1426	1446	YX	1090	N747YX	EWR	SYR	39	195	13	30	2023-09-06 13:00:00	Other
25275	9	4	648	659	-11	801	830	YX	1378	N411YX	LGA	PIT	52	335	6	59	2023-09-04 06:00:00	Other
25286	11	13	2119	2129	-10	2236	2300	YX	1841	N210JQ	LGA	DCA	45	214	21	29	2023-11-13 21:00:00	Other
25292	5	17	750	759	-9	1000	1002	AA	952	N581UW	LGA	CLT	90	544	7	59	2023-05-17 07:00:00	CLT
25302	6	16	820	827	-7	1029	1045	9E	1603	N902XJ	LGA	MCI	153	1107	8	27	2023-06-16 08:00:00	Other
25303	9	6	1614	1625	-11	1749	1800	YX	1921	N203JQ	LGA	DCA	42	214	16	25	2023-09-06 16:00:00	Other
25305	4	18	2008	2015	-7	2116	2134	B6	500	N334JB	LGA	BOS	40	184	20	15	2023-04-18 20:00:00	BOS
25309	8	4	1051	1059	-8	1217	1224	9E	1119	N304PQ	LGA	SYR	38	198	10	59	2023-08-04 10:00:00	Other
25310	12	30	1902	1915	-13	2011	2059	YX	1770	N217JQ	LGA	PIT	54	335	19	15	2023-12-30 19:00:00	Other
25314	10	7	658	705	-7	945	1005	DL	497	N111NG	LGA	TPA	149	1010	7	5	2023-10-07 07:00:00	Other
25318	2	7	1306	1315	-9	1400	1425	B6	803	N284JB	LGA	BOS	35	184	13	15	2023-02-07 13:00:00	BOS
25320	8	22	725	735	-10	932	1000	DL	168	N377DA	LGA	DEN	207	1620	7	35	2023-08-22 07:00:00	Other
25334	10	11	809	815	-6	1313	1303	UA	108	N76062	EWR	HNL	624	4962	8	15	2023-10-11 08:00:00	Other
25342	12	1	1751	1759	-8	2007	2026	YX	1340	N447YX	LGA	IND	110	660	17	59	2023-12-01 17:00:00	Other
25345	11	10	1502	1510	-8	1655	1714	YX	1343	N424YX	JFK	CLE	91	425	15	10	2023-11-10 15:00:00	Other
25347	10	19	650	700	-10	801	819	AA	513	N763US	LGA	DCA	42	214	7	0	2023-10-19 07:00:00	Other
25348	8	22	1511	1517	-6	1751	1815	NK	683	N636NK	EWR	LAX	307	2454	15	17	2023-08-22 15:00:00	LAX
25360	4	29	1353	1359	-6	1508	1518	YX	1445	N201JQ	JFK	BOS	39	187	13	59	2023-04-29 13:00:00	BOS
25365	5	11	921	928	-7	1141	1153	UA	868	N469UA	EWR	ATL	103	746	9	28	2023-05-11 09:00:00	ATL
25370	1	19	751	800	-9	925	930	9E	1703	N301PQ	JFK	ROC	50	264	8	0	2023-01-19 08:00:00	Other
25381	3	18	1453	1459	-6	1635	1644	B6	650	N281JB	JFK	BNA	138	765	14	59	2023-03-18 14:00:00	Other
25394	11	27	1048	1057	-9	1242	1307	9E	1502	N331PQ	LGA	MYR	94	563	10	57	2023-11-27 10:00:00	Other
25402	10	9	2120	2129	-9	2226	2302	9E	1646	N306PQ	LGA	BUF	47	292	21	29	2023-10-09 21:00:00	Other
25408	12	26	1057	1104	-7	1200	1215	9E	1356	N341PQ	JFK	ITH	40	189	11	4	2023-12-26 11:00:00	Other
25409	10	31	818	830	-12	1132	1152	B6	527	N2084J	JFK	RSW	169	1074	8	30	2023-10-31 08:00:00	Other
25434	9	19	752	800	-8	1057	1104	B6	799	N947JB	JFK	LAX	335	2475	8	0	2023-09-19 08:00:00	LAX
25436	5	19	1123	1129	-6	1407	1439	UA	473	N443UA	EWR	AUS	198	1504	11	29	2023-05-19 11:00:00	Other
25453	5	18	754	800	-6	929	938	UA	848	N29717	LGA	ORD	114	733	8	0	2023-05-18 08:00:00	ORD
25454	10	30	1943	1950	-7	2151	2148	9E	1393	N910XJ	JFK	RIC	60	288	19	50	2023-10-30 19:00:00	Other
25456	12	16	754	805	-11	918	941	9E	1468	N309PQ	JFK	PWM	52	273	8	5	2023-12-16 08:00:00	Other
25457	11	10	1341	1350	-9	1518	1540	9E	1473	N478PX	LGA	BHM	141	866	13	50	2023-11-10 13:00:00	Other
25460	1	22	1251	1300	-9	1509	1507	AA	935	N987NN	JFK	CLT	104	541	13	0	2023-01-22 13:00:00	CLT
25465	1	24	1323	1330	-7	1438	1453	YX	1908	N201JQ	JFK	PWM	52	273	13	30	2023-01-24 13:00:00	Other
25467	8	29	852	900	-8	1216	1222	AA	568	N323RM	JFK	MIA	148	1089	9	0	2023-08-29 09:00:00	MIA
25476	10	21	1253	1259	-6	1535	1612	DL	537	N112DN	LGA	FLL	139	1076	12	59	2023-10-21 12:00:00	FLL
25477	4	2	949	959	-10	1140	1218	9E	1316	N903XJ	LGA	MYR	91	563	9	59	2023-04-02 09:00:00	Other
25484	10	22	1614	1620	-6	1807	1835	9E	1684	N907XJ	JFK	CLT	83	541	16	20	2023-10-22 16:00:00	CLT
25491	10	10	654	700	-6	915	934	UA	202	N37545	EWR	LAS	290	2227	7	0	2023-10-10 07:00:00	Other
25494	10	12	1852	1859	-7	2032	2104	9E	1537	N491PX	LGA	GSO	71	461	18	59	2023-10-12 18:00:00	Other
25497	2	7	1554	1603	-9	1854	1911	UA	826	N76254	EWR	DFW	211	1372	16	3	2023-02-07 16:00:00	Other
25508	9	1	936	945	-9	1100	1134	9E	1429	N490PX	LGA	BGR	60	378	9	45	2023-09-01 09:00:00	Other
25525	11	23	1820	1828	-8	2106	2146	F9	1474	N609FR	LGA	MCO	138	950	18	28	2023-11-23 18:00:00	MCO
25526	4	12	705	711	-6	858	915	AA	323	N819NN	LGA	CLT	73	544	7	11	2023-04-12 07:00:00	CLT
25527	9	3	528	535	-7	758	810	B6	102	N627JB	EWR	MCO	122	937	5	35	2023-09-03 05:00:00	MCO
25531	6	23	1052	1100	-8	1221	1231	YX	1291	N408YX	LGA	PIT	65	335	11	0	2023-06-23 11:00:00	Other
25535	3	24	1338	1344	-6	1506	1513	B6	938	N265JB	JFK	BUF	60	301	13	44	2023-03-24 13:00:00	Other
25540	10	13	1547	1555	-8	1731	1751	YX	1092	N979RP	EWR	CMH	80	463	15	55	2023-10-13 15:00:00	Other
25547	4	11	1908	1915	-7	2014	2058	UA	718	N820UA	LGA	ORD	104	733	19	15	2023-04-11 19:00:00	ORD
25550	12	30	1340	1349	-9	1533	1614	9E	1415	N298PQ	LGA	IND	88	660	13	49	2023-12-30 13:00:00	Other
25552	6	8	853	859	-6	1052	1056	YX	1389	N872RW	LGA	ILM	85	500	8	59	2023-06-08 08:00:00	Other
25555	1	10	2154	2200	-6	2318	2339	B6	391	N375JB	LGA	BNA	108	764	22	0	2023-01-10 22:00:00	Other
25563	3	27	1042	1055	-13	1310	1310	G4	1016	193NV	EWR	TYS	108	631	10	55	2023-03-27 10:00:00	Other
25575	4	8	1515	1521	-6	1757	1809	UA	245	N873UA	EWR	MCO	135	937	15	21	2023-04-08 15:00:00	MCO
25579	9	13	728	735	-7	1026	1037	DL	790	N3740C	JFK	PBI	148	1028	7	35	2023-09-13 07:00:00	Other
25582	9	1	623	630	-7	909	918	UA	417	N449UA	EWR	SRQ	142	1034	6	30	2023-09-01 06:00:00	Other
25595	1	9	1248	1256	-8	1422	1458	AA	516	N801NN	LGA	ORD	114	733	12	56	2023-01-09 12:00:00	ORD
25596	7	11	723	730	-7	1002	1035	AA	3	N116AN	JFK	LAX	314	2475	7	30	2023-07-11 07:00:00	LAX
25597	4	7	1338	1345	-7	1537	1600	B6	850	N239JB	LGA	CHS	98	641	13	45	2023-04-07 13:00:00	Other
25598	8	3	1509	1515	-6	1800	1822	DL	182	N198DN	JFK	LAX	310	2475	15	15	2023-08-03 15:00:00	LAX
25605	9	14	1322	1329	-7	1516	1532	AA	934	N9026C	JFK	CLT	84	541	13	29	2023-09-14 13:00:00	CLT
25608	5	12	1453	1459	-6	1743	1750	B6	569	N621JB	EWR	MCO	122	937	14	59	2023-05-12 14:00:00	MCO
25616	10	3	749	759	-10	934	1006	YX	1140	N758YX	EWR	MYR	80	550	7	59	2023-10-03 07:00:00	Other
25617	5	13	1233	1240	-7	1425	1457	9E	1280	N908XJ	LGA	CVG	93	585	12	40	2023-05-13 12:00:00	Other
25618	9	19	1953	1959	-6	2311	2319	DL	563	N308DN	LGA	FLL	167	1076	19	59	2023-09-19 19:00:00	FLL
25620	12	26	1946	1952	-6	2049	2120	YX	1031	N657RW	LGA	IAD	46	229	19	52	2023-12-26 19:00:00	Other
25623	9	24	1252	1259	-7	1448	1454	9E	1423	N292PQ	JFK	DTW	83	509	12	59	2023-09-24 12:00:00	Other
25626	1	23	1709	1718	-9	1853	1922	YX	1257	N863RW	EWR	CMH	68	463	17	18	2023-01-23 17:00:00	Other
25630	11	21	752	800	-8	1041	1034	DL	908	N368NB	JFK	MSY	191	1182	8	0	2023-11-21 08:00:00	Other
25632	1	20	748	755	-7	902	920	YX	1193	N729YX	EWR	PWM	49	284	7	55	2023-01-20 07:00:00	Other
25634	5	26	2052	2100	-8	2210	2243	UA	427	N468UA	LGA	ORD	98	733	21	0	2023-05-26 21:00:00	ORD
25635	7	13	1353	1400	-7	1533	1521	AA	392	N703UW	LGA	DCA	44	214	14	0	2023-07-13 14:00:00	Other
25636	1	25	650	659	-9	925	943	B6	871	N580JB	LGA	DEN	236	1620	6	59	2023-01-25 06:00:00	Other
25640	2	8	852	900	-8	1215	1235	YX	1219	N432YX	LGA	IAH	214	1416	9	0	2023-02-08 09:00:00	Other
25651	2	2	1622	1635	-13	1955	1957	B6	739	N986JB	EWR	LAX	353	2454	16	35	2023-02-02 16:00:00	LAX
25652	2	27	1205	1213	-8	1404	1452	YX	1238	N119HQ	LGA	MSP	150	1020	12	13	2023-02-27 12:00:00	Other
25659	8	13	1110	1118	-8	1355	1414	DL	359	N871DN	JFK	TPA	130	1005	11	18	2023-08-13 11:00:00	Other
25662	12	13	827	835	-8	1114	1137	YX	1798	N211JQ	JFK	JAX	132	828	8	35	2023-12-13 08:00:00	Other
25664	1	28	2049	2057	-8	2227	2244	UA	153	N898UA	EWR	RDU	70	416	20	57	2023-01-28 20:00:00	Other
25671	5	26	2123	2129	-6	2311	2320	YX	1319	N434YX	LGA	CLE	68	419	21	29	2023-05-26 21:00:00	Other
25673	5	18	645	653	-8	854	910	YX	1071	N651RW	EWR	IND	99	645	6	53	2023-05-18 06:00:00	Other
25674	3	16	2003	2015	-12	2336	2354	UA	882	N19130	EWR	SFO	352	2565	20	15	2023-03-16 20:00:00	Other
25677	11	30	806	814	-8	950	1006	YX	1291	N108HQ	LGA	ILM	79	500	8	14	2023-11-30 08:00:00	Other
25678	4	24	608	615	-7	908	914	DL	282	N128DU	LGA	DFW	210	1389	6	15	2023-04-24 06:00:00	Other
25684	8	6	2120	2130	-10	2309	2334	YX	875	N760YX	EWR	GSO	74	445	21	30	2023-08-06 21:00:00	Other
25691	9	5	1537	1545	-8	1642	1658	9E	1746	N305PQ	LGA	PVD	29	143	15	45	2023-09-05 15:00:00	Other
25693	10	22	1454	1500	-6	1703	1713	9E	1578	N181GJ	EWR	CVG	94	569	15	0	2023-10-22 15:00:00	Other
25699	10	4	1829	1835	-6	1959	2015	YX	1160	N723YX	EWR	PIT	56	319	18	35	2023-10-04 18:00:00	Other
25704	3	13	1138	1145	-7	1416	1513	AS	8	N943AK	JFK	PDX	317	2454	11	45	2023-03-13 11:00:00	Other
25706	1	31	1052	1059	-7	1312	1255	YX	1121	N755YX	EWR	MYR	91	550	10	59	2023-01-31 10:00:00	Other
25710	6	20	1449	1455	-6	1648	1710	YX	1423	N414YX	LGA	CVG	91	585	14	55	2023-06-20 14:00:00	Other
25711	11	13	921	929	-8	1108	1126	YX	1141	N760YX	EWR	STL	129	872	9	29	2023-11-13 09:00:00	Other
25713	7	17	1022	1030	-8	1400	1358	YX	942	N651RW	EWR	EYW	180	1196	10	30	2023-07-17 10:00:00	Other
25718	11	25	620	630	-10	1002	1007	UA	424	N12114	EWR	PHX	310	2133	6	30	2023-11-25 06:00:00	Other
25722	5	22	722	730	-8	1018	1026	B6	319	N623JB	JFK	PBI	146	1028	7	30	2023-05-22 07:00:00	Other
25726	5	6	2054	2100	-6	2215	2235	YX	1616	N226JQ	JFK	DCA	51	213	21	0	2023-05-06 21:00:00	Other
25745	4	7	1153	1200	-7	1447	1456	B6	145	N658JB	LGA	MCO	136	950	12	0	2023-04-07 12:00:00	MCO
25748	9	20	738	745	-7	933	957	YX	1208	N760YX	EWR	GRR	91	605	7	45	2023-09-20 07:00:00	Other
25749	2	4	739	745	-6	1054	1114	AA	575	N918NN	LGA	MIA	158	1096	7	45	2023-02-04 07:00:00	MIA
25752	8	30	1650	1700	-10	1857	1900	YX	963	N113HQ	LGA	DSM	151	1031	17	0	2023-08-30 17:00:00	Other
25756	10	15	1046	1052	-6	1211	1234	9E	1377	N176PQ	LGA	BNA	121	764	10	52	2023-10-15 10:00:00	Other
25765	12	19	1200	1207	-7	1355	1427	DL	350	N104DU	JFK	MSP	155	1029	12	7	2023-12-19 12:00:00	Other
25768	5	9	2052	2059	-7	2400	2350	B6	681	N547JB	EWR	MCO	156	937	20	59	2023-05-09 20:00:00	MCO
25774	4	1	839	849	-10	1114	1045	YX	1237	N434YX	LGA	ILM	99	500	8	49	2023-04-01 08:00:00	Other
25775	7	26	652	659	-7	836	856	YX	1022	N424YX	LGA	DTW	78	502	6	59	2023-07-26 06:00:00	Other
25784	3	22	1135	1145	-10	1437	1459	AS	8	N238AK	JFK	PDX	337	2454	11	45	2023-03-22 11:00:00	Other
25785	8	31	1541	1550	-9	1649	1731	9E	1276	N935XJ	LGA	CHO	49	305	15	50	2023-08-31 15:00:00	Other
25786	12	18	1621	1629	-8	1811	1905	UA	635	N812UA	LGA	DEN	211	1620	16	29	2023-12-18 16:00:00	Other
25790	12	26	1437	1445	-8	1601	1615	YX	1025	N638RW	EWR	IAD	45	212	14	45	2023-12-26 14:00:00	Other
25793	9	16	1151	1200	-9	1305	1324	YX	1953	N246JQ	LGA	BOS	44	184	12	0	2023-09-16 12:00:00	BOS
25802	9	21	613	619	-6	820	818	AA	319	N965NN	JFK	CLT	89	541	6	19	2023-09-21 06:00:00	CLT
25813	9	15	854	900	-6	1117	1127	UA	896	N17316	EWR	ATL	101	746	9	0	2023-09-15 09:00:00	ATL
25815	10	7	622	630	-8	750	808	UA	254	N14230	EWR	CLE	61	404	6	30	2023-10-07 06:00:00	Other
25817	11	7	2045	2055	-10	2228	2257	9E	1555	N490PX	LGA	ILM	71	500	20	55	2023-11-07 20:00:00	Other
25820	6	6	1352	1405	-13	1542	1558	YX	1378	N445YX	LGA	ILM	79	500	14	5	2023-06-06 14:00:00	Other
25826	4	21	2021	2029	-8	2224	2242	YX	1098	N446YX	LGA	MEM	145	963	20	29	2023-04-21 20:00:00	Other
25831	8	20	1119	1130	-11	1226	1242	B6	625	N337JB	JFK	ACK	44	199	11	30	2023-08-20 11:00:00	Other
25832	4	23	1452	1459	-7	1658	1705	DL	480	N341NB	LGA	DTW	74	502	14	59	2023-04-23 14:00:00	Other
25834	10	14	1509	1515	-6	1755	1741	YX	1286	N440YX	JFK	IND	110	665	15	15	2023-10-14 15:00:00	Other
25837	7	17	1320	1329	-9	1452	1518	9E	1113	N936XJ	LGA	CLE	66	419	13	29	2023-07-17 13:00:00	Other
25846	8	16	1108	1115	-7	1209	1234	B6	206	N348JB	LGA	BOS	33	184	11	15	2023-08-16 11:00:00	BOS
25857	5	10	752	800	-8	937	1020	YX	1586	N234JQ	JFK	CLT	85	541	8	0	2023-05-10 08:00:00	CLT
25862	4	24	622	630	-8	742	818	AA	898	N943AN	LGA	ORD	106	733	6	30	2023-04-24 06:00:00	ORD
25867	9	14	1425	1432	-7	1617	1630	YX	1392	N128HQ	LGA	ILM	79	500	14	32	2023-09-14 14:00:00	Other
25868	9	11	734	740	-6	940	953	UA	893	N29717	EWR	MSY	153	1167	7	40	2023-09-11 07:00:00	Other
25875	8	22	1159	1205	-6	1312	1332	AA	631	N754UW	LGA	DCA	44	214	12	5	2023-08-22 12:00:00	Other
25881	5	3	1121	1130	-9	1248	1320	YX	1637	N234JQ	LGA	PIT	57	335	11	30	2023-05-03 11:00:00	Other
25884	6	18	1521	1527	-6	1716	1729	DL	964	N307DU	EWR	MSP	146	1008	15	27	2023-06-18 15:00:00	Other
25886	12	16	1520	1529	-9	1629	1700	9E	1399	N184GJ	JFK	PWM	44	273	15	29	2023-12-16 15:00:00	Other
25900	4	5	548	555	-7	754	754	NK	473	N506NK	LGA	CLT	82	544	5	55	2023-04-05 05:00:00	CLT
25904	2	26	1146	1200	-14	1331	1356	AA	955	N935AN	LGA	RDU	72	431	12	0	2023-02-26 12:00:00	Other
25913	2	9	1707	1715	-8	1824	1833	B6	414	N193JB	LGA	BOS	40	184	17	15	2023-02-09 17:00:00	BOS
25915	1	14	753	800	-7	1127	1120	B6	59	N2039J	JFK	SAN	327	2446	8	0	2023-01-14 08:00:00	Other
25923	4	11	821	830	-9	1004	1032	9E	1426	N200PQ	LGA	ILM	78	500	8	30	2023-04-11 08:00:00	Other
25924	3	4	1944	1955	-11	2104	2118	UA	917	N488UA	EWR	IAD	47	212	19	55	2023-03-04 19:00:00	Other
25927	7	19	1718	1729	-11	1935	1951	YX	1063	N447YX	LGA	SDF	105	659	17	29	2023-07-19 17:00:00	Other
25931	10	11	1203	1211	-8	1326	1345	YX	1795	N218JQ	JFK	BUF	57	301	12	11	2023-10-11 12:00:00	Other
25937	4	26	1053	1100	-7	1331	1416	AA	115	N108NN	JFK	LAX	322	2475	11	0	2023-04-26 11:00:00	LAX
25938	3	18	1946	1954	-8	2239	2320	B6	607	N988JT	EWR	LAX	328	2454	19	54	2023-03-18 19:00:00	LAX
25943	11	13	2120	2130	-10	2314	2336	OO	1194	N293SY	JFK	CLE	82	425	21	30	2023-11-13 21:00:00	Other
25949	10	3	703	710	-7	938	1008	UA	782	N68453	EWR	PBI	133	1023	7	10	2023-10-03 07:00:00	Other
25951	11	8	2124	2130	-6	2318	2336	OO	1194	N303SY	JFK	CLE	84	425	21	30	2023-11-08 21:00:00	Other
25952	5	18	1535	1542	-7	1700	1739	YX	1570	N234JQ	LGA	STL	123	888	15	42	2023-05-18 15:00:00	Other
25956	5	28	902	909	-7	1007	1043	YX	1214	N127HQ	JFK	BOS	43	187	9	9	2023-05-28 09:00:00	BOS
25959	3	8	1853	1900	-7	2104	2127	9E	1503	N294PQ	JFK	IND	107	665	19	0	2023-03-08 19:00:00	Other
25966	10	28	754	800	-6	910	911	B6	37	N216JB	JFK	BOS	42	187	8	0	2023-10-28 08:00:00	BOS
25969	10	12	1953	1959	-6	2253	2313	DL	526	N345DN	LGA	FLL	156	1076	19	59	2023-10-12 19:00:00	FLL
25971	9	12	2010	2017	-7	23	23	NK	355	N624NK	EWR	SJU	220	1608	20	17	2023-09-12 20:00:00	Other
25982	10	31	952	959	-7	1328	1311	AA	573	N902AN	LGA	DFW	231	1389	9	59	2023-10-31 09:00:00	Other
25984	8	28	621	630	-9	1028	926	NK	402	N929NK	LGA	MCO	125	950	6	30	2023-08-28 06:00:00	MCO
25987	10	30	1908	1916	-8	2139	2157	UA	791	N47293	EWR	PHX	309	2133	19	16	2023-10-30 19:00:00	Other
25988	1	5	1323	1330	-7	1545	1555	YX	1337	N121HQ	LGA	LIT	178	1085	13	30	2023-01-05 13:00:00	Other
25989	10	7	1015	1025	-10	1211	1232	9E	1656	N326PQ	LGA	AVL	96	599	10	25	2023-10-07 10:00:00	Other
25990	5	28	1926	1933	-7	2122	2203	YX	1604	N225JQ	LGA	OMA	143	1148	19	33	2023-05-28 19:00:00	Other
25994	11	17	1054	1100	-6	1323	1354	B6	140	N987JT	JFK	LAS	303	2248	11	0	2023-11-17 11:00:00	Other
25997	8	17	751	759	-8	951	1010	YX	1082	N102HQ	LGA	CVG	101	585	7	59	2023-08-17 07:00:00	Other
26002	12	16	1303	1311	-8	1443	1501	DL	973	N929AT	EWR	DTW	81	488	13	11	2023-12-16 13:00:00	Other
26007	6	30	1622	1630	-8	1751	1817	DL	637	N119DU	LGA	ORD	112	733	16	30	2023-06-30 16:00:00	ORD
26015	10	25	1635	1643	-8	1804	1822	UA	763	N27722	EWR	CLE	66	404	16	43	2023-10-25 16:00:00	Other
26016	5	6	1405	1411	-6	1554	1612	YX	1088	N742YX	EWR	ILM	68	488	14	11	2023-05-06 14:00:00	Other
26022	6	21	628	635	-7	817	828	YX	1414	N422YX	JFK	RDU	77	427	6	35	2023-06-21 06:00:00	Other
26034	11	26	921	929	-8	1057	1117	YX	1901	N220JQ	LGA	BNA	129	764	9	29	2023-11-26 09:00:00	Other
26038	11	8	1149	1159	-10	1430	1436	OO	1187	N255SY	LGA	SDF	121	659	11	59	2023-11-08 11:00:00	Other
26043	5	19	704	712	-8	853	926	YX	1209	N410YX	LGA	DTW	79	502	7	12	2023-05-19 07:00:00	Other
26045	1	27	2034	2043	-9	2220	2240	9E	1667	N181PQ	LGA	RDU	72	431	20	43	2023-01-27 20:00:00	Other
26052	6	4	1032	1043	-11	1243	1245	UA	561	N27292	EWR	CHS	102	628	10	43	2023-06-04 10:00:00	Other
26056	4	26	1308	1315	-7	1418	1431	B6	743	N354JB	LGA	BOS	33	184	13	15	2023-04-26 13:00:00	BOS
26058	11	2	854	900	-6	1126	1202	AS	13	N978AK	JFK	SAN	313	2446	9	0	2023-11-02 09:00:00	Other
26060	11	6	1151	1159	-8	1333	1400	9E	1498	N676CA	LGA	ILM	78	500	11	59	2023-11-06 11:00:00	Other
26064	4	19	858	905	-7	1129	1142	B6	419	N187JB	JFK	ATL	107	760	9	5	2023-04-19 09:00:00	ATL
26069	9	1	1247	1300	-13	1444	1509	UA	901	N817UA	EWR	MSY	156	1167	13	0	2023-09-01 13:00:00	Other
26070	10	7	858	905	-7	1055	1111	DL	181	N303DN	LGA	DTW	80	502	9	5	2023-10-07 09:00:00	Other
26076	5	1	944	950	-6	1110	1113	9E	1324	N924XJ	JFK	PWM	47	273	9	50	2023-05-01 09:00:00	Other
26078	12	13	637	645	-8	945	1002	AA	547	N933NN	LGA	MIA	168	1096	6	45	2023-12-13 06:00:00	MIA
26082	7	6	2004	2014	-10	2125	2158	YX	1058	N413YX	LGA	PIT	59	335	20	14	2023-07-06 20:00:00	Other
26088	5	3	716	722	-6	1005	1017	UA	680	N428UA	EWR	TPA	142	997	7	22	2023-05-03 07:00:00	Other
26094	5	31	1120	1128	-8	1238	1259	UA	359	N69810	EWR	ORD	104	719	11	28	2023-05-31 11:00:00	ORD
26095	6	23	820	827	-7	1006	1006	YX	1073	N655RW	EWR	RIC	72	277	8	27	2023-06-23 08:00:00	Other
26096	9	16	1242	1248	-6	1444	1437	YX	1313	N108HQ	JFK	CLE	72	425	12	48	2023-09-16 12:00:00	Other
26099	8	3	952	959	-7	1400	1416	AA	805	N9025B	JFK	STT	197	1623	9	59	2023-08-03 09:00:00	Other
26104	1	14	2053	2100	-7	2305	2336	YX	1412	N134HQ	JFK	IND	96	665	21	0	2023-01-14 21:00:00	Other
26109	9	7	1023	1030	-7	1259	1328	B6	159	N766JB	LGA	PBI	137	1035	10	30	2023-09-07 10:00:00	Other
26113	8	29	1006	1015	-9	1148	1202	AA	179	N760US	LGA	STL	133	888	10	15	2023-08-29 10:00:00	Other
26116	10	17	1749	1759	-10	2042	2105	F9	443	N369FR	LGA	MCO	141	950	17	59	2023-10-17 17:00:00	MCO
26121	3	9	837	845	-8	1029	1046	YX	1750	N227JQ	LGA	STL	145	888	8	45	2023-03-09 08:00:00	Other
26122	2	8	1133	1145	-12	1321	1345	YX	1285	N406YX	JFK	CLE	87	425	11	45	2023-02-08 11:00:00	Other
26129	3	31	1411	1417	-6	1627	1634	9E	1556	N131EV	LGA	CVG	110	585	14	17	2023-03-31 14:00:00	Other
26135	10	4	1420	1435	-15	1627	1640	UA	332	N892UA	EWR	CLT	84	529	14	35	2023-10-04 14:00:00	CLT
26138	11	23	851	857	-6	1122	1202	B6	222	N603JB	LGA	MCO	129	950	8	57	2023-11-23 08:00:00	MCO
26141	1	16	1428	1435	-7	1543	1553	UA	542	N73251	EWR	BOS	42	200	14	35	2023-01-16 14:00:00	BOS
26147	2	25	1723	1729	-6	1905	1923	YX	1277	N419YX	JFK	RDU	76	427	17	29	2023-02-25 17:00:00	Other
26149	11	1	1643	1654	-11	2007	1956	AA	969	N924NN	LGA	DFW	198	1389	16	54	2023-11-01 16:00:00	Other
26154	9	2	1653	1703	-10	1846	1921	UA	933	N47293	EWR	PHX	268	2133	17	3	2023-09-02 17:00:00	Other
26164	6	5	550	600	-10	709	712	B6	842	N358JB	EWR	BOS	39	200	6	0	2023-06-05 06:00:00	BOS
26174	2	7	521	530	-9	755	836	B6	235	N613JB	EWR	TPA	135	997	5	30	2023-02-07 05:00:00	Other
26175	4	21	1044	1050	-6	1234	1236	AA	904	N815AW	LGA	STL	129	888	10	50	2023-04-21 10:00:00	Other
26176	9	23	921	929	-8	1108	1116	YX	1312	N406YX	JFK	CLE	69	425	9	29	2023-09-23 09:00:00	Other
26179	2	7	1619	1628	-9	1737	1818	YX	1250	N869RW	LGA	CHO	61	305	16	28	2023-02-07 16:00:00	Other
26182	9	25	608	615	-7	909	909	UA	240	N27287	EWR	AUS	210	1504	6	15	2023-09-25 06:00:00	Other
26192	6	15	2103	2110	-7	2221	2243	YX	1401	N421YX	LGA	ORF	50	296	21	10	2023-06-15 21:00:00	Other
26194	4	19	909	924	-15	1056	1133	YX	976	N741YX	EWR	AVL	84	583	9	24	2023-04-19 09:00:00	Other
26196	2	6	657	705	-8	909	949	DL	193	N365DN	LGA	ATL	105	762	7	5	2023-02-06 07:00:00	ATL
26198	8	2	833	842	-9	950	1025	9E	1267	N600LR	LGA	CHO	51	305	8	42	2023-08-02 08:00:00	Other
26199	2	21	1127	1136	-9	1309	1321	YX	1065	N728YX	EWR	CLE	78	404	11	36	2023-02-21 11:00:00	Other
26202	10	23	1454	1500	-6	1605	1630	YX	1159	N741YX	EWR	PIT	53	319	15	0	2023-10-23 15:00:00	Other
26207	12	5	1621	1628	-7	1746	1803	YX	1097	N721YX	EWR	PIT	61	319	16	28	2023-12-05 16:00:00	Other
26211	11	5	955	1003	-8	1209	1233	UA	529	N37471	EWR	DEN	225	1605	10	3	2023-11-05 10:00:00	Other
26216	7	18	1016	1024	-8	1258	1314	AA	216	N921AN	EWR	DFW	177	1372	10	24	2023-07-18 10:00:00	Other
26217	8	31	1653	1701	-8	1920	1952	AA	779	N984NN	LGA	DFW	169	1389	17	1	2023-08-31 17:00:00	Other
26224	5	8	1443	1450	-7	1649	1656	B6	356	N279JB	JFK	DTW	88	509	14	50	2023-05-08 14:00:00	Other
26230	2	28	1457	1505	-8	1647	1658	YX	1496	N206JQ	JFK	PIT	70	340	15	5	2023-02-28 15:00:00	Other
26232	1	30	1830	1839	-9	2204	2204	UA	571	N16709	EWR	SNA	361	2434	18	39	2023-01-30 18:00:00	Other
26235	5	10	1349	1355	-6	1605	1615	YX	1036	N729YX	EWR	SDF	98	642	13	55	2023-05-10 13:00:00	Other
26241	7	30	853	900	-7	1039	1044	YX	1347	N225JQ	JFK	PIT	66	340	9	0	2023-07-30 09:00:00	Other
26243	9	28	1203	1210	-7	1322	1342	YX	1382	N427YX	LGA	RIC	55	292	12	10	2023-09-28 12:00:00	Other
26244	1	18	1649	1659	-10	1759	1827	9E	1502	N479PX	LGA	PWM	47	269	16	59	2023-01-18 16:00:00	Other
26254	12	25	1651	1700	-9	2005	2033	DL	840	N341NB	JFK	AUS	214	1521	17	0	2023-12-25 17:00:00	Other
26255	10	3	1556	1604	-8	1807	1829	UA	503	N77530	EWR	ATL	100	746	16	4	2023-10-03 16:00:00	ATL
26267	10	19	712	722	-10	916	943	9E	1645	N195PQ	LGA	CVG	97	585	7	22	2023-10-19 07:00:00	Other
26275	6	9	548	600	-12	645	707	UA	388	N24715	EWR	BOS	35	200	6	0	2023-06-09 06:00:00	BOS
26279	9	17	944	955	-11	1106	1133	9E	1467	N138EV	JFK	RIC	55	288	9	55	2023-09-17 09:00:00	Other
26284	2	20	1532	1540	-8	1749	1806	B6	865	N569JB	JFK	CHS	105	636	15	40	2023-02-20 15:00:00	Other
26292	10	25	720	729	-9	1003	1024	UA	922	N33714	LGA	IAH	192	1416	7	29	2023-10-25 07:00:00	Other
26295	10	11	550	600	-10	716	722	AA	704	N840AW	LGA	DCA	48	214	6	0	2023-10-11 06:00:00	Other
26300	10	16	1450	1459	-9	1747	1805	DL	969	N365NW	LGA	TPA	143	1010	14	59	2023-10-16 14:00:00	Other
26303	2	27	1617	1625	-8	1719	1737	9E	1435	N916XJ	LGA	PVD	28	143	16	25	2023-02-27 16:00:00	Other
26304	2	19	1628	1635	-7	1743	1808	YX	1517	N216JQ	LGA	DCA	48	214	16	35	2023-02-19 16:00:00	Other
26317	4	17	1051	1100	-9	2140	1413	B6	191	N651JB	JFK	FLL	NA	1069	11	0	2023-04-17 11:00:00	FLL
26319	11	5	949	959	-10	1058	1135	YX	1821	N218JQ	JFK	DCA	43	213	9	59	2023-11-05 09:00:00	Other
26321	4	25	807	816	-9	1038	1040	YX	1563	N212JQ	LGA	MCI	166	1107	8	16	2023-04-25 08:00:00	Other
26322	10	25	1622	1629	-7	1738	1758	YX	1321	N115HQ	JFK	ORF	48	290	16	29	2023-10-25 16:00:00	Other
26324	8	7	657	705	-8	949	932	B6	125	N947JB	JFK	LAS	301	2248	7	5	2023-08-07 07:00:00	Other
26337	2	20	2038	2045	-7	2200	2234	DL	451	N107DU	LGA	ORD	121	733	20	45	2023-02-20 20:00:00	ORD
26342	1	5	1417	1429	-12	1506	1529	B6	346	N318JB	JFK	ORH	28	150	14	29	2023-01-05 14:00:00	Other
26345	10	28	1126	1135	-9	1252	1329	YX	1333	N444YX	JFK	RDU	67	427	11	35	2023-10-28 11:00:00	Other
26365	2	7	648	659	-11	904	943	B6	771	N768JB	LGA	DEN	234	1620	6	59	2023-02-07 06:00:00	Other
26369	7	22	854	900	-6	1039	1037	OO	985	N306SY	JFK	BNA	129	765	9	0	2023-07-22 09:00:00	Other
26371	1	8	944	955	-11	1159	1208	G4	71	327NV	EWR	AVL	98	583	9	55	2023-01-08 09:00:00	Other
26374	4	18	1714	1727	-13	2046	2104	YX	951	N644RW	EWR	EYW	175	1196	17	27	2023-04-18 17:00:00	Other
26375	5	22	1922	1930	-8	2212	2228	B6	662	N585JB	LGA	PBI	144	1035	19	30	2023-05-22 19:00:00	Other
26377	11	4	1222	1229	-7	1415	1438	DL	967	N316DU	JFK	MSP	153	1029	12	29	2023-11-04 12:00:00	Other
26381	2	19	1217	1225	-8	1405	1436	NK	630	N680NK	LGA	DTW	84	502	12	25	2023-02-19 12:00:00	Other
26382	8	13	750	800	-10	859	926	YX	1346	N245JQ	LGA	BOS	40	184	8	0	2023-08-13 08:00:00	BOS
26386	6	5	840	850	-10	1014	1028	9E	1686	N921XJ	LGA	MKE	114	738	8	50	2023-06-05 08:00:00	Other
26388	4	25	1040	1050	-10	1319	1325	F9	523	N303FR	LGA	ATL	118	762	10	50	2023-04-25 10:00:00	ATL
26392	5	28	752	800	-8	959	1017	B6	317	N306JB	JFK	SAV	106	718	8	0	2023-05-28 08:00:00	Other
26394	11	27	1703	1710	-7	1822	1832	UA	580	N897UA	EWR	IAD	51	212	17	10	2023-11-27 17:00:00	Other
26396	1	22	831	845	-14	1024	1059	9E	1646	N197PQ	LGA	ILM	94	500	8	45	2023-01-22 08:00:00	Other
26400	12	1	1208	1215	-7	1418	1444	UA	848	N37507	EWR	DEN	224	1605	12	15	2023-12-01 12:00:00	Other
26404	5	11	1441	1447	-6	1634	1655	YX	1145	N729YX	EWR	CVG	91	569	14	47	2023-05-11 14:00:00	Other
26407	9	19	1648	1659	-11	2005	2028	AA	49	N104NN	JFK	SFO	345	2586	16	59	2023-09-19 16:00:00	Other
26413	3	23	817	827	-10	1051	1104	B6	923	N779JB	LGA	MSY	174	1183	8	27	2023-03-23 08:00:00	Other
26447	9	2	1049	1055	-6	1255	1317	UA	481	N423UA	EWR	JAX	110	820	10	55	2023-09-02 10:00:00	Other
26453	10	12	1924	1930	-6	2314	2343	UA	532	N37563	EWR	SJU	198	1608	19	30	2023-10-12 19:00:00	Other
26454	11	8	1821	1829	-8	1959	2024	9E	1464	N182GJ	LGA	BHM	123	866	18	29	2023-11-08 18:00:00	Other
26456	12	4	1909	1916	-7	2220	2257	UA	287	N27263	EWR	PHX	280	2133	19	16	2023-12-04 19:00:00	Other
26460	10	5	1154	1200	-6	1300	1324	YX	1853	N243JQ	LGA	BOS	33	184	12	0	2023-10-05 12:00:00	BOS
26462	6	13	1101	1110	-9	1230	1240	YX	1403	N413YX	JFK	ORF	55	290	11	10	2023-06-13 11:00:00	Other
26474	8	15	722	730	-8	900	908	B6	314	N329JB	JFK	ORD	113	740	7	30	2023-08-15 07:00:00	ORD
26478	11	15	1950	2000	-10	2100	2120	AA	703	N712US	LGA	DCA	45	214	20	0	2023-11-15 20:00:00	Other
26482	10	18	731	738	-7	942	1003	UA	385	N24706	EWR	JAX	106	820	7	38	2023-10-18 07:00:00	Other
26484	3	23	1023	1029	-6	1403	1332	UA	878	N454UA	EWR	MTJ	304	1795	10	29	2023-03-23 10:00:00	Other
26488	1	27	606	615	-9	934	935	DL	739	N128DU	LGA	IAH	241	1416	6	15	2023-01-27 06:00:00	Other
26490	2	25	1135	1145	-10	1255	1258	9E	1325	N181GJ	JFK	ITH	51	189	11	45	2023-02-25 11:00:00	Other
26496	2	18	1221	1228	-7	1516	1528	UA	829	N836UA	EWR	PBI	156	1023	12	28	2023-02-18 12:00:00	Other
26499	10	2	1833	1840	-7	2114	2135	NK	304	N959NK	LGA	DFW	183	1389	18	40	2023-10-02 18:00:00	Other
26501	1	20	924	930	-6	1233	1248	B6	50	N630JB	JFK	SRQ	157	1041	9	30	2023-01-20 09:00:00	Other
26503	12	3	1221	1227	-6	1351	1343	AA	829	N744P	LGA	BOS	42	184	12	27	2023-12-03 12:00:00	BOS
26507	7	9	1139	1145	-6	1322	1313	YX	1411	N236JQ	LGA	DCA	59	214	11	45	2023-07-09 11:00:00	Other
26508	12	5	735	744	-9	938	952	AA	673	N977NN	EWR	CLT	94	529	7	44	2023-12-05 07:00:00	CLT
26510	2	5	943	950	-7	1220	1215	UA	756	N13954	EWR	DEN	214	1605	9	50	2023-02-05 09:00:00	Other
26514	9	21	1622	1630	-8	1916	1935	B6	776	N988JT	EWR	LAX	331	2454	16	30	2023-09-21 16:00:00	LAX
26515	4	24	1212	1221	-9	1342	1358	YX	1258	N443YX	LGA	PIT	58	335	12	21	2023-04-24 12:00:00	Other
26517	6	7	550	600	-10	900	905	B6	882	N705JB	JFK	MIA	159	1089	6	0	2023-06-07 06:00:00	MIA
26522	9	7	923	929	-6	1121	1154	YX	1206	N724YX	EWR	HHH	96	687	9	29	2023-09-07 09:00:00	Other
26525	8	18	1420	1430	-10	1536	1557	YX	1013	N425YX	LGA	BUF	49	292	14	30	2023-08-18 14:00:00	Other
26534	7	26	832	840	-8	1010	1034	YX	1083	N109HQ	LGA	ILM	77	500	8	40	2023-07-26 08:00:00	Other
26535	6	20	1306	1316	-10	1408	1436	B6	880	N306JB	JFK	ACK	37	199	13	16	2023-06-20 13:00:00	Other
26539	5	31	743	750	-7	1009	1050	UA	265	N27253	EWR	IAH	179	1400	7	50	2023-05-31 07:00:00	Other
26545	5	23	852	900	-8	1100	1133	DL	196	N776DE	JFK	DEN	212	1626	9	0	2023-05-23 09:00:00	Other
26549	4	19	2043	2050	-7	2201	2201	YX	992	N745YX	EWR	PVD	33	160	20	50	2023-04-19 20:00:00	Other
26551	7	10	1022	1029	-7	1234	1236	YX	896	N855RW	EWR	CLT	96	529	10	29	2023-07-10 10:00:00	CLT
26552	2	6	819	830	-11	932	1020	B6	399	N203JB	JFK	BNA	108	765	8	30	2023-02-06 08:00:00	Other
26556	10	4	1348	1400	-12	1553	1604	YX	1296	N124HQ	LGA	CAE	89	617	14	0	2023-10-04 14:00:00	Other
26558	6	9	520	530	-10	745	841	B6	41	N964JT	JFK	LAX	305	2475	5	30	2023-06-09 05:00:00	LAX
26560	1	5	638	645	-7	915	1005	UA	906	N37502	EWR	SEA	307	2402	6	45	2023-01-05 06:00:00	Other
26566	5	3	824	830	-6	1010	1027	9E	1470	N691CA	JFK	RDU	71	427	8	30	2023-05-03 08:00:00	Other
26568	4	11	2122	2130	-8	2319	2327	YX	1128	N438YX	JFK	RDU	64	427	21	30	2023-04-11 21:00:00	Other
26574	2	26	950	959	-9	1310	1308	NK	286	N694NK	LGA	MCO	140	950	9	59	2023-02-26 09:00:00	MCO
26577	11	24	1627	1635	-8	1918	1940	WN	997	N7844A	LGA	DAL	201	1381	16	35	2023-11-24 16:00:00	Other
26582	11	8	2053	2059	-6	2233	2258	YX	1100	N753YX	EWR	GSO	73	445	20	59	2023-11-08 20:00:00	Other
26586	12	16	1014	1020	-6	1140	1156	9E	1496	N325PQ	JFK	ROC	52	264	10	20	2023-12-16 10:00:00	Other
26589	5	22	739	745	-6	1035	1052	DL	319	N388DA	JFK	RSW	152	1074	7	45	2023-05-22 07:00:00	Other
26596	6	30	619	629	-10	743	756	UA	992	N896UA	LGA	ORD	116	733	6	29	2023-06-30 06:00:00	ORD
26611	2	14	1548	1557	-9	1939	1950	AA	594	N339SU	JFK	PHX	327	2153	15	57	2023-02-14 15:00:00	Other
26620	10	9	1820	1830	-10	2024	2056	9E	1498	N912XJ	LGA	TYS	100	647	18	30	2023-10-09 18:00:00	Other
26628	10	21	1553	1559	-6	1902	1912	DL	510	N3752	JFK	MIA	140	1089	15	59	2023-10-21 15:00:00	MIA
26637	11	18	1824	1830	-6	1941	2007	OO	1216	N306SY	JFK	BNA	110	765	18	30	2023-11-18 18:00:00	Other
26642	8	14	1151	1159	-8	1437	1517	NK	815	N680NK	LGA	MIA	146	1096	11	59	2023-08-14 11:00:00	MIA
26651	2	12	1049	1055	-6	1401	1413	NK	969	N962NK	LGA	MIA	160	1096	10	55	2023-02-12 10:00:00	MIA
26652	11	8	1727	1736	-9	2034	2013	DL	317	N399DA	LGA	DEN	260	1620	17	36	2023-11-08 17:00:00	Other
26654	12	15	2050	2100	-10	2158	2212	AA	841	N836AW	LGA	BOS	39	184	21	0	2023-12-15 21:00:00	BOS
26666	11	24	1556	1610	-14	1816	1840	9E	1582	N601LR	LGA	MCI	164	1107	16	10	2023-11-24 16:00:00	Other
26668	1	3	1014	1020	-6	1215	1237	9E	1520	N166PQ	JFK	CHS	96	636	10	20	2023-01-03 10:00:00	Other
26669	2	24	833	840	-7	1055	1106	9E	1302	N905XJ	JFK	DTW	109	509	8	40	2023-02-24 08:00:00	Other
26670	8	27	920	929	-9	1208	1222	AA	483	N895NN	LGA	DFW	192	1389	9	29	2023-08-27 09:00:00	Other
26671	4	10	1754	1800	-6	1918	1938	YX	1505	N230JQ	LGA	BOS	36	184	18	0	2023-04-10 18:00:00	BOS
26674	11	14	1751	1759	-8	2008	2026	YX	1404	N112HQ	LGA	IND	97	660	17	59	2023-11-14 17:00:00	Other
26675	8	9	2032	2040	-8	2144	2217	9E	1216	N293PQ	LGA	CHO	50	305	20	40	2023-08-09 20:00:00	Other
26676	4	10	646	700	-14	940	1016	AS	14	N247AK	JFK	SEA	326	2422	7	0	2023-04-10 07:00:00	Other
26682	1	4	1202	1210	-8	1420	1443	B6	642	N531JL	JFK	DEN	215	1626	12	10	2023-01-04 12:00:00	Other
26686	4	4	657	705	-8	939	1011	DL	610	N345NB	LGA	TPA	138	1010	7	5	2023-04-04 07:00:00	Other
26687	10	31	1039	1050	-11	1146	1210	9E	1670	N293PQ	JFK	BTV	48	266	10	50	2023-10-31 10:00:00	Other
26688	12	13	1021	1030	-9	1205	1227	AA	868	N177XF	LGA	STL	143	888	10	30	2023-12-13 10:00:00	Other
26689	3	31	1752	1800	-8	1938	1959	YX	1618	N221JQ	LGA	CMH	85	479	18	0	2023-03-31 18:00:00	Other
26691	9	7	1552	1559	-7	1822	1737	YX	1827	N214JQ	LGA	BGR	60	378	15	59	2023-09-07 15:00:00	Other
26703	9	1	1221	1229	-8	1402	1415	DL	855	N935AT	EWR	DTW	77	488	12	29	2023-09-01 12:00:00	Other
26704	2	5	1703	1711	-8	1808	1835	YX	1097	N724YX	EWR	BTV	45	266	17	11	2023-02-05 17:00:00	Other
26712	7	12	1054	1100	-6	1217	1233	UA	563	N16701	EWR	CLE	61	404	11	0	2023-07-12 11:00:00	Other
26721	4	9	1127	1135	-8	1342	1338	AA	680	N836AW	LGA	CLT	86	544	11	35	2023-04-09 11:00:00	CLT
26725	1	2	704	710	-6	949	1021	DL	680	N775DE	LGA	FLL	147	1076	7	10	2023-01-02 07:00:00	FLL
26734	2	22	1447	1455	-8	1702	1711	AA	665	N803NN	LGA	CLT	90	544	14	55	2023-02-22 14:00:00	CLT
26736	2	4	1828	1834	-6	2135	2145	AA	252	N890NN	EWR	DFW	204	1372	18	34	2023-02-04 18:00:00	Other
26750	9	26	1924	1930	-6	2142	2202	UA	281	N62889	EWR	JAX	115	820	19	30	2023-09-26 19:00:00	Other
26753	4	2	2044	2050	-6	2236	2250	OO	1044	N241SY	JFK	CLE	80	425	20	50	2023-04-02 20:00:00	Other
26756	8	29	950	957	-7	1251	1249	UA	387	N24706	EWR	AUS	207	1504	9	57	2023-08-29 09:00:00	Other
26772	2	10	924	930	-6	1022	1045	YX	1043	N732YX	EWR	PVD	33	160	9	30	2023-02-10 09:00:00	Other
26776	11	24	1322	1329	-7	1631	1640	DL	295	N180DN	JFK	LAX	337	2475	13	29	2023-11-24 13:00:00	LAX
26779	3	28	1529	1536	-7	1902	1853	DL	1000	N127DU	LGA	IAH	238	1416	15	36	2023-03-28 15:00:00	Other
26780	11	15	750	759	-9	1045	1110	AA	343	N837NN	LGA	MIA	155	1096	7	59	2023-11-15 07:00:00	MIA
26781	1	30	1836	1845	-9	2035	2107	9E	1550	N933XJ	LGA	CLT	88	544	18	45	2023-01-30 18:00:00	CLT
26784	3	24	835	849	-14	946	955	9E	1498	N902XJ	LGA	ALB	31	136	8	49	2023-03-24 08:00:00	Other
26787	3	30	1312	1320	-8	1435	1453	YX	1679	N236JQ	LGA	RIC	58	292	13	20	2023-03-30 13:00:00	Other
26791	5	4	1922	1929	-7	2137	2157	YX	1618	N245JQ	LGA	OMA	171	1148	19	29	2023-05-04 19:00:00	Other
26794	12	20	1926	1935	-9	2047	2134	YX	1771	N210JQ	JFK	PIT	54	340	19	35	2023-12-20 19:00:00	Other
26799	2	9	820	830	-10	1059	1042	B6	65	N197JB	JFK	DTW	105	509	8	30	2023-02-09 08:00:00	Other
26804	10	24	1347	1359	-12	1559	1626	B6	964	N517JB	LGA	ATL	107	762	13	59	2023-10-24 13:00:00	ATL
26810	9	17	1320	1329	-9	1445	1508	UA	664	N17317	EWR	CLE	68	404	13	29	2023-09-17 13:00:00	Other
26817	3	24	1159	1210	-11	1311	1326	YX	1259	N104HQ	JFK	BOS	42	187	12	10	2023-03-24 12:00:00	BOS
26827	6	20	723	730	-7	954	1048	AS	13	N297AK	JFK	SEA	297	2422	7	30	2023-06-20 07:00:00	Other
26844	5	24	1621	1629	-8	1741	1805	YX	1268	N122HQ	LGA	PIT	59	335	16	29	2023-05-24 16:00:00	Other
26845	11	2	1020	1029	-9	1136	1203	YX	1763	N204JQ	LGA	DCA	51	214	10	29	2023-11-02 10:00:00	Other
26847	6	23	721	730	-9	851	908	B6	403	N203JB	JFK	ORD	109	740	7	30	2023-06-23 07:00:00	ORD
26854	7	20	904	915	-11	1009	1035	B6	725	N231JB	LGA	BOS	38	184	9	15	2023-07-20 09:00:00	BOS
26855	12	9	1831	1839	-8	2130	2200	UA	437	N14228	EWR	SMF	335	2500	18	39	2023-12-09 18:00:00	Other
26857	3	29	550	600	-10	842	911	DL	297	N145DQ	LGA	DFW	207	1389	6	0	2023-03-29 06:00:00	Other
26864	7	20	1223	1231	-8	1409	1414	DL	695	N953AT	EWR	DTW	80	488	12	31	2023-07-20 12:00:00	Other
26868	5	9	1347	1355	-8	1526	1550	YX	1226	N430YX	JFK	RDU	76	427	13	55	2023-05-09 13:00:00	Other
26870	12	13	1950	1959	-9	2329	2305	NK	156	N663NK	LGA	MCO	145	950	19	59	2023-12-13 19:00:00	MCO
26874	1	4	1845	1855	-10	2056	2111	AA	734	N717UW	LGA	CLT	92	544	18	55	2023-01-04 18:00:00	CLT
26884	11	29	551	600	-9	714	726	AA	237	N748UW	LGA	DCA	49	214	6	0	2023-11-29 06:00:00	Other
26887	11	29	1726	1732	-6	1958	2023	UA	833	N38443	EWR	LAS	308	2227	17	32	2023-11-29 17:00:00	Other
26888	5	7	1345	1355	-10	1536	1550	YX	1226	N114HQ	JFK	RDU	65	427	13	55	2023-05-07 13:00:00	Other
26890	4	7	1128	1135	-7	1357	1338	AA	680	N802AW	LGA	CLT	112	544	11	35	2023-04-07 11:00:00	CLT
26904	3	24	1342	1349	-7	1624	1629	B6	742	N729JB	LGA	DEN	248	1620	13	49	2023-03-24 13:00:00	Other
26905	3	3	720	729	-9	842	907	YX	1282	N453YX	JFK	DCA	54	213	7	29	2023-03-03 07:00:00	Other
26928	5	25	650	700	-10	826	847	9E	1336	N922XJ	LGA	STL	129	888	7	0	2023-05-25 07:00:00	Other
26933	10	5	1853	1859	-6	2142	2206	UA	166	N16703	EWR	SNA	324	2434	18	59	2023-10-05 18:00:00	Other
26955	3	15	718	730	-12	1109	1120	AS	15	N263AK	JFK	SFO	387	2586	7	30	2023-03-15 07:00:00	Other
26959	10	31	1049	1100	-11	1411	1406	B6	772	N827JB	LGA	TPA	162	1010	11	0	2023-10-31 11:00:00	Other
26961	11	4	808	820	-12	1043	1129	B6	53	N971JT	JFK	SAN	321	2446	8	20	2023-11-04 08:00:00	Other
26963	7	18	1154	1200	-6	1423	1353	YX	1085	N121HQ	LGA	MEM	138	963	12	0	2023-07-18 12:00:00	Other
26976	9	21	1009	1015	-6	1136	1150	UA	706	N33286	LGA	ORD	109	733	10	15	2023-09-21 10:00:00	ORD
26978	1	18	1647	1655	-8	1914	1925	WN	764	N444WN	LGA	MCI	182	1107	16	55	2023-01-18 16:00:00	Other
26979	9	22	844	850	-6	1043	1058	NK	287	N678NK	LGA	CLT	94	544	8	50	2023-09-22 08:00:00	CLT
26986	5	9	1123	1130	-7	1421	1440	UA	290	N14106	EWR	LAX	331	2454	11	30	2023-05-09 11:00:00	LAX
26990	12	5	1659	1706	-7	1851	1930	9E	1364	N272PQ	LGA	DSM	145	1031	17	6	2023-12-05 17:00:00	Other
26994	6	3	2053	2100	-7	2353	2359	NK	1057	N618NK	EWR	MIA	151	1085	21	0	2023-06-03 21:00:00	MIA
27010	10	23	840	850	-10	1002	1033	9E	1655	N314PQ	LGA	CHO	52	305	8	50	2023-10-23 08:00:00	Other
27014	6	6	826	836	-10	1029	1058	9E	1471	N927XJ	LGA	GRR	102	618	8	36	2023-06-06 08:00:00	Other
27015	1	9	603	610	-7	709	721	B6	69	N304JB	LGA	BOS	41	184	6	10	2023-01-09 06:00:00	BOS
27018	5	16	754	800	-6	902	928	YX	1712	N208JQ	LGA	BOS	42	184	8	0	2023-05-16 08:00:00	BOS
27026	8	10	1248	1305	-17	1403	1429	YX	853	N761YX	EWR	PIT	53	319	13	5	2023-08-10 13:00:00	Other
27027	10	7	1046	1055	-9	1252	1300	G4	482	207NV	EWR	TYS	98	631	10	55	2023-10-07 10:00:00	Other
27043	3	7	1657	1705	-8	1933	1902	YX	1761	N203JQ	LGA	CLE	80	419	17	5	2023-03-07 17:00:00	Other
27048	11	21	1250	1300	-10	1603	1615	AA	224	N146AA	LGA	MIA	154	1096	13	0	2023-11-21 13:00:00	MIA
27049	8	29	1119	1130	-11	1325	1338	UA	213	N16701	EWR	SAV	105	708	11	30	2023-08-29 11:00:00	Other
27051	11	19	1303	1310	-7	1431	1449	UA	372	N435UA	LGA	ORD	119	733	13	10	2023-11-19 13:00:00	ORD
27052	12	25	1948	1955	-7	2052	2139	YX	1210	N437YX	LGA	BNA	103	764	19	55	2023-12-25 19:00:00	Other
27056	6	9	1234	1240	-6	1414	1428	YX	1420	N403YX	JFK	RDU	73	427	12	40	2023-06-09 12:00:00	Other
27058	5	14	1233	1241	-8	1605	1637	AA	230	N9016	JFK	STT	193	1623	12	41	2023-05-14 12:00:00	Other
27066	11	9	929	940	-11	1131	1143	YX	1317	N101HQ	JFK	CMH	84	483	9	40	2023-11-09 09:00:00	Other
27067	1	28	1753	1806	-13	2044	2112	UA	1025	N445UA	EWR	PBI	145	1023	18	6	2023-01-28 18:00:00	Other
27069	9	1	752	800	-8	907	926	YX	1881	N244JQ	LGA	BOS	37	184	8	0	2023-09-01 08:00:00	BOS
27077	11	13	1152	1200	-8	1356	1439	YX	1305	N438YX	LGA	XNA	166	1147	12	0	2023-11-13 12:00:00	Other
27079	12	25	1226	1236	-10	1428	1528	UA	543	N66831	EWR	LAS	275	2227	12	36	2023-12-25 12:00:00	Other
27083	1	18	1649	1659	-10	1927	1947	DL	411	N396DN	LGA	ATL	123	762	16	59	2023-01-18 16:00:00	ATL
27084	11	25	1810	1820	-10	2115	2132	UA	718	N37468	EWR	RSW	159	1068	18	20	2023-11-25 18:00:00	Other
27088	8	9	1158	1204	-6	1409	1416	DL	748	N375DA	EWR	ATL	99	746	12	4	2023-08-09 12:00:00	ATL
27093	10	26	1426	1434	-8	1541	1556	B6	906	N317JB	JFK	BUF	55	301	14	34	2023-10-26 14:00:00	Other
27096	2	5	1024	1030	-6	1238	1311	YX	1611	N229JQ	LGA	MCI	167	1107	10	30	2023-02-05 10:00:00	Other
27119	1	20	721	730	-9	954	1008	B6	528	N375JB	JFK	JAX	130	828	7	30	2023-01-20 07:00:00	Other
27124	2	17	931	940	-9	1145	1211	9E	1416	N914XJ	LGA	CVG	112	585	9	40	2023-02-17 09:00:00	Other
27126	7	26	1459	1505	-6	1743	1821	DL	313	N320NB	LGA	PBI	141	1035	15	5	2023-07-26 15:00:00	Other
27128	2	11	854	900	-6	1201	1231	YX	1051	N728YX	EWR	AUS	221	1504	9	0	2023-02-11 09:00:00	Other
27131	2	23	1729	1735	-6	2039	2101	DL	447	N320US	JFK	AUS	221	1521	17	35	2023-02-23 17:00:00	Other
27134	10	17	2235	2241	-6	2346	13	9E	1432	N197PQ	JFK	SYR	39	209	22	41	2023-10-17 22:00:00	Other
27139	6	13	554	601	-7	751	759	AA	987	N575UW	EWR	CLT	85	529	6	1	2023-06-13 06:00:00	CLT
27149	10	2	552	600	-8	834	905	NK	46	N661NK	LGA	FLL	143	1076	6	0	2023-10-02 06:00:00	FLL
27156	3	24	1222	1230	-8	1415	1415	AA	468	N979AN	LGA	ORD	128	733	12	30	2023-03-24 12:00:00	ORD
27158	2	17	553	600	-7	746	801	AA	908	N662AW	EWR	CLT	90	529	6	0	2023-02-17 06:00:00	CLT
27159	12	1	947	955	-8	1230	1255	B6	664	N358JB	EWR	MCO	138	937	9	55	2023-12-01 09:00:00	MCO
27163	7	12	618	629	-11	744	813	AA	783	N750UW	LGA	RDU	65	431	6	29	2023-07-12 06:00:00	Other
27172	4	7	837	845	-8	1007	1019	YX	1204	N102HQ	LGA	RIC	54	292	8	45	2023-04-07 08:00:00	Other
27173	5	18	1623	1630	-7	1753	1822	YX	1161	N858RW	EWR	RDU	69	416	16	30	2023-05-18 16:00:00	Other
27176	8	30	1553	1600	-7	1719	1740	AA	604	N876NN	LGA	ORD	109	733	16	0	2023-08-30 16:00:00	ORD
27196	4	19	1950	1959	-9	2300	2311	DL	573	N340NW	LGA	TPA	136	1010	19	59	2023-04-19 19:00:00	Other
27198	6	4	1618	1625	-7	1845	1828	YX	1308	N424YX	LGA	GSP	94	610	16	25	2023-06-04 16:00:00	Other
27201	10	25	1154	1200	-6	1302	1316	AA	759	N830AW	LGA	DCA	42	214	12	0	2023-10-25 12:00:00	Other
27205	3	28	551	600	-9	834	902	B6	145	N537JT	EWR	FLL	147	1065	6	0	2023-03-28 06:00:00	FLL
27206	11	9	717	730	-13	954	1030	UA	611	N33264	EWR	MCO	126	937	7	30	2023-11-09 07:00:00	MCO
27211	12	13	922	930	-8	1023	1044	YX	1067	N770YX	EWR	PVD	37	160	9	30	2023-12-13 09:00:00	Other
27212	8	28	818	829	-11	1135	1208	AA	47	N113AN	JFK	SFO	340	2586	8	29	2023-08-28 08:00:00	Other
27213	2	26	1754	1800	-6	2036	2041	UA	849	N895UA	LGA	DEN	251	1620	18	0	2023-02-26 18:00:00	Other
27214	12	1	723	730	-7	922	951	DL	533	N319US	JFK	MSP	156	1029	7	30	2023-12-01 07:00:00	Other
27223	1	10	948	1000	-12	1123	1159	9E	1634	N313PQ	EWR	RDU	70	416	10	0	2023-01-10 10:00:00	Other
27231	1	31	1655	1705	-10	1819	1836	YX	1742	N219YX	LGA	BTV	45	258	17	5	2023-01-31 17:00:00	Other
27232	1	6	950	959	-9	1229	1256	NK	303	N620NK	LGA	MCO	134	950	9	59	2023-01-06 09:00:00	MCO
27233	3	21	1619	1629	-10	1909	1946	B6	746	N323JB	LGA	PBI	147	1035	16	29	2023-03-21 16:00:00	Other
27235	6	3	2237	2245	-8	47	106	F9	872	N369FR	LGA	ATL	108	762	22	45	2023-06-03 22:00:00	ATL
27237	4	20	811	820	-9	1021	1038	YX	1560	N228JQ	LGA	CLT	85	544	8	20	2023-04-20 08:00:00	CLT
27240	11	19	2237	2255	-18	2355	15	B6	62	N239JB	JFK	BTV	52	266	22	55	2023-11-19 22:00:00	Other
27245	10	4	845	855	-10	1001	1033	9E	1434	N915XJ	LGA	ORF	50	296	8	55	2023-10-04 08:00:00	Other
27248	8	25	621	630	-9	931	924	UA	708	N41140	EWR	LAX	314	2454	6	30	2023-08-25 06:00:00	LAX
27249	10	10	1414	1420	-6	1618	1634	UA	356	N37267	EWR	DEN	217	1605	14	20	2023-10-10 14:00:00	Other
27259	9	2	1452	1459	-7	1600	1637	YX	1361	N411YX	JFK	DCA	44	213	14	59	2023-09-02 14:00:00	Other
27260	5	9	838	849	-11	1152	1208	UA	862	N17254	EWR	AUS	211	1504	8	49	2023-05-09 08:00:00	Other
27261	10	22	1853	1859	-6	2107	2123	9E	1482	N935XJ	LGA	CLT	85	544	18	59	2023-10-22 18:00:00	CLT
27264	4	3	621	630	-9	1018	1010	AA	32	N108NN	JFK	SFO	389	2586	6	30	2023-04-03 06:00:00	Other
27271	11	10	2153	2159	-6	2317	2321	UA	451	N23708	EWR	BUF	58	282	21	59	2023-11-10 21:00:00	Other
27283	10	31	1322	1329	-7	1624	1641	B6	70	N603JB	LGA	FLL	153	1076	13	29	2023-10-31 13:00:00	FLL
27287	8	25	605	615	-10	846	836	UA	342	N17296	EWR	JAX	107	820	6	15	2023-08-25 06:00:00	Other
27289	12	24	654	700	-6	1138	1204	UA	546	N13720	EWR	STT	192	1634	7	0	2023-12-24 07:00:00	Other
27300	12	15	1752	1759	-7	1958	2011	YX	1207	N112HQ	LGA	DSM	142	1031	17	59	2023-12-15 17:00:00	Other
27305	11	10	1444	1450	-6	1649	1619	OO	1195	N254SY	JFK	IAD	77	228	14	50	2023-11-10 14:00:00	Other
27307	5	16	1313	1323	-10	1459	1537	YX	1619	N235JQ	LGA	CLT	85	544	13	23	2023-05-16 13:00:00	CLT
27308	8	21	1054	1100	-6	1245	1310	9E	1301	N306PQ	JFK	CLT	78	541	11	0	2023-08-21 11:00:00	CLT
27314	6	21	708	715	-7	823	831	B6	1022	N283JB	LGA	BOS	35	184	7	15	2023-06-21 07:00:00	BOS
27319	11	27	2104	2110	-6	2207	2232	9E	1584	N303PQ	JFK	BWI	38	184	21	10	2023-11-27 21:00:00	Other
27320	4	19	1911	1917	-6	2115	2145	YX	1550	N240JQ	LGA	MCI	153	1107	19	17	2023-04-19 19:00:00	Other
27323	8	28	1451	1458	-7	1602	1624	YX	889	N748YX	EWR	BUF	50	282	14	58	2023-08-28 14:00:00	Other
27326	4	12	1454	1500	-6	1649	1707	AA	682	N916AN	LGA	CLT	77	544	15	0	2023-04-12 15:00:00	CLT
27333	1	26	751	800	-9	1047	1128	B6	855	N929JB	JFK	LAX	315	2475	8	0	2023-01-26 08:00:00	LAX
27336	8	26	1133	1140	-7	1300	1312	YX	964	N104HQ	JFK	ORF	52	290	11	40	2023-08-26 11:00:00	Other
27347	9	22	751	800	-9	907	924	YX	1830	N860RW	LGA	BOS	40	184	8	0	2023-09-22 08:00:00	BOS
27348	6	1	1830	1837	-7	2026	2055	YX	1814	N882RW	LGA	CLT	82	544	18	37	2023-06-01 18:00:00	CLT
27349	3	17	1943	1951	-8	2202	2214	YX	1135	N724YX	EWR	IND	113	645	19	51	2023-03-17 19:00:00	Other
27351	9	2	1448	1455	-7	1722	1805	B6	280	N656JB	LGA	PBI	131	1035	14	55	2023-09-02 14:00:00	Other
27367	3	9	1252	1300	-8	1439	1448	OO	1387	N157SY	LGA	ORD	130	733	13	0	2023-03-09 13:00:00	ORD
27373	8	4	652	700	-8	959	1015	AS	13	N253AK	JFK	SFO	338	2586	7	0	2023-08-04 07:00:00	Other
27379	11	10	823	830	-7	1044	1110	DL	502	N707TW	JFK	ATL	123	760	8	30	2023-11-10 08:00:00	ATL
27381	2	25	1834	1843	-9	2224	2209	DL	459	N818DA	EWR	SLC	314	1969	18	43	2023-02-25 18:00:00	Other
27385	8	29	905	915	-10	1015	1035	B6	707	N307JB	LGA	BOS	35	184	9	15	2023-08-29 09:00:00	BOS
27395	9	26	624	630	-6	859	938	UA	754	N797UA	EWR	SFO	314	2565	6	30	2023-09-26 06:00:00	Other
27405	3	16	1203	1210	-7	1300	1315	YX	1250	N136HQ	JFK	ORH	35	150	12	10	2023-03-16 12:00:00	Other
27412	9	7	1137	1143	-6	1315	1328	OO	1276	N243SY	JFK	ORD	119	740	11	43	2023-09-07 11:00:00	ORD
27413	8	20	909	915	-6	1040	1113	9E	1265	N927XJ	JFK	CLE	71	425	9	15	2023-08-20 09:00:00	Other
27415	3	26	1046	1056	-10	1405	1405	UA	439	N19117	EWR	MIA	156	1085	10	56	2023-03-26 10:00:00	MIA
27418	11	26	1531	1537	-6	1911	1857	DL	211	N303DU	LGA	DFW	231	1389	15	37	2023-11-26 15:00:00	Other
27420	12	16	944	952	-8	1125	1129	YX	1728	N213JQ	JFK	DCA	43	213	9	52	2023-12-16 09:00:00	Other
27425	5	10	615	623	-8	759	821	YX	1194	N109HQ	LGA	CMH	80	479	6	23	2023-05-10 06:00:00	Other
27430	9	30	2021	2027	-6	2145	2146	YX	1189	N756YX	EWR	ITH	32	172	20	27	2023-09-30 20:00:00	Other
27438	1	31	1116	1125	-9	1420	1434	NK	600	N684NK	EWR	FLL	163	1065	11	25	2023-01-31 11:00:00	FLL
27440	8	2	816	825	-9	1059	1108	AA	476	N128UW	EWR	DFW	181	1372	8	25	2023-08-02 08:00:00	Other
27461	1	24	1939	1947	-8	2055	2122	YX	1135	N638RW	EWR	PIT	55	319	19	47	2023-01-24 19:00:00	Other
27465	9	26	806	815	-9	912	933	B6	104	N192JB	LGA	BOS	38	184	8	15	2023-09-26 08:00:00	BOS
27470	10	27	1420	1430	-10	1538	1552	YX	1086	N725YX	EWR	PWM	50	284	14	30	2023-10-27 14:00:00	Other
27473	3	22	1249	1259	-10	1429	1456	9E	1545	N135EV	LGA	GSO	77	461	12	59	2023-03-22 12:00:00	Other
27475	2	15	821	830	-9	1004	1020	B6	399	N328JB	JFK	BNA	127	765	8	30	2023-02-15 08:00:00	Other
27477	8	19	1139	1146	-7	1345	1403	YX	1015	N413YX	JFK	IND	90	665	11	46	2023-08-19 11:00:00	Other
27480	12	11	652	659	-7	852	912	AA	180	N894NN	LGA	CLT	96	544	6	59	2023-12-11 06:00:00	CLT
27481	11	14	751	800	-9	950	1005	9E	1674	N131EV	JFK	CLT	84	541	8	0	2023-11-14 08:00:00	CLT
27485	10	12	2051	2059	-8	2146	2219	YX	1774	N212JQ	LGA	BOS	33	184	20	59	2023-10-12 20:00:00	BOS
27486	10	19	1624	1630	-6	1736	1755	YX	1738	N824MD	LGA	DCA	44	214	16	30	2023-10-19 16:00:00	Other
27488	5	2	1831	1837	-6	2044	2100	YX	993	N742YX	EWR	IND	97	645	18	37	2023-05-02 18:00:00	Other
27501	8	24	924	930	-6	1129	1159	YX	1351	N815MD	LGA	HHH	93	701	9	30	2023-08-24 09:00:00	Other
27502	7	22	711	719	-8	958	1020	DL	609	N351DN	EWR	SLC	257	1969	7	19	2023-07-22 07:00:00	Other
27504	12	5	840	848	-8	1042	1049	9E	1617	N918XJ	LGA	STL	132	888	8	48	2023-12-05 08:00:00	Other
27506	10	9	750	800	-10	1041	1127	AA	320	N117AN	JFK	SNA	319	2454	8	0	2023-10-09 08:00:00	Other
27516	11	14	648	659	-11	953	1019	UA	80	N76522	EWR	SNA	336	2434	6	59	2023-11-14 06:00:00	Other
27518	11	25	1924	1931	-7	2133	2155	9E	1465	N316PQ	JFK	DTW	92	509	19	31	2023-11-25 19:00:00	Other
27531	3	8	1833	1840	-7	2152	2210	AS	11	N403AS	JFK	SAN	351	2446	18	40	2023-03-08 18:00:00	Other
27533	11	9	2113	2120	-7	2228	2239	9E	1550	N906XJ	JFK	ITH	45	189	21	20	2023-11-09 21:00:00	Other
27539	8	28	1905	1915	-10	2146	2214	DL	504	N102DU	LGA	IAH	192	1416	19	15	2023-08-28 19:00:00	Other
27541	9	17	2118	2125	-7	2227	2250	YX	1872	N211JQ	LGA	DCA	44	214	21	25	2023-09-17 21:00:00	Other
27544	8	26	2021	2029	-8	2123	2218	YX	1325	N241JQ	JFK	DCA	40	213	20	29	2023-08-26 20:00:00	Other
27545	1	16	1722	1729	-7	2114	2114	B6	46	N956JT	JFK	PHX	324	2153	17	29	2023-01-16 17:00:00	Other
27549	10	21	1929	1940	-11	2200	2211	YX	1255	N407YX	JFK	CVG	99	589	19	40	2023-10-21 19:00:00	Other
27552	2	26	708	715	-7	818	828	UA	547	N33284	EWR	BOS	42	200	7	15	2023-02-26 07:00:00	BOS
27558	10	27	622	630	-8	820	836	UA	577	N846UA	EWR	IND	95	645	6	30	2023-10-27 06:00:00	Other
27568	11	25	1108	1115	-7	1411	1433	DL	412	N303DN	JFK	FLL	161	1069	11	15	2023-11-25 11:00:00	FLL
27573	11	21	1631	1640	-9	1937	1954	B6	616	N804JB	JFK	RSW	159	1074	16	40	2023-11-21 16:00:00	Other
27574	12	15	908	915	-7	1019	1045	9E	1419	N912XJ	LGA	PWM	50	269	9	15	2023-12-15 09:00:00	Other
27576	3	9	819	829	-10	1010	1033	YX	1110	N728YX	EWR	GSO	66	445	8	29	2023-03-09 08:00:00	Other
27585	7	22	1551	1600	-9	1723	1803	9E	1157	N335PQ	LGA	STL	125	888	16	0	2023-07-22 16:00:00	Other
27587	3	10	724	730	-6	1008	1033	B6	225	N526JL	JFK	MCO	133	944	7	30	2023-03-10 07:00:00	MCO
27596	10	23	1349	1359	-10	1557	1622	9E	1559	N315PQ	LGA	OMA	155	1148	13	59	2023-10-23 13:00:00	Other
27597	1	17	1513	1530	-17	1724	1742	NK	577	N512NK	LGA	CLT	92	544	15	30	2023-01-17 15:00:00	CLT
27598	8	31	834	847	-13	1103	1115	UA	711	N828UA	EWR	ATL	103	746	8	47	2023-08-31 08:00:00	ATL
27602	9	27	2241	2250	-9	2349	21	9E	1468	N303PQ	JFK	ROC	43	264	22	50	2023-09-27 22:00:00	Other
27605	10	28	851	859	-8	957	1023	YX	1764	N203JQ	LGA	BOS	41	184	8	59	2023-10-28 08:00:00	BOS
27610	3	28	1043	1057	-14	1314	1303	YX	1247	N871RW	LGA	AVL	116	599	10	57	2023-03-28 10:00:00	Other
27614	1	8	2025	2040	-15	2227	2239	9E	1583	N330PQ	LGA	GSO	86	461	20	40	2023-01-08 20:00:00	Other
27617	1	8	2018	2025	-7	2332	2356	AA	1095	N958AN	LGA	MIA	168	1096	20	25	2023-01-08 20:00:00	MIA
27621	4	5	852	900	-8	1005	1026	YX	1483	N228JQ	LGA	BOS	35	184	9	0	2023-04-05 09:00:00	BOS
27622	4	28	1322	1330	-8	1436	1442	B6	41	N279JB	JFK	SYR	52	209	13	30	2023-04-28 13:00:00	Other
27623	10	12	1029	1036	-7	1406	1330	UA	224	N17301	EWR	TPA	183	997	10	36	2023-10-12 10:00:00	Other
27624	8	28	655	705	-10	849	932	UA	357	N47291	EWR	PHX	277	2133	7	5	2023-08-28 07:00:00	Other
27625	10	18	1542	1550	-8	1741	1803	9E	1644	N602LR	LGA	CLT	81	544	15	50	2023-10-18 15:00:00	CLT
27626	9	6	722	730	-8	841	903	YX	1306	N102HQ	JFK	ORF	47	290	7	30	2023-09-06 07:00:00	Other
27631	10	20	1023	1030	-7	1312	1340	B6	249	N591JB	JFK	SAT	206	1587	10	30	2023-10-20 10:00:00	Other
27640	8	3	2050	2100	-10	2238	2306	YX	978	N442YX	JFK	RDU	68	427	21	0	2023-08-03 21:00:00	Other
27641	5	13	1249	1300	-11	1421	1448	OO	1495	N107SY	LGA	ORD	116	733	13	0	2023-05-13 13:00:00	ORD
27644	2	7	621	630	-9	722	743	B6	209	N281JB	JFK	BOS	36	187	6	30	2023-02-07 06:00:00	BOS
27649	6	20	841	849	-8	1000	1033	YX	1338	N107HQ	LGA	CLE	60	419	8	49	2023-06-20 08:00:00	Other
27656	10	24	1352	1359	-7	1543	1602	YX	1169	N746YX	EWR	DTW	82	488	13	59	2023-10-24 13:00:00	Other
27664	9	14	1353	1359	-6	1557	1617	YX	1307	N420YX	JFK	CVG	95	589	13	59	2023-09-14 13:00:00	Other
27672	8	28	728	734	-6	1017	1021	B6	150	N746JB	JFK	MCO	129	944	7	34	2023-08-28 07:00:00	MCO
27673	3	26	639	646	-7	951	954	UA	845	N57286	EWR	RSW	160	1068	6	46	2023-03-26 06:00:00	Other
27676	5	15	1506	1515	-9	1604	1634	YX	1652	N214JQ	LGA	SYR	43	198	15	15	2023-05-15 15:00:00	Other
27680	12	12	852	900	-8	1019	1111	9E	1617	N326PQ	LGA	STL	131	888	9	0	2023-12-12 09:00:00	Other
27682	8	2	1324	1330	-6	1448	1442	YX	860	N739YX	EWR	SYR	37	195	13	30	2023-08-02 13:00:00	Other
27689	10	27	1717	1725	-8	1913	1943	YX	1157	N763YX	EWR	CVG	94	569	17	25	2023-10-27 17:00:00	Other
27693	1	19	953	1003	-10	1303	1309	UA	961	N27252	EWR	DFW	214	1372	10	3	2023-01-19 10:00:00	Other
27695	9	30	844	850	-6	1032	1058	NK	287	N686NK	LGA	CLT	86	544	8	50	2023-09-30 08:00:00	CLT
27697	5	2	926	935	-9	1209	1229	B6	222	N656JB	LGA	MCO	140	950	9	35	2023-05-02 09:00:00	MCO
27700	10	5	1051	1103	-12	1346	1404	NK	826	N626NK	EWR	AUS	212	1504	11	3	2023-10-05 11:00:00	Other
27701	11	15	554	600	-6	907	859	AA	12	N109NN	JFK	LAX	338	2475	6	0	2023-11-15 06:00:00	LAX
27702	5	9	1617	1625	-8	1746	1803	YX	1312	N420YX	JFK	BNA	116	765	16	25	2023-05-09 16:00:00	Other
27707	12	12	1753	1800	-7	2055	2109	UA	663	N17104	EWR	SAN	338	2425	18	0	2023-12-12 18:00:00	Other
27711	3	17	2005	2015	-10	2321	2354	UA	882	N17126	EWR	SFO	342	2565	20	15	2023-03-17 20:00:00	Other
27714	8	26	1732	1739	-7	2017	2035	UA	244	N17296	EWR	SRQ	133	1034	17	39	2023-08-26 17:00:00	Other
27718	5	29	1922	1929	-7	2101	2119	YX	1331	N126HQ	JFK	BOS	37	187	19	29	2023-05-29 19:00:00	BOS
27726	5	8	519	528	-9	634	703	AA	962	N915AN	EWR	ORD	120	719	5	28	2023-05-08 05:00:00	ORD
27728	5	5	1552	1559	-7	1740	1815	YX	1703	N810MD	LGA	CLT	82	544	15	59	2023-05-05 15:00:00	CLT
27738	5	17	1254	1300	-6	1512	1502	AA	358	N154UW	LGA	CLT	88	544	13	0	2023-05-17 13:00:00	CLT
27740	7	28	1022	1029	-7	1205	1241	DL	430	N333DX	LGA	MSP	141	1020	10	29	2023-07-28 10:00:00	Other
27745	12	4	1152	1200	-8	1351	1406	YX	1246	N119HQ	LGA	DTW	87	502	12	0	2023-12-04 12:00:00	Other
27747	3	22	1409	1415	-6	1538	1543	YX	1113	N753YX	EWR	PIT	57	319	14	15	2023-03-22 14:00:00	Other
27759	5	29	1213	1225	-12	1335	1359	YX	1231	N433YX	LGA	BNA	100	764	12	25	2023-05-29 12:00:00	Other
27762	4	21	2119	2129	-10	2234	2258	9E	1267	N691CA	LGA	BUF	50	292	21	29	2023-04-21 21:00:00	Other
27764	9	25	953	959	-6	1222	1201	YX	1354	N437YX	LGA	GSP	104	610	9	59	2023-09-25 09:00:00	Other
27769	11	12	1301	1310	-9	1425	1441	9E	1544	N137EV	JFK	BGR	60	382	13	10	2023-11-12 13:00:00	Other
27772	9	4	553	601	-8	831	900	B6	497	N521JB	LGA	FLL	135	1076	6	1	2023-09-04 06:00:00	FLL
27786	11	15	754	800	-6	1022	1049	DL	183	N532DN	JFK	DEN	223	1626	8	0	2023-11-15 08:00:00	Other
27787	9	17	1033	1043	-10	1337	1353	DL	1000	N113DQ	LGA	SRQ	162	1047	10	43	2023-09-17 10:00:00	Other
27788	7	11	923	930	-7	1027	1100	YX	1338	N217JQ	LGA	DCA	43	214	9	30	2023-07-11 09:00:00	Other
27793	10	29	1343	1350	-7	1535	1521	9E	1680	N676CA	LGA	RIC	52	292	13	50	2023-10-29 13:00:00	Other
27797	10	14	622	630	-8	803	822	YX	1360	N430YX	JFK	RDU	73	427	6	30	2023-10-14 06:00:00	Other
27801	4	25	757	805	-8	1014	1025	DL	831	N3757D	EWR	ATL	111	746	8	5	2023-04-25 08:00:00	ATL
27806	2	7	518	525	-7	804	820	UA	195	N18112	EWR	IAH	198	1400	5	25	2023-02-07 05:00:00	Other
27809	12	2	810	820	-10	1125	1135	DL	254	N130DU	LGA	DFW	212	1389	8	20	2023-12-02 08:00:00	Other
27814	8	1	1353	1400	-7	1554	1557	9E	1206	N132EV	JFK	RDU	76	427	14	0	2023-08-01 14:00:00	Other
27822	8	30	827	835	-8	1046	1057	9E	1247	N926XJ	JFK	CHS	98	636	8	35	2023-08-30 08:00:00	Other
27823	2	4	522	530	-8	713	635	B6	173	N905JB	JFK	BOS	44	187	5	30	2023-02-04 05:00:00	BOS
27824	2	25	618	625	-7	903	900	UA	670	N880UA	LGA	DEN	259	1620	6	25	2023-02-25 06:00:00	Other
27829	2	10	1935	1945	-10	2208	2210	9E	1299	N136EV	JFK	CLT	103	541	19	45	2023-02-10 19:00:00	CLT
27845	6	1	1554	1600	-6	1814	1855	AA	1036	N944NN	LGA	DFW	169	1389	16	0	2023-06-01 16:00:00	Other
27850	9	6	1141	1155	-14	1329	1354	YX	1832	N245JQ	LGA	CMH	70	479	11	55	2023-09-06 11:00:00	Other
27854	3	22	2020	2030	-10	2120	2142	9E	1317	N935XJ	LGA	BGM	35	147	20	30	2023-03-22 20:00:00	Other
27855	6	7	616	626	-10	753	753	UA	992	N33289	LGA	ORD	115	733	6	26	2023-06-07 06:00:00	ORD
27858	2	19	2017	2025	-8	2148	2224	YX	1319	N821MD	LGA	ORF	51	296	20	25	2023-02-19 20:00:00	Other
27866	4	7	1444	1450	-6	1650	1617	9E	1302	N292PQ	LGA	ORF	90	296	14	50	2023-04-07 14:00:00	Other
27873	4	19	1125	1135	-10	1320	1338	AA	680	N760US	LGA	CLT	77	544	11	35	2023-04-19 11:00:00	CLT
27888	11	10	1318	1329	-11	1523	1545	9E	1542	N910XJ	LGA	CVG	102	585	13	29	2023-11-10 13:00:00	Other
27890	3	22	1535	1542	-7	1745	1750	YX	1272	N427YX	LGA	DTW	91	502	15	42	2023-03-22 15:00:00	Other
27896	9	4	2049	2055	-6	2323	2347	B6	30	N968JT	JFK	SAN	305	2446	20	55	2023-09-04 20:00:00	Other
27901	7	4	1622	1630	-8	1805	1810	YX	1348	N225JQ	LGA	BNA	108	764	16	30	2023-07-04 16:00:00	Other
27908	8	25	2024	2030	-6	2152	2211	DL	355	N108DQ	LGA	ORD	113	733	20	30	2023-08-25 20:00:00	ORD
27912	4	18	1651	1659	-8	1943	2007	UA	531	N435UA	EWR	FLL	147	1065	16	59	2023-04-18 16:00:00	FLL
27918	1	19	1335	1345	-10	1504	1522	9E	1702	N197PQ	LGA	BUF	54	292	13	45	2023-01-19 13:00:00	Other
27920	3	31	1250	1300	-10	1546	1601	UA	224	N57286	EWR	SAT	215	1569	13	0	2023-03-31 13:00:00	Other
27923	2	26	1752	1800	-8	1939	2000	YX	1498	N824MD	LGA	CMH	92	479	18	0	2023-02-26 18:00:00	Other
27930	11	11	552	600	-8	920	935	AA	24	N116AN	JFK	SFO	357	2586	6	0	2023-11-11 06:00:00	Other
27934	12	25	936	944	-8	1104	1143	YX	1290	N107HQ	LGA	CLE	63	419	9	44	2023-12-25 09:00:00	Other
27937	1	2	1813	1820	-7	2117	2146	AS	316	N237AK	EWR	SEA	329	2402	18	20	2023-01-02 18:00:00	Other
27946	9	6	2102	2113	-11	2251	2313	UA	611	N27270	EWR	MSP	135	1008	21	13	2023-09-06 21:00:00	Other
27955	3	21	1519	1529	-10	1659	1733	YX	1395	N451YX	JFK	CLE	73	425	15	29	2023-03-21 15:00:00	Other
27957	7	15	1015	1025	-10	1238	1255	YX	1380	N205JQ	LGA	SDF	107	659	10	25	2023-07-15 10:00:00	Other
27959	8	29	722	735	-13	843	852	B6	164	N274JB	JFK	PWM	51	273	7	35	2023-08-29 07:00:00	Other
27968	5	28	1923	1934	-11	2030	2113	9E	1286	N906XJ	LGA	MKE	102	738	19	34	2023-05-28 19:00:00	Other
27976	8	9	618	630	-12	948	932	B6	5	N989JT	JFK	SFO	364	2586	6	30	2023-08-09 06:00:00	Other
27980	11	1	1109	1115	-6	1226	1236	B6	234	N198JB	LGA	BOS	35	184	11	15	2023-11-01 11:00:00	BOS
27981	10	3	919	929	-10	1040	1057	AA	684	N753US	LGA	PIT	57	335	9	29	2023-10-03 09:00:00	Other
27984	1	24	1046	1055	-9	1201	1233	YX	1904	N810MD	LGA	ORF	51	296	10	55	2023-01-24 10:00:00	Other
27985	11	8	608	615	-7	817	813	DL	964	N981AT	EWR	MSP	171	1008	6	15	2023-11-08 06:00:00	Other
27996	5	2	943	950	-7	1137	1211	9E	1345	N933XJ	LGA	GRR	97	618	9	50	2023-05-02 09:00:00	Other
28001	2	25	1724	1730	-6	1900	1904	YX	1537	N237JQ	JFK	DCA	60	213	17	30	2023-02-25 17:00:00	Other
28008	11	27	1949	1959	-10	2218	2235	YX	1125	N753YX	EWR	SDF	118	642	19	59	2023-11-27 19:00:00	Other
28009	12	18	1246	1255	-9	1602	1605	UA	448	N36469	EWR	RSW	158	1068	12	55	2023-12-18 12:00:00	Other
28014	2	21	1316	1327	-11	1523	1551	UA	321	N805UA	EWR	MSY	170	1167	13	27	2023-02-21 13:00:00	Other
28018	6	6	1644	1650	-6	1911	1854	YX	1278	N109HQ	LGA	DSM	147	1031	16	50	2023-06-06 16:00:00	Other
28028	7	19	453	501	-8	818	843	B6	748	N957JB	JFK	BQN	187	1576	5	1	2023-07-19 05:00:00	Other
28030	10	16	841	848	-7	1021	1042	9E	1606	N305PQ	JFK	RDU	74	427	8	48	2023-10-16 08:00:00	Other
28034	8	1	800	808	-8	1008	1028	YX	1082	N411YX	LGA	CVG	101	585	8	8	2023-08-01 08:00:00	Other
28035	3	4	551	600	-9	839	915	NK	52	N676NK	LGA	FLL	151	1076	6	0	2023-03-04 06:00:00	FLL
28044	5	9	1106	1115	-9	1310	1319	YX	1217	N870RW	LGA	AVL	97	599	11	15	2023-05-09 11:00:00	Other
28045	4	25	1123	1130	-7	1348	1400	DL	782	N351NB	LGA	MSY	167	1183	11	30	2023-04-25 11:00:00	Other
28046	10	10	736	745	-9	940	959	B6	855	N524JB	LGA	CHS	98	641	7	45	2023-10-10 07:00:00	Other
28052	1	25	1206	1212	-6	1410	1455	YX	1354	N129HQ	LGA	MSP	157	1020	12	12	2023-01-25 12:00:00	Other
28057	5	8	1354	1400	-6	1603	1619	NK	36	N635NK	EWR	ATL	100	746	14	0	2023-05-08 14:00:00	ATL
28059	6	9	553	601	-8	748	759	AA	987	N523UW	EWR	CLT	89	529	6	1	2023-06-09 06:00:00	CLT
28077	10	5	700	710	-10	932	1008	UA	782	N38479	EWR	PBI	127	1023	7	10	2023-10-05 07:00:00	Other
28082	2	16	2133	2140	-7	23	41	B6	394	N568JB	JFK	PBI	142	1028	21	40	2023-02-16 21:00:00	Other
28090	11	3	1649	1658	-9	1913	1948	B6	922	N520JB	LGA	ATL	112	762	16	58	2023-11-03 16:00:00	ATL
28099	12	27	652	659	-7	812	827	NK	267	N536NK	EWR	PIT	61	319	6	59	2023-12-27 06:00:00	Other
28103	1	28	542	550	-8	853	901	AA	685	N941NN	LGA	DFW	212	1389	5	50	2023-01-28 05:00:00	Other
28111	2	6	723	730	-7	1003	1035	UA	726	N76505	EWR	BZN	263	1882	7	30	2023-02-06 07:00:00	Other
28119	4	10	729	735	-6	925	948	DL	285	N340NB	JFK	MSP	146	1029	7	35	2023-04-10 07:00:00	Other
28121	11	23	1710	1720	-10	1935	2002	B6	849	N768JB	LGA	JAX	119	833	17	20	2023-11-23 17:00:00	Other
28124	7	30	2024	2030	-6	2139	2207	YX	1089	N437YX	JFK	BOS	39	187	20	30	2023-07-30 20:00:00	BOS
28135	5	23	1500	1510	-10	1629	1639	9E	1316	N909XJ	LGA	IAD	45	229	15	10	2023-05-23 15:00:00	Other
28143	3	24	1147	1155	-8	1317	1317	NK	282	N656NK	EWR	PIT	66	319	11	55	2023-03-24 11:00:00	Other
28151	11	4	1958	2005	-7	2254	2322	DL	425	N774DE	LGA	RSW	158	1080	20	5	2023-11-04 20:00:00	Other
28156	11	22	1521	1528	-7	1803	1848	UA	632	N408UA	EWR	AUS	203	1504	15	28	2023-11-22 15:00:00	Other
28164	9	14	922	929	-7	1201	1246	DL	295	N816DN	JFK	SLC	260	1990	9	29	2023-09-14 09:00:00	Other
28165	1	31	634	640	-6	835	836	YX	1304	N420YX	LGA	STL	161	888	6	40	2023-01-31 06:00:00	Other
28173	11	11	854	900	-6	1122	1136	9E	1458	N300PQ	LGA	SAV	116	722	9	0	2023-11-11 09:00:00	Other
28176	10	3	1123	1129	-6	1410	1439	DL	460	N3757D	JFK	MIA	143	1089	11	29	2023-10-03 11:00:00	MIA
28184	2	25	1605	1613	-8	1709	1726	UA	148	N47281	EWR	BOS	43	200	16	13	2023-02-25 16:00:00	BOS
28185	1	27	751	800	-9	911	941	YX	1320	N428YX	LGA	DCA	58	214	8	0	2023-01-27 08:00:00	Other
28192	3	16	1424	1430	-6	1526	1600	YX	1175	N747YX	EWR	ORF	46	284	14	30	2023-03-16 14:00:00	Other
28208	1	15	1252	1300	-8	1403	1432	YX	1746	N810MD	LGA	RIC	49	292	13	0	2023-01-15 13:00:00	Other
28211	1	20	729	735	-6	928	950	B6	41	N766JB	JFK	MSP	145	1029	7	35	2023-01-20 07:00:00	Other
28225	8	3	819	827	-8	940	1006	YX	916	N653RW	EWR	RIC	53	277	8	27	2023-08-03 08:00:00	Other
28236	5	25	1412	1418	-6	1532	1551	9E	1437	N319PQ	LGA	MKE	108	738	14	18	2023-05-25 14:00:00	Other
28243	5	26	1212	1220	-8	1336	1348	YX	1617	N206JQ	LGA	PWM	51	269	12	20	2023-05-26 12:00:00	Other
28245	5	27	1006	1015	-9	1220	1223	YX	1236	N443YX	LGA	CAE	99	617	10	15	2023-05-27 10:00:00	Other
28249	10	21	721	729	-8	911	931	UA	432	N37307	EWR	CLT	76	529	7	29	2023-10-21 07:00:00	CLT
28250	3	25	1639	1645	-6	2010	2007	B6	778	N547JB	JFK	MIA	167	1089	16	45	2023-03-25 16:00:00	MIA
28253	9	20	805	815	-10	1005	1025	9E	1573	N928XJ	LGA	GRR	93	618	8	15	2023-09-20 08:00:00	Other
28259	6	13	1816	1826	-10	1912	1940	YX	1116	N741YX	EWR	ALB	30	143	18	26	2023-06-13 18:00:00	Other
28268	4	18	618	630	-12	911	931	B6	430	N775JB	LGA	TPA	150	1010	6	30	2023-04-18 06:00:00	Other
28278	8	17	637	645	-8	913	926	UA	649	N482UA	EWR	DFW	180	1372	6	45	2023-08-17 06:00:00	Other
28290	10	9	659	710	-11	946	1005	DL	505	N102DN	LGA	MCO	140	950	7	10	2023-10-09 07:00:00	MCO
28291	4	11	1244	1254	-10	1413	1441	YX	1245	N132HQ	JFK	PIT	59	340	12	54	2023-04-11 12:00:00	Other
28304	6	21	922	930	-8	1108	1139	DL	209	N375DN	LGA	DTW	73	502	9	30	2023-06-21 09:00:00	Other
28306	9	15	1125	1131	-6	1312	1332	AA	942	N849NN	JFK	CLT	84	541	11	31	2023-09-15 11:00:00	CLT
28309	7	3	1642	1648	-6	2014	1955	AA	420	N842NN	LGA	MIA	153	1096	16	48	2023-07-03 16:00:00	MIA
28312	7	12	551	600	-9	730	746	DL	637	N893AT	EWR	DTW	83	488	6	0	2023-07-12 06:00:00	Other
28327	5	27	1912	1919	-7	2124	2205	UA	406	N77552	EWR	LAS	278	2227	19	19	2023-05-27 19:00:00	Other
28328	2	11	2128	2137	-9	2359	5	UA	169	N36469	EWR	ATL	119	746	21	37	2023-02-11 21:00:00	ATL
28329	10	10	1514	1521	-7	1739	1746	YX	1286	N406YX	JFK	IND	106	665	15	21	2023-10-10 15:00:00	Other
28330	3	24	1947	1954	-7	2251	2320	B6	607	N992JB	EWR	LAX	342	2454	19	54	2023-03-24 19:00:00	LAX
28334	5	18	1654	1700	-6	2006	2000	DL	344	N105DU	JFK	DFW	206	1391	17	0	2023-05-18 17:00:00	Other
28335	1	23	1948	1959	-11	2201	2227	DL	1018	N376NW	EWR	ATL	101	746	19	59	2023-01-23 19:00:00	ATL
28339	7	17	623	630	-7	907	921	UA	566	N57299	EWR	TPA	143	997	6	30	2023-07-17 06:00:00	Other
28353	9	10	1454	1500	-6	1650	1718	YX	1419	N432YX	LGA	CVG	92	585	15	0	2023-09-10 15:00:00	Other
28355	10	18	1548	1555	-7	1732	1831	DL	95	N912DU	JFK	PHX	268	2153	15	55	2023-10-18 15:00:00	Other
28356	2	28	804	815	-11	1135	1156	AA	607	N344PP	JFK	MIA	145	1089	8	15	2023-02-28 08:00:00	MIA
28357	11	11	947	955	-8	1053	1113	YX	1895	N215JQ	JFK	BOS	37	187	9	55	2023-11-11 09:00:00	BOS
28358	2	7	732	740	-8	1123	1122	B6	5	N982JB	JFK	SFO	358	2586	7	40	2023-02-07 07:00:00	Other
28359	1	26	600	610	-10	721	721	B6	69	N317JB	LGA	BOS	47	184	6	10	2023-01-26 06:00:00	BOS
28360	10	24	1020	1030	-10	1350	1339	DL	529	N123DQ	JFK	SAT	246	1587	10	30	2023-10-24 10:00:00	Other
28362	6	7	1608	1615	-7	1833	1840	DL	811	N362NB	JFK	MSY	163	1182	16	15	2023-06-07 16:00:00	Other
28364	6	24	1509	1519	-10	1716	1735	DL	389	N382DN	LGA	MSP	140	1020	15	19	2023-06-24 15:00:00	Other
28370	4	5	952	1000	-8	1057	1115	YX	1449	N217JQ	JFK	BOS	39	187	10	0	2023-04-05 10:00:00	BOS
28377	4	27	910	919	-9	1134	1159	YX	1579	N216JQ	LGA	SDF	110	659	9	19	2023-04-27 09:00:00	Other
28379	4	28	1817	1829	-12	1945	2004	YX	1169	N437YX	LGA	PIT	59	335	18	29	2023-04-28 18:00:00	Other
28382	9	1	543	550	-7	812	839	AA	568	N861NN	LGA	DFW	185	1389	5	50	2023-09-01 05:00:00	Other
28398	2	15	1505	1515	-10	1618	1638	9E	1301	N272PQ	LGA	SYR	43	198	15	15	2023-02-15 15:00:00	Other
28400	9	22	1808	1815	-7	1923	1942	B6	424	N216JB	LGA	BOS	35	184	18	15	2023-09-22 18:00:00	BOS
28404	6	24	454	500	-6	748	812	NK	299	N925NK	EWR	OAK	336	2555	5	0	2023-06-24 05:00:00	Other
28405	4	18	551	600	-9	854	902	B6	698	N763JB	LGA	FLL	152	1076	6	0	2023-04-18 06:00:00	FLL
28414	2	11	1523	1529	-6	1636	1702	YX	1509	N224JQ	LGA	DCA	45	214	15	29	2023-02-11 15:00:00	Other
28423	10	9	1210	1219	-9	1320	1355	9E	1534	N691CA	LGA	BUF	46	292	12	19	2023-10-09 12:00:00	Other
28424	10	30	2009	2016	-7	2150	2211	9E	1403	N146PQ	EWR	RDU	77	416	20	16	2023-10-30 20:00:00	Other
28429	3	28	704	715	-11	957	953	9E	1462	N490PX	LGA	JAX	132	833	7	15	2023-03-28 07:00:00	Other
28433	10	25	1136	1145	-9	1435	1459	AS	6	N937AK	JFK	PDX	340	2454	11	45	2023-10-25 11:00:00	Other
28434	6	1	1823	1830	-7	2057	2113	YX	1329	N410YX	LGA	OKC	173	1341	18	30	2023-06-01 18:00:00	Other
28435	6	4	920	930	-10	1039	1101	AA	742	N747UW	LGA	PIT	57	335	9	30	2023-06-04 09:00:00	Other
28445	2	3	1903	1910	-7	2200	2217	UA	550	N647UA	EWR	IAH	182	1400	19	10	2023-02-03 19:00:00	Other
28448	12	11	930	940	-10	1149	1210	YX	1309	N427YX	JFK	CVG	99	589	9	40	2023-12-11 09:00:00	Other
28449	8	16	754	800	-6	953	1007	AA	793	N539UW	LGA	CLT	89	544	8	0	2023-08-16 08:00:00	CLT
28452	1	25	1355	1402	-7	1709	1637	UA	323	N848UA	EWR	ATL	132	746	14	2	2023-01-25 14:00:00	ATL
28463	10	10	1424	1430	-6	1523	1540	YX	1118	N728YX	EWR	PVD	38	160	14	30	2023-10-10 14:00:00	Other
28467	4	28	1053	1059	-6	1225	1240	9E	1394	N228PQ	LGA	RIC	65	292	10	59	2023-04-28 10:00:00	Other
28468	10	30	810	820	-10	1041	1044	9E	1701	N315PQ	LGA	IND	122	660	8	20	2023-10-30 08:00:00	Other
28476	7	24	1602	1610	-8	1744	1805	YX	1081	N870RW	LGA	GSO	80	461	16	10	2023-07-24 16:00:00	Other
28477	7	19	1319	1329	-10	1607	1621	UA	544	N17254	EWR	AUS	196	1504	13	29	2023-07-19 13:00:00	Other
28482	11	12	1752	1800	-8	2015	2036	UA	868	N837UA	LGA	DEN	239	1620	18	0	2023-11-12 18:00:00	Other
28487	7	4	1001	1012	-11	1129	1156	AA	685	N740UW	LGA	STL	126	888	10	12	2023-07-04 10:00:00	Other
28488	4	15	1147	1155	-8	1443	1510	DL	375	N348NB	LGA	TPA	144	1010	11	55	2023-04-15 11:00:00	Other
28491	11	7	2027	2036	-9	2301	2321	DL	895	N120DU	LGA	JAX	111	833	20	36	2023-11-07 20:00:00	Other
28493	6	18	1724	1730	-6	1913	1927	YX	1315	N433YX	LGA	CMH	78	479	17	30	2023-06-18 17:00:00	Other
28500	11	22	753	759	-6	952	955	YX	1281	N135HQ	LGA	CMH	86	479	7	59	2023-11-22 07:00:00	Other
28505	12	30	944	950	-6	1102	1142	YX	1720	N210JQ	LGA	BNA	102	764	9	50	2023-12-30 09:00:00	Other
28507	11	20	1025	1035	-10	1244	1255	B6	867	N784JB	LGA	CHS	96	641	10	35	2023-11-20 10:00:00	Other
28526	2	15	1243	1250	-7	1547	1559	B6	43	N597JB	JFK	TPA	152	1005	12	50	2023-02-15 12:00:00	Other
28528	8	17	1101	1111	-10	1414	1434	DL	486	N3745B	LGA	MIA	164	1096	11	11	2023-08-17 11:00:00	MIA
28530	5	2	1918	1925	-7	2041	2124	OO	1117	N307SY	JFK	ORD	117	740	19	25	2023-05-02 19:00:00	ORD
28531	11	9	747	759	-12	948	1024	YX	1286	N113HQ	JFK	CVG	98	589	7	59	2023-11-09 07:00:00	Other
28538	9	24	752	759	-7	914	928	YX	1124	N744YX	EWR	PIT	56	319	7	59	2023-09-24 07:00:00	Other
28539	12	30	1951	2005	-14	2042	2123	9E	1370	N919XJ	LGA	ALB	32	136	20	5	2023-12-30 20:00:00	Other
28545	9	20	1114	1120	-6	1252	1319	9E	1612	N299PQ	LGA	RDU	69	431	11	20	2023-09-20 11:00:00	Other
28553	2	8	758	810	-12	917	942	YX	1619	N241JQ	LGA	BTV	48	258	8	10	2023-02-08 08:00:00	Other
28560	4	20	536	545	-9	815	832	B6	357	N640JB	JFK	PBI	134	1028	5	45	2023-04-20 05:00:00	Other
28561	10	1	2053	2100	-7	2209	2236	UA	650	N836UA	LGA	ORD	102	733	21	0	2023-10-01 21:00:00	ORD
28562	9	4	650	659	-9	930	958	AA	290	N701UW	JFK	AUS	198	1521	6	59	2023-09-04 06:00:00	Other
28564	7	19	1043	1050	-7	1251	1315	9E	1140	N181GJ	LGA	CVG	99	585	10	50	2023-07-19 10:00:00	Other
28576	12	21	1340	1350	-10	1518	1531	9E	1352	N929XJ	JFK	RIC	57	288	13	50	2023-12-21 13:00:00	Other
28586	1	10	1821	1829	-8	2012	2050	9E	1416	N315PQ	LGA	CHS	90	641	18	29	2023-01-10 18:00:00	Other
28590	11	15	1537	1545	-8	1924	1859	DL	813	N3757D	JFK	MIA	158	1089	15	45	2023-11-15 15:00:00	MIA
28592	4	8	1151	1159	-8	1451	1455	UA	629	N47280	EWR	TPA	149	997	11	59	2023-04-08 11:00:00	Other
28593	2	4	853	900	-7	1022	1046	OO	1061	N242SY	JFK	BNA	118	765	9	0	2023-02-04 09:00:00	Other
28602	1	29	1712	1718	-6	1917	1932	YX	1136	N649RW	EWR	GSP	100	594	17	18	2023-01-29 17:00:00	Other
28604	2	20	1409	1415	-6	1517	1541	9E	1465	N341PQ	JFK	BTV	46	266	14	15	2023-02-20 14:00:00	Other
28608	8	27	1442	1455	-13	1640	1724	B6	27	N323JB	JFK	MSY	157	1182	14	55	2023-08-27 14:00:00	Other
28612	4	1	1139	1145	-6	1446	1500	AS	11	N472AS	JFK	SEA	327	2422	11	45	2023-04-01 11:00:00	Other
28613	10	25	913	930	-17	1244	1245	AS	7	N946AK	JFK	SEA	354	2422	9	30	2023-10-25 09:00:00	Other
28615	2	7	1000	1010	-10	1214	1235	9E	1364	N921XJ	LGA	MYR	87	563	10	10	2023-02-07 10:00:00	Other
28616	4	5	949	955	-6	1236	1227	AA	714	N402AN	EWR	PHX	328	2133	9	55	2023-04-05 09:00:00	Other
28618	10	14	1353	1400	-7	1554	1555	9E	1494	N279PQ	JFK	RDU	76	427	14	0	2023-10-14 14:00:00	Other
28620	11	13	1148	1200	-12	1331	1339	YX	1158	N755YX	EWR	BNA	111	748	12	0	2023-11-13 12:00:00	Other
28621	5	25	855	901	-6	1037	1040	YX	1326	N420YX	LGA	BUF	51	292	9	1	2023-05-25 09:00:00	Other
28626	11	8	1302	1310	-8	1413	1443	YX	1387	N121HQ	LGA	RIC	53	292	13	10	2023-11-08 13:00:00	Other
28630	3	24	553	600	-7	718	721	AA	461	N774XF	LGA	DCA	50	214	6	0	2023-03-24 06:00:00	Other
28635	2	19	1423	1430	-7	1702	1713	DL	120	N3737C	JFK	DEN	250	1626	14	30	2023-02-19 14:00:00	Other
28636	6	3	1854	1900	-6	2044	2117	AA	784	N8027D	JFK	CLT	88	541	19	0	2023-06-03 19:00:00	CLT
28637	10	30	2016	2025	-9	2257	2250	WN	164	N224WN	LGA	DEN	242	1620	20	25	2023-10-30 20:00:00	Other
28639	8	14	1220	1229	-9	1509	1529	UA	642	N809UA	EWR	SAT	204	1569	12	29	2023-08-14 12:00:00	Other
28640	9	18	854	900	-6	1020	1029	YX	1101	N747YX	EWR	DCA	44	199	9	0	2023-09-18 09:00:00	Other
28646	1	1	1152	1200	-8	1524	1601	YX	1360	N420YX	LGA	EYW	193	1207	12	0	2023-01-01 12:00:00	Other
28647	4	29	721	729	-8	1016	1043	B6	171	N635JB	JFK	BUR	324	2465	7	29	2023-04-29 07:00:00	Other
28654	12	28	550	600	-10	855	910	UA	292	N17289	EWR	FLL	160	1065	6	0	2023-12-28 06:00:00	FLL
28660	9	17	1250	1259	-9	1349	1403	9E	1431	N300PQ	JFK	ITH	43	189	12	59	2023-09-17 12:00:00	Other
28670	5	17	1006	1014	-8	1228	1240	9E	1440	N600LR	JFK	SAV	105	718	10	14	2023-05-17 10:00:00	Other
28680	6	23	1604	1610	-6	1807	1805	OO	1272	N257SY	JFK	ORD	122	740	16	10	2023-06-23 16:00:00	ORD
28692	8	17	1238	1250	-12	1325	1358	9E	1245	N917XJ	LGA	PVD	25	143	12	50	2023-08-17 12:00:00	Other
28695	1	25	1252	1300	-8	1358	1425	YX	1846	N220JQ	LGA	BOS	33	184	13	0	2023-01-25 13:00:00	BOS
28704	12	12	1940	1950	-10	2212	2227	YX	1147	N753YX	EWR	MCI	175	1092	19	50	2023-12-12 19:00:00	Other
28705	8	17	1522	1529	-7	1707	1737	YX	930	N733YX	EWR	MYR	80	550	15	29	2023-08-17 15:00:00	Other
28706	1	17	2018	2025	-7	2225	2242	UA	671	N61887	EWR	CVG	101	569	20	25	2023-01-17 20:00:00	Other
28708	12	8	1732	1740	-8	2025	2100	AS	75	N492AS	EWR	PDX	313	2434	17	40	2023-12-08 17:00:00	Other
28710	11	14	1404	1411	-7	1524	1544	UA	568	N412UA	EWR	BNA	111	748	14	11	2023-11-14 14:00:00	Other
28721	12	21	1921	1929	-8	2058	2115	YX	1347	N404YX	JFK	PIT	63	340	19	29	2023-12-21 19:00:00	Other
28723	1	2	820	828	-8	1044	1101	YX	1122	N723YX	EWR	CVG	107	569	8	28	2023-01-02 08:00:00	Other
28726	3	22	1949	1959	-10	2127	2158	YX	1217	N730YX	EWR	ILM	71	488	19	59	2023-03-22 19:00:00	Other
28728	12	18	751	800	-9	1007	1032	DL	888	N603AT	EWR	ATL	107	746	8	0	2023-12-18 08:00:00	ATL
28729	4	30	1139	1145	-6	1355	1443	DL	189	N842DN	JFK	LAS	289	2248	11	45	2023-04-30 11:00:00	Other
28736	8	5	844	850	-6	1141	1152	B6	536	N980JT	EWR	LAX	327	2454	8	50	2023-08-05 08:00:00	LAX
28739	10	22	1120	1130	-10	1416	1449	DL	390	N107DU	LGA	RSW	158	1080	11	30	2023-10-22 11:00:00	Other
28748	10	13	650	659	-9	916	914	YX	1303	N114HQ	LGA	MSP	176	1020	6	59	2023-10-13 06:00:00	Other
28750	1	20	1014	1020	-6	1218	1224	AA	732	N314PD	EWR	CLT	92	529	10	20	2023-01-20 10:00:00	CLT
28755	10	3	1350	1359	-9	1623	1627	9E	1413	N279PQ	JFK	SAV	116	718	13	59	2023-10-03 13:00:00	Other
28759	3	9	925	940	-15	1055	1144	YX	1304	N421YX	JFK	BNA	118	765	9	40	2023-03-09 09:00:00	Other
28763	6	1	916	925	-9	1026	1101	YX	1854	N237JQ	LGA	DCA	42	214	9	25	2023-06-01 09:00:00	Other
28764	1	24	551	600	-9	840	926	B6	587	N985JT	EWR	LAX	327	2454	6	0	2023-01-24 06:00:00	LAX
28770	3	28	2035	2045	-10	5	2359	B6	487	N587JB	JFK	AUS	241	1521	20	45	2023-03-28 20:00:00	Other
28772	9	20	2055	2106	-11	2258	2310	UA	658	N39461	EWR	CLT	78	529	21	6	2023-09-20 21:00:00	CLT
28775	5	23	1821	1829	-8	2018	2052	YX	1225	N104HQ	LGA	IND	98	660	18	29	2023-05-23 18:00:00	Other
28785	1	26	2141	2155	-14	2254	2307	B6	991	N306JB	JFK	SYR	49	209	21	55	2023-01-26 21:00:00	Other
28796	10	3	1343	1349	-6	1607	1645	AA	975	N977NN	LGA	DFW	179	1389	13	49	2023-10-03 13:00:00	Other
28799	10	23	1319	1329	-10	1528	1548	9E	1700	N928XJ	LGA	IND	105	660	13	29	2023-10-23 13:00:00	Other
28806	9	3	1053	1100	-7	1221	1251	UA	846	N835UA	EWR	MEM	128	946	11	0	2023-09-03 11:00:00	Other
28811	3	7	1726	1735	-9	2043	2101	DL	463	N321US	JFK	AUS	219	1521	17	35	2023-03-07 17:00:00	Other
28812	10	25	1426	1435	-9	1549	1602	YX	1094	N764YX	EWR	MKE	114	725	14	35	2023-10-25 14:00:00	Other
28815	2	16	1508	1515	-7	1627	1632	B6	162	N324JB	LGA	BOS	39	184	15	15	2023-02-16 15:00:00	BOS
28816	7	14	600	610	-10	758	747	DL	387	N103DU	LGA	ORD	115	733	6	10	2023-07-14 06:00:00	ORD
28819	1	11	1406	1415	-9	1605	1613	YX	1873	N875RW	LGA	CMH	84	479	14	15	2023-01-11 14:00:00	Other
28820	9	1	1819	1830	-11	2121	2134	UA	895	N17311	EWR	PDX	332	2434	18	30	2023-09-01 18:00:00	Other
28824	4	21	2116	2125	-9	2240	2255	WN	1033	N8643A	LGA	MDW	111	725	21	25	2023-04-21 21:00:00	Other
28828	2	25	933	943	-10	1211	1141	YX	1259	N115HQ	JFK	BNA	160	765	9	43	2023-02-25 09:00:00	Other
28836	5	8	1954	2000	-6	2114	2118	B6	516	N184JB	LGA	PWM	48	269	20	0	2023-05-08 20:00:00	Other
28837	11	22	2129	2140	-11	2253	2336	YX	1244	N417YX	JFK	RDU	66	427	21	40	2023-11-22 21:00:00	Other
28841	9	2	1949	1959	-10	2231	2258	NK	162	N661NK	LGA	MCO	124	950	19	59	2023-09-02 19:00:00	MCO
28856	12	6	1022	1029	-7	1242	1304	YX	1807	N245JQ	LGA	MCI	156	1107	10	29	2023-12-06 10:00:00	Other
28858	9	21	1020	1029	-9	1140	1155	AA	200	N819AW	LGA	BNA	106	764	10	29	2023-09-21 10:00:00	Other
28864	9	4	621	630	-9	804	846	UA	178	N12238	LGA	DEN	207	1620	6	30	2023-09-04 06:00:00	Other
28870	5	14	1748	1756	-8	2053	2108	AA	736	N341RW	LGA	MIA	140	1096	17	56	2023-05-14 17:00:00	MIA
28877	12	24	758	805	-7	1038	1108	UA	404	N37462	EWR	MCO	133	937	8	5	2023-12-24 08:00:00	MCO
28884	9	16	1015	1025	-10	1204	1229	9E	1624	N482PX	LGA	GSO	69	461	10	25	2023-09-16 10:00:00	Other
28894	5	18	621	629	-8	807	815	AA	959	N856NN	LGA	ORD	117	733	6	29	2023-05-18 06:00:00	ORD
28901	12	9	916	925	-9	1058	1113	9E	1672	N302PQ	LGA	PIT	56	335	9	25	2023-12-09 09:00:00	Other
28914	2	14	2049	2059	-10	2228	2254	YX	1041	N744YX	EWR	GSO	74	445	20	59	2023-02-14 20:00:00	Other
28916	11	4	1134	1140	-6	1352	1409	YX	1313	N447YX	JFK	IND	109	665	11	40	2023-11-04 11:00:00	Other
28919	2	1	1927	1935	-8	2359	30	B6	466	N651JB	EWR	SJU	183	1608	19	35	2023-02-01 19:00:00	Other
28921	12	7	955	1003	-8	1208	1233	UA	537	N53442	EWR	DEN	225	1605	10	3	2023-12-07 10:00:00	Other
28930	7	24	945	955	-10	1222	1212	YX	1068	N870RW	LGA	SDF	104	659	9	55	2023-07-24 09:00:00	Other
28933	1	27	2010	2020	-10	2114	2131	9E	1632	N916XJ	LGA	PVD	31	143	20	20	2023-01-27 20:00:00	Other
28934	5	18	704	712	-8	958	1013	DL	350	N347NB	LGA	PBI	146	1035	7	12	2023-05-18 07:00:00	Other
28936	10	22	1216	1222	-6	1328	1339	YX	1272	N135HQ	JFK	BOS	46	187	12	22	2023-10-22 12:00:00	BOS
28939	3	22	607	615	-8	709	728	B6	72	N334JB	LGA	BOS	33	184	6	15	2023-03-22 06:00:00	BOS
28940	12	5	848	855	-7	1041	1056	YX	1109	N758YX	EWR	GSO	86	445	8	55	2023-12-05 08:00:00	Other
28941	7	20	624	630	-6	911	921	UA	566	N62892	EWR	TPA	136	997	6	30	2023-07-20 06:00:00	Other
28957	11	20	1528	1538	-10	1653	1657	NK	558	N954NK	EWR	BNA	113	748	15	38	2023-11-20 15:00:00	Other
28964	2	15	1051	1100	-9	1218	1243	YX	1180	N123HQ	LGA	DCA	50	214	11	0	2023-02-15 11:00:00	Other
28978	10	28	911	930	-19	1253	1232	AS	13	N290AK	JFK	SAN	361	2446	9	30	2023-10-28 09:00:00	Other
28983	7	26	800	813	-13	918	949	YX	1431	N202JQ	LGA	BUF	49	292	8	13	2023-07-26 08:00:00	Other
28984	2	10	1638	1650	-12	1826	1835	YX	1554	N823MD	LGA	PIT	68	335	16	50	2023-02-10 16:00:00	Other
28986	10	17	923	930	-7	1104	1127	YX	1260	N443YX	JFK	CMH	74	483	9	30	2023-10-17 09:00:00	Other
28987	9	1	853	900	-7	1245	1222	AS	15	N453AS	JFK	SFO	363	2586	9	0	2023-09-01 09:00:00	Other
28988	11	26	1719	1729	-10	1923	1936	YX	1334	N132HQ	LGA	CMH	90	479	17	29	2023-11-26 17:00:00	Other
28990	1	29	1713	1730	-17	1944	2020	YX	1338	N806MD	LGA	SDF	117	659	17	30	2023-01-29 17:00:00	Other
28991	10	18	1414	1420	-6	1544	1610	YX	1788	N213JQ	LGA	CMH	72	479	14	20	2023-10-18 14:00:00	Other
28995	11	18	818	829	-11	1136	1202	YX	1146	N638RW	EWR	EYW	166	1196	8	29	2023-11-18 08:00:00	Other
28997	10	6	1545	1554	-9	1830	1853	UA	596	N77575	EWR	TPA	141	997	15	54	2023-10-06 15:00:00	Other
29003	12	5	835	845	-10	1101	1121	9E	1570	N305PQ	LGA	OMA	162	1148	8	45	2023-12-05 08:00:00	Other
29005	3	13	1708	1715	-7	1923	1937	YX	1674	N227JQ	LGA	IND	93	660	17	15	2023-03-13 17:00:00	Other
29006	10	16	950	959	-9	1118	1148	YX	1719	N235JQ	JFK	CMH	67	483	9	59	2023-10-16 09:00:00	Other
29012	1	22	623	630	-7	728	743	B6	222	N337JB	JFK	BOS	42	187	6	30	2023-01-22 06:00:00	BOS
29013	3	28	554	600	-6	925	945	AA	52	N106NN	JFK	LAX	359	2475	6	0	2023-03-28 06:00:00	LAX
29016	9	3	754	800	-6	939	1038	DL	183	N516DA	JFK	DEN	207	1626	8	0	2023-09-03 08:00:00	Other
29020	7	13	653	659	-6	843	834	YX	1067	N106HQ	LGA	PIT	62	335	6	59	2023-07-13 06:00:00	Other
29024	4	19	826	838	-12	1009	1037	YX	959	N857RW	EWR	GSO	65	445	8	38	2023-04-19 08:00:00	Other
29028	8	31	1126	1135	-9	1422	1441	DL	666	N336NB	LGA	PBI	142	1035	11	35	2023-08-31 11:00:00	Other
29029	12	26	1033	1040	-7	1241	1255	YX	1223	N406YX	LGA	AVL	98	599	10	40	2023-12-26 10:00:00	Other
29037	10	17	653	659	-6	800	835	AA	992	N981AN	EWR	ORD	103	719	6	59	2023-10-17 06:00:00	ORD
29039	10	31	2106	2117	-11	2314	2330	UA	200	N47524	EWR	CVG	101	569	21	17	2023-10-31 21:00:00	Other
29040	3	25	854	900	-6	1141	1143	B6	458	N982JB	JFK	ATL	124	760	9	0	2023-03-25 09:00:00	ATL
29041	10	3	1928	1938	-10	2211	2245	UA	712	N27261	EWR	RSW	144	1068	19	38	2023-10-03 19:00:00	Other
29045	5	3	1554	1600	-6	1830	1852	B6	400	N793JB	EWR	MCO	129	937	16	0	2023-05-03 16:00:00	MCO
29047	11	11	1519	1526	-7	1622	1640	YX	1128	N754YX	EWR	MHT	41	209	15	26	2023-11-11 15:00:00	Other
29048	9	25	854	900	-6	1056	1106	9E	1684	N304PQ	JFK	CVG	85	589	9	0	2023-09-25 09:00:00	Other
29060	6	18	652	658	-6	753	815	AA	573	N814AW	LGA	DCA	42	214	6	58	2023-06-18 06:00:00	Other
29064	12	5	2049	2100	-11	2205	2250	AA	116	N991NN	LGA	ORD	105	733	21	0	2023-12-05 21:00:00	ORD
29074	8	2	719	729	-10	952	956	YX	996	N427YX	LGA	OMA	184	1148	7	29	2023-08-02 07:00:00	Other
29079	8	29	1445	1455	-10	1736	1803	B6	120	N587JB	LGA	MCO	139	950	14	55	2023-08-29 14:00:00	MCO
29082	4	25	2038	2045	-7	2331	10	B6	34	N961JT	JFK	SAN	328	2446	20	45	2023-04-25 20:00:00	Other
29084	10	7	1746	1755	-9	1900	1928	9E	1629	N910XJ	LGA	BUF	50	292	17	55	2023-10-07 17:00:00	Other
29088	7	13	650	659	-9	838	905	AA	290	N944NN	LGA	CLT	80	544	6	59	2023-07-13 06:00:00	CLT
29093	3	7	1248	1256	-8	1449	1410	YX	1146	N638RW	EWR	MHT	44	209	12	56	2023-03-07 12:00:00	Other
29100	5	22	952	1000	-8	1256	1326	DL	140	N916DU	JFK	SLC	266	1990	10	0	2023-05-22 10:00:00	Other
29112	11	10	836	849	-13	1051	1112	YX	1285	N424YX	LGA	CVG	107	585	8	49	2023-11-10 08:00:00	Other
29113	9	1	523	530	-7	800	810	B6	40	N990JL	JFK	LAX	305	2475	5	30	2023-09-01 05:00:00	LAX
29115	5	23	2152	2200	-8	2312	2346	YX	1366	N403YX	LGA	RDU	66	431	22	0	2023-05-23 22:00:00	Other
29117	10	15	1204	1211	-7	1347	1345	YX	1795	N224JQ	JFK	BUF	57	301	12	11	2023-10-15 12:00:00	Other
29119	11	30	1718	1728	-10	1859	1930	YX	1117	N721YX	EWR	CMH	78	463	17	28	2023-11-30 17:00:00	Other
29130	5	9	1108	1115	-7	1413	1423	DL	532	N386DN	JFK	FLL	145	1069	11	15	2023-05-09 11:00:00	FLL
29151	11	28	650	659	-9	805	830	AA	955	N824AW	LGA	DCA	50	214	6	59	2023-11-28 06:00:00	Other
29152	4	18	1738	1745	-7	2031	2052	B6	21	N793JB	LGA	TPA	146	1010	17	45	2023-04-18 17:00:00	Other
29158	12	31	1247	1254	-7	1528	1609	NK	346	N692NK	EWR	FLL	146	1065	12	54	2023-12-31 12:00:00	FLL
29165	10	28	1422	1432	-10	1540	1540	B6	818	N284JB	JFK	ACK	36	199	14	32	2023-10-28 14:00:00	Other
29171	2	9	1212	1225	-13	1423	1454	YX	1242	N115HQ	LGA	DAY	95	549	12	25	2023-02-09 12:00:00	Other
29173	2	7	1920	1929	-9	2045	2048	UA	524	N27722	EWR	BOS	49	200	19	29	2023-02-07 19:00:00	BOS
29174	2	3	738	747	-9	925	924	YX	1234	N448YX	JFK	DCA	84	213	7	47	2023-02-03 07:00:00	Other
29180	12	30	1540	1549	-9	1646	1731	9E	1539	N904XJ	LGA	CHO	47	305	15	49	2023-12-30 15:00:00	Other
29185	3	13	1154	1203	-9	1355	1428	YX	1287	N132HQ	LGA	MSP	145	1020	12	3	2023-03-13 12:00:00	Other
29188	7	31	1444	1455	-11	1653	1710	DL	520	N372NW	LGA	DTW	93	502	14	55	2023-07-31 14:00:00	Other
29192	11	9	2048	2055	-7	2230	2254	YX	1768	N220JQ	JFK	PIT	73	340	20	55	2023-11-09 20:00:00	Other
29196	10	31	1838	1845	-7	2137	2147	UA	452	N27268	EWR	PBI	142	1023	18	45	2023-10-31 18:00:00	Other
29203	7	31	1355	1401	-6	1604	1607	YX	859	N859RW	EWR	GRR	95	605	14	1	2023-07-31 14:00:00	Other
29204	4	11	955	1003	-8	1158	1222	UA	464	N478UA	EWR	SAV	100	708	10	3	2023-04-11 10:00:00	Other
29207	2	25	1258	1310	-12	1451	1517	YX	1202	N407YX	LGA	CLE	90	419	13	10	2023-02-25 13:00:00	Other
29208	2	26	1820	1830	-10	2127	2151	DL	483	N140DU	LGA	IAH	217	1416	18	30	2023-02-26 18:00:00	Other
29209	11	18	1947	1959	-12	2154	2235	YX	1125	N747YX	EWR	SDF	99	642	19	59	2023-11-18 19:00:00	Other
29211	5	2	1130	1137	-7	1258	1304	YX	1129	N654RW	EWR	PIT	64	319	11	37	2023-05-02 11:00:00	Other
29212	2	8	1053	1100	-7	1410	1425	AA	112	N112AN	JFK	LAX	353	2475	11	0	2023-02-08 11:00:00	LAX
29215	7	8	1849	1859	-10	2147	2149	AS	85	N570AS	EWR	SAN	321	2425	18	59	2023-07-08 18:00:00	Other
29217	1	18	805	815	-10	1116	1136	AA	639	N959NN	LGA	DFW	229	1389	8	15	2023-01-18 08:00:00	Other
29228	4	25	819	829	-10	1020	1114	YX	1083	N420YX	JFK	CVG	103	589	8	29	2023-04-25 08:00:00	Other
6	12	7	2127	2129	-2	35	100	B6	756	N991JT	JFK	LAX	347	2475	21	29	2023-12-07 21:00:00	LAX
17	5	31	1123	1125	-2	1356	1438	UA	249	N63890	EWR	SEA	294	2402	11	25	2023-05-31 11:00:00	Other
20	11	21	1340	1345	-5	1646	1700	AA	364	N844NN	LGA	DFW	213	1389	13	45	2023-11-21 13:00:00	Other
27	3	26	856	900	-4	1214	1202	B6	359	N281JB	JFK	PBI	153	1028	9	0	2023-03-26 09:00:00	Other
29	7	25	1326	1329	-3	1423	1446	YX	1400	N214JQ	LGA	MVY	38	175	13	29	2023-07-25 13:00:00	Other
30	10	11	1325	1329	-4	1910	1639	AA	57	N452AN	JFK	MIA	NA	1089	13	29	2023-10-11 13:00:00	MIA
33	4	3	725	730	-5	1012	1035	UA	397	N77544	EWR	FLL	146	1065	7	30	2023-04-03 07:00:00	FLL
34	8	24	1737	1740	-3	2040	1943	9E	1269	N925XJ	LGA	DSM	140	1031	17	40	2023-08-24 17:00:00	Other
36	6	18	835	837	-2	1003	1031	9E	1569	N295PQ	LGA	RDU	68	431	8	37	2023-06-18 08:00:00	Other
45	3	8	725	730	-5	1024	1012	UA	513	N804UA	LGA	DEN	260	1620	7	30	2023-03-08 07:00:00	Other
46	1	23	1423	1425	-2	1528	1551	9E	1688	N326PQ	JFK	BTV	47	266	14	25	2023-01-23 14:00:00	Other
49	3	24	1402	1405	-3	1529	1540	UA	622	N478UA	EWR	BNA	125	748	14	5	2023-03-24 14:00:00	Other
50	5	6	657	700	-3	940	1017	DL	376	N334DN	JFK	MIA	138	1089	7	0	2023-05-06 07:00:00	MIA
53	7	1	705	710	-5	950	1009	B6	691	N506JB	EWR	MIA	142	1085	7	10	2023-07-01 07:00:00	MIA
68	2	1	625	630	-5	942	907	B6	718	N597JB	JFK	ATL	125	760	6	30	2023-02-01 06:00:00	ATL
76	11	15	1051	1055	-4	1237	1257	YX	1049	N742YX	EWR	MYR	87	550	10	55	2023-11-15 10:00:00	Other
78	11	8	1852	1855	-3	2024	2030	WN	876	N7845A	LGA	MDW	126	725	18	55	2023-11-08 18:00:00	Other
81	10	5	915	919	-4	1050	1115	9E	1495	N479PX	LGA	STL	132	888	9	19	2023-10-05 09:00:00	Other
84	1	26	925	929	-4	1239	1239	UA	572	N17752	EWR	TPA	166	997	9	29	2023-01-26 09:00:00	Other
89	4	9	1104	1108	-4	1409	1431	DL	568	N374DX	LGA	MIA	154	1096	11	8	2023-04-09 11:00:00	MIA
90	9	22	1254	1259	-5	1442	1452	9E	1552	N315PQ	LGA	RDU	69	431	12	59	2023-09-22 12:00:00	Other
98	6	2	856	859	-3	1113	1116	YX	1232	N638RW	EWR	HHH	103	687	8	59	2023-06-02 08:00:00	Other
105	1	12	1451	1455	-4	1656	1717	9E	1531	N923XJ	JFK	CLT	97	541	14	55	2023-01-12 14:00:00	CLT
109	9	7	1125	1129	-4	1352	1417	UA	552	N39423	EWR	MCO	124	937	11	29	2023-09-07 11:00:00	MCO
110	1	9	851	856	-5	1110	1124	UA	561	N884UA	EWR	SAV	112	708	8	56	2023-01-09 08:00:00	Other
112	3	3	1817	1820	-3	2054	2115	UA	439	N33203	EWR	LAS	299	2227	18	20	2023-03-03 18:00:00	Other
116	7	1	1650	1655	-5	1948	2020	AS	6	N976AK	JFK	SEA	321	2422	16	55	2023-07-01 16:00:00	Other
126	1	26	1055	1100	-5	1254	1256	YX	1121	N742YX	EWR	MYR	99	550	11	0	2023-01-26 11:00:00	Other
130	1	18	2157	2159	-2	2309	2327	YX	1192	N729YX	EWR	PWM	52	284	21	59	2023-01-18 21:00:00	Other
144	9	30	1326	1330	-4	1600	1628	NK	23	N512NK	EWR	MCO	127	937	13	30	2023-09-30 13:00:00	MCO
145	10	18	2042	2047	-5	2302	2314	UA	229	N37419	EWR	ATL	101	746	20	47	2023-10-18 20:00:00	ATL
152	6	8	921	925	-4	1032	1100	YX	1779	N211JQ	LGA	DCA	45	214	9	25	2023-06-08 09:00:00	Other
154	4	13	1657	1659	-2	1826	1848	OO	1445	N202SY	LGA	ORD	108	733	16	59	2023-04-13 16:00:00	ORD
159	8	9	2054	2059	-5	3	16	B6	26	N662JB	JFK	SLC	271	1990	20	59	2023-08-09 20:00:00	Other
162	8	1	2126	2130	-4	2246	2324	YX	1330	N860RW	JFK	RIC	54	288	21	30	2023-08-01 21:00:00	Other
166	5	13	848	852	-4	1050	1118	9E	1290	N301PQ	LGA	SAV	105	722	8	52	2023-05-13 08:00:00	Other
172	5	25	1257	1300	-3	1701	1653	DL	725	N816DN	JFK	SJU	199	1598	13	0	2023-05-25 13:00:00	Other
173	6	17	1915	1920	-5	2107	2136	DL	552	N362NB	LGA	MSY	155	1183	19	20	2023-06-17 19:00:00	Other
175	8	7	1027	1029	-2	1214	1241	DL	413	N316DN	LGA	MSP	132	1020	10	29	2023-08-07 10:00:00	Other
176	10	25	658	700	-2	912	934	DL	167	N303DN	LGA	ATL	107	762	7	0	2023-10-25 07:00:00	ATL
177	7	24	1545	1550	-5	1655	1732	9E	1303	N676CA	LGA	CHO	53	305	15	50	2023-07-24 15:00:00	Other
184	5	12	1826	1830	-4	2200	2155	DL	125	N879DN	JFK	SEA	351	2422	18	30	2023-05-12 18:00:00	Other
192	10	2	1548	1550	-2	1836	1851	UA	507	N17312	EWR	FLL	142	1065	15	50	2023-10-02 15:00:00	FLL
197	1	1	755	800	-5	1009	1027	9E	1520	N927XJ	JFK	CHS	104	636	8	0	2023-01-01 08:00:00	Other
205	12	7	1517	1519	-2	1634	1640	YX	1073	N765YX	EWR	SYR	51	195	15	19	2023-12-07 15:00:00	Other
208	7	2	1413	1415	-2	1609	1538	B6	187	N324JB	LGA	BOS	32	184	14	15	2023-07-02 14:00:00	BOS
214	2	19	1157	1200	-3	1455	1518	B6	720	N653JB	LGA	FLL	146	1076	12	0	2023-02-19 12:00:00	FLL
215	4	25	956	1000	-4	1118	1131	YX	968	N741YX	EWR	BUF	55	282	10	0	2023-04-25 10:00:00	Other
217	11	9	2127	2130	-3	24	28	B6	121	N593JB	LGA	FLL	149	1076	21	30	2023-11-09 21:00:00	FLL
223	1	9	1156	1200	-4	1255	1303	9E	1457	N200PQ	JFK	ITH	40	189	12	0	2023-01-09 12:00:00	Other
224	5	23	1940	1945	-5	2125	2152	9E	1475	N921XJ	EWR	CVG	89	569	19	45	2023-05-23 19:00:00	Other
231	1	13	1925	1929	-4	2158	2310	AA	94	N115NN	JFK	LAX	315	2475	19	29	2023-01-13 19:00:00	LAX
236	3	13	1340	1345	-5	1507	1534	YX	1256	N112HQ	LGA	CLE	66	419	13	45	2023-03-13 13:00:00	Other
242	11	25	1924	1929	-5	2229	2243	DL	534	N371DN	LGA	FLL	153	1076	19	29	2023-11-25 19:00:00	FLL
248	7	11	1027	1030	-3	1347	1358	YX	942	N642RW	EWR	EYW	170	1196	10	30	2023-07-11 10:00:00	Other
255	3	21	2154	2159	-5	2335	2331	B6	38	N324JB	JFK	BUF	62	301	21	59	2023-03-21 21:00:00	Other
258	10	15	735	740	-5	933	947	AA	498	N925AN	JFK	CLT	88	541	7	40	2023-10-15 07:00:00	CLT
260	6	18	1451	1455	-4	1716	1715	9E	1545	N232PQ	JFK	CVG	90	589	14	55	2023-06-18 14:00:00	Other
261	1	30	1638	1642	-4	1808	1829	UA	98	N847UA	EWR	RDU	67	416	16	42	2023-01-30 16:00:00	Other
265	5	18	955	958	-3	1206	1211	AA	914	N150UW	JFK	CLT	87	541	9	58	2023-05-18 09:00:00	CLT
268	3	21	1157	1200	-3	1310	1321	OO	1141	N305SY	JFK	IAD	47	228	12	0	2023-03-21 12:00:00	Other
269	10	11	1326	1330	-4	1505	1525	9E	1437	N297PQ	JFK	CLE	78	425	13	30	2023-10-11 13:00:00	Other
278	11	18	1600	1603	-3	1842	1905	UA	69	N78524	EWR	PBI	139	1023	16	3	2023-11-18 16:00:00	Other
279	2	22	1327	1330	-3	1704	1707	B6	567	N969JT	JFK	SFO	368	2586	13	30	2023-02-22 13:00:00	Other
280	11	6	654	659	-5	853	910	9E	1650	N316PQ	JFK	DTW	88	509	6	59	2023-11-06 06:00:00	Other
281	3	21	1724	1729	-5	2006	2008	YX	1273	N425YX	LGA	ATL	122	762	17	29	2023-03-21 17:00:00	ATL
288	4	6	830	835	-5	1034	1101	9E	1382	N313PQ	LGA	SAV	105	722	8	35	2023-04-06 08:00:00	Other
290	10	5	1323	1325	-2	1452	1510	9E	1485	N916XJ	LGA	CLE	64	419	13	25	2023-10-05 13:00:00	Other
291	6	24	1257	1259	-2	1601	1615	AA	668	N306RC	JFK	MIA	150	1089	12	59	2023-06-24 12:00:00	MIA
300	2	9	1031	1035	-4	1239	1320	B6	713	N621JB	LGA	DEN	225	1620	10	35	2023-02-09 10:00:00	Other
303	6	2	1523	1526	-3	1826	1842	DL	414	N301DV	LGA	MIA	163	1096	15	26	2023-06-02 15:00:00	MIA
315	6	14	824	829	-5	1133	1121	AA	361	N865NN	LGA	DFW	209	1389	8	29	2023-06-14 08:00:00	Other
319	4	18	715	720	-5	1008	1030	DL	486	N357NW	JFK	AUS	212	1521	7	20	2023-04-18 07:00:00	Other
324	6	9	1954	1959	-5	2150	2229	DL	980	N964AT	EWR	ATL	96	746	19	59	2023-06-09 19:00:00	ATL
330	1	5	1848	1850	-2	2212	2157	B6	84	N2084J	JFK	MCO	152	944	18	50	2023-01-05 18:00:00	MCO
331	6	30	1510	1515	-5	1748	1815	DL	225	N141DU	LGA	DFW	187	1389	15	15	2023-06-30 15:00:00	Other
333	1	17	1154	1159	-5	1350	1410	YX	1898	N818MD	LGA	STL	147	888	11	59	2023-01-17 11:00:00	Other
334	10	6	727	730	-3	908	915	AA	223	N867NN	LGA	ORD	112	733	7	30	2023-10-06 07:00:00	ORD
338	3	22	1936	1940	-4	2140	2201	9E	1548	N232PQ	LGA	CVG	96	585	19	40	2023-03-22 19:00:00	Other
339	4	13	1256	1259	-3	1411	1422	9E	1326	N315PQ	JFK	ORF	51	290	12	59	2023-04-13 12:00:00	Other
349	3	28	824	829	-5	1059	1101	9E	1509	N134EV	LGA	IND	125	660	8	29	2023-03-28 08:00:00	Other
356	5	27	1739	1744	-5	2006	2039	UA	814	N14250	EWR	MCO	123	937	17	44	2023-05-27 17:00:00	MCO
357	7	3	1650	1652	-2	1858	1918	DL	727	N3761R	EWR	ATL	107	746	16	52	2023-07-03 16:00:00	ATL
361	6	20	2032	2035	-3	2145	2224	YX	1915	N818MD	LGA	MSN	107	812	20	35	2023-06-20 20:00:00	Other
366	3	31	1337	1340	-3	1543	1548	9E	1411	N309PQ	LGA	TYS	109	647	13	40	2023-03-31 13:00:00	Other
367	3	21	1356	1359	-3	1622	1635	DL	172	N377DE	JFK	DEN	239	1626	13	59	2023-03-21 13:00:00	Other
370	4	6	1957	1959	-2	2300	2320	DL	543	N395DZ	LGA	MIA	160	1096	19	59	2023-04-06 19:00:00	MIA
371	10	7	740	745	-5	942	959	B6	855	N625JB	LGA	CHS	94	641	7	45	2023-10-07 07:00:00	Other
376	9	30	855	900	-5	1018	1056	9E	1545	N330PQ	LGA	STL	120	888	9	0	2023-09-30 09:00:00	Other
380	6	15	1857	1859	-2	2005	2038	YX	1069	N859RW	LGA	IAD	48	229	18	59	2023-06-15 18:00:00	Other
384	3	3	1656	1700	-4	1953	2022	UA	139	N2749U	EWR	SFO	327	2565	17	0	2023-03-03 17:00:00	Other
386	12	14	1112	1115	-3	1216	1236	B6	227	N323JB	LGA	BOS	38	184	11	15	2023-12-14 11:00:00	BOS
388	6	6	1703	1708	-5	1902	1913	9E	1611	N195PQ	JFK	RDU	67	427	17	8	2023-06-06 17:00:00	Other
393	7	8	557	600	-3	820	838	UA	739	N481UA	LGA	IAH	186	1416	6	0	2023-07-08 06:00:00	Other
405	8	15	859	903	-4	1052	1103	YX	896	N754YX	EWR	CMH	75	463	9	3	2023-08-15 09:00:00	Other
406	10	23	723	725	-2	904	915	WN	360	N8640D	LGA	STL	130	888	7	25	2023-10-23 07:00:00	Other
410	10	5	557	600	-3	659	725	WN	83	N932WN	LGA	MDW	103	725	6	0	2023-10-05 06:00:00	Other
411	4	19	825	829	-4	1051	1114	YX	1083	N405YX	JFK	CVG	95	589	8	29	2023-04-19 08:00:00	Other
412	9	17	1054	1059	-5	1211	1214	9E	1606	N309PQ	JFK	SYR	49	209	10	59	2023-09-17 10:00:00	Other
415	4	11	1420	1425	-5	1607	1633	YX	944	N748YX	EWR	GRR	89	605	14	25	2023-04-11 14:00:00	Other
416	4	22	1640	1645	-5	1854	1839	YX	1224	N871RW	LGA	ILM	86	500	16	45	2023-04-22 16:00:00	Other
438	5	23	1751	1755	-4	1910	1927	YX	1650	N214JQ	LGA	DCA	56	214	17	55	2023-05-23 17:00:00	Other
445	2	22	826	830	-4	1126	1157	NK	320	N685NK	LGA	IAH	212	1416	8	30	2023-02-22 08:00:00	Other
448	4	18	2046	2050	-4	2214	2249	9E	1277	N197PQ	LGA	GSO	68	461	20	50	2023-04-18 20:00:00	Other
450	2	27	945	949	-4	1326	1329	AA	952	N407AN	EWR	PHX	319	2133	9	49	2023-02-27 09:00:00	Other
451	8	5	1726	1730	-4	1859	1915	AA	733	N767UW	LGA	ORD	116	733	17	30	2023-08-05 17:00:00	ORD
453	1	29	1726	1730	-4	2058	2040	DL	109	N876DN	JFK	LAS	356	2248	17	30	2023-01-29 17:00:00	Other
466	5	29	855	900	-5	1015	1027	YX	1164	N721YX	EWR	DCA	39	199	9	0	2023-05-29 09:00:00	Other
482	5	11	556	600	-4	748	808	YX	1624	N243JQ	LGA	CLT	81	544	6	0	2023-05-11 06:00:00	CLT
494	2	19	1933	1935	-2	2144	2157	9E	1299	N153PQ	JFK	CLT	91	541	19	35	2023-02-19 19:00:00	CLT
500	3	6	1155	1200	-5	1613	1654	DL	746	N854DN	JFK	SJU	181	1598	12	0	2023-03-06 12:00:00	Other
502	10	26	825	830	-5	1023	1012	UA	586	N75435	EWR	CLE	64	404	8	30	2023-10-26 08:00:00	Other
507	3	17	1456	1500	-4	1623	1635	YX	1261	N131HQ	LGA	DCA	58	214	15	0	2023-03-17 15:00:00	Other
508	2	16	2025	2030	-5	2204	2210	YX	1538	N206JQ	LGA	PIT	65	335	20	30	2023-02-16 20:00:00	Other
510	5	3	2046	2050	-4	2233	2259	OO	1141	N297SY	JFK	CLE	76	425	20	50	2023-05-03 20:00:00	Other
513	11	25	805	810	-5	1014	1014	9E	1583	N908XJ	JFK	CLE	79	425	8	10	2023-11-25 08:00:00	Other
520	11	26	1956	2000	-4	2340	2214	YX	1883	N209JQ	JFK	CLT	112	541	20	0	2023-11-26 20:00:00	CLT
545	2	9	2254	2259	-5	339	349	B6	308	N564JB	JFK	PSE	198	1617	22	59	2023-02-09 22:00:00	Other
549	10	26	2113	2115	-2	2344	2351	DL	814	N502DX	JFK	ATL	109	760	21	15	2023-10-26 21:00:00	ATL
550	8	27	1352	1355	-3	1507	1534	OO	955	N311SY	JFK	BOS	35	187	13	55	2023-08-27 13:00:00	BOS
555	9	20	1855	1900	-5	2015	2039	AA	767	N804NN	LGA	ORD	111	733	19	0	2023-09-20 19:00:00	ORD
569	4	21	726	730	-4	1017	1035	UA	397	N37531	EWR	FLL	145	1065	7	30	2023-04-21 07:00:00	FLL
593	7	17	800	805	-5	955	1003	AA	492	N842NN	EWR	CLT	87	529	8	5	2023-07-17 08:00:00	CLT
611	5	14	1908	1912	-4	2204	2222	DL	428	N361NB	LGA	PBI	129	1035	19	12	2023-05-14 19:00:00	Other
614	10	8	1700	1705	-5	1811	1829	YX	1076	N726YX	EWR	ROC	48	246	17	5	2023-10-08 17:00:00	Other
616	11	3	1615	1620	-5	1737	1754	9E	1675	N298PQ	JFK	ORF	56	290	16	20	2023-11-03 16:00:00	Other
623	3	2	1845	1850	-5	2116	2123	9E	1393	N228PQ	LGA	SAV	117	722	18	50	2023-03-02 18:00:00	Other
627	4	3	2045	2049	-4	2205	2227	YX	966	N739YX	EWR	MKE	117	725	20	49	2023-04-03 20:00:00	Other
628	2	15	742	745	-3	1046	1114	AA	575	N982AN	LGA	MIA	153	1096	7	45	2023-02-15 07:00:00	MIA
630	5	26	642	645	-3	838	914	UA	444	N77543	EWR	PHX	274	2133	6	45	2023-05-26 06:00:00	Other
635	1	24	1138	1140	-2	1245	1310	WN	245	N7835A	LGA	MDW	114	725	11	40	2023-01-24 11:00:00	Other
643	8	11	2157	2159	-2	2248	2304	9E	1190	N926XJ	LGA	BDL	26	101	21	59	2023-08-11 21:00:00	Other
647	3	6	1818	1820	-2	2046	2059	YX	1712	N231JQ	LGA	SDF	111	659	18	20	2023-03-06 18:00:00	Other
648	3	22	1221	1225	-4	1453	1514	UA	288	N47293	EWR	MCO	128	937	12	25	2023-03-22 12:00:00	MCO
659	9	16	1149	1152	-3	1250	1308	UA	265	N38446	EWR	BOS	42	200	11	52	2023-09-16 11:00:00	BOS
662	1	6	2207	2210	-3	302	317	NK	436	N923NK	EWR	SJU	214	1608	22	10	2023-01-06 22:00:00	Other
667	1	1	1551	1555	-4	1815	1827	NK	478	N531NK	EWR	ATL	104	746	15	55	2023-01-01 15:00:00	ATL
675	9	29	515	520	-5	1003	906	B6	921	N630JB	JFK	BQN	259	1576	5	20	2023-09-29 05:00:00	Other
681	11	1	1926	1929	-3	2153	2203	9E	1522	N937XJ	JFK	MCI	167	1113	19	29	2023-11-01 19:00:00	Other
686	6	5	2225	2230	-5	101	203	B6	972	N992JB	JFK	SFO	311	2586	22	30	2023-06-05 22:00:00	Other
690	3	4	1021	1025	-4	1137	1205	YX	1717	N224JQ	LGA	DCA	45	214	10	25	2023-03-04 10:00:00	Other
694	4	9	1116	1118	-2	1415	1425	DL	429	N399DA	LGA	PBI	148	1035	11	18	2023-04-09 11:00:00	Other
706	9	18	1011	1015	-4	1124	1150	UA	706	N17229	LGA	ORD	104	733	10	15	2023-09-18 10:00:00	ORD
709	6	12	707	710	-3	950	958	DL	567	N376DN	LGA	MCO	138	950	7	10	2023-06-12 07:00:00	MCO
711	1	6	1515	1520	-5	1617	1651	9E	1614	N915XJ	LGA	ROC	43	254	15	20	2023-01-06 15:00:00	Other
716	4	3	1454	1459	-5	1638	1650	NK	24	N527NK	EWR	MYR	86	550	14	59	2023-04-03 14:00:00	Other
718	12	5	940	945	-5	1255	1256	B6	652	N585JB	LGA	MCO	155	950	9	45	2023-12-05 09:00:00	MCO
725	5	17	1511	1515	-4	1804	1817	UA	911	N480UA	EWR	SRQ	150	1034	15	15	2023-05-17 15:00:00	Other
729	2	28	2156	2159	-3	146	133	B6	895	N977JE	JFK	SFO	370	2586	21	59	2023-02-28 21:00:00	Other
732	5	18	1527	1530	-3	1817	1854	AA	58	N115NN	JFK	LAX	320	2475	15	30	2023-05-18 15:00:00	LAX
734	7	21	1623	1628	-5	1743	1800	YX	900	N726YX	EWR	BGR	58	393	16	28	2023-07-21 16:00:00	Other
737	3	3	925	930	-5	1101	1057	9E	1486	N296PQ	JFK	PWM	50	273	9	30	2023-03-03 09:00:00	Other
741	3	2	756	759	-3	1112	1109	B6	174	N775JB	LGA	PBI	164	1035	7	59	2023-03-02 07:00:00	Other
743	2	1	1041	1045	-4	1324	1345	UA	652	N17265	EWR	MCO	136	937	10	45	2023-02-01 10:00:00	MCO
748	10	16	1949	1952	-3	2215	2216	YX	1143	N750YX	EWR	SAV	104	708	19	52	2023-10-16 19:00:00	Other
749	4	21	712	715	-3	929	940	WN	561	N7853B	LGA	ATL	106	762	7	15	2023-04-21 07:00:00	ATL
757	2	16	1416	1420	-4	1703	1654	YX	1581	N220JQ	LGA	MCI	182	1107	14	20	2023-02-16 14:00:00	Other
761	2	9	1735	1740	-5	2030	2110	B6	914	N980JT	JFK	LAX	320	2475	17	40	2023-02-09 17:00:00	LAX
762	2	19	957	1000	-3	1200	1228	UA	756	N45956	EWR	DEN	219	1605	10	0	2023-02-19 10:00:00	Other
767	3	1	1425	1430	-5	1733	1732	UA	886	N78005	EWR	LAX	339	2454	14	30	2023-03-01 14:00:00	LAX
770	6	19	727	730	-3	1001	1022	AA	154	N927NN	LGA	DFW	185	1389	7	30	2023-06-19 07:00:00	Other
776	10	12	925	930	-5	1241	1246	DL	100	N839DN	JFK	SLC	278	1990	9	30	2023-10-12 09:00:00	Other
779	6	4	755	800	-5	1011	1026	DL	217	N334DN	LGA	ATL	105	762	8	0	2023-06-04 08:00:00	ATL
781	7	31	1225	1229	-4	1454	1517	UA	615	N467UA	LGA	IAH	185	1416	12	29	2023-07-31 12:00:00	Other
784	1	10	1931	1935	-4	2157	2206	9E	1518	N195PQ	JFK	MSP	160	1029	19	35	2023-01-10 19:00:00	Other
787	9	5	716	720	-4	838	847	9E	1577	N482PX	LGA	RIC	51	292	7	20	2023-09-05 07:00:00	Other
790	12	3	720	724	-4	1008	1000	UA	641	N850UA	LGA	DEN	240	1620	7	24	2023-12-03 07:00:00	Other
798	11	27	1315	1320	-5	1535	1543	9E	1616	N927XJ	JFK	CHS	109	636	13	20	2023-11-27 13:00:00	Other
804	2	8	1051	1055	-4	1347	1413	NK	969	N967NK	LGA	MIA	150	1096	10	55	2023-02-08 10:00:00	MIA
808	5	26	709	712	-3	1017	1013	DL	350	N344NB	LGA	PBI	152	1035	7	12	2023-05-26 07:00:00	Other
818	12	14	832	836	-4	1050	1048	NK	295	N672NK	LGA	CLT	94	544	8	36	2023-12-14 08:00:00	CLT
821	2	7	956	959	-3	1250	1313	B6	789	N959JB	JFK	FLL	145	1069	9	59	2023-02-07 09:00:00	FLL
824	1	25	626	630	-4	912	931	UA	354	N37504	EWR	MCO	138	937	6	30	2023-01-25 06:00:00	MCO
831	4	18	755	800	-5	1109	1115	DL	547	N381DN	JFK	RSW	161	1074	8	0	2023-04-18 08:00:00	Other
834	10	22	1836	1840	-4	1954	2002	UA	272	N77552	EWR	BOS	46	200	18	40	2023-10-22 18:00:00	BOS
841	9	20	603	605	-2	732	725	YX	1795	N875RW	LGA	DCA	63	214	6	5	2023-09-20 06:00:00	Other
843	2	2	855	900	-5	1039	1045	WN	131	N755SA	LGA	MDW	129	725	9	0	2023-02-02 09:00:00	Other
849	6	21	1916	1920	-4	2110	2136	9E	1682	N602LR	LGA	MCI	141	1107	19	20	2023-06-21 19:00:00	Other
850	11	25	823	825	-2	930	952	YX	1864	N237JQ	EWR	BOS	43	200	8	25	2023-11-25 08:00:00	BOS
853	12	6	940	945	-5	1051	1120	WN	467	N966WN	LGA	BNA	108	764	9	45	2023-12-06 09:00:00	Other
856	3	29	710	715	-5	1014	953	9E	1462	N928XJ	LGA	JAX	124	833	7	15	2023-03-29 07:00:00	Other
865	12	10	2056	2059	-3	39	41	DL	262	N520DE	JFK	SAN	328	2446	20	59	2023-12-10 20:00:00	Other
883	4	28	1815	1820	-5	1930	1947	9E	1420	N904XJ	LGA	PWM	44	269	18	20	2023-04-28 18:00:00	Other
886	1	12	1602	1605	-3	1840	1811	9E	1560	N678CA	LGA	ILM	78	500	16	5	2023-01-12 16:00:00	Other
888	11	16	1852	1855	-3	2021	2037	AA	732	N750UW	LGA	ORD	113	733	18	55	2023-11-16 18:00:00	ORD
890	5	28	1526	1530	-4	1638	1658	B6	567	N228JB	JFK	BOS	40	187	15	30	2023-05-28 15:00:00	BOS
891	3	8	1554	1559	-5	1805	1826	YX	1300	N123HQ	JFK	CVG	102	589	15	59	2023-03-08 15:00:00	Other
893	10	22	1141	1145	-4	1359	1406	B6	946	N2060J	JFK	ATL	106	760	11	45	2023-10-22 11:00:00	ATL
905	5	17	1650	1655	-5	1814	1833	YX	1607	N208JQ	LGA	DCA	43	214	16	55	2023-05-17 16:00:00	Other
908	3	21	2115	2120	-5	2218	2216	9E	1443	N131EV	LGA	ALB	31	136	21	20	2023-03-21 21:00:00	Other
912	7	12	655	700	-5	838	850	9E	1137	N183GJ	LGA	STL	131	888	7	0	2023-07-12 07:00:00	Other
917	6	11	1558	1600	-2	1728	1733	YX	1146	N731YX	EWR	PIT	55	319	16	0	2023-06-11 16:00:00	Other
918	5	19	1618	1620	-2	1816	1837	9E	1522	N936XJ	LGA	CLT	82	544	16	20	2023-05-19 16:00:00	CLT
932	2	23	1510	1515	-5	1629	1648	9E	1421	N904XJ	LGA	ORF	50	296	15	15	2023-02-23 15:00:00	Other
939	9	20	555	600	-5	705	720	YX	1930	N225JQ	LGA	BOS	40	184	6	0	2023-09-20 06:00:00	BOS
948	4	8	515	520	-5	627	636	NK	270	N516NK	EWR	PIT	53	319	5	20	2023-04-08 05:00:00	Other
950	9	15	1456	1459	-3	1726	1713	YX	1336	N423YX	JFK	IND	96	665	14	59	2023-09-15 14:00:00	Other
951	6	6	1955	1959	-4	2330	2258	DL	473	N330DX	LGA	MCO	135	950	19	59	2023-06-06 19:00:00	MCO
953	5	5	1953	1955	-2	2307	2359	DL	536	N718TW	JFK	SFO	334	2586	19	55	2023-05-05 19:00:00	Other
955	3	18	1527	1530	-3	1910	1926	B6	998	N648JB	JFK	SJU	199	1598	15	30	2023-03-18 15:00:00	Other
963	7	15	1055	1100	-5	1405	1411	DL	426	N3732J	JFK	MIA	167	1089	11	0	2023-07-15 11:00:00	MIA
974	11	10	703	705	-2	947	949	YX	1832	N221JQ	LGA	JAX	130	833	7	5	2023-11-10 07:00:00	Other
979	9	11	722	725	-3	951	959	DL	184	N509DT	JFK	LAS	302	2248	7	25	2023-09-11 07:00:00	Other
981	10	14	1054	1059	-5	1415	1410	DL	576	N3743H	LGA	MIA	149	1096	10	59	2023-10-14 10:00:00	MIA
989	4	23	1023	1025	-2	1235	1225	AA	596	N524UW	EWR	CLT	95	529	10	25	2023-04-23 10:00:00	CLT
1004	7	10	1503	1505	-2	1710	1712	AA	626	N956AN	LGA	CLT	87	544	15	5	2023-07-10 15:00:00	CLT
1005	5	17	1525	1530	-5	1814	1827	UA	837	N27255	EWR	DFW	192	1372	15	30	2023-05-17 15:00:00	Other
1008	4	29	1748	1750	-2	1859	1920	YX	1518	N242JQ	LGA	DCA	46	214	17	50	2023-04-29 17:00:00	Other
1009	11	11	840	845	-5	1132	1121	9E	1758	N315PQ	LGA	OMA	178	1148	8	45	2023-11-11 08:00:00	Other
1015	8	14	1046	1050	-4	1337	1408	DL	347	N117DU	LGA	RSW	151	1080	10	50	2023-08-14 10:00:00	Other
1018	2	22	1226	1230	-4	1402	1417	YX	1568	N880RW	LGA	BNA	128	764	12	30	2023-02-22 12:00:00	Other
1021	11	19	1058	1100	-2	1323	1354	B6	140	N964JT	JFK	LAS	300	2248	11	0	2023-11-19 11:00:00	Other
1023	10	27	1702	1705	-3	1818	1827	UA	409	N14231	EWR	BOS	43	200	17	5	2023-10-27 17:00:00	BOS
1028	5	19	1030	1035	-5	1301	1309	B6	386	N657JB	LGA	DEN	240	1620	10	35	2023-05-19 10:00:00	Other
1035	5	16	955	1000	-5	1118	1141	YX	1311	N425YX	JFK	BNA	114	765	10	0	2023-05-16 10:00:00	Other
1041	2	19	1501	1505	-4	1632	1638	9E	1421	N478PX	LGA	ORF	59	296	15	5	2023-02-19 15:00:00	Other
1044	7	11	1200	1205	-5	1314	1334	9E	1189	N176PQ	JFK	BUF	52	301	12	5	2023-07-11 12:00:00	Other
1052	3	1	725	730	-5	1023	948	DL	1005	N347NW	LGA	MSP	166	1020	7	30	2023-03-01 07:00:00	Other
1057	4	19	1443	1447	-4	1551	1623	9E	1330	N305PQ	LGA	CHO	53	305	14	47	2023-04-19 14:00:00	Other
1059	2	25	811	815	-4	1101	1101	YX	1611	N880RW	LGA	MCI	204	1107	8	15	2023-02-25 08:00:00	Other
1065	10	5	850	855	-5	1031	1056	9E	1427	N922XJ	LGA	RDU	75	431	8	55	2023-10-05 08:00:00	Other
1067	6	28	1655	1700	-5	1823	1855	9E	1468	N307PQ	LGA	RDU	65	431	17	0	2023-06-28 17:00:00	Other
1070	5	21	1425	1429	-4	1643	1700	DL	138	N347DN	LGA	ATL	107	762	14	29	2023-05-21 14:00:00	ATL
1071	2	22	655	700	-5	1032	1028	DL	104	N807DN	JFK	SEA	376	2422	7	0	2023-02-22 07:00:00	Other
1073	9	27	1937	1942	-5	2155	2220	9E	1463	N930XJ	JFK	SAV	114	718	19	42	2023-09-27 19:00:00	Other
1078	4	8	633	636	-3	924	942	UA	267	N434UA	EWR	FLL	156	1065	6	36	2023-04-08 06:00:00	FLL
1079	4	19	1925	1929	-4	2216	2237	DL	395	N339DN	LGA	MCO	127	950	19	29	2023-04-19 19:00:00	MCO
1084	1	23	858	900	-2	1042	1030	YX	1126	N635RW	EWR	DCA	48	199	9	0	2023-01-23 09:00:00	Other
1086	3	16	1458	1500	-2	2349	1816	DL	113	N114DU	LGA	DFW	NA	1389	15	0	2023-03-16 15:00:00	Other
1087	3	3	1155	1158	-3	1429	1428	UA	262	N437UA	EWR	ATL	126	746	11	58	2023-03-03 11:00:00	ATL
1094	11	30	727	730	-3	1004	1025	DL	184	N504DZ	JFK	LAS	303	2248	7	30	2023-11-30 07:00:00	Other
1095	1	26	700	705	-5	1015	1014	B6	187	N615JB	LGA	PBI	166	1035	7	5	2023-01-26 07:00:00	Other
1108	10	6	626	630	-4	914	939	AA	333	N306SP	JFK	MIA	148	1089	6	30	2023-10-06 06:00:00	MIA
1117	9	17	957	959	-2	1158	1215	9E	1633	N538CA	LGA	CVG	101	585	9	59	2023-09-17 09:00:00	Other
1119	10	26	755	800	-5	1040	1107	UA	567	N14107	EWR	FLL	136	1065	8	0	2023-10-26 08:00:00	FLL
1122	10	27	556	600	-4	850	905	NK	46	N669NK	LGA	FLL	140	1076	6	0	2023-10-27 06:00:00	FLL
1127	7	24	630	635	-5	815	830	YX	1096	N131HQ	JFK	RDU	75	427	6	35	2023-07-24 06:00:00	Other
1131	11	1	2238	2241	-3	2355	13	9E	1453	N181PQ	JFK	SYR	43	209	22	41	2023-11-01 22:00:00	Other
1135	11	30	820	825	-5	957	1004	YX	1327	N444YX	LGA	CLE	72	419	8	25	2023-11-30 08:00:00	Other
1140	4	8	1307	1310	-3	1526	1552	AA	882	N318SF	JFK	PHX	294	2153	13	10	2023-04-08 13:00:00	Other
1149	12	23	1159	1201	-2	1405	1431	DL	381	N951AT	EWR	ATL	106	746	12	1	2023-12-23 12:00:00	ATL
1150	4	10	1246	1250	-4	1409	1441	9E	1185	N186PQ	LGA	CLE	64	419	12	50	2023-04-10 12:00:00	Other
1153	1	25	1254	1259	-5	1506	1516	YX	1769	N201JQ	LGA	CLT	108	544	12	59	2023-01-25 12:00:00	CLT
1158	2	23	951	955	-4	1203	1218	9E	1358	N936XJ	JFK	IND	109	665	9	55	2023-02-23 09:00:00	Other
1161	9	15	600	605	-5	703	725	YX	1863	N875RW	LGA	DCA	42	214	6	5	2023-09-15 06:00:00	Other
1162	3	11	1554	1557	-3	1819	1830	UA	498	N17730	EWR	JAX	111	820	15	57	2023-03-11 15:00:00	Other
1171	2	10	916	920	-4	1139	1207	YX	1551	N210JQ	LGA	SDF	119	659	9	20	2023-02-10 09:00:00	Other
1173	1	9	803	805	-2	1021	1115	DL	383	N727TW	JFK	LAS	302	2248	8	5	2023-01-09 08:00:00	Other
1174	10	9	1155	1200	-5	1447	1525	UA	825	N19130	EWR	SFO	333	2565	12	0	2023-10-09 12:00:00	Other
1176	10	25	955	959	-4	1250	1307	UA	585	N77261	EWR	RSW	141	1068	9	59	2023-10-25 09:00:00	Other
1179	6	27	1627	1629	-2	2043	1935	AA	976	N786AN	JFK	MIA	136	1089	16	29	2023-06-27 16:00:00	MIA
1181	9	2	1713	1717	-4	1913	1938	UA	858	N68817	EWR	DEN	210	1605	17	17	2023-09-02 17:00:00	Other
1184	2	6	522	525	-3	806	820	UA	195	N67134	EWR	IAH	190	1400	5	25	2023-02-06 05:00:00	Other
1225	2	8	1611	1615	-4	1757	1814	YX	1308	N132HQ	JFK	RDU	78	427	16	15	2023-02-08 16:00:00	Other
1234	1	11	1626	1629	-3	1724	1738	9E	1640	N914XJ	LGA	PVD	29	143	16	29	2023-01-11 16:00:00	Other
1238	10	25	1842	1845	-3	2024	2045	YX	1145	N755YX	EWR	CMH	73	463	18	45	2023-10-25 18:00:00	Other
1241	5	11	1137	1141	-4	1254	1315	YX	1656	N233JQ	LGA	BUF	50	292	11	41	2023-05-11 11:00:00	Other
1243	9	12	1247	1250	-3	1457	1508	OO	1245	N311SY	LGA	SDF	109	659	12	50	2023-09-12 12:00:00	Other
1248	4	18	2154	2159	-5	200	158	B6	654	N954JB	JFK	SJU	204	1598	21	59	2023-04-18 21:00:00	Other
1258	10	31	836	840	-4	935	1007	YX	1727	N202JQ	EWR	BOS	32	200	8	40	2023-10-31 08:00:00	BOS
1259	2	25	2125	2130	-5	111	46	B6	34	N978JB	JFK	SAN	387	2446	21	30	2023-02-25 21:00:00	Other
1261	9	27	1155	1200	-5	1308	1324	YX	1953	N244JQ	LGA	BOS	35	184	12	0	2023-09-27 12:00:00	BOS
1265	11	8	1314	1316	-2	1553	1627	AA	643	N945NN	EWR	DFW	198	1372	13	16	2023-11-08 13:00:00	Other
1267	4	27	1455	1459	-4	1654	1705	DL	528	N331NB	LGA	MSP	146	1020	14	59	2023-04-27 14:00:00	Other
1268	3	23	2155	2159	-4	2251	2301	YX	1689	N220JQ	LGA	PVD	32	143	21	59	2023-03-23 21:00:00	Other
1270	3	11	1518	1523	-5	1652	1646	YX	1165	N859RW	EWR	BTV	48	266	15	23	2023-03-11 15:00:00	Other
1276	6	15	918	920	-2	1120	1119	9E	1666	N138EV	LGA	ILM	80	500	9	20	2023-06-15 09:00:00	Other
1281	8	21	1451	1455	-4	1639	1725	YX	1322	N218JQ	JFK	CLT	78	541	14	55	2023-08-21 14:00:00	CLT
1287	12	21	1501	1506	-5	1628	1705	YX	1260	N136HQ	JFK	RDU	65	427	15	6	2023-12-21 15:00:00	Other
1290	1	31	2017	2020	-3	2119	2131	9E	1632	N904XJ	LGA	PVD	26	143	20	20	2023-01-31 20:00:00	Other
1296	11	18	1226	1229	-3	1534	1542	AA	959	N323RM	JFK	MIA	155	1089	12	29	2023-11-18 12:00:00	MIA
1299	9	29	1126	1129	-3	1420	1356	DL	361	N864DN	JFK	ATL	122	760	11	29	2023-09-29 11:00:00	ATL
1301	3	28	1645	1650	-5	1822	1823	YX	1665	N225JQ	LGA	RIC	67	292	16	50	2023-03-28 16:00:00	Other
1303	6	16	858	900	-2	1012	1034	YX	1839	N235JQ	LGA	BOS	41	184	9	0	2023-06-16 09:00:00	BOS
1311	9	17	1535	1540	-5	1812	1800	9E	1662	N303PQ	LGA	CHS	115	641	15	40	2023-09-17 15:00:00	Other
1316	2	8	1127	1130	-3	1439	1434	DL	198	N841DN	JFK	LAS	348	2248	11	30	2023-02-08 11:00:00	Other
1324	8	31	1311	1315	-4	1431	1435	B6	131	N265JB	LGA	BOS	33	184	13	15	2023-08-31 13:00:00	BOS
1329	2	14	2127	2130	-3	2348	2359	9E	1290	N676CA	JFK	SAV	112	718	21	30	2023-02-14 21:00:00	Other
1332	3	21	1830	1832	-2	2142	2150	UA	762	N81449	EWR	SEA	330	2402	18	32	2023-03-21 18:00:00	Other
1345	4	20	1946	1950	-4	2241	2316	DL	538	N3735D	JFK	TPA	138	1005	19	50	2023-04-20 19:00:00	Other
1346	3	22	726	730	-4	905	917	AA	254	N953NN	LGA	ORD	123	733	7	30	2023-03-22 07:00:00	ORD
1354	9	2	1254	1259	-5	1405	1428	9E	1542	N937XJ	LGA	PWM	43	269	12	59	2023-09-02 12:00:00	Other
1356	10	30	1708	1710	-2	1936	1932	DL	871	N3761R	EWR	ATL	114	746	17	10	2023-10-30 17:00:00	ATL
1360	12	20	1805	1810	-5	2007	2029	DL	391	N118DY	LGA	MSP	154	1020	18	10	2023-12-20 18:00:00	Other
1362	8	1	1757	1759	-2	2027	2106	AA	35	N115NN	JFK	LAX	307	2475	17	59	2023-08-01 17:00:00	LAX
1363	8	13	1646	1650	-4	1854	1915	9E	1204	N306PQ	JFK	DTW	91	509	16	50	2023-08-13 16:00:00	Other
1364	8	27	1126	1129	-3	1339	1338	UA	213	N12754	EWR	SAV	107	708	11	29	2023-08-27 11:00:00	Other
1379	11	5	1713	1715	-2	1844	1854	UA	857	N852UA	LGA	ORD	115	733	17	15	2023-11-05 17:00:00	ORD
1383	5	21	928	930	-2	1133	1200	UA	850	N490UA	LGA	DEN	221	1620	9	30	2023-05-21 09:00:00	Other
1407	2	23	1350	1355	-5	1510	1519	YX	995	N743YX	EWR	ROC	51	246	13	55	2023-02-23 13:00:00	Other
1410	8	2	1003	1005	-2	1151	1204	B6	53	N193JB	JFK	DTW	83	509	10	5	2023-08-02 10:00:00	Other
1411	7	26	2050	2052	-2	29	111	DL	573	N831DN	JFK	SJU	200	1598	20	52	2023-07-26 20:00:00	Other
1415	8	1	1156	1200	-4	1445	1445	DL	167	N420DX	JFK	LAX	315	2475	12	0	2023-08-01 12:00:00	LAX
1425	1	4	925	930	-5	1135	1207	YX	1803	N241JQ	LGA	IND	104	660	9	30	2023-01-04 09:00:00	Other
1431	10	23	1856	1900	-4	2229	2308	UA	192	N37420	EWR	BQN	189	1585	19	0	2023-10-23 19:00:00	Other
1437	11	17	1355	1400	-5	1648	1717	UA	156	N78009	EWR	SFO	333	2565	14	0	2023-11-17 14:00:00	Other
1442	7	13	1950	1955	-5	2248	2249	DL	153	N930DZ	JFK	DEN	243	1626	19	55	2023-07-13 19:00:00	Other
1443	12	21	1224	1229	-5	1523	1544	YX	1208	N430YX	LGA	OKC	208	1341	12	29	2023-12-21 12:00:00	Other
1444	11	24	956	1000	-4	1136	1145	AA	748	N710UW	LGA	ORD	124	733	10	0	2023-11-24 10:00:00	ORD
1448	7	12	1015	1020	-5	1130	1157	9E	1324	N676CA	JFK	ROC	50	264	10	20	2023-07-12 10:00:00	Other
1451	6	2	654	659	-5	830	834	AA	627	N824NN	EWR	ORD	100	719	6	59	2023-06-02 06:00:00	ORD
1459	10	15	1412	1415	-3	1538	1538	B6	232	N3132J	JFK	MKE	110	745	14	15	2023-10-15 14:00:00	Other
1463	3	28	830	835	-5	1100	1101	9E	1517	N147PQ	LGA	SAV	121	722	8	35	2023-03-28 08:00:00	Other
1467	3	18	2125	2127	-2	46	2355	YX	1121	N723YX	EWR	MCI	174	1092	21	27	2023-03-18 21:00:00	Other
1476	6	19	2027	2030	-3	2222	2248	UA	307	N67846	EWR	PHX	276	2133	20	30	2023-06-19 20:00:00	Other
1484	4	29	1055	1100	-5	1502	1413	B6	191	N655JB	JFK	FLL	157	1069	11	0	2023-04-29 11:00:00	FLL
1488	10	3	1526	1530	-4	1723	1748	B6	798	N2060J	JFK	MCI	144	1113	15	30	2023-10-03 15:00:00	Other
1489	4	4	640	644	-4	830	854	YX	1134	N441YX	LGA	DTW	88	502	6	44	2023-04-04 06:00:00	Other
1492	3	6	1158	1203	-5	1444	1445	UA	901	N453UA	LGA	DEN	256	1620	12	3	2023-03-06 12:00:00	Other
1495	2	9	1656	1659	-3	1854	1910	9E	1391	N176PQ	LGA	ILM	80	500	16	59	2023-02-09 16:00:00	Other
1498	12	1	1427	1429	-2	1802	1809	B6	539	N980JT	JFK	SFO	368	2586	14	29	2023-12-01 14:00:00	Other
1508	10	4	1917	1921	-4	2127	2138	YX	1736	N243JQ	LGA	OMA	166	1148	19	21	2023-10-04 19:00:00	Other
1509	12	24	1042	1045	-3	1224	1230	YX	1815	N209JQ	JFK	ORD	125	740	10	45	2023-12-24 10:00:00	ORD
1511	5	16	1958	2000	-2	2210	2213	9E	1385	N602LR	LGA	CAE	93	617	20	0	2023-05-16 20:00:00	Other
1513	11	18	1308	1312	-4	1458	1509	YX	1055	N748YX	EWR	CMH	76	463	13	12	2023-11-18 13:00:00	Other
1522	8	23	555	600	-5	840	916	AA	362	N959NN	LGA	MIA	135	1096	6	0	2023-08-23 06:00:00	MIA
1532	7	1	1320	1325	-5	1440	1437	YX	1377	N228JQ	EWR	BOS	45	200	13	25	2023-07-01 13:00:00	BOS
1534	8	21	756	800	-4	1034	1115	AA	478	N335RT	JFK	MIA	134	1089	8	0	2023-08-21 08:00:00	MIA
1538	1	6	1800	1805	-5	1930	2004	9E	1525	N309PQ	LGA	CLE	70	419	18	5	2023-01-06 18:00:00	Other
1544	11	27	633	635	-2	811	833	YX	1876	N240JQ	LGA	CMH	82	479	6	35	2023-11-27 06:00:00	Other
1548	3	17	1957	1959	-2	2119	2133	YX	1193	N745YX	EWR	PIT	62	319	19	59	2023-03-17 19:00:00	Other
1550	3	17	928	930	-2	1119	1119	9E	1474	N279PQ	JFK	CLE	81	425	9	30	2023-03-17 09:00:00	Other
1551	11	29	1010	1012	-2	1222	1225	OO	1188	N317SY	LGA	MEM	162	963	10	12	2023-11-29 10:00:00	Other
1553	8	8	726	729	-3	914	910	AA	778	N865NN	LGA	ORD	106	733	7	29	2023-08-08 07:00:00	ORD
1561	4	13	1527	1530	-3	1639	1700	YX	1018	N754YX	EWR	PIT	51	319	15	30	2023-04-13 15:00:00	Other
1571	10	16	1835	1840	-5	1943	1955	YX	1066	N736YX	EWR	ALB	30	143	18	40	2023-10-16 18:00:00	Other
1572	7	1	717	719	-2	953	1027	UA	503	N17294	EWR	FLL	133	1065	7	19	2023-07-01 07:00:00	FLL
1577	9	15	1926	1929	-3	2222	2226	DL	231	N315DU	LGA	DFW	184	1389	19	29	2023-09-15 19:00:00	Other
1586	10	31	1953	1958	-5	2259	2308	DL	315	N3752	LGA	MIA	154	1096	19	58	2023-10-31 19:00:00	MIA
1598	4	3	1025	1030	-5	1154	1210	AA	150	N939NN	LGA	ORD	128	733	10	30	2023-04-03 10:00:00	ORD
1609	9	19	1433	1436	-3	1610	1629	YX	1875	N818MD	LGA	MEM	134	963	14	36	2023-09-19 14:00:00	Other
1626	6	17	1159	1204	-5	1408	1419	DL	983	N395DN	EWR	ATL	100	746	12	4	2023-06-17 12:00:00	ATL
1632	6	11	625	630	-5	819	837	AA	348	N845NN	JFK	CLT	81	541	6	30	2023-06-11 06:00:00	CLT
1635	4	13	857	859	-2	1157	1204	UA	377	N27271	EWR	PBI	160	1023	8	59	2023-04-13 08:00:00	Other
1637	7	8	925	930	-5	1101	1113	AA	798	N845NN	LGA	ORD	113	733	9	30	2023-07-08 09:00:00	ORD
1638	10	18	1028	1030	-2	1326	1343	B6	668	N510JB	LGA	RSW	146	1080	10	30	2023-10-18 10:00:00	Other
1643	3	16	831	835	-4	1045	1115	DL	553	N188DN	JFK	ATL	101	760	8	35	2023-03-16 08:00:00	ATL
1651	10	28	700	705	-5	929	1000	DL	327	N360NW	LGA	PBI	134	1035	7	5	2023-10-28 07:00:00	Other
1654	1	13	1227	1229	-2	1347	1355	YX	1808	N232JQ	LGA	PWM	50	269	12	29	2023-01-13 12:00:00	Other
1660	2	20	556	600	-4	732	717	YX	1530	N238JQ	LGA	BOS	43	184	6	0	2023-02-20 06:00:00	BOS
1669	1	27	1930	1935	-5	2125	2206	9E	1518	N903XJ	JFK	MSP	152	1029	19	35	2023-01-27 19:00:00	Other
1670	6	21	1157	1201	-4	1332	1339	9E	1557	N293PQ	JFK	BUF	58	301	12	1	2023-06-21 12:00:00	Other
1671	8	2	1655	1659	-4	1818	1834	YX	1040	N426YX	JFK	ORF	55	290	16	59	2023-08-02 16:00:00	Other
1678	2	7	1020	1025	-5	1330	1354	B6	302	N565JB	JFK	SAT	232	1587	10	25	2023-02-07 10:00:00	Other
1689	12	17	1238	1241	-3	1546	1544	UA	814	N68891	EWR	TPA	156	997	12	41	2023-12-17 12:00:00	Other
1690	11	8	831	836	-5	1036	1103	9E	1526	N930XJ	LGA	TYS	95	647	8	36	2023-11-08 08:00:00	Other
1692	9	27	1058	1100	-2	1316	1327	UA	241	N458UA	EWR	ATL	109	746	11	0	2023-09-27 11:00:00	ATL
1697	3	27	947	950	-3	1253	1244	B6	229	N779JB	LGA	MCO	140	950	9	50	2023-03-27 09:00:00	MCO
1699	5	27	925	930	-5	1032	1114	AA	941	N812AW	LGA	ORD	102	733	9	30	2023-05-27 09:00:00	ORD
1701	6	4	2007	2011	-4	2214	2254	YX	1337	N401YX	JFK	IND	91	665	20	11	2023-06-04 20:00:00	Other
1703	10	12	1756	1759	-3	2122	2110	B6	944	N993JE	JFK	LAX	345	2475	17	59	2023-10-12 17:00:00	LAX
1706	4	23	1455	1500	-5	1751	1814	AA	766	N897NN	LGA	MIA	155	1096	15	0	2023-04-23 15:00:00	MIA
1726	9	12	956	959	-3	1133	1156	YX	1806	N201JQ	JFK	CMH	77	483	9	59	2023-09-12 09:00:00	Other
1732	12	25	730	735	-5	1026	1057	DL	813	N324DX	JFK	FLL	152	1069	7	35	2023-12-25 07:00:00	FLL
1736	10	26	1953	1956	-3	2214	2221	DL	918	N3754A	EWR	ATL	100	746	19	56	2023-10-26 19:00:00	ATL
1737	7	29	1928	1930	-2	2255	2229	B6	551	N517JB	LGA	PBI	170	1035	19	30	2023-07-29 19:00:00	Other
1746	6	8	1241	1245	-4	1601	1608	B6	616	N2044J	JFK	FLL	173	1069	12	45	2023-06-08 12:00:00	FLL
1748	5	9	1118	1120	-2	1410	1435	DL	511	N3765	JFK	MIA	149	1089	11	20	2023-05-09 11:00:00	MIA
1749	2	27	726	730	-4	1004	1023	DL	182	N3773D	LGA	DEN	245	1620	7	30	2023-02-27 07:00:00	Other
1750	3	1	558	600	-2	827	807	YX	1249	N403YX	LGA	CMH	96	479	6	0	2023-03-01 06:00:00	Other
1758	8	30	1924	1929	-5	2124	2143	9E	1215	N935XJ	JFK	RDU	75	427	19	29	2023-08-30 19:00:00	Other
1760	2	22	1005	1010	-5	1159	1219	AA	100	N552UW	JFK	CLT	87	541	10	10	2023-02-22 10:00:00	CLT
1761	3	28	1912	1915	-3	2028	2045	WN	334	N8321D	LGA	MDW	117	725	19	15	2023-03-28 19:00:00	Other
1765	4	11	600	605	-5	834	901	UA	780	N37419	EWR	TPA	135	997	6	5	2023-04-11 06:00:00	Other
1767	6	16	656	700	-4	950	1000	DL	201	N178DZ	JFK	LAX	309	2475	7	0	2023-06-16 07:00:00	LAX
1768	7	24	940	945	-5	1105	1135	9E	1106	N917XJ	LGA	BGR	51	378	9	45	2023-07-24 09:00:00	Other
1770	5	10	519	523	-4	756	820	UA	177	N47280	EWR	IAH	187	1400	5	23	2023-05-10 05:00:00	Other
1772	8	12	1157	1200	-3	1347	1348	9E	1235	N905XJ	JFK	RDU	68	427	12	0	2023-08-12 12:00:00	Other
1781	3	29	1558	1600	-2	1705	1723	YX	1630	N215JQ	LGA	BOS	34	184	16	0	2023-03-29 16:00:00	BOS
1790	10	24	1025	1029	-4	1129	1203	YX	1810	N215JQ	LGA	DCA	43	214	10	29	2023-10-24 10:00:00	Other
1794	10	22	1856	1859	-3	2141	2206	UA	166	N24706	EWR	SNA	324	2434	18	59	2023-10-22 18:00:00	Other
1796	2	4	702	705	-3	946	1015	DL	605	N391DN	LGA	FLL	147	1076	7	5	2023-02-04 07:00:00	FLL
1798	11	22	1934	1937	-3	2142	2245	B6	412	N989JT	JFK	LAS	285	2248	19	37	2023-11-22 19:00:00	Other
1802	3	23	726	730	-4	901	857	YX	1691	N205JQ	LGA	BUF	62	292	7	30	2023-03-23 07:00:00	Other
1804	9	20	1157	1200	-3	1446	1450	DL	187	N412DX	JFK	LAX	323	2475	12	0	2023-09-20 12:00:00	LAX
1806	10	3	1025	1029	-4	1136	1155	AA	186	N819AW	LGA	BNA	101	764	10	29	2023-10-03 10:00:00	Other
1813	2	16	1025	1030	-5	1134	1135	9E	1447	N153PQ	JFK	BWI	41	184	10	30	2023-02-16 10:00:00	Other
1818	8	12	530	535	-5	804	810	B6	93	N506JB	EWR	MCO	123	937	5	35	2023-08-12 05:00:00	MCO
1826	8	12	1456	1500	-4	1648	1710	YX	838	N740YX	EWR	GRR	94	605	15	0	2023-08-12 15:00:00	Other
1827	9	28	1350	1355	-5	1527	1538	AA	761	N826AW	LGA	RDU	74	431	13	55	2023-09-28 13:00:00	Other
1836	5	15	937	941	-4	1123	1153	UA	546	N415UA	EWR	CHS	82	628	9	41	2023-05-15 09:00:00	Other
1838	5	22	2226	2230	-4	9	4	9E	1526	N932XJ	JFK	SYR	41	209	22	30	2023-05-22 22:00:00	Other
1845	5	10	1110	1115	-5	1350	1414	B6	204	N796JB	EWR	PBI	133	1023	11	15	2023-05-10 11:00:00	Other
1849	10	14	2055	2100	-5	2213	2226	B6	62	N323JB	JFK	BTV	44	266	21	0	2023-10-14 21:00:00	Other
1850	5	22	1228	1230	-2	1523	1527	DL	299	N112DU	LGA	DFW	191	1389	12	30	2023-05-22 12:00:00	Other
1859	9	18	827	830	-3	1101	1123	UA	134	N12003	EWR	LAX	304	2454	8	30	2023-09-18 08:00:00	LAX
1875	4	4	1157	1159	-2	1436	1510	UA	166	N402UA	EWR	FLL	141	1065	11	59	2023-04-04 11:00:00	FLL
1878	8	2	842	846	-4	1006	1006	YX	902	N640RW	EWR	ALB	31	143	8	46	2023-08-02 08:00:00	Other
1883	5	5	1858	1900	-2	2008	2028	YX	1023	N865RW	EWR	DCA	37	199	19	0	2023-05-05 19:00:00	Other
1884	9	1	1657	1659	-2	1808	1823	UA	436	N15710	EWR	BOS	37	200	16	59	2023-09-01 16:00:00	BOS
1886	10	12	1702	1707	-5	1925	1932	DL	871	N935AT	EWR	ATL	116	746	17	7	2023-10-12 17:00:00	ATL
1890	3	25	606	610	-4	729	730	NK	282	N521NK	EWR	PIT	61	319	6	10	2023-03-25 06:00:00	Other
1906	4	16	858	900	-2	1127	1144	9E	1342	N331PQ	JFK	JAX	118	828	9	0	2023-04-16 09:00:00	Other
1911	7	4	1535	1540	-5	1819	1846	DL	336	N141DU	LGA	IAH	194	1416	15	40	2023-07-04 15:00:00	Other
1919	8	3	700	705	-5	903	919	DL	231	N913DU	JFK	PHX	276	2153	7	5	2023-08-03 07:00:00	Other
1924	7	19	1357	1359	-2	1647	1646	AA	533	N907AN	EWR	DFW	192	1372	13	59	2023-07-19 13:00:00	Other
1930	8	30	658	700	-2	930	912	UA	116	N27477	EWR	DEN	229	1605	7	0	2023-08-30 07:00:00	Other
1933	12	11	853	856	-3	1046	1056	9E	1378	N482PX	LGA	CLE	70	419	8	56	2023-12-11 08:00:00	Other
1934	7	6	1534	1539	-5	1749	1804	B6	737	N193JB	JFK	CHS	90	636	15	39	2023-07-06 15:00:00	Other
1935	12	30	1418	1422	-4	1531	1540	B6	33	N354JB	JFK	SYR	47	209	14	22	2023-12-30 14:00:00	Other
1936	4	3	648	650	-2	753	800	B6	200	N323JB	JFK	BOS	35	187	6	50	2023-04-03 06:00:00	BOS
1944	1	18	555	600	-5	755	754	YX	1857	N823MD	LGA	STL	156	888	6	0	2023-01-18 06:00:00	Other
1949	7	12	1127	1132	-5	1320	1339	AA	616	N916AN	LGA	CLT	77	544	11	32	2023-07-12 11:00:00	CLT
1950	3	31	2115	2120	-5	2219	2216	9E	1443	N195PQ	LGA	ALB	36	136	21	20	2023-03-31 21:00:00	Other
1965	3	6	1931	1935	-4	2153	2202	9E	1550	N909XJ	JFK	DTW	104	509	19	35	2023-03-06 19:00:00	Other
1971	8	1	1708	1711	-3	1829	1847	UA	490	N822UA	LGA	ORD	108	733	17	11	2023-08-01 17:00:00	ORD
1972	3	23	1755	1759	-4	1913	1933	B6	2	N603JB	JFK	BUF	61	301	17	59	2023-03-23 17:00:00	Other
1979	2	2	1239	1241	-2	1512	1441	9E	1328	N905XJ	JFK	CLT	107	541	12	41	2023-02-02 12:00:00	CLT
1992	6	8	1056	1100	-4	1327	1349	AA	778	N800NN	LGA	DFW	177	1389	11	0	2023-06-08 11:00:00	Other
1995	4	15	754	759	-5	905	927	YX	940	N752YX	EWR	BTV	42	266	7	59	2023-04-15 07:00:00	Other
2005	7	7	805	810	-5	937	955	9E	1198	N337PQ	JFK	RIC	51	288	8	10	2023-07-07 08:00:00	Other
2012	9	27	1846	1850	-4	2058	2108	9E	1774	N147PQ	LGA	MCI	160	1107	18	50	2023-09-27 18:00:00	Other
2013	4	20	1106	1110	-4	1224	1225	OO	1054	N614CZ	EWR	BOS	41	200	11	10	2023-04-20 11:00:00	BOS
2020	1	14	837	840	-3	1033	1015	YX	1319	N106HQ	JFK	BOS	40	187	8	40	2023-01-14 08:00:00	BOS
2038	12	13	1557	1559	-2	1905	1919	B6	308	N984JB	JFK	LAX	340	2475	15	59	2023-12-13 15:00:00	LAX
2041	4	8	1255	1259	-4	1355	1420	YX	1539	N244JQ	LGA	BOS	33	184	12	59	2023-04-08 12:00:00	BOS
2053	11	18	558	600	-2	831	908	UA	896	N855UA	LGA	IAH	195	1416	6	0	2023-11-18 06:00:00	Other
2055	11	10	938	940	-2	1238	1236	NK	1029	N979NK	EWR	MCO	140	937	9	40	2023-11-10 09:00:00	MCO
2056	4	21	2045	2050	-5	2154	2212	9E	1195	N490PX	LGA	SCE	39	208	20	50	2023-04-21 20:00:00	Other
2062	2	3	1257	1300	-3	1420	1425	YX	1575	N214JQ	LGA	BOS	39	184	13	0	2023-02-03 13:00:00	BOS
2072	5	10	827	829	-2	1121	1125	AA	339	N943NN	LGA	DFW	183	1389	8	29	2023-05-10 08:00:00	Other
2077	8	3	626	630	-4	757	815	9E	1261	N922XJ	LGA	CLE	65	419	6	30	2023-08-03 06:00:00	Other
2078	5	8	1226	1229	-3	1507	1521	DL	528	N393DN	JFK	MCO	136	944	12	29	2023-05-08 12:00:00	MCO
2083	4	12	1833	1838	-5	2007	2021	UA	422	N78285	EWR	ORD	105	719	18	38	2023-04-12 18:00:00	ORD
2091	4	8	1725	1730	-5	1955	1955	9E	1222	N349PQ	JFK	MCI	172	1113	17	30	2023-04-08 17:00:00	Other
2094	6	23	556	600	-4	806	820	UA	446	N497UA	EWR	ATL	110	746	6	0	2023-06-23 06:00:00	ATL
2101	3	21	1817	1819	-2	2129	2120	B6	280	N656JB	JFK	LAS	340	2248	18	19	2023-03-21 18:00:00	Other
2103	8	17	1326	1330	-4	1520	1534	YX	1016	N433YX	LGA	CAE	96	617	13	30	2023-08-17 13:00:00	Other
2107	3	8	632	635	-3	921	915	B6	801	N828JB	LGA	DEN	260	1620	6	35	2023-03-08 06:00:00	Other
2112	12	2	1744	1746	-2	2008	2029	DL	557	N876DN	JFK	ATL	125	760	17	46	2023-12-02 17:00:00	ATL
2119	6	6	628	630	-2	858	921	UA	709	N37295	EWR	TPA	130	997	6	30	2023-06-06 06:00:00	Other
2122	4	8	751	755	-4	905	924	YX	1213	N870RW	LGA	CHO	59	305	7	55	2023-04-08 07:00:00	Other
2128	10	25	1137	1140	-3	1358	1400	DL	847	N101DU	LGA	MSY	160	1183	11	40	2023-10-25 11:00:00	Other
2129	9	26	606	608	-2	753	755	DL	780	N991AT	EWR	DTW	74	488	6	8	2023-09-26 06:00:00	Other
2133	11	6	2215	2220	-5	2319	2342	OO	1190	N247SY	JFK	BOS	42	187	22	20	2023-11-06 22:00:00	BOS
2134	6	18	1946	1950	-4	2102	2125	AA	978	N873NN	EWR	ORD	107	719	19	50	2023-06-18 19:00:00	ORD
2135	10	3	1455	1459	-4	1820	1839	DL	245	N703TW	JFK	SFO	349	2586	14	59	2023-10-03 14:00:00	Other
2136	2	5	1326	1330	-4	1438	1453	YX	1620	N228JQ	JFK	PWM	47	273	13	30	2023-02-05 13:00:00	Other
2138	10	13	755	800	-5	1004	1009	9E	1488	N925XJ	JFK	CLT	84	541	8	0	2023-10-13 08:00:00	CLT
2146	3	7	1657	1659	-2	1920	1910	9E	1472	N302PQ	LGA	ILM	76	500	16	59	2023-03-07 16:00:00	Other
2149	10	30	625	630	-5	919	931	UA	924	N17311	EWR	TPA	143	997	6	30	2023-10-30 06:00:00	Other
2150	11	25	2018	2020	-2	2355	2357	UA	720	N19117	EWR	SFO	360	2565	20	20	2023-11-25 20:00:00	Other
2152	10	12	1056	1059	-3	1320	1342	DL	267	N390DN	LGA	ATL	117	762	10	59	2023-10-12 10:00:00	ATL
2154	8	2	850	855	-5	1103	1114	9E	1106	N479PX	LGA	GRR	93	618	8	55	2023-08-02 08:00:00	Other
2157	12	30	1603	1608	-5	1738	1758	9E	1352	N186PQ	JFK	RIC	53	288	16	8	2023-12-30 16:00:00	Other
2168	3	1	1245	1250	-5	1425	1430	9E	1337	N329PQ	LGA	MKE	132	738	12	50	2023-03-01 12:00:00	Other
2170	4	9	1545	1550	-5	1657	1730	B6	258	N3023J	JFK	MKE	107	745	15	50	2023-04-09 15:00:00	Other
2175	12	15	1825	1830	-5	2019	2056	9E	1633	N297PQ	LGA	GSP	94	610	18	30	2023-12-15 18:00:00	Other
2177	8	29	1626	1629	-3	1741	1740	B6	733	N283JB	LGA	MVY	37	175	16	29	2023-08-29 16:00:00	Other
2200	5	11	725	730	-5	1035	1055	AS	15	N492AS	JFK	SFO	346	2586	7	30	2023-05-11 07:00:00	Other
2208	6	17	946	950	-4	1114	1146	9E	1723	N302PQ	LGA	CLE	66	419	9	50	2023-06-17 09:00:00	Other
2210	3	15	928	930	-2	1236	1303	AA	831	N101NN	JFK	SNA	333	2454	9	30	2023-03-15 09:00:00	Other
2211	3	27	1408	1410	-2	1622	1611	YX	1179	N730YX	EWR	ILM	82	488	14	10	2023-03-27 14:00:00	Other
2213	2	14	1457	1459	-2	1616	1628	B6	946	N249JB	JFK	BUF	61	301	14	59	2023-02-14 14:00:00	Other
2215	2	13	542	545	-3	822	853	NK	212	N637NK	EWR	FLL	139	1065	5	45	2023-02-13 05:00:00	FLL
2225	10	4	603	605	-2	843	845	WN	1228	N412WN	LGA	HOU	191	1428	6	5	2023-10-04 06:00:00	Other
2227	10	12	608	610	-2	746	746	DL	415	N117DU	LGA	ORD	125	733	6	10	2023-10-12 06:00:00	ORD
2231	5	16	1427	1430	-3	1643	1653	B6	806	N3123J	JFK	MCI	167	1113	14	30	2023-05-16 14:00:00	Other
2232	11	8	920	925	-5	1218	1233	UA	570	N37252	EWR	FLL	143	1065	9	25	2023-11-08 09:00:00	FLL
2237	10	26	555	600	-5	748	805	AA	215	N162UW	LGA	CLT	79	544	6	0	2023-10-26 06:00:00	CLT
2241	4	17	731	735	-4	911	948	DL	285	N348NB	JFK	MSP	135	1029	7	35	2023-04-17 07:00:00	Other
2243	4	12	725	729	-4	905	929	UA	453	N808UA	EWR	CLT	72	529	7	29	2023-04-12 07:00:00	CLT
2247	7	25	648	650	-2	952	957	AA	745	N817NN	LGA	MIA	162	1096	6	50	2023-07-25 06:00:00	MIA
2249	7	29	627	630	-3	920	922	B6	46	N529JB	JFK	SRQ	142	1041	6	30	2023-07-29 06:00:00	Other
2250	1	20	947	950	-3	1208	1251	UA	840	N54711	EWR	JAC	247	1874	9	50	2023-01-20 09:00:00	Other
2256	3	19	1154	1158	-4	1420	1428	UA	262	N496UA	EWR	ATL	122	746	11	58	2023-03-19 11:00:00	ATL
2258	7	13	1121	1124	-3	1409	1433	DL	169	N875DN	JFK	SEA	322	2422	11	24	2023-07-13 11:00:00	Other
2265	7	19	1956	2000	-4	2153	2222	YX	862	N721YX	EWR	IND	91	645	20	0	2023-07-19 20:00:00	Other
2266	9	2	625	630	-5	850	931	AA	835	N949NN	JFK	DFW	172	1391	6	30	2023-09-02 06:00:00	Other
2267	12	1	555	600	-5	759	813	DL	529	N354DN	LGA	MSP	162	1020	6	0	2023-12-01 06:00:00	Other
2269	3	29	1257	1259	-2	1550	1548	AA	985	N315SD	JFK	PHX	325	2153	12	59	2023-03-29 12:00:00	Other
2271	12	13	1551	1555	-4	1849	1905	B6	735	N976JT	EWR	LAX	327	2454	15	55	2023-12-13 15:00:00	LAX
2279	3	7	1411	1415	-4	1542	1541	9E	1580	N908XJ	JFK	BTV	54	266	14	15	2023-03-07 14:00:00	Other
2284	12	4	1857	1859	-2	2058	2106	AA	618	N740UW	LGA	CLT	93	544	18	59	2023-12-04 18:00:00	CLT
2286	9	2	727	730	-3	942	1003	DL	184	N519DT	JFK	LAS	276	2248	7	30	2023-09-02 07:00:00	Other
2289	2	15	1624	1629	-5	1951	1955	AA	95	N107NN	JFK	LAX	359	2475	16	29	2023-02-15 16:00:00	LAX
2292	9	19	645	650	-5	935	1015	DL	113	N103DY	JFK	SLC	266	1990	6	50	2023-09-19 06:00:00	Other
2295	9	8	910	915	-5	1019	1035	B6	183	N192JB	JFK	PWM	47	273	9	15	2023-09-08 09:00:00	Other
2297	4	12	542	545	-3	834	851	AA	409	N866NN	EWR	MIA	149	1085	5	45	2023-04-12 05:00:00	MIA
2315	9	14	1554	1557	-3	1814	1839	DL	311	N506DA	JFK	LAS	290	2248	15	57	2023-09-14 15:00:00	Other
2322	4	2	726	729	-3	843	851	YX	961	N748YX	EWR	ROC	46	246	7	29	2023-04-02 07:00:00	Other
2325	6	17	825	830	-5	1125	1140	UA	689	N17139	EWR	SEA	321	2402	8	30	2023-06-17 08:00:00	Other
2326	6	10	640	645	-5	910	937	YX	1149	N647RW	EWR	DFW	184	1372	6	45	2023-06-10 06:00:00	Other
2328	11	7	646	650	-4	817	832	YX	1793	N879RW	LGA	PIT	68	335	6	50	2023-11-07 06:00:00	Other
2333	5	21	1210	1215	-5	1411	1422	YX	1229	N871RW	LGA	DAY	85	549	12	15	2023-05-21 12:00:00	Other
2335	12	16	1656	1659	-3	2024	2028	AS	4	N247AK	JFK	SEA	340	2422	16	59	2023-12-16 16:00:00	Other
2337	3	29	1345	1350	-5	1650	1648	B6	570	N623JB	JFK	MCO	138	944	13	50	2023-03-29 13:00:00	MCO
2338	11	29	2226	2230	-4	2341	2358	9E	1447	N187GJ	JFK	PWM	47	273	22	30	2023-11-29 22:00:00	Other
2339	1	6	1115	1119	-4	1336	1355	9E	1403	N335PQ	LGA	AVL	96	599	11	19	2023-01-06 11:00:00	Other
2342	6	8	556	600	-4	736	746	DL	803	N932AT	EWR	DTW	80	488	6	0	2023-06-08 06:00:00	Other
2344	3	22	1103	1108	-5	1353	1431	DL	636	N315DN	LGA	MIA	144	1096	11	8	2023-03-22 11:00:00	MIA
2347	10	16	1209	1211	-2	1329	1345	YX	1795	N238JQ	JFK	BUF	56	301	12	11	2023-10-16 12:00:00	Other
2359	9	2	1521	1526	-5	1642	1713	9E	1561	N337PQ	JFK	BNA	97	765	15	26	2023-09-02 15:00:00	Other
2366	4	18	1812	1815	-3	2027	2057	DL	187	N314DN	LGA	ATL	111	762	18	15	2023-04-18 18:00:00	ATL
2369	3	20	1412	1417	-5	1615	1634	9E	1556	N294PQ	LGA	CVG	102	585	14	17	2023-03-20 14:00:00	Other
2373	4	10	1317	1319	-2	1414	1435	B6	300	N179JB	JFK	BOS	38	187	13	19	2023-04-10 13:00:00	BOS
2375	3	27	1856	1859	-3	2053	2058	YX	1189	N859RW	EWR	CMH	82	463	18	59	2023-03-27 18:00:00	Other
2380	5	11	1657	1700	-3	1831	1909	DL	885	N358NB	LGA	DTW	78	502	17	0	2023-05-11 17:00:00	Other
2388	3	5	1854	1859	-5	2052	2100	YX	1091	N857RW	EWR	CMH	78	463	18	59	2023-03-05 18:00:00	Other
2402	2	17	626	630	-4	945	1020	AA	32	N116AN	JFK	SFO	355	2586	6	30	2023-02-17 06:00:00	Other
2403	3	25	1053	1056	-3	1240	1315	DL	430	N334NW	LGA	MSP	144	1020	10	56	2023-03-25 10:00:00	Other
2406	8	22	1556	1559	-3	1717	1734	YX	899	N753YX	EWR	PIT	57	319	15	59	2023-08-22 15:00:00	Other
2407	1	16	2040	2045	-5	2205	2214	9E	1555	N607LR	LGA	ORF	47	296	20	45	2023-01-16 20:00:00	Other
2408	10	31	1651	1655	-4	1848	1847	YX	1028	N862RW	EWR	RDU	84	416	16	55	2023-10-31 16:00:00	Other
2413	11	25	555	600	-5	900	921	DL	432	N117DU	LGA	IAH	210	1416	6	0	2023-11-25 06:00:00	Other
2419	11	8	1607	1610	-3	1930	1932	UA	585	N18119	EWR	LAX	353	2454	16	10	2023-11-08 16:00:00	LAX
2422	6	13	1152	1155	-3	1437	1450	DL	619	N105DX	LGA	MCO	136	950	11	55	2023-06-13 11:00:00	MCO
2424	6	2	642	645	-3	923	935	AA	963	N866NN	JFK	DFW	192	1391	6	45	2023-06-02 06:00:00	Other
2432	3	7	757	759	-2	1047	1054	UA	666	N37293	EWR	MCO	136	937	7	59	2023-03-07 07:00:00	MCO
2443	8	14	708	710	-2	909	910	9E	1105	N330PQ	JFK	DTW	86	509	7	10	2023-08-14 07:00:00	Other
2450	2	5	1824	1829	-5	2050	2050	9E	1292	N195PQ	LGA	CHS	112	641	18	29	2023-02-05 18:00:00	Other
2453	1	21	954	959	-5	1134	1143	9E	1601	N187GJ	JFK	PIT	63	340	9	59	2023-01-21 09:00:00	Other
2455	7	14	557	600	-3	830	837	UA	170	N17254	EWR	IAH	188	1400	6	0	2023-07-14 06:00:00	Other
2457	2	18	1947	1950	-3	2118	2153	9E	1434	N908XJ	JFK	RDU	69	427	19	50	2023-02-18 19:00:00	Other
2462	12	22	1324	1329	-5	1613	1647	UA	568	N889UA	EWR	AUS	208	1504	13	29	2023-12-22 13:00:00	Other
2463	6	7	856	900	-4	1004	1025	WN	57	N8558Z	LGA	MDW	106	725	9	0	2023-06-07 09:00:00	Other
2468	9	23	1255	1259	-4	1418	1403	9E	1431	N306PQ	JFK	ITH	45	189	12	59	2023-09-23 12:00:00	Other
2474	4	19	2127	2130	-3	2307	2309	9E	1199	N296PQ	JFK	RIC	52	288	21	30	2023-04-19 21:00:00	Other
2477	6	13	658	700	-2	851	914	UA	138	N67846	EWR	DEN	209	1605	7	0	2023-06-13 07:00:00	Other
2479	12	25	556	600	-4	747	836	UA	488	N13113	EWR	DEN	210	1605	6	0	2023-12-25 06:00:00	Other
2482	1	27	813	815	-2	1359	1324	DL	793	N6704Z	JFK	STT	197	1623	8	15	2023-01-27 08:00:00	Other
2484	1	17	655	700	-5	952	1027	DL	1008	N853DN	JFK	RSW	157	1074	7	0	2023-01-17 07:00:00	Other
2486	6	22	1156	1200	-4	1349	1401	YX	1766	N878RW	LGA	CMH	75	479	12	0	2023-06-22 12:00:00	Other
2491	11	26	1113	1118	-5	1321	1309	YX	1301	N422YX	JFK	RDU	84	427	11	18	2023-11-26 11:00:00	Other
2495	9	5	1034	1037	-3	1212	1158	9E	1591	N348PQ	JFK	BTV	51	266	10	37	2023-09-05 10:00:00	Other
2508	1	24	753	755	-2	921	920	YX	1193	N745YX	EWR	PWM	51	284	7	55	2023-01-24 07:00:00	Other
2510	9	3	1858	1900	-2	2000	2030	UA	627	N14735	EWR	BNA	98	748	19	0	2023-09-03 19:00:00	Other
2513	5	22	943	945	-2	1237	1326	DL	97	N710TW	JFK	SFO	326	2586	9	45	2023-05-22 09:00:00	Other
2515	12	7	1957	1959	-2	2253	2338	AA	943	N336TM	LGA	MIA	145	1096	19	59	2023-12-07 19:00:00	MIA
2519	8	11	1157	1159	-2	1333	1351	YX	832	N651RW	EWR	CMH	73	463	11	59	2023-08-11 11:00:00	Other
2522	9	13	1057	1059	-2	1245	1300	NK	627	N915NK	LGA	DTW	81	502	10	59	2023-09-13 10:00:00	Other
2523	7	13	2025	2029	-4	28	2345	B6	629	N565JB	LGA	RSW	141	1080	20	29	2023-07-13 20:00:00	Other
2524	5	13	1927	1932	-5	2137	2206	9E	1291	N602LR	JFK	MSP	155	1029	19	32	2023-05-13 19:00:00	Other
2525	3	24	1255	1259	-4	1407	1422	9E	1530	N228PQ	LGA	SCE	49	208	12	59	2023-03-24 12:00:00	Other
2531	1	31	1026	1030	-4	1402	1357	AA	3	N105NN	JFK	LAX	365	2475	10	30	2023-01-31 10:00:00	LAX
2532	5	19	1053	1056	-3	1333	1348	UA	657	N17289	EWR	MCO	128	937	10	56	2023-05-19 10:00:00	MCO
2534	6	5	2055	2059	-4	2223	2231	YX	1842	N210JQ	LGA	RIC	49	292	20	59	2023-06-05 20:00:00	Other
2536	6	5	1554	1559	-5	1724	1726	YX	1220	N722YX	EWR	PWM	52	284	15	59	2023-06-05 15:00:00	Other
2542	3	25	1927	1930	-3	2050	2106	AA	125	N966NN	LGA	ORD	114	733	19	30	2023-03-25 19:00:00	ORD
2543	4	18	1155	1200	-5	1322	1333	YX	1132	N412YX	LGA	BNA	117	764	12	0	2023-04-18 12:00:00	Other
2544	6	8	1558	1600	-2	1701	1737	YX	1798	N246JQ	LGA	BOS	33	184	16	0	2023-06-08 16:00:00	BOS
2554	11	15	2058	2100	-2	2204	2212	DL	206	N118DU	LGA	BOS	43	184	21	0	2023-11-15 21:00:00	BOS
2560	8	1	815	819	-4	929	958	YX	872	N743YX	EWR	PIT	54	319	8	19	2023-08-01 08:00:00	Other
2564	5	5	1047	1050	-3	1215	1240	WN	963	N8689C	LGA	STL	128	888	10	50	2023-05-05 10:00:00	Other
2570	2	22	727	730	-3	948	921	B6	406	N274JB	JFK	ORD	156	740	7	30	2023-02-22 07:00:00	ORD
2572	1	18	1125	1130	-5	1412	1434	DL	209	N856DN	JFK	LAS	318	2248	11	30	2023-01-18 11:00:00	Other
2582	11	14	1731	1736	-5	1951	2013	DL	317	N3768	LGA	DEN	223	1620	17	36	2023-11-14 17:00:00	Other
2589	6	28	1452	1457	-5	1733	1740	YX	1882	N215JQ	JFK	JAX	108	828	14	57	2023-06-28 14:00:00	Other
2596	7	23	533	535	-2	823	807	B6	100	N524JB	EWR	MCO	137	937	5	35	2023-07-23 05:00:00	MCO
2597	3	23	952	955	-3	1131	1139	OO	1190	N250SY	JFK	PIT	76	340	9	55	2023-03-23 09:00:00	Other
2599	12	3	2257	2259	-2	20	30	9E	1691	N927XJ	JFK	ROC	60	264	22	59	2023-12-03 22:00:00	Other
2602	12	1	603	605	-2	716	729	YX	1772	N234JQ	LGA	DCA	51	214	6	5	2023-12-01 06:00:00	Other
2611	3	24	921	925	-4	1122	1127	AA	667	N895NN	EWR	CLT	88	529	9	25	2023-03-24 09:00:00	CLT
2617	12	7	1712	1714	-2	2009	2020	B6	407	N2059J	JFK	SAN	333	2446	17	14	2023-12-07 17:00:00	Other
2618	3	29	1247	1251	-4	1454	1501	YX	1294	N427YX	LGA	DAY	100	549	12	51	2023-03-29 12:00:00	Other
2619	3	9	1812	1814	-2	2058	2119	UA	499	N36272	EWR	FLL	139	1065	18	14	2023-03-09 18:00:00	FLL
2630	6	3	558	600	-2	741	753	DL	380	N373DX	LGA	DTW	82	502	6	0	2023-06-03 06:00:00	Other
2636	1	26	1032	1035	-3	1234	1320	B6	796	N805JB	LGA	DEN	213	1620	10	35	2023-01-26 10:00:00	Other
2638	7	29	952	955	-3	1137	1200	9E	1143	N917XJ	LGA	MEM	133	963	9	55	2023-07-29 09:00:00	Other
2644	4	19	1250	1255	-5	1425	1445	WN	340	N8852Q	LGA	STL	128	888	12	55	2023-04-19 12:00:00	Other
2646	11	26	1222	1225	-3	1347	1353	YX	1274	N426YX	LGA	DCA	60	214	12	25	2023-11-26 12:00:00	Other
2648	3	21	1926	1929	-3	2026	2042	YX	1657	N238JQ	LGA	PVD	31	143	19	29	2023-03-21 19:00:00	Other
2650	4	10	945	950	-5	1132	1140	9E	1278	N923XJ	EWR	RDU	68	416	9	50	2023-04-10 09:00:00	Other
2653	4	21	723	728	-5	944	950	YX	948	N736YX	EWR	SDF	102	642	7	28	2023-04-21 07:00:00	Other
2655	4	14	2025	2030	-5	2206	2221	YX	1453	N210JQ	JFK	PIT	62	340	20	30	2023-04-14 20:00:00	Other
2671	8	11	1932	1935	-3	2133	2213	9E	1299	N183GJ	JFK	CLT	78	541	19	35	2023-08-11 19:00:00	CLT
2674	2	2	1146	1150	-4	1231	1303	YX	1502	N241JQ	LGA	BDL	24	101	11	50	2023-02-02 11:00:00	Other
2677	10	22	800	805	-5	1044	1053	UA	240	N33203	EWR	IAH	192	1400	8	5	2023-10-22 08:00:00	Other
2679	12	19	658	700	-2	940	1000	NK	1004	N693NK	LGA	PBI	137	1035	7	0	2023-12-19 07:00:00	Other
2680	7	6	1123	1125	-2	1322	1334	YX	1025	N112HQ	LGA	AVL	94	599	11	25	2023-07-06 11:00:00	Other
2686	4	21	1256	1259	-3	1455	1459	9E	1336	N331PQ	JFK	DTW	90	509	12	59	2023-04-21 12:00:00	Other
2703	6	30	658	700	-2	851	902	9E	1469	N325PQ	JFK	DTW	83	509	7	0	2023-06-30 07:00:00	Other
2709	4	20	1354	1359	-5	1503	1520	9E	1388	N324PQ	JFK	SYR	46	209	13	59	2023-04-20 13:00:00	Other
2721	10	6	1356	1359	-3	1600	1625	DL	196	N3757D	LGA	DEN	218	1620	13	59	2023-10-06 13:00:00	Other
2727	7	12	1637	1640	-3	1913	2000	DL	242	N511DE	JFK	SAN	310	2446	16	40	2023-07-12 16:00:00	Other
2733	9	19	718	720	-2	849	855	WN	613	N8515X	LGA	BNA	133	764	7	20	2023-09-19 07:00:00	Other
2738	10	15	1812	1815	-3	1937	1958	DL	607	N115DU	LGA	ORD	100	733	18	15	2023-10-15 18:00:00	ORD
2742	5	28	1509	1514	-5	1638	1714	OO	1145	N316SY	JFK	PIT	66	340	15	14	2023-05-28 15:00:00	Other
2760	10	22	726	729	-3	1031	1042	DL	285	N844DN	JFK	SEA	327	2422	7	29	2023-10-22 07:00:00	Other
2765	4	24	834	838	-4	1116	1152	UA	291	N48127	EWR	SAN	321	2425	8	38	2023-04-24 08:00:00	Other
2773	2	5	1821	1825	-4	2115	2138	AA	225	N950AN	JFK	DFW	199	1391	18	25	2023-02-05 18:00:00	Other
2780	5	21	611	615	-4	749	815	DL	938	N954AT	EWR	MSP	142	1008	6	15	2023-05-21 06:00:00	Other
2781	12	3	1001	1003	-2	1226	1233	UA	537	N34455	EWR	DEN	225	1605	10	3	2023-12-03 10:00:00	Other
2782	5	28	632	635	-3	939	1012	AA	32	N102NN	JFK	SFO	345	2586	6	35	2023-05-28 06:00:00	Other
2784	10	29	1955	2000	-5	2243	2239	B6	29	N613JB	JFK	DEN	251	1626	20	0	2023-10-29 20:00:00	Other
2791	5	14	1852	1855	-3	2242	2153	DL	284	N126DU	LGA	DFW	245	1389	18	55	2023-05-14 18:00:00	Other
2794	9	27	701	705	-4	947	1000	DL	520	N927DZ	JFK	TPA	149	1005	7	5	2023-09-27 07:00:00	Other
2800	12	6	1923	1925	-2	20	25	DL	674	N827DN	JFK	SJU	197	1598	19	25	2023-12-06 19:00:00	Other
2801	4	5	1655	1700	-5	2106	2038	B6	252	N709JB	JFK	SJC	382	2569	17	0	2023-04-05 17:00:00	Other
2803	12	11	1933	1935	-2	2144	2202	9E	1402	N348PQ	JFK	DTW	85	509	19	35	2023-12-11 19:00:00	Other
2808	1	29	2045	2050	-5	2236	2253	YX	1787	N209JQ	JFK	CMH	90	483	20	50	2023-01-29 20:00:00	Other
2809	11	1	2125	2129	-4	2335	2335	OO	1206	N246SY	JFK	CLE	78	425	21	29	2023-11-01 21:00:00	Other
2814	4	4	1356	1400	-4	1618	1619	YX	1286	N118HQ	LGA	CVG	98	585	14	0	2023-04-04 14:00:00	Other
2816	2	14	1727	1729	-2	2002	2041	B6	735	N586JB	JFK	PBI	138	1028	17	29	2023-02-14 17:00:00	Other
2818	2	18	2056	2100	-4	2218	2239	AA	264	N829AW	EWR	ORD	117	719	21	0	2023-02-18 21:00:00	ORD
2822	9	4	1958	2000	-2	2314	2341	DL	95	N881DN	JFK	SLC	264	1990	20	0	2023-09-04 20:00:00	Other
2823	6	20	1311	1315	-4	1524	1529	9E	1482	N147PQ	JFK	CHS	101	636	13	15	2023-06-20 13:00:00	Other
2833	11	11	836	841	-5	1025	1040	YX	1789	N213JQ	LGA	CMH	85	479	8	41	2023-11-11 08:00:00	Other
2834	6	28	1540	1542	-2	1833	1853	DL	625	N3772H	JFK	PBI	128	1028	15	42	2023-06-28 15:00:00	Other
2836	5	28	2125	2130	-5	11	28	B6	20	N519JB	LGA	TPA	137	1010	21	30	2023-05-28 21:00:00	Other
2844	8	21	1700	1705	-5	2037	2012	NK	687	N629NK	EWR	FLL	133	1065	17	5	2023-08-21 17:00:00	FLL
2845	9	22	935	940	-5	1047	1111	9E	1619	N485PX	LGA	BTV	46	258	9	40	2023-09-22 09:00:00	Other
2846	11	10	2135	2140	-5	2326	2336	YX	1244	N434YX	JFK	RDU	81	427	21	40	2023-11-10 21:00:00	Other
2851	9	7	555	600	-5	702	722	AA	740	N820AW	LGA	DCA	36	214	6	0	2023-09-07 06:00:00	Other
2853	5	25	1122	1125	-3	1351	1438	UA	249	N64844	EWR	SEA	294	2402	11	25	2023-05-25 11:00:00	Other
2861	2	5	705	710	-5	946	1021	UA	778	N27251	EWR	DFW	195	1372	7	10	2023-02-05 07:00:00	Other
2870	2	14	1248	1250	-2	1439	1505	9E	1378	N691CA	LGA	DAY	92	549	12	50	2023-02-14 12:00:00	Other
2881	10	30	556	600	-4	901	905	NK	46	N684NK	LGA	FLL	151	1076	6	0	2023-10-30 06:00:00	FLL
2891	4	8	1545	1550	-5	1755	1803	YX	1466	N209JQ	LGA	CLT	96	544	15	50	2023-04-08 15:00:00	CLT
2899	2	12	837	842	-5	1046	1112	YX	996	N725YX	EWR	SDF	100	642	8	42	2023-02-12 08:00:00	Other
2900	2	13	1245	1250	-5	1404	1416	9E	1309	N138EV	LGA	BTV	44	258	12	50	2023-02-13 12:00:00	Other
2904	2	3	812	815	-3	1140	1156	AA	607	N342RX	JFK	MIA	168	1089	8	15	2023-02-03 08:00:00	MIA
2907	7	31	1854	1859	-5	2036	2110	9E	1135	N922XJ	LGA	STL	127	888	18	59	2023-07-31 18:00:00	Other
2908	5	8	855	900	-5	1005	1022	9E	1551	N605LR	LGA	SYR	41	198	9	0	2023-05-08 09:00:00	Other
2910	5	4	1956	2000	-4	2126	2151	B6	517	N283JB	JFK	RDU	67	427	20	0	2023-05-04 20:00:00	Other
2911	12	1	1905	1910	-5	2048	2101	UA	183	N421UA	EWR	RDU	70	416	19	10	2023-12-01 19:00:00	Other
2919	2	27	610	615	-5	926	935	UA	825	N12114	EWR	LAX	352	2454	6	15	2023-02-27 06:00:00	LAX
2920	6	22	1353	1355	-2	1647	1655	DL	311	N171DN	JFK	LAX	317	2475	13	55	2023-06-22 13:00:00	LAX
2924	5	7	1913	1915	-2	2329	2244	DL	153	N172DN	JFK	LAX	352	2475	19	15	2023-05-07 19:00:00	LAX
2926	12	4	1551	1554	-3	1704	1720	YX	1857	N242JQ	JFK	BOS	34	187	15	54	2023-12-04 15:00:00	BOS
2927	11	19	1056	1059	-3	1311	1322	YX	1108	N653RW	EWR	IND	91	645	10	59	2023-11-19 10:00:00	Other
2928	4	10	612	615	-3	859	935	UA	288	N34137	EWR	SFO	322	2565	6	15	2023-04-10 06:00:00	Other
2938	1	30	1950	1955	-5	2119	2135	9E	1679	N197PQ	EWR	RDU	69	416	19	55	2023-01-30 19:00:00	Other
2944	10	18	1131	1133	-2	1232	1244	YX	1338	N436YX	JFK	ORH	33	150	11	33	2023-10-18 11:00:00	Other
2949	1	18	1527	1529	-2	1656	1704	9E	1621	N916XJ	LGA	ORF	51	296	15	29	2023-01-18 15:00:00	Other
2952	9	30	1740	1745	-5	1945	2010	DL	1002	N950AT	EWR	ATL	100	746	17	45	2023-09-30 17:00:00	ATL
2959	4	7	1926	1929	-3	2020	2042	YX	1494	N220JQ	LGA	PVD	28	143	19	29	2023-04-07 19:00:00	Other
2970	8	10	807	810	-3	1057	1055	DL	166	N145DQ	LGA	DFW	196	1389	8	10	2023-08-10 08:00:00	Other
2986	5	19	1157	1200	-3	1330	1341	AA	562	N802AW	LGA	RDU	73	431	12	0	2023-05-19 12:00:00	Other
2990	3	7	1955	2000	-5	2148	2205	9E	1400	N147PQ	LGA	GSO	73	461	20	0	2023-03-07 20:00:00	Other
2993	9	14	1158	1200	-2	1433	1436	DL	341	N521DT	JFK	LAS	294	2248	12	0	2023-09-14 12:00:00	Other
2995	10	19	1625	1629	-4	1904	1911	B6	838	N708JB	LGA	JAX	124	833	16	29	2023-10-19 16:00:00	Other
3003	6	12	925	929	-4	1126	1139	YX	1129	N758YX	EWR	AVL	88	583	9	29	2023-06-12 09:00:00	Other
3010	5	9	1738	1742	-4	2048	2058	UA	563	N37295	EWR	SMF	330	2500	17	42	2023-05-09 17:00:00	Other
3011	3	19	1557	1559	-2	1835	1849	AA	612	N350RV	JFK	PHX	297	2153	15	59	2023-03-19 15:00:00	Other
3016	2	25	700	705	-5	929	936	DL	747	N3734B	EWR	ATL	119	746	7	5	2023-02-25 07:00:00	ATL
3017	11	9	657	659	-2	821	825	B6	674	N236JB	JFK	DCA	53	213	6	59	2023-11-09 06:00:00	Other
3028	1	17	1125	1129	-4	1311	1334	YX	1839	N204JQ	LGA	CMH	84	479	11	29	2023-01-17 11:00:00	Other
3029	2	12	637	640	-3	914	950	UA	325	N27261	EWR	SAN	324	2425	6	40	2023-02-12 06:00:00	Other
3046	2	2	2208	2210	-2	234	317	NK	391	N616NK	EWR	SJU	189	1608	22	10	2023-02-02 22:00:00	Other
3047	12	4	757	800	-3	1004	1008	DL	506	N129DN	LGA	DTW	83	502	8	0	2023-12-04 08:00:00	Other
3052	6	29	1408	1413	-5	1604	1554	YX	1346	N428YX	JFK	PIT	62	340	14	13	2023-06-29 14:00:00	Other
3056	11	20	1857	1859	-2	2143	2216	B6	157	N905JB	JFK	ONT	295	2429	18	59	2023-11-20 18:00:00	Other
3065	4	6	635	640	-5	828	831	9E	1354	N920XJ	LGA	CLE	70	419	6	40	2023-04-06 06:00:00	Other
3074	8	9	902	905	-3	1202	1210	YX	976	N119HQ	LGA	IAH	198	1416	9	5	2023-08-09 09:00:00	Other
3080	7	9	703	705	-2	941	940	WN	820	N460WN	LGA	DAL	198	1381	7	5	2023-07-09 07:00:00	Other
3088	4	28	1256	1300	-4	1406	1421	YX	1539	N242JQ	LGA	BOS	36	184	13	0	2023-04-28 13:00:00	BOS
3089	4	2	655	700	-5	951	1016	DL	364	N372DN	JFK	MIA	141	1089	7	0	2023-04-02 07:00:00	MIA
3090	8	2	1006	1010	-4	1155	1215	AA	601	N920NN	LGA	CLT	75	544	10	10	2023-08-02 10:00:00	CLT
3098	3	9	625	630	-5	814	824	YX	1611	N245JQ	LGA	CMH	84	479	6	30	2023-03-09 06:00:00	Other
3099	1	17	657	700	-3	825	843	YX	1871	N818MD	LGA	PIT	62	335	7	0	2023-01-17 07:00:00	Other
3103	5	15	1549	1551	-2	1801	1836	DL	426	N3732J	JFK	ATL	102	760	15	51	2023-05-15 15:00:00	ATL
3113	1	26	1949	1952	-3	2256	2301	UA	261	N17105	EWR	TPA	163	997	19	52	2023-01-26 19:00:00	Other
3143	11	12	1521	1526	-5	1759	1814	YX	1795	N240JQ	LGA	JAX	124	833	15	26	2023-11-12 15:00:00	Other
3146	3	24	1043	1045	-2	1428	1421	B6	40	N967JT	JFK	SFO	382	2586	10	45	2023-03-24 10:00:00	Other
3161	8	10	726	730	-4	852	908	B6	314	N231JB	JFK	ORD	121	740	7	30	2023-08-10 07:00:00	ORD
3163	10	1	1125	1130	-5	1426	1437	DL	877	N313DU	LGA	PBI	154	1035	11	30	2023-10-01 11:00:00	Other
3164	11	22	555	600	-5	710	719	UA	420	N17316	EWR	IAD	52	212	6	0	2023-11-22 06:00:00	Other
3167	4	10	1442	1446	-4	1725	1739	UA	388	N14731	EWR	SRQ	146	1034	14	46	2023-04-10 14:00:00	Other
3173	3	26	555	600	-5	709	709	UA	756	N484UA	EWR	IAD	54	212	6	0	2023-03-26 06:00:00	Other
3175	10	30	756	800	-4	1120	1104	DL	156	N171DZ	JFK	LAX	333	2475	8	0	2023-10-30 08:00:00	LAX
3176	8	13	1308	1311	-3	1503	1535	9E	1280	N937XJ	LGA	IND	94	660	13	11	2023-08-13 13:00:00	Other
3179	2	21	1246	1250	-4	1451	1430	9E	1284	N186PQ	LGA	MKE	133	738	12	50	2023-02-21 12:00:00	Other
3187	2	16	946	950	-4	1221	1220	WN	193	N211WN	LGA	MCI	185	1107	9	50	2023-02-16 09:00:00	Other
3189	4	9	1156	1159	-3	1257	1326	YX	1445	N215JQ	LGA	BOS	37	184	11	59	2023-04-09 11:00:00	BOS
3199	1	20	631	635	-4	930	945	B6	517	N625JB	LGA	TPA	153	1010	6	35	2023-01-20 06:00:00	Other
3200	10	8	1954	1958	-4	2253	2314	DL	315	N3752	LGA	MIA	157	1096	19	58	2023-10-08 19:00:00	MIA
3203	11	27	2050	2055	-5	2223	2254	YX	1768	N246JQ	JFK	PIT	71	340	20	55	2023-11-27 20:00:00	Other
3219	6	10	840	843	-3	1044	1117	DL	163	N337NB	JFK	ATL	102	760	8	43	2023-06-10 08:00:00	ATL
3223	9	16	1047	1051	-4	1322	1357	DL	373	N316DU	LGA	TPA	137	1010	10	51	2023-09-16 10:00:00	Other
3225	12	2	2027	2030	-3	2158	2226	AA	727	N708UW	LGA	ORD	129	733	20	30	2023-12-02 20:00:00	ORD
3240	12	5	1756	1759	-3	2053	2120	DL	197	N122DU	JFK	DFW	203	1391	17	59	2023-12-05 17:00:00	Other
3244	8	13	1958	2000	-2	2206	2222	YX	897	N757YX	EWR	IND	102	645	20	0	2023-08-13 20:00:00	Other
3252	7	6	1342	1347	-5	1506	1521	AA	530	N316RK	EWR	ORD	106	719	13	47	2023-07-06 13:00:00	ORD
3261	2	17	820	825	-5	959	1039	9E	1438	N314PQ	LGA	ILM	83	500	8	25	2023-02-17 08:00:00	Other
3263	12	15	1556	1559	-3	1823	1840	B6	932	N258JB	JFK	JAX	122	828	15	59	2023-12-15 15:00:00	Other
3265	8	9	1742	1745	-3	1950	1946	YX	884	N744YX	EWR	CMH	77	463	17	45	2023-08-09 17:00:00	Other
3273	12	28	915	920	-5	1311	1239	AA	719	N319TE	LGA	MIA	190	1096	9	20	2023-12-28 09:00:00	MIA
3275	8	20	1225	1230	-5	1431	1525	NK	400	N624NK	LGA	IAH	169	1416	12	30	2023-08-20 12:00:00	Other
3283	6	3	557	600	-3	756	814	DL	868	N953AT	EWR	ATL	99	746	6	0	2023-06-03 06:00:00	ATL
3288	5	13	957	1000	-3	1235	1304	UA	687	N14731	LGA	IAH	191	1416	10	0	2023-05-13 10:00:00	Other
3296	7	1	1527	1529	-2	1710	1718	9E	1108	N924XJ	JFK	BGR	63	382	15	29	2023-07-01 15:00:00	Other
3297	6	17	937	942	-5	1113	1156	YX	1294	N404YX	JFK	CMH	75	483	9	42	2023-06-17 09:00:00	Other
3299	6	20	556	600	-4	750	754	DL	427	N374NW	LGA	DTW	85	502	6	0	2023-06-20 06:00:00	Other
3302	10	23	556	600	-4	844	902	B6	462	N531JL	LGA	FLL	143	1076	6	0	2023-10-23 06:00:00	FLL
3305	9	9	1005	1010	-5	1141	1218	9E	1558	N349PQ	EWR	DTW	74	488	10	10	2023-09-09 10:00:00	Other
3308	1	25	945	950	-5	1216	1251	UA	840	N38727	EWR	JAC	248	1874	9	50	2023-01-25 09:00:00	Other
3322	7	5	829	831	-2	1017	1044	9E	1170	N917XJ	LGA	GSP	88	610	8	31	2023-07-05 08:00:00	Other
3329	3	23	1621	1625	-4	1907	1930	WN	863	N8782Q	LGA	DAL	204	1381	16	25	2023-03-23 16:00:00	Other
3332	4	7	1356	1359	-3	1623	1635	DL	170	N398DA	JFK	DEN	232	1626	13	59	2023-04-07 13:00:00	Other
3337	9	21	925	930	-5	1204	1240	AS	8	N277AK	JFK	SEA	304	2422	9	30	2023-09-21 09:00:00	Other
3342	2	7	946	950	-4	1251	1314	B6	574	N655JB	JFK	RSW	162	1074	9	50	2023-02-07 09:00:00	Other
3352	12	1	1955	1959	-4	2128	2158	9E	1355	N937XJ	JFK	RIC	56	288	19	59	2023-12-01 19:00:00	Other
3357	5	25	1647	1650	-3	1840	1832	9E	1533	N602LR	JFK	PWM	50	273	16	50	2023-05-25 16:00:00	Other
3367	6	20	2152	2155	-3	115	142	DL	347	N718TW	JFK	SFO	322	2586	21	55	2023-06-20 21:00:00	Other
3376	2	24	1000	1005	-5	1216	1223	AA	729	N897NN	LGA	CLT	97	544	10	5	2023-02-24 10:00:00	CLT
3377	11	3	1816	1820	-4	2027	2028	YX	1346	N419YX	LGA	MCI	169	1107	18	20	2023-11-03 18:00:00	Other
3379	5	9	1650	1655	-5	1956	2016	AA	3	N110AN	JFK	LAX	328	2475	16	55	2023-05-09 16:00:00	LAX
3381	6	2	1257	1259	-2	1558	1606	AA	661	N950AN	EWR	MIA	148	1085	12	59	2023-06-02 12:00:00	MIA
3385	4	23	1452	1455	-3	1807	1758	AA	358	N907NN	LGA	DFW	221	1389	14	55	2023-04-23 14:00:00	Other
3386	8	31	1502	1505	-3	1808	1821	DL	300	N320NB	LGA	PBI	144	1035	15	5	2023-08-31 15:00:00	Other
3388	9	25	828	830	-2	1106	1057	B6	961	N516JB	LGA	ATL	107	762	8	30	2023-09-25 08:00:00	ATL
3391	10	15	558	600	-2	847	856	B6	1	N625JB	JFK	FLL	143	1069	6	0	2023-10-15 06:00:00	FLL
3398	10	23	1412	1416	-4	1627	1624	9E	1575	N184GJ	JFK	CVG	93	589	14	16	2023-10-23 14:00:00	Other
3403	3	6	1724	1729	-5	1951	2008	YX	1273	N438YX	LGA	ATL	113	762	17	29	2023-03-06 17:00:00	ATL
3419	3	13	2025	2030	-5	2202	2203	9E	1402	N916XJ	LGA	ORF	54	296	20	30	2023-03-13 20:00:00	Other
3422	1	9	2003	2005	-2	2238	2315	NK	309	N529NK	EWR	IAH	193	1400	20	5	2023-01-09 20:00:00	Other
3425	3	20	600	605	-5	918	910	B6	110	N949JT	EWR	MCO	160	937	6	5	2023-03-20 06:00:00	MCO
3428	6	7	921	926	-5	1025	1049	B6	631	N375JB	JFK	BTV	46	266	9	26	2023-06-07 09:00:00	Other
3432	7	17	2157	2159	-2	2346	2337	YX	847	N757YX	EWR	BGR	55	393	21	59	2023-07-17 21:00:00	Other
3434	5	19	753	755	-2	1048	1100	UA	719	N27261	EWR	PBI	147	1023	7	55	2023-05-19 07:00:00	Other
3436	2	24	1205	1210	-5	1325	1342	YX	1233	N424YX	JFK	ORF	60	290	12	10	2023-02-24 12:00:00	Other
3438	5	5	1957	2000	-3	2147	2218	9E	1385	N349PQ	LGA	CAE	85	617	20	0	2023-05-05 20:00:00	Other
3444	3	23	800	805	-5	931	939	9E	1532	N292PQ	JFK	ROC	58	264	8	5	2023-03-23 08:00:00	Other
3445	4	6	928	930	-2	1150	1159	B6	866	N231JB	LGA	SAV	109	722	9	30	2023-04-06 09:00:00	Other
3448	4	29	1840	1845	-5	2043	2020	YX	1057	N728YX	EWR	PIT	61	319	18	45	2023-04-29 18:00:00	Other
3450	8	5	1955	1959	-4	2231	2259	B6	19	N618JB	LGA	TPA	138	1010	19	59	2023-08-05 19:00:00	Other
3451	8	13	1242	1247	-5	1519	1533	AA	432	N991NN	LGA	DFW	186	1389	12	47	2023-08-13 12:00:00	Other
3457	5	26	751	755	-4	906	924	9E	1454	N181GJ	JFK	BUF	52	301	7	55	2023-05-26 07:00:00	Other
3460	6	21	725	730	-5	911	925	9E	1497	N904XJ	LGA	GSO	77	461	7	30	2023-06-21 07:00:00	Other
3463	3	1	1456	1459	-3	1622	1629	YX	1043	N638RW	EWR	ORF	54	284	14	59	2023-03-01 14:00:00	Other
3466	8	5	1355	1359	-4	1504	1517	YX	1358	N207JQ	JFK	ACK	44	199	13	59	2023-08-05 13:00:00	Other
3470	1	5	1157	1200	-3	1517	1530	UA	873	N57111	EWR	SFO	345	2565	12	0	2023-01-05 12:00:00	Other
3478	8	26	628	630	-2	908	931	AA	662	N951NN	JFK	DFW	178	1391	6	30	2023-08-26 06:00:00	Other
3479	2	4	726	730	-4	949	1020	9E	1387	N919XJ	LGA	JAX	121	833	7	30	2023-02-04 07:00:00	Other
3490	1	17	1905	1910	-5	2208	2217	UA	632	N642UA	EWR	IAH	202	1400	19	10	2023-01-17 19:00:00	Other
3491	5	13	925	930	-5	1134	1200	UA	850	N806UA	LGA	DEN	224	1620	9	30	2023-05-13 09:00:00	Other
3494	5	8	743	745	-2	919	921	UA	839	N495UA	EWR	ORD	118	719	7	45	2023-05-08 07:00:00	ORD
3496	6	23	953	957	-4	1233	1249	UA	502	N27724	EWR	AUS	187	1504	9	57	2023-06-23 09:00:00	Other
3500	3	2	1415	1417	-2	1552	1546	YX	1113	N641RW	EWR	PIT	70	319	14	17	2023-03-02 14:00:00	Other
3505	7	29	1424	1429	-5	1557	1604	9E	1199	N134EV	JFK	SYR	49	209	14	29	2023-07-29 14:00:00	Other
3513	2	11	1625	1627	-2	1754	1817	YX	1047	N723YX	EWR	CLE	72	404	16	27	2023-02-11 16:00:00	Other
3516	9	20	1725	1729	-4	2006	2035	AA	38	N117AN	JFK	LAX	324	2475	17	29	2023-09-20 17:00:00	LAX
3517	11	10	1512	1515	-3	1738	1759	DL	249	N851DN	JFK	DEN	245	1626	15	15	2023-11-10 15:00:00	Other
3521	10	8	843	848	-5	1114	1131	YX	1759	N223JQ	JFK	JAX	132	828	8	48	2023-10-08 08:00:00	Other
3528	2	7	600	605	-5	756	819	DL	427	N363NB	LGA	MSP	154	1020	6	5	2023-02-07 06:00:00	Other
3530	4	19	1550	1555	-5	1703	1727	YX	1209	N871RW	LGA	RIC	54	292	15	55	2023-04-19 15:00:00	Other
3533	8	12	636	640	-4	800	815	UA	242	N27515	EWR	CLE	61	404	6	40	2023-08-12 06:00:00	Other
3541	6	12	731	735	-4	849	853	UA	273	N27290	EWR	BUF	51	282	7	35	2023-06-12 07:00:00	Other
3544	8	27	1857	1859	-2	2112	2113	9E	1270	N915XJ	LGA	GSP	106	610	18	59	2023-08-27 18:00:00	Other
3548	12	4	605	610	-5	931	934	DL	438	N102DU	LGA	IAH	243	1416	6	10	2023-12-04 06:00:00	Other
3549	10	10	1110	1115	-5	1244	1305	AA	487	N710UW	LGA	RDU	70	431	11	15	2023-10-10 11:00:00	Other
3551	4	18	1926	1930	-4	2132	2148	YX	1080	N403YX	LGA	LIT	155	1085	19	30	2023-04-18 19:00:00	Other
3558	6	18	1345	1350	-5	1516	1539	9E	1461	N195PQ	LGA	CLE	67	419	13	50	2023-06-18 13:00:00	Other
3570	9	4	1114	1118	-4	1348	1414	DL	429	N927DZ	JFK	TPA	132	1005	11	18	2023-09-04 11:00:00	Other
3576	2	14	956	1000	-4	1605	1605	HA	22	N381HA	JFK	HNL	642	4983	10	0	2023-02-14 10:00:00	Other
3577	4	23	750	755	-5	1008	956	AA	891	N184US	LGA	CLT	97	544	7	55	2023-04-23 07:00:00	CLT
3580	1	17	2048	2050	-2	2247	2302	9E	1708	N319PQ	LGA	GSP	101	610	20	50	2023-01-17 20:00:00	Other
3583	9	22	606	610	-4	749	818	YX	1330	N115HQ	LGA	DTW	77	502	6	10	2023-09-22 06:00:00	Other
3585	12	26	727	731	-4	1017	1049	AA	531	N355PU	LGA	DFW	201	1389	7	31	2023-12-26 07:00:00	Other
3588	6	29	817	820	-3	1058	1126	AA	337	N931NN	JFK	DFW	177	1391	8	20	2023-06-29 08:00:00	Other
3590	1	29	1924	1929	-5	2053	2116	YX	1869	N235JQ	LGA	PIT	66	335	19	29	2023-01-29 19:00:00	Other
3598	9	10	1957	1959	-2	2244	2259	DL	439	N306DN	LGA	MCO	134	950	19	59	2023-09-10 19:00:00	MCO
3601	10	18	1139	1142	-3	1415	1438	UA	600	N24224	EWR	PBI	140	1023	11	42	2023-10-18 11:00:00	Other
3608	6	30	557	600	-3	858	859	B6	529	N644JB	LGA	FLL	133	1076	6	0	2023-06-30 06:00:00	FLL
3611	9	13	727	729	-2	937	929	AA	531	N967AN	JFK	CLT	96	541	7	29	2023-09-13 07:00:00	CLT
3620	11	24	1615	1620	-5	1920	1930	AA	436	N917NN	JFK	DFW	202	1391	16	20	2023-11-24 16:00:00	Other
3622	9	8	628	630	-2	925	942	AA	354	N341RW	JFK	MIA	145	1089	6	30	2023-09-08 06:00:00	MIA
3625	4	5	1245	1249	-4	1406	1421	9E	1325	N490PX	LGA	BGR	56	378	12	49	2023-04-05 12:00:00	Other
3636	5	21	1455	1500	-5	1613	1630	YX	1711	N245JQ	LGA	BOS	40	184	15	0	2023-05-21 15:00:00	BOS
3637	8	8	822	827	-5	951	1006	YX	916	N861RW	EWR	RIC	57	277	8	27	2023-08-08 08:00:00	Other
3638	4	3	806	810	-4	1307	1318	UA	131	N69063	EWR	HNL	634	4962	8	10	2023-04-03 08:00:00	Other
3639	2	20	2022	2025	-3	2131	2201	YX	1560	N204JQ	JFK	DCA	44	213	20	25	2023-02-20 20:00:00	Other
3640	9	20	706	710	-4	913	933	UA	848	N61886	EWR	DEN	214	1605	7	10	2023-09-20 07:00:00	Other
3647	8	28	1021	1024	-3	1302	1317	DL	340	N105DU	LGA	IAH	196	1416	10	24	2023-08-28 10:00:00	Other
3649	8	1	626	630	-4	833	846	UA	160	N73256	LGA	DEN	227	1620	6	30	2023-08-01 06:00:00	Other
3655	9	4	1527	1530	-3	1814	1833	UA	488	N17128	EWR	LAX	314	2454	15	30	2023-09-04 15:00:00	LAX
3657	3	25	1815	1819	-4	2104	2120	B6	280	N640JB	JFK	LAS	306	2248	18	19	2023-03-25 18:00:00	Other
3670	12	11	1321	1324	-3	1610	1645	UA	709	N17719	EWR	SNA	329	2434	13	24	2023-12-11 13:00:00	Other
3671	3	17	2123	2127	-4	2353	2355	YX	1121	N729YX	EWR	MCI	179	1092	21	27	2023-03-17 21:00:00	Other
3673	7	22	1257	1300	-3	1554	1555	B6	561	N505JB	EWR	RSW	162	1068	13	0	2023-07-22 13:00:00	Other
3675	1	17	813	815	-2	1110	1135	B6	262	N973JT	JFK	FLL	144	1069	8	15	2023-01-17 08:00:00	FLL
3677	12	3	927	930	-3	1056	1117	YX	1713	N229JQ	LGA	MSN	132	812	9	30	2023-12-03 09:00:00	Other
3683	10	18	2033	2035	-2	2230	2252	9E	1637	N181PQ	LGA	CAE	88	617	20	35	2023-10-18 20:00:00	Other
3684	5	8	1755	1759	-4	2035	2059	AA	202	N962NN	LGA	DFW	188	1389	17	59	2023-05-08 17:00:00	Other
3686	11	7	1424	1429	-5	1528	1546	9E	1669	N197PQ	LGA	SYR	42	198	14	29	2023-11-07 14:00:00	Other
3694	8	20	1357	1359	-2	1618	1650	AA	512	N948AN	EWR	DFW	167	1372	13	59	2023-08-20 13:00:00	Other
3701	11	14	625	630	-5	757	824	9E	1712	N295PQ	LGA	STL	128	888	6	30	2023-11-14 06:00:00	Other
3703	2	2	645	650	-5	956	1016	AA	877	N329SL	LGA	MIA	168	1096	6	50	2023-02-02 06:00:00	MIA
3706	3	14	2010	2015	-5	2241	2320	WN	675	N8681M	LGA	DAL	187	1381	20	15	2023-03-14 20:00:00	Other
3709	9	15	617	619	-2	808	818	AA	319	N933NN	JFK	CLT	88	541	6	19	2023-09-15 06:00:00	CLT
3711	8	23	1256	1259	-3	1512	1539	DL	107	N391DN	LGA	ATL	103	762	12	59	2023-08-23 12:00:00	ATL
3726	2	6	836	840	-4	1146	1206	AA	783	N338RS	LGA	MIA	152	1096	8	40	2023-02-06 08:00:00	MIA
3728	11	10	1452	1455	-3	1734	1805	B6	134	N517JB	LGA	MCO	139	950	14	55	2023-11-10 14:00:00	MCO
3733	7	26	817	820	-3	1044	1109	YX	1432	N246JQ	JFK	JAX	120	828	8	20	2023-07-26 08:00:00	Other
3735	6	7	1025	1030	-5	1126	1140	B6	996	N328JB	JFK	BOS	38	187	10	30	2023-06-07 10:00:00	BOS
3739	4	1	1120	1125	-5	1314	1312	OO	1031	N323SY	JFK	ORD	120	740	11	25	2023-04-01 11:00:00	ORD
3764	12	29	829	832	-3	1139	1150	DL	542	N3773D	LGA	RSW	169	1080	8	32	2023-12-29 08:00:00	Other
3769	11	5	905	910	-5	1033	1106	AA	970	N820NN	JFK	ORD	115	740	9	10	2023-11-05 09:00:00	ORD
3772	5	8	1052	1055	-3	1420	1449	DL	715	N693DL	JFK	STT	191	1623	10	55	2023-05-08 10:00:00	Other
3777	9	15	556	600	-4	723	734	AA	542	N971NN	LGA	ORD	107	733	6	0	2023-09-15 06:00:00	ORD
3779	10	13	556	600	-4	743	734	UA	344	N66825	EWR	ORD	121	719	6	0	2023-10-13 06:00:00	ORD
3780	12	16	1325	1329	-4	1711	1636	UA	473	N14250	EWR	FLL	159	1065	13	29	2023-12-16 13:00:00	FLL
3805	6	17	1127	1130	-3	1253	1302	YX	1403	N428YX	JFK	ORF	54	290	11	30	2023-06-17 11:00:00	Other
3811	12	1	855	900	-5	1207	1245	AS	111	N471AS	EWR	SFO	343	2565	9	0	2023-12-01 09:00:00	Other
3819	12	19	1555	1600	-5	1726	1740	9E	1507	N147PQ	JFK	ORF	53	290	16	0	2023-12-19 16:00:00	Other
3820	2	12	2156	2200	-4	2312	2323	AA	758	N826AW	LGA	DCA	43	214	22	0	2023-02-12 22:00:00	Other
3826	8	21	1026	1030	-4	1253	1324	UA	313	N17303	EWR	TPA	121	997	10	30	2023-08-21 10:00:00	Other
3835	1	21	802	805	-3	1046	1040	DL	1002	N379DA	EWR	ATL	120	746	8	5	2023-01-21 08:00:00	ATL
3843	11	29	1855	1900	-5	2159	2222	UA	733	N47293	EWR	SEA	338	2402	19	0	2023-11-29 19:00:00	Other
3846	3	1	1246	1249	-3	1540	1549	UA	866	N410UA	EWR	PBI	154	1023	12	49	2023-03-01 12:00:00	Other
3847	8	24	1555	1600	-5	1714	1749	9E	1198	N331PQ	LGA	BGR	55	378	16	0	2023-08-24 16:00:00	Other
3856	5	12	2054	2059	-5	18	53	B6	316	N834JB	JFK	BQN	189	1576	20	59	2023-05-12 20:00:00	Other
3857	10	10	1626	1629	-3	1917	1935	AA	87	N103NN	JFK	LAX	329	2475	16	29	2023-10-10 16:00:00	LAX
3859	6	7	1711	1715	-4	1950	2106	DL	309	N702TW	JFK	SFO	313	2586	17	15	2023-06-07 17:00:00	Other
3862	7	29	1131	1134	-3	1409	1426	NK	840	N697NK	EWR	MCO	126	937	11	34	2023-07-29 11:00:00	MCO
3866	7	6	1345	1350	-5	1516	1535	9E	1282	N916XJ	LGA	BHM	118	866	13	50	2023-07-06 13:00:00	Other
3871	10	4	557	600	-3	840	857	B6	126	N665JB	EWR	FLL	132	1065	6	0	2023-10-04 06:00:00	FLL
3875	1	10	1530	1535	-5	1821	1859	OO	1623	N114SY	LGA	IAH	205	1416	15	35	2023-01-10 15:00:00	Other
3876	3	28	1656	1658	-2	1818	1829	9E	1541	N308PQ	JFK	PWM	52	273	16	58	2023-03-28 16:00:00	Other
3877	9	2	730	734	-4	1017	1021	B6	167	N729JB	JFK	MCO	129	944	7	34	2023-09-02 07:00:00	MCO
3878	12	28	757	802	-5	1023	1050	DL	886	N361NB	JFK	MSY	173	1182	8	2	2023-12-28 08:00:00	Other
3883	5	18	530	535	-5	823	843	AA	425	N815NN	EWR	MIA	145	1085	5	35	2023-05-18 05:00:00	MIA
3888	11	28	555	600	-5	736	743	YX	1043	N761YX	EWR	BNA	133	748	6	0	2023-11-28 06:00:00	Other
3893	1	24	1057	1100	-3	1339	1418	B6	63	N605JB	EWR	FLL	142	1065	11	0	2023-01-24 11:00:00	FLL
3894	11	29	940	945	-5	1222	1236	DL	887	N896DN	JFK	MCO	137	944	9	45	2023-11-29 09:00:00	MCO
3905	11	29	1424	1429	-5	1633	1651	YX	1911	N226JQ	LGA	CHS	96	641	14	29	2023-11-29 14:00:00	Other
3912	9	26	1156	1159	-3	1503	1505	UA	940	N841UA	EWR	SAT	206	1569	11	59	2023-09-26 11:00:00	Other
3915	5	18	924	929	-5	1049	1046	B6	611	N279JB	JFK	BTV	47	266	9	29	2023-05-18 09:00:00	Other
3916	3	17	940	945	-5	1041	1114	9E	1373	N329PQ	JFK	PWM	45	273	9	45	2023-03-17 09:00:00	Other
3920	3	23	656	700	-4	1001	1008	UA	845	N27277	EWR	RSW	146	1068	7	0	2023-03-23 07:00:00	Other
3929	6	3	1446	1449	-3	1644	1655	B6	381	N317JB	JFK	DTW	82	509	14	49	2023-06-03 14:00:00	Other
3930	6	18	955	958	-3	1241	1250	UA	502	N33203	EWR	AUS	196	1504	9	58	2023-06-18 09:00:00	Other
3940	5	17	825	830	-5	957	1005	OO	1175	N310SY	JFK	BNA	122	765	8	30	2023-05-17 08:00:00	Other
3943	12	18	715	720	-5	830	906	YX	1112	N762YX	EWR	MKE	101	725	7	20	2023-12-18 07:00:00	Other
3956	2	16	1915	1920	-5	2151	2215	9E	1408	N936XJ	LGA	JAX	125	833	19	20	2023-02-16 19:00:00	Other
3961	10	2	1058	1100	-2	1336	1406	B6	298	N561JB	JFK	SLC	257	1990	11	0	2023-10-02 11:00:00	Other
3962	3	15	716	720	-4	913	938	9E	1511	N903XJ	LGA	CVG	93	585	7	20	2023-03-15 07:00:00	Other
3966	10	4	700	705	-5	954	1015	DL	943	N3756	LGA	MIA	145	1096	7	5	2023-10-04 07:00:00	MIA
3967	3	26	816	820	-4	1114	1139	UA	497	N2749U	EWR	SFO	335	2565	8	20	2023-03-26 08:00:00	Other
3973	1	27	655	700	-5	1022	1027	DL	1008	N806DN	JFK	RSW	180	1074	7	0	2023-01-27 07:00:00	Other
3974	5	8	824	829	-5	1024	1054	9E	1462	N301PQ	LGA	IND	96	660	8	29	2023-05-08 08:00:00	Other
3979	5	9	2056	2100	-4	10	54	AA	55	N106NN	JFK	SFO	336	2586	21	0	2023-05-09 21:00:00	Other
3984	11	9	842	845	-3	1134	1121	9E	1653	N931XJ	LGA	OMA	193	1148	8	45	2023-11-09 08:00:00	Other
3992	10	14	856	900	-4	1123	1145	DL	136	N394DX	LGA	ATL	115	762	9	0	2023-10-14 09:00:00	ATL
3993	7	27	1200	1205	-5	1451	1504	B6	674	N929JB	JFK	LAX	316	2475	12	5	2023-07-27 12:00:00	LAX
4001	12	29	855	900	-5	1156	1201	B6	150	N521JB	LGA	PBI	160	1035	9	0	2023-12-29 09:00:00	Other
4002	8	2	956	1000	-4	1255	1252	UA	387	N16709	EWR	AUS	188	1504	10	0	2023-08-02 10:00:00	Other
4003	5	6	640	645	-5	830	849	UA	477	N27733	EWR	CHS	89	628	6	45	2023-05-06 06:00:00	Other
4004	10	20	2026	2029	-3	2141	2218	AA	114	N917AN	LGA	ORD	107	733	20	29	2023-10-20 20:00:00	ORD
4006	3	10	755	800	-5	956	1019	YX	1624	N235JQ	JFK	CLT	90	541	8	0	2023-03-10 08:00:00	CLT
4009	9	18	827	832	-5	1027	1041	YX	1332	N440YX	LGA	OMA	164	1148	8	32	2023-09-18 08:00:00	Other
4011	7	11	602	605	-3	804	817	DL	684	N988AT	EWR	ATL	101	746	6	5	2023-07-11 06:00:00	ATL
4017	3	5	1057	1059	-2	1206	1222	YX	1078	N732YX	EWR	DCA	48	199	10	59	2023-03-05 10:00:00	Other
4020	10	31	1221	1226	-5	1601	1529	AA	161	N954NN	LGA	DFW	231	1389	12	26	2023-10-31 12:00:00	Other
4029	10	29	1736	1740	-4	2018	2008	YX	1324	N418YX	LGA	SDF	111	659	17	40	2023-10-29 17:00:00	Other
4033	7	20	1500	1505	-5	1710	1712	AA	626	N301NW	LGA	CLT	81	544	15	5	2023-07-20 15:00:00	CLT
4035	11	15	1052	1057	-5	1250	1307	9E	1502	N482PX	LGA	MYR	85	563	10	57	2023-11-15 10:00:00	Other
4042	4	3	1926	1929	-3	2137	2200	YX	1553	N210JQ	LGA	OMA	171	1148	19	29	2023-04-03 19:00:00	Other
4043	11	3	915	920	-5	1022	1040	9E	1516	N932XJ	JFK	IAD	47	228	9	20	2023-11-03 09:00:00	Other
4047	11	12	1810	1815	-5	2022	2109	9E	1540	N137EV	JFK	MCI	160	1113	18	15	2023-11-12 18:00:00	Other
4049	4	20	1457	1459	-2	1739	1801	DL	303	N3772H	LGA	PBI	139	1035	14	59	2023-04-20 14:00:00	Other
4058	5	15	1942	1945	-3	2135	2152	9E	1475	N308PQ	EWR	CVG	88	569	19	45	2023-05-15 19:00:00	Other
4064	2	13	1024	1029	-5	1140	1152	YX	1017	N746YX	EWR	DCA	45	199	10	29	2023-02-13 10:00:00	Other
4067	5	5	1557	1559	-2	1758	1836	DL	765	N344NB	JFK	MSY	158	1182	15	59	2023-05-05 15:00:00	Other
4070	6	7	1147	1150	-3	1521	1546	DL	185	N544US	JFK	STT	197	1623	11	50	2023-06-07 11:00:00	Other
4077	4	18	1541	1546	-5	1724	1729	YX	1159	N110HQ	JFK	DCA	55	213	15	46	2023-04-18 15:00:00	Other
4085	12	19	1731	1735	-4	2033	2045	AS	75	N284AK	EWR	PDX	334	2434	17	35	2023-12-19 17:00:00	Other
4089	2	21	1156	1200	-4	1258	1324	YX	1486	N222JQ	LGA	BOS	34	184	12	0	2023-02-21 12:00:00	BOS
4099	3	15	1025	1030	-5	1130	1136	9E	1554	N329PQ	JFK	BWI	35	184	10	30	2023-03-15 10:00:00	Other
4103	3	6	730	735	-5	1019	1043	DL	597	N926DZ	JFK	TPA	144	1005	7	35	2023-03-06 07:00:00	Other
4113	6	4	646	650	-4	921	1002	DL	107	N510DE	JFK	SEA	296	2422	6	50	2023-06-04 06:00:00	Other
4119	11	6	657	700	-3	1030	1033	DL	173	N718TW	JFK	SFO	368	2586	7	0	2023-11-06 07:00:00	Other
4126	5	19	555	600	-5	731	753	DL	355	N349DX	LGA	DTW	77	502	6	0	2023-05-19 06:00:00	Other
4129	8	21	1235	1240	-5	1401	1417	AA	781	N905NN	LGA	ORD	111	733	12	40	2023-08-21 12:00:00	ORD
4135	12	6	1158	1200	-2	1317	1337	OO	1149	N271SY	JFK	BUF	57	301	12	0	2023-12-06 12:00:00	Other
4141	6	15	1625	1630	-5	1738	1805	9E	1540	N313PQ	LGA	PWM	42	269	16	30	2023-06-15 16:00:00	Other
4143	3	14	1724	1729	-5	2022	2044	B6	446	N592JB	JFK	SAN	324	2446	17	29	2023-03-14 17:00:00	Other
4146	1	29	755	800	-5	923	936	9E	1589	N299PQ	JFK	BUF	62	301	8	0	2023-01-29 08:00:00	Other
4147	10	21	827	830	-3	1033	1104	YX	1708	N206JQ	LGA	SDF	108	659	8	30	2023-10-21 08:00:00	Other
4154	2	2	2055	2057	-2	2243	2240	UA	76	N24702	EWR	CLE	77	404	20	57	2023-02-02 20:00:00	Other
4162	10	30	1825	1830	-5	1944	1959	YX	1848	N221JQ	LGA	DCA	49	214	18	30	2023-10-30 18:00:00	Other
4169	9	5	927	929	-2	1218	1246	DL	295	N913DU	JFK	SLC	258	1990	9	29	2023-09-05 09:00:00	Other
4180	4	19	2242	2245	-3	18	4	B6	6	N317JB	JFK	SYR	44	209	22	45	2023-04-19 22:00:00	Other
4182	5	13	1751	1756	-5	2057	2108	AA	736	N343RY	LGA	MIA	151	1096	17	56	2023-05-13 17:00:00	MIA
4183	3	15	1540	1545	-5	1859	1907	UA	429	N37018	EWR	SFO	344	2565	15	45	2023-03-15 15:00:00	Other
4185	6	8	2051	2055	-4	2221	2258	YX	1862	N240JQ	JFK	PIT	57	340	20	55	2023-06-08 20:00:00	Other
4186	3	5	1517	1520	-3	1817	1845	DL	113	N126DU	LGA	DFW	210	1389	15	20	2023-03-05 15:00:00	Other
4198	4	10	817	820	-3	921	954	9E	1304	N933XJ	LGA	IAD	45	229	8	20	2023-04-10 08:00:00	Other
4200	3	17	1453	1458	-5	1629	1635	9E	1546	N302PQ	JFK	RIC	61	288	14	58	2023-03-17 14:00:00	Other
4215	11	6	822	825	-3	925	952	YX	1864	N203JQ	EWR	BOS	36	200	8	25	2023-11-06 08:00:00	BOS
4217	2	20	758	800	-2	945	946	B6	399	N304JB	JFK	BNA	140	765	8	0	2023-02-20 08:00:00	Other
4222	5	2	2025	2030	-5	2158	2221	YX	1577	N201JQ	JFK	PIT	64	340	20	30	2023-05-02 20:00:00	Other
4235	3	12	1556	1600	-4	1912	1921	AA	98	N110AN	JFK	LAX	347	2475	16	0	2023-03-12 16:00:00	LAX
4237	11	8	656	700	-4	946	1015	DL	921	N355NW	JFK	AUS	199	1521	7	0	2023-11-08 07:00:00	Other
4238	1	28	758	800	-2	1105	1128	AA	903	N928NN	JFK	DFW	214	1391	8	0	2023-01-28 08:00:00	Other
4242	7	5	1003	1007	-4	1235	1249	UA	82	N27269	EWR	DFW	172	1372	10	7	2023-07-05 10:00:00	Other
4249	12	8	1927	1929	-2	2118	2132	YX	1759	N860RW	LGA	CMH	75	479	19	29	2023-12-08 19:00:00	Other
4251	3	9	1354	1359	-5	1529	1557	YX	1179	N657RW	EWR	ILM	74	488	13	59	2023-03-09 13:00:00	Other
4253	6	30	748	751	-3	957	1014	UA	235	N17301	EWR	LAS	283	2227	7	51	2023-06-30 07:00:00	Other
4255	9	6	1255	1300	-5	1538	1606	UA	129	N24702	EWR	SNA	322	2434	13	0	2023-09-06 13:00:00	Other
4256	11	24	1406	1411	-5	1524	1544	UA	568	N469UA	EWR	BNA	117	748	14	11	2023-11-24 14:00:00	Other
4258	3	11	1748	1751	-3	1940	2001	B6	380	N216JB	JFK	DTW	86	509	17	51	2023-03-11 17:00:00	Other
4261	2	15	947	950	-3	1209	1220	WN	193	N240WN	LGA	MCI	179	1107	9	50	2023-02-15 09:00:00	Other
4266	2	19	855	859	-4	1200	1226	UA	244	N16732	EWR	SNA	348	2434	8	59	2023-02-19 08:00:00	Other
4273	6	19	635	640	-5	816	831	9E	1591	N319PQ	LGA	CMH	77	479	6	40	2023-06-19 06:00:00	Other
4278	4	11	1257	1300	-3	1527	1546	UA	659	N27520	EWR	MCO	124	937	13	0	2023-04-11 13:00:00	MCO
4279	6	15	1403	1405	-2	1537	1551	OO	1777	N163SY	LGA	ORD	117	733	14	5	2023-06-15 14:00:00	ORD
4280	7	12	2033	2037	-4	2348	2352	B6	565	N934JB	JFK	LAX	318	2475	20	37	2023-07-12 20:00:00	LAX
4286	8	25	755	759	-4	1006	943	OO	941	N254SY	JFK	ORD	123	740	7	59	2023-08-25 07:00:00	ORD
4287	8	21	2200	2205	-5	2325	2354	9E	1250	N932XJ	JFK	BTV	48	266	22	5	2023-08-21 22:00:00	Other
4289	2	10	632	635	-3	822	827	YX	1492	N219YX	LGA	CMH	86	479	6	35	2023-02-10 06:00:00	Other
4292	12	2	1357	1400	-3	1704	1717	UA	393	N77014	EWR	SFO	341	2565	14	0	2023-12-02 14:00:00	Other
4298	4	29	555	600	-5	757	819	DL	751	N934AT	EWR	ATL	109	746	6	0	2023-04-29 06:00:00	ATL
4299	9	22	1438	1440	-2	1612	1612	9E	1500	N485PX	LGA	ORF	55	296	14	40	2023-09-22 14:00:00	Other
4301	12	24	951	955	-4	1140	1210	NK	520	N628NK	EWR	CHS	88	628	9	55	2023-12-24 09:00:00	Other
4303	9	11	1007	1009	-2	1204	1213	UA	507	N23707	EWR	CLT	89	529	10	9	2023-09-11 10:00:00	CLT
4315	3	19	750	755	-5	1059	1104	B6	174	N561JB	LGA	PBI	171	1035	7	55	2023-03-19 07:00:00	Other
4316	1	10	555	600	-5	928	924	AA	51	N102NN	JFK	LAX	362	2475	6	0	2023-01-10 06:00:00	LAX
4317	10	18	1857	1900	-3	2041	2058	YX	1366	N134HQ	JFK	RDU	68	427	19	0	2023-10-18 19:00:00	Other
4319	9	19	1607	1610	-3	1907	1938	DL	238	N901DN	JFK	SLC	269	1990	16	10	2023-09-19 16:00:00	Other
4330	10	17	1837	1840	-3	2123	2150	B6	44	N957JB	JFK	SMF	323	2521	18	40	2023-10-17 18:00:00	Other
4337	4	2	705	710	-5	851	853	B6	372	N192JB	JFK	ORD	131	740	7	10	2023-04-02 07:00:00	ORD
4341	4	4	705	710	-5	1047	1105	UA	528	N27733	EWR	STT	197	1634	7	10	2023-04-04 07:00:00	Other
4342	2	8	1255	1300	-5	1450	1510	9E	1380	N132EV	JFK	DTW	92	509	13	0	2023-02-08 13:00:00	Other
4345	9	27	1841	1845	-4	2001	2010	WN	1285	N7722B	LGA	BNA	112	764	18	45	2023-09-27 18:00:00	Other
4346	2	24	1927	1929	-2	2332	2240	UA	203	N47282	EWR	SAN	388	2425	19	29	2023-02-24 19:00:00	Other
4352	10	30	948	950	-2	1155	1212	9E	1490	N146PQ	EWR	CVG	102	569	9	50	2023-10-30 09:00:00	Other
4354	8	2	1237	1240	-3	1414	1359	NK	331	N519NK	EWR	BNA	103	748	12	40	2023-08-02 12:00:00	Other
4360	10	31	856	859	-3	1003	1023	YX	1764	N810MD	LGA	BOS	32	184	8	59	2023-10-31 08:00:00	BOS
4362	6	23	557	600	-3	842	903	AA	1	N101NN	JFK	LAX	316	2475	6	0	2023-06-23 06:00:00	LAX
4365	10	2	1401	1406	-5	1459	1522	UA	706	N408UA	EWR	BOS	38	200	14	6	2023-10-02 14:00:00	BOS
4367	8	17	1633	1638	-5	1810	1817	9E	1160	N302PQ	LGA	PWM	45	269	16	38	2023-08-17 16:00:00	Other
4385	10	1	521	525	-4	801	824	B6	38	N943JT	JFK	LAX	314	2475	5	25	2023-10-01 05:00:00	LAX
4389	6	3	940	945	-5	1138	1209	9E	1434	N491PX	LGA	GRR	87	618	9	45	2023-06-03 09:00:00	Other
4390	4	18	1700	1705	-5	1848	1850	NK	24	N509NK	EWR	MYR	83	550	17	5	2023-04-18 17:00:00	Other
4403	10	4	1908	1910	-2	2109	2122	9E	1611	N923XJ	JFK	CVG	89	589	19	10	2023-10-04 19:00:00	Other
4404	11	27	1309	1311	-2	1437	1447	UA	85	N27239	EWR	ORD	119	719	13	11	2023-11-27 13:00:00	ORD
4406	11	10	1231	1236	-5	1516	1543	NK	349	N922NK	EWR	FLL	148	1065	12	36	2023-11-10 12:00:00	FLL
4408	7	24	1342	1345	-3	1540	1547	YX	1038	N128HQ	LGA	CAE	98	617	13	45	2023-07-24 13:00:00	Other
4416	1	19	856	900	-4	1156	1228	AA	881	N323RM	LGA	MIA	152	1096	9	0	2023-01-19 09:00:00	MIA
4421	8	19	1236	1240	-4	1527	1545	NK	294	N905NK	EWR	FLL	141	1065	12	40	2023-08-19 12:00:00	FLL
4425	11	14	1857	1900	-3	2236	2225	DL	512	N514DE	JFK	SEA	357	2422	19	0	2023-11-14 19:00:00	Other
4426	3	28	956	959	-3	1233	1221	9E	1481	N183GJ	JFK	SAV	121	718	9	59	2023-03-28 09:00:00	Other
4429	11	3	1521	1525	-4	1758	1809	YX	1770	N222JQ	LGA	JAX	126	833	15	25	2023-11-03 15:00:00	Other
4436	4	7	618	620	-2	855	905	B6	224	N662JB	JFK	MCO	132	944	6	20	2023-04-07 06:00:00	MCO
4454	11	2	1852	1857	-5	2112	2118	DL	446	N103DU	LGA	MSY	174	1183	18	57	2023-11-02 18:00:00	Other
4456	12	16	2029	2034	-5	2141	2205	NK	1005	N644NK	LGA	ORD	110	733	20	34	2023-12-16 20:00:00	ORD
4457	7	26	1345	1350	-5	1520	1531	YX	1062	N108HQ	JFK	PIT	62	340	13	50	2023-07-26 13:00:00	Other
4465	8	21	1056	1100	-4	1249	1319	YX	877	N865RW	EWR	IND	88	645	11	0	2023-08-21 11:00:00	Other
4476	10	30	726	730	-4	925	913	DL	646	N112DU	LGA	ORD	128	733	7	30	2023-10-30 07:00:00	ORD
4477	5	28	1855	1859	-4	2117	2214	UA	573	N75436	EWR	PDX	294	2434	18	59	2023-05-28 18:00:00	Other
4483	3	14	802	806	-4	908	935	B6	59	N197JB	JFK	ROC	49	264	8	6	2023-03-14 08:00:00	Other
4485	3	23	1301	1303	-2	1442	1439	UA	682	N37274	EWR	ORD	137	719	13	3	2023-03-23 13:00:00	ORD
4489	9	25	1926	1929	-3	2140	2133	AA	760	N8001N	JFK	CLT	92	541	19	29	2023-09-25 19:00:00	CLT
4491	2	20	555	600	-5	745	801	AA	908	N114UW	EWR	CLT	89	529	6	0	2023-02-20 06:00:00	CLT
4505	8	30	953	955	-2	1152	1147	9E	1262	N324PQ	EWR	RDU	70	416	9	55	2023-08-30 09:00:00	Other
4509	5	29	1816	1819	-3	2116	2159	B6	245	N775JB	JFK	SJC	321	2569	18	19	2023-05-29 18:00:00	Other
4518	4	17	1925	1929	-4	2134	2226	DL	104	N860DN	JFK	DEN	224	1626	19	29	2023-04-17 19:00:00	Other
4519	2	17	556	600	-4	815	809	AA	260	N971UY	LGA	CLT	99	544	6	0	2023-02-17 06:00:00	CLT
4524	2	11	751	755	-4	1040	1115	AS	86	N930VA	EWR	LAX	321	2454	7	55	2023-02-11 07:00:00	LAX
4528	5	1	754	759	-5	1044	1101	AA	322	N967AN	JFK	DFW	194	1391	7	59	2023-05-01 07:00:00	Other
4532	5	31	1319	1324	-5	1628	1628	UA	466	N459UA	EWR	RSW	151	1068	13	24	2023-05-31 13:00:00	Other
4533	8	14	1000	1003	-3	1215	1202	B6	53	N247JB	JFK	DTW	89	509	10	3	2023-08-14 10:00:00	Other
4546	11	3	1724	1729	-5	1837	1904	YX	1136	N741YX	EWR	PIT	53	319	17	29	2023-11-03 17:00:00	Other
4549	8	4	1104	1109	-5	1240	1304	YX	1053	N423YX	LGA	CMH	76	479	11	9	2023-08-04 11:00:00	Other
4552	7	5	1249	1252	-3	1430	1502	DL	428	N103DU	JFK	DTW	78	509	12	52	2023-07-05 12:00:00	Other
4556	10	26	1325	1329	-4	1550	1558	DL	102	N3756	LGA	DEN	237	1620	13	29	2023-10-26 13:00:00	Other
4563	3	8	622	625	-3	821	831	YX	1253	N401YX	LGA	STL	163	888	6	25	2023-03-08 06:00:00	Other
4567	9	30	1545	1548	-3	1735	1757	UA	420	N806UA	EWR	IND	92	645	15	48	2023-09-30 15:00:00	Other
4568	10	23	1958	2000	-2	2248	2315	AA	691	N306NY	LGA	MIA	138	1096	20	0	2023-10-23 20:00:00	MIA
4572	5	24	832	834	-2	1011	1033	YX	993	N752YX	EWR	GSO	69	445	8	34	2023-05-24 08:00:00	Other
4575	6	24	1146	1149	-3	1256	1322	9E	1744	N331PQ	LGA	BUF	48	292	11	49	2023-06-24 11:00:00	Other
4593	9	8	1055	1100	-5	1405	1400	AA	715	N846NN	LGA	DFW	217	1389	11	0	2023-09-08 11:00:00	Other
4597	11	11	1548	1550	-2	1856	1905	DL	196	N172DN	JFK	LAX	321	2475	15	50	2023-11-11 15:00:00	LAX
4618	7	13	1947	1950	-3	2247	2217	9E	1143	N294PQ	LGA	IND	115	660	19	50	2023-07-13 19:00:00	Other
4623	1	19	750	755	-5	938	940	YX	1844	N879RW	LGA	MKE	118	738	7	55	2023-01-19 07:00:00	Other
4630	8	16	657	659	-2	1002	958	AA	256	N823AW	JFK	AUS	204	1521	6	59	2023-08-16 06:00:00	Other
4642	4	10	1752	1755	-3	2032	2030	WN	207	N8552Z	LGA	ATL	104	762	17	55	2023-04-10 17:00:00	ATL
4648	3	14	1157	1200	-3	1435	1435	DL	284	N812DN	JFK	ATL	108	760	12	0	2023-03-14 12:00:00	ATL
4650	2	2	2123	2125	-2	2248	2247	YX	1525	N222JQ	LGA	ROC	53	254	21	25	2023-02-02 21:00:00	Other
4662	6	13	731	733	-2	917	926	UA	498	N47282	EWR	CLT	82	529	7	33	2023-06-13 07:00:00	CLT
4666	4	9	1753	1756	-3	2054	2112	UA	767	N818UA	EWR	MIA	147	1085	17	56	2023-04-09 17:00:00	MIA
4675	10	17	1324	1329	-5	1525	1548	9E	1700	N335PQ	LGA	IND	90	660	13	29	2023-10-17 13:00:00	Other
4681	6	20	841	845	-4	1125	1122	YX	1898	N229JQ	JFK	JAX	126	828	8	45	2023-06-20 08:00:00	Other
4685	12	29	1957	1959	-2	2339	2323	DL	339	N389DN	LGA	MIA	184	1096	19	59	2023-12-29 19:00:00	MIA
4697	3	3	1955	2000	-5	2252	2205	9E	1400	N319PQ	LGA	GSO	90	461	20	0	2023-03-03 20:00:00	Other
4708	10	4	1851	1855	-4	2119	2150	DL	748	N328DN	LGA	MCO	120	950	18	55	2023-10-04 18:00:00	MCO
4709	10	14	1411	1416	-5	1508	1535	YX	1170	N725YX	EWR	BOS	35	200	14	16	2023-10-14 14:00:00	BOS
4710	5	8	615	620	-5	946	945	UA	380	N14118	EWR	SFO	361	2565	6	20	2023-05-08 06:00:00	Other
4713	7	21	655	700	-5	1025	956	DL	442	N828DN	JFK	TPA	153	1005	7	0	2023-07-21 07:00:00	Other
4728	7	19	558	600	-2	810	820	DL	258	N357DN	LGA	ATL	108	762	6	0	2023-07-19 06:00:00	ATL
4732	12	12	940	945	-5	1128	1147	9E	1423	N935XJ	EWR	RDU	65	416	9	45	2023-12-12 09:00:00	Other
4742	7	10	1815	1820	-5	2045	2052	9E	1249	N691CA	JFK	CHS	100	636	18	20	2023-07-10 18:00:00	Other
4752	3	13	1152	1155	-3	1440	1518	DL	313	N106DU	LGA	DFW	205	1389	11	55	2023-03-13 11:00:00	Other
4758	2	24	1755	1800	-5	1927	1927	YX	1565	N211JQ	JFK	PWM	53	273	18	0	2023-02-24 18:00:00	Other
4759	9	19	1125	1130	-5	1325	1353	YX	1865	N880RW	LGA	MCI	153	1107	11	30	2023-09-19 11:00:00	Other
4765	4	8	2127	2130	-3	4	14	DL	467	N901DN	JFK	ATL	121	760	21	30	2023-04-08 21:00:00	ATL
4766	4	7	816	820	-4	1037	1044	B6	821	N809JB	LGA	MSY	168	1183	8	20	2023-04-07 08:00:00	Other
4770	10	30	1102	1107	-5	1326	1340	UA	446	N76288	EWR	JAX	119	820	11	7	2023-10-30 11:00:00	Other
4790	5	12	1025	1029	-4	1214	1259	YX	1613	N211JQ	LGA	IND	92	660	10	29	2023-05-12 10:00:00	Other
4792	5	14	1445	1448	-3	1605	1630	B6	797	N521JB	LGA	BNA	108	764	14	48	2023-05-14 14:00:00	Other
4793	6	11	1514	1519	-5	1709	1735	DL	389	N350DN	LGA	MSP	148	1020	15	19	2023-06-11 15:00:00	Other
4796	8	13	756	759	-3	931	938	YX	916	N855RW	EWR	RIC	51	277	7	59	2023-08-13 07:00:00	Other
4806	11	14	1024	1027	-3	1317	1336	DL	378	N337DN	LGA	TPA	143	1010	10	27	2023-11-14 10:00:00	Other
4816	4	21	1157	1200	-3	1325	1331	AA	645	N318SF	EWR	ORD	107	719	12	0	2023-04-21 12:00:00	ORD
4818	1	17	628	630	-2	933	935	B6	93	N998JE	LGA	MCO	139	950	6	30	2023-01-17 06:00:00	MCO
4822	12	28	1824	1829	-5	2127	2144	F9	1410	N717FR	LGA	MCO	149	950	18	29	2023-12-28 18:00:00	MCO
4826	10	27	1951	1955	-4	2308	2307	UA	612	N37563	EWR	SMF	347	2500	19	55	2023-10-27 19:00:00	Other
4828	11	1	1025	1029	-4	1329	1334	DL	538	N106DU	JFK	SAT	226	1587	10	29	2023-11-01 10:00:00	Other
4834	9	15	546	549	-3	835	853	AA	1	N105NN	JFK	LAX	318	2475	5	49	2023-09-15 05:00:00	LAX
4842	7	22	831	835	-4	949	1010	YX	1404	N243JQ	LGA	BNA	119	764	8	35	2023-07-22 08:00:00	Other
4843	3	3	1224	1227	-3	1344	1357	YX	1063	N745YX	EWR	BUF	52	282	12	27	2023-03-03 12:00:00	Other
4847	6	13	1451	1455	-4	1553	1626	9E	1658	N929XJ	JFK	BWI	38	184	14	55	2023-06-13 14:00:00	Other
4851	8	3	838	840	-2	1012	1022	UA	192	N17279	EWR	CLE	59	404	8	40	2023-08-03 08:00:00	Other
4852	5	18	1427	1429	-2	1712	1731	UA	842	N479UA	EWR	PBI	143	1023	14	29	2023-05-18 14:00:00	Other
4854	6	16	733	735	-2	929	936	UA	930	N38446	EWR	MSY	156	1167	7	35	2023-06-16 07:00:00	Other
4856	9	20	1051	1056	-5	1218	1243	YX	1159	N647RW	EWR	RDU	66	416	10	56	2023-09-20 10:00:00	Other
4858	8	13	1646	1649	-3	1938	2028	DL	143	N528DE	JFK	SEA	325	2422	16	49	2023-08-13 16:00:00	Other
4861	9	20	2121	2126	-5	2241	2300	YX	1891	N228JQ	LGA	PIT	54	335	21	26	2023-09-20 21:00:00	Other
4864	11	15	1119	1123	-4	1428	1425	NK	1029	N629NK	EWR	MCO	137	937	11	23	2023-11-15 11:00:00	MCO
4867	1	27	1724	1729	-5	1947	2008	9E	1418	N299PQ	JFK	MCI	179	1113	17	29	2023-01-27 17:00:00	Other
4869	8	15	1628	1630	-2	2019	1943	B6	57	N706JB	JFK	TPA	166	1005	16	30	2023-08-15 16:00:00	Other
4873	1	17	1210	1215	-5	1315	1325	B6	324	N279JB	LGA	BOS	42	184	12	15	2023-01-17 12:00:00	BOS
4875	8	13	1715	1720	-5	1908	1900	9E	1231	N136EV	LGA	BNA	120	764	17	20	2023-08-13 17:00:00	Other
4884	9	19	727	730	-3	840	900	YX	1083	N725YX	EWR	MKE	107	725	7	30	2023-09-19 07:00:00	Other
4892	12	9	1023	1027	-4	1323	1332	UA	682	N78540	EWR	IAH	214	1400	10	27	2023-12-09 10:00:00	Other
4893	4	4	1920	1925	-5	2037	2055	AA	886	N776XF	LGA	BNA	109	764	19	25	2023-04-04 19:00:00	Other
4907	1	10	925	930	-5	1034	1057	9E	1577	N166PQ	JFK	PWM	53	273	9	30	2023-01-10 09:00:00	Other
4910	7	20	1123	1128	-5	1418	1445	AA	534	N887NN	LGA	MIA	141	1096	11	28	2023-07-20 11:00:00	MIA
4911	7	22	2049	2051	-2	2211	2144	YX	940	N647RW	EWR	PHL	22	80	20	51	2023-07-22 20:00:00	Other
4918	7	19	1425	1429	-4	1554	1604	9E	1199	N935XJ	JFK	SYR	45	209	14	29	2023-07-19 14:00:00	Other
4924	10	10	811	813	-2	1014	1032	9E	1562	N306PQ	LGA	GRR	94	618	8	13	2023-10-10 08:00:00	Other
4931	5	27	1252	1255	-3	1438	1445	9E	1376	N604LR	JFK	RDU	71	427	12	55	2023-05-27 12:00:00	Other
4933	11	21	651	655	-4	857	901	UA	454	N476UA	EWR	CLT	94	529	6	55	2023-11-21 06:00:00	CLT
4942	5	10	1846	1850	-4	1959	2019	9E	1322	N187GJ	LGA	PWM	51	269	18	50	2023-05-10 18:00:00	Other
4946	7	24	1428	1430	-2	1607	1619	YX	1040	N445YX	LGA	CLE	66	419	14	30	2023-07-24 14:00:00	Other
4952	11	29	856	859	-3	1229	1257	AA	519	N303RE	JFK	PHX	305	2153	8	59	2023-11-29 08:00:00	Other
4959	5	12	1854	1859	-5	2011	2029	YX	1710	N219YX	LGA	BOS	35	184	18	59	2023-05-12 18:00:00	BOS
4963	1	6	732	737	-5	1023	1044	DL	360	N386DN	JFK	MCO	142	944	7	37	2023-01-06 07:00:00	MCO
4966	8	20	2145	2150	-5	2251	2314	UA	311	N4888U	EWR	BOS	46	200	21	50	2023-08-20 21:00:00	BOS
4967	8	3	1356	1400	-4	1534	1557	9E	1206	N272PQ	JFK	RDU	70	427	14	0	2023-08-03 14:00:00	Other
4968	5	17	912	914	-2	1209	1206	UA	501	N465UA	EWR	MCO	135	937	9	14	2023-05-17 09:00:00	MCO
4972	2	27	815	820	-5	1021	1046	9E	1277	N928XJ	LGA	CVG	103	585	8	20	2023-02-27 08:00:00	Other
4988	1	7	1843	1845	-2	2103	2126	DL	206	N372NW	LGA	ATL	113	762	18	45	2023-01-07 18:00:00	ATL
4989	8	3	757	759	-2	1106	1110	AA	478	N378SC	JFK	MIA	148	1089	7	59	2023-08-03 07:00:00	MIA
5001	5	19	1327	1329	-2	1453	1515	YX	1323	N118HQ	JFK	PIT	64	340	13	29	2023-05-19 13:00:00	Other
5010	9	1	1457	1459	-2	1635	1637	YX	1361	N127HQ	JFK	DCA	50	213	14	59	2023-09-01 14:00:00	Other
5012	3	7	1636	1640	-4	1940	2000	DL	236	N193DN	JFK	SEA	334	2422	16	40	2023-03-07 16:00:00	Other
5015	2	19	826	830	-4	951	1029	DL	611	N123DQ	LGA	ORD	118	733	8	30	2023-02-19 08:00:00	ORD
5019	1	19	624	629	-5	844	900	UA	867	N882UA	LGA	DEN	230	1620	6	29	2023-01-19 06:00:00	Other
5021	8	10	655	659	-4	911	912	NK	939	N693NK	EWR	PHX	296	2133	6	59	2023-08-10 06:00:00	Other
5026	6	20	1120	1124	-4	1350	1443	DL	183	N842DN	JFK	SEA	298	2422	11	24	2023-06-20 11:00:00	Other
5029	2	19	1855	1859	-4	2026	2056	YX	1256	N132HQ	LGA	PIT	65	335	18	59	2023-02-19 18:00:00	Other
5040	3	28	1145	1150	-5	1325	1327	9E	1426	N915XJ	LGA	MKE	122	738	11	50	2023-03-28 11:00:00	Other
5043	3	5	952	955	-3	1157	1208	DL	989	N980AT	EWR	DTW	95	488	9	55	2023-03-05 09:00:00	Other
5044	3	13	1007	1010	-3	1243	1253	YX	1129	N656RW	EWR	JAX	130	820	10	10	2023-03-13 10:00:00	Other
5047	4	12	2126	2129	-3	2240	2258	9E	1267	N200PQ	LGA	BUF	51	292	21	29	2023-04-12 21:00:00	Other
5048	4	15	825	829	-4	1013	1005	OO	1060	N244SY	JFK	BNA	111	765	8	29	2023-04-15 08:00:00	Other
5051	5	21	1948	1950	-2	2148	2240	B6	47	N2047J	JFK	PHX	277	2153	19	50	2023-05-21 19:00:00	Other
5053	10	9	920	925	-5	1103	1113	YX	1326	N406YX	LGA	GSO	75	461	9	25	2023-10-09 09:00:00	Other
5061	8	24	2128	2130	-2	20	2338	YX	910	N742YX	EWR	DTW	116	488	21	30	2023-08-24 21:00:00	Other
5073	9	5	626	630	-4	820	833	AA	319	N121UW	JFK	CLT	87	541	6	30	2023-09-05 06:00:00	CLT
5074	11	19	630	635	-5	803	819	YX	1124	N760YX	EWR	CLE	70	404	6	35	2023-11-19 06:00:00	Other
5084	10	10	1901	1903	-2	2153	2159	UA	873	N69838	EWR	PBI	138	1023	19	3	2023-10-10 19:00:00	Other
5086	10	12	1726	1730	-4	1913	1904	OO	1239	N312SY	JFK	MKE	133	745	17	30	2023-10-12 17:00:00	Other
5092	10	28	1430	1434	-4	1609	1556	B6	906	N324JB	JFK	BUF	59	301	14	34	2023-10-28 14:00:00	Other
5096	8	17	843	846	-3	1015	1028	YX	1396	N239JQ	LGA	PIT	54	335	8	46	2023-08-17 08:00:00	Other
5097	11	26	1541	1546	-5	1731	1738	YX	1318	N126HQ	JFK	BNA	132	765	15	46	2023-11-26 15:00:00	Other
5104	11	10	1658	1700	-2	1816	1838	YX	1878	N225JQ	LGA	DCA	48	214	17	0	2023-11-10 17:00:00	Other
5110	2	17	1257	1259	-2	1447	1506	DL	749	N354NW	LGA	DTW	84	502	12	59	2023-02-17 12:00:00	Other
5117	8	16	712	715	-3	833	840	WN	819	N8746Q	LGA	BNA	114	764	7	15	2023-08-16 07:00:00	Other
5119	4	24	1456	1500	-4	1637	1644	9E	1385	N485PX	EWR	RDU	73	416	15	0	2023-04-24 15:00:00	Other
5124	2	2	826	830	-4	1049	1118	DL	537	N842DN	JFK	ATL	126	760	8	30	2023-02-02 08:00:00	ATL
5126	10	26	1656	1659	-3	1926	1954	UA	566	N57299	EWR	PBI	129	1023	16	59	2023-10-26 16:00:00	Other
5128	10	6	625	630	-5	832	836	UA	577	N842UA	EWR	IND	91	645	6	30	2023-10-06 06:00:00	Other
5152	4	16	728	730	-2	1025	1108	AS	15	N459AS	JFK	SFO	335	2586	7	30	2023-04-16 07:00:00	Other
5162	7	22	628	630	-2	907	921	UA	566	N25201	EWR	TPA	135	997	6	30	2023-07-22 06:00:00	Other
5166	12	5	1701	1705	-4	2035	2052	AA	930	N326SJ	JFK	PHX	313	2153	17	5	2023-12-05 17:00:00	Other
5167	7	13	636	640	-4	802	815	UA	255	N37295	EWR	CLE	62	404	6	40	2023-07-13 06:00:00	Other
5170	3	9	1726	1729	-3	2027	2040	UA	475	N17272	EWR	IAH	200	1400	17	29	2023-03-09 17:00:00	Other
5171	7	4	820	825	-5	951	1023	9E	1154	N914XJ	LGA	STL	129	888	8	25	2023-07-04 08:00:00	Other
5173	7	8	958	1000	-2	1305	1317	AA	70	N102NN	JFK	LAX	328	2475	10	0	2023-07-08 10:00:00	LAX
5175	8	7	1318	1320	-2	1433	1454	YX	1360	N882RW	LGA	DCA	47	214	13	20	2023-08-07 13:00:00	Other
5180	1	9	1517	1520	-3	1706	1721	YX	1463	N445YX	JFK	CMH	80	483	15	20	2023-01-09 15:00:00	Other
5188	11	3	823	825	-2	1134	1149	UA	201	N223UA	EWR	SFO	324	2565	8	25	2023-11-03 08:00:00	Other
5189	4	23	750	754	-4	918	958	DL	907	N315NB	LGA	MSP	134	1020	7	54	2023-04-23 07:00:00	Other
5190	10	31	1513	1515	-2	1633	1654	YX	1311	N424YX	JFK	DCA	54	213	15	15	2023-10-31 15:00:00	Other
5191	7	30	827	830	-3	1118	1140	UA	424	N13110	EWR	SEA	321	2402	8	30	2023-07-30 08:00:00	Other
5192	6	24	1703	1705	-2	1939	1914	DL	949	N327NB	LGA	DTW	79	502	17	5	2023-06-24 17:00:00	Other
5200	11	26	857	900	-3	1213	1233	AA	70	N117AN	JFK	LAX	341	2475	9	0	2023-11-26 09:00:00	LAX
5208	9	9	1005	1009	-4	1148	1217	AA	758	N905AN	LGA	CLT	79	544	10	9	2023-09-09 10:00:00	CLT
5218	2	20	556	600	-4	931	915	DL	309	N106DU	LGA	DFW	250	1389	6	0	2023-02-20 06:00:00	Other
5223	11	24	2012	2015	-3	2331	2328	UA	929	N17133	EWR	FLL	164	1065	20	15	2023-11-24 20:00:00	FLL
5226	10	28	1139	1142	-3	1410	1438	UA	600	N13248	EWR	PBI	131	1023	11	42	2023-10-28 11:00:00	Other
5227	9	23	1351	1355	-4	1748	1651	DL	284	N179DN	JFK	LAX	325	2475	13	55	2023-09-23 13:00:00	LAX
5241	11	3	1718	1720	-2	1932	1940	9E	1546	N919XJ	LGA	CVG	100	585	17	20	2023-11-03 17:00:00	Other
5245	11	11	755	800	-5	1010	1026	9E	1671	N600LR	JFK	CHS	110	636	8	0	2023-11-11 08:00:00	Other
5247	5	21	1027	1029	-2	1230	1259	YX	1613	N216JQ	LGA	IND	98	660	10	29	2023-05-21 10:00:00	Other
5261	8	12	806	810	-4	1155	1218	DL	575	N6703D	JFK	STT	200	1623	8	10	2023-08-12 08:00:00	Other
5264	8	22	1425	1429	-4	1624	1640	UA	670	N38467	EWR	DEN	213	1605	14	29	2023-08-22 14:00:00	Other
5268	5	30	540	545	-5	649	709	NK	273	N517NK	EWR	PIT	49	319	5	45	2023-05-30 05:00:00	Other
5276	11	12	1726	1730	-4	1837	1854	OO	1173	N614CZ	JFK	BOS	34	187	17	30	2023-11-12 17:00:00	BOS
5284	5	28	701	705	-4	908	923	DL	764	N809DN	EWR	ATL	102	746	7	5	2023-05-28 07:00:00	ATL
5286	1	25	1710	1715	-5	2005	2037	UA	151	N27015	EWR	SFO	310	2565	17	15	2023-01-25 17:00:00	Other
5287	8	22	1409	1412	-3	1603	1626	9E	1108	N691CA	LGA	CVG	87	585	14	12	2023-08-22 14:00:00	Other
5302	9	16	606	608	-2	742	755	DL	780	N927AT	EWR	DTW	72	488	6	8	2023-09-16 06:00:00	Other
5308	9	15	1019	1022	-3	1208	1220	YX	1059	N753YX	EWR	ILM	77	488	10	22	2023-09-15 10:00:00	Other
5310	8	31	1513	1515	-2	1624	1633	YX	1331	N878RW	LGA	ACK	36	202	15	15	2023-08-31 15:00:00	Other
5328	11	11	852	857	-5	1107	1119	9E	1761	N491PX	LGA	GSP	106	610	8	57	2023-11-11 08:00:00	Other
5334	6	27	628	630	-2	835	840	WN	426	N470WN	LGA	DEN	221	1620	6	30	2023-06-27 06:00:00	Other
5340	6	7	1058	1100	-2	1211	1230	YX	1920	N239JQ	LGA	BOS	34	184	11	0	2023-06-07 11:00:00	BOS
5345	6	1	823	825	-2	1008	1035	YX	1321	N124HQ	LGA	GRR	91	618	8	25	2023-06-01 08:00:00	Other
5365	1	24	727	730	-3	959	1008	B6	528	N317JB	JFK	JAX	128	828	7	30	2023-01-24 07:00:00	Other
5366	3	7	1351	1355	-4	1531	1548	9E	1514	N325PQ	JFK	RDU	77	427	13	55	2023-03-07 13:00:00	Other
5379	12	1	1011	1015	-4	1143	1154	UA	459	N458UA	LGA	ORD	120	733	10	15	2023-12-01 10:00:00	ORD
5380	4	20	1515	1520	-5	1638	1655	9E	1350	N922XJ	LGA	MKE	113	738	15	20	2023-04-20 15:00:00	Other
5381	5	25	2157	2159	-2	2311	2330	YX	1184	N402YX	JFK	BOS	38	187	21	59	2023-05-25 21:00:00	BOS
5389	6	29	832	836	-4	1017	1030	9E	1549	N933XJ	LGA	RDU	70	431	8	36	2023-06-29 08:00:00	Other
5395	7	16	1125	1130	-5	1426	1437	AA	101	N117AN	JFK	LAX	326	2475	11	30	2023-07-16 11:00:00	LAX
5398	4	23	1727	1730	-3	1913	1932	NK	53	N601NK	LGA	DTW	74	502	17	30	2023-04-23 17:00:00	Other
5401	3	22	627	630	-3	819	820	WN	264	N8760L	LGA	STL	142	888	6	30	2023-03-22 06:00:00	Other
5408	2	19	1706	1709	-3	1914	1932	AA	592	N923US	LGA	CLT	96	544	17	9	2023-02-19 17:00:00	CLT
5409	1	23	752	755	-3	913	940	YX	1844	N880RW	LGA	MKE	117	738	7	55	2023-01-23 07:00:00	Other
5410	9	28	2147	2150	-3	2242	2245	9E	1510	N330PQ	LGA	BDL	22	101	21	50	2023-09-28 21:00:00	Other
5412	4	5	1551	1555	-4	1837	1840	DL	703	N340NB	JFK	MSY	167	1182	15	55	2023-04-05 15:00:00	Other
5424	11	26	2225	2230	-5	30	2358	9E	1447	N135EV	JFK	PWM	42	273	22	30	2023-11-26 22:00:00	Other
5425	12	30	1524	1528	-4	1732	1747	YX	1121	N751YX	EWR	CHS	95	628	15	28	2023-12-30 15:00:00	Other
5432	11	7	725	730	-5	940	957	9E	1432	N132EV	JFK	SAV	104	718	7	30	2023-11-07 07:00:00	Other
5443	1	25	841	843	-2	1033	1023	YX	1176	N744YX	EWR	MKE	121	725	8	43	2023-01-25 08:00:00	Other
5446	9	28	1520	1525	-5	1704	1729	YX	1850	N229JQ	JFK	CMH	77	483	15	25	2023-09-28 15:00:00	Other
5449	1	8	1926	1930	-4	2100	2120	DL	1067	N135DQ	LGA	BNA	128	764	19	30	2023-01-08 19:00:00	Other
5450	7	22	1155	1200	-5	1429	1443	UA	675	N775UA	EWR	LAX	299	2454	12	0	2023-07-22 12:00:00	LAX
5453	1	24	938	940	-2	1423	1444	UA	668	N68807	EWR	SJU	194	1608	9	40	2023-01-24 09:00:00	Other
5456	11	23	1456	1459	-3	1646	1709	DL	750	N352DN	LGA	DTW	81	502	14	59	2023-11-23 14:00:00	Other
5457	2	5	656	700	-4	1033	1050	DL	267	N856DN	JFK	PHX	307	2153	7	0	2023-02-05 07:00:00	Other
5458	8	31	1155	1200	-5	1442	1454	UA	437	N17296	EWR	TPA	139	997	12	0	2023-08-31 12:00:00	Other
5460	8	22	851	855	-4	1028	1058	9E	1109	N921XJ	JFK	CVG	81	589	8	55	2023-08-22 08:00:00	Other
5462	5	23	2157	2200	-3	2330	2347	9E	1447	N341PQ	JFK	ROC	49	264	22	0	2023-05-23 22:00:00	Other
5463	11	29	2025	2029	-4	2130	2147	AA	989	N824AW	LGA	BOS	45	184	20	29	2023-11-29 20:00:00	BOS
5474	12	21	910	914	-4	1039	1035	9E	1368	N331PQ	LGA	ALB	30	136	9	14	2023-12-21 09:00:00	Other
5476	5	15	858	900	-2	1209	1214	AS	131	N560AS	EWR	SFO	336	2565	9	0	2023-05-15 09:00:00	Other
5478	4	25	1757	1800	-3	2053	2138	DL	253	N115DN	JFK	SLC	269	1990	18	0	2023-04-25 18:00:00	Other
5482	2	13	2032	2035	-3	2316	2255	YX	1014	N743YX	EWR	GRR	98	605	20	35	2023-02-13 20:00:00	Other
5488	9	17	1624	1629	-5	1744	1800	9E	1728	N153PQ	JFK	ROC	50	264	16	29	2023-09-17 16:00:00	Other
5506	3	21	954	959	-5	1115	1137	9E	1502	N314PQ	LGA	BGR	55	378	9	59	2023-03-21 09:00:00	Other
5510	11	9	1132	1136	-4	1328	1352	AA	749	N917NN	LGA	CLT	82	544	11	36	2023-11-09 11:00:00	CLT
5514	7	29	1325	1329	-4	1509	1508	9E	1131	N303PQ	JFK	RIC	67	288	13	29	2023-07-29 13:00:00	Other
5515	5	15	1227	1229	-2	1530	1538	UA	783	N479UA	EWR	SAT	212	1569	12	29	2023-05-15 12:00:00	Other
5518	3	19	2055	2100	-5	2400	1	B6	48	N804JB	EWR	PBI	161	1023	21	0	2023-03-19 21:00:00	Other
5524	1	27	1254	1259	-5	1427	1427	9E	1563	N308PQ	JFK	BUF	59	301	12	59	2023-01-27 12:00:00	Other
5526	10	11	1245	1250	-5	1358	1426	9E	1535	N915XJ	LGA	RIC	55	292	12	50	2023-10-11 12:00:00	Other
5527	2	25	1811	1815	-4	2112	2128	B6	235	N821JB	EWR	TPA	159	997	18	15	2023-02-25 18:00:00	Other
5530	9	25	1422	1426	-4	1726	1739	UA	243	N27263	EWR	SEA	329	2402	14	26	2023-09-25 14:00:00	Other
5540	7	17	2037	2040	-3	13	29	AA	768	N102NN	JFK	SFO	347	2586	20	40	2023-07-17 20:00:00	Other
5544	3	8	927	930	-3	1049	1114	YX	1691	N217JQ	LGA	IAD	49	229	9	30	2023-03-08 09:00:00	Other
5545	11	13	2157	2159	-2	2312	2339	B6	172	N258JB	JFK	ROC	54	264	21	59	2023-11-13 21:00:00	Other
5550	12	24	1527	1529	-2	1715	1733	NK	1003	N962NK	LGA	DTW	82	502	15	29	2023-12-24 15:00:00	Other
5553	9	21	2010	2015	-5	2156	2221	9E	1631	N910XJ	LGA	ILM	77	500	20	15	2023-09-21 20:00:00	Other
5574	2	5	642	645	-3	936	955	NK	822	N625NK	EWR	AUS	212	1504	6	45	2023-02-05 06:00:00	Other
5588	1	15	757	759	-2	839	900	YX	1183	N725YX	EWR	PHL	19	80	7	59	2023-01-15 07:00:00	Other
5590	2	1	555	600	-5	904	754	YX	1583	N880RW	LGA	STL	169	888	6	0	2023-02-01 06:00:00	Other
5601	9	12	1057	1059	-2	1217	1232	9E	1676	N929XJ	LGA	BUF	50	292	10	59	2023-09-12 10:00:00	Other
5609	9	30	950	955	-5	1257	1249	DL	388	N349DX	LGA	MCO	138	950	9	55	2023-09-30 09:00:00	MCO
5613	7	17	928	930	-2	1124	1136	NK	453	N694NK	EWR	CHS	92	628	9	30	2023-07-17 09:00:00	Other
5616	12	30	1027	1030	-3	1148	1234	YX	1109	N721YX	EWR	GSO	66	445	10	30	2023-12-30 10:00:00	Other
5620	12	1	828	830	-2	1059	1110	DL	200	N721TW	JFK	ATL	120	760	8	30	2023-12-01 08:00:00	ATL
5625	10	27	1057	1100	-3	1427	1406	B6	298	N649JB	JFK	SLC	307	1990	11	0	2023-10-27 11:00:00	Other
5626	6	21	1426	1429	-3	1621	1648	YX	1254	N729YX	EWR	IND	92	645	14	29	2023-06-21 14:00:00	Other
5631	10	1	616	620	-4	725	745	NK	369	N697NK	EWR	BNA	104	748	6	20	2023-10-01 06:00:00	Other
5636	2	24	1331	1335	-4	1646	1656	DL	538	N372NW	JFK	AUS	226	1521	13	35	2023-02-24 13:00:00	Other
5638	12	22	1324	1329	-5	1429	1451	YX	1784	N214JQ	LGA	SYR	42	198	13	29	2023-12-22 13:00:00	Other
5641	4	20	1454	1459	-5	1658	1717	YX	1528	N212JQ	JFK	CLT	87	541	14	59	2023-04-20 14:00:00	CLT
5647	1	24	2150	2155	-5	2321	2307	B6	991	N192JB	JFK	SYR	50	209	21	55	2023-01-24 21:00:00	Other
5650	1	23	757	800	-3	1113	1146	B6	16	N661JB	JFK	PHX	290	2153	8	0	2023-01-23 08:00:00	Other
5651	1	22	1206	1211	-5	1320	1334	YX	1171	N750YX	EWR	PWM	50	284	12	11	2023-01-22 12:00:00	Other
5684	1	27	1345	1350	-5	1500	1513	9E	1710	N307PQ	JFK	ORF	56	290	13	50	2023-01-27 13:00:00	Other
5698	5	22	1452	1455	-3	1825	1810	B6	526	N554JB	JFK	FLL	165	1069	14	55	2023-05-22 14:00:00	FLL
5701	5	22	2217	2220	-3	2342	2355	9E	1548	N923XJ	JFK	BTV	51	266	22	20	2023-05-22 22:00:00	Other
5713	11	12	1856	1859	-3	2202	2247	DL	278	N502DX	JFK	PHX	283	2153	18	59	2023-11-12 18:00:00	Other
5730	6	29	1114	1119	-5	1354	1428	DL	406	N347NB	LGA	TPA	132	1010	11	19	2023-06-29 11:00:00	Other
5733	11	29	1817	1820	-3	2024	1959	YX	1886	N201JQ	JFK	DCA	43	213	18	20	2023-11-29 18:00:00	Other
5737	11	19	1411	1416	-5	1556	1613	YX	1866	N202JQ	LGA	CMH	77	479	14	16	2023-11-19 14:00:00	Other
5743	7	1	1103	1108	-5	1339	1407	UA	225	N47291	EWR	PBI	124	1023	11	8	2023-07-01 11:00:00	Other
5751	4	3	655	700	-5	952	1014	DL	607	N127DU	LGA	IAH	212	1416	7	0	2023-04-03 07:00:00	Other
5752	2	14	758	800	-2	941	942	UA	837	N77258	LGA	ORD	129	733	8	0	2023-02-14 08:00:00	ORD
5754	8	13	741	745	-4	900	901	UA	199	N78511	EWR	BOS	43	200	7	45	2023-08-13 07:00:00	BOS
5768	5	18	521	523	-2	746	820	UA	177	N17300	EWR	IAH	183	1400	5	23	2023-05-18 05:00:00	Other
5770	10	6	741	745	-4	909	918	9E	1417	N307PQ	JFK	BUF	53	301	7	45	2023-10-06 07:00:00	Other
5775	4	14	1254	1259	-5	1452	1522	9E	1289	N341PQ	LGA	TYS	98	647	12	59	2023-04-14 12:00:00	Other
5778	5	18	1958	2000	-2	2110	2123	AA	560	N710UW	LGA	DCA	51	214	20	0	2023-05-18 20:00:00	Other
5779	12	15	1240	1242	-2	1528	1545	UA	814	N66897	EWR	TPA	143	997	12	42	2023-12-15 12:00:00	Other
5786	4	14	904	908	-4	1006	1025	B6	567	N183JB	JFK	BTV	44	266	9	8	2023-04-14 09:00:00	Other
5787	5	30	1856	1900	-4	2008	2028	YX	1023	N864RW	EWR	DCA	40	199	19	0	2023-05-30 19:00:00	Other
5796	10	10	1755	1759	-4	2059	2110	B6	944	N937JB	JFK	LAX	331	2475	17	59	2023-10-10 17:00:00	LAX
5800	10	30	605	610	-5	909	905	WN	705	N259WN	LGA	HOU	212	1428	6	10	2023-10-30 06:00:00	Other
5806	8	18	1224	1229	-5	1504	1517	OO	1371	N140SY	LGA	IAH	190	1416	12	29	2023-08-18 12:00:00	Other
5810	10	2	1943	1948	-5	2242	2240	UA	605	N68802	EWR	MCO	131	937	19	48	2023-10-02 19:00:00	MCO
5811	3	17	1612	1617	-5	1736	1741	UA	197	N54241	EWR	BUF	52	282	16	17	2023-03-17 16:00:00	Other
5813	5	14	1715	1720	-5	1900	1854	9E	1378	N131EV	LGA	BUF	51	292	17	20	2023-05-14 17:00:00	Other
5821	5	15	1122	1125	-3	1410	1429	AA	739	N878NN	LGA	DFW	177	1389	11	25	2023-05-15 11:00:00	Other
5827	3	21	1956	1959	-3	2251	2257	UA	428	N27251	EWR	LAS	324	2227	19	59	2023-03-21 19:00:00	Other
5828	5	15	1425	1429	-4	1617	1612	9E	1510	N335PQ	JFK	RIC	51	288	14	29	2023-05-15 14:00:00	Other
5832	11	26	1116	1120	-4	1449	1429	UA	831	N37420	EWR	MIA	174	1085	11	20	2023-11-26 11:00:00	MIA
5836	3	7	540	545	-5	844	853	NK	203	N629NK	EWR	FLL	136	1065	5	45	2023-03-07 05:00:00	FLL
5837	3	5	1134	1138	-4	1348	1345	DL	287	N114DU	EWR	MSP	173	1008	11	38	2023-03-05 11:00:00	Other
5838	9	15	1651	1655	-4	1756	1828	YX	1823	N215JQ	LGA	PWM	46	269	16	55	2023-09-15 16:00:00	Other
5840	2	21	1253	1258	-5	1440	1500	OO	1136	N693CA	EWR	DTW	86	488	12	58	2023-02-21 12:00:00	Other
5848	3	6	1956	2000	-4	2102	2119	DL	545	N122DU	LGA	BOS	38	184	20	0	2023-03-06 20:00:00	BOS
5851	9	21	1154	1159	-5	1426	1457	UA	736	N39450	EWR	IAH	182	1400	11	59	2023-09-21 11:00:00	Other
5853	10	27	1601	1606	-5	1743	1810	YX	1161	N642RW	EWR	MYR	79	550	16	6	2023-10-27 16:00:00	Other
5863	12	11	922	925	-3	1052	1058	9E	1553	N604LR	JFK	IAD	52	228	9	25	2023-12-11 09:00:00	Other
5871	3	5	1456	1500	-4	1615	1625	YX	1748	N215JQ	LGA	BOS	34	184	15	0	2023-03-05 15:00:00	BOS
5875	12	31	1107	1110	-3	1242	1327	DL	489	N102DN	LGA	MSP	133	1020	11	10	2023-12-31 11:00:00	Other
5879	8	15	1125	1130	-5	1423	1435	AA	94	N101NN	JFK	LAX	328	2475	11	30	2023-08-15 11:00:00	LAX
5891	9	15	1556	1559	-3	1704	1723	YX	1081	N739YX	EWR	DCA	44	199	15	59	2023-09-15 15:00:00	Other
5895	6	8	1226	1230	-4	1354	1417	B6	87	N646JB	JFK	RDU	67	427	12	30	2023-06-08 12:00:00	Other
5899	10	30	2056	2059	-3	2159	2219	YX	1784	N209JQ	LGA	BOS	32	184	20	59	2023-10-30 20:00:00	BOS
5906	10	24	1158	1200	-2	1513	1525	UA	825	N14107	EWR	SFO	355	2565	12	0	2023-10-24 12:00:00	Other
5917	11	1	728	730	-2	936	933	AA	515	N949NN	EWR	CLT	98	529	7	30	2023-11-01 07:00:00	CLT
5927	8	30	1822	1824	-2	2016	2044	DL	323	N384DN	LGA	MSP	144	1020	18	24	2023-08-30 18:00:00	Other
5932	12	7	2054	2059	-5	2216	2242	9E	1353	N491PX	LGA	ORF	49	296	20	59	2023-12-07 20:00:00	Other
5933	9	13	1026	1030	-4	1345	1354	YX	1194	N763YX	EWR	EYW	167	1196	10	30	2023-09-13 10:00:00	Other
5939	10	11	1054	1059	-5	1342	1359	NK	236	N634NK	LGA	MCO	137	950	10	59	2023-10-11 10:00:00	MCO
5942	12	15	1410	1415	-5	1724	1742	YX	1012	N979RP	EWR	EYW	173	1196	14	15	2023-12-15 14:00:00	Other
5944	7	25	942	946	-4	1150	1200	UA	716	N73276	LGA	DEN	217	1620	9	46	2023-07-25 09:00:00	Other
5946	5	24	1218	1222	-4	1358	1355	9E	1534	N153PQ	JFK	BUF	51	301	12	22	2023-05-24 12:00:00	Other
5949	8	1	1750	1754	-4	1902	1929	B6	86	N348JB	JFK	PWM	51	273	17	54	2023-08-01 17:00:00	Other
5952	4	4	556	600	-4	742	735	UA	363	N17279	EWR	ORD	124	719	6	0	2023-04-04 06:00:00	ORD
5964	4	24	1523	1525	-2	1657	1710	WN	778	N8665D	LGA	STL	132	888	15	25	2023-04-24 15:00:00	Other
5965	10	28	830	832	-2	1138	1139	DL	221	N121DU	JFK	DFW	199	1391	8	32	2023-10-28 08:00:00	Other
5967	12	23	1050	1053	-3	1320	1328	YX	1263	N440YX	LGA	SDF	111	659	10	53	2023-12-23 10:00:00	Other
5972	7	28	1658	1700	-2	1848	1857	DL	792	N963AT	EWR	DTW	82	488	17	0	2023-07-28 17:00:00	Other
5982	10	3	756	800	-4	1029	1055	DL	156	N840MH	JFK	LAX	308	2475	8	0	2023-10-03 08:00:00	LAX
5983	1	12	930	933	-3	1257	1255	UA	928	N12216	EWR	AUS	233	1504	9	33	2023-01-12 09:00:00	Other
5991	6	12	956	959	-3	1230	1256	DL	720	N117DX	JFK	MCO	131	944	9	59	2023-06-12 09:00:00	MCO
6003	4	26	2006	2010	-4	2227	2304	B6	35	N651JB	JFK	DEN	229	1626	20	10	2023-04-26 20:00:00	Other
6006	1	28	1141	1144	-3	1609	1648	NK	1110	N656NK	EWR	SJU	181	1608	11	44	2023-01-28 11:00:00	Other
6008	12	20	1731	1735	-4	2032	2045	AS	75	N978AK	EWR	PDX	328	2434	17	35	2023-12-20 17:00:00	Other
6018	2	16	1151	1155	-4	1331	1327	YX	1533	N882RW	LGA	DCA	79	214	11	55	2023-02-16 11:00:00	Other
6022	10	14	937	940	-3	1048	1104	YX	1727	N243JQ	JFK	DCA	46	213	9	40	2023-10-14 09:00:00	Other
6031	10	2	703	705	-2	944	1000	DL	489	N804DN	JFK	TPA	134	1005	7	5	2023-10-02 07:00:00	Other
6032	5	9	955	1000	-5	1057	1124	YX	1573	N204JQ	JFK	BOS	34	187	10	0	2023-05-09 10:00:00	BOS
6034	2	26	605	610	-5	735	728	DL	403	N143DU	JFK	BOS	43	187	6	10	2023-02-26 06:00:00	BOS
6035	9	13	1823	1828	-5	2033	2041	YX	1366	N872RW	LGA	MCI	162	1107	18	28	2023-09-13 18:00:00	Other
6040	1	18	1359	1402	-3	1604	1604	UA	195	N874UA	EWR	MSP	159	1008	14	2	2023-01-18 14:00:00	Other
6049	6	1	1613	1618	-5	1734	1759	YX	1772	N239JQ	LGA	BNA	102	764	16	18	2023-06-01 16:00:00	Other
6055	11	23	1440	1445	-5	1555	1613	UA	82	N14731	EWR	BUF	57	282	14	45	2023-11-23 14:00:00	Other
6058	9	30	1225	1229	-4	1350	1344	DL	577	N110DU	JFK	BOS	39	187	12	29	2023-09-30 12:00:00	BOS
6059	7	31	555	600	-5	838	908	NK	47	N668NK	LGA	FLL	146	1076	6	0	2023-07-31 06:00:00	FLL
6066	6	9	855	857	-2	1003	1017	YX	1191	N751YX	EWR	ALB	31	143	8	57	2023-06-09 08:00:00	Other
6071	3	17	1328	1330	-2	1650	1707	B6	585	N985JT	JFK	SFO	349	2586	13	30	2023-03-17 13:00:00	Other
6086	6	24	1533	1536	-3	1818	1735	9E	1504	N305PQ	LGA	ILM	82	500	15	36	2023-06-24 15:00:00	Other
6091	9	28	1021	1025	-4	1228	1232	9E	1724	N485PX	LGA	AVL	95	599	10	25	2023-09-28 10:00:00	Other
6092	8	15	1621	1625	-4	1758	1823	YX	849	N732YX	EWR	GSO	76	445	16	25	2023-08-15 16:00:00	Other
6108	4	7	1602	1606	-4	1717	1730	YX	1039	N657RW	EWR	PWM	43	284	16	6	2023-04-07 16:00:00	Other
6109	3	17	1546	1550	-4	1730	1748	9E	1468	N932XJ	LGA	CLE	80	419	15	50	2023-03-17 15:00:00	Other
6112	8	22	1122	1127	-5	1423	1435	DL	792	N117DU	LGA	SRQ	139	1047	11	27	2023-08-22 11:00:00	Other
6114	12	21	1946	1950	-4	2111	2140	OO	1204	N316SY	LGA	BNA	114	764	19	50	2023-12-21 19:00:00	Other
6115	6	11	856	900	-4	1009	1051	YX	1332	N436YX	JFK	DCA	54	213	9	0	2023-06-11 09:00:00	Other
6116	2	26	2045	2050	-5	2234	2253	YX	1528	N231JQ	JFK	CMH	81	483	20	50	2023-02-26 20:00:00	Other
6120	9	18	1342	1345	-3	1545	1550	9E	1734	N920XJ	LGA	CAE	94	617	13	45	2023-09-18 13:00:00	Other
6121	7	30	1912	1915	-3	2139	2214	DL	526	N131DU	LGA	IAH	181	1416	19	15	2023-07-30 19:00:00	Other
6124	6	3	1028	1030	-2	1253	1304	DL	124	N306DN	LGA	ATL	103	762	10	30	2023-06-03 10:00:00	ATL
6127	5	23	1050	1055	-5	1240	1259	9E	1484	N316PQ	LGA	GSO	73	461	10	55	2023-05-23 10:00:00	Other
6135	1	6	754	759	-5	1026	1041	UA	502	N77530	EWR	JAX	120	820	7	59	2023-01-06 07:00:00	Other
6137	2	5	1828	1830	-2	2032	2056	9E	1454	N929XJ	JFK	CVG	104	589	18	30	2023-02-05 18:00:00	Other
6138	12	27	827	830	-3	1142	1204	B6	3	N2151J	JFK	SFO	337	2586	8	30	2023-12-27 08:00:00	Other
6141	1	22	947	950	-3	1108	1130	WN	943	N8669B	LGA	MDW	121	725	9	50	2023-01-22 09:00:00	Other
6143	6	1	1656	1659	-3	1900	1919	YX	1110	N745YX	EWR	IND	91	645	16	59	2023-06-01 16:00:00	Other
6151	7	11	625	630	-5	753	815	9E	1288	N146PQ	LGA	CLE	63	419	6	30	2023-07-11 06:00:00	Other
6157	2	27	748	750	-2	931	937	UA	668	N17244	EWR	ORD	129	719	7	50	2023-02-27 07:00:00	ORD
6161	4	26	731	735	-4	1036	1032	NK	432	N674NK	EWR	MCO	145	937	7	35	2023-04-26 07:00:00	MCO
6163	7	5	710	715	-5	915	931	DL	642	N375DA	EWR	ATL	100	746	7	15	2023-07-05 07:00:00	ATL
6171	9	8	1043	1047	-4	1248	1255	UA	535	N47293	EWR	CHS	91	628	10	47	2023-09-08 10:00:00	Other
6173	5	31	556	600	-4	911	908	AA	452	N892NN	LGA	MIA	157	1096	6	0	2023-05-31 06:00:00	MIA
6188	11	15	1927	1929	-2	2026	2057	B6	913	N324JB	JFK	DCA	39	213	19	29	2023-11-15 19:00:00	Other
6197	9	30	827	829	-2	1116	1140	AA	337	N111ZM	JFK	SNA	324	2454	8	29	2023-09-30 08:00:00	Other
6201	12	9	945	950	-5	1302	1305	NK	1008	N908NK	LGA	MIA	170	1096	9	50	2023-12-09 09:00:00	MIA
6204	5	13	1127	1130	-3	1333	1337	AA	740	N764US	LGA	CLT	79	544	11	30	2023-05-13 11:00:00	CLT
6207	2	25	1607	1610	-3	1903	1929	DL	415	N337DN	LGA	MIA	147	1096	16	10	2023-02-25 16:00:00	MIA
6209	6	2	711	715	-4	950	1008	UA	779	N79541	EWR	SNA	301	2434	7	15	2023-06-02 07:00:00	Other
6210	5	28	1913	1915	-2	2040	2106	OO	1498	N167SY	LGA	ORD	122	733	19	15	2023-05-28 19:00:00	ORD
6211	8	13	1013	1015	-2	1224	1254	UA	566	N14011	EWR	IAH	167	1400	10	15	2023-08-13 10:00:00	Other
6216	4	20	655	700	-5	938	1006	DL	534	N873DN	JFK	TPA	135	1005	7	0	2023-04-20 07:00:00	Other
6218	12	12	1526	1530	-4	1705	1722	B6	29	N197JB	JFK	ORD	130	740	15	30	2023-12-12 15:00:00	ORD
6220	4	19	746	749	-3	937	958	9E	1266	N330PQ	JFK	CVG	91	589	7	49	2023-04-19 07:00:00	Other
6221	11	7	715	720	-5	840	900	WN	345	N7867A	LGA	BNA	116	764	7	20	2023-11-07 07:00:00	Other
6222	12	9	543	545	-2	832	844	UA	166	N47512	EWR	IAH	208	1400	5	45	2023-12-09 05:00:00	Other
6224	12	6	1816	1820	-4	1942	1959	YX	1848	N242JQ	JFK	DCA	55	213	18	20	2023-12-06 18:00:00	Other
6230	3	15	1455	1500	-5	1720	1725	9E	1385	N901XJ	JFK	CHS	92	636	15	0	2023-03-15 15:00:00	Other
6234	6	13	1726	1729	-3	2036	2040	AA	153	N840NN	JFK	MIA	147	1089	17	29	2023-06-13 17:00:00	MIA
6237	6	9	1725	1730	-5	1956	1957	9E	1700	N936XJ	LGA	SAV	106	722	17	30	2023-06-09 17:00:00	Other
6240	9	18	1433	1435	-2	1627	1640	UA	353	N477UA	EWR	CLT	86	529	14	35	2023-09-18 14:00:00	CLT
6241	5	4	616	619	-3	840	850	AA	966	N451AN	EWR	PHX	287	2133	6	19	2023-05-04 06:00:00	Other
6245	7	7	1056	1100	-4	1323	1348	AA	615	N917AN	LGA	DFW	178	1389	11	0	2023-07-07 11:00:00	Other
6249	1	24	1002	1005	-3	1312	1319	NK	26	N658NK	EWR	MIA	159	1085	10	5	2023-01-24 10:00:00	MIA
6251	1	6	2055	2100	-5	2219	2249	9E	1486	N605LR	JFK	BUF	57	301	21	0	2023-01-06 21:00:00	Other
6259	7	24	1720	1725	-5	1933	2007	B6	706	N599JB	LGA	JAX	118	833	17	25	2023-07-24 17:00:00	Other
6260	3	1	1310	1315	-5	1440	1450	9E	1477	N299PQ	JFK	BUF	63	301	13	15	2023-03-01 13:00:00	Other
6263	11	30	2055	2059	-4	2350	17	B6	740	N537JT	LGA	RSW	157	1080	20	59	2023-11-30 20:00:00	Other
6267	3	8	921	926	-5	1215	1222	UA	518	N61898	EWR	MCO	127	937	9	26	2023-03-08 09:00:00	MCO
6280	12	8	1945	1950	-5	2205	2227	YX	1147	N752YX	EWR	MCI	161	1092	19	50	2023-12-08 19:00:00	Other
6283	6	19	1924	1929	-5	2030	2101	YX	1888	N212JQ	LGA	DCA	44	214	19	29	2023-06-19 19:00:00	Other
6294	9	12	1734	1736	-2	1943	1959	YX	1374	N445YX	LGA	SDF	106	659	17	36	2023-09-12 17:00:00	Other
6302	6	20	1800	1805	-5	1949	1957	9E	1559	N906XJ	LGA	MEM	138	963	18	5	2023-06-20 18:00:00	Other
6305	4	8	828	830	-2	959	1017	OO	1060	N604CZ	JFK	BNA	129	765	8	30	2023-04-08 08:00:00	Other
6312	8	8	1957	2000	-3	2115	2130	YX	1383	N225JQ	LGA	BOS	48	184	20	0	2023-08-08 20:00:00	BOS
6315	5	22	758	800	-2	1102	1150	DL	305	N704X	JFK	SFO	329	2586	8	0	2023-05-22 08:00:00	Other
6330	10	21	1953	1955	-2	2243	2307	UA	612	N75428	EWR	SMF	328	2500	19	55	2023-10-21 19:00:00	Other
6333	12	18	826	830	-4	1154	1217	AA	860	N108NN	JFK	SNA	331	2454	8	30	2023-12-18 08:00:00	Other
6338	4	7	844	849	-5	1018	955	9E	1368	N916XJ	LGA	ALB	46	136	8	49	2023-04-07 08:00:00	Other
6339	5	6	1815	1820	-5	2017	2053	9E	1460	N314PQ	JFK	IND	92	665	18	20	2023-05-06 18:00:00	Other
6344	1	2	1226	1230	-4	1505	1459	DL	458	N898DN	JFK	DEN	238	1626	12	30	2023-01-02 12:00:00	Other
6349	3	6	1654	1659	-5	1850	1910	9E	1472	N301PQ	LGA	ILM	74	500	16	59	2023-03-06 16:00:00	Other
6370	11	4	643	645	-2	944	953	UA	886	N47284	EWR	MIA	146	1085	6	45	2023-11-04 06:00:00	MIA
6373	6	16	627	629	-2	759	809	AA	1002	N815AW	LGA	RDU	66	431	6	29	2023-06-16 06:00:00	Other
6379	3	29	1259	1303	-4	1554	1559	UA	866	N848UA	EWR	PBI	152	1023	13	3	2023-03-29 13:00:00	Other
6385	1	22	1327	1330	-3	1443	1459	YX	1796	N201JQ	JFK	DCA	48	213	13	30	2023-01-22 13:00:00	Other
6390	2	16	927	930	-3	1301	1258	AA	114	N113AN	JFK	SNA	347	2454	9	30	2023-02-16 09:00:00	Other
6395	10	11	1912	1915	-3	2036	2040	B6	441	N328JB	LGA	BOS	42	184	19	15	2023-10-11 19:00:00	BOS
6399	3	3	2125	2129	-4	39	55	DL	199	N181DN	JFK	LAX	332	2475	21	29	2023-03-03 21:00:00	LAX
6415	7	11	1456	1500	-4	1623	1655	YX	1097	N404YX	LGA	STL	127	888	15	0	2023-07-11 15:00:00	Other
6425	8	5	956	1000	-4	1248	1313	AA	64	N102NN	JFK	LAX	324	2475	10	0	2023-08-05 10:00:00	LAX
6429	2	9	1212	1217	-5	1314	1339	YX	1042	N753YX	EWR	PWM	45	284	12	17	2023-02-09 12:00:00	Other
6445	11	30	802	805	-3	1022	1034	DL	910	N967AT	EWR	ATL	114	746	8	5	2023-11-30 08:00:00	ATL
6448	10	6	755	800	-5	1102	1134	DL	278	N707TW	JFK	SFO	339	2586	8	0	2023-10-06 08:00:00	Other
6451	11	11	1909	1913	-4	2208	2226	UA	578	N77530	EWR	FLL	153	1065	19	13	2023-11-11 19:00:00	FLL
6455	12	13	745	750	-5	1021	1036	NK	143	N621NK	EWR	LAS	313	2227	7	50	2023-12-13 07:00:00	Other
6460	10	31	1515	1520	-5	1726	1724	UA	332	N38268	EWR	CLT	100	529	15	20	2023-10-31 15:00:00	CLT
6473	3	19	1218	1220	-2	1519	1514	DL	544	N363DN	JFK	MCO	157	944	12	20	2023-03-19 12:00:00	MCO
6474	5	7	2046	2050	-4	2234	2254	9E	1423	N604LR	LGA	ILM	74	500	20	50	2023-05-07 20:00:00	Other
6479	8	21	656	700	-4	946	1007	DL	358	N3733Z	JFK	RSW	143	1074	7	0	2023-08-21 07:00:00	Other
6481	4	13	1418	1420	-2	1637	1651	9E	1363	N298PQ	JFK	SAV	107	718	14	20	2023-04-13 14:00:00	Other
6483	6	6	1256	1259	-3	1529	1536	YX	1326	N134HQ	LGA	OKC	187	1341	12	59	2023-06-06 12:00:00	Other
6486	9	21	2042	2045	-3	2354	2359	NK	1026	N664NK	EWR	MIA	151	1085	20	45	2023-09-21 20:00:00	MIA
6492	4	24	1720	1725	-5	1916	1940	9E	1427	N337PQ	JFK	CVG	102	589	17	25	2023-04-24 17:00:00	Other
6503	5	1	1555	1558	-3	1855	1915	B6	240	N648JB	JFK	PBI	151	1028	15	58	2023-05-01 15:00:00	Other
6506	5	14	1857	1900	-3	2218	2212	B6	124	N998JE	JFK	ONT	342	2429	19	0	2023-05-14 19:00:00	Other
6515	12	15	1055	1100	-5	1253	1329	9E	1701	N295PQ	LGA	IND	94	660	11	0	2023-12-15 11:00:00	Other
6522	2	23	912	917	-5	1204	1214	UA	496	N41135	EWR	MCO	133	937	9	17	2023-02-23 09:00:00	MCO
6523	4	14	2052	2055	-3	2254	2308	UA	474	N441UA	EWR	CVG	85	569	20	55	2023-04-14 20:00:00	Other
6525	1	10	1612	1615	-3	1726	1752	UA	540	N21723	EWR	BNA	108	748	16	15	2023-01-10 16:00:00	Other
6530	4	5	638	640	-2	919	942	B6	759	N569JB	JFK	MIA	137	1089	6	40	2023-04-05 06:00:00	MIA
6537	10	8	641	645	-4	940	948	UA	243	N37522	EWR	FLL	153	1065	6	45	2023-10-08 06:00:00	FLL
6539	2	8	1525	1529	-4	1650	1657	YX	1106	N754YX	EWR	ROC	47	246	15	29	2023-02-08 15:00:00	Other
6543	5	7	1100	1105	-5	1156	1211	9E	1322	N176PQ	LGA	BDL	29	101	11	5	2023-05-07 11:00:00	Other
6548	11	1	1550	1555	-5	1713	1735	YX	1090	N865RW	EWR	MKE	113	725	15	55	2023-11-01 15:00:00	Other
6555	5	17	1508	1510	-2	1802	1816	UA	394	N17301	EWR	AUS	212	1504	15	10	2023-05-17 15:00:00	Other
6563	8	10	1107	1110	-3	1430	1420	DL	712	N864DN	JFK	FLL	154	1069	11	10	2023-08-10 11:00:00	FLL
6570	5	8	1247	1250	-3	1350	1359	9E	1269	N326PQ	JFK	ITH	38	189	12	50	2023-05-08 12:00:00	Other
6575	1	27	615	620	-5	914	927	UA	311	N12114	EWR	FLL	159	1065	6	20	2023-01-27 06:00:00	FLL
6582	5	7	1346	1350	-4	1610	1628	9E	1430	N605LR	LGA	JAX	116	833	13	50	2023-05-07 13:00:00	Other
6594	8	23	557	601	-4	827	839	B6	191	N970JB	JFK	MCO	120	944	6	1	2023-08-23 06:00:00	MCO
6596	5	27	1027	1030	-3	1148	1140	B6	930	N228JB	JFK	BOS	45	187	10	30	2023-05-27 10:00:00	BOS
6600	1	21	523	525	-2	823	820	UA	206	N14102	EWR	IAH	210	1400	5	25	2023-01-21 05:00:00	Other
6601	11	8	1706	1711	-5	1844	1914	AA	640	N922US	EWR	CLT	79	529	17	11	2023-11-08 17:00:00	CLT
6602	7	9	941	945	-4	1055	1120	9E	1208	N929XJ	LGA	BTV	45	258	9	45	2023-07-09 09:00:00	Other
6605	8	21	1125	1129	-4	1325	1338	UA	213	N37295	EWR	SAV	98	708	11	29	2023-08-21 11:00:00	Other
6611	5	4	1824	1829	-5	2036	2059	UA	855	N812UA	LGA	DEN	221	1620	18	29	2023-05-04 18:00:00	Other
6616	3	19	813	817	-4	1152	1211	UA	794	N59053	EWR	SJU	193	1608	8	17	2023-03-19 08:00:00	Other
6629	11	16	558	601	-3	811	832	UA	555	N69806	EWR	DEN	225	1605	6	1	2023-11-16 06:00:00	Other
6631	5	17	747	750	-3	1036	1050	UA	265	N47281	EWR	IAH	194	1400	7	50	2023-05-17 07:00:00	Other
6646	6	8	2155	2200	-5	2259	2323	9E	1626	N300PQ	JFK	ITH	39	189	22	0	2023-06-08 22:00:00	Other
6653	3	10	1445	1450	-5	1617	1634	9E	1520	N916XJ	EWR	RDU	78	416	14	50	2023-03-10 14:00:00	Other
6655	1	22	1757	1759	-2	2122	2116	AA	137	N940NN	JFK	MIA	164	1089	17	59	2023-01-22 17:00:00	MIA
6663	8	5	1108	1110	-2	1227	1239	YX	1076	N431YX	JFK	ORF	55	290	11	10	2023-08-05 11:00:00	Other
6664	2	9	1650	1655	-5	1901	1925	WN	675	N1808U	LGA	MCI	165	1107	16	55	2023-02-09 16:00:00	Other
6665	4	17	855	900	-5	1215	1217	AA	728	N338RS	LGA	MIA	173	1096	9	0	2023-04-17 09:00:00	MIA
6666	2	12	1827	1830	-3	2004	2036	AA	922	N906NN	LGA	ORD	111	733	18	30	2023-02-12 18:00:00	ORD
6669	4	12	1432	1435	-3	1616	1658	B6	739	N3023J	JFK	MCI	143	1113	14	35	2023-04-12 14:00:00	Other
6673	1	8	855	900	-5	1523	1525	DL	101	N183DN	JFK	HNL	661	4983	9	0	2023-01-08 09:00:00	Other
6678	1	16	1141	1144	-3	1606	1648	NK	1110	N603NK	EWR	SJU	188	1608	11	44	2023-01-16 11:00:00	Other
6683	8	16	2200	2205	-5	2325	2354	9E	1250	N320PQ	JFK	BTV	49	266	22	5	2023-08-16 22:00:00	Other
6689	7	18	457	500	-3	754	808	AA	352	N855NN	EWR	MIA	153	1085	5	0	2023-07-18 05:00:00	MIA
6693	3	28	645	650	-5	747	800	B6	200	N179JB	JFK	BOS	33	187	6	50	2023-03-28 06:00:00	BOS
6695	2	20	1732	1735	-3	1855	1907	YX	1549	N225JQ	LGA	DCA	55	214	17	35	2023-02-20 17:00:00	Other
6698	3	7	605	610	-5	728	728	DL	402	N145DQ	JFK	BOS	36	187	6	10	2023-03-07 06:00:00	BOS
6700	5	15	657	700	-3	941	1009	DL	535	N308DN	LGA	MIA	140	1096	7	0	2023-05-15 07:00:00	MIA
6719	5	4	1930	1935	-5	2045	2112	9E	1286	N176PQ	LGA	MKE	111	738	19	35	2023-05-04 19:00:00	Other
6726	2	26	556	600	-4	826	809	AA	901	N804NN	JFK	CLT	103	541	6	0	2023-02-26 06:00:00	CLT
6741	11	12	1156	1159	-3	1333	1345	DL	618	N132DU	LGA	ORD	120	733	11	59	2023-11-12 11:00:00	ORD
6757	3	21	758	800	-2	1147	1159	B6	193	N2029J	JFK	SJU	203	1598	8	0	2023-03-21 08:00:00	Other
6758	5	19	1726	1730	-4	1926	1944	YX	1654	N232JQ	LGA	LIT	153	1085	17	30	2023-05-19 17:00:00	Other
6762	10	2	1256	1300	-4	1402	1416	UA	427	N37567	EWR	BOS	38	200	13	0	2023-10-02 13:00:00	BOS
6763	7	15	845	850	-5	1052	1135	9E	1167	N907XJ	LGA	JAX	112	833	8	50	2023-07-15 08:00:00	Other
6764	8	13	1158	1200	-2	1309	1325	YX	1353	N202JQ	LGA	BOS	42	184	12	0	2023-08-13 12:00:00	BOS
6766	1	16	1810	1814	-4	2016	2040	YX	1177	N732YX	EWR	IND	96	645	18	14	2023-01-16 18:00:00	Other
6772	10	5	1554	1559	-5	1652	1721	YX	1250	N108HQ	JFK	BOS	34	187	15	59	2023-10-05 15:00:00	BOS
6776	10	9	2101	2104	-3	2320	2339	UA	574	N17302	EWR	LAS	287	2227	21	4	2023-10-09 21:00:00	Other
6777	7	3	1027	1029	-2	1129	1146	YX	1428	N215JQ	LGA	MVY	39	175	10	29	2023-07-03 10:00:00	Other
6795	5	3	557	600	-3	734	749	DL	760	N923AT	EWR	DTW	79	488	6	0	2023-05-03 06:00:00	Other
6797	3	25	557	600	-3	748	757	AA	956	N669AW	EWR	CLT	91	529	6	0	2023-03-25 06:00:00	CLT
6800	5	5	1845	1850	-5	2122	2145	UA	639	N17300	EWR	MCO	126	937	18	50	2023-05-05 18:00:00	MCO
6805	2	25	1056	1100	-4	1330	1412	B6	170	N615JB	EWR	PBI	138	1023	11	0	2023-02-25 11:00:00	Other
6811	2	22	757	800	-3	1046	1030	OO	1172	N613CZ	JFK	MSP	193	1029	8	0	2023-02-22 08:00:00	Other
6816	9	30	626	630	-4	738	801	UA	955	N12754	LGA	ORD	108	733	6	30	2023-09-30 06:00:00	ORD
6829	10	15	1954	1959	-5	2134	2137	9E	1686	N295PQ	LGA	CHO	59	305	19	59	2023-10-15 19:00:00	Other
6838	6	5	1329	1334	-5	1625	1635	UA	482	N452UA	EWR	RSW	153	1068	13	34	2023-06-05 13:00:00	Other
6844	3	12	1707	1712	-5	1909	1907	YX	1037	N727YX	EWR	GSO	81	445	17	12	2023-03-12 17:00:00	Other
6854	2	6	1125	1129	-4	1411	1438	AA	458	N772AN	JFK	MIA	139	1089	11	29	2023-02-06 11:00:00	MIA
6856	7	31	1151	1156	-5	1349	1400	AA	765	N912NN	JFK	CLT	81	541	11	56	2023-07-31 11:00:00	CLT
6865	3	10	1218	1220	-2	1326	1344	9E	1542	N309PQ	LGA	BTV	45	258	12	20	2023-03-10 12:00:00	Other
6869	9	3	1954	1959	-5	2136	2153	YX	1373	N413YX	JFK	PIT	63	340	19	59	2023-09-03 19:00:00	Other
6874	1	19	750	755	-5	912	920	YX	1193	N750YX	EWR	PWM	54	284	7	55	2023-01-19 07:00:00	Other
6882	6	28	1340	1345	-5	1537	1534	9E	1461	N299PQ	LGA	CLE	93	419	13	45	2023-06-28 13:00:00	Other
6885	2	13	700	705	-5	1226	1204	UA	574	N13716	EWR	STT	219	1634	7	5	2023-02-13 07:00:00	Other
6887	4	20	1627	1632	-5	1732	1752	YX	1577	N206JQ	LGA	BTV	45	258	16	32	2023-04-20 16:00:00	Other
6898	7	31	707	710	-3	910	922	9E	1229	N325PQ	LGA	CHS	93	641	7	10	2023-07-31 07:00:00	Other
6900	9	22	1043	1047	-4	1340	1353	NK	511	N658NK	EWR	FLL	149	1065	10	47	2023-09-22 10:00:00	FLL
6903	3	20	1756	1800	-4	1926	1922	AA	487	N838AW	LGA	DCA	47	214	18	0	2023-03-20 18:00:00	Other
6907	3	31	945	950	-5	1140	1143	9E	1475	N913XJ	EWR	RDU	68	416	9	50	2023-03-31 09:00:00	Other
6915	1	9	2027	2029	-2	2255	2302	YX	1180	N643RW	EWR	SDF	112	642	20	29	2023-01-09 20:00:00	Other
6925	6	21	1156	1159	-3	1418	1428	UA	448	N424UA	EWR	ATL	110	746	11	59	2023-06-21 11:00:00	ATL
6937	8	6	1625	1629	-4	1845	1857	AA	470	N315SD	JFK	PHX	291	2153	16	29	2023-08-06 16:00:00	Other
6939	5	26	751	755	-4	1037	1049	AA	599	N930AN	EWR	DFW	199	1372	7	55	2023-05-26 07:00:00	Other
6944	2	8	756	800	-4	932	950	UA	668	N73275	EWR	ORD	118	719	8	0	2023-02-08 08:00:00	ORD
6947	12	9	1424	1429	-5	1536	1545	YX	1222	N420YX	JFK	BOS	51	187	14	29	2023-12-09 14:00:00	BOS
6949	9	22	1608	1610	-2	1916	1938	DL	238	N866DN	JFK	SLC	271	1990	16	10	2023-09-22 16:00:00	Other
6951	11	7	1738	1740	-2	2014	2048	UA	711	N29124	EWR	IAH	189	1400	17	40	2023-11-07 17:00:00	Other
6957	5	6	953	955	-2	1134	1134	OO	1138	N319SY	JFK	PIT	75	340	9	55	2023-05-06 09:00:00	Other
6960	10	10	1824	1829	-5	2136	2157	DL	225	N818DA	JFK	SLC	280	1990	18	29	2023-10-10 18:00:00	Other
6970	9	28	924	929	-5	1113	1124	YX	1192	N744YX	EWR	STL	121	872	9	29	2023-09-28 09:00:00	Other
6971	9	5	1837	1840	-3	2121	2149	UA	763	N63820	EWR	SEA	303	2402	18	40	2023-09-05 18:00:00	Other
6975	1	8	1155	1200	-5	1345	1352	9E	1672	N131EV	JFK	RDU	83	427	12	0	2023-01-08 12:00:00	Other
6979	6	21	2024	2029	-5	5	2357	AS	17	N964AK	JFK	SFO	325	2586	20	29	2023-06-21 20:00:00	Other
6983	2	26	1818	1820	-2	2001	2011	DL	378	N110DU	LGA	ORD	129	733	18	20	2023-02-26 18:00:00	ORD
6985	8	10	1851	1855	-4	2147	2200	AS	10	N263AK	JFK	SAN	322	2446	18	55	2023-08-10 18:00:00	Other
6986	5	25	1824	1827	-3	1952	1958	YX	1168	N729YX	EWR	IAD	46	212	18	27	2023-05-25 18:00:00	Other
6988	8	2	1055	1100	-5	1336	1343	UA	253	N419UA	EWR	DFW	175	1372	11	0	2023-08-02 11:00:00	Other
6991	8	24	828	830	-2	1041	1121	DL	174	N128DU	JFK	DFW	171	1391	8	30	2023-08-24 08:00:00	Other
6992	1	15	556	601	-5	1035	1055	B6	691	N948JB	JFK	SJU	197	1598	6	1	2023-01-15 06:00:00	Other
6996	9	26	824	829	-5	1056	1140	AA	337	N105NN	JFK	SNA	306	2454	8	29	2023-09-26 08:00:00	Other
6999	4	3	844	847	-3	1028	1050	9E	1381	N933XJ	LGA	CLE	74	419	8	47	2023-04-03 08:00:00	Other
7013	3	4	957	959	-2	1331	1304	UA	437	N18243	EWR	FLL	149	1065	9	59	2023-03-04 09:00:00	FLL
7016	9	15	1125	1129	-4	1420	1417	UA	552	N36476	EWR	MCO	150	937	11	29	2023-09-15 11:00:00	MCO
7018	1	21	710	715	-5	1011	1040	AS	14	N237AK	JFK	SEA	332	2422	7	15	2023-01-21 07:00:00	Other
7021	7	15	1525	1530	-5	1839	1845	AA	55	N108NN	JFK	LAX	332	2475	15	30	2023-07-15 15:00:00	LAX
7030	2	15	956	1000	-4	1223	1228	UA	756	N27964	EWR	DEN	224	1605	10	0	2023-02-15 10:00:00	Other
7033	1	19	1636	1640	-4	1831	1850	YX	1442	N124HQ	LGA	GSO	92	461	16	40	2023-01-19 16:00:00	Other
7037	5	17	750	755	-5	952	1010	9E	1363	N131EV	JFK	CVG	97	589	7	55	2023-05-17 07:00:00	Other
7039	12	8	1932	1935	-3	2115	2118	OO	1192	N614CZ	JFK	IAD	47	228	19	35	2023-12-08 19:00:00	Other
7042	9	28	855	900	-5	1051	1050	9E	1664	N905XJ	JFK	RDU	81	427	9	0	2023-09-28 09:00:00	Other
7048	4	3	558	600	-2	731	735	UA	363	N27252	EWR	ORD	124	719	6	0	2023-04-03 06:00:00	ORD
7052	4	20	755	800	-5	912	935	9E	1393	N928XJ	JFK	ROC	52	264	8	0	2023-04-20 08:00:00	Other
7055	1	7	1637	1640	-3	1848	1901	9E	1576	N319PQ	LGA	CVG	98	585	16	40	2023-01-07 16:00:00	Other
7067	4	26	2156	2159	-3	2301	2316	YX	1561	N243JQ	LGA	PWM	45	269	21	59	2023-04-26 21:00:00	Other
7076	2	17	727	730	-3	927	924	AA	270	N840NN	LGA	ORD	119	733	7	30	2023-02-17 07:00:00	ORD
7089	12	2	1446	1449	-3	1701	1655	AA	100	N303RE	JFK	CLT	92	541	14	49	2023-12-02 14:00:00	CLT
7096	4	29	1537	1540	-3	1826	1804	UA	348	N69885	EWR	DEN	220	1605	15	40	2023-04-29 15:00:00	Other
7099	6	2	1555	1600	-5	1811	1727	YX	1220	N741YX	EWR	PWM	61	284	16	0	2023-06-02 16:00:00	Other
7104	11	8	2016	2020	-4	3	2357	UA	720	N12116	EWR	SFO	377	2565	20	20	2023-11-08 20:00:00	Other
7105	3	24	2155	2159	-4	2245	2301	YX	1689	N206JQ	LGA	PVD	27	143	21	59	2023-03-24 21:00:00	Other
7106	10	1	731	735	-4	905	922	UA	934	N26215	EWR	RDU	68	416	7	35	2023-10-01 07:00:00	Other
7107	7	22	1210	1215	-5	1509	1511	B6	238	N507JT	JFK	AUS	217	1521	12	15	2023-07-22 12:00:00	Other
7108	8	23	1557	1600	-3	1855	1907	AS	68	N251AK	EWR	SEA	320	2402	16	0	2023-08-23 16:00:00	Other
7109	11	13	959	1003	-4	1208	1233	UA	529	N66828	EWR	DEN	227	1605	10	3	2023-11-13 10:00:00	Other
7110	8	7	628	630	-2	809	828	YX	1080	N442YX	JFK	RDU	71	427	6	30	2023-08-07 06:00:00	Other
7117	12	10	1127	1131	-4	1328	1337	YX	1151	N763YX	EWR	MEM	160	946	11	31	2023-12-10 11:00:00	Other
7126	11	10	528	530	-2	824	844	AA	244	N326RP	JFK	MIA	149	1089	5	30	2023-11-10 05:00:00	MIA
7127	1	7	1116	1120	-4	1326	1353	9E	1677	N304PQ	LGA	SAV	105	722	11	20	2023-01-07 11:00:00	Other
7130	9	13	1948	1950	-2	2230	2303	DL	890	N866DN	JFK	TPA	142	1005	19	50	2023-09-13 19:00:00	Other
7148	6	4	1350	1355	-5	1517	1523	9E	1730	N937XJ	LGA	BUF	50	292	13	55	2023-06-04 13:00:00	Other
7155	6	8	2043	2045	-2	48	59	DL	721	N869DN	JFK	SJU	210	1598	20	45	2023-06-08 20:00:00	Other
7164	8	9	1057	1100	-3	1259	1320	B6	102	N834JB	LGA	DEN	220	1620	11	0	2023-08-09 11:00:00	Other
7168	5	18	944	947	-3	1232	1241	B6	222	N519JB	LGA	MCO	130	950	9	47	2023-05-18 09:00:00	MCO
7171	6	30	1755	1800	-5	1858	1932	YX	1868	N202JQ	LGA	BOS	33	184	18	0	2023-06-30 18:00:00	BOS
7184	3	18	1521	1525	-4	1824	1847	DL	422	N315DN	LGA	MIA	166	1096	15	25	2023-03-18 15:00:00	MIA
7187	1	13	1426	1430	-4	1707	1731	UA	957	N227UA	EWR	LAX	313	2454	14	30	2023-01-13 14:00:00	LAX
7194	7	7	1125	1129	-4	1238	1246	9E	1134	N676CA	LGA	SYR	42	198	11	29	2023-07-07 11:00:00	Other
7207	1	4	1557	1602	-5	1711	1736	UA	952	N38727	EWR	PIT	55	319	16	2	2023-01-04 16:00:00	Other
7228	7	6	641	645	-4	933	953	UA	244	N454UA	EWR	FLL	153	1065	6	45	2023-07-06 06:00:00	FLL
7242	9	16	725	730	-5	844	907	AA	236	N950NN	LGA	ORD	104	733	7	30	2023-09-16 07:00:00	ORD
7243	2	6	715	720	-5	949	1005	WN	534	N735SA	LGA	DEN	242	1620	7	20	2023-02-06 07:00:00	Other
7249	9	30	1726	1729	-3	2004	2035	AA	38	N105NN	JFK	LAX	316	2475	17	29	2023-09-30 17:00:00	LAX
7270	12	21	559	601	-2	849	902	B6	46	N784JB	LGA	FLL	143	1076	6	1	2023-12-21 06:00:00	FLL
7271	12	22	526	529	-3	757	829	B6	41	N561JB	EWR	PBI	136	1023	5	29	2023-12-22 05:00:00	Other
7285	6	14	1012	1015	-3	1139	1150	YX	1114	N762YX	EWR	BGR	59	393	10	15	2023-06-14 10:00:00	Other
7287	4	17	1925	1930	-5	2056	2125	YX	1151	N117HQ	JFK	DCA	58	213	19	30	2023-04-17 19:00:00	Other
7289	3	31	1427	1430	-3	1719	1737	B6	23	N706JB	JFK	PBI	148	1028	14	30	2023-03-31 14:00:00	Other
7297	6	8	2013	2017	-4	2235	2239	YX	1077	N739YX	EWR	SDF	93	642	20	17	2023-06-08 20:00:00	Other
7298	12	16	655	659	-4	853	912	AA	180	N801NN	LGA	CLT	84	544	6	59	2023-12-16 06:00:00	CLT
7304	3	4	1127	1130	-3	1346	1335	AA	106	N972AN	LGA	CLT	98	544	11	30	2023-03-04 11:00:00	CLT
7306	1	12	1327	1329	-2	1648	1700	YX	1444	N429YX	LGA	IAH	233	1416	13	29	2023-01-12 13:00:00	Other
7310	8	3	1447	1450	-3	1732	1720	WN	526	N408WN	LGA	ATL	130	762	14	50	2023-08-03 14:00:00	ATL
7317	5	21	726	729	-3	831	905	UA	839	N407UA	EWR	ORD	106	719	7	29	2023-05-21 07:00:00	ORD
7329	1	25	1154	1159	-5	1335	1345	9E	1405	N136EV	LGA	MKE	126	738	11	59	2023-01-25 11:00:00	Other
7345	2	22	827	830	-3	1012	1030	9E	1417	N937XJ	JFK	RDU	74	427	8	30	2023-02-22 08:00:00	Other
7378	2	27	1135	1138	-3	1321	1342	AA	732	N754UW	EWR	CLT	83	529	11	38	2023-02-27 11:00:00	CLT
7379	9	18	1943	1948	-5	2141	2118	9E	1522	N936XJ	LGA	ROC	44	254	19	48	2023-09-18 19:00:00	Other
7384	4	25	1612	1617	-5	1833	1820	AA	840	N557UW	JFK	CLT	88	541	16	17	2023-04-25 16:00:00	CLT
7385	2	21	1510	1515	-5	1835	1829	UA	379	N2645U	EWR	SFO	362	2565	15	15	2023-02-21 15:00:00	Other
7387	9	15	1624	1626	-2	1819	1854	UA	694	N409UA	LGA	DEN	215	1620	16	26	2023-09-15 16:00:00	Other
7389	7	7	827	829	-2	1022	1029	AA	800	N827NN	JFK	ORD	113	740	8	29	2023-07-07 08:00:00	ORD
7390	1	9	1937	1940	-3	2103	2130	YX	1469	N428YX	JFK	DCA	57	213	19	40	2023-01-09 19:00:00	Other
7391	6	10	1619	1622	-3	1750	1820	YX	1098	N729YX	EWR	GSO	65	445	16	22	2023-06-10 16:00:00	Other
7393	4	10	931	935	-4	1057	1100	YX	1480	N217JQ	JFK	DCA	56	213	9	35	2023-04-10 09:00:00	Other
7398	2	3	1627	1630	-3	2016	2007	DL	230	N868DN	JFK	SLC	290	1990	16	30	2023-02-03 16:00:00	Other
7401	2	19	2155	2200	-5	2332	2356	YX	1316	N409YX	LGA	RDU	77	431	22	0	2023-02-19 22:00:00	Other
7410	1	10	2220	2225	-5	216	158	B6	1011	N903JB	JFK	SFO	366	2586	22	25	2023-01-10 22:00:00	Other
7414	1	21	826	829	-3	1002	1009	YX	1176	N749YX	EWR	MKE	120	725	8	29	2023-01-21 08:00:00	Other
7417	1	10	656	700	-4	943	1009	B6	409	N571JB	JFK	PBI	148	1028	7	0	2023-01-10 07:00:00	Other
7422	1	8	1825	1830	-5	2054	2118	UA	964	N17279	EWR	LAS	301	2227	18	30	2023-01-08 18:00:00	Other
7423	1	13	831	835	-4	1208	1241	AA	55	N112AN	JFK	SFO	356	2586	8	35	2023-01-13 08:00:00	Other
7425	2	10	1726	1730	-4	1928	1947	9E	1395	N301PQ	LGA	DSM	151	1031	17	30	2023-02-10 17:00:00	Other
7429	9	17	1530	1534	-4	1649	1703	9E	1526	N330PQ	LGA	ROC	46	254	15	34	2023-09-17 15:00:00	Other
7430	1	7	1957	1959	-2	2110	2150	AA	850	N746UW	LGA	BNA	111	764	19	59	2023-01-07 19:00:00	Other
7439	9	20	830	833	-3	1056	1100	B6	419	N206JB	JFK	ATL	106	760	8	33	2023-09-20 08:00:00	ATL
7445	5	17	1556	1558	-2	1807	1827	DL	765	N344NB	JFK	MSY	176	1182	15	58	2023-05-17 15:00:00	Other
7448	8	7	558	600	-2	720	732	UA	310	N17550	EWR	ORD	109	719	6	0	2023-08-07 06:00:00	ORD
7454	4	5	2233	2237	-4	37	2355	UA	530	N23721	EWR	BTV	43	266	22	37	2023-04-05 22:00:00	Other
7460	10	20	1143	1145	-2	1419	1440	DL	589	N302DN	JFK	MCO	133	944	11	45	2023-10-20 11:00:00	MCO
7467	5	28	1426	1429	-3	1617	1612	9E	1510	N232PQ	JFK	RIC	53	288	14	29	2023-05-28 14:00:00	Other
7468	10	14	1701	1706	-5	1913	1907	9E	1412	N306PQ	JFK	RDU	73	427	17	6	2023-10-14 17:00:00	Other
7475	3	9	1712	1717	-5	1824	1843	YX	1069	N755YX	EWR	ROC	47	246	17	17	2023-03-09 17:00:00	Other
7478	10	3	726	730	-4	841	906	DL	595	N127DU	LGA	ORD	103	733	7	30	2023-10-03 07:00:00	ORD
7482	6	28	835	840	-5	1028	1100	9E	1685	N302PQ	JFK	CHS	86	636	8	40	2023-06-28 08:00:00	Other
7486	5	22	712	715	-3	911	947	DL	237	N919DU	JFK	PHX	273	2153	7	15	2023-05-22 07:00:00	Other
7488	6	30	1724	1729	-5	2026	2042	AA	1005	N323SG	JFK	AUS	208	1521	17	29	2023-06-30 17:00:00	Other
7494	12	17	1747	1750	-3	2019	2029	9E	1392	N676CA	JFK	MCI	164	1113	17	50	2023-12-17 17:00:00	Other
7497	3	19	1858	1900	-2	1959	2022	YX	1747	N218JQ	LGA	BOS	35	184	19	0	2023-03-19 19:00:00	BOS
7507	6	25	1054	1059	-5	1237	1255	NK	650	N675NK	LGA	DTW	73	502	10	59	2023-06-25 10:00:00	Other
7513	12	18	1105	1107	-2	1329	1340	UA	476	N25201	EWR	JAX	123	820	11	7	2023-12-18 11:00:00	Other
7515	6	8	1933	1935	-2	2139	2213	9E	1579	N905XJ	JFK	MCI	153	1113	19	35	2023-06-08 19:00:00	Other
7520	9	19	1342	1346	-4	1601	1600	9E	1714	N336PQ	JFK	CHS	96	636	13	46	2023-09-19 13:00:00	Other
7525	9	28	856	900	-4	1020	1029	YX	1101	N731YX	EWR	DCA	43	199	9	0	2023-09-28 09:00:00	Other
7531	5	24	1554	1556	-2	1806	1814	YX	1341	N406YX	LGA	TYS	102	647	15	56	2023-05-24 15:00:00	Other
7544	9	11	1546	1550	-4	2100	1849	UA	631	N35271	EWR	TPA	141	997	15	50	2023-09-11 15:00:00	Other
7552	4	4	1236	1240	-4	1426	1447	NK	581	N668NK	LGA	DTW	86	502	12	40	2023-04-04 12:00:00	Other
7554	10	18	1313	1315	-2	1423	1450	UA	584	N882UA	LGA	ORD	110	733	13	15	2023-10-18 13:00:00	ORD
7555	4	7	558	600	-2	808	755	DL	346	N392DN	LGA	DTW	98	502	6	0	2023-04-07 06:00:00	Other
7556	11	17	1657	1659	-2	1923	1939	DL	141	N319DN	LGA	ATL	116	762	16	59	2023-11-17 16:00:00	ATL
7570	3	5	1740	1745	-5	2012	2030	WN	800	N8648A	LGA	ATL	118	762	17	45	2023-03-05 17:00:00	ATL
7572	1	7	658	700	-2	946	1023	DL	99	N808DN	JFK	SEA	313	2422	7	0	2023-01-07 07:00:00	Other
7583	2	23	1726	1730	-4	1958	1947	9E	1395	N480PX	LGA	DSM	178	1031	17	30	2023-02-23 17:00:00	Other
7585	10	29	1229	1232	-3	1358	1351	YX	1272	N435YX	JFK	BOS	47	187	12	32	2023-10-29 12:00:00	BOS
7589	8	9	1330	1335	-5	1446	1452	YX	905	N729YX	EWR	BTV	48	266	13	35	2023-08-09 13:00:00	Other
7593	10	15	1849	1854	-5	2029	2029	AA	731	N359PX	LGA	ORD	98	733	18	54	2023-10-15 18:00:00	ORD
7607	3	13	1255	1259	-4	1405	1422	9E	1530	N182GJ	LGA	SCE	43	208	12	59	2023-03-13 12:00:00	Other
7615	8	14	1622	1625	-3	1915	1935	AA	84	N101NN	JFK	LAX	320	2475	16	25	2023-08-14 16:00:00	LAX
7618	7	14	535	539	-4	1046	933	B6	500	N913JB	JFK	SJU	223	1598	5	39	2023-07-14 05:00:00	Other
7620	5	7	1816	1820	-4	1935	1947	9E	1529	N309PQ	LGA	PWM	48	269	18	20	2023-05-07 18:00:00	Other
7621	10	22	925	928	-3	1109	1130	YX	1164	N765YX	EWR	MEM	142	946	9	28	2023-10-22 09:00:00	Other
7622	3	31	756	800	-4	1008	1019	YX	1624	N231JQ	JFK	CLT	88	541	8	0	2023-03-31 08:00:00	CLT
7624	8	26	755	759	-4	951	1004	DL	467	N385DZ	LGA	MSP	153	1020	7	59	2023-08-26 07:00:00	Other
7627	10	8	2057	2100	-3	2348	8	AA	82	N112AN	JFK	LAX	317	2475	21	0	2023-10-08 21:00:00	LAX
7629	10	18	1823	1825	-2	2109	2125	WN	1198	N8573Z	LGA	TPA	145	1010	18	25	2023-10-18 18:00:00	Other
7646	3	8	2006	2010	-4	2329	2340	B6	67	N961JT	JFK	LAX	357	2475	20	10	2023-03-08 20:00:00	LAX
7650	2	1	753	757	-4	1009	910	9E	1403	N607LR	LGA	BDL	22	101	7	57	2023-02-01 07:00:00	Other
7651	5	4	1356	1400	-4	1512	1518	YX	1110	N647RW	EWR	DCA	46	199	14	0	2023-05-04 14:00:00	Other
7653	6	14	845	850	-5	1014	1010	YX	1787	N215JQ	EWR	BOS	45	200	8	50	2023-06-14 08:00:00	BOS
7654	10	31	700	705	-5	944	1000	DL	327	N364NW	LGA	PBI	139	1035	7	5	2023-10-31 07:00:00	Other
7661	3	28	655	700	-5	759	810	YX	1732	N245JQ	EWR	BOS	37	200	7	0	2023-03-28 07:00:00	BOS
7664	5	3	1002	1007	-5	1210	1216	YX	1045	N647RW	EWR	AVL	90	583	10	7	2023-05-03 10:00:00	Other
7667	11	16	1728	1730	-2	1837	1854	OO	1173	N293SY	JFK	BOS	45	187	17	30	2023-11-16 17:00:00	BOS
7670	5	20	1158	1200	-2	1418	1438	DL	320	N350DN	LGA	ATL	110	762	12	0	2023-05-20 12:00:00	ATL
7671	6	18	622	626	-4	751	753	UA	992	N73275	LGA	ORD	116	733	6	26	2023-06-18 06:00:00	ORD
7682	12	2	858	902	-4	1237	1237	AA	860	N116AN	JFK	SNA	356	2454	9	2	2023-12-02 09:00:00	Other
7684	9	26	752	755	-3	1056	1106	AA	128	N944AN	LGA	MIA	166	1096	7	55	2023-09-26 07:00:00	MIA
7686	12	3	1055	1100	-5	1243	1250	AA	868	N808AW	LGA	STL	137	888	11	0	2023-12-03 11:00:00	Other
7696	7	23	651	654	-3	927	952	UA	664	N27511	EWR	PBI	139	1023	6	54	2023-07-23 06:00:00	Other
7698	8	4	1926	1930	-4	2231	2229	B6	531	N504JB	LGA	PBI	144	1035	19	30	2023-08-04 19:00:00	Other
7702	2	18	957	1000	-3	1250	1314	UA	692	N401UA	LGA	IAH	203	1416	10	0	2023-02-18 10:00:00	Other
7705	9	11	957	1000	-3	1121	1136	UA	441	N39728	EWR	BNA	112	748	10	0	2023-09-11 10:00:00	Other
7707	4	7	1625	1629	-4	1727	1749	YX	1454	N218JQ	JFK	BOS	38	187	16	29	2023-04-07 16:00:00	BOS
7715	2	15	1510	1515	-5	1822	1751	UA	695	N34455	EWR	DEN	239	1605	15	15	2023-02-15 15:00:00	Other
7727	2	16	2050	2055	-5	2238	2249	9E	1453	N915XJ	LGA	RDU	75	431	20	55	2023-02-16 20:00:00	Other
7730	1	19	1442	1445	-3	1738	1717	B6	791	N594JB	LGA	MSY	199	1183	14	45	2023-01-19 14:00:00	Other
7734	4	11	1827	1829	-2	2017	2048	YX	1125	N419YX	LGA	IND	88	660	18	29	2023-04-11 18:00:00	Other
7737	9	25	820	825	-5	1106	1118	AA	332	N891NN	LGA	DFW	190	1389	8	25	2023-09-25 08:00:00	Other
7739	2	1	1450	1455	-5	1719	1750	9E	1274	N936XJ	JFK	JAX	124	828	14	55	2023-02-01 14:00:00	Other
7742	2	6	1728	1730	-2	1922	1926	9E	1369	N134EV	JFK	RDU	70	427	17	30	2023-02-06 17:00:00	Other
7745	9	1	841	846	-5	1025	1028	YX	1967	N233JQ	LGA	PIT	56	335	8	46	2023-09-01 08:00:00	Other
7748	7	5	1047	1050	-3	1224	1212	9E	1215	N538CA	JFK	BTV	49	266	10	50	2023-07-05 10:00:00	Other
7755	3	27	725	730	-5	907	855	YX	1629	N203JQ	LGA	ORF	73	296	7	30	2023-03-27 07:00:00	Other
7766	7	21	1019	1023	-4	1143	1158	UA	556	N27213	EWR	ORD	111	719	10	23	2023-07-21 10:00:00	ORD
7767	5	20	1420	1425	-5	1603	1603	9E	1375	N298PQ	JFK	ROC	49	264	14	25	2023-05-20 14:00:00	Other
7776	1	2	2000	2002	-2	2147	2218	YX	1438	N826MD	LGA	CLE	79	419	20	2	2023-01-02 20:00:00	Other
7779	10	15	1141	1145	-4	1320	1343	9E	1546	N134EV	LGA	RDU	76	431	11	45	2023-10-15 11:00:00	Other
7780	10	17	2245	2250	-5	8	27	9E	1421	N305PQ	JFK	ROC	45	264	22	50	2023-10-17 22:00:00	Other
7781	7	20	1654	1659	-5	1900	1844	AA	813	N773XF	LGA	STL	129	888	16	59	2023-07-20 16:00:00	Other
7782	7	10	1520	1525	-5	1738	1737	9E	1148	N935XJ	LGA	ILM	81	500	15	25	2023-07-10 15:00:00	Other
7787	11	3	808	810	-2	1035	1049	B6	188	N760JB	JFK	ATL	115	760	8	10	2023-11-03 08:00:00	ATL
7789	9	1	1352	1357	-5	1602	1615	9E	1545	N908XJ	LGA	TYS	93	647	13	57	2023-09-01 13:00:00	Other
7803	10	15	1135	1140	-5	1340	1348	AA	919	N840NN	JFK	CLT	92	541	11	40	2023-10-15 11:00:00	CLT
7808	5	31	1147	1150	-3	1328	1346	DL	611	N942AT	EWR	MSP	134	1008	11	50	2023-05-31 11:00:00	Other
7814	10	29	1852	1857	-5	2132	2118	DL	426	N101DU	LGA	MSY	174	1183	18	57	2023-10-29 18:00:00	Other
7815	9	7	1356	1359	-3	1733	1701	DL	385	N349NB	LGA	IAH	199	1416	13	59	2023-09-07 13:00:00	Other
7817	3	18	1026	1029	-3	1232	1247	9E	1313	N279PQ	LGA	CLT	102	544	10	29	2023-03-18 10:00:00	CLT
7821	8	12	757	759	-2	1049	1110	AA	478	N306RC	JFK	MIA	146	1089	7	59	2023-08-12 07:00:00	MIA
7823	12	14	626	630	-4	930	1014	AA	23	N113AN	JFK	SFO	340	2586	6	30	2023-12-14 06:00:00	Other
7830	10	30	851	855	-4	1010	1024	YX	1104	N746YX	EWR	PWM	43	284	8	55	2023-10-30 08:00:00	Other
7833	8	14	802	805	-3	1007	1014	DL	447	N324NB	JFK	MSP	150	1029	8	5	2023-08-14 08:00:00	Other
7835	3	20	1958	2000	-2	2134	2158	YX	1614	N239JQ	JFK	PIT	57	340	20	0	2023-03-20 20:00:00	Other
7840	5	19	755	800	-5	1124	1110	AA	512	N980NN	EWR	MIA	163	1085	8	0	2023-05-19 08:00:00	MIA
7841	1	24	945	950	-5	1230	1300	B6	260	N564JB	LGA	MCO	136	950	9	50	2023-01-24 09:00:00	MCO
7844	10	9	1056	1100	-4	1312	1327	UA	228	N4901U	EWR	ATL	113	746	11	0	2023-10-09 11:00:00	ATL
7859	9	1	1155	1200	-5	1352	1350	9E	1675	N147PQ	JFK	RDU	71	427	12	0	2023-09-01 12:00:00	Other
7862	1	18	1811	1815	-4	2118	2140	UA	503	N2250U	EWR	SFO	332	2565	18	15	2023-01-18 18:00:00	Other
7867	12	31	1629	1634	-5	1908	2008	DL	279	N531DA	JFK	SAN	320	2446	16	34	2023-12-31 16:00:00	Other
7870	4	21	1955	2000	-5	2145	2211	DL	726	N333NB	LGA	DTW	73	502	20	0	2023-04-21 20:00:00	Other
7875	1	16	846	849	-3	1032	1111	9E	1514	N917XJ	LGA	MEM	141	963	8	49	2023-01-16 08:00:00	Other
7881	12	28	755	800	-5	932	1030	DL	533	N343NB	JFK	MSP	132	1029	8	0	2023-12-28 08:00:00	Other
7883	12	2	1924	1929	-5	2132	2131	YX	1081	N755YX	EWR	STL	157	872	19	29	2023-12-02 19:00:00	Other
7886	4	27	958	1000	-2	1206	1211	AA	684	N536UW	LGA	CLT	95	544	10	0	2023-04-27 10:00:00	CLT
7887	11	5	1547	1550	-3	1704	1730	9E	1412	N908XJ	LGA	ORF	52	296	15	50	2023-11-05 15:00:00	Other
7917	12	11	1920	1924	-4	2117	2129	UA	513	N62849	EWR	DTW	77	488	19	24	2023-12-11 19:00:00	Other
7921	6	17	637	640	-3	900	908	AA	571	N336RU	JFK	PHX	284	2153	6	40	2023-06-17 06:00:00	Other
7931	1	29	732	735	-3	1030	1042	DL	662	N343NW	JFK	TPA	149	1005	7	35	2023-01-29 07:00:00	Other
7935	5	25	1618	1620	-2	1815	1837	9E	1522	N200PQ	LGA	CLT	86	544	16	20	2023-05-25 16:00:00	CLT
7936	4	12	1832	1835	-3	2021	2121	DL	162	N3765	LGA	DEN	206	1620	18	35	2023-04-12 18:00:00	Other
7939	7	14	1124	1128	-4	1448	1437	B6	252	N536JB	JFK	SAT	210	1587	11	28	2023-07-14 11:00:00	Other
7948	12	3	657	700	-3	1020	1049	AS	11	N278AK	JFK	SFO	348	2586	7	0	2023-12-03 07:00:00	Other
7949	3	7	1156	1159	-3	1446	1502	UA	831	N443UA	EWR	SRQ	144	1034	11	59	2023-03-07 11:00:00	Other
7955	8	21	1551	1555	-4	1800	1849	B6	500	N625JB	JFK	JAX	104	828	15	55	2023-08-21 15:00:00	Other
7960	3	3	1632	1635	-3	1801	1808	YX	1641	N223JQ	LGA	DCA	54	214	16	35	2023-03-03 16:00:00	Other
7966	12	13	2156	2200	-4	2335	2349	9E	1579	N600LR	JFK	BUF	61	301	22	0	2023-12-13 22:00:00	Other
7968	6	17	1516	1520	-4	1648	1723	9E	1511	N914XJ	LGA	GSO	72	461	15	20	2023-06-17 15:00:00	Other
7970	7	26	1934	1939	-5	2119	2129	YX	1076	N121HQ	LGA	CMH	72	479	19	39	2023-07-26 19:00:00	Other
7971	1	23	947	950	-3	1229	1220	WN	204	N959WN	LGA	MCI	155	1107	9	50	2023-01-23 09:00:00	Other
7985	2	4	1115	1118	-3	1420	1441	B6	77	N784JB	LGA	FLL	160	1076	11	18	2023-02-04 11:00:00	FLL
7986	1	5	757	800	-3	1056	1129	DL	218	N107DU	LGA	DFW	210	1389	8	0	2023-01-05 08:00:00	Other
7989	4	25	1626	1629	-3	1802	1825	OO	1009	N246SY	JFK	ORD	126	740	16	29	2023-04-25 16:00:00	ORD
7991	8	28	658	700	-2	954	1007	DL	358	N374DA	JFK	RSW	151	1074	7	0	2023-08-28 07:00:00	Other
7995	11	6	1455	1500	-5	1625	1639	OO	1204	N247SY	JFK	BNA	120	765	15	0	2023-11-06 15:00:00	Other
7999	7	5	1007	1010	-3	1202	1215	AA	620	N952AA	LGA	CLT	82	544	10	10	2023-07-05 10:00:00	CLT
8007	12	23	1936	1940	-4	11	36	UA	553	N37513	EWR	SJU	195	1608	19	40	2023-12-23 19:00:00	Other
8011	5	26	845	848	-3	1028	1049	9E	1396	N916XJ	LGA	MEM	135	963	8	48	2023-05-26 08:00:00	Other
8012	1	22	746	751	-5	958	1027	UA	919	N67134	EWR	DEN	223	1605	7	51	2023-01-22 07:00:00	Other
8016	12	9	725	730	-5	1016	1031	UA	417	N33289	EWR	SRQ	148	1034	7	30	2023-12-09 07:00:00	Other
8018	8	8	1414	1418	-4	1550	1610	B6	223	N317JB	JFK	RDU	74	427	14	18	2023-08-08 14:00:00	Other
8021	11	10	1257	1259	-2	1424	1416	YX	1816	N239JQ	LGA	BOS	40	184	12	59	2023-11-10 12:00:00	BOS
8023	4	14	1515	1520	-5	1719	1715	YX	1126	N438YX	JFK	RDU	77	427	15	20	2023-04-14 15:00:00	Other
8035	4	26	1125	1129	-4	1234	1300	UA	349	N24702	EWR	ORD	113	719	11	29	2023-04-26 11:00:00	ORD
8036	6	1	1711	1714	-3	1826	1851	9E	1431	N348PQ	LGA	BUF	47	292	17	14	2023-06-01 17:00:00	Other
8040	6	8	1025	1029	-4	1202	1219	YX	1204	N979RP	EWR	GSO	69	445	10	29	2023-06-08 10:00:00	Other
8041	5	11	1157	1202	-5	1305	1337	YX	1207	N433YX	JFK	BOS	41	187	12	2	2023-05-11 12:00:00	BOS
8043	4	27	1613	1617	-4	1903	1820	AA	840	N142AN	JFK	CLT	82	541	16	17	2023-04-27 16:00:00	CLT
8049	5	17	1331	1335	-4	1452	1511	9E	1449	N304PQ	LGA	RIC	49	292	13	35	2023-05-17 13:00:00	Other
8051	5	22	1657	1700	-3	1809	1832	YX	1668	N203JQ	EWR	BOS	40	200	17	0	2023-05-22 17:00:00	BOS
8058	4	7	1445	1450	-5	1602	1623	9E	1347	N348PQ	LGA	CHO	61	305	14	50	2023-04-07 14:00:00	Other
8064	12	15	611	615	-4	857	933	DL	438	N120DU	LGA	IAH	196	1416	6	15	2023-12-15 06:00:00	Other
8065	3	11	2039	2042	-3	2352	2	B6	35	N991JT	JFK	SAN	353	2446	20	42	2023-03-11 20:00:00	Other
8076	9	16	1611	1615	-4	1715	1740	WN	876	N8687A	LGA	MDW	100	725	16	15	2023-09-16 16:00:00	Other
8084	3	4	1125	1129	-4	1419	1428	DL	189	N192DN	JFK	LAS	327	2248	11	29	2023-03-04 11:00:00	Other
8087	9	21	752	757	-5	1106	1104	UA	601	N47291	EWR	FLL	160	1065	7	57	2023-09-21 07:00:00	FLL
8090	1	14	646	650	-4	943	1016	AA	990	N341SV	LGA	MIA	153	1096	6	50	2023-01-14 06:00:00	MIA
8094	10	9	1713	1715	-2	1830	1851	UA	844	N33284	LGA	ORD	107	733	17	15	2023-10-09 17:00:00	ORD
8097	5	21	1833	1838	-5	2043	2119	9E	1298	N304PQ	JFK	SAV	107	718	18	38	2023-05-21 18:00:00	Other
8109	8	16	1720	1725	-5	1911	1916	YX	968	N446YX	JFK	CLE	76	425	17	25	2023-08-16 17:00:00	Other
8113	5	24	1611	1615	-4	1814	1831	DL	337	N141DU	LGA	CHS	94	641	16	15	2023-05-24 16:00:00	Other
8116	1	27	1210	1215	-5	1312	1325	B6	324	N334JB	LGA	BOS	38	184	12	15	2023-01-27 12:00:00	BOS
8121	4	3	959	1003	-4	1200	1214	AA	684	N918NN	LGA	CLT	90	544	10	3	2023-04-03 10:00:00	CLT
8132	9	14	1523	1525	-2	1715	1719	YX	1915	N224JQ	JFK	PIT	67	340	15	25	2023-09-14 15:00:00	Other
8133	9	13	1435	1440	-5	1558	1612	9E	1500	N480PX	LGA	ORF	54	296	14	40	2023-09-13 14:00:00	Other
8134	5	30	1515	1520	-5	1720	1746	9E	1342	N183GJ	JFK	CHS	90	636	15	20	2023-05-30 15:00:00	Other
8140	6	6	1000	1003	-3	1142	1159	OO	1271	N260SY	LGA	MEM	142	963	10	3	2023-06-06 10:00:00	Other
8143	5	18	1217	1222	-5	1341	1355	9E	1534	N691CA	JFK	BUF	55	301	12	22	2023-05-18 12:00:00	Other
8144	12	24	1128	1130	-2	1432	1448	AA	434	N996NN	JFK	AUS	218	1521	11	30	2023-12-24 11:00:00	Other
8157	3	7	1341	1344	-3	1633	1650	AA	464	N998NN	EWR	DFW	208	1372	13	44	2023-03-07 13:00:00	Other
8159	4	25	1158	1200	-2	1307	1325	YX	1548	N882RW	LGA	BTV	42	258	12	0	2023-04-25 12:00:00	Other
8161	12	6	1204	1209	-5	1343	1400	YX	1262	N417YX	JFK	RDU	75	427	12	9	2023-12-06 12:00:00	Other
8163	9	28	1654	1659	-5	1859	1914	YX	1084	N757YX	EWR	IND	95	645	16	59	2023-09-28 16:00:00	Other
8164	3	7	606	610	-4	951	920	WN	551	N8711Q	LGA	HOU	208	1428	6	10	2023-03-07 06:00:00	Other
8176	3	8	1325	1330	-5	1723	1707	B6	585	N945JT	JFK	SFO	383	2586	13	30	2023-03-08 13:00:00	Other
8178	1	31	1856	1900	-4	2014	2027	YX	1882	N215JQ	LGA	BOS	31	184	19	0	2023-01-31 19:00:00	BOS
8188	12	28	925	930	-5	1200	1244	AS	12	N921AK	JFK	SAN	300	2446	9	30	2023-12-28 09:00:00	Other
8193	5	16	1121	1125	-4	1319	1338	YX	1241	N421YX	LGA	MSP	151	1020	11	25	2023-05-16 11:00:00	Other
8196	2	2	1225	1229	-4	1423	1416	YX	1586	N860RW	LGA	BNA	150	764	12	29	2023-02-02 12:00:00	Other
8204	11	21	1827	1829	-2	2140	2144	AS	168	N937AK	EWR	SEA	331	2402	18	29	2023-11-21 18:00:00	Other
8216	3	7	2003	2005	-2	2227	2233	9E	1433	N918XJ	LGA	GRR	101	618	20	5	2023-03-07 20:00:00	Other
8219	11	10	1550	1555	-5	1857	1905	B6	744	N979JT	EWR	LAX	345	2454	15	55	2023-11-10 15:00:00	LAX
8227	2	26	2213	2215	-2	203	141	B6	680	N992JB	JFK	LAX	374	2475	22	15	2023-02-26 22:00:00	LAX
8235	10	4	955	959	-4	1249	1256	DL	235	N177DN	JFK	LAX	306	2475	9	59	2023-10-04 09:00:00	LAX
8236	6	15	1457	1500	-3	1716	1742	B6	676	N304JB	JFK	ATL	110	760	15	0	2023-06-15 15:00:00	ATL
8237	5	13	613	615	-2	723	727	YX	1163	N651RW	EWR	IAD	40	212	6	15	2023-05-13 06:00:00	Other
8245	4	27	1031	1035	-4	1302	1305	WN	589	N470WN	LGA	ATL	124	762	10	35	2023-04-27 10:00:00	ATL
8253	11	1	1627	1629	-2	1836	1859	YX	1129	N742YX	EWR	SDF	106	642	16	29	2023-11-01 16:00:00	Other
8255	1	24	1745	1749	-4	1926	1935	9E	1529	N607LR	JFK	RDU	73	427	17	49	2023-01-24 17:00:00	Other
8259	7	11	1042	1045	-3	1235	1310	WN	838	N421LV	LGA	ATL	100	762	10	45	2023-07-11 10:00:00	ATL
8260	9	11	954	959	-5	1216	1223	9E	1470	N176PQ	JFK	SAV	110	718	9	59	2023-09-11 09:00:00	Other
8264	12	23	2124	2129	-5	2307	2322	9E	1608	N136EV	JFK	RIC	55	288	21	29	2023-12-23 21:00:00	Other
8275	11	17	727	730	-3	904	908	9E	1551	N480PX	LGA	RIC	63	292	7	30	2023-11-17 07:00:00	Other
8286	2	26	557	600	-3	914	920	AA	389	N70020	JFK	MIA	147	1089	6	0	2023-02-26 06:00:00	MIA
8293	7	4	1021	1023	-2	1150	1158	YX	882	N754YX	EWR	BGR	69	393	10	23	2023-07-04 10:00:00	Other
8295	8	17	1027	1030	-3	1240	1237	YX	873	N651RW	EWR	CLT	83	529	10	30	2023-08-17 10:00:00	CLT
8302	12	26	1041	1045	-4	1211	1230	YX	1815	N201JQ	JFK	ORD	113	740	10	45	2023-12-26 10:00:00	ORD
8307	4	18	1750	1755	-5	2021	2101	AA	211	N969AN	LGA	DFW	190	1389	17	55	2023-04-18 17:00:00	Other
8313	12	23	1625	1630	-5	1937	2014	AA	816	N116AN	JFK	SFO	342	2586	16	30	2023-12-23 16:00:00	Other
8319	7	26	1055	1100	-5	1357	1403	NK	438	N685NK	EWR	FLL	152	1065	11	0	2023-07-26 11:00:00	FLL
8327	10	27	939	942	-3	1221	1152	B6	958	N508JL	JFK	CHS	104	636	9	42	2023-10-27 09:00:00	Other
8329	9	7	1655	1659	-4	2012	1917	YX	1377	N424YX	JFK	CVG	112	589	16	59	2023-09-07 16:00:00	Other
8342	6	13	1436	1440	-4	1555	1610	YX	1320	N428YX	LGA	BUF	46	292	14	40	2023-06-13 14:00:00	Other
8352	12	1	1517	1520	-3	1756	1752	DL	478	N1201P	JFK	ATL	124	760	15	20	2023-12-01 15:00:00	ATL
8357	8	21	926	930	-4	1159	1243	B6	66	N531JL	LGA	FLL	135	1076	9	30	2023-08-21 09:00:00	FLL
8363	11	4	700	705	-5	946	955	DL	499	N889DN	JFK	TPA	142	1005	7	5	2023-11-04 07:00:00	Other
8369	1	3	1544	1549	-5	2233	1830	B6	733	N599JB	JFK	ATL	NA	760	15	49	2023-01-03 15:00:00	ATL
8370	12	21	1227	1229	-2	1521	1548	DL	559	N371DN	LGA	FLL	143	1076	12	29	2023-12-21 12:00:00	FLL
8377	3	8	2125	2130	-5	2225	2237	YX	1195	N723YX	EWR	PVD	33	160	21	30	2023-03-08 21:00:00	Other
8391	4	27	1843	1845	-2	2121	2147	UA	234	N211UA	EWR	LAX	309	2454	18	45	2023-04-27 18:00:00	LAX
8395	9	1	625	629	-4	747	756	UA	955	N831UA	LGA	ORD	112	733	6	29	2023-09-01 06:00:00	ORD
8397	7	12	1245	1250	-5	1515	1527	YX	1041	N435YX	LGA	OKC	186	1341	12	50	2023-07-12 12:00:00	Other
8405	12	11	1723	1726	-3	1845	1848	UA	128	N843UA	EWR	IAD	51	212	17	26	2023-12-11 17:00:00	Other
8406	7	12	2112	2117	-5	2253	2319	YX	1015	N403YX	LGA	MEM	132	963	21	17	2023-07-12 21:00:00	Other
8419	2	14	1420	1425	-5	1549	1625	9E	1439	N297PQ	LGA	GSO	68	461	14	25	2023-02-14 14:00:00	Other
8422	3	2	2252	2255	-3	10	3	YX	1634	N207JQ	JFK	BWI	43	184	22	55	2023-03-02 22:00:00	Other
8423	6	9	656	700	-4	916	937	UA	533	N78509	EWR	IAH	177	1400	7	0	2023-06-09 07:00:00	Other
8427	2	6	1158	1201	-3	1401	1423	DL	902	N978AT	EWR	ATL	106	746	12	1	2023-02-06 12:00:00	ATL
8430	3	1	915	918	-3	1244	1232	YX	1369	N417YX	LGA	IAH	229	1416	9	18	2023-03-01 09:00:00	Other
8432	8	9	2045	2050	-5	2211	2228	YX	1366	N216JQ	LGA	ORF	50	296	20	50	2023-08-09 20:00:00	Other
8434	7	30	1159	1204	-5	1351	1406	YX	1078	N427YX	LGA	DTW	85	502	12	4	2023-07-30 12:00:00	Other
8435	5	17	1852	1855	-3	2321	2310	DL	694	N921DU	JFK	SJU	222	1598	18	55	2023-05-17 18:00:00	Other
8436	3	17	945	950	-5	1048	1114	9E	1562	N923XJ	JFK	SYR	45	209	9	50	2023-03-17 09:00:00	Other
8442	11	27	1808	1810	-2	2203	2126	DL	348	N172DN	JFK	LAX	324	2475	18	10	2023-11-27 18:00:00	LAX
8450	1	30	617	620	-3	1007	1001	AA	531	N425AN	EWR	PHX	326	2133	6	20	2023-01-30 06:00:00	Other
8462	11	4	1556	1600	-4	1809	1833	DL	174	N350DN	LGA	ATL	111	762	16	0	2023-11-04 16:00:00	ATL
8469	3	14	645	650	-5	802	829	YX	1670	N879RW	LGA	PIT	58	335	6	50	2023-03-14 06:00:00	Other
8471	11	11	856	900	-4	1152	1206	B6	160	N565JB	LGA	PBI	144	1035	9	0	2023-11-11 09:00:00	Other
8480	11	22	1017	1020	-3	1216	1205	9E	1426	N927XJ	LGA	RIC	76	292	10	20	2023-11-22 10:00:00	Other
8481	11	29	1046	1051	-5	1340	1401	UA	587	N27287	EWR	RSW	152	1068	10	51	2023-11-29 10:00:00	Other
8487	8	25	756	800	-4	1014	1007	AA	793	N556UW	LGA	CLT	89	544	8	0	2023-08-25 08:00:00	CLT
8489	5	5	625	630	-5	919	929	B6	701	N595JB	JFK	IAH	205	1417	6	30	2023-05-05 06:00:00	Other
8495	2	5	1454	1459	-5	1700	1658	9E	1324	N316PQ	JFK	CLE	81	425	14	59	2023-02-05 14:00:00	Other
8508	9	21	1827	1829	-2	2111	2134	AS	164	N247AK	EWR	SEA	301	2402	18	29	2023-09-21 18:00:00	Other
8515	7	23	716	720	-4	853	840	WN	1255	N437WN	LGA	MDW	105	725	7	20	2023-07-23 07:00:00	Other
8518	12	8	2254	2259	-5	11	38	9E	1691	N304PQ	JFK	ROC	51	264	22	59	2023-12-08 22:00:00	Other
8521	7	31	635	640	-5	813	830	YX	1406	N227JQ	LGA	CMH	76	479	6	40	2023-07-31 06:00:00	Other
8524	7	12	710	715	-5	906	929	DL	642	N3764D	EWR	ATL	95	746	7	15	2023-07-12 07:00:00	ATL
8538	5	15	556	600	-4	719	735	UA	375	N36247	EWR	ORD	110	719	6	0	2023-05-15 06:00:00	ORD
8546	2	11	1652	1655	-3	1935	1931	UA	906	N64844	EWR	DEN	231	1605	16	55	2023-02-11 16:00:00	Other
8551	5	26	1826	1829	-3	2105	2137	DL	487	N144DU	LGA	IAH	188	1416	18	29	2023-05-26 18:00:00	Other
8552	6	10	801	805	-4	956	1010	WN	563	N419WN	LGA	DEN	216	1620	8	5	2023-06-10 08:00:00	Other
8559	4	25	1232	1235	-3	1546	1542	AA	201	N809NN	LGA	DFW	205	1389	12	35	2023-04-25 12:00:00	Other
8561	10	3	1341	1346	-5	1504	1519	YX	1777	N246JQ	JFK	ORF	54	290	13	46	2023-10-03 13:00:00	Other
8572	10	9	1936	1938	-2	2241	2245	UA	712	N27251	EWR	RSW	157	1068	19	38	2023-10-09 19:00:00	Other
8586	4	27	1458	1500	-2	1722	1704	YX	1042	N721YX	EWR	CLT	102	529	15	0	2023-04-27 15:00:00	CLT
8595	1	18	927	930	-3	1040	1057	9E	1695	N133EV	JFK	ORF	51	290	9	30	2023-01-18 09:00:00	Other
8598	12	14	1509	1514	-5	1622	1635	B6	39	N306JB	JFK	BTV	53	266	15	14	2023-12-14 15:00:00	Other
8619	12	28	1040	1045	-5	1254	1302	9E	1397	N324PQ	LGA	PNS	166	1030	10	45	2023-12-28 10:00:00	Other
8635	5	25	626	630	-4	938	931	B6	925	N531JL	JFK	FLL	165	1069	6	30	2023-05-25 06:00:00	FLL
8637	2	22	1636	1639	-3	1935	2002	B6	747	N709JB	JFK	MIA	150	1089	16	39	2023-02-22 16:00:00	MIA
8652	1	16	1154	1159	-5	1501	1517	B6	896	N945JT	JFK	LAX	343	2475	11	59	2023-01-16 11:00:00	LAX
8654	1	25	1628	1630	-2	2001	1946	NK	377	N676NK	LGA	FLL	189	1076	16	30	2023-01-25 16:00:00	FLL
8655	4	27	755	800	-5	1002	1021	9E	1374	N927XJ	LGA	IND	106	660	8	0	2023-04-27 08:00:00	Other
8668	10	25	556	600	-4	822	819	UA	387	N39728	EWR	ATL	101	746	6	0	2023-10-25 06:00:00	ATL
8680	3	24	1855	1859	-4	2125	2131	DL	829	N939AT	EWR	ATL	113	746	18	59	2023-03-24 18:00:00	ATL
8686	10	25	1937	1940	-3	2238	2243	B6	104	N2060J	JFK	ONT	319	2429	19	40	2023-10-25 19:00:00	Other
8687	8	22	1256	1300	-4	1531	1601	UA	87	N453UA	EWR	RSW	139	1068	13	0	2023-08-22 13:00:00	Other
8692	7	20	1115	1119	-4	1402	1423	DL	329	N302NB	LGA	TPA	136	1010	11	19	2023-07-20 11:00:00	Other
8693	11	28	1955	1959	-4	2158	2158	9E	1419	N906XJ	JFK	RIC	58	288	19	59	2023-11-28 19:00:00	Other
8696	3	21	1538	1540	-2	1855	1852	AA	116	N921AN	JFK	MIA	160	1089	15	40	2023-03-21 15:00:00	MIA
8700	8	22	1627	1630	-3	1924	1941	NK	267	N683NK	LGA	FLL	134	1076	16	30	2023-08-22 16:00:00	FLL
8706	9	11	855	900	-5	1204	1208	AS	122	N587AS	EWR	SFO	346	2565	9	0	2023-09-11 09:00:00	Other
8716	3	16	2224	2229	-5	126	155	B6	707	N595JB	JFK	LAX	335	2475	22	29	2023-03-16 22:00:00	LAX
8718	11	27	2055	2100	-5	2347	21	AA	52	N109NN	JFK	LAX	328	2475	21	0	2023-11-27 21:00:00	LAX
8731	7	24	601	605	-4	745	759	UA	257	N37420	EWR	MSP	140	1008	6	5	2023-07-24 06:00:00	Other
8740	5	8	1720	1723	-3	1942	1945	AA	921	N410AN	EWR	PHX	284	2133	17	23	2023-05-08 17:00:00	Other
8743	2	9	2058	2100	-2	2234	2239	AA	264	N826AW	EWR	ORD	115	719	21	0	2023-02-09 21:00:00	ORD
8755	6	14	1057	1100	-3	1243	1309	9E	1587	N937XJ	JFK	CLT	83	541	11	0	2023-06-14 11:00:00	CLT
8756	5	4	1951	1954	-3	2330	2353	UA	211	N61882	EWR	BQN	196	1585	19	54	2023-05-04 19:00:00	Other
8759	8	27	1727	1729	-2	1852	1909	UA	195	N17752	EWR	CLE	66	404	17	29	2023-08-27 17:00:00	Other
8771	8	20	1557	1559	-2	1708	1734	YX	899	N741YX	EWR	PIT	52	319	15	59	2023-08-20 15:00:00	Other
8774	3	6	1327	1329	-2	1611	1559	UA	393	N837UA	EWR	ATL	114	746	13	29	2023-03-06 13:00:00	ATL
8777	8	12	1310	1315	-5	1504	1528	9E	1114	N182GJ	JFK	CHS	89	636	13	15	2023-08-12 13:00:00	Other
8779	10	14	1855	1857	-2	2145	2205	DL	803	N389DN	LGA	TPA	150	1010	18	57	2023-10-14 18:00:00	Other
8780	6	18	1911	1915	-4	2031	2051	UA	904	N481UA	LGA	ORD	107	733	19	15	2023-06-18 19:00:00	ORD
8782	10	27	1355	1359	-4	1525	1553	9E	1401	N916XJ	LGA	GSO	70	461	13	59	2023-10-27 13:00:00	Other
8784	9	12	1049	1054	-5	1318	1324	UA	481	N17285	EWR	JAX	117	820	10	54	2023-09-12 10:00:00	Other
8786	11	25	1455	1500	-5	1802	1830	YX	1307	N405YX	LGA	MIA	168	1096	15	0	2023-11-25 15:00:00	MIA
8788	4	21	816	820	-4	931	954	9E	1304	N320PQ	LGA	IAD	44	229	8	20	2023-04-21 08:00:00	Other
8794	10	30	1756	1800	-4	2030	2027	9E	1531	N319PQ	LGA	MCI	184	1107	18	0	2023-10-30 18:00:00	Other
8797	7	12	1625	1630	-5	1938	1959	B6	230	N527JL	JFK	SJC	349	2569	16	30	2023-07-12 16:00:00	Other
8798	2	26	1405	1410	-5	1607	1620	YX	1131	N855RW	EWR	DTW	95	488	14	10	2023-02-26 14:00:00	Other
8805	11	2	1155	1200	-5	1507	1512	NK	1203	N676NK	LGA	FLL	152	1076	12	0	2023-11-02 12:00:00	FLL
8810	10	27	1622	1627	-5	1728	1745	UA	698	N77571	EWR	IAD	42	212	16	27	2023-10-27 16:00:00	Other
8818	8	19	1325	1329	-4	1505	1554	AA	782	N318SF	JFK	PHX	255	2153	13	29	2023-08-19 13:00:00	Other
8822	3	24	2054	2059	-5	2225	2234	YX	1648	N228JQ	JFK	DCA	58	213	20	59	2023-03-24 20:00:00	Other
8823	9	2	1928	1933	-5	2225	2237	UA	630	N47284	EWR	SMF	325	2500	19	33	2023-09-02 19:00:00	Other
8833	5	7	1644	1647	-3	1808	1826	UA	774	N37255	EWR	CLE	60	404	16	47	2023-05-07 16:00:00	Other
8837	5	23	1313	1316	-3	1531	1540	YX	1655	N237JQ	LGA	SDF	99	659	13	16	2023-05-23 13:00:00	Other
8840	4	24	1913	1915	-2	2155	2244	DL	160	N180DN	JFK	LAX	318	2475	19	15	2023-04-24 19:00:00	LAX
8844	2	20	1040	1045	-5	1214	1225	9E	1433	N923XJ	LGA	RIC	66	292	10	45	2023-02-20 10:00:00	Other
8846	5	6	1958	2000	-2	2233	2256	B6	84	N2016J	JFK	MCO	124	944	20	0	2023-05-06 20:00:00	MCO
8848	2	2	2157	2159	-2	2255	2306	YX	1100	N751YX	EWR	PVD	38	160	21	59	2023-02-02 21:00:00	Other
8851	8	30	1651	1655	-4	1952	2013	AS	6	N941AK	JFK	SEA	319	2422	16	55	2023-08-30 16:00:00	Other
8857	11	30	1620	1625	-5	1801	1806	9E	1530	N181PQ	JFK	BUF	58	301	16	25	2023-11-30 16:00:00	Other
8858	3	17	1447	1450	-3	1605	1626	9E	1476	N913XJ	LGA	MKE	119	738	14	50	2023-03-17 14:00:00	Other
8860	2	24	1000	1005	-5	1258	1320	NK	30	N665NK	EWR	MIA	152	1085	10	5	2023-02-24 10:00:00	MIA
8863	11	6	1438	1440	-2	1608	1627	AA	192	N873NN	LGA	ORD	122	733	14	40	2023-11-06 14:00:00	ORD
8870	11	4	1158	1200	-2	1459	1519	UA	835	N13138	EWR	LAX	334	2454	12	0	2023-11-04 12:00:00	LAX
8873	11	7	658	700	-2	950	1015	DL	921	N319US	JFK	AUS	206	1521	7	0	2023-11-07 07:00:00	Other
8878	10	30	1939	1942	-3	2134	2135	YX	1323	N445YX	JFK	PIT	75	340	19	42	2023-10-30 19:00:00	Other
8880	2	19	2025	2030	-5	2153	2201	9E	1388	N232PQ	LGA	ORF	54	296	20	30	2023-02-19 20:00:00	Other
8886	10	10	1436	1440	-4	1646	1710	WN	1018	N942WN	LGA	ATL	110	762	14	40	2023-10-10 14:00:00	ATL
8897	1	8	1342	1345	-3	1632	1705	DL	174	N175DN	JFK	LAX	330	2475	13	45	2023-01-08 13:00:00	LAX
8899	8	12	623	625	-2	856	913	UA	216	N854UA	EWR	AUS	194	1504	6	25	2023-08-12 06:00:00	Other
8906	1	3	1510	1515	-5	1619	1650	9E	1417	N228PQ	LGA	BUF	52	292	15	15	2023-01-03 15:00:00	Other
8908	4	28	739	744	-5	929	1009	UA	758	N68880	EWR	DEN	208	1605	7	44	2023-04-28 07:00:00	Other
8912	3	28	555	600	-5	917	859	UA	916	N852UA	LGA	IAH	234	1416	6	0	2023-03-28 06:00:00	Other
8916	7	1	1737	1741	-4	2035	2017	YX	1044	N423YX	LGA	OKC	202	1341	17	41	2023-07-01 17:00:00	Other
8918	5	18	953	955	-2	1149	1210	WN	139	N472WN	LGA	MCI	154	1107	9	55	2023-05-18 09:00:00	Other
8922	5	23	657	700	-3	1005	1014	DL	376	N376DA	JFK	MIA	155	1089	7	0	2023-05-23 07:00:00	MIA
8923	2	21	1056	1059	-3	1409	1400	B6	672	N537JT	JFK	LAS	346	2248	10	59	2023-02-21 10:00:00	Other
8925	2	13	827	830	-3	1019	1051	9E	1349	N132EV	JFK	CLT	91	541	8	30	2023-02-13 08:00:00	CLT
8938	6	11	1453	1455	-2	1722	1722	YX	1807	N879RW	JFK	CLT	97	541	14	55	2023-06-11 14:00:00	CLT
8946	3	9	621	625	-4	848	900	UA	192	N820UA	LGA	DEN	244	1620	6	25	2023-03-09 06:00:00	Other
8948	2	15	1832	1835	-3	2059	2109	DL	799	N923AT	EWR	ATL	119	746	18	35	2023-02-15 18:00:00	ATL
8951	12	31	1056	1100	-4	1249	1322	B6	694	N821JB	LGA	DEN	206	1620	11	0	2023-12-31 11:00:00	Other
8952	5	13	1410	1415	-5	1650	1609	AA	336	N838AW	LGA	STL	146	888	14	15	2023-05-13 14:00:00	Other
8960	4	10	1343	1348	-5	1453	1516	9E	1206	N331PQ	LGA	BUF	49	292	13	48	2023-04-10 13:00:00	Other
8962	6	28	1716	1720	-4	1916	1929	AA	796	N197UW	LGA	CLT	92	544	17	20	2023-06-28 17:00:00	CLT
8964	8	4	1326	1330	-4	1551	1538	YX	1016	N123HQ	LGA	CAE	91	617	13	30	2023-08-04 13:00:00	Other
8966	6	15	727	730	-3	928	959	DL	200	N382DA	LGA	DEN	210	1620	7	30	2023-06-15 07:00:00	Other
8967	10	9	1947	1952	-5	2216	2216	YX	1143	N757YX	EWR	SAV	109	708	19	52	2023-10-09 19:00:00	Other
8972	4	14	802	805	-3	955	955	OO	1011	N313SY	JFK	ORD	113	740	8	5	2023-04-14 08:00:00	ORD
8980	10	8	1750	1755	-5	1921	1940	YX	1711	N222JQ	JFK	DCA	48	213	17	55	2023-10-08 17:00:00	Other
9002	7	19	2036	2040	-4	2	29	AA	768	N101NN	JFK	SFO	355	2586	20	40	2023-07-19 20:00:00	Other
9005	12	21	747	751	-4	900	916	YX	1334	N102HQ	LGA	ORF	50	296	7	51	2023-12-21 07:00:00	Other
9006	11	14	1346	1349	-3	1550	1600	YX	1295	N409YX	LGA	MSP	158	1020	13	49	2023-11-14 13:00:00	Other
9008	11	5	1822	1825	-3	2053	2126	DL	752	N320DN	LGA	MCO	116	950	18	25	2023-11-05 18:00:00	MCO
9012	1	6	1822	1825	-3	2105	2140	WN	642	N219WN	LGA	TPA	145	1010	18	25	2023-01-06 18:00:00	Other
9015	11	8	725	730	-5	902	908	9E	1551	N478PX	LGA	RIC	53	292	7	30	2023-11-08 07:00:00	Other
9019	5	6	1751	1756	-5	2050	2108	AA	646	N843NN	EWR	MIA	151	1085	17	56	2023-05-06 17:00:00	MIA
9023	11	24	1521	1525	-4	1808	1830	UA	803	N643UA	EWR	IAH	202	1400	15	25	2023-11-24 15:00:00	Other
9026	9	29	725	730	-5	925	955	DL	188	N3738B	LGA	DEN	206	1620	7	30	2023-09-29 07:00:00	Other
9031	12	20	1219	1223	-4	1407	1420	NK	30	N939NK	EWR	MYR	83	550	12	23	2023-12-20 12:00:00	Other
9034	11	19	701	705	-4	933	947	B6	255	N590JB	JFK	JAX	116	828	7	5	2023-11-19 07:00:00	Other
9035	2	10	1656	1659	-3	1821	1820	YX	1121	N749YX	EWR	IAD	51	212	16	59	2023-02-10 16:00:00	Other
9044	3	14	1455	1459	-4	1858	1724	9E	1594	N924XJ	JFK	IND	99	665	14	59	2023-03-14 14:00:00	Other
9045	12	12	1418	1420	-2	1725	1723	UA	571	N811UA	EWR	IAH	213	1400	14	20	2023-12-12 14:00:00	Other
9050	4	7	643	648	-5	942	939	AA	514	N341SV	JFK	PHX	330	2153	6	48	2023-04-07 06:00:00	Other
9053	1	23	2118	2122	-4	2313	2327	UA	742	N69806	EWR	CLT	82	529	21	22	2023-01-23 21:00:00	CLT
9064	6	2	1657	1700	-3	1959	1959	DL	110	N883DN	JFK	LAS	270	2248	17	0	2023-06-02 17:00:00	Other
9071	11	9	1458	1502	-4	1710	1706	DL	914	N948AT	EWR	MSP	169	1008	15	2	2023-11-09 15:00:00	Other
9072	2	22	558	600	-2	849	912	B6	740	N563JB	LGA	FLL	145	1076	6	0	2023-02-22 06:00:00	FLL
9082	4	29	751	754	-3	933	958	DL	907	N352NW	LGA	MSP	137	1020	7	54	2023-04-29 07:00:00	Other
9086	7	31	925	930	-5	1109	1057	B6	499	N274JB	JFK	BUF	65	301	9	30	2023-07-31 09:00:00	Other
9088	1	28	1005	1010	-5	1231	1240	9E	1610	N902XJ	LGA	CVG	106	585	10	10	2023-01-28 10:00:00	Other
9091	10	12	800	805	-5	1028	1029	UA	819	N37563	EWR	DEN	224	1605	8	5	2023-10-12 08:00:00	Other
9094	9	12	1007	1009	-2	1306	1315	DL	407	N117DU	LGA	IAH	194	1416	10	9	2023-09-12 10:00:00	Other
9101	8	24	1643	1645	-2	1945	1919	UA	675	N11206	EWR	LAS	283	2227	16	45	2023-08-24 16:00:00	Other
9104	3	17	1259	1303	-4	1425	1439	UA	682	N73256	EWR	ORD	115	719	13	3	2023-03-17 13:00:00	ORD
9114	4	11	958	1000	-2	1234	1329	DL	146	N816DN	JFK	SLC	243	1990	10	0	2023-04-11 10:00:00	Other
9117	7	9	558	600	-2	841	909	AA	653	N918NN	JFK	MIA	139	1089	6	0	2023-07-09 06:00:00	MIA
9126	9	15	1102	1107	-5	1306	1333	UA	432	N67845	EWR	PHX	282	2133	11	7	2023-09-15 11:00:00	Other
9128	3	13	758	800	-2	1149	1159	B6	193	N2027J	JFK	SJU	192	1598	8	0	2023-03-13 08:00:00	Other
9137	10	30	1628	1633	-5	1905	1920	UA	823	N33289	EWR	LAS	315	2227	16	33	2023-10-30 16:00:00	Other
9148	6	12	1900	1902	-2	2203	2239	B6	26	N636JB	JFK	SLC	249	1990	19	2	2023-06-12 19:00:00	Other
9153	12	8	956	1000	-4	1257	1324	DL	255	N171DN	JFK	LAX	333	2475	10	0	2023-12-08 10:00:00	LAX
9159	3	30	728	730	-2	1126	1108	AS	15	N274AK	JFK	SFO	369	2586	7	30	2023-03-30 07:00:00	Other
9170	2	2	1056	1100	-4	1353	1406	AA	103	N761AJ	JFK	MIA	151	1089	11	0	2023-02-02 11:00:00	MIA
9171	9	4	1426	1430	-4	1541	1557	YX	1343	N132HQ	LGA	BUF	50	292	14	30	2023-09-04 14:00:00	Other
9174	11	13	1054	1059	-5	1358	1415	UA	574	N488UA	EWR	AUS	222	1504	10	59	2023-11-13 10:00:00	Other
9175	5	23	1102	1105	-3	1208	1232	9E	1544	N298PQ	JFK	BTV	46	266	11	5	2023-05-23 11:00:00	Other
9186	8	6	1250	1255	-5	1603	1557	B6	18	N605JB	LGA	TPA	160	1010	12	55	2023-08-06 12:00:00	Other
9201	11	19	1724	1728	-4	1901	1930	YX	1117	N739YX	EWR	CMH	75	463	17	28	2023-11-19 17:00:00	Other
9202	3	18	1245	1250	-5	1351	1358	9E	1308	N909XJ	JFK	ITH	45	189	12	50	2023-03-18 12:00:00	Other
9208	12	11	858	900	-2	1043	1110	AA	947	N902NN	JFK	ORD	116	740	9	0	2023-12-11 09:00:00	ORD
9218	11	29	1236	1240	-4	1347	1358	NK	558	N528NK	EWR	BNA	113	748	12	40	2023-11-29 12:00:00	Other
9220	8	25	1034	1038	-4	1206	1205	9E	1191	N936XJ	JFK	BTV	52	266	10	38	2023-08-25 10:00:00	Other
9234	11	12	2032	2036	-4	2318	2321	DL	895	N115DU	LGA	JAX	123	833	20	36	2023-11-12 20:00:00	Other
9236	6	30	1257	1259	-2	1437	1500	DL	812	N112DN	LGA	DTW	74	502	12	59	2023-06-30 12:00:00	Other
9238	10	19	1858	1900	-2	2126	2155	UA	865	N227UA	EWR	LAX	288	2454	19	0	2023-10-19 19:00:00	LAX
9239	7	11	1727	1730	-3	2035	2140	DL	262	N707TW	JFK	SFO	339	2586	17	30	2023-07-11 17:00:00	Other
9244	10	5	1108	1112	-4	1351	1414	UA	139	N77543	EWR	FLL	130	1065	11	12	2023-10-05 11:00:00	FLL
9247	6	5	1122	1125	-3	1328	1335	YX	1312	N439YX	LGA	AVL	89	599	11	25	2023-06-05 11:00:00	Other
9248	11	16	846	849	-3	953	1021	9E	1521	N914XJ	LGA	BTV	48	258	8	49	2023-11-16 08:00:00	Other
9270	11	17	1808	1810	-2	2032	2042	9E	1490	N932XJ	JFK	SAV	109	718	18	10	2023-11-17 18:00:00	Other
9272	3	16	457	500	-3	738	812	AA	449	N903AN	EWR	MIA	138	1085	5	0	2023-03-16 05:00:00	MIA
9286	7	24	1556	1559	-3	1820	1851	UA	687	N37295	EWR	SAN	297	2425	15	59	2023-07-24 15:00:00	Other
9288	5	23	1805	1810	-5	2001	2030	9E	1390	N902XJ	LGA	GRR	93	618	18	10	2023-05-23 18:00:00	Other
9291	8	20	724	729	-5	854	909	AA	212	N984NN	LGA	ORD	110	733	7	29	2023-08-20 07:00:00	ORD
9308	9	1	915	920	-5	1120	1127	9E	1678	N138EV	LGA	ILM	72	500	9	20	2023-09-01 09:00:00	Other
9310	11	23	1057	1100	-3	1244	1255	YX	1261	N101HQ	JFK	RDU	72	427	11	0	2023-11-23 11:00:00	Other
9315	9	30	1123	1125	-2	1401	1422	DL	429	N819DN	JFK	TPA	134	1005	11	25	2023-09-30 11:00:00	Other
9316	4	4	1455	1500	-5	1708	1712	9E	1294	N319PQ	LGA	GSP	91	610	15	0	2023-04-04 15:00:00	Other
9324	1	24	1752	1755	-3	2103	2127	AA	625	N836NN	LGA	DFW	216	1389	17	55	2023-01-24 17:00:00	Other
9330	5	14	1009	1011	-2	1130	1155	YX	1718	N223JQ	LGA	BNA	115	764	10	11	2023-05-14 10:00:00	Other
9332	9	27	600	602	-2	739	801	DL	980	N982AT	EWR	MSP	136	1008	6	2	2023-09-27 06:00:00	Other
9336	11	10	1047	1051	-4	1326	1329	F9	529	N372FR	LGA	ATL	130	762	10	51	2023-11-10 10:00:00	ATL
9337	2	24	1426	1430	-4	1738	1713	DL	120	N3749D	JFK	DEN	274	1626	14	30	2023-02-24 14:00:00	Other
9344	2	14	1448	1450	-2	1705	1731	DL	354	N394DX	LGA	ATL	116	762	14	50	2023-02-14 14:00:00	ATL
9348	6	9	1558	1600	-2	1830	1910	AS	83	N979AK	EWR	SEA	303	2402	16	0	2023-06-09 16:00:00	Other
9354	11	7	1305	1310	-5	1414	1441	9E	1544	N153PQ	JFK	BGR	56	382	13	10	2023-11-07 13:00:00	Other
9360	3	27	1410	1413	-3	1600	1550	YX	1627	N215JQ	LGA	PIT	67	335	14	13	2023-03-27 14:00:00	Other
9361	5	4	1921	1925	-4	2053	2124	OO	1117	N253SY	JFK	ORD	113	740	19	25	2023-05-04 19:00:00	ORD
9365	4	6	1458	1500	-2	1710	1725	9E	1261	N313PQ	JFK	CHS	101	636	15	0	2023-04-06 15:00:00	Other
9370	9	24	754	759	-5	1051	1110	AA	128	N989NN	LGA	MIA	153	1096	7	59	2023-09-24 07:00:00	MIA
9378	7	26	1745	1750	-5	2014	2022	9E	1286	N601LR	LGA	SAV	102	722	17	50	2023-07-26 17:00:00	Other
9379	8	1	856	901	-5	1108	1113	9E	1275	N184GJ	LGA	AVL	87	599	9	1	2023-08-01 09:00:00	Other
9381	4	25	2055	2100	-5	2203	2251	YX	1012	N856RW	LGA	ORD	110	733	21	0	2023-04-25 21:00:00	ORD
9387	12	5	558	600	-2	916	910	DL	253	N304DU	LGA	DFW	222	1389	6	0	2023-12-05 06:00:00	Other
9413	4	11	1835	1840	-5	2000	2010	B6	853	N183JB	EWR	BOS	48	200	18	40	2023-04-11 18:00:00	BOS
9416	10	31	725	730	-5	1048	1039	UA	942	N15751	LGA	IAH	225	1416	7	30	2023-10-31 07:00:00	Other
9424	11	16	625	630	-5	801	819	9E	1759	N298PQ	LGA	RDU	67	431	6	30	2023-11-16 06:00:00	Other
9430	5	21	1847	1850	-3	2034	2114	YX	1062	N657RW	EWR	IND	89	645	18	50	2023-05-21 18:00:00	Other
9433	1	9	1224	1227	-3	1529	1540	UA	799	N494UA	LGA	IAH	214	1416	12	27	2023-01-09 12:00:00	Other
9435	5	11	1238	1243	-5	1422	1457	9E	1343	N932XJ	JFK	CLT	76	541	12	43	2023-05-11 12:00:00	CLT
9441	12	1	1756	1800	-4	2040	2058	UA	766	N68453	EWR	MCO	130	937	18	0	2023-12-01 18:00:00	MCO
9449	8	8	926	930	-4	1302	1245	B6	24	N947JB	JFK	SEA	315	2422	9	30	2023-08-08 09:00:00	Other
9453	3	26	701	705	-4	956	1024	DL	549	N378DN	LGA	MIA	154	1096	7	5	2023-03-26 07:00:00	MIA
9469	2	11	1410	1415	-5	1706	1746	UA	186	N29124	EWR	SFO	340	2565	14	15	2023-02-11 14:00:00	Other
9471	9	10	727	730	-3	1002	1027	AA	140	N907AN	LGA	DFW	183	1389	7	30	2023-09-10 07:00:00	Other
9477	11	8	555	600	-5	837	836	DL	287	N350DN	LGA	ATL	112	762	6	0	2023-11-08 06:00:00	ATL
9485	9	30	711	715	-4	815	840	B6	709	N258JB	JFK	DCA	42	213	7	15	2023-09-30 07:00:00	Other
9496	1	4	1957	2000	-3	2312	2311	B6	68	N821JB	JFK	TPA	171	1005	20	0	2023-01-04 20:00:00	Other
9498	8	23	925	930	-5	1054	1132	9E	1271	N909XJ	LGA	STL	119	888	9	30	2023-08-23 09:00:00	Other
9499	7	5	1544	1549	-5	1908	1933	B6	215	N944JT	JFK	SFO	360	2586	15	49	2023-07-05 15:00:00	Other
9500	12	30	557	600	-3	657	711	B6	94	N267JB	JFK	BOS	37	187	6	0	2023-12-30 06:00:00	BOS
9503	4	26	640	645	-5	937	934	B6	913	N184JB	JFK	PBI	150	1028	6	45	2023-04-26 06:00:00	Other
9506	10	5	1126	1130	-4	1405	1451	AA	610	N934NN	LGA	MIA	138	1096	11	30	2023-10-05 11:00:00	MIA
9509	6	29	1140	1145	-5	1419	1445	AS	7	N442AS	JFK	PDX	317	2454	11	45	2023-06-29 11:00:00	Other
9520	10	2	1254	1259	-5	1404	1403	9E	1381	N135EV	JFK	ITH	38	189	12	59	2023-10-02 12:00:00	Other
9521	5	31	543	545	-2	654	709	NK	273	N517NK	EWR	PIT	50	319	5	45	2023-05-31 05:00:00	Other
9527	6	6	1934	1936	-2	2202	2141	YX	1088	N858RW	EWR	DTW	82	488	19	36	2023-06-06 19:00:00	Other
9534	4	21	1926	1929	-3	2158	2237	DL	395	N398DN	LGA	MCO	124	950	19	29	2023-04-21 19:00:00	MCO
9540	8	19	1500	1505	-5	1756	1821	DL	300	N318NB	LGA	PBI	143	1035	15	5	2023-08-19 15:00:00	Other
9541	2	6	740	745	-5	1053	1102	UA	325	N39461	EWR	SAN	346	2425	7	45	2023-02-06 07:00:00	Other
9557	7	1	625	630	-5	934	954	AA	27	N113AN	JFK	SFO	337	2586	6	30	2023-07-01 06:00:00	Other
9563	2	1	1707	1712	-5	1811	1831	UA	159	N415UA	EWR	BOS	38	200	17	12	2023-02-01 17:00:00	BOS
9569	12	29	557	600	-3	755	820	AA	225	N179UW	LGA	CLT	93	544	6	0	2023-12-29 06:00:00	CLT
9575	4	10	846	849	-3	945	957	9E	1368	N491PX	LGA	ALB	34	136	8	49	2023-04-10 08:00:00	Other
9576	10	31	1825	1829	-4	2046	2055	9E	1588	N138EV	JFK	CHS	105	636	18	29	2023-10-31 18:00:00	Other
9577	1	1	1657	1700	-3	1843	1848	DL	1010	N128DU	LGA	ORD	126	733	17	0	2023-01-01 17:00:00	ORD
9581	10	28	837	840	-3	1051	1113	9E	1392	N935XJ	LGA	OMA	172	1148	8	40	2023-10-28 08:00:00	Other
9584	11	7	1329	1333	-4	1432	1445	UA	637	N27267	EWR	BOS	42	200	13	33	2023-11-07 13:00:00	BOS
9590	9	13	1355	1359	-4	1637	1648	UA	489	N454UA	EWR	DFW	191	1372	13	59	2023-09-13 13:00:00	Other
9592	11	25	828	830	-2	1142	1151	DL	241	N122DU	JFK	DFW	207	1391	8	30	2023-11-25 08:00:00	Other
9593	11	7	725	730	-5	907	925	WN	1023	N8581Z	LGA	STL	141	888	7	30	2023-11-07 07:00:00	Other
9601	3	24	1505	1510	-5	1701	1715	DL	935	N894AT	EWR	MSP	162	1008	15	10	2023-03-24 15:00:00	Other
9608	12	20	1424	1429	-5	1632	1655	YX	1854	N224JQ	LGA	IND	100	660	14	29	2023-12-20 14:00:00	Other
9613	11	16	1624	1629	-5	1819	1837	YX	1269	N105HQ	LGA	GSP	88	610	16	29	2023-11-16 16:00:00	Other
9619	12	14	1954	1959	-5	2111	2148	9E	1528	N691CA	JFK	ORF	52	290	19	59	2023-12-14 19:00:00	Other
9620	4	7	944	947	-3	1153	1158	DL	888	N978AT	EWR	DTW	89	488	9	47	2023-04-07 09:00:00	Other
9623	4	26	520	523	-3	812	818	UA	188	N37278	EWR	IAH	206	1400	5	23	2023-04-26 05:00:00	Other
9625	8	22	1345	1348	-3	1510	1525	AA	507	N943NN	EWR	ORD	111	719	13	48	2023-08-22 13:00:00	ORD
9639	7	5	1256	1259	-3	1404	1425	YX	1390	N242JQ	LGA	BOS	36	184	12	59	2023-07-05 12:00:00	BOS
9641	10	1	803	805	-2	1031	1053	UA	240	N24224	EWR	IAH	179	1400	8	5	2023-10-01 08:00:00	Other
9646	3	29	1552	1555	-3	1829	1840	DL	779	N335NB	JFK	MSY	175	1182	15	55	2023-03-29 15:00:00	Other
9651	12	3	1524	1529	-5	1913	1834	UA	782	N47570	EWR	IAH	240	1400	15	29	2023-12-03 15:00:00	Other
9657	11	15	832	836	-4	1110	1157	DL	241	N143DU	JFK	DFW	185	1391	8	36	2023-11-15 08:00:00	Other
9658	9	1	746	750	-4	956	945	9E	1548	N232PQ	JFK	RDU	68	427	7	50	2023-09-01 07:00:00	Other
9660	7	24	1056	1100	-4	1325	1321	YX	1017	N123HQ	LGA	XNA	164	1147	11	0	2023-07-24 11:00:00	Other
9662	8	8	1856	1900	-4	2014	2040	YX	855	N647RW	EWR	PIT	53	319	19	0	2023-08-08 19:00:00	Other
9669	12	29	1211	1216	-5	1356	1455	UA	689	N33292	LGA	DEN	206	1620	12	16	2023-12-29 12:00:00	Other
9670	3	23	1250	1255	-5	1513	1526	YX	1697	N824MD	LGA	SDF	116	659	12	55	2023-03-23 12:00:00	Other
9684	6	19	2045	2050	-5	2303	2352	DL	162	N862DN	JFK	LAS	283	2248	20	50	2023-06-19 20:00:00	Other
9686	3	2	955	959	-4	1356	1301	UA	748	N73251	EWR	IAH	227	1400	9	59	2023-03-02 09:00:00	Other
9689	6	13	656	700	-4	855	902	UA	494	N826UA	EWR	CHS	93	628	7	0	2023-06-13 07:00:00	Other
9699	11	5	703	705	-2	926	949	YX	1832	N205JQ	LGA	JAX	125	833	7	5	2023-11-05 07:00:00	Other
9703	9	13	1055	1059	-4	1139	1159	YX	1075	N748YX	EWR	AVP	25	93	10	59	2023-09-13 10:00:00	Other
9707	12	14	725	730	-5	947	1045	DL	175	N542DE	JFK	LAS	291	2248	7	30	2023-12-14 07:00:00	Other
9709	10	23	813	816	-3	928	950	YX	1096	N761YX	EWR	ROC	46	246	8	16	2023-10-23 08:00:00	Other
9712	8	27	1141	1145	-4	1244	1303	UA	693	N17289	EWR	PWM	43	284	11	45	2023-08-27 11:00:00	Other
9713	12	22	1920	1925	-5	2218	2305	AS	82	N293AK	EWR	SFO	338	2565	19	25	2023-12-22 19:00:00	Other
9714	12	14	2022	2025	-3	2147	2200	YX	1715	N242JQ	LGA	DCA	63	214	20	25	2023-12-14 20:00:00	Other
9716	11	27	1025	1027	-2	1317	1336	DL	378	N368DN	LGA	TPA	157	1010	10	27	2023-11-27 10:00:00	Other
9724	9	17	1416	1420	-4	1623	1632	UA	381	N61881	EWR	DEN	210	1605	14	20	2023-09-17 14:00:00	Other
9730	10	25	1357	1401	-4	1645	1648	UA	455	N456UA	EWR	DFW	188	1372	14	1	2023-10-25 14:00:00	Other
9739	6	11	958	1000	-2	1107	1110	B6	996	N247JB	JFK	BOS	37	187	10	0	2023-06-11 10:00:00	BOS
9742	11	13	1437	1440	-3	1702	1715	WN	679	N8575Z	LGA	MSY	171	1183	14	40	2023-11-13 14:00:00	Other
9751	1	25	1754	1759	-5	2216	2126	F9	1074	N304FR	LGA	MIA	210	1096	17	59	2023-01-25 17:00:00	MIA
9755	4	7	925	930	-5	1104	1102	UA	854	N435UA	EWR	BNA	120	748	9	30	2023-04-07 09:00:00	Other
9759	8	31	843	845	-2	958	1027	DL	299	N113DQ	LGA	ORD	111	733	8	45	2023-08-31 08:00:00	ORD
9764	12	19	2116	2120	-4	2238	2307	YX	1779	N209JQ	JFK	ORF	50	290	21	20	2023-12-19 21:00:00	Other
9769	9	7	1425	1429	-4	1750	1732	B6	134	N809JB	LGA	MCO	137	950	14	29	2023-09-07 14:00:00	MCO
9772	5	30	1058	1100	-2	1238	1323	9E	1288	N181GJ	LGA	MCI	139	1107	11	0	2023-05-30 11:00:00	Other
9773	12	2	1558	1600	-2	1747	1757	9E	1416	N695CA	JFK	RDU	75	427	16	0	2023-12-02 16:00:00	Other
9777	4	21	1028	1030	-2	1332	1317	B6	39	N973JT	JFK	LAS	297	2248	10	30	2023-04-21 10:00:00	Other
9789	2	9	1410	1415	-5	1658	1735	UA	725	N227UA	EWR	SFO	313	2565	14	15	2023-02-09 14:00:00	Other
9791	1	15	1538	1540	-2	1736	1824	DL	145	N176DZ	JFK	ATL	98	760	15	40	2023-01-15 15:00:00	ATL
9795	6	23	1254	1259	-5	1418	1428	9E	1546	N341PQ	LGA	PWM	42	269	12	59	2023-06-23 12:00:00	Other
9801	4	26	1442	1445	-3	1658	1700	WN	653	N8328A	LGA	MSY	175	1183	14	45	2023-04-26 14:00:00	Other
9810	2	23	1156	1200	-4	1417	1434	DL	296	N823DN	JFK	ATL	122	760	12	0	2023-02-23 12:00:00	ATL
9815	12	19	1610	1615	-5	1803	1854	DL	747	N333NB	JFK	MSY	151	1182	16	15	2023-12-19 16:00:00	Other
9818	10	27	645	648	-3	941	1001	AA	892	N966NN	LGA	MIA	140	1096	6	48	2023-10-27 06:00:00	MIA
9824	11	13	1427	1430	-3	1636	1659	B6	805	N3065J	JFK	MCI	167	1113	14	30	2023-11-13 14:00:00	Other
9840	2	16	1930	1935	-5	2143	2157	9E	1299	N296PQ	JFK	CLT	98	541	19	35	2023-02-16 19:00:00	CLT
9843	10	20	1858	1900	-2	2143	2155	UA	865	N204UA	EWR	LAX	305	2454	19	0	2023-10-20 19:00:00	LAX
9846	1	17	1523	1527	-4	1831	1833	UA	1017	N405UA	EWR	SRQ	153	1034	15	27	2023-01-17 15:00:00	Other
9848	3	28	2130	2135	-5	2251	2253	9E	1454	N137EV	JFK	ITH	41	189	21	35	2023-03-28 21:00:00	Other
9853	12	1	1821	1825	-4	2045	2051	9E	1504	N695CA	JFK	IND	108	665	18	25	2023-12-01 18:00:00	Other
9854	11	29	1331	1336	-5	1531	1550	9E	1617	N695CA	JFK	CVG	102	589	13	36	2023-11-29 13:00:00	Other
9861	4	3	855	859	-4	1044	1109	9E	1188	N311PQ	LGA	MEM	147	963	8	59	2023-04-03 08:00:00	Other
9865	12	25	1926	1930	-4	2214	2239	B6	203	N794JB	LGA	FLL	150	1076	19	30	2023-12-25 19:00:00	FLL
9873	10	31	1655	1659	-4	1914	1908	YX	1243	N101HQ	LGA	DSM	165	1031	16	59	2023-10-31 16:00:00	Other
9881	8	30	711	715	-4	943	935	WN	577	N272WN	LGA	ATL	119	762	7	15	2023-08-30 07:00:00	ATL
9888	7	17	1657	1700	-3	1833	1857	DL	792	N919AT	EWR	DTW	78	488	17	0	2023-07-17 17:00:00	Other
9894	11	27	926	929	-3	1241	1239	B6	801	N974JT	JFK	FLL	158	1069	9	29	2023-11-27 09:00:00	FLL
9914	10	3	912	915	-3	1023	1035	B6	168	N328JB	JFK	PWM	53	273	9	15	2023-10-03 09:00:00	Other
9917	12	2	852	855	-3	1029	1046	9E	1689	N324PQ	JFK	RDU	77	427	8	55	2023-12-02 08:00:00	Other
9922	10	27	757	800	-3	1018	1022	DL	901	N855DN	EWR	ATL	107	746	8	0	2023-10-27 08:00:00	ATL
9932	3	19	1731	1735	-4	2100	2053	UA	563	N27270	EWR	SAN	347	2425	17	35	2023-03-19 17:00:00	Other
9935	12	1	1956	2000	-4	2308	2324	AS	13	N280AK	JFK	PDX	340	2454	20	0	2023-12-01 20:00:00	Other
9942	4	28	1751	1755	-4	2127	2107	AA	678	N306SW	LGA	MIA	179	1096	17	55	2023-04-28 17:00:00	MIA
9945	6	13	2118	2122	-4	2335	2338	YX	1213	N732YX	EWR	AVL	96	583	21	22	2023-06-13 21:00:00	Other
9957	9	14	815	820	-5	1003	1014	9E	1642	N306PQ	JFK	CLE	73	425	8	20	2023-09-14 08:00:00	Other
9959	12	16	825	829	-4	1115	1135	UA	806	N39423	EWR	TPA	147	997	8	29	2023-12-16 08:00:00	Other
9976	6	19	2146	2149	-3	2235	2242	YX	1148	N728YX	EWR	PHL	20	80	21	49	2023-06-19 21:00:00	Other
9980	6	5	1201	1204	-3	1406	1419	DL	983	N390DA	EWR	ATL	101	746	12	4	2023-06-05 12:00:00	ATL
9982	4	7	621	625	-4	921	923	UA	217	N66848	EWR	SAN	340	2425	6	25	2023-04-07 06:00:00	Other
9989	7	10	827	829	-2	1110	1118	AA	299	N921AN	LGA	DFW	191	1389	8	29	2023-07-10 08:00:00	Other
9993	8	21	823	826	-3	949	1008	YX	1034	N121HQ	LGA	CLE	64	419	8	26	2023-08-21 08:00:00	Other
9996	11	18	555	600	-5	759	833	DL	735	N685DA	JFK	ATL	104	760	6	0	2023-11-18 06:00:00	ATL
9998	4	23	1324	1329	-5	1525	1539	9E	1413	N320PQ	LGA	CVG	99	585	13	29	2023-04-23 13:00:00	Other
10018	2	26	1026	1030	-4	1251	1313	DL	330	N114DU	LGA	MCI	187	1107	10	30	2023-02-26 10:00:00	Other
10021	5	10	1550	1552	-2	1837	1920	DL	379	N3748Y	JFK	MIA	141	1089	15	52	2023-05-10 15:00:00	MIA
10025	4	6	1438	1441	-3	1631	1645	YX	1265	N102HQ	JFK	CMH	80	483	14	41	2023-04-06 14:00:00	Other
10028	10	2	655	700	-5	906	934	UA	202	N27539	EWR	LAS	287	2227	7	0	2023-10-02 07:00:00	Other
10039	11	30	1725	1730	-5	1843	1854	OO	1173	N247SY	JFK	BOS	49	187	17	30	2023-11-30 17:00:00	BOS
10041	10	19	2013	2016	-3	2144	2211	9E	1403	N926XJ	EWR	RDU	68	416	20	16	2023-10-19 20:00:00	Other
10051	5	12	841	845	-4	1047	1050	9E	1560	N485PX	LGA	AVL	82	599	8	45	2023-05-12 08:00:00	Other
10055	11	20	1416	1420	-4	1535	1551	YX	1311	N127HQ	LGA	BUF	50	292	14	20	2023-11-20 14:00:00	Other
10059	1	29	836	840	-4	1030	1057	YX	1747	N246JQ	LGA	STL	155	888	8	40	2023-01-29 08:00:00	Other
10062	6	27	910	915	-5	1125	1114	9E	1666	N310PQ	LGA	ILM	77	500	9	15	2023-06-27 09:00:00	Other
10067	1	8	1056	1059	-3	1403	1337	UA	292	N808UA	EWR	ATL	113	746	10	59	2023-01-08 10:00:00	ATL
10068	11	14	658	700	-2	1011	1033	DL	173	N172DZ	JFK	SFO	348	2586	7	0	2023-11-14 07:00:00	Other
10069	9	28	1431	1436	-5	1633	1629	YX	1875	N824MD	LGA	MEM	145	963	14	36	2023-09-28 14:00:00	Other
10073	3	17	2227	2230	-3	15	10	9E	1445	N926XJ	JFK	BUF	61	301	22	30	2023-03-17 22:00:00	Other
10075	8	28	1857	1900	-3	2104	2119	UA	56	N73251	EWR	SAV	102	708	19	0	2023-08-28 19:00:00	Other
10077	6	27	1156	1200	-4	1504	1450	DL	198	N415DX	JFK	LAX	325	2475	12	0	2023-06-27 12:00:00	LAX
10081	9	23	1112	1115	-3	1254	1308	NK	21	N684NK	EWR	MYR	84	550	11	15	2023-09-23 11:00:00	Other
10082	5	26	611	615	-4	856	920	UA	245	N409UA	EWR	AUS	207	1504	6	15	2023-05-26 06:00:00	Other
10091	9	27	1356	1359	-3	1642	1648	UA	489	N491UA	EWR	DFW	205	1372	13	59	2023-09-27 13:00:00	Other
10094	2	6	558	600	-2	720	722	YX	1136	N751YX	EWR	IAD	54	212	6	0	2023-02-06 06:00:00	Other
10102	3	7	1547	1550	-3	1726	1736	9E	1453	N485PX	LGA	CHO	57	305	15	50	2023-03-07 15:00:00	Other
10107	3	28	942	946	-4	1323	1341	UA	602	N27421	EWR	SJU	198	1608	9	46	2023-03-28 09:00:00	Other
10109	1	6	1512	1515	-3	1811	1832	UA	747	N27263	EWR	RSW	155	1068	15	15	2023-01-06 15:00:00	Other
10120	12	22	1254	1259	-5	1354	1410	9E	1356	N924XJ	JFK	ITH	41	189	12	59	2023-12-22 12:00:00	Other
10124	4	6	1122	1126	-4	1424	1432	UA	848	N881UA	EWR	AUS	220	1504	11	26	2023-04-06 11:00:00	Other
10129	8	1	1415	1420	-5	1635	1715	DL	325	N131DU	LGA	IAH	177	1416	14	20	2023-08-01 14:00:00	Other
10137	11	10	855	900	-5	1047	1047	UA	728	N434UA	EWR	ORD	132	719	9	0	2023-11-10 09:00:00	ORD
10140	12	21	1314	1318	-4	1510	1528	YX	1311	N114HQ	LGA	DAY	87	549	13	18	2023-12-21 13:00:00	Other
10151	5	8	656	700	-4	938	1007	UA	270	N805UA	EWR	FLL	139	1065	7	0	2023-05-08 07:00:00	FLL
10156	1	20	1055	1059	-4	1251	1317	YX	1262	N636RW	EWR	GRR	93	605	10	59	2023-01-20 10:00:00	Other
10160	8	26	826	830	-4	1059	1128	AA	476	N956AN	EWR	DFW	173	1372	8	30	2023-08-26 08:00:00	Other
10167	12	8	847	849	-2	1045	1054	AA	563	N980UY	EWR	CLT	81	529	8	49	2023-12-08 08:00:00	CLT
10176	5	3	1216	1220	-4	1313	1338	YX	1207	N445YX	JFK	BOS	33	187	12	20	2023-05-03 12:00:00	BOS
10181	12	26	2048	2050	-2	2214	2235	9E	1593	N325PQ	JFK	BUF	52	301	20	50	2023-12-26 20:00:00	Other
10182	10	25	654	659	-5	906	914	YX	1303	N436YX	LGA	MSP	172	1020	6	59	2023-10-25 06:00:00	Other
10184	3	19	1446	1450	-4	1552	1626	9E	1476	N936XJ	LGA	MKE	111	738	14	50	2023-03-19 14:00:00	Other
10189	9	7	606	608	-2	745	755	DL	780	N994AT	EWR	DTW	77	488	6	8	2023-09-07 06:00:00	Other
10192	9	4	1611	1615	-4	1804	1807	YX	1839	N207JQ	JFK	ORF	49	290	16	15	2023-09-04 16:00:00	Other
10204	12	5	1911	1916	-5	2156	2257	UA	287	N37278	EWR	PHX	266	2133	19	16	2023-12-05 19:00:00	Other
10210	9	28	1406	1409	-3	1550	1604	9E	1544	N306PQ	JFK	RDU	72	427	14	9	2023-09-28 14:00:00	Other
10216	6	22	1345	1350	-5	1511	1535	9E	1694	N308PQ	LGA	BHM	123	866	13	50	2023-06-22 13:00:00	Other
10224	9	22	1430	1432	-2	1628	1630	YX	1392	N423YX	LGA	ILM	82	500	14	32	2023-09-22 14:00:00	Other
10226	5	7	1657	1700	-3	1902	1920	DL	916	N949AT	EWR	ATL	106	746	17	0	2023-05-07 17:00:00	ATL
10227	6	8	708	710	-2	1026	1015	DL	995	N373DA	LGA	MIA	159	1096	7	10	2023-06-08 07:00:00	MIA
10228	4	3	1340	1345	-5	1454	1511	YX	1568	N818MD	LGA	DCA	47	214	13	45	2023-04-03 13:00:00	Other
10232	1	29	1257	1300	-3	1457	1517	AA	710	N152UW	LGA	CLT	93	544	13	0	2023-01-29 13:00:00	CLT
10238	5	3	1627	1630	-3	1744	1756	YX	1015	N855RW	EWR	BUF	50	282	16	30	2023-05-03 16:00:00	Other
10248	8	27	2127	2132	-5	2330	2349	YX	900	N728YX	EWR	CHS	91	628	21	32	2023-08-27 21:00:00	Other
10270	5	15	2056	2100	-4	2343	2359	NK	977	N654NK	EWR	MIA	145	1085	21	0	2023-05-15 21:00:00	MIA
10273	3	17	1023	1025	-2	1246	1309	DL	122	N384DN	LGA	ATL	113	762	10	25	2023-03-17 10:00:00	ATL
10274	8	28	956	958	-2	1108	1129	YX	1327	N212JQ	JFK	BOS	33	187	9	58	2023-08-28 09:00:00	BOS
10281	2	18	1143	1145	-2	1456	1513	AS	8	N491AS	JFK	PDX	350	2454	11	45	2023-02-18 11:00:00	Other
10303	12	14	2055	2059	-4	2209	2219	YX	1331	N430YX	JFK	BOS	50	187	20	59	2023-12-14 20:00:00	BOS
10305	7	24	1912	1915	-3	2210	2214	DL	526	N106DU	LGA	IAH	188	1416	19	15	2023-07-24 19:00:00	Other
10316	7	6	1354	1359	-5	1507	1523	9E	1199	N341PQ	JFK	SYR	43	209	13	59	2023-07-06 13:00:00	Other
10317	11	2	1345	1348	-3	1513	1529	MQ	1034	N760MQ	EWR	ORD	120	719	13	48	2023-11-02 13:00:00	ORD
10319	11	25	1826	1830	-4	2121	2135	NK	739	N637NK	EWR	MCO	135	937	18	30	2023-11-25 18:00:00	MCO
10320	2	12	728	730	-2	1018	1010	UA	779	N24202	LGA	DEN	230	1620	7	30	2023-02-12 07:00:00	Other
10321	3	18	925	929	-4	1231	1241	UA	729	N424UA	EWR	RSW	167	1068	9	29	2023-03-18 09:00:00	Other
10323	10	20	1248	1250	-2	1353	1359	9E	1381	N928XJ	JFK	ITH	39	189	12	50	2023-10-20 12:00:00	Other
10324	4	12	652	655	-3	849	859	9E	1229	N182GJ	JFK	DTW	84	509	6	55	2023-04-12 06:00:00	Other
10325	5	4	1327	1329	-2	1456	1503	9E	1444	N176PQ	JFK	BGR	66	382	13	29	2023-05-04 13:00:00	Other
10326	5	17	711	715	-4	948	949	9E	1428	N348PQ	LGA	JAX	118	833	7	15	2023-05-17 07:00:00	Other
10331	3	9	1153	1158	-5	1413	1428	UA	262	N487UA	EWR	ATL	116	746	11	58	2023-03-09 11:00:00	ATL
10338	9	21	925	930	-5	1249	1243	AA	822	N342RX	LGA	MIA	163	1096	9	30	2023-09-21 09:00:00	MIA
10348	11	21	1300	1305	-5	1606	1602	UA	528	N36207	EWR	MCO	158	937	13	5	2023-11-21 13:00:00	MCO
10351	10	19	1925	1929	-4	2320	2333	DL	666	N826DN	JFK	SJU	202	1598	19	29	2023-10-19 19:00:00	Other
10352	4	10	2154	2159	-5	2252	2308	DL	445	N106DU	LGA	SYR	38	198	21	59	2023-04-10 21:00:00	Other
10357	11	21	1726	1729	-3	1937	1958	YX	1850	N220JQ	LGA	IND	109	660	17	29	2023-11-21 17:00:00	Other
10364	10	16	1245	1250	-5	1346	1359	9E	1381	N901XJ	JFK	ITH	41	189	12	50	2023-10-16 12:00:00	Other
10365	10	5	826	830	-4	1112	1120	DL	221	N145DQ	JFK	DFW	196	1391	8	30	2023-10-05 08:00:00	Other
10382	3	29	954	959	-5	1215	1202	YX	1073	N736YX	EWR	CLT	89	529	9	59	2023-03-29 09:00:00	CLT
10384	8	18	641	645	-4	839	807	AA	445	N715UW	LGA	DCA	43	214	6	45	2023-08-18 06:00:00	Other
10390	3	16	843	845	-2	1041	1103	9E	1599	N920XJ	LGA	AVL	86	599	8	45	2023-03-16 08:00:00	Other
10395	8	4	607	610	-3	836	835	WN	817	N1802U	LGA	DAL	184	1381	6	10	2023-08-04 06:00:00	Other
10400	2	11	1827	1829	-2	2057	2122	UA	818	N37464	EWR	LAS	302	2227	18	29	2023-02-11 18:00:00	Other
10403	8	5	1526	1530	-4	1616	1642	YX	874	N758YX	EWR	ALB	29	143	15	30	2023-08-05 15:00:00	Other
10404	1	16	1255	1300	-5	1547	1619	B6	1100	N564JB	JFK	MIA	138	1089	13	0	2023-01-16 13:00:00	MIA
10410	5	7	1813	1815	-2	2010	2028	DL	738	N608AT	EWR	MSP	153	1008	18	15	2023-05-07 18:00:00	Other
10412	6	29	1457	1459	-2	1656	1644	YX	1335	N103HQ	JFK	DCA	68	213	14	59	2023-06-29 14:00:00	Other
10415	8	25	558	600	-2	756	752	DL	329	N375NC	LGA	DTW	83	502	6	0	2023-08-25 06:00:00	Other
10419	11	1	805	810	-5	1102	1133	AA	317	N354PT	JFK	DFW	196	1391	8	10	2023-11-01 08:00:00	Other
10421	3	10	654	659	-5	826	830	9E	1490	N678CA	LGA	RIC	54	292	6	59	2023-03-10 06:00:00	Other
10422	3	15	838	842	-4	1022	1033	YX	1309	N449YX	LGA	GSO	66	461	8	42	2023-03-15 08:00:00	Other
10426	8	16	1555	1600	-5	1840	1907	AS	68	N934AK	EWR	SEA	308	2402	16	0	2023-08-16 16:00:00	Other
10432	5	30	1512	1514	-2	1750	1802	UA	238	N14250	EWR	MCO	137	937	15	14	2023-05-30 15:00:00	MCO
10436	10	8	1458	1503	-5	1758	1809	UA	490	N26232	EWR	MIA	153	1085	15	3	2023-10-08 15:00:00	MIA
10437	6	5	1453	1455	-2	1656	1715	9E	1545	N933XJ	JFK	CVG	90	589	14	55	2023-06-05 14:00:00	Other
10439	7	5	1624	1629	-5	1903	1855	AA	494	N329SL	JFK	PHX	302	2153	16	29	2023-07-05 16:00:00	Other
10441	11	8	1830	1835	-5	2106	2109	UA	527	N37437	EWR	DEN	242	1605	18	35	2023-11-08 18:00:00	Other
10447	8	7	1426	1430	-4	1619	1611	AA	172	N819NN	LGA	ORD	117	733	14	30	2023-08-07 14:00:00	ORD
10448	12	29	951	955	-4	1338	1320	DL	875	N331DN	LGA	FLL	184	1076	9	55	2023-12-29 09:00:00	FLL
10455	5	10	2227	2230	-3	7	7	YX	1653	N208JQ	JFK	PWM	50	273	22	30	2023-05-10 22:00:00	Other
10465	8	21	1557	1559	-2	1752	1759	YX	1009	N419YX	LGA	DTW	85	502	15	59	2023-08-21 15:00:00	Other
10467	1	30	1357	1359	-2	1557	1551	9E	1691	N919XJ	LGA	RDU	78	431	13	59	2023-01-30 13:00:00	Other
10469	11	2	1127	1130	-3	1431	1436	DL	887	N375NC	LGA	PBI	153	1035	11	30	2023-11-02 11:00:00	Other
10476	8	11	1212	1215	-3	1416	1429	UA	576	N27261	LGA	DEN	226	1620	12	15	2023-08-11 12:00:00	Other
10478	2	21	613	615	-2	852	853	DL	732	N721TW	JFK	ATL	127	760	6	15	2023-02-21 06:00:00	ATL
10484	2	24	756	800	-4	1010	939	9E	1404	N337PQ	JFK	BUF	78	301	8	0	2023-02-24 08:00:00	Other
10500	3	30	2047	2050	-3	2302	2259	9E	1428	N604LR	LGA	CAE	91	617	20	50	2023-03-30 20:00:00	Other
10509	8	1	1255	1259	-4	1429	1439	9E	1149	N482PX	LGA	RIC	52	292	12	59	2023-08-01 12:00:00	Other
10515	4	16	1955	2000	-5	2145	2209	YX	1104	N441YX	JFK	RDU	72	427	20	0	2023-04-16 20:00:00	Other
10524	4	8	1301	1304	-3	1359	1421	YX	971	N979RP	EWR	BOS	37	200	13	4	2023-04-08 13:00:00	BOS
10528	8	1	1627	1629	-2	1833	1857	UA	572	N497UA	LGA	DEN	216	1620	16	29	2023-08-01 16:00:00	Other
10534	4	28	755	800	-5	1009	1017	9E	1344	N935XJ	JFK	CHS	101	636	8	0	2023-04-28 08:00:00	Other
10537	12	30	754	759	-5	909	946	UA	649	N892UA	EWR	ORD	110	719	7	59	2023-12-30 07:00:00	ORD
10541	1	26	1458	1500	-2	1756	1755	B6	936	N641JB	LGA	JAX	149	833	15	0	2023-01-26 15:00:00	Other
10544	9	19	1655	1700	-5	140	2014	B6	1005	N972JT	JFK	FLL	NA	1069	17	0	2023-09-19 17:00:00	FLL
10545	4	25	1226	1230	-4	1342	1405	9E	1299	N298PQ	LGA	MKE	114	738	12	30	2023-04-25 12:00:00	Other
10546	3	25	901	905	-4	1022	1024	B6	635	N267JB	JFK	BTV	42	266	9	5	2023-03-25 09:00:00	Other
10554	8	10	658	700	-2	944	1005	UA	232	N498UA	EWR	FLL	143	1065	7	0	2023-08-10 07:00:00	FLL
10559	11	27	1556	1559	-3	1834	1839	DL	174	N361DN	LGA	ATL	136	762	15	59	2023-11-27 15:00:00	ATL
10560	3	19	1455	1458	-3	1651	1635	9E	1546	N695CA	JFK	RIC	63	288	14	58	2023-03-19 14:00:00	Other
10562	8	28	702	705	-3	952	1019	DL	469	N351DN	LGA	FLL	147	1076	7	5	2023-08-28 07:00:00	FLL
10564	1	9	1843	1845	-2	2053	2119	DL	897	N978AT	EWR	ATL	106	746	18	45	2023-01-09 18:00:00	ATL
10566	2	14	2046	2050	-4	2149	2213	YX	1154	N855RW	EWR	DCA	44	199	20	50	2023-02-14 20:00:00	Other
10567	1	10	1232	1235	-3	1509	1539	UA	286	N27255	EWR	TPA	141	997	12	35	2023-01-10 12:00:00	Other
10570	7	23	738	742	-4	1019	1029	B6	164	N554JB	JFK	MCO	132	944	7	42	2023-07-23 07:00:00	MCO
10573	3	20	645	650	-5	800	829	YX	1670	N878RW	LGA	PIT	59	335	6	50	2023-03-20 06:00:00	Other
10579	5	22	1320	1325	-5	1609	1550	UA	433	N78540	EWR	ATL	111	746	13	25	2023-05-22 13:00:00	ATL
10582	8	3	1310	1315	-5	1459	1529	9E	1114	N905XJ	JFK	CHS	84	636	13	15	2023-08-03 13:00:00	Other
10584	11	16	2145	2150	-5	2258	2307	UA	599	N14735	EWR	BTV	52	266	21	50	2023-11-16 21:00:00	Other
10586	11	21	1056	1100	-4	1341	1422	AA	2	N109NN	JFK	LAX	319	2475	11	0	2023-11-21 11:00:00	LAX
10587	6	23	844	846	-2	953	1006	YX	1191	N728YX	EWR	ALB	34	143	8	46	2023-06-23 08:00:00	Other
10589	8	22	605	610	-5	751	820	9E	1095	N931XJ	LGA	CLT	82	544	6	10	2023-08-22 06:00:00	CLT
10592	12	31	1511	1515	-4	1644	1654	YX	1717	N205JQ	JFK	ORF	61	290	15	15	2023-12-31 15:00:00	Other
10594	3	12	656	700	-4	940	1006	UA	279	N24706	EWR	FLL	143	1065	7	0	2023-03-12 07:00:00	FLL
10596	11	24	1721	1725	-4	1837	1845	9E	1408	N937XJ	LGA	SYR	46	198	17	25	2023-11-24 17:00:00	Other
10598	6	8	945	950	-5	1029	1100	9E	1621	N306PQ	LGA	ALB	29	136	9	50	2023-06-08 09:00:00	Other
10600	5	2	942	946	-4	1328	1341	UA	582	N75436	EWR	SJU	202	1608	9	46	2023-05-02 09:00:00	Other
10612	4	21	1726	1730	-4	2029	2004	B6	157	N317JB	JFK	ATL	116	760	17	30	2023-04-21 17:00:00	ATL
10614	4	22	1627	1629	-2	2013	1939	AA	109	N793AN	JFK	MIA	191	1089	16	29	2023-04-22 16:00:00	MIA
10620	9	9	1233	1236	-3	1337	1410	9E	1614	N902XJ	LGA	BUF	47	292	12	36	2023-09-09 12:00:00	Other
10624	9	21	1857	1900	-3	2126	2133	DL	198	N309DN	LGA	ATL	104	762	19	0	2023-09-21 19:00:00	ATL
10632	4	6	1910	1915	-5	2128	2145	YX	1176	N872RW	LGA	SDF	111	659	19	15	2023-04-06 19:00:00	Other
10638	8	16	1927	1929	-2	2145	2137	AA	602	N4032T	JFK	CLT	85	541	19	29	2023-08-16 19:00:00	CLT
10639	1	1	1256	1300	-4	1614	1622	B6	896	N943JT	JFK	LAX	353	2475	13	0	2023-01-01 13:00:00	LAX
10644	11	3	1436	1440	-4	1619	1644	UA	359	N23707	EWR	CLT	81	529	14	40	2023-11-03 14:00:00	CLT
10651	11	3	925	929	-4	1029	1049	YX	1079	N747YX	EWR	SYR	40	195	9	29	2023-11-03 09:00:00	Other
10655	7	23	1308	1312	-4	1457	1518	YX	948	N721YX	EWR	CVG	94	569	13	12	2023-07-23 13:00:00	Other
10658	6	19	1733	1736	-3	1844	1912	B6	103	N306JB	JFK	PWM	45	273	17	36	2023-06-19 17:00:00	Other
10670	12	5	727	730	-3	1115	1030	UA	616	N27270	EWR	MCO	153	937	7	30	2023-12-05 07:00:00	MCO
10671	4	26	1122	1125	-3	1424	1445	DL	817	N344DN	LGA	FLL	157	1076	11	25	2023-04-26 11:00:00	FLL
10672	3	23	1540	1545	-5	1930	1907	UA	429	N204UA	EWR	SFO	366	2565	15	45	2023-03-23 15:00:00	Other
10691	9	10	1543	1545	-2	1915	1859	DL	886	N345NB	JFK	AUS	206	1521	15	45	2023-09-10 15:00:00	Other
10694	2	16	848	850	-2	1059	1121	9E	1330	N915XJ	LGA	GSP	98	610	8	50	2023-02-16 08:00:00	Other
10699	12	15	1155	1200	-5	1323	1337	YX	1708	N824MD	LGA	BGR	60	378	12	0	2023-12-15 12:00:00	Other
10700	6	13	1209	1212	-3	1409	1405	YX	1393	N103HQ	LGA	MEM	152	963	12	12	2023-06-13 12:00:00	Other
10704	11	24	728	730	-2	1019	1030	UA	762	N27260	EWR	PBI	154	1023	7	30	2023-11-24 07:00:00	Other
10705	7	26	1848	1851	-3	2051	2121	DL	675	N373DA	EWR	ATL	94	746	18	51	2023-07-26 18:00:00	ATL
10706	3	13	713	715	-2	854	904	DL	568	N138DU	LGA	ORD	109	733	7	15	2023-03-13 07:00:00	ORD
10709	5	12	1927	1929	-2	2128	2151	YX	1258	N425YX	LGA	MCI	150	1107	19	29	2023-05-12 19:00:00	Other
10716	1	6	1557	1600	-3	1814	1830	9E	1416	N348PQ	LGA	CHS	103	641	16	0	2023-01-06 16:00:00	Other
10720	8	5	657	659	-2	932	941	UA	257	N822UA	EWR	MCO	120	937	6	59	2023-08-05 06:00:00	MCO
10721	8	12	1141	1143	-2	1358	1412	UA	346	N449UA	EWR	ATL	102	746	11	43	2023-08-12 11:00:00	ATL
10730	2	23	2209	2211	-2	2355	2336	UA	673	N47275	EWR	BNA	121	748	22	11	2023-02-23 22:00:00	Other
10736	11	27	1604	1608	-4	1855	1910	UA	69	N79521	EWR	PBI	148	1023	16	8	2023-11-27 16:00:00	Other
10751	12	14	2025	2030	-5	2212	2256	9E	1497	N272PQ	LGA	GRR	88	618	20	30	2023-12-14 20:00:00	Other
10754	4	5	628	630	-2	937	900	UA	192	N854UA	LGA	DEN	279	1620	6	30	2023-04-05 06:00:00	Other
10762	2	3	1356	1359	-3	1636	1617	YX	1587	N201JQ	LGA	CHS	113	641	13	59	2023-02-03 13:00:00	Other
10767	6	28	811	815	-4	1045	1132	B6	238	N994JL	JFK	FLL	132	1069	8	15	2023-06-28 08:00:00	FLL
10769	8	31	1457	1500	-3	1709	1704	9E	1152	N136EV	LGA	RDU	72	431	15	0	2023-08-31 15:00:00	Other
10772	3	27	615	620	-5	800	807	9E	1604	N929XJ	LGA	RDU	78	431	6	20	2023-03-27 06:00:00	Other
10773	6	18	741	744	-3	1002	956	9E	1746	N935XJ	JFK	CLT	86	541	7	44	2023-06-18 07:00:00	CLT
10787	5	3	645	648	-3	906	939	AA	556	N316RK	JFK	PHX	293	2153	6	48	2023-05-03 06:00:00	Other
10790	8	30	1424	1429	-5	1625	1640	UA	670	N62892	EWR	DEN	217	1605	14	29	2023-08-30 14:00:00	Other
10805	4	11	1155	1159	-4	1349	1423	UA	355	N36476	EWR	DEN	198	1605	11	59	2023-04-11 11:00:00	Other
10823	6	25	1309	1314	-5	1511	1535	9E	1737	N602LR	LGA	IND	95	660	13	14	2023-06-25 13:00:00	Other
10829	8	11	2031	2035	-4	2336	2330	UA	219	N17310	EWR	AUS	193	1504	20	35	2023-08-11 20:00:00	Other
10853	1	19	833	835	-2	1149	1241	AA	55	N110AN	JFK	SFO	344	2586	8	35	2023-01-19 08:00:00	Other
10860	12	19	1824	1829	-5	2114	2150	AS	158	N224AK	EWR	SEA	327	2402	18	29	2023-12-19 18:00:00	Other
10862	12	14	557	601	-4	840	913	UA	62	N458UA	EWR	AUS	207	1504	6	1	2023-12-14 06:00:00	Other
10866	10	2	730	735	-5	857	922	UA	934	N73283	EWR	RDU	68	416	7	35	2023-10-02 07:00:00	Other
10876	6	2	1057	1059	-2	1313	1321	UA	515	N13718	EWR	JAX	113	820	10	59	2023-06-02 10:00:00	Other
10883	9	22	1805	1810	-5	2001	2028	9E	1635	N176PQ	LGA	GSP	90	610	18	10	2023-09-22 18:00:00	Other
10888	4	18	834	837	-3	1004	1023	YX	978	N730YX	EWR	PIT	62	319	8	37	2023-04-18 08:00:00	Other
10894	2	22	1836	1838	-2	1946	2000	B6	854	N216JB	JFK	BOS	43	187	18	38	2023-02-22 18:00:00	BOS
10895	1	30	624	629	-5	908	900	UA	867	N4888U	LGA	DEN	257	1620	6	29	2023-01-30 06:00:00	Other
10902	7	25	601	605	-4	738	759	UA	257	N67845	EWR	MSP	140	1008	6	5	2023-07-25 06:00:00	Other
10903	4	11	712	715	-3	851	945	DL	266	N703TW	JFK	PHX	258	2153	7	15	2023-04-11 07:00:00	Other
10910	9	27	1531	1535	-4	1640	1704	9E	1526	N187GJ	LGA	ROC	43	254	15	35	2023-09-27 15:00:00	Other
10915	10	15	656	659	-3	844	906	9E	1379	N315PQ	JFK	DTW	86	509	6	59	2023-10-15 06:00:00	Other
10917	3	13	1450	1455	-5	1652	1657	9E	1557	N905XJ	JFK	RDU	78	427	14	55	2023-03-13 14:00:00	Other
10923	3	20	558	600	-2	716	730	WN	992	N8711Q	LGA	MDW	110	725	6	0	2023-03-20 06:00:00	Other
10924	6	19	858	900	-2	1015	1025	WN	57	N8552Z	LGA	MDW	105	725	9	0	2023-06-19 09:00:00	Other
10927	7	31	2155	2159	-4	50	111	B6	543	N985JT	JFK	LAX	316	2475	21	59	2023-07-31 21:00:00	LAX
10942	5	13	1220	1225	-5	1344	1410	9E	1415	N913XJ	LGA	CHO	68	305	12	25	2023-05-13 12:00:00	Other
10947	11	20	1926	1929	-3	2129	2133	9E	1557	N905XJ	JFK	RDU	80	427	19	29	2023-11-20 19:00:00	Other
10950	6	23	1456	1459	-3	1700	1705	AA	142	N9012	JFK	CLT	85	541	14	59	2023-06-23 14:00:00	CLT
10954	10	14	826	830	-4	1127	1150	DL	316	N525DA	JFK	SAN	331	2446	8	30	2023-10-14 08:00:00	Other
10955	11	2	1228	1232	-4	1539	1528	NK	469	N616NK	LGA	IAH	211	1416	12	32	2023-11-02 12:00:00	Other
10956	5	26	1655	1700	-5	1800	1830	YX	1702	N213JQ	LGA	BOS	36	184	17	0	2023-05-26 17:00:00	BOS
10959	10	9	1056	1100	-4	1238	1258	YX	1139	N730YX	EWR	ILM	81	488	11	0	2023-10-09 11:00:00	Other
10960	12	26	2020	2025	-5	2230	2300	UA	648	N37541	EWR	DEN	210	1605	20	25	2023-12-26 20:00:00	Other
10967	8	25	1526	1529	-3	1707	1724	YX	835	N752YX	EWR	CMH	70	463	15	29	2023-08-25 15:00:00	Other
10969	1	12	1237	1241	-4	1439	1441	9E	1460	N166PQ	JFK	CLT	93	541	12	41	2023-01-12 12:00:00	CLT
10981	11	24	1656	1658	-2	1834	1839	OO	1211	N241SY	JFK	MKE	132	745	16	58	2023-11-24 16:00:00	Other
10983	2	18	1121	1125	-4	1304	1322	9E	1460	N931XJ	LGA	RDU	66	431	11	25	2023-02-18 11:00:00	Other
10986	1	28	1525	1530	-5	1631	1649	B6	468	N354JB	JFK	BOS	49	187	15	30	2023-01-28 15:00:00	BOS
10992	2	19	1955	2000	-5	2108	2114	9E	1428	N314PQ	LGA	PVD	32	143	20	0	2023-02-19 20:00:00	Other
10997	3	8	1117	1120	-3	1419	1451	DL	590	N140DU	LGA	IAH	202	1416	11	20	2023-03-08 11:00:00	Other
10998	11	9	1426	1428	-2	1747	1743	UA	444	N75428	EWR	AUS	219	1504	14	28	2023-11-09 14:00:00	Other
11001	5	25	1653	1658	-5	1901	1906	YX	1012	N644RW	EWR	GSP	101	594	16	58	2023-05-25 16:00:00	Other
11004	8	9	955	959	-4	1143	1201	AA	516	N162UW	EWR	CLT	76	529	9	59	2023-08-09 09:00:00	CLT
11006	9	20	1856	1859	-3	2026	2101	9E	1599	N920XJ	LGA	GSO	71	461	18	59	2023-09-20 18:00:00	Other
11011	2	8	740	745	-5	1050	1102	UA	325	N78438	EWR	SAN	334	2425	7	45	2023-02-08 07:00:00	Other
11013	12	27	1123	1125	-2	1433	1447	DL	394	N136DQ	LGA	IAH	228	1416	11	25	2023-12-27 11:00:00	Other
11019	5	4	1024	1029	-5	1228	1209	9E	1369	N920XJ	LGA	BUF	49	292	10	29	2023-05-04 10:00:00	Other
11027	2	12	1725	1730	-5	1924	1947	9E	1395	N902XJ	LGA	DSM	143	1031	17	30	2023-02-12 17:00:00	Other
11028	12	1	1342	1345	-3	1653	1700	AA	369	N967AN	LGA	DFW	226	1389	13	45	2023-12-01 13:00:00	Other
11032	11	7	1635	1640	-5	1842	1917	DL	544	N870DN	JFK	ATL	108	760	16	40	2023-11-07 16:00:00	ATL
11040	7	10	1258	1300	-2	1652	1613	AA	212	N338ST	LGA	MIA	161	1096	13	0	2023-07-10 13:00:00	MIA
11043	11	19	1757	1759	-2	2044	2115	AA	649	N306NY	LGA	DFW	200	1389	17	59	2023-11-19 17:00:00	Other
11049	7	25	605	610	-5	803	813	DL	202	N112DN	LGA	MSP	143	1020	6	10	2023-07-25 06:00:00	Other
11053	4	12	1813	1815	-2	2006	2028	DL	679	N951AT	EWR	MSP	140	1008	18	15	2023-04-12 18:00:00	Other
11059	8	22	1555	1559	-4	1707	1734	YX	970	N101HQ	JFK	BOS	36	187	15	59	2023-08-22 15:00:00	BOS
11060	3	13	803	805	-2	928	947	9E	1497	N183GJ	JFK	BUF	52	301	8	5	2023-03-13 08:00:00	Other
11062	4	25	800	805	-5	1007	1010	B6	439	N229JB	JFK	CHS	97	636	8	5	2023-04-25 08:00:00	Other
11068	10	23	1823	1825	-2	2006	2010	WN	880	N8872Q	LGA	STL	129	888	18	25	2023-10-23 18:00:00	Other
11069	11	10	1725	1729	-4	2026	2048	B6	949	N988JT	JFK	LAX	346	2475	17	29	2023-11-10 17:00:00	LAX
11073	10	12	1606	1611	-5	1744	1803	AA	692	N709UW	LGA	RDU	77	431	16	11	2023-10-12 16:00:00	Other
11075	4	9	1527	1529	-2	1759	1826	AA	234	N950NN	EWR	DFW	184	1372	15	29	2023-04-09 15:00:00	Other
11078	2	9	956	1000	-4	1413	1359	YX	1245	N826MD	LGA	EYW	191	1207	10	0	2023-02-09 10:00:00	Other
11079	8	18	825	829	-4	1123	1208	AA	47	N112AN	JFK	SFO	324	2586	8	29	2023-08-18 08:00:00	Other
11080	5	1	1453	1457	-4	1621	1635	YX	1698	N218JQ	JFK	DCA	57	213	14	57	2023-05-01 14:00:00	Other
11084	5	5	1656	1659	-3	1825	1842	UA	673	N497UA	EWR	STL	126	872	16	59	2023-05-05 16:00:00	Other
11093	8	10	558	600	-2	709	718	UA	353	N830UA	EWR	IAD	42	212	6	0	2023-08-10 06:00:00	Other
11095	8	3	1636	1640	-4	1923	2000	DL	230	N526DE	JFK	SAN	313	2446	16	40	2023-08-03 16:00:00	Other
11100	10	21	1518	1520	-2	1702	1734	DL	980	N120DN	LGA	MSP	145	1020	15	20	2023-10-21 15:00:00	Other
11112	1	14	1056	1100	-4	1307	1318	YX	1262	N646RW	EWR	GRR	88	605	11	0	2023-01-14 11:00:00	Other
11113	2	16	755	759	-4	925	929	YX	1126	N724YX	EWR	ROC	48	246	7	59	2023-02-16 07:00:00	Other
11119	11	24	625	630	-5	815	839	AA	927	N944NN	JFK	CLT	88	541	6	30	2023-11-24 06:00:00	CLT
11128	4	23	1805	1810	-5	2111	2046	9E	1214	N181PQ	JFK	SAV	112	718	18	10	2023-04-23 18:00:00	Other
11132	11	22	1141	1145	-4	1438	1510	UA	676	N37465	EWR	SAT	212	1569	11	45	2023-11-22 11:00:00	Other
11135	8	14	1754	1759	-5	2024	2030	9E	1220	N326PQ	JFK	CHS	99	636	17	59	2023-08-14 17:00:00	Other
11138	2	24	1856	1900	-4	2130	2127	9E	1409	N337PQ	JFK	IND	127	665	19	0	2023-02-24 19:00:00	Other
11141	4	24	1613	1616	-3	1738	1752	9E	1313	N309PQ	JFK	ORF	57	290	16	16	2023-04-24 16:00:00	Other
11151	7	15	1210	1215	-5	1415	1429	UA	595	N33264	LGA	DEN	224	1620	12	15	2023-07-15 12:00:00	Other
11156	8	14	456	500	-4	749	807	AA	339	N997NN	EWR	MIA	146	1085	5	0	2023-08-14 05:00:00	MIA
11157	10	17	1956	2000	-4	2218	2240	DL	287	N309DN	LGA	ATL	99	762	20	0	2023-10-17 20:00:00	ATL
11161	9	21	555	600	-5	855	905	NK	47	N680NK	LGA	FLL	142	1076	6	0	2023-09-21 06:00:00	FLL
11169	9	14	1757	1800	-3	1919	1930	YX	1907	N205JQ	LGA	BOS	45	184	18	0	2023-09-14 18:00:00	BOS
11177	10	7	2005	2009	-4	2321	2342	AS	15	N913AK	JFK	SFO	319	2586	20	9	2023-10-07 20:00:00	Other
11183	4	4	1723	1727	-4	2042	2104	YX	951	N861RW	EWR	EYW	157	1196	17	27	2023-04-04 17:00:00	Other
11185	12	19	603	605	-2	758	815	DL	942	N925AT	EWR	MSP	148	1008	6	5	2023-12-19 06:00:00	Other
11187	3	6	1005	1010	-5	1310	1322	DL	995	N319DN	LGA	MCO	134	950	10	10	2023-03-06 10:00:00	MCO
11188	4	20	1926	1930	-4	2059	2103	UA	773	N65832	EWR	MSN	120	799	19	30	2023-04-20 19:00:00	Other
11193	4	19	1427	1430	-3	1633	1655	WN	897	N8670A	LGA	ATL	108	762	14	30	2023-04-19 14:00:00	ATL
11194	12	4	1755	1800	-5	2006	2031	9E	1362	N335PQ	LGA	MCI	168	1107	18	0	2023-12-04 18:00:00	Other
11203	8	3	954	959	-5	1143	1210	9E	1182	N132EV	EWR	CVG	87	569	9	59	2023-08-03 09:00:00	Other
11208	2	18	1825	1829	-4	2112	2147	B6	893	N536JB	EWR	FLL	137	1065	18	29	2023-02-18 18:00:00	FLL
11217	4	10	757	800	-3	1052	1120	DL	182	N825MH	JFK	LAX	301	2475	8	0	2023-04-10 08:00:00	LAX
11227	8	19	845	847	-2	1137	1115	UA	711	N77535	EWR	ATL	98	746	8	47	2023-08-19 08:00:00	ATL
11232	12	4	557	602	-5	801	817	AA	911	N161UW	EWR	CLT	93	529	6	2	2023-12-04 06:00:00	CLT
11234	1	12	1631	1635	-4	1803	1801	9E	1628	N138EV	JFK	SYR	45	209	16	35	2023-01-12 16:00:00	Other
11237	8	20	2232	2236	-4	2347	2359	UA	381	N407UA	EWR	BUF	48	282	22	36	2023-08-20 22:00:00	Other
11239	12	3	1125	1130	-5	1454	1435	WN	547	N8834L	LGA	DAL	235	1381	11	30	2023-12-03 11:00:00	Other
11240	11	15	1822	1825	-3	2057	2126	DL	752	N360DN	LGA	MCO	133	950	18	25	2023-11-15 18:00:00	MCO
11241	11	5	1438	1441	-3	1756	1749	UA	759	N77542	EWR	MIA	150	1085	14	41	2023-11-05 14:00:00	MIA
11245	2	6	1341	1345	-4	1501	1525	9E	1298	N330PQ	LGA	PIT	55	335	13	45	2023-02-06 13:00:00	Other
11246	12	9	1211	1215	-4	1416	1444	UA	848	N41135	EWR	DEN	226	1605	12	15	2023-12-09 12:00:00	Other
11248	6	20	1443	1445	-2	1555	1615	9E	1763	N924XJ	LGA	ROC	44	254	14	45	2023-06-20 14:00:00	Other
11257	1	30	1622	1626	-4	1756	1820	YX	1163	N733YX	EWR	GSO	74	445	16	26	2023-01-30 16:00:00	Other
11266	8	6	1257	1300	-3	1612	1534	DL	377	N913DU	JFK	ATL	162	760	13	0	2023-08-06 13:00:00	ATL
11268	1	3	1126	1130	-4	1423	1432	UA	290	N876UA	EWR	MTJ	273	1795	11	30	2023-01-03 11:00:00	Other
11274	6	18	1855	1859	-4	2011	2038	YX	1191	N858RW	LGA	IAD	50	229	18	59	2023-06-18 18:00:00	Other
11282	11	2	1415	1420	-5	1552	1608	9E	1437	N695CA	LGA	BHM	129	866	14	20	2023-11-02 14:00:00	Other
11283	3	18	1309	1313	-4	1545	1547	UA	317	N873UA	EWR	JAX	131	820	13	13	2023-03-18 13:00:00	Other
11285	12	23	2157	2200	-3	2315	2318	YX	1269	N422YX	JFK	BOS	44	187	22	0	2023-12-23 22:00:00	BOS
11293	10	2	1855	1859	-4	2050	2125	YX	1310	N410YX	LGA	XNA	149	1147	18	59	2023-10-02 18:00:00	Other
11295	9	15	746	750	-4	927	939	9E	1664	N153PQ	JFK	RDU	73	427	7	50	2023-09-15 07:00:00	Other
11296	6	21	656	700	-4	942	1003	DL	548	N842DN	JFK	TPA	140	1005	7	0	2023-06-21 07:00:00	Other
11298	3	9	1658	1700	-2	2028	2007	AA	405	N906AN	LGA	DFW	223	1389	17	0	2023-03-09 17:00:00	Other
11315	7	17	850	855	-5	1039	1049	YX	1065	N408YX	LGA	GSO	81	461	8	55	2023-07-17 08:00:00	Other
11316	4	25	1628	1630	-2	1903	1901	UA	762	N776UA	EWR	LAS	292	2227	16	30	2023-04-25 16:00:00	Other
11321	9	29	811	815	-4	1031	1006	OO	1229	N614CZ	JFK	ORD	115	740	8	15	2023-09-29 08:00:00	ORD
11324	10	5	2057	2059	-2	2204	2230	YX	1041	N755YX	EWR	BTV	48	266	20	59	2023-10-05 20:00:00	Other
11332	4	25	1505	1510	-5	1635	1647	UA	637	N37277	EWR	ORD	113	719	15	10	2023-04-25 15:00:00	ORD
11338	12	23	656	700	-4	949	1008	UA	264	N47291	EWR	FLL	148	1065	7	0	2023-12-23 07:00:00	FLL
11342	3	16	556	600	-4	910	945	AA	52	N105NN	JFK	LAX	347	2475	6	0	2023-03-16 06:00:00	LAX
11343	4	24	837	840	-3	1055	1114	DL	498	N704X	JFK	ATL	114	760	8	40	2023-04-24 08:00:00	ATL
11344	1	18	1840	1845	-5	2121	2134	DL	205	N366NW	LGA	ATL	115	762	18	45	2023-01-18 18:00:00	ATL
11350	7	30	957	1000	-3	1202	1209	YX	901	N746YX	EWR	CHS	97	628	10	0	2023-07-30 10:00:00	Other
11364	4	26	1417	1421	-4	1737	1706	UA	250	N15751	EWR	DFW	227	1372	14	21	2023-04-26 14:00:00	Other
11366	4	13	2132	2135	-3	2227	2303	OO	1013	N312SY	JFK	IAD	42	228	21	35	2023-04-13 21:00:00	Other
11370	8	5	1526	1530	-4	1709	1725	YX	1019	N416YX	LGA	CLE	72	419	15	30	2023-08-05 15:00:00	Other
11371	8	8	827	829	-2	1017	1047	9E	1200	N301PQ	LGA	MCI	148	1107	8	29	2023-08-08 08:00:00	Other
11372	3	15	600	605	-5	723	751	DL	427	N128DU	LGA	ORD	111	733	6	5	2023-03-15 06:00:00	ORD
11373	1	5	828	830	-2	1203	1205	DL	126	N727TW	JFK	SAN	342	2446	8	30	2023-01-05 08:00:00	Other
11375	3	18	607	610	-3	732	730	NK	282	N535NK	EWR	PIT	63	319	6	10	2023-03-18 06:00:00	Other
11376	10	18	1936	1940	-4	2140	2243	B6	104	N952JB	JFK	ONT	290	2429	19	40	2023-10-18 19:00:00	Other
11379	2	8	754	759	-5	1011	1024	YX	1239	N118HQ	LGA	MSP	172	1020	7	59	2023-02-08 07:00:00	Other
11380	11	2	701	705	-4	1007	1000	DL	353	N329NW	LGA	PBI	144	1035	7	5	2023-11-02 07:00:00	Other
11382	10	11	708	710	-2	1001	1005	DL	505	N301DV	LGA	MCO	143	950	7	10	2023-10-11 07:00:00	MCO
11395	4	20	558	600	-2	815	830	UA	371	N63899	EWR	DEN	232	1605	6	0	2023-04-20 06:00:00	Other
11398	3	14	556	600	-4	701	717	YX	1757	N233JQ	JFK	BOS	38	187	6	0	2023-03-14 06:00:00	BOS
11404	12	21	1504	1509	-5	1646	1705	YX	1251	N413YX	LGA	ILM	77	500	15	9	2023-12-21 15:00:00	Other
11408	9	12	2013	2015	-2	2112	2138	B6	527	N306JB	LGA	BOS	33	184	20	15	2023-09-12 20:00:00	BOS
11419	6	16	558	600	-2	705	706	B6	504	N355JB	JFK	BOS	41	187	6	0	2023-06-16 06:00:00	BOS
11429	8	9	1130	1135	-5	1238	1323	DL	466	N121DU	LGA	ORD	106	733	11	35	2023-08-09 11:00:00	ORD
11432	12	19	1111	1115	-4	1242	1255	YX	1765	N216JQ	LGA	RIC	59	292	11	15	2023-12-19 11:00:00	Other
11433	6	30	1345	1350	-5	1532	1527	9E	1562	N935XJ	JFK	BGR	60	382	13	50	2023-06-30 13:00:00	Other
11435	5	23	1853	1855	-2	2247	2310	DL	694	N904DN	JFK	SJU	211	1598	18	55	2023-05-23 18:00:00	Other
11437	5	18	958	1000	-2	1301	1326	DL	140	N821DN	JFK	SLC	271	1990	10	0	2023-05-18 10:00:00	Other
11438	9	17	1152	1155	-3	1402	1420	WN	1010	N8832H	LGA	ATL	114	762	11	55	2023-09-17 11:00:00	ATL
11441	8	19	927	930	-3	1050	1104	YX	1380	N232JQ	LGA	PWM	46	269	9	30	2023-08-19 09:00:00	Other
11443	6	1	557	600	-3	726	735	UA	394	N39297	EWR	ORD	108	719	6	0	2023-06-01 06:00:00	ORD
11445	11	9	557	600	-3	815	813	DL	519	N354DN	LGA	MSP	168	1020	6	0	2023-11-09 06:00:00	Other
11451	12	22	1106	1110	-4	1414	1432	DL	590	N313DN	LGA	MIA	146	1096	11	10	2023-12-22 11:00:00	MIA
11452	1	28	1356	1359	-3	1647	1709	AA	513	N344PP	EWR	DFW	204	1372	13	59	2023-01-28 13:00:00	Other
11457	3	9	2117	2120	-3	2241	2238	9E	1508	N187GJ	LGA	BTV	47	258	21	20	2023-03-09 21:00:00	Other
11465	1	29	1026	1030	-4	1130	1135	9E	1660	N341PQ	JFK	BWI	39	184	10	30	2023-01-29 10:00:00	Other
11467	9	4	1450	1455	-5	1608	1643	9E	1532	N917XJ	LGA	ORF	52	296	14	55	2023-09-04 14:00:00	Other
11468	8	26	1021	1024	-3	1217	1227	9E	1238	N482PX	LGA	GSO	73	461	10	24	2023-08-26 10:00:00	Other
11476	3	5	826	830	-4	957	1013	9E	1591	N905XJ	JFK	ROC	61	264	8	30	2023-03-05 08:00:00	Other
11485	4	25	2213	2215	-2	114	131	DL	101	N842MH	JFK	LAX	327	2475	22	15	2023-04-25 22:00:00	LAX
11496	11	10	1455	1500	-5	1603	1627	9E	1488	N691CA	LGA	PWM	47	269	15	0	2023-11-10 15:00:00	Other
11498	7	26	1717	1720	-3	1933	1930	AA	630	N133AN	LGA	CLT	86	544	17	20	2023-07-26 17:00:00	CLT
11511	5	21	1715	1720	-5	1850	1854	9E	1378	N307PQ	LGA	BUF	47	292	17	20	2023-05-21 17:00:00	Other
11513	11	18	643	645	-2	952	953	UA	886	N77552	EWR	MIA	151	1085	6	45	2023-11-18 06:00:00	MIA
11515	4	26	832	835	-3	1123	1142	DL	335	N143DU	JFK	DFW	212	1391	8	35	2023-04-26 08:00:00	Other
11530	12	12	821	825	-4	1138	1140	NK	571	N958NK	EWR	MIA	157	1085	8	25	2023-12-12 08:00:00	MIA
11533	11	19	610	615	-5	858	920	UA	701	N37462	EWR	FLL	139	1065	6	15	2023-11-19 06:00:00	FLL
11550	3	22	807	810	-3	1107	1050	DL	354	N3732J	JFK	DEN	263	1626	8	10	2023-03-22 08:00:00	Other
11551	3	1	1657	1701	-4	1848	1904	DL	912	N998AT	EWR	DTW	93	488	17	1	2023-03-01 17:00:00	Other
11564	4	11	2342	2345	-3	313	335	B6	147	N2043J	JFK	SJU	192	1598	23	45	2023-04-11 23:00:00	Other
11565	4	9	603	605	-2	756	818	DL	792	N356NW	LGA	MSP	145	1020	6	5	2023-04-09 06:00:00	Other
11566	4	4	925	929	-4	1118	1120	YX	1164	N826MD	LGA	CLE	74	419	9	29	2023-04-04 09:00:00	Other
11567	12	8	1511	1514	-3	1801	1816	UA	788	N33289	EWR	PBI	141	1023	15	14	2023-12-08 15:00:00	Other
11572	3	12	932	935	-3	1224	1243	B6	403	N323JB	JFK	MCO	134	944	9	35	2023-03-12 09:00:00	MCO
11575	3	9	1652	1655	-3	2007	2015	AS	81	N283AK	EWR	SEA	342	2402	16	55	2023-03-09 16:00:00	Other
11580	6	3	838	840	-2	1136	1201	DL	330	N373DA	JFK	SAN	313	2446	8	40	2023-06-03 08:00:00	Other
11581	10	19	541	545	-4	837	853	AA	46	N113AN	JFK	LAX	310	2475	5	45	2023-10-19 05:00:00	LAX
11583	12	9	1513	1518	-5	1819	1820	UA	782	N37567	EWR	IAH	217	1400	15	18	2023-12-09 15:00:00	Other
11584	4	2	707	710	-3	953	1010	WN	57	N8839Q	LGA	DAL	206	1381	7	10	2023-04-02 07:00:00	Other
11593	2	14	1426	1429	-3	1702	1720	UA	406	N14106	EWR	MCO	132	937	14	29	2023-02-14 14:00:00	MCO
11611	7	22	812	816	-4	1049	1107	UA	583	N76517	EWR	BZN	252	1882	8	16	2023-07-22 08:00:00	Other
11613	10	19	1151	1155	-4	1421	1452	DL	172	N419DX	JFK	LAX	290	2475	11	55	2023-10-19 11:00:00	LAX
11614	3	1	633	635	-2	925	956	AA	921	N877NN	LGA	MIA	146	1096	6	35	2023-03-01 06:00:00	MIA
11617	7	13	1124	1128	-4	1413	1437	B6	252	N651JB	JFK	SAT	213	1587	11	28	2023-07-13 11:00:00	Other
11619	3	29	957	1000	-3	1258	1246	UA	680	N769UA	EWR	MCO	137	937	10	0	2023-03-29 10:00:00	MCO
11624	12	19	1626	1629	-3	1936	2023	DL	98	N542DE	JFK	PHX	291	2153	16	29	2023-12-19 16:00:00	Other
11626	8	27	627	630	-3	926	926	NK	402	N655NK	LGA	MCO	129	950	6	30	2023-08-27 06:00:00	MCO
11632	5	20	958	1000	-2	1244	1304	DL	122	N183DN	JFK	LAX	318	2475	10	0	2023-05-20 10:00:00	LAX
11641	8	28	1917	1920	-3	2221	2243	DL	593	N104DU	LGA	RSW	162	1080	19	20	2023-08-28 19:00:00	Other
11651	12	7	1624	1629	-5	1724	1756	B6	508	N231JB	JFK	BOS	42	187	16	29	2023-12-07 16:00:00	BOS
11652	11	30	2255	2259	-4	2350	19	B6	904	N368JB	JFK	SYR	42	209	22	59	2023-11-30 22:00:00	Other
11663	5	4	1225	1230	-5	1445	1508	YX	1664	N215JQ	LGA	SDF	107	659	12	30	2023-05-04 12:00:00	Other
11666	6	17	1155	1159	-4	1436	1454	UA	762	N77530	EWR	SNA	320	2434	11	59	2023-06-17 11:00:00	Other
11670	12	1	1058	1100	-2	1353	1414	B6	321	N552JB	JFK	SLC	275	1990	11	0	2023-12-01 11:00:00	Other
11677	3	18	856	900	-4	1103	1103	YX	1358	N821MD	LGA	CMH	97	479	9	0	2023-03-18 09:00:00	Other
11679	10	6	617	620	-3	920	914	B6	463	N979JT	EWR	LAX	321	2454	6	20	2023-10-06 06:00:00	LAX
11682	6	17	626	630	-4	744	750	B6	1011	N354JB	JFK	BUF	55	301	6	30	2023-06-17 06:00:00	Other
11688	4	23	805	810	-5	1206	1207	DL	660	N6710E	JFK	STT	199	1623	8	10	2023-04-23 08:00:00	Other
11690	9	28	2044	2046	-2	2158	2215	UA	744	N69816	EWR	BNA	106	748	20	46	2023-09-28 20:00:00	Other
11697	11	30	1255	1259	-4	1455	1456	YX	1804	N217JQ	LGA	STL	140	888	12	59	2023-11-30 12:00:00	Other
11699	9	2	711	715	-4	928	929	DL	787	N776DE	EWR	ATL	106	746	7	15	2023-09-02 07:00:00	ATL
11700	1	4	945	950	-5	1102	1130	WN	128	N735SA	LGA	BNA	120	764	9	50	2023-01-04 09:00:00	Other
11709	9	1	1536	1539	-3	1723	1743	YX	1380	N446YX	JFK	RDU	69	427	15	39	2023-09-01 15:00:00	Other
11711	12	15	812	817	-5	954	1018	9E	1659	N479PX	LGA	RDU	75	431	8	17	2023-12-15 08:00:00	Other
11714	8	24	1619	1624	-5	1738	1750	UA	581	N77544	EWR	IAD	40	212	16	24	2023-08-24 16:00:00	Other
11715	5	16	1307	1311	-4	1418	1426	YX	1093	N750YX	EWR	MHT	42	209	13	11	2023-05-16 13:00:00	Other
11717	2	23	1008	1010	-2	1424	1400	DL	298	N179DN	JFK	SFO	383	2586	10	10	2023-02-23 10:00:00	Other
11719	8	24	837	840	-3	1150	1055	YX	1036	N872RW	LGA	IND	105	660	8	40	2023-08-24 08:00:00	Other
11721	9	27	1116	1120	-4	1411	1416	UA	235	N47284	EWR	PBI	148	1023	11	20	2023-09-27 11:00:00	Other
11723	1	17	2001	2005	-4	2256	2330	WN	438	N8826Q	LGA	DAL	215	1381	20	5	2023-01-17 20:00:00	Other
11729	8	25	2026	2030	-4	2227	2248	YX	926	N746YX	EWR	GRR	92	605	20	30	2023-08-25 20:00:00	Other
11734	12	3	1251	1255	-4	1556	1605	UA	448	N77431	EWR	RSW	163	1068	12	55	2023-12-03 12:00:00	Other
11735	2	14	1545	1550	-5	1646	1736	9E	1376	N920XJ	LGA	CHO	49	305	15	50	2023-02-14 15:00:00	Other
11739	12	26	1314	1318	-4	1430	1450	YX	1051	N639RW	EWR	PIT	60	319	13	18	2023-12-26 13:00:00	Other
11747	11	6	1045	1050	-5	1153	1217	9E	1567	N136EV	JFK	ROC	50	264	10	50	2023-11-06 10:00:00	Other
11751	11	5	1557	1600	-3	1745	1755	OO	1193	N240SY	JFK	ORD	128	740	16	0	2023-11-05 16:00:00	ORD
11753	6	22	950	955	-5	1143	1151	9E	1706	N200PQ	EWR	RDU	81	416	9	55	2023-06-22 09:00:00	Other
11757	2	6	1003	1005	-2	1316	1319	NK	27	N683NK	EWR	MIA	146	1085	10	5	2023-02-06 10:00:00	MIA
11762	5	5	738	740	-2	903	927	DL	552	N102DU	LGA	ORD	108	733	7	40	2023-05-05 07:00:00	ORD
11764	8	3	635	640	-5	753	815	UA	242	N27292	EWR	CLE	61	404	6	40	2023-08-03 06:00:00	Other
11767	1	29	1647	1650	-3	1837	1858	9E	1560	N292PQ	LGA	ILM	84	500	16	50	2023-01-29 16:00:00	Other
11775	5	25	1101	1106	-5	1457	1420	UA	829	N4888U	EWR	MIA	183	1085	11	6	2023-05-25 11:00:00	MIA
11779	8	16	1248	1250	-2	1348	1357	9E	1283	N313PQ	JFK	ITH	37	189	12	50	2023-08-16 12:00:00	Other
11781	9	2	925	929	-4	1136	1146	YX	1206	N758YX	EWR	HHH	97	687	9	29	2023-09-02 09:00:00	Other
11784	10	23	2011	2015	-4	2145	2213	YX	1775	N206JQ	JFK	PIT	57	340	20	15	2023-10-23 20:00:00	Other
11786	8	25	1325	1330	-5	1600	1622	UA	523	N37305	EWR	AUS	188	1504	13	30	2023-08-25 13:00:00	Other
11793	6	20	905	907	-2	1011	1030	B6	631	N306JB	JFK	BTV	44	266	9	7	2023-06-20 09:00:00	Other
11802	8	11	1827	1830	-3	2105	2131	UA	398	N27722	EWR	SNA	313	2434	18	30	2023-08-11 18:00:00	Other
11804	1	29	615	620	-5	916	927	UA	311	N17133	EWR	FLL	147	1065	6	20	2023-01-29 06:00:00	FLL
11809	1	26	626	630	-4	933	935	B6	93	N997JL	LGA	MCO	158	950	6	30	2023-01-26 06:00:00	MCO
11817	8	22	1426	1429	-3	1544	1605	YX	1382	N203JQ	LGA	BUF	54	292	14	29	2023-08-22 14:00:00	Other
11818	10	26	1924	1929	-5	2226	2246	DL	402	N109DU	LGA	RSW	154	1080	19	29	2023-10-26 19:00:00	Other
11822	5	18	1028	1030	-2	1323	1353	AA	77	N117AN	JFK	LAX	316	2475	10	30	2023-05-18 10:00:00	LAX
11829	3	24	1250	1255	-5	1431	1452	9E	1312	N933XJ	LGA	CLE	78	419	12	55	2023-03-24 12:00:00	Other
11833	12	23	703	705	-2	943	1018	DL	351	N362DN	LGA	PBI	138	1035	7	5	2023-12-23 07:00:00	Other
11834	8	14	1526	1530	-4	1834	1931	DL	269	N718TW	JFK	SFO	327	2586	15	30	2023-08-14 15:00:00	Other
11839	10	29	655	700	-5	917	909	9E	1598	N910XJ	JFK	DTW	101	509	7	0	2023-10-29 07:00:00	Other
11844	8	30	1501	1505	-4	1705	1718	AA	525	N942AN	LGA	CLT	89	544	15	5	2023-08-30 15:00:00	CLT
11847	12	14	953	955	-2	1150	1210	NK	520	N690NK	EWR	CHS	94	628	9	55	2023-12-14 09:00:00	Other
11850	9	30	1802	1807	-5	2032	2057	UA	633	N805UA	EWR	DFW	176	1372	18	7	2023-09-30 18:00:00	Other
11859	7	21	1728	1731	-3	2010	2025	AA	193	N429AN	EWR	DFW	195	1372	17	31	2023-07-21 17:00:00	Other
11861	4	7	1643	1645	-2	1924	1959	B6	284	N659JB	LGA	PBI	143	1035	16	45	2023-04-07 16:00:00	Other
11862	6	1	1925	1929	-4	2121	2140	YX	1348	N424YX	LGA	CVG	85	585	19	29	2023-06-01 19:00:00	Other
11867	6	4	1913	1915	-2	2205	2237	DL	155	N195DN	JFK	LAX	300	2475	19	15	2023-06-04 19:00:00	LAX
11870	7	25	803	806	-3	1011	1015	B6	386	N206JB	JFK	CHS	98	636	8	6	2023-07-25 08:00:00	Other
11887	11	16	1139	1142	-3	1239	1315	YX	1904	N214JQ	LGA	DCA	46	214	11	42	2023-11-16 11:00:00	Other
11889	5	8	1455	1459	-4	1704	1727	DL	129	N365NB	JFK	MSP	157	1029	14	59	2023-05-08 14:00:00	Other
11892	1	25	830	835	-5	1101	1100	9E	1556	N918XJ	LGA	TYS	114	647	8	35	2023-01-25 08:00:00	Other
11894	11	26	1210	1215	-5	1428	1448	UA	688	N35271	LGA	DEN	235	1620	12	15	2023-11-26 12:00:00	Other
11895	11	17	828	830	-2	1124	1133	UA	134	N14016	EWR	LAX	321	2454	8	30	2023-11-17 08:00:00	LAX
11896	10	5	1305	1310	-5	1425	1435	YX	1746	N222JQ	LGA	DCA	61	214	13	10	2023-10-05 13:00:00	Other
11897	9	16	1403	1408	-5	1518	1533	YX	1092	N741YX	EWR	ORF	46	284	14	8	2023-09-16 14:00:00	Other
11899	1	24	1603	1607	-4	1853	1907	UA	283	N27263	EWR	MCO	137	937	16	7	2023-01-24 16:00:00	MCO
11900	5	5	618	623	-5	746	758	UA	923	N21723	EWR	RDU	62	416	6	23	2023-05-05 06:00:00	Other
11903	11	26	1623	1628	-5	1754	1803	YX	1135	N655RW	EWR	PIT	63	319	16	28	2023-11-26 16:00:00	Other
11909	11	23	927	929	-2	1017	1036	YX	1105	N745YX	EWR	ALB	30	143	9	29	2023-11-23 09:00:00	Other
11918	8	21	656	700	-4	938	955	DL	169	N169DZ	JFK	LAX	283	2475	7	0	2023-08-21 07:00:00	LAX
11932	7	24	1945	1950	-5	2158	2217	9E	1143	N913XJ	LGA	IND	101	660	19	50	2023-07-24 19:00:00	Other
11943	1	29	1106	1109	-3	1358	1418	UA	176	N17285	EWR	FLL	147	1065	11	9	2023-01-29 11:00:00	FLL
11946	12	10	757	800	-3	1037	1032	DL	888	N608AT	EWR	ATL	118	746	8	0	2023-12-10 08:00:00	ATL
11948	6	12	726	730	-4	855	910	DL	434	N135DQ	LGA	ORD	114	733	7	30	2023-06-12 07:00:00	ORD
11957	3	6	841	845	-4	950	1020	YX	1683	N214JQ	LGA	DCA	45	214	8	45	2023-03-06 08:00:00	Other
11975	4	3	1851	1853	-2	2104	2111	YX	970	N640RW	EWR	CHS	93	628	18	53	2023-04-03 18:00:00	Other
11977	6	15	1442	1445	-3	1546	1618	9E	1536	N308PQ	LGA	ORF	49	296	14	45	2023-06-15 14:00:00	Other
11984	7	11	853	858	-5	1028	1050	9E	1184	N292PQ	LGA	RDU	64	431	8	58	2023-07-11 08:00:00	Other
11985	12	29	2045	2050	-5	2300	2321	UA	853	N27270	EWR	MSY	162	1167	20	50	2023-12-29 20:00:00	Other
11986	9	23	956	959	-3	1251	1313	YX	1060	N731YX	EWR	AUS	202	1504	9	59	2023-09-23 09:00:00	Other
11988	8	3	1248	1250	-2	1514	1527	YX	1020	N412YX	LGA	OKC	186	1341	12	50	2023-08-03 12:00:00	Other
11990	4	13	636	640	-4	953	942	B6	759	N703JB	JFK	MIA	170	1089	6	40	2023-04-13 06:00:00	MIA
11996	10	18	1916	1920	-4	2100	2117	YX	1796	N239JQ	LGA	CMH	73	479	19	20	2023-10-18 19:00:00	Other
12004	4	20	1038	1040	-2	1157	1214	YX	1473	N236JQ	LGA	DCA	50	214	10	40	2023-04-20 10:00:00	Other
12005	2	11	1054	1059	-5	1346	1358	UA	269	N27263	EWR	PBI	148	1023	10	59	2023-02-11 10:00:00	Other
12015	1	30	546	550	-4	909	901	AA	685	N813NN	LGA	DFW	236	1389	5	50	2023-01-30 05:00:00	Other
12020	6	21	1126	1130	-4	1226	1239	YX	1375	N422YX	JFK	ORH	30	150	11	30	2023-06-21 11:00:00	Other
12033	10	25	1226	1229	-3	1336	1352	YX	1799	N209JQ	LGA	BOS	44	184	12	29	2023-10-25 12:00:00	BOS
12039	1	26	1128	1130	-2	1450	1440	DL	608	N723TW	JFK	FLL	167	1069	11	30	2023-01-26 11:00:00	FLL
12053	8	3	1527	1529	-2	1714	1737	YX	930	N754YX	EWR	MYR	78	550	15	29	2023-08-03 15:00:00	Other
12060	3	29	1656	1659	-3	1912	1914	YX	1195	N752YX	EWR	IND	114	645	16	59	2023-03-29 16:00:00	Other
12063	9	4	610	615	-5	819	836	UA	411	N17301	EWR	JAX	105	820	6	15	2023-09-04 06:00:00	Other
12066	8	25	1258	1300	-2	1451	1509	UA	715	N851UA	EWR	MSY	150	1167	13	0	2023-08-25 13:00:00	Other
12067	5	3	1040	1045	-5	1347	1347	NK	526	N687NK	EWR	FLL	150	1065	10	45	2023-05-03 10:00:00	FLL
12068	11	9	1540	1542	-2	1824	1841	UA	619	N33264	EWR	MCO	128	937	15	42	2023-11-09 15:00:00	MCO
12078	3	20	855	900	-5	956	1030	9E	1485	N478PX	LGA	PWM	45	269	9	0	2023-03-20 09:00:00	Other
12079	8	22	1411	1415	-4	1604	1602	AA	603	N831AW	LGA	RDU	84	431	14	15	2023-08-22 14:00:00	Other
12083	6	5	1806	1808	-2	2049	2130	DL	915	N335NW	JFK	AUS	193	1521	18	8	2023-06-05 18:00:00	Other
12085	4	4	1348	1350	-2	1507	1519	9E	1206	N920XJ	LGA	BUF	52	292	13	50	2023-04-04 13:00:00	Other
12087	12	5	1250	1255	-5	1558	1644	AA	951	N342SX	JFK	PHX	287	2153	12	55	2023-12-05 12:00:00	Other
12098	4	19	1958	2000	-2	2230	2250	B6	47	N537JT	JFK	PHX	308	2153	20	0	2023-04-19 20:00:00	Other
12101	12	7	628	630	-2	828	905	WN	103	N566WN	LGA	DEN	224	1620	6	30	2023-12-07 06:00:00	Other
12111	7	10	1311	1315	-4	1533	1529	9E	1129	N927XJ	JFK	CHS	116	636	13	15	2023-07-10 13:00:00	Other
12114	4	2	1549	1551	-2	1900	1920	DL	367	N372DN	JFK	MIA	148	1089	15	51	2023-04-02 15:00:00	MIA
12132	7	1	820	825	-5	1020	1023	9E	1253	N920XJ	LGA	STL	150	888	8	25	2023-07-01 08:00:00	Other
12144	1	28	1442	1445	-3	1728	1752	DL	435	N322DN	LGA	PBI	146	1035	14	45	2023-01-28 14:00:00	Other
12146	3	9	1553	1555	-2	1754	1840	DL	779	N344NB	JFK	MSY	164	1182	15	55	2023-03-09 15:00:00	Other
12151	12	14	1959	2001	-2	44	57	UA	553	N37516	EWR	SJU	199	1608	20	1	2023-12-14 20:00:00	Other
12162	4	14	1924	1928	-4	2157	2233	UA	458	N897UA	EWR	IAH	186	1400	19	28	2023-04-14 19:00:00	Other
12163	10	4	906	910	-4	1211	1216	UA	914	N17312	EWR	MIA	141	1085	9	10	2023-10-04 09:00:00	MIA
12164	9	28	1428	1430	-2	1602	1614	AA	192	N940NN	LGA	ORD	108	733	14	30	2023-09-28 14:00:00	ORD
12166	6	23	800	805	-5	1002	1009	AA	607	N873NN	EWR	CLT	88	529	8	5	2023-06-23 08:00:00	CLT
12172	4	11	750	755	-5	1136	1156	UA	715	N76065	EWR	SJU	201	1608	7	55	2023-04-11 07:00:00	Other
12178	5	1	912	915	-3	1028	1040	9E	1549	N315PQ	JFK	ORF	54	290	9	15	2023-05-01 09:00:00	Other
12183	8	25	925	928	-3	1239	1228	AA	291	N112AN	JFK	SNA	315	2454	9	28	2023-08-25 09:00:00	Other
12188	12	20	1754	1759	-5	1912	1939	9E	1606	N915XJ	LGA	BUF	49	292	17	59	2023-12-20 17:00:00	Other
12192	3	10	806	810	-4	1039	1050	DL	354	N775DE	JFK	DEN	238	1626	8	10	2023-03-10 08:00:00	Other
12193	4	10	655	659	-4	820	831	AA	305	N866NN	EWR	ORD	106	719	6	59	2023-04-10 06:00:00	ORD
12205	6	18	755	800	-5	1001	1014	UA	881	N27292	EWR	DEN	206	1605	8	0	2023-06-18 08:00:00	Other
12208	3	23	802	805	-3	946	947	9E	1497	N314PQ	JFK	BUF	63	301	8	5	2023-03-23 08:00:00	Other
12210	4	16	1706	1710	-4	1846	1849	YX	1526	N815MD	LGA	BNA	128	764	17	10	2023-04-16 17:00:00	Other
12213	9	16	2135	2140	-5	2245	2302	UA	261	N16713	EWR	MKE	105	725	21	40	2023-09-16 21:00:00	Other
12214	6	16	755	800	-5	1018	1030	DL	341	N118DY	LGA	ATL	113	762	8	0	2023-06-16 08:00:00	ATL
12215	1	31	1103	1107	-4	1405	1418	UA	553	N78448	EWR	MIA	150	1085	11	7	2023-01-31 11:00:00	MIA
12217	9	28	1237	1242	-5	1348	1408	9E	1623	N915XJ	LGA	BTV	48	258	12	42	2023-09-28 12:00:00	Other
12222	11	22	827	830	-3	1034	1104	YX	1286	N425YX	JFK	CVG	108	589	8	30	2023-11-22 08:00:00	Other
12229	11	22	2056	2100	-4	2325	21	AA	52	N102NN	JFK	LAX	309	2475	21	0	2023-11-22 21:00:00	LAX
12230	2	6	732	735	-3	1035	1049	DL	448	N333DX	JFK	FLL	144	1069	7	35	2023-02-06 07:00:00	FLL
12248	1	12	1353	1355	-2	1628	1637	NK	420	N941NK	EWR	LAS	306	2227	13	55	2023-01-12 13:00:00	Other
12249	3	29	1257	1300	-3	1457	1502	AA	639	N154UW	LGA	CLT	87	544	13	0	2023-03-29 13:00:00	CLT
12259	5	25	1655	1700	-5	1848	1858	9E	1433	N306PQ	LGA	CLE	70	419	17	0	2023-05-25 17:00:00	Other
12263	8	2	1454	1459	-5	1709	1719	YX	1015	N119HQ	JFK	IND	96	665	14	59	2023-08-02 14:00:00	Other
12267	4	3	945	950	-5	1142	1213	9E	1227	N478PX	LGA	GRR	102	618	9	50	2023-04-03 09:00:00	Other
12275	9	6	1856	1900	-4	2107	2133	DL	198	N331DN	LGA	ATL	100	762	19	0	2023-09-06 19:00:00	ATL
12278	6	9	1225	1229	-4	1334	1341	B6	891	N273JB	LGA	ACK	43	202	12	29	2023-06-09 12:00:00	Other
12283	6	30	945	950	-5	1141	1206	9E	1672	N319PQ	JFK	IND	95	665	9	50	2023-06-30 09:00:00	Other
12289	11	10	827	829	-2	1005	1005	9E	1492	N908XJ	LGA	MKE	123	738	8	29	2023-11-10 08:00:00	Other
12290	9	12	2127	2130	-3	2307	2302	9E	1557	N915XJ	LGA	CHO	59	305	21	30	2023-09-12 21:00:00	Other
12296	8	22	926	930	-4	1055	1052	UA	543	N76288	EWR	BOS	54	200	9	30	2023-08-22 09:00:00	BOS
12300	5	18	2055	2100	-5	15	54	AA	55	N116AN	JFK	SFO	341	2586	21	0	2023-05-18 21:00:00	Other
12328	6	28	1531	1536	-5	1712	1735	9E	1504	N314PQ	LGA	ILM	75	500	15	36	2023-06-28 15:00:00	Other
12329	7	3	1037	1040	-3	1242	1300	WN	791	N7731A	LGA	ATL	109	762	10	40	2023-07-03 10:00:00	ATL
12332	12	14	2250	2255	-5	9	17	B6	61	N284JB	JFK	BTV	52	266	22	55	2023-12-14 22:00:00	Other
12334	8	24	1349	1354	-5	1520	1534	9E	1174	N341PQ	JFK	BGR	63	382	13	54	2023-08-24 13:00:00	Other
12335	8	12	733	735	-2	1025	1026	DL	390	N381DZ	JFK	MCO	148	944	7	35	2023-08-12 07:00:00	MCO
12341	1	29	1135	1140	-5	1357	1403	YX	1433	N438YX	LGA	DTW	109	502	11	40	2023-01-29 11:00:00	Other
12344	10	18	1731	1735	-4	2028	2042	UA	626	N47284	EWR	RSW	146	1068	17	35	2023-10-18 17:00:00	Other
12346	1	29	747	751	-4	1040	1027	UA	919	N17122	EWR	DEN	262	1605	7	51	2023-01-29 07:00:00	Other
12351	5	12	631	635	-4	743	810	9E	1307	N479PX	LGA	PIT	54	335	6	35	2023-05-12 06:00:00	Other
12356	8	2	1111	1116	-5	1247	1309	9E	1257	N134EV	LGA	RDU	68	431	11	16	2023-08-02 11:00:00	Other
12361	9	28	1939	1942	-3	2202	2220	9E	1463	N306PQ	JFK	SAV	105	718	19	42	2023-09-28 19:00:00	Other
12363	10	12	930	935	-5	1241	1232	B6	302	N568JB	EWR	MCO	168	937	9	35	2023-10-12 09:00:00	MCO
12367	7	9	1829	1833	-4	2242	2138	UA	730	N827UA	EWR	PDX	331	2434	18	33	2023-07-09 18:00:00	Other
12381	4	10	1757	1800	-3	2049	2138	DL	253	N118DY	JFK	SLC	259	1990	18	0	2023-04-10 18:00:00	Other
12403	12	1	626	630	-4	928	944	AA	63	N306SW	JFK	MIA	155	1089	6	30	2023-12-01 06:00:00	MIA
12408	4	18	838	840	-2	1047	1114	DL	498	N712TW	JFK	ATL	108	760	8	40	2023-04-18 08:00:00	ATL
12409	3	24	931	935	-4	1107	1108	YX	1683	N218JQ	LGA	DCA	53	214	9	35	2023-03-24 09:00:00	Other
12410	11	15	822	825	-3	1015	1004	YX	1327	N431YX	LGA	CLE	76	419	8	25	2023-11-15 08:00:00	Other
12423	9	30	1937	1942	-5	2120	2157	UA	431	N455UA	EWR	MCI	139	1092	19	42	2023-09-30 19:00:00	Other
12424	2	11	727	730	-3	940	1023	DL	182	N397DA	LGA	DEN	225	1620	7	30	2023-02-11 07:00:00	Other
12426	1	31	1147	1151	-4	1357	1359	YX	1175	N731YX	EWR	MEM	170	946	11	51	2023-01-31 11:00:00	Other
12429	2	10	955	1000	-5	1338	1359	YX	1245	N821MD	LGA	EYW	193	1207	10	0	2023-02-10 10:00:00	Other
12432	11	15	1255	1300	-5	1427	1458	YX	1304	N126HQ	LGA	STL	133	888	13	0	2023-11-15 13:00:00	Other
12435	6	15	938	943	-5	1104	1140	9E	1721	N600LR	LGA	STL	120	888	9	43	2023-06-15 09:00:00	Other
12438	2	22	2132	2135	-3	2347	2349	UA	235	N852UA	EWR	CVG	105	569	21	35	2023-02-22 21:00:00	Other
12446	6	12	1250	1255	-5	1409	1430	WN	354	N8743K	LGA	STL	122	888	12	55	2023-06-12 12:00:00	Other
12455	4	21	2155	2200	-5	2313	2332	YX	1085	N127HQ	LGA	RIC	55	292	22	0	2023-04-21 22:00:00	Other
12462	3	18	1850	1855	-5	2200	2212	NK	1025	N944NK	LGA	FLL	156	1076	18	55	2023-03-18 18:00:00	FLL
12469	1	28	1458	1500	-2	1859	1854	DL	417	N846DN	JFK	PHX	316	2153	15	0	2023-01-28 15:00:00	Other
12472	8	5	2130	2135	-5	2249	2319	YX	1027	N119HQ	JFK	DCA	46	213	21	35	2023-08-05 21:00:00	Other
12473	6	15	1255	1259	-4	1519	1458	NK	517	N605NK	LGA	MYR	81	563	12	59	2023-06-15 12:00:00	Other
12481	6	25	1359	1402	-3	1742	1623	B6	754	N779JB	LGA	DEN	236	1620	14	2	2023-06-25 14:00:00	Other
12483	2	21	925	930	-5	1039	1057	9E	1399	N691CA	JFK	PWM	45	273	9	30	2023-02-21 09:00:00	Other
12512	7	13	1553	1555	-2	1913	1937	B6	215	N992JB	JFK	SFO	349	2586	15	55	2023-07-13 15:00:00	Other
12522	1	24	625	630	-5	800	814	B6	464	N337JB	JFK	ORD	126	740	6	30	2023-01-24 06:00:00	ORD
12523	1	28	1025	1030	-5	1242	1251	9E	1592	N306PQ	JFK	SAV	110	718	10	30	2023-01-28 10:00:00	Other
12526	2	6	839	842	-3	1052	1115	YX	981	N643RW	EWR	CVG	93	569	8	42	2023-02-06 08:00:00	Other
12527	7	28	1647	1650	-3	1801	1833	YX	1416	N209JQ	LGA	BUF	49	292	16	50	2023-07-28 16:00:00	Other
12528	6	10	955	1000	-5	1147	1201	YX	1331	N412YX	LGA	GSP	86	610	10	0	2023-06-10 10:00:00	Other
12544	11	11	1142	1145	-3	1433	1440	DL	590	N360DN	JFK	MCO	141	944	11	45	2023-11-11 11:00:00	MCO
12546	3	22	1536	1540	-4	1828	1852	UA	822	N649UA	EWR	IAH	198	1400	15	40	2023-03-22 15:00:00	Other
12549	4	11	1300	1305	-5	1428	1454	DL	437	N136DQ	LGA	ORD	105	733	13	5	2023-04-11 13:00:00	ORD
12572	11	25	1555	1600	-5	1826	1840	DL	174	N302DN	LGA	ATL	121	762	16	0	2023-11-25 16:00:00	ATL
12573	8	1	1926	1929	-3	2058	2144	9E	1215	N272PQ	JFK	RDU	68	427	19	29	2023-08-01 19:00:00	Other
12577	2	26	724	729	-5	1025	1041	UA	685	N24702	LGA	IAH	210	1416	7	29	2023-02-26 07:00:00	Other
12586	5	30	1748	1750	-2	2040	2101	B6	753	N556JB	JFK	PBI	139	1028	17	50	2023-05-30 17:00:00	Other
12587	9	27	1614	1619	-5	1725	1753	YX	1921	N823MD	LGA	DCA	40	214	16	19	2023-09-27 16:00:00	Other
12603	6	6	1418	1421	-3	1626	1700	YX	1879	N220JQ	JFK	SAV	105	718	14	21	2023-06-06 14:00:00	Other
12608	5	16	656	700	-4	803	816	YX	1638	N243JQ	EWR	BOS	44	200	7	0	2023-05-16 07:00:00	BOS
12609	12	6	1155	1159	-4	1352	1400	9E	1430	N329PQ	LGA	ILM	73	500	11	59	2023-12-06 11:00:00	Other
12619	8	2	2027	2030	-3	2232	2248	YX	926	N756YX	EWR	GRR	93	605	20	30	2023-08-02 20:00:00	Other
12630	11	7	1353	1358	-5	1540	1615	9E	1605	N927XJ	LGA	CAE	90	617	13	58	2023-11-07 13:00:00	Other
12636	7	8	1306	1310	-4	1409	1416	B6	481	N354JB	JFK	MVY	38	173	13	10	2023-07-08 13:00:00	Other
12643	4	6	1752	1755	-3	2013	1920	YX	1518	N810MD	LGA	DCA	105	214	17	55	2023-04-06 17:00:00	Other
12647	8	15	1057	1100	-3	1351	1411	DL	409	N3760C	JFK	MIA	155	1089	11	0	2023-08-15 11:00:00	MIA
12650	7	30	2157	2200	-3	2328	2341	YX	1026	N406YX	LGA	RDU	72	431	22	0	2023-07-30 22:00:00	Other
12656	12	28	725	730	-5	926	1023	UA	211	N27283	EWR	LAS	267	2227	7	30	2023-12-28 07:00:00	Other
12657	5	10	1419	1422	-3	1632	1640	UA	782	N28478	EWR	DEN	223	1605	14	22	2023-05-10 14:00:00	Other
12664	3	8	631	635	-4	944	956	AA	921	N917AN	LGA	MIA	152	1096	6	35	2023-03-08 06:00:00	MIA
12665	4	20	1136	1140	-4	1503	1455	DL	210	N176DN	JFK	LAX	344	2475	11	40	2023-04-20 11:00:00	LAX
12672	10	12	757	800	-3	1106	1105	B6	764	N988JT	JFK	LAX	340	2475	8	0	2023-10-12 08:00:00	LAX
12677	5	2	2211	2215	-4	54	131	DL	101	N827MH	JFK	LAX	322	2475	22	15	2023-05-02 22:00:00	LAX
12692	4	7	1053	1055	-2	1301	1250	WN	862	N208WN	LGA	STL	150	888	10	55	2023-04-07 10:00:00	Other
12693	12	28	822	825	-3	1209	1140	NK	571	N691NK	EWR	MIA	174	1085	8	25	2023-12-28 08:00:00	MIA
12695	4	17	756	800	-4	1050	1120	DL	182	N832MH	JFK	LAX	326	2475	8	0	2023-04-17 08:00:00	LAX
12703	7	17	708	710	-2	954	1008	DL	261	N352NB	LGA	TPA	140	1010	7	10	2023-07-17 07:00:00	Other
12708	12	12	555	600	-5	816	843	DL	284	N332DN	LGA	ATL	112	762	6	0	2023-12-12 06:00:00	ATL
12719	10	24	845	848	-3	1053	1124	9E	1618	N926XJ	LGA	SAV	103	722	8	48	2023-10-24 08:00:00	Other
12720	2	15	755	800	-5	1045	1106	UA	171	N407UA	EWR	PBI	141	1023	8	0	2023-02-15 08:00:00	Other
12724	3	20	1222	1225	-3	1508	1514	UA	288	N17285	EWR	MCO	144	937	12	25	2023-03-20 12:00:00	MCO
12726	7	27	843	845	-2	1015	1027	DL	312	N115DU	LGA	ORD	108	733	8	45	2023-07-27 08:00:00	ORD
12729	8	13	1139	1142	-3	1353	1406	YX	974	N106HQ	JFK	IND	94	665	11	42	2023-08-13 11:00:00	Other
12751	1	7	1245	1250	-5	1534	1559	B6	42	N618JB	JFK	TPA	144	1005	12	50	2023-01-07 12:00:00	Other
12769	7	21	1554	1559	-5	1748	1757	YX	1030	N439YX	LGA	DTW	82	502	15	59	2023-07-21 15:00:00	Other
12792	1	9	2257	2259	-2	344	349	B6	332	N589JB	JFK	PSE	199	1617	22	59	2023-01-09 22:00:00	Other
12796	6	19	2154	2159	-5	2243	2256	9E	1586	N279PQ	LGA	BDL	29	101	21	59	2023-06-19 21:00:00	Other
12797	8	3	1625	1630	-5	2239	1940	NK	267	N668NK	LGA	FLL	NA	1076	16	30	2023-08-03 16:00:00	FLL
12800	6	15	756	800	-4	946	1011	UA	811	N13718	EWR	IND	87	645	8	0	2023-06-15 08:00:00	Other
12805	12	22	1154	1159	-5	1334	1359	YX	1746	N237JQ	LGA	CMH	73	479	11	59	2023-12-22 11:00:00	Other
12806	1	31	1116	1119	-3	1411	1421	UA	284	N13113	EWR	PBI	142	1023	11	19	2023-01-31 11:00:00	Other
12814	9	19	1655	1700	-5	1906	1908	9E	1432	N187GJ	JFK	DTW	87	509	17	0	2023-09-19 17:00:00	Other
12826	8	8	755	800	-5	1049	1047	B6	633	N929JB	JFK	LAX	324	2475	8	0	2023-08-08 08:00:00	LAX
12828	3	17	1146	1150	-4	1340	1400	YX	1363	N109HQ	LGA	DTW	87	502	11	50	2023-03-17 11:00:00	Other
12836	11	4	655	700	-5	838	846	UA	844	N78506	EWR	ORD	121	719	7	0	2023-11-04 07:00:00	ORD
12839	3	19	604	609	-5	919	915	NK	52	N680NK	LGA	FLL	170	1076	6	9	2023-03-19 06:00:00	FLL
12842	8	29	1927	1930	-3	2255	2236	UA	645	N17301	EWR	FLL	162	1065	19	30	2023-08-29 19:00:00	FLL
12849	8	30	1455	1459	-4	1625	1644	UA	547	N440UA	EWR	RDU	68	416	14	59	2023-08-30 14:00:00	Other
12852	5	21	1909	1912	-3	2150	2222	DL	428	N329NB	LGA	PBI	134	1035	19	12	2023-05-21 19:00:00	Other
12863	3	20	1454	1459	-5	1646	1650	NK	24	N515NK	EWR	MYR	88	550	14	59	2023-03-20 14:00:00	Other
12871	8	10	2024	2029	-5	2330	2357	AS	17	N538AS	JFK	SFO	338	2586	20	29	2023-08-10 20:00:00	Other
12875	2	6	1350	1355	-5	1632	1706	B6	698	N558JB	JFK	IAH	195	1417	13	55	2023-02-06 13:00:00	Other
12880	5	2	1355	1359	-4	1522	1520	9E	1483	N600LR	JFK	SYR	44	209	13	59	2023-05-02 13:00:00	Other
12885	8	2	957	1000	-3	1109	1130	DL	324	N132DU	LGA	BOS	36	184	10	0	2023-08-02 10:00:00	BOS
12889	8	17	1924	1929	-5	2149	2203	9E	1211	N183GJ	JFK	MSP	152	1029	19	29	2023-08-17 19:00:00	Other
12890	12	5	855	900	-5	1140	1136	9E	1396	N186GJ	LGA	SAV	120	722	9	0	2023-12-05 09:00:00	Other
12897	9	12	1026	1030	-4	1315	1328	B6	191	N993JE	JFK	LAX	330	2475	10	30	2023-09-12 10:00:00	LAX
12900	6	5	1055	1100	-5	1344	1412	AA	275	N906AN	JFK	MIA	145	1089	11	0	2023-06-05 11:00:00	MIA
12903	7	28	920	925	-5	1209	1241	DL	741	N702TW	JFK	SLC	265	1990	9	25	2023-07-28 09:00:00	Other
12907	8	19	941	946	-5	1148	1200	UA	698	N33262	LGA	DEN	204	1620	9	46	2023-08-19 09:00:00	Other
12914	6	21	1939	1943	-4	2245	2257	DL	362	N3757D	LGA	MIA	153	1096	19	43	2023-06-21 19:00:00	MIA
12916	9	27	1056	1100	-4	1219	1225	YX	1932	N230JQ	LGA	BOS	36	184	11	0	2023-09-27 11:00:00	BOS
12920	10	29	557	600	-3	914	917	B6	38	N987JT	JFK	LAX	356	2475	6	0	2023-10-29 06:00:00	LAX
12921	9	16	856	900	-4	1018	1038	B6	782	N358JB	LGA	BNA	109	764	9	0	2023-09-16 09:00:00	Other
12928	7	1	922	925	-3	1115	1142	YX	949	N762YX	EWR	HHH	93	687	9	25	2023-07-01 09:00:00	Other
12931	10	4	1356	1359	-3	1646	1655	UA	930	N13718	LGA	IAH	198	1416	13	59	2023-10-04 13:00:00	Other
12935	3	20	1158	1200	-2	1346	1407	YX	1274	N416YX	LGA	MEM	146	963	12	0	2023-03-20 12:00:00	Other
12941	5	10	857	859	-2	1144	1211	UA	399	N57299	EWR	MIA	134	1085	8	59	2023-05-10 08:00:00	MIA
12942	11	17	1144	1149	-5	1302	1325	YX	1767	N878RW	LGA	BGR	58	378	11	49	2023-11-17 11:00:00	Other
12946	8	6	925	930	-5	1134	1200	YX	1351	N880RW	LGA	HHH	103	701	9	30	2023-08-06 09:00:00	Other
12947	10	26	731	735	-4	1004	1038	DL	754	N377DA	JFK	PBI	129	1028	7	35	2023-10-26 07:00:00	Other
12951	12	26	1922	1925	-3	2131	2241	DL	139	N543DE	JFK	LAS	285	2248	19	25	2023-12-26 19:00:00	Other
12952	11	30	1137	1140	-3	1323	1326	OO	1176	N296SY	JFK	ORD	124	740	11	40	2023-11-30 11:00:00	ORD
12955	6	8	1354	1358	-4	1543	1604	YX	1085	N732YX	EWR	GRR	88	605	13	58	2023-06-08 13:00:00	Other
12956	4	25	625	630	-5	731	745	UA	477	N13750	EWR	BOS	35	200	6	30	2023-04-25 06:00:00	BOS
12957	5	19	1911	1915	-4	2040	2106	OO	1498	N128SY	LGA	ORD	118	733	19	15	2023-05-19 19:00:00	ORD
12963	12	8	1727	1729	-2	2034	2046	AA	896	N987NN	JFK	MIA	159	1089	17	29	2023-12-08 17:00:00	MIA
12966	4	13	1013	1015	-2	1132	1157	9E	1310	N930XJ	LGA	ORF	48	296	10	15	2023-04-13 10:00:00	Other
12983	9	17	1056	1059	-3	1248	1316	YX	1121	N722YX	EWR	IND	97	645	10	59	2023-09-17 10:00:00	Other
12984	6	22	1124	1129	-5	1424	1436	UA	756	N493UA	EWR	MIA	157	1085	11	29	2023-06-22 11:00:00	MIA
12989	4	20	1913	1915	-2	2054	2111	UA	501	N437UA	EWR	RDU	61	416	19	15	2023-04-20 19:00:00	Other
12996	4	11	953	955	-2	1225	1255	B6	81	N583JB	JFK	IAH	173	1417	9	55	2023-04-11 09:00:00	Other
13006	9	22	941	946	-5	1038	1047	9E	1703	N176PQ	LGA	BDL	22	101	9	46	2023-09-22 09:00:00	Other
13008	11	30	805	810	-5	1013	1017	UA	219	N443UA	EWR	GSP	97	594	8	10	2023-11-30 08:00:00	Other
13010	6	22	1653	1655	-2	1926	1955	AS	87	N921VA	EWR	LAX	303	2454	16	55	2023-06-22 16:00:00	LAX
13014	8	14	1625	1629	-4	1919	1935	AA	744	N780AN	JFK	MIA	137	1089	16	29	2023-08-14 16:00:00	MIA
13015	9	28	726	729	-3	1026	1031	DL	790	N3769L	JFK	PBI	149	1028	7	29	2023-09-28 07:00:00	Other
13021	8	15	805	810	-5	1028	1036	B6	759	N571JB	LGA	ATL	111	762	8	10	2023-08-15 08:00:00	ATL
13050	1	10	835	840	-5	1100	1120	B6	28	N636JB	JFK	MSY	162	1182	8	40	2023-01-10 08:00:00	Other
13051	12	3	1730	1735	-5	1924	1939	NK	47	N528NK	LGA	DTW	88	502	17	35	2023-12-03 17:00:00	Other
13057	5	23	726	730	-4	956	935	9E	1405	N300PQ	LGA	CHS	92	641	7	30	2023-05-23 07:00:00	Other
13058	11	7	2149	2154	-5	2255	2300	YX	1083	N653RW	EWR	ALB	32	143	21	54	2023-11-07 21:00:00	Other
13065	7	2	1454	1459	-5	1725	1746	DL	781	N707TW	JFK	ATL	107	760	14	59	2023-07-02 14:00:00	ATL
13066	10	26	1508	1510	-2	1839	1819	DL	190	N197DN	JFK	LAX	340	2475	15	10	2023-10-26 15:00:00	LAX
13085	12	1	755	800	-5	859	923	B6	684	N3142J	JFK	BOS	42	187	8	0	2023-12-01 08:00:00	BOS
13096	10	7	1821	1825	-4	2204	2136	AA	130	N818NN	JFK	MIA	172	1089	18	25	2023-10-07 18:00:00	MIA
13098	3	29	1926	1929	-3	2219	2232	DL	433	N341DN	LGA	MCO	141	950	19	29	2023-03-29 19:00:00	MCO
13102	8	17	642	646	-4	835	852	UA	672	N820UA	EWR	IND	89	645	6	46	2023-08-17 06:00:00	Other
13103	11	27	655	700	-5	1033	1020	DL	285	N776DE	JFK	RSW	170	1074	7	0	2023-11-27 07:00:00	Other
13107	5	16	1324	1329	-5	1533	1547	9E	1521	N602LR	LGA	IND	99	660	13	29	2023-05-16 13:00:00	Other
13109	8	19	1028	1030	-2	1313	1324	UA	313	N27258	EWR	TPA	135	997	10	30	2023-08-19 10:00:00	Other
13124	2	14	941	945	-4	1107	1135	WN	91	N268WN	LGA	BNA	119	764	9	45	2023-02-14 09:00:00	Other
13129	11	12	1724	1728	-4	2054	2030	UA	881	N17229	EWR	PBI	145	1023	17	28	2023-11-12 17:00:00	Other
13138	10	1	2108	2110	-2	2247	2309	YX	1268	N446YX	LGA	MEM	121	963	21	10	2023-10-01 21:00:00	Other
13141	4	17	1328	1330	-2	1647	1716	B6	525	N982JB	JFK	SFO	357	2586	13	30	2023-04-17 13:00:00	Other
13148	4	24	834	839	-5	1132	1156	UA	425	N17719	EWR	SNA	331	2434	8	39	2023-04-24 08:00:00	Other
13153	2	5	1432	1436	-4	1734	1736	DL	465	N302DN	LGA	MCO	155	950	14	36	2023-02-05 14:00:00	MCO
13154	7	23	1425	1430	-5	1545	1612	AA	186	N856NN	LGA	ORD	106	733	14	30	2023-07-23 14:00:00	ORD
13162	1	24	2140	2145	-5	55	56	B6	249	N561JB	LGA	FLL	176	1076	21	45	2023-01-24 21:00:00	FLL
13164	9	11	908	910	-2	1204	1214	B6	220	N662JB	JFK	FLL	150	1069	9	10	2023-09-11 09:00:00	FLL
13170	8	16	856	900	-4	1211	1210	AS	109	N549AS	EWR	SFO	313	2565	9	0	2023-08-16 09:00:00	Other
13172	5	18	1753	1755	-2	1909	1927	YX	1650	N209JQ	LGA	DCA	53	214	17	55	2023-05-18 17:00:00	Other
13178	8	5	1748	1750	-2	2024	2032	YX	1023	N413YX	LGA	OKC	194	1341	17	50	2023-08-05 17:00:00	Other
13181	2	19	1257	1300	-3	1406	1433	9E	1386	N695CA	LGA	BGR	55	378	13	0	2023-02-19 13:00:00	Other
13190	8	4	1052	1055	-3	1341	1414	DL	347	N322NB	LGA	RSW	144	1080	10	55	2023-08-04 10:00:00	Other
13191	12	22	726	730	-4	1022	1025	DL	526	N108DN	LGA	MCO	132	950	7	30	2023-12-22 07:00:00	MCO
13195	1	20	625	630	-5	811	820	YX	1902	N210JQ	LGA	RDU	76	431	6	30	2023-01-20 06:00:00	Other
13198	7	14	1556	1559	-3	1947	2000	DL	280	N710TW	JFK	SFO	368	2586	15	59	2023-07-14 15:00:00	Other
13202	9	1	1551	1555	-4	1911	1917	AA	98	N927NN	JFK	MIA	161	1089	15	55	2023-09-01 15:00:00	MIA
13207	3	6	1615	1620	-5	1841	1852	9E	1456	N330PQ	LGA	AVL	94	599	16	20	2023-03-06 16:00:00	Other
13209	3	17	1945	1950	-5	2159	2215	YX	1680	N882RW	LGA	IND	113	660	19	50	2023-03-17 19:00:00	Other
13210	6	19	1053	1056	-3	1349	1420	B6	582	N947JB	JFK	SFO	324	2586	10	56	2023-06-19 10:00:00	Other
13213	2	28	1345	1350	-5	1524	1525	9E	1474	N604LR	LGA	BUF	57	292	13	50	2023-02-28 13:00:00	Other
13214	8	14	802	805	-3	1145	1209	DL	560	N831DN	JFK	SJU	188	1598	8	5	2023-08-14 08:00:00	Other
13217	1	8	737	740	-3	1054	1059	UA	308	N33203	EWR	IAH	229	1400	7	40	2023-01-08 07:00:00	Other
13230	6	4	911	915	-4	1033	1043	YX	1806	N203JQ	JFK	DCA	48	213	9	15	2023-06-04 09:00:00	Other
13238	10	25	1425	1430	-5	1537	1553	YX	1293	N436YX	LGA	BUF	57	292	14	30	2023-10-25 14:00:00	Other
13245	1	28	1706	1710	-4	1835	1845	9E	1686	N604LR	JFK	BUF	59	301	17	10	2023-01-28 17:00:00	Other
13258	11	30	558	600	-2	723	718	YX	1891	N232JQ	LGA	BOS	41	184	6	0	2023-11-30 06:00:00	BOS
13264	6	16	858	900	-2	1200	1235	DL	99	N174DZ	JFK	SFO	333	2586	9	0	2023-06-16 09:00:00	Other
13269	10	5	2125	2128	-3	2247	2309	YX	1061	N763YX	EWR	MSN	114	799	21	28	2023-10-05 21:00:00	Other
13277	1	7	1455	1500	-5	1647	1717	YX	1751	N238JQ	LGA	CLT	84	544	15	0	2023-01-07 15:00:00	CLT
13280	9	5	2155	2159	-4	2351	2357	YX	1142	N761YX	EWR	ILM	70	488	21	59	2023-09-05 21:00:00	Other
13299	3	8	917	920	-3	1042	1115	9E	1342	N330PQ	LGA	PIT	57	335	9	20	2023-03-08 09:00:00	Other
13306	9	14	912	915	-3	1118	1058	DL	438	N124DU	LGA	ORD	114	733	9	15	2023-09-14 09:00:00	ORD
13308	9	20	1653	1657	-4	1923	1958	AA	983	N816NN	LGA	DFW	188	1389	16	57	2023-09-20 16:00:00	Other
13309	9	14	755	800	-5	957	1016	9E	1639	N292PQ	JFK	CHS	94	636	8	0	2023-09-14 08:00:00	Other
13310	2	5	724	729	-5	838	905	9E	1462	N908XJ	LGA	BUF	55	292	7	29	2023-02-05 07:00:00	Other
13322	9	20	2157	2159	-2	2254	2310	DL	946	N141DU	LGA	BOS	37	184	21	59	2023-09-20 21:00:00	BOS
13323	4	15	1715	1720	-5	2143	2038	AA	868	N343RY	JFK	AUS	273	1521	17	20	2023-04-15 17:00:00	Other
13331	2	3	827	830	-3	1035	1040	B6	65	N198JB	JFK	DTW	95	509	8	30	2023-02-03 08:00:00	Other
13332	9	19	1035	1040	-5	1224	1230	YX	1383	N427YX	JFK	RDU	79	427	10	40	2023-09-19 10:00:00	Other
13334	2	19	1006	1010	-4	1332	1400	DL	298	N183DN	JFK	SFO	354	2586	10	10	2023-02-19 10:00:00	Other
13336	3	10	1727	1729	-2	2100	2047	UA	563	N27269	EWR	SAN	350	2425	17	29	2023-03-10 17:00:00	Other
13341	4	19	2231	2235	-4	32	6	YX	1452	N234JQ	JFK	PWM	48	273	22	35	2023-04-19 22:00:00	Other
13342	6	4	1257	1300	-3	1542	1548	UA	579	N12125	EWR	MCO	137	937	13	0	2023-06-04 13:00:00	MCO
13348	1	27	726	730	-4	944	954	B6	976	N644JB	JFK	CHS	114	636	7	30	2023-01-27 07:00:00	Other
13355	11	19	1645	1650	-5	1815	1850	9E	1747	N932XJ	LGA	STL	131	888	16	50	2023-11-19 16:00:00	Other
13356	11	8	1116	1120	-4	1303	1319	9E	1750	N232PQ	LGA	CMH	78	479	11	20	2023-11-08 11:00:00	Other
13370	8	8	1043	1048	-5	1308	1310	UA	399	N39726	EWR	JAX	115	820	10	48	2023-08-08 10:00:00	Other
13372	2	21	1451	1455	-4	1648	1700	YX	1529	N234JQ	JFK	CMH	94	483	14	55	2023-02-21 14:00:00	Other
13373	1	22	2045	2050	-5	2237	2253	YX	1787	N235JQ	JFK	CMH	91	483	20	50	2023-01-22 20:00:00	Other
13395	8	11	1710	1715	-5	1813	1842	B6	321	N304JB	LGA	BOS	38	184	17	15	2023-08-11 17:00:00	BOS
13397	2	7	1803	1805	-2	1955	2013	UA	79	N820UA	EWR	CLT	82	529	18	5	2023-02-07 18:00:00	CLT
13400	9	8	1225	1229	-4	1327	1344	DL	577	N102DU	JFK	BOS	40	187	12	29	2023-09-08 12:00:00	BOS
13406	11	16	1924	1929	-5	2110	2139	AA	472	N9013A	JFK	CLT	86	541	19	29	2023-11-16 19:00:00	CLT
13408	2	4	952	955	-3	1207	1215	9E	1358	N691CA	JFK	IND	109	665	9	55	2023-02-04 09:00:00	Other
13416	1	26	1725	1729	-4	2115	2056	AA	1052	N303RG	JFK	AUS	256	1521	17	29	2023-01-26 17:00:00	Other
13420	7	22	2201	2205	-4	2258	2331	9E	1238	N908XJ	JFK	ITH	37	189	22	5	2023-07-22 22:00:00	Other
13425	7	4	1121	1124	-3	1403	1443	DL	169	N868DN	JFK	SEA	310	2422	11	24	2023-07-04 11:00:00	Other
13434	8	10	1655	1700	-5	1838	1843	AA	794	N733UW	LGA	STL	135	888	17	0	2023-08-10 17:00:00	Other
13436	1	1	1820	1822	-2	2136	2134	AA	784	N949NN	EWR	DFW	208	1372	18	22	2023-01-01 18:00:00	Other
13440	11	10	1716	1720	-4	1843	1900	WN	1075	N920WN	LGA	MDW	128	725	17	20	2023-11-10 17:00:00	Other
13445	7	29	803	805	-2	1014	1003	AA	492	N812NN	EWR	CLT	84	529	8	5	2023-07-29 08:00:00	CLT
13449	12	15	555	600	-5	838	905	WN	1059	N8844Q	LGA	DAL	192	1381	6	0	2023-12-15 06:00:00	Other
13450	3	20	2045	2050	-5	2229	2248	9E	1600	N903XJ	LGA	GSO	77	461	20	50	2023-03-20 20:00:00	Other
13453	11	15	1702	1706	-4	1901	1931	NK	271	N671NK	EWR	IND	99	645	17	6	2023-11-15 17:00:00	Other
13459	3	9	1454	1459	-5	1627	1624	YX	1711	N213JQ	LGA	BOS	36	184	14	59	2023-03-09 14:00:00	BOS
13464	5	4	2156	2159	-3	2255	2308	DL	939	N109DU	LGA	BOS	37	184	21	59	2023-05-04 21:00:00	BOS
13465	10	5	950	953	-3	1143	1213	9E	1533	N480PX	LGA	GSP	92	610	9	53	2023-10-05 09:00:00	Other
13472	4	19	1920	1925	-5	2138	2156	YX	1152	N114HQ	LGA	XNA	163	1147	19	25	2023-04-19 19:00:00	Other
13482	4	12	1722	1725	-3	1927	2010	DL	892	N381DN	JFK	ATL	103	760	17	25	2023-04-12 17:00:00	ATL
13483	7	19	1852	1855	-3	2201	2200	AS	10	N954AK	JFK	SAN	310	2446	18	55	2023-07-19 18:00:00	Other
13486	5	12	1254	1259	-5	1439	1459	DL	766	N314NB	LGA	DTW	78	502	12	59	2023-05-12 12:00:00	Other
13487	5	3	948	950	-2	1055	1126	9E	1496	N929XJ	LGA	ROC	44	254	9	50	2023-05-03 09:00:00	Other
13511	10	21	701	705	-4	946	1015	DL	290	N393DA	JFK	RSW	144	1074	7	5	2023-10-21 07:00:00	Other
13517	9	22	1742	1747	-5	1853	1918	YX	1073	N726YX	EWR	BUF	46	282	17	47	2023-09-22 17:00:00	Other
13526	9	2	733	735	-2	1022	1037	DL	790	N3759	JFK	PBI	132	1028	7	35	2023-09-02 07:00:00	Other
13530	3	31	555	600	-5	839	859	UA	916	N897UA	LGA	IAH	203	1416	6	0	2023-03-31 06:00:00	Other
13537	12	24	2155	2159	-4	2333	2329	B6	28	N328JB	JFK	BUF	58	301	21	59	2023-12-24 21:00:00	Other
13543	6	8	2113	2115	-2	2243	2322	YX	1290	N433YX	JFK	RDU	69	427	21	15	2023-06-08 21:00:00	Other
13544	8	22	1106	1110	-4	1333	1420	DL	712	N927DZ	JFK	FLL	129	1069	11	10	2023-08-22 11:00:00	FLL
13546	12	18	1455	1459	-4	1628	1702	DL	602	N332NB	LGA	DTW	75	502	14	59	2023-12-18 14:00:00	Other
13547	6	2	1554	1559	-5	1725	1723	YX	1869	N860RW	LGA	ACK	44	202	15	59	2023-06-02 15:00:00	Other
13567	10	4	546	549	-3	823	853	AA	1	N108NN	JFK	LAX	316	2475	5	49	2023-10-04 05:00:00	LAX
13569	5	14	1921	1925	-4	2205	2150	YX	1249	N118HQ	LGA	XNA	160	1147	19	25	2023-05-14 19:00:00	Other
13573	11	12	707	710	-3	1124	1035	DL	309	N508DA	JFK	SEA	365	2422	7	10	2023-11-12 07:00:00	Other
13576	1	2	517	520	-3	756	818	UA	206	N29124	EWR	IAH	195	1400	5	20	2023-01-02 05:00:00	Other
13595	11	27	1156	1200	-4	1455	1510	B6	322	N579JB	JFK	SLC	272	1990	12	0	2023-11-27 12:00:00	Other
13612	7	6	1455	1459	-4	1647	1640	YX	1050	N137HQ	JFK	DCA	58	213	14	59	2023-07-06 14:00:00	Other
13616	8	25	1350	1354	-4	1520	1534	9E	1174	N325PQ	JFK	BGR	60	382	13	54	2023-08-25 13:00:00	Other
13617	4	15	1336	1340	-4	1703	1643	UA	719	N891UA	LGA	IAH	218	1416	13	40	2023-04-15 13:00:00	Other
13623	12	3	1536	1540	-4	1856	1846	DL	352	N306DN	LGA	MCO	150	950	15	40	2023-12-03 15:00:00	MCO
13635	11	28	955	959	-4	1115	1135	YX	1821	N202JQ	JFK	DCA	48	213	9	59	2023-11-28 09:00:00	Other
13640	8	25	555	600	-5	743	715	WN	462	N221WN	LGA	MDW	112	725	6	0	2023-08-25 06:00:00	Other
13661	9	11	1325	1329	-4	1634	1511	MQ	1032	N765ST	EWR	ORD	131	719	13	29	2023-09-11 13:00:00	ORD
13665	4	20	1410	1415	-5	1510	1516	B6	286	N354JB	JFK	ORH	30	150	14	15	2023-04-20 14:00:00	Other
13669	8	30	1757	1800	-3	1907	1931	YX	1364	N227JQ	LGA	BOS	44	184	18	0	2023-08-30 18:00:00	BOS
13679	8	7	1419	1423	-4	1538	1548	UA	477	N29717	EWR	BNA	113	748	14	23	2023-08-07 14:00:00	Other
13684	2	18	1025	1030	-5	1136	1146	YX	1490	N238JQ	JFK	BOS	45	187	10	30	2023-02-18 10:00:00	BOS
13688	7	5	1831	1836	-5	2038	2055	YX	1039	N420YX	LGA	OMA	168	1148	18	36	2023-07-05 18:00:00	Other
13698	3	24	925	929	-4	1233	1250	NK	1021	N673NK	LGA	MIA	155	1096	9	29	2023-03-24 09:00:00	MIA
13704	8	3	1701	1705	-4	2018	2010	NK	501	N968NK	EWR	FLL	177	1065	17	5	2023-08-03 17:00:00	FLL
13710	12	15	2110	2115	-5	2320	2308	9E	1355	N930XJ	JFK	RIC	56	288	21	15	2023-12-15 21:00:00	Other
13712	9	6	925	929	-4	1209	1246	DL	295	N851DN	JFK	SLC	263	1990	9	29	2023-09-06 09:00:00	Other
13717	1	24	1313	1315	-2	1442	1444	9E	1563	N607LR	JFK	BUF	62	301	13	15	2023-01-24 13:00:00	Other
13718	1	9	2246	2250	-4	2346	2358	YX	1761	N238JQ	JFK	BWI	36	184	22	50	2023-01-09 22:00:00	Other
13722	5	6	2131	2135	-4	2331	13	DL	496	N879DN	JFK	ATL	99	760	21	35	2023-05-06 21:00:00	ATL
13726	7	24	1857	1900	-3	2132	2118	YX	1049	N123HQ	LGA	XNA	158	1147	19	0	2023-07-24 19:00:00	Other
13731	12	2	2205	2210	-5	40	52	NK	573	N968NK	EWR	ATL	128	746	22	10	2023-12-02 22:00:00	ATL
13736	5	6	1505	1510	-5	1608	1631	9E	1283	N186PQ	LGA	SCE	40	208	15	10	2023-05-06 15:00:00	Other
13738	4	20	1255	1300	-5	1446	1505	AA	426	N187US	LGA	CLT	79	544	13	0	2023-04-20 13:00:00	CLT
13740	2	27	820	825	-5	1003	1039	9E	1438	N292PQ	LGA	ILM	80	500	8	25	2023-02-27 08:00:00	Other
13742	5	23	1122	1125	-3	1325	1400	UA	568	N69840	EWR	LAS	274	2227	11	25	2023-05-23 11:00:00	Other
13750	3	10	1106	1110	-4	1208	1219	OO	1235	N610CZ	EWR	BOS	42	200	11	10	2023-03-10 11:00:00	BOS
13751	11	15	558	600	-2	749	752	DL	747	N894AT	EWR	DTW	81	488	6	0	2023-11-15 06:00:00	Other
13755	5	24	1703	1708	-5	1845	1906	9E	1433	N485PX	LGA	CLE	70	419	17	8	2023-05-24 17:00:00	Other
13760	10	12	935	939	-4	1054	1106	YX	1114	N731YX	EWR	MHT	38	209	9	39	2023-10-12 09:00:00	Other
13764	2	15	700	705	-5	1151	1204	UA	574	N24736	EWR	STT	199	1634	7	5	2023-02-15 07:00:00	Other
13772	8	31	1923	1925	-2	2126	2151	9E	1199	N348PQ	JFK	DTW	83	509	19	25	2023-08-31 19:00:00	Other
13773	12	8	826	830	-4	1130	1217	AA	860	N113AN	JFK	SNA	345	2454	8	30	2023-12-08 08:00:00	Other
13777	11	25	2227	2229	-2	143	157	B6	655	N923JB	JFK	LAX	349	2475	22	29	2023-11-25 22:00:00	LAX
13780	6	6	1424	1429	-5	1735	1653	B6	744	N665JB	LGA	MSY	173	1183	14	29	2023-06-06 14:00:00	Other
13783	8	27	1749	1753	-4	2052	2049	UA	503	N69888	EWR	TPA	149	997	17	53	2023-08-27 17:00:00	Other
13787	6	3	1313	1315	-2	1546	1538	9E	1415	N925XJ	LGA	SAV	100	722	13	15	2023-06-03 13:00:00	Other
13788	11	27	1445	1449	-4	1705	1655	AA	105	N820NN	JFK	CLT	96	541	14	49	2023-11-27 14:00:00	CLT
13789	9	25	956	1000	-4	1206	1202	B6	60	N258JB	JFK	DTW	84	509	10	0	2023-09-25 10:00:00	Other
13791	11	28	1305	1310	-5	1429	1441	9E	1544	N187GJ	JFK	BGR	58	382	13	10	2023-11-28 13:00:00	Other
13795	5	10	756	800	-4	1140	1150	DL	305	N722TW	JFK	SFO	358	2586	8	0	2023-05-10 08:00:00	Other
13798	10	8	900	905	-5	1038	1111	DL	181	N117DX	LGA	DTW	75	502	9	5	2023-10-08 09:00:00	Other
13800	12	6	926	929	-3	1235	1259	B6	675	N661JB	LGA	RSW	156	1080	9	29	2023-12-06 09:00:00	Other
13810	7	1	636	640	-4	754	815	UA	255	N27271	EWR	CLE	59	404	6	40	2023-07-01 06:00:00	Other
13830	1	4	1656	1659	-3	2020	2024	AA	687	N945AN	LGA	DFW	214	1389	16	59	2023-01-04 16:00:00	Other
13831	7	1	1153	1156	-3	1335	1403	AA	765	N986NN	JFK	CLT	74	541	11	56	2023-07-01 11:00:00	CLT
13832	9	5	1012	1015	-3	1127	1205	AA	735	N818AW	LGA	ORD	100	733	10	15	2023-09-05 10:00:00	ORD
13835	10	9	1155	1200	-5	1418	1452	UA	801	N2749U	EWR	LAX	296	2454	12	0	2023-10-09 12:00:00	LAX
13837	3	13	1751	1755	-4	2124	2058	DL	596	N103DY	LGA	MCO	151	950	17	55	2023-03-13 17:00:00	MCO
13839	3	31	2227	2232	-5	2358	2359	9E	1560	N319PQ	JFK	SYR	49	209	22	32	2023-03-31 22:00:00	Other
13840	3	21	1504	1507	-3	1754	1809	UA	947	N17730	EWR	SRQ	155	1034	15	7	2023-03-21 15:00:00	Other
13841	4	21	958	1000	-2	1126	1129	YX	1501	N225JQ	LGA	BOS	35	184	10	0	2023-04-21 10:00:00	BOS
13845	1	2	1652	1655	-3	1950	1959	UA	193	N206UA	EWR	LAX	322	2454	16	55	2023-01-02 16:00:00	LAX
13848	5	14	2112	2115	-3	2305	2310	YX	1363	N869RW	LGA	ILM	69	500	21	15	2023-05-14 21:00:00	Other
13859	8	8	1815	1820	-5	2012	2053	9E	1099	N316PQ	JFK	IND	95	665	18	20	2023-08-08 18:00:00	Other
13860	4	6	658	700	-2	1020	1020	DL	202	N180DN	JFK	LAX	347	2475	7	0	2023-04-06 07:00:00	LAX
13861	4	6	1833	1837	-4	2107	2100	YX	934	N640RW	EWR	IND	107	645	18	37	2023-04-06 18:00:00	Other
13862	8	24	755	759	-4	1006	1012	UA	673	N37516	EWR	DEN	214	1605	7	59	2023-08-24 07:00:00	Other
13869	5	4	907	910	-3	1100	1110	YX	1270	N424YX	LGA	GSO	70	461	9	10	2023-05-04 09:00:00	Other
13870	7	2	1609	1612	-3	1756	1743	YX	888	N724YX	EWR	ROC	50	246	16	12	2023-07-02 16:00:00	Other
13878	1	18	824	829	-5	959	1014	UA	238	N880UA	EWR	BNA	120	748	8	29	2023-01-18 08:00:00	Other
13881	7	4	1920	1925	-5	2123	2124	YX	1057	N118HQ	LGA	DTW	83	502	19	25	2023-07-04 19:00:00	Other
13882	11	21	839	841	-2	1043	1040	YX	1789	N225JQ	LGA	CMH	98	479	8	41	2023-11-21 08:00:00	Other
13883	11	1	1841	1845	-4	2029	2047	YX	1147	N744YX	EWR	CMH	75	463	18	45	2023-11-01 18:00:00	Other
13885	5	17	826	829	-3	1120	1125	AA	339	N979NN	LGA	DFW	198	1389	8	29	2023-05-17 08:00:00	Other
13891	12	5	1128	1130	-2	1341	1402	DL	956	N870DN	JFK	ATL	121	760	11	30	2023-12-05 11:00:00	ATL
13903	8	23	758	800	-2	943	1011	DL	732	N361NB	JFK	MSY	141	1182	8	0	2023-08-23 08:00:00	Other
13909	11	8	1225	1230	-5	1348	1400	YX	1077	N754YX	EWR	PIT	64	319	12	30	2023-11-08 12:00:00	Other
13911	11	10	1525	1530	-5	1821	1847	DL	575	N399DA	JFK	PBI	153	1028	15	30	2023-11-10 15:00:00	Other
13912	9	21	1623	1627	-4	1840	1843	9E	1614	N295PQ	LGA	CLT	89	544	16	27	2023-09-21 16:00:00	CLT
13920	9	14	1417	1422	-5	1552	1559	DL	867	N314DU	LGA	ORD	114	733	14	22	2023-09-14 14:00:00	ORD
13927	10	24	1625	1630	-5	1735	1755	YX	1738	N860RW	LGA	DCA	44	214	16	30	2023-10-24 16:00:00	Other
13928	8	8	1432	1435	-3	1552	1609	YX	895	N746YX	EWR	IAD	46	212	14	35	2023-08-08 14:00:00	Other
13932	7	22	2027	2029	-2	2254	2254	YX	917	N739YX	EWR	SDF	98	642	20	29	2023-07-22 20:00:00	Other
13944	1	26	640	645	-5	959	955	NK	926	N607NK	EWR	AUS	241	1504	6	45	2023-01-26 06:00:00	Other
13945	1	25	558	600	-2	809	749	DL	480	N132DU	LGA	ORD	138	733	6	0	2023-01-25 06:00:00	ORD
13967	5	6	2156	2200	-4	2303	2335	9E	1519	N299PQ	JFK	ORF	44	290	22	0	2023-05-06 22:00:00	Other
13977	6	17	758	800	-2	1001	1030	DL	341	N119DN	LGA	ATL	101	762	8	0	2023-06-17 08:00:00	ATL
13979	5	16	1057	1100	-3	1244	1245	AA	530	N810AW	LGA	STL	131	888	11	0	2023-05-16 11:00:00	Other
13985	2	8	1145	1150	-5	1230	1303	YX	1502	N203JQ	LGA	BDL	23	101	11	50	2023-02-08 11:00:00	Other
13997	4	28	938	942	-4	1048	1109	UA	448	N33714	EWR	BOS	41	200	9	42	2023-04-28 09:00:00	BOS
14007	8	15	858	900	-2	1047	1043	YX	1314	N211JQ	JFK	PIT	65	340	9	0	2023-08-15 09:00:00	Other
14008	5	19	1501	1505	-4	1630	1643	UA	606	N812UA	LGA	ORD	123	733	15	5	2023-05-19 15:00:00	ORD
14010	9	29	857	900	-3	1200	1206	B6	73	N509JB	LGA	FLL	164	1076	9	0	2023-09-29 09:00:00	FLL
14012	10	8	854	859	-5	1025	1052	9E	1622	N335PQ	LGA	CLE	70	419	8	59	2023-10-08 08:00:00	Other
14022	8	10	1056	1100	-4	1206	1230	YX	1397	N221JQ	LGA	BOS	43	184	11	0	2023-08-10 11:00:00	BOS
14024	8	26	603	605	-2	810	817	DL	667	N303DN	EWR	ATL	96	746	6	5	2023-08-26 06:00:00	ATL
14035	4	13	2045	2050	-5	2233	2254	9E	1337	N228PQ	LGA	ILM	74	500	20	50	2023-04-13 20:00:00	Other
14040	8	2	1127	1130	-3	1423	1435	DL	792	N109DU	LGA	SRQ	141	1047	11	30	2023-08-02 11:00:00	Other
14047	12	14	722	726	-4	849	911	UA	914	N434UA	EWR	RDU	66	416	7	26	2023-12-14 07:00:00	Other
14053	12	14	1258	1300	-2	1429	1457	9E	1658	N919XJ	LGA	RDU	64	431	13	0	2023-12-14 13:00:00	Other
14064	1	30	1854	1859	-5	2204	2147	UA	821	N27255	EWR	LAS	342	2227	18	59	2023-01-30 18:00:00	Other
14068	7	7	556	600	-4	817	838	UA	739	N407UA	LGA	IAH	180	1416	6	0	2023-07-07 06:00:00	Other
14077	12	16	1018	1020	-2	1229	1300	DL	780	N992AT	EWR	ATL	114	746	10	20	2023-12-16 10:00:00	ATL
14081	10	16	626	630	-4	732	748	YX	1707	N882RW	LGA	DCA	49	214	6	30	2023-10-16 06:00:00	Other
14085	8	9	837	842	-5	955	1024	9E	1267	N925XJ	LGA	CHO	51	305	8	42	2023-08-09 08:00:00	Other
14088	11	25	657	700	-3	809	814	B6	953	N368JB	LGA	BOS	38	184	7	0	2023-11-25 07:00:00	BOS
14097	11	22	1956	2000	-4	2247	2326	AA	35	N101NN	JFK	LAX	319	2475	20	0	2023-11-22 20:00:00	LAX
14107	4	12	1724	1727	-3	2102	2104	YX	951	N649RW	EWR	EYW	165	1196	17	27	2023-04-12 17:00:00	Other
14109	11	23	620	625	-5	742	801	UA	948	N872UA	LGA	ORD	116	733	6	25	2023-11-23 06:00:00	ORD
14111	1	27	558	600	-2	920	912	UA	1014	N15751	LGA	IAH	237	1416	6	0	2023-01-27 06:00:00	Other
14114	8	30	755	759	-4	1112	1109	AA	117	N938AN	LGA	MIA	150	1096	7	59	2023-08-30 07:00:00	MIA
14121	5	31	1731	1734	-3	1846	1911	YX	1120	N724YX	EWR	PIT	52	319	17	34	2023-05-31 17:00:00	Other
14129	5	28	1309	1314	-5	1619	1621	UA	497	N27266	EWR	FLL	144	1065	13	14	2023-05-28 13:00:00	FLL
14134	11	1	1256	1300	-4	1604	1612	AA	224	N319TE	LGA	MIA	171	1096	13	0	2023-11-01 13:00:00	MIA
14136	2	8	1828	1830	-2	2031	2047	9E	1384	N306PQ	LGA	CLT	82	544	18	30	2023-02-08 18:00:00	CLT
14146	4	5	2055	2100	-5	2231	2251	YX	1012	N655RW	LGA	ORD	121	733	21	0	2023-04-05 21:00:00	ORD
14158	5	23	936	940	-4	1211	1257	B6	108	N986JB	JFK	LAX	307	2475	9	40	2023-05-23 09:00:00	LAX
14161	4	18	2151	2156	-5	35	59	NK	655	N663NK	EWR	MCO	131	937	21	56	2023-04-18 21:00:00	MCO
14179	8	28	1253	1255	-2	1443	1501	DL	411	N116DU	JFK	DTW	89	509	12	55	2023-08-28 12:00:00	Other
14185	11	1	1155	1200	-5	1302	1323	YX	1823	N235JQ	LGA	BOS	33	184	12	0	2023-11-01 12:00:00	BOS
14193	5	13	1240	1245	-5	1457	1542	NK	81	N616NK	EWR	DFW	175	1372	12	45	2023-05-13 12:00:00	Other
14194	2	28	1441	1445	-4	1707	1725	WN	167	N7865A	LGA	MSY	174	1183	14	45	2023-02-28 14:00:00	Other
14196	8	16	1821	1824	-3	2029	2044	DL	323	N125DN	LGA	MSP	142	1020	18	24	2023-08-16 18:00:00	Other
14203	12	5	822	825	-3	930	952	YX	1768	N216JQ	EWR	BOS	37	200	8	25	2023-12-05 08:00:00	BOS
14206	9	24	729	733	-4	1027	1027	NK	433	N684NK	EWR	MCO	130	937	7	33	2023-09-24 07:00:00	MCO
14214	11	19	756	759	-3	1307	1256	AA	328	N9008U	JFK	STT	226	1623	7	59	2023-11-19 07:00:00	Other
14222	11	23	757	800	-3	1122	1145	DL	125	N533DT	JFK	PHX	278	2153	8	0	2023-11-23 08:00:00	Other
14226	1	11	1625	1630	-5	1836	1910	DL	842	N390DA	JFK	MSY	170	1182	16	30	2023-01-11 16:00:00	Other
14230	5	28	1715	1717	-2	2007	2029	B6	212	N618JB	LGA	FLL	144	1076	17	17	2023-05-28 17:00:00	FLL
14235	12	9	730	735	-5	952	1012	9E	1367	N933XJ	JFK	SAV	110	718	7	35	2023-12-09 07:00:00	Other
14236	10	4	1143	1147	-4	1430	1435	DL	589	N354DN	JFK	MCO	127	944	11	47	2023-10-04 11:00:00	MCO
14241	9	12	1555	1600	-5	1727	1744	AA	762	N916AN	LGA	ORD	117	733	16	0	2023-09-12 16:00:00	ORD
14247	5	5	640	645	-5	744	759	UA	510	N17264	EWR	BOS	39	200	6	45	2023-05-05 06:00:00	BOS
14249	11	1	1325	1330	-5	1601	1625	NK	329	N628NK	LGA	DFW	193	1389	13	30	2023-11-01 13:00:00	Other
14255	12	3	656	700	-4	934	946	UA	211	N14107	EWR	LAS	306	2227	7	0	2023-12-03 07:00:00	Other
14259	10	24	646	650	-4	1039	1016	DL	103	N115DN	JFK	SLC	300	1990	6	50	2023-10-24 06:00:00	Other
14270	2	18	2112	2115	-3	35	45	B6	647	N988JT	JFK	LAX	357	2475	21	15	2023-02-18 21:00:00	LAX
14282	12	23	1856	1859	-3	2158	2217	AS	8	N903AK	JFK	SAN	328	2446	18	59	2023-12-23 18:00:00	Other
14284	11	17	1049	1054	-5	1204	1218	9E	1430	N921XJ	JFK	SYR	47	209	10	54	2023-11-17 10:00:00	Other
14287	4	16	1302	1305	-3	1424	1454	DL	437	N129DU	LGA	ORD	108	733	13	5	2023-04-16 13:00:00	ORD
14289	10	18	1339	1342	-3	1529	1544	AA	606	N337PJ	EWR	CLT	76	529	13	42	2023-10-18 13:00:00	CLT
14290	4	4	1657	1700	-3	1932	1936	DL	334	N325DN	LGA	ATL	111	762	17	0	2023-04-04 17:00:00	ATL
14303	10	16	1558	1600	-2	1758	1836	UA	389	N17306	EWR	LAS	279	2227	16	0	2023-10-16 16:00:00	Other
14325	5	10	1820	1825	-5	2014	2025	9E	1453	N325PQ	LGA	MEM	143	963	18	25	2023-05-10 18:00:00	Other
14329	10	21	1725	1729	-4	2035	2037	AA	36	N104NN	JFK	LAX	329	2475	17	29	2023-10-21 17:00:00	LAX
14332	7	28	841	845	-4	959	1009	YX	885	N744YX	EWR	ROC	47	246	8	45	2023-07-28 08:00:00	Other
14343	8	26	725	730	-5	917	933	UA	709	N15710	EWR	MSY	151	1167	7	30	2023-08-26 07:00:00	Other
14344	3	1	1946	1950	-4	2136	2153	9E	1538	N335PQ	JFK	RDU	75	427	19	50	2023-03-01 19:00:00	Other
14349	9	24	1136	1140	-4	1253	1307	NK	262	N648NK	EWR	PIT	55	319	11	40	2023-09-24 11:00:00	Other
14351	8	19	1255	1300	-5	1458	1534	DL	377	N880DN	JFK	ATL	98	760	13	0	2023-08-19 13:00:00	ATL
14356	5	16	944	949	-5	1045	1122	9E	1496	N903XJ	LGA	ROC	46	254	9	49	2023-05-16 09:00:00	Other
14357	2	26	2222	2225	-3	248	330	NK	391	N652NK	EWR	SJU	188	1608	22	25	2023-02-26 22:00:00	Other
14358	8	7	730	735	-5	1022	1037	DL	629	N3748Y	JFK	PBI	139	1028	7	35	2023-08-07 07:00:00	Other
14361	1	18	1842	1845	-3	2132	2147	UA	983	N91007	EWR	LAX	317	2454	18	45	2023-01-18 18:00:00	LAX
14365	5	30	1550	1552	-2	1935	1920	DL	379	N774DE	JFK	MIA	144	1089	15	52	2023-05-30 15:00:00	MIA
14367	12	21	1613	1615	-2	1905	1935	UA	194	N226UA	EWR	SFO	321	2565	16	15	2023-12-21 16:00:00	Other
14369	5	17	652	655	-3	815	830	WN	37	N261WN	LGA	STL	127	888	6	55	2023-05-17 06:00:00	Other
14371	1	8	1624	1629	-5	1753	1800	YX	1852	N211JQ	JFK	BOS	48	187	16	29	2023-01-08 16:00:00	BOS
14381	12	22	2149	2153	-4	2252	2309	9E	1670	N912XJ	LGA	BTV	47	258	21	53	2023-12-22 21:00:00	Other
14388	3	27	956	959	-3	1229	1221	9E	1481	N131EV	JFK	SAV	115	718	9	59	2023-03-27 09:00:00	Other
14393	2	28	2056	2059	-3	2255	2302	YX	1145	N747YX	EWR	CMH	78	463	20	59	2023-02-28 20:00:00	Other
14396	9	10	1010	1013	-3	1150	1150	YX	1150	N753YX	EWR	BGR	60	393	10	13	2023-09-10 10:00:00	Other
14407	4	13	1055	1100	-5	1325	1416	B6	205	N978JB	JFK	LAX	309	2475	11	0	2023-04-13 11:00:00	LAX
14410	1	10	2117	2120	-3	2347	2346	9E	1414	N935XJ	JFK	SAV	99	718	21	20	2023-01-10 21:00:00	Other
14423	9	25	1028	1030	-2	1305	1323	B6	367	N547JB	JFK	MCO	128	944	10	30	2023-09-25 10:00:00	MCO
14433	2	10	1857	1859	-2	2214	2219	UA	742	N37437	EWR	SEA	342	2402	18	59	2023-02-10 18:00:00	Other
14435	10	29	727	729	-2	1043	1042	DL	285	N894DN	JFK	SEA	348	2422	7	29	2023-10-29 07:00:00	Other
14438	9	24	1527	1529	-2	1731	1728	YX	1302	N126HQ	JFK	CLE	76	425	15	29	2023-09-24 15:00:00	Other
14445	10	14	1104	1108	-4	1329	1344	UA	524	N37313	EWR	LAS	293	2227	11	8	2023-10-14 11:00:00	Other
14452	2	12	1704	1708	-4	1955	1959	UA	160	N47284	EWR	MCO	134	937	17	8	2023-02-12 17:00:00	MCO
14460	3	5	620	625	-5	746	810	WN	1015	N7855A	LGA	BNA	127	764	6	25	2023-03-05 06:00:00	Other
14464	2	23	725	729	-4	1118	856	YX	1152	N979RP	EWR	BUF	59	282	7	29	2023-02-23 07:00:00	Other
14468	4	26	725	730	-5	852	855	9E	1250	N292PQ	LGA	BUF	52	292	7	30	2023-04-26 07:00:00	Other
14473	5	27	1518	1520	-2	1626	1656	9E	1274	N600LR	JFK	BWI	39	184	15	20	2023-05-27 15:00:00	Other
14474	2	5	930	935	-5	1114	1145	DL	642	N303DN	LGA	DTW	86	502	9	35	2023-02-05 09:00:00	Other
14476	11	11	1156	1200	-4	1315	1337	OO	1172	N259SY	JFK	BUF	64	301	12	0	2023-11-11 12:00:00	Other
14482	9	2	1554	1559	-5	1825	1901	AA	887	N934NN	JFK	DFW	174	1391	15	59	2023-09-02 15:00:00	Other
14483	5	28	755	757	-2	911	921	YX	1065	N856RW	EWR	PWM	52	284	7	57	2023-05-28 07:00:00	Other
14501	2	13	1455	1500	-5	1708	1734	OO	1164	N317SY	JFK	MSP	172	1029	15	0	2023-02-13 15:00:00	Other
14514	4	9	1254	1259	-5	1447	1514	9E	1332	N916XJ	LGA	DAY	86	549	12	59	2023-04-09 12:00:00	Other
14518	4	9	1455	1459	-4	1637	1656	9E	1183	N324PQ	JFK	CLE	68	425	14	59	2023-04-09 14:00:00	Other
14537	10	14	625	630	-5	924	920	UA	189	N424UA	EWR	DFW	214	1372	6	30	2023-10-14 06:00:00	Other
14545	11	1	924	929	-5	1034	1049	YX	1079	N858RW	EWR	SYR	43	195	9	29	2023-11-01 09:00:00	Other
14550	11	27	1523	1525	-2	1641	1700	YX	1843	N878RW	LGA	DCA	52	214	15	25	2023-11-27 15:00:00	Other
14551	1	17	1658	1700	-2	1823	1819	B6	1029	N266JB	EWR	BOS	52	200	17	0	2023-01-17 17:00:00	BOS
14562	10	27	1552	1555	-3	1740	1748	YX	1763	N232JQ	JFK	CMH	79	483	15	55	2023-10-27 15:00:00	Other
14563	5	26	1455	1459	-4	1614	1620	UA	732	N478UA	EWR	IAD	50	212	14	59	2023-05-26 14:00:00	Other
14571	12	22	1410	1415	-5	1534	1558	UA	128	N464UA	LGA	ORD	115	733	14	15	2023-12-22 14:00:00	ORD
14577	10	19	757	800	-3	1054	1107	UA	567	N17139	EWR	FLL	147	1065	8	0	2023-10-19 08:00:00	FLL
14586	11	1	1053	1056	-3	1426	1404	DL	986	N102DU	LGA	SRQ	170	1047	10	56	2023-11-01 10:00:00	Other
14591	7	22	1042	1046	-4	1312	1340	B6	325	N585JB	JFK	MCO	130	944	10	46	2023-07-22 10:00:00	MCO
14594	3	31	1157	1159	-2	1436	1455	UA	750	N17285	EWR	IAH	198	1400	11	59	2023-03-31 11:00:00	Other
14597	6	11	1015	1020	-5	1200	1218	9E	1576	N305PQ	LGA	MYR	82	563	10	20	2023-06-11 10:00:00	Other
14598	8	27	1645	1650	-5	1812	1837	9E	1201	N491PX	LGA	PIT	60	335	16	50	2023-08-27 16:00:00	Other
14601	12	23	1850	1855	-5	2138	2217	DL	981	N115DU	LGA	SRQ	142	1047	18	55	2023-12-23 18:00:00	Other
14609	1	18	626	630	-4	755	820	YX	1902	N205JQ	LGA	RDU	70	431	6	30	2023-01-18 06:00:00	Other
14613	7	6	1711	1715	-4	2112	2106	DL	262	N727TW	JFK	SFO	362	2586	17	15	2023-07-06 17:00:00	Other
14618	3	2	1427	1429	-2	1725	1720	UA	408	N17122	EWR	MCO	142	937	14	29	2023-03-02 14:00:00	MCO
14620	1	22	1926	1929	-3	2130	2116	YX	1869	N204JQ	LGA	PIT	76	335	19	29	2023-01-22 19:00:00	Other
14621	4	9	1151	1155	-4	1439	1441	UA	275	N73259	EWR	MCO	143	937	11	55	2023-04-09 11:00:00	MCO
14623	2	16	555	600	-5	805	838	UA	429	N69838	EWR	DEN	230	1605	6	0	2023-02-16 06:00:00	Other
14624	10	26	1711	1715	-4	1833	1841	B6	355	N228JB	LGA	BOS	44	184	17	15	2023-10-26 17:00:00	BOS
14633	11	18	1457	1459	-2	1808	1821	B6	230	N978JB	JFK	LAX	345	2475	14	59	2023-11-18 14:00:00	LAX
14635	10	7	742	745	-3	936	932	UA	934	N29717	EWR	RDU	69	416	7	45	2023-10-07 07:00:00	Other
14636	10	18	1412	1415	-3	1539	1550	UA	923	N12225	LGA	ORD	108	733	14	15	2023-10-18 14:00:00	ORD
14644	6	20	941	946	-5	1134	1200	UA	916	N76529	LGA	DEN	206	1620	9	46	2023-06-20 09:00:00	Other
14655	10	22	1130	1133	-3	1423	1435	UA	139	N17302	EWR	FLL	148	1065	11	33	2023-10-22 11:00:00	FLL
14657	6	11	1927	1929	-2	2121	2136	9E	1636	N303PQ	JFK	RDU	68	427	19	29	2023-06-11 19:00:00	Other
14659	5	16	2125	2130	-5	2348	2358	DL	90	N342DN	LGA	ATL	121	762	21	30	2023-05-16 21:00:00	ATL
14660	10	29	1632	1634	-2	1931	1947	UA	611	N17311	EWR	MIA	152	1085	16	34	2023-10-29 16:00:00	MIA
14667	4	19	1200	1205	-5	1446	1516	UA	166	N77259	EWR	FLL	144	1065	12	5	2023-04-19 12:00:00	FLL
14688	2	18	1036	1040	-4	1304	1327	DL	122	N115DN	LGA	ATL	117	762	10	40	2023-02-18 10:00:00	ATL
14693	10	30	1325	1330	-5	1506	1525	9E	1616	N316PQ	JFK	CLE	82	425	13	30	2023-10-30 13:00:00	Other
14698	11	6	1057	1059	-2	1311	1310	YX	1089	N766YX	EWR	MSP	160	1008	10	59	2023-11-06 10:00:00	Other
14703	9	6	721	725	-4	948	959	DL	184	N507DZ	JFK	LAS	296	2248	7	25	2023-09-06 07:00:00	Other
14708	8	2	728	730	-2	958	1030	AA	129	N853NN	LGA	DFW	176	1389	7	30	2023-08-02 07:00:00	Other
14710	4	29	1139	1144	-5	1437	1458	UA	361	N27252	EWR	SEA	311	2402	11	44	2023-04-29 11:00:00	Other
14714	8	22	942	946	-4	1402	1341	UA	465	N47512	EWR	SJU	230	1608	9	46	2023-08-22 09:00:00	Other
14715	9	30	1125	1130	-5	1311	1329	YX	1393	N433YX	LGA	DTW	78	502	11	30	2023-09-30 11:00:00	Other
14716	10	9	1338	1340	-2	1554	1607	UA	875	N471UA	EWR	ATL	111	746	13	40	2023-10-09 13:00:00	ATL
14722	2	21	825	830	-5	946	958	YX	1526	N214JQ	LGA	SYR	44	198	8	30	2023-02-21 08:00:00	Other
14726	4	3	555	600	-5	913	904	B6	481	N935JB	EWR	LAX	357	2454	6	0	2023-04-03 06:00:00	LAX
14728	10	17	2117	2120	-3	2246	2320	YX	1767	N227JQ	JFK	CMH	71	483	21	20	2023-10-17 21:00:00	Other
14731	5	31	1926	1930	-4	2142	2159	YX	1087	N739YX	EWR	SDF	91	642	19	30	2023-05-31 19:00:00	Other
14739	4	19	756	800	-4	1043	1058	DL	315	N848DN	JFK	LAS	320	2248	8	0	2023-04-19 08:00:00	Other
14743	3	7	610	615	-5	1023	933	UA	312	N223UA	EWR	SFO	358	2565	6	15	2023-03-07 06:00:00	Other
14747	11	9	1658	1700	-2	1956	2009	B6	627	N809JB	LGA	PBI	141	1035	17	0	2023-11-09 17:00:00	Other
14761	1	7	1058	1100	-2	1203	1247	YX	1287	N446YX	LGA	DCA	43	214	11	0	2023-01-07 11:00:00	Other
14762	6	8	1558	1600	-2	1826	1844	DL	182	N318DX	LGA	ATL	109	762	16	0	2023-06-08 16:00:00	ATL
14764	1	27	1555	1559	-4	1703	1711	9E	1705	N153PQ	LGA	ALB	36	136	15	59	2023-01-27 15:00:00	Other
14776	6	15	1025	1029	-4	1155	1234	9E	1667	N313PQ	LGA	GSO	67	461	10	29	2023-06-15 10:00:00	Other
14788	2	10	1415	1419	-4	1602	1609	9E	1412	N376CA	LGA	CLE	77	419	14	19	2023-02-10 14:00:00	Other
14791	3	23	711	715	-4	1019	1021	UA	651	N17272	EWR	BZN	281	1882	7	15	2023-03-23 07:00:00	Other
14794	9	29	756	800	-4	1048	1022	YX	1318	N126HQ	JFK	CVG	98	589	8	0	2023-09-29 08:00:00	Other
14799	7	11	556	600	-4	703	715	WN	14	N8871Q	LGA	MDW	101	725	6	0	2023-07-11 06:00:00	Other
14800	5	3	1555	1600	-5	1657	1720	UA	140	N458UA	EWR	BOS	38	200	16	0	2023-05-03 16:00:00	BOS
14801	12	17	856	900	-4	1048	1042	YX	1838	N243JQ	JFK	ORF	57	290	9	0	2023-12-17 09:00:00	Other
14805	10	8	733	737	-4	922	939	UA	432	N854UA	EWR	CLT	86	529	7	37	2023-10-08 07:00:00	CLT
14807	5	29	1328	1330	-2	1642	1651	AA	419	N848NN	JFK	MIA	149	1089	13	30	2023-05-29 13:00:00	MIA
14811	9	19	857	900	-3	1030	1040	OO	1266	N296SY	JFK	PIT	61	340	9	0	2023-09-19 09:00:00	Other
14819	5	10	817	821	-4	1027	1056	YX	1610	N860RW	LGA	HHH	112	701	8	21	2023-05-10 08:00:00	Other
14826	3	25	725	730	-5	920	945	DL	1005	N327NB	LGA	MSP	148	1020	7	30	2023-03-25 07:00:00	Other
14831	10	1	952	955	-3	1354	1455	DL	69	N174DN	JFK	HNL	582	4983	9	55	2023-10-01 09:00:00	Other
14833	7	29	742	747	-5	1000	950	UA	728	N25705	EWR	MSY	155	1167	7	47	2023-07-29 07:00:00	Other
14834	5	25	755	800	-5	902	928	YX	1712	N231JQ	LGA	BOS	37	184	8	0	2023-05-25 08:00:00	BOS
14836	9	21	1343	1346	-3	1510	1519	YX	1866	N217JQ	JFK	ORF	56	290	13	46	2023-09-21 13:00:00	Other
14842	9	3	456	500	-4	734	813	AA	405	N323RM	EWR	MIA	135	1085	5	0	2023-09-03 05:00:00	MIA
14843	6	30	1257	1259	-2	1540	1531	DL	134	N375DN	LGA	ATL	122	762	12	59	2023-06-30 12:00:00	ATL
14847	2	12	1942	1945	-3	2206	2235	B6	166	N258JB	LGA	JAX	118	833	19	45	2023-02-12 19:00:00	Other
14850	3	31	1627	1629	-2	1948	2008	DL	216	N882DN	JFK	SLC	284	1990	16	29	2023-03-31 16:00:00	Other
14856	1	19	1325	1329	-4	1453	1500	YX	1754	N209JQ	LGA	DCA	54	214	13	29	2023-01-19 13:00:00	Other
14858	5	1	1026	1030	-4	1258	1353	AA	3	N117AN	JFK	LAX	311	2475	10	30	2023-05-01 10:00:00	LAX
14863	5	17	1441	1445	-4	1736	1752	B6	292	N775JB	LGA	PBI	138	1035	14	45	2023-05-17 14:00:00	Other
14865	5	22	756	800	-4	1116	1110	UA	602	N27268	EWR	FLL	161	1065	8	0	2023-05-22 08:00:00	FLL
14872	3	11	1828	1830	-2	2131	2138	UA	915	N796UA	EWR	LAX	329	2454	18	30	2023-03-11 18:00:00	LAX
14875	10	18	1842	1845	-3	1947	2015	WN	1035	N903WN	LGA	BNA	109	764	18	45	2023-10-18 18:00:00	Other
14888	5	23	1451	1455	-4	1645	1650	9E	1471	N306PQ	JFK	RDU	70	427	14	55	2023-05-23 14:00:00	Other
14891	6	25	856	900	-4	1010	1024	9E	1550	N187GJ	JFK	IAD	48	228	9	0	2023-06-25 09:00:00	Other
14893	12	29	842	845	-3	1053	1103	9E	1485	N330PQ	JFK	CLT	88	541	8	45	2023-12-29 08:00:00	CLT
14895	8	12	755	800	-5	1014	1052	UA	227	N651UA	EWR	IAH	175	1400	8	0	2023-08-12 08:00:00	Other
14904	6	18	1024	1029	-5	1210	1234	9E	1667	N330PQ	LGA	GSO	72	461	10	29	2023-06-18 10:00:00	Other
14907	10	7	725	729	-4	1013	1024	UA	922	N38727	LGA	IAH	206	1416	7	29	2023-10-07 07:00:00	Other
14911	4	19	1340	1343	-3	1518	1540	AA	591	N992AN	EWR	CLT	73	529	13	43	2023-04-19 13:00:00	CLT
14914	5	5	1707	1710	-3	1832	1849	YX	1660	N815MD	LGA	BNA	110	764	17	10	2023-05-05 17:00:00	Other
14924	8	23	924	927	-3	1051	1056	YX	885	N754YX	EWR	PWM	55	284	9	27	2023-08-23 09:00:00	Other
14936	1	13	1532	1534	-2	1705	1714	YX	1870	N215JQ	JFK	DCA	58	213	15	34	2023-01-13 15:00:00	Other
14966	9	22	745	750	-5	836	910	9E	1694	N937XJ	JFK	BWI	35	184	7	50	2023-09-22 07:00:00	Other
14970	3	1	1256	1300	-4	1439	1448	OO	1376	N604UX	LGA	ORD	139	733	13	0	2023-03-01 13:00:00	ORD
14971	2	24	826	830	-4	1453	1450	UA	129	N68061	EWR	HNL	642	4962	8	30	2023-02-24 08:00:00	Other
14972	3	31	726	730	-4	841	855	YX	1629	N206JQ	LGA	ORF	51	296	7	30	2023-03-31 07:00:00	Other
14983	11	20	2135	2140	-5	2308	2336	YX	1244	N131HQ	JFK	RDU	73	427	21	40	2023-11-20 21:00:00	Other
14984	7	21	757	759	-2	1021	1005	AA	812	N561UW	LGA	CLT	84	544	7	59	2023-07-21 07:00:00	CLT
14988	6	24	1805	1810	-5	1926	1958	9E	1570	N186PQ	LGA	BGR	55	378	18	10	2023-06-24 18:00:00	Other
14994	3	21	2025	2030	-5	2144	2203	9E	1402	N485PX	LGA	ORF	49	296	20	30	2023-03-21 20:00:00	Other
15000	6	14	1026	1028	-2	1316	1310	UA	92	N824UA	EWR	DFW	198	1372	10	28	2023-06-14 10:00:00	Other
15012	10	10	2141	2145	-4	27	50	B6	516	N556JB	JFK	FLL	146	1069	21	45	2023-10-10 21:00:00	FLL
15014	1	6	928	933	-5	1236	1255	UA	928	N76522	EWR	AUS	220	1504	9	33	2023-01-06 09:00:00	Other
15016	4	4	1920	1925	-5	2139	2149	9E	1408	N293PQ	JFK	DTW	94	509	19	25	2023-04-04 19:00:00	Other
15023	10	13	1956	2000	-4	2253	2306	UA	941	N77573	EWR	MIA	144	1085	20	0	2023-10-13 20:00:00	MIA
15028	8	3	746	750	-4	1004	1005	YX	830	N723YX	EWR	GRR	97	605	7	50	2023-08-03 07:00:00	Other
15034	10	8	1303	1305	-2	1522	1541	UA	109	N17301	EWR	LAS	289	2227	13	5	2023-10-08 13:00:00	Other
15042	6	22	1623	1626	-3	1749	1814	9E	1596	N337PQ	LGA	BGR	59	378	16	26	2023-06-22 16:00:00	Other
15048	6	16	1020	1025	-5	1246	1238	9E	1517	N480PX	LGA	CLT	94	544	10	25	2023-06-16 10:00:00	CLT
15053	4	14	828	830	-2	1005	1032	9E	1426	N314PQ	LGA	ILM	83	500	8	30	2023-04-14 08:00:00	Other
15058	11	29	1852	1856	-4	2131	2203	DL	811	N319DN	LGA	TPA	143	1010	18	56	2023-11-29 18:00:00	Other
15065	6	4	1411	1414	-3	1600	1607	YX	1905	N237JQ	LGA	CMH	76	479	14	14	2023-06-04 14:00:00	Other
15066	10	13	1033	1035	-2	1311	1305	WN	916	N217JC	LGA	ATL	114	762	10	35	2023-10-13 10:00:00	ATL
15067	4	17	640	644	-4	813	836	AA	305	N932AN	EWR	ORD	107	719	6	44	2023-04-17 06:00:00	ORD
15069	9	18	655	659	-4	954	1005	DL	657	N367NW	JFK	AUS	202	1521	6	59	2023-09-18 06:00:00	Other
15070	7	3	1330	1335	-5	1508	1520	9E	1160	N485PX	LGA	ROA	65	405	13	35	2023-07-03 13:00:00	Other
15078	8	10	1157	1159	-2	1340	1351	YX	832	N657RW	EWR	CMH	74	463	11	59	2023-08-10 11:00:00	Other
15083	8	21	2053	2055	-2	2309	2308	OO	961	N322SY	JFK	CLE	81	425	20	55	2023-08-21 20:00:00	Other
15084	5	14	917	920	-3	1036	1100	9E	1491	N936XJ	JFK	RIC	55	288	9	20	2023-05-14 09:00:00	Other
15090	11	1	1155	1200	-5	1339	1353	YX	1369	N131HQ	JFK	RDU	87	427	12	0	2023-11-01 12:00:00	Other
15091	8	29	1928	1933	-5	2217	2237	UA	502	N17311	EWR	SMF	328	2500	19	33	2023-08-29 19:00:00	Other
15099	6	12	641	645	-4	916	1009	DL	127	N544US	JFK	SLC	251	1990	6	45	2023-06-12 06:00:00	Other
15101	12	29	1721	1725	-4	1957	2008	YX	1151	N743YX	EWR	JAX	138	820	17	25	2023-12-29 17:00:00	Other
15111	4	3	1318	1321	-3	1542	1546	UA	366	N27734	EWR	JAX	119	820	13	21	2023-04-03 13:00:00	Other
15119	9	9	1326	1330	-4	1610	1638	UA	746	N787UA	EWR	SFO	317	2565	13	30	2023-09-09 13:00:00	Other
15121	3	8	1956	1959	-3	2209	2242	DL	448	N188DN	JFK	ATL	108	760	19	59	2023-03-08 19:00:00	ATL
15129	10	23	1824	1829	-5	2047	2055	9E	1627	N319PQ	JFK	CHS	86	636	18	29	2023-10-23 18:00:00	Other
15132	8	1	1150	1155	-5	1331	1346	9E	1235	N907XJ	JFK	RDU	72	427	11	55	2023-08-01 11:00:00	Other
15136	5	8	1555	1600	-5	1714	1722	AA	741	N829AW	LGA	DCA	44	214	16	0	2023-05-08 16:00:00	Other
15137	10	10	1656	1700	-4	1846	1854	9E	1469	N181PQ	LGA	RDU	67	431	17	0	2023-10-10 17:00:00	Other
15138	11	27	1917	1919	-2	2215	2233	DL	506	N320US	LGA	PBI	151	1035	19	19	2023-11-27 19:00:00	Other
15139	5	21	641	645	-4	834	845	YX	1039	N858RW	EWR	GSP	91	594	6	45	2023-05-21 06:00:00	Other
15140	4	15	812	815	-3	1015	1102	UA	227	N466UA	EWR	LAS	281	2227	8	15	2023-04-15 08:00:00	Other
15146	9	28	1518	1520	-2	1752	1754	B6	627	N526JL	JFK	JAX	120	828	15	20	2023-09-28 15:00:00	Other
15150	3	26	556	600	-4	800	806	AA	949	N971NN	JFK	CLT	96	541	6	0	2023-03-26 06:00:00	CLT
15154	10	22	1356	1400	-4	1608	1623	9E	1559	N928XJ	LGA	OMA	158	1148	14	0	2023-10-22 14:00:00	Other
15155	10	7	1124	1129	-5	1436	1439	DL	460	N3752	JFK	MIA	161	1089	11	29	2023-10-07 11:00:00	MIA
15158	12	2	814	818	-4	1048	1049	YX	1825	N824MD	LGA	IND	119	660	8	18	2023-12-02 08:00:00	Other
15167	4	22	1456	1459	-3	1817	1801	UA	214	N494UA	EWR	AUS	220	1504	14	59	2023-04-22 14:00:00	Other
15169	12	5	1555	1559	-4	1728	1742	YX	1285	N403YX	JFK	BNA	123	765	15	59	2023-12-05 15:00:00	Other
15171	2	5	613	615	-2	845	853	DL	732	N717TW	JFK	ATL	126	760	6	15	2023-02-05 06:00:00	ATL
15174	7	6	1454	1459	-5	1659	1708	AA	128	N704US	JFK	CLT	83	541	14	59	2023-07-06 14:00:00	CLT
15189	4	22	1257	1300	-3	1559	1611	AA	230	N423AN	LGA	MIA	158	1096	13	0	2023-04-22 13:00:00	MIA
15200	2	16	1326	1330	-4	1549	1554	UA	321	N819UA	EWR	MSY	177	1167	13	30	2023-02-16 13:00:00	Other
15207	9	14	826	830	-4	1106	1129	UA	289	N13138	EWR	SAN	313	2425	8	30	2023-09-14 08:00:00	Other
15212	2	16	755	800	-5	912	927	YX	1556	N246JQ	LGA	BOS	42	184	8	0	2023-02-16 08:00:00	BOS
15214	7	29	713	715	-2	950	1011	B6	376	N632JB	LGA	TPA	140	1010	7	15	2023-07-29 07:00:00	Other
15215	5	14	1924	1929	-5	2103	2108	YX	1672	N224JQ	LGA	BNA	112	764	19	29	2023-05-14 19:00:00	Other
15235	8	5	1651	1655	-4	1835	1856	9E	1196	N133EV	LGA	MYR	81	563	16	55	2023-08-05 16:00:00	Other
15238	5	11	656	700	-4	950	1005	UA	869	N415UA	EWR	MIA	143	1085	7	0	2023-05-11 07:00:00	MIA
15240	11	22	1854	1859	-5	2125	2151	UA	388	N14118	EWR	LAS	290	2227	18	59	2023-11-22 18:00:00	Other
15241	5	23	1109	1111	-2	1313	1341	UA	452	N47281	EWR	PHX	269	2133	11	11	2023-05-23 11:00:00	Other
15252	4	10	848	853	-5	1120	1109	YX	1131	N131HQ	LGA	AGS	107	678	8	53	2023-04-10 08:00:00	Other
15253	11	6	624	629	-5	724	741	UA	281	N68453	EWR	BOS	36	200	6	29	2023-11-06 06:00:00	BOS
15256	8	2	856	900	-4	1022	1037	OO	959	N240SY	JFK	BNA	107	765	9	0	2023-08-02 09:00:00	Other
15275	8	23	824	829	-5	940	957	9E	1118	N917XJ	LGA	ROC	50	254	8	29	2023-08-23 08:00:00	Other
15276	12	23	1142	1145	-3	1442	1508	AS	5	N971AK	JFK	PDX	323	2454	11	45	2023-12-23 11:00:00	Other
15279	9	22	1357	1359	-2	1645	1702	UA	447	N437UA	EWR	RSW	150	1068	13	59	2023-09-22 13:00:00	Other
15284	6	13	924	929	-5	1226	1222	AA	626	N997NN	LGA	DFW	207	1389	9	29	2023-06-13 09:00:00	Other
15286	11	13	1257	1259	-2	1449	1504	DL	756	N343NW	LGA	DTW	89	502	12	59	2023-11-13 12:00:00	Other
15288	9	13	759	803	-4	1113	1117	AA	496	N846NN	EWR	MIA	163	1085	8	3	2023-09-13 08:00:00	MIA
15290	5	9	1943	1945	-2	2322	2337	DL	89	N174DN	JFK	SFO	340	2586	19	45	2023-05-09 19:00:00	Other
15292	5	30	1941	1945	-4	2131	2152	9E	1475	N901XJ	EWR	CVG	83	569	19	45	2023-05-30 19:00:00	Other
15294	7	23	1255	1300	-5	1356	1408	9E	1235	N916XJ	LGA	ORH	35	146	13	0	2023-07-23 13:00:00	Other
15301	6	4	1923	1928	-5	2227	2230	DL	637	N364NB	LGA	TPA	147	1010	19	28	2023-06-04 19:00:00	Other
15303	11	14	601	605	-4	718	729	YX	1828	N240JQ	LGA	DCA	51	214	6	5	2023-11-14 06:00:00	Other
15315	3	5	825	830	-5	1031	1051	9E	1420	N602LR	JFK	CLT	90	541	8	30	2023-03-05 08:00:00	CLT
15320	6	29	1955	2000	-5	2106	2134	YX	1896	N823MD	LGA	BOS	43	184	20	0	2023-06-29 20:00:00	BOS
15323	7	17	1456	1459	-3	1654	1708	AA	128	N9002U	JFK	CLT	90	541	14	59	2023-07-17 14:00:00	CLT
15330	8	17	728	730	-2	944	1030	AS	73	N921VA	EWR	LAX	295	2454	7	30	2023-08-17 07:00:00	LAX
15332	8	16	756	800	-4	952	1038	DL	164	N529DT	JFK	DEN	209	1626	8	0	2023-08-16 08:00:00	Other
15337	3	15	1641	1645	-4	2010	2010	DL	173	N378DA	JFK	SAN	337	2446	16	45	2023-03-15 16:00:00	Other
15345	11	11	956	1000	-4	1309	1312	DL	259	N177DN	JFK	LAX	341	2475	10	0	2023-11-11 10:00:00	LAX
15351	3	15	715	717	-2	839	905	B6	408	N375JB	JFK	ORD	112	740	7	17	2023-03-15 07:00:00	ORD
15357	3	10	841	845	-4	1020	1031	YX	1621	N213JQ	LGA	PIT	69	335	8	45	2023-03-10 08:00:00	Other
15365	2	10	1425	1430	-5	1626	1625	AA	846	N758US	LGA	RDU	83	431	14	30	2023-02-10 14:00:00	Other
15367	12	7	1355	1359	-4	1610	1644	DL	159	N383DZ	LGA	ATL	106	762	13	59	2023-12-07 13:00:00	ATL
15369	10	11	946	950	-4	1103	1113	YX	1791	N244JQ	JFK	BOS	46	187	9	50	2023-10-11 09:00:00	BOS
15376	4	15	757	800	-3	1052	1017	9E	1344	N279PQ	JFK	CHS	103	636	8	0	2023-04-15 08:00:00	Other
15377	10	25	2236	2240	-4	2359	18	9E	1608	N325PQ	JFK	PWM	43	273	22	40	2023-10-25 22:00:00	Other
15379	11	6	1750	1755	-5	2047	2104	UA	657	N17122	EWR	SAN	333	2425	17	55	2023-11-06 17:00:00	Other
15381	5	9	1156	1200	-4	1411	1430	DL	370	N873DN	JFK	ATL	108	760	12	0	2023-05-09 12:00:00	ATL
15398	2	10	613	615	-2	846	853	DL	732	N704X	JFK	ATL	121	760	6	15	2023-02-10 06:00:00	ATL
15399	11	20	1326	1329	-3	1615	1640	DL	295	N180DN	JFK	LAX	301	2475	13	29	2023-11-20 13:00:00	LAX
15405	10	18	1840	1845	-5	2017	2045	YX	1145	N766YX	EWR	CMH	73	463	18	45	2023-10-18 18:00:00	Other
15418	10	8	2247	2250	-3	119	155	F9	908	N233FR	LGA	DFW	189	1389	22	50	2023-10-08 22:00:00	Other
15427	4	26	655	700	-5	1014	1007	AS	93	N938AK	EWR	SEA	323	2402	7	0	2023-04-26 07:00:00	Other
15428	11	13	1919	1924	-5	2119	2129	UA	504	N38443	EWR	DTW	90	488	19	24	2023-11-13 19:00:00	Other
15433	11	27	655	700	-5	817	823	YX	1861	N220JQ	LGA	BOS	38	184	7	0	2023-11-27 07:00:00	BOS
15434	3	17	2127	2129	-2	2329	2309	9E	1328	N314PQ	JFK	RIC	65	288	21	29	2023-03-17 21:00:00	Other
15436	2	23	1724	1727	-3	1952	2025	YX	1225	N136HQ	LGA	ATL	125	762	17	27	2023-02-23 17:00:00	ATL
15455	2	5	1257	1300	-3	1435	1444	YX	1513	N818MD	LGA	BNA	123	764	13	0	2023-02-05 13:00:00	Other
15470	2	10	1917	1920	-3	2207	2254	DL	165	N3762Y	JFK	SAN	333	2446	19	20	2023-02-10 19:00:00	Other
15484	10	10	1345	1350	-5	1513	1525	YX	1793	N224JQ	LGA	BNA	116	764	13	50	2023-10-10 13:00:00	Other
15487	7	17	1750	1755	-5	2033	2006	YX	1101	N410YX	LGA	IND	110	660	17	55	2023-07-17 17:00:00	Other
15491	3	12	1143	1145	-2	1327	1331	YX	1348	N806MD	LGA	ROA	83	405	11	45	2023-03-12 11:00:00	Other
15494	9	29	856	900	-4	1004	1026	YX	1404	N869RW	LGA	BUF	46	292	9	0	2023-09-29 09:00:00	Other
15497	5	30	1610	1615	-5	1757	1800	9E	1483	N300PQ	JFK	ORF	52	290	16	15	2023-05-30 16:00:00	Other
15502	11	29	1644	1649	-5	1817	1827	9E	1463	N330PQ	LGA	BGR	56	378	16	49	2023-11-29 16:00:00	Other
15507	9	14	2043	2047	-4	2233	2304	YX	1088	N638RW	EWR	GRR	89	605	20	47	2023-09-14 20:00:00	Other
15508	9	26	2151	2155	-4	124	118	B6	936	N943JT	JFK	SFO	328	2586	21	55	2023-09-26 21:00:00	Other
15509	5	25	1159	1202	-3	1315	1337	YX	1207	N117HQ	JFK	BOS	34	187	12	2	2023-05-25 12:00:00	BOS
15517	4	23	2157	2200	-3	2317	2335	9E	1412	N297PQ	JFK	ORF	51	290	22	0	2023-04-23 22:00:00	Other
15524	9	7	1703	1705	-2	2001	1856	B6	398	N206JB	JFK	RDU	69	427	17	5	2023-09-07 17:00:00	Other
15529	10	5	1148	1152	-4	1327	1347	YX	1059	N762YX	EWR	CMH	69	463	11	52	2023-10-05 11:00:00	Other
15530	9	3	1818	1821	-3	2017	2027	YX	1316	N134HQ	LGA	LIT	151	1085	18	21	2023-09-03 18:00:00	Other
15534	3	23	1805	1810	-5	1941	1935	DL	444	N111NG	JFK	BOS	44	187	18	10	2023-03-23 18:00:00	BOS
15540	8	11	725	729	-4	933	949	AA	442	N350RV	JFK	PHX	285	2153	7	29	2023-08-11 07:00:00	Other
15549	3	2	1225	1229	-4	1322	1339	UA	492	N37541	EWR	BOS	36	200	12	29	2023-03-02 12:00:00	BOS
15551	2	2	2045	2050	-5	2237	2253	YX	1528	N238JQ	JFK	CMH	92	483	20	50	2023-02-02 20:00:00	Other
15552	2	14	2250	2255	-5	2353	3	YX	1508	N217JQ	JFK	BWI	37	184	22	55	2023-02-14 22:00:00	Other
15556	2	24	1157	1200	-3	1549	1523	DL	221	N172DN	JFK	LAX	385	2475	12	0	2023-02-24 12:00:00	LAX
15566	1	19	850	855	-5	1054	1114	9E	1429	N302PQ	JFK	DTW	94	509	8	55	2023-01-19 08:00:00	Other
15571	11	6	2005	2009	-4	8	2342	AS	16	N491AS	JFK	SFO	382	2586	20	9	2023-11-06 20:00:00	Other
15573	8	27	1545	1550	-5	1844	1815	9E	1103	N137EV	LGA	CLT	117	544	15	50	2023-08-27 15:00:00	CLT
15576	6	18	1725	1730	-5	1912	1922	9E	1593	N602LR	JFK	BUF	51	301	17	30	2023-06-18 17:00:00	Other
15578	2	21	2055	2100	-5	2220	2231	9E	1448	N691CA	JFK	ORF	50	290	21	0	2023-02-21 21:00:00	Other
15585	2	24	2058	2100	-2	2357	1	B6	48	N651JB	EWR	PBI	139	1023	21	0	2023-02-24 21:00:00	Other
15588	8	28	2018	2022	-4	2201	2220	DL	802	N988AT	EWR	DTW	76	488	20	22	2023-08-28 20:00:00	Other
15590	2	27	926	930	-4	1157	1212	UA	842	N491UA	LGA	DEN	234	1620	9	30	2023-02-27 09:00:00	Other
15591	7	17	1015	1020	-5	1131	1157	9E	1324	N306PQ	JFK	ROC	51	264	10	20	2023-07-17 10:00:00	Other
15592	2	15	812	815	-3	1124	1156	AA	607	N336SR	JFK	MIA	158	1089	8	15	2023-02-15 08:00:00	MIA
15596	11	9	1725	1729	-4	2030	2032	UA	898	N68802	EWR	SRQ	152	1034	17	29	2023-11-09 17:00:00	Other
15612	10	14	1750	1755	-5	1902	1931	9E	1629	N311PQ	LGA	BUF	51	292	17	55	2023-10-14 17:00:00	Other
15638	3	19	1624	1629	-5	1911	1915	DL	365	N831DN	JFK	PHX	299	2153	16	29	2023-03-19 16:00:00	Other
15648	8	4	555	600	-5	654	727	AA	588	N813AW	LGA	DCA	42	214	6	0	2023-08-04 06:00:00	Other
15649	5	3	1718	1720	-2	1943	2017	B6	432	N794JB	JFK	LAS	304	2248	17	20	2023-05-03 17:00:00	Other
15650	8	18	1556	1600	-4	1725	1740	AA	604	N813NN	LGA	ORD	115	733	16	0	2023-08-18 16:00:00	ORD
15652	3	13	555	600	-5	800	850	UA	270	N69826	EWR	LAS	287	2227	6	0	2023-03-13 06:00:00	Other
15662	12	8	1533	1538	-5	1721	1733	OO	1171	N323SY	JFK	ORD	123	740	15	38	2023-12-08 15:00:00	ORD
15667	3	21	1855	1900	-5	2000	2022	YX	1747	N210JQ	LGA	BOS	40	184	19	0	2023-03-21 19:00:00	BOS
15670	3	4	1458	1500	-2	1710	1727	9E	1385	N905XJ	JFK	CHS	103	636	15	0	2023-03-04 15:00:00	Other
15673	2	23	858	900	-2	1228	1235	YX	1219	N128HQ	LGA	IAH	224	1416	9	0	2023-02-23 09:00:00	Other
15675	7	17	2046	2050	-4	2205	2229	YX	1413	N205JQ	LGA	ORF	54	296	20	50	2023-07-17 20:00:00	Other
15677	1	17	733	735	-2	1014	1035	DL	428	N311DN	JFK	MCO	134	944	7	35	2023-01-17 07:00:00	MCO
15686	1	22	1756	1759	-3	1938	1954	YX	1288	N126HQ	JFK	RDU	78	427	17	59	2023-01-22 17:00:00	Other
15688	9	15	525	530	-5	815	841	AA	801	N324RN	JFK	MIA	146	1089	5	30	2023-09-15 05:00:00	MIA
15690	6	9	1625	1627	-2	1831	1852	YX	1187	N645RW	EWR	SDF	94	642	16	27	2023-06-09 16:00:00	Other
15699	3	22	1353	1355	-2	1459	1519	YX	1050	N641RW	EWR	ROC	48	246	13	55	2023-03-22 13:00:00	Other
15701	4	13	1355	1400	-5	1553	1619	YX	1286	N411YX	LGA	CVG	91	585	14	0	2023-04-13 14:00:00	Other
15704	11	13	1455	1500	-5	1604	1627	9E	1488	N601LR	LGA	PWM	44	269	15	0	2023-11-13 15:00:00	Other
15706	12	13	1846	1849	-3	2245	2229	AS	8	N277AK	JFK	SAN	327	2446	18	49	2023-12-13 18:00:00	Other
15708	8	22	745	750	-5	1017	1104	UA	479	N47282	EWR	FLL	134	1065	7	50	2023-08-22 07:00:00	FLL
15709	10	19	2210	2215	-5	2325	2349	YX	1714	N207JQ	JFK	BOS	42	187	22	15	2023-10-19 22:00:00	BOS
15718	5	15	658	700	-2	918	924	DL	216	N330DX	LGA	ATL	106	762	7	0	2023-05-15 07:00:00	ATL
15727	12	5	1955	1959	-4	2334	2338	AA	943	N983AN	LGA	MIA	165	1096	19	59	2023-12-05 19:00:00	MIA
15732	9	19	719	723	-4	1009	1015	B6	209	N646JB	EWR	TPA	145	997	7	23	2023-09-19 07:00:00	Other
15740	9	5	1127	1130	-3	1404	1437	B6	930	N763JB	JFK	MIA	139	1089	11	30	2023-09-05 11:00:00	MIA
15754	5	10	1616	1621	-5	1728	1747	YX	1015	N647RW	EWR	BUF	48	282	16	21	2023-05-10 16:00:00	Other
15756	12	13	1417	1420	-3	1627	1645	9E	1471	N187GJ	LGA	CVG	108	585	14	20	2023-12-13 14:00:00	Other
15757	7	21	1621	1624	-3	1754	1750	UA	601	N37538	EWR	IAD	64	212	16	24	2023-07-21 16:00:00	Other
15766	9	1	1050	1055	-5	1313	1317	UA	481	N424UA	EWR	JAX	115	820	10	55	2023-09-01 10:00:00	Other
15775	10	29	1454	1459	-5	1607	1625	9E	1647	N538CA	JFK	BWI	42	184	14	59	2023-10-29 14:00:00	Other
15791	8	14	1256	1259	-3	1548	1617	AA	515	N324SH	JFK	MIA	149	1089	12	59	2023-08-14 12:00:00	MIA
15792	6	30	1058	1100	-2	1309	1334	DL	310	N356DN	LGA	ATL	101	762	11	0	2023-06-30 11:00:00	ATL
15794	10	18	1757	1800	-3	1908	1931	YX	1033	N762YX	EWR	BUF	53	282	18	0	2023-10-18 18:00:00	Other
15795	11	7	1453	1455	-2	1707	1727	DL	470	N185DN	JFK	ATL	107	760	14	55	2023-11-07 14:00:00	ATL
15798	7	1	1605	1610	-5	1840	1832	YX	1055	N872RW	LGA	MCI	168	1107	16	10	2023-07-01 16:00:00	Other
15805	9	2	1106	1110	-4	1319	1344	DL	341	N727TW	JFK	LAS	284	2248	11	10	2023-09-02 11:00:00	Other
15811	4	18	2125	2130	-5	2310	2309	9E	1199	N676CA	JFK	RIC	55	288	21	30	2023-04-18 21:00:00	Other
15822	7	3	1122	1124	-2	1426	1443	DL	169	N850DN	JFK	SEA	318	2422	11	24	2023-07-03 11:00:00	Other
15825	12	23	925	930	-5	1137	1216	YX	1758	N244JQ	LGA	MCI	164	1107	9	30	2023-12-23 09:00:00	Other
15832	1	9	1154	1159	-5	1325	1343	YX	1215	N855RW	EWR	CLE	69	404	11	59	2023-01-09 11:00:00	Other
15834	8	20	955	1000	-5	1100	1120	YX	1381	N234JQ	LGA	MVY	41	175	10	0	2023-08-20 10:00:00	Other
15835	4	29	1324	1329	-5	1453	1503	9E	1356	N924XJ	JFK	BGR	60	382	13	29	2023-04-29 13:00:00	Other
15842	4	11	1405	1410	-5	1639	1656	UA	372	N76522	EWR	MCO	126	937	14	10	2023-04-11 14:00:00	MCO
15843	3	3	927	929	-2	1251	1310	YX	1186	N856RW	EWR	EYW	180	1196	9	29	2023-03-03 09:00:00	Other
15846	6	15	1027	1030	-3	1310	1326	B6	397	N562JB	JFK	MCO	135	944	10	30	2023-06-15 10:00:00	MCO
15848	1	27	701	705	-4	1025	1008	DL	425	N361NB	LGA	PBI	174	1035	7	5	2023-01-27 07:00:00	Other
15865	6	12	755	800	-5	908	929	YX	1843	N240JQ	LGA	BOS	42	184	8	0	2023-06-12 08:00:00	BOS
15872	8	28	1256	1300	-4	1445	1507	AA	599	N897NN	LGA	CLT	86	544	13	0	2023-08-28 13:00:00	CLT
15882	10	13	557	600	-3	931	927	AA	26	N106NN	JFK	SFO	362	2586	6	0	2023-10-13 06:00:00	Other
15888	12	11	625	630	-5	952	1014	AA	23	N112AN	JFK	SFO	357	2586	6	30	2023-12-11 06:00:00	Other
15918	6	20	1040	1045	-5	1328	1411	DL	947	N916DU	JFK	SLC	258	1990	10	45	2023-06-20 10:00:00	Other
15923	1	15	1258	1300	-2	1408	1425	YX	1846	N224JQ	LGA	BOS	37	184	13	0	2023-01-15 13:00:00	BOS
15936	3	12	1030	1035	-5	1150	1158	YX	1103	N753YX	EWR	DCA	44	199	10	35	2023-03-12 10:00:00	Other
15944	4	17	1121	1125	-4	1300	1312	OO	1031	N254SY	JFK	ORD	116	740	11	25	2023-04-17 11:00:00	ORD
15945	4	24	1956	1959	-3	2135	2145	9E	1442	N485PX	EWR	RDU	69	416	19	59	2023-04-24 19:00:00	Other
15950	4	5	700	705	-5	931	1002	DL	396	N101DQ	LGA	MCO	121	950	7	5	2023-04-05 07:00:00	MCO
15960	9	25	1224	1229	-5	1529	1544	AA	645	N322TH	JFK	MIA	147	1089	12	29	2023-09-25 12:00:00	MIA
15964	2	22	1601	1605	-4	1943	1935	AS	83	N925VA	EWR	LAX	360	2454	16	5	2023-02-22 16:00:00	LAX
15967	3	9	557	600	-3	714	717	YX	1757	N214JQ	JFK	BOS	40	187	6	0	2023-03-09 06:00:00	BOS
15982	10	10	546	550	-4	827	850	AA	530	N339PL	LGA	DFW	190	1389	5	50	2023-10-10 05:00:00	Other
15986	10	26	1412	1416	-4	1617	1624	9E	1575	N184GJ	JFK	CVG	97	589	14	16	2023-10-26 14:00:00	Other
15989	9	14	1426	1430	-4	1617	1614	AA	192	N987NN	LGA	ORD	112	733	14	30	2023-09-14 14:00:00	ORD
16001	10	25	1128	1130	-2	1410	1451	AA	610	N998NN	LGA	MIA	142	1096	11	30	2023-10-25 11:00:00	MIA
16007	4	23	1944	1947	-3	2236	2250	UA	537	N27546	EWR	TPA	146	997	19	47	2023-04-23 19:00:00	Other
16018	8	25	628	630	-2	801	748	B6	774	N284JB	JFK	BUF	54	301	6	30	2023-08-25 06:00:00	Other
16024	12	20	1655	1659	-4	1851	1928	9E	1475	N605LR	LGA	CVG	88	585	16	59	2023-12-20 16:00:00	Other
16025	12	22	1028	1030	-2	1330	1346	B6	759	N766JB	JFK	RSW	156	1074	10	30	2023-12-22 10:00:00	Other
16031	3	10	755	800	-5	932	946	B6	399	N258JB	JFK	BNA	129	765	8	0	2023-03-10 08:00:00	Other
16032	2	12	1756	1800	-4	2002	1942	UA	905	N812UA	LGA	ORD	116	733	18	0	2023-02-12 18:00:00	ORD
16038	5	26	920	925	-5	1210	1222	DL	205	N145DQ	LGA	DFW	186	1389	9	25	2023-05-26 09:00:00	Other
16040	2	25	2124	2129	-5	116	118	DL	109	N1602	JFK	SFO	378	2586	21	29	2023-02-25 21:00:00	Other
16041	2	23	1217	1220	-3	1543	1549	DL	323	N136DQ	LGA	DFW	223	1389	12	20	2023-02-23 12:00:00	Other
16045	4	21	941	945	-4	1144	1156	9E	1233	N604LR	EWR	CVG	92	569	9	45	2023-04-21 09:00:00	Other
16048	11	3	1400	1405	-5	1530	1553	YX	1069	N766YX	EWR	CLE	67	404	14	5	2023-11-03 14:00:00	Other
16049	11	3	1554	1559	-5	1844	1904	AA	994	N806NN	LGA	DFW	194	1389	15	59	2023-11-03 15:00:00	Other
16054	5	30	1657	1700	-3	1907	1926	DL	916	N3746H	EWR	ATL	104	746	17	0	2023-05-30 17:00:00	ATL
16059	6	15	2155	2159	-4	2317	2341	DL	902	N339NB	JFK	BUF	50	301	21	59	2023-06-15 21:00:00	Other
16062	2	1	556	600	-4	831	808	AA	908	N9004F	EWR	CLT	99	529	6	0	2023-02-01 06:00:00	CLT
16075	1	13	706	710	-4	1036	956	9E	1553	N197PQ	LGA	JAX	142	833	7	10	2023-01-13 07:00:00	Other
16081	4	24	705	710	-5	1013	1007	DL	352	N3735D	LGA	PBI	160	1035	7	10	2023-04-24 07:00:00	Other
16098	8	16	924	929	-5	1254	1232	UA	578	N17262	EWR	PBI	160	1023	9	29	2023-08-16 09:00:00	Other
16105	2	3	701	705	-4	1023	1008	DL	380	N340NB	LGA	PBI	167	1035	7	5	2023-02-03 07:00:00	Other
16113	8	19	1355	1359	-4	1545	1632	DL	551	N395DN	LGA	DEN	203	1620	13	59	2023-08-19 13:00:00	Other
16124	5	26	627	630	-3	931	931	B6	925	N709JB	JFK	FLL	157	1069	6	30	2023-05-26 06:00:00	FLL
16125	10	18	1927	1932	-5	2223	2230	UA	506	N77543	EWR	SAN	308	2425	19	32	2023-10-18 19:00:00	Other
16126	12	13	723	726	-3	853	911	UA	914	N63899	EWR	RDU	68	416	7	26	2023-12-13 07:00:00	Other
16134	6	7	725	730	-5	901	925	9E	1497	N918XJ	LGA	GSO	71	461	7	30	2023-06-07 07:00:00	Other
16142	10	18	808	810	-2	1204	1207	UA	770	N67052	EWR	SJU	209	1608	8	10	2023-10-18 08:00:00	Other
16146	12	20	1444	1446	-2	1555	1618	9E	1639	N482PX	LGA	ROC	46	254	14	46	2023-12-20 14:00:00	Other
16147	3	5	948	950	-2	1339	1329	AA	1004	N407AN	EWR	PHX	314	2133	9	50	2023-03-05 09:00:00	Other
16152	3	3	925	930	-5	1234	1257	AA	814	N306SW	LGA	MIA	154	1096	9	30	2023-03-03 09:00:00	MIA
16154	10	8	927	930	-3	1233	1241	B6	905	N661JB	JFK	MIA	157	1089	9	30	2023-10-08 09:00:00	MIA
16155	3	18	1450	1455	-5	1729	1723	9E	1492	N929XJ	JFK	SAV	118	718	14	55	2023-03-18 14:00:00	Other
16159	10	23	657	700	-3	831	842	UA	831	N77510	EWR	ORD	112	719	7	0	2023-10-23 07:00:00	ORD
16160	1	5	627	630	-3	903	919	UA	258	N27252	EWR	LAS	300	2227	6	30	2023-01-05 06:00:00	Other
16164	12	14	1106	1109	-3	1250	1326	DL	489	N365DN	LGA	MSP	134	1020	11	9	2023-12-14 11:00:00	Other
16174	11	13	748	750	-2	1008	1009	YX	1062	N764YX	EWR	GRR	106	605	7	50	2023-11-13 07:00:00	Other
16178	1	15	656	700	-4	938	1012	UA	772	N874UA	LGA	IAH	202	1416	7	0	2023-01-15 07:00:00	Other
16184	9	19	1500	1502	-2	1648	1657	DL	757	N992AT	EWR	MSP	143	1008	15	2	2023-09-19 15:00:00	Other
16190	10	15	843	848	-5	1021	1042	9E	1606	N676CA	JFK	RDU	76	427	8	48	2023-10-15 08:00:00	Other
16195	7	24	2154	2158	-4	2248	2301	9E	1265	N901XJ	LGA	PVD	31	143	21	58	2023-07-24 21:00:00	Other
16199	12	22	1132	1135	-3	1248	1305	WN	797	N274WN	LGA	MDW	105	725	11	35	2023-12-22 11:00:00	Other
16201	10	14	558	600	-2	838	850	UA	163	N37561	EWR	IAH	194	1400	6	0	2023-10-14 06:00:00	Other
16204	5	27	756	800	-4	1030	1104	DL	172	N827MH	JFK	LAX	303	2475	8	0	2023-05-27 08:00:00	LAX
16210	3	17	800	805	-5	927	947	9E	1497	N292PQ	JFK	BUF	59	301	8	5	2023-03-17 08:00:00	Other
16221	2	15	1227	1229	-2	1334	1355	YX	1542	N212JQ	LGA	PWM	42	269	12	29	2023-02-15 12:00:00	Other
16222	11	18	957	1000	-3	1203	1232	YX	1061	N861RW	EWR	SDF	101	642	10	0	2023-11-18 10:00:00	Other
16227	3	23	1025	1029	-4	1245	1300	YX	1647	N240JQ	LGA	IND	119	660	10	29	2023-03-23 10:00:00	Other
16228	8	8	1343	1346	-3	1617	1640	UA	229	N87527	LGA	IAH	195	1416	13	46	2023-08-08 13:00:00	Other
16229	7	30	1454	1459	-5	1703	1736	9E	1169	N931XJ	JFK	IND	104	665	14	59	2023-07-30 14:00:00	Other
16234	6	17	816	820	-4	1053	1126	AA	337	N936AN	JFK	DFW	181	1391	8	20	2023-06-17 08:00:00	Other
16243	7	25	857	900	-3	1157	1210	AS	16	N291BT	JFK	SFO	323	2586	9	0	2023-07-25 09:00:00	Other
16244	10	3	1826	1830	-4	1959	2007	UA	398	N37274	EWR	ORD	102	719	18	30	2023-10-03 18:00:00	ORD
16255	9	28	1354	1359	-5	1658	1701	DL	385	N327NB	LGA	IAH	194	1416	13	59	2023-09-28 13:00:00	Other
16257	6	3	1843	1845	-2	2102	2213	DL	476	N913DU	EWR	SLC	235	1969	18	45	2023-06-03 18:00:00	Other
16262	2	27	1021	1025	-4	1150	1205	YX	1578	N223JQ	LGA	DCA	46	214	10	25	2023-02-27 10:00:00	Other
16272	8	2	1440	1445	-5	1616	1634	9E	1156	N341PQ	LGA	ORF	57	296	14	45	2023-08-02 14:00:00	Other
16283	4	18	1903	1905	-2	2143	2149	DL	408	N900DU	JFK	ATL	104	760	19	5	2023-04-18 19:00:00	ATL
16284	4	24	1716	1720	-4	2026	2038	AA	868	N316SE	JFK	AUS	224	1521	17	20	2023-04-24 17:00:00	Other
16286	3	1	857	900	-3	1057	1053	9E	1589	N916XJ	LGA	MSN	142	812	9	0	2023-03-01 09:00:00	Other
16292	9	12	1520	1525	-5	1646	1650	NK	394	N536NK	EWR	BNA	115	748	15	25	2023-09-12 15:00:00	Other
16296	7	31	1456	1500	-4	1606	1617	9E	1235	N917XJ	LGA	ORH	36	146	15	0	2023-07-31 15:00:00	Other
16301	9	20	1913	1915	-2	2258	2219	DL	141	N174DN	JFK	LAX	320	2475	19	15	2023-09-20 19:00:00	LAX
16304	3	3	1842	1845	-3	2127	2134	DL	187	N376DN	LGA	ATL	136	762	18	45	2023-03-03 18:00:00	ATL
16308	9	15	1205	1208	-3	1322	1320	YX	1891	N815MD	LGA	ALB	29	136	12	8	2023-09-15 12:00:00	Other
16311	1	7	1025	1030	-5	1229	1256	9E	1500	N914XJ	LGA	GSP	93	610	10	30	2023-01-07 10:00:00	Other
16316	12	4	1901	1905	-4	2353	2357	UA	201	N27477	EWR	BQN	198	1585	19	5	2023-12-04 19:00:00	Other
16317	5	13	1019	1023	-4	1258	1308	NK	24	N527NK	EWR	MCO	125	937	10	23	2023-05-13 10:00:00	MCO
16318	11	14	1547	1550	-3	1827	1905	DL	196	N172DN	JFK	LAX	318	2475	15	50	2023-11-14 15:00:00	LAX
16322	8	6	724	729	-5	1027	1028	AA	3	N110AN	JFK	LAX	339	2475	7	29	2023-08-06 07:00:00	LAX
16323	3	14	1157	1200	-3	1413	1358	9E	1374	N184GJ	LGA	STL	121	888	12	0	2023-03-14 12:00:00	Other
16351	3	21	946	950	-4	1059	1114	9E	1562	N936XJ	JFK	SYR	46	209	9	50	2023-03-21 09:00:00	Other
16355	3	29	1325	1330	-5	1629	1641	UA	514	N47280	EWR	FLL	162	1065	13	30	2023-03-29 13:00:00	FLL
16365	8	8	1147	1152	-5	1317	1309	UA	237	N37561	EWR	BOS	51	200	11	52	2023-08-08 11:00:00	BOS
16383	3	16	826	830	-4	959	1007	AA	126	N807NN	LGA	ORD	115	733	8	30	2023-03-16 08:00:00	ORD
16385	4	24	1403	1407	-4	1521	1545	YX	1464	N202JQ	LGA	PIT	58	335	14	7	2023-04-24 14:00:00	Other
16390	11	12	1355	1359	-4	1458	1518	YX	1880	N246JQ	LGA	BOS	33	184	13	59	2023-11-12 13:00:00	BOS
16391	7	23	1924	1929	-5	2140	2209	9E	1209	N299PQ	JFK	MCI	158	1113	19	29	2023-07-23 19:00:00	Other
16394	11	16	2052	2055	-3	10	2354	DL	422	N919DU	JFK	MCO	156	944	20	55	2023-11-16 20:00:00	MCO
16399	6	11	1436	1440	-4	1543	1609	YX	1217	N642RW	EWR	IAD	40	212	14	40	2023-06-11 14:00:00	Other
16400	10	13	949	954	-5	1105	1133	9E	1579	N903XJ	JFK	RIC	53	288	9	54	2023-10-13 09:00:00	Other
16405	2	9	825	830	-5	956	1000	9E	1449	N331PQ	JFK	IAD	49	228	8	30	2023-02-09 08:00:00	Other
16406	2	12	2024	2029	-5	2252	2304	YX	973	N726YX	EWR	SDF	102	642	20	29	2023-02-12 20:00:00	Other
16409	2	22	1100	1105	-5	1322	1345	DL	330	N102DU	LGA	MCI	178	1107	11	5	2023-02-22 11:00:00	Other
16429	11	22	1752	1756	-4	2010	2105	B6	663	N794JB	JFK	PSP	298	2378	17	56	2023-11-22 17:00:00	Other
16443	5	9	944	949	-5	1101	1122	9E	1496	N913XJ	LGA	ROC	47	254	9	49	2023-05-09 09:00:00	Other
16450	11	18	2016	2021	-5	2350	2338	B6	550	N990JL	EWR	LAX	348	2454	20	21	2023-11-18 20:00:00	LAX
16455	3	12	803	806	-3	930	935	B6	59	N368JB	JFK	ROC	49	264	8	6	2023-03-12 08:00:00	Other
16456	12	1	1828	1830	-2	1948	2000	YX	1742	N237JQ	LGA	BOS	40	184	18	30	2023-12-01 18:00:00	BOS
16458	9	9	1428	1430	-2	1643	1646	9E	1555	N691CA	JFK	CLT	94	541	14	30	2023-09-09 14:00:00	CLT
16461	5	30	819	822	-3	956	1035	YX	1094	N855RW	EWR	DTW	71	488	8	22	2023-05-30 08:00:00	Other
16469	4	9	1724	1729	-5	1852	1916	AA	741	N906NN	JFK	ORD	110	740	17	29	2023-04-09 17:00:00	ORD
16476	4	6	840	845	-5	1013	1031	YX	978	N754YX	EWR	PIT	56	319	8	45	2023-04-06 08:00:00	Other
16487	3	10	1308	1313	-5	1550	1547	UA	317	N889UA	EWR	JAX	139	820	13	13	2023-03-10 13:00:00	Other
16498	2	16	1026	1029	-3	1320	1332	UA	844	N832UA	EWR	MTJ	262	1795	10	29	2023-02-16 10:00:00	Other
16505	4	17	2240	2245	-5	17	17	9E	1358	N676CA	JFK	ROC	49	264	22	45	2023-04-17 22:00:00	Other
16506	8	24	1635	1639	-4	1939	1930	OO	944	N323SY	LGA	OKC	179	1341	16	39	2023-08-24 16:00:00	Other
16510	4	24	715	720	-5	1004	957	9E	1341	N478PX	LGA	JAX	132	833	7	20	2023-04-24 07:00:00	Other
16525	5	14	1322	1325	-3	1708	1550	UA	433	N37277	EWR	ATL	106	746	13	25	2023-05-14 13:00:00	ATL
16536	9	1	626	629	-3	752	814	AA	967	N717UW	LGA	RDU	65	431	6	29	2023-09-01 06:00:00	Other
16539	8	13	1955	1959	-4	2113	2127	YX	1368	N201JQ	EWR	BOS	44	200	19	59	2023-08-13 19:00:00	BOS
16547	4	17	1143	1145	-2	1321	1348	YX	1074	N106HQ	JFK	CMH	79	483	11	45	2023-04-17 11:00:00	Other
16548	9	20	1925	1930	-5	2221	2225	UA	526	N880UA	EWR	SRQ	143	1034	19	30	2023-09-20 19:00:00	Other
16552	9	17	2043	2045	-2	2341	2359	NK	1026	N661NK	EWR	MIA	156	1085	20	45	2023-09-17 20:00:00	MIA
16554	11	2	1512	1517	-5	1622	1647	9E	1514	N600LR	LGA	MKE	112	738	15	17	2023-11-02 15:00:00	Other
16555	2	16	1410	1415	-5	1556	1613	YX	1595	N215JQ	LGA	CMH	84	479	14	15	2023-02-16 14:00:00	Other
16557	9	30	1927	1929	-2	2146	2211	UA	804	N17265	EWR	DFW	173	1372	19	29	2023-09-30 19:00:00	Other
16559	6	4	1321	1324	-3	1504	1557	AA	1021	N378SC	JFK	PHX	262	2153	13	24	2023-06-04 13:00:00	Other
16564	10	27	906	910	-4	1246	1210	B6	53	N987JT	JFK	SAN	346	2446	9	10	2023-10-27 09:00:00	Other
16573	6	3	924	929	-5	1105	1139	YX	1129	N742YX	EWR	AVL	82	583	9	29	2023-06-03 09:00:00	Other
16576	5	27	1425	1429	-4	1550	1612	9E	1510	N349PQ	JFK	RIC	55	288	14	29	2023-05-27 14:00:00	Other
16579	5	14	1059	1102	-3	1228	1229	UA	491	N27258	EWR	BNA	107	748	11	2	2023-05-14 11:00:00	Other
16600	3	10	908	910	-2	1031	1039	YX	1642	N214JQ	JFK	DCA	60	213	9	10	2023-03-10 09:00:00	Other
16602	11	29	1521	1526	-5	1658	1726	YX	1782	N207JQ	JFK	CMH	81	483	15	26	2023-11-29 15:00:00	Other
16611	10	13	1049	1052	-3	1317	1310	DL	464	N320DN	LGA	MSP	146	1020	10	52	2023-10-13 10:00:00	Other
16613	8	25	2018	2020	-2	2215	2240	9E	1155	N602LR	LGA	GRR	93	618	20	20	2023-08-25 20:00:00	Other
16619	5	12	1033	1035	-2	1245	1305	WN	638	N969WN	LGA	ATL	106	762	10	35	2023-05-12 10:00:00	ATL
16624	10	22	1445	1450	-5	1650	1703	9E	1570	N676CA	LGA	GSP	92	610	14	50	2023-10-22 14:00:00	Other
16625	11	22	1155	1200	-5	1328	1337	OO	1172	N322SY	JFK	BUF	66	301	12	0	2023-11-22 12:00:00	Other
16629	12	27	727	730	-3	1047	1044	DL	961	N920DU	JFK	MIA	154	1089	7	30	2023-12-27 07:00:00	MIA
16635	1	30	1803	1807	-4	1921	1945	YX	1249	N745YX	EWR	PIT	58	319	18	7	2023-01-30 18:00:00	Other
16641	11	10	2149	2152	-3	2245	2303	9E	1408	N300PQ	LGA	SYR	41	198	21	52	2023-11-10 21:00:00	Other
16643	8	29	655	700	-5	827	850	9E	1122	N132EV	LGA	STL	129	888	7	0	2023-08-29 07:00:00	Other
16653	4	20	1515	1520	-5	1831	1847	B6	45	N646JB	JFK	RSW	160	1074	15	20	2023-04-20 15:00:00	Other
16655	2	21	1624	1629	-5	1948	1955	AA	95	N116AN	JFK	LAX	360	2475	16	29	2023-02-21 16:00:00	LAX
16667	9	1	1913	1915	-2	2156	2233	DL	558	N365DN	JFK	MCO	127	944	19	15	2023-09-01 19:00:00	MCO
16699	3	23	1815	1820	-5	1934	1950	9E	1566	N918XJ	LGA	PWM	49	269	18	20	2023-03-23 18:00:00	Other
16713	3	26	901	905	-4	1024	1041	9E	1529	N136EV	JFK	RIC	60	288	9	5	2023-03-26 09:00:00	Other
16717	2	25	936	940	-4	1050	1108	9E	1452	N296PQ	JFK	SYR	49	209	9	40	2023-02-25 09:00:00	Other
16721	10	23	1822	1825	-3	2124	2134	DL	848	N338NW	JFK	AUS	207	1521	18	25	2023-10-23 18:00:00	Other
16723	9	20	943	947	-4	1037	1102	YX	1117	N742YX	EWR	PVD	35	160	9	47	2023-09-20 09:00:00	Other
16727	11	12	756	800	-4	1009	1012	YX	1052	N724YX	EWR	CMH	89	463	8	0	2023-11-12 08:00:00	Other
16728	10	11	727	730	-3	1059	1042	AA	275	N9021H	JFK	AUS	251	1521	7	30	2023-10-11 07:00:00	Other
16733	8	15	1441	1445	-4	1637	1635	YX	1081	N433YX	LGA	STL	129	888	14	45	2023-08-15 14:00:00	Other
16735	6	11	1331	1335	-4	1443	1455	YX	1246	N739YX	EWR	ORF	48	284	13	35	2023-06-11 13:00:00	Other
16740	5	26	2005	2007	-2	2117	2129	UA	527	N873UA	EWR	BOS	47	200	20	7	2023-05-26 20:00:00	BOS
16743	5	12	952	957	-5	1122	1137	YX	1030	N739YX	EWR	BGR	65	393	9	57	2023-05-12 09:00:00	Other
16745	1	11	1256	1259	-3	1456	1516	YX	1769	N239JQ	LGA	CLT	89	544	12	59	2023-01-11 12:00:00	CLT
16748	5	5	1756	1800	-4	2031	2110	DL	344	N338NB	JFK	DFW	185	1391	18	0	2023-05-05 18:00:00	Other
16749	11	19	2056	2100	-4	2308	2302	NK	1026	N703NK	EWR	DTW	86	488	21	0	2023-11-19 21:00:00	Other
16758	12	17	557	600	-3	733	740	UA	372	N17126	EWR	ORD	121	719	6	0	2023-12-17 06:00:00	ORD
16770	1	17	1945	1950	-5	2133	2159	YX	1312	N412YX	JFK	RDU	78	427	19	50	2023-01-17 19:00:00	Other
16781	5	6	1741	1745	-4	2033	2057	UA	259	N841UA	EWR	AUS	206	1504	17	45	2023-05-06 17:00:00	Other
16783	6	24	1358	1401	-3	1605	1607	YX	1085	N645RW	EWR	GRR	89	605	14	1	2023-06-24 14:00:00	Other
16784	7	13	1612	1615	-3	1810	1840	DL	342	N110DU	LGA	CHS	88	641	16	15	2023-07-13 16:00:00	Other
16799	2	2	522	525	-3	832	820	UA	195	N19136	EWR	IAH	222	1400	5	25	2023-02-02 05:00:00	Other
16801	12	3	757	800	-3	1028	1026	9E	1590	N301PQ	JFK	CHS	111	636	8	0	2023-12-03 08:00:00	Other
16806	7	26	1306	1311	-5	1512	1535	9E	1308	N137EV	LGA	IND	97	660	13	11	2023-07-26 13:00:00	Other
16814	9	14	755	800	-5	1051	1134	DL	293	N707TW	JFK	SFO	330	2586	8	0	2023-09-14 08:00:00	Other
16818	12	23	1155	1159	-4	1437	1512	UA	621	N17316	EWR	SAN	320	2425	11	59	2023-12-23 11:00:00	Other
16819	7	17	1100	1105	-5	1216	1243	9E	1313	N319PQ	LGA	BUF	46	292	11	5	2023-07-17 11:00:00	Other
16824	9	2	1353	1355	-2	1630	1656	DL	284	N177DN	JFK	LAX	304	2475	13	55	2023-09-02 13:00:00	LAX
16825	9	24	1426	1429	-3	1619	1621	AA	761	N802AW	LGA	RDU	69	431	14	29	2023-09-24 14:00:00	Other
16828	4	27	1025	1030	-5	1203	1209	AA	150	N856NN	LGA	ORD	117	733	10	30	2023-04-27 10:00:00	ORD
16833	9	25	757	800	-3	1045	1055	DL	166	N832MH	JFK	LAX	312	2475	8	0	2023-09-25 08:00:00	LAX
16835	10	6	1518	1520	-2	1643	1658	B6	792	N247JB	LGA	BNA	115	764	15	20	2023-10-06 15:00:00	Other
16836	4	18	1925	1929	-4	2152	2226	DL	104	N810DN	JFK	DEN	227	1626	19	29	2023-04-18 19:00:00	Other
16840	6	30	652	655	-3	942	948	B6	296	N977JE	JFK	LAX	319	2475	6	55	2023-06-30 06:00:00	LAX
16848	8	29	1850	1855	-5	2035	2058	9E	1172	N295PQ	LGA	MEM	137	963	18	55	2023-08-29 18:00:00	Other
16849	10	22	718	723	-5	1002	1015	B6	195	N607JB	EWR	TPA	141	997	7	23	2023-10-22 07:00:00	Other
16851	10	15	608	610	-2	905	915	NK	175	N920NK	EWR	FLL	148	1065	6	10	2023-10-15 06:00:00	FLL
16857	3	23	1654	1658	-4	1812	1829	9E	1541	N324PQ	JFK	PWM	50	273	16	58	2023-03-23 16:00:00	Other
16863	5	12	1427	1429	-2	1717	1731	B6	685	N281JB	JFK	TPA	139	1005	14	29	2023-05-12 14:00:00	Other
16866	2	22	1545	1550	-5	1738	1728	YX	1609	N209JQ	LGA	BUF	58	292	15	50	2023-02-22 15:00:00	Other
16867	3	13	657	659	-2	814	830	9E	1490	N923XJ	LGA	RIC	54	292	6	59	2023-03-13 06:00:00	Other
16874	5	26	1753	1755	-2	1913	1927	YX	1650	N206JQ	LGA	DCA	51	214	17	55	2023-05-26 17:00:00	Other
16879	11	18	707	709	-2	1019	1025	DL	329	N302DU	EWR	SLC	276	1969	7	9	2023-11-18 07:00:00	Other
16890	3	20	1954	1959	-5	2154	2209	YX	1130	N744YX	EWR	DTW	82	488	19	59	2023-03-20 19:00:00	Other
16897	4	9	1143	1148	-5	1358	1410	9E	1419	N920XJ	LGA	CHS	106	641	11	48	2023-04-09 11:00:00	Other
16898	1	3	1640	1642	-2	1831	1852	YX	1442	N132HQ	LGA	GSO	82	461	16	42	2023-01-03 16:00:00	Other
16900	10	18	2034	2039	-5	2225	2249	9E	1665	N200PQ	LGA	MYR	81	563	20	39	2023-10-18 20:00:00	Other
16905	8	10	1726	1729	-3	2032	2140	DL	250	N704X	JFK	SFO	344	2586	17	29	2023-08-10 17:00:00	Other
16906	1	3	1720	1725	-5	1905	1916	9E	1714	N480PX	LGA	BNA	124	764	17	25	2023-01-03 17:00:00	Other
16908	9	19	1946	1950	-4	2231	2303	DL	890	N921DU	JFK	TPA	141	1005	19	50	2023-09-19 19:00:00	Other
16913	5	14	2217	2220	-3	2342	2355	9E	1548	N131EV	JFK	BTV	52	266	22	20	2023-05-14 22:00:00	Other
16914	5	28	1423	1425	-2	1626	1650	WN	958	N551WN	LGA	ATL	101	762	14	25	2023-05-28 14:00:00	ATL
16915	3	8	1410	1415	-5	1524	1541	9E	1580	N184GJ	JFK	BTV	48	266	14	15	2023-03-08 14:00:00	Other
16917	10	29	1358	1400	-2	1559	1617	YX	1153	N750YX	EWR	CVG	101	569	14	0	2023-10-29 14:00:00	Other
16923	1	10	925	929	-4	1235	1254	NK	1108	N669NK	LGA	MIA	158	1096	9	29	2023-01-10 09:00:00	MIA
16925	3	20	2149	2153	-4	2302	2315	9E	1391	N678CA	LGA	BUF	53	292	21	53	2023-03-20 21:00:00	Other
16928	12	12	1444	1449	-5	1645	1659	AA	716	N153UW	LGA	CLT	92	544	14	49	2023-12-12 14:00:00	CLT
16933	2	15	1758	1800	-2	2014	2021	DL	417	N352NW	LGA	MSP	164	1020	18	0	2023-02-15 18:00:00	Other
16949	7	21	928	930	-2	1030	1052	UA	458	N35236	EWR	BOS	35	200	9	30	2023-07-21 09:00:00	BOS
16960	12	28	1656	1700	-4	1900	1830	YX	1714	N212JQ	LGA	BOS	51	184	17	0	2023-12-28 17:00:00	BOS
16962	7	13	1156	1200	-4	1436	1454	B6	238	N655JB	JFK	AUS	202	1521	12	0	2023-07-13 12:00:00	Other
16963	2	4	1711	1716	-5	2001	2022	UA	456	N87507	EWR	IAH	201	1400	17	16	2023-02-04 17:00:00	Other
16970	7	26	2155	2159	-4	2307	2327	YX	1069	N416YX	JFK	BOS	42	187	21	59	2023-07-26 21:00:00	BOS
16971	5	12	1458	1500	-2	1805	1817	AA	834	N976AN	LGA	MIA	144	1096	15	0	2023-05-12 15:00:00	MIA
16972	3	19	1921	1925	-4	2229	2149	9E	1550	N325PQ	JFK	DTW	88	509	19	25	2023-03-19 19:00:00	Other
16973	12	8	1300	1305	-5	1537	1602	UA	536	N62883	EWR	MCO	132	937	13	5	2023-12-08 13:00:00	MCO
16981	7	2	1418	1420	-2	1553	1555	YX	1353	N235JQ	LGA	BNA	122	764	14	20	2023-07-02 14:00:00	Other
16986	10	29	736	740	-4	923	947	AA	498	N815NN	JFK	CLT	82	541	7	40	2023-10-29 07:00:00	CLT
16995	1	8	857	900	-3	1211	1229	B6	364	N934JB	JFK	LAX	333	2475	9	0	2023-01-08 09:00:00	LAX
17002	6	2	1011	1015	-4	1132	1150	YX	1114	N724YX	EWR	BGR	61	393	10	15	2023-06-02 10:00:00	Other
17013	3	9	1140	1145	-5	1315	1331	YX	1348	N806MD	LGA	ROA	73	405	11	45	2023-03-09 11:00:00	Other
17014	1	4	1502	1507	-5	1816	1811	UA	606	N27733	EWR	PBI	146	1023	15	7	2023-01-04 15:00:00	Other
17015	10	23	1841	1845	-4	2019	2045	YX	1145	N764YX	EWR	CMH	68	463	18	45	2023-10-23 18:00:00	Other
17017	8	28	754	759	-5	1049	1109	AA	117	N826NN	LGA	MIA	149	1096	7	59	2023-08-28 07:00:00	MIA
17022	4	6	558	600	-2	728	730	WN	890	N8823Q	LGA	MDW	118	725	6	0	2023-04-06 06:00:00	Other
17027	11	3	2155	2159	-4	2255	2316	DL	424	N124DU	LGA	BOS	41	184	21	59	2023-11-03 21:00:00	BOS
17029	7	20	1001	1005	-4	1254	1257	DL	236	N176DN	JFK	LAX	316	2475	10	5	2023-07-20 10:00:00	LAX
17036	6	20	1955	2000	-5	2153	2210	9E	1452	N927XJ	LGA	DAY	86	549	20	0	2023-06-20 20:00:00	Other
17040	9	14	835	840	-5	948	956	B6	51	N193JB	EWR	BOS	35	200	8	40	2023-09-14 08:00:00	BOS
17051	2	13	1107	1110	-3	1410	1440	DL	148	N845DN	JFK	SLC	274	1990	11	10	2023-02-13 11:00:00	Other
17069	6	3	1041	1046	-5	1248	1310	DL	913	N361NB	LGA	MSY	148	1183	10	46	2023-06-03 10:00:00	Other
17071	12	2	1054	1059	-5	1436	1428	YX	1126	N740YX	EWR	AUS	254	1504	10	59	2023-12-02 10:00:00	Other
17081	9	30	656	659	-3	942	1011	AA	3	N110AN	JFK	LAX	321	2475	6	59	2023-09-30 06:00:00	LAX
17092	5	3	1125	1129	-4	1422	1432	B6	19	N599JB	LGA	TPA	143	1010	11	29	2023-05-03 11:00:00	Other
17096	8	15	1259	1304	-5	1355	1413	YX	829	N723YX	EWR	MDT	31	141	13	4	2023-08-15 13:00:00	Other
17100	12	31	1705	1709	-4	1858	1924	9E	1534	N311PQ	JFK	DTW	80	509	17	9	2023-12-31 17:00:00	Other
17105	8	9	1744	1746	-2	1946	1945	YX	1332	N824MD	LGA	CMH	74	479	17	46	2023-08-09 17:00:00	Other
17114	1	17	1556	1600	-4	1719	1745	WN	61	N8582Z	LGA	BNA	121	764	16	0	2023-01-17 16:00:00	Other
17115	1	7	1354	1359	-5	1647	1709	AA	948	N963NN	EWR	DFW	213	1372	13	59	2023-01-07 13:00:00	Other
17116	2	19	657	659	-2	848	839	AA	949	N962AN	EWR	ORD	121	719	6	59	2023-02-19 06:00:00	ORD
17123	5	14	1958	2000	-2	2328	2335	B6	69	N968JT	JFK	LAX	334	2475	20	0	2023-05-14 20:00:00	LAX
17124	7	2	1257	1300	-3	1459	1537	DL	395	N873DN	JFK	ATL	102	760	13	0	2023-07-02 13:00:00	ATL
17125	9	21	2035	2037	-2	2307	2317	UA	781	N47570	EWR	LAS	299	2227	20	37	2023-09-21 20:00:00	Other
17128	8	23	925	929	-4	1206	1221	UA	400	N17122	EWR	MCO	121	937	9	29	2023-08-23 09:00:00	MCO
17137	8	21	958	1000	-2	1101	1130	DL	324	N141DU	LGA	BOS	43	184	10	0	2023-08-21 10:00:00	BOS
17143	8	13	727	730	-3	919	933	UA	709	N829UA	EWR	MSY	151	1167	7	30	2023-08-13 07:00:00	Other
17146	10	16	1755	1759	-4	2023	2050	UA	630	N77571	EWR	IAH	165	1400	17	59	2023-10-16 17:00:00	Other
17150	11	1	1948	1950	-2	2201	2227	YX	1076	N767YX	EWR	MCI	157	1092	19	50	2023-11-01 19:00:00	Other
17154	11	30	1643	1645	-2	1747	1813	B6	498	N236JB	JFK	BOS	49	187	16	45	2023-11-30 16:00:00	BOS
17168	5	8	900	902	-2	1107	1124	YX	1169	N639RW	EWR	MCI	163	1092	9	2	2023-05-08 09:00:00	Other
17171	4	11	1100	1102	-2	1339	1400	UA	247	N493UA	EWR	PBI	134	1023	11	2	2023-04-11 11:00:00	Other
17172	7	30	1607	1609	-2	1807	1825	9E	1293	N901XJ	LGA	AVL	91	599	16	9	2023-07-30 16:00:00	Other
17176	2	21	1032	1036	-4	1403	1400	AA	431	N318SF	LGA	DFW	223	1389	10	36	2023-02-21 10:00:00	Other
17178	1	23	942	945	-3	1140	1135	WN	92	N7817J	LGA	BNA	117	764	9	45	2023-01-23 09:00:00	Other
17179	3	30	842	847	-5	1037	1050	9E	1516	N320PQ	LGA	CLE	76	419	8	47	2023-03-30 08:00:00	Other
17183	11	2	555	600	-5	848	857	B6	90	N519JB	LGA	MCO	133	950	6	0	2023-11-02 06:00:00	MCO
17185	1	28	1157	1159	-2	1336	1343	YX	1215	N723YX	EWR	CLE	76	404	11	59	2023-01-28 11:00:00	Other
17187	6	10	945	950	-5	1114	1146	9E	1723	N326PQ	LGA	CLE	65	419	9	50	2023-06-10 09:00:00	Other
17188	1	17	820	825	-5	1007	1032	9E	1641	N904XJ	LGA	GSO	74	461	8	25	2023-01-17 08:00:00	Other
17201	11	21	1831	1835	-4	1955	2014	YX	1165	N730YX	EWR	PIT	66	319	18	35	2023-11-21 18:00:00	Other
17204	8	10	935	940	-5	1243	1207	9E	1242	N331PQ	JFK	IND	116	665	9	40	2023-08-10 09:00:00	Other
17208	2	20	1524	1529	-5	1631	1702	YX	1509	N233JQ	LGA	DCA	49	214	15	29	2023-02-20 15:00:00	Other
17214	8	27	1257	1259	-2	1453	1504	DL	628	N367DN	LGA	DTW	87	502	12	59	2023-08-27 12:00:00	Other
17215	10	24	1137	1140	-3	1344	1348	AA	919	N960AN	JFK	CLT	88	541	11	40	2023-10-24 11:00:00	CLT
17222	10	22	1755	1758	-3	2038	2104	F9	443	N331FR	LGA	MCO	130	950	17	58	2023-10-22 17:00:00	MCO
17224	8	14	1648	1650	-2	1906	1900	WN	686	N8323C	LGA	MCI	166	1107	16	50	2023-08-14 16:00:00	Other
17228	4	27	651	655	-4	912	928	B6	120	N306JB	LGA	JAX	122	833	6	55	2023-04-27 06:00:00	Other
17230	9	18	1627	1629	-2	2040	1942	AA	487	N316RK	LGA	MIA	154	1096	16	29	2023-09-18 16:00:00	MIA
17231	5	3	655	700	-5	908	935	DL	103	N108DN	LGA	ATL	107	762	7	0	2023-05-03 07:00:00	ATL
17242	7	28	1720	1725	-5	1910	1914	9E	1220	N311PQ	JFK	BUF	53	301	17	25	2023-07-28 17:00:00	Other
17247	7	7	1513	1515	-2	1839	1820	DL	194	N199DN	JFK	LAX	331	2475	15	15	2023-07-07 15:00:00	LAX
17250	9	20	1445	1447	-2	1759	1752	UA	521	N433UA	EWR	MIA	155	1085	14	47	2023-09-20 14:00:00	MIA
17253	8	27	1457	1500	-3	1645	1636	UA	483	N17306	LGA	ORD	134	733	15	0	2023-08-27 15:00:00	ORD
17257	1	29	1840	1845	-5	2052	2107	9E	1550	N301PQ	LGA	CLT	98	544	18	45	2023-01-29 18:00:00	CLT
17258	3	25	900	905	-5	1151	1154	B6	266	N279JB	JFK	JAX	132	828	9	5	2023-03-25 09:00:00	Other
17262	7	31	1055	1059	-4	1218	1224	9E	1134	N600LR	LGA	SYR	44	198	10	59	2023-07-31 10:00:00	Other
17264	7	17	1030	1034	-4	1134	1156	UA	396	N15712	EWR	BOS	36	200	10	34	2023-07-17 10:00:00	BOS
17273	10	28	618	620	-2	842	841	UA	736	N27255	LGA	DEN	248	1620	6	20	2023-10-28 06:00:00	Other
17279	2	4	1214	1216	-2	1406	1339	YX	1042	N728YX	EWR	PWM	51	284	12	16	2023-02-04 12:00:00	Other
17282	5	10	2025	2029	-4	2216	2230	YX	1080	N729YX	EWR	ILM	69	488	20	29	2023-05-10 20:00:00	Other
17286	10	14	1242	1247	-5	1354	1414	YX	1305	N436YX	LGA	ORF	53	296	12	47	2023-10-14 12:00:00	Other
17287	12	24	857	900	-3	1208	1227	AA	68	N109NN	JFK	LAX	334	2475	9	0	2023-12-24 09:00:00	LAX
17292	3	1	1122	1125	-3	1439	1445	AA	838	N841NN	LGA	MIA	157	1096	11	25	2023-03-01 11:00:00	MIA
17297	7	11	1309	1314	-5	1458	1520	YX	1042	N447YX	LGA	MSP	150	1020	13	14	2023-07-11 13:00:00	Other
17303	1	29	1930	1935	-5	2135	2159	9E	1656	N279PQ	JFK	DTW	100	509	19	35	2023-01-29 19:00:00	Other
17304	10	20	1755	1800	-5	2001	2011	NK	246	N660NK	EWR	IND	91	645	18	0	2023-10-20 18:00:00	Other
17307	5	27	1056	1100	-4	1347	1438	DL	94	N722TW	JFK	SFO	318	2586	11	0	2023-05-27 11:00:00	Other
17316	7	26	1353	1356	-3	1603	1635	NK	73	N956NK	EWR	DFW	168	1372	13	56	2023-07-26 13:00:00	Other
17325	5	20	1557	1600	-3	1724	1755	WN	184	N8613K	LGA	STL	129	888	16	0	2023-05-20 16:00:00	Other
17353	11	7	955	1000	-5	1147	1220	AA	727	N155UW	LGA	CLT	81	544	10	0	2023-11-07 10:00:00	CLT
17362	10	1	728	733	-5	947	952	UA	440	N4901U	EWR	SAV	97	708	7	33	2023-10-01 07:00:00	Other
17365	8	25	1716	1718	-2	1853	1853	UA	630	N14106	EWR	ORD	114	719	17	18	2023-08-25 17:00:00	ORD
17366	9	26	1154	1159	-5	1306	1307	B6	857	N337JB	LGA	ACK	40	202	11	59	2023-09-26 11:00:00	Other
17371	8	7	855	900	-5	1012	1035	9E	1166	N910XJ	JFK	IAD	43	228	9	0	2023-08-07 09:00:00	Other
17375	5	30	831	834	-3	1004	1033	YX	993	N643RW	EWR	GSO	69	445	8	34	2023-05-30 08:00:00	Other
17377	7	8	1150	1155	-5	1359	1410	9E	1307	N929XJ	LGA	CLT	92	544	11	55	2023-07-08 11:00:00	CLT
17382	12	3	1440	1445	-5	1715	1706	B6	867	N306JB	JFK	CHS	110	636	14	45	2023-12-03 14:00:00	Other
17385	1	18	1136	1140	-4	1445	1450	WN	289	N8649A	LGA	DAL	230	1381	11	40	2023-01-18 11:00:00	Other
17386	3	13	1557	1600	-3	1909	1924	UA	761	N12116	EWR	LAX	321	2454	16	0	2023-03-13 16:00:00	LAX
17389	10	24	1124	1129	-5	1252	1307	9E	1465	N184GJ	LGA	ORF	53	296	11	29	2023-10-24 11:00:00	Other
17391	2	16	1926	1929	-3	2202	2208	DL	275	N105DU	LGA	MCI	188	1107	19	29	2023-02-16 19:00:00	Other
17392	12	27	656	700	-4	958	1000	NK	1004	N626NK	LGA	PBI	158	1035	7	0	2023-12-27 07:00:00	Other
17404	3	11	1655	1700	-5	1839	1911	9E	1587	N306PQ	JFK	CLT	84	541	17	0	2023-03-11 17:00:00	CLT
17411	11	13	1157	1200	-3	1338	1337	OO	1172	N240SY	JFK	BUF	68	301	12	0	2023-11-13 12:00:00	Other
17415	2	21	925	930	-5	1303	1258	AA	114	N115NN	JFK	SNA	366	2454	9	30	2023-02-21 09:00:00	Other
17429	11	15	1430	1435	-5	1552	1616	9E	1493	N302PQ	JFK	RIC	57	288	14	35	2023-11-15 14:00:00	Other
17432	9	26	957	1000	-3	1301	1256	B6	331	N593JB	JFK	PBI	157	1028	10	0	2023-09-26 10:00:00	Other
17434	7	2	1305	1307	-2	1540	1556	UA	172	N29124	EWR	MCO	126	937	13	7	2023-07-02 13:00:00	MCO
17436	12	14	1418	1420	-2	1712	1723	UA	571	N17306	EWR	IAH	192	1400	14	20	2023-12-14 14:00:00	Other
17439	5	25	752	755	-3	1110	1056	AS	87	N272AK	EWR	LAX	322	2454	7	55	2023-05-25 07:00:00	LAX
17442	12	11	851	855	-4	1021	1023	YX	1122	N744YX	EWR	ORF	63	284	8	55	2023-12-11 08:00:00	Other
17449	4	7	2154	2159	-5	1	2359	UA	673	N27269	EWR	DTW	85	488	21	59	2023-04-07 21:00:00	Other
17460	8	3	1301	1305	-4	1503	1511	YX	923	N641RW	EWR	CVG	89	569	13	5	2023-08-03 13:00:00	Other
17469	8	6	1821	1825	-4	2122	2139	AS	147	N474AS	EWR	SEA	302	2402	18	25	2023-08-06 18:00:00	Other
17473	4	30	911	915	-4	1213	1250	AA	336	N108NN	JFK	SNA	326	2454	9	15	2023-04-30 09:00:00	Other
17479	11	1	2150	2155	-5	2319	2324	9E	1548	N912XJ	LGA	ROC	48	254	21	55	2023-11-01 21:00:00	Other
17481	12	25	2027	2030	-3	2323	2343	UA	670	N17321	EWR	DFW	196	1372	20	30	2023-12-25 20:00:00	Other
17484	9	6	1844	1849	-5	2038	2119	9E	1760	N905XJ	JFK	IND	89	665	18	49	2023-09-06 18:00:00	Other
17485	4	14	1810	1815	-5	1934	1949	B6	2	N358JB	JFK	BUF	50	301	18	15	2023-04-14 18:00:00	Other
17490	8	28	800	805	-5	1156	1209	DL	560	N846DN	JFK	SJU	198	1598	8	5	2023-08-28 08:00:00	Other
17504	3	17	455	500	-5	744	812	AA	449	N803NN	EWR	MIA	143	1085	5	0	2023-03-17 05:00:00	MIA
17508	7	25	735	740	-5	1027	1030	B6	210	N520JB	LGA	MCO	134	950	7	40	2023-07-25 07:00:00	MCO
17510	9	1	1925	1929	-4	2116	2143	9E	1646	N292PQ	JFK	RDU	65	427	19	29	2023-09-01 19:00:00	Other
17511	1	15	1925	1927	-2	2042	2102	YX	1135	N725YX	EWR	PIT	50	319	19	27	2023-01-15 19:00:00	Other
17515	10	12	555	600	-5	759	802	AA	928	N967NN	EWR	CLT	93	529	6	0	2023-10-12 06:00:00	CLT
17520	2	1	2155	2200	-5	2312	2309	9E	1265	N931XJ	JFK	ITH	43	189	22	0	2023-02-01 22:00:00	Other
17525	2	22	827	830	-3	1047	1051	9E	1349	N310PQ	JFK	CLT	93	541	8	30	2023-02-22 08:00:00	CLT
17526	12	8	1459	1501	-2	1643	1704	DL	742	N371NW	LGA	DTW	80	502	15	1	2023-12-08 15:00:00	Other
17529	7	14	1200	1205	-5	1404	1334	9E	1189	N133EV	JFK	BUF	52	301	12	5	2023-07-14 12:00:00	Other
17534	1	29	955	1000	-5	1235	1241	DL	947	N107DU	LGA	MSY	191	1183	10	0	2023-01-29 10:00:00	Other
17537	10	10	2154	2159	-5	2259	2312	UA	445	N47281	EWR	SYR	37	195	21	59	2023-10-10 21:00:00	Other
17540	11	12	608	610	-2	902	915	NK	190	N962NK	EWR	FLL	154	1065	6	10	2023-11-12 06:00:00	FLL
17542	10	2	957	1000	-3	1225	1236	DL	136	N302DN	LGA	ATL	100	762	10	0	2023-10-02 10:00:00	ATL
17546	1	30	749	751	-2	1025	1027	UA	919	N19141	EWR	DEN	240	1605	7	51	2023-01-30 07:00:00	Other
17547	6	6	1008	1010	-2	1152	1214	AA	783	N970AN	LGA	CLT	81	544	10	10	2023-06-06 10:00:00	CLT
17558	4	8	712	715	-3	952	952	DL	244	N705TW	JFK	PHX	311	2153	7	15	2023-04-08 07:00:00	Other
17570	6	13	726	730	-4	1118	1022	AA	154	N931AN	LGA	DFW	257	1389	7	30	2023-06-13 07:00:00	Other
17573	10	5	705	710	-5	1110	1107	B6	552	N504JB	EWR	SJU	217	1608	7	10	2023-10-05 07:00:00	Other
17600	3	6	2225	2229	-4	250	319	B6	296	N535JB	JFK	PSE	187	1617	22	29	2023-03-06 22:00:00	Other
17602	6	11	924	929	-5	1036	1110	YX	1233	N729YX	EWR	PIT	50	319	9	29	2023-06-11 09:00:00	Other
17604	4	3	830	835	-5	918	945	9E	1369	N600LR	LGA	BDL	26	101	8	35	2023-04-03 08:00:00	Other
17619	2	15	858	901	-3	1242	1229	UA	601	N873UA	EWR	SAT	243	1569	9	1	2023-02-15 09:00:00	Other
17621	10	10	1304	1308	-4	1556	1557	UA	688	N14120	EWR	MCO	135	937	13	8	2023-10-10 13:00:00	MCO
17626	11	22	607	610	-3	915	916	NK	190	N957NK	EWR	FLL	167	1065	6	10	2023-11-22 06:00:00	FLL
17633	7	4	1014	1018	-4	1158	1216	NK	21	N668NK	EWR	MYR	80	550	10	18	2023-07-04 10:00:00	Other
17635	1	26	1304	1309	-5	1456	1452	UA	775	N439UA	EWR	RDU	83	416	13	9	2023-01-26 13:00:00	Other
17638	3	10	926	930	-4	1151	1212	UA	876	N873UA	LGA	DEN	238	1620	9	30	2023-03-10 09:00:00	Other
17647	11	2	558	600	-2	831	830	DL	287	N397DN	LGA	ATL	121	762	6	0	2023-11-02 06:00:00	ATL
17651	10	26	854	859	-5	958	1023	YX	1835	N244JQ	LGA	BOS	40	184	8	59	2023-10-26 08:00:00	BOS
17654	11	18	1342	1345	-3	1631	1700	AA	364	N343PN	LGA	DFW	202	1389	13	45	2023-11-18 13:00:00	Other
17655	8	26	1537	1541	-4	1821	1846	UA	440	N17294	EWR	FLL	143	1065	15	41	2023-08-26 15:00:00	FLL
17658	2	19	947	950	-3	1113	1135	YX	976	N741YX	EWR	MKE	118	725	9	50	2023-02-19 09:00:00	Other
17659	3	2	1355	1400	-5	1620	1624	YX	1254	N131HQ	LGA	IND	129	660	14	0	2023-03-02 14:00:00	Other
17661	1	9	2147	2149	-2	2259	2307	B6	70	N198JB	JFK	BTV	51	266	21	49	2023-01-09 21:00:00	Other
17667	12	21	1456	1459	-3	1647	1702	DL	602	N301NB	LGA	DTW	82	502	14	59	2023-12-21 14:00:00	Other
17669	7	6	2207	2210	-3	120	114	DL	299	N829MH	JFK	LAX	313	2475	22	10	2023-07-06 22:00:00	LAX
17672	12	4	1457	1459	-2	1558	1618	9E	1492	N348PQ	JFK	BWI	38	184	14	59	2023-12-04 14:00:00	Other
17676	5	17	1547	1552	-5	1734	1738	9E	1414	N307PQ	LGA	CHO	57	305	15	52	2023-05-17 15:00:00	Other
17686	3	5	627	630	-3	907	935	B6	92	N997JL	LGA	MCO	136	950	6	30	2023-03-05 06:00:00	MCO
17688	10	12	1603	1606	-3	1756	1810	YX	1161	N653RW	EWR	MYR	87	550	16	6	2023-10-12 16:00:00	Other
17694	11	24	1047	1050	-3	1250	1301	YX	1089	N746YX	EWR	MSP	161	1008	10	50	2023-11-24 10:00:00	Other
17700	7	19	2046	2050	-4	2317	2241	9E	1160	N478PX	LGA	ROA	106	405	20	50	2023-07-19 20:00:00	Other
17747	3	12	803	805	-2	952	958	OO	1148	N297SY	JFK	ORD	123	740	8	5	2023-03-12 08:00:00	ORD
17762	8	3	955	959	-4	1135	1155	YX	1328	N225JQ	JFK	CMH	73	483	9	59	2023-08-03 09:00:00	Other
17763	12	8	1716	1719	-3	1911	1924	AA	647	N104UW	EWR	CLT	81	529	17	19	2023-12-08 17:00:00	CLT
17771	9	7	1025	1030	-5	1214	1239	YX	1102	N740YX	EWR	DTW	76	488	10	30	2023-09-07 10:00:00	Other
17776	5	14	2026	2030	-4	2203	2200	YX	1601	N239JQ	LGA	DCA	44	214	20	30	2023-05-14 20:00:00	Other
17779	1	24	1355	1359	-4	1634	1647	YX	1889	N237JQ	LGA	JAX	129	833	13	59	2023-01-24 13:00:00	Other
17782	4	14	941	944	-3	1104	1116	YX	962	N646RW	EWR	PWM	53	284	9	44	2023-04-14 09:00:00	Other
17786	5	3	1013	1017	-4	1152	1152	UA	672	N17229	EWR	ORD	108	719	10	17	2023-05-03 10:00:00	ORD
17792	5	1	1103	1105	-2	1404	1455	DL	110	N712TW	JFK	SFO	322	2586	11	5	2023-05-01 11:00:00	Other
17793	12	22	1957	2000	-3	2152	2221	OO	1172	N614CZ	JFK	CLE	76	425	20	0	2023-12-22 20:00:00	Other
17796	12	26	1128	1130	-2	1453	1448	AA	434	N984NN	JFK	AUS	229	1521	11	30	2023-12-26 11:00:00	Other
17799	2	3	555	600	-5	907	912	UA	898	N14704	LGA	IAH	230	1416	6	0	2023-02-03 06:00:00	Other
17800	12	14	603	605	-2	724	735	WN	1019	N479WN	LGA	MDW	111	725	6	5	2023-12-14 06:00:00	Other
17801	4	3	1627	1630	-3	1807	1808	YX	1550	N226JQ	LGA	PIT	68	335	16	30	2023-04-03 16:00:00	Other
17812	7	6	723	725	-2	853	900	WN	966	N8763L	LGA	STL	120	888	7	25	2023-07-06 07:00:00	Other
17814	8	31	1120	1125	-5	1359	1349	YX	1339	N222JQ	LGA	CHS	103	641	11	25	2023-08-31 11:00:00	Other
17821	10	4	1013	1016	-3	1223	1240	AA	769	N921US	EWR	PHX	281	2133	10	16	2023-10-04 10:00:00	Other
17825	8	21	1127	1130	-3	1229	1300	YX	1367	N818MD	LGA	DCA	41	214	11	30	2023-08-21 11:00:00	Other
17831	2	15	711	715	-4	843	900	WN	965	N8328A	LGA	BNA	126	764	7	15	2023-02-15 07:00:00	Other
17833	2	18	651	655	-4	807	808	UA	547	N33266	EWR	BOS	39	200	6	55	2023-02-18 06:00:00	BOS
17843	10	18	907	910	-3	1159	1216	UA	914	N27258	EWR	MIA	139	1085	9	10	2023-10-18 09:00:00	MIA
17844	3	5	2052	2055	-3	2307	2308	9E	1428	N478PX	LGA	CAE	96	617	20	55	2023-03-05 20:00:00	Other
17849	12	11	1430	1434	-4	1533	1547	YX	1065	N742YX	EWR	BOS	39	200	14	34	2023-12-11 14:00:00	BOS
17851	10	14	1958	2000	-2	2127	2153	YX	1101	N724YX	EWR	STL	127	872	20	0	2023-10-14 20:00:00	Other
17852	6	8	1951	1955	-4	2209	2249	DL	437	N843DN	JFK	ATL	102	760	19	55	2023-06-08 19:00:00	ATL
17863	4	7	2225	2229	-4	2339	2354	B6	72	N247JB	JFK	BTV	45	266	22	29	2023-04-07 22:00:00	Other
17869	5	29	1116	1121	-5	1241	1311	YX	1648	N218JQ	LGA	PIT	54	335	11	21	2023-05-29 11:00:00	Other
17879	8	16	1725	1730	-5	1926	1957	YX	1363	N215JQ	LGA	SDF	99	659	17	30	2023-08-16 17:00:00	Other
17880	5	12	2126	2130	-4	2238	2250	YX	1696	N202JQ	LGA	PWM	44	269	21	30	2023-05-12 21:00:00	Other
17893	1	14	1838	1843	-5	2136	2209	DL	526	N869DN	EWR	SLC	275	1969	18	43	2023-01-14 18:00:00	Other
17903	10	25	802	805	-3	1039	1040	DL	115	N506DA	JFK	PHX	292	2153	8	5	2023-10-25 08:00:00	Other
17904	9	29	555	600	-5	736	758	YX	1317	N437YX	LGA	CMH	80	479	6	0	2023-09-29 06:00:00	Other
17911	4	28	858	900	-2	1026	1023	9E	1296	N348PQ	JFK	IAD	46	228	9	0	2023-04-28 09:00:00	Other
17913	9	26	1736	1740	-4	1939	1933	9E	1669	N147PQ	LGA	MEM	144	963	17	40	2023-09-26 17:00:00	Other
17917	8	16	647	650	-3	848	903	NK	939	N692NK	EWR	PHX	266	2133	6	50	2023-08-16 06:00:00	Other
17919	9	17	1925	1929	-4	2105	2126	YX	1390	N871RW	LGA	CMH	77	479	19	29	2023-09-17 19:00:00	Other
17924	9	27	1116	1118	-2	1420	1439	DL	416	N318DU	LGA	RSW	158	1080	11	18	2023-09-27 11:00:00	Other
17931	8	28	1606	1608	-2	1718	1739	YX	841	N655RW	EWR	ROC	42	246	16	8	2023-08-28 16:00:00	Other
17935	1	5	925	929	-4	1322	1251	UA	928	N14249	EWR	AUS	217	1504	9	29	2023-01-05 09:00:00	Other
17940	3	10	1357	1400	-3	1534	1550	OO	1388	N200SY	LGA	ORD	117	733	14	0	2023-03-10 14:00:00	ORD
17947	3	2	823	826	-3	1125	1045	UA	902	N833UA	EWR	ATL	125	746	8	26	2023-03-02 08:00:00	ATL
17954	5	24	1917	1919	-2	2215	2205	UA	406	N37538	EWR	LAS	309	2227	19	19	2023-05-24 19:00:00	Other
17959	8	14	1552	1555	-3	1913	1931	B6	201	N929JB	JFK	SFO	336	2586	15	55	2023-08-14 15:00:00	Other
17960	11	2	1401	1405	-4	1610	1615	9E	1535	N272PQ	JFK	CVG	103	589	14	5	2023-11-02 14:00:00	Other
17962	2	1	826	830	-4	1034	1040	B6	65	N184JB	JFK	DTW	98	509	8	30	2023-02-01 08:00:00	Other
17966	8	17	2012	2016	-4	2243	2249	B6	38	N973JT	JFK	PHX	294	2153	20	16	2023-08-17 20:00:00	Other
17971	1	28	850	855	-5	1047	1114	9E	1429	N279PQ	JFK	DTW	98	509	8	55	2023-01-28 08:00:00	Other
17972	5	1	1114	1117	-3	1253	1315	YX	1673	N824MD	LGA	CMH	75	479	11	17	2023-05-01 11:00:00	Other
17973	12	2	1736	1740	-4	2047	2100	AS	75	N703AL	EWR	PDX	345	2434	17	40	2023-12-02 17:00:00	Other
17976	8	6	1626	1629	-3	1819	1857	UA	572	N425UA	LGA	DEN	211	1620	16	29	2023-08-06 16:00:00	Other
17988	10	23	931	935	-4	1208	1216	B6	23	N979JT	JFK	LAS	310	2248	9	35	2023-10-23 09:00:00	Other
17991	12	22	1837	1840	-3	2017	2034	YX	1225	N426YX	JFK	RDU	67	427	18	40	2023-12-22 18:00:00	Other
17998	9	21	851	855	-4	1100	1118	YX	1831	N234JQ	LGA	SDF	97	659	8	55	2023-09-21 08:00:00	Other
18000	7	12	1520	1525	-5	1654	1737	9E	1148	N296PQ	LGA	ILM	70	500	15	25	2023-07-12 15:00:00	Other
18009	3	26	1224	1229	-5	1347	1349	YX	1088	N740YX	EWR	BUF	61	282	12	29	2023-03-26 12:00:00	Other
18024	8	9	1253	1258	-5	1428	1451	YX	1083	N425YX	JFK	RDU	68	427	12	58	2023-08-09 12:00:00	Other
18028	10	5	855	900	-5	1042	1107	AA	543	N157UW	EWR	CLT	77	529	9	0	2023-10-05 09:00:00	CLT
18029	2	21	558	600	-2	916	910	WN	921	N734SA	LGA	DAL	229	1381	6	0	2023-02-21 06:00:00	Other
18033	2	12	726	730	-4	1026	1031	NK	25	N522NK	EWR	MCO	146	937	7	30	2023-02-12 07:00:00	MCO
18042	6	11	2050	2055	-5	2217	2233	DL	1026	N107DU	JFK	BOS	43	187	20	55	2023-06-11 20:00:00	BOS
18052	6	19	1723	1725	-2	1833	1914	OO	1275	N296SY	JFK	BOS	36	187	17	25	2023-06-19 17:00:00	BOS
18054	12	12	921	925	-4	1034	1058	9E	1553	N600LR	JFK	IAD	43	228	9	25	2023-12-12 09:00:00	Other
18064	8	3	1952	1955	-3	2222	2249	DL	141	N900DU	JFK	DEN	244	1626	19	55	2023-08-03 19:00:00	Other
18065	10	20	1055	1059	-4	1401	1410	DL	576	N387DA	LGA	MIA	163	1096	10	59	2023-10-20 10:00:00	MIA
18068	3	1	1954	1959	-5	2237	2308	NK	181	N673NK	LGA	MCO	140	950	19	59	2023-03-01 19:00:00	MCO
18087	3	11	727	730	-3	1053	1026	DL	377	N307DX	JFK	MCO	126	944	7	30	2023-03-11 07:00:00	MCO
18090	12	28	606	610	-4	815	821	B6	844	N516JB	LGA	CHS	103	641	6	10	2023-12-28 06:00:00	Other
18101	10	13	1828	1830	-2	2048	2101	DL	801	N935AT	EWR	ATL	119	746	18	30	2023-10-13 18:00:00	ATL
18104	8	7	1256	1259	-3	1417	1425	YX	1349	N245JQ	LGA	BOS	51	184	12	59	2023-08-07 12:00:00	BOS
18113	9	22	1010	1013	-3	1139	1150	YX	1150	N745YX	EWR	BGR	61	393	10	13	2023-09-22 10:00:00	Other
18124	4	10	620	624	-4	723	733	UA	676	N449UA	EWR	IAD	39	212	6	24	2023-04-10 06:00:00	Other
18128	7	6	840	845	-5	1048	1105	9E	1188	N305PQ	LGA	SAV	100	722	8	45	2023-07-06 08:00:00	Other
18129	4	11	1433	1435	-2	1710	1750	UA	79	N76021	EWR	SFO	308	2565	14	35	2023-04-11 14:00:00	Other
18133	6	23	657	700	-3	1016	1001	UA	936	N57286	EWR	MIA	173	1085	7	0	2023-06-23 07:00:00	MIA
18136	3	18	1410	1415	-5	1718	1732	UA	755	N91007	EWR	SFO	314	2565	14	15	2023-03-18 14:00:00	Other
18140	12	23	2153	2157	-4	2305	2332	YX	1292	N126HQ	JFK	DCA	40	213	21	57	2023-12-23 21:00:00	Other
18148	11	16	753	755	-2	944	1010	DL	549	N362DN	LGA	MSP	152	1020	7	55	2023-11-16 07:00:00	Other
18151	10	5	1915	1920	-5	2043	2121	YX	1796	N213JQ	LGA	CMH	72	479	19	20	2023-10-05 19:00:00	Other
18152	9	4	1914	1917	-3	2121	2123	AA	652	N980UY	LGA	CLT	74	544	19	17	2023-09-04 19:00:00	CLT
18160	6	24	1455	1459	-4	1550	1616	B6	761	N323JB	JFK	HYA	38	196	14	59	2023-06-24 14:00:00	Other
18166	6	9	924	927	-3	1222	1239	B6	81	N508JL	LGA	FLL	153	1076	9	27	2023-06-09 09:00:00	FLL
18168	3	25	951	955	-4	1206	1227	9E	1329	N302PQ	LGA	MCI	171	1107	9	55	2023-03-25 09:00:00	Other
18171	12	11	1728	1730	-2	1928	1926	OO	1194	N244SY	JFK	MKE	143	745	17	30	2023-12-11 17:00:00	Other
18181	5	31	829	833	-4	1116	1147	UA	301	N27503	EWR	SAN	304	2425	8	33	2023-05-31 08:00:00	Other
18182	11	1	2211	2214	-3	23	45	NK	559	N926NK	EWR	ATL	111	746	22	14	2023-11-01 22:00:00	ATL
18184	7	4	556	600	-4	837	859	B6	428	N598JB	LGA	FLL	140	1076	6	0	2023-07-04 06:00:00	FLL
18190	12	28	1506	1510	-4	1657	1714	YX	1241	N110HQ	JFK	CMH	81	483	15	10	2023-12-28 15:00:00	Other
18192	11	7	1048	1051	-3	1344	1401	UA	587	N47284	EWR	RSW	150	1068	10	51	2023-11-07 10:00:00	Other
18203	12	20	1040	1045	-5	1236	1306	9E	1529	N490PX	LGA	CLT	81	544	10	45	2023-12-20 10:00:00	CLT
18204	10	17	725	729	-4	1022	1042	DL	285	N871DN	JFK	SEA	331	2422	7	29	2023-10-17 07:00:00	Other
18232	1	21	1139	1144	-5	1605	1648	NK	1110	N635NK	EWR	SJU	186	1608	11	44	2023-01-21 11:00:00	Other
18238	1	18	1726	1729	-3	1858	1854	B6	494	N354JB	JFK	ROC	57	264	17	29	2023-01-18 17:00:00	Other
18241	10	13	1426	1429	-3	1647	1653	UA	933	N894UA	LGA	DEN	237	1620	14	29	2023-10-13 14:00:00	Other
18242	8	6	1716	1720	-4	1939	1929	AA	615	N178US	LGA	CLT	85	544	17	20	2023-08-06 17:00:00	CLT
18250	2	11	1626	1630	-4	1824	1840	B6	386	N324JB	JFK	DTW	87	509	16	30	2023-02-11 16:00:00	Other
18251	12	23	957	1000	-3	1251	1320	DL	255	N177DN	JFK	LAX	320	2475	10	0	2023-12-23 10:00:00	LAX
18255	3	28	805	810	-5	1020	1013	AA	993	N191UW	LGA	CLT	104	544	8	10	2023-03-28 08:00:00	CLT
18274	1	7	1320	1325	-5	1542	1607	YX	1825	N233JQ	LGA	JAX	123	833	13	25	2023-01-07 13:00:00	Other
18277	1	27	1926	1930	-4	2234	2300	DL	326	N121DU	LGA	DFW	226	1389	19	30	2023-01-27 19:00:00	Other
18278	8	19	1846	1851	-5	2058	2122	DL	660	N977AT	EWR	ATL	98	746	18	51	2023-08-19 18:00:00	ATL
18282	7	18	1016	1018	-2	1206	1216	NK	21	N670NK	EWR	MYR	84	550	10	18	2023-07-18 10:00:00	Other
18288	8	3	740	742	-2	1022	1029	B6	150	N584JB	JFK	MCO	124	944	7	42	2023-08-03 07:00:00	MCO
18292	11	6	726	730	-4	914	917	AA	130	N946NN	LGA	ORD	124	733	7	30	2023-11-06 07:00:00	ORD
18298	8	31	641	645	-4	923	926	DL	366	N133DU	LGA	IAH	197	1416	6	45	2023-08-31 06:00:00	Other
18303	8	23	643	645	-2	804	807	AA	445	N837AW	LGA	DCA	42	214	6	45	2023-08-23 06:00:00	Other
18311	8	11	455	500	-5	646	658	AA	725	N934NN	EWR	CLT	82	529	5	0	2023-08-11 05:00:00	CLT
18313	4	18	1856	1859	-3	2046	2058	YX	1040	N655RW	EWR	CMH	76	463	18	59	2023-04-18 18:00:00	Other
18316	5	29	957	1000	-3	1427	1455	HA	21	N375HA	JFK	HNL	586	4983	10	0	2023-05-29 10:00:00	Other
18330	3	6	2002	2005	-3	2247	2250	DL	345	N337NW	LGA	ATL	109	762	20	5	2023-03-06 20:00:00	ATL
18336	5	8	1526	1530	-4	1829	1854	AA	58	N105NN	JFK	LAX	329	2475	15	30	2023-05-08 15:00:00	LAX
18342	2	19	852	855	-3	1024	1044	OO	1061	N301SY	JFK	BNA	131	765	8	55	2023-02-19 08:00:00	Other
18346	2	19	1927	1929	-2	2235	2259	DL	306	N117DU	LGA	DFW	224	1389	19	29	2023-02-19 19:00:00	Other
18348	4	24	1326	1330	-4	1628	1716	B6	525	N942JB	JFK	SFO	339	2586	13	30	2023-04-24 13:00:00	Other
18365	5	18	2141	2145	-4	2335	2358	UA	634	N17289	EWR	MCI	149	1092	21	45	2023-05-18 21:00:00	Other
18367	3	8	1631	1635	-4	1804	1808	YX	1641	N878RW	LGA	DCA	50	214	16	35	2023-03-08 16:00:00	Other
18378	12	14	655	700	-5	946	1033	AA	1	N115NN	JFK	LAX	323	2475	7	0	2023-12-14 07:00:00	LAX
18380	12	16	1119	1121	-2	1455	1440	DL	863	N318DX	LGA	PBI	167	1035	11	21	2023-12-16 11:00:00	Other
18387	8	14	826	830	-4	1053	1114	UA	120	N14011	EWR	LAX	298	2454	8	30	2023-08-14 08:00:00	LAX
18389	4	27	1225	1230	-5	1338	1405	9E	1299	N479PX	LGA	MKE	111	738	12	30	2023-04-27 12:00:00	Other
18391	3	24	1732	1735	-3	2058	2057	DL	268	N178DN	JFK	LAX	358	2475	17	35	2023-03-24 17:00:00	LAX
18394	8	23	1515	1518	-3	1746	1811	UA	617	N433UA	EWR	TPA	127	997	15	18	2023-08-23 15:00:00	Other
18396	10	19	1731	1735	-4	2030	2042	UA	626	N27255	EWR	RSW	155	1068	17	35	2023-10-19 17:00:00	Other
18398	11	4	1056	1100	-4	1258	1321	YX	1408	N437YX	LGA	CVG	99	585	11	0	2023-11-04 11:00:00	Other
18406	9	12	1128	1130	-2	1417	1446	AA	643	N350RV	LGA	MIA	148	1096	11	30	2023-09-12 11:00:00	MIA
18407	5	4	1455	1500	-5	1640	1644	9E	1480	N479PX	EWR	RDU	66	416	15	0	2023-05-04 15:00:00	Other
18436	2	4	1137	1140	-3	1700	1635	DL	716	N930DZ	JFK	SJU	196	1598	11	40	2023-02-04 11:00:00	Other
18437	12	20	1507	1510	-3	1625	1700	YX	1774	N211JQ	JFK	BNA	109	765	15	10	2023-12-20 15:00:00	Other
18438	10	27	1005	1010	-5	1140	1142	YX	1357	N107HQ	JFK	ORF	59	290	10	10	2023-10-27 10:00:00	Other
18439	1	10	1450	1455	-5	1714	1723	YX	1836	N220JQ	JFK	IND	95	665	14	55	2023-01-10 14:00:00	Other
18442	2	9	1330	1335	-5	1453	1526	AA	156	N860NN	LGA	ORD	118	733	13	35	2023-02-09 13:00:00	ORD
18445	1	29	2011	2015	-4	2245	2315	UA	872	N27261	EWR	MCO	133	937	20	15	2023-01-29 20:00:00	MCO
18449	10	26	754	759	-5	909	928	YX	1082	N758YX	EWR	PIT	54	319	7	59	2023-10-26 07:00:00	Other
18451	11	4	835	840	-5	1002	1018	OO	1175	N293SY	JFK	BNA	120	765	8	40	2023-11-04 08:00:00	Other
18455	11	3	1310	1312	-2	1453	1506	YX	1836	N214JQ	LGA	STL	136	888	13	12	2023-11-03 13:00:00	Other
18459	5	11	658	700	-2	916	924	DL	216	N103DY	LGA	ATL	109	762	7	0	2023-05-11 07:00:00	ATL
18471	6	2	903	905	-2	1151	1156	B6	397	N804JB	JFK	MCO	130	944	9	5	2023-06-02 09:00:00	MCO
18475	9	4	2226	2229	-3	224	223	B6	303	N809JB	JFK	BQN	203	1576	22	29	2023-09-04 22:00:00	Other
18477	1	24	1550	1555	-5	1706	1720	OO	1280	N295SY	EWR	BOS	46	200	15	55	2023-01-24 15:00:00	BOS
18484	5	26	555	600	-5	703	723	YX	1690	N203JQ	LGA	DCA	44	214	6	0	2023-05-26 06:00:00	Other
18489	10	5	1555	1557	-2	1822	1839	DL	294	N529DT	JFK	LAS	289	2248	15	57	2023-10-05 15:00:00	Other
18493	10	11	1702	1705	-3	1946	1856	B6	372	N337JB	JFK	RDU	71	427	17	5	2023-10-11 17:00:00	Other
18497	5	26	955	1000	-5	1057	1124	YX	1573	N230JQ	JFK	BOS	38	187	10	0	2023-05-26 10:00:00	BOS
18498	9	15	1325	1330	-5	1504	1505	9E	1465	N930XJ	JFK	RIC	52	288	13	30	2023-09-15 13:00:00	Other
18502	3	18	1502	1504	-2	1728	1718	YX	1047	N864RW	EWR	GRR	116	605	15	4	2023-03-18 15:00:00	Other
18514	8	31	644	649	-5	911	933	UA	255	N68891	EWR	SAN	303	2425	6	49	2023-08-31 06:00:00	Other
18515	3	1	1058	1100	-2	1215	1228	YX	1754	N211JQ	LGA	BOS	34	184	11	0	2023-03-01 11:00:00	BOS
18517	8	10	2042	2045	-3	2243	2256	DL	375	N360NB	LGA	MSY	156	1183	20	45	2023-08-10 20:00:00	Other
18519	1	11	1654	1656	-2	1905	1927	YX	1219	N855RW	EWR	SAV	108	708	16	56	2023-01-11 16:00:00	Other
18527	5	23	1751	1756	-5	2059	2108	AA	736	N304RB	LGA	MIA	147	1096	17	56	2023-05-23 17:00:00	MIA
18531	2	26	1630	1635	-5	1846	1916	DL	748	N120DU	JFK	MSY	176	1182	16	35	2023-02-26 16:00:00	Other
18535	1	23	955	1000	-5	1138	1159	9E	1634	N305PQ	EWR	RDU	81	416	10	0	2023-01-23 10:00:00	Other
18536	2	22	1101	1105	-4	1357	1431	DL	617	N337DN	LGA	MIA	152	1096	11	5	2023-02-22 11:00:00	MIA
18547	1	19	1323	1325	-2	1453	1445	YX	1890	N201JQ	JFK	IAD	54	228	13	25	2023-01-19 13:00:00	Other
18550	11	23	1400	1405	-5	1637	1712	B6	533	N526JL	EWR	MCO	132	937	14	5	2023-11-23 14:00:00	MCO
18553	4	26	1857	1900	-3	2009	2026	UA	734	N457UA	EWR	IAD	45	212	19	0	2023-04-26 19:00:00	Other
18555	12	17	706	710	-4	825	902	DL	607	N306DU	LGA	ORD	110	733	7	10	2023-12-17 07:00:00	ORD
18557	8	9	2130	2135	-5	2236	2302	9E	1209	N320PQ	JFK	ITH	40	189	21	35	2023-08-09 21:00:00	Other
18563	2	27	1624	1627	-3	1750	1812	UA	757	N39475	EWR	CLE	67	404	16	27	2023-02-27 16:00:00	Other
18566	1	8	920	925	-5	1138	1151	9E	1674	N903XJ	JFK	IND	111	665	9	25	2023-01-08 09:00:00	Other
18568	11	26	1751	1755	-4	1958	1954	YX	1817	N221JQ	LGA	CMH	84	479	17	55	2023-11-26 17:00:00	Other
18574	1	26	1325	1329	-4	1511	1501	YX	1746	N202JQ	LGA	RIC	66	292	13	29	2023-01-26 13:00:00	Other
18576	8	6	941	945	-4	1059	1115	9E	1177	N930XJ	JFK	DCA	52	213	9	45	2023-08-06 09:00:00	Other
18580	12	24	1856	1900	-4	2129	2147	DL	192	N106DN	LGA	ATL	117	762	19	0	2023-12-24 19:00:00	ATL
18581	12	13	956	1000	-4	1302	1332	AA	236	N891NN	LGA	DFW	211	1389	10	0	2023-12-13 10:00:00	Other
18589	4	28	906	910	-4	1312	1239	AA	509	N924NN	JFK	MIA	208	1089	9	10	2023-04-28 09:00:00	MIA
18597	10	10	559	602	-3	805	808	DL	961	N921AT	EWR	MSP	144	1008	6	2	2023-10-10 06:00:00	Other
18617	12	5	1623	1627	-4	1716	1734	YX	1143	N758YX	EWR	ALB	28	143	16	27	2023-12-05 16:00:00	Other
18619	11	6	746	750	-4	955	1019	9E	1706	N182GJ	LGA	MCI	167	1107	7	50	2023-11-06 07:00:00	Other
18622	6	4	2024	2029	-5	2313	2326	B6	188	N520JB	LGA	MCO	124	950	20	29	2023-06-04 20:00:00	MCO
18629	3	6	945	950	-5	1121	1123	9E	1549	N182GJ	LGA	ROC	49	254	9	50	2023-03-06 09:00:00	Other
18632	5	6	1105	1110	-5	1240	1311	9E	1423	N146PQ	LGA	ILM	69	500	11	10	2023-05-06 11:00:00	Other
18641	8	30	628	630	-2	829	835	WN	459	N8813Q	LGA	DEN	218	1620	6	30	2023-08-30 06:00:00	Other
18642	4	30	1516	1520	-4	1620	1655	9E	1350	N914XJ	LGA	MKE	101	738	15	20	2023-04-30 15:00:00	Other
18646	5	4	755	800	-5	1051	1119	UA	481	N214UA	EWR	SFO	316	2565	8	0	2023-05-04 08:00:00	Other
18647	5	11	1416	1420	-4	1603	1649	9E	1502	N311PQ	JFK	CLT	79	541	14	20	2023-05-11 14:00:00	CLT
18648	1	24	1227	1230	-3	1451	1502	DL	317	N833DN	JFK	ATL	122	760	12	30	2023-01-24 12:00:00	ATL
18653	3	8	1320	1325	-5	1539	1547	9E	1541	N922XJ	LGA	IND	107	660	13	25	2023-03-08 13:00:00	Other
18658	10	17	1920	1925	-5	2137	2159	YX	1780	N218JQ	LGA	SDF	102	659	19	25	2023-10-17 19:00:00	Other
18659	11	18	2331	2335	-4	39	49	B6	573	N3138J	JFK	BOS	36	187	23	35	2023-11-18 23:00:00	BOS
18665	6	8	1131	1135	-4	1321	1341	AA	779	N905NN	LGA	CLT	83	544	11	35	2023-06-08 11:00:00	CLT
18667	9	29	800	803	-3	1114	1117	AA	496	N986NN	EWR	MIA	159	1085	8	3	2023-09-29 08:00:00	MIA
18669	9	27	933	937	-4	1244	1233	UA	650	N485UA	EWR	PBI	159	1023	9	37	2023-09-27 09:00:00	Other
18670	5	16	856	901	-5	1015	1040	YX	1326	N429YX	LGA	BUF	51	292	9	1	2023-05-16 09:00:00	Other
18674	8	23	858	900	-2	1155	1220	DL	82	N705TW	JFK	SFO	333	2586	9	0	2023-08-23 09:00:00	Other
18680	2	1	955	959	-4	1354	1309	B6	917	N595JB	JFK	TPA	163	1005	9	59	2023-02-01 09:00:00	Other
18682	1	14	1556	1600	-4	1717	1735	9E	1481	N917XJ	LGA	BGR	55	378	16	0	2023-01-14 16:00:00	Other
18683	12	19	1221	1225	-4	1317	1349	DL	560	N128DU	JFK	BOS	41	187	12	25	2023-12-19 12:00:00	BOS
18689	3	21	901	905	-4	1019	1041	9E	1529	N311PQ	JFK	RIC	54	288	9	5	2023-03-21 09:00:00	Other
18690	9	21	1657	1659	-2	1853	1857	YX	1797	N818MD	LGA	RDU	74	431	16	59	2023-09-21 16:00:00	Other
18699	4	27	1650	1654	-4	1906	1920	B6	121	N247JB	JFK	SAV	112	718	16	54	2023-04-27 16:00:00	Other
18725	4	6	655	700	-5	932	942	DL	174	N374DA	LGA	DEN	242	1620	7	0	2023-04-06 07:00:00	Other
18732	5	8	1128	1132	-4	1412	1434	DL	404	N337NB	JFK	PBI	135	1028	11	32	2023-05-08 11:00:00	Other
18733	2	2	1727	1730	-3	1947	1952	9E	1322	N490PX	LGA	CVG	117	585	17	30	2023-02-02 17:00:00	Other
18741	7	26	635	639	-4	851	918	UA	665	N47284	EWR	DFW	169	1372	6	39	2023-07-26 06:00:00	Other
18744	12	29	857	900	-3	1131	1227	AA	68	N113AN	JFK	LAX	304	2475	9	0	2023-12-29 09:00:00	LAX
18745	7	6	1054	1059	-5	1227	1250	9E	1284	N691CA	LGA	RDU	66	431	10	59	2023-07-06 10:00:00	Other
18756	10	31	1714	1716	-2	1904	1917	9E	1400	N186PQ	JFK	RDU	84	427	17	16	2023-10-31 17:00:00	Other
18759	11	22	1515	1517	-2	1658	1725	YX	1059	N767YX	EWR	DTW	80	488	15	17	2023-11-22 15:00:00	Other
18763	11	15	2215	2220	-5	2339	2342	OO	1190	N293SY	JFK	BOS	49	187	22	20	2023-11-15 22:00:00	BOS
18764	11	2	656	700	-4	957	1005	DL	620	N377NW	JFK	AUS	214	1521	7	0	2023-11-02 07:00:00	Other
18766	3	26	1633	1636	-3	1951	1939	9E	1319	N330PQ	LGA	OKC	234	1341	16	36	2023-03-26 16:00:00	Other
18771	6	16	1726	1729	-3	1942	1950	YX	1347	N402YX	LGA	SDF	105	659	17	29	2023-06-16 17:00:00	Other
18772	1	2	701	705	-4	859	850	UA	560	N13138	EWR	ORD	131	719	7	5	2023-01-02 07:00:00	ORD
18773	3	9	730	735	-5	1013	1037	DL	597	N844DN	JFK	TPA	137	1005	7	35	2023-03-09 07:00:00	Other
18797	11	5	630	633	-3	1002	1014	AA	856	N331TK	JFK	PHX	288	2153	6	33	2023-11-05 06:00:00	Other
18800	11	18	2225	2229	-4	127	157	B6	655	N980JT	JFK	LAX	338	2475	22	29	2023-11-18 22:00:00	LAX
18802	11	17	507	509	-2	801	823	AA	405	N336SR	EWR	MIA	144	1085	5	9	2023-11-17 05:00:00	MIA
18816	7	12	1555	1559	-4	1812	1757	YX	1030	N403YX	LGA	DTW	88	502	15	59	2023-07-12 15:00:00	Other
18831	2	8	1500	1505	-5	1636	1658	YX	1496	N219YX	JFK	PIT	70	340	15	5	2023-02-08 15:00:00	Other
18838	2	21	807	810	-3	1251	1310	DL	696	N846DN	JFK	SJU	191	1598	8	10	2023-02-21 08:00:00	Other
18841	4	1	1548	1550	-2	1732	1733	B6	730	N656JB	LGA	BNA	131	764	15	50	2023-04-01 15:00:00	Other
18843	10	13	955	1000	-5	1251	1301	DL	235	N174DN	JFK	LAX	330	2475	10	0	2023-10-13 10:00:00	LAX
18844	4	13	1121	1125	-4	1254	1312	OO	1031	N604CZ	JFK	ORD	113	740	11	25	2023-04-13 11:00:00	ORD
18846	5	5	756	800	-4	900	921	YX	1712	N234JQ	LGA	BOS	35	184	8	0	2023-05-05 08:00:00	BOS
18854	8	29	1931	1935	-4	2242	2250	DL	130	N176DN	JFK	LAX	318	2475	19	35	2023-08-29 19:00:00	LAX
18859	9	14	819	824	-5	949	1001	YX	1355	N103HQ	JFK	DCA	45	213	8	24	2023-09-14 08:00:00	Other
18865	6	2	1251	1256	-5	1444	1459	9E	1483	N147PQ	JFK	DTW	80	509	12	56	2023-06-02 12:00:00	Other
18868	4	11	455	500	-5	725	756	AA	301	N935AN	EWR	DFW	169	1372	5	0	2023-04-11 05:00:00	Other
18872	8	18	1158	1200	-2	1310	1340	YX	1336	N244JQ	LGA	ORF	52	296	12	0	2023-08-18 12:00:00	Other
18878	10	3	1024	1029	-5	1145	1213	9E	1461	N300PQ	LGA	RIC	53	292	10	29	2023-10-03 10:00:00	Other
18879	1	31	726	730	-4	938	956	YX	1323	N128HQ	LGA	DTW	99	502	7	30	2023-01-31 07:00:00	Other
18883	5	8	1653	1655	-2	1939	2029	DL	164	N395DN	JFK	SAN	324	2446	16	55	2023-05-08 16:00:00	Other
18886	1	3	1021	1025	-4	1316	1333	UA	177	N795UA	EWR	IAH	208	1400	10	25	2023-01-03 10:00:00	Other
18887	8	4	1117	1119	-2	1409	1423	DL	317	N339NB	LGA	TPA	133	1010	11	19	2023-08-04 11:00:00	Other
18889	3	3	841	846	-5	1018	1032	YX	1096	N724YX	EWR	PIT	65	319	8	46	2023-03-03 08:00:00	Other
18892	5	18	2010	2012	-2	2258	2311	UA	505	N33292	EWR	PBI	138	1023	20	12	2023-05-18 20:00:00	Other
18897	9	12	1810	1815	-5	2052	2113	UA	453	N38727	EWR	BZN	255	1882	18	15	2023-09-12 18:00:00	Other
18904	1	5	1206	1210	-4	1415	1443	B6	642	N605JB	JFK	DEN	220	1626	12	10	2023-01-05 12:00:00	Other
18912	12	16	727	729	-2	1052	1043	AA	738	N334SM	JFK	MIA	152	1089	7	29	2023-12-16 07:00:00	MIA
18914	10	5	2126	2129	-3	2240	2300	YX	1738	N815MD	LGA	BUF	49	292	21	29	2023-10-05 21:00:00	Other
18915	11	3	643	645	-2	900	905	WN	785	N7733B	LGA	DEN	232	1620	6	45	2023-11-03 06:00:00	Other
18916	5	30	1439	1444	-5	1712	1651	9E	1344	N918XJ	LGA	ILM	73	500	14	44	2023-05-30 14:00:00	Other
18922	3	28	612	615	-3	714	727	B6	72	N281JB	LGA	BOS	36	184	6	15	2023-03-28 06:00:00	BOS
18926	7	13	1833	1836	-3	2214	2055	YX	1039	N411YX	LGA	OMA	180	1148	18	36	2023-07-13 18:00:00	Other
18927	12	5	805	810	-5	949	1014	9E	1508	N932XJ	JFK	CLE	82	425	8	10	2023-12-05 08:00:00	Other
18936	3	25	556	600	-4	737	739	AA	999	N904AN	LGA	ORD	125	733	6	0	2023-03-25 06:00:00	ORD
18937	11	28	1617	1620	-3	1921	1944	B6	88	N597JB	JFK	AUS	214	1521	16	20	2023-11-28 16:00:00	Other
18945	1	13	1457	1500	-3	1900	1813	B6	23	N706JB	JFK	PBI	185	1028	15	0	2023-01-13 15:00:00	Other
18952	12	7	1048	1050	-2	1330	1400	DL	384	N317DN	LGA	TPA	138	1010	10	50	2023-12-07 10:00:00	Other
18958	3	13	555	600	-5	746	807	YX	1249	N408YX	LGA	CMH	80	479	6	0	2023-03-13 06:00:00	Other
18959	3	8	1545	1550	-5	1708	1736	9E	1453	N917XJ	LGA	CHO	52	305	15	50	2023-03-08 15:00:00	Other
18961	8	26	728	730	-2	941	948	AA	442	N310RF	JFK	PHX	273	2153	7	30	2023-08-26 07:00:00	Other
18965	3	21	656	700	-4	801	824	YX	1606	N207JQ	LGA	BOS	43	184	7	0	2023-03-21 07:00:00	BOS
18972	7	6	1940	1943	-3	2256	2257	DL	300	N391DA	LGA	MIA	148	1096	19	43	2023-07-06 19:00:00	MIA
18975	2	16	2152	2155	-3	2258	2310	DL	728	N845DN	JFK	BOS	40	187	21	55	2023-02-16 21:00:00	BOS
18978	12	11	837	840	-3	941	1009	YX	1819	N209JQ	EWR	BOS	39	200	8	40	2023-12-11 08:00:00	BOS
18982	8	28	759	803	-4	1010	1006	AA	468	N997NN	EWR	CLT	92	529	8	3	2023-08-28 08:00:00	CLT
18985	4	11	1224	1229	-5	1311	1325	YX	1028	N722YX	EWR	AVP	27	93	12	29	2023-04-11 12:00:00	Other
18989	7	25	1248	1250	-2	NA	1527	YX	1041	N122HQ	LGA	OKC	NA	1341	12	50	2023-07-25 12:00:00	Other
18993	12	22	1402	1405	-3	1606	1617	YX	1030	N748YX	EWR	DTW	84	488	14	5	2023-12-22 14:00:00	Other
18994	5	25	1645	1650	-5	1849	1920	9E	1552	N302PQ	JFK	CLT	81	541	16	50	2023-05-25 16:00:00	CLT
18999	5	17	1915	1920	-5	2102	2120	AA	323	N844NN	EWR	CLT	82	529	19	20	2023-05-17 19:00:00	CLT
19003	5	27	2055	2100	-5	2303	2329	9E	1293	N311PQ	JFK	CHS	92	636	21	0	2023-05-27 21:00:00	Other
19007	3	1	1627	1630	-3	1821	1816	AA	136	N830NN	LGA	ORD	132	733	16	30	2023-03-01 16:00:00	ORD
19008	6	14	732	735	-3	950	936	UA	930	N62894	EWR	MSY	170	1167	7	35	2023-06-14 07:00:00	Other
19015	9	17	956	1000	-4	1231	1308	UA	816	N219UA	EWR	SFO	309	2565	10	0	2023-09-17 10:00:00	Other
19018	7	5	555	600	-5	707	708	UA	425	N27255	EWR	BOS	41	200	6	0	2023-07-05 06:00:00	BOS
19019	3	15	1130	1132	-2	1243	1259	YX	1676	N205JQ	JFK	DCA	51	213	11	32	2023-03-15 11:00:00	Other
19028	10	29	1921	1925	-4	2158	2236	DL	836	N505DZ	JFK	MCO	132	944	19	25	2023-10-29 19:00:00	MCO
19047	5	21	1815	1820	-5	2015	2045	9E	1460	N936XJ	JFK	IND	92	665	18	20	2023-05-21 18:00:00	Other
19048	10	4	1952	1955	-3	2123	2145	9E	1403	N300PQ	EWR	RDU	66	416	19	55	2023-10-04 19:00:00	Other
19051	7	5	2144	2146	-2	2335	2350	YX	921	N979RP	EWR	GSO	64	445	21	46	2023-07-05 21:00:00	Other
19052	10	30	756	800	-4	1001	952	OO	1230	N259SY	JFK	ORD	149	740	8	0	2023-10-30 08:00:00	ORD
19055	2	25	1201	1205	-4	1553	1507	B6	33	N634JB	JFK	MCO	140	944	12	5	2023-02-25 12:00:00	MCO
19059	1	21	730	735	-5	1027	1035	DL	428	N309DN	JFK	MCO	145	944	7	35	2023-01-21 07:00:00	MCO
19064	11	16	1132	1136	-4	1334	1352	AA	749	N315PE	LGA	CLT	88	544	11	36	2023-11-16 11:00:00	CLT
19074	7	15	956	1000	-4	1246	1303	UA	119	N16709	EWR	RSW	146	1068	10	0	2023-07-15 10:00:00	Other
19075	10	8	1810	1814	-4	2059	2110	UA	797	N37267	EWR	TPA	144	997	18	14	2023-10-08 18:00:00	Other
19077	7	3	847	852	-5	1006	1017	UA	553	N27511	EWR	ORF	44	284	8	52	2023-07-03 08:00:00	Other
19078	1	16	756	759	-3	1042	1112	AA	903	N972NN	JFK	DFW	199	1391	7	59	2023-01-16 07:00:00	Other
19082	10	2	757	800	-3	1008	1035	DL	168	N538DN	JFK	DEN	220	1626	8	0	2023-10-02 08:00:00	Other
19091	3	29	1545	1550	-5	1731	1748	9E	1468	N183GJ	LGA	CLE	78	419	15	50	2023-03-29 15:00:00	Other
19093	9	1	1757	1800	-3	1957	2044	DL	309	N3749D	LGA	DEN	208	1620	18	0	2023-09-01 18:00:00	Other
19095	6	17	1354	1359	-5	1508	1523	9E	1567	N184GJ	JFK	SYR	44	209	13	59	2023-06-17 13:00:00	Other
19105	10	23	1810	1815	-5	1943	1958	DL	607	N104DU	LGA	ORD	117	733	18	15	2023-10-23 18:00:00	ORD
19106	11	6	1454	1459	-5	1558	1618	9E	1563	N931XJ	JFK	BWI	40	184	14	59	2023-11-06 14:00:00	Other
19111	9	4	1624	1629	-5	1815	1843	YX	1210	N858RW	EWR	CVG	86	569	16	29	2023-09-04 16:00:00	Other
19116	2	14	855	900	-5	1042	1053	9E	1473	N479PX	LGA	MSN	123	812	9	0	2023-02-14 09:00:00	Other
19119	11	30	2006	2010	-4	2200	2225	DL	568	N344DN	LGA	DTW	81	502	20	10	2023-11-30 20:00:00	Other
19127	8	9	1349	1354	-5	1523	1534	9E	1174	N336PQ	JFK	BGR	61	382	13	54	2023-08-09 13:00:00	Other
19132	12	10	555	600	-5	728	740	UA	372	N14107	EWR	ORD	122	719	6	0	2023-12-10 06:00:00	ORD
19135	1	30	925	929	-4	1143	1203	9E	1441	N349PQ	LGA	GRR	110	618	9	29	2023-01-30 09:00:00	Other
19139	4	12	1451	1455	-4	1617	1656	9E	1379	N923XJ	JFK	RDU	61	427	14	55	2023-04-12 14:00:00	Other
19143	11	14	1603	1606	-3	1758	1812	9E	1440	N324PQ	JFK	CLT	78	541	16	6	2023-11-14 16:00:00	CLT
19162	3	5	1126	1130	-4	1251	1254	YX	1133	N743YX	EWR	PWM	59	284	11	30	2023-03-05 11:00:00	Other
19166	9	15	958	1000	-2	1118	1140	AA	982	N737US	LGA	ORD	105	733	10	0	2023-09-15 10:00:00	ORD
19177	11	16	625	630	-5	755	824	9E	1712	N316PQ	LGA	STL	128	888	6	30	2023-11-16 06:00:00	Other
19181	6	28	1323	1325	-2	1451	1505	9E	1485	N909XJ	JFK	RIC	56	288	13	25	2023-06-28 13:00:00	Other
19190	9	21	1142	1147	-5	1415	1435	DL	623	N345DN	JFK	MCO	129	944	11	47	2023-09-21 11:00:00	MCO
19207	6	16	857	900	-3	1031	1042	UA	706	N16713	EWR	CLE	65	404	9	0	2023-06-16 09:00:00	Other
19216	6	13	1525	1530	-5	1751	1811	B6	650	N534JB	JFK	JAX	125	828	15	30	2023-06-13 15:00:00	Other
19220	9	16	1750	1755	-5	1909	1928	9E	1611	N920XJ	LGA	ORF	47	296	17	55	2023-09-16 17:00:00	Other
19226	10	9	1958	2000	-2	2302	2317	AA	83	N104NN	JFK	LAX	309	2475	20	0	2023-10-09 20:00:00	LAX
19227	1	1	1724	1729	-5	2014	2035	UA	564	N832UA	EWR	PBI	145	1023	17	29	2023-01-01 17:00:00	Other
19231	9	22	1227	1229	-2	1450	1457	AA	988	N318SF	JFK	PHX	293	2153	12	29	2023-09-22 12:00:00	Other
19232	12	8	1639	1642	-3	1854	1916	UA	910	N17139	EWR	DEN	226	1605	16	42	2023-12-08 16:00:00	Other
19233	8	16	1057	1059	-2	1307	1337	DL	251	N396DN	LGA	ATL	105	762	10	59	2023-08-16 10:00:00	ATL
19236	3	19	1557	1559	-2	1833	1826	YX	1300	N427YX	JFK	CVG	107	589	15	59	2023-03-19 15:00:00	Other
19242	3	31	1858	1900	-2	2041	2047	YX	1192	N864RW	EWR	CLE	73	404	19	0	2023-03-31 19:00:00	Other
19247	8	21	801	805	-4	1146	1209	DL	560	N909DN	JFK	SJU	193	1598	8	5	2023-08-21 08:00:00	Other
19255	1	27	628	630	-2	901	904	UA	271	N898UA	EWR	ATL	130	746	6	30	2023-01-27 06:00:00	ATL
19257	8	18	640	645	-5	848	847	UA	379	N76526	EWR	CHS	89	628	6	45	2023-08-18 06:00:00	Other
19264	9	6	2155	2200	-5	2334	2336	DL	368	N365NB	JFK	BUF	52	301	22	0	2023-09-06 22:00:00	Other
19265	12	12	923	925	-2	1046	1120	DL	885	N112DU	LGA	ORD	118	733	9	25	2023-12-12 09:00:00	ORD
19271	9	11	846	848	-2	1131	1131	YX	1846	N218JQ	JFK	JAX	127	828	8	48	2023-09-11 08:00:00	Other
19273	1	16	915	920	-5	1043	1128	9E	1620	N335PQ	LGA	CLE	65	419	9	20	2023-01-16 09:00:00	Other
19287	11	20	755	800	-5	1014	1049	DL	183	N512DE	JFK	DEN	229	1626	8	0	2023-11-20 08:00:00	Other
19288	3	19	701	705	-4	947	1004	DL	386	N3759	LGA	PBI	154	1035	7	5	2023-03-19 07:00:00	Other
19295	5	8	1013	1018	-5	1306	1320	NK	27	N668NK	EWR	MIA	141	1085	10	18	2023-05-08 10:00:00	MIA
19300	5	7	1443	1445	-2	1550	1612	9E	1400	N176PQ	LGA	ROC	43	254	14	45	2023-05-07 14:00:00	Other
19301	5	23	616	620	-4	809	845	AA	966	N400AN	EWR	PHX	265	2133	6	20	2023-05-23 06:00:00	Other
19302	5	1	625	630	-5	818	745	UA	510	N27239	EWR	BOS	55	200	6	30	2023-05-01 06:00:00	BOS
19309	5	24	1046	1049	-3	1238	1302	YX	1040	N979RP	EWR	MSP	146	1008	10	49	2023-05-24 10:00:00	Other
19312	11	24	1925	1928	-3	2229	2230	UA	705	N76528	EWR	IAH	210	1400	19	28	2023-11-24 19:00:00	Other
19324	12	19	1520	1525	-5	1745	1830	UA	782	N62849	EWR	IAH	187	1400	15	25	2023-12-19 15:00:00	Other
19337	3	19	1958	2000	-2	2126	2136	9E	1583	N182GJ	LGA	CHO	59	305	20	0	2023-03-19 20:00:00	Other
19339	2	12	2115	2120	-5	2227	2226	9E	1367	N138EV	LGA	ALB	27	136	21	20	2023-02-12 21:00:00	Other
19343	8	11	556	600	-4	911	905	NK	43	N685NK	LGA	FLL	142	1076	6	0	2023-08-11 06:00:00	FLL
19345	5	23	1857	1859	-2	2134	2204	AS	88	N428AS	EWR	PDX	302	2434	18	59	2023-05-23 18:00:00	Other
19348	4	21	845	850	-5	1054	1047	9E	1274	N914XJ	LGA	RDU	66	431	8	50	2023-04-21 08:00:00	Other
19349	3	26	954	959	-5	1251	1320	NK	1021	N684NK	LGA	MIA	157	1096	9	59	2023-03-26 09:00:00	MIA
19350	11	14	558	600	-2	900	905	WN	1091	N8775Q	LGA	DAL	209	1381	6	0	2023-11-14 06:00:00	Other
19351	8	22	715	719	-4	1005	1020	DL	589	N315DN	EWR	SLC	258	1969	7	19	2023-08-22 07:00:00	Other
19353	10	5	855	900	-5	1131	1202	AS	13	N263AK	JFK	SAN	316	2446	9	0	2023-10-05 09:00:00	Other
19365	1	14	1425	1429	-4	1717	1749	B6	91	N974JT	JFK	AUS	204	1521	14	29	2023-01-14 14:00:00	Other
19372	8	26	1106	1110	-4	1345	1420	DL	712	N914DU	JFK	FLL	138	1069	11	10	2023-08-26 11:00:00	FLL
19375	8	2	2041	2045	-4	2232	2256	DL	375	N314NB	LGA	MSY	147	1183	20	45	2023-08-02 20:00:00	Other
19376	11	8	1642	1645	-3	1933	2000	B6	616	N975JT	JFK	RSW	150	1074	16	45	2023-11-08 16:00:00	Other
19388	11	6	1851	1855	-4	2018	2030	WN	876	N7729A	LGA	MDW	125	725	18	55	2023-11-06 18:00:00	Other
19390	6	29	1633	1635	-2	1822	1756	9E	1524	N538CA	LGA	SYR	41	198	16	35	2023-06-29 16:00:00	Other
19397	1	10	915	918	-3	1217	1234	UA	696	N17285	EWR	FLL	151	1065	9	18	2023-01-10 09:00:00	FLL
19398	11	28	1547	1550	-3	1852	1856	DL	971	N331NW	LGA	TPA	161	1010	15	50	2023-11-28 15:00:00	Other
19399	6	14	1556	1559	-3	1851	1741	YX	1384	N108HQ	JFK	BNA	131	765	15	59	2023-06-14 15:00:00	Other
19400	8	1	2105	2110	-5	2213	2249	9E	1228	N133EV	JFK	BWI	36	184	21	10	2023-08-01 21:00:00	Other
19401	3	22	1315	1320	-5	1411	1432	YX	1267	N425YX	JFK	BOS	33	187	13	20	2023-03-22 13:00:00	BOS
19404	5	4	2158	2200	-2	2321	2335	9E	1519	N147PQ	JFK	ORF	52	290	22	0	2023-05-04 22:00:00	Other
19405	5	6	1102	1105	-3	1417	1455	DL	110	N712TW	JFK	SFO	353	2586	11	5	2023-05-06 11:00:00	Other
19409	10	26	1207	1211	-4	1338	1345	YX	1795	N224JQ	JFK	BUF	55	301	12	11	2023-10-26 12:00:00	Other
19414	11	26	512	516	-4	754	815	NK	21	N530NK	EWR	MCO	139	937	5	16	2023-11-26 05:00:00	MCO
19418	11	24	1638	1640	-2	1902	1917	DL	544	N841DN	JFK	ATL	111	760	16	40	2023-11-24 16:00:00	ATL
19420	11	13	1231	1236	-5	1516	1543	NK	349	N901NK	EWR	FLL	146	1065	12	36	2023-11-13 12:00:00	FLL
19421	8	28	1011	1015	-4	1150	1205	AA	585	N758US	LGA	ORD	116	733	10	15	2023-08-28 10:00:00	ORD
19424	4	15	1256	1300	-4	1606	1610	UA	741	N12116	EWR	LAX	317	2454	13	0	2023-04-15 13:00:00	LAX
19427	12	10	1236	1240	-4	1504	1519	OO	1164	N296SY	LGA	SDF	128	659	12	40	2023-12-10 12:00:00	Other
19438	3	3	1126	1129	-3	1329	1329	AA	239	N663AW	EWR	CLT	87	529	11	29	2023-03-03 11:00:00	CLT
19444	1	3	1945	1950	-5	2232	2315	DL	1080	N345NB	JFK	PBI	140	1028	19	50	2023-01-03 19:00:00	Other
19446	12	13	941	945	-4	1425	1440	UA	558	N37516	EWR	SJU	200	1608	9	45	2023-12-13 09:00:00	Other
19448	11	20	1556	1559	-3	1809	1827	DL	879	N3737C	EWR	ATL	111	746	15	59	2023-11-20 15:00:00	ATL
19449	6	5	640	645	-5	915	926	UA	840	N498UA	EWR	DFW	185	1372	6	45	2023-06-05 06:00:00	Other
19457	5	31	1045	1050	-5	1211	1240	WN	963	N8683D	LGA	STL	116	888	10	50	2023-05-31 10:00:00	Other
19463	11	26	1825	1827	-2	2200	2145	UA	254	N27520	EWR	AUS	237	1504	18	27	2023-11-26 18:00:00	Other
19464	11	27	646	650	-4	807	832	YX	1793	N824MD	LGA	PIT	63	335	6	50	2023-11-27 06:00:00	Other
19473	3	12	556	600	-4	843	823	DL	841	N317NB	EWR	ATL	127	746	6	0	2023-03-12 06:00:00	ATL
19474	7	17	1353	1356	-3	1701	1635	NK	73	N641NK	EWR	DFW	186	1372	13	56	2023-07-17 13:00:00	Other
19478	6	2	1044	1049	-5	1239	1318	YX	1813	N233JQ	LGA	IND	91	660	10	49	2023-06-02 10:00:00	Other
19479	5	30	710	715	-5	933	949	9E	1428	N337PQ	LGA	JAX	114	833	7	15	2023-05-30 07:00:00	Other
19481	12	16	1316	1320	-4	1508	1534	YX	1722	N210JQ	LGA	CLT	89	544	13	20	2023-12-16 13:00:00	CLT
19483	1	23	1353	1355	-2	1656	1700	B6	635	N639JB	JFK	MCO	153	944	13	55	2023-01-23 13:00:00	MCO
19493	2	26	1628	1630	-2	1818	1834	YX	1291	N129HQ	JFK	CMH	85	483	16	30	2023-02-26 16:00:00	Other
19494	10	19	1738	1740	-2	1926	1938	YX	1287	N101HQ	LGA	CMH	76	479	17	40	2023-10-19 17:00:00	Other
19499	9	25	1253	1255	-2	1426	1455	G4	156	253NV	EWR	DSM	133	1017	12	55	2023-09-25 12:00:00	Other
19509	8	5	1056	1059	-3	1235	1306	DL	413	N377DN	LGA	MSP	140	1020	10	59	2023-08-05 10:00:00	Other
19514	1	6	733	735	-2	1038	1053	DL	889	N880DN	JFK	MIA	155	1089	7	35	2023-01-06 07:00:00	MIA
19525	11	1	2026	2030	-4	15	4	AA	932	N101NN	JFK	SFO	353	2586	20	30	2023-11-01 20:00:00	Other
19531	3	23	1422	1427	-5	1620	1627	YX	1207	N653RW	EWR	MYR	80	550	14	27	2023-03-23 14:00:00	Other
19533	5	18	1454	1459	-5	1635	1727	DL	129	N343NB	JFK	MSP	142	1029	14	59	2023-05-18 14:00:00	Other
19536	7	17	924	929	-5	1047	1051	YX	959	N745YX	EWR	MHT	43	209	9	29	2023-07-17 09:00:00	Other
19541	5	5	2045	2047	-2	2209	2158	YX	1119	N751YX	EWR	PVD	37	160	20	47	2023-05-05 20:00:00	Other
19545	7	5	1922	1925	-3	2235	2250	AS	83	N472AS	EWR	SFO	333	2565	19	25	2023-07-05 19:00:00	Other
19547	5	31	2154	2157	-3	2332	2359	UA	615	N471UA	EWR	MSP	133	1008	21	57	2023-05-31 21:00:00	Other
19551	12	28	756	759	-3	1023	1026	YX	1309	N109HQ	JFK	CVG	105	589	7	59	2023-12-28 07:00:00	Other
19553	1	21	624	629	-5	748	805	UA	1031	N808UA	LGA	ORD	119	733	6	29	2023-01-21 06:00:00	ORD
19560	12	5	2050	2055	-5	2355	2354	DL	424	N803DN	JFK	MCO	149	944	20	55	2023-12-05 20:00:00	MCO
19562	12	21	1850	1855	-5	2159	2211	UA	466	N37508	EWR	RSW	152	1068	18	55	2023-12-21 18:00:00	Other
19565	5	1	1257	1300	-3	1513	1552	UA	808	N36962	EWR	LAX	296	2454	13	0	2023-05-01 13:00:00	LAX
19570	12	22	1203	1207	-4	1359	1427	DL	350	N142DU	JFK	MSP	153	1029	12	7	2023-12-22 12:00:00	Other
19574	10	18	701	705	-4	946	1010	DL	943	N394DA	LGA	MIA	141	1096	7	5	2023-10-18 07:00:00	MIA
19582	2	9	1126	1130	-4	1302	1327	9E	1460	N176PQ	LGA	RDU	71	431	11	30	2023-02-09 11:00:00	Other
19585	10	24	1255	1300	-5	1456	1520	YX	1141	N754YX	EWR	SDF	103	642	13	0	2023-10-24 13:00:00	Other
19591	8	30	2113	2115	-2	2233	2240	WN	1102	N8819L	LGA	MDW	108	725	21	15	2023-08-30 21:00:00	Other
19595	12	21	1856	1859	-3	2157	2204	UA	703	N37528	EWR	IAH	200	1400	18	59	2023-12-21 18:00:00	Other
19602	11	25	728	730	-2	1035	1045	DL	985	N776DE	JFK	MIA	151	1089	7	30	2023-11-25 07:00:00	MIA
19605	9	21	926	930	-4	1041	1102	YX	1814	N226JQ	JFK	DCA	46	213	9	30	2023-09-21 09:00:00	Other
19606	8	14	1410	1415	-5	1545	1555	9E	1255	N324PQ	LGA	BHM	120	866	14	15	2023-08-14 14:00:00	Other
19611	12	12	1330	1333	-3	1621	1634	UA	80	N37465	EWR	PBI	151	1023	13	33	2023-12-12 13:00:00	Other
19612	3	1	1347	1350	-3	1608	1631	DL	140	N340NW	LGA	ATL	119	762	13	50	2023-03-01 13:00:00	ATL
19616	3	2	1500	1505	-5	1646	1658	YX	1614	N231JQ	JFK	PIT	80	340	15	5	2023-03-02 15:00:00	Other
19628	11	5	526	530	-4	830	844	AA	244	N318TD	JFK	MIA	156	1089	5	30	2023-11-05 05:00:00	MIA
19634	5	18	955	959	-4	1116	1126	9E	1527	N136EV	JFK	SYR	46	209	9	59	2023-05-18 09:00:00	Other
19635	3	31	1346	1349	-3	1507	1515	9E	1451	N200PQ	JFK	ORF	50	290	13	49	2023-03-31 13:00:00	Other
19637	10	4	855	900	-5	1004	1027	YX	1835	N204JQ	LGA	BOS	33	184	9	0	2023-10-04 09:00:00	BOS
19638	5	24	1550	1552	-2	2034	1920	DL	379	N3745B	JFK	MIA	232	1089	15	52	2023-05-24 15:00:00	MIA
19641	5	4	1611	1614	-3	1909	1926	AA	506	N997NN	LGA	MIA	147	1096	16	14	2023-05-04 16:00:00	MIA
19642	11	21	656	700	-4	1006	1033	AS	12	N464AS	JFK	SFO	333	2586	7	0	2023-11-21 07:00:00	Other
19651	10	5	1442	1445	-3	1652	1715	WN	1018	N7747C	LGA	ATL	108	762	14	45	2023-10-05 14:00:00	ATL
19653	4	4	720	722	-2	958	1017	UA	632	N412UA	EWR	TPA	133	997	7	22	2023-04-04 07:00:00	Other
19654	9	19	556	600	-4	743	802	AA	228	N167US	LGA	CLT	78	544	6	0	2023-09-19 06:00:00	CLT
19656	9	27	931	935	-4	1230	1225	UA	482	N87531	EWR	MCO	143	937	9	35	2023-09-27 09:00:00	MCO
19665	1	13	556	600	-4	729	722	YX	1245	N723YX	EWR	IAD	57	212	6	0	2023-01-13 06:00:00	Other
19668	11	26	1355	1400	-5	1708	1711	B6	491	N709JB	JFK	FLL	175	1069	14	0	2023-11-26 14:00:00	FLL
19676	12	18	2108	2110	-2	214	209	DL	651	N927DZ	JFK	SJU	224	1598	21	10	2023-12-18 21:00:00	Other
19685	4	11	1815	1820	-5	1920	1947	9E	1420	N490PX	LGA	PWM	50	269	18	20	2023-04-11 18:00:00	Other
19693	9	15	758	800	-2	919	924	YX	1830	N232JQ	LGA	BOS	45	184	8	0	2023-09-15 08:00:00	BOS
19694	11	6	1445	1450	-5	1705	1716	9E	1582	N138EV	LGA	MCI	178	1107	14	50	2023-11-06 14:00:00	Other
19698	6	10	1532	1534	-2	1715	1740	YX	1412	N405YX	JFK	CMH	75	483	15	34	2023-06-10 15:00:00	Other
19699	2	9	830	835	-5	1041	1104	9E	1390	N919XJ	LGA	TYS	101	647	8	35	2023-02-09 08:00:00	Other
19716	1	7	1111	1115	-4	1225	1244	B6	1007	N324JB	JFK	BUF	58	301	11	15	2023-01-07 11:00:00	Other
19719	7	31	1254	1259	-5	1418	1429	9E	1182	N325PQ	LGA	PWM	45	269	12	59	2023-07-31 12:00:00	Other
19722	9	27	1916	1920	-4	2100	2121	YX	1889	N824MD	LGA	CMH	77	479	19	20	2023-09-27 19:00:00	Other
19730	9	9	625	630	-5	915	919	B6	41	N793JB	JFK	TPA	140	1005	6	30	2023-09-09 06:00:00	Other
19732	9	4	949	954	-5	1238	1257	UA	620	N17264	EWR	RSW	140	1068	9	54	2023-09-04 09:00:00	Other
19740	4	9	857	900	-3	1025	1030	9E	1432	N182GJ	JFK	ORF	56	290	9	0	2023-04-09 09:00:00	Other
19749	10	31	1541	1545	-4	1652	1724	YX	1739	N211JQ	JFK	BOS	32	187	15	45	2023-10-31 15:00:00	BOS
19750	2	4	701	705	-4	952	1014	B6	180	N651JB	LGA	PBI	151	1035	7	5	2023-02-04 07:00:00	Other
19760	4	21	757	800	-3	1055	1115	DL	547	N388DA	JFK	RSW	145	1074	8	0	2023-04-21 08:00:00	Other
19761	3	23	825	830	-5	1044	1122	9E	1463	N903XJ	JFK	JAX	114	828	8	30	2023-03-23 08:00:00	Other
19775	3	19	1254	1258	-4	1416	1427	YX	1068	N728YX	EWR	PIT	61	319	12	58	2023-03-19 12:00:00	Other
19788	11	18	839	841	-2	1027	1040	YX	1789	N210JQ	LGA	CMH	80	479	8	41	2023-11-18 08:00:00	Other
19791	8	11	1656	1700	-4	1821	1843	AA	794	N808AW	LGA	STL	123	888	17	0	2023-08-11 17:00:00	Other
19797	3	30	1637	1641	-4	2000	1955	NK	339	N662NK	LGA	FLL	141	1076	16	41	2023-03-30 16:00:00	FLL
19799	3	10	555	600	-5	805	824	DL	841	N934AT	EWR	ATL	112	746	6	0	2023-03-10 06:00:00	ATL
19802	6	4	1224	1229	-5	1444	1502	DL	335	N356DN	LGA	ATL	110	762	12	29	2023-06-04 12:00:00	ATL
19803	2	6	1158	1200	-2	1509	1518	UA	799	N14115	EWR	LAX	349	2454	12	0	2023-02-06 12:00:00	LAX
19805	5	25	1101	1106	-5	1411	1405	UA	240	N813UA	EWR	PBI	163	1023	11	6	2023-05-25 11:00:00	Other
19806	3	28	1024	1029	-5	1312	1300	YX	1647	N225JQ	LGA	IND	129	660	10	29	2023-03-28 10:00:00	Other
19809	7	3	1135	1139	-4	1236	1251	YX	1385	N218JQ	JFK	MVY	35	173	11	39	2023-07-03 11:00:00	Other
19814	10	14	954	959	-5	1141	1148	YX	1719	N219YX	JFK	CMH	81	483	9	59	2023-10-14 09:00:00	Other
19817	10	2	1550	1555	-5	1716	1740	AA	801	N831NN	JFK	ORD	108	740	15	55	2023-10-02 15:00:00	ORD
19825	5	19	1651	1655	-4	2015	2043	AS	13	N431AS	JFK	SFO	344	2586	16	55	2023-05-19 16:00:00	Other
19831	8	8	1346	1350	-4	1538	1609	YX	1355	N203JQ	LGA	CLT	81	544	13	50	2023-08-08 13:00:00	CLT
19832	8	14	1727	1730	-3	2005	2030	AS	74	N562AS	EWR	PDX	310	2434	17	30	2023-08-14 17:00:00	Other
19834	11	4	556	600	-4	849	900	B6	47	N584JB	LGA	FLL	150	1076	6	0	2023-11-04 06:00:00	FLL
19836	4	26	2015	2020	-5	2213	2234	9E	1355	N478PX	LGA	GSP	96	610	20	20	2023-04-26 20:00:00	Other
19851	11	27	858	900	-2	1201	1236	AS	15	N955AK	JFK	SFO	339	2586	9	0	2023-11-27 09:00:00	Other
19852	11	14	828	830	-2	1414	1438	UA	119	N76065	EWR	HNL	617	4962	8	30	2023-11-14 08:00:00	Other
19854	6	3	757	800	-3	1101	1111	AA	528	N935AN	EWR	MIA	154	1085	8	0	2023-06-03 08:00:00	MIA
19855	2	1	555	600	-5	822	749	DL	419	N123DQ	LGA	ORD	134	733	6	0	2023-02-01 06:00:00	ORD
19858	10	1	1611	1615	-4	1740	1727	9E	1664	N304PQ	LGA	ALB	31	136	16	15	2023-10-01 16:00:00	Other
19865	7	19	601	605	-4	803	817	DL	684	N937AT	EWR	ATL	106	746	6	5	2023-07-19 06:00:00	ATL
19866	10	2	1155	1200	-5	1315	1339	9E	1525	N485PX	LGA	PIT	58	335	12	0	2023-10-02 12:00:00	Other
19868	12	18	852	855	-3	1026	1039	UA	66	N35236	EWR	CLE	62	404	8	55	2023-12-18 08:00:00	Other
19874	3	26	1016	1020	-4	1336	1334	DL	922	N144DU	LGA	SRQ	186	1047	10	20	2023-03-26 10:00:00	Other
19875	5	6	1223	1227	-4	1335	1345	YX	1051	N858RW	EWR	PWM	50	284	12	27	2023-05-06 12:00:00	Other
19876	7	3	831	834	-3	1020	1033	UA	90	N827UA	EWR	DTW	77	488	8	34	2023-07-03 08:00:00	Other
19881	5	8	1113	1115	-2	1357	1423	DL	532	N370DN	JFK	FLL	144	1069	11	15	2023-05-08 11:00:00	FLL
19882	10	8	1112	1117	-5	1302	1310	NK	20	N676NK	EWR	MYR	90	550	11	17	2023-10-08 11:00:00	Other
19888	8	13	956	1000	-4	1214	1213	UA	450	N39423	EWR	DEN	227	1605	10	0	2023-08-13 10:00:00	Other
19896	4	5	741	744	-3	1018	1009	UA	758	N36444	EWR	DEN	241	1605	7	44	2023-04-05 07:00:00	Other
19901	12	1	1051	1055	-4	1345	1414	B6	20	N993JE	JFK	SEA	325	2422	10	55	2023-12-01 10:00:00	Other
19910	3	15	854	859	-5	1032	1109	9E	1316	N331PQ	LGA	MEM	130	963	8	59	2023-03-15 08:00:00	Other
19913	7	18	546	550	-4	812	831	AA	482	N906NN	LGA	DFW	181	1389	5	50	2023-07-18 05:00:00	Other
19916	2	23	1542	1545	-3	1924	1922	DL	265	N178DN	JFK	LAX	382	2475	15	45	2023-02-23 15:00:00	LAX
19927	2	18	757	800	-3	1055	1114	AA	804	N315RJ	JFK	DFW	209	1391	8	0	2023-02-18 08:00:00	Other
19928	7	12	1016	1020	-4	1156	1241	9E	1158	N915XJ	LGA	CLT	78	544	10	20	2023-07-12 10:00:00	CLT
19938	8	29	1111	1116	-5	1244	1308	9E	1257	N903XJ	LGA	RDU	67	431	11	16	2023-08-29 11:00:00	Other
19943	12	3	1924	1928	-4	2239	2230	UA	703	N17317	EWR	IAH	213	1400	19	28	2023-12-03 19:00:00	Other
19947	12	20	1455	1459	-4	1630	1706	9E	1519	N913XJ	JFK	CLE	71	425	14	59	2023-12-20 14:00:00	Other
19950	10	22	950	955	-5	1228	1245	DL	310	N121DZ	JFK	MCO	137	944	9	55	2023-10-22 09:00:00	MCO
19966	10	18	2119	2124	-5	2232	2259	YX	1088	N760YX	EWR	MKE	105	725	21	24	2023-10-18 21:00:00	Other
19968	6	7	835	840	-5	1050	1100	9E	1685	N308PQ	JFK	CHS	108	636	8	40	2023-06-07 08:00:00	Other
19969	2	19	722	725	-3	1043	1050	DL	520	N363NW	JFK	AUS	237	1521	7	25	2023-02-19 07:00:00	Other
19978	7	5	1345	1350	-5	1512	1535	9E	1282	N480PX	LGA	BHM	120	866	13	50	2023-07-05 13:00:00	Other
19980	5	13	657	700	-3	937	1009	DL	535	N380DN	LGA	MIA	141	1096	7	0	2023-05-13 07:00:00	MIA
19981	8	9	615	620	-5	903	908	NK	421	N963NK	EWR	MCO	133	937	6	20	2023-08-09 06:00:00	MCO
19994	4	24	555	600	-5	904	859	UA	814	N838UA	LGA	IAH	218	1416	6	0	2023-04-24 06:00:00	Other
19996	1	13	1450	1455	-5	1606	1626	9E	1505	N601LR	JFK	ROC	51	264	14	55	2023-01-13 14:00:00	Other
20007	3	26	1838	1840	-2	2030	2017	AA	973	N822NN	LGA	ORD	136	733	18	40	2023-03-26 18:00:00	ORD
20011	2	9	1956	2000	-4	2204	2231	9E	1394	N186PQ	LGA	OMA	165	1148	20	0	2023-02-09 20:00:00	Other
20012	10	29	1807	1810	-3	2051	2025	DL	679	N365NW	LGA	MSP	165	1020	18	10	2023-10-29 18:00:00	Other
20014	10	1	754	759	-5	905	928	YX	1082	N750YX	EWR	PIT	53	319	7	59	2023-10-01 07:00:00	Other
20018	12	8	1655	1700	-5	2003	2027	DL	87	N190DN	JFK	LAX	326	2475	17	0	2023-12-08 17:00:00	LAX
20022	7	4	2157	2159	-2	2325	2341	DL	707	N302NB	JFK	BUF	49	301	21	59	2023-07-04 21:00:00	Other
20024	10	13	1355	1400	-5	1549	1555	9E	1494	N925XJ	JFK	RDU	73	427	14	0	2023-10-13 14:00:00	Other
20026	9	3	656	659	-3	943	953	DL	657	N319US	JFK	AUS	195	1521	6	59	2023-09-03 06:00:00	Other
20037	1	2	959	1002	-3	1256	1250	UA	654	N17265	EWR	LAS	310	2227	10	2	2023-01-02 10:00:00	Other
20048	2	14	1335	1339	-4	1519	1519	MQ	985	N217NN	EWR	ORD	131	719	13	39	2023-02-14 13:00:00	ORD
20049	6	10	1655	1700	-5	1909	1934	UA	885	N75432	EWR	LAS	289	2227	17	0	2023-06-10 17:00:00	Other
20052	2	14	2010	2015	-5	2335	2359	AS	18	N560AS	JFK	SFO	348	2586	20	15	2023-02-14 20:00:00	Other
20053	11	11	1955	2000	-5	2303	2308	UA	705	N57299	EWR	IAH	219	1400	20	0	2023-11-11 20:00:00	Other
20057	1	2	757	800	-3	1226	1255	DL	276	N917DU	JFK	SJU	186	1598	8	0	2023-01-02 08:00:00	Other
20065	12	22	1338	1342	-4	1532	1545	AA	645	N538UW	EWR	CLT	82	529	13	42	2023-12-22 13:00:00	CLT
20067	7	6	1157	1159	-2	1348	1351	YX	852	N747YX	EWR	CMH	70	463	11	59	2023-07-06 11:00:00	Other
20071	1	3	827	830	-3	1128	1140	UA	264	N12021	EWR	LAX	318	2454	8	30	2023-01-03 08:00:00	LAX
20072	11	4	803	805	-2	1107	1120	DL	319	N706TW	JFK	PDX	338	2454	8	5	2023-11-04 08:00:00	Other
20082	11	27	1924	1928	-4	2229	2230	UA	705	N14235	EWR	IAH	215	1400	19	28	2023-11-27 19:00:00	Other
20084	11	2	1120	1122	-2	1422	1428	UA	153	N47288	EWR	FLL	152	1065	11	22	2023-11-02 11:00:00	FLL
20086	5	23	1308	1312	-4	1555	1603	UA	714	N69804	EWR	MCO	139	937	13	12	2023-05-23 13:00:00	MCO
20090	6	24	458	500	-2	753	808	AA	439	N929NN	EWR	MIA	146	1085	5	0	2023-06-24 05:00:00	MIA
20104	10	13	1757	1759	-2	2030	2037	DL	312	N846DN	JFK	PHX	306	2153	17	59	2023-10-13 17:00:00	Other
20107	7	11	1223	1225	-2	1431	1435	WN	375	N8611F	LGA	DEN	225	1620	12	25	2023-07-11 12:00:00	Other
20114	3	30	1817	1821	-4	2008	2020	YX	1128	N724YX	EWR	CMH	73	463	18	21	2023-03-30 18:00:00	Other
20115	4	2	1231	1235	-4	1400	1427	9E	1293	N314PQ	JFK	RDU	68	427	12	35	2023-04-02 12:00:00	Other
20118	3	26	1146	1150	-4	1344	1348	DL	287	N923AT	EWR	MSP	160	1008	11	50	2023-03-26 11:00:00	Other
20130	6	15	1925	1930	-5	2102	2129	YX	1313	N424YX	JFK	RDU	69	427	19	30	2023-06-15 19:00:00	Other
20138	10	12	857	900	-3	1014	1029	YX	1051	N752YX	EWR	DCA	43	199	9	0	2023-10-12 09:00:00	Other
20146	8	15	1901	1906	-5	2049	2048	UA	417	N67501	EWR	CLE	71	404	19	6	2023-08-15 19:00:00	Other
20151	10	14	1339	1343	-4	1636	1638	NK	71	N947NK	EWR	DFW	209	1372	13	43	2023-10-14 13:00:00	Other
20159	9	4	1054	1059	-5	1322	1346	B6	191	N988JT	JFK	LAX	307	2475	10	59	2023-09-04 10:00:00	LAX
20162	10	26	1752	1757	-5	1927	1950	YX	1720	N203JQ	LGA	CMH	72	479	17	57	2023-10-26 17:00:00	Other
20169	5	17	1953	1955	-2	2237	2307	AS	86	N923VA	EWR	LAX	308	2454	19	55	2023-05-17 19:00:00	LAX
20171	6	5	1015	1020	-5	1404	1430	AA	1049	N3014R	JFK	STT	208	1623	10	20	2023-06-05 10:00:00	Other
20176	2	21	745	750	-5	932	937	UA	668	N73251	EWR	ORD	120	719	7	50	2023-02-21 07:00:00	ORD
20181	11	9	844	848	-4	1052	1049	9E	1696	N921XJ	LGA	STL	152	888	8	48	2023-11-09 08:00:00	Other
20185	10	4	1725	1727	-2	2004	2016	UA	775	N86534	EWR	MCO	124	937	17	27	2023-10-04 17:00:00	MCO
20188	11	10	1558	1600	-2	1756	1757	9E	1486	N316PQ	JFK	RDU	80	427	16	0	2023-11-10 16:00:00	Other
20193	10	9	2245	2250	-5	14	27	9E	1421	N293PQ	JFK	ROC	49	264	22	50	2023-10-09 22:00:00	Other
20195	5	9	1240	1243	-3	1437	1457	9E	1343	N932XJ	JFK	CLT	89	541	12	43	2023-05-09 12:00:00	CLT
20200	1	9	1359	1403	-4	1646	1659	UA	792	N76522	EWR	MCO	133	937	14	3	2023-01-09 14:00:00	MCO
20201	1	20	1146	1150	-4	1247	1301	9E	1484	N181PQ	LGA	ALB	36	136	11	50	2023-01-20 11:00:00	Other
20212	9	10	827	830	-3	1128	1134	AA	597	N880NN	EWR	DFW	178	1372	8	30	2023-09-10 08:00:00	Other
20215	5	18	1837	1840	-3	2047	2108	9E	1308	N307PQ	JFK	CLT	86	541	18	40	2023-05-18 18:00:00	CLT
20220	1	25	812	815	-3	1117	1145	UA	550	N223UA	EWR	SFO	323	2565	8	15	2023-01-25 08:00:00	Other
20221	8	14	1055	1100	-5	1349	1430	DL	254	N703TW	JFK	SFO	330	2586	11	0	2023-08-14 11:00:00	Other
20225	9	12	1010	1015	-5	1150	1150	UA	706	N77542	LGA	ORD	112	733	10	15	2023-09-12 10:00:00	ORD
20227	9	25	1246	1250	-4	1503	1448	NK	483	N690NK	LGA	MYR	80	563	12	50	2023-09-25 12:00:00	Other
20228	3	23	1145	1150	-5	1333	1327	9E	1426	N914XJ	LGA	MKE	139	738	11	50	2023-03-23 11:00:00	Other
20229	3	22	900	905	-5	1031	1041	9E	1529	N336PQ	JFK	RIC	59	288	9	5	2023-03-22 09:00:00	Other
20236	12	30	556	600	-4	741	755	DL	737	N607AT	EWR	DTW	73	488	6	0	2023-12-30 06:00:00	Other
20243	2	2	728	730	-2	1108	1054	AA	1	N112AN	JFK	LAX	362	2475	7	30	2023-02-02 07:00:00	LAX
20248	1	25	702	705	-3	1157	1204	UA	657	N29717	EWR	STT	206	1634	7	5	2023-01-25 07:00:00	Other
20249	3	11	808	810	-2	1310	1315	DL	738	N6713Y	JFK	STT	198	1623	8	10	2023-03-11 08:00:00	Other
20251	1	2	743	745	-2	1006	1033	YX	1133	N741YX	EWR	SDF	111	642	7	45	2023-01-02 07:00:00	Other
20253	5	1	841	846	-5	1020	1050	YX	1713	N220JQ	LGA	CMH	76	479	8	46	2023-05-01 08:00:00	Other
20254	3	25	1244	1248	-4	1611	1554	UA	717	N18220	EWR	MIA	158	1085	12	48	2023-03-25 12:00:00	MIA
20256	6	26	743	745	-2	959	1000	YX	1802	N237JQ	LGA	OMA	167	1148	7	45	2023-06-26 07:00:00	Other
20258	2	5	1426	1430	-4	1552	1603	9E	1423	N606LR	LGA	BGR	49	378	14	30	2023-02-05 14:00:00	Other
20260	11	20	1155	1200	-5	1357	1358	9E	1453	N329PQ	JFK	CLT	88	541	12	0	2023-11-20 12:00:00	CLT
20267	12	31	1410	1415	-5	1525	1601	9E	1352	N137EV	JFK	RIC	56	288	14	15	2023-12-31 14:00:00	Other
20268	5	31	2115	2120	-5	2251	2246	9E	1550	N320PQ	LGA	BTV	51	258	21	20	2023-05-31 21:00:00	Other
20269	11	26	1024	1029	-5	1210	1226	9E	1513	N319PQ	LGA	RDU	75	431	10	29	2023-11-26 10:00:00	Other
20271	9	22	1155	1200	-5	1509	1450	DL	187	N414DZ	JFK	LAX	333	2475	12	0	2023-09-22 12:00:00	LAX
20272	7	24	1925	1929	-4	2142	2139	YX	1064	N431YX	LGA	CVG	106	585	19	29	2023-07-24 19:00:00	Other
20277	2	5	2015	2019	-4	2205	2220	DL	954	N985AT	EWR	DTW	84	488	20	19	2023-02-05 20:00:00	Other
20280	4	30	1121	1125	-4	1258	1318	DL	540	N135DQ	LGA	ORD	108	733	11	25	2023-04-30 11:00:00	ORD
20282	1	8	557	600	-3	855	912	B6	646	N663JB	EWR	FLL	150	1065	6	0	2023-01-08 06:00:00	FLL
20290	4	10	1425	1429	-4	1544	1604	9E	1405	N935XJ	JFK	RIC	51	288	14	29	2023-04-10 14:00:00	Other
20305	2	2	1236	1240	-4	1509	1505	UA	482	N442UA	EWR	MSY	185	1167	12	40	2023-02-02 12:00:00	Other
20319	12	8	2155	2200	-5	2329	2349	9E	1579	N604LR	JFK	BUF	51	301	22	0	2023-12-08 22:00:00	Other
20324	5	5	1455	1500	-5	1754	1807	DL	114	N102DU	LGA	DFW	203	1389	15	0	2023-05-05 15:00:00	Other
20325	6	29	1055	1100	-5	1314	1320	B6	129	N595JB	LGA	DEN	230	1620	11	0	2023-06-29 11:00:00	Other
20329	7	11	1626	1629	-3	1850	1936	AA	91	N113AN	JFK	LAX	306	2475	16	29	2023-07-11 16:00:00	LAX
20338	11	27	630	635	-5	932	1005	DL	115	N128DN	JFK	SLC	277	1990	6	35	2023-11-27 06:00:00	Other
20347	5	13	555	600	-5	737	753	DL	355	N387DN	LGA	DTW	80	502	6	0	2023-05-13 06:00:00	Other
20356	8	4	606	610	-4	803	813	DL	189	N101DQ	LGA	MSP	151	1020	6	10	2023-08-04 06:00:00	Other
20361	7	25	758	800	-2	1011	1029	DL	283	N324DX	LGA	ATL	106	762	8	0	2023-07-25 08:00:00	ATL
20362	4	8	641	645	-4	813	817	NK	399	N642NK	EWR	BNA	130	748	6	45	2023-04-08 06:00:00	Other
20364	5	12	1327	1330	-3	1623	1651	AA	419	N813NN	JFK	MIA	141	1089	13	30	2023-05-12 13:00:00	MIA
20369	7	20	1720	1725	-5	1948	2007	B6	706	N827JB	LGA	JAX	119	833	17	25	2023-07-20 17:00:00	Other
20373	8	11	1954	1959	-5	2107	2127	YX	1368	N217JQ	EWR	BOS	45	200	19	59	2023-08-11 19:00:00	BOS
20377	11	8	1446	1450	-4	1618	1619	OO	1195	N324SY	JFK	IAD	54	228	14	50	2023-11-08 14:00:00	Other
20378	12	2	1953	1955	-2	2310	2257	UA	703	N14230	EWR	IAH	231	1400	19	55	2023-12-02 19:00:00	Other
20381	7	8	1057	1100	-3	1305	1320	B6	111	N531JL	LGA	DEN	220	1620	11	0	2023-07-08 11:00:00	Other
20384	1	16	1912	1915	-3	2224	2250	DL	227	N179DN	JFK	LAX	344	2475	19	15	2023-01-16 19:00:00	LAX
20394	7	23	1627	1629	-2	1833	1855	AA	494	N852NN	JFK	PHX	278	2153	16	29	2023-07-23 16:00:00	Other
20399	11	12	1530	1535	-5	1638	1702	NK	558	N607NK	EWR	BNA	110	748	15	35	2023-11-12 15:00:00	Other
20400	12	16	946	950	-4	1120	1142	YX	1720	N211JQ	LGA	BNA	121	764	9	50	2023-12-16 09:00:00	Other
20402	4	30	920	924	-4	1222	1133	YX	976	N646RW	EWR	AVL	98	583	9	24	2023-04-30 09:00:00	Other
20409	10	9	913	915	-2	1216	1228	AA	790	N320TF	LGA	MIA	157	1096	9	15	2023-10-09 09:00:00	MIA
20412	3	6	1303	1305	-2	1400	1416	B6	327	N368JB	JFK	BOS	40	187	13	5	2023-03-06 13:00:00	BOS
20433	6	16	655	700	-5	919	920	DL	287	N921DU	JFK	PHX	291	2153	7	0	2023-06-16 07:00:00	Other
20438	11	19	1638	1642	-4	1853	1916	UA	934	N19117	EWR	DEN	226	1605	16	42	2023-11-19 16:00:00	Other
20442	8	27	806	810	-4	941	951	9E	1178	N294PQ	JFK	RIC	57	288	8	10	2023-08-27 08:00:00	Other
20443	2	16	2025	2030	-5	2145	2204	YX	1604	N233JQ	LGA	IAD	49	229	20	30	2023-02-16 20:00:00	Other
20453	6	2	1741	1745	-4	2041	2013	UA	537	N27255	EWR	ATL	102	746	17	45	2023-06-02 17:00:00	ATL
20461	2	3	950	955	-5	1116	1128	9E	1443	N905XJ	LGA	ROC	52	254	9	55	2023-02-03 09:00:00	Other
20466	10	25	843	848	-5	1049	1124	9E	1618	N293PQ	LGA	SAV	105	722	8	48	2023-10-25 08:00:00	Other
20470	6	30	712	714	-2	1109	1112	B6	613	N529JB	EWR	SJU	211	1608	7	14	2023-06-30 07:00:00	Other
20473	6	5	950	955	-5	1217	1214	YX	1362	N806MD	LGA	SDF	95	659	9	55	2023-06-05 09:00:00	Other
20485	6	15	815	820	-5	953	1017	AA	1018	N887NN	JFK	ORD	116	740	8	20	2023-06-15 08:00:00	ORD
20489	2	20	1028	1030	-2	1342	1356	AA	3	N110AN	JFK	LAX	343	2475	10	30	2023-02-20 10:00:00	LAX
20494	6	3	1256	1300	-4	1435	1500	DL	812	N371NW	LGA	DTW	78	502	13	0	2023-06-03 13:00:00	Other
20497	6	22	605	610	-5	759	815	9E	1457	N337PQ	LGA	CLT	87	544	6	10	2023-06-22 06:00:00	CLT
20498	9	29	727	730	-3	1014	939	9E	1707	N292PQ	LGA	CVG	121	585	7	30	2023-09-29 07:00:00	Other
20504	4	26	1718	1720	-2	2001	2017	B6	416	N645JB	JFK	LAS	297	2248	17	20	2023-04-26 17:00:00	Other
20507	4	28	1246	1250	-4	1449	1502	9E	1272	N147PQ	JFK	CHS	98	636	12	50	2023-04-28 12:00:00	Other
20511	9	23	1458	1503	-5	1755	1758	UA	69	N27253	EWR	PBI	155	1023	15	3	2023-09-23 15:00:00	Other
20513	10	3	1428	1431	-3	1703	1701	B6	593	N598JB	JFK	JAX	115	828	14	31	2023-10-03 14:00:00	Other
20528	6	12	625	629	-4	854	850	UA	444	N872UA	EWR	JAX	120	820	6	29	2023-06-12 06:00:00	Other
20531	6	29	657	700	-3	930	1003	DL	548	N807DN	JFK	TPA	131	1005	7	0	2023-06-29 07:00:00	Other
20532	1	27	737	740	-3	1039	1041	UA	861	N68821	EWR	MCO	147	937	7	40	2023-01-27 07:00:00	MCO
20548	11	3	1935	1940	-5	2125	2208	DL	411	N359NB	JFK	MSP	155	1029	19	40	2023-11-03 19:00:00	Other
20557	3	1	1205	1210	-5	1436	1441	YX	1407	N430YX	LGA	CVG	114	585	12	10	2023-03-01 12:00:00	Other
20558	8	18	1827	1830	-3	2030	2045	YX	1018	N425YX	LGA	OMA	162	1148	18	30	2023-08-18 18:00:00	Other
20569	7	27	653	655	-2	906	909	B6	660	N633JB	LGA	DEN	210	1620	6	55	2023-07-27 06:00:00	Other
20574	8	22	1652	1655	-3	2001	2013	AS	6	N956AK	JFK	SEA	323	2422	16	55	2023-08-22 16:00:00	Other
20590	6	21	1530	1535	-5	1708	1714	9E	1731	N341PQ	LGA	CHO	75	305	15	35	2023-06-21 15:00:00	Other
20596	4	8	1621	1625	-4	1804	1802	YX	1231	N109HQ	JFK	BNA	128	765	16	25	2023-04-08 16:00:00	Other
20597	6	21	915	920	-5	1103	1115	9E	1714	N905XJ	JFK	CLE	70	425	9	20	2023-06-21 09:00:00	Other
20602	4	15	1010	1015	-5	1216	1230	9E	1440	N186PQ	LGA	AVL	98	599	10	15	2023-04-15 10:00:00	Other
20607	8	17	1625	1629	-4	1845	1907	9E	1089	N319PQ	JFK	CLT	84	541	16	29	2023-08-17 16:00:00	CLT
20609	1	14	626	630	-4	937	943	B6	1033	N768JB	JFK	FLL	156	1069	6	30	2023-01-14 06:00:00	FLL
20622	10	15	1124	1129	-5	1355	1356	DL	113	N821DN	JFK	ATL	115	760	11	29	2023-10-15 11:00:00	ATL
20626	4	27	826	829	-3	938	958	UA	231	N479UA	EWR	BOS	46	200	8	29	2023-04-27 08:00:00	BOS
20627	11	13	1342	1345	-3	1625	1700	B6	518	N505JB	JFK	MCO	132	944	13	45	2023-11-13 13:00:00	MCO
20631	5	16	754	759	-5	931	926	YX	1132	N750YX	EWR	DCA	64	199	7	59	2023-05-16 07:00:00	Other
20635	5	28	757	800	-3	912	940	WN	37	N8522P	LGA	STL	114	888	8	0	2023-05-28 08:00:00	Other
20637	12	8	1841	1845	-4	2018	2047	YX	1125	N766YX	EWR	CMH	72	463	18	45	2023-12-08 18:00:00	Other
20642	5	12	1056	1100	-4	1257	1326	YX	1277	N108HQ	JFK	IND	94	665	11	0	2023-05-12 11:00:00	Other
20645	8	25	2056	2100	-4	2207	2220	DL	341	N130DU	LGA	BOS	47	184	21	0	2023-08-25 21:00:00	BOS
20653	12	12	1456	1459	-3	1557	1622	YX	1769	N229JQ	LGA	BOS	38	184	14	59	2023-12-12 14:00:00	BOS
20662	6	16	1140	1145	-5	1244	1305	YX	1306	N121HQ	JFK	BOS	33	187	11	45	2023-06-16 11:00:00	BOS
20664	4	27	1105	1110	-5	1232	1225	OO	1054	N324SY	EWR	BOS	50	200	11	10	2023-04-27 11:00:00	BOS
20667	12	4	1356	1359	-3	1503	1522	AA	636	N808AW	LGA	DCA	47	214	13	59	2023-12-04 13:00:00	Other
20676	8	1	1820	1824	-4	1954	2000	UA	592	N884UA	LGA	ORD	110	733	18	24	2023-08-01 18:00:00	ORD
20678	10	2	1325	1330	-5	1530	1544	YX	1356	N872RW	LGA	IND	96	660	13	30	2023-10-02 13:00:00	Other
20688	9	22	2105	2110	-5	2307	2301	YX	1320	N103HQ	LGA	GSO	77	461	21	10	2023-09-22 21:00:00	Other
20689	12	30	1142	1145	-3	1325	1350	9E	1350	N304PQ	LGA	STL	119	888	11	45	2023-12-30 11:00:00	Other
20690	10	16	1650	1653	-3	1855	1918	YX	1078	N725YX	EWR	SDF	93	642	16	53	2023-10-16 16:00:00	Other
20693	1	9	1518	1522	-4	1621	1639	YX	1204	N729YX	EWR	MHT	43	209	15	22	2023-01-09 15:00:00	Other
20696	5	16	1056	1100	-4	1200	1230	YX	1583	N225JQ	LGA	BOS	40	184	11	0	2023-05-16 11:00:00	BOS
20699	4	6	740	744	-4	1023	1045	UA	664	N37277	EWR	PBI	135	1023	7	44	2023-04-06 07:00:00	Other
20700	6	24	1828	1830	-2	2155	2151	DL	774	N132DU	LGA	RSW	155	1080	18	30	2023-06-24 18:00:00	Other
20707	7	24	1727	1730	-3	1916	1926	NK	48	N613NK	LGA	DTW	82	502	17	30	2023-07-24 17:00:00	Other
20713	6	1	1254	1259	-5	1606	1615	AA	668	N303RG	JFK	MIA	154	1089	12	59	2023-06-01 12:00:00	MIA
20716	2	9	1713	1718	-5	1914	1932	YX	999	N643RW	EWR	GSP	97	594	17	18	2023-02-09 17:00:00	Other
20724	9	16	558	600	-2	735	751	DL	392	N397DN	LGA	DTW	75	502	6	0	2023-09-16 06:00:00	Other
20735	12	15	620	625	-5	943	1001	AA	448	N420AN	EWR	PHX	288	2133	6	25	2023-12-15 06:00:00	Other
20739	1	7	1802	1806	-4	2116	2128	AA	1087	N303RG	EWR	MIA	151	1085	18	6	2023-01-07 18:00:00	MIA
20741	9	13	1120	1125	-5	1417	1422	DL	429	N866DN	JFK	TPA	149	1005	11	25	2023-09-13 11:00:00	Other
20750	8	2	1825	1829	-4	2127	2142	AA	151	N832NN	JFK	MIA	129	1089	18	29	2023-08-02 18:00:00	MIA
20752	10	18	1522	1525	-3	1758	1827	DL	783	N120DN	JFK	MCO	131	944	15	25	2023-10-18 15:00:00	MCO
20753	1	22	1526	1530	-4	1831	1850	B6	604	N588JB	EWR	MIA	159	1085	15	30	2023-01-22 15:00:00	MIA
20762	10	26	1027	1030	-3	1239	1255	DL	794	N819DN	EWR	ATL	103	746	10	30	2023-10-26 10:00:00	ATL
20771	8	17	556	558	-2	907	908	AA	635	N327SK	JFK	MIA	153	1089	5	58	2023-08-17 05:00:00	MIA
20776	3	10	926	929	-3	1303	1314	YX	1186	N638RW	EWR	EYW	180	1196	9	29	2023-03-10 09:00:00	Other
20793	5	9	1527	1530	-3	1641	1643	B6	849	N206JB	EWR	BOS	38	200	15	30	2023-05-09 15:00:00	BOS
20794	4	27	1122	1126	-4	1429	1432	UA	848	N841UA	EWR	AUS	224	1504	11	26	2023-04-27 11:00:00	Other
20796	7	5	1151	1156	-5	1346	1400	AA	765	N970NN	JFK	CLT	80	541	11	56	2023-07-05 11:00:00	CLT
20802	8	2	1748	1750	-2	2029	2018	UA	419	N77259	EWR	ATL	102	746	17	50	2023-08-02 17:00:00	ATL
20813	6	19	1154	1159	-5	1332	1349	YX	1076	N742YX	EWR	CMH	73	463	11	59	2023-06-19 11:00:00	Other
20814	9	8	1140	1145	-5	1429	1455	AS	9	N943AK	JFK	SEA	323	2422	11	45	2023-09-08 11:00:00	Other
20824	3	8	946	950	-4	1321	1329	AA	1004	N436AN	EWR	PHX	300	2133	9	50	2023-03-08 09:00:00	Other
20830	8	19	625	630	-5	936	959	AA	28	N112AN	JFK	SFO	349	2586	6	30	2023-08-19 06:00:00	Other
20833	4	15	641	645	-4	806	817	NK	399	N602NK	EWR	BNA	123	748	6	45	2023-04-15 06:00:00	Other
20842	4	6	1355	1400	-5	1621	1638	YX	1210	N117HQ	LGA	ATL	117	762	14	0	2023-04-06 14:00:00	ATL
20843	5	19	2050	2054	-4	2152	2219	YX	1010	N643RW	EWR	MHT	39	209	20	54	2023-05-19 20:00:00	Other
20852	8	19	1524	1526	-2	1716	1713	9E	1173	N538CA	JFK	BNA	100	765	15	26	2023-08-19 15:00:00	Other
20853	10	30	556	600	-4	856	908	UA	884	N77536	LGA	IAH	211	1416	6	0	2023-10-30 06:00:00	Other
20855	5	8	1211	1213	-2	1439	1502	UA	858	N76503	EWR	DFW	189	1372	12	13	2023-05-08 12:00:00	Other
20860	11	11	1136	1140	-4	1325	1326	OO	1176	N247SY	JFK	ORD	132	740	11	40	2023-11-11 11:00:00	ORD
20861	8	15	712	715	-3	905	908	UA	384	N47275	EWR	CLT	78	529	7	15	2023-08-15 07:00:00	CLT
20872	8	19	1611	1615	-4	1729	1801	9E	1260	N314PQ	LGA	RIC	49	292	16	15	2023-08-19 16:00:00	Other
20875	2	15	1553	1555	-2	1813	1829	NK	417	N628NK	EWR	ATL	119	746	15	55	2023-02-15 15:00:00	ATL
20879	5	11	1121	1126	-5	1308	1258	YX	1642	N246JQ	JFK	DCA	57	213	11	26	2023-05-11 11:00:00	Other
20880	3	6	609	614	-5	758	757	AA	1001	N868NN	EWR	ORD	136	719	6	14	2023-03-06 06:00:00	ORD
20884	5	17	802	805	-3	1016	1028	DL	897	N3751B	EWR	ATL	110	746	8	5	2023-05-17 08:00:00	ATL
20888	2	18	1756	1800	-4	1948	1957	OO	1174	N258SY	JFK	ORD	136	740	18	0	2023-02-18 18:00:00	ORD
20892	2	23	705	710	-5	1017	1012	UA	278	N17279	EWR	BZN	273	1882	7	10	2023-02-23 07:00:00	Other
20908	8	3	812	814	-2	1004	1020	9E	1151	N479PX	LGA	GSP	85	610	8	14	2023-08-03 08:00:00	Other
20911	9	24	1058	1100	-2	1259	1327	UA	241	N460UA	EWR	ATL	99	746	11	0	2023-09-24 11:00:00	ATL
20912	3	26	1235	1240	-5	1440	1447	NK	652	N670NK	LGA	DTW	90	502	12	40	2023-03-26 12:00:00	Other
20915	4	24	1033	1035	-2	1150	1157	B6	146	N283JB	JFK	BUF	54	301	10	35	2023-04-24 10:00:00	Other
20917	7	19	724	729	-5	945	956	YX	1019	N867RW	LGA	OMA	164	1148	7	29	2023-07-19 07:00:00	Other
20924	8	8	658	700	-2	950	954	DL	525	N341NW	JFK	AUS	202	1521	7	0	2023-08-08 07:00:00	Other
20931	5	10	708	710	-2	1011	1028	B6	280	N923JB	JFK	LAX	319	2475	7	10	2023-05-10 07:00:00	LAX
20932	12	9	1702	1705	-3	2027	2052	AA	930	N334TL	JFK	PHX	296	2153	17	5	2023-12-09 17:00:00	Other
20933	12	26	1655	1700	-5	1751	1830	YX	1714	N229JQ	LGA	BOS	33	184	17	0	2023-12-26 17:00:00	BOS
20935	8	16	1904	1907	-3	2152	2222	UA	606	N17262	EWR	SEA	318	2402	19	7	2023-08-16 19:00:00	Other
20941	4	14	1216	1220	-4	1334	1349	YX	1257	N112HQ	JFK	ORF	48	290	12	20	2023-04-14 12:00:00	Other
20942	11	17	1746	1749	-3	2056	2105	AA	957	N927NN	JFK	AUS	225	1521	17	49	2023-11-17 17:00:00	Other
20953	1	6	1656	1659	-3	1843	1900	YX	1845	N810MD	LGA	CMH	80	479	16	59	2023-01-06 16:00:00	Other
20965	4	14	1417	1420	-3	1741	1745	B6	694	N760JB	LGA	RSW	180	1080	14	20	2023-04-14 14:00:00	Other
20970	12	28	820	825	-5	1127	1146	DL	254	N125DU	LGA	DFW	199	1389	8	25	2023-12-28 08:00:00	Other
20975	8	14	1920	1925	-5	2143	2151	9E	1199	N313PQ	JFK	DTW	90	509	19	25	2023-08-14 19:00:00	Other
20977	2	5	1940	1945	-5	2125	2142	9E	1434	N936XJ	JFK	RDU	79	427	19	45	2023-02-05 19:00:00	Other
20978	4	26	655	700	-5	1002	1011	AS	14	N919AK	JFK	SEA	329	2422	7	0	2023-04-26 07:00:00	Other
20979	12	19	756	800	-4	942	1030	DL	533	N341NB	JFK	MSP	147	1029	8	0	2023-12-19 08:00:00	Other
20986	12	23	1505	1510	-5	1812	1820	DL	796	N820DN	JFK	MIA	156	1089	15	10	2023-12-23 15:00:00	MIA
20999	9	22	1115	1118	-3	1418	1438	DL	416	N312DU	LGA	RSW	154	1080	11	18	2023-09-22 11:00:00	Other
21000	6	13	624	626	-2	758	753	UA	992	N76265	LGA	ORD	108	733	6	26	2023-06-13 06:00:00	ORD
21002	10	14	854	859	-5	1005	1023	YX	1835	N208JQ	LGA	BOS	39	184	8	59	2023-10-14 08:00:00	BOS
21006	10	30	1826	1830	-4	2056	2056	9E	1498	N480PX	LGA	TYS	116	647	18	30	2023-10-30 18:00:00	Other
21017	2	25	655	659	-4	849	828	YX	1029	N640RW	EWR	BNA	143	748	6	59	2023-02-25 06:00:00	Other
21018	12	25	2151	2155	-4	2315	2342	UA	485	N17262	EWR	RDU	63	416	21	55	2023-12-25 21:00:00	Other
21020	3	9	1905	1910	-5	2222	2230	AS	182	N936AK	EWR	SEA	339	2402	19	10	2023-03-09 19:00:00	Other
21032	1	29	1155	1200	-5	1353	1411	YX	1898	N218JQ	LGA	STL	156	888	12	0	2023-01-29 12:00:00	Other
21036	9	26	1343	1345	-2	1618	1550	9E	1734	N491PX	LGA	CAE	99	617	13	45	2023-09-26 13:00:00	Other
21037	2	12	1524	1529	-5	1656	1702	YX	1509	N226JQ	LGA	DCA	53	214	15	29	2023-02-12 15:00:00	Other
21040	8	21	942	945	-3	1138	1205	YX	1047	N419YX	LGA	SDF	90	659	9	45	2023-08-21 09:00:00	Other
21044	12	4	1826	1829	-3	2144	2134	AA	400	N906AN	JFK	MIA	167	1089	18	29	2023-12-04 18:00:00	MIA
21057	5	18	542	545	-3	645	705	NK	416	N601NK	EWR	BNA	104	748	5	45	2023-05-18 05:00:00	Other
21062	9	20	1905	1910	-5	2119	2122	9E	1667	N300PQ	JFK	CVG	91	589	19	10	2023-09-20 19:00:00	Other
21063	10	18	1957	1959	-2	2259	2313	DL	526	N384DN	LGA	FLL	148	1076	19	59	2023-10-18 19:00:00	FLL
21067	1	23	2154	2159	-5	2306	2309	9E	1443	N922XJ	LGA	SCE	42	208	21	59	2023-01-23 21:00:00	Other
21070	9	24	1026	1029	-3	1209	1238	YX	1102	N656RW	EWR	DTW	77	488	10	29	2023-09-24 10:00:00	Other
21077	9	4	2100	2102	-2	2236	2304	UA	611	N411UA	EWR	MSP	133	1008	21	2	2023-09-04 21:00:00	Other
21104	9	28	1057	1100	-3	1311	1332	DL	283	N319DN	LGA	ATL	110	762	11	0	2023-09-28 11:00:00	ATL
21108	3	5	950	955	-5	1151	1154	9E	1452	N676CA	JFK	CLE	89	425	9	55	2023-03-05 09:00:00	Other
21112	9	7	1429	1433	-4	1611	1555	B6	931	N304JB	JFK	BUF	65	301	14	33	2023-09-07 14:00:00	Other
21119	6	7	815	820	-5	947	959	YX	1224	N657RW	EWR	RIC	55	277	8	20	2023-06-07 08:00:00	Other
21121	8	18	836	840	-4	1136	1140	DL	290	N721TW	JFK	SAN	296	2446	8	40	2023-08-18 08:00:00	Other
21123	9	27	725	729	-4	1020	1045	DL	299	N514DE	JFK	SEA	324	2422	7	29	2023-09-27 07:00:00	Other
21124	12	25	1555	1559	-4	1741	1808	B6	357	N354JB	JFK	DTW	79	509	15	59	2023-12-25 15:00:00	Other
21131	7	1	2155	2159	-4	2311	2321	YX	865	N733YX	EWR	MHT	40	209	21	59	2023-07-01 21:00:00	Other
21135	10	7	602	605	-3	807	830	WN	783	N956WN	LGA	DEN	212	1620	6	5	2023-10-07 06:00:00	Other
21136	1	20	901	906	-5	1212	1233	UA	221	N17730	EWR	SNA	344	2434	9	6	2023-01-20 09:00:00	Other
21140	9	15	1756	1800	-4	1935	1950	9E	1548	N308PQ	LGA	STL	119	888	18	0	2023-09-15 18:00:00	Other
21149	8	15	2155	2158	-3	2250	2300	9E	1239	N294PQ	LGA	PVD	27	143	21	58	2023-08-15 21:00:00	Other
21155	9	7	1125	1130	-5	1325	1352	9E	1627	N905XJ	LGA	MCI	150	1107	11	30	2023-09-07 11:00:00	Other
21156	12	16	959	1003	-4	1156	1233	UA	537	N47284	EWR	DEN	215	1605	10	3	2023-12-16 10:00:00	Other
21157	2	10	556	600	-4	913	915	DL	309	N140DU	LGA	DFW	223	1389	6	0	2023-02-10 06:00:00	Other
21159	4	15	810	815	-5	1055	1117	AA	332	N981NN	LGA	DFW	190	1389	8	15	2023-04-15 08:00:00	Other
21160	11	4	902	905	-3	1018	1032	B6	963	N206JB	JFK	BUF	56	301	9	5	2023-11-04 09:00:00	Other
21162	10	19	1756	1800	-4	2034	2105	AA	182	N932NN	LGA	DFW	186	1389	18	0	2023-10-19 18:00:00	Other
21164	6	19	2147	2152	-5	2252	2315	9E	1590	N300PQ	LGA	ROC	44	254	21	52	2023-06-19 21:00:00	Other
21167	12	20	555	600	-5	804	831	DL	803	N930AT	EWR	ATL	105	746	6	0	2023-12-20 06:00:00	ATL
21169	1	14	1032	1035	-3	1238	1320	B6	796	N645JB	LGA	DEN	220	1620	10	35	2023-01-14 10:00:00	Other
21171	4	11	856	900	-4	1138	1217	YX	1110	N419YX	LGA	IAH	180	1416	9	0	2023-04-11 09:00:00	Other
21173	3	20	940	945	-5	1139	1204	9E	1537	N915XJ	LGA	TYS	98	647	9	45	2023-03-20 09:00:00	Other
21176	11	26	756	800	-4	1113	1113	B6	78	N2060J	JFK	IAH	229	1417	8	0	2023-11-26 08:00:00	Other
21177	6	21	626	630	-4	752	804	UA	301	N14235	EWR	CLE	58	404	6	30	2023-06-21 06:00:00	Other
21184	3	21	1649	1654	-5	1816	1840	YX	1090	N635RW	EWR	MKE	125	725	16	54	2023-03-21 16:00:00	Other
21185	7	20	807	812	-5	1110	1120	AA	427	N936NN	EWR	MIA	153	1085	8	12	2023-07-20 08:00:00	MIA
21188	9	13	1556	1559	-3	1743	1803	YX	1217	N979RP	EWR	MYR	84	550	15	59	2023-09-13 15:00:00	Other
21195	4	12	658	700	-2	1037	1101	B6	550	N556JB	EWR	SJU	190	1608	7	0	2023-04-12 07:00:00	Other
21204	11	6	1251	1255	-4	1459	1500	9E	1611	N326PQ	JFK	DTW	95	509	12	55	2023-11-06 12:00:00	Other
21214	6	24	1148	1152	-4	1258	1310	UA	911	N37257	EWR	PWM	46	284	11	52	2023-06-24 11:00:00	Other
21216	12	8	1923	1925	-2	2133	2158	DL	453	N108DQ	LGA	MSY	170	1183	19	25	2023-12-08 19:00:00	Other
21220	3	20	720	725	-5	1005	954	UA	452	N840UA	EWR	JAX	138	820	7	25	2023-03-20 07:00:00	Other
21229	7	1	1745	1750	-5	1853	1857	9E	1109	N326PQ	LGA	ALB	34	136	17	50	2023-07-01 17:00:00	Other
21230	3	26	1627	1629	-2	1827	1818	DL	476	N122DU	LGA	ORD	150	733	16	29	2023-03-26 16:00:00	ORD
21234	6	29	1506	1509	-3	1739	1815	B6	587	N517JB	EWR	MCO	121	937	15	9	2023-06-29 15:00:00	MCO
21237	2	25	857	900	-3	1132	1119	AA	931	N378SC	JFK	ORD	160	740	9	0	2023-02-25 09:00:00	ORD
21246	10	15	1655	1659	-4	2010	2015	AS	75	N569AS	EWR	LAX	304	2454	16	59	2023-10-15 16:00:00	LAX
21250	9	10	1725	1730	-5	2022	1954	AA	951	N419AN	EWR	PHX	311	2133	17	30	2023-09-10 17:00:00	Other
21254	3	22	2012	2015	-3	2126	2131	B6	556	N193JB	LGA	BOS	41	184	20	15	2023-03-22 20:00:00	BOS
21257	5	27	1256	1300	-4	1551	1614	AA	224	N430AN	LGA	MIA	150	1096	13	0	2023-05-27 13:00:00	MIA
21262	5	17	1130	1132	-2	1411	1434	DL	404	N352NB	JFK	PBI	139	1028	11	32	2023-05-17 11:00:00	Other
21264	12	8	1957	1959	-2	2307	2338	AA	943	N314PD	LGA	MIA	157	1096	19	59	2023-12-08 19:00:00	MIA
21267	4	5	1642	1645	-3	1942	2003	B6	702	N625JB	JFK	MIA	140	1089	16	45	2023-04-05 16:00:00	MIA
21274	6	11	1155	1200	-5	1312	1331	9E	1501	N915XJ	LGA	ORF	50	296	12	0	2023-06-11 12:00:00	Other
21277	10	24	1257	1259	-2	1533	1535	AA	972	N335SN	JFK	PHX	307	2153	12	59	2023-10-24 12:00:00	Other
21278	10	13	912	915	-3	1122	1102	DL	898	N141DU	LGA	ORD	130	733	9	15	2023-10-13 09:00:00	ORD
21279	9	14	1226	1229	-3	1438	1457	AA	988	N833NN	JFK	PHX	280	2153	12	29	2023-09-14 12:00:00	Other
21281	3	26	805	810	-5	1039	1013	AA	993	N925UY	LGA	CLT	124	544	8	10	2023-03-26 08:00:00	CLT
21283	4	2	1925	1929	-4	2121	2135	OO	1026	N250SY	JFK	ORD	129	740	19	29	2023-04-02 19:00:00	ORD
21285	11	27	1026	1030	-4	1404	1411	YX	1332	N126HQ	LGA	EYW	191	1207	10	30	2023-11-27 10:00:00	Other
21292	12	1	555	600	-5	711	709	YX	1845	N231JQ	JFK	BOS	44	187	6	0	2023-12-01 06:00:00	BOS
21297	7	5	927	930	-3	1115	1139	DL	189	N351DN	LGA	DTW	74	502	9	30	2023-07-05 09:00:00	Other
21301	11	29	1250	1255	-5	1353	1414	DL	548	N110DU	JFK	BOS	45	187	12	55	2023-11-29 12:00:00	BOS
21307	3	21	1603	1608	-5	1734	1742	UA	490	N37253	EWR	BNA	114	748	16	8	2023-03-21 16:00:00	Other
21335	6	4	711	716	-5	853	909	UA	498	N24729	EWR	CLT	77	529	7	16	2023-06-04 07:00:00	CLT
21338	9	16	1840	1845	-5	2016	2045	YX	1198	N646RW	EWR	CMH	74	463	18	45	2023-09-16 18:00:00	Other
21340	3	5	1326	1330	-4	1526	1546	YX	1639	N214JQ	LGA	CLT	91	544	13	30	2023-03-05 13:00:00	CLT
21342	2	7	1451	1455	-4	1707	1727	9E	1402	N910XJ	JFK	SAV	108	718	14	55	2023-02-07 14:00:00	Other
21354	8	22	1841	1845	-4	2022	2132	DL	96	N814DN	JFK	PHX	263	2153	18	45	2023-08-22 18:00:00	Other
21358	12	22	1055	1100	-5	1353	1405	B6	892	N629JB	JFK	MIA	152	1089	11	0	2023-12-22 11:00:00	MIA
21366	2	23	954	959	-5	1141	1143	9E	1413	N186PQ	JFK	PIT	69	340	9	59	2023-02-23 09:00:00	Other
21368	11	6	947	950	-3	1140	1137	YX	1774	N218JQ	LGA	MSN	141	812	9	50	2023-11-06 09:00:00	Other
21370	2	1	1825	1830	-5	2039	2056	9E	1454	N307PQ	JFK	CVG	113	589	18	30	2023-02-01 18:00:00	Other
21372	7	23	1456	1459	-3	1745	1814	DL	721	N368NB	JFK	AUS	202	1521	14	59	2023-07-23 14:00:00	Other
21373	11	30	922	927	-5	1133	1120	OO	1201	N316SY	JFK	PIT	83	340	9	27	2023-11-30 09:00:00	Other
21380	3	29	957	959	-2	1114	1130	YX	1664	N202JQ	LGA	BOS	34	184	9	59	2023-03-29 09:00:00	BOS
21384	5	8	1310	1315	-5	1421	1431	B6	277	N258JB	JFK	BOS	39	187	13	15	2023-05-08 13:00:00	BOS
21385	3	22	1308	1310	-2	1522	1541	NK	37	N622NK	EWR	ATL	112	746	13	10	2023-03-22 13:00:00	ATL
21387	7	27	1011	1016	-5	1207	1236	AA	654	N918US	EWR	PHX	269	2133	10	16	2023-07-27 10:00:00	Other
21394	5	4	1755	1800	-5	1916	1925	AA	472	N819AW	LGA	DCA	57	214	18	0	2023-05-04 18:00:00	Other
21406	12	22	856	900	-4	1309	1227	AA	68	N113AN	JFK	LAX	348	2475	9	0	2023-12-22 09:00:00	LAX
21412	9	24	757	800	-3	1052	1052	B6	52	N625JB	JFK	MCO	132	944	8	0	2023-09-24 08:00:00	MCO
21417	6	11	557	600	-3	704	716	UA	455	N17289	EWR	IAD	40	212	6	0	2023-06-11 06:00:00	Other
21429	2	12	1456	1500	-4	1620	1630	YX	988	N642RW	EWR	ORF	58	284	15	0	2023-02-12 15:00:00	Other
21430	8	4	752	755	-3	948	1000	DL	467	N377DN	LGA	MSP	149	1020	7	55	2023-08-04 07:00:00	Other
21448	3	31	1536	1538	-2	1720	1716	UA	685	N68811	EWR	CLE	70	404	15	38	2023-03-31 15:00:00	Other
21452	12	25	1057	1059	-2	1155	1214	UA	212	N41135	EWR	BOS	38	200	10	59	2023-12-25 10:00:00	BOS
21455	11	7	606	610	-4	851	915	NK	190	N961NK	EWR	FLL	139	1065	6	10	2023-11-07 06:00:00	FLL
21457	5	26	1230	1235	-5	1400	1421	B6	85	N283JB	JFK	RDU	71	427	12	35	2023-05-26 12:00:00	Other
21458	4	10	924	929	-5	1029	1044	B6	859	N239JB	JFK	BOS	44	187	9	29	2023-04-10 09:00:00	BOS
21462	7	23	1248	1250	-2	1539	1527	YX	1041	N137HQ	LGA	OKC	195	1341	12	50	2023-07-23 12:00:00	Other
21466	3	8	1006	1011	-5	1256	1317	UA	748	N38458	EWR	IAH	198	1400	10	11	2023-03-08 10:00:00	Other
21469	2	13	1855	1859	-4	2052	2102	YX	1033	N749YX	EWR	CMH	77	463	18	59	2023-02-13 18:00:00	Other
21486	12	16	2104	2108	-4	2338	2348	UA	815	N37504	EWR	JAX	128	820	21	8	2023-12-16 21:00:00	Other
21488	7	30	2154	2158	-4	2246	2301	9E	1265	N901XJ	LGA	PVD	29	143	21	58	2023-07-30 21:00:00	Other
21494	2	9	1727	1730	-3	2016	1904	YX	1537	N202JQ	JFK	DCA	NA	213	17	30	2023-02-09 17:00:00	Other
21504	3	22	1653	1658	-5	1931	1933	UA	472	N77431	EWR	DEN	254	1605	16	58	2023-03-22 16:00:00	Other
21506	12	16	2145	2149	-4	2248	2301	YX	1039	N751YX	EWR	MHT	37	209	21	49	2023-12-16 21:00:00	Other
21508	4	16	1957	2000	-3	2102	2128	YX	1458	N239JQ	LGA	BOS	34	184	20	0	2023-04-16 20:00:00	BOS
21514	6	30	1447	1450	-3	1617	1651	YX	1784	N243JQ	LGA	CMH	76	479	14	50	2023-06-30 14:00:00	Other
21515	5	2	1815	1820	-5	2052	2111	9E	1426	N937XJ	JFK	JAX	122	828	18	20	2023-05-02 18:00:00	Other
21542	7	22	1154	1159	-5	1441	1500	UA	94	N433UA	EWR	RSW	145	1068	11	59	2023-07-22 11:00:00	Other
21551	4	12	614	619	-5	757	850	AA	906	N452AN	EWR	PHX	258	2133	6	19	2023-04-12 06:00:00	Other
21554	1	20	838	842	-4	1050	1115	YX	1122	N746YX	EWR	CVG	103	569	8	42	2023-01-20 08:00:00	Other
21562	1	9	1730	1735	-5	1908	1934	AA	234	N344PP	JFK	ORD	116	740	17	35	2023-01-09 17:00:00	ORD
21565	7	5	1107	1110	-3	1327	1347	DL	306	N523DE	JFK	LAS	293	2248	11	10	2023-07-05 11:00:00	Other
21566	9	22	1058	1100	-2	1259	1323	YX	1323	N112HQ	LGA	XNA	159	1147	11	0	2023-09-22 11:00:00	Other
21573	2	25	1648	1650	-2	2008	1947	DL	880	N3736C	LGA	DEN	280	1620	16	50	2023-02-25 16:00:00	Other
21582	5	17	1256	1259	-3	1451	1446	DL	460	N130DU	LGA	ORD	118	733	12	59	2023-05-17 12:00:00	ORD
21585	10	27	2021	2025	-4	2316	2320	WN	931	N413WN	LGA	DAL	202	1381	20	25	2023-10-27 20:00:00	Other
21587	6	1	1303	1305	-2	1505	1527	B6	1003	N566JB	LGA	SAV	100	722	13	5	2023-06-01 13:00:00	Other
21588	10	5	958	1000	-2	1145	1202	B6	59	N238JB	JFK	DTW	80	509	10	0	2023-10-05 10:00:00	Other
21593	2	26	1504	1506	-2	1758	1806	UA	590	N23708	EWR	TPA	147	997	15	6	2023-02-26 15:00:00	Other
21594	7	27	602	604	-2	752	806	AA	770	N549UW	EWR	CLT	79	529	6	4	2023-07-27 06:00:00	CLT
21608	12	12	1252	1257	-5	1447	1513	9E	1536	N293PQ	JFK	DTW	92	509	12	57	2023-12-12 12:00:00	Other
21610	5	13	1437	1440	-3	1733	1625	YX	1698	N239JQ	JFK	DCA	NA	213	14	40	2023-05-13 14:00:00	Other
21616	11	22	1026	1030	-4	1148	1148	B6	58	N661JB	JFK	BOS	48	187	10	30	2023-11-22 10:00:00	BOS
21617	8	24	1108	1110	-2	1348	1420	DL	712	N817DN	JFK	FLL	135	1069	11	10	2023-08-24 11:00:00	FLL
21640	10	17	1427	1429	-2	1627	1653	UA	933	N4888U	LGA	DEN	220	1620	14	29	2023-10-17 14:00:00	Other
21641	10	3	1956	1959	-3	2236	2300	DL	597	N318DU	LGA	IAH	186	1416	19	59	2023-10-03 19:00:00	Other
21642	2	6	1626	1630	-4	1734	1759	9E	1426	N910XJ	JFK	SYR	45	209	16	30	2023-02-06 16:00:00	Other
21646	12	20	959	1003	-4	1203	1233	UA	537	N39416	EWR	DEN	222	1605	10	3	2023-12-20 10:00:00	Other
21652	9	12	1650	1655	-5	1928	2015	AS	6	N288AK	JFK	SEA	310	2422	16	55	2023-09-12 16:00:00	Other
21657	2	12	618	620	-2	908	949	B6	510	N978JB	EWR	LAX	322	2454	6	20	2023-02-12 06:00:00	LAX
21664	12	12	1847	1849	-2	2215	2229	AS	8	N964AK	JFK	SAN	356	2446	18	49	2023-12-12 18:00:00	Other
21665	4	8	1658	1700	-2	1946	2021	UA	143	N209UA	EWR	SFO	331	2565	17	0	2023-04-08 17:00:00	Other
21668	8	1	1915	1920	-5	2223	2244	DL	593	N302NB	LGA	RSW	143	1080	19	20	2023-08-01 19:00:00	Other
21669	3	16	925	930	-5	1151	1212	UA	876	N818UA	LGA	DEN	241	1620	9	30	2023-03-16 09:00:00	Other
21673	7	29	1050	1055	-5	1339	1414	DL	361	N339NB	LGA	RSW	153	1080	10	55	2023-07-29 10:00:00	Other
21682	4	23	1258	1300	-2	1536	1546	UA	659	N37514	EWR	MCO	131	937	13	0	2023-04-23 13:00:00	MCO
21688	3	20	555	559	-4	910	917	AA	152	N329SL	JFK	MIA	166	1089	5	59	2023-03-20 05:00:00	MIA
21690	11	8	1102	1105	-3	1350	1352	UA	532	N57111	EWR	LAS	321	2227	11	5	2023-11-08 11:00:00	Other
21706	10	16	1528	1530	-2	1802	1838	UA	728	N77014	EWR	SFO	305	2565	15	30	2023-10-16 15:00:00	Other
21708	8	16	1942	1945	-3	2143	2202	UA	705	N17302	EWR	MSY	156	1167	19	45	2023-08-16 19:00:00	Other
21715	6	6	1458	1500	-2	1749	1807	NK	645	N665NK	LGA	FLL	148	1076	15	0	2023-06-06 15:00:00	FLL
21716	12	29	607	610	-3	749	814	YX	1332	N422YX	LGA	CMH	77	479	6	10	2023-12-29 06:00:00	Other
21721	10	4	855	900	-5	1016	1032	YX	1180	N864RW	EWR	ORF	53	284	9	0	2023-10-04 09:00:00	Other
21725	12	23	1717	1720	-3	1815	1853	YX	1268	N433YX	LGA	DCA	44	214	17	20	2023-12-23 17:00:00	Other
21733	1	17	1432	1435	-3	1638	1651	9E	1421	N295PQ	LGA	CVG	105	585	14	35	2023-01-17 14:00:00	Other
21750	3	6	557	600	-3	900	910	WN	972	N256WN	LGA	DAL	210	1381	6	0	2023-03-06 06:00:00	Other
21756	4	4	1926	1929	-3	2357	2200	YX	1553	N224JQ	LGA	OMA	NA	1148	19	29	2023-04-04 19:00:00	Other
21758	3	20	1926	1929	-3	2035	2100	YX	1735	N818MD	LGA	DCA	45	214	19	29	2023-03-20 19:00:00	Other
21762	4	27	645	650	-5	754	820	9E	1333	N294PQ	LGA	RIC	50	292	6	50	2023-04-27 06:00:00	Other
21765	8	31	1326	1329	-3	1434	1437	9E	1225	N131EV	LGA	BGM	31	147	13	29	2023-08-31 13:00:00	Other
21768	7	19	2114	2117	-3	2321	2313	YX	910	N763YX	EWR	ILM	89	488	21	17	2023-07-19 21:00:00	Other
21770	5	26	1622	1625	-3	1805	1809	AA	716	N802AW	LGA	RDU	73	431	16	25	2023-05-26 16:00:00	Other
21775	3	28	1124	1129	-5	1248	1256	YX	1054	N755YX	EWR	PIT	63	319	11	29	2023-03-28 11:00:00	Other
21776	4	29	1707	1709	-2	1845	1915	DL	818	N331NW	LGA	DTW	77	502	17	9	2023-04-29 17:00:00	Other
21781	1	4	1820	1825	-5	2124	2139	AA	1098	N953NN	JFK	DFW	213	1391	18	25	2023-01-04 18:00:00	Other
21783	2	27	1753	1755	-2	2041	2124	AA	544	N335PH	LGA	DFW	204	1389	17	55	2023-02-27 17:00:00	Other
21788	1	6	1757	1800	-3	2105	2125	UA	236	N17272	EWR	AUS	219	1504	18	0	2023-01-06 18:00:00	Other
21790	9	1	1425	1427	-2	1601	1619	UA	185	N449UA	EWR	MSP	137	1008	14	27	2023-09-01 14:00:00	Other
21794	2	23	1345	1350	-5	1550	1606	9E	1456	N695CA	LGA	TYS	106	647	13	50	2023-02-23 13:00:00	Other
21795	2	24	1322	1325	-3	1619	1642	AA	766	N969NN	JFK	MIA	152	1089	13	25	2023-02-24 13:00:00	MIA
21799	3	19	2007	2011	-4	2136	2152	YX	1378	N442YX	LGA	ORF	59	296	20	11	2023-03-19 20:00:00	Other
21801	7	24	2045	2050	-5	2230	2225	YX	1444	N878RW	LGA	MSN	119	812	20	50	2023-07-24 20:00:00	Other
21812	9	3	1142	1145	-3	1357	1420	WN	207	N464WN	LGA	DAL	178	1381	11	45	2023-09-03 11:00:00	Other
21813	6	20	1156	1200	-4	1301	1311	B6	891	N355JB	LGA	ACK	36	202	12	0	2023-06-20 12:00:00	Other
21816	11	5	725	730	-5	1023	1043	NK	557	N602NK	EWR	MIA	156	1085	7	30	2023-11-05 07:00:00	MIA
21823	6	30	1645	1650	-5	1829	1854	YX	1278	N135HQ	LGA	DSM	146	1031	16	50	2023-06-30 16:00:00	Other
21828	11	30	1324	1329	-5	1531	1557	DL	251	N377DA	LGA	DEN	226	1620	13	29	2023-11-30 13:00:00	Other
21831	7	13	1610	1615	-5	1749	1802	9E	1187	N307PQ	LGA	RIC	70	292	16	15	2023-07-13 16:00:00	Other
21834	4	8	555	600	-5	817	830	UA	371	N69829	EWR	DEN	233	1605	6	0	2023-04-08 06:00:00	Other
21835	9	17	1656	1700	-4	1848	1855	DL	148	N959AT	EWR	DTW	85	488	17	0	2023-09-17 17:00:00	Other
21847	7	21	1056	1100	-4	1158	1231	YX	1447	N208JQ	LGA	BOS	32	184	11	0	2023-07-21 11:00:00	BOS
21850	2	4	2112	2115	-3	2248	2246	9E	1448	N676CA	JFK	ORF	49	290	21	15	2023-02-04 21:00:00	Other
21859	12	10	947	949	-2	1117	1141	9E	1682	N928XJ	LGA	MSN	128	812	9	49	2023-12-10 09:00:00	Other
21866	11	8	852	855	-3	1020	1046	9E	1752	N186GJ	JFK	RDU	72	427	8	55	2023-11-08 08:00:00	Other
21871	2	14	1926	1929	-3	2205	2241	DL	582	N387DA	JFK	TPA	144	1005	19	29	2023-02-14 19:00:00	Other
21872	1	19	1128	1130	-2	1236	1247	YX	1147	N646RW	EWR	BTV	47	266	11	30	2023-01-19 11:00:00	Other
21875	2	19	657	700	-3	941	1010	DL	605	N318DX	LGA	FLL	147	1076	7	0	2023-02-19 07:00:00	FLL
21878	8	10	642	645	-3	947	959	DL	100	N536US	JFK	SLC	270	1990	6	45	2023-08-10 06:00:00	Other
21883	5	20	2055	2100	-5	2349	2359	NK	977	N693NK	EWR	MIA	147	1085	21	0	2023-05-20 21:00:00	MIA
21885	12	16	2156	2159	-3	2303	2321	UA	457	N35271	EWR	BUF	48	282	21	59	2023-12-16 21:00:00	Other
21886	12	10	727	730	-3	952	1019	DL	173	N325DN	LGA	ATL	121	762	7	30	2023-12-10 07:00:00	ATL
21890	8	30	725	730	-5	945	946	9E	1278	N902XJ	LGA	CVG	97	585	7	30	2023-08-30 07:00:00	Other
21895	2	16	726	730	-4	1048	1023	DL	182	N393DA	LGA	DEN	240	1620	7	30	2023-02-16 07:00:00	Other
21899	6	30	2248	2250	-2	26	33	9E	1661	N928XJ	JFK	ROC	49	264	22	50	2023-06-30 22:00:00	Other
21901	8	9	1342	1346	-4	1607	1640	UA	229	N27246	LGA	IAH	188	1416	13	46	2023-08-09 13:00:00	Other
21906	9	14	856	900	-4	1136	1200	B6	55	N2060J	JFK	SAN	317	2446	9	0	2023-09-14 09:00:00	Other
21907	7	23	941	946	-5	1400	1341	UA	488	N62895	EWR	SJU	211	1608	9	46	2023-07-23 09:00:00	Other
21918	2	21	1256	1300	-4	1437	1448	OO	1317	N105SY	LGA	ORD	131	733	13	0	2023-02-21 13:00:00	ORD
21919	12	9	645	650	-5	809	825	WN	343	N7873A	LGA	BNA	113	764	6	50	2023-12-09 06:00:00	Other
21924	9	5	1657	1700	-3	1807	1840	YX	1799	N217JQ	JFK	BOS	35	187	17	0	2023-09-05 17:00:00	BOS
21925	1	26	1723	1725	-2	2009	2022	YX	1340	N104HQ	LGA	ATL	144	762	17	25	2023-01-26 17:00:00	ATL
21926	8	20	628	630	-2	849	925	UA	597	N216UA	EWR	SFO	302	2565	6	30	2023-08-20 06:00:00	Other
21928	10	18	724	729	-5	1006	1032	DL	781	N396DN	JFK	FLL	137	1069	7	29	2023-10-18 07:00:00	FLL
21965	12	20	832	836	-4	1136	1210	UA	578	N465UA	EWR	SAT	215	1569	8	36	2023-12-20 08:00:00	Other
21967	12	8	1547	1550	-3	1821	1829	B6	922	N594JB	JFK	ATL	113	760	15	50	2023-12-08 15:00:00	ATL
21970	5	14	1247	1252	-5	1337	1402	9E	1320	N904XJ	LGA	ALB	28	136	12	52	2023-05-14 12:00:00	Other
21973	12	1	1227	1229	-2	1442	1456	9E	1574	N935XJ	LGA	SAV	114	722	12	29	2023-12-01 12:00:00	Other
21976	12	24	1043	1045	-2	1228	1302	9E	1397	N602LR	LGA	PNS	144	1030	10	45	2023-12-24 10:00:00	Other
21977	2	27	1413	1415	-2	1520	1527	B6	339	N228JB	LGA	BOS	34	184	14	15	2023-02-27 14:00:00	BOS
21983	10	23	2055	2100	-5	2219	2236	UA	650	N461UA	LGA	ORD	110	733	21	0	2023-10-23 21:00:00	ORD
21988	11	22	1255	1257	-2	1541	1610	DL	133	N131DU	LGA	DFW	183	1389	12	57	2023-11-22 12:00:00	Other
21991	6	12	1218	1222	-4	1424	1452	OO	1263	N260SY	LGA	SDF	100	659	12	22	2023-06-12 12:00:00	Other
21995	6	13	647	650	-3	951	955	AA	951	N946AN	LGA	MIA	152	1096	6	50	2023-06-13 06:00:00	MIA
22006	1	10	1831	1833	-2	2004	2017	UA	259	N23721	EWR	CLE	64	404	18	33	2023-01-10 18:00:00	Other
22012	9	30	656	700	-4	753	810	B6	989	N281JB	LGA	BOS	36	184	7	0	2023-09-30 07:00:00	BOS
22023	3	2	2152	2154	-2	2331	2328	UA	537	N14219	EWR	ORD	135	719	21	54	2023-03-02 21:00:00	ORD
22028	10	7	1502	1505	-3	1748	1758	UA	66	N37527	EWR	PBI	144	1023	15	5	2023-10-07 15:00:00	Other
22031	10	23	657	700	-3	815	820	YX	1734	N216JQ	LGA	BOS	35	184	7	0	2023-10-23 07:00:00	BOS
22033	5	2	606	610	-4	718	750	DL	405	N142DU	LGA	ORD	106	733	6	10	2023-05-02 06:00:00	ORD
22034	1	14	1327	1330	-3	1615	1654	DL	116	N145DQ	LGA	DFW	187	1389	13	30	2023-01-14 13:00:00	Other
22037	4	17	1717	1719	-2	1904	1915	DL	764	N945AT	EWR	DTW	80	488	17	19	2023-04-17 17:00:00	Other
22040	4	9	1055	1100	-5	1205	1229	UA	463	N474UA	EWR	BNA	106	748	11	0	2023-04-09 11:00:00	Other
22047	11	22	1435	1440	-5	1645	1646	YX	1266	N437YX	JFK	CVG	91	589	14	40	2023-11-22 14:00:00	Other
22066	5	22	2011	2015	-4	2130	2155	9E	1536	N936XJ	LGA	RIC	49	292	20	15	2023-05-22 20:00:00	Other
22068	1	20	2154	2158	-4	2258	2312	UA	1012	N891UA	EWR	SYR	39	195	21	58	2023-01-20 21:00:00	Other
22071	2	12	827	829	-2	938	944	YX	1153	N742YX	EWR	BOS	46	200	8	29	2023-02-12 08:00:00	BOS
22075	8	6	704	708	-4	947	947	UA	415	N435UA	EWR	IAH	188	1400	7	8	2023-08-06 07:00:00	Other
22078	8	28	1135	1138	-3	1300	1247	YX	1345	N211JQ	JFK	MVY	38	173	11	38	2023-08-28 11:00:00	Other
22082	9	12	1648	1650	-2	2000	2020	AS	11	N419AS	JFK	SFO	336	2586	16	50	2023-09-12 16:00:00	Other
22087	9	13	958	1000	-2	1150	1159	YX	1181	N641RW	EWR	GSO	74	445	10	0	2023-09-13 10:00:00	Other
22096	10	2	1142	1145	-3	1440	1459	AS	8	N413AS	JFK	SEA	323	2422	11	45	2023-10-02 11:00:00	Other
22102	7	20	1802	1805	-3	1959	2032	9E	1202	N485PX	LGA	TYS	102	647	18	5	2023-07-20 18:00:00	Other
22111	2	14	558	600	-2	908	925	OO	1484	N108SY	LGA	IAH	212	1416	6	0	2023-02-14 06:00:00	Other
22112	5	17	1828	1830	-2	2127	2200	B6	51	N955JB	JFK	SMF	321	2521	18	30	2023-05-17 18:00:00	Other
22113	4	19	1150	1155	-5	1421	1510	DL	375	N340NW	LGA	TPA	131	1010	11	55	2023-04-19 11:00:00	Other
22128	2	3	624	629	-5	933	944	AA	381	N901AN	LGA	DFW	212	1389	6	29	2023-02-03 06:00:00	Other
22136	4	7	1122	1125	-3	1311	1316	DL	540	N115DU	LGA	ORD	133	733	11	25	2023-04-07 11:00:00	ORD
22137	8	14	1125	1127	-2	1428	1435	DL	792	N112DU	LGA	SRQ	148	1047	11	27	2023-08-14 11:00:00	Other
22142	11	15	954	959	-5	1159	1220	9E	1523	N186PQ	JFK	IND	100	665	9	59	2023-11-15 09:00:00	Other
22144	12	1	506	509	-3	807	823	AA	411	N326RP	EWR	MIA	149	1085	5	9	2023-12-01 05:00:00	MIA
22147	9	2	1250	1255	-5	1443	1501	DL	497	N107DU	JFK	DTW	85	509	12	55	2023-09-02 12:00:00	Other
22158	5	12	1115	1120	-5	1356	1435	DL	511	N3756	JFK	MIA	142	1089	11	20	2023-05-12 11:00:00	MIA
22168	1	30	1045	1050	-5	1204	1230	9E	1638	N316PQ	LGA	RIC	58	292	10	50	2023-01-30 10:00:00	Other
22169	4	17	1145	1150	-5	1344	1359	9E	1253	N228PQ	JFK	CLT	95	541	11	50	2023-04-17 11:00:00	CLT
22172	12	27	915	920	-5	1316	1240	UA	495	N17303	EWR	RSW	189	1068	9	20	2023-12-27 09:00:00	Other
22174	10	6	1845	1849	-4	2114	2119	9E	1691	N304PQ	JFK	IND	125	665	18	49	2023-10-06 18:00:00	Other
22176	3	21	1107	1110	-3	1214	1219	OO	1235	N242SY	EWR	BOS	46	200	11	10	2023-03-21 11:00:00	BOS
22185	12	1	602	605	-3	722	735	WN	1019	N444WN	LGA	MDW	111	725	6	5	2023-12-01 06:00:00	Other
22189	2	2	741	744	-3	1114	1114	UA	601	N27255	EWR	SAT	254	1569	7	44	2023-02-02 07:00:00	Other
22190	8	31	1537	1540	-3	1756	1804	B6	717	N368JB	JFK	CHS	95	636	15	40	2023-08-31 15:00:00	Other
22199	10	26	1455	1500	-5	1706	1713	9E	1578	N186GJ	EWR	CVG	88	569	15	0	2023-10-26 15:00:00	Other
22200	11	17	1010	1015	-5	1109	1131	YX	1867	N202JQ	LGA	ALB	30	136	10	15	2023-11-17 10:00:00	Other
22210	10	30	1559	1604	-5	1749	1807	AA	392	N553UW	EWR	CLT	85	529	16	4	2023-10-30 16:00:00	CLT
22215	5	24	1613	1615	-2	1719	1735	B6	362	N304JB	LGA	BOS	39	184	16	15	2023-05-24 16:00:00	BOS
22223	4	9	945	950	-5	1056	1114	9E	1418	N293PQ	JFK	SYR	45	209	9	50	2023-04-09 09:00:00	Other
22225	11	22	1327	1330	-3	1555	1634	NK	329	N609NK	LGA	DFW	190	1389	13	30	2023-11-22 13:00:00	Other
22226	12	14	654	659	-5	811	847	MQ	1056	N303DD	EWR	ORD	108	719	6	59	2023-12-14 06:00:00	ORD
22235	10	27	1600	1604	-4	1813	1829	UA	503	N77530	EWR	ATL	108	746	16	4	2023-10-27 16:00:00	ATL
22250	8	7	827	829	-2	939	957	9E	1118	N902XJ	LGA	ROC	45	254	8	29	2023-08-07 08:00:00	Other
22252	9	2	1213	1215	-2	1432	1429	UA	723	N37273	LGA	DEN	209	1620	12	15	2023-09-02 12:00:00	Other
22253	12	21	1055	1100	-5	1209	1226	YX	1840	N242JQ	LGA	BOS	36	184	11	0	2023-12-21 11:00:00	BOS
22254	1	19	1056	1059	-3	1153	1216	YX	1731	N231JQ	JFK	BOS	36	187	10	59	2023-01-19 10:00:00	BOS
22256	12	16	952	955	-3	1133	1157	NK	604	N530NK	LGA	DTW	80	502	9	55	2023-12-16 09:00:00	Other
22257	10	28	1741	1745	-4	2101	2100	UA	470	N47570	EWR	SEA	351	2402	17	45	2023-10-28 17:00:00	Other
22259	12	30	1308	1311	-3	1442	1501	DL	973	N991AT	EWR	DTW	73	488	13	11	2023-12-30 13:00:00	Other
22264	9	15	901	905	-4	1051	1111	DL	195	N337DN	LGA	DTW	72	502	9	5	2023-09-15 09:00:00	Other
22267	6	22	622	625	-3	806	809	9E	1632	N316PQ	LGA	RDU	72	431	6	25	2023-06-22 06:00:00	Other
22268	2	10	1025	1029	-4	1157	1152	YX	1017	N729YX	EWR	DCA	46	199	10	29	2023-02-10 10:00:00	Other
22271	11	20	1444	1449	-5	1606	1620	9E	1601	N181PQ	LGA	CHO	57	305	14	49	2023-11-20 14:00:00	Other
22272	8	13	1915	1920	-5	2154	2207	9E	1289	N929XJ	LGA	JAX	118	833	19	20	2023-08-13 19:00:00	Other
22282	1	16	1038	1042	-4	1405	1426	UA	518	N27253	EWR	PHX	306	2133	10	42	2023-01-16 10:00:00	Other
22283	6	8	1525	1530	-5	1750	1811	B6	650	N537JT	JFK	JAX	115	828	15	30	2023-06-08 15:00:00	Other
22285	2	4	830	835	-5	1044	1121	YX	1257	N423YX	LGA	ATL	117	762	8	35	2023-02-04 08:00:00	ATL
22286	10	30	955	1000	-5	1314	1321	UA	558	N13138	EWR	LAX	347	2454	10	0	2023-10-30 10:00:00	LAX
22288	8	17	701	705	-4	901	932	B6	125	N945JT	JFK	LAS	276	2248	7	5	2023-08-17 07:00:00	Other
22293	3	16	857	900	-3	1017	1027	YX	1086	N732YX	EWR	DCA	40	199	9	0	2023-03-16 09:00:00	Other
22299	10	3	2127	2130	-3	2245	2302	9E	1686	N909XJ	LGA	CHO	55	305	21	30	2023-10-03 21:00:00	Other
22301	8	23	1854	1856	-2	2056	2102	YX	918	N650RW	EWR	CMH	76	463	18	56	2023-08-23 18:00:00	Other
22302	4	5	854	859	-5	1047	1109	9E	1188	N316PQ	LGA	MEM	147	963	8	59	2023-04-05 08:00:00	Other
22319	1	4	1453	1455	-2	1643	1706	9E	1659	N306PQ	JFK	CLE	75	425	14	55	2023-01-04 14:00:00	Other
22320	4	28	1157	1200	-3	1248	1308	YX	1217	N409YX	JFK	ORH	28	150	12	0	2023-04-28 12:00:00	Other
22321	3	30	543	545	-2	818	852	NK	203	N963NK	EWR	FLL	139	1065	5	45	2023-03-30 05:00:00	FLL
22327	6	6	632	635	-3	850	925	DL	472	N125DU	LGA	IAH	179	1416	6	35	2023-06-06 06:00:00	Other
22332	7	5	1126	1129	-3	1241	1246	9E	1134	N936XJ	LGA	SYR	39	198	11	29	2023-07-05 11:00:00	Other
22335	3	8	1026	1030	-4	1339	1354	AA	3	N109NN	JFK	LAX	349	2475	10	30	2023-03-08 10:00:00	LAX
22343	2	4	2235	2240	-5	2342	2348	YX	1508	N207JQ	JFK	BWI	41	184	22	40	2023-02-04 22:00:00	Other
22354	8	28	1301	1305	-4	1415	1429	YX	853	N749YX	EWR	PIT	56	319	13	5	2023-08-28 13:00:00	Other
22360	5	22	936	940	-4	1117	1140	DL	950	N983AT	EWR	DTW	77	488	9	40	2023-05-22 09:00:00	Other
22367	5	16	940	945	-5	1222	1301	B6	60	N955JB	JFK	SAN	324	2446	9	45	2023-05-16 09:00:00	Other
22369	3	16	945	947	-2	1132	1158	DL	989	N919AT	EWR	DTW	86	488	9	47	2023-03-16 09:00:00	Other
22377	11	7	706	709	-3	1042	1025	DL	329	N316DU	EWR	SLC	312	1969	7	9	2023-11-07 07:00:00	Other
22380	8	6	1250	1255	-5	1403	1428	9E	1192	N341PQ	JFK	ORF	46	290	12	55	2023-08-06 12:00:00	Other
22388	8	25	925	930	-5	1255	1245	B6	24	N935JB	JFK	SEA	327	2422	9	30	2023-08-25 09:00:00	Other
22390	10	29	1823	1825	-2	2127	2134	DL	848	N321US	JFK	AUS	222	1521	18	25	2023-10-29 18:00:00	Other
22396	1	22	1956	1959	-3	2253	2336	AS	91	N932AK	EWR	SFO	325	2565	19	59	2023-01-22 19:00:00	Other
22399	10	23	1051	1056	-5	1344	1404	DL	983	N102DU	LGA	SRQ	143	1047	10	56	2023-10-23 10:00:00	Other
22400	1	21	1258	1300	-2	1432	1447	YX	1149	N746YX	EWR	GSO	76	445	13	0	2023-01-21 13:00:00	Other
22401	11	26	1839	1844	-5	2154	2200	UA	446	N16709	EWR	SNA	350	2434	18	44	2023-11-26 18:00:00	Other
22404	10	25	1026	1030	-4	1240	1255	DL	794	N3768	EWR	ATL	102	746	10	30	2023-10-25 10:00:00	ATL
22407	8	7	831	835	-4	1059	1057	9E	1247	N691CA	JFK	CHS	102	636	8	35	2023-08-07 08:00:00	Other
22411	7	22	2047	2052	-5	31	111	DL	573	N849DN	JFK	SJU	192	1598	20	52	2023-07-22 20:00:00	Other
22415	4	6	1255	1259	-4	1453	1500	B6	809	N806JB	JFK	CHS	93	636	12	59	2023-04-06 12:00:00	Other
22416	6	6	1657	1700	-3	2003	1944	DL	357	N309DN	LGA	ATL	143	762	17	0	2023-06-06 17:00:00	ATL
22418	8	6	1216	1220	-4	1335	1356	AA	507	N841NN	EWR	ORD	108	719	12	20	2023-08-06 12:00:00	ORD
22423	4	15	758	800	-2	1011	1032	DL	105	N336DX	LGA	ATL	110	762	8	0	2023-04-15 08:00:00	ATL
22430	3	8	2045	2050	-5	2228	2253	YX	1653	N239JQ	JFK	CMH	83	483	20	50	2023-03-08 20:00:00	Other
22435	12	27	1757	1759	-2	1924	1939	UA	657	N17329	EWR	BNA	120	748	17	59	2023-12-27 17:00:00	Other
22440	6	13	2024	2029	-5	2153	2200	YX	1135	N649RW	EWR	BTV	44	266	20	29	2023-06-13 20:00:00	Other
22465	3	6	1311	1313	-2	1539	1547	UA	317	N809UA	EWR	JAX	121	820	13	13	2023-03-06 13:00:00	Other
22470	8	25	1418	1420	-2	1603	1552	YX	852	N754YX	EWR	MKE	116	725	14	20	2023-08-25 14:00:00	Other
22477	6	19	815	820	-5	953	959	YX	1224	N862RW	EWR	RIC	54	277	8	20	2023-06-19 08:00:00	Other
22478	11	19	1225	1230	-5	1509	1535	YX	1229	N104HQ	LGA	OKC	201	1341	12	30	2023-11-19 12:00:00	Other
22479	11	7	1533	1535	-2	1815	1842	NK	848	N625NK	EWR	FLL	140	1065	15	35	2023-11-07 15:00:00	FLL
22483	7	20	840	843	-3	1140	1134	UA	497	N87527	EWR	SAT	201	1569	8	43	2023-07-20 08:00:00	Other
22499	7	17	1317	1320	-3	1426	1455	YX	1403	N245JQ	LGA	DCA	47	214	13	20	2023-07-17 13:00:00	Other
22508	3	24	1157	1200	-3	1433	1407	YX	1274	N449YX	LGA	MEM	171	963	12	0	2023-03-24 12:00:00	Other
22510	12	28	1132	1135	-3	1345	1343	AA	167	N947AN	JFK	CLT	89	541	11	35	2023-12-28 11:00:00	CLT
22512	5	31	1424	1429	-5	1608	1612	9E	1510	N604LR	JFK	RIC	54	288	14	29	2023-05-31 14:00:00	Other
22514	6	1	1505	1510	-5	1710	1709	DL	964	N896AT	EWR	MSP	151	1008	15	10	2023-06-01 15:00:00	Other
22519	4	21	2026	2030	-4	2334	2331	B6	67	N821JB	JFK	TPA	148	1005	20	30	2023-04-21 20:00:00	Other
22521	7	5	1113	1118	-5	1411	1430	DL	811	N129DU	LGA	SRQ	148	1047	11	18	2023-07-05 11:00:00	Other
22523	11	29	824	829	-5	948	1005	9E	1492	N478PX	LGA	MKE	120	738	8	29	2023-11-29 08:00:00	Other
22525	8	3	1526	1531	-5	1750	1819	9E	1101	N330PQ	LGA	JAX	118	833	15	31	2023-08-03 15:00:00	Other
22543	10	10	930	933	-3	1325	1330	B6	990	N998JE	JFK	SJU	200	1598	9	33	2023-10-10 09:00:00	Other
22552	5	1	1924	1929	-5	7	2147	9E	1513	N906XJ	JFK	DTW	NA	509	19	29	2023-05-01 19:00:00	Other
22555	7	25	556	600	-4	846	908	NK	47	N670NK	LGA	FLL	149	1076	6	0	2023-07-25 06:00:00	FLL
22557	1	4	756	800	-4	1011	1042	DL	215	N337NW	LGA	ATL	118	762	8	0	2023-01-04 08:00:00	ATL
22559	3	24	1053	1055	-2	1248	1250	WN	968	N202WN	LGA	STL	147	888	10	55	2023-03-24 10:00:00	Other
22561	2	28	1955	2000	-5	2230	2231	9E	1394	N146PQ	LGA	OMA	181	1148	20	0	2023-02-28 20:00:00	Other
22564	6	27	727	730	-3	849	848	UA	532	N466UA	EWR	BTV	48	266	7	30	2023-06-27 07:00:00	Other
22565	4	20	815	820	-5	1157	1215	DL	296	N704X	JFK	SFO	362	2586	8	20	2023-04-20 08:00:00	Other
22573	12	14	725	729	-4	1036	1043	AA	738	N310RF	JFK	MIA	149	1089	7	29	2023-12-14 07:00:00	MIA
22581	9	16	826	830	-4	1018	1002	OO	1244	N259SY	JFK	BNA	109	765	8	30	2023-09-16 08:00:00	Other
22589	5	11	903	905	-2	1132	1156	B6	378	N535JB	JFK	MCO	124	944	9	5	2023-05-11 09:00:00	MCO
22597	9	26	717	720	-3	841	847	9E	1577	N200PQ	LGA	RIC	52	292	7	20	2023-09-26 07:00:00	Other
22599	10	4	2055	2100	-5	2216	2245	YX	1768	N219YX	JFK	DCA	41	213	21	0	2023-10-04 21:00:00	Other
22604	12	1	1256	1259	-3	1444	1451	9E	1658	N919XJ	LGA	RDU	83	431	12	59	2023-12-01 12:00:00	Other
22605	12	31	1822	1824	-2	2126	2146	AA	383	N912AN	LGA	MIA	157	1096	18	24	2023-12-31 18:00:00	MIA
22610	8	5	1002	1005	-3	1328	1255	DL	223	N401DZ	JFK	LAX	328	2475	10	5	2023-08-05 10:00:00	LAX
22612	6	1	1306	1311	-5	1455	1519	YX	1327	N401YX	LGA	MSP	143	1020	13	11	2023-06-01 13:00:00	Other
22620	2	27	1255	1259	-4	1608	1608	B6	43	N623JB	JFK	TPA	152	1005	12	59	2023-02-27 12:00:00	Other
22624	4	26	713	715	-2	926	945	DL	266	N717TW	JFK	PHX	292	2153	7	15	2023-04-26 07:00:00	Other
22627	7	30	1658	1700	-2	1809	1837	YX	1370	N228JQ	LGA	BOS	36	184	17	0	2023-07-30 17:00:00	BOS
22628	6	21	1624	1626	-2	1801	1814	9E	1596	N183GJ	LGA	BGR	57	378	16	26	2023-06-21 16:00:00	Other
22636	1	28	858	900	-2	1157	1209	UA	573	N14107	EWR	MCO	141	937	9	0	2023-01-28 09:00:00	MCO
22641	2	7	1101	1105	-4	1345	1415	B6	690	N2084J	JFK	PBI	144	1028	11	5	2023-02-07 11:00:00	Other
22642	10	1	703	705	-2	946	1000	DL	489	N918DU	JFK	TPA	137	1005	7	5	2023-10-01 07:00:00	Other
22644	7	20	1525	1528	-3	1727	1728	DL	754	N938AT	EWR	MSP	143	1008	15	28	2023-07-20 15:00:00	Other
22645	3	5	1011	1014	-3	1320	1332	B6	44	N267JB	EWR	MCO	148	937	10	14	2023-03-05 10:00:00	MCO
22648	12	16	1108	1110	-2	1247	1327	DL	489	N355DN	LGA	MSP	146	1020	11	10	2023-12-16 11:00:00	Other
22649	8	17	1442	1445	-3	1553	1613	YX	840	N757YX	LGA	IAD	47	229	14	45	2023-08-17 14:00:00	Other
22650	1	14	1958	2002	-4	2227	2316	B6	68	N537JT	JFK	TPA	125	1005	20	2	2023-01-14 20:00:00	Other
22667	4	3	1856	1859	-3	2048	2058	YX	1040	N654RW	EWR	CMH	73	463	18	59	2023-04-03 18:00:00	Other
22671	2	23	825	830	-5	1154	1134	UA	220	N12012	EWR	LAX	342	2454	8	30	2023-02-23 08:00:00	LAX
22674	4	24	1957	1959	-2	2206	2205	9E	1380	N315PQ	EWR	CVG	98	569	19	59	2023-04-24 19:00:00	Other
22675	4	29	2231	2235	-4	2339	2359	DL	435	N128DU	JFK	BOS	34	187	22	35	2023-04-29 22:00:00	BOS
22679	7	16	801	805	-4	1102	1014	DL	467	N371NB	JFK	MSP	146	1029	8	5	2023-07-16 08:00:00	Other
22701	12	24	1113	1117	-4	1247	1314	NK	18	N677NK	EWR	MYR	77	550	11	17	2023-12-24 11:00:00	Other
22705	3	14	1101	1105	-4	1451	1411	UA	851	N17272	EWR	MIA	154	1085	11	5	2023-03-14 11:00:00	MIA
22707	5	17	657	700	-3	904	904	9E	1310	N605LR	JFK	DTW	87	509	7	0	2023-05-17 07:00:00	Other
22710	12	11	855	900	-5	1145	1133	9E	1396	N228PQ	LGA	SAV	118	722	9	0	2023-12-11 09:00:00	Other
22721	8	24	901	905	-4	1126	1212	YX	976	N423YX	LGA	IAH	179	1416	9	5	2023-08-24 09:00:00	Other
22725	1	16	1154	1159	-5	1332	1345	9E	1405	N303PQ	LGA	MKE	108	738	11	59	2023-01-16 11:00:00	Other
22733	3	16	555	600	-5	817	836	UA	438	N34137	EWR	DEN	232	1605	6	0	2023-03-16 06:00:00	Other
22734	9	4	1341	1346	-5	1627	1640	UA	257	N481UA	LGA	IAH	191	1416	13	46	2023-09-04 13:00:00	Other
22736	10	4	1054	1059	-5	1357	1430	DL	271	N171DZ	JFK	SFO	338	2586	10	59	2023-10-04 10:00:00	Other
22739	12	21	1155	1159	-4	1317	1331	YX	1046	N722YX	EWR	PIT	55	319	11	59	2023-12-21 11:00:00	Other
22743	3	5	1316	1320	-4	1609	1609	UA	737	N48127	EWR	MCO	134	937	13	20	2023-03-05 13:00:00	MCO
22744	1	12	855	900	-5	1024	1045	WN	138	N242WN	LGA	MDW	120	725	9	0	2023-01-12 09:00:00	Other
22751	3	17	827	830	-3	1136	1146	AA	676	N9013A	JFK	EGE	259	1746	8	30	2023-03-17 08:00:00	Other
22756	3	24	1255	1259	-4	1400	1420	YX	1710	N242JQ	LGA	BOS	33	184	12	59	2023-03-24 12:00:00	BOS
22757	10	5	1946	1949	-3	2320	2255	B6	326	N709JB	JFK	PDX	312	2454	19	49	2023-10-05 19:00:00	Other
22762	11	1	2022	2025	-3	31	24	B6	679	N2039J	JFK	SJU	201	1598	20	25	2023-11-01 20:00:00	Other
22769	2	2	918	923	-5	1050	1053	B6	603	N231JB	JFK	BUF	66	301	9	23	2023-02-02 09:00:00	Other
22773	6	29	1032	1035	-3	1149	1216	AA	148	N836NN	LGA	ORD	105	733	10	35	2023-06-29 10:00:00	ORD
22777	5	6	1057	1059	-2	1256	1301	NK	629	N677NK	LGA	DTW	77	502	10	59	2023-05-06 10:00:00	Other
22782	10	2	934	938	-4	1040	1039	9E	1643	N300PQ	LGA	BDL	25	101	9	38	2023-10-02 09:00:00	Other
22785	4	10	1515	1520	-5	1646	1655	9E	1350	N478PX	LGA	MKE	108	738	15	20	2023-04-10 15:00:00	Other
22786	1	1	1533	1536	-3	1814	1849	DL	1022	N392DN	JFK	MCO	137	944	15	36	2023-01-01 15:00:00	MCO
22787	3	26	807	810	-3	1037	1050	DL	354	N379DA	JFK	DEN	243	1626	8	10	2023-03-26 08:00:00	Other
22789	7	13	1245	1250	-5	1338	1359	9E	1271	N902XJ	LGA	PVD	31	143	12	50	2023-07-13 12:00:00	Other
22792	6	29	2025	2030	-5	2143	2205	YX	1399	N119HQ	JFK	BOS	45	187	20	30	2023-06-29 20:00:00	BOS
22794	10	30	855	900	-5	1055	1036	OO	1181	N246SY	JFK	BNA	136	765	9	0	2023-10-30 09:00:00	Other
22795	5	7	1903	1905	-2	2126	2149	DL	424	N919DU	JFK	ATL	112	760	19	5	2023-05-07 19:00:00	ATL
22797	10	17	1147	1150	-3	1258	1305	WN	1238	N429WN	LGA	MDW	102	725	11	50	2023-10-17 11:00:00	Other
22798	11	14	2216	2218	-2	42	59	NK	262	N619NK	EWR	LAS	306	2227	22	18	2023-11-14 22:00:00	Other
22799	7	6	1158	1200	-2	1307	1321	YX	1018	N133HQ	JFK	BOS	38	187	12	0	2023-07-06 12:00:00	BOS
22801	12	11	1118	1120	-2	1412	1424	DL	428	N808DN	JFK	TPA	154	1005	11	20	2023-12-11 11:00:00	Other
22802	2	23	2100	2105	-5	2203	2211	9E	1264	N491PX	LGA	BGM	35	147	21	5	2023-02-23 21:00:00	Other
22803	8	5	1356	1400	-4	1753	1621	B6	580	N521JB	LGA	DEN	246	1620	14	0	2023-08-05 14:00:00	Other
22805	11	22	1052	1055	-3	1412	1414	B6	22	N942JB	JFK	SEA	348	2422	10	55	2023-11-22 10:00:00	Other
22806	1	9	1028	1030	-2	1155	1135	9E	1660	N183GJ	JFK	BWI	38	184	10	30	2023-01-09 10:00:00	Other
22814	11	11	1021	1025	-4	1223	1247	9E	1688	N927XJ	LGA	CAE	100	617	10	25	2023-11-11 10:00:00	Other
22819	7	20	1726	1730	-4	1932	1926	YX	1029	N113HQ	LGA	CMH	76	479	17	30	2023-07-20 17:00:00	Other
22826	4	17	1858	1900	-2	2016	2026	UA	734	N432UA	EWR	IAD	49	212	19	0	2023-04-17 19:00:00	Other
22829	11	4	1522	1525	-3	1808	1827	DL	785	N379DN	JFK	MCO	139	944	15	25	2023-11-04 15:00:00	MCO
22833	7	31	1627	1630	-3	1928	1959	B6	230	N632JB	JFK	SJC	331	2569	16	30	2023-07-31 16:00:00	Other
22834	7	19	1027	1029	-2	1215	1236	YX	896	N723YX	EWR	CLT	87	529	10	29	2023-07-19 10:00:00	CLT
22836	11	3	824	829	-5	957	1013	YX	1848	N860RW	LGA	MSN	129	812	8	29	2023-11-03 08:00:00	Other
22837	7	6	2026	2030	-4	2155	2207	YX	1089	N122HQ	JFK	BOS	44	187	20	30	2023-07-06 20:00:00	BOS
22845	10	30	1045	1050	-5	1244	1235	WN	891	N555LV	LGA	STL	145	888	10	50	2023-10-30 10:00:00	Other
22852	1	16	845	850	-5	1038	1118	9E	1464	N478PX	LGA	GSP	91	610	8	50	2023-01-16 08:00:00	Other
22853	6	1	1226	1229	-3	1513	1538	UA	833	N494UA	EWR	SAT	207	1569	12	29	2023-06-01 12:00:00	Other
22854	6	17	1322	1325	-3	1450	1505	9E	1485	N228PQ	JFK	RIC	52	288	13	25	2023-06-17 13:00:00	Other
22859	10	16	1827	1830	-3	2156	2140	AA	130	N934NN	JFK	MIA	157	1089	18	30	2023-10-16 18:00:00	MIA
22862	1	15	555	600	-5	837	919	AA	165	N306SP	JFK	MIA	132	1089	6	0	2023-01-15 06:00:00	MIA
22864	2	20	1710	1712	-2	1851	1850	UA	754	N36247	EWR	ORD	130	719	17	12	2023-02-20 17:00:00	ORD
22876	12	3	956	959	-3	1137	1135	YX	1765	N209JQ	JFK	DCA	51	213	9	59	2023-12-03 09:00:00	Other
22878	9	1	951	956	-5	1204	1222	UA	561	N37278	EWR	LAS	282	2227	9	56	2023-09-01 09:00:00	Other
22880	5	3	935	940	-5	1222	1238	B6	44	N318JB	EWR	MCO	134	937	9	40	2023-05-03 09:00:00	MCO
22888	9	5	2055	2059	-4	2219	2238	UA	232	N39416	EWR	ORD	95	719	20	59	2023-09-05 20:00:00	ORD
22889	2	15	556	600	-4	749	809	AA	260	N172US	LGA	CLT	89	544	6	0	2023-02-15 06:00:00	CLT
22890	3	11	455	500	-5	742	806	AA	210	N910NN	EWR	DFW	201	1372	5	0	2023-03-11 05:00:00	Other
22902	7	23	1423	1428	-5	1555	1620	B6	236	N503JB	JFK	RDU	67	427	14	28	2023-07-23 14:00:00	Other
22909	2	7	1255	1300	-5	1434	1447	YX	1012	N731YX	EWR	GSO	76	445	13	0	2023-02-07 13:00:00	Other
22914	8	13	2143	2147	-4	2351	4	YX	900	N747YX	EWR	CHS	86	628	21	47	2023-08-13 21:00:00	Other
22917	5	12	555	600	-5	741	735	UA	375	N37518	EWR	ORD	111	719	6	0	2023-05-12 06:00:00	ORD
22935	7	13	958	1000	-2	1513	1455	HA	20	N374HA	JFK	HNL	633	4983	10	0	2023-07-13 10:00:00	Other
22944	5	5	557	600	-3	753	801	AA	231	N162UW	LGA	CLT	84	544	6	0	2023-05-05 06:00:00	CLT
22945	7	4	648	650	-2	945	942	NK	437	N615NK	EWR	MCO	131	937	6	50	2023-07-04 06:00:00	MCO
22948	2	2	1056	1100	-4	1252	1256	YX	980	N753YX	EWR	MYR	94	550	11	0	2023-02-02 11:00:00	Other
22956	12	26	1526	1529	-3	1826	1825	UA	532	N27270	EWR	MCO	139	937	15	29	2023-12-26 15:00:00	MCO
22957	3	15	606	609	-3	914	915	NK	52	N664NK	LGA	FLL	160	1076	6	9	2023-03-15 06:00:00	FLL
22958	4	13	2047	2050	-3	2240	2259	OO	1044	N604CZ	JFK	CLE	71	425	20	50	2023-04-13 20:00:00	Other
22965	11	2	650	655	-5	1006	957	B6	428	N523JB	LGA	TPA	152	1010	6	55	2023-11-02 06:00:00	Other
22966	6	9	845	850	-5	1004	1010	YX	1787	N824MD	EWR	BOS	36	200	8	50	2023-06-09 08:00:00	BOS
22969	4	4	2040	2045	-5	2305	2326	YX	1162	N826MD	JFK	IND	98	665	20	45	2023-04-04 20:00:00	Other
22973	5	2	1236	1240	-4	1357	1419	9E	1296	N314PQ	LGA	BGR	58	378	12	40	2023-05-02 12:00:00	Other
22984	2	9	1803	1806	-3	2049	2112	UA	907	N27261	EWR	PBI	141	1023	18	6	2023-02-09 18:00:00	Other
22996	5	17	1853	1855	-2	2115	2137	NK	262	N958NK	EWR	LAS	298	2227	18	55	2023-05-17 18:00:00	Other
22999	5	9	710	715	-5	956	949	9E	1428	N294PQ	LGA	JAX	116	833	7	15	2023-05-09 07:00:00	Other
23000	3	3	738	742	-4	1013	1019	UA	848	N14118	EWR	DEN	240	1605	7	42	2023-03-03 07:00:00	Other
23001	7	28	855	900	-5	1033	1037	OO	985	N240SY	JFK	BNA	106	765	9	0	2023-07-28 09:00:00	Other
23003	8	7	746	750	-4	931	945	9E	1167	N153PQ	JFK	RDU	70	427	7	50	2023-08-07 07:00:00	Other
23012	8	19	1538	1540	-2	1757	1804	B6	717	N206JB	JFK	CHS	87	636	15	40	2023-08-19 15:00:00	Other
23016	10	13	1418	1421	-3	1706	1717	UA	270	N841UA	EWR	AUS	212	1504	14	21	2023-10-13 14:00:00	Other
23017	7	10	546	550	-4	829	831	AA	482	N315PE	LGA	DFW	199	1389	5	50	2023-07-10 05:00:00	Other
23018	7	1	555	600	-5	813	837	UA	170	N27252	EWR	IAH	174	1400	6	0	2023-07-01 06:00:00	Other
23023	5	3	1625	1629	-4	1918	1939	AA	106	N758AN	JFK	MIA	147	1089	16	29	2023-05-03 16:00:00	MIA
23026	4	3	557	600	-3	848	911	AA	431	N843NN	LGA	MIA	149	1096	6	0	2023-04-03 06:00:00	MIA
23028	5	17	1610	1615	-5	2030	1831	DL	337	N103DU	LGA	CHS	NA	641	16	15	2023-05-17 16:00:00	Other
23030	4	27	1018	1021	-3	1111	1139	YX	1500	N241JQ	LGA	PVD	32	143	10	21	2023-04-27 10:00:00	Other
23040	11	28	2127	2129	-2	2304	2325	YX	1068	N731YX	EWR	ILM	73	488	21	29	2023-11-28 21:00:00	Other
23057	3	19	1837	1840	-3	2045	2112	YX	1285	N113HQ	LGA	OMA	167	1148	18	40	2023-03-19 18:00:00	Other
23061	8	11	1342	1346	-4	1610	1640	UA	229	N35271	LGA	IAH	187	1416	13	46	2023-08-11 13:00:00	Other
23071	5	28	631	635	-4	925	948	AA	362	N338ST	JFK	MIA	150	1089	6	35	2023-05-28 06:00:00	MIA
23079	10	8	1005	1009	-4	1119	1158	AA	965	N701UW	LGA	ORD	105	733	10	9	2023-10-08 10:00:00	ORD
23087	12	21	1354	1359	-5	1505	1522	YX	1707	N201JQ	LGA	BOS	38	184	13	59	2023-12-21 13:00:00	BOS
23091	8	5	2045	2048	-3	2340	2357	UA	553	N17245	EWR	SLC	271	1969	20	48	2023-08-05 20:00:00	Other
23097	8	4	1725	1730	-5	2038	2141	DL	250	N710TW	JFK	SFO	345	2586	17	30	2023-08-04 17:00:00	Other
23099	2	4	1451	1455	-4	1743	1805	B6	140	N956JT	JFK	MCO	135	944	14	55	2023-02-04 14:00:00	MCO
23102	3	17	2357	2359	-2	336	343	B6	979	N706JB	JFK	SJU	194	1598	23	59	2023-03-17 23:00:00	Other
23106	1	27	1011	1016	-5	1317	1328	DL	1077	N328DN	LGA	MCO	156	950	10	16	2023-01-27 10:00:00	MCO
23111	9	3	1713	1717	-4	1929	1938	UA	858	N68821	EWR	DEN	206	1605	17	17	2023-09-03 17:00:00	Other
23113	11	8	929	933	-4	1300	1258	NK	1181	N650NK	EWR	PHX	304	2133	9	33	2023-11-08 09:00:00	Other
23118	11	20	1327	1330	-3	1425	1459	B6	531	N368JB	JFK	BOS	34	187	13	30	2023-11-20 13:00:00	BOS
23131	10	19	1905	1910	-5	2131	2200	UA	336	N37427	EWR	IAH	179	1400	19	10	2023-10-19 19:00:00	Other
23141	11	3	556	600	-4	657	715	B6	102	N318JB	JFK	BOS	45	187	6	0	2023-11-03 06:00:00	BOS
23150	5	30	625	630	-5	1032	1020	B6	599	N999JQ	JFK	SJU	218	1598	6	30	2023-05-30 06:00:00	Other
23165	5	11	658	700	-2	954	1007	UA	270	N27263	EWR	FLL	143	1065	7	0	2023-05-11 07:00:00	FLL
23171	1	17	1013	1015	-2	1153	1221	YX	1286	N430YX	JFK	RDU	77	427	10	15	2023-01-17 10:00:00	Other
23172	3	29	2133	2138	-5	2344	2359	UA	314	N460UA	EWR	SAV	102	708	21	38	2023-03-29 21:00:00	Other
23175	8	7	1628	1630	-2	1932	1943	B6	57	N807JB	JFK	TPA	154	1005	16	30	2023-08-07 16:00:00	Other
23182	2	8	855	900	-5	1052	1103	OO	1169	N256SY	JFK	ORD	134	740	9	0	2023-02-08 09:00:00	ORD
23184	3	26	1353	1357	-4	1609	1559	UA	664	N444UA	EWR	CHS	113	628	13	57	2023-03-26 13:00:00	Other
23191	8	29	555	600	-5	832	835	WN	870	N8739L	LGA	DAL	188	1381	6	0	2023-08-29 06:00:00	Other
23192	8	5	853	858	-5	1030	1050	9E	1165	N131EV	LGA	RDU	71	431	8	58	2023-08-05 08:00:00	Other
23195	4	19	1547	1550	-3	1738	1804	UA	746	N67501	EWR	MSY	150	1167	15	50	2023-04-19 15:00:00	Other
23199	3	18	700	705	-5	1015	1024	DL	549	N392DN	LGA	MIA	164	1096	7	5	2023-03-18 07:00:00	MIA
23200	9	24	1146	1150	-4	1250	1305	YX	1325	N410YX	JFK	BOS	34	187	11	50	2023-09-24 11:00:00	BOS
23202	10	29	1513	1515	-2	1903	1857	DL	258	N718TW	JFK	SFO	385	2586	15	15	2023-10-29 15:00:00	Other
23205	9	26	1317	1320	-3	1535	1523	YX	1350	N406YX	LGA	MSP	143	1020	13	20	2023-09-26 13:00:00	Other
23207	4	7	1717	1720	-3	2046	2059	B6	252	N784JB	JFK	SJC	365	2569	17	20	2023-04-07 17:00:00	Other
23209	12	20	1247	1252	-5	1446	1508	9E	1351	N926XJ	JFK	DTW	87	509	12	52	2023-12-20 12:00:00	Other
23210	2	15	1839	1843	-4	2155	2209	DL	459	N854DN	EWR	SLC	287	1969	18	43	2023-02-15 18:00:00	Other
23211	4	8	811	815	-4	956	1009	YX	1447	N209JQ	LGA	ORD	129	733	8	15	2023-04-08 08:00:00	ORD
23213	6	5	2133	2137	-4	2327	2351	YX	1157	N741YX	EWR	CLT	80	529	21	37	2023-06-05 21:00:00	CLT
23214	6	4	558	600	-2	826	904	B6	530	N983JT	EWR	LAX	295	2454	6	0	2023-06-04 06:00:00	LAX
23215	12	26	655	700	-5	1005	1049	DL	117	N535DN	JFK	PHX	278	2153	7	0	2023-12-26 07:00:00	Other
23216	11	20	728	730	-2	930	952	DL	525	N365NB	JFK	MSP	151	1029	7	30	2023-11-20 07:00:00	Other
23220	8	23	725	729	-4	907	909	AA	212	N885NN	LGA	ORD	110	733	7	29	2023-08-23 07:00:00	ORD
23225	8	12	612	615	-3	818	836	UA	342	N68842	EWR	JAX	106	820	6	15	2023-08-12 06:00:00	Other
23226	4	4	922	925	-3	1024	1059	YX	1111	N102HQ	JFK	BOS	33	187	9	25	2023-04-04 09:00:00	BOS
23228	2	15	955	1000	-5	1137	1202	9E	1430	N315PQ	EWR	RDU	74	416	10	0	2023-02-15 10:00:00	Other
23229	8	6	2143	2145	-2	32	47	B6	144	N768JB	LGA	FLL	144	1076	21	45	2023-08-06 21:00:00	FLL
23233	8	15	557	601	-4	830	839	B6	191	N2039J	JFK	MCO	124	944	6	1	2023-08-15 06:00:00	MCO
23238	10	29	2153	2155	-2	135	142	DL	300	N717TW	JFK	SFO	367	2586	21	55	2023-10-29 21:00:00	Other
23243	5	12	1718	1723	-5	1916	1945	AA	921	N400AN	EWR	PHX	272	2133	17	23	2023-05-12 17:00:00	Other
23251	10	19	1057	1100	-3	1159	1209	B6	58	N281JB	JFK	BOS	44	187	11	0	2023-10-19 11:00:00	BOS
23255	3	31	1432	1437	-5	1647	1654	NK	883	N691NK	EWR	MSY	173	1167	14	37	2023-03-31 14:00:00	Other
23270	6	23	621	625	-4	758	809	9E	1632	N925XJ	LGA	RDU	67	431	6	25	2023-06-23 06:00:00	Other
23284	3	24	1511	1514	-3	1702	1655	UA	715	N27239	EWR	ORD	126	719	15	14	2023-03-24 15:00:00	ORD
23293	5	11	825	830	-5	952	1005	OO	1175	N319SY	JFK	BNA	108	765	8	30	2023-05-11 08:00:00	Other
23295	3	24	653	655	-2	751	809	B6	200	N334JB	JFK	BOS	39	187	6	55	2023-03-24 06:00:00	BOS
23302	11	11	1112	1117	-5	1259	1310	NK	20	N669NK	EWR	MYR	93	550	11	17	2023-11-11 11:00:00	Other
23304	3	12	2018	2023	-5	2215	2243	YX	1075	N746YX	EWR	GRR	94	605	20	23	2023-03-12 20:00:00	Other
23305	7	12	1828	1832	-4	1944	1948	YX	884	N639RW	EWR	ALB	39	143	18	32	2023-07-12 18:00:00	Other
23306	3	20	1055	1100	-5	1207	1233	YX	1244	N423YX	LGA	DCA	45	214	11	0	2023-03-20 11:00:00	Other
23308	12	6	1511	1515	-4	1713	1759	DL	244	N809DN	JFK	DEN	224	1626	15	15	2023-12-06 15:00:00	Other
23315	12	20	631	635	-4	737	759	B6	681	N328JB	JFK	DCA	45	213	6	35	2023-12-20 06:00:00	Other
23322	1	23	921	925	-4	1119	1144	9E	1386	N200PQ	EWR	CVG	97	569	9	25	2023-01-23 09:00:00	Other
23324	3	19	1838	1840	-2	2009	2020	UA	461	N840UA	EWR	ORD	109	719	18	40	2023-03-19 18:00:00	ORD
23328	1	22	945	949	-4	1309	1329	AA	1088	N432AN	EWR	PHX	294	2133	9	49	2023-01-22 09:00:00	Other
23329	6	13	1140	1145	-5	1420	1427	UA	518	N17265	EWR	DFW	193	1372	11	45	2023-06-13 11:00:00	Other
23330	9	21	1738	1740	-2	2035	2034	B6	64	N793JB	JFK	TPA	154	1005	17	40	2023-09-21 17:00:00	Other
23337	1	5	1003	1005	-2	1408	1319	NK	26	N667NK	EWR	MIA	177	1085	10	5	2023-01-05 10:00:00	MIA
23338	9	22	954	959	-5	1258	1307	UA	620	N838UA	EWR	RSW	150	1068	9	59	2023-09-22 09:00:00	Other
23342	8	19	1056	1059	-3	1227	1255	YX	859	N763YX	EWR	ILM	72	488	10	59	2023-08-19 10:00:00	Other
23343	6	7	1043	1045	-2	1311	1411	DL	947	N930DZ	JFK	SLC	250	1990	10	45	2023-06-07 10:00:00	Other
23344	10	27	656	700	-4	901	915	DL	515	N301NB	JFK	MSP	152	1029	7	0	2023-10-27 07:00:00	Other
23348	5	1	1052	1056	-4	1315	1321	UA	98	N47280	EWR	ATL	110	746	10	56	2023-05-01 10:00:00	ATL
23353	4	21	726	730	-4	852	855	9E	1250	N933XJ	LGA	BUF	48	292	7	30	2023-04-21 07:00:00	Other
23360	11	20	557	600	-3	731	739	DL	437	N109DU	LGA	ORD	120	733	6	0	2023-11-20 06:00:00	ORD
23365	2	27	1225	1229	-4	1451	1506	YX	1614	N202JQ	LGA	SDF	112	659	12	29	2023-02-27 12:00:00	Other
23368	2	7	625	630	-5	912	935	B6	92	N952JB	LGA	MCO	130	950	6	30	2023-02-07 06:00:00	MCO
23371	3	29	1428	1430	-2	1657	1642	UA	204	N405UA	EWR	MSY	167	1167	14	30	2023-03-29 14:00:00	Other
23377	5	22	1757	1759	-2	2047	2137	DL	246	N803DN	JFK	SLC	254	1990	17	59	2023-05-22 17:00:00	Other
23383	12	31	1152	1155	-3	1414	1509	DL	347	N526DE	JFK	LAS	299	2248	11	55	2023-12-31 11:00:00	Other
23389	7	6	1527	1531	-4	1849	1835	B6	477	N517JB	EWR	MCO	130	937	15	31	2023-07-06 15:00:00	MCO
23395	1	4	1505	1509	-4	1806	1816	UA	676	N36207	EWR	TPA	149	997	15	9	2023-01-04 15:00:00	Other
23397	4	12	725	730	-5	845	855	9E	1250	N331PQ	LGA	BUF	52	292	7	30	2023-04-12 07:00:00	Other
23406	10	10	557	600	-3	709	718	UA	397	N37277	EWR	IAD	40	212	6	0	2023-10-10 06:00:00	Other
23416	7	30	1556	1559	-3	1817	1808	YX	1094	N406YX	LGA	TYS	93	647	15	59	2023-07-30 15:00:00	Other
23418	2	28	857	900	-3	1247	1250	AS	17	N926AK	JFK	SFO	380	2586	9	0	2023-02-28 09:00:00	Other
23424	7	5	1627	1629	-2	2021	1947	AA	420	N928NN	LGA	MIA	190	1096	16	29	2023-07-05 16:00:00	MIA
23425	7	25	655	700	-5	954	1007	DL	373	N3736C	JFK	RSW	150	1074	7	0	2023-07-25 07:00:00	Other
23431	3	9	1943	1945	-2	2200	2220	B6	684	N273JB	LGA	SAV	102	722	19	45	2023-03-09 19:00:00	Other
23435	11	24	1256	1300	-4	1528	1621	DL	200	N523DE	JFK	PDX	319	2454	13	0	2023-11-24 13:00:00	Other
23442	9	20	1404	1409	-5	1536	1604	9E	1544	N604LR	JFK	RDU	68	427	14	9	2023-09-20 14:00:00	Other
23452	10	31	755	800	-5	1024	1029	DL	168	N514DE	JFK	DEN	245	1626	8	0	2023-10-31 08:00:00	Other
23453	12	7	556	600	-4	806	833	UA	569	N897UA	LGA	DEN	228	1620	6	0	2023-12-07 06:00:00	Other
23455	7	11	1142	1145	-3	1343	1404	YX	999	N442YX	JFK	IND	99	665	11	45	2023-07-11 11:00:00	Other
23459	6	4	1905	1910	-5	2119	2126	YX	1317	N871RW	LGA	IND	92	660	19	10	2023-06-04 19:00:00	Other
23481	11	10	1417	1419	-2	1641	1642	9E	1525	N298PQ	LGA	TYS	108	647	14	19	2023-11-10 14:00:00	Other
23482	8	28	1557	1559	-2	1758	1743	YX	1040	N103HQ	JFK	ORF	66	290	15	59	2023-08-28 15:00:00	Other
23484	6	7	1525	1530	-5	1751	1711	YX	1885	N208JQ	LGA	DCA	51	214	15	30	2023-06-07 15:00:00	Other
23489	5	9	1056	1100	-4	1421	1438	DL	94	N722TW	JFK	SFO	360	2586	11	0	2023-05-09 11:00:00	Other
23492	6	13	923	927	-4	1216	1239	B6	81	N592JB	LGA	FLL	152	1076	9	27	2023-06-13 09:00:00	FLL
23496	5	31	1657	1700	-3	1858	1926	DL	916	N3740C	EWR	ATL	100	746	17	0	2023-05-31 17:00:00	ATL
23498	5	11	1608	1610	-2	1736	1739	9E	1318	N904XJ	LGA	PWM	55	269	16	10	2023-05-11 16:00:00	Other
23506	12	17	831	836	-5	1038	1048	NK	295	N667NK	LGA	CLT	98	544	8	36	2023-12-17 08:00:00	CLT
23517	12	17	1827	1829	-2	2035	2014	AA	635	N836AW	LGA	RDU	83	431	18	29	2023-12-17 18:00:00	Other
23524	5	28	2024	2029	-5	2207	2230	YX	1080	N753YX	EWR	ILM	74	488	20	29	2023-05-28 20:00:00	Other
23530	11	14	1554	1559	-5	1845	1905	B6	973	N784JB	JFK	TPA	145	1005	15	59	2023-11-14 15:00:00	Other
23537	11	18	625	630	-5	918	923	B6	388	N804JB	JFK	PBI	154	1028	6	30	2023-11-18 06:00:00	Other
23550	11	6	1710	1715	-5	1845	1854	UA	857	N896UA	LGA	ORD	128	733	17	15	2023-11-06 17:00:00	ORD
23576	7	5	926	930	-4	1220	1250	B6	35	N935JB	JFK	SFO	335	2586	9	30	2023-07-05 09:00:00	Other
23577	6	21	558	600	-2	834	844	B6	96	N715JB	LGA	MCO	129	950	6	0	2023-06-21 06:00:00	MCO
23580	5	15	1428	1430	-2	1720	1740	AA	106	N793AN	JFK	MIA	136	1089	14	30	2023-05-15 14:00:00	MIA
23582	10	11	1641	1645	-4	1942	1953	NK	594	N947NK	EWR	FLL	153	1065	16	45	2023-10-11 16:00:00	FLL
23589	3	18	1053	1055	-2	1410	1350	DL	976	N325DN	JFK	MCO	151	944	10	55	2023-03-18 10:00:00	MCO
23592	10	17	1014	1016	-2	1213	1243	AA	769	N156UW	EWR	PHX	259	2133	10	16	2023-10-17 10:00:00	Other
23602	8	29	2024	2029	-5	2150	2155	YX	1070	N871RW	LGA	BUF	50	292	20	29	2023-08-29 20:00:00	Other
23609	11	29	625	630	-5	920	944	AA	65	N335RT	JFK	MIA	153	1089	6	30	2023-11-29 06:00:00	MIA
23615	12	31	615	620	-5	904	935	NK	182	N928NK	EWR	FLL	142	1065	6	20	2023-12-31 06:00:00	FLL
23621	8	29	1107	1112	-5	1403	1428	DL	723	N354DN	LGA	FLL	149	1076	11	12	2023-08-29 11:00:00	FLL
23623	8	20	2036	2039	-3	2304	2325	UA	638	N37278	EWR	DFW	166	1372	20	39	2023-08-20 20:00:00	Other
23630	8	31	2054	2059	-5	2332	16	B6	26	N585JB	JFK	SLC	254	1990	20	59	2023-08-31 20:00:00	Other
23631	9	22	1459	1503	-4	1742	1758	UA	69	N17262	EWR	PBI	144	1023	15	3	2023-09-22 15:00:00	Other
23635	1	20	1402	1406	-4	1614	1635	UA	865	N69824	EWR	DEN	227	1605	14	6	2023-01-20 14:00:00	Other
23640	8	17	2154	2159	-5	2244	2304	9E	1190	N927XJ	LGA	BDL	25	101	21	59	2023-08-17 21:00:00	Other
23644	12	6	1827	1830	-3	2142	2219	B6	219	N977JE	JFK	SFO	349	2586	18	30	2023-12-06 18:00:00	Other
23648	2	3	1325	1330	-5	1509	1456	YX	988	N755YX	EWR	ORF	58	284	13	30	2023-02-03 13:00:00	Other
23652	6	28	1354	1359	-5	1457	1523	9E	1567	N131EV	JFK	SYR	42	209	13	59	2023-06-28 13:00:00	Other
23659	10	21	1156	1159	-3	1301	1317	UA	419	N464UA	EWR	PWM	49	284	11	59	2023-10-21 11:00:00	Other
23662	8	2	835	840	-5	1019	1022	UA	192	N17309	EWR	CLE	64	404	8	40	2023-08-02 08:00:00	Other
23670	10	19	1355	1359	-4	1634	1655	UA	930	N18220	LGA	IAH	190	1416	13	59	2023-10-19 13:00:00	Other
23671	7	17	754	759	-5	953	1002	AA	452	N915AN	JFK	CLT	89	541	7	59	2023-07-17 07:00:00	CLT
23672	12	10	1903	1905	-2	2306	2239	DL	522	N513DA	JFK	SEA	329	2422	19	5	2023-12-10 19:00:00	Other
23675	8	4	833	838	-5	1035	1105	YX	1341	N224JQ	LGA	SDF	103	659	8	38	2023-08-04 08:00:00	Other
23676	9	12	1427	1432	-5	1622	1638	AA	534	N321TG	JFK	CLT	80	541	14	32	2023-09-12 14:00:00	CLT
23682	7	27	757	759	-2	1052	1059	UA	597	N27276	EWR	PBI	152	1023	7	59	2023-07-27 07:00:00	Other
23697	10	25	1810	1812	-2	2149	2211	B6	680	N958JB	JFK	SJU	183	1598	18	12	2023-10-25 18:00:00	Other
23702	6	9	1916	1920	-4	2130	2136	9E	1682	N320PQ	LGA	MCI	150	1107	19	20	2023-06-09 19:00:00	Other
23710	9	16	1343	1346	-3	1511	1519	YX	1866	N213JQ	JFK	ORF	48	290	13	46	2023-09-16 13:00:00	Other
23717	8	2	608	610	-2	812	813	DL	189	N382DN	LGA	MSP	154	1020	6	10	2023-08-02 06:00:00	Other
23720	10	15	1326	1330	-4	1511	1525	9E	1437	N341PQ	JFK	CLE	80	425	13	30	2023-10-15 13:00:00	Other
23723	11	12	1831	1835	-4	2055	2109	UA	527	N67845	EWR	DEN	232	1605	18	35	2023-11-12 18:00:00	Other
23730	7	30	1922	1925	-3	2153	2155	9E	1143	N604LR	LGA	IND	97	660	19	25	2023-07-30 19:00:00	Other
23732	8	10	928	930	-2	1100	1052	YX	833	N754YX	EWR	MHT	42	209	9	30	2023-08-10 09:00:00	Other
23738	2	1	1543	1545	-2	1709	1732	YX	1187	N867RW	LGA	RIC	62	292	15	45	2023-02-01 15:00:00	Other
23744	11	4	1354	1359	-5	1615	1631	DL	169	N303DN	LGA	ATL	113	762	13	59	2023-11-04 13:00:00	ATL
23750	11	2	825	830	-5	952	959	9E	1543	N137EV	JFK	ORF	55	290	8	30	2023-11-02 08:00:00	Other
23756	5	21	2002	2005	-3	2209	2229	YX	1079	N739YX	EWR	IND	92	645	20	5	2023-05-21 20:00:00	Other
23763	1	14	825	830	-5	1150	1146	AA	738	N9022G	JFK	EGE	248	1746	8	30	2023-01-14 08:00:00	Other
23767	12	22	1648	1652	-4	1920	1953	UA	555	N37532	EWR	TPA	136	997	16	52	2023-12-22 16:00:00	Other
23781	5	2	2048	2050	-2	2232	2259	OO	1141	N244SY	JFK	CLE	77	425	20	50	2023-05-02 20:00:00	Other
23783	5	23	1501	1505	-4	1649	1711	9E	1418	N918XJ	LGA	AVL	87	599	15	5	2023-05-23 15:00:00	Other
23796	7	14	1527	1530	-3	1850	1845	AA	55	N107NN	JFK	LAX	335	2475	15	30	2023-07-14 15:00:00	LAX
23799	1	14	1504	1507	-3	1714	1750	YX	1189	N723YX	EWR	JAX	112	820	15	7	2023-01-14 15:00:00	Other
23803	8	28	1841	1845	-4	2058	2132	DL	96	N846DN	JFK	PHX	275	2153	18	45	2023-08-28 18:00:00	Other
23809	11	7	1454	1459	-5	1710	1741	DL	332	N348DN	LGA	ATL	106	762	14	59	2023-11-07 14:00:00	ATL
23811	7	5	756	759	-3	948	1005	AA	812	N978UY	LGA	CLT	81	544	7	59	2023-07-05 07:00:00	CLT
23815	5	16	751	755	-4	1108	1107	AS	87	N931AK	EWR	LAX	312	2454	7	55	2023-05-16 07:00:00	LAX
23821	2	24	628	630	-2	738	743	B6	209	N306JB	JFK	BOS	39	187	6	30	2023-02-24 06:00:00	BOS
23824	12	10	625	630	-5	956	1014	AA	23	N102NN	JFK	SFO	369	2586	6	30	2023-12-10 06:00:00	Other
23826	5	15	1710	1715	-5	1834	1842	B6	396	N228JB	LGA	BOS	39	184	17	15	2023-05-15 17:00:00	BOS
23829	11	21	1118	1123	-5	1403	1359	DL	859	N312DU	LGA	MSY	203	1183	11	23	2023-11-21 11:00:00	Other
23830	8	20	1054	1059	-5	1302	1337	DL	251	N334DN	LGA	ATL	97	762	10	59	2023-08-20 10:00:00	ATL
23842	4	14	1725	1727	-2	2114	2104	YX	951	N726YX	EWR	EYW	175	1196	17	27	2023-04-14 17:00:00	Other
23843	9	12	1158	1200	-2	1439	1455	DL	297	N110DX	LGA	MCO	131	950	12	0	2023-09-12 12:00:00	MCO
23847	3	13	1453	1457	-4	1636	1716	DL	450	N364NB	JFK	MSP	139	1029	14	57	2023-03-13 14:00:00	Other
23851	5	11	1554	1559	-5	1721	1734	YX	1041	N727YX	EWR	MKE	114	725	15	59	2023-05-11 15:00:00	Other
23852	10	27	745	750	-5	851	927	9E	1484	N135EV	LGA	ROC	46	254	7	50	2023-10-27 07:00:00	Other
23866	1	13	1158	1200	-2	1407	1344	9E	1489	N605LR	JFK	RDU	101	427	12	0	2023-01-13 12:00:00	Other
23871	3	4	2224	2229	-5	302	319	B6	296	N643JB	JFK	PSE	201	1617	22	29	2023-03-04 22:00:00	Other
23877	2	21	1824	1828	-4	2022	2039	YX	1124	N724YX	EWR	CLT	84	529	18	28	2023-02-21 18:00:00	CLT
23878	7	2	731	735	-4	1012	1047	DL	562	N103DY	JFK	FLL	138	1069	7	35	2023-07-02 07:00:00	FLL
23880	3	31	2026	2029	-3	2257	2300	UA	581	N27539	EWR	DEN	225	1605	20	29	2023-03-31 20:00:00	Other
23882	10	5	555	600	-5	739	735	AA	129	N835NN	LGA	ORD	113	733	6	0	2023-10-05 06:00:00	ORD
23883	3	24	958	1000	-2	1309	1320	UA	753	N14016	EWR	SFO	339	2565	10	0	2023-03-24 10:00:00	Other
23888	2	19	727	730	-3	907	921	B6	406	N317JB	JFK	ORD	124	740	7	30	2023-02-19 07:00:00	ORD
23892	12	13	728	730	-2	918	925	WN	992	N8671D	LGA	STL	146	888	7	30	2023-12-13 07:00:00	Other
23899	12	19	1007	1010	-3	1143	1210	YX	1249	N443YX	LGA	GSO	75	461	10	10	2023-12-19 10:00:00	Other
23905	7	7	845	850	-5	1007	1039	9E	1105	N200PQ	LGA	BHM	117	866	8	50	2023-07-07 08:00:00	Other
23915	2	2	1744	1746	-2	2142	2110	NK	31	N940NK	EWR	LAX	356	2454	17	46	2023-02-02 17:00:00	LAX
23929	5	9	1522	1526	-4	1819	1842	DL	398	N310DN	LGA	MIA	151	1096	15	26	2023-05-09 15:00:00	MIA
23932	12	19	605	610	-5	821	843	UA	371	N27733	EWR	ATL	105	746	6	10	2023-12-19 06:00:00	ATL
23934	2	26	947	950	-3	1120	1135	YX	976	N755YX	EWR	MKE	129	725	9	50	2023-02-26 09:00:00	Other
23937	2	24	1140	1145	-5	1254	1258	9E	1325	N315PQ	JFK	ITH	49	189	11	45	2023-02-24 11:00:00	Other
23943	11	27	1555	1600	-5	1804	1757	9E	1486	N324PQ	JFK	RDU	76	427	16	0	2023-11-27 16:00:00	Other
23959	4	28	801	805	-4	1045	1112	AA	557	N978UY	EWR	DFW	190	1372	8	5	2023-04-28 08:00:00	Other
23962	5	9	658	700	-2	1021	1045	DL	175	N710TW	JFK	SFO	353	2586	7	0	2023-05-09 07:00:00	Other
23973	10	20	756	800	-4	1101	1145	DL	278	N727TW	JFK	SFO	328	2586	8	0	2023-10-20 08:00:00	Other
23975	7	1	1606	1610	-4	1733	1754	9E	1223	N298PQ	JFK	ROC	53	264	16	10	2023-07-01 16:00:00	Other
23978	2	17	935	940	-5	1430	1444	UA	583	N37419	EWR	SJU	196	1608	9	40	2023-02-17 09:00:00	Other
23979	1	6	927	930	-3	1217	1232	DL	401	N374DX	LGA	MCO	138	950	9	30	2023-01-06 09:00:00	MCO
23984	11	28	1727	1729	-2	2110	2050	UA	757	N47284	EWR	PDX	330	2434	17	29	2023-11-28 17:00:00	Other
23990	1	27	803	805	-2	1040	1040	DL	1002	N3738B	EWR	ATL	128	746	8	5	2023-01-27 08:00:00	ATL
23991	4	6	1958	2000	-2	2215	2221	YX	1177	N102HQ	LGA	CVG	106	585	20	0	2023-04-06 20:00:00	Other
23992	6	15	1606	1610	-4	1757	1805	OO	1272	N310SY	JFK	ORD	122	740	16	10	2023-06-15 16:00:00	ORD
23993	12	15	1126	1130	-4	1417	1454	DL	179	N174DZ	JFK	LAX	312	2475	11	30	2023-12-15 11:00:00	LAX
23995	9	26	2122	2126	-4	2251	2300	YX	1891	N230JQ	LGA	PIT	58	335	21	26	2023-09-26 21:00:00	Other
23996	12	8	1355	1400	-5	1556	1617	YX	1130	N748YX	EWR	CVG	95	569	14	0	2023-12-08 14:00:00	Other
23997	2	20	1535	1540	-5	1737	1802	9E	1348	N910XJ	LGA	GSP	104	610	15	40	2023-02-20 15:00:00	Other
23998	4	7	728	730	-2	1006	1000	UA	649	N484UA	LGA	DEN	242	1620	7	30	2023-04-07 07:00:00	Other
24000	2	22	742	745	-3	1052	1105	B6	246	N2060J	JFK	FLL	148	1069	7	45	2023-02-22 07:00:00	FLL
24004	4	8	1348	1350	-2	1522	1525	WN	836	N7856A	LGA	BNA	132	764	13	50	2023-04-08 13:00:00	Other
24006	5	9	1655	1659	-4	1958	2023	DL	270	N505DZ	JFK	SEA	335	2422	16	59	2023-05-09 16:00:00	Other
24009	10	2	2154	2159	-5	2311	2318	UA	414	N34222	EWR	ROC	40	246	21	59	2023-10-02 21:00:00	Other
24015	11	4	702	705	-3	953	1010	DL	948	N37700	LGA	MIA	153	1096	7	5	2023-11-04 07:00:00	MIA
24025	4	2	558	600	-2	847	911	AA	431	N834NN	LGA	MIA	144	1096	6	0	2023-04-02 06:00:00	MIA
24026	5	6	1126	1128	-2	1255	1259	UA	359	N57286	EWR	ORD	110	719	11	28	2023-05-06 11:00:00	ORD
24030	5	7	556	600	-4	925	925	B6	5	N986JB	JFK	SFO	362	2586	6	0	2023-05-07 06:00:00	Other
24036	9	22	1456	1500	-4	1635	1621	UA	742	N17264	EWR	IAD	54	212	15	0	2023-09-22 15:00:00	Other
24039	11	22	850	855	-5	1057	1056	YX	1101	N856RW	EWR	GSO	86	445	8	55	2023-11-22 08:00:00	Other
24042	5	13	1246	1250	-4	1348	1359	9E	1269	N348PQ	JFK	ITH	42	189	12	50	2023-05-13 12:00:00	Other
24050	10	15	657	700	-3	939	1010	AA	12	N113AN	JFK	LAX	318	2475	7	0	2023-10-15 07:00:00	LAX
24058	11	13	633	635	-2	832	833	YX	1876	N209JQ	LGA	CMH	83	479	6	35	2023-11-13 06:00:00	Other
24059	11	1	840	843	-3	1150	1217	UA	564	N471UA	EWR	SAT	231	1569	8	43	2023-11-01 08:00:00	Other
24060	11	17	1737	1740	-3	2038	2048	UA	711	N685UA	EWR	IAH	192	1400	17	40	2023-11-17 17:00:00	Other
24061	12	1	757	759	-2	1240	1256	AA	329	N9029F	JFK	STT	193	1623	7	59	2023-12-01 07:00:00	Other
24067	2	1	704	707	-3	909	854	YX	1122	N731YX	EWR	CLE	80	404	7	7	2023-02-01 07:00:00	Other
24069	9	6	639	644	-5	758	827	9E	1542	N904XJ	LGA	CLE	60	419	6	44	2023-09-06 06:00:00	Other
24075	4	21	619	622	-3	843	856	UA	170	N37518	EWR	LAS	295	2227	6	22	2023-04-21 06:00:00	Other
24078	10	13	945	950	-5	1103	1115	YX	1308	N105HQ	LGA	DCA	46	214	9	50	2023-10-13 09:00:00	Other
24085	1	21	641	645	-4	810	823	UA	326	N37474	EWR	CLE	64	404	6	45	2023-01-21 06:00:00	Other
24087	4	18	1657	1659	-2	1755	1819	UA	435	N882UA	EWR	BOS	39	200	16	59	2023-04-18 16:00:00	BOS
24089	10	18	1446	1449	-3	1628	1655	AA	500	N808NN	JFK	CLT	78	541	14	49	2023-10-18 14:00:00	CLT
24091	4	6	1058	1100	-2	1347	1413	B6	191	N569JB	JFK	FLL	146	1069	11	0	2023-04-06 11:00:00	FLL
24092	1	8	725	730	-5	1031	1117	AS	58	N928VA	JFK	SFO	329	2586	7	30	2023-01-08 07:00:00	Other
24093	10	18	1007	1010	-3	1128	1142	YX	1357	N435YX	JFK	ORF	55	290	10	10	2023-10-18 10:00:00	Other
24095	12	14	1757	1759	-2	1950	2028	YX	1340	N437YX	LGA	IND	88	660	17	59	2023-12-14 17:00:00	Other
24108	8	31	1754	1759	-5	2047	2110	F9	395	N622FR	LGA	MCO	132	950	17	59	2023-08-31 17:00:00	MCO
24115	5	20	1525	1527	-2	1814	1824	UA	837	N47288	EWR	DFW	204	1372	15	27	2023-05-20 15:00:00	Other
24120	5	20	1346	1350	-4	1510	1522	YX	1706	N246JQ	JFK	BOS	48	187	13	50	2023-05-20 13:00:00	BOS
24126	2	7	1447	1450	-3	1558	1614	9E	1377	N138EV	LGA	PWM	43	269	14	50	2023-02-07 14:00:00	Other
24127	5	13	1540	1544	-4	1820	1854	UA	756	N469UA	EWR	FLL	145	1065	15	44	2023-05-13 15:00:00	FLL
24132	2	10	1155	1200	-5	1257	1324	YX	1486	N219YX	LGA	BOS	38	184	12	0	2023-02-10 12:00:00	BOS
24133	6	13	844	849	-5	1106	1128	B6	119	N520JB	LGA	JAX	122	833	8	49	2023-06-13 08:00:00	Other
24139	7	13	1955	2000	-5	2315	2208	9E	1107	N325PQ	LGA	DAY	91	549	20	0	2023-07-13 20:00:00	Other
24140	5	12	1249	1254	-5	1521	1550	NK	332	N606NK	LGA	DFW	189	1389	12	54	2023-05-12 12:00:00	Other
24150	5	23	1044	1046	-2	1250	1310	DL	849	N347NB	LGA	MSY	160	1183	10	46	2023-05-23 10:00:00	Other
24153	7	12	1917	1920	-3	2138	2143	YX	1343	N246JQ	LGA	CHS	89	641	19	20	2023-07-12 19:00:00	Other
24159	5	31	1719	1723	-4	1926	1945	AA	921	N437AN	EWR	PHX	265	2133	17	23	2023-05-31 17:00:00	Other
24163	12	11	945	950	-5	1250	1330	B6	32	N934JB	JFK	SFO	343	2586	9	50	2023-12-11 09:00:00	Other
24168	1	4	1932	1935	-3	2239	2305	DL	570	N878DN	JFK	MIA	163	1089	19	35	2023-01-04 19:00:00	MIA
24169	8	27	1152	1155	-3	1429	1355	G4	181	215NV	EWR	GRR	90	605	11	55	2023-08-27 11:00:00	Other
24176	6	21	1643	1645	-2	1859	1938	OO	1262	N324SY	LGA	OKC	176	1341	16	45	2023-06-21 16:00:00	Other
24195	3	31	1111	1115	-4	1359	1352	YX	1296	N430YX	LGA	XNA	199	1147	11	15	2023-03-31 11:00:00	Other
24198	6	24	1453	1455	-2	1837	1626	9E	1658	N176PQ	JFK	BWI	52	184	14	55	2023-06-24 14:00:00	Other
24210	9	20	1943	1946	-3	2154	2200	9E	1442	N313PQ	JFK	DTW	81	509	19	46	2023-09-20 19:00:00	Other
24222	9	18	954	959	-5	1128	1126	YX	1408	N442YX	JFK	ORF	60	290	9	59	2023-09-18 09:00:00	Other
24235	12	19	924	929	-5	1112	1132	YX	1238	N132HQ	JFK	CLE	71	425	9	29	2023-12-19 09:00:00	Other
24238	5	18	1211	1215	-4	1344	1404	B6	85	N198JB	JFK	RDU	69	427	12	15	2023-05-18 12:00:00	Other
24240	11	19	2056	2059	-3	2314	2342	DL	343	N112DN	LGA	ATL	109	762	20	59	2023-11-19 20:00:00	ATL
24242	7	31	958	1000	-2	1243	1252	UA	403	N39728	EWR	AUS	202	1504	10	0	2023-07-31 10:00:00	Other
24252	5	10	1043	1047	-4	1221	1248	YX	995	N740YX	EWR	CMH	73	463	10	47	2023-05-10 10:00:00	Other
24253	8	20	1302	1305	-3	1420	1442	UA	494	N873UA	LGA	ORD	110	733	13	5	2023-08-20 13:00:00	ORD
24255	12	13	2154	2156	-2	2312	2316	UA	849	N429UA	EWR	ORF	59	284	21	56	2023-12-13 21:00:00	Other
24256	3	20	1456	1500	-4	1542	1608	YX	1728	N245JQ	LGA	BDL	25	101	15	0	2023-03-20 15:00:00	Other
24270	6	30	1929	1934	-5	2225	2248	AA	98	N105NN	JFK	LAX	320	2475	19	34	2023-06-30 19:00:00	LAX
24282	2	13	1021	1025	-4	1250	1307	DL	840	N121DU	LGA	MSY	172	1183	10	25	2023-02-13 10:00:00	Other
24283	6	7	855	900	-5	1015	1037	UA	244	N16217	LGA	ORD	109	733	9	0	2023-06-07 09:00:00	ORD
24286	12	1	757	800	-3	1108	1112	AA	96	N833NN	EWR	MIA	151	1085	8	0	2023-12-01 08:00:00	MIA
24287	7	8	1020	1024	-4	1303	1314	AA	216	N926NN	EWR	DFW	186	1372	10	24	2023-07-08 10:00:00	Other
24298	11	14	2019	2024	-5	2141	2201	9E	1618	N138EV	LGA	CHO	51	305	20	24	2023-11-14 20:00:00	Other
24311	5	8	2012	2015	-3	2149	2155	9E	1536	N306PQ	LGA	RIC	51	292	20	15	2023-05-08 20:00:00	Other
24316	9	10	1955	1959	-4	2226	2219	YX	1375	N101HQ	LGA	CVG	93	585	19	59	2023-09-10 19:00:00	Other
24330	8	20	1334	1337	-3	1553	1634	YX	1064	N116HQ	LGA	IAH	176	1416	13	37	2023-08-20 13:00:00	Other
24338	1	16	602	605	-3	750	819	DL	1057	N964AT	EWR	MSP	144	1008	6	5	2023-01-16 06:00:00	Other
24348	12	1	1111	1115	-4	1414	1423	UA	144	N17289	EWR	FLL	148	1065	11	15	2023-12-01 11:00:00	FLL
24354	3	3	1555	1559	-4	1656	1724	OO	1233	N253SY	EWR	BOS	35	200	15	59	2023-03-03 15:00:00	BOS
24355	7	27	822	825	-3	1057	1108	AA	500	N127UW	EWR	DFW	169	1372	8	25	2023-07-27 08:00:00	Other
24356	5	14	1624	1629	-5	1805	1815	AA	747	N806NN	LGA	ORD	129	733	16	29	2023-05-14 16:00:00	ORD
24360	2	28	1555	1600	-5	1724	1725	YX	1570	N201JQ	LGA	BOS	38	184	16	0	2023-02-28 16:00:00	BOS
24363	1	30	2226	2230	-4	2344	2354	9E	1551	N929XJ	JFK	SYR	47	209	22	30	2023-01-30 22:00:00	Other
24364	10	31	745	750	-5	900	923	9E	1607	N922XJ	LGA	BUF	54	292	7	50	2023-10-31 07:00:00	Other
24366	9	14	855	900	-5	1046	1044	YX	1097	N726YX	EWR	MSN	119	799	9	0	2023-09-14 09:00:00	Other
24374	2	6	1545	1550	-5	1703	1736	9E	1376	N184GJ	LGA	CHO	50	305	15	50	2023-02-06 15:00:00	Other
24386	11	17	925	930	-5	1213	1256	AS	6	N440AS	JFK	SEA	321	2422	9	30	2023-11-17 09:00:00	Other
24389	5	7	1545	1550	-5	1722	1729	9E	1402	N298PQ	LGA	BGR	57	378	15	50	2023-05-07 15:00:00	Other
24393	9	4	627	630	-3	841	850	B6	245	N623JB	JFK	JAX	110	828	6	30	2023-09-04 06:00:00	Other
24394	12	15	1713	1715	-2	1816	1842	B6	387	N236JB	LGA	BOS	36	184	17	15	2023-12-15 17:00:00	BOS
24395	9	22	1656	1700	-4	1830	1843	YX	1305	N407YX	LGA	BHM	123	866	17	0	2023-09-22 17:00:00	Other
24407	11	6	507	509	-2	752	823	AA	405	N334SM	EWR	MIA	136	1085	5	9	2023-11-06 05:00:00	MIA
24411	1	25	1047	1049	-2	1339	1335	F9	648	N349FR	LGA	ATL	135	762	10	49	2023-01-25 10:00:00	ATL
24412	6	17	1256	1300	-4	1405	1426	YX	1847	N213JQ	LGA	BOS	42	184	13	0	2023-06-17 13:00:00	BOS
24426	9	8	655	659	-4	1008	1003	AA	290	N887NN	JFK	AUS	199	1521	6	59	2023-09-08 06:00:00	Other
24437	5	24	707	710	-3	1018	1012	DL	600	N339DN	LGA	FLL	153	1076	7	10	2023-05-24 07:00:00	FLL
24440	11	1	848	853	-5	1006	1008	9E	1521	N302PQ	LGA	PVD	29	143	8	53	2023-11-01 08:00:00	Other
24442	10	2	1405	1408	-3	1621	1617	9E	1575	N133EV	JFK	CVG	85	589	14	8	2023-10-02 14:00:00	Other
24447	3	1	1556	1559	-3	1746	1802	UA	714	N414UA	EWR	DTW	87	488	15	59	2023-03-01 15:00:00	Other
24452	4	7	1258	1300	-2	1500	1456	OO	1122	N554CA	EWR	DTW	96	488	13	0	2023-04-07 13:00:00	Other
24462	9	23	1621	1625	-4	1754	1820	YX	1072	N861RW	EWR	GSO	73	445	16	25	2023-09-23 16:00:00	Other
24469	12	3	1433	1435	-2	1733	1710	WN	691	N556WN	LGA	ATL	140	762	14	35	2023-12-03 14:00:00	ATL
24476	12	18	1821	1825	-4	2140	2137	UA	711	N67827	EWR	RSW	153	1068	18	25	2023-12-18 18:00:00	Other
24480	6	20	811	815	-4	1057	1121	DL	363	N706TW	JFK	SAN	310	2446	8	15	2023-06-20 08:00:00	Other
24485	1	22	826	829	-3	1102	1141	AA	738	N9004F	JFK	EGE	252	1746	8	29	2023-01-22 08:00:00	Other
24487	10	31	1055	1100	-5	1432	1405	AA	718	N890NN	LGA	DFW	229	1389	11	0	2023-10-31 11:00:00	Other
24489	11	13	1840	1845	-5	2134	2147	UA	472	N37305	EWR	PBI	141	1023	18	45	2023-11-13 18:00:00	Other
24497	6	30	1645	1650	-5	2005	2013	AS	12	N253AK	JFK	SFO	349	2586	16	50	2023-06-30 16:00:00	Other
24499	8	20	1440	1445	-5	1547	1613	YX	840	N758YX	LGA	IAD	42	229	14	45	2023-08-20 14:00:00	Other
24505	1	14	954	959	-5	1138	1220	9E	1514	N303PQ	LGA	MEM	126	963	9	59	2023-01-14 09:00:00	Other
24507	12	21	1711	1715	-4	1839	1859	UA	291	N37502	EWR	CLE	64	404	17	15	2023-12-21 17:00:00	Other
24510	9	1	1645	1650	-5	1835	1915	9E	1617	N228PQ	JFK	DTW	78	509	16	50	2023-09-01 16:00:00	Other
24512	2	17	927	930	-3	1041	1114	YX	1557	N209JQ	LGA	IAD	50	229	9	30	2023-02-17 09:00:00	Other
24513	6	4	1458	1500	-2	1709	1706	B6	381	N348JB	JFK	DTW	85	509	15	0	2023-06-04 15:00:00	Other
24515	12	15	826	829	-3	1108	1130	UA	477	N17296	EWR	MCO	129	937	8	29	2023-12-15 08:00:00	MCO
24518	4	24	1705	1710	-5	1857	1910	YX	1457	N201JQ	LGA	CMH	81	479	17	10	2023-04-24 17:00:00	Other
24522	9	28	1227	1229	-2	1341	1344	DL	577	N104DU	JFK	BOS	36	187	12	29	2023-09-28 12:00:00	BOS
24527	2	6	1957	2000	-3	2223	2227	9E	1442	N314PQ	LGA	CVG	99	585	20	0	2023-02-06 20:00:00	Other
24535	3	23	755	800	-5	939	950	B6	847	N593JB	JFK	RDU	67	427	8	0	2023-03-23 08:00:00	Other
24538	10	25	722	725	-3	1003	1018	DL	169	N514DE	JFK	LAS	318	2248	7	25	2023-10-25 07:00:00	Other
24544	4	9	936	939	-3	1124	1159	9E	1359	N313PQ	EWR	CVG	87	569	9	39	2023-04-09 09:00:00	Other
24546	10	2	817	820	-3	1050	1140	DL	295	N908DN	JFK	PDX	304	2454	8	20	2023-10-02 08:00:00	Other
24549	9	19	1527	1530	-3	1915	1849	DL	569	N380DN	LGA	FLL	156	1076	15	30	2023-09-19 15:00:00	FLL
24559	2	18	730	735	-5	1017	1025	UA	242	N665UA	EWR	LAS	314	2227	7	35	2023-02-18 07:00:00	Other
24562	1	29	1827	1830	-3	2006	2029	9E	1397	N478PX	LGA	RDU	75	431	18	30	2023-01-29 18:00:00	Other
24564	12	9	1255	1259	-4	1446	1502	DL	748	N323US	LGA	DTW	84	502	12	59	2023-12-09 12:00:00	Other
24570	12	17	1757	1800	-3	2105	2121	UA	690	N69020	EWR	SFO	329	2565	18	0	2023-12-17 18:00:00	Other
24576	3	17	743	745	-2	1037	1058	AA	592	N862NN	LGA	MIA	149	1096	7	45	2023-03-17 07:00:00	MIA
24580	3	13	903	905	-2	1245	1236	AA	168	N970NN	JFK	MIA	189	1089	9	5	2023-03-13 09:00:00	MIA
24582	5	10	1654	1659	-5	1822	1842	UA	673	N421UA	EWR	STL	124	872	16	59	2023-05-10 16:00:00	Other
24593	5	3	700	705	-5	951	1007	DL	428	N353NB	LGA	RSW	157	1080	7	5	2023-05-03 07:00:00	Other
24595	7	8	606	610	-4	818	833	B6	233	N229JB	JFK	JAX	113	828	6	10	2023-07-08 06:00:00	Other
24600	2	8	1255	1300	-5	1406	1425	YX	1575	N241JQ	LGA	BOS	35	184	13	0	2023-02-08 13:00:00	BOS
24602	9	1	1635	1639	-4	1930	1930	OO	1247	N324SY	LGA	OKC	207	1341	16	39	2023-09-01 16:00:00	Other
24603	3	3	1916	1918	-2	2225	2245	UA	465	N874UA	EWR	SLC	276	1969	19	18	2023-03-03 19:00:00	Other
24611	3	1	1756	1800	-4	1932	1942	UA	954	N895UA	LGA	ORD	131	733	18	0	2023-03-01 18:00:00	ORD
24617	5	4	2128	2130	-2	55	56	B6	653	N976JT	JFK	LAX	344	2475	21	30	2023-05-04 21:00:00	LAX
24626	4	10	655	700	-5	1009	1002	B6	761	N643JB	EWR	MIA	167	1085	7	0	2023-04-10 07:00:00	MIA
24632	9	4	1424	1429	-5	1619	1657	UA	952	N419UA	LGA	DEN	208	1620	14	29	2023-09-04 14:00:00	Other
24636	7	1	1056	1100	-4	1242	1309	9E	1214	N324PQ	JFK	CLT	74	541	11	0	2023-07-01 11:00:00	CLT
24645	7	17	940	945	-5	1103	1115	9E	1197	N183GJ	JFK	DCA	56	213	9	45	2023-07-17 09:00:00	Other
24646	3	27	803	805	-2	1013	958	OO	1148	N240SY	JFK	ORD	140	740	8	5	2023-03-27 08:00:00	ORD
24654	11	28	1417	1421	-4	1727	1732	B6	651	N510JB	EWR	RSW	168	1068	14	21	2023-11-28 14:00:00	Other
24656	6	16	1256	1259	-3	1407	1425	YX	1847	N208JQ	LGA	BOS	32	184	12	59	2023-06-16 12:00:00	BOS
24657	3	28	1658	1700	-2	1934	1942	DL	994	N171DN	JFK	ATL	125	760	17	0	2023-03-28 17:00:00	ATL
24660	5	22	1324	1329	-5	1436	1503	YX	1719	N234JQ	JFK	SYR	46	209	13	29	2023-05-22 13:00:00	Other
24662	2	13	1020	1025	-5	1215	1224	AA	843	N155UW	EWR	CLT	90	529	10	25	2023-02-13 10:00:00	CLT
24668	2	10	1155	1200	-5	1439	1523	DL	221	N174DN	JFK	LAX	323	2475	12	0	2023-02-10 12:00:00	LAX
24677	11	29	1938	1940	-2	2052	2104	YX	1164	N760YX	EWR	BOS	44	200	19	40	2023-11-29 19:00:00	BOS
24700	5	31	1753	1755	-2	2012	2025	WN	390	N298WN	LGA	ATL	108	762	17	55	2023-05-31 17:00:00	ATL
24701	3	25	555	600	-5	836	908	B6	772	N585JB	LGA	FLL	146	1076	6	0	2023-03-25 06:00:00	FLL
24705	6	18	1810	1815	-5	1922	1938	B6	456	N375JB	LGA	BOS	34	184	18	15	2023-06-18 18:00:00	BOS
24712	11	6	1658	1700	-2	1913	1919	YX	1227	N401YX	LGA	DSM	170	1031	17	0	2023-11-06 17:00:00	Other
24713	8	19	1641	1645	-4	1951	2010	AS	11	N448AS	JFK	SFO	326	2586	16	45	2023-08-19 16:00:00	Other
24717	3	14	1955	1959	-4	2246	2257	UA	428	N27270	EWR	LAS	304	2227	19	59	2023-03-14 19:00:00	Other
24721	8	1	802	806	-4	1006	1015	B6	370	N229JB	JFK	CHS	94	636	8	6	2023-08-01 08:00:00	Other
24723	4	26	2055	2059	-4	2322	2334	YX	1158	N416YX	LGA	ATL	119	762	20	59	2023-04-26 20:00:00	ATL
24730	11	22	1146	1150	-4	1342	1339	YX	1107	N745YX	EWR	RDU	86	416	11	50	2023-11-22 11:00:00	Other
24741	3	7	1930	1935	-5	2140	2157	9E	1354	N314PQ	JFK	CLT	86	541	19	35	2023-03-07 19:00:00	CLT
24756	12	12	1216	1220	-4	1429	1446	9E	1574	N325PQ	LGA	SAV	113	722	12	20	2023-12-12 12:00:00	Other
24777	10	8	1557	1600	-3	1837	1912	AS	72	N214AK	EWR	SEA	312	2402	16	0	2023-10-08 16:00:00	Other
24778	2	27	556	600	-4	806	829	DL	810	N929AT	EWR	ATL	112	746	6	0	2023-02-27 06:00:00	ATL
24779	10	4	1226	1231	-5	1400	1427	DL	479	N894AT	EWR	MSP	136	1008	12	31	2023-10-04 12:00:00	Other
24784	4	9	1238	1241	-3	1409	1415	YX	1258	N105HQ	LGA	PIT	60	335	12	41	2023-04-09 12:00:00	Other
24785	11	24	2056	2100	-4	2221	2239	UA	441	N882UA	LGA	ORD	122	733	21	0	2023-11-24 21:00:00	ORD
24789	11	19	740	745	-5	1003	1030	NK	152	N956NK	EWR	LAS	305	2227	7	45	2023-11-19 07:00:00	Other
24790	5	28	856	859	-3	1008	1044	UA	671	N14231	EWR	ORD	101	719	8	59	2023-05-28 08:00:00	ORD
24791	5	24	1829	1832	-3	2041	2051	YX	990	N856RW	EWR	CVG	87	569	18	32	2023-05-24 18:00:00	Other
24795	1	16	1726	1730	-4	1921	1938	YX	1303	N446YX	LGA	ORD	119	733	17	30	2023-01-16 17:00:00	ORD
24798	7	12	1701	1705	-4	1851	1921	9E	1322	N479PX	LGA	LIT	141	1085	17	5	2023-07-12 17:00:00	Other
24799	4	6	1624	1629	-5	2008	2008	DL	215	N906DN	JFK	SLC	304	1990	16	29	2023-04-06 16:00:00	Other
24806	2	24	1401	1403	-2	1746	1705	UA	272	N67846	EWR	DFW	223	1372	14	3	2023-02-24 14:00:00	Other
24816	1	9	1356	1400	-4	1555	1631	DL	879	N983AT	EWR	ATL	101	746	14	0	2023-01-09 14:00:00	ATL
24821	12	21	2047	2050	-3	2248	2321	UA	853	N17311	EWR	MSY	159	1167	20	50	2023-12-21 20:00:00	Other
24823	12	19	2057	2100	-3	2233	2245	YX	1211	N104HQ	LGA	BHM	121	866	21	0	2023-12-19 21:00:00	Other
24832	6	21	723	725	-2	853	900	WN	1257	N8718Q	LGA	STL	118	888	7	25	2023-06-21 07:00:00	Other
24834	11	10	1653	1658	-5	1803	1823	YX	1139	N733YX	EWR	PWM	50	284	16	58	2023-11-10 16:00:00	Other
24837	9	22	1745	1750	-5	2019	2040	UA	602	N77510	EWR	IAH	193	1400	17	50	2023-09-22 17:00:00	Other
24842	8	14	1927	1930	-3	2303	2251	AA	81	N117AN	JFK	LAX	311	2475	19	30	2023-08-14 19:00:00	LAX
24843	8	5	556	600	-4	736	746	DL	621	N943AT	EWR	DTW	83	488	6	0	2023-08-05 06:00:00	Other
24861	5	8	1335	1340	-5	1516	1510	9E	1444	N329PQ	JFK	BGR	66	382	13	40	2023-05-08 13:00:00	Other
24863	6	3	1123	1126	-3	1332	1340	OO	1270	N247SY	JFK	CHS	96	636	11	26	2023-06-03 11:00:00	Other
24865	6	12	1106	1110	-4	1307	1323	DL	913	N365NB	LGA	MSY	156	1183	11	10	2023-06-12 11:00:00	Other
24867	12	23	1811	1815	-4	1956	2004	UA	480	N37422	EWR	RDU	63	416	18	15	2023-12-23 18:00:00	Other
24870	5	9	1635	1640	-5	1918	1907	B6	118	N358JB	JFK	SAV	104	718	16	40	2023-05-09 16:00:00	Other
24879	7	2	1925	1930	-5	2238	2257	B6	309	N804JB	JFK	PDX	340	2454	19	30	2023-07-02 19:00:00	Other
24882	9	27	1248	1250	-2	1432	1430	WN	291	N564WN	LGA	STL	128	888	12	50	2023-09-27 12:00:00	Other
24883	5	31	1957	2000	-3	2110	2148	OO	1174	N246SY	JFK	BNA	102	765	20	0	2023-05-31 20:00:00	Other
24891	6	6	1132	1135	-3	1401	1434	B6	30	N190JB	JFK	MCO	128	944	11	35	2023-06-06 11:00:00	MCO
24894	2	19	1115	1117	-2	1304	1330	YX	1037	N751YX	EWR	DTW	85	488	11	17	2023-02-19 11:00:00	Other
24899	10	25	1132	1136	-4	1252	1308	UA	331	N69826	EWR	ORD	115	719	11	36	2023-10-25 11:00:00	ORD
24901	3	5	823	826	-3	946	1003	UA	506	N17752	EWR	BNA	118	748	8	26	2023-03-05 08:00:00	Other
24904	5	27	1454	1459	-5	1738	1750	B6	569	N558JB	EWR	MCO	132	937	14	59	2023-05-27 14:00:00	MCO
24911	11	27	1325	1329	-4	1541	1558	9E	1758	N929XJ	LGA	OMA	175	1148	13	29	2023-11-27 13:00:00	Other
24916	5	27	1354	1359	-5	1627	1655	UA	594	N27260	EWR	IAH	181	1400	13	59	2023-05-27 13:00:00	Other
24921	11	29	1945	1950	-5	2142	2216	9E	1623	N936XJ	LGA	CHS	91	641	19	50	2023-11-29 19:00:00	Other
24925	9	22	2140	2144	-4	2307	2322	YX	1146	N979RP	EWR	BGR	62	393	21	44	2023-09-22 21:00:00	Other
24927	3	1	1025	1030	-5	1237	1254	9E	1499	N228PQ	JFK	SAV	111	718	10	30	2023-03-01 10:00:00	Other
24937	11	29	555	600	-5	729	709	YX	1884	N215JQ	JFK	BOS	40	187	6	0	2023-11-29 06:00:00	BOS
24941	11	24	632	635	-3	957	1005	DL	115	N106DN	JFK	SLC	290	1990	6	35	2023-11-24 06:00:00	Other
24944	6	10	730	733	-3	920	923	UA	498	N37295	EWR	CLT	75	529	7	33	2023-06-10 07:00:00	CLT
24947	10	10	1755	1759	-4	2002	2037	DL	312	N909DN	JFK	PHX	285	2153	17	59	2023-10-10 17:00:00	Other
24956	10	7	1258	1300	-2	1751	1625	AS	4	N969AK	JFK	SFO	363	2586	13	0	2023-10-07 13:00:00	Other
24966	6	14	733	737	-4	952	1000	UA	235	N17302	EWR	LAS	278	2227	7	37	2023-06-14 07:00:00	Other
24968	3	30	1546	1551	-5	1755	1746	YX	1042	N732YX	EWR	CMH	86	463	15	51	2023-03-30 15:00:00	Other
24973	9	25	1024	1029	-5	1232	1213	9E	1509	N134EV	LGA	RIC	49	292	10	29	2023-09-25 10:00:00	Other
24976	5	3	855	900	-5	1158	1217	AA	796	N378SC	LGA	MIA	150	1096	9	0	2023-05-03 09:00:00	MIA
24978	5	25	1946	1950	-4	2146	2152	9E	1379	N335PQ	LGA	GSO	80	461	19	50	2023-05-25 19:00:00	Other
24984	8	14	928	930	-2	1129	1147	YX	924	N742YX	EWR	HHH	95	687	9	30	2023-08-14 09:00:00	Other
24985	3	19	618	620	-2	912	1000	DL	325	N113DX	JFK	SLC	279	1990	6	20	2023-03-19 06:00:00	Other
24988	11	17	712	715	-3	917	930	DL	745	N363NB	LGA	CHS	90	641	7	15	2023-11-17 07:00:00	Other
24991	8	21	1226	1229	-3	1447	1521	AA	432	N909NN	LGA	DFW	163	1389	12	29	2023-08-21 12:00:00	Other
24992	1	9	1530	1535	-5	1836	1859	OO	1623	N163SY	LGA	IAH	209	1416	15	35	2023-01-09 15:00:00	Other
24998	8	11	1715	1717	-2	1945	1938	UA	680	N45440	EWR	DEN	219	1605	17	17	2023-08-11 17:00:00	Other
25003	8	10	807	810	-3	1246	1211	UA	639	N67052	EWR	SJU	204	1608	8	10	2023-08-10 08:00:00	Other
25005	4	12	1513	1515	-2	1710	1751	9E	1437	N308PQ	JFK	IND	90	665	15	15	2023-04-12 15:00:00	Other
25007	10	25	1855	1859	-4	2149	2206	UA	166	N17752	EWR	SNA	330	2434	18	59	2023-10-25 18:00:00	Other
25009	10	21	1010	1014	-4	1153	1141	YX	1068	N765YX	EWR	IAD	59	212	10	14	2023-10-21 10:00:00	Other
25018	1	14	625	630	-5	844	907	B6	806	N2102J	JFK	ATL	100	760	6	30	2023-01-14 06:00:00	ATL
25019	9	2	1625	1630	-5	1732	1810	9E	1540	N918XJ	LGA	ROC	47	254	16	30	2023-09-02 16:00:00	Other
25030	8	10	1727	1730	-3	2033	2030	AS	74	N589AS	EWR	PDX	343	2434	17	30	2023-08-10 17:00:00	Other
25032	2	20	955	1000	-5	1111	1134	AA	768	N757UW	LGA	DCA	53	214	10	0	2023-02-20 10:00:00	Other
25033	1	7	1054	1059	-5	1236	1319	DL	415	N346NB	LGA	MSP	139	1020	10	59	2023-01-07 10:00:00	Other
25039	2	24	1627	1630	-3	2146	1959	DL	179	N806DN	JFK	SAN	NA	2446	16	30	2023-02-24 16:00:00	Other
25041	2	20	920	925	-5	1120	1129	AA	644	N812NN	EWR	CLT	91	529	9	25	2023-02-20 09:00:00	CLT
25047	4	19	1717	1720	-3	2001	2038	AA	868	N327SK	JFK	AUS	201	1521	17	20	2023-04-19 17:00:00	Other
25056	5	11	1304	1309	-5	1513	1534	YX	1111	N655RW	EWR	SAV	106	708	13	9	2023-05-11 13:00:00	Other
25072	9	9	725	729	-4	1045	1042	AA	599	N322TH	JFK	MIA	159	1089	7	29	2023-09-09 07:00:00	MIA
25086	2	8	1458	1500	-2	1731	1734	OO	1164	N259SY	JFK	MSP	186	1029	15	0	2023-02-08 15:00:00	Other
25089	11	21	841	845	-4	1024	1026	OO	1185	N241SY	JFK	BNA	132	765	8	45	2023-11-21 08:00:00	Other
25090	9	27	1856	1900	-4	2247	2308	UA	206	N75436	EWR	BQN	201	1585	19	0	2023-09-27 19:00:00	Other
25095	7	7	713	715	-2	910	931	DL	642	N3764D	EWR	ATL	97	746	7	15	2023-07-07 07:00:00	ATL
25097	4	18	2047	2050	-3	2203	2227	YX	1517	N236JQ	LGA	RIC	58	292	20	50	2023-04-18 20:00:00	Other
25104	11	4	1429	1434	-5	1546	1546	UA	565	N433UA	EWR	BOS	46	200	14	34	2023-11-04 14:00:00	BOS
25110	5	17	1748	1751	-3	2026	2101	UA	557	N17289	EWR	SAN	311	2425	17	51	2023-05-17 17:00:00	Other
25130	7	24	1418	1420	-2	1553	1552	YX	846	N761YX	EWR	MKE	108	725	14	20	2023-07-24 14:00:00	Other
25131	11	20	1021	1025	-4	1143	1205	UA	79	N37305	EWR	ORD	112	719	10	25	2023-11-20 10:00:00	ORD
25136	12	1	1857	1859	-2	2050	2106	AA	618	N118US	LGA	CLT	86	544	18	59	2023-12-01 18:00:00	CLT
25140	3	25	2136	2140	-4	2259	2324	YX	1081	N751YX	EWR	MKE	115	725	21	40	2023-03-25 21:00:00	Other
25143	10	11	2225	2229	-4	2343	2352	B6	159	N216JB	JFK	ROC	53	264	22	29	2023-10-11 22:00:00	Other
25144	5	15	1350	1355	-5	1456	1525	YX	1663	N815MD	LGA	DCA	44	214	13	55	2023-05-15 13:00:00	Other
25153	3	25	1122	1125	-3	1503	1445	AA	838	N310RF	LGA	MIA	160	1096	11	25	2023-03-25 11:00:00	MIA
25154	4	9	1053	1055	-2	1253	1255	G4	918	330NV	EWR	VPS	144	988	10	55	2023-04-09 10:00:00	Other
25155	8	21	1202	1205	-3	1353	1405	YX	1060	N426YX	LGA	DTW	82	502	12	5	2023-08-21 12:00:00	Other
25165	4	11	1546	1550	-4	1716	1729	9E	1314	N232PQ	LGA	BGR	57	378	15	50	2023-04-11 15:00:00	Other
25169	12	6	1256	1259	-3	1345	1404	9E	1685	N184GJ	LGA	PVD	29	143	12	59	2023-12-06 12:00:00	Other
25171	5	26	1655	1700	-5	1827	1858	9E	1433	N916XJ	LGA	CLE	62	419	17	0	2023-05-26 17:00:00	Other
25179	1	28	2030	2035	-5	2357	2359	B6	539	N625JB	JFK	AUS	239	1521	20	35	2023-01-28 20:00:00	Other
25183	1	5	1629	1633	-4	1817	1845	YX	1442	N418YX	LGA	GSO	86	461	16	33	2023-01-05 16:00:00	Other
25188	6	29	1706	1708	-2	1849	1913	9E	1611	N184GJ	JFK	RDU	73	427	17	8	2023-06-29 17:00:00	Other
25192	1	16	755	800	-5	922	927	YX	1884	N215JQ	LGA	BOS	40	184	8	0	2023-01-16 08:00:00	BOS
25194	6	15	642	645	-3	930	935	AA	963	N826NN	JFK	DFW	197	1391	6	45	2023-06-15 06:00:00	Other
25197	7	9	816	820	-4	1110	1125	AA	279	N905AN	JFK	DFW	194	1391	8	20	2023-07-09 08:00:00	Other
25204	3	19	1858	1900	-2	2021	2034	YX	1301	N103HQ	LGA	PIT	60	335	19	0	2023-03-19 19:00:00	Other
25213	8	17	831	835	-4	1048	1057	9E	1247	N313PQ	JFK	CHS	96	636	8	35	2023-08-17 08:00:00	Other
25219	11	15	1330	1333	-3	1438	1445	UA	637	N77259	EWR	BOS	43	200	13	33	2023-11-15 13:00:00	BOS
25221	10	24	1127	1129	-2	1439	1437	AA	979	N969NN	JFK	AUS	213	1521	11	29	2023-10-24 11:00:00	Other
25228	2	7	856	900	-4	1017	1044	9E	1427	N331PQ	JFK	RIC	57	288	9	0	2023-02-07 09:00:00	Other
25232	5	13	1652	1655	-3	1944	2029	DL	164	N377DE	JFK	SAN	315	2446	16	55	2023-05-13 16:00:00	Other
25237	5	30	2025	2029	-4	2339	2326	B6	180	N505JB	LGA	MCO	131	950	20	29	2023-05-30 20:00:00	MCO
25240	1	31	2028	2030	-2	2233	2229	9E	1417	N929XJ	LGA	ROA	82	405	20	30	2023-01-31 20:00:00	Other
25243	7	29	1440	1445	-5	1612	1634	YX	1425	N224JQ	LGA	ORF	55	296	14	45	2023-07-29 14:00:00	Other
25244	6	1	1044	1049	-5	1231	1302	YX	1125	N754YX	EWR	MSP	140	1008	10	49	2023-06-01 10:00:00	Other
25245	12	4	1345	1350	-5	1656	1705	UA	912	N490UA	LGA	IAH	227	1416	13	50	2023-12-04 13:00:00	Other
25248	5	13	815	820	-5	1159	1219	DL	699	N846DN	JFK	SJU	194	1598	8	20	2023-05-13 08:00:00	Other
25249	11	8	2125	2129	-4	20	34	B6	355	N964JT	JFK	LAS	325	2248	21	29	2023-11-08 21:00:00	Other
25253	5	18	2057	2100	-3	2334	2357	DL	244	N911DQ	JFK	LAS	290	2248	21	0	2023-05-18 21:00:00	Other
25255	3	6	1057	1059	-2	1302	1321	UA	907	N452UA	EWR	MSY	162	1167	10	59	2023-03-06 10:00:00	Other
25258	3	8	1453	1455	-2	1735	1750	9E	1326	N601LR	JFK	JAX	120	828	14	55	2023-03-08 14:00:00	Other
25262	6	22	1956	2000	-4	2151	2210	9E	1452	N184GJ	LGA	DAY	84	549	20	0	2023-06-22 20:00:00	Other
25269	1	12	1357	1400	-3	1550	1554	YX	1233	N755YX	EWR	CMH	85	463	14	0	2023-01-12 14:00:00	Other
25270	1	30	2016	2020	-4	2212	2221	YX	1774	N230JQ	LGA	CMH	90	479	20	20	2023-01-30 20:00:00	Other
25277	11	5	1454	1459	-5	1600	1618	9E	1563	N901XJ	JFK	BWI	40	184	14	59	2023-11-05 14:00:00	Other
25278	9	13	1225	1229	-4	1439	1457	AA	988	N341RW	JFK	PHX	293	2153	12	29	2023-09-13 12:00:00	Other
25282	3	6	1931	1935	-4	2136	2157	9E	1354	N305PQ	JFK	CLT	87	541	19	35	2023-03-06 19:00:00	CLT
25290	5	1	744	749	-5	948	958	9E	1347	N908XJ	JFK	CVG	100	589	7	49	2023-05-01 07:00:00	Other
25293	5	12	1827	1830	-3	2026	2041	B6	533	N328JB	JFK	DTW	83	509	18	30	2023-05-12 18:00:00	Other
25298	8	2	1815	1820	-5	2040	2052	9E	1220	N602LR	JFK	CHS	89	636	18	20	2023-08-02 18:00:00	Other
25307	10	19	1726	1730	-4	1910	1909	9E	1593	N305PQ	LGA	BNA	128	764	17	30	2023-10-19 17:00:00	Other
25308	8	26	655	700	-5	1015	955	DL	169	N178DZ	JFK	LAX	339	2475	7	0	2023-08-26 07:00:00	LAX
25313	10	14	1917	1920	-3	2232	2233	DL	133	N839MH	JFK	LAX	313	2475	19	20	2023-10-14 19:00:00	LAX
25324	10	13	936	940	-4	1314	1341	UA	536	N27539	EWR	SJU	189	1608	9	40	2023-10-13 09:00:00	Other
25326	5	12	1200	1205	-5	1339	1353	OO	1123	N258SY	JFK	ORD	126	740	12	5	2023-05-12 12:00:00	ORD
25327	1	3	756	800	-4	1044	1110	UA	941	N27252	EWR	TPA	141	997	8	0	2023-01-03 08:00:00	Other
25329	5	12	913	915	-2	1048	1043	YX	1608	N243JQ	JFK	DCA	69	213	9	15	2023-05-12 09:00:00	Other
25336	3	4	1113	1115	-2	1415	1422	AA	477	N755AN	JFK	MIA	153	1089	11	15	2023-03-04 11:00:00	MIA
25337	11	25	935	940	-5	1131	1135	YX	1291	N409YX	LGA	ILM	85	500	9	40	2023-11-25 09:00:00	Other
25338	6	1	1425	1429	-4	1921	1731	UA	900	N417UA	EWR	PBI	NA	1023	14	29	2023-06-01 14:00:00	Other
25339	12	20	1816	1820	-4	2014	2016	OO	1193	N294SY	JFK	ORD	131	740	18	20	2023-12-20 18:00:00	ORD
25340	6	13	1420	1425	-5	1725	1711	UA	614	N27268	EWR	IAH	223	1400	14	25	2023-06-13 14:00:00	Other
25353	2	2	758	800	-2	1036	1058	UA	395	N17128	EWR	EGE	261	1725	8	0	2023-02-02 08:00:00	Other
25357	10	30	1457	1459	-2	1619	1632	9E	1612	N915XJ	LGA	ORF	61	296	14	59	2023-10-30 14:00:00	Other
25361	8	29	1538	1540	-2	1747	1804	B6	717	N203JB	JFK	CHS	101	636	15	40	2023-08-29 15:00:00	Other
25363	5	8	824	829	-5	1014	1018	9E	1477	N181GJ	LGA	CLE	71	419	8	29	2023-05-08 08:00:00	Other
25366	2	22	927	929	-2	1031	1044	YX	1043	N744YX	EWR	PVD	32	160	9	29	2023-02-22 09:00:00	Other
25371	4	20	1813	1815	-2	2037	2057	DL	187	N113DX	LGA	ATL	105	762	18	15	2023-04-20 18:00:00	ATL
25372	11	17	1545	1550	-5	1834	1856	DL	971	N372NW	LGA	TPA	144	1010	15	50	2023-11-17 15:00:00	Other
25374	8	10	1104	1108	-4	1405	1407	UA	211	N17301	EWR	PBI	135	1023	11	8	2023-08-10 11:00:00	Other
25379	3	13	657	700	-3	1006	952	UA	318	N14107	EWR	MCO	135	937	7	0	2023-03-13 07:00:00	MCO
25395	9	5	1257	1259	-2	1428	1422	YX	1893	N216JQ	LGA	BOS	49	184	12	59	2023-09-05 12:00:00	BOS
25400	3	9	1125	1130	-5	1312	1314	AA	115	N769US	LGA	ORD	129	733	11	30	2023-03-09 11:00:00	ORD
25415	3	9	1902	1905	-3	2039	2051	AA	138	N764US	LGA	RDU	66	431	19	5	2023-03-09 19:00:00	Other
25417	6	1	651	653	-2	859	910	YX	1156	N646RW	EWR	IND	87	645	6	53	2023-06-01 06:00:00	Other
25422	8	22	1836	1840	-4	2118	2144	B6	735	N566JB	JFK	MCO	120	944	18	40	2023-08-22 18:00:00	MCO
25426	11	19	1927	1929	-2	2043	2104	YX	1349	N421YX	LGA	PIT	57	335	19	29	2023-11-19 19:00:00	Other
25440	12	28	1556	1559	-3	1840	1840	B6	932	N358JB	JFK	JAX	136	828	15	59	2023-12-28 15:00:00	Other
25441	8	26	1728	1730	-2	1949	1952	YX	857	N743YX	EWR	IND	109	645	17	30	2023-08-26 17:00:00	Other
25442	6	21	1956	1959	-3	2314	2309	AA	789	N916AN	LGA	MIA	160	1096	19	59	2023-06-21 19:00:00	MIA
25447	4	28	900	905	-5	1144	1146	YX	1135	N401YX	LGA	ATL	119	762	9	5	2023-04-28 09:00:00	ATL
25463	1	21	715	720	-5	1013	1038	AA	434	N967AN	JFK	MIA	154	1089	7	20	2023-01-21 07:00:00	MIA
25471	4	14	1925	1929	-4	2154	2226	DL	104	N819DN	JFK	DEN	222	1626	19	29	2023-04-14 19:00:00	Other
25473	12	29	1030	1035	-5	1150	1230	WN	1155	N7746C	LGA	STL	114	888	10	35	2023-12-29 10:00:00	Other
25480	4	7	557	600	-3	723	719	AA	671	N753US	LGA	DCA	52	214	6	0	2023-04-07 06:00:00	Other
25493	4	22	843	848	-5	1157	1153	UA	397	N17265	EWR	FLL	153	1065	8	48	2023-04-22 08:00:00	FLL
25502	11	7	1835	1840	-5	2050	2109	YX	1106	N640RW	EWR	IND	113	645	18	40	2023-11-07 18:00:00	Other
25503	3	20	801	806	-5	915	935	B6	59	N258JB	JFK	ROC	54	264	8	6	2023-03-20 08:00:00	Other
25512	11	5	1646	1650	-4	1829	1840	AA	221	N705UW	LGA	STL	130	888	16	50	2023-11-05 16:00:00	Other
25514	7	20	1527	1530	-3	1733	1753	B6	673	N3008J	JFK	MCI	164	1113	15	30	2023-07-20 15:00:00	Other
25520	10	3	1442	1445	-3	1600	1613	YX	1305	N419YX	LGA	ORF	53	296	14	45	2023-10-03 14:00:00	Other
25523	5	9	1857	1859	-2	1954	2029	YX	1710	N245JQ	LGA	BOS	36	184	18	59	2023-05-09 18:00:00	BOS
25528	3	29	1051	1056	-5	1252	1315	DL	430	N339NW	LGA	MSP	157	1020	10	56	2023-03-29 10:00:00	Other
25530	7	24	1848	1850	-2	2044	2122	YX	1374	N227JQ	LGA	CLT	89	544	18	50	2023-07-24 18:00:00	CLT
25537	2	13	1710	1712	-2	1851	1850	UA	754	N37419	EWR	ORD	113	719	17	12	2023-02-13 17:00:00	ORD
25539	9	2	1054	1059	-5	1250	1318	YX	1121	N752YX	EWR	IND	91	645	10	59	2023-09-02 10:00:00	Other
25541	4	21	1158	1200	-2	1343	1400	YX	1558	N222JQ	LGA	STL	129	888	12	0	2023-04-21 12:00:00	Other
25542	4	23	2024	2029	-5	2155	2213	YX	1143	N115HQ	JFK	ORF	55	290	20	29	2023-04-23 20:00:00	Other
25543	4	25	1547	1550	-3	1716	1729	9E	1314	N341PQ	LGA	BGR	55	378	15	50	2023-04-25 15:00:00	Other
25549	12	9	908	912	-4	1042	1114	9E	1689	N186GJ	JFK	RDU	69	427	9	12	2023-12-09 09:00:00	Other
25556	9	21	725	730	-5	930	939	9E	1707	N187GJ	LGA	CVG	92	585	7	30	2023-09-21 07:00:00	Other
25557	1	23	2116	2120	-4	2324	2346	YX	1195	N733YX	EWR	IND	100	645	21	20	2023-01-23 21:00:00	Other
25566	5	18	2115	2120	-5	2225	2246	9E	1550	N349PQ	LGA	BTV	46	258	21	20	2023-05-18 21:00:00	Other
25568	8	13	556	600	-4	844	909	AA	635	N327SK	JFK	MIA	139	1089	6	0	2023-08-13 06:00:00	MIA
25577	12	3	656	659	-3	802	830	AA	929	N768US	LGA	DCA	47	214	6	59	2023-12-03 06:00:00	Other
25580	9	15	1657	1700	-3	1900	1908	9E	1478	N200PQ	JFK	DTW	78	509	17	0	2023-09-15 17:00:00	Other
25581	7	8	1027	1030	-3	1136	1153	YX	960	N724YX	EWR	DCA	44	199	10	30	2023-07-08 10:00:00	Other
25583	5	21	1434	1436	-2	1706	1741	AA	860	N867NN	JFK	DFW	180	1391	14	36	2023-05-21 14:00:00	Other
25588	3	13	1106	1110	-4	1212	1219	OO	1235	N315SY	EWR	BOS	41	200	11	10	2023-03-13 11:00:00	BOS
25594	4	28	1359	1404	-5	1508	1523	YX	947	N855RW	EWR	ROC	45	246	14	4	2023-04-28 14:00:00	Other
25614	10	6	1941	1946	-5	2149	2200	9E	1391	N133EV	JFK	DTW	82	509	19	46	2023-10-06 19:00:00	Other
25622	2	20	1654	1659	-5	1909	1919	YX	1210	N119HQ	JFK	CVG	116	589	16	59	2023-02-20 16:00:00	Other
25624	2	4	2018	2020	-2	2247	2328	YX	1191	N432YX	LGA	ATL	125	762	20	20	2023-02-04 20:00:00	ATL
25627	8	9	957	1000	-3	1305	1313	AA	64	N107NN	JFK	LAX	332	2475	10	0	2023-08-09 10:00:00	LAX
25631	6	15	2126	2129	-3	2312	2331	YX	1134	N641RW	EWR	GSO	66	445	21	29	2023-06-15 21:00:00	Other
25638	8	2	2118	2121	-3	2351	2359	NK	228	N652NK	EWR	IAH	177	1400	21	21	2023-08-02 21:00:00	Other
25643	12	2	2052	2055	-3	2354	2354	DL	424	N841DN	JFK	MCO	145	944	20	55	2023-12-02 20:00:00	MCO
25649	1	1	1533	1537	-4	1725	1746	YX	1756	N213JQ	JFK	CMH	84	483	15	37	2023-01-01 15:00:00	Other
25650	4	12	1745	1750	-5	1927	2029	9E	1234	N316PQ	JFK	MCI	143	1113	17	50	2023-04-12 17:00:00	Other
25663	2	17	840	845	-5	1054	1125	9E	1481	N490PX	LGA	AVL	109	599	8	45	2023-02-17 08:00:00	Other
25665	1	24	1402	1405	-3	1512	1520	B6	45	N324JB	JFK	BTV	50	266	14	5	2023-01-24 14:00:00	Other
25670	5	20	957	1000	-3	1118	1124	YX	1573	N205JQ	JFK	BOS	43	187	10	0	2023-05-20 10:00:00	BOS
25679	2	15	708	710	-2	1016	1012	UA	278	N27253	EWR	BZN	266	1882	7	10	2023-02-15 07:00:00	Other
25687	10	25	914	917	-3	1154	1213	UA	694	N27263	EWR	PBI	124	1023	9	17	2023-10-25 09:00:00	Other
25689	6	18	835	840	-5	1039	1100	9E	1685	N131EV	JFK	CHS	94	636	8	40	2023-06-18 08:00:00	Other
25690	4	7	725	730	-5	939	947	B6	308	N283JB	JFK	SAV	112	718	7	30	2023-04-07 07:00:00	Other
25696	9	6	2112	2117	-5	2157	2224	YX	1106	N753YX	EWR	PHL	21	80	21	17	2023-09-06 21:00:00	Other
25697	8	24	1354	1359	-5	1542	1558	YX	825	N739YX	EWR	DTW	79	488	13	59	2023-08-24 13:00:00	Other
25698	1	20	948	951	-3	1201	1205	UA	716	N444UA	EWR	CHS	107	628	9	51	2023-01-20 09:00:00	Other
25712	11	30	1833	1835	-2	2001	2014	YX	1165	N748YX	EWR	PIT	56	319	18	35	2023-11-30 18:00:00	Other
25727	3	6	1631	1635	-4	1859	1916	DL	779	N145DQ	JFK	MSY	169	1182	16	35	2023-03-06 16:00:00	Other
25728	2	5	1525	1529	-4	1649	1707	YX	1151	N722YX	EWR	MKE	114	725	15	29	2023-02-05 15:00:00	Other
25743	8	26	1815	1820	-5	2045	2054	YX	1319	N246JQ	JFK	IND	110	665	18	20	2023-08-26 18:00:00	Other
25746	3	29	935	940	-5	1243	1244	B6	82	N729JB	JFK	IAH	208	1417	9	40	2023-03-29 09:00:00	Other
25750	7	12	636	640	-4	810	830	YX	1406	N206JQ	LGA	CMH	75	479	6	40	2023-07-12 06:00:00	Other
25757	11	15	1555	1600	-5	1717	1736	9E	1553	N186GJ	JFK	ROC	57	264	16	0	2023-11-15 16:00:00	Other
25763	8	21	732	735	-3	854	852	B6	164	N197JB	JFK	PWM	57	273	7	35	2023-08-21 07:00:00	Other
25766	1	19	657	700	-3	1001	1027	DL	1008	N898DN	JFK	RSW	155	1074	7	0	2023-01-19 07:00:00	Other
25771	11	4	725	730	-5	900	915	UA	943	N34460	EWR	RDU	76	416	7	30	2023-11-04 07:00:00	Other
25773	10	14	826	830	-4	1125	1118	AA	501	N335SN	JFK	PHX	318	2153	8	30	2023-10-14 08:00:00	Other
25777	6	25	1127	1129	-2	1419	1345	YX	1833	N219YX	LGA	CHS	101	641	11	29	2023-06-25 11:00:00	Other
25778	10	8	1712	1715	-3	2006	2030	NK	250	N908NK	EWR	OAK	331	2555	17	15	2023-10-08 17:00:00	Other
25779	7	22	1531	1535	-4	1815	1855	DL	507	N3759	JFK	PBI	143	1028	15	35	2023-07-22 15:00:00	Other
25781	10	13	2055	2100	-5	2228	2254	9E	1425	N133EV	JFK	RIC	57	288	21	0	2023-10-13 21:00:00	Other
25787	7	4	556	600	-4	832	908	NK	47	N676NK	LGA	FLL	137	1076	6	0	2023-07-04 06:00:00	FLL
25788	6	15	556	600	-4	707	718	YX	1832	N202JQ	LGA	BOS	38	184	6	0	2023-06-15 06:00:00	BOS
25794	8	20	1201	1205	-4	1322	1333	9E	1170	N313PQ	JFK	BUF	53	301	12	5	2023-08-20 12:00:00	Other
25795	5	25	1955	2000	-5	2126	2148	OO	1174	N301SY	JFK	BNA	118	765	20	0	2023-05-25 20:00:00	Other
25796	1	29	1256	1300	-4	1403	1411	B6	363	N328JB	JFK	BOS	41	187	13	0	2023-01-29 13:00:00	BOS
25798	12	18	1726	1729	-3	2019	2038	UA	663	N27253	EWR	SAN	317	2425	17	29	2023-12-18 17:00:00	Other
25799	12	2	856	900	-4	1211	1233	AA	68	N105NN	JFK	LAX	354	2475	9	0	2023-12-02 09:00:00	LAX
25810	11	2	645	650	-5	758	821	9E	1541	N136EV	LGA	ROC	49	254	6	50	2023-11-02 06:00:00	Other
25811	10	10	801	805	-4	945	1004	OO	1161	N269SY	JFK	ORD	118	740	8	5	2023-10-10 08:00:00	ORD
25830	3	15	725	730	-5	857	910	9E	1404	N184GJ	LGA	BNA	107	764	7	30	2023-03-15 07:00:00	Other
25835	2	7	1456	1500	-4	1848	1854	DL	371	N838DN	JFK	PHX	303	2153	15	0	2023-02-07 15:00:00	Other
25840	4	26	2047	2050	-3	2243	2254	9E	1337	N326PQ	LGA	ILM	84	500	20	50	2023-04-26 20:00:00	Other
25841	10	12	1827	1830	-3	2021	2056	9E	1498	N478PX	LGA	TYS	95	647	18	30	2023-10-12 18:00:00	Other
25855	10	19	1322	1327	-5	1620	1639	NK	1013	N650NK	EWR	MIA	153	1085	13	27	2023-10-19 13:00:00	MIA
25856	11	26	1105	1107	-2	1309	1326	DL	480	N371DN	LGA	MSP	149	1020	11	7	2023-11-26 11:00:00	Other
25860	4	11	851	855	-4	1207	1245	DL	296	N723TW	JFK	SFO	324	2586	8	55	2023-04-11 08:00:00	Other
25869	8	22	1822	1825	-3	1959	2022	DL	296	N119DU	LGA	ORD	118	733	18	25	2023-08-22 18:00:00	ORD
25878	9	6	1747	1750	-3	2011	2040	UA	602	N77539	EWR	IAH	181	1400	17	50	2023-09-06 17:00:00	Other
25882	11	10	1506	1510	-4	1830	1804	NK	329	N608NK	LGA	DFW	224	1389	15	10	2023-11-10 15:00:00	Other
25883	2	6	1043	1045	-2	1401	1407	DL	565	N354NB	LGA	RSW	148	1080	10	45	2023-02-06 10:00:00	Other
25889	3	18	642	645	-3	824	828	YX	1074	N756YX	EWR	CLE	82	404	6	45	2023-03-18 06:00:00	Other
25897	4	1	1755	1800	-5	2200	2150	B6	299	N992JB	JFK	SFO	385	2586	18	0	2023-04-01 18:00:00	Other
25901	4	21	845	849	-4	1132	1111	9E	1318	N341PQ	LGA	CHS	95	641	8	49	2023-04-21 08:00:00	Other
25902	6	8	1225	1229	-4	1532	1535	DL	554	N368NW	JFK	AUS	202	1521	12	29	2023-06-08 12:00:00	Other
25909	12	30	1326	1330	-4	1603	1650	DL	294	N405DX	JFK	LAX	312	2475	13	30	2023-12-30 13:00:00	LAX
25910	4	5	854	856	-2	1050	1103	YX	1535	N810MD	LGA	CMH	88	479	8	56	2023-04-05 08:00:00	Other
25922	2	28	612	615	-3	1008	928	UA	322	N788UA	EWR	SFO	360	2565	6	15	2023-02-28 06:00:00	Other
25925	11	12	1124	1129	-5	1423	1424	DL	426	N805DN	JFK	TPA	154	1005	11	29	2023-11-12 11:00:00	Other
25929	10	9	1954	1957	-3	2301	2320	DL	806	N3757D	JFK	MIA	152	1089	19	57	2023-10-09 19:00:00	MIA
25935	3	5	611	615	-4	838	853	DL	763	N723TW	JFK	ATL	119	760	6	15	2023-03-05 06:00:00	ATL
25940	7	3	755	759	-4	1015	1013	UA	690	N17296	EWR	DEN	206	1605	7	59	2023-07-03 07:00:00	Other
25941	3	22	1357	1359	-2	1509	1513	OO	1268	N240SY	JFK	BOS	34	187	13	59	2023-03-22 13:00:00	BOS
25946	1	15	1714	1718	-4	1857	1932	YX	1136	N647RW	EWR	GSP	83	594	17	18	2023-01-15 17:00:00	Other
25953	6	6	627	630	-3	743	752	B6	1011	N279JB	JFK	BUF	55	301	6	30	2023-06-06 06:00:00	Other
25955	8	20	1335	1340	-5	1704	1743	DL	582	N802DN	JFK	SJU	185	1598	13	40	2023-08-20 13:00:00	Other
25962	10	1	1312	1316	-4	1925	1618	UA	444	N37263	EWR	FLL	NA	1065	13	16	2023-10-01 13:00:00	FLL
25981	2	6	742	745	-3	1050	1114	AA	575	N315RJ	LGA	MIA	154	1096	7	45	2023-02-06 07:00:00	MIA
25983	9	24	1433	1436	-3	1621	1629	YX	1875	N204JQ	LGA	MEM	133	963	14	36	2023-09-24 14:00:00	Other
25986	4	8	835	838	-3	1026	1037	YX	959	N739YX	EWR	GSO	84	445	8	38	2023-04-08 08:00:00	Other
25992	10	24	1545	1547	-2	1739	1751	YX	1052	N656RW	EWR	DTW	83	488	15	47	2023-10-24 15:00:00	Other
25993	9	14	802	806	-4	928	938	B6	364	N279JB	JFK	BNA	117	765	8	6	2023-09-14 08:00:00	Other
25995	6	1	1847	1850	-3	2043	2114	YX	1145	N722YX	EWR	IND	90	645	18	50	2023-06-01 18:00:00	Other
26004	11	16	1328	1333	-5	1613	1634	UA	188	N38467	EWR	PBI	146	1023	13	33	2023-11-16 13:00:00	Other
26011	8	19	1335	1340	-5	1701	1743	DL	582	N897DN	JFK	SJU	190	1598	13	40	2023-08-19 13:00:00	Other
26012	3	22	856	900	-4	1053	1103	YX	1358	N871RW	LGA	CMH	85	479	9	0	2023-03-22 09:00:00	Other
26018	8	4	1855	1900	-5	2112	2051	YX	1324	N860RW	LGA	PIT	65	335	19	0	2023-08-04 19:00:00	Other
26031	4	10	1255	1300	-5	1544	1619	B6	316	N645JB	JFK	SLC	253	1990	13	0	2023-04-10 13:00:00	Other
26057	2	6	758	800	-2	1331	1259	B6	202	N913JB	JFK	SJU	242	1598	8	0	2023-02-06 08:00:00	Other
26059	1	19	957	959	-2	1051	1117	9E	1450	N691CA	LGA	PVD	31	143	9	59	2023-01-19 09:00:00	Other
26061	2	14	733	735	-2	1017	1043	DL	578	N3730B	JFK	TPA	139	1005	7	35	2023-02-14 07:00:00	Other
26062	1	19	954	959	-5	1242	1309	B6	1041	N640JB	JFK	TPA	147	1005	9	59	2023-01-19 09:00:00	Other
26066	4	3	2057	2100	-3	2234	2251	YX	1012	N743YX	LGA	ORD	134	733	21	0	2023-04-03 21:00:00	ORD
26072	9	3	1655	1700	-5	1829	1903	9E	1512	N491PX	LGA	RDU	64	431	17	0	2023-09-03 17:00:00	Other
26073	9	21	559	604	-5	848	900	B6	431	N794JB	LGA	TPA	143	1010	6	4	2023-09-21 06:00:00	Other
26074	10	15	925	930	-5	1222	1228	B6	45	N2084J	JFK	SRQ	157	1041	9	30	2023-10-15 09:00:00	Other
26081	12	7	1527	1529	-2	1730	1733	NK	1003	N969NK	LGA	DTW	86	502	15	29	2023-12-07 15:00:00	Other
26083	11	15	1932	1935	-3	2339	2320	DL	346	N178DN	JFK	SFO	384	2586	19	35	2023-11-15 19:00:00	Other
26087	6	9	818	820	-2	931	958	B6	806	N504JB	LGA	BNA	108	764	8	20	2023-06-09 08:00:00	Other
26091	1	23	754	758	-4	1132	1122	AA	658	N802NN	LGA	MIA	180	1096	7	58	2023-01-23 07:00:00	MIA
26097	8	6	555	600	-5	734	746	DL	621	N993AT	EWR	DTW	81	488	6	0	2023-08-06 06:00:00	Other
26098	9	12	1924	1929	-5	2135	2133	AA	760	N8027D	JFK	CLT	94	541	19	29	2023-09-12 19:00:00	CLT
26107	5	3	1040	1045	-5	1229	1247	YX	995	N753YX	EWR	CMH	70	463	10	45	2023-05-03 10:00:00	Other
26110	8	19	1656	1700	-4	1807	1836	YX	1333	N229JQ	LGA	BOS	42	184	17	0	2023-08-19 17:00:00	BOS
26118	6	11	1833	1837	-4	2028	2101	YX	1324	N412YX	LGA	OMA	153	1148	18	37	2023-06-11 18:00:00	Other
26126	10	4	1904	1909	-5	2154	2238	AS	79	N581AS	EWR	SFO	331	2565	19	9	2023-10-04 19:00:00	Other
26131	2	5	1826	1830	-4	2008	2029	9E	1279	N482PX	LGA	RDU	79	431	18	30	2023-02-05 18:00:00	Other
26137	10	31	1550	1555	-5	1712	1715	WN	785	N209WN	LGA	MDW	122	725	15	55	2023-10-31 15:00:00	Other
26146	5	5	826	830	-4	1013	1032	9E	1537	N136EV	LGA	ILM	77	500	8	30	2023-05-05 08:00:00	Other
26150	11	30	556	600	-4	701	719	UA	420	N27274	EWR	IAD	42	212	6	0	2023-11-30 06:00:00	Other
26155	7	16	633	635	-2	823	827	YX	1096	N138HQ	JFK	RDU	74	427	6	35	2023-07-16 06:00:00	Other
26159	9	14	1208	1210	-2	1359	1428	UA	885	N37561	EWR	DEN	208	1605	12	10	2023-09-14 12:00:00	Other
26161	2	27	649	654	-5	1023	1037	UA	448	N12125	EWR	PHX	316	2133	6	54	2023-02-27 06:00:00	Other
26163	5	21	1925	1930	-5	2145	2203	UA	291	N27268	EWR	PHX	286	2133	19	30	2023-05-21 19:00:00	Other
26166	1	1	845	850	-5	1046	1128	9E	1601	N309PQ	LGA	CHS	102	641	8	50	2023-01-01 08:00:00	Other
26169	10	25	1530	1535	-5	1652	1707	UA	661	N37560	EWR	ORD	111	719	15	35	2023-10-25 15:00:00	ORD
26173	10	23	755	800	-5	1014	1029	DL	168	N524DE	JFK	DEN	229	1626	8	0	2023-10-23 08:00:00	Other
26181	3	19	1526	1530	-4	1841	1831	NK	1022	N615NK	EWR	MCO	152	937	15	30	2023-03-19 15:00:00	MCO
26186	2	21	800	805	-5	1104	1115	DL	350	N717TW	JFK	LAS	333	2248	8	5	2023-02-21 08:00:00	Other
26200	11	8	1048	1050	-2	1321	1345	B6	39	N570JB	EWR	MCO	125	937	10	50	2023-11-08 10:00:00	MCO
26203	12	12	855	900	-5	1120	1129	YX	1038	N746YX	EWR	IND	107	645	9	0	2023-12-12 09:00:00	Other
26205	9	5	1855	1859	-4	2038	2054	YX	1420	N443YX	JFK	RDU	72	427	18	59	2023-09-05 18:00:00	Other
26213	11	21	1726	1730	-4	1854	1854	OO	1173	N254SY	JFK	BOS	48	187	17	30	2023-11-21 17:00:00	BOS
26214	2	9	1825	1830	-5	1950	2000	YX	1488	N234JQ	JFK	BOS	46	187	18	30	2023-02-09 18:00:00	BOS
26221	3	17	1011	1013	-2	1258	1319	UA	748	N17244	EWR	IAH	196	1400	10	13	2023-03-17 10:00:00	Other
26231	6	4	1355	1400	-5	1548	1553	YX	1378	N821MD	LGA	ILM	84	500	14	0	2023-06-04 14:00:00	Other
26234	1	11	657	700	-3	954	1015	DL	1007	N375DA	JFK	DFW	207	1391	7	0	2023-01-11 07:00:00	Other
26239	8	28	600	605	-5	822	817	DL	667	N368NB	EWR	ATL	109	746	6	5	2023-08-28 06:00:00	ATL
26242	3	1	1627	1629	-2	1748	1756	YX	1151	N744YX	EWR	BUF	58	282	16	29	2023-03-01 16:00:00	Other
26248	3	22	1306	1310	-4	1550	1619	UA	483	N455UA	EWR	RSW	150	1068	13	10	2023-03-22 13:00:00	Other
26251	10	26	2125	2130	-5	2242	2300	9E	1641	N146PQ	JFK	BWI	38	184	21	30	2023-10-26 21:00:00	Other
26253	7	3	954	959	-5	1430	1510	DL	94	N172DN	JFK	HNL	611	4983	9	59	2023-07-03 09:00:00	Other
26258	4	15	825	830	-5	1041	1105	9E	1424	N307PQ	LGA	SAV	104	722	8	30	2023-04-15 08:00:00	Other
26260	3	9	843	848	-5	1043	1112	9E	1442	N301PQ	LGA	CHS	87	641	8	48	2023-03-09 08:00:00	Other
26262	3	10	1654	1659	-5	2022	2020	AA	95	N116AN	JFK	LAX	357	2475	16	59	2023-03-10 16:00:00	LAX
26263	12	13	1048	1050	-2	1345	1400	DL	384	N304DN	LGA	TPA	158	1010	10	50	2023-12-13 10:00:00	Other
26265	5	15	1211	1215	-4	1340	1404	B6	85	N348JB	JFK	RDU	69	427	12	15	2023-05-15 12:00:00	Other
26270	5	5	844	846	-2	1039	1043	9E	1477	N931XJ	LGA	CLE	72	419	8	46	2023-05-05 08:00:00	Other
26274	8	28	1225	1229	-4	1434	1457	OO	945	N287SY	LGA	SDF	106	659	12	29	2023-08-28 12:00:00	Other
26280	2	1	925	930	-5	1108	1057	9E	1470	N184GJ	JFK	ORF	62	290	9	30	2023-02-01 09:00:00	Other
26283	3	17	1514	1519	-5	1640	1659	YX	1736	N220JQ	JFK	DCA	56	213	15	19	2023-03-17 15:00:00	Other
26288	9	29	556	600	-4	708	720	YX	1930	N207JQ	LGA	BOS	34	184	6	0	2023-09-29 06:00:00	BOS
26290	11	2	2040	2043	-3	2315	2330	UA	767	N37278	EWR	LAS	297	2227	20	43	2023-11-02 20:00:00	Other
26299	5	19	655	700	-5	845	904	9E	1310	N932XJ	JFK	DTW	81	509	7	0	2023-05-19 07:00:00	Other
26311	3	13	1118	1120	-2	1439	1419	UA	623	N47282	EWR	PBI	177	1023	11	20	2023-03-13 11:00:00	Other
26323	12	15	2025	2029	-4	2121	2202	9E	1510	N147PQ	JFK	BWI	36	184	20	29	2023-12-15 20:00:00	Other
26326	8	4	858	901	-3	1105	1113	9E	1275	N294PQ	LGA	AVL	89	599	9	1	2023-08-04 09:00:00	Other
26327	5	26	1610	1615	-5	1719	1800	9E	1483	N232PQ	JFK	ORF	55	290	16	15	2023-05-26 16:00:00	Other
26329	3	24	1703	1705	-2	1834	1849	YX	1692	N243JQ	LGA	BNA	124	764	17	5	2023-03-24 17:00:00	Other
26334	2	2	1139	1144	-5	1247	1257	UA	397	N37547	EWR	BOS	41	200	11	44	2023-02-02 11:00:00	BOS
26335	3	14	934	936	-2	1244	1252	B6	82	N796JB	JFK	IAH	202	1417	9	36	2023-03-14 09:00:00	Other
26340	5	17	755	800	-5	933	938	UA	848	N15751	LGA	ORD	118	733	8	0	2023-05-17 08:00:00	ORD
26344	11	29	607	610	-3	855	920	WN	635	N8652B	LGA	HOU	205	1428	6	10	2023-11-29 06:00:00	Other
26349	1	19	813	815	-2	1116	1135	B6	262	N949JT	JFK	FLL	154	1069	8	15	2023-01-19 08:00:00	FLL
26350	7	11	1542	1546	-4	1721	1735	YX	1381	N221JQ	JFK	DCA	43	213	15	46	2023-07-11 15:00:00	Other
26353	10	11	1530	1535	-5	1655	1707	UA	661	N36469	EWR	ORD	119	719	15	35	2023-10-11 15:00:00	ORD
26363	1	28	616	618	-2	846	849	UA	867	N833UA	LGA	DEN	245	1620	6	18	2023-01-28 06:00:00	Other
26364	3	27	1013	1018	-5	1108	1132	YX	1663	N215JQ	LGA	PVD	27	143	10	18	2023-03-27 10:00:00	Other
26367	3	21	1838	1840	-2	2102	2112	YX	1285	N108HQ	LGA	OMA	180	1148	18	40	2023-03-21 18:00:00	Other
26402	9	18	2033	2037	-4	2316	2317	UA	781	N37305	EWR	LAS	300	2227	20	37	2023-09-18 20:00:00	Other
26410	3	6	1855	1900	-5	2122	2127	9E	1503	N905XJ	JFK	IND	119	665	19	0	2023-03-06 19:00:00	Other
26419	10	12	1805	1807	-2	2051	2057	UA	338	N883UA	EWR	DFW	184	1372	18	7	2023-10-12 18:00:00	Other
26423	9	28	1024	1029	-5	1227	1231	9E	1484	N914XJ	LGA	MYR	90	563	10	29	2023-09-28 10:00:00	Other
26424	7	5	1309	1314	-5	1512	1535	9E	1308	N307PQ	LGA	IND	91	660	13	14	2023-07-05 13:00:00	Other
26425	11	7	1355	1359	-4	1609	1638	DL	169	N114DN	LGA	ATL	108	762	13	59	2023-11-07 13:00:00	ATL
26426	8	15	2051	2056	-5	2247	2302	YX	932	N736YX	EWR	CMH	72	463	20	56	2023-08-15 20:00:00	Other
26435	9	18	1635	1640	-5	1738	1807	9E	1437	N137EV	JFK	PWM	42	273	16	40	2023-09-18 16:00:00	Other
26438	12	9	1507	1512	-5	1629	1655	9E	1700	N292PQ	JFK	ROC	55	264	15	12	2023-12-09 15:00:00	Other
26444	10	13	1827	1829	-2	2111	2129	DL	227	N525DA	JFK	LAS	320	2248	18	29	2023-10-13 18:00:00	Other
26449	7	10	950	955	-5	1156	1212	YX	1068	N826MD	LGA	SDF	101	659	9	55	2023-07-10 09:00:00	Other
26458	2	7	1957	1959	-2	2229	2242	DL	433	N717TW	JFK	ATL	116	760	19	59	2023-02-07 19:00:00	ATL
26459	7	12	1528	1530	-2	1728	1812	B6	542	N368JB	JFK	ATL	98	760	15	30	2023-07-12 15:00:00	ATL
26464	9	21	658	700	-2	1028	1025	AS	13	N973AK	JFK	SFO	348	2586	7	0	2023-09-21 07:00:00	Other
26465	11	18	948	951	-3	1141	1153	9E	1442	N478PX	LGA	CLE	67	419	9	51	2023-11-18 09:00:00	Other
26466	9	28	1102	1107	-5	1253	1333	UA	432	N39423	EWR	PHX	270	2133	11	7	2023-09-28 11:00:00	Other
26470	8	25	2055	2100	-5	2239	2253	9E	1175	N904XJ	LGA	RDU	64	431	21	0	2023-08-25 21:00:00	Other
26471	7	26	555	600	-5	854	923	AA	27	N108NN	JFK	SFO	326	2586	6	0	2023-07-26 06:00:00	Other
26479	10	24	1126	1130	-4	1335	1351	YX	1295	N413YX	JFK	IND	105	665	11	30	2023-10-24 11:00:00	Other
26492	11	1	1054	1059	-5	1204	1219	9E	1611	N600LR	JFK	SYR	49	209	10	59	2023-11-01 10:00:00	Other
26505	8	28	942	945	-3	1104	1115	9E	1177	N695CA	JFK	DCA	52	213	9	45	2023-08-28 09:00:00	Other
26512	11	2	1719	1722	-3	1928	1947	AA	941	N404AN	EWR	PHX	278	2133	17	22	2023-11-02 17:00:00	Other
26516	6	19	607	610	-3	823	831	B6	269	N229JB	JFK	JAX	117	828	6	10	2023-06-19 06:00:00	Other
26518	6	2	715	720	-5	850	914	9E	1643	N315PQ	LGA	GSO	69	461	7	20	2023-06-02 07:00:00	Other
26520	12	20	702	705	-3	935	1018	DL	351	N398DN	LGA	PBI	130	1035	7	5	2023-12-20 07:00:00	Other
26521	8	15	1154	1159	-5	1448	1453	UA	437	N14235	EWR	TPA	148	997	11	59	2023-08-15 11:00:00	Other
26529	3	25	1543	1545	-2	1913	1907	UA	429	N78009	EWR	SFO	326	2565	15	45	2023-03-25 15:00:00	Other
26531	12	22	1525	1530	-5	1800	1808	B6	922	N2059J	JFK	ATL	106	760	15	30	2023-12-22 15:00:00	ATL
26532	5	25	711	715	-4	921	947	DL	237	N861DN	JFK	PHX	288	2153	7	15	2023-05-25 07:00:00	Other
26533	2	14	915	920	-5	1138	1207	YX	1551	N242JQ	LGA	SDF	110	659	9	20	2023-02-14 09:00:00	Other
26536	11	12	1153	1155	-2	1329	1325	WN	267	N203WN	LGA	MDW	123	725	11	55	2023-11-12 11:00:00	Other
26537	9	5	1948	1950	-2	2220	2303	DL	890	N835DN	JFK	TPA	131	1005	19	50	2023-09-05 19:00:00	Other
26540	11	25	755	759	-4	940	1000	YX	1052	N764YX	EWR	CMH	79	463	7	59	2023-11-25 07:00:00	Other
26547	3	26	1024	1029	-5	1244	1258	9E	1512	N918XJ	LGA	CVG	109	585	10	29	2023-03-26 10:00:00	Other
26548	9	21	2125	2129	-4	2225	2236	9E	1738	N912XJ	LGA	ALB	32	136	21	29	2023-09-21 21:00:00	Other
26572	9	22	2043	2048	-5	2334	2335	UA	465	N57286	EWR	IAH	176	1400	20	48	2023-09-22 20:00:00	Other
26578	9	17	745	747	-2	1052	1045	B6	672	N935JB	EWR	LAX	311	2454	7	47	2023-09-17 07:00:00	LAX
26585	10	11	1732	1734	-2	1936	1940	UA	75	N34222	EWR	CLT	91	529	17	34	2023-10-11 17:00:00	CLT
26587	4	7	955	959	-4	1230	1218	9E	1316	N293PQ	LGA	MYR	91	563	9	59	2023-04-07 09:00:00	Other
26590	1	25	825	830	-5	1103	1116	9E	1427	N901XJ	JFK	JAX	130	828	8	30	2023-01-25 08:00:00	Other
26598	10	11	2126	2130	-4	18	33	B6	28	N993JE	JFK	SAN	337	2446	21	30	2023-10-11 21:00:00	Other
26608	3	22	1654	1656	-2	1904	1908	DL	772	N115DU	JFK	DTW	95	509	16	56	2023-03-22 16:00:00	Other
26612	7	10	954	959	-5	1454	1505	DL	94	N171DN	JFK	HNL	628	4983	9	59	2023-07-10 09:00:00	Other
26613	1	16	1956	1959	-3	104	57	UA	664	N69826	EWR	SJU	190	1608	19	59	2023-01-16 19:00:00	Other
26615	8	14	747	752	-5	902	913	AA	600	N12028	LGA	DCA	49	214	7	52	2023-08-14 07:00:00	Other
26619	7	5	1018	1023	-5	1159	1158	YX	882	N724YX	EWR	BGR	61	393	10	23	2023-07-05 10:00:00	Other
26624	6	30	1450	1455	-5	1718	1702	9E	1722	N187GJ	JFK	CLE	71	425	14	55	2023-06-30 14:00:00	Other
26626	8	24	953	955	-2	1141	1155	G4	58	190NV	EWR	AVL	85	583	9	55	2023-08-24 09:00:00	Other
26634	4	9	1455	1459	-4	1625	1624	YX	1540	N244JQ	LGA	BOS	43	184	14	59	2023-04-09 14:00:00	BOS
26636	6	15	1932	1935	-3	2048	2136	OO	1277	N260SY	JFK	BNA	106	765	19	35	2023-06-15 19:00:00	Other
26638	10	26	1216	1220	-4	1442	1518	NK	734	N665NK	EWR	MCO	125	937	12	20	2023-10-26 12:00:00	MCO
26640	12	12	835	839	-4	1208	1249	AA	529	N319TE	JFK	PHX	312	2153	8	39	2023-12-12 08:00:00	Other
26644	5	29	1450	1455	-5	1717	1717	9E	1556	N181PQ	JFK	IND	97	665	14	55	2023-05-29 14:00:00	Other
26648	8	3	1726	1729	-3	1930	1951	YX	1042	N126HQ	LGA	SDF	103	659	17	29	2023-08-03 17:00:00	Other
26657	8	23	1520	1525	-5	1651	1713	9E	1290	N296PQ	JFK	PWM	51	273	15	25	2023-08-23 15:00:00	Other
26659	8	15	1138	1143	-5	1406	1412	UA	346	N461UA	EWR	ATL	110	746	11	43	2023-08-15 11:00:00	ATL
26660	12	30	948	950	-2	1143	1216	YX	1796	N213JQ	JFK	IND	92	665	9	50	2023-12-30 09:00:00	Other
26662	3	24	1152	1156	-4	1446	1507	DL	413	N334NW	LGA	TPA	143	1010	11	56	2023-03-24 11:00:00	Other
26667	9	21	1057	1059	-2	1338	1413	DL	173	N532DN	JFK	SEA	304	2422	10	59	2023-09-21 10:00:00	Other
26673	12	3	1434	1437	-3	1553	1545	9E	1436	N320PQ	LGA	PVD	30	143	14	37	2023-12-03 14:00:00	Other
26677	3	18	1217	1220	-3	1451	1453	B6	966	N605JB	JFK	ATL	125	760	12	20	2023-03-18 12:00:00	ATL
26680	1	29	758	803	-5	1057	1113	UA	941	N77259	EWR	TPA	147	997	8	3	2023-01-29 08:00:00	Other
26685	7	13	824	829	-5	1116	1118	AA	299	N969AN	LGA	DFW	203	1389	8	29	2023-07-13 08:00:00	Other
26695	2	8	1327	1330	-3	1757	1823	B6	329	N703JB	JFK	SJU	187	1598	13	30	2023-02-08 13:00:00	Other
26697	1	27	555	600	-5	720	735	WN	940	N8508W	LGA	MDW	114	725	6	0	2023-01-27 06:00:00	Other
26706	8	6	557	601	-4	709	707	B6	389	N355JB	JFK	BOS	38	187	6	1	2023-08-06 06:00:00	BOS
26709	9	2	949	952	-3	1238	1244	UA	464	N63899	EWR	AUS	191	1504	9	52	2023-09-02 09:00:00	Other
26717	9	30	1712	1716	-4	1843	1910	YX	1797	N815MD	LGA	RDU	64	431	17	16	2023-09-30 17:00:00	Other
26718	11	14	1155	1200	-5	1454	1516	AA	494	N935AN	JFK	AUS	206	1521	12	0	2023-11-14 12:00:00	Other
26723	2	2	954	959	-5	1321	1324	B6	213	N946JL	JFK	LAX	354	2475	9	59	2023-02-02 09:00:00	LAX
26726	10	27	1445	1450	-5	1641	1654	9E	1502	N937XJ	JFK	CLT	82	541	14	50	2023-10-27 14:00:00	CLT
26729	5	14	1041	1043	-2	1246	1317	YX	1114	N731YX	EWR	SDF	100	642	10	43	2023-05-14 10:00:00	Other
26733	5	19	2157	2200	-3	2313	2327	DL	632	N127DU	JFK	BOS	44	187	22	0	2023-05-19 22:00:00	BOS
26737	2	7	2155	2159	-4	2305	2327	YX	1064	N730YX	EWR	PWM	44	284	21	59	2023-02-07 21:00:00	Other
26743	8	22	845	850	-5	1053	1113	9E	1282	N349PQ	LGA	TVC	99	655	8	50	2023-08-22 08:00:00	Other
26746	5	9	457	500	-3	742	754	AA	186	N305NX	EWR	DFW	195	1372	5	0	2023-05-09 05:00:00	Other
26749	7	18	1255	1259	-4	1741	1617	AA	536	N302SS	JFK	MIA	154	1089	12	59	2023-07-18 12:00:00	MIA
26752	4	13	1626	1629	-3	1808	1848	DL	698	N142DU	JFK	DTW	82	509	16	29	2023-04-13 16:00:00	Other
26754	10	3	1051	1055	-4	1256	1325	WN	993	N919WN	LGA	ATL	105	762	10	55	2023-10-03 10:00:00	ATL
26760	9	4	1826	1829	-3	2122	2144	AA	139	N820NN	JFK	MIA	136	1089	18	29	2023-09-04 18:00:00	MIA
26766	6	7	739	744	-5	906	932	9E	1551	N195PQ	JFK	RDU	69	427	7	44	2023-06-07 07:00:00	Other
26771	5	25	1646	1650	-4	1808	1829	9E	1478	N293PQ	LGA	BGR	55	378	16	50	2023-05-25 16:00:00	Other
26774	3	30	1010	1015	-5	1321	1314	UA	417	N57286	EWR	SRQ	151	1034	10	15	2023-03-30 10:00:00	Other
26775	1	9	1526	1530	-4	1858	1858	B6	269	N807JB	JFK	LAX	365	2475	15	30	2023-01-09 15:00:00	LAX
26792	1	9	1504	1508	-4	1626	1646	YX	1170	N655RW	EWR	RIC	56	277	15	8	2023-01-09 15:00:00	Other
26795	9	26	2056	2100	-4	2218	2227	B6	66	N368JB	JFK	BTV	48	266	21	0	2023-09-26 21:00:00	Other
26796	2	20	758	800	-2	1028	1030	OO	1172	N297SY	JFK	MSP	173	1029	8	0	2023-02-20 08:00:00	Other
26798	6	18	1300	1304	-4	1426	1438	UA	111	N37525	EWR	ORD	110	719	13	4	2023-06-18 13:00:00	ORD
26803	10	29	1530	1535	-5	1653	1637	9E	1444	N176PQ	LGA	BDL	22	101	15	35	2023-10-29 15:00:00	Other
26816	5	13	555	600	-5	723	738	UA	768	N418UA	LGA	ORD	121	733	6	0	2023-05-13 06:00:00	ORD
26820	8	21	942	946	-4	1324	1341	UA	465	N47569	EWR	SJU	199	1608	9	46	2023-08-21 09:00:00	Other
26821	11	19	1413	1415	-2	1538	1601	OO	1792	N145SY	LGA	ORD	124	733	14	15	2023-11-19 14:00:00	ORD
26834	2	2	757	800	-3	1013	1027	9E	1278	N331PQ	JFK	MSP	167	1029	8	0	2023-02-02 08:00:00	Other
26839	12	4	606	610	-4	911	936	DL	106	N109DN	JFK	SLC	280	1990	6	10	2023-12-04 06:00:00	Other
26843	11	16	1555	1557	-2	1729	1759	YX	1155	N747YX	EWR	CMH	70	463	15	57	2023-11-16 15:00:00	Other
26858	11	6	1524	1529	-5	1700	1731	9E	1472	N904XJ	LGA	GSO	74	461	15	29	2023-11-06 15:00:00	Other
26859	5	23	1116	1118	-2	1459	1435	DL	884	N358DN	LGA	FLL	163	1076	11	18	2023-05-23 11:00:00	FLL
26871	4	27	807	810	-3	1318	1318	UA	131	N68061	EWR	HNL	609	4962	8	10	2023-04-27 08:00:00	Other
26875	8	1	1955	2000	-5	2125	2204	YX	1359	N225JQ	JFK	PIT	64	340	20	0	2023-08-01 20:00:00	Other
26876	10	12	1824	1829	-5	2034	2026	YX	1261	N403YX	JFK	CMH	81	483	18	29	2023-10-12 18:00:00	Other
26880	2	18	2052	2056	-4	2300	2313	UA	324	N73291	EWR	SAV	100	708	20	56	2023-02-18 20:00:00	Other
26882	4	6	1209	1213	-4	1505	1457	UA	793	N33203	EWR	DFW	216	1372	12	13	2023-04-06 12:00:00	Other
26892	8	23	1456	1500	-4	1602	1616	9E	1207	N482PX	LGA	ORH	34	146	15	0	2023-08-23 15:00:00	Other
26894	6	8	1643	1647	-4	1810	1820	YX	1142	N647RW	EWR	BGR	61	393	16	47	2023-06-08 16:00:00	Other
26896	8	2	655	659	-4	837	905	AA	278	N942AN	LGA	CLT	79	544	6	59	2023-08-02 06:00:00	CLT
26899	6	15	558	603	-5	729	735	UA	758	N14235	EWR	ORD	111	719	6	3	2023-06-15 06:00:00	ORD
26908	11	13	626	630	-4	908	931	UA	879	N13018	EWR	LAX	308	2454	6	30	2023-11-13 06:00:00	LAX
26910	2	25	1854	1859	-5	2027	2032	YX	978	N646RW	EWR	BGR	57	393	18	59	2023-02-25 18:00:00	Other
26912	1	14	2154	2159	-5	2259	2307	DL	619	N120DU	LGA	BOS	36	184	21	59	2023-01-14 21:00:00	BOS
26916	9	23	824	829	-5	1155	1150	AA	712	N313SB	JFK	MIA	161	1089	8	29	2023-09-23 08:00:00	MIA
26917	2	18	1630	1635	-5	1801	1843	YX	1218	N407YX	LGA	GSO	72	461	16	35	2023-02-18 16:00:00	Other
26919	1	19	1723	1725	-2	2019	2047	B6	76	N978JB	JFK	SEA	308	2422	17	25	2023-01-19 17:00:00	Other
26921	2	28	1345	1347	-2	1654	1654	UA	491	N27269	EWR	FLL	144	1065	13	47	2023-02-28 13:00:00	FLL
26923	1	25	1426	1429	-3	1619	1631	NK	575	N644NK	LGA	MYR	99	563	14	29	2023-01-25 14:00:00	Other
26925	3	1	1627	1629	-2	1755	1758	YX	1082	N748YX	EWR	PIT	61	319	16	29	2023-03-01 16:00:00	Other
26936	2	14	658	700	-2	810	822	YX	1485	N229JQ	LGA	BOS	41	184	7	0	2023-02-14 07:00:00	BOS
26938	2	10	1146	1150	-4	1233	1303	YX	1502	N224JQ	LGA	BDL	23	101	11	50	2023-02-10 11:00:00	Other
26941	9	23	957	1000	-3	1201	1208	YX	1354	N115HQ	LGA	GSP	101	610	10	0	2023-09-23 10:00:00	Other
26945	1	25	726	730	-4	1017	1055	DL	105	N825DN	JFK	SEA	321	2422	7	30	2023-01-25 07:00:00	Other
26966	5	29	1842	1845	-3	2041	2019	B6	2	N355JB	JFK	BUF	47	301	18	45	2023-05-29 18:00:00	Other
26968	1	8	2157	2200	-3	2322	2339	B6	391	N249JB	LGA	BNA	122	764	22	0	2023-01-08 22:00:00	Other
26970	10	9	1557	1559	-2	1952	1914	DL	862	N345NB	JFK	AUS	222	1521	15	59	2023-10-09 15:00:00	Other
26971	3	13	1456	1500	-4	1621	1635	YX	1261	N118HQ	LGA	DCA	56	214	15	0	2023-03-13 15:00:00	Other
26972	7	26	702	705	-3	851	932	UA	372	N77259	EWR	PHX	266	2133	7	5	2023-07-26 07:00:00	Other
26975	1	31	1552	1557	-5	1804	1815	YX	1159	N732YX	EWR	CHS	105	628	15	57	2023-01-31 15:00:00	Other
26977	2	10	1054	1057	-3	1300	1306	YX	1062	N733YX	EWR	CLT	99	529	10	57	2023-02-10 10:00:00	CLT
26980	3	31	2155	2200	-5	2306	2323	UA	523	N457UA	EWR	ORF	49	284	22	0	2023-03-31 22:00:00	Other
26981	1	18	1317	1322	-5	1442	1455	UA	110	N37422	EWR	ORD	116	719	13	22	2023-01-18 13:00:00	ORD
26995	1	30	1956	2000	-4	2220	2224	9E	1652	N320PQ	LGA	CVG	112	585	20	0	2023-01-30 20:00:00	Other
26996	5	10	1151	1155	-4	1343	1409	DL	409	N355NB	LGA	MSP	151	1020	11	55	2023-05-10 11:00:00	Other
27000	12	3	950	954	-4	1133	1152	9E	1451	N304PQ	EWR	RDU	76	416	9	54	2023-12-03 09:00:00	Other
27002	11	8	556	600	-4	901	859	AA	12	N112AN	JFK	LAX	343	2475	6	0	2023-11-08 06:00:00	LAX
27003	9	5	856	900	-4	1211	1210	AS	122	N517AS	EWR	SFO	332	2565	9	0	2023-09-05 09:00:00	Other
27020	1	2	1040	1045	-5	1352	1405	DL	127	N177DN	JFK	LAX	342	2475	10	45	2023-01-02 10:00:00	LAX
27022	9	16	625	629	-4	812	829	AA	319	N909AN	JFK	CLT	83	541	6	29	2023-09-16 06:00:00	CLT
27023	6	8	957	959	-2	1249	1230	9E	1533	N300PQ	JFK	SAV	113	718	9	59	2023-06-08 09:00:00	Other
27031	5	28	658	700	-2	910	945	WN	614	N913WN	LGA	DAL	172	1381	7	0	2023-05-28 07:00:00	Other
27038	7	26	627	630	-3	901	921	NK	418	N919NK	LGA	MCO	132	950	6	30	2023-07-26 06:00:00	MCO
27062	2	1	1102	1106	-4	1244	1242	UA	753	N445UA	EWR	BNA	136	748	11	6	2023-02-01 11:00:00	Other
27065	11	3	750	755	-5	1040	1049	NK	430	N665NK	EWR	MCO	142	937	7	55	2023-11-03 07:00:00	MCO
27068	6	4	1834	1839	-5	2045	2059	9E	1441	N925XJ	LGA	GRR	91	618	18	39	2023-06-04 18:00:00	Other
27072	8	31	2026	2030	-4	2146	2211	DL	355	N131DU	LGA	ORD	108	733	20	30	2023-08-31 20:00:00	ORD
27078	5	5	958	1000	-2	1309	1329	DL	140	N810DN	JFK	SLC	270	1990	10	0	2023-05-05 10:00:00	Other
27080	11	25	1125	1130	-5	1258	1254	YX	1072	N725YX	EWR	BUF	51	282	11	30	2023-11-25 11:00:00	Other
27085	11	29	2055	2059	-4	2238	2301	YX	1780	N204JQ	JFK	CMH	77	483	20	59	2023-11-29 20:00:00	Other
27099	2	16	725	730	-5	1009	1030	DL	425	N106DN	LGA	MCO	138	950	7	30	2023-02-16 07:00:00	MCO
27109	3	12	555	600	-5	749	755	DL	378	N314DN	LGA	DTW	88	502	6	0	2023-03-12 06:00:00	Other
27113	3	8	1455	1500	-5	1609	1625	YX	1748	N230JQ	LGA	BOS	40	184	15	0	2023-03-08 15:00:00	BOS
27114	8	16	1912	1915	-3	2150	2210	AA	314	N306NY	LGA	DFW	178	1389	19	15	2023-08-16 19:00:00	Other
27125	10	13	956	1000	-4	1227	1229	YX	1329	N135HQ	LGA	SDF	112	659	10	0	2023-10-13 10:00:00	Other
27141	11	12	2254	2259	-5	6	30	9E	1753	N330PQ	JFK	ROC	51	264	22	59	2023-11-12 22:00:00	Other
27145	8	21	817	820	-3	923	938	YX	1071	N117HQ	LGA	BUF	49	292	8	20	2023-08-21 08:00:00	Other
27153	11	13	857	900	-3	1147	1210	AS	85	N486AS	EWR	LAX	321	2454	9	0	2023-11-13 09:00:00	LAX
27155	12	7	1930	1935	-5	2259	2342	DL	344	N175DN	JFK	SFO	367	2586	19	35	2023-12-07 19:00:00	Other
27166	12	24	905	908	-3	1028	1059	YX	1040	N728YX	EWR	MKE	117	725	9	8	2023-12-24 09:00:00	Other
27175	1	15	1125	1130	-5	1317	1353	YX	1184	N736YX	EWR	IND	91	645	11	30	2023-01-15 11:00:00	Other
27183	6	6	1256	1259	-3	1419	1428	9E	1546	N601LR	LGA	PWM	47	269	12	59	2023-06-06 12:00:00	Other
27189	11	5	1452	1455	-3	1554	1609	YX	1128	N736YX	EWR	MHT	39	209	14	55	2023-11-05 14:00:00	Other
27193	5	29	824	829	-5	1127	1223	AA	56	N110AN	JFK	SFO	324	2586	8	29	2023-05-29 08:00:00	Other
27199	3	28	855	900	-5	1023	1030	9E	1485	N908XJ	LGA	PWM	55	269	9	0	2023-03-28 09:00:00	Other
27200	7	13	1527	1529	-2	1920	1853	AS	82	N967AK	EWR	SFO	348	2565	15	29	2023-07-13 15:00:00	Other
27202	3	12	2156	2200	-4	2354	2348	YX	1375	N107HQ	LGA	RDU	85	431	22	0	2023-03-12 22:00:00	Other
27215	7	23	1656	1659	-3	1902	1924	YX	1066	N422YX	JFK	CVG	100	589	16	59	2023-07-23 16:00:00	Other
27220	12	6	1512	1517	-5	1645	1651	YX	1037	N647RW	EWR	PIT	52	319	15	17	2023-12-06 15:00:00	Other
27238	3	18	1654	1657	-3	1851	1848	YX	1279	N425YX	LGA	RDU	82	431	16	57	2023-03-18 16:00:00	Other
27244	2	26	1034	1039	-5	1229	1248	YX	1062	N723YX	EWR	CLT	93	529	10	39	2023-02-26 10:00:00	CLT
27253	5	7	1107	1111	-4	1337	1419	DL	449	N382DA	LGA	PBI	127	1035	11	11	2023-05-07 11:00:00	Other
27263	5	26	635	640	-5	823	919	NK	160	N643NK	EWR	LAS	274	2227	6	40	2023-05-26 06:00:00	Other
27266	1	27	2020	2025	-5	2134	2201	YX	1831	N241JQ	JFK	DCA	47	213	20	25	2023-01-27 20:00:00	Other
27268	9	7	1109	1113	-4	1246	1310	9E	1612	N187GJ	LGA	RDU	65	431	11	13	2023-09-07 11:00:00	Other
27276	7	30	1201	1204	-3	1412	1416	DL	766	N3749D	EWR	ATL	106	746	12	4	2023-07-30 12:00:00	ATL
27292	4	29	617	620	-3	805	818	AA	849	N557UW	EWR	CLT	87	529	6	20	2023-04-29 06:00:00	CLT
27297	6	29	2035	2040	-5	2154	2216	9E	1639	N316PQ	LGA	CHO	52	305	20	40	2023-06-29 20:00:00	Other
27301	12	21	1854	1859	-5	2201	2227	UA	172	N25705	EWR	SNA	332	2434	18	59	2023-12-21 18:00:00	Other
27303	4	26	925	930	-5	1156	1159	B6	866	N267JB	LGA	SAV	111	722	9	30	2023-04-26 09:00:00	Other
27309	1	14	1012	1016	-4	1220	1231	YX	1206	N855RW	EWR	GSP	86	594	10	16	2023-01-14 10:00:00	Other
27311	9	28	948	950	-2	1109	1130	9E	1743	N678CA	LGA	BGR	57	378	9	50	2023-09-28 09:00:00	Other
27324	8	13	1647	1650	-3	1757	1832	YX	1370	N205JQ	LGA	BUF	50	292	16	50	2023-08-13 16:00:00	Other
27332	11	11	1257	1259	-2	1632	1641	AA	974	N316RK	JFK	PHX	309	2153	12	59	2023-11-11 12:00:00	Other
27334	11	9	1943	1945	-2	2238	2257	B6	210	N784JB	LGA	FLL	148	1076	19	45	2023-11-09 19:00:00	FLL
27335	4	10	800	805	-5	958	1030	DL	828	N145DQ	JFK	MSY	157	1182	8	5	2023-04-10 08:00:00	Other
27341	10	17	838	840	-2	949	1012	YX	1748	N207JQ	LGA	DCA	42	214	8	40	2023-10-17 08:00:00	Other
27345	8	26	1550	1555	-5	1923	1931	B6	201	N929JB	JFK	SFO	363	2586	15	55	2023-08-26 15:00:00	Other
27346	10	12	1956	1959	-3	2315	2316	AS	76	N568AS	EWR	LAX	344	2454	19	59	2023-10-12 19:00:00	LAX
27352	5	13	745	750	-5	852	918	9E	1518	N309PQ	JFK	BWI	39	184	7	50	2023-05-13 07:00:00	Other
27354	4	27	1901	1906	-5	2149	2220	DL	438	N385DZ	EWR	SLC	269	1969	19	6	2023-04-27 19:00:00	Other
27355	4	9	556	600	-4	806	824	DL	751	N990AT	EWR	ATL	112	746	6	0	2023-04-09 06:00:00	ATL
27357	1	24	2153	2155	-2	2311	2310	DL	817	N906DN	JFK	BOS	41	187	21	55	2023-01-24 21:00:00	BOS
27360	6	3	755	800	-5	1011	1036	DL	598	N133DU	JFK	JAX	118	828	8	0	2023-06-03 08:00:00	Other
27362	11	13	747	752	-5	908	926	YX	1097	N647RW	EWR	PIT	59	319	7	52	2023-11-13 07:00:00	Other
27364	3	11	1212	1215	-3	1524	1535	UA	804	N229UA	EWR	SFO	344	2565	12	15	2023-03-11 12:00:00	Other
27372	12	17	702	705	-3	1022	1014	DL	566	N340DN	LGA	FLL	171	1076	7	5	2023-12-17 07:00:00	FLL
27374	4	6	1742	1744	-2	1934	1940	YX	1118	N434YX	LGA	CMH	78	479	17	44	2023-04-06 17:00:00	Other
27375	11	8	749	752	-3	918	926	YX	1097	N864RW	EWR	PIT	66	319	7	52	2023-11-08 07:00:00	Other
27376	11	25	1819	1824	-5	2042	2056	DL	809	N979AT	EWR	ATL	116	746	18	24	2023-11-25 18:00:00	ATL
27383	9	1	927	930	-3	1231	1246	DL	911	N707TW	JFK	SLC	261	1990	9	30	2023-09-01 09:00:00	Other
27384	7	26	1245	1250	-5	1349	1359	9E	1271	N919XJ	LGA	PVD	31	143	12	50	2023-07-26 12:00:00	Other
27391	11	20	857	900	-3	1116	1138	B6	23	N3121J	JFK	MSY	178	1182	9	0	2023-11-20 09:00:00	Other
27392	4	20	1041	1045	-4	1342	1348	AA	404	N898NN	LGA	DFW	205	1389	10	45	2023-04-20 10:00:00	Other
27394	2	15	1222	1225	-3	1426	1436	NK	630	N658NK	LGA	DTW	88	502	12	25	2023-02-15 12:00:00	Other
27397	10	30	2156	2159	-3	2307	2321	UA	430	N433UA	EWR	BUF	54	282	21	59	2023-10-30 21:00:00	Other
27406	12	15	726	729	-3	1032	1043	AA	738	N336TM	JFK	MIA	148	1089	7	29	2023-12-15 07:00:00	MIA
27417	6	8	640	642	-2	945	944	NK	202	N951NK	EWR	FLL	159	1065	6	42	2023-06-08 06:00:00	FLL
27427	4	19	1134	1137	-3	1250	1304	YX	1033	N722YX	EWR	PIT	56	319	11	37	2023-04-19 11:00:00	Other
27432	8	22	1342	1347	-5	1602	1641	AA	785	N841NN	LGA	DFW	172	1389	13	47	2023-08-22 13:00:00	Other
27435	9	7	657	700	-3	956	1020	DL	171	N191DN	JFK	SFO	333	2586	7	0	2023-09-07 07:00:00	Other
27436	7	2	759	803	-4	1040	1046	B6	294	N640JB	EWR	MCO	119	937	8	3	2023-07-02 08:00:00	MCO
27441	11	17	2150	2155	-5	2300	2311	9E	1506	N920XJ	LGA	PWM	47	269	21	55	2023-11-17 21:00:00	Other
27443	1	15	928	930	-2	1232	1248	B6	50	N806JB	JFK	SRQ	146	1041	9	30	2023-01-15 09:00:00	Other
27451	10	31	555	600	-5	924	859	DL	233	N107DU	LGA	DFW	232	1389	6	0	2023-10-31 06:00:00	Other
27454	1	4	2024	2029	-5	2242	2302	YX	1180	N646RW	EWR	SDF	116	642	20	29	2023-01-04 20:00:00	Other
27457	11	1	1604	1608	-4	1836	1842	UA	692	N17730	EWR	ATL	127	746	16	8	2023-11-01 16:00:00	ATL
27458	2	24	1255	1300	-5	1526	1510	9E	1380	N932XJ	JFK	DTW	123	509	13	0	2023-02-24 13:00:00	Other
27478	3	24	1550	1555	-5	1826	1827	NK	425	N639NK	EWR	ATL	118	746	15	55	2023-03-24 15:00:00	ATL
27495	11	16	1226	1230	-4	1355	1403	YX	1785	N204JQ	LGA	MKE	116	738	12	30	2023-11-16 12:00:00	Other
27500	7	3	1200	1204	-4	1411	1419	DL	766	N3756	EWR	ATL	107	746	12	4	2023-07-03 12:00:00	ATL
27507	7	3	1156	1201	-5	1349	1339	9E	1189	N304PQ	JFK	BUF	50	301	12	1	2023-07-03 12:00:00	Other
27513	4	27	1342	1345	-3	1646	1709	YX	1236	N872RW	LGA	IAH	218	1416	13	45	2023-04-27 13:00:00	Other
27521	10	9	1523	1525	-2	1812	1849	AS	78	N974AK	EWR	SFO	320	2565	15	25	2023-10-09 15:00:00	Other
27523	10	6	1725	1730	-5	1846	1908	9E	1585	N292PQ	JFK	BUF	56	301	17	30	2023-10-06 17:00:00	Other
27524	4	7	1550	1555	-5	1705	1727	9E	1384	N337PQ	LGA	BGR	49	378	15	55	2023-04-07 15:00:00	Other
27525	9	21	547	549	-2	849	853	AA	1	N108NN	JFK	LAX	333	2475	5	49	2023-09-21 05:00:00	LAX
27527	5	10	911	915	-4	1034	1111	AA	943	N338ST	JFK	ORD	117	740	9	15	2023-05-10 09:00:00	ORD
27529	7	3	1748	1750	-2	1918	1938	9E	1320	N917XJ	LGA	BGR	58	378	17	50	2023-07-03 17:00:00	Other
27537	4	17	757	800	-3	910	911	B6	273	N317JB	JFK	BOS	34	187	8	0	2023-04-17 08:00:00	BOS
27543	5	25	1443	1446	-3	1704	1704	9E	1314	N920XJ	LGA	MCI	167	1107	14	46	2023-05-25 14:00:00	Other
27555	11	15	1857	1900	-3	2142	2206	DL	862	N340NW	JFK	AUS	200	1521	19	0	2023-11-15 19:00:00	Other
27560	12	25	1729	1731	-2	2043	2047	AA	896	N906AN	JFK	MIA	157	1089	17	31	2023-12-25 17:00:00	MIA
27562	9	12	1907	1910	-3	2140	2152	YX	1352	N426YX	LGA	OKC	195	1341	19	10	2023-09-12 19:00:00	Other
27570	2	27	1707	1710	-3	2000	2014	B6	671	N603JB	LGA	MCO	134	950	17	10	2023-02-27 17:00:00	MCO
27572	5	10	1025	1029	-4	1152	1206	YX	1600	N233JQ	LGA	DCA	44	214	10	29	2023-05-10 10:00:00	Other
27575	3	2	1048	1053	-5	1244	1224	YX	1059	N644RW	EWR	PIT	63	319	10	53	2023-03-02 10:00:00	Other
27589	6	23	726	730	-4	932	916	UA	419	N27239	EWR	RDU	97	416	7	30	2023-06-23 07:00:00	Other
27599	12	18	2021	2025	-4	2222	2250	9E	1511	N330PQ	JFK	CLT	90	541	20	25	2023-12-18 20:00:00	CLT
27600	4	30	1458	1500	-2	1706	1707	AA	682	N863NN	LGA	CLT	97	544	15	0	2023-04-30 15:00:00	CLT
27607	12	6	555	600	-5	720	740	UA	372	N13113	EWR	ORD	111	719	6	0	2023-12-06 06:00:00	ORD
27613	2	13	955	1000	-5	1115	1134	YX	1536	N239JQ	LGA	BOS	33	184	10	0	2023-02-13 10:00:00	BOS
27628	2	13	1249	1254	-5	1407	1423	YX	1008	N751YX	EWR	PIT	60	319	12	54	2023-02-13 12:00:00	Other
27630	9	22	1311	1313	-2	1534	1602	UA	720	N27260	EWR	MCO	127	937	13	13	2023-09-22 13:00:00	MCO
27638	1	21	902	905	-3	1018	1024	B6	706	N283JB	JFK	BTV	49	266	9	5	2023-01-21 09:00:00	Other
27643	1	25	1447	1450	-3	1609	1619	B6	1082	N279JB	JFK	BUF	60	301	14	50	2023-01-25 14:00:00	Other
27645	8	2	654	659	-5	843	856	YX	999	N406YX	LGA	DTW	82	502	6	59	2023-08-02 06:00:00	Other
27646	4	21	936	940	-4	1219	1239	B6	421	N649JB	JFK	TPA	135	1005	9	40	2023-04-21 09:00:00	Other
27653	9	27	1054	1059	-5	1251	1255	YX	1185	N740YX	EWR	MEM	144	946	10	59	2023-09-27 10:00:00	Other
27654	3	21	1926	1929	-3	2148	2159	9E	1437	N147PQ	JFK	MSP	164	1029	19	29	2023-03-21 19:00:00	Other
27674	8	17	1124	1129	-5	1331	1401	DL	309	N840DN	JFK	ATL	105	760	11	29	2023-08-17 11:00:00	ATL
27683	4	13	658	700	-2	941	1015	DL	202	N16065	JFK	LAX	311	2475	7	0	2023-04-13 07:00:00	LAX
27684	1	8	1016	1020	-4	1232	1255	DL	233	N988AT	EWR	ATL	118	746	10	20	2023-01-08 10:00:00	ATL
27690	10	20	2136	2138	-2	2332	2315	UA	629	N14115	EWR	ORD	104	719	21	38	2023-10-20 21:00:00	ORD
27696	6	15	1656	1700	-4	1817	1844	AA	1031	N810AW	LGA	STL	118	888	17	0	2023-06-15 17:00:00	Other
27703	5	1	1757	1759	-2	1917	1940	UA	791	N844UA	LGA	ORD	109	733	17	59	2023-05-01 17:00:00	ORD
27723	2	7	1625	1629	-4	1808	1816	UA	98	N810UA	EWR	RDU	74	416	16	29	2023-02-07 16:00:00	Other
27724	12	28	1033	1035	-2	1157	1230	WN	1155	N941WN	LGA	STL	122	888	10	35	2023-12-28 10:00:00	Other
27725	8	14	602	605	-3	805	819	UA	493	N62892	EWR	DEN	223	1605	6	5	2023-08-14 06:00:00	Other
27727	9	15	1151	1154	-3	1253	1310	UA	265	N37530	EWR	BOS	38	200	11	54	2023-09-15 11:00:00	BOS
27731	6	22	802	805	-3	1021	1009	AA	607	N855NN	EWR	CLT	93	529	8	5	2023-06-22 08:00:00	CLT
27736	10	20	644	646	-2	907	918	AA	510	N331TK	JFK	PHX	291	2153	6	46	2023-10-20 06:00:00	Other
27752	9	3	1554	1556	-2	1744	1751	YX	1052	N725YX	EWR	CMH	68	463	15	56	2023-09-03 15:00:00	Other
27754	3	20	1342	1345	-3	1510	1534	YX	1256	N434YX	LGA	CLE	67	419	13	45	2023-03-20 13:00:00	Other
27757	11	8	956	1000	-4	1320	1312	DL	259	N172DN	JFK	LAX	340	2475	10	0	2023-11-08 10:00:00	LAX
27761	9	25	1224	1229	-5	1414	1419	9E	1499	N601LR	JFK	RDU	69	427	12	29	2023-09-25 12:00:00	Other
27766	10	20	1857	1859	-2	2218	2155	UA	873	N81449	EWR	PBI	147	1023	18	59	2023-10-20 18:00:00	Other
27767	3	21	2025	2029	-4	2201	2210	UA	533	N24702	EWR	CLE	64	404	20	29	2023-03-21 20:00:00	Other
27775	5	2	1138	1140	-2	1425	1455	DL	201	N174DN	JFK	LAX	318	2475	11	40	2023-05-02 11:00:00	LAX
27783	11	29	913	915	-2	1031	1053	UA	230	N73251	LGA	ORD	115	733	9	15	2023-11-29 09:00:00	ORD
27784	4	28	626	630	-4	902	957	DL	298	N110DX	JFK	SLC	259	1990	6	30	2023-04-28 06:00:00	Other
27795	9	16	555	600	-5	847	915	AA	432	N308RD	LGA	MIA	144	1096	6	0	2023-09-16 06:00:00	MIA
27802	11	26	1655	1659	-4	1908	1857	YX	1903	N220JQ	LGA	RDU	87	431	16	59	2023-11-26 16:00:00	Other
27805	11	16	758	800	-2	1031	1113	B6	78	N2060J	JFK	IAH	181	1417	8	0	2023-11-16 08:00:00	Other
27807	7	13	1057	1100	-3	1336	1403	NK	438	N672NK	EWR	FLL	138	1065	11	0	2023-07-13 11:00:00	FLL
27815	10	22	854	859	-5	1147	1210	UA	560	N76502	EWR	SAT	210	1569	8	59	2023-10-22 08:00:00	Other
27821	4	13	1825	1830	-5	2020	2101	UA	779	N34137	EWR	DEN	206	1605	18	30	2023-04-13 18:00:00	Other
27825	12	3	1717	1720	-3	2003	2002	B6	828	N585JB	LGA	JAX	137	833	17	20	2023-12-03 17:00:00	Other
27833	6	28	855	900	-5	1021	1024	9E	1550	N195PQ	JFK	IAD	48	228	9	0	2023-06-28 09:00:00	Other
27838	1	25	1455	1500	-5	1712	1730	B6	895	N3077J	JFK	MCI	176	1113	15	0	2023-01-25 15:00:00	Other
27842	11	7	1234	1237	-3	1520	1533	NK	469	N616NK	LGA	IAH	192	1416	12	37	2023-11-07 12:00:00	Other
27849	2	20	1858	1900	-2	2109	2127	9E	1409	N310PQ	JFK	IND	112	665	19	0	2023-02-20 19:00:00	Other
27857	11	11	1555	1559	-4	1927	1916	AA	568	N957AN	LGA	DFW	210	1389	15	59	2023-11-11 15:00:00	Other
27859	4	28	1033	1035	-2	1248	1305	WN	589	N265WN	LGA	ATL	116	762	10	35	2023-04-28 10:00:00	ATL
27860	7	23	812	815	-3	1249	1300	UA	113	N69063	EWR	HNL	588	4962	8	15	2023-07-23 08:00:00	Other
27868	2	7	1813	1815	-2	2058	2132	NK	661	N673NK	EWR	FLL	142	1065	18	15	2023-02-07 18:00:00	FLL
27876	12	7	757	800	-3	943	1020	AA	518	N931NN	JFK	CLT	82	541	8	0	2023-12-07 08:00:00	CLT
27878	6	18	1455	1459	-4	1657	1705	AA	142	N9012	JFK	CLT	83	541	14	59	2023-06-18 14:00:00	CLT
27885	1	8	657	700	-3	953	1024	B6	321	N987JT	JFK	LAX	326	2475	7	0	2023-01-08 07:00:00	LAX
27905	7	30	557	600	-3	852	859	B6	428	N556JB	LGA	FLL	153	1076	6	0	2023-07-30 06:00:00	FLL
27907	11	21	1243	1245	-2	1419	1435	WN	593	N7842A	LGA	STL	137	888	12	45	2023-11-21 12:00:00	Other
27921	10	28	1327	1329	-2	1637	1601	AA	972	N318TD	JFK	PHX	329	2153	13	29	2023-10-28 13:00:00	Other
27926	9	25	1452	1456	-4	1717	1719	OO	1254	N296SY	JFK	IND	101	665	14	56	2023-09-25 14:00:00	Other
27929	2	19	1022	1025	-3	1139	1205	YX	1578	N224JQ	LGA	DCA	47	214	10	25	2023-02-19 10:00:00	Other
27938	5	15	943	945	-2	1259	1326	DL	97	N722TW	JFK	SFO	343	2586	9	45	2023-05-15 09:00:00	Other
27952	5	15	755	800	-5	947	1020	YX	1586	N227JQ	JFK	CLT	81	541	8	0	2023-05-15 08:00:00	CLT
27958	1	17	1826	1830	-4	2002	2031	YX	1814	N221JQ	JFK	ORD	122	740	18	30	2023-01-17 18:00:00	ORD
27963	1	13	1626	1630	-4	1849	1900	9E	1542	N313PQ	LGA	AVL	100	599	16	30	2023-01-13 16:00:00	Other
27966	9	22	625	630	-5	925	920	UA	819	N488UA	EWR	DFW	189	1372	6	30	2023-09-22 06:00:00	Other
27970	1	27	1413	1417	-4	1523	1522	YX	1209	N743YX	EWR	ALB	37	143	14	17	2023-01-27 14:00:00	Other
27972	9	22	757	759	-2	1042	1054	AA	309	N843NN	JFK	DFW	194	1391	7	59	2023-09-22 07:00:00	Other
27974	2	7	732	735	-3	945	1011	UA	861	N36444	EWR	ATL	110	746	7	35	2023-02-07 07:00:00	ATL
27979	1	7	1631	1636	-5	1920	2010	DL	289	N710TW	JFK	SLC	264	1990	16	36	2023-01-07 16:00:00	Other
27982	1	26	728	730	-2	1027	1054	AA	1	N111ZM	JFK	LAX	323	2475	7	30	2023-01-26 07:00:00	LAX
27987	5	9	1921	1925	-4	2213	2150	YX	1249	N406YX	LGA	XNA	168	1147	19	25	2023-05-09 19:00:00	Other
27988	8	23	758	800	-2	916	938	YX	854	N753YX	EWR	MKE	107	725	8	0	2023-08-23 08:00:00	Other
27993	2	9	1957	1959	-2	2259	2308	NK	187	N679NK	LGA	MCO	144	950	19	59	2023-02-09 19:00:00	MCO
27998	12	14	1758	1800	-2	2113	2125	UA	871	N17126	EWR	LAX	321	2454	18	0	2023-12-14 18:00:00	LAX
28012	10	27	1411	1415	-4	1519	1533	B6	286	N306JB	LGA	BOS	43	184	14	15	2023-10-27 14:00:00	BOS
28016	12	5	2106	2110	-4	2218	2232	9E	1510	N909XJ	JFK	BWI	42	184	21	10	2023-12-05 21:00:00	Other
28019	9	26	955	959	-4	1309	1310	AA	250	N317PG	JFK	MIA	172	1089	9	59	2023-09-26 09:00:00	MIA
28022	7	12	924	929	-5	1203	1220	AA	508	N995NN	LGA	DFW	177	1389	9	29	2023-07-12 09:00:00	Other
28023	8	8	656	700	-4	825	818	YX	1352	N878RW	LGA	DCA	45	214	7	0	2023-08-08 07:00:00	Other
28033	1	14	1655	1659	-4	1847	1848	B6	493	N307JB	JFK	RDU	75	427	16	59	2023-01-14 16:00:00	Other
28040	7	19	1305	1307	-2	1548	1556	UA	172	N67134	EWR	MCO	125	937	13	7	2023-07-19 13:00:00	MCO
28041	2	20	958	1000	-2	1156	1207	B6	65	N355JB	JFK	DTW	97	509	10	0	2023-02-20 10:00:00	Other
28060	2	9	1452	1455	-3	1706	1657	9E	1324	N604LR	JFK	CLE	78	425	14	55	2023-02-09 14:00:00	Other
28062	10	9	1339	1343	-4	1457	1518	9E	1681	N297PQ	JFK	BGR	60	382	13	43	2023-10-09 13:00:00	Other
28064	9	1	1913	1915	-2	2158	2210	AA	370	N971AN	LGA	DFW	186	1389	19	15	2023-09-01 19:00:00	Other
28067	11	22	755	759	-4	1122	1116	UA	684	N37555	EWR	MIA	180	1085	7	59	2023-11-22 07:00:00	MIA
28070	3	11	1207	1210	-3	1412	1445	WN	395	N8319F	LGA	ATL	105	762	12	10	2023-03-11 12:00:00	ATL
28076	10	8	2120	2123	-3	2200	2230	YX	1073	N753YX	EWR	PHL	20	80	21	23	2023-10-08 21:00:00	Other
28079	1	26	617	620	-3	924	927	UA	311	N13138	EWR	FLL	170	1065	6	20	2023-01-26 06:00:00	FLL
28080	10	16	922	927	-5	1100	1130	YX	1862	N201JQ	LGA	CMH	69	479	9	27	2023-10-16 09:00:00	Other
28083	2	23	557	601	-4	849	914	B6	913	N638JB	JFK	FLL	150	1069	6	1	2023-02-23 06:00:00	FLL
28089	7	29	1458	1500	-2	1709	1727	YX	1091	N118HQ	LGA	IND	112	660	15	0	2023-07-29 15:00:00	Other
28096	7	24	1535	1539	-4	1831	1844	UA	462	N27256	EWR	FLL	150	1065	15	39	2023-07-24 15:00:00	FLL
28101	5	30	1051	1055	-4	1154	1212	YX	1681	N815MD	JFK	ACK	39	199	10	55	2023-05-30 10:00:00	Other
28108	4	20	1345	1349	-4	1447	1457	9E	1224	N478PX	LGA	BGM	42	147	13	49	2023-04-20 13:00:00	Other
28110	8	9	1222	1225	-3	1433	1435	WN	360	N8684F	LGA	DEN	220	1620	12	25	2023-08-09 12:00:00	Other
28115	1	19	657	700	-3	1005	1009	B6	409	N656JB	JFK	PBI	144	1028	7	0	2023-01-19 07:00:00	Other
28117	1	15	728	730	-2	1038	1055	DL	105	N900DU	JFK	SEA	321	2422	7	30	2023-01-15 07:00:00	Other
28127	6	7	1030	1035	-5	1156	1216	AA	148	N905AN	LGA	ORD	109	733	10	35	2023-06-07 10:00:00	ORD
28132	8	22	1528	1530	-2	1729	1812	B6	520	N284JB	JFK	ATL	99	760	15	30	2023-08-22 15:00:00	ATL
28134	1	26	2117	2122	-5	2324	2327	UA	742	N66828	EWR	CLT	99	529	21	22	2023-01-26 21:00:00	CLT
28139	9	27	954	959	-5	1157	1214	9E	1568	N348PQ	JFK	IND	100	665	9	59	2023-09-27 09:00:00	Other
28141	7	5	634	639	-5	902	918	UA	665	N855UA	EWR	DFW	179	1372	6	39	2023-07-05 06:00:00	Other
28166	7	26	810	814	-4	1003	1020	9E	1170	N915XJ	LGA	GSP	91	610	8	14	2023-07-26 08:00:00	Other
28167	11	26	1854	1859	-5	2202	2144	DL	199	N395DZ	LGA	ATL	137	762	18	59	2023-11-26 18:00:00	ATL
28177	10	22	2124	2129	-5	2243	2248	YX	1352	N115HQ	LGA	BUF	53	292	21	29	2023-10-22 21:00:00	Other
28178	1	20	822	825	-3	1045	1107	YX	1299	N418YX	JFK	CVG	104	589	8	25	2023-01-20 08:00:00	Other
28179	5	6	1000	1005	-5	1243	1312	B6	901	N599JB	JFK	MIA	140	1089	10	5	2023-05-06 10:00:00	MIA
28180	4	12	1039	1041	-2	1223	1250	UA	339	N16713	EWR	CHS	82	628	10	41	2023-04-12 10:00:00	Other
28181	2	27	1552	1555	-3	1706	1735	WN	851	N8835Q	LGA	MDW	113	725	15	55	2023-02-27 15:00:00	Other
28187	4	16	601	606	-5	858	902	UA	780	N37462	EWR	TPA	138	997	6	6	2023-04-16 06:00:00	Other
28188	1	5	1147	1150	-3	1348	1329	YX	1790	N208JQ	LGA	RIC	67	292	11	50	2023-01-05 11:00:00	Other
28197	10	24	810	812	-2	1116	1053	B6	128	N976JT	JFK	LAS	312	2248	8	12	2023-10-24 08:00:00	Other
28203	11	25	1025	1027	-2	1325	1336	DL	378	N364DX	LGA	TPA	162	1010	10	27	2023-11-25 10:00:00	Other
28204	4	18	1341	1345	-4	1638	1709	YX	1236	N870RW	LGA	IAH	212	1416	13	45	2023-04-18 13:00:00	Other
28210	11	2	1445	1449	-4	1644	1655	AA	510	N945AN	JFK	CLT	86	541	14	49	2023-11-02 14:00:00	CLT
28219	1	29	857	900	-3	1215	1229	B6	364	N968JT	JFK	LAX	351	2475	9	0	2023-01-29 09:00:00	LAX
28231	3	22	1527	1529	-2	1640	1633	YX	1032	N723YX	EWR	PVD	36	160	15	29	2023-03-22 15:00:00	Other
28242	7	20	601	605	-4	807	819	UA	516	N33292	EWR	DEN	224	1605	6	5	2023-07-20 06:00:00	Other
28244	6	14	626	630	-4	737	741	B6	199	N265JB	JFK	BOS	40	187	6	30	2023-06-14 06:00:00	BOS
28247	11	15	757	800	-3	943	1019	AA	508	N965AN	JFK	CLT	86	541	8	0	2023-11-15 08:00:00	CLT
28248	6	7	823	828	-5	939	959	9E	1481	N301PQ	LGA	BUF	52	292	8	28	2023-06-07 08:00:00	Other
28263	4	22	1757	1800	-3	2123	2110	DL	338	N335NB	JFK	DFW	211	1391	18	0	2023-04-22 18:00:00	Other
28266	6	15	700	705	-5	901	932	UA	459	N27266	EWR	PHX	279	2133	7	5	2023-06-15 07:00:00	Other
28272	9	22	647	652	-5	900	905	YX	1168	N760YX	EWR	IND	92	645	6	52	2023-09-22 06:00:00	Other
28282	2	8	945	950	-5	1052	1118	9E	1452	N607LR	JFK	SYR	48	209	9	50	2023-02-08 09:00:00	Other
28288	2	12	732	735	-3	1038	1049	DL	448	N351DN	JFK	FLL	159	1069	7	35	2023-02-12 07:00:00	FLL
28296	11	26	1057	1100	-3	1353	1420	DL	175	N502DX	JFK	SEA	320	2422	11	0	2023-11-26 11:00:00	Other
28302	8	13	1358	1400	-2	1558	1615	DL	650	N386DA	EWR	ATL	97	746	14	0	2023-08-13 14:00:00	ATL
28307	3	6	2250	2255	-5	2359	3	YX	1634	N215JQ	JFK	BWI	42	184	22	55	2023-03-06 22:00:00	Other
28315	8	27	1825	1829	-4	2130	2109	YX	1023	N443YX	LGA	OKC	202	1341	18	29	2023-08-27 18:00:00	Other
28320	4	16	842	845	-3	1041	1051	9E	1440	N181GJ	LGA	AVL	92	599	8	45	2023-04-16 08:00:00	Other
28321	3	23	1745	1750	-5	2132	2131	AA	953	N107NN	JFK	SFO	378	2586	17	50	2023-03-23 17:00:00	Other
28322	2	9	1127	1130	-3	1430	1449	DL	471	N323US	LGA	SRQ	165	1047	11	30	2023-02-09 11:00:00	Other
28323	8	6	2036	2040	-4	2204	2218	9E	1216	N320PQ	LGA	CHO	62	305	20	40	2023-08-06 20:00:00	Other
28333	3	18	655	700	-5	1004	1015	B6	145	N594JB	EWR	FLL	157	1065	7	0	2023-03-18 07:00:00	FLL
28336	3	23	1133	1135	-2	1405	1435	DL	467	N345NW	JFK	TPA	134	1005	11	35	2023-03-23 11:00:00	Other
28340	12	17	740	744	-4	938	952	AA	673	N810NN	EWR	CLT	95	529	7	44	2023-12-17 07:00:00	CLT
28342	3	2	1026	1029	-3	1349	1256	YX	1046	N751YX	EWR	IND	134	645	10	29	2023-03-02 10:00:00	Other
28345	5	18	851	855	-4	1131	1222	AA	342	N106NN	JFK	SNA	311	2454	8	55	2023-05-18 08:00:00	Other
28347	12	11	2156	2159	-3	2312	2315	UA	73	N77431	EWR	BOS	41	200	21	59	2023-12-11 21:00:00	BOS
28348	2	15	624	629	-5	844	805	UA	606	N847UA	LGA	ORD	159	733	6	29	2023-02-15 06:00:00	ORD
28352	11	20	627	630	-3	906	926	UA	302	N14106	EWR	MCO	132	937	6	30	2023-11-20 06:00:00	MCO
28365	8	18	856	900	-4	1024	1037	UA	204	N33264	LGA	ORD	109	733	9	0	2023-08-18 09:00:00	ORD
28368	6	8	1057	1100	-3	1400	1416	B6	203	N2105J	JFK	LAX	310	2475	11	0	2023-06-08 11:00:00	LAX
28378	2	12	1028	1030	-2	1132	1146	YX	1490	N240JQ	JFK	BOS	41	187	10	30	2023-02-12 10:00:00	BOS
28380	6	23	1453	1455	-2	1701	1702	9E	1722	N187GJ	JFK	CLE	73	425	14	55	2023-06-23 14:00:00	Other
28381	2	12	1542	1545	-3	1713	1720	YX	1247	N406YX	JFK	DCA	62	213	15	45	2023-02-12 15:00:00	Other
28386	8	19	658	700	-2	849	912	UA	116	N75433	EWR	DEN	208	1605	7	0	2023-08-19 07:00:00	Other
28387	2	13	937	940	-3	1427	1444	UA	583	N62896	EWR	SJU	206	1608	9	40	2023-02-13 09:00:00	Other
28388	5	27	955	1000	-5	1057	1123	YX	1164	N729YX	EWR	DCA	37	199	10	0	2023-05-27 10:00:00	Other
28389	10	12	1956	2000	-4	2132	2140	YX	1044	N731YX	EWR	PIT	57	319	20	0	2023-10-12 20:00:00	Other
28393	10	16	1154	1159	-5	1319	1341	9E	1368	N335PQ	LGA	PIT	52	335	11	59	2023-10-16 11:00:00	Other
28401	12	21	1518	1520	-2	1804	1834	UA	782	N13110	EWR	IAH	198	1400	15	20	2023-12-21 15:00:00	Other
28403	6	15	1341	1344	-3	1527	1543	AA	664	N553UW	EWR	CLT	76	529	13	44	2023-06-15 13:00:00	CLT
28406	6	30	1045	1050	-5	1208	1223	YX	1383	N427YX	JFK	BNA	103	765	10	50	2023-06-30 10:00:00	Other
28408	8	9	1141	1143	-2	1418	1433	NK	816	N639NK	EWR	MCO	129	937	11	43	2023-08-09 11:00:00	MCO
28415	11	7	1051	1055	-4	1236	1257	YX	1049	N733YX	EWR	MYR	84	550	10	55	2023-11-07 10:00:00	Other
28420	3	21	802	806	-4	920	935	B6	59	N355JB	JFK	ROC	59	264	8	6	2023-03-21 08:00:00	Other
28421	2	26	1006	1010	-4	1304	1322	DL	943	N344DN	LGA	MCO	145	950	10	10	2023-02-26 10:00:00	MCO
28422	5	30	1203	1205	-2	1404	1435	UA	620	N495UA	LGA	DEN	204	1620	12	5	2023-05-30 12:00:00	Other
28441	12	15	1712	1715	-3	1849	1854	UA	833	N803UA	LGA	ORD	115	733	17	15	2023-12-15 17:00:00	ORD
28442	4	7	2106	2109	-3	2341	2348	YX	1045	N655RW	EWR	JAX	125	820	21	9	2023-04-07 21:00:00	Other
28443	3	11	1453	1455	-2	1548	1611	OO	1277	N313SY	JFK	BWI	39	184	14	55	2023-03-11 14:00:00	Other
28444	12	20	555	600	-5	656	729	AA	231	N822AW	LGA	DCA	40	214	6	0	2023-12-20 06:00:00	Other
28465	3	12	1158	1200	-2	1516	1515	DL	210	N185DN	JFK	LAX	338	2475	12	0	2023-03-12 12:00:00	LAX
28466	8	22	2125	2130	-5	2312	2338	YX	910	N733YX	EWR	DTW	78	488	21	30	2023-08-22 21:00:00	Other
28472	4	2	1543	1545	-2	1809	1824	DL	310	N398DN	LGA	ATL	117	762	15	45	2023-04-02 15:00:00	ATL
28489	5	20	1340	1345	-5	1450	1524	9E	1452	N490PX	LGA	ORF	56	296	13	45	2023-05-20 13:00:00	Other
28490	8	5	456	500	-4	635	658	AA	725	N871NN	EWR	CLT	76	529	5	0	2023-08-05 05:00:00	CLT
28495	10	20	557	600	-3	817	823	DL	429	N549US	JFK	ATL	112	760	6	0	2023-10-20 06:00:00	ATL
28499	9	25	927	929	-2	1155	1154	YX	1206	N753YX	EWR	HHH	99	687	9	29	2023-09-25 09:00:00	Other
28501	11	2	1954	1958	-4	2254	2308	DL	339	N774DE	LGA	MIA	155	1096	19	58	2023-11-02 19:00:00	MIA
28503	1	6	925	930	-5	1320	1310	AA	413	N105NN	JFK	SNA	376	2454	9	30	2023-01-06 09:00:00	Other
28512	6	12	1450	1455	-5	1702	1722	YX	1807	N882RW	JFK	CLT	93	541	14	55	2023-06-12 14:00:00	CLT
28522	1	28	927	929	-2	1225	1239	UA	572	N23721	EWR	TPA	152	997	9	29	2023-01-28 09:00:00	Other
28527	5	28	1326	1329	-3	1537	1534	YX	1075	N657RW	EWR	DTW	74	488	13	29	2023-05-28 13:00:00	Other
28529	6	29	757	800	-3	1029	1026	B6	995	N613JB	LGA	ATL	100	762	8	0	2023-06-29 08:00:00	ATL
28544	12	30	1910	1915	-5	2208	2219	UA	482	N36476	EWR	PBI	144	1023	19	15	2023-12-30 19:00:00	Other
28548	7	17	1026	1030	-4	1323	1334	DL	539	N112DU	JFK	SAT	218	1587	10	30	2023-07-17 10:00:00	Other
28550	11	18	1110	1112	-2	1409	1428	DL	476	N103DY	JFK	MIA	153	1089	11	12	2023-11-18 11:00:00	MIA
28555	7	24	1104	1108	-4	1402	1407	UA	225	N37278	EWR	PBI	144	1023	11	8	2023-07-24 11:00:00	Other
28557	1	3	702	705	-3	835	850	UA	560	N19117	EWR	ORD	119	719	7	5	2023-01-03 07:00:00	ORD
28558	1	20	1559	1603	-4	1855	1911	UA	930	N78540	EWR	DFW	210	1372	16	3	2023-01-20 16:00:00	Other
28563	3	13	1206	1210	-4	1338	1349	YX	1276	N438YX	LGA	BNA	121	764	12	10	2023-03-13 12:00:00	Other
28572	3	26	556	600	-4	755	757	AA	956	N111US	EWR	CLT	88	529	6	0	2023-03-26 06:00:00	CLT
28578	11	27	1725	1729	-4	2026	2027	UA	779	N24202	EWR	MCO	141	937	17	29	2023-11-27 17:00:00	MCO
28581	8	5	826	830	-4	945	948	B6	760	N193JB	JFK	BOS	36	187	8	30	2023-08-05 08:00:00	BOS
28582	2	20	555	600	-5	800	809	AA	260	N509AY	LGA	CLT	93	544	6	0	2023-02-20 06:00:00	CLT
28584	1	16	901	905	-4	1022	1033	YX	1131	N656RW	EWR	SYR	41	195	9	5	2023-01-16 09:00:00	Other
28587	11	21	656	700	-4	1027	1015	DL	921	N347NW	JFK	AUS	238	1521	7	0	2023-11-21 07:00:00	Other
28589	5	3	715	720	-5	912	956	DL	167	N387DA	LGA	DEN	210	1620	7	20	2023-05-03 07:00:00	Other
28601	3	10	920	925	-5	1022	1050	9E	1339	N302PQ	JFK	IAD	45	228	9	25	2023-03-10 09:00:00	Other
28617	8	14	813	815	-2	924	932	B6	95	N348JB	LGA	BOS	39	184	8	15	2023-08-14 08:00:00	BOS
28623	1	25	946	951	-5	1150	1205	UA	716	N439UA	EWR	CHS	102	628	9	51	2023-01-25 09:00:00	Other
28631	2	28	756	800	-4	906	927	YX	1556	N226JQ	LGA	BOS	35	184	8	0	2023-02-28 08:00:00	BOS
28633	8	6	2146	2150	-4	2242	2251	9E	1131	N490PX	LGA	BGM	34	147	21	50	2023-08-06 21:00:00	Other
28641	1	12	703	707	-4	840	854	YX	1234	N655RW	EWR	CLE	71	404	7	7	2023-01-12 07:00:00	Other
28650	4	20	1324	1329	-5	1553	1548	YX	1160	N431YX	LGA	MCI	165	1107	13	29	2023-04-20 13:00:00	Other
28652	2	1	2154	2158	-4	2256	2312	UA	896	N68822	EWR	SYR	36	195	21	58	2023-02-01 21:00:00	Other
28655	9	8	811	815	-4	957	1006	OO	1282	N322SY	JFK	ORD	119	740	8	15	2023-09-08 08:00:00	ORD
28657	10	13	2153	2155	-2	110	119	B6	912	N979JT	JFK	SFO	351	2586	21	55	2023-10-13 21:00:00	Other
28668	3	12	828	830	-2	1014	1017	OO	1217	N255SY	JFK	BNA	135	765	8	30	2023-03-12 08:00:00	Other
28676	3	31	1325	1329	-4	1458	1522	9E	1425	N197PQ	LGA	RDU	70	431	13	29	2023-03-31 13:00:00	Other
28677	7	6	855	900	-5	1008	1024	9E	1185	N605LR	JFK	IAD	41	228	9	0	2023-07-06 09:00:00	Other
28678	9	8	1126	1130	-4	1435	1446	AA	643	N944NN	LGA	MIA	149	1096	11	30	2023-09-08 11:00:00	MIA
28696	6	5	1156	1201	-5	1319	1339	9E	1557	N138EV	JFK	BUF	55	301	12	1	2023-06-05 12:00:00	Other
28702	3	11	1756	1800	-4	1947	2001	YX	1128	N729YX	EWR	CMH	77	463	18	0	2023-03-11 18:00:00	Other
28717	7	13	1238	1240	-2	1407	1420	WN	964	N478WN	LGA	STL	133	888	12	40	2023-07-13 12:00:00	Other
28718	9	21	1551	1555	-4	1706	1740	AA	833	N964AN	JFK	ORD	112	740	15	55	2023-09-21 15:00:00	ORD
28720	10	10	1956	1959	-3	2252	2319	DL	579	N305DN	JFK	FLL	149	1069	19	59	2023-10-10 19:00:00	FLL
28724	11	24	823	825	-2	1127	1126	UA	469	N662UA	EWR	MCO	148	937	8	25	2023-11-24 08:00:00	MCO
28730	2	20	1057	1059	-2	1408	1400	DL	570	N355DN	JFK	MCO	136	944	10	59	2023-02-20 10:00:00	MCO
28734	4	1	945	950	-5	1249	1232	YX	1462	N879RW	LGA	HHH	121	701	9	50	2023-04-01 09:00:00	Other
28737	5	5	1057	1059	-2	1214	1240	9E	1494	N936XJ	LGA	RIC	54	292	10	59	2023-05-05 10:00:00	Other
28751	2	16	1007	1012	-5	1153	1151	UA	669	N27270	EWR	ORD	129	719	10	12	2023-02-16 10:00:00	ORD
28753	6	13	1346	1348	-2	1651	1703	B6	135	N505JB	LGA	FLL	164	1076	13	48	2023-06-13 13:00:00	FLL
28766	6	23	458	500	-2	801	808	AA	439	N928NN	EWR	MIA	150	1085	5	0	2023-06-23 05:00:00	MIA
28768	8	29	1326	1330	-4	1602	1623	UA	591	N797UA	EWR	SFO	313	2565	13	30	2023-08-29 13:00:00	Other
28769	3	10	735	740	-5	1042	1047	NK	856	N941NK	EWR	AUS	230	1504	7	40	2023-03-10 07:00:00	Other
28771	2	2	1624	1629	-5	1928	1946	B6	716	N355JB	LGA	PBI	166	1035	16	29	2023-02-02 16:00:00	Other
28777	12	20	1356	1400	-4	1549	1614	YX	1280	N123HQ	LGA	CAE	89	617	14	0	2023-12-20 14:00:00	Other
28781	10	22	1435	1438	-3	1556	1612	YX	1867	N239JQ	LGA	PIT	58	335	14	38	2023-10-22 14:00:00	Other
28786	3	4	1325	1330	-5	1450	1504	9E	1477	N147PQ	JFK	BUF	61	301	13	30	2023-03-04 13:00:00	Other
28787	8	13	655	700	-5	1006	1022	DL	153	N704X	JFK	SFO	339	2586	7	0	2023-08-13 07:00:00	Other
28798	10	23	811	815	-4	1054	1116	AA	314	N803NN	LGA	DFW	191	1389	8	15	2023-10-23 08:00:00	Other
28801	3	26	1439	1441	-2	1600	1609	YX	1063	N643RW	EWR	RIC	55	277	14	41	2023-03-26 14:00:00	Other
28803	6	10	1514	1518	-4	1708	1722	YX	1318	N420YX	JFK	RDU	67	427	15	18	2023-06-10 15:00:00	Other
28825	9	26	606	610	-4	741	743	DL	444	N130DU	LGA	ORD	114	733	6	10	2023-09-26 06:00:00	ORD
28826	7	14	1127	1129	-2	1251	1237	YX	1074	N127HQ	JFK	ORH	36	150	11	29	2023-07-14 11:00:00	Other
28830	11	13	755	800	-5	1050	1115	DL	170	N1200K	JFK	LAX	323	2475	8	0	2023-11-13 08:00:00	LAX
28831	6	3	1257	1300	-3	1442	1509	UA	937	N879UA	EWR	MSY	150	1167	13	0	2023-06-03 13:00:00	Other
28832	8	3	1020	1025	-5	1234	1240	DL	653	N3733Z	EWR	ATL	104	746	10	25	2023-08-03 10:00:00	ATL
28834	1	7	954	959	-5	1337	1313	B6	888	N994JL	JFK	FLL	141	1069	9	59	2023-01-07 09:00:00	FLL
28838	5	6	1852	1855	-3	2142	2206	AS	12	N933AK	JFK	SAN	329	2446	18	55	2023-05-06 18:00:00	Other
28840	7	25	1357	1401	-4	1739	1607	YX	859	N864RW	EWR	GRR	91	605	14	1	2023-07-25 14:00:00	Other
28844	1	22	1442	1445	-3	1557	1618	9E	1625	N299PQ	LGA	BGR	54	378	14	45	2023-01-22 14:00:00	Other
28845	10	15	800	805	-5	1013	1029	UA	819	N77559	EWR	DEN	213	1605	8	5	2023-10-15 08:00:00	Other
28852	4	25	1647	1652	-5	1902	1853	9E	1334	N303PQ	LGA	AVL	92	599	16	52	2023-04-25 16:00:00	Other
28861	3	18	1733	1735	-2	2051	2031	UA	385	N424UA	EWR	TPA	164	997	17	35	2023-03-18 17:00:00	Other
28862	1	14	701	705	-4	936	1014	DL	741	N353NW	LGA	TPA	134	1010	7	5	2023-01-14 07:00:00	Other
28869	1	6	952	955	-3	1146	1208	G4	785	260NV	EWR	AVL	92	583	9	55	2023-01-06 09:00:00	Other
28871	10	21	2154	2159	-5	2336	2350	UA	363	N17752	EWR	MEM	133	946	21	59	2023-10-21 21:00:00	Other
28872	3	1	1755	1759	-4	2042	2028	YX	1298	N410YX	LGA	MCI	199	1107	17	59	2023-03-01 17:00:00	Other
28876	4	18	1624	1629	-5	1925	1947	B6	134	N547JB	LGA	FLL	153	1076	16	29	2023-04-18 16:00:00	FLL
28879	2	28	1248	1250	-2	1555	1558	UA	687	N76519	EWR	MIA	145	1085	12	50	2023-02-28 12:00:00	MIA
28881	2	17	628	630	-2	850	858	UA	437	N24224	EWR	JAX	122	820	6	30	2023-02-17 06:00:00	Other
28882	3	9	706	710	-4	901	915	AA	321	N939AN	LGA	CLT	77	544	7	10	2023-03-09 07:00:00	CLT
28885	5	17	955	1000	-5	1140	1141	YX	1311	N406YX	JFK	BNA	122	765	10	0	2023-05-17 10:00:00	Other
28892	4	26	1325	1329	-4	1555	1601	DL	197	N315DN	LGA	ATL	119	762	13	29	2023-04-26 13:00:00	ATL
28915	11	4	1337	1342	-5	1535	1544	AA	606	N909AN	EWR	CLT	88	529	13	42	2023-11-04 13:00:00	CLT
28929	10	19	1653	1655	-2	1924	2004	B6	106	N634JB	JFK	BUR	307	2465	16	55	2023-10-19 16:00:00	Other
28945	5	5	1041	1045	-4	1254	1207	9E	1505	N602LR	JFK	BTV	44	266	10	45	2023-05-05 10:00:00	Other
28948	9	8	756	759	-3	1102	1054	AA	309	N800NN	JFK	DFW	213	1391	7	59	2023-09-08 07:00:00	Other
28950	7	24	1056	1100	-4	1412	1430	DL	266	N707TW	JFK	SFO	327	2586	11	0	2023-07-24 11:00:00	Other
28952	4	4	1430	1434	-4	1653	1651	NK	788	N618NK	EWR	MSY	183	1167	14	34	2023-04-04 14:00:00	Other
28981	7	10	457	500	-3	646	658	AA	744	N123NN	EWR	CLT	82	529	5	0	2023-07-10 05:00:00	CLT
28989	6	30	1811	1815	-4	2108	2105	AA	210	N915AN	LGA	DFW	199	1389	18	15	2023-06-30 18:00:00	Other
28993	1	30	1053	1055	-2	1208	1233	YX	1904	N810MD	LGA	ORF	57	296	10	55	2023-01-30 10:00:00	Other
28996	2	10	1027	1031	-4	1245	1305	DL	788	N3732J	EWR	ATL	119	746	10	31	2023-02-10 10:00:00	ATL
28999	10	18	1446	1450	-4	1629	1654	9E	1502	N325PQ	JFK	CLT	77	541	14	50	2023-10-18 14:00:00	CLT
29009	8	29	2026	2030	-4	2242	2234	9E	1180	N302PQ	LGA	CAE	94	617	20	30	2023-08-29 20:00:00	Other
29017	5	10	630	635	-5	744	810	9E	1307	N491PX	LGA	PIT	56	335	6	35	2023-05-10 06:00:00	Other
29018	8	24	731	735	-4	934	1000	DL	168	N3742C	LGA	DEN	208	1620	7	35	2023-08-24 07:00:00	Other
29021	8	30	825	830	-5	1116	1140	UA	530	N41135	EWR	SEA	316	2402	8	30	2023-08-30 08:00:00	Other
29026	3	5	1805	1810	-5	2026	2039	9E	1564	N301PQ	JFK	CVG	104	589	18	10	2023-03-05 18:00:00	Other
29036	8	29	1831	1835	-4	2026	2045	DL	773	N943AT	EWR	MSP	147	1008	18	35	2023-08-29 18:00:00	Other
29043	1	9	602	607	-5	729	724	YX	1879	N234JQ	JFK	BOS	41	187	6	7	2023-01-09 06:00:00	BOS
29044	3	8	654	659	-5	955	1031	B6	722	N612JB	LGA	RSW	155	1080	6	59	2023-03-08 06:00:00	Other
29051	11	9	720	724	-4	1022	1000	UA	235	N844UA	LGA	DEN	272	1620	7	24	2023-11-09 07:00:00	Other
29055	6	2	1257	1301	-4	1812	1556	UA	814	N476UA	EWR	TPA	NA	997	13	1	2023-06-02 13:00:00	Other
29059	12	4	1128	1130	-2	1431	1434	DL	984	N310DN	LGA	MCO	158	950	11	30	2023-12-04 11:00:00	MCO
29063	9	27	625	630	-5	906	924	NK	510	N656NK	EWR	MCO	140	937	6	30	2023-09-27 06:00:00	MCO
29065	4	7	1741	1743	-2	2022	2042	UA	351	N79541	EWR	TPA	140	997	17	43	2023-04-07 17:00:00	Other
29068	1	6	1525	1530	-5	1642	1712	B6	296	N3102J	JFK	MKE	119	745	15	30	2023-01-06 15:00:00	Other
29078	5	24	658	700	-2	918	924	DL	216	N389DN	LGA	ATL	112	762	7	0	2023-05-24 07:00:00	ATL
29081	12	13	1917	1920	-3	2221	2306	AS	82	N949AK	EWR	SFO	329	2565	19	20	2023-12-13 19:00:00	Other
29087	2	25	810	815	-5	923	950	YX	1550	N215JQ	LGA	DCA	50	214	8	15	2023-02-25 08:00:00	Other
29091	8	27	728	730	-2	1003	1023	B6	39	N516JB	EWR	PBI	135	1023	7	30	2023-08-27 07:00:00	Other
29095	7	24	935	940	-5	1156	1208	9E	1267	N601LR	JFK	IND	95	665	9	40	2023-07-24 09:00:00	Other
29098	7	27	1254	1259	-5	1451	1450	9E	1149	N904XJ	LGA	RDU	91	431	12	59	2023-07-27 12:00:00	Other
29103	1	26	1148	1150	-2	1409	1355	UA	629	N808UA	EWR	CHS	113	628	11	50	2023-01-26 11:00:00	Other
29104	8	29	2121	2126	-5	2229	2249	9E	1193	N926XJ	LGA	ROC	42	254	21	26	2023-08-29 21:00:00	Other
29106	2	7	1755	1759	-4	2055	2126	F9	940	N316FR	LGA	MIA	148	1096	17	59	2023-02-07 17:00:00	MIA
29121	3	29	927	930	-3	1114	1119	9E	1474	N907XJ	JFK	CLE	84	425	9	30	2023-03-29 09:00:00	Other
29124	4	17	2210	2214	-4	2356	2359	9E	1322	N927XJ	JFK	BUF	61	301	22	14	2023-04-17 22:00:00	Other
29133	5	29	1824	1827	-3	2005	2041	DL	402	N101DQ	LGA	MSP	135	1020	18	27	2023-05-29 18:00:00	Other
29134	3	22	1122	1125	-3	1345	1413	DL	346	N355NW	LGA	ATL	118	762	11	25	2023-03-22 11:00:00	ATL
29136	12	12	1126	1129	-3	1436	1447	AA	910	N922AN	JFK	AUS	227	1521	11	29	2023-12-12 11:00:00	Other
29138	9	25	855	900	-5	1042	1050	9E	1664	N296PQ	JFK	RDU	69	427	9	0	2023-09-25 09:00:00	Other
29139	11	8	925	929	-4	1058	1117	YX	1901	N239JQ	LGA	BNA	118	764	9	29	2023-11-08 09:00:00	Other
29144	2	13	1957	2000	-3	2222	2231	9E	1394	N176PQ	LGA	OMA	175	1148	20	0	2023-02-13 20:00:00	Other
29145	5	4	1455	1459	-4	1637	1705	DL	570	N363NB	LGA	MSP	135	1020	14	59	2023-05-04 14:00:00	Other
29148	2	7	655	700	-5	952	1028	DL	104	N930DZ	JFK	SEA	339	2422	7	0	2023-02-07 07:00:00	Other
29150	4	12	1956	2000	-4	2155	2227	9E	1207	N927XJ	JFK	CHS	88	636	20	0	2023-04-12 20:00:00	Other
29153	4	20	555	600	-5	838	859	UA	814	N838UA	LGA	IAH	201	1416	6	0	2023-04-20 06:00:00	Other
29156	3	13	838	842	-4	1025	1033	YX	1309	N114HQ	LGA	GSO	84	461	8	42	2023-03-13 08:00:00	Other
29159	3	23	925	930	-5	1118	1119	9E	1474	N695CA	JFK	CLE	87	425	9	30	2023-03-23 09:00:00	Other
29164	10	18	1314	1318	-4	1556	1623	AA	395	N941AN	EWR	DFW	184	1372	13	18	2023-10-18 13:00:00	Other
29168	1	1	1957	1959	-2	32	57	UA	664	N28457	EWR	SJU	193	1608	19	59	2023-01-01 19:00:00	Other
29169	2	22	656	700	-4	1112	1025	DL	211	N172DN	JFK	LAX	384	2475	7	0	2023-02-22 07:00:00	LAX
29181	8	10	557	601	-4	829	839	B6	191	N2039J	JFK	MCO	130	944	6	1	2023-08-10 06:00:00	MCO
29183	1	16	1527	1529	-2	1814	1839	AA	784	N930NN	EWR	DFW	200	1372	15	29	2023-01-16 15:00:00	Other
29189	6	2	1217	1222	-5	1334	1355	9E	1698	N195PQ	JFK	BUF	53	301	12	22	2023-06-02 12:00:00	Other
29190	11	14	2015	2020	-5	2140	2206	YX	1859	N235JQ	LGA	RIC	51	292	20	20	2023-11-14 20:00:00	Other
29197	3	7	1005	1010	-5	1219	1235	9E	1440	N324PQ	LGA	MYR	85	563	10	10	2023-03-07 10:00:00	Other
29198	11	2	631	635	-4	808	819	YX	1124	N763YX	EWR	CLE	70	404	6	35	2023-11-02 06:00:00	Other
29206	12	9	1536	1538	-2	1709	1733	OO	1171	N614CZ	JFK	ORD	126	740	15	38	2023-12-09 15:00:00	ORD
29216	2	6	1824	1828	-4	2029	2027	9E	1279	N311PQ	LGA	RDU	65	431	18	28	2023-02-06 18:00:00	Other
5	2	9	930	930	0	1238	1248	B6	51	N563JB	JFK	SRQ	154	1041	9	30	2023-02-09 09:00:00	Other
13	9	23	748	745	3	1028	957	9E	1539	N324PQ	JFK	CLT	103	541	7	45	2023-09-23 07:00:00	CLT
23	7	23	800	800	0	910	927	YX	1387	N214JQ	LGA	BOS	40	184	8	0	2023-07-23 08:00:00	BOS
35	1	1	802	800	2	959	1013	AA	675	N914NN	EWR	CLT	91	529	8	0	2023-01-01 08:00:00	CLT
38	9	4	1144	1145	-1	1250	1303	UA	874	N24729	EWR	PWM	48	284	11	45	2023-09-04 11:00:00	Other
43	9	1	1224	1225	-1	1426	1441	UA	885	N38443	EWR	DEN	211	1605	12	25	2023-09-01 12:00:00	Other
58	3	26	2059	2100	-1	2244	2251	OO	1765	N163SY	LGA	ORD	136	733	21	0	2023-03-26 21:00:00	ORD
60	1	6	1300	1259	1	1422	1425	9E	1630	N329PQ	JFK	BTV	48	266	12	59	2023-01-06 12:00:00	Other
70	10	8	810	810	0	1055	1104	B6	239	N588JB	LGA	MCO	146	950	8	10	2023-10-08 08:00:00	MCO
71	12	11	1556	1557	-1	1739	1759	YX	1096	N769YX	EWR	CMH	76	463	15	57	2023-12-11 15:00:00	Other
73	1	9	2009	1959	10	106	57	UA	664	N61887	EWR	SJU	217	1608	19	59	2023-01-09 19:00:00	Other
74	12	28	1111	1110	1	1445	1432	DL	590	N322DN	LGA	MIA	173	1096	11	10	2023-12-28 11:00:00	MIA
83	4	3	1731	1729	2	2103	2039	AA	226	N953AN	JFK	MIA	145	1089	17	29	2023-04-03 17:00:00	MIA
85	5	10	1758	1759	-1	2141	2146	AA	917	N117AN	JFK	SFO	363	2586	17	59	2023-05-10 17:00:00	Other
101	4	28	1441	1435	6	1726	1750	UA	79	N786UA	EWR	SFO	303	2565	14	35	2023-04-28 14:00:00	Other
106	9	2	1014	1015	-1	1229	1254	UA	711	N29981	EWR	IAH	169	1400	10	15	2023-09-02 10:00:00	Other
117	8	24	1022	1017	5	1310	1311	UA	313	N17314	EWR	TPA	131	997	10	17	2023-08-24 10:00:00	Other
120	1	3	713	714	-1	1007	1022	B6	187	N651JB	LGA	PBI	143	1035	7	14	2023-01-03 07:00:00	Other
124	12	29	659	700	-1	1023	1057	DL	802	N703TW	JFK	SFO	340	2586	7	0	2023-12-29 07:00:00	Other
139	3	17	1202	1159	3	1450	1455	UA	702	N37549	EWR	TPA	136	997	11	59	2023-03-17 11:00:00	Other
140	3	21	1704	1659	5	1953	2011	B6	347	N247JB	JFK	MCO	139	944	16	59	2023-03-21 16:00:00	MCO
143	1	21	2009	2010	-1	2105	2129	UA	601	N439UA	EWR	BOS	38	200	20	10	2023-01-21 20:00:00	BOS
157	10	3	2101	2059	2	2252	2323	B6	895	N637JB	LGA	MSY	146	1183	20	59	2023-10-03 20:00:00	Other
158	9	26	1431	1432	-1	1648	1638	AA	534	N323SG	JFK	CLT	89	541	14	32	2023-09-26 14:00:00	CLT
169	6	23	2152	2152	0	2256	2315	9E	1590	N325PQ	LGA	ROC	41	254	21	52	2023-06-23 21:00:00	Other
191	1	18	2155	2149	6	2303	2307	B6	70	N346JB	JFK	BTV	48	266	21	49	2023-01-18 21:00:00	Other
202	3	26	1836	1837	-1	2120	2100	YX	1034	N638RW	EWR	IND	116	645	18	37	2023-03-26 18:00:00	Other
206	9	30	2251	2250	1	112	144	F9	932	N336FR	LGA	DFW	176	1389	22	50	2023-09-30 22:00:00	Other
227	8	16	1610	1610	0	1753	1815	OO	957	N243SY	JFK	ORD	111	740	16	10	2023-08-16 16:00:00	ORD
230	7	9	831	830	1	1149	1125	DL	188	N118DU	JFK	DFW	208	1391	8	30	2023-07-09 08:00:00	Other
239	8	19	900	901	-1	1118	1112	9E	1275	N309PQ	LGA	AVL	93	599	9	1	2023-08-19 09:00:00	Other
240	7	22	1102	1059	3	1355	1408	UA	148	N64809	EWR	FLL	144	1065	10	59	2023-07-22 10:00:00	FLL
243	3	9	1926	1927	-1	2110	2132	AA	761	N963AN	JFK	CLT	81	541	19	27	2023-03-09 19:00:00	CLT
245	1	1	619	620	-1	751	745	WN	2	N8679A	LGA	MDW	137	725	6	20	2023-01-01 06:00:00	Other
250	5	12	1625	1623	2	1845	1853	UA	713	N823UA	LGA	DEN	236	1620	16	23	2023-05-12 16:00:00	Other
253	5	31	1159	1200	-1	1445	1523	B6	807	N977JE	JFK	LAX	317	2475	12	0	2023-05-31 12:00:00	LAX
254	4	17	1425	1425	0	1634	1633	YX	944	N758YX	EWR	GRR	93	605	14	25	2023-04-17 14:00:00	Other
259	7	6	704	700	4	1025	1015	AS	13	N928AK	JFK	SFO	349	2586	7	0	2023-07-06 07:00:00	Other
264	8	21	2108	2058	10	2249	2302	YX	875	N749YX	EWR	GSO	63	445	20	58	2023-08-21 20:00:00	Other
267	8	27	1659	1659	0	1933	1951	UA	414	N27273	EWR	SAN	298	2425	16	59	2023-08-27 16:00:00	Other
272	9	1	1605	1558	7	1718	1732	YX	1099	N757YX	EWR	ORF	50	284	15	58	2023-09-01 15:00:00	Other
277	3	15	811	810	1	1148	1207	B6	927	N2017J	JFK	BQN	191	1576	8	10	2023-03-15 08:00:00	Other
287	8	19	2038	2039	-1	2307	2325	UA	638	N14235	EWR	DFW	167	1372	20	39	2023-08-19 20:00:00	Other
295	10	28	1745	1743	2	1916	1918	UA	203	N76288	EWR	CLE	67	404	17	43	2023-10-28 17:00:00	Other
307	5	10	1538	1538	0	1902	1835	AA	228	N960AN	EWR	DFW	218	1372	15	38	2023-05-10 15:00:00	Other
309	9	23	1701	1700	1	2022	1933	DL	573	N871DN	JFK	ATL	103	760	17	0	2023-09-23 17:00:00	ATL
310	3	31	1451	1450	1	1632	1634	9E	1520	N604LR	EWR	RDU	82	416	14	50	2023-03-31 14:00:00	Other
314	6	30	759	755	4	1053	1100	AA	320	N801AW	JFK	AUS	199	1521	7	55	2023-06-30 07:00:00	Other
317	3	4	1428	1429	-1	1607	1631	NK	519	N616NK	LGA	MYR	87	563	14	29	2023-03-04 14:00:00	Other
329	7	14	1627	1621	6	1759	1803	UA	621	N27733	EWR	CLE	63	404	16	21	2023-07-14 16:00:00	Other
332	11	24	1658	1649	9	1952	1955	B6	440	N805JB	JFK	MCO	139	944	16	49	2023-11-24 16:00:00	MCO
337	4	29	914	912	2	1059	1102	YX	979	N725YX	EWR	CLE	68	404	9	12	2023-04-29 09:00:00	Other
340	2	4	1301	1300	1	1601	1629	AA	919	N435AN	LGA	MIA	156	1096	13	0	2023-02-04 13:00:00	MIA
341	5	19	1940	1930	10	2135	2127	YX	1248	N417YX	JFK	DCA	56	213	19	30	2023-05-19 19:00:00	Other
355	8	13	1455	1455	0	1701	1714	YX	935	N763YX	EWR	IND	99	645	14	55	2023-08-13 14:00:00	Other
358	2	26	1959	1959	0	2212	2229	DL	900	N3772H	EWR	ATL	111	746	19	59	2023-02-26 19:00:00	ATL
372	1	7	1643	1642	1	1820	1834	YX	1207	N862RW	EWR	RDU	73	416	16	42	2023-01-07 16:00:00	Other
373	2	14	1704	1700	4	2003	2023	B6	204	N715JB	EWR	FLL	146	1065	17	0	2023-02-14 17:00:00	FLL
375	4	21	821	820	1	1128	1215	DL	296	N705TW	JFK	SFO	336	2586	8	20	2023-04-21 08:00:00	Other
378	4	14	1635	1625	10	1751	1813	DL	436	N103DU	LGA	ORD	112	733	16	25	2023-04-14 16:00:00	ORD
381	5	4	1628	1629	-1	1915	1859	UA	870	N891UA	LGA	DEN	266	1620	16	29	2023-05-04 16:00:00	Other
389	11	19	1730	1729	1	2025	2055	AA	92	N110AN	JFK	LAX	324	2475	17	29	2023-11-19 17:00:00	LAX
397	10	2	804	805	-1	1043	1053	UA	240	N37555	EWR	IAH	185	1400	8	5	2023-10-02 08:00:00	Other
403	4	7	2054	2044	10	2345	2359	UA	587	N489UA	EWR	MIA	149	1085	20	44	2023-04-07 20:00:00	MIA
407	12	27	1000	1000	0	1553	1630	DL	109	N833MH	JFK	HNL	621	4983	10	0	2023-12-27 10:00:00	Other
418	12	1	830	830	0	1137	1133	UA	124	N14019	EWR	LAX	312	2454	8	30	2023-12-01 08:00:00	LAX
426	5	31	1329	1329	0	1503	1515	YX	1323	N127HQ	JFK	PIT	59	340	13	29	2023-05-31 13:00:00	Other
430	11	17	1833	1830	3	2150	2209	B6	60	N985JT	JFK	LAX	340	2475	18	30	2023-11-17 18:00:00	LAX
437	4	28	925	924	1	1145	1149	UA	803	N23707	EWR	ATL	115	746	9	24	2023-04-28 09:00:00	ATL
447	8	9	1329	1325	4	1602	1614	UA	157	N14107	EWR	MCO	122	937	13	25	2023-08-09 13:00:00	MCO
454	3	1	1110	1110	0	1400	1415	DL	673	N128DN	LGA	MCO	140	950	11	10	2023-03-01 11:00:00	MCO
461	2	11	1044	1045	-1	1358	1407	DL	565	N329NB	LGA	RSW	173	1080	10	45	2023-02-11 10:00:00	Other
471	6	12	1346	1346	0	1633	1640	UA	284	N897UA	LGA	IAH	201	1416	13	46	2023-06-12 13:00:00	Other
476	1	8	1244	1245	-1	1414	1400	YX	1286	N448YX	JFK	BOS	51	187	12	45	2023-01-08 12:00:00	BOS
477	1	1	1659	1700	-1	1852	1906	DL	479	N367NW	LGA	DTW	88	502	17	0	2023-01-01 17:00:00	Other
487	2	17	1909	1859	10	2244	2219	UA	742	N68805	EWR	SEA	336	2402	18	59	2023-02-17 18:00:00	Other
489	6	7	2059	2100	-1	2343	44	B6	325	N976JT	JFK	SFO	308	2586	21	0	2023-06-07 21:00:00	Other
498	1	26	1303	1253	10	1620	1607	AA	585	N807NN	EWR	MIA	168	1085	12	53	2023-01-26 12:00:00	MIA
499	3	19	1030	1030	0	1308	1339	UA	401	N17017	EWR	LAX	307	2454	10	30	2023-03-19 10:00:00	LAX
506	3	25	505	500	5	805	812	AA	449	N883NN	EWR	MIA	154	1085	5	0	2023-03-25 05:00:00	MIA
514	2	12	759	800	-1	1016	1045	WN	512	N925WN	LGA	DEN	233	1620	8	0	2023-02-12 08:00:00	Other
515	6	14	2216	2210	6	104	114	DL	103	N184DN	JFK	LAX	308	2475	22	10	2023-06-14 22:00:00	LAX
532	6	29	1355	1348	7	1604	1554	YX	1231	N747YX	EWR	CVG	91	569	13	48	2023-06-29 13:00:00	Other
540	1	21	1924	1925	-1	2223	2249	B6	674	N987JT	EWR	LAX	324	2454	19	25	2023-01-21 19:00:00	LAX
541	10	18	1413	1406	7	1535	1522	UA	706	N484UA	EWR	BOS	53	200	14	6	2023-10-18 14:00:00	BOS
544	10	24	1841	1840	1	2137	2152	AA	613	N854NN	EWR	MIA	131	1085	18	40	2023-10-24 18:00:00	MIA
546	10	16	1141	1135	6	1309	1328	OO	1203	N613CZ	JFK	ORD	110	740	11	35	2023-10-16 11:00:00	ORD
557	3	24	2138	2130	8	2249	2248	UA	409	N27270	EWR	BTV	42	266	21	30	2023-03-24 21:00:00	Other
561	7	2	1527	1528	-1	1842	1849	DL	222	N313DN	JFK	FLL	155	1069	15	28	2023-07-02 15:00:00	FLL
563	2	15	1629	1630	-1	1948	2007	DL	230	N811DZ	JFK	SLC	299	1990	16	30	2023-02-15 16:00:00	Other
566	4	20	1419	1420	-1	1524	1545	WN	71	N8642E	LGA	MDW	108	725	14	20	2023-04-20 14:00:00	Other
576	12	19	734	735	-1	1233	1244	DL	677	N506DA	JFK	SJU	217	1598	7	35	2023-12-19 07:00:00	Other
581	3	17	1609	1600	9	1920	1924	UA	761	N17104	EWR	LAX	335	2454	16	0	2023-03-17 16:00:00	LAX
586	5	31	1902	1855	7	2106	2137	NK	262	N978NK	EWR	LAS	275	2227	18	55	2023-05-31 18:00:00	Other
587	7	4	2253	2250	3	4	33	9E	1260	N678CA	JFK	ROC	45	264	22	50	2023-07-04 22:00:00	Other
598	9	21	643	641	2	926	937	NK	485	N629NK	LGA	MCO	136	950	6	41	2023-09-21 06:00:00	MCO
604	1	8	1851	1850	1	2155	2200	B6	84	N2048J	JFK	MCO	142	944	18	50	2023-01-08 18:00:00	MCO
607	2	16	1049	1040	9	1312	1327	DL	122	N124DX	LGA	ATL	119	762	10	40	2023-02-16 10:00:00	ATL
610	2	24	1129	1130	-1	1225	1237	9E	1332	N916XJ	LGA	BGM	38	147	11	30	2023-02-24 11:00:00	Other
620	3	11	1443	1441	2	1724	1730	UA	574	N37273	EWR	LAS	313	2227	14	41	2023-03-11 14:00:00	Other
622	4	17	2129	2129	0	2337	2340	UA	585	N843UA	EWR	MCI	156	1092	21	29	2023-04-17 21:00:00	Other
624	8	9	1410	1405	5	1638	1646	UA	406	N418UA	EWR	DFW	185	1372	14	5	2023-08-09 14:00:00	Other
625	12	16	1518	1515	3	1647	1654	UA	699	N855UA	LGA	ORD	121	733	15	15	2023-12-16 15:00:00	ORD
633	3	31	807	800	7	1102	1105	UA	859	N91007	EWR	LAX	325	2454	8	0	2023-03-31 08:00:00	LAX
638	4	27	1145	1140	5	1257	1305	WN	152	N467WN	LGA	MDW	114	725	11	40	2023-04-27 11:00:00	Other
642	9	10	2009	1959	10	2318	2324	AS	83	N966AK	EWR	SFO	344	2565	19	59	2023-09-10 19:00:00	Other
644	1	5	1725	1715	10	1842	1850	WN	591	N8805L	LGA	MDW	109	725	17	15	2023-01-05 17:00:00	Other
655	6	17	758	759	-1	947	958	AA	558	N667AW	JFK	CLT	78	541	7	59	2023-06-17 07:00:00	CLT
673	3	6	804	804	0	1239	1301	B6	927	N2016J	JFK	BQN	181	1576	8	4	2023-03-06 08:00:00	Other
685	11	23	705	705	0	923	947	B6	255	N588JB	JFK	JAX	114	828	7	5	2023-11-23 07:00:00	Other
691	9	14	1405	1358	7	1612	1611	9E	1632	N919XJ	LGA	GSP	89	610	13	58	2023-09-14 13:00:00	Other
692	5	7	525	523	2	753	820	UA	177	N27273	EWR	IAH	187	1400	5	23	2023-05-07 05:00:00	Other
702	3	11	1926	1927	-1	2130	2132	AA	761	N858NN	JFK	CLT	95	541	19	27	2023-03-11 19:00:00	CLT
704	1	14	1806	1807	-1	1949	1945	YX	1249	N732YX	EWR	PIT	50	319	18	7	2023-01-14 18:00:00	Other
707	8	8	1428	1429	-1	1611	1626	YX	1308	N221JQ	LGA	MEM	136	963	14	29	2023-08-08 14:00:00	Other
710	11	28	1309	1300	9	1620	1615	AA	224	N124AA	LGA	MIA	168	1096	13	0	2023-11-28 13:00:00	MIA
720	9	1	1559	1559	0	1846	1901	AA	887	N979NN	JFK	DFW	183	1391	15	59	2023-09-01 15:00:00	Other
723	9	24	1702	1700	2	1907	1908	9E	1432	N925XJ	JFK	DTW	81	509	17	0	2023-09-24 17:00:00	Other
724	5	6	1025	1024	1	1157	1205	UA	672	N421UA	EWR	ORD	116	719	10	24	2023-05-06 10:00:00	ORD
733	6	28	1155	1150	5	1603	1546	DL	185	N6709	JFK	STT	212	1623	11	50	2023-06-28 11:00:00	Other
736	4	18	1701	1701	0	1844	1842	UA	420	N16234	EWR	ORD	115	719	17	1	2023-04-18 17:00:00	ORD
738	11	27	902	900	2	1134	1136	9E	1458	N320PQ	LGA	SAV	116	722	9	0	2023-11-27 09:00:00	Other
740	12	31	509	510	-1	744	802	B6	207	N623JB	JFK	MCO	130	944	5	10	2023-12-31 05:00:00	MCO
750	11	12	1849	1840	9	2022	2020	WN	1114	N490WN	LGA	BNA	116	764	18	40	2023-11-12 18:00:00	Other
753	5	24	1035	1035	0	1221	1309	B6	386	N584JB	LGA	DEN	204	1620	10	35	2023-05-24 10:00:00	Other
755	2	3	1400	1400	0	1633	1619	YX	1130	N650RW	EWR	CVG	103	569	14	0	2023-02-03 14:00:00	Other
756	11	10	814	810	4	1030	1049	B6	188	N612JB	JFK	ATL	117	760	8	10	2023-11-10 08:00:00	ATL
768	6	24	1612	1613	-1	1918	1748	YX	1188	N749YX	EWR	PIT	60	319	16	13	2023-06-24 16:00:00	Other
771	9	29	2024	2017	7	42	23	NK	355	N690NK	EWR	SJU	225	1608	20	17	2023-09-29 20:00:00	Other
785	9	9	959	955	4	1249	1258	B6	219	N520JB	LGA	MCO	138	950	9	55	2023-09-09 09:00:00	MCO
797	5	21	1830	1829	1	2005	2036	YX	1368	N425YX	JFK	RDU	72	427	18	29	2023-05-21 18:00:00	Other
816	7	20	930	924	6	1238	1235	AA	302	N113AN	JFK	SNA	311	2454	9	24	2023-07-20 09:00:00	Other
817	7	26	1002	1000	2	1240	1255	DL	572	N329DN	JFK	MCO	128	944	10	0	2023-07-26 10:00:00	MCO
822	2	22	1045	1045	0	1312	1330	WN	881	N460WN	LGA	ATL	119	762	10	45	2023-02-22 10:00:00	ATL
826	8	19	1628	1629	-1	1916	1930	AA	84	N102NN	JFK	LAX	321	2475	16	29	2023-08-19 16:00:00	LAX
839	9	19	1832	1830	2	2110	2103	B6	139	N337JB	JFK	ATL	112	760	18	30	2023-09-19 18:00:00	ATL
840	6	22	2039	2040	-1	2322	2304	B6	952	N324JB	LGA	ATL	111	762	20	40	2023-06-22 20:00:00	ATL
846	10	27	1840	1840	0	2235	2150	B6	44	N907JB	JFK	SMF	365	2521	18	40	2023-10-27 18:00:00	Other
854	7	7	702	700	2	903	927	DL	177	N124DX	LGA	ATL	100	762	7	0	2023-07-07 07:00:00	ATL
867	10	5	1708	1708	0	1906	1920	AA	737	N991AN	LGA	CLT	80	544	17	8	2023-10-05 17:00:00	CLT
869	11	17	703	700	3	947	1005	DL	353	N337NW	LGA	PBI	139	1035	7	0	2023-11-17 07:00:00	Other
871	2	6	659	700	-1	816	822	YX	1485	N229JQ	LGA	BOS	34	184	7	0	2023-02-06 07:00:00	BOS
872	8	20	1939	1940	-1	2127	2236	DL	141	N892DN	JFK	DEN	196	1626	19	40	2023-08-20 19:00:00	Other
873	5	30	1704	1657	7	1942	1956	UA	867	N448UA	EWR	PBI	138	1023	16	57	2023-05-30 16:00:00	Other
875	8	15	709	700	9	942	944	UA	257	N37413	EWR	MCO	124	937	7	0	2023-08-15 07:00:00	MCO
884	2	4	2101	2059	2	2246	2229	OO	1167	N259SY	JFK	IAD	48	228	20	59	2023-02-04 20:00:00	Other
913	2	20	1035	1029	6	1304	1305	UA	234	N827UA	EWR	ATL	125	746	10	29	2023-02-20 10:00:00	ATL
914	11	27	1141	1142	-1	1306	1315	UA	358	N411UA	EWR	ORD	117	719	11	42	2023-11-27 11:00:00	ORD
915	6	18	1747	1745	2	1914	1920	AA	658	N918AN	EWR	ORD	114	719	17	45	2023-06-18 17:00:00	ORD
923	10	29	1550	1550	0	1938	1928	UA	359	N67134	EWR	SFO	382	2565	15	50	2023-10-29 15:00:00	Other
926	10	20	631	630	1	807	758	9E	1540	N933XJ	LGA	PIT	63	335	6	30	2023-10-20 06:00:00	Other
933	8	1	645	635	10	830	805	UA	436	N424UA	EWR	ORD	126	719	6	35	2023-08-01 06:00:00	ORD
938	5	11	1655	1655	0	1921	2029	DL	164	N3765	JFK	SAN	310	2446	16	55	2023-05-11 16:00:00	Other
962	2	13	1911	1910	1	2108	2119	AA	730	N926NN	JFK	CLT	78	541	19	10	2023-02-13 19:00:00	CLT
968	3	17	2209	2159	10	2339	2322	UA	793	N493UA	EWR	ORF	52	284	21	59	2023-03-17 21:00:00	Other
971	5	30	2107	2059	8	2319	2318	YX	1155	N733YX	EWR	CVG	84	569	20	59	2023-05-30 20:00:00	Other
975	2	5	900	900	0	1154	1209	NK	454	N682NK	EWR	MCO	145	937	9	0	2023-02-05 09:00:00	MCO
978	3	3	1638	1630	8	1945	1950	B6	131	N623JB	LGA	FLL	158	1076	16	30	2023-03-03 16:00:00	FLL
983	12	25	2225	2220	5	104	153	B6	901	N976JT	JFK	SFO	310	2586	22	20	2023-12-25 22:00:00	Other
988	4	5	1934	1925	9	2332	2242	UA	813	N29124	EWR	LAX	347	2454	19	25	2023-04-05 19:00:00	LAX
990	2	21	708	705	3	945	949	DL	193	N102DN	LGA	ATL	126	762	7	5	2023-02-21 07:00:00	ATL
993	1	17	1655	1655	0	1839	1847	OO	1682	N205SY	LGA	ORD	119	733	16	55	2023-01-17 16:00:00	ORD
995	2	22	1408	1400	8	1736	1719	B6	523	N608JB	JFK	FLL	147	1069	14	0	2023-02-22 14:00:00	FLL
998	10	21	712	710	2	942	1005	DL	505	N358DN	LGA	MCO	132	950	7	10	2023-10-21 07:00:00	MCO
1001	8	27	1832	1829	3	2128	2136	AS	147	N266AK	EWR	SEA	319	2402	18	29	2023-08-27 18:00:00	Other
1010	5	28	1507	1459	8	1623	1627	YX	1232	N407YX	LGA	BUF	47	292	14	59	2023-05-28 14:00:00	Other
1020	12	8	1307	1259	8	1613	1617	AA	215	N302SS	LGA	MIA	151	1096	12	59	2023-12-08 12:00:00	MIA
1029	6	10	2121	2112	9	2357	2344	UA	310	N78524	EWR	LAS	300	2227	21	12	2023-06-10 21:00:00	Other
1033	3	20	1505	1455	10	1625	1631	OO	1108	N322SY	JFK	BNA	114	765	14	55	2023-03-20 14:00:00	Other
1046	5	10	1757	1757	0	2035	2056	DL	574	N356DN	LGA	MCO	129	950	17	57	2023-05-10 17:00:00	MCO
1051	8	11	2012	2013	-1	2217	2255	YX	1033	N435YX	JFK	IND	93	665	20	13	2023-08-11 20:00:00	Other
1053	11	12	2057	2050	7	2252	2248	9E	1595	N931XJ	LGA	CLE	78	419	20	50	2023-11-12 20:00:00	Other
1060	12	17	601	600	1	855	917	DL	253	N301DU	LGA	DFW	204	1389	6	0	2023-12-17 06:00:00	Other
1061	10	15	2223	2218	5	19	59	NK	238	N939NK	EWR	LAS	270	2227	22	18	2023-10-15 22:00:00	Other
1066	9	30	904	900	4	1023	1044	UA	700	N24729	EWR	ORD	101	719	9	0	2023-09-30 09:00:00	ORD
1077	6	16	1639	1635	4	1743	1756	9E	1524	N932XJ	LGA	SYR	41	198	16	35	2023-06-16 16:00:00	Other
1082	4	25	1902	1900	2	2026	2026	UA	734	N428UA	EWR	IAD	50	212	19	0	2023-04-25 19:00:00	Other
1093	11	9	1801	1759	2	2104	2120	DL	204	N104DU	JFK	DFW	209	1391	17	59	2023-11-09 17:00:00	Other
1102	7	3	1731	1725	6	1952	2007	B6	706	N709JB	LGA	JAX	119	833	17	25	2023-07-03 17:00:00	Other
1104	3	20	1132	1130	2	1401	1435	WN	119	N454WN	LGA	DAL	194	1381	11	30	2023-03-20 11:00:00	Other
1110	8	1	715	715	0	926	929	DL	626	N3733Z	EWR	ATL	104	746	7	15	2023-08-01 07:00:00	ATL
1116	8	12	906	900	6	1047	1047	B6	623	N375JB	LGA	BNA	107	764	9	0	2023-08-12 09:00:00	Other
1128	8	20	959	1000	-1	1259	1303	UA	495	N433UA	EWR	RSW	148	1068	10	0	2023-08-20 10:00:00	Other
1151	5	2	1839	1830	9	2045	2101	UA	846	N13110	EWR	DEN	210	1605	18	30	2023-05-02 18:00:00	Other
1159	9	28	1537	1535	2	1654	1710	UA	695	N12125	EWR	ORD	105	719	15	35	2023-09-28 15:00:00	ORD
1168	9	24	714	715	-1	1008	1021	UA	157	N33289	EWR	SNA	325	2434	7	15	2023-09-24 07:00:00	Other
1175	11	24	1724	1725	-1	2036	2100	NK	277	N908NK	EWR	OAK	352	2555	17	25	2023-11-24 17:00:00	Other
1195	11	3	1700	1700	0	1855	1854	DL	961	N982AT	EWR	DTW	91	488	17	0	2023-11-03 17:00:00	Other
1200	6	24	1153	1143	10	1416	1412	UA	448	N488UA	EWR	ATL	111	746	11	43	2023-06-24 11:00:00	ATL
1209	9	4	1501	1500	1	1627	1636	UA	606	N38257	LGA	ORD	105	733	15	0	2023-09-04 15:00:00	ORD
1212	12	6	631	630	1	937	944	AA	620	N338ST	JFK	MIA	162	1089	6	30	2023-12-06 06:00:00	MIA
1228	9	15	1031	1030	1	1252	1246	DL	824	N385DN	EWR	ATL	110	746	10	30	2023-09-15 10:00:00	ATL
1253	9	30	2123	2123	0	2212	2230	YX	1101	N745YX	EWR	PHL	20	80	21	23	2023-09-30 21:00:00	Other
1256	7	18	1207	1205	2	1341	1328	AA	84	N767UW	LGA	DCA	45	214	12	5	2023-07-18 12:00:00	Other
1275	5	25	2000	1952	8	2248	2302	UA	753	N27274	EWR	SAN	315	2425	19	52	2023-05-25 19:00:00	Other
1277	8	17	859	900	-1	1113	1117	NK	134	N964NK	EWR	LAS	281	2227	9	0	2023-08-17 09:00:00	Other
1283	3	21	1656	1656	0	1850	1908	DL	772	N127DU	JFK	DTW	86	509	16	56	2023-03-21 16:00:00	Other
1288	4	2	1657	1655	2	1823	1822	YX	1520	N878RW	LGA	ROC	49	254	16	55	2023-04-02 16:00:00	Other
1293	3	7	831	830	1	1156	1157	NK	308	N673NK	LGA	IAH	208	1416	8	30	2023-03-07 08:00:00	Other
1294	4	1	1950	1950	0	2329	2333	DL	565	N3762Y	JFK	RSW	150	1074	19	50	2023-04-01 19:00:00	Other
1305	11	26	1358	1359	-1	1653	1638	DL	169	N363DN	LGA	ATL	135	762	13	59	2023-11-26 13:00:00	ATL
1310	12	13	801	800	1	1252	1313	DL	677	N532DN	JFK	SJU	198	1598	8	0	2023-12-13 08:00:00	Other
1314	1	6	2019	2015	4	2305	2315	UA	872	N27270	EWR	MCO	129	937	20	15	2023-01-06 20:00:00	MCO
1330	2	17	1920	1920	0	2237	2254	DL	165	N3763D	JFK	SAN	345	2446	19	20	2023-02-17 19:00:00	Other
1331	2	3	721	720	1	1040	1037	DL	399	N371DN	JFK	MIA	172	1089	7	20	2023-02-03 07:00:00	MIA
1337	3	20	1230	1227	3	1542	1547	B6	343	N615JB	JFK	SLC	291	1990	12	27	2023-03-20 12:00:00	Other
1348	12	22	1237	1228	9	1435	1500	UA	848	N37508	EWR	DEN	219	1605	12	28	2023-12-22 12:00:00	Other
1350	12	24	1525	1525	0	1646	1643	B6	39	N599JB	JFK	BTV	48	266	15	25	2023-12-24 15:00:00	Other
1355	8	6	1459	1459	0	1715	1722	YX	1015	N423YX	JFK	IND	95	665	14	59	2023-08-06 14:00:00	Other
1361	5	2	941	940	1	1231	1250	UA	703	N76502	EWR	RSW	148	1068	9	40	2023-05-02 09:00:00	Other
1366	12	26	1932	1929	3	2146	2219	DL	879	N927DZ	JFK	ATL	109	760	19	29	2023-12-26 19:00:00	ATL
1367	1	27	902	900	2	1127	1150	DL	402	N776DE	JFK	DEN	228	1626	9	0	2023-01-27 09:00:00	Other
1369	5	14	1101	1056	5	1340	1348	UA	657	N36207	EWR	MCO	127	937	10	56	2023-05-14 10:00:00	MCO
1370	6	25	1307	1259	8	2019	1606	AA	661	N943AN	EWR	MIA	NA	1085	12	59	2023-06-25 12:00:00	MIA
1375	9	7	1559	1600	-1	2021	1835	DL	172	N101DQ	LGA	ATL	112	762	16	0	2023-09-07 16:00:00	ATL
1376	2	21	1221	1215	6	1559	1530	UA	839	N78009	EWR	SFO	370	2565	12	15	2023-02-21 12:00:00	Other
1381	9	27	709	710	-1	904	933	UA	848	N69806	EWR	DEN	201	1605	7	10	2023-09-27 07:00:00	Other
1382	12	11	539	535	4	838	841	NK	261	N619NK	EWR	IAH	211	1400	5	35	2023-12-11 05:00:00	Other
1384	7	25	1315	1305	10	NA	1440	UA	99	N27290	EWR	ORD	NA	719	13	5	2023-07-25 13:00:00	ORD
1401	5	31	1454	1455	-1	1633	1650	9E	1471	N295PQ	JFK	RDU	78	427	14	55	2023-05-31 14:00:00	Other
1423	7	11	707	700	7	1006	1007	DL	373	N383DN	JFK	RSW	147	1074	7	0	2023-07-11 07:00:00	Other
1424	11	19	2044	2044	0	2337	2358	B6	526	N834JB	JFK	FLL	143	1069	20	44	2023-11-19 20:00:00	FLL
1453	4	23	1314	1315	-1	1440	1445	YX	1515	N234JQ	LGA	RIC	56	292	13	15	2023-04-23 13:00:00	Other
1456	5	19	1945	1945	0	2221	2304	DL	768	N369NB	JFK	PBI	133	1028	19	45	2023-05-19 19:00:00	Other
1466	5	25	600	600	0	818	825	DL	750	N703TW	JFK	ATL	112	760	6	0	2023-05-25 06:00:00	ATL
1472	5	23	1142	1135	7	1524	1440	NK	526	N668NK	EWR	FLL	188	1065	11	35	2023-05-23 11:00:00	FLL
1477	1	14	525	525	0	800	820	UA	206	N14107	EWR	IAH	178	1400	5	25	2023-01-14 05:00:00	Other
1482	8	12	730	730	0	1000	1005	DL	165	N525DA	JFK	LAS	299	2248	7	30	2023-08-12 07:00:00	Other
1486	10	2	1602	1600	2	1817	1835	DL	161	N360DN	LGA	ATL	104	762	16	0	2023-10-02 16:00:00	ATL
1496	11	18	1129	1129	0	1359	1424	DL	426	N900DU	JFK	TPA	136	1005	11	29	2023-11-18 11:00:00	Other
1521	2	15	1836	1830	6	2007	2036	AA	922	N812NN	LGA	ORD	122	733	18	30	2023-02-15 18:00:00	ORD
1524	4	28	1854	1855	-1	2225	2158	DL	460	N140DU	LGA	IAH	221	1416	18	55	2023-04-28 18:00:00	Other
1525	10	28	954	948	6	1102	1112	UA	426	N76265	EWR	BOS	45	200	9	48	2023-10-28 09:00:00	BOS
1529	4	7	1700	1659	1	1842	1850	YX	937	N750YX	EWR	GSO	83	445	16	59	2023-04-07 16:00:00	Other
1531	1	18	2204	2159	5	117	126	B6	768	N985JT	JFK	LAX	344	2475	21	59	2023-01-18 21:00:00	LAX
1535	5	10	1439	1429	10	1634	1646	UA	352	N35204	EWR	MSY	156	1167	14	29	2023-05-10 14:00:00	Other
1540	6	19	1028	1029	-1	1207	1234	9E	1667	N931XJ	LGA	GSO	68	461	10	29	2023-06-19 10:00:00	Other
1547	9	5	1136	1130	6	1230	1242	B6	786	N307JB	JFK	ACK	35	199	11	30	2023-09-05 11:00:00	Other
1555	5	5	1929	1920	9	2131	2140	9E	1308	N297PQ	JFK	CLT	79	541	19	20	2023-05-05 19:00:00	CLT
1559	2	28	2029	2020	9	2221	2221	YX	1519	N220JQ	LGA	CMH	81	479	20	20	2023-02-28 20:00:00	Other
1563	3	27	1304	1300	4	1605	1555	B6	142	N657JB	LGA	MCO	152	950	13	0	2023-03-27 13:00:00	MCO
1576	11	28	1734	1728	6	2043	2030	UA	881	N33266	EWR	PBI	148	1023	17	28	2023-11-28 17:00:00	Other
1585	3	6	1352	1350	2	1711	1619	B6	957	N216JB	LGA	CHS	98	641	13	50	2023-03-06 13:00:00	Other
1588	4	3	2109	2059	10	2239	2232	UA	773	N806UA	EWR	MSN	125	799	20	59	2023-04-03 20:00:00	Other
1590	11	7	1729	1729	0	2101	2055	AA	92	N107NN	JFK	LAX	366	2475	17	29	2023-11-07 17:00:00	LAX
1593	8	24	619	620	-1	808	815	DL	775	N980AT	EWR	MSP	138	1008	6	20	2023-08-24 06:00:00	Other
1597	3	30	1023	1017	6	1220	1152	UA	696	N66808	EWR	ORD	123	719	10	17	2023-03-30 10:00:00	ORD
1607	8	22	1455	1455	0	1706	1710	DL	498	N330NB	LGA	DTW	86	502	14	55	2023-08-22 14:00:00	Other
1610	2	16	823	817	6	1320	1311	UA	764	N76064	EWR	SJU	189	1608	8	17	2023-02-16 08:00:00	Other
1611	5	17	1956	1955	1	2312	2312	B6	698	N934JB	EWR	LAX	313	2454	19	55	2023-05-17 19:00:00	LAX
1617	11	17	2307	2259	8	214	209	F9	1483	N716FR	LGA	MIA	151	1096	22	59	2023-11-17 22:00:00	MIA
1641	3	29	1846	1847	-1	2131	2148	UA	824	N36472	EWR	TPA	141	997	18	47	2023-03-29 18:00:00	Other
1647	11	25	1629	1630	-1	1942	1945	B6	991	N974JT	JFK	FLL	165	1069	16	30	2023-11-25 16:00:00	FLL
1648	10	3	1527	1525	2	1837	1849	AS	78	N579AS	EWR	SFO	342	2565	15	25	2023-10-03 15:00:00	Other
1652	4	3	1211	1210	1	1335	1349	YX	1123	N410YX	LGA	BNA	117	764	12	10	2023-04-03 12:00:00	Other
1655	3	10	1404	1359	5	1601	1611	YX	1092	N727YX	EWR	MSP	151	1008	13	59	2023-03-10 13:00:00	Other
1658	10	15	2001	1953	8	2355	2259	UA	941	N36469	EWR	MIA	157	1085	19	53	2023-10-15 19:00:00	MIA
1662	12	6	1412	1405	7	1918	1904	B6	304	N805JB	JFK	SJU	201	1598	14	5	2023-12-06 14:00:00	Other
1675	8	1	1858	1859	-1	2045	2110	AA	602	N70020	JFK	CLT	80	541	18	59	2023-08-01 18:00:00	CLT
1688	7	12	1907	1900	7	2117	2118	YX	1049	N440YX	LGA	XNA	157	1147	19	0	2023-07-12 19:00:00	Other
1694	2	12	759	800	-1	1041	1114	AA	804	N874NN	JFK	DFW	190	1391	8	0	2023-02-12 08:00:00	Other
1698	6	22	2025	2025	0	2145	2208	AA	793	N751UW	LGA	ORD	102	733	20	25	2023-06-22 20:00:00	ORD
1702	4	11	1538	1535	3	1827	1839	DL	379	N120DU	LGA	IAH	178	1416	15	35	2023-04-11 15:00:00	Other
1711	6	12	1639	1629	10	2220	1935	AA	976	N774AN	JFK	MIA	NA	1089	16	29	2023-06-12 16:00:00	MIA
1723	11	8	2000	1950	10	2256	2317	DL	816	N308DN	JFK	MIA	141	1089	19	50	2023-11-08 19:00:00	MIA
1725	1	16	2149	2149	0	2305	2307	B6	70	N193JB	JFK	BTV	48	266	21	49	2023-01-16 21:00:00	Other
1738	3	27	1629	1630	-1	1932	1932	NK	540	N626NK	EWR	MCO	148	937	16	30	2023-03-27 16:00:00	MCO
1747	5	2	2006	1957	9	2131	2120	UA	882	N485UA	EWR	IAD	47	212	19	57	2023-05-02 19:00:00	Other
1751	4	25	1359	1400	-1	1515	1523	YX	1242	N435YX	LGA	DCA	47	214	14	0	2023-04-25 14:00:00	Other
1771	12	3	600	600	0	922	859	NK	479	N650NK	LGA	MCO	143	950	6	0	2023-12-03 06:00:00	MCO
1773	10	28	1619	1613	6	1718	1733	9E	1507	N292PQ	LGA	SYR	40	198	16	13	2023-10-28 16:00:00	Other
1777	6	7	1819	1820	-1	2059	2045	9E	1647	N691CA	JFK	CVG	93	589	18	20	2023-06-07 18:00:00	Other
1785	9	15	1432	1430	2	1703	1727	AA	675	N826NN	JFK	DFW	185	1391	14	30	2023-09-15 14:00:00	Other
1788	8	8	1833	1827	6	2142	2144	AA	151	N982NN	JFK	MIA	147	1089	18	27	2023-08-08 18:00:00	MIA
1793	12	27	1134	1135	-1	1436	1343	AA	167	N922NN	JFK	CLT	102	541	11	35	2023-12-27 11:00:00	CLT
1800	2	21	1201	1201	0	1331	1336	AA	439	N828AW	EWR	ORD	124	719	12	1	2023-02-21 12:00:00	ORD
1814	5	3	702	700	2	950	1006	DL	575	N909DN	JFK	TPA	145	1005	7	0	2023-05-03 07:00:00	Other
1820	12	1	1958	1955	3	2311	2320	DL	427	N3743H	LGA	RSW	167	1080	19	55	2023-12-01 19:00:00	Other
1825	8	29	719	710	9	959	1003	UA	529	N17285	EWR	PDX	321	2434	7	10	2023-08-29 07:00:00	Other
1841	12	12	602	600	2	854	904	B6	919	N658JB	JFK	FLL	149	1069	6	0	2023-12-12 06:00:00	FLL
1846	6	18	931	930	1	1207	1228	B6	168	N521JB	LGA	PBI	131	1035	9	30	2023-06-18 09:00:00	Other
1847	11	17	1252	1245	7	1550	1557	B6	75	N598JB	LGA	FLL	155	1076	12	45	2023-11-17 12:00:00	FLL
1851	6	18	1925	1925	0	2119	2124	YX	1341	N428YX	LGA	DTW	77	502	19	25	2023-06-18 19:00:00	Other
1854	3	24	632	630	2	1119	942	AA	374	N989NN	LGA	DFW	303	1389	6	30	2023-03-24 06:00:00	Other
1857	9	3	1714	1705	9	2014	2012	NK	865	N901NK	EWR	FLL	129	1065	17	5	2023-09-03 17:00:00	FLL
1865	2	5	1100	1100	0	1441	1425	AA	112	N112AN	JFK	LAX	369	2475	11	0	2023-02-05 11:00:00	LAX
1873	5	10	1854	1855	-1	2251	2310	DL	694	N824DN	JFK	SJU	193	1598	18	55	2023-05-10 18:00:00	Other
1876	4	8	837	838	-1	1127	1152	UA	291	N19130	EWR	SAN	321	2425	8	38	2023-04-08 08:00:00	Other
1877	9	2	943	943	0	1226	1241	B6	331	N796JB	JFK	PBI	133	1028	9	43	2023-09-02 09:00:00	Other
1881	4	14	745	740	5	1056	1041	UA	664	N27273	EWR	PBI	168	1023	7	40	2023-04-14 07:00:00	Other
1889	9	3	1633	1630	3	1857	1923	NK	510	N905NK	EWR	MCO	124	937	16	30	2023-09-03 16:00:00	MCO
1896	6	23	1809	1759	10	2129	2103	B6	699	N503JB	LGA	MCO	153	950	17	59	2023-06-23 17:00:00	MCO
1908	5	18	2207	2202	5	2314	2326	UA	493	N21723	EWR	ROC	38	246	22	2	2023-05-18 22:00:00	Other
1912	3	24	1959	2000	-1	2201	2214	9E	1483	N538CA	LGA	GSP	98	610	20	0	2023-03-24 20:00:00	Other
1913	8	16	1428	1429	-1	1615	1630	UA	305	N805UA	EWR	CLT	85	529	14	29	2023-08-16 14:00:00	CLT
1915	5	11	2034	2030	4	2303	2300	DL	326	N377DN	LGA	ATL	101	762	20	30	2023-05-11 20:00:00	ATL
1916	11	25	1607	1558	9	1859	1920	DL	383	N776DE	LGA	MIA	153	1096	15	58	2023-11-25 15:00:00	MIA
1921	10	4	1837	1830	7	2143	2137	UA	638	N35953	EWR	SFO	322	2565	18	30	2023-10-04 18:00:00	Other
1927	7	27	1539	1539	0	2135	1844	UA	462	N17264	EWR	FLL	205	1065	15	39	2023-07-27 15:00:00	FLL
1932	2	9	1005	1003	2	1257	1309	UA	853	N27205	EWR	DFW	200	1372	10	3	2023-02-09 10:00:00	Other
1940	11	21	1256	1255	1	1514	1500	9E	1611	N232PQ	JFK	DTW	95	509	12	55	2023-11-21 12:00:00	Other
1945	7	20	1848	1843	5	1957	2007	UA	559	N453UA	EWR	BOS	41	200	18	43	2023-07-20 18:00:00	BOS
1951	1	25	605	605	0	758	819	DL	1057	N919AT	EWR	MSP	153	1008	6	5	2023-01-25 06:00:00	Other
1952	9	24	528	520	8	911	906	B6	921	N662JB	JFK	BQN	201	1576	5	20	2023-09-24 05:00:00	Other
1955	4	11	1559	1600	-1	1705	1710	9E	1256	N307PQ	LGA	PVD	34	143	16	0	2023-04-11 16:00:00	Other
1956	5	21	1602	1559	3	1702	1721	UA	140	N33289	EWR	BOS	41	200	15	59	2023-05-21 15:00:00	BOS
1963	12	1	1600	1600	0	1804	1755	OO	1171	N322SY	JFK	ORD	145	740	16	0	2023-12-01 16:00:00	ORD
1968	8	11	1137	1129	8	1246	1254	UA	383	N53441	EWR	BNA	108	748	11	29	2023-08-11 11:00:00	Other
1978	7	17	1300	1300	0	1627	1613	AA	212	N904NN	LGA	MIA	165	1096	13	0	2023-07-17 13:00:00	MIA
1983	5	14	750	750	0	901	929	9E	1493	N337PQ	JFK	ROC	48	264	7	50	2023-05-14 07:00:00	Other
1987	4	24	1510	1510	0	1655	1704	OO	1048	N251SY	JFK	PIT	68	340	15	10	2023-04-24 15:00:00	Other
2002	9	4	1302	1259	3	1507	1504	DL	789	N118DY	LGA	DTW	76	502	12	59	2023-09-04 12:00:00	Other
2007	8	22	1533	1526	7	1811	1849	DL	209	N319DN	JFK	FLL	133	1069	15	26	2023-08-22 15:00:00	FLL
2019	2	26	808	805	3	1031	1040	DL	886	N374DA	EWR	ATL	116	746	8	5	2023-02-26 08:00:00	ATL
2028	6	24	1459	1454	5	1923	1730	NK	283	N937NK	EWR	IAH	186	1400	14	54	2023-06-24 14:00:00	Other
2032	8	19	1455	1450	5	1607	1615	WN	298	N8879Q	LGA	MDW	101	725	14	50	2023-08-19 14:00:00	Other
2040	6	28	534	530	4	818	821	B6	41	N991JT	JFK	LAX	327	2475	5	30	2023-06-28 05:00:00	LAX
2049	1	23	1242	1240	2	1447	1505	UA	555	N430UA	EWR	MSY	171	1167	12	40	2023-01-23 12:00:00	Other
2051	5	1	1129	1130	-1	1314	1336	YX	1310	N419YX	LGA	DTW	77	502	11	30	2023-05-01 11:00:00	Other
2054	2	3	1842	1840	2	2344	2335	B6	702	N949JT	JFK	SJU	204	1598	18	40	2023-02-03 18:00:00	Other
2057	1	17	818	817	1	1259	1311	UA	864	N66057	EWR	SJU	182	1608	8	17	2023-01-17 08:00:00	Other
2064	3	28	1843	1840	3	2124	2125	DL	159	N373DA	LGA	DEN	246	1620	18	40	2023-03-28 18:00:00	Other
2086	10	19	1301	1301	0	1535	1607	UA	485	N27724	EWR	SNA	307	2434	13	1	2023-10-19 13:00:00	Other
2087	5	8	2128	2129	-1	2253	2306	YX	1013	N732YX	EWR	PIT	59	319	21	29	2023-05-08 21:00:00	Other
2089	7	21	1649	1640	9	1932	2000	DL	242	N531DA	JFK	SAN	317	2446	16	40	2023-07-21 16:00:00	Other
2093	1	26	1323	1323	0	1430	1434	B6	363	N206JB	JFK	BOS	37	187	13	23	2023-01-26 13:00:00	BOS
2102	5	3	2000	1959	1	2349	2357	UA	577	N67815	EWR	SJU	204	1608	19	59	2023-05-03 19:00:00	Other
2109	8	5	1814	1808	6	2103	2058	UA	510	N17264	EWR	MCO	138	937	18	8	2023-08-05 18:00:00	MCO
2126	1	24	1139	1140	-1	1337	1403	YX	1433	N448YX	LGA	DTW	82	502	11	40	2023-01-24 11:00:00	Other
2139	3	27	1704	1700	4	2025	2026	B6	370	N526JL	JFK	PDX	348	2454	17	0	2023-03-27 17:00:00	Other
2166	6	23	1121	1122	-1	1424	1425	DL	462	N833DN	JFK	TPA	144	1005	11	22	2023-06-23 11:00:00	Other
2173	3	23	2035	2030	5	2400	2344	B6	69	N517JB	JFK	TPA	151	1005	20	30	2023-03-23 20:00:00	Other
2179	7	23	1533	1525	8	1649	1700	UA	569	N477UA	EWR	ORD	110	719	15	25	2023-07-23 15:00:00	ORD
2185	5	4	1603	1555	8	1725	1727	YX	1294	N821MD	LGA	RIC	53	292	15	55	2023-05-04 15:00:00	Other
2212	1	6	1244	1245	-1	1354	1400	YX	1286	N103HQ	JFK	BOS	32	187	12	45	2023-01-06 12:00:00	BOS
2222	6	23	1340	1335	5	1447	1452	YX	1198	N723YX	EWR	BTV	48	266	13	35	2023-06-23 13:00:00	Other
2233	9	25	1537	1530	7	1753	1748	B6	831	N593JB	JFK	MCI	155	1113	15	30	2023-09-25 15:00:00	Other
2239	9	10	914	915	-1	1024	1050	UA	226	N839UA	LGA	ORD	105	733	9	15	2023-09-10 09:00:00	ORD
2242	7	13	1758	1759	-1	2107	2104	DL	96	N142DU	JFK	DFW	203	1391	17	59	2023-07-13 17:00:00	Other
2245	6	28	1509	1459	10	1701	1656	OO	1267	N244SY	JFK	PIT	67	340	14	59	2023-06-28 14:00:00	Other
2246	4	3	1829	1829	0	2156	2145	UA	469	N29717	EWR	SNA	353	2434	18	29	2023-04-03 18:00:00	Other
2270	10	24	1130	1126	4	1416	1430	DL	460	N3752	JFK	MIA	136	1089	11	26	2023-10-24 11:00:00	MIA
2273	8	6	656	657	-1	942	940	B6	238	N944JT	JFK	LAX	323	2475	6	57	2023-08-06 06:00:00	LAX
2275	8	12	928	929	-1	1236	1221	UA	400	N13113	EWR	MCO	157	937	9	29	2023-08-12 09:00:00	MCO
2276	3	3	1124	1115	9	1404	1352	YX	1296	N118HQ	LGA	XNA	178	1147	11	15	2023-03-03 11:00:00	Other
2298	3	14	1647	1637	10	1900	1911	UA	942	N37531	EWR	PHX	285	2133	16	37	2023-03-14 16:00:00	Other
2303	6	27	606	600	6	709	706	B6	504	N375JB	JFK	BOS	43	187	6	0	2023-06-27 06:00:00	BOS
2311	12	29	825	817	8	927	959	YX	1314	N419YX	JFK	DCA	43	213	8	17	2023-12-29 08:00:00	Other
2317	2	24	1731	1729	2	2242	2059	B6	914	N935JB	JFK	LAX	403	2475	17	29	2023-02-24 17:00:00	LAX
2319	10	9	1110	1110	0	1314	1346	UA	524	N17311	EWR	LAS	278	2227	11	10	2023-10-09 11:00:00	Other
2330	1	11	1547	1545	2	1848	1922	DL	278	N171DN	JFK	LAX	335	2475	15	45	2023-01-11 15:00:00	LAX
2343	9	12	729	730	-1	847	907	AA	236	N926NN	LGA	ORD	109	733	7	30	2023-09-12 07:00:00	ORD
2381	8	21	1100	1100	0	1338	1412	AA	224	N830NN	JFK	MIA	138	1089	11	0	2023-08-21 11:00:00	MIA
2384	11	26	822	822	0	1037	1016	9E	1756	N605LR	LGA	BHM	152	866	8	22	2023-11-26 08:00:00	Other
2391	6	26	1247	1245	2	1546	1415	9E	1460	N146PQ	LGA	MKE	135	738	12	45	2023-06-26 12:00:00	Other
2394	7	10	1753	1751	2	2111	2050	B6	632	N986JB	EWR	LAX	315	2454	17	51	2023-07-10 17:00:00	LAX
2397	2	19	1335	1330	5	1649	1707	B6	567	N978JB	JFK	SFO	345	2586	13	30	2023-02-19 13:00:00	Other
2411	1	12	1659	1650	9	1856	1903	NK	52	N643NK	LGA	DTW	87	502	16	50	2023-01-12 16:00:00	Other
2421	9	12	1805	1805	0	1951	2018	DL	383	N375NC	LGA	MSP	137	1020	18	5	2023-09-12 18:00:00	Other
2425	1	29	620	620	0	1025	1001	AA	531	N446AN	EWR	PHX	336	2133	6	20	2023-01-29 06:00:00	Other
2430	1	24	1840	1841	-1	2142	2150	UA	893	N883UA	EWR	TPA	147	997	18	41	2023-01-24 18:00:00	Other
2437	6	25	1236	1230	6	1521	1525	NK	352	N643NK	LGA	DFW	195	1389	12	30	2023-06-25 12:00:00	Other
2444	10	20	731	730	1	1042	1042	AA	275	N9006	JFK	AUS	218	1521	7	30	2023-10-20 07:00:00	Other
2451	2	18	734	735	-1	1016	1043	DL	578	N818DA	JFK	TPA	141	1005	7	35	2023-02-18 07:00:00	Other
2458	7	13	1649	1649	0	1817	1822	YX	900	N657RW	EWR	BGR	58	393	16	49	2023-07-13 16:00:00	Other
2480	3	12	1304	1255	9	1442	1452	9E	1312	N181GJ	LGA	CLE	73	419	12	55	2023-03-12 12:00:00	Other
2487	2	3	911	906	5	1227	1233	UA	208	N24702	EWR	SNA	349	2434	9	6	2023-02-03 09:00:00	Other
2498	1	10	906	900	6	1027	1113	AA	1062	N917AN	JFK	ORD	112	740	9	0	2023-01-10 09:00:00	ORD
2500	4	14	1419	1420	-1	1516	1545	WN	71	N8678E	LGA	MDW	98	725	14	20	2023-04-14 14:00:00	Other
2502	3	31	911	905	6	1039	1031	B6	620	N266JB	JFK	BUF	60	301	9	5	2023-03-31 09:00:00	Other
2507	10	4	1305	1302	3	1550	1605	B6	651	N658JB	EWR	RSW	138	1068	13	2	2023-10-04 13:00:00	Other
2511	4	12	2050	2045	5	2250	2326	YX	1162	N136HQ	JFK	IND	89	665	20	45	2023-04-12 20:00:00	Other
2512	7	3	1959	2000	-1	59	2359	B6	241	N2084J	JFK	SJU	191	1598	20	0	2023-07-03 20:00:00	Other
2514	9	28	811	808	3	957	1001	YX	1398	N869RW	LGA	ILM	84	500	8	8	2023-09-28 08:00:00	Other
2521	9	22	1538	1535	3	1831	1825	UA	957	N654UA	EWR	IAH	196	1400	15	35	2023-09-22 15:00:00	Other
2545	6	11	1445	1445	0	1725	1752	B6	308	N579JB	LGA	PBI	141	1035	14	45	2023-06-11 14:00:00	Other
2553	11	12	1737	1731	6	1918	1914	MQ	1187	N770JM	EWR	ORD	124	719	17	31	2023-11-12 17:00:00	ORD
2555	3	1	1306	1305	1	1526	1537	NK	37	N617NK	EWR	ATL	117	746	13	5	2023-03-01 13:00:00	ATL
2561	3	19	1628	1629	-1	1739	1752	YX	1112	N856RW	EWR	DCA	45	199	16	29	2023-03-19 16:00:00	Other
2565	7	11	1310	1300	10	1512	1534	DL	395	N918DU	JFK	ATL	102	760	13	0	2023-07-11 13:00:00	ATL
2577	9	21	1928	1929	-1	2229	2231	AS	79	N928VA	EWR	LAX	319	2454	19	29	2023-09-21 19:00:00	LAX
2579	8	24	1406	1404	2	1608	1610	YX	838	N649RW	EWR	GRR	92	605	14	4	2023-08-24 14:00:00	Other
2587	8	7	644	645	-1	930	926	UA	649	N410UA	EWR	DFW	192	1372	6	45	2023-08-07 06:00:00	Other
2593	5	13	603	600	3	844	850	WN	614	N8681M	LGA	DAL	180	1381	6	0	2023-05-13 06:00:00	Other
2600	2	26	707	705	2	1008	1014	DL	653	N333NW	LGA	TPA	147	1010	7	5	2023-02-26 07:00:00	Other
2604	8	24	2120	2110	10	23	2354	B6	159	N615JB	LGA	MCO	125	950	21	10	2023-08-24 21:00:00	MCO
2613	2	25	908	901	7	1203	1203	UA	711	N87513	EWR	PBI	148	1023	9	1	2023-02-25 09:00:00	Other
2621	5	18	1000	1000	0	1307	1304	DL	122	N178DN	JFK	LAX	303	2475	10	0	2023-05-18 10:00:00	LAX
2622	2	16	1159	1200	-1	1414	1434	DL	296	N903DN	JFK	ATL	116	760	12	0	2023-02-16 12:00:00	ATL
2623	11	15	1454	1455	-1	1711	1727	DL	470	N195DN	JFK	ATL	113	760	14	55	2023-11-15 14:00:00	ATL
2633	4	6	2038	2029	9	2321	2213	YX	1143	N436YX	JFK	ORF	91	290	20	29	2023-04-06 20:00:00	Other
2658	9	29	1713	1710	3	1918	1926	9E	1528	N914XJ	LGA	CVG	89	585	17	10	2023-09-29 17:00:00	Other
2662	8	17	737	735	2	1044	1042	DL	791	N3739P	JFK	MIA	153	1089	7	35	2023-08-17 07:00:00	MIA
2663	9	22	515	515	0	823	810	NK	23	N524NK	EWR	MCO	136	937	5	15	2023-09-22 05:00:00	MCO
2673	12	2	759	800	-1	933	954	B6	807	N3138J	JFK	RDU	74	427	8	0	2023-12-02 08:00:00	Other
2683	10	6	2203	2203	0	44	59	NK	241	N621NK	EWR	IAH	199	1400	22	3	2023-10-06 22:00:00	Other
2693	4	27	859	900	-1	1213	1217	YX	1110	N418YX	LGA	IAH	218	1416	9	0	2023-04-27 09:00:00	Other
2704	11	28	1738	1730	8	1923	1938	YX	1334	N424YX	LGA	CMH	78	479	17	30	2023-11-28 17:00:00	Other
2713	11	28	1940	1935	5	2315	2320	DL	346	N177DN	JFK	SFO	339	2586	19	35	2023-11-28 19:00:00	Other
2716	11	19	1250	1250	0	1453	1508	DL	790	N875DN	EWR	ATL	101	746	12	50	2023-11-19 12:00:00	ATL
2725	6	2	1248	1245	3	1416	1442	9E	1761	N341PQ	LGA	RDU	65	431	12	45	2023-06-02 12:00:00	Other
2736	3	26	1818	1810	8	1929	1935	DL	444	N102DU	JFK	BOS	37	187	18	10	2023-03-26 18:00:00	BOS
2745	2	1	957	950	7	1241	1145	YX	1616	N232JQ	LGA	BNA	145	764	9	50	2023-02-01 09:00:00	Other
2748	12	24	1756	1752	4	2043	2127	NK	275	N904NK	EWR	OAK	327	2555	17	52	2023-12-24 17:00:00	Other
2751	4	2	1936	1928	8	2138	2150	9E	1225	N931XJ	JFK	CLT	85	541	19	28	2023-04-02 19:00:00	CLT
2755	7	30	2149	2139	10	2307	2302	B6	747	N179JB	JFK	SYR	43	209	21	39	2023-07-30 21:00:00	Other
2759	2	8	1853	1845	8	2316	2340	B6	702	N957JB	JFK	SJU	184	1598	18	45	2023-02-08 18:00:00	Other
2762	12	15	1426	1421	5	1647	1653	UA	78	N850UA	LGA	DEN	227	1620	14	21	2023-12-15 14:00:00	Other
2778	11	22	2129	2129	0	1	59	B6	766	N979JT	JFK	LAX	312	2475	21	29	2023-11-22 21:00:00	LAX
2783	3	27	1129	1129	0	1441	1432	B6	20	N564JB	LGA	TPA	158	1010	11	29	2023-03-27 11:00:00	Other
2786	6	10	2112	2105	7	2333	2349	UA	828	N37278	EWR	DFW	172	1372	21	5	2023-06-10 21:00:00	Other
2795	4	11	721	720	1	912	945	WN	490	N952WN	LGA	DEN	206	1620	7	20	2023-04-11 07:00:00	Other
2799	9	17	1159	1200	-1	1414	1416	DL	943	N997AT	EWR	ATL	113	746	12	0	2023-09-17 12:00:00	ATL
2802	9	5	1114	1111	3	1310	1326	DL	784	N139DU	LGA	CHS	86	641	11	11	2023-09-05 11:00:00	Other
2805	12	20	2129	2120	9	2241	2250	YX	1712	N232JQ	LGA	DCA	40	214	21	20	2023-12-20 21:00:00	Other
2806	11	24	2138	2135	3	230	231	B6	648	N973JT	JFK	SJU	191	1598	21	35	2023-11-24 21:00:00	Other
2820	11	11	1828	1829	-1	2154	2134	AA	393	N955NN	JFK	MIA	158	1089	18	29	2023-11-11 18:00:00	MIA
2824	6	9	2105	2057	8	2235	2237	YX	1096	N751YX	EWR	PIT	49	319	20	57	2023-06-09 20:00:00	Other
2829	3	31	1007	1003	4	1210	1214	AA	760	N908NN	LGA	CLT	87	544	10	3	2023-03-31 10:00:00	CLT
2847	5	26	1620	1621	-1	1739	1747	YX	1015	N646RW	EWR	BUF	48	282	16	21	2023-05-26 16:00:00	Other
2862	10	13	859	900	-1	1016	1029	YX	1051	N747YX	EWR	DCA	44	199	9	0	2023-10-13 09:00:00	Other
2863	8	12	714	715	-1	915	929	DL	626	N3767	EWR	ATL	96	746	7	15	2023-08-12 07:00:00	ATL
2867	5	19	1505	1457	8	1644	1641	UA	572	N872UA	EWR	RDU	72	416	14	57	2023-05-19 14:00:00	Other
2872	2	4	735	735	0	1037	1049	DL	448	N336DX	JFK	FLL	152	1069	7	35	2023-02-04 07:00:00	FLL
2878	3	23	759	800	-1	1119	1130	DL	610	N385DN	JFK	RSW	153	1074	8	0	2023-03-23 08:00:00	Other
2879	10	25	1722	1720	2	1933	1940	9E	1481	N491PX	LGA	CVG	93	585	17	20	2023-10-25 17:00:00	Other
2884	7	24	2133	2125	8	2250	2248	YX	1090	N427YX	LGA	ORF	53	296	21	25	2023-07-24 21:00:00	Other
2890	5	11	1646	1645	1	1956	2001	AA	506	N814NN	LGA	MIA	149	1096	16	45	2023-05-11 16:00:00	MIA
2895	3	31	1032	1029	3	1206	1209	9E	1408	N485PX	LGA	BUF	57	292	10	29	2023-03-31 10:00:00	Other
2901	12	1	1953	1945	8	2121	2122	OO	1192	N316SY	JFK	IAD	52	228	19	45	2023-12-01 19:00:00	Other
2909	5	4	1953	1952	1	2048	2106	YX	1032	N742YX	EWR	ALB	31	143	19	52	2023-05-04 19:00:00	Other
2913	3	12	923	920	3	1214	1220	UA	507	N73283	EWR	PBI	153	1023	9	20	2023-03-12 09:00:00	Other
2955	8	21	1632	1630	2	1910	1952	B6	216	N547JB	JFK	SJC	312	2569	16	30	2023-08-21 16:00:00	Other
2965	5	15	600	600	0	846	902	B6	513	N640JB	LGA	FLL	142	1076	6	0	2023-05-15 06:00:00	FLL
2967	1	26	1601	1559	2	1912	1956	AA	681	N306SP	JFK	PHX	279	2153	15	59	2023-01-26 15:00:00	Other
2971	1	17	1949	1950	-1	2138	2150	9E	1639	N605LR	JFK	RDU	76	427	19	50	2023-01-17 19:00:00	Other
2972	3	19	2058	2058	0	2320	2253	YX	1101	N858RW	EWR	GSO	85	445	20	58	2023-03-19 20:00:00	Other
2974	4	2	2123	2120	3	2242	2250	WN	830	N8754S	LGA	MDW	115	725	21	20	2023-04-02 21:00:00	Other
2979	8	8	946	946	0	1137	1200	UA	698	N76529	LGA	DEN	214	1620	9	46	2023-08-08 09:00:00	Other
2980	6	22	1548	1549	-1	1859	1933	B6	242	N983JT	JFK	SFO	330	2586	15	49	2023-06-22 15:00:00	Other
2983	7	26	1714	1715	-1	1849	1855	YX	1388	N878RW	LGA	DCA	54	214	17	15	2023-07-26 17:00:00	Other
2998	12	29	1300	1300	0	1603	1556	UA	536	N27270	EWR	MCO	154	937	13	0	2023-12-29 13:00:00	MCO
3004	3	3	1425	1415	10	1619	1613	YX	1740	N243JQ	LGA	CMH	89	479	14	15	2023-03-03 14:00:00	Other
3025	3	19	1055	1056	-1	1236	1315	DL	430	N364NW	LGA	MSP	146	1020	10	56	2023-03-19 10:00:00	Other
3031	7	30	620	615	5	847	836	UA	356	N17279	EWR	JAX	122	820	6	15	2023-07-30 06:00:00	Other
3040	9	3	1931	1929	2	2118	2203	9E	1637	N348PQ	JFK	MSP	143	1029	19	29	2023-09-03 19:00:00	Other
3041	8	8	2152	2150	2	2304	2314	UA	311	N808UA	EWR	BOS	44	200	21	50	2023-08-08 21:00:00	BOS
3042	6	10	2058	2055	3	2341	2357	B6	100	N589JB	EWR	FLL	138	1065	20	55	2023-06-10 20:00:00	FLL
3045	11	23	1300	1300	0	1501	1538	DL	334	N336DX	LGA	ATL	103	762	13	0	2023-11-23 13:00:00	ATL
3053	3	22	1825	1825	0	2017	2016	DL	369	N113DQ	LGA	ORD	130	733	18	25	2023-03-22 18:00:00	ORD
3063	1	14	1308	1300	8	1636	1637	B6	650	N964JT	JFK	SFO	350	2586	13	0	2023-01-14 13:00:00	Other
3066	7	4	1010	1006	4	1157	1219	UA	471	N28457	EWR	DEN	200	1605	10	6	2023-07-04 10:00:00	Other
3077	6	20	1709	1659	10	1951	1954	UA	599	N73270	EWR	MCO	132	937	16	59	2023-06-20 16:00:00	MCO
3079	3	20	1832	1833	-1	2126	2127	UA	660	N36272	EWR	MCO	133	937	18	33	2023-03-20 18:00:00	MCO
3083	5	27	1536	1529	7	1710	1712	YX	1036	N760YX	EWR	CLE	61	404	15	29	2023-05-27 15:00:00	Other
3112	12	6	1738	1729	9	2025	2046	AA	896	N851NN	JFK	MIA	135	1089	17	29	2023-12-06 17:00:00	MIA
3116	1	26	2004	2000	4	2230	2241	B6	33	N966JT	JFK	DEN	227	1626	20	0	2023-01-26 20:00:00	Other
3122	4	9	1025	1020	5	1256	1312	UA	652	N38955	EWR	IAH	180	1400	10	20	2023-04-09 10:00:00	Other
3128	5	12	700	700	0	944	1005	UA	869	N411UA	EWR	MIA	140	1085	7	0	2023-05-12 07:00:00	MIA
3130	7	27	1044	1045	-1	1244	1310	WN	838	N490WN	LGA	ATL	104	762	10	45	2023-07-27 10:00:00	ATL
3131	2	28	1122	1119	3	1435	1427	UA	469	N27251	EWR	AUS	226	1504	11	19	2023-02-28 11:00:00	Other
3133	1	24	1025	1020	5	1217	1224	AA	732	N314PD	EWR	CLT	85	529	10	20	2023-01-24 10:00:00	CLT
3141	5	24	2102	2100	2	2258	2317	OO	1141	N311SY	JFK	CLE	79	425	21	0	2023-05-24 21:00:00	Other
3144	3	4	1506	1504	2	1721	1718	YX	1047	N638RW	EWR	GRR	103	605	15	4	2023-03-04 15:00:00	Other
3149	4	22	1519	1512	7	1631	1627	DL	445	N139DU	LGA	SYR	40	198	15	12	2023-04-22 15:00:00	Other
3156	2	6	1937	1929	8	2235	2303	DL	157	N856DN	JFK	PDX	336	2454	19	29	2023-02-06 19:00:00	Other
3157	10	25	1609	1600	9	1905	1913	DL	510	N37700	JFK	MIA	138	1089	16	0	2023-10-25 16:00:00	MIA
3178	6	15	604	605	-1	846	845	WN	1050	N754SW	LGA	HOU	197	1428	6	5	2023-06-15 06:00:00	Other
3180	12	27	1417	1415	2	1622	1645	YX	1738	N205JQ	LGA	OMA	160	1148	14	15	2023-12-27 14:00:00	Other
3181	1	8	1620	1620	0	1859	1855	DL	530	N140DU	JFK	MSY	187	1182	16	20	2023-01-08 16:00:00	Other
3186	11	9	700	700	0	811	823	YX	1861	N214JQ	LGA	BOS	38	184	7	0	2023-11-09 07:00:00	BOS
3212	10	5	1439	1435	4	1553	1602	UA	564	N830UA	EWR	BNA	111	748	14	35	2023-10-05 14:00:00	Other
3214	11	16	1200	1200	0	1444	1508	B6	25	N998JE	JFK	MCO	136	944	12	0	2023-11-16 12:00:00	MCO
3218	5	27	1849	1850	-1	2129	2151	UA	802	N66831	EWR	TPA	141	997	18	50	2023-05-27 18:00:00	Other
3243	4	18	525	523	2	756	818	UA	188	N27276	EWR	IAH	194	1400	5	23	2023-04-18 05:00:00	Other
3260	8	5	1039	1037	2	1331	1344	B6	272	N746JB	JFK	SLC	270	1990	10	37	2023-08-05 10:00:00	Other
3264	8	11	600	600	0	831	820	DL	245	N118DY	LGA	ATL	121	762	6	0	2023-08-11 06:00:00	ATL
3266	1	8	1242	1235	7	1539	1606	AA	223	N346PR	LGA	DFW	211	1389	12	35	2023-01-08 12:00:00	Other
3267	2	11	1715	1716	-1	1817	1833	YX	1040	N730YX	EWR	BOS	41	200	17	16	2023-02-11 17:00:00	BOS
3269	9	28	1430	1430	0	1626	1628	9E	1615	N932XJ	LGA	ILM	79	500	14	30	2023-09-28 14:00:00	Other
3272	1	12	1920	1916	4	2227	2238	UA	835	N27263	EWR	SEA	319	2402	19	16	2023-01-12 19:00:00	Other
3287	10	21	910	910	0	1228	1210	B6	53	N970JB	JFK	SAN	331	2446	9	10	2023-10-21 09:00:00	Other
3289	4	27	1510	1510	0	1728	1720	9E	1294	N935XJ	LGA	GSP	100	610	15	10	2023-04-27 15:00:00	Other
3295	10	30	1910	1911	-1	2237	2241	UA	663	N14731	EWR	SLC	297	1969	19	11	2023-10-30 19:00:00	Other
3298	8	8	1639	1630	9	1927	1943	B6	57	N592JB	JFK	TPA	138	1005	16	30	2023-08-08 16:00:00	Other
3314	12	20	2138	2130	8	2251	2308	B6	162	N318JB	JFK	ROC	51	264	21	30	2023-12-20 21:00:00	Other
3317	6	19	1919	1913	6	2211	2208	UA	663	N77559	EWR	MCO	138	937	19	13	2023-06-19 19:00:00	MCO
3318	3	12	836	835	1	1103	1115	DL	553	N174DZ	JFK	ATL	118	760	8	35	2023-03-12 08:00:00	ATL
3321	4	7	1332	1325	7	1458	1500	WN	836	N8708Q	LGA	BNA	123	764	13	25	2023-04-07 13:00:00	Other
3325	12	19	1749	1745	4	2027	2050	UA	705	N14228	EWR	IAH	188	1400	17	45	2023-12-19 17:00:00	Other
3330	8	31	2110	2110	0	2217	2250	YX	1325	N212JQ	JFK	DCA	41	213	21	10	2023-08-31 21:00:00	Other
3339	12	15	704	700	4	1021	1035	AS	11	N963AK	JFK	SFO	338	2586	7	0	2023-12-15 07:00:00	Other
3340	12	8	925	920	5	1227	1255	UA	712	N17104	EWR	SFO	340	2565	9	20	2023-12-08 09:00:00	Other
3343	5	23	1832	1832	0	2023	2051	YX	990	N859RW	EWR	CVG	92	569	18	32	2023-05-23 18:00:00	Other
3361	4	19	1317	1309	8	1423	1423	UA	555	N4901U	EWR	BOS	41	200	13	9	2023-04-19 13:00:00	BOS
3365	3	13	1403	1359	4	1701	1705	UA	614	N53442	EWR	IAH	212	1400	13	59	2023-03-13 13:00:00	Other
3366	4	24	1346	1345	1	1500	1510	YX	997	N726YX	EWR	PIT	57	319	13	45	2023-04-24 13:00:00	Other
3368	3	17	2059	2100	-1	43	23	B6	487	N570JB	JFK	AUS	244	1521	21	0	2023-03-17 21:00:00	Other
3374	3	28	2154	2148	6	2327	2325	UA	537	N37293	EWR	ORD	113	719	21	48	2023-03-28 21:00:00	ORD
3383	5	25	1822	1812	10	2028	2058	UA	828	N36476	EWR	LAS	284	2227	18	12	2023-05-25 18:00:00	Other
3389	8	7	1543	1540	3	1814	1804	B6	717	N231JB	JFK	CHS	113	636	15	40	2023-08-07 15:00:00	Other
3402	3	10	1009	1010	-1	1254	1318	DL	995	N378DN	LGA	MCO	137	950	10	10	2023-03-10 10:00:00	MCO
3404	2	14	2029	2030	-1	2143	2150	B6	359	N249JB	JFK	BOS	37	187	20	30	2023-02-14 20:00:00	BOS
3408	4	27	939	940	-1	1216	1239	B6	421	N655JB	JFK	TPA	141	1005	9	40	2023-04-27 09:00:00	Other
3412	11	1	1900	1900	0	2225	2225	DL	207	N503DZ	JFK	SEA	332	2422	19	0	2023-11-01 19:00:00	Other
3413	12	17	1733	1729	4	2149	2046	AA	896	N815NN	JFK	MIA	173	1089	17	29	2023-12-17 17:00:00	MIA
3424	7	21	1020	1020	0	1138	1137	YX	1428	N202JQ	LGA	MVY	36	175	10	20	2023-07-21 10:00:00	Other
3433	8	15	2239	2236	3	2344	2359	UA	381	N438UA	EWR	BUF	42	282	22	36	2023-08-15 22:00:00	Other
3439	8	25	1200	1200	0	1442	1445	DL	167	N409DX	JFK	LAX	301	2475	12	0	2023-08-25 12:00:00	LAX
3443	11	4	605	600	5	841	815	DL	820	N911DQ	EWR	ATL	106	746	6	0	2023-11-04 06:00:00	ATL
3446	5	27	1834	1827	7	2123	2140	UA	483	N419UA	EWR	FLL	150	1065	18	27	2023-05-27 18:00:00	FLL
3452	5	19	714	715	-1	943	940	WN	604	N485WN	LGA	ATL	114	762	7	15	2023-05-19 07:00:00	ATL
3453	10	24	1159	1200	-1	1436	1450	DL	963	N812DN	JFK	TPA	130	1005	12	0	2023-10-24 12:00:00	Other
3456	6	23	1126	1121	5	1346	1330	UA	259	N25705	EWR	SAV	106	708	11	21	2023-06-23 11:00:00	Other
3459	9	18	1630	1630	0	1930	1937	AA	91	N117AN	JFK	LAX	339	2475	16	30	2023-09-18 16:00:00	LAX
3461	7	12	723	715	8	930	935	WN	489	N416WN	LGA	ATL	103	762	7	15	2023-07-12 07:00:00	ATL
3464	2	5	2258	2259	-1	402	349	B6	308	N775JB	JFK	PSE	216	1617	22	59	2023-02-05 22:00:00	Other
3469	10	5	1551	1550	1	1654	1704	9E	1437	N936XJ	LGA	PVD	33	143	15	50	2023-10-05 15:00:00	Other
3471	11	12	1030	1025	5	1150	1205	UA	79	N15710	EWR	ORD	115	719	10	25	2023-11-12 10:00:00	ORD
3477	4	28	1800	1800	0	2115	2138	DL	253	N394DX	JFK	SLC	265	1990	18	0	2023-04-28 18:00:00	Other
3501	11	26	1630	1620	10	1732	1736	UA	786	N29129	EWR	BOS	44	200	16	20	2023-11-26 16:00:00	BOS
3502	2	12	1844	1845	-1	2356	2340	B6	702	N913JB	JFK	SJU	217	1598	18	45	2023-02-12 18:00:00	Other
3507	8	24	1758	1759	-1	2101	2114	DL	293	N178DN	JFK	LAX	301	2475	17	59	2023-08-24 17:00:00	LAX
3512	4	11	1948	1945	3	2107	2120	YX	964	N732YX	EWR	PIT	57	319	19	45	2023-04-11 19:00:00	Other
3515	12	31	1057	1055	2	1248	1310	G4	988	204NV	EWR	TYS	93	631	10	55	2023-12-31 10:00:00	Other
3525	12	31	1329	1329	0	1615	1649	DL	394	N127DU	LGA	IAH	205	1416	13	29	2023-12-31 13:00:00	Other
3545	1	16	809	800	9	1135	1128	B6	855	N980JT	JFK	LAX	345	2475	8	0	2023-01-16 08:00:00	LAX
3555	5	16	1019	1019	0	1306	1332	UA	622	N489UA	EWR	RSW	146	1068	10	19	2023-05-16 10:00:00	Other
3562	7	13	1606	1559	7	1906	1851	UA	687	N37465	EWR	SAN	315	2425	15	59	2023-07-13 15:00:00	Other
3566	8	5	709	710	-1	949	1018	DL	759	N3739P	LGA	MIA	135	1096	7	10	2023-08-05 07:00:00	MIA
3567	5	24	735	735	0	1031	1042	DL	444	N371DN	JFK	FLL	148	1069	7	35	2023-05-24 07:00:00	FLL
3575	3	23	1959	2000	-1	2112	2127	YX	1619	N238JQ	LGA	BOS	40	184	20	0	2023-03-23 20:00:00	BOS
3584	1	18	937	933	4	1250	1255	UA	928	N73283	EWR	AUS	221	1504	9	33	2023-01-18 09:00:00	Other
3599	2	2	1006	1000	6	1155	1145	UA	86	N78511	EWR	RDU	78	416	10	0	2023-02-02 10:00:00	Other
3612	12	5	1737	1738	-1	2017	2104	AS	83	N569AS	EWR	SAN	307	2425	17	38	2023-12-05 17:00:00	Other
3615	8	25	559	600	-1	826	802	AA	205	N997NN	LGA	CLT	101	544	6	0	2023-08-25 06:00:00	CLT
3623	1	22	2042	2035	7	2222	2204	YX	1765	N237JQ	LGA	DCA	51	214	20	35	2023-01-22 20:00:00	Other
3633	2	9	1255	1255	0	1434	1455	WN	338	N8813Q	LGA	STL	134	888	12	55	2023-02-09 12:00:00	Other
3645	11	9	1525	1526	-1	1651	1704	UA	789	N18220	EWR	ORD	124	719	15	26	2023-11-09 15:00:00	ORD
3648	12	9	554	555	-1	922	910	AA	576	N317PG	LGA	DFW	225	1389	5	55	2023-12-09 05:00:00	Other
3651	5	9	1559	1559	0	1653	1704	YX	1674	N823MD	LGA	BDL	23	101	15	59	2023-05-09 15:00:00	Other
3654	10	7	1729	1730	-1	1836	1855	YX	1293	N104HQ	LGA	BUF	49	292	17	30	2023-10-07 17:00:00	Other
3656	9	28	1735	1729	6	2014	2035	AA	38	N103NN	JFK	LAX	315	2475	17	29	2023-09-28 17:00:00	LAX
3668	12	14	1454	1448	6	1605	1615	YX	1066	N726YX	EWR	IAD	44	212	14	48	2023-12-14 14:00:00	Other
3669	4	16	2030	2030	0	2157	2221	YX	1453	N212JQ	JFK	PIT	62	340	20	30	2023-04-16 20:00:00	Other
3672	6	8	1453	1446	7	1630	1632	AA	786	N812AW	LGA	RDU	67	431	14	46	2023-06-08 14:00:00	Other
3685	5	24	1234	1229	5	1448	1502	DL	320	N382DN	LGA	ATL	110	762	12	29	2023-05-24 12:00:00	ATL
3697	10	29	2207	2159	8	2312	2315	UA	157	N53441	EWR	BOS	33	200	21	59	2023-10-29 21:00:00	BOS
3707	5	3	1051	1045	6	1345	1336	B6	133	N973JT	JFK	MCO	137	944	10	45	2023-05-03 10:00:00	MCO
3708	11	5	1657	1658	-1	1814	1823	YX	1139	N722YX	EWR	PWM	46	284	16	58	2023-11-05 16:00:00	Other
3715	10	23	1719	1715	4	1839	1835	WN	1190	N912WN	LGA	MDW	111	725	17	15	2023-10-23 17:00:00	Other
3732	7	19	1126	1121	5	1313	1312	UA	574	N477UA	EWR	DTW	75	488	11	21	2023-07-19 11:00:00	Other
3734	6	2	958	959	-1	1105	1124	UA	475	N471UA	EWR	BNA	99	748	9	59	2023-06-02 09:00:00	Other
3740	12	3	1111	1110	1	1423	1415	NK	72	N647NK	EWR	DFW	224	1372	11	10	2023-12-03 11:00:00	Other
3742	3	31	629	630	-1	814	820	WN	264	N8849Q	LGA	STL	139	888	6	30	2023-03-31 06:00:00	Other
3743	4	12	1418	1419	-1	1627	1637	9E	1410	N485PX	LGA	CHS	86	641	14	19	2023-04-12 14:00:00	Other
3749	8	30	1101	1053	8	1428	1350	B6	277	N504JB	EWR	MCO	137	937	10	53	2023-08-30 10:00:00	MCO
3753	10	4	1958	1959	-1	2244	2325	AA	729	N840NN	LGA	MIA	141	1096	19	59	2023-10-04 19:00:00	MIA
3770	7	11	1438	1428	10	1630	1640	UA	450	N37466	EWR	DEN	212	1605	14	28	2023-07-11 14:00:00	Other
3784	2	17	1133	1130	3	1253	1237	9E	1332	N330PQ	LGA	BGM	35	147	11	30	2023-02-17 11:00:00	Other
3806	11	3	1030	1030	0	1249	1250	B6	867	N641JB	LGA	CHS	105	641	10	30	2023-11-03 10:00:00	Other
3809	8	2	1430	1430	0	1636	1643	YX	975	N431YX	JFK	CVG	92	589	14	30	2023-08-02 14:00:00	Other
3810	3	2	935	935	0	1258	1257	B6	26	N766JB	LGA	PBI	174	1035	9	35	2023-03-02 09:00:00	Other
3814	8	14	1006	1000	6	1123	1120	YX	1381	N229JQ	LGA	MVY	38	175	10	0	2023-08-14 10:00:00	Other
3827	10	5	2307	2259	8	26	15	B6	436	N284JB	JFK	BOS	42	187	22	59	2023-10-05 22:00:00	BOS
3836	10	9	1559	1600	-1	1828	1912	AS	72	N419AS	EWR	SEA	306	2402	16	0	2023-10-09 16:00:00	Other
3842	4	7	1624	1621	3	1811	1805	UA	100	N29717	EWR	RDU	76	416	16	21	2023-04-07 16:00:00	Other
3852	8	23	2048	2048	0	2337	2357	UA	553	N73270	EWR	SLC	261	1969	20	48	2023-08-23 20:00:00	Other
3853	10	12	1944	1944	0	2312	2329	DL	321	N171DN	JFK	SFO	348	2586	19	44	2023-10-12 19:00:00	Other
3860	4	12	1426	1421	5	1644	1706	UA	250	N13716	EWR	DFW	170	1372	14	21	2023-04-12 14:00:00	Other
3869	9	12	1605	1556	9	1819	1823	UA	435	N37305	EWR	ATL	104	746	15	56	2023-09-12 15:00:00	ATL
3881	5	16	2151	2146	5	11	2349	UA	731	N68834	EWR	DTW	82	488	21	46	2023-05-16 21:00:00	Other
3887	5	10	2001	2000	1	2115	2123	AA	560	N776XF	LGA	DCA	54	214	20	0	2023-05-10 20:00:00	Other
3903	4	2	1806	1800	6	1956	1959	YX	1457	N218JQ	LGA	CMH	79	479	18	0	2023-04-02 18:00:00	Other
3919	5	22	1202	1200	2	1444	1500	DL	201	N401DZ	JFK	LAX	312	2475	12	0	2023-05-22 12:00:00	LAX
3922	3	1	1202	1200	2	1504	1518	B6	749	N547JB	LGA	FLL	150	1076	12	0	2023-03-01 12:00:00	FLL
3923	7	8	1114	1110	4	1552	1323	DL	713	N341NB	LGA	MSY	NA	1183	11	10	2023-07-08 11:00:00	Other
3925	3	23	2049	2043	6	2340	2258	B6	548	N368JB	JFK	DTW	111	509	20	43	2023-03-23 20:00:00	Other
3926	5	9	2009	2000	9	2125	2123	AA	560	N714US	LGA	DCA	54	214	20	0	2023-05-09 20:00:00	Other
3927	11	28	1623	1623	0	1740	1739	UA	133	N29129	EWR	BOS	44	200	16	23	2023-11-28 16:00:00	BOS
3931	6	29	848	845	3	1119	1137	B6	84	N527JL	JFK	IAH	177	1417	8	45	2023-06-29 08:00:00	Other
3935	9	1	739	739	0	1026	1029	B6	219	N521JB	LGA	MCO	128	950	7	39	2023-09-01 07:00:00	MCO
3950	9	2	900	900	0	1046	1058	AA	761	N717UW	LGA	RDU	71	431	9	0	2023-09-02 09:00:00	Other
3965	3	27	1659	1650	9	1941	1916	B6	118	N328JB	JFK	SAV	119	718	16	50	2023-03-27 16:00:00	Other
3982	7	11	559	600	-1	753	820	DL	671	N6714Q	JFK	ATL	97	760	6	0	2023-07-11 06:00:00	ATL
3999	2	18	1244	1245	-1	1456	1530	WN	881	N8545V	LGA	ATL	112	762	12	45	2023-02-18 12:00:00	ATL
4000	4	20	1506	1505	1	1640	1643	UA	563	N879UA	LGA	ORD	111	733	15	5	2023-04-20 15:00:00	ORD
4010	8	13	801	759	2	1031	1013	UA	673	N27269	EWR	DEN	236	1605	7	59	2023-08-13 07:00:00	Other
4014	5	30	1455	1456	-1	1710	1713	9E	1523	N331PQ	LGA	CVG	91	585	14	56	2023-05-30 14:00:00	Other
4028	4	3	1953	1950	3	2247	2256	B6	176	N584JB	LGA	FLL	145	1076	19	50	2023-04-03 19:00:00	FLL
4034	2	27	646	644	2	930	928	B6	771	N603JB	LGA	DEN	254	1620	6	44	2023-02-27 06:00:00	Other
4040	7	1	716	715	1	931	1000	WN	829	N927WN	LGA	HOU	180	1428	7	15	2023-07-01 07:00:00	Other
4061	1	13	1845	1845	0	2132	2147	UA	983	N12020	EWR	LAX	304	2454	18	45	2023-01-13 18:00:00	LAX
4063	6	20	2029	2029	0	2342	2335	B6	171	N649JB	LGA	FLL	165	1076	20	29	2023-06-20 20:00:00	FLL
4066	2	6	2009	2005	4	2306	2358	AA	928	N896NN	LGA	MIA	142	1096	20	5	2023-02-06 20:00:00	MIA
4069	4	3	1533	1529	4	1835	1852	AA	121	N106NN	JFK	LAX	337	2475	15	29	2023-04-03 15:00:00	LAX
4078	8	25	1014	1007	7	1215	1220	UA	450	N76516	EWR	DEN	208	1605	10	7	2023-08-25 10:00:00	Other
4081	6	26	908	907	1	1017	1030	B6	631	N231JB	JFK	BTV	44	266	9	7	2023-06-26 09:00:00	Other
4084	3	13	1629	1629	0	2006	1946	B6	746	N265JB	LGA	PBI	177	1035	16	29	2023-03-13 16:00:00	Other
4092	1	8	2159	2155	4	2310	2307	B6	991	N329JB	JFK	SYR	44	209	21	55	2023-01-08 21:00:00	Other
4093	1	10	1515	1515	0	1842	1840	UA	726	N2341U	EWR	SFO	344	2565	15	15	2023-01-10 15:00:00	Other
4095	12	25	846	846	0	1048	1119	YX	1091	N724YX	EWR	IND	96	645	8	46	2023-12-25 08:00:00	Other
4117	5	21	1859	1855	4	2108	2122	DL	808	N3761R	EWR	ATL	103	746	18	55	2023-05-21 18:00:00	ATL
4118	5	19	559	600	-1	702	710	DL	610	N132DU	LGA	BOS	40	184	6	0	2023-05-19 06:00:00	BOS
4124	1	17	1934	1929	5	2150	2200	DL	698	N371NW	LGA	MSY	175	1183	19	29	2023-01-17 19:00:00	Other
4167	8	20	1629	1629	0	1832	1922	DL	464	N704X	JFK	ATL	98	760	16	29	2023-08-20 16:00:00	ATL
4170	12	23	2124	2125	-1	2239	2300	WN	1079	N8308K	LGA	BNA	108	764	21	25	2023-12-23 21:00:00	Other
4171	1	9	749	745	4	917	923	YX	1349	N417YX	JFK	DCA	60	213	7	45	2023-01-09 07:00:00	Other
4172	9	12	1154	1155	-1	1318	1310	WN	693	N8840Q	LGA	MDW	108	725	11	55	2023-09-12 11:00:00	Other
4187	12	19	916	910	6	1019	1022	B6	946	N329JB	JFK	BOS	40	187	9	10	2023-12-19 09:00:00	BOS
4191	5	21	2059	2059	0	2	2350	B6	681	N584JB	EWR	MCO	132	937	20	59	2023-05-21 20:00:00	MCO
4195	6	9	729	729	0	910	919	AA	1016	N800NN	LGA	ORD	109	733	7	29	2023-06-09 07:00:00	ORD
4208	2	14	1533	1530	3	1822	1846	DL	939	N356DN	JFK	MIA	148	1089	15	30	2023-02-14 15:00:00	MIA
4210	3	29	739	735	4	1034	1053	DL	464	N350DN	JFK	FLL	144	1069	7	35	2023-03-29 07:00:00	FLL
4226	4	24	1605	1555	10	1737	1727	YX	1209	N821MD	LGA	RIC	55	292	15	55	2023-04-24 15:00:00	Other
4228	11	5	1359	1400	-1	1627	1704	UA	474	N854UA	EWR	DFW	183	1372	14	0	2023-11-05 14:00:00	Other
4233	5	16	1429	1429	0	1646	1653	B6	712	N775JB	LGA	MSY	164	1183	14	29	2023-05-16 14:00:00	Other
4234	10	4	1528	1529	-1	1703	1706	YX	1344	N402YX	JFK	BNA	111	765	15	29	2023-10-04 15:00:00	Other
4264	4	6	1129	1125	4	1334	1413	DL	319	N317US	LGA	ATL	105	762	11	25	2023-04-06 11:00:00	ATL
4269	8	22	1519	1518	1	1745	1811	UA	617	N431UA	EWR	TPA	128	997	15	18	2023-08-22 15:00:00	Other
4277	5	20	1336	1330	6	1437	1449	B6	516	N193JB	LGA	PWM	41	269	13	30	2023-05-20 13:00:00	Other
4281	12	31	1111	1101	10	1244	1308	UA	751	N75436	EWR	MSP	128	1008	11	1	2023-12-31 11:00:00	Other
4304	11	2	1536	1537	-1	1848	1844	DL	761	N379DN	JFK	FLL	156	1069	15	37	2023-11-02 15:00:00	FLL
4311	9	14	1405	1400	5	1527	1525	YX	1092	N861RW	EWR	ORF	54	284	14	0	2023-09-14 14:00:00	Other
4314	7	6	1301	1259	2	1518	1531	DL	116	N326DN	LGA	ATL	101	762	12	59	2023-07-06 12:00:00	ATL
4325	6	30	1905	1859	6	2152	2151	AS	95	N272AK	EWR	SAN	318	2425	18	59	2023-06-30 18:00:00	Other
4333	12	23	1444	1445	-1	1620	1615	YX	1025	N639RW	EWR	IAD	51	212	14	45	2023-12-23 14:00:00	Other
4351	2	5	1139	1130	9	1258	1308	UA	562	N17128	EWR	ORD	109	719	11	30	2023-02-05 11:00:00	ORD
4357	5	22	1352	1349	3	1537	1522	9E	1330	N320PQ	LGA	BNA	119	764	13	49	2023-05-22 13:00:00	Other
4361	1	13	1342	1335	7	1702	1644	UA	566	N37267	EWR	FLL	162	1065	13	35	2023-01-13 13:00:00	FLL
4364	9	27	2006	1959	7	2310	2319	DL	563	N369DN	LGA	FLL	150	1076	19	59	2023-09-27 19:00:00	FLL
4371	5	8	1159	1200	-1	1514	1500	DL	201	N419DX	JFK	LAX	345	2475	12	0	2023-05-08 12:00:00	LAX
4375	6	21	1749	1750	-1	2037	2049	UA	655	N62889	EWR	TPA	136	997	17	50	2023-06-21 17:00:00	Other
4378	7	18	2051	2045	6	2250	2256	DL	393	N331NB	LGA	MSY	156	1183	20	45	2023-07-18 20:00:00	Other
4380	11	9	830	830	0	1443	1438	UA	119	N76055	EWR	HNL	640	4962	8	30	2023-11-09 08:00:00	Other
4381	3	23	1523	1515	8	1702	1705	OO	1199	N241SY	JFK	PIT	78	340	15	15	2023-03-23 15:00:00	Other
4392	11	22	1029	1030	-1	1331	1356	B6	945	N627JB	JFK	AUS	199	1521	10	30	2023-11-22 10:00:00	Other
4393	9	13	1058	1059	-1	1237	1309	DL	499	N388DN	LGA	MSP	139	1020	10	59	2023-09-13 10:00:00	Other
4399	12	18	1706	1702	4	1850	1856	DL	937	N995AT	EWR	DTW	78	488	17	2	2023-12-18 17:00:00	Other
4407	10	21	739	729	10	946	955	UA	401	N13138	EWR	PHX	280	2133	7	29	2023-10-21 07:00:00	Other
4418	7	8	632	625	7	859	855	WN	792	N8578Q	LGA	DAL	183	1381	6	25	2023-07-08 06:00:00	Other
4431	3	6	925	923	2	1128	1143	UA	783	N416UA	EWR	MCI	164	1092	9	23	2023-03-06 09:00:00	Other
4438	4	15	830	830	0	1244	1227	B6	193	N999JQ	JFK	SJU	199	1598	8	30	2023-04-15 08:00:00	Other
4439	12	5	1008	1003	5	1207	1233	UA	537	N62884	EWR	DEN	217	1605	10	3	2023-12-05 10:00:00	Other
4442	1	11	559	600	-1	732	749	DL	480	N135DQ	LGA	ORD	118	733	6	0	2023-01-11 06:00:00	ORD
4448	5	22	604	600	4	839	850	WN	614	N8796L	LGA	DAL	182	1381	6	0	2023-05-22 06:00:00	Other
4458	1	6	822	820	2	1003	1031	UA	964	N12225	EWR	DTW	78	488	8	20	2023-01-06 08:00:00	Other
4459	6	1	1648	1640	8	1928	1907	B6	120	N247JB	JFK	SAV	103	718	16	40	2023-06-01 16:00:00	Other
4475	9	27	805	805	0	1030	1032	DL	125	N524DE	JFK	PHX	281	2153	8	5	2023-09-27 08:00:00	Other
4481	5	31	745	745	0	909	921	UA	839	N75432	EWR	ORD	104	719	7	45	2023-05-31 07:00:00	ORD
4482	8	4	604	600	4	747	746	DL	621	N953AT	EWR	DTW	86	488	6	0	2023-08-04 06:00:00	Other
4493	12	17	1445	1440	5	1707	1715	WN	683	N872CB	LGA	MSY	181	1183	14	40	2023-12-17 14:00:00	Other
4499	8	29	1808	1759	9	2011	2008	YX	1035	N432YX	LGA	MCI	160	1107	17	59	2023-08-29 17:00:00	Other
4510	3	1	839	840	-1	1124	1128	DL	553	N856DN	JFK	ATL	117	760	8	40	2023-03-01 08:00:00	ATL
4512	2	28	734	735	-1	1054	1046	UA	289	N75426	EWR	IAH	198	1400	7	35	2023-02-28 07:00:00	Other
4514	12	26	1359	1400	-1	1653	1719	B6	622	N2059J	JFK	RSW	150	1074	14	0	2023-12-26 14:00:00	Other
4515	5	4	1100	1056	4	1309	1306	UA	871	N873UA	EWR	MSY	156	1167	10	56	2023-05-04 10:00:00	Other
4525	6	21	2158	2159	-1	2336	2341	DL	902	N344NB	JFK	BUF	50	301	21	59	2023-06-21 21:00:00	Other
4526	11	9	907	906	1	1153	1211	UA	694	N4901U	EWR	PBI	144	1023	9	6	2023-11-09 09:00:00	Other
4530	4	10	1350	1345	5	1617	1700	DL	260	N176DN	JFK	LAX	298	2475	13	45	2023-04-10 13:00:00	LAX
4539	8	13	2005	1959	6	2155	2152	YX	1084	N426YX	LGA	ILM	75	500	19	59	2023-08-13 19:00:00	Other
4540	7	4	1904	1859	5	2155	2204	NK	26	N908NK	EWR	LAX	309	2454	18	59	2023-07-04 18:00:00	LAX
4541	9	11	1835	1835	0	2241	2152	B6	240	N746JB	JFK	SJC	350	2569	18	35	2023-09-11 18:00:00	Other
4547	11	10	1406	1405	1	1644	1639	UA	885	N25705	EWR	ATL	124	746	14	5	2023-11-10 14:00:00	ATL
4557	11	8	906	901	5	1147	1226	AA	569	N766AN	JFK	MIA	135	1089	9	1	2023-11-08 09:00:00	MIA
4561	3	10	2158	2159	-1	132	133	B6	943	N934JB	JFK	SFO	365	2586	21	59	2023-03-10 21:00:00	Other
4570	2	22	1958	1959	-1	2140	2154	YX	1156	N862RW	EWR	ILM	79	488	19	59	2023-02-22 19:00:00	Other
4582	6	5	1228	1229	-1	1456	1517	UA	438	N412UA	LGA	IAH	184	1416	12	29	2023-06-05 12:00:00	Other
4583	9	14	825	820	5	1107	1133	DL	334	N504DZ	JFK	SAN	317	2446	8	20	2023-09-14 08:00:00	Other
4599	1	28	2035	2029	6	2336	2346	UA	724	N17279	EWR	MIA	153	1085	20	29	2023-01-28 20:00:00	MIA
4606	2	9	1600	1557	3	1819	1816	AA	110	N873NN	JFK	CLT	91	541	15	57	2023-02-09 15:00:00	CLT
4608	10	6	1801	1755	6	2006	2038	B6	244	N612JB	JFK	LAS	291	2248	17	55	2023-10-06 17:00:00	Other
4610	1	19	1619	1620	-1	1927	1951	AA	579	N820AW	LGA	MIA	160	1096	16	20	2023-01-19 16:00:00	MIA
4614	2	12	1840	1830	10	2139	2134	UA	681	N17017	EWR	LAX	297	2454	18	30	2023-02-12 18:00:00	LAX
4616	4	6	1143	1140	3	1338	1341	YX	1170	N106HQ	LGA	MEM	149	963	11	40	2023-04-06 11:00:00	Other
4617	1	23	1101	1100	1	1304	1256	YX	1121	N749YX	EWR	MYR	101	550	11	0	2023-01-23 11:00:00	Other
4632	7	10	1729	1730	-1	2055	2140	DL	262	N721TW	JFK	SFO	339	2586	17	30	2023-07-10 17:00:00	Other
4633	1	25	2037	2030	7	2156	2150	B6	397	N279JB	JFK	BOS	45	187	20	30	2023-01-25 20:00:00	BOS
4636	9	12	841	835	6	1028	1035	YX	1828	N234JQ	LGA	CMH	75	479	8	35	2023-09-12 08:00:00	Other
4643	3	22	1739	1740	-1	2135	2105	NK	32	N924NK	EWR	LAX	380	2454	17	40	2023-03-22 17:00:00	LAX
4658	7	30	807	759	8	949	1002	AA	452	N987AN	JFK	CLT	79	541	7	59	2023-07-30 07:00:00	CLT
4663	4	23	2025	2025	0	2319	2347	AA	688	N854NN	LGA	MIA	147	1096	20	25	2023-04-23 20:00:00	MIA
4667	8	8	1434	1435	-1	1632	1654	YX	935	N732YX	EWR	IND	92	645	14	35	2023-08-08 14:00:00	Other
4670	12	3	958	955	3	1207	1156	AA	936	N192UW	EWR	CLT	103	529	9	55	2023-12-03 09:00:00	CLT
4703	1	13	1704	1656	8	1928	1927	YX	1219	N653RW	EWR	SAV	119	708	16	56	2023-01-13 16:00:00	Other
4712	8	27	611	605	6	813	819	UA	493	N69824	EWR	DEN	212	1605	6	5	2023-08-27 06:00:00	Other
4727	9	15	1517	1514	3	1658	1710	9E	1538	N147PQ	LGA	RDU	67	431	15	14	2023-09-15 15:00:00	Other
4730	1	5	659	700	-1	1029	1024	B6	321	N993JE	JFK	LAX	343	2475	7	0	2023-01-05 07:00:00	LAX
4744	10	12	1602	1555	7	1907	1904	DL	973	N3757D	LGA	MIA	154	1096	15	55	2023-10-12 15:00:00	MIA
4747	2	26	2159	2159	0	2304	2301	9E	1446	N138EV	LGA	PVD	32	143	21	59	2023-02-26 21:00:00	Other
4775	11	20	1101	1055	6	1327	1335	WN	30	N237WN	LGA	ATL	115	762	10	55	2023-11-20 10:00:00	ATL
4776	8	10	1518	1510	8	1824	1823	DL	649	N322DN	JFK	MCO	129	944	15	10	2023-08-10 15:00:00	MCO
4779	11	14	914	915	-1	1024	1036	B6	969	N229JB	JFK	BOS	41	187	9	15	2023-11-14 09:00:00	BOS
4780	2	17	1316	1315	1	1450	1450	UA	282	N37413	EWR	ORD	112	719	13	15	2023-02-17 13:00:00	ORD
4782	6	5	834	835	-1	950	1010	9E	1718	N197PQ	JFK	ORF	47	290	8	35	2023-06-05 08:00:00	Other
4783	2	5	1600	1600	0	1734	1807	OO	1165	N247SY	JFK	ORD	125	740	16	0	2023-02-05 16:00:00	ORD
4786	7	23	744	745	-1	902	915	WN	592	N8736J	LGA	STL	120	888	7	45	2023-07-23 07:00:00	Other
4794	1	5	1257	1255	2	1614	1601	B6	42	N635JB	JFK	TPA	172	1005	12	55	2023-01-05 12:00:00	Other
4795	7	3	725	725	0	840	900	WN	966	N8813Q	LGA	STL	123	888	7	25	2023-07-03 07:00:00	Other
4798	5	1	1716	1715	1	1821	1842	B6	396	N328JB	LGA	BOS	40	184	17	15	2023-05-01 17:00:00	BOS
4804	8	15	1359	1400	-1	1627	1618	DL	650	N3755D	EWR	ATL	111	746	14	0	2023-08-15 14:00:00	ATL
4815	3	25	1156	1156	0	1455	1507	DL	413	N360NW	LGA	TPA	159	1010	11	56	2023-03-25 11:00:00	Other
4819	7	14	1018	1018	0	1158	1216	NK	21	N662NK	EWR	MYR	83	550	10	18	2023-07-14 10:00:00	Other
4824	7	11	1314	1305	9	1520	1440	UA	99	N56859	EWR	ORD	119	719	13	5	2023-07-11 13:00:00	ORD
4829	7	1	2007	1959	8	2250	2319	DL	478	N325DN	LGA	FLL	143	1076	19	59	2023-07-01 19:00:00	FLL
4832	9	30	1758	1759	-1	1931	1955	YX	1387	N435YX	JFK	CMH	73	483	17	59	2023-09-30 17:00:00	Other
4837	6	19	1319	1320	-1	1427	1440	WN	67	N8857Q	LGA	BNA	108	764	13	20	2023-06-19 13:00:00	Other
4839	12	19	701	700	1	916	946	DL	173	N366NW	LGA	ATL	108	762	7	0	2023-12-19 07:00:00	ATL
4844	6	27	928	920	8	1101	1115	9E	1714	N306PQ	JFK	CLE	68	425	9	20	2023-06-27 09:00:00	Other
4853	6	13	2235	2225	10	239	222	NK	1058	N604NK	EWR	SJU	224	1608	22	25	2023-06-13 22:00:00	Other
4857	9	24	803	800	3	1105	1037	B6	138	N992JB	JFK	LAS	303	2248	8	0	2023-09-24 08:00:00	Other
4862	4	24	1851	1850	1	2055	2109	9E	1306	N916XJ	LGA	GRR	94	618	18	50	2023-04-24 18:00:00	Other
4871	3	22	1736	1729	7	2119	2042	B6	718	N603JB	JFK	PSP	365	2378	17	29	2023-03-22 17:00:00	Other
4877	2	24	1739	1729	10	1934	1932	YX	1063	N740YX	EWR	CMH	82	463	17	29	2023-02-24 17:00:00	Other
4882	8	9	931	930	1	1236	1246	DL	722	N6705Y	JFK	SLC	275	1990	9	30	2023-08-09 09:00:00	Other
4886	12	23	959	1000	-1	1311	1336	UA	567	N34131	EWR	SFO	345	2565	10	0	2023-12-23 10:00:00	Other
4889	3	26	1428	1429	-1	1658	1641	UA	204	N820UA	EWR	MSY	185	1167	14	29	2023-03-26 14:00:00	Other
4894	5	29	1006	959	7	1131	1128	YX	1630	N214JQ	LGA	BOS	37	184	9	59	2023-05-29 09:00:00	BOS
4899	8	19	1509	1459	10	1754	1806	DL	182	N171DZ	JFK	LAX	317	2475	14	59	2023-08-19 14:00:00	LAX
4902	10	6	806	805	1	1041	1024	DL	901	N870DN	EWR	ATL	107	746	8	5	2023-10-06 08:00:00	ATL
4904	6	15	1329	1330	-1	1603	1623	UA	772	N796UA	EWR	SFO	313	2565	13	30	2023-06-15 13:00:00	Other
4906	10	28	1030	1030	0	1256	1323	B6	346	N594JB	JFK	MCO	127	944	10	30	2023-10-28 10:00:00	MCO
4915	10	19	915	915	0	1152	1225	AA	573	N824NN	LGA	DFW	190	1389	9	15	2023-10-19 09:00:00	Other
4916	7	6	1155	1155	0	1320	1341	G4	834	278NV	EWR	VPS	122	988	11	55	2023-07-06 11:00:00	Other
4934	4	6	1934	1929	5	2155	2119	OO	1061	N255SY	JFK	BNA	127	765	19	29	2023-04-06 19:00:00	Other
4936	1	14	1537	1529	8	1809	1839	AA	784	N942NN	EWR	DFW	190	1372	15	29	2023-01-14 15:00:00	Other
4945	3	6	2040	2030	10	2327	2336	UA	792	N873UA	EWR	DFW	206	1372	20	30	2023-03-06 20:00:00	Other
4947	11	7	929	923	6	1223	1230	B6	371	N706JB	JFK	MCO	134	944	9	23	2023-11-07 09:00:00	MCO
4976	9	21	1823	1824	-1	2055	2052	UA	506	N69847	EWR	ATL	102	746	18	24	2023-09-21 18:00:00	ATL
4980	6	29	1014	1010	4	1205	1214	AA	783	N948AN	LGA	CLT	84	544	10	10	2023-06-29 10:00:00	CLT
4982	5	15	1730	1730	0	1913	1915	OO	1151	N259SY	JFK	MKE	129	745	17	30	2023-05-15 17:00:00	Other
4992	7	20	2047	2040	7	22	29	AA	768	N109NN	JFK	SFO	344	2586	20	40	2023-07-20 20:00:00	Other
4994	12	21	1634	1634	0	1910	2008	DL	279	N521DT	JFK	SAN	320	2446	16	34	2023-12-21 16:00:00	Other
5005	5	14	2034	2029	5	2206	2206	UA	443	N27253	EWR	ORD	117	719	20	29	2023-05-14 20:00:00	ORD
5007	4	3	1436	1430	6	1529	1535	9E	1416	N131EV	LGA	ORH	26	146	14	30	2023-04-03 14:00:00	Other
5013	4	24	1958	1959	-1	2155	2200	YX	1060	N725YX	EWR	ILM	74	488	19	59	2023-04-24 19:00:00	Other
5018	5	18	1200	1200	0	1446	1500	DL	201	N412DX	JFK	LAX	308	2475	12	0	2023-05-18 12:00:00	LAX
5024	3	18	2135	2135	0	2351	2338	UA	484	N18220	EWR	CHS	102	628	21	35	2023-03-18 21:00:00	Other
5031	8	4	1356	1355	1	1558	1600	WN	128	N8577Z	LGA	MSY	164	1183	13	55	2023-08-04 13:00:00	Other
5033	12	24	1109	1110	-1	1410	1418	DL	486	N832DN	JFK	MIA	158	1089	11	10	2023-12-24 11:00:00	MIA
5035	8	21	924	920	4	1118	1127	9E	1237	N331PQ	LGA	ILM	71	500	9	20	2023-08-21 09:00:00	Other
5038	11	5	739	730	9	943	951	DL	525	N376NW	JFK	MSP	152	1029	7	30	2023-11-05 07:00:00	Other
5039	10	19	1244	1245	-1	1530	1557	AA	603	N987AM	EWR	MIA	148	1085	12	45	2023-10-19 12:00:00	MIA
5041	8	21	1215	1210	5	1352	1409	YX	1303	N211JQ	LGA	CMH	69	479	12	10	2023-08-21 12:00:00	Other
5046	7	4	1528	1525	3	1659	1700	WN	236	N7888A	LGA	STL	123	888	15	25	2023-07-04 15:00:00	Other
5049	4	17	2028	2020	8	2320	2320	WN	565	N8690A	LGA	DAL	190	1381	20	20	2023-04-17 20:00:00	Other
5054	11	1	808	805	3	1158	1204	DL	668	N534DT	JFK	SJU	202	1598	8	5	2023-11-01 08:00:00	Other
5068	6	28	1055	1048	7	1259	1310	UA	515	N14731	EWR	JAX	103	820	10	48	2023-06-28 10:00:00	Other
5083	10	7	1759	1759	0	2053	2051	DL	187	N129DU	JFK	DFW	198	1391	17	59	2023-10-07 17:00:00	Other
5107	2	4	2048	2045	3	2232	2208	UA	435	N421UA	EWR	BUF	54	282	20	45	2023-02-04 20:00:00	Other
5108	12	30	1835	1829	6	2119	2144	F9	1410	N389FR	LGA	MCO	138	950	18	29	2023-12-30 18:00:00	MCO
5111	9	14	1147	1140	7	1444	1435	DL	133	N119DU	LGA	DFW	192	1389	11	40	2023-09-14 11:00:00	Other
5112	9	21	1703	1655	8	1947	2000	AS	78	N921VA	EWR	LAX	316	2454	16	55	2023-09-21 16:00:00	LAX
5118	3	21	1129	1130	-1	1432	1434	DL	1010	N351DN	LGA	MCO	141	950	11	30	2023-03-21 11:00:00	MCO
5138	7	31	1510	1510	0	1755	1810	DL	200	N106DU	LGA	DFW	180	1389	15	10	2023-07-31 15:00:00	Other
5142	11	1	1724	1715	9	1856	1837	B6	381	N258JB	LGA	BOS	39	184	17	15	2023-11-01 17:00:00	BOS
5147	8	6	1258	1258	0	1432	1451	YX	1083	N438YX	JFK	RDU	69	427	12	58	2023-08-06 12:00:00	Other
5150	11	2	1457	1455	2	1621	1629	OO	1212	N614CZ	JFK	IAD	49	228	14	55	2023-11-02 14:00:00	Other
5161	5	4	1539	1529	10	1927	1845	DL	398	N107DN	LGA	MIA	143	1096	15	29	2023-05-04 15:00:00	MIA
5163	2	27	1803	1800	3	1926	1942	UA	905	N875UA	LGA	ORD	116	733	18	0	2023-02-27 18:00:00	ORD
5165	7	2	1704	1659	5	1948	1948	UA	699	N463UA	EWR	DFW	184	1372	16	59	2023-07-02 16:00:00	Other
5183	9	9	630	630	0	913	920	UA	819	N472UA	EWR	DFW	186	1372	6	30	2023-09-09 06:00:00	Other
5193	5	13	1117	1118	-1	1357	1435	DL	884	N367DN	LGA	FLL	138	1076	11	18	2023-05-13 11:00:00	FLL
5195	4	6	1528	1529	-1	1801	1802	YX	1139	N123HQ	JFK	IND	106	665	15	29	2023-04-06 15:00:00	Other
5201	1	7	1837	1829	8	2149	2142	AA	201	N931AN	JFK	MIA	147	1089	18	29	2023-01-07 18:00:00	MIA
5207	1	31	1314	1315	-1	1552	1632	B6	374	N651JB	EWR	PBI	140	1023	13	15	2023-01-31 13:00:00	Other
5209	9	18	1801	1800	1	2025	1939	9E	1441	N310PQ	LGA	BHM	127	866	18	0	2023-09-18 18:00:00	Other
5211	9	6	2005	2000	5	2212	2232	DL	302	N108DN	LGA	ATL	102	762	20	0	2023-09-06 20:00:00	ATL
5221	1	26	1852	1850	2	2119	2120	9E	1465	N908XJ	LGA	SAV	121	722	18	50	2023-01-26 18:00:00	Other
5229	9	30	1502	1459	3	1557	1634	YX	1361	N430YX	JFK	DCA	40	213	14	59	2023-09-30 14:00:00	Other
5233	9	23	1322	1321	1	1618	1636	AA	638	N916NN	EWR	MIA	155	1085	13	21	2023-09-23 13:00:00	MIA
5249	6	13	851	850	1	1045	1053	NK	314	N657NK	LGA	CLT	91	544	8	50	2023-06-13 08:00:00	CLT
5250	5	2	1120	1112	8	1419	1429	DL	612	N389DN	LGA	MIA	147	1096	11	12	2023-05-02 11:00:00	MIA
5253	10	3	1659	1700	-1	1941	2001	DL	86	N183DN	JFK	LAX	304	2475	17	0	2023-10-03 17:00:00	LAX
5259	8	1	1534	1529	5	1847	1852	AA	91	N804NN	JFK	MIA	147	1089	15	29	2023-08-01 15:00:00	MIA
5262	4	5	1045	1039	6	1233	1244	UA	706	N873UA	EWR	MSP	153	1008	10	39	2023-04-05 10:00:00	Other
5265	5	5	1702	1655	7	1951	2007	AS	82	N268AK	EWR	SEA	314	2402	16	55	2023-05-05 16:00:00	Other
5272	12	7	1100	1100	0	1354	1414	AA	209	N872NN	JFK	MIA	149	1089	11	0	2023-12-07 11:00:00	MIA
5274	7	18	2005	1959	6	2339	2357	UA	484	N69819	EWR	SJU	194	1608	19	59	2023-07-18 19:00:00	Other
5277	12	20	1441	1440	1	1632	1651	AA	100	N315RJ	JFK	CLT	80	541	14	40	2023-12-20 14:00:00	CLT
5282	4	20	1038	1035	3	1259	1305	WN	589	N8859Q	LGA	ATL	110	762	10	35	2023-04-20 10:00:00	ATL
5289	9	20	1329	1329	0	1451	1511	MQ	1032	N778RH	EWR	ORD	112	719	13	29	2023-09-20 13:00:00	ORD
5290	2	4	2154	2145	9	2331	2313	9E	1400	N131EV	JFK	ROC	57	264	21	45	2023-02-04 21:00:00	Other
5297	3	2	1434	1435	-1	1723	1735	DL	486	N350DN	LGA	MCO	141	950	14	35	2023-03-02 14:00:00	MCO
5304	9	11	604	605	-1	715	725	YX	1863	N810MD	LGA	DCA	45	214	6	5	2023-09-11 06:00:00	Other
5312	3	20	1009	1010	-1	1316	1318	DL	995	N113DX	LGA	MCO	159	950	10	10	2023-03-20 10:00:00	MCO
5321	9	19	1920	1915	5	2226	2219	DL	141	N172DN	JFK	LAX	324	2475	19	15	2023-09-19 19:00:00	LAX
5323	11	15	810	810	0	1046	1049	B6	188	N779JB	JFK	ATL	112	760	8	10	2023-11-15 08:00:00	ATL
5325	3	29	2102	2059	3	2259	2254	UA	114	N24729	EWR	MEM	142	946	20	59	2023-03-29 20:00:00	Other
5327	8	1	1534	1530	4	1836	1839	UA	607	N228UA	EWR	SFO	334	2565	15	30	2023-08-01 15:00:00	Other
5332	9	12	1720	1715	5	1817	1841	B6	380	N318JB	LGA	BOS	32	184	17	15	2023-09-12 17:00:00	BOS
5336	8	11	1514	1515	-1	1802	1822	DL	182	N199DN	JFK	LAX	314	2475	15	15	2023-08-11 15:00:00	LAX
5342	4	19	1800	1800	0	2108	2118	UA	414	N78005	EWR	SFO	342	2565	18	0	2023-04-19 18:00:00	Other
5348	11	8	1620	1620	0	1903	1930	AA	436	N875NN	JFK	DFW	199	1391	16	20	2023-11-08 16:00:00	Other
5353	9	12	855	855	0	1007	1033	9E	1722	N335PQ	LGA	CHO	50	305	8	55	2023-09-12 08:00:00	Other
5354	3	25	1929	1929	0	2213	2159	9E	1437	N604LR	JFK	MSP	144	1029	19	29	2023-03-25 19:00:00	Other
5359	10	3	1821	1815	6	1918	1944	UA	371	N69806	EWR	BNA	98	748	18	15	2023-10-03 18:00:00	Other
5361	3	26	1522	1520	2	1726	1710	WN	1205	N8571Z	LGA	STL	157	888	15	20	2023-03-26 15:00:00	Other
5363	4	21	846	845	1	1039	1051	9E	1440	N917XJ	LGA	AVL	85	599	8	45	2023-04-21 08:00:00	Other
5364	12	7	1544	1543	1	1827	1912	DL	850	N345NB	JFK	AUS	207	1521	15	43	2023-12-07 15:00:00	Other
5367	8	29	1959	1950	9	2254	2246	DL	208	N131DU	LGA	DFW	195	1389	19	50	2023-08-29 19:00:00	Other
5370	4	10	1800	1800	0	2055	2136	AA	847	N108NN	JFK	SFO	323	2586	18	0	2023-04-10 18:00:00	Other
5371	2	3	630	630	0	1016	1020	AA	32	N110AN	JFK	SFO	361	2586	6	30	2023-02-03 06:00:00	Other
5374	10	28	859	900	-1	1216	1218	AA	1	N117AN	JFK	LAX	347	2475	9	0	2023-10-28 09:00:00	LAX
5376	3	24	659	700	-1	947	1015	B6	145	N536JB	EWR	FLL	147	1065	7	0	2023-03-24 07:00:00	FLL
5377	7	13	1027	1023	4	1141	1158	UA	556	N73276	EWR	ORD	108	719	10	23	2023-07-13 10:00:00	ORD
5382	10	26	2036	2030	6	2214	2201	B6	2	N317JB	JFK	BUF	59	301	20	30	2023-10-26 20:00:00	Other
5399	5	27	1158	1159	-1	1342	1423	UA	857	N75436	EWR	DEN	202	1605	11	59	2023-05-27 11:00:00	Other
5416	3	4	1451	1445	6	1649	1646	YX	1388	N447YX	JFK	CMH	86	483	14	45	2023-03-04 14:00:00	Other
5418	2	18	708	659	9	852	839	AA	949	N940NN	EWR	ORD	118	719	6	59	2023-02-18 06:00:00	ORD
5419	8	13	719	710	9	1001	1003	UA	529	N17306	EWR	PDX	317	2434	7	10	2023-08-13 07:00:00	Other
5421	11	6	1600	1559	1	1807	1827	DL	879	N905DN	EWR	ATL	102	746	15	59	2023-11-06 15:00:00	ATL
5422	5	25	1600	1559	1	1700	1721	UA	140	N897UA	EWR	BOS	35	200	15	59	2023-05-25 15:00:00	BOS
5427	5	23	1135	1130	5	1426	1456	UA	230	N67134	EWR	SFO	323	2565	11	30	2023-05-23 11:00:00	Other
5428	3	24	1201	1159	2	1432	1431	UA	388	N57286	EWR	DEN	242	1605	11	59	2023-03-24 11:00:00	Other
5430	11	16	1648	1642	6	1925	1916	UA	934	N41140	EWR	DEN	235	1605	16	42	2023-11-16 16:00:00	Other
5431	11	9	758	759	-1	1042	1110	AA	343	N927NN	LGA	MIA	145	1096	7	59	2023-11-09 07:00:00	MIA
5444	8	18	1157	1155	2	1515	1455	DL	477	N117DX	LGA	MCO	133	950	11	55	2023-08-18 11:00:00	MCO
5451	12	26	1732	1731	1	2052	2047	AA	896	N330TJ	JFK	MIA	155	1089	17	31	2023-12-26 17:00:00	MIA
5454	4	6	1843	1838	5	2109	2021	UA	422	N37257	EWR	ORD	117	719	18	38	2023-04-06 18:00:00	ORD
5469	6	17	1539	1531	8	2041	1849	DL	595	N319DN	LGA	FLL	241	1076	15	31	2023-06-17 15:00:00	FLL
5473	10	2	1450	1450	0	1738	1759	DL	329	N317DU	LGA	PBI	139	1035	14	50	2023-10-02 14:00:00	Other
5489	1	8	2202	2153	9	2313	2338	UA	596	N431UA	EWR	ORD	102	719	21	53	2023-01-08 21:00:00	ORD
5493	4	13	1959	2000	-1	2113	2128	YX	1458	N227JQ	LGA	BOS	42	184	20	0	2023-04-13 20:00:00	BOS
5495	1	18	2130	2122	8	2318	2327	UA	742	N81449	EWR	CLT	80	529	21	22	2023-01-18 21:00:00	CLT
5505	2	28	1242	1241	1	1714	1729	AA	258	N90024	JFK	STT	189	1623	12	41	2023-02-28 12:00:00	Other
5519	6	1	1540	1540	0	1705	1720	9E	1448	N311PQ	JFK	SYR	43	209	15	40	2023-06-01 15:00:00	Other
5520	6	26	1022	1020	2	1216	1218	9E	1576	N482PX	LGA	MYR	81	563	10	20	2023-06-26 10:00:00	Other
5532	2	6	2005	2000	5	2301	2231	9E	1394	N605LR	LGA	OMA	190	1148	20	0	2023-02-06 20:00:00	Other
5534	9	24	1145	1143	2	1314	1328	OO	1234	N296SY	JFK	ORD	114	740	11	43	2023-09-24 11:00:00	ORD
5535	8	18	1117	1111	6	1403	1434	DL	486	N3762Y	LGA	MIA	149	1096	11	11	2023-08-18 11:00:00	MIA
5536	4	1	1109	1059	10	1415	1403	NK	261	N635NK	LGA	MCO	145	950	10	59	2023-04-01 10:00:00	MCO
5541	5	12	1702	1700	2	2008	2021	UA	763	N2138U	EWR	SFO	302	2565	17	0	2023-05-12 17:00:00	Other
5557	4	29	725	720	5	922	956	DL	174	N383DN	LGA	DEN	213	1620	7	20	2023-04-29 07:00:00	Other
5561	7	30	1432	1430	2	1644	1650	WN	547	N7875A	LGA	ATL	105	762	14	30	2023-07-30 14:00:00	ATL
5567	9	2	2213	2210	3	126	107	B6	653	N985JT	JFK	LAX	318	2475	22	10	2023-09-02 22:00:00	LAX
5576	3	10	1807	1804	3	1949	2009	YX	1269	N132HQ	LGA	CMH	81	479	18	4	2023-03-10 18:00:00	Other
5580	11	9	1441	1435	6	1709	1710	WN	693	N912WN	LGA	ATL	116	762	14	35	2023-11-09 14:00:00	ATL
5581	2	20	637	630	7	924	927	UA	564	N27270	EWR	TPA	143	997	6	30	2023-02-20 06:00:00	Other
5589	3	31	2104	2100	4	16	2347	NK	275	N962NK	EWR	LAS	350	2227	21	0	2023-03-31 21:00:00	Other
5593	5	14	1203	1159	4	1410	1422	UA	247	N413UA	EWR	ATL	102	746	11	59	2023-05-14 11:00:00	ATL
5596	5	23	600	600	0	922	902	B6	513	N646JB	LGA	FLL	162	1076	6	0	2023-05-23 06:00:00	FLL
5597	5	23	1829	1825	4	1944	2015	WN	184	N8517F	LGA	STL	118	888	18	25	2023-05-23 18:00:00	Other
5608	6	6	2023	2015	8	2211	2134	B6	556	N281JB	LGA	BOS	32	184	20	15	2023-06-06 20:00:00	BOS
5627	6	6	1846	1839	7	2205	2148	DL	476	N109DN	EWR	SLC	249	1969	18	39	2023-06-06 18:00:00	Other
5634	4	16	1330	1329	1	1552	1601	DL	197	N380DN	LGA	ATL	119	762	13	29	2023-04-16 13:00:00	ATL
5652	8	22	1830	1830	0	2122	2142	UA	343	N77012	EWR	SFO	313	2565	18	30	2023-08-22 18:00:00	Other
5657	6	8	850	851	-1	1024	1030	YX	1840	N229JQ	LGA	MKE	108	738	8	51	2023-06-08 08:00:00	Other
5663	1	1	1856	1851	5	2018	2015	UA	727	N47414	EWR	IAD	43	212	18	51	2023-01-01 18:00:00	Other
5678	3	2	1704	1655	9	2003	1925	WN	703	N8846Q	LGA	MCI	200	1107	16	55	2023-03-02 16:00:00	Other
5687	1	2	1120	1110	10	1418	1432	DL	697	N109DN	LGA	MIA	154	1096	11	10	2023-01-02 11:00:00	MIA
5690	8	31	1630	1629	1	1847	1922	DL	464	N722TW	JFK	ATL	110	760	16	29	2023-08-31 16:00:00	ATL
5692	8	7	804	800	4	1018	1011	DL	732	N359NB	JFK	MSY	160	1182	8	0	2023-08-07 08:00:00	Other
5699	9	30	800	800	0	912	911	B6	39	N337JB	JFK	BOS	36	187	8	0	2023-09-30 08:00:00	BOS
5700	3	25	1105	1100	5	1505	1406	UA	851	N17254	EWR	MIA	171	1085	11	0	2023-03-25 11:00:00	MIA
5706	7	6	1607	1559	8	1915	1852	AA	722	N970NN	JFK	DFW	193	1391	15	59	2023-07-06 15:00:00	Other
5707	12	18	1711	1709	2	1911	1924	9E	1534	N296PQ	JFK	DTW	82	509	17	9	2023-12-18 17:00:00	Other
5710	3	7	1731	1730	1	2102	2045	AS	87	N214AK	EWR	PDX	356	2434	17	30	2023-03-07 17:00:00	Other
5711	5	26	2036	2029	7	2353	2345	AA	749	N814NN	LGA	MIA	157	1096	20	29	2023-05-26 20:00:00	MIA
5715	7	31	1455	1455	0	1702	1706	9E	1162	N902XJ	LGA	GSP	91	610	14	55	2023-07-31 14:00:00	Other
5729	8	25	1559	1559	0	1851	1907	UA	602	N27274	EWR	SEA	318	2402	15	59	2023-08-25 15:00:00	Other
5739	3	21	2128	2127	1	2356	2355	YX	1121	N736YX	EWR	MCI	170	1092	21	27	2023-03-21 21:00:00	Other
5742	2	1	1729	1730	-1	2059	2120	DL	885	N717TW	JFK	SFO	365	2586	17	30	2023-02-01 17:00:00	Other
5750	11	30	1115	1115	0	1422	1419	B6	137	N784JB	EWR	FLL	159	1065	11	15	2023-11-30 11:00:00	FLL
5755	7	3	1551	1550	1	1850	1920	DL	679	N3738B	JFK	MIA	144	1089	15	50	2023-07-03 15:00:00	MIA
5758	1	4	1945	1941	4	2256	2248	UA	336	N67815	EWR	PBI	163	1023	19	41	2023-01-04 19:00:00	Other
5762	2	25	623	615	8	946	928	UA	322	N206UA	EWR	SFO	365	2565	6	15	2023-02-25 06:00:00	Other
5767	12	4	1529	1530	-1	1646	1704	NK	572	N969NK	EWR	BNA	118	748	15	30	2023-12-04 15:00:00	Other
5772	12	6	707	705	2	959	1007	DL	509	N809DN	JFK	TPA	145	1005	7	5	2023-12-06 07:00:00	Other
5773	1	20	2001	2002	-1	2300	2316	B6	68	N828JB	JFK	TPA	147	1005	20	2	2023-01-20 20:00:00	Other
5777	9	14	1400	1359	1	1749	1655	UA	589	N899UA	LGA	IAH	243	1416	13	59	2023-09-14 13:00:00	Other
5784	4	25	2000	1954	6	2340	2353	UA	218	N69885	EWR	BQN	196	1585	19	54	2023-04-25 19:00:00	Other
5788	12	12	1826	1827	-1	2132	2145	UA	250	N17730	EWR	AUS	228	1504	18	27	2023-12-12 18:00:00	Other
5791	2	27	759	800	-1	1103	1107	AA	585	N905AU	EWR	DFW	211	1372	8	0	2023-02-27 08:00:00	Other
5793	5	17	900	900	0	1141	1224	B6	164	N2039J	JFK	BUR	318	2465	9	0	2023-05-17 09:00:00	Other
5795	6	13	1816	1815	1	2006	2020	YX	1297	N129HQ	LGA	LIT	152	1085	18	15	2023-06-13 18:00:00	Other
5797	10	22	602	602	0	801	808	DL	961	N949AT	EWR	MSP	148	1008	6	2	2023-10-22 06:00:00	Other
5801	10	15	1758	1759	-1	1955	2034	DL	293	N393DA	LGA	DEN	200	1620	17	59	2023-10-15 17:00:00	Other
5817	7	2	1105	1102	3	1306	1316	UA	377	N68823	EWR	PHX	275	2133	11	2	2023-07-02 11:00:00	Other
5820	11	17	2019	2017	2	2116	2127	YX	1138	N654RW	EWR	PVD	34	160	20	17	2023-11-17 20:00:00	Other
5850	3	5	904	859	5	1014	1034	YX	1672	N212JQ	EWR	BOS	41	200	8	59	2023-03-05 08:00:00	BOS
5859	2	18	1759	1759	0	2022	2039	B6	158	N636JB	JFK	ATL	114	760	17	59	2023-02-18 17:00:00	ATL
5873	3	17	1807	1800	7	2007	1959	YX	1618	N209JQ	LGA	CMH	88	479	18	0	2023-03-17 18:00:00	Other
5876	7	20	1429	1420	9	1642	1638	9E	1124	N187GJ	LGA	CVG	97	585	14	20	2023-07-20 14:00:00	Other
5881	5	28	1707	1700	7	1912	1939	B6	906	N564JB	LGA	ATL	104	762	17	0	2023-05-28 17:00:00	ATL
5883	5	2	1605	1559	6	1811	1846	AA	591	N303RG	JFK	PHX	284	2153	15	59	2023-05-02 15:00:00	Other
5885	2	22	1253	1250	3	1510	1531	DL	207	N357DN	LGA	ATL	117	762	12	50	2023-02-22 12:00:00	ATL
5887	5	13	756	755	1	1016	956	AA	587	N865NN	EWR	CLT	77	529	7	55	2023-05-13 07:00:00	CLT
5889	7	27	1559	1559	0	1748	1734	YX	926	N748YX	EWR	PIT	55	319	15	59	2023-07-27 15:00:00	Other
5897	4	20	1122	1122	0	1327	1319	YX	1072	N421YX	JFK	CLE	74	425	11	22	2023-04-20 11:00:00	Other
5901	6	30	1202	1200	2	1416	1435	DL	335	N335DN	LGA	ATL	98	762	12	0	2023-06-30 12:00:00	ATL
5909	9	16	934	930	4	1210	1229	B6	159	N566JB	LGA	PBI	137	1035	9	30	2023-09-16 09:00:00	Other
5914	12	1	2107	2100	7	2232	2235	WN	909	N208WN	LGA	MDW	124	725	21	0	2023-12-01 21:00:00	Other
5915	2	22	1504	1503	1	1854	1802	UA	590	N27277	EWR	TPA	144	997	15	3	2023-02-22 15:00:00	Other
5918	10	4	1448	1445	3	1725	1746	B6	124	N729JB	LGA	MCO	124	950	14	45	2023-10-04 14:00:00	MCO
5925	3	19	2156	2155	1	2339	2335	UA	842	N62894	EWR	RDU	84	416	21	55	2023-03-19 21:00:00	Other
5935	6	21	1259	1255	4	1617	1557	B6	18	N656JB	LGA	TPA	162	1010	12	55	2023-06-21 12:00:00	Other
5945	3	12	2018	2014	4	2203	2220	DL	1006	N930AT	EWR	DTW	84	488	20	14	2023-03-12 20:00:00	Other
5954	9	1	633	630	3	819	835	WN	567	N8825Q	LGA	DEN	207	1620	6	30	2023-09-01 06:00:00	Other
5956	8	30	1651	1650	1	1844	1915	9E	1204	N676CA	JFK	DTW	89	509	16	50	2023-08-30 16:00:00	Other
5958	6	13	1844	1839	5	2140	2148	AA	670	N950AN	EWR	MIA	147	1085	18	39	2023-06-13 18:00:00	MIA
5975	1	27	1710	1711	-1	1827	1835	YX	1214	N745YX	EWR	BTV	53	266	17	11	2023-01-27 17:00:00	Other
5986	11	12	658	659	-1	907	915	UA	449	N474UA	EWR	CHS	104	628	6	59	2023-11-12 06:00:00	Other
5988	4	21	1707	1705	2	1945	2010	NK	582	N681NK	EWR	FLL	140	1065	17	5	2023-04-21 17:00:00	FLL
5994	2	25	1435	1434	1	1742	1736	UA	272	N459UA	EWR	DFW	218	1372	14	34	2023-02-25 14:00:00	Other
5997	12	2	816	810	6	1050	1049	B6	180	N206JB	JFK	ATL	130	760	8	10	2023-12-02 08:00:00	ATL
6002	8	6	929	929	0	1109	1057	B6	475	N184JB	JFK	BUF	61	301	9	29	2023-08-06 09:00:00	Other
6011	8	25	1230	1225	5	1426	1441	UA	702	N37422	EWR	DEN	209	1605	12	25	2023-08-25 12:00:00	Other
6016	10	27	2103	2053	10	4	2359	UA	538	N37319	EWR	AUS	209	1504	20	53	2023-10-27 20:00:00	Other
6023	3	25	2101	2100	1	2354	1	B6	48	N805JB	EWR	PBI	155	1023	21	0	2023-03-25 21:00:00	Other
6033	9	22	1940	1935	5	2339	2329	DL	338	N703TW	JFK	SFO	363	2586	19	35	2023-09-22 19:00:00	Other
6036	4	12	1204	1159	5	1411	1421	UA	254	N492UA	EWR	ATL	104	746	11	59	2023-04-12 11:00:00	ATL
6037	1	19	745	745	0	1043	1102	UA	351	N66893	EWR	SAN	331	2425	7	45	2023-01-19 07:00:00	Other
6041	12	1	1830	1829	1	2202	2152	AS	158	N936AK	EWR	SEA	335	2402	18	29	2023-12-01 18:00:00	Other
6048	3	29	1904	1905	-1	2032	2051	AA	138	N821AW	LGA	RDU	72	431	19	5	2023-03-29 19:00:00	Other
6072	10	6	1441	1435	6	1554	1602	YX	1094	N753YX	EWR	MKE	110	725	14	35	2023-10-06 14:00:00	Other
6078	6	19	959	959	0	1217	1235	DL	157	N379DN	LGA	ATL	106	762	9	59	2023-06-19 09:00:00	ATL
6100	9	13	835	830	5	1125	1120	DL	194	N102DU	JFK	DFW	199	1391	8	30	2023-09-13 08:00:00	Other
6122	1	17	1129	1130	-1	1420	1449	DL	541	N371NW	LGA	SRQ	153	1047	11	30	2023-01-17 11:00:00	Other
6136	3	7	1628	1629	-1	1852	1819	YX	1170	N654RW	EWR	CLE	77	404	16	29	2023-03-07 16:00:00	Other
6140	8	31	922	922	0	1054	1124	9E	1271	N153PQ	LGA	STL	133	888	9	22	2023-08-31 09:00:00	Other
6144	11	2	1114	1115	-1	1443	1435	DL	899	N324DX	LGA	FLL	158	1076	11	15	2023-11-02 11:00:00	FLL
6155	3	20	1328	1329	-1	1639	1639	NK	647	N669NK	LGA	FLL	164	1076	13	29	2023-03-20 13:00:00	FLL
6160	6	25	905	900	5	1023	1034	B6	806	N184JB	LGA	BNA	117	764	9	0	2023-06-25 09:00:00	Other
6164	10	7	1200	1200	0	1439	1525	UA	825	N21108	EWR	SFO	317	2565	12	0	2023-10-07 12:00:00	Other
6179	1	17	1530	1530	0	1829	1850	B6	604	N623JB	EWR	MIA	152	1085	15	30	2023-01-17 15:00:00	MIA
6182	1	12	959	959	0	1306	1324	B6	226	N976JT	JFK	LAX	337	2475	9	59	2023-01-12 09:00:00	LAX
6183	7	18	1038	1038	0	1208	1225	B6	78	N562JB	JFK	RDU	71	427	10	38	2023-07-18 10:00:00	Other
6184	2	21	940	940	0	1231	1230	DL	181	N367DN	LGA	ATL	122	762	9	40	2023-02-21 09:00:00	ATL
6187	10	13	704	705	-1	945	955	DL	489	N813DN	JFK	TPA	140	1005	7	5	2023-10-13 07:00:00	Other
6208	1	11	1200	1159	1	1330	1345	9E	1405	N922XJ	LGA	MKE	122	738	11	59	2023-01-11 11:00:00	Other
6227	3	6	1627	1627	0	1800	1756	YX	1061	N654RW	EWR	BUF	54	282	16	27	2023-03-06 16:00:00	Other
6229	6	6	1518	1518	0	1726	1722	YX	1318	N129HQ	JFK	RDU	70	427	15	18	2023-06-06 15:00:00	Other
6236	5	14	833	829	4	1151	1223	AA	56	N104NN	JFK	SFO	339	2586	8	29	2023-05-14 08:00:00	Other
6248	8	10	2139	2130	9	2253	2255	9E	1121	N915XJ	LGA	PWM	44	269	21	30	2023-08-10 21:00:00	Other
6264	8	26	1910	1909	1	2258	2308	UA	185	N68802	EWR	BQN	201	1585	19	9	2023-08-26 19:00:00	Other
6265	4	2	1645	1645	0	1810	1813	YX	1479	N818MD	LGA	DCA	44	214	16	45	2023-04-02 16:00:00	Other
6268	11	16	2123	2124	-1	2320	2329	NK	279	N625NK	LGA	DTW	82	502	21	24	2023-11-16 21:00:00	Other
6286	2	12	1702	1659	3	1852	1841	UA	836	N878UA	LGA	ORD	113	733	16	59	2023-02-12 16:00:00	ORD
6290	6	12	1647	1640	7	2000	2020	AS	92	N526AS	EWR	SFO	338	2565	16	40	2023-06-12 16:00:00	Other
6292	12	17	834	830	4	1112	1113	B6	103	N662JB	LGA	JAX	130	833	8	30	2023-12-17 08:00:00	Other
6300	11	11	933	930	3	1203	1202	9E	1612	N919XJ	LGA	MCI	176	1107	9	30	2023-11-11 09:00:00	Other
6310	5	24	1559	1559	0	1755	1806	YX	1167	N724YX	EWR	DTW	84	488	15	59	2023-05-24 15:00:00	Other
6314	4	7	1634	1629	5	1925	1939	AA	109	N780AN	JFK	MIA	141	1089	16	29	2023-04-07 16:00:00	MIA
6320	7	14	711	705	6	1044	1019	DL	493	N325DN	LGA	FLL	169	1076	7	5	2023-07-14 07:00:00	FLL
6322	8	27	1109	1100	9	1420	1408	B6	655	N591JB	JFK	FLL	148	1069	11	0	2023-08-27 11:00:00	FLL
6323	4	30	2050	2050	0	2222	2227	YX	1517	N243JQ	LGA	RIC	62	292	20	50	2023-04-30 20:00:00	Other
6324	6	6	1607	1559	8	1945	1854	AA	1036	N884NN	LGA	DFW	210	1389	15	59	2023-06-06 15:00:00	Other
6327	6	2	1445	1440	5	1645	1607	YX	1136	N642RW	EWR	BUF	55	282	14	40	2023-06-02 14:00:00	Other
6328	4	27	1644	1639	5	1947	1950	NK	312	N672NK	LGA	FLL	152	1076	16	39	2023-04-27 16:00:00	FLL
6329	10	21	1700	1700	0	1938	1957	DL	571	N121DZ	LGA	MCO	125	950	17	0	2023-10-21 17:00:00	MCO
6334	2	25	2109	2105	4	2351	2359	B6	69	N568JB	EWR	MCO	133	937	21	5	2023-02-25 21:00:00	MCO
6345	11	10	1945	1945	0	2239	2252	DL	877	N874DN	JFK	TPA	146	1005	19	45	2023-11-10 19:00:00	Other
6347	12	14	700	655	5	938	950	B6	177	N968JT	JFK	LAS	291	2248	6	55	2023-12-14 06:00:00	Other
6351	2	9	1700	1655	5	1919	1952	DL	880	N774DE	LGA	DEN	222	1620	16	55	2023-02-09 16:00:00	Other
6354	3	2	1928	1927	1	2302	2159	YX	1290	N408YX	LGA	XNA	219	1147	19	27	2023-03-02 19:00:00	Other
6362	3	29	2012	2005	7	2257	2313	B6	642	N703JB	JFK	PBI	141	1028	20	5	2023-03-29 20:00:00	Other
6365	9	18	1040	1030	10	1334	1323	B6	367	N571JB	JFK	MCO	144	944	10	30	2023-09-18 10:00:00	MCO
6376	6	21	859	900	-1	1022	1024	9E	1550	N137EV	JFK	IAD	52	228	9	0	2023-06-21 09:00:00	Other
6378	12	16	900	900	0	1205	1216	AA	134	N895NN	EWR	DFW	206	1372	9	0	2023-12-16 09:00:00	Other
6380	5	19	1805	1800	5	2050	2036	UA	904	N37295	EWR	PHX	295	2133	18	0	2023-05-19 18:00:00	Other
6389	3	29	829	830	-1	1248	1232	AA	55	N107NN	JFK	SFO	395	2586	8	30	2023-03-29 08:00:00	Other
6396	1	6	609	601	8	1120	1055	B6	691	N956JT	JFK	SJU	218	1598	6	1	2023-01-06 06:00:00	Other
6401	5	23	2108	2059	9	2343	22	B6	34	N964JT	JFK	SAN	302	2446	20	59	2023-05-23 20:00:00	Other
6419	7	14	1636	1630	6	1930	1838	UA	550	N415UA	EWR	CHS	110	628	16	30	2023-07-14 16:00:00	Other
6424	8	2	1635	1635	0	1800	1842	DL	491	N123DQ	LGA	ORD	113	733	16	35	2023-08-02 16:00:00	ORD
6426	2	27	1240	1230	10	1605	1554	UA	554	N13750	EWR	SNA	357	2434	12	30	2023-02-27 12:00:00	Other
6427	2	22	1705	1705	0	1854	1900	NK	24	N527NK	EWR	MYR	83	550	17	5	2023-02-22 17:00:00	Other
6435	4	17	1508	1500	8	1612	1622	YX	1025	N864RW	EWR	BTV	45	266	15	0	2023-04-17 15:00:00	Other
6437	7	24	834	835	-1	1130	1058	9E	1274	N294PQ	JFK	CHS	119	636	8	35	2023-07-24 08:00:00	Other
6441	2	27	1137	1130	7	1311	1320	DL	584	N113DQ	LGA	ORD	118	733	11	30	2023-02-27 11:00:00	ORD
6449	9	17	930	930	0	1247	1241	B6	930	N593JB	JFK	MIA	156	1089	9	30	2023-09-17 09:00:00	MIA
6453	7	13	1940	1930	10	2310	2221	UA	439	N38443	EWR	MCO	118	937	19	30	2023-07-13 19:00:00	MCO
6461	12	18	1935	1928	7	2211	2230	UA	703	N77431	EWR	IAH	191	1400	19	28	2023-12-18 19:00:00	Other
6462	5	27	2000	1954	6	2342	2353	UA	211	N68891	EWR	BQN	201	1585	19	54	2023-05-27 19:00:00	Other
6464	10	3	1836	1834	2	2138	2146	AA	613	N336RU	EWR	MIA	144	1085	18	34	2023-10-03 18:00:00	MIA
6468	12	6	1559	1558	1	1909	1920	DL	389	N3765	LGA	MIA	145	1096	15	58	2023-12-06 15:00:00	MIA
6472	10	12	600	600	0	852	847	UA	884	N806UA	LGA	IAH	203	1416	6	0	2023-10-12 06:00:00	Other
6475	1	21	1927	1928	-1	2055	2107	AA	277	N346PR	EWR	ORD	122	719	19	28	2023-01-21 19:00:00	ORD
6493	1	1	2200	2155	5	17	5	B6	267	N236JB	JFK	MSP	173	1029	21	55	2023-01-01 21:00:00	Other
6494	2	10	1737	1730	7	2102	2120	DL	245	N727TW	JFK	SFO	357	2586	17	30	2023-02-10 17:00:00	Other
6499	8	8	930	930	0	1219	1246	DL	722	N546US	JFK	SLC	271	1990	9	30	2023-08-08 09:00:00	Other
6504	3	1	714	715	-1	947	955	WN	758	N8566Z	LGA	ATL	121	762	7	15	2023-03-01 07:00:00	ATL
6508	5	23	2030	2020	10	2315	2357	AS	18	N979AK	JFK	SFO	314	2586	20	20	2023-05-23 20:00:00	Other
6517	11	25	1159	1200	-1	1454	1510	B6	322	N627JB	JFK	SLC	274	1990	12	0	2023-11-25 12:00:00	Other
6518	3	29	1350	1350	0	1517	1519	9E	1335	N928XJ	LGA	BUF	58	292	13	50	2023-03-29 13:00:00	Other
6531	9	25	954	955	-1	1419	1455	DL	72	N183DN	JFK	HNL	602	4983	9	55	2023-09-25 09:00:00	Other
6534	6	18	1100	1100	0	1352	1412	AA	275	N932NN	JFK	MIA	145	1089	11	0	2023-06-18 11:00:00	MIA
6545	3	23	1149	1150	-1	1304	1319	YX	1649	N818MD	LGA	PWM	50	269	11	50	2023-03-23 11:00:00	Other
6550	12	4	1437	1435	2	1700	1710	WN	691	N7732A	LGA	ATL	124	762	14	35	2023-12-04 14:00:00	ATL
6559	5	23	504	500	4	746	812	NK	282	N958NK	EWR	OAK	320	2555	5	0	2023-05-23 05:00:00	Other
6560	10	1	1602	1600	2	1926	1836	UA	389	N27273	EWR	LAS	289	2227	16	0	2023-10-01 16:00:00	Other
6567	3	9	859	900	-1	1026	1031	B6	620	N337JB	JFK	BUF	59	301	9	0	2023-03-09 09:00:00	Other
6578	1	20	1721	1712	9	1900	1831	UA	167	N452UA	EWR	BOS	43	200	17	12	2023-01-20 17:00:00	BOS
6580	4	11	811	810	1	1110	1139	AA	559	N310RF	JFK	MIA	153	1089	8	10	2023-04-11 08:00:00	MIA
6588	5	18	1520	1520	0	1756	1821	UA	801	N648UA	EWR	IAH	192	1400	15	20	2023-05-18 15:00:00	Other
6590	2	2	1558	1559	-1	1857	1924	B6	672	N2017J	JFK	FLL	156	1069	15	59	2023-02-02 15:00:00	FLL
6592	4	21	1755	1754	1	2044	2049	UA	749	N24224	EWR	MCO	129	937	17	54	2023-04-21 17:00:00	MCO
6595	7	31	945	939	6	1038	1048	B6	413	N284JB	JFK	MVY	33	173	9	39	2023-07-31 09:00:00	Other
6598	4	7	2135	2130	5	18	7	B6	440	N705JB	JFK	JAX	138	828	21	30	2023-04-07 21:00:00	Other
6599	12	30	1300	1300	0	1549	1617	B6	824	N523JB	LGA	SRQ	149	1047	13	0	2023-12-30 13:00:00	Other
6603	1	2	1652	1651	1	1945	2005	DL	181	N839DN	JFK	SEA	319	2422	16	51	2023-01-02 16:00:00	Other
6604	3	27	1827	1825	2	2141	2139	UA	499	N14231	EWR	FLL	155	1065	18	25	2023-03-27 18:00:00	FLL
6612	12	17	2225	2220	5	146	153	B6	901	N969JT	JFK	SFO	346	2586	22	20	2023-12-17 22:00:00	Other
6614	3	22	1218	1215	3	1504	1450	WN	995	N955WN	LGA	DEN	264	1620	12	15	2023-03-22 12:00:00	Other
6617	4	30	809	759	10	1113	1101	AA	313	N800NN	JFK	DFW	204	1391	7	59	2023-04-30 07:00:00	Other
6618	2	18	1016	1015	1	1207	1241	9E	1371	N695CA	LGA	MEM	145	963	10	15	2023-02-18 10:00:00	Other
6619	10	28	1654	1655	-1	1804	1813	YX	1727	N878RW	EWR	BOS	45	200	16	55	2023-10-28 16:00:00	BOS
6621	3	28	1659	1659	0	1833	1840	UA	459	N47275	EWR	ORD	117	719	16	59	2023-03-28 16:00:00	ORD
6633	3	24	701	659	2	1007	1005	UA	279	N53441	EWR	FLL	157	1065	6	59	2023-03-24 06:00:00	FLL
6640	6	25	1155	1156	-1	1419	1403	AA	982	N959NN	JFK	CLT	93	541	11	56	2023-06-25 11:00:00	CLT
6642	1	27	1509	1507	2	1751	1750	YX	1189	N731YX	EWR	JAX	137	820	15	7	2023-01-27 15:00:00	Other
6645	9	14	2009	2010	-1	2247	2331	B6	62	N961JT	JFK	LAX	311	2475	20	10	2023-09-14 20:00:00	LAX
6649	5	25	1438	1435	3	1646	1648	B6	874	N266JB	JFK	CHS	103	636	14	35	2023-05-25 14:00:00	Other
6674	5	3	1635	1635	0	1932	2013	DL	208	N911DQ	JFK	SLC	269	1990	16	35	2023-05-03 16:00:00	Other
6676	10	12	1610	1605	5	1753	1758	YX	1723	N209JQ	LGA	STL	140	888	16	5	2023-10-12 16:00:00	Other
6690	9	26	2112	2110	2	2336	2357	DL	142	N530DE	JFK	LAS	289	2248	21	10	2023-09-26 21:00:00	Other
6699	11	24	1749	1740	9	2059	2052	AS	89	N275AK	EWR	SAN	340	2425	17	40	2023-11-24 17:00:00	Other
6701	1	14	1917	1916	1	2220	2238	UA	835	N17752	EWR	SEA	331	2402	19	16	2023-01-14 19:00:00	Other
6706	6	12	1028	1029	-1	1126	1146	YX	1893	N213JQ	LGA	MVY	40	175	10	29	2023-06-12 10:00:00	Other
6708	9	3	2152	2150	2	2259	2314	UA	365	N493UA	EWR	BOS	40	200	21	50	2023-09-03 21:00:00	BOS
6713	7	27	1624	1620	4	1803	1802	UA	621	N13750	EWR	CLE	64	404	16	20	2023-07-27 16:00:00	Other
6727	4	7	1724	1725	-1	1916	1940	9E	1427	N313PQ	JFK	CVG	97	589	17	25	2023-04-07 17:00:00	Other
6743	10	19	1547	1547	0	1730	1751	YX	1052	N647RW	EWR	DTW	79	488	15	47	2023-10-19 15:00:00	Other
6744	1	1	1102	1100	2	1313	1318	YX	1262	N741YX	EWR	GRR	107	605	11	0	2023-01-01 11:00:00	Other
6745	2	19	1347	1340	7	1616	1621	DL	145	N348NW	LGA	ATL	119	762	13	40	2023-02-19 13:00:00	ATL
6748	2	4	1824	1825	-1	2158	2156	DL	126	N855DN	JFK	SEA	334	2422	18	25	2023-02-04 18:00:00	Other
6754	3	6	735	729	6	950	953	YX	1409	N134HQ	JFK	CVG	106	589	7	29	2023-03-06 07:00:00	Other
6761	10	20	1505	1455	10	1809	1811	B6	1008	N569JB	JFK	MIA	156	1089	14	55	2023-10-20 14:00:00	MIA
6782	6	19	1915	1914	1	2042	2056	UA	535	N27269	EWR	CLE	63	404	19	14	2023-06-19 19:00:00	Other
6785	1	26	826	827	-1	1057	1115	YX	1133	N743YX	EWR	SDF	116	642	8	27	2023-01-26 08:00:00	Other
6789	7	20	631	630	1	850	846	UA	174	N27246	LGA	DEN	236	1620	6	30	2023-07-20 06:00:00	Other
6804	10	2	1637	1627	10	1832	1843	9E	1550	N341PQ	LGA	CLT	81	544	16	27	2023-10-02 16:00:00	CLT
6808	9	6	630	630	0	913	942	AA	354	N350RV	JFK	MIA	139	1089	6	30	2023-09-06 06:00:00	MIA
6818	1	13	933	923	10	1044	1039	B6	1038	N284JB	JFK	BOS	39	187	9	23	2023-01-13 09:00:00	BOS
6824	7	12	1530	1520	10	1659	1700	WN	767	N871HK	LGA	STL	125	888	15	20	2023-07-12 15:00:00	Other
6834	6	30	2035	2030	5	2146	2205	YX	1399	N434YX	JFK	BOS	34	187	20	30	2023-06-30 20:00:00	BOS
6835	11	18	1209	1210	-1	1453	1527	YX	1162	N722YX	EWR	DFW	192	1372	12	10	2023-11-18 12:00:00	Other
6842	10	24	1602	1559	3	1910	1904	AA	991	N891NN	LGA	DFW	194	1389	15	59	2023-10-24 15:00:00	Other
6847	10	26	1054	1054	0	1306	1317	YX	1151	N721YX	EWR	SAV	100	708	10	54	2023-10-26 10:00:00	Other
6849	5	27	1000	958	2	1208	1211	AA	914	N180US	JFK	CLT	86	541	9	58	2023-05-27 09:00:00	CLT
6853	9	11	1304	1304	0	1409	1415	YX	1045	N657RW	EWR	MDT	32	141	13	4	2023-09-11 13:00:00	Other
6868	3	21	1539	1530	9	1750	1804	B6	827	N3115J	JFK	MCI	164	1113	15	30	2023-03-21 15:00:00	Other
6884	3	3	814	815	-1	1040	1103	DL	356	N350DN	LGA	ATL	123	762	8	15	2023-03-03 08:00:00	ATL
6901	6	13	1728	1729	-1	2025	2042	AA	1005	N323SG	JFK	AUS	218	1521	17	29	2023-06-13 17:00:00	Other
6913	10	14	1228	1229	-1	1538	1535	UA	325	N837UA	EWR	SAT	232	1569	12	29	2023-10-14 12:00:00	Other
6914	1	9	2006	2000	6	2201	2212	DL	876	N346NB	LGA	DTW	80	502	20	0	2023-01-09 20:00:00	Other
6918	10	10	1954	1955	-1	2146	2155	YX	1166	N743YX	EWR	CMH	77	463	19	55	2023-10-10 19:00:00	Other
6940	8	11	840	840	0	1110	1140	DL	290	N703TW	JFK	SAN	314	2446	8	40	2023-08-11 08:00:00	Other
6942	8	4	857	858	-1	1045	1050	9E	1165	N181PQ	LGA	RDU	68	431	8	58	2023-08-04 08:00:00	Other
6946	1	16	2049	2043	6	2233	2240	9E	1667	N917XJ	LGA	RDU	66	431	20	43	2023-01-16 20:00:00	Other
6965	11	21	1202	1200	2	1500	1502	B6	664	N958JB	JFK	PBI	155	1028	12	0	2023-11-21 12:00:00	Other
6972	12	7	1509	1510	-1	1747	1828	DL	319	N525DA	JFK	LAS	311	2248	15	10	2023-12-07 15:00:00	Other
6995	3	8	1040	1040	0	1301	1327	DL	122	N129DN	LGA	ATL	115	762	10	40	2023-03-08 10:00:00	ATL
6997	5	4	859	900	-1	1152	1217	AA	796	N303RG	LGA	MIA	142	1096	9	0	2023-05-04 09:00:00	MIA
7000	5	20	624	616	8	908	916	UA	365	N27274	EWR	SAN	314	2425	6	16	2023-05-20 06:00:00	Other
7001	11	28	1601	1600	1	1755	1757	9E	1486	N295PQ	JFK	RDU	75	427	16	0	2023-11-28 16:00:00	Other
7003	7	8	1432	1430	2	1624	1631	UA	317	N425UA	EWR	CLT	87	529	14	30	2023-07-08 14:00:00	CLT
7011	6	20	929	929	0	1304	1221	UA	516	N68811	EWR	MCO	176	937	9	29	2023-06-20 09:00:00	MCO
7014	10	11	1335	1330	5	1449	1449	YX	1249	N113HQ	JFK	BOS	38	187	13	30	2023-10-11 13:00:00	BOS
7017	5	1	1129	1127	2	1411	1440	DL	205	N811DZ	JFK	SEA	302	2422	11	27	2023-05-01 11:00:00	Other
7019	7	4	758	759	-1	1032	1059	UA	597	N47291	EWR	PBI	135	1023	7	59	2023-07-04 07:00:00	Other
7023	4	9	1536	1528	8	1811	1829	UA	735	N648UA	EWR	IAH	190	1400	15	28	2023-04-09 15:00:00	Other
7024	12	17	1109	1059	10	1402	1358	B6	38	N653JB	EWR	MCO	144	937	10	59	2023-12-17 10:00:00	MCO
7029	8	29	1459	1459	0	1748	1814	DL	703	N366NB	JFK	AUS	204	1521	14	59	2023-08-29 14:00:00	Other
7031	2	4	559	600	-1	723	722	YX	1136	N740YX	EWR	IAD	50	212	6	0	2023-02-04 06:00:00	Other
7047	2	17	1838	1830	8	2152	2201	DL	126	N828DN	JFK	SEA	345	2422	18	30	2023-02-17 18:00:00	Other
7053	1	31	1229	1230	-1	1438	1436	AA	516	N943NN	LGA	ORD	140	733	12	30	2023-01-31 12:00:00	ORD
7056	12	8	1325	1325	0	1444	1500	WN	338	N551WN	LGA	BNA	114	764	13	25	2023-12-08 13:00:00	Other
7057	8	20	1255	1248	7	1533	1553	NK	294	N954NK	EWR	FLL	138	1065	12	48	2023-08-20 12:00:00	FLL
7069	7	31	931	932	-1	1149	1201	B6	364	N197JB	JFK	ATL	103	760	9	32	2023-07-31 09:00:00	ATL
7071	6	8	1529	1529	0	1715	1721	YX	1837	N202JQ	JFK	DCA	46	213	15	29	2023-06-08 15:00:00	Other
7077	7	21	1848	1840	8	2102	2102	YX	898	N638RW	EWR	IND	102	645	18	40	2023-07-21 18:00:00	Other
7078	1	11	1628	1620	8	1922	1957	DL	244	N887DN	JFK	SLC	271	1990	16	20	2023-01-11 16:00:00	Other
7092	3	5	1919	1920	-1	2211	2221	UA	824	N441UA	EWR	TPA	144	997	19	20	2023-03-05 19:00:00	Other
7102	10	31	727	725	2	1002	1018	DL	169	N521DT	JFK	LAS	314	2248	7	25	2023-10-31 07:00:00	Other
7124	5	23	840	841	-1	1127	1155	UA	596	N34222	EWR	SAT	202	1569	8	41	2023-05-23 08:00:00	Other
7125	7	10	1337	1332	5	1602	1555	NK	31	N637NK	EWR	ATL	110	746	13	32	2023-07-10 13:00:00	ATL
7128	7	6	758	751	7	1025	1014	UA	208	N47275	EWR	LAS	290	2227	7	51	2023-07-06 07:00:00	Other
7132	8	24	729	729	0	1013	943	UA	207	N467UA	LGA	DEN	211	1620	7	29	2023-08-24 07:00:00	Other
7133	3	18	2101	2101	0	2258	2302	YX	1210	N739YX	EWR	CMH	89	463	21	1	2023-03-18 21:00:00	Other
7136	12	16	1558	1550	8	1702	1720	YX	1747	N237JQ	JFK	BOS	38	187	15	50	2023-12-16 15:00:00	BOS
7138	9	21	1129	1130	-1	1325	1323	YX	1386	N104HQ	LGA	CMH	77	479	11	30	2023-09-21 11:00:00	Other
7146	7	3	1802	1800	2	2030	2015	DL	334	N103DY	LGA	MSP	156	1020	18	0	2023-07-03 18:00:00	Other
7156	2	13	1121	1120	1	1450	1451	DL	572	N116DU	LGA	IAH	209	1416	11	20	2023-02-13 11:00:00	Other
7162	12	17	1833	1829	4	2145	2132	DL	586	N371DN	LGA	MCO	154	950	18	29	2023-12-17 18:00:00	MCO
7166	11	30	1525	1526	-1	1706	1726	YX	1782	N226JQ	JFK	CMH	76	483	15	26	2023-11-30 15:00:00	Other
7172	10	3	1941	1942	-1	2044	2105	UA	885	N443UA	EWR	IAD	43	212	19	42	2023-10-03 19:00:00	Other
7176	11	5	1858	1859	-1	2045	2050	UA	647	N444UA	EWR	RDU	72	416	18	59	2023-11-05 18:00:00	Other
7185	9	13	1051	1051	0	1333	1357	DL	373	N313DU	LGA	TPA	146	1010	10	51	2023-09-13 10:00:00	Other
7188	11	15	1846	1843	3	2105	2144	DL	250	N541DE	JFK	LAS	300	2248	18	43	2023-11-15 18:00:00	Other
7192	3	23	1505	1459	6	1710	1706	DL	527	N324NB	LGA	DTW	97	502	14	59	2023-03-23 14:00:00	Other
7193	2	4	1708	1708	0	1856	1915	DL	876	N317US	LGA	DTW	86	502	17	8	2023-02-04 17:00:00	Other
7201	11	11	1824	1825	-1	2046	2125	B6	269	N529JB	JFK	LAS	297	2248	18	25	2023-11-11 18:00:00	Other
7208	9	3	1748	1741	7	2027	2141	DL	238	N514DE	JFK	SLC	259	1990	17	41	2023-09-03 17:00:00	Other
7209	2	2	959	1000	-1	1341	1348	DL	298	N178DN	JFK	SFO	360	2586	10	0	2023-02-02 10:00:00	Other
7217	8	2	1031	1030	1	1133	1139	B6	769	N339JB	LGA	HYA	39	197	10	30	2023-08-02 10:00:00	Other
7221	1	22	1336	1330	6	1812	1823	B6	356	N527JL	JFK	SJU	196	1598	13	30	2023-01-22 13:00:00	Other
7226	1	8	1454	1455	-1	1652	1706	9E	1659	N135EV	JFK	CLE	85	425	14	55	2023-01-08 14:00:00	Other
7239	6	20	1730	1730	0	1930	1922	9E	1593	N293PQ	JFK	BUF	55	301	17	30	2023-06-20 17:00:00	Other
7244	12	11	828	825	3	1129	1149	UA	234	N786UA	EWR	SFO	333	2565	8	25	2023-12-11 08:00:00	Other
7246	10	7	2005	2000	5	2308	2306	UA	941	N39415	EWR	MIA	152	1085	20	0	2023-10-07 20:00:00	MIA
7248	11	3	1300	1251	9	1408	1413	9E	1635	N919XJ	LGA	BTV	45	258	12	51	2023-11-03 12:00:00	Other
7252	1	26	1111	1110	1	1424	1420	DL	1092	N387DN	LGA	PBI	167	1035	11	10	2023-01-26 11:00:00	Other
7257	4	27	1159	1200	-1	1330	1333	YX	1132	N131HQ	LGA	BNA	119	764	12	0	2023-04-27 12:00:00	Other
7267	8	28	1540	1541	-1	1842	1846	UA	440	N17300	EWR	FLL	162	1065	15	41	2023-08-28 15:00:00	FLL
7280	2	24	2014	2015	-1	2323	2339	B6	511	N508JL	JFK	RSW	153	1074	20	15	2023-02-24 20:00:00	Other
7286	11	1	1414	1415	-1	1717	1726	B6	67	N521JB	LGA	TPA	156	1010	14	15	2023-11-01 14:00:00	Other
7288	6	27	1257	1255	2	1427	1430	WN	354	N8699A	LGA	STL	125	888	12	55	2023-06-27 12:00:00	Other
7293	4	12	1856	1855	1	2111	2158	AA	372	N316PF	LGA	DFW	170	1389	18	55	2023-04-12 18:00:00	Other
7294	1	10	1659	1659	0	1906	1947	DL	411	N362DN	LGA	ATL	106	762	16	59	2023-01-10 16:00:00	ATL
7301	10	18	1259	1300	-1	1403	1416	UA	427	N77543	EWR	BOS	43	200	13	0	2023-10-18 13:00:00	BOS
7302	6	29	2130	2130	0	2237	2310	9E	1659	N538CA	JFK	BWI	38	184	21	30	2023-06-29 21:00:00	Other
7305	8	9	732	732	0	1018	1014	B6	281	N536JB	EWR	MCO	128	937	7	32	2023-08-09 07:00:00	MCO
7307	8	19	1704	1700	4	2006	2011	B6	611	N651JB	JFK	PBI	143	1028	17	0	2023-08-19 17:00:00	Other
7311	2	19	955	955	0	1214	1218	9E	1358	N138EV	JFK	IND	110	665	9	55	2023-02-19 09:00:00	Other
7319	7	31	1822	1820	2	2042	2052	9E	1249	N294PQ	JFK	CHS	90	636	18	20	2023-07-31 18:00:00	Other
7328	7	13	2214	2215	-1	143	115	DL	93	N832MH	JFK	LAX	333	2475	22	15	2023-07-13 22:00:00	LAX
7335	6	14	702	700	2	858	914	UA	138	N38459	EWR	DEN	202	1605	7	0	2023-06-14 07:00:00	Other
7344	2	20	1839	1830	9	2100	2047	9E	1384	N311PQ	LGA	CLT	95	544	18	30	2023-02-20 18:00:00	CLT
7350	5	31	834	830	4	1118	1148	UA	354	N12754	EWR	SNA	310	2434	8	30	2023-05-31 08:00:00	Other
7361	4	24	2030	2030	0	2212	2221	YX	1453	N207JQ	JFK	PIT	69	340	20	30	2023-04-24 20:00:00	Other
7363	2	3	919	915	4	1145	1158	DL	591	N131DU	JFK	MSY	180	1182	9	15	2023-02-03 09:00:00	Other
7365	3	25	759	800	-1	1122	1107	AA	834	N301NW	JFK	DFW	224	1391	8	0	2023-03-25 08:00:00	Other
7369	6	19	1150	1145	5	1419	1427	UA	518	N27261	EWR	DFW	180	1372	11	45	2023-06-19 11:00:00	Other
7370	8	19	730	730	0	926	933	UA	709	N17730	EWR	MSY	146	1167	7	30	2023-08-19 07:00:00	Other
7380	1	21	1820	1816	4	2141	2128	AA	705	N910NN	EWR	DFW	223	1372	18	16	2023-01-21 18:00:00	Other
7381	12	15	905	900	5	1042	1107	YX	1740	N207JQ	JFK	CMH	73	483	9	0	2023-12-15 09:00:00	Other
7405	8	24	949	946	3	1342	1341	UA	465	N67501	EWR	SJU	197	1608	9	46	2023-08-24 09:00:00	Other
7418	11	2	559	600	-1	855	905	NK	47	N673NK	LGA	FLL	154	1076	6	0	2023-11-02 06:00:00	FLL
7419	6	16	1534	1530	4	1837	1851	AA	59	N117AN	JFK	LAX	331	2475	15	30	2023-06-16 15:00:00	LAX
7424	7	26	701	659	2	849	905	AA	290	N895NN	LGA	CLT	81	544	6	59	2023-07-26 06:00:00	CLT
7436	2	23	1033	1030	3	1326	1340	B6	789	N998JE	JFK	FLL	149	1069	10	30	2023-02-23 10:00:00	FLL
7444	7	31	1653	1650	3	1905	1915	9E	1232	N930XJ	JFK	DTW	92	509	16	50	2023-07-31 16:00:00	Other
7447	4	21	2249	2250	-1	34	12	9E	1417	N901XJ	JFK	SYR	39	209	22	50	2023-04-21 22:00:00	Other
7451	11	27	1111	1112	-1	1427	1428	DL	476	N353DN	JFK	MIA	163	1089	11	12	2023-11-27 11:00:00	MIA
7456	6	29	1445	1446	-1	1622	1632	AA	786	N760US	LGA	RDU	69	431	14	46	2023-06-29 14:00:00	Other
7473	7	2	1536	1531	5	1854	1849	DL	483	N379DN	LGA	FLL	155	1076	15	31	2023-07-02 15:00:00	FLL
7504	1	12	2123	2120	3	50	2346	9E	1414	N326PQ	JFK	SAV	124	718	21	20	2023-01-12 21:00:00	Other
7505	2	26	1537	1529	8	1840	1838	UA	229	N27292	EWR	AUS	214	1504	15	29	2023-02-26 15:00:00	Other
7512	1	9	1549	1545	4	1705	1725	YX	1363	N867RW	LGA	CHO	52	305	15	45	2023-01-09 15:00:00	Other
7527	2	24	500	500	0	817	815	AA	434	N879NN	EWR	MIA	154	1085	5	0	2023-02-24 05:00:00	MIA
7529	10	26	1919	1920	-1	2045	2050	WN	927	N8533S	LGA	MDW	118	725	19	20	2023-10-26 19:00:00	Other
7533	8	9	1834	1835	-1	2030	2045	DL	773	N970AT	EWR	MSP	146	1008	18	35	2023-08-09 18:00:00	Other
7535	11	15	1059	1050	9	1354	1354	B6	527	N637JB	EWR	FLL	147	1065	10	50	2023-11-15 10:00:00	FLL
7536	3	27	1959	2000	-1	2250	2250	B6	47	N558JB	JFK	PHX	327	2153	20	0	2023-03-27 20:00:00	Other
7540	4	22	958	959	-1	1317	1319	B6	528	N657JB	JFK	RSW	169	1074	9	59	2023-04-22 09:00:00	Other
7541	1	18	1849	1845	4	1958	2009	UA	727	N477UA	EWR	IAD	44	212	18	45	2023-01-18 18:00:00	Other
7545	9	5	1514	1515	-1	1741	1816	DL	819	N394DX	JFK	MCO	121	944	15	15	2023-09-05 15:00:00	MCO
7577	1	24	1714	1715	-1	2016	2037	DL	297	N416DX	JFK	LAX	330	2475	17	15	2023-01-24 17:00:00	LAX
7580	7	31	1932	1929	3	2246	2335	DL	303	N723TW	JFK	SFO	337	2586	19	29	2023-07-31 19:00:00	Other
7588	9	5	1722	1720	2	1832	1840	WN	638	N8898L	LGA	MDW	101	725	17	20	2023-09-05 17:00:00	Other
7595	10	9	1333	1329	4	1538	1548	9E	1700	N341PQ	LGA	IND	94	660	13	29	2023-10-09 13:00:00	Other
7601	3	30	1400	1350	10	1529	1527	9E	1399	N300PQ	LGA	BNA	119	764	13	50	2023-03-30 13:00:00	Other
7603	11	28	1837	1830	7	2009	2012	UA	421	N76505	EWR	ORD	113	719	18	30	2023-11-28 18:00:00	ORD
7612	2	7	958	959	-1	1252	1309	B6	917	N510JB	JFK	TPA	145	1005	9	59	2023-02-07 09:00:00	Other
7619	3	27	1037	1032	5	1233	1203	YX	1114	N750YX	EWR	ORF	56	284	10	32	2023-03-27 10:00:00	Other
7623	9	22	603	600	3	734	734	UA	363	N37305	EWR	ORD	107	719	6	0	2023-09-22 06:00:00	ORD
7628	12	5	1529	1530	-1	1702	1723	B6	29	N317JB	JFK	ORD	115	740	15	30	2023-12-05 15:00:00	ORD
7630	8	8	2100	2100	0	2216	2234	UA	685	N852UA	EWR	MSN	111	799	21	0	2023-08-08 21:00:00	Other
7631	9	28	801	800	1	1139	1157	DL	705	N514DE	JFK	SJU	196	1598	8	0	2023-09-28 08:00:00	Other
7636	5	10	1630	1629	1	1821	1851	UA	810	N841UA	EWR	MSY	152	1167	16	29	2023-05-10 16:00:00	Other
7640	3	23	1504	1459	5	1647	1650	NK	24	N517NK	EWR	MYR	79	550	14	59	2023-03-23 14:00:00	Other
7652	8	8	1429	1429	0	1633	1657	UA	754	N460UA	LGA	DEN	223	1620	14	29	2023-08-08 14:00:00	Other
7658	7	30	1244	1245	-1	1346	1405	YX	994	N103HQ	JFK	BOS	35	187	12	45	2023-07-30 12:00:00	BOS
7672	1	12	2127	2120	7	2400	2253	9E	1597	N604LR	JFK	RIC	66	288	21	20	2023-01-12 21:00:00	Other
7675	1	31	1635	1629	6	1944	1944	UA	660	N78438	EWR	FLL	165	1065	16	29	2023-01-31 16:00:00	FLL
7676	2	19	753	745	8	1229	1246	B6	595	N632JB	EWR	SJU	190	1608	7	45	2023-02-19 07:00:00	Other
7688	12	21	1929	1929	0	2147	2219	DL	879	N880DN	JFK	ATL	105	760	19	29	2023-12-21 19:00:00	ATL
7695	9	11	1403	1355	8	1651	1645	WN	158	N8612K	LGA	HOU	185	1428	13	55	2023-09-11 13:00:00	Other
7697	4	4	734	735	-1	1004	1031	DL	345	N331DN	JFK	MCO	130	944	7	35	2023-04-04 07:00:00	MCO
7703	5	29	1400	1401	-1	1530	1545	YX	1095	N733YX	EWR	RDU	65	416	14	1	2023-05-29 14:00:00	Other
7704	3	3	919	920	-1	1143	1207	YX	1685	N241JQ	LGA	SDF	117	659	9	20	2023-03-03 09:00:00	Other
7719	11	16	1352	1350	2	1521	1540	9E	1473	N306PQ	LGA	BHM	117	866	13	50	2023-11-16 13:00:00	Other
7741	11	15	1412	1402	10	1542	1545	UA	775	N24706	EWR	STL	128	872	14	2	2023-11-15 14:00:00	Other
7751	4	6	931	930	1	1238	1241	B6	734	N2038J	JFK	FLL	143	1069	9	30	2023-04-06 09:00:00	FLL
7770	10	4	1113	1112	1	1355	1414	UA	139	N37522	EWR	FLL	139	1065	11	12	2023-10-04 11:00:00	FLL
7790	8	27	2044	2035	9	2216	2239	9E	1140	N310PQ	LGA	ILM	73	500	20	35	2023-08-27 20:00:00	Other
7791	5	26	1316	1315	1	1422	1431	B6	277	N197JB	JFK	BOS	38	187	13	15	2023-05-26 13:00:00	BOS
7794	9	22	1030	1029	1	1139	1155	AA	200	N803AW	LGA	BNA	101	764	10	29	2023-09-22 10:00:00	Other
7810	3	19	1804	1804	0	1951	2023	DL	425	N340NB	LGA	MSP	146	1020	18	4	2023-03-19 18:00:00	Other
7813	9	23	804	759	5	937	928	YX	1124	N752YX	EWR	PIT	58	319	7	59	2023-09-23 07:00:00	Other
7829	1	16	1454	1455	-1	1623	1630	9E	1649	N319PQ	JFK	RIC	54	288	14	55	2023-01-16 14:00:00	Other
7834	2	28	2037	2030	7	2301	2317	YX	1260	N107HQ	LGA	CVG	107	585	20	30	2023-02-28 20:00:00	Other
7839	2	15	1647	1642	5	1941	1950	UA	640	N37295	EWR	MIA	155	1085	16	42	2023-02-15 16:00:00	MIA
7842	12	21	720	720	0	931	946	B6	314	N2016J	JFK	SAV	103	718	7	20	2023-12-21 07:00:00	Other
7851	8	9	1419	1418	1	1546	1610	B6	223	N197JB	JFK	RDU	65	427	14	18	2023-08-09 14:00:00	Other
7854	5	20	1315	1314	1	1632	1621	UA	497	N17265	EWR	FLL	139	1065	13	14	2023-05-20 13:00:00	FLL
7857	11	14	605	600	5	809	755	DL	392	N372NW	LGA	DTW	83	502	6	0	2023-11-14 06:00:00	Other
7869	6	21	1035	1035	0	1215	1223	B6	87	N705JB	JFK	RDU	74	427	10	35	2023-06-21 10:00:00	Other
7871	5	4	1759	1755	4	2002	2025	WN	878	N8554X	LGA	DEN	222	1620	17	55	2023-05-04 17:00:00	Other
7879	9	10	554	549	5	845	853	AA	1	N112AN	JFK	LAX	314	2475	5	49	2023-09-10 05:00:00	LAX
7897	7	18	1002	1000	2	1216	1238	DL	144	N350DN	LGA	ATL	108	762	10	0	2023-07-18 10:00:00	ATL
7905	7	10	859	900	-1	1019	1037	OO	985	N253SY	JFK	BNA	115	765	9	0	2023-07-10 09:00:00	Other
7906	6	8	735	735	0	1016	1029	DL	768	N355DN	EWR	SLC	250	1969	7	35	2023-06-08 07:00:00	Other
7911	7	29	1105	1059	6	1257	1255	NK	522	N626NK	LGA	DTW	83	502	10	59	2023-07-29 10:00:00	Other
7919	6	10	1201	1200	1	1523	1500	DL	646	N317DN	JFK	MCO	130	944	12	0	2023-06-10 12:00:00	MCO
7920	5	27	2136	2130	6	2345	13	DL	451	N859DN	JFK	ATL	97	760	21	30	2023-05-27 21:00:00	ATL
7922	6	4	836	830	6	1044	1048	9E	1510	N348PQ	JFK	CHS	95	636	8	30	2023-06-04 08:00:00	Other
7926	11	26	1805	1759	6	2020	2007	9E	1443	N931XJ	LGA	MEM	157	963	17	59	2023-11-26 17:00:00	Other
7928	4	23	1545	1545	0	1838	1910	DL	242	N1602	JFK	LAX	326	2475	15	45	2023-04-23 15:00:00	LAX
7934	8	26	1059	1059	0	1246	1313	UA	362	N37465	EWR	PHX	267	2133	10	59	2023-08-26 10:00:00	Other
7977	11	18	1830	1830	0	2148	2205	B6	60	N984JB	JFK	LAX	340	2475	18	30	2023-11-18 18:00:00	LAX
8006	9	17	1202	1200	2	1446	1455	DL	297	N113DX	LGA	MCO	139	950	12	0	2023-09-17 12:00:00	MCO
8034	5	14	730	730	0	953	1016	DL	413	N367DN	LGA	MCO	122	950	7	30	2023-05-14 07:00:00	MCO
8037	11	17	729	730	-1	935	952	DL	525	N357NB	JFK	MSP	148	1029	7	30	2023-11-17 07:00:00	Other
8053	12	19	946	945	1	1051	1120	WN	467	N7702A	LGA	BNA	109	764	9	45	2023-12-19 09:00:00	Other
8055	6	6	941	940	1	1214	1245	B6	998	N558JB	JFK	TPA	132	1005	9	40	2023-06-06 09:00:00	Other
8062	12	24	1929	1926	3	2221	2251	DL	799	N319DN	JFK	MIA	146	1089	19	26	2023-12-24 19:00:00	MIA
8070	11	28	901	900	1	1023	1047	UA	460	N47533	EWR	ORD	110	719	9	0	2023-11-28 09:00:00	ORD
8071	7	17	1929	1930	-1	2238	2249	B6	63	N977JE	JFK	LAX	315	2475	19	30	2023-07-17 19:00:00	LAX
8072	3	5	2102	2100	2	2245	2243	UA	812	N454UA	LGA	ORD	130	733	21	0	2023-03-05 21:00:00	ORD
8077	5	8	1344	1345	-1	1633	1640	WN	239	N8669B	LGA	HOU	206	1428	13	45	2023-05-08 13:00:00	Other
8078	11	9	605	600	5	848	910	B6	831	N504JB	EWR	MIA	143	1085	6	0	2023-11-09 06:00:00	MIA
8086	1	1	644	645	-1	936	959	UA	972	N78509	EWR	MIA	154	1085	6	45	2023-01-01 06:00:00	MIA
8095	8	23	1258	1259	-1	1423	1425	YX	1349	N215JQ	LGA	BOS	36	184	12	59	2023-08-23 12:00:00	BOS
8105	4	13	1629	1625	4	1854	1920	WN	822	N8504G	LGA	DAL	180	1381	16	25	2023-04-13 16:00:00	Other
8108	8	25	2130	2130	0	2257	2304	UA	685	N811UA	EWR	MSN	118	799	21	30	2023-08-25 21:00:00	Other
8119	5	7	2154	2155	-1	2301	2316	YX	1661	N216JQ	LGA	ROC	45	254	21	55	2023-05-07 21:00:00	Other
8123	1	13	2127	2122	5	2328	2327	UA	742	N53442	EWR	CLT	88	529	21	22	2023-01-13 21:00:00	CLT
8129	3	2	2205	2159	6	2344	2339	UA	533	N17264	EWR	CLE	72	404	21	59	2023-03-02 21:00:00	Other
8131	8	27	1848	1840	8	2139	2144	B6	735	N510JB	JFK	MCO	138	944	18	40	2023-08-27 18:00:00	MCO
8137	10	4	1800	1800	0	2033	2059	B6	732	N635JB	JFK	PBI	130	1028	18	0	2023-10-04 18:00:00	Other
8138	4	16	1346	1341	5	1604	1558	9E	1254	N324PQ	LGA	IND	111	660	13	41	2023-04-16 13:00:00	Other
8146	6	18	1406	1407	-1	1540	1558	9E	1617	N600LR	JFK	RDU	65	427	14	7	2023-06-18 14:00:00	Other
8147	7	2	1301	1302	-1	1521	1555	NK	840	N601NK	EWR	MCO	123	937	13	2	2023-07-02 13:00:00	MCO
8152	3	31	1129	1121	8	1439	1438	DL	926	N851DN	JFK	SEA	338	2422	11	21	2023-03-31 11:00:00	Other
8155	4	27	2128	2125	3	2250	2255	WN	1033	N8684F	LGA	MDW	109	725	21	25	2023-04-27 21:00:00	Other
8165	3	31	2108	2059	9	16	2351	UA	391	N840UA	EWR	DFW	226	1372	20	59	2023-03-31 20:00:00	Other
8171	9	15	1031	1030	1	1346	1323	B6	367	N958JB	JFK	MCO	154	944	10	30	2023-09-15 10:00:00	MCO
8181	7	11	600	600	0	817	835	WN	492	N939WN	LGA	HOU	179	1428	6	0	2023-07-11 06:00:00	Other
8187	5	10	859	900	-1	1015	1015	WN	62	N950WN	LGA	MDW	107	725	9	0	2023-05-10 09:00:00	Other
8192	10	4	1229	1229	0	1517	1544	AA	612	N326SJ	JFK	MIA	145	1089	12	29	2023-10-04 12:00:00	MIA
8202	8	1	1614	1609	5	1812	1825	9E	1266	N325PQ	LGA	AVL	83	599	16	9	2023-08-01 16:00:00	Other
8217	5	1	1150	1150	0	1350	1359	9E	1332	N348PQ	JFK	CLT	89	541	11	50	2023-05-01 11:00:00	CLT
8218	6	10	1459	1455	4	1708	1715	9E	1545	N302PQ	JFK	CVG	92	589	14	55	2023-06-10 14:00:00	Other
8225	2	1	1221	1220	1	1529	1505	WN	410	N8786Q	LGA	DEN	254	1620	12	20	2023-02-01 12:00:00	Other
8230	12	15	2129	2130	-1	21	107	B6	358	N985JT	JFK	LAX	312	2475	21	30	2023-12-15 21:00:00	LAX
8233	12	1	2035	2035	0	2328	2347	B6	60	N632JB	JFK	TPA	147	1005	20	35	2023-12-01 20:00:00	Other
8239	7	8	629	630	-1	937	949	DL	109	N6706Q	JFK	SLC	278	1990	6	30	2023-07-08 06:00:00	Other
8241	6	18	648	642	6	938	931	AA	1000	N970AN	EWR	DFW	197	1372	6	42	2023-06-18 06:00:00	Other
8247	11	29	1439	1429	10	1750	1809	B6	530	N942JB	JFK	SFO	348	2586	14	29	2023-11-29 14:00:00	Other
8249	9	11	929	930	-1	1048	1054	UA	451	N67846	EWR	BOS	51	200	9	30	2023-09-11 09:00:00	BOS
8254	1	29	1240	1233	7	1518	1459	UA	757	N37506	EWR	DEN	253	1605	12	33	2023-01-29 12:00:00	Other
8256	8	3	1059	1100	-1	1353	1403	NK	422	N665NK	EWR	FLL	134	1065	11	0	2023-08-03 11:00:00	FLL
8257	3	9	1408	1405	3	1527	1540	UA	622	N4888U	EWR	BNA	119	748	14	5	2023-03-09 14:00:00	Other
8265	9	17	1729	1730	-1	1923	1930	NK	48	N631NK	LGA	DTW	95	502	17	30	2023-09-17 17:00:00	Other
8269	4	12	1144	1145	-1	1339	1443	DL	189	N833DN	JFK	LAS	272	2248	11	45	2023-04-12 11:00:00	Other
8271	8	2	739	740	-1	1013	1030	B6	196	N506JB	LGA	MCO	117	950	7	40	2023-08-02 07:00:00	MCO
8273	1	18	1628	1625	3	1946	1940	WN	575	N225WN	LGA	DAL	231	1381	16	25	2023-01-18 16:00:00	Other
8278	8	9	1607	1605	2	1801	1839	DL	627	N340NB	JFK	MSY	154	1182	16	5	2023-08-09 16:00:00	Other
8279	7	20	602	601	1	835	839	B6	204	N973JT	JFK	MCO	128	944	6	1	2023-07-20 06:00:00	MCO
8281	11	2	1147	1145	2	1435	1445	DL	1011	N301DV	LGA	MCO	140	950	11	45	2023-11-02 11:00:00	MCO
8299	1	28	1629	1630	-1	1954	2007	DL	244	N826DN	JFK	SLC	305	1990	16	30	2023-01-28 16:00:00	Other
8306	7	20	730	730	0	1019	1032	AS	80	N922VA	EWR	LAX	312	2454	7	30	2023-07-20 07:00:00	LAX
8309	4	4	1629	1629	0	1916	1915	DL	337	N877DN	JFK	PHX	319	2153	16	29	2023-04-04 16:00:00	Other
8311	9	25	709	659	10	834	830	YX	1958	N879RW	LGA	PIT	58	335	6	59	2023-09-25 06:00:00	Other
8317	5	20	604	605	-1	835	830	WN	604	N251WN	LGA	ATL	120	762	6	5	2023-05-20 06:00:00	ATL
8325	1	5	1425	1425	0	1741	1740	B6	342	N638JB	LGA	PBI	175	1035	14	25	2023-01-05 14:00:00	Other
8326	1	15	1554	1550	4	1701	1730	WN	591	N8328A	LGA	MDW	108	725	15	50	2023-01-15 15:00:00	Other
8330	2	24	1633	1630	3	1838	1829	AA	139	N852NN	LGA	ORD	146	733	16	30	2023-02-24 16:00:00	ORD
8348	1	27	829	830	-1	1029	1027	9E	1611	N232PQ	JFK	RDU	84	427	8	30	2023-01-27 08:00:00	Other
8353	5	1	1029	1025	4	1252	1303	DL	121	N386DN	LGA	ATL	118	762	10	25	2023-05-01 10:00:00	ATL
8360	9	15	1816	1815	1	2134	2128	AA	751	N941AN	LGA	MIA	153	1096	18	15	2023-09-15 18:00:00	MIA
8368	2	9	1503	1503	0	1701	1657	YX	1111	N862RW	EWR	STL	139	872	15	3	2023-02-09 15:00:00	Other
8374	10	26	1606	1604	2	1811	1831	B6	25	N661JB	JFK	MSY	154	1182	16	4	2023-10-26 16:00:00	Other
8376	9	25	829	830	-1	1131	1134	AA	597	N964AN	EWR	DFW	189	1372	8	30	2023-09-25 08:00:00	Other
8385	10	3	1632	1629	3	1747	1757	AA	977	N769US	LGA	BNA	103	764	16	29	2023-10-03 16:00:00	Other
8392	4	5	1528	1529	-1	1727	1727	YX	1073	N101HQ	JFK	CLE	73	425	15	29	2023-04-05 15:00:00	Other
8401	10	2	2010	2000	10	2226	2232	DL	287	N318DX	LGA	ATL	101	762	20	0	2023-10-02 20:00:00	ATL
8410	4	28	1959	1959	0	2256	2311	DL	573	N366NW	LGA	TPA	147	1010	19	59	2023-04-28 19:00:00	Other
8411	11	10	1833	1829	4	2142	2144	AS	168	N265AK	EWR	SEA	334	2402	18	29	2023-11-10 18:00:00	Other
8413	3	6	1140	1140	0	1447	1450	WN	258	N8796L	LGA	DAL	204	1381	11	40	2023-03-06 11:00:00	Other
8414	12	6	1258	1259	-1	1538	1611	NK	331	N632NK	LGA	DFW	184	1389	12	59	2023-12-06 12:00:00	Other
8415	6	19	1308	1307	1	1420	1433	9E	1585	N913XJ	LGA	BTV	49	258	13	7	2023-06-19 13:00:00	Other
8418	3	25	937	930	7	1317	1254	B6	591	N535JB	JFK	RSW	162	1074	9	30	2023-03-25 09:00:00	Other
8431	12	24	1954	1954	0	2233	2312	DL	611	N308DN	LGA	PBI	137	1035	19	54	2023-12-24 19:00:00	Other
8437	2	8	1826	1825	1	2120	2139	B6	21	N598JB	LGA	TPA	138	1010	18	25	2023-02-08 18:00:00	Other
8439	4	12	1902	1855	7	2001	2023	B6	794	N229JB	JFK	BOS	40	187	18	55	2023-04-12 18:00:00	BOS
8446	3	5	1200	1159	1	1500	1502	UA	831	N443UA	EWR	SRQ	151	1034	11	59	2023-03-05 11:00:00	Other
8474	6	11	1156	1155	1	1339	1341	G4	1056	206NV	EWR	VPS	137	988	11	55	2023-06-11 11:00:00	Other
8494	3	14	1835	1825	10	2153	2151	AS	91	N973AK	EWR	SAN	320	2425	18	25	2023-03-14 18:00:00	Other
8502	5	15	1558	1558	0	1802	1827	DL	765	N343NB	JFK	MSY	154	1182	15	58	2023-05-15 15:00:00	Other
8507	11	10	1949	1950	-1	2200	2227	YX	1076	N747YX	EWR	MCI	169	1092	19	50	2023-11-10 19:00:00	Other
8509	6	3	1104	1054	10	1355	1342	B6	349	N566JB	EWR	MCO	130	937	10	54	2023-06-03 10:00:00	MCO
8547	2	14	714	715	-1	831	900	WN	965	N8577Z	LGA	BNA	116	764	7	15	2023-02-14 07:00:00	Other
8557	5	1	726	720	6	919	956	DL	167	N388DA	LGA	DEN	208	1620	7	20	2023-05-01 07:00:00	Other
8562	6	7	929	930	-1	1117	1135	B6	70	N506JB	JFK	DTW	85	509	9	30	2023-06-07 09:00:00	Other
8566	8	27	1755	1745	10	2016	2005	WN	981	N8543Z	LGA	DEN	219	1620	17	45	2023-08-27 17:00:00	Other
8568	10	7	730	730	0	1103	1043	NK	553	N981NK	EWR	MIA	159	1085	7	30	2023-10-07 07:00:00	MIA
8569	3	2	754	755	-1	1028	958	AA	608	N883NN	EWR	CLT	92	529	7	55	2023-03-02 07:00:00	CLT
8570	4	23	1419	1420	-1	1608	1650	UA	808	N853UA	LGA	DEN	216	1620	14	20	2023-04-23 14:00:00	Other
8579	8	14	1820	1815	5	2258	2127	AA	595	N976AN	LGA	MIA	156	1096	18	15	2023-08-14 18:00:00	MIA
8581	9	29	1331	1329	2	1504	1511	MQ	1032	N764JD	EWR	ORD	108	719	13	29	2023-09-29 13:00:00	ORD
8589	1	30	1723	1718	5	1924	1932	YX	1136	N636RW	EWR	GSP	96	594	17	18	2023-01-30 17:00:00	Other
8591	2	11	2159	2200	-1	2323	2312	9E	1265	N921XJ	JFK	ITH	50	189	22	0	2023-02-11 22:00:00	Other
8593	12	24	1229	1230	-1	1540	1532	B6	37	N3145J	JFK	TPA	155	1005	12	30	2023-12-24 12:00:00	Other
8602	8	13	752	750	2	924	945	9E	1167	N538CA	JFK	RDU	68	427	7	50	2023-08-13 07:00:00	Other
8603	2	19	934	930	4	1204	1212	UA	842	N815UA	LGA	DEN	249	1620	9	30	2023-02-19 09:00:00	Other
8604	7	15	1716	1711	5	1914	1847	UA	514	N846UA	LGA	ORD	116	733	17	11	2023-07-15 17:00:00	ORD
8607	8	9	1649	1650	-1	1835	1915	9E	1204	N303PQ	JFK	DTW	81	509	16	50	2023-08-09 16:00:00	Other
8624	11	22	1633	1629	4	1950	2005	AA	836	N117AN	JFK	SFO	353	2586	16	29	2023-11-22 16:00:00	Other
8629	2	22	959	1000	-1	1241	1228	UA	756	N13954	EWR	DEN	243	1605	10	0	2023-02-22 10:00:00	Other
8640	1	2	1135	1130	5	1310	1335	AA	119	N826AW	LGA	ORD	128	733	11	30	2023-01-02 11:00:00	ORD
8644	7	29	1931	1929	2	2240	2209	9E	1209	N906XJ	JFK	MCI	155	1113	19	29	2023-07-29 19:00:00	Other
8659	10	16	1230	1229	1	1547	1547	DL	537	N327DN	LGA	FLL	156	1076	12	29	2023-10-16 12:00:00	FLL
8660	3	28	922	923	-1	1127	1117	YX	1297	N445YX	LGA	CLE	83	419	9	23	2023-03-28 09:00:00	Other
8662	5	16	1502	1459	3	1637	1642	AA	197	N871NN	LGA	ORD	114	733	14	59	2023-05-16 14:00:00	ORD
8673	12	6	1702	1659	3	1818	1832	YX	1780	N882RW	LGA	BOS	37	184	16	59	2023-12-06 16:00:00	BOS
8676	3	30	1056	1055	1	1351	1354	B6	165	N547JB	EWR	PBI	140	1023	10	55	2023-03-30 10:00:00	Other
8678	10	1	1814	1815	-1	2019	2028	YX	1289	N419YX	LGA	IND	92	660	18	15	2023-10-01 18:00:00	Other
8694	9	10	1830	1824	6	2135	2137	AA	169	N928AN	JFK	MIA	153	1089	18	24	2023-09-10 18:00:00	MIA
8703	3	9	1603	1600	3	1912	1924	UA	761	N13138	EWR	LAX	341	2454	16	0	2023-03-09 16:00:00	LAX
8707	2	18	642	640	2	957	950	UA	325	N37518	EWR	SAN	345	2425	6	40	2023-02-18 06:00:00	Other
8713	8	23	1654	1650	4	1854	1837	9E	1201	N491PX	LGA	PIT	55	335	16	50	2023-08-23 16:00:00	Other
8715	11	8	1959	1959	0	2158	2218	YX	1051	N762YX	EWR	GSP	92	594	19	59	2023-11-08 19:00:00	Other
8717	3	17	745	735	10	1041	1053	DL	464	N302DN	JFK	FLL	149	1069	7	35	2023-03-17 07:00:00	FLL
8724	8	7	1739	1739	0	2111	2035	UA	244	N17314	EWR	SRQ	141	1034	17	39	2023-08-07 17:00:00	Other
8725	11	22	1826	1825	1	2030	2051	9E	1580	N308PQ	JFK	IND	91	665	18	25	2023-11-22 18:00:00	Other
8727	11	28	1432	1427	5	1648	1632	AA	638	N998NN	EWR	CLT	83	529	14	27	2023-11-28 14:00:00	CLT
8733	2	17	1154	1155	-1	1310	1327	YX	1533	N882RW	LGA	DCA	55	214	11	55	2023-02-17 11:00:00	Other
8735	11	11	1226	1226	0	1536	1540	DL	510	N362NB	JFK	AUS	228	1521	12	26	2023-11-11 12:00:00	Other
8738	2	2	1808	1800	8	1930	1927	YX	1488	N217JQ	JFK	BOS	51	187	18	0	2023-02-02 18:00:00	BOS
8741	9	11	1434	1432	2	1829	1638	AA	534	N324SH	JFK	CLT	86	541	14	32	2023-09-11 14:00:00	CLT
8754	5	12	1002	1000	2	1250	1303	AA	606	N910NN	LGA	DFW	193	1389	10	0	2023-05-12 10:00:00	Other
8760	3	2	2158	2159	-1	2325	2322	UA	523	N497UA	EWR	ORF	57	284	21	59	2023-03-02 21:00:00	Other
8761	11	9	2102	2055	7	2228	2236	9E	1417	N331PQ	LGA	ORF	55	296	20	55	2023-11-09 20:00:00	Other
8766	10	9	2004	1959	5	2251	2316	AS	76	N972AK	EWR	LAX	307	2454	19	59	2023-10-09 19:00:00	LAX
8767	1	16	600	600	0	808	830	UA	491	N41140	EWR	DEN	215	1605	6	0	2023-01-16 06:00:00	Other
8770	4	25	2002	2000	2	2102	2128	YX	1458	N245JQ	LGA	BOS	35	184	20	0	2023-04-25 20:00:00	BOS
8781	10	15	1939	1940	-1	2221	2226	DL	1007	N373DX	JFK	ATL	113	760	19	40	2023-10-15 19:00:00	ATL
8789	5	27	829	830	-1	1135	1138	UA	481	N787UA	EWR	SFO	300	2565	8	30	2023-05-27 08:00:00	Other
8799	12	23	1730	1729	1	2135	2054	B6	921	N967JT	JFK	LAX	322	2475	17	29	2023-12-23 17:00:00	LAX
8808	6	9	2006	2000	6	2148	2159	YX	1286	N133HQ	JFK	PIT	63	340	20	0	2023-06-09 20:00:00	Other
8815	9	19	1959	1949	10	2307	2255	B6	344	N709JB	JFK	PDX	325	2454	19	49	2023-09-19 19:00:00	Other
8817	12	3	1441	1440	1	1648	1644	UA	362	N456UA	EWR	CLT	105	529	14	40	2023-12-03 14:00:00	CLT
8821	7	3	1034	1030	4	1329	1337	B6	284	N663JB	JFK	SLC	264	1990	10	30	2023-07-03 10:00:00	Other
8826	3	16	1823	1820	3	2024	2026	9E	1494	N606LR	LGA	MEM	144	963	18	20	2023-03-16 18:00:00	Other
8831	7	7	838	830	8	1108	1114	UA	130	N16009	EWR	LAX	297	2454	8	30	2023-07-07 08:00:00	LAX
8832	11	20	705	705	0	935	947	B6	255	N779JB	JFK	JAX	116	828	7	5	2023-11-20 07:00:00	Other
8834	2	19	1527	1520	7	1838	1845	DL	114	N132DU	LGA	DFW	224	1389	15	20	2023-02-19 15:00:00	Other
8852	2	14	629	630	-1	953	1006	DL	255	N883DN	JFK	SLC	296	1990	6	30	2023-02-14 06:00:00	Other
8861	12	28	1019	1020	-1	1204	1209	YX	1308	N416YX	LGA	ROA	75	405	10	20	2023-12-28 10:00:00	Other
8865	3	15	1049	1050	-1	1210	1238	YX	1758	N210JQ	LGA	BNA	112	764	10	50	2023-03-15 10:00:00	Other
8872	2	20	1329	1326	3	1537	1541	B6	254	N323JB	JFK	MSP	166	1029	13	26	2023-02-20 13:00:00	Other
8874	7	4	635	630	5	931	954	AA	27	N117AN	JFK	SFO	335	2586	6	30	2023-07-04 06:00:00	Other
8882	9	13	1229	1229	0	1516	1520	B6	75	N566JB	JFK	IAH	205	1417	12	29	2023-09-13 12:00:00	Other
8896	9	24	1146	1147	-1	1259	1317	YX	1066	N722YX	EWR	PIT	57	319	11	47	2023-09-24 11:00:00	Other
8903	5	7	2203	2157	6	16	2359	UA	615	N406UA	EWR	MSP	158	1008	21	57	2023-05-07 21:00:00	Other
8905	4	7	1134	1125	9	1403	1413	DL	319	N349NW	LGA	ATL	116	762	11	25	2023-04-07 11:00:00	ATL
8914	10	17	2022	2015	7	2256	2244	B6	42	N971JT	JFK	PHX	269	2153	20	15	2023-10-17 20:00:00	Other
8915	8	23	631	630	1	832	835	WN	459	N8822Q	LGA	DEN	212	1620	6	30	2023-08-23 06:00:00	Other
8917	5	29	1651	1650	1	1907	1920	9E	1552	N335PQ	JFK	CLT	79	541	16	50	2023-05-29 16:00:00	CLT
8919	9	1	1932	1930	2	2045	2045	B6	501	N247JB	LGA	PWM	48	269	19	30	2023-09-01 19:00:00	Other
8920	4	7	731	730	1	949	944	DL	180	N355NB	JFK	MSP	174	1029	7	30	2023-04-07 07:00:00	Other
8927	7	25	1153	1149	4	1422	1434	UA	635	N73291	EWR	SAN	301	2425	11	49	2023-07-25 11:00:00	Other
8931	4	9	1144	1145	-1	1356	1444	DL	189	N873DN	JFK	LAS	287	2248	11	45	2023-04-09 11:00:00	Other
8935	4	10	1658	1659	-1	1826	1840	UA	717	N841UA	LGA	ORD	108	733	16	59	2023-04-10 16:00:00	ORD
8944	10	26	1857	1856	1	2036	2045	UA	648	N37437	EWR	RDU	64	416	18	56	2023-10-26 18:00:00	Other
8955	8	21	559	600	-1	708	715	WN	462	N8327A	LGA	MDW	102	725	6	0	2023-08-21 06:00:00	Other
8963	7	17	1647	1645	2	1745	1756	B6	750	N206JB	LGA	MVY	36	175	16	45	2023-07-17 16:00:00	Other
8965	4	5	1230	1230	0	1517	1535	AA	588	N466AN	EWR	MIA	142	1085	12	30	2023-04-05 12:00:00	MIA
8974	8	9	1654	1654	0	1905	1922	DL	708	N391DA	EWR	ATL	101	746	16	54	2023-08-09 16:00:00	ATL
8982	12	6	1800	1759	1	2042	2126	DL	96	N803DN	JFK	SLC	266	1990	17	59	2023-12-06 17:00:00	Other
8985	3	16	1357	1349	8	1622	1629	B6	742	N805JB	LGA	DEN	235	1620	13	49	2023-03-16 13:00:00	Other
8987	1	5	604	600	4	1101	1049	B6	691	N905JB	JFK	SJU	209	1598	6	0	2023-01-05 06:00:00	Other
8988	1	6	614	615	-1	921	931	UA	929	N14107	EWR	LAX	338	2454	6	15	2023-01-06 06:00:00	LAX
8990	12	3	720	720	0	854	900	WN	343	N218WN	LGA	BNA	138	764	7	20	2023-12-03 07:00:00	Other
8993	10	28	900	900	0	1151	1206	UA	914	N17317	EWR	MIA	138	1085	9	0	2023-10-28 09:00:00	MIA
8995	4	24	1040	1030	10	1313	1317	B6	39	N913JB	JFK	LAS	305	2248	10	30	2023-04-24 10:00:00	Other
8997	9	15	1108	1100	8	1348	1332	DL	283	N347DN	LGA	ATL	110	762	11	0	2023-09-15 11:00:00	ATL
9003	1	13	1914	1915	-1	2113	2126	AA	819	N934AN	JFK	CLT	91	541	19	15	2023-01-13 19:00:00	CLT
9021	8	14	1900	1859	1	2040	2029	UA	500	N66841	EWR	BNA	105	748	18	59	2023-08-14 18:00:00	Other
9022	12	21	1109	1110	-1	1310	1327	DL	489	N384DN	LGA	MSP	150	1020	11	10	2023-12-21 11:00:00	Other
9032	5	21	2000	2000	0	2210	2226	DL	912	N3771K	EWR	ATL	103	746	20	0	2023-05-21 20:00:00	ATL
9047	7	5	609	600	9	719	718	UA	368	N26215	EWR	IAD	42	212	6	0	2023-07-05 06:00:00	Other
9055	6	29	1105	1059	6	1256	1318	YX	1141	N642RW	EWR	IND	90	645	10	59	2023-06-29 10:00:00	Other
9058	1	8	1230	1230	0	1351	1402	YX	1145	N643RW	EWR	PIT	61	319	12	30	2023-01-08 12:00:00	Other
9062	1	17	1459	1500	-1	1908	1854	DL	417	N898DN	JFK	PHX	342	2153	15	0	2023-01-17 15:00:00	Other
9068	3	12	1629	1630	-1	1819	1819	DL	766	N140DU	LGA	RDU	76	431	16	30	2023-03-12 16:00:00	Other
9069	3	4	603	601	2	850	850	UA	270	N416UA	EWR	LAS	318	2227	6	1	2023-03-04 06:00:00	Other
9074	8	22	814	814	0	1012	1019	9E	1151	N915XJ	LGA	GSP	87	610	8	14	2023-08-22 08:00:00	Other
9090	11	6	1054	1055	-1	1310	1335	WN	30	N7735A	LGA	ATL	111	762	10	55	2023-11-06 10:00:00	ATL
9096	1	21	1510	1510	0	1638	1648	UA	702	N17279	EWR	ORD	118	719	15	10	2023-01-21 15:00:00	ORD
9098	12	9	809	801	8	1125	1120	AA	96	N722US	EWR	MIA	164	1085	8	1	2023-12-09 08:00:00	MIA
9099	12	24	829	830	-1	1144	1151	DL	254	N302DU	LGA	DFW	199	1389	8	30	2023-12-24 08:00:00	Other
9102	4	23	800	800	0	1017	1017	9E	1344	N602LR	JFK	CHS	99	636	8	0	2023-04-23 08:00:00	Other
9107	12	8	1318	1318	0	1557	1635	AA	650	N913AN	EWR	DFW	192	1372	13	18	2023-12-08 13:00:00	Other
9112	9	23	559	600	-1	801	810	DL	841	N893AT	EWR	ATL	100	746	6	0	2023-09-23 06:00:00	ATL
9113	3	12	1625	1620	5	1847	1844	YX	1084	N755YX	EWR	MCI	165	1092	16	20	2023-03-12 16:00:00	Other
9115	2	15	1442	1441	1	1804	1754	AA	806	N883NN	JFK	DFW	221	1391	14	41	2023-02-15 14:00:00	Other
9134	1	18	2306	2259	7	344	349	B6	332	N640JB	JFK	PSE	192	1617	22	59	2023-01-18 22:00:00	Other
9139	12	13	1349	1350	-1	1556	1554	OO	1185	N614CZ	JFK	CLE	97	425	13	50	2023-12-13 13:00:00	Other
9140	7	31	730	730	0	956	1007	9E	1167	N906XJ	LGA	JAX	121	833	7	30	2023-07-31 07:00:00	Other
9147	12	26	1602	1555	7	1857	1956	DL	281	N703TW	JFK	SFO	328	2586	15	55	2023-12-26 15:00:00	Other
9149	5	22	1511	1510	1	1803	1816	UA	394	N27274	EWR	AUS	207	1504	15	10	2023-05-22 15:00:00	Other
9160	11	25	929	929	0	1217	1227	UA	210	N37468	EWR	MCO	137	937	9	29	2023-11-25 09:00:00	MCO
9162	10	10	1637	1635	2	1917	1931	B6	525	N768JB	EWR	MCO	134	937	16	35	2023-10-10 16:00:00	MCO
9165	6	30	1208	1200	8	1444	1500	UA	768	N2332U	EWR	SFO	313	2565	12	0	2023-06-30 12:00:00	Other
9173	5	13	1551	1552	-1	1838	1920	DL	379	N3754A	JFK	MIA	141	1089	15	52	2023-05-13 15:00:00	MIA
9188	3	7	2230	2220	10	2356	2359	B6	348	N534JB	LGA	BNA	120	764	22	20	2023-03-07 22:00:00	Other
9189	11	28	2233	2223	10	311	313	NK	361	N650NK	EWR	SJU	203	1608	22	23	2023-11-28 22:00:00	Other
9191	6	30	1306	1302	4	1538	1555	NK	1060	N604NK	EWR	MCO	126	937	13	2	2023-06-30 13:00:00	MCO
9206	3	15	1124	1115	9	1222	1229	B6	245	N324JB	LGA	BOS	38	184	11	15	2023-03-15 11:00:00	BOS
9209	7	21	1904	1900	4	2200	2208	UA	584	N27269	EWR	RSW	144	1068	19	0	2023-07-21 19:00:00	Other
9215	5	8	1303	1304	-1	1401	1418	UA	182	N14704	EWR	BOS	36	200	13	4	2023-05-08 13:00:00	BOS
9216	12	3	1935	1925	10	2308	2236	DL	339	N3743H	LGA	MIA	165	1096	19	25	2023-12-03 19:00:00	MIA
9223	5	31	2206	2200	6	2322	2327	DL	632	N103DU	JFK	BOS	43	187	22	0	2023-05-31 22:00:00	BOS
9224	11	28	729	730	-1	910	915	DL	597	N110DU	LGA	ORD	114	733	7	30	2023-11-28 07:00:00	ORD
9231	8	11	1538	1529	9	1652	1704	UA	552	N818UA	EWR	ORD	108	719	15	29	2023-08-11 15:00:00	ORD
9242	10	15	1959	1959	0	2302	2307	DL	803	N325DN	LGA	TPA	155	1010	19	59	2023-10-15 19:00:00	Other
9256	11	7	1159	1200	-1	1638	1645	DL	700	N925DZ	JFK	SJU	191	1598	12	0	2023-11-07 12:00:00	Other
9258	2	23	807	800	7	1102	1030	OO	1172	N607CZ	JFK	MSP	195	1029	8	0	2023-02-23 08:00:00	Other
9271	3	25	2041	2042	-1	2400	2	B6	35	N945JT	JFK	SAN	345	2446	20	42	2023-03-25 20:00:00	Other
9279	3	13	1735	1725	10	2050	2035	WN	904	N495WN	LGA	HOU	219	1428	17	25	2023-03-13 17:00:00	Other
9296	8	15	800	755	5	921	916	NK	234	N527NK	EWR	PIT	50	319	7	55	2023-08-15 07:00:00	Other
9302	7	19	1551	1550	1	1731	1732	9E	1303	N316PQ	LGA	CHO	58	305	15	50	2023-07-19 15:00:00	Other
9313	5	30	1630	1630	0	1943	1937	NK	321	N676NK	LGA	FLL	146	1076	16	30	2023-05-30 16:00:00	FLL
9314	5	29	610	610	0	753	813	AA	329	N947NN	JFK	CLT	84	541	6	10	2023-05-29 06:00:00	CLT
9317	6	18	1304	1302	2	1529	1555	NK	1060	N611NK	EWR	MCO	122	937	13	2	2023-06-18 13:00:00	MCO
9327	5	24	1328	1319	9	1525	1605	AA	946	N323SG	JFK	PHX	273	2153	13	19	2023-05-24 13:00:00	Other
9335	4	11	1634	1629	5	1752	1825	OO	1009	N307SY	JFK	ORD	111	740	16	29	2023-04-11 16:00:00	ORD
9345	10	10	1146	1145	1	1442	1459	AS	6	N918AK	JFK	PDX	332	2454	11	45	2023-10-10 11:00:00	Other
9349	1	27	735	735	0	1032	1042	DL	662	N343NW	JFK	TPA	162	1005	7	35	2023-01-27 07:00:00	Other
9355	7	13	1459	1455	4	1757	1803	B6	130	N561JB	LGA	MCO	140	950	14	55	2023-07-13 14:00:00	MCO
9362	12	13	559	600	-1	726	740	UA	372	N34131	EWR	ORD	122	719	6	0	2023-12-13 06:00:00	ORD
9367	5	8	1616	1607	9	1729	1729	UA	140	N447UA	EWR	BOS	39	200	16	7	2023-05-08 16:00:00	BOS
9369	3	2	941	935	6	1207	1212	9E	1366	N601LR	LGA	GRR	117	618	9	35	2023-03-02 09:00:00	Other
9371	9	13	1709	1707	2	1845	1843	UA	793	N19136	EWR	ORD	110	719	17	7	2023-09-13 17:00:00	ORD
9374	12	21	1758	1759	-1	1918	1939	9E	1606	N478PX	LGA	BUF	53	292	17	59	2023-12-21 17:00:00	Other
9377	7	13	724	725	-1	854	850	WN	124	N7859B	LGA	BNA	114	764	7	25	2023-07-13 07:00:00	Other
9401	12	18	841	839	2	1209	1249	AA	529	N339SU	JFK	PHX	294	2153	8	39	2023-12-18 08:00:00	Other
9407	10	10	1559	1549	10	1853	1852	UA	353	N412UA	EWR	AUS	205	1504	15	49	2023-10-10 15:00:00	Other
9420	1	18	738	730	8	1116	1113	AS	15	N952AK	JFK	SFO	371	2586	7	30	2023-01-18 07:00:00	Other
9432	6	19	705	700	5	856	914	UA	138	N73283	EWR	DEN	204	1605	7	0	2023-06-19 07:00:00	Other
9444	11	8	1924	1920	4	2319	2245	DL	200	N895DN	JFK	PDX	351	2454	19	20	2023-11-08 19:00:00	Other
9447	8	17	1932	1933	-1	2223	2237	UA	502	N27287	EWR	SMF	327	2500	19	33	2023-08-17 19:00:00	Other
9456	2	27	1947	1945	2	2233	2301	B6	185	N556JB	LGA	FLL	146	1076	19	45	2023-02-27 19:00:00	FLL
9458	9	15	1840	1834	6	2140	2146	AA	647	N336RU	EWR	MIA	155	1085	18	34	2023-09-15 18:00:00	MIA
9460	10	28	559	600	-1	716	730	WN	33	N903WN	LGA	BNA	115	764	6	0	2023-10-28 06:00:00	Other
9464	6	14	710	710	0	948	958	DL	567	N383DZ	LGA	MCO	136	950	7	10	2023-06-14 07:00:00	MCO
9497	8	28	1549	1550	-1	1750	1815	9E	1103	N313PQ	LGA	CLT	87	544	15	50	2023-08-28 15:00:00	CLT
9502	11	26	1657	1658	-1	1853	1839	OO	1211	N316SY	JFK	MKE	129	745	16	58	2023-11-26 16:00:00	Other
9508	4	9	1646	1645	1	1945	1959	B6	284	N608JB	LGA	PBI	152	1035	16	45	2023-04-09 16:00:00	Other
9514	3	27	1450	1445	5	1615	1609	YX	1043	N751YX	EWR	ORF	56	284	14	45	2023-03-27 14:00:00	Other
9517	4	4	819	820	-1	925	948	YX	1538	N245JQ	LGA	IAD	48	229	8	20	2023-04-04 08:00:00	Other
9542	8	7	1738	1730	8	2046	2046	B6	626	N644JB	JFK	MIA	161	1089	17	30	2023-08-07 17:00:00	MIA
9547	5	19	1833	1829	4	2144	2142	AS	171	N293AK	EWR	SEA	325	2402	18	29	2023-05-19 18:00:00	Other
9551	5	25	1355	1352	3	1516	1519	YX	1116	N864RW	EWR	PIT	57	319	13	52	2023-05-25 13:00:00	Other
9558	11	20	1959	2000	-1	2155	2214	YX	1883	N223JQ	JFK	CLT	88	541	20	0	2023-11-20 20:00:00	CLT
9562	6	11	1651	1648	3	1839	1837	9E	1604	N915XJ	LGA	PIT	57	335	16	48	2023-06-11 16:00:00	Other
9564	11	6	801	800	1	1042	1113	B6	78	N834JB	JFK	IAH	197	1417	8	0	2023-11-06 08:00:00	Other
9566	6	14	1700	1650	10	1853	1855	WN	122	N8678E	LGA	MCI	156	1107	16	50	2023-06-14 16:00:00	Other
9567	9	16	1541	1540	1	1732	1802	9E	1756	N308PQ	LGA	IND	92	660	15	40	2023-09-16 15:00:00	Other
9588	10	28	1508	1506	2	1616	1625	UA	707	N498UA	EWR	IAD	43	212	15	6	2023-10-28 15:00:00	Other
9591	1	4	814	815	-1	1116	1127	UA	617	N27015	EWR	LAX	327	2454	8	15	2023-01-04 08:00:00	LAX
9594	12	24	1109	1110	-1	1302	1327	DL	489	N354DN	LGA	MSP	150	1020	11	10	2023-12-24 11:00:00	Other
9597	7	24	730	730	0	1046	1043	DL	562	N371DN	JFK	FLL	161	1069	7	30	2023-07-24 07:00:00	FLL
9606	1	7	1828	1825	3	2142	2139	AA	1098	N935AN	JFK	DFW	216	1391	18	25	2023-01-07 18:00:00	Other
9621	8	1	1259	1300	-1	1549	1613	AA	198	N306RC	LGA	MIA	145	1096	13	0	2023-08-01 13:00:00	MIA
9632	7	15	1145	1140	5	1349	1400	WN	607	N8555Z	LGA	ATL	106	762	11	40	2023-07-15 11:00:00	ATL
9643	11	1	1105	1057	8	1351	1335	F9	529	N232FR	LGA	ATL	123	762	10	57	2023-11-01 10:00:00	ATL
9644	8	3	733	730	3	926	927	9E	1127	N904XJ	LGA	GSO	77	461	7	30	2023-08-03 07:00:00	Other
9648	12	8	1837	1834	3	2136	2149	AA	972	N959NN	EWR	MIA	151	1085	18	34	2023-12-08 18:00:00	MIA
9661	1	27	1845	1844	1	2109	2120	UA	431	N13138	EWR	DEN	228	1605	18	44	2023-01-27 18:00:00	Other
9671	12	5	2007	1959	8	2315	2329	DL	710	N104DN	JFK	FLL	161	1069	19	59	2023-12-05 19:00:00	FLL
9679	1	24	1844	1845	-1	2156	2147	UA	983	N14016	EWR	LAX	320	2454	18	45	2023-01-24 18:00:00	LAX
9681	9	11	829	830	-1	1041	1057	B6	961	N504JB	LGA	ATL	108	762	8	30	2023-09-11 08:00:00	ATL
9687	10	5	1830	1830	0	2118	2137	UA	638	N26970	EWR	SFO	312	2565	18	30	2023-10-05 18:00:00	Other
9692	4	24	2209	2200	9	2318	2332	YX	1117	N439YX	JFK	BOS	36	187	22	0	2023-04-24 22:00:00	BOS
9697	8	16	1347	1345	2	1629	1635	WN	641	N8689C	LGA	HOU	195	1428	13	45	2023-08-16 13:00:00	Other
9711	5	21	2056	2055	1	2349	2357	B6	98	N585JB	EWR	FLL	142	1065	20	55	2023-05-21 20:00:00	FLL
9722	3	14	1619	1620	-1	1849	1834	9E	1456	N916XJ	LGA	AVL	91	599	16	20	2023-03-14 16:00:00	Other
9726	4	7	1334	1329	5	1520	1522	9E	1298	N902XJ	LGA	RDU	78	431	13	29	2023-04-07 13:00:00	Other
9749	9	24	1725	1715	10	1901	1851	UA	546	N14249	LGA	ORD	113	733	17	15	2023-09-24 17:00:00	ORD
9761	7	17	1519	1520	-1	1704	1700	WN	767	N8555Z	LGA	STL	135	888	15	20	2023-07-17 15:00:00	Other
9766	1	6	1635	1636	-1	1848	1900	UA	211	N16701	EWR	SAV	102	708	16	36	2023-01-06 16:00:00	Other
9770	4	4	1532	1529	3	1819	1837	B6	668	N329JB	LGA	PBI	135	1035	15	29	2023-04-04 15:00:00	Other
9776	5	21	745	741	4	942	1011	UA	826	N77258	EWR	DEN	214	1605	7	41	2023-05-21 07:00:00	Other
9778	7	12	1728	1723	5	1958	2035	B6	64	N517JB	JFK	TPA	135	1005	17	23	2023-07-12 17:00:00	Other
9779	2	21	934	929	5	1103	1056	UA	710	N1902U	EWR	IAD	47	212	9	29	2023-02-21 09:00:00	Other
9780	10	10	642	643	-1	944	949	DL	624	N328NW	JFK	AUS	209	1521	6	43	2023-10-10 06:00:00	Other
9786	10	19	1035	1035	0	1253	1305	WN	916	N298WN	LGA	ATL	114	762	10	35	2023-10-19 10:00:00	ATL
9787	2	16	1428	1429	-1	1707	1650	UA	807	N842UA	EWR	MSY	173	1167	14	29	2023-02-16 14:00:00	Other
9788	5	8	1103	1100	3	1321	1323	9E	1288	N137EV	LGA	MCI	162	1107	11	0	2023-05-08 11:00:00	Other
9790	1	3	1625	1625	0	1917	1930	DL	827	N107DU	JFK	DFW	210	1391	16	25	2023-01-03 16:00:00	Other
9797	12	31	1705	1700	5	1922	1936	DL	453	N395DN	LGA	MSY	170	1183	17	0	2023-12-31 17:00:00	Other
9800	11	21	1945	1935	10	2255	2323	DL	346	N842MH	JFK	SFO	323	2586	19	35	2023-11-21 19:00:00	Other
9802	2	27	646	640	6	933	957	B6	819	N562JB	EWR	MIA	146	1085	6	40	2023-02-27 06:00:00	MIA
9805	4	14	832	830	2	1040	1105	9E	1424	N200PQ	LGA	SAV	106	722	8	30	2023-04-14 08:00:00	Other
9814	7	17	604	600	4	835	839	B6	86	N571JB	LGA	MCO	132	950	6	0	2023-07-17 06:00:00	MCO
9826	8	22	2103	2056	7	2239	2302	YX	932	N730YX	EWR	CMH	67	463	20	56	2023-08-22 20:00:00	Other
9830	10	25	758	759	-1	1014	1037	DL	297	N388DN	LGA	ATL	106	762	7	59	2023-10-25 07:00:00	ATL
9831	8	3	1553	1553	0	1937	1924	DL	461	N385DZ	LGA	FLL	204	1076	15	53	2023-08-03 15:00:00	FLL
9835	8	27	834	830	4	1207	1140	UA	530	N19136	EWR	SEA	330	2402	8	30	2023-08-27 08:00:00	Other
9837	12	26	1540	1535	5	1647	1653	B6	39	N267JB	JFK	BTV	49	266	15	35	2023-12-26 15:00:00	Other
9847	8	3	1428	1424	4	1715	1725	UA	218	N78511	EWR	SEA	318	2402	14	24	2023-08-03 14:00:00	Other
9864	9	15	1631	1629	2	1937	1942	AA	487	N304RB	LGA	MIA	154	1096	16	29	2023-09-15 16:00:00	MIA
9868	5	14	1529	1530	-1	1747	1811	B6	650	N794JB	JFK	ATL	102	760	15	30	2023-05-14 15:00:00	ATL
9870	10	25	1509	1459	10	1623	1632	9E	1612	N480PX	LGA	ORF	50	296	14	59	2023-10-25 14:00:00	Other
9879	7	17	1450	1450	0	1717	1720	WN	547	N968WN	LGA	ATL	114	762	14	50	2023-07-17 14:00:00	ATL
9883	5	5	928	929	-1	1039	1046	B6	611	N358JB	JFK	BTV	44	266	9	29	2023-05-05 09:00:00	Other
9887	8	22	1711	1702	9	1955	2026	B6	795	N793JB	JFK	FLL	135	1069	17	2	2023-08-22 17:00:00	FLL
9895	7	24	1910	1905	5	2046	2042	YX	877	N754YX	EWR	PWM	56	284	19	5	2023-07-24 19:00:00	Other
9897	6	16	1023	1020	3	1421	1348	YX	1218	N865RW	EWR	EYW	169	1196	10	20	2023-06-16 10:00:00	Other
9898	4	8	2206	2159	7	2321	2322	UA	476	N64809	EWR	ORF	50	284	21	59	2023-04-08 21:00:00	Other
9902	11	6	1210	1205	5	1447	1445	WN	34	N484WN	LGA	DEN	248	1620	12	5	2023-11-06 12:00:00	Other
9903	7	23	2043	2035	8	2233	2240	9E	1156	N319PQ	LGA	ILM	81	500	20	35	2023-07-23 20:00:00	Other
9907	10	19	2059	2100	-1	2330	8	AA	82	N108NN	JFK	LAX	300	2475	21	0	2023-10-19 21:00:00	LAX
9913	4	6	1629	1629	0	1900	1809	AA	827	N810NN	LGA	ORD	122	733	16	29	2023-04-06 16:00:00	ORD
9919	2	12	814	815	-1	1110	1134	UA	477	N229UA	EWR	SFO	315	2565	8	15	2023-02-12 08:00:00	Other
9926	5	7	1010	1000	10	1325	1329	DL	140	N802DN	JFK	SLC	279	1990	10	0	2023-05-07 10:00:00	Other
9946	4	15	1030	1027	3	1140	1202	UA	624	N478UA	EWR	ORD	102	719	10	27	2023-04-15 10:00:00	ORD
9950	7	9	709	710	-1	936	958	DL	460	N386DN	LGA	MCO	128	950	7	10	2023-07-09 07:00:00	MCO
9952	8	28	1552	1553	-1	1854	1924	DL	461	N372DN	LGA	FLL	164	1076	15	53	2023-08-28 15:00:00	FLL
9955	5	12	1408	1409	-1	1615	1629	DL	794	N3741S	EWR	ATL	102	746	14	9	2023-05-12 14:00:00	ATL
9956	4	26	1459	1500	-1	1623	1622	YX	1025	N746YX	EWR	BTV	52	266	15	0	2023-04-26 15:00:00	Other
9961	3	11	1815	1815	0	2133	2137	UA	516	N13716	EWR	SNA	351	2434	18	15	2023-03-11 18:00:00	Other
9963	4	10	1830	1829	1	2055	2145	UA	469	N17719	EWR	SNA	298	2434	18	29	2023-04-10 18:00:00	Other
9965	5	12	1454	1455	-1	1612	1631	OO	1084	N610CZ	JFK	IAD	44	228	14	55	2023-05-12 14:00:00	Other
9981	6	9	1705	1700	5	1920	1939	B6	971	N565JB	LGA	ATL	102	762	17	0	2023-06-09 17:00:00	ATL
9987	8	1	1800	1759	1	2014	2027	UA	700	N855UA	LGA	DEN	223	1620	17	59	2023-08-01 17:00:00	Other
9997	4	24	1831	1830	1	2144	2159	B6	29	N526JL	JFK	SLC	275	1990	18	30	2023-04-24 18:00:00	Other
10005	7	15	1358	1355	3	1506	1535	OO	980	N310SY	JFK	BOS	35	187	13	55	2023-07-15 13:00:00	BOS
10010	5	20	715	715	0	959	1011	UA	680	N27269	EWR	TPA	138	997	7	15	2023-05-20 07:00:00	Other
10012	5	10	1849	1850	-1	2202	2151	UA	802	N39297	EWR	TPA	148	997	18	50	2023-05-10 18:00:00	Other
10019	3	5	2129	2130	-1	2227	2237	YX	1195	N863RW	EWR	PVD	34	160	21	30	2023-03-05 21:00:00	Other
10022	9	9	1139	1129	10	1454	1439	DL	495	N375DA	JFK	MIA	168	1089	11	29	2023-09-09 11:00:00	MIA
10023	8	19	1932	1933	-1	2212	2237	UA	502	N27258	EWR	SMF	313	2500	19	33	2023-08-19 19:00:00	Other
10029	3	11	936	934	2	1112	1124	YX	1080	N727YX	EWR	CLE	70	404	9	34	2023-03-11 09:00:00	Other
10032	11	3	825	825	0	1247	1333	UA	119	N68061	EWR	HNL	594	4962	8	25	2023-11-03 08:00:00	Other
10034	12	10	510	510	0	819	825	AA	411	N875NN	EWR	MIA	159	1085	5	10	2023-12-10 05:00:00	MIA
10035	5	16	1513	1510	3	1804	1816	UA	394	N27287	EWR	AUS	207	1504	15	10	2023-05-16 15:00:00	Other
10040	4	6	1822	1815	7	2027	2024	DL	504	N921AT	EWR	MSP	162	1008	18	15	2023-04-06 18:00:00	Other
10043	11	18	2135	2127	8	2306	2315	UA	821	N75436	EWR	RDU	66	416	21	27	2023-11-18 21:00:00	Other
10044	7	26	1609	1559	10	1729	1734	YX	926	N743YX	EWR	PIT	54	319	15	59	2023-07-26 15:00:00	Other
10053	12	8	1759	1759	0	2000	1950	MQ	1164	N765ST	EWR	ORD	115	719	17	59	2023-12-08 17:00:00	ORD
10057	10	16	634	635	-1	920	946	AA	557	N835NN	LGA	DFW	183	1389	6	35	2023-10-16 06:00:00	Other
10061	4	1	1459	1459	0	1732	1737	YX	1116	N129HQ	JFK	IND	113	665	14	59	2023-04-01 14:00:00	Other
10066	9	8	907	900	7	1017	1030	WN	1274	N8658A	LGA	MDW	100	725	9	0	2023-09-08 09:00:00	Other
10085	8	30	1733	1725	8	1901	1913	9E	1195	N341PQ	JFK	BUF	52	301	17	25	2023-08-30 17:00:00	Other
10089	11	17	600	600	0	841	905	WN	1091	N8545V	LGA	DAL	196	1381	6	0	2023-11-17 06:00:00	Other
10103	3	27	2049	2045	4	2355	44	AA	58	N113AN	JFK	LAX	343	2475	20	45	2023-03-27 20:00:00	LAX
10117	9	22	2010	2000	10	2236	2232	DL	302	N381DZ	LGA	ATL	106	762	20	0	2023-09-22 20:00:00	ATL
10128	9	28	1110	1110	0	1158	1215	YX	1388	N441YX	JFK	ORH	30	150	11	10	2023-09-28 11:00:00	Other
10133	12	9	604	605	-1	737	749	AA	336	N932NN	LGA	ORD	116	733	6	5	2023-12-09 06:00:00	ORD
10139	9	25	1955	1948	7	2150	2152	AA	313	N534UW	EWR	CLT	87	529	19	48	2023-09-25 19:00:00	CLT
10154	12	7	1716	1714	2	1935	1951	DL	557	N856DN	JFK	ATL	105	760	17	14	2023-12-07 17:00:00	ATL
10161	5	6	1054	1055	-1	1335	1350	DL	372	N380DN	JFK	MCO	133	944	10	55	2023-05-06 10:00:00	MCO
10162	11	7	1903	1900	3	2013	2021	UA	815	N78285	EWR	BOS	45	200	19	0	2023-11-07 19:00:00	BOS
10163	3	12	645	645	0	846	854	UA	493	N25201	EWR	CHS	94	628	6	45	2023-03-12 06:00:00	Other
10179	6	14	837	830	7	1118	1058	UA	933	N27733	EWR	ATL	128	746	8	30	2023-06-14 08:00:00	ATL
10186	4	18	1504	1459	5	1711	1717	YX	1528	N221JQ	JFK	CLT	89	541	14	59	2023-04-18 14:00:00	CLT
10190	1	29	459	500	-1	801	817	AA	499	N893NN	EWR	MIA	148	1085	5	0	2023-01-29 05:00:00	MIA
10193	2	22	1207	1205	2	1310	1315	B6	64	N179JB	JFK	BOS	38	187	12	5	2023-02-22 12:00:00	BOS
10194	2	17	759	800	-1	1032	1021	9E	1374	N232PQ	JFK	CHS	110	636	8	0	2023-02-17 08:00:00	Other
10199	5	22	1435	1436	-1	1727	1741	AA	860	N905NN	JFK	DFW	180	1391	14	36	2023-05-22 14:00:00	Other
10213	2	10	1732	1727	5	2027	2036	UA	577	N480UA	EWR	FLL	148	1065	17	27	2023-02-10 17:00:00	FLL
10217	8	9	2054	2055	-1	2344	2347	B6	30	N985JT	JFK	SAN	322	2446	20	55	2023-08-09 20:00:00	Other
10231	2	19	2101	2100	1	2235	2243	UA	781	N412UA	LGA	ORD	119	733	21	0	2023-02-19 21:00:00	ORD
10239	9	29	651	650	1	956	1015	DL	113	N101DQ	JFK	SLC	268	1990	6	50	2023-09-29 06:00:00	Other
10247	4	25	2352	2345	7	336	335	B6	147	N971JT	JFK	SJU	192	1598	23	45	2023-04-25 23:00:00	Other
10256	3	25	831	828	3	939	951	YX	1157	N742YX	EWR	ALB	28	143	8	28	2023-03-25 08:00:00	Other
10257	5	3	1055	1056	-1	1413	1405	UA	418	N877UA	EWR	MIA	156	1085	10	56	2023-05-03 10:00:00	MIA
10259	7	11	559	600	-1	823	838	UA	739	N482UA	LGA	IAH	180	1416	6	0	2023-07-11 06:00:00	Other
10264	12	1	1059	1057	2	1400	1416	DL	875	N380DN	LGA	FLL	146	1076	10	57	2023-12-01 10:00:00	FLL
10267	1	12	1434	1435	-1	1544	1553	UA	542	N18220	EWR	BOS	36	200	14	35	2023-01-12 14:00:00	BOS
10269	6	7	2058	2058	0	103	55	B6	331	N534JB	JFK	BQN	201	1576	20	58	2023-06-07 20:00:00	Other
10275	6	12	1302	1259	3	1444	1458	NK	517	N624NK	LGA	MYR	80	563	12	59	2023-06-12 12:00:00	Other
10278	4	4	937	935	2	1217	1237	B6	26	N763JB	LGA	PBI	134	1035	9	35	2023-04-04 09:00:00	Other
10282	8	4	1706	1700	6	1945	2010	DL	83	N830MH	JFK	LAX	314	2475	17	0	2023-08-04 17:00:00	LAX
10283	10	14	1931	1932	-1	2203	2230	UA	506	N37551	EWR	SAN	312	2425	19	32	2023-10-14 19:00:00	Other
10300	8	20	1510	1505	5	1744	1821	DL	300	N353NB	LGA	PBI	132	1035	15	5	2023-08-20 15:00:00	Other
10308	1	20	956	955	1	1158	1215	9E	1508	N136EV	JFK	IND	103	665	9	55	2023-01-20 09:00:00	Other
10332	8	31	809	810	-1	1250	1211	UA	639	N76054	EWR	SJU	252	1608	8	10	2023-08-31 08:00:00	Other
10339	6	24	732	730	2	1006	1048	AS	13	N924AK	JFK	SEA	306	2422	7	30	2023-06-24 07:00:00	Other
10341	7	7	1930	1930	0	2308	2249	B6	63	N968JT	JFK	LAX	336	2475	19	30	2023-07-07 19:00:00	LAX
10344	3	2	901	900	1	1013	1032	YX	1645	N235JQ	LGA	BOS	33	184	9	0	2023-03-02 09:00:00	BOS
10345	4	29	947	945	2	1305	1244	NK	25	N514NK	EWR	MCO	139	937	9	45	2023-04-29 09:00:00	MCO
10354	4	5	2109	2100	9	27	2359	B6	219	N547JB	LGA	FLL	142	1076	21	0	2023-04-05 21:00:00	FLL
10355	5	7	2058	2059	-1	2304	2256	UA	408	N841UA	EWR	MEM	148	946	20	59	2023-05-07 20:00:00	Other
10371	11	25	755	745	10	1058	1053	UA	576	N17529	EWR	SAN	333	2425	7	45	2023-11-25 07:00:00	Other
10372	3	24	604	600	4	831	824	DL	841	N944AT	EWR	ATL	121	746	6	0	2023-03-24 06:00:00	ATL
10379	5	14	1750	1745	5	2040	2057	UA	259	N78509	EWR	AUS	197	1504	17	45	2023-05-14 17:00:00	Other
10386	12	20	1629	1629	0	1809	1829	OO	1168	N244SY	LGA	ORD	121	733	16	29	2023-12-20 16:00:00	ORD
10393	9	21	1914	1912	2	2139	2144	DL	1002	N951AT	EWR	ATL	106	746	19	12	2023-09-21 19:00:00	ATL
10394	2	9	1840	1840	0	2343	2342	DL	691	N834DN	JFK	SJU	203	1598	18	40	2023-02-09 18:00:00	Other
10401	12	19	959	1000	-1	1243	1302	UA	246	N17272	EWR	PBI	136	1023	10	0	2023-12-19 10:00:00	Other
10402	11	10	1356	1355	1	1642	1659	B6	533	N504JB	EWR	MCO	138	937	13	55	2023-11-10 13:00:00	MCO
10406	11	11	1230	1230	0	1519	1523	UA	704	N226UA	EWR	IAH	202	1400	12	30	2023-11-11 12:00:00	Other
10423	7	21	559	600	-1	942	912	AA	377	N341RW	LGA	MIA	159	1096	6	0	2023-07-21 06:00:00	MIA
10424	1	12	1453	1445	8	1735	1725	WN	175	N431WN	LGA	MSY	190	1183	14	45	2023-01-12 14:00:00	Other
10429	11	5	1358	1359	-1	1600	1638	DL	169	N309DN	LGA	ATL	97	762	13	59	2023-11-05 13:00:00	ATL
10438	8	29	700	700	0	1006	1022	DL	153	N183DN	JFK	SFO	335	2586	7	0	2023-08-29 07:00:00	Other
10443	5	18	1143	1140	3	1300	1305	WN	145	N792SW	LGA	MDW	103	725	11	40	2023-05-18 11:00:00	Other
10451	5	21	2134	2125	9	2251	2255	WN	1129	N8316H	LGA	MDW	105	725	21	25	2023-05-21 21:00:00	Other
10454	9	27	1444	1436	8	1634	1629	YX	1875	N879RW	LGA	MEM	141	963	14	36	2023-09-27 14:00:00	Other
10463	1	2	2105	2059	6	122	2325	YX	1195	N733YX	EWR	IND	NA	645	20	59	2023-01-02 20:00:00	Other
10464	12	22	2059	2059	0	2239	2251	AA	64	N9016	JFK	RDU	69	427	20	59	2023-12-22 20:00:00	Other
10468	12	23	1740	1740	0	2035	2100	DL	895	N917DU	JFK	FLL	149	1069	17	40	2023-12-23 17:00:00	FLL
10471	6	28	1916	1917	-1	2133	2118	AA	1015	N545UW	LGA	CLT	86	544	19	17	2023-06-28 19:00:00	CLT
10482	12	7	1404	1359	5	1609	1622	9E	1577	N336PQ	JFK	CHS	91	636	13	59	2023-12-07 13:00:00	Other
10488	11	15	1754	1755	-1	2209	2104	UA	657	N29129	EWR	SAN	355	2425	17	55	2023-11-15 17:00:00	Other
10492	2	16	1946	1946	0	2250	2300	B6	782	N615JB	JFK	RNO	329	2411	19	46	2023-02-16 19:00:00	Other
10493	11	3	800	800	0	1039	1022	DL	910	N909DN	EWR	ATL	112	746	8	0	2023-11-03 08:00:00	ATL
10494	8	17	1251	1247	4	1443	1500	UA	702	N27213	EWR	DEN	212	1605	12	47	2023-08-17 12:00:00	Other
10495	7	18	948	948	0	1159	1156	YX	857	N755YX	EWR	CVG	93	569	9	48	2023-07-18 09:00:00	Other
10496	4	26	1259	1250	9	1534	1502	9E	1272	N186PQ	JFK	CHS	101	636	12	50	2023-04-26 12:00:00	Other
10499	7	7	730	730	0	1009	1038	UA	503	N27260	EWR	FLL	139	1065	7	30	2023-07-07 07:00:00	FLL
10501	8	11	2130	2131	-1	2310	2324	UA	681	N61882	EWR	RDU	66	416	21	31	2023-08-11 21:00:00	Other
10511	12	31	559	600	-1	815	843	DL	284	N372NW	LGA	ATL	108	762	6	0	2023-12-31 06:00:00	ATL
10520	12	24	903	900	3	1139	1150	DL	141	N387DN	LGA	ATL	110	762	9	0	2023-12-24 09:00:00	ATL
10522	10	13	812	812	0	1106	1053	B6	128	N993JE	JFK	LAS	321	2248	8	12	2023-10-13 08:00:00	Other
10523	5	12	1538	1530	8	1828	1858	B6	229	N977JE	JFK	LAX	316	2475	15	30	2023-05-12 15:00:00	LAX
10527	3	10	1701	1700	1	1855	1902	9E	1446	N602LR	JFK	RDU	76	427	17	0	2023-03-10 17:00:00	Other
10535	8	21	1502	1500	2	1713	1745	DL	282	N314DN	LGA	ATL	97	762	15	0	2023-08-21 15:00:00	ATL
10538	3	19	719	720	-1	1025	1039	AA	385	N323RM	JFK	MIA	162	1089	7	20	2023-03-19 07:00:00	MIA
10543	7	5	2105	2058	7	2331	2344	UA	655	N47293	EWR	DFW	170	1372	20	58	2023-07-05 20:00:00	Other
10547	1	27	815	805	10	938	934	B6	58	N206JB	JFK	ROC	56	264	8	5	2023-01-27 08:00:00	Other
10551	3	17	1228	1229	-1	1337	1351	9E	1321	N915XJ	LGA	SYR	41	198	12	29	2023-03-17 12:00:00	Other
10568	2	6	1447	1440	7	1624	1641	YX	1329	N408YX	JFK	CMH	77	483	14	40	2023-02-06 14:00:00	Other
10569	3	14	950	950	0	1139	1114	9E	1562	N336PQ	JFK	SYR	45	209	9	50	2023-03-14 09:00:00	Other
10574	7	11	1044	1045	-1	1205	1220	WN	976	N490WN	LGA	STL	121	888	10	45	2023-07-11 10:00:00	Other
10575	8	22	1734	1725	9	1958	2015	WN	771	N8680C	LGA	HOU	173	1428	17	25	2023-08-22 17:00:00	Other
10580	10	10	1144	1145	-1	1355	1406	B6	946	N828JB	JFK	ATL	109	760	11	45	2023-10-10 11:00:00	ATL
10581	8	14	1000	1000	0	1250	1255	DL	554	N125DN	JFK	MCO	130	944	10	0	2023-08-14 10:00:00	MCO
10583	1	29	2049	2045	4	2208	2208	UA	500	N39726	EWR	BUF	54	282	20	45	2023-01-29 20:00:00	Other
10585	1	19	1831	1829	2	2005	2014	UA	510	N67812	EWR	ORD	109	719	18	29	2023-01-19 18:00:00	ORD
10616	6	6	1753	1745	8	2149	2058	B6	699	N703JB	LGA	MCO	132	950	17	45	2023-06-06 17:00:00	MCO
10619	8	20	2117	2115	2	2225	2240	WN	1102	N500WR	LGA	MDW	98	725	21	15	2023-08-20 21:00:00	Other
10630	7	15	1121	1120	1	1257	1305	OO	979	N317SY	JFK	ORD	120	740	11	20	2023-07-15 11:00:00	ORD
10633	7	23	753	745	8	854	901	UA	213	N26208	EWR	BOS	39	200	7	45	2023-07-23 07:00:00	BOS
10650	12	8	1734	1730	4	2003	2049	DL	224	N522DA	JFK	LAS	296	2248	17	30	2023-12-08 17:00:00	Other
10654	10	7	2028	2026	2	2229	2238	YX	1119	N729YX	EWR	AVL	93	583	20	26	2023-10-07 20:00:00	Other
10657	11	28	1522	1515	7	1750	1759	DL	249	N888DU	JFK	DEN	229	1626	15	15	2023-11-28 15:00:00	Other
10666	3	11	1403	1404	-1	1630	1706	UA	256	N77535	EWR	DFW	188	1372	14	4	2023-03-11 14:00:00	Other
10674	11	26	1946	1942	4	2144	2147	UA	504	N27290	EWR	DTW	82	488	19	42	2023-11-26 19:00:00	Other
10675	12	23	939	940	-1	1127	1141	YX	1242	N115HQ	JFK	CMH	80	483	9	40	2023-12-23 09:00:00	Other
10678	4	11	1920	1921	-1	2100	2130	AA	603	N188US	LGA	CLT	73	544	19	21	2023-04-11 19:00:00	CLT
10685	3	4	1333	1330	3	1445	1500	WN	362	N8722L	LGA	MDW	115	725	13	30	2023-03-04 13:00:00	Other
10692	12	20	1133	1129	4	1408	1435	DL	984	N326DN	LGA	MCO	129	950	11	29	2023-12-20 11:00:00	MCO
10696	12	13	1956	1955	1	2257	2300	DL	854	N901DN	JFK	TPA	151	1005	19	55	2023-12-13 19:00:00	Other
10707	9	28	1641	1634	7	1940	1930	B6	562	N655JB	EWR	MCO	146	937	16	34	2023-09-28 16:00:00	MCO
10718	11	17	2148	2140	8	57	59	NK	1156	N706NK	EWR	LAX	345	2454	21	40	2023-11-17 21:00:00	LAX
10719	1	8	715	715	0	1009	1034	B6	158	N644JB	EWR	FLL	150	1065	7	15	2023-01-08 07:00:00	FLL
10722	8	2	605	600	5	852	909	AA	635	N329SL	JFK	MIA	135	1089	6	0	2023-08-02 06:00:00	MIA
10723	10	14	1842	1840	2	2141	2152	AA	613	N358PW	EWR	MIA	151	1085	18	40	2023-10-14 18:00:00	MIA
10733	1	26	1633	1633	0	1959	1950	UA	860	N37277	EWR	RSW	184	1068	16	33	2023-01-26 16:00:00	Other
10740	2	9	1440	1441	-1	1748	1754	AA	806	N903NN	JFK	DFW	212	1391	14	41	2023-02-09 14:00:00	Other
10742	7	4	959	1000	-1	1142	1155	YX	936	N745YX	EWR	GSO	70	445	10	0	2023-07-04 10:00:00	Other
10755	10	31	1244	1245	-1	1544	1557	AA	603	N466AN	EWR	MIA	163	1085	12	45	2023-10-31 12:00:00	MIA
10756	12	28	1515	1515	0	1728	1756	UA	598	N893UA	LGA	DEN	200	1620	15	15	2023-12-28 15:00:00	Other
10764	3	14	1843	1833	10	2145	2142	AA	897	N357PV	EWR	DFW	181	1372	18	33	2023-03-14 18:00:00	Other
10795	12	26	1731	1731	0	2001	1950	AA	733	N585UW	LGA	CLT	115	544	17	31	2023-12-26 17:00:00	CLT
10796	2	21	2004	2005	-1	2307	2330	WN	392	N8536Z	LGA	DAL	226	1381	20	5	2023-02-21 20:00:00	Other
10820	10	30	1000	959	1	1222	1244	DL	136	N326DN	LGA	ATL	117	762	9	59	2023-10-30 09:00:00	ATL
10831	4	28	1936	1929	7	2052	2100	YX	1475	N823MD	LGA	DCA	49	214	19	29	2023-04-28 19:00:00	Other
10836	4	11	1133	1125	8	1408	1436	DL	427	N3737C	JFK	TPA	132	1005	11	25	2023-04-11 11:00:00	Other
10838	9	22	1659	1700	-1	1919	1933	DL	573	N887DN	JFK	ATL	103	760	17	0	2023-09-22 17:00:00	ATL
10839	4	25	1044	1045	-1	1337	1336	B6	139	N954JB	JFK	MCO	145	944	10	45	2023-04-25 10:00:00	MCO
10846	4	23	1504	1459	5	1629	1632	B6	580	N183JB	JFK	BNA	121	765	14	59	2023-04-23 14:00:00	Other
10849	8	2	1318	1310	8	1419	1416	B6	459	N317JB	JFK	MVY	32	173	13	10	2023-08-02 13:00:00	Other
10850	8	14	1206	1158	8	1423	1414	YX	844	N653RW	EWR	SDF	114	642	11	58	2023-08-14 11:00:00	Other
10854	8	31	2305	2259	6	307	258	B6	243	N645JB	JFK	PSE	212	1617	22	59	2023-08-31 22:00:00	Other
10891	7	22	2059	2059	0	2245	2305	YX	956	N740YX	EWR	CMH	72	463	20	59	2023-07-22 20:00:00	Other
10893	3	30	1154	1155	-1	1436	1449	B6	34	N583JB	JFK	MCO	135	944	11	55	2023-03-30 11:00:00	MCO
10899	1	31	1456	1455	1	1620	1626	9E	1505	N933XJ	JFK	ROC	55	264	14	55	2023-01-31 14:00:00	Other
10904	2	3	602	603	-1	932	949	AA	463	N436AN	EWR	PHX	303	2133	6	3	2023-02-03 06:00:00	Other
10908	10	5	1709	1705	4	1854	1856	B6	372	N281JB	JFK	RDU	70	427	17	5	2023-10-05 17:00:00	Other
10914	10	27	2010	2010	0	2324	2338	DL	185	N876DN	JFK	PDX	334	2454	20	10	2023-10-27 20:00:00	Other
10921	2	6	949	940	9	1111	1109	9E	1470	N908XJ	JFK	ORF	57	290	9	40	2023-02-06 09:00:00	Other
10928	8	20	710	710	0	859	910	9E	1105	N329PQ	JFK	DTW	80	509	7	10	2023-08-20 07:00:00	Other
10934	11	28	2040	2040	0	2232	2254	9E	1414	N315PQ	LGA	MYR	87	563	20	40	2023-11-28 20:00:00	Other
10936	8	28	759	759	0	939	921	AA	600	N837AW	LGA	DCA	65	214	7	59	2023-08-28 07:00:00	Other
10938	6	4	1125	1121	4	1307	1311	YX	1852	N234JQ	LGA	PIT	61	335	11	21	2023-06-04 11:00:00	Other
10944	4	22	559	600	-1	710	725	WN	575	N8718Q	LGA	MDW	107	725	6	0	2023-04-22 06:00:00	Other
10946	4	24	1834	1825	9	2128	2131	AS	179	N934AK	EWR	SEA	316	2402	18	25	2023-04-24 18:00:00	Other
10951	1	19	1304	1259	5	1437	1427	9E	1563	N310PQ	JFK	BUF	56	301	12	59	2023-01-19 12:00:00	Other
10952	4	5	1430	1430	0	1826	1826	B6	295	N796JB	JFK	SJU	190	1598	14	30	2023-04-05 14:00:00	Other
10953	12	18	1424	1420	4	1624	1654	9E	1673	N695CA	LGA	MCI	154	1107	14	20	2023-12-18 14:00:00	Other
10961	5	26	1134	1134	0	1317	1325	DL	583	N144DU	LGA	ORD	104	733	11	34	2023-05-26 11:00:00	ORD
10963	6	16	1158	1159	-1	1424	1418	9E	1676	N600LR	LGA	MCI	163	1107	11	59	2023-06-16 11:00:00	Other
10965	4	11	1951	1950	1	2206	2236	9E	1340	N307PQ	LGA	JAX	113	833	19	50	2023-04-11 19:00:00	Other
10968	2	3	1104	1100	4	1215	1227	DL	355	N117DU	LGA	BOS	37	184	11	0	2023-02-03 11:00:00	BOS
10970	1	24	1043	1042	1	1355	1426	UA	518	N27274	EWR	PHX	296	2133	10	42	2023-01-24 10:00:00	Other
10974	8	8	1650	1650	0	1949	2006	B6	186	N827JB	LGA	FLL	154	1076	16	50	2023-08-08 16:00:00	FLL
10975	9	20	1109	1110	-1	1406	1420	DL	414	N363DN	JFK	FLL	153	1069	11	10	2023-09-20 11:00:00	FLL
10978	9	13	929	930	-1	1228	1229	AA	225	N960NN	EWR	DFW	194	1372	9	30	2023-09-13 09:00:00	Other
10988	10	10	1405	1406	-1	1514	1522	UA	706	N4901U	EWR	BOS	45	200	14	6	2023-10-10 14:00:00	BOS
10995	11	8	1959	2000	-1	28	59	B6	679	N2039J	JFK	SJU	181	1598	20	0	2023-11-08 20:00:00	Other
11058	8	13	1029	1030	-1	1138	1152	YX	833	N748YX	EWR	MHT	44	209	10	30	2023-08-13 10:00:00	Other
11067	10	2	1951	1942	9	2223	2224	UA	88	N14242	EWR	DFW	173	1372	19	42	2023-10-02 19:00:00	Other
11072	8	16	1608	1608	0	1720	1739	YX	841	N654RW	EWR	ROC	44	246	16	8	2023-08-16 16:00:00	Other
11082	8	2	2002	2000	2	2121	2139	UA	356	N477UA	EWR	ORD	110	719	20	0	2023-08-02 20:00:00	ORD
11088	3	5	1759	1759	0	2121	2116	AA	840	N318SF	LGA	MIA	153	1096	17	59	2023-03-05 17:00:00	MIA
11102	9	1	1554	1553	1	1844	1924	DL	569	N330DX	LGA	FLL	145	1076	15	53	2023-09-01 15:00:00	FLL
11109	7	24	2158	2157	1	15	2317	UA	410	N15712	EWR	ROC	59	246	21	57	2023-07-24 21:00:00	Other
11111	2	13	1601	1555	6	1810	1829	NK	417	N693NK	EWR	ATL	105	746	15	55	2023-02-13 15:00:00	ATL
11114	3	2	1212	1209	3	1348	1351	AA	1008	N772XF	LGA	RDU	75	431	12	9	2023-03-02 12:00:00	Other
11115	2	17	757	750	7	1110	1117	B6	660	N943JT	EWR	LAX	330	2454	7	50	2023-02-17 07:00:00	LAX
11123	2	17	932	930	2	1127	1133	YX	1252	N113HQ	LGA	CLE	74	419	9	30	2023-02-17 09:00:00	Other
11131	3	17	1600	1555	5	1836	1836	B6	670	N307JB	JFK	ATL	127	760	15	55	2023-03-17 15:00:00	ATL
11139	11	20	1004	1000	4	1230	1321	UA	562	N12114	EWR	LAX	302	2454	10	0	2023-11-20 10:00:00	LAX
11148	2	21	737	730	7	950	948	DL	953	N372NW	LGA	MSP	151	1020	7	30	2023-02-21 07:00:00	Other
11150	5	12	1514	1514	0	1647	1714	OO	1145	N311SY	JFK	PIT	66	340	15	14	2023-05-12 15:00:00	Other
11159	12	29	1354	1355	-1	1625	1705	WN	1115	N460WN	LGA	HOU	194	1428	13	55	2023-12-29 13:00:00	Other
11166	4	9	800	800	0	1113	1110	AA	479	N871NN	EWR	MIA	159	1085	8	0	2023-04-09 08:00:00	MIA
11174	4	24	2219	2215	4	120	131	DL	101	N830MH	JFK	LAX	330	2475	22	15	2023-04-24 22:00:00	LAX
11175	10	5	1708	1700	8	1839	1844	AA	987	N748UW	LGA	STL	128	888	17	0	2023-10-05 17:00:00	Other
11178	10	6	802	800	2	1215	1157	DL	671	N537DT	JFK	SJU	211	1598	8	0	2023-10-06 08:00:00	Other
11179	4	17	1349	1345	4	1607	1600	B6	850	N307JB	LGA	CHS	109	641	13	45	2023-04-17 13:00:00	Other
11195	7	17	759	759	0	1054	1113	AA	127	N965NN	LGA	MIA	153	1096	7	59	2023-07-17 07:00:00	MIA
11201	6	4	638	630	8	930	954	AA	29	N116AN	JFK	SFO	321	2586	6	30	2023-06-04 06:00:00	Other
11218	5	27	949	950	-1	1123	1137	OO	1138	N301SY	JFK	PIT	64	340	9	50	2023-05-27 09:00:00	Other
11221	8	25	1459	1459	0	1816	1814	DL	703	N371NB	JFK	AUS	195	1521	14	59	2023-08-25 14:00:00	Other
11229	6	21	1632	1629	3	1944	1935	AA	976	N761AJ	JFK	MIA	143	1089	16	29	2023-06-21 16:00:00	MIA
11247	3	6	2053	2046	7	2	2306	YX	1075	N653RW	EWR	GRR	113	605	20	46	2023-03-06 20:00:00	Other
11249	1	29	738	730	8	1015	1008	B6	528	N317JB	JFK	JAX	128	828	7	30	2023-01-29 07:00:00	Other
11256	1	20	2000	1959	1	38	57	UA	664	N69816	EWR	SJU	191	1608	19	59	2023-01-20 19:00:00	Other
11258	12	15	1131	1129	2	1446	1447	AA	910	N813NN	JFK	AUS	210	1521	11	29	2023-12-15 11:00:00	Other
11259	10	29	630	630	0	918	931	UA	924	N17302	EWR	TPA	146	997	6	30	2023-10-29 06:00:00	Other
11262	12	15	1556	1546	10	1853	1915	DL	204	N315DU	LGA	DFW	200	1389	15	46	2023-12-15 15:00:00	Other
11265	4	21	1258	1259	-1	1414	1422	9E	1326	N297PQ	JFK	ORF	50	290	12	59	2023-04-21 12:00:00	Other
11270	1	2	1430	1425	5	1549	1555	WN	367	N8523W	LGA	MDW	119	725	14	25	2023-01-02 14:00:00	Other
11272	2	16	847	840	7	1111	1128	DL	537	N864DN	JFK	ATL	116	760	8	40	2023-02-16 08:00:00	ATL
11277	7	30	1510	1505	5	1713	1712	AA	626	N305NX	LGA	CLT	84	544	15	5	2023-07-30 15:00:00	CLT
11311	9	6	1805	1805	0	1958	2018	DL	383	N347NW	LGA	MSP	135	1020	18	5	2023-09-06 18:00:00	Other
11314	11	10	1759	1759	0	2038	2112	B6	125	N999JQ	JFK	MCO	134	944	17	59	2023-11-10 17:00:00	MCO
11319	12	21	1437	1430	7	1754	1755	UA	846	N17126	EWR	LAX	347	2454	14	30	2023-12-21 14:00:00	LAX
11320	3	23	1419	1420	-1	1551	1545	WN	414	N8603F	LGA	MDW	128	725	14	20	2023-03-23 14:00:00	Other
11325	12	8	1854	1850	4	2243	2249	DL	276	N531DA	JFK	PHX	293	2153	18	50	2023-12-08 18:00:00	Other
11330	12	14	1254	1254	0	1540	1609	NK	346	N636NK	EWR	FLL	145	1065	12	54	2023-12-14 12:00:00	FLL
11331	5	6	836	829	7	1021	1036	YX	1086	N751YX	EWR	MEM	139	946	8	29	2023-05-06 08:00:00	Other
11337	5	25	1432	1431	1	1613	1604	9E	1444	N924XJ	JFK	BGR	58	382	14	31	2023-05-25 14:00:00	Other
11339	7	21	650	649	1	955	933	UA	267	N37471	EWR	SAN	335	2425	6	49	2023-07-21 06:00:00	Other
11345	3	10	816	810	6	1246	1315	DL	738	N6704Z	JFK	STT	179	1623	8	10	2023-03-10 08:00:00	Other
11349	6	2	1619	1620	-1	2013	1959	DL	218	N863DN	JFK	SLC	278	1990	16	20	2023-06-02 16:00:00	Other
11351	3	9	1353	1344	9	1715	1650	AA	464	N949NN	EWR	DFW	236	1372	13	44	2023-03-09 13:00:00	Other
11354	11	17	814	815	-1	1017	1030	9E	1761	N676CA	LGA	GSP	99	610	8	15	2023-11-17 08:00:00	Other
11369	9	20	1503	1455	8	1843	1811	B6	1021	N206JB	JFK	MIA	189	1089	14	55	2023-09-20 14:00:00	MIA
11389	11	2	1829	1829	0	2132	2137	UA	578	N78501	EWR	FLL	153	1065	18	29	2023-11-02 18:00:00	FLL
11391	1	13	1701	1659	2	1924	1947	DL	411	N335DN	LGA	ATL	112	762	16	59	2023-01-13 16:00:00	ATL
11396	4	29	1548	1549	-1	1922	1849	UA	714	N419UA	EWR	RSW	157	1068	15	49	2023-04-29 15:00:00	Other
11405	2	26	929	930	-1	1253	1258	AS	9	N551AS	JFK	SEA	360	2422	9	30	2023-02-26 09:00:00	Other
11411	5	14	1825	1815	10	2126	2135	DL	343	N175DN	JFK	LAX	331	2475	18	15	2023-05-14 18:00:00	LAX
11412	5	6	1708	1709	-1	1847	1915	DL	885	N367NW	LGA	DTW	81	502	17	9	2023-05-06 17:00:00	Other
11420	5	16	947	947	0	1213	1241	B6	222	N521JB	LGA	MCO	126	950	9	47	2023-05-16 09:00:00	MCO
11436	2	18	1728	1728	0	2015	2019	UA	845	N37293	EWR	MCO	127	937	17	28	2023-02-18 17:00:00	MCO
11442	2	20	914	915	-1	1141	1158	DL	591	N126DU	JFK	MSY	187	1182	9	15	2023-02-20 09:00:00	Other
11450	8	15	1940	1941	-1	2050	2113	UA	721	N13718	EWR	IAD	49	212	19	41	2023-08-15 19:00:00	Other
11454	12	2	904	905	-1	1034	1030	B6	939	N229JB	JFK	BUF	69	301	9	5	2023-12-02 09:00:00	Other
11459	2	1	733	730	3	1104	1002	9E	1304	N485PX	LGA	MCI	203	1107	7	30	2023-02-01 07:00:00	Other
11460	2	9	1859	1900	-1	2038	2045	UA	755	N14704	EWR	ORD	113	719	19	0	2023-02-09 19:00:00	ORD
11471	3	12	1516	1510	6	1845	1835	B6	865	N184JB	LGA	SRQ	162	1047	15	10	2023-03-12 15:00:00	Other
11477	8	27	750	744	6	950	958	9E	1287	N936XJ	JFK	CLT	85	541	7	44	2023-08-27 07:00:00	CLT
11487	10	27	1136	1135	1	1406	1420	WN	768	N8687A	LGA	DAL	195	1381	11	35	2023-10-27 11:00:00	Other
11493	1	11	1807	1807	0	1929	1945	YX	1249	N740YX	EWR	PIT	58	319	18	7	2023-01-11 18:00:00	Other
11494	9	17	1759	1800	-1	2108	2103	DL	339	N194DN	JFK	LAX	321	2475	18	0	2023-09-17 18:00:00	LAX
11495	12	8	1134	1130	4	1418	1436	DL	713	N374DX	LGA	MCO	135	950	11	30	2023-12-08 11:00:00	MCO
11502	7	24	1626	1621	5	1805	1821	UA	259	N16709	EWR	CLT	75	529	16	21	2023-07-24 16:00:00	CLT
11506	10	19	1545	1545	0	1841	1845	B6	508	N579JB	JFK	MCO	139	944	15	45	2023-10-19 15:00:00	MCO
11514	5	24	828	829	-1	958	1011	AA	126	N957NN	LGA	ORD	118	733	8	29	2023-05-24 08:00:00	ORD
11527	2	17	810	800	10	1003	950	B6	814	N665JB	JFK	RDU	82	427	8	0	2023-02-17 08:00:00	Other
11532	4	14	1625	1621	4	1835	1805	UA	100	N17730	EWR	RDU	77	416	16	21	2023-04-14 16:00:00	Other
11538	3	1	1000	1000	0	1137	1202	9E	1527	N184GJ	EWR	RDU	70	416	10	0	2023-03-01 10:00:00	Other
11539	10	7	1421	1415	6	1607	1538	B6	232	N3065J	JFK	MKE	107	745	14	15	2023-10-07 14:00:00	Other
11544	2	5	1914	1915	-1	2242	2250	DL	214	N178DZ	JFK	LAX	358	2475	19	15	2023-02-05 19:00:00	LAX
11548	6	22	1447	1437	10	1628	1602	UA	116	N496UA	EWR	IAD	62	212	14	37	2023-06-22 14:00:00	Other
11549	8	14	1427	1420	7	1725	1715	DL	325	N133DU	LGA	IAH	194	1416	14	20	2023-08-14 14:00:00	Other
11559	2	9	759	800	-1	1058	1114	AA	804	N848NN	JFK	DFW	205	1391	8	0	2023-02-09 08:00:00	Other
11562	4	8	1759	1800	-1	2056	2118	UA	414	N76010	EWR	SFO	329	2565	18	0	2023-04-08 18:00:00	Other
11569	9	10	1147	1138	9	1528	1440	UA	850	N443UA	EWR	MIA	163	1085	11	38	2023-09-10 11:00:00	MIA
11577	2	23	2024	2025	-1	2308	2339	B6	67	N506JB	JFK	TPA	142	1005	20	25	2023-02-23 20:00:00	Other
11595	6	23	1107	1100	7	1417	1405	DL	934	N119DN	JFK	FLL	169	1069	11	0	2023-06-23 11:00:00	FLL
11596	12	20	1131	1130	1	1442	1453	AA	718	N834NN	LGA	MIA	146	1096	11	30	2023-12-20 11:00:00	MIA
11598	7	28	1128	1129	-1	1225	1246	UA	249	N27519	EWR	BOS	36	200	11	29	2023-07-28 11:00:00	BOS
11605	6	3	929	929	0	1159	1221	UA	516	N57286	EWR	MCO	125	937	9	29	2023-06-03 09:00:00	MCO
11615	10	11	612	608	4	807	754	DL	743	N986AT	EWR	DTW	84	488	6	8	2023-10-11 06:00:00	Other
11622	2	26	1820	1820	0	2009	2002	UA	445	N34455	EWR	ORD	127	719	18	20	2023-02-26 18:00:00	ORD
11629	10	5	1949	1942	7	2219	2224	UA	88	N73251	EWR	DFW	179	1372	19	42	2023-10-05 19:00:00	Other
11630	9	13	1117	1107	10	1325	1333	UA	432	N69804	EWR	PHX	287	2133	11	7	2023-09-13 11:00:00	Other
11631	8	11	658	659	-1	802	819	AA	445	N177XF	LGA	DCA	44	214	6	59	2023-08-11 06:00:00	Other
11649	10	23	1430	1429	1	1636	1653	UA	933	N472UA	LGA	DEN	226	1620	14	29	2023-10-23 14:00:00	Other
11656	6	11	951	950	1	1237	1326	B6	38	N929JB	JFK	SFO	324	2586	9	50	2023-06-11 09:00:00	Other
11658	4	28	1757	1754	3	2029	2104	UA	506	N38459	EWR	SAN	299	2425	17	54	2023-04-28 17:00:00	Other
11659	7	6	1938	1939	-1	2130	2129	YX	1076	N132HQ	LGA	CMH	83	479	19	39	2023-07-06 19:00:00	Other
11662	12	22	845	836	9	1035	1048	NK	295	N684NK	LGA	CLT	84	544	8	36	2023-12-22 08:00:00	CLT
11667	9	15	1901	1855	6	2201	2208	DL	442	N313DU	EWR	SLC	268	1969	18	55	2023-09-15 18:00:00	Other
11685	11	12	1909	1910	-1	2214	2230	DL	147	N179DN	JFK	LAX	321	2475	19	10	2023-11-12 19:00:00	LAX
11716	1	30	1950	1945	5	2246	2249	B6	504	N2102J	JFK	LAS	333	2248	19	45	2023-01-30 19:00:00	Other
11722	7	21	1759	1800	-1	2020	2026	YX	1014	N442YX	LGA	TUL	177	1231	18	0	2023-07-21 18:00:00	Other
11724	8	20	852	845	7	1046	1117	9E	1169	N187GJ	LGA	SAV	95	722	8	45	2023-08-20 08:00:00	Other
11756	5	23	829	830	-1	939	1001	YX	1644	N237JQ	JFK	BOS	37	187	8	30	2023-05-23 08:00:00	BOS
11759	3	13	1304	1255	9	1519	1526	YX	1697	N878RW	LGA	SDF	108	659	12	55	2023-03-13 12:00:00	Other
11760	5	5	755	756	-1	1028	1025	B6	927	N796JB	LGA	ATL	111	762	7	56	2023-05-05 07:00:00	ATL
11771	11	25	1540	1539	1	1842	1850	UA	724	N24224	EWR	RSW	159	1068	15	39	2023-11-25 15:00:00	Other
11773	8	7	909	900	9	1218	1146	B6	50	N929JB	JFK	SAN	323	2446	9	0	2023-08-07 09:00:00	Other
11783	12	6	1630	1629	1	1929	1952	AA	722	N330TJ	LGA	MIA	145	1096	16	29	2023-12-06 16:00:00	MIA
11785	3	15	1329	1330	-1	1442	1443	B6	41	N375JB	JFK	SYR	48	209	13	30	2023-03-15 13:00:00	Other
11792	11	29	902	902	0	1224	1236	NK	1181	N692NK	EWR	PHX	306	2133	9	2	2023-11-29 09:00:00	Other
11794	5	4	1138	1130	8	1434	1437	DL	631	N105DU	LGA	IAH	202	1416	11	30	2023-05-04 11:00:00	Other
11799	9	5	1315	1316	-1	1509	1526	9E	1620	N200PQ	JFK	CHS	87	636	13	16	2023-09-05 13:00:00	Other
11805	6	20	2119	2119	0	2223	2219	9E	1741	N491PX	LGA	ALB	35	136	21	19	2023-06-20 21:00:00	Other
11827	6	21	1358	1359	-1	1621	1636	DL	175	N390DN	LGA	ATL	110	762	13	59	2023-06-21 13:00:00	ATL
11837	6	9	1039	1035	4	1201	1216	AA	148	N966AN	LGA	ORD	108	733	10	35	2023-06-09 10:00:00	ORD
11840	3	16	850	850	0	1031	1049	9E	1431	N490PX	LGA	RDU	70	431	8	50	2023-03-16 08:00:00	Other
11846	1	13	1500	1500	0	1608	1652	OO	1748	N143SY	LGA	ORD	107	733	15	0	2023-01-13 15:00:00	ORD
11853	11	29	810	810	0	1257	1310	DL	668	N542DE	JFK	SJU	197	1598	8	10	2023-11-29 08:00:00	Other
11854	9	8	759	800	-1	1028	1030	DL	524	N721TW	JFK	ATL	97	760	8	0	2023-09-08 08:00:00	ATL
11864	7	1	949	950	-1	1128	1146	9E	1300	N916XJ	LGA	CLE	65	419	9	50	2023-07-01 09:00:00	Other
11871	7	24	1658	1659	-1	1824	1831	B6	329	N317JB	JFK	BOS	42	187	16	59	2023-07-24 16:00:00	BOS
11873	7	6	1704	1655	9	2002	1955	AS	78	N929VA	EWR	LAX	316	2454	16	55	2023-07-06 16:00:00	LAX
11886	12	22	1159	1159	0	1440	1514	UA	586	N17279	EWR	AUS	201	1504	11	59	2023-12-22 11:00:00	Other
11890	12	8	1854	1853	1	2058	2122	YX	1068	N757YX	EWR	IND	98	645	18	53	2023-12-08 18:00:00	Other
11902	7	11	2200	2159	1	2322	2321	YX	865	N641RW	EWR	MHT	42	209	21	59	2023-07-11 21:00:00	Other
11908	8	16	1259	1300	-1	1609	1612	AA	198	N335SN	LGA	MIA	159	1096	13	0	2023-08-16 13:00:00	MIA
11912	11	14	1336	1336	0	1541	1550	9E	1617	N314PQ	JFK	CVG	93	589	13	36	2023-11-14 13:00:00	Other
11919	3	19	532	528	4	851	832	UA	188	N78501	EWR	IAH	224	1400	5	28	2023-03-19 05:00:00	Other
11923	4	7	1102	1055	7	1336	1350	DL	870	N388DN	JFK	MCO	132	944	10	55	2023-04-07 10:00:00	MCO
11925	4	8	705	705	0	1003	1024	DL	496	N369DN	LGA	MIA	153	1096	7	5	2023-04-08 07:00:00	MIA
11926	4	11	1620	1620	0	1852	1911	UA	123	N41135	EWR	MCO	127	937	16	20	2023-04-11 16:00:00	MCO
11927	12	25	733	730	3	957	1019	DL	320	N333DX	LGA	ATL	113	762	7	30	2023-12-25 07:00:00	ATL
11944	2	9	2054	2055	-1	2327	2254	OO	1166	N301SY	JFK	CLE	87	425	20	55	2023-02-09 20:00:00	Other
11945	4	28	1005	1000	5	1225	1236	B6	16	N999JQ	JFK	PHX	279	2153	10	0	2023-04-28 10:00:00	Other
11950	3	4	1650	1650	0	1839	1848	OO	1224	N308SY	JFK	ORD	134	740	16	50	2023-03-04 16:00:00	ORD
11955	2	6	2037	2030	7	2329	2353	UA	795	N17133	EWR	LAX	323	2454	20	30	2023-02-06 20:00:00	LAX
11956	9	24	1049	1047	2	1341	1353	NK	511	N663NK	EWR	FLL	152	1065	10	47	2023-09-24 10:00:00	FLL
11960	11	30	1639	1629	10	1922	1927	UA	543	N69818	EWR	MCO	130	937	16	29	2023-11-30 16:00:00	MCO
11962	1	12	1630	1629	1	1951	1946	B6	804	N267JB	LGA	PBI	156	1035	16	29	2023-01-12 16:00:00	Other
11964	12	17	1427	1428	-1	1722	1743	UA	638	N429UA	EWR	AUS	211	1504	14	28	2023-12-17 14:00:00	Other
11974	2	12	1649	1640	9	1953	2000	DL	251	N509DT	JFK	SEA	337	2422	16	40	2023-02-12 16:00:00	Other
11987	4	13	1029	1030	-1	1156	1216	B6	83	N306JB	JFK	RDU	65	427	10	30	2023-04-13 10:00:00	Other
11989	7	23	2152	2149	3	2328	2338	YX	1048	N138HQ	JFK	DCA	52	213	21	49	2023-07-23 21:00:00	Other
11995	9	29	1809	1800	9	2040	2100	AA	196	N905NN	LGA	DFW	181	1389	18	0	2023-09-29 18:00:00	Other
12007	10	11	559	600	-1	718	725	WN	83	N8518R	LGA	MDW	115	725	6	0	2023-10-11 06:00:00	Other
12017	7	25	603	600	3	831	837	UA	170	N27274	EWR	IAH	181	1400	6	0	2023-07-25 06:00:00	Other
12019	11	15	1246	1245	1	1503	1519	UA	413	N478UA	EWR	ATL	112	746	12	45	2023-11-15 12:00:00	ATL
12022	3	21	2159	2200	-1	2313	2313	UA	567	N899UA	EWR	BOS	45	200	22	0	2023-03-21 22:00:00	BOS
12035	1	23	1701	1700	1	2009	2023	B6	214	N594JB	EWR	FLL	166	1065	17	0	2023-01-23 17:00:00	FLL
12046	1	26	1748	1746	2	2108	2110	NK	28	N902NK	EWR	LAX	326	2454	17	46	2023-01-26 17:00:00	LAX
12054	2	1	1958	1959	-1	2211	2242	DL	433	N1603	JFK	ATL	119	760	19	59	2023-02-01 19:00:00	ATL
12056	1	21	1629	1630	-1	1924	2007	DL	244	N873DN	JFK	SLC	270	1990	16	30	2023-01-21 16:00:00	Other
12061	11	9	1946	1944	2	2146	2147	AA	637	N920NN	EWR	CLT	83	529	19	44	2023-11-09 19:00:00	CLT
12070	11	16	1714	1715	-1	1903	1854	UA	857	N814UA	LGA	ORD	115	733	17	15	2023-11-16 17:00:00	ORD
12072	7	24	754	755	-1	943	1000	DL	490	N346DN	LGA	MSP	140	1020	7	55	2023-07-24 07:00:00	Other
12075	4	5	1456	1455	1	1748	1744	9E	1290	N330PQ	JFK	JAX	119	828	14	55	2023-04-05 14:00:00	Other
12076	9	1	1734	1734	0	2007	2029	AA	203	N406AN	EWR	DFW	181	1372	17	34	2023-09-01 17:00:00	Other
12086	7	2	909	905	4	1101	1110	9E	1302	N927XJ	LGA	AVL	90	599	9	5	2023-07-02 09:00:00	Other
12088	8	1	1055	1053	2	1236	1239	UA	338	N13750	EWR	RDU	65	416	10	53	2023-08-01 10:00:00	Other
12097	11	6	859	900	-1	1032	1047	UA	728	N444UA	EWR	ORD	121	719	9	0	2023-11-06 09:00:00	ORD
12099	3	10	1628	1629	-1	1833	1827	YX	1372	N104HQ	LGA	ILM	82	500	16	29	2023-03-10 16:00:00	Other
12108	9	28	1407	1408	-1	1617	1624	9E	1661	N923XJ	LGA	IND	96	660	14	8	2023-09-28 14:00:00	Other
12112	10	13	905	859	6	1212	1210	UA	560	N77296	EWR	SAT	215	1569	8	59	2023-10-13 08:00:00	Other
12119	4	20	2129	2129	0	3	2335	YX	975	N654RW	EWR	GSP	82	594	21	29	2023-04-20 21:00:00	Other
12127	8	9	1049	1048	1	1255	1310	UA	399	N17753	EWR	JAX	107	820	10	48	2023-08-09 10:00:00	Other
12134	7	17	1800	1800	0	2041	2044	DL	279	N3756	LGA	DEN	220	1620	18	0	2023-07-17 18:00:00	Other
12137	11	28	2029	2020	9	2355	2357	UA	360	N19141	EWR	SFO	342	2565	20	20	2023-11-28 20:00:00	Other
12139	11	7	1605	1559	6	1814	1839	DL	174	N377DN	LGA	ATL	109	762	15	59	2023-11-07 15:00:00	ATL
12140	10	26	1859	1900	-1	2132	2141	DL	184	N116DN	LGA	ATL	111	762	19	0	2023-10-26 19:00:00	ATL
12149	11	23	1909	1910	-1	2157	2230	DL	147	N172DN	JFK	LAX	327	2475	19	10	2023-11-23 19:00:00	LAX
12158	4	8	834	835	-1	1119	1205	DL	306	N3737C	JFK	SAN	321	2446	8	35	2023-04-08 08:00:00	Other
12165	11	9	615	615	0	822	813	DL	964	N891AT	EWR	MSP	164	1008	6	15	2023-11-09 06:00:00	Other
12186	3	31	1004	955	9	1205	1205	G4	131	243NV	EWR	CVG	96	569	9	55	2023-03-31 09:00:00	Other
12194	5	30	1909	1907	2	2222	2225	UA	689	N493UA	EWR	SLC	285	1969	19	7	2023-05-30 19:00:00	Other
12196	5	4	906	900	6	1155	1202	B6	338	N216JB	JFK	PBI	147	1028	9	0	2023-05-04 09:00:00	Other
12219	7	22	1053	1052	1	1328	1350	B6	289	N516JB	EWR	MCO	131	937	10	52	2023-07-22 10:00:00	MCO
12220	9	4	1702	1700	2	1935	2011	B6	769	N709JB	JFK	PBI	127	1028	17	0	2023-09-04 17:00:00	Other
12221	10	2	2102	2056	6	2236	2251	9E	1476	N479PX	LGA	RDU	70	431	20	56	2023-10-02 20:00:00	Other
12223	11	11	943	935	8	1322	1322	DL	230	N111NG	LGA	PHX	313	2149	9	35	2023-11-11 09:00:00	Other
12225	3	21	2030	2029	1	2158	2153	9E	1588	N601LR	JFK	BWI	37	184	20	29	2023-03-21 20:00:00	Other
12236	12	20	952	950	2	1142	1153	AA	643	N576UW	EWR	CLT	82	529	9	50	2023-12-20 09:00:00	CLT
12237	2	15	707	705	2	1001	1008	DL	380	N324NB	LGA	PBI	149	1035	7	5	2023-02-15 07:00:00	Other
12241	6	29	1943	1939	4	2221	2245	NK	1057	N645NK	EWR	MIA	134	1085	19	39	2023-06-29 19:00:00	MIA
12260	9	4	1216	1215	1	1439	1425	WN	153	N8733M	LGA	DEN	206	1620	12	15	2023-09-04 12:00:00	Other
12274	2	12	859	900	-1	1446	1525	DL	101	N833MH	JFK	HNL	609	4983	9	0	2023-02-12 09:00:00	Other
12277	1	21	849	849	0	1129	1124	YX	1238	N745YX	EWR	SAV	119	708	8	49	2023-01-21 08:00:00	Other
12279	4	26	1958	1959	-1	2248	2319	DL	426	N344DN	LGA	FLL	145	1076	19	59	2023-04-26 19:00:00	FLL
12284	10	29	900	855	5	1034	1055	9E	1427	N301PQ	LGA	RDU	70	431	8	55	2023-10-29 08:00:00	Other
12292	5	4	758	759	-1	1041	1101	AA	322	N980AN	JFK	DFW	191	1391	7	59	2023-05-04 07:00:00	Other
12308	7	26	1845	1836	9	2149	2149	AA	538	N959NN	EWR	MIA	148	1085	18	36	2023-07-26 18:00:00	MIA
12309	2	19	1238	1230	8	1403	1438	AA	451	N343PN	LGA	ORD	118	733	12	30	2023-02-19 12:00:00	ORD
12322	6	14	659	700	-1	950	1003	DL	548	N817DN	JFK	TPA	143	1005	7	0	2023-06-14 07:00:00	Other
12324	4	17	818	819	-1	1053	1032	YX	1273	N410YX	LGA	CVG	105	585	8	19	2023-04-17 08:00:00	Other
12326	1	28	1114	1115	-1	1416	1433	DL	987	N370DN	LGA	FLL	152	1076	11	15	2023-01-28 11:00:00	FLL
12331	2	15	1658	1650	8	1856	1848	OO	1165	N279SY	JFK	ORD	140	740	16	50	2023-02-15 16:00:00	ORD
12336	6	7	1557	1555	2	1759	1829	UA	220	N17302	EWR	LAS	274	2227	15	55	2023-06-07 15:00:00	Other
12353	3	28	1700	1659	1	1815	1819	UA	475	N460UA	EWR	BOS	37	200	16	59	2023-03-28 16:00:00	BOS
12371	1	9	1132	1125	7	1414	1434	NK	600	N687NK	EWR	FLL	142	1065	11	25	2023-01-09 11:00:00	FLL
12372	6	23	1225	1225	0	1400	1347	AA	1025	N740UW	LGA	BNA	109	764	12	25	2023-06-23 12:00:00	Other
12379	8	8	1859	1859	0	2030	2109	9E	1120	N917XJ	LGA	STL	122	888	18	59	2023-08-08 18:00:00	Other
12383	11	27	1505	1502	3	1657	1706	DL	914	N932AT	EWR	MSP	149	1008	15	2	2023-11-27 15:00:00	Other
12389	6	16	610	610	0	801	745	DL	478	N115DU	LGA	ORD	123	733	6	10	2023-06-16 06:00:00	ORD
12394	6	19	811	812	-1	1032	1101	UA	282	N17529	EWR	IAH	184	1400	8	12	2023-06-19 08:00:00	Other
12396	1	1	1315	1310	5	1613	1615	UA	141	N871UA	EWR	PBI	150	1023	13	10	2023-01-01 13:00:00	Other
12402	4	3	2131	2130	1	111	56	B6	604	N978JB	JFK	LAX	357	2475	21	30	2023-04-03 21:00:00	LAX
12412	9	24	1247	1247	0	1536	1554	NK	340	N631NK	EWR	FLL	152	1065	12	47	2023-09-24 12:00:00	FLL
12418	1	22	2218	2211	7	2344	2349	UA	763	N87513	EWR	BNA	124	748	22	11	2023-01-22 22:00:00	Other
12419	9	7	608	600	8	710	709	YX	1916	N232JQ	JFK	BOS	42	187	6	0	2023-09-07 06:00:00	BOS
12420	5	25	1509	1506	3	1700	1710	DL	513	N332NB	LGA	DTW	78	502	15	6	2023-05-25 15:00:00	Other
12421	1	21	1332	1332	0	1534	1535	AA	638	N950NN	EWR	CLT	88	529	13	32	2023-01-21 13:00:00	CLT
12431	12	3	1516	1514	2	1812	1816	UA	788	N36207	EWR	PBI	153	1023	15	14	2023-12-03 15:00:00	Other
12440	6	18	1630	1630	0	1851	1905	B6	120	N193JB	JFK	SAV	107	718	16	30	2023-06-18 16:00:00	Other
12441	9	28	614	615	-1	853	909	UA	240	N27292	EWR	AUS	197	1504	6	15	2023-09-28 06:00:00	Other
12449	7	10	1324	1320	4	1436	1440	WN	61	N8677A	LGA	BNA	109	764	13	20	2023-07-10 13:00:00	Other
12453	8	2	1110	1101	9	1232	1237	YX	1061	N433YX	JFK	BNA	112	765	11	1	2023-08-02 11:00:00	Other
12463	2	18	759	800	-1	1026	1024	DL	637	N130DU	JFK	CHS	95	636	8	0	2023-02-18 08:00:00	Other
12466	6	6	1055	1045	10	1216	1220	WN	1023	N8615E	LGA	STL	120	888	10	45	2023-06-06 10:00:00	Other
12502	12	28	559	600	-1	929	916	AA	433	N925AN	LGA	MIA	180	1096	6	0	2023-12-28 06:00:00	MIA
12507	1	29	1246	1247	-1	1438	1441	YX	1242	N752YX	EWR	CMH	87	463	12	47	2023-01-29 12:00:00	Other
12520	2	4	1203	1200	3	1509	1518	UA	799	N21108	EWR	LAX	337	2454	12	0	2023-02-04 12:00:00	LAX
12521	11	17	829	830	-1	1047	1110	DL	502	N704X	JFK	ATL	115	760	8	30	2023-11-17 08:00:00	ATL
12532	5	28	2100	2100	0	2259	2317	OO	1141	N316SY	JFK	CLE	72	425	21	0	2023-05-28 21:00:00	Other
12542	9	23	1454	1454	0	1708	1749	NK	256	N977NK	EWR	IAH	175	1400	14	54	2023-09-23 14:00:00	Other
12556	3	29	1801	1800	1	2156	2116	UA	858	N76504	EWR	MIA	208	1085	18	0	2023-03-29 18:00:00	MIA
12559	7	12	1649	1650	-1	1952	2029	DL	155	N529DT	JFK	SEA	328	2422	16	50	2023-07-12 16:00:00	Other
12566	4	3	1757	1750	7	2014	2025	WN	802	N8843S	LGA	DEN	237	1620	17	50	2023-04-03 17:00:00	Other
12580	6	1	942	935	7	1058	1101	B6	617	N184JB	JFK	BUF	58	301	9	35	2023-06-01 09:00:00	Other
12581	2	18	604	605	-1	808	819	DL	427	N338NW	LGA	MSP	161	1020	6	5	2023-02-18 06:00:00	Other
12583	9	18	943	942	1	1212	1152	B6	976	N638JB	JFK	CHS	116	636	9	42	2023-09-18 09:00:00	Other
12588	2	1	1732	1730	2	1949	2000	DL	475	N776DE	EWR	ATL	122	746	17	30	2023-02-01 17:00:00	ATL
12590	5	22	2105	2059	6	2313	2318	YX	1155	N729YX	EWR	CVG	90	569	20	59	2023-05-22 20:00:00	Other
12600	3	30	1801	1800	1	2125	2143	DL	261	N827DN	JFK	SLC	304	1990	18	0	2023-03-30 18:00:00	Other
12610	11	17	637	630	7	906	931	B6	216	N641JB	JFK	MCO	131	944	6	30	2023-11-17 06:00:00	MCO
12613	11	12	1527	1525	2	1651	1700	YX	1843	N860RW	LGA	DCA	50	214	15	25	2023-11-12 15:00:00	Other
12617	8	8	2119	2120	-1	2257	2246	YX	1389	N218JQ	LGA	BUF	50	292	21	20	2023-08-08 21:00:00	Other
12623	9	22	1801	1757	4	1939	1954	YX	1807	N219YX	LGA	CMH	75	479	17	57	2023-09-22 17:00:00	Other
12624	6	21	746	744	2	935	932	9E	1551	N319PQ	JFK	RDU	74	427	7	44	2023-06-21 07:00:00	Other
12632	8	2	611	610	1	829	835	WN	817	N8850Q	LGA	DAL	173	1381	6	10	2023-08-02 06:00:00	Other
12633	1	11	2008	2000	8	2137	2131	AA	857	N824AW	LGA	DCA	45	214	20	0	2023-01-11 20:00:00	Other
12635	12	1	800	800	0	932	947	UA	649	N15710	EWR	ORD	123	719	8	0	2023-12-01 08:00:00	ORD
12649	8	26	2043	2039	4	2312	2325	UA	638	N37307	EWR	DFW	177	1372	20	39	2023-08-26 20:00:00	Other
12652	3	29	1210	1210	0	1349	1349	YX	1276	N420YX	LGA	BNA	127	764	12	10	2023-03-29 12:00:00	Other
12654	12	20	2023	2020	3	2312	2354	B6	452	N3145J	JFK	AUS	210	1521	20	20	2023-12-20 20:00:00	Other
12658	8	20	1459	1459	0	1558	1615	B6	584	N324JB	JFK	HYA	35	196	14	59	2023-08-20 14:00:00	Other
12667	12	26	1634	1634	0	1855	2008	DL	279	N516DA	JFK	SAN	298	2446	16	34	2023-12-26 16:00:00	Other
12668	9	8	1632	1622	10	1732	1728	B6	924	N375JB	LGA	MVY	37	175	16	22	2023-09-08 16:00:00	Other
12674	1	18	2139	2130	9	2249	2243	B6	106	N354JB	JFK	BOS	42	187	21	30	2023-01-18 21:00:00	BOS
12679	12	27	1731	1725	6	1856	1900	WN	1048	N7740A	LGA	MDW	107	725	17	25	2023-12-27 17:00:00	Other
12684	3	17	1732	1729	3	1924	1920	UA	79	N75426	EWR	STL	144	872	17	29	2023-03-17 17:00:00	Other
12688	5	26	2131	2122	9	2245	2258	UA	902	N37257	EWR	BNA	109	748	21	22	2023-05-26 21:00:00	Other
12704	3	15	1359	1359	0	1550	1513	OO	1268	N251SY	JFK	BOS	47	187	13	59	2023-03-15 13:00:00	BOS
12705	9	6	2009	2010	-1	2214	2223	9E	1690	N228PQ	EWR	CVG	88	569	20	10	2023-09-06 20:00:00	Other
12706	8	11	1751	1741	10	2054	2141	DL	214	N504DZ	JFK	SLC	276	1990	17	41	2023-08-11 17:00:00	Other
12707	4	28	1301	1300	1	1530	1610	UA	741	N17139	EWR	LAX	302	2454	13	0	2023-04-28 13:00:00	LAX
12713	2	5	1535	1535	0	1853	1859	OO	1422	N213SY	LGA	IAH	224	1416	15	35	2023-02-05 15:00:00	Other
12728	7	9	653	650	3	1015	934	AA	781	N928AN	EWR	DFW	196	1372	6	50	2023-07-09 06:00:00	Other
12732	3	2	2243	2240	3	44	27	B6	532	N193JB	JFK	RDU	78	427	22	40	2023-03-02 22:00:00	Other
12735	12	12	1506	1506	0	1719	1724	9E	1385	N935XJ	EWR	CVG	105	569	15	6	2023-12-12 15:00:00	Other
12737	4	24	2121	2112	9	29	2359	UA	776	N69829	EWR	MCO	136	937	21	12	2023-04-24 21:00:00	MCO
12738	9	29	1200	1200	0	1331	1349	AA	519	N817AW	LGA	RDU	69	431	12	0	2023-09-29 12:00:00	Other
12748	5	25	1917	1915	2	2155	2215	UA	779	N427UA	EWR	DFW	183	1372	19	15	2023-05-25 19:00:00	Other
12757	12	19	1210	1200	10	1500	1508	NK	1186	N679NK	LGA	FLL	140	1076	12	0	2023-12-19 12:00:00	FLL
12767	12	9	1417	1411	6	1537	1544	UA	132	N37308	EWR	BNA	114	748	14	11	2023-12-09 14:00:00	Other
12770	5	21	1456	1455	1	1812	1810	B6	526	N591JB	JFK	FLL	154	1069	14	55	2023-05-21 14:00:00	FLL
12772	3	6	1715	1715	0	1947	1957	9E	1348	N908XJ	JFK	MCI	189	1113	17	15	2023-03-06 17:00:00	Other
12781	6	29	1429	1429	0	1643	1644	9E	1518	N915XJ	LGA	MCI	168	1107	14	29	2023-06-29 14:00:00	Other
12793	10	9	1116	1107	9	1309	1329	UA	406	N68452	EWR	PHX	275	2133	11	7	2023-10-09 11:00:00	Other
12794	12	27	1831	1830	1	2210	2144	AA	400	N855NN	JFK	MIA	182	1089	18	30	2023-12-27 18:00:00	MIA
12795	5	28	2058	2059	-1	2207	2237	UA	840	N481UA	EWR	MSN	105	799	20	59	2023-05-28 20:00:00	Other
12804	4	27	1737	1729	8	2013	2038	B6	640	N535JB	JFK	PSP	316	2378	17	29	2023-04-27 17:00:00	Other
12808	4	21	655	645	10	927	951	UA	672	N47533	EWR	SEA	307	2402	6	45	2023-04-21 06:00:00	Other
12810	1	15	1827	1825	2	2114	2138	AA	1098	N339PL	JFK	DFW	197	1391	18	25	2023-01-15 18:00:00	Other
12813	12	15	926	925	1	1107	1120	DL	885	N130DU	LGA	ORD	109	733	9	25	2023-12-15 09:00:00	ORD
12815	10	23	1839	1840	-1	2143	2152	AA	613	N905AN	EWR	MIA	141	1085	18	40	2023-10-23 18:00:00	MIA
12816	3	19	2029	2030	-1	2338	2355	UA	825	N29129	EWR	LAX	339	2454	20	30	2023-03-19 20:00:00	LAX
12818	10	10	1736	1730	6	1925	1930	NK	47	N906NK	LGA	DTW	82	502	17	30	2023-10-10 17:00:00	Other
12820	10	28	1749	1750	-1	2103	2058	UA	615	N14735	EWR	PDX	350	2434	17	50	2023-10-28 17:00:00	Other
12822	2	24	705	705	0	1139	1204	UA	574	N17752	EWR	STT	192	1634	7	5	2023-02-24 07:00:00	Other
12823	11	29	729	730	-1	936	951	DL	525	N347NW	JFK	MSP	157	1029	7	30	2023-11-29 07:00:00	Other
12829	12	6	937	930	7	1235	1240	B6	781	N949JT	JFK	FLL	150	1069	9	30	2023-12-06 09:00:00	FLL
12844	4	22	1329	1329	0	1554	1601	DL	144	N395DZ	LGA	ATL	121	762	13	29	2023-04-22 13:00:00	ATL
12853	2	20	945	940	5	1246	1304	B6	574	N584JB	JFK	RSW	162	1074	9	40	2023-02-20 09:00:00	Other
12859	11	10	1632	1633	-1	1925	1936	UA	160	N434UA	EWR	TPA	144	997	16	33	2023-11-10 16:00:00	Other
12862	7	3	1258	1255	3	1548	1557	B6	18	N766JB	LGA	TPA	145	1010	12	55	2023-07-03 12:00:00	Other
12867	4	7	1319	1320	-1	1545	1545	NK	36	N694NK	EWR	ATL	121	746	13	20	2023-04-07 13:00:00	ATL
12868	6	18	1522	1523	-1	1654	1714	9E	1560	N908XJ	JFK	BNA	107	765	15	23	2023-06-18 15:00:00	Other
12869	9	2	1319	1320	-1	1449	1501	YX	1413	N867RW	LGA	STL	129	888	13	20	2023-09-02 13:00:00	Other
12870	1	12	1800	1800	0	1942	1926	YX	1805	N241JQ	LGA	BOS	41	184	18	0	2023-01-12 18:00:00	BOS
12878	1	10	802	800	2	936	950	UA	759	N37290	EWR	ORD	108	719	8	0	2023-01-10 08:00:00	ORD
12886	11	21	2204	2159	5	2359	2318	YX	1255	N138HQ	JFK	BOS	48	187	21	59	2023-11-21 21:00:00	BOS
12894	12	25	2000	1959	1	2214	2320	AS	77	N282AK	EWR	LAX	286	2454	19	59	2023-12-25 19:00:00	LAX
12909	4	9	1551	1552	-1	1739	1805	YX	970	N654RW	EWR	MCI	144	1092	15	52	2023-04-09 15:00:00	Other
12910	11	22	1838	1830	8	2007	2012	UA	421	N17285	EWR	ORD	102	719	18	30	2023-11-22 18:00:00	ORD
12911	10	17	1307	1259	8	1457	1535	AA	972	N321RL	JFK	PHX	270	2153	12	59	2023-10-17 12:00:00	Other
12915	12	28	1559	1600	-1	1834	1844	YX	1075	N769YX	EWR	ATL	119	746	16	0	2023-12-28 16:00:00	ATL
12923	5	8	1739	1740	-1	2052	2053	NK	31	N977NK	EWR	LAX	334	2454	17	40	2023-05-08 17:00:00	LAX
12924	3	8	1748	1747	1	1922	1925	AA	694	N912NN	LGA	ORD	119	733	17	47	2023-03-08 17:00:00	ORD
12937	3	31	1529	1529	0	1719	1728	NK	519	N635NK	LGA	MYR	87	563	15	29	2023-03-31 15:00:00	Other
12959	5	12	1919	1920	-1	2051	2124	OO	1117	N258SY	JFK	ORD	120	740	19	20	2023-05-12 19:00:00	ORD
12960	12	13	1853	1853	0	2116	2122	YX	1068	N730YX	EWR	IND	106	645	18	53	2023-12-13 18:00:00	Other
12965	11	9	1945	1945	0	2221	2252	DL	877	N925DZ	JFK	TPA	141	1005	19	45	2023-11-09 19:00:00	Other
12968	1	16	2022	2020	2	2128	2131	9E	1632	N927XJ	LGA	PVD	30	143	20	20	2023-01-16 20:00:00	Other
12969	2	18	2136	2136	0	2341	2349	YX	1035	N655RW	EWR	GSP	102	594	21	36	2023-02-18 21:00:00	Other
12972	12	11	900	900	0	1139	1115	NK	520	N642NK	EWR	CHS	103	628	9	0	2023-12-11 09:00:00	Other
12974	11	17	1706	1700	6	1958	2011	NK	596	N634NK	EWR	FLL	149	1065	17	0	2023-11-17 17:00:00	FLL
12985	6	19	725	725	0	943	945	WN	590	N8868L	LGA	ATL	108	762	7	25	2023-06-19 07:00:00	ATL
12987	5	25	1306	1259	7	1624	1609	UA	688	N35236	EWR	MIA	162	1085	12	59	2023-05-25 12:00:00	MIA
12994	2	18	1139	1135	4	1439	1454	DL	471	N310DN	LGA	SRQ	150	1047	11	35	2023-02-18 11:00:00	Other
12997	1	17	730	729	1	858	844	UA	890	N419UA	EWR	BOS	41	200	7	29	2023-01-17 07:00:00	BOS
12998	7	30	1658	1654	4	1859	1922	DL	727	N377DE	EWR	ATL	103	746	16	54	2023-07-30 16:00:00	ATL
13004	1	10	1815	1810	5	2003	2024	9E	1523	N920XJ	LGA	MYR	85	563	18	10	2023-01-10 18:00:00	Other
13007	2	1	1821	1822	-1	2100	2112	YX	1228	N826MD	LGA	IND	123	660	18	22	2023-02-01 18:00:00	Other
13012	9	17	1605	1605	0	1846	1832	B6	27	N192JB	JFK	MSY	175	1182	16	5	2023-09-17 16:00:00	Other
13030	2	18	1312	1304	8	1552	1610	B6	553	N807JB	JFK	MCO	132	944	13	4	2023-02-18 13:00:00	MCO
13031	9	27	1710	1707	3	1858	1843	UA	793	N33132	EWR	ORD	113	719	17	7	2023-09-27 17:00:00	ORD
13035	6	30	2211	2210	1	102	114	DL	103	N828MH	JFK	LAX	307	2475	22	10	2023-06-30 22:00:00	LAX
13053	8	1	1124	1121	3	1311	1312	UA	556	N492UA	EWR	DTW	77	488	11	21	2023-08-01 11:00:00	Other
13055	3	22	809	810	-1	1203	1215	DL	738	N900PC	JFK	STT	197	1623	8	10	2023-03-22 08:00:00	Other
13060	4	8	2102	2102	0	2346	2359	UA	722	N38467	EWR	PBI	144	1023	21	2	2023-04-08 21:00:00	Other
13062	12	8	1740	1740	0	2048	2058	DL	418	N106DN	LGA	MIA	155	1096	17	40	2023-12-08 17:00:00	MIA
13064	4	12	727	728	-1	920	950	YX	948	N753YX	EWR	SDF	91	642	7	28	2023-04-12 07:00:00	Other
13067	11	20	759	800	-1	1018	1005	9E	1674	N928XJ	JFK	CLT	93	541	8	0	2023-11-20 08:00:00	CLT
13077	8	18	1630	1630	0	1902	1920	UA	391	N799UA	EWR	LAX	291	2454	16	30	2023-08-18 16:00:00	LAX
13083	9	7	939	940	-1	1139	1152	9E	1731	N936XJ	JFK	IND	99	665	9	40	2023-09-07 09:00:00	Other
13091	1	19	2036	2030	6	2202	2150	B6	397	N334JB	JFK	BOS	36	187	20	30	2023-01-19 20:00:00	BOS
13099	2	14	1454	1455	-1	1714	1727	9E	1402	N147PQ	JFK	SAV	104	718	14	55	2023-02-14 14:00:00	Other
13108	10	21	1239	1235	4	1459	1449	YX	1156	N726YX	EWR	CHS	97	628	12	35	2023-10-21 12:00:00	Other
13113	12	23	2122	2123	-1	2333	2351	UA	248	N27519	EWR	ATL	104	746	21	23	2023-12-23 21:00:00	ATL
13126	4	7	1502	1457	5	1723	1716	DL	410	N344NB	JFK	MSP	168	1029	14	57	2023-04-07 14:00:00	Other
13135	1	31	900	900	0	1342	1229	YX	1443	N403YX	LGA	IAH	245	1416	9	0	2023-01-31 09:00:00	Other
13139	4	23	1446	1440	6	1659	1710	WN	897	N8669B	LGA	ATL	116	762	14	40	2023-04-23 14:00:00	ATL
13165	2	19	1539	1540	-1	1739	1802	9E	1348	N905XJ	LGA	GSP	100	610	15	40	2023-02-19 15:00:00	Other
13168	6	9	1252	1252	0	1440	1502	DL	529	N132DU	JFK	DTW	82	509	12	52	2023-06-09 12:00:00	Other
13171	8	24	928	928	0	1227	1228	AA	291	N116AN	JFK	SNA	305	2454	9	28	2023-08-24 09:00:00	Other
13173	3	16	2244	2240	4	20	27	B6	532	N238JB	JFK	RDU	66	427	22	40	2023-03-16 22:00:00	Other
13185	3	9	900	900	0	1039	1043	UA	241	N443UA	LGA	ORD	120	733	9	0	2023-03-09 09:00:00	ORD
13189	6	22	1724	1725	-1	1909	1914	OO	1275	N260SY	JFK	BOS	38	187	17	25	2023-06-22 17:00:00	BOS
13193	1	22	1017	1008	9	1345	1328	UA	807	N405UA	EWR	IAH	233	1400	10	8	2023-01-22 10:00:00	Other
13219	6	13	1704	1659	5	2006	1954	UA	599	N17301	EWR	MCO	148	937	16	59	2023-06-13 16:00:00	MCO
13226	4	21	655	655	0	906	928	B6	120	N307JB	LGA	JAX	111	833	6	55	2023-04-21 06:00:00	Other
13227	4	16	1425	1420	5	1624	1650	UA	808	N824UA	LGA	DEN	219	1620	14	20	2023-04-16 14:00:00	Other
13240	9	13	1003	1000	3	1218	1236	DL	145	N313DN	LGA	ATL	109	762	10	0	2023-09-13 10:00:00	ATL
13247	1	18	1453	1445	8	1728	1725	WN	175	N934WN	LGA	MSY	182	1183	14	45	2023-01-18 14:00:00	Other
13249	9	2	839	840	-1	1152	1140	DL	334	N516DA	JFK	SAN	295	2446	8	40	2023-09-02 08:00:00	Other
13253	1	9	1504	1500	4	1655	1652	OO	1748	N120SY	LGA	ORD	123	733	15	0	2023-01-09 15:00:00	ORD
13257	3	3	525	525	0	741	700	AA	913	N912NN	EWR	ORD	146	719	5	25	2023-03-03 05:00:00	ORD
13263	7	3	1332	1325	7	1614	1623	B6	337	N605JB	JFK	PBI	136	1028	13	25	2023-07-03 13:00:00	Other
13275	1	1	1513	1512	1	1724	1721	OO	1267	N295SY	EWR	MSP	171	1008	15	12	2023-01-01 15:00:00	Other
13278	6	2	1530	1530	0	1740	1811	B6	650	N655JB	JFK	JAX	112	828	15	30	2023-06-02 15:00:00	Other
13285	7	5	614	615	-1	854	908	B6	40	N655JB	EWR	PBI	137	1023	6	15	2023-07-05 06:00:00	Other
13297	2	17	908	900	8	1101	1031	B6	603	N190JB	JFK	BUF	60	301	9	0	2023-02-17 09:00:00	Other
13305	12	28	1209	1210	-1	1331	1359	YX	1835	N201JQ	JFK	MKE	119	745	12	10	2023-12-28 12:00:00	Other
13325	10	10	1647	1645	2	1920	1939	UA	465	N33132	EWR	SAN	316	2425	16	45	2023-10-10 16:00:00	Other
13329	1	14	1243	1235	8	1516	1539	UA	286	N17279	EWR	TPA	132	997	12	35	2023-01-14 12:00:00	Other
13330	7	27	737	735	2	938	1000	DL	182	N3755D	LGA	DEN	215	1620	7	35	2023-07-27 07:00:00	Other
13337	4	11	1704	1701	3	1820	1842	UA	420	N17229	EWR	ORD	108	719	17	1	2023-04-11 17:00:00	ORD
13343	9	28	1755	1745	10	1936	1937	YX	1338	N423YX	LGA	CMH	78	479	17	45	2023-09-28 17:00:00	Other
13349	3	10	843	842	1	1027	1041	9E	1523	N187GJ	LGA	ILM	76	500	8	42	2023-03-10 08:00:00	Other
13357	4	22	1059	1100	-1	1245	1303	9E	1188	N490PX	LGA	MEM	143	963	11	0	2023-04-22 11:00:00	Other
13359	3	26	1514	1514	0	1638	1642	YX	1156	N744YX	EWR	PIT	62	319	15	14	2023-03-26 15:00:00	Other
13379	2	26	1604	1605	-1	1810	1823	9E	1472	N337PQ	JFK	CLT	94	541	16	5	2023-02-26 16:00:00	CLT
13381	2	23	2154	2154	0	2334	2328	UA	519	N87531	EWR	ORD	128	719	21	54	2023-02-23 21:00:00	ORD
13382	12	1	2109	2100	9	2358	3	DL	142	N520DE	JFK	LAS	325	2248	21	0	2023-12-01 21:00:00	Other
13387	5	16	2108	2059	9	2330	2335	UA	696	N810UA	EWR	JAX	116	820	20	59	2023-05-16 20:00:00	Other
13422	6	22	659	700	-1	953	1040	DL	181	N717TW	JFK	SFO	327	2586	7	0	2023-06-22 07:00:00	Other
13428	11	7	1904	1859	5	2204	2151	UA	388	N12109	EWR	LAS	326	2227	18	59	2023-11-07 18:00:00	Other
13439	5	4	1831	1825	6	2009	2025	DL	348	N139DU	LGA	ORD	115	733	18	25	2023-05-04 18:00:00	ORD
13454	10	6	1420	1420	0	1541	1553	YX	1761	N216JQ	LGA	BNA	118	764	14	20	2023-10-06 14:00:00	Other
13455	2	28	1357	1355	2	1635	1548	9E	1418	N331PQ	JFK	RDU	71	427	13	55	2023-02-28 13:00:00	Other
13468	6	7	2037	2030	7	2137	2139	YX	1090	N645RW	EWR	MDT	32	141	20	30	2023-06-07 20:00:00	Other
13477	3	8	1819	1820	-1	2002	2008	YX	1747	N231JQ	LGA	BNA	117	764	18	20	2023-03-08 18:00:00	Other
13496	5	4	1350	1350	0	1526	1523	9E	1393	N480PX	LGA	BNA	119	764	13	50	2023-05-04 13:00:00	Other
13507	10	5	910	900	10	1020	1007	B6	749	N358JB	JFK	ACK	41	199	9	0	2023-10-05 09:00:00	Other
13509	7	16	1535	1525	10	1651	1657	UA	569	N33266	EWR	ORD	104	719	15	25	2023-07-16 15:00:00	ORD
13510	3	9	2114	2115	-1	2304	2257	9E	1397	N478PX	LGA	ROA	76	405	21	15	2023-03-09 21:00:00	Other
13513	7	22	2124	2119	5	29	34	B6	25	N537JT	JFK	SLC	262	1990	21	19	2023-07-22 21:00:00	Other
13515	7	26	1243	1234	9	1525	1534	UA	658	N842UA	EWR	SAT	199	1569	12	34	2023-07-26 12:00:00	Other
13520	12	31	1212	1205	7	1413	1445	WN	33	N7720F	LGA	DEN	222	1620	12	5	2023-12-31 12:00:00	Other
13528	5	13	2129	2129	0	2253	2306	YX	1013	N725YX	EWR	PIT	54	319	21	29	2023-05-13 21:00:00	Other
13531	4	26	1609	1610	-1	1909	1920	B6	705	N705JB	LGA	MCO	152	950	16	10	2023-04-26 16:00:00	MCO
13539	9	28	1659	1659	0	1940	1940	OO	1264	N242SY	LGA	OKC	182	1341	16	59	2023-09-28 16:00:00	Other
13540	2	10	2034	2029	5	2324	2331	UA	860	N37257	EWR	TPA	151	997	20	29	2023-02-10 20:00:00	Other
13541	4	24	1859	1900	-1	2008	2026	UA	734	N440UA	EWR	IAD	44	212	19	0	2023-04-24 19:00:00	Other
13551	11	14	1507	1500	7	1702	1710	9E	1448	N933XJ	EWR	CVG	95	569	15	0	2023-11-14 15:00:00	Other
13565	7	24	730	730	0	1138	1029	B6	691	N517JB	EWR	MIA	190	1085	7	30	2023-07-24 07:00:00	MIA
13570	12	13	1541	1540	1	1706	1715	WN	718	N929WN	LGA	MDW	128	725	15	40	2023-12-13 15:00:00	Other
13577	5	31	749	750	-1	1030	1045	NK	833	N630NK	EWR	AUS	191	1504	7	50	2023-05-31 07:00:00	Other
13583	12	19	1358	1359	-1	1602	1615	YX	1254	N111HQ	LGA	MSP	154	1020	13	59	2023-12-19 13:00:00	Other
13586	2	23	2120	2120	0	2352	2349	9E	1290	N931XJ	JFK	SAV	109	718	21	20	2023-02-23 21:00:00	Other
13597	2	21	1522	1515	7	1648	1648	9E	1421	N491PX	LGA	ORF	50	296	15	15	2023-02-21 15:00:00	Other
13603	9	13	830	830	0	957	1005	OO	1275	N317SY	JFK	BNA	114	765	8	30	2023-09-13 08:00:00	Other
13607	11	22	1559	1559	0	1736	1744	YX	1132	N736YX	EWR	CLE	65	404	15	59	2023-11-22 15:00:00	Other
13610	10	5	1854	1855	-1	2144	2210	NK	1016	N674NK	LGA	MIA	142	1096	18	55	2023-10-05 18:00:00	MIA
13626	8	20	859	900	-1	958	1034	B6	623	N216JB	LGA	BNA	96	764	9	0	2023-08-20 09:00:00	Other
13653	3	5	1454	1455	-1	1706	1720	9E	1448	N602LR	JFK	CLT	87	541	14	55	2023-03-05 14:00:00	CLT
13656	3	26	602	600	2	915	911	AA	471	N304RB	LGA	MIA	161	1096	6	0	2023-03-26 06:00:00	MIA
13668	3	9	659	700	-1	937	1016	DL	399	N301DV	JFK	MIA	142	1089	7	0	2023-03-09 07:00:00	MIA
13670	8	15	1638	1630	8	1912	1920	UA	391	N27959	EWR	LAX	294	2454	16	30	2023-08-15 16:00:00	LAX
13672	7	15	1034	1035	-1	1316	1329	UA	326	N27276	EWR	TPA	129	997	10	35	2023-07-15 10:00:00	Other
13673	11	29	2001	2000	1	2319	2326	AA	35	N107NN	JFK	LAX	324	2475	20	0	2023-11-29 20:00:00	LAX
13674	6	29	1159	1200	-1	1358	1435	DL	335	N315DN	LGA	ATL	101	762	12	0	2023-06-29 12:00:00	ATL
13676	11	26	2001	1959	2	2238	2227	DL	926	N830DN	EWR	ATL	131	746	19	59	2023-11-26 19:00:00	ATL
13692	9	14	704	700	4	924	925	DL	182	N105DX	LGA	ATL	115	762	7	0	2023-09-14 07:00:00	ATL
13695	5	1	1800	1755	5	2017	2025	WN	390	N233LV	LGA	ATL	110	762	17	55	2023-05-01 17:00:00	ATL
13703	4	24	1138	1130	8	1448	1437	DL	583	N104DU	LGA	IAH	212	1416	11	30	2023-04-24 11:00:00	Other
13705	7	30	1353	1347	6	1523	1521	AA	530	N887NN	EWR	ORD	114	719	13	47	2023-07-30 13:00:00	ORD
13713	4	16	2109	2109	0	2335	2341	UA	462	N17752	EWR	JAX	118	820	21	9	2023-04-16 21:00:00	Other
13716	8	11	1520	1520	0	1639	1700	WN	749	N8530W	LGA	STL	123	888	15	20	2023-08-11 15:00:00	Other
13721	9	4	2002	1959	3	2319	2258	NK	162	N668NK	LGA	MCO	124	950	19	59	2023-09-04 19:00:00	MCO
13725	12	5	1019	1015	4	1352	1345	DL	412	N103DU	LGA	IAH	233	1416	10	15	2023-12-05 10:00:00	Other
13727	9	23	1516	1510	6	1719	1710	DL	625	N103DU	LGA	DTW	75	502	15	10	2023-09-23 15:00:00	Other
13729	3	2	1858	1859	-1	2042	2032	YX	1033	N747YX	EWR	BGR	59	393	18	59	2023-03-02 18:00:00	Other
13743	11	17	1234	1229	5	1528	1535	B6	978	N523JB	LGA	TPA	149	1010	12	29	2023-11-17 12:00:00	Other
13748	9	4	737	735	2	855	852	B6	183	N284JB	JFK	PWM	55	273	7	35	2023-09-04 07:00:00	Other
13753	4	26	807	800	7	1029	1032	DL	140	N345DN	LGA	ATL	116	762	8	0	2023-04-26 08:00:00	ATL
13758	5	2	934	929	5	1052	1101	UA	923	N447UA	EWR	BNA	108	748	9	29	2023-05-02 09:00:00	Other
13761	9	14	1104	1100	4	1337	1332	DL	283	N391DN	LGA	ATL	113	762	11	0	2023-09-14 11:00:00	ATL
13762	12	5	1001	1000	1	1246	1312	DL	255	N179DN	JFK	LAX	316	2475	10	0	2023-12-05 10:00:00	LAX
13768	7	6	1439	1440	-1	1736	1738	DL	398	N126DN	LGA	MCO	128	950	14	40	2023-07-06 14:00:00	MCO
13771	4	15	659	700	-1	817	809	OO	990	N261SY	EWR	BOS	40	200	7	0	2023-04-15 07:00:00	BOS
13779	6	15	2015	2005	10	2245	2240	WN	1193	N500WR	LGA	DAL	193	1381	20	5	2023-06-15 20:00:00	Other
13782	3	7	831	830	1	1002	1000	9E	1558	N308PQ	JFK	IAD	52	228	8	30	2023-03-07 08:00:00	Other
13793	7	21	1614	1615	-1	1827	1840	DL	342	N129DU	LGA	CHS	94	641	16	15	2023-07-21 16:00:00	Other
13794	10	22	1726	1727	-1	1954	2016	UA	775	N76522	EWR	MCO	124	937	17	27	2023-10-22 17:00:00	MCO
13803	12	7	1540	1541	-1	1834	1848	UA	527	N76522	EWR	FLL	146	1065	15	41	2023-12-07 15:00:00	FLL
13808	1	25	1201	1200	1	1457	1530	UA	873	N12109	EWR	SFO	331	2565	12	0	2023-01-25 12:00:00	Other
13811	2	9	625	620	5	918	949	B6	510	N991JT	EWR	LAX	324	2454	6	20	2023-02-09 06:00:00	LAX
13812	12	7	1000	951	9	1245	1302	B6	487	N974JT	LGA	FLL	139	1076	9	51	2023-12-07 09:00:00	FLL
13818	9	20	1130	1129	1	1341	1356	DL	361	N808DN	JFK	ATL	107	760	11	29	2023-09-20 11:00:00	ATL
13819	10	23	602	600	2	820	819	UA	387	N23707	EWR	ATL	105	746	6	0	2023-10-23 06:00:00	ATL
13824	12	5	1454	1444	10	1552	1605	B6	384	N304JB	JFK	BOS	36	187	14	44	2023-12-05 14:00:00	BOS
13825	6	11	1300	1300	0	1607	1643	AS	4	N483AS	JFK	SFO	330	2586	13	0	2023-06-11 13:00:00	Other
13836	9	25	1500	1459	1	1701	1705	AA	484	N804NN	LGA	CLT	83	544	14	59	2023-09-25 14:00:00	CLT
13838	2	1	2015	2015	0	8	2359	AS	18	N949AK	JFK	SFO	374	2586	20	15	2023-02-01 20:00:00	Other
13849	12	27	1904	1855	9	2050	2105	9E	1492	N478PX	LGA	STL	132	888	18	55	2023-12-27 18:00:00	Other
13851	8	6	1702	1659	3	2012	1951	UA	414	N19141	EWR	SAN	317	2425	16	59	2023-08-06 16:00:00	Other
13852	11	28	1335	1330	5	1515	1511	YX	1299	N423YX	JFK	PIT	69	340	13	30	2023-11-28 13:00:00	Other
13866	5	18	2009	2007	2	2122	2129	UA	527	N809UA	EWR	BOS	46	200	20	7	2023-05-18 20:00:00	BOS
13875	8	4	645	645	0	916	926	DL	366	N143DU	LGA	IAH	190	1416	6	45	2023-08-04 06:00:00	Other
13890	2	23	1705	1700	5	2140	2022	B6	739	N943JT	EWR	LAX	429	2454	17	0	2023-02-23 17:00:00	LAX
13893	2	18	944	945	-1	1222	1257	DL	943	N388DN	LGA	MCO	130	950	9	45	2023-02-18 09:00:00	MCO
13895	7	19	1601	1600	1	1902	1849	AA	818	N868NN	LGA	DFW	189	1389	16	0	2023-07-19 16:00:00	Other
13897	1	24	1659	1659	0	1840	1848	B6	493	N337JB	JFK	RDU	70	427	16	59	2023-01-24 16:00:00	Other
13900	3	11	1329	1329	0	1632	1656	DL	785	N373NW	JFK	AUS	212	1521	13	29	2023-03-11 13:00:00	Other
13907	5	17	2229	2230	-1	2345	2357	YX	1139	N736YX	EWR	PWM	52	284	22	30	2023-05-17 22:00:00	Other
13914	8	31	929	930	-1	1219	1230	AS	8	N979AK	JFK	SEA	320	2422	9	30	2023-08-31 09:00:00	Other
13916	10	14	600	600	0	819	830	DL	260	N360DN	LGA	ATL	115	762	6	0	2023-10-14 06:00:00	ATL
13926	4	6	1029	1030	-1	1159	1153	YX	929	N751YX	EWR	DCA	42	199	10	30	2023-04-06 10:00:00	Other
13938	7	11	915	915	0	1039	1048	YX	849	N746YX	EWR	BUF	48	282	9	15	2023-07-11 09:00:00	Other
13939	7	5	755	747	8	951	950	UA	728	N829UA	EWR	MSY	156	1167	7	47	2023-07-05 07:00:00	Other
13941	9	6	2110	2110	0	2342	2357	DL	142	N529DT	JFK	LAS	291	2248	21	10	2023-09-06 21:00:00	Other
13948	12	30	1925	1925	0	2233	2305	AS	82	N413AS	EWR	SFO	325	2565	19	25	2023-12-30 19:00:00	Other
13966	12	15	758	759	-1	951	1003	AA	743	N938NN	LGA	CLT	84	544	7	59	2023-12-15 07:00:00	CLT
13969	7	27	1625	1625	0	1915	1859	UA	131	N17296	EWR	LAS	289	2227	16	25	2023-07-27 16:00:00	Other
13986	10	12	721	713	8	1029	1024	DL	304	N302DU	EWR	SLC	272	1969	7	13	2023-10-12 07:00:00	Other
14004	5	11	1436	1429	7	1656	1700	DL	138	N369DN	LGA	ATL	107	762	14	29	2023-05-11 14:00:00	ATL
14009	2	21	734	735	-1	1022	1043	DL	578	N387DA	JFK	TPA	152	1005	7	35	2023-02-21 07:00:00	Other
14014	5	19	1319	1319	0	1532	1605	AA	946	N324SH	JFK	PHX	294	2153	13	19	2023-05-19 13:00:00	Other
14018	3	19	2229	2230	-1	153	219	B6	144	N959JB	JFK	SJU	188	1598	22	30	2023-03-19 22:00:00	Other
14030	3	9	1459	1457	2	1715	1716	DL	450	N368NB	JFK	MSP	167	1029	14	57	2023-03-09 14:00:00	Other
14037	4	22	1015	1013	2	1319	1253	YX	961	N654RW	EWR	JAX	135	820	10	13	2023-04-22 10:00:00	Other
14051	11	25	1149	1145	4	1504	1510	UA	676	N38459	EWR	SAT	237	1569	11	45	2023-11-25 11:00:00	Other
14054	11	8	1737	1731	6	2000	1914	MQ	1187	N772MR	EWR	ORD	154	719	17	31	2023-11-08 17:00:00	ORD
14056	9	25	838	830	8	1130	1123	UA	134	N13018	EWR	LAX	293	2454	8	30	2023-09-25 08:00:00	LAX
14057	7	16	1423	1424	-1	1736	1725	UA	231	N77530	EWR	SEA	338	2402	14	24	2023-07-16 14:00:00	Other
14067	2	1	721	715	6	1100	900	WN	965	N8777Q	LGA	BNA	79	764	7	15	2023-02-01 07:00:00	Other
14072	5	25	800	800	0	1032	1025	DL	206	N121DZ	LGA	ATL	106	762	8	0	2023-05-25 08:00:00	ATL
14084	4	17	1205	1200	5	1356	1354	9E	1293	N348PQ	JFK	RDU	75	427	12	0	2023-04-17 12:00:00	Other
14092	3	16	1958	1959	-1	2246	2320	DL	606	N389DN	LGA	MIA	146	1096	19	59	2023-03-16 19:00:00	MIA
14093	9	8	1959	2000	-1	51	3	B6	88	N2086J	JFK	SJU	202	1598	20	0	2023-09-08 20:00:00	Other
14104	5	3	1739	1729	10	2034	2048	AA	318	N906AN	JFK	MIA	143	1089	17	29	2023-05-03 17:00:00	MIA
14115	12	8	1405	1355	10	1656	1716	AA	369	N865NN	LGA	DFW	195	1389	13	55	2023-12-08 13:00:00	Other
14120	4	19	944	945	-1	1238	1235	B6	366	N238JB	JFK	MCO	137	944	9	45	2023-04-19 09:00:00	MCO
14124	7	12	1437	1435	2	1636	1654	YX	962	N855RW	EWR	IND	99	645	14	35	2023-07-12 14:00:00	Other
14127	9	24	658	659	-1	942	1005	DL	657	N347NW	JFK	AUS	194	1521	6	59	2023-09-24 06:00:00	Other
14130	6	30	833	827	6	958	1006	YX	1073	N979RP	EWR	RIC	54	277	8	27	2023-06-30 08:00:00	Other
14133	2	19	937	936	1	1229	1253	B6	200	N634JB	JFK	FLL	150	1069	9	36	2023-02-19 09:00:00	FLL
14138	3	25	1501	1459	2	1650	1650	NK	24	N536NK	EWR	MYR	92	550	14	59	2023-03-25 14:00:00	Other
14144	12	2	1749	1749	0	1926	1944	B6	403	N229JB	JFK	RDU	79	427	17	49	2023-12-02 17:00:00	Other
14150	8	10	707	708	-1	1018	947	UA	415	N403UA	EWR	IAH	201	1400	7	8	2023-08-10 07:00:00	Other
14157	5	25	744	745	-1	1119	1052	DL	319	N3756	JFK	RSW	159	1074	7	45	2023-05-25 07:00:00	Other
14166	7	19	1006	1000	6	1257	1252	UA	403	N24729	EWR	AUS	197	1504	10	0	2023-07-19 10:00:00	Other
14171	11	27	1650	1650	0	2017	2029	AA	195	N420AN	EWR	PHX	302	2133	16	50	2023-11-27 16:00:00	Other
14182	1	19	1511	1507	4	1751	1750	YX	1189	N729YX	EWR	JAX	127	820	15	7	2023-01-19 15:00:00	Other
14189	10	15	600	600	0	818	830	DL	260	N125DN	LGA	ATL	116	762	6	0	2023-10-15 06:00:00	ATL
14198	12	19	1744	1735	9	2017	2020	WN	593	N425LV	LGA	DEN	231	1620	17	35	2023-12-19 17:00:00	Other
14201	5	23	1245	1245	0	1521	1542	NK	81	N608NK	EWR	DFW	184	1372	12	45	2023-05-23 12:00:00	Other
14202	12	28	1737	1729	8	2028	2111	UA	450	N37560	EWR	PHX	256	2133	17	29	2023-12-28 17:00:00	Other
14204	12	23	630	630	0	819	838	AA	906	N834NN	JFK	CLT	89	541	6	30	2023-12-23 06:00:00	CLT
14205	4	20	1342	1343	-1	1558	1540	AA	591	N988NN	EWR	CLT	74	529	13	43	2023-04-20 13:00:00	CLT
14210	11	26	1429	1430	-1	1740	1749	UA	869	N12125	EWR	LAX	346	2454	14	30	2023-11-26 14:00:00	LAX
14216	11	9	1729	1730	-1	1920	1938	YX	1334	N406YX	LGA	CMH	83	479	17	30	2023-11-09 17:00:00	Other
14218	6	8	612	610	2	743	745	DL	478	N133DU	LGA	ORD	116	733	6	10	2023-06-08 06:00:00	ORD
14221	4	10	2158	2159	-1	2346	2359	UA	571	N804UA	EWR	MSP	139	1008	21	59	2023-04-10 21:00:00	Other
14229	8	2	2059	2100	-1	5	24	AA	80	N112AN	JFK	LAX	324	2475	21	0	2023-08-02 21:00:00	LAX
14245	4	22	1429	1429	0	1629	1604	9E	1405	N931XJ	JFK	RIC	58	288	14	29	2023-04-22 14:00:00	Other
14251	12	15	1415	1408	7	1613	1633	UA	195	N68821	EWR	DEN	212	1605	14	8	2023-12-15 14:00:00	Other
14252	7	30	1439	1440	-1	1729	1743	DL	398	N316DN	LGA	MCO	131	950	14	40	2023-07-30 14:00:00	MCO
14257	3	3	730	725	5	1008	954	UA	452	N847UA	EWR	JAX	126	820	7	25	2023-03-03 07:00:00	Other
14264	3	29	759	800	-1	1112	1103	AA	604	N159AN	EWR	DFW	210	1372	8	0	2023-03-29 08:00:00	Other
14265	7	5	804	759	5	1055	1113	AA	127	N925NN	LGA	MIA	143	1096	7	59	2023-07-05 07:00:00	MIA
14268	8	29	2209	2200	9	2315	2318	YX	845	N856RW	EWR	MHT	37	209	22	0	2023-08-29 22:00:00	Other
14281	9	13	1625	1625	0	1811	1820	YX	1072	N729YX	EWR	GSO	75	445	16	25	2023-09-13 16:00:00	Other
14292	9	21	1556	1550	6	1819	1807	9E	1662	N292PQ	LGA	CHS	98	641	15	50	2023-09-21 15:00:00	Other
14307	4	4	754	755	-1	1144	1156	UA	715	N69063	EWR	SJU	194	1608	7	55	2023-04-04 07:00:00	Other
14317	9	9	807	805	2	1038	1024	DL	925	N376DA	EWR	ATL	108	746	8	5	2023-09-09 08:00:00	ATL
14322	7	31	703	700	3	815	816	B6	803	N307JB	LGA	BOS	42	184	7	0	2023-07-31 07:00:00	BOS
14324	7	30	1750	1750	0	2145	2051	DL	506	N352DN	LGA	MCO	143	950	17	50	2023-07-30 17:00:00	MCO
14345	2	17	1559	1600	-1	1720	1726	OO	1171	N310SY	JFK	BOS	38	187	16	0	2023-02-17 16:00:00	BOS
14347	4	6	2056	2055	1	2305	2308	UA	474	N435UA	EWR	CVG	91	569	20	55	2023-04-06 20:00:00	Other
14352	2	5	1605	1559	6	1927	1924	B6	672	N2060J	JFK	FLL	172	1069	15	59	2023-02-05 15:00:00	FLL
14375	10	11	1606	1600	6	1918	1913	DL	510	N3767	JFK	MIA	156	1089	16	0	2023-10-11 16:00:00	MIA
14378	6	1	1659	1655	4	1937	2029	DL	167	N3742C	JFK	SAN	314	2446	16	55	2023-06-01 16:00:00	Other
14390	9	20	1030	1029	1	1158	1200	YX	1945	N213JQ	LGA	DCA	47	214	10	29	2023-09-20 10:00:00	Other
14411	5	22	1116	1117	-1	1331	1342	YX	1201	N122HQ	LGA	XNA	163	1147	11	17	2023-05-22 11:00:00	Other
14417	2	1	922	914	8	1157	1138	UA	752	N872UA	EWR	IND	118	645	9	14	2023-02-01 09:00:00	Other
14427	4	8	1454	1455	-1	1749	1758	AA	358	N306PB	LGA	DFW	207	1389	14	55	2023-04-08 14:00:00	Other
14434	2	9	2134	2130	4	2245	2259	UA	791	N68834	EWR	ORF	48	284	21	30	2023-02-09 21:00:00	Other
14437	10	2	1928	1929	-1	2208	2234	DL	836	N522DA	JFK	MCO	124	944	19	29	2023-10-02 19:00:00	MCO
14446	4	15	959	1000	-1	1154	1201	B6	65	N337JB	JFK	DTW	74	509	10	0	2023-04-15 10:00:00	Other
14447	1	27	1929	1929	0	2211	2212	YX	1291	N123HQ	LGA	LIT	190	1085	19	29	2023-01-27 19:00:00	Other
14454	5	22	1733	1730	3	1949	1954	9E	1384	N305PQ	JFK	MCI	160	1113	17	30	2023-05-22 17:00:00	Other
14458	3	1	1938	1930	8	2129	2129	YX	1396	N105HQ	JFK	DCA	68	213	19	30	2023-03-01 19:00:00	Other
14467	3	6	1457	1455	2	1721	1727	9E	1492	N695CA	JFK	SAV	110	718	14	55	2023-03-06 14:00:00	Other
14477	5	17	1702	1659	3	1829	1839	UA	771	N465UA	EWR	ORD	117	719	16	59	2023-05-17 16:00:00	ORD
14487	2	20	1728	1729	-1	2012	2020	UA	820	N57111	EWR	LAS	315	2227	17	29	2023-02-20 17:00:00	Other
14494	7	1	1557	1554	3	1919	1857	AA	722	N882NN	JFK	DFW	204	1391	15	54	2023-07-01 15:00:00	Other
14505	1	26	1521	1515	6	1806	1840	UA	726	N2140U	EWR	SFO	323	2565	15	15	2023-01-26 15:00:00	Other
14510	8	7	714	715	-1	927	935	WN	466	N7715E	LGA	ATL	114	762	7	15	2023-08-07 07:00:00	ATL
14520	12	31	1716	1706	10	1825	1850	UA	421	N34460	EWR	ORD	103	719	17	6	2023-12-31 17:00:00	ORD
14522	2	6	1850	1850	0	2125	2123	9E	1331	N606LR	LGA	SAV	96	722	18	50	2023-02-06 18:00:00	Other
14523	6	5	1509	1459	10	1657	1713	UA	970	N47275	EWR	PHX	266	2133	14	59	2023-06-05 14:00:00	Other
14527	4	14	1030	1030	0	1245	1317	B6	39	N958JB	JFK	LAS	283	2248	10	30	2023-04-14 10:00:00	Other
14544	8	19	1424	1424	0	1715	1725	UA	218	N27239	EWR	SEA	323	2402	14	24	2023-08-19 14:00:00	Other
14549	6	6	1232	1229	3	1348	1400	YX	1279	N434YX	JFK	ORF	55	290	12	29	2023-06-06 12:00:00	Other
14565	8	21	1532	1530	2	1735	1812	B6	520	N206JB	JFK	ATL	94	760	15	30	2023-08-21 15:00:00	ATL
14567	9	30	1634	1629	5	1750	1806	9E	1574	N134EV	JFK	ORF	50	290	16	29	2023-09-30 16:00:00	Other
14573	2	19	2044	2045	-1	2325	2356	UA	292	N69835	EWR	FLL	137	1065	20	45	2023-02-19 20:00:00	FLL
14575	5	10	2028	2029	-1	2328	2335	UA	250	N37534	EWR	AUS	199	1504	20	29	2023-05-10 20:00:00	Other
14590	2	24	1304	1305	-1	1408	1416	B6	336	N193JB	JFK	BOS	43	187	13	5	2023-02-24 13:00:00	BOS
14619	2	7	1530	1530	0	1828	1849	DL	632	N372DN	JFK	FLL	139	1069	15	30	2023-02-07 15:00:00	FLL
14625	3	26	2203	2159	4	2307	2308	DL	96	N136DQ	LGA	SYR	38	198	21	59	2023-03-26 21:00:00	Other
14629	3	11	922	923	-1	1141	1152	YX	1132	N739YX	EWR	MCI	167	1092	9	23	2023-03-11 09:00:00	Other
14631	12	16	1848	1843	5	2143	2213	DL	442	N302DU	EWR	SLC	273	1969	18	43	2023-12-16 18:00:00	Other
14632	7	7	1754	1754	0	1915	1929	B6	93	N281JB	JFK	PWM	47	273	17	54	2023-07-07 17:00:00	Other
14640	12	23	659	700	-1	1035	1049	DL	117	N524DE	JFK	PHX	290	2153	7	0	2023-12-23 07:00:00	Other
14647	8	11	955	955	0	1106	1125	WN	946	N8570W	LGA	BNA	112	764	9	55	2023-08-11 09:00:00	Other
14652	1	12	1032	1029	3	1501	1521	B6	1083	N999JQ	JFK	SJU	185	1598	10	29	2023-01-12 10:00:00	Other
14668	6	4	1235	1235	0	1453	1455	WN	339	N447WN	LGA	ATL	109	762	12	35	2023-06-04 12:00:00	ATL
14671	7	1	759	800	-1	1011	1029	DL	178	N515DE	JFK	DEN	226	1626	8	0	2023-07-01 08:00:00	Other
14672	1	2	559	600	-1	735	738	UA	1031	N35236	LGA	ORD	126	733	6	0	2023-01-02 06:00:00	ORD
14677	4	17	1558	1559	-1	1827	1820	YX	988	N855RW	EWR	SAV	117	708	15	59	2023-04-17 15:00:00	Other
14680	3	9	1002	959	3	1214	1221	9E	1481	N131EV	JFK	SAV	109	718	9	59	2023-03-09 09:00:00	Other
14684	4	14	1655	1645	10	1839	1855	WN	196	N8751R	LGA	MCI	144	1107	16	45	2023-04-14 16:00:00	Other
14687	7	29	709	700	9	907	916	DL	243	N707TW	JFK	PHX	264	2153	7	0	2023-07-29 07:00:00	Other
14699	2	25	1950	1945	5	2159	2220	B6	656	N267JB	LGA	SAV	110	722	19	45	2023-02-25 19:00:00	Other
14701	11	20	730	730	0	1021	1051	AS	90	N577AS	EWR	SEA	319	2402	7	30	2023-11-20 07:00:00	Other
14707	2	23	1839	1840	-1	2143	2151	YX	1188	N126HQ	LGA	TUL	209	1231	18	40	2023-02-23 18:00:00	Other
14737	8	28	1825	1825	0	2130	2118	DL	803	N116DU	JFK	JAX	124	828	18	25	2023-08-28 18:00:00	Other
14740	2	18	2145	2135	10	2314	2320	YX	1013	N752YX	EWR	MKE	122	725	21	35	2023-02-18 21:00:00	Other
14742	5	1	1437	1435	2	1716	1750	UA	80	N78005	EWR	SFO	313	2565	14	35	2023-05-01 14:00:00	Other
14744	4	24	906	900	6	1205	1153	UA	470	N27276	EWR	MCO	144	937	9	0	2023-04-24 09:00:00	MCO
14756	8	2	2039	2030	9	2201	2211	DL	355	N132DU	LGA	ORD	115	733	20	30	2023-08-02 20:00:00	ORD
14759	8	25	659	700	-1	955	1007	DL	358	N3747D	JFK	RSW	147	1074	7	0	2023-08-25 07:00:00	Other
14763	11	24	1058	1059	-1	1354	1415	DL	376	N342NW	LGA	PBI	154	1035	10	59	2023-11-24 10:00:00	Other
14766	1	29	618	615	3	937	933	UA	348	N225UA	EWR	SFO	360	2565	6	15	2023-01-29 06:00:00	Other
14772	2	8	1837	1835	2	2048	2109	DL	799	N955AT	EWR	ATL	109	746	18	35	2023-02-08 18:00:00	ATL
14779	2	13	857	850	7	1213	1249	DL	313	N718TW	JFK	SFO	341	2586	8	50	2023-02-13 08:00:00	Other
14780	2	3	931	930	1	1309	1248	B6	51	N570JB	JFK	SRQ	177	1041	9	30	2023-02-03 09:00:00	Other
14784	10	3	1708	1705	3	1820	1827	UA	409	N37263	EWR	BOS	43	200	17	5	2023-10-03 17:00:00	BOS
14785	9	4	1417	1409	8	1535	1526	UA	135	N39726	EWR	BOS	45	200	14	9	2023-09-04 14:00:00	BOS
14796	11	14	1631	1630	1	1828	1819	DL	563	N115DU	LGA	ORD	118	733	16	30	2023-11-14 16:00:00	ORD
14802	1	5	1854	1850	4	2229	2236	UA	340	N34137	EWR	PHX	298	2133	18	50	2023-01-05 18:00:00	Other
14810	2	24	1840	1835	5	2106	2109	DL	799	N982AT	EWR	ATL	119	746	18	35	2023-02-24 18:00:00	ATL
14814	7	20	903	855	8	1114	1059	9E	1125	N329PQ	JFK	CVG	92	589	8	55	2023-07-20 08:00:00	Other
14837	2	7	1400	1400	0	1647	1709	AA	685	N724AN	JFK	MIA	140	1089	14	0	2023-02-07 14:00:00	MIA
14841	7	31	1538	1529	9	1736	1724	YX	854	N750YX	EWR	CMH	77	463	15	29	2023-07-31 15:00:00	Other
14846	9	14	1228	1229	-1	1525	1544	AA	645	N964NN	JFK	MIA	153	1089	12	29	2023-09-14 12:00:00	MIA
14849	2	9	703	700	3	1020	1024	B6	301	N943JT	JFK	LAX	325	2475	7	0	2023-02-09 07:00:00	LAX
14868	11	16	902	902	0	1241	1236	NK	1181	N619NK	EWR	PHX	300	2133	9	2	2023-11-16 09:00:00	Other
14876	11	26	1533	1529	4	1709	1707	UA	789	N36207	EWR	ORD	117	719	15	29	2023-11-26 15:00:00	ORD
14880	12	27	1832	1832	0	2218	2150	AA	972	N907AN	EWR	MIA	182	1085	18	32	2023-12-27 18:00:00	MIA
14882	5	31	1028	1019	9	1218	1228	9E	1403	N326PQ	LGA	MYR	81	563	10	19	2023-05-31 10:00:00	Other
14884	5	27	2201	2200	1	2317	2339	OO	1100	N317SY	JFK	IAD	43	228	22	0	2023-05-27 22:00:00	Other
14886	7	17	1659	1700	-1	1841	1837	YX	1370	N241JQ	LGA	BOS	54	184	17	0	2023-07-17 17:00:00	BOS
14892	3	18	1230	1230	0	1612	1532	B6	34	N587JB	JFK	MCO	159	944	12	30	2023-03-18 12:00:00	MCO
14897	4	21	2016	2010	6	2242	2304	B6	35	N510JB	JFK	DEN	224	1626	20	10	2023-04-21 20:00:00	Other
14898	3	13	729	730	-1	944	1012	UA	513	N457UA	LGA	DEN	223	1620	7	30	2023-03-13 07:00:00	Other
14899	1	21	2051	2051	0	2158	2214	UA	500	N815UA	EWR	BUF	52	282	20	51	2023-01-21 20:00:00	Other
14909	7	31	1601	1559	2	1913	1907	UA	400	N17289	EWR	SEA	332	2402	15	59	2023-07-31 15:00:00	Other
14910	6	8	1830	1820	10	1958	2012	DL	375	N135DQ	LGA	ORD	114	733	18	20	2023-06-08 18:00:00	ORD
14912	6	8	1701	1700	1	1953	2010	DL	100	N845MH	JFK	LAX	310	2475	17	0	2023-06-08 17:00:00	LAX
14916	6	16	2206	2159	7	2344	2352	UA	421	N818UA	EWR	MEM	134	946	21	59	2023-06-16 21:00:00	Other
14942	11	27	1826	1825	1	2023	2020	WN	1008	N235WN	LGA	STL	144	888	18	25	2023-11-27 18:00:00	Other
14947	8	20	1029	1030	-1	1351	1358	YX	914	N651RW	EWR	EYW	171	1196	10	30	2023-08-20 10:00:00	Other
14950	4	28	2134	2126	8	2332	2329	NK	278	N695NK	LGA	DTW	78	502	21	26	2023-04-28 21:00:00	Other
14951	4	26	1945	1945	0	2243	2248	NK	920	N616NK	EWR	MIA	149	1085	19	45	2023-04-26 19:00:00	MIA
14960	5	19	549	550	-1	815	847	AA	575	N990NN	LGA	DFW	181	1389	5	50	2023-05-19 05:00:00	Other
14961	6	15	1137	1135	2	1418	1410	WN	47	N7752B	LGA	DAL	191	1381	11	35	2023-06-15 11:00:00	Other
14980	1	17	1300	1300	0	1553	1625	AA	1045	N422AN	LGA	MIA	150	1096	13	0	2023-01-17 13:00:00	MIA
14985	6	12	928	923	5	1030	1035	B6	513	N304JB	JFK	MVY	37	173	9	23	2023-06-12 09:00:00	Other
14989	2	13	734	735	-1	1019	1035	DL	383	N305DN	JFK	MCO	131	944	7	35	2023-02-13 07:00:00	MCO
15001	10	15	1432	1430	2	1536	1547	B6	523	N318JB	JFK	BOS	38	187	14	30	2023-10-15 14:00:00	BOS
15006	10	30	644	639	5	926	916	UA	401	N13113	EWR	PHX	318	2133	6	39	2023-10-30 06:00:00	Other
15017	9	22	725	725	0	839	900	WN	613	N940WN	LGA	BNA	105	764	7	25	2023-09-22 07:00:00	Other
15025	8	10	643	641	2	926	924	AA	762	N945NN	EWR	DFW	195	1372	6	41	2023-08-10 06:00:00	Other
15027	11	5	659	655	4	927	952	B6	186	N989JT	JFK	LAS	293	2248	6	55	2023-11-05 06:00:00	Other
15029	6	19	1100	1100	0	1331	1357	B6	203	N944JT	JFK	LAX	304	2475	11	0	2023-06-19 11:00:00	LAX
15033	8	2	1939	1939	0	2231	2245	NK	812	N651NK	EWR	MIA	132	1085	19	39	2023-08-02 19:00:00	MIA
15036	11	24	803	800	3	1005	1020	9E	1651	N302PQ	LGA	CHS	101	641	8	0	2023-11-24 08:00:00	Other
15038	7	11	1358	1359	-1	1500	1531	YX	1391	N210JQ	LGA	BOS	36	184	13	59	2023-07-11 13:00:00	BOS
15043	4	23	1305	1300	5	1608	1611	B6	630	N520JB	EWR	RSW	152	1068	13	0	2023-04-23 13:00:00	Other
15044	8	10	1110	1100	10	1310	1251	UA	671	N441UA	EWR	MEM	134	946	11	0	2023-08-10 11:00:00	Other
15045	11	27	1329	1325	4	1506	1454	B6	894	N197JB	JFK	DCA	50	213	13	25	2023-11-27 13:00:00	Other
15046	9	27	2015	2015	0	2151	2154	UA	426	N62849	EWR	ORD	107	719	20	15	2023-09-27 20:00:00	ORD
15062	1	26	802	800	2	1022	1027	9E	1396	N200PQ	JFK	MSP	146	1029	8	0	2023-01-26 08:00:00	Other
15076	5	12	1454	1451	3	1740	1745	DL	470	N322DN	LGA	MCO	126	950	14	51	2023-05-12 14:00:00	MCO
15087	3	7	607	600	7	940	912	UA	607	N24702	LGA	IAH	204	1416	6	0	2023-03-07 06:00:00	Other
15092	7	7	1025	1025	0	1208	1230	AA	537	N182UW	EWR	CLT	81	529	10	25	2023-07-07 10:00:00	CLT
15102	12	27	1654	1652	2	2029	1953	UA	555	N37541	EWR	TPA	159	997	16	52	2023-12-27 16:00:00	Other
15104	7	21	713	705	8	920	932	UA	372	N27256	EWR	PHX	283	2133	7	5	2023-07-21 07:00:00	Other
15110	10	22	610	608	2	811	754	DL	743	N951AT	EWR	DTW	80	488	6	8	2023-10-22 06:00:00	Other
15130	12	11	1629	1630	-1	1820	1849	9E	1395	N146PQ	JFK	DTW	86	509	16	30	2023-12-11 16:00:00	Other
15143	12	11	1655	1655	0	1957	1945	B6	900	N516JB	LGA	ATL	115	762	16	55	2023-12-11 16:00:00	ATL
15145	11	24	1740	1740	0	2030	2048	UA	711	N13138	EWR	IAH	209	1400	17	40	2023-11-24 17:00:00	Other
15151	4	13	1754	1750	4	1948	2029	9E	1234	N315PQ	JFK	MCI	145	1113	17	50	2023-04-13 17:00:00	Other
15157	1	25	1632	1625	7	1946	1940	WN	575	N263WN	LGA	DAL	225	1381	16	25	2023-01-25 16:00:00	Other
15163	8	4	1459	1459	0	1618	1611	YX	874	N760YX	EWR	ALB	33	143	14	59	2023-08-04 14:00:00	Other
15185	11	7	1750	1749	1	2051	2105	AA	957	N326SJ	JFK	AUS	218	1521	17	49	2023-11-07 17:00:00	Other
15188	4	8	1556	1555	1	1931	1953	B6	896	N706JB	JFK	SJU	195	1598	15	55	2023-04-08 15:00:00	Other
15201	1	12	730	731	-1	1053	1105	UA	513	N21108	EWR	PHX	298	2133	7	31	2023-01-12 07:00:00	Other
15204	7	7	839	840	-1	1006	1022	UA	651	N37278	EWR	CLE	60	404	8	40	2023-07-07 08:00:00	Other
15206	6	13	2102	2059	3	2222	2229	UA	770	N23708	EWR	BNA	106	748	20	59	2023-06-13 20:00:00	Other
15218	6	21	2028	2029	-1	2336	2335	B6	171	N640JB	LGA	FLL	148	1076	20	29	2023-06-21 20:00:00	FLL
15222	8	19	1554	1553	1	1849	1924	DL	461	N101DQ	LGA	FLL	147	1076	15	53	2023-08-19 15:00:00	FLL
15224	4	30	1020	1020	0	1316	1245	DL	733	N373DA	EWR	ATL	111	746	10	20	2023-04-30 10:00:00	ATL
15227	1	29	1603	1559	4	1809	1809	AA	112	N904NN	JFK	CLT	94	541	15	59	2023-01-29 15:00:00	CLT
15228	5	16	1158	1159	-1	1458	1507	NK	978	N679NK	LGA	MIA	149	1096	11	59	2023-05-16 11:00:00	MIA
15239	5	2	1501	1500	1	1604	1622	YX	1116	N727YX	EWR	BTV	46	266	15	0	2023-05-02 15:00:00	Other
15243	1	16	1930	1930	0	2154	2200	9E	1564	N320PQ	LGA	OMA	168	1148	19	30	2023-01-16 19:00:00	Other
15244	12	8	1529	1529	0	1727	1748	DL	105	N370NW	LGA	MSP	147	1020	15	29	2023-12-08 15:00:00	Other
15248	4	18	1650	1647	3	1902	1910	UA	651	N24729	EWR	ATL	106	746	16	47	2023-04-18 16:00:00	ATL
15283	10	23	1426	1426	0	1639	1640	UA	356	N17294	EWR	DEN	228	1605	14	26	2023-10-23 14:00:00	Other
15285	6	20	1505	1459	6	1828	1800	UA	77	N410UA	EWR	PBI	160	1023	14	59	2023-06-20 14:00:00	Other
15289	4	28	1209	1205	4	1400	1422	YX	1145	N126HQ	LGA	MSP	141	1020	12	5	2023-04-28 12:00:00	Other
15299	4	26	1909	1900	9	2024	2030	WN	52	N8570W	LGA	MDW	116	725	19	0	2023-04-26 19:00:00	Other
15305	2	22	2132	2125	7	2302	2246	YX	1590	N215JQ	LGA	PWM	41	269	21	25	2023-02-22 21:00:00	Other
15308	5	5	2234	2235	-1	10	2359	DL	458	N117DU	JFK	BOS	46	187	22	35	2023-05-05 22:00:00	BOS
15314	1	22	740	735	5	1036	1035	DL	428	N311DN	JFK	MCO	144	944	7	35	2023-01-22 07:00:00	MCO
15316	9	2	1459	1459	0	1658	1706	B6	349	N307JB	JFK	DTW	84	509	14	59	2023-09-02 14:00:00	Other
15324	9	12	1501	1502	-1	1642	1657	DL	757	N945AT	EWR	MSP	137	1008	15	2	2023-09-12 15:00:00	Other
15326	3	28	658	659	-1	854	851	YX	1284	N444YX	LGA	RDU	76	431	6	59	2023-03-28 06:00:00	Other
15329	12	15	1528	1525	3	1748	1758	UA	135	N17529	EWR	DEN	215	1605	15	25	2023-12-15 15:00:00	Other
15331	12	29	902	902	0	1135	1140	B6	22	N3077J	JFK	MSY	177	1182	9	2	2023-12-29 09:00:00	Other
15340	9	28	1032	1029	3	1238	1233	UA	507	N27734	EWR	CLT	90	529	10	29	2023-09-28 10:00:00	CLT
15344	6	16	1128	1129	-1	1241	1304	UA	382	N35271	EWR	ORD	110	719	11	29	2023-06-16 11:00:00	ORD
15370	9	25	1506	1459	7	1700	1709	YX	1205	N745YX	EWR	CVG	91	569	14	59	2023-09-25 14:00:00	Other
15382	4	3	720	720	0	1008	1039	AA	351	N336RU	JFK	MIA	143	1089	7	20	2023-04-03 07:00:00	MIA
15389	9	11	1241	1231	10	1524	1528	AA	557	N896NN	LGA	DFW	188	1389	12	31	2023-09-11 12:00:00	Other
15391	4	2	1535	1536	-1	1840	1853	DL	899	N101DU	LGA	IAH	211	1416	15	36	2023-04-02 15:00:00	Other
15392	9	25	1901	1900	1	2207	2151	UA	559	N37556	EWR	IAH	193	1400	19	0	2023-09-25 19:00:00	Other
15394	11	1	728	729	-1	1059	1042	DL	309	N864DN	JFK	SEA	345	2422	7	29	2023-11-01 07:00:00	Other
15415	8	27	1429	1429	0	1546	1603	9E	1179	N153PQ	JFK	SYR	48	209	14	29	2023-08-27 14:00:00	Other
15423	10	28	1914	1910	4	2158	2200	UA	336	N57286	EWR	IAH	189	1400	19	10	2023-10-28 19:00:00	Other
15438	3	5	2202	2157	5	2344	2333	UA	903	N13718	EWR	MSN	127	799	21	57	2023-03-05 21:00:00	Other
15450	10	30	1523	1520	3	1741	1734	DL	980	N309DU	LGA	MSP	168	1020	15	20	2023-10-30 15:00:00	Other
15451	6	20	1122	1122	0	1403	1425	DL	462	N807DN	JFK	TPA	140	1005	11	22	2023-06-20 11:00:00	Other
15452	12	22	1857	1855	2	2303	2247	B6	40	N653JB	JFK	PHX	293	2153	18	55	2023-12-22 18:00:00	Other
15458	12	18	1159	1200	-1	1451	1519	UA	765	N34131	EWR	LAX	321	2454	12	0	2023-12-18 12:00:00	LAX
15463	12	14	1453	1445	8	1553	1629	B6	776	N805JB	LGA	BNA	103	764	14	45	2023-12-14 14:00:00	Other
15465	11	6	1608	1608	0	1846	1910	UA	69	N472UA	EWR	PBI	135	1023	16	8	2023-11-06 16:00:00	Other
15472	10	20	1300	1300	0	1455	1511	UA	878	N47517	EWR	MSY	149	1167	13	0	2023-10-20 13:00:00	Other
15475	4	2	1027	1018	9	1323	1305	B6	44	N358JB	EWR	MCO	133	937	10	18	2023-04-02 10:00:00	MCO
15476	9	6	1329	1321	8	1620	1636	AA	638	N804NN	EWR	MIA	142	1085	13	21	2023-09-06 13:00:00	MIA
15482	10	1	1858	1859	-1	2149	2206	UA	166	N16732	EWR	SNA	308	2434	18	59	2023-10-01 18:00:00	Other
15505	11	18	600	600	0	853	915	WN	635	N286WN	LGA	HOU	203	1428	6	0	2023-11-18 06:00:00	Other
15521	11	1	759	800	-1	920	939	UA	853	N461UA	LGA	ORD	112	733	8	0	2023-11-01 08:00:00	ORD
15527	5	2	2058	2059	-1	2230	2254	9E	1557	N913XJ	LGA	RDU	66	431	20	59	2023-05-02 20:00:00	Other
15528	6	5	1602	1557	5	1826	1824	UA	470	N37465	EWR	ATL	105	746	15	57	2023-06-05 15:00:00	ATL
15544	7	22	1929	1925	4	2145	2152	9E	1226	N146PQ	JFK	DTW	77	509	19	25	2023-07-22 19:00:00	Other
15548	4	13	724	715	9	924	945	DL	266	N710TW	JFK	PHX	271	2153	7	15	2023-04-13 07:00:00	Other
15555	12	17	1729	1729	0	2030	2050	UA	749	N17312	EWR	PDX	328	2434	17	29	2023-12-17 17:00:00	Other
15563	6	10	1739	1735	4	1914	1917	UA	673	N13720	EWR	CLE	62	404	17	35	2023-06-10 17:00:00	Other
15565	3	16	921	915	6	1159	1217	UA	517	N445UA	EWR	TPA	129	997	9	15	2023-03-16 09:00:00	Other
15568	4	22	1430	1425	5	1649	1626	YX	1056	N865RW	EWR	MYR	98	550	14	25	2023-04-22 14:00:00	Other
15570	11	4	1058	1059	-1	1204	1218	YX	1152	N766YX	EWR	DCA	40	199	10	59	2023-11-04 10:00:00	Other
15583	7	13	1344	1334	10	1636	1635	UA	94	N470UA	EWR	RSW	150	1068	13	34	2023-07-13 13:00:00	Other
15586	11	19	1400	1400	0	1556	1617	YX	1154	N747YX	EWR	CVG	89	569	14	0	2023-11-19 14:00:00	Other
15587	3	22	812	805	7	1007	958	OO	1148	N254SY	JFK	ORD	127	740	8	5	2023-03-22 08:00:00	ORD
15605	9	21	1949	1945	4	2313	2309	DL	838	N384DA	JFK	MIA	159	1089	19	45	2023-09-21 19:00:00	MIA
15609	8	29	1857	1850	7	2122	2110	9E	1246	N341PQ	LGA	MCI	165	1107	18	50	2023-08-29 18:00:00	Other
15621	10	2	1428	1424	4	1718	1723	B6	299	N637JB	JFK	MCO	130	944	14	24	2023-10-02 14:00:00	MCO
15624	12	21	707	705	2	1023	1018	DL	351	N311DN	LGA	PBI	138	1035	7	5	2023-12-21 07:00:00	Other
15625	3	20	1204	1155	9	1325	1317	NK	282	N630NK	EWR	PIT	59	319	11	55	2023-03-20 11:00:00	Other
15635	9	1	1240	1240	0	1535	1545	NK	340	N974NK	EWR	FLL	158	1065	12	40	2023-09-01 12:00:00	FLL
15641	2	19	1737	1730	7	2100	2120	DL	245	N718TW	JFK	SFO	355	2586	17	30	2023-02-19 17:00:00	Other
15642	4	12	2022	2020	2	2239	2320	WN	565	N8683D	LGA	DAL	174	1381	20	20	2023-04-12 20:00:00	Other
15654	2	25	800	800	0	930	939	9E	1404	N298PQ	JFK	BUF	65	301	8	0	2023-02-25 08:00:00	Other
15655	8	27	805	805	0	1018	1014	DL	447	N366NB	JFK	MSP	154	1029	8	5	2023-08-27 08:00:00	Other
15663	7	20	635	630	5	821	838	AA	288	N947AN	JFK	CLT	86	541	6	30	2023-07-20 06:00:00	CLT
15674	5	5	1124	1125	-1	1403	1436	DL	447	N3741S	JFK	TPA	137	1005	11	25	2023-05-05 11:00:00	Other
15682	2	12	1334	1335	-1	1451	1456	9E	1466	N176PQ	LGA	ROC	47	254	13	35	2023-02-12 13:00:00	Other
15684	12	3	1325	1325	0	1511	1500	WN	338	N228WN	LGA	BNA	139	764	13	25	2023-12-03 13:00:00	Other
15697	9	28	1901	1859	2	2147	2202	AA	370	N936NN	LGA	DFW	187	1389	18	59	2023-09-28 18:00:00	Other
15731	8	1	1533	1526	7	1844	1849	DL	209	N358DN	JFK	FLL	147	1069	15	26	2023-08-01 15:00:00	FLL
15753	9	24	1433	1430	3	1635	1642	YX	1419	N401YX	LGA	CVG	90	585	14	30	2023-09-24 14:00:00	Other
15755	9	22	1356	1355	1	1641	1645	WN	158	N8778Q	LGA	HOU	197	1428	13	55	2023-09-22 13:00:00	Other
15763	10	16	559	600	-1	847	854	UA	227	N17303	EWR	AUS	197	1504	6	0	2023-10-16 06:00:00	Other
15768	7	18	1139	1130	9	1449	1435	DL	811	N119DU	LGA	SRQ	159	1047	11	30	2023-07-18 11:00:00	Other
15776	2	9	703	700	3	1038	1051	DL	273	N174DN	JFK	SFO	337	2586	7	0	2023-02-09 07:00:00	Other
15779	7	2	705	700	5	1015	1015	AS	13	N493AS	JFK	SFO	333	2586	7	0	2023-07-02 07:00:00	Other
15784	10	23	1144	1145	-1	1419	1445	DL	1005	N343DN	LGA	MCO	126	950	11	45	2023-10-23 11:00:00	MCO
15804	8	31	1137	1129	8	1423	1401	DL	309	N846DN	JFK	ATL	105	760	11	29	2023-08-31 11:00:00	ATL
15809	2	1	934	929	5	1233	1239	UA	495	N39728	EWR	TPA	148	997	9	29	2023-02-01 09:00:00	Other
15827	8	16	1236	1236	0	1539	1547	AA	509	N895NN	EWR	MIA	154	1085	12	36	2023-08-16 12:00:00	MIA
15828	5	19	701	700	1	940	950	UA	793	N897UA	EWR	DFW	196	1372	7	0	2023-05-19 07:00:00	Other
15839	5	27	2058	2055	3	2320	2306	YX	1044	N747YX	EWR	GSP	91	594	20	55	2023-05-27 20:00:00	Other
15847	12	12	1156	1155	1	1304	1325	WN	263	N7748A	LGA	MDW	114	725	11	55	2023-12-12 11:00:00	Other
15852	6	1	1329	1330	-1	1432	1442	B6	39	N203JB	JFK	SYR	41	209	13	30	2023-06-01 13:00:00	Other
15855	1	22	604	605	-1	755	819	DL	1057	N966AT	EWR	MSP	155	1008	6	5	2023-01-22 06:00:00	Other
15859	4	5	835	835	0	1249	1155	DL	335	N121DU	JFK	DFW	286	1391	8	35	2023-04-05 08:00:00	Other
15870	7	30	906	905	1	1104	1124	9E	1123	N335PQ	LGA	GRR	98	618	9	5	2023-07-30 09:00:00	Other
15876	4	9	2000	1955	5	2137	2152	YX	1219	N409YX	LGA	CMH	72	479	19	55	2023-04-09 19:00:00	Other
15886	11	21	1655	1655	0	2014	1950	B6	198	N623JB	EWR	PBI	170	1023	16	55	2023-11-21 16:00:00	Other
15892	2	10	1729	1720	9	2046	2035	WN	473	N8698B	LGA	HOU	233	1428	17	20	2023-02-10 17:00:00	Other
15895	9	13	1150	1143	7	1337	1328	OO	1276	N259SY	JFK	ORD	119	740	11	43	2023-09-13 11:00:00	ORD
15898	11	18	1945	1945	0	2124	2122	OO	1209	N603CZ	JFK	IAD	56	228	19	45	2023-11-18 19:00:00	Other
15909	5	31	949	946	3	1332	1341	UA	582	N69885	EWR	SJU	200	1608	9	46	2023-05-31 09:00:00	Other
15914	7	29	1358	1359	-1	1507	1517	YX	1401	N204JQ	JFK	ACK	47	199	13	59	2023-07-29 13:00:00	Other
15916	12	19	1728	1729	-1	2018	2057	AA	86	N113AN	JFK	LAX	324	2475	17	29	2023-12-19 17:00:00	LAX
15946	2	18	1658	1659	-1	1931	2002	UA	236	N39297	EWR	PBI	131	1023	16	59	2023-02-18 16:00:00	Other
15947	12	6	1658	1659	-1	1845	1909	DL	876	N313DN	LGA	DTW	80	502	16	59	2023-12-06 16:00:00	Other
15949	6	27	919	919	0	1055	1123	YX	1814	N214JQ	LGA	CMH	72	479	9	19	2023-06-27 09:00:00	Other
15963	11	2	1402	1402	0	1532	1545	UA	775	N24736	EWR	STL	129	872	14	2	2023-11-02 14:00:00	Other
15971	9	5	1701	1659	2	1901	1915	9E	1454	N482PX	LGA	CVG	87	585	16	59	2023-09-05 16:00:00	Other
15980	12	12	1108	1100	8	1419	1415	B6	321	N712JB	JFK	SLC	288	1990	11	0	2023-12-12 11:00:00	Other
15981	6	28	2106	2059	7	2249	2305	YX	1244	N742YX	EWR	CMH	68	463	20	59	2023-06-28 20:00:00	Other
15988	4	29	1557	1555	2	1723	1727	YX	1209	N429YX	LGA	RIC	55	292	15	55	2023-04-29 15:00:00	Other
15991	12	31	1302	1300	2	1518	1543	DL	315	N388DN	LGA	ATL	112	762	13	0	2023-12-31 13:00:00	ATL
15997	11	11	1932	1929	3	2124	2138	AA	472	N924NN	JFK	CLT	91	541	19	29	2023-11-11 19:00:00	CLT
16003	7	11	1355	1355	0	1552	1600	WN	139	N8565Z	LGA	MSY	153	1183	13	55	2023-07-11 13:00:00	Other
16010	1	24	1644	1640	4	2007	1950	NK	720	N659NK	EWR	FLL	173	1065	16	40	2023-01-24 16:00:00	FLL
16013	9	28	1004	959	5	1306	1310	AA	250	N919NN	JFK	MIA	153	1089	9	59	2023-09-28 09:00:00	MIA
16019	10	1	1900	1900	0	2147	2155	UA	865	N213UA	EWR	LAX	300	2454	19	0	2023-10-01 19:00:00	LAX
16039	12	16	704	659	5	1020	1035	DL	309	N517DN	JFK	SEA	327	2422	6	59	2023-12-16 06:00:00	Other
16043	12	28	1507	1457	10	1722	1820	B6	774	N651JB	JFK	RNO	291	2411	14	57	2023-12-28 14:00:00	Other
16044	10	23	654	655	-1	816	824	UA	352	N16703	EWR	BNA	106	748	6	55	2023-10-23 06:00:00	Other
16056	12	24	1108	1100	8	1406	1404	B6	892	N579JB	JFK	MIA	155	1089	11	0	2023-12-24 11:00:00	MIA
16057	1	14	1437	1435	2	1733	1754	B6	1081	N228JB	JFK	FLL	139	1069	14	35	2023-01-14 14:00:00	FLL
16067	5	23	704	705	-1	920	923	DL	764	N831DN	EWR	ATL	109	746	7	5	2023-05-23 07:00:00	ATL
16068	2	18	1810	1800	10	1957	1941	UA	671	N847UA	EWR	STL	137	872	18	0	2023-02-18 18:00:00	Other
16078	10	25	1609	1610	-1	1921	1936	DL	225	N915DU	JFK	SLC	281	1990	16	10	2023-10-25 16:00:00	Other
16087	4	27	605	605	0	916	905	WN	842	N8796L	LGA	HOU	222	1428	6	5	2023-04-27 06:00:00	Other
16089	9	28	1612	1610	2	1903	1938	DL	238	N876DN	JFK	SLC	265	1990	16	10	2023-09-28 16:00:00	Other
16102	9	25	1321	1315	6	1438	1438	B6	907	N328JB	JFK	DCA	55	213	13	15	2023-09-25 13:00:00	Other
16118	4	3	950	948	2	1140	1200	DL	597	N360DN	LGA	DTW	85	502	9	48	2023-04-03 09:00:00	Other
16128	4	3	1718	1715	3	1825	1842	B6	381	N203JB	LGA	BOS	38	184	17	15	2023-04-03 17:00:00	BOS
16129	12	15	1048	1040	8	1213	1235	WN	1155	N203WN	LGA	STL	127	888	10	40	2023-12-15 10:00:00	Other
16143	2	13	1058	1059	-1	1412	1359	UA	269	N27252	EWR	PBI	166	1023	10	59	2023-02-13 10:00:00	Other
16153	3	29	2031	2030	1	2330	2322	B6	934	N913JB	JFK	MCO	139	944	20	30	2023-03-29 20:00:00	MCO
16165	10	26	1959	1955	4	2223	2232	DL	89	N822DN	JFK	DEN	230	1626	19	55	2023-10-26 19:00:00	Other
16172	3	28	1644	1645	-1	1807	1813	YX	1641	N860RW	LGA	DCA	55	214	16	45	2023-03-28 16:00:00	Other
16175	10	1	1259	1259	0	1656	1612	AA	206	N342SX	LGA	MIA	200	1096	12	59	2023-10-01 12:00:00	MIA
16207	7	17	1732	1730	2	1938	1926	YX	1029	N423YX	LGA	CMH	89	479	17	30	2023-07-17 17:00:00	Other
16212	7	19	1028	1029	-1	1212	1241	DL	430	N372DN	LGA	MSP	144	1020	10	29	2023-07-19 10:00:00	Other
16216	11	5	2107	2100	7	2341	2359	B6	179	N623JB	LGA	MCO	120	950	21	0	2023-11-05 21:00:00	MCO
16219	3	2	1025	1025	0	1246	1228	AA	877	N538UW	EWR	CLT	87	529	10	25	2023-03-02 10:00:00	CLT
16220	3	19	737	735	2	1038	1031	DL	377	N369DN	JFK	MCO	155	944	7	35	2023-03-19 07:00:00	MCO
16223	8	10	1034	1025	9	1304	1240	DL	653	N395DN	EWR	ATL	107	746	10	25	2023-08-10 10:00:00	ATL
16226	11	3	2012	2005	7	2321	2321	DL	425	N301DU	LGA	RSW	161	1080	20	5	2023-11-03 20:00:00	Other
16245	12	12	848	849	-1	1015	1026	9E	1474	N182GJ	LGA	BUF	55	292	8	49	2023-12-12 08:00:00	Other
16249	4	25	2255	2245	10	8	4	B6	6	N355JB	JFK	SYR	45	209	22	45	2023-04-25 22:00:00	Other
16250	5	1	1953	1954	-1	2343	2353	UA	211	N37466	EWR	BQN	200	1585	19	54	2023-05-01 19:00:00	Other
16251	7	13	2106	2100	6	2346	2229	YX	1086	N118HQ	LGA	BUF	63	292	21	0	2023-07-13 21:00:00	Other
16252	9	29	929	929	0	1135	1146	YX	1110	N856RW	EWR	AVL	88	583	9	29	2023-09-29 09:00:00	Other
16256	11	21	1930	1931	-1	2303	2245	UA	484	N78506	EWR	MIA	167	1085	19	31	2023-11-21 19:00:00	MIA
16261	12	8	1137	1132	5	1330	1339	AA	167	N902NN	JFK	CLT	85	541	11	32	2023-12-08 11:00:00	CLT
16263	3	13	1314	1315	-1	1607	1630	DL	269	N190DN	JFK	LAX	331	2475	13	15	2023-03-13 13:00:00	LAX
16265	3	20	1458	1458	0	1627	1635	9E	1546	N695CA	JFK	RIC	61	288	14	58	2023-03-20 14:00:00	Other
16269	5	27	2217	2209	8	2355	2332	UA	509	N12754	EWR	ORF	54	284	22	9	2023-05-27 22:00:00	Other
16276	10	26	737	735	2	857	922	UA	934	N13227	EWR	RDU	59	416	7	35	2023-10-26 07:00:00	Other
16291	8	21	1741	1741	0	2043	2141	DL	214	N510DE	JFK	SLC	248	1990	17	41	2023-08-21 17:00:00	Other
16297	11	18	1531	1525	6	1803	1830	UA	803	N643UA	EWR	IAH	187	1400	15	25	2023-11-18 15:00:00	Other
16306	12	8	1501	1459	2	1753	1814	NK	600	N675NK	LGA	FLL	151	1076	14	59	2023-12-08 14:00:00	FLL
16325	2	3	1834	1830	4	2218	2206	B6	66	N946JL	JFK	LAX	343	2475	18	30	2023-02-03 18:00:00	LAX
16337	12	28	2004	1959	5	2301	2304	DL	854	N925DZ	JFK	TPA	155	1005	19	59	2023-12-28 19:00:00	Other
16349	2	20	1116	1117	-1	1408	1415	UA	271	N47282	EWR	TPA	148	997	11	17	2023-02-20 11:00:00	Other
16362	2	1	700	700	0	1037	1012	UA	685	N818UA	LGA	IAH	232	1416	7	0	2023-02-01 07:00:00	Other
16372	9	14	729	729	0	1027	1045	DL	299	N542DE	JFK	SEA	324	2422	7	29	2023-09-14 07:00:00	Other
16374	7	13	1508	1500	8	1730	1745	DL	295	N377DN	LGA	ATL	112	762	15	0	2023-07-13 15:00:00	ATL
16386	11	10	1028	1029	-1	1221	1226	9E	1513	N232PQ	LGA	RDU	77	431	10	29	2023-11-10 10:00:00	Other
16389	6	13	1905	1859	6	2154	2230	DL	214	N841DN	JFK	PDX	304	2454	18	59	2023-06-13 18:00:00	Other
16395	5	8	1029	1029	0	1225	1239	YX	1246	N128HQ	LGA	GSP	89	610	10	29	2023-05-08 10:00:00	Other
16398	12	12	1229	1230	-1	1522	1523	UA	702	N78009	EWR	IAH	201	1400	12	30	2023-12-12 12:00:00	Other
16407	4	10	1301	1300	1	1655	1605	UA	639	N37528	EWR	MIA	200	1085	13	0	2023-04-10 13:00:00	MIA
16410	1	7	1807	1807	0	1928	1945	YX	1249	N722YX	EWR	PIT	51	319	18	7	2023-01-07 18:00:00	Other
16426	6	17	855	850	5	1109	1138	9E	1575	N925XJ	LGA	JAX	112	833	8	50	2023-06-17 08:00:00	Other
16427	9	15	815	815	0	919	933	B6	104	N337JB	LGA	BOS	39	184	8	15	2023-09-15 08:00:00	BOS
16432	3	4	629	629	0	732	746	DL	402	N112DU	JFK	BOS	35	187	6	29	2023-03-04 06:00:00	BOS
16454	10	20	1202	1159	3	1311	1317	UA	419	N409UA	EWR	PWM	47	284	11	59	2023-10-20 11:00:00	Other
16477	2	9	1658	1659	-1	1919	1933	YX	990	N640RW	EWR	SDF	114	642	16	59	2023-02-09 16:00:00	Other
16478	6	13	2033	2025	8	2144	2208	AA	793	N836AW	LGA	ORD	108	733	20	25	2023-06-13 20:00:00	ORD
16479	7	7	818	815	3	1117	1121	DL	301	N706TW	JFK	SAN	315	2446	8	15	2023-07-07 08:00:00	Other
16481	9	29	529	530	-1	821	841	AA	801	N341RW	JFK	MIA	151	1089	5	30	2023-09-29 05:00:00	MIA
16484	6	23	1233	1229	4	1514	1517	UA	778	N492UA	LGA	IAH	186	1416	12	29	2023-06-23 12:00:00	Other
16489	1	8	1315	1315	0	1608	1542	YX	1834	N246JQ	LGA	IND	111	660	13	15	2023-01-08 13:00:00	Other
16492	4	23	2215	2215	0	117	131	DL	101	N839MH	JFK	LAX	324	2475	22	15	2023-04-23 22:00:00	LAX
16495	3	10	959	1000	-1	1216	1207	B6	65	N284JB	JFK	DTW	88	509	10	0	2023-03-10 10:00:00	Other
16503	10	17	659	700	-1	818	842	UA	831	N76522	EWR	ORD	105	719	7	0	2023-10-17 07:00:00	ORD
16508	6	28	1833	1834	-1	2043	2045	DL	1010	N895AT	EWR	MSP	145	1008	18	34	2023-06-28 18:00:00	Other
16509	12	6	955	954	1	1138	1152	9E	1451	N182GJ	EWR	RDU	69	416	9	54	2023-12-06 09:00:00	Other
16522	10	16	1029	1030	-1	1336	1340	AA	236	N912NN	JFK	MIA	163	1089	10	30	2023-10-16 10:00:00	MIA
16523	11	21	900	901	-1	1205	1226	AA	569	N761AJ	JFK	MIA	153	1089	9	1	2023-11-21 09:00:00	MIA
16524	10	22	2154	2155	-1	2313	2315	B6	894	N279JB	JFK	SYR	44	209	21	55	2023-10-22 21:00:00	Other
16526	5	21	1021	1019	2	1310	1332	UA	622	N435UA	EWR	RSW	153	1068	10	19	2023-05-21 10:00:00	Other
16532	1	10	1635	1635	0	1750	1801	9E	1628	N136EV	JFK	SYR	48	209	16	35	2023-01-10 16:00:00	Other
16550	6	15	800	800	0	1010	1029	DL	193	N504DZ	JFK	DEN	211	1626	8	0	2023-06-15 08:00:00	Other
16561	10	7	1516	1510	6	1841	1748	DL	992	N169DZ	JFK	ATL	117	760	15	10	2023-10-07 15:00:00	ATL
16566	2	13	1250	1250	0	1420	1430	9E	1284	N601LR	LGA	MKE	111	738	12	50	2023-02-13 12:00:00	Other
16568	11	19	1430	1430	0	1729	1740	AA	243	N843NN	JFK	DFW	207	1391	14	30	2023-11-19 14:00:00	Other
16570	12	23	1759	1750	9	1946	1934	MQ	1164	N271NN	EWR	ORD	116	719	17	50	2023-12-23 17:00:00	ORD
16572	1	26	2224	2225	-1	134	158	B6	1011	N929JB	JFK	SFO	346	2586	22	25	2023-01-26 22:00:00	Other
16577	12	22	600	601	-1	904	902	B6	46	N570JB	LGA	FLL	144	1076	6	1	2023-12-22 06:00:00	FLL
16582	2	12	1124	1115	9	1427	1433	DL	875	N392DN	LGA	FLL	153	1076	11	15	2023-02-12 11:00:00	FLL
16604	9	30	1626	1626	0	1856	1911	UA	571	N41135	EWR	MCO	123	937	16	26	2023-09-30 16:00:00	MCO
16606	8	2	1838	1838	0	2032	2038	B6	333	N197JB	JFK	RDU	71	427	18	38	2023-08-02 18:00:00	Other
16620	3	7	1833	1830	3	2114	2042	YX	1646	N878RW	LGA	STL	143	888	18	30	2023-03-07 18:00:00	Other
16627	2	27	1800	1800	0	2034	2041	UA	849	N876UA	LGA	DEN	239	1620	18	0	2023-02-27 18:00:00	Other
16642	3	23	1645	1645	0	1820	1813	YX	1641	N815MD	LGA	DCA	44	214	16	45	2023-03-23 16:00:00	Other
16646	10	15	1559	1600	-1	1835	1833	DL	161	N383DZ	LGA	ATL	117	762	16	0	2023-10-15 16:00:00	ATL
16658	6	7	610	605	5	837	845	WN	1050	N211WN	LGA	HOU	184	1428	6	5	2023-06-07 06:00:00	Other
16659	8	17	1400	1359	1	1547	1558	YX	825	N722YX	EWR	DTW	84	488	13	59	2023-08-17 13:00:00	Other
16671	5	22	759	755	4	1154	1156	UA	781	N67058	EWR	SJU	193	1608	7	55	2023-05-22 07:00:00	Other
16673	1	17	705	700	5	1003	1015	DL	1007	N131DU	JFK	DFW	218	1391	7	0	2023-01-17 07:00:00	Other
16681	2	8	1941	1940	1	2225	2258	DL	587	N349DX	LGA	MIA	146	1096	19	40	2023-02-08 19:00:00	MIA
16684	1	23	1050	1049	1	1421	1335	F9	648	N376FR	LGA	ATL	111	762	10	49	2023-01-23 10:00:00	ATL
16687	10	16	1452	1445	7	1719	1715	WN	1018	N244WN	LGA	ATL	104	762	14	45	2023-10-16 14:00:00	ATL
16689	11	5	1830	1830	0	2120	2137	AA	998	N847NN	EWR	MIA	144	1085	18	30	2023-11-05 18:00:00	MIA
16692	11	1	1901	1855	6	2032	2025	WN	676	N8562Z	LGA	MDW	111	725	18	55	2023-11-01 18:00:00	Other
16694	6	30	1927	1927	0	2112	2130	YX	1901	N227JQ	LGA	CMH	75	479	19	27	2023-06-30 19:00:00	Other
16695	7	17	1059	1059	0	1306	1318	YX	899	N859RW	EWR	IND	98	645	10	59	2023-07-17 10:00:00	Other
16702	7	4	1902	1859	3	2202	2158	NK	416	N644NK	LGA	IAH	192	1416	18	59	2023-07-04 18:00:00	Other
16715	8	11	2216	2207	9	2359	3	YX	898	N749YX	EWR	MEM	133	946	22	7	2023-08-11 22:00:00	Other
16725	2	23	1304	1305	-1	1706	1700	AA	933	N378SC	JFK	PHX	329	2153	13	5	2023-02-23 13:00:00	Other
16736	1	12	550	550	0	905	901	AA	685	N965AN	LGA	DFW	216	1389	5	50	2023-01-12 05:00:00	Other
16738	4	28	1705	1705	0	1846	1850	9E	1255	N131EV	JFK	BUF	53	301	17	5	2023-04-28 17:00:00	Other
16739	6	29	1717	1707	10	1958	2029	B6	810	N508JL	JFK	MIA	136	1089	17	7	2023-06-29 17:00:00	MIA
16761	9	26	1729	1730	-1	1849	1915	OO	1294	N607CZ	JFK	MKE	121	745	17	30	2023-09-26 17:00:00	Other
16765	7	31	659	700	-1	1007	950	DL	183	N177DZ	JFK	LAX	325	2475	7	0	2023-07-31 07:00:00	LAX
16774	2	24	1515	1515	0	1803	1751	UA	695	N37468	EWR	DEN	257	1605	15	15	2023-02-24 15:00:00	Other
16779	5	1	1104	1054	10	1240	1306	DL	409	N368NW	LGA	MSP	135	1020	10	54	2023-05-01 10:00:00	Other
16794	10	12	1339	1340	-1	1600	1607	UA	875	N495UA	EWR	ATL	112	746	13	40	2023-10-12 13:00:00	ATL
16809	3	12	1425	1420	5	1629	1637	9E	1553	N295PQ	LGA	CHS	104	641	14	20	2023-03-12 14:00:00	Other
16810	5	18	2020	2020	0	2301	2255	WN	361	N415WN	LGA	DEN	228	1620	20	20	2023-05-18 20:00:00	Other
16815	6	25	815	815	0	1058	1121	DL	363	N706TW	JFK	SAN	324	2446	8	15	2023-06-25 08:00:00	Other
16820	8	28	2005	1959	6	2306	2254	AS	72	N922VA	EWR	LAX	320	2454	19	59	2023-08-28 19:00:00	LAX
16826	1	30	739	740	-1	1022	1041	UA	861	N37471	EWR	MCO	141	937	7	40	2023-01-30 07:00:00	MCO
16827	10	8	1109	1110	-1	1402	1420	DL	388	N312DN	JFK	FLL	155	1069	11	10	2023-10-08 11:00:00	FLL
16830	6	5	935	935	0	1237	1259	B6	589	N307JB	JFK	RSW	154	1074	9	35	2023-06-05 09:00:00	Other
16842	2	28	1116	1117	-1	1427	1415	UA	271	N37295	EWR	TPA	137	997	11	17	2023-02-28 11:00:00	Other
16846	11	26	1249	1250	-1	1403	1359	9E	1456	N678CA	JFK	ITH	48	189	12	50	2023-11-26 12:00:00	Other
16852	7	15	1101	1100	1	1438	1421	DL	266	N171DN	JFK	SFO	343	2586	11	0	2023-07-15 11:00:00	Other
16855	8	23	707	705	2	929	932	B6	125	N989JT	JFK	LAS	282	2248	7	5	2023-08-23 07:00:00	Other
16862	11	29	938	934	4	1215	1236	NK	430	N674NK	EWR	MCO	135	937	9	34	2023-11-29 09:00:00	MCO
16864	3	5	1835	1829	6	2139	2129	UA	309	N27477	EWR	TPA	140	997	18	29	2023-03-05 18:00:00	Other
16881	8	29	1612	1605	7	1850	1903	AA	798	N974AN	LGA	DFW	189	1389	16	5	2023-08-29 16:00:00	Other
16883	10	11	1853	1854	-1	2044	2029	AA	731	N806NN	LGA	ORD	119	733	18	54	2023-10-11 18:00:00	ORD
16887	3	11	1825	1825	0	2138	2151	AS	91	N413AS	EWR	SAN	352	2425	18	25	2023-03-11 18:00:00	Other
16891	5	29	600	600	0	820	850	WN	614	N8618N	LGA	DAL	175	1381	6	0	2023-05-29 06:00:00	Other
16895	12	27	2021	2020	1	2326	2354	B6	452	N3115J	JFK	AUS	222	1521	20	20	2023-12-27 20:00:00	Other
16922	12	22	800	800	0	955	1030	DL	533	N315NB	JFK	MSP	152	1029	8	0	2023-12-22 08:00:00	Other
16929	5	28	2147	2147	0	2243	2255	YX	1005	N760YX	EWR	MDT	29	141	21	47	2023-05-28 21:00:00	Other
16937	1	29	2236	2235	1	2350	2359	9E	1693	N538CA	JFK	BTV	47	266	22	35	2023-01-29 22:00:00	Other
16940	4	23	2007	2000	7	2157	2211	DL	726	N370NB	LGA	DTW	75	502	20	0	2023-04-23 20:00:00	Other
16943	9	23	1505	1506	-1	1614	1630	YX	1153	N747YX	EWR	BUF	47	282	15	6	2023-09-23 15:00:00	Other
16946	5	13	544	545	-1	730	752	NK	504	N530NK	LGA	CLT	81	544	5	45	2023-05-13 05:00:00	CLT
16950	9	22	1609	1600	9	1839	1905	AS	75	N553AS	EWR	SEA	297	2402	16	0	2023-09-22 16:00:00	Other
16951	12	28	1651	1650	1	1956	2044	DL	98	N515DE	JFK	PHX	265	2153	16	50	2023-12-28 16:00:00	Other
16953	1	31	735	730	5	1028	923	9E	1568	N920XJ	LGA	CLE	79	419	7	30	2023-01-31 07:00:00	Other
16955	8	18	1320	1314	6	1509	1518	YX	1021	N405YX	LGA	MSP	150	1020	13	14	2023-08-18 13:00:00	Other
16961	3	6	559	600	-1	807	755	DL	378	N105DX	LGA	DTW	86	502	6	0	2023-03-06 06:00:00	Other
16965	10	17	1135	1135	0	1303	1328	OO	1203	N257SY	JFK	ORD	110	740	11	35	2023-10-17 11:00:00	ORD
16966	11	6	1444	1436	8	1730	1744	UA	759	N78285	EWR	MIA	144	1085	14	36	2023-11-06 14:00:00	MIA
16978	11	14	1958	1955	3	2309	2320	DL	425	N3745B	LGA	RSW	153	1080	19	55	2023-11-14 19:00:00	Other
16980	1	19	1844	1835	9	2249	2150	AS	11	N272AK	JFK	SAN	338	2446	18	35	2023-01-19 18:00:00	Other
16989	1	25	1113	1106	7	1251	1242	UA	850	N429UA	EWR	BNA	130	748	11	6	2023-01-25 11:00:00	Other
16994	8	6	710	700	10	937	944	UA	257	N68807	EWR	MCO	124	937	7	0	2023-08-06 07:00:00	MCO
17008	3	19	1953	1945	8	2311	2304	NK	1019	N609NK	EWR	MIA	175	1085	19	45	2023-03-19 19:00:00	MIA
17009	10	20	630	630	0	944	938	UA	719	N791UA	EWR	SFO	307	2565	6	30	2023-10-20 06:00:00	Other
17010	8	9	1459	1459	0	1555	1615	B6	584	N216JB	JFK	HYA	37	196	14	59	2023-08-09 14:00:00	Other
17011	3	29	2136	2130	6	14	7	B6	481	N339JB	JFK	JAX	122	828	21	30	2023-03-29 21:00:00	Other
17025	8	16	1906	1859	7	2110	2208	AS	78	N287AK	EWR	SAN	287	2425	18	59	2023-08-16 18:00:00	Other
17039	10	24	649	650	-1	941	956	B6	766	N588JB	JFK	RSW	144	1074	6	50	2023-10-24 06:00:00	Other
17043	9	12	1453	1454	-1	1624	1639	UA	687	N451UA	EWR	RDU	67	416	14	54	2023-09-12 14:00:00	Other
17044	3	23	1824	1825	-1	2022	2020	WN	644	N417WN	LGA	STL	146	888	18	25	2023-03-23 18:00:00	Other
17046	4	14	1532	1525	7	NA	1843	AS	83	N924VA	EWR	LAX	NA	2454	15	25	2023-04-14 15:00:00	LAX
17049	3	14	1737	1728	9	2030	2020	UA	839	N68807	EWR	MCO	139	937	17	28	2023-03-14 17:00:00	MCO
17056	1	1	1606	1603	3	1845	1903	UA	425	N47281	EWR	MCO	134	937	16	3	2023-01-01 16:00:00	MCO
17060	5	7	629	630	-1	905	931	B6	925	N565JB	JFK	FLL	137	1069	6	30	2023-05-07 06:00:00	FLL
17061	12	19	1902	1900	2	2119	2141	DL	905	N945AT	EWR	ATL	102	746	19	0	2023-12-19 19:00:00	ATL
17062	3	10	825	825	0	953	1019	DL	853	N115DU	LGA	ORD	118	733	8	25	2023-03-10 08:00:00	ORD
17065	10	26	1102	1100	2	1315	1327	UA	228	N448UA	EWR	ATL	105	746	11	0	2023-10-26 11:00:00	ATL
17073	9	17	2008	2000	8	2259	2301	DL	632	N306DU	LGA	IAH	200	1416	20	0	2023-09-17 20:00:00	Other
17079	11	7	1139	1130	9	1428	1453	DL	986	N301DU	LGA	SRQ	149	1047	11	30	2023-11-07 11:00:00	Other
17084	5	19	1808	1800	8	2101	2111	UA	218	N28478	EWR	MIA	145	1085	18	0	2023-05-19 18:00:00	MIA
17085	4	28	2125	2120	5	2355	2358	DL	149	N126DN	LGA	ATL	112	762	21	20	2023-04-28 21:00:00	ATL
17097	4	19	1729	1730	-1	1920	1947	9E	1258	N914XJ	LGA	CVG	93	585	17	30	2023-04-19 17:00:00	Other
17103	7	3	2035	2030	5	141	18	AA	768	N102NN	JFK	SFO	337	2586	20	30	2023-07-03 20:00:00	Other
17109	2	23	1634	1635	-1	1752	1808	YX	1517	N824MD	LGA	DCA	54	214	16	35	2023-02-23 16:00:00	Other
17120	5	16	1435	1430	5	1643	1655	WN	958	N8543Z	LGA	ATL	108	762	14	30	2023-05-16 14:00:00	ATL
17126	9	22	1347	1339	8	1636	1645	B6	449	N591JB	JFK	AUS	200	1521	13	39	2023-09-22 13:00:00	Other
17133	4	14	2159	2159	0	2332	2336	UA	485	N27258	EWR	ORD	100	719	21	59	2023-04-14 21:00:00	ORD
17134	10	17	1949	1944	5	2246	2329	DL	321	N171DN	JFK	SFO	332	2586	19	44	2023-10-17 19:00:00	Other
17136	10	24	1147	1140	7	1416	1425	WN	768	N8731J	LGA	DAL	191	1381	11	40	2023-10-24 11:00:00	Other
17140	5	2	1519	1520	-1	1644	1655	9E	1437	N491PX	LGA	MKE	111	738	15	20	2023-05-02 15:00:00	Other
17141	2	19	1649	1650	-1	1943	1947	DL	880	N393DA	LGA	DEN	257	1620	16	50	2023-02-19 16:00:00	Other
17157	3	30	2004	2005	-1	2257	2313	B6	642	N627JB	JFK	PBI	131	1028	20	5	2023-03-30 20:00:00	Other
17165	4	11	1635	1635	0	1900	2013	DL	215	N850DN	JFK	SLC	245	1990	16	35	2023-04-11 16:00:00	Other
17173	11	7	1100	1100	0	1444	1420	DL	175	N511DE	JFK	SEA	359	2422	11	0	2023-11-07 11:00:00	Other
17202	2	13	617	615	2	933	928	UA	322	N223UA	EWR	SFO	320	2565	6	15	2023-02-13 06:00:00	Other
17210	1	24	1824	1825	-1	2031	2016	DL	423	N124DU	LGA	ORD	132	733	18	25	2023-01-24 18:00:00	ORD
17211	4	3	1547	1545	2	1841	1824	DL	310	N303DN	LGA	ATL	120	762	15	45	2023-04-03 15:00:00	ATL
17216	5	22	1431	1430	1	1554	1602	B6	956	N184JB	JFK	BUF	53	301	14	30	2023-05-22 14:00:00	Other
17221	7	27	659	700	-1	822	830	YX	1339	N205JQ	JFK	BOS	42	187	7	0	2023-07-27 07:00:00	BOS
17240	2	10	618	615	3	858	928	UA	322	N788UA	EWR	SFO	318	2565	6	15	2023-02-10 06:00:00	Other
17278	1	27	839	840	-1	1214	1201	UA	652	N76508	EWR	FLL	171	1065	8	40	2023-01-27 08:00:00	FLL
17280	5	14	1230	1229	1	1519	1548	B6	325	N746JB	JFK	SLC	259	1990	12	29	2023-05-14 12:00:00	Other
17294	6	21	2255	2250	5	44	21	9E	1735	N293PQ	JFK	SYR	40	209	22	50	2023-06-21 22:00:00	Other
17295	1	13	801	800	1	1020	1058	UA	444	N18112	EWR	EGE	225	1725	8	0	2023-01-13 08:00:00	Other
17299	11	4	2235	2229	6	121	153	B6	655	N979JT	JFK	LAX	321	2475	22	29	2023-11-04 22:00:00	LAX
17300	7	19	2027	2023	4	2309	2257	UA	638	N87527	EWR	LAS	301	2227	20	23	2023-07-19 20:00:00	Other
17302	12	8	512	510	2	758	825	AA	411	N979AN	EWR	MIA	144	1085	5	10	2023-12-08 05:00:00	MIA
17310	4	5	1454	1449	5	1754	1750	UA	74	N37277	EWR	PBI	144	1023	14	49	2023-04-05 14:00:00	Other
17312	7	3	1200	1155	5	1420	1418	YX	999	N135HQ	JFK	IND	110	665	11	55	2023-07-03 11:00:00	Other
17315	1	8	625	625	0	755	810	WN	1101	N930WN	LGA	BNA	129	764	6	25	2023-01-08 06:00:00	Other
17318	4	13	1745	1744	1	1901	1918	YX	960	N654RW	EWR	PIT	54	319	17	44	2023-04-13 17:00:00	Other
17322	3	11	1315	1315	0	1418	1425	B6	833	N190JB	LGA	BOS	47	184	13	15	2023-03-11 13:00:00	BOS
17323	3	8	755	745	10	1225	1246	B6	613	N586JB	EWR	SJU	183	1608	7	45	2023-03-08 07:00:00	Other
17328	3	22	1158	1159	-1	1441	1505	UA	750	N17254	EWR	IAH	199	1400	11	59	2023-03-22 11:00:00	Other
17330	2	1	830	825	5	1113	1024	DL	611	N126DU	LGA	ORD	133	733	8	25	2023-02-01 08:00:00	ORD
17333	9	11	631	630	1	908	852	B6	245	N658JB	JFK	JAX	125	828	6	30	2023-09-11 06:00:00	Other
17340	11	19	1455	1453	2	1734	1804	NK	848	N976NK	EWR	FLL	141	1065	14	53	2023-11-19 14:00:00	FLL
17348	4	7	2014	2015	-1	2321	2320	WN	605	N8688J	LGA	DAL	203	1381	20	15	2023-04-07 20:00:00	Other
17352	10	17	1832	1825	7	2131	2125	WN	1198	N8899H	LGA	TPA	141	1010	18	25	2023-10-17 18:00:00	Other
17357	9	17	1000	1000	0	1146	1140	AA	982	N767UW	LGA	ORD	125	733	10	0	2023-09-17 10:00:00	ORD
17359	3	17	1104	1103	1	1330	1356	UA	589	N27268	EWR	LAS	297	2227	11	3	2023-03-17 11:00:00	Other
17367	7	1	1259	1300	-1	1412	1426	YX	1390	N218JQ	LGA	BOS	47	184	13	0	2023-07-01 13:00:00	BOS
17372	6	4	929	930	-1	1205	1235	AS	9	N534AS	JFK	SEA	295	2422	9	30	2023-06-04 09:00:00	Other
17376	2	8	2035	2029	6	2320	2338	B6	658	N547JB	LGA	PBI	147	1035	20	29	2023-02-08 20:00:00	Other
17378	5	20	2133	2129	4	39	19	UA	65	N14250	EWR	MCO	128	937	21	29	2023-05-20 21:00:00	MCO
17380	7	6	2029	2030	-1	2242	2247	UA	723	N27277	EWR	MSY	151	1167	20	30	2023-07-06 20:00:00	Other
17383	1	17	1033	1029	4	1238	1254	YX	1786	N823MD	LGA	CLT	96	544	10	29	2023-01-17 10:00:00	CLT
17399	1	4	600	600	0	848	905	WN	483	N411WN	LGA	DAL	215	1381	6	0	2023-01-04 06:00:00	Other
17419	6	22	1905	1858	7	2102	2108	YX	1128	N646RW	EWR	GSP	97	594	18	58	2023-06-22 18:00:00	Other
17423	4	11	1038	1030	8	1157	1216	B6	83	N179JB	JFK	RDU	64	427	10	30	2023-04-11 10:00:00	Other
17435	1	5	2030	2029	1	2324	2305	UA	580	N826UA	EWR	ATL	118	746	20	29	2023-01-05 20:00:00	ATL
17445	11	19	1621	1615	6	1721	1738	B6	360	N339JB	LGA	BOS	38	184	16	15	2023-11-19 16:00:00	BOS
17446	9	18	934	930	4	1246	1243	AA	822	N330TJ	LGA	MIA	156	1096	9	30	2023-09-18 09:00:00	MIA
17458	2	5	2019	2020	-1	2213	2221	YX	1519	N860RW	LGA	CMH	82	479	20	20	2023-02-05 20:00:00	Other
17462	4	22	1507	1459	8	1656	1705	DL	528	N315NB	LGA	MSP	132	1020	14	59	2023-04-22 14:00:00	Other
17464	2	1	707	700	7	1157	1050	DL	267	N907DN	JFK	PHX	341	2153	7	0	2023-02-01 07:00:00	Other
17465	1	27	1300	1300	0	1605	1626	B6	44	N655JB	JFK	RSW	156	1074	13	0	2023-01-27 13:00:00	Other
17467	6	1	1329	1330	-1	1604	1624	B6	570	N715JB	JFK	MCO	134	944	13	30	2023-06-01 13:00:00	MCO
17472	6	7	1511	1510	1	1819	1820	DL	840	N397DN	JFK	MCO	154	944	15	10	2023-06-07 15:00:00	MCO
17482	3	18	1459	1455	4	1618	1611	OO	1277	N293SY	JFK	BWI	43	184	14	55	2023-03-18 14:00:00	Other
17496	4	8	821	815	6	1037	1102	UA	227	N443UA	EWR	LAS	294	2227	8	15	2023-04-08 08:00:00	Other
17497	2	2	659	700	-1	1028	1025	DL	211	N177DN	JFK	LAX	355	2475	7	0	2023-02-02 07:00:00	LAX
17502	3	4	1852	1848	4	2148	2140	UA	660	N26208	EWR	MCO	137	937	18	48	2023-03-04 18:00:00	MCO
17505	11	10	1606	1559	7	1831	1827	DL	879	N887DN	EWR	ATL	116	746	15	59	2023-11-10 15:00:00	ATL
17513	8	14	1929	1929	0	2235	2308	DL	183	N534DT	JFK	SEA	314	2422	19	29	2023-08-14 19:00:00	Other
17517	11	3	901	900	1	1028	1054	AA	970	N968AN	JFK	ORD	125	740	9	0	2023-11-03 09:00:00	ORD
17538	9	15	1729	1730	-1	1920	1908	9E	1649	N931XJ	JFK	BUF	50	301	17	30	2023-09-15 17:00:00	Other
17552	4	21	1509	1510	-1	1811	1830	B6	774	N228JB	LGA	SRQ	149	1047	15	10	2023-04-21 15:00:00	Other
17555	7	11	2009	2010	-1	2208	2242	B6	30	N517JB	JFK	DEN	217	1626	20	10	2023-07-11 20:00:00	Other
17559	12	21	709	700	9	930	928	DL	978	N925DZ	EWR	ATL	103	746	7	0	2023-12-21 07:00:00	ATL
17564	5	20	1945	1935	10	2238	2245	B6	26	N784JB	JFK	ABQ	248	1826	19	35	2023-05-20 19:00:00	Other
17575	7	9	950	950	0	1237	1206	9E	1248	N605LR	JFK	IND	117	665	9	50	2023-07-09 09:00:00	Other
17582	6	2	939	930	9	1208	1235	AS	9	N516AS	JFK	SEA	291	2422	9	30	2023-06-02 09:00:00	Other
17584	2	18	1134	1135	-1	1236	1245	UA	625	N14115	EWR	BOS	39	200	11	35	2023-02-18 11:00:00	BOS
17591	3	2	1612	1613	-1	1718	1728	UA	143	N27261	EWR	BOS	38	200	16	13	2023-03-02 16:00:00	BOS
17595	12	7	800	800	0	1049	1113	AA	341	N865NN	LGA	MIA	143	1096	8	0	2023-12-07 08:00:00	MIA
17607	4	20	1800	1759	1	2119	2116	B6	895	N520JB	JFK	FLL	156	1069	17	59	2023-04-20 17:00:00	FLL
17616	4	19	2139	2140	-1	139	134	DL	111	N706TW	JFK	SFO	361	2586	21	40	2023-04-19 21:00:00	Other
17624	10	22	1204	1200	4	1447	1452	UA	801	N781UA	EWR	LAX	316	2454	12	0	2023-10-22 12:00:00	LAX
17657	5	4	1400	1400	0	1541	1520	YX	1606	N221JQ	LGA	BOS	50	184	14	0	2023-05-04 14:00:00	BOS
17660	4	22	1629	1629	0	1806	1809	AA	827	N869NN	LGA	ORD	112	733	16	29	2023-04-22 16:00:00	ORD
17666	7	18	838	829	9	953	958	9E	1133	N479PX	LGA	ROC	47	254	8	29	2023-07-18 08:00:00	Other
17671	10	21	615	615	0	851	909	UA	656	N78524	EWR	TPA	133	997	6	15	2023-10-21 06:00:00	Other
17678	8	3	1650	1650	0	1848	1900	WN	686	N8642E	LGA	MCI	156	1107	16	50	2023-08-03 16:00:00	Other
17682	3	14	1722	1722	0	2052	2037	UA	68	N77539	EWR	SMF	346	2500	17	22	2023-03-14 17:00:00	Other
17685	9	12	1657	1655	2	1900	1920	UA	946	N38417	EWR	DEN	223	1605	16	55	2023-09-12 16:00:00	Other
17703	6	27	900	900	0	958	1025	WN	57	N8301J	LGA	MDW	103	725	9	0	2023-06-27 09:00:00	Other
17706	2	19	1005	1000	5	1255	1310	B6	917	N569JB	JFK	TPA	147	1005	10	0	2023-02-19 10:00:00	Other
17710	5	21	1454	1453	1	1650	1648	UA	360	N427UA	EWR	CLT	84	529	14	53	2023-05-21 14:00:00	CLT
17711	9	10	1600	1600	0	1852	1905	AS	75	N293AK	EWR	SEA	313	2402	16	0	2023-09-10 16:00:00	Other
17720	5	14	1457	1455	2	1651	1645	WN	845	N8574Z	LGA	STL	129	888	14	55	2023-05-14 14:00:00	Other
17727	3	21	619	620	-1	755	807	9E	1604	N336PQ	LGA	RDU	73	431	6	20	2023-03-21 06:00:00	Other
17728	9	13	1515	1515	0	1719	1751	DL	239	N863DN	JFK	DEN	216	1626	15	15	2023-09-13 15:00:00	Other
17736	2	14	1833	1825	8	2146	2141	AA	153	N947NN	JFK	MIA	150	1089	18	25	2023-02-14 18:00:00	MIA
17738	3	16	743	735	8	1030	1043	UA	277	N659UA	EWR	IAH	186	1400	7	35	2023-03-16 07:00:00	Other
17742	11	19	1526	1526	0	1712	1726	YX	1782	N234JQ	JFK	CMH	77	483	15	26	2023-11-19 15:00:00	Other
17745	11	9	1507	1459	8	1719	1726	DL	501	N966AT	EWR	ATL	107	746	14	59	2023-11-09 14:00:00	ATL
17748	7	12	2034	2030	4	2220	2211	DL	370	N138DU	LGA	ORD	119	733	20	30	2023-07-12 20:00:00	ORD
17756	12	2	2159	2159	0	2343	2350	B6	494	N284JB	JFK	RDU	78	427	21	59	2023-12-02 21:00:00	Other
17764	5	12	1929	1929	0	2255	2258	B6	349	N570JB	JFK	PDX	350	2454	19	29	2023-05-12 19:00:00	Other
17768	5	26	1847	1837	10	2113	2055	YX	1614	N238JQ	LGA	CLT	87	544	18	37	2023-05-26 18:00:00	CLT
17773	4	10	2030	2029	1	2341	2352	DL	565	N3765	JFK	RSW	147	1074	20	29	2023-04-10 20:00:00	Other
17778	9	9	1247	1245	2	1532	1458	YX	1800	N204JQ	LGA	CLT	110	544	12	45	2023-09-09 12:00:00	CLT
17781	2	18	1733	1729	4	2059	2059	B6	914	N993JE	JFK	LAX	355	2475	17	29	2023-02-18 17:00:00	LAX
17789	9	21	1733	1729	4	2033	2035	AA	38	N111ZM	JFK	LAX	333	2475	17	29	2023-09-21 17:00:00	LAX
17808	4	19	1659	1700	-1	2003	2025	DL	259	N174DN	JFK	LAX	335	2475	17	0	2023-04-19 17:00:00	LAX
17813	3	17	1820	1820	0	2115	2125	B6	276	N653JB	LGA	MCO	141	950	18	20	2023-03-17 18:00:00	MCO
17819	12	16	1511	1510	1	1817	1845	DL	151	N527DE	JFK	SEA	335	2422	15	10	2023-12-16 15:00:00	Other
17822	2	16	1425	1425	0	1617	1625	9E	1439	N200PQ	LGA	GSO	82	461	14	25	2023-02-16 14:00:00	Other
17834	6	17	1829	1830	-1	1930	1955	WN	240	N8643A	LGA	MDW	106	725	18	30	2023-06-17 18:00:00	Other
17835	10	29	1809	1810	-1	2123	2120	UA	883	N786UA	EWR	LAX	336	2454	18	10	2023-10-29 18:00:00	LAX
17848	3	10	1304	1300	4	1512	1502	AA	639	N560UW	LGA	CLT	93	544	13	0	2023-03-10 13:00:00	CLT
17862	12	24	1224	1223	1	1359	1420	NK	30	N985NK	EWR	MYR	77	550	12	23	2023-12-24 12:00:00	Other
17868	1	27	1714	1715	-1	2034	2044	DL	297	N183DN	JFK	LAX	348	2475	17	15	2023-01-27 17:00:00	LAX
17874	10	26	1814	1815	-1	2025	1958	DL	607	N101DU	LGA	ORD	117	733	18	15	2023-10-26 18:00:00	ORD
17878	4	3	1609	1600	9	1941	1934	AS	90	N942AK	EWR	SFO	363	2565	16	0	2023-04-03 16:00:00	Other
17885	5	20	1203	1159	4	1403	1423	UA	857	N69810	EWR	DEN	215	1605	11	59	2023-05-20 11:00:00	Other
17887	1	18	1559	1600	-1	1932	1957	DL	464	N195DN	JFK	SFO	359	2586	16	0	2023-01-18 16:00:00	Other
17888	4	2	1540	1540	0	1706	1720	B6	258	N3102J	JFK	MKE	125	745	15	40	2023-04-02 15:00:00	Other
17900	6	3	1959	1959	0	2303	2325	DL	152	N874DN	JFK	PDX	298	2454	19	59	2023-06-03 19:00:00	Other
17922	9	16	1545	1545	0	1831	1845	B6	541	N665JB	JFK	MCO	131	944	15	45	2023-09-16 15:00:00	MCO
17928	8	2	1046	1045	1	1216	1220	WN	950	N7815L	LGA	STL	129	888	10	45	2023-08-02 10:00:00	Other
17936	6	5	1720	1720	0	1929	1954	B6	153	N729JB	JFK	ATL	105	760	17	20	2023-06-05 17:00:00	ATL
17956	12	22	800	800	0	1029	1051	UA	864	N17326	EWR	HDN	235	1728	8	0	2023-12-22 08:00:00	Other
17969	6	26	1118	1118	0	1411	1430	DL	1029	N125DU	LGA	SRQ	140	1047	11	18	2023-06-26 11:00:00	Other
17983	4	7	1631	1629	2	1833	1818	DL	436	N125DU	LGA	ORD	130	733	16	29	2023-04-07 16:00:00	ORD
17992	8	9	2006	1959	7	2259	2305	AS	72	N924VA	EWR	LAX	316	2454	19	59	2023-08-09 19:00:00	LAX
17993	11	21	709	710	-1	1028	1035	DL	309	N541DE	JFK	SEA	335	2422	7	10	2023-11-21 07:00:00	Other
17999	2	6	1757	1750	7	2032	2035	WN	769	N281WN	LGA	ATL	107	762	17	50	2023-02-06 17:00:00	ATL
18012	6	28	1929	1930	-1	2239	2257	B6	376	N607JB	JFK	PDX	323	2454	19	30	2023-06-28 19:00:00	Other
18017	2	11	1037	1037	0	1328	1340	UA	413	N470UA	EWR	SRQ	159	1034	10	37	2023-02-11 10:00:00	Other
18026	5	31	705	705	0	850	924	DL	780	N351NB	JFK	MSP	145	1029	7	5	2023-05-31 07:00:00	Other
18045	7	12	845	845	0	1048	1118	9E	1188	N601LR	LGA	SAV	95	722	8	45	2023-07-12 08:00:00	Other
18048	2	14	830	830	0	1008	1011	AA	128	N920NN	LGA	ORD	116	733	8	30	2023-02-14 08:00:00	ORD
18058	6	27	1048	1040	8	1257	1300	WN	1008	N489WN	LGA	ATL	108	762	10	40	2023-06-27 10:00:00	ATL
18070	10	14	1525	1525	0	1722	1722	YX	1772	N227JQ	JFK	PIT	71	340	15	25	2023-10-14 15:00:00	Other
18073	11	30	1417	1417	0	1646	1659	YX	1854	N231JQ	JFK	JAX	128	828	14	17	2023-11-30 14:00:00	Other
18081	5	21	714	712	2	955	1013	DL	350	N337NB	LGA	PBI	139	1035	7	12	2023-05-21 07:00:00	Other
18084	8	4	1043	1040	3	1202	1215	9E	1288	N923XJ	LGA	BNA	113	764	10	40	2023-08-04 10:00:00	Other
18086	5	17	1145	1145	0	1423	1446	AS	8	N403AS	JFK	PDX	315	2454	11	45	2023-05-17 11:00:00	Other
18095	3	21	2147	2142	5	10	2359	UA	314	N15710	EWR	SAV	109	708	21	42	2023-03-21 21:00:00	Other
18099	9	16	1434	1434	0	1606	1556	B6	931	N368JB	JFK	BUF	53	301	14	34	2023-09-16 14:00:00	Other
18109	6	3	1029	1030	-1	1147	1140	B6	996	N306JB	JFK	BOS	36	187	10	30	2023-06-03 10:00:00	BOS
18111	4	24	800	750	10	1012	1036	UA	227	N69829	EWR	LAS	292	2227	7	50	2023-04-24 07:00:00	Other
18119	5	9	656	655	1	827	830	AA	313	N952AA	EWR	ORD	110	719	6	55	2023-05-09 06:00:00	ORD
18122	11	5	1853	1848	5	2048	2048	9E	1406	N320PQ	LGA	STL	132	888	18	48	2023-11-05 18:00:00	Other
18123	9	8	910	910	0	1103	1129	9E	1716	N299PQ	LGA	CVG	85	585	9	10	2023-09-08 09:00:00	Other
18125	8	17	1130	1130	0	1243	1255	UA	383	N53442	EWR	BNA	100	748	11	30	2023-08-17 11:00:00	Other
18126	9	6	1714	1715	-1	1842	1851	UA	546	N54711	LGA	ORD	104	733	17	15	2023-09-06 17:00:00	ORD
18127	3	26	2108	2059	9	2337	2318	YX	1173	N724YX	EWR	IND	114	645	20	59	2023-03-26 20:00:00	Other
18135	3	7	759	800	-1	1131	1135	DL	333	N3741S	JFK	SAN	365	2446	8	0	2023-03-07 08:00:00	Other
18137	12	18	759	759	0	1107	1116	UA	686	N27520	EWR	MIA	152	1085	7	59	2023-12-18 07:00:00	MIA
18144	11	28	2003	1957	6	2255	2243	DL	402	N303DN	JFK	ATL	110	760	19	57	2023-11-28 19:00:00	ATL
18147	7	24	758	759	-1	1129	1110	AA	502	N335SN	JFK	MIA	158	1089	7	59	2023-07-24 07:00:00	MIA
18158	3	31	810	800	10	906	922	YX	1749	N245JQ	LGA	BOS	36	184	8	0	2023-03-31 08:00:00	BOS
18163	10	12	759	800	-1	1056	1107	UA	567	N17139	EWR	FLL	145	1065	8	0	2023-10-12 08:00:00	FLL
18174	9	25	1559	1600	-1	1754	1754	OO	1255	N261SY	JFK	ORD	118	740	16	0	2023-09-25 16:00:00	ORD
18180	7	17	506	501	5	838	843	B6	748	N999JQ	JFK	BQN	197	1576	5	1	2023-07-17 05:00:00	Other
18186	8	27	1450	1448	2	1641	1655	AA	436	N802NN	JFK	CLT	80	541	14	48	2023-08-27 14:00:00	CLT
18191	4	13	2101	2055	6	2309	2308	UA	474	N837UA	EWR	CVG	86	569	20	55	2023-04-13 20:00:00	Other
18195	12	22	1429	1430	-1	1636	1650	YX	1228	N435YX	JFK	CVG	104	589	14	30	2023-12-22 14:00:00	Other
18197	9	6	703	700	3	951	952	UA	417	N808UA	EWR	SRQ	143	1034	7	0	2023-09-06 07:00:00	Other
18201	6	3	1916	1913	3	2157	2208	UA	663	N37521	EWR	MCO	131	937	19	13	2023-06-03 19:00:00	MCO
18210	3	29	1734	1729	5	2037	2053	AA	974	N341RW	JFK	AUS	217	1521	17	29	2023-03-29 17:00:00	Other
18221	10	1	2059	2059	0	2219	2222	UA	337	N422UA	EWR	IAD	38	212	20	59	2023-10-01 20:00:00	Other
18222	11	12	603	600	3	842	820	DL	820	N935AT	EWR	ATL	128	746	6	0	2023-11-12 06:00:00	ATL
18224	5	29	1545	1545	0	1839	1903	DL	236	N197DN	JFK	LAX	310	2475	15	45	2023-05-29 15:00:00	LAX
18233	10	14	1134	1125	9	1432	1345	B6	13	N779JB	JFK	PHX	307	2153	11	25	2023-10-14 11:00:00	Other
18234	4	21	1551	1550	1	1700	1730	B6	258	N3008J	JFK	MKE	108	745	15	50	2023-04-21 15:00:00	Other
18240	5	17	1801	1759	2	2125	2146	AA	917	N106NN	JFK	SFO	342	2586	17	59	2023-05-17 17:00:00	Other
18245	8	5	1024	1025	-1	1154	1200	UA	539	N17309	EWR	ORD	113	719	10	25	2023-08-05 10:00:00	ORD
18259	10	31	605	605	0	919	855	WN	317	N8696E	LGA	DAL	228	1381	6	5	2023-10-31 06:00:00	Other
18261	10	24	1327	1325	2	1615	1632	B6	110	N536JB	LGA	FLL	144	1076	13	25	2023-10-24 13:00:00	FLL
18279	9	5	1531	1530	1	1825	1832	UA	488	N14115	EWR	LAX	313	2454	15	30	2023-09-05 15:00:00	LAX
18308	6	14	1434	1429	5	1740	1730	B6	191	N768JB	EWR	FLL	154	1065	14	29	2023-06-14 14:00:00	FLL
18309	11	27	1617	1615	2	1709	1738	B6	360	N328JB	LGA	BOS	32	184	16	15	2023-11-27 16:00:00	BOS
18315	10	15	759	800	-1	1002	1029	DL	168	N523DE	JFK	DEN	218	1626	8	0	2023-10-15 08:00:00	Other
18320	6	3	947	945	2	1259	1240	B6	998	N729JB	JFK	TPA	140	1005	9	45	2023-06-03 09:00:00	Other
18329	9	27	805	800	5	1105	1134	DL	293	N717TW	JFK	SFO	323	2586	8	0	2023-09-27 08:00:00	Other
18334	6	6	609	610	-1	714	725	WN	600	N449WN	LGA	MDW	102	725	6	10	2023-06-06 06:00:00	Other
18341	7	22	1021	1020	1	1129	1137	YX	1354	N230JQ	LGA	MVY	36	175	10	20	2023-07-22 10:00:00	Other
18349	3	22	2244	2245	-1	114	144	F9	513	N378FR	LGA	MCO	124	950	22	45	2023-03-22 22:00:00	MCO
18359	8	24	1744	1745	-1	1952	1923	AA	506	N947AN	EWR	ORD	118	719	17	45	2023-08-24 17:00:00	ORD
18363	2	5	2030	2025	5	2351	2350	AS	85	N926VA	EWR	LAX	354	2454	20	25	2023-02-05 20:00:00	LAX
18371	12	5	1925	1920	5	2207	2306	AS	82	N947AK	EWR	SFO	320	2565	19	20	2023-12-05 19:00:00	Other
18376	10	25	2112	2113	-1	2302	2317	UA	544	N17244	EWR	CHS	81	628	21	13	2023-10-25 21:00:00	Other
18377	6	29	1802	1800	2	1954	2015	9E	1570	N480PX	LGA	TYS	84	647	18	0	2023-06-29 18:00:00	Other
18379	3	25	1854	1850	4	2236	2024	YX	1208	N740YX	EWR	PIT	NA	319	18	50	2023-03-25 18:00:00	Other
18397	7	23	1131	1130	1	1422	1419	UA	470	N429UA	EWR	MCO	142	937	11	30	2023-07-23 11:00:00	MCO
18403	7	22	726	722	4	1014	1015	UA	738	N27246	EWR	SNA	325	2434	7	22	2023-07-22 07:00:00	Other
18410	6	30	2116	2110	6	2231	2235	WN	1228	N209WN	LGA	MDW	108	725	21	10	2023-06-30 21:00:00	Other
18422	4	3	1533	1529	4	1827	1829	DL	446	N386DN	LGA	MCO	137	950	15	29	2023-04-03 15:00:00	MCO
18425	2	1	1829	1830	-1	2207	2206	B6	66	N976JT	JFK	LAX	370	2475	18	30	2023-02-01 18:00:00	LAX
18428	6	29	920	915	5	1118	1114	9E	1666	N604LR	LGA	ILM	71	500	9	15	2023-06-29 09:00:00	Other
18443	5	22	559	600	-1	821	825	DL	750	N705TW	JFK	ATL	115	760	6	0	2023-05-22 06:00:00	ATL
18457	4	14	1436	1429	7	1651	1702	DL	144	N360DN	LGA	ATL	115	762	14	29	2023-04-14 14:00:00	ATL
18463	10	19	735	735	0	1036	1045	AA	777	N917AN	JFK	MIA	150	1089	7	35	2023-10-19 07:00:00	MIA
18466	10	27	804	759	5	1010	1013	YX	1362	N439YX	LGA	CVG	103	585	7	59	2023-10-27 07:00:00	Other
18468	9	2	1316	1312	4	1550	1541	UA	120	N14102	EWR	LAS	278	2227	13	12	2023-09-02 13:00:00	Other
18470	3	24	1518	1519	-1	1626	1659	YX	1736	N205JQ	JFK	DCA	49	213	15	19	2023-03-24 15:00:00	Other
18472	6	8	959	1000	-1	1246	1304	UA	837	N776UA	EWR	SFO	303	2565	10	0	2023-06-08 10:00:00	Other
18474	2	7	1559	1600	-1	1705	1725	YX	1570	N204JQ	LGA	BOS	32	184	16	0	2023-02-07 16:00:00	BOS
18479	10	6	1339	1329	10	1641	1639	AA	57	N956NN	JFK	MIA	151	1089	13	29	2023-10-06 13:00:00	MIA
18482	12	3	1644	1645	-1	1802	1813	B6	508	N206JB	JFK	BOS	41	187	16	45	2023-12-03 16:00:00	BOS
18487	4	21	846	838	8	1134	1152	UA	291	N33103	EWR	SAN	324	2425	8	38	2023-04-21 08:00:00	Other
18495	4	13	2140	2138	2	2358	15	NK	262	N964NK	EWR	LAS	289	2227	21	38	2023-04-13 21:00:00	Other
18501	11	20	1858	1856	2	2200	2203	DL	811	N111DC	LGA	TPA	148	1010	18	56	2023-11-20 18:00:00	Other
18505	10	9	2107	2108	-1	2252	2308	NK	1015	N651NK	EWR	DTW	77	488	21	8	2023-10-09 21:00:00	Other
18511	9	1	1942	1935	7	2217	2240	DL	141	N177DN	JFK	LAX	298	2475	19	35	2023-09-01 19:00:00	LAX
18513	6	24	1354	1355	-1	1724	1655	DL	311	N177DN	JFK	LAX	346	2475	13	55	2023-06-24 13:00:00	LAX
18520	10	12	901	900	1	1043	1032	YX	1180	N656RW	EWR	ORF	50	284	9	0	2023-10-12 09:00:00	Other
18525	1	6	1354	1355	-1	1623	1637	NK	420	N926NK	EWR	LAS	312	2227	13	55	2023-01-06 13:00:00	Other
18540	10	9	2014	2015	-1	2234	2246	B6	893	N605JB	LGA	ATL	112	762	20	15	2023-10-09 20:00:00	ATL
18544	5	16	939	940	-1	1122	1140	DL	950	N998AT	EWR	DTW	80	488	9	40	2023-05-16 09:00:00	Other
18546	3	31	1729	1730	-1	2031	2039	AS	87	N973AK	EWR	PDX	338	2434	17	30	2023-03-31 17:00:00	Other
18558	10	18	1416	1410	6	1700	1705	NK	71	N925NK	EWR	DFW	195	1372	14	10	2023-10-18 14:00:00	Other
18561	5	4	852	850	2	1102	1047	9E	1359	N479PX	LGA	RDU	75	431	8	50	2023-05-04 08:00:00	Other
18567	11	1	828	829	-1	951	943	YX	1391	N446YX	LGA	BUF	53	292	8	29	2023-11-01 08:00:00	Other
18571	9	24	957	955	2	1434	1455	DL	72	N174DZ	JFK	HNL	607	4983	9	55	2023-09-24 09:00:00	Other
18578	6	28	829	830	-1	1141	1140	UA	525	N18119	EWR	SEA	319	2402	8	30	2023-06-28 08:00:00	Other
18582	11	20	1925	1920	5	2208	2254	AS	88	N917AK	EWR	SFO	314	2565	19	20	2023-11-20 19:00:00	Other
18591	10	8	1730	1729	1	2016	2037	AA	36	N108NN	JFK	LAX	314	2475	17	29	2023-10-08 17:00:00	LAX
18594	8	31	1048	1038	10	1345	1345	B6	272	N659JB	JFK	SLC	266	1990	10	38	2023-08-31 10:00:00	Other
18610	2	9	1629	1630	-1	1917	1959	DL	179	N387DA	JFK	SAN	324	2446	16	30	2023-02-09 16:00:00	Other
18611	6	6	1705	1700	5	1930	1934	UA	885	N17265	EWR	LAS	277	2227	17	0	2023-06-06 17:00:00	Other
18613	4	17	1847	1845	2	2009	2020	YX	1057	N736YX	EWR	PIT	55	319	18	45	2023-04-17 18:00:00	Other
18615	6	29	1231	1225	6	1435	1347	AA	1025	N833AW	LGA	BNA	160	764	12	25	2023-06-29 12:00:00	Other
18618	5	31	1644	1645	-1	1928	2004	DL	254	N844MH	JFK	LAX	303	2475	16	45	2023-05-31 16:00:00	LAX
18625	10	6	1600	1550	10	1806	1807	9E	1604	N298PQ	LGA	CHS	95	641	15	50	2023-10-06 15:00:00	Other
18638	10	7	1317	1315	2	1533	1520	DL	752	N376NW	LGA	DTW	79	502	13	15	2023-10-07 13:00:00	Other
18645	9	29	1406	1401	5	1630	1648	UA	489	N426UA	EWR	DFW	178	1372	14	1	2023-09-29 14:00:00	Other
18657	12	9	1224	1225	-1	1335	1353	YX	1234	N103HQ	LGA	DCA	49	214	12	25	2023-12-09 12:00:00	Other
18660	11	9	1350	1340	10	1523	1510	9E	1415	N132EV	JFK	ORF	57	290	13	40	2023-11-09 13:00:00	Other
18678	4	15	1019	1020	-1	1245	1312	UA	652	N45956	EWR	IAH	178	1400	10	20	2023-04-15 10:00:00	Other
18693	1	12	856	855	1	1100	1100	9E	1482	N336PQ	LGA	RDU	73	431	8	55	2023-01-12 08:00:00	Other
18703	9	5	1937	1929	8	2144	2136	YX	1190	N736YX	EWR	DTW	82	488	19	29	2023-09-05 19:00:00	Other
18708	5	10	1827	1819	8	2139	2159	B6	245	N588JB	JFK	SJC	347	2569	18	19	2023-05-10 18:00:00	Other
18709	7	28	1507	1459	8	1608	1611	YX	897	N657RW	EWR	ALB	32	143	14	59	2023-07-28 14:00:00	Other
18712	3	22	959	959	0	1302	1304	UA	437	N39297	EWR	FLL	137	1065	9	59	2023-03-22 09:00:00	FLL
18714	4	13	1853	1849	4	2145	2204	UA	532	N61887	EWR	PDX	321	2434	18	49	2023-04-13 18:00:00	Other
18717	11	2	2031	2025	6	2315	2313	DL	819	N128DU	JFK	JAX	130	828	20	25	2023-11-02 20:00:00	Other
18719	1	20	1404	1402	2	1633	1637	UA	323	N840UA	EWR	ATL	118	746	14	2	2023-01-20 14:00:00	ATL
18729	7	31	1702	1700	2	1826	1820	AA	346	N832AW	LGA	DCA	59	214	17	0	2023-07-31 17:00:00	Other
18730	6	7	2004	2000	4	2248	2313	UA	787	N14731	EWR	SEA	298	2402	20	0	2023-06-07 20:00:00	Other
18737	4	15	1200	1155	5	1442	1441	UA	275	N37252	EWR	MCO	131	937	11	55	2023-04-15 11:00:00	MCO
18747	5	7	1114	1110	4	1319	1335	YX	1277	N101HQ	JFK	IND	101	665	11	10	2023-05-07 11:00:00	Other
18757	7	13	1458	1459	-1	1718	1719	YX	1037	N126HQ	JFK	IND	102	665	14	59	2023-07-13 14:00:00	Other
18767	1	4	830	830	0	1059	1135	DL	661	N516DA	JFK	LAS	300	2248	8	30	2023-01-04 08:00:00	Other
18768	1	12	1632	1630	2	1813	1820	DL	932	N138DU	LGA	BNA	138	764	16	30	2023-01-12 16:00:00	Other
18788	2	23	903	900	3	1133	1149	B6	281	N328JB	JFK	JAX	122	828	9	0	2023-02-23 09:00:00	Other
18790	3	28	1827	1820	7	2138	2120	WN	191	N484WN	LGA	TPA	163	1010	18	20	2023-03-28 18:00:00	Other
18803	8	9	1901	1900	1	2039	2040	YX	855	N763YX	EWR	PIT	53	319	19	0	2023-08-09 19:00:00	Other
18807	11	29	1523	1519	4	1632	1640	YX	1119	N747YX	EWR	SYR	44	195	15	19	2023-11-29 15:00:00	Other
18811	9	6	1136	1135	1	1416	1420	WN	289	N8507C	LGA	DAL	176	1381	11	35	2023-09-06 11:00:00	Other
18813	12	9	1549	1550	-1	1840	1914	DL	189	N833MH	JFK	LAX	318	2475	15	50	2023-12-09 15:00:00	LAX
18818	8	12	659	659	0	1006	1009	AA	306	N307TA	JFK	MIA	150	1089	6	59	2023-08-12 06:00:00	MIA
18836	3	3	2119	2120	-1	2249	2255	9E	1487	N296PQ	JFK	ROC	53	264	21	20	2023-03-03 21:00:00	Other
18840	1	28	1248	1245	3	1506	1530	WN	994	N8761L	LGA	ATL	115	762	12	45	2023-01-28 12:00:00	ATL
18845	8	11	1407	1400	7	1601	1557	9E	1206	N131EV	JFK	RDU	67	427	14	0	2023-08-11 14:00:00	Other
18855	1	30	2043	2036	7	2343	2340	UA	967	N75426	EWR	TPA	147	997	20	36	2023-01-30 20:00:00	Other
18858	12	23	1559	1600	-1	1717	1736	OO	1173	N324SY	JFK	IAD	48	228	16	0	2023-12-23 16:00:00	Other
18860	6	22	1536	1530	6	1814	1833	UA	522	N12114	EWR	LAX	312	2454	15	30	2023-06-22 15:00:00	LAX
18864	12	10	1730	1730	0	2120	2050	DL	895	N820DN	JFK	FLL	168	1069	17	30	2023-12-10 17:00:00	FLL
18882	8	21	1938	1929	9	2225	2335	DL	292	N723TW	JFK	SFO	312	2586	19	29	2023-08-21 19:00:00	Other
18894	5	31	950	951	-1	1145	1203	UA	546	N27734	EWR	CHS	91	628	9	51	2023-05-31 09:00:00	Other
18895	1	4	1335	1335	0	1653	1652	B6	765	N607JB	EWR	RSW	175	1068	13	35	2023-01-04 13:00:00	Other
18899	6	28	2044	2037	7	2345	2352	B6	708	N942JB	JFK	LAX	325	2475	20	37	2023-06-28 20:00:00	LAX
18905	11	30	1928	1925	3	2235	2236	DL	339	N374DA	LGA	MIA	157	1096	19	25	2023-11-30 19:00:00	MIA
18906	10	6	1525	1525	0	1723	1729	YX	1763	N245JQ	JFK	CMH	76	483	15	25	2023-10-06 15:00:00	Other
18907	8	7	930	930	0	1132	1159	YX	1351	N875RW	LGA	HHH	101	701	9	30	2023-08-07 09:00:00	Other
18908	5	2	1719	1720	-1	2003	2046	B6	928	N942JB	JFK	LAX	321	2475	17	20	2023-05-02 17:00:00	LAX
18910	12	13	838	839	-1	1216	1249	AA	529	N310RF	JFK	PHX	319	2153	8	39	2023-12-13 08:00:00	Other
18921	2	25	1405	1402	3	1545	1534	UA	605	N37255	EWR	BNA	136	748	14	2	2023-02-25 14:00:00	Other
18923	5	19	801	800	1	1041	1104	DL	172	N836MH	JFK	LAX	306	2475	8	0	2023-05-19 08:00:00	LAX
18934	6	8	1404	1405	-1	1640	1641	UA	523	N37531	EWR	DFW	188	1372	14	5	2023-06-08 14:00:00	Other
18941	7	20	1832	1829	3	2013	2015	AA	596	N804AW	LGA	RDU	69	431	18	29	2023-07-20 18:00:00	Other
18942	8	13	1102	1059	3	1348	1346	B6	171	N4064J	JFK	LAX	317	2475	10	59	2023-08-13 10:00:00	LAX
18949	1	25	1744	1744	0	2010	1936	UA	296	N13716	EWR	STL	133	872	17	44	2023-01-25 17:00:00	Other
18954	1	26	1808	1759	9	2147	2116	AA	137	N923AN	JFK	MIA	181	1089	17	59	2023-01-26 17:00:00	MIA
18960	8	4	1310	1311	-1	1514	1535	9E	1280	N927XJ	LGA	IND	98	660	13	11	2023-08-04 13:00:00	Other
18962	8	20	2016	2010	6	2200	2235	B6	31	N599JB	JFK	DEN	200	1626	20	10	2023-08-20 20:00:00	Other
18971	2	17	1754	1754	0	2210	2141	AA	904	N107NN	JFK	SFO	368	2586	17	54	2023-02-17 17:00:00	Other
18979	3	29	1422	1421	1	1719	1746	B6	768	N760JB	LGA	RSW	160	1080	14	21	2023-03-29 14:00:00	Other
18986	3	20	2001	1955	6	2259	2308	DL	562	N376DN	JFK	MCO	142	944	19	55	2023-03-20 19:00:00	MCO
19013	9	21	1352	1350	2	1621	1615	B6	728	N643JB	LGA	DEN	213	1620	13	50	2023-09-21 13:00:00	Other
19014	6	17	951	951	0	1248	1253	UA	643	N27270	EWR	RSW	144	1068	9	51	2023-06-17 09:00:00	Other
19029	12	20	2003	2000	3	2323	2337	UA	363	N29124	EWR	SFO	333	2565	20	0	2023-12-20 20:00:00	Other
19035	11	9	1324	1325	-1	1437	1500	WN	336	N267WN	LGA	BNA	119	764	13	25	2023-11-09 13:00:00	Other
19036	4	20	1759	1750	9	2011	2006	9E	1260	N490PX	LGA	DSM	163	1031	17	50	2023-04-20 17:00:00	Other
19041	3	28	1159	1159	0	1456	1455	UA	750	N898UA	EWR	IAH	211	1400	11	59	2023-03-28 11:00:00	Other
19053	5	26	1458	1459	-1	1614	1627	YX	1232	N442YX	LGA	BUF	47	292	14	59	2023-05-26 14:00:00	Other
19054	9	23	1434	1428	6	1536	1555	YX	1191	N762YX	EWR	MKE	99	725	14	28	2023-09-23 14:00:00	Other
19058	9	1	2138	2130	8	44	41	B6	800	N505JB	JFK	RSW	147	1074	21	30	2023-09-01 21:00:00	Other
19085	3	30	1758	1759	-1	2005	1940	UA	806	N836UA	LGA	ORD	133	733	17	59	2023-03-30 17:00:00	ORD
19086	6	29	1836	1829	7	2118	2140	AA	179	N945AN	JFK	MIA	132	1089	18	29	2023-06-29 18:00:00	MIA
19089	10	4	1644	1645	-1	1952	2015	AS	10	N947AK	JFK	SFO	332	2586	16	45	2023-10-04 16:00:00	Other
19090	9	24	1604	1600	4	1811	1835	DL	172	N394DX	LGA	ATL	102	762	16	0	2023-09-24 16:00:00	ATL
19101	7	17	2017	2010	7	2207	2214	9E	1173	N480PX	LGA	GSO	79	461	20	10	2023-07-17 20:00:00	Other
19102	6	11	1130	1130	0	1410	1346	9E	1676	N678CA	LGA	MCI	154	1107	11	30	2023-06-11 11:00:00	Other
19124	4	13	1005	1000	5	1200	1201	B6	65	N206JB	JFK	DTW	84	509	10	0	2023-04-13 10:00:00	Other
19131	5	10	2158	2157	1	2351	2359	UA	615	N76505	EWR	MSP	145	1008	21	57	2023-05-10 21:00:00	Other
19146	5	29	1504	1505	-1	1627	1643	UA	606	N483UA	LGA	ORD	106	733	15	5	2023-05-29 15:00:00	ORD
19147	3	21	1457	1457	0	1709	1716	DL	450	N329NB	JFK	MSP	155	1029	14	57	2023-03-21 14:00:00	Other
19149	10	24	1029	1030	-1	1129	1159	YX	1074	N766YX	EWR	DCA	40	199	10	30	2023-10-24 10:00:00	Other
19160	4	19	935	935	0	1319	1250	B6	62	N796JB	EWR	FLL	147	1065	9	35	2023-04-19 09:00:00	FLL
19164	4	10	1602	1555	7	1809	1822	NK	387	N635NK	EWR	ATL	105	746	15	55	2023-04-10 15:00:00	ATL
19165	8	11	1139	1135	4	1443	1442	UA	674	N76502	EWR	MIA	157	1085	11	35	2023-08-11 11:00:00	MIA
19169	2	26	1300	1300	0	1700	1649	AS	4	N508AS	JFK	SFO	391	2586	13	0	2023-02-26 13:00:00	Other
19171	3	20	1833	1830	3	2023	2014	B6	30	N592JB	JFK	BNA	113	765	18	30	2023-03-20 18:00:00	Other
19179	9	29	941	940	1	1346	1341	UA	575	N37516	EWR	SJU	206	1608	9	40	2023-09-29 09:00:00	Other
19186	5	21	715	715	0	917	947	DL	237	N866DN	JFK	PHX	278	2153	7	15	2023-05-21 07:00:00	Other
19206	5	26	2120	2120	0	2316	2320	YX	1092	N864RW	EWR	MEM	143	946	21	20	2023-05-26 21:00:00	Other
19211	4	4	1050	1045	5	1338	1336	B6	139	N2038J	JFK	MCO	142	944	10	45	2023-04-04 10:00:00	MCO
19214	9	10	740	740	0	951	1001	B6	14	N994JL	JFK	PHX	283	2153	7	40	2023-09-10 07:00:00	Other
19217	6	15	1118	1118	0	1427	1417	UA	257	N17254	EWR	PBI	153	1023	11	18	2023-06-15 11:00:00	Other
19218	5	10	559	600	-1	834	849	B6	590	N583JB	JFK	TPA	130	1005	6	0	2023-05-10 06:00:00	Other
19224	3	30	1358	1359	-1	1535	1513	OO	1268	N313SY	JFK	BOS	55	187	13	59	2023-03-30 13:00:00	BOS
19249	12	31	1530	1530	0	1637	1704	NK	572	N957NK	EWR	BNA	109	748	15	30	2023-12-31 15:00:00	Other
19261	9	22	607	608	-1	754	755	DL	780	N925AT	EWR	DTW	74	488	6	8	2023-09-22 06:00:00	Other
19266	9	19	1840	1835	5	2134	2137	B6	927	N663JB	JFK	MCO	136	944	18	35	2023-09-19 18:00:00	MCO
19278	11	18	800	800	0	1059	1125	B6	46	N231JB	JFK	SRQ	146	1041	8	0	2023-11-18 08:00:00	Other
19281	3	16	858	859	-1	1107	1117	YX	1191	N979RP	EWR	AVL	89	583	8	59	2023-03-16 08:00:00	Other
19290	4	6	1928	1929	-1	2143	2135	OO	1026	N305SY	JFK	ORD	130	740	19	29	2023-04-06 19:00:00	ORD
19292	5	7	1314	1315	-1	1428	1445	YX	1646	N222JQ	LGA	RIC	50	292	13	15	2023-05-07 13:00:00	Other
19298	6	15	1555	1554	1	1926	1857	AA	923	N882NN	JFK	DFW	205	1391	15	54	2023-06-15 15:00:00	Other
19299	2	21	702	700	2	1049	1050	DL	273	N703TW	JFK	SFO	374	2586	7	0	2023-02-21 07:00:00	Other
19318	3	22	1729	1729	0	2016	2039	AA	226	N874NN	JFK	MIA	144	1089	17	29	2023-03-22 17:00:00	MIA
19322	6	27	1258	1259	-1	1617	1615	AA	668	N337PJ	JFK	MIA	151	1089	12	59	2023-06-27 12:00:00	MIA
19323	8	22	1552	1553	-1	1831	1924	DL	461	N381DZ	LGA	FLL	136	1076	15	53	2023-08-22 15:00:00	FLL
19327	3	2	1402	1400	2	1722	1713	B6	23	N627JB	JFK	PBI	175	1028	14	0	2023-03-02 14:00:00	Other
19331	4	11	735	735	0	1018	1048	DL	424	N352DN	JFK	FLL	146	1069	7	35	2023-04-11 07:00:00	FLL
19334	11	14	1240	1230	10	1357	1403	YX	1785	N221JQ	LGA	MKE	116	738	12	30	2023-11-14 12:00:00	Other
19344	9	20	1533	1528	5	1723	1732	YX	1047	N755YX	EWR	DTW	81	488	15	28	2023-09-20 15:00:00	Other
19352	3	4	1200	1159	1	1335	1349	YX	1038	N721YX	EWR	CLE	74	404	11	59	2023-03-04 11:00:00	Other
19367	4	2	1125	1126	-1	1335	1353	9E	1200	N307PQ	LGA	MCI	165	1107	11	26	2023-04-02 11:00:00	Other
19382	2	5	2105	2059	6	26	17	B6	34	N976JT	JFK	SAN	354	2446	20	59	2023-02-05 20:00:00	Other
19396	8	13	701	700	1	948	955	DL	169	N829MH	JFK	LAX	314	2475	7	0	2023-08-13 07:00:00	LAX
19407	2	10	2059	2059	0	2220	2229	OO	1167	N261SY	JFK	IAD	55	228	20	59	2023-02-10 20:00:00	Other
19415	8	5	754	752	2	947	1007	DL	732	N371NB	JFK	MSY	151	1182	7	52	2023-08-05 07:00:00	Other
19417	11	18	600	600	0	812	836	UA	742	N845UA	LGA	DEN	228	1620	6	0	2023-11-18 06:00:00	Other
19431	1	21	1119	1120	-1	1409	1448	B6	384	N593JB	JFK	SLC	269	1990	11	20	2023-01-21 11:00:00	Other
19433	4	10	1000	955	5	1432	1528	DL	238	N194DN	JFK	HNL	594	4983	9	55	2023-04-10 09:00:00	Other
19434	2	13	1003	959	4	1137	1114	UA	111	N472UA	EWR	BOS	42	200	9	59	2023-02-13 09:00:00	BOS
19440	3	2	1232	1229	3	1340	1355	YX	1671	N233JQ	LGA	PWM	43	269	12	29	2023-03-02 12:00:00	Other
19455	8	19	800	800	0	1116	1115	AA	478	N314RH	JFK	MIA	147	1089	8	0	2023-08-19 08:00:00	MIA
19489	10	8	648	648	0	947	1001	AA	892	N906AN	LGA	MIA	153	1096	6	48	2023-10-08 06:00:00	MIA
19495	7	19	1701	1700	1	2040	2010	DL	90	N838MH	JFK	LAX	319	2475	17	0	2023-07-19 17:00:00	LAX
19506	5	2	1502	1458	4	1624	1628	9E	1386	N310PQ	LGA	ORF	54	296	14	58	2023-05-02 14:00:00	Other
19507	1	26	1845	1845	0	2203	2130	DL	358	N112DU	JFK	JAX	145	828	18	45	2023-01-26 18:00:00	Other
19529	5	25	807	805	2	1104	1057	UA	647	N69838	EWR	MCO	136	937	8	5	2023-05-25 08:00:00	MCO
19537	9	12	900	900	0	1012	1035	UA	226	N14237	LGA	ORD	108	733	9	0	2023-09-12 09:00:00	ORD
19546	4	26	1855	1856	-1	2016	2021	UA	620	N877UA	EWR	BOS	39	200	18	56	2023-04-26 18:00:00	BOS
19557	3	3	1512	1510	2	1749	1737	NK	883	N625NK	EWR	MSY	191	1167	15	10	2023-03-03 15:00:00	Other
19569	9	15	1900	1853	7	2114	2125	DL	1002	N983AT	EWR	ATL	102	746	18	53	2023-09-15 18:00:00	ATL
19572	4	19	1854	1854	0	2140	2150	UA	590	N36476	EWR	MCO	124	937	18	54	2023-04-19 18:00:00	MCO
19577	4	10	806	759	7	1048	1042	UA	598	N211UA	EWR	MCO	131	937	7	59	2023-04-10 07:00:00	MCO
19592	12	11	1654	1655	-1	2008	1950	B6	191	N537JT	EWR	PBI	161	1023	16	55	2023-12-11 16:00:00	Other
19604	9	23	809	800	9	1025	1010	B6	285	N763JB	JFK	MSY	150	1182	8	0	2023-09-23 08:00:00	Other
19614	2	26	1241	1240	1	1457	1521	DL	207	N101DQ	LGA	ATL	118	762	12	40	2023-02-26 12:00:00	ATL
19622	6	5	1615	1608	7	1734	1750	AA	551	N827NN	LGA	ORD	107	733	16	8	2023-06-05 16:00:00	ORD
19624	4	10	710	700	10	958	1006	DL	534	N376DA	JFK	TPA	140	1005	7	0	2023-04-10 07:00:00	Other
19639	10	24	2133	2129	4	2231	2238	9E	1671	N331PQ	LGA	ALB	37	136	21	29	2023-10-24 21:00:00	Other
19643	5	18	1200	1150	10	1353	1346	DL	611	N932AT	EWR	MSP	139	1008	11	50	2023-05-18 11:00:00	Other
19647	3	3	1859	1859	0	2157	2103	AA	671	N802NN	LGA	CLT	136	544	18	59	2023-03-03 18:00:00	CLT
19650	10	18	1701	1659	2	1950	2015	AS	75	N551AS	EWR	LAX	292	2454	16	59	2023-10-18 16:00:00	LAX
19661	10	8	1830	1830	0	2112	2137	UA	638	N17963	EWR	SFO	303	2565	18	30	2023-10-08 18:00:00	Other
19670	12	22	1759	1750	9	1944	1934	MQ	1164	N211NN	EWR	ORD	119	719	17	50	2023-12-22 17:00:00	ORD
19671	9	20	1634	1630	4	1931	1944	B6	207	N599JB	LGA	FLL	151	1076	16	30	2023-09-20 16:00:00	FLL
19679	11	23	702	700	2	810	825	AA	696	N809AW	LGA	BOS	41	184	7	0	2023-11-23 07:00:00	BOS
19688	1	26	802	800	2	927	936	9E	1589	N691CA	JFK	BUF	59	301	8	0	2023-01-26 08:00:00	Other
19696	4	5	1403	1404	-1	1632	1625	UA	716	N62883	EWR	DEN	234	1605	14	4	2023-04-05 14:00:00	Other
19710	12	19	1052	1048	4	1313	1317	9E	1427	N337PQ	LGA	CHS	98	641	10	48	2023-12-19 10:00:00	Other
19714	2	26	629	630	-1	934	1000	AA	877	N916AN	LGA	MIA	145	1096	6	30	2023-02-26 06:00:00	MIA
19718	10	10	1937	1929	8	2228	2233	DL	869	N801DZ	JFK	TPA	148	1005	19	29	2023-10-10 19:00:00	Other
19720	2	11	1003	1003	0	1303	1309	UA	608	N76514	EWR	FLL	160	1065	10	3	2023-02-11 10:00:00	FLL
19721	3	27	2042	2042	0	2400	7	B6	35	N979JT	JFK	SAN	360	2446	20	42	2023-03-27 20:00:00	Other
19737	4	12	601	600	1	703	715	YX	1492	N208JQ	LGA	BOS	36	184	6	0	2023-04-12 06:00:00	BOS
19752	2	8	2016	2015	1	2301	2328	DL	263	N847DN	JFK	LAS	312	2248	20	15	2023-02-08 20:00:00	Other
19754	1	29	841	842	-1	1105	1115	YX	1122	N725YX	EWR	CVG	113	569	8	42	2023-01-29 08:00:00	Other
19755	10	5	1902	1903	-1	2050	2110	YX	1054	N725YX	EWR	DTW	77	488	19	3	2023-10-05 19:00:00	Other
19759	7	30	1044	1037	7	1402	1344	B6	284	N768JB	JFK	SLC	276	1990	10	37	2023-07-30 10:00:00	Other
19763	1	29	1945	1935	10	16	30	B6	536	N613JB	EWR	SJU	186	1608	19	35	2023-01-29 19:00:00	Other
19764	7	8	1541	1539	2	2020	1844	UA	462	N17262	EWR	FLL	219	1065	15	39	2023-07-08 15:00:00	FLL
19768	4	12	1019	1017	2	1130	1152	UA	624	N36247	EWR	ORD	107	719	10	17	2023-04-12 10:00:00	ORD
19772	7	2	737	730	7	936	908	B6	327	N355JB	JFK	ORD	129	740	7	30	2023-07-02 07:00:00	ORD
19783	12	15	1430	1430	0	1624	1656	B6	785	N3121J	JFK	MCI	152	1113	14	30	2023-12-15 14:00:00	Other
19784	12	25	1934	1929	5	2126	2223	B6	415	N967JT	JFK	LAS	268	2248	19	29	2023-12-25 19:00:00	Other
19790	11	3	1419	1415	4	1702	1713	UA	639	N19130	EWR	MCO	139	937	14	15	2023-11-03 14:00:00	MCO
19798	4	24	716	710	6	1046	1020	DL	558	N382DN	LGA	FLL	174	1076	7	10	2023-04-24 07:00:00	FLL
19800	12	14	801	800	1	1049	1128	AA	794	N915NN	JFK	DFW	182	1391	8	0	2023-12-14 08:00:00	Other
19804	4	7	754	755	-1	1116	1107	AA	142	N324RA	LGA	MIA	152	1096	7	55	2023-04-07 07:00:00	MIA
19823	1	7	1412	1410	2	1648	1706	DL	1031	N117DX	LGA	MCO	136	950	14	10	2023-01-07 14:00:00	MCO
19824	8	15	957	950	7	1129	1115	WN	930	N8810L	LGA	BNA	116	764	9	50	2023-08-15 09:00:00	Other
19839	12	30	1928	1921	7	2113	2125	NK	79	N617NK	LGA	DTW	76	502	19	21	2023-12-30 19:00:00	Other
19840	2	12	1138	1138	0	1340	1342	AA	732	N665AW	EWR	CLT	88	529	11	38	2023-02-12 11:00:00	CLT
19848	5	31	759	800	-1	1002	1048	DL	324	N862DN	JFK	LAS	282	2248	8	0	2023-05-31 08:00:00	Other
19857	7	12	1132	1130	2	1402	1431	DL	374	N849DN	JFK	TPA	128	1005	11	30	2023-07-12 11:00:00	Other
19859	6	1	758	759	-1	921	928	UA	240	N838UA	EWR	BOS	48	200	7	59	2023-06-01 07:00:00	BOS
19867	1	12	1738	1730	8	1934	1938	YX	1303	N423YX	LGA	ORD	123	733	17	30	2023-01-12 17:00:00	ORD
19872	5	22	951	950	1	1055	1111	YX	1572	N860RW	LGA	PVD	29	143	9	50	2023-05-22 09:00:00	Other
19884	5	20	915	910	5	1213	1236	AA	707	N921NN	JFK	MIA	140	1089	9	10	2023-05-20 09:00:00	MIA
19894	9	23	705	705	0	957	1000	DL	520	N876DN	JFK	TPA	141	1005	7	5	2023-09-23 07:00:00	Other
19895	10	23	807	800	7	1052	1112	AA	461	N805NN	EWR	MIA	142	1085	8	0	2023-10-23 08:00:00	MIA
19920	11	19	730	730	0	909	915	UA	943	N17294	EWR	RDU	69	416	7	30	2023-11-19 07:00:00	Other
19921	2	19	2018	2016	2	2230	2238	UA	855	N47282	EWR	MSY	163	1167	20	16	2023-02-19 20:00:00	Other
19930	7	27	1132	1129	3	1308	1254	UA	407	N15710	EWR	BNA	99	748	11	29	2023-07-27 11:00:00	Other
19949	6	5	1205	1200	5	1336	1338	AA	546	N768US	LGA	RDU	65	431	12	0	2023-06-05 12:00:00	Other
19955	1	23	1904	1855	9	2158	2221	DL	556	N139DU	LGA	IAH	205	1416	18	55	2023-01-23 18:00:00	Other
19970	8	5	1504	1505	-1	1731	1821	DL	300	N353NB	LGA	PBI	131	1035	15	5	2023-08-05 15:00:00	Other
19986	7	16	1922	1917	5	2124	2120	AA	797	N945NN	LGA	CLT	86	544	19	17	2023-07-16 19:00:00	CLT
19991	3	28	2202	2159	3	25	10	UA	484	N460UA	EWR	CHS	100	628	21	59	2023-03-28 21:00:00	Other
19993	7	18	1343	1340	3	1558	1604	B6	785	N187JB	LGA	SAV	111	722	13	40	2023-07-18 13:00:00	Other
19998	2	8	804	800	4	1125	1107	AA	585	N163AA	EWR	DFW	207	1372	8	0	2023-02-08 08:00:00	Other
20000	11	29	559	600	-1	849	908	UA	896	N801UA	LGA	IAH	205	1416	6	0	2023-11-29 06:00:00	Other
20001	2	18	2204	2204	0	2315	2327	YX	1178	N438YX	JFK	BOS	44	187	22	4	2023-02-18 22:00:00	BOS
20003	1	9	1829	1830	-1	2148	2206	B6	67	N968JT	JFK	LAX	348	2475	18	30	2023-01-09 18:00:00	LAX
20009	8	1	1005	1005	0	1256	1257	DL	223	N174DN	JFK	LAX	321	2475	10	5	2023-08-01 10:00:00	LAX
20020	10	18	1917	1915	2	2206	2215	DL	416	N329NW	LGA	PBI	136	1035	19	15	2023-10-18 19:00:00	Other
20030	6	15	859	900	-1	1008	1025	WN	57	N8848Q	LGA	MDW	105	725	9	0	2023-06-15 09:00:00	Other
20034	11	8	2159	2159	0	2303	2315	UA	171	N67827	EWR	BOS	36	200	21	59	2023-11-08 21:00:00	BOS
20041	1	30	1006	1000	6	1342	1348	DL	318	N183DN	JFK	SFO	371	2586	10	0	2023-01-30 10:00:00	Other
20045	3	11	906	905	1	1145	1210	WN	390	N8759Q	LGA	TPA	136	1010	9	5	2023-03-11 09:00:00	Other
20047	9	22	2014	2010	4	2254	2252	UA	959	N37307	EWR	DFW	175	1372	20	10	2023-09-22 20:00:00	Other
20051	5	1	1234	1235	-1	1519	1542	AA	191	N968AN	LGA	DFW	192	1389	12	35	2023-05-01 12:00:00	Other
20064	2	20	1831	1825	6	2143	2151	AS	91	N407AS	EWR	SAN	340	2425	18	25	2023-02-20 18:00:00	Other
20068	5	19	1258	1259	-1	1441	1459	DL	766	N358NB	LGA	DTW	80	502	12	59	2023-05-19 12:00:00	Other
20075	12	3	1007	1000	7	1637	1605	HA	16	N389HA	JFK	HNL	637	4983	10	0	2023-12-03 10:00:00	Other
20088	11	18	1318	1310	8	1601	1615	NK	76	N970NK	EWR	DFW	193	1372	13	10	2023-11-18 13:00:00	Other
20096	11	28	1349	1349	0	1547	1600	YX	1295	N428YX	LGA	MSP	155	1020	13	49	2023-11-28 13:00:00	Other
20110	1	20	1701	1700	1	2009	2020	DL	1021	N522DA	JFK	SEA	317	2422	17	0	2023-01-20 17:00:00	Other
20143	8	24	2051	2052	-1	117	111	DL	555	N879DN	JFK	SJU	191	1598	20	52	2023-08-24 20:00:00	Other
20148	10	6	813	810	3	1052	1133	AA	293	N884NN	JFK	DFW	191	1391	8	10	2023-10-06 08:00:00	Other
20155	2	17	2345	2345	0	425	430	B6	342	N534JB	JFK	BQN	195	1576	23	45	2023-02-17 23:00:00	Other
20163	1	13	1120	1114	6	1253	1320	YX	1325	N418YX	LGA	ROA	79	405	11	14	2023-01-13 11:00:00	Other
20172	1	11	1733	1730	3	2055	2120	DL	998	N174DN	JFK	SFO	359	2586	17	30	2023-01-11 17:00:00	Other
20180	3	29	802	755	7	1118	1055	UA	277	N27260	EWR	IAH	210	1400	7	55	2023-03-29 07:00:00	Other
20186	8	30	1149	1150	-1	1311	1336	9E	1213	N146PQ	LGA	PIT	60	335	11	50	2023-08-30 11:00:00	Other
20199	4	12	1856	1849	7	2144	2204	UA	532	N77430	EWR	PDX	317	2434	18	49	2023-04-12 18:00:00	Other
20203	4	27	1148	1141	7	1434	1446	DL	392	N357DN	LGA	MCO	131	950	11	41	2023-04-27 11:00:00	MCO
20206	10	5	1959	2000	-1	2228	2236	DL	378	N394DX	JFK	ATL	102	760	20	0	2023-10-05 20:00:00	ATL
20207	11	16	1449	1450	-1	1645	1656	9E	1434	N329PQ	JFK	CLT	87	541	14	50	2023-11-16 14:00:00	CLT
20208	3	30	1332	1325	7	1450	1500	WN	941	N8675A	LGA	BNA	114	764	13	25	2023-03-30 13:00:00	Other
20210	5	9	1355	1349	6	1521	1522	9E	1330	N315PQ	LGA	BNA	114	764	13	49	2023-05-09 13:00:00	Other
20223	4	9	1810	1800	10	2112	2118	UA	414	N27015	EWR	SFO	313	2565	18	0	2023-04-09 18:00:00	Other
20233	9	23	1518	1509	9	1709	1718	YX	1069	N760YX	EWR	GSP	87	594	15	9	2023-09-23 15:00:00	Other
20239	5	29	1424	1425	-1	1618	1627	YX	1154	N725YX	EWR	MYR	80	550	14	25	2023-05-29 14:00:00	Other
20242	6	12	1856	1855	1	2024	2018	AA	903	N742PS	LGA	BNA	121	764	18	55	2023-06-12 18:00:00	Other
20250	5	18	1716	1717	-1	1919	1901	9E	1277	N905XJ	JFK	BUF	55	301	17	17	2023-05-18 17:00:00	Other
20266	9	19	1728	1729	-1	2336	2040	AA	130	N924AN	JFK	MIA	NA	1089	17	29	2023-09-19 17:00:00	MIA
20275	7	26	2153	2150	3	2258	2251	9E	1145	N912XJ	LGA	BGM	35	147	21	50	2023-07-26 21:00:00	Other
20281	12	21	801	800	1	946	947	UA	649	N77538	EWR	ORD	119	719	8	0	2023-12-21 08:00:00	ORD
20284	10	5	2159	2200	-1	2314	2321	UA	157	N801UA	EWR	BOS	48	200	22	0	2023-10-05 22:00:00	BOS
20289	6	12	1037	1030	7	1142	1140	B6	996	N197JB	JFK	BOS	46	187	10	30	2023-06-12 10:00:00	BOS
20299	3	30	1950	1940	10	2252	2309	DL	638	N123DW	JFK	FLL	137	1069	19	40	2023-03-30 19:00:00	FLL
20301	9	25	805	805	0	1026	1024	DL	925	N925DZ	EWR	ATL	100	746	8	5	2023-09-25 08:00:00	ATL
20302	7	29	631	630	1	829	838	AA	288	N932NN	JFK	CLT	83	541	6	30	2023-07-29 06:00:00	CLT
20308	6	5	705	705	0	837	853	9E	1491	N909XJ	LGA	STL	121	888	7	5	2023-06-05 07:00:00	Other
20316	9	15	929	929	0	1125	1146	YX	1110	N743YX	EWR	AVL	87	583	9	29	2023-09-15 09:00:00	Other
20318	2	17	1600	1600	0	1755	1754	YX	1237	N452YX	JFK	BNA	134	765	16	0	2023-02-17 16:00:00	Other
20321	4	26	1044	1045	-1	1430	1348	AA	404	N967AN	LGA	DFW	233	1389	10	45	2023-04-26 10:00:00	Other
20327	2	6	2042	2035	7	2325	2352	UA	635	N27273	EWR	MIA	138	1085	20	35	2023-02-06 20:00:00	MIA
20334	10	6	600	600	0	815	818	DL	730	N706TW	JFK	ATL	112	760	6	0	2023-10-06 06:00:00	ATL
20342	6	8	559	600	-1	913	910	AA	466	N306SP	LGA	MIA	164	1096	6	0	2023-06-08 06:00:00	MIA
20344	8	13	1216	1215	1	1458	1511	B6	225	N779JB	JFK	AUS	204	1521	12	15	2023-08-13 12:00:00	Other
20349	10	17	706	659	7	905	914	YX	1303	N417YX	LGA	MSP	139	1020	6	59	2023-10-17 06:00:00	Other
20352	12	21	644	645	-1	755	827	YX	1836	N878RW	LGA	BNA	108	764	6	45	2023-12-21 06:00:00	Other
20363	4	27	1007	1006	1	1353	1311	UA	560	N37420	EWR	FLL	156	1065	10	6	2023-04-27 10:00:00	FLL
20365	12	20	710	710	0	836	902	DL	607	N131DU	LGA	ORD	111	733	7	10	2023-12-20 07:00:00	ORD
20366	3	21	1731	1729	2	2100	2110	YX	1122	N656RW	EWR	EYW	177	1196	17	29	2023-03-21 17:00:00	Other
20367	12	7	659	700	-1	948	1018	DL	769	N387DA	JFK	FLL	137	1069	7	0	2023-12-07 07:00:00	FLL
20371	1	5	801	800	1	926	950	UA	759	N12221	EWR	ORD	109	719	8	0	2023-01-05 08:00:00	ORD
20375	10	25	1933	1929	4	2231	2233	DL	869	N822DN	JFK	TPA	136	1005	19	29	2023-10-25 19:00:00	Other
20382	5	17	1508	1500	8	1759	1756	UA	268	N77538	EWR	TPA	142	997	15	0	2023-05-17 15:00:00	Other
20392	8	17	634	630	4	934	926	B6	757	N531JL	JFK	FLL	152	1069	6	30	2023-08-17 06:00:00	FLL
20437	8	17	1013	1007	6	1217	1220	UA	450	N78511	EWR	DEN	213	1605	10	7	2023-08-17 10:00:00	Other
20446	7	3	1458	1459	-1	1712	1746	DL	781	N722TW	JFK	ATL	108	760	14	59	2023-07-03 14:00:00	ATL
20448	10	16	703	700	3	817	815	UA	468	N37551	EWR	BOS	44	200	7	0	2023-10-16 07:00:00	BOS
20459	12	4	1520	1517	3	1719	1725	YX	1030	N748YX	EWR	DTW	81	488	15	17	2023-12-04 15:00:00	Other
20465	4	23	1447	1445	2	1708	1728	B6	777	N508JL	LGA	JAX	123	833	14	45	2023-04-23 14:00:00	Other
20471	1	30	1956	1952	4	2237	2301	UA	261	N34137	EWR	TPA	143	997	19	52	2023-01-30 19:00:00	Other
20479	7	21	1406	1400	6	1618	1618	DL	666	N3764D	EWR	ATL	101	746	14	0	2023-07-21 14:00:00	ATL
20483	4	21	759	800	-1	922	938	UA	781	N835UA	LGA	ORD	111	733	8	0	2023-04-21 08:00:00	ORD
20491	8	2	1613	1608	5	1733	1739	YX	841	N641RW	EWR	ROC	49	246	16	8	2023-08-02 16:00:00	Other
20495	5	15	1504	1455	9	1758	1810	B6	526	N639JB	JFK	FLL	140	1069	14	55	2023-05-15 14:00:00	FLL
20509	5	5	1332	1330	2	1557	1603	B6	940	N509JB	LGA	ATL	115	762	13	30	2023-05-05 13:00:00	ATL
20523	2	23	1307	1303	4	1632	1548	UA	133	N37255	EWR	LAS	367	2227	13	3	2023-02-23 13:00:00	Other
20524	1	12	826	825	1	1056	1107	YX	1299	N416YX	JFK	CVG	110	589	8	25	2023-01-12 08:00:00	Other
20534	12	26	1114	1111	3	1246	1312	YX	1261	N105HQ	LGA	RDU	69	431	11	11	2023-12-26 11:00:00	Other
20535	6	29	1531	1530	1	1750	1755	B6	853	N3121J	JFK	MCI	177	1113	15	30	2023-06-29 15:00:00	Other
20536	1	19	603	600	3	826	839	DL	380	N358DN	LGA	ATL	114	762	6	0	2023-01-19 06:00:00	ATL
20540	9	28	1723	1720	3	1932	1928	AA	773	N936AN	LGA	CLT	86	544	17	20	2023-09-28 17:00:00	CLT
20551	12	4	1830	1830	0	2008	2012	UA	423	N36272	EWR	ORD	114	719	18	30	2023-12-04 18:00:00	ORD
20552	9	17	1022	1017	5	1223	1232	YX	1926	N212JQ	LGA	CLT	90	544	10	17	2023-09-17 10:00:00	CLT
20556	5	24	1655	1645	10	2130	2001	AA	506	N324RN	LGA	MIA	203	1096	16	45	2023-05-24 16:00:00	MIA
20560	12	31	510	510	0	748	825	B6	488	N961JT	EWR	LAX	314	2454	5	10	2023-12-31 05:00:00	LAX
20562	6	28	1652	1645	7	1906	1922	AA	611	N940NN	JFK	PHX	289	2153	16	45	2023-06-28 16:00:00	Other
20572	8	3	611	605	6	815	819	UA	493	N63820	EWR	DEN	218	1605	6	5	2023-08-03 06:00:00	Other
20575	11	13	1830	1830	0	2131	2205	B6	60	N986JB	JFK	LAX	330	2475	18	30	2023-11-13 18:00:00	LAX
20582	8	17	1327	1325	2	1546	1557	B6	776	N568JB	LGA	ATL	109	762	13	25	2023-08-17 13:00:00	ATL
20585	12	12	1129	1130	-1	1301	1311	YX	1274	N109HQ	JFK	BNA	122	765	11	30	2023-12-12 11:00:00	Other
20588	5	10	1939	1932	7	2212	2206	9E	1291	N131EV	JFK	MSP	155	1029	19	32	2023-05-10 19:00:00	Other
20589	3	12	2130	2129	1	2318	2309	9E	1328	N305PQ	JFK	RIC	58	288	21	29	2023-03-12 21:00:00	Other
20591	9	8	804	800	4	1254	1157	DL	705	N537DT	JFK	SJU	204	1598	8	0	2023-09-08 08:00:00	Other
20592	8	11	958	959	-1	1301	1256	NK	224	N618NK	LGA	MCO	133	950	9	59	2023-08-11 09:00:00	MCO
20594	9	22	603	600	3	744	751	DL	392	N126DN	LGA	DTW	75	502	6	0	2023-09-22 06:00:00	Other
20600	7	12	1427	1420	7	1646	1715	DL	336	N114DU	LGA	IAH	181	1416	14	20	2023-07-12 14:00:00	Other
20611	5	22	721	720	1	1032	1006	NK	453	N663NK	EWR	MCO	130	937	7	20	2023-05-22 07:00:00	MCO
20612	7	13	2100	2100	0	2321	2246	OO	1250	N202SY	LGA	ORD	120	733	21	0	2023-07-13 21:00:00	ORD
20620	4	12	829	829	0	956	1005	OO	1060	N280SY	JFK	BNA	96	765	8	29	2023-04-12 08:00:00	Other
20624	3	25	759	800	-1	1101	1024	DL	932	N399DA	EWR	ATL	119	746	8	0	2023-03-25 08:00:00	ATL
20625	1	5	2156	2156	0	2253	2314	YX	1203	N728YX	EWR	MHT	39	209	21	56	2023-01-05 21:00:00	Other
20629	6	16	734	735	-1	849	855	B6	193	N229JB	JFK	PWM	50	273	7	35	2023-06-16 07:00:00	Other
20632	1	16	1900	1859	1	2150	2208	DL	501	N362DN	LGA	PBI	135	1035	18	59	2023-01-16 18:00:00	Other
20636	5	19	714	715	-1	956	947	DL	167	N376DA	LGA	DEN	245	1620	7	15	2023-05-19 07:00:00	Other
20650	3	1	1900	1900	0	2030	2033	YX	1033	N856RW	EWR	BGR	58	393	19	0	2023-03-01 19:00:00	Other
20655	2	17	901	900	1	1218	1149	B6	281	N354JB	JFK	JAX	129	828	9	0	2023-02-17 09:00:00	Other
20666	2	5	2201	2158	3	2309	2315	YX	1102	N641RW	EWR	SYR	41	195	21	58	2023-02-05 21:00:00	Other
20673	4	22	1233	1231	2	1337	1410	AA	880	N957AN	LGA	ORD	100	733	12	31	2023-04-22 12:00:00	ORD
20684	11	6	1059	1100	-1	1403	1354	B6	140	N995JL	JFK	LAS	334	2248	11	0	2023-11-06 11:00:00	Other
20685	8	2	1358	1359	-1	1546	1558	YX	825	N728YX	EWR	DTW	74	488	13	59	2023-08-02 13:00:00	Other
20692	1	20	1115	1115	0	1405	1419	DL	515	N340NW	JFK	TPA	151	1005	11	15	2023-01-20 11:00:00	Other
20702	4	7	1915	1914	1	2029	2051	UA	581	N806UA	EWR	BNA	113	748	19	14	2023-04-07 19:00:00	Other
20706	6	6	708	709	-1	1106	1110	B6	613	N552JB	EWR	SJU	206	1608	7	9	2023-06-06 07:00:00	Other
20708	11	24	2112	2105	7	2357	4	B6	179	N804JB	LGA	MCO	139	950	21	5	2023-11-24 21:00:00	MCO
20711	5	7	2036	2035	1	2249	2256	YX	1028	N731YX	EWR	GRR	106	605	20	35	2023-05-07 20:00:00	Other
20715	1	22	2136	2130	6	2336	2341	UA	938	N38727	EWR	MSP	146	1008	21	30	2023-01-22 21:00:00	Other
20717	12	26	1404	1359	5	1606	1635	DL	190	N3773D	LGA	DEN	216	1620	13	59	2023-12-26 13:00:00	Other
20718	9	15	1632	1630	2	1911	1922	UA	469	N216UA	EWR	LAX	303	2454	16	30	2023-09-15 16:00:00	LAX
20722	4	15	1532	1524	8	1923	1842	UA	695	N47288	EWR	FLL	165	1065	15	24	2023-04-15 15:00:00	FLL
20726	8	23	1138	1130	8	1420	1437	B6	738	N618JB	JFK	MIA	138	1089	11	30	2023-08-23 11:00:00	MIA
20731	11	5	1353	1345	8	1634	1653	B6	651	N703JB	EWR	RSW	145	1068	13	45	2023-11-05 13:00:00	Other
20732	12	20	1603	1600	3	1709	1740	WN	1117	N8641B	LGA	BNA	106	764	16	0	2023-12-20 16:00:00	Other
20740	3	30	2123	2120	3	2219	2222	YX	1737	N214JQ	LGA	BDL	22	101	21	20	2023-03-30 21:00:00	Other
20742	2	16	607	600	7	844	839	DL	348	N384DN	LGA	ATL	124	762	6	0	2023-02-16 06:00:00	ATL
20749	1	22	2120	2120	0	2354	2253	9E	1597	N306PQ	JFK	RIC	63	288	21	20	2023-01-22 21:00:00	Other
20758	11	20	1506	1500	6	1639	1631	9E	1424	N308PQ	JFK	SYR	47	209	15	0	2023-11-20 15:00:00	Other
20759	7	18	1550	1549	1	2004	1920	DL	679	N393DA	JFK	MIA	157	1089	15	49	2023-07-18 15:00:00	MIA
20770	7	6	1152	1152	0	1255	1309	UA	249	N37504	EWR	BOS	40	200	11	52	2023-07-06 11:00:00	BOS
20784	12	21	1543	1541	2	1836	1854	UA	716	N37542	EWR	RSW	153	1068	15	41	2023-12-21 15:00:00	Other
20805	4	3	1116	1114	2	1336	1340	UA	374	N34460	EWR	PHX	304	2133	11	14	2023-04-03 11:00:00	Other
20811	12	1	1854	1853	1	2118	2122	YX	1068	N862RW	EWR	IND	108	645	18	53	2023-12-01 18:00:00	Other
20841	7	10	1336	1329	7	1530	1553	AA	802	N308RD	JFK	PHX	266	2153	13	29	2023-07-10 13:00:00	Other
20849	10	14	2059	2100	-1	2214	2237	YX	1865	N208JQ	JFK	DCA	46	213	21	0	2023-10-14 21:00:00	Other
20858	2	10	609	610	-1	911	920	WN	535	N8311Q	LGA	HOU	220	1428	6	10	2023-02-10 06:00:00	Other
20859	3	19	1458	1459	-1	1643	1644	B6	650	N348JB	JFK	BNA	136	765	14	59	2023-03-19 14:00:00	Other
20871	12	27	1209	1210	-1	1659	1656	B6	967	N965JT	JFK	SJU	194	1598	12	10	2023-12-27 12:00:00	Other
20881	2	19	810	805	5	1032	1040	DL	886	N776DE	EWR	ATL	119	746	8	5	2023-02-19 08:00:00	ATL
20882	12	3	1414	1405	9	1920	1903	B6	304	N568JB	JFK	SJU	184	1598	14	5	2023-12-03 14:00:00	Other
20885	10	27	800	800	0	1105	1029	DL	168	N517DN	JFK	DEN	237	1626	8	0	2023-10-27 08:00:00	Other
20895	9	18	829	830	-1	1049	1057	B6	961	N504JB	LGA	ATL	114	762	8	30	2023-09-18 08:00:00	ATL
20904	12	21	1147	1147	0	1348	1409	YX	1032	N654RW	EWR	CVG	91	569	11	47	2023-12-21 11:00:00	Other
20905	11	1	700	700	0	955	1015	AA	301	N9013A	JFK	AUS	215	1521	7	0	2023-11-01 07:00:00	Other
20906	1	23	2129	2130	-1	2301	2243	B6	106	N643JB	JFK	BOS	55	187	21	30	2023-01-23 21:00:00	BOS
20918	4	21	1839	1840	-1	1950	2010	B6	853	N229JB	EWR	BOS	35	200	18	40	2023-04-21 18:00:00	BOS
20919	2	13	1406	1405	1	1606	1626	YX	1038	N647RW	EWR	IND	100	645	14	5	2023-02-13 14:00:00	Other
20921	9	13	959	1000	-1	1447	1500	HA	19	N382HA	JFK	HNL	618	4983	10	0	2023-09-13 10:00:00	Other
20944	4	4	1310	1310	0	1551	1552	AA	882	N335SN	JFK	PHX	317	2153	13	10	2023-04-04 13:00:00	Other
20945	11	16	1317	1315	2	1613	1610	B6	290	N804JB	LGA	PBI	152	1035	13	15	2023-11-16 13:00:00	Other
20947	4	4	1158	1159	-1	1459	1511	NK	325	N671NK	LGA	DFW	202	1389	11	59	2023-04-04 11:00:00	Other
20957	1	12	1803	1800	3	2135	2117	DL	418	N112DU	JFK	DFW	216	1391	18	0	2023-01-12 18:00:00	Other
20971	12	21	1558	1559	-1	1710	1724	YX	1792	N226JQ	LGA	BOS	42	184	15	59	2023-12-21 15:00:00	BOS
20982	12	7	2009	2001	8	59	57	UA	553	N27519	EWR	SJU	188	1608	20	1	2023-12-07 20:00:00	Other
21001	6	12	1521	1520	1	1744	1752	YX	1322	N439YX	JFK	IND	106	665	15	20	2023-06-12 15:00:00	Other
21003	11	22	1627	1628	-1	1751	1758	YX	1081	N858RW	EWR	ORF	59	284	16	28	2023-11-22 16:00:00	Other
21013	10	16	2008	2009	-1	2313	2342	AS	15	N552AS	JFK	SFO	325	2586	20	9	2023-10-16 20:00:00	Other
21016	9	28	826	820	6	1115	1133	DL	334	N530DE	JFK	SAN	314	2446	8	20	2023-09-28 08:00:00	Other
21026	4	2	1246	1237	9	1552	1551	AA	635	N451AN	JFK	MIA	155	1089	12	37	2023-04-02 12:00:00	MIA
21029	8	29	1158	1150	8	1327	1336	9E	1213	N320PQ	LGA	PIT	54	335	11	50	2023-08-29 11:00:00	Other
21031	4	13	1100	1100	0	1345	1410	B6	91	N784JB	JFK	AUS	190	1521	11	0	2023-04-13 11:00:00	Other
21038	10	20	2204	2155	9	2331	2315	B6	894	N354JB	JFK	SYR	40	209	21	55	2023-10-20 21:00:00	Other
21042	6	23	1832	1825	7	2137	2139	AS	174	N491AS	EWR	SEA	302	2402	18	25	2023-06-23 18:00:00	Other
21050	1	15	749	750	-1	923	956	AA	675	N805NN	EWR	CLT	73	529	7	50	2023-01-15 07:00:00	CLT
21053	6	3	2059	2100	-1	2224	2239	YX	1815	N211JQ	JFK	DCA	41	213	21	0	2023-06-03 21:00:00	Other
21065	4	24	2149	2150	-1	2239	2246	9E	1200	N491PX	LGA	BDL	26	101	21	50	2023-04-24 21:00:00	Other
21074	1	7	607	600	7	856	912	B6	833	N746JB	LGA	FLL	146	1076	6	0	2023-01-07 06:00:00	FLL
21075	5	12	1555	1551	4	1715	1749	B6	37	N306JB	JFK	ORD	117	740	15	51	2023-05-12 15:00:00	ORD
21085	12	16	2250	2250	0	142	203	F9	1175	N370FR	LGA	DFW	205	1389	22	50	2023-12-16 22:00:00	Other
21088	4	25	904	905	-1	1024	1031	B6	556	N339JB	JFK	BUF	57	301	9	5	2023-04-25 09:00:00	Other
21093	1	27	1756	1755	1	2017	2040	WN	403	N8502Z	LGA	DEN	228	1620	17	55	2023-01-27 17:00:00	Other
21098	2	16	905	905	0	1036	1046	YX	1058	N753YX	EWR	PIT	63	319	9	5	2023-02-16 09:00:00	Other
21102	12	17	1626	1623	3	1738	1739	UA	123	N21108	EWR	BOS	35	200	16	23	2023-12-17 16:00:00	BOS
21103	1	13	1907	1905	2	2217	2224	DL	977	N380DA	LGA	RSW	154	1080	19	5	2023-01-13 19:00:00	Other
21106	10	5	1454	1455	-1	1611	1628	OO	1207	N254SY	JFK	IAD	51	228	14	55	2023-10-05 14:00:00	Other
21109	12	30	948	948	0	1120	1133	YX	1099	N761YX	EWR	CLE	59	404	9	48	2023-12-30 09:00:00	Other
21122	7	27	1536	1528	8	1733	1728	DL	754	N926AT	EWR	MSP	142	1008	15	28	2023-07-27 15:00:00	Other
21125	2	22	1943	1935	8	2200	2202	9E	1444	N131EV	JFK	DTW	96	509	19	35	2023-02-22 19:00:00	Other
21129	4	9	1842	1838	4	1950	2021	UA	422	N422UA	EWR	ORD	103	719	18	38	2023-04-09 18:00:00	ORD
21134	9	11	1405	1355	10	1723	1651	DL	284	N1201P	JFK	LAX	334	2475	13	55	2023-09-11 13:00:00	LAX
21145	12	30	1716	1710	6	2033	2017	B6	412	N504JB	LGA	MCO	166	950	17	10	2023-12-30 17:00:00	MCO
21147	6	27	503	501	2	918	843	B6	957	N955JB	JFK	BQN	230	1576	5	1	2023-06-27 05:00:00	Other
21158	7	2	602	600	2	813	827	DL	258	N125DN	LGA	ATL	105	762	6	0	2023-07-02 06:00:00	ATL
21182	7	17	1346	1345	1	1541	1546	9E	1275	N146PQ	LGA	CAE	92	617	13	45	2023-07-17 13:00:00	Other
21186	12	12	1808	1759	9	2114	2112	B6	117	N995JL	JFK	MCO	157	944	17	59	2023-12-12 17:00:00	MCO
21199	11	20	2238	2229	9	2344	2348	B6	102	N2086J	JFK	BOS	36	187	22	29	2023-11-20 22:00:00	BOS
21203	9	23	559	600	-1	912	915	AA	432	N321TG	LGA	MIA	161	1096	6	0	2023-09-23 06:00:00	MIA
21205	7	14	1500	1459	1	1719	1746	DL	781	N707TW	JFK	ATL	107	760	14	59	2023-07-14 14:00:00	ATL
21231	11	25	1525	1519	6	1712	1723	NK	1035	N630NK	LGA	DTW	83	502	15	19	2023-11-25 15:00:00	Other
21244	7	28	1940	1940	0	2210	2135	9E	1204	N676CA	EWR	RDU	64	416	19	40	2023-07-28 19:00:00	Other
21245	8	26	734	735	-1	1015	1037	DL	629	N399DA	JFK	PBI	131	1028	7	35	2023-08-26 07:00:00	Other
21247	4	5	1313	1303	10	1559	1559	UA	775	N17279	EWR	PBI	133	1023	13	3	2023-04-05 13:00:00	Other
21248	10	19	601	600	1	812	819	UA	387	N15751	EWR	ATL	103	746	6	0	2023-10-19 06:00:00	ATL
21253	8	8	2129	2126	3	2324	2249	9E	1193	N931XJ	LGA	ROC	49	254	21	26	2023-08-08 21:00:00	Other
21261	9	26	1350	1341	9	1538	1544	AA	640	N923US	EWR	CLT	90	529	13	41	2023-09-26 13:00:00	CLT
21266	6	28	1303	1303	0	1439	1448	DL	889	N932AT	EWR	DTW	76	488	13	3	2023-06-28 13:00:00	Other
21273	7	22	630	630	0	859	855	WN	842	N8842L	LGA	DAL	191	1381	6	30	2023-07-22 06:00:00	Other
21290	5	17	620	620	0	844	845	AA	966	N452AN	EWR	PHX	276	2133	6	20	2023-05-17 06:00:00	Other
21293	9	20	1853	1853	0	2205	2209	B6	71	N980JT	JFK	SEA	317	2422	18	53	2023-09-20 18:00:00	Other
21298	1	17	1354	1355	-1	1651	1710	WN	737	N8695D	LGA	HOU	215	1428	13	55	2023-01-17 13:00:00	Other
21303	2	15	1234	1230	4	1416	1438	AA	451	N977NN	LGA	ORD	132	733	12	30	2023-02-15 12:00:00	ORD
21312	2	27	759	800	-1	1024	1030	OO	1172	N324SY	JFK	MSP	161	1029	8	0	2023-02-27 08:00:00	Other
21315	6	20	1101	1100	1	1409	1432	DL	314	N722TW	JFK	SFO	336	2586	11	0	2023-06-20 11:00:00	Other
21327	9	23	1628	1629	-1	1851	1801	YX	1371	N435YX	JFK	ORF	73	290	16	29	2023-09-23 16:00:00	Other
21330	2	2	1729	1730	-1	2120	2120	DL	885	N727TW	JFK	SFO	366	2586	17	30	2023-02-02 17:00:00	Other
21332	3	11	647	645	2	755	821	NK	437	N623NK	EWR	BNA	109	748	6	45	2023-03-11 06:00:00	Other
21344	2	13	712	705	7	1003	1008	DL	380	N328NB	LGA	PBI	138	1035	7	5	2023-02-13 07:00:00	Other
21348	7	21	734	735	-1	1102	1037	DL	645	N3768	JFK	PBI	162	1028	7	35	2023-07-21 07:00:00	Other
21355	12	1	2100	2055	5	2244	2254	YX	1709	N207JQ	JFK	PIT	64	340	20	55	2023-12-01 20:00:00	Other
21386	11	16	830	830	0	1121	1140	B6	371	N306JB	JFK	MCO	139	944	8	30	2023-11-16 08:00:00	MCO
21389	1	8	737	730	7	950	954	B6	976	N179JB	JFK	CHS	101	636	7	30	2023-01-08 07:00:00	Other
21390	9	30	1829	1830	-1	2100	2137	UA	674	N27957	EWR	SFO	304	2565	18	30	2023-09-30 18:00:00	Other
21405	5	1	646	640	6	900	949	DL	104	N828DN	JFK	SEA	286	2422	6	40	2023-05-01 06:00:00	Other
21407	9	16	705	705	0	947	1000	DL	520	N818DA	JFK	TPA	137	1005	7	5	2023-09-16 07:00:00	Other
21410	7	6	1829	1830	-1	2143	2131	UA	414	N27733	EWR	SNA	323	2434	18	30	2023-07-06 18:00:00	Other
21411	3	20	2134	2125	9	2252	2301	9E	1555	N309PQ	JFK	ORF	46	290	21	25	2023-03-20 21:00:00	Other
21415	7	9	1357	1347	10	1537	1453	YX	923	N728YX	EWR	PVD	40	160	13	47	2023-07-09 13:00:00	Other
21416	5	29	1551	1550	1	1701	1720	WN	584	N8823Q	LGA	MDW	102	725	15	50	2023-05-29 15:00:00	Other
21431	4	28	1418	1418	0	1616	1624	YX	1047	N725YX	EWR	CVG	95	569	14	18	2023-04-28 14:00:00	Other
21435	5	31	1840	1840	0	2040	2108	9E	1308	N182GJ	JFK	CLT	79	541	18	40	2023-05-31 18:00:00	CLT
21449	3	29	1929	1925	4	2155	2149	9E	1550	N137EV	JFK	DTW	96	509	19	25	2023-03-29 19:00:00	Other
21450	8	18	1014	1015	-1	1235	1254	UA	566	N26970	EWR	IAH	169	1400	10	15	2023-08-18 10:00:00	Other
21467	10	11	1113	1107	6	1318	1329	UA	406	N37504	EWR	PHX	285	2133	11	7	2023-10-11 11:00:00	Other
21473	12	21	1509	1510	-1	1813	1835	DL	204	N307DU	LGA	DFW	213	1389	15	10	2023-12-21 15:00:00	Other
21474	10	4	1302	1259	3	1446	1503	DL	752	N343NW	LGA	DTW	76	502	12	59	2023-10-04 12:00:00	Other
21480	9	5	633	630	3	819	840	WN	1121	N8879Q	LGA	DEN	206	1620	6	30	2023-09-05 06:00:00	Other
21483	3	19	1755	1751	4	2001	2001	B6	380	N281JB	JFK	DTW	90	509	17	51	2023-03-19 17:00:00	Other
21491	6	5	1202	1159	3	1403	1418	9E	1676	N923XJ	LGA	MCI	149	1107	11	59	2023-06-05 11:00:00	Other
21510	5	15	1431	1421	10	1542	1603	9E	1386	N176PQ	LGA	ORF	53	296	14	21	2023-05-15 14:00:00	Other
21513	2	21	2114	2115	-1	45	45	B6	647	N993JE	JFK	LAX	365	2475	21	15	2023-02-21 21:00:00	LAX
21528	4	11	2108	2102	6	2327	2335	UA	268	N69885	EWR	ATL	95	746	21	2	2023-04-11 21:00:00	ATL
21532	3	8	1029	1029	0	1153	1215	9E	1449	N297PQ	LGA	BGR	62	378	10	29	2023-03-08 10:00:00	Other
21536	2	17	1135	1130	5	1310	1320	DL	584	N135DQ	LGA	ORD	114	733	11	30	2023-02-17 11:00:00	ORD
21539	2	15	1428	1425	3	1623	1625	9E	1439	N931XJ	LGA	GSO	82	461	14	25	2023-02-15 14:00:00	Other
21544	12	29	1206	1200	6	1527	1508	NK	1186	N681NK	LGA	FLL	169	1076	12	0	2023-12-29 12:00:00	FLL
21548	5	14	2201	2159	2	2342	2344	B6	517	N358JB	JFK	RDU	71	427	21	59	2023-05-14 21:00:00	Other
21550	4	29	1301	1300	1	1551	1610	UA	741	N14118	EWR	LAX	316	2454	13	0	2023-04-29 13:00:00	LAX
21568	7	11	650	650	0	942	957	AA	745	N925AN	LGA	MIA	151	1096	6	50	2023-07-11 06:00:00	MIA
21586	1	13	1247	1245	2	1449	1458	9E	1539	N925XJ	LGA	DAY	92	549	12	45	2023-01-13 12:00:00	Other
21589	1	16	830	830	0	1027	1027	9E	1611	N307PQ	JFK	RDU	67	427	8	30	2023-01-16 08:00:00	Other
21597	2	3	1735	1735	0	2136	2105	B6	914	N981JT	JFK	LAX	348	2475	17	35	2023-02-03 17:00:00	LAX
21600	10	8	2042	2040	2	48	46	NK	334	N628NK	EWR	SJU	219	1608	20	40	2023-10-08 20:00:00	Other
21609	5	25	2030	2029	1	2332	2335	UA	250	N66808	EWR	AUS	204	1504	20	29	2023-05-25 20:00:00	Other
21615	4	21	2021	2020	1	2308	2320	WN	565	N8668A	LGA	DAL	197	1381	20	20	2023-04-21 20:00:00	Other
21618	4	3	1952	1948	4	2249	2302	UA	382	N402UA	EWR	FLL	158	1065	19	48	2023-04-03 19:00:00	FLL
21629	9	22	1129	1129	0	1436	1447	AA	643	N338PK	LGA	MIA	154	1096	11	29	2023-09-22 11:00:00	MIA
21633	1	13	1000	955	5	1211	1215	9E	1508	N136EV	JFK	IND	104	665	9	55	2023-01-13 09:00:00	Other
21643	5	15	1724	1723	1	1858	1851	YX	1022	N861RW	EWR	ROC	48	246	17	23	2023-05-15 17:00:00	Other
21651	12	11	702	700	2	1018	1049	AS	11	N274AK	JFK	SFO	346	2586	7	0	2023-12-11 07:00:00	Other
21655	6	8	1826	1826	0	2000	1940	YX	1116	N641RW	EWR	ALB	33	143	18	26	2023-06-08 18:00:00	Other
21662	2	20	2038	2039	-1	2258	2253	B6	532	N323JB	JFK	DTW	92	509	20	39	2023-02-20 20:00:00	Other
21674	9	1	945	946	-1	1327	1341	UA	575	N47524	EWR	SJU	199	1608	9	46	2023-09-01 09:00:00	Other
21678	10	19	1728	1729	-1	1918	2002	AA	551	N313SB	JFK	PHX	268	2153	17	29	2023-10-19 17:00:00	Other
21681	5	24	1651	1645	6	2039	1855	WN	187	N8314L	LGA	MCI	NA	1107	16	45	2023-05-24 16:00:00	Other
21692	5	4	1639	1630	9	1918	1932	NK	525	N639NK	EWR	MCO	131	937	16	30	2023-05-04 16:00:00	MCO
21707	11	13	714	705	9	1032	1007	DL	499	N917DU	JFK	TPA	147	1005	7	5	2023-11-13 07:00:00	Other
21717	5	25	837	835	2	1116	1110	DL	537	N6701	JFK	ATL	103	760	8	35	2023-05-25 08:00:00	ATL
21718	6	22	1629	1630	-1	1757	1817	DL	637	N134DU	LGA	ORD	110	733	16	30	2023-06-22 16:00:00	ORD
21734	9	21	1706	1700	6	1926	1933	DL	573	N857DZ	JFK	ATL	116	760	17	0	2023-09-21 17:00:00	ATL
21737	10	14	1722	1721	1	1913	1929	AA	737	N986NN	LGA	CLT	88	544	17	21	2023-10-14 17:00:00	CLT
21741	1	31	1910	1910	0	2126	2134	9E	1598	N131EV	JFK	CHS	103	636	19	10	2023-01-31 19:00:00	Other
21742	1	22	732	730	2	1029	1055	DL	105	N928DU	JFK	SEA	322	2422	7	30	2023-01-22 07:00:00	Other
21748	3	2	933	933	0	1256	1300	B6	62	N644JB	EWR	FLL	146	1065	9	33	2023-03-02 09:00:00	FLL
21749	3	15	1305	1256	9	1425	1410	YX	1146	N855RW	EWR	MHT	47	209	12	56	2023-03-15 12:00:00	Other
21753	4	15	729	725	4	845	905	WN	704	N7734H	LGA	STL	119	888	7	25	2023-04-15 07:00:00	Other
21761	8	12	951	952	-1	1226	1240	UA	387	N17262	EWR	AUS	189	1504	9	52	2023-08-12 09:00:00	Other
21766	8	18	629	630	-1	912	931	AA	662	N912NN	JFK	DFW	187	1391	6	30	2023-08-18 06:00:00	Other
21767	5	21	726	727	-1	934	951	YX	1007	N739YX	EWR	SDF	103	642	7	27	2023-05-21 07:00:00	Other
21771	6	10	754	755	-1	911	941	UA	991	N14250	EWR	RDU	61	416	7	55	2023-06-10 07:00:00	Other
21773	8	17	1747	1739	8	2037	2035	UA	244	N27267	EWR	SRQ	142	1034	17	39	2023-08-17 17:00:00	Other
21774	10	9	2159	2200	-1	2310	2333	9E	1539	N232PQ	JFK	BTV	48	266	22	0	2023-10-09 22:00:00	Other
21777	2	8	2156	2150	6	2257	2303	9E	1312	N904XJ	LGA	SCE	38	208	21	50	2023-02-08 21:00:00	Other
21782	5	18	1620	1621	-1	1720	1737	YX	1584	N205JQ	LGA	PVD	34	143	16	21	2023-05-18 16:00:00	Other
21784	5	11	1944	1935	9	2205	2245	B6	26	N703JB	JFK	ABQ	242	1826	19	35	2023-05-11 19:00:00	Other
21800	9	18	839	840	-1	1024	1030	B6	904	N355JB	JFK	RDU	78	427	8	40	2023-09-18 08:00:00	Other
21808	6	6	1733	1729	4	2015	1937	YX	1147	N723YX	EWR	DTW	89	488	17	29	2023-06-06 17:00:00	Other
21819	1	25	1006	1000	6	1257	1325	DL	421	N176DN	JFK	LAX	323	2475	10	0	2023-01-25 10:00:00	LAX
21821	8	20	1429	1430	-1	1542	1603	9E	1300	N331PQ	LGA	ROC	44	254	14	30	2023-08-20 14:00:00	Other
21822	8	30	1200	1200	0	1433	1443	UA	660	N772UA	EWR	LAX	299	2454	12	0	2023-08-30 12:00:00	LAX
21827	2	18	2145	2145	0	2254	2256	B6	105	N375JB	JFK	BOS	42	187	21	45	2023-02-18 21:00:00	BOS
21833	8	28	1909	1905	4	2024	2030	WN	822	N8812Q	LGA	MDW	109	725	19	5	2023-08-28 19:00:00	Other
21838	10	31	1711	1710	1	1943	1935	DL	708	N607AT	EWR	ATL	127	746	17	10	2023-10-31 17:00:00	ATL
21839	2	24	1636	1627	9	1947	1851	YX	1015	N746YX	EWR	MCI	217	1092	16	27	2023-02-24 16:00:00	Other
21845	7	13	1505	1459	6	1750	1822	B6	438	N505JB	JFK	FLL	138	1069	14	59	2023-07-13 14:00:00	FLL
21867	11	22	2103	2055	8	5	2353	B6	884	N821JB	LGA	PBI	140	1035	20	55	2023-11-22 20:00:00	Other
21873	4	6	614	615	-1	904	910	NK	25	N529NK	EWR	MCO	127	937	6	15	2023-04-06 06:00:00	MCO
21882	3	22	1759	1800	-1	2124	2143	DL	261	N914DU	JFK	SLC	302	1990	18	0	2023-03-22 18:00:00	Other
21892	9	27	1000	1000	0	1314	1254	B6	331	N571JB	JFK	PBI	155	1028	10	0	2023-09-27 10:00:00	Other
21894	11	20	801	800	1	920	919	B6	40	N523JB	JFK	BTV	47	266	8	0	2023-11-20 08:00:00	Other
21927	11	3	1619	1610	9	1927	1936	DL	103	N887DN	JFK	SLC	292	1990	16	10	2023-11-03 16:00:00	Other
21932	10	15	801	755	6	1050	1049	NK	407	N665NK	EWR	MCO	139	937	7	55	2023-10-15 07:00:00	MCO
21933	9	2	801	755	6	953	955	WN	1391	N7749B	LGA	DEN	213	1620	7	55	2023-09-02 07:00:00	Other
21936	3	25	1637	1629	8	2012	1937	UA	502	N27292	EWR	RSW	177	1068	16	29	2023-03-25 16:00:00	Other
21939	10	26	2011	2005	6	2256	2318	DL	597	N304DU	LGA	IAH	197	1416	20	5	2023-10-26 20:00:00	Other
21941	7	30	2206	2159	7	2356	7	YX	928	N653RW	EWR	DTW	83	488	21	59	2023-07-30 21:00:00	Other
21943	10	21	1016	1015	1	1240	1311	UA	676	N672UA	EWR	IAH	179	1400	10	15	2023-10-21 10:00:00	Other
21944	5	24	1503	1500	3	1849	1756	UA	268	N17245	EWR	TPA	198	997	15	0	2023-05-24 15:00:00	Other
21946	7	27	659	700	-1	946	956	DL	442	N893DN	JFK	TPA	132	1005	7	0	2023-07-27 07:00:00	Other
21964	12	11	806	807	-1	1106	1139	UA	54	N77543	EWR	DFW	197	1372	8	7	2023-12-11 08:00:00	Other
21966	1	1	719	719	0	1033	1042	B6	932	N645JB	JFK	FLL	164	1069	7	19	2023-01-01 07:00:00	FLL
21968	3	3	1159	1200	-1	1459	1521	UA	529	N29129	EWR	LAX	338	2454	12	0	2023-03-03 12:00:00	LAX
21971	5	16	1927	1928	-1	2221	2230	DL	617	N361NB	LGA	TPA	142	1010	19	28	2023-05-16 19:00:00	Other
21979	4	2	1029	1030	-1	1128	1136	9E	1411	N326PQ	JFK	BWI	40	184	10	30	2023-04-02 10:00:00	Other
21990	5	17	1125	1118	7	1431	1435	DL	884	N325DN	LGA	FLL	154	1076	11	18	2023-05-17 11:00:00	FLL
21992	10	12	726	725	1	907	915	WN	360	N8557Q	LGA	STL	136	888	7	25	2023-10-12 07:00:00	Other
21996	3	6	2004	1959	5	47	57	UA	599	N68891	EWR	SJU	187	1608	19	59	2023-03-06 19:00:00	Other
22004	11	16	1028	1020	8	1259	1325	UA	675	N14240	EWR	IAH	189	1400	10	20	2023-11-16 10:00:00	Other
22005	2	20	1009	1010	-1	1213	1219	AA	100	N157UW	JFK	CLT	98	541	10	10	2023-02-20 10:00:00	CLT
22029	11	20	1205	1200	5	1424	1519	UA	835	N643UA	EWR	LAX	297	2454	12	0	2023-11-20 12:00:00	LAX
22036	10	1	1100	1059	1	1327	1337	UA	524	N27292	EWR	LAS	296	2227	10	59	2023-10-01 10:00:00	Other
22042	10	30	1722	1713	9	1936	1951	DL	534	N807DN	JFK	ATL	114	760	17	13	2023-10-30 17:00:00	ATL
22051	7	16	1101	1100	1	1423	1403	NK	438	N664NK	EWR	FLL	168	1065	11	0	2023-07-16 11:00:00	FLL
22054	6	1	1208	1205	3	1428	1353	OO	1205	N246SY	JFK	ORD	115	740	12	5	2023-06-01 12:00:00	ORD
22062	9	8	954	955	-1	1409	1244	DL	294	N340DN	JFK	MCO	182	944	9	55	2023-09-08 09:00:00	MCO
22063	9	4	1314	1305	9	1423	1429	YX	1080	N746YX	EWR	PIT	54	319	13	5	2023-09-04 13:00:00	Other
22069	4	7	2158	2159	-1	1	2359	UA	571	N27253	EWR	MSP	153	1008	21	59	2023-04-07 21:00:00	Other
22072	3	2	2039	2039	0	2252	2253	B6	548	N231JB	JFK	DTW	105	509	20	39	2023-03-02 20:00:00	Other
22077	11	2	1035	1030	5	1251	1255	DL	800	N883DN	EWR	ATL	113	746	10	30	2023-11-02 10:00:00	ATL
22098	11	8	956	955	1	1216	1220	WN	464	N259WN	LGA	MCI	173	1107	9	55	2023-11-08 09:00:00	Other
22109	2	1	1716	1708	8	1916	1915	DL	876	N338NW	LGA	DTW	97	502	17	8	2023-02-01 17:00:00	Other
22126	1	18	2128	2120	8	2346	2346	YX	1195	N731YX	EWR	IND	114	645	21	20	2023-01-18 21:00:00	Other
22130	9	14	1910	1900	10	2033	2030	WN	1229	N8670A	LGA	MDW	105	725	19	0	2023-09-14 19:00:00	Other
22138	7	12	2014	2015	-1	2134	2135	B6	449	N236JB	LGA	BOS	41	184	20	15	2023-07-12 20:00:00	BOS
22146	4	13	1016	1015	1	1304	1314	UA	379	N27251	EWR	SRQ	152	1034	10	15	2023-04-13 10:00:00	Other
22155	10	2	921	919	2	1105	1115	9E	1495	N341PQ	LGA	STL	117	888	9	19	2023-10-02 09:00:00	Other
22161	5	29	959	1000	-1	1228	1303	AA	606	N343PN	LGA	DFW	173	1389	10	0	2023-05-29 10:00:00	Other
22165	4	27	740	730	10	912	910	B6	756	N821JB	JFK	RDU	75	427	7	30	2023-04-27 07:00:00	Other
22167	9	5	1731	1730	1	2005	2034	AS	81	N968AK	EWR	PDX	302	2434	17	30	2023-09-05 17:00:00	Other
22177	4	20	654	645	9	937	934	B6	913	N266JB	JFK	PBI	146	1028	6	45	2023-04-20 06:00:00	Other
22178	12	12	1728	1729	-1	2034	2050	UA	749	N27273	EWR	PDX	328	2434	17	29	2023-12-12 17:00:00	Other
22182	5	28	1621	1615	6	1730	1755	WN	161	N500WR	LGA	BNA	101	764	16	15	2023-05-28 16:00:00	Other
22192	6	15	1656	1655	1	1844	1856	UA	306	N33714	EWR	CLT	71	529	16	55	2023-06-15 16:00:00	CLT
22193	5	14	2015	2015	0	2147	2134	B6	540	N328JB	LGA	BOS	40	184	20	15	2023-05-14 20:00:00	BOS
22214	5	16	1614	1615	-1	1810	1831	DL	337	N105DU	LGA	CHS	93	641	16	15	2023-05-16 16:00:00	Other
22220	10	7	1254	1255	-1	1454	1508	OO	1163	N613CZ	LGA	OMA	162	1148	12	55	2023-10-07 12:00:00	Other
22222	7	16	1204	1155	9	1600	1455	DL	501	N393DN	LGA	MCO	162	950	11	55	2023-07-16 11:00:00	MCO
22231	4	24	2234	2235	-1	18	6	YX	1452	N235JQ	JFK	PWM	47	273	22	35	2023-04-24 22:00:00	Other
22234	5	15	2010	2000	10	2218	2251	DL	424	N395DN	JFK	ATL	101	760	20	0	2023-05-15 20:00:00	ATL
22236	1	26	1816	1816	0	2133	2128	AA	705	N352PS	EWR	DFW	220	1372	18	16	2023-01-26 18:00:00	Other
22239	3	20	1629	1629	0	1752	1818	DL	476	N117DU	LGA	ORD	113	733	16	29	2023-03-20 16:00:00	ORD
22242	8	4	606	559	7	940	951	B6	3	N516JB	JFK	SJU	192	1598	5	59	2023-08-04 05:00:00	Other
22244	9	12	800	800	0	1146	1157	DL	705	N521DT	JFK	SJU	208	1598	8	0	2023-09-12 08:00:00	Other
22249	8	27	1933	1929	4	2146	2208	9E	1187	N602LR	JFK	MCI	161	1113	19	29	2023-08-27 19:00:00	Other
22266	7	28	1032	1029	3	1208	1227	9E	1207	N927XJ	LGA	MYR	81	563	10	29	2023-07-28 10:00:00	Other
22269	12	2	730	730	0	1009	1012	DL	173	N304DN	LGA	ATL	135	762	7	30	2023-12-02 07:00:00	ATL
22274	6	1	1255	1245	10	1432	1442	9E	1761	N308PQ	LGA	RDU	71	431	12	45	2023-06-01 12:00:00	Other
22281	9	10	1004	1000	4	1358	1204	9E	1613	N320PQ	LGA	GSO	79	461	10	0	2023-09-10 10:00:00	Other
22290	7	15	1931	1929	2	2211	2225	DL	153	N882DN	JFK	DEN	220	1626	19	29	2023-07-15 19:00:00	Other
22292	3	17	1154	1150	4	1320	1315	WN	1023	N8308K	LGA	MDW	119	725	11	50	2023-03-17 11:00:00	Other
22294	7	20	1328	1329	-1	1610	1557	UA	733	N17306	EWR	ATL	103	746	13	29	2023-07-20 13:00:00	ATL
22300	10	1	1129	1129	0	1355	1424	UA	741	N37295	EWR	SAN	311	2425	11	29	2023-10-01 11:00:00	Other
22305	10	12	1201	1200	1	1451	1449	DL	324	N525DA	JFK	LAS	319	2248	12	0	2023-10-12 12:00:00	Other
22310	5	11	2155	2155	0	48	141	DL	108	N703TW	JFK	SFO	329	2586	21	55	2023-05-11 21:00:00	Other
22311	9	24	1328	1320	8	1441	1445	WN	515	N7868K	LGA	BNA	107	764	13	20	2023-09-24 13:00:00	Other
22316	3	29	1735	1730	5	2113	2105	DL	268	N186DN	JFK	LAX	365	2475	17	30	2023-03-29 17:00:00	LAX
22322	2	19	1849	1844	5	2203	2209	B6	50	N2044J	JFK	SMF	339	2521	18	44	2023-02-19 18:00:00	Other
22323	6	26	1204	1200	4	1540	1435	DL	335	N396DN	LGA	ATL	111	762	12	0	2023-06-26 12:00:00	ATL
22326	11	13	1737	1729	8	2107	2043	UA	841	N26210	EWR	MIA	163	1085	17	29	2023-11-13 17:00:00	MIA
22328	9	18	2014	2015	-1	2334	2315	WN	574	N8641B	LGA	DAL	187	1381	20	15	2023-09-18 20:00:00	Other
22338	6	5	1104	1059	5	1227	1250	UA	877	N883UA	EWR	MEM	127	946	10	59	2023-06-05 10:00:00	Other
22346	7	13	1503	1459	4	1815	1806	UA	207	N486UA	EWR	MIA	152	1085	14	59	2023-07-13 14:00:00	MIA
22347	7	28	1528	1526	2	1657	1714	9E	1192	N303PQ	JFK	BNA	112	765	15	26	2023-07-28 15:00:00	Other
22348	1	16	1502	1500	2	1741	1813	B6	23	N633JB	JFK	PBI	133	1028	15	0	2023-01-16 15:00:00	Other
22351	5	28	2046	2045	1	2332	20	AA	95	N102NN	JFK	LAX	302	2475	20	45	2023-05-28 20:00:00	LAX
22357	12	9	944	945	-1	1520	1615	DL	109	N830MH	JFK	HNL	613	4983	9	45	2023-12-09 09:00:00	Other
22358	7	21	2104	2100	4	2345	24	AA	87	N108NN	JFK	LAX	309	2475	21	0	2023-07-21 21:00:00	LAX
22363	9	18	1431	1430	1	1655	1646	9E	1448	N901XJ	JFK	CLT	88	541	14	30	2023-09-18 14:00:00	CLT
22368	12	5	1123	1115	8	1428	1419	B6	127	N794JB	EWR	FLL	163	1065	11	15	2023-12-05 11:00:00	FLL
22385	5	1	901	900	1	1015	1015	WN	62	N479WN	LGA	MDW	104	725	9	0	2023-05-01 09:00:00	Other
22393	11	9	1829	1830	-1	2127	2137	AA	998	N924NN	EWR	MIA	147	1085	18	30	2023-11-09 18:00:00	MIA
22398	4	30	730	729	1	935	929	UA	453	N873UA	EWR	CLT	94	529	7	29	2023-04-30 07:00:00	CLT
22413	8	13	602	600	2	903	910	AA	362	N316SE	LGA	MIA	143	1096	6	0	2023-08-13 06:00:00	MIA
22417	10	14	831	830	1	1115	1123	UA	124	N14019	EWR	LAX	302	2454	8	30	2023-10-14 08:00:00	LAX
22419	7	18	826	823	3	1112	1114	DL	188	N3759	JFK	DFW	178	1391	8	23	2023-07-18 08:00:00	Other
22434	9	12	1442	1435	7	1613	1601	UA	598	N425UA	EWR	BNA	116	748	14	35	2023-09-12 14:00:00	Other
22445	10	4	2004	2000	4	2211	2213	B6	489	N238JB	JFK	DTW	79	509	20	0	2023-10-04 20:00:00	Other
22451	4	17	722	715	7	939	945	DL	266	N704X	JFK	PHX	294	2153	7	15	2023-04-17 07:00:00	Other
22452	11	11	1234	1229	5	1541	1542	AA	959	N304RB	JFK	MIA	155	1089	12	29	2023-11-11 12:00:00	MIA
22456	10	20	930	930	0	1248	1246	DL	100	N904DN	JFK	SLC	276	1990	9	30	2023-10-20 09:00:00	Other
22469	7	8	1531	1530	1	1654	1705	UA	569	N840UA	EWR	ORD	115	719	15	30	2023-07-08 15:00:00	ORD
22482	3	20	1708	1702	6	2024	2024	B6	771	N984JB	EWR	LAX	344	2454	17	2	2023-03-20 17:00:00	LAX
22485	6	4	1200	1200	0	1440	1500	DL	209	N419DX	JFK	LAX	303	2475	12	0	2023-06-04 12:00:00	LAX
22488	2	27	2135	2135	0	7	2349	UA	235	N819UA	EWR	CVG	98	569	21	35	2023-02-27 21:00:00	Other
22489	2	8	1631	1630	1	1939	2007	DL	230	N906DN	JFK	SLC	287	1990	16	30	2023-02-08 16:00:00	Other
22492	7	8	959	956	3	1117	1128	YX	889	N758YX	EWR	BNA	108	748	9	56	2023-07-08 09:00:00	Other
22502	10	7	1400	1400	0	1622	1614	DL	787	N3765	EWR	ATL	111	746	14	0	2023-10-07 14:00:00	ATL
22507	7	14	1403	1400	3	1651	1655	AA	805	N958AN	LGA	DFW	193	1389	14	0	2023-07-14 14:00:00	Other
22511	11	30	2059	2059	0	2242	2255	9E	1436	N302PQ	LGA	ROA	64	405	20	59	2023-11-30 20:00:00	Other
22518	7	24	2300	2258	2	302	258	B6	256	N547JB	JFK	PSE	202	1617	22	58	2023-07-24 22:00:00	Other
22528	3	28	1851	1850	1	2009	2020	B6	959	N3112J	EWR	BOS	35	200	18	50	2023-03-28 18:00:00	BOS
22531	12	25	1333	1329	4	1614	1649	DL	394	N102DU	LGA	IAH	204	1416	13	29	2023-12-25 13:00:00	Other
22534	6	12	742	735	7	1052	1047	DL	1028	N398DA	JFK	MIA	146	1089	7	35	2023-06-12 07:00:00	MIA
22535	11	2	1300	1259	1	1437	1447	9E	1538	N915XJ	LGA	CLE	69	419	12	59	2023-11-02 12:00:00	Other
22547	6	6	2008	1959	9	2153	2138	UA	458	N77261	EWR	ORD	107	719	19	59	2023-06-06 19:00:00	ORD
22549	9	26	1950	1945	5	2137	2214	DL	795	N321US	JFK	MSP	140	1029	19	45	2023-09-26 19:00:00	Other
22551	4	12	2029	2030	-1	2134	2212	YX	1477	N214JQ	LGA	BNA	101	764	20	30	2023-04-12 20:00:00	Other
22553	6	12	710	700	10	946	1000	AS	96	N523AS	EWR	SEA	304	2402	7	0	2023-06-12 07:00:00	Other
22554	7	8	1124	1124	0	1420	1440	DL	169	N718TW	JFK	SEA	316	2422	11	24	2023-07-08 11:00:00	Other
22569	8	1	2055	2055	0	2256	2309	OO	961	N240SY	JFK	CLE	80	425	20	55	2023-08-01 20:00:00	Other
22570	12	25	1643	1641	2	1944	1947	B6	17	N580JB	JFK	PBI	148	1028	16	41	2023-12-25 16:00:00	Other
22576	7	17	658	659	-1	840	830	YX	1433	N214JQ	LGA	BNA	126	764	6	59	2023-07-17 06:00:00	Other
22582	10	26	1804	1755	9	1913	1926	YX	1711	N246JQ	JFK	DCA	40	213	17	55	2023-10-26 17:00:00	Other
22583	5	8	844	845	-1	1056	1050	9E	1560	N904XJ	LGA	AVL	90	599	8	45	2023-05-08 08:00:00	Other
22594	2	12	1825	1815	10	2107	2125	AA	252	N955AN	EWR	DFW	188	1372	18	15	2023-02-12 18:00:00	Other
22602	9	24	1230	1229	1	1602	1525	UA	659	N807UA	LGA	IAH	190	1416	12	29	2023-09-24 12:00:00	Other
22608	7	19	729	719	10	1017	1027	UA	503	N62892	EWR	FLL	143	1065	7	19	2023-07-19 07:00:00	FLL
22619	1	2	805	800	5	1314	1256	B6	212	N2002J	JFK	SJU	192	1598	8	0	2023-01-02 08:00:00	Other
22621	10	17	2110	2111	-1	2340	2359	UA	478	N27274	EWR	MCO	127	937	21	11	2023-10-17 21:00:00	MCO
22625	3	25	1757	1755	2	2129	2124	DL	637	N343NW	JFK	AUS	239	1521	17	55	2023-03-25 17:00:00	Other
22626	7	2	1137	1133	4	1243	1244	B6	641	N283JB	JFK	ACK	45	199	11	33	2023-07-02 11:00:00	Other
22630	4	8	1434	1435	-1	1734	1750	UA	79	N224UA	EWR	SFO	335	2565	14	35	2023-04-08 14:00:00	Other
22632	12	1	1659	1659	0	1926	1939	DL	131	N342DN	LGA	ATL	121	762	16	59	2023-12-01 16:00:00	ATL
22635	10	17	1623	1615	8	1841	1900	WN	858	N277WN	LGA	DAL	175	1381	16	15	2023-10-17 16:00:00	Other
22651	5	26	833	829	4	951	1011	AA	126	N906NN	LGA	ORD	105	733	8	29	2023-05-26 08:00:00	ORD
22656	6	5	1843	1843	0	1953	2007	UA	693	N883UA	EWR	BOS	42	200	18	43	2023-06-05 18:00:00	BOS
22660	7	15	1650	1651	-1	1857	1905	NK	247	N679NK	EWR	IND	94	645	16	51	2023-07-15 16:00:00	Other
22670	3	27	913	914	-1	1212	1223	UA	423	N27734	EWR	MIA	159	1085	9	14	2023-03-27 09:00:00	MIA
22684	5	29	1840	1830	10	2145	2205	UA	430	N12125	EWR	SFO	316	2565	18	30	2023-05-29 18:00:00	Other
22685	1	16	1701	1659	2	2033	2022	AA	95	N106NN	JFK	LAX	353	2475	16	59	2023-01-16 16:00:00	LAX
22688	7	3	1058	1059	-1	1246	1313	UA	377	N64844	EWR	PHX	267	2133	10	59	2023-07-03 10:00:00	Other
22693	9	10	800	800	0	1117	1134	DL	293	N723TW	JFK	SFO	349	2586	8	0	2023-09-10 08:00:00	Other
22697	6	24	629	630	-1	903	928	B6	50	N323JB	JFK	SRQ	138	1041	6	30	2023-06-24 06:00:00	Other
22702	5	29	954	955	-1	1148	1205	G4	407	313NV	EWR	SAV	93	708	9	55	2023-05-29 09:00:00	Other
22708	9	4	1503	1459	4	1841	1842	UA	440	N17303	EWR	ANC	429	3370	14	59	2023-09-04 14:00:00	Other
22712	5	14	2029	2020	9	2217	2153	YX	1334	N102HQ	LGA	ORF	54	296	20	20	2023-05-14 20:00:00	Other
22715	7	19	1240	1237	3	1414	1414	AA	801	N887NN	LGA	ORD	112	733	12	37	2023-07-19 12:00:00	ORD
22724	11	29	1025	1015	10	1320	1321	B6	633	N945JT	EWR	LAX	332	2454	10	15	2023-11-29 10:00:00	LAX
22726	7	31	1840	1830	10	2016	2008	UA	369	N75425	EWR	ORD	114	719	18	30	2023-07-31 18:00:00	ORD
22729	6	23	844	845	-1	1100	1105	9E	1554	N605LR	LGA	SAV	114	722	8	45	2023-06-23 08:00:00	Other
22732	10	21	1300	1255	5	1534	1600	B6	16	N571JB	LGA	TPA	134	1010	12	55	2023-10-21 12:00:00	Other
22746	1	26	828	829	-1	1107	1100	9E	1677	N138EV	LGA	SAV	132	722	8	29	2023-01-26 08:00:00	Other
22749	8	6	934	929	5	1242	1232	UA	578	N35236	EWR	PBI	170	1023	9	29	2023-08-06 09:00:00	Other
22761	1	8	659	700	-1	955	1005	UA	647	N14230	EWR	TPA	155	997	7	0	2023-01-08 07:00:00	Other
22767	3	3	1959	2000	-1	2109	2122	AA	790	N748UW	LGA	DCA	50	214	20	0	2023-03-03 20:00:00	Other
22774	8	22	649	650	-1	928	1001	AA	726	N877NN	LGA	MIA	135	1096	6	50	2023-08-22 06:00:00	MIA
22791	8	9	829	830	-1	1059	1114	UA	120	N91007	EWR	LAX	306	2454	8	30	2023-08-09 08:00:00	LAX
22808	6	24	714	715	-1	1000	1033	DL	327	N528DE	JFK	SEA	312	2422	7	15	2023-06-24 07:00:00	Other
22810	2	10	1407	1359	8	1716	1712	B6	147	N907JB	LGA	MCO	141	950	13	59	2023-02-10 13:00:00	MCO
22815	3	26	837	830	7	1033	1017	OO	1217	N610CZ	JFK	BNA	142	765	8	30	2023-03-26 08:00:00	Other
22823	6	1	1816	1817	-1	2111	2125	UA	780	N495UA	EWR	RSW	151	1068	18	17	2023-06-01 18:00:00	Other
22825	11	25	1638	1630	8	1947	1934	B6	824	N828JB	EWR	TPA	165	997	16	30	2023-11-25 16:00:00	Other
22830	12	17	1704	1705	-1	2013	2013	DL	826	N511DE	JFK	MCO	143	944	17	5	2023-12-17 17:00:00	MCO
22831	2	20	559	600	-1	1001	945	AA	463	N919US	EWR	PHX	336	2133	6	0	2023-02-20 06:00:00	Other
22835	2	17	947	940	7	1311	1304	B6	574	N615JB	JFK	RSW	163	1074	9	40	2023-02-17 09:00:00	Other
22851	11	18	1620	1620	0	1833	1842	9E	1455	N176PQ	LGA	CHS	91	641	16	20	2023-11-18 16:00:00	Other
22858	2	18	615	610	5	817	841	B6	31	N552JB	JFK	MSY	158	1182	6	10	2023-02-18 06:00:00	Other
22865	4	4	731	729	2	1020	1030	NK	432	N683NK	EWR	MCO	126	937	7	29	2023-04-04 07:00:00	MCO
22870	9	21	1028	1029	-1	1222	1229	OO	1246	N324SY	LGA	MEM	132	963	10	29	2023-09-21 10:00:00	Other
22871	8	20	1859	1859	0	2022	2109	9E	1120	N932XJ	LGA	STL	117	888	18	59	2023-08-20 18:00:00	Other
22873	9	13	1918	1915	3	2229	2219	DL	141	N706TW	JFK	LAX	318	2475	19	15	2023-09-13 19:00:00	LAX
22877	10	16	1504	1500	4	1627	1648	9E	1504	N195PQ	EWR	RDU	64	416	15	0	2023-10-16 15:00:00	Other
22879	10	3	1059	1059	0	1324	1337	UA	524	N57299	EWR	LAS	288	2227	10	59	2023-10-03 10:00:00	Other
22883	11	21	929	930	-1	1111	1116	AA	748	N750UW	LGA	ORD	119	733	9	30	2023-11-21 09:00:00	ORD
22884	2	15	659	700	-1	1001	1010	DL	605	N371DN	LGA	FLL	158	1076	7	0	2023-02-15 07:00:00	FLL
22885	7	9	1101	1100	1	1420	1348	AA	615	N931NN	LGA	DFW	219	1389	11	0	2023-07-09 11:00:00	Other
22894	1	18	1828	1825	3	2137	2156	DL	132	N897DN	JFK	SEA	332	2422	18	25	2023-01-18 18:00:00	Other
22895	8	13	2129	2130	-1	1	2344	YX	893	N730YX	EWR	CLT	79	529	21	30	2023-08-13 21:00:00	CLT
22900	9	29	1429	1430	-1	1551	1553	YX	1060	N728YX	EWR	ROC	41	246	14	30	2023-09-29 14:00:00	Other
22907	11	5	1101	1100	1	1403	1405	AA	218	N983NN	JFK	MIA	156	1089	11	0	2023-11-05 11:00:00	MIA
22910	7	9	707	658	9	807	815	AA	465	N770UW	LGA	DCA	43	214	6	58	2023-07-09 06:00:00	Other
22921	6	13	911	905	6	1223	1209	YX	1289	N129HQ	LGA	IAH	212	1416	9	5	2023-06-13 09:00:00	Other
22926	9	24	630	630	0	936	942	B6	5	N942JB	JFK	SFO	338	2586	6	30	2023-09-24 06:00:00	Other
22933	3	20	1103	1059	4	1210	1222	YX	1078	N722YX	EWR	DCA	44	199	10	59	2023-03-20 10:00:00	Other
22939	11	5	1944	1945	-1	2114	2122	OO	1209	N315SY	JFK	IAD	51	228	19	45	2023-11-05 19:00:00	Other
22940	4	16	604	600	4	808	830	UA	371	N65832	EWR	DEN	203	1605	6	0	2023-04-16 06:00:00	Other
22943	10	14	1754	1755	-1	1852	1903	9E	1536	N918XJ	LGA	PVD	34	143	17	55	2023-10-14 17:00:00	Other
22951	4	28	2251	2250	1	16	12	9E	1417	N302PQ	JFK	SYR	41	209	22	50	2023-04-28 22:00:00	Other
22961	9	6	911	905	6	1049	1111	DL	195	N352DN	LGA	DTW	74	502	9	5	2023-09-06 09:00:00	Other
22962	7	19	1600	1600	0	1717	1742	YX	1351	N203JQ	LGA	BOS	39	184	16	0	2023-07-19 16:00:00	BOS
22963	12	1	1329	1330	-1	1506	1511	YX	1259	N447YX	JFK	PIT	78	340	13	30	2023-12-01 13:00:00	Other
22983	8	4	704	705	-1	941	1019	DL	469	N113DX	LGA	FLL	137	1076	7	5	2023-08-04 07:00:00	FLL
22992	5	10	1621	1621	0	1718	1737	YX	1584	N206JQ	LGA	PVD	35	143	16	21	2023-05-10 16:00:00	Other
22997	8	9	1528	1528	0	1721	1728	DL	737	N943AT	EWR	MSP	150	1008	15	28	2023-08-09 15:00:00	Other
23008	12	27	1406	1400	6	1808	1718	AA	897	N334TL	JFK	MIA	163	1089	14	0	2023-12-27 14:00:00	MIA
23020	2	20	1004	955	9	1223	1218	9E	1358	N197PQ	JFK	IND	113	665	9	55	2023-02-20 09:00:00	Other
23024	2	24	2201	2159	2	2339	2325	9E	1343	N319PQ	LGA	BGR	59	378	21	59	2023-02-24 21:00:00	Other
23043	8	24	818	810	8	1014	1019	B6	370	N284JB	JFK	CHS	85	636	8	10	2023-08-24 08:00:00	Other
23047	8	29	2000	1959	1	2317	2329	DL	665	N894DN	JFK	MIA	162	1089	19	59	2023-08-29 19:00:00	MIA
23049	12	14	2223	2224	-1	313	325	NK	364	N607NK	EWR	SJU	196	1608	22	24	2023-12-14 22:00:00	Other
23064	10	24	745	745	0	1028	1020	NK	138	N611NK	EWR	LAS	304	2227	7	45	2023-10-24 07:00:00	Other
23065	6	22	744	744	0	931	956	9E	1746	N906XJ	JFK	CLT	86	541	7	44	2023-06-22 07:00:00	CLT
23070	2	16	1550	1550	0	1819	1836	DL	345	N320DN	LGA	ATL	120	762	15	50	2023-02-16 15:00:00	ATL
23072	5	19	1201	1201	0	1343	1357	YX	1263	N429YX	LGA	MEM	134	963	12	1	2023-05-19 12:00:00	Other
23073	7	17	1207	1200	7	1434	1435	DL	277	N345DN	LGA	ATL	116	762	12	0	2023-07-17 12:00:00	ATL
23074	3	25	1610	1600	10	1908	1903	UA	769	N467UA	EWR	FLL	159	1065	16	0	2023-03-25 16:00:00	FLL
23075	9	30	1803	1759	4	1956	2029	DL	269	N913DU	JFK	PHX	272	2153	17	59	2023-09-30 17:00:00	Other
23077	7	4	926	925	1	1206	1231	B6	298	N584JB	JFK	PBI	137	1028	9	25	2023-07-04 09:00:00	Other
23080	4	7	1128	1127	1	1421	1425	UA	247	N442UA	EWR	PBI	158	1023	11	27	2023-04-07 11:00:00	Other
23084	2	4	1543	1540	3	1849	1859	DL	579	N125DN	LGA	FLL	155	1076	15	40	2023-02-04 15:00:00	FLL
23089	11	3	1526	1517	9	1722	1725	YX	1059	N767YX	EWR	DTW	86	488	15	17	2023-11-03 15:00:00	Other
23090	2	13	1729	1727	2	2016	2036	UA	577	N497UA	EWR	FLL	136	1065	17	27	2023-02-13 17:00:00	FLL
23103	11	10	715	715	0	938	955	WN	1163	N8853Q	LGA	ATL	122	762	7	15	2023-11-10 07:00:00	ATL
23110	2	2	710	705	5	942	949	DL	193	N129DN	LGA	ATL	129	762	7	5	2023-02-02 07:00:00	ATL
23114	5	27	1500	1500	0	1605	1618	YX	1683	N202JQ	LGA	MVY	42	175	15	0	2023-05-27 15:00:00	Other
23120	7	31	1338	1330	8	1647	1647	B6	117	N627JB	LGA	FLL	167	1076	13	30	2023-07-31 13:00:00	FLL
23121	1	16	1835	1830	5	2133	2145	NK	1113	N948NK	LGA	FLL	141	1076	18	30	2023-01-16 18:00:00	FLL
23125	2	8	1819	1820	-1	1946	2008	YX	1602	N230JQ	LGA	BNA	117	764	18	20	2023-02-08 18:00:00	Other
23137	6	5	1145	1145	0	1408	1427	UA	518	N27270	EWR	DFW	179	1372	11	45	2023-06-05 11:00:00	Other
23140	8	24	1459	1459	0	1613	1615	B6	584	N284JB	JFK	HYA	38	196	14	59	2023-08-24 14:00:00	Other
23147	2	1	2234	2225	9	212	158	B6	895	N964JT	JFK	SFO	374	2586	22	25	2023-02-01 22:00:00	Other
23148	5	17	1625	1615	10	1912	1935	AA	96	N108NN	JFK	LAX	323	2475	16	15	2023-05-17 16:00:00	LAX
23152	6	11	825	825	0	1208	1225	DL	748	N686DA	JFK	STT	197	1623	8	25	2023-06-11 08:00:00	Other
23163	10	15	2002	2000	2	2300	2224	YX	1143	N732YX	EWR	SAV	116	708	20	0	2023-10-15 20:00:00	Other
23168	11	17	1854	1855	-1	2149	2203	UA	663	N489UA	EWR	DFW	195	1372	18	55	2023-11-17 18:00:00	Other
23169	7	6	705	705	0	829	853	9E	1137	N916XJ	LGA	STL	119	888	7	5	2023-07-06 07:00:00	Other
23174	5	23	1608	1605	3	1856	1916	B6	764	N648JB	JFK	PBI	141	1028	16	5	2023-05-23 16:00:00	Other
23178	3	7	2202	2156	6	6	2358	UA	752	N61898	EWR	DTW	88	488	21	56	2023-03-07 21:00:00	Other
23181	8	13	2117	2110	7	2208	2211	9E	1284	N915XJ	LGA	ALB	28	136	21	10	2023-08-13 21:00:00	Other
23193	6	18	1529	1529	0	1717	1737	UA	87	N16713	EWR	CHS	88	628	15	29	2023-06-18 15:00:00	Other
23204	12	18	2001	1958	3	2302	2313	DL	545	N331DN	LGA	FLL	157	1076	19	58	2023-12-18 19:00:00	FLL
23212	8	13	1428	1429	-1	1633	1643	YX	975	N420YX	JFK	CVG	97	589	14	29	2023-08-13 14:00:00	Other
23237	11	28	1133	1129	4	1429	1445	B6	322	N804JB	JFK	SLC	275	1990	11	29	2023-11-28 11:00:00	Other
23241	3	5	1304	1300	4	1452	1502	AA	639	N544UW	LGA	CLT	89	544	13	0	2023-03-05 13:00:00	CLT
23245	9	23	1837	1830	7	2019	2009	UA	424	N19117	EWR	ORD	105	719	18	30	2023-09-23 18:00:00	ORD
23249	4	4	956	948	8	1149	1200	DL	597	N332DN	LGA	DTW	83	502	9	48	2023-04-04 09:00:00	Other
23257	8	6	1739	1735	4	2000	2005	YX	1348	N224JQ	LGA	IND	99	660	17	35	2023-08-06 17:00:00	Other
23258	12	22	532	530	2	839	912	NK	347	N921NK	EWR	PHX	289	2133	5	30	2023-12-22 05:00:00	Other
23263	10	29	1928	1929	-1	2135	2131	YX	1101	N744YX	EWR	STL	145	872	19	29	2023-10-29 19:00:00	Other
23271	1	24	1109	1110	-1	1405	1440	DL	156	N915DU	JFK	SLC	278	1990	11	10	2023-01-24 11:00:00	Other
23287	10	30	1958	1959	-1	2314	2316	NK	1155	N710NK	EWR	LAX	344	2454	19	59	2023-10-30 19:00:00	LAX
23291	9	28	1819	1820	-1	2034	2104	DL	240	N514DE	JFK	LAS	285	2248	18	20	2023-09-28 18:00:00	Other
23292	8	21	900	900	0	1011	1030	YX	1343	N228JQ	LGA	BOS	44	184	9	0	2023-08-21 09:00:00	BOS
23294	4	4	1453	1449	4	1740	1750	UA	74	N17254	EWR	PBI	144	1023	14	49	2023-04-04 14:00:00	Other
23297	3	4	1130	1130	0	1300	1310	UA	586	N16703	EWR	RDU	70	416	11	30	2023-03-04 11:00:00	Other
23298	6	13	1430	1420	10	1601	1540	WN	479	N8540V	LGA	MDW	104	725	14	20	2023-06-13 14:00:00	Other
23300	12	9	1559	1559	0	1936	1923	B6	82	N569JB	JFK	AUS	246	1521	15	59	2023-12-09 15:00:00	Other
23303	4	19	1630	1630	0	1908	1934	B6	320	N187JB	JFK	MCO	127	944	16	30	2023-04-19 16:00:00	MCO
23309	1	29	1824	1815	9	2042	2027	9E	1565	N915XJ	LGA	DSM	172	1031	18	15	2023-01-29 18:00:00	Other
23311	6	20	1513	1505	8	1851	1830	B6	191	N624JB	EWR	FLL	164	1065	15	5	2023-06-20 15:00:00	FLL
23323	8	28	1358	1359	-1	1536	1530	B6	221	N3085J	JFK	MKE	113	745	13	59	2023-08-28 13:00:00	Other
23333	11	12	1601	1559	2	1747	1750	AA	131	N870NN	LGA	ORD	119	733	15	59	2023-11-12 15:00:00	ORD
23341	7	10	638	630	8	924	921	UA	566	N14214	EWR	TPA	145	997	6	30	2023-07-10 06:00:00	Other
23345	7	23	1648	1640	8	1815	1805	WN	68	N917WN	LGA	MDW	115	725	16	40	2023-07-23 16:00:00	Other
23354	2	25	1159	1200	-1	1450	1515	DL	311	N332NW	LGA	TPA	146	1010	12	0	2023-02-25 12:00:00	Other
23355	3	6	1115	1115	0	1409	1433	DL	919	N323DN	LGA	FLL	139	1076	11	15	2023-03-06 11:00:00	FLL
23359	7	17	1400	1359	1	1642	1646	AA	533	N339PL	EWR	DFW	187	1372	13	59	2023-07-17 13:00:00	Other
23363	5	15	700	700	0	955	1006	UA	820	N17289	EWR	RSW	150	1068	7	0	2023-05-15 07:00:00	Other
23367	6	28	1022	1022	0	1138	1150	YX	1212	N736YX	LGA	IAD	52	229	10	22	2023-06-28 10:00:00	Other
23370	11	20	1158	1159	-1	1425	1426	YX	1163	N762YX	EWR	SAV	109	708	11	59	2023-11-20 11:00:00	Other
23374	2	26	1233	1230	3	1336	1353	9E	1297	N479PX	LGA	SCE	47	208	12	30	2023-02-26 12:00:00	Other
23376	11	6	1334	1329	5	1608	1636	UA	465	N33284	EWR	FLL	135	1065	13	29	2023-11-06 13:00:00	FLL
23381	5	18	703	700	3	939	1000	DL	192	N188DN	JFK	LAX	312	2475	7	0	2023-05-18 07:00:00	LAX
23382	2	11	1045	1040	5	1318	1327	DL	122	N316DN	LGA	ATL	126	762	10	40	2023-02-11 10:00:00	ATL
23384	12	2	631	630	1	831	839	AA	906	N870NN	JFK	CLT	93	541	6	30	2023-12-02 06:00:00	CLT
23386	3	11	1155	1155	0	1349	1409	9E	1470	N310PQ	LGA	TYS	93	647	11	55	2023-03-11 11:00:00	Other
23390	11	3	1351	1352	-1	1628	1657	AA	978	N967NN	LGA	DFW	191	1389	13	52	2023-11-03 13:00:00	Other
23399	12	16	2037	2030	7	2350	2359	B6	619	N988JT	JFK	LAX	327	2475	20	30	2023-12-16 20:00:00	LAX
23414	10	6	2107	2059	8	2225	2236	9E	1631	N176PQ	LGA	MSN	112	812	20	59	2023-10-06 20:00:00	Other
23419	8	27	630	630	0	830	835	WN	459	N8890Q	LGA	DEN	217	1620	6	30	2023-08-27 06:00:00	Other
23420	12	11	1359	1400	-1	1647	1717	UA	393	N228UA	EWR	SFO	322	2565	14	0	2023-12-11 14:00:00	Other
23430	10	7	1504	1459	5	1803	1800	DL	190	N199DN	JFK	LAX	301	2475	14	59	2023-10-07 14:00:00	LAX
23433	1	25	630	630	0	755	752	B6	1056	N179JB	JFK	BUF	61	301	6	30	2023-01-25 06:00:00	Other
23434	3	13	833	826	7	1214	1135	UA	273	N425UA	EWR	FLL	161	1065	8	26	2023-03-13 08:00:00	FLL
23450	6	19	734	733	1	919	926	UA	498	N27253	EWR	CLT	78	529	7	33	2023-06-19 07:00:00	CLT
23451	7	12	725	719	6	1022	1020	DL	609	N393DN	EWR	SLC	276	1969	7	19	2023-07-12 07:00:00	Other
23456	4	1	651	645	6	936	936	UA	725	N16234	EWR	PBI	137	1023	6	45	2023-04-01 06:00:00	Other
23458	10	12	603	604	-1	859	900	B6	405	N623JB	LGA	TPA	147	1010	6	4	2023-10-12 06:00:00	Other
23460	9	27	1636	1635	1	1854	1859	DL	788	N334NB	JFK	MSY	168	1182	16	35	2023-09-27 16:00:00	Other
23462	10	19	629	630	-1	924	904	B6	199	N975JT	JFK	MCO	139	944	6	30	2023-10-19 06:00:00	MCO
23463	12	18	2107	2100	7	2352	36	B6	26	N962JT	JFK	SAN	324	2446	21	0	2023-12-18 21:00:00	Other
23474	7	13	559	600	-1	658	718	UA	368	N896UA	EWR	IAD	40	212	6	0	2023-07-13 06:00:00	Other
23476	8	7	603	601	2	839	839	B6	191	N2039J	JFK	MCO	132	944	6	1	2023-08-07 06:00:00	MCO
23508	3	7	1839	1830	9	2158	2146	NK	1025	N604NK	LGA	FLL	138	1076	18	30	2023-03-07 18:00:00	FLL
23515	7	26	949	946	3	1351	1341	UA	488	N47505	EWR	SJU	203	1608	9	46	2023-07-26 09:00:00	Other
23516	4	2	559	600	-1	738	755	DL	699	N947AT	EWR	DTW	83	488	6	0	2023-04-02 06:00:00	Other
23525	10	23	1136	1135	1	1405	1420	WN	768	N8739L	LGA	DAL	187	1381	11	35	2023-10-23 11:00:00	Other
23528	6	21	1724	1725	-1	1851	1914	OO	1275	N311SY	JFK	BOS	35	187	17	25	2023-06-21 17:00:00	BOS
23540	4	10	1837	1837	0	2041	2100	YX	934	N979RP	EWR	IND	93	645	18	37	2023-04-10 18:00:00	Other
23543	11	17	905	902	3	1239	1236	NK	1181	N627NK	EWR	PHX	296	2133	9	2	2023-11-17 09:00:00	Other
23551	5	15	1830	1820	10	2103	2120	WN	494	N8515X	LGA	TPA	137	1010	18	20	2023-05-15 18:00:00	Other
23553	3	23	2008	1959	9	2226	2235	DL	805	N337NB	LGA	MSY	170	1183	19	59	2023-03-23 19:00:00	Other
23554	12	16	1627	1620	7	1920	1922	B6	465	N561JB	EWR	PBI	150	1023	16	20	2023-12-16 16:00:00	Other
23557	8	14	2118	2110	8	2222	2250	YX	1325	N210JQ	JFK	DCA	42	213	21	10	2023-08-14 21:00:00	Other
23560	4	23	2059	2100	-1	13	47	AA	54	N106NN	JFK	SFO	343	2586	21	0	2023-04-23 21:00:00	Other
23561	12	5	1051	1049	2	1445	1429	YX	1842	N860RW	LGA	EYW	201	1207	10	49	2023-12-05 10:00:00	Other
23566	5	3	948	940	8	1244	1250	UA	703	N67815	EWR	RSW	145	1068	9	40	2023-05-03 09:00:00	Other
23568	2	3	738	730	8	954	1002	9E	1304	N920XJ	LGA	MCI	171	1107	7	30	2023-02-03 07:00:00	Other
23587	11	12	1718	1715	3	2040	2030	WN	384	N443WN	LGA	HOU	220	1428	17	15	2023-11-12 17:00:00	Other
23590	6	5	1255	1255	0	1435	1455	G4	540	205NV	EWR	TYS	82	631	12	55	2023-06-05 12:00:00	Other
23596	5	18	1550	1551	-1	1817	1836	DL	426	N3745B	JFK	ATL	111	760	15	51	2023-05-18 15:00:00	ATL
23605	9	7	1345	1345	0	1601	1608	B6	970	N627JB	LGA	SAV	100	722	13	45	2023-09-07 13:00:00	Other
23606	11	15	1932	1930	2	1	2240	UA	571	N27015	EWR	LAX	345	2454	19	30	2023-11-15 19:00:00	LAX
23607	3	9	1351	1350	1	1540	1527	9E	1399	N326PQ	LGA	BNA	122	764	13	50	2023-03-09 13:00:00	Other
23608	8	23	1503	1457	6	1752	1758	UA	63	N821UA	EWR	PBI	138	1023	14	57	2023-08-23 14:00:00	Other
23612	2	21	1723	1718	5	2056	2040	B6	75	N968JT	JFK	SEA	371	2422	17	18	2023-02-21 17:00:00	Other
23613	5	19	1233	1229	4	1503	1533	UA	609	N894UA	LGA	IAH	187	1416	12	29	2023-05-19 12:00:00	Other
23624	6	20	1136	1129	7	1311	1320	UA	722	N403UA	EWR	DTW	76	488	11	29	2023-06-20 11:00:00	Other
23645	5	20	926	925	1	1236	1239	DL	648	N104DU	JFK	SAT	221	1587	9	25	2023-05-20 09:00:00	Other
23664	9	2	1517	1517	0	1735	1815	NK	861	N631NK	EWR	LAX	298	2454	15	17	2023-09-02 15:00:00	LAX
23666	4	26	2034	2027	7	2350	2337	UA	627	N434UA	EWR	RSW	153	1068	20	27	2023-04-26 20:00:00	Other
23677	4	6	912	912	0	1055	1102	YX	979	N726YX	EWR	CLE	68	404	9	12	2023-04-06 09:00:00	Other
23692	10	7	1524	1520	4	1730	1650	OO	1218	N295SY	JFK	BNA	126	765	15	20	2023-10-07 15:00:00	Other
23706	5	8	1920	1915	5	2212	2237	DL	153	N179DN	JFK	LAX	328	2475	19	15	2023-05-08 19:00:00	LAX
23713	7	17	1025	1015	10	1248	1254	UA	587	N24976	EWR	IAH	181	1400	10	15	2023-07-17 10:00:00	Other
23715	6	23	1026	1023	3	1222	1150	YX	1162	N640RW	EWR	IAD	88	212	10	23	2023-06-23 10:00:00	Other
23716	11	19	917	914	3	1022	1035	B6	969	N228JB	JFK	BOS	40	187	9	14	2023-11-19 09:00:00	BOS
23719	3	20	1020	1013	7	1307	1319	UA	748	N73291	EWR	IAH	205	1400	10	13	2023-03-20 10:00:00	Other
23722	3	22	1457	1457	0	1742	1758	UA	76	N12125	EWR	PBI	150	1023	14	57	2023-03-22 14:00:00	Other
23726	12	6	1808	1759	9	2039	2119	AA	656	N835NN	LGA	DFW	187	1389	17	59	2023-12-06 17:00:00	Other
23734	9	3	1403	1357	6	1551	1603	YX	1056	N758YX	EWR	GRR	89	605	13	57	2023-09-03 13:00:00	Other
23735	7	10	936	930	6	1042	1052	YX	959	N752YX	EWR	MHT	39	209	9	30	2023-07-10 09:00:00	Other
23739	9	12	1010	1000	10	1145	1136	UA	441	N36272	EWR	BNA	116	748	10	0	2023-09-12 10:00:00	Other
23745	4	3	1654	1655	-1	1817	1822	YX	1520	N810MD	LGA	ROC	57	254	16	55	2023-04-03 16:00:00	Other
23751	8	22	733	730	3	924	1005	DL	165	N542DE	JFK	LAS	272	2248	7	30	2023-08-22 07:00:00	Other
23754	8	2	1724	1725	-1	1857	1916	OO	960	N240SY	JFK	BOS	36	187	17	25	2023-08-02 17:00:00	BOS
23757	5	18	1509	1509	0	1714	1718	9E	1377	N310PQ	LGA	GSP	95	610	15	9	2023-05-18 15:00:00	Other
23760	2	21	1359	1350	9	1542	1525	9E	1474	N482PX	LGA	BUF	73	292	13	50	2023-02-21 13:00:00	Other
23765	6	10	1937	1938	-1	2222	2245	B6	312	N990JL	JFK	LAS	293	2248	19	38	2023-06-10 19:00:00	Other
23774	8	10	908	909	-1	1156	1111	UA	197	N27724	EWR	MCI	154	1092	9	9	2023-08-10 09:00:00	Other
23784	1	2	1149	1147	2	1311	1318	YX	1126	N657RW	EWR	PIT	60	319	11	47	2023-01-02 11:00:00	Other
23786	6	10	710	709	1	1110	1110	B6	613	N796JB	EWR	SJU	208	1608	7	9	2023-06-10 07:00:00	Other
23793	2	23	1838	1829	9	2220	2130	B6	292	N663JB	JFK	LAS	376	2248	18	29	2023-02-23 18:00:00	Other
23795	1	25	728	725	3	1037	1039	UA	506	N805UA	EWR	SRQ	163	1034	7	25	2023-01-25 07:00:00	Other
23804	5	4	1644	1645	-1	1831	1855	WN	187	N8756S	LGA	MCI	152	1107	16	45	2023-05-04 16:00:00	Other
23806	4	28	1552	1550	2	1729	1730	B6	258	N3044J	JFK	MKE	108	745	15	50	2023-04-28 15:00:00	Other
23825	7	7	1733	1731	2	2104	2025	AA	193	N437AN	EWR	DFW	181	1372	17	31	2023-07-07 17:00:00	Other
23828	1	24	1106	1100	6	1320	1318	UA	953	N445UA	EWR	MCI	170	1092	11	0	2023-01-24 11:00:00	Other
23836	1	7	2025	2025	0	2224	2248	YX	1239	N747YX	EWR	CVG	89	569	20	25	2023-01-07 20:00:00	Other
23839	7	25	1504	1505	-1	1843	1712	AA	626	N857NN	LGA	CLT	85	544	15	5	2023-07-25 15:00:00	CLT
23849	5	14	800	800	0	1039	1104	DL	172	N835MH	JFK	LAX	311	2475	8	0	2023-05-14 08:00:00	LAX
23850	11	7	853	850	3	1124	1137	YX	1847	N220JQ	JFK	JAX	124	828	8	50	2023-11-07 08:00:00	Other
23860	6	25	1205	1205	0	1406	1351	9E	1499	N138EV	LGA	PIT	60	335	12	5	2023-06-25 12:00:00	Other
23867	12	24	1027	1026	1	1330	1402	AA	770	N977UY	EWR	PHX	277	2133	10	26	2023-12-24 10:00:00	Other
23868	5	10	958	959	-1	1108	1128	YX	1630	N246JQ	LGA	BOS	36	184	9	59	2023-05-10 09:00:00	BOS
23869	9	30	1505	1506	-1	1614	1625	UA	742	N439UA	EWR	IAD	49	212	15	6	2023-09-30 15:00:00	Other
23873	4	9	2105	2105	0	14	4	B6	576	N641JB	JFK	PBI	141	1028	21	5	2023-04-09 21:00:00	Other
23885	12	26	758	759	-1	1050	1048	AA	629	N9002U	JFK	EGE	228	1746	7	59	2023-12-26 07:00:00	Other
23889	8	21	1731	1725	6	1928	1916	YX	968	N114HQ	JFK	CLE	75	425	17	25	2023-08-21 17:00:00	Other
23890	8	7	1903	1859	4	2250	2029	UA	500	N75426	EWR	BNA	112	748	18	59	2023-08-07 18:00:00	Other
23902	3	27	2113	2112	1	14	2359	UA	867	N61886	EWR	MCO	146	937	21	12	2023-03-27 21:00:00	MCO
23912	2	24	1105	1100	5	1303	1242	UA	543	N15710	LGA	ORD	145	733	11	0	2023-02-24 11:00:00	ORD
23926	2	6	1105	1105	0	1420	1431	DL	617	N312DN	LGA	MIA	143	1096	11	5	2023-02-06 11:00:00	MIA
23936	5	21	949	945	4	1258	1326	DL	97	N707TW	JFK	SFO	329	2586	9	45	2023-05-21 09:00:00	Other
23954	8	1	2131	2125	6	2243	2245	WN	514	N8559Q	LGA	MDW	104	725	21	25	2023-08-01 21:00:00	Other
23965	4	30	1334	1329	5	1609	1601	DL	197	N338DN	LGA	ATL	113	762	13	29	2023-04-30 13:00:00	ATL
23966	6	20	2201	2159	2	2353	2341	DL	902	N330NB	JFK	BUF	52	301	21	59	2023-06-20 21:00:00	Other
23969	9	22	740	730	10	1111	1048	B6	36	N992JB	JFK	SFO	356	2586	7	30	2023-09-22 07:00:00	Other
23982	9	17	740	740	0	957	1005	AA	543	N326SJ	JFK	PHX	287	2153	7	40	2023-09-17 07:00:00	Other
23989	1	26	2041	2036	5	2337	2301	UA	963	N38473	EWR	MSY	199	1167	20	36	2023-01-26 20:00:00	Other
24002	4	3	2109	2110	-1	2347	2358	B6	69	N641JB	EWR	MCO	126	937	21	10	2023-04-03 21:00:00	MCO
24010	3	29	1344	1345	-1	1455	1511	YX	1741	N875RW	LGA	DCA	46	214	13	45	2023-03-29 13:00:00	Other
24011	9	10	1828	1825	3	2010	2001	UA	714	N17311	LGA	ORD	111	733	18	25	2023-09-10 18:00:00	ORD
24012	10	16	919	917	2	1208	1213	UA	694	N27270	EWR	PBI	145	1023	9	17	2023-10-16 09:00:00	Other
24016	12	21	922	919	3	1055	1114	YX	1249	N117HQ	LGA	GSO	68	461	9	19	2023-12-21 09:00:00	Other
24028	5	18	1204	1159	5	1430	1422	UA	247	N411UA	EWR	ATL	116	746	11	59	2023-05-18 11:00:00	ATL
24033	11	17	1900	1858	2	2045	2037	UA	421	N14242	EWR	ORD	114	719	18	58	2023-11-17 18:00:00	ORD
24035	5	14	2205	2159	6	2339	2347	UA	816	N17719	EWR	RDU	70	416	21	59	2023-05-14 21:00:00	Other
24044	9	8	953	950	3	1141	1142	9E	1540	N133EV	EWR	RDU	65	416	9	50	2023-09-08 09:00:00	Other
24045	2	1	955	950	5	1311	1314	B6	574	N591JB	JFK	RSW	164	1074	9	50	2023-02-01 09:00:00	Other
24046	4	26	1711	1705	6	2201	2010	NK	582	N673NK	EWR	FLL	170	1065	17	5	2023-04-26 17:00:00	FLL
24048	1	16	1700	1700	0	2000	2008	B6	390	N996JL	JFK	MCO	131	944	17	0	2023-01-16 17:00:00	MCO
24070	7	28	1901	1900	1	2248	2125	YX	937	N858RW	EWR	SAV	108	708	19	0	2023-07-28 19:00:00	Other
24082	11	21	1327	1327	0	1615	1642	NK	1024	N643NK	EWR	MIA	153	1085	13	27	2023-11-21 13:00:00	MIA
24090	1	12	800	800	0	932	936	9E	1589	N133EV	JFK	BUF	59	301	8	0	2023-01-12 08:00:00	Other
24096	3	4	646	639	7	939	952	UA	751	N27520	EWR	SEA	322	2402	6	39	2023-03-04 06:00:00	Other
24097	9	21	1520	1520	0	1624	1623	9E	1620	N316PQ	LGA	BDL	23	101	15	20	2023-09-21 15:00:00	Other
24105	5	20	804	800	4	1026	1031	UA	220	N214UA	EWR	LAS	278	2227	8	0	2023-05-20 08:00:00	Other
24109	3	25	559	600	-1	855	911	AA	471	N945NN	LGA	MIA	150	1096	6	0	2023-03-25 06:00:00	MIA
24124	11	2	2241	2241	0	2349	13	9E	1453	N909XJ	JFK	SYR	45	209	22	41	2023-11-02 22:00:00	Other
24129	5	7	726	720	6	934	956	DL	167	N3732J	LGA	DEN	227	1620	7	20	2023-05-07 07:00:00	Other
24130	4	11	835	835	0	1423	1159	DL	306	N3765	JFK	SAN	NA	2446	8	35	2023-04-11 08:00:00	Other
24134	9	11	907	900	7	1204	1200	B6	55	N2039J	JFK	SAN	330	2446	9	0	2023-09-11 09:00:00	Other
24136	9	4	1359	1359	0	1635	1655	AA	642	N403AN	EWR	DFW	174	1372	13	59	2023-09-04 13:00:00	Other
24145	7	2	1044	1045	-1	1332	1411	DL	741	N876DN	JFK	SLC	257	1990	10	45	2023-07-02 10:00:00	Other
24156	8	22	1908	1905	3	2014	2030	WN	822	N8688J	LGA	MDW	105	725	19	5	2023-08-22 19:00:00	Other
24160	8	16	1101	1059	2	1257	1313	UA	362	N68807	EWR	PHX	264	2133	10	59	2023-08-16 10:00:00	Other
24166	7	13	1133	1133	0	1238	1244	B6	641	N284JB	JFK	ACK	43	199	11	33	2023-07-13 11:00:00	Other
24167	10	2	1600	1600	0	1728	1744	AA	727	N919NN	LGA	ORD	105	733	16	0	2023-10-02 16:00:00	ORD
24187	8	17	940	940	0	1150	1207	9E	1242	N329PQ	JFK	IND	97	665	9	40	2023-08-17 09:00:00	Other
24188	3	24	1921	1915	6	2046	2045	WN	334	N8850Q	LGA	MDW	118	725	19	15	2023-03-24 19:00:00	Other
24192	9	25	940	940	0	1348	1341	UA	575	N37525	EWR	SJU	198	1608	9	40	2023-09-25 09:00:00	Other
24199	6	15	2003	1959	4	2127	2138	UA	458	N12221	EWR	ORD	110	719	19	59	2023-06-15 19:00:00	ORD
24224	2	21	709	705	4	1236	1204	UA	574	N17752	EWR	STT	225	1634	7	5	2023-02-21 07:00:00	Other
24232	6	6	1832	1830	2	2101	2045	DL	416	N376DN	LGA	MSP	141	1020	18	30	2023-06-06 18:00:00	Other
24237	8	14	1509	1459	10	1810	1806	UA	194	N840UA	EWR	MIA	152	1085	14	59	2023-08-14 14:00:00	MIA
24245	5	2	1541	1540	1	1748	1804	UA	357	N64809	EWR	DEN	207	1605	15	40	2023-05-02 15:00:00	Other
24250	11	21	1412	1411	1	1554	1544	UA	568	N489UA	EWR	BNA	134	748	14	11	2023-11-21 14:00:00	Other
24266	10	14	631	630	1	756	801	UA	935	N29717	LGA	ORD	120	733	6	30	2023-10-14 06:00:00	ORD
24268	2	17	1252	1249	3	1635	1549	UA	829	N466UA	EWR	PBI	203	1023	12	49	2023-02-17 12:00:00	Other
24272	4	9	2102	2059	3	2235	2234	YX	1486	N245JQ	JFK	DCA	48	213	20	59	2023-04-09 20:00:00	Other
24284	4	29	1505	1500	5	1801	1810	UA	791	N58101	EWR	LAX	323	2454	15	0	2023-04-29 15:00:00	LAX
24294	7	6	2104	2100	4	2347	2359	B6	29	N929JB	JFK	SAN	312	2446	21	0	2023-07-06 21:00:00	Other
24301	10	1	724	725	-1	934	950	WN	579	N8576Z	LGA	ATL	101	762	7	25	2023-10-01 07:00:00	ATL
24302	7	30	759	750	9	1003	1005	YX	866	N741YX	EWR	GRR	99	605	7	50	2023-07-30 07:00:00	Other
24305	5	27	1205	1159	6	1456	1507	NK	978	N674NK	LGA	MIA	147	1096	11	59	2023-05-27 11:00:00	MIA
24306	9	17	1558	1559	-1	1900	1904	AA	362	N916NN	LGA	DFW	192	1389	15	59	2023-09-17 15:00:00	Other
24314	1	12	1529	1520	9	1842	1844	AA	122	N103NN	JFK	LAX	323	2475	15	20	2023-01-12 15:00:00	LAX
24323	3	7	715	715	0	1027	1040	AS	14	N975AK	JFK	SEA	332	2422	7	15	2023-03-07 07:00:00	Other
24326	10	19	649	650	-1	941	1016	DL	103	N120DN	JFK	SLC	261	1990	6	50	2023-10-19 06:00:00	Other
24327	6	2	1704	1656	8	2019	2014	B6	1052	N784JB	JFK	MIA	147	1089	16	56	2023-06-02 16:00:00	MIA
24329	10	17	1646	1645	1	1921	1939	UA	465	N34137	EWR	SAN	306	2425	16	45	2023-10-17 16:00:00	Other
24343	11	17	2132	2128	4	2221	2230	YX	1126	N724YX	EWR	PHL	31	80	21	28	2023-11-17 21:00:00	Other
24351	7	4	2029	2029	0	2324	2335	B6	156	N827JB	LGA	FLL	149	1076	20	29	2023-07-04 20:00:00	FLL
24362	4	23	1331	1329	2	1644	1640	DL	499	N332NW	JFK	AUS	226	1521	13	29	2023-04-23 13:00:00	Other
24370	6	23	832	831	1	1047	1044	9E	1530	N902XJ	LGA	GSP	99	610	8	31	2023-06-23 08:00:00	Other
24378	6	4	1256	1250	6	1447	1447	9E	1447	N925XJ	LGA	RDU	72	431	12	50	2023-06-04 12:00:00	Other
24382	5	23	1311	1311	0	1432	1445	UA	108	N33292	EWR	ORD	108	719	13	11	2023-05-23 13:00:00	ORD
24399	4	18	1929	1929	0	2104	2112	OO	1061	N247SY	JFK	BNA	112	765	19	29	2023-04-18 19:00:00	Other
24408	5	2	1230	1225	5	1435	1455	WN	961	N7875A	LGA	DEN	216	1620	12	25	2023-05-02 12:00:00	Other
24410	3	19	736	729	7	1010	1035	UA	651	N17265	EWR	BZN	253	1882	7	29	2023-03-19 07:00:00	Other
24418	2	7	738	738	0	844	907	YX	1113	N654RW	EWR	ORF	49	284	7	38	2023-02-07 07:00:00	Other
24425	7	12	1028	1029	-1	1220	1236	YX	896	N736YX	EWR	CLT	78	529	10	29	2023-07-12 10:00:00	CLT
24428	8	31	1955	1945	10	2201	2212	UA	583	N68880	EWR	DEN	212	1605	19	45	2023-08-31 19:00:00	Other
24430	9	25	1247	1242	5	1441	1351	9E	1613	N308PQ	LGA	BGM	28	147	12	42	2023-09-25 12:00:00	Other
24431	12	17	1719	1709	10	1919	1924	9E	1534	N349PQ	JFK	DTW	84	509	17	9	2023-12-17 17:00:00	Other
24432	11	18	1524	1525	-1	1756	1824	DL	318	N521DT	JFK	LAS	307	2248	15	25	2023-11-18 15:00:00	Other
24433	9	4	1528	1529	-1	1726	1724	YX	1052	N657RW	EWR	CMH	68	463	15	29	2023-09-04 15:00:00	Other
24434	4	10	1959	2000	-1	2152	2211	DL	726	N355NB	LGA	DTW	78	502	20	0	2023-04-10 20:00:00	Other
24444	7	25	600	600	0	905	909	AA	653	N308TB	JFK	MIA	157	1089	6	0	2023-07-25 06:00:00	MIA
24449	5	3	603	600	3	849	858	UA	245	N406UA	EWR	AUS	200	1504	6	0	2023-05-03 06:00:00	Other
24450	11	23	559	600	-1	748	755	DL	392	N329NW	LGA	DTW	80	502	6	0	2023-11-23 06:00:00	Other
24453	11	19	1529	1530	-1	1808	1840	B6	323	N283JB	JFK	MCO	129	944	15	30	2023-11-19 15:00:00	MCO
24454	7	13	2118	2110	8	2337	2249	9E	1258	N306PQ	JFK	BWI	45	184	21	10	2023-07-13 21:00:00	Other
24456	11	16	1249	1247	2	1550	1554	AA	646	N341SV	EWR	MIA	158	1085	12	47	2023-11-16 12:00:00	MIA
24458	8	22	1914	1906	8	2044	2048	UA	417	N37536	EWR	CLE	63	404	19	6	2023-08-22 19:00:00	Other
24464	5	16	742	741	1	851	907	UA	198	N465UA	EWR	BNA	107	748	7	41	2023-05-16 07:00:00	Other
24468	12	31	658	659	-1	927	1035	DL	309	N546DN	JFK	SEA	301	2422	6	59	2023-12-31 06:00:00	Other
24475	12	5	2128	2129	-1	2347	14	DL	596	N506DA	JFK	ATL	119	760	21	29	2023-12-05 21:00:00	ATL
24479	12	6	729	730	-1	955	1025	DL	175	N531DA	JFK	LAS	287	2248	7	30	2023-12-06 07:00:00	Other
24483	6	7	710	700	10	1011	1040	DL	181	N703TW	JFK	SFO	332	2586	7	0	2023-06-07 07:00:00	Other
24498	9	22	1159	1200	-1	1447	1508	UA	854	N77012	EWR	SFO	321	2565	12	0	2023-09-22 12:00:00	Other
24516	7	4	1400	1400	0	1601	1530	YX	1035	N409YX	LGA	BUF	46	292	14	0	2023-07-04 14:00:00	Other
24520	1	7	1838	1835	3	2138	2218	AS	150	N293AK	JFK	SAN	319	2446	18	35	2023-01-07 18:00:00	Other
24552	5	7	1835	1835	0	2131	2121	DL	156	N3745B	LGA	DEN	251	1620	18	35	2023-05-07 18:00:00	Other
24554	6	12	1406	1407	-1	1600	1558	9E	1617	N316PQ	JFK	RDU	84	427	14	7	2023-06-12 14:00:00	Other
24560	3	12	1231	1226	5	1538	1540	UA	634	N417UA	LGA	IAH	217	1416	12	26	2023-03-12 12:00:00	Other
24592	1	29	1530	1530	0	1652	1649	B6	468	N192JB	JFK	BOS	51	187	15	30	2023-01-29 15:00:00	BOS
24597	5	11	1923	1915	8	2207	2237	DL	153	N176DN	JFK	LAX	311	2475	19	15	2023-05-11 19:00:00	LAX
24606	10	2	2105	2059	6	2305	2257	UA	579	N27205	EWR	MSP	136	1008	20	59	2023-10-02 20:00:00	Other
24609	2	18	1519	1515	4	1737	1745	WN	250	N7824A	LGA	MCI	180	1107	15	15	2023-02-18 15:00:00	Other
24623	10	5	1339	1339	0	1704	1645	B6	425	N2047J	JFK	AUS	218	1521	13	39	2023-10-05 13:00:00	Other
24628	6	15	1929	1930	-1	2152	2257	B6	376	N640JB	JFK	PDX	308	2454	19	30	2023-06-15 19:00:00	Other
24629	12	23	836	835	1	1042	1059	9E	1601	N913XJ	JFK	CVG	89	589	8	35	2023-12-23 08:00:00	Other
24630	5	16	1529	1530	-1	1726	1730	AA	649	N830NN	EWR	CLT	79	529	15	30	2023-05-16 15:00:00	CLT
24635	5	13	2114	2115	-1	2308	2256	DL	853	N110DU	JFK	BUF	52	301	21	15	2023-05-13 21:00:00	Other
24637	7	6	1607	1605	2	1954	1920	DL	272	N3746H	LGA	MIA	178	1096	16	5	2023-07-06 16:00:00	MIA
24638	11	8	1235	1226	9	1525	1540	DL	510	N353NB	JFK	AUS	203	1521	12	26	2023-11-08 12:00:00	Other
24648	6	1	720	720	0	919	945	WN	543	N945WN	LGA	DEN	208	1620	7	20	2023-06-01 07:00:00	Other
24650	5	10	1509	1509	0	1750	1718	9E	1377	N935XJ	LGA	GSP	118	610	15	9	2023-05-10 15:00:00	Other
24665	7	31	1331	1329	2	1619	1621	UA	544	N17312	EWR	AUS	191	1504	13	29	2023-07-31 13:00:00	Other
24669	12	27	1929	1920	9	2128	2216	UA	395	N27273	EWR	LAS	273	2227	19	20	2023-12-27 19:00:00	Other
24680	12	1	658	650	8	959	1004	NK	821	N630NK	EWR	LAX	331	2454	6	50	2023-12-01 06:00:00	LAX
24693	9	2	1724	1725	-1	1952	2030	B6	116	N508JL	JFK	BUR	303	2465	17	25	2023-09-02 17:00:00	Other
24695	6	23	1529	1530	-1	1843	1833	UA	522	N14102	EWR	LAX	322	2454	15	30	2023-06-23 15:00:00	LAX
24703	2	24	1505	1500	5	1808	1734	OO	1164	N258SY	JFK	MSP	217	1029	15	0	2023-02-24 15:00:00	Other
24704	1	22	1749	1746	3	2045	2110	NK	28	N903NK	EWR	LAX	328	2454	17	46	2023-01-22 17:00:00	LAX
24718	4	25	1901	1855	6	2101	2101	UA	423	N29717	EWR	CLT	80	529	18	55	2023-04-25 18:00:00	CLT
24719	12	1	830	830	0	1144	1200	DL	340	N519DT	JFK	SAN	336	2446	8	30	2023-12-01 08:00:00	Other
24733	4	5	705	705	0	943	1004	DL	352	N3747D	LGA	PBI	126	1035	7	5	2023-04-05 07:00:00	Other
24735	3	29	916	915	1	1052	1120	AA	983	N306RC	JFK	ORD	127	740	9	15	2023-03-29 09:00:00	ORD
24743	1	7	658	659	-1	823	840	AA	1086	N868NN	EWR	ORD	103	719	6	59	2023-01-07 06:00:00	ORD
24745	10	12	1904	1905	-1	2208	2145	UA	362	N14115	EWR	LAS	329	2227	19	5	2023-10-12 19:00:00	Other
24748	1	26	1042	1040	2	1317	1327	DL	124	N389DN	LGA	ATL	138	762	10	40	2023-01-26 10:00:00	ATL
24749	5	13	2109	2102	7	2334	2334	UA	508	N67846	EWR	ATL	97	746	21	2	2023-05-13 21:00:00	ATL
24755	11	29	1946	1945	1	2117	2122	OO	1209	N316SY	JFK	IAD	47	228	19	45	2023-11-29 19:00:00	Other
24760	4	9	1033	1024	9	1246	1254	DL	733	N350NA	EWR	ATL	108	746	10	24	2023-04-09 10:00:00	ATL
24764	12	23	1235	1236	-1	1512	1528	UA	543	N47275	EWR	LAS	300	2227	12	36	2023-12-23 12:00:00	Other
24768	5	12	1206	1159	7	1442	1455	UA	821	N35271	EWR	TPA	131	997	11	59	2023-05-12 11:00:00	Other
24774	5	12	1111	1106	5	1405	1420	UA	829	N474UA	EWR	MIA	143	1085	11	6	2023-05-12 11:00:00	MIA
24780	6	28	1049	1048	1	1304	1316	F9	580	N343FR	LGA	ATL	102	762	10	48	2023-06-28 10:00:00	ATL
24803	7	11	804	805	-1	951	1014	DL	467	N362NB	JFK	MSP	145	1029	8	5	2023-07-11 08:00:00	Other
24811	2	8	1319	1315	4	1601	1632	B6	344	N510JB	EWR	PBI	143	1023	13	15	2023-02-08 13:00:00	Other
24820	6	11	2156	2155	1	2318	2318	9E	1626	N316PQ	JFK	ITH	41	189	21	55	2023-06-11 21:00:00	Other
24822	7	23	2205	2157	8	2326	2321	UA	324	N438UA	EWR	BOS	47	200	21	57	2023-07-23 21:00:00	BOS
24830	10	25	1134	1132	2	1423	1421	UA	521	N24729	EWR	DFW	190	1372	11	32	2023-10-25 11:00:00	Other
24831	10	31	2007	1959	8	2204	2200	YX	1166	N751YX	EWR	CMH	84	463	19	59	2023-10-31 19:00:00	Other
24847	2	1	903	900	3	1120	1114	UA	518	N23707	EWR	CLT	92	529	9	0	2023-02-01 09:00:00	CLT
24851	4	19	1059	1059	0	1511	1448	DL	660	N549US	JFK	STT	217	1623	10	59	2023-04-19 10:00:00	Other
24855	12	14	1151	1149	2	1427	1450	DL	601	N349DX	JFK	MCO	132	944	11	49	2023-12-14 11:00:00	MCO
24856	3	18	1833	1825	8	1952	2000	WN	334	N8558Z	LGA	MDW	118	725	18	25	2023-03-18 18:00:00	Other
24872	11	30	1759	1800	-1	2009	2024	YX	1159	N753YX	EWR	CVG	102	569	18	0	2023-11-30 18:00:00	Other
24877	4	9	1830	1830	0	2103	2148	DL	338	N357NB	JFK	DFW	183	1391	18	30	2023-04-09 18:00:00	Other
24878	8	25	717	715	2	928	935	WN	577	N219WN	LGA	ATL	104	762	7	15	2023-08-25 07:00:00	ATL
24881	11	2	600	601	-1	815	832	UA	555	N61881	EWR	DEN	223	1605	6	1	2023-11-02 06:00:00	Other
24895	5	2	1010	1000	10	1110	1127	AA	454	N823AW	LGA	DCA	42	214	10	0	2023-05-02 10:00:00	Other
24898	12	20	1601	1559	2	1801	1802	9E	1513	N600LR	LGA	RDU	66	431	15	59	2023-12-20 15:00:00	Other
24902	9	14	1315	1316	-1	1513	1526	9E	1620	N923XJ	JFK	CHS	96	636	13	16	2023-09-14 13:00:00	Other
24905	4	18	1558	1549	9	1858	1849	UA	714	N409UA	EWR	RSW	159	1068	15	49	2023-04-18 15:00:00	Other
24928	4	11	1345	1345	0	1630	1700	DL	260	N172DN	JFK	LAX	287	2475	13	45	2023-04-11 13:00:00	LAX
24929	6	3	1502	1500	2	1734	1714	UA	970	N37257	EWR	PHX	302	2133	15	0	2023-06-03 15:00:00	Other
24943	3	29	1726	1725	1	1914	1905	OO	1095	N313SY	JFK	MKE	137	745	17	25	2023-03-29 17:00:00	Other
24952	10	2	947	945	2	1138	1156	9E	1395	N695CA	EWR	CVG	83	569	9	45	2023-10-02 09:00:00	Other
24955	4	2	1900	1850	10	2044	2032	YX	1546	N236JQ	LGA	PIT	56	335	18	50	2023-04-02 18:00:00	Other
24961	5	1	1003	1000	3	1214	1300	UA	377	N16009	EWR	LAX	291	2454	10	0	2023-05-01 10:00:00	LAX
24965	3	5	1959	1959	0	33	57	UA	599	N66893	EWR	SJU	187	1608	19	59	2023-03-05 19:00:00	Other
24970	1	13	704	705	-1	944	949	DL	204	N311DN	LGA	ATL	123	762	7	5	2023-01-13 07:00:00	ATL
24975	4	2	1628	1629	-1	1817	1818	DL	436	N135DQ	LGA	ORD	126	733	16	29	2023-04-02 16:00:00	ORD
24980	7	4	1356	1355	1	1641	1655	DL	264	N175DN	JFK	LAX	312	2475	13	55	2023-07-04 13:00:00	LAX
24982	6	15	1705	1705	0	1941	1859	DL	1009	N933AT	EWR	DTW	119	488	17	5	2023-06-15 17:00:00	Other
24983	12	30	2115	2115	0	15	25	B6	726	N238JB	JFK	PBI	146	1028	21	15	2023-12-30 21:00:00	Other
24987	1	13	2124	2125	-1	2254	2247	YX	1783	N225JQ	LGA	ROC	46	254	21	25	2023-01-13 21:00:00	Other
24995	8	20	1602	1556	6	1738	1751	YX	835	N728YX	EWR	CMH	72	463	15	56	2023-08-20 15:00:00	Other
25001	3	21	1116	1115	1	1408	1422	AA	477	N796AN	JFK	MIA	149	1089	11	15	2023-03-21 11:00:00	MIA
25004	3	26	1101	1059	2	1401	1426	B6	27	N507JT	JFK	SEA	329	2422	10	59	2023-03-26 10:00:00	Other
25006	1	14	1517	1515	2	1822	1840	UA	726	N2749U	EWR	SFO	336	2565	15	15	2023-01-14 15:00:00	Other
25010	10	14	602	601	1	904	904	AA	948	N972NN	EWR	DFW	200	1372	6	1	2023-10-14 06:00:00	Other
25014	2	8	1816	1806	10	2059	2112	UA	907	N16234	EWR	PBI	137	1023	18	6	2023-02-08 18:00:00	Other
25021	1	12	759	800	-1	925	930	9E	1703	N197PQ	JFK	ROC	54	264	8	0	2023-01-12 08:00:00	Other
25028	12	1	1234	1230	4	1536	1544	AA	935	N316RK	JFK	MIA	151	1089	12	30	2023-12-01 12:00:00	MIA
25029	6	2	1829	1830	-1	2311	2155	DL	129	N870DN	JFK	SEA	295	2422	18	30	2023-06-02 18:00:00	Other
25037	12	25	1159	1200	-1	1443	1505	B6	672	N952JB	JFK	PBI	138	1028	12	0	2023-12-25 12:00:00	Other
25045	11	17	1100	1059	1	1428	1411	UA	630	N39416	EWR	MIA	155	1085	10	59	2023-11-17 10:00:00	MIA
25063	8	20	1444	1445	-1	1650	1655	9E	1146	N907XJ	LGA	GSP	89	610	14	45	2023-08-20 14:00:00	Other
25064	6	2	759	800	-1	925	949	OO	1182	N322SY	JFK	ORD	108	740	8	0	2023-06-02 08:00:00	ORD
25071	6	26	2037	2035	2	2351	2329	B6	873	N505JB	EWR	TPA	159	997	20	35	2023-06-26 20:00:00	Other
25073	6	8	1953	1954	-1	2346	2353	UA	223	N62892	EWR	BQN	203	1585	19	54	2023-06-08 19:00:00	Other
25074	2	27	1504	1505	-1	1801	1818	B6	204	N562JB	EWR	FLL	147	1065	15	5	2023-02-27 15:00:00	FLL
25075	5	14	1737	1729	8	2013	1955	9E	1458	N134EV	LGA	SAV	97	722	17	29	2023-05-14 17:00:00	Other
25076	7	19	1126	1126	0	1352	1335	UA	227	N458UA	EWR	SAV	102	708	11	26	2023-07-19 11:00:00	Other
25080	10	12	836	830	6	1010	1010	B6	349	N274JB	JFK	ORD	127	740	8	30	2023-10-12 08:00:00	ORD
25092	5	2	2001	2000	1	2114	2130	B6	333	N337JB	JFK	BOS	46	187	20	0	2023-05-02 20:00:00	BOS
25094	2	15	1159	1159	0	1450	1502	UA	801	N481UA	EWR	SRQ	156	1034	11	59	2023-02-15 11:00:00	Other
25096	1	13	1006	1005	1	1316	1309	UA	471	N880UA	EWR	SRQ	165	1034	10	5	2023-01-13 10:00:00	Other
25099	2	14	1054	1049	5	1344	1335	F9	565	N360FR	LGA	ATL	123	762	10	49	2023-02-14 10:00:00	ATL
25111	5	15	951	947	4	1245	1241	B6	222	N503JB	LGA	MCO	125	950	9	47	2023-05-15 09:00:00	MCO
25113	6	7	1647	1645	2	1918	1952	UA	649	N77019	EWR	SFO	305	2565	16	45	2023-06-07 16:00:00	Other
25115	8	19	603	600	3	819	840	WN	947	N8881L	LGA	HOU	177	1428	6	0	2023-08-19 06:00:00	Other
25119	2	22	1737	1730	7	2127	2120	DL	245	N717TW	JFK	SFO	378	2586	17	30	2023-02-22 17:00:00	Other
25124	8	30	2014	2015	-1	2144	2142	YX	836	N753YX	EWR	BTV	48	266	20	15	2023-08-30 20:00:00	Other
25145	10	27	1457	1455	2	1750	1811	B6	1008	N633JB	JFK	MIA	138	1089	14	55	2023-10-27 14:00:00	MIA
25150	10	14	2004	2000	4	2233	2247	B6	388	N957JB	JFK	LAS	295	2248	20	0	2023-10-14 20:00:00	Other
25157	12	24	1217	1210	7	1646	1656	B6	967	N959JB	JFK	SJU	185	1598	12	10	2023-12-24 12:00:00	Other
25158	4	16	948	945	3	1123	1200	DL	597	N378DN	LGA	DTW	74	502	9	45	2023-04-16 09:00:00	Other
25162	3	15	700	700	0	1006	1016	DL	399	N354DN	JFK	MIA	161	1089	7	0	2023-03-15 07:00:00	MIA
25178	1	18	1019	1020	-1	1228	1224	AA	732	N953AN	EWR	CLT	83	529	10	20	2023-01-18 10:00:00	CLT
25198	2	21	1734	1730	4	2142	2120	DL	245	N723TW	JFK	SFO	397	2586	17	30	2023-02-21 17:00:00	Other
25222	11	14	1459	1454	5	1717	1718	OO	1191	N253SY	JFK	IND	104	665	14	54	2023-11-14 14:00:00	Other
25231	12	16	1334	1325	9	1656	1648	YX	1305	N414YX	LGA	MIA	182	1096	13	25	2023-12-16 13:00:00	MIA
25247	2	28	954	955	-1	1232	1218	9E	1358	N923XJ	JFK	IND	107	665	9	55	2023-02-28 09:00:00	Other
25252	4	27	903	900	3	1020	1015	WN	61	N401WN	LGA	MDW	110	725	9	0	2023-04-27 09:00:00	Other
25254	1	14	801	800	1	1324	1259	B6	212	N958JB	JFK	SJU	228	1598	8	0	2023-01-14 08:00:00	Other
25259	12	5	954	955	-1	1105	1110	YX	1852	N234JQ	JFK	BOS	36	187	9	55	2023-12-05 09:00:00	BOS
25260	4	26	1719	1719	0	1905	1915	DL	764	N993AT	EWR	DTW	83	488	17	19	2023-04-26 17:00:00	Other
25264	2	28	2039	2030	9	2255	2254	YX	1094	N744YX	EWR	IND	110	645	20	30	2023-02-28 20:00:00	Other
25267	1	19	1402	1402	0	1548	1604	UA	195	N849UA	EWR	MSP	142	1008	14	2	2023-01-19 14:00:00	Other
25273	2	4	925	923	2	1050	1053	B6	603	N249JB	JFK	BUF	63	301	9	23	2023-02-04 09:00:00	Other
25274	11	7	2039	2040	-1	2243	2254	B6	499	N317JB	JFK	DTW	96	509	20	40	2023-11-07 20:00:00	Other
25283	11	11	1314	1315	-1	1651	1647	B6	276	N3044J	JFK	SAT	255	1587	13	15	2023-11-11 13:00:00	Other
25287	12	14	929	929	0	1140	1151	UA	790	N12238	EWR	SAV	105	708	9	29	2023-12-14 09:00:00	Other
25289	9	1	2009	2000	9	2309	2309	B6	821	N580JB	JFK	RNO	314	2411	20	0	2023-09-01 20:00:00	Other
25296	9	18	1329	1329	0	1537	1545	9E	1616	N303PQ	LGA	TYS	94	647	13	29	2023-09-18 13:00:00	Other
25297	2	25	832	830	2	1454	1450	UA	129	N76065	EWR	HNL	644	4962	8	30	2023-02-25 08:00:00	Other
25299	7	1	714	715	-1	851	917	DL	125	N109DU	LGA	DTW	77	502	7	15	2023-07-01 07:00:00	Other
25304	5	9	1128	1129	-1	1527	1525	B6	183	N662JB	JFK	SJU	196	1598	11	29	2023-05-09 11:00:00	Other
25316	12	3	1852	1853	-1	2153	2122	YX	1068	N755YX	EWR	IND	127	645	18	53	2023-12-03 18:00:00	Other
25321	4	6	1721	1720	1	1855	1850	WN	211	N8748Q	LGA	MDW	115	725	17	20	2023-04-06 17:00:00	Other
25323	11	3	1936	1936	0	2120	2140	AA	320	N908AN	EWR	CLT	74	529	19	36	2023-11-03 19:00:00	CLT
25343	8	3	1057	1052	5	1340	1350	B6	277	N524JB	EWR	MCO	121	937	10	52	2023-08-03 10:00:00	MCO
25359	10	16	1329	1330	-1	1519	1515	YX	1147	N724YX	EWR	GSO	70	445	13	30	2023-10-16 13:00:00	Other
25362	2	26	1331	1326	5	1550	1541	B6	254	N183JB	JFK	MSP	179	1029	13	26	2023-02-26 13:00:00	Other
25367	2	23	704	705	-1	956	1014	DL	653	N309US	LGA	TPA	148	1010	7	5	2023-02-23 07:00:00	Other
25373	6	19	1107	1100	7	1347	1413	B6	848	N608JB	JFK	FLL	134	1069	11	0	2023-06-19 11:00:00	FLL
25375	7	9	1305	1305	0	1647	1610	UA	412	N78438	EWR	FLL	154	1065	13	5	2023-07-09 13:00:00	FLL
25376	6	16	629	630	-1	915	931	B6	993	N729JB	JFK	FLL	145	1069	6	30	2023-06-16 06:00:00	FLL
25380	10	12	1653	1645	8	1939	1939	UA	465	N14106	EWR	SAN	330	2425	16	45	2023-10-12 16:00:00	Other
25383	3	20	1507	1506	1	1808	1804	UA	609	N87507	EWR	TPA	152	997	15	6	2023-03-20 15:00:00	Other
25393	3	14	642	640	2	956	957	DL	103	N835DN	JFK	SEA	324	2422	6	40	2023-03-14 06:00:00	Other
25398	6	9	1707	1659	8	1907	1911	AA	989	N435AN	EWR	PHX	276	2133	16	59	2023-06-09 16:00:00	Other
25399	10	5	1250	1250	0	1502	1508	OO	1195	N309SY	LGA	SDF	108	659	12	50	2023-10-05 12:00:00	Other
25401	7	10	1103	1055	8	1235	1245	G4	144	299NV	EWR	DSM	134	1017	10	55	2023-07-10 10:00:00	Other
25404	1	22	1528	1529	-1	1720	1719	9E	1419	N313PQ	JFK	BNA	140	765	15	29	2023-01-22 15:00:00	Other
25406	2	13	2208	2209	-1	2315	2323	UA	551	N17262	EWR	BOS	45	200	22	9	2023-02-13 22:00:00	BOS
25410	12	7	1708	1705	3	1856	1913	DL	876	N306DN	LGA	DTW	83	502	17	5	2023-12-07 17:00:00	Other
25413	5	5	854	845	9	1108	1051	9E	1560	N296PQ	LGA	AVL	93	599	8	45	2023-05-05 08:00:00	Other
25418	3	27	1920	1915	5	2051	2045	WN	334	N8805L	LGA	MDW	126	725	19	15	2023-03-27 19:00:00	Other
25430	4	15	1509	1500	9	1832	1740	DL	137	N185DN	JFK	ATL	121	760	15	0	2023-04-15 15:00:00	ATL
25433	10	16	2228	2218	10	24	59	NK	238	N927NK	EWR	LAS	275	2227	22	18	2023-10-16 22:00:00	Other
25449	4	19	1939	1939	0	2255	2255	DL	543	N315DN	LGA	MIA	151	1096	19	39	2023-04-19 19:00:00	MIA
25451	12	24	609	610	-1	857	918	NK	261	N625NK	EWR	IAH	199	1400	6	10	2023-12-24 06:00:00	Other
25452	12	15	1318	1315	3	1615	1638	DL	123	N145DQ	LGA	DFW	206	1389	13	15	2023-12-15 13:00:00	Other
25462	2	5	2009	2000	9	2138	2135	AA	760	N769US	LGA	DCA	69	214	20	0	2023-02-05 20:00:00	Other
25469	1	11	1708	1707	1	2006	2007	UA	194	N27266	EWR	MCO	134	937	17	7	2023-01-11 17:00:00	MCO
25470	12	20	530	530	0	842	912	NK	347	N653NK	EWR	PHX	293	2133	5	30	2023-12-20 05:00:00	Other
25504	12	15	1550	1550	0	1847	1931	B6	219	N988JT	JFK	SFO	333	2586	15	50	2023-12-15 15:00:00	Other
25505	9	22	1316	1310	6	1437	1423	B6	557	N328JB	JFK	BOS	48	187	13	10	2023-09-22 13:00:00	BOS
25524	8	13	1912	1909	3	2247	2308	UA	185	N61886	EWR	BQN	192	1585	19	9	2023-08-13 19:00:00	Other
25532	11	16	629	630	-1	1113	1125	B6	567	N996JL	JFK	SJU	195	1598	6	30	2023-11-16 06:00:00	Other
25551	12	15	708	659	9	952	1000	B6	237	N2086J	JFK	MCO	126	944	6	59	2023-12-15 06:00:00	MCO
25558	12	7	749	745	4	1000	1020	UA	808	N12116	EWR	DEN	226	1605	7	45	2023-12-07 07:00:00	Other
25560	11	15	1830	1830	0	1953	2007	OO	1216	N613CZ	JFK	BNA	111	765	18	30	2023-11-15 18:00:00	Other
25569	1	8	750	740	10	1129	1122	B6	6	N984JB	JFK	SFO	359	2586	7	40	2023-01-08 07:00:00	Other
25571	12	7	2003	2001	2	2342	2346	B6	307	N968JT	JFK	SFO	366	2586	20	1	2023-12-07 20:00:00	Other
25578	8	6	1448	1445	3	1743	1810	B6	162	N645JB	EWR	FLL	151	1065	14	45	2023-08-06 14:00:00	FLL
25586	7	24	1539	1530	9	1830	1839	UA	624	N788UA	EWR	SFO	327	2565	15	30	2023-07-24 15:00:00	Other
25592	3	22	624	615	9	820	817	DL	980	N991AT	EWR	MSP	159	1008	6	15	2023-03-22 06:00:00	Other
25593	4	21	603	600	3	913	915	AA	52	N108NN	JFK	LAX	333	2475	6	0	2023-04-21 06:00:00	LAX
25599	7	13	1704	1700	4	1927	1914	YX	952	N641RW	EWR	CVG	95	569	17	0	2023-07-13 17:00:00	Other
25604	1	22	2044	2045	-1	2249	2234	DL	516	N126DU	LGA	ORD	114	733	20	45	2023-01-22 20:00:00	ORD
25607	1	27	1625	1620	5	1838	1835	9E	1698	N279PQ	JFK	CLT	100	541	16	20	2023-01-27 16:00:00	CLT
25612	2	18	1520	1520	0	1636	1655	YX	1577	N243JQ	LGA	ORF	50	296	15	20	2023-02-18 15:00:00	Other
25613	7	1	1719	1712	7	2020	2029	B6	64	N640JB	JFK	TPA	136	1005	17	12	2023-07-01 17:00:00	Other
25625	10	16	700	700	0	915	934	DL	167	N339DN	LGA	ATL	102	762	7	0	2023-10-16 07:00:00	ATL
25628	2	2	1739	1730	9	2058	2050	AS	88	N562AS	EWR	PDX	359	2434	17	30	2023-02-02 17:00:00	Other
25629	10	27	1855	1850	5	2121	2148	NK	734	N522NK	EWR	MCO	124	937	18	50	2023-10-27 18:00:00	MCO
25633	3	7	1703	1700	3	2059	2022	UA	139	N2341U	EWR	SFO	352	2565	17	0	2023-03-07 17:00:00	Other
25644	1	25	2029	2029	0	102	2344	UA	312	N17122	EWR	FLL	173	1065	20	29	2023-01-25 20:00:00	FLL
25645	4	9	1800	1759	1	2102	2106	F9	889	N380FR	LGA	MIA	156	1096	17	59	2023-04-09 17:00:00	MIA
25648	6	15	1814	1815	-1	2006	2020	YX	1297	N427YX	LGA	LIT	152	1085	18	15	2023-06-15 18:00:00	Other
25655	10	20	811	810	1	1216	1207	UA	770	N77066	EWR	SJU	211	1608	8	10	2023-10-20 08:00:00	Other
25657	7	24	1159	1200	-1	1401	1417	9E	1269	N348PQ	LGA	MCI	149	1107	12	0	2023-07-24 12:00:00	Other
25666	6	22	1042	1040	2	1330	1337	B6	349	N503JB	EWR	MCO	138	937	10	40	2023-06-22 10:00:00	MCO
25672	4	13	1920	1914	6	2041	2051	UA	581	N812UA	EWR	BNA	105	748	19	14	2023-04-13 19:00:00	Other
25675	11	7	1110	1105	5	1401	1426	DL	577	N3757D	LGA	MIA	147	1096	11	5	2023-11-07 11:00:00	MIA
25676	11	16	1951	1945	6	2240	2252	DL	877	N836DN	JFK	TPA	146	1005	19	45	2023-11-16 19:00:00	Other
25701	1	3	754	754	0	1100	1111	AA	658	N924NN	LGA	MIA	149	1096	7	54	2023-01-03 07:00:00	MIA
25714	12	22	857	849	8	1109	1119	9E	1596	N197PQ	LGA	SAV	100	722	8	49	2023-12-22 08:00:00	Other
25715	1	13	2103	2100	3	2304	2309	YX	1413	N448YX	LGA	GSO	82	461	21	0	2023-01-13 21:00:00	Other
25716	5	14	1906	1905	1	2237	2236	B6	28	N706JB	JFK	SLC	276	1990	19	5	2023-05-14 19:00:00	Other
25719	7	15	1204	1159	5	1447	1453	UA	454	N27273	EWR	TPA	134	997	11	59	2023-07-15 11:00:00	Other
25723	5	26	1428	1429	-1	1600	1612	9E	1510	N341PQ	JFK	RIC	54	288	14	29	2023-05-26 14:00:00	Other
25725	8	10	806	759	7	1119	1110	AA	478	N350RV	JFK	MIA	142	1089	7	59	2023-08-10 07:00:00	MIA
25731	9	23	1435	1430	5	1543	1554	YX	1202	N746YX	EWR	DCA	44	199	14	30	2023-09-23 14:00:00	Other
25734	11	25	2135	2125	10	26	17	B6	658	N306JB	EWR	MCO	138	937	21	25	2023-11-25 21:00:00	MCO
25736	12	3	1224	1223	1	1535	1540	DL	559	N346DN	LGA	FLL	153	1076	12	23	2023-12-03 12:00:00	FLL
25739	4	22	800	751	9	1102	1052	UA	664	N821UA	EWR	PBI	156	1023	7	51	2023-04-22 07:00:00	Other
25741	11	30	1528	1529	-1	1742	1746	9E	1632	N480PX	LGA	AVL	90	599	15	29	2023-11-30 15:00:00	Other
25742	4	13	2137	2130	7	2329	2336	YX	975	N725YX	EWR	GSP	81	594	21	30	2023-04-13 21:00:00	Other
25760	3	10	2101	2059	2	2208	2222	YX	1746	N223JQ	LGA	BOS	35	184	20	59	2023-03-10 20:00:00	BOS
25764	4	10	631	630	1	758	816	AA	898	N924AN	LGA	ORD	110	733	6	30	2023-04-10 06:00:00	ORD
25772	5	3	2005	1959	6	2257	2319	DL	446	N389DN	LGA	FLL	144	1076	19	59	2023-05-03 19:00:00	FLL
25801	3	12	1220	1215	5	1533	1535	UA	804	N218UA	EWR	SFO	330	2565	12	15	2023-03-12 12:00:00	Other
25803	3	11	1629	1630	-1	2000	2008	B6	237	N937JB	JFK	SFO	358	2586	16	30	2023-03-11 16:00:00	Other
25804	9	2	1258	1259	-1	1403	1413	B6	847	N328JB	JFK	ACK	39	199	12	59	2023-09-02 12:00:00	Other
25806	8	11	1115	1115	0	1310	1325	DL	694	N330NB	LGA	MSY	159	1183	11	15	2023-08-11 11:00:00	Other
25809	2	11	1134	1135	-1	1246	1245	UA	625	N58101	EWR	BOS	49	200	11	35	2023-02-11 11:00:00	BOS
25812	11	5	1130	1130	0	1417	1435	WN	536	N8612K	LGA	DAL	178	1381	11	30	2023-11-05 11:00:00	Other
25814	8	10	1348	1342	6	1611	1540	AA	511	N357PV	EWR	CLT	94	529	13	42	2023-08-10 13:00:00	CLT
25821	9	24	1524	1520	4	1640	1651	9E	1601	N676CA	JFK	SYR	43	209	15	20	2023-09-24 15:00:00	Other
25825	5	18	929	929	0	1121	1121	YX	1257	N425YX	LGA	CLE	72	419	9	29	2023-05-18 09:00:00	Other
25828	3	6	1300	1255	5	1403	1405	UA	492	N67827	EWR	BOS	42	200	12	55	2023-03-06 12:00:00	BOS
25839	6	5	801	800	1	948	947	OO	1258	N297SY	JFK	ORD	124	740	8	0	2023-06-05 08:00:00	ORD
25844	5	4	1843	1840	3	1958	2010	B6	922	N249JB	EWR	BOS	37	200	18	40	2023-05-04 18:00:00	BOS
25847	5	29	605	600	5	702	725	WN	618	N8727M	LGA	MDW	98	725	6	0	2023-05-29 06:00:00	Other
25848	1	30	1036	1035	1	1212	1235	WN	1003	N901WN	LGA	STL	142	888	10	35	2023-01-30 10:00:00	Other
25849	1	2	839	840	-1	1030	1045	YX	1151	N724YX	EWR	GSO	86	445	8	40	2023-01-02 08:00:00	Other
25851	11	1	600	600	0	908	907	B6	946	N665JB	JFK	FLL	162	1069	6	0	2023-11-01 06:00:00	FLL
25853	10	15	1707	1700	7	1930	2027	DL	256	N526DE	JFK	SAN	293	2446	17	0	2023-10-15 17:00:00	Other
25854	2	21	1348	1348	0	1619	1617	YX	990	N756YX	EWR	SDF	116	642	13	48	2023-02-21 13:00:00	Other
25858	1	31	1848	1849	-1	2147	2201	B6	1063	N552JB	JFK	TPA	152	1005	18	49	2023-01-31 18:00:00	Other
25859	11	28	1330	1329	1	1619	1637	DL	295	N408DX	JFK	LAX	318	2475	13	29	2023-11-28 13:00:00	LAX
25861	12	6	2105	2100	5	2228	2235	WN	909	N482WN	LGA	MDW	111	725	21	0	2023-12-06 21:00:00	Other
25871	4	18	1200	1200	0	1323	1331	AA	645	N938NN	EWR	ORD	108	719	12	0	2023-04-18 12:00:00	ORD
25874	4	13	1230	1230	0	1455	1526	NK	325	N646NK	LGA	DFW	176	1389	12	30	2023-04-13 12:00:00	Other
25879	11	27	1336	1330	6	1725	1634	NK	329	N643NK	LGA	DFW	254	1389	13	30	2023-11-27 13:00:00	Other
25892	10	5	1508	1500	8	1629	1626	YX	1841	N211JQ	LGA	BOS	41	184	15	0	2023-10-05 15:00:00	BOS
25903	11	25	809	810	-1	1250	1310	DL	668	N546DN	JFK	SJU	198	1598	8	10	2023-11-25 08:00:00	Other
25905	6	12	1826	1820	6	2213	2109	DL	1047	N125DU	JFK	JAX	119	828	18	20	2023-06-12 18:00:00	Other
25908	12	31	1728	1729	-1	2041	2038	B6	449	N784JB	JFK	MCO	142	944	17	29	2023-12-31 17:00:00	MCO
25912	7	20	1440	1440	0	1730	1743	DL	398	N359DN	LGA	MCO	132	950	14	40	2023-07-20 14:00:00	MCO
25916	5	26	1605	1605	0	1844	1911	AA	960	N936NN	LGA	DFW	181	1389	16	5	2023-05-26 16:00:00	Other
25918	9	1	1955	1955	0	2250	2328	DL	611	N822DN	JFK	FLL	136	1069	19	55	2023-09-01 19:00:00	FLL
25920	12	4	2254	2255	-1	7	15	B6	61	N274JB	JFK	BTV	47	266	22	55	2023-12-04 22:00:00	Other
25928	4	13	1500	1500	0	1751	1810	UA	791	N17126	EWR	LAX	316	2454	15	0	2023-04-13 15:00:00	LAX
25939	11	5	2006	2001	5	58	57	UA	541	N37514	EWR	SJU	197	1608	20	1	2023-11-05 20:00:00	Other
25944	10	25	1204	1200	4	1459	1452	UA	801	N210UA	EWR	LAX	329	2454	12	0	2023-10-25 12:00:00	LAX
25947	8	13	1844	1840	4	2142	2153	DL	369	N330DX	EWR	SLC	282	1969	18	40	2023-08-13 18:00:00	Other
25948	10	26	1229	1230	-1	1516	1541	AA	354	N843NN	LGA	DFW	200	1389	12	30	2023-10-26 12:00:00	Other
25973	2	14	1125	1125	0	1443	1502	AA	808	N895NN	LGA	MIA	166	1096	11	25	2023-02-14 11:00:00	MIA
25975	5	5	1019	1020	-1	1310	1312	UA	705	N29985	EWR	IAH	187	1400	10	20	2023-05-05 10:00:00	Other
25976	5	13	1635	1629	6	1757	1810	YX	1691	N231JQ	JFK	BOS	39	187	16	29	2023-05-13 16:00:00	BOS
25977	4	14	645	640	5	1018	942	B6	759	N793JB	JFK	MIA	160	1089	6	40	2023-04-14 06:00:00	MIA
25979	2	4	1334	1325	9	1636	1635	NK	347	N669NK	LGA	FLL	160	1076	13	25	2023-02-04 13:00:00	FLL
25985	12	14	1729	1730	-1	1936	2049	DL	245	N525DA	JFK	LAS	282	2248	17	30	2023-12-14 17:00:00	Other
26003	2	25	559	600	-1	847	915	NK	52	N671NK	LGA	FLL	143	1076	6	0	2023-02-25 06:00:00	FLL
26019	1	18	1728	1720	8	2043	2035	WN	542	N8509U	LGA	HOU	238	1428	17	20	2023-01-18 17:00:00	Other
26020	2	22	1317	1315	2	1452	1450	9E	1393	N297PQ	JFK	BUF	66	301	13	15	2023-02-22 13:00:00	Other
26023	12	27	822	815	7	1042	1038	DL	736	N305DU	LGA	CHS	106	641	8	15	2023-12-27 08:00:00	Other
26026	1	24	1713	1705	8	1859	1849	AA	914	N328RR	EWR	ORD	128	719	17	5	2023-01-24 17:00:00	ORD
26028	11	11	1545	1540	5	1736	1733	B6	404	N229JB	JFK	RDU	78	427	15	40	2023-11-11 15:00:00	Other
26029	9	15	2003	1955	8	2128	2135	YX	1068	N641RW	EWR	PIT	54	319	19	55	2023-09-15 19:00:00	Other
26032	1	16	1239	1240	-1	1409	1428	YX	1410	N870RW	LGA	ORF	47	296	12	40	2023-01-16 12:00:00	Other
26041	10	20	731	725	6	951	1018	DL	169	N536DN	JFK	LAS	294	2248	7	25	2023-10-20 07:00:00	Other
26042	1	16	2037	2035	2	2344	2352	UA	724	N27258	EWR	MIA	145	1085	20	35	2023-01-16 20:00:00	MIA
26049	12	28	700	700	0	922	928	DL	978	N918DU	EWR	ATL	111	746	7	0	2023-12-28 07:00:00	ATL
26053	9	4	1746	1745	1	1916	1923	AA	634	N961NN	EWR	ORD	101	719	17	45	2023-09-04 17:00:00	ORD
26067	11	16	2120	2117	3	2249	2259	UA	638	N64809	EWR	CLE	64	404	21	17	2023-11-16 21:00:00	Other
26071	1	1	1723	1720	3	2009	2005	WN	400	N8537Z	LGA	DEN	261	1620	17	20	2023-01-01 17:00:00	Other
26075	5	18	1731	1729	2	2054	2054	AA	318	N306SP	JFK	MIA	160	1089	17	29	2023-05-18 17:00:00	MIA
26077	6	27	1511	1502	9	NA	1809	NK	645	N677NK	LGA	FLL	NA	1076	15	2	2023-06-27 15:00:00	FLL
26084	11	19	713	710	3	948	1009	DL	419	N368DN	LGA	MCO	129	950	7	10	2023-11-19 07:00:00	MCO
26085	7	23	1911	1910	1	2134	2124	YX	1031	N870RW	LGA	IND	113	660	19	10	2023-07-23 19:00:00	Other
26086	8	25	658	649	9	957	933	UA	255	N66841	EWR	SAN	310	2425	6	49	2023-08-25 06:00:00	Other
26090	7	13	1758	1759	-1	2101	2114	DL	715	N329NW	JFK	AUS	205	1521	17	59	2023-07-13 17:00:00	Other
26101	4	13	1120	1111	9	1436	1419	DL	429	N3766	LGA	PBI	173	1035	11	11	2023-04-13 11:00:00	Other
26108	2	5	1515	1510	5	1650	1648	UA	612	N29717	EWR	ORD	118	719	15	10	2023-02-05 15:00:00	ORD
26112	8	30	609	610	-1	754	747	DL	371	N141DU	LGA	ORD	119	733	6	10	2023-08-30 06:00:00	ORD
26119	8	23	1306	1305	1	1540	1610	UA	396	N66848	EWR	FLL	132	1065	13	5	2023-08-23 13:00:00	FLL
26120	12	9	1741	1740	1	2054	2055	DL	755	N3741S	LGA	RSW	170	1080	17	40	2023-12-09 17:00:00	Other
26125	11	16	1102	1055	7	1419	1402	NK	260	N607NK	LGA	MCO	137	950	10	55	2023-11-16 10:00:00	MCO
26128	9	15	2147	2148	-1	2326	2341	YX	1115	N647RW	EWR	GSO	68	445	21	48	2023-09-15 21:00:00	Other
26133	11	21	2104	2100	4	2212	2241	AA	636	N807NN	EWR	ORD	104	719	21	0	2023-11-21 21:00:00	ORD
26134	7	28	1535	1529	6	1736	1737	YX	955	N727YX	EWR	MYR	83	550	15	29	2023-07-28 15:00:00	Other
26139	11	25	1054	1055	-1	1246	1305	G4	509	306NV	EWR	VPS	140	988	10	55	2023-11-25 10:00:00	Other
26144	2	23	830	830	0	1135	1157	NK	320	N682NK	LGA	IAH	218	1416	8	30	2023-02-23 08:00:00	Other
26145	8	2	1458	1459	-1	1710	1736	9E	1150	N935XJ	JFK	IND	95	665	14	59	2023-08-02 14:00:00	Other
26148	3	24	705	705	0	1013	1024	DL	549	N110DX	LGA	MIA	157	1096	7	5	2023-03-24 07:00:00	MIA
26156	11	30	2002	2000	2	2314	2319	AA	965	N940AN	LGA	MIA	161	1096	20	0	2023-11-30 20:00:00	MIA
26157	7	27	559	600	-1	710	715	WN	14	N8720L	LGA	MDW	101	725	6	0	2023-07-27 06:00:00	Other
26160	1	14	1912	1910	2	2141	2228	DL	977	N3758Y	LGA	RSW	130	1080	19	10	2023-01-14 19:00:00	Other
26165	11	4	928	929	-1	1211	1227	UA	210	N77572	EWR	MCO	130	937	9	29	2023-11-04 09:00:00	MCO
26167	12	23	1424	1420	4	1636	1646	B6	785	N3115J	JFK	MCI	159	1113	14	20	2023-12-23 14:00:00	Other
26170	4	17	1104	1100	4	1440	1407	B6	834	N592JB	JFK	MIA	179	1089	11	0	2023-04-17 11:00:00	MIA
26171	11	12	1631	1629	2	1857	1905	UA	791	N811UA	LGA	DEN	233	1620	16	29	2023-11-12 16:00:00	Other
26177	11	15	1553	1554	-1	1714	1720	YX	1899	N237JQ	JFK	BOS	45	187	15	54	2023-11-15 15:00:00	BOS
26185	1	27	1607	1559	8	1713	1729	OO	1276	N320SY	JFK	IAD	47	228	15	59	2023-01-27 15:00:00	Other
26189	1	30	949	950	-1	1216	1218	9E	1610	N482PX	LGA	CVG	103	585	9	50	2023-01-30 09:00:00	Other
26191	8	21	1658	1649	9	1820	1822	YX	878	N744YX	EWR	BGR	58	393	16	49	2023-08-21 16:00:00	Other
26193	3	25	1814	1805	9	2131	2124	AA	1003	N826NN	EWR	MIA	164	1085	18	5	2023-03-25 18:00:00	MIA
26209	7	17	958	955	3	1116	1125	WN	973	N8583Z	LGA	BNA	114	764	9	55	2023-07-17 09:00:00	Other
26212	6	28	1806	1800	6	2107	2110	DL	368	N183DN	JFK	LAX	325	2475	18	0	2023-06-28 18:00:00	LAX
26245	4	2	1701	1659	2	1855	1840	UA	717	N831UA	LGA	ORD	127	733	16	59	2023-04-02 16:00:00	ORD
26249	3	28	1829	1825	4	2153	2139	AS	182	N287AK	EWR	SEA	343	2402	18	25	2023-03-28 18:00:00	Other
26252	9	7	1241	1231	10	1429	1427	DL	513	N925AT	EWR	MSP	138	1008	12	31	2023-09-07 12:00:00	Other
26257	10	27	2023	2015	8	2321	2315	UA	742	N37530	EWR	TPA	135	997	20	15	2023-10-27 20:00:00	Other
26268	5	12	1429	1429	0	1640	1700	DL	138	N365DN	LGA	ATL	107	762	14	29	2023-05-12 14:00:00	ATL
26271	4	5	1344	1335	9	1642	1525	UA	190	N37274	EWR	MSP	209	1008	13	35	2023-04-05 13:00:00	Other
26285	10	29	2022	2020	2	2147	2200	YX	1025	N741YX	EWR	BGR	53	393	20	20	2023-10-29 20:00:00	Other
26286	5	17	1230	1229	1	1504	1502	DL	320	N353DN	LGA	ATL	113	762	12	29	2023-05-17 12:00:00	ATL
26289	5	16	1442	1435	7	1630	1648	B6	874	N324JB	JFK	CHS	92	636	14	35	2023-05-16 14:00:00	Other
26296	11	22	831	832	-1	958	951	9E	1489	N915XJ	LGA	PWM	46	269	8	32	2023-11-22 08:00:00	Other
26305	4	2	1503	1455	8	1744	1738	B6	777	N627JB	LGA	JAX	115	833	14	55	2023-04-02 14:00:00	Other
26307	12	1	700	700	0	1023	1015	DL	181	N179DN	JFK	LAX	337	2475	7	0	2023-12-01 07:00:00	LAX
26309	4	13	735	730	5	908	910	B6	756	N633JB	JFK	RDU	64	427	7	30	2023-04-13 07:00:00	Other
26313	4	12	910	910	0	1045	1110	YX	1182	N405YX	LGA	GSO	64	461	9	10	2023-04-12 09:00:00	Other
26318	5	14	1653	1654	-1	1923	2000	NK	630	N601NK	EWR	FLL	135	1065	16	54	2023-05-14 16:00:00	FLL
26328	2	26	2100	2100	0	2319	2230	9E	1482	N304PQ	LGA	RIC	52	292	21	0	2023-02-26 21:00:00	Other
26331	4	3	1522	1520	2	1709	1710	WN	1053	N8606C	LGA	STL	136	888	15	20	2023-04-03 15:00:00	Other
26341	11	20	1728	1729	-1	2039	2032	UA	898	N67815	EWR	SRQ	143	1034	17	29	2023-11-20 17:00:00	Other
26346	6	16	1722	1717	5	2016	2029	B6	72	N629JB	JFK	TPA	146	1005	17	17	2023-06-16 17:00:00	Other
26348	6	13	1928	1929	-1	2232	2252	DL	926	N3750D	JFK	TPA	150	1005	19	29	2023-06-13 19:00:00	Other
26352	11	22	1613	1614	-1	1910	1956	UA	826	N17289	EWR	PHX	276	2133	16	14	2023-11-22 16:00:00	Other
26370	4	26	2206	2159	7	2346	2321	UA	286	N27734	EWR	BOS	50	200	21	59	2023-04-26 21:00:00	BOS
26391	12	28	1255	1255	0	1457	1510	G4	987	233NV	EWR	TYS	98	631	12	55	2023-12-28 12:00:00	Other
26393	5	27	1132	1129	3	1312	1324	UA	804	N16732	EWR	CLT	81	529	11	29	2023-05-27 11:00:00	CLT
26395	10	3	1850	1849	1	2112	2119	9E	1691	N906XJ	JFK	IND	93	665	18	49	2023-10-03 18:00:00	Other
26401	4	29	933	924	9	1337	1326	UA	528	N13750	EWR	STT	195	1634	9	24	2023-04-29 09:00:00	Other
26411	8	18	940	930	10	1204	1159	YX	1351	N823MD	LGA	HHH	104	701	9	30	2023-08-18 09:00:00	Other
26418	3	31	2005	2000	5	2208	2201	YX	1217	N724YX	EWR	ILM	75	488	20	0	2023-03-31 20:00:00	Other
26429	6	9	607	603	4	724	735	UA	758	N33264	EWR	ORD	104	719	6	3	2023-06-09 06:00:00	ORD
26430	7	24	1256	1255	1	1616	1557	B6	18	N274JB	LGA	TPA	167	1010	12	55	2023-07-24 12:00:00	Other
26433	6	23	1833	1830	3	1937	1946	YX	1116	N746YX	EWR	ALB	37	143	18	30	2023-06-23 18:00:00	Other
26437	10	4	805	800	5	1018	1016	B6	289	N2084J	JFK	SAV	99	718	8	0	2023-10-04 08:00:00	Other
26457	2	3	700	700	0	854	901	YX	1235	N429YX	LGA	RDU	85	431	7	0	2023-02-03 07:00:00	Other
26468	12	22	2049	2050	-1	2226	2233	YX	1860	N243JQ	LGA	ORF	49	296	20	50	2023-12-22 20:00:00	Other
26475	7	27	928	929	-1	1145	1159	YX	1392	N818MD	LGA	HHH	102	701	9	29	2023-07-27 09:00:00	Other
26489	12	28	1048	1040	8	1339	1422	UA	446	N17294	EWR	PHX	269	2133	10	40	2023-12-28 10:00:00	Other
26493	3	27	1706	1700	6	2006	2001	UA	447	N19951	EWR	LAX	326	2454	17	0	2023-03-27 17:00:00	LAX
26495	4	24	1823	1815	8	2010	2028	DL	679	N979AT	EWR	MSP	139	1008	18	15	2023-04-24 18:00:00	Other
26497	8	23	1839	1840	-1	2031	2102	YX	876	N760YX	EWR	IND	91	645	18	40	2023-08-23 18:00:00	Other
26502	5	17	1808	1759	9	1947	1940	UA	709	N468UA	LGA	ORD	109	733	17	59	2023-05-17 17:00:00	ORD
26509	5	16	1228	1229	-1	1515	1532	AA	541	N972AN	LGA	DFW	187	1389	12	29	2023-05-16 12:00:00	Other
26511	11	10	1450	1450	0	1710	1656	9E	1434	N176PQ	JFK	CLT	101	541	14	50	2023-11-10 14:00:00	CLT
26519	1	30	1146	1140	6	1303	1310	WN	245	N249WN	LGA	MDW	120	725	11	40	2023-01-30 11:00:00	Other
26526	12	3	1024	1020	4	1443	1340	DL	550	N126DU	JFK	SAT	280	1587	10	20	2023-12-03 10:00:00	Other
26528	12	15	1528	1525	3	1843	1830	UA	782	N37462	EWR	IAH	196	1400	15	25	2023-12-15 15:00:00	Other
26530	5	16	600	600	0	721	725	WN	618	N8840Q	LGA	MDW	116	725	6	0	2023-05-16 06:00:00	Other
26538	6	15	2201	2157	4	2258	2254	9E	1668	N186PQ	LGA	PVD	35	143	21	57	2023-06-15 21:00:00	Other
26542	4	14	1951	1941	10	2159	2210	YX	1005	N744YX	EWR	SDF	94	642	19	41	2023-04-14 19:00:00	Other
26543	6	4	1455	1455	0	1733	1717	9E	1739	N600LR	JFK	IND	99	665	14	55	2023-06-04 14:00:00	Other
26557	12	26	1959	1959	0	2324	2323	DL	339	N385DZ	LGA	MIA	147	1096	19	59	2023-12-26 19:00:00	MIA
26561	11	21	1713	1711	2	2025	2019	UA	537	N57299	EWR	FLL	166	1065	17	11	2023-11-21 17:00:00	FLL
26567	5	11	1200	1200	0	1439	1446	NK	980	N611NK	EWR	MCO	124	937	12	0	2023-05-11 12:00:00	MCO
26569	2	28	1952	1950	2	2248	2328	DL	614	N3766	JFK	RSW	151	1074	19	50	2023-02-28 19:00:00	Other
26576	7	21	947	939	8	1101	1048	B6	413	N184JB	JFK	MVY	39	173	9	39	2023-07-21 09:00:00	Other
26594	3	2	659	659	0	1106	1016	NK	856	N621NK	EWR	AUS	272	1504	6	59	2023-03-02 06:00:00	Other
26599	4	30	1732	1730	2	2007	2030	AS	87	N238AK	EWR	PDX	298	2434	17	30	2023-04-30 17:00:00	Other
26602	1	1	1240	1231	9	1346	1343	UA	902	N27519	EWR	BOS	43	200	12	31	2023-01-01 12:00:00	BOS
26606	2	14	1715	1715	0	2034	2037	DL	283	N417DX	JFK	LAX	330	2475	17	15	2023-02-14 17:00:00	LAX
26614	7	16	849	850	-1	1005	1019	YX	1384	N229JQ	LGA	MKE	106	738	8	50	2023-07-16 08:00:00	Other
26621	3	28	625	625	0	929	923	UA	218	N37464	EWR	SAN	347	2425	6	25	2023-03-28 06:00:00	Other
26622	3	30	1659	1650	9	1925	1900	9E	1383	N908XJ	LGA	DSM	161	1031	16	50	2023-03-30 16:00:00	Other
26623	7	31	631	630	1	749	748	B6	794	N267JB	JFK	BUF	55	301	6	30	2023-07-31 06:00:00	Other
26625	11	29	1229	1229	0	1537	1542	AA	959	N324SH	JFK	MIA	159	1089	12	29	2023-11-29 12:00:00	MIA
26629	7	16	2044	2040	4	2336	2304	B6	746	N187JB	LGA	ATL	116	762	20	40	2023-07-16 20:00:00	ATL
26633	9	12	1644	1645	-1	1949	1953	NK	628	N602NK	EWR	FLL	143	1065	16	45	2023-09-12 16:00:00	FLL
26645	5	2	1639	1630	9	1738	1758	YX	1004	N641RW	EWR	DCA	40	199	16	30	2023-05-02 16:00:00	Other
26647	12	10	1533	1526	7	1717	1704	UA	353	N37290	EWR	ORD	118	719	15	26	2023-12-10 15:00:00	ORD
26663	9	21	1952	1950	2	2234	2303	DL	890	N855DN	JFK	TPA	140	1005	19	50	2023-09-21 19:00:00	Other
26665	12	5	1103	1055	8	1329	1335	WN	30	N264LV	LGA	ATL	124	762	10	55	2023-12-05 10:00:00	ATL
26672	7	27	816	817	-1	1127	1135	B6	211	N595JB	JFK	FLL	166	1069	8	17	2023-07-27 08:00:00	FLL
26683	8	14	604	600	4	715	715	WN	14	N1803U	LGA	MDW	108	725	6	0	2023-08-14 06:00:00	Other
26732	8	28	745	744	1	950	958	9E	1287	N307PQ	JFK	CLT	92	541	7	44	2023-08-28 07:00:00	CLT
26742	10	1	834	829	5	1149	1140	AA	320	N116AN	JFK	SNA	318	2454	8	29	2023-10-01 08:00:00	Other
26758	10	25	1518	1515	3	1912	1857	DL	258	N727TW	JFK	SFO	380	2586	15	15	2023-10-25 15:00:00	Other
26761	4	4	1856	1855	1	2028	2040	WN	839	N8534Z	LGA	BNA	116	764	18	55	2023-04-04 18:00:00	Other
26763	2	28	1934	1930	4	2103	2128	AA	127	N973NN	LGA	ORD	128	733	19	30	2023-02-28 19:00:00	ORD
26765	8	5	1042	1038	4	1213	1225	B6	71	N705JB	JFK	RDU	71	427	10	38	2023-08-05 10:00:00	Other
26769	5	28	1127	1127	0	1406	1422	DL	410	N336DX	LGA	MCO	132	950	11	27	2023-05-28 11:00:00	MCO
26777	6	3	1127	1121	6	1433	1420	UA	257	N27269	EWR	PBI	159	1023	11	21	2023-06-03 11:00:00	Other
26782	2	4	1336	1336	0	1654	1707	YX	1123	N856RW	EWR	EYW	165	1196	13	36	2023-02-04 13:00:00	Other
26797	5	18	2129	2130	-1	2350	2358	DL	90	N301DV	LGA	ATL	113	762	21	30	2023-05-18 21:00:00	ATL
26800	5	8	1159	1200	-1	1407	1430	DL	370	N865DN	JFK	ATL	102	760	12	0	2023-05-08 12:00:00	ATL
26805	8	7	1423	1424	-1	1705	1725	UA	218	N36272	EWR	SEA	313	2402	14	24	2023-08-07 14:00:00	Other
26806	8	7	1959	2000	-1	2105	2130	YX	1383	N214JQ	LGA	BOS	44	184	20	0	2023-08-07 20:00:00	BOS
26807	5	20	1628	1629	-1	1833	1851	UA	810	N893UA	EWR	MSY	162	1167	16	29	2023-05-20 16:00:00	Other
26813	2	20	1908	1859	9	2055	2032	YX	978	N646RW	EWR	BGR	59	393	18	59	2023-02-20 18:00:00	Other
26823	12	7	1302	1255	7	1504	1505	G4	58	205NV	EWR	AVL	83	583	12	55	2023-12-07 12:00:00	Other
26826	3	4	706	700	6	1012	1028	DL	103	N917DU	JFK	SEA	326	2422	7	0	2023-03-04 07:00:00	Other
26829	3	5	2119	2120	-1	2242	2242	YX	1650	N236JQ	LGA	ROC	53	254	21	20	2023-03-05 21:00:00	Other
26830	1	2	1759	1759	0	2131	2146	B6	46	N715JB	JFK	PHX	310	2153	17	59	2023-01-02 17:00:00	Other
26832	6	24	1830	1830	0	2109	2008	UA	456	N451UA	EWR	ORD	116	719	18	30	2023-06-24 18:00:00	ORD
26838	6	9	900	900	0	1012	1025	WN	57	N8756S	LGA	MDW	99	725	9	0	2023-06-09 09:00:00	Other
26840	12	19	958	959	-1	1133	1200	YX	1717	N209JQ	JFK	CMH	73	483	9	59	2023-12-19 09:00:00	Other
26848	6	28	1000	950	10	1108	1115	WN	701	N8861Q	LGA	BNA	110	764	9	50	2023-06-28 09:00:00	Other
26851	12	13	1947	1944	3	2143	2221	DL	955	N358NW	JFK	MSP	148	1029	19	44	2023-12-13 19:00:00	Other
26853	4	21	1359	1359	0	1612	1633	DL	170	N3752	JFK	DEN	217	1626	13	59	2023-04-21 13:00:00	Other
26865	1	12	1836	1830	6	2034	2031	YX	1814	N230JQ	JFK	ORD	124	740	18	30	2023-01-12 18:00:00	ORD
26869	10	10	1012	1013	-1	1136	1150	YX	1113	N762YX	EWR	BGR	59	393	10	13	2023-10-10 10:00:00	Other
26901	10	20	1259	1300	-1	1705	1607	B6	561	N627JB	JFK	FLL	160	1069	13	0	2023-10-20 13:00:00	FLL
26909	4	9	934	930	4	1235	1241	B6	734	N999JQ	JFK	FLL	150	1069	9	30	2023-04-09 09:00:00	FLL
26914	10	20	633	630	3	922	919	B6	39	N652JB	JFK	TPA	144	1005	6	30	2023-10-20 06:00:00	Other
26924	1	6	1531	1530	1	1702	1722	YX	1770	N216JQ	JFK	RIC	62	288	15	30	2023-01-06 15:00:00	Other
26927	12	24	1030	1030	0	1332	1346	B6	759	N592JB	JFK	RSW	163	1074	10	30	2023-12-24 10:00:00	Other
26929	7	22	1958	1959	-1	2249	2317	DL	478	N313DN	LGA	FLL	145	1076	19	59	2023-07-22 19:00:00	FLL
26931	8	6	1504	1501	3	1807	1810	DL	487	N327NB	LGA	TPA	142	1010	15	1	2023-08-06 15:00:00	Other
26934	5	8	2019	2020	-1	2252	2255	WN	361	N493WN	LGA	DEN	236	1620	20	20	2023-05-08 20:00:00	Other
26939	2	6	1519	1515	4	1643	1648	9E	1421	N296PQ	LGA	ORF	49	296	15	15	2023-02-06 15:00:00	Other
26952	10	1	1801	1756	5	2019	2105	UA	615	N892UA	EWR	PDX	300	2434	17	56	2023-10-01 17:00:00	Other
26953	6	23	1359	1400	-1	1513	1530	YX	1848	N224JQ	LGA	BOS	34	184	14	0	2023-06-23 14:00:00	BOS
26967	3	20	1756	1750	6	2151	2131	AA	953	N103NN	JFK	SFO	379	2586	17	50	2023-03-20 17:00:00	Other
26973	12	9	932	930	2	1123	1141	DL	506	N398DN	LGA	DTW	81	502	9	30	2023-12-09 09:00:00	Other
26974	5	28	1729	1729	0	1856	1923	AA	808	N804NN	JFK	ORD	111	740	17	29	2023-05-28 17:00:00	ORD
26983	2	20	1029	1029	0	1233	1254	YX	1527	N860RW	LGA	CLT	97	544	10	29	2023-02-20 10:00:00	CLT
26988	11	13	1634	1633	1	1935	1936	UA	160	N76528	EWR	TPA	148	997	16	33	2023-11-13 16:00:00	Other
26992	7	4	1940	1940	0	2249	2312	DL	513	N899DN	JFK	FLL	156	1069	19	40	2023-07-04 19:00:00	FLL
26999	6	12	2001	2000	1	2104	2118	B6	533	N355JB	LGA	PWM	40	269	20	0	2023-06-12 20:00:00	Other
27004	4	26	1936	1930	6	2309	2257	AA	42	N105NN	JFK	LAX	327	2475	19	30	2023-04-26 19:00:00	LAX
27011	1	6	1205	1200	5	1513	1518	UA	897	N19117	EWR	LAX	347	2454	12	0	2023-01-06 12:00:00	LAX
27029	8	21	630	630	0	813	833	AA	276	N649AW	JFK	CLT	82	541	6	30	2023-08-21 06:00:00	CLT
27035	8	24	1655	1649	6	2039	2028	DL	143	N531DA	JFK	SEA	343	2422	16	49	2023-08-24 16:00:00	Other
27037	6	23	1201	1159	2	1405	1418	9E	1676	N310PQ	LGA	MCI	148	1107	11	59	2023-06-23 11:00:00	Other
27040	12	19	1644	1638	6	1857	1911	UA	137	N27292	EWR	JAX	111	820	16	38	2023-12-19 16:00:00	Other
27045	6	13	1258	1259	-1	1411	1450	DL	1048	N128DU	LGA	ORD	104	733	12	59	2023-06-13 12:00:00	ORD
27046	10	1	602	600	2	746	802	AA	928	N558UW	EWR	CLT	77	529	6	0	2023-10-01 06:00:00	CLT
27047	4	19	1131	1130	1	1253	1320	YX	1508	N211JQ	LGA	PIT	56	335	11	30	2023-04-19 11:00:00	Other
27057	11	26	710	710	0	1007	1026	DL	782	N398DA	JFK	FLL	149	1069	7	10	2023-11-26 07:00:00	FLL
27063	7	22	1437	1430	7	1628	1640	UA	450	N68453	EWR	DEN	212	1605	14	30	2023-07-22 14:00:00	Other
27064	2	28	2000	1959	1	2310	2314	UA	280	N37508	EWR	AUS	225	1504	19	59	2023-02-28 19:00:00	Other
27071	1	22	954	950	4	1237	1251	UA	840	N21723	EWR	JAC	256	1874	9	50	2023-01-22 09:00:00	Other
27086	11	3	1840	1835	5	2210	2156	UA	431	N27287	EWR	SMF	350	2500	18	35	2023-11-03 18:00:00	Other
27089	7	12	1535	1529	6	1828	1819	UA	353	N17566	EWR	SRQ	142	1034	15	29	2023-07-12 15:00:00	Other
27090	12	25	1634	1634	0	1853	2008	DL	279	N525DA	JFK	SAN	296	2446	16	34	2023-12-25 16:00:00	Other
27100	6	22	747	737	10	1005	1000	UA	235	N17303	EWR	LAS	289	2227	7	37	2023-06-22 07:00:00	Other
27104	6	13	609	610	-1	736	812	DL	228	N341DN	LGA	MSP	127	1020	6	10	2023-06-13 06:00:00	Other
27105	12	19	2109	2100	9	2352	10	B6	726	N508JL	JFK	PBI	128	1028	21	0	2023-12-19 21:00:00	Other
27108	11	21	930	929	1	1233	1239	B6	801	N965JT	JFK	FLL	150	1069	9	29	2023-11-21 09:00:00	FLL
27110	8	16	1024	1017	7	1345	1311	UA	313	N27273	EWR	TPA	147	997	10	17	2023-08-16 10:00:00	Other
27111	4	3	1559	1559	0	1852	1908	AA	558	N947AN	LGA	DFW	204	1389	15	59	2023-04-03 15:00:00	Other
27118	1	6	1003	1003	0	1314	1309	UA	961	N27270	EWR	DFW	216	1372	10	3	2023-01-06 10:00:00	Other
27130	5	18	1645	1645	0	2012	2001	AA	506	N885NN	LGA	MIA	154	1096	16	45	2023-05-18 16:00:00	MIA
27133	8	2	2134	2125	9	2241	2245	WN	514	N8606C	LGA	MDW	106	725	21	25	2023-08-02 21:00:00	Other
27136	11	22	1202	1202	0	1423	1415	YX	1411	N418YX	LGA	MEM	153	963	12	2	2023-11-22 12:00:00	Other
27144	6	15	1329	1329	0	1608	1630	UA	482	N459UA	EWR	RSW	143	1068	13	29	2023-06-15 13:00:00	Other
27148	5	25	1629	1630	-1	1803	1826	DL	459	N120DU	LGA	ORD	118	733	16	30	2023-05-25 16:00:00	ORD
27151	5	27	804	755	9	1035	1056	AS	87	N955AK	EWR	LAX	290	2454	7	55	2023-05-27 07:00:00	LAX
27152	10	29	1808	1759	9	2038	1956	YX	1287	N103HQ	LGA	CMH	81	479	17	59	2023-10-29 17:00:00	Other
27154	9	22	2159	2200	-1	119	59	DL	93	N839MH	JFK	LAX	317	2475	22	0	2023-09-22 22:00:00	LAX
27164	12	11	1508	1458	10	1624	1628	YX	1078	N736YX	EWR	ORF	52	284	14	58	2023-12-11 14:00:00	Other
27165	4	13	1549	1545	4	1754	1805	9E	1261	N232PQ	JFK	CHS	91	636	15	45	2023-04-13 15:00:00	Other
27169	12	5	1705	1655	10	2003	1950	B6	191	N580JB	EWR	PBI	157	1023	16	55	2023-12-05 16:00:00	Other
27170	10	24	2112	2111	1	2342	2359	UA	478	N27269	EWR	MCO	123	937	21	11	2023-10-24 21:00:00	MCO
27177	5	14	2102	2059	3	2245	2300	YX	1159	N653RW	EWR	CMH	74	463	20	59	2023-05-14 20:00:00	Other
27178	5	17	1803	1800	3	2037	2020	9E	1463	N914XJ	LGA	TYS	99	647	18	0	2023-05-17 18:00:00	Other
27185	8	25	927	927	0	1042	1056	YX	885	N739YX	EWR	PWM	50	284	9	27	2023-08-25 09:00:00	Other
27194	1	26	1820	1810	10	2022	2024	9E	1523	N920XJ	LGA	MYR	101	563	18	10	2023-01-26 18:00:00	Other
27197	5	20	1300	1255	5	1436	1445	9E	1376	N297PQ	JFK	RDU	70	427	12	55	2023-05-20 12:00:00	Other
27216	2	1	1550	1541	9	1818	1810	UA	493	N37419	EWR	DEN	238	1605	15	41	2023-02-01 15:00:00	Other
27225	8	25	1959	1959	0	2209	2224	DL	746	N3746H	EWR	ATL	96	746	19	59	2023-08-25 19:00:00	ATL
27243	12	28	1452	1450	2	1728	1715	9E	1614	N146PQ	LGA	CVG	99	585	14	50	2023-12-28 14:00:00	Other
27251	7	11	1309	1259	10	1445	1448	DL	825	N112DU	LGA	ORD	121	733	12	59	2023-07-11 12:00:00	ORD
27254	9	16	1749	1750	-1	2039	2040	UA	602	N17306	EWR	IAH	198	1400	17	50	2023-09-16 17:00:00	Other
27258	2	4	559	600	-1	851	908	B6	563	N586JB	EWR	FLL	144	1065	6	0	2023-02-04 06:00:00	FLL
27275	1	13	708	705	3	1022	1011	DL	693	N396DN	LGA	FLL	170	1076	7	5	2023-01-13 07:00:00	FLL
27281	12	19	1126	1120	6	1641	1618	DL	323	N882DN	JFK	SJU	235	1598	11	20	2023-12-19 11:00:00	Other
27313	4	22	939	930	9	1234	1241	B6	734	N950JT	JFK	FLL	153	1069	9	30	2023-04-22 09:00:00	FLL
27322	1	4	1100	1100	0	1350	1358	DL	644	N898DN	JFK	LAS	299	2248	11	0	2023-01-04 11:00:00	Other
27342	6	15	1535	1530	5	1821	1833	UA	522	N41135	EWR	LAX	315	2454	15	30	2023-06-15 15:00:00	LAX
27344	11	19	905	900	5	1207	1236	AS	15	N546AS	JFK	SFO	343	2586	9	0	2023-11-19 09:00:00	Other
27359	3	17	1124	1118	6	1425	1425	DL	469	N3735D	LGA	PBI	142	1035	11	18	2023-03-17 11:00:00	Other
27363	3	28	1558	1550	8	1914	1858	UA	769	N412UA	EWR	FLL	173	1065	15	50	2023-03-28 15:00:00	FLL
27377	4	7	835	836	-1	1203	1151	UA	564	N13750	EWR	SAT	237	1569	8	36	2023-04-07 08:00:00	Other
27386	2	13	832	829	3	1028	1031	YX	1103	N643RW	EWR	CMH	78	463	8	29	2023-02-13 08:00:00	Other
27402	12	6	1112	1112	0	1410	1428	DL	486	N376DN	JFK	MIA	152	1089	11	12	2023-12-06 11:00:00	MIA
27414	10	23	1659	1700	-1	1908	1935	DL	308	N112DN	LGA	ATL	105	762	17	0	2023-10-23 17:00:00	ATL
27444	4	5	734	730	4	906	910	9E	1282	N308PQ	LGA	BNA	118	764	7	30	2023-04-05 07:00:00	Other
27459	12	7	705	700	5	916	935	UA	512	N24211	EWR	ATL	106	746	7	0	2023-12-07 07:00:00	ATL
27468	8	9	2134	2125	9	2231	2245	WN	514	N8307K	LGA	MDW	102	725	21	25	2023-08-09 21:00:00	Other
27472	12	14	1550	1550	0	1909	1951	DL	281	N722TW	JFK	SFO	342	2586	15	50	2023-12-14 15:00:00	Other
27484	7	19	709	659	10	855	856	YX	1022	N104HQ	LGA	DTW	79	502	6	59	2023-07-19 06:00:00	Other
27487	12	1	1115	1115	0	1447	1419	B6	127	N649JB	EWR	FLL	154	1065	11	15	2023-12-01 11:00:00	FLL
27492	12	5	1932	1929	3	2121	2133	9E	1488	N135EV	JFK	RDU	78	427	19	29	2023-12-05 19:00:00	Other
27505	9	13	1559	1600	-1	1750	1754	OO	1273	N317SY	JFK	ORD	118	740	16	0	2023-09-13 16:00:00	ORD
27510	10	11	934	929	5	1210	1236	DL	209	N320DN	LGA	MCO	133	950	9	29	2023-10-11 09:00:00	MCO
27514	8	11	1501	1502	-1	1743	1812	NK	496	N660NK	LGA	FLL	143	1076	15	2	2023-08-11 15:00:00	FLL
27517	12	25	1501	1500	1	1730	1745	DL	159	N114DN	LGA	ATL	110	762	15	0	2023-12-25 15:00:00	ATL
27526	2	18	855	845	10	1127	1135	WN	512	N7733B	LGA	DEN	248	1620	8	45	2023-02-18 08:00:00	Other
27535	5	15	2106	2100	6	2344	2357	DL	244	N928DU	JFK	LAS	292	2248	21	0	2023-05-15 21:00:00	Other
27536	10	17	807	805	2	1103	1135	AA	49	N102NN	JFK	SFO	328	2586	8	5	2023-10-17 08:00:00	Other
27542	7	10	611	610	1	715	725	WN	486	N450WN	LGA	MDW	101	725	6	10	2023-07-10 06:00:00	Other
27546	2	2	849	849	0	1132	1117	UA	487	N842UA	EWR	SAV	119	708	8	49	2023-02-02 08:00:00	Other
27551	5	23	702	659	3	815	827	AA	558	N765US	LGA	DCA	42	214	6	59	2023-05-23 06:00:00	Other
27553	12	29	1519	1517	2	1635	1700	UA	752	N68880	EWR	ORD	102	719	15	17	2023-12-29 15:00:00	ORD
27577	4	23	1539	1530	9	1838	1846	AA	58	N101NN	JFK	LAX	329	2475	15	30	2023-04-23 15:00:00	LAX
27578	11	26	600	600	0	849	906	B6	527	N603JB	EWR	FLL	146	1065	6	0	2023-11-26 06:00:00	FLL
27580	1	15	1000	1000	0	1259	1323	UA	811	N2749U	EWR	SFO	333	2565	10	0	2023-01-15 10:00:00	Other
27582	11	8	1234	1230	4	1504	1523	UA	704	N792UA	EWR	IAH	183	1400	12	30	2023-11-08 12:00:00	Other
27593	9	11	1403	1359	4	1631	1629	DL	165	N339DN	LGA	ATL	106	762	13	59	2023-09-11 13:00:00	ATL
27608	10	16	845	840	5	951	1007	YX	1849	N205JQ	EWR	BOS	43	200	8	40	2023-10-16 08:00:00	BOS
27619	9	14	1855	1854	1	2133	2201	UA	480	N14731	EWR	SNA	313	2434	18	54	2023-09-14 18:00:00	Other
27632	11	18	1316	1315	1	1519	1552	DL	470	N829MH	JFK	ATL	103	760	13	15	2023-11-18 13:00:00	ATL
27633	4	4	2104	2055	9	2234	2248	YX	958	N722YX	EWR	GSO	68	445	20	55	2023-04-04 20:00:00	Other
27636	10	15	1317	1312	5	1450	1506	YX	1820	N206JQ	LGA	STL	129	888	13	12	2023-10-15 13:00:00	Other
27657	5	12	720	720	0	933	945	WN	527	N7748A	LGA	DEN	227	1620	7	20	2023-05-12 07:00:00	Other
27660	8	4	1028	1018	10	1213	1216	NK	22	N676NK	EWR	MYR	83	550	10	18	2023-08-04 10:00:00	Other
27666	5	27	1119	1120	-1	1411	1435	DL	511	N3745B	JFK	MIA	149	1089	11	20	2023-05-27 11:00:00	MIA
27670	7	27	1602	1559	3	1855	1849	UA	353	N17265	EWR	SRQ	144	1034	15	59	2023-07-27 15:00:00	Other
27685	7	31	1938	1939	-1	2247	2245	NK	836	N613NK	EWR	MIA	162	1085	19	39	2023-07-31 19:00:00	MIA
27686	7	30	1249	1250	-1	1339	1359	9E	1271	N602LR	LGA	PVD	29	143	12	50	2023-07-30 12:00:00	Other
27698	9	25	1244	1235	9	1525	1533	B6	29	N665JB	JFK	MCO	131	944	12	35	2023-09-25 12:00:00	MCO
27699	7	6	1458	1459	-1	1826	1823	DL	721	N352NB	JFK	AUS	197	1521	14	59	2023-07-06 14:00:00	Other
27705	7	18	1159	1200	-1	1522	1445	DL	181	N418DX	JFK	LAX	331	2475	12	0	2023-07-18 12:00:00	LAX
27712	2	21	1930	1929	1	2150	2212	YX	1185	N442YX	LGA	LIT	179	1085	19	29	2023-02-21 19:00:00	Other
27716	12	2	721	715	6	1025	1020	WN	687	N8908Q	LGA	DAL	226	1381	7	15	2023-12-02 07:00:00	Other
27722	9	30	629	630	-1	915	919	B6	41	N708JB	JFK	TPA	145	1005	6	30	2023-09-30 06:00:00	Other
27729	4	18	1531	1530	1	1739	1730	UA	636	N27733	EWR	DTW	81	488	15	30	2023-04-18 15:00:00	Other
27732	2	20	2200	2159	1	2333	2322	UA	506	N839UA	EWR	ORF	50	284	21	59	2023-02-20 21:00:00	Other
27741	3	8	1707	1701	6	1854	1904	DL	912	N998AT	EWR	DTW	90	488	17	1	2023-03-08 17:00:00	Other
27743	10	1	1501	1500	1	1702	1707	9E	1578	N909XJ	EWR	CVG	83	569	15	0	2023-10-01 15:00:00	Other
27744	2	14	1528	1529	-1	1714	1733	YX	1150	N725YX	EWR	CMH	76	463	15	29	2023-02-14 15:00:00	Other
27748	4	23	1528	1520	8	1825	1815	WN	822	N8630B	LGA	DAL	208	1381	15	20	2023-04-23 15:00:00	Other
27753	9	8	1358	1359	-1	1532	1553	YX	1876	N208JQ	LGA	CMH	76	479	13	59	2023-09-08 13:00:00	Other
27763	1	12	759	800	-1	1031	1058	UA	444	N58101	EWR	EGE	243	1725	8	0	2023-01-12 08:00:00	Other
27765	11	29	1550	1545	5	1734	1738	AA	194	N9008U	JFK	ORD	126	740	15	45	2023-11-29 15:00:00	ORD
27776	6	21	929	929	0	1034	1051	UA	489	N79521	EWR	BOS	35	200	9	29	2023-06-21 09:00:00	BOS
27777	2	11	605	605	0	902	910	B6	110	N995JL	EWR	MCO	150	937	6	5	2023-02-11 06:00:00	MCO
27785	8	24	1959	2000	-1	2234	2139	B6	739	N279JB	JFK	BUF	70	301	20	0	2023-08-24 20:00:00	Other
27789	4	15	950	946	4	1422	1341	UA	539	N34455	EWR	SJU	198	1608	9	46	2023-04-15 09:00:00	Other
27790	11	22	1145	1145	0	1457	1440	DL	590	N121DZ	JFK	MCO	155	944	11	45	2023-11-22 11:00:00	MCO
27794	2	21	1801	1800	1	1921	1941	AA	468	N751UW	LGA	DCA	58	214	18	0	2023-02-21 18:00:00	Other
27798	4	6	2201	2159	2	2352	2322	UA	476	N498UA	EWR	ORF	80	284	21	59	2023-04-06 21:00:00	Other
27803	8	11	1339	1330	9	1506	1508	9E	1116	N348PQ	JFK	RIC	57	288	13	30	2023-08-11 13:00:00	Other
27808	10	10	1059	1100	-1	1354	1408	AA	3	N106NN	JFK	LAX	334	2475	11	0	2023-10-10 11:00:00	LAX
27810	4	7	1626	1627	-1	1823	1835	YX	1216	N433YX	JFK	CMH	89	483	16	27	2023-04-07 16:00:00	Other
27813	3	4	859	900	-1	1214	1212	UA	423	N27255	EWR	MIA	152	1085	9	0	2023-03-04 09:00:00	MIA
27819	9	28	1458	1459	-1	1748	1839	DL	262	N717TW	JFK	SFO	329	2586	14	59	2023-09-28 14:00:00	Other
27836	5	6	1003	1000	3	1211	1238	DL	121	N340DN	LGA	ATL	105	762	10	0	2023-05-06 10:00:00	ATL
27846	11	4	608	602	6	802	808	DL	964	N991AT	EWR	MSP	145	1008	6	2	2023-11-04 06:00:00	Other
27862	4	18	600	600	0	742	755	DL	346	N309DN	LGA	DTW	78	502	6	0	2023-04-18 06:00:00	Other
27870	8	25	1359	1359	0	1558	1632	DL	551	N3742C	LGA	DEN	214	1620	13	59	2023-08-25 13:00:00	Other
27877	10	22	753	754	-1	907	908	UA	207	N14235	EWR	BOS	44	200	7	54	2023-10-22 07:00:00	BOS
27880	12	8	905	900	5	1157	1216	AA	134	N885NN	EWR	DFW	188	1372	9	0	2023-12-08 09:00:00	Other
27884	7	21	1009	1000	9	1547	1455	HA	20	N378HA	JFK	HNL	636	4983	10	0	2023-07-21 10:00:00	Other
27893	11	12	600	600	0	831	836	DL	287	N375DN	LGA	ATL	124	762	6	0	2023-11-12 06:00:00	ATL
27894	9	29	1831	1830	1	2128	2139	UA	674	N204UA	EWR	SFO	315	2565	18	30	2023-09-29 18:00:00	Other
27904	6	15	829	830	-1	1042	1058	UA	933	N12754	EWR	ATL	109	746	8	30	2023-06-15 08:00:00	ATL
27922	9	8	1116	1115	1	1410	1436	DL	912	N103DY	LGA	FLL	147	1076	11	15	2023-09-08 11:00:00	FLL
27935	9	13	802	800	2	1026	1035	DL	183	N529DT	JFK	DEN	224	1626	8	0	2023-09-13 08:00:00	Other
27936	3	19	1345	1345	0	1653	1640	WN	75	N8627B	LGA	TPA	165	1010	13	45	2023-03-19 13:00:00	Other
27943	12	28	515	510	5	826	802	B6	207	N587JB	JFK	MCO	162	944	5	10	2023-12-28 05:00:00	MCO
27944	8	23	1000	1000	0	1453	1455	HA	20	N379HA	JFK	HNL	622	4983	10	0	2023-08-23 10:00:00	Other
27947	12	3	937	929	8	1239	1259	B6	675	N715JB	LGA	RSW	159	1080	9	29	2023-12-03 09:00:00	Other
27948	12	31	1520	1515	5	1806	1816	B6	544	N657JB	EWR	MCO	136	937	15	15	2023-12-31 15:00:00	MCO
27949	3	17	648	648	0	849	911	UA	846	N77539	EWR	MSY	161	1167	6	48	2023-03-17 06:00:00	Other
27953	10	20	2059	2057	2	15	3	UA	915	N14704	EWR	AUS	200	1504	20	57	2023-10-20 20:00:00	Other
27961	12	6	1523	1520	3	1730	1752	DL	478	N1200K	JFK	ATL	95	760	15	20	2023-12-06 15:00:00	ATL
27967	8	31	804	805	-1	1004	1014	DL	447	N301NB	JFK	MSP	145	1029	8	5	2023-08-31 08:00:00	Other
27978	4	27	1459	1500	-1	1608	1624	YX	1010	N655RW	EWR	ORF	48	284	15	0	2023-04-27 15:00:00	Other
27990	4	26	1430	1429	1	1636	1641	UA	204	N421UA	EWR	MSY	165	1167	14	29	2023-04-26 14:00:00	Other
27997	6	11	1606	1557	9	1816	1824	UA	470	N487UA	EWR	ATL	104	746	15	57	2023-06-11 15:00:00	ATL
28003	4	30	1505	1505	0	1636	1636	9E	1400	N908XJ	JFK	PWM	54	273	15	5	2023-04-30 15:00:00	Other
28004	6	15	901	900	1	1206	1235	DL	99	N177DN	JFK	SFO	332	2586	9	0	2023-06-15 09:00:00	Other
28017	6	18	715	710	5	1004	958	DL	567	N391DN	LGA	MCO	124	950	7	10	2023-06-18 07:00:00	MCO
28021	3	28	2138	2130	8	21	2356	B6	105	N603JB	JFK	ATL	123	760	21	30	2023-03-28 21:00:00	ATL
28029	2	9	1922	1920	2	2147	2215	9E	1408	N320PQ	LGA	JAX	124	833	19	20	2023-02-09 19:00:00	Other
28031	10	26	1259	1300	-1	1425	1430	YX	1056	N762YX	EWR	PIT	56	319	13	0	2023-10-26 13:00:00	Other
28054	2	14	1327	1327	0	1545	1551	UA	321	N875UA	EWR	MSY	175	1167	13	27	2023-02-14 13:00:00	Other
28085	2	14	1959	1959	0	2252	2308	DL	546	N367DN	JFK	MCO	131	944	19	59	2023-02-14 19:00:00	MCO
28091	11	6	801	800	1	1017	1042	DL	321	N388DN	LGA	ATL	107	762	8	0	2023-11-06 08:00:00	ATL
28092	1	18	959	1000	-1	1313	1325	DL	421	N178DN	JFK	LAX	343	2475	10	0	2023-01-18 10:00:00	LAX
28114	4	28	1259	1300	-1	1612	1605	UA	639	N37532	EWR	MIA	164	1085	13	0	2023-04-28 13:00:00	MIA
28118	11	9	2052	2045	7	1	15	B6	445	N589JB	JFK	AUS	223	1521	20	45	2023-11-09 20:00:00	Other
28128	5	5	2117	2117	0	2325	2328	YX	1044	N731YX	EWR	GSP	85	594	21	17	2023-05-05 21:00:00	Other
28129	3	17	854	855	-1	1155	1223	DL	184	N185DN	JFK	LAX	332	2475	8	55	2023-03-17 08:00:00	LAX
28130	11	27	1427	1428	-1	1748	1743	UA	444	N47275	EWR	AUS	231	1504	14	28	2023-11-27 14:00:00	Other
28131	4	11	2200	2159	1	2352	2359	UA	571	N37278	EWR	MSP	137	1008	21	59	2023-04-11 21:00:00	Other
28137	2	24	947	945	2	1214	1224	B6	848	N592JB	LGA	CHS	106	641	9	45	2023-02-24 09:00:00	Other
28138	1	22	1323	1315	8	1440	1425	B6	901	N329JB	LGA	BOS	43	184	13	15	2023-01-22 13:00:00	BOS
28144	9	15	1758	1759	-1	1950	2029	DL	269	N876DN	JFK	PHX	273	2153	17	59	2023-09-15 17:00:00	Other
28150	10	22	1905	1859	6	2211	2158	DL	608	N303DU	EWR	SLC	272	1969	18	59	2023-10-22 18:00:00	Other
28153	2	22	1054	1054	0	1336	1340	F9	565	N343FR	LGA	ATL	124	762	10	54	2023-02-22 10:00:00	ATL
28158	2	8	1854	1850	4	2137	2202	B6	932	N657JB	JFK	TPA	142	1005	18	50	2023-02-08 18:00:00	Other
28162	12	31	1640	1635	5	1942	1952	NK	1006	N929NK	LGA	FLL	160	1076	16	35	2023-12-31 16:00:00	FLL
28175	10	4	705	700	5	832	845	9E	1389	N479PX	LGA	STL	122	888	7	0	2023-10-04 07:00:00	Other
28182	4	17	1943	1933	10	2206	2239	B6	28	N640JB	JFK	ABQ	245	1826	19	33	2023-04-17 19:00:00	Other
28193	6	3	600	600	0	824	850	WN	634	N8812Q	LGA	DAL	169	1381	6	0	2023-06-03 06:00:00	Other
28199	2	3	1546	1545	1	1729	1736	YX	1571	N209JQ	LGA	PIT	67	335	15	45	2023-02-03 15:00:00	Other
28202	5	7	901	900	1	1154	1219	AA	796	N350RV	LGA	MIA	142	1096	9	0	2023-05-07 09:00:00	MIA
28223	11	14	1946	1945	1	2054	2122	OO	1209	N324SY	JFK	IAD	47	228	19	45	2023-11-14 19:00:00	Other
28240	6	22	900	900	0	1048	1110	YX	1074	N753YX	EWR	MCI	140	1092	9	0	2023-06-22 09:00:00	Other
28255	7	26	900	900	0	1008	1019	B6	510	N247JB	JFK	BTV	45	266	9	0	2023-07-26 09:00:00	Other
28258	4	25	1523	1521	2	1824	1809	UA	245	N17272	EWR	MCO	141	937	15	21	2023-04-25 15:00:00	MCO
28261	1	21	1613	1610	3	1911	1929	DL	474	N367DN	LGA	MIA	157	1096	16	10	2023-01-21 16:00:00	MIA
28262	6	13	1945	1939	6	2236	2245	NK	1057	N653NK	EWR	MIA	150	1085	19	39	2023-06-13 19:00:00	MIA
28276	1	16	1459	1500	-1	1712	1729	9E	1492	N166PQ	JFK	MSP	150	1029	15	0	2023-01-16 15:00:00	Other
28279	6	30	1517	1515	2	1627	1636	YX	1822	N860RW	LGA	ACK	43	202	15	15	2023-06-30 15:00:00	Other
28281	8	20	1654	1655	-1	1927	2009	AA	744	N780AN	JFK	MIA	133	1089	16	55	2023-08-20 16:00:00	MIA
28284	9	15	1528	1529	-1	1745	1744	YX	1182	N649RW	EWR	IND	102	645	15	29	2023-09-15 15:00:00	Other
28286	7	29	1703	1655	8	2057	2023	AA	50	N116AN	JFK	SFO	374	2586	16	55	2023-07-29 16:00:00	Other
28292	3	4	2129	2126	3	2225	2237	YX	1079	N725YX	EWR	ALB	29	143	21	26	2023-03-04 21:00:00	Other
28293	1	13	1731	1730	1	2029	2050	AS	89	N581AS	EWR	PDX	335	2434	17	30	2023-01-13 17:00:00	Other
28301	12	20	1906	1859	7	2205	2217	AS	8	N954AK	JFK	SAN	331	2446	18	59	2023-12-20 18:00:00	Other
28308	12	30	604	605	-1	833	920	WN	641	N8674B	LGA	HOU	189	1428	6	5	2023-12-30 06:00:00	Other
28324	10	31	1944	1940	4	2258	2246	DL	218	N311DU	LGA	DFW	223	1389	19	40	2023-10-31 19:00:00	Other
28326	1	9	830	830	0	1100	1116	9E	1427	N136EV	JFK	JAX	122	828	8	30	2023-01-09 08:00:00	Other
28346	7	5	1528	1529	-1	1755	1737	YX	955	N761YX	EWR	MYR	115	550	15	29	2023-07-05 15:00:00	Other
28354	1	15	1228	1229	-1	1345	1357	YX	1348	N103HQ	JFK	ORF	55	290	12	29	2023-01-15 12:00:00	Other
28363	1	22	1855	1845	10	2134	2134	DL	205	N112DN	LGA	ATL	139	762	18	45	2023-01-22 18:00:00	ATL
28366	10	18	1904	1900	4	2119	2124	YX	1270	N412YX	LGA	IND	99	660	19	0	2023-10-18 19:00:00	Other
28375	7	2	1946	1940	6	2228	2236	DL	221	N131DU	LGA	DFW	197	1389	19	40	2023-07-02 19:00:00	Other
28376	6	28	1740	1730	10	1917	1926	NK	52	N655NK	LGA	DTW	77	502	17	30	2023-06-28 17:00:00	Other
28390	11	13	722	720	2	933	916	9E	1689	N919XJ	LGA	GSO	77	461	7	20	2023-11-13 07:00:00	Other
28411	6	5	2022	2020	2	2229	2216	9E	1745	N279PQ	LGA	MYR	84	563	20	20	2023-06-05 20:00:00	Other
28412	3	5	2142	2142	0	2349	2359	UA	314	N16703	EWR	SAV	104	708	21	42	2023-03-05 21:00:00	Other
28426	5	20	1629	1619	10	1923	1924	UA	367	N17730	EWR	SNA	325	2434	16	19	2023-05-20 16:00:00	Other
28437	2	11	1039	1029	10	1334	1338	UA	819	N47275	EWR	MIA	152	1085	10	29	2023-02-11 10:00:00	MIA
28450	11	25	1317	1310	7	1650	1642	B6	276	N3085J	JFK	SAT	249	1587	13	10	2023-11-25 13:00:00	Other
28455	10	30	1520	1513	7	1734	1711	YX	1259	N410YX	JFK	CLE	86	425	15	13	2023-10-30 15:00:00	Other
28473	12	19	2030	2030	0	9	2359	B6	619	N992JB	JFK	LAX	322	2475	20	30	2023-12-19 20:00:00	LAX
28475	12	17	1334	1335	-1	1628	1643	DL	791	N838DN	JFK	RSW	154	1074	13	35	2023-12-17 13:00:00	Other
28478	1	16	808	805	3	1104	1115	DL	383	N705TW	JFK	LAS	311	2248	8	5	2023-01-16 08:00:00	Other
28483	5	27	1307	1304	3	1415	1418	UA	182	N842UA	EWR	BOS	40	200	13	4	2023-05-27 13:00:00	BOS
28486	1	8	641	640	1	943	945	WN	737	N7884G	LGA	HOU	225	1428	6	40	2023-01-08 06:00:00	Other
28498	10	18	1433	1434	-1	1548	1556	B6	906	N229JB	JFK	BUF	53	301	14	34	2023-10-18 14:00:00	Other
28516	7	11	849	850	-1	1134	1152	B6	554	N980JT	EWR	LAX	309	2454	8	50	2023-07-11 08:00:00	LAX
28536	10	17	1801	1759	2	2059	2105	AA	158	N782AN	JFK	MIA	148	1089	17	59	2023-10-17 17:00:00	MIA
28537	3	28	1900	1900	0	2227	2216	UA	485	N818UA	EWR	SLC	290	1969	19	0	2023-03-28 19:00:00	Other
28542	12	21	730	730	0	914	925	WN	1201	N8729H	LGA	STL	126	888	7	30	2023-12-21 07:00:00	Other
28543	9	6	1604	1600	4	1720	1744	AA	762	N858NN	LGA	ORD	100	733	16	0	2023-09-06 16:00:00	ORD
28554	2	1	1534	1535	-1	1858	1859	OO	1422	N139SY	LGA	IAH	239	1416	15	35	2023-02-01 15:00:00	Other
28556	12	3	1423	1415	8	1555	1531	B6	310	N375JB	LGA	BOS	48	184	14	15	2023-12-03 14:00:00	BOS
28559	11	22	1905	1900	5	2146	2206	DL	862	N375NC	JFK	AUS	195	1521	19	0	2023-11-22 19:00:00	Other
28566	4	2	2101	2053	8	2246	2247	YX	1279	N867RW	LGA	ILM	73	500	20	53	2023-04-02 20:00:00	Other
28569	7	7	1110	1100	10	1415	1320	B6	111	N531JL	LGA	DEN	233	1620	11	0	2023-07-07 11:00:00	Other
28571	11	16	1944	1945	-1	2152	2200	9E	1667	N901XJ	EWR	CVG	88	569	19	45	2023-11-16 19:00:00	Other
28573	6	24	614	615	-1	909	908	B6	45	N652JB	EWR	PBI	142	1023	6	15	2023-06-24 06:00:00	Other
28574	11	15	2134	2135	-1	227	231	B6	648	N955JB	JFK	SJU	212	1598	21	35	2023-11-15 21:00:00	Other
28575	2	27	1542	1537	5	1843	1846	AA	841	N876NN	EWR	DFW	199	1372	15	37	2023-02-27 15:00:00	Other
28577	4	23	1506	1500	6	1816	1802	UA	214	N453UA	EWR	AUS	233	1504	15	0	2023-04-23 15:00:00	Other
28580	11	17	802	759	3	1248	1259	B6	180	N2039J	JFK	SJU	203	1598	7	59	2023-11-17 07:00:00	Other
28600	9	22	1418	1418	0	1549	1555	DL	867	N108DQ	LGA	ORD	106	733	14	18	2023-09-22 14:00:00	ORD
28607	5	25	1758	1757	1	2048	2056	DL	574	N380DN	LGA	MCO	144	950	17	57	2023-05-25 17:00:00	MCO
28614	4	5	1830	1830	0	2057	2111	DL	187	N369DN	LGA	ATL	109	762	18	30	2023-04-05 18:00:00	ATL
28629	8	31	1009	1010	-1	1202	1226	AA	601	N572UW	LGA	CLT	82	544	10	10	2023-08-31 10:00:00	CLT
28638	1	7	1040	1030	10	1335	1351	AA	104	N773AN	JFK	MIA	142	1089	10	30	2023-01-07 10:00:00	MIA
28651	10	25	1803	1759	4	2045	2050	UA	630	N27519	EWR	IAH	186	1400	17	59	2023-10-25 17:00:00	Other
28659	9	1	1714	1715	-1	1835	1840	WN	1052	N8663A	LGA	MDW	107	725	17	15	2023-09-01 17:00:00	Other
28661	1	20	2143	2140	3	103	127	DL	110	N704X	JFK	SFO	340	2586	21	40	2023-01-20 21:00:00	Other
28685	7	3	1112	1110	2	1329	1347	DL	306	N501DA	JFK	LAS	287	2248	11	10	2023-07-03 11:00:00	Other
28687	1	28	1954	1955	-1	2117	2144	9E	1475	N607LR	JFK	BNA	122	765	19	55	2023-01-28 19:00:00	Other
28690	12	7	2159	2159	0	223	254	B6	313	N655JB	JFK	BQN	184	1576	21	59	2023-12-07 21:00:00	Other
28694	5	10	1259	1300	-1	1630	1653	DL	725	N881DN	JFK	SJU	191	1598	13	0	2023-05-10 13:00:00	Other
28698	6	8	830	830	0	1103	1140	DL	363	N706TW	JFK	SAN	304	2446	8	30	2023-06-08 08:00:00	Other
28709	3	30	1334	1333	1	1640	1700	DL	785	N356NW	JFK	AUS	219	1521	13	33	2023-03-30 13:00:00	Other
28711	1	12	1435	1430	5	1635	1623	AA	229	N744P	LGA	ORD	127	733	14	30	2023-01-12 14:00:00	ORD
28713	1	26	2026	2019	7	2210	2220	DL	1090	N974AT	EWR	DTW	83	488	20	19	2023-01-26 20:00:00	Other
28714	1	19	1805	1800	5	1936	1936	AA	398	N750UW	LGA	DCA	53	214	18	0	2023-01-19 18:00:00	Other
28716	8	19	830	830	0	1016	948	B6	760	N355JB	JFK	BOS	47	187	8	30	2023-08-19 08:00:00	BOS
28722	10	7	739	740	-1	937	955	DL	515	N347NB	JFK	MSP	138	1029	7	40	2023-10-07 07:00:00	Other
28731	1	19	1508	1509	-1	1805	1816	UA	676	N27263	EWR	TPA	156	997	15	9	2023-01-19 15:00:00	Other
28733	8	13	2103	2100	3	2225	2220	DL	341	N127DU	LGA	BOS	42	184	21	0	2023-08-13 21:00:00	BOS
28735	2	14	1204	1205	-1	1504	1520	B6	602	N2059J	JFK	FLL	144	1069	12	5	2023-02-14 12:00:00	FLL
28746	3	9	1215	1216	-1	1522	1527	NK	351	N670NK	LGA	DFW	217	1389	12	16	2023-03-09 12:00:00	Other
28749	2	26	1624	1625	-1	1811	1820	AA	405	N805AW	LGA	RDU	72	431	16	25	2023-02-26 16:00:00	Other
28760	4	2	1700	1700	0	1843	1902	9E	1323	N678CA	JFK	RDU	68	427	17	0	2023-04-02 17:00:00	Other
28765	1	19	1000	1000	0	1314	1316	UA	779	N840UA	LGA	IAH	226	1416	10	0	2023-01-19 10:00:00	Other
28774	2	8	1458	1459	-1	1758	1833	AA	373	N997NN	LGA	MIA	146	1096	14	59	2023-02-08 14:00:00	MIA
28776	10	20	1758	1759	-1	2026	2037	DL	312	N805DN	JFK	PHX	285	2153	17	59	2023-10-20 17:00:00	Other
28778	6	21	1807	1800	7	2305	2035	DL	337	N3739P	LGA	DEN	248	1620	18	0	2023-06-21 18:00:00	Other
28779	5	23	1520	1510	10	1821	1816	UA	394	N47275	EWR	AUS	195	1504	15	10	2023-05-23 15:00:00	Other
28788	2	16	1841	1835	6	2040	2020	B6	29	N559JB	JFK	BNA	131	765	18	35	2023-02-16 18:00:00	Other
28793	10	3	2145	2145	0	2336	2336	YX	1246	N127HQ	JFK	RDU	71	427	21	45	2023-10-03 21:00:00	Other
28797	1	11	1714	1715	-1	2015	2037	UA	151	N77006	EWR	SFO	332	2565	17	15	2023-01-11 17:00:00	Other
28800	8	6	630	630	0	840	830	WN	789	N909WN	LGA	DEN	224	1620	6	30	2023-08-06 06:00:00	Other
28804	4	11	1623	1620	3	1721	1755	WN	166	N8816Q	LGA	BNA	95	764	16	20	2023-04-11 16:00:00	Other
28807	2	1	704	705	-1	1144	1008	DL	380	N347NB	LGA	PBI	157	1035	7	5	2023-02-01 07:00:00	Other
28809	4	17	948	946	2	1135	1147	9E	1329	N331PQ	JFK	CLE	74	425	9	46	2023-04-17 09:00:00	Other
28839	8	13	1936	1928	8	2132	2129	YX	1386	N218JQ	LGA	CMH	73	479	19	28	2023-08-13 19:00:00	Other
28849	7	10	1835	1830	5	2204	2147	AA	165	N931NN	JFK	MIA	161	1089	18	30	2023-07-10 18:00:00	MIA
28851	1	2	1459	1450	9	1623	1641	AA	778	N775XF	LGA	RDU	63	431	14	50	2023-01-02 14:00:00	Other
28855	5	19	655	655	0	824	830	WN	37	N491WN	LGA	STL	127	888	6	55	2023-05-19 06:00:00	Other
28883	4	13	1728	1729	-1	1900	1916	AA	741	N980NN	JFK	ORD	113	740	17	29	2023-04-13 17:00:00	ORD
28895	4	8	2003	1959	4	2310	2325	DL	524	N3771K	JFK	PBI	148	1028	19	59	2023-04-08 19:00:00	Other
28896	7	18	729	730	-1	1000	1032	AS	80	N926VA	EWR	LAX	306	2454	7	30	2023-07-18 07:00:00	LAX
28898	3	30	1559	1555	4	1901	1912	B6	253	N639JB	JFK	PBI	156	1028	15	55	2023-03-30 15:00:00	Other
28899	1	22	1107	1107	0	1412	1418	UA	553	N66897	EWR	MIA	162	1085	11	7	2023-01-22 11:00:00	MIA
28902	2	11	616	615	1	854	853	DL	732	N593NW	JFK	ATL	122	760	6	15	2023-02-11 06:00:00	ATL
28903	4	13	1529	1529	0	1753	1826	AA	234	N933NN	EWR	DFW	175	1372	15	29	2023-04-13 15:00:00	Other
28907	12	10	1442	1440	2	1714	1715	WN	683	N8501V	LGA	MSY	185	1183	14	40	2023-12-10 14:00:00	Other
28917	8	14	1506	1501	5	1752	1810	DL	487	N314NB	LGA	TPA	142	1010	15	1	2023-08-14 15:00:00	Other
28920	2	12	1011	1012	-1	1129	1151	UA	669	N33262	EWR	ORD	109	719	10	12	2023-02-12 10:00:00	ORD
28931	1	18	2202	2159	3	2324	2334	YX	1250	N653RW	EWR	PIT	63	319	21	59	2023-01-18 21:00:00	Other
28938	10	14	759	800	-1	1048	1103	DL	156	N835MH	JFK	LAX	315	2475	8	0	2023-10-14 08:00:00	LAX
28943	7	24	1042	1034	8	1201	1156	UA	396	N13716	EWR	BOS	49	200	10	34	2023-07-24 10:00:00	BOS
28955	11	26	930	930	0	1300	1253	B6	103	N947JB	JFK	LAX	345	2475	9	30	2023-11-26 09:00:00	LAX
28956	7	27	704	705	-1	937	932	B6	136	N989JT	JFK	LAS	282	2248	7	5	2023-07-27 07:00:00	Other
28960	10	18	2100	2059	1	2209	2222	UA	337	N457UA	EWR	IAD	41	212	20	59	2023-10-18 20:00:00	Other
28963	3	21	1855	1850	5	2155	2135	UA	303	N47282	EWR	PHX	321	2133	18	50	2023-03-21 18:00:00	Other
28966	5	5	1503	1458	5	1625	1628	9E	1386	N349PQ	LGA	ORF	52	296	14	58	2023-05-05 14:00:00	Other
28971	8	2	734	735	-1	847	853	B6	164	N284JB	JFK	PWM	52	273	7	35	2023-08-02 07:00:00	Other
28974	10	6	2009	2005	4	2207	2212	9E	1594	N902XJ	LGA	DAY	86	549	20	5	2023-10-06 20:00:00	Other
28975	1	4	1236	1229	7	1531	1544	UA	531	N27722	EWR	RSW	158	1068	12	29	2023-01-04 12:00:00	Other
28998	1	30	1100	1100	0	1324	1318	UA	953	N25705	EWR	MCI	174	1092	11	0	2023-01-30 11:00:00	Other
29008	5	24	628	629	-1	901	954	DL	306	N118DY	JFK	SLC	245	1990	6	29	2023-05-24 06:00:00	Other
29015	7	3	958	959	-1	1148	1201	AA	537	N162UW	EWR	CLT	78	529	9	59	2023-07-03 09:00:00	CLT
29025	10	11	735	729	6	1035	1042	DL	285	N895DN	JFK	SEA	328	2422	7	29	2023-10-11 07:00:00	Other
29031	9	19	1409	1359	10	1621	1629	DL	165	N330DX	LGA	ATL	108	762	13	59	2023-09-19 13:00:00	ATL
29032	12	29	630	630	0	847	935	UA	856	N12021	EWR	LAX	278	2454	6	30	2023-12-29 06:00:00	LAX
29033	12	18	601	601	0	846	913	UA	62	N880UA	EWR	AUS	204	1504	6	1	2023-12-18 06:00:00	Other
29042	5	5	605	605	0	905	905	WN	913	N8836Q	LGA	HOU	206	1428	6	5	2023-05-05 06:00:00	Other
29066	10	14	2009	2010	-1	2303	2338	DL	185	N913DU	JFK	PDX	328	2454	20	10	2023-10-14 20:00:00	Other
29069	2	6	2128	2129	-1	27	55	DL	208	N174DN	JFK	LAX	337	2475	21	29	2023-02-06 21:00:00	LAX
29099	12	29	1212	1210	2	1517	1513	UA	240	N27260	EWR	PBI	164	1023	12	10	2023-12-29 12:00:00	Other
29108	7	21	1428	1429	-1	1544	1606	YX	1429	N226JQ	LGA	BUF	50	292	14	29	2023-07-21 14:00:00	Other
29111	4	11	559	600	-1	848	906	UA	158	N14219	EWR	FLL	146	1065	6	0	2023-04-11 06:00:00	FLL
29116	12	7	559	600	-1	842	857	B6	84	N571JB	LGA	MCO	127	950	6	0	2023-12-07 06:00:00	MCO
29122	8	29	1633	1630	3	1922	1952	B6	216	N509JB	JFK	SJC	328	2569	16	30	2023-08-29 16:00:00	Other
29123	12	10	2003	2000	3	2129	2122	AA	701	N702UW	LGA	DCA	63	214	20	0	2023-12-10 20:00:00	Other
29126	5	8	1134	1125	9	1420	1438	UA	249	N66814	EWR	SEA	317	2402	11	25	2023-05-08 11:00:00	Other
29149	5	28	1858	1848	10	2038	2050	AA	652	N991NN	LGA	CLT	81	544	18	48	2023-05-28 18:00:00	CLT
29154	10	22	1206	1159	7	1425	1440	DL	255	N117DX	LGA	ATL	109	762	11	59	2023-10-22 11:00:00	ATL
29160	1	17	2127	2120	7	2341	2359	DL	982	N366NW	LGA	ATL	118	762	21	20	2023-01-17 21:00:00	ATL
29177	8	8	2020	2020	0	2204	2240	9E	1155	N936XJ	LGA	GRR	84	618	20	20	2023-08-08 20:00:00	Other
29178	8	21	1358	1358	0	1609	1644	NK	67	N910NK	EWR	DFW	165	1372	13	58	2023-08-21 13:00:00	Other
29179	12	15	608	600	8	740	750	DL	444	N145DQ	LGA	ORD	114	733	6	0	2023-12-15 06:00:00	ORD
29193	10	7	1647	1648	-1	1938	1957	AA	188	N900UW	EWR	DFW	193	1372	16	48	2023-10-07 16:00:00	Other
29199	7	31	1423	1423	0	1537	1548	UA	501	N29717	EWR	BNA	113	748	14	23	2023-07-31 14:00:00	Other
29205	2	24	1458	1459	-1	1923	1853	DL	371	N825DN	JFK	PHX	358	2153	14	59	2023-02-24 14:00:00	Other
29210	12	23	2001	2000	1	2155	2221	OO	1172	N254SY	JFK	CLE	75	425	20	0	2023-12-23 20:00:00	Other
29214	9	13	2121	2117	4	2231	2224	YX	1106	N749YX	EWR	PHL	36	80	21	17	2023-09-13 21:00:00	Other
29218	10	16	1950	1945	5	2215	2251	DL	218	N315DU	LGA	DFW	174	1389	19	45	2023-10-16 19:00:00	Other
29219	4	26	1756	1749	7	2111	2106	NK	31	N924NK	EWR	LAX	324	2454	17	49	2023-04-26 17:00:00	LAX
29227	9	28	701	700	1	1014	1005	UA	899	N18223	EWR	MIA	155	1085	7	0	2023-09-28 07:00:00	MIA
9	3	25	1914	1740	94	2221	2105	NK	32	N975NK	EWR	LAX	340	2454	17	40	2023-03-25 17:00:00	LAX
14	9	19	1356	1341	15	1544	1544	AA	640	N182UW	EWR	CLT	82	529	13	41	2023-09-19 13:00:00	CLT
15	7	24	1519	1500	19	1624	1617	9E	1235	N138EV	LGA	ORH	34	146	15	0	2023-07-24 15:00:00	Other
16	7	17	1659	1620	39	1833	1802	UA	621	N17753	EWR	CLE	64	404	16	20	2023-07-17 16:00:00	Other
18	1	13	1446	1355	51	1717	1710	WN	737	N8735L	LGA	HOU	191	1428	13	55	2023-01-13 13:00:00	Other
21	3	28	1933	1920	13	2224	2202	9E	1461	N135EV	LGA	JAX	133	833	19	20	2023-03-28 19:00:00	Other
31	3	4	15	2135	160	117	2247	B6	6	N273JB	JFK	SYR	44	209	21	35	2023-03-04 21:00:00	Other
40	5	3	1437	1421	16	1701	1706	UA	243	N15712	EWR	DFW	184	1372	14	21	2023-05-03 14:00:00	Other
41	8	3	1953	1915	38	2149	2117	9E	1139	N916XJ	LGA	CLE	69	419	19	15	2023-08-03 19:00:00	Other
48	7	4	1742	1725	17	2047	2015	WN	43	N910WN	LGA	HOU	197	1428	17	25	2023-07-04 17:00:00	Other
56	9	6	1503	1447	16	1753	1752	UA	521	N443UA	EWR	MIA	140	1085	14	47	2023-09-06 14:00:00	MIA
57	6	5	2255	2045	130	308	59	DL	721	N873DN	JFK	SJU	204	1598	20	45	2023-06-05 20:00:00	Other
63	4	25	1201	659	1742	1315	818	AA	518	N808AW	LGA	DCA	42	214	6	59	2023-04-25 06:00:00	Other
75	11	9	2156	2108	48	2356	2308	NK	1026	N941NK	EWR	DTW	93	488	21	8	2023-11-09 21:00:00	Other
80	3	11	1811	1629	102	2134	2003	UA	942	N77431	EWR	PHX	293	2133	16	29	2023-03-11 16:00:00	Other
91	1	11	1905	1833	32	2054	2017	UA	259	N13716	EWR	CLE	65	404	18	33	2023-01-11 18:00:00	Other
95	1	15	1920	1800	80	2125	2037	UA	956	N432UA	LGA	DEN	209	1620	18	0	2023-01-15 18:00:00	Other
100	2	1	1625	1550	35	1756	1733	9E	1376	N932XJ	LGA	CHO	65	305	15	50	2023-02-01 15:00:00	Other
104	2	21	1817	1720	57	2130	2035	WN	473	N8842L	LGA	HOU	215	1428	17	20	2023-02-21 17:00:00	Other
111	2	22	41	2245	116	321	145	F9	490	N364FR	LGA	MCO	130	950	22	45	2023-02-22 22:00:00	MCO
114	6	16	2010	1930	40	2119	2045	B6	533	N328JB	LGA	PWM	46	269	19	30	2023-06-16 19:00:00	Other
115	10	16	2056	2025	31	2258	2250	WN	164	N7836A	LGA	DEN	205	1620	20	25	2023-10-16 20:00:00	Other
129	10	6	1915	1841	34	2034	2009	YX	1024	N647RW	EWR	ORF	52	284	18	41	2023-10-06 18:00:00	Other
134	5	8	1015	949	26	1058	1056	YX	1675	N210JQ	LGA	BDL	21	101	9	49	2023-05-08 09:00:00	Other
136	2	21	1347	1230	77	1645	1545	B6	602	N2016J	JFK	FLL	153	1069	12	30	2023-02-21 12:00:00	FLL
142	6	25	1839	1705	94	2208	2002	B6	799	N991JT	EWR	LAX	345	2454	17	5	2023-06-25 17:00:00	LAX
155	1	17	2301	2145	76	32	2313	9E	1578	N937XJ	JFK	ROC	54	264	21	45	2023-01-17 21:00:00	Other
165	8	16	1626	1502	84	1928	1812	NK	496	N659NK	LGA	FLL	161	1076	15	2	2023-08-16 15:00:00	FLL
167	6	4	1223	1200	23	1431	1443	UA	855	N211UA	EWR	LAX	281	2454	12	0	2023-06-04 12:00:00	LAX
170	6	30	1547	1429	78	1744	1657	UA	990	N439UA	LGA	DEN	215	1620	14	29	2023-06-30 14:00:00	Other
171	3	26	2307	2159	68	56	2359	UA	752	N27261	EWR	DTW	88	488	21	59	2023-03-26 21:00:00	Other
178	6	28	912	850	22	1102	1053	NK	314	N682NK	LGA	CLT	90	544	8	50	2023-06-28 08:00:00	CLT
180	3	24	2038	1924	74	2234	2126	AA	316	N804NN	EWR	CLT	81	529	19	24	2023-03-24 19:00:00	CLT
181	8	8	1604	1550	14	1757	1815	9E	1103	N931XJ	LGA	CLT	84	544	15	50	2023-08-08 15:00:00	CLT
182	9	29	723	700	23	1017	952	UA	417	N807UA	EWR	SRQ	152	1034	7	0	2023-09-29 07:00:00	Other
198	4	14	2231	2130	61	53	7	B6	440	N809JB	JFK	JAX	115	828	21	30	2023-04-14 21:00:00	Other
211	2	26	1643	1320	203	1857	1552	NK	36	N620NK	EWR	ATL	108	746	13	20	2023-02-26 13:00:00	ATL
212	4	26	1921	1829	52	2222	2141	AA	183	N903AN	JFK	MIA	149	1089	18	29	2023-04-26 18:00:00	MIA
216	12	7	1916	1755	81	2159	2108	B6	117	N974JT	JFK	MCO	137	944	17	55	2023-12-07 17:00:00	MCO
218	3	12	1849	1751	58	2108	2001	B6	380	N197JB	JFK	DTW	91	509	17	51	2023-03-12 17:00:00	Other
221	7	11	1751	1712	39	1935	1924	AA	363	N583UW	EWR	CLT	77	529	17	12	2023-07-11 17:00:00	CLT
222	2	21	1147	815	212	1449	1156	AA	607	N326SJ	JFK	MIA	158	1089	8	15	2023-02-21 08:00:00	MIA
226	8	18	1625	1530	55	1802	1737	9E	1133	N348PQ	LGA	ILM	76	500	15	30	2023-08-18 15:00:00	Other
229	3	1	1811	1729	42	2017	1918	B6	442	N569JB	JFK	RDU	73	427	17	29	2023-03-01 17:00:00	Other
237	6	16	2155	1915	160	22	2233	DL	585	N371DN	JFK	MCO	131	944	19	15	2023-06-16 19:00:00	MCO
246	3	29	1536	1520	16	1718	1710	WN	1205	N8626B	LGA	STL	140	888	15	20	2023-03-29 15:00:00	Other
270	8	17	1045	1003	42	1230	1208	OO	956	N293SY	LGA	MEM	134	963	10	3	2023-08-17 10:00:00	Other
273	4	2	2058	1610	288	2338	1920	DL	418	N127DN	JFK	MCO	133	944	16	10	2023-04-02 16:00:00	MCO
274	3	2	1853	1729	84	2222	2047	B6	997	N2016J	JFK	FLL	151	1069	17	29	2023-03-02 17:00:00	FLL
276	9	11	2122	2025	57	28	2306	DL	840	N137DU	JFK	JAX	116	828	20	25	2023-09-11 20:00:00	Other
284	4	8	1142	1035	67	1310	1157	B6	146	N197JB	JFK	BUF	62	301	10	35	2023-04-08 10:00:00	Other
285	9	15	1542	1530	12	1822	1832	UA	488	N14118	EWR	LAX	310	2454	15	30	2023-09-15 15:00:00	LAX
298	3	22	2037	1955	42	46	2358	DL	350	N702TW	JFK	SFO	384	2586	19	55	2023-03-22 19:00:00	Other
305	8	20	1510	1455	15	1703	1724	B6	27	N193JB	JFK	MSY	145	1182	14	55	2023-08-20 14:00:00	Other
313	3	17	2122	1959	83	23	2335	DL	151	N868DN	JFK	PDX	319	2454	19	59	2023-03-17 19:00:00	Other
320	3	17	1950	1929	21	2307	2255	DL	206	N415DX	JFK	LAX	327	2475	19	29	2023-03-17 19:00:00	LAX
336	3	5	1015	956	19	1310	1306	B6	229	N793JB	LGA	MCO	146	950	9	56	2023-03-05 09:00:00	MCO
351	1	1	1019	950	29	1218	1210	UA	144	N26970	EWR	DEN	219	1605	9	50	2023-01-01 09:00:00	Other
363	3	6	1141	959	102	1341	1220	UA	508	N810UA	EWR	SAV	106	708	9	59	2023-03-06 09:00:00	Other
368	7	11	1441	1305	96	1725	1610	UA	412	N75435	EWR	FLL	142	1065	13	5	2023-07-11 13:00:00	FLL
383	10	30	1521	1430	51	1708	1622	AA	599	N766US	LGA	RDU	77	431	14	30	2023-10-30 14:00:00	Other
385	8	2	2035	1830	125	38	2228	B6	569	N948JB	JFK	SJU	194	1598	18	30	2023-08-02 18:00:00	Other
387	3	20	701	630	31	1018	1007	B6	5	N964JT	JFK	SFO	358	2586	6	30	2023-03-20 06:00:00	Other
395	12	15	1145	1117	28	1319	1314	NK	18	N667NK	EWR	MYR	82	550	11	17	2023-12-15 11:00:00	Other
408	6	19	1424	1355	29	1557	1523	9E	1625	N304PQ	LGA	BUF	54	292	13	55	2023-06-19 13:00:00	Other
414	8	10	1959	1929	30	2202	2225	DL	337	N822DN	JFK	ATL	98	760	19	29	2023-08-10 19:00:00	ATL
422	3	24	1542	1530	12	1822	1804	B6	827	N3104J	JFK	MCI	191	1113	15	30	2023-03-24 15:00:00	Other
427	3	12	1310	1200	70	1430	1325	WN	1023	N7734H	LGA	MDW	116	725	12	0	2023-03-12 12:00:00	Other
428	1	3	1751	1705	46	1925	1846	UA	851	N433UA	EWR	ORD	121	719	17	5	2023-01-03 17:00:00	ORD
441	9	22	1712	1655	17	1908	1920	UA	946	N69840	EWR	DEN	209	1605	16	55	2023-09-22 16:00:00	Other
456	3	31	1410	1300	70	1600	1456	OO	1275	N679CA	EWR	DTW	84	488	13	0	2023-03-31 13:00:00	Other
462	10	4	749	729	20	1055	1041	DL	781	N356DN	JFK	FLL	136	1069	7	29	2023-10-04 07:00:00	FLL
478	5	29	2113	2037	36	2244	2215	YX	988	N656RW	EWR	BGR	58	393	20	37	2023-05-29 20:00:00	Other
479	9	24	2023	1922	61	2148	2100	UA	503	N16701	EWR	CLE	59	404	19	22	2023-09-24 19:00:00	Other
481	8	12	2027	1915	72	8	2233	DL	453	N372DN	JFK	MCO	124	944	19	15	2023-08-12 19:00:00	MCO
486	7	17	1855	1753	62	2050	1941	B6	520	N358JB	JFK	BNA	113	765	17	53	2023-07-17 17:00:00	Other
503	9	10	1113	1100	13	NA	1225	YX	1932	N224JQ	LGA	BOS	NA	184	11	0	2023-09-10 11:00:00	BOS
504	8	2	1939	1909	30	2310	2308	UA	185	N63820	EWR	BQN	189	1585	19	9	2023-08-02 19:00:00	Other
511	6	16	2235	2055	100	2341	2233	DL	1026	N120DU	JFK	BOS	39	187	20	55	2023-06-16 20:00:00	BOS
521	11	26	44	2132	192	151	2244	YX	1065	N751YX	EWR	MHT	41	209	21	32	2023-11-26 21:00:00	Other
527	6	28	2120	1929	111	2334	2136	9E	1636	N186PQ	JFK	RDU	64	427	19	29	2023-06-28 19:00:00	Other
529	10	22	2146	2129	17	2309	2302	9E	1646	N931XJ	LGA	BUF	53	292	21	29	2023-10-22 21:00:00	Other
530	5	22	2246	2100	106	37	2320	B6	889	N564JB	LGA	MSY	151	1183	21	0	2023-05-22 21:00:00	Other
533	10	12	1459	1359	60	1819	1711	B6	527	N779JB	JFK	RSW	168	1074	13	59	2023-10-12 13:00:00	Other
534	9	9	1502	1355	67	1751	1651	DL	284	N179DN	JFK	LAX	320	2475	13	55	2023-09-09 13:00:00	LAX
538	7	18	2203	1829	214	2336	2015	AA	596	N810AW	LGA	RDU	66	431	18	29	2023-07-18 18:00:00	Other
548	9	5	1106	1018	48	1244	1214	NK	21	N683NK	EWR	MYR	80	550	10	18	2023-09-05 10:00:00	Other
552	9	9	2242	1740	302	153	2034	B6	64	N527JL	JFK	TPA	141	1005	17	40	2023-09-09 17:00:00	Other
556	12	11	1519	1435	44	1808	1710	WN	691	N224WN	LGA	ATL	114	762	14	35	2023-12-11 14:00:00	ATL
558	3	31	2148	2050	58	2350	2250	OO	1194	N614CZ	JFK	CLE	84	425	20	50	2023-03-31 20:00:00	Other
559	12	10	24	2250	94	305	203	F9	1175	N328FR	LGA	DFW	200	1389	22	50	2023-12-10 22:00:00	Other
560	6	11	2208	2057	71	2329	2237	YX	1096	N745YX	EWR	PIT	56	319	20	57	2023-06-11 20:00:00	Other
567	4	25	1101	1044	17	1320	1254	UA	807	N881UA	EWR	MSY	171	1167	10	44	2023-04-25 10:00:00	Other
571	6	24	853	759	54	1020	922	YX	1200	N746YX	EWR	DCA	49	199	7	59	2023-06-24 07:00:00	Other
573	5	14	2255	2159	56	246	158	B6	418	N615JB	JFK	SJU	186	1598	21	59	2023-05-14 21:00:00	Other
585	2	27	1709	1630	39	2037	2007	DL	230	N804DN	JFK	SLC	291	1990	16	30	2023-02-27 16:00:00	Other
589	6	8	1349	1330	19	1447	1443	YX	1859	N216JQ	LGA	MVY	40	175	13	30	2023-06-08 13:00:00	Other
601	2	21	2211	2028	103	43	2309	B6	35	N638JB	JFK	DEN	245	1626	20	28	2023-02-21 20:00:00	Other
605	6	26	1450	1302	108	1731	1555	NK	1060	N632NK	EWR	MCO	124	937	13	2	2023-06-26 13:00:00	MCO
608	5	4	1851	1835	16	2114	2137	B6	271	N956JT	JFK	LAS	300	2248	18	35	2023-05-04 18:00:00	Other
617	11	20	1411	1350	21	1557	1540	9E	1473	N937XJ	LGA	BHM	129	866	13	50	2023-11-20 13:00:00	Other
619	11	6	746	730	16	1018	1030	UA	762	N27239	EWR	PBI	127	1023	7	30	2023-11-06 07:00:00	Other
632	6	24	2320	1430	530	145	1725	UA	267	N87531	EWR	SEA	294	2402	14	30	2023-06-24 14:00:00	Other
640	7	1	2358	2225	93	330	222	NK	837	N621NK	EWR	SJU	195	1608	22	25	2023-07-01 22:00:00	Other
651	3	24	1326	1315	11	1645	1706	DL	746	N881DN	JFK	SJU	183	1598	13	15	2023-03-24 13:00:00	Other
657	10	28	1840	1829	11	2202	2129	DL	227	N533DT	JFK	LAS	339	2248	18	29	2023-10-28 18:00:00	Other
664	6	26	1140	930	130	1319	1111	YX	1192	N856RW	EWR	STL	121	872	9	30	2023-06-26 09:00:00	Other
672	1	2	1649	1625	24	2050	1930	DL	827	N124DU	JFK	DFW	273	1391	16	25	2023-01-02 16:00:00	Other
679	4	16	1504	1429	35	1757	1722	UA	388	N24729	EWR	SRQ	155	1034	14	29	2023-04-16 14:00:00	Other
680	1	20	2209	2156	13	2314	2314	YX	1203	N749YX	EWR	MHT	42	209	21	56	2023-01-20 21:00:00	Other
682	12	3	1850	1829	21	2227	2134	AA	400	N902NN	JFK	MIA	172	1089	18	29	2023-12-03 18:00:00	MIA
688	11	30	721	635	46	851	815	UA	280	N26210	EWR	CLE	66	404	6	35	2023-11-30 06:00:00	Other
696	4	22	1805	1659	66	2009	1840	UA	717	N819UA	LGA	ORD	121	733	16	59	2023-04-22 16:00:00	ORD
697	7	4	2218	2000	138	2353	2138	B6	756	N187JB	JFK	BUF	52	301	20	0	2023-07-04 20:00:00	Other
699	10	2	1659	1645	14	2005	1953	NK	594	N609NK	EWR	FLL	142	1065	16	45	2023-10-02 16:00:00	FLL
703	7	24	1951	1930	21	2238	2249	B6	63	N934JB	JFK	LAX	304	2475	19	30	2023-07-24 19:00:00	LAX
705	7	6	1454	1435	19	1622	1609	YX	920	N742YX	EWR	IAD	44	212	14	35	2023-07-06 14:00:00	Other
712	8	6	1137	1046	51	1455	1340	B6	312	N705JB	JFK	MCO	142	944	10	46	2023-08-06 10:00:00	MCO
714	4	20	2136	2010	86	48	2344	B6	66	N983JT	JFK	LAX	325	2475	20	10	2023-04-20 20:00:00	LAX
715	7	10	1330	1255	35	1513	1501	DL	428	N112DU	JFK	DTW	78	509	12	55	2023-07-10 12:00:00	Other
717	12	27	2147	1959	108	101	2305	NK	156	N660NK	LGA	MCO	147	950	19	59	2023-12-27 19:00:00	MCO
722	8	14	1717	1703	14	2045	1953	UA	643	N36247	EWR	MCO	148	937	17	3	2023-08-14 17:00:00	MCO
728	7	4	1727	1700	27	1934	1855	9E	1120	N916XJ	LGA	RDU	68	431	17	0	2023-07-04 17:00:00	Other
730	5	3	2114	2059	15	2223	2232	UA	840	N883UA	EWR	MSN	110	799	20	59	2023-05-03 20:00:00	Other
759	2	23	2024	1929	55	2314	2208	DL	275	N105DU	LGA	MCI	197	1107	19	29	2023-02-23 19:00:00	Other
760	12	30	2044	2002	42	2341	2321	AA	943	N912AN	LGA	MIA	150	1096	20	2	2023-12-30 20:00:00	MIA
763	10	14	1327	1310	17	1540	1529	DL	787	N804DN	EWR	ATL	110	746	13	10	2023-10-14 13:00:00	ATL
769	12	12	1212	1200	12	1502	1504	B6	672	N2059J	JFK	PBI	151	1028	12	0	2023-12-12 12:00:00	Other
783	1	11	834	732	62	1043	1004	UA	714	N27261	EWR	MSY	167	1167	7	32	2023-01-11 07:00:00	Other
799	11	6	1831	1800	31	2158	2121	UA	854	N217UA	EWR	SFO	341	2565	18	0	2023-11-06 18:00:00	Other
801	6	21	2132	2052	40	2234	2221	UA	647	N16732	EWR	MKE	97	725	20	52	2023-06-21 20:00:00	Other
815	9	22	929	915	14	1052	1039	9E	1579	N324PQ	JFK	IAD	50	228	9	15	2023-09-22 09:00:00	Other
819	8	10	1854	1700	114	2035	1903	9E	1145	N480PX	LGA	RDU	69	431	17	0	2023-08-10 17:00:00	Other
823	6	16	1548	1359	109	1716	1531	UA	831	N425UA	EWR	STL	117	872	13	59	2023-06-16 13:00:00	Other
829	6	14	2013	1730	163	2154	1926	NK	52	N943NK	LGA	DTW	74	502	17	30	2023-06-14 17:00:00	Other
830	1	9	636	615	21	954	933	UA	348	N796UA	EWR	SFO	352	2565	6	15	2023-01-09 06:00:00	Other
832	7	21	1340	1311	29	1554	1535	9E	1308	N927XJ	LGA	IND	106	660	13	11	2023-07-21 13:00:00	Other
833	1	11	1028	800	148	1216	943	UA	943	N23708	LGA	ORD	116	733	8	0	2023-01-11 08:00:00	ORD
837	12	1	2051	2030	21	2357	2343	UA	907	N12114	EWR	FLL	161	1065	20	30	2023-12-01 20:00:00	FLL
838	7	11	1118	1100	18	1355	1408	B6	670	N809JB	JFK	FLL	141	1069	11	0	2023-07-11 11:00:00	FLL
844	8	31	1338	1326	12	1552	1551	NK	32	N602NK	EWR	ATL	110	746	13	26	2023-08-31 13:00:00	ATL
851	3	28	2116	2053	23	34	2359	NK	278	N971NK	EWR	IAH	216	1400	20	53	2023-03-28 20:00:00	Other
861	8	13	1812	1755	17	2042	2100	DL	89	N135DQ	JFK	DFW	186	1391	17	55	2023-08-13 17:00:00	Other
870	3	3	1754	1640	74	2021	1909	B6	118	N306JB	JFK	SAV	120	718	16	40	2023-03-03 16:00:00	Other
889	7	25	1045	1030	15	1315	1326	UA	548	N17133	EWR	LAX	295	2454	10	30	2023-07-25 10:00:00	LAX
897	9	13	1136	1059	37	1339	1301	9E	1427	N200PQ	JFK	CLT	94	541	10	59	2023-09-13 10:00:00	CLT
899	6	27	1640	1521	79	NA	1812	UA	798	N69838	EWR	TPA	NA	997	15	21	2023-06-27 15:00:00	Other
911	8	1	1214	1138	36	1309	1248	YX	1345	N246JQ	JFK	MVY	32	173	11	38	2023-08-01 11:00:00	Other
916	1	11	1631	1415	136	1954	1735	UA	814	N782UA	EWR	SFO	347	2565	14	15	2023-01-11 14:00:00	Other
920	5	30	1110	1050	20	1337	1308	9E	1514	N298PQ	LGA	CLT	88	544	10	50	2023-05-30 10:00:00	CLT
935	3	19	2029	1959	30	2247	2133	YX	1193	N752YX	EWR	PIT	56	319	19	59	2023-03-19 19:00:00	Other
936	3	8	1620	1459	81	1911	1807	UA	215	N454UA	EWR	AUS	207	1504	14	59	2023-03-08 14:00:00	Other
937	8	14	1424	1315	69	1532	1435	B6	131	N184JB	LGA	BOS	40	184	13	15	2023-08-14 13:00:00	BOS
946	1	24	1254	1200	54	1431	1357	AA	1091	N801AW	LGA	RDU	73	431	12	0	2023-01-24 12:00:00	Other
947	4	17	752	735	17	1102	1036	UA	664	N37553	EWR	PBI	158	1023	7	35	2023-04-17 07:00:00	Other
957	10	8	1754	1725	29	2006	1957	B6	911	N520JB	LGA	ATL	111	762	17	25	2023-10-08 17:00:00	ATL
961	2	20	2053	2020	33	2332	2248	UA	176	N68807	EWR	ATL	119	746	20	20	2023-02-20 20:00:00	ATL
964	3	20	1607	1545	22	1935	1941	DL	358	N723TW	JFK	SFO	359	2586	15	45	2023-03-20 15:00:00	Other
965	11	25	1338	1227	71	1520	1343	AA	851	N803AW	LGA	BOS	40	184	12	27	2023-11-25 12:00:00	BOS
966	1	12	1436	1400	36	1741	1706	UA	683	N17279	EWR	IAH	210	1400	14	0	2023-01-12 14:00:00	Other
967	4	27	2245	2137	68	41	2340	UA	354	N69835	EWR	CLT	82	529	21	37	2023-04-27 21:00:00	CLT
969	8	27	2100	2020	40	2307	2240	9E	1155	N138EV	LGA	GRR	96	618	20	20	2023-08-27 20:00:00	Other
987	7	12	1646	1635	11	1851	1858	UA	402	N479UA	EWR	JAX	102	820	16	35	2023-07-12 16:00:00	Other
997	1	18	1642	1559	43	1803	1729	OO	1276	N260SY	JFK	IAD	51	228	15	59	2023-01-18 15:00:00	Other
1000	5	22	1943	1915	28	2232	2237	DL	153	N178DN	JFK	LAX	309	2475	19	15	2023-05-22 19:00:00	LAX
1007	10	20	1845	1759	46	2143	2105	AA	158	N787AL	JFK	MIA	141	1089	17	59	2023-10-20 17:00:00	MIA
1013	5	31	1825	1759	26	1929	1940	UA	709	N418UA	LGA	ORD	99	733	17	59	2023-05-31 17:00:00	ORD
1019	4	18	1648	1550	58	1901	1800	B6	809	N663JB	JFK	CHS	98	636	15	50	2023-04-18 15:00:00	Other
1022	8	26	1827	1630	117	2058	1903	B6	97	N329JB	JFK	SAV	107	718	16	30	2023-08-26 16:00:00	Other
1026	5	7	1530	1510	20	1755	1818	B6	139	N516JB	LGA	MCO	124	950	15	10	2023-05-07 15:00:00	MCO
1031	2	3	2101	1929	92	2248	2122	9E	1445	N482PX	LGA	BHM	124	866	19	29	2023-02-03 19:00:00	Other
1040	9	26	1258	1231	27	1431	1427	DL	513	N895AT	EWR	MSP	134	1008	12	31	2023-09-26 12:00:00	Other
1042	3	30	2316	2010	186	149	2304	B6	36	N659JB	JFK	DEN	243	1626	20	10	2023-03-30 20:00:00	Other
1043	12	7	1405	1350	15	1655	1702	NK	72	N930NK	EWR	DFW	194	1372	13	50	2023-12-07 13:00:00	Other
1047	9	9	930	1359	1171	1209	1655	UA	589	N826UA	LGA	IAH	192	1416	13	59	2023-09-09 13:00:00	Other
1097	5	3	2041	2026	15	2325	2330	UA	250	N27477	EWR	AUS	196	1504	20	26	2023-05-03 20:00:00	Other
1100	5	1	1025	1000	25	1228	1236	B6	16	N957JB	JFK	PHX	280	2153	10	0	2023-05-01 10:00:00	Other
1111	4	10	1449	1145	184	1609	1331	9E	1204	N918XJ	LGA	BHM	115	866	11	45	2023-04-10 11:00:00	Other
1120	12	14	754	730	24	1047	1057	AS	10	N468AS	JFK	SEA	314	2422	7	30	2023-12-14 07:00:00	Other
1121	1	3	2002	1729	153	2249	2035	UA	564	N877UA	EWR	PBI	140	1023	17	29	2023-01-03 17:00:00	Other
1124	8	15	2348	2250	58	145	36	9E	1232	N926XJ	JFK	ROC	49	264	22	50	2023-08-15 22:00:00	Other
1129	12	28	2101	1849	132	106	2203	NK	996	N661NK	LGA	MIA	173	1096	18	49	2023-12-28 18:00:00	MIA
1137	3	14	1100	1040	20	1330	1315	WN	395	N401WN	LGA	ATL	111	762	10	40	2023-03-14 10:00:00	ATL
1141	10	10	1722	1645	37	2012	1953	NK	594	N972NK	EWR	FLL	147	1065	16	45	2023-10-10 16:00:00	FLL
1146	6	5	1219	1200	19	1445	1443	UA	855	N213UA	EWR	LAX	293	2454	12	0	2023-06-05 12:00:00	LAX
1154	7	1	2043	1958	45	2303	2244	DL	153	N126DN	JFK	DEN	214	1626	19	58	2023-07-01 19:00:00	Other
1172	4	22	2302	2044	138	208	2359	UA	587	N410UA	EWR	MIA	159	1085	20	44	2023-04-22 20:00:00	MIA
1180	2	9	1528	1400	88	1820	1706	UA	596	N48127	EWR	IAH	203	1400	14	0	2023-02-09 14:00:00	Other
1182	4	3	1140	1115	25	1408	1352	YX	1163	N129HQ	LGA	XNA	174	1147	11	15	2023-04-03 11:00:00	Other
1183	4	30	1636	1614	22	1927	1913	UA	434	N15712	EWR	SNA	311	2434	16	14	2023-04-30 16:00:00	Other
1189	4	12	2137	2045	52	9	2359	B6	447	N589JB	JFK	AUS	187	1521	20	45	2023-04-12 20:00:00	Other
1190	3	11	623	600	23	906	912	UA	607	N47280	LGA	IAH	194	1416	6	0	2023-03-11 06:00:00	Other
1191	4	2	1342	1159	103	1458	1320	OO	1004	N295SY	JFK	IAD	52	228	11	59	2023-04-02 11:00:00	Other
1192	12	3	1558	1402	116	1742	1545	UA	764	N15710	EWR	STL	138	872	14	2	2023-12-03 14:00:00	Other
1196	8	11	1457	1300	117	1715	1534	DL	377	N876DN	JFK	ATL	107	760	13	0	2023-08-11 13:00:00	ATL
1197	12	9	1113	1100	13	1227	1228	9E	1446	N311PQ	JFK	BTV	43	266	11	0	2023-12-09 11:00:00	Other
1198	7	22	2321	2142	99	215	53	B6	652	N661JB	JFK	RSW	152	1074	21	42	2023-07-22 21:00:00	Other
1199	5	11	1106	1055	11	1358	1407	DL	345	N895DN	JFK	SEA	321	2422	10	55	2023-05-11 10:00:00	Other
1204	8	6	856	830	26	1129	1114	UA	120	N12004	EWR	LAX	303	2454	8	30	2023-08-06 08:00:00	LAX
1210	8	8	1725	1629	56	1929	1907	9E	1089	N136EV	JFK	CLT	89	541	16	29	2023-08-08 16:00:00	CLT
1213	4	7	1036	1025	11	1312	1309	DL	125	N358DN	LGA	ATL	116	762	10	25	2023-04-07 10:00:00	ATL
1214	2	23	2216	2125	51	2359	2247	YX	1525	N207JQ	LGA	ROC	57	254	21	25	2023-02-23 21:00:00	Other
1217	7	20	1717	1649	28	1855	1822	YX	900	N639RW	EWR	BGR	58	393	16	49	2023-07-20 16:00:00	Other
1219	6	4	1141	1115	26	1241	1225	B6	56	N273JB	EWR	BOS	40	200	11	15	2023-06-04 11:00:00	BOS
1222	9	22	1844	1830	14	2011	2009	UA	424	N58101	EWR	ORD	106	719	18	30	2023-09-22 18:00:00	ORD
1224	4	5	1303	2103	960	1639	2354	UA	356	N17279	EWR	DFW	203	1372	21	3	2023-04-05 21:00:00	Other
1232	5	14	1817	1723	54	2031	1945	AA	921	N416AN	EWR	PHX	289	2133	17	23	2023-05-14 17:00:00	Other
1242	4	14	1624	1459	85	1924	1802	B6	194	N563JB	EWR	FLL	155	1065	14	59	2023-04-14 14:00:00	FLL
1249	9	25	1542	1359	103	1721	1553	YX	1876	N202JQ	LGA	CMH	79	479	13	59	2023-09-25 13:00:00	Other
1251	6	23	2211	2129	42	2304	2232	9E	1500	N306PQ	LGA	BGM	29	147	21	29	2023-06-23 21:00:00	Other
1260	2	28	1422	1330	52	1813	1707	B6	567	N990JL	JFK	SFO	385	2586	13	30	2023-02-28 13:00:00	Other
1262	8	31	853	840	13	1154	1055	YX	1036	N404YX	LGA	IND	112	660	8	40	2023-08-31 08:00:00	Other
1263	9	18	2209	2125	44	1	2326	NK	271	N915NK	LGA	DTW	73	502	21	25	2023-09-18 21:00:00	Other
1266	10	9	2249	2229	20	141	144	B6	618	N964JT	JFK	LAX	316	2475	22	29	2023-10-09 22:00:00	LAX
1272	8	1	1159	1108	51	1440	1407	UA	211	N27421	EWR	PBI	138	1023	11	8	2023-08-01 11:00:00	Other
1278	11	16	1401	1329	32	1712	1637	DL	295	N417DX	JFK	LAX	346	2475	13	29	2023-11-16 13:00:00	LAX
1279	9	26	2335	2113	142	105	2313	UA	611	N17296	EWR	MSP	131	1008	21	13	2023-09-26 21:00:00	Other
1280	10	3	1357	1200	117	1649	1507	B6	799	N962JT	JFK	LAX	327	2475	12	0	2023-10-03 12:00:00	LAX
1282	9	8	1040	1025	15	1249	1232	9E	1724	N485PX	LGA	AVL	90	599	10	25	2023-09-08 10:00:00	Other
1285	4	3	1613	1455	78	1750	1657	9E	1414	N181GJ	JFK	RDU	74	427	14	55	2023-04-03 14:00:00	Other
1295	8	24	2252	2130	82	31	2323	YX	1330	N878RW	JFK	RIC	52	288	21	30	2023-08-24 21:00:00	Other
1300	12	10	1935	1915	20	2227	2237	UA	721	N63890	EWR	SEA	312	2402	19	15	2023-12-10 19:00:00	Other
1304	6	3	2106	1913	113	2334	2205	UA	568	N37295	EWR	SAN	295	2425	19	13	2023-06-03 19:00:00	Other
1313	8	11	1947	1930	17	2050	2045	B6	415	N198JB	LGA	PWM	46	269	19	30	2023-08-11 19:00:00	Other
1325	1	19	1645	1630	15	1945	1953	UA	819	N14107	EWR	LAX	322	2454	16	30	2023-01-19 16:00:00	LAX
1326	7	26	1404	1329	35	1521	1446	UA	443	N37278	EWR	ORF	50	284	13	29	2023-07-26 13:00:00	Other
1334	6	5	2049	1900	109	47	2255	B6	485	N834JB	EWR	SJU	207	1608	19	0	2023-06-05 19:00:00	Other
1335	2	3	1527	1515	12	1727	1727	YX	1532	N228JQ	LGA	STL	140	888	15	15	2023-02-03 15:00:00	Other
1336	5	31	1940	1900	40	2203	2215	UA	573	N36472	EWR	PDX	301	2434	19	0	2023-05-31 19:00:00	Other
1344	12	18	923	900	23	1200	1216	AA	134	N981AN	EWR	DFW	190	1372	9	0	2023-12-18 09:00:00	Other
1352	11	19	736	700	36	905	843	UA	844	N38451	EWR	ORD	119	719	7	0	2023-11-19 07:00:00	ORD
1365	7	14	2145	1929	136	120	2308	DL	195	N529DT	JFK	SEA	347	2422	19	29	2023-07-14 19:00:00	Other
1372	6	18	1706	1625	41	1946	1936	AA	101	N106NN	JFK	LAX	309	2475	16	25	2023-06-18 16:00:00	LAX
1388	2	23	2138	2120	18	2232	2226	9E	1367	N915XJ	LGA	ALB	29	136	21	20	2023-02-23 21:00:00	Other
1392	2	24	2220	2105	75	2319	2211	9E	1264	N916XJ	LGA	BGM	35	147	21	5	2023-02-24 21:00:00	Other
1400	2	21	1648	1625	23	1739	1737	9E	1435	N919XJ	LGA	PVD	27	143	16	25	2023-02-21 16:00:00	Other
1413	12	22	803	750	13	1051	1036	NK	143	N608NK	EWR	LAS	313	2227	7	50	2023-12-22 07:00:00	Other
1417	6	5	1149	1050	59	1449	1406	DL	449	N116DU	LGA	RSW	153	1080	10	50	2023-06-05 10:00:00	Other
1418	8	24	1710	1531	99	1928	1818	9E	1101	N602LR	LGA	JAX	105	833	15	31	2023-08-24 15:00:00	Other
1422	10	13	2037	2025	12	2321	2250	WN	164	N774SW	LGA	DEN	252	1620	20	25	2023-10-13 20:00:00	Other
1426	3	26	832	820	12	1015	1004	YX	1209	N724YX	EWR	RDU	81	416	8	20	2023-03-26 08:00:00	Other
1429	1	15	1834	1815	19	2127	2132	NK	754	N675NK	EWR	FLL	143	1065	18	15	2023-01-15 18:00:00	FLL
1435	6	15	1740	1711	29	1914	1847	UA	636	N469UA	LGA	ORD	113	733	17	11	2023-06-15 17:00:00	ORD
1440	8	5	1700	1644	16	1938	1950	B6	113	N955JB	JFK	MCO	128	944	16	44	2023-08-05 16:00:00	MCO
1445	9	10	2039	1900	99	2335	2155	UA	643	N778UA	EWR	LAX	310	2454	19	0	2023-09-10 19:00:00	LAX
1447	2	28	1346	1219	87	1608	1452	B6	916	N228JB	JFK	ATL	114	760	12	19	2023-02-28 12:00:00	ATL
1458	1	17	2205	2120	45	2313	2254	9E	1692	N913XJ	LGA	CHO	54	305	21	20	2023-01-17 21:00:00	Other
1465	3	12	1421	1355	26	1726	1708	B6	142	N524JB	LGA	MCO	148	950	13	55	2023-03-12 13:00:00	MCO
1471	3	12	2154	2029	85	42	2335	UA	792	N431UA	EWR	DFW	199	1372	20	29	2023-03-12 20:00:00	Other
1478	6	12	1930	1755	95	2158	2025	WN	859	N8622A	LGA	ATL	110	762	17	55	2023-06-12 17:00:00	ATL
1485	8	3	1121	1015	66	1233	1155	AA	124	N9017P	LGA	ORD	109	733	10	15	2023-08-03 10:00:00	ORD
1494	12	30	2102	2045	17	2355	2352	B6	889	N638JB	JFK	MCO	123	944	20	45	2023-12-30 20:00:00	MCO
1504	9	24	2346	1959	227	237	2324	AS	83	N931AK	EWR	SFO	316	2565	19	59	2023-09-24 19:00:00	Other
1514	2	21	2131	1920	131	2352	2215	9E	1408	N606LR	LGA	JAX	120	833	19	20	2023-02-21 19:00:00	Other
1518	12	15	804	750	14	1018	1036	NK	143	N604NK	EWR	LAS	289	2227	7	50	2023-12-15 07:00:00	Other
1523	4	24	2110	2059	11	2234	2232	UA	773	N881UA	EWR	MSN	113	799	20	59	2023-04-24 20:00:00	Other
1527	11	15	1722	1700	22	2046	2045	AA	956	N334SM	JFK	PHX	301	2153	17	0	2023-11-15 17:00:00	Other
1541	10	21	1613	1546	27	1843	1845	DL	111	N357DN	LGA	MCO	130	950	15	46	2023-10-21 15:00:00	MCO
1543	5	29	1007	859	68	1123	1029	YX	1043	N732YX	EWR	BOS	38	200	8	59	2023-05-29 08:00:00	BOS
1554	9	22	2229	2159	30	2336	2317	9E	1531	N912XJ	LGA	ROC	43	254	21	59	2023-09-22 21:00:00	Other
1557	8	11	938	925	13	1226	1223	AA	291	N110AN	JFK	SNA	310	2454	9	25	2023-08-11 09:00:00	Other
1566	12	1	1529	1459	30	1800	1726	DL	511	N717JL	EWR	ATL	119	746	14	59	2023-12-01 14:00:00	ATL
1570	7	14	1310	1205	65	1508	1407	YX	1078	N422YX	LGA	DTW	82	502	12	5	2023-07-14 12:00:00	Other
1574	1	7	953	720	153	1205	949	DL	1053	N3762Y	EWR	ATL	110	746	7	20	2023-01-07 07:00:00	ATL
1582	3	10	2219	2120	59	12	2344	B6	368	N569JB	LGA	CHS	94	641	21	20	2023-03-10 21:00:00	Other
1584	2	1	1758	1717	41	1852	1827	YX	1044	N644RW	EWR	PVD	31	160	17	17	2023-02-01 17:00:00	Other
1592	6	26	1321	1155	86	1533	1418	YX	1287	N403YX	JFK	IND	94	665	11	55	2023-06-26 11:00:00	Other
1596	8	19	1315	1255	20	1514	1513	9E	1212	N311PQ	LGA	CLT	80	544	12	55	2023-08-19 12:00:00	CLT
1599	1	22	1825	1800	25	2003	1928	YX	1146	N741YX	EWR	ROC	49	246	18	0	2023-01-22 18:00:00	Other
1601	5	26	1358	1344	14	1654	1658	B6	92	N715JB	JFK	AUS	205	1521	13	44	2023-05-26 13:00:00	Other
1605	2	3	1732	1708	24	1936	1915	DL	876	N332NW	LGA	DTW	83	502	17	8	2023-02-03 17:00:00	Other
1608	7	11	1739	1510	149	2017	1759	UA	631	N69838	EWR	TPA	128	997	15	10	2023-07-11 15:00:00	Other
1616	10	23	917	900	17	1246	1209	B6	79	N643JB	JFK	AUS	215	1521	9	0	2023-10-23 09:00:00	Other
1621	3	15	812	800	12	934	946	B6	399	N283JB	JFK	BNA	110	765	8	0	2023-03-15 08:00:00	Other
1623	6	1	1141	1120	21	1350	1400	B6	37	N2043J	JFK	LAS	278	2248	11	20	2023-06-01 11:00:00	Other
1627	7	1	1831	1750	41	2140	2100	NK	518	N955NK	LGA	FLL	166	1076	17	50	2023-07-01 17:00:00	FLL
1636	6	12	1937	1859	38	2208	2105	AA	784	N12028	JFK	CLT	85	541	18	59	2023-06-12 18:00:00	CLT
1644	1	14	806	751	15	1015	1027	UA	919	N17126	EWR	DEN	221	1605	7	51	2023-01-14 07:00:00	Other
1646	1	1	613	600	13	834	836	DL	178	N342NW	LGA	ATL	124	762	6	0	2023-01-01 06:00:00	ATL
1656	5	14	1435	1422	13	1650	1640	UA	782	N497UA	EWR	DEN	227	1605	14	22	2023-05-14 14:00:00	Other
1657	7	31	1828	1659	89	1944	1823	UA	380	N459UA	EWR	BOS	41	200	16	59	2023-07-31 16:00:00	BOS
1663	6	16	1418	1355	23	1704	1635	WN	717	N8830Q	LGA	HOU	193	1428	13	55	2023-06-16 13:00:00	Other
1664	10	3	1709	1645	24	1912	1911	UA	909	N48127	EWR	PHX	285	2133	16	45	2023-10-03 16:00:00	Other
1666	6	20	738	650	48	1003	934	UA	319	N66808	EWR	SAN	301	2425	6	50	2023-06-20 06:00:00	Other
1681	2	8	2326	2259	27	352	349	B6	308	N615JB	JFK	PSE	191	1617	22	59	2023-02-08 22:00:00	Other
1682	1	17	1643	1555	48	1908	1816	9E	1459	N937XJ	JFK	CHS	97	636	15	55	2023-01-17 15:00:00	Other
1695	4	1	1704	1630	34	1815	1756	YX	955	N864RW	EWR	BUF	51	282	16	30	2023-04-01 16:00:00	Other
1704	1	21	2122	2100	22	2358	2336	YX	1412	N418YX	JFK	IND	118	665	21	0	2023-01-21 21:00:00	Other
1707	6	13	1959	1820	99	2112	2012	DL	375	N101DU	LGA	ORD	102	733	18	20	2023-06-13 18:00:00	ORD
1710	4	6	1732	1630	62	1939	1758	YX	945	N654RW	EWR	DCA	83	199	16	30	2023-04-06 16:00:00	Other
1713	4	19	1301	1145	76	1411	1331	9E	1204	N922XJ	LGA	BHM	109	866	11	45	2023-04-19 11:00:00	Other
1714	2	28	1119	1100	19	1256	1228	YX	1612	N878RW	LGA	BOS	49	184	11	0	2023-02-28 11:00:00	BOS
1718	7	7	2239	2200	39	11	2328	B6	166	N281JB	JFK	ROC	47	264	22	0	2023-07-07 22:00:00	Other
1727	10	2	1119	946	93	1239	1125	YX	1751	N810MD	LGA	MSN	114	812	9	46	2023-10-02 09:00:00	Other
1728	6	7	2027	1930	57	2343	2228	B6	690	N636JB	LGA	PBI	170	1035	19	30	2023-06-07 19:00:00	Other
1734	7	7	15	1900	315	221	2119	UA	573	N478UA	EWR	SAV	101	708	19	0	2023-07-07 19:00:00	Other
1740	6	8	2112	1915	117	2339	2204	AA	403	N865NN	LGA	DFW	177	1389	19	15	2023-06-08 19:00:00	Other
1741	8	24	1912	1745	87	2124	1946	YX	884	N761YX	EWR	CMH	79	463	17	45	2023-08-24 17:00:00	Other
1743	1	7	1855	1820	35	2208	2130	DL	462	N102DU	JFK	DFW	220	1391	18	20	2023-01-07 18:00:00	Other
1756	7	1	1703	1559	64	1826	1728	YX	995	N434YX	JFK	BOS	37	187	15	59	2023-07-01 15:00:00	BOS
1766	3	25	2308	2225	43	33	2348	B6	185	N203JB	JFK	ROC	56	264	22	25	2023-03-25 22:00:00	Other
1774	9	11	1729	1620	69	2042	1824	9E	1615	N296PQ	LGA	ILM	76	500	16	20	2023-09-11 16:00:00	Other
1780	6	12	906	845	21	1014	1028	UA	808	N27258	EWR	ORD	103	719	8	45	2023-06-12 08:00:00	ORD
1784	6	24	1841	1830	11	2303	2142	UA	445	N2748U	EWR	SFO	324	2565	18	30	2023-06-24 18:00:00	Other
1786	5	20	1626	1607	19	1809	1731	UA	724	N475UA	EWR	IAD	40	212	16	7	2023-05-20 16:00:00	Other
1787	6	17	1626	1610	16	1902	1900	UA	255	N17105	EWR	MCO	127	937	16	10	2023-06-17 16:00:00	MCO
1791	7	27	2020	1954	26	2357	2353	UA	197	N69840	EWR	BQN	195	1585	19	54	2023-07-27 19:00:00	Other
1805	6	17	1439	1427	12	1551	1552	UA	619	N38727	EWR	BNA	109	748	14	27	2023-06-17 14:00:00	Other
1808	4	13	1137	1100	37	1419	1400	UA	249	N36476	EWR	TPA	138	997	11	0	2023-04-13 11:00:00	Other
1811	7	28	2038	1939	59	3	2129	YX	1076	N433YX	LGA	CMH	76	479	19	39	2023-07-28 19:00:00	Other
1821	4	6	1524	1445	39	1747	1720	WN	851	N8820L	LGA	ATL	115	762	14	45	2023-04-06 14:00:00	ATL
1824	7	10	1055	953	62	1342	1316	B6	23	N632JB	JFK	SEA	326	2422	9	53	2023-07-10 09:00:00	Other
1832	3	5	2235	2156	39	28	2358	UA	752	N75428	EWR	DTW	84	488	21	56	2023-03-05 21:00:00	Other
1833	2	4	1514	1455	19	1803	1723	YX	1564	N244JQ	JFK	IND	112	665	14	55	2023-02-04 14:00:00	Other
1834	6	25	1051	1030	21	1326	1325	B6	397	N805JB	JFK	MCO	131	944	10	30	2023-06-25 10:00:00	MCO
1835	6	25	913	900	13	1227	1210	AS	136	N962AK	EWR	SFO	339	2565	9	0	2023-06-25 09:00:00	Other
1842	2	4	2013	1959	14	2252	2308	DL	546	N375DN	JFK	MCO	129	944	19	59	2023-02-04 19:00:00	MCO
1843	8	6	1300	1159	61	1557	1453	UA	437	N27258	EWR	TPA	154	997	11	59	2023-08-06 11:00:00	Other
1856	12	4	1004	949	15	1227	1203	9E	1442	N601LR	LGA	PNS	172	1030	9	49	2023-12-04 09:00:00	Other
1863	8	8	2036	1930	66	2352	2242	B6	614	N524JB	LGA	RSW	155	1080	19	30	2023-08-08 19:00:00	Other
1866	4	7	2329	2245	44	30	4	B6	6	N231JB	JFK	SYR	48	209	22	45	2023-04-07 22:00:00	Other
1867	3	24	1108	950	78	1421	1310	B6	26	N507JT	LGA	PBI	160	1035	9	50	2023-03-24 09:00:00	Other
1868	2	13	1836	1825	11	2136	2141	AA	153	N967AN	JFK	MIA	145	1089	18	25	2023-02-13 18:00:00	MIA
1870	1	13	1428	1400	28	1643	1627	DL	879	N317US	EWR	ATL	113	746	14	0	2023-01-13 14:00:00	ATL
1874	8	5	1414	1100	194	1656	1403	NK	422	N683NK	EWR	FLL	136	1065	11	0	2023-08-05 11:00:00	FLL
1904	3	19	2231	2220	11	2339	2344	UA	495	N37290	EWR	BUF	50	282	22	20	2023-03-19 22:00:00	Other
1905	7	2	1608	1320	168	1804	1453	9E	1168	N133EV	LGA	RIC	78	292	13	20	2023-07-02 13:00:00	Other
1914	1	12	1355	1159	116	1544	1345	9E	1405	N330PQ	LGA	MKE	126	738	11	59	2023-01-12 11:00:00	Other
1918	7	14	1629	1259	210	1744	1426	YX	1390	N227JQ	LGA	BOS	41	184	12	59	2023-07-14 12:00:00	BOS
1920	3	26	2005	1924	41	2200	2126	AA	316	N915AN	EWR	CLT	82	529	19	24	2023-03-26 19:00:00	CLT
1922	6	8	2143	2129	14	2307	2255	YX	1300	N134HQ	LGA	RIC	56	292	21	29	2023-06-08 21:00:00	Other
1923	3	18	905	800	65	1231	1103	AA	604	N928AM	EWR	DFW	230	1372	8	0	2023-03-18 08:00:00	Other
1929	7	4	1801	1747	14	2021	2021	UA	692	N27239	EWR	LAS	286	2227	17	47	2023-07-04 17:00:00	Other
1931	8	12	1149	1100	49	1432	1404	NK	422	N664NK	EWR	FLL	142	1065	11	0	2023-08-12 11:00:00	FLL
1939	6	21	1710	1645	25	1925	1900	9E	1614	N232PQ	JFK	DTW	75	509	16	45	2023-06-21 16:00:00	Other
1954	5	8	1417	1357	20	1559	1604	UA	644	N820UA	EWR	CHS	90	628	13	57	2023-05-08 13:00:00	Other
1957	8	18	1613	1518	55	1844	1808	UA	617	N13720	EWR	TPA	134	997	15	18	2023-08-18 15:00:00	Other
1961	7	5	2059	2025	34	2313	2247	B6	649	N656JB	LGA	MSY	158	1183	20	25	2023-07-05 20:00:00	Other
1967	2	2	1529	1515	14	1838	1832	UA	657	N17294	EWR	RSW	163	1068	15	15	2023-02-02 15:00:00	Other
1970	3	27	1450	1435	15	1757	1750	UA	80	N792UA	EWR	SFO	341	2565	14	35	2023-03-27 14:00:00	Other
1973	9	18	1919	1855	24	2132	2030	WN	1285	N8702L	LGA	BNA	112	764	18	55	2023-09-18 18:00:00	Other
1976	1	23	1842	1815	27	2214	2132	NK	754	N659NK	EWR	FLL	165	1065	18	15	2023-01-23 18:00:00	FLL
1977	9	7	1607	1554	13	2019	1924	B6	224	N968JT	JFK	SFO	365	2586	15	54	2023-09-07 15:00:00	Other
1981	11	12	1431	1404	27	1911	1903	B6	304	N579JB	JFK	SJU	188	1598	14	4	2023-11-12 14:00:00	Other
1985	6	3	1541	1427	74	1651	1552	UA	619	N13720	EWR	BNA	104	748	14	27	2023-06-03 14:00:00	Other
1994	5	26	2017	1900	77	2300	2215	UA	573	N36476	EWR	PDX	290	2434	19	0	2023-05-26 19:00:00	Other
1997	4	17	1843	1715	88	2029	1842	B6	381	N324JB	LGA	BOS	35	184	17	15	2023-04-17 17:00:00	BOS
2000	6	20	1554	1530	24	1750	1755	B6	853	N3058J	JFK	MCI	147	1113	15	30	2023-06-20 15:00:00	Other
2003	6	20	1213	1201	12	1332	1339	9E	1557	N319PQ	JFK	BUF	57	301	12	1	2023-06-20 12:00:00	Other
2010	10	7	1600	1515	45	1837	1741	YX	1286	N432YX	JFK	IND	101	665	15	15	2023-10-07 15:00:00	Other
2015	4	9	1325	1229	56	1557	1533	UA	566	N855UA	LGA	IAH	192	1416	12	29	2023-04-09 12:00:00	Other
2016	3	7	858	830	28	1109	1051	9E	1420	N923XJ	JFK	CLT	86	541	8	30	2023-03-07 08:00:00	CLT
2018	6	10	2103	2043	20	2346	10	B6	31	N964JT	JFK	SAN	323	2446	20	43	2023-06-10 20:00:00	Other
2022	1	11	919	830	49	1123	1040	B6	65	N236JB	JFK	DTW	85	509	8	30	2023-01-11 08:00:00	Other
2024	12	16	1213	1149	24	1400	1350	9E	1542	N200PQ	LGA	RDU	69	431	11	49	2023-12-16 11:00:00	Other
2027	1	21	1000	600	240	1232	839	DL	380	N310DN	LGA	ATL	121	762	6	0	2023-01-21 06:00:00	ATL
2029	3	13	1914	1859	15	2159	2130	DL	829	N318NB	EWR	ATL	117	746	18	59	2023-03-13 18:00:00	ATL
2033	7	21	2052	1955	57	2318	2249	DL	153	N806DN	JFK	DEN	212	1626	19	55	2023-07-21 19:00:00	Other
2036	3	6	1546	1529	17	1740	1658	YX	1140	N746YX	EWR	PIT	67	319	15	29	2023-03-06 15:00:00	Other
2037	7	18	1300	1134	86	1549	1426	NK	840	N923NK	EWR	MCO	142	937	11	34	2023-07-18 11:00:00	MCO
2046	7	16	1320	1230	50	1556	1525	NK	292	N601NK	LGA	DFW	187	1389	12	30	2023-07-16 12:00:00	Other
2050	9	26	1645	1600	45	1836	1728	DL	525	N127DU	LGA	BOS	48	184	16	0	2023-09-26 16:00:00	BOS
2059	11	19	1749	1725	24	2046	2100	NK	277	N953NK	EWR	OAK	334	2555	17	25	2023-11-19 17:00:00	Other
2060	9	13	1047	1030	17	1405	1335	B6	826	N584JB	JFK	FLL	180	1069	10	30	2023-09-13 10:00:00	FLL
2061	1	31	1618	1445	93	1909	1717	B6	791	N661JB	LGA	MSY	190	1183	14	45	2023-01-31 14:00:00	Other
2070	2	16	2152	2000	112	107	2354	AS	18	N288AK	JFK	SFO	355	2586	20	0	2023-02-16 20:00:00	Other
2071	4	4	1213	1155	18	1500	1449	B6	33	N648JB	JFK	MCO	128	944	11	55	2023-04-04 11:00:00	MCO
2073	6	3	2210	2050	80	21	2301	UA	483	N68811	EWR	CHS	90	628	20	50	2023-06-03 20:00:00	Other
2079	12	17	2005	1930	35	2310	2230	B6	15	N809JB	LGA	TPA	148	1010	19	30	2023-12-17 19:00:00	Other
2081	10	29	1737	1645	52	2048	1850	WN	102	N280WN	LGA	MCI	186	1107	16	45	2023-10-29 16:00:00	Other
2088	9	22	1747	1720	27	1856	1840	WN	638	N8800L	LGA	MDW	103	725	17	20	2023-09-22 17:00:00	Other
2090	9	28	2009	1949	20	2244	2210	9E	1751	N923XJ	LGA	CHS	109	641	19	49	2023-09-28 19:00:00	Other
2092	6	21	1914	1900	14	2018	2030	UA	650	N69818	EWR	BNA	102	748	19	0	2023-06-21 19:00:00	Other
2100	7	24	1935	1825	70	2134	2043	DL	334	N104DN	LGA	MSP	143	1020	18	25	2023-07-24 18:00:00	Other
2111	7	31	2312	2210	62	132	36	NK	239	N982NK	EWR	LAS	294	2227	22	10	2023-07-31 22:00:00	Other
2114	1	5	1047	829	138	1240	1014	UA	238	N808UA	EWR	BNA	121	748	8	29	2023-01-05 08:00:00	Other
2115	12	5	1506	1150	196	1642	1337	9E	1382	N176PQ	LGA	PIT	59	335	11	50	2023-12-05 11:00:00	Other
2123	6	6	2016	1745	151	2313	2013	9E	1644	N147PQ	JFK	CHS	96	636	17	45	2023-06-06 17:00:00	Other
2127	6	16	1554	1529	25	1722	1721	YX	1837	N242JQ	JFK	DCA	44	213	15	29	2023-06-16 15:00:00	Other
2130	1	11	923	830	53	1148	1027	9E	1611	N314PQ	JFK	RDU	71	427	8	30	2023-01-11 08:00:00	Other
2137	1	21	1743	1710	33	1908	1845	9E	1686	N582CA	JFK	BUF	57	301	17	10	2023-01-21 17:00:00	Other
2161	6	1	1202	1140	22	1309	1305	WN	148	N752SW	LGA	MDW	99	725	11	40	2023-06-01 11:00:00	Other
2169	8	24	1333	1300	33	1520	1509	UA	715	N827UA	EWR	MSY	147	1167	13	0	2023-08-24 13:00:00	Other
2174	8	4	1307	1116	111	1443	1309	9E	1257	N925XJ	LGA	RDU	70	431	11	16	2023-08-04 11:00:00	Other
2178	4	9	1836	1540	176	2054	1804	UA	348	N47414	EWR	DEN	205	1605	15	40	2023-04-09 15:00:00	Other
2183	8	10	1652	1543	69	1827	1745	AA	660	N980NN	JFK	ORD	119	740	15	43	2023-08-10 15:00:00	ORD
2190	4	28	2032	1825	127	2301	2111	UA	760	N69818	EWR	LAS	273	2227	18	25	2023-04-28 18:00:00	Other
2193	7	2	1524	1459	25	1655	1645	UA	564	N496UA	EWR	RDU	72	416	14	59	2023-07-02 14:00:00	Other
2195	8	13	2209	2055	74	123	2347	B6	30	N990JL	JFK	SAN	324	2446	20	55	2023-08-13 20:00:00	Other
2199	9	24	2130	1945	105	2340	2214	DL	795	N354NW	JFK	MSP	145	1029	19	45	2023-09-24 19:00:00	Other
2205	3	19	1714	1658	16	1935	1933	UA	472	N38454	EWR	DEN	230	1605	16	58	2023-03-19 16:00:00	Other
2207	2	16	1643	1620	23	1847	1852	9E	1379	N937XJ	LGA	AVL	101	599	16	20	2023-02-16 16:00:00	Other
2214	1	3	1010	950	20	1306	1311	B6	657	N641JB	JFK	RSW	155	1074	9	50	2023-01-03 09:00:00	Other
2221	5	14	1219	1200	19	1340	1325	WN	979	N7749B	LGA	MDW	112	725	12	0	2023-05-14 12:00:00	Other
2229	3	31	2014	1859	75	2321	2214	UA	595	N62849	EWR	PDX	325	2434	18	59	2023-03-31 18:00:00	Other
2234	3	18	1418	1406	12	1621	1638	UA	795	N14118	EWR	DEN	219	1605	14	6	2023-03-18 14:00:00	Other
2240	5	19	1745	1545	120	1936	1753	9E	1511	N315PQ	EWR	CVG	89	569	15	45	2023-05-19 15:00:00	Other
2248	4	28	1642	1550	52	1859	1804	UA	746	N17529	EWR	MSY	164	1167	15	50	2023-04-28 15:00:00	Other
2252	3	26	1944	1800	104	2149	1959	YX	1618	N217JQ	LGA	CMH	88	479	18	0	2023-03-26 18:00:00	Other
2260	9	15	2212	2200	12	13	2358	YX	1142	N751YX	EWR	ILM	69	488	22	0	2023-09-15 22:00:00	Other
2264	10	4	1907	1730	97	2044	1906	OO	1170	N256SY	JFK	BOS	34	187	17	30	2023-10-04 17:00:00	BOS
2272	4	10	2051	2000	51	2247	2209	9E	1398	N930XJ	JFK	RDU	66	427	20	0	2023-04-10 20:00:00	Other
2282	5	14	1001	946	15	1353	1341	UA	582	N68802	EWR	SJU	202	1608	9	46	2023-05-14 09:00:00	Other
2285	2	4	1121	938	103	1403	1231	AA	662	N9015D	LGA	EGE	238	1739	9	38	2023-02-04 09:00:00	Other
2287	7	29	1539	1440	59	1810	1736	UA	719	N34131	EWR	LAX	296	2454	14	40	2023-07-29 14:00:00	LAX
2294	3	19	2109	2050	19	2218	2220	9E	1315	N935XJ	LGA	IAD	48	229	20	50	2023-03-19 20:00:00	Other
2300	1	12	844	829	15	1031	1014	UA	238	N891UA	EWR	BNA	125	748	8	29	2023-01-12 08:00:00	Other
2302	9	28	1403	1315	48	1540	1438	B6	907	N324JB	JFK	DCA	43	213	13	15	2023-09-28 13:00:00	Other
2310	9	8	1842	1655	107	NA	1920	UA	946	N38446	EWR	DEN	NA	1605	16	55	2023-09-08 16:00:00	Other
2313	6	13	1935	1850	45	2052	2020	WN	746	N477WN	LGA	BNA	110	764	18	50	2023-06-13 18:00:00	Other
2316	6	19	1952	1935	17	2150	2125	YX	1377	N869RW	LGA	CMH	77	479	19	35	2023-06-19 19:00:00	Other
2320	10	15	2158	2059	59	10	2323	B6	895	N768JB	LGA	MSY	171	1183	20	59	2023-10-15 20:00:00	Other
2336	2	3	1140	1120	20	1328	1325	YX	1294	N872RW	LGA	ROA	76	405	11	20	2023-02-03 11:00:00	Other
2341	1	6	1141	1110	31	1438	1432	DL	697	N127DN	LGA	MIA	154	1096	11	10	2023-01-06 11:00:00	MIA
2348	6	6	1618	1600	18	1940	1844	DL	182	N395DZ	LGA	ATL	139	762	16	0	2023-06-06 16:00:00	ATL
2350	4	22	1953	1725	148	2300	1940	9E	1427	N132EV	JFK	CVG	117	589	17	25	2023-04-22 17:00:00	Other
2353	3	26	1445	1300	105	1746	1556	B6	43	N648JB	JFK	TPA	154	1005	13	0	2023-03-26 13:00:00	Other
2354	6	25	1832	1759	33	2120	2101	DL	106	N119DU	JFK	DFW	188	1391	17	59	2023-06-25 17:00:00	Other
2358	3	23	1957	1940	17	2341	2225	B6	47	N570JB	JFK	PHX	351	2153	19	40	2023-03-23 19:00:00	Other
2361	9	2	944	2115	749	1248	55	AA	49	N101NN	JFK	SFO	335	2586	21	15	2023-09-02 21:00:00	Other
2364	4	28	1731	1700	31	2108	2008	AA	877	N941AN	LGA	DFW	228	1389	17	0	2023-04-28 17:00:00	Other
2368	4	30	2032	1930	62	2333	2231	UA	461	N67845	EWR	PBI	151	1023	19	30	2023-04-30 19:00:00	Other
2390	2	22	842	817	25	1314	1311	UA	764	N66051	EWR	SJU	179	1608	8	17	2023-02-22 08:00:00	Other
2399	10	20	1613	1550	23	1919	1851	UA	507	N17317	EWR	FLL	153	1065	15	50	2023-10-20 15:00:00	FLL
2417	9	22	2022	1929	53	2322	2231	AS	79	N921VA	EWR	LAX	324	2454	19	29	2023-09-22 19:00:00	LAX
2426	8	6	2351	2245	66	223	139	F9	740	N308FR	LGA	DFW	191	1389	22	45	2023-08-06 22:00:00	Other
2429	8	2	2224	2102	82	21	2304	UA	489	N38459	EWR	MSP	146	1008	21	2	2023-08-02 21:00:00	Other
2434	4	30	1635	1500	95	1804	1624	YX	1574	N245JQ	LGA	BOS	39	184	15	0	2023-04-30 15:00:00	BOS
2435	3	2	2027	2015	12	2144	2131	B6	556	N267JB	LGA	BOS	36	184	20	15	2023-03-02 20:00:00	BOS
2440	2	1	1942	1845	57	2253	2147	UA	872	N17002	EWR	LAX	316	2454	18	45	2023-02-01 18:00:00	LAX
2441	5	26	1540	1255	165	1726	1445	WN	348	N8618N	LGA	STL	121	888	12	55	2023-05-26 12:00:00	Other
2445	1	31	1532	1455	37	1736	1700	YX	1788	N234JQ	JFK	CMH	97	483	14	55	2023-01-31 14:00:00	Other
2446	3	12	2010	1945	25	2301	2249	B6	455	N907JB	JFK	LAS	302	2248	19	45	2023-03-12 19:00:00	Other
2447	3	15	2255	2050	125	43	2259	9E	1428	N490PX	LGA	CAE	83	617	20	50	2023-03-15 20:00:00	Other
2459	3	18	1731	1713	18	1906	1855	UA	784	N457UA	EWR	ORD	119	719	17	13	2023-03-18 17:00:00	ORD
2461	11	17	715	700	15	1026	1033	AS	12	N975AK	JFK	SFO	335	2586	7	0	2023-11-17 07:00:00	Other
2464	3	29	1030	1000	30	1228	1201	B6	65	N375JB	JFK	DTW	95	509	10	0	2023-03-29 10:00:00	Other
2475	4	9	1419	1359	20	1623	1635	DL	170	N396DA	JFK	DEN	219	1626	13	59	2023-04-09 13:00:00	Other
2476	4	8	1221	800	261	1523	1055	B6	861	N564JB	JFK	TPA	151	1005	8	0	2023-04-08 08:00:00	Other
2492	6	5	1520	1304	136	1653	1438	UA	111	N76269	EWR	ORD	105	719	13	4	2023-06-05 13:00:00	ORD
2504	2	26	1933	1830	63	2304	2201	DL	126	N895DN	JFK	SEA	344	2422	18	30	2023-02-26 18:00:00	Other
2506	2	21	1548	1537	11	1850	1846	AA	841	N959NN	EWR	DFW	205	1372	15	37	2023-02-21 15:00:00	Other
2509	10	8	2031	1959	32	2312	2316	AS	76	N941AK	EWR	LAX	306	2454	19	59	2023-10-08 19:00:00	LAX
2516	5	12	1742	1615	87	1849	1750	WN	161	N8667D	LGA	BNA	106	764	16	15	2023-05-12 16:00:00	Other
2527	2	6	1944	1929	15	2117	2121	OO	1175	N256SY	JFK	BNA	122	765	19	29	2023-02-06 19:00:00	Other
2528	6	15	958	946	12	1202	1200	UA	916	N77258	LGA	DEN	209	1620	9	46	2023-06-15 09:00:00	Other
2539	6	7	1840	1730	70	2016	1927	YX	1315	N109HQ	LGA	CMH	82	479	17	30	2023-06-07 17:00:00	Other
2546	5	6	2313	2230	43	237	203	B6	907	N944JT	JFK	SFO	355	2586	22	30	2023-05-06 22:00:00	Other
2548	4	11	1526	1459	27	1629	1620	UA	674	N446UA	EWR	IAD	44	212	14	59	2023-04-11 14:00:00	Other
2549	2	22	2026	1857	89	2307	2131	UA	387	N37541	EWR	DEN	249	1605	18	57	2023-02-22 18:00:00	Other
2550	6	17	1320	1300	20	1728	1616	B6	616	N2027J	JFK	FLL	164	1069	13	0	2023-06-17 13:00:00	FLL
2558	1	16	1749	1708	41	1951	1915	DL	988	N331NW	LGA	DTW	74	502	17	8	2023-01-16 17:00:00	Other
2568	4	30	829	815	14	1211	1147	AA	293	N893NN	JFK	AUS	228	1521	8	15	2023-04-30 08:00:00	Other
2571	6	15	1512	1459	13	1624	1616	B6	761	N355JB	JFK	HYA	38	196	14	59	2023-06-15 14:00:00	Other
2580	3	22	1236	1225	11	1518	1531	AA	526	N406AN	EWR	MIA	141	1085	12	25	2023-03-22 12:00:00	MIA
2583	3	18	2306	2230	36	247	219	B6	144	N2029J	JFK	SJU	195	1598	22	30	2023-03-18 22:00:00	Other
2586	9	10	1017	959	18	NA	1223	9E	1470	N134EV	JFK	SAV	NA	718	9	59	2023-09-10 09:00:00	Other
2591	5	1	1642	1620	22	1936	1936	AA	96	N116AN	JFK	LAX	322	2475	16	20	2023-05-01 16:00:00	LAX
2592	6	1	1417	1359	18	1638	1651	UA	260	N24212	EWR	DFW	169	1372	13	59	2023-06-01 13:00:00	Other
2595	10	1	823	600	143	941	718	UA	397	N813UA	EWR	IAD	43	212	6	0	2023-10-01 06:00:00	Other
2609	7	17	1413	1359	14	1547	1536	9E	1282	N131EV	LGA	BHM	131	866	13	59	2023-07-17 13:00:00	Other
2610	9	11	1133	1000	93	1326	1219	9E	1716	N691CA	LGA	CVG	90	585	10	0	2023-09-11 10:00:00	Other
2614	5	16	1641	1535	66	1922	1843	B6	61	N504JB	JFK	MCO	135	944	15	35	2023-05-16 15:00:00	MCO
2615	2	13	1757	1740	17	2109	2105	NK	31	N916NK	EWR	LAX	345	2454	17	40	2023-02-13 17:00:00	LAX
2628	11	27	835	817	18	1046	1044	YX	1312	N107HQ	LGA	GRR	101	618	8	17	2023-11-27 08:00:00	Other
2632	9	29	1753	1714	39	1942	1859	YX	1333	N408YX	EWR	ORD	101	719	17	14	2023-09-29 17:00:00	ORD
2634	5	3	1809	1755	14	2002	2025	WN	878	N8791D	LGA	DEN	211	1620	17	55	2023-05-03 17:00:00	Other
2637	6	12	1854	1627	147	2020	1800	YX	1370	N869RW	LGA	RIC	52	292	16	27	2023-06-12 16:00:00	Other
2639	10	4	703	630	33	904	840	WN	1091	N8878L	LGA	DEN	218	1620	6	30	2023-10-04 06:00:00	Other
2645	4	18	2013	1955	18	2116	2105	YX	946	N721YX	EWR	AVP	25	93	19	55	2023-04-18 19:00:00	Other
2654	4	16	1533	1430	63	1758	1652	UA	417	N13718	EWR	ATL	115	746	14	30	2023-04-16 14:00:00	ATL
2659	7	10	851	730	81	1107	945	B6	276	N507JT	JFK	SAV	107	718	7	30	2023-07-10 07:00:00	Other
2661	2	26	1951	1859	52	2255	2219	UA	742	N69804	EWR	SEA	336	2402	18	59	2023-02-26 18:00:00	Other
2665	10	6	948	859	49	1204	1116	OO	1187	N254SY	LGA	OMA	171	1148	8	59	2023-10-06 08:00:00	Other
2672	4	13	1938	1925	13	2154	2242	UA	813	N58101	EWR	LAX	292	2454	19	25	2023-04-13 19:00:00	LAX
2678	11	27	1529	1453	36	1816	1804	NK	848	N611NK	EWR	FLL	156	1065	14	53	2023-11-27 14:00:00	FLL
2681	11	11	1754	1558	116	2047	1920	DL	383	N37700	LGA	MIA	149	1096	15	58	2023-11-11 15:00:00	MIA
2684	8	11	1343	1325	18	1600	1557	B6	776	N796JB	LGA	ATL	105	762	13	25	2023-08-11 13:00:00	ATL
2685	1	31	1833	1800	33	1945	1927	YX	1729	N201JQ	JFK	BOS	33	187	18	0	2023-01-31 18:00:00	BOS
2687	1	3	1006	950	16	1204	1201	AA	950	N907AA	EWR	CLT	85	529	9	50	2023-01-03 09:00:00	CLT
2689	9	20	1759	1740	19	2037	2034	B6	64	N709JB	JFK	TPA	140	1005	17	40	2023-09-20 17:00:00	Other
2690	8	10	2054	1958	56	2229	2129	OO	949	N296SY	LGA	MKE	124	738	19	58	2023-08-10 19:00:00	Other
2692	3	9	1347	1305	42	1517	1414	B6	327	N231JB	JFK	BOS	64	187	13	5	2023-03-09 13:00:00	BOS
2695	7	10	1656	1500	116	1811	1635	9E	1150	N482PX	LGA	MKE	100	738	15	0	2023-07-10 15:00:00	Other
2698	8	25	1045	847	118	1311	1115	UA	711	N874UA	EWR	ATL	97	746	8	47	2023-08-25 08:00:00	ATL
2707	12	15	1733	1436	177	2116	1744	UA	206	N27273	EWR	MIA	151	1085	14	36	2023-12-15 14:00:00	MIA
2708	4	9	821	805	16	938	939	9E	1393	N905XJ	JFK	ROC	46	264	8	5	2023-04-09 08:00:00	Other
2712	7	15	1633	1424	129	2012	1725	UA	231	N73270	EWR	SEA	324	2402	14	24	2023-07-15 14:00:00	Other
2717	2	18	1410	1345	25	1713	1717	B6	302	N552JB	JFK	SAT	224	1587	13	45	2023-02-18 13:00:00	Other
2718	10	21	2253	2230	23	225	145	B6	618	N987JT	JFK	LAX	341	2475	22	30	2023-10-21 22:00:00	LAX
2720	1	26	1133	1106	27	1305	1242	UA	850	N405UA	EWR	BNA	123	748	11	6	2023-01-26 11:00:00	Other
2731	3	16	1839	1825	14	2130	2125	AS	91	N292AK	EWR	SAN	328	2425	18	25	2023-03-16 18:00:00	Other
2739	4	5	2139	2120	19	2250	2216	9E	1319	N914XJ	LGA	ALB	32	136	21	20	2023-04-05 21:00:00	Other
2740	4	7	1638	1540	58	1859	1826	DL	137	N106DN	JFK	ATL	113	760	15	40	2023-04-07 15:00:00	ATL
2743	5	26	1905	1759	66	2155	2056	F9	625	N312FR	LGA	MCO	144	950	17	59	2023-05-26 17:00:00	MCO
2744	6	11	1352	1300	52	1554	1509	UA	937	N880UA	EWR	MSY	158	1167	13	0	2023-06-11 13:00:00	Other
2747	2	13	2100	2015	45	2353	2328	DL	263	N844DN	JFK	LAS	321	2248	20	15	2023-02-13 20:00:00	Other
2749	12	14	853	837	16	1145	1143	UA	806	N17285	EWR	TPA	141	997	8	37	2023-12-14 08:00:00	Other
2750	4	6	2123	2035	48	2332	2305	DL	841	N3738B	EWR	ATL	107	746	20	35	2023-04-06 20:00:00	ATL
2776	1	11	1145	928	137	1429	1244	UA	696	N16701	EWR	FLL	140	1065	9	28	2023-01-11 09:00:00	FLL
2777	7	12	957	940	17	1226	1238	B6	779	N593JB	JFK	TPA	127	1005	9	40	2023-07-12 09:00:00	Other
2779	3	2	1333	1220	73	1531	1427	9E	1458	N602LR	LGA	STL	154	888	12	20	2023-03-02 12:00:00	Other
2789	6	28	2026	1834	112	2138	2014	YX	1103	N656RW	EWR	ORF	45	284	18	34	2023-06-28 18:00:00	Other
2792	5	18	2349	2059	170	330	53	B6	316	N703JB	JFK	BQN	192	1576	20	59	2023-05-18 20:00:00	Other
2804	9	10	1115	845	150	1340	1048	UA	738	N4888U	EWR	GSP	95	594	8	45	2023-09-10 08:00:00	Other
2810	5	25	630	600	30	929	902	B6	142	N612JB	EWR	FLL	163	1065	6	0	2023-05-25 06:00:00	FLL
2825	7	18	1946	1700	166	2209	1949	AA	799	N953AN	LGA	DFW	183	1389	17	0	2023-07-18 17:00:00	Other
2830	2	21	1000	940	20	1224	1211	9E	1416	N916XJ	LGA	CVG	103	585	9	40	2023-02-21 09:00:00	Other
2831	9	10	810	750	20	1009	939	9E	1664	N181GJ	JFK	RDU	79	427	7	50	2023-09-10 07:00:00	Other
2835	5	7	2203	2129	34	2327	2306	YX	1013	N723YX	EWR	PIT	51	319	21	29	2023-05-07 21:00:00	Other
2837	2	9	1849	1815	34	2145	2126	NK	661	N670NK	EWR	FLL	152	1065	18	15	2023-02-09 18:00:00	FLL
2838	3	13	1335	1249	46	1458	1421	9E	1449	N606LR	LGA	BGR	53	378	12	49	2023-03-13 12:00:00	Other
2839	9	10	2025	1510	315	2322	1748	DL	966	N177DN	JFK	ATL	120	760	15	10	2023-09-10 15:00:00	ATL
2840	7	29	649	630	19	919	924	UA	727	N75851	EWR	LAX	300	2454	6	30	2023-07-29 06:00:00	LAX
2841	5	18	1650	1629	21	1838	1843	DL	248	N344NB	JFK	DTW	77	509	16	29	2023-05-18 16:00:00	Other
2843	7	28	2140	1945	115	12	2212	UA	603	N47414	EWR	DEN	229	1605	19	45	2023-07-28 19:00:00	Other
2856	12	23	1827	1740	47	2119	2100	WN	787	N946WN	LGA	HOU	207	1428	17	40	2023-12-23 17:00:00	Other
2858	4	20	1748	1737	11	1950	1915	AA	686	N802NN	LGA	ORD	114	733	17	37	2023-04-20 17:00:00	ORD
2860	6	11	738	710	28	1009	1011	DL	308	N360NB	LGA	TPA	134	1010	7	10	2023-06-11 07:00:00	Other
2865	7	13	2159	2051	68	2302	2144	YX	940	N756YX	EWR	PHL	26	80	20	51	2023-07-13 20:00:00	Other
2868	1	2	1909	1829	40	2236	2142	AA	201	N899NN	JFK	MIA	154	1089	18	29	2023-01-02 18:00:00	MIA
2869	5	21	1340	1329	11	1542	1547	9E	1521	N923XJ	LGA	IND	93	660	13	29	2023-05-21 13:00:00	Other
2882	3	3	2050	1959	51	2348	2307	DL	433	N126DN	LGA	MCO	146	950	19	59	2023-03-03 19:00:00	MCO
2883	10	2	741	710	31	1023	959	B6	183	N709JB	EWR	PBI	137	1023	7	10	2023-10-02 07:00:00	Other
2896	2	10	1149	1110	39	1517	1420	DL	507	N330DX	JFK	MIA	159	1089	11	10	2023-02-10 11:00:00	MIA
2915	2	21	1209	1125	44	1514	1502	AA	808	N945NN	LGA	MIA	156	1096	11	25	2023-02-21 11:00:00	MIA
2916	3	2	1626	1559	27	1830	1741	B6	816	N623JB	LGA	BNA	130	764	15	59	2023-03-02 15:00:00	Other
2917	9	10	1947	1900	47	2110	2039	AA	767	N983AN	LGA	ORD	110	733	19	0	2023-09-10 19:00:00	ORD
2923	2	11	856	840	16	1124	1128	DL	537	N801DZ	JFK	ATL	121	760	8	40	2023-02-11 08:00:00	ATL
2931	3	11	915	800	75	1401	1259	B6	193	N973JT	JFK	SJU	202	1598	8	0	2023-03-11 08:00:00	Other
2946	1	23	2015	1929	46	2154	2116	YX	1869	N212JQ	LGA	PIT	59	335	19	29	2023-01-23 19:00:00	Other
2954	10	2	1415	834	341	1647	1134	UA	274	N76523	EWR	SAN	309	2425	8	34	2023-10-02 08:00:00	Other
2962	10	9	1727	1135	352	1911	1328	OO	1203	N324SY	JFK	ORD	113	740	11	35	2023-10-09 11:00:00	ORD
2968	1	31	2019	1929	50	2323	2212	YX	1291	N402YX	LGA	LIT	203	1085	19	29	2023-01-31 19:00:00	Other
2973	11	17	1116	1059	17	1445	1415	DL	376	N342NW	LGA	PBI	144	1035	10	59	2023-11-17 10:00:00	Other
2976	6	9	1525	1429	56	1649	1554	UA	116	N489UA	EWR	IAD	44	212	14	29	2023-06-09 14:00:00	Other
2981	11	2	1640	1555	45	1928	1900	UA	803	N651UA	EWR	IAH	196	1400	15	55	2023-11-02 15:00:00	Other
2987	6	26	1524	940	344	1818	1203	B6	574	N563JB	JFK	DEN	241	1626	9	40	2023-06-26 09:00:00	Other
2992	2	16	1908	1840	28	8	2022	UA	445	N33284	EWR	ORD	NA	719	18	40	2023-02-16 18:00:00	ORD
2994	6	26	736	705	31	1022	1007	DL	610	N339DN	LGA	FLL	137	1076	7	5	2023-06-26 07:00:00	FLL
2999	6	26	2323	2051	152	149	2144	YX	1215	N655RW	EWR	PHL	24	80	20	51	2023-06-26 20:00:00	Other
3005	11	19	2101	2045	16	11	2354	B6	911	N563JB	JFK	MCO	130	944	20	45	2023-11-19 20:00:00	MCO
3013	3	31	852	650	122	958	800	B6	200	N279JB	JFK	BOS	40	187	6	50	2023-03-31 06:00:00	BOS
3014	6	10	1633	1600	33	1936	1916	B6	810	N763JB	JFK	PBI	131	1028	16	0	2023-06-10 16:00:00	Other
3015	3	15	1946	1859	47	2132	2044	UA	209	N459UA	EWR	RDU	63	416	18	59	2023-03-15 18:00:00	Other
3018	6	6	1712	1700	12	1902	1844	AA	1031	N814AW	LGA	STL	123	888	17	0	2023-06-06 17:00:00	Other
3021	2	28	858	749	69	1104	931	YX	1296	N404YX	LGA	CHO	62	305	7	49	2023-02-28 07:00:00	Other
3033	3	30	1220	1056	84	1533	1405	UA	439	N37545	EWR	MIA	172	1085	10	56	2023-03-30 10:00:00	MIA
3039	11	27	851	805	46	1103	1034	UA	828	N33103	EWR	DEN	220	1605	8	5	2023-11-27 08:00:00	Other
3049	5	11	1650	1629	21	1824	1816	UA	100	N465UA	EWR	RDU	63	416	16	29	2023-05-11 16:00:00	Other
3050	3	14	2106	1755	191	2353	2058	DL	596	N310DN	LGA	MCO	140	950	17	55	2023-03-14 17:00:00	MCO
3051	5	9	1313	1259	14	1449	1446	DL	460	N127DU	LGA	ORD	113	733	12	59	2023-05-09 12:00:00	ORD
3055	3	23	1714	1659	15	1946	2011	B6	347	N334JB	JFK	MCO	129	944	16	59	2023-03-23 16:00:00	MCO
3057	8	12	2231	2013	138	136	2255	YX	1033	N440YX	JFK	IND	109	665	20	13	2023-08-12 20:00:00	Other
3059	5	28	1731	1715	16	1943	1945	WN	390	N8527Q	LGA	ATL	103	762	17	15	2023-05-28 17:00:00	ATL
3060	8	23	924	859	25	1110	1048	YX	982	N431YX	JFK	CMH	76	483	8	59	2023-08-23 08:00:00	Other
3068	6	7	1736	1608	88	1909	1750	AA	551	N970NN	LGA	ORD	107	733	16	8	2023-06-07 16:00:00	ORD
3070	11	2	2225	2214	11	43	45	NK	559	N901NK	EWR	ATL	115	746	22	14	2023-11-02 22:00:00	ATL
3073	8	22	2126	2000	86	2359	2309	B6	651	N606JB	JFK	RNO	314	2411	20	0	2023-08-22 20:00:00	Other
3078	9	8	2125	2015	70	2346	2246	B6	917	N712JB	LGA	ATL	112	762	20	15	2023-09-08 20:00:00	ATL
3081	7	5	1951	1929	22	2340	2239	DL	389	N362NB	LGA	PBI	178	1035	19	29	2023-07-05 19:00:00	Other
3082	3	1	1943	1910	33	2245	2227	DL	638	N128DN	JFK	FLL	145	1069	19	10	2023-03-01 19:00:00	FLL
3085	4	6	1509	1455	14	1822	1758	AA	358	N950AN	LGA	DFW	216	1389	14	55	2023-04-06 14:00:00	Other
3097	5	18	2029	1930	59	2320	2245	UA	228	N69829	EWR	LAX	317	2454	19	30	2023-05-18 19:00:00	LAX
3101	12	8	1638	1625	13	1851	1845	WN	1157	N436WN	LGA	MCI	162	1107	16	25	2023-12-08 16:00:00	Other
3102	7	5	1620	1559	21	1748	1734	YX	926	N726YX	EWR	PIT	47	319	15	59	2023-07-05 15:00:00	Other
3107	7	1	1841	1830	11	2139	2131	UA	414	N38727	EWR	SNA	325	2434	18	30	2023-07-01 18:00:00	Other
3118	4	19	1150	925	145	1403	1202	DL	173	N391DN	LGA	ATL	103	762	9	25	2023-04-19 09:00:00	ATL
3119	4	26	1853	1825	28	2211	2131	AS	179	N478AS	EWR	SEA	338	2402	18	25	2023-04-26 18:00:00	Other
3120	4	19	1016	959	17	1240	1309	DL	893	N312DN	LGA	MCO	125	950	9	59	2023-04-19 09:00:00	MCO
3129	9	9	1823	1500	203	2225	1805	AA	991	N930NN	LGA	DFW	212	1389	15	0	2023-09-09 15:00:00	Other
3135	6	14	1340	1318	22	1639	1541	B6	677	N537JT	JFK	MSY	173	1182	13	18	2023-06-14 13:00:00	Other
3136	9	6	1129	1030	59	1240	1154	B6	596	N203JB	JFK	BUF	50	301	10	30	2023-09-06 10:00:00	Other
3140	5	7	856	805	51	1102	1030	DL	894	N102DU	JFK	MSY	152	1182	8	5	2023-05-07 08:00:00	Other
3147	6	8	2142	2130	12	41	56	B6	708	N968JT	JFK	LAX	317	2475	21	30	2023-06-08 21:00:00	LAX
3150	6	21	1626	1557	29	1847	1824	UA	470	N64844	EWR	ATL	107	746	15	57	2023-06-21 15:00:00	ATL
3152	4	22	232	2030	362	518	2322	B6	832	N965JT	JFK	MCO	137	944	20	30	2023-04-22 20:00:00	MCO
3153	6	24	1136	1059	37	1334	1311	DL	531	N372DN	LGA	MSP	156	1020	10	59	2023-06-24 10:00:00	Other
3162	11	20	1221	1205	16	1351	1350	YX	1365	N416YX	LGA	BNA	118	764	12	5	2023-11-20 12:00:00	Other
3165	3	17	1408	1355	13	1646	1645	AA	985	N834NN	JFK	PHX	317	2153	13	55	2023-03-17 13:00:00	Other
3170	6	11	2254	2159	55	32	2359	UA	609	N77537	EWR	DTW	79	488	21	59	2023-06-11 21:00:00	Other
3172	7	23	831	810	21	1210	1218	DL	594	N6711M	JFK	STT	194	1623	8	10	2023-07-23 08:00:00	Other
3174	6	29	2046	2010	36	2223	2143	9E	1655	N906XJ	LGA	ORF	57	296	20	10	2023-06-29 20:00:00	Other
3183	8	22	1218	1152	26	1315	1309	UA	237	N69839	EWR	BOS	35	200	11	52	2023-08-22 11:00:00	BOS
3201	9	13	1333	600	453	1447	722	AA	740	N758US	LGA	DCA	50	214	6	0	2023-09-13 06:00:00	Other
3211	7	23	851	811	40	1006	949	YX	875	N754YX	EWR	MKE	110	725	8	11	2023-07-23 08:00:00	Other
3213	7	13	2243	2150	53	NA	2314	UA	324	N37252	EWR	BOS	NA	200	21	50	2023-07-13 21:00:00	BOS
3216	4	29	621	600	21	918	908	NK	52	N687NK	LGA	FLL	146	1076	6	0	2023-04-29 06:00:00	FLL
3221	3	24	1945	1900	45	2252	2230	B6	29	N999JQ	JFK	SLC	282	1990	19	0	2023-03-24 19:00:00	Other
3224	5	29	2003	1848	75	2201	2050	AA	652	N996NN	LGA	CLT	76	544	18	48	2023-05-29 18:00:00	CLT
3226	6	27	1348	1259	49	1538	1500	DL	812	N303DN	LGA	DTW	86	502	12	59	2023-06-27 12:00:00	Other
3235	1	2	2143	1935	128	21	2254	DL	650	N398DN	JFK	MCO	127	944	19	35	2023-01-02 19:00:00	MCO
3236	6	14	1643	1438	125	2111	1837	B6	322	N612JB	JFK	SJU	209	1598	14	38	2023-06-14 14:00:00	Other
3245	5	21	1949	1830	79	2232	2200	B6	51	N2086J	JFK	SMF	318	2521	18	30	2023-05-21 18:00:00	Other
3247	3	17	1612	1600	12	1908	1903	UA	769	N410UA	EWR	FLL	155	1065	16	0	2023-03-17 16:00:00	FLL
3250	3	25	1713	1553	80	1850	1732	B6	267	N3065J	JFK	MKE	122	745	15	53	2023-03-25 15:00:00	Other
3256	3	27	847	614	153	1013	757	AA	1001	N808NN	EWR	ORD	121	719	6	14	2023-03-27 06:00:00	ORD
3257	1	13	846	800	46	1002	950	UA	759	N36247	EWR	ORD	105	719	8	0	2023-01-13 08:00:00	ORD
3268	5	20	1247	1125	82	1450	1400	UA	568	N37513	EWR	LAS	282	2227	11	25	2023-05-20 11:00:00	Other
3294	6	30	1851	1718	93	2010	1853	UA	819	N12114	EWR	ORD	98	719	17	18	2023-06-30 17:00:00	ORD
3307	4	11	2153	2140	13	47	134	DL	111	N717TW	JFK	SFO	328	2586	21	40	2023-04-11 21:00:00	Other
3310	7	25	1826	1520	186	2003	1700	WN	767	N8309C	LGA	STL	123	888	15	20	2023-07-25 15:00:00	Other
3313	8	28	2335	2145	110	225	47	B6	144	N537JT	LGA	FLL	154	1076	21	45	2023-08-28 21:00:00	FLL
3319	4	22	43	2050	233	343	28	UA	634	N14120	EWR	SFO	326	2565	20	50	2023-04-22 20:00:00	Other
3324	10	29	1841	1720	81	2149	2038	B6	750	N998JE	JFK	MIA	155	1089	17	20	2023-10-29 17:00:00	MIA
3328	12	4	718	705	13	834	835	9E	1693	N931XJ	LGA	ROC	51	254	7	5	2023-12-04 07:00:00	Other
3333	9	10	1210	1129	41	1550	1356	DL	361	N868DN	JFK	ATL	108	760	11	29	2023-09-10 11:00:00	ATL
3334	6	23	1447	1259	108	1724	1458	NK	517	N692NK	LGA	MYR	99	563	12	59	2023-06-23 12:00:00	Other
3336	11	28	2146	1931	135	2357	2155	9E	1465	N325PQ	JFK	DTW	91	509	19	31	2023-11-28 19:00:00	Other
3347	7	16	1229	1200	29	1428	1417	9E	1269	N935XJ	LGA	MCI	158	1107	12	0	2023-07-16 12:00:00	Other
3349	1	26	2346	1800	346	54	1936	AA	398	N807AW	LGA	DCA	46	214	18	0	2023-01-26 18:00:00	Other
3350	7	22	1816	1711	65	1942	1847	UA	514	N878UA	LGA	ORD	112	733	17	11	2023-07-22 17:00:00	ORD
3355	1	8	828	620	128	1132	927	UA	311	N67134	EWR	FLL	152	1065	6	20	2023-01-08 06:00:00	FLL
3363	1	14	1133	1100	33	1324	1328	YX	1135	N740YX	EWR	MCI	151	1092	11	0	2023-01-14 11:00:00	Other
3370	6	7	24	2159	145	154	2352	UA	421	N838UA	EWR	MEM	125	946	21	59	2023-06-07 21:00:00	Other
3372	10	1	2115	1929	106	2242	2138	OO	1225	N614CZ	JFK	ORD	112	740	19	29	2023-10-01 19:00:00	ORD
3387	2	26	858	615	163	1222	928	UA	322	N217UA	EWR	SFO	353	2565	6	15	2023-02-26 06:00:00	Other
3392	2	16	1642	1550	52	1845	1812	9E	1483	N695CA	LGA	CLT	92	544	15	50	2023-02-16 15:00:00	CLT
3401	4	30	701	650	11	817	800	B6	200	N198JB	JFK	BOS	33	187	6	50	2023-04-30 06:00:00	BOS
3406	9	5	1107	1050	17	1234	1230	WN	1019	N8816Q	LGA	STL	118	888	10	50	2023-09-05 10:00:00	Other
3409	9	11	2006	1759	127	2223	2024	UA	422	N62894	EWR	DEN	206	1605	17	59	2023-09-11 17:00:00	Other
3410	9	11	803	1613	950	1001	1814	AA	418	N857NN	EWR	CLT	79	529	16	13	2023-09-11 16:00:00	CLT
3417	5	11	1551	1500	51	1905	1810	UA	856	N14107	EWR	LAX	322	2454	15	0	2023-05-11 15:00:00	LAX
3427	8	30	1615	1515	60	1810	1738	B6	658	N3121J	JFK	MCI	154	1113	15	15	2023-08-30 15:00:00	Other
3437	4	29	1116	1102	14	1433	1400	UA	247	N845UA	EWR	PBI	148	1023	11	2	2023-04-29 11:00:00	Other
3441	3	5	2151	2101	50	30	2359	UA	418	N39418	EWR	MCO	129	937	21	1	2023-03-05 21:00:00	MCO
3458	7	5	741	730	11	952	946	B6	276	N526JL	JFK	SAV	97	718	7	30	2023-07-05 07:00:00	Other
3462	3	24	1557	1340	137	1744	1516	AA	150	N826NN	LGA	ORD	124	733	13	40	2023-03-24 13:00:00	ORD
3468	8	31	2125	1959	86	142	2357	UA	462	N62849	EWR	SJU	215	1608	19	59	2023-08-31 19:00:00	Other
3472	10	16	1148	1130	18	1253	1253	YX	1853	N206JQ	LGA	BOS	35	184	11	30	2023-10-16 11:00:00	BOS
3474	9	24	1757	1730	27	1959	1915	OO	1294	N311SY	JFK	MKE	117	745	17	30	2023-09-24 17:00:00	Other
3483	10	20	1053	951	62	1258	1229	UA	156	N14120	EWR	LAS	278	2227	9	51	2023-10-20 09:00:00	Other
3485	5	4	1703	1548	75	1948	1856	UA	756	N17300	EWR	FLL	146	1065	15	48	2023-05-04 15:00:00	FLL
3489	7	10	2045	2015	30	2206	2135	B6	449	N203JB	LGA	BOS	37	184	20	15	2023-07-10 20:00:00	BOS
3492	10	20	1353	1325	28	1714	1632	B6	110	N637JB	LGA	FLL	164	1076	13	25	2023-10-20 13:00:00	FLL
3497	4	26	2237	2215	22	158	131	DL	101	N837MH	JFK	LAX	309	2475	22	15	2023-04-26 22:00:00	LAX
3503	4	21	1755	1616	99	1926	1752	9E	1313	N308PQ	JFK	ORF	67	290	16	16	2023-04-21 16:00:00	Other
3504	5	24	2234	2159	35	2335	2321	UA	173	N69833	EWR	BOS	35	200	21	59	2023-05-24 21:00:00	BOS
3508	2	28	1533	1320	133	1815	1552	NK	36	N625NK	EWR	ATL	109	746	13	20	2023-02-28 13:00:00	ATL
3514	8	22	1532	1459	33	1805	1810	B6	441	N997JL	JFK	MCO	120	944	14	59	2023-08-22 14:00:00	MCO
3538	3	31	1210	1118	52	1515	1425	DL	469	N3773D	LGA	PBI	137	1035	11	18	2023-03-31 11:00:00	Other
3552	7	1	2004	1805	119	2234	2056	UA	339	N17719	EWR	JAC	242	1874	18	5	2023-07-01 18:00:00	Other
3559	4	21	1721	1658	23	1813	1812	YX	1021	N655RW	EWR	ALB	35	143	16	58	2023-04-21 16:00:00	Other
3564	4	2	645	629	16	932	914	B6	224	N665JB	JFK	MCO	139	944	6	29	2023-04-02 06:00:00	MCO
3578	3	15	1237	1150	47	1348	1315	WN	1023	N8743K	LGA	MDW	104	725	11	50	2023-03-15 11:00:00	Other
3589	8	5	1059	1046	13	1335	1340	B6	312	N665JB	JFK	MCO	130	944	10	46	2023-08-05 10:00:00	MCO
3600	9	28	1606	1434	92	1724	1556	B6	931	N206JB	JFK	BUF	56	301	14	34	2023-09-28 14:00:00	Other
3602	9	7	1014	1915	899	1300	2219	DL	141	N174DN	JFK	LAX	315	2475	19	15	2023-09-07 19:00:00	LAX
3605	2	28	1215	1203	12	1516	1457	DL	456	N368NW	JFK	PBI	136	1028	12	3	2023-02-28 12:00:00	Other
3613	2	21	1516	1459	17	1732	1717	DL	426	N301NB	LGA	MSP	171	1020	14	59	2023-02-21 14:00:00	Other
3614	12	21	1850	1832	18	2146	2150	AA	972	N804NN	EWR	MIA	147	1085	18	32	2023-12-21 18:00:00	MIA
3616	6	26	746	605	101	1020	845	WN	1050	N211WN	LGA	HOU	194	1428	6	5	2023-06-26 06:00:00	Other
3618	1	3	1925	1905	20	2231	2230	DL	433	N407DX	JFK	LAX	344	2475	19	5	2023-01-03 19:00:00	LAX
3621	6	25	1809	1315	294	1946	1435	B6	156	N239JB	LGA	BOS	46	184	13	15	2023-06-25 13:00:00	BOS
3628	8	12	2145	1940	125	19	2225	WN	579	N8880G	LGA	DAL	186	1381	19	40	2023-08-12 19:00:00	Other
3630	1	20	1555	1529	26	1854	1839	UA	774	N460UA	EWR	MIA	156	1085	15	29	2023-01-20 15:00:00	MIA
3642	9	7	933	857	36	1131	1121	9E	1677	N538CA	LGA	SAV	99	722	8	57	2023-09-07 08:00:00	Other
3650	2	9	1106	1045	21	1416	1407	DL	565	N365NB	LGA	RSW	168	1080	10	45	2023-02-09 10:00:00	Other
3663	1	31	904	815	49	1343	1324	DL	793	N699DL	JFK	STT	182	1623	8	15	2023-01-31 08:00:00	Other
3664	8	7	2216	1759	257	151	2044	B6	233	N949JT	JFK	LAS	304	2248	17	59	2023-08-07 17:00:00	Other
3666	7	14	1835	1530	185	NA	1839	UA	624	N209UA	EWR	SFO	NA	2565	15	30	2023-07-14 15:00:00	Other
3676	5	24	2231	1717	314	125	2029	B6	212	N580JB	LGA	FLL	148	1076	17	17	2023-05-24 17:00:00	FLL
3679	5	14	1514	1455	19	1627	1631	OO	1084	N259SY	JFK	IAD	50	228	14	55	2023-05-14 14:00:00	Other
3693	6	5	1541	1530	11	1825	1833	UA	522	N14118	EWR	LAX	306	2454	15	30	2023-06-05 15:00:00	LAX
3700	9	17	1858	1820	38	2137	2104	DL	240	N501DA	JFK	LAS	291	2248	18	20	2023-09-17 18:00:00	Other
3702	6	22	1004	936	28	1349	1340	B6	1034	N913JB	JFK	SJU	195	1598	9	36	2023-06-22 09:00:00	Other
3704	8	13	2112	2059	13	58	53	B6	737	N965JT	EWR	SJU	195	1608	20	59	2023-08-13 20:00:00	Other
3710	9	7	1530	1424	66	1806	1723	B6	317	N629JB	JFK	MCO	128	944	14	24	2023-09-07 14:00:00	MCO
3713	6	26	1848	1100	468	NA	1253	YX	1292	N110HQ	JFK	CLE	NA	425	11	0	2023-06-26 11:00:00	Other
3717	1	12	1230	1205	25	1407	1348	AA	504	N855NN	EWR	ORD	126	719	12	5	2023-01-12 12:00:00	ORD
3718	5	14	2202	2054	68	2324	2219	YX	1010	N723YX	EWR	MHT	41	209	20	54	2023-05-14 20:00:00	Other
3723	12	27	1618	1600	18	1927	1908	B6	658	N715JB	EWR	RSW	167	1068	16	0	2023-12-27 16:00:00	Other
3725	7	16	1938	1529	249	2322	1837	UA	400	N38443	EWR	SEA	335	2402	15	29	2023-07-16 15:00:00	Other
3731	3	10	1754	1714	40	1935	1855	UA	784	N17233	EWR	ORD	112	719	17	14	2023-03-10 17:00:00	ORD
3736	6	23	1629	1559	30	1916	1833	UA	457	N27258	EWR	LAS	301	2227	15	59	2023-06-23 15:00:00	Other
3748	6	20	1933	1850	43	2048	2020	WN	746	N7832A	LGA	BNA	108	764	18	50	2023-06-20 18:00:00	Other
3761	6	24	1603	1424	99	NA	1731	UA	233	N441UA	EWR	MIA	NA	1085	14	24	2023-06-24 14:00:00	MIA
3765	6	5	823	715	68	1038	931	DL	810	N3768	EWR	ATL	103	746	7	15	2023-06-05 07:00:00	ATL
3767	3	8	1815	1729	46	2005	1918	B6	442	N193JB	JFK	RDU	71	427	17	29	2023-03-08 17:00:00	Other
3773	3	2	1906	1850	16	2247	2230	UA	303	N67134	EWR	PHX	311	2133	18	50	2023-03-02 18:00:00	Other
3774	1	12	1248	1233	15	1608	1555	UA	866	N831UA	EWR	SAT	236	1569	12	33	2023-01-12 12:00:00	Other
3778	7	2	2115	2053	22	2251	2255	9E	1173	N490PX	LGA	GSO	69	461	20	53	2023-07-02 20:00:00	Other
3781	5	5	1525	1510	15	1740	1750	DL	132	N193DN	JFK	ATL	110	760	15	10	2023-05-05 15:00:00	ATL
3785	3	6	2117	2020	57	151	114	B6	979	N903JB	JFK	SJU	181	1598	20	20	2023-03-06 20:00:00	Other
3788	5	18	2335	2159	96	309	158	B6	418	N593JB	JFK	SJU	192	1598	21	59	2023-05-18 21:00:00	Other
3794	8	15	1804	1655	69	2058	1944	UA	140	N54711	EWR	DFW	188	1372	16	55	2023-08-15 16:00:00	Other
3795	7	12	1908	1357	311	2105	1616	9E	1183	N319PQ	LGA	TYS	88	647	13	57	2023-07-12 13:00:00	Other
3797	2	20	1544	1529	15	1839	1836	UA	737	N27274	EWR	FLL	147	1065	15	29	2023-02-20 15:00:00	FLL
3800	5	5	1441	1429	12	1647	1702	DL	138	N108DN	LGA	ATL	107	762	14	29	2023-05-05 14:00:00	ATL
3801	7	18	2222	1429	473	2347	1604	9E	1199	N272PQ	JFK	SYR	41	209	14	29	2023-07-18 14:00:00	Other
3802	12	25	1503	1440	23	1711	1655	B6	867	N273JB	JFK	CHS	92	636	14	40	2023-12-25 14:00:00	Other
3807	4	28	1656	1559	57	1849	1846	AA	549	N306RC	JFK	PHX	270	2153	15	59	2023-04-28 15:00:00	Other
3812	11	21	2246	2140	66	146	55	B6	26	N988JT	JFK	SAN	297	2446	21	40	2023-11-21 21:00:00	Other
3818	4	17	1940	1801	99	2251	2108	AA	597	N901NN	EWR	MIA	159	1085	18	1	2023-04-17 18:00:00	MIA
3822	2	28	1819	1800	19	2017	1957	OO	1174	N305SY	JFK	ORD	131	740	18	0	2023-02-28 18:00:00	ORD
3828	3	20	2208	2048	80	113	2356	UA	280	N24211	EWR	FLL	160	1065	20	48	2023-03-20 20:00:00	FLL
3829	5	13	1929	1750	99	2213	2053	B6	673	N506JB	LGA	MCO	126	950	17	50	2023-05-13 17:00:00	MCO
3831	2	18	2040	1950	50	2314	2259	DL	566	N335NB	JFK	PBI	135	1028	19	50	2023-02-18 19:00:00	Other
3834	12	21	1841	1815	26	2121	2120	WN	735	N7735A	LGA	TPA	141	1010	18	15	2023-12-21 18:00:00	Other
3838	6	6	1517	1459	18	1704	1651	YX	1781	N240JQ	LGA	MEM	133	963	14	59	2023-06-06 14:00:00	Other
3840	9	22	2022	2005	17	2238	2217	9E	1583	N325PQ	LGA	GRR	89	618	20	5	2023-09-22 20:00:00	Other
3841	8	10	1953	1935	18	2244	2240	DL	130	N177DN	JFK	LAX	323	2475	19	35	2023-08-10 19:00:00	LAX
3844	4	1	2049	1754	175	2359	2104	UA	506	N67815	EWR	SAN	339	2425	17	54	2023-04-01 17:00:00	Other
3863	9	10	1652	1115	337	1747	1235	B6	229	N306JB	LGA	BOS	33	184	11	15	2023-09-10 11:00:00	BOS
3868	12	10	1503	1419	44	1649	1616	YX	1822	N216JQ	LGA	CMH	84	479	14	19	2023-12-10 14:00:00	Other
3889	6	12	1305	1230	35	1542	1525	NK	352	N903NK	LGA	DFW	193	1389	12	30	2023-06-12 12:00:00	Other
3890	1	13	931	918	13	1304	1234	UA	696	N27253	EWR	FLL	175	1065	9	18	2023-01-13 09:00:00	FLL
3899	6	29	1548	755	473	1755	1001	DL	604	N365DN	LGA	MSP	156	1020	7	55	2023-06-29 07:00:00	Other
3906	6	14	1858	1829	29	2135	2142	AS	174	N481AS	EWR	SEA	309	2402	18	29	2023-06-14 18:00:00	Other
3908	6	3	1621	1530	51	1748	1658	B6	584	N216JB	JFK	BOS	41	187	15	30	2023-06-03 15:00:00	BOS
3909	3	24	1637	1415	142	1938	1749	B6	768	N643JB	LGA	RSW	156	1080	14	15	2023-03-24 14:00:00	Other
3910	8	6	1530	1517	13	1648	1634	UA	474	N33289	EWR	BOS	48	200	15	17	2023-08-06 15:00:00	BOS
3911	4	28	1910	1859	11	2134	2124	DL	741	N392DA	EWR	ATL	108	746	18	59	2023-04-28 18:00:00	ATL
3913	4	20	1320	1300	20	1609	1615	B6	669	N509JB	LGA	FLL	143	1076	13	0	2023-04-20 13:00:00	FLL
3914	6	30	36	2159	157	138	2323	UA	396	N27277	EWR	BOS	35	200	21	59	2023-06-30 21:00:00	BOS
3918	4	13	1744	1555	109	2047	1957	B6	233	N991JT	JFK	SFO	336	2586	15	55	2023-04-13 15:00:00	Other
3924	7	14	1748	939	489	1858	1048	B6	413	N323JB	JFK	MVY	39	173	9	39	2023-07-14 09:00:00	Other
3932	2	15	1631	1530	61	1755	1713	YX	1592	N218JQ	JFK	DCA	58	213	15	30	2023-02-15 15:00:00	Other
3934	2	26	1857	1835	22	2159	2142	UA	479	N37506	EWR	FLL	140	1065	18	35	2023-02-26 18:00:00	FLL
3942	1	11	933	835	58	1155	1100	9E	1556	N917XJ	LGA	TYS	99	647	8	35	2023-01-11 08:00:00	Other
3946	3	17	2213	2200	13	2327	2313	UA	567	N871UA	EWR	BOS	41	200	22	0	2023-03-17 22:00:00	BOS
3947	2	10	1627	1559	28	1900	1846	B6	630	N612JB	JFK	JAX	130	828	15	59	2023-02-10 15:00:00	Other
3951	2	21	2002	1945	17	2240	2254	B6	658	N206JB	LGA	PBI	138	1035	19	45	2023-02-21 19:00:00	Other
3953	4	17	1753	1709	44	1932	1915	DL	818	N375NC	LGA	DTW	77	502	17	9	2023-04-17 17:00:00	Other
3960	5	29	1913	1850	23	2145	2145	UA	639	N17265	EWR	MCO	127	937	18	50	2023-05-29 18:00:00	MCO
3964	8	20	2022	1935	47	2129	2122	OO	962	N257SY	JFK	BNA	101	765	19	35	2023-08-20 19:00:00	Other
3969	4	15	1947	1859	48	37	2308	DL	643	N903DN	JFK	SJU	195	1598	18	59	2023-04-15 18:00:00	Other
3971	1	6	1908	1835	33	2153	2141	UA	1025	N34137	EWR	PBI	132	1023	18	35	2023-01-06 18:00:00	Other
3975	4	29	1449	1425	24	1708	1626	YX	1056	N725YX	EWR	MYR	90	550	14	25	2023-04-29 14:00:00	Other
3977	4	3	1509	1045	264	1807	1336	B6	139	N999JQ	JFK	MCO	132	944	10	45	2023-04-03 10:00:00	MCO
3980	11	9	2002	1844	78	NA	2200	UA	446	N24729	EWR	SNA	NA	2434	18	44	2023-11-09 18:00:00	Other
3981	4	30	1848	1719	89	2021	1915	DL	764	N980AT	EWR	DTW	76	488	17	19	2023-04-30 17:00:00	Other
3985	5	17	1716	1659	17	1917	1919	YX	1025	N752YX	EWR	IND	100	645	16	59	2023-05-17 16:00:00	Other
3987	9	7	2052	1500	352	2259	1621	UA	742	N418UA	EWR	IAD	60	212	15	0	2023-09-07 15:00:00	Other
3988	9	7	2125	2000	85	109	2306	UA	504	N66893	EWR	MIA	164	1085	20	0	2023-09-07 20:00:00	MIA
3995	2	3	2127	1905	142	23	2218	DL	582	N371NW	JFK	TPA	141	1005	19	5	2023-02-03 19:00:00	Other
3996	9	18	1444	1329	75	1612	1508	UA	664	N27273	EWR	CLE	64	404	13	29	2023-09-18 13:00:00	Other
3997	1	4	1920	1423	297	2141	1618	NK	1268	N524NK	LGA	CLT	107	544	14	23	2023-01-04 14:00:00	CLT
4007	10	6	1044	1030	14	1155	1154	B6	562	N231JB	JFK	BUF	52	301	10	30	2023-10-06 10:00:00	Other
4008	11	16	2203	2140	23	108	59	NK	1156	N703NK	EWR	LAX	339	2454	21	40	2023-11-16 21:00:00	LAX
4015	3	14	1111	1059	12	1358	1311	YX	1190	N745YX	EWR	MSP	148	1008	10	59	2023-03-14 10:00:00	Other
4016	9	25	2115	1930	105	2350	2212	UA	959	N17294	EWR	DFW	189	1372	19	30	2023-09-25 19:00:00	Other
4026	9	10	2219	2110	69	152	2357	DL	147	N527DE	JFK	LAS	309	2248	21	10	2023-09-10 21:00:00	Other
4037	8	13	1724	1705	19	1910	1920	9E	1294	N916XJ	LGA	LIT	147	1085	17	5	2023-08-13 17:00:00	Other
4041	8	13	2205	2145	20	100	56	B6	634	N523JB	JFK	RSW	144	1074	21	45	2023-08-13 21:00:00	Other
4045	7	20	5	1925	280	247	2240	DL	389	N366NB	LGA	PBI	140	1035	19	25	2023-07-20 19:00:00	Other
4050	12	3	1126	1103	23	1407	1336	UA	476	N37561	EWR	JAX	133	820	11	3	2023-12-03 11:00:00	Other
4054	3	30	1808	1754	14	2052	2049	UA	839	N12116	EWR	MCO	126	937	17	54	2023-03-30 17:00:00	MCO
4056	9	23	1834	1520	194	2144	1754	B6	627	N729JB	JFK	JAX	112	828	15	20	2023-09-23 15:00:00	Other
4065	11	26	1659	1630	29	2038	1947	B6	308	N988JT	JFK	LAX	356	2475	16	30	2023-11-26 16:00:00	LAX
4068	1	14	1206	1150	16	1401	1355	UA	629	N890UA	EWR	CHS	91	628	11	50	2023-01-14 11:00:00	Other
4094	7	26	1625	1345	160	1839	1547	YX	1038	N405YX	LGA	CAE	91	617	13	45	2023-07-26 13:00:00	Other
4101	7	10	2008	1850	78	2151	2020	WN	591	N910WN	LGA	BNA	104	764	18	50	2023-07-10 18:00:00	Other
4105	1	20	2031	1954	37	113	50	UA	247	N62889	EWR	BQN	184	1585	19	54	2023-01-20 19:00:00	Other
4106	1	3	2320	2129	111	35	2247	YX	1203	N726YX	EWR	MHT	38	209	21	29	2023-01-03 21:00:00	Other
4107	3	21	2104	2015	49	47	2354	UA	882	N34137	EWR	SFO	372	2565	20	15	2023-03-21 20:00:00	Other
4111	5	4	950	900	50	1127	1027	YX	994	N747YX	EWR	DCA	41	199	9	0	2023-05-04 09:00:00	Other
4112	6	2	2249	2059	110	126	2350	B6	710	N635JB	EWR	MCO	127	937	20	59	2023-06-02 20:00:00	MCO
4116	9	15	2108	2029	39	2244	2209	AA	124	N754UW	LGA	ORD	110	733	20	29	2023-09-15 20:00:00	ORD
4120	2	16	2303	2045	138	119	2234	DL	451	N101DU	LGA	ORD	159	733	20	45	2023-02-16 20:00:00	ORD
4122	11	5	716	659	17	1017	1021	AA	536	N986NN	LGA	MIA	152	1096	6	59	2023-11-05 06:00:00	MIA
4132	4	2	2005	1840	85	35	2210	B6	50	N903JB	JFK	SMF	NA	2521	18	40	2023-04-02 18:00:00	Other
4136	3	1	1615	1540	35	1837	1824	DL	134	N706TW	JFK	ATL	116	760	15	40	2023-03-01 15:00:00	ATL
4139	12	11	2036	2007	29	2337	2321	UA	496	N61886	EWR	MIA	155	1085	20	7	2023-12-11 20:00:00	MIA
4142	5	21	1839	1720	79	2127	2025	WN	944	N8761L	LGA	HOU	195	1428	17	20	2023-05-21 17:00:00	Other
4144	2	1	1446	1300	106	1541	1425	YX	1575	N214JQ	LGA	BOS	34	184	13	0	2023-02-01 13:00:00	BOS
4150	4	17	1045	1025	20	1323	1303	DL	125	N374DX	LGA	ATL	121	762	10	25	2023-04-17 10:00:00	ATL
4153	6	7	2240	2121	79	111	2359	NK	283	N619NK	EWR	IAH	186	1400	21	21	2023-06-07 21:00:00	Other
4157	3	14	1155	1131	24	1351	1241	UA	646	N839UA	EWR	BOS	41	200	11	31	2023-03-14 11:00:00	BOS
4159	9	12	1547	1516	31	1839	1808	DL	208	N309DU	LGA	DFW	201	1389	15	16	2023-09-12 15:00:00	Other
4164	4	23	1400	1343	17	1521	1518	YX	1108	N118HQ	EWR	ORD	105	719	13	43	2023-04-23 13:00:00	ORD
4165	2	2	2216	2150	26	2330	2314	UA	873	N69826	EWR	IAD	39	212	21	50	2023-02-02 21:00:00	Other
4166	7	16	1340	1300	40	2055	1614	B6	498	N2002J	JFK	FLL	NA	1069	13	0	2023-07-16 13:00:00	FLL
4168	12	19	1745	1729	16	2042	2054	B6	921	N987JT	JFK	LAX	325	2475	17	29	2023-12-19 17:00:00	LAX
4173	6	30	1755	1730	25	2046	2030	AS	90	N587AS	EWR	PDX	325	2434	17	30	2023-06-30 17:00:00	Other
4181	11	3	2214	2150	24	2319	2257	UA	231	N77259	EWR	SYR	39	195	21	50	2023-11-03 21:00:00	Other
4184	11	27	1707	1649	18	1829	1827	9E	1463	N293PQ	LGA	BGR	52	378	16	49	2023-11-27 16:00:00	Other
4190	3	22	1502	1450	12	1629	1634	9E	1520	N478PX	EWR	RDU	69	416	14	50	2023-03-22 14:00:00	Other
4193	11	3	2210	2045	85	139	17	B6	445	N593JB	JFK	AUS	198	1521	20	45	2023-11-03 20:00:00	Other
4197	11	17	900	848	12	1047	1049	9E	1696	N917XJ	LGA	STL	128	888	8	48	2023-11-17 08:00:00	Other
4201	11	7	1801	1645	76	2255	2000	B6	616	N3085J	JFK	RSW	NA	1074	16	45	2023-11-07 16:00:00	Other
4211	1	11	1111	810	181	1341	1055	DL	404	N382DN	LGA	ATL	114	762	8	10	2023-01-11 08:00:00	ATL
4224	8	19	1500	1225	155	1654	1441	UA	702	N69847	EWR	DEN	199	1605	12	25	2023-08-19 12:00:00	Other
4225	10	1	703	608	55	857	755	DL	743	N894AT	EWR	DTW	73	488	6	8	2023-10-01 06:00:00	Other
4230	5	20	2047	2015	32	110	20	B6	708	N958JB	JFK	SJU	211	1598	20	15	2023-05-20 20:00:00	Other
4241	1	1	1630	1530	60	1929	1842	B6	390	N641JB	JFK	MCO	148	944	15	30	2023-01-01 15:00:00	MCO
4245	1	12	1939	1859	40	2124	2035	UA	870	N436UA	EWR	MSN	120	799	18	59	2023-01-12 18:00:00	Other
4247	7	15	2058	1753	185	8	2049	UA	525	N34455	EWR	TPA	129	997	17	53	2023-07-15 17:00:00	Other
4260	7	26	1702	1347	195	1808	1453	YX	923	N855RW	EWR	PVD	34	160	13	47	2023-07-26 13:00:00	Other
4262	3	28	750	730	20	935	900	B6	399	N187JB	JFK	BNA	140	765	7	30	2023-03-28 07:00:00	Other
4267	12	31	943	930	13	1209	1256	AS	6	N471AS	JFK	SEA	302	2422	9	30	2023-12-31 09:00:00	Other
4268	8	11	1632	1525	67	1759	1713	9E	1290	N538CA	JFK	PWM	51	273	15	25	2023-08-11 15:00:00	Other
4272	7	5	1838	1808	30	2114	2130	DL	715	N320US	JFK	AUS	188	1521	18	8	2023-07-05 18:00:00	Other
4274	2	25	1235	1219	16	1502	1452	B6	916	N317JB	JFK	ATL	124	760	12	19	2023-02-25 12:00:00	ATL
4275	5	19	822	759	23	1107	1100	AA	322	N932NN	JFK	DFW	188	1391	7	59	2023-05-19 07:00:00	Other
4276	9	17	721	632	49	836	750	B6	979	N2043J	JFK	BUF	50	301	6	32	2023-09-17 06:00:00	Other
4290	1	31	2034	1940	54	2343	2253	DL	711	N371NW	LGA	TPA	151	1010	19	40	2023-01-31 19:00:00	Other
4300	7	23	831	730	61	951	908	B6	327	N317JB	JFK	ORD	109	740	7	30	2023-07-23 07:00:00	ORD
4306	7	26	952	935	17	1142	1150	WN	120	N210WN	LGA	MCI	147	1107	9	35	2023-07-26 09:00:00	Other
4312	12	8	2207	2135	32	254	231	B6	654	N2039J	JFK	SJU	188	1598	21	35	2023-12-08 21:00:00	Other
4321	9	3	1520	1440	40	1758	1736	UA	884	N14118	EWR	LAX	306	2454	14	40	2023-09-03 14:00:00	LAX
4322	9	19	1553	1534	19	1832	1837	UA	378	N447UA	EWR	AUS	194	1504	15	34	2023-09-19 15:00:00	Other
4324	3	2	1843	1828	15	2247	2145	UA	516	N15712	EWR	SNA	383	2434	18	28	2023-03-02 18:00:00	Other
4326	2	12	1822	1755	27	2145	2136	AA	809	N323RM	LGA	MIA	155	1096	17	55	2023-02-12 17:00:00	MIA
4334	2	17	1144	1054	50	1448	1340	F9	565	N373FR	LGA	ATL	136	762	10	54	2023-02-17 10:00:00	ATL
4339	1	6	2037	1940	57	2146	2110	DL	677	N107DU	JFK	BOS	34	187	19	40	2023-01-06 19:00:00	BOS
4340	8	15	2114	1959	75	28	2310	AA	608	N820NN	LGA	MIA	170	1096	19	59	2023-08-15 19:00:00	MIA
4343	9	18	1141	1125	16	1437	1422	DL	429	N851DN	JFK	TPA	144	1005	11	25	2023-09-18 11:00:00	Other
4349	3	3	1300	1115	105	1556	1422	AA	477	N789AN	JFK	MIA	147	1089	11	15	2023-03-03 11:00:00	MIA
4358	1	30	1706	1620	46	2027	1951	AA	579	N722US	LGA	MIA	153	1096	16	20	2023-01-30 16:00:00	MIA
4363	5	30	2214	2120	54	2354	2320	YX	1092	N655RW	EWR	MEM	128	946	21	20	2023-05-30 21:00:00	Other
4373	10	13	1817	1739	38	2107	2003	9E	1468	N935XJ	LGA	SBN	113	651	17	39	2023-10-13 17:00:00	Other
4376	6	8	1733	1629	64	1901	1811	UA	822	N13718	EWR	CLE	62	404	16	29	2023-06-08 16:00:00	Other
4394	8	8	1745	1700	45	1900	1839	YX	1040	N421YX	JFK	ORF	52	290	17	0	2023-08-08 17:00:00	Other
4396	6	2	2150	1929	141	2251	2100	YX	1799	N235JQ	LGA	DCA	43	214	19	29	2023-06-02 19:00:00	Other
4397	2	1	751	735	16	1135	950	B6	42	N821JB	JFK	MSP	173	1029	7	35	2023-02-01 07:00:00	Other
4398	2	16	1040	1000	40	1708	1605	HA	22	N375HA	JFK	HNL	654	4983	10	0	2023-02-16 10:00:00	Other
4410	5	17	1616	1550	26	1911	1952	B6	227	N943JT	JFK	SFO	334	2586	15	50	2023-05-17 15:00:00	Other
4412	7	22	2050	2029	21	2344	2357	AS	17	N536AS	JFK	SFO	329	2586	20	29	2023-07-22 20:00:00	Other
4413	2	18	1735	1429	186	2025	1720	UA	406	N12109	EWR	MCO	127	937	14	29	2023-02-18 14:00:00	MCO
4414	9	17	1844	1759	45	2126	2058	NK	510	N630NK	EWR	MCO	134	937	17	59	2023-09-17 17:00:00	MCO
4415	12	10	1605	1459	66	1904	1814	NK	600	N687NK	LGA	FLL	161	1076	14	59	2023-12-10 14:00:00	FLL
4420	7	25	1643	1231	252	1815	1414	DL	695	N938AT	EWR	DTW	72	488	12	31	2023-07-25 12:00:00	Other
4424	7	27	1840	1759	41	2138	2104	B6	752	N534JB	JFK	MCO	126	944	17	59	2023-07-27 17:00:00	MCO
4428	5	26	2119	2100	19	15	2359	NK	977	N642NK	EWR	MIA	155	1085	21	0	2023-05-26 21:00:00	MIA
4434	11	19	2050	2005	45	14	2350	B6	306	N969JT	JFK	SFO	338	2586	20	5	2023-11-19 20:00:00	Other
4450	7	20	1713	1702	11	2057	2014	B6	64	N562JB	JFK	TPA	147	1005	17	2	2023-07-20 17:00:00	Other
4453	2	17	1547	1510	37	1927	1835	B6	828	N283JB	LGA	SRQ	176	1047	15	10	2023-02-17 15:00:00	Other
4460	5	25	1831	1741	50	2026	1945	9E	1404	N307PQ	LGA	MYR	90	563	17	41	2023-05-25 17:00:00	Other
4463	5	10	1725	1659	26	2030	2023	DL	270	N511DE	JFK	SEA	333	2422	16	59	2023-05-10 16:00:00	Other
4480	1	24	2121	2043	38	2301	2240	9E	1667	N478PX	LGA	RDU	70	431	20	43	2023-01-24 20:00:00	Other
4486	6	17	1830	1538	172	2014	1710	UA	797	N37437	EWR	ORD	108	719	15	38	2023-06-17 15:00:00	ORD
4488	6	3	1657	1629	28	1901	1843	DL	266	N362NB	JFK	DTW	77	509	16	29	2023-06-03 16:00:00	Other
4495	4	26	2143	2109	34	13	2341	UA	462	N14731	EWR	JAX	112	820	21	9	2023-04-26 21:00:00	Other
4496	3	24	1950	1929	21	2213	2159	9E	1437	N306PQ	JFK	MSP	171	1029	19	29	2023-03-24 19:00:00	Other
4501	2	4	1406	1344	22	1707	1655	B6	698	N789JB	JFK	IAH	207	1417	13	44	2023-02-04 13:00:00	Other
4503	8	30	1234	1159	35	1517	1453	UA	586	N17303	EWR	IAH	192	1400	11	59	2023-08-30 11:00:00	Other
4513	3	6	1552	1515	37	1733	1632	B6	158	N328JB	LGA	BOS	47	184	15	15	2023-03-06 15:00:00	BOS
4520	11	21	1542	1515	27	1710	1654	UA	918	N73276	LGA	ORD	114	733	15	15	2023-11-21 15:00:00	ORD
4529	2	19	1808	1740	28	2156	2105	NK	31	N971NK	EWR	LAX	382	2454	17	40	2023-02-19 17:00:00	LAX
4535	4	27	2221	2155	26	2329	2316	9E	1259	N195PQ	LGA	ROC	44	254	21	55	2023-04-27 21:00:00	Other
4538	10	23	1849	1710	99	2215	2009	B6	115	N2039J	JFK	MCO	131	944	17	10	2023-10-23 17:00:00	MCO
4550	4	6	1518	1503	15	1843	1804	DL	303	N3747D	LGA	PBI	164	1035	15	3	2023-04-06 15:00:00	Other
4553	6	22	2041	1939	62	2339	2247	B6	128	N913JB	JFK	ONT	310	2429	19	39	2023-06-22 19:00:00	Other
4562	8	25	1111	1059	12	1304	1259	NK	500	N706NK	LGA	DTW	80	502	10	59	2023-08-25 10:00:00	Other
4564	1	12	2239	2155	44	2340	2306	DL	892	N110DU	LGA	SYR	40	198	21	55	2023-01-12 21:00:00	Other
4584	2	20	541	530	11	714	708	AA	870	N920NN	EWR	ORD	126	719	5	30	2023-02-20 05:00:00	ORD
4586	8	27	1610	1459	71	1804	1707	9E	1263	N909XJ	JFK	CLE	77	425	14	59	2023-08-27 14:00:00	Other
4587	5	15	1625	1600	25	1744	1722	AA	741	N817AW	LGA	DCA	41	214	16	0	2023-05-15 16:00:00	Other
4589	10	20	753	715	38	1019	1020	UA	147	N57286	EWR	SNA	300	2434	7	15	2023-10-20 07:00:00	Other
4596	11	21	2117	2029	48	121	2315	DL	819	N121DU	JFK	JAX	138	828	20	29	2023-11-21 20:00:00	Other
4603	8	13	714	657	17	1004	940	B6	238	N990JL	JFK	LAX	317	2475	6	57	2023-08-13 06:00:00	LAX
4604	4	16	2202	1856	186	114	2204	NK	619	N657NK	EWR	FLL	148	1065	18	56	2023-04-16 18:00:00	FLL
4615	1	22	1244	1215	29	1448	1450	UA	715	N13227	LGA	DEN	219	1620	12	15	2023-01-22 12:00:00	Other
4620	3	10	1632	1535	57	1823	1733	9E	1479	N294PQ	LGA	ILM	79	500	15	35	2023-03-10 15:00:00	Other
4622	2	3	2025	1825	120	2327	2139	B6	21	N784JB	LGA	TPA	143	1010	18	25	2023-02-03 18:00:00	Other
4628	7	24	1149	1129	20	1302	1254	UA	407	N17752	EWR	BNA	104	748	11	29	2023-07-24 11:00:00	Other
4629	6	10	1203	1048	75	1445	1316	F9	580	N311FR	LGA	ATL	105	762	10	48	2023-06-10 10:00:00	ATL
4635	11	10	636	607	29	948	909	AA	952	N826NN	EWR	DFW	221	1372	6	7	2023-11-10 06:00:00	Other
4647	5	31	1536	1500	36	1630	1613	9E	1490	N183GJ	LGA	PVD	31	143	15	0	2023-05-31 15:00:00	Other
4661	11	27	1310	1259	11	1535	1537	DL	280	N377DN	LGA	ATL	125	762	12	59	2023-11-27 12:00:00	ATL
4665	3	27	1421	1410	11	1657	1656	UA	408	N27251	EWR	MCO	136	937	14	10	2023-03-27 14:00:00	MCO
4668	7	21	1425	940	285	1712	1238	B6	779	N593JB	JFK	TPA	141	1005	9	40	2023-07-21 09:00:00	Other
4671	9	3	2030	1930	60	2319	2247	B6	344	N653JB	JFK	PDX	319	2454	19	30	2023-09-03 19:00:00	Other
4672	1	13	1815	1800	15	2000	2020	DL	478	N323US	LGA	MSP	138	1020	18	0	2023-01-13 18:00:00	Other
4676	9	20	1722	1659	23	1931	1923	DL	892	N378DA	EWR	ATL	106	746	16	59	2023-09-20 16:00:00	ATL
4682	6	11	1224	1159	25	1329	1317	UA	912	N39728	EWR	PWM	49	284	11	59	2023-06-11 11:00:00	Other
4684	1	26	1817	1640	97	2203	1950	NK	720	N674NK	EWR	FLL	198	1065	16	40	2023-01-26 16:00:00	FLL
4688	1	10	845	810	35	1055	1055	DL	404	N354DN	LGA	ATL	110	762	8	10	2023-01-10 08:00:00	ATL
4690	9	30	2042	1959	43	2333	2324	AS	83	N978AK	EWR	SFO	318	2565	19	59	2023-09-30 19:00:00	Other
4691	7	18	2254	2059	115	13	2233	UA	703	N828UA	EWR	MSN	115	799	20	59	2023-07-18 20:00:00	Other
4699	3	24	957	855	62	1339	1223	DL	184	N174DN	JFK	LAX	365	2475	8	55	2023-03-24 08:00:00	LAX
4702	4	6	1352	1229	83	1455	1351	9E	1192	N490PX	LGA	SYR	38	198	12	29	2023-04-06 12:00:00	Other
4717	11	2	1602	1546	16	1906	1845	DL	122	N112DN	LGA	MCO	140	950	15	46	2023-11-02 15:00:00	MCO
4718	4	27	1402	1310	52	1535	1441	UA	111	N27273	EWR	ORD	113	719	13	10	2023-04-27 13:00:00	ORD
4719	4	17	18	2225	113	422	227	NK	353	N698NK	EWR	SJU	227	1608	22	25	2023-04-17 22:00:00	Other
4724	5	19	1355	1329	26	1602	1602	DL	188	N311DN	LGA	ATL	105	762	13	29	2023-05-19 13:00:00	ATL
4733	12	5	1250	1220	30	1439	1435	DL	977	N134DU	JFK	MSP	149	1029	12	20	2023-12-05 12:00:00	Other
4736	3	13	1236	1150	46	1355	1315	WN	1023	N8818Q	LGA	MDW	109	725	11	50	2023-03-13 11:00:00	Other
4737	3	15	1435	1345	50	1612	1511	YX	1741	N815MD	LGA	DCA	43	214	13	45	2023-03-15 13:00:00	Other
4739	3	4	1839	1800	39	2030	1957	OO	1236	N296SY	JFK	ORD	124	740	18	0	2023-03-04 18:00:00	ORD
4740	3	13	1116	1035	41	1533	1337	B6	137	N907JB	JFK	MCO	168	944	10	35	2023-03-13 10:00:00	MCO
4741	7	14	2316	2159	77	29	2327	YX	1069	N428YX	JFK	BOS	45	187	21	59	2023-07-14 21:00:00	BOS
4748	11	18	1601	1540	21	1846	1845	DL	785	N303DN	JFK	MCO	129	944	15	40	2023-11-18 15:00:00	MCO
4751	8	26	2227	2210	17	37	33	NK	226	N953NK	EWR	LAS	293	2227	22	10	2023-08-26 22:00:00	Other
4754	5	22	1243	1230	13	1606	1534	AA	637	N438AN	EWR	MIA	185	1085	12	30	2023-05-22 12:00:00	MIA
4756	12	10	1158	1100	58	1551	1334	B6	694	N629JB	LGA	DEN	NA	1620	11	0	2023-12-10 11:00:00	Other
4762	2	24	1550	1450	60	1821	1731	DL	354	N325DN	LGA	ATL	128	762	14	50	2023-02-24 14:00:00	ATL
4769	1	2	521	500	21	755	815	AA	499	N907NN	EWR	MIA	136	1085	5	0	2023-01-02 05:00:00	MIA
4799	4	23	1636	1620	16	1916	1911	UA	123	N13113	EWR	MCO	136	937	16	20	2023-04-23 16:00:00	MCO
4809	11	13	807	755	12	1055	1049	NK	430	N660NK	EWR	MCO	136	937	7	55	2023-11-13 07:00:00	MCO
4812	2	20	1934	1729	125	2253	2039	UA	597	N47284	EWR	RSW	167	1068	17	29	2023-02-20 17:00:00	Other
4814	3	19	849	830	19	1141	1140	UA	578	N12006	EWR	LAX	307	2454	8	30	2023-03-19 08:00:00	LAX
4825	8	9	817	759	18	1131	1110	AA	478	N324SH	JFK	MIA	154	1089	7	59	2023-08-09 07:00:00	MIA
4827	12	6	1703	1630	33	1950	1948	B6	154	N556JB	LGA	FLL	135	1076	16	30	2023-12-06 16:00:00	FLL
4835	8	8	607	530	37	904	810	B6	36	N967JT	JFK	LAX	335	2475	5	30	2023-08-08 05:00:00	LAX
4838	2	6	2015	1959	16	2227	2242	DL	433	N6714Q	JFK	ATL	102	760	19	59	2023-02-06 19:00:00	ATL
4850	2	17	1937	1840	57	2125	2022	UA	445	N403UA	EWR	ORD	112	719	18	40	2023-02-17 18:00:00	ORD
4855	9	24	1735	1635	60	1938	1859	DL	788	N336NB	JFK	MSY	149	1182	16	35	2023-09-24 16:00:00	Other
4859	7	20	1252	1008	164	1539	1317	B6	479	N971JT	JFK	RSW	151	1074	10	8	2023-07-20 10:00:00	Other
4863	5	21	2136	2102	34	2347	2334	UA	508	N68843	EWR	ATL	104	746	21	2	2023-05-21 21:00:00	ATL
4865	6	25	1252	1030	142	1654	1326	UA	685	N41135	EWR	LAX	328	2454	10	30	2023-06-25 10:00:00	LAX
4866	1	26	2249	2230	19	33	2354	9E	1551	N131EV	JFK	SYR	43	209	22	30	2023-01-26 22:00:00	Other
4878	2	18	1643	1030	373	1941	1353	B6	77	N629JB	LGA	FLL	143	1076	10	30	2023-02-18 10:00:00	FLL
4880	4	13	1004	935	29	1253	1229	B6	228	N595JB	LGA	MCO	144	950	9	35	2023-04-13 09:00:00	MCO
4887	12	26	1707	1655	12	2007	2031	AA	646	N420AN	EWR	PHX	270	2133	16	55	2023-12-26 16:00:00	Other
4895	8	21	1547	1530	17	1729	1705	UA	552	N76254	EWR	ORD	111	719	15	30	2023-08-21 15:00:00	ORD
4896	8	30	800	715	45	1052	959	DL	438	N119DN	LGA	MCO	138	950	7	15	2023-08-30 07:00:00	MCO
4898	9	12	2147	2130	17	18	3	DL	844	N527DE	JFK	ATL	121	760	21	30	2023-09-12 21:00:00	ATL
4901	1	19	40	2000	280	336	2332	B6	735	N962JT	JFK	LAX	336	2475	20	0	2023-01-19 20:00:00	LAX
4908	9	22	703	600	63	1013	853	B6	1	N956JT	JFK	FLL	159	1069	6	0	2023-09-22 06:00:00	FLL
4917	7	25	845	745	60	1020	917	UA	702	N41135	EWR	ORD	111	719	7	45	2023-07-25 07:00:00	ORD
4920	1	25	1525	1455	30	1820	1750	9E	1391	N600LR	JFK	JAX	140	828	14	55	2023-01-25 14:00:00	Other
4921	11	27	814	750	24	1035	1019	9E	1706	N937XJ	LGA	MCI	179	1107	7	50	2023-11-27 07:00:00	Other
4937	3	27	1352	1311	41	1806	1528	YX	1199	N743YX	EWR	HHH	NA	687	13	11	2023-03-27 13:00:00	Other
4939	7	9	1014	1300	1274	1215	1509	UA	735	N803UA	EWR	MSY	162	1167	13	0	2023-07-09 13:00:00	Other
4940	6	11	1734	1715	19	2047	2106	DL	309	N722TW	JFK	SFO	329	2586	17	15	2023-06-11 17:00:00	Other
4941	1	20	1636	1600	36	1836	1820	YX	1244	N747YX	EWR	CVG	101	569	16	0	2023-01-20 16:00:00	Other
4943	3	4	1117	1105	12	1459	1431	DL	636	N384DN	LGA	MIA	169	1096	11	5	2023-03-04 11:00:00	MIA
4948	4	3	1952	1924	28	2138	2126	AA	292	N835NN	EWR	CLT	81	529	19	24	2023-04-03 19:00:00	CLT
4954	3	26	1530	1421	69	1903	1746	B6	768	N568JB	LGA	RSW	165	1080	14	21	2023-03-26 14:00:00	Other
4984	10	10	957	900	57	1253	1218	AA	1	N113AN	JFK	LAX	328	2475	9	0	2023-10-10 09:00:00	LAX
4997	4	5	1944	1900	44	2222	2150	DL	408	N3758Y	JFK	ATL	107	760	19	0	2023-04-05 19:00:00	ATL
5002	4	27	1701	1630	31	1925	1901	UA	762	N776UA	EWR	LAS	298	2227	16	30	2023-04-27 16:00:00	Other
5008	1	11	2348	2030	198	254	6	AA	57	N113AN	JFK	LAX	341	2475	20	30	2023-01-11 20:00:00	LAX
5023	8	25	929	800	89	1043	940	9E	1184	N916XJ	LGA	ORF	50	296	8	0	2023-08-25 08:00:00	Other
5028	12	3	1809	1729	40	2156	2032	UA	732	N14731	EWR	SRQ	176	1034	17	29	2023-12-03 17:00:00	Other
5034	5	14	2046	1900	106	2231	2030	WN	53	N8737L	LGA	MDW	114	725	19	0	2023-05-14 19:00:00	Other
5037	9	17	1937	1850	47	2326	2221	DL	205	N507DZ	JFK	SEA	319	2422	18	50	2023-09-17 18:00:00	Other
5042	5	4	1337	1025	192	1532	1254	YX	1613	N211JQ	LGA	IND	92	660	10	25	2023-05-04 10:00:00	Other
5063	11	4	2012	2001	11	3	2357	UA	541	N37513	EWR	SJU	214	1608	20	1	2023-11-04 20:00:00	Other
5069	11	15	1516	1408	68	1726	1633	UA	382	N69885	EWR	DEN	221	1605	14	8	2023-11-15 14:00:00	Other
5071	9	10	1714	943	451	1940	1153	B6	976	N304JB	JFK	CHS	112	636	9	43	2023-09-10 09:00:00	Other
5076	6	29	1453	1420	33	1636	1552	YX	1063	N762YX	EWR	MKE	130	725	14	20	2023-06-29 14:00:00	Other
5082	1	23	2032	2015	17	2310	2315	UA	872	N35236	EWR	MCO	136	937	20	15	2023-01-23 20:00:00	MCO
5087	4	16	1655	1300	235	1959	1619	B6	316	N706JB	JFK	SLC	267	1990	13	0	2023-04-16 13:00:00	Other
5094	10	4	2147	2129	18	2249	2236	9E	1671	N478PX	LGA	ALB	27	136	21	29	2023-10-04 21:00:00	Other
5095	7	23	2122	2007	75	2245	2137	UA	522	N27722	EWR	BNA	105	748	20	7	2023-07-23 20:00:00	Other
5100	4	16	1819	1422	237	2015	1618	YX	1567	N207JQ	LGA	CMH	79	479	14	22	2023-04-16 14:00:00	Other
5106	4	30	2010	1600	250	2123	1730	YX	1468	N879RW	LGA	BOS	33	184	16	0	2023-04-30 16:00:00	BOS
5109	3	27	1200	1000	120	1415	1201	B6	65	N283JB	JFK	DTW	97	509	10	0	2023-03-27 10:00:00	Other
5116	8	15	1629	1605	24	1943	1903	AA	798	N994NN	LGA	DFW	199	1389	16	5	2023-08-15 16:00:00	Other
5122	7	13	1206	1129	37	1319	1304	UA	316	N446UA	EWR	ORD	106	719	11	29	2023-07-13 11:00:00	ORD
5125	6	5	2213	2110	63	28	29	DL	173	N507DZ	JFK	SAN	295	2446	21	10	2023-06-05 21:00:00	Other
5132	1	11	2127	1822	185	321	2112	YX	1343	N109HQ	LGA	IND	NA	660	18	22	2023-01-11 18:00:00	Other
5133	5	13	1850	1830	20	2201	2156	AA	173	N921AN	JFK	MIA	155	1089	18	30	2023-05-13 18:00:00	MIA
5134	9	22	1828	1800	28	2036	2029	DL	327	N358DN	LGA	ATL	102	762	18	0	2023-09-22 18:00:00	ATL
5136	7	25	2209	2050	79	2330	2225	YX	1444	N878RW	LGA	MSN	113	812	20	50	2023-07-25 20:00:00	Other
5140	4	1	1402	1311	51	1620	1528	YX	1048	N644RW	EWR	HHH	114	687	13	11	2023-04-01 13:00:00	Other
5143	2	24	2008	1930	38	2217	2128	AA	127	N925AN	LGA	ORD	150	733	19	30	2023-02-24 19:00:00	ORD
5145	3	11	2149	2059	50	2353	2325	UA	892	N893UA	EWR	MSY	163	1167	20	59	2023-03-11 20:00:00	Other
5146	2	1	816	700	76	1051	818	YX	1019	N754YX	EWR	DCA	48	199	7	0	2023-02-01 07:00:00	Other
5154	12	2	641	610	31	942	916	NK	182	N982NK	EWR	FLL	161	1065	6	10	2023-12-02 06:00:00	FLL
5155	11	26	1658	1559	59	1809	1713	DL	503	N132DU	LGA	BOS	38	184	15	59	2023-11-26 15:00:00	BOS
5157	6	28	2004	1935	29	2159	2139	OO	1273	N243SY	JFK	ORD	115	740	19	35	2023-06-28 19:00:00	ORD
5158	7	21	2023	1929	54	2251	2224	B6	24	N806JB	JFK	ABQ	243	1826	19	29	2023-07-21 19:00:00	Other
5164	8	25	951	939	12	1419	1340	B6	796	N972JT	JFK	SJU	216	1598	9	39	2023-08-25 09:00:00	Other
5176	7	12	1527	1450	37	1820	1815	B6	176	N580JB	EWR	FLL	134	1065	14	50	2023-07-12 14:00:00	FLL
5177	2	17	1611	1515	56	1912	1829	UA	379	N2136U	EWR	SFO	332	2565	15	15	2023-02-17 15:00:00	Other
5197	8	5	1414	1230	104	1704	1531	UA	87	N419UA	EWR	RSW	153	1068	12	30	2023-08-05 12:00:00	Other
5204	1	17	1814	1759	15	2108	2104	B6	761	N705JB	LGA	MCO	137	950	17	59	2023-01-17 17:00:00	MCO
5206	4	14	1702	1629	33	1815	1758	9E	1295	N197PQ	LGA	BUF	53	292	16	29	2023-04-14 16:00:00	Other
5212	5	7	2051	2027	24	2157	2150	UA	882	N435UA	EWR	IAD	38	212	20	27	2023-05-07 20:00:00	Other
5215	8	10	2228	2217	11	2354	2326	UA	707	N491UA	EWR	SYR	38	195	22	17	2023-08-10 22:00:00	Other
5217	10	22	1451	1411	40	1555	1537	B6	52	N273JB	JFK	ROC	50	264	14	11	2023-10-22 14:00:00	Other
5228	8	5	1321	1255	26	1510	1501	DL	411	N106DU	JFK	DTW	88	509	12	55	2023-08-05 12:00:00	Other
5231	3	3	1615	1559	16	1914	1902	UA	769	N456UA	EWR	FLL	155	1065	15	59	2023-03-03 15:00:00	FLL
5232	12	3	1617	1550	27	1906	1905	DL	189	N174DN	JFK	LAX	322	2475	15	50	2023-12-03 15:00:00	LAX
5237	9	29	1454	1323	91	1615	1455	UA	99	N77510	EWR	ORD	105	719	13	23	2023-09-29 13:00:00	ORD
5238	7	8	2249	1855	234	137	2213	DL	612	N120DU	LGA	RSW	151	1080	18	55	2023-07-08 18:00:00	Other
5243	8	25	1722	1703	19	1956	1953	UA	643	N79521	EWR	MCO	121	937	17	3	2023-08-25 17:00:00	MCO
5244	9	26	2056	2025	31	54	2331	B6	161	N703JB	LGA	FLL	198	1076	20	25	2023-09-26 20:00:00	FLL
5248	3	9	1506	1446	20	1810	1753	AA	836	N306NY	JFK	DFW	216	1391	14	46	2023-03-09 14:00:00	Other
5271	6	22	1816	1729	47	1952	1912	UA	102	N27239	EWR	RDU	71	416	17	29	2023-06-22 17:00:00	Other
5273	10	9	2003	1934	29	2210	2155	9E	1391	N933XJ	JFK	DTW	85	509	19	34	2023-10-09 19:00:00	Other
5279	2	2	1514	1500	14	1858	1854	DL	371	N848DN	JFK	PHX	318	2153	15	0	2023-02-02 15:00:00	Other
5281	2	25	956	917	39	1302	1205	UA	381	N37295	EWR	HDN	285	1728	9	17	2023-02-25 09:00:00	Other
5285	3	21	946	930	16	1247	1245	AS	9	N413AS	JFK	SEA	334	2422	9	30	2023-03-21 09:00:00	Other
5291	5	1	1652	1531	81	1904	1812	B6	650	N536JB	JFK	ATL	112	760	15	31	2023-05-01 15:00:00	ATL
5293	11	19	1635	1610	25	1908	1932	UA	585	N48127	EWR	LAX	307	2454	16	10	2023-11-19 16:00:00	LAX
5295	12	27	1414	1355	19	1719	1705	WN	1115	N283WN	LGA	HOU	228	1428	13	55	2023-12-27 13:00:00	Other
5317	7	16	1923	1753	90	2203	2044	UA	709	N37257	EWR	IAH	198	1400	17	53	2023-07-16 17:00:00	Other
5319	4	19	1941	1825	76	2143	2015	WN	194	N8702L	LGA	STL	129	888	18	25	2023-04-19 18:00:00	Other
5329	12	4	1751	1642	69	2000	1916	UA	910	N41135	EWR	DEN	219	1605	16	42	2023-12-04 16:00:00	Other
5331	1	12	1348	1303	45	1602	1544	UA	220	N37277	EWR	LAS	288	2227	13	3	2023-01-12 13:00:00	Other
5339	7	7	2116	2000	76	100	2359	B6	241	N2002J	JFK	SJU	192	1598	20	0	2023-07-07 20:00:00	Other
5349	3	20	1623	1529	54	1847	1754	UA	837	N486UA	EWR	MSY	172	1167	15	29	2023-03-20 15:00:00	Other
5362	3	18	1925	1859	26	2300	2305	DL	721	N892DN	JFK	SJU	194	1598	18	59	2023-03-18 18:00:00	Other
5375	3	9	606	525	41	753	700	AA	913	N986NN	EWR	ORD	125	719	5	25	2023-03-09 05:00:00	ORD
5391	4	8	1603	1531	32	1844	1812	B6	602	N656JB	JFK	ATL	125	760	15	31	2023-04-08 15:00:00	ATL
5392	3	12	1656	1613	43	1827	1745	UA	490	N38268	EWR	BNA	121	748	16	13	2023-03-12 16:00:00	Other
5396	1	7	2140	2105	35	2334	2329	B6	422	N351JB	LGA	CHS	93	641	21	5	2023-01-07 21:00:00	Other
5397	10	6	1954	1932	22	932	2230	UA	506	N27515	EWR	SAN	NA	2425	19	32	2023-10-06 19:00:00	Other
5413	8	8	1844	1825	19	1957	2022	DL	296	N109DU	LGA	ORD	107	733	18	25	2023-08-08 18:00:00	ORD
5414	4	16	1457	1404	53	1646	1625	UA	716	N37462	EWR	DEN	209	1605	14	4	2023-04-16 14:00:00	Other
5415	9	24	2155	2015	100	18	2246	B6	917	N630JB	LGA	ATL	104	762	20	15	2023-09-24 20:00:00	ATL
5417	10	16	2105	1302	483	2400	1605	B6	651	N658JB	EWR	RSW	146	1068	13	2	2023-10-16 13:00:00	Other
5436	9	19	1631	1359	152	125	1648	UA	489	N437UA	EWR	DFW	NA	1372	13	59	2023-09-19 13:00:00	Other
5439	2	9	1758	1729	29	2111	2046	AA	241	N879NN	JFK	MIA	162	1089	17	29	2023-02-09 17:00:00	MIA
5442	10	20	1916	1900	16	2344	2308	UA	192	N37468	EWR	BQN	221	1585	19	0	2023-10-20 19:00:00	Other
5445	8	24	1801	1750	11	2100	2020	WN	284	N259WN	LGA	ATL	101	762	17	50	2023-08-24 17:00:00	ATL
5447	10	21	2334	2214	80	138	45	NK	555	N966NK	EWR	ATL	107	746	22	14	2023-10-21 22:00:00	ATL
5455	3	25	1945	1928	17	2157	2150	9E	1354	N304PQ	JFK	CLT	96	541	19	28	2023-03-25 19:00:00	CLT
5459	8	4	1838	1729	69	2122	1927	YX	1008	N419YX	LGA	CMH	81	479	17	29	2023-08-04 17:00:00	Other
5471	4	21	1645	1629	16	1757	1759	YX	967	N643RW	EWR	PIT	53	319	16	29	2023-04-21 16:00:00	Other
5472	1	24	933	905	28	1103	1046	9E	1630	N331PQ	JFK	RIC	56	288	9	5	2023-01-24 09:00:00	Other
5475	3	10	1725	1659	26	1955	1931	UA	600	N850UA	EWR	ATL	113	746	16	59	2023-03-10 16:00:00	ATL
5477	4	12	2014	1959	15	3	2252	NK	178	N671NK	LGA	MCO	128	950	19	59	2023-04-12 19:00:00	MCO
5480	2	4	1700	1648	12	2004	2010	B6	747	N658JB	JFK	MIA	154	1089	16	48	2023-02-04 16:00:00	MIA
5483	1	26	2222	2150	32	2329	2314	UA	985	N63820	EWR	IAD	45	212	21	50	2023-01-26 21:00:00	Other
5498	9	14	1401	1345	16	1628	1608	B6	970	N806JB	LGA	SAV	109	722	13	45	2023-09-14 13:00:00	Other
5501	7	30	2027	1700	207	2318	2011	B6	627	N568JB	JFK	PBI	137	1028	17	0	2023-07-30 17:00:00	Other
5507	3	3	618	600	18	921	918	AA	152	N302SA	JFK	MIA	161	1089	6	0	2023-03-03 06:00:00	MIA
5508	5	11	2117	2020	57	2341	2320	WN	608	N8841L	LGA	DAL	178	1381	20	20	2023-05-11 20:00:00	Other
5512	9	2	1215	1147	28	1340	1344	YX	1103	N724YX	EWR	MEM	126	946	11	47	2023-09-02 11:00:00	Other
5521	4	18	2047	2027	20	2352	2337	UA	627	N412UA	EWR	RSW	151	1068	20	27	2023-04-18 20:00:00	Other
5522	5	16	1036	1014	22	1246	1240	9E	1440	N131EV	JFK	SAV	104	718	10	14	2023-05-16 10:00:00	Other
5523	7	16	2044	1959	45	112	2329	DL	681	N882DN	JFK	MIA	140	1089	19	59	2023-07-16 19:00:00	MIA
5525	7	5	1449	1435	14	1646	1654	YX	962	N755YX	EWR	IND	91	645	14	35	2023-07-05 14:00:00	Other
5556	4	12	2036	1859	97	2202	2041	AA	195	N810AW	LGA	RDU	63	431	18	59	2023-04-12 18:00:00	Other
5558	1	31	1243	1130	73	1500	1352	AA	108	N335PH	LGA	CLT	94	544	11	30	2023-01-31 11:00:00	CLT
5562	7	29	10	2023	227	228	2257	UA	638	N87527	EWR	LAS	286	2227	20	23	2023-07-29 20:00:00	Other
5570	12	14	1749	1629	80	2114	1952	AA	722	N959AN	LGA	MIA	158	1096	16	29	2023-12-14 16:00:00	MIA
5573	1	27	1026	1015	11	1127	1130	B6	234	N273JB	LGA	BOS	37	184	10	15	2023-01-27 10:00:00	BOS
5575	8	18	1840	1330	310	1948	1447	B6	480	N307JB	JFK	BOS	43	187	13	30	2023-08-18 13:00:00	BOS
5578	1	8	1342	1315	27	1641	1632	B6	374	N652JB	EWR	PBI	152	1023	13	15	2023-01-08 13:00:00	Other
5592	7	21	1943	1820	83	2206	2054	9E	1115	N131EV	JFK	IND	113	665	18	20	2023-07-21 18:00:00	Other
5602	6	21	1801	1745	16	2038	2010	WN	34	N8825Q	LGA	DEN	247	1620	17	45	2023-06-21 17:00:00	Other
5618	4	18	2114	2045	29	2225	2217	YX	1474	N227JQ	LGA	DCA	49	214	20	45	2023-04-18 20:00:00	Other
5623	10	30	1024	940	44	1410	1222	B6	13	N508JL	JFK	PHX	334	2153	9	40	2023-10-30 09:00:00	Other
5629	9	13	1724	1655	29	2018	2015	AS	6	N265AK	JFK	SEA	319	2422	16	55	2023-09-13 16:00:00	Other
5630	10	1	2042	2030	12	2204	2211	YX	1829	N235JQ	LGA	BNA	104	764	20	30	2023-10-01 20:00:00	Other
5640	6	14	1220	1134	46	1505	1426	NK	1060	N604NK	EWR	MCO	141	937	11	34	2023-06-14 11:00:00	MCO
5643	5	24	1913	1900	13	2022	2028	YX	1023	N655RW	EWR	DCA	40	199	19	0	2023-05-24 19:00:00	Other
5644	7	26	1448	1418	30	1557	1549	9E	1212	N480PX	LGA	BTV	43	258	14	18	2023-07-26 14:00:00	Other
5654	5	9	2301	1915	226	112	2215	UA	779	N420UA	EWR	DFW	173	1372	19	15	2023-05-09 19:00:00	Other
5665	8	25	932	900	32	1102	1035	9E	1166	N146PQ	JFK	IAD	43	228	9	0	2023-08-25 09:00:00	Other
5669	4	16	631	605	26	909	813	B6	31	N621JB	JFK	MSY	196	1182	6	5	2023-04-16 06:00:00	Other
5674	7	23	1915	1644	151	2210	1950	B6	123	N2016J	JFK	MCO	140	944	16	44	2023-07-23 16:00:00	MCO
5677	6	25	1250	830	260	1522	1055	NK	160	N958NK	EWR	LAS	309	2227	8	30	2023-06-25 08:00:00	Other
5680	6	25	1120	1013	67	1311	1148	YX	1114	N856RW	EWR	BGR	58	393	10	13	2023-06-25 10:00:00	Other
5681	6	8	1430	1330	60	1722	1629	B6	570	N796JB	JFK	MCO	138	944	13	30	2023-06-08 13:00:00	MCO
5689	9	14	2005	1900	65	2238	2122	9E	1606	N307PQ	LGA	IND	95	660	19	0	2023-09-14 19:00:00	Other
5704	7	10	1647	1523	84	1939	1825	NK	701	N632NK	EWR	LAX	312	2454	15	23	2023-07-10 15:00:00	LAX
5714	9	7	1815	1629	106	2220	1844	YX	1316	N870RW	LGA	LIT	149	1085	16	29	2023-09-07 16:00:00	Other
5722	1	12	2037	1950	47	2204	2117	YX	1222	N728YX	EWR	IAD	44	212	19	50	2023-01-12 19:00:00	Other
5728	12	2	1948	1935	13	2142	2117	UA	176	N15710	EWR	CLE	73	404	19	35	2023-12-02 19:00:00	Other
5736	6	24	2151	2100	51	111	23	AA	97	N117AN	JFK	LAX	336	2475	21	0	2023-06-24 21:00:00	LAX
5740	1	13	1135	1120	15	1420	1451	DL	655	N121DU	LGA	IAH	197	1416	11	20	2023-01-13 11:00:00	Other
5741	1	15	1725	1627	58	2027	1947	UA	730	N890UA	EWR	AUS	207	1504	16	27	2023-01-15 16:00:00	Other
5746	2	15	2214	2157	17	4	2359	UA	722	N14704	EWR	DTW	88	488	21	57	2023-02-15 21:00:00	Other
5753	4	17	1819	1725	54	1958	1915	OO	977	N324SY	JFK	MKE	120	745	17	25	2023-04-17 17:00:00	Other
5760	6	10	2154	2140	14	1	2359	UA	680	N17300	EWR	SAV	102	708	21	40	2023-06-10 21:00:00	Other
5761	11	13	2045	1959	46	2337	2316	NK	1156	N705NK	EWR	LAX	321	2454	19	59	2023-11-13 19:00:00	LAX
5765	7	29	848	815	33	1322	1300	UA	113	N76054	EWR	HNL	584	4962	8	15	2023-07-29 08:00:00	Other
5774	1	12	1524	1445	39	1814	1717	B6	791	N804JB	LGA	MSY	194	1183	14	45	2023-01-12 14:00:00	Other
5798	9	13	1448	1419	29	1726	1703	YX	1809	N241JQ	JFK	JAX	120	828	14	19	2023-09-13 14:00:00	Other
5815	8	13	1932	1920	12	2212	2226	UA	645	N17272	EWR	FLL	139	1065	19	20	2023-08-13 19:00:00	FLL
5816	9	17	1023	830	113	1202	1002	OO	1244	N254SY	JFK	BNA	132	765	8	30	2023-09-17 08:00:00	Other
5822	9	10	1055	1016	39	1349	1240	AA	803	N926UW	EWR	PHX	272	2133	10	16	2023-09-10 10:00:00	Other
5823	6	7	2034	2016	18	2210	2215	DL	1046	N949AT	EWR	DTW	75	488	20	16	2023-06-07 20:00:00	Other
5829	2	9	2212	2045	87	46	25	UA	684	N14106	EWR	SFO	315	2565	20	45	2023-02-09 20:00:00	Other
5835	1	16	1012	1000	12	1117	1124	UA	778	N489UA	EWR	IAD	44	212	10	0	2023-01-16 10:00:00	Other
5839	4	7	2130	2059	31	2330	2256	YX	1058	N742YX	EWR	CMH	88	463	20	59	2023-04-07 20:00:00	Other
5841	7	18	1541	1515	26	1916	1822	DL	194	N178DZ	JFK	LAX	339	2475	15	15	2023-07-18 15:00:00	LAX
5843	10	5	1348	1330	18	1455	1439	B6	35	N281JB	JFK	SYR	41	209	13	30	2023-10-05 13:00:00	Other
5860	1	10	915	855	20	1120	1124	9E	1524	N232PQ	LGA	CHS	99	641	8	55	2023-01-10 08:00:00	Other
5866	10	1	1630	1540	50	1812	1804	UA	845	N69840	EWR	DEN	197	1605	15	40	2023-10-01 15:00:00	Other
5874	5	17	2104	1959	65	19	2300	UA	873	N27260	EWR	TPA	141	997	19	59	2023-05-17 19:00:00	Other
5880	3	10	2019	1950	29	2225	2202	9E	1538	N903XJ	JFK	RDU	80	427	19	50	2023-03-10 19:00:00	Other
5884	6	30	1012	959	13	1219	1235	DL	157	N325DN	LGA	ATL	102	762	9	59	2023-06-30 09:00:00	ATL
5886	11	20	645	600	45	906	833	UA	411	N17285	EWR	ATL	112	746	6	0	2023-11-20 06:00:00	ATL
5896	7	28	718	610	68	1000	747	DL	387	N105DU	LGA	ORD	152	733	6	10	2023-07-28 06:00:00	ORD
5898	8	1	957	920	37	1155	1128	9E	1237	N187GJ	LGA	ILM	78	500	9	20	2023-08-01 09:00:00	Other
5905	4	13	2106	1933	93	2330	2239	B6	28	N547JB	JFK	ABQ	235	1826	19	33	2023-04-13 19:00:00	Other
5921	1	4	2247	2121	86	117	2359	UA	557	N16701	EWR	JAX	126	820	21	21	2023-01-04 21:00:00	Other
5923	11	17	1937	1755	102	2208	2035	WN	1066	N8629A	LGA	ATL	117	762	17	55	2023-11-17 17:00:00	ATL
5926	12	2	1902	1535	207	2133	1750	DL	105	N320US	LGA	MSP	159	1020	15	35	2023-12-02 15:00:00	Other
5938	8	27	1011	959	12	1155	1154	YX	1328	N233JQ	JFK	CMH	82	483	9	59	2023-08-27 09:00:00	Other
5943	1	11	1759	1725	34	1935	1913	AA	234	N915NN	JFK	ORD	124	740	17	25	2023-01-11 17:00:00	ORD
5950	9	9	126	1904	382	355	2202	NK	770	N663NK	EWR	MCO	127	937	19	4	2023-09-09 19:00:00	MCO
5953	4	6	1424	1350	34	1722	1648	B6	512	N625JB	JFK	MCO	133	944	13	50	2023-04-06 13:00:00	MCO
5960	3	15	36	2159	157	149	2317	YX	1743	N879RW	LGA	DCA	46	214	21	59	2023-03-15 21:00:00	Other
5963	8	29	1221	1029	112	1434	1249	YX	993	N126HQ	LGA	XNA	161	1147	10	29	2023-08-29 10:00:00	Other
5966	9	22	1024	900	84	1313	1209	B6	83	N507JT	JFK	AUS	204	1521	9	0	2023-09-22 09:00:00	Other
5971	11	16	1542	1525	17	1758	1758	UA	858	N37536	EWR	DEN	231	1605	15	25	2023-11-16 15:00:00	Other
5973	10	26	1125	1100	25	1517	1436	DL	271	N710TW	JFK	SFO	371	2586	11	0	2023-10-26 11:00:00	Other
5987	7	18	1435	1405	30	1710	1646	UA	422	N463UA	EWR	DFW	190	1372	14	5	2023-07-18 14:00:00	Other
5996	1	31	1907	1729	98	2217	2046	AA	257	N334SM	JFK	MIA	159	1089	17	29	2023-01-31 17:00:00	MIA
5999	11	12	1755	1540	135	1932	1715	WN	729	N8606C	LGA	MDW	124	725	15	40	2023-11-12 15:00:00	Other
6005	11	28	2009	1756	133	2327	2105	B6	663	N775JB	JFK	PSP	318	2378	17	56	2023-11-28 17:00:00	Other
6009	11	9	849	800	49	1222	1145	DL	125	N541DE	JFK	PHX	305	2153	8	0	2023-11-09 08:00:00	Other
6012	6	24	1115	1045	30	1335	1255	9E	1690	N301PQ	LGA	CAE	118	617	10	45	2023-06-24 10:00:00	Other
6015	7	4	1526	1430	56	1739	1650	WN	57	N490WN	LGA	ATL	106	762	14	30	2023-07-04 14:00:00	ATL
6021	5	2	2157	2130	27	2349	2334	B6	347	N821JB	LGA	CHS	91	641	21	30	2023-05-02 21:00:00	Other
6025	8	24	1405	1338	27	1555	1545	AA	118	N90024	JFK	CLT	80	541	13	38	2023-08-24 13:00:00	CLT
6026	5	13	932	909	23	1041	1043	YX	1214	N107HQ	JFK	BOS	37	187	9	9	2023-05-13 09:00:00	BOS
6028	9	17	1742	1545	117	2105	1845	B6	541	N807JB	JFK	MCO	168	944	15	45	2023-09-17 15:00:00	MCO
6042	7	20	629	600	29	804	732	AA	819	N820NN	EWR	ORD	115	719	6	0	2023-07-20 06:00:00	ORD
6043	8	4	1726	1654	32	1929	1922	DL	708	N375DA	EWR	ATL	103	746	16	54	2023-08-04 16:00:00	ATL
6051	6	7	2351	2229	82	231	153	B6	678	N929JB	JFK	LAX	315	2475	22	29	2023-06-07 22:00:00	LAX
6057	12	27	1327	1258	29	1601	1536	B6	945	N653JB	LGA	ATL	130	762	12	58	2023-12-27 12:00:00	ATL
6067	7	16	2125	2025	60	2244	2156	YX	927	N747YX	EWR	DCA	40	199	20	25	2023-07-16 20:00:00	Other
6073	8	19	2123	2000	83	125	2359	B6	228	N2027J	JFK	SJU	188	1598	20	0	2023-08-19 20:00:00	Other
6076	4	5	47	2130	197	229	2336	YX	975	N649RW	EWR	GSP	87	594	21	30	2023-04-05 21:00:00	Other
6079	3	4	809	735	34	1101	1043	UA	277	N77867	EWR	IAH	196	1400	7	35	2023-03-04 07:00:00	Other
6081	7	5	1917	1900	17	2158	2148	UA	349	N781UA	EWR	LAX	309	2454	19	0	2023-07-05 19:00:00	LAX
6094	4	19	1201	1140	21	1326	1305	WN	152	N272WN	LGA	MDW	118	725	11	40	2023-04-19 11:00:00	Other
6097	1	28	1318	1132	106	1640	1434	UA	951	N805UA	EWR	MTJ	291	1795	11	32	2023-01-28 11:00:00	Other
6098	6	6	1511	1445	26	1808	1752	B6	308	N712JB	LGA	PBI	144	1035	14	45	2023-06-06 14:00:00	Other
6099	2	17	1751	1630	81	1922	1756	YX	1597	N225JQ	LGA	ROC	58	254	16	30	2023-02-17 16:00:00	Other
6101	1	12	2012	1959	13	2257	2256	NK	194	N669NK	LGA	MCO	139	950	19	59	2023-01-12 19:00:00	MCO
6103	11	30	1224	915	189	1344	1053	UA	230	N14235	LGA	ORD	119	733	9	15	2023-11-30 09:00:00	ORD
6105	7	7	1344	1259	45	1737	1555	UA	558	N76526	EWR	SNA	318	2434	12	59	2023-07-07 12:00:00	Other
6106	4	18	1747	1734	13	1951	1933	AA	600	N905AN	EWR	CLT	83	529	17	34	2023-04-18 17:00:00	CLT
6107	7	5	1914	1830	44	2248	2151	DL	612	N112DU	LGA	RSW	172	1080	18	30	2023-07-05 18:00:00	Other
6113	9	29	1710	1520	110	1831	1703	B6	823	N281JB	LGA	BNA	103	764	15	20	2023-09-29 15:00:00	Other
6118	12	20	1736	1715	21	1901	1842	B6	387	N279JB	LGA	BOS	35	184	17	15	2023-12-20 17:00:00	BOS
6128	10	1	2206	2104	62	27	2339	UA	574	N47281	EWR	LAS	279	2227	21	4	2023-10-01 21:00:00	Other
6129	12	23	2333	2259	34	44	17	B6	968	N641JB	JFK	BOS	41	187	22	59	2023-12-23 22:00:00	BOS
6132	3	8	2108	2053	15	2255	2247	YX	1401	N826MD	LGA	ILM	76	500	20	53	2023-03-08 20:00:00	Other
6150	3	2	2047	2029	18	2244	2158	UA	741	N16703	EWR	MSN	134	799	20	29	2023-03-02 20:00:00	Other
6152	6	19	1406	1347	19	1526	1520	AA	659	N829NN	EWR	ORD	109	719	13	47	2023-06-19 13:00:00	ORD
6158	11	12	1025	929	56	1317	1227	UA	210	N27503	EWR	MCO	140	937	9	29	2023-11-12 09:00:00	MCO
6159	1	8	1746	1729	17	2056	2048	B6	192	N805JB	LGA	FLL	155	1076	17	29	2023-01-08 17:00:00	FLL
6162	7	5	813	700	73	1004	902	9E	1121	N907XJ	JFK	DTW	78	509	7	0	2023-07-05 07:00:00	Other
6178	8	4	2013	1929	44	2155	2106	YX	1378	N224JQ	LGA	DCA	51	214	19	29	2023-08-04 19:00:00	Other
6185	9	12	1220	1129	51	1320	1230	B6	567	N317JB	JFK	MVY	38	173	11	29	2023-09-12 11:00:00	Other
6192	10	1	2118	2015	63	2234	2138	B6	494	N228JB	LGA	BOS	36	184	20	15	2023-10-01 20:00:00	BOS
6193	7	14	13	1928	285	213	2130	YX	1435	N224JQ	LGA	CMH	71	479	19	28	2023-07-14 19:00:00	Other
6202	3	23	1406	1240	86	1657	1550	B6	253	N766JB	JFK	PBI	144	1028	12	40	2023-03-23 12:00:00	Other
6205	4	3	1434	1417	17	1629	1634	9E	1413	N184GJ	LGA	CVG	97	585	14	17	2023-04-03 14:00:00	Other
6217	1	31	1812	1729	43	2102	2041	B6	824	N566JB	JFK	PBI	142	1028	17	29	2023-01-31 17:00:00	Other
6239	7	22	2011	1959	12	2241	2305	AS	79	N925VA	EWR	LAX	296	2454	19	59	2023-07-22 19:00:00	LAX
6242	5	14	1730	1655	35	2020	2007	AS	82	N296AK	EWR	SEA	321	2402	16	55	2023-05-14 16:00:00	Other
6246	5	4	1732	1700	32	2030	2021	UA	137	N213UA	EWR	SFO	321	2565	17	0	2023-05-04 17:00:00	Other
6253	9	23	1713	1649	24	1915	1914	YX	1226	N650RW	EWR	SDF	93	642	16	49	2023-09-23 16:00:00	Other
6256	3	15	54	2200	174	312	59	NK	733	N678NK	EWR	MCO	116	937	22	0	2023-03-15 22:00:00	MCO
6272	10	18	813	800	13	1048	1054	NK	407	N669NK	EWR	MCO	125	937	8	0	2023-10-18 08:00:00	MCO
6273	8	10	1135	1045	50	1318	1216	YX	1061	N422YX	JFK	BNA	112	765	10	45	2023-08-10 10:00:00	Other
6276	2	23	2057	2023	34	2240	2205	UA	447	N69804	EWR	ORD	130	719	20	23	2023-02-23 20:00:00	ORD
6277	3	13	2213	1810	243	229	2150	B6	326	N978JB	JFK	SFO	365	2586	18	10	2023-03-13 18:00:00	Other
6284	12	14	1218	1149	29	1332	1328	9E	1526	N918XJ	LGA	ORF	49	296	11	49	2023-12-14 11:00:00	Other
6288	11	5	827	630	117	1132	944	AA	65	N328TC	JFK	MIA	153	1089	6	30	2023-11-05 06:00:00	MIA
6289	7	23	1334	1312	22	1429	1421	YX	886	N657RW	EWR	MDT	29	141	13	12	2023-07-23 13:00:00	Other
6296	2	27	712	700	12	1016	1028	DL	104	N858DZ	JFK	SEA	336	2422	7	0	2023-02-27 07:00:00	Other
6299	7	1	2236	2107	89	45	2312	UA	206	N37471	EWR	CVG	81	569	21	7	2023-07-01 21:00:00	Other
6301	12	3	2041	2017	24	2204	2127	YX	1106	N656RW	EWR	PVD	28	160	20	17	2023-12-03 20:00:00	Other
6304	2	26	1728	1700	28	1842	1828	YX	1596	N235JQ	LGA	BOS	46	184	17	0	2023-02-26 17:00:00	BOS
6311	3	14	1820	1800	20	2019	2041	UA	747	N476UA	LGA	DEN	214	1620	18	0	2023-03-14 18:00:00	Other
6316	7	7	1553	1455	58	1925	1756	UA	69	N27260	EWR	PBI	151	1023	14	55	2023-07-07 14:00:00	Other
6332	4	14	2100	2004	56	2254	2151	YX	1043	N748YX	EWR	CLE	65	404	20	4	2023-04-14 20:00:00	Other
6336	1	5	1038	1005	33	1606	1309	UA	471	N898UA	EWR	SRQ	NA	1034	10	5	2023-01-05 10:00:00	Other
6341	9	26	1929	1859	30	2127	2101	9E	1599	N485PX	LGA	GSO	78	461	18	59	2023-09-26 18:00:00	Other
6350	6	27	2036	1825	131	2339	2139	AS	174	N442AS	EWR	SEA	324	2402	18	25	2023-06-27 18:00:00	Other
6352	8	3	1528	1429	59	1646	1604	9E	1179	N929XJ	JFK	SYR	44	209	14	29	2023-08-03 14:00:00	Other
6355	5	9	2326	2045	161	217	2359	B6	472	N2039J	JFK	AUS	201	1521	20	45	2023-05-09 20:00:00	Other
6356	4	2	1554	1455	59	1832	1744	9E	1290	N691CA	JFK	JAX	121	828	14	55	2023-04-02 14:00:00	Other
6357	6	9	1021	900	81	1255	1205	AS	15	N952AK	JFK	SAN	309	2446	9	0	2023-06-09 09:00:00	Other
6359	3	26	2243	2030	133	17	2219	DL	468	N145DQ	LGA	ORD	132	733	20	30	2023-03-26 20:00:00	ORD
6363	9	5	1956	1927	29	2149	2146	9E	1744	N131EV	LGA	CLT	73	544	19	27	2023-09-05 19:00:00	CLT
6367	5	29	2046	1929	77	2153	2108	YX	1672	N228JQ	LGA	BNA	105	764	19	29	2023-05-29 19:00:00	Other
6371	3	13	909	825	44	1046	959	9E	1323	N914XJ	LGA	MKE	117	738	8	25	2023-03-13 08:00:00	Other
6372	12	18	757	700	57	1314	1204	UA	546	N27733	EWR	STT	235	1634	7	0	2023-12-18 07:00:00	Other
6374	12	19	1008	955	13	1255	1320	DL	875	N333DX	LGA	FLL	143	1076	9	55	2023-12-19 09:00:00	FLL
6375	1	15	1056	1045	11	1305	1319	UA	144	N4888U	EWR	JAX	103	820	10	45	2023-01-15 10:00:00	Other
6377	8	20	2112	2059	13	100	53	B6	737	N965JT	EWR	SJU	197	1608	20	59	2023-08-20 20:00:00	Other
6387	10	11	1015	929	46	1200	1121	UA	366	N440UA	EWR	CMH	79	463	9	29	2023-10-11 09:00:00	Other
6388	6	29	1702	1630	32	1938	1924	NK	541	N625NK	EWR	MCO	122	937	16	30	2023-06-29 16:00:00	MCO
6393	1	27	1302	1240	22	1415	1428	YX	1410	N806MD	LGA	ORF	54	296	12	40	2023-01-27 12:00:00	Other
6397	2	4	921	900	21	1159	1209	UA	496	N67134	EWR	MCO	130	937	9	0	2023-02-04 09:00:00	MCO
6402	2	25	1048	1030	18	1748	1329	B6	39	N995JL	JFK	LAS	NA	2248	10	30	2023-02-25 10:00:00	Other
6403	8	6	1239	1107	92	1549	1416	UA	135	N27271	EWR	FLL	170	1065	11	7	2023-08-06 11:00:00	FLL
6414	4	27	2108	1959	69	35	2319	DL	426	N318DX	LGA	FLL	171	1076	19	59	2023-04-27 19:00:00	FLL
6416	1	27	2041	1959	42	11	2324	DL	986	N379DN	JFK	MIA	176	1089	19	59	2023-01-27 19:00:00	MIA
6422	9	24	2236	2130	66	45	3	DL	844	N521DT	JFK	ATL	99	760	21	30	2023-09-24 21:00:00	ATL
6423	6	17	1729	1703	26	2010	1953	UA	532	N79541	EWR	SAN	308	2425	17	3	2023-06-17 17:00:00	Other
6428	2	5	1610	1530	40	1727	1649	B6	409	N228JB	JFK	BOS	50	187	15	30	2023-02-05 15:00:00	BOS
6430	3	28	905	829	36	1226	1146	B6	60	N612JB	JFK	SAN	353	2446	8	29	2023-03-28 08:00:00	Other
6440	10	15	1211	1136	35	1335	1308	UA	331	N36476	EWR	ORD	103	719	11	36	2023-10-15 11:00:00	ORD
6444	3	14	1221	1145	36	1640	1504	DL	654	N145DQ	LGA	IAH	217	1416	11	45	2023-03-14 11:00:00	Other
6447	1	19	1510	1459	11	1659	1717	DL	487	N358NB	LGA	MSP	144	1020	14	59	2023-01-19 14:00:00	Other
6463	1	27	1342	1253	49	1707	1607	AA	585	N937AN	EWR	MIA	170	1085	12	53	2023-01-27 12:00:00	MIA
6467	4	14	1920	1855	25	2220	2200	B6	230	N607JB	EWR	FLL	148	1065	18	55	2023-04-14 18:00:00	FLL
6482	2	9	2012	2000	12	2223	2241	B6	35	N566JB	JFK	DEN	226	1626	20	0	2023-02-09 20:00:00	Other
6487	1	21	1937	1600	217	2046	1726	OO	1279	N268SY	JFK	BOS	40	187	16	0	2023-01-21 16:00:00	BOS
6496	7	22	2306	2200	66	30	2328	B6	166	N203JB	JFK	ROC	50	264	22	0	2023-07-22 22:00:00	Other
6502	9	10	1907	1400	307	2032	1537	DL	533	N131DU	LGA	ORD	110	733	14	0	2023-09-10 14:00:00	ORD
6507	8	17	1606	1554	12	1948	1925	DL	663	N395DN	JFK	MIA	161	1089	15	54	2023-08-17 15:00:00	MIA
6510	3	25	753	735	18	1105	1102	DL	538	N343NW	JFK	AUS	230	1521	7	35	2023-03-25 07:00:00	Other
6514	4	17	1134	1044	50	1348	1254	UA	807	N827UA	EWR	MSY	169	1167	10	44	2023-04-17 10:00:00	Other
6516	10	30	1628	1559	29	1751	1732	B6	989	N258JB	JFK	BUF	61	301	15	59	2023-10-30 15:00:00	Other
6529	10	28	1103	1035	28	1244	1233	UA	473	N13750	EWR	CLT	77	529	10	35	2023-10-28 10:00:00	CLT
6535	8	19	827	735	52	1127	1026	DL	390	N317DN	JFK	MCO	124	944	7	35	2023-08-19 07:00:00	MCO
6540	7	24	743	645	58	1038	959	DL	109	N6701	JFK	SLC	258	1990	6	45	2023-07-24 06:00:00	Other
6544	8	11	2226	2114	72	50	2346	UA	106	N27251	EWR	LAS	297	2227	21	14	2023-08-11 21:00:00	Other
6554	5	15	1340	1300	40	1617	1614	AA	224	N464AA	LGA	MIA	139	1096	13	0	2023-05-15 13:00:00	MIA
6556	4	16	2229	1745	284	126	2052	B6	21	N571JB	LGA	TPA	154	1010	17	45	2023-04-16 17:00:00	Other
6566	7	28	1953	1929	24	2352	2308	DL	195	N537DT	JFK	SEA	338	2422	19	29	2023-07-28 19:00:00	Other
6573	1	10	1158	1130	28	1454	1440	DL	608	N333DX	JFK	FLL	151	1069	11	30	2023-01-10 11:00:00	FLL
6581	9	2	1041	1015	26	1229	1205	AA	735	N737US	LGA	ORD	110	733	10	15	2023-09-02 10:00:00	ORD
6585	4	16	1435	1404	31	1538	1523	YX	947	N647RW	EWR	ROC	42	246	14	4	2023-04-16 14:00:00	Other
6587	9	8	39	2022	257	344	2344	AS	16	N979AK	JFK	SFO	328	2586	20	22	2023-09-08 20:00:00	Other
6589	2	27	1746	1730	16	2048	2040	DL	108	N805DN	JFK	LAS	335	2248	17	30	2023-02-27 17:00:00	Other
6591	7	28	1833	1705	88	2149	2010	NK	523	N694NK	EWR	FLL	144	1065	17	5	2023-07-28 17:00:00	FLL
6607	4	24	2004	1800	124	2349	2116	UA	767	N69833	EWR	MIA	174	1085	18	0	2023-04-24 18:00:00	MIA
6620	4	7	2007	1744	143	2249	2055	B6	641	N955JB	JFK	PBI	140	1028	17	44	2023-04-07 17:00:00	Other
6624	12	21	2108	2029	39	151	121	B6	683	N998JE	JFK	SJU	192	1598	20	29	2023-12-21 20:00:00	Other
6626	9	19	1238	1200	38	1410	1349	AA	519	N748UW	LGA	RDU	68	431	12	0	2023-09-19 12:00:00	Other
6632	1	11	1156	949	127	1529	1329	AA	1088	N423AN	EWR	PHX	310	2133	9	49	2023-01-11 09:00:00	Other
6638	3	5	1733	1722	11	2110	2037	UA	68	N27266	EWR	SMF	372	2500	17	22	2023-03-05 17:00:00	Other
6643	11	17	1952	1925	27	2314	2236	DL	339	N377DA	LGA	MIA	158	1096	19	25	2023-11-17 19:00:00	MIA
6644	6	27	1842	1359	283	2215	1636	DL	175	N370DN	LGA	ATL	100	762	13	59	2023-06-27 13:00:00	ATL
6648	2	21	1921	1829	52	2156	2121	UA	636	N33286	EWR	MCO	125	937	18	29	2023-02-21 18:00:00	MCO
6661	1	9	1337	1300	37	1629	1619	B6	1100	N746JB	JFK	MIA	142	1089	13	0	2023-01-09 13:00:00	MIA
6667	3	29	1954	1833	81	2259	2142	AA	897	N994NN	EWR	DFW	201	1372	18	33	2023-03-29 18:00:00	Other
6668	1	2	1744	1729	15	1922	1914	UA	317	N54711	EWR	CLE	68	404	17	29	2023-01-02 17:00:00	Other
6670	8	1	1756	1712	44	1939	1924	AA	349	N119NN	EWR	CLT	80	529	17	12	2023-08-01 17:00:00	CLT
6671	8	17	2205	2030	95	41	2324	B6	669	N504JB	EWR	TPA	134	997	20	30	2023-08-17 20:00:00	Other
6702	12	18	1728	1559	89	1924	1802	9E	1513	N183GJ	LGA	RDU	77	431	15	59	2023-12-18 15:00:00	Other
6705	4	15	929	905	24	1154	1142	B6	419	N348JB	JFK	ATL	105	760	9	5	2023-04-15 09:00:00	ATL
6707	6	3	1603	951	372	1852	1253	UA	643	N27287	EWR	RSW	154	1068	9	51	2023-06-03 09:00:00	Other
6714	7	5	1622	1559	23	1750	1737	YX	1080	N414YX	JFK	BNA	107	765	15	59	2023-07-05 15:00:00	Other
6715	12	31	707	642	25	950	943	B6	275	N329JB	JFK	TPA	141	1005	6	42	2023-12-31 06:00:00	Other
6717	8	30	1424	1346	38	1711	1640	UA	229	N87513	LGA	IAH	201	1416	13	46	2023-08-30 13:00:00	Other
6720	12	14	1936	1855	41	2027	2030	WN	853	N212WN	LGA	MDW	99	725	18	55	2023-12-14 18:00:00	Other
6728	5	9	1126	1111	15	1335	1341	UA	452	N27276	EWR	PHX	288	2133	11	11	2023-05-09 11:00:00	Other
6729	12	18	817	800	17	1140	1155	AA	49	N109NN	JFK	SFO	346	2586	8	0	2023-12-18 08:00:00	Other
6732	12	31	1627	1559	28	1812	1808	B6	357	N337JB	JFK	DTW	81	509	15	59	2023-12-31 15:00:00	Other
6733	4	17	1420	1330	50	1906	1641	UA	468	N27269	EWR	FLL	165	1065	13	30	2023-04-17 13:00:00	FLL
6734	7	15	2155	2142	13	117	53	B6	652	N656JB	JFK	RSW	141	1074	21	42	2023-07-15 21:00:00	Other
6735	7	17	2141	2126	15	2338	2250	9E	1217	N131EV	LGA	ROC	54	254	21	26	2023-07-17 21:00:00	Other
6742	6	6	2049	2030	19	2258	2214	DL	457	N104DU	LGA	ORD	111	733	20	30	2023-06-06 20:00:00	ORD
6746	2	16	2045	2029	16	2342	2354	B6	787	N593JB	JFK	MIA	152	1089	20	29	2023-02-16 20:00:00	MIA
6750	7	9	224	2139	285	333	2302	B6	747	N265JB	JFK	SYR	35	209	21	39	2023-07-09 21:00:00	Other
6753	9	2	830	815	15	1142	1110	B6	672	N942JB	EWR	LAX	315	2454	8	15	2023-09-02 08:00:00	LAX
6756	8	9	1241	1053	108	1508	1350	B6	277	N506JB	EWR	MCO	123	937	10	53	2023-08-09 10:00:00	MCO
6768	8	25	2154	2135	19	2354	2302	9E	1209	N315PQ	JFK	ITH	40	189	21	35	2023-08-25 21:00:00	Other
6769	6	23	2108	1959	69	13	2302	NK	172	N674NK	LGA	MCO	155	950	19	59	2023-06-23 19:00:00	MCO
6771	9	2	1104	745	199	1219	917	UA	862	N12125	EWR	ORD	104	719	7	45	2023-09-02 07:00:00	ORD
6774	12	17	1906	1850	16	2227	2159	B6	980	N571JB	EWR	TPA	150	997	18	50	2023-12-17 18:00:00	Other
6775	3	24	1641	1629	12	1821	1827	YX	1372	N440YX	LGA	ILM	77	500	16	29	2023-03-24 16:00:00	Other
6778	3	11	945	900	45	1145	1118	YX	1191	N645RW	EWR	AVL	87	583	9	0	2023-03-11 09:00:00	Other
6781	1	18	38	2259	99	503	347	B6	157	N2038J	JFK	SJU	184	1598	22	59	2023-01-18 22:00:00	Other
6791	9	15	1135	630	305	1442	916	B6	85	N579JB	LGA	MCO	147	950	6	30	2023-09-15 06:00:00	MCO
6793	12	11	2132	1955	97	53	2309	DL	755	N392DA	LGA	RSW	167	1080	19	55	2023-12-11 19:00:00	Other
6796	5	26	2155	2119	36	24	2359	B6	464	N615JB	JFK	JAX	115	828	21	19	2023-05-26 21:00:00	Other
6799	7	28	2226	2210	16	155	36	NK	239	N951NK	EWR	LAS	309	2227	22	10	2023-07-28 22:00:00	Other
6802	10	20	2211	2025	106	15	2250	WN	164	N949WN	LGA	DEN	221	1620	20	25	2023-10-20 20:00:00	Other
6809	4	29	1207	1150	17	1505	1450	NK	923	N609NK	EWR	MCO	138	937	11	50	2023-04-29 11:00:00	MCO
6821	11	5	1747	1729	18	2044	2040	AA	917	N940AN	JFK	MIA	143	1089	17	29	2023-11-05 17:00:00	MIA
6826	9	24	1830	1810	20	2027	2028	9E	1635	N921XJ	LGA	GSP	85	610	18	10	2023-09-24 18:00:00	Other
6828	5	21	1454	2215	999	1815	122	DL	101	N829MH	JFK	LAX	307	2475	22	15	2023-05-21 22:00:00	LAX
6836	8	8	916	905	11	1209	1210	YX	976	N404YX	LGA	IAH	198	1416	9	5	2023-08-08 09:00:00	Other
6837	8	29	1404	1300	64	1548	1507	AA	599	N948AN	LGA	CLT	80	544	13	0	2023-08-29 13:00:00	CLT
6843	4	9	1313	1209	64	1439	1353	AA	507	N815AW	LGA	RDU	67	431	12	9	2023-04-09 12:00:00	Other
6846	8	12	2150	1959	111	39	2259	B6	19	N640JB	LGA	TPA	143	1010	19	59	2023-08-12 19:00:00	Other
6859	5	3	1719	1621	58	1849	1805	UA	100	N62892	EWR	RDU	62	416	16	21	2023-05-03 16:00:00	Other
6862	3	30	1951	1930	21	2325	2236	B6	28	N658JB	JFK	ABQ	295	1826	19	30	2023-03-30 19:00:00	Other
6863	8	28	1144	1007	97	1341	1214	YX	873	N651RW	EWR	CLT	91	529	10	7	2023-08-28 10:00:00	CLT
6873	12	23	714	631	43	1032	1018	AA	448	N972UY	EWR	PHX	286	2133	6	31	2023-12-23 06:00:00	Other
6875	7	13	2009	1925	44	15	2250	AS	83	N513AS	EWR	SFO	358	2565	19	25	2023-07-13 19:00:00	Other
6877	1	18	1036	1016	20	1306	1328	DL	1077	N373DX	LGA	MCO	134	950	10	16	2023-01-18 10:00:00	MCO
6881	12	16	802	655	67	1046	1011	NK	821	N641NK	EWR	LAX	319	2454	6	55	2023-12-16 06:00:00	LAX
6883	7	21	2337	2217	80	33	2326	UA	725	N76526	EWR	SYR	37	195	22	17	2023-07-21 22:00:00	Other
6891	4	20	2043	1956	47	2306	2215	YX	953	N739YX	EWR	IND	93	645	19	56	2023-04-20 19:00:00	Other
6893	4	22	2323	2159	84	332	158	B6	654	N999JQ	JFK	SJU	197	1598	21	59	2023-04-22 21:00:00	Other
6894	6	20	2221	2155	26	38	2357	B6	548	N265JB	JFK	DTW	77	509	21	55	2023-06-20 21:00:00	Other
6897	7	28	1643	1529	74	1935	1834	UA	462	N27304	EWR	FLL	145	1065	15	29	2023-07-28 15:00:00	FLL
6902	1	27	1028	1000	28	1140	1124	UA	778	N24702	EWR	IAD	45	212	10	0	2023-01-27 10:00:00	Other
6904	4	3	736	722	14	1020	1017	UA	632	N454UA	EWR	TPA	139	997	7	22	2023-04-03 07:00:00	Other
6909	8	12	2015	1920	55	2219	2137	DL	429	N330NB	LGA	MSY	161	1183	19	20	2023-08-12 19:00:00	Other
6912	4	2	938	900	38	1255	1219	UA	721	N798UA	EWR	SFO	334	2565	9	0	2023-04-02 09:00:00	Other
6919	4	1	633	615	18	939	913	UA	252	N16703	EWR	AUS	229	1504	6	15	2023-04-01 06:00:00	Other
6921	6	21	1836	1747	49	2015	1953	YX	1070	N859RW	EWR	CMH	69	463	17	47	2023-06-21 17:00:00	Other
6926	4	29	2202	2138	24	22	15	NK	262	N979NK	EWR	LAS	294	2227	21	38	2023-04-29 21:00:00	Other
6927	3	14	2302	1955	187	255	2329	DL	918	N368DN	JFK	MIA	155	1089	19	55	2023-03-14 19:00:00	MIA
6931	10	25	1209	1140	29	1445	1425	WN	768	N8562Z	LGA	DAL	192	1381	11	40	2023-10-25 11:00:00	Other
6932	4	3	1656	1629	27	1823	1749	YX	1454	N219YX	JFK	BOS	39	187	16	29	2023-04-03 16:00:00	BOS
6935	7	2	2114	1839	155	16	2148	AA	538	N937AN	EWR	MIA	144	1085	18	39	2023-07-02 18:00:00	MIA
6952	5	1	1837	1815	22	2015	2028	DL	738	N951AT	EWR	MSP	134	1008	18	15	2023-05-01 18:00:00	Other
6954	3	9	1128	1109	19	1422	1424	DL	919	N126DN	LGA	FLL	141	1076	11	9	2023-03-09 11:00:00	FLL
6956	9	4	716	700	16	1015	1015	AS	13	N253AK	JFK	SFO	331	2586	7	0	2023-09-04 07:00:00	Other
6959	5	27	1833	1344	289	2126	1658	B6	92	N634JB	JFK	AUS	199	1521	13	44	2023-05-27 13:00:00	Other
6963	3	27	1006	930	36	1254	1159	B6	971	N348JB	LGA	SAV	124	722	9	30	2023-03-27 09:00:00	Other
6980	6	24	2114	2029	45	3	2335	B6	171	N589JB	LGA	FLL	149	1076	20	29	2023-06-24 20:00:00	FLL
6982	8	1	1646	1635	11	1809	1842	DL	491	N125DU	LGA	ORD	109	733	16	35	2023-08-01 16:00:00	ORD
6993	4	14	1521	1510	11	1715	1720	9E	1294	N301PQ	LGA	GSP	93	610	15	10	2023-04-14 15:00:00	Other
7005	4	14	737	710	27	1047	1020	DL	558	N361DN	LGA	FLL	158	1076	7	10	2023-04-14 07:00:00	FLL
7007	7	25	1243	1100	103	1536	1411	AA	237	N302SS	JFK	MIA	149	1089	11	0	2023-07-25 11:00:00	MIA
7010	7	21	1144	1110	34	1446	1420	DL	732	N806DN	JFK	FLL	142	1069	11	10	2023-07-21 11:00:00	FLL
7022	4	1	2004	1925	39	2207	2130	YX	1077	N441YX	LGA	MEM	157	963	19	25	2023-04-01 19:00:00	Other
7028	8	30	2217	1959	138	105	2258	NK	145	N677NK	LGA	MCO	143	950	19	59	2023-08-30 19:00:00	MCO
7035	5	11	1433	1410	23	1717	1718	B6	52	N644JB	JFK	SRQ	140	1041	14	10	2023-05-11 14:00:00	Other
7036	4	6	1719	1659	20	1958	1850	YX	937	N743YX	EWR	GSO	76	445	16	59	2023-04-06 16:00:00	Other
7038	10	23	2101	1940	81	2400	2243	B6	104	N998JE	JFK	ONT	321	2429	19	40	2023-10-23 19:00:00	Other
7041	2	26	1622	1555	27	1936	1919	AA	605	N839NN	LGA	DFW	215	1389	15	55	2023-02-26 15:00:00	Other
7043	8	3	1712	1541	91	2023	1846	UA	440	N17309	EWR	FLL	161	1065	15	41	2023-08-03 15:00:00	FLL
7044	3	16	1925	1729	116	2054	1918	B6	442	N355JB	JFK	RDU	65	427	17	29	2023-03-16 17:00:00	Other
7045	7	30	2235	2136	59	2340	2229	YX	940	N859RW	EWR	PHL	21	80	21	36	2023-07-30 21:00:00	Other
7065	4	5	915	830	45	1241	1227	B6	193	N958JB	JFK	SJU	185	1598	8	30	2023-04-05 08:00:00	Other
7072	1	16	929	915	14	1115	1125	YX	1840	N244JQ	LGA	CMH	76	479	9	15	2023-01-16 09:00:00	Other
7081	12	16	759	600	119	922	722	YX	1102	N770YX	EWR	IAD	47	212	6	0	2023-12-16 06:00:00	Other
7086	1	16	2337	1855	282	55	2046	DL	341	N133DU	LGA	BNA	118	764	18	55	2023-01-16 18:00:00	Other
7087	12	17	1813	1800	13	2027	2036	UA	845	N817UA	LGA	DEN	222	1620	18	0	2023-12-17 18:00:00	Other
7113	3	23	1826	1629	117	2110	1938	UA	663	N812UA	EWR	MIA	140	1085	16	29	2023-03-23 16:00:00	MIA
7129	9	22	907	833	34	1125	1100	B6	419	N258JB	JFK	ATL	113	760	8	33	2023-09-22 08:00:00	ATL
7131	5	13	1217	1159	18	1459	1455	UA	821	N76515	EWR	TPA	142	997	11	59	2023-05-13 11:00:00	Other
7135	2	3	1617	1330	167	1732	1448	DL	382	N134DU	JFK	BOS	40	187	13	30	2023-02-03 13:00:00	BOS
7142	3	18	1525	1506	19	1901	1804	UA	609	N37257	EWR	TPA	164	997	15	6	2023-03-18 15:00:00	Other
7143	3	13	2022	1850	92	2331	2208	B6	662	N796JB	JFK	FLL	156	1069	18	50	2023-03-13 18:00:00	FLL
7151	6	27	1030	915	75	1132	1035	B6	927	N247JB	LGA	BOS	41	184	9	15	2023-06-27 09:00:00	BOS
7159	6	6	2351	2149	122	47	2242	YX	1148	N729YX	EWR	PHL	26	80	21	49	2023-06-06 21:00:00	Other
7161	3	9	1850	1825	25	2047	2020	WN	644	N7824A	LGA	STL	142	888	18	25	2023-03-09 18:00:00	Other
7163	12	24	2215	2155	20	2329	2342	UA	485	N75428	EWR	RDU	58	416	21	55	2023-12-24 21:00:00	Other
7170	10	27	2144	2055	49	2321	2238	DL	375	N106DU	LGA	ORD	116	733	20	55	2023-10-27 20:00:00	ORD
7181	12	19	1802	1710	52	2046	2035	DL	87	N195DN	JFK	LAX	316	2475	17	10	2023-12-19 17:00:00	LAX
7196	1	20	1233	1159	34	1342	1325	9E	1488	N902XJ	LGA	ROC	46	254	11	59	2023-01-20 11:00:00	Other
7198	5	17	1733	1720	13	2046	2025	WN	944	N8610A	LGA	HOU	198	1428	17	20	2023-05-17 17:00:00	Other
7202	4	26	2117	1959	78	2307	2142	UA	483	N17294	EWR	CLE	67	404	19	59	2023-04-26 19:00:00	Other
7206	4	16	2300	1840	260	152	2210	B6	50	N2002J	JFK	SMF	319	2521	18	40	2023-04-16 18:00:00	Other
7213	9	7	1953	1859	54	117	2154	AS	10	N278AK	JFK	SAN	337	2446	18	59	2023-09-07 18:00:00	Other
7220	7	21	2323	2140	103	245	58	B6	760	N946JL	JFK	SFO	337	2586	21	40	2023-07-21 21:00:00	Other
7229	10	11	2328	2155	93	245	119	B6	912	N923JB	JFK	SFO	357	2586	21	55	2023-10-11 21:00:00	Other
7232	7	17	1110	1059	11	1246	1250	UA	688	N420UA	EWR	MEM	131	946	10	59	2023-07-17 10:00:00	Other
7234	2	23	1545	1532	13	1754	1757	YX	1224	N433YX	LGA	DTW	101	502	15	32	2023-02-23 15:00:00	Other
7245	5	14	1715	1647	28	1856	1826	UA	774	N36247	EWR	CLE	69	404	16	47	2023-05-14 16:00:00	Other
7247	7	14	1846	1759	47	NA	2114	DL	715	N366NW	JFK	AUS	NA	1521	17	59	2023-07-14 17:00:00	Other
7251	7	15	1834	1701	93	2032	1915	DL	743	N343NB	LGA	DTW	80	502	17	1	2023-07-15 17:00:00	Other
7262	1	20	1209	910	179	1343	1101	9E	1700	N691CA	LGA	MSN	123	812	9	10	2023-01-20 09:00:00	Other
7264	9	10	1948	1830	78	2118	2010	YX	1218	N740YX	EWR	PIT	54	319	18	30	2023-09-10 18:00:00	Other
7265	3	15	1921	1759	82	2200	2102	YX	1289	N121HQ	LGA	OKC	197	1341	17	59	2023-03-15 17:00:00	Other
7277	2	14	1036	900	96	1339	1202	UA	495	N12109	EWR	TPA	142	997	9	0	2023-02-14 09:00:00	Other
7278	1	30	1542	1515	27	1857	1840	UA	726	N2639U	EWR	SFO	342	2565	15	15	2023-01-30 15:00:00	Other
7303	6	21	2058	2037	21	21	2352	B6	708	N929JB	JFK	LAX	323	2475	20	37	2023-06-21 20:00:00	LAX
7312	5	1	2243	2059	104	1	2232	UA	840	N877UA	EWR	MSN	109	799	20	59	2023-05-01 20:00:00	Other
7313	2	2	1719	1655	24	1904	1853	9E	1370	N184GJ	LGA	RDU	81	431	16	55	2023-02-02 16:00:00	Other
7322	11	22	1229	1159	30	1435	1436	OO	1187	N240SY	LGA	SDF	103	659	11	59	2023-11-22 11:00:00	Other
7323	1	12	2126	2100	26	128	38	B6	362	N929JB	JFK	SFO	350	2586	21	0	2023-01-12 21:00:00	Other
7324	3	5	821	810	11	1246	1310	DL	725	N878DN	JFK	SJU	186	1598	8	10	2023-03-05 08:00:00	Other
7325	1	23	1728	1630	58	1905	1829	AA	146	N845NN	LGA	ORD	120	733	16	30	2023-01-23 16:00:00	ORD
7327	6	21	1711	1527	104	1835	1729	DL	964	N895AT	EWR	MSP	125	1008	15	27	2023-06-21 15:00:00	Other
7354	4	13	1834	1759	35	2124	2117	B6	697	N946JL	EWR	LAX	309	2454	17	59	2023-04-13 17:00:00	LAX
7356	10	17	1344	1303	41	1548	1508	AA	721	N914AN	LGA	CLT	88	544	13	3	2023-10-17 13:00:00	CLT
7357	7	26	2208	2131	37	6	2339	UA	527	N444UA	EWR	MCI	146	1092	21	31	2023-07-26 21:00:00	Other
7360	2	3	2209	2105	64	13	2329	B6	377	N519JB	LGA	CHS	92	641	21	5	2023-02-03 21:00:00	Other
7373	7	16	940	700	160	1124	912	UA	126	N69806	EWR	DEN	206	1605	7	0	2023-07-16 07:00:00	Other
7374	11	27	1933	1920	13	2240	2254	AS	88	N921AK	EWR	SFO	334	2565	19	20	2023-11-27 19:00:00	Other
7377	11	25	1526	1500	26	1737	1710	9E	1448	N695CA	EWR	CVG	97	569	15	0	2023-11-25 15:00:00	Other
7383	9	16	1137	755	222	1328	1006	DL	89	N119DU	LGA	CHS	91	641	7	55	2023-09-16 07:00:00	Other
7386	9	13	1942	1930	12	2249	2253	AA	87	N101NN	JFK	LAX	318	2475	19	30	2023-09-13 19:00:00	LAX
7388	5	29	1742	1729	13	2054	2054	AA	318	N303RG	JFK	MIA	156	1089	17	29	2023-05-29 17:00:00	MIA
7394	7	7	1543	1530	13	1904	1827	UA	672	N647UA	EWR	IAH	179	1400	15	30	2023-07-07 15:00:00	Other
7397	7	23	2112	2030	42	2242	2207	YX	1089	N430YX	JFK	BOS	44	187	20	30	2023-07-23 20:00:00	BOS
7411	7	4	1201	957	124	1520	1249	UA	403	N25705	EWR	AUS	201	1504	9	57	2023-07-04 09:00:00	Other
7415	12	8	625	600	25	912	909	NK	479	N634NK	LGA	MCO	137	950	6	0	2023-12-08 06:00:00	MCO
7421	8	7	1856	1815	41	2227	2127	AA	595	N825NN	LGA	MIA	154	1096	18	15	2023-08-07 18:00:00	MIA
7428	6	26	1014	943	31	1149	1140	9E	1721	N348PQ	LGA	STL	122	888	9	43	2023-06-26 09:00:00	Other
7433	2	13	1001	805	116	1324	1125	B6	246	N999JQ	JFK	FLL	147	1069	8	5	2023-02-13 08:00:00	FLL
7434	4	28	1119	1100	19	1244	1229	UA	463	N495UA	EWR	BNA	114	748	11	0	2023-04-28 11:00:00	Other
7440	10	28	1239	1145	54	1454	1406	B6	946	N985JT	JFK	ATL	108	760	11	45	2023-10-28 11:00:00	ATL
7441	2	24	1049	1029	20	1512	1345	UA	183	N69840	EWR	PHX	339	2133	10	29	2023-02-24 10:00:00	Other
7442	1	19	2307	1929	218	231	2259	B6	27	N706JB	JFK	SLC	270	1990	19	29	2023-01-19 19:00:00	Other
7452	5	1	1508	1445	23	1627	1612	9E	1400	N921XJ	LGA	ROC	46	254	14	45	2023-05-01 14:00:00	Other
7455	11	18	1547	1526	21	1655	1704	UA	789	N37462	EWR	ORD	113	719	15	26	2023-11-18 15:00:00	ORD
7470	4	15	2026	1904	82	2311	2123	9E	1311	N313PQ	JFK	MSP	137	1029	19	4	2023-04-15 19:00:00	Other
7477	3	4	753	1630	923	1137	2007	DL	216	N836DN	JFK	SLC	316	1990	16	30	2023-03-04 16:00:00	Other
7480	3	15	1631	1559	32	1746	1741	B6	816	N612JB	LGA	BNA	105	764	15	59	2023-03-15 15:00:00	Other
7523	8	10	1844	1650	114	2230	2006	B6	186	N584JB	LGA	FLL	177	1076	16	50	2023-08-10 16:00:00	FLL
7530	3	17	955	855	60	1301	1218	DL	214	N108DQ	LGA	DFW	222	1389	8	55	2023-03-17 08:00:00	Other
7534	9	10	1312	1250	22	1633	1552	B6	17	N789JB	LGA	TPA	148	1010	12	50	2023-09-10 12:00:00	Other
7538	7	15	725	702	23	1104	1010	AA	318	N329SL	JFK	MIA	148	1089	7	2	2023-07-15 07:00:00	MIA
7539	3	14	1331	1259	32	1609	1422	9E	1530	N299PQ	LGA	SCE	37	208	12	59	2023-03-14 12:00:00	Other
7546	6	11	1755	1530	145	2054	1833	UA	522	N29124	EWR	LAX	318	2454	15	30	2023-06-11 15:00:00	LAX
7548	3	2	1444	1425	19	1700	1609	DL	815	N133DU	LGA	ORD	144	733	14	25	2023-03-02 14:00:00	ORD
7551	6	16	1827	1542	165	2148	1853	DL	625	N3746H	JFK	PBI	172	1028	15	42	2023-06-16 15:00:00	Other
7553	8	29	2038	1930	68	2318	2239	B6	55	N983JT	JFK	LAX	310	2475	19	30	2023-08-29 19:00:00	LAX
7559	1	14	2134	2115	19	2243	2300	UA	224	N479UA	EWR	ORD	104	719	21	15	2023-01-14 21:00:00	ORD
7560	9	6	1949	1835	74	2238	2152	B6	240	N531JL	JFK	SJC	330	2569	18	35	2023-09-06 18:00:00	Other
7561	8	13	1226	1120	66	1331	1231	9E	1115	N182GJ	LGA	ALB	28	136	11	20	2023-08-13 11:00:00	Other
7569	6	24	2120	1515	365	3	1650	UA	715	N666UA	EWR	ORD	97	719	15	15	2023-06-24 15:00:00	ORD
7571	4	20	2021	1855	86	2316	2158	DL	460	N132DU	LGA	IAH	189	1416	18	55	2023-04-20 18:00:00	Other
7578	9	29	1037	955	42	1227	1210	WN	1081	N273WN	LGA	MCI	148	1107	9	55	2023-09-29 09:00:00	Other
7582	8	25	1323	950	213	1518	1158	YX	1025	N427YX	LGA	GSP	91	610	9	50	2023-08-25 09:00:00	Other
7584	12	17	2021	1815	126	2259	2144	DL	197	N130DU	JFK	DFW	186	1391	18	15	2023-12-17 18:00:00	Other
7591	7	11	1640	1624	16	1749	1750	UA	601	N77552	EWR	IAD	43	212	16	24	2023-07-11 16:00:00	Other
7598	3	12	1839	1825	14	2001	2016	DL	369	N120DU	LGA	ORD	112	733	18	25	2023-03-12 18:00:00	ORD
7599	9	11	1933	1841	52	2109	2030	UA	805	N68817	EWR	RDU	64	416	18	41	2023-09-11 18:00:00	Other
7605	4	15	337	2156	341	607	59	NK	655	N672NK	EWR	MCO	129	937	21	56	2023-04-15 21:00:00	MCO
7608	4	2	1535	1315	140	1915	1647	UA	675	N19141	EWR	SFO	371	2565	13	15	2023-04-02 13:00:00	Other
7609	10	9	1105	1029	36	1255	1244	9E	1436	N922XJ	LGA	MYR	85	563	10	29	2023-10-09 10:00:00	Other
7634	4	21	2020	2000	20	2143	2126	AA	521	N740UW	LGA	DCA	48	214	20	0	2023-04-21 20:00:00	Other
7639	7	4	905	845	20	1113	1105	9E	1188	N315PQ	LGA	SAV	99	722	8	45	2023-07-04 08:00:00	Other
7644	4	1	2054	1941	73	2259	2210	YX	1005	N741YX	EWR	SDF	105	642	19	41	2023-04-01 19:00:00	Other
7648	5	22	1412	1300	72	1644	1610	UA	808	N41140	EWR	LAX	309	2454	13	0	2023-05-22 13:00:00	LAX
7649	7	6	2218	2035	103	57	2330	UA	232	N47275	EWR	AUS	188	1504	20	35	2023-07-06 20:00:00	Other
7655	5	3	2225	2159	26	28	10	UA	467	N470UA	EWR	CHS	91	628	21	59	2023-05-03 21:00:00	Other
7663	7	9	833	820	13	1049	1040	DL	751	N881DN	EWR	ATL	105	746	8	20	2023-07-09 08:00:00	ATL
7666	4	7	1924	1850	34	2134	2105	9E	1306	N331PQ	LGA	GRR	105	618	18	50	2023-04-07 18:00:00	Other
7668	2	26	1343	1330	13	1540	1546	YX	1515	N810MD	LGA	CLT	96	544	13	30	2023-02-26 13:00:00	CLT
7685	9	1	2038	1657	221	2211	1842	UA	92	N493UA	EWR	RDU	66	416	16	57	2023-09-01 16:00:00	Other
7690	3	7	1014	955	19	1400	1340	B6	16	N948JB	JFK	PHX	320	2153	9	55	2023-03-07 09:00:00	Other
7693	4	21	1230	1159	31	1428	1423	UA	355	N69888	EWR	DEN	216	1605	11	59	2023-04-21 11:00:00	Other
7700	1	10	1221	1130	51	1518	1434	DL	209	N878DN	JFK	LAS	333	2248	11	30	2023-01-10 11:00:00	Other
7706	7	15	1916	1630	166	2035	1806	OO	968	N253SY	LGA	MKE	106	738	16	30	2023-07-15 16:00:00	Other
7708	1	20	959	940	19	1303	1302	B6	186	N775JB	JFK	BUR	338	2465	9	40	2023-01-20 09:00:00	Other
7710	4	25	1638	1627	11	1826	1835	YX	1216	N109HQ	JFK	CMH	87	483	16	27	2023-04-25 16:00:00	Other
7716	11	3	1643	1245	238	1804	1416	AA	979	N825AW	LGA	BNA	114	764	12	45	2023-11-03 12:00:00	Other
7720	9	25	2259	2159	60	15	2320	UA	168	N26226	EWR	BOS	48	200	21	59	2023-09-25 21:00:00	BOS
7732	8	14	1859	1830	29	2200	2131	UA	398	N54711	EWR	SNA	314	2434	18	30	2023-08-14 18:00:00	Other
7744	12	9	2021	1959	22	2312	2305	NK	156	N660NK	LGA	MCO	141	950	19	59	2023-12-09 19:00:00	MCO
7746	8	4	2017	1954	23	2224	2248	DL	337	N886DN	JFK	ATL	99	760	19	54	2023-08-04 19:00:00	ATL
7753	1	6	2236	2220	16	2355	2343	B6	202	N179JB	JFK	ROC	56	264	22	20	2023-01-06 22:00:00	Other
7754	8	10	1624	1510	74	1859	1810	DL	187	N137DU	LGA	DFW	187	1389	15	10	2023-08-10 15:00:00	Other
7760	9	29	1436	1359	37	1633	1625	DL	210	N3772H	LGA	DEN	204	1620	13	59	2023-09-29 13:00:00	Other
7761	3	24	2235	2048	107	124	2356	UA	280	N14230	EWR	FLL	145	1065	20	48	2023-03-24 20:00:00	FLL
7764	3	23	126	2240	166	226	2235	YX	1713	N223JQ	JFK	PWM	45	273	22	40	2023-03-23 22:00:00	Other
7765	3	24	1721	1659	22	1959	1931	UA	600	N468UA	EWR	ATL	112	746	16	59	2023-03-24 16:00:00	ATL
7771	10	7	1527	1453	34	1659	1638	UA	653	N801UA	EWR	RDU	72	416	14	53	2023-10-07 14:00:00	Other
7785	2	16	1330	1300	30	1550	1537	B6	706	N535JB	LGA	MSY	175	1183	13	0	2023-02-16 13:00:00	Other
7796	5	23	1513	1445	28	1709	1700	WN	706	N8842L	LGA	MSY	160	1183	14	45	2023-05-23 14:00:00	Other
7798	4	26	1005	930	35	1138	1102	UA	854	N457UA	EWR	BNA	113	748	9	30	2023-04-26 09:00:00	Other
7801	3	13	1854	1840	14	2148	2210	AS	11	N264AK	JFK	SAN	328	2446	18	40	2023-03-13 18:00:00	Other
7806	12	25	944	930	14	1217	1252	B6	96	N2151J	JFK	LAX	304	2475	9	30	2023-12-25 09:00:00	LAX
7809	6	3	2304	2105	119	118	2349	UA	828	N27283	EWR	DFW	169	1372	21	5	2023-06-03 21:00:00	Other
7816	9	1	105	1916	349	443	2313	B6	448	N827JB	EWR	SJU	190	1608	19	16	2023-09-01 19:00:00	Other
7819	7	21	632	600	32	919	837	UA	170	N27304	EWR	IAH	178	1400	6	0	2023-07-21 06:00:00	Other
7824	7	8	1631	1529	62	2001	1832	B6	463	N994JL	JFK	MCO	138	944	15	29	2023-07-08 15:00:00	MCO
7843	11	20	2207	2024	103	2326	2201	9E	1618	N485PX	LGA	CHO	56	305	20	24	2023-11-20 20:00:00	Other
7858	11	30	1638	1546	52	1755	1738	YX	1318	N401YX	JFK	BNA	117	765	15	46	2023-11-30 15:00:00	Other
7861	8	6	743	730	13	1036	1043	DL	545	N101DQ	JFK	FLL	148	1069	7	30	2023-08-06 07:00:00	FLL
7866	7	26	1447	1329	78	1643	1553	AA	802	N931NN	JFK	PHX	272	2153	13	29	2023-07-26 13:00:00	Other
7876	9	4	823	810	13	1159	1211	UA	806	N78060	EWR	SJU	193	1608	8	10	2023-09-04 08:00:00	Other
7880	1	26	2032	2007	25	2245	2209	YX	1254	N740YX	EWR	CMH	85	463	20	7	2023-01-26 20:00:00	Other
7892	3	16	126	2340	106	442	325	B6	334	N656JB	JFK	BQN	178	1576	23	40	2023-03-16 23:00:00	Other
7898	5	25	2132	2120	12	2325	2320	YX	1092	N640RW	EWR	MEM	137	946	21	20	2023-05-25 21:00:00	Other
7901	2	3	2326	2259	27	411	348	B6	342	N834JB	JFK	BQN	200	1576	22	59	2023-02-03 22:00:00	Other
7903	1	3	1211	1130	41	1340	1311	UA	88	N17752	EWR	RDU	69	416	11	30	2023-01-03 11:00:00	Other
7908	9	10	1356	830	326	1606	1006	9E	1755	N910XJ	JFK	ORF	67	290	8	30	2023-09-10 08:00:00	Other
7910	11	22	1704	1529	95	2020	1836	B6	700	N586JB	LGA	PBI	163	1035	15	29	2023-11-22 15:00:00	Other
7914	7	14	1703	1559	64	1835	1749	9E	1224	N904XJ	LGA	BGR	65	378	15	59	2023-07-14 15:00:00	Other
7915	2	6	1652	1627	25	1815	1757	YX	1011	N731YX	EWR	BUF	51	282	16	27	2023-02-06 16:00:00	Other
7918	1	2	1452	1400	52	1803	1705	UA	141	N27270	EWR	PBI	154	1023	14	0	2023-01-02 14:00:00	Other
7924	6	14	2248	2206	42	2357	2320	UA	817	N12754	EWR	SYR	39	195	22	6	2023-06-14 22:00:00	Other
7925	5	11	1707	1630	37	1910	1858	YX	1640	N244JQ	LGA	IND	98	660	16	30	2023-05-11 16:00:00	Other
7947	3	16	2158	2130	28	2318	2255	B6	185	N306JB	JFK	ROC	51	264	21	30	2023-03-16 21:00:00	Other
7950	9	11	1059	959	60	1241	1203	AA	329	N917UY	EWR	CLT	84	529	9	59	2023-09-11 09:00:00	CLT
7954	8	26	1758	1529	149	2040	1832	B6	441	N975JT	JFK	MCO	134	944	15	29	2023-08-26 15:00:00	MCO
7958	1	13	1333	1235	58	1632	1539	UA	286	N27276	EWR	TPA	152	997	12	35	2023-01-13 12:00:00	Other
7961	11	22	1157	1059	58	1435	1415	UA	574	N39726	EWR	AUS	199	1504	10	59	2023-11-22 10:00:00	Other
7962	10	22	1615	1559	16	1917	1914	DL	862	N347NB	JFK	AUS	217	1521	15	59	2023-10-22 15:00:00	Other
7964	12	17	2202	2110	52	26	2353	DL	806	N3738B	JFK	ATL	110	760	21	10	2023-12-17 21:00:00	ATL
7965	5	21	1845	1820	25	2058	2118	B6	432	N2043J	JFK	LAS	288	2248	18	20	2023-05-21 18:00:00	Other
7967	8	26	1850	1825	25	2033	2020	YX	1054	N133HQ	JFK	CMH	84	483	18	25	2023-08-26 18:00:00	Other
7972	12	18	1025	730	175	1247	1008	B6	251	N354JB	JFK	JAX	124	828	7	30	2023-12-18 07:00:00	Other
7979	1	3	1237	1205	32	1558	1517	B6	689	N2027J	JFK	FLL	147	1069	12	5	2023-01-03 12:00:00	FLL
7984	11	17	1644	1625	19	1852	1845	WN	1180	N7879A	LGA	MCI	162	1107	16	25	2023-11-17 16:00:00	Other
7987	1	29	1530	1507	23	1800	1750	YX	1189	N756YX	EWR	JAX	125	820	15	7	2023-01-29 15:00:00	Other
7992	7	27	2320	2135	105	226	20	B6	76	N197JB	JFK	MCO	128	944	21	35	2023-07-27 21:00:00	MCO
7996	12	18	1913	1835	38	2107	2109	UA	535	N37474	EWR	DEN	203	1605	18	35	2023-12-18 18:00:00	Other
8014	4	27	1556	1545	11	1831	1823	DL	310	N124DX	LGA	ATL	115	762	15	45	2023-04-27 15:00:00	ATL
8015	9	15	1337	1300	37	1630	1604	B6	595	N558JB	JFK	FLL	141	1069	13	0	2023-09-15 13:00:00	FLL
8020	4	28	2216	2055	81	7	2302	YX	974	N748YX	EWR	MYR	89	550	20	55	2023-04-28 20:00:00	Other
8026	4	16	2003	1720	163	2244	2017	B6	416	N605JB	JFK	LAS	298	2248	17	20	2023-04-16 17:00:00	Other
8030	6	28	1834	1815	19	2009	1938	B6	456	N197JB	LGA	BOS	48	184	18	15	2023-06-28 18:00:00	BOS
8031	12	21	2220	2130	50	2335	2308	B6	162	N239JB	JFK	ROC	50	264	21	30	2023-12-21 21:00:00	Other
8033	5	11	1912	1800	72	2120	2020	9E	1463	N919XJ	LGA	TYS	87	647	18	0	2023-05-11 18:00:00	Other
8044	7	5	5	2217	108	108	2326	UA	725	N498UA	EWR	SYR	32	195	22	17	2023-07-05 22:00:00	Other
8046	2	21	1628	1600	28	1743	1725	YX	1570	N240JQ	LGA	BOS	34	184	16	0	2023-02-21 16:00:00	BOS
8052	4	16	913	750	83	1058	947	AA	545	N803NN	EWR	CLT	79	529	7	50	2023-04-16 07:00:00	CLT
8057	6	20	2321	2136	105	39	2315	UA	753	N33289	EWR	ORD	98	719	21	36	2023-06-20 21:00:00	ORD
8066	8	8	1919	1824	55	2038	2000	UA	592	N827UA	LGA	ORD	109	733	18	24	2023-08-08 18:00:00	ORD
8067	6	18	2116	2037	39	2303	2253	UA	307	N62884	EWR	PHX	263	2133	20	37	2023-06-18 20:00:00	Other
8069	12	8	720	700	20	1022	1025	DL	331	N316DU	EWR	SLC	278	1969	7	0	2023-12-08 07:00:00	Other
8093	7	7	1022	932	50	1227	1201	B6	364	N281JB	JFK	ATL	104	760	9	32	2023-07-07 09:00:00	ATL
8096	5	19	1710	1659	11	1850	1840	UA	616	N419UA	LGA	ORD	122	733	16	59	2023-05-19 16:00:00	ORD
8098	5	3	2050	1954	56	34	2353	UA	211	N39423	EWR	BQN	200	1585	19	54	2023-05-03 19:00:00	Other
8100	7	13	1140	852	168	1255	1017	UA	553	N845UA	EWR	ORF	48	284	8	52	2023-07-13 08:00:00	Other
8102	7	6	1858	1539	199	2147	1844	UA	462	N75433	EWR	FLL	132	1065	15	39	2023-07-06 15:00:00	FLL
8104	12	19	1703	1644	19	1943	2002	AA	678	N402AN	EWR	DFW	185	1372	16	44	2023-12-19 16:00:00	Other
8111	6	6	18	2035	223	150	2232	9E	1514	N905XJ	LGA	ILM	78	500	20	35	2023-06-06 20:00:00	Other
8112	5	22	1820	1742	38	2120	2059	UA	563	N408UA	EWR	SMF	319	2500	17	42	2023-05-22 17:00:00	Other
8114	1	26	2312	2034	158	154	2359	UA	978	N37290	EWR	SMF	325	2500	20	34	2023-01-26 20:00:00	Other
8117	12	14	1353	1155	118	1528	1415	G4	140	203NV	EWR	DSM	136	1017	11	55	2023-12-14 11:00:00	Other
8118	9	8	1641	1550	51	2209	1826	UA	851	N37567	EWR	LAS	326	2227	15	50	2023-09-08 15:00:00	Other
8120	7	27	1752	1415	217	1939	1603	AA	622	N804AW	LGA	RDU	84	431	14	15	2023-07-27 14:00:00	Other
8130	8	26	2041	1959	42	38	2357	UA	462	N68821	EWR	SJU	215	1608	19	59	2023-08-26 19:00:00	Other
8136	6	9	1753	1729	24	2042	2040	AA	153	N887NN	JFK	MIA	147	1089	17	29	2023-06-09 17:00:00	MIA
8145	6	2	1407	1350	17	1526	1522	OO	1212	N256SY	JFK	BOS	38	187	13	50	2023-06-02 13:00:00	BOS
8150	12	16	1824	1805	19	2130	2136	DL	840	N315NB	JFK	AUS	222	1521	18	5	2023-12-16 18:00:00	Other
8153	12	8	1210	1149	21	1337	1328	9E	1526	N912XJ	LGA	ORF	57	296	11	49	2023-12-08 11:00:00	Other
8156	2	3	1458	1400	58	1715	1627	DL	780	N3758Y	EWR	ATL	114	746	14	0	2023-02-03 14:00:00	ATL
8158	4	12	2125	2100	25	43	47	AA	54	N102NN	JFK	SFO	349	2586	21	0	2023-04-12 21:00:00	Other
8160	4	23	1603	1508	55	1739	1715	DL	833	N935AT	EWR	MSP	132	1008	15	8	2023-04-23 15:00:00	Other
8166	5	12	1913	1715	118	2149	2019	B6	70	N585JB	JFK	TPA	134	1005	17	15	2023-05-12 17:00:00	Other
8173	7	5	2330	2255	35	149	149	F9	757	N230FR	LGA	DFW	174	1389	22	55	2023-07-05 22:00:00	Other
8185	8	1	1525	1500	25	1659	1655	YX	1081	N132HQ	LGA	STL	128	888	15	0	2023-08-01 15:00:00	Other
8197	6	23	1649	1624	25	1823	1750	UA	758	N37560	EWR	IAD	48	212	16	24	2023-06-23 16:00:00	Other
8201	10	2	1003	930	33	1301	1241	B6	905	N579JB	JFK	MIA	153	1089	9	30	2023-10-02 09:00:00	MIA
8208	10	26	617	600	17	910	854	UA	227	N57286	EWR	AUS	207	1504	6	0	2023-10-26 06:00:00	Other
8221	9	23	616	600	16	730	734	UA	363	N27251	EWR	ORD	102	719	6	0	2023-09-23 06:00:00	ORD
8223	8	10	1416	1405	11	1702	1650	WN	289	N942WN	LGA	HOU	190	1428	14	5	2023-08-10 14:00:00	Other
8228	1	10	1404	1344	20	1700	1655	B6	785	N536JB	JFK	IAH	189	1417	13	44	2023-01-10 13:00:00	Other
8238	4	3	942	905	37	1249	1142	B6	419	N355JB	JFK	ATL	130	760	9	5	2023-04-03 09:00:00	ATL
8240	10	2	1622	1502	80	1920	1815	NK	587	N663NK	LGA	FLL	142	1076	15	2	2023-10-02 15:00:00	FLL
8246	8	5	1609	1534	35	1753	1744	YX	1079	N404YX	JFK	CMH	77	483	15	34	2023-08-05 15:00:00	Other
8248	9	10	1956	1915	41	2329	2219	DL	141	N175DN	JFK	LAX	336	2475	19	15	2023-09-10 19:00:00	LAX
8261	9	30	1302	1212	50	1434	1339	YX	1299	N115HQ	JFK	ORF	53	290	12	12	2023-09-30 12:00:00	Other
8270	7	25	14	2055	199	201	2309	OO	987	N308SY	JFK	CLE	71	425	20	55	2023-07-25 20:00:00	Other
8276	7	10	1121	1050	31	1310	1315	9E	1140	N153PQ	LGA	CVG	90	585	10	50	2023-07-10 10:00:00	Other
8280	7	28	38	2217	141	145	2326	UA	725	N24729	EWR	SYR	41	195	22	17	2023-07-28 22:00:00	Other
8282	8	12	1030	2250	700	1151	25	9E	1279	N935XJ	JFK	SYR	51	209	22	50	2023-08-12 22:00:00	Other
8291	12	28	1543	1451	52	1711	1640	DL	99	N120DU	LGA	ORD	114	733	14	51	2023-12-28 14:00:00	ORD
8292	3	27	1546	1530	16	1732	1708	UA	685	N33714	EWR	CLE	78	404	15	30	2023-03-27 15:00:00	Other
8312	7	17	2101	1629	272	2400	1904	DL	694	N331NB	JFK	MSP	158	1029	16	29	2023-07-17 16:00:00	Other
8314	8	15	2014	1910	64	2158	2144	UA	326	N37466	EWR	LAS	263	2227	19	10	2023-08-15 19:00:00	Other
8315	4	2	1212	1159	13	1424	1429	YX	986	N729YX	EWR	SAV	102	708	11	59	2023-04-02 11:00:00	Other
8322	5	6	1540	1514	26	1816	1802	UA	238	N27270	EWR	MCO	122	937	15	14	2023-05-06 15:00:00	MCO
8328	2	1	1028	1015	13	1221	1130	B6	218	N239JB	LGA	BOS	34	184	10	15	2023-02-01 10:00:00	BOS
8332	10	3	1359	1325	34	1509	1450	WN	481	N463WN	LGA	BNA	103	764	13	25	2023-10-03 13:00:00	Other
8336	7	27	1629	1559	30	1746	1749	9E	1224	N183GJ	LGA	BGR	58	378	15	59	2023-07-27 15:00:00	Other
8338	2	16	1942	1929	13	2125	2121	OO	1175	N317SY	JFK	BNA	140	765	19	29	2023-02-16 19:00:00	Other
8341	1	1	1	2038	203	328	3	UA	628	N25201	EWR	SMF	367	2500	20	38	2023-01-01 20:00:00	Other
8344	2	25	1658	1625	33	1827	1821	9E	1279	N134EV	LGA	RDU	72	431	16	25	2023-02-25 16:00:00	Other
8359	3	27	1923	1859	24	2318	2305	DL	721	N884DN	JFK	SJU	193	1598	18	59	2023-03-27 18:00:00	Other
8361	6	23	2235	2037	118	2355	2210	B6	74	N358JB	JFK	BTV	43	266	20	37	2023-06-23 20:00:00	Other
8364	11	26	2003	1859	64	2230	2106	AA	613	N751UW	LGA	CLT	98	544	18	59	2023-11-26 18:00:00	CLT
8366	3	5	2038	1940	58	2342	2249	B6	687	N306JB	LGA	PBI	140	1035	19	40	2023-03-05 19:00:00	Other
8367	12	18	1036	940	56	1352	1315	UA	712	N14118	EWR	SFO	336	2565	9	40	2023-12-18 09:00:00	Other
8372	9	5	2124	2110	14	26	32	UA	692	N12114	EWR	SFO	328	2565	21	10	2023-09-05 21:00:00	Other
8373	7	1	1856	1550	186	2207	1920	DL	679	N3753	JFK	MIA	149	1089	15	50	2023-07-01 15:00:00	MIA
8380	5	2	2243	1840	243	2350	2010	B6	922	N228JB	EWR	BOS	46	200	18	40	2023-05-02 18:00:00	BOS
8383	2	26	2013	1954	19	44	50	UA	233	N78448	EWR	BQN	179	1585	19	54	2023-02-26 19:00:00	Other
8384	4	29	1408	1350	18	1854	1648	B6	512	N566JB	JFK	MCO	144	944	13	50	2023-04-29 13:00:00	MCO
8386	6	9	1656	1640	16	1915	1855	B6	988	N510JB	LGA	CHS	100	641	16	40	2023-06-09 16:00:00	Other
8388	3	27	2055	1952	63	2203	2106	YX	1079	N753YX	EWR	ALB	29	143	19	52	2023-03-27 19:00:00	Other
8390	12	23	1515	1457	18	1804	1820	B6	774	N821JB	JFK	RNO	318	2411	14	57	2023-12-23 14:00:00	Other
8394	5	18	2046	1930	76	2156	2114	AA	895	N918NN	LGA	ORD	106	733	19	30	2023-05-18 19:00:00	ORD
8399	2	1	2057	2029	28	2336	2248	YX	1014	N745YX	EWR	GRR	112	605	20	29	2023-02-01 20:00:00	Other
8400	8	12	2156	2059	57	134	16	B6	26	N559JB	JFK	SLC	285	1990	20	59	2023-08-12 20:00:00	Other
8412	5	22	2204	2146	18	2352	2349	UA	731	N38443	EWR	DTW	77	488	21	46	2023-05-22 21:00:00	Other
8424	5	22	2125	1855	150	102	2149	B6	899	N563JB	JFK	MCO	137	944	18	55	2023-05-22 18:00:00	MCO
8438	6	17	2002	1759	123	2355	2056	F9	511	N611FR	LGA	MCO	206	950	17	59	2023-06-17 17:00:00	MCO
8441	4	20	2121	2005	76	2347	2245	B6	165	N507JT	LGA	JAX	113	833	20	5	2023-04-20 20:00:00	Other
8443	5	24	1023	600	263	1222	814	DL	815	N947AT	EWR	ATL	103	746	6	0	2023-05-24 06:00:00	ATL
8449	8	18	856	845	11	1133	1007	YX	1312	N882RW	EWR	BOS	40	200	8	45	2023-08-18 08:00:00	BOS
8454	3	1	1640	1429	131	1807	1609	UA	706	N853UA	EWR	RDU	66	416	14	29	2023-03-01 14:00:00	Other
8455	1	31	1626	1330	176	1736	1448	DL	427	N111NG	JFK	BOS	32	187	13	30	2023-01-31 13:00:00	BOS
8458	9	26	1819	1750	29	2146	2040	UA	602	N77538	EWR	IAH	181	1400	17	50	2023-09-26 17:00:00	Other
8463	3	10	1843	1755	48	2012	1920	YX	1682	N810MD	LGA	DCA	56	214	17	55	2023-03-10 17:00:00	Other
8465	8	2	2048	1825	143	2212	2022	DL	296	N121DU	LGA	ORD	116	733	18	25	2023-08-02 18:00:00	ORD
8472	8	12	710	644	26	919	856	YX	890	N855RW	EWR	IND	98	645	6	44	2023-08-12 06:00:00	Other
8477	4	16	2240	2125	75	116	25	DL	251	N873DN	JFK	LAS	296	2248	21	25	2023-04-16 21:00:00	Other
8478	7	10	2138	2120	18	2320	2247	YX	1439	N214JQ	LGA	BUF	45	292	21	20	2023-07-10 21:00:00	Other
8484	9	24	1529	1459	30	1704	1620	9E	1715	N923XJ	JFK	BWI	40	184	14	59	2023-09-24 14:00:00	Other
8485	8	25	927	840	47	1210	1140	DL	290	N721TW	JFK	SAN	294	2446	8	40	2023-08-25 08:00:00	Other
8486	6	19	1215	1045	90	1431	1319	UA	738	N29968	EWR	IAH	169	1400	10	45	2023-06-19 10:00:00	Other
8490	5	27	1931	1700	151	2157	2000	DL	344	N101DU	JFK	DFW	166	1391	17	0	2023-05-27 17:00:00	Other
8492	4	14	1837	1820	17	2133	2116	AA	800	N962NN	EWR	DFW	188	1372	18	20	2023-04-14 18:00:00	Other
8493	5	4	1028	1008	20	1201	1139	YX	1037	N744YX	EWR	BUF	44	282	10	8	2023-05-04 10:00:00	Other
8496	7	7	2336	1859	277	232	2158	NK	416	N650NK	LGA	IAH	187	1416	18	59	2023-07-07 18:00:00	Other
8500	2	16	2148	2128	20	2342	2334	UA	832	N47293	EWR	MSP	149	1008	21	28	2023-02-16 21:00:00	Other
8506	7	14	1218	1159	19	1512	1453	UA	454	N76529	EWR	TPA	139	997	11	59	2023-07-14 11:00:00	Other
8517	7	26	824	710	74	1112	1003	UA	549	N17312	EWR	PDX	322	2434	7	10	2023-07-26 07:00:00	Other
8519	10	1	1230	1205	25	1510	1503	NK	734	N671NK	EWR	MCO	131	937	12	5	2023-10-01 12:00:00	MCO
8527	1	2	850	829	21	1209	1138	UA	573	N37257	EWR	MCO	132	937	8	29	2023-01-02 08:00:00	MCO
8530	4	5	1915	1855	20	2101	2040	WN	839	N8800L	LGA	BNA	128	764	18	55	2023-04-05 18:00:00	Other
8531	6	2	1246	1020	146	1550	1332	DL	491	N106DU	LGA	SRQ	163	1047	10	20	2023-06-02 10:00:00	Other
8543	7	20	2058	2035	23	2259	2240	9E	1156	N329PQ	LGA	ILM	73	500	20	35	2023-07-20 20:00:00	Other
8545	5	29	1818	1730	48	2127	2121	DL	209	N702TW	JFK	SFO	320	2586	17	30	2023-05-29 17:00:00	Other
8548	7	15	1004	919	45	1258	1215	B6	58	N2016J	JFK	SAN	322	2446	9	19	2023-07-15 09:00:00	Other
8550	12	27	1812	1553	139	2144	1900	B6	87	N570JB	EWR	FLL	179	1065	15	53	2023-12-27 15:00:00	FLL
8556	3	16	1253	1237	16	1532	1551	AA	713	N451AN	JFK	MIA	135	1089	12	37	2023-03-16 12:00:00	MIA
8560	4	7	2319	2159	80	258	158	B6	654	N954JB	JFK	SJU	198	1598	21	59	2023-04-07 21:00:00	Other
8582	1	29	1511	1500	11	1732	1718	DL	487	N347NB	LGA	MSP	167	1020	15	0	2023-01-29 15:00:00	Other
8584	4	3	2026	1838	108	2204	2021	UA	422	N15751	EWR	ORD	121	719	18	38	2023-04-03 18:00:00	ORD
8592	12	27	1501	1430	31	1830	1741	UA	374	N17327	EWR	MIA	155	1085	14	30	2023-12-27 14:00:00	MIA
8597	7	18	2119	1929	110	51	2308	DL	195	N503DZ	JFK	SEA	331	2422	19	29	2023-07-18 19:00:00	Other
8599	7	19	1657	1215	282	1850	1408	YX	1059	N404YX	LGA	CMH	78	479	12	15	2023-07-19 12:00:00	Other
8605	6	23	13	2250	83	117	21	9E	1735	N302PQ	JFK	SYR	39	209	22	50	2023-06-23 22:00:00	Other
8610	4	29	2142	2050	52	50	28	UA	634	N19136	EWR	SFO	330	2565	20	50	2023-04-29 20:00:00	Other
8628	8	29	1949	1915	34	2126	2116	9E	1139	N479PX	LGA	CLE	71	419	19	15	2023-08-29 19:00:00	Other
8631	11	18	1021	857	84	1211	1119	9E	1761	N490PX	LGA	GSP	92	610	8	57	2023-11-18 08:00:00	Other
8636	5	15	1914	1520	234	2149	1821	UA	801	N648UA	EWR	IAH	180	1400	15	20	2023-05-15 15:00:00	Other
8638	6	29	1150	1005	105	1336	1204	B6	70	N328JB	JFK	DTW	81	509	10	5	2023-06-29 10:00:00	Other
8643	6	23	832	655	97	1138	948	B6	296	N987JT	JFK	LAX	321	2475	6	55	2023-06-23 06:00:00	LAX
8657	1	23	617	600	17	918	859	B6	48	N588JB	EWR	PBI	159	1023	6	0	2023-01-23 06:00:00	Other
8661	1	11	1240	1100	100	1339	1227	DL	387	N130DU	LGA	BOS	34	184	11	0	2023-01-11 11:00:00	BOS
8666	1	14	1624	1555	29	1823	1839	DL	145	N704X	JFK	ATL	98	760	15	55	2023-01-14 15:00:00	ATL
8671	5	7	2046	2030	16	2230	2211	9E	1547	N228PQ	LGA	CHO	55	305	20	30	2023-05-07 20:00:00	Other
8675	9	18	1137	1125	12	1352	1349	B6	22	N568JB	LGA	DEN	213	1620	11	25	2023-09-18 11:00:00	Other
8698	10	21	1727	1645	42	2012	1939	UA	465	N17139	EWR	SAN	313	2425	16	45	2023-10-21 16:00:00	Other
8699	2	16	947	930	17	1119	1120	B6	744	N184JB	LGA	BNA	128	764	9	30	2023-02-16 09:00:00	Other
8701	12	4	1434	1345	49	1656	1623	B6	882	N639JB	LGA	MSY	183	1183	13	45	2023-12-04 13:00:00	Other
8705	2	19	1617	1600	17	1925	1919	UA	872	N17105	EWR	LAX	349	2454	16	0	2023-02-19 16:00:00	LAX
8711	11	6	1257	1103	114	1412	1242	9E	1629	N480PX	LGA	ORF	57	296	11	3	2023-11-06 11:00:00	Other
8712	6	23	614	600	14	843	829	DL	849	N175DZ	JFK	ATL	112	760	6	0	2023-06-23 06:00:00	ATL
8723	12	11	1835	1810	25	2125	2120	UA	871	N229UA	EWR	LAX	310	2454	18	10	2023-12-11 18:00:00	LAX
8730	2	22	1147	1130	17	1353	1331	YX	1567	N237JQ	LGA	CMH	94	479	11	30	2023-02-22 11:00:00	Other
8734	9	14	1226	1029	117	1436	1231	9E	1484	N181PQ	LGA	MYR	83	563	10	29	2023-09-14 10:00:00	Other
8742	2	7	1700	1605	55	1914	1823	9E	1472	N695CA	JFK	CLT	90	541	16	5	2023-02-07 16:00:00	CLT
8745	4	9	1800	1659	61	1917	1819	UA	435	N403UA	EWR	BOS	53	200	16	59	2023-04-09 16:00:00	BOS
8747	4	2	2216	2200	16	2315	2308	YX	950	N642RW	EWR	MDT	32	141	22	0	2023-04-02 22:00:00	Other
8751	8	19	2233	2210	23	27	33	NK	226	N921NK	EWR	LAS	273	2227	22	10	2023-08-19 22:00:00	Other
8753	6	8	1233	1211	22	1407	1342	9E	1501	N490PX	LGA	ORF	72	296	12	11	2023-06-08 12:00:00	Other
8773	4	23	900	835	25	1228	1159	DL	306	N3737C	JFK	SAN	324	2446	8	35	2023-04-23 08:00:00	Other
8776	7	19	656	630	26	821	806	YX	997	N430YX	JFK	ORF	51	290	6	30	2023-07-19 06:00:00	Other
8796	1	14	2032	1935	57	2240	2206	9E	1518	N929XJ	JFK	MSP	147	1029	19	35	2023-01-14 19:00:00	Other
8801	3	14	2146	2000	106	56	2309	B6	123	N558JB	JFK	ONT	327	2429	20	0	2023-03-14 20:00:00	Other
8803	3	6	2316	2229	47	18	2328	B6	265	N231JB	JFK	ORH	34	150	22	29	2023-03-06 22:00:00	Other
8804	6	26	1616	1550	26	1905	1758	YX	1788	N236JQ	JFK	CMH	74	483	15	50	2023-06-26 15:00:00	Other
8807	5	8	2111	2100	11	2307	2317	OO	1141	N322SY	JFK	CLE	82	425	21	0	2023-05-08 21:00:00	Other
8811	4	17	1953	1915	38	2128	2113	9E	1305	N272PQ	LGA	CLE	68	419	19	15	2023-04-17 19:00:00	Other
8812	10	5	1137	1125	12	1336	1349	B6	21	N570JB	LGA	DEN	215	1620	11	25	2023-10-05 11:00:00	Other
8819	1	12	1025	940	45	1326	1302	B6	186	N588JB	JFK	BUR	337	2465	9	40	2023-01-12 09:00:00	Other
8820	7	1	1630	1539	51	1905	1844	UA	462	N17279	EWR	FLL	132	1065	15	39	2023-07-01 15:00:00	FLL
8845	12	27	1342	1330	12	1547	1542	NK	504	N661NK	LGA	CLT	102	544	13	30	2023-12-27 13:00:00	CLT
8862	6	14	1924	1900	24	2331	2255	B6	485	N807JB	EWR	SJU	209	1608	19	0	2023-06-14 19:00:00	Other
8869	7	8	1902	1834	28	2030	2014	YX	871	N856RW	EWR	ORF	49	284	18	34	2023-07-08 18:00:00	Other
8884	3	17	1603	1540	23	1838	1826	DL	134	N343DN	JFK	ATL	127	760	15	40	2023-03-17 15:00:00	ATL
8885	12	27	2001	1912	49	2323	2230	NK	112	N668NK	EWR	FLL	172	1065	19	12	2023-12-27 19:00:00	FLL
8889	12	15	1942	1925	17	2239	2305	AS	82	N440AS	EWR	SFO	323	2565	19	25	2023-12-15 19:00:00	Other
8890	2	4	1049	830	139	1316	1141	AA	650	N9025B	JFK	EGE	247	1746	8	30	2023-02-04 08:00:00	Other
8891	6	21	1643	1625	18	1853	1900	WN	1214	N8581Z	LGA	DAL	174	1381	16	25	2023-06-21 16:00:00	Other
8895	8	25	1503	1435	28	1617	1609	YX	895	N743YX	EWR	IAD	40	212	14	35	2023-08-25 14:00:00	Other
8907	9	24	2327	2159	88	32	2321	YX	1221	N725YX	EWR	ROC	42	246	21	59	2023-09-24 21:00:00	Other
8921	6	4	1613	1600	13	1935	1855	AA	1036	N970NN	LGA	DFW	197	1389	16	0	2023-06-04 16:00:00	Other
8930	7	5	941	659	162	1057	833	9E	1190	N906XJ	JFK	BUF	49	301	6	59	2023-07-05 06:00:00	Other
8940	7	26	2211	2110	61	2300	2212	9E	1312	N478PX	LGA	ALB	32	136	21	10	2023-07-26 21:00:00	Other
8945	7	9	135	1925	370	428	2250	AS	83	N517AS	EWR	SFO	323	2565	19	25	2023-07-09 19:00:00	Other
8949	12	5	2400	2335	25	49	49	B6	585	N318JB	JFK	BOS	33	187	23	35	2023-12-05 23:00:00	BOS
8953	1	26	2012	1935	37	2324	2239	B6	307	N766JB	LGA	MCO	160	950	19	35	2023-01-26 19:00:00	MCO
8954	2	2	1654	1520	94	2019	1845	DL	114	N129DU	LGA	DFW	244	1389	15	20	2023-02-02 15:00:00	Other
8961	7	3	2155	2025	90	14	2243	UA	260	N68843	EWR	PHX	262	2133	20	25	2023-07-03 20:00:00	Other
8968	2	20	2309	2245	24	10	2351	B6	482	N183JB	JFK	BOS	34	187	22	45	2023-02-20 22:00:00	BOS
8975	7	26	2111	1935	96	2233	2122	OO	989	N259SY	JFK	BNA	109	765	19	35	2023-07-26 19:00:00	Other
8984	7	5	1136	1121	15	1322	1312	UA	574	N492UA	EWR	DTW	73	488	11	21	2023-07-05 11:00:00	Other
8991	2	20	2015	1959	16	2239	2242	DL	433	N180DN	JFK	ATL	122	760	19	59	2023-02-20 19:00:00	ATL
8992	9	9	2211	1929	162	119	2234	DL	324	N504DZ	JFK	MCO	130	944	19	29	2023-09-09 19:00:00	MCO
8996	8	16	2249	2145	64	145	35	B6	70	N354JB	JFK	MCO	137	944	21	45	2023-08-16 21:00:00	MCO
8998	3	15	2149	2029	80	20	2319	B6	162	N547JB	LGA	JAX	101	833	20	29	2023-03-15 20:00:00	Other
9009	2	26	1650	1615	35	1827	1814	YX	1308	N451YX	JFK	RDU	70	427	16	15	2023-02-26 16:00:00	Other
9014	3	3	2212	2028	104	39	2309	B6	36	N566JB	JFK	DEN	227	1626	20	28	2023-03-03 20:00:00	Other
9016	9	5	1618	1557	21	1802	1805	NK	263	N683NK	EWR	IND	86	645	15	57	2023-09-05 15:00:00	Other
9018	7	26	1530	1510	20	1814	1800	UA	631	N62883	EWR	TPA	133	997	15	10	2023-07-26 15:00:00	Other
9033	7	14	1236	1200	36	1531	1443	UA	675	N212UA	EWR	LAX	309	2454	12	0	2023-07-14 12:00:00	LAX
9037	6	7	1734	1700	34	2115	1954	AA	1017	N869NN	LGA	DFW	183	1389	17	0	2023-06-07 17:00:00	Other
9038	11	16	1622	1558	24	1907	1920	DL	383	N373DA	LGA	MIA	146	1096	15	58	2023-11-16 15:00:00	MIA
9043	7	24	1954	1935	19	2144	2214	9E	1328	N691CA	JFK	CLT	80	541	19	35	2023-07-24 19:00:00	CLT
9046	7	20	1638	1625	13	1737	1755	9E	1165	N936XJ	LGA	SYR	39	198	16	25	2023-07-20 16:00:00	Other
9049	8	13	742	730	12	932	908	B6	314	N197JB	JFK	ORD	129	740	7	30	2023-08-13 07:00:00	ORD
9060	6	13	1555	1530	25	1838	1851	AA	59	N105NN	JFK	LAX	322	2475	15	30	2023-06-13 15:00:00	LAX
9061	5	7	1046	1029	17	1156	1200	YX	1063	N732YX	EWR	ORF	46	284	10	29	2023-05-07 10:00:00	Other
9070	7	31	1927	1753	94	2040	1941	B6	520	N229JB	JFK	BNA	108	765	17	53	2023-07-31 17:00:00	Other
9079	8	5	1913	1820	53	2106	2058	9E	1187	N200PQ	JFK	MCI	147	1113	18	20	2023-08-05 18:00:00	Other
9080	3	18	2352	1849	303	257	2159	B6	83	N952JB	JFK	MCO	158	944	18	49	2023-03-18 18:00:00	MCO
9087	1	12	1801	1659	62	2031	1933	YX	1130	N636RW	EWR	SDF	115	642	16	59	2023-01-12 16:00:00	Other
9100	12	23	959	924	35	1309	1242	UA	902	N37531	EWR	MIA	143	1085	9	24	2023-12-23 09:00:00	MIA
9106	6	26	1852	1841	11	2244	2123	DL	118	N899DN	JFK	PHX	308	2153	18	41	2023-06-26 18:00:00	Other
9110	5	21	738	715	23	1012	1011	UA	680	N17302	EWR	TPA	133	997	7	15	2023-05-21 07:00:00	Other
9116	10	31	1654	1635	19	1828	1811	9E	1418	N917XJ	LGA	PIT	64	335	16	35	2023-10-31 16:00:00	Other
9141	7	5	1749	1450	179	2040	1808	B6	130	N804JB	LGA	MCO	141	950	14	50	2023-07-05 14:00:00	MCO
9150	7	15	1952	1851	61	2214	2121	DL	675	N3760C	EWR	ATL	105	746	18	51	2023-07-15 18:00:00	ATL
9151	12	1	2329	2255	34	108	15	B6	61	N265JB	JFK	BTV	48	266	22	55	2023-12-01 22:00:00	Other
9155	2	19	2229	2159	30	225	133	B6	895	N977JE	JFK	SFO	359	2586	21	59	2023-02-19 21:00:00	Other
9156	8	22	741	610	91	920	754	9E	1214	N315PQ	LGA	RDU	68	431	6	10	2023-08-22 06:00:00	Other
9158	6	6	1712	1700	12	1958	1939	B6	971	N589JB	LGA	ATL	123	762	17	0	2023-06-06 17:00:00	ATL
9161	10	5	1640	1455	105	1956	1811	B6	1008	N510JB	JFK	MIA	156	1089	14	55	2023-10-05 14:00:00	MIA
9164	10	19	1635	1620	15	1855	1910	WN	858	N458WN	LGA	DAL	182	1381	16	20	2023-10-19 16:00:00	Other
9167	9	7	2326	2059	147	41	2231	YX	1899	N824MD	LGA	PWM	48	269	20	59	2023-09-07 20:00:00	Other
9185	12	28	1316	1259	17	1705	1616	UA	448	N68452	EWR	RSW	201	1068	12	59	2023-12-28 12:00:00	Other
9187	10	3	1609	1515	54	1729	1650	UA	573	N478UA	LGA	ORD	105	733	15	15	2023-10-03 15:00:00	ORD
9192	5	14	1426	1409	17	1634	1629	DL	794	N385DN	EWR	ATL	104	746	14	9	2023-05-14 14:00:00	ATL
9197	4	10	917	720	117	1116	956	DL	174	N3766	LGA	DEN	201	1620	7	20	2023-04-10 07:00:00	Other
9199	4	5	2156	2000	116	2309	2127	YX	1458	N230JQ	LGA	BOS	33	184	20	0	2023-04-05 20:00:00	BOS
9200	2	14	1046	1024	22	1308	1303	YX	1275	N107HQ	LGA	SDF	112	659	10	24	2023-02-14 10:00:00	Other
9212	4	1	1543	1315	148	1855	1647	UA	675	N14120	EWR	SFO	347	2565	13	15	2023-04-01 13:00:00	Other
9213	6	7	1431	1420	11	1653	1630	9E	1548	N920XJ	LGA	TYS	98	647	14	20	2023-06-07 14:00:00	Other
9222	3	5	1612	1559	13	1732	1729	OO	1228	N310SY	JFK	IAD	51	228	15	59	2023-03-05 15:00:00	Other
9226	9	23	1615	1600	15	1830	1754	OO	1255	N614CZ	JFK	ORD	123	740	16	0	2023-09-23 16:00:00	ORD
9243	6	25	2151	1837	194	22	2101	YX	1324	N418YX	LGA	OMA	168	1148	18	37	2023-06-25 18:00:00	Other
9250	3	12	2131	2100	31	2356	2347	NK	275	N947NK	EWR	LAS	300	2227	21	0	2023-03-12 21:00:00	Other
9251	4	15	2044	1820	144	2320	2053	9E	1371	N228PQ	JFK	IND	96	665	18	20	2023-04-15 18:00:00	Other
9252	1	27	1750	1729	21	2132	2048	B6	192	N834JB	LGA	FLL	172	1076	17	29	2023-01-27 17:00:00	FLL
9254	2	22	2150	2115	35	202	45	B6	647	N937JB	JFK	LAX	378	2475	21	15	2023-02-22 21:00:00	LAX
9255	3	6	1652	1640	12	1941	2000	DL	236	N411DX	JFK	SEA	322	2422	16	40	2023-03-06 16:00:00	Other
9257	1	7	2238	2159	39	137	126	B6	768	N990JL	JFK	LAX	327	2475	21	59	2023-01-07 21:00:00	LAX
9259	12	19	2019	1855	84	40	2247	B6	40	N634JB	JFK	PHX	285	2153	18	55	2023-12-19 18:00:00	Other
9260	3	4	1258	1106	112	1549	1405	UA	623	N37287	EWR	PBI	149	1023	11	6	2023-03-04 11:00:00	Other
9261	7	11	1705	1635	30	1915	1903	UA	402	N877UA	EWR	JAX	109	820	16	35	2023-07-11 16:00:00	Other
9269	2	3	2022	2000	22	2246	2245	DL	352	N312US	LGA	ATL	103	762	20	0	2023-02-03 20:00:00	ATL
9273	3	14	2031	1944	47	2332	2300	B6	179	N507JT	LGA	FLL	156	1076	19	44	2023-03-14 19:00:00	FLL
9275	7	25	1242	1143	59	1517	1412	UA	360	N449UA	EWR	ATL	118	746	11	43	2023-07-25 11:00:00	ATL
9280	1	14	2137	1945	112	40	2315	AA	125	N9023N	JFK	MIA	136	1089	19	45	2023-01-14 19:00:00	MIA
9284	1	12	2328	2159	89	48	2330	UA	574	N849UA	EWR	PIT	52	319	21	59	2023-01-12 21:00:00	Other
9285	7	3	1612	1600	12	1828	1844	DL	168	N357DN	LGA	ATL	110	762	16	0	2023-07-03 16:00:00	ATL
9295	3	30	1445	1415	30	1602	1532	B6	330	N216JB	LGA	BOS	34	184	14	15	2023-03-30 14:00:00	BOS
9300	9	11	1025	955	30	1318	1249	DL	388	N127DN	LGA	MCO	134	950	9	55	2023-09-11 09:00:00	MCO
9301	12	7	750	730	20	914	925	WN	992	N8314L	LGA	STL	127	888	7	30	2023-12-07 07:00:00	Other
9311	10	20	1519	1505	14	1707	1638	OO	1218	N607CZ	JFK	BNA	140	765	15	5	2023-10-20 15:00:00	Other
9326	4	20	2327	2245	42	41	4	B6	6	N324JB	JFK	SYR	42	209	22	45	2023-04-20 22:00:00	Other
9333	6	2	2249	2110	99	104	2342	UA	310	N69833	EWR	LAS	274	2227	21	10	2023-06-02 21:00:00	Other
9353	1	3	2105	1900	125	2339	2228	AS	23	N266AK	EWR	PDX	312	2434	19	0	2023-01-03 19:00:00	Other
9359	10	20	2002	1948	14	2300	2240	UA	605	N14228	EWR	MCO	127	937	19	48	2023-10-20 19:00:00	MCO
9363	1	13	838	750	48	1219	1107	AA	1097	N954AN	EWR	MIA	187	1085	7	50	2023-01-13 07:00:00	MIA
9366	1	30	2019	1959	20	2306	2308	DL	627	N306DN	JFK	MCO	134	944	19	59	2023-01-30 19:00:00	MCO
9385	10	10	1314	1229	45	1432	1407	AA	970	N809NN	LGA	ORD	112	733	12	29	2023-10-10 12:00:00	ORD
9386	5	7	2012	1959	13	2159	2145	9E	1563	N904XJ	EWR	RDU	63	416	19	59	2023-05-07 19:00:00	Other
9389	2	1	1613	1600	13	1757	1749	DL	457	N143DU	LGA	ORD	133	733	16	0	2023-02-01 16:00:00	ORD
9391	6	7	1841	1717	84	2140	2029	B6	224	N561JB	LGA	FLL	161	1076	17	17	2023-06-07 17:00:00	FLL
9392	4	10	810	759	11	1031	1101	AA	313	N814NN	JFK	DFW	179	1391	7	59	2023-04-10 07:00:00	Other
9397	7	1	1318	1300	18	1606	1616	B6	498	N2002J	JFK	FLL	139	1069	13	0	2023-07-01 13:00:00	FLL
9398	6	24	2223	2052	91	105	2354	B6	31	N934JB	JFK	SAN	313	2446	20	52	2023-06-24 20:00:00	Other
9404	5	7	2144	2059	45	9	2300	YX	1159	N755YX	EWR	CMH	78	463	20	59	2023-05-07 20:00:00	Other
9421	4	17	1946	1849	57	2253	2204	UA	532	N37427	EWR	PDX	330	2434	18	49	2023-04-17 18:00:00	Other
9423	6	27	1614	1459	75	NA	1658	YX	1293	N102HQ	JFK	CLE	NA	425	14	59	2023-06-27 14:00:00	Other
9431	7	14	834	759	35	1201	1059	UA	597	N17294	EWR	PBI	170	1023	7	59	2023-07-14 07:00:00	Other
9440	2	8	2035	2023	12	2	2342	UA	391	N17262	EWR	SLC	271	1969	20	23	2023-02-08 20:00:00	Other
9442	3	17	2051	2015	36	2349	2338	B6	818	N584JB	JFK	MIA	143	1089	20	15	2023-03-17 20:00:00	MIA
9443	12	5	1553	1458	55	1757	1704	9E	1428	N480PX	LGA	MEM	149	963	14	58	2023-12-05 14:00:00	Other
9445	7	21	2303	2130	93	135	9	B6	173	N625JB	LGA	MCO	127	950	21	30	2023-07-21 21:00:00	MCO
9448	3	5	1110	850	140	1219	1021	YX	1623	N226JQ	JFK	BTV	53	266	8	50	2023-03-05 08:00:00	Other
9452	8	20	2002	1929	33	2224	2247	DL	706	N399DA	JFK	TPA	125	1005	19	29	2023-08-20 19:00:00	Other
9457	9	22	2047	2015	32	2333	2310	DL	439	N344DN	LGA	MCO	133	950	20	15	2023-09-22 20:00:00	MCO
9462	3	24	2153	2115	38	8	2345	YX	1341	N113HQ	JFK	IND	113	665	21	15	2023-03-24 21:00:00	Other
9482	6	24	2342	2048	174	252	2357	UA	718	N69829	EWR	SLC	280	1969	20	48	2023-06-24 20:00:00	Other
9483	10	29	2037	2021	16	16	2338	B6	542	N990JL	EWR	LAX	366	2454	20	21	2023-10-29 20:00:00	LAX
9484	9	26	1451	1440	11	1750	1743	UA	884	N17128	EWR	LAX	314	2454	14	40	2023-09-26 14:00:00	LAX
9486	7	4	1806	1745	21	2036	2010	WN	32	N8555Z	LGA	DEN	218	1620	17	45	2023-07-04 17:00:00	Other
9487	9	26	748	730	18	856	900	YX	1083	N655RW	EWR	MKE	105	725	7	30	2023-09-26 07:00:00	Other
9493	1	27	1627	1430	117	1924	1731	UA	957	N78001	EWR	LAX	318	2454	14	30	2023-01-27 14:00:00	LAX
9495	10	8	1902	1825	37	2103	2050	UA	551	N13110	EWR	DEN	210	1605	18	25	2023-10-08 18:00:00	Other
9510	1	6	2012	1959	13	2112	2117	B6	980	N190JB	EWR	BOS	37	200	19	59	2023-01-06 19:00:00	BOS
9515	5	21	1335	1030	185	1446	1140	B6	930	N258JB	JFK	BOS	38	187	10	30	2023-05-21 10:00:00	BOS
9516	9	14	1232	1129	63	1328	1230	B6	567	N355JB	JFK	MVY	33	173	11	29	2023-09-14 11:00:00	Other
9518	1	6	1650	1630	20	1937	1953	UA	819	N12116	EWR	LAX	321	2454	16	30	2023-01-06 16:00:00	LAX
9519	6	27	1253	1725	1168	1418	1914	OO	1275	N241SY	JFK	BOS	41	187	17	25	2023-06-27 17:00:00	BOS
9522	1	24	2002	1940	22	2255	2253	DL	711	N350NA	LGA	TPA	149	1010	19	40	2023-01-24 19:00:00	Other
9523	1	27	1632	1600	32	2004	1957	DL	464	N195DN	JFK	SFO	349	2586	16	0	2023-01-27 16:00:00	Other
9525	5	14	1955	1935	20	2245	2245	B6	26	N646JB	JFK	ABQ	253	1826	19	35	2023-05-14 19:00:00	Other
9526	10	14	1904	1825	39	2150	2134	DL	848	N349NW	JFK	AUS	208	1521	18	25	2023-10-14 18:00:00	Other
9545	11	19	832	759	33	1341	1259	B6	180	N2059J	JFK	SJU	219	1598	7	59	2023-11-19 07:00:00	Other
9549	12	28	1659	1638	21	1952	1944	NK	501	N634NK	EWR	MCO	150	937	16	38	2023-12-28 16:00:00	MCO
9552	2	1	1539	1525	14	1740	1730	WN	598	N8775Q	LGA	STL	158	888	15	25	2023-02-01 15:00:00	Other
9560	12	26	1702	1645	17	1800	1801	9E	1370	N480PX	LGA	ALB	33	136	16	45	2023-12-26 16:00:00	Other
9565	6	4	2020	1918	62	2221	2100	UA	535	N37278	EWR	CLE	61	404	19	18	2023-06-04 19:00:00	Other
9572	6	19	1856	1751	65	2048	1943	B6	648	N329JB	JFK	BNA	113	765	17	51	2023-06-19 17:00:00	Other
9578	6	28	1854	1832	22	2013	1948	YX	1116	N859RW	EWR	ALB	33	143	18	32	2023-06-28 18:00:00	Other
9582	12	12	1902	1820	42	2049	2015	WN	979	N8643A	LGA	STL	141	888	18	20	2023-12-12 18:00:00	Other
9583	6	28	733	715	18	1049	1008	UA	940	N37252	EWR	SNA	326	2434	7	15	2023-06-28 07:00:00	Other
9616	2	28	1855	1729	86	2240	2042	B6	689	N526JL	JFK	PSP	374	2378	17	29	2023-02-28 17:00:00	Other
9618	2	26	1345	1320	25	1502	1445	WN	733	N952WN	LGA	MDW	123	725	13	20	2023-02-26 13:00:00	Other
9626	3	15	2049	2027	22	2242	2253	UA	892	N883UA	EWR	MSY	142	1167	20	27	2023-03-15 20:00:00	Other
9627	8	22	2107	2000	67	2228	2139	UA	356	N38446	EWR	ORD	110	719	20	0	2023-08-22 20:00:00	ORD
9633	5	11	1548	1535	13	1823	1843	B6	61	N517JB	JFK	MCO	127	944	15	35	2023-05-11 15:00:00	MCO
9645	8	17	2028	1955	33	2342	2328	DL	489	N825DN	JFK	FLL	153	1069	19	55	2023-08-17 19:00:00	FLL
9654	7	2	1256	1215	41	1452	1409	YX	1059	N414YX	LGA	CMH	77	479	12	15	2023-07-02 12:00:00	Other
9667	3	16	2014	1849	85	2254	2159	B6	83	N2043J	JFK	MCO	128	944	18	49	2023-03-16 18:00:00	MCO
9668	8	24	1724	1440	164	2059	1736	UA	701	N17133	EWR	LAX	309	2454	14	40	2023-08-24 14:00:00	LAX
9675	1	14	920	829	51	1240	1159	AA	694	N719AN	JFK	MIA	139	1089	8	29	2023-01-14 08:00:00	MIA
9676	10	23	1000	938	22	1132	1125	UA	611	N838UA	EWR	STL	125	872	9	38	2023-10-23 09:00:00	Other
9677	3	15	1849	1749	60	2103	1950	YX	1128	N727YX	EWR	CMH	67	463	17	49	2023-03-15 17:00:00	Other
9682	6	8	1955	1930	25	2313	2241	UA	836	N27526	EWR	FLL	153	1065	19	30	2023-06-08 19:00:00	FLL
9690	10	21	2226	2155	31	2355	2325	B6	31	N337JB	JFK	BUF	56	301	21	55	2023-10-21 21:00:00	Other
9694	9	11	2032	1626	246	2222	1745	UA	731	N73283	EWR	IAD	43	212	16	26	2023-09-11 16:00:00	Other
9701	5	2	1708	1630	38	2005	2009	B6	78	N923JB	JFK	SEA	321	2422	16	30	2023-05-02 16:00:00	Other
9702	7	4	1235	1200	35	1434	1435	DL	277	N127DN	LGA	ATL	100	762	12	0	2023-07-04 12:00:00	ATL
9705	6	23	653	600	53	1002	908	NK	51	N667NK	LGA	FLL	159	1076	6	0	2023-06-23 06:00:00	FLL
9710	5	30	2008	1952	16	2250	2302	UA	753	N17265	EWR	SAN	321	2425	19	52	2023-05-30 19:00:00	Other
9715	4	6	2006	1929	37	2302	2159	9E	1311	N604LR	JFK	MSP	171	1029	19	29	2023-04-06 19:00:00	Other
9717	4	11	2114	2000	74	2258	2151	B6	482	N358JB	JFK	RDU	62	427	20	0	2023-04-11 20:00:00	Other
9720	8	7	2313	1859	254	231	2149	AS	78	N251AK	EWR	SAN	327	2425	18	59	2023-08-07 18:00:00	Other
9743	6	12	1931	1554	217	2238	1857	AA	923	N867NN	JFK	DFW	208	1391	15	54	2023-06-12 15:00:00	Other
9747	1	27	1854	1830	24	2033	2029	9E	1397	N920XJ	LGA	RDU	74	431	18	30	2023-01-27 18:00:00	Other
9754	8	19	722	700	22	1010	1010	NK	240	N919NK	EWR	OAK	325	2555	7	0	2023-08-19 07:00:00	Other
9760	3	5	1333	1104	149	1446	1219	B6	56	N239JB	EWR	BOS	47	200	11	4	2023-03-05 11:00:00	BOS
9763	3	10	1554	1525	29	1904	1847	DL	422	N310DN	LGA	MIA	157	1096	15	25	2023-03-10 15:00:00	MIA
9765	7	11	1247	1035	132	1356	1201	B6	56	N281JB	JFK	ROC	49	264	10	35	2023-07-11 10:00:00	Other
9767	4	29	1125	1105	20	1544	1455	DL	113	N707TW	JFK	SFO	330	2586	11	5	2023-04-29 11:00:00	Other
9771	12	19	1335	1218	77	1844	1704	B6	967	N970JB	JFK	SJU	222	1598	12	18	2023-12-19 12:00:00	Other
9782	11	27	2325	2230	55	410	327	B6	286	N659JB	JFK	PSE	203	1617	22	30	2023-11-27 22:00:00	Other
9783	5	9	1922	1900	22	2101	2057	YX	1303	N441YX	LGA	CMH	75	479	19	0	2023-05-09 19:00:00	Other
9784	11	22	1921	1900	21	2036	2021	UA	815	N14235	EWR	BOS	43	200	19	0	2023-11-22 19:00:00	BOS
9785	2	23	1722	1659	23	1846	1820	YX	1121	N746YX	EWR	IAD	53	212	16	59	2023-02-23 16:00:00	Other
9799	2	17	2157	2005	112	2	2233	9E	1360	N915XJ	LGA	GRR	97	618	20	5	2023-02-17 20:00:00	Other
9812	9	14	2015	1840	95	2326	2150	B6	45	N949JT	JFK	SMF	317	2521	18	40	2023-09-14 18:00:00	Other
9827	3	31	934	700	154	1304	1020	DL	202	N171DN	JFK	LAX	353	2475	7	0	2023-03-31 07:00:00	LAX
9828	11	28	2126	1935	111	2306	2117	UA	185	N17752	EWR	CLE	68	404	19	35	2023-11-28 19:00:00	Other
9829	2	10	1834	1815	19	2144	2125	AA	252	N997NN	EWR	DFW	217	1372	18	15	2023-02-10 18:00:00	Other
9832	12	3	16	2017	239	238	2253	YX	1153	N762YX	EWR	SDF	119	642	20	17	2023-12-03 20:00:00	Other
9841	9	26	2121	2029	52	2249	2209	AA	124	N737US	LGA	ORD	111	733	20	29	2023-09-26 20:00:00	ORD
9849	11	6	1215	1059	76	1508	1404	AA	218	N907NN	JFK	MIA	143	1089	10	59	2023-11-06 10:00:00	MIA
9855	8	14	1415	1330	45	1525	1447	B6	480	N307JB	JFK	BOS	42	187	13	30	2023-08-14 13:00:00	BOS
9857	3	16	2146	2115	31	116	18	B6	323	N627JB	JFK	DFW	241	1391	21	15	2023-03-16 21:00:00	Other
9858	4	29	1055	1038	17	1326	1247	UA	339	N899UA	EWR	CHS	94	628	10	38	2023-04-29 10:00:00	Other
9859	5	11	1714	1647	27	1856	1855	YX	1012	N747YX	EWR	GSP	83	594	16	47	2023-05-11 16:00:00	Other
9867	7	19	1532	1520	12	1747	1700	WN	767	N8828L	LGA	STL	134	888	15	20	2023-07-19 15:00:00	Other
9871	5	4	2217	2159	18	158	158	B6	708	N913JB	JFK	SJU	194	1598	21	59	2023-05-04 21:00:00	Other
9874	5	20	1921	1759	82	2044	1924	B6	421	N317JB	JFK	ROC	53	264	17	59	2023-05-20 17:00:00	Other
9878	6	25	1647	1420	147	1825	1552	YX	1063	N742YX	EWR	MKE	120	725	14	20	2023-06-25 14:00:00	Other
9882	1	12	2331	2139	112	201	2325	B6	592	N337JB	JFK	RDU	77	427	21	39	2023-01-12 21:00:00	Other
9884	3	12	1556	1045	311	1914	1349	B6	137	N958JB	JFK	MCO	151	944	10	45	2023-03-12 10:00:00	MCO
9889	5	12	1920	1827	53	2025	1958	YX	1168	N749YX	EWR	IAD	40	212	18	27	2023-05-12 18:00:00	Other
9899	7	8	1940	1838	62	2208	2038	B6	345	N273JB	JFK	RDU	67	427	18	38	2023-07-08 18:00:00	Other
9900	2	20	1949	1915	34	2305	2233	B6	639	N598JB	JFK	FLL	148	1069	19	15	2023-02-20 19:00:00	FLL
9904	3	26	1505	1450	15	1632	1617	9E	1430	N137EV	LGA	ORF	54	296	14	50	2023-03-26 14:00:00	Other
9911	1	7	1533	1435	58	1711	1630	WN	685	N8697C	LGA	STL	140	888	14	35	2023-01-07 14:00:00	Other
9912	7	31	725	700	25	953	939	UA	432	N414UA	EWR	IAH	176	1400	7	0	2023-07-31 07:00:00	Other
9915	4	29	1809	1750	19	2116	2050	UA	407	N26970	EWR	LAX	304	2454	17	50	2023-04-29 17:00:00	LAX
9920	3	15	1758	1705	53	2003	1928	9E	1393	N903XJ	LGA	SAV	97	722	17	5	2023-03-15 17:00:00	Other
9934	6	19	1751	1705	46	2039	2002	B6	799	N987JT	EWR	LAX	313	2454	17	5	2023-06-19 17:00:00	LAX
9936	11	13	1037	705	212	1403	1018	DL	948	N3753	LGA	MIA	149	1096	7	5	2023-11-13 07:00:00	MIA
9938	7	27	1638	1530	68	1749	1659	YX	1045	N442YX	LGA	ORF	51	296	15	30	2023-07-27 15:00:00	Other
9940	12	11	1134	1110	24	1432	1424	DL	382	N372NW	LGA	PBI	153	1035	11	10	2023-12-11 11:00:00	Other
9943	8	15	1354	1330	24	1511	1447	B6	480	N184JB	JFK	BOS	41	187	13	30	2023-08-15 13:00:00	BOS
9949	3	31	1836	1650	106	2124	1957	NK	653	N661NK	EWR	FLL	140	1065	16	50	2023-03-31 16:00:00	FLL
9953	1	18	2019	1959	20	2315	2308	DL	627	N303DN	JFK	MCO	134	944	19	59	2023-01-18 19:00:00	MCO
9958	5	1	1126	1115	11	1437	1415	NK	833	N646NK	EWR	AUS	207	1504	11	15	2023-05-01 11:00:00	Other
9962	12	3	2013	1959	14	2221	2200	YX	1210	N446YX	LGA	BNA	150	764	19	59	2023-12-03 19:00:00	Other
9967	6	6	954	935	19	1111	1103	B6	617	N273JB	JFK	BUF	55	301	9	35	2023-06-06 09:00:00	Other
9968	5	13	1314	1300	14	1610	1614	AA	224	N463AA	LGA	MIA	145	1096	13	0	2023-05-13 13:00:00	MIA
9970	9	11	1419	1400	19	NA	1527	YX	1177	N654RW	EWR	MKE	NA	725	14	0	2023-09-11 14:00:00	Other
9971	1	13	2336	2230	66	110	2359	9E	1499	N279PQ	JFK	BGR	63	382	22	30	2023-01-13 22:00:00	Other
9972	6	23	1620	1559	21	1819	1813	NK	292	N684NK	EWR	IND	87	645	15	59	2023-06-23 15:00:00	Other
9973	3	21	1218	1150	28	1407	1348	DL	287	N923AT	EWR	MSP	151	1008	11	50	2023-03-21 11:00:00	Other
9977	8	25	1041	900	101	1157	1019	B6	485	N197JB	JFK	BTV	49	266	9	0	2023-08-25 09:00:00	Other
9978	7	24	2203	2130	33	50	9	B6	173	N531JL	LGA	MCO	139	950	21	30	2023-07-24 21:00:00	MCO
9979	7	27	1801	1745	16	2048	2035	WN	44	N8831L	LGA	HOU	191	1428	17	45	2023-07-27 17:00:00	Other
9983	9	29	2158	2059	59	18	2257	UA	611	N14235	EWR	MSP	161	1008	20	59	2023-09-29 20:00:00	Other
9984	1	5	1303	1220	43	1833	1706	DL	357	N835DN	JFK	SJU	247	1598	12	20	2023-01-05 12:00:00	Other
9994	9	18	1629	1615	14	1741	1741	B6	354	N187JB	LGA	BOS	38	184	16	15	2023-09-18 16:00:00	BOS
9999	3	5	1738	1650	48	2054	1947	DL	924	N3764D	LGA	DEN	274	1620	16	50	2023-03-05 16:00:00	Other
10000	9	13	1317	1250	27	1501	1448	NK	483	N959NK	LGA	MYR	83	563	12	50	2023-09-13 12:00:00	Other
10003	9	7	1048	935	73	1154	1051	B6	608	N304JB	JFK	BTV	43	266	9	35	2023-09-07 09:00:00	Other
10014	4	16	1629	1455	94	1811	1631	OO	984	N313SY	JFK	BNA	127	765	14	55	2023-04-16 14:00:00	Other
10017	5	14	2219	2100	79	138	54	AA	55	N105NN	JFK	SFO	357	2586	21	0	2023-05-14 21:00:00	Other
10026	1	13	2034	1959	35	201	57	UA	664	N37434	EWR	SJU	221	1608	19	59	2023-01-13 19:00:00	Other
10033	11	4	1632	1526	66	1730	1640	YX	1128	N754YX	EWR	MHT	42	209	15	26	2023-11-04 15:00:00	Other
10037	8	21	1728	1716	12	1907	1852	UA	490	N485UA	LGA	ORD	112	733	17	16	2023-08-21 17:00:00	ORD
10038	8	28	1950	1935	15	2242	2213	9E	1299	N908XJ	JFK	CLT	97	541	19	35	2023-08-28 19:00:00	CLT
10047	6	12	1818	1657	81	2006	1854	9E	1675	N902XJ	LGA	CLE	76	419	16	57	2023-06-12 16:00:00	Other
10060	2	3	2321	2200	81	33	2335	B6	357	N375JB	LGA	BNA	113	764	22	0	2023-02-03 22:00:00	Other
10065	9	15	806	750	16	1051	1057	NK	997	N935NK	EWR	LAX	319	2454	7	50	2023-09-15 07:00:00	LAX
10070	4	30	1647	1625	22	1808	1813	DL	436	N143DU	LGA	ORD	105	733	16	25	2023-04-30 16:00:00	ORD
10076	6	3	2014	1940	34	2210	2146	YX	1424	N429YX	JFK	RDU	74	427	19	40	2023-06-03 19:00:00	Other
10078	4	6	1409	1340	29	1646	1609	B6	581	N266JB	JFK	JAX	117	828	13	40	2023-04-06 13:00:00	Other
10084	5	1	2127	2027	60	23	2337	UA	675	N404UA	EWR	RSW	150	1068	20	27	2023-05-01 20:00:00	Other
10095	8	14	737	725	12	907	850	WN	114	N7888A	LGA	BNA	122	764	7	25	2023-08-14 07:00:00	Other
10096	5	19	1717	1615	62	1822	1735	B6	362	N368JB	LGA	BOS	37	184	16	15	2023-05-19 16:00:00	BOS
10099	12	18	1030	934	56	1332	1240	B6	127	N827JB	EWR	FLL	153	1065	9	34	2023-12-18 09:00:00	FLL
10100	1	5	1744	1729	15	2054	2059	B6	1037	N967JT	JFK	LAX	342	2475	17	29	2023-01-05 17:00:00	LAX
10106	6	12	44	2100	224	154	2246	OO	1646	N203SY	LGA	ORD	100	733	21	0	2023-06-12 21:00:00	ORD
10123	5	26	1143	1106	37	1449	1420	UA	829	N453UA	EWR	MIA	165	1085	11	6	2023-05-26 11:00:00	MIA
10141	2	17	1055	1010	45	1421	1322	DL	943	N329DN	LGA	MCO	178	950	10	10	2023-02-17 10:00:00	MCO
10143	10	15	1953	1359	354	2256	1711	B6	527	N519JB	JFK	RSW	159	1074	13	59	2023-10-15 13:00:00	Other
10148	7	15	922	901	21	1136	1113	9E	1302	N137EV	LGA	AVL	86	599	9	1	2023-07-15 09:00:00	Other
10150	4	17	2132	1930	122	20	2241	B6	127	N974JT	JFK	ONT	324	2429	19	30	2023-04-17 19:00:00	Other
10152	9	15	1632	1615	17	1900	1905	WN	1031	N8771D	LGA	DAL	180	1381	16	15	2023-09-15 16:00:00	Other
10159	5	18	1746	1700	46	2053	2000	UA	507	N784UA	EWR	LAX	316	2454	17	0	2023-05-18 17:00:00	LAX
10166	3	10	1711	1659	12	1904	1850	YX	1367	N103HQ	LGA	GSO	76	461	16	59	2023-03-10 16:00:00	Other
10171	6	11	2006	1932	34	2329	2229	UA	520	N75429	EWR	PBI	170	1023	19	32	2023-06-11 19:00:00	Other
10174	9	23	1749	1545	124	2024	1843	DL	436	N119DN	LGA	MCO	123	950	15	45	2023-09-23 15:00:00	MCO
10178	12	8	807	748	19	1150	1106	B6	546	N570JB	JFK	RSW	159	1074	7	48	2023-12-08 07:00:00	Other
10185	7	5	2311	2114	117	116	2344	UA	224	N17311	EWR	LAS	276	2227	21	14	2023-07-05 21:00:00	Other
10187	7	15	707	649	18	938	933	UA	267	N37516	EWR	SAN	307	2425	6	49	2023-07-15 06:00:00	Other
10197	4	17	1852	1735	77	2113	1937	9E	1317	N232PQ	LGA	MYR	94	563	17	35	2023-04-17 17:00:00	Other
10200	5	20	1603	1530	33	1901	1811	B6	629	N229JB	JFK	JAX	121	828	15	30	2023-05-20 15:00:00	Other
10207	10	13	1235	1216	19	1355	1341	NK	245	N611NK	EWR	PIT	64	319	12	16	2023-10-13 12:00:00	Other
10208	4	6	1128	1044	44	1331	1254	UA	807	N809UA	EWR	MSY	162	1167	10	44	2023-04-06 10:00:00	Other
10212	1	5	2218	1900	198	58	2228	AS	23	N564AS	EWR	PDX	315	2434	19	0	2023-01-05 19:00:00	Other
10230	7	7	1119	1046	33	1406	1342	B6	325	N592JB	JFK	MCO	147	944	10	46	2023-07-07 10:00:00	MCO
10237	7	11	2113	2055	18	2223	2237	DL	807	N119DU	JFK	BOS	40	187	20	55	2023-07-11 20:00:00	BOS
10240	3	30	1641	1520	81	1950	1847	B6	45	N584JB	JFK	RSW	153	1074	15	20	2023-03-30 15:00:00	Other
10242	12	2	1548	1500	48	1730	1639	OO	1188	N322SY	JFK	BNA	140	765	15	0	2023-12-02 15:00:00	Other
10243	6	30	1939	1830	69	2324	2142	UA	445	N2645U	EWR	SFO	329	2565	18	30	2023-06-30 18:00:00	Other
10249	11	16	2028	1957	31	2254	2243	DL	402	N384DN	JFK	ATL	105	760	19	57	2023-11-16 19:00:00	ATL
10252	7	30	2219	2150	29	25	2358	UA	527	N477UA	EWR	MCI	157	1092	21	50	2023-07-30 21:00:00	Other
10254	3	26	1930	1856	34	2037	2021	UA	690	N817UA	EWR	BOS	41	200	18	56	2023-03-26 18:00:00	BOS
10260	3	11	734	639	55	1126	952	UA	751	N37516	EWR	SEA	323	2402	6	39	2023-03-11 06:00:00	Other
10262	6	8	1740	1700	40	2040	2028	B6	1032	N972JT	JFK	FLL	154	1069	17	0	2023-06-08 17:00:00	FLL
10263	7	6	1626	1454	92	1848	1724	B6	26	N607JB	JFK	MSY	149	1182	14	54	2023-07-06 14:00:00	Other
10268	9	8	2235	1855	220	103	2150	DL	785	N358DN	LGA	MCO	126	950	18	55	2023-09-08 18:00:00	MCO
10272	2	22	2032	1945	47	2207	2059	UA	524	N27260	EWR	BOS	51	200	19	45	2023-02-22 19:00:00	BOS
10277	3	31	1548	1455	53	1707	1628	OO	1152	N614CZ	JFK	IAD	49	228	14	55	2023-03-31 14:00:00	Other
10290	3	26	1920	1905	15	2050	2040	WN	815	N917WN	LGA	MDW	125	725	19	5	2023-03-26 19:00:00	Other
10296	6	30	801	730	31	926	916	UA	419	N37252	EWR	RDU	62	416	7	30	2023-06-30 07:00:00	Other
10302	8	31	1057	954	63	1409	1252	B6	142	N520JB	LGA	PBI	159	1035	9	54	2023-08-31 09:00:00	Other
10309	7	24	1715	1600	75	2015	1910	AS	74	N549AS	EWR	SEA	325	2402	16	0	2023-07-24 16:00:00	Other
10311	4	26	2014	1948	26	2308	2302	UA	382	N878UA	EWR	FLL	152	1065	19	48	2023-04-26 19:00:00	FLL
10315	1	11	916	745	91	1212	1102	UA	351	N69885	EWR	SAN	329	2425	7	45	2023-01-11 07:00:00	Other
10322	6	23	1532	1430	62	1647	1606	B6	271	N3121J	JFK	MKE	111	745	14	30	2023-06-23 14:00:00	Other
10327	10	27	1029	940	49	1427	1341	UA	536	N27568	EWR	SJU	211	1608	9	40	2023-10-27 09:00:00	Other
10328	8	18	1527	1502	25	1830	1812	NK	496	N664NK	LGA	FLL	156	1076	15	2	2023-08-18 15:00:00	FLL
10330	8	1	1838	1753	45	2005	1941	B6	498	N283JB	JFK	BNA	103	765	17	53	2023-08-01 17:00:00	Other
10333	1	5	2004	1950	14	2125	2117	YX	1222	N743YX	EWR	IAD	51	212	19	50	2023-01-05 19:00:00	Other
10340	6	8	2206	2152	14	2311	2315	9E	1590	N311PQ	LGA	ROC	45	254	21	52	2023-06-08 21:00:00	Other
10342	1	13	1600	1455	65	1806	1710	AA	756	N178US	LGA	CLT	89	544	14	55	2023-01-13 14:00:00	CLT
10349	3	15	103	2135	208	242	2338	UA	484	N33203	EWR	CHS	79	628	21	35	2023-03-15 21:00:00	Other
10358	4	28	2252	2235	17	22	2359	DL	435	N123DQ	JFK	BOS	39	187	22	35	2023-04-28 22:00:00	BOS
10366	10	19	2028	2015	13	2223	2244	B6	42	N958JB	JFK	PHX	265	2153	20	15	2023-10-19 20:00:00	Other
10387	7	4	1638	1626	12	1928	1850	9E	1104	N306PQ	JFK	CLT	80	541	16	26	2023-07-04 16:00:00	CLT
10388	11	5	1522	1510	12	1815	1828	DL	540	N351DN	LGA	FLL	144	1076	15	10	2023-11-05 15:00:00	FLL
10392	6	5	1340	1250	50	1628	1603	B6	616	N2086J	JFK	FLL	143	1069	12	50	2023-06-05 12:00:00	FLL
10396	9	26	1709	1630	39	1940	1922	UA	469	N225UA	EWR	LAX	303	2454	16	30	2023-09-26 16:00:00	LAX
10397	10	3	1639	1330	189	2053	1727	B6	277	N659JB	JFK	SJU	208	1598	13	30	2023-10-03 13:00:00	Other
10407	1	19	1800	1635	85	1935	1801	9E	1628	N184GJ	JFK	SYR	45	209	16	35	2023-01-19 16:00:00	Other
10413	11	20	1018	946	32	1335	1318	B6	666	N709JB	LGA	RSW	155	1080	9	46	2023-11-20 09:00:00	Other
10418	4	4	1314	1200	74	1414	1317	B6	64	N238JB	JFK	BOS	32	187	12	0	2023-04-04 12:00:00	BOS
10425	1	29	2050	2020	30	2235	2222	9E	1473	N479PX	LGA	GSO	81	461	20	20	2023-01-29 20:00:00	Other
10431	9	8	1013	1000	13	1154	1159	YX	1181	N858RW	EWR	GSO	66	445	10	0	2023-09-08 10:00:00	Other
10435	3	11	2155	2129	26	2304	2301	OO	1150	N305SY	JFK	IAD	49	228	21	29	2023-03-11 21:00:00	Other
10442	6	21	1944	1725	139	2212	2007	B6	901	N523JB	LGA	JAX	114	833	17	25	2023-06-21 17:00:00	Other
10445	12	16	1950	1910	40	2229	2241	DL	138	N183DN	JFK	LAX	308	2475	19	10	2023-12-16 19:00:00	LAX
10446	5	13	1200	1140	20	1427	1438	B6	165	N506JB	LGA	PBI	129	1035	11	40	2023-05-13 11:00:00	Other
10450	5	15	1417	1130	167	1613	1337	AA	740	N838AW	LGA	CLT	76	544	11	30	2023-05-15 11:00:00	CLT
10459	3	12	906	759	67	1045	936	UA	506	N17753	EWR	BNA	123	748	7	59	2023-03-12 07:00:00	Other
10461	3	13	2306	2140	86	229	41	B6	392	N828JB	JFK	PBI	145	1028	21	40	2023-03-13 21:00:00	Other
10462	3	10	1431	1259	92	1534	1420	YX	1710	N229JQ	LGA	BOS	34	184	12	59	2023-03-10 12:00:00	BOS
10477	11	16	908	857	11	1204	1202	B6	222	N705JB	LGA	MCO	138	950	8	57	2023-11-16 08:00:00	MCO
10485	7	11	1131	1037	54	1429	1344	B6	284	N651JB	JFK	SLC	278	1990	10	37	2023-07-11 10:00:00	Other
10508	6	21	1647	1530	77	2020	1835	B6	570	N2016J	JFK	MCO	132	944	15	30	2023-06-21 15:00:00	MCO
10512	6	24	1016	1002	14	1152	1204	B6	70	N355JB	JFK	DTW	76	509	10	2	2023-06-24 10:00:00	Other
10513	2	12	2006	1955	11	2303	2309	NK	968	N641NK	EWR	MIA	148	1085	19	55	2023-02-12 19:00:00	MIA
10514	9	11	1756	1729	27	2133	2043	B6	207	N834JB	LGA	FLL	161	1076	17	29	2023-09-11 17:00:00	FLL
10526	9	13	2058	2030	28	2331	2307	DL	908	N116DU	LGA	JAX	118	833	20	30	2023-09-13 20:00:00	Other
10529	4	14	1306	1250	16	1415	1357	YX	1456	N214JQ	LGA	PVD	33	143	12	50	2023-04-14 12:00:00	Other
10536	11	26	745	700	45	1049	1006	B6	223	N2039J	JFK	FLL	159	1069	7	0	2023-11-26 07:00:00	FLL
10539	6	13	8	2259	69	415	257	B6	146	N954JB	JFK	SJU	213	1598	22	59	2023-06-13 22:00:00	Other
10540	1	4	1118	1059	19	1416	1427	B6	384	N630JB	JFK	SLC	272	1990	10	59	2023-01-04 10:00:00	Other
10548	7	25	1740	1535	125	2054	1855	DL	507	N3757D	JFK	PBI	156	1028	15	35	2023-07-25 15:00:00	Other
10552	9	11	2036	1529	307	2345	1848	DL	569	N386DN	LGA	FLL	159	1076	15	29	2023-09-11 15:00:00	FLL
10561	2	19	811	750	21	1138	1117	B6	660	N981JT	EWR	LAX	359	2454	7	50	2023-02-19 07:00:00	LAX
10563	5	18	1906	1842	24	2026	2025	UA	441	N77431	EWR	ORD	106	719	18	42	2023-05-18 18:00:00	ORD
10571	11	2	1012	955	17	1201	1154	G4	64	294NV	EWR	AVL	81	583	9	55	2023-11-02 09:00:00	Other
10593	9	3	1800	1645	75	2042	1951	B6	125	N2059J	JFK	MCO	121	944	16	45	2023-09-03 16:00:00	MCO
10597	4	14	1508	1445	23	1722	1700	WN	653	N1802U	LGA	MSY	164	1183	14	45	2023-04-14 14:00:00	Other
10599	6	5	1717	1655	22	1958	2043	AS	12	N224AK	JFK	SFO	315	2586	16	55	2023-06-05 16:00:00	Other
10602	1	11	1648	1500	108	1841	1652	OO	1748	N143SY	LGA	ORD	126	733	15	0	2023-01-11 15:00:00	ORD
10603	3	13	1856	1812	44	2129	2040	9E	1343	N901XJ	JFK	SAV	115	718	18	12	2023-03-13 18:00:00	Other
10605	6	2	904	800	64	1230	1111	AA	528	N861NN	EWR	MIA	154	1085	8	0	2023-06-02 08:00:00	MIA
10606	6	28	1629	1550	39	1810	1747	9E	1516	N906XJ	LGA	STL	135	888	15	50	2023-06-28 15:00:00	Other
10607	8	31	1414	1347	27	1654	1641	AA	785	N931AN	LGA	DFW	188	1389	13	47	2023-08-31 13:00:00	Other
10608	5	17	1644	1630	14	1831	1809	9E	1478	N908XJ	LGA	BGR	63	378	16	30	2023-05-17 16:00:00	Other
10609	12	6	1635	1618	17	1800	1755	YX	1802	N219YX	LGA	MKE	117	738	16	18	2023-12-06 16:00:00	Other
10611	7	31	1644	1630	14	2048	1940	NK	278	N687NK	LGA	FLL	157	1076	16	30	2023-07-31 16:00:00	FLL
10617	12	11	1554	1515	39	1706	1658	9E	1700	N335PQ	JFK	ROC	51	264	15	15	2023-12-11 15:00:00	Other
10621	7	29	1024	1006	18	1232	1219	UA	471	N829UA	EWR	DEN	215	1605	10	6	2023-07-29 10:00:00	Other
10629	3	27	1112	1000	72	1509	1323	DL	133	N193DN	JFK	LAX	351	2475	10	0	2023-03-27 10:00:00	LAX
10637	8	14	1514	1502	12	1815	1812	NK	496	N658NK	LGA	FLL	150	1076	15	2	2023-08-14 15:00:00	FLL
10656	2	27	921	745	96	1036	903	UA	613	N39297	EWR	ORF	48	284	7	45	2023-02-27 07:00:00	Other
10659	6	6	1034	954	40	1316	1257	B6	237	N703JB	LGA	MCO	128	950	9	54	2023-06-06 09:00:00	MCO
10664	10	21	1446	1431	15	1725	1701	B6	593	N608JB	JFK	JAX	109	828	14	31	2023-10-21 14:00:00	Other
10673	10	14	1401	1348	13	1525	1529	MQ	1023	N635RW	EWR	ORD	114	719	13	48	2023-10-14 13:00:00	ORD
10677	12	12	2057	2035	22	2350	2347	B6	60	N583JB	JFK	TPA	150	1005	20	35	2023-12-12 20:00:00	Other
10686	9	15	2027	2011	16	2229	2239	YX	1364	N436YX	JFK	IND	95	665	20	11	2023-09-15 20:00:00	Other
10698	8	17	2148	2025	83	2349	2255	WN	303	N923WN	LGA	DEN	224	1620	20	25	2023-08-17 20:00:00	Other
10701	4	12	2022	1959	23	29	2357	UA	536	N36447	EWR	SJU	200	1608	19	59	2023-04-12 19:00:00	Other
10702	2	24	2047	1935	72	2345	2249	NK	968	N635NK	EWR	MIA	143	1085	19	35	2023-02-24 19:00:00	MIA
10708	4	17	1515	1420	55	1648	1545	WN	71	N8708Q	LGA	MDW	107	725	14	20	2023-04-17 14:00:00	Other
10713	1	11	2204	1935	149	4	2154	9E	1426	N187GJ	JFK	CLT	81	541	19	35	2023-01-11 19:00:00	CLT
10715	7	16	1129	1000	89	1720	1255	DL	572	N359DN	JFK	MCO	172	944	10	0	2023-07-16 10:00:00	MCO
10717	12	26	2256	2055	121	109	2334	B6	880	N583JB	LGA	ATL	110	762	20	55	2023-12-26 20:00:00	ATL
10725	6	7	2247	2030	137	39	2240	9E	1568	N695CA	LGA	CAE	94	617	20	30	2023-06-07 20:00:00	Other
10726	6	8	2029	2000	29	2133	2118	B6	533	N184JB	LGA	PWM	44	269	20	0	2023-06-08 20:00:00	Other
10727	1	12	2126	2027	59	2259	2214	UA	153	N27724	EWR	RDU	70	416	20	27	2023-01-12 20:00:00	Other
10732	6	25	1922	1549	213	2114	1743	AA	855	N902NN	JFK	ORD	116	740	15	49	2023-06-25 15:00:00	ORD
10734	9	23	1818	1759	19	2028	2049	UA	859	N852UA	EWR	DFW	169	1372	17	59	2023-09-23 17:00:00	Other
10735	7	20	2044	2030	14	2250	2247	UA	723	N27268	EWR	MSY	156	1167	20	30	2023-07-20 20:00:00	Other
10739	6	3	1927	1800	87	2228	2138	DL	264	N804DN	JFK	SLC	240	1990	18	0	2023-06-03 18:00:00	Other
10743	5	12	826	810	16	1315	1318	UA	127	N76064	EWR	HNL	602	4962	8	10	2023-05-12 08:00:00	Other
10745	3	18	732	645	47	1033	1002	B6	851	N662JB	EWR	MIA	156	1085	6	45	2023-03-18 06:00:00	MIA
10746	1	17	1911	1859	12	2150	2212	DL	667	N341NW	JFK	TPA	145	1005	18	59	2023-01-17 18:00:00	Other
10747	7	19	1811	1753	18	2101	2049	UA	525	N63820	EWR	TPA	133	997	17	53	2023-07-19 17:00:00	Other
10752	2	11	2307	2105	122	118	2355	NK	287	N901NK	EWR	LAS	291	2227	21	5	2023-02-11 21:00:00	Other
10757	1	23	1405	1350	15	1506	1514	9E	1690	N181GJ	LGA	ROC	44	254	13	50	2023-01-23 13:00:00	Other
10759	7	21	1939	1755	104	2211	2057	B6	558	N505JB	LGA	MCO	125	950	17	55	2023-07-21 17:00:00	MCO
10760	9	23	2322	2157	85	58	2334	YX	1356	N409YX	JFK	DCA	43	213	21	57	2023-09-23 21:00:00	Other
10768	4	29	1351	1147	124	1707	1438	UA	487	N17752	EWR	SRQ	169	1034	11	47	2023-04-29 11:00:00	Other
10771	4	16	2039	1955	44	2339	2309	DL	505	N348DN	JFK	MCO	133	944	19	55	2023-04-16 19:00:00	MCO
10776	6	29	1141	2055	886	1255	2233	DL	1026	N134DU	JFK	BOS	36	187	20	55	2023-06-29 20:00:00	BOS
10777	5	8	1926	1907	19	2344	2225	UA	689	N406UA	EWR	SLC	283	1969	19	7	2023-05-08 19:00:00	Other
10778	1	16	2028	1941	47	2153	2130	AA	850	N834AW	LGA	BNA	114	764	19	41	2023-01-16 19:00:00	Other
10781	1	21	1441	1315	86	1605	1444	9E	1563	N232PQ	JFK	BUF	54	301	13	15	2023-01-21 13:00:00	Other
10783	8	4	1951	1930	21	2049	2046	YX	842	N729YX	EWR	PVD	34	160	19	30	2023-08-04 19:00:00	Other
10785	7	10	901	830	31	1108	1055	NK	147	N646NK	EWR	LAS	282	2227	8	30	2023-07-10 08:00:00	Other
10786	5	13	959	935	24	1256	1259	B6	570	N358JB	JFK	RSW	150	1074	9	35	2023-05-13 09:00:00	Other
10789	9	11	2057	2000	57	2326	2248	DL	95	N820DN	JFK	DEN	223	1626	20	0	2023-09-11 20:00:00	Other
10793	4	7	1758	1548	130	2054	1856	UA	695	N17294	EWR	FLL	141	1065	15	48	2023-04-07 15:00:00	FLL
10797	1	14	1353	1330	23	1459	1500	WN	412	N472WN	LGA	MDW	103	725	13	30	2023-01-14 13:00:00	Other
10798	4	29	2124	1730	234	27	2056	DL	569	N343NW	JFK	AUS	210	1521	17	30	2023-04-29 17:00:00	Other
10804	4	17	1615	1525	50	1757	1710	WN	778	N8517F	LGA	STL	127	888	15	25	2023-04-17 15:00:00	Other
10806	4	5	2049	2020	29	2333	2321	B6	67	N784JB	JFK	TPA	143	1005	20	20	2023-04-05 20:00:00	Other
10807	4	15	1944	1729	135	2155	1928	B6	403	N284JB	JFK	RDU	79	427	17	29	2023-04-15 17:00:00	Other
10808	2	7	833	810	23	1054	1109	B6	761	N562JB	JFK	LAS	302	2248	8	10	2023-02-07 08:00:00	Other
10809	4	28	2158	2045	73	225	2359	B6	447	N588JB	JFK	AUS	240	1521	20	45	2023-04-28 20:00:00	Other
10811	4	13	2051	1906	105	2351	2221	DL	438	N828DN	EWR	SLC	268	1969	19	6	2023-04-13 19:00:00	Other
10812	6	23	2338	2158	100	113	2359	YX	1115	N752YX	EWR	MEM	131	946	21	58	2023-06-23 21:00:00	Other
10813	7	5	1801	1736	25	1918	1912	B6	93	N368JB	JFK	PWM	51	273	17	36	2023-07-05 17:00:00	Other
10817	1	15	27	2259	88	506	347	B6	157	N2084J	JFK	SJU	186	1598	22	59	2023-01-15 22:00:00	Other
10818	3	16	1553	1540	13	1841	1852	AA	116	N972AN	JFK	MIA	141	1089	15	40	2023-03-16 15:00:00	MIA
10819	2	24	1955	1925	30	2138	2125	AA	142	N778XF	LGA	RDU	79	431	19	25	2023-02-24 19:00:00	Other
10821	10	31	1600	1245	195	1927	1552	B6	39	N612JB	JFK	TPA	162	1005	12	45	2023-10-31 12:00:00	Other
10824	8	11	1554	1530	24	1842	1833	UA	405	N14107	EWR	LAX	315	2454	15	30	2023-08-11 15:00:00	LAX
10825	4	4	1521	1500	21	1836	1802	UA	214	N473UA	EWR	AUS	205	1504	15	0	2023-04-04 15:00:00	Other
10827	10	29	1432	1415	17	1750	1710	WN	689	N8322X	LGA	HOU	207	1428	14	15	2023-10-29 14:00:00	Other
10833	8	9	743	730	13	908	911	DL	335	N113DQ	LGA	ORD	108	733	7	30	2023-08-09 07:00:00	ORD
10834	7	28	2113	1954	79	105	2353	UA	197	N67812	EWR	BQN	190	1585	19	54	2023-07-28 19:00:00	Other
10835	9	18	1002	935	27	1115	1051	B6	608	N324JB	JFK	BTV	42	266	9	35	2023-09-18 09:00:00	Other
10842	10	18	2042	2029	13	2228	2210	DL	997	N894AT	EWR	DTW	78	488	20	29	2023-10-18 20:00:00	Other
10851	9	7	1015	1000	15	1253	1302	NK	856	N640NK	EWR	AUS	190	1504	10	0	2023-09-07 10:00:00	Other
10864	12	19	1957	1730	147	2228	2039	B6	449	N556JB	JFK	MCO	123	944	17	30	2023-12-19 17:00:00	MCO
10865	5	14	1434	1412	22	1716	1700	UA	384	N73251	EWR	MCO	132	937	14	12	2023-05-14 14:00:00	MCO
10867	3	4	1817	1800	17	1936	1942	UA	937	N879UA	LGA	ORD	117	733	18	0	2023-03-04 18:00:00	ORD
10872	11	13	1848	1830	18	2016	2010	B6	566	N355JB	JFK	BUF	62	301	18	30	2023-11-13 18:00:00	Other
10873	2	22	1855	1829	26	2202	2147	B6	893	N570JB	EWR	FLL	147	1065	18	29	2023-02-22 18:00:00	FLL
10874	11	17	2036	1930	66	2137	2057	YX	1818	N231JQ	LGA	BOS	39	184	19	30	2023-11-17 19:00:00	BOS
10885	2	6	1920	1859	21	2204	2208	DL	436	N128DN	LGA	PBI	132	1035	18	59	2023-02-06 18:00:00	Other
10886	9	12	1947	1900	47	2248	2122	9E	1606	N337PQ	LGA	IND	104	660	19	0	2023-09-12 19:00:00	Other
10887	8	30	1910	1840	30	2218	2144	B6	735	N652JB	JFK	MCO	165	944	18	40	2023-08-30 18:00:00	MCO
10890	6	8	902	810	52	1313	1211	UA	830	N76054	EWR	SJU	210	1608	8	10	2023-06-08 08:00:00	Other
10896	7	7	1836	1334	302	2148	1635	UA	94	N469UA	EWR	RSW	154	1068	13	34	2023-07-07 13:00:00	Other
10897	9	7	2145	1935	130	112	2145	9E	1442	N305PQ	JFK	DTW	86	509	19	35	2023-09-07 19:00:00	Other
10901	12	24	1009	925	44	1221	1200	DL	95	N102DU	LGA	SAV	110	722	9	25	2023-12-24 09:00:00	Other
10905	12	8	1714	1629	45	1947	1913	DL	747	N355NB	JFK	MSY	164	1182	16	29	2023-12-08 16:00:00	Other
10909	12	20	1623	1530	53	1900	1835	B6	324	N715JB	JFK	MCO	127	944	15	30	2023-12-20 15:00:00	MCO
10920	11	23	1559	1350	129	1725	1520	9E	1612	N903XJ	LGA	CHO	55	305	13	50	2023-11-23 13:00:00	Other
10929	8	1	837	820	17	1103	1109	YX	1376	N210JQ	JFK	JAX	114	828	8	20	2023-08-01 08:00:00	Other
10932	2	15	1038	1025	13	1406	1354	B6	302	N598JB	JFK	SAT	251	1587	10	25	2023-02-15 10:00:00	Other
10943	1	12	1724	1633	51	2058	1950	UA	860	N76269	EWR	RSW	162	1068	16	33	2023-01-12 16:00:00	Other
10958	10	20	1439	1315	84	1549	1438	B6	882	N307JB	JFK	DCA	42	213	13	15	2023-10-20 13:00:00	Other
10966	7	13	1520	1454	26	1740	1724	B6	26	N595JB	JFK	MSY	170	1182	14	54	2023-07-13 14:00:00	Other
10973	7	25	1846	1710	96	2210	2027	B6	642	N637JB	JFK	MIA	169	1089	17	10	2023-07-25 17:00:00	MIA
10982	11	27	814	800	14	1150	1124	AA	812	N979NN	JFK	DFW	236	1391	8	0	2023-11-27 08:00:00	Other
10984	8	10	828	600	148	1115	835	WN	468	N458WN	LGA	HOU	204	1428	6	0	2023-08-10 06:00:00	Other
10993	9	18	1205	900	185	1404	1106	9E	1684	N316PQ	JFK	CVG	93	589	9	0	2023-09-18 09:00:00	Other
10999	11	20	2303	2223	40	329	313	NK	361	N606NK	EWR	SJU	188	1608	22	23	2023-11-20 22:00:00	Other
11012	7	14	1324	1259	25	1503	1439	9E	1168	N920XJ	LGA	RIC	54	292	12	59	2023-07-14 12:00:00	Other
11014	2	26	1912	1800	72	2108	1941	UA	671	N819UA	EWR	STL	139	872	18	0	2023-02-26 18:00:00	Other
11018	4	10	1737	1630	67	2029	1932	NK	488	N643NK	EWR	MCO	137	937	16	30	2023-04-10 16:00:00	MCO
11021	7	9	127	1959	328	402	2305	AS	79	N929VA	EWR	LAX	304	2454	19	59	2023-07-09 19:00:00	LAX
11024	7	17	2335	2010	205	220	2242	B6	30	N537JT	JFK	DEN	254	1626	20	10	2023-07-17 20:00:00	Other
11026	1	14	1213	1200	13	1404	1303	9E	1457	N134EV	JFK	ITH	38	189	12	0	2023-01-14 12:00:00	Other
11031	7	15	2030	1959	31	2334	2305	AS	79	N930VA	EWR	LAX	322	2454	19	59	2023-07-15 19:00:00	LAX
11037	11	16	2019	2005	14	2330	2350	B6	306	N980JT	JFK	SFO	344	2586	20	5	2023-11-16 20:00:00	Other
11038	2	10	1826	1815	11	2138	2137	UA	438	N2644U	EWR	SFO	336	2565	18	15	2023-02-10 18:00:00	Other
11048	2	3	2111	1729	222	15	2041	B6	735	N562JB	JFK	PBI	142	1028	17	29	2023-02-03 17:00:00	Other
11050	7	21	1719	1700	19	1949	1837	YX	1370	N242JQ	LGA	BOS	37	184	17	0	2023-07-21 17:00:00	BOS
11051	1	1	1437	1400	37	1743	1716	B6	600	N2048J	JFK	FLL	162	1069	14	0	2023-01-01 14:00:00	FLL
11052	11	19	2031	2015	16	2323	2328	UA	929	N12116	EWR	FLL	139	1065	20	15	2023-11-19 20:00:00	FLL
11061	7	21	1543	1318	145	1650	1434	B6	689	N348JB	JFK	ACK	46	199	13	18	2023-07-21 13:00:00	Other
11070	12	3	2017	1820	117	2153	1959	YX	1848	N216JQ	JFK	DCA	60	213	18	20	2023-12-03 18:00:00	Other
11074	5	17	2043	1915	88	2310	2215	UA	779	N420UA	EWR	DFW	178	1372	19	15	2023-05-17 19:00:00	Other
11076	10	3	1356	1237	79	1542	1445	DL	952	N117DU	JFK	MSP	143	1029	12	37	2023-10-03 12:00:00	Other
11077	12	23	2124	2105	19	2332	2336	UA	853	N66837	EWR	MSY	162	1167	21	5	2023-12-23 21:00:00	Other
11083	3	30	2053	2026	27	33	2330	UA	265	N75426	EWR	AUS	211	1504	20	26	2023-03-30 20:00:00	Other
11086	12	21	1915	1815	60	2151	2144	DL	197	N115DU	JFK	DFW	189	1391	18	15	2023-12-21 18:00:00	Other
11105	5	13	1838	1827	11	2121	2140	UA	483	N431UA	EWR	FLL	148	1065	18	27	2023-05-13 18:00:00	FLL
11107	3	8	1250	1130	80	1356	1237	9E	1394	N606LR	LGA	BGM	29	147	11	30	2023-03-08 11:00:00	Other
11120	3	3	1306	1220	46	1559	1522	B6	34	N563JB	JFK	MCO	142	944	12	20	2023-03-03 12:00:00	MCO
11121	11	2	1020	805	135	1205	959	B6	827	N3058J	JFK	RDU	79	427	8	5	2023-11-02 08:00:00	Other
11125	4	25	1812	1720	52	2124	2038	AA	868	N335RT	JFK	AUS	223	1521	17	20	2023-04-25 17:00:00	Other
11126	7	17	1552	1529	23	1940	1852	AA	98	N848NN	JFK	MIA	199	1089	15	29	2023-07-17 15:00:00	MIA
11134	12	4	1636	1535	61	1816	1750	DL	105	N342NW	LGA	MSP	142	1020	15	35	2023-12-04 15:00:00	Other
11137	7	29	1758	855	543	2011	1114	9E	1123	N478PX	LGA	GRR	96	618	8	55	2023-07-29 08:00:00	Other
11140	7	3	1759	1610	109	2033	1837	UA	379	N807UA	EWR	ATL	120	746	16	10	2023-07-03 16:00:00	ATL
11142	7	19	1158	1130	28	1451	1431	DL	374	N894DN	JFK	TPA	132	1005	11	30	2023-07-19 11:00:00	Other
11143	7	29	943	745	118	1102	901	UA	213	N38257	EWR	BOS	44	200	7	45	2023-07-29 07:00:00	BOS
11149	6	22	2102	2037	25	44	2352	B6	708	N937JB	JFK	LAX	361	2475	20	37	2023-06-22 20:00:00	LAX
11155	7	5	1510	1459	11	1617	1616	B6	604	N318JB	JFK	HYA	39	196	14	59	2023-07-05 14:00:00	Other
11162	7	19	1924	1900	24	2049	2035	WN	843	N499WN	LGA	MDW	110	725	19	0	2023-07-19 19:00:00	Other
11163	3	7	2218	2129	49	8	2318	YX	1365	N112HQ	LGA	CLE	78	419	21	29	2023-03-07 21:00:00	Other
11173	12	15	2325	1829	296	207	2144	F9	1410	N322FR	LGA	MCO	129	950	18	29	2023-12-15 18:00:00	MCO
11182	6	20	2040	1925	75	2306	2224	DL	656	N103DU	LGA	IAH	182	1416	19	25	2023-06-20 19:00:00	Other
11192	4	16	2328	2159	89	33	2316	YX	1561	N231JQ	LGA	PWM	44	269	21	59	2023-04-16 21:00:00	Other
11197	4	5	2306	2035	151	16	2203	YX	1554	N227JQ	LGA	DCA	43	214	20	35	2023-04-05 20:00:00	Other
11198	1	17	910	829	41	1155	1159	AA	694	N727AN	JFK	MIA	141	1089	8	29	2023-01-17 08:00:00	MIA
11209	12	3	753	730	23	1107	1039	UA	630	N15712	LGA	IAH	234	1416	7	30	2023-12-03 07:00:00	Other
11211	6	9	1634	1559	35	1912	1827	UA	500	N408UA	EWR	JAX	138	820	15	59	2023-06-09 15:00:00	Other
11212	9	26	1538	1418	80	1826	1707	UA	370	N33203	EWR	MCO	137	937	14	18	2023-09-26 14:00:00	MCO
11215	2	27	1022	850	92	1407	1219	B6	758	N967JT	JFK	LAX	375	2475	8	50	2023-02-27 08:00:00	LAX
11226	1	23	1858	1825	33	2029	2016	DL	423	N102DU	LGA	ORD	116	733	18	25	2023-01-23 18:00:00	ORD
11261	9	23	830	730	60	1036	955	DL	188	N311DU	LGA	DEN	225	1620	7	30	2023-09-23 07:00:00	Other
11273	5	24	1721	1615	66	2009	1906	UA	580	N18112	EWR	MCO	137	937	16	15	2023-05-24 16:00:00	MCO
11286	10	1	1122	1101	21	1241	1249	UA	654	N17719	EWR	MEM	125	946	11	1	2023-10-01 11:00:00	Other
11288	8	13	1800	1659	61	2021	1831	B6	317	N206JB	JFK	BOS	42	187	16	59	2023-08-13 16:00:00	BOS
11306	7	8	1713	1520	113	1850	1717	YX	1081	N826MD	LGA	GSO	73	461	15	20	2023-07-08 15:00:00	Other
11307	3	26	1023	1005	18	1246	1227	UA	786	N68836	EWR	DEN	232	1605	10	5	2023-03-26 10:00:00	Other
11309	2	17	847	830	17	1152	1155	B6	59	N789JB	JFK	SAN	348	2446	8	30	2023-02-17 08:00:00	Other
11322	12	16	724	700	24	1028	1025	DL	331	N316DU	EWR	SLC	273	1969	7	0	2023-12-16 07:00:00	Other
11328	12	13	1639	1600	39	1846	1822	YX	1229	N115HQ	JFK	CVG	103	589	16	0	2023-12-13 16:00:00	Other
11340	6	18	1934	1845	49	2050	2024	UA	456	N439UA	EWR	ORD	105	719	18	45	2023-06-18 18:00:00	ORD
11348	3	10	843	825	18	929	935	9E	1500	N309PQ	LGA	BDL	21	101	8	25	2023-03-10 08:00:00	Other
11352	5	13	1754	1629	85	1922	1815	AA	747	N968AN	LGA	ORD	112	733	16	29	2023-05-13 16:00:00	ORD
11356	12	11	1004	845	79	1146	1020	YX	1849	N243JQ	LGA	DCA	60	214	8	45	2023-12-11 08:00:00	Other
11359	3	23	948	755	113	1356	1113	AS	86	N927VA	EWR	LAX	391	2454	7	55	2023-03-23 07:00:00	LAX
11360	1	14	1256	1200	56	1555	1527	DL	900	N118DU	LGA	IAH	191	1416	12	0	2023-01-14 12:00:00	Other
11383	1	3	917	830	47	1042	1019	AA	134	N947NN	LGA	ORD	120	733	8	30	2023-01-03 08:00:00	ORD
11386	11	30	1321	1233	48	1535	1459	UA	233	N17333	EWR	MSY	171	1167	12	33	2023-11-30 12:00:00	Other
11387	10	7	1552	1459	53	1757	1701	YX	1259	N443YX	JFK	CLE	71	425	14	59	2023-10-07 14:00:00	Other
11397	4	2	1455	1429	26	1639	1626	YX	1585	N232JQ	LGA	STL	137	888	14	29	2023-04-02 14:00:00	Other
11402	9	24	2244	2150	54	2338	2245	9E	1510	N538CA	LGA	BDL	23	101	21	50	2023-09-24 21:00:00	Other
11406	3	12	34	2040	234	410	37	B6	732	N958JB	JFK	SJU	191	1598	20	40	2023-03-12 20:00:00	Other
11407	1	19	1415	1400	15	1724	1702	UA	141	N408UA	EWR	PBI	160	1023	14	0	2023-01-19 14:00:00	Other
11409	7	21	2153	2125	28	2306	2245	WN	535	N8875B	LGA	MDW	110	725	21	25	2023-07-21 21:00:00	Other
11410	7	30	1448	1428	20	1700	1640	UA	450	N75432	EWR	DEN	220	1605	14	28	2023-07-30 14:00:00	Other
11415	8	8	2127	1959	88	125	2357	UA	462	N68821	EWR	SJU	200	1608	19	59	2023-08-08 19:00:00	Other
11416	4	18	2024	1959	25	2343	2315	B6	544	N946JL	EWR	LAX	340	2454	19	59	2023-04-18 19:00:00	LAX
11421	1	19	2212	2000	132	107	2245	DL	385	N344NW	LGA	ATL	127	762	20	0	2023-01-19 20:00:00	ATL
11422	2	18	646	600	46	848	814	DL	926	N955AT	EWR	MSP	162	1008	6	0	2023-02-18 06:00:00	Other
11427	1	14	1640	1620	20	1817	1835	9E	1698	N182GJ	JFK	CLT	75	541	16	20	2023-01-14 16:00:00	CLT
11431	2	6	2031	1959	32	2223	2210	9E	1419	N936XJ	EWR	CVG	94	569	19	59	2023-02-06 19:00:00	Other
11439	12	25	1454	1440	14	1657	1715	WN	683	N8573Z	LGA	MSY	167	1183	14	40	2023-12-25 14:00:00	Other
11446	6	17	935	600	215	1217	903	AA	1	N101NN	JFK	LAX	310	2475	6	0	2023-06-17 06:00:00	LAX
11456	4	22	1451	1429	22	1720	1651	UA	417	N39728	EWR	ATL	117	746	14	29	2023-04-22 14:00:00	ATL
11463	12	12	800	559	121	1244	1051	B6	581	N952JB	JFK	SJU	200	1598	5	59	2023-12-12 05:00:00	Other
11470	4	2	2309	2215	54	43	2352	UA	485	N37287	EWR	ORD	118	719	22	15	2023-04-02 22:00:00	ORD
11472	8	4	1520	1508	12	1700	1705	9E	1111	N293PQ	EWR	RDU	83	416	15	8	2023-08-04 15:00:00	Other
11486	6	30	1949	1930	19	2344	2249	B6	71	N988JT	JFK	LAX	334	2475	19	30	2023-06-30 19:00:00	LAX
11489	9	12	1049	1000	49	1159	1128	YX	1327	N135HQ	LGA	DCA	42	214	10	0	2023-09-12 10:00:00	Other
11505	5	21	1446	1430	16	1626	1618	AA	852	N748UW	LGA	RDU	68	431	14	30	2023-05-21 14:00:00	Other
11507	7	31	1901	1730	91	2140	2040	B6	112	N507JT	JFK	BUR	320	2465	17	30	2023-07-31 17:00:00	Other
11516	6	5	2021	1955	26	2240	2312	B6	728	N943JT	EWR	LAX	294	2454	19	55	2023-06-05 19:00:00	LAX
11523	8	2	1559	1541	18	2022	1846	UA	440	N27273	EWR	FLL	187	1065	15	41	2023-08-02 15:00:00	FLL
11524	2	1	1816	1629	107	1908	1738	9E	1435	N918XJ	LGA	PVD	28	143	16	29	2023-02-01 16:00:00	Other
11525	2	18	934	915	19	1114	1125	YX	1569	N234JQ	LGA	CMH	78	479	9	15	2023-02-18 09:00:00	Other
11526	11	20	1555	1540	15	1835	1845	DL	785	N391DN	JFK	MCO	130	944	15	40	2023-11-20 15:00:00	MCO
11529	10	10	923	910	13	1243	1216	UA	914	N27304	EWR	MIA	159	1085	9	10	2023-10-10 09:00:00	MIA
11540	4	2	2053	1849	124	1	2143	B6	82	N959JB	JFK	MCO	133	944	18	49	2023-04-02 18:00:00	MCO
11586	7	6	1222	1205	17	1403	1407	YX	1078	N433YX	LGA	DTW	77	502	12	5	2023-07-06 12:00:00	Other
11594	6	1	1721	1559	82	1836	1723	YX	1869	N880RW	LGA	ACK	41	202	15	59	2023-06-01 15:00:00	Other
11602	7	18	2037	1855	102	2214	2016	AA	708	N770UW	LGA	BNA	125	764	18	55	2023-07-18 18:00:00	Other
11610	4	30	2009	1720	169	2251	2025	WN	879	N8729H	LGA	HOU	194	1428	17	20	2023-04-30 17:00:00	Other
11636	5	31	1044	949	55	1205	1149	YX	1686	N220JQ	LGA	STL	116	888	9	49	2023-05-31 09:00:00	Other
11637	6	14	1935	1440	295	2146	1655	WN	473	N7819A	LGA	MSY	173	1183	14	40	2023-06-14 14:00:00	Other
11638	5	1	2100	1914	106	2218	2051	UA	629	N841UA	EWR	BNA	105	748	19	14	2023-05-01 19:00:00	Other
11640	9	7	942	930	12	1128	1147	YX	1110	N733YX	EWR	AVL	86	583	9	30	2023-09-07 09:00:00	Other
11645	10	11	1359	1345	14	1605	1608	B6	953	N708JB	LGA	SAV	103	722	13	45	2023-10-11 13:00:00	Other
11650	11	6	2202	2150	12	2317	2257	UA	231	N37555	EWR	SYR	39	195	21	50	2023-11-06 21:00:00	Other
11660	6	13	1643	1628	15	1754	1755	UA	790	N442UA	EWR	IAD	41	212	16	28	2023-06-13 16:00:00	Other
11671	6	26	1833	1640	113	1353	2008	DL	170	N520DE	JFK	SEA	NA	2422	16	40	2023-06-26 16:00:00	Other
11672	3	20	1848	1825	23	2208	2125	AS	91	N298AK	EWR	SAN	350	2425	18	25	2023-03-20 18:00:00	Other
11675	9	26	2140	2117	23	2256	2224	YX	1106	N758YX	EWR	PHL	35	80	21	17	2023-09-26 21:00:00	Other
11681	3	18	910	755	75	1207	1113	AS	86	N922VA	EWR	LAX	325	2454	7	55	2023-03-18 07:00:00	LAX
11683	5	5	1811	1730	41	1958	1907	YX	1120	N863RW	EWR	PIT	51	319	17	30	2023-05-05 17:00:00	Other
11707	12	11	2233	2129	64	16	2316	AA	268	N834AW	LGA	RDU	73	431	21	29	2023-12-11 21:00:00	Other
11708	2	18	1922	1729	113	2237	2057	AA	923	N339SU	JFK	AUS	224	1521	17	29	2023-02-18 17:00:00	Other
11718	3	19	1626	1610	16	1930	1900	WN	830	N8813Q	LGA	MCO	153	950	16	10	2023-03-19 16:00:00	MCO
11720	4	30	2153	2045	68	57	2359	B6	447	N715JB	JFK	AUS	211	1521	20	45	2023-04-30 20:00:00	Other
11730	11	18	1702	1645	17	1953	2003	B6	164	N505JB	LGA	FLL	145	1076	16	45	2023-11-18 16:00:00	FLL
11731	9	29	1843	1646	117	2118	1944	AA	203	N964NN	EWR	DFW	179	1372	16	46	2023-09-29 16:00:00	Other
11732	7	13	1232	1155	37	1403	1346	9E	1262	N316PQ	JFK	RDU	64	427	11	55	2023-07-13 11:00:00	Other
11736	3	10	1843	1745	58	2143	2057	B6	21	N537JT	LGA	TPA	147	1010	17	45	2023-03-10 17:00:00	Other
11737	4	14	1421	1340	41	1657	1609	B6	581	N337JB	JFK	JAX	120	828	13	40	2023-04-14 13:00:00	Other
11738	4	7	1807	1750	17	2023	2025	WN	802	N8534Z	LGA	DEN	234	1620	17	50	2023-04-07 17:00:00	Other
11740	2	26	1815	1700	75	2022	1940	DL	942	N849DN	JFK	ATL	112	760	17	0	2023-02-26 17:00:00	ATL
11743	10	3	1822	1759	23	2100	2055	F9	443	N709FR	LGA	MCO	129	950	17	59	2023-10-03 17:00:00	MCO
11745	2	10	2307	1929	218	205	2259	DL	306	N132DU	LGA	DFW	219	1389	19	29	2023-02-10 19:00:00	Other
11746	3	5	1456	1429	27	1639	1631	NK	519	N923NK	LGA	MYR	80	563	14	29	2023-03-05 14:00:00	Other
11749	12	16	2024	2000	24	2234	2221	OO	1172	N320SY	JFK	CLE	85	425	20	0	2023-12-16 20:00:00	Other
11754	4	17	1507	1250	137	1614	1357	YX	1456	N228JQ	LGA	PVD	28	143	12	50	2023-04-17 12:00:00	Other
11774	1	2	933	2159	694	1038	2326	UA	477	N840UA	EWR	ORF	46	284	21	59	2023-01-02 21:00:00	Other
11787	9	26	1723	1630	53	2057	1944	B6	207	N558JB	LGA	FLL	176	1076	16	30	2023-09-26 16:00:00	FLL
11795	1	5	1957	1940	17	2056	2110	DL	677	N115DU	JFK	BOS	32	187	19	40	2023-01-05 19:00:00	BOS
11796	4	22	2228	2052	96	126	2357	UA	109	N38454	EWR	SRQ	158	1034	20	52	2023-04-22 20:00:00	Other
11808	6	16	2311	2234	37	18	2348	UA	817	N25705	EWR	SYR	34	195	22	34	2023-06-16 22:00:00	Other
11812	11	17	2206	2016	110	52	2322	B6	17	N510JB	LGA	TPA	145	1010	20	16	2023-11-17 20:00:00	Other
11821	1	26	1524	1453	31	1658	1640	UA	185	N69829	EWR	RDU	80	416	14	53	2023-01-26 14:00:00	Other
11831	2	19	2131	2059	32	2312	2302	YX	1145	N730YX	EWR	CMH	83	463	20	59	2023-02-19 20:00:00	Other
11835	3	16	1539	1445	54	1911	1836	B6	319	N656JB	JFK	SJU	192	1598	14	45	2023-03-16 14:00:00	Other
11838	3	12	1853	1740	73	2207	2105	NK	32	N946NK	EWR	LAX	331	2454	17	40	2023-03-12 17:00:00	LAX
11842	8	17	1544	1529	15	1704	1654	UA	376	N821UA	EWR	BNA	104	748	15	29	2023-08-17 15:00:00	Other
11843	3	14	2041	1959	42	2243	2158	YX	1217	N753YX	EWR	ILM	71	488	19	59	2023-03-14 19:00:00	Other
11848	2	11	1459	1445	14	1637	1630	WN	60	N279WN	LGA	BNA	125	764	14	45	2023-02-11 14:00:00	Other
11849	5	21	1923	1740	103	2239	2053	NK	31	N951NK	EWR	LAX	320	2454	17	40	2023-05-21 17:00:00	LAX
11865	5	26	1755	1729	26	2118	2054	AA	318	N338RS	JFK	MIA	166	1089	17	29	2023-05-26 17:00:00	MIA
11876	12	7	1023	949	34	1308	1300	B6	781	N952JB	JFK	FLL	141	1069	9	49	2023-12-07 09:00:00	FLL
11880	12	15	1014	950	24	1208	1219	9E	1702	N676CA	EWR	CVG	85	569	9	50	2023-12-15 09:00:00	Other
11888	8	4	615	600	15	751	732	UA	310	N24224	EWR	ORD	113	719	6	0	2023-08-04 06:00:00	ORD
11891	9	20	2039	2010	29	2300	2301	B6	25	N809JB	JFK	ABQ	241	1826	20	10	2023-09-20 20:00:00	Other
11893	1	30	1613	1559	14	1812	1809	AA	112	N945AN	JFK	CLT	88	541	15	59	2023-01-30 15:00:00	CLT
11898	4	1	2219	1955	144	217	2358	DL	108	N706TW	JFK	SFO	366	2586	19	55	2023-04-01 19:00:00	Other
11901	8	4	1417	1330	47	1652	1558	B6	33	N648JB	JFK	LAS	297	2248	13	30	2023-08-04 13:00:00	Other
11905	6	30	1837	1755	42	2051	2025	WN	859	N8880G	LGA	ATL	101	762	17	55	2023-06-30 17:00:00	ATL
11907	8	23	2252	2105	107	121	15	DL	1399	N842MH	JFK	LAX	293	2475	21	5	2023-08-23 21:00:00	LAX
11910	2	23	955	930	25	1328	1246	AA	266	N969AN	LGA	DFW	231	1389	9	30	2023-02-23 09:00:00	Other
11914	3	19	1556	1320	156	1742	1453	YX	1679	N222JQ	LGA	RIC	63	292	13	20	2023-03-19 13:00:00	Other
11917	9	13	827	730	57	1134	1030	AS	80	N928VA	EWR	LAX	316	2454	7	30	2023-09-13 07:00:00	LAX
11924	2	22	1430	1407	23	1717	1718	UA	596	N38446	EWR	IAH	207	1400	14	7	2023-02-22 14:00:00	Other
11929	8	2	1014	930	44	1241	1154	YX	907	N653RW	EWR	TVC	103	644	9	30	2023-08-02 09:00:00	Other
11935	5	5	1001	947	14	1247	1241	B6	222	N516JB	LGA	MCO	135	950	9	47	2023-05-05 09:00:00	MCO
11938	8	2	1840	1740	60	2034	2007	9E	1100	N926XJ	LGA	CVG	90	585	17	40	2023-08-02 17:00:00	Other
11941	2	26	1407	1304	63	1729	1610	B6	553	N593JB	JFK	MCO	142	944	13	4	2023-02-26 13:00:00	MCO
11947	1	4	1931	1820	71	2143	2037	9E	1643	N138EV	JFK	CVG	106	589	18	20	2023-01-04 18:00:00	Other
11952	7	25	2239	1929	190	24	2144	9E	1245	N293PQ	JFK	RDU	67	427	19	29	2023-07-25 19:00:00	Other
11953	3	15	2121	2030	51	2251	2219	DL	468	N144DU	LGA	ORD	113	733	20	30	2023-03-15 20:00:00	ORD
11965	2	16	1443	1430	13	1622	1610	UA	679	N877UA	EWR	RDU	69	416	14	30	2023-02-16 14:00:00	Other
11973	11	25	709	655	14	843	839	UA	652	N27260	EWR	CLE	65	404	6	55	2023-11-25 06:00:00	Other
11976	2	24	1637	1550	47	1903	1836	DL	345	N348DN	LGA	ATL	120	762	15	50	2023-02-24 15:00:00	ATL
11978	6	29	2242	1529	433	2	1704	UA	715	N76532	EWR	ORD	103	719	15	29	2023-06-29 15:00:00	ORD
11979	4	6	1517	1459	18	1739	1724	9E	1437	N308PQ	JFK	IND	102	665	14	59	2023-04-06 14:00:00	Other
11991	8	16	1718	1630	48	2000	1952	B6	216	N587JB	JFK	SJC	305	2569	16	30	2023-08-16 16:00:00	Other
12000	12	17	2201	2055	66	59	15	B6	731	N806JB	LGA	RSW	154	1080	20	55	2023-12-17 20:00:00	Other
12002	7	3	1959	1930	29	NA	2257	B6	309	N508JL	JFK	PDX	NA	2454	19	30	2023-07-03 19:00:00	Other
12006	11	22	1012	949	23	1233	1203	9E	1510	N153PQ	LGA	PNS	169	1030	9	49	2023-11-22 09:00:00	Other
12008	4	21	1307	1240	27	1429	1419	9E	1212	N320PQ	LGA	BGR	57	378	12	40	2023-04-21 12:00:00	Other
12014	5	9	841	645	116	1111	856	UA	866	N840UA	EWR	MSY	169	1167	6	45	2023-05-09 06:00:00	Other
12021	7	31	1237	1217	20	1409	1341	AA	806	N733UW	LGA	BNA	118	764	12	17	2023-07-31 12:00:00	Other
12024	2	22	2000	1725	155	2144	1912	AA	218	N963AN	JFK	ORD	134	740	17	25	2023-02-22 17:00:00	ORD
12025	9	14	1440	1315	85	1616	1431	B6	270	N273JB	LGA	BOS	40	184	13	15	2023-09-14 13:00:00	BOS
12027	9	7	1506	1455	11	1837	1628	OO	1257	N253SY	JFK	IAD	65	228	14	55	2023-09-07 14:00:00	Other
12031	6	25	2118	1735	223	2323	1957	9E	1464	N914XJ	LGA	CVG	91	585	17	35	2023-06-25 17:00:00	Other
12034	2	12	1359	1300	59	1551	1507	DL	749	N328NB	LGA	DTW	79	502	13	0	2023-02-12 13:00:00	Other
12037	5	5	2134	2059	35	2348	2312	UA	374	N14704	EWR	CVG	92	569	20	59	2023-05-05 20:00:00	Other
12042	11	26	1128	1019	69	1338	1240	9E	1450	N135EV	LGA	CLT	99	544	10	19	2023-11-26 10:00:00	CLT
12043	2	16	1011	829	102	1224	1106	B6	879	N607JB	LGA	MSY	170	1183	8	29	2023-02-16 08:00:00	Other
12049	3	30	1844	1829	15	2217	2145	UA	516	N17730	EWR	SNA	361	2434	18	29	2023-03-30 18:00:00	Other
12057	5	24	2204	1959	125	105	2306	DL	446	N368DN	LGA	FLL	155	1076	19	59	2023-05-24 19:00:00	FLL
12058	6	25	2147	1605	342	58	1920	DL	326	N3760C	LGA	MIA	149	1096	16	5	2023-06-25 16:00:00	MIA
12059	7	25	2342	1930	252	241	2255	B6	309	N794JB	JFK	PDX	324	2454	19	30	2023-07-25 19:00:00	Other
12062	5	21	1431	1354	37	1640	1623	B6	720	N562JB	LGA	DEN	218	1620	13	54	2023-05-21 13:00:00	Other
12082	10	7	1708	1643	25	2035	2000	B6	821	N519JB	EWR	MIA	168	1085	16	43	2023-10-07 16:00:00	MIA
12092	1	25	1643	1559	44	1851	1815	DL	586	N123DW	LGA	DTW	91	502	15	59	2023-01-25 15:00:00	Other
12100	3	1	1750	1729	21	2052	2026	UA	475	N38459	EWR	IAH	204	1400	17	29	2023-03-01 17:00:00	Other
12104	7	17	2016	1959	17	2247	2224	DL	764	N3747D	EWR	ATL	106	746	19	59	2023-07-17 19:00:00	ATL
12105	9	10	2325	2250	35	155	118	F9	842	N233FR	LGA	ATL	110	762	22	50	2023-09-10 22:00:00	ATL
12107	4	10	931	850	41	1054	1017	9E	1357	N272PQ	LGA	PWM	53	269	8	50	2023-04-10 08:00:00	Other
12109	8	10	1422	1314	68	1623	1525	YX	1021	N445YX	LGA	MSP	154	1020	13	14	2023-08-10 13:00:00	Other
12113	6	17	1015	1000	15	1457	1455	HA	20	N380HA	JFK	HNL	590	4983	10	0	2023-06-17 10:00:00	Other
12118	6	16	1346	1129	137	1604	1345	YX	1833	N243JQ	LGA	CHS	112	641	11	29	2023-06-16 11:00:00	Other
12122	6	2	1539	1519	20	1851	1842	DL	656	N384DN	JFK	FLL	152	1069	15	19	2023-06-02 15:00:00	FLL
12123	12	3	2142	1949	113	107	2319	UA	778	N13716	EWR	SLC	281	1969	19	49	2023-12-03 19:00:00	Other
12124	3	5	1817	1800	17	2009	1942	UA	937	N453UA	LGA	ORD	130	733	18	0	2023-03-05 18:00:00	ORD
12129	5	19	1605	1545	20	1905	1903	DL	236	N1201P	JFK	LAX	335	2475	15	45	2023-05-19 15:00:00	LAX
12136	3	27	2025	2007	18	2134	2130	UA	375	N39728	EWR	BOS	42	200	20	7	2023-03-27 20:00:00	BOS
12138	3	7	843	800	43	1212	1103	AA	604	N988AL	EWR	DFW	210	1372	8	0	2023-03-07 08:00:00	Other
12150	6	13	2212	2159	13	2319	2330	YX	1209	N647RW	EWR	PWM	43	284	21	59	2023-06-13 21:00:00	Other
12153	10	4	650	634	16	934	850	AA	995	N461AN	EWR	PHX	308	2133	6	34	2023-10-04 06:00:00	Other
12161	10	28	1424	1359	25	1614	1602	YX	1169	N739YX	EWR	DTW	90	488	13	59	2023-10-28 13:00:00	Other
12169	6	27	1408	1350	18	1811	1539	9E	1461	N337PQ	LGA	CLE	68	419	13	50	2023-06-27 13:00:00	Other
12173	2	3	1946	1845	61	2213	2134	DL	194	N368DN	LGA	ATL	107	762	18	45	2023-02-03 18:00:00	ATL
12174	8	30	2024	1459	325	2349	1822	B6	422	N506JB	JFK	FLL	170	1069	14	59	2023-08-30 14:00:00	FLL
12175	10	16	746	730	16	920	926	9E	1576	N479PX	LGA	GSO	70	461	7	30	2023-10-16 07:00:00	Other
12177	6	7	1314	1250	24	1544	1442	9E	1512	N918XJ	LGA	STL	118	888	12	50	2023-06-07 12:00:00	Other
12189	1	28	1646	1230	256	1844	1436	AA	516	N987NN	LGA	ORD	138	733	12	30	2023-01-28 12:00:00	ORD
12190	12	22	2118	2100	18	20	34	AA	50	N112AN	JFK	LAX	329	2475	21	0	2023-12-22 21:00:00	LAX
12195	9	24	2121	1949	92	15	2255	B6	344	N637JB	JFK	PDX	319	2454	19	49	2023-09-24 19:00:00	Other
12201	11	21	832	815	17	1101	1058	B6	188	N203JB	JFK	ATL	129	760	8	15	2023-11-21 08:00:00	ATL
12203	11	5	815	750	25	1106	1055	UA	112	N17139	EWR	FLL	148	1065	7	50	2023-11-05 07:00:00	FLL
12204	6	22	2023	1950	33	2154	2147	9E	1572	N926XJ	EWR	RDU	71	416	19	50	2023-06-22 19:00:00	Other
12218	7	19	1126	1100	26	1507	1411	DL	426	N3752	JFK	MIA	155	1089	11	0	2023-07-19 11:00:00	MIA
12233	4	7	1722	1700	22	1933	1908	B6	347	N375JB	JFK	DTW	96	509	17	0	2023-04-07 17:00:00	Other
12244	12	17	2030	1959	31	2251	2221	YX	1791	N237JQ	LGA	CLT	91	544	19	59	2023-12-17 19:00:00	CLT
12247	3	4	1849	1829	20	2142	2147	B6	940	N603JB	EWR	FLL	148	1065	18	29	2023-03-04 18:00:00	FLL
12250	11	1	940	929	11	1144	1147	YX	1120	N744YX	EWR	AVL	102	583	9	29	2023-11-01 09:00:00	Other
12251	9	12	1818	1700	78	1922	1816	UA	108	N496UA	EWR	BOS	35	200	17	0	2023-09-12 17:00:00	BOS
12255	12	27	929	915	14	1111	1117	9E	1585	N341PQ	JFK	RDU	76	427	9	15	2023-12-27 09:00:00	Other
12256	8	3	926	915	11	1057	1048	YX	828	N757YX	EWR	BUF	48	282	9	15	2023-08-03 09:00:00	Other
12258	9	15	1720	1700	20	1939	1935	DL	427	N350DN	LGA	ATL	107	762	17	0	2023-09-15 17:00:00	ATL
12266	5	16	1338	1319	19	1611	1605	AA	946	N308RD	JFK	PHX	298	2153	13	19	2023-05-16 13:00:00	Other
12282	6	6	1643	1605	38	1825	1740	WN	529	N7877H	LGA	BNA	110	764	16	5	2023-06-06 16:00:00	Other
12287	6	2	1324	1300	24	1521	1509	UA	937	N897UA	EWR	MSY	153	1167	13	0	2023-06-02 13:00:00	Other
12295	5	8	1141	1009	92	1400	1241	UA	257	N27734	EWR	JAX	112	820	10	9	2023-05-08 10:00:00	Other
12299	7	2	2023	1943	40	2328	2257	DL	300	N373DA	LGA	MIA	151	1096	19	43	2023-07-02 19:00:00	MIA
12303	7	4	1636	1459	97	1811	1656	OO	977	N614CZ	JFK	PIT	65	340	14	59	2023-07-04 14:00:00	Other
12306	12	20	1625	1559	26	1923	1910	B6	965	N948JB	JFK	FLL	147	1069	15	59	2023-12-20 15:00:00	FLL
12307	6	6	1659	1529	90	1841	1651	UA	490	N14704	EWR	BNA	118	748	15	29	2023-06-06 15:00:00	Other
12315	2	13	1024	1000	24	1233	1228	UA	756	N29981	EWR	DEN	207	1605	10	0	2023-02-13 10:00:00	Other
12330	12	25	1411	1347	24	1547	1530	MQ	1001	N771JV	EWR	ORD	113	719	13	47	2023-12-25 13:00:00	ORD
12339	12	30	1447	1430	17	1621	1627	YX	1251	N117HQ	LGA	ILM	75	500	14	30	2023-12-30 14:00:00	Other
12350	9	25	818	750	28	1037	1025	NK	148	N609NK	EWR	LAS	284	2227	7	50	2023-09-25 07:00:00	Other
12364	9	17	2016	1440	336	2312	1743	UA	884	N29124	EWR	LAX	324	2454	14	40	2023-09-17 14:00:00	LAX
12365	4	13	1904	1700	124	2153	2025	DL	259	N176DN	JFK	LAX	304	2475	17	0	2023-04-13 17:00:00	LAX
12374	2	28	946	815	91	1454	1324	DL	708	N549US	JFK	STT	192	1623	8	15	2023-02-28 08:00:00	Other
12378	7	19	1201	1020	101	1339	1137	YX	1428	N209JQ	LGA	MVY	39	175	10	20	2023-07-19 10:00:00	Other
12382	10	9	2136	2035	61	2331	2252	9E	1637	N324PQ	LGA	CAE	91	617	20	35	2023-10-09 20:00:00	Other
12397	7	23	1051	1030	21	1230	1225	YX	936	N752YX	EWR	GSO	72	445	10	30	2023-07-23 10:00:00	Other
12398	9	10	1310	747	323	1604	1045	B6	672	N982JB	EWR	LAX	329	2454	7	47	2023-09-10 07:00:00	LAX
12407	3	28	1253	930	203	1612	1241	B6	820	N2038J	JFK	FLL	160	1069	9	30	2023-03-28 09:00:00	FLL
12415	7	16	1237	1143	54	1452	1412	UA	360	N471UA	EWR	ATL	106	746	11	43	2023-07-16 11:00:00	ATL
12417	8	18	1856	1645	131	2216	1951	B6	113	N2039J	JFK	MCO	131	944	16	45	2023-08-18 16:00:00	MCO
12439	2	27	1103	1044	19	1448	1420	B6	40	N993JE	JFK	SFO	373	2586	10	44	2023-02-27 10:00:00	Other
12445	3	6	859	805	54	1114	1040	DL	932	N3750D	EWR	ATL	111	746	8	5	2023-03-06 08:00:00	ATL
12447	3	14	1502	1314	108	1824	1620	B6	570	N618JB	JFK	MCO	142	944	13	14	2023-03-14 13:00:00	MCO
12452	1	11	1806	1642	84	2122	1953	UA	875	N27274	EWR	SAN	338	2425	16	42	2023-01-11 16:00:00	Other
12465	2	4	1628	1500	88	1838	1712	9E	1405	N182GJ	EWR	MSP	167	1008	15	0	2023-02-04 15:00:00	Other
12467	9	8	1019	955	24	1702	1258	B6	219	N523JB	LGA	MCO	NA	950	9	55	2023-09-08 09:00:00	MCO
12468	2	17	1228	1148	40	1548	1450	NK	971	N614NK	EWR	MCO	177	937	11	48	2023-02-17 11:00:00	MCO
12475	9	27	2122	2005	77	2318	2217	9E	1583	N309PQ	LGA	GRR	90	618	20	5	2023-09-27 20:00:00	Other
12476	7	22	1734	1703	31	2051	1953	UA	659	N27260	EWR	MCO	158	937	17	3	2023-07-22 17:00:00	MCO
12480	1	3	1413	1345	28	1713	1650	WN	805	N8620H	LGA	HOU	219	1428	13	45	2023-01-03 13:00:00	Other
12487	6	26	11	2040	211	225	2253	DL	489	N365NB	LGA	MSY	155	1183	20	40	2023-06-26 20:00:00	Other
12490	8	5	1854	1830	24	2155	2136	NK	687	N619NK	EWR	FLL	139	1065	18	30	2023-08-05 18:00:00	FLL
12491	3	6	841	810	31	1308	1310	DL	725	N818DA	JFK	SJU	181	1598	8	10	2023-03-06 08:00:00	Other
12496	4	30	1833	1335	298	1927	1443	9E	1224	N919XJ	LGA	BGM	27	147	13	35	2023-04-30 13:00:00	Other
12500	6	29	1331	1303	28	1506	1448	DL	889	N951AT	EWR	DTW	74	488	13	3	2023-06-29 13:00:00	Other
12514	9	28	1935	1915	20	2045	2040	B6	474	N193JB	LGA	BOS	35	184	19	15	2023-09-28 19:00:00	BOS
12515	8	26	949	929	20	1111	1057	B6	475	N184JB	JFK	BUF	55	301	9	29	2023-08-26 09:00:00	Other
12518	8	28	629	535	54	905	810	B6	93	N520JB	EWR	MCO	129	937	5	35	2023-08-28 05:00:00	MCO
12524	9	10	1024	850	94	1332	1115	NK	1236	N656NK	EWR	PHX	287	2133	8	50	2023-09-10 08:00:00	Other
12534	1	22	1136	1049	47	1409	1335	F9	648	N323FR	LGA	ATL	130	762	10	49	2023-01-22 10:00:00	ATL
12537	5	22	1040	1024	16	1158	1205	UA	672	N421UA	EWR	ORD	110	719	10	24	2023-05-22 10:00:00	ORD
12538	6	2	1759	1605	114	2053	1916	B6	810	N956JT	JFK	PBI	152	1028	16	5	2023-06-02 16:00:00	Other
12550	4	21	1127	1114	13	1346	1340	UA	374	N39423	EWR	PHX	284	2133	11	14	2023-04-21 11:00:00	Other
12554	7	27	1517	1340	97	1851	1743	DL	602	N919DU	JFK	SJU	195	1598	13	40	2023-07-27 13:00:00	Other
12565	6	16	1336	1325	11	1553	1557	B6	1014	N529JB	LGA	ATL	110	762	13	25	2023-06-16 13:00:00	ATL
12584	9	24	939	900	39	1242	1209	B6	83	N809JB	JFK	AUS	195	1521	9	0	2023-09-24 09:00:00	Other
12585	8	10	1827	1455	212	1948	1638	OO	953	N316SY	JFK	IAD	50	228	14	55	2023-08-10 14:00:00	Other
12596	6	1	1950	1856	54	2228	2204	NK	516	N620NK	LGA	IAH	186	1416	18	56	2023-06-01 18:00:00	Other
12602	1	13	1954	1930	24	2232	2255	UA	294	N47281	EWR	AUS	184	1504	19	30	2023-01-13 19:00:00	Other
12604	6	7	2140	1959	101	59	2309	AA	789	N854NN	LGA	MIA	168	1096	19	59	2023-06-07 19:00:00	MIA
12607	1	8	2156	2129	27	2342	2259	OO	1282	N311SY	JFK	IAD	48	228	21	29	2023-01-08 21:00:00	Other
12620	6	26	1628	1045	343	2001	1324	UA	738	N24979	EWR	IAH	184	1400	10	45	2023-06-26 10:00:00	Other
12621	9	17	833	715	78	939	840	B6	709	N273JB	JFK	DCA	48	213	7	15	2023-09-17 07:00:00	Other
12622	9	21	1750	1730	20	1944	1930	NK	48	N615NK	LGA	DTW	73	502	17	30	2023-09-21 17:00:00	Other
12627	2	5	1014	1000	14	1341	1348	DL	298	N174DN	JFK	SFO	366	2586	10	0	2023-02-05 10:00:00	Other
12628	3	8	1929	1855	34	2202	2144	DL	187	N359DN	LGA	ATL	111	762	18	55	2023-03-08 18:00:00	ATL
12631	1	23	1919	1855	24	2214	2223	AA	464	N359PX	LGA	DFW	196	1389	18	55	2023-01-23 18:00:00	Other
12638	2	4	913	900	13	1204	1234	DL	191	N176DN	JFK	LAX	331	2475	9	0	2023-02-04 09:00:00	LAX
12640	1	12	1554	1529	25	1826	1756	YX	1248	N635RW	EWR	IND	115	645	15	29	2023-01-12 15:00:00	Other
12644	1	12	1534	1239	175	1854	1542	UA	899	N24736	EWR	SRQ	164	1034	12	39	2023-01-12 12:00:00	Other
12646	10	1	939	737	122	1114	939	UA	432	N27734	EWR	CLT	75	529	7	37	2023-10-01 07:00:00	CLT
12659	6	21	1721	1610	71	2011	1900	UA	255	N14107	EWR	MCO	135	937	16	10	2023-06-21 16:00:00	MCO
12666	6	2	1932	1830	62	2328	2138	UA	445	N795UA	EWR	SFO	308	2565	18	30	2023-06-02 18:00:00	Other
12671	2	26	1207	1130	37	1403	1351	AA	107	N987NN	LGA	CLT	89	544	11	30	2023-02-26 11:00:00	CLT
12673	5	28	1445	1359	46	1713	1649	AA	641	N905AU	EWR	DFW	176	1372	13	59	2023-05-28 13:00:00	Other
12681	8	15	2248	1929	199	233	2225	DL	337	N808DN	JFK	ATL	109	760	19	29	2023-08-15 19:00:00	ATL
12683	1	27	1237	1225	12	1430	1412	YX	1811	N229JQ	JFK	ORD	134	740	12	25	2023-01-27 12:00:00	ORD
12696	5	28	1942	1820	82	2145	2040	WN	981	N8519R	LGA	MSY	150	1183	18	20	2023-05-28 18:00:00	Other
12700	2	12	1620	1558	22	1843	1831	UA	478	N33286	EWR	JAX	119	820	15	58	2023-02-12 15:00:00	Other
12701	6	2	1923	1855	28	2335	2116	9E	1663	N131EV	JFK	DTW	77	509	18	55	2023-06-02 18:00:00	Other
12714	4	15	941	759	102	1254	1101	AA	313	N833NN	JFK	DFW	204	1391	7	59	2023-04-15 07:00:00	Other
12716	2	21	2155	2128	27	23	2334	UA	832	N37257	EWR	MSP	183	1008	21	28	2023-02-21 21:00:00	Other
12718	9	8	1953	1859	54	2	2303	DL	699	N812DN	JFK	SJU	196	1598	18	59	2023-09-08 18:00:00	Other
12722	1	26	1810	1755	15	2009	2007	DL	626	N363NB	EWR	MSP	144	1008	17	55	2023-01-26 17:00:00	Other
12723	6	7	1744	1719	25	1858	1854	UA	898	N17122	EWR	ORD	101	719	17	19	2023-06-07 17:00:00	ORD
12731	4	6	1302	1220	42	1418	1344	9E	1401	N480PX	LGA	BTV	43	258	12	20	2023-04-06 12:00:00	Other
12734	8	11	1607	1510	57	1850	1823	DL	649	N347DN	JFK	MCO	136	944	15	10	2023-08-11 15:00:00	MCO
12740	7	1	1859	1835	24	2059	2038	B6	345	N231JB	JFK	RDU	67	427	18	35	2023-07-01 18:00:00	Other
12743	4	23	1757	1745	12	1927	1930	WN	313	N872CB	LGA	STL	129	888	17	45	2023-04-23 17:00:00	Other
12749	3	4	914	900	14	1213	1149	B6	266	N339JB	JFK	JAX	134	828	9	0	2023-03-04 09:00:00	Other
12755	9	19	1137	1125	12	1342	1349	B6	22	N966JT	LGA	DEN	221	1620	11	25	2023-09-19 11:00:00	Other
12760	9	10	1229	1215	14	1429	1347	AA	992	N715UW	LGA	BNA	113	764	12	15	2023-09-10 12:00:00	Other
12761	9	8	1634	1529	65	1946	1706	YX	1395	N441YX	JFK	BNA	142	765	15	29	2023-09-08 15:00:00	Other
12780	9	17	1655	1629	26	1848	1855	UA	933	N47281	EWR	PHX	274	2133	16	29	2023-09-17 16:00:00	Other
12784	12	3	107	2125	222	224	2301	9E	1443	N305PQ	JFK	BTV	49	266	21	25	2023-12-03 21:00:00	Other
12786	2	2	628	615	13	942	931	UA	825	N19141	EWR	LAX	340	2454	6	15	2023-02-02 06:00:00	LAX
12802	10	21	1330	1318	12	1609	1623	AA	395	N301NW	EWR	DFW	192	1372	13	18	2023-10-21 13:00:00	Other
12824	4	3	2111	1957	74	2211	2120	UA	815	N488UA	EWR	IAD	40	212	19	57	2023-04-03 19:00:00	Other
12830	10	12	1441	1430	11	1704	1650	WN	711	N8815L	LGA	MSY	181	1183	14	30	2023-10-12 14:00:00	Other
12838	6	30	1002	910	52	1128	1059	YX	1789	N203JQ	JFK	PIT	62	340	9	10	2023-06-30 09:00:00	Other
12851	7	18	2350	2107	163	146	2312	UA	206	N75435	EWR	CVG	92	569	21	7	2023-07-18 21:00:00	Other
12854	11	10	745	710	35	1056	1011	B6	331	N639JB	EWR	MCO	139	937	7	10	2023-11-10 07:00:00	MCO
12857	9	9	1712	1655	17	NA	2002	B6	116	N566JB	JFK	BUR	NA	2465	16	55	2023-09-09 16:00:00	Other
12872	3	13	827	800	27	1046	1019	YX	1624	N246JQ	JFK	CLT	97	541	8	0	2023-03-13 08:00:00	CLT
12876	5	6	1143	1125	18	1349	1405	DL	320	N363NW	LGA	ATL	106	762	11	25	2023-05-06 11:00:00	ATL
12882	11	24	2010	1959	11	2312	2306	NK	166	N677NK	LGA	MCO	142	950	19	59	2023-11-24 19:00:00	MCO
12888	6	8	2029	1745	164	2147	1920	AA	658	N913NN	EWR	ORD	101	719	17	45	2023-06-08 17:00:00	ORD
12895	7	28	1612	1559	13	NA	1851	UA	687	N37295	EWR	SAN	NA	2425	15	59	2023-07-28 15:00:00	Other
12899	9	4	1720	1703	17	2012	1953	UA	811	N76529	EWR	MCO	134	937	17	3	2023-09-04 17:00:00	MCO
12901	4	16	2156	2126	30	2343	2329	NK	278	N647NK	LGA	DTW	78	502	21	26	2023-04-16 21:00:00	Other
12905	12	11	2213	2150	23	2330	2258	YX	1829	N205JQ	LGA	ALB	35	136	21	50	2023-12-11 21:00:00	Other
12906	12	10	616	600	16	901	908	NK	479	N609NK	LGA	MCO	136	950	6	0	2023-12-10 06:00:00	MCO
12908	1	11	1829	1815	14	2153	2140	UA	503	N2138U	EWR	SFO	334	2565	18	15	2023-01-11 18:00:00	Other
12913	3	14	2132	1959	93	126	2357	UA	599	N38417	EWR	SJU	198	1608	19	59	2023-03-14 19:00:00	Other
12917	2	1	617	600	17	1024	912	B6	563	N526JL	EWR	FLL	146	1065	6	0	2023-02-01 06:00:00	FLL
12919	3	14	47	2130	197	346	59	B6	672	N969JT	JFK	LAX	337	2475	21	30	2023-03-14 21:00:00	LAX
12932	1	25	1856	1845	11	2130	2119	DL	897	N978AT	EWR	ATL	133	746	18	45	2023-01-25 18:00:00	ATL
12933	6	14	1511	1407	64	1801	1558	9E	1617	N931XJ	JFK	RDU	75	427	14	7	2023-06-14 14:00:00	Other
12940	9	24	1728	1629	59	1934	1844	YX	1316	N408YX	LGA	LIT	150	1085	16	29	2023-09-24 16:00:00	Other
12961	7	15	1450	1427	23	1639	1619	UA	180	N490UA	EWR	MSP	144	1008	14	27	2023-07-15 14:00:00	Other
12978	12	25	2151	1830	201	24	2207	B6	43	N966JT	JFK	SMF	306	2521	18	30	2023-12-25 18:00:00	Other
12979	4	9	1756	1743	13	2042	2042	UA	351	N16234	EWR	TPA	143	997	17	43	2023-04-09 17:00:00	Other
12981	6	15	842	705	97	1127	1005	DL	377	N336NB	LGA	PBI	141	1035	7	5	2023-06-15 07:00:00	Other
12991	1	11	1756	1710	46	1946	1919	AA	484	N708UW	LGA	STL	136	888	17	10	2023-01-11 17:00:00	Other
12999	5	24	2121	2054	27	2246	2219	YX	1010	N747YX	EWR	MHT	36	209	20	54	2023-05-24 20:00:00	Other
13001	6	28	1447	1405	42	1707	1646	UA	523	N491UA	EWR	DFW	176	1372	14	5	2023-06-28 14:00:00	Other
13002	12	9	2247	2234	13	2400	2359	OO	1169	N322SY	JFK	BOS	41	187	22	34	2023-12-09 22:00:00	BOS
13013	4	27	1350	1200	110	1642	1456	B6	145	N661JB	LGA	MCO	144	950	12	0	2023-04-27 12:00:00	MCO
13018	6	7	1548	1531	17	1856	1849	DL	595	N335DN	LGA	FLL	151	1076	15	31	2023-06-07 15:00:00	FLL
13023	8	25	1228	1100	88	1517	1404	NK	422	N676NK	EWR	FLL	144	1065	11	0	2023-08-25 11:00:00	FLL
13026	3	10	2152	2127	25	41	36	DL	259	N823DN	JFK	LAS	321	2248	21	27	2023-03-10 21:00:00	Other
13027	3	7	1008	956	12	1300	1300	UA	89	N27733	EWR	DFW	197	1372	9	56	2023-03-07 09:00:00	Other
13032	1	13	1955	1929	26	2125	2122	9E	1657	N918XJ	LGA	BHM	118	866	19	29	2023-01-13 19:00:00	Other
13034	7	24	2301	2245	16	118	108	F9	472	N390FR	LGA	ATL	108	762	22	45	2023-07-24 22:00:00	ATL
13037	9	7	2105	1900	125	45	2133	DL	198	N327DN	LGA	ATL	110	762	19	0	2023-09-07 19:00:00	ATL
13041	6	23	2255	2109	106	43	2317	UA	657	N444UA	EWR	MCI	140	1092	21	9	2023-06-23 21:00:00	Other
13046	4	3	2156	2045	71	6	2243	YX	1490	N222JQ	JFK	CMH	71	483	20	45	2023-04-03 20:00:00	Other
13047	11	17	1732	1637	55	1857	1824	9E	1451	N485PX	LGA	PIT	60	335	16	37	2023-11-17 16:00:00	Other
13049	7	31	1751	1215	336	2035	1511	B6	238	N608JB	JFK	AUS	194	1521	12	15	2023-07-31 12:00:00	Other
13052	10	7	1522	1429	53	1804	1729	B6	262	N570JB	LGA	PBI	142	1035	14	29	2023-10-07 14:00:00	Other
13054	1	11	1023	803	140	1315	1113	UA	941	N47282	EWR	TPA	144	997	8	3	2023-01-11 08:00:00	Other
13056	8	10	722	600	82	1014	839	DL	222	N137DU	LGA	DFW	199	1389	6	0	2023-08-10 06:00:00	Other
13061	9	11	1414	1145	149	1622	1406	B6	964	N982JB	JFK	ATL	107	760	11	45	2023-09-11 11:00:00	ATL
13076	7	8	1251	1217	34	1428	1407	YX	852	N858RW	EWR	CMH	72	463	12	17	2023-07-08 12:00:00	Other
13078	4	15	1911	1510	241	2036	1631	9E	1195	N184GJ	LGA	SCE	39	208	15	10	2023-04-15 15:00:00	Other
13079	8	11	1750	1725	25	2018	2007	B6	688	N580JB	LGA	JAX	121	833	17	25	2023-08-11 17:00:00	Other
13080	7	17	2302	2229	33	22	2352	UA	205	N416UA	EWR	PWM	48	284	22	29	2023-07-17 22:00:00	Other
13084	9	24	1321	1020	181	1431	1150	WN	135	N8570W	LGA	BNA	104	764	10	20	2023-09-24 10:00:00	Other
13086	7	4	1344	1325	19	1515	1505	9E	1131	N131EV	JFK	RIC	64	288	13	25	2023-07-04 13:00:00	Other
13095	3	2	2005	1954	11	43	50	UA	219	N63890	EWR	BQN	183	1585	19	54	2023-03-02 19:00:00	Other
13101	2	28	2006	1838	88	2124	2000	B6	854	N228JB	JFK	BOS	34	187	18	38	2023-02-28 18:00:00	BOS
13105	1	30	1929	1749	100	2105	1935	9E	1529	N605LR	JFK	RDU	67	427	17	49	2023-01-30 17:00:00	Other
13115	5	21	1952	1941	11	2042	2043	YX	1147	N653RW	EWR	AVP	24	93	19	41	2023-05-21 19:00:00	Other
13116	1	3	1625	1540	45	1918	1857	AA	120	N954AN	JFK	MIA	151	1089	15	40	2023-01-03 15:00:00	MIA
13117	7	20	2024	1959	25	2348	2329	DL	681	N843DN	JFK	MIA	154	1089	19	59	2023-07-20 19:00:00	MIA
13119	6	9	2134	2029	65	7	2315	UA	828	N37257	EWR	DFW	184	1372	20	29	2023-06-09 20:00:00	Other
13120	3	19	2042	2000	42	20	2311	B6	934	N971JT	JFK	MCO	164	944	20	0	2023-03-19 20:00:00	MCO
13121	12	30	1347	840	307	1610	1151	B6	74	N519JB	JFK	IAH	179	1417	8	40	2023-12-30 08:00:00	Other
13125	1	30	1514	1459	15	1645	1652	B6	917	N636JB	JFK	RDU	72	427	14	59	2023-01-30 14:00:00	Other
13133	5	26	1921	1855	26	2118	2137	NK	262	N956NK	EWR	LAS	272	2227	18	55	2023-05-26 18:00:00	Other
13134	7	11	1556	1545	11	1755	1715	WN	879	N564WN	LGA	MDW	157	725	15	45	2023-07-11 15:00:00	Other
13144	1	13	1812	1630	102	2012	1910	DL	842	N130DU	JFK	MSY	161	1182	16	30	2023-01-13 16:00:00	Other
13145	3	30	1512	1500	12	1803	1802	UA	215	N486UA	EWR	AUS	213	1504	15	0	2023-03-30 15:00:00	Other
13146	5	14	2157	2007	110	107	2325	UA	689	N16713	EWR	SLC	281	1969	20	7	2023-05-14 20:00:00	Other
13156	1	20	2111	1929	102	2229	2127	AA	133	N822NN	LGA	ORD	114	733	19	29	2023-01-20 19:00:00	ORD
13157	5	21	1833	1750	43	2125	2101	B6	753	N705JB	JFK	PBI	145	1028	17	50	2023-05-21 17:00:00	Other
13177	6	10	1045	930	75	1340	1235	AS	9	N596AS	JFK	SEA	324	2422	9	30	2023-06-10 09:00:00	Other
13183	11	28	1007	955	12	1200	1220	WN	464	N7736A	LGA	MCI	158	1107	9	55	2023-11-28 09:00:00	Other
13203	6	20	842	830	12	1109	1058	UA	933	N39726	EWR	ATL	97	746	8	30	2023-06-20 08:00:00	ATL
13216	5	23	2216	2113	63	52	2359	UA	843	N37295	EWR	MCO	135	937	21	13	2023-05-23 21:00:00	MCO
13222	8	24	1534	1500	34	1821	1745	DL	282	N123DW	LGA	ATL	130	762	15	0	2023-08-24 15:00:00	ATL
13223	4	4	1515	1500	15	1832	1810	UA	791	N29129	EWR	LAX	339	2454	15	0	2023-04-04 15:00:00	LAX
13243	8	10	715	659	16	844	833	AA	484	N982NN	EWR	ORD	112	719	6	59	2023-08-10 06:00:00	ORD
13248	4	20	1946	1935	11	2135	2112	9E	1198	N147PQ	LGA	MKE	121	738	19	35	2023-04-20 19:00:00	Other
13251	2	20	1745	1725	20	1940	1912	AA	218	N976NN	JFK	ORD	128	740	17	25	2023-02-20 17:00:00	ORD
13252	4	4	1012	1000	12	1307	1300	UA	365	N14001	EWR	LAX	322	2454	10	0	2023-04-04 10:00:00	LAX
13261	1	26	1038	925	73	1353	1259	AA	179	N303RE	JFK	MIA	170	1089	9	25	2023-01-26 09:00:00	MIA
13265	3	25	2230	2150	40	40	2353	UA	412	N871UA	EWR	MEM	161	946	21	50	2023-03-25 21:00:00	Other
13266	7	22	2152	2000	112	25	2309	B6	667	N621JB	JFK	RNO	313	2411	20	0	2023-07-22 20:00:00	Other
13267	8	6	1530	1500	30	1909	1857	B6	664	N955JB	JFK	BQN	192	1576	15	0	2023-08-06 15:00:00	Other
13268	10	6	2131	2059	32	2346	2323	B6	895	N593JB	LGA	MSY	169	1183	20	59	2023-10-06 20:00:00	Other
13272	10	10	2109	2015	54	2325	2246	B6	893	N706JB	LGA	ATL	114	762	20	15	2023-10-10 20:00:00	ATL
13279	7	11	732	710	22	1019	1003	UA	549	N17301	EWR	PDX	326	2434	7	10	2023-07-11 07:00:00	Other
13283	5	29	1644	1556	48	1845	1814	YX	1341	N430YX	LGA	TYS	92	647	15	56	2023-05-29 15:00:00	Other
13284	9	8	1431	1415	16	1549	1540	9E	1616	N136EV	LGA	BTV	43	258	14	15	2023-09-08 14:00:00	Other
13287	7	8	1606	1530	36	1824	1711	YX	1080	N126HQ	JFK	BNA	147	765	15	30	2023-07-08 15:00:00	Other
13290	7	22	2119	1940	99	2344	2244	B6	110	N970JB	JFK	ONT	302	2429	19	40	2023-07-22 19:00:00	Other
13300	12	23	525	510	15	803	802	B6	207	N509JB	JFK	MCO	127	944	5	10	2023-12-23 05:00:00	MCO
13302	6	9	2106	2000	66	2250	2254	B6	32	N646JB	JFK	DEN	206	1626	20	0	2023-06-09 20:00:00	Other
13303	7	27	917	900	17	1045	1043	UA	555	N37278	EWR	ORD	107	719	9	0	2023-07-27 09:00:00	ORD
13313	4	28	1117	1056	21	1503	1405	UA	401	N17244	EWR	MIA	196	1085	10	56	2023-04-28 10:00:00	MIA
13318	2	17	2341	2145	116	234	44	B6	199	N634JB	LGA	MCO	150	950	21	45	2023-02-17 21:00:00	MCO
13320	1	2	1500	1317	103	1737	1611	UA	792	N17254	EWR	MCO	129	937	13	17	2023-01-02 13:00:00	MCO
13321	11	20	805	730	35	948	915	DL	597	N3739P	LGA	ORD	123	733	7	30	2023-11-20 07:00:00	ORD
13324	11	20	2232	2155	37	2339	2321	B6	330	N579JB	JFK	BOS	32	187	21	55	2023-11-20 21:00:00	BOS
13326	6	8	1508	1457	11	1849	1804	UA	717	N412UA	EWR	MIA	183	1085	14	57	2023-06-08 14:00:00	MIA
13327	8	16	2213	2146	27	2319	2315	UA	233	N62892	EWR	MKE	97	725	21	46	2023-08-16 21:00:00	Other
13333	8	22	714	610	64	948	851	B6	79	N595JB	LGA	MCO	118	950	6	10	2023-08-22 06:00:00	MCO
13344	3	10	2027	1959	28	2321	2304	NK	181	N680NK	LGA	MCO	139	950	19	59	2023-03-10 19:00:00	MCO
13347	5	7	1459	1310	109	1608	1441	YX	1245	N872RW	LGA	ORF	49	296	13	10	2023-05-07 13:00:00	Other
13351	1	14	1513	1435	38	1613	1553	UA	542	N803UA	EWR	BOS	37	200	14	35	2023-01-14 14:00:00	BOS
13352	10	4	1940	1849	51	2158	2119	9E	1691	N314PQ	JFK	IND	93	665	18	49	2023-10-04 18:00:00	Other
13354	3	11	1908	1759	69	2019	1933	B6	2	N588JB	JFK	BUF	53	301	17	59	2023-03-11 17:00:00	Other
13361	11	27	1916	1855	21	2213	2212	DL	435	N315DU	EWR	SLC	270	1969	18	55	2023-11-27 18:00:00	Other
13362	5	3	953	730	143	1117	900	B6	376	N198JB	JFK	BNA	113	765	7	30	2023-05-03 07:00:00	Other
13365	6	6	1836	1759	37	2148	2101	DL	679	N135DQ	JFK	DFW	195	1391	17	59	2023-06-06 17:00:00	Other
13377	9	29	1046	1030	16	1325	1333	UA	660	N17126	EWR	LAX	302	2454	10	30	2023-09-29 10:00:00	LAX
13384	10	6	1156	1138	18	1359	1348	AA	719	N923AN	LGA	CLT	94	544	11	38	2023-10-06 11:00:00	CLT
13386	9	5	1814	1525	169	1944	1719	YX	1915	N232JQ	JFK	PIT	59	340	15	25	2023-09-05 15:00:00	Other
13404	1	11	1056	830	146	1341	1118	DL	614	N895DN	JFK	ATL	117	760	8	30	2023-01-11 08:00:00	ATL
13415	1	4	1256	1235	21	1542	1539	UA	286	N27251	EWR	TPA	150	997	12	35	2023-01-04 12:00:00	Other
13419	11	21	1951	1818	93	2212	2028	UA	777	N66825	EWR	CLT	87	529	18	18	2023-11-21 18:00:00	CLT
13431	4	12	2053	2000	53	2232	2201	YX	1060	N750YX	EWR	ILM	68	488	20	0	2023-04-12 20:00:00	Other
13435	7	1	1514	1359	75	1705	1558	YX	848	N645RW	EWR	DTW	76	488	13	59	2023-07-01 13:00:00	Other
13438	6	6	1210	1156	14	1355	1403	AA	982	N830NN	JFK	CLT	83	541	11	56	2023-06-06 11:00:00	CLT
13448	9	22	1738	1725	13	1954	1957	B6	935	N520JB	LGA	ATL	105	762	17	25	2023-09-22 17:00:00	ATL
13456	5	14	1101	1024	37	1248	1205	UA	672	N37531	EWR	ORD	112	719	10	24	2023-05-14 10:00:00	ORD
13457	7	23	2132	2025	67	2248	2209	AA	628	N773XF	LGA	ORD	113	733	20	25	2023-07-23 20:00:00	ORD
13458	7	31	1831	1800	31	24	2044	DL	279	N774DE	LGA	DEN	NA	1620	18	0	2023-07-31 18:00:00	Other
13463	12	2	1650	1550	60	1751	1713	B6	463	N274JB	JFK	BOS	40	187	15	50	2023-12-02 15:00:00	BOS
13489	10	6	2028	1946	42	2141	2112	YX	1765	N213JQ	EWR	BOS	38	200	19	46	2023-10-06 19:00:00	BOS
13490	7	2	1738	1713	25	2003	2003	UA	659	N33292	EWR	MCO	123	937	17	13	2023-07-02 17:00:00	MCO
13493	8	1	1944	1825	79	2146	2052	UA	352	N41135	EWR	DEN	212	1605	18	25	2023-08-01 18:00:00	Other
13494	9	29	1101	1045	16	1222	1225	WN	968	N8710M	LGA	STL	122	888	10	45	2023-09-29 10:00:00	Other
13504	10	23	2203	2145	18	44	50	B6	516	N566JB	JFK	FLL	139	1069	21	45	2023-10-23 21:00:00	FLL
13508	6	16	1708	1655	13	1941	2020	AS	6	N918AK	JFK	SEA	305	2422	16	55	2023-06-16 16:00:00	Other
13514	4	20	1817	1755	22	2032	2025	WN	376	N287WN	LGA	ATL	106	762	17	55	2023-04-20 17:00:00	ATL
13519	9	15	1627	1540	47	1948	1853	OO	1860	N105SY	LGA	IAH	226	1416	15	40	2023-09-15 15:00:00	Other
13536	11	20	2229	2129	60	58	14	DL	825	N529DT	JFK	ATL	114	760	21	29	2023-11-20 21:00:00	ATL
13538	6	5	1812	1800	12	2029	2027	YX	1302	N138HQ	LGA	TUL	165	1231	18	0	2023-06-05 18:00:00	Other
13556	5	30	1819	1800	19	2202	2111	UA	218	N64809	EWR	MIA	178	1085	18	0	2023-05-30 18:00:00	MIA
13558	10	23	922	833	49	1133	1100	B6	394	N265JB	JFK	ATL	109	760	8	33	2023-10-23 08:00:00	ATL
13571	1	13	2052	2005	47	2315	2330	WN	438	N8834L	LGA	DAL	173	1381	20	5	2023-01-13 20:00:00	Other
13572	5	18	1859	1829	30	2059	2051	YX	1258	N405YX	LGA	MCI	157	1107	18	29	2023-05-18 18:00:00	Other
13574	8	20	2021	2000	21	2236	2222	YX	897	N744YX	EWR	IND	86	645	20	0	2023-08-20 20:00:00	Other
13591	5	3	2234	2050	104	9	2254	9E	1423	N304PQ	LGA	ILM	71	500	20	50	2023-05-03 20:00:00	Other
13593	6	6	2017	2000	17	2159	2134	YX	1896	N878RW	LGA	BOS	31	184	20	0	2023-06-06 20:00:00	BOS
13594	5	11	2232	2055	97	108	2354	B6	169	N708JB	LGA	FLL	134	1076	20	55	2023-05-11 20:00:00	FLL
13596	5	29	1948	1929	19	2213	2224	DL	412	N378DN	LGA	MCO	122	950	19	29	2023-05-29 19:00:00	MCO
13598	8	31	1652	1620	32	1952	1910	UA	463	N19141	EWR	MCO	132	937	16	20	2023-08-31 16:00:00	MCO
13599	4	29	1724	1700	24	1911	1847	AA	617	N750UW	LGA	STL	148	888	17	0	2023-04-29 17:00:00	Other
13605	3	13	752	715	37	929	855	WN	571	N919WN	LGA	BNA	124	764	7	15	2023-03-13 07:00:00	Other
13608	10	30	1138	1113	25	1334	1311	9E	1437	N330PQ	LGA	RDU	73	431	11	13	2023-10-30 11:00:00	Other
13609	11	12	7	2159	128	326	139	B6	923	N983JT	JFK	SFO	361	2586	21	59	2023-11-12 21:00:00	Other
13614	1	5	1235	1220	15	1449	1505	WN	470	N8647A	LGA	DEN	234	1620	12	20	2023-01-05 12:00:00	Other
13618	6	24	1549	1520	29	1734	1652	9E	1675	N341PQ	LGA	PWM	47	269	15	20	2023-06-24 15:00:00	Other
13619	3	27	615	600	15	925	906	UA	154	N24211	EWR	FLL	166	1065	6	0	2023-03-27 06:00:00	FLL
13622	1	12	1715	1659	16	2018	1947	DL	411	N387DN	LGA	ATL	128	762	16	59	2023-01-12 16:00:00	ATL
13624	4	18	1720	1645	35	1906	1855	WN	196	N8617E	LGA	MCI	153	1107	16	45	2023-04-18 16:00:00	Other
13625	6	25	1913	1745	88	2200	2040	WN	726	N8624J	LGA	TPA	144	1010	17	45	2023-06-25 17:00:00	Other
13627	8	15	802	730	32	1058	1023	B6	39	N982JB	EWR	PBI	143	1023	7	30	2023-08-15 07:00:00	Other
13634	5	12	927	915	12	1222	1225	UA	288	N78509	EWR	FLL	140	1065	9	15	2023-05-12 09:00:00	FLL
13636	2	26	1933	1915	18	2225	2233	B6	639	N563JB	JFK	FLL	141	1069	19	15	2023-02-26 19:00:00	FLL
13637	7	9	1800	1225	335	2012	1441	UA	720	N62889	EWR	DEN	207	1605	12	25	2023-07-09 12:00:00	Other
13638	12	2	1531	1502	29	1735	1706	DL	891	N950AT	EWR	MSP	161	1008	15	2	2023-12-02 15:00:00	Other
13639	6	2	2219	2010	129	2341	2158	YX	1342	N433YX	LGA	PIT	57	335	20	10	2023-06-02 20:00:00	Other
13643	6	4	1942	1840	62	2156	2108	9E	1380	N907XJ	JFK	CLT	85	541	18	40	2023-06-04 18:00:00	CLT
13644	7	17	1901	1840	21	2018	2018	AA	750	N946AN	LGA	ORD	108	733	18	40	2023-07-17 18:00:00	ORD
13647	8	16	1541	1440	61	1808	1736	UA	701	N14120	EWR	LAX	299	2454	14	40	2023-08-16 14:00:00	LAX
13650	8	20	1513	1409	64	1629	1526	UA	121	N73291	EWR	BOS	48	200	14	9	2023-08-20 14:00:00	BOS
13651	7	1	2003	1943	20	2251	2257	DL	300	N3762Y	LGA	MIA	147	1096	19	43	2023-07-01 19:00:00	MIA
13663	9	9	2127	2059	28	2334	2323	B6	919	N789JB	LGA	MSY	168	1183	20	59	2023-09-09 20:00:00	Other
13678	7	29	1649	1620	29	1929	1910	UA	485	N58101	EWR	MCO	122	937	16	20	2023-07-29 16:00:00	MCO
13687	2	3	2114	1959	75	2	2256	NK	187	N683NK	LGA	MCO	131	950	19	59	2023-02-03 19:00:00	MCO
13691	2	4	850	800	50	1151	1114	AA	804	N866NN	JFK	DFW	201	1391	8	0	2023-02-04 08:00:00	Other
13696	7	18	942	900	42	1100	1019	B6	510	N354JB	JFK	BTV	47	266	9	0	2023-07-18 09:00:00	Other
13697	1	18	1457	1425	32	1803	1743	B6	342	N534JB	LGA	PBI	143	1035	14	25	2023-01-18 14:00:00	Other
13706	10	13	1958	1940	18	2258	2243	B6	104	N994JL	JFK	ONT	333	2429	19	40	2023-10-13 19:00:00	Other
13707	9	3	1840	1815	25	2117	2135	DL	879	N327NW	JFK	AUS	192	1521	18	15	2023-09-03 18:00:00	Other
13708	1	2	2303	2040	143	14	2158	UA	80	N17730	EWR	BOS	46	200	20	40	2023-01-02 20:00:00	BOS
13714	8	1	1806	1717	49	2035	1938	UA	680	N27503	EWR	DEN	218	1605	17	17	2023-08-01 17:00:00	Other
13723	4	10	2225	2150	35	2316	2246	9E	1200	N919XJ	LGA	BDL	29	101	21	50	2023-04-10 21:00:00	Other
13728	4	22	716	700	16	952	1002	B6	616	N929JB	JFK	PSP	317	2378	7	0	2023-04-22 07:00:00	Other
13732	2	3	1919	1642	157	2104	1829	UA	98	N824UA	EWR	RDU	77	416	16	42	2023-02-03 16:00:00	Other
13735	5	22	1646	1629	17	1847	1859	UA	713	N490UA	LGA	DEN	218	1620	16	29	2023-05-22 16:00:00	Other
13749	7	25	206	2228	218	545	223	B6	275	N760JB	JFK	BQN	196	1576	22	28	2023-07-25 22:00:00	Other
13769	11	27	914	849	25	1020	1021	9E	1521	N912XJ	LGA	BTV	43	258	8	49	2023-11-27 08:00:00	Other
13790	3	17	2210	2025	105	208	2344	AS	85	N928VA	EWR	LAX	336	2454	20	25	2023-03-17 20:00:00	LAX
13797	4	7	1845	1810	35	1949	1935	DL	405	N123DQ	JFK	BOS	37	187	18	10	2023-04-07 18:00:00	BOS
13802	5	1	1634	1500	94	1851	1740	DL	132	N196DN	JFK	ATL	114	760	15	0	2023-05-01 15:00:00	ATL
13807	1	19	636	600	36	845	830	UA	491	N18112	EWR	DEN	220	1605	6	0	2023-01-19 06:00:00	Other
13809	11	2	1208	1157	11	1349	1353	YX	1104	N730YX	EWR	ILM	81	488	11	57	2023-11-02 11:00:00	Other
13821	1	11	1819	1735	44	2121	2105	B6	1037	N969JT	JFK	LAX	330	2475	17	35	2023-01-11 17:00:00	LAX
13822	6	19	2041	1648	233	6	1955	AA	521	N901NN	LGA	MIA	160	1096	16	48	2023-06-19 16:00:00	MIA
13826	9	3	2133	2110	23	27	35	UA	692	N14102	EWR	SFO	325	2565	21	10	2023-09-03 21:00:00	Other
13827	12	28	1941	1930	11	2301	2239	B6	203	N809JB	LGA	FLL	174	1076	19	30	2023-12-28 19:00:00	FLL
13846	3	20	1651	1610	41	1958	1920	DL	457	N357DN	JFK	MCO	152	944	16	10	2023-03-20 16:00:00	MCO
13847	12	18	1649	1629	20	1950	1943	UA	861	N53441	EWR	MIA	152	1085	16	29	2023-12-18 16:00:00	MIA
13855	8	18	2106	2045	21	2326	2306	B6	728	N206JB	LGA	ATL	105	762	20	45	2023-08-18 20:00:00	ATL
13857	9	10	1006	955	11	1458	1258	B6	219	N504JB	LGA	MCO	139	950	9	55	2023-09-10 09:00:00	MCO
13863	7	6	1437	1400	37	1610	1521	AA	392	N776XF	LGA	DCA	48	214	14	0	2023-07-06 14:00:00	Other
13872	8	3	1635	1455	100	1800	1639	OO	953	N260SY	JFK	IAD	44	228	14	55	2023-08-03 14:00:00	Other
13876	5	26	1456	1430	26	1649	1653	B6	806	N3044J	JFK	MCI	140	1113	14	30	2023-05-26 14:00:00	Other
13887	6	26	2259	1859	240	212	2143	DL	213	N103DY	LGA	ATL	163	762	18	59	2023-06-26 18:00:00	ATL
13888	12	8	1924	1830	54	2114	2056	9E	1633	N937XJ	LGA	GSP	90	610	18	30	2023-12-08 18:00:00	Other
13892	1	13	1623	1530	53	1946	1846	DL	1073	N324DX	JFK	MIA	172	1089	15	30	2023-01-13 15:00:00	MIA
13898	10	2	818	738	40	1028	1003	UA	385	N17752	EWR	JAX	110	820	7	38	2023-10-02 07:00:00	Other
13904	5	11	1919	1700	139	2201	2000	UA	507	N777UA	EWR	LAX	293	2454	17	0	2023-05-11 17:00:00	LAX
13905	8	25	1052	1020	32	1252	1240	9E	1142	N904XJ	LGA	CLT	80	544	10	20	2023-08-25 10:00:00	CLT
13908	2	28	1108	1040	28	1326	1327	DL	122	N353DN	LGA	ATL	112	762	10	40	2023-02-28 10:00:00	ATL
13913	4	9	2226	2159	27	2334	2308	DL	874	N115DU	LGA	BOS	49	184	21	59	2023-04-09 21:00:00	BOS
13915	6	7	956	820	96	1236	1126	AA	337	N324RN	JFK	DFW	179	1391	8	20	2023-06-07 08:00:00	Other
13917	3	10	2248	2230	18	339	319	B6	144	N641JB	JFK	SJU	193	1598	22	30	2023-03-10 22:00:00	Other
13918	7	24	1612	1501	71	1906	1810	DL	512	N336NB	LGA	TPA	152	1010	15	1	2023-07-24 15:00:00	Other
13925	9	1	1238	1140	58	1355	1312	YX	1299	N119HQ	JFK	ORF	51	290	11	40	2023-09-01 11:00:00	Other
13936	2	12	1533	1510	23	1741	1737	NK	847	N622NK	EWR	MSY	164	1167	15	10	2023-02-12 15:00:00	Other
13940	10	16	1534	1453	41	1840	1800	NK	837	N656NK	EWR	FLL	160	1065	14	53	2023-10-16 14:00:00	FLL
13949	8	27	1527	1459	28	1812	1822	B6	422	N519JB	JFK	FLL	138	1069	14	59	2023-08-27 14:00:00	FLL
13955	3	31	2008	1735	153	2255	2009	B6	152	N595JB	JFK	ATL	118	760	17	35	2023-03-31 17:00:00	ATL
13958	8	24	1126	1050	36	1232	1214	9E	1119	N316PQ	LGA	SYR	43	198	10	50	2023-08-24 10:00:00	Other
13959	11	19	1407	1345	22	1659	1700	B6	518	N995JL	JFK	MCO	131	944	13	45	2023-11-19 13:00:00	MCO
13960	3	20	1625	930	415	1853	1218	B6	16	N994JL	JFK	PHX	305	2153	9	30	2023-03-20 09:00:00	Other
13963	6	25	1301	1200	61	1536	1435	DL	335	N311DN	LGA	ATL	111	762	12	0	2023-06-25 12:00:00	ATL
13964	7	13	1747	1659	48	2105	2007	UA	617	N413UA	EWR	RSW	150	1068	16	59	2023-07-13 16:00:00	Other
13976	1	20	1201	1129	32	1354	1334	YX	1839	N221JQ	LGA	CMH	82	479	11	29	2023-01-20 11:00:00	Other
13982	2	1	725	630	55	1042	932	B6	239	N632JB	JFK	MCO	145	944	6	30	2023-02-01 06:00:00	MCO
13983	12	3	1200	1140	20	1335	1326	OO	1156	N306SY	JFK	ORD	125	740	11	40	2023-12-03 11:00:00	ORD
13990	6	25	2123	1738	225	2325	1918	UA	236	N16709	EWR	CLE	63	404	17	38	2023-06-25 17:00:00	Other
13991	4	14	2117	2015	62	21	2359	AS	18	N924AK	JFK	SFO	333	2586	20	15	2023-04-14 20:00:00	Other
13992	2	3	1802	1729	33	2111	2046	UA	479	N27261	EWR	FLL	154	1065	17	29	2023-02-03 17:00:00	FLL
13996	8	11	2047	2022	25	2228	2220	DL	802	N933AT	EWR	DTW	75	488	20	22	2023-08-11 20:00:00	Other
14001	12	27	1619	1605	14	1907	1910	WN	971	N942WN	LGA	DAL	208	1381	16	5	2023-12-27 16:00:00	Other
14011	2	24	1026	950	36	1300	1220	WN	193	N7822A	LGA	MCI	190	1107	9	50	2023-02-24 09:00:00	Other
14019	3	13	757	744	13	1021	1039	UA	227	N17285	EWR	LAS	291	2227	7	44	2023-03-13 07:00:00	Other
14021	1	22	1007	914	53	1223	1138	UA	849	N815UA	EWR	IND	108	645	9	14	2023-01-22 09:00:00	Other
14036	8	25	826	759	27	1017	1010	YX	1082	N443YX	LGA	CVG	85	585	7	59	2023-08-25 07:00:00	Other
14043	6	23	2141	2029	72	57	2357	AS	17	N529AS	JFK	SFO	339	2586	20	29	2023-06-23 20:00:00	Other
14044	7	28	1657	1459	118	2005	1806	UA	207	N14731	EWR	MIA	143	1085	14	59	2023-07-28 14:00:00	MIA
14045	2	10	1020	1000	20	1329	1314	UA	692	N854UA	LGA	IAH	225	1416	10	0	2023-02-10 10:00:00	Other
14048	5	7	1546	1502	44	1833	1810	DL	556	N349NB	LGA	TPA	137	1010	15	2	2023-05-07 15:00:00	Other
14062	4	20	1607	1529	38	1739	1730	9E	1263	N296PQ	LGA	ILM	70	500	15	29	2023-04-20 15:00:00	Other
14063	9	29	802	700	62	1139	1008	B6	266	N984JB	JFK	LAX	320	2475	7	0	2023-09-29 07:00:00	LAX
14071	1	15	953	938	15	1230	1301	B6	586	N526JL	LGA	FLL	131	1076	9	38	2023-01-15 09:00:00	FLL
14074	5	1	1618	1600	18	1804	1720	UA	140	N429UA	EWR	BOS	40	200	16	0	2023-05-01 16:00:00	BOS
14076	9	29	1317	1259	18	1508	1454	9E	1423	N331PQ	JFK	DTW	83	509	12	59	2023-09-29 12:00:00	Other
14079	1	29	1653	1605	48	1923	1835	WN	764	N445WN	LGA	MCI	187	1107	16	5	2023-01-29 16:00:00	Other
14083	3	26	1634	1555	39	1957	1912	B6	253	N639JB	JFK	PBI	168	1028	15	55	2023-03-26 15:00:00	Other
14091	10	26	919	900	19	1253	1206	B6	70	N645JB	LGA	FLL	170	1076	9	0	2023-10-26 09:00:00	FLL
14102	5	9	1401	1330	31	1645	1624	B6	554	N637JB	JFK	MCO	130	944	13	30	2023-05-09 13:00:00	MCO
14112	11	20	1617	1537	40	1946	1857	DL	211	N303DU	LGA	DFW	232	1389	15	37	2023-11-20 15:00:00	Other
14117	1	12	2152	1935	137	51	2239	B6	307	N568JB	LGA	MCO	143	950	19	35	2023-01-12 19:00:00	MCO
14132	4	17	1236	1059	97	1442	1324	YX	1549	N215JQ	LGA	MCI	159	1107	10	59	2023-04-17 10:00:00	Other
14135	7	9	2007	1215	472	2301	1429	UA	595	N54241	LGA	DEN	241	1620	12	15	2023-07-09 12:00:00	Other
14137	1	19	1533	1511	22	1715	1707	YX	1738	N242JQ	JFK	PIT	72	340	15	11	2023-01-19 15:00:00	Other
14140	3	29	1643	1600	43	1936	1910	B6	781	N656JB	LGA	MCO	141	950	16	0	2023-03-29 16:00:00	MCO
14148	4	17	819	700	79	1135	1006	DL	534	N903DN	JFK	TPA	165	1005	7	0	2023-04-17 07:00:00	Other
14154	9	12	1512	1432	40	1613	1540	B6	847	N329JB	JFK	ACK	43	199	14	32	2023-09-12 14:00:00	Other
14155	9	7	2132	1426	426	153	1739	UA	243	N17294	EWR	SEA	309	2402	14	26	2023-09-07 14:00:00	Other
14160	3	23	2043	2015	28	2321	2320	WN	675	N8833L	LGA	DAL	202	1381	20	15	2023-03-23 20:00:00	Other
14164	4	25	2158	2120	38	19	2358	DL	149	N303DN	LGA	ATL	117	762	21	20	2023-04-25 21:00:00	ATL
14170	7	9	1232	1200	32	1350	1311	B6	697	N284JB	LGA	ACK	38	202	12	0	2023-07-09 12:00:00	Other
14173	7	15	1844	1501	223	2216	1810	DL	512	N349NB	LGA	TPA	178	1010	15	1	2023-07-15 15:00:00	Other
14177	3	30	1521	1459	22	1650	1632	B6	650	N247JB	JFK	BNA	124	765	14	59	2023-03-30 14:00:00	Other
14178	5	11	2106	2029	37	2355	2335	UA	250	N37538	EWR	AUS	195	1504	20	29	2023-05-11 20:00:00	Other
14181	8	29	1942	1859	43	2217	2144	DL	177	N375DN	LGA	ATL	128	762	18	59	2023-08-29 18:00:00	ATL
14186	2	6	1126	1049	37	1334	1335	F9	565	N384FR	LGA	ATL	104	762	10	49	2023-02-06 10:00:00	ATL
14190	7	14	1847	1307	340	2236	1556	UA	172	N14115	EWR	MCO	141	937	13	7	2023-07-14 13:00:00	MCO
14195	7	14	1655	1500	115	1752	1617	9E	1235	N478PX	LGA	ORH	34	146	15	0	2023-07-14 15:00:00	Other
14197	6	7	1941	1913	28	2225	2205	UA	568	N27255	EWR	SAN	301	2425	19	13	2023-06-07 19:00:00	Other
14199	12	22	1405	1218	107	1901	1704	B6	967	N956JT	JFK	SJU	204	1598	12	18	2023-12-22 12:00:00	Other
14207	7	25	2003	1639	204	2223	1931	OO	970	N315SY	LGA	OKC	179	1341	16	39	2023-07-25 16:00:00	Other
14212	12	27	2142	2029	73	207	121	B6	683	N956JT	JFK	SJU	183	1598	20	29	2023-12-27 20:00:00	Other
14215	12	13	1134	1100	34	1437	1415	B6	321	N534JB	JFK	SLC	281	1990	11	0	2023-12-13 11:00:00	Other
14217	5	31	728	659	29	842	827	AA	558	N742PS	LGA	DCA	45	214	6	59	2023-05-31 06:00:00	Other
14223	5	28	1247	1235	12	1552	1545	UA	688	N481UA	EWR	MIA	152	1085	12	35	2023-05-28 12:00:00	MIA
14225	5	15	1226	1115	71	1501	1414	B6	204	N623JB	EWR	PBI	136	1023	11	15	2023-05-15 11:00:00	Other
14227	4	30	2100	2011	49	2317	2231	DL	841	N3735D	EWR	ATL	114	746	20	11	2023-04-30 20:00:00	ATL
14228	9	10	1055	1030	25	1405	1246	DL	824	N3752	EWR	ATL	111	746	10	30	2023-09-10 10:00:00	ATL
14238	7	26	744	730	14	959	1007	9E	1167	N335PQ	LGA	JAX	115	833	7	30	2023-07-26 07:00:00	Other
14248	8	4	2221	1840	221	126	2153	DL	369	N331DN	EWR	SLC	253	1969	18	40	2023-08-04 18:00:00	Other
14258	11	21	1812	1711	61	2020	1914	AA	640	N581UW	EWR	CLT	97	529	17	11	2023-11-21 17:00:00	CLT
14261	6	20	2138	2030	68	2338	2247	UA	924	N27287	EWR	MSY	155	1167	20	30	2023-06-20 20:00:00	Other
14277	1	23	2058	1935	83	206	30	B6	536	N649JB	EWR	SJU	213	1608	19	35	2023-01-23 19:00:00	Other
14288	6	19	936	925	11	1218	1231	B6	360	N651JB	JFK	PBI	133	1028	9	25	2023-06-19 09:00:00	Other
14293	1	13	1707	1559	68	1950	1846	B6	719	N763JB	JFK	JAX	135	828	15	59	2023-01-13 15:00:00	Other
14295	7	21	1214	1159	15	1451	1453	UA	606	N37313	EWR	IAH	191	1400	11	59	2023-07-21 11:00:00	Other
14297	8	28	1941	1925	16	2244	2151	9E	1199	N602LR	JFK	DTW	80	509	19	25	2023-08-28 19:00:00	Other
14298	11	10	2003	1945	18	2223	2215	DL	980	N366NB	JFK	MSP	164	1029	19	45	2023-11-10 19:00:00	Other
14299	6	19	1120	1048	32	1335	1316	F9	580	N359FR	LGA	ATL	110	762	10	48	2023-06-19 10:00:00	ATL
14300	2	17	2127	2025	62	44	2358	AS	85	N923VA	EWR	LAX	341	2454	20	25	2023-02-17 20:00:00	LAX
14302	7	29	1551	1427	84	1735	1619	UA	180	N476UA	EWR	MSP	144	1008	14	27	2023-07-29 14:00:00	Other
14309	8	24	1102	950	72	1154	1101	9E	1208	N303PQ	LGA	ALB	30	136	9	50	2023-08-24 09:00:00	Other
14310	6	7	1754	1645	69	2017	1938	OO	1262	N251SY	LGA	OKC	182	1341	16	45	2023-06-07 16:00:00	Other
14314	12	14	1830	1710	80	2310	2208	B6	451	N587JB	EWR	SJU	198	1608	17	10	2023-12-14 17:00:00	Other
14319	9	10	1707	1359	188	1942	1626	B6	981	N523JB	LGA	ATL	120	762	13	59	2023-09-10 13:00:00	ATL
14331	9	9	1855	1310	345	2056	1500	YX	1396	N444YX	LGA	GSO	80	461	13	10	2023-09-09 13:00:00	Other
14334	7	14	1632	1610	22	1905	1815	OO	983	N320SY	JFK	ORD	144	740	16	10	2023-07-14 16:00:00	ORD
14338	4	18	1927	1825	62	2051	2015	WN	194	N8781Q	LGA	STL	126	888	18	25	2023-04-18 18:00:00	Other
14339	9	14	1035	1015	20	1347	1313	UA	711	N73259	EWR	IAH	218	1400	10	15	2023-09-14 10:00:00	Other
14353	2	26	2018	1959	19	2315	2307	DL	424	N342DN	LGA	MCO	131	950	19	59	2023-02-26 19:00:00	MCO
14359	4	22	830	800	30	936	911	B6	273	N267JB	JFK	BOS	33	187	8	0	2023-04-22 08:00:00	BOS
14373	4	30	1716	1400	196	2221	1715	B6	489	N2044J	JFK	FLL	190	1069	14	0	2023-04-30 14:00:00	FLL
14382	6	30	1223	1135	48	1443	1410	WN	47	N423WN	LGA	DAL	180	1381	11	35	2023-06-30 11:00:00	Other
14385	2	5	1643	1630	13	1841	1847	DL	123	N353NW	JFK	DTW	89	509	16	30	2023-02-05 16:00:00	Other
14398	7	14	48	1858	350	355	2225	B6	309	N634JB	JFK	PDX	350	2454	18	58	2023-07-14 18:00:00	Other
14400	2	6	1656	1600	56	1820	1726	OO	1171	N247SY	JFK	BOS	39	187	16	0	2023-02-06 16:00:00	BOS
14401	4	29	908	850	18	1035	1009	YX	1513	N212JQ	JFK	BOS	34	187	8	50	2023-04-29 08:00:00	BOS
14402	3	10	1736	1710	26	2130	2012	UA	271	N489UA	EWR	PBI	181	1023	17	10	2023-03-10 17:00:00	Other
14412	10	16	1716	1645	31	2003	2015	AS	10	N469AS	JFK	SFO	321	2586	16	45	2023-10-16 16:00:00	Other
14413	2	2	1731	1707	24	2017	2007	UA	187	N27268	EWR	MCO	138	937	17	7	2023-02-02 17:00:00	MCO
14420	9	4	1709	1530	99	1926	1812	B6	651	N284JB	JFK	ATL	99	760	15	30	2023-09-04 15:00:00	ATL
14425	6	3	2242	2112	90	29	2344	UA	310	N76288	EWR	LAS	268	2227	21	12	2023-06-03 21:00:00	Other
14426	8	1	1346	1305	41	1453	1440	UA	92	N17311	EWR	ORD	105	719	13	5	2023-08-01 13:00:00	ORD
14436	3	27	720	615	65	842	727	B6	72	N375JB	LGA	BOS	40	184	6	15	2023-03-27 06:00:00	BOS
14439	2	5	1858	1833	25	2037	2017	UA	243	N15751	EWR	CLE	66	404	18	33	2023-02-05 18:00:00	Other
14444	9	29	1658	1643	15	2002	2000	B6	850	N506JB	EWR	MIA	165	1085	16	43	2023-09-29 16:00:00	MIA
14450	5	10	1555	1456	59	1805	1713	9E	1523	N538CA	LGA	CVG	98	585	14	56	2023-05-10 14:00:00	Other
14457	8	27	2141	829	792	2329	1032	AA	780	N887NN	JFK	ORD	123	740	8	29	2023-08-27 08:00:00	ORD
14459	3	28	1907	1830	37	2238	2159	B6	29	N659JB	JFK	SLC	302	1990	18	30	2023-03-28 18:00:00	Other
14469	4	5	1025	945	40	1146	1115	9E	1365	N272PQ	LGA	ROC	48	254	9	45	2023-04-05 09:00:00	Other
14470	8	31	1757	1725	32	1934	1913	9E	1195	N921XJ	JFK	BUF	51	301	17	25	2023-08-31 17:00:00	Other
14478	10	3	2221	2159	22	2353	2357	YX	1107	N724YX	EWR	ILM	75	488	21	59	2023-10-03 21:00:00	Other
14481	2	20	1034	1000	34	1238	1228	UA	756	N25982	EWR	DEN	219	1605	10	0	2023-02-20 10:00:00	Other
14486	11	25	1954	1629	205	2258	1949	AA	734	N303RG	LGA	MIA	150	1096	16	29	2023-11-25 16:00:00	MIA
14488	4	22	1159	1147	12	1349	1401	YX	956	N645RW	EWR	IND	92	645	11	47	2023-04-22 11:00:00	Other
14492	9	4	919	610	189	1159	850	B6	498	N982JB	EWR	LAX	307	2454	6	10	2023-09-04 06:00:00	LAX
14507	3	14	1553	1459	54	1910	1806	DL	573	N314NB	LGA	TPA	147	1010	14	59	2023-03-14 14:00:00	Other
14509	4	1	1906	1755	71	2148	1947	DL	436	N116DU	LGA	ORD	123	733	17	55	2023-04-01 17:00:00	ORD
14511	6	14	130	2100	270	411	25	UA	711	N12109	EWR	SFO	326	2565	21	0	2023-06-14 21:00:00	Other
14516	6	3	1330	1126	124	1444	1258	YX	1847	N211JQ	JFK	DCA	48	213	11	26	2023-06-03 11:00:00	Other
14528	6	11	1848	1717	91	2051	1938	UA	719	N38454	EWR	DEN	214	1605	17	17	2023-06-11 17:00:00	Other
14529	4	15	938	745	113	1101	920	YX	1150	N433YX	JFK	DCA	43	213	7	45	2023-04-15 07:00:00	Other
14533	9	10	1542	1454	48	1850	1749	NK	256	N525NK	EWR	IAH	211	1400	14	54	2023-09-10 14:00:00	Other
14534	5	30	1116	1000	76	1519	1356	B6	957	N2016J	JFK	SJU	222	1598	10	0	2023-05-30 10:00:00	Other
14536	8	1	958	900	58	1258	1151	UA	473	N78501	EWR	SAT	199	1569	9	0	2023-08-01 09:00:00	Other
14538	6	29	1803	1718	45	1944	1853	UA	819	N12109	EWR	ORD	109	719	17	18	2023-06-29 17:00:00	ORD
14542	1	3	1612	1559	13	1921	1921	B6	600	N2017J	JFK	FLL	146	1069	15	59	2023-01-03 15:00:00	FLL
14546	7	6	2122	2000	82	2245	2138	B6	756	N348JB	JFK	BUF	50	301	20	0	2023-07-06 20:00:00	Other
14547	7	30	714	700	14	1014	1010	AS	86	N288AK	EWR	SEA	339	2402	7	0	2023-07-30 07:00:00	Other
14554	4	2	2028	2014	14	2215	2220	DL	908	N953AT	EWR	DTW	82	488	20	14	2023-04-02 20:00:00	Other
14558	8	20	2007	1939	28	2212	2242	B6	101	N949JT	JFK	ONT	284	2429	19	39	2023-08-20 19:00:00	Other
14568	10	5	1445	1429	16	1642	1627	9E	1552	N937XJ	LGA	ILM	79	500	14	29	2023-10-05 14:00:00	Other
14570	1	8	2222	2156	26	2323	2314	YX	1203	N753YX	EWR	MHT	40	209	21	56	2023-01-08 21:00:00	Other
14572	8	15	1333	1300	33	1643	1614	B6	474	N2002J	JFK	FLL	164	1069	13	0	2023-08-15 13:00:00	FLL
14576	6	1	1838	1730	68	2012	1932	NK	52	N683NK	LGA	DTW	72	502	17	30	2023-06-01 17:00:00	Other
14578	10	21	1225	1155	30	1338	1326	AA	976	N773XF	LGA	BNA	110	764	11	55	2023-10-21 11:00:00	Other
14584	6	30	1902	1832	30	2019	1948	YX	1116	N747YX	EWR	ALB	36	143	18	32	2023-06-30 18:00:00	Other
14587	10	9	2118	2025	53	2332	2250	WN	164	N776WN	LGA	DEN	212	1620	20	25	2023-10-09 20:00:00	Other
14589	3	3	1722	1629	53	1831	1742	UA	143	N478UA	EWR	BOS	33	200	16	29	2023-03-03 16:00:00	BOS
14593	12	18	1331	605	446	1525	815	9E	1654	N176PQ	LGA	CLT	87	544	6	5	2023-12-18 06:00:00	CLT
14599	6	24	1512	1300	132	1637	1415	B6	880	N339JB	JFK	ACK	38	199	13	0	2023-06-24 13:00:00	Other
14602	6	29	1841	1630	131	2041	1905	B6	120	N274JB	JFK	SAV	97	718	16	30	2023-06-29 16:00:00	Other
14607	5	22	1351	1329	22	1525	1515	YX	1323	N420YX	JFK	PIT	64	340	13	29	2023-05-22 13:00:00	Other
14608	9	16	1103	1046	17	1252	1248	YX	1102	N751YX	EWR	DTW	76	488	10	46	2023-09-16 10:00:00	Other
14614	4	13	2000	1935	25	2157	2132	AA	314	N848NN	EWR	CLT	80	529	19	35	2023-04-13 19:00:00	CLT
14615	5	3	1617	1505	72	1721	1643	UA	606	N802UA	LGA	ORD	101	733	15	5	2023-05-03 15:00:00	ORD
14627	12	15	1814	1659	75	2050	1946	DL	131	N104DN	LGA	ATL	119	762	16	59	2023-12-15 16:00:00	ATL
14630	2	3	1804	1655	69	2008	1847	OO	1461	N620UX	LGA	ORD	125	733	16	55	2023-02-03 16:00:00	ORD
14634	10	28	941	922	19	1340	1326	UA	527	N24736	EWR	STT	204	1634	9	22	2023-10-28 09:00:00	Other
14637	8	8	1610	1530	40	1917	1833	UA	405	N34137	EWR	LAX	330	2454	15	30	2023-08-08 15:00:00	LAX
14650	5	11	1505	1445	20	1657	1632	9E	1480	N482PX	EWR	RDU	64	416	14	45	2023-05-11 14:00:00	Other
14658	7	15	1828	1805	23	2052	2051	DL	191	N330DX	LGA	ATL	115	762	18	5	2023-07-15 18:00:00	ATL
14661	7	6	1610	1455	75	1913	1756	UA	69	N37456	EWR	PBI	149	1023	14	55	2023-07-06 14:00:00	Other
14663	4	17	2017	1930	47	2322	2259	B6	341	N706JB	JFK	PDX	338	2454	19	30	2023-04-17 19:00:00	Other
14664	7	29	1309	1132	97	1448	1339	AA	616	N843NN	LGA	CLT	76	544	11	32	2023-07-29 11:00:00	CLT
14665	9	29	2249	2200	49	135	59	DL	93	N171DN	JFK	LAX	305	2475	22	0	2023-09-29 22:00:00	LAX
14669	5	1	1228	940	168	1508	1239	B6	438	N651JB	JFK	TPA	145	1005	9	40	2023-05-01 09:00:00	Other
14674	7	19	1909	1730	99	2257	2040	B6	112	N606JB	JFK	BUR	318	2465	17	30	2023-07-19 17:00:00	Other
14675	6	5	1140	1029	71	1438	1336	B6	965	N613JB	JFK	MIA	151	1089	10	29	2023-06-05 10:00:00	MIA
14676	12	27	2217	2200	17	47	115	NK	1131	N710NK	EWR	LAX	312	2454	22	0	2023-12-27 22:00:00	LAX
14679	4	16	2342	2211	91	57	2334	UA	452	N855UA	EWR	BUF	46	282	22	11	2023-04-16 22:00:00	Other
14682	7	28	803	730	33	1015	947	9E	1305	N933XJ	LGA	CVG	90	585	7	30	2023-07-28 07:00:00	Other
14692	3	27	2118	2100	18	2312	2251	OO	1765	N167SY	LGA	ORD	140	733	21	0	2023-03-27 21:00:00	ORD
14696	10	5	2117	2100	17	8	16	DL	153	N518DQ	JFK	SAN	308	2446	21	0	2023-10-05 21:00:00	Other
14702	11	23	907	730	97	1200	1039	UA	947	N27733	LGA	IAH	203	1416	7	30	2023-11-23 07:00:00	Other
14711	9	20	1537	1456	41	1748	1719	OO	1254	N295SY	JFK	IND	97	665	14	56	2023-09-20 14:00:00	Other
14717	9	3	1502	1359	63	1615	1530	B6	246	N3112J	JFK	MKE	109	745	13	59	2023-09-03 13:00:00	Other
14732	1	26	835	800	35	1006	950	UA	759	N73270	EWR	ORD	107	719	8	0	2023-01-26 08:00:00	ORD
14736	6	24	1450	1405	45	1824	1646	UA	523	N462UA	EWR	DFW	173	1372	14	5	2023-06-24 14:00:00	Other
14746	3	14	2233	2120	73	2320	2222	YX	1737	N234JQ	LGA	BDL	23	101	21	20	2023-03-14 21:00:00	Other
14754	9	5	1027	1015	12	1305	1315	DL	407	N134DU	LGA	IAH	179	1416	10	15	2023-09-05 10:00:00	Other
14758	9	7	2309	2130	99	53	2302	9E	1557	N310PQ	LGA	CHO	78	305	21	30	2023-09-07 21:00:00	Other
14767	3	12	2027	1950	37	21	2333	DL	633	N3768	JFK	RSW	182	1074	19	50	2023-03-12 19:00:00	Other
14769	6	28	1144	1129	15	1346	1313	OO	1269	N246SY	JFK	ORD	123	740	11	29	2023-06-28 11:00:00	ORD
14778	3	21	1402	1300	62	1628	1537	B6	736	N796JB	LGA	MSY	169	1183	13	0	2023-03-21 13:00:00	Other
14795	9	14	1831	1810	21	2041	2028	9E	1659	N316PQ	LGA	GSP	100	610	18	10	2023-09-14 18:00:00	Other
14797	10	27	1522	1506	16	1631	1625	UA	707	N808UA	EWR	IAD	46	212	15	6	2023-10-27 15:00:00	Other
14798	8	8	1718	1415	183	1819	1538	B6	173	N206JB	LGA	BOS	42	184	14	15	2023-08-08 14:00:00	BOS
14803	4	6	933	849	44	1034	955	9E	1368	N315PQ	LGA	ALB	32	136	8	49	2023-04-06 08:00:00	Other
14813	2	4	1219	1042	97	1532	1426	UA	453	N47281	EWR	PHX	293	2133	10	42	2023-02-04 10:00:00	Other
14816	2	16	2201	1800	241	6	1941	UA	671	N832UA	EWR	STL	150	872	18	0	2023-02-16 18:00:00	Other
14821	6	28	2125	2038	47	2342	2324	UA	503	N438UA	EWR	IAH	172	1400	20	38	2023-06-28 20:00:00	Other
14840	10	23	2006	1929	37	2314	2246	DL	402	N109DU	LGA	RSW	148	1080	19	29	2023-10-23 19:00:00	Other
14852	10	13	1709	1546	83	1959	1845	DL	111	N328DN	LGA	MCO	134	950	15	46	2023-10-13 15:00:00	MCO
14867	8	7	809	745	24	944	917	UA	684	N18112	EWR	ORD	109	719	7	45	2023-08-07 07:00:00	ORD
14873	4	22	1548	1425	83	1808	1633	NK	786	N624NK	EWR	MSY	165	1167	14	25	2023-04-22 14:00:00	Other
14874	7	28	17	2117	180	210	2319	YX	1015	N401YX	LGA	MEM	129	963	21	17	2023-07-28 21:00:00	Other
14885	6	14	2124	1900	144	2248	2030	UA	650	N66831	EWR	BNA	115	748	19	0	2023-06-14 19:00:00	Other
14887	6	23	1349	1259	50	1617	1536	YX	1326	N435YX	LGA	OKC	183	1341	12	59	2023-06-23 12:00:00	Other
14901	10	6	1948	1834	74	2111	2005	OO	1241	N242SY	JFK	BNA	119	765	18	34	2023-10-06 18:00:00	Other
14902	3	25	948	929	19	1313	1241	UA	729	N441UA	EWR	RSW	166	1068	9	29	2023-03-25 09:00:00	Other
14905	6	15	1642	1629	13	1903	1853	DL	888	N329NB	JFK	MSP	147	1029	16	29	2023-06-15 16:00:00	Other
14913	6	26	1116	953	83	1308	1145	DL	1027	N988AT	EWR	DTW	78	488	9	53	2023-06-26 09:00:00	Other
14915	2	3	2238	2053	105	6	2303	YX	1338	N871RW	LGA	ILM	68	500	20	53	2023-02-03 20:00:00	Other
14921	3	4	1431	1131	180	1740	1443	UA	488	N33264	EWR	AUS	223	1504	11	31	2023-03-04 11:00:00	Other
14927	7	30	820	800	20	1018	1038	DL	178	N523DE	JFK	DEN	217	1626	8	0	2023-07-30 08:00:00	Other
14930	9	10	2104	1424	400	8	1723	B6	317	N566JB	JFK	MCO	136	944	14	24	2023-09-10 14:00:00	MCO
14939	4	16	1508	1025	283	1619	1136	YX	1449	N246JQ	JFK	BOS	35	187	10	25	2023-04-16 10:00:00	BOS
14941	9	28	2020	1830	110	2253	2103	B6	139	N206JB	JFK	ATL	119	760	18	30	2023-09-28 18:00:00	ATL
14945	8	11	1732	1700	32	2003	1949	AA	779	N354PT	LGA	DFW	181	1389	17	0	2023-08-11 17:00:00	Other
14948	12	27	943	930	13	1217	1252	B6	96	N962JT	JFK	LAX	310	2475	9	30	2023-12-27 09:00:00	LAX
14952	1	25	2250	2100	110	18	2252	YX	1263	N862RW	LGA	ORD	116	733	21	0	2023-01-25 21:00:00	ORD
14955	11	27	2141	1935	126	120	2246	DL	1007	N517DN	JFK	MCO	153	944	19	35	2023-11-27 19:00:00	MCO
14958	7	25	2317	1945	212	106	2212	UA	603	N37536	EWR	DEN	207	1605	19	45	2023-07-25 19:00:00	Other
14959	11	4	1341	1330	11	1543	1525	9E	1677	N908XJ	JFK	CLE	77	425	13	30	2023-11-04 13:00:00	Other
14962	8	20	1830	1745	45	2021	2005	WN	981	N8704Q	LGA	DEN	207	1620	17	45	2023-08-20 17:00:00	Other
14986	12	4	1119	1054	25	1412	1332	F9	999	N305FR	LGA	ATL	131	762	10	54	2023-12-04 10:00:00	ATL
14991	10	1	2148	2030	78	2338	2257	B6	29	N605JB	JFK	DEN	210	1626	20	30	2023-10-01 20:00:00	Other
14996	10	13	2131	2029	62	2321	2210	DL	997	N947AT	EWR	DTW	86	488	20	29	2023-10-13 20:00:00	Other
15007	2	28	2142	2128	14	2339	2334	UA	832	N17279	EWR	MSP	156	1008	21	28	2023-02-28 21:00:00	Other
15013	9	30	1302	1246	16	1553	1553	NK	628	N696NK	EWR	FLL	153	1065	12	46	2023-09-30 12:00:00	FLL
15019	3	10	1847	1830	17	2140	2139	AA	897	N810NN	EWR	DFW	192	1372	18	30	2023-03-10 18:00:00	Other
15022	5	21	722	645	37	1004	952	UA	730	N37419	EWR	SEA	315	2402	6	45	2023-05-21 06:00:00	Other
15026	10	19	1830	1800	30	2129	2055	UA	459	N66803	EWR	SRQ	149	1034	18	0	2023-10-19 18:00:00	Other
15031	1	13	1244	1210	34	1546	1509	DL	603	N349DX	JFK	MCO	158	944	12	10	2023-01-13 12:00:00	MCO
15035	5	28	1832	1759	33	2058	2107	AA	971	N928AN	JFK	DFW	172	1391	17	59	2023-05-28 17:00:00	Other
15037	4	12	1256	1225	31	1501	1455	WN	901	N910WN	LGA	DEN	208	1620	12	25	2023-04-12 12:00:00	Other
15039	10	1	1850	1757	53	2025	1954	YX	1720	N824MD	LGA	CMH	69	479	17	57	2023-10-01 17:00:00	Other
15050	10	1	942	840	62	1113	1030	B6	880	N267JB	JFK	RDU	67	427	8	40	2023-10-01 08:00:00	Other
15051	2	3	2201	2122	39	3	2327	UA	654	N75426	EWR	CLT	79	529	21	22	2023-02-03 21:00:00	CLT
15064	12	11	1708	1648	20	1850	1839	AA	212	N830AW	LGA	STL	128	888	16	48	2023-12-11 16:00:00	Other
15068	8	30	711	700	11	925	850	9E	1122	N910XJ	LGA	STL	128	888	7	0	2023-08-30 07:00:00	Other
15072	6	12	1455	1259	116	1636	1450	DL	1048	N110DU	LGA	ORD	125	733	12	59	2023-06-12 12:00:00	ORD
15074	12	28	2046	2029	17	2334	2339	B6	60	N657JB	JFK	TPA	148	1005	20	29	2023-12-28 20:00:00	Other
15075	5	12	1542	1530	12	1758	1811	B6	650	N828JB	JFK	ATL	104	760	15	30	2023-05-12 15:00:00	ATL
15088	6	3	1549	1530	19	1704	1658	YX	1117	N750YX	EWR	BNA	104	748	15	30	2023-06-03 15:00:00	Other
15093	4	27	1341	1329	12	1610	1601	DL	197	N327DN	LGA	ATL	118	762	13	29	2023-04-27 13:00:00	ATL
15094	7	27	1524	1450	34	1738	1720	WN	547	N946WN	LGA	ATL	107	762	14	50	2023-07-27 14:00:00	ATL
15096	12	10	828	730	58	1056	1045	DL	175	N507DZ	JFK	LAS	306	2248	7	30	2023-12-10 07:00:00	Other
15108	5	3	2004	1859	65	2154	2041	AA	186	N751UW	LGA	RDU	69	431	18	59	2023-05-03 18:00:00	Other
15112	2	5	1031	950	41	1354	1314	B6	574	N653JB	JFK	RSW	170	1074	9	50	2023-02-05 09:00:00	Other
15115	3	29	1506	1455	11	1759	1744	9E	1412	N272PQ	JFK	JAX	126	828	14	55	2023-03-29 14:00:00	Other
15123	4	27	2232	2213	19	2341	2333	UA	466	N47284	EWR	PWM	47	284	22	13	2023-04-27 22:00:00	Other
15127	1	22	2212	2155	17	2341	2310	DL	817	N837DN	JFK	BOS	32	187	21	55	2023-01-22 21:00:00	BOS
15131	10	2	744	650	54	1037	959	NK	250	N925NK	EWR	OAK	317	2555	6	50	2023-10-02 06:00:00	Other
15135	1	11	1327	1215	72	1526	1450	YX	1295	N433YX	LGA	DAY	91	549	12	15	2023-01-11 12:00:00	Other
15141	6	27	2033	1550	283	2307	1758	YX	1788	N222JQ	JFK	CMH	83	483	15	50	2023-06-27 15:00:00	Other
15147	1	21	1745	1729	16	1914	1915	UA	684	N25705	EWR	CLE	69	404	17	29	2023-01-21 17:00:00	Other
15152	7	27	1717	1632	45	1844	1812	9E	1179	N197PQ	LGA	PWM	48	269	16	32	2023-07-27 16:00:00	Other
15156	8	18	651	630	21	939	922	B6	42	N793JB	JFK	SRQ	149	1041	6	30	2023-08-18 06:00:00	Other
15164	4	21	1642	1629	13	1939	1947	B6	134	N612JB	LGA	FLL	154	1076	16	29	2023-04-21 16:00:00	FLL
15175	9	5	2248	2230	18	8	2344	9E	1692	N310PQ	JFK	ITH	37	189	22	30	2023-09-05 22:00:00	Other
15177	2	10	1318	1250	28	1652	1558	UA	687	N13248	EWR	MIA	156	1085	12	50	2023-02-10 12:00:00	MIA
15178	6	29	1146	943	123	1336	1140	9E	1721	N919XJ	LGA	STL	137	888	9	43	2023-06-29 09:00:00	Other
15181	10	7	1725	1545	100	2052	1859	DL	862	N331NB	JFK	AUS	209	1521	15	45	2023-10-07 15:00:00	Other
15183	5	28	2019	1922	57	2237	2207	9E	1298	N925XJ	JFK	SAV	100	718	19	22	2023-05-28 19:00:00	Other
15184	10	6	1823	1659	84	2106	2015	AS	75	N492AS	EWR	LAX	315	2454	16	59	2023-10-06 16:00:00	LAX
15187	8	26	1253	1050	123	1454	1314	9E	1295	N305PQ	LGA	CVG	95	585	10	50	2023-08-26 10:00:00	Other
15190	9	6	1654	1640	14	1854	1845	WN	505	N241WN	LGA	MCI	152	1107	16	40	2023-09-06 16:00:00	Other
15192	1	15	1707	1653	14	1850	1828	9E	1503	N183GJ	JFK	BGR	69	382	16	53	2023-01-15 16:00:00	Other
15193	5	25	1826	1720	66	1939	1857	B6	29	N923JB	JFK	BNA	114	765	17	20	2023-05-25 17:00:00	Other
15195	4	30	1326	1259	27	1536	1459	9E	1336	N340CA	JFK	DTW	79	509	12	59	2023-04-30 12:00:00	Other
15197	12	25	1109	1040	29	1228	1235	WN	1155	N439WN	LGA	STL	127	888	10	40	2023-12-25 10:00:00	Other
15205	4	6	1201	1150	11	1314	1315	WN	925	N8608N	LGA	MDW	113	725	11	50	2023-04-06 11:00:00	Other
15208	12	11	47	1959	288	313	2242	B6	880	N807JB	LGA	ATL	116	762	19	59	2023-12-11 19:00:00	ATL
15216	3	2	2125	2000	85	107	2309	B6	123	N629JB	JFK	ONT	368	2429	20	0	2023-03-02 20:00:00	Other
15219	7	19	837	820	17	1155	1125	AA	279	N936NN	JFK	DFW	186	1391	8	20	2023-07-19 08:00:00	Other
15221	3	19	1944	1720	144	2339	2038	B6	997	N2044J	JFK	FLL	173	1069	17	20	2023-03-19 17:00:00	FLL
15223	4	14	2144	2130	14	21	2327	YX	1128	N123HQ	JFK	RDU	115	427	21	30	2023-04-14 21:00:00	Other
15229	6	25	1931	1615	196	2145	1745	WN	1053	N8642E	LGA	BNA	119	764	16	15	2023-06-25 16:00:00	Other
15234	8	27	2000	1800	120	2333	2114	AA	151	N886NN	JFK	MIA	176	1089	18	0	2023-08-27 18:00:00	MIA
15237	4	23	1735	1649	46	2054	2015	B6	406	N956JT	JFK	SAN	327	2446	16	49	2023-04-23 16:00:00	Other
15247	4	13	2232	2130	62	28	2334	B6	339	N603JB	LGA	CHS	98	641	21	30	2023-04-13 21:00:00	Other
15254	8	1	1540	1459	41	1714	1644	UA	547	N495UA	EWR	RDU	68	416	14	59	2023-08-01 14:00:00	Other
15257	3	21	1319	1305	14	1416	1414	B6	327	N247JB	JFK	BOS	37	187	13	5	2023-03-21 13:00:00	BOS
15261	7	28	2025	1916	69	40	2313	B6	391	N527JL	EWR	SJU	198	1608	19	16	2023-07-28 19:00:00	Other
15263	1	11	1517	1200	197	1829	1518	UA	897	N67134	EWR	LAX	328	2454	12	0	2023-01-11 12:00:00	LAX
15265	10	25	1511	1459	12	1659	1653	9E	1523	N181GJ	LGA	RDU	66	431	14	59	2023-10-25 14:00:00	Other
15271	1	12	1539	1449	50	1941	1750	B6	656	N965JT	EWR	MCO	144	937	14	49	2023-01-12 14:00:00	MCO
15272	9	10	2053	1615	278	2150	1741	B6	354	N306JB	LGA	BOS	33	184	16	15	2023-09-10 16:00:00	BOS
15273	8	24	2333	2250	43	151	144	F9	740	N331FR	LGA	DFW	171	1389	22	50	2023-08-24 22:00:00	Other
15282	7	29	1333	1205	88	1458	1334	9E	1189	N931XJ	JFK	BUF	56	301	12	5	2023-07-29 12:00:00	Other
15297	8	15	2138	2120	18	2301	2246	YX	1389	N230JQ	LGA	BUF	49	292	21	20	2023-08-15 21:00:00	Other
15298	6	9	2115	2055	20	4	2357	B6	100	N760JB	EWR	FLL	139	1065	20	55	2023-06-09 20:00:00	FLL
15300	2	23	1432	1415	17	1752	1749	B6	736	N597JB	LGA	RSW	163	1080	14	15	2023-02-23 14:00:00	Other
15302	10	27	1517	1329	108	1918	1726	B6	277	N974JT	JFK	SJU	209	1598	13	29	2023-10-27 13:00:00	Other
15304	11	7	1939	1759	100	2205	2026	YX	1404	N425YX	LGA	IND	111	660	17	59	2023-11-07 17:00:00	Other
15307	3	21	1114	1100	14	1234	1236	YX	1380	N430YX	LGA	PIT	60	335	11	0	2023-03-21 11:00:00	Other
15309	11	13	2018	1944	34	2214	2147	AA	637	N865NN	EWR	CLT	84	529	19	44	2023-11-13 19:00:00	CLT
15310	1	9	1049	1000	49	1315	1219	AA	818	N357PV	LGA	CLT	85	544	10	0	2023-01-09 10:00:00	CLT
15317	3	14	1825	1545	160	2306	1907	UA	429	N57016	EWR	SFO	341	2565	15	45	2023-03-14 15:00:00	Other
15318	3	1	2028	1959	29	2301	2308	DL	562	N305DN	JFK	MCO	134	944	19	59	2023-03-01 19:00:00	MCO
15319	12	6	1940	1800	100	2149	2036	UA	845	N890UA	LGA	DEN	223	1620	18	0	2023-12-06 18:00:00	Other
15321	10	16	2124	1830	174	2347	2137	UA	638	N17963	EWR	SFO	292	2565	18	30	2023-10-16 18:00:00	Other
15322	3	24	1939	1430	309	2122	1622	AA	880	N774XF	LGA	RDU	78	431	14	30	2023-03-24 14:00:00	Other
15325	11	4	1040	1026	14	1228	1233	UA	486	N837UA	EWR	CLT	84	529	10	26	2023-11-04 10:00:00	CLT
15334	12	22	715	700	15	932	946	DL	173	N366NW	LGA	ATL	108	762	7	0	2023-12-22 07:00:00	ATL
15336	2	22	1949	1927	22	2113	2103	YX	998	N730YX	EWR	PIT	58	319	19	27	2023-02-22 19:00:00	Other
15342	4	23	1449	1355	54	1602	1525	B6	835	N375JB	JFK	BUF	53	301	13	55	2023-04-23 13:00:00	Other
15349	7	10	1247	1215	32	1501	1429	UA	595	N76505	LGA	DEN	223	1620	12	15	2023-07-10 12:00:00	Other
15356	10	10	1905	1800	65	2111	2022	YX	1289	N429YX	LGA	IND	100	660	18	0	2023-10-10 18:00:00	Other
15374	9	25	1900	1720	100	2021	1900	YX	1952	N224JQ	LGA	BNA	112	764	17	20	2023-09-25 17:00:00	Other
15378	7	18	2224	1754	270	2335	1929	B6	93	N198JB	JFK	PWM	43	273	17	54	2023-07-18 17:00:00	Other
15383	2	3	2013	1830	103	2203	2029	9E	1279	N538CA	LGA	RDU	74	431	18	30	2023-02-03 18:00:00	Other
15388	11	29	2031	1915	76	2317	2219	B6	737	N763JB	JFK	PBI	145	1028	19	15	2023-11-29 19:00:00	Other
15390	5	29	2007	1946	21	2344	2258	UA	788	N37514	EWR	FLL	161	1065	19	46	2023-05-29 19:00:00	FLL
15395	1	19	2053	2030	23	2312	2210	YX	1804	N880RW	LGA	PIT	68	335	20	30	2023-01-19 20:00:00	Other
15397	2	28	1949	1929	20	2114	2116	YX	1591	N208JQ	LGA	PIT	60	335	19	29	2023-02-28 19:00:00	Other
15400	2	9	957	751	126	1205	1027	UA	816	N19117	EWR	DEN	211	1605	7	51	2023-02-09 07:00:00	Other
15402	4	6	1736	1400	216	2034	1715	B6	489	N2016J	JFK	FLL	154	1069	14	0	2023-04-06 14:00:00	FLL
15403	11	22	1603	1538	25	1711	1654	YX	1386	N445YX	LGA	PHL	36	96	15	38	2023-11-22 15:00:00	Other
15404	1	26	2114	2020	54	2359	2329	YX	1297	N404YX	LGA	ATL	139	762	20	20	2023-01-26 20:00:00	ATL
15407	8	25	2252	2225	27	226	231	NK	813	N654NK	EWR	SJU	194	1608	22	25	2023-08-25 22:00:00	Other
15410	8	26	1515	1450	25	1641	1615	WN	298	N1801U	LGA	MDW	109	725	14	50	2023-08-26 14:00:00	Other
15419	9	9	1434	1410	24	NA	1610	9E	1506	N279PQ	JFK	CLE	NA	425	14	10	2023-09-09 14:00:00	Other
15420	12	17	1856	1820	36	2025	2015	WN	979	N1810U	LGA	STL	125	888	18	20	2023-12-17 18:00:00	Other
15421	1	11	1128	955	93	1426	1315	B6	1005	N537JT	JFK	MIA	149	1089	9	55	2023-01-11 09:00:00	MIA
15437	9	20	1711	1629	42	2037	1942	AA	487	N990AN	LGA	MIA	169	1096	16	29	2023-09-20 16:00:00	MIA
15439	3	3	1719	1625	54	1811	1737	9E	1539	N479PX	LGA	PVD	30	143	16	25	2023-03-03 16:00:00	Other
15446	3	27	929	905	24	1208	1142	B6	458	N236JB	JFK	ATL	127	760	9	5	2023-03-27 09:00:00	ATL
15447	11	22	2013	1920	53	2157	2107	YX	1797	N824MD	LGA	PIT	56	335	19	20	2023-11-22 19:00:00	Other
15453	9	8	18	2100	198	149	2252	YX	1862	N208JQ	JFK	PIT	53	340	21	0	2023-09-08 21:00:00	Other
15457	5	17	1716	1659	17	2020	2000	UA	741	N411UA	EWR	RSW	155	1068	16	59	2023-05-17 16:00:00	Other
15460	9	11	1942	1800	102	2255	2105	NK	865	N639NK	EWR	FLL	154	1065	18	0	2023-09-11 18:00:00	FLL
15471	3	11	1534	1500	34	1746	1657	YX	1762	N201JQ	LGA	STL	159	888	15	0	2023-03-11 15:00:00	Other
15477	4	27	2029	1935	54	2311	2132	AA	314	N847NN	EWR	CLT	91	529	19	35	2023-04-27 19:00:00	CLT
15478	3	13	1817	1749	28	2004	1950	YX	1128	N756YX	EWR	CMH	72	463	17	49	2023-03-13 17:00:00	Other
15481	6	28	1825	1730	55	2121	2040	B6	130	N580JB	JFK	BUR	335	2465	17	30	2023-06-28 17:00:00	Other
15498	7	18	2110	1930	100	2354	2229	UA	419	N27213	EWR	PBI	130	1023	19	30	2023-07-18 19:00:00	Other
15513	7	4	2130	2029	61	2258	2200	YX	1086	N869RW	LGA	BUF	46	292	20	29	2023-07-04 20:00:00	Other
15516	10	15	1814	1714	60	2124	2030	B6	988	N954JB	JFK	FLL	157	1069	17	14	2023-10-15 17:00:00	FLL
15520	9	11	2216	1930	166	106	2236	UA	697	N79541	EWR	SLC	265	1969	19	30	2023-09-11 19:00:00	Other
15522	2	22	852	755	57	1201	1110	AA	958	N861NN	EWR	MIA	158	1085	7	55	2023-02-22 07:00:00	MIA
15523	3	17	1228	1155	33	1554	1518	DL	313	N130DU	LGA	DFW	229	1389	11	55	2023-03-17 11:00:00	Other
15526	9	24	834	757	37	1125	1104	UA	601	N76523	EWR	FLL	146	1065	7	57	2023-09-24 07:00:00	FLL
15532	3	13	2330	2129	121	43	2300	UA	701	N27273	EWR	BNA	109	748	21	29	2023-03-13 21:00:00	Other
15535	5	28	1250	1229	21	1410	1413	AA	945	N805NN	LGA	ORD	106	733	12	29	2023-05-28 12:00:00	ORD
15539	12	16	1918	1859	19	2140	2151	UA	395	N36469	EWR	LAS	288	2227	18	59	2023-12-16 18:00:00	Other
15550	12	19	1949	1722	147	2135	1932	AA	647	N105UW	EWR	CLT	77	529	17	22	2023-12-19 17:00:00	CLT
15553	1	16	2056	2045	11	18	25	UA	771	N41140	EWR	SFO	327	2565	20	45	2023-01-16 20:00:00	Other
15554	7	1	1336	1325	11	1547	1557	B6	796	N623JB	LGA	ATL	104	762	13	25	2023-07-01 13:00:00	ATL
15562	2	28	1450	1347	63	1605	1502	B6	46	N267JB	JFK	BTV	44	266	13	47	2023-02-28 13:00:00	Other
15572	9	21	1012	930	42	1305	1220	AS	14	N493AS	JFK	SAN	322	2446	9	30	2023-09-21 09:00:00	Other
15574	1	19	1723	1710	13	1953	1907	YX	1905	N823MD	LGA	CLE	95	419	17	10	2023-01-19 17:00:00	Other
15575	1	19	2310	2153	77	29	2338	UA	596	N408UA	EWR	ORD	109	719	21	53	2023-01-19 21:00:00	ORD
15580	3	7	2127	1830	177	154	2210	B6	326	N979JT	JFK	SFO	399	2586	18	30	2023-03-07 18:00:00	Other
15582	7	26	1418	1350	28	1615	1610	YX	1397	N244JQ	LGA	CLT	79	544	13	50	2023-07-26 13:00:00	CLT
15599	7	10	1249	1135	74	1535	1441	DL	683	N362NB	LGA	PBI	140	1035	11	35	2023-07-10 11:00:00	Other
15600	8	3	1426	1359	27	1603	1536	9E	1255	N310PQ	LGA	BHM	116	866	13	59	2023-08-03 13:00:00	Other
15602	12	8	842	825	17	1150	1140	NK	571	N920NK	EWR	MIA	151	1085	8	25	2023-12-08 08:00:00	MIA
15603	9	10	2115	2100	15	2221	2224	YX	1801	N879RW	LGA	BOS	34	184	21	0	2023-09-10 21:00:00	BOS
15606	1	12	1752	1729	23	2107	2048	B6	192	N566JB	LGA	FLL	149	1076	17	29	2023-01-12 17:00:00	FLL
15616	8	17	2400	2225	95	353	231	NK	813	N612NK	EWR	SJU	201	1608	22	25	2023-08-17 22:00:00	Other
15617	6	3	2359	2140	139	214	2359	UA	680	N68822	EWR	SAV	102	708	21	40	2023-06-03 21:00:00	Other
15618	7	31	2212	2115	57	2336	2245	UA	104	N17753	EWR	BNA	103	748	21	15	2023-07-31 21:00:00	Other
15619	1	11	1000	759	121	1135	945	UA	1030	N810UA	EWR	RDU	68	416	7	59	2023-01-11 07:00:00	Other
15620	12	30	1650	1634	16	1927	2008	DL	279	N503DZ	JFK	SAN	319	2446	16	34	2023-12-30 16:00:00	Other
15622	1	13	1942	1815	87	2312	2132	NK	754	N674NK	EWR	FLL	169	1065	18	15	2023-01-13 18:00:00	FLL
15626	1	28	1012	956	16	1306	1255	UA	840	N24715	EWR	JAC	267	1874	9	56	2023-01-28 09:00:00	Other
15628	4	30	1632	1620	12	1959	1911	UA	123	N12116	EWR	MCO	154	937	16	20	2023-04-30 16:00:00	MCO
15630	11	25	2319	2100	139	36	2232	B6	330	N3085J	JFK	BOS	43	187	21	0	2023-11-25 21:00:00	BOS
15634	8	12	1706	1629	37	1940	1857	UA	572	N851UA	LGA	DEN	235	1620	16	29	2023-08-12 16:00:00	Other
15644	3	23	1807	1725	42	2043	2037	B6	719	N973JT	JFK	PBI	136	1028	17	25	2023-03-23 17:00:00	Other
15646	1	23	1343	1259	44	1525	1506	DL	843	N332NB	LGA	DTW	76	502	12	59	2023-01-23 12:00:00	Other
15653	7	4	1744	1710	34	2046	2006	DL	230	N503DZ	JFK	LAS	292	2248	17	10	2023-07-04 17:00:00	Other
15664	12	23	1719	1652	27	1925	1931	9E	1681	N324PQ	LGA	MCI	161	1107	16	52	2023-12-23 16:00:00	Other
15681	5	31	2035	1846	109	2151	2008	UA	667	N36272	EWR	BOS	48	200	18	46	2023-05-31 18:00:00	BOS
15703	8	22	2026	1935	51	2243	2250	DL	130	N178DN	JFK	LAX	294	2475	19	35	2023-08-22 19:00:00	LAX
15707	10	15	1837	1730	67	2024	1930	NK	47	N677NK	LGA	DTW	74	502	17	30	2023-10-15 17:00:00	Other
15715	4	14	1338	1323	15	1754	1632	B6	916	N809JB	JFK	MIA	225	1089	13	23	2023-04-14 13:00:00	MIA
15719	10	1	1457	1445	12	1727	1707	B6	685	N521JB	LGA	MSY	154	1183	14	45	2023-10-01 14:00:00	Other
15723	2	2	1045	1025	20	1243	1247	9E	1364	N582CA	LGA	MYR	97	563	10	25	2023-02-02 10:00:00	Other
15725	7	23	2142	1500	402	5	1707	B6	315	N504JB	JFK	DTW	91	509	15	0	2023-07-23 15:00:00	Other
15726	6	13	1014	945	29	1130	1133	9E	1451	N336PQ	LGA	BGR	53	378	9	45	2023-06-13 09:00:00	Other
15735	3	11	2314	2200	74	19	2324	UA	495	N34460	EWR	BUF	47	282	22	0	2023-03-11 22:00:00	Other
15737	3	2	1750	1729	21	2139	2039	AA	226	N951AA	JFK	MIA	161	1089	17	29	2023-03-02 17:00:00	MIA
15742	6	17	1055	917	98	1354	1231	AA	366	N107NN	JFK	SNA	323	2454	9	17	2023-06-17 09:00:00	Other
15744	10	18	1217	1135	42	1341	1329	YX	1333	N127HQ	JFK	RDU	65	427	11	35	2023-10-18 11:00:00	Other
15745	10	10	1121	1100	21	1216	1209	B6	58	N279JB	JFK	BOS	39	187	11	0	2023-10-10 11:00:00	BOS
15751	2	13	1210	955	135	1409	1145	B6	744	N228JB	LGA	BNA	141	764	9	55	2023-02-13 09:00:00	Other
15762	3	16	1745	1730	15	2021	2031	DL	107	N861DN	JFK	LAS	315	2248	17	30	2023-03-16 17:00:00	Other
15765	6	13	2004	1915	49	2307	2233	DL	585	N316DN	JFK	MCO	136	944	19	15	2023-06-13 19:00:00	MCO
15772	1	11	919	800	79	1218	1028	B6	122	N203JB	JFK	SAV	107	718	8	0	2023-01-11 08:00:00	Other
15778	4	10	906	759	67	1221	1108	AA	142	N926NN	LGA	MIA	158	1096	7	59	2023-04-10 07:00:00	MIA
15785	3	6	1724	1659	25	1833	1812	UA	731	N826UA	EWR	BOS	47	200	16	59	2023-03-06 16:00:00	BOS
15786	7	27	810	750	20	949	946	9E	1186	N936XJ	JFK	RDU	67	427	7	50	2023-07-27 07:00:00	Other
15793	6	11	2327	1735	352	44	1917	UA	673	N27722	EWR	CLE	63	404	17	35	2023-06-11 17:00:00	Other
15803	2	26	1724	1656	28	1911	1836	AA	812	N979NN	EWR	ORD	131	719	16	56	2023-02-26 16:00:00	ORD
15807	11	16	1923	1840	43	2047	2020	WN	1114	N567WN	LGA	BNA	109	764	18	40	2023-11-16 18:00:00	Other
15808	6	3	1106	1045	21	1325	1319	UA	738	N27964	EWR	IAH	161	1400	10	45	2023-06-03 10:00:00	Other
15815	4	4	632	620	12	1109	816	AA	849	N109UW	EWR	CLT	NA	529	6	20	2023-04-04 06:00:00	CLT
15818	4	23	2111	1705	246	39	2010	NK	582	N660NK	EWR	FLL	154	1065	17	5	2023-04-23 17:00:00	FLL
15820	2	18	2204	2140	24	46	41	B6	394	N805JB	JFK	PBI	139	1028	21	40	2023-02-18 21:00:00	Other
15830	1	25	1027	959	28	1310	1304	B6	457	N339JB	JFK	MCO	141	944	9	59	2023-01-25 09:00:00	MCO
15833	9	19	2031	2000	31	2314	2312	UA	630	N37527	EWR	SMF	318	2500	20	0	2023-09-19 20:00:00	Other
15837	5	29	826	730	56	958	907	9E	1431	N905XJ	LGA	ORF	63	296	7	30	2023-05-29 07:00:00	Other
15838	7	15	1029	630	239	1217	838	AA	288	N904AN	JFK	CLT	78	541	6	30	2023-07-15 06:00:00	CLT
15844	7	10	1213	924	169	1449	1235	AA	302	N116AN	JFK	SNA	300	2454	9	24	2023-07-10 09:00:00	Other
15851	8	25	1004	845	79	1133	1027	DL	299	N112DU	LGA	ORD	116	733	8	45	2023-08-25 08:00:00	ORD
15864	9	10	1127	1050	37	1418	1230	YX	1816	N233JQ	LGA	BNA	114	764	10	50	2023-09-10 10:00:00	Other
15866	3	13	2134	2105	29	59	50	AA	54	N107NN	JFK	SFO	345	2586	21	5	2023-03-13 21:00:00	Other
15880	6	11	2338	2210	88	154	36	NK	280	N936NK	EWR	LAS	295	2227	22	10	2023-06-11 22:00:00	Other
15881	10	6	1336	1303	33	1520	1508	AA	721	N990AN	LGA	CLT	82	544	13	3	2023-10-06 13:00:00	CLT
15889	2	20	1702	1651	11	1959	1959	UA	640	N17294	EWR	MIA	153	1085	16	51	2023-02-20 16:00:00	MIA
15896	4	30	1025	859	86	1443	1208	UA	384	N854UA	EWR	MIA	178	1085	8	59	2023-04-30 08:00:00	MIA
15897	1	12	1331	1311	20	1641	1626	UA	199	N846UA	EWR	AUS	216	1504	13	11	2023-01-12 13:00:00	Other
15903	3	14	1014	940	34	1544	1344	UA	602	N75425	EWR	SJU	219	1608	9	40	2023-03-14 09:00:00	Other
15905	2	28	1556	1525	31	1749	1730	WN	598	N8673F	LGA	STL	144	888	15	25	2023-02-28 15:00:00	Other
15906	12	11	2142	1959	103	49	2304	B6	412	N639JB	LGA	MCO	148	950	19	59	2023-12-11 19:00:00	MCO
15907	4	1	909	830	39	1319	1227	B6	193	N994JL	JFK	SJU	192	1598	8	30	2023-04-01 08:00:00	Other
15908	10	5	2040	1604	276	2245	1831	B6	25	N662JB	JFK	MSY	151	1182	16	4	2023-10-05 16:00:00	Other
15925	1	20	1935	1859	36	2251	2216	UA	755	N39450	EWR	RSW	153	1068	18	59	2023-01-20 18:00:00	Other
15931	3	11	2135	2048	47	17	2357	UA	280	N823UA	EWR	FLL	135	1065	20	48	2023-03-11 20:00:00	FLL
15933	6	6	1705	1650	15	1929	1855	WN	122	N8851Q	LGA	MCI	150	1107	16	50	2023-06-06 16:00:00	Other
15943	1	19	2002	1929	33	2201	2103	YX	1766	N210JQ	LGA	DCA	68	214	19	29	2023-01-19 19:00:00	Other
15953	7	12	2153	2114	39	1	2344	UA	224	N27256	EWR	LAS	281	2227	21	14	2023-07-12 21:00:00	Other
15955	11	16	1844	1755	49	2140	2100	B6	263	N649JB	LGA	MCO	138	950	17	55	2023-11-16 17:00:00	MCO
15957	12	27	17	2105	192	310	2357	UA	503	N69885	EWR	MCO	153	937	21	5	2023-12-27 21:00:00	MCO
15958	3	28	1759	1555	124	2029	1827	NK	425	N608NK	EWR	ATL	123	746	15	55	2023-03-28 15:00:00	ATL
15959	4	18	1125	1050	35	1323	1235	NK	393	N942NK	EWR	MYR	83	550	10	50	2023-04-18 10:00:00	Other
15961	12	30	954	901	53	1319	1215	UA	299	N17104	EWR	FLL	181	1065	9	1	2023-12-30 09:00:00	FLL
15966	6	7	1609	1530	39	1757	1733	9E	1511	N482PX	LGA	GSO	73	461	15	30	2023-06-07 15:00:00	Other
15968	7	19	1125	1105	20	1249	1243	9E	1313	N676CA	LGA	BUF	47	292	11	5	2023-07-19 11:00:00	Other
15969	10	27	2005	1645	200	2219	1911	UA	909	N656UA	EWR	PHX	280	2133	16	45	2023-10-27 16:00:00	Other
15970	6	5	2019	1947	32	2303	2256	DL	856	N361NB	LGA	TPA	138	1010	19	47	2023-06-05 19:00:00	Other
15974	7	21	1325	1129	116	1507	1237	YX	1074	N444YX	JFK	ORH	32	150	11	29	2023-07-21 11:00:00	Other
15976	3	19	834	750	44	1131	1117	B6	688	N935JB	EWR	LAX	332	2454	7	50	2023-03-19 07:00:00	LAX
15979	4	3	1741	1730	11	2059	2039	AS	87	N928AK	EWR	PDX	342	2434	17	30	2023-04-03 17:00:00	Other
15983	4	18	919	838	41	1228	1152	UA	291	N12125	EWR	SAN	338	2425	8	38	2023-04-18 08:00:00	Other
15985	12	19	2011	2000	11	2335	2337	UA	363	N34137	EWR	SFO	335	2565	20	0	2023-12-19 20:00:00	Other
15990	11	20	906	855	11	1015	1020	UA	442	N814UA	EWR	ORF	52	284	8	55	2023-11-20 08:00:00	Other
15995	1	11	1001	600	241	1143	735	WN	940	N8512U	LGA	MDW	114	725	6	0	2023-01-11 06:00:00	Other
15998	6	16	1045	1006	39	1226	1132	YX	1073	N642RW	EWR	IAD	70	212	10	6	2023-06-16 10:00:00	Other
15999	5	9	1548	1525	23	1713	1710	WN	845	N8547V	LGA	STL	129	888	15	25	2023-05-09 15:00:00	Other
16011	12	14	1835	1824	11	2047	2107	DL	789	N963AT	EWR	ATL	103	746	18	24	2023-12-14 18:00:00	ATL
16014	6	30	2340	1950	230	143	2148	AA	340	N927NN	EWR	CLT	71	529	19	50	2023-06-30 19:00:00	CLT
16015	3	5	1743	1630	73	2045	1945	NK	339	N684NK	LGA	FLL	145	1076	16	30	2023-03-05 16:00:00	FLL
16022	6	16	1556	1429	87	1759	1648	YX	1254	N728YX	EWR	IND	108	645	14	29	2023-06-16 14:00:00	Other
16027	9	18	1045	1025	20	1339	1326	DL	362	N113DQ	JFK	SAT	210	1587	10	25	2023-09-18 10:00:00	Other
16030	11	15	1541	1527	14	1726	1724	YX	1279	N403YX	LGA	CLE	70	419	15	27	2023-11-15 15:00:00	Other
16035	2	1	2019	1830	109	2221	2029	9E	1279	N491PX	LGA	RDU	80	431	18	30	2023-02-01 18:00:00	Other
16042	5	5	2240	2159	41	226	205	B6	285	N562JB	JFK	PSE	195	1617	21	59	2023-05-05 21:00:00	Other
16051	3	14	2215	2156	19	7	2358	UA	752	N67845	EWR	DTW	73	488	21	56	2023-03-14 21:00:00	Other
16052	10	5	2041	2015	26	2308	2310	DL	411	N375DN	LGA	MCO	125	950	20	15	2023-10-05 20:00:00	MCO
16072	10	2	2130	2033	57	2321	2247	9E	1637	N919XJ	LGA	CAE	85	617	20	33	2023-10-02 20:00:00	Other
16073	1	19	1749	1702	47	2141	2045	AA	1063	N433AN	EWR	PHX	303	2133	17	2	2023-01-19 17:00:00	Other
16083	4	6	655	600	55	843	747	9E	1428	N916XJ	LGA	STL	131	888	6	0	2023-04-06 06:00:00	Other
16086	3	24	1654	1630	24	2020	2008	B6	237	N987JT	JFK	SFO	363	2586	16	30	2023-03-24 16:00:00	Other
16088	12	4	1746	1711	35	1933	1914	AA	647	N169UW	EWR	CLT	79	529	17	11	2023-12-04 17:00:00	CLT
16093	8	13	1129	1112	17	1444	1428	DL	723	N324DX	LGA	FLL	174	1076	11	12	2023-08-13 11:00:00	FLL
16107	3	14	1622	1600	22	1806	1720	AA	180	N814AW	LGA	DCA	48	214	16	0	2023-03-14 16:00:00	Other
16108	9	6	1108	1030	38	1404	1337	B6	826	N625JB	JFK	FLL	150	1069	10	30	2023-09-06 10:00:00	FLL
16110	4	23	1826	1744	42	2123	2055	B6	641	N952JB	JFK	PBI	142	1028	17	44	2023-04-23 17:00:00	Other
16112	4	27	1559	1125	274	1738	1312	OO	1031	N310SY	JFK	ORD	126	740	11	25	2023-04-27 11:00:00	ORD
16120	5	21	1804	1710	54	2010	1955	DL	156	N3735D	LGA	DEN	218	1620	17	10	2023-05-21 17:00:00	Other
16122	5	28	1709	1645	24	1922	1910	WN	361	N8697C	LGA	DEN	227	1620	16	45	2023-05-28 16:00:00	Other
16123	6	23	2058	1959	59	2357	2258	DL	473	N332DN	LGA	MCO	153	950	19	59	2023-06-23 19:00:00	MCO
16130	8	25	1543	1215	208	1727	1408	YX	1039	N137HQ	LGA	CMH	73	479	12	15	2023-08-25 12:00:00	Other
16131	1	1	537	520	17	926	818	UA	206	N13113	EWR	IAH	258	1400	5	20	2023-01-01 05:00:00	Other
16135	8	1	1756	1539	137	2002	1804	B6	717	N354JB	JFK	CHS	93	636	15	39	2023-08-01 15:00:00	Other
16136	12	17	859	840	19	1148	1138	DL	174	N522DA	JFK	DEN	227	1626	8	40	2023-12-17 08:00:00	Other
16149	3	23	924	848	36	1124	1112	9E	1442	N181GJ	LGA	CHS	93	641	8	48	2023-03-23 08:00:00	Other
16169	5	26	1515	1400	75	1752	1701	AA	948	N905AN	LGA	DFW	181	1389	14	0	2023-05-26 14:00:00	Other
16170	5	27	1007	946	21	1409	1341	UA	582	N69840	EWR	SJU	208	1608	9	46	2023-05-27 09:00:00	Other
16176	1	26	1019	959	20	1208	1144	UA	88	N69829	EWR	RDU	78	416	9	59	2023-01-26 09:00:00	Other
16182	1	25	9	2200	129	304	59	NK	790	N686NK	EWR	MCO	157	937	22	0	2023-01-25 22:00:00	MCO
16186	7	6	2158	2025	93	7	2247	B6	649	N796JB	LGA	MSY	151	1183	20	25	2023-07-06 20:00:00	Other
16188	10	27	1114	1100	14	1350	1335	NK	138	N646NK	EWR	LAS	317	2227	11	0	2023-10-27 11:00:00	Other
16191	6	10	854	705	109	1127	1005	DL	377	N314NB	LGA	PBI	134	1035	7	5	2023-06-10 07:00:00	Other
16192	4	14	1023	900	83	1352	1202	B6	331	N354JB	JFK	PBI	183	1028	9	0	2023-04-14 09:00:00	Other
16215	12	16	1859	1829	30	2159	2150	AS	158	N280AK	EWR	SEA	342	2402	18	29	2023-12-16 18:00:00	Other
16230	6	26	1437	1107	210	NA	1416	UA	161	N64809	EWR	FLL	NA	1065	11	7	2023-06-26 11:00:00	FLL
16231	4	11	1555	1531	24	1803	1812	B6	602	N612JB	JFK	ATL	99	760	15	31	2023-04-11 15:00:00	ATL
16233	2	15	840	829	11	1216	1213	AA	929	N834NN	JFK	AUS	229	1521	8	29	2023-02-15 08:00:00	Other
16242	3	27	1632	1549	43	1942	1849	UA	791	N482UA	EWR	RSW	164	1068	15	49	2023-03-27 15:00:00	Other
16246	3	20	1923	1845	38	2230	2152	NK	689	N676NK	EWR	FLL	159	1065	18	45	2023-03-20 18:00:00	FLL
16253	1	12	2118	1950	88	2352	2159	YX	1312	N403YX	JFK	RDU	82	427	19	50	2023-01-12 19:00:00	Other
16279	10	7	2118	2104	14	2322	2339	UA	574	N17285	EWR	LAS	279	2227	21	4	2023-10-07 21:00:00	Other
16281	3	26	1306	1130	96	1514	1335	AA	106	N908NN	LGA	CLT	101	544	11	30	2023-03-26 11:00:00	CLT
16287	6	3	850	759	51	1033	1004	AA	1030	N977NN	LGA	CLT	77	544	7	59	2023-06-03 07:00:00	CLT
16290	3	20	1504	1420	44	1623	1545	WN	414	N7814B	LGA	MDW	106	725	14	20	2023-03-20 14:00:00	Other
16294	5	25	1401	1325	36	1608	1550	UA	433	N14249	EWR	ATL	102	746	13	25	2023-05-25 13:00:00	ATL
16303	2	3	1604	1530	34	1918	1850	B6	527	N615JB	EWR	MIA	165	1085	15	30	2023-02-03 15:00:00	MIA
16307	9	18	1022	959	23	1249	1232	YX	1947	N244JQ	LGA	HHH	111	701	9	59	2023-09-18 09:00:00	Other
16314	5	20	1631	1614	17	1853	1836	UA	482	N17233	EWR	JAX	112	820	16	14	2023-05-20 16:00:00	Other
16315	1	16	1831	1815	16	2032	2027	9E	1565	N604LR	LGA	DSM	143	1031	18	15	2023-01-16 18:00:00	Other
16320	7	9	1006	710	176	1343	1003	UA	549	N27258	EWR	PDX	328	2434	7	10	2023-07-09 07:00:00	Other
16328	4	22	1724	1521	123	2018	1809	UA	245	N432UA	EWR	MCO	139	937	15	21	2023-04-22 15:00:00	MCO
16329	6	6	1526	1502	24	1857	1754	AA	159	N316RK	LGA	DFW	198	1389	15	2	2023-06-06 15:00:00	Other
16333	3	29	1703	1647	16	1923	1910	UA	730	N33714	EWR	ATL	112	746	16	47	2023-03-29 16:00:00	ATL
16339	8	8	1603	1546	17	1757	1735	YX	1342	N220JQ	JFK	DCA	49	213	15	46	2023-08-08 15:00:00	Other
16350	4	20	2231	2159	32	235	205	B6	281	N561JB	JFK	PSE	203	1617	21	59	2023-04-20 21:00:00	Other
16358	7	31	2011	1945	26	2252	2212	UA	603	N39423	EWR	DEN	252	1605	19	45	2023-07-31 19:00:00	Other
16363	5	2	1447	1240	127	1823	1552	AA	644	N442AN	JFK	MIA	173	1089	12	40	2023-05-02 12:00:00	MIA
16366	11	6	2059	1929	90	2231	2123	YX	1837	N232JQ	LGA	BNA	114	764	19	29	2023-11-06 19:00:00	Other
16368	1	8	1524	1500	24	1734	1729	UA	794	N19117	EWR	DEN	223	1605	15	0	2023-01-08 15:00:00	Other
16373	6	11	1636	1549	47	1834	1743	AA	855	N897NN	JFK	ORD	123	740	15	49	2023-06-11 15:00:00	ORD
16375	12	7	2210	2059	71	2341	2238	UA	506	N801UA	EWR	MSN	124	799	20	59	2023-12-07 20:00:00	Other
16376	8	25	1944	1930	14	2257	2247	B6	297	N663JB	JFK	PDX	328	2454	19	30	2023-08-25 19:00:00	Other
16380	11	22	1705	1558	67	2051	1920	DL	383	N3773D	LGA	MIA	158	1096	15	58	2023-11-22 15:00:00	MIA
16384	8	1	1606	1513	53	1934	1806	UA	617	N47280	EWR	TPA	129	997	15	13	2023-08-01 15:00:00	Other
16392	6	28	759	610	109	926	745	DL	478	N121DU	LGA	ORD	110	733	6	10	2023-06-28 06:00:00	ORD
16397	8	6	1954	1929	25	2217	2204	9E	1211	N132EV	JFK	MSP	141	1029	19	29	2023-08-06 19:00:00	Other
16403	10	7	2102	1910	112	2306	2122	9E	1611	N131EV	JFK	CVG	91	589	19	10	2023-10-07 19:00:00	Other
16413	8	6	2109	2000	69	25	2309	B6	651	N793JB	JFK	RNO	316	2411	20	0	2023-08-06 20:00:00	Other
16418	4	12	1321	935	226	NA	1250	B6	62	N592JB	EWR	FLL	NA	1065	9	35	2023-04-12 09:00:00	FLL
16420	10	17	2040	2010	30	2253	2301	B6	24	N809JB	JFK	ABQ	232	1826	20	10	2023-10-17 20:00:00	Other
16421	5	8	1935	1855	40	2218	2153	DL	284	N118DU	LGA	DFW	183	1389	18	55	2023-05-08 18:00:00	Other
16422	10	4	1555	1535	20	1719	1707	UA	661	N37534	EWR	ORD	109	719	15	35	2023-10-04 15:00:00	ORD
16423	5	15	1813	1750	23	2047	2101	B6	753	N561JB	JFK	PBI	138	1028	17	50	2023-05-15 17:00:00	Other
16425	6	6	1529	1048	281	1824	1316	F9	580	N387FR	LGA	ATL	105	762	10	48	2023-06-06 10:00:00	ATL
16431	9	11	746	645	61	1025	919	UA	217	N37502	EWR	LAS	296	2227	6	45	2023-09-11 06:00:00	Other
16433	1	11	2004	1829	95	2222	2050	9E	1416	N319PQ	LGA	CHS	93	641	18	29	2023-01-11 18:00:00	Other
16447	5	19	1400	1330	30	1627	1603	B6	940	N535JB	LGA	ATL	107	762	13	30	2023-05-19 13:00:00	ATL
16452	3	26	2022	1922	60	2336	2237	UA	762	N33714	EWR	SEA	330	2402	19	22	2023-03-26 19:00:00	Other
16457	9	29	1927	1739	108	2123	1949	9E	1470	N294PQ	LGA	LIT	142	1085	17	39	2023-09-29 17:00:00	Other
16459	4	21	1213	1147	26	1509	1438	UA	487	N17730	EWR	SRQ	135	1034	11	47	2023-04-21 11:00:00	Other
16462	6	15	1925	1859	26	2049	2039	YX	1241	N753YX	EWR	PIT	52	319	18	59	2023-06-15 18:00:00	Other
16465	1	23	1607	1555	12	1715	1735	WN	958	N8699A	LGA	MDW	108	725	15	55	2023-01-23 15:00:00	Other
16466	6	4	1919	1729	110	2101	1912	UA	102	N33284	EWR	RDU	66	416	17	29	2023-06-04 17:00:00	Other
16468	1	31	1602	1545	17	1744	1732	YX	1293	N872RW	LGA	RIC	58	292	15	45	2023-01-31 15:00:00	Other
16480	8	17	917	830	47	1042	957	UA	236	N474UA	EWR	BNA	100	748	8	30	2023-08-17 08:00:00	Other
16486	11	28	1119	1059	20	1411	1417	DL	253	N117DU	LGA	DFW	202	1389	10	59	2023-11-28 10:00:00	Other
16488	8	21	745	630	75	1059	924	UA	708	N14115	EWR	LAX	281	2454	6	30	2023-08-21 06:00:00	LAX
16497	8	6	1819	1808	11	2115	2058	UA	510	N76265	EWR	MCO	123	937	18	8	2023-08-06 18:00:00	MCO
16500	9	11	1636	1610	26	NA	1743	YX	1363	N871RW	LGA	CHO	NA	305	16	10	2023-09-11 16:00:00	Other
16507	1	5	2058	2045	13	2338	2355	DL	323	N802DN	JFK	LAS	305	2248	20	45	2023-01-05 20:00:00	Other
16528	8	18	1558	1459	59	1909	1822	B6	422	N506JB	JFK	FLL	147	1069	14	59	2023-08-18 14:00:00	FLL
16537	7	28	1214	1100	74	1410	1320	B6	111	N531JL	LGA	DEN	212	1620	11	0	2023-07-28 11:00:00	Other
16538	11	27	803	715	48	1032	955	WN	203	N483WN	LGA	ATL	122	762	7	15	2023-11-27 07:00:00	ATL
16542	12	27	2151	2059	52	2335	2233	B6	162	N229JB	JFK	ROC	56	264	20	59	2023-12-27 20:00:00	Other
16543	5	31	1949	1856	53	2140	2101	UA	704	N78448	EWR	CLT	76	529	18	56	2023-05-31 18:00:00	CLT
16544	4	3	2049	2020	29	2307	2300	DL	318	N352DN	LGA	ATL	111	762	20	20	2023-04-03 20:00:00	ATL
16545	2	3	1945	1905	40	2254	2222	AS	91	N428AS	EWR	SAN	346	2425	19	5	2023-02-03 19:00:00	Other
16549	7	26	1023	956	27	1310	1259	UA	119	N416UA	EWR	RSW	144	1068	9	56	2023-07-26 09:00:00	Other
16558	1	25	1857	1837	20	2315	2155	UA	428	N844UA	EWR	MIA	201	1085	18	37	2023-01-25 18:00:00	MIA
16565	7	21	2122	2010	72	119	2356	B6	271	N923JB	JFK	SFO	338	2586	20	10	2023-07-21 20:00:00	Other
16571	9	11	911	900	11	1011	1030	WN	1274	N8324A	LGA	MDW	103	725	9	0	2023-09-11 09:00:00	Other
16583	1	17	819	758	21	1112	1122	AA	658	N853NN	LGA	MIA	147	1096	7	58	2023-01-17 07:00:00	MIA
16585	3	30	1029	1000	29	1235	1201	B6	65	N247JB	JFK	DTW	95	509	10	0	2023-03-30 10:00:00	Other
16589	9	13	1444	1342	62	1601	1458	B6	557	N317JB	JFK	BOS	46	187	13	42	2023-09-13 13:00:00	BOS
16593	4	21	1713	1659	14	2014	2007	UA	531	N489UA	EWR	FLL	155	1065	16	59	2023-04-21 16:00:00	FLL
16596	8	15	1952	1600	232	2133	1740	AA	604	N896NN	LGA	ORD	108	733	16	0	2023-08-15 16:00:00	ORD
16607	10	25	2103	2047	16	2327	2314	UA	229	N69816	EWR	ATL	103	746	20	47	2023-10-25 20:00:00	ATL
16617	4	23	755	730	25	948	955	WN	490	N268WN	LGA	DEN	213	1620	7	30	2023-04-23 07:00:00	Other
16621	9	17	2030	2002	28	2231	2152	YX	1373	N421YX	JFK	PIT	66	340	20	2	2023-09-17 20:00:00	Other
16663	2	18	1431	1406	25	1654	1635	UA	765	N61887	EWR	DEN	239	1605	14	6	2023-02-18 14:00:00	Other
16666	8	8	1437	1359	38	1638	1639	DL	148	N329DN	LGA	ATL	105	762	13	59	2023-08-08 13:00:00	ATL
16669	7	15	2109	1559	310	102	1907	UA	400	N67845	EWR	SEA	328	2402	15	59	2023-07-15 15:00:00	Other
16674	1	4	1648	1635	13	1820	1816	B6	883	N323JB	LGA	BNA	128	764	16	35	2023-01-04 16:00:00	Other
16676	7	20	153	2245	188	409	108	F9	472	N326FR	LGA	ATL	103	762	22	45	2023-07-20 22:00:00	ATL
16677	2	3	1441	1425	16	1754	1743	B6	316	N568JB	LGA	PBI	158	1035	14	25	2023-02-03 14:00:00	Other
16680	4	30	2025	1930	55	2325	2257	AA	42	N102NN	JFK	LAX	311	2475	19	30	2023-04-30 19:00:00	LAX
16682	5	25	712	700	12	1017	1007	UA	270	N459UA	EWR	FLL	156	1065	7	0	2023-05-25 07:00:00	FLL
16690	5	6	1525	1455	30	1812	1810	B6	526	N607JB	JFK	FLL	149	1069	14	55	2023-05-06 14:00:00	FLL
16700	11	10	1631	1540	51	1857	1818	B6	595	N2084J	JFK	JAX	128	828	15	40	2023-11-10 15:00:00	Other
16708	7	16	1648	1624	24	1753	1750	UA	601	N37554	EWR	IAD	44	212	16	24	2023-07-16 16:00:00	Other
16710	6	14	1414	1400	14	1645	1530	YX	1848	N211JQ	LGA	BOS	44	184	14	0	2023-06-14 14:00:00	BOS
16712	11	25	2130	2029	61	29	2340	B6	61	N3112J	JFK	TPA	153	1005	20	29	2023-11-25 20:00:00	Other
16726	1	3	2132	1929	123	41	2239	UA	454	N37253	EWR	DFW	214	1372	19	29	2023-01-03 19:00:00	Other
16731	7	2	1610	1559	11	1824	1843	DL	168	N309US	LGA	ATL	110	762	15	59	2023-07-02 15:00:00	ATL
16746	7	18	2258	1950	188	108	2217	9E	1143	N676CA	LGA	IND	106	660	19	50	2023-07-18 19:00:00	Other
16753	8	24	1323	1051	152	1524	1316	9E	1136	N478PX	LGA	IND	103	660	10	51	2023-08-24 10:00:00	Other
16755	9	9	838	815	23	1008	953	YX	1793	N823MD	LGA	BNA	116	764	8	15	2023-09-09 08:00:00	Other
16759	9	29	2311	2059	132	146	15	DL	163	N537DT	JFK	SAN	309	2446	20	59	2023-09-29 20:00:00	Other
16760	9	17	1728	1705	23	1838	1825	WN	638	N920WN	LGA	MDW	107	725	17	5	2023-09-17 17:00:00	Other
16763	3	25	1037	959	38	1357	1303	NK	272	N632NK	LGA	MCO	145	950	9	59	2023-03-25 09:00:00	MCO
16772	8	16	1313	1259	14	1431	1438	9E	1149	N925XJ	LGA	RIC	53	292	12	59	2023-08-16 12:00:00	Other
16775	11	11	1026	915	71	1330	1245	DL	110	N503DZ	JFK	SLC	285	1990	9	15	2023-11-11 09:00:00	Other
16785	7	28	2239	2045	114	128	2256	DL	393	N320NB	LGA	MSY	171	1183	20	45	2023-07-28 20:00:00	Other
16787	10	6	1552	1530	22	1830	1833	UA	454	N12125	EWR	LAX	306	2454	15	30	2023-10-06 15:00:00	LAX
16790	1	16	1121	1100	21	1406	1406	AA	104	N774AN	JFK	MIA	143	1089	11	0	2023-01-16 11:00:00	MIA
16797	8	6	1655	1550	65	1935	1816	9E	1103	N309PQ	LGA	CLT	83	544	15	50	2023-08-06 15:00:00	CLT
16800	10	28	1457	1342	75	1642	1544	AA	606	N870NN	EWR	CLT	80	529	13	42	2023-10-28 13:00:00	CLT
16803	6	29	1504	1440	24	1721	1655	WN	473	N7848A	LGA	MSY	155	1183	14	40	2023-06-29 14:00:00	Other
16804	9	11	1914	1630	164	2236	1935	B6	776	N943JT	EWR	LAX	336	2454	16	30	2023-09-11 16:00:00	LAX
16808	9	27	2139	2029	70	2245	2209	AA	124	N765US	LGA	ORD	102	733	20	29	2023-09-27 20:00:00	ORD
16811	4	23	648	545	63	957	851	AA	409	N908AN	EWR	MIA	157	1085	5	45	2023-04-23 05:00:00	MIA
16813	1	14	1302	1200	62	1536	1515	DL	337	N357NB	LGA	TPA	130	1010	12	0	2023-01-14 12:00:00	Other
16832	11	26	1123	955	88	1704	1618	DL	99	N844MH	JFK	HNL	611	4983	9	55	2023-11-26 09:00:00	Other
16841	5	5	1943	1929	14	2131	2147	9E	1513	N302PQ	JFK	DTW	81	509	19	29	2023-05-05 19:00:00	Other
16850	10	9	1341	1325	16	1640	1632	B6	110	N526JL	LGA	FLL	162	1076	13	25	2023-10-09 13:00:00	FLL
16854	4	17	1005	755	130	1251	1113	AS	86	N929VA	EWR	LAX	315	2454	7	55	2023-04-17 07:00:00	LAX
16856	10	6	718	705	13	945	928	UA	367	N37534	EWR	DEN	235	1605	7	5	2023-10-06 07:00:00	Other
16868	11	2	2023	1959	24	2201	2138	OO	1198	N243SY	LGA	MKE	124	738	19	59	2023-11-02 19:00:00	Other
16875	1	25	2104	2030	34	8	6	AA	57	N105NN	JFK	LAX	334	2475	20	30	2023-01-25 20:00:00	LAX
16885	6	1	2017	1950	27	2157	2152	9E	1432	N691CA	LGA	GSO	72	461	19	50	2023-06-01 19:00:00	Other
16886	4	15	1954	1510	284	2113	1642	YX	1566	N818MD	LGA	ROC	52	254	15	10	2023-04-15 15:00:00	Other
16892	5	20	1935	1830	65	2241	2155	DL	125	N827DN	JFK	SEA	310	2422	18	30	2023-05-20 18:00:00	Other
16894	6	27	1625	1519	66	1836	1735	DL	389	N123DW	LGA	MSP	155	1020	15	19	2023-06-27 15:00:00	Other
16896	9	24	1500	1447	13	1807	1752	UA	521	N446UA	EWR	MIA	165	1085	14	47	2023-09-24 14:00:00	MIA
16904	6	24	1133	1459	1234	1512	1842	UA	474	N17279	EWR	ANC	416	3370	14	59	2023-06-24 14:00:00	Other
16907	1	3	1218	1159	19	1323	1327	YX	1846	N233JQ	LGA	BOS	37	184	11	59	2023-01-03 11:00:00	BOS
16911	2	3	1959	1850	69	2223	2120	9E	1331	N676CA	LGA	SAV	104	722	18	50	2023-02-03 18:00:00	Other
16924	8	28	1033	815	138	1327	1128	B6	197	N775JB	JFK	FLL	150	1069	8	15	2023-08-28 08:00:00	FLL
16926	9	28	2140	2015	85	2300	2154	UA	426	N38451	EWR	ORD	104	719	20	15	2023-09-28 20:00:00	ORD
16935	4	28	1501	1410	51	1743	1656	UA	372	N66831	EWR	MCO	134	937	14	10	2023-04-28 14:00:00	MCO
16944	4	5	1458	1110	228	1755	1258	YX	1020	N747YX	LGA	ORD	173	733	11	10	2023-04-05 11:00:00	ORD
16954	9	7	846	715	91	957	846	YX	1928	N225JQ	LGA	BNA	106	764	7	15	2023-09-07 07:00:00	Other
16957	8	25	919	730	109	1040	911	DL	335	N109DU	LGA	ORD	114	733	7	30	2023-08-25 07:00:00	ORD
16958	10	4	1501	1450	11	1734	1759	DL	329	N303DU	LGA	PBI	134	1035	14	50	2023-10-04 14:00:00	Other
16968	7	19	1842	1702	100	2149	2014	B6	64	N580JB	JFK	TPA	133	1005	17	2	2023-07-19 17:00:00	Other
16976	7	5	2350	2225	85	330	222	NK	837	N605NK	EWR	SJU	194	1608	22	25	2023-07-05 22:00:00	Other
16979	10	30	1510	1448	22	1645	1615	YX	1086	N745YX	EWR	IAD	57	212	14	48	2023-10-30 14:00:00	Other
16982	12	30	756	525	151	1127	825	B6	41	N636JB	EWR	PBI	176	1023	5	25	2023-12-30 05:00:00	Other
16991	12	24	1837	1825	12	2128	2130	WN	818	N8713M	LGA	TPA	142	1010	18	25	2023-12-24 18:00:00	Other
16998	3	23	1808	1659	69	2048	2005	UA	594	N495UA	EWR	FLL	140	1065	16	59	2023-03-23 16:00:00	FLL
17000	10	27	830	800	30	1158	1103	DL	156	N844MH	JFK	LAX	337	2475	8	0	2023-10-27 08:00:00	LAX
17003	1	17	1644	1600	44	2002	1957	DL	464	N180DN	JFK	SFO	334	2586	16	0	2023-01-17 16:00:00	Other
17006	2	26	713	700	13	1009	1002	UA	776	N27256	EWR	PBI	145	1023	7	0	2023-02-26 07:00:00	Other
17012	8	25	737	710	27	1038	1008	DL	433	N358NB	LGA	TPA	137	1010	7	10	2023-08-25 07:00:00	Other
17016	4	29	1059	1020	39	1357	1312	UA	652	N29971	EWR	IAH	192	1400	10	20	2023-04-29 10:00:00	Other
17032	3	11	1144	1130	14	1315	1310	UA	586	N13750	EWR	RDU	70	416	11	30	2023-03-11 11:00:00	Other
17034	4	3	1858	1847	11	2156	2148	UA	736	N68880	EWR	TPA	136	997	18	47	2023-04-03 18:00:00	Other
17042	2	11	1558	1430	88	1744	1618	NK	24	N506NK	EWR	MYR	90	550	14	30	2023-02-11 14:00:00	Other
17048	4	2	917	810	67	1241	1105	B6	51	N564JB	JFK	SRQ	166	1041	8	10	2023-04-02 08:00:00	Other
17052	4	23	1437	1400	37	1744	1706	B6	648	N509JB	JFK	IAH	223	1417	14	0	2023-04-23 14:00:00	Other
17053	1	9	1732	1700	32	2015	2008	B6	390	N2029J	JFK	MCO	128	944	17	0	2023-01-09 17:00:00	MCO
17054	6	30	2135	2100	35	102	16	B6	26	N566JB	JFK	SLC	262	1990	21	0	2023-06-30 21:00:00	Other
17057	5	21	1235	1120	75	1443	1407	B6	38	N980JT	JFK	LAS	285	2248	11	20	2023-05-21 11:00:00	Other
17058	3	5	1859	1815	44	2219	2126	NK	689	N675NK	EWR	FLL	145	1065	18	15	2023-03-05 18:00:00	FLL
17067	5	24	1514	1300	134	1655	1447	DL	965	N932AT	EWR	DTW	82	488	13	0	2023-05-24 13:00:00	Other
17074	4	14	1847	1820	27	2043	2040	NK	271	N671NK	EWR	IND	88	645	18	20	2023-04-14 18:00:00	Other
17086	1	9	2328	2029	179	132	2305	UA	580	N27266	EWR	ATL	99	746	20	29	2023-01-09 20:00:00	ATL
17089	5	1	1629	1459	90	1746	1619	B6	421	N283JB	JFK	ROC	52	264	14	59	2023-05-01 14:00:00	Other
17090	1	11	8	2115	173	118	2246	9E	1661	N311PQ	JFK	ORF	52	290	21	15	2023-01-11 21:00:00	Other
17091	5	14	1439	1420	19	1631	1649	9E	1502	N138EV	JFK	CLT	81	541	14	20	2023-05-14 14:00:00	CLT
17093	9	10	1258	1215	43	1656	1605	DL	732	N3769L	JFK	SJU	198	1598	12	15	2023-09-10 12:00:00	Other
17095	12	10	2053	1959	54	2324	2239	B6	685	N519JB	LGA	MSY	188	1183	19	59	2023-12-10 19:00:00	Other
17102	9	1	1856	1730	86	2156	2046	B6	787	N952JB	JFK	MIA	143	1089	17	30	2023-09-01 17:00:00	MIA
17110	11	20	2218	2015	123	55	2256	B6	145	N534JB	JFK	ATL	120	760	20	15	2023-11-20 20:00:00	ATL
17112	3	29	1441	1421	20	1721	1706	UA	256	N39728	EWR	DFW	195	1372	14	21	2023-03-29 14:00:00	Other
17127	9	25	2314	2227	47	42	2344	YX	1067	N756YX	EWR	MHT	41	209	22	27	2023-09-25 22:00:00	Other
17132	8	14	1807	1755	12	2011	2025	WN	322	N8629A	LGA	DEN	212	1620	17	55	2023-08-14 17:00:00	Other
17144	7	16	1925	1905	20	2050	2040	WN	843	N8305E	LGA	MDW	111	725	19	5	2023-07-16 19:00:00	Other
17145	3	25	2102	2045	17	2305	2245	9E	1373	N606LR	JFK	CLE	84	425	20	45	2023-03-25 20:00:00	Other
17152	7	30	2106	2010	56	24	2356	B6	271	N989JT	JFK	SFO	333	2586	20	10	2023-07-30 20:00:00	Other
17155	8	14	955	930	25	1241	1243	B6	66	N629JB	LGA	FLL	144	1076	9	30	2023-08-14 09:00:00	FLL
17158	2	14	1855	1840	15	2315	2342	DL	691	N859DN	JFK	SJU	174	1598	18	40	2023-02-14 18:00:00	Other
17161	12	12	2029	1506	323	2238	1719	DL	626	N312DU	EWR	MSP	160	1008	15	6	2023-12-12 15:00:00	Other
17163	8	20	2229	2150	39	37	2353	B6	426	N198JB	JFK	DTW	77	509	21	50	2023-08-20 21:00:00	Other
17174	4	9	1344	1327	17	1611	1552	UA	366	N892UA	EWR	JAX	119	820	13	27	2023-04-09 13:00:00	Other
17182	7	19	1946	1829	77	2242	2133	UA	730	N17306	EWR	PDX	327	2434	18	29	2023-07-19 18:00:00	Other
17184	1	22	821	800	21	1102	1028	B6	122	N304JB	JFK	SAV	120	718	8	0	2023-01-22 08:00:00	Other
17190	11	26	2105	2025	40	2347	2245	UA	617	N47288	EWR	SAV	123	708	20	25	2023-11-26 20:00:00	Other
17191	6	8	1812	1730	42	2053	2027	AS	95	N596AS	EWR	SAN	307	2425	17	30	2023-06-08 17:00:00	Other
17196	7	29	2319	2159	80	24	2327	YX	1069	N126HQ	JFK	BOS	36	187	21	59	2023-07-29 21:00:00	BOS
17203	3	25	1610	1557	13	1844	1830	UA	498	N13716	EWR	JAX	131	820	15	57	2023-03-25 15:00:00	Other
17217	11	20	1239	1200	39	1536	1509	NK	1203	N659NK	LGA	FLL	148	1076	12	0	2023-11-20 12:00:00	FLL
17218	9	9	1614	1600	14	1742	1714	9E	1486	N916XJ	LGA	PVD	34	143	16	0	2023-09-09 16:00:00	Other
17227	8	9	1230	1215	15	1519	1511	B6	225	N627JB	JFK	AUS	200	1521	12	15	2023-08-09 12:00:00	Other
17233	4	1	2105	1915	110	2228	2058	UA	718	N891UA	LGA	ORD	123	733	19	15	2023-04-01 19:00:00	ORD
17245	6	23	1121	1050	31	1439	1406	DL	449	N138DU	LGA	RSW	162	1080	10	50	2023-06-23 10:00:00	Other
17246	9	19	1941	1919	22	2133	2138	9E	1729	N305PQ	LGA	CLT	85	544	19	19	2023-09-19 19:00:00	CLT
17251	8	15	1451	1415	36	1639	1538	B6	173	N328JB	LGA	BOS	38	184	14	15	2023-08-15 14:00:00	BOS
17252	7	12	1848	1830	18	2116	2120	UA	585	N47275	EWR	MCO	116	937	18	30	2023-07-12 18:00:00	MCO
17260	4	19	1116	1045	31	1401	1347	NK	489	N681NK	EWR	FLL	142	1065	10	45	2023-04-19 10:00:00	FLL
17261	9	4	1501	1418	43	1624	1548	9E	1586	N903XJ	LGA	BTV	45	258	14	18	2023-09-04 14:00:00	Other
17263	6	4	1622	1559	23	1834	1825	UA	500	N27270	EWR	JAX	109	820	15	59	2023-06-04 15:00:00	Other
17265	3	23	1550	1530	20	1906	1926	B6	998	N641JB	JFK	SJU	177	1598	15	30	2023-03-23 15:00:00	Other
17267	3	21	1702	1629	33	1939	1907	UA	906	N37290	LGA	DEN	242	1620	16	29	2023-03-21 16:00:00	Other
17270	7	17	1820	1800	20	2119	2026	YX	1014	N404YX	LGA	TUL	190	1231	18	0	2023-07-17 18:00:00	Other
17283	6	22	1843	1659	104	2158	2007	UA	780	N65832	EWR	RSW	167	1068	16	59	2023-06-22 16:00:00	Other
17289	10	2	1207	1136	31	1315	1308	UA	331	N39423	EWR	ORD	103	719	11	36	2023-10-02 11:00:00	ORD
17293	2	24	1635	1600	35	1741	1726	OO	1171	N279SY	JFK	BOS	40	187	16	0	2023-02-24 16:00:00	BOS
17296	1	27	1629	1530	59	2038	1849	DL	722	N113DX	JFK	FLL	184	1069	15	30	2023-01-27 15:00:00	FLL
17306	6	11	2021	2000	21	2343	2313	UA	787	N38727	EWR	SEA	301	2402	20	0	2023-06-11 20:00:00	Other
17314	3	30	2015	1950	25	2252	2305	DL	601	N372NW	JFK	TPA	137	1005	19	50	2023-03-30 19:00:00	Other
17317	7	21	1012	930	42	1313	1243	B6	72	N706JB	LGA	FLL	145	1076	9	30	2023-07-21 09:00:00	FLL
17319	6	10	2336	2136	120	54	2315	UA	753	N37267	EWR	ORD	115	719	21	36	2023-06-10 21:00:00	ORD
17324	8	1	1427	702	445	1721	1010	AA	306	N327SK	JFK	MIA	149	1089	7	2	2023-08-01 07:00:00	MIA
17326	8	27	1849	1716	93	2028	1852	UA	490	N838UA	LGA	ORD	118	733	17	16	2023-08-27 17:00:00	ORD
17329	6	28	1111	1030	41	1211	1158	B6	60	N506JB	JFK	ROC	43	264	10	30	2023-06-28 10:00:00	Other
17338	1	8	1945	1910	35	2230	2217	UA	632	N642UA	EWR	IAH	197	1400	19	10	2023-01-08 19:00:00	Other
17339	6	25	1741	1645	56	2018	1910	WN	639	N915WN	LGA	ATL	120	762	16	45	2023-06-25 16:00:00	ATL
17342	6	12	1630	1530	60	1923	1839	UA	788	N27015	EWR	SFO	321	2565	15	30	2023-06-12 15:00:00	Other
17345	5	23	719	630	49	1025	931	B6	925	N566JB	JFK	FLL	154	1069	6	30	2023-05-23 06:00:00	FLL
17360	2	5	714	700	14	1029	1024	B6	301	N985JT	JFK	LAX	355	2475	7	0	2023-02-05 07:00:00	LAX
17363	7	26	1248	1225	23	1436	1435	WN	375	N8877Q	LGA	DEN	207	1620	12	25	2023-07-26 12:00:00	Other
17374	6	13	1614	1600	14	1828	1844	DL	182	N103DY	LGA	ATL	113	762	16	0	2023-06-13 16:00:00	ATL
17379	11	16	1740	1715	25	2041	2030	WN	384	N7887A	LGA	HOU	200	1428	17	15	2023-11-16 17:00:00	Other
17387	8	6	1725	1710	15	1959	2009	DL	216	N508DA	JFK	LAS	294	2248	17	10	2023-08-06 17:00:00	Other
17390	9	22	1532	1514	18	1637	1630	UA	595	N33289	EWR	BOS	37	200	15	14	2023-09-22 15:00:00	BOS
17393	1	3	825	745	40	1025	1010	B6	976	N2002J	JFK	CHS	90	636	7	45	2023-01-03 07:00:00	Other
17396	1	10	1409	1350	19	1535	1514	9E	1690	N920XJ	LGA	ROC	47	254	13	50	2023-01-10 13:00:00	Other
17398	4	27	2014	1855	79	2343	2206	AS	12	N954AK	JFK	SAN	326	2446	18	55	2023-04-27 18:00:00	Other
17413	5	7	1142	1130	12	1401	1424	B6	33	N763JB	JFK	MCO	114	944	11	30	2023-05-07 11:00:00	MCO
17417	7	13	1859	1559	180	2305	2000	DL	280	N727TW	JFK	SFO	360	2586	15	59	2023-07-13 15:00:00	Other
17422	1	2	1458	1329	89	1809	1642	AA	866	N455AN	JFK	MIA	154	1089	13	29	2023-01-02 13:00:00	MIA
17431	7	22	1314	1259	15	1503	1429	YX	1442	N226JQ	LGA	PWM	47	269	12	59	2023-07-22 12:00:00	Other
17438	6	26	1209	1000	129	1616	1304	UA	837	N221UA	EWR	SFO	327	2565	10	0	2023-06-26 10:00:00	Other
17443	7	2	1648	1629	19	1904	1853	DL	694	N371NB	JFK	MSP	143	1029	16	29	2023-07-02 16:00:00	Other
17452	5	10	2147	2129	18	2317	2320	YX	1319	N135HQ	LGA	CLE	69	419	21	29	2023-05-10 21:00:00	Other
17455	9	18	1651	1516	95	1943	1808	DL	208	N316DU	LGA	DFW	191	1389	15	16	2023-09-18 15:00:00	Other
17457	6	6	1452	1429	23	1732	1648	YX	1254	N728YX	EWR	IND	100	645	14	29	2023-06-06 14:00:00	Other
17466	5	18	1717	1659	18	1943	1922	UA	520	N810UA	EWR	ATL	112	746	16	59	2023-05-18 16:00:00	ATL
17470	5	19	2040	2029	11	2334	2345	AA	749	N328RR	LGA	MIA	145	1096	20	29	2023-05-19 20:00:00	MIA
17471	9	18	1001	950	11	1210	1142	9E	1540	N923XJ	EWR	RDU	74	416	9	50	2023-09-18 09:00:00	Other
17475	7	1	1447	1424	23	1801	1731	UA	207	N418UA	EWR	MIA	160	1085	14	24	2023-07-01 14:00:00	MIA
17477	11	22	1126	1112	14	1443	1428	DL	476	N336DX	JFK	MIA	175	1089	11	12	2023-11-22 11:00:00	MIA
17478	9	10	1539	1009	330	1832	1315	DL	407	N117DU	LGA	IAH	206	1416	10	9	2023-09-10 10:00:00	Other
17492	3	20	1008	950	18	1242	1229	AA	1004	N448AN	EWR	PHX	300	2133	9	50	2023-03-20 09:00:00	Other
17498	4	13	1422	1345	37	1648	1640	WN	246	N8309C	LGA	HOU	182	1428	13	45	2023-04-13 13:00:00	Other
17499	2	27	1441	1318	83	1651	1554	UA	560	N13720	EWR	JAX	117	820	13	18	2023-02-27 13:00:00	Other
17509	11	22	1504	1453	11	1807	1804	NK	848	N644NK	EWR	FLL	164	1065	14	53	2023-11-22 14:00:00	FLL
17512	1	13	1415	1359	16	1647	1709	AA	513	N978NN	EWR	DFW	183	1372	13	59	2023-01-13 13:00:00	Other
17524	3	23	2212	2048	84	129	2356	UA	280	N25201	EWR	FLL	157	1065	20	48	2023-03-23 20:00:00	FLL
17528	2	8	1157	1130	27	1348	1320	DL	584	N118DU	LGA	ORD	132	733	11	30	2023-02-08 11:00:00	ORD
17553	12	18	1159	959	120	1354	1207	9E	1455	N605LR	JFK	CLE	72	425	9	59	2023-12-18 09:00:00	Other
17561	1	10	1104	1025	39	1257	1247	9E	1522	N607LR	LGA	MYR	90	563	10	25	2023-01-10 10:00:00	Other
17571	9	1	2140	2110	30	17	2354	B6	177	N821JB	LGA	MCO	129	950	21	10	2023-09-01 21:00:00	MCO
17574	3	2	1058	1045	13	1420	1407	DL	583	N359NB	LGA	RSW	174	1080	10	45	2023-03-02 10:00:00	Other
17576	7	26	2003	1930	33	2228	2249	B6	63	N929JB	JFK	LAX	307	2475	19	30	2023-07-26 19:00:00	LAX
17583	1	12	1218	1130	48	1404	1326	AA	119	N774XF	LGA	ORD	127	733	11	30	2023-01-12 11:00:00	ORD
17585	12	26	1621	1544	37	1928	1850	NK	19	N975NK	EWR	MCO	155	937	15	44	2023-12-26 15:00:00	MCO
17588	9	24	2044	1957	47	2247	2217	9E	1507	N919XJ	LGA	CVG	87	585	19	57	2023-09-24 19:00:00	Other
17589	4	23	2234	2159	35	24	10	UA	443	N62883	EWR	CHS	92	628	21	59	2023-04-23 21:00:00	Other
17596	11	16	1800	1649	71	2058	1955	B6	440	N510JB	JFK	MCO	141	944	16	49	2023-11-16 16:00:00	MCO
17597	9	1	1458	1429	29	1703	1626	YX	1813	N221JQ	LGA	MEM	141	963	14	29	2023-09-01 14:00:00	Other
17603	4	6	29	2245	104	131	4	B6	6	N197JB	JFK	SYR	42	209	22	45	2023-04-06 22:00:00	Other
17606	4	5	1049	715	214	1223	904	DL	510	N134DU	LGA	ORD	129	733	7	15	2023-04-05 07:00:00	ORD
17612	1	24	1145	1120	25	1541	1451	DL	655	N139DU	LGA	IAH	270	1416	11	20	2023-01-24 11:00:00	Other
17628	7	29	1642	1330	192	1905	1558	B6	34	N563JB	JFK	LAS	292	2248	13	30	2023-07-29 13:00:00	Other
17639	6	7	1447	1400	47	1655	1624	DL	841	N823DN	EWR	ATL	97	746	14	0	2023-06-07 14:00:00	ATL
17640	8	4	1220	1055	85	1439	1317	UA	399	N442UA	EWR	JAX	105	820	10	55	2023-08-04 10:00:00	Other
17642	2	12	1611	1555	16	1834	1829	NK	417	N621NK	EWR	ATL	105	746	15	55	2023-02-12 15:00:00	ATL
17644	1	13	2101	1759	182	24	2104	B6	761	N566JB	LGA	MCO	145	950	17	59	2023-01-13 17:00:00	MCO
17645	8	15	1108	1020	48	1304	1240	9E	1142	N914XJ	LGA	CLT	87	544	10	20	2023-08-15 10:00:00	CLT
17646	11	7	1734	1715	19	2009	2030	WN	384	N7876A	LGA	HOU	194	1428	17	15	2023-11-07 17:00:00	Other
17652	9	7	715	700	15	923	927	UA	384	N482UA	EWR	ATL	99	746	7	0	2023-09-07 07:00:00	ATL
17656	4	14	1731	1625	66	2216	1807	AA	662	N177XF	LGA	RDU	NA	431	16	25	2023-04-14 16:00:00	Other
17664	4	5	2231	2138	53	114	2359	UA	290	N452UA	EWR	SAV	102	708	21	38	2023-04-05 21:00:00	Other
17665	6	8	1935	1920	15	2226	2319	DL	367	N707TW	JFK	SFO	322	2586	19	20	2023-06-08 19:00:00	Other
17670	4	3	1847	1830	17	2148	2148	DL	338	N335NB	JFK	DFW	194	1391	18	30	2023-04-03 18:00:00	Other
17674	5	6	2100	2047	13	2249	2258	YX	1044	N729YX	EWR	GSP	83	594	20	47	2023-05-06 20:00:00	Other
17680	4	4	614	600	14	901	905	WN	926	N8792Q	LGA	DAL	201	1381	6	0	2023-04-04 06:00:00	Other
17681	11	16	1536	1345	111	1827	1700	AA	364	N905NN	LGA	DFW	194	1389	13	45	2023-11-16 13:00:00	Other
17683	9	11	1744	1710	34	2109	2027	DL	146	N529DT	JFK	SAN	325	2446	17	10	2023-09-11 17:00:00	Other
17684	8	12	2012	1950	22	2159	2125	AA	707	N907AN	EWR	ORD	123	719	19	50	2023-08-12 19:00:00	ORD
17692	9	22	2055	1853	122	2357	2209	B6	71	N935JB	JFK	SEA	294	2422	18	53	2023-09-22 18:00:00	Other
17696	3	7	715	635	40	1103	915	B6	801	N536JB	LGA	DEN	265	1620	6	35	2023-03-07 06:00:00	Other
17698	4	10	929	810	79	1224	1106	B6	51	N570JB	JFK	SRQ	146	1041	8	10	2023-04-10 08:00:00	Other
17701	10	18	950	900	50	1249	1206	B6	70	N606JB	LGA	FLL	147	1076	9	0	2023-10-18 09:00:00	FLL
17715	8	1	2128	2059	29	2255	2239	9E	1229	N336PQ	LGA	RIC	54	292	20	59	2023-08-01 20:00:00	Other
17719	3	28	2103	1950	73	2400	2249	B6	455	N2002J	JFK	LAS	327	2248	19	50	2023-03-28 19:00:00	Other
17725	4	17	944	810	94	1259	1139	AA	559	N303RG	JFK	MIA	165	1089	8	10	2023-04-17 08:00:00	MIA
17744	5	22	2332	2159	93	111	2344	B6	517	N266JB	JFK	RDU	71	427	21	59	2023-05-22 21:00:00	Other
17758	7	15	1738	1655	43	2004	1917	YX	1063	N869RW	LGA	SDF	107	659	16	55	2023-07-15 16:00:00	Other
17765	7	22	1730	1700	30	2008	2011	B6	627	N536JB	JFK	PBI	144	1028	17	0	2023-07-22 17:00:00	Other
17767	6	19	2319	1929	230	236	2239	DL	481	N362NB	LGA	PBI	164	1035	19	29	2023-06-19 19:00:00	Other
17772	5	4	2347	2100	167	311	47	AA	55	N111ZM	JFK	SFO	344	2586	21	0	2023-05-04 21:00:00	Other
17784	11	26	2046	2029	17	2350	2329	UA	605	N17302	EWR	MCO	145	937	20	29	2023-11-26 20:00:00	MCO
17790	11	25	2100	1929	91	2245	2133	9E	1557	N320PQ	JFK	RDU	72	427	19	29	2023-11-25 19:00:00	Other
17795	3	16	1648	1400	168	1928	1719	B6	541	N2027J	JFK	FLL	139	1069	14	0	2023-03-16 14:00:00	FLL
17797	8	12	1900	1727	93	2148	2001	YX	837	N855RW	EWR	ATL	110	746	17	27	2023-08-12 17:00:00	ATL
17803	5	7	1919	1850	29	2155	2145	UA	639	N35236	EWR	MCO	124	937	18	50	2023-05-07 18:00:00	MCO
17815	9	17	2151	2130	21	2400	3	DL	844	N520DE	JFK	ATL	111	760	21	30	2023-09-17 21:00:00	ATL
17817	5	10	714	645	29	821	759	UA	510	N68834	EWR	BOS	41	200	6	45	2023-05-10 06:00:00	BOS
17824	7	21	2048	2010	38	2229	2214	9E	1173	N919XJ	LGA	GSO	82	461	20	10	2023-07-21 20:00:00	Other
17829	4	18	1628	1555	33	1926	1858	AA	900	N700UW	LGA	DFW	194	1389	15	55	2023-04-18 15:00:00	Other
17841	7	2	1754	1729	25	2018	1951	YX	860	N733YX	EWR	IND	97	645	17	29	2023-07-02 17:00:00	Other
17846	10	24	2219	2155	24	220	142	DL	300	N710TW	JFK	SFO	373	2586	21	55	2023-10-24 21:00:00	Other
17847	7	21	2204	1959	125	38	2259	B6	19	N580JB	LGA	TPA	136	1010	19	59	2023-07-21 19:00:00	Other
17864	4	25	1815	1759	16	2104	2100	DL	533	N114DN	LGA	MCO	140	950	17	59	2023-04-25 17:00:00	MCO
17865	5	10	1944	1929	15	2208	2224	DL	412	N342DN	LGA	MCO	125	950	19	29	2023-05-10 19:00:00	MCO
17870	10	24	1436	1159	157	1542	1317	UA	419	N443UA	EWR	PWM	50	284	11	59	2023-10-24 11:00:00	Other
17881	2	28	1809	1715	54	2028	1957	9E	1294	N298PQ	JFK	MCI	182	1113	17	15	2023-02-28 17:00:00	Other
17882	4	2	2101	1959	62	2331	2234	DL	723	N347NB	LGA	MSY	178	1183	19	59	2023-04-02 19:00:00	Other
17884	1	13	2251	2200	51	8	2339	B6	391	N190JB	LGA	BNA	114	764	22	0	2023-01-13 22:00:00	Other
17886	1	12	1850	1755	55	2058	2040	WN	403	N8625A	LGA	DEN	217	1620	17	55	2023-01-12 17:00:00	Other
17892	7	24	1348	1300	48	1707	1555	B6	561	N516JB	EWR	RSW	172	1068	13	0	2023-07-24 13:00:00	Other
17894	3	10	2144	2128	16	3	2333	UA	869	N27260	EWR	MSP	139	1008	21	28	2023-03-10 21:00:00	Other
17898	5	14	1347	1330	17	1640	1645	UA	383	N773UA	EWR	SFO	329	2565	13	30	2023-05-14 13:00:00	Other
17901	12	10	1732	1713	19	2107	2016	UA	264	N27526	EWR	TPA	179	997	17	13	2023-12-10 17:00:00	Other
17902	10	29	2003	1859	64	2304	2129	YX	1310	N421YX	LGA	XNA	183	1147	18	59	2023-10-29 18:00:00	Other
17905	4	2	1616	1535	41	1809	1733	9E	1352	N937XJ	LGA	ILM	74	500	15	35	2023-04-02 15:00:00	Other
17906	6	25	1514	1328	106	1741	1440	YX	1163	N736YX	EWR	SYR	38	195	13	28	2023-06-25 13:00:00	Other
17909	9	25	906	650	136	1212	959	NK	268	N980NK	EWR	OAK	321	2555	6	50	2023-09-25 06:00:00	Other
17918	11	20	1015	959	16	1215	1156	NK	595	N648NK	LGA	DTW	84	502	9	59	2023-11-20 09:00:00	Other
17939	8	1	1753	1705	48	1950	1921	9E	1294	N478PX	LGA	LIT	141	1085	17	5	2023-08-01 17:00:00	Other
17943	2	23	1121	1106	15	1339	1326	UA	864	N27276	EWR	MSY	178	1167	11	6	2023-02-23 11:00:00	Other
17950	9	5	1918	1803	75	2105	1953	9E	1548	N137EV	LGA	STL	119	888	18	3	2023-09-05 18:00:00	Other
17968	6	22	2045	1959	46	2332	2305	AS	88	N930VA	EWR	LAX	308	2454	19	59	2023-06-22 19:00:00	LAX
17979	2	20	1600	1357	123	1849	1704	UA	491	N492UA	EWR	FLL	147	1065	13	57	2023-02-20 13:00:00	FLL
17980	5	22	1632	1615	17	1800	1800	9E	1483	N314PQ	JFK	ORF	54	290	16	15	2023-05-22 16:00:00	Other
17986	8	9	2053	2010	43	2256	2235	B6	31	N779JB	JFK	DEN	213	1626	20	10	2023-08-09 20:00:00	Other
17990	11	19	1114	1015	59	1405	1325	B6	565	N729JB	JFK	FLL	146	1069	10	15	2023-11-19 10:00:00	FLL
17995	5	25	1519	1455	24	1846	1810	B6	526	N585JB	JFK	FLL	185	1069	14	55	2023-05-25 14:00:00	FLL
18005	7	14	1510	1330	100	1843	1558	B6	34	N630JB	JFK	LAS	328	2248	13	30	2023-07-14 13:00:00	Other
18008	6	27	1207	1100	67	1546	1320	B6	129	N618JB	LGA	DEN	NA	1620	11	0	2023-06-27 11:00:00	Other
18011	8	30	1205	1111	54	1333	1248	UA	682	N423UA	LGA	ORD	107	733	11	11	2023-08-30 11:00:00	ORD
18016	7	21	613	1935	638	807	2214	9E	1328	N304PQ	JFK	CLT	87	541	19	35	2023-07-21 19:00:00	CLT
18021	7	1	953	815	98	1232	1132	B6	211	N2027J	JFK	FLL	136	1069	8	15	2023-07-01 08:00:00	FLL
18031	6	11	1843	1529	194	2117	1737	UA	87	N21723	EWR	CHS	91	628	15	29	2023-06-11 15:00:00	Other
18032	6	4	1916	1753	83	2145	2044	UA	745	N17301	EWR	IAH	175	1400	17	53	2023-06-04 17:00:00	Other
18036	12	15	2123	2050	33	2231	2218	9E	1628	N183GJ	LGA	SYR	38	198	20	50	2023-12-15 20:00:00	Other
18037	4	18	1613	1529	44	1907	1837	B6	668	N239JB	LGA	PBI	148	1035	15	29	2023-04-18 15:00:00	Other
18038	10	10	1028	812	136	1246	1053	B6	128	N983JT	JFK	LAS	295	2248	8	12	2023-10-10 08:00:00	Other
18047	6	15	1326	1302	24	1444	1426	YX	1106	N750YX	EWR	PIT	51	319	13	2	2023-06-15 13:00:00	Other
18049	8	18	1453	1440	13	1732	1736	UA	701	N17133	EWR	LAX	318	2454	14	40	2023-08-18 14:00:00	LAX
18055	7	20	2110	2005	65	2301	2215	YX	893	N864RW	EWR	GSP	86	594	20	5	2023-07-20 20:00:00	Other
18062	4	5	2206	1830	216	101	2148	DL	338	N320NB	JFK	DFW	208	1391	18	30	2023-04-05 18:00:00	Other
18069	12	28	2021	1959	22	2343	2323	DL	339	N312DN	LGA	MIA	164	1096	19	59	2023-12-28 19:00:00	MIA
18071	4	30	2017	1915	62	2121	2036	B6	465	N197JB	LGA	BOS	34	184	19	15	2023-04-30 19:00:00	BOS
18075	1	14	1156	1130	26	1429	1432	UA	284	N18112	EWR	PBI	135	1023	11	30	2023-01-14 11:00:00	Other
18076	7	4	1619	1429	110	1834	1630	UA	317	N807UA	EWR	CLT	78	529	14	29	2023-07-04 14:00:00	CLT
18078	10	9	1507	1450	17	1705	1703	9E	1570	N325PQ	LGA	GSP	98	610	14	50	2023-10-09 14:00:00	Other
18079	6	22	1429	1402	27	1620	1623	B6	754	N586JB	LGA	DEN	204	1620	14	2	2023-06-22 14:00:00	Other
18080	8	10	1709	1655	14	2035	2020	AS	6	N268AK	JFK	SEA	353	2422	16	55	2023-08-10 16:00:00	Other
18083	12	5	2019	1950	29	2347	2317	DL	799	N353DN	JFK	MIA	164	1089	19	50	2023-12-05 19:00:00	MIA
18089	6	14	2142	1659	283	36	1954	UA	599	N12216	EWR	MCO	145	937	16	59	2023-06-14 16:00:00	MCO
18096	3	17	1430	1406	24	1647	1638	UA	795	N17122	EWR	DEN	224	1605	14	6	2023-03-17 14:00:00	Other
18102	7	13	1714	1629	45	1946	1855	AA	494	N831NN	JFK	PHX	293	2153	16	29	2023-07-13 16:00:00	Other
18103	7	22	1040	1025	15	1256	1255	YX	1380	N231JQ	LGA	SDF	104	659	10	25	2023-07-22 10:00:00	Other
18105	9	9	1030	1009	21	1221	1213	UA	507	N73259	EWR	CLT	80	529	10	9	2023-09-09 10:00:00	CLT
18108	11	19	1733	1707	26	1914	1848	UA	673	N37577	EWR	ORD	116	719	17	7	2023-11-19 17:00:00	ORD
18112	2	4	2014	1917	57	2326	2235	UA	383	N36476	EWR	MIA	149	1085	19	17	2023-02-04 19:00:00	MIA
18131	3	28	1925	1905	20	2253	2236	DL	206	N176DN	JFK	LAX	347	2475	19	5	2023-03-28 19:00:00	LAX
18132	11	18	1202	1000	122	1515	1318	UA	263	N228UA	EWR	SFO	335	2565	10	0	2023-11-18 10:00:00	Other
18139	3	22	1514	1459	15	1706	1656	9E	1310	N935XJ	JFK	CLE	78	425	14	59	2023-03-22 14:00:00	Other
18145	9	27	2011	1959	12	2256	2324	AS	83	N288AK	EWR	SFO	322	2565	19	59	2023-09-27 19:00:00	Other
18149	10	27	1424	925	299	1548	1113	YX	1326	N136HQ	LGA	GSO	69	461	9	25	2023-10-27 09:00:00	Other
18153	9	23	1723	1707	16	1854	1843	UA	793	N14120	EWR	ORD	103	719	17	7	2023-09-23 17:00:00	ORD
18154	10	26	815	759	16	1026	1037	DL	297	N339DN	LGA	ATL	108	762	7	59	2023-10-26 07:00:00	ATL
18159	7	4	1333	1255	38	1448	1421	9E	1216	N294PQ	JFK	ORF	47	290	12	55	2023-07-04 12:00:00	Other
18161	7	24	1634	1503	91	1921	1752	UA	327	N27277	EWR	MCO	134	937	15	3	2023-07-24 15:00:00	MCO
18164	6	14	1426	1347	39	1614	1520	AA	659	N335PH	EWR	ORD	113	719	13	47	2023-06-14 13:00:00	ORD
18167	10	27	1847	1829	18	2212	2144	AS	154	N251AK	EWR	SEA	344	2402	18	29	2023-10-27 18:00:00	Other
18173	2	11	1908	1857	11	2110	2131	NK	295	N673NK	EWR	IND	89	645	18	57	2023-02-11 18:00:00	Other
18177	1	24	1619	1602	17	1744	1736	UA	952	N439UA	EWR	PIT	56	319	16	2	2023-01-24 16:00:00	Other
18187	9	29	929	859	30	1140	1116	OO	1238	N283SY	LGA	OMA	164	1148	8	59	2023-09-29 08:00:00	Other
18189	5	27	1313	1302	11	1555	1612	UA	688	N24211	EWR	MIA	145	1085	13	2	2023-05-27 13:00:00	MIA
18196	12	13	611	600	11	735	732	YX	1853	N882RW	LGA	DCA	51	214	6	0	2023-12-13 06:00:00	Other
18209	12	15	1614	1559	15	1937	1920	DL	389	N3769L	LGA	MIA	167	1096	15	59	2023-12-15 15:00:00	MIA
18215	3	24	1847	1745	62	2132	2057	B6	21	N507JT	LGA	TPA	147	1010	17	45	2023-03-24 17:00:00	Other
18217	3	20	1643	1629	14	1852	1844	YX	1057	N863RW	EWR	GSP	92	594	16	29	2023-03-20 16:00:00	Other
18223	12	3	1822	1755	27	2143	2035	WN	1040	N8723Q	LGA	ATL	148	762	17	55	2023-12-03 17:00:00	ATL
18228	9	5	1130	1059	31	1243	1232	9E	1676	N305PQ	LGA	BUF	49	292	10	59	2023-09-05 10:00:00	Other
18236	9	13	1509	1435	34	1704	1647	9E	1698	N604LR	LGA	CVG	97	585	14	35	2023-09-13 14:00:00	Other
18247	3	9	2009	1430	339	2148	1622	AA	880	N758US	LGA	RDU	65	431	14	30	2023-03-09 14:00:00	Other
18249	11	22	819	800	19	1148	1114	B6	535	N2084J	JFK	RSW	169	1074	8	0	2023-11-22 08:00:00	Other
18257	8	12	2101	1559	302	9	1859	AA	704	N934AN	JFK	DFW	200	1391	15	59	2023-08-12 15:00:00	Other
18258	8	1	1603	1546	17	1711	1735	YX	1342	N246JQ	JFK	DCA	41	213	15	46	2023-08-01 15:00:00	Other
18267	6	9	1743	1430	193	1933	1656	B6	853	N3112J	JFK	MCI	148	1113	14	30	2023-06-09 14:00:00	Other
18268	1	14	2118	1915	123	23	2250	DL	227	N174DN	JFK	LAX	332	2475	19	15	2023-01-14 19:00:00	LAX
18269	8	18	1333	1310	23	1452	1416	B6	459	N355JB	JFK	MVY	38	173	13	10	2023-08-18 13:00:00	Other
18272	12	8	1412	1245	87	1508	1353	AA	530	N884NN	LGA	BOS	32	184	12	45	2023-12-08 12:00:00	BOS
18276	6	18	849	830	19	1145	1140	UA	689	N13110	EWR	SEA	321	2402	8	30	2023-06-18 08:00:00	Other
18283	3	18	1001	827	94	1251	1104	B6	923	N613JB	LGA	MSY	190	1183	8	27	2023-03-18 08:00:00	Other
18284	9	6	1651	1629	22	1809	1757	AA	993	N776XF	LGA	BNA	106	764	16	29	2023-09-06 16:00:00	Other
18286	7	7	2010	1210	480	2112	1325	WN	821	N7845A	LGA	MDW	106	725	12	10	2023-07-07 12:00:00	Other
18294	1	12	2154	2027	87	9	2228	YX	1396	N439YX	JFK	PIT	68	340	20	27	2023-01-12 20:00:00	Other
18297	5	25	2202	2117	45	10	2336	UA	861	N68842	EWR	MSY	157	1167	21	17	2023-05-25 21:00:00	Other
18300	10	8	1927	1910	17	2142	2122	9E	1611	N676CA	JFK	CVG	95	589	19	10	2023-10-08 19:00:00	Other
18305	4	20	1919	1859	20	2318	2308	DL	643	N842DN	JFK	SJU	201	1598	18	59	2023-04-20 18:00:00	Other
18314	2	6	1005	950	15	1112	1118	9E	1452	N349PQ	JFK	SYR	46	209	9	50	2023-02-06 09:00:00	Other
18323	9	16	1741	1655	46	2021	2015	AS	6	N236AK	JFK	SEA	312	2422	16	55	2023-09-16 16:00:00	Other
18325	4	3	619	600	19	840	832	DL	313	N105DX	LGA	ATL	116	762	6	0	2023-04-03 06:00:00	ATL
18328	8	30	801	705	56	1134	1019	DL	469	N102DN	LGA	FLL	153	1076	7	5	2023-08-30 07:00:00	FLL
18331	11	19	1009	955	14	1618	1618	DL	99	N840MH	JFK	HNL	626	4983	9	55	2023-11-19 09:00:00	Other
18354	5	9	1935	1859	36	2111	2035	YX	1262	N408YX	LGA	PIT	56	335	18	59	2023-05-09 18:00:00	Other
18355	10	29	1932	1747	105	2150	2001	9E	1573	N695CA	LGA	GSP	97	610	17	47	2023-10-29 17:00:00	Other
18356	6	12	1547	1530	17	1834	1833	UA	522	N17105	EWR	LAX	313	2454	15	30	2023-06-12 15:00:00	LAX
18357	9	21	1730	1716	14	1940	1924	9E	1688	N935XJ	LGA	DSM	142	1031	17	16	2023-09-21 17:00:00	Other
18366	4	10	736	600	96	1029	904	B6	481	N967JT	EWR	LAX	303	2454	6	0	2023-04-10 06:00:00	LAX
18368	3	23	2214	2125	49	28	2301	9E	1555	N133EV	JFK	ORF	61	290	21	25	2023-03-23 21:00:00	Other
18369	7	6	2156	2030	86	2309	2200	B6	66	N206JB	JFK	BTV	51	266	20	30	2023-07-06 20:00:00	Other
18370	8	17	1928	1906	22	2103	2048	UA	417	N37532	EWR	CLE	65	404	19	6	2023-08-17 19:00:00	Other
18373	7	19	2308	2159	69	206	111	B6	543	N964JT	JFK	LAX	313	2475	21	59	2023-07-19 21:00:00	LAX
18374	3	31	1806	1651	75	1951	1834	YX	1123	N753YX	EWR	CLE	72	404	16	51	2023-03-31 16:00:00	Other
18384	7	19	1623	1559	24	1757	1734	YX	926	N722YX	EWR	PIT	67	319	15	59	2023-07-19 15:00:00	Other
18402	2	3	2059	2015	44	44	2359	AS	18	N975AK	JFK	SFO	364	2586	20	15	2023-02-03 20:00:00	Other
18413	3	6	1524	1510	14	1829	1824	DL	598	N111DC	LGA	FLL	143	1076	15	10	2023-03-06 15:00:00	FLL
18416	9	24	1349	1310	39	1704	1601	B6	965	N612JB	JFK	TPA	139	1005	13	10	2023-09-24 13:00:00	Other
18418	5	15	1422	1359	23	1702	1633	DL	163	N384DA	JFK	DEN	225	1626	13	59	2023-05-15 13:00:00	Other
18427	6	18	1621	1559	22	1928	1907	UA	153	N27260	EWR	SEA	324	2402	15	59	2023-06-18 15:00:00	Other
18430	7	7	2240	2050	110	153	12	DL	158	N520DE	JFK	SAN	319	2446	20	50	2023-07-07 20:00:00	Other
18431	5	19	623	600	23	853	844	B6	94	N624JB	LGA	MCO	130	950	6	0	2023-05-19 06:00:00	MCO
18432	11	22	1404	1329	35	1604	1545	9E	1542	N910XJ	LGA	CVG	87	585	13	29	2023-11-22 13:00:00	Other
18444	2	28	931	917	14	1210	1214	UA	496	N19130	EWR	MCO	126	937	9	17	2023-02-28 09:00:00	MCO
18454	11	9	1025	830	115	1320	1200	DL	340	N506DA	JFK	SAN	335	2446	8	30	2023-11-09 08:00:00	Other
18456	2	1	2021	1945	36	2306	2249	B6	439	N2043J	JFK	LAS	326	2248	19	45	2023-02-01 19:00:00	Other
18460	12	15	811	800	11	950	1014	DL	561	N333NB	LGA	MSP	142	1020	8	0	2023-12-15 08:00:00	Other
18465	6	4	2146	2110	36	2325	2306	YX	1301	N423YX	LGA	GSO	71	461	21	10	2023-06-04 21:00:00	Other
18478	5	11	1807	1751	16	2048	2101	UA	557	N27273	EWR	SAN	308	2425	17	51	2023-05-11 17:00:00	Other
18480	3	13	1152	959	113	1312	1113	UA	489	N453UA	EWR	BOS	35	200	9	59	2023-03-13 09:00:00	BOS
18481	7	8	1132	1055	37	1510	1352	B6	40	N625JB	EWR	PBI	170	1023	10	55	2023-07-08 10:00:00	Other
18483	12	27	10	2140	150	309	40	B6	664	N279JB	EWR	MCO	154	937	21	40	2023-12-27 21:00:00	MCO
18494	12	18	852	750	62	1014	929	YX	1314	N439YX	JFK	DCA	43	213	7	50	2023-12-18 07:00:00	Other
18499	9	13	2111	2059	12	2337	2323	B6	919	N665JB	LGA	MSY	174	1183	20	59	2023-09-13 20:00:00	Other
18504	7	12	1618	1559	19	1745	1734	YX	926	N747YX	EWR	PIT	55	319	15	59	2023-07-12 15:00:00	Other
18506	4	20	2112	2052	20	18	2357	UA	109	N69888	EWR	SRQ	139	1034	20	52	2023-04-20 20:00:00	Other
18521	5	5	2122	2055	27	5	2354	B6	169	N529JB	LGA	FLL	141	1076	20	55	2023-05-05 20:00:00	FLL
18522	9	25	1258	1150	68	1516	1356	9E	1427	N313PQ	JFK	CLT	83	541	11	50	2023-09-25 11:00:00	CLT
18523	4	30	1332	1105	147	1637	1455	DL	209	N704X	JFK	SFO	337	2586	11	5	2023-04-30 11:00:00	Other
18532	7	1	1112	1100	12	1358	1413	B6	670	N558JB	JFK	FLL	138	1069	11	0	2023-07-01 11:00:00	FLL
18533	6	21	1715	1655	20	1853	1824	YX	1092	N726YX	EWR	BUF	48	282	16	55	2023-06-21 16:00:00	Other
18537	2	21	1542	1530	12	1914	1855	AA	120	N105NN	JFK	LAX	360	2475	15	30	2023-02-21 15:00:00	LAX
18539	11	7	849	800	49	958	921	YX	1812	N226JQ	LGA	BOS	41	184	8	0	2023-11-07 08:00:00	BOS
18541	8	2	1521	1503	18	1750	1752	UA	314	N17309	EWR	MCO	122	937	15	3	2023-08-02 15:00:00	MCO
18556	4	6	2217	2159	18	218	158	B6	654	N903JB	JFK	SJU	201	1598	21	59	2023-04-06 21:00:00	Other
18559	3	16	1358	1329	29	1654	1656	DL	785	N327NW	JFK	AUS	212	1521	13	29	2023-03-16 13:00:00	Other
18562	4	9	1928	1915	13	2041	2036	B6	465	N281JB	LGA	BOS	45	184	19	15	2023-04-09 19:00:00	BOS
18564	4	14	1508	1326	102	1617	1435	9E	1338	N935XJ	JFK	ITH	38	189	13	26	2023-04-14 13:00:00	Other
18577	4	17	1420	1400	20	1658	1638	YX	1210	N410YX	LGA	ATL	120	762	14	0	2023-04-17 14:00:00	ATL
18583	11	20	2109	2030	39	2241	2201	NK	1038	N973NK	LGA	ORD	124	733	20	30	2023-11-20 20:00:00	ORD
18584	9	30	1219	1200	19	1422	1416	DL	943	N939AT	EWR	ATL	100	746	12	0	2023-09-30 12:00:00	ATL
18590	7	13	1448	1359	49	1716	1646	AA	533	N820NN	EWR	DFW	177	1372	13	59	2023-07-13 13:00:00	Other
18592	11	3	1720	1645	35	2056	2015	AS	9	N585AS	JFK	SFO	358	2586	16	45	2023-11-03 16:00:00	Other
18595	11	18	2031	1827	124	2328	2145	UA	254	N38443	EWR	AUS	213	1504	18	27	2023-11-18 18:00:00	Other
18596	9	9	33	1400	633	242	1614	DL	820	N924AT	EWR	ATL	103	746	14	0	2023-09-09 14:00:00	ATL
18601	5	23	1710	1540	90	1853	1804	UA	378	N37513	EWR	DEN	197	1605	15	40	2023-05-23 15:00:00	Other
18607	7	12	1445	1429	16	1627	1630	UA	317	N845UA	EWR	CLT	73	529	14	29	2023-07-12 14:00:00	CLT
18630	10	26	1833	1755	38	2050	2020	WN	510	N8576Z	LGA	DEN	239	1620	17	55	2023-10-26 17:00:00	Other
18635	8	2	1009	958	11	1114	1130	YX	1327	N228JQ	JFK	BOS	37	187	9	58	2023-08-02 09:00:00	BOS
18636	5	24	1411	1348	23	1836	1703	B6	130	N524JB	LGA	FLL	224	1076	13	48	2023-05-24 13:00:00	FLL
18637	7	24	2257	2135	82	144	20	B6	76	N368JB	JFK	MCO	132	944	21	35	2023-07-24 21:00:00	MCO
18643	12	21	2012	1846	86	2253	2211	B6	149	N2017J	JFK	ONT	316	2429	18	46	2023-12-21 18:00:00	Other
18644	9	29	1110	1051	19	1408	1357	DL	373	N313DU	LGA	TPA	149	1010	10	51	2023-09-29 10:00:00	Other
18652	3	12	1012	959	13	1244	1221	9E	1481	N600LR	JFK	SAV	115	718	9	59	2023-03-12 09:00:00	Other
18656	5	20	921	755	86	1326	1156	UA	781	N76064	EWR	SJU	199	1608	7	55	2023-05-20 07:00:00	Other
18668	8	25	1115	1038	37	1238	1225	B6	71	N793JB	JFK	RDU	67	427	10	38	2023-08-25 10:00:00	Other
18673	1	3	1916	1833	43	2044	2011	UA	510	N35204	EWR	ORD	116	719	18	33	2023-01-03 18:00:00	ORD
18679	9	18	2142	2129	13	2258	2236	9E	1738	N919XJ	LGA	ALB	29	136	21	29	2023-09-18 21:00:00	Other
18681	7	18	1319	1255	24	1608	1557	B6	18	N206JB	LGA	TPA	147	1010	12	55	2023-07-18 12:00:00	Other
18684	10	9	1728	1530	118	2032	1829	UA	796	N643UA	EWR	IAH	187	1400	15	30	2023-10-09 15:00:00	Other
18686	6	27	1225	909	196	1612	1210	B6	111	N983JT	JFK	LAX	340	2475	9	9	2023-06-27 09:00:00	LAX
18688	4	16	2144	2120	24	2303	2254	9E	1288	N324PQ	LGA	BGR	54	378	21	20	2023-04-16 21:00:00	Other
18691	9	26	806	705	61	1113	1015	DL	961	N3761R	LGA	MIA	153	1096	7	5	2023-09-26 07:00:00	MIA
18694	1	2	1822	1729	53	2120	2042	B6	776	N658JB	JFK	PSP	330	2378	17	29	2023-01-02 17:00:00	Other
18697	7	31	1802	1750	12	1927	1930	UA	209	N24729	EWR	CLE	65	404	17	50	2023-07-31 17:00:00	Other
18715	12	13	1958	1720	158	2225	2002	B6	828	N566JB	LGA	JAX	120	833	17	20	2023-12-13 17:00:00	Other
18718	2	1	1107	1055	12	1427	1420	NK	969	N534NK	LGA	MIA	150	1096	10	55	2023-02-01 10:00:00	MIA
18724	9	12	1253	1237	16	1437	1445	DL	969	N133DU	JFK	MSP	145	1029	12	37	2023-09-12 12:00:00	Other
18738	4	23	2126	2100	26	2226	2219	DL	380	N131DU	LGA	BOS	34	184	21	0	2023-04-23 21:00:00	BOS
18739	1	2	1814	1800	14	2240	2257	DL	778	N908DN	JFK	SJU	182	1598	18	0	2023-01-02 18:00:00	Other
18743	7	30	1526	1459	27	1621	1611	YX	897	N863RW	EWR	ALB	31	143	14	59	2023-07-30 14:00:00	Other
18748	9	10	2314	1755	319	219	2035	B6	261	N999JQ	JFK	LAS	294	2248	17	55	2023-09-10 17:00:00	Other
18750	1	23	2224	2000	144	25	2224	9E	1652	N582CA	LGA	CVG	97	585	20	0	2023-01-23 20:00:00	Other
18754	3	5	1731	1715	16	2119	2044	DL	268	N175DN	JFK	LAX	368	2475	17	15	2023-03-05 17:00:00	LAX
18760	1	10	1132	835	177	1335	1100	9E	1556	N319PQ	LGA	TYS	102	647	8	35	2023-01-10 08:00:00	Other
18762	4	2	1449	1201	168	1613	1335	AA	416	N762US	EWR	ORD	117	719	12	1	2023-04-02 12:00:00	ORD
18769	7	17	925	900	25	1233	1201	B6	99	N980JT	JFK	LAX	332	2475	9	0	2023-07-17 09:00:00	LAX
18775	3	13	2036	1950	46	2327	2305	DL	601	N376NW	JFK	TPA	151	1005	19	50	2023-03-13 19:00:00	Other
18778	5	1	2016	1743	153	2313	2042	UA	362	N17233	EWR	TPA	149	997	17	43	2023-05-01 17:00:00	Other
18780	6	24	1057	915	102	1359	1237	AA	844	N334SM	LGA	MIA	156	1096	9	15	2023-06-24 09:00:00	MIA
18781	11	24	2213	2157	16	2331	2330	UA	487	N892UA	EWR	ORD	116	719	21	57	2023-11-24 21:00:00	ORD
18785	1	14	1256	1155	61	1455	1440	DL	376	N342NW	LGA	ATL	99	762	11	55	2023-01-14 11:00:00	ATL
18789	6	10	55	2059	236	223	2233	UA	899	N448UA	EWR	MSN	119	799	20	59	2023-06-10 20:00:00	Other
18791	4	3	836	800	36	1042	1019	YX	1461	N203JQ	JFK	CLT	85	541	8	0	2023-04-03 08:00:00	CLT
18793	12	18	2159	2058	61	111	58	DL	338	N529DT	JFK	PHX	287	2153	20	58	2023-12-18 20:00:00	Other
18795	6	17	518	507	11	904	902	B6	618	N905JB	JFK	SJU	207	1598	5	7	2023-06-17 05:00:00	Other
18808	9	29	1248	1143	65	1428	1328	OO	1234	N306SY	JFK	ORD	116	740	11	43	2023-09-29 11:00:00	ORD
18820	2	6	2158	2100	58	2310	2255	YX	1187	N426YX	LGA	RIC	46	292	21	0	2023-02-06 21:00:00	Other
18825	7	12	2003	1925	38	2129	2055	B6	541	N307JB	JFK	BOS	42	187	19	25	2023-07-12 19:00:00	BOS
18827	12	17	1933	1859	34	2218	2151	UA	395	N37549	EWR	LAS	298	2227	18	59	2023-12-17 18:00:00	Other
18830	9	11	1855	1625	150	1311	1913	UA	571	N12114	EWR	MCO	NA	937	16	25	2023-09-11 16:00:00	MCO
18835	6	7	1718	1700	18	2015	2024	B6	825	N279JB	JFK	RSW	158	1074	17	0	2023-06-07 17:00:00	Other
18853	5	3	945	930	15	1159	1159	B6	934	N339JB	LGA	SAV	112	722	9	30	2023-05-03 09:00:00	Other
18863	9	19	1611	1550	21	1823	1826	UA	851	N77572	EWR	LAS	284	2227	15	50	2023-09-19 15:00:00	Other
18866	7	1	2218	2140	38	12	2343	YX	1060	N116HQ	JFK	CLE	73	425	21	40	2023-07-01 21:00:00	Other
18870	4	14	2135	2030	65	26	2331	B6	67	N705JB	JFK	TPA	147	1005	20	30	2023-04-14 20:00:00	Other
18880	11	9	1519	1500	19	1650	1649	9E	1435	N316PQ	EWR	RDU	69	416	15	0	2023-11-09 15:00:00	Other
18885	3	8	2005	1954	11	45	50	UA	219	N66841	EWR	BQN	178	1585	19	54	2023-03-08 19:00:00	Other
18900	8	4	2152	2025	87	9	2255	WN	767	N939WN	LGA	DEN	225	1620	20	25	2023-08-04 20:00:00	Other
18901	9	25	1605	1345	140	1806	1550	9E	1734	N491PX	LGA	CAE	91	617	13	45	2023-09-25 13:00:00	Other
18911	4	14	2109	2030	39	8	2322	B6	832	N956JT	JFK	MCO	135	944	20	30	2023-04-14 20:00:00	MCO
18918	6	7	1944	1858	46	2112	2046	9E	1537	N485PX	LGA	BHM	123	866	18	58	2023-06-07 18:00:00	Other
18920	9	9	2328	2059	149	215	2351	B6	691	N958JB	EWR	MCO	128	937	20	59	2023-09-09 20:00:00	MCO
18925	3	15	2128	2043	45	2340	2258	B6	548	N203JB	JFK	DTW	86	509	20	43	2023-03-15 20:00:00	Other
18930	2	23	2020	1849	91	2306	2159	B6	82	N2048J	JFK	MCO	132	944	18	49	2023-02-23 18:00:00	MCO
18953	8	26	2144	2054	50	10	2340	UA	388	N36444	EWR	IAH	178	1400	20	54	2023-08-26 20:00:00	Other
18957	4	17	2247	2150	57	2332	2246	9E	1200	N490PX	LGA	BDL	25	101	21	50	2023-04-17 21:00:00	Other
18967	2	17	1552	1515	37	1746	1648	9E	1421	N479PX	LGA	ORF	66	296	15	15	2023-02-17 15:00:00	Other
18969	3	30	1018	930	48	1237	1159	B6	971	N329JB	LGA	SAV	116	722	9	30	2023-03-30 09:00:00	Other
18973	11	2	922	853	29	1011	1008	9E	1521	N935XJ	LGA	PVD	31	143	8	53	2023-11-02 08:00:00	Other
18976	6	14	1354	1302	52	1547	1426	YX	1106	N724YX	EWR	PIT	66	319	13	2	2023-06-14 13:00:00	Other
18980	7	7	2212	2200	12	2309	2257	9E	1213	N936XJ	LGA	BDL	26	101	22	0	2023-07-07 22:00:00	Other
18988	3	26	1647	1503	104	2014	1804	DL	329	N371DA	LGA	PBI	168	1035	15	3	2023-03-26 15:00:00	Other
18995	1	16	2200	2025	95	17	2242	UA	671	N39418	EWR	CVG	94	569	20	25	2023-01-16 20:00:00	Other
19010	2	2	2108	2025	43	2335	2248	YX	1129	N731YX	EWR	CVG	114	569	20	25	2023-02-02 20:00:00	Other
19011	9	10	1744	1711	33	1930	1915	DL	913	N327NW	LGA	DTW	79	502	17	11	2023-09-10 17:00:00	Other
19012	8	25	1050	834	136	1246	1033	UA	83	N898UA	EWR	DTW	77	488	8	34	2023-08-25 08:00:00	Other
19016	5	4	1924	1910	14	2037	2036	UA	800	N38458	EWR	IAD	42	212	19	10	2023-05-04 19:00:00	Other
19021	7	28	2237	2130	67	124	2324	YX	1366	N882RW	JFK	RIC	60	288	21	30	2023-07-28 21:00:00	Other
19022	12	8	2252	2030	142	132	2343	UA	907	N41135	EWR	FLL	143	1065	20	30	2023-12-08 20:00:00	FLL
19024	12	8	1849	1825	24	2131	2130	WN	818	N1808U	LGA	TPA	145	1010	18	25	2023-12-08 18:00:00	Other
19027	10	2	1802	1720	42	2034	2005	WN	1201	N8645A	LGA	HOU	185	1428	17	20	2023-10-02 17:00:00	Other
19032	6	20	1009	956	13	1212	1222	UA	586	N37295	EWR	LAS	279	2227	9	56	2023-06-20 09:00:00	Other
19033	7	25	2116	1929	107	11	2308	DL	195	N511DE	JFK	SEA	329	2422	19	29	2023-07-25 19:00:00	Other
19037	7	18	2038	1915	83	2342	2214	DL	526	N119DU	LGA	IAH	200	1416	19	15	2023-07-18 19:00:00	Other
19042	1	4	2239	2159	40	2343	2318	UA	633	N76519	EWR	BOS	37	200	21	59	2023-01-04 21:00:00	BOS
19046	1	4	1917	1745	92	2116	2020	WN	400	N8307K	LGA	DEN	221	1620	17	45	2023-01-04 17:00:00	Other
19050	12	28	1215	1131	44	1446	1404	UA	655	N77430	EWR	JAX	133	820	11	31	2023-12-28 11:00:00	Other
19057	8	1	2255	2159	56	22	2352	UA	681	N27253	EWR	RDU	63	416	21	59	2023-08-01 21:00:00	Other
19073	1	13	1846	1829	17	2121	2154	YX	1357	N871RW	LGA	OKC	180	1341	18	29	2023-01-13 18:00:00	Other
19076	3	15	1359	1259	60	1552	1514	9E	1455	N138EV	LGA	DAY	84	549	12	59	2023-03-15 12:00:00	Other
19079	8	7	716	700	16	1017	1020	NK	811	N972NK	EWR	SLC	265	1969	7	0	2023-08-07 07:00:00	Other
19084	9	5	1404	1301	63	1559	1511	UA	901	N69826	EWR	MSY	145	1167	13	1	2023-09-05 13:00:00	Other
19097	5	30	2011	1959	12	2302	2321	DL	581	N399DA	JFK	TPA	136	1005	19	59	2023-05-30 19:00:00	Other
19103	4	28	1646	1629	17	1839	1848	DL	698	N123DQ	JFK	DTW	83	509	16	29	2023-04-28 16:00:00	Other
19107	11	14	1903	1631	152	2206	1945	NK	316	N692NK	LGA	FLL	143	1076	16	31	2023-11-14 16:00:00	FLL
19108	5	14	2146	2122	24	2309	2258	UA	902	N38446	EWR	BNA	102	748	21	22	2023-05-14 21:00:00	Other
19110	5	7	1915	1900	15	2030	2033	YX	1710	N208JQ	LGA	BOS	43	184	19	0	2023-05-07 19:00:00	BOS
19113	7	28	1958	1930	28	NA	2229	B6	551	N516JB	LGA	PBI	NA	1035	19	30	2023-07-28 19:00:00	Other
19120	8	9	2052	2000	52	2338	2341	DL	88	N923DZ	JFK	SLC	261	1990	20	0	2023-08-09 20:00:00	Other
19125	7	30	1632	1539	53	1835	1804	B6	737	N239JB	JFK	CHS	95	636	15	39	2023-07-30 15:00:00	Other
19137	7	27	719	705	14	904	932	UA	372	N27253	EWR	PHX	264	2133	7	5	2023-07-27 07:00:00	Other
19150	4	4	926	900	26	1042	1035	WN	305	N952WN	LGA	MDW	114	725	9	0	2023-04-04 09:00:00	Other
19152	6	29	2032	1959	33	2319	2309	AA	789	N350RV	LGA	MIA	139	1096	19	59	2023-06-29 19:00:00	MIA
19153	3	5	1723	1630	53	2045	1950	B6	131	N583JB	LGA	FLL	155	1076	16	30	2023-03-05 16:00:00	FLL
19157	12	23	1328	1259	29	1653	1652	AA	951	N313SB	JFK	PHX	305	2153	12	59	2023-12-23 12:00:00	Other
19158	8	25	1113	1035	38	1223	1201	B6	49	N358JB	JFK	ROC	51	264	10	35	2023-08-25 10:00:00	Other
19159	8	2	1212	1015	117	1345	1155	AA	124	N763US	LGA	ORD	112	733	10	15	2023-08-02 10:00:00	ORD
19170	4	30	1150	1129	21	1524	1432	B6	20	N633JB	LGA	TPA	157	1010	11	29	2023-04-30 11:00:00	Other
19175	6	14	1956	1859	57	2109	2021	DL	1043	N130DU	LGA	BOS	43	184	18	59	2023-06-14 18:00:00	BOS
19178	12	17	152	2255	177	649	347	B6	126	N558JB	JFK	SJU	213	1598	22	55	2023-12-17 22:00:00	Other
19182	3	6	1840	1825	15	2128	2134	AA	133	N942AN	JFK	DFW	196	1391	18	25	2023-03-06 18:00:00	Other
19188	11	5	2247	2230	17	13	7	9E	1500	N935XJ	JFK	SYR	44	209	22	30	2023-11-05 22:00:00	Other
19194	9	29	1231	1200	31	1508	1508	UA	854	N37018	EWR	SFO	311	2565	12	0	2023-09-29 12:00:00	Other
19195	2	27	1144	1117	27	1359	1330	YX	1037	N753YX	EWR	DTW	95	488	11	17	2023-02-27 11:00:00	Other
19197	3	3	2022	2007	15	2246	2305	UA	428	N75425	EWR	LAS	300	2227	20	7	2023-03-03 20:00:00	Other
19200	12	13	1110	1041	29	1404	1344	UA	242	N77530	EWR	TPA	140	997	10	41	2023-12-13 10:00:00	Other
19209	9	11	2110	1915	115	2237	2051	UA	750	N494UA	LGA	ORD	109	733	19	15	2023-09-11 19:00:00	ORD
19215	6	8	1747	1715	32	1909	1846	B6	413	N183JB	LGA	BOS	44	184	17	15	2023-06-08 17:00:00	BOS
19223	9	10	1140	833	187	1518	1100	B6	419	N284JB	JFK	ATL	115	760	8	33	2023-09-10 08:00:00	ATL
19229	7	4	1321	1229	52	1435	1400	YX	991	N124HQ	JFK	ORF	49	290	12	29	2023-07-04 12:00:00	Other
19230	3	6	1757	1729	28	2019	1954	9E	1380	N303PQ	LGA	CVG	106	585	17	29	2023-03-06 17:00:00	Other
19239	8	2	2038	2025	13	2246	2255	WN	767	N959WN	LGA	DEN	222	1620	20	25	2023-08-02 20:00:00	Other
19243	6	28	1020	943	37	1245	1309	B6	23	N537JT	JFK	SEA	308	2422	9	43	2023-06-28 09:00:00	Other
19244	1	23	1936	1845	51	2158	2134	DL	205	N339DN	LGA	ATL	107	762	18	45	2023-01-23 18:00:00	ATL
19245	7	18	2206	1935	151	12	2214	9E	1328	N602LR	JFK	CLT	78	541	19	35	2023-07-18 19:00:00	CLT
19246	10	3	953	900	53	1133	1050	9E	1606	N320PQ	JFK	RDU	66	427	9	0	2023-10-03 09:00:00	Other
19248	1	23	1205	1148	17	1452	1446	UA	320	N25201	EWR	MCO	145	937	11	48	2023-01-23 11:00:00	MCO
19252	8	4	1500	1315	105	1558	1435	B6	131	N206JB	LGA	BOS	41	184	13	15	2023-08-04 13:00:00	BOS
19256	12	2	1913	1459	254	2203	1814	DL	355	N344NW	LGA	PBI	148	1035	14	59	2023-12-02 14:00:00	Other
19260	6	30	2130	2102	28	2244	2236	UA	899	N823UA	EWR	MSN	106	799	21	2	2023-06-30 21:00:00	Other
19262	11	26	1704	1610	54	1855	1750	WN	1143	N7879A	LGA	BNA	127	764	16	10	2023-11-26 16:00:00	Other
19263	3	9	957	939	18	1206	1159	9E	1488	N307PQ	EWR	CVG	92	569	9	39	2023-03-09 09:00:00	Other
19268	7	11	1514	1459	15	1644	1645	UA	564	N487UA	EWR	RDU	66	416	14	59	2023-07-11 14:00:00	Other
19272	6	8	1521	1405	76	1814	1723	B6	50	N507JT	JFK	SRQ	145	1041	14	5	2023-06-08 14:00:00	Other
19275	10	27	1228	1217	11	1405	1411	NK	20	N661NK	EWR	MYR	79	550	12	17	2023-10-27 12:00:00	Other
19276	12	28	1031	952	39	1350	1257	NK	997	N978NK	EWR	MCO	163	937	9	52	2023-12-28 09:00:00	MCO
19304	5	23	1949	1915	34	2114	2106	OO	1498	N114SY	LGA	ORD	105	733	19	15	2023-05-23 19:00:00	ORD
19306	3	31	1712	1647	25	2019	2007	DL	324	N674DL	JFK	SEA	325	2422	16	47	2023-03-31 16:00:00	Other
19308	6	17	2127	2112	15	2330	2344	UA	310	N87513	EWR	LAS	286	2227	21	12	2023-06-17 21:00:00	Other
19310	5	6	1145	1125	20	1422	1445	DL	884	N389DN	LGA	FLL	136	1076	11	25	2023-05-06 11:00:00	FLL
19311	8	8	1602	1455	67	1719	1643	9E	1156	N904XJ	LGA	ORF	50	296	14	55	2023-08-08 14:00:00	Other
19325	7	1	2147	2110	37	40	35	UA	567	N17126	EWR	SFO	327	2565	21	10	2023-07-01 21:00:00	Other
19330	7	20	804	655	69	1042	909	B6	660	N703JB	LGA	DEN	241	1620	6	55	2023-07-20 06:00:00	Other
19335	2	15	831	800	31	1106	1050	UA	446	N14115	EWR	EGE	252	1725	8	0	2023-02-15 08:00:00	Other
19336	6	2	2205	2005	120	2345	2206	DL	840	N357NB	LGA	DTW	77	502	20	5	2023-06-02 20:00:00	Other
19340	9	18	1228	1152	36	1325	1308	UA	265	N36469	EWR	BOS	36	200	11	52	2023-09-18 11:00:00	BOS
19354	4	3	1540	1415	85	1646	1532	B6	304	N329JB	LGA	BOS	39	184	14	15	2023-04-03 14:00:00	BOS
19363	5	1	1953	1900	53	2107	2026	UA	800	N443UA	EWR	IAD	45	212	19	0	2023-05-01 19:00:00	Other
19366	4	26	1645	1630	15	1942	1934	B6	320	N355JB	JFK	MCO	144	944	16	30	2023-04-26 16:00:00	MCO
19369	8	11	815	759	16	1110	1108	AA	117	N822NN	LGA	MIA	154	1096	7	59	2023-08-11 07:00:00	MIA
19370	4	23	1208	900	188	1339	1038	UA	235	N73270	LGA	ORD	103	733	9	0	2023-04-23 09:00:00	ORD
19381	6	24	1950	1830	80	2104	1955	WN	240	N8512U	LGA	MDW	112	725	18	30	2023-06-24 18:00:00	Other
19385	1	1	1117	1103	14	1409	1410	UA	172	N489UA	EWR	PBI	147	1023	11	3	2023-01-01 11:00:00	Other
19402	6	3	1937	1900	37	2111	2040	YX	1241	N723YX	EWR	PIT	61	319	19	0	2023-06-03 19:00:00	Other
19411	11	20	1041	1012	29	1254	1225	OO	1188	N243SY	LGA	MEM	159	963	10	12	2023-11-20 10:00:00	Other
19412	9	22	1823	1535	168	2017	1710	UA	695	N19117	EWR	ORD	105	719	15	35	2023-09-22 15:00:00	ORD
19413	8	22	1513	1330	103	1900	1731	B6	258	N954JB	JFK	SJU	193	1598	13	30	2023-08-22 13:00:00	Other
19419	6	16	2117	2100	17	6	23	AA	97	N108NN	JFK	LAX	313	2475	21	0	2023-06-16 21:00:00	LAX
19425	3	28	1657	1459	118	1816	1619	B6	443	N375JB	JFK	ROC	51	264	14	59	2023-03-28 14:00:00	Other
19435	8	8	2041	2030	11	2338	2324	B6	669	N506JB	EWR	TPA	146	997	20	30	2023-08-08 20:00:00	Other
19445	4	17	2109	1830	159	21	2136	UA	801	N78540	EWR	PBI	163	1023	18	30	2023-04-17 18:00:00	Other
19447	5	7	1455	1440	15	1703	1710	WN	958	N8814K	LGA	ATL	106	762	14	40	2023-05-07 14:00:00	ATL
19452	11	21	2239	2005	154	218	2350	B6	306	N993JE	JFK	SFO	337	2586	20	5	2023-11-21 20:00:00	Other
19454	1	24	1432	1359	33	1606	1536	AA	184	N924NN	EWR	ORD	123	719	13	59	2023-01-24 13:00:00	ORD
19456	2	28	2138	1959	99	2350	2219	YX	1204	N442YX	LGA	CMH	92	479	19	59	2023-02-28 19:00:00	Other
19458	12	20	1441	1400	41	1752	1719	B6	622	N597JB	JFK	RSW	148	1074	14	0	2023-12-20 14:00:00	Other
19461	11	29	1206	1142	24	1319	1315	YX	1904	N232JQ	LGA	DCA	44	214	11	42	2023-11-29 11:00:00	Other
19466	4	23	805	500	185	1108	756	AA	301	N800NN	EWR	DFW	202	1372	5	0	2023-04-23 05:00:00	Other
19467	11	5	1850	1825	25	2129	2130	WN	840	N8509U	LGA	TPA	132	1010	18	25	2023-11-05 18:00:00	Other
19468	2	12	1935	1859	36	2240	2219	UA	742	N75433	EWR	SEA	327	2402	18	59	2023-02-12 18:00:00	Other
19472	6	26	1235	915	200	1555	1207	UA	516	N12221	EWR	MCO	127	937	9	15	2023-06-26 09:00:00	MCO
19477	7	15	751	719	32	1044	1020	DL	609	N116DN	EWR	SLC	271	1969	7	19	2023-07-15 07:00:00	Other
19484	11	5	1220	1159	21	1439	1436	OO	1187	N254SY	LGA	SDF	102	659	11	59	2023-11-05 11:00:00	Other
19486	12	17	2241	2059	102	2352	2233	DL	136	N121DU	JFK	BOS	40	187	20	59	2023-12-17 20:00:00	BOS
19500	3	19	1222	1205	17	1339	1315	B6	64	N236JB	JFK	BOS	43	187	12	5	2023-03-19 12:00:00	BOS
19502	6	11	2149	2114	35	40	2359	B6	480	N794JB	JFK	JAX	124	828	21	14	2023-06-11 21:00:00	Other
19510	1	11	2143	1959	104	22	2308	DL	627	N339DN	JFK	MCO	128	944	19	59	2023-01-11 19:00:00	MCO
19511	7	10	658	627	31	840	816	YX	1010	N109HQ	LGA	CMH	78	479	6	27	2023-07-10 06:00:00	Other
19513	1	8	1008	950	18	1212	1215	UA	854	N29978	EWR	DEN	207	1605	9	50	2023-01-08 09:00:00	Other
19520	7	14	1232	1730	1142	1448	1926	YX	1029	N137HQ	LGA	CMH	74	479	17	30	2023-07-14 17:00:00	Other
19522	1	4	1852	1829	23	2019	2014	UA	510	N37462	EWR	ORD	107	719	18	29	2023-01-04 18:00:00	ORD
19532	9	11	1549	1525	24	1850	1719	YX	1915	N218JQ	JFK	PIT	55	340	15	25	2023-09-11 15:00:00	Other
19535	5	9	1648	1630	18	1955	1953	B6	955	N552JB	JFK	FLL	154	1069	16	30	2023-05-09 16:00:00	FLL
19542	8	16	2305	2250	15	146	115	F9	451	N718FR	LGA	ATL	111	762	22	50	2023-08-16 22:00:00	ATL
19549	11	26	335	2125	370	621	17	B6	658	N355JB	EWR	MCO	141	937	21	25	2023-11-26 21:00:00	MCO
19555	4	17	1723	1705	18	1925	1928	YX	1510	N234JQ	LGA	IND	100	660	17	5	2023-04-17 17:00:00	Other
19559	6	15	1905	1825	40	2141	2139	AS	174	N524AS	EWR	SEA	305	2402	18	25	2023-06-15 18:00:00	Other
19566	5	7	1914	1900	14	2035	2030	WN	53	N8801Q	LGA	MDW	114	725	19	0	2023-05-07 19:00:00	Other
19567	3	2	1542	1514	28	1810	1745	UA	97	N17264	EWR	ATL	120	746	15	14	2023-03-02 15:00:00	ATL
19568	7	27	1758	1546	132	1949	1735	YX	1381	N201JQ	JFK	DCA	76	213	15	46	2023-07-27 15:00:00	Other
19571	2	10	2005	1857	68	2224	2131	NK	295	N659NK	EWR	IND	107	645	18	57	2023-02-10 18:00:00	Other
19573	7	29	905	843	22	1208	1134	UA	497	N815UA	EWR	SAT	196	1569	8	43	2023-07-29 08:00:00	Other
19576	8	10	1206	1155	11	1445	1455	DL	477	N124DX	LGA	MCO	136	950	11	55	2023-08-10 11:00:00	MCO
19579	6	18	1414	1330	44	1806	1734	B6	322	N556JB	JFK	SJU	200	1598	13	30	2023-06-18 13:00:00	Other
19580	9	29	1716	1550	86	1958	1859	DL	986	N104DU	LGA	TPA	141	1010	15	50	2023-09-29 15:00:00	Other
19587	2	14	2118	2100	18	9	18	B6	34	N944JT	JFK	SAN	335	2446	21	0	2023-02-14 21:00:00	Other
19590	2	3	728	715	13	842	827	B6	934	N190JB	LGA	BOS	40	184	7	15	2023-02-03 07:00:00	BOS
19594	9	12	1003	840	83	1109	956	B6	51	N375JB	EWR	BOS	33	200	8	40	2023-09-12 08:00:00	BOS
19599	2	24	1942	1900	42	2050	2019	DL	610	N127DU	LGA	BOS	39	184	19	0	2023-02-24 19:00:00	BOS
19600	9	8	1612	1600	12	1930	1754	OO	1273	N243SY	JFK	ORD	141	740	16	0	2023-09-08 16:00:00	ORD
19607	9	5	1345	1300	45	1619	1614	B6	595	N2017J	JFK	FLL	133	1069	13	0	2023-09-05 13:00:00	FLL
19608	6	22	933	900	33	1137	1117	YX	1232	N856RW	EWR	HHH	104	687	9	0	2023-06-22 09:00:00	Other
19610	6	17	1407	1334	33	1540	1451	B6	622	N179JB	JFK	BOS	47	187	13	34	2023-06-17 13:00:00	BOS
19613	12	15	919	849	30	1051	1057	9E	1472	N918XJ	LGA	GSO	69	461	8	49	2023-12-15 08:00:00	Other
19618	8	3	1529	1500	29	1704	1655	YX	1081	N102HQ	LGA	STL	130	888	15	0	2023-08-03 15:00:00	Other
19631	8	1	2159	2129	30	2257	2247	9E	1230	N491PX	LGA	SYR	39	198	21	29	2023-08-01 21:00:00	Other
19646	8	19	1815	1734	41	2131	2041	AA	35	N113AN	JFK	LAX	311	2475	17	34	2023-08-19 17:00:00	LAX
19659	9	23	1543	1359	104	1657	1528	YX	1827	N245JQ	LGA	MKE	101	738	13	59	2023-09-23 13:00:00	Other
19660	3	8	1709	1641	28	2026	1955	NK	339	N670NK	LGA	FLL	153	1076	16	41	2023-03-08 16:00:00	FLL
19663	6	17	1803	1659	64	1938	1831	B6	406	N247JB	JFK	BOS	38	187	16	59	2023-06-17 16:00:00	BOS
19666	10	1	2231	1910	201	39	2152	YX	1304	N421YX	LGA	OKC	167	1341	19	10	2023-10-01 19:00:00	Other
19672	3	25	1108	1055	13	1226	1225	WN	1023	N8567Z	LGA	MDW	114	725	10	55	2023-03-25 10:00:00	Other
19678	8	8	1735	1556	99	1950	1846	DL	215	N902DN	JFK	DEN	232	1626	15	56	2023-08-08 15:00:00	Other
19689	7	21	1354	1046	188	1640	1342	B6	325	N621JB	JFK	MCO	128	944	10	46	2023-07-21 10:00:00	MCO
19692	8	4	2220	2144	36	21	2322	YX	912	N757YX	EWR	BGR	65	393	21	44	2023-08-04 21:00:00	Other
19697	7	7	1836	1455	221	2223	1805	B6	261	N569JB	LGA	PBI	173	1035	14	55	2023-07-07 14:00:00	Other
19703	11	19	2208	2055	73	2345	2257	9E	1555	N341PQ	LGA	ILM	71	500	20	55	2023-11-19 20:00:00	Other
19706	10	15	1736	1645	51	2042	1953	NK	594	N608NK	EWR	FLL	157	1065	16	45	2023-10-15 16:00:00	FLL
19715	9	17	1703	1650	13	1919	1905	WN	152	N8502Z	LGA	MSY	175	1183	16	50	2023-09-17 16:00:00	Other
19723	9	18	1025	1013	12	1202	1150	YX	1150	N758YX	EWR	BGR	58	393	10	13	2023-09-18 10:00:00	Other
19725	7	6	1551	1540	11	1713	1705	WN	726	N7886A	LGA	MDW	115	725	15	40	2023-07-06 15:00:00	Other
19729	3	19	2051	2025	26	2255	2300	WN	891	N8805L	LGA	DEN	222	1620	20	25	2023-03-19 20:00:00	Other
19734	1	11	2155	1950	125	2340	2150	9E	1639	N926XJ	JFK	RDU	71	427	19	50	2023-01-11 19:00:00	Other
19742	8	1	1641	1440	121	1913	1743	DL	380	N342DN	LGA	MCO	123	950	14	40	2023-08-01 14:00:00	MCO
19744	12	10	2143	2050	53	11	2306	9E	1505	N918XJ	LGA	CAE	106	617	20	50	2023-12-10 20:00:00	Other
19745	3	31	1617	1555	22	1929	1912	B6	253	N796JB	JFK	PBI	143	1028	15	55	2023-03-31 15:00:00	Other
19751	3	31	2128	2027	61	36	2337	UA	700	N430UA	EWR	RSW	163	1068	20	27	2023-03-31 20:00:00	Other
19773	5	12	2017	1959	18	2144	2152	YX	1050	N979RP	EWR	GSO	65	445	19	59	2023-05-12 19:00:00	Other
19777	2	21	2118	2030	48	2318	2248	9E	1477	N920XJ	LGA	GSP	95	610	20	30	2023-02-21 20:00:00	Other
19778	6	23	957	920	37	1132	1115	9E	1714	N294PQ	JFK	CLE	66	425	9	20	2023-06-23 09:00:00	Other
19787	7	4	1202	1134	28	1428	1426	NK	840	N626NK	EWR	MCO	124	937	11	34	2023-07-04 11:00:00	MCO
19792	5	29	730	710	20	1017	1012	DL	600	N384DN	LGA	FLL	141	1076	7	10	2023-05-29 07:00:00	FLL
19794	9	12	1857	1530	207	2152	1838	UA	764	N77012	EWR	SFO	315	2565	15	30	2023-09-12 15:00:00	Other
19801	7	27	1727	1708	19	1931	1936	AA	771	N417AN	EWR	PHX	271	2133	17	8	2023-07-27 17:00:00	Other
19810	9	12	2250	2159	51	2400	2313	9E	1751	N904XJ	LGA	SYR	37	198	21	59	2023-09-12 21:00:00	Other
19820	2	3	2237	1959	158	114	2308	DL	546	N390DN	JFK	MCO	135	944	19	59	2023-02-03 19:00:00	MCO
19821	7	27	2050	1659	231	2327	1948	UA	699	N15710	EWR	DFW	174	1372	16	59	2023-07-27 16:00:00	Other
19822	4	22	1817	1730	47	2120	2030	WN	822	N8659D	LGA	DAL	212	1381	17	30	2023-04-22 17:00:00	Other
19827	9	10	2151	2030	81	55	2257	B6	31	N569JB	JFK	DEN	241	1626	20	30	2023-09-10 20:00:00	Other
19841	3	23	2341	2230	71	322	219	B6	144	N2002J	JFK	SJU	176	1598	22	30	2023-03-23 22:00:00	Other
19843	3	3	1921	1835	46	2153	2020	B6	30	N760JB	JFK	BNA	129	765	18	35	2023-03-03 18:00:00	Other
19845	4	6	2254	2237	17	1	2355	UA	530	N17730	EWR	BTV	45	266	22	37	2023-04-06 22:00:00	Other
19847	10	11	1823	1729	54	2157	2037	AA	36	N102NN	JFK	LAX	366	2475	17	29	2023-10-11 17:00:00	LAX
19850	7	14	800	705	55	1011	932	UA	372	N47291	EWR	PHX	286	2133	7	5	2023-07-14 07:00:00	Other
19856	7	13	2019	1920	59	2342	2118	9E	1155	N917XJ	LGA	CLE	80	419	19	20	2023-07-13 19:00:00	Other
19861	9	8	1203	1131	32	1357	1332	AA	942	N872NN	JFK	CLT	78	541	11	31	2023-09-08 11:00:00	CLT
19863	1	23	2020	1940	40	2232	2137	9E	1639	N331PQ	JFK	RDU	70	427	19	40	2023-01-23 19:00:00	Other
19877	5	28	1634	1623	11	1835	1853	UA	713	N834UA	LGA	DEN	219	1620	16	23	2023-05-28 16:00:00	Other
19883	5	10	1518	1450	28	1758	1758	DL	363	N351NB	LGA	PBI	131	1035	14	50	2023-05-10 14:00:00	Other
19886	7	18	1737	1650	47	1931	1900	WN	704	N8608N	LGA	MCI	157	1107	16	50	2023-07-18 16:00:00	Other
19889	9	30	1546	1530	16	1711	1716	YX	1418	N406YX	LGA	RDU	64	431	15	30	2023-09-30 15:00:00	Other
19890	10	5	2211	2200	11	121	59	DL	88	N177DN	JFK	LAX	322	2475	22	0	2023-10-05 22:00:00	LAX
19897	2	13	1313	1240	33	1610	1553	AA	508	N406AN	EWR	MIA	143	1085	12	40	2023-02-13 12:00:00	MIA
19899	5	4	1733	1720	13	2045	2059	B6	245	N760JB	JFK	SJC	340	2569	17	20	2023-05-04 17:00:00	Other
19903	7	28	751	600	111	921	715	WN	14	N8610A	LGA	MDW	123	725	6	0	2023-07-28 06:00:00	Other
19904	12	15	2018	1959	19	2342	2338	AA	943	N344PP	LGA	MIA	158	1096	19	59	2023-12-15 19:00:00	MIA
19905	6	16	1321	1155	86	1554	1418	YX	1287	N132HQ	JFK	IND	111	665	11	55	2023-06-16 11:00:00	Other
19906	12	6	1429	1340	49	1612	1543	AA	645	N915US	EWR	CLT	79	529	13	40	2023-12-06 13:00:00	CLT
19912	9	11	1934	1829	65	2154	2059	YX	1321	N872RW	LGA	TUL	169	1231	18	29	2023-09-11 18:00:00	Other
19914	8	13	1512	1459	13	1727	1735	9E	1150	N183GJ	JFK	IND	100	665	14	59	2023-08-13 14:00:00	Other
19915	9	11	2131	1412	439	2310	1537	B6	54	N317JB	JFK	ROC	45	264	14	12	2023-09-11 14:00:00	Other
19917	12	21	2205	1959	126	22	2251	DL	368	N123DQ	LGA	JAX	115	833	19	59	2023-12-21 19:00:00	Other
19923	5	11	1320	920	240	1504	1120	NK	543	N641NK	EWR	CHS	82	628	9	20	2023-05-11 09:00:00	Other
19926	3	30	1427	1410	17	1725	1656	UA	408	N33262	EWR	MCO	129	937	14	10	2023-03-30 14:00:00	MCO
19929	1	29	2228	2153	35	1	2338	UA	596	N485UA	EWR	ORD	127	719	21	53	2023-01-29 21:00:00	ORD
19931	6	4	733	720	13	921	934	UA	249	N33203	LGA	DEN	206	1620	7	20	2023-06-04 07:00:00	Other
19932	10	6	646	634	12	911	850	B6	776	N561JB	LGA	DEN	242	1620	6	34	2023-10-06 06:00:00	Other
19941	2	21	1026	1000	26	1157	1134	AA	768	N837AW	LGA	DCA	51	214	10	0	2023-02-21 10:00:00	Other
19944	1	15	619	600	19	936	912	B6	646	N590JB	EWR	FLL	129	1065	6	0	2023-01-15 06:00:00	FLL
19948	6	8	1817	1800	17	2008	2012	9E	1719	N929XJ	LGA	DSM	140	1031	18	0	2023-06-08 18:00:00	Other
19951	1	4	1807	1633	94	2107	1948	UA	660	N37471	EWR	FLL	153	1065	16	33	2023-01-04 16:00:00	FLL
19957	7	28	2011	1255	436	6	1505	G4	347	327NV	EWR	SAV	106	708	12	55	2023-07-28 12:00:00	Other
19958	3	16	2204	2120	44	2350	2329	NK	292	N969NK	LGA	DTW	82	502	21	20	2023-03-16 21:00:00	Other
19961	11	27	1650	1530	80	1848	1723	B6	29	N657JB	JFK	ORD	126	740	15	30	2023-11-27 15:00:00	ORD
19967	12	18	1658	1530	88	1923	1808	B6	922	N796JB	JFK	ATL	115	760	15	30	2023-12-18 15:00:00	ATL
19977	4	18	716	655	21	942	928	B6	120	N274JB	LGA	JAX	119	833	6	55	2023-04-18 06:00:00	Other
19982	3	10	1214	1150	24	1357	1348	DL	287	N926AT	EWR	MSP	147	1008	11	50	2023-03-10 11:00:00	Other
19989	6	16	1629	1525	64	1803	1700	WN	274	N569WN	LGA	STL	136	888	15	25	2023-06-16 15:00:00	Other
19992	2	1	1617	1543	34	1848	1824	B6	645	N821JB	JFK	ATL	124	760	15	43	2023-02-01 15:00:00	ATL
19999	12	16	1219	1150	29	1537	1505	NK	346	N954NK	EWR	FLL	175	1065	11	50	2023-12-16 11:00:00	FLL
20002	5	29	1841	1650	111	2034	1832	9E	1533	N927XJ	JFK	PWM	48	273	16	50	2023-05-29 16:00:00	Other
20019	6	16	1958	1915	43	2239	2203	9E	1748	N919XJ	LGA	JAX	128	833	19	15	2023-06-16 19:00:00	Other
20021	7	24	1719	1659	20	2011	2007	UA	617	N432UA	EWR	RSW	150	1068	16	59	2023-07-24 16:00:00	Other
20023	1	20	2216	1710	306	59	2011	NK	599	N606NK	EWR	MCO	139	937	17	10	2023-01-20 17:00:00	MCO
20025	3	9	2130	2059	31	3	2353	UA	418	N38458	EWR	MCO	124	937	20	59	2023-03-09 20:00:00	MCO
20029	5	23	1939	1855	44	2223	2149	B6	899	N569JB	JFK	MCO	136	944	18	55	2023-05-23 18:00:00	MCO
20033	2	28	1845	1829	16	2104	2054	YX	1005	N861RW	EWR	IND	111	645	18	29	2023-02-28 18:00:00	Other
20038	1	16	1736	1710	26	1937	1919	AA	484	N4032T	LGA	STL	137	888	17	10	2023-01-16 17:00:00	Other
20055	6	7	2117	2100	17	2219	2216	DL	441	N142DU	LGA	BOS	38	184	21	0	2023-06-07 21:00:00	BOS
20060	8	11	2058	2039	19	2325	2325	UA	638	N66803	EWR	DFW	175	1372	20	39	2023-08-11 20:00:00	Other
20069	12	30	2245	2224	21	338	325	NK	364	N628NK	EWR	SJU	217	1608	22	24	2023-12-30 22:00:00	Other
20076	8	21	2008	1859	69	2219	2144	DL	177	N367DN	LGA	ATL	96	762	18	59	2023-08-21 18:00:00	ATL
20077	6	3	2246	2059	107	1	2229	UA	770	N27734	EWR	BNA	105	748	20	59	2023-06-03 20:00:00	Other
20081	3	5	926	804	82	1228	1121	B6	727	N629JB	JFK	IAH	218	1417	8	4	2023-03-05 08:00:00	Other
20083	3	13	1715	1546	89	2016	1907	B6	704	N640JB	EWR	RSW	158	1068	15	46	2023-03-13 15:00:00	Other
20097	1	22	817	805	12	1045	1115	DL	383	N707TW	JFK	LAS	300	2248	8	5	2023-01-22 08:00:00	Other
20099	11	18	939	800	99	1244	1114	B6	535	N2060J	JFK	RSW	152	1074	8	0	2023-11-18 08:00:00	Other
20102	4	29	1804	1749	15	2139	2106	NK	31	N903NK	EWR	LAX	330	2454	17	49	2023-04-29 17:00:00	LAX
20108	4	23	813	730	43	1044	947	B6	308	N339JB	JFK	SAV	115	718	7	30	2023-04-23 07:00:00	Other
20120	4	7	1921	1859	22	2222	2215	UA	444	N442UA	EWR	SLC	275	1969	18	59	2023-04-07 18:00:00	Other
20122	9	8	9	2130	159	240	18	B6	177	N520JB	LGA	MCO	123	950	21	30	2023-09-08 21:00:00	MCO
20124	6	25	1020	909	71	1310	1210	B6	111	N929JB	JFK	LAX	332	2475	9	9	2023-06-25 09:00:00	LAX
20132	4	1	2243	2135	68	16	2253	9E	1331	N137EV	JFK	ITH	43	189	21	35	2023-04-01 21:00:00	Other
20135	1	22	2210	1910	180	121	2227	DL	709	N382DN	JFK	FLL	165	1069	19	10	2023-01-22 19:00:00	FLL
20136	7	4	1419	1334	45	1530	1451	B6	505	N206JB	JFK	BOS	39	187	13	34	2023-07-04 13:00:00	BOS
20144	8	18	1312	1259	13	1425	1438	9E	1149	N935XJ	LGA	RIC	56	292	12	59	2023-08-18 12:00:00	Other
20153	8	11	1827	1750	37	2103	2021	9E	1259	N928XJ	LGA	SAV	103	722	17	50	2023-08-11 17:00:00	Other
20154	6	3	1703	1530	93	1925	1811	B6	650	N559JB	JFK	JAX	109	828	15	30	2023-06-03 15:00:00	Other
20156	7	24	1942	1925	17	2156	2152	9E	1226	N182GJ	JFK	DTW	87	509	19	25	2023-07-24 19:00:00	Other
20157	4	30	1111	1100	11	1344	1416	B6	205	N2105J	JFK	LAX	314	2475	11	0	2023-04-30 11:00:00	LAX
20158	8	25	2222	2107	75	6	2312	UA	193	N36444	EWR	CVG	78	569	21	7	2023-08-25 21:00:00	Other
20160	8	16	1643	1548	55	2042	1908	DL	482	N3739P	JFK	PBI	190	1028	15	48	2023-08-16 15:00:00	Other
20161	1	22	1019	955	24	1218	1151	9E	1535	N337PQ	JFK	CLE	83	425	9	55	2023-01-22 09:00:00	Other
20164	5	24	1958	1915	43	2328	2237	DL	153	N177DN	JFK	LAX	331	2475	19	15	2023-05-24 19:00:00	LAX
20166	8	1	647	601	46	928	839	B6	191	N903JB	JFK	MCO	128	944	6	1	2023-08-01 06:00:00	MCO
20167	4	2	826	759	27	1111	1106	UA	397	N38727	EWR	FLL	147	1065	7	59	2023-04-02 07:00:00	FLL
20168	7	8	1701	1555	66	2026	1836	DL	229	N807DN	JFK	DEN	256	1626	15	55	2023-07-08 15:00:00	Other
20174	11	6	2014	1959	15	2312	2329	DL	716	N316DN	JFK	FLL	144	1069	19	59	2023-11-06 19:00:00	FLL
20178	1	8	1200	1130	30	1500	1513	AA	909	N958AN	LGA	MIA	156	1096	11	30	2023-01-08 11:00:00	MIA
20182	8	30	842	800	42	1210	1112	AA	410	N946AN	EWR	MIA	164	1085	8	0	2023-08-30 08:00:00	MIA
20192	7	5	2107	1840	147	2256	2018	AA	750	N972NN	LGA	ORD	120	733	18	40	2023-07-05 18:00:00	ORD
20196	3	15	2113	2030	43	9	2344	B6	69	N506JB	JFK	TPA	131	1005	20	30	2023-03-15 20:00:00	Other
20197	2	3	41	2029	252	245	2302	YX	1052	N744YX	EWR	SDF	100	642	20	29	2023-02-03 20:00:00	Other
20198	1	7	841	615	146	1156	933	UA	348	N785UA	EWR	SFO	323	2565	6	15	2023-01-07 06:00:00	Other
20202	9	24	1956	1843	73	2116	2005	UA	673	N472UA	EWR	BOS	36	200	18	43	2023-09-24 18:00:00	BOS
20204	6	14	2028	1655	213	2151	1824	YX	1092	N751YX	EWR	BUF	49	282	16	55	2023-06-14 16:00:00	Other
20209	12	7	1759	1728	31	2047	2030	UA	858	N12238	EWR	PBI	133	1023	17	28	2023-12-07 17:00:00	Other
20213	2	4	1042	959	43	1232	1220	9E	1361	N326PQ	LGA	MEM	140	963	9	59	2023-02-04 09:00:00	Other
20219	10	5	1907	1325	342	2153	1632	B6	110	N571JB	LGA	FLL	140	1076	13	25	2023-10-05 13:00:00	FLL
20231	5	21	1719	1615	64	2041	1906	UA	580	N12125	EWR	MCO	153	937	16	15	2023-05-21 16:00:00	MCO
20232	7	10	1527	1420	67	1803	1705	UA	496	N24224	EWR	IAH	184	1400	14	20	2023-07-10 14:00:00	Other
20235	8	10	935	734	121	1230	1021	B6	150	N564JB	JFK	MCO	131	944	7	34	2023-08-10 07:00:00	MCO
20238	6	25	1736	1700	36	2059	1944	DL	357	N347DN	LGA	ATL	119	762	17	0	2023-06-25 17:00:00	ATL
20247	10	20	1747	1730	17	1926	1904	OO	1239	N251SY	JFK	MKE	118	745	17	30	2023-10-20 17:00:00	Other
20259	5	17	1847	1820	27	2050	2033	NK	274	N660NK	EWR	IND	95	645	18	20	2023-05-17 18:00:00	Other
20263	1	22	727	700	27	1020	1009	B6	409	N703JB	JFK	PBI	151	1028	7	0	2023-01-22 07:00:00	Other
20279	9	14	1521	1502	19	1828	1815	NK	622	N670NK	LGA	FLL	154	1076	15	2	2023-09-14 15:00:00	FLL
20285	5	8	2133	2115	18	2256	2256	DL	853	N137DU	JFK	BUF	54	301	21	15	2023-05-08 21:00:00	Other
20293	3	20	2028	1640	228	2351	2002	B6	78	N942JB	JFK	SEA	319	2422	16	40	2023-03-20 16:00:00	Other
20304	7	12	900	845	15	1046	1027	DL	312	N110DU	LGA	ORD	120	733	8	45	2023-07-12 08:00:00	ORD
20312	4	2	2150	2130	20	2357	2334	B6	339	N627JB	LGA	CHS	94	641	21	30	2023-04-02 21:00:00	Other
20313	3	15	1800	1650	70	2109	1957	NK	653	N684NK	EWR	FLL	140	1065	16	50	2023-03-15 16:00:00	FLL
20320	9	5	1223	959	144	1456	1256	NK	250	N623NK	LGA	MCO	122	950	9	59	2023-09-05 09:00:00	MCO
20323	4	15	2345	2135	130	224	13	DL	467	N860DN	JFK	ATL	101	760	21	35	2023-04-15 21:00:00	ATL
20333	10	1	1951	1835	76	2247	2137	B6	903	N703JB	JFK	MCO	128	944	18	35	2023-10-01 18:00:00	MCO
20350	8	28	1344	1330	14	1503	1447	B6	480	N329JB	JFK	BOS	34	187	13	30	2023-08-28 13:00:00	BOS
20353	5	26	1816	1614	122	2055	1930	B6	758	N969JT	EWR	LAX	308	2454	16	14	2023-05-26 16:00:00	LAX
20354	12	15	1824	1810	14	2052	2135	DL	345	N843MH	JFK	LAX	302	2475	18	10	2023-12-15 18:00:00	LAX
20374	3	15	1427	1400	27	1740	1713	B6	23	N821JB	JFK	PBI	141	1028	14	0	2023-03-15 14:00:00	Other
20379	5	23	1230	857	213	1409	1050	9E	1359	N920XJ	LGA	RDU	74	431	8	57	2023-05-23 08:00:00	Other
20390	10	12	1006	940	26	1129	1104	YX	1727	N228JQ	JFK	DCA	45	213	9	40	2023-10-12 09:00:00	Other
20391	9	12	1027	840	107	1152	1030	B6	904	N274JB	JFK	RDU	65	427	8	40	2023-09-12 08:00:00	Other
20414	4	5	1812	1730	42	2005	1932	NK	53	N695NK	LGA	DTW	82	502	17	30	2023-04-05 17:00:00	Other
20419	8	4	2235	2059	96	12	2239	YX	848	N736YX	EWR	PIT	51	319	20	59	2023-08-04 20:00:00	Other
20420	6	26	1606	1417	109	2031	1714	DL	418	N106DU	LGA	IAH	190	1416	14	17	2023-06-26 14:00:00	Other
20423	4	11	2036	1755	161	2247	2055	AS	92	N506AS	EWR	SAN	288	2425	17	55	2023-04-11 17:00:00	Other
20444	1	9	1114	1100	14	1238	1247	YX	1287	N413YX	LGA	DCA	44	214	11	0	2023-01-09 11:00:00	Other
20445	4	20	2101	2030	31	2226	2211	9E	1431	N200PQ	LGA	CHO	52	305	20	30	2023-04-20 20:00:00	Other
20451	2	1	952	923	29	1111	1039	B6	915	N206JB	JFK	BOS	31	187	9	23	2023-02-01 09:00:00	BOS
20456	12	10	2136	1955	101	101	2309	DL	755	N381DN	LGA	RSW	184	1080	19	55	2023-12-10 19:00:00	Other
20458	7	14	1132	1105	27	1312	1243	9E	1313	N294PQ	LGA	BUF	52	292	11	5	2023-07-14 11:00:00	Other
20468	3	3	1929	1729	120	2301	2053	AA	974	N316RK	JFK	AUS	233	1521	17	29	2023-03-03 17:00:00	Other
20478	8	3	1221	1200	21	1449	1454	UA	437	N77259	EWR	TPA	125	997	12	0	2023-08-03 12:00:00	Other
20484	7	31	1103	1052	11	1347	1350	B6	289	N516JB	EWR	MCO	128	937	10	52	2023-07-31 10:00:00	MCO
20487	12	14	1937	1905	32	2232	2239	DL	522	N544DN	JFK	SEA	320	2422	19	5	2023-12-14 19:00:00	Other
20499	7	23	2131	1930	121	2240	2045	B6	432	N375JB	LGA	PWM	43	269	19	30	2023-07-23 19:00:00	Other
20500	5	27	2002	1930	32	2056	2044	YX	1134	N753YX	EWR	ALB	30	143	19	30	2023-05-27 19:00:00	Other
20503	6	20	1652	1610	42	1910	1827	YX	1408	N437YX	LGA	TYS	101	647	16	10	2023-06-20 16:00:00	Other
20512	6	20	1752	1729	23	2013	2024	DL	601	N3738B	JFK	ATL	103	760	17	29	2023-06-20 17:00:00	ATL
20527	6	20	2305	2226	39	330	225	B6	331	N705JB	JFK	BQN	201	1576	22	26	2023-06-20 22:00:00	Other
20539	10	7	2035	1759	156	2344	2057	B6	732	N603JB	JFK	PBI	143	1028	17	59	2023-10-07 17:00:00	Other
20542	9	18	1857	1835	22	2242	2152	B6	240	N563JB	JFK	SJC	348	2569	18	35	2023-09-18 18:00:00	Other
20545	3	15	2145	1800	225	2304	1922	AA	487	N703UW	LGA	DCA	41	214	18	0	2023-03-15 18:00:00	Other
20546	4	15	1802	1305	297	1952	1454	DL	437	N123DQ	LGA	ORD	130	733	13	5	2023-04-15 13:00:00	ORD
20547	2	4	1053	945	68	1304	1222	YX	1544	N823MD	LGA	IND	105	660	9	45	2023-02-04 09:00:00	Other
20550	8	7	1841	1755	46	2237	2103	F9	395	N339FR	LGA	MCO	128	950	17	55	2023-08-07 17:00:00	MCO
20553	6	24	1801	1745	16	2112	2001	9E	1452	N306PQ	LGA	CLT	80	544	17	45	2023-06-24 17:00:00	CLT
20561	6	11	754	659	55	932	834	AA	627	N967NN	EWR	ORD	118	719	6	59	2023-06-11 06:00:00	ORD
20563	5	20	1745	1715	30	1943	1934	UA	264	N12109	EWR	DEN	214	1605	17	15	2023-05-20 17:00:00	Other
20565	6	13	1229	1140	49	1341	1305	UA	506	N402UA	EWR	BNA	113	748	11	40	2023-06-13 11:00:00	Other
20566	8	8	1136	930	126	1348	1136	NK	435	N696NK	EWR	CHS	97	628	9	30	2023-08-08 09:00:00	Other
20567	9	25	2331	2150	101	26	2245	9E	1510	N929XJ	LGA	BDL	23	101	21	50	2023-09-25 21:00:00	Other
20573	9	25	2022	2000	22	2253	2222	YX	1957	N233JQ	JFK	CLT	86	541	20	0	2023-09-25 20:00:00	CLT
20577	1	11	724	630	54	1038	757	YX	1732	N880RW	LGA	RIC	51	292	6	30	2023-01-11 06:00:00	Other
20595	2	19	1609	1555	14	1851	1857	B6	682	N375JB	EWR	MCO	137	937	15	55	2023-02-19 15:00:00	MCO
20599	9	23	940	915	25	1102	1039	9E	1579	N923XJ	JFK	IAD	50	228	9	15	2023-09-23 09:00:00	Other
20604	10	29	1351	1245	66	1616	1519	UA	389	N478UA	EWR	ATL	113	746	12	45	2023-10-29 12:00:00	ATL
20613	8	25	1326	1255	31	1444	1427	9E	1192	N909XJ	JFK	ORF	49	290	12	55	2023-08-25 12:00:00	Other
20615	10	31	2023	1915	68	2214	2102	OO	1694	N207SY	LGA	ORD	117	733	19	15	2023-10-31 19:00:00	ORD
20619	1	31	1642	1608	34	2044	1947	UA	189	N27263	EWR	PHX	335	2133	16	8	2023-01-31 16:00:00	Other
20634	5	1	946	925	21	1254	1312	DL	97	N703TW	JFK	SFO	335	2586	9	25	2023-05-01 09:00:00	Other
20639	7	30	1741	1658	43	1852	1841	B6	2	N375JB	JFK	BUF	54	301	16	58	2023-07-30 16:00:00	Other
20657	6	6	1706	1655	11	2048	2015	AS	6	N934AK	JFK	SEA	314	2422	16	55	2023-06-06 16:00:00	Other
20660	1	22	2158	2129	29	2315	2228	9E	1379	N310PQ	LGA	BGM	34	147	21	29	2023-01-22 21:00:00	Other
20668	1	12	2021	2005	16	2335	2315	NK	309	N525NK	EWR	IAH	209	1400	20	5	2023-01-12 20:00:00	Other
20675	5	23	823	800	23	1046	1036	DL	579	N141DU	JFK	JAX	120	828	8	0	2023-05-23 08:00:00	Other
20681	10	30	1423	1400	23	1649	1627	9E	1538	N695CA	LGA	MCI	177	1107	14	0	2023-10-30 14:00:00	Other
20683	12	24	1643	1629	14	1914	1940	NK	477	N668NK	LGA	IAH	193	1416	16	29	2023-12-24 16:00:00	Other
20691	6	11	2022	1225	477	2216	1347	AA	1025	N807AW	LGA	BNA	127	764	12	25	2023-06-11 12:00:00	Other
20698	8	8	1313	1155	78	1506	1345	9E	1235	N691CA	JFK	RDU	70	427	11	55	2023-08-08 11:00:00	Other
20701	12	25	2219	2155	24	2330	2314	UA	471	N17300	EWR	PWM	51	284	21	55	2023-12-25 21:00:00	Other
20710	10	19	1010	900	70	1138	1049	OO	1226	N244SY	JFK	PIT	64	340	9	0	2023-10-19 09:00:00	Other
20712	1	12	1533	1507	26	1956	1811	UA	606	N16701	EWR	PBI	171	1023	15	7	2023-01-12 15:00:00	Other
20727	10	24	1937	1759	98	2249	2110	B6	944	N964JT	JFK	LAX	331	2475	17	59	2023-10-24 17:00:00	LAX
20730	12	31	1611	1555	16	1849	1906	B6	634	N630JB	LGA	PBI	138	1035	15	55	2023-12-31 15:00:00	Other
20737	5	6	1654	1534	80	1814	1727	YX	1313	N424YX	LGA	GSO	65	461	15	34	2023-05-06 15:00:00	Other
20744	7	6	1613	1559	14	1716	1726	YX	943	N654RW	EWR	PWM	46	284	15	59	2023-07-06 15:00:00	Other
20747	10	10	1536	1359	97	1831	1711	B6	527	N558JB	JFK	RSW	156	1074	13	59	2023-10-10 13:00:00	Other
20755	6	8	1726	1711	15	1856	1847	UA	636	N429UA	LGA	ORD	107	733	17	11	2023-06-08 17:00:00	ORD
20756	4	6	1943	1925	18	2114	2053	YX	1252	N116HQ	JFK	BOS	33	187	19	25	2023-04-06 19:00:00	BOS
20757	7	5	1804	1530	154	2107	1835	B6	463	N2016J	JFK	MCO	137	944	15	30	2023-07-05 15:00:00	MCO
20763	7	18	1052	800	172	1259	1038	DL	178	N519DT	JFK	DEN	226	1626	8	0	2023-07-18 08:00:00	Other
20768	4	13	2029	1945	44	2245	2207	B6	612	N228JB	LGA	SAV	110	722	19	45	2023-04-13 19:00:00	Other
20769	6	13	1716	1700	16	1853	1855	9E	1468	N605LR	LGA	RDU	74	431	17	0	2023-06-13 17:00:00	Other
20773	1	1	859	844	15	1207	1209	UA	786	N17265	EWR	RSW	164	1068	8	44	2023-01-01 08:00:00	Other
20774	10	10	1947	1920	27	2300	2235	DL	133	N171DN	JFK	LAX	320	2475	19	20	2023-10-10 19:00:00	LAX
20777	3	16	1707	1620	47	1920	1844	YX	1084	N651RW	EWR	MCI	163	1092	16	20	2023-03-16 16:00:00	Other
20779	5	2	1423	1213	130	1703	1457	UA	858	N36207	EWR	DFW	183	1372	12	13	2023-05-02 12:00:00	Other
20780	6	16	1940	1746	114	2143	2018	YX	1845	N810MD	LGA	IND	99	660	17	46	2023-06-16 17:00:00	Other
20781	7	31	1648	1200	288	1933	1500	UA	609	N2135U	EWR	SFO	312	2565	12	0	2023-07-31 12:00:00	Other
20782	5	19	920	759	81	NA	928	UA	225	N415UA	EWR	BOS	NA	200	7	59	2023-05-19 07:00:00	BOS
20783	9	17	929	730	119	1119	956	UA	572	N14118	EWR	PHX	272	2133	7	30	2023-09-17 07:00:00	Other
20786	9	6	2331	2259	32	309	302	B6	274	N634JB	JFK	PSE	200	1617	22	59	2023-09-06 22:00:00	Other
20789	3	15	1553	1445	68	1708	1600	B6	587	N228JB	JFK	BOS	43	187	14	45	2023-03-15 14:00:00	BOS
20790	4	17	1922	1744	98	2106	1940	YX	1118	N414YX	LGA	CMH	78	479	17	44	2023-04-17 17:00:00	Other
20815	3	12	1856	1800	56	2205	2143	DL	261	N859DN	JFK	SLC	275	1990	18	0	2023-03-12 18:00:00	Other
20817	4	16	753	730	23	1133	1125	B6	557	N954JB	JFK	SJU	191	1598	7	30	2023-04-16 07:00:00	Other
20818	6	2	31	2159	152	437	205	B6	302	N562JB	JFK	PSE	210	1617	21	59	2023-06-02 21:00:00	Other
20822	6	12	1732	1655	37	1951	1856	UA	306	N24715	EWR	CLT	94	529	16	55	2023-06-12 16:00:00	CLT
20823	9	23	953	900	53	1108	1044	UA	390	N78506	EWR	ORD	103	719	9	0	2023-09-23 09:00:00	ORD
20825	5	13	819	705	74	1032	923	DL	764	N872DN	EWR	ATL	100	746	7	5	2023-05-13 07:00:00	ATL
20829	6	12	746	700	46	1001	927	DL	192	N389DN	LGA	ATL	108	762	7	0	2023-06-12 07:00:00	ATL
20831	10	4	1718	1655	23	2001	2002	B6	106	N612JB	JFK	BUR	310	2465	16	55	2023-10-04 16:00:00	Other
20832	12	25	1626	1129	297	1918	1455	DL	254	N317DU	LGA	DFW	199	1389	11	29	2023-12-25 11:00:00	Other
20838	2	1	2218	2159	19	2310	2310	DL	793	N107DU	LGA	SYR	38	198	21	59	2023-02-01 21:00:00	Other
20847	8	25	1203	817	226	1323	949	YX	1384	N203JQ	LGA	BUF	50	292	8	17	2023-08-25 08:00:00	Other
20848	2	14	1055	1030	25	1418	1346	UA	183	N68807	EWR	PHX	293	2133	10	30	2023-02-14 10:00:00	Other
20850	1	16	2258	2059	119	110	2307	UA	482	N877UA	EWR	MEM	162	946	20	59	2023-01-16 20:00:00	Other
20851	1	3	1758	1659	59	1939	1848	B6	493	N358JB	JFK	RDU	73	427	16	59	2023-01-03 16:00:00	Other
20863	4	25	1826	1815	11	2032	2028	DL	679	N988AT	EWR	MSP	148	1008	18	15	2023-04-25 18:00:00	Other
20865	6	12	2232	2052	100	2331	2221	UA	647	N23708	EWR	MKE	93	725	20	52	2023-06-12 20:00:00	Other
20866	4	4	1417	1300	77	1709	1556	B6	43	N537JT	JFK	TPA	135	1005	13	0	2023-04-04 13:00:00	Other
20867	12	23	622	610	12	812	820	DL	430	N364DX	LGA	MSP	145	1020	6	10	2023-12-23 06:00:00	Other
20887	8	15	1302	1145	77	1405	1303	UA	693	N38727	EWR	PWM	43	284	11	45	2023-08-15 11:00:00	Other
20891	6	23	939	907	32	1055	1030	B6	631	N375JB	JFK	BTV	48	266	9	7	2023-06-23 09:00:00	Other
20898	9	9	2115	2000	75	2351	2228	UA	279	N14115	EWR	PHX	272	2133	20	0	2023-09-09 20:00:00	Other
20899	3	21	746	730	16	1144	1108	AS	15	N224AK	JFK	SFO	386	2586	7	30	2023-03-21 07:00:00	Other
20901	1	2	1502	1442	20	1849	1753	AA	907	N956AN	JFK	DFW	256	1391	14	42	2023-01-02 14:00:00	Other
20907	7	7	2121	1648	273	2256	1821	9E	1210	N491PX	LGA	BUF	60	292	16	48	2023-07-07 16:00:00	Other
20910	6	30	1523	1405	78	1755	1646	UA	523	N27724	EWR	DFW	176	1372	14	5	2023-06-30 14:00:00	Other
20916	2	21	1800	1745	15	2104	2112	F9	940	N373FR	LGA	MIA	150	1096	17	45	2023-02-21 17:00:00	MIA
20920	5	19	2017	1959	18	2256	2250	NK	170	N677NK	LGA	MCO	123	950	19	59	2023-05-19 19:00:00	MCO
20922	12	1	1701	1644	17	1948	1950	B6	449	N905JB	JFK	MCO	134	944	16	44	2023-12-01 16:00:00	MCO
20926	4	10	1533	1515	18	1858	1815	DL	446	N111DC	LGA	MCO	156	950	15	15	2023-04-10 15:00:00	MCO
20927	3	27	2247	2100	107	33	2250	YX	1342	N409YX	LGA	GSO	89	461	21	0	2023-03-27 21:00:00	Other
20937	3	26	1959	1930	29	2309	2236	B6	28	N547JB	JFK	ABQ	290	1826	19	30	2023-03-26 19:00:00	Other
20940	10	24	1610	1518	52	1753	1724	DL	592	N319DN	LGA	DTW	81	502	15	18	2023-10-24 15:00:00	Other
20943	5	18	1059	1024	35	1224	1205	UA	672	N76505	EWR	ORD	109	719	10	24	2023-05-18 10:00:00	ORD
20951	3	2	706	600	66	935	805	9E	1362	N294PQ	LGA	CLT	100	544	6	0	2023-03-02 06:00:00	CLT
20952	2	3	2301	1814	287	110	2040	YX	1049	N730YX	EWR	IND	107	645	18	14	2023-02-03 18:00:00	Other
20969	9	24	2200	2010	110	35	2301	B6	25	N624JB	JFK	ABQ	240	1826	20	10	2023-09-24 20:00:00	Other
20972	5	24	2205	2115	50	2305	2232	DL	738	N129DU	LGA	SYR	37	198	21	15	2023-05-24 21:00:00	Other
20973	2	28	1500	1355	65	1647	1545	DL	409	N133DU	LGA	RDU	68	431	13	55	2023-02-28 13:00:00	Other
20980	9	20	1823	1729	54	2109	2030	B6	678	N603JB	LGA	MCO	139	950	17	29	2023-09-20 17:00:00	MCO
20984	8	1	2056	1830	146	2223	2008	UA	354	N37471	EWR	ORD	104	719	18	30	2023-08-01 18:00:00	ORD
20985	12	13	1744	1653	51	2302	2151	NK	606	N645NK	EWR	SJU	231	1608	16	53	2023-12-13 16:00:00	Other
20987	12	7	1816	1749	27	1946	1944	B6	403	N283JB	JFK	RDU	68	427	17	49	2023-12-07 17:00:00	Other
20993	6	18	1333	1301	32	1613	1556	UA	814	N434UA	EWR	TPA	138	997	13	1	2023-06-18 13:00:00	Other
20996	9	2	1605	1510	55	1837	1823	DL	819	N109DN	JFK	MCO	124	944	15	10	2023-09-02 15:00:00	MCO
21007	9	13	1419	1359	20	1725	1701	DL	385	N317DU	LGA	IAH	208	1416	13	59	2023-09-13 13:00:00	Other
21009	6	24	1923	1735	108	2249	1956	UA	892	N27251	EWR	DEN	219	1605	17	35	2023-06-24 17:00:00	Other
21011	8	3	951	920	31	1237	1215	B6	50	N946JL	JFK	SAN	323	2446	9	20	2023-08-03 09:00:00	Other
21022	6	23	2318	1837	281	323	2238	B6	740	N999JQ	JFK	SJU	197	1598	18	37	2023-06-23 18:00:00	Other
21025	2	27	1727	1715	12	1847	1833	B6	414	N306JB	LGA	BOS	35	184	17	15	2023-02-27 17:00:00	BOS
21028	12	17	1412	1350	22	1936	1834	B6	960	N526JL	JFK	BQN	204	1576	13	50	2023-12-17 13:00:00	Other
21033	8	16	1516	1459	17	1845	1810	B6	441	N2060J	JFK	MCO	165	944	14	59	2023-08-16 14:00:00	MCO
21043	7	2	1208	1145	23	1327	1313	YX	1411	N878RW	LGA	DCA	47	214	11	45	2023-07-02 11:00:00	Other
21046	12	11	1544	1501	43	1740	1704	DL	742	N341NW	LGA	DTW	77	502	15	1	2023-12-11 15:00:00	Other
21047	9	25	2119	1955	84	2331	2216	9E	1775	N299PQ	LGA	IND	98	660	19	55	2023-09-25 19:00:00	Other
21049	9	29	2242	2059	103	34	2311	UA	215	N27734	EWR	CVG	83	569	20	59	2023-09-29 20:00:00	Other
21056	3	27	2050	1929	81	2337	2234	UA	501	N37295	EWR	IAH	199	1400	19	29	2023-03-27 19:00:00	Other
21058	12	20	946	914	32	1051	1035	9E	1368	N324PQ	LGA	ALB	30	136	9	14	2023-12-20 09:00:00	Other
21064	8	7	2325	1624	421	114	1750	UA	581	N27568	EWR	IAD	48	212	16	24	2023-08-07 16:00:00	Other
21076	10	6	2035	1935	60	2338	2329	DL	321	N822DX	JFK	SFO	326	2586	19	35	2023-10-06 19:00:00	Other
21080	8	20	2110	1959	71	2357	2329	DL	665	N801DZ	JFK	MIA	138	1089	19	59	2023-08-20 19:00:00	MIA
21084	9	25	2141	2022	79	54	2344	AS	16	N296AK	JFK	SFO	328	2586	20	22	2023-09-25 20:00:00	Other
21087	8	20	1518	1459	19	1900	1842	UA	368	N17285	EWR	ANC	439	3370	14	59	2023-08-20 14:00:00	Other
21094	4	1	1526	1459	27	1734	1724	9E	1437	N326PQ	JFK	IND	101	665	14	59	2023-04-01 14:00:00	Other
21097	12	7	1847	1834	13	2155	2149	AA	972	N335SN	EWR	MIA	143	1085	18	34	2023-12-07 18:00:00	MIA
21120	5	5	2250	1820	270	123	2118	B6	432	N974JT	JFK	LAS	300	2248	18	20	2023-05-05 18:00:00	Other
21127	6	10	1620	1510	70	1953	1852	UA	474	N27277	EWR	ANC	420	3370	15	10	2023-06-10 15:00:00	Other
21138	11	10	1855	1844	11	2212	2200	UA	446	N27722	EWR	SNA	341	2434	18	44	2023-11-10 18:00:00	Other
21139	1	15	1305	1229	36	1551	1544	UA	531	N47282	EWR	RSW	139	1068	12	29	2023-01-15 12:00:00	Other
21141	9	17	819	659	80	1114	1005	DL	657	N358NW	JFK	AUS	212	1521	6	59	2023-09-17 06:00:00	Other
21148	2	24	1751	1545	126	1936	1736	YX	1571	N224JQ	LGA	PIT	70	335	15	45	2023-02-24 15:00:00	Other
21151	8	7	1719	1629	50	NA	1857	UA	572	N460UA	LGA	DEN	NA	1620	16	29	2023-08-07 16:00:00	Other
21153	11	22	2019	1959	20	2312	2306	NK	166	N658NK	LGA	MCO	139	950	19	59	2023-11-22 19:00:00	MCO
21168	9	12	1232	1159	33	1529	1505	UA	940	N878UA	EWR	SAT	216	1569	11	59	2023-09-12 11:00:00	Other
21170	7	18	524	501	23	902	843	B6	748	N952JB	JFK	BQN	197	1576	5	1	2023-07-18 05:00:00	Other
21172	11	12	1438	1359	39	1605	1541	YX	1815	N234JQ	LGA	PIT	64	335	13	59	2023-11-12 13:00:00	Other
21178	9	13	1455	1302	113	1743	1605	B6	684	N634JB	EWR	RSW	150	1068	13	2	2023-09-13 13:00:00	Other
21192	9	11	1543	1410	93	1924	1610	9E	1506	N925XJ	JFK	CLE	71	425	14	10	2023-09-11 14:00:00	Other
21193	4	1	346	2159	347	725	158	B6	654	N905JB	JFK	SJU	193	1598	21	59	2023-04-01 21:00:00	Other
21196	1	27	840	829	11	1055	1101	9E	1603	N331PQ	LGA	IND	103	660	8	29	2023-01-27 08:00:00	Other
21198	4	30	1948	1730	138	2137	1900	YX	1454	N204JQ	JFK	BOS	43	187	17	30	2023-04-30 17:00:00	BOS
21209	1	23	2012	1840	92	2314	2149	YX	1294	N870RW	LGA	TUL	191	1231	18	40	2023-01-23 18:00:00	Other
21213	9	9	948	815	93	1111	1006	9E	1545	N485PX	LGA	STL	117	888	8	15	2023-09-09 08:00:00	Other
21217	3	11	1340	1255	45	1535	1457	9E	1457	N678CA	JFK	DTW	83	509	12	55	2023-03-11 12:00:00	Other
21218	11	19	2242	2230	12	7	7	9E	1500	N228PQ	JFK	SYR	45	209	22	30	2023-11-19 22:00:00	Other
21222	9	9	945	930	15	1221	1226	UA	650	N17564	EWR	PBI	141	1023	9	30	2023-09-09 09:00:00	Other
21226	2	17	917	905	12	1107	1046	YX	1058	N724YX	EWR	PIT	64	319	9	5	2023-02-17 09:00:00	Other
21227	5	6	1805	1750	15	2005	2029	9E	1315	N319PQ	JFK	MCI	155	1113	17	50	2023-05-06 17:00:00	Other
21232	10	4	2117	2010	67	2332	2230	UA	854	N17529	EWR	DEN	222	1605	20	10	2023-10-04 20:00:00	Other
21236	9	8	2259	1730	329	204	2028	AS	84	N566AS	EWR	SAN	315	2425	17	30	2023-09-08 17:00:00	Other
21251	7	4	1911	1650	141	2222	2006	B6	199	N527JL	LGA	FLL	153	1076	16	50	2023-07-04 16:00:00	FLL
21252	8	7	1924	1825	59	2241	2125	WN	948	N8561Z	LGA	TPA	149	1010	18	25	2023-08-07 18:00:00	Other
21255	7	20	2112	1830	162	109	2228	B6	588	N966JT	JFK	SJU	191	1598	18	30	2023-07-20 18:00:00	Other
21260	7	30	1537	1523	14	1801	1825	NK	701	N646NK	EWR	LAX	306	2454	15	23	2023-07-30 15:00:00	LAX
21265	5	7	1443	1425	18	1633	1627	YX	1154	N721YX	EWR	MYR	79	550	14	25	2023-05-07 14:00:00	Other
21282	3	7	2315	2259	16	31	23	YX	1632	N233JQ	JFK	PWM	52	273	22	59	2023-03-07 22:00:00	Other
21289	3	25	2140	1830	190	33	2130	UA	309	N37420	EWR	TPA	157	997	18	30	2023-03-25 18:00:00	Other
21291	11	15	2353	2340	13	56	54	B6	573	N3085J	JFK	BOS	44	187	23	40	2023-11-15 23:00:00	BOS
21296	10	1	1459	1419	40	1739	1703	YX	1722	N231JQ	JFK	JAX	119	828	14	19	2023-10-01 14:00:00	Other
21299	10	12	2103	2025	38	2327	2250	WN	164	N7859B	LGA	DEN	243	1620	20	25	2023-10-12 20:00:00	Other
21306	5	9	1825	1800	25	2201	2130	UA	430	N17126	EWR	SFO	353	2565	18	0	2023-05-09 18:00:00	Other
21308	8	2	1838	1755	43	2112	2057	B6	540	N504JB	LGA	MCO	127	950	17	55	2023-08-02 17:00:00	MCO
21319	7	4	1936	1718	138	2040	1853	UA	647	N33132	EWR	ORD	96	719	17	18	2023-07-04 17:00:00	ORD
21320	6	24	1033	1007	26	1318	1249	UA	92	N27253	EWR	DFW	176	1372	10	7	2023-06-24 10:00:00	Other
21323	6	6	2058	1930	88	2315	2116	YX	1810	N824MD	LGA	PIT	59	335	19	30	2023-06-06 19:00:00	Other
21325	5	16	601	1530	871	834	1840	DL	434	N107DN	JFK	MCO	132	944	15	30	2023-05-16 15:00:00	MCO
21328	1	22	2350	2029	201	305	2346	UA	724	N77530	EWR	MIA	168	1085	20	29	2023-01-22 20:00:00	MIA
21329	6	15	1315	1300	15	1618	1609	AA	239	N334SM	LGA	MIA	147	1096	13	0	2023-06-15 13:00:00	MIA
21334	4	17	1242	955	167	1352	1115	9E	1418	N921XJ	JFK	SYR	39	209	9	55	2023-04-17 09:00:00	Other
21337	6	25	2021	1858	83	2208	2046	9E	1537	N479PX	LGA	BHM	122	866	18	58	2023-06-25 18:00:00	Other
21341	10	26	1449	1411	38	1559	1537	B6	52	N216JB	JFK	ROC	50	264	14	11	2023-10-26 14:00:00	Other
21349	12	27	1111	900	131	1338	1135	B6	180	N318JB	JFK	ATL	124	760	9	0	2023-12-27 09:00:00	ATL
21350	3	26	1948	1820	88	2300	2144	DL	124	N867DN	JFK	SEA	326	2422	18	20	2023-03-26 18:00:00	Other
21352	2	14	1104	950	74	1336	1300	B6	244	N827JB	LGA	MCO	125	950	9	50	2023-02-14 09:00:00	MCO
21359	6	26	1233	830	243	1601	1125	DL	208	N104DU	JFK	DFW	217	1391	8	30	2023-06-26 08:00:00	Other
21363	12	29	1743	1715	28	1927	1859	UA	291	N37561	EWR	CLE	64	404	17	15	2023-12-29 17:00:00	Other
21364	12	2	836	825	11	1147	1149	UA	234	N227UA	EWR	SFO	337	2565	8	25	2023-12-02 08:00:00	Other
21365	5	24	1130	1115	15	1336	1319	YX	1217	N826MD	LGA	AVL	94	599	11	15	2023-05-24 11:00:00	Other
21379	3	10	810	730	40	935	917	AA	254	N357PV	LGA	ORD	121	733	7	30	2023-03-10 07:00:00	ORD
21383	5	4	1645	1610	35	1924	1920	B6	767	N703JB	LGA	MCO	129	950	16	10	2023-05-04 16:00:00	MCO
21393	5	14	2145	2030	75	2328	2214	DL	448	N101DU	LGA	ORD	125	733	20	30	2023-05-14 20:00:00	ORD
21397	6	25	1153	1135	18	1411	1442	UA	884	N37287	EWR	MIA	NA	1085	11	35	2023-06-25 11:00:00	MIA
21401	4	30	1512	1343	89	1703	1518	YX	1108	N117HQ	EWR	ORD	107	719	13	43	2023-04-30 13:00:00	ORD
21408	7	22	1622	1607	15	1842	1821	YX	932	N742YX	EWR	CHS	99	628	16	7	2023-07-22 16:00:00	Other
21428	1	29	1958	1927	31	2246	2217	YX	1359	N442YX	LGA	XNA	206	1147	19	27	2023-01-29 19:00:00	Other
21436	7	10	1751	1323	268	2115	1630	B6	286	N281JB	JFK	MCO	145	944	13	23	2023-07-10 13:00:00	MCO
21447	2	27	1146	1125	21	1441	1502	AA	808	N302SA	LGA	MIA	144	1096	11	25	2023-02-27 11:00:00	MIA
21451	3	27	2302	2055	127	108	2301	YX	1242	N402YX	LGA	MEM	165	963	20	55	2023-03-27 20:00:00	Other
21454	4	5	2237	2140	57	216	133	DL	108	N705TW	JFK	SFO	365	2586	21	40	2023-04-05 21:00:00	Other
21459	9	3	2300	2215	45	135	115	DL	93	N836MH	JFK	LAX	310	2475	22	15	2023-09-03 22:00:00	LAX
21463	6	22	616	600	16	755	754	DL	427	N345NW	LGA	DTW	72	502	6	0	2023-06-22 06:00:00	Other
21471	8	25	1456	1355	61	1632	1534	YX	1302	N244JQ	JFK	BOS	64	187	13	55	2023-08-25 13:00:00	BOS
21477	5	30	1547	1529	18	1714	1708	UA	660	N24706	EWR	CLE	56	404	15	29	2023-05-30 15:00:00	Other
21479	4	7	652	625	27	930	910	B6	93	N503JB	LGA	MCO	133	950	6	25	2023-04-07 06:00:00	MCO
21481	12	27	640	600	40	758	743	UA	372	N17316	EWR	ORD	105	719	6	0	2023-12-27 06:00:00	ORD
21484	7	21	635	605	30	845	819	UA	516	N39423	EWR	DEN	222	1605	6	5	2023-07-21 06:00:00	Other
21485	4	23	1853	1838	15	2020	2021	UA	422	N17272	EWR	ORD	103	719	18	38	2023-04-23 18:00:00	ORD
21490	8	22	1610	1555	15	1818	1849	B6	500	N608JB	JFK	JAX	105	828	15	55	2023-08-22 15:00:00	Other
21492	4	29	1249	1230	19	1550	1458	B6	860	N184JB	JFK	ATL	124	760	12	30	2023-04-29 12:00:00	ATL
21497	5	25	1313	1245	28	1539	1542	NK	81	N645NK	EWR	DFW	181	1372	12	45	2023-05-25 12:00:00	Other
21502	11	4	1724	1540	104	1944	1820	B6	595	N990JL	JFK	JAX	121	828	15	40	2023-11-04 15:00:00	Other
21503	9	22	1236	1037	119	1350	1158	9E	1591	N930XJ	JFK	BTV	50	266	10	37	2023-09-22 10:00:00	Other
21509	6	12	1839	1729	70	2014	1903	YX	1118	N729YX	EWR	PIT	68	319	17	29	2023-06-12 17:00:00	Other
21522	6	28	2053	1959	54	2308	2258	DL	473	N119DN	LGA	MCO	119	950	19	59	2023-06-28 19:00:00	MCO
21524	4	2	2136	2055	41	2313	2250	9E	1390	N937XJ	LGA	ILM	73	500	20	55	2023-04-02 20:00:00	Other
21525	2	18	1521	1505	16	1754	1806	NK	522	N648NK	EWR	MCO	127	937	15	5	2023-02-18 15:00:00	MCO
21533	4	16	1945	1639	186	2320	1950	NK	312	N660NK	LGA	FLL	176	1076	16	39	2023-04-16 16:00:00	FLL
21538	9	25	1420	1359	21	1659	1627	9E	1460	N320PQ	JFK	SAV	106	718	13	59	2023-09-25 13:00:00	Other
21552	4	8	1120	1044	36	1346	1254	UA	807	N806UA	EWR	MSY	179	1167	10	44	2023-04-08 10:00:00	Other
21558	6	4	2317	2135	102	22	2321	YX	1333	N114HQ	JFK	DCA	38	213	21	35	2023-06-04 21:00:00	Other
21569	5	24	2052	2029	23	2350	2335	UA	250	N37555	EWR	AUS	190	1504	20	29	2023-05-24 20:00:00	Other
21572	7	14	307	1850	497	433	2020	UA	522	N64844	EWR	BNA	102	748	18	50	2023-07-14 18:00:00	Other
21583	11	29	1846	1830	16	2149	2204	B6	44	N995JL	JFK	SMF	343	2521	18	30	2023-11-29 18:00:00	Other
21592	1	8	2120	2100	20	2228	2221	YX	1816	N246JQ	LGA	PWM	51	269	21	0	2023-01-08 21:00:00	Other
21607	3	30	2127	2055	32	9	2356	B6	323	N585JB	JFK	DFW	198	1391	20	55	2023-03-30 20:00:00	Other
21620	10	3	1641	1629	12	1754	1800	9E	1661	N909XJ	JFK	ROC	47	264	16	29	2023-10-03 16:00:00	Other
21623	6	25	1004	930	34	1205	1204	B6	452	N281JB	JFK	ATL	100	760	9	30	2023-06-25 09:00:00	ATL
21624	4	27	2057	1705	232	49	2014	B6	625	N766JB	LGA	MCO	176	950	17	5	2023-04-27 17:00:00	MCO
21625	3	7	1447	1415	32	1612	1543	YX	1113	N649RW	EWR	PIT	61	319	14	15	2023-03-07 14:00:00	Other
21628	7	11	2056	2035	21	2351	2330	UA	232	N27270	EWR	AUS	192	1504	20	35	2023-07-11 20:00:00	Other
21630	7	23	1909	1845	24	2154	2132	DL	103	N828DN	JFK	PHX	263	2153	18	45	2023-07-23 18:00:00	Other
21632	10	7	957	939	18	1354	1336	B6	990	N971JT	JFK	SJU	206	1598	9	39	2023-10-07 09:00:00	Other
21637	6	13	1903	1830	33	2131	2138	UA	445	N793UA	EWR	SFO	309	2565	18	30	2023-06-13 18:00:00	Other
21644	4	17	1225	1159	26	1510	1445	UA	275	N36272	EWR	MCO	141	937	11	59	2023-04-17 11:00:00	MCO
21647	4	23	2003	1925	38	2318	2304	AS	91	N936AK	EWR	SFO	332	2565	19	25	2023-04-23 19:00:00	Other
21653	8	10	549	2059	530	1000	53	B6	737	N950JT	EWR	SJU	222	1608	20	59	2023-08-10 20:00:00	Other
21660	8	10	2159	2129	30	2344	2314	YX	1003	N439YX	LGA	RDU	68	431	21	29	2023-08-10 21:00:00	Other
21686	6	23	2345	2016	209	131	2215	DL	1046	N953AT	EWR	DTW	74	488	20	16	2023-06-23 20:00:00	Other
21691	2	16	2251	2120	91	2345	2226	9E	1367	N482PX	LGA	ALB	32	136	21	20	2023-02-16 21:00:00	Other
21693	8	14	1641	1610	31	1902	1815	OO	957	N260SY	JFK	ORD	140	740	16	10	2023-08-14 16:00:00	ORD
21694	11	19	2228	2210	18	2400	2338	B6	28	N231JB	JFK	BUF	62	301	22	10	2023-11-19 22:00:00	Other
21695	12	23	1342	1325	17	1624	1630	B6	154	N531JL	LGA	FLL	143	1076	13	25	2023-12-23 13:00:00	FLL
21699	1	3	1541	1108	273	1840	1420	UA	176	N17245	EWR	FLL	155	1065	11	8	2023-01-03 11:00:00	FLL
21703	4	30	2035	1820	135	2335	2121	B6	263	N766JB	LGA	MCO	152	950	18	20	2023-04-30 18:00:00	MCO
21711	5	23	1512	1500	12	1758	1810	UA	856	N17126	EWR	LAX	305	2454	15	0	2023-05-23 15:00:00	LAX
21723	2	21	1937	1755	102	2233	2136	AA	809	N867NN	LGA	MIA	147	1096	17	55	2023-02-21 17:00:00	MIA
21730	8	8	2121	1959	82	21	2317	DL	456	N333DX	LGA	FLL	143	1076	19	59	2023-08-08 19:00:00	FLL
21731	5	4	1120	1102	18	1407	1400	UA	240	N27724	EWR	PBI	143	1023	11	2	2023-05-04 11:00:00	Other
21732	5	20	2219	2145	34	2333	2253	YX	1005	N979RP	EWR	MDT	32	141	21	45	2023-05-20 21:00:00	Other
21738	8	10	1944	1845	59	2136	2109	9E	1221	N933XJ	JFK	CVG	91	589	18	45	2023-08-10 18:00:00	Other
21739	2	17	1500	1441	19	1814	1754	AA	806	N877NN	JFK	DFW	210	1391	14	41	2023-02-17 14:00:00	Other
21746	10	13	1847	1830	17	2146	2103	B6	130	N236JB	JFK	ATL	149	760	18	30	2023-10-13 18:00:00	ATL
21754	7	28	1650	1500	110	1820	1705	9E	1171	N176PQ	LGA	RDU	65	431	15	0	2023-07-28 15:00:00	Other
21755	12	3	1615	1600	15	1745	1740	WN	1117	N8841L	LGA	BNA	123	764	16	0	2023-12-03 16:00:00	Other
21778	11	16	1109	1047	22	1258	1257	YX	1326	N407YX	LGA	GSP	89	610	10	47	2023-11-16 10:00:00	Other
21797	9	14	847	759	48	1104	1010	B6	285	N807JB	JFK	MSY	171	1182	7	59	2023-09-14 07:00:00	Other
21802	7	16	2023	1859	84	2131	2028	DL	822	N129DU	LGA	BOS	42	184	18	59	2023-07-16 18:00:00	BOS
21809	9	9	2027	1610	257	114	1938	DL	238	N890DN	JFK	SLC	298	1990	16	10	2023-09-09 16:00:00	Other
21810	1	12	2304	2120	104	130	2359	DL	982	N369NW	LGA	ATL	126	762	21	20	2023-01-12 21:00:00	ATL
21825	4	25	1940	1859	41	2122	2041	AA	195	N822AW	LGA	RDU	74	431	18	59	2023-04-25 18:00:00	Other
21841	10	17	1738	1715	23	2025	2010	WN	841	N8626B	LGA	HOU	187	1428	17	15	2023-10-17 17:00:00	Other
21843	4	23	1808	1754	14	2105	2049	UA	749	N36207	EWR	MCO	135	937	17	54	2023-04-23 17:00:00	MCO
21854	2	25	1858	1800	58	2002	1941	AA	468	N802AW	LGA	DCA	44	214	18	0	2023-02-25 18:00:00	Other
21855	3	3	1641	1629	12	1819	1819	YX	1170	N857RW	EWR	CLE	74	404	16	29	2023-03-03 16:00:00	Other
21856	8	31	1741	1702	39	2022	2026	B6	795	N591JB	JFK	FLL	138	1069	17	2	2023-08-31 17:00:00	FLL
21858	4	5	2043	1929	74	2321	2200	YX	1553	N228JQ	LGA	OMA	180	1148	19	29	2023-04-05 19:00:00	Other
21860	6	22	2031	1959	32	2210	2226	UA	710	N68843	EWR	DEN	198	1605	19	59	2023-06-22 19:00:00	Other
21864	1	15	1648	1559	49	1851	1825	B6	527	N193JB	JFK	CHS	89	636	15	59	2023-01-15 15:00:00	Other
21880	8	11	1444	1225	139	1638	1441	UA	702	N39418	EWR	DEN	212	1605	12	25	2023-08-11 12:00:00	Other
21896	7	11	729	600	89	1052	908	NK	47	N669NK	LGA	FLL	154	1076	6	0	2023-07-11 06:00:00	FLL
21897	5	5	1843	1825	18	2143	2131	AS	171	N288AK	EWR	SEA	315	2402	18	25	2023-05-05 18:00:00	Other
21902	9	29	1841	1759	42	2137	2058	NK	510	N603NK	EWR	MCO	133	937	17	59	2023-09-29 17:00:00	MCO
21903	4	14	1915	1830	45	2027	2017	YX	1546	N241JQ	LGA	PIT	52	335	18	30	2023-04-14 18:00:00	Other
21909	5	23	2244	2230	14	131	203	B6	907	N945JT	JFK	SFO	316	2586	22	30	2023-05-23 22:00:00	Other
21910	3	26	1915	1859	16	2110	2058	YX	1189	N739YX	EWR	CMH	81	463	18	59	2023-03-26 18:00:00	Other
21911	6	19	1423	1149	154	1548	1322	9E	1744	N176PQ	LGA	BUF	52	292	11	49	2023-06-19 11:00:00	Other
21923	7	23	1744	1659	45	1901	1823	UA	380	N39726	EWR	BOS	37	200	16	59	2023-07-23 16:00:00	BOS
21929	7	21	2054	2030	24	2228	2211	DL	370	N104DU	LGA	ORD	117	733	20	30	2023-07-21 20:00:00	ORD
21930	7	14	1748	1645	63	1848	1756	B6	750	N203JB	LGA	MVY	37	175	16	45	2023-07-14 16:00:00	Other
21938	5	7	2001	1855	66	2201	2035	WN	272	N8323C	LGA	BNA	145	764	18	55	2023-05-07 18:00:00	Other
21952	6	23	1719	1700	19	2110	1954	AA	1017	N925AN	LGA	DFW	217	1389	17	0	2023-06-23 17:00:00	Other
21955	7	17	1249	1215	34	1444	1429	UA	595	N27213	LGA	DEN	216	1620	12	15	2023-07-17 12:00:00	Other
21957	9	15	1006	955	11	1429	1455	DL	72	N171DN	JFK	HNL	599	4983	9	55	2023-09-15 09:00:00	Other
21962	8	14	911	900	11	1131	1117	NK	134	N621NK	EWR	LAS	289	2227	9	0	2023-08-14 09:00:00	Other
21969	7	5	2050	1925	85	19	2231	UA	662	N17262	EWR	FLL	161	1065	19	25	2023-07-05 19:00:00	FLL
21981	6	12	1957	1859	58	2053	2021	DL	1043	N142DU	LGA	BOS	32	184	18	59	2023-06-12 18:00:00	BOS
21986	1	9	719	605	74	959	910	B6	112	N949JT	EWR	MCO	137	937	6	5	2023-01-09 06:00:00	MCO
21994	5	28	1708	1646	22	1818	1820	9E	1542	N186PQ	LGA	BTV	44	258	16	46	2023-05-28 16:00:00	Other
22007	6	9	1346	1330	16	1611	1603	B6	1014	N768JB	LGA	ATL	106	762	13	30	2023-06-09 13:00:00	ATL
22016	6	25	1801	1729	32	2113	2042	AA	1005	N323SG	JFK	AUS	202	1521	17	29	2023-06-25 17:00:00	Other
22020	10	7	1027	1000	27	1316	1254	B6	313	N805JB	JFK	PBI	138	1028	10	0	2023-10-07 10:00:00	Other
22024	2	26	1557	1540	17	1819	1809	YX	1222	N104HQ	JFK	IND	118	665	15	40	2023-02-26 15:00:00	Other
22027	10	23	1447	1259	108	1635	1500	DL	752	N331NW	LGA	DTW	78	502	12	59	2023-10-23 12:00:00	Other
22032	2	17	1743	1657	46	2029	1931	UA	581	N893UA	EWR	ATL	132	746	16	57	2023-02-17 16:00:00	ATL
22039	1	12	2231	2155	36	22	2310	DL	817	N844DN	JFK	BOS	41	187	21	55	2023-01-12 21:00:00	BOS
22041	8	3	1531	1505	26	1723	1712	AA	609	N813NN	LGA	CLT	81	544	15	5	2023-08-03 15:00:00	CLT
22045	6	4	1302	1152	70	1518	1435	UA	801	N12218	EWR	SAN	294	2425	11	52	2023-06-04 11:00:00	Other
22046	3	21	1154	915	159	1334	1120	AA	983	N843NN	JFK	ORD	117	740	9	15	2023-03-21 09:00:00	ORD
22052	8	16	1857	1820	37	2211	2110	WN	940	N8830Q	LGA	TPA	167	1010	18	20	2023-08-16 18:00:00	Other
22053	12	1	810	709	61	1132	1025	DL	331	N303DU	EWR	SLC	279	1969	7	9	2023-12-01 07:00:00	Other
22081	9	10	1041	948	53	1215	1124	UA	441	N12221	EWR	BNA	105	748	9	48	2023-09-10 09:00:00	Other
22083	10	19	1314	1230	44	1453	1411	MQ	1191	N764JD	EWR	ORD	120	719	12	30	2023-10-19 12:00:00	ORD
22085	6	10	914	902	12	1113	1112	YX	1074	N725YX	EWR	MCI	153	1092	9	2	2023-06-10 09:00:00	Other
22088	3	13	1317	1218	59	1619	1514	UA	702	N37468	EWR	TPA	155	997	12	18	2023-03-13 12:00:00	Other
22090	1	11	1750	1720	30	2008	2007	YX	1475	N138HQ	LGA	IND	106	660	17	20	2023-01-11 17:00:00	Other
22091	5	25	1041	1029	12	1153	1206	YX	1600	N815MD	LGA	DCA	43	214	10	29	2023-05-25 10:00:00	Other
22093	7	21	1506	1455	11	1746	1756	UA	69	N27260	EWR	PBI	133	1023	14	55	2023-07-21 14:00:00	Other
22095	1	9	1620	1328	172	1727	1439	B6	363	N249JB	JFK	BOS	39	187	13	28	2023-01-09 13:00:00	BOS
22099	3	3	8	2039	209	232	2253	B6	548	N193JB	JFK	DTW	87	509	20	39	2023-03-03 20:00:00	Other
22101	10	13	2115	1859	136	2309	2123	9E	1482	N146PQ	LGA	CLT	85	544	18	59	2023-10-13 18:00:00	CLT
22106	1	19	1401	1259	62	1516	1417	YX	1775	N818MD	LGA	SYR	44	198	12	59	2023-01-19 12:00:00	Other
22107	5	16	1911	1717	114	2159	2029	B6	212	N598JB	LGA	FLL	148	1076	17	17	2023-05-16 17:00:00	FLL
22114	2	17	1620	1549	31	1828	1738	YX	1198	N872RW	LGA	RIC	79	292	15	49	2023-02-17 15:00:00	Other
22115	3	23	613	601	12	906	851	UA	270	N75425	EWR	LAS	327	2227	6	1	2023-03-23 06:00:00	Other
22125	8	15	1050	1035	15	1203	1201	B6	49	N206JB	JFK	ROC	51	264	10	35	2023-08-15 10:00:00	Other
22127	7	18	1532	1440	52	1835	1743	DL	398	N105DX	LGA	MCO	146	950	14	40	2023-07-18 14:00:00	MCO
22131	1	12	2024	2000	24	2329	2311	B6	1004	N624JB	JFK	MCO	145	944	20	0	2023-01-12 20:00:00	MCO
22134	4	30	1734	1510	144	1954	1704	OO	1048	N241SY	JFK	PIT	63	340	15	10	2023-04-30 15:00:00	Other
22139	6	6	2333	2245	48	152	106	F9	872	N307FR	LGA	ATL	104	762	22	45	2023-06-06 22:00:00	ATL
22140	2	18	1856	1700	116	2218	2022	B6	739	N977JE	EWR	LAX	354	2454	17	0	2023-02-18 17:00:00	LAX
22143	7	21	2158	2102	56	48	3	B6	156	N656JB	LGA	FLL	142	1076	21	2	2023-07-21 21:00:00	FLL
22145	8	1	1257	1240	17	1402	1359	NK	331	N519NK	EWR	BNA	104	748	12	40	2023-08-01 12:00:00	Other
22148	3	16	1352	1320	32	1623	1609	UA	737	N19136	EWR	MCO	124	937	13	20	2023-03-16 13:00:00	MCO
22149	9	18	1538	1520	18	1708	1650	OO	1270	N259SY	JFK	BNA	115	765	15	20	2023-09-18 15:00:00	Other
22154	8	8	1949	1929	20	2153	2225	DL	337	N841DN	JFK	ATL	102	760	19	29	2023-08-08 19:00:00	ATL
22159	8	24	1239	805	274	1536	1100	DL	149	N833MH	JFK	LAX	325	2475	8	5	2023-08-24 08:00:00	LAX
22163	3	30	2119	2100	19	2314	2244	AA	248	N766US	EWR	ORD	132	719	21	0	2023-03-30 21:00:00	ORD
22171	2	27	2227	2030	117	NA	2150	B6	359	N375JB	JFK	BOS	NA	187	20	30	2023-02-27 20:00:00	BOS
22175	1	29	2013	1926	47	2237	2146	UA	208	N438UA	EWR	IND	117	645	19	26	2023-01-29 19:00:00	Other
22186	12	10	1934	1909	25	2253	2250	UA	287	N27239	EWR	PHX	287	2133	19	9	2023-12-10 19:00:00	Other
22191	3	14	1315	1220	55	1451	1348	YX	1281	N107HQ	JFK	ORF	53	290	12	20	2023-03-14 12:00:00	Other
22195	5	10	1331	1315	16	1436	1431	B6	809	N206JB	LGA	BOS	41	184	13	15	2023-05-10 13:00:00	BOS
22224	6	7	2328	2159	89	42	2337	YX	1068	N743YX	EWR	BGR	53	393	21	59	2023-06-07 21:00:00	Other
22227	10	12	1716	1626	50	2012	1911	UA	533	N13138	EWR	MCO	135	937	16	26	2023-10-12 16:00:00	MCO
22228	2	17	821	755	26	1127	1104	B6	180	N775JB	LGA	PBI	157	1035	7	55	2023-02-17 07:00:00	Other
22238	6	12	1530	1459	31	1712	1644	YX	1335	N440YX	JFK	DCA	61	213	14	59	2023-06-12 14:00:00	Other
22261	1	13	830	805	25	1104	1115	DL	383	N706TW	JFK	LAS	287	2248	8	5	2023-01-13 08:00:00	Other
22270	9	11	2110	1755	195	2	2035	B6	261	N998JE	JFK	LAS	312	2248	17	55	2023-09-11 17:00:00	Other
22278	6	1	1408	1345	23	1629	1640	WN	256	N8503A	LGA	HOU	184	1428	13	45	2023-06-01 13:00:00	Other
22289	5	7	2329	2250	39	31	12	9E	1526	N147PQ	JFK	SYR	42	209	22	50	2023-05-07 22:00:00	Other
22295	8	7	1721	1700	21	2110	2010	DL	83	N839MH	JFK	LAX	350	2475	17	0	2023-08-07 17:00:00	LAX
22296	2	20	2237	2159	38	2323	2301	9E	1446	N186PQ	LGA	PVD	30	143	21	59	2023-02-20 21:00:00	Other
22297	3	3	1746	1715	31	1949	1923	AA	611	N993AN	LGA	CLT	98	544	17	15	2023-03-03 17:00:00	CLT
22298	11	22	1329	1310	19	1626	1642	B6	276	N3121J	JFK	SAT	211	1587	13	10	2023-11-22 13:00:00	Other
22308	4	8	848	619	149	1117	850	AA	906	N416AN	EWR	PHX	291	2133	6	19	2023-04-08 06:00:00	Other
22309	6	1	2205	2145	20	13	2358	UA	657	N27258	EWR	MCI	137	1092	21	45	2023-06-01 21:00:00	Other
22315	4	6	1034	855	99	1327	1218	DL	213	N134DU	LGA	DFW	199	1389	8	55	2023-04-06 08:00:00	Other
22318	3	28	1202	1110	52	1359	1258	OO	1567	N131SY	LGA	ORD	127	733	11	10	2023-03-28 11:00:00	ORD
22325	12	22	1622	1600	22	1842	1844	YX	1075	N861RW	EWR	ATL	108	746	16	0	2023-12-22 16:00:00	ATL
22331	6	16	1559	1350	129	1722	1527	9E	1562	N299PQ	JFK	BGR	57	382	13	50	2023-06-16 13:00:00	Other
22333	3	12	1552	1529	23	1904	1832	UA	860	N13720	EWR	DFW	205	1372	15	29	2023-03-12 15:00:00	Other
22334	10	24	1711	1700	11	2012	2009	DL	86	N828MH	JFK	LAX	326	2475	17	0	2023-10-24 17:00:00	LAX
22336	1	2	734	720	14	1008	949	DL	1053	N377DA	EWR	ATL	111	746	7	20	2023-01-02 07:00:00	ATL
22341	6	20	1037	1016	21	1241	1240	AA	827	N913US	EWR	PHX	266	2133	10	16	2023-06-20 10:00:00	Other
22352	4	30	1124	1045	39	1423	1336	B6	139	N913JB	JFK	MCO	150	944	10	45	2023-04-30 10:00:00	MCO
22355	5	1	2032	1959	33	2314	2231	DL	790	N365NB	LGA	MSY	170	1183	19	59	2023-05-01 19:00:00	Other
22359	9	2	1505	1430	35	1756	1730	B6	226	N935JB	JFK	LAX	302	2475	14	30	2023-09-02 14:00:00	LAX
22362	4	23	1158	1100	58	1315	1229	UA	463	N410UA	EWR	BNA	109	748	11	0	2023-04-23 11:00:00	Other
22364	7	10	1628	1610	18	1849	1837	UA	379	N818UA	EWR	ATL	111	746	16	10	2023-07-10 16:00:00	ATL
22365	9	18	2304	2200	64	213	136	DL	318	N723TW	JFK	SFO	331	2586	22	0	2023-09-18 22:00:00	Other
22370	2	23	1838	1700	98	2130	2014	B6	224	N775JB	EWR	PBI	136	1023	17	0	2023-02-23 17:00:00	Other
22371	10	16	631	600	31	819	802	AA	928	N958AN	EWR	CLT	88	529	6	0	2023-10-16 06:00:00	CLT
22375	6	3	1650	1629	21	1856	1843	YX	1153	N722YX	EWR	CHS	92	628	16	29	2023-06-03 16:00:00	Other
22376	9	29	1511	1131	220	1724	1332	AA	942	N955AN	JFK	CLT	86	541	11	31	2023-09-29 11:00:00	CLT
22378	12	17	1106	845	141	1253	1108	OO	1167	N271SY	LGA	MEM	145	963	8	45	2023-12-17 08:00:00	Other
22384	8	10	1254	1220	34	1440	1345	9E	1244	N907XJ	LGA	MKE	128	738	12	20	2023-08-10 12:00:00	Other
22397	2	17	1014	959	15	1154	1143	9E	1413	N905XJ	JFK	PIT	70	340	9	59	2023-02-17 09:00:00	Other
22406	3	26	2041	2011	30	2311	2212	YX	1217	N732YX	EWR	ILM	78	488	20	11	2023-03-26 20:00:00	Other
22409	4	30	1057	1000	57	1218	1127	AA	433	N716UW	LGA	DCA	56	214	10	0	2023-04-30 10:00:00	Other
22410	7	14	812	710	62	1119	1003	UA	549	N17301	EWR	PDX	316	2434	7	10	2023-07-14 07:00:00	Other
22414	7	29	1122	945	97	1254	1135	9E	1285	N926XJ	LGA	BGR	55	378	9	45	2023-07-29 09:00:00	Other
22438	1	3	807	730	37	1140	1052	AA	1	N105NN	JFK	LAX	359	2475	7	30	2023-01-03 07:00:00	LAX
22444	11	29	1830	1740	50	2240	2048	UA	711	N33103	EWR	IAH	208	1400	17	40	2023-11-29 17:00:00	Other
22446	1	25	44	2139	185	235	2325	B6	592	N203JB	JFK	RDU	89	427	21	39	2023-01-25 21:00:00	Other
22453	7	1	1925	1725	120	2055	1914	OO	986	N293SY	JFK	BOS	35	187	17	25	2023-07-01 17:00:00	BOS
22461	8	4	1345	1318	27	1505	1434	B6	672	N284JB	JFK	ACK	41	199	13	18	2023-08-04 13:00:00	Other
22463	8	26	1512	1240	152	1656	1430	DL	466	N128DU	LGA	ORD	123	733	12	40	2023-08-26 12:00:00	ORD
22464	3	8	1943	1927	16	2212	2159	YX	1290	N106HQ	LGA	XNA	172	1147	19	27	2023-03-08 19:00:00	Other
22474	6	30	1714	1555	79	1953	1907	B6	326	N923JB	JFK	LAX	315	2475	15	55	2023-06-30 15:00:00	LAX
22476	8	7	155	2259	176	536	258	B6	243	N561JB	JFK	PSE	207	1617	22	59	2023-08-07 22:00:00	Other
22480	8	27	1654	1608	46	1814	1739	YX	841	N647RW	EWR	ROC	42	246	16	8	2023-08-27 16:00:00	Other
22486	10	27	843	830	13	1015	1012	UA	586	N68823	EWR	CLE	64	404	8	30	2023-10-27 08:00:00	Other
22487	6	9	1002	758	124	1201	1008	DL	958	N320NB	JFK	MSY	152	1182	7	58	2023-06-09 07:00:00	Other
22490	3	8	1542	1527	15	1724	1731	YX	1213	N723YX	EWR	CMH	79	463	15	27	2023-03-08 15:00:00	Other
22494	1	9	1450	1359	51	1744	1712	B6	154	N949JT	LGA	MCO	132	950	13	59	2023-01-09 13:00:00	MCO
22498	2	19	1758	1530	148	2036	1804	B6	797	N3112J	JFK	MCI	186	1113	15	30	2023-02-19 15:00:00	Other
22500	8	1	2119	2100	19	2308	2254	9E	1175	N490PX	LGA	RDU	68	431	21	0	2023-08-01 21:00:00	Other
22501	6	15	1854	1459	235	2142	1800	UA	77	N458UA	EWR	PBI	141	1023	14	59	2023-06-15 14:00:00	Other
22505	1	13	1648	1559	49	1836	1815	DL	586	N102DN	LGA	DTW	77	502	15	59	2023-01-13 15:00:00	Other
22532	1	29	1031	959	32	1314	1304	B6	457	N203JB	JFK	MCO	140	944	9	59	2023-01-29 09:00:00	MCO
22539	12	22	1810	1737	33	2056	2059	AA	678	N989AU	EWR	DFW	186	1372	17	37	2023-12-22 17:00:00	Other
22540	6	13	1921	1900	21	2038	2030	UA	650	N66803	EWR	BNA	105	748	19	0	2023-06-13 19:00:00	Other
22558	2	3	1604	1500	64	1819	1642	9E	1424	N316PQ	EWR	RDU	80	416	15	0	2023-02-03 15:00:00	Other
22572	3	25	816	659	77	1115	1031	B6	722	N526JL	LGA	RSW	156	1080	6	59	2023-03-25 06:00:00	Other
22577	6	4	1738	1720	18	2054	1954	B6	153	N583JB	JFK	ATL	159	760	17	20	2023-06-04 17:00:00	ATL
22578	8	2	1709	1645	24	2001	1957	UA	499	N2846U	EWR	SFO	326	2565	16	45	2023-08-02 16:00:00	Other
22585	11	30	1323	1247	36	1610	1550	UA	834	N64809	EWR	TPA	143	997	12	47	2023-11-30 12:00:00	Other
22598	4	18	2016	1956	20	2234	2215	YX	953	N646RW	EWR	IND	101	645	19	56	2023-04-18 19:00:00	Other
22614	10	13	1350	1255	55	1541	1455	G4	135	253NV	EWR	DSM	153	1017	12	55	2023-10-13 12:00:00	Other
22631	3	15	1429	1328	61	1809	1645	AA	796	N324RN	JFK	MIA	155	1089	13	28	2023-03-15 13:00:00	MIA
22634	7	31	1908	1830	38	2235	2157	B6	45	N948JB	JFK	SMF	358	2521	18	30	2023-07-31 18:00:00	Other
22637	10	12	857	800	57	1102	1009	9E	1488	N313PQ	JFK	CLT	87	541	8	0	2023-10-12 08:00:00	CLT
22640	6	24	1759	1421	218	2113	1700	YX	1879	N233JQ	JFK	SAV	111	718	14	21	2023-06-24 14:00:00	Other
22652	8	27	1959	1840	79	2202	2023	AA	532	N705UW	LGA	RDU	69	431	18	40	2023-08-27 18:00:00	Other
22658	1	23	1720	1705	15	1849	1849	AA	914	N912NN	EWR	ORD	116	719	17	5	2023-01-23 17:00:00	ORD
22662	10	10	2028	1909	79	2312	2215	UA	778	N78509	EWR	FLL	145	1065	19	9	2023-10-10 19:00:00	FLL
22665	12	24	1013	950	23	1259	1305	NK	1008	N961NK	LGA	MIA	146	1096	9	50	2023-12-24 09:00:00	MIA
22672	10	8	2110	2050	20	2308	2301	YX	1080	N763YX	EWR	GSP	87	594	20	50	2023-10-08 20:00:00	Other
22676	4	25	1611	1549	22	1740	1732	B6	730	N663JB	LGA	BNA	114	764	15	49	2023-04-25 15:00:00	Other
22680	3	31	2143	1830	193	112	2159	B6	29	N952JB	JFK	SLC	293	1990	18	30	2023-03-31 18:00:00	Other
22717	7	28	2125	1759	206	44	2104	DL	96	N106DU	JFK	DFW	200	1391	17	59	2023-07-28 17:00:00	Other
22720	7	28	2300	2215	45	303	115	DL	93	N830MH	JFK	LAX	328	2475	22	15	2023-07-28 22:00:00	LAX
22722	8	26	842	830	12	1053	1114	UA	120	N91007	EWR	LAX	283	2454	8	30	2023-08-26 08:00:00	LAX
22735	5	5	1644	1630	14	1932	1937	NK	321	N657NK	LGA	FLL	148	1076	16	30	2023-05-05 16:00:00	FLL
22737	1	19	2037	2025	12	2357	2333	B6	443	N558JB	JFK	PBI	152	1028	20	25	2023-01-19 20:00:00	Other
22738	12	4	1906	1830	36	2225	2137	AA	972	N842NN	EWR	MIA	162	1085	18	30	2023-12-04 18:00:00	MIA
22742	4	2	2048	1930	78	2211	2129	YX	1272	N427YX	JFK	DCA	52	213	19	30	2023-04-02 19:00:00	Other
22750	9	11	2229	2030	119	200	2342	UA	792	N41140	EWR	LAX	338	2454	20	30	2023-09-11 20:00:00	LAX
22758	4	22	1320	1250	30	1529	1513	YX	1286	N136HQ	LGA	CVG	98	585	12	50	2023-04-22 12:00:00	Other
22763	7	28	1806	1729	37	2115	2043	AA	138	N931NN	JFK	MIA	142	1089	17	29	2023-07-28 17:00:00	MIA
22765	2	9	1548	1430	78	1719	1625	AA	846	N776XF	LGA	RDU	73	431	14	30	2023-02-09 14:00:00	Other
22771	11	28	2114	1935	99	2335	2211	9E	1449	N341PQ	LGA	SAV	106	722	19	35	2023-11-28 19:00:00	Other
22772	8	8	1022	915	67	1121	1045	WN	484	N500WR	LGA	MDW	101	725	9	15	2023-08-08 09:00:00	Other
22775	1	11	1929	1830	59	2110	2038	AA	1048	N927NN	LGA	ORD	119	733	18	30	2023-01-11 18:00:00	ORD
22779	8	16	2135	2059	36	125	53	B6	737	N952JB	EWR	SJU	202	1608	20	59	2023-08-16 20:00:00	Other
22783	1	11	2206	2155	11	2336	2310	DL	817	N822DN	JFK	BOS	33	187	21	55	2023-01-11 21:00:00	BOS
22784	4	21	844	830	14	1112	1027	9E	1378	N329PQ	JFK	RDU	66	427	8	30	2023-04-21 08:00:00	Other
22800	12	23	1255	1200	55	1545	1508	NK	1186	N708NK	LGA	FLL	149	1076	12	0	2023-12-23 12:00:00	FLL
22813	3	29	1118	1000	78	1449	1336	DL	143	N819DN	JFK	SLC	305	1990	10	0	2023-03-29 10:00:00	Other
22817	5	16	1712	1659	13	2003	2023	DL	270	N532DN	JFK	SEA	322	2422	16	59	2023-05-16 16:00:00	Other
22822	4	1	2113	2029	44	2337	2300	UA	522	N27519	EWR	DEN	227	1605	20	29	2023-04-01 20:00:00	Other
22824	6	25	2157	1905	172	2338	2042	YX	1109	N721YX	EWR	PWM	47	284	19	5	2023-06-25 19:00:00	Other
22840	3	11	1201	959	122	1439	1303	NK	272	N652NK	LGA	MCO	129	950	9	59	2023-03-11 09:00:00	MCO
22843	1	17	1011	1000	11	1120	1124	UA	778	N437UA	EWR	IAD	43	212	10	0	2023-01-17 10:00:00	Other
22844	8	20	1916	1759	77	2201	2114	DL	293	N171DN	JFK	LAX	321	2475	17	59	2023-08-20 17:00:00	LAX
22848	8	1	1319	1300	19	1603	1601	UA	87	N434UA	EWR	RSW	149	1068	13	0	2023-08-01 13:00:00	Other
22855	10	30	1831	1729	62	2144	2048	B6	944	N937JB	JFK	LAX	334	2475	17	29	2023-10-30 17:00:00	LAX
22861	3	8	1911	1829	42	2236	2147	B6	940	N587JB	EWR	FLL	143	1065	18	29	2023-03-08 18:00:00	FLL
22863	5	29	1831	1820	11	2055	2045	9E	1460	N310PQ	JFK	IND	92	665	18	20	2023-05-29 18:00:00	Other
22867	9	11	2005	1825	100	2301	2125	WN	1223	N8661A	LGA	TPA	146	1010	18	25	2023-09-11 18:00:00	Other
22868	7	14	1150	846	184	1357	1050	UA	330	N37567	EWR	MYR	88	550	8	46	2023-07-14 08:00:00	Other
22881	7	15	1941	1657	164	2159	1846	YX	944	N863RW	EWR	RDU	80	416	16	57	2023-07-15 16:00:00	Other
22882	7	5	2236	2149	47	2359	2338	YX	1048	N437YX	JFK	DCA	46	213	21	49	2023-07-05 21:00:00	Other
22887	4	30	2216	2055	81	42	2314	YX	972	N752YX	EWR	GRR	84	605	20	55	2023-04-30 20:00:00	Other
22892	12	4	1032	859	93	1200	1057	AA	947	N918NN	JFK	ORD	119	740	8	59	2023-12-04 08:00:00	ORD
22904	11	22	1520	1450	30	1721	1716	9E	1582	N181PQ	LGA	MCI	144	1107	14	50	2023-11-22 14:00:00	Other
22915	2	18	924	659	145	1221	1031	B6	692	N629JB	LGA	RSW	157	1080	6	59	2023-02-18 06:00:00	Other
22919	7	19	1203	940	143	1420	1203	B6	466	N618JB	JFK	DEN	232	1626	9	40	2023-07-19 09:00:00	Other
22924	10	1	1014	935	39	1141	1051	B6	575	N368JB	JFK	BTV	51	266	9	35	2023-10-01 09:00:00	Other
22925	12	28	956	831	85	1245	1141	B6	74	N625JB	JFK	IAH	197	1417	8	31	2023-12-28 08:00:00	Other
22927	4	22	2021	1745	156	2324	1924	YX	1503	N202JQ	JFK	DCA	102	213	17	45	2023-04-22 17:00:00	Other
22929	7	28	1204	1149	15	1448	1434	UA	635	N78506	EWR	SAN	305	2425	11	49	2023-07-28 11:00:00	Other
22936	5	15	1713	1655	18	1952	2016	AA	3	N103NN	JFK	LAX	318	2475	16	55	2023-05-15 16:00:00	LAX
22938	5	23	843	759	44	1141	1109	UA	602	N17296	EWR	FLL	150	1065	7	59	2023-05-23 07:00:00	FLL
22946	7	26	1523	1459	24	1805	1822	B6	438	N504JB	JFK	FLL	143	1069	14	59	2023-07-26 14:00:00	FLL
22950	3	12	911	1924	827	1106	2126	AA	316	N872NN	EWR	CLT	84	529	19	24	2023-03-12 19:00:00	CLT
22955	2	22	612	600	12	848	838	UA	429	N69830	EWR	DEN	249	1605	6	0	2023-02-22 06:00:00	Other
22959	7	29	1725	1645	40	2025	1957	UA	521	N2243U	EWR	SFO	318	2565	16	45	2023-07-29 16:00:00	Other
22960	8	25	1230	735	295	1502	1037	DL	629	N3767	JFK	PBI	132	1028	7	35	2023-08-25 07:00:00	Other
22967	7	25	2051	1555	296	2336	1937	B6	215	N980JT	JFK	SFO	328	2586	15	55	2023-07-25 15:00:00	Other
22978	12	1	1919	1905	14	2134	2134	YX	1253	N414YX	LGA	IND	110	660	19	5	2023-12-01 19:00:00	Other
22980	4	16	1536	900	396	1824	1202	B6	331	N306JB	JFK	PBI	149	1028	9	0	2023-04-16 09:00:00	Other
22982	6	22	1944	1834	70	2052	2013	UA	456	N37525	EWR	ORD	100	719	18	34	2023-06-22 18:00:00	ORD
22987	10	1	1223	1059	84	1457	1413	DL	162	N533DT	JFK	SEA	307	2422	10	59	2023-10-01 10:00:00	Other
22990	8	13	4	2140	144	103	2303	B6	729	N279JB	JFK	SYR	41	209	21	40	2023-08-13 21:00:00	Other
22993	1	16	1013	959	14	1111	1117	9E	1450	N320PQ	LGA	PVD	31	143	9	59	2023-01-16 09:00:00	Other
23011	6	17	1732	1659	33	1858	1826	YX	1137	N752YX	EWR	BOS	39	200	16	59	2023-06-17 16:00:00	BOS
23019	1	23	1912	1844	28	2133	2120	UA	431	N57111	EWR	DEN	219	1605	18	44	2023-01-23 18:00:00	Other
23031	4	2	2049	1955	54	27	2358	DL	324	N702TW	JFK	SFO	366	2586	19	55	2023-04-02 19:00:00	Other
23034	4	23	1902	1743	79	2202	2042	UA	351	N37257	EWR	TPA	142	997	17	43	2023-04-23 17:00:00	Other
23036	10	25	2142	2059	43	2326	2257	UA	579	N78524	EWR	MSP	141	1008	20	59	2023-10-25 20:00:00	Other
23041	4	16	1552	1147	245	1935	1438	UA	487	N33714	EWR	SRQ	158	1034	11	47	2023-04-16 11:00:00	Other
23045	9	8	2043	1200	523	1	1507	B6	832	N961JT	JFK	LAX	318	2475	12	0	2023-09-08 12:00:00	LAX
23052	3	11	1822	1810	12	1934	1935	DL	444	N111NG	JFK	BOS	37	187	18	10	2023-03-11 18:00:00	BOS
23055	7	27	1852	1700	112	2209	2008	UA	617	N434UA	EWR	RSW	149	1068	17	0	2023-07-27 17:00:00	Other
23056	4	21	1702	1620	42	1939	1911	UA	123	N19136	EWR	MCO	128	937	16	20	2023-04-21 16:00:00	MCO
23068	4	9	1647	1525	82	1912	1843	AS	83	N925VA	EWR	LAX	300	2454	15	25	2023-04-09 15:00:00	LAX
23076	2	24	1039	1000	39	1648	1605	HA	22	N396HA	JFK	HNL	639	4983	10	0	2023-02-24 10:00:00	Other
23078	7	6	1912	1805	67	2131	2033	UA	435	N37295	EWR	ATL	108	746	18	5	2023-07-06 18:00:00	ATL
23086	2	5	2214	2159	15	2330	2327	YX	1064	N740YX	EWR	PWM	47	284	21	59	2023-02-05 21:00:00	Other
23092	2	1	948	900	48	1641	1525	DL	101	N825MH	JFK	HNL	662	4983	9	0	2023-02-01 09:00:00	Other
23107	10	9	1157	1057	60	1431	1335	F9	521	N361FR	LGA	ATL	113	762	10	57	2023-10-09 10:00:00	ATL
23109	4	8	1111	1030	41	1351	1317	B6	39	N958JB	JFK	LAS	306	2248	10	30	2023-04-08 10:00:00	Other
23112	4	7	1101	946	75	1502	1341	UA	539	N75433	EWR	SJU	209	1608	9	46	2023-04-07 09:00:00	Other
23119	8	5	2321	1959	202	219	2305	AS	72	N927VA	EWR	LAX	323	2454	19	59	2023-08-05 19:00:00	LAX
23127	7	31	2109	2030	39	2320	2258	UA	451	N77259	EWR	ATL	96	746	20	30	2023-07-31 20:00:00	ATL
23128	4	2	821	810	11	1301	1318	UA	131	N76054	EWR	HNL	613	4962	8	10	2023-04-02 08:00:00	Other
23136	5	8	2307	2059	128	105	2312	UA	374	N17753	EWR	CVG	86	569	20	59	2023-05-08 20:00:00	Other
23139	3	25	2128	2050	38	123	16	B6	487	N623JB	JFK	AUS	252	1521	20	50	2023-03-25 20:00:00	Other
23144	4	12	1957	1941	16	1	2254	UA	484	N36272	EWR	MIA	156	1085	19	41	2023-04-12 19:00:00	MIA
23149	7	26	2027	1925	62	2324	2231	UA	662	N78540	EWR	FLL	147	1065	19	25	2023-07-26 19:00:00	FLL
23151	3	1	1331	1300	31	1430	1425	YX	1710	N240JQ	LGA	BOS	34	184	13	0	2023-03-01 13:00:00	BOS
23155	3	8	1205	1151	14	1515	1457	NK	541	N661NK	EWR	FLL	157	1065	11	51	2023-03-08 11:00:00	FLL
23156	10	2	1032	730	182	1235	955	DL	173	N387DA	LGA	DEN	206	1620	7	30	2023-10-02 07:00:00	Other
23159	9	10	1056	959	57	1606	1310	AA	250	N927NN	JFK	MIA	160	1089	9	59	2023-09-10 09:00:00	MIA
23164	4	21	930	915	15	1154	1154	YX	1482	N879RW	LGA	HHH	98	701	9	15	2023-04-21 09:00:00	Other
23167	6	6	2200	2055	65	2345	2233	DL	1026	N127DU	JFK	BOS	42	187	20	55	2023-06-06 20:00:00	BOS
23173	4	11	1527	1515	12	1805	1815	DL	446	N119DN	LGA	MCO	130	950	15	15	2023-04-11 15:00:00	MCO
23177	1	27	1535	1455	40	1644	1617	9E	1382	N186PQ	JFK	BWI	39	184	14	55	2023-01-27 14:00:00	Other
23179	1	11	1324	1229	55	1451	1416	YX	1862	N818MD	LGA	BNA	119	764	12	29	2023-01-11 12:00:00	Other
23180	7	30	1312	1145	87	1422	1303	UA	712	N17300	EWR	PWM	50	284	11	45	2023-07-30 11:00:00	Other
23188	4	16	1715	1630	45	1823	1758	YX	945	N649RW	EWR	DCA	42	199	16	30	2023-04-16 16:00:00	Other
23194	8	18	1846	1830	16	2238	2200	B6	65	N977JE	JFK	SEA	339	2422	18	30	2023-08-18 18:00:00	Other
23218	2	17	2206	2129	37	120	55	DL	208	N176DZ	JFK	LAX	352	2475	21	29	2023-02-17 21:00:00	LAX
23223	1	23	856	829	27	1019	1014	UA	238	N16703	EWR	BNA	114	748	8	29	2023-01-23 08:00:00	Other
23224	7	14	1903	1630	153	NA	1920	UA	408	N787UA	EWR	LAX	NA	2454	16	30	2023-07-14 16:00:00	LAX
23231	3	27	2055	1715	220	2259	1923	AA	611	N179UW	LGA	CLT	94	544	17	15	2023-03-27 17:00:00	CLT
23242	4	18	1809	1755	14	2133	2055	AS	92	N260AK	EWR	SAN	336	2425	17	55	2023-04-18 17:00:00	Other
23246	3	14	1645	1555	50	1916	1836	B6	670	N216JB	JFK	ATL	106	760	15	55	2023-03-14 15:00:00	ATL
23248	6	17	628	615	13	902	908	B6	45	N556JB	EWR	PBI	132	1023	6	15	2023-06-17 06:00:00	Other
23253	7	6	2343	2131	132	130	2339	UA	527	N459UA	EWR	MCI	146	1092	21	31	2023-07-06 21:00:00	Other
23256	11	15	1131	1105	26	1411	1352	UA	532	N57111	EWR	LAS	310	2227	11	5	2023-11-15 11:00:00	Other
23264	7	24	2041	2020	21	2256	2241	9E	1174	N676CA	LGA	GRR	99	618	20	20	2023-07-24 20:00:00	Other
23266	10	8	938	745	113	1123	918	9E	1417	N292PQ	JFK	BUF	64	301	7	45	2023-10-08 07:00:00	Other
23267	9	7	854	819	35	1004	951	YX	1851	N215JQ	LGA	BUF	46	292	8	19	2023-09-07 08:00:00	Other
23268	3	23	1014	1000	14	1348	1320	UA	753	N12003	EWR	SFO	366	2565	10	0	2023-03-23 10:00:00	Other
23272	7	14	1124	955	89	1318	1148	9E	1289	N336PQ	EWR	RDU	98	416	9	55	2023-07-14 09:00:00	Other
23276	10	12	959	900	59	1320	1209	B6	79	N964JT	JFK	AUS	229	1521	9	0	2023-10-12 09:00:00	Other
23279	6	3	2330	2259	31	334	254	B6	146	N996JL	JFK	SJU	213	1598	22	59	2023-06-03 22:00:00	Other
23280	6	15	2044	1959	45	2341	2319	DL	588	N320DN	LGA	FLL	161	1076	19	59	2023-06-15 19:00:00	FLL
23283	7	24	1557	1543	14	1844	1841	UA	331	N37422	EWR	AUS	197	1504	15	43	2023-07-24 15:00:00	Other
23296	4	17	2051	1957	54	2159	2120	UA	815	N478UA	EWR	IAD	43	212	19	57	2023-04-17 19:00:00	Other
23301	7	7	16	2258	78	427	252	B6	132	N995JL	JFK	SJU	198	1598	22	58	2023-07-07 22:00:00	Other
23310	6	24	750	735	15	1027	1029	DL	768	N350DN	EWR	SLC	261	1969	7	35	2023-06-24 07:00:00	Other
23326	3	25	1634	1410	144	1937	1727	B6	336	N661JB	EWR	PBI	154	1023	14	10	2023-03-25 14:00:00	Other
23334	10	5	2025	1906	79	2202	2109	YX	1340	N406YX	LGA	CMH	74	479	19	6	2023-10-05 19:00:00	Other
23339	10	30	1159	1140	19	1442	1400	DL	847	N302DU	LGA	MSY	183	1183	11	40	2023-10-30 11:00:00	Other
23340	8	22	1552	1529	23	1735	1724	AA	660	N959AN	JFK	ORD	120	740	15	29	2023-08-22 15:00:00	ORD
23347	9	22	1026	1000	26	1306	1254	B6	331	N658JB	JFK	PBI	141	1028	10	0	2023-09-22 10:00:00	Other
23349	7	10	1358	1145	133	1716	1455	AS	9	N973AK	JFK	SEA	337	2422	11	45	2023-07-10 11:00:00	Other
23351	7	27	931	920	11	1225	1215	B6	58	N985JT	JFK	SAN	293	2446	9	20	2023-07-27 09:00:00	Other
23361	1	22	1327	1300	27	1439	1425	YX	1846	N205JQ	LGA	BOS	46	184	13	0	2023-01-22 13:00:00	BOS
23403	2	9	1727	1543	104	1951	1824	B6	645	N653JB	JFK	ATL	118	760	15	43	2023-02-09 15:00:00	ATL
23407	7	5	1916	1515	241	2102	1707	DL	515	N113DQ	LGA	ORD	111	733	15	15	2023-07-05 15:00:00	ORD
23411	8	27	1818	1750	28	2053	2020	WN	284	N7815L	LGA	ATL	112	762	17	50	2023-08-27 17:00:00	ATL
23421	8	10	2117	2022	55	2328	2220	DL	802	N919AT	EWR	DTW	82	488	20	22	2023-08-10 20:00:00	Other
23426	10	12	933	915	18	1058	1102	DL	898	N133DU	LGA	ORD	126	733	9	15	2023-10-12 09:00:00	ORD
23428	5	10	1748	1720	28	2033	2025	WN	944	N8605E	LGA	HOU	197	1428	17	20	2023-05-10 17:00:00	Other
23429	3	1	2118	2044	34	5	2359	B6	579	N584JB	JFK	FLL	141	1069	20	44	2023-03-01 20:00:00	FLL
23432	5	7	2050	2036	14	2313	2247	YX	1044	N729YX	EWR	GSP	91	594	20	36	2023-05-07 20:00:00	Other
23436	9	23	1549	1534	15	1836	1837	UA	378	N484UA	EWR	AUS	198	1504	15	34	2023-09-23 15:00:00	Other
23438	9	29	1921	1800	81	2140	2103	DL	339	N178DN	JFK	LAX	294	2475	18	0	2023-09-29 18:00:00	LAX
23440	1	20	1935	1905	30	2107	2111	AA	452	N177XF	LGA	RDU	67	431	19	5	2023-01-20 19:00:00	Other
23441	7	21	1941	1850	51	2118	2036	9E	1176	N490PX	LGA	BHM	123	866	18	50	2023-07-21 18:00:00	Other
23443	6	16	2110	1959	71	14	2319	DL	588	N102DN	LGA	FLL	148	1076	19	59	2023-06-16 19:00:00	FLL
23448	12	27	1228	1150	38	1555	1505	NK	346	N614NK	EWR	FLL	182	1065	11	50	2023-12-27 11:00:00	FLL
23449	5	4	653	615	38	958	925	UA	864	N73860	EWR	LAX	321	2454	6	15	2023-05-04 06:00:00	LAX
23457	6	23	1447	1325	82	1705	1548	NK	33	N621NK	EWR	ATL	105	746	13	25	2023-06-23 13:00:00	ATL
23467	4	15	628	600	28	835	819	DL	751	N977AT	EWR	ATL	107	746	6	0	2023-04-15 06:00:00	ATL
23469	7	21	2222	2030	112	100	2248	YX	880	N725YX	EWR	GRR	97	605	20	30	2023-07-21 20:00:00	Other
23475	3	19	643	630	13	750	755	WN	331	N8529Z	LGA	MDW	114	725	6	30	2023-03-19 06:00:00	Other
23478	3	5	1707	1625	42	1856	1806	AA	406	N825AW	LGA	RDU	67	431	16	25	2023-03-05 16:00:00	Other
23483	1	19	1741	1729	12	2043	2042	B6	776	N712JB	JFK	PSP	324	2378	17	29	2023-01-19 17:00:00	Other
23486	3	12	647	630	17	945	901	UA	454	N405UA	EWR	ATL	153	746	6	30	2023-03-12 06:00:00	ATL
23500	5	22	1613	1540	33	1915	1847	DL	576	N310DN	LGA	FLL	145	1076	15	40	2023-05-22 15:00:00	FLL
23502	6	2	944	933	11	1135	1138	B6	70	N247JB	JFK	DTW	79	509	9	33	2023-06-02 09:00:00	Other
23505	8	11	2145	2000	105	2321	2139	B6	739	N368JB	JFK	BUF	53	301	20	0	2023-08-11 20:00:00	Other
23513	7	4	2156	2130	26	2335	2344	YX	1443	N221JQ	JFK	CMH	68	483	21	30	2023-07-04 21:00:00	Other
23518	11	16	2222	2130	52	120	59	B6	445	N595JB	JFK	AUS	204	1521	21	30	2023-11-16 21:00:00	Other
23521	7	21	2051	1859	112	6	2158	NK	416	N663NK	LGA	IAH	195	1416	18	59	2023-07-21 18:00:00	Other
23522	6	6	1544	1530	14	1816	1811	B6	650	N563JB	JFK	JAX	120	828	15	30	2023-06-06 15:00:00	Other
23529	9	21	2221	2200	21	149	136	DL	318	N704X	JFK	SFO	343	2586	22	0	2023-09-21 22:00:00	Other
23532	11	8	1714	1700	14	1955	2009	B6	627	N598JB	LGA	PBI	132	1035	17	0	2023-11-08 17:00:00	Other
23535	6	30	2143	2130	13	2313	2344	YX	1914	N212JQ	JFK	CMH	68	483	21	30	2023-06-30 21:00:00	Other
23536	4	13	2050	1902	108	2344	2218	UA	444	N816UA	EWR	SLC	260	1969	19	2	2023-04-13 19:00:00	Other
23544	11	12	1647	1631	16	2007	1945	NK	316	N674NK	LGA	FLL	157	1076	16	31	2023-11-12 16:00:00	FLL
23564	8	25	1019	1007	12	1253	1309	NK	678	N603NK	EWR	AUS	190	1504	10	7	2023-08-25 10:00:00	Other
23567	3	23	1700	1636	24	2219	1939	9E	1319	N908XJ	LGA	OKC	NA	1341	16	36	2023-03-23 16:00:00	Other
23575	6	15	1911	1835	36	2040	2041	YX	1223	N856RW	EWR	CMH	71	463	18	35	2023-06-15 18:00:00	Other
23579	11	14	1742	1729	13	2047	2055	AA	92	N110AN	JFK	LAX	334	2475	17	29	2023-11-14 17:00:00	LAX
23586	2	5	1847	1830	17	2331	2332	DL	691	N893DN	JFK	SJU	202	1598	18	30	2023-02-05 18:00:00	Other
23588	8	3	1837	1825	12	2012	2015	WN	765	N960WN	LGA	STL	130	888	18	25	2023-08-03 18:00:00	Other
23610	1	2	1703	1400	183	1938	1712	UA	566	N36207	EWR	FLL	138	1065	14	0	2023-01-02 14:00:00	FLL
23618	10	13	956	935	21	1107	1050	B6	575	N238JB	JFK	BTV	49	266	9	35	2023-10-13 09:00:00	Other
23620	5	3	1652	1612	40	1901	1833	UA	482	N25705	EWR	JAX	109	820	16	12	2023-05-03 16:00:00	Other
23634	1	14	2331	2259	32	428	348	B6	371	N587JB	JFK	BQN	204	1576	22	59	2023-01-14 22:00:00	Other
23641	12	29	1610	1455	75	1857	1749	9E	1390	N335PQ	JFK	JAX	140	828	14	55	2023-12-29 14:00:00	Other
23650	8	4	2209	2130	39	50	9	B6	159	N598JB	LGA	MCO	126	950	21	30	2023-08-04 21:00:00	MCO
23651	7	9	1958	1834	84	2205	2045	DL	793	N929AT	EWR	MSP	134	1008	18	34	2023-07-09 18:00:00	Other
23654	7	26	1410	1329	41	1632	1557	UA	733	N27269	EWR	ATL	98	746	13	29	2023-07-26 13:00:00	ATL
23658	12	15	1928	1916	12	2200	2229	DL	978	N505DZ	JFK	MCO	132	944	19	16	2023-12-15 19:00:00	MCO
23667	10	22	1116	730	226	1435	1049	B6	34	N983JT	JFK	SFO	347	2586	7	30	2023-10-22 07:00:00	Other
23668	7	31	1002	946	16	1154	1141	DL	808	N923AT	EWR	DTW	96	488	9	46	2023-07-31 09:00:00	Other
23669	6	29	2215	2157	18	2309	2254	9E	1668	N348PQ	LGA	PVD	33	143	21	57	2023-06-29 21:00:00	Other
23678	8	25	1217	1204	13	1426	1416	DL	748	N3758Y	EWR	ATL	96	746	12	4	2023-08-25 12:00:00	ATL
23679	3	28	2140	1916	144	35	2200	UA	428	N27509	EWR	LAS	313	2227	19	16	2023-03-28 19:00:00	Other
23680	1	11	1537	1345	112	1651	1522	9E	1702	N314PQ	LGA	BUF	52	292	13	45	2023-01-11 13:00:00	Other
23684	11	26	1226	1200	26	1405	1346	AA	722	N770UW	LGA	RDU	76	431	12	0	2023-11-26 12:00:00	Other
23689	4	24	1406	1319	47	1520	1435	B6	300	N238JB	JFK	BOS	33	187	13	19	2023-04-24 13:00:00	BOS
23690	6	4	1011	956	15	1220	1222	UA	586	N27255	EWR	LAS	274	2227	9	56	2023-06-04 09:00:00	Other
23696	1	29	1614	1520	54	2008	1845	DL	116	N127DU	LGA	DFW	250	1389	15	20	2023-01-29 15:00:00	Other
23704	9	17	2204	2015	109	45	2246	B6	917	N529JB	LGA	ATL	127	762	20	15	2023-09-17 20:00:00	ATL
23708	1	11	934	740	114	1347	1122	B6	6	N943JT	JFK	SFO	387	2586	7	40	2023-01-11 07:00:00	Other
23711	9	6	1752	1715	37	1914	1841	B6	380	N329JB	LGA	BOS	45	184	17	15	2023-09-06 17:00:00	BOS
23712	8	16	1503	1430	33	1734	1730	B6	204	N934JB	JFK	LAX	299	2475	14	30	2023-08-16 14:00:00	LAX
23714	9	9	807	755	12	1022	1006	DL	89	N119DU	LGA	CHS	113	641	7	55	2023-09-09 07:00:00	Other
23718	1	29	1454	1430	24	1641	1614	DL	882	N108DQ	LGA	ORD	133	733	14	30	2023-01-29 14:00:00	ORD
23724	7	11	759	730	29	952	945	B6	276	N517JB	JFK	SAV	99	718	7	30	2023-07-11 07:00:00	Other
23727	1	31	956	730	146	1148	920	DL	634	N126DU	LGA	ORD	134	733	7	30	2023-01-31 07:00:00	ORD
23729	2	27	2130	2116	14	142	19	B6	333	N558JB	JFK	DFW	198	1391	21	16	2023-02-27 21:00:00	Other
23731	4	21	2134	1941	113	37	2254	UA	484	N33284	EWR	MIA	148	1085	19	41	2023-04-21 19:00:00	MIA
23740	8	19	1152	1055	57	1408	1317	UA	399	N474UA	EWR	JAX	109	820	10	55	2023-08-19 10:00:00	Other
23742	7	21	2145	1920	145	26	2235	DL	141	N175DN	JFK	LAX	315	2475	19	20	2023-07-21 19:00:00	LAX
23743	10	29	1540	1525	15	1855	1832	B6	699	N651JB	LGA	PBI	141	1035	15	25	2023-10-29 15:00:00	Other
23748	1	11	1701	1630	31	2025	2000	B6	365	N942JB	JFK	LAX	342	2475	16	30	2023-01-11 16:00:00	LAX
23753	7	25	2232	2015	137	51	2255	DL	274	N313DN	LGA	ATL	99	762	20	15	2023-07-25 20:00:00	ATL
23769	10	2	2046	2030	16	2255	2307	DL	883	N121DU	LGA	JAX	110	833	20	30	2023-10-02 20:00:00	Other
23787	6	15	2026	2000	26	2332	2343	DL	105	N893DN	JFK	SLC	259	1990	20	0	2023-06-15 20:00:00	Other
23791	4	9	1639	1615	24	1924	1905	WN	742	N8697C	LGA	MCO	138	950	16	15	2023-04-09 16:00:00	MCO
23794	6	26	1111	1025	46	1252	1200	YX	1858	N217JQ	LGA	BNA	124	764	10	25	2023-06-26 10:00:00	Other
23797	10	6	2011	1955	16	2147	2145	9E	1403	N184GJ	EWR	RDU	64	416	19	55	2023-10-06 19:00:00	Other
23798	3	20	2209	2140	29	107	41	B6	392	N605JB	JFK	PBI	144	1028	21	40	2023-03-20 21:00:00	Other
23802	6	12	1603	1517	46	1734	1634	UA	616	N27260	EWR	BOS	35	200	15	17	2023-06-12 15:00:00	BOS
23805	11	20	913	850	23	1139	1137	YX	1847	N211JQ	JFK	JAX	123	828	8	50	2023-11-20 08:00:00	Other
23814	5	31	1830	1800	30	1952	1946	9E	1364	N480PX	LGA	ORF	54	296	18	0	2023-05-31 18:00:00	Other
23822	7	6	750	710	40	1020	1011	DL	261	N331NB	LGA	TPA	134	1010	7	10	2023-07-06 07:00:00	Other
23823	7	18	2302	2236	26	11	2359	UA	399	N37263	EWR	BUF	49	282	22	36	2023-07-18 22:00:00	Other
23833	8	2	1326	1255	31	1518	1501	DL	411	N102DU	JFK	DTW	83	509	12	55	2023-08-02 12:00:00	Other
23835	12	30	1253	1150	63	1622	1505	NK	346	N922NK	EWR	FLL	189	1065	11	50	2023-12-30 11:00:00	FLL
23840	5	27	2125	2100	25	11	38	UA	682	N41135	EWR	SFO	320	2565	21	0	2023-05-27 21:00:00	Other
23857	7	31	741	720	21	1005	934	UA	220	N437UA	LGA	DEN	225	1620	7	20	2023-07-31 07:00:00	Other
23864	4	12	1956	1925	31	2226	2242	UA	813	N18112	EWR	LAX	306	2454	19	25	2023-04-12 19:00:00	LAX
23875	8	17	1114	1059	15	1307	1313	UA	362	N37434	EWR	PHX	267	2133	10	59	2023-08-17 10:00:00	Other
23893	7	10	1220	1149	31	1443	1434	UA	635	N14237	EWR	SAN	301	2425	11	49	2023-07-10 11:00:00	Other
23895	9	19	1928	1841	47	2112	2030	UA	805	N37420	EWR	RDU	72	416	18	41	2023-09-19 18:00:00	Other
23898	10	8	1541	1525	16	1817	1804	9E	1601	N921XJ	LGA	JAX	132	833	15	25	2023-10-08 15:00:00	Other
23904	11	28	2045	2005	40	2328	2308	NK	265	N655NK	EWR	IAH	193	1400	20	5	2023-11-28 20:00:00	Other
23907	3	24	1830	1237	353	2128	1551	AA	713	N411AN	JFK	MIA	152	1089	12	37	2023-03-24 12:00:00	MIA
23911	8	14	2225	2210	15	41	33	NK	226	N976NK	EWR	LAS	294	2227	22	10	2023-08-14 22:00:00	Other
23921	12	17	2254	2010	164	8	2141	B6	870	N358JB	JFK	DCA	46	213	20	10	2023-12-17 20:00:00	Other
23923	3	10	1939	1815	84	2043	1937	B6	461	N354JB	LGA	BOS	34	184	18	15	2023-03-10 18:00:00	BOS
23927	8	11	1540	1525	15	1729	1734	YX	847	N739YX	EWR	GSP	86	594	15	25	2023-08-11 15:00:00	Other
23933	5	12	2115	2036	39	9	2247	YX	1044	N731YX	EWR	GSP	88	594	20	36	2023-05-12 20:00:00	Other
23938	9	25	932	915	17	1129	1058	DL	490	N127DU	LGA	ORD	111	733	9	15	2023-09-25 09:00:00	ORD
23939	10	6	1328	1259	29	1453	1422	YX	1799	N246JQ	LGA	BOS	34	184	12	59	2023-10-06 12:00:00	BOS
23940	2	17	1946	1850	56	2112	2011	B6	910	N339JB	EWR	BOS	38	200	18	50	2023-02-17 18:00:00	BOS
23944	7	18	1728	1713	15	2008	2003	UA	659	N76533	EWR	MCO	125	937	17	13	2023-07-18 17:00:00	MCO
23947	2	22	1846	1800	46	2106	1942	UA	905	N818UA	LGA	ORD	130	733	18	0	2023-02-22 18:00:00	ORD
23952	1	13	1423	1259	84	1605	1500	DL	454	N928AT	EWR	DTW	82	488	12	59	2023-01-13 12:00:00	Other
23955	4	4	1640	1629	11	1800	1759	YX	967	N739YX	EWR	PIT	55	319	16	29	2023-04-04 16:00:00	Other
23956	4	1	1855	1740	75	2308	2105	NK	31	N943NK	EWR	LAX	326	2454	17	40	2023-04-01 17:00:00	LAX
23970	4	16	1	2245	76	103	4	B6	6	N323JB	JFK	SYR	41	209	22	45	2023-04-16 22:00:00	Other
23976	6	12	1223	1211	12	1349	1357	9E	1499	N337PQ	LGA	PIT	55	335	12	11	2023-06-12 12:00:00	Other
23981	4	23	936	900	36	1216	1153	UA	470	N47282	EWR	MCO	130	937	9	0	2023-04-23 09:00:00	MCO
23983	4	18	1315	1300	15	1410	1421	YX	1539	N219YX	LGA	BOS	38	184	13	0	2023-04-18 13:00:00	BOS
24003	3	14	847	815	32	1154	1122	AA	575	N965AN	LGA	DFW	197	1389	8	15	2023-03-14 08:00:00	Other
24020	3	31	2039	1948	51	2328	2302	UA	421	N27253	EWR	FLL	138	1065	19	48	2023-03-31 19:00:00	FLL
24027	7	16	2041	1940	61	3	2253	UA	434	N27519	EWR	MIA	148	1085	19	40	2023-07-16 19:00:00	MIA
24038	4	7	834	820	14	1212	1139	UA	454	N225UA	EWR	SFO	354	2565	8	20	2023-04-07 08:00:00	Other
24040	8	29	2315	2250	25	137	115	F9	451	N233FR	LGA	ATL	119	762	22	50	2023-08-29 22:00:00	ATL
24052	11	14	1257	1230	27	1554	1553	AA	433	N929NN	LGA	DFW	190	1389	12	30	2023-11-14 12:00:00	Other
24054	9	9	803	1540	983	1058	1853	OO	1860	N166SY	LGA	IAH	203	1416	15	40	2023-09-09 15:00:00	Other
24055	6	30	2020	1928	52	2300	2220	UA	568	N37534	EWR	SAN	315	2425	19	28	2023-06-30 19:00:00	Other
24056	11	3	1856	1759	57	2143	2106	AA	197	N887NN	LGA	DFW	192	1389	17	59	2023-11-03 17:00:00	Other
24064	3	11	1821	1725	56	2126	2037	B6	719	N907JB	JFK	PBI	138	1028	17	25	2023-03-11 17:00:00	Other
24083	10	4	1016	929	47	1148	1121	UA	366	N422UA	EWR	CMH	65	463	9	29	2023-10-04 09:00:00	Other
24098	12	30	1616	1600	16	1957	1908	B6	658	N633JB	EWR	RSW	194	1068	16	0	2023-12-30 16:00:00	Other
24101	7	2	2114	2030	44	2227	2214	DL	370	N116DU	LGA	ORD	114	733	20	30	2023-07-02 20:00:00	ORD
24111	2	1	1540	1515	25	1849	1840	UA	638	N2138U	EWR	SFO	343	2565	15	15	2023-02-01 15:00:00	Other
24113	6	25	1853	1729	84	2123	2024	DL	601	N3735D	JFK	ATL	110	760	17	29	2023-06-25 17:00:00	ATL
24114	8	9	1510	1455	15	1744	1805	B6	249	N618JB	LGA	PBI	127	1035	14	55	2023-08-09 14:00:00	Other
24122	12	2	1007	2120	767	1142	2239	9E	1479	N305PQ	JFK	ITH	44	189	21	20	2023-12-02 21:00:00	Other
24125	10	1	2125	2000	85	2236	2123	AA	517	N708UW	LGA	DCA	37	214	20	0	2023-10-01 20:00:00	Other
24138	6	30	1637	1529	68	1752	1704	UA	715	N815UA	EWR	ORD	108	719	15	29	2023-06-30 15:00:00	ORD
24142	6	25	2111	1608	303	2240	1750	AA	551	N880NN	LGA	ORD	105	733	16	8	2023-06-25 16:00:00	ORD
24152	7	14	845	751	54	1143	1014	UA	208	N17272	EWR	LAS	296	2227	7	51	2023-07-14 07:00:00	Other
24154	6	12	2143	1815	208	59	2124	AA	776	N860NN	LGA	MIA	161	1096	18	15	2023-06-12 18:00:00	MIA
24171	4	21	1310	1217	53	1511	1433	DL	844	N397DA	EWR	ATL	101	746	12	17	2023-04-21 12:00:00	ATL
24173	7	3	924	855	29	1126	1106	9E	1310	N336PQ	LGA	TVC	87	655	8	55	2023-07-03 08:00:00	Other
24174	6	15	2016	1958	18	2249	2244	DL	166	N383DZ	JFK	DEN	219	1626	19	58	2023-06-15 19:00:00	Other
24179	6	28	1149	1119	30	1424	1424	DL	948	N327DN	LGA	FLL	134	1076	11	19	2023-06-28 11:00:00	FLL
24183	12	3	1720	1659	21	1839	1821	YX	1138	N753YX	EWR	BTV	46	266	16	59	2023-12-03 16:00:00	Other
24185	5	20	2300	2159	61	51	2344	B6	517	N324JB	JFK	RDU	68	427	21	59	2023-05-20 21:00:00	Other
24189	10	30	1339	1327	12	1626	1639	NK	1013	N627NK	EWR	MIA	154	1085	13	27	2023-10-30 13:00:00	MIA
24202	7	10	1259	1247	12	1505	1500	UA	720	N13248	EWR	DEN	217	1605	12	47	2023-07-10 12:00:00	Other
24204	7	18	1522	1430	52	1914	1735	B6	217	N967JT	JFK	LAX	345	2475	14	30	2023-07-18 14:00:00	LAX
24229	5	4	1214	1159	15	1408	1401	UA	534	N37534	EWR	OMA	148	1134	11	59	2023-05-04 11:00:00	Other
24243	4	17	1630	1607	23	1744	1731	YX	1039	N747YX	EWR	PWM	46	284	16	7	2023-04-17 16:00:00	Other
24249	8	7	1720	1649	31	2107	2028	DL	143	N514DE	JFK	SEA	359	2422	16	49	2023-08-07 16:00:00	Other
24254	11	30	917	800	77	1052	922	9E	1552	N326PQ	JFK	BWI	46	184	8	0	2023-11-30 08:00:00	Other
24259	5	13	2009	1957	12	2110	2120	UA	882	N14704	EWR	IAD	42	212	19	57	2023-05-13 19:00:00	Other
24260	1	8	2057	2020	37	2336	2304	DL	299	N856DN	JFK	ATL	113	760	20	20	2023-01-08 20:00:00	ATL
24265	9	26	1849	1830	19	2017	2004	YX	1798	N216JQ	LGA	DCA	44	214	18	30	2023-09-26 18:00:00	Other
24273	8	8	1635	1553	42	1948	1924	DL	461	N359DN	LGA	FLL	155	1076	15	53	2023-08-08 15:00:00	FLL
24274	12	10	1436	1420	16	1745	1723	UA	571	N17321	EWR	IAH	214	1400	14	20	2023-12-10 14:00:00	Other
24278	10	26	2114	2029	45	2246	2232	YX	1363	N429YX	LGA	ILM	73	500	20	29	2023-10-26 20:00:00	Other
24280	8	4	1736	1700	36	2038	2011	B6	611	N621JB	JFK	PBI	143	1028	17	0	2023-08-04 17:00:00	Other
24292	12	2	1406	1336	30	1626	1550	9E	1541	N186PQ	JFK	CVG	107	589	13	36	2023-12-02 13:00:00	Other
24296	12	28	1536	1500	36	1741	1621	B6	463	N273JB	JFK	BOS	40	187	15	0	2023-12-28 15:00:00	BOS
24299	4	10	1534	1515	19	1833	1808	UA	546	N77543	EWR	TPA	135	997	15	15	2023-04-10 15:00:00	Other
24300	8	24	1848	1834	14	2037	2014	YX	851	N642RW	EWR	ORF	58	284	18	34	2023-08-24 18:00:00	Other
24310	12	24	1138	915	143	1423	1218	UA	477	N68822	EWR	MCO	125	937	9	15	2023-12-24 09:00:00	MCO
24319	2	3	1912	1845	27	2225	2147	UA	872	N14019	EWR	LAX	317	2454	18	45	2023-02-03 18:00:00	LAX
24325	10	11	1834	1807	27	2147	2057	UA	338	N846UA	EWR	DFW	216	1372	18	7	2023-10-11 18:00:00	Other
24328	7	7	1609	1555	14	1844	1836	DL	229	N870DN	JFK	DEN	221	1626	15	55	2023-07-07 15:00:00	Other
24332	1	14	1648	1450	118	1827	1649	NK	575	N616NK	LGA	MYR	81	563	14	50	2023-01-14 14:00:00	Other
24336	1	12	2320	2147	93	125	2359	UA	630	N24736	EWR	CHS	99	628	21	47	2023-01-12 21:00:00	Other
24341	4	5	2232	2130	62	36	14	DL	467	N816DN	JFK	ATL	104	760	21	30	2023-04-05 21:00:00	ATL
24342	12	15	1600	1543	17	1834	1849	DL	772	N368DN	JFK	MCO	126	944	15	43	2023-12-15 15:00:00	MCO
24369	1	3	945	915	30	1209	1154	YX	1782	N218JQ	LGA	SDF	115	659	9	15	2023-01-03 09:00:00	Other
24372	1	31	1008	955	13	1301	1258	UA	559	N17272	EWR	PBI	141	1023	9	55	2023-01-31 09:00:00	Other
24377	1	2	1127	1049	38	1415	1325	UA	482	N24702	EWR	ATL	109	746	10	49	2023-01-02 10:00:00	ATL
24381	7	25	2353	2030	203	110	2200	B6	66	N238JB	JFK	BTV	49	266	20	30	2023-07-25 20:00:00	Other
24383	3	15	1947	1815	92	2110	2017	YX	1667	N204JQ	LGA	STL	121	888	18	15	2023-03-15 18:00:00	Other
24401	2	15	1745	1725	20	2111	2046	B6	747	N599JB	JFK	MIA	156	1089	17	25	2023-02-15 17:00:00	MIA
24405	7	4	1930	1559	211	2116	1813	UA	758	N47291	EWR	PHX	261	2133	15	59	2023-07-04 15:00:00	Other
24414	9	1	1848	1615	153	2044	1840	DL	393	N127DU	LGA	CHS	90	641	16	15	2023-09-01 16:00:00	Other
24417	11	7	1511	1458	13	1631	1628	YX	1088	N766YX	EWR	ORF	51	284	14	58	2023-11-07 14:00:00	Other
24419	7	4	616	600	16	804	814	AA	218	N507AY	LGA	CLT	79	544	6	0	2023-07-04 06:00:00	CLT
24421	8	16	1930	1759	91	2211	2044	B6	233	N970JB	JFK	LAS	281	2248	17	59	2023-08-16 17:00:00	Other
24422	4	2	733	710	23	1106	1105	UA	528	N39728	EWR	STT	198	1634	7	10	2023-04-02 07:00:00	Other
24424	7	15	1919	1845	34	NA	2132	DL	103	N930DZ	JFK	PHX	NA	2153	18	45	2023-07-15 18:00:00	Other
24436	2	15	725	700	25	844	822	YX	1485	N235JQ	LGA	BOS	39	184	7	0	2023-02-15 07:00:00	BOS
24438	2	24	834	817	17	1348	1311	UA	764	N78060	EWR	SJU	188	1608	8	17	2023-02-24 08:00:00	Other
24460	9	19	955	935	20	1104	1051	B6	608	N228JB	JFK	BTV	45	266	9	35	2023-09-19 09:00:00	Other
24463	4	4	2240	2159	41	52	2359	UA	571	N57286	EWR	MSP	153	1008	21	59	2023-04-04 21:00:00	Other
24470	5	21	1537	1523	14	1656	1657	YX	1052	N736YX	EWR	BGR	58	393	15	23	2023-05-21 15:00:00	Other
24471	6	15	2044	1913	91	2345	2208	UA	663	N17557	EWR	MCO	147	937	19	13	2023-06-15 19:00:00	MCO
24478	10	2	943	929	14	1156	1154	YX	1040	N979RP	EWR	HHH	98	687	9	29	2023-10-02 09:00:00	Other
24491	6	6	1617	1529	48	1920	1835	UA	569	N498UA	EWR	FLL	144	1065	15	29	2023-06-06 15:00:00	FLL
24493	10	23	1221	1205	16	1429	1425	WN	590	N925WN	LGA	DEN	223	1620	12	5	2023-10-23 12:00:00	Other
24495	8	20	2126	2110	16	2350	2354	B6	159	N618JB	LGA	MCO	115	950	21	10	2023-08-20 21:00:00	MCO
24496	8	20	2353	2025	208	220	2321	B6	531	N535JB	LGA	PBI	124	1035	20	25	2023-08-20 20:00:00	Other
24500	10	7	918	2230	648	1030	2356	9E	1608	N906XJ	JFK	PWM	52	273	22	30	2023-10-07 22:00:00	Other
24504	10	25	1319	1300	19	1612	1607	B6	561	N585JB	JFK	FLL	148	1069	13	0	2023-10-25 13:00:00	FLL
24514	3	13	2052	1929	83	5	2245	UA	394	N77258	EWR	SAN	316	2425	19	29	2023-03-13 19:00:00	Other
24517	5	8	2035	2015	20	2157	2134	B6	540	N355JB	LGA	BOS	34	184	20	15	2023-05-08 20:00:00	BOS
24519	10	20	948	929	19	1120	1114	AA	604	N834AW	LGA	STL	124	888	9	29	2023-10-20 09:00:00	Other
24524	8	12	2146	2131	15	7	2339	UA	505	N76265	EWR	MCI	161	1092	21	31	2023-08-12 21:00:00	Other
24541	3	11	1402	1240	82	1704	1550	B6	253	N592JB	JFK	PBI	143	1028	12	40	2023-03-11 12:00:00	Other
24542	11	9	1625	1600	25	1751	1740	WN	1143	N8647A	LGA	BNA	120	764	16	0	2023-11-09 16:00:00	Other
24543	4	14	1859	1800	59	2001	1925	AA	447	N776XF	LGA	DCA	41	214	18	0	2023-04-14 18:00:00	Other
24547	8	7	1741	1729	12	2045	2043	AA	126	N314RH	JFK	MIA	149	1089	17	29	2023-08-07 17:00:00	MIA
24548	9	24	921	855	26	1053	1056	YX	1895	N240JQ	LGA	RDU	65	431	8	55	2023-09-24 08:00:00	Other
24553	3	9	1116	1040	36	1340	1315	WN	395	N7727A	LGA	ATL	113	762	10	40	2023-03-09 10:00:00	ATL
24556	2	16	2303	1930	213	117	2128	AA	127	N933NN	LGA	ORD	160	733	19	30	2023-02-16 19:00:00	ORD
24558	3	15	1514	1413	61	1659	1550	YX	1627	N227JQ	LGA	PIT	58	335	14	13	2023-03-15 14:00:00	Other
24563	4	21	2024	1959	25	2326	2252	NK	178	N657NK	LGA	MCO	135	950	19	59	2023-04-21 19:00:00	MCO
24567	7	14	2210	1932	158	142	2250	AA	88	N116AN	JFK	LAX	338	2475	19	32	2023-07-14 19:00:00	LAX
24569	11	20	1343	1316	27	1537	1529	AA	736	N757UW	LGA	CLT	89	544	13	16	2023-11-20 13:00:00	CLT
24572	1	8	2318	2259	19	404	348	B6	371	N656JB	JFK	BQN	198	1576	22	59	2023-01-08 22:00:00	Other
24577	2	19	1627	1527	60	1755	1712	UA	657	N16709	EWR	CLE	65	404	15	27	2023-02-19 15:00:00	Other
24579	7	5	2022	1939	43	2158	2111	UA	740	N13718	EWR	IAD	41	212	19	39	2023-07-05 19:00:00	Other
24584	6	22	2219	2041	98	32	2256	UA	924	N25705	EWR	MSY	155	1167	20	41	2023-06-22 20:00:00	Other
24591	11	22	1119	1051	28	1416	1329	F9	1032	N367FR	LGA	ATL	123	762	10	51	2023-11-22 10:00:00	ATL
24596	3	31	717	620	57	1053	1000	DL	325	N358DN	JFK	SLC	295	1990	6	20	2023-03-31 06:00:00	Other
24599	10	23	1207	1135	32	1348	1328	OO	1203	N306SY	JFK	ORD	121	740	11	35	2023-10-23 11:00:00	ORD
24615	2	16	2027	2000	27	2302	2311	B6	889	N959JB	JFK	MCO	137	944	20	0	2023-02-16 20:00:00	MCO
24618	2	3	949	930	19	1155	1133	YX	1252	N438YX	LGA	CLE	79	419	9	30	2023-02-03 09:00:00	Other
24621	11	22	2131	2044	47	18	2358	B6	526	N592JB	JFK	FLL	139	1069	20	44	2023-11-22 20:00:00	FLL
24627	1	26	1617	1250	207	2021	1559	B6	42	N558JB	JFK	TPA	179	1005	12	50	2023-01-26 12:00:00	Other
24633	4	28	900	845	15	1056	1041	YX	1237	N867RW	LGA	ILM	83	500	8	45	2023-04-28 08:00:00	Other
24639	9	11	1425	1401	24	1545	1523	YX	1116	N746YX	EWR	PWM	44	284	14	1	2023-09-11 14:00:00	Other
24640	6	2	2303	2230	33	235	203	B6	972	N945JT	JFK	SFO	323	2586	22	30	2023-06-02 22:00:00	Other
24641	3	10	1724	1710	14	1829	1823	UA	731	N17285	EWR	BOS	34	200	17	10	2023-03-10 17:00:00	BOS
24647	5	1	1308	1125	103	1552	1436	DL	447	N3754A	JFK	TPA	145	1005	11	25	2023-05-01 11:00:00	Other
24652	5	27	1952	1935	17	2217	2245	B6	26	N760JB	JFK	ABQ	234	1826	19	35	2023-05-27 19:00:00	Other
24663	8	5	1316	1259	17	1454	1458	NK	401	N655NK	LGA	MYR	81	563	12	59	2023-08-05 12:00:00	Other
24666	4	26	914	900	14	1036	1020	DL	823	N113DQ	LGA	BOS	36	184	9	0	2023-04-26 09:00:00	BOS
24673	1	6	2123	2043	40	2230	2202	UA	344	N69833	EWR	BOS	34	200	20	43	2023-01-06 20:00:00	BOS
24686	6	16	2215	2130	45	52	9	B6	188	N706JB	LGA	MCO	131	950	21	30	2023-06-16 21:00:00	MCO
24687	5	24	1805	1615	110	2033	1901	AA	591	N342SX	JFK	PHX	285	2153	16	15	2023-05-24 16:00:00	Other
24688	3	2	1744	1729	15	2200	2053	AA	974	N310RF	JFK	AUS	293	1521	17	29	2023-03-02 17:00:00	Other
24689	7	20	2100	2016	44	2316	2248	B6	38	N997JL	JFK	PHX	271	2153	20	16	2023-07-20 20:00:00	Other
24692	5	27	936	914	22	1219	1206	UA	501	N17265	EWR	MCO	134	937	9	14	2023-05-27 09:00:00	MCO
24694	7	23	2009	1842	87	2152	2020	AA	750	N925AN	LGA	ORD	124	733	18	42	2023-07-23 18:00:00	ORD
24698	4	16	2059	1929	90	2233	2112	OO	1061	N254SY	JFK	BNA	117	765	19	29	2023-04-16 19:00:00	Other
24699	1	11	1503	1255	128	1648	1455	WN	365	N212WN	LGA	STL	136	888	12	55	2023-01-11 12:00:00	Other
24707	3	15	1047	950	57	1244	1211	9E	1506	N295PQ	JFK	IND	95	665	9	50	2023-03-15 09:00:00	Other
24726	9	14	930	805	85	1053	927	AA	757	N826AW	LGA	DCA	49	214	8	5	2023-09-14 08:00:00	Other
24734	6	14	2141	2059	42	13	22	B6	31	N942JB	JFK	SAN	315	2446	20	59	2023-06-14 20:00:00	Other
24738	3	21	2113	2059	14	2308	2304	UA	677	N890UA	EWR	CLT	79	529	20	59	2023-03-21 20:00:00	CLT
24740	6	7	1639	1559	40	1908	1827	UA	500	N4901U	EWR	JAX	120	820	15	59	2023-06-07 15:00:00	Other
24746	3	10	1829	1800	29	2016	1942	UA	937	N841UA	LGA	ORD	118	733	18	0	2023-03-10 18:00:00	ORD
24754	1	18	2328	2230	58	31	2354	9E	1551	N294PQ	JFK	SYR	43	209	22	30	2023-01-18 22:00:00	Other
24757	3	15	1112	939	93	1259	1159	9E	1488	N304PQ	EWR	CVG	88	569	9	39	2023-03-15 09:00:00	Other
24761	9	13	2301	2159	62	14	2326	YX	1808	N237JQ	LGA	BGR	53	378	21	59	2023-09-13 21:00:00	Other
24766	2	19	2148	1809	219	35	2110	B6	292	N966JT	JFK	LAS	319	2248	18	9	2023-02-19 18:00:00	Other
24770	10	10	1404	1329	35	1750	1726	B6	277	N534JB	JFK	SJU	193	1598	13	29	2023-10-10 13:00:00	Other
24773	4	9	2121	2059	22	2316	2318	YX	1030	N650RW	EWR	IND	89	645	20	59	2023-04-09 20:00:00	Other
24776	8	31	1431	1359	32	1546	1530	B6	221	N3044J	JFK	MKE	112	745	13	59	2023-08-31 13:00:00	Other
24783	3	2	1538	1515	23	1705	1632	B6	158	N267JB	LGA	BOS	39	184	15	15	2023-03-02 15:00:00	BOS
24800	8	28	847	816	31	1123	1107	UA	563	N76514	EWR	BZN	252	1882	8	16	2023-08-28 08:00:00	Other
24805	3	22	920	908	12	1031	1025	B6	965	N358JB	JFK	BOS	35	187	9	8	2023-03-22 09:00:00	BOS
24814	12	25	2107	2050	17	2312	2321	UA	853	N27263	EWR	MSY	165	1167	20	50	2023-12-25 20:00:00	Other
24835	10	29	2136	1929	127	22	2203	9E	1457	N330PQ	JFK	MCI	190	1113	19	29	2023-10-29 19:00:00	Other
24838	3	14	1312	1216	56	1638	1527	NK	351	N682NK	LGA	DFW	186	1389	12	16	2023-03-14 12:00:00	Other
24840	9	17	1949	1935	14	2123	2113	OO	1276	N296SY	JFK	IAD	52	228	19	35	2023-09-17 19:00:00	Other
24841	10	5	2032	2010	22	2230	2230	UA	854	N77572	EWR	DEN	215	1605	20	10	2023-10-05 20:00:00	Other
24848	6	11	807	745	22	1007	946	UA	930	N67827	EWR	MSY	152	1167	7	45	2023-06-11 07:00:00	Other
24852	7	16	1345	1329	16	1601	1509	YX	1062	N410YX	JFK	PIT	67	340	13	29	2023-07-16 13:00:00	Other
24857	7	5	2122	2015	67	2314	2142	YX	855	N756YX	EWR	BTV	49	266	20	15	2023-07-05 20:00:00	Other
24862	6	12	1442	1324	78	1709	1557	AA	1021	N335RT	JFK	PHX	299	2153	13	24	2023-06-12 13:00:00	Other
24874	4	17	1649	940	429	1948	1239	B6	421	N657JB	JFK	TPA	152	1005	9	40	2023-04-17 09:00:00	Other
24875	7	3	2212	2100	72	2358	2230	UA	104	N27734	EWR	BNA	109	748	21	0	2023-07-03 21:00:00	Other
24887	5	29	1848	1659	109	1947	1821	UA	458	N456UA	EWR	BOS	36	200	16	59	2023-05-29 16:00:00	BOS
24892	9	5	1605	1524	41	1835	1812	UA	547	N27277	EWR	MCO	122	937	15	24	2023-09-05 15:00:00	MCO
24897	10	1	1822	1759	23	2052	2050	UA	630	N37561	EWR	IAH	183	1400	17	59	2023-10-01 17:00:00	Other
24900	3	17	2142	2045	57	102	2351	NK	278	N530NK	EWR	IAH	223	1400	20	45	2023-03-17 20:00:00	Other
24903	7	8	1133	1110	23	1407	1347	DL	306	N509DT	JFK	LAS	301	2248	11	10	2023-07-08 11:00:00	Other
24907	4	14	1557	1529	28	1855	1837	B6	668	N179JB	LGA	PBI	155	1035	15	29	2023-04-14 15:00:00	Other
24910	3	25	1548	1339	129	1731	1532	9E	1425	N910XJ	LGA	RDU	74	431	13	39	2023-03-25 13:00:00	Other
24918	1	20	1221	1200	21	1524	1530	UA	873	N17126	EWR	SFO	347	2565	12	0	2023-01-20 12:00:00	Other
24922	7	23	2159	2030	89	2355	2247	UA	723	N37278	EWR	MSY	148	1167	20	30	2023-07-23 20:00:00	Other
24923	6	27	733	537	116	1151	933	B6	618	N949JT	JFK	SJU	227	1598	5	37	2023-06-27 05:00:00	Other
24924	1	6	1256	1235	21	1553	1606	AA	223	N966NN	LGA	DFW	210	1389	12	35	2023-01-06 12:00:00	Other
24935	11	28	1150	1129	21	1410	1335	AA	177	N952AA	JFK	CLT	99	541	11	29	2023-11-28 11:00:00	CLT
24938	4	29	1234	1220	14	1443	1422	YX	1074	N412YX	JFK	CMH	83	483	12	20	2023-04-29 12:00:00	Other
24939	6	10	2125	2059	26	2241	2229	UA	770	N29717	EWR	BNA	105	748	20	59	2023-06-10 20:00:00	Other
24957	8	30	1913	1900	13	2136	2121	YX	1028	N133HQ	LGA	XNA	167	1147	19	0	2023-08-30 19:00:00	Other
24959	6	7	1642	1628	14	1810	1755	UA	790	N457UA	EWR	IAD	48	212	16	28	2023-06-07 16:00:00	Other
24960	4	2	1119	500	379	1420	806	AA	210	N951NN	EWR	DFW	216	1372	5	0	2023-04-02 05:00:00	Other
24967	4	4	1113	1050	23	1246	1236	AA	904	N804AW	LGA	STL	131	888	10	50	2023-04-04 10:00:00	Other
24971	6	26	1353	1330	23	1707	1647	B6	135	N651JB	LGA	FLL	154	1076	13	30	2023-06-26 13:00:00	FLL
25000	7	16	2217	1950	147	37	2246	DL	221	N125DU	LGA	DFW	184	1389	19	50	2023-07-16 19:00:00	Other
25015	6	3	1839	1825	14	2116	2111	DL	866	N102DU	JFK	JAX	119	828	18	25	2023-06-03 18:00:00	Other
25016	6	2	1916	1845	31	2118	2023	AA	959	N901NN	LGA	ORD	109	733	18	45	2023-06-02 18:00:00	ORD
25043	2	25	1018	929	49	1325	1245	NK	970	N664NK	LGA	MIA	149	1096	9	29	2023-02-25 09:00:00	MIA
25052	4	4	1851	1735	76	2111	2009	B6	157	N584JB	JFK	ATL	107	760	17	35	2023-04-04 17:00:00	ATL
25053	5	19	1809	1515	174	2112	1817	UA	911	N455UA	EWR	SRQ	152	1034	15	15	2023-05-19 15:00:00	Other
25058	12	1	2025	2000	25	2336	2310	WN	990	N7852A	LGA	DAL	220	1381	20	0	2023-12-01 20:00:00	Other
25060	11	6	1811	1759	12	2254	2253	DL	665	N891DN	JFK	SJU	200	1598	17	59	2023-11-06 17:00:00	Other
25061	6	2	1402	1346	16	1626	1640	UA	284	N889UA	LGA	IAH	179	1416	13	46	2023-06-02 13:00:00	Other
25077	10	14	1103	1040	23	1356	1345	WN	1011	N8689C	LGA	TPA	148	1010	10	40	2023-10-14 10:00:00	Other
25079	4	23	1654	1629	25	1810	1755	UA	667	N823UA	EWR	IAD	49	212	16	29	2023-04-23 16:00:00	Other
25084	6	14	1608	1550	18	1752	1747	9E	1516	N303PQ	LGA	STL	123	888	15	50	2023-06-14 15:00:00	Other
25088	10	5	1042	659	223	1159	835	AA	992	N949AN	EWR	ORD	103	719	6	59	2023-10-05 06:00:00	ORD
25093	8	5	1021	945	36	1133	1115	9E	1177	N602LR	JFK	DCA	47	213	9	45	2023-08-05 09:00:00	Other
25100	5	21	1718	1629	49	1851	1831	YX	1300	N127HQ	JFK	CMH	73	483	16	29	2023-05-21 16:00:00	Other
25105	9	25	1816	1747	29	1950	1918	YX	1073	N740YX	EWR	BUF	48	282	17	47	2023-09-25 17:00:00	Other
25106	3	10	1913	1849	24	2203	2159	B6	83	N2043J	JFK	MCO	143	944	18	49	2023-03-10 18:00:00	MCO
25116	7	14	842	820	22	1005	947	YX	1087	N133HQ	LGA	BUF	57	292	8	20	2023-07-14 08:00:00	Other
25139	5	7	2255	2150	65	2334	2246	YX	1700	N214JQ	LGA	BDL	26	101	21	50	2023-05-07 21:00:00	Other
25141	2	27	1009	850	79	1210	1119	9E	1366	N298PQ	LGA	CHS	90	641	8	50	2023-02-27 08:00:00	Other
25146	5	2	914	856	18	1213	1211	UA	607	N429UA	EWR	SAT	215	1569	8	56	2023-05-02 08:00:00	Other
25151	7	13	1721	1455	146	1913	1706	9E	1162	N915XJ	LGA	GSP	90	610	14	55	2023-07-13 14:00:00	Other
25160	8	24	1231	1200	31	1451	1443	UA	660	N221UA	EWR	LAX	289	2454	12	0	2023-08-24 12:00:00	LAX
25163	7	22	1845	1830	15	2141	2147	AA	165	N960AN	JFK	MIA	146	1089	18	30	2023-07-22 18:00:00	MIA
25170	11	16	1527	1510	17	1831	1828	DL	540	N341DN	LGA	FLL	152	1076	15	10	2023-11-16 15:00:00	FLL
25174	1	9	838	810	28	1053	1109	B6	859	N592JB	JFK	LAS	298	2248	8	10	2023-01-09 08:00:00	Other
25175	5	26	1503	1452	11	1629	1620	YX	1048	N729YX	EWR	RIC	56	277	14	52	2023-05-26 14:00:00	Other
25176	8	5	2141	2056	45	2326	2302	YX	932	N650RW	EWR	CMH	75	463	20	56	2023-08-05 20:00:00	Other
25185	3	4	1030	1000	30	1648	1605	HA	22	N382HA	JFK	HNL	641	4983	10	0	2023-03-04 10:00:00	Other
25186	6	17	1023	945	38	1325	1242	NK	890	N607NK	EWR	AUS	208	1504	9	45	2023-06-17 09:00:00	Other
25195	2	24	1700	1610	50	1951	1916	B6	750	N625JB	LGA	MCO	145	950	16	10	2023-02-24 16:00:00	MCO
25199	9	8	624	608	16	816	755	DL	780	N923AT	EWR	DTW	76	488	6	8	2023-09-08 06:00:00	Other
25203	4	4	1528	1457	31	1752	1716	DL	410	N317NB	JFK	MSP	165	1029	14	57	2023-04-04 14:00:00	Other
25206	1	10	2108	1959	69	28	2336	AS	91	N931AK	EWR	SFO	356	2565	19	59	2023-01-10 19:00:00	Other
25212	5	11	1702	1615	47	1810	1735	B6	362	N216JB	LGA	BOS	47	184	16	15	2023-05-11 16:00:00	BOS
25220	9	18	1843	1824	19	2255	2137	AA	169	N922AN	JFK	MIA	161	1089	18	24	2023-09-18 18:00:00	MIA
25224	12	22	2127	2040	47	14	2340	B6	327	N585JB	EWR	MCO	131	937	20	40	2023-12-22 20:00:00	MCO
25225	6	12	650	603	47	759	735	UA	758	N78509	EWR	ORD	106	719	6	3	2023-06-12 06:00:00	ORD
25227	4	3	1936	1435	301	2233	1750	UA	79	N225UA	EWR	SFO	333	2565	14	35	2023-04-03 14:00:00	Other
25233	1	25	1512	1259	133	1646	1427	9E	1563	N937XJ	JFK	BUF	59	301	12	59	2023-01-25 12:00:00	Other
25256	11	20	1451	1358	53	1652	1615	9E	1605	N181GJ	LGA	CAE	92	617	13	58	2023-11-20 13:00:00	Other
25265	10	31	2113	2029	44	26	2341	UA	853	N37263	EWR	RSW	158	1068	20	29	2023-10-31 20:00:00	Other
25266	6	6	1552	1529	23	1839	1827	UA	411	N37560	EWR	AUS	201	1504	15	29	2023-06-06 15:00:00	Other
25276	2	11	1507	1445	22	1952	1938	B6	883	N2059J	JFK	BQN	195	1576	14	45	2023-02-11 14:00:00	Other
25280	5	1	1459	1359	60	1706	1633	DL	163	N3763D	JFK	DEN	210	1626	13	59	2023-05-01 13:00:00	Other
25281	3	15	1220	1130	50	1506	1434	DL	1010	N310DN	LGA	MCO	131	950	11	30	2023-03-15 11:00:00	MCO
25300	6	2	1838	1820	18	NA	2139	DL	633	N336NW	JFK	AUS	NA	1521	18	20	2023-06-02 18:00:00	Other
25301	9	30	1200	1145	15	1412	1406	B6	964	N662JB	JFK	ATL	100	760	11	45	2023-09-30 11:00:00	ATL
25312	8	26	1913	1845	28	2048	2030	WN	458	N7836A	LGA	STL	136	888	18	45	2023-08-26 18:00:00	Other
25317	3	14	1712	1640	32	2047	2002	B6	78	N984JB	JFK	SEA	340	2422	16	40	2023-03-14 16:00:00	Other
25322	12	18	2054	1700	234	11	2038	UA	465	N12125	EWR	SFO	348	2565	17	0	2023-12-18 17:00:00	Other
25325	1	6	920	830	50	1219	1207	DL	284	N128DU	JFK	AUS	220	1521	8	30	2023-01-06 08:00:00	Other
25328	11	14	2151	1945	126	2359	2200	9E	1667	N933XJ	EWR	CVG	89	569	19	45	2023-11-14 19:00:00	Other
25330	3	14	1014	919	55	1150	1058	9E	1534	N337PQ	LGA	CHO	50	305	9	19	2023-03-14 09:00:00	Other
25331	4	30	2339	2012	207	131	2221	YX	941	N757YX	EWR	DTW	69	488	20	12	2023-04-30 20:00:00	Other
25333	11	22	1558	1430	88	1903	1738	B6	670	N3077J	JFK	IAH	201	1417	14	30	2023-11-22 14:00:00	Other
25350	12	23	1805	1559	126	2106	1910	B6	965	N948JB	JFK	FLL	154	1069	15	59	2023-12-23 15:00:00	FLL
25351	7	26	1640	1620	20	1915	1900	WN	598	N8824Q	LGA	DAL	176	1381	16	20	2023-07-26 16:00:00	Other
25352	9	29	1153	1129	24	1542	1439	DL	495	N3761R	JFK	MIA	188	1089	11	29	2023-09-29 11:00:00	MIA
25355	9	24	1111	1057	14	1402	1331	F9	553	N309FR	LGA	ATL	100	762	10	57	2023-09-24 10:00:00	ATL
25356	7	11	2102	2016	46	2256	2248	B6	38	N949JT	JFK	PHX	269	2153	20	16	2023-07-11 20:00:00	Other
25382	9	25	1432	1405	27	1538	1526	AA	412	N745VJ	LGA	DCA	45	214	14	5	2023-09-25 14:00:00	Other
25389	7	5	2038	2020	18	2352	2314	B6	578	N942JB	EWR	LAX	337	2454	20	20	2023-07-05 20:00:00	LAX
25390	5	10	1818	1755	23	2029	2025	WN	390	N247WN	LGA	ATL	111	762	17	55	2023-05-10 17:00:00	ATL
25391	1	30	921	906	15	1358	1233	UA	221	N24715	EWR	SNA	NA	2434	9	6	2023-01-30 09:00:00	Other
25392	1	31	1745	1729	16	2044	2046	UA	552	N17279	EWR	FLL	161	1065	17	29	2023-01-31 17:00:00	FLL
25397	1	22	1956	1945	11	2337	2300	DL	673	N304DN	LGA	MIA	172	1096	19	45	2023-01-22 19:00:00	MIA
25403	3	14	2012	1835	97	2142	1957	B6	890	N192JB	JFK	BOS	50	187	18	35	2023-03-14 18:00:00	BOS
25421	12	11	2131	2020	71	2302	2209	OO	1190	N307SY	LGA	MKE	120	738	20	20	2023-12-11 20:00:00	Other
25423	1	9	2043	2015	28	9	2359	AS	18	N953AK	JFK	SFO	356	2586	20	15	2023-01-09 20:00:00	Other
25427	6	10	2254	2225	29	239	222	NK	1058	N641NK	EWR	SJU	202	1608	22	25	2023-06-10 22:00:00	Other
25428	3	27	1647	1613	34	1816	1741	UA	490	N425UA	EWR	BNA	126	748	16	13	2023-03-27 16:00:00	Other
25431	2	14	2035	2000	35	2249	2227	9E	1442	N582CA	LGA	CVG	107	585	20	0	2023-02-14 20:00:00	Other
25435	6	24	1044	1032	12	1224	1223	B6	87	N715JB	JFK	RDU	67	427	10	32	2023-06-24 10:00:00	Other
25443	11	2	1452	1438	14	1627	1612	YX	1817	N239JQ	LGA	PIT	59	335	14	38	2023-11-02 14:00:00	Other
25444	2	28	39	2015	264	136	2131	B6	541	N318JB	LGA	BOS	35	184	20	15	2023-02-28 20:00:00	BOS
25446	4	24	2213	2159	14	2354	2359	UA	673	N27271	EWR	DTW	73	488	21	59	2023-04-24 21:00:00	Other
25448	3	19	1104	1050	14	1249	1301	YX	1119	N740YX	EWR	DTW	85	488	10	50	2023-03-19 10:00:00	Other
25455	4	1	1553	1510	43	1905	1830	B6	774	N190JB	LGA	SRQ	170	1047	15	10	2023-04-01 15:00:00	Other
25461	5	7	1541	1515	26	1753	1751	9E	1556	N695CA	JFK	IND	100	665	15	15	2023-05-07 15:00:00	Other
25464	7	21	1110	1008	62	1423	1317	B6	479	N2039J	JFK	RSW	153	1074	10	8	2023-07-21 10:00:00	Other
25466	9	24	1812	1725	47	2045	1957	B6	935	N516JB	LGA	ATL	103	762	17	25	2023-09-24 17:00:00	ATL
25474	11	14	2150	2000	110	218	59	B6	679	N2027J	JFK	SJU	185	1598	20	0	2023-11-14 20:00:00	Other
25479	9	23	2107	2000	67	2313	2228	UA	279	N48127	EWR	PHX	281	2133	20	0	2023-09-23 20:00:00	Other
25481	1	19	2043	2015	28	133	2359	AS	18	N975AK	JFK	SFO	342	2586	20	15	2023-01-19 20:00:00	Other
25485	10	22	1120	1100	20	1422	1406	B6	298	N613JB	JFK	SLC	271	1990	11	0	2023-10-22 11:00:00	Other
25490	7	15	2350	2258	52	355	258	B6	256	N570JB	JFK	PSE	211	1617	22	58	2023-07-15 22:00:00	Other
25492	4	6	1720	1650	30	1940	1900	9E	1260	N490PX	LGA	DSM	175	1031	16	50	2023-04-06 16:00:00	Other
25495	4	29	941	929	12	1112	1044	B6	859	N190JB	JFK	BOS	35	187	9	29	2023-04-29 09:00:00	BOS
25499	2	21	2011	1915	56	2308	2233	B6	639	N589JB	JFK	FLL	144	1069	19	15	2023-02-21 19:00:00	FLL
25506	8	24	2127	2000	87	2327	2244	B6	345	N907JB	JFK	LAS	273	2248	20	0	2023-08-24 20:00:00	Other
25510	9	2	1439	1412	27	1609	1605	YX	1392	N122HQ	LGA	ILM	71	500	14	12	2023-09-02 14:00:00	Other
25513	12	27	1000	948	12	1134	1129	UA	599	N47281	EWR	CLE	65	404	9	48	2023-12-27 09:00:00	Other
25515	2	10	2005	1929	36	2302	2241	DL	582	N395DN	JFK	TPA	154	1005	19	29	2023-02-10 19:00:00	Other
25529	11	17	1225	1147	38	1513	1457	NK	349	N977NK	EWR	FLL	148	1065	11	47	2023-11-17 11:00:00	FLL
25533	8	3	1906	1830	36	2146	2147	AA	151	N324RA	JFK	MIA	138	1089	18	30	2023-08-03 18:00:00	MIA
25534	6	15	1704	1645	19	1942	1952	UA	649	N2639U	EWR	SFO	314	2565	16	45	2023-06-15 16:00:00	Other
25536	3	19	1536	1514	22	1654	1655	UA	715	N16217	EWR	ORD	111	719	15	14	2023-03-19 15:00:00	ORD
25538	6	25	2140	1730	250	2352	1927	YX	1315	N424YX	LGA	CMH	79	479	17	30	2023-06-25 17:00:00	Other
25544	3	15	632	559	33	937	917	AA	152	N302SA	JFK	MIA	156	1089	5	59	2023-03-15 05:00:00	MIA
25546	7	27	52	2030	262	158	2200	B6	66	N284JB	JFK	BTV	45	266	20	30	2023-07-27 20:00:00	Other
25548	3	2	1544	1529	15	2229	1835	AA	51	N995NN	EWR	DFW	NA	1372	15	29	2023-03-02 15:00:00	Other
25553	11	30	1737	1700	37	1902	1838	YX	1878	N225JQ	LGA	DCA	60	214	17	0	2023-11-30 17:00:00	Other
25559	9	12	1254	1231	23	1420	1413	DL	656	N113DQ	LGA	ORD	111	733	12	31	2023-09-12 12:00:00	ORD
25567	3	14	2004	1725	159	NA	1940	9E	1578	N905XJ	JFK	CVG	NA	589	17	25	2023-03-14 17:00:00	Other
25570	11	24	1632	1530	62	1930	1840	B6	323	N206JB	JFK	MCO	139	944	15	30	2023-11-24 15:00:00	MCO
25572	4	13	1140	1110	30	1243	1225	OO	1054	N301SY	EWR	BOS	45	200	11	10	2023-04-13 11:00:00	BOS
25573	6	10	2019	2000	19	2320	2314	UA	787	N850UA	EWR	SEA	321	2402	20	0	2023-06-10 20:00:00	Other
25576	7	26	2113	2005	68	2302	2215	YX	893	N654RW	EWR	GSP	83	594	20	5	2023-07-26 20:00:00	Other
25585	2	21	1713	1627	46	2106	2002	UA	894	N38458	EWR	PHX	314	2133	16	27	2023-02-21 16:00:00	Other
25601	5	30	2114	2100	14	37	2359	NK	977	N694NK	EWR	MIA	157	1085	21	0	2023-05-30 21:00:00	MIA
25606	6	26	1648	1629	19	2012	1853	DL	888	N339NB	JFK	MSP	139	1029	16	29	2023-06-26 16:00:00	Other
25611	4	28	1304	1145	79	1525	1443	DL	189	N859DN	JFK	LAS	289	2248	11	45	2023-04-28 11:00:00	Other
25619	9	27	1102	1030	32	1335	1328	B6	191	N944JT	JFK	LAX	315	2475	10	30	2023-09-27 10:00:00	LAX
25621	3	10	1107	1030	37	1240	1210	AA	147	N957NN	LGA	ORD	117	733	10	30	2023-03-10 10:00:00	ORD
25637	7	16	1205	1100	65	1531	1357	B6	185	N2105J	JFK	LAX	336	2475	11	0	2023-07-16 11:00:00	LAX
25641	1	22	1503	1430	33	1731	1711	YX	1305	N128HQ	LGA	IND	116	660	14	30	2023-01-22 14:00:00	Other
25642	7	31	1613	1559	14	1818	1813	UA	758	N27276	EWR	PHX	278	2133	15	59	2023-07-31 15:00:00	Other
25646	2	22	2057	1712	225	2236	1850	UA	754	N17245	EWR	ORD	127	719	17	12	2023-02-22 17:00:00	ORD
25647	1	11	935	715	140	1044	827	B6	1066	N193JB	LGA	BOS	37	184	7	15	2023-01-11 07:00:00	BOS
25661	1	8	1029	950	39	1219	1201	AA	950	N185UW	EWR	CLT	89	529	9	50	2023-01-08 09:00:00	CLT
25668	3	12	2032	2000	32	2200	2136	9E	1583	N306PQ	LGA	CHO	59	305	20	0	2023-03-12 20:00:00	Other
25682	4	5	921	815	66	1201	1127	B6	229	N2047J	JFK	FLL	136	1069	8	15	2023-04-05 08:00:00	FLL
25686	8	20	2028	1815	133	2135	1938	B6	354	N284JB	LGA	BOS	42	184	18	15	2023-08-20 18:00:00	BOS
25688	3	13	843	829	14	1204	1158	UA	618	N839UA	EWR	SAT	237	1569	8	29	2023-03-13 08:00:00	Other
25692	7	9	753	730	23	937	908	B6	327	N267JB	JFK	ORD	128	740	7	30	2023-07-09 07:00:00	ORD
25694	11	22	1651	1637	14	1849	1824	9E	1451	N918XJ	LGA	PIT	61	335	16	37	2023-11-22 16:00:00	Other
25703	12	16	1821	1729	52	2102	2027	UA	766	N39418	EWR	MCO	133	937	17	29	2023-12-16 17:00:00	MCO
25707	12	23	1140	924	136	1424	1232	DL	396	N345DN	LGA	MCO	128	950	9	24	2023-12-23 09:00:00	MCO
25708	1	9	1852	1833	19	2033	2017	UA	259	N16732	EWR	CLE	64	404	18	33	2023-01-09 18:00:00	Other
25709	7	26	653	610	43	914	835	WN	842	N8818Q	LGA	DAL	181	1381	6	10	2023-07-26 06:00:00	Other
25720	3	20	1929	1849	40	2225	2159	B6	83	N2047J	JFK	MCO	144	944	18	49	2023-03-20 18:00:00	MCO
25721	1	29	2151	2120	31	25	2359	DL	982	N375NC	LGA	ATL	130	762	21	20	2023-01-29 21:00:00	ATL
25724	8	18	1234	1209	25	1413	1329	YX	995	N427YX	JFK	BOS	41	187	12	9	2023-08-18 12:00:00	BOS
25729	8	14	2142	1959	103	47	2317	DL	456	N320DN	LGA	FLL	159	1076	19	59	2023-08-14 19:00:00	FLL
25732	12	19	847	825	22	1037	1037	YX	1122	N770YX	EWR	GSP	87	594	8	25	2023-12-19 08:00:00	Other
25733	3	15	1058	1042	16	1328	1351	AA	443	N902AN	LGA	DFW	184	1389	10	42	2023-03-15 10:00:00	Other
25737	9	26	925	745	100	1047	918	9E	1464	N907XJ	JFK	BUF	54	301	7	45	2023-09-26 07:00:00	Other
25738	1	26	1113	1055	18	1243	1233	YX	1904	N810MD	LGA	ORF	64	296	10	55	2023-01-26 10:00:00	Other
25740	7	26	1633	1529	64	2001	1852	AA	98	N909NN	JFK	MIA	173	1089	15	29	2023-07-26 15:00:00	MIA
25747	12	3	1945	1924	21	2154	2129	UA	513	N69813	EWR	DTW	86	488	19	24	2023-12-03 19:00:00	Other
25751	7	22	1736	1543	113	2016	1841	UA	331	N77431	EWR	AUS	195	1504	15	43	2023-07-22 15:00:00	Other
25753	6	25	2125	1629	296	2344	1857	UA	745	N467UA	LGA	DEN	227	1620	16	29	2023-06-25 16:00:00	Other
25754	5	28	1740	1717	23	1902	1844	YX	1022	N864RW	EWR	ROC	40	246	17	17	2023-05-28 17:00:00	Other
25761	3	17	905	810	55	1230	1207	B6	927	N2044J	JFK	BQN	185	1576	8	10	2023-03-17 08:00:00	Other
25762	2	13	1020	955	25	1235	1218	9E	1358	N315PQ	JFK	IND	100	665	9	55	2023-02-13 09:00:00	Other
25767	7	20	1737	1559	98	2025	1850	B6	522	N634JB	JFK	JAX	139	828	15	59	2023-07-20 15:00:00	Other
25776	7	6	612	529	43	859	820	B6	37	N961JT	JFK	LAX	327	2475	5	29	2023-07-06 05:00:00	LAX
25783	4	15	1948	1530	258	2241	1835	UA	594	N27722	EWR	MIA	146	1085	15	30	2023-04-15 15:00:00	MIA
25789	12	29	849	838	11	1141	1208	UA	578	N17272	EWR	SAT	207	1569	8	38	2023-12-29 08:00:00	Other
25791	9	21	1606	1542	24	1731	1706	B6	373	N283JB	JFK	BOS	37	187	15	42	2023-09-21 15:00:00	BOS
25792	8	11	1935	1830	65	2042	2008	UA	354	N67845	EWR	ORD	103	719	18	30	2023-08-11 18:00:00	ORD
25800	5	14	1759	1730	29	2020	1954	9E	1384	N935XJ	JFK	MCI	174	1113	17	30	2023-05-14 17:00:00	Other
25807	4	5	2211	2055	76	2353	2247	9E	1438	N296PQ	LGA	RDU	69	431	20	55	2023-04-05 20:00:00	Other
25816	8	10	1415	1038	217	1739	1345	B6	272	N2039J	JFK	SLC	281	1990	10	38	2023-08-10 10:00:00	Other
25819	1	26	1810	1712	58	2127	2021	UA	434	N461UA	EWR	TPA	165	997	17	12	2023-01-26 17:00:00	Other
25822	6	28	1914	1800	74	2132	2035	DL	337	N3759	LGA	DEN	223	1620	18	0	2023-06-28 18:00:00	Other
25824	9	7	2105	1929	96	119	2136	9E	1433	N136EV	JFK	RDU	69	427	19	29	2023-09-07 19:00:00	Other
25827	5	23	1031	905	86	1318	1156	B6	378	N809JB	JFK	MCO	135	944	9	5	2023-05-23 09:00:00	MCO
25838	5	28	1114	1100	14	1401	1438	DL	94	N718TW	JFK	SFO	320	2586	11	0	2023-05-28 11:00:00	Other
25842	2	21	2212	2159	13	2309	2310	DL	793	N133DU	LGA	SYR	39	198	21	59	2023-02-21 21:00:00	Other
25843	1	20	1622	1259	203	1750	1427	9E	1563	N228PQ	JFK	BUF	58	301	12	59	2023-01-20 12:00:00	Other
25850	12	27	1044	1015	29	1328	1326	B6	639	N988JT	EWR	LAX	305	2454	10	15	2023-12-27 10:00:00	LAX
25852	2	11	832	730	62	1205	1052	AA	887	N341SV	JFK	MIA	176	1089	7	30	2023-02-11 07:00:00	MIA
25864	5	4	1934	1854	40	2210	2150	UA	639	N27421	EWR	MCO	125	937	18	54	2023-05-04 18:00:00	MCO
25866	5	6	1052	825	147	1419	1226	DL	699	N857DZ	JFK	SJU	187	1598	8	25	2023-05-06 08:00:00	Other
25870	11	27	1845	1655	110	2136	1950	B6	198	N565JB	EWR	PBI	148	1023	16	55	2023-11-27 16:00:00	Other
25877	9	20	1949	1920	29	2127	2121	YX	1889	N882RW	LGA	CMH	72	479	19	20	2023-09-20 19:00:00	Other
25885	3	4	1622	1559	23	2009	1927	B6	328	N942JB	JFK	LAX	380	2475	15	59	2023-03-04 15:00:00	LAX
25888	3	10	1151	1115	36	1445	1411	UA	255	N14107	EWR	TPA	146	997	11	15	2023-03-10 11:00:00	Other
25890	4	9	1715	1700	15	1837	1830	9E	1400	N181PQ	JFK	PWM	48	273	17	0	2023-04-09 17:00:00	Other
25896	2	13	1720	1630	50	2035	1959	DL	179	N391DA	JFK	SAN	347	2446	16	30	2023-02-13 16:00:00	Other
25899	3	11	1508	1400	68	1837	1751	AA	985	N308RD	JFK	PHX	303	2153	14	0	2023-03-11 14:00:00	Other
25906	7	10	1126	955	91	1232	1120	UA	384	N76514	EWR	BNA	105	748	9	55	2023-07-10 09:00:00	Other
25907	2	25	1251	1057	114	1418	1234	UA	568	N417UA	EWR	BNA	124	748	10	57	2023-02-25 10:00:00	Other
25914	3	28	1132	908	144	1239	1025	B6	635	N179JB	JFK	BTV	49	266	9	8	2023-03-28 09:00:00	Other
25919	1	23	2110	2014	56	5	2320	UA	554	N17254	EWR	IAH	200	1400	20	14	2023-01-23 20:00:00	Other
25921	1	21	1344	1330	14	1515	1500	WN	412	N248WN	LGA	MDW	120	725	13	30	2023-01-21 13:00:00	Other
25926	2	22	2028	2015	13	2218	2131	B6	541	N318JB	LGA	BOS	32	184	20	15	2023-02-22 20:00:00	BOS
25932	8	8	1454	1359	55	1606	1530	YX	1350	N224JQ	LGA	BOS	42	184	13	59	2023-08-08 13:00:00	BOS
25933	5	31	947	830	77	1121	1005	OO	1175	N614CZ	JFK	BNA	111	765	8	30	2023-05-31 08:00:00	Other
25934	11	2	1944	1915	29	2108	2054	UA	706	N844UA	LGA	ORD	112	733	19	15	2023-11-02 19:00:00	ORD
25936	11	22	858	825	33	1031	952	YX	1864	N210JQ	EWR	BOS	39	200	8	25	2023-11-22 08:00:00	BOS
25945	7	12	2129	2058	31	2354	2344	UA	655	N27251	EWR	DFW	171	1372	20	58	2023-07-12 20:00:00	Other
25950	1	1	1524	1503	21	1743	1738	UA	551	N12754	EWR	JAX	119	820	15	3	2023-01-01 15:00:00	Other
25960	9	25	1447	1315	92	1603	1450	UA	619	N17752	LGA	ORD	109	733	13	15	2023-09-25 13:00:00	ORD
25963	8	11	2004	1630	214	2221	1903	B6	97	N355JB	JFK	SAV	110	718	16	30	2023-08-11 16:00:00	Other
25970	12	25	2258	2129	89	333	217	B6	654	N996JL	JFK	SJU	186	1598	21	29	2023-12-25 21:00:00	Other
25972	6	24	1710	1630	40	2222	1920	UA	507	N229UA	EWR	LAX	307	2454	16	30	2023-06-24 16:00:00	LAX
25974	3	13	1743	1730	13	2028	1959	YX	1271	N821MD	LGA	SDF	111	659	17	30	2023-03-13 17:00:00	Other
25978	3	27	1856	1840	16	2138	2112	YX	1285	N416YX	LGA	OMA	198	1148	18	40	2023-03-27 18:00:00	Other
25999	7	17	908	759	69	1110	1013	YX	866	N757YX	EWR	GRR	91	605	7	59	2023-07-17 07:00:00	Other
26005	6	19	1439	1425	14	1708	1711	UA	614	N476UA	EWR	IAH	184	1400	14	25	2023-06-19 14:00:00	Other
26006	6	6	1046	940	66	1156	1112	9E	1577	N914XJ	LGA	BTV	48	258	9	40	2023-06-06 09:00:00	Other
26009	1	31	1602	1545	17	1745	1726	YX	1361	N138HQ	JFK	DCA	61	213	15	45	2023-01-31 15:00:00	Other
26014	4	3	1835	1800	35	1940	1922	AA	447	N755US	LGA	DCA	43	214	18	0	2023-04-03 18:00:00	Other
26017	5	28	2246	2159	47	2349	2310	DL	123	N144DU	LGA	BOS	45	184	21	59	2023-05-28 21:00:00	BOS
26027	3	16	1752	1740	12	2110	2134	DL	360	N712TW	JFK	SFO	357	2586	17	40	2023-03-16 17:00:00	Other
26030	5	24	2010	1929	41	2331	2258	B6	349	N656JB	JFK	PDX	309	2454	19	29	2023-05-24 19:00:00	Other
26033	5	6	2249	2159	50	9	2344	B6	517	N355JB	JFK	RDU	61	427	21	59	2023-05-06 21:00:00	Other
26037	6	19	1912	1850	22	2034	2020	WN	746	N416WN	LGA	BNA	111	764	18	50	2023-06-19 18:00:00	Other
26039	8	10	1922	1900	22	2048	2035	WN	818	N7721E	LGA	MDW	110	725	19	0	2023-08-10 19:00:00	Other
26040	7	8	1433	1415	18	1538	1538	B6	187	N358JB	LGA	BOS	32	184	14	15	2023-07-08 14:00:00	BOS
26046	10	12	2217	2155	22	2330	2315	B6	894	N249JB	JFK	SYR	43	209	21	55	2023-10-12 21:00:00	Other
26047	9	9	1444	1425	19	1646	1556	AA	123	N818AW	LGA	BNA	131	764	14	25	2023-09-09 14:00:00	Other
26054	9	11	27	2214	133	222	45	NK	590	N950NK	EWR	ATL	98	746	22	14	2023-09-11 22:00:00	ATL
26055	3	28	1522	1455	27	1816	1738	B6	868	N565JB	LGA	JAX	141	833	14	55	2023-03-28 14:00:00	Other
26068	9	19	4	2230	94	120	2359	OO	1250	N261SY	JFK	BOS	40	187	22	30	2023-09-19 22:00:00	BOS
26079	5	26	1628	1550	38	1810	1802	YX	1621	N219YX	JFK	CMH	78	483	15	50	2023-05-26 15:00:00	Other
26106	9	12	2228	2000	148	4	2137	9E	1777	N928XJ	LGA	ORF	50	296	20	0	2023-09-12 20:00:00	Other
26111	6	2	818	755	23	1109	1056	AS	89	N929AK	EWR	LAX	295	2454	7	55	2023-06-02 07:00:00	LAX
26115	6	26	755	700	55	900	830	YX	1780	N243JQ	JFK	BOS	43	187	7	0	2023-06-26 07:00:00	BOS
26123	12	23	1901	1843	18	2159	2213	DL	442	N311DU	EWR	SLC	270	1969	18	43	2023-12-23 18:00:00	Other
26127	2	18	1944	1933	11	2246	2245	UA	824	N38454	EWR	MIA	142	1085	19	33	2023-02-18 19:00:00	MIA
26153	7	8	1219	1125	54	1407	1334	YX	899	N641RW	EWR	IND	91	645	11	25	2023-07-08 11:00:00	Other
26162	3	2	2204	2100	64	54	1	B6	48	N589JB	EWR	PBI	141	1023	21	0	2023-03-02 21:00:00	Other
26168	4	12	2007	1825	102	2123	2025	DL	340	N143DU	LGA	ORD	105	733	18	25	2023-04-12 18:00:00	ORD
26180	3	7	817	800	17	1302	1259	B6	193	N2086J	JFK	SJU	183	1598	8	0	2023-03-07 08:00:00	Other
26183	3	1	2157	2140	17	126	127	DL	108	N703TW	JFK	SFO	353	2586	21	40	2023-03-01 21:00:00	Other
26184	5	27	1928	1915	13	2139	2215	UA	779	N437UA	EWR	DFW	169	1372	19	15	2023-05-27 19:00:00	Other
26190	1	23	1825	1755	30	2046	2040	WN	403	N8790Q	LGA	DEN	224	1620	17	55	2023-01-23 17:00:00	Other
26195	4	5	2150	1810	220	2315	1935	DL	405	N121DU	JFK	BOS	32	187	18	10	2023-04-05 18:00:00	BOS
26204	5	29	1026	915	71	1136	1043	YX	1608	N238JQ	JFK	DCA	49	213	9	15	2023-05-29 09:00:00	Other
26220	4	21	1442	1430	12	1832	1826	B6	295	N763JB	JFK	SJU	198	1598	14	30	2023-04-21 14:00:00	Other
26222	4	5	1730	1700	30	2031	2008	AA	877	N892NN	LGA	DFW	207	1389	17	0	2023-04-05 17:00:00	Other
26223	9	17	926	915	11	1052	1039	9E	1579	N336PQ	JFK	IAD	50	228	9	15	2023-09-17 09:00:00	Other
26226	2	27	1801	1750	11	1942	1939	B6	430	N192JB	JFK	RDU	74	427	17	50	2023-02-27 17:00:00	Other
26227	11	4	827	815	12	1033	1016	AA	987	N867NN	LGA	CLT	97	544	8	15	2023-11-04 08:00:00	CLT
26229	4	28	725	645	40	1016	936	UA	725	N27268	EWR	PBI	150	1023	6	45	2023-04-28 06:00:00	Other
26236	3	16	1323	1300	23	1513	1502	AA	639	N553UW	LGA	CLT	80	544	13	0	2023-03-16 13:00:00	CLT
26246	3	22	1616	1545	31	1844	1824	DL	337	N317DN	LGA	ATL	116	762	15	45	2023-03-22 15:00:00	ATL
26247	6	20	2221	2130	51	2332	2254	UA	396	N37293	EWR	BOS	36	200	21	30	2023-06-20 21:00:00	BOS
26256	5	31	615	600	15	737	735	UA	375	N76269	EWR	ORD	105	719	6	0	2023-05-31 06:00:00	ORD
26273	5	25	2145	2130	15	2352	13	DL	451	N827DN	JFK	ATL	108	760	21	30	2023-05-25 21:00:00	ATL
26277	3	8	2019	2000	19	2348	2309	B6	123	N597JB	JFK	ONT	353	2429	20	0	2023-03-08 20:00:00	Other
26281	12	22	953	929	24	1251	1253	UA	660	N39728	EWR	EYW	156	1196	9	29	2023-12-22 09:00:00	Other
26282	5	11	1009	900	69	1257	1210	AS	16	N588AS	JFK	SAN	320	2446	9	0	2023-05-11 09:00:00	Other
26312	7	2	1832	1705	87	2016	1859	DL	792	N934AT	EWR	DTW	84	488	17	5	2023-07-02 17:00:00	Other
26314	3	5	1705	1557	68	1927	1830	UA	498	N54711	EWR	JAX	120	820	15	57	2023-03-05 15:00:00	Other
26332	9	11	1346	1225	81	1643	1445	WN	458	N267WN	LGA	DEN	238	1620	12	25	2023-09-11 12:00:00	Other
26336	5	9	2040	2012	28	2348	2311	UA	505	N78509	EWR	PBI	156	1023	20	12	2023-05-09 20:00:00	Other
26347	9	6	1848	1740	68	2112	2034	B6	64	N591JB	JFK	TPA	131	1005	17	40	2023-09-06 17:00:00	Other
26351	10	29	1919	1859	20	2238	2143	YX	1267	N443YX	LGA	TUL	213	1231	18	59	2023-10-29 18:00:00	Other
26354	6	12	2026	1934	52	2319	2248	AA	98	N110AN	JFK	LAX	307	2475	19	34	2023-06-12 19:00:00	LAX
26357	6	8	2109	1959	70	16	2319	DL	588	N374DX	LGA	FLL	153	1076	19	59	2023-06-08 19:00:00	FLL
26358	12	22	2042	2010	32	2206	2141	B6	870	N273JB	JFK	DCA	42	213	20	10	2023-12-22 20:00:00	Other
26360	8	21	742	715	27	1014	959	DL	438	N347DN	LGA	MCO	120	950	7	15	2023-08-21 07:00:00	MCO
26368	8	22	2249	2025	144	151	2321	B6	531	N903JB	LGA	PBI	153	1035	20	25	2023-08-22 20:00:00	Other
26372	5	13	1103	1030	33	1326	1323	B6	147	N706JB	JFK	MCO	122	944	10	30	2023-05-13 10:00:00	MCO
26378	4	29	2059	1455	364	2244	1631	OO	984	N305SY	JFK	BNA	127	765	14	55	2023-04-29 14:00:00	Other
26380	7	30	1202	1035	87	1438	1329	UA	326	N845UA	EWR	TPA	135	997	10	35	2023-07-30 10:00:00	Other
26383	6	26	1656	1350	186	2037	1605	YX	1288	N439YX	JFK	CVG	109	589	13	50	2023-06-26 13:00:00	Other
26384	1	11	1212	1006	126	1349	1151	UA	784	N816UA	LGA	ORD	120	733	10	6	2023-01-11 10:00:00	ORD
26385	1	15	1853	1615	158	2042	1734	B6	434	N354JB	LGA	BOS	72	184	16	15	2023-01-15 16:00:00	BOS
26387	3	19	1522	1506	16	1844	1804	UA	609	N27263	EWR	TPA	171	997	15	6	2023-03-19 15:00:00	Other
26389	8	12	1340	1230	70	1617	1524	B6	29	N2039J	JFK	MCO	124	944	12	30	2023-08-12 12:00:00	MCO
26398	9	25	1010	930	40	1309	1228	B6	46	N635JB	JFK	SRQ	147	1041	9	30	2023-09-25 09:00:00	Other
26399	6	9	22	2259	83	420	257	B6	146	N949JT	JFK	SJU	213	1598	22	59	2023-06-09 22:00:00	Other
26403	9	24	2008	1920	48	2154	2121	YX	1889	N230JQ	LGA	CMH	74	479	19	20	2023-09-24 19:00:00	Other
26405	1	30	2102	2029	33	2349	2344	UA	312	N17105	EWR	FLL	143	1065	20	29	2023-01-30 20:00:00	FLL
26412	7	28	1953	1925	28	2149	2055	B6	541	N323JB	JFK	BOS	40	187	19	25	2023-07-28 19:00:00	BOS
26415	3	19	42	2359	43	409	343	B6	979	N796JB	JFK	SJU	187	1598	23	59	2023-03-19 23:00:00	Other
26420	1	23	1514	1359	75	1656	1549	9E	1613	N184GJ	JFK	RDU	77	427	13	59	2023-01-23 13:00:00	Other
26427	7	17	1640	1610	30	1851	1837	UA	379	N813UA	EWR	ATL	102	746	16	10	2023-07-17 16:00:00	ATL
26431	5	25	2130	2102	28	2354	2334	UA	508	N37474	EWR	ATL	108	746	21	2	2023-05-25 21:00:00	ATL
26436	6	1	44	2146	178	314	31	NK	283	N530NK	EWR	IAH	174	1400	21	46	2023-06-01 21:00:00	Other
26439	9	10	2127	2059	28	2338	2331	YX	1147	N865RW	EWR	SDF	96	642	20	59	2023-09-10 20:00:00	Other
26440	4	30	1632	1621	11	1835	1809	YX	1052	N654RW	EWR	RDU	79	416	16	21	2023-04-30 16:00:00	Other
26450	9	14	1918	1849	29	2205	2109	DL	451	N141DU	LGA	MSY	163	1183	18	49	2023-09-14 18:00:00	Other
26455	5	26	2219	1930	169	31	2203	UA	291	N57286	EWR	PHX	270	2133	19	30	2023-05-26 19:00:00	Other
26461	8	14	1105	930	95	1403	1245	B6	24	N979JT	JFK	SEA	324	2422	9	30	2023-08-14 09:00:00	Other
26467	10	6	2228	2145	43	136	50	B6	516	N709JB	JFK	FLL	143	1069	21	45	2023-10-06 21:00:00	FLL
26469	5	22	1753	1717	36	1950	1925	AA	757	N973UY	LGA	CLT	84	544	17	17	2023-05-22 17:00:00	CLT
26477	12	7	2048	2030	18	2332	2343	UA	907	N13138	EWR	FLL	140	1065	20	30	2023-12-07 20:00:00	FLL
26481	7	24	1317	1305	12	1612	1610	UA	412	N37313	EWR	FLL	150	1065	13	5	2023-07-24 13:00:00	FLL
26483	8	16	1742	1712	30	1905	1856	AA	794	N808AW	LGA	STL	117	888	17	12	2023-08-16 17:00:00	Other
26504	6	21	1846	1829	17	2104	2055	UA	454	N485UA	EWR	DEN	237	1605	18	29	2023-06-21 18:00:00	Other
26506	7	31	2301	2159	62	104	2352	UA	636	N459UA	EWR	RDU	71	416	21	59	2023-07-31 21:00:00	Other
26524	9	8	1851	1829	22	2319	2134	AS	164	N296AK	EWR	SEA	320	2402	18	29	2023-09-08 18:00:00	Other
26550	8	11	1303	1038	145	1430	1225	B6	71	N594JB	JFK	RDU	67	427	10	38	2023-08-11 10:00:00	Other
26554	12	4	1524	1420	64	1752	1704	B6	945	N768JB	LGA	ATL	117	762	14	20	2023-12-04 14:00:00	ATL
26564	12	5	717	655	22	948	1011	NK	821	N637NK	EWR	LAX	309	2454	6	55	2023-12-05 06:00:00	LAX
26565	9	4	1817	1753	24	2119	2044	UA	871	N27261	EWR	IAH	213	1400	17	53	2023-09-04 17:00:00	Other
26570	7	7	1456	1400	56	1646	1530	YX	1391	N242JQ	LGA	BOS	42	184	14	0	2023-07-07 14:00:00	BOS
26571	6	6	2319	2230	49	155	206	B6	972	N968JT	JFK	SFO	315	2586	22	30	2023-06-06 22:00:00	Other
26573	7	14	1735	1701	34	1915	1915	DL	743	N364NB	LGA	DTW	78	502	17	1	2023-07-14 17:00:00	Other
26579	9	10	728	630	58	948	852	B6	245	N589JB	JFK	JAX	119	828	6	30	2023-09-10 06:00:00	Other
26584	1	23	1027	1003	24	1306	1309	UA	961	N35236	EWR	DFW	191	1372	10	3	2023-01-23 10:00:00	Other
26593	11	19	1547	1530	17	1737	1740	YX	1283	N428YX	JFK	CMH	79	483	15	30	2023-11-19 15:00:00	Other
26597	4	15	2305	2237	28	13	2355	UA	530	N62889	EWR	BTV	49	266	22	37	2023-04-15 22:00:00	Other
26600	9	1	1258	829	269	1556	1119	AA	332	N865NN	LGA	DFW	183	1389	8	29	2023-09-01 08:00:00	Other
26601	5	4	1910	1855	15	2109	2101	UA	442	N14731	EWR	CLT	80	529	18	55	2023-05-04 18:00:00	CLT
26609	10	12	904	729	95	1140	955	UA	401	N13110	EWR	PHX	301	2133	7	29	2023-10-12 07:00:00	Other
26617	6	10	1149	1130	19	1448	1443	AA	113	N103NN	JFK	LAX	328	2475	11	30	2023-06-10 11:00:00	LAX
26631	5	22	2011	1950	21	2311	2258	UA	703	N419UA	EWR	RSW	155	1068	19	50	2023-05-22 19:00:00	Other
26632	1	31	1206	1000	126	1312	1124	UA	778	N422UA	EWR	IAD	51	212	10	0	2023-01-31 10:00:00	Other
26643	2	8	1301	1225	36	1503	1454	YX	1242	N412YX	LGA	DAY	88	549	12	25	2023-02-08 12:00:00	Other
26653	5	24	1100	1029	31	1315	1303	DL	121	N338DN	LGA	ATL	109	762	10	29	2023-05-24 10:00:00	ATL
26690	1	20	1619	1508	71	1731	1646	YX	1170	N638RW	EWR	RIC	51	277	15	8	2023-01-20 15:00:00	Other
26692	4	22	957	940	17	1312	1250	UA	650	N73256	EWR	RSW	166	1068	9	40	2023-04-22 09:00:00	Other
26694	3	11	1714	1655	19	1854	1902	DL	920	N349NB	LGA	DTW	80	502	16	55	2023-03-11 16:00:00	Other
26696	9	27	1430	1345	45	1655	1608	B6	970	N624JB	LGA	SAV	108	722	13	45	2023-09-27 13:00:00	Other
26701	5	19	2125	2100	25	34	54	AA	55	N104NN	JFK	SFO	335	2586	21	0	2023-05-19 21:00:00	Other
26714	5	3	1120	1100	20	1406	1400	UA	242	N17244	EWR	TPA	142	997	11	0	2023-05-03 11:00:00	Other
26719	2	9	1710	1630	40	1833	1803	YX	1517	N815MD	LGA	DCA	53	214	16	30	2023-02-09 16:00:00	Other
26720	7	14	1643	1525	78	1812	1714	9E	1318	N187GJ	JFK	PWM	52	273	15	25	2023-07-14 15:00:00	Other
26722	7	1	2147	1959	108	137	2357	UA	484	N69885	EWR	SJU	201	1608	19	59	2023-07-01 19:00:00	Other
26731	3	29	2132	2059	33	33	2358	B6	1007	N634JB	EWR	PBI	143	1023	20	59	2023-03-29 20:00:00	Other
26738	1	8	2048	2000	48	2220	2128	AA	857	N757UW	LGA	DCA	60	214	20	0	2023-01-08 20:00:00	Other
26744	11	19	1948	1929	19	2131	2133	9E	1557	N602LR	JFK	RDU	75	427	19	29	2023-11-19 19:00:00	Other
26747	8	30	751	530	141	1046	810	B6	36	N986JB	JFK	LAX	313	2475	5	30	2023-08-30 05:00:00	LAX
26751	7	10	1724	1705	19	2006	1939	B6	759	N746JB	LGA	ATL	112	762	17	5	2023-07-10 17:00:00	ATL
26755	2	15	2055	2005	50	2352	2358	AA	928	N815NN	LGA	MIA	156	1096	20	5	2023-02-15 20:00:00	MIA
26768	7	11	1646	1600	46	1847	1850	DL	168	N368DN	LGA	ATL	104	762	16	0	2023-07-11 16:00:00	ATL
26770	7	28	2051	2000	51	2334	2140	YX	1348	N235JQ	LGA	BNA	110	764	20	0	2023-07-28 20:00:00	Other
26773	5	19	1151	1129	22	1457	1443	DL	969	N337NB	LGA	PBI	150	1035	11	29	2023-05-19 11:00:00	Other
26778	9	23	1335	1310	25	1536	1512	9E	1709	N195PQ	LGA	AVL	85	599	13	10	2023-09-23 13:00:00	Other
26783	9	25	2145	2050	55	2303	2227	YX	1965	N823MD	LGA	MSN	112	812	20	50	2023-09-25 20:00:00	Other
26785	7	15	1006	945	21	1158	1155	9E	1132	N912XJ	LGA	GSP	88	610	9	45	2023-07-15 09:00:00	Other
26790	9	11	1854	1645	129	2237	1953	UA	870	N793UA	EWR	SFO	328	2565	16	45	2023-09-11 16:00:00	Other
26802	8	31	918	900	18	1140	1117	NK	134	N649NK	EWR	LAS	279	2227	9	0	2023-08-31 09:00:00	Other
26811	8	8	1030	725	185	1146	850	WN	114	N295WN	LGA	BNA	115	764	7	25	2023-08-08 07:00:00	Other
26812	6	30	1156	1145	11	1503	1455	AS	10	N214AK	JFK	SEA	328	2422	11	45	2023-06-30 11:00:00	Other
26818	7	16	1057	1020	37	1308	1241	9E	1158	N300PQ	LGA	CLT	86	544	10	20	2023-07-16 10:00:00	CLT
26819	9	11	2042	1833	129	2335	2145	B6	71	N978JB	JFK	SEA	311	2422	18	33	2023-09-11 18:00:00	Other
26828	9	9	1120	1100	20	1405	1406	AA	103	N111ZM	JFK	LAX	321	2475	11	0	2023-09-09 11:00:00	LAX
26835	6	19	2000	1917	43	2205	2118	AA	1015	N583UW	LGA	CLT	82	544	19	17	2023-06-19 19:00:00	CLT
26836	11	25	1905	1711	114	2204	2019	UA	537	N27274	EWR	FLL	159	1065	17	11	2023-11-25 17:00:00	FLL
26837	1	2	1429	1340	49	1730	1645	WN	805	N7734H	LGA	HOU	220	1428	13	40	2023-01-02 13:00:00	Other
26841	12	24	1113	1100	13	1404	1424	B6	321	N2059J	JFK	SLC	269	1990	11	0	2023-12-24 11:00:00	Other
26842	9	25	1256	1240	16	1500	1425	WN	637	N437WN	LGA	STL	123	888	12	40	2023-09-25 12:00:00	Other
26849	12	10	1941	1713	148	2131	1926	YX	1296	N441YX	LGA	CMH	86	479	17	13	2023-12-10 17:00:00	Other
26860	5	12	2214	2059	75	31	2312	UA	374	N29717	EWR	CVG	85	569	20	59	2023-05-12 20:00:00	Other
26862	9	6	2239	2145	54	15	2336	YX	1301	N134HQ	JFK	RDU	63	427	21	45	2023-09-06 21:00:00	Other
26878	5	2	2231	2138	53	32	15	NK	262	N628NK	EWR	LAS	281	2227	21	38	2023-05-02 21:00:00	Other
26881	11	28	1841	1830	11	2157	2138	UA	300	N24224	EWR	FLL	155	1065	18	30	2023-11-28 18:00:00	FLL
26886	1	27	1517	1455	22	1835	1818	AA	1044	N832NN	LGA	DFW	227	1389	14	55	2023-01-27 14:00:00	Other
26889	4	28	2007	1925	42	2208	2130	UA	621	N64844	EWR	CHS	87	628	19	25	2023-04-28 19:00:00	Other
26891	6	6	2204	1645	319	1	1922	AA	611	N925NN	JFK	PHX	271	2153	16	45	2023-06-06 16:00:00	Other
26893	10	6	1050	910	100	1353	1214	B6	205	N592JB	JFK	FLL	160	1069	9	10	2023-10-06 09:00:00	FLL
26898	9	16	1626	1530	56	1905	1838	UA	764	N780UA	EWR	SFO	312	2565	15	30	2023-09-16 15:00:00	Other
26900	9	15	18	2030	228	247	2342	UA	792	N29129	EWR	LAX	306	2454	20	30	2023-09-15 20:00:00	LAX
26906	7	13	1810	1753	17	2114	2049	UA	525	N37413	EWR	TPA	132	997	17	53	2023-07-13 17:00:00	Other
26918	4	16	2314	2059	135	149	2332	UA	268	N14704	EWR	ATL	118	746	20	59	2023-04-16 20:00:00	ATL
26922	3	18	2127	2115	12	2302	2247	UA	701	N433UA	EWR	BNA	131	748	21	15	2023-03-18 21:00:00	Other
26926	4	17	1845	1755	50	2130	2101	AA	211	N338PK	LGA	DFW	195	1389	17	55	2023-04-17 17:00:00	Other
26930	2	7	1504	1441	23	1822	1754	AA	806	N909NN	JFK	DFW	227	1391	14	41	2023-02-07 14:00:00	Other
26937	12	1	745	730	15	900	908	YX	1334	N136HQ	LGA	ORF	54	296	7	30	2023-12-01 07:00:00	Other
26942	3	27	2146	1929	137	2335	2135	OO	1166	N312SY	JFK	ORD	136	740	19	29	2023-03-27 19:00:00	ORD
26943	2	21	1519	1505	14	1804	1815	DL	751	N327NW	LGA	TPA	147	1010	15	5	2023-02-21 15:00:00	Other
26944	7	18	1719	1429	170	1920	1630	UA	317	N409UA	EWR	CLT	78	529	14	29	2023-07-18 14:00:00	CLT
26946	7	19	2223	2125	58	2339	2248	YX	1090	N110HQ	LGA	ORF	50	296	21	25	2023-07-19 21:00:00	Other
26947	8	25	1555	1529	26	1813	1737	YX	981	N103HQ	JFK	CLE	77	425	15	29	2023-08-25 15:00:00	Other
26948	1	1	1000	700	180	1322	1019	UA	852	N12116	EWR	LAX	358	2454	7	0	2023-01-01 07:00:00	LAX
26950	5	25	2131	1955	96	8	2307	DL	544	N368DN	JFK	MCO	140	944	19	55	2023-05-25 19:00:00	MCO
26951	9	8	911	810	61	1040	951	9E	1467	N601LR	JFK	RIC	55	288	8	10	2023-09-08 08:00:00	Other
26957	8	31	1433	1420	13	1557	1540	WN	147	N8504G	LGA	MDW	105	725	14	20	2023-08-31 14:00:00	Other
26960	6	8	1402	1229	93	1629	1517	UA	438	N477UA	LGA	IAH	184	1416	12	29	2023-06-08 12:00:00	Other
26962	6	4	2004	1950	14	2155	2148	AA	340	N893NN	EWR	CLT	80	529	19	50	2023-06-04 19:00:00	CLT
26969	1	17	1640	1455	105	1802	1626	9E	1505	N602LR	JFK	ROC	56	264	14	55	2023-01-17 14:00:00	Other
26982	6	21	1947	1915	32	2335	2204	AA	403	N805NN	LGA	DFW	176	1389	19	15	2023-06-21 19:00:00	Other
26987	3	24	2151	2135	16	2327	2328	YX	1334	N104HQ	JFK	RDU	72	427	21	35	2023-03-24 21:00:00	Other
26989	10	1	1217	1130	47	1409	1352	YX	1863	N815MD	LGA	IND	90	660	11	30	2023-10-01 11:00:00	Other
26993	3	1	1159	1000	119	1459	1314	UA	722	N840UA	LGA	IAH	216	1416	10	0	2023-03-01 10:00:00	Other
26997	5	12	3	2159	124	120	2321	UA	173	N69806	EWR	BOS	38	200	21	59	2023-05-12 21:00:00	BOS
27001	8	28	2335	2100	155	353	105	NK	307	N617NK	EWR	SJU	242	1608	21	0	2023-08-28 21:00:00	Other
27005	3	3	1121	1300	1341	1325	1502	AA	639	N551UW	LGA	CLT	98	544	13	0	2023-03-03 13:00:00	CLT
27006	3	2	2048	2020	28	2400	2333	DL	247	N869DN	JFK	LAS	338	2248	20	20	2023-03-02 20:00:00	Other
27012	4	17	2255	2213	42	4	2333	UA	466	N27252	EWR	PWM	43	284	22	13	2023-04-17 22:00:00	Other
27013	8	16	1108	1048	20	1336	1310	UA	399	N17730	EWR	JAX	117	820	10	48	2023-08-16 10:00:00	Other
27019	6	30	2032	1959	33	2311	2319	DL	588	N316DN	LGA	FLL	134	1076	19	59	2023-06-30 19:00:00	FLL
27024	4	30	2125	1815	190	2256	2028	DL	679	N953AT	EWR	MSP	126	1008	18	15	2023-04-30 18:00:00	Other
27033	10	13	1729	1455	154	2029	1811	B6	1008	N821JB	JFK	MIA	155	1089	14	55	2023-10-13 14:00:00	MIA
27041	2	27	1412	1345	27	1725	1717	B6	302	N595JB	JFK	SAT	227	1587	13	45	2023-02-27 13:00:00	Other
27055	3	27	1902	1845	17	2036	2020	YX	1208	N728YX	EWR	PIT	63	319	18	45	2023-03-27 18:00:00	Other
27074	12	6	1014	1000	14	1208	1232	YX	1034	N765YX	EWR	SDF	95	642	10	0	2023-12-06 10:00:00	Other
27075	5	2	1230	1056	94	1516	1405	UA	418	N47282	EWR	MIA	144	1085	10	56	2023-05-02 10:00:00	MIA
27076	6	3	1751	1659	52	2121	2000	B6	873	N509JB	EWR	TPA	176	997	16	59	2023-06-03 16:00:00	Other
27082	6	2	2315	2155	80	230	141	DL	111	N712TW	JFK	SFO	309	2586	21	55	2023-06-02 21:00:00	Other
27091	2	5	1312	1000	192	1411	1124	UA	691	N16217	EWR	IAD	43	212	10	0	2023-02-05 10:00:00	Other
27095	5	4	2218	2159	19	2	1	YX	1228	N445YX	JFK	RDU	70	427	21	59	2023-05-04 21:00:00	Other
27098	7	19	1634	1430	124	1858	1643	YX	1000	N102HQ	JFK	CVG	93	589	14	30	2023-07-19 14:00:00	Other
27102	9	7	123	2159	204	233	2338	UA	680	N17245	EWR	ORD	101	719	21	59	2023-09-07 21:00:00	ORD
27115	2	24	2122	2029	53	28	2344	B6	561	N569JB	JFK	FLL	150	1069	20	29	2023-02-24 20:00:00	FLL
27116	10	11	1426	1415	11	1556	1538	B6	232	N3102J	JFK	MKE	131	745	14	15	2023-10-11 14:00:00	Other
27117	1	16	905	830	35	1151	1203	DL	243	N138DU	LGA	DFW	202	1389	8	30	2023-01-16 08:00:00	Other
27120	12	20	1813	1729	44	2108	2050	UA	749	N37295	EWR	PDX	328	2434	17	29	2023-12-20 17:00:00	Other
27123	7	30	1718	1700	18	2009	1949	AA	799	N934NN	LGA	DFW	182	1389	17	0	2023-07-30 17:00:00	Other
27137	3	27	658	620	38	1024	1000	DL	325	N118DY	JFK	SLC	306	1990	6	20	2023-03-27 06:00:00	Other
27142	11	16	809	700	69	1057	946	UA	220	N12109	EWR	LAS	314	2227	7	0	2023-11-16 07:00:00	Other
27143	12	17	1751	1652	59	2041	1934	B6	900	N520JB	LGA	ATL	110	762	16	52	2023-12-17 16:00:00	ATL
27146	6	24	2135	1630	305	2347	1905	B6	120	N368JB	JFK	SAV	97	718	16	30	2023-06-24 16:00:00	Other
27150	8	25	955	930	25	1139	1142	DL	175	N343DN	LGA	DTW	80	502	9	30	2023-08-25 09:00:00	Other
27161	6	24	1006	929	37	1204	1100	9E	1565	N337PQ	JFK	DCA	56	213	9	29	2023-06-24 09:00:00	Other
27167	9	9	1120	730	230	1409	949	UA	472	N4901U	EWR	SAV	107	708	7	30	2023-09-09 07:00:00	Other
27168	8	13	1944	1925	19	2241	2250	AS	76	N585AS	EWR	SFO	336	2565	19	25	2023-08-13 19:00:00	Other
27171	2	26	2038	1959	39	2346	2311	DL	449	N366DX	LGA	FLL	141	1076	19	59	2023-02-26 19:00:00	FLL
27174	7	28	1315	1116	119	1446	1309	9E	1284	N932XJ	LGA	RDU	65	431	11	16	2023-07-28 11:00:00	Other
27179	8	8	1632	1620	12	1832	1821	UA	247	N14731	EWR	CLT	84	529	16	20	2023-08-08 16:00:00	CLT
27180	8	25	1135	826	189	1312	1008	YX	1034	N103HQ	LGA	CLE	70	419	8	26	2023-08-25 08:00:00	Other
27181	6	6	1052	1040	12	1224	1200	NK	429	N509NK	EWR	BNA	109	748	10	40	2023-06-06 10:00:00	Other
27184	1	30	1714	1424	170	2036	1744	B6	91	N648JB	JFK	AUS	239	1521	14	24	2023-01-30 14:00:00	Other
27186	7	29	2330	2102	148	247	3	B6	156	N592JB	LGA	FLL	177	1076	21	2	2023-07-29 21:00:00	FLL
27187	7	12	713	700	13	956	950	DL	183	N176DZ	JFK	LAX	300	2475	7	0	2023-07-12 07:00:00	LAX
27192	6	24	1250	1152	58	1412	1309	UA	295	N67501	EWR	BOS	44	200	11	52	2023-06-24 11:00:00	BOS
27195	2	17	2222	2155	27	2338	2333	UA	83	N37252	EWR	MKE	107	725	21	55	2023-02-17 21:00:00	Other
27207	4	27	719	655	24	905	830	WN	38	N788SA	LGA	STL	145	888	6	55	2023-04-27 06:00:00	Other
27208	3	11	2243	2000	163	124	2311	B6	934	N998JE	JFK	MCO	126	944	20	0	2023-03-11 20:00:00	MCO
27210	3	30	1319	1042	157	1613	1351	AA	443	N932NN	LGA	DFW	214	1389	10	42	2023-03-30 10:00:00	Other
27222	5	25	1659	1630	29	2010	1917	NK	525	N651NK	EWR	MCO	140	937	16	30	2023-05-25 16:00:00	MCO
27226	12	3	2203	2150	13	2329	2316	9E	1640	N293PQ	LGA	BUF	58	292	21	50	2023-12-03 21:00:00	Other
27227	9	22	1035	1016	19	1249	1240	AA	803	N184US	EWR	PHX	291	2133	10	16	2023-09-22 10:00:00	Other
27228	1	9	755	729	26	919	905	9E	1683	N601LR	LGA	BUF	53	292	7	29	2023-01-09 07:00:00	Other
27229	8	24	2147	2102	45	6	2304	UA	489	N68834	EWR	MSP	147	1008	21	2	2023-08-24 21:00:00	Other
27236	4	1	1516	1456	20	1750	1700	YX	1042	N724YX	EWR	CLT	99	529	14	56	2023-04-01 14:00:00	CLT
27247	3	23	1658	1645	13	2013	2007	B6	778	N2060J	JFK	MIA	144	1089	16	45	2023-03-23 16:00:00	MIA
27250	8	13	1120	1100	20	1412	1411	DL	409	N774DE	JFK	MIA	148	1089	11	0	2023-08-13 11:00:00	MIA
27257	12	1	835	800	35	1102	1042	DL	320	N384DN	LGA	ATL	125	762	8	0	2023-12-01 08:00:00	ATL
27262	11	22	1639	1540	59	1831	1809	B6	805	N3132J	JFK	MCI	148	1113	15	40	2023-11-22 15:00:00	Other
27267	1	23	1251	1230	21	1419	1436	AA	516	N936AN	LGA	ORD	107	733	12	30	2023-01-23 12:00:00	ORD
27270	8	16	2353	2111	162	231	2359	NK	228	N651NK	EWR	IAH	189	1400	21	11	2023-08-16 21:00:00	Other
27274	8	25	1208	1111	57	1450	1434	DL	486	N3751B	LGA	MIA	138	1096	11	11	2023-08-25 11:00:00	MIA
27277	7	4	2035	2010	25	2319	2242	B6	30	N523JB	JFK	DEN	257	1626	20	10	2023-07-04 20:00:00	Other
27278	11	22	2116	2005	71	2352	2308	NK	265	N692NK	EWR	IAH	196	1400	20	5	2023-11-22 20:00:00	Other
27285	11	26	1342	1245	57	1647	1552	B6	38	N705JB	JFK	TPA	161	1005	12	45	2023-11-26 12:00:00	Other
27286	12	11	822	805	17	956	941	9E	1555	N294PQ	JFK	PWM	50	273	8	5	2023-12-11 08:00:00	Other
27288	2	17	2136	1902	154	25	2235	AA	406	N816NN	LGA	DFW	203	1389	19	2	2023-02-17 19:00:00	Other
27291	1	30	1421	1406	15	1717	1635	UA	865	N28457	EWR	DEN	249	1605	14	6	2023-01-30 14:00:00	Other
27293	6	9	1714	1700	14	2022	2043	B6	79	N967JT	JFK	SEA	309	2422	17	0	2023-06-09 17:00:00	Other
27294	1	15	2109	1959	70	2336	2308	DL	627	N330DX	JFK	MCO	125	944	19	59	2023-01-15 19:00:00	MCO
27298	10	4	956	933	23	1351	1330	B6	990	N956JT	JFK	SJU	209	1598	9	33	2023-10-04 09:00:00	Other
27302	8	13	2216	2110	66	2333	2250	YX	1325	N217JQ	JFK	DCA	40	213	21	10	2023-08-13 21:00:00	Other
27306	6	9	1019	755	144	1259	1056	AS	89	N288AK	EWR	LAX	305	2454	7	55	2023-06-09 07:00:00	LAX
27315	7	4	2047	1759	168	2322	2056	F9	411	N610FR	LGA	MCO	125	950	17	59	2023-07-04 17:00:00	MCO
27316	1	23	2303	2155	68	3	2306	DL	892	N107DU	LGA	SYR	39	198	21	55	2023-01-23 21:00:00	Other
27317	9	25	2001	1935	26	2332	2329	DL	338	N722TW	JFK	SFO	326	2586	19	35	2023-09-25 19:00:00	Other
27321	7	5	1606	1540	26	1723	1705	WN	726	N7736A	LGA	MDW	103	725	15	40	2023-07-05 15:00:00	Other
27327	6	13	2220	2159	21	2359	2359	UA	609	N17265	EWR	DTW	76	488	21	59	2023-06-13 21:00:00	Other
27329	5	2	1056	1045	11	1349	1347	NK	526	N678NK	EWR	FLL	145	1065	10	45	2023-05-02 10:00:00	FLL
27330	11	9	1946	1930	16	2251	2240	UA	571	N795UA	EWR	LAX	329	2454	19	30	2023-11-09 19:00:00	LAX
27331	8	11	1909	1808	61	2154	2058	UA	510	N12221	EWR	MCO	131	937	18	8	2023-08-11 18:00:00	MCO
27340	5	18	1116	1055	21	1259	1259	9E	1484	N331PQ	LGA	GSO	73	461	10	55	2023-05-18 10:00:00	Other
27353	2	20	2325	2229	56	42	2352	B6	192	N307JB	JFK	ROC	54	264	22	29	2023-02-20 22:00:00	Other
27356	4	12	2052	2030	22	2334	2331	B6	67	N586JB	JFK	TPA	138	1005	20	30	2023-04-12 20:00:00	Other
27358	6	26	1143	1023	80	1437	1158	YX	1114	N653RW	EWR	BGR	62	393	10	23	2023-06-26 10:00:00	Other
27365	7	12	2001	1920	41	2238	2208	9E	1317	N329PQ	LGA	JAX	110	833	19	20	2023-07-12 19:00:00	Other
27366	5	19	1019	910	69	1235	1123	B6	463	N229JB	JFK	CHS	104	636	9	10	2023-05-19 09:00:00	Other
27370	9	30	2018	2001	17	2226	2224	UA	279	N13110	EWR	PHX	275	2133	20	1	2023-09-30 20:00:00	Other
27371	9	8	1041	929	72	1151	1101	YX	1814	N220JQ	JFK	DCA	42	213	9	29	2023-09-08 09:00:00	Other
27380	6	19	915	845	30	1148	1137	B6	84	N2039J	JFK	IAH	185	1417	8	45	2023-06-19 08:00:00	Other
27382	2	28	1844	1829	15	2132	2121	UA	636	N33294	EWR	MCO	130	937	18	29	2023-02-28 18:00:00	MCO
27393	7	27	2011	2000	11	2158	2131	YX	1430	N815MD	LGA	BOS	42	184	20	0	2023-07-27 20:00:00	BOS
27396	9	7	1733	1700	33	NA	1852	9E	1590	N349PQ	LGA	CLE	NA	419	17	0	2023-09-07 17:00:00	Other
27398	7	22	943	929	14	1053	1051	YX	959	N745YX	EWR	MHT	41	209	9	29	2023-07-22 09:00:00	Other
27404	4	2	1713	1658	15	1901	1835	AA	753	N906AN	EWR	ORD	131	719	16	58	2023-04-02 16:00:00	ORD
27410	3	1	943	905	38	1049	1024	B6	635	N192JB	JFK	BTV	47	266	9	5	2023-03-01 09:00:00	Other
27416	4	18	1823	1720	63	2106	2025	WN	879	N478WN	LGA	HOU	194	1428	17	20	2023-04-18 17:00:00	Other
27421	8	20	2301	2250	11	101	115	F9	451	N362FR	LGA	ATL	95	762	22	50	2023-08-20 22:00:00	ATL
27434	3	14	1612	1540	32	1923	1826	DL	134	N331DN	JFK	ATL	106	760	15	40	2023-03-14 15:00:00	ATL
27437	10	14	1713	1645	28	2001	1909	B6	685	N586JB	LGA	MSY	176	1183	16	45	2023-10-14 16:00:00	Other
27439	6	24	1547	1530	17	1902	1750	WN	36	N488WN	LGA	ATL	112	762	15	30	2023-06-24 15:00:00	ATL
27445	4	5	1726	1559	87	2022	1907	B6	320	N339JB	JFK	MCO	130	944	15	59	2023-04-05 15:00:00	MCO
27447	5	26	1404	1345	19	1640	1640	WN	239	N8509U	LGA	HOU	193	1428	13	45	2023-05-26 13:00:00	Other
27449	3	2	1714	1650	24	1934	1900	NK	53	N615NK	LGA	DTW	101	502	16	50	2023-03-02 16:00:00	Other
27460	5	6	1119	1102	17	1225	1229	UA	491	N27255	EWR	BNA	103	748	11	2	2023-05-06 11:00:00	Other
27464	10	1	1750	1650	60	1940	1905	WN	141	N8655D	LGA	MSY	153	1183	16	50	2023-10-01 16:00:00	Other
27474	6	27	1749	1729	20	2126	2040	AA	153	N935NN	JFK	MIA	150	1089	17	29	2023-06-27 17:00:00	MIA
27476	3	14	1457	1405	52	1625	1540	UA	622	N453UA	EWR	BNA	113	748	14	5	2023-03-14 14:00:00	Other
27479	3	13	1458	1446	12	1756	1753	AA	836	N954NN	JFK	DFW	203	1391	14	46	2023-03-13 14:00:00	Other
27483	6	4	2005	1918	47	2155	2128	UA	857	N497UA	EWR	CLT	81	529	19	18	2023-06-04 19:00:00	CLT
27494	4	1	1144	1113	31	1601	1432	YX	929	N740YX	EWR	AUS	273	1504	11	13	2023-04-01 11:00:00	Other
27497	5	20	1600	1457	63	1744	1645	NK	23	N523NK	EWR	MYR	80	550	14	57	2023-05-20 14:00:00	Other
27499	2	22	2103	2005	58	10	2250	DL	352	N345NW	LGA	ATL	114	762	20	5	2023-02-22 20:00:00	ATL
27503	1	12	2156	2109	47	35	8	B6	210	N653JB	LGA	MCO	139	950	21	9	2023-01-12 21:00:00	MCO
27511	7	6	1545	1530	15	1729	1711	YX	1420	N202JQ	LGA	DCA	56	214	15	30	2023-07-06 15:00:00	Other
27512	1	15	1802	1720	42	2047	2035	WN	542	N260WN	LGA	HOU	197	1428	17	20	2023-01-15 17:00:00	Other
27519	7	18	1624	1526	58	2022	1849	DL	222	N344DN	JFK	FLL	156	1069	15	26	2023-07-18 15:00:00	FLL
27530	7	4	1324	1156	88	1518	1403	AA	765	N941NN	JFK	CLT	81	541	11	56	2023-07-04 11:00:00	CLT
27532	7	26	2310	2228	42	252	223	B6	275	N508JL	JFK	BQN	196	1576	22	28	2023-07-26 22:00:00	Other
27534	12	21	645	620	25	946	935	NK	182	N985NK	EWR	FLL	143	1065	6	20	2023-12-21 06:00:00	FLL
27547	9	1	2212	2159	13	2322	2321	YX	1067	N640RW	EWR	MHT	39	209	21	59	2023-09-01 21:00:00	Other
27550	1	27	1231	1207	24	1525	1528	UA	232	N77530	EWR	SNA	335	2434	12	7	2023-01-27 12:00:00	Other
27567	3	26	2110	1959	71	2348	2235	DL	805	N338NB	LGA	MSY	182	1183	19	59	2023-03-26 19:00:00	Other
27571	7	9	1947	1650	177	2338	2018	AS	11	N264AK	JFK	SFO	361	2586	16	50	2023-07-09 16:00:00	Other
27581	1	11	1350	1115	155	1526	1312	9E	1681	N302PQ	LGA	RDU	67	431	11	15	2023-01-11 11:00:00	Other
27584	10	27	1114	900	134	1247	1049	OO	1226	N293SY	JFK	PIT	72	340	9	0	2023-10-27 09:00:00	Other
27586	3	14	1409	1215	114	1716	1446	YX	1407	N110HQ	LGA	CVG	92	585	12	15	2023-03-14 12:00:00	Other
27594	6	22	1133	1112	21	1422	1406	UA	259	N54241	EWR	TPA	146	997	11	12	2023-06-22 11:00:00	Other
27603	5	19	1056	1040	16	1342	1335	B6	338	N729JB	JFK	PBI	146	1028	10	40	2023-05-19 10:00:00	Other
27604	11	14	834	820	14	1122	1135	DL	258	N135DQ	LGA	DFW	188	1389	8	20	2023-11-14 08:00:00	Other
27606	7	12	1146	1133	13	1249	1244	B6	641	N284JB	JFK	ACK	43	199	11	33	2023-07-12 11:00:00	Other
27609	3	18	1201	1100	61	1517	1448	DL	108	N723TW	JFK	SFO	350	2586	11	0	2023-03-18 11:00:00	Other
27616	2	26	1542	1529	13	1756	1752	YX	1135	N645RW	EWR	CVG	106	569	15	29	2023-02-26 15:00:00	Other
27618	1	10	1450	1435	15	1654	1651	9E	1421	N916XJ	LGA	CVG	95	585	14	35	2023-01-10 14:00:00	Other
27620	9	4	1619	1550	29	1825	1816	YX	1862	N211JQ	LGA	CLT	77	544	15	50	2023-09-04 15:00:00	CLT
27627	7	10	1831	1529	182	2048	1654	UA	394	N409UA	EWR	BNA	111	748	15	29	2023-07-10 15:00:00	Other
27629	12	4	1312	1020	172	1703	1340	DL	550	N126DU	JFK	SAT	264	1587	10	20	2023-12-04 10:00:00	Other
27634	9	15	2114	2100	14	2305	2252	YX	1862	N213JQ	JFK	PIT	62	340	21	0	2023-09-15 21:00:00	Other
27651	12	10	1944	1815	89	2258	2039	9E	1504	N195PQ	JFK	IND	104	665	18	15	2023-12-10 18:00:00	Other
27659	7	31	1047	1007	40	1307	1249	UA	82	N35260	EWR	DFW	172	1372	10	7	2023-07-31 10:00:00	Other
27661	7	17	1244	1023	141	1357	1158	UA	556	N77537	EWR	ORD	108	719	10	23	2023-07-17 10:00:00	ORD
27667	9	8	1239	1158	41	1538	1513	NK	1028	N661NK	LGA	MIA	164	1096	11	58	2023-09-08 11:00:00	MIA
27668	6	19	2200	1707	293	140	2029	B6	810	N834JB	JFK	MIA	172	1089	17	7	2023-06-19 17:00:00	MIA
27669	1	11	2113	1759	194	17	2104	B6	761	N712JB	LGA	MCO	132	950	17	59	2023-01-11 17:00:00	MCO
27675	7	23	1540	1459	41	1732	1652	YX	1005	N430YX	JFK	CLE	79	425	14	59	2023-07-23 14:00:00	Other
27677	7	1	2107	2009	58	2231	2139	UA	522	N23721	EWR	BNA	109	748	20	9	2023-07-01 20:00:00	Other
27678	4	10	1108	759	189	1327	1109	B6	618	N969JT	EWR	LAX	294	2454	7	59	2023-04-10 07:00:00	LAX
27687	9	12	2238	2110	88	37	2309	YX	1322	N109HQ	LGA	MEM	149	963	21	10	2023-09-12 21:00:00	Other
27708	2	23	1709	1649	20	1815	1757	YX	987	N657RW	EWR	MDT	35	141	16	49	2023-02-23 16:00:00	Other
27710	5	23	1700	1640	20	1952	2020	AS	90	N494AS	EWR	SFO	318	2565	16	40	2023-05-23 16:00:00	Other
27713	2	24	2351	2039	192	211	2253	B6	532	N348JB	JFK	DTW	113	509	20	39	2023-02-24 20:00:00	Other
27715	11	17	2041	2030	11	2157	2201	NK	1038	N973NK	LGA	ORD	114	733	20	30	2023-11-17 20:00:00	ORD
27719	1	11	1245	1230	15	1427	1424	YX	1242	N740YX	EWR	CMH	80	463	12	30	2023-01-11 12:00:00	Other
27721	9	29	1627	1339	168	1945	1645	B6	449	N595JB	JFK	AUS	198	1521	13	39	2023-09-29 13:00:00	Other
27735	1	6	1007	950	17	1316	1314	B6	657	N709JB	JFK	RSW	158	1074	9	50	2023-01-06 09:00:00	Other
27739	5	11	855	840	15	1042	1028	YX	1047	N642RW	EWR	PIT	51	319	8	40	2023-05-11 08:00:00	Other
27746	1	6	1858	1529	209	2030	1707	YX	1258	N742YX	EWR	MKE	113	725	15	29	2023-01-06 15:00:00	Other
27751	7	24	1848	1836	12	2201	2149	AA	538	N835NN	EWR	MIA	160	1085	18	36	2023-07-24 18:00:00	MIA
27755	3	29	2005	1916	49	2304	2200	UA	428	N66841	EWR	LAS	319	2227	19	16	2023-03-29 19:00:00	Other
27758	6	12	1706	1459	127	2033	1705	AA	142	N9029F	JFK	CLT	118	541	14	59	2023-06-12 14:00:00	CLT
27768	5	15	1829	1756	33	2116	2108	AA	646	N937AN	EWR	MIA	139	1085	17	56	2023-05-15 17:00:00	MIA
27770	3	9	1957	1945	12	2254	2249	B6	455	N955JB	JFK	LAS	326	2248	19	45	2023-03-09 19:00:00	Other
27779	7	26	1337	1225	72	1520	1420	YX	1033	N869RW	LGA	DAY	81	549	12	25	2023-07-26 12:00:00	Other
27796	12	8	1841	1800	41	2012	1944	9E	1650	N925XJ	LGA	MSN	121	812	18	0	2023-12-08 18:00:00	Other
27800	1	1	1626	1559	27	1725	1717	UA	156	N36247	EWR	BOS	40	200	15	59	2023-01-01 15:00:00	BOS
27811	5	3	1425	1410	15	1650	1700	UA	594	N47288	EWR	IAH	181	1400	14	10	2023-05-03 14:00:00	Other
27816	5	21	1718	1645	33	1936	1910	WN	361	N8600F	LGA	DEN	223	1620	16	45	2023-05-21 16:00:00	Other
27818	8	3	2331	2228	63	307	223	B6	264	N766JB	JFK	BQN	187	1576	22	28	2023-08-03 22:00:00	Other
27820	1	25	1825	1730	55	2115	2020	YX	1338	N869RW	LGA	SDF	127	659	17	30	2023-01-25 17:00:00	Other
27826	7	21	1431	1420	11	1658	1705	UA	496	N421UA	EWR	IAH	182	1400	14	20	2023-07-21 14:00:00	Other
27828	5	26	1359	1301	58	1624	1529	B6	931	N588JB	JFK	ATL	113	760	13	1	2023-05-26 13:00:00	ATL
27830	2	24	1823	1455	208	2119	1725	YX	1564	N230JQ	JFK	IND	131	665	14	55	2023-02-24 14:00:00	Other
27834	7	25	1637	1430	127	1950	1737	UA	571	N24715	EWR	SLC	266	1969	14	30	2023-07-25 14:00:00	Other
27835	9	22	1943	1930	13	2245	2237	UA	709	N17312	EWR	RSW	153	1068	19	30	2023-09-22 19:00:00	Other
27837	8	25	1321	810	311	1533	1036	B6	759	N656JB	LGA	ATL	103	762	8	10	2023-08-25 08:00:00	ATL
27839	12	12	1851	1840	11	2015	2020	WN	1079	N495WN	LGA	BNA	120	764	18	40	2023-12-12 18:00:00	Other
27847	2	27	1	2245	76	NA	2351	B6	482	N267JB	JFK	BOS	NA	187	22	45	2023-02-27 22:00:00	BOS
27848	7	4	725	705	20	913	932	UA	372	N17303	EWR	PHX	268	2133	7	5	2023-07-04 07:00:00	Other
27852	7	26	1156	1129	27	1430	1418	UA	470	N37422	EWR	MCO	123	937	11	29	2023-07-26 11:00:00	MCO
27856	8	2	1549	1457	52	1812	1758	UA	63	N809UA	EWR	PBI	124	1023	14	57	2023-08-02 14:00:00	Other
27863	1	19	1758	1710	48	2006	1919	AA	484	N807AW	LGA	STL	157	888	17	10	2023-01-19 17:00:00	Other
27865	3	11	1645	1614	31	1745	1727	UA	143	N893UA	EWR	BOS	38	200	16	14	2023-03-11 16:00:00	BOS
27869	8	1	1859	1815	44	2204	2128	AA	595	N892NN	LGA	MIA	142	1096	18	15	2023-08-01 18:00:00	MIA
27872	2	16	1510	1155	195	1629	1324	NK	294	N691NK	EWR	PIT	57	319	11	55	2023-02-16 11:00:00	Other
27874	3	11	959	904	55	1205	1147	B6	458	N775JB	JFK	ATL	105	760	9	4	2023-03-11 09:00:00	ATL
27875	1	6	817	759	18	926	900	YX	1183	N753YX	EWR	PHL	36	80	7	59	2023-01-06 07:00:00	Other
27879	2	5	51	2220	151	209	2343	B6	192	N206JB	JFK	ROC	53	264	22	20	2023-02-05 22:00:00	Other
27886	10	23	1952	1940	12	2222	2226	DL	1007	N392DN	JFK	ATL	103	760	19	40	2023-10-23 19:00:00	ATL
27892	8	20	2028	2010	18	2310	2351	B6	259	N944JT	JFK	SFO	306	2586	20	10	2023-08-20 20:00:00	Other
27895	8	17	2141	2114	27	6	2346	UA	106	N27292	EWR	LAS	280	2227	21	14	2023-08-17 21:00:00	Other
27898	5	29	2256	2156	60	27	2344	UA	816	N63890	EWR	RDU	67	416	21	56	2023-05-29 21:00:00	Other
27899	2	17	2228	2015	133	2354	2131	B6	541	N247JB	LGA	BOS	40	184	20	15	2023-02-17 20:00:00	BOS
27900	5	13	851	715	96	950	827	B6	947	N368JB	LGA	BOS	36	184	7	15	2023-05-13 07:00:00	BOS
27903	11	29	1657	1635	22	1945	1940	WN	997	N243WN	LGA	DAL	201	1381	16	35	2023-11-29 16:00:00	Other
27906	6	24	1842	1650	112	1938	1801	B6	959	N339JB	LGA	MVY	34	175	16	50	2023-06-24 16:00:00	Other
27909	6	5	835	800	35	1118	1100	UA	752	N47280	EWR	PBI	135	1023	8	0	2023-06-05 08:00:00	Other
27911	1	5	928	835	53	1152	1040	YX	1435	N132HQ	LGA	ILM	103	500	8	35	2023-01-05 08:00:00	Other
27914	3	27	1048	1035	13	1214	1157	B6	143	N274JB	JFK	BUF	61	301	10	35	2023-03-27 10:00:00	Other
27915	9	29	2216	2200	16	2321	2319	UA	522	N35236	EWR	ROC	41	246	22	0	2023-09-29 22:00:00	Other
27928	5	13	2230	2209	21	2334	2332	UA	509	N474UA	EWR	ORF	41	284	22	9	2023-05-13 22:00:00	Other
27933	1	15	805	735	30	1057	1049	DL	513	N324DX	JFK	FLL	136	1069	7	35	2023-01-15 07:00:00	FLL
27939	8	13	1910	1859	11	2155	2149	AS	78	N287AK	EWR	SAN	312	2425	18	59	2023-08-13 18:00:00	Other
27940	4	17	1002	946	16	1352	1341	UA	539	N45440	EWR	SJU	197	1608	9	46	2023-04-17 09:00:00	Other
27945	2	17	914	855	19	1041	1021	YX	1566	N212JQ	JFK	BOS	42	187	8	55	2023-02-17 08:00:00	BOS
27954	7	25	1803	1330	273	2043	1558	B6	34	N536JB	JFK	LAS	294	2248	13	30	2023-07-25 13:00:00	Other
27975	6	20	2115	2030	45	2214	2139	YX	1090	N739YX	EWR	MDT	32	141	20	30	2023-06-20 20:00:00	Other
27986	4	5	2230	2110	80	146	2358	B6	69	N705JB	EWR	MCO	123	937	21	10	2023-04-05 21:00:00	MCO
27991	7	26	908	600	188	1053	746	DL	637	N929AT	EWR	DTW	77	488	6	0	2023-07-26 06:00:00	Other
27992	5	11	2212	2146	26	2	2349	UA	731	N66841	EWR	DTW	78	488	21	46	2023-05-11 21:00:00	Other
27994	8	6	2300	2150	70	57	2353	B6	426	N317JB	JFK	DTW	78	509	21	50	2023-08-06 21:00:00	Other
27995	6	7	2231	2155	36	2333	2317	UA	495	N39726	EWR	ROC	41	246	21	55	2023-06-07 21:00:00	Other
28005	6	2	1808	1515	173	2233	1819	NK	896	N652NK	EWR	LAX	313	2454	15	15	2023-06-02 15:00:00	LAX
28010	12	16	2006	1954	12	2320	2344	DL	193	N546DN	JFK	PDX	329	2454	19	54	2023-12-16 19:00:00	Other
28013	11	24	1549	1531	18	1815	1756	9E	1591	N324PQ	JFK	IND	106	665	15	31	2023-11-24 15:00:00	Other
28015	4	2	1947	1930	17	2217	2156	YX	1079	N133HQ	LGA	LIT	177	1085	19	30	2023-04-02 19:00:00	Other
28020	5	25	1542	1530	12	1828	1840	DL	434	N101DQ	JFK	MCO	140	944	15	30	2023-05-25 15:00:00	MCO
28024	12	6	1253	1054	119	1416	1218	9E	1365	N927XJ	JFK	SYR	46	209	10	54	2023-12-06 10:00:00	Other
28025	10	3	2244	2030	134	50	2257	B6	29	N599JB	JFK	DEN	219	1626	20	30	2023-10-03 20:00:00	Other
28026	5	7	1241	1230	11	1406	1405	9E	1383	N935XJ	LGA	MKE	115	738	12	30	2023-05-07 12:00:00	Other
28027	7	21	2221	2130	51	102	2344	YX	919	N861RW	EWR	CLT	78	529	21	30	2023-07-21 21:00:00	CLT
28036	8	3	1246	1230	16	1523	1525	NK	280	N614NK	LGA	DFW	200	1389	12	30	2023-08-03 12:00:00	Other
28042	7	24	1223	1130	53	1515	1437	B6	755	N598JB	JFK	MIA	149	1089	11	30	2023-07-24 11:00:00	MIA
28043	8	10	1851	1830	21	2141	2142	UA	343	N204UA	EWR	SFO	322	2565	18	30	2023-08-10 18:00:00	Other
28050	7	11	1005	929	36	1235	1220	AA	508	N933NN	LGA	DFW	188	1389	9	29	2023-07-11 09:00:00	Other
28058	8	10	1819	1759	20	2024	2027	UA	700	N802UA	LGA	DEN	225	1620	17	59	2023-08-10 17:00:00	Other
28063	8	6	1451	1435	16	1637	1609	YX	895	N748YX	EWR	IAD	43	212	14	35	2023-08-06 14:00:00	Other
28066	11	29	1930	1905	25	13	2357	UA	208	N61898	EWR	BQN	194	1585	19	5	2023-11-29 19:00:00	Other
28071	1	23	2153	2055	58	2303	2203	9E	1526	N182GJ	LGA	ALB	34	136	20	55	2023-01-23 20:00:00	Other
28072	7	20	2336	2250	46	115	37	9E	1260	N182GJ	JFK	ROC	55	264	22	50	2023-07-20 22:00:00	Other
28073	5	12	1740	1654	46	2019	2000	NK	630	N633NK	EWR	FLL	131	1065	16	54	2023-05-12 16:00:00	FLL
28078	7	4	1827	1510	197	2108	1800	UA	631	N68842	EWR	TPA	134	997	15	10	2023-07-04 15:00:00	Other
28086	11	12	831	800	31	947	939	UA	853	N454UA	LGA	ORD	118	733	8	0	2023-11-12 08:00:00	ORD
28094	5	26	1651	1559	52	1847	1806	YX	1167	N746YX	EWR	DTW	79	488	15	59	2023-05-26 15:00:00	Other
28098	7	9	1458	1440	18	1737	1738	DL	398	N379DN	LGA	MCO	137	950	14	40	2023-07-09 14:00:00	MCO
28100	8	5	1843	1825	18	1950	2000	WN	818	N8874Q	LGA	MDW	109	725	18	25	2023-08-05 18:00:00	Other
28102	12	4	841	750	51	951	920	YX	1314	N427YX	JFK	DCA	46	213	7	50	2023-12-04 07:00:00	Other
28104	11	28	1549	1519	30	1703	1640	YX	1119	N745YX	EWR	SYR	43	195	15	19	2023-11-28 15:00:00	Other
28116	7	24	1857	1815	42	2116	2019	YX	1009	N109HQ	LGA	LIT	155	1085	18	15	2023-07-24 18:00:00	Other
28145	7	29	1706	1459	127	1836	1645	UA	564	N874UA	EWR	RDU	62	416	14	59	2023-07-29 14:00:00	Other
28146	7	7	1326	1300	26	1745	1614	B6	498	N2084J	JFK	FLL	174	1069	13	0	2023-07-07 13:00:00	FLL
28148	12	1	1831	1820	11	2037	2015	WN	979	N1802U	LGA	STL	148	888	18	20	2023-12-01 18:00:00	Other
28155	3	26	1456	1435	21	1803	1750	UA	80	N209UA	EWR	SFO	337	2565	14	35	2023-03-26 14:00:00	Other
28159	1	8	1748	1735	13	2100	2105	B6	1037	N968JT	JFK	LAX	331	2475	17	35	2023-01-08 17:00:00	LAX
28160	3	2	1614	1559	15	1825	1802	UA	714	N478UA	EWR	DTW	102	488	15	59	2023-03-02 15:00:00	Other
28161	1	31	1100	929	91	1344	1203	9E	1441	N678CA	LGA	GRR	113	618	9	29	2023-01-31 09:00:00	Other
28172	7	10	2042	1850	112	2343	2122	YX	1374	N230JQ	LGA	CLT	105	544	18	50	2023-07-10 18:00:00	CLT
28174	4	5	827	800	27	1039	1033	DL	329	N334DN	LGA	ATL	107	762	8	0	2023-04-05 08:00:00	ATL
28190	3	20	1601	1500	61	1814	1704	UA	384	N837UA	EWR	CLT	84	529	15	0	2023-03-20 15:00:00	CLT
28195	5	17	2131	2057	34	23	2359	UA	457	N431UA	EWR	SRQ	148	1034	20	57	2023-05-17 20:00:00	Other
28198	1	11	1619	1600	19	1729	1726	OO	1279	N297SY	JFK	BOS	35	187	16	0	2023-01-11 16:00:00	BOS
28200	7	21	720	700	20	1023	1010	AS	86	N918AK	EWR	SEA	321	2402	7	0	2023-07-21 07:00:00	Other
28215	4	1	1111	700	251	1624	1101	B6	550	N806JB	EWR	SJU	219	1608	7	0	2023-04-01 07:00:00	Other
28216	4	24	1511	1430	41	1808	1733	AA	795	N821NN	JFK	DFW	201	1391	14	30	2023-04-24 14:00:00	Other
28217	11	27	2023	2001	22	124	57	UA	541	N47517	EWR	SJU	208	1608	20	1	2023-11-27 20:00:00	Other
28218	2	23	2003	1455	308	2333	1820	AA	374	N948NN	LGA	DFW	231	1389	14	55	2023-02-23 14:00:00	Other
28222	10	3	2004	1950	14	2252	2303	DL	869	N913DU	JFK	TPA	130	1005	19	50	2023-10-03 19:00:00	Other
28226	7	18	1809	1751	18	2106	2050	B6	632	N985JT	EWR	LAX	326	2454	17	51	2023-07-18 17:00:00	LAX
28230	5	4	1412	945	267	1653	1235	B6	378	N197JB	JFK	MCO	131	944	9	45	2023-05-04 09:00:00	MCO
28234	1	4	2345	2216	89	254	149	B6	1011	N969JT	JFK	SFO	351	2586	22	16	2023-01-04 22:00:00	Other
28251	5	30	1740	1723	17	1952	1945	AA	921	N464AA	EWR	PHX	277	2133	17	23	2023-05-30 17:00:00	Other
28254	12	8	1237	1140	57	1410	1334	9E	1376	N691CA	LGA	CLE	72	419	11	40	2023-12-08 11:00:00	Other
28256	7	6	1533	1448	45	1908	1750	NK	701	N621NK	EWR	LAX	325	2454	14	48	2023-07-06 14:00:00	LAX
28257	2	10	1247	1235	12	1546	1608	AA	210	N891NN	LGA	DFW	216	1389	12	35	2023-02-10 12:00:00	Other
28265	12	7	1527	1514	13	1650	1635	B6	39	N206JB	JFK	BTV	55	266	15	14	2023-12-07 15:00:00	Other
28267	8	17	1601	1530	31	1852	1833	UA	405	N18119	EWR	LAX	313	2454	15	30	2023-08-17 15:00:00	LAX
28274	7	10	1054	1037	17	1406	1325	UA	326	N17296	EWR	TPA	162	997	10	37	2023-07-10 10:00:00	Other
28283	7	5	2148	2130	18	2322	2329	9E	1221	N927XJ	JFK	RIC	55	288	21	30	2023-07-05 21:00:00	Other
28289	10	30	1347	1251	56	1457	1413	9E	1560	N491PX	LGA	BTV	42	258	12	51	2023-10-30 12:00:00	Other
28310	1	7	2156	2130	26	2307	2243	B6	106	N206JB	JFK	BOS	44	187	21	30	2023-01-07 21:00:00	BOS
28316	6	25	1329	1145	104	1612	1445	AS	7	N583AS	JFK	PDX	315	2454	11	45	2023-06-25 11:00:00	Other
28338	9	27	811	651	80	924	814	YX	1051	N731YX	EWR	BTV	46	266	6	51	2023-09-27 06:00:00	Other
28341	9	29	2119	2029	50	2252	2220	DL	1014	N950AT	EWR	DTW	73	488	20	29	2023-09-29 20:00:00	Other
28350	10	25	2321	2259	22	246	302	B6	259	N554JB	JFK	PSE	188	1617	22	59	2023-10-25 22:00:00	Other
28351	4	30	2218	1906	192	101	2220	DL	438	N363DN	EWR	SLC	248	1969	19	6	2023-04-30 19:00:00	Other
28369	5	6	2120	1900	140	2257	2037	YX	1011	N644RW	EWR	PIT	58	319	19	0	2023-05-06 19:00:00	Other
28372	12	23	2244	2055	109	134	15	B6	731	N571JB	LGA	RSW	150	1080	20	55	2023-12-23 20:00:00	Other
28383	3	17	2128	1730	238	2351	1959	YX	1712	N232JQ	LGA	SDF	119	659	17	30	2023-03-17 17:00:00	Other
28385	5	17	2152	2059	53	2359	2305	UA	255	N66837	EWR	CLT	84	529	20	59	2023-05-17 20:00:00	CLT
28391	5	23	1902	1850	12	2123	2155	UA	136	N772UA	EWR	LAX	294	2454	18	50	2023-05-23 18:00:00	LAX
28397	2	3	10	1729	401	139	1921	UA	282	N27267	EWR	STL	129	872	17	29	2023-02-03 17:00:00	Other
28399	7	22	2050	1939	71	5	2245	NK	836	N656NK	EWR	MIA	166	1085	19	39	2023-07-22 19:00:00	MIA
28407	7	15	1025	1010	15	1300	1257	UA	344	N895UA	LGA	IAH	188	1416	10	10	2023-07-15 10:00:00	Other
28409	7	23	1830	1815	15	2145	2110	WN	974	N418WN	LGA	TPA	157	1010	18	15	2023-07-23 18:00:00	Other
28413	7	14	2222	1930	172	131	2249	B6	63	N986JB	JFK	LAX	331	2475	19	30	2023-07-14 19:00:00	LAX
28417	8	22	1741	1730	11	2040	2046	B6	626	N586JB	JFK	MIA	135	1089	17	30	2023-08-22 17:00:00	MIA
28418	9	13	2024	1959	25	2202	2142	OO	1283	N246SY	JFK	BOS	53	187	19	59	2023-09-13 19:00:00	BOS
28425	9	8	2040	1450	350	2346	1759	DL	347	N307DU	LGA	PBI	152	1035	14	50	2023-09-08 14:00:00	Other
28430	9	10	1610	1500	70	1810	1706	AA	484	N951AA	LGA	CLT	84	544	15	0	2023-09-10 15:00:00	CLT
28431	6	10	1129	820	189	1332	1040	DL	960	N835DN	EWR	ATL	97	746	8	20	2023-06-10 08:00:00	ATL
28432	8	30	1747	1659	48	1948	1917	UA	741	N27283	EWR	PHX	256	2133	16	59	2023-08-30 16:00:00	Other
28436	4	30	1647	1210	277	1830	1440	UA	853	N24211	LGA	DEN	201	1620	12	10	2023-04-30 12:00:00	Other
28438	6	11	2004	1859	65	2216	2204	AS	90	N478AS	EWR	PDX	293	2434	18	59	2023-06-11 18:00:00	Other
28439	3	27	1023	1000	23	1325	1255	UA	401	N12010	EWR	LAX	325	2454	10	0	2023-03-27 10:00:00	LAX
28440	3	13	2210	2154	16	2337	2318	UA	495	N27268	EWR	BUF	51	282	21	54	2023-03-13 21:00:00	Other
28451	1	23	1008	950	18	1126	1115	9E	1666	N930XJ	JFK	SYR	46	209	9	50	2023-01-23 09:00:00	Other
28453	5	29	1200	1136	24	1434	1446	UA	473	N443UA	EWR	AUS	192	1504	11	36	2023-05-29 11:00:00	Other
28454	12	27	1000	805	115	1138	948	B6	373	N368JB	JFK	BNA	129	765	8	5	2023-12-27 08:00:00	Other
28458	7	21	1331	1300	31	1612	1614	B6	498	N2060J	JFK	FLL	139	1069	13	0	2023-07-21 13:00:00	FLL
28459	3	5	1742	1729	13	2047	2047	B6	997	N2102J	JFK	FLL	150	1069	17	29	2023-03-05 17:00:00	FLL
28460	6	26	2207	1920	167	NA	2319	DL	367	N721TW	JFK	SFO	NA	2586	19	20	2023-06-26 19:00:00	Other
28470	9	12	1916	1830	46	2037	1954	B6	93	N323JB	JFK	PWM	45	273	18	30	2023-09-12 18:00:00	Other
28471	7	28	1625	1530	55	1830	1753	B6	673	N3062J	JFK	MCI	161	1113	15	30	2023-07-28 15:00:00	Other
28474	10	23	2307	2250	17	135	155	F9	908	N346FR	LGA	DFW	182	1389	22	50	2023-10-23 22:00:00	Other
28481	7	9	1225	1155	30	1416	1341	G4	834	292NV	EWR	VPS	141	988	11	55	2023-07-09 11:00:00	Other
28502	4	22	1714	1700	14	2034	2021	UA	143	N2644U	EWR	SFO	317	2565	17	0	2023-04-22 17:00:00	Other
28509	12	10	1159	800	239	1531	1113	B6	74	N2060J	JFK	IAH	237	1417	8	0	2023-12-10 08:00:00	Other
28510	2	3	926	810	76	1213	1109	B6	119	N193JB	LGA	JAX	143	833	8	10	2023-02-03 08:00:00	Other
28511	7	28	2002	1925	37	2354	2240	DL	389	N315NB	LGA	PBI	146	1035	19	25	2023-07-28 19:00:00	Other
28514	11	11	1837	1620	137	2004	1736	UA	786	N17139	EWR	BOS	34	200	16	20	2023-11-11 16:00:00	BOS
28518	3	14	1734	1720	14	2134	2038	B6	997	N2086J	JFK	FLL	173	1069	17	20	2023-03-14 17:00:00	FLL
28520	2	20	1943	1924	19	2152	2129	AA	327	N966NN	EWR	CLT	91	529	19	24	2023-02-20 19:00:00	CLT
28525	1	16	1408	1229	99	1634	1505	9E	1383	N607LR	LGA	SDF	103	659	12	29	2023-01-16 12:00:00	Other
28534	12	28	1424	1356	28	1557	1610	YX	1254	N417YX	LGA	MSP	134	1020	13	56	2023-12-28 13:00:00	Other
28535	5	1	1509	1410	59	1753	1700	UA	594	N27276	EWR	IAH	197	1400	14	10	2023-05-01 14:00:00	Other
28546	4	14	1032	959	33	1408	1330	YX	1038	N757YX	EWR	EYW	182	1196	9	59	2023-04-14 09:00:00	Other
28547	12	18	1512	1430	42	1722	1656	B6	785	N3113J	JFK	MCI	157	1113	14	30	2023-12-18 14:00:00	Other
28567	8	11	1532	1359	93	1828	1648	UA	574	N17264	EWR	MCO	136	937	13	59	2023-08-11 13:00:00	MCO
28597	7	11	1212	1158	14	1442	1414	YX	858	N855RW	EWR	SDF	104	642	11	58	2023-07-11 11:00:00	Other
28598	7	31	1713	1629	44	1923	1837	UA	550	N13720	EWR	CHS	94	628	16	29	2023-07-31 16:00:00	Other
28603	3	10	1949	1820	89	2253	2125	B6	276	N645JB	LGA	MCO	142	950	18	20	2023-03-10 18:00:00	MCO
28606	4	29	1100	1000	60	1449	1329	DL	146	N878DN	JFK	SLC	263	1990	10	0	2023-04-29 10:00:00	Other
28609	11	10	1143	1129	14	1442	1431	UA	245	N17245	EWR	PBI	147	1023	11	29	2023-11-10 11:00:00	Other
28619	9	10	1718	1454	144	1854	1639	UA	687	N422UA	EWR	RDU	71	416	14	54	2023-09-10 14:00:00	Other
28622	11	9	1625	1559	26	1745	1713	DL	503	N103DU	LGA	BOS	56	184	15	59	2023-11-09 15:00:00	BOS
28624	3	2	2309	2100	129	38	2230	OO	1226	N247SY	JFK	IAD	57	228	21	0	2023-03-02 21:00:00	Other
28627	6	12	1825	1740	45	2140	2117	DL	261	N106DN	JFK	SLC	261	1990	17	40	2023-06-12 17:00:00	Other
28628	3	16	1934	1920	14	2159	2202	9E	1461	N135EV	LGA	JAX	113	833	19	20	2023-03-16 19:00:00	Other
28644	2	27	2207	2154	13	23	2328	UA	519	N37253	EWR	ORD	111	719	21	54	2023-02-27 21:00:00	ORD
28649	7	30	704	612	52	903	832	UA	358	N487UA	EWR	ATL	100	746	6	12	2023-07-30 06:00:00	ATL
28653	1	3	1824	1720	64	2128	2022	NK	1165	N685NK	EWR	MCO	131	937	17	20	2023-01-03 17:00:00	MCO
28656	6	20	1412	1300	72	1818	1548	UA	579	N14102	EWR	MCO	209	937	13	0	2023-06-20 13:00:00	MCO
28663	12	17	949	825	84	1243	1146	DL	254	N130DU	LGA	DFW	203	1389	8	25	2023-12-17 08:00:00	Other
28669	9	6	1212	1200	12	1510	1507	B6	832	N977JE	JFK	LAX	315	2475	12	0	2023-09-06 12:00:00	LAX
28671	4	8	2119	1950	89	7	2256	B6	176	N606JB	LGA	FLL	151	1076	19	50	2023-04-08 19:00:00	FLL
28672	1	25	2051	1929	82	2237	2109	YX	1469	N128HQ	JFK	DCA	69	213	19	29	2023-01-25 19:00:00	Other
28673	3	20	2234	2200	34	2346	2311	UA	307	N484UA	EWR	SYR	47	195	22	0	2023-03-20 22:00:00	Other
28675	12	18	1016	955	21	1220	1210	NK	520	N624NK	EWR	CHS	99	628	9	55	2023-12-18 09:00:00	Other
28688	5	19	1856	1842	14	2204	2157	UA	748	N62884	EWR	SEA	323	2402	18	42	2023-05-19 18:00:00	Other
28699	11	30	1647	1553	54	1835	1757	AA	217	N744P	LGA	DTW	80	502	15	53	2023-11-30 15:00:00	Other
28701	8	17	1606	1553	13	1907	1924	DL	461	N114DN	LGA	FLL	160	1076	15	53	2023-08-17 15:00:00	FLL
28703	2	27	859	730	89	1142	1033	B6	239	N643JB	JFK	MCO	134	944	7	30	2023-02-27 07:00:00	MCO
28712	6	29	1700	1629	31	1104	1857	UA	745	N832UA	LGA	DEN	NA	1620	16	29	2023-06-29 16:00:00	Other
28719	12	28	2140	2129	11	2238	2244	AA	841	N773XF	LGA	BOS	33	184	21	29	2023-12-28 21:00:00	BOS
28738	1	26	1311	1159	72	1423	1325	9E	1488	N479PX	LGA	ROC	48	254	11	59	2023-01-26 11:00:00	Other
28742	5	24	2126	2113	13	26	2359	UA	843	N17301	EWR	MCO	127	937	21	13	2023-05-24 21:00:00	MCO
28743	2	4	1244	1030	134	1425	1245	YX	1584	N213JQ	LGA	STL	136	888	10	30	2023-02-04 10:00:00	Other
28744	8	19	1740	1725	15	2052	2030	B6	103	N583JB	JFK	BUR	335	2465	17	25	2023-08-19 17:00:00	Other
28747	1	15	914	855	19	1103	1114	9E	1429	N176PQ	JFK	DTW	80	509	8	55	2023-01-15 08:00:00	Other
28757	1	11	1232	930	182	1339	1059	YX	1773	N210JQ	JFK	DCA	45	213	9	30	2023-01-11 09:00:00	Other
28762	7	22	1701	1539	82	1947	1844	UA	462	N14242	EWR	FLL	147	1065	15	39	2023-07-22 15:00:00	FLL
28767	11	17	1718	1707	11	1848	1848	UA	673	N37577	EWR	ORD	117	719	17	7	2023-11-17 17:00:00	ORD
28782	7	13	1202	1116	46	1347	1309	9E	1284	N331PQ	LGA	RDU	70	431	11	16	2023-07-13 11:00:00	Other
28790	7	24	2120	2025	55	2342	2243	UA	260	N75433	EWR	PHX	276	2133	20	25	2023-07-24 20:00:00	Other
28813	7	28	1048	930	78	1258	1154	YX	935	N749YX	EWR	TVC	98	644	9	30	2023-07-28 09:00:00	Other
28817	9	24	1133	959	94	1411	1301	UA	464	N29717	EWR	AUS	188	1504	9	59	2023-09-24 09:00:00	Other
28818	2	23	1137	950	107	1237	1111	9E	1318	N296PQ	LGA	PVD	26	143	9	50	2023-02-23 09:00:00	Other
28822	7	18	11	2255	76	222	118	F9	472	N606FR	LGA	ATL	109	762	22	55	2023-07-18 22:00:00	ATL
28827	9	25	1941	1843	58	2108	2005	UA	673	N467UA	EWR	BOS	52	200	18	43	2023-09-25 18:00:00	BOS
28833	1	22	2149	2120	29	2327	2249	YX	1826	N215JQ	LGA	IAD	57	229	21	20	2023-01-22 21:00:00	Other
28842	3	26	1916	1750	86	2124	1955	NK	53	N655NK	LGA	DTW	93	502	17	50	2023-03-26 17:00:00	Other
28846	4	14	1758	1725	33	1952	1929	9E	1323	N315PQ	JFK	RDU	69	427	17	25	2023-04-14 17:00:00	Other
28857	7	14	1014	915	59	1220	1114	9E	1292	N306PQ	JFK	CLE	77	425	9	15	2023-07-14 09:00:00	Other
28859	6	20	1144	1113	31	1319	1308	YX	1374	N116HQ	LGA	CMH	74	479	11	13	2023-06-20 11:00:00	Other
28866	7	23	2257	2100	117	8	2230	UA	104	N37518	EWR	BNA	106	748	21	0	2023-07-23 21:00:00	Other
28868	9	10	1829	1759	30	2232	2109	B6	962	N923JB	JFK	LAX	341	2475	17	59	2023-09-10 17:00:00	LAX
28874	6	18	951	937	14	1042	1050	B6	513	N283JB	JFK	MVY	37	173	9	37	2023-06-18 09:00:00	Other
28880	9	13	750	620	90	934	841	UA	379	N811UA	LGA	DEN	205	1620	6	20	2023-09-13 06:00:00	Other
28890	8	10	1832	1815	17	2219	2127	AA	595	N949NN	LGA	MIA	187	1096	18	15	2023-08-10 18:00:00	MIA
28893	3	9	139	2340	119	554	425	B6	334	N591JB	JFK	BQN	178	1576	23	40	2023-03-09 23:00:00	Other
28906	1	15	2217	2159	18	2306	2300	YX	1737	N210JQ	LGA	BDL	28	101	21	59	2023-01-15 21:00:00	Other
28909	2	25	1417	1355	22	1727	1700	WN	683	N207WN	LGA	TPA	153	1010	13	55	2023-02-25 13:00:00	Other
28910	3	14	1201	1130	31	1410	1402	DL	875	N340NB	LGA	MSY	169	1183	11	30	2023-03-14 11:00:00	Other
28912	7	27	2128	2040	48	38	2304	B6	746	N187JB	LGA	ATL	106	762	20	40	2023-07-27 20:00:00	ATL
28918	10	14	1341	1330	11	1641	1630	YX	1245	N126HQ	LGA	OKC	214	1341	13	30	2023-10-14 13:00:00	Other
28922	9	11	1341	1235	66	1628	1533	B6	29	N507JT	JFK	MCO	138	944	12	35	2023-09-11 12:00:00	MCO
28926	7	1	1353	1334	19	1528	1451	B6	505	N323JB	JFK	BOS	37	187	13	34	2023-07-01 13:00:00	BOS
28928	8	28	2114	2102	12	2258	2304	UA	489	N37456	EWR	MSP	135	1008	21	2	2023-08-28 21:00:00	Other
28932	6	4	1345	1330	15	1453	1442	B6	39	N339JB	JFK	SYR	47	209	13	30	2023-06-04 13:00:00	Other
28935	4	14	2115	2055	20	2320	2248	YX	958	N745YX	EWR	GSO	73	445	20	55	2023-04-14 20:00:00	Other
28944	10	9	2137	2110	27	2349	9	DL	137	N534DT	JFK	LAS	286	2248	21	10	2023-10-09 21:00:00	Other
28947	5	4	1824	1754	30	2149	2104	UA	545	N67815	EWR	SAN	341	2425	17	54	2023-05-04 17:00:00	Other
28962	4	17	1709	1655	14	1959	2005	AS	80	N953AK	EWR	SEA	323	2402	16	55	2023-04-17 16:00:00	Other
28965	3	18	825	715	70	1203	952	DL	251	N717TW	JFK	PHX	301	2153	7	15	2023-03-18 07:00:00	Other
28967	1	14	1525	1500	25	1835	1854	DL	417	N809DN	JFK	PHX	282	2153	15	0	2023-01-14 15:00:00	Other
28969	12	15	1742	1729	13	2046	2050	B6	70	N934JB	JFK	SEA	332	2422	17	29	2023-12-15 17:00:00	Other
28970	2	21	1730	1716	14	1912	1830	UA	701	N17294	EWR	BOS	48	200	17	16	2023-02-21 17:00:00	BOS
28976	1	13	653	620	33	953	1001	AA	531	N417AN	EWR	PHX	273	2133	6	20	2023-01-13 06:00:00	Other
28977	6	16	2040	1826	134	2319	2158	B6	49	N966JT	JFK	SMF	312	2521	18	26	2023-06-16 18:00:00	Other
28979	6	5	2119	2057	22	2246	2237	YX	1096	N748YX	EWR	PIT	52	319	20	57	2023-06-05 20:00:00	Other
28982	5	24	1604	1510	54	1830	1816	UA	394	N27251	EWR	AUS	190	1504	15	10	2023-05-24 15:00:00	Other
29002	8	13	1210	915	175	1329	1035	B6	707	N274JB	LGA	BOS	39	184	9	15	2023-08-13 09:00:00	BOS
29004	2	25	1944	1825	79	2239	2138	AA	225	N301PA	JFK	DFW	202	1391	18	25	2023-02-25 18:00:00	Other
29007	1	4	2128	2045	43	2305	2208	UA	500	N17272	EWR	BUF	52	282	20	45	2023-01-04 20:00:00	Other
29014	6	30	1549	1402	107	1719	1535	UA	831	N894UA	EWR	STL	119	872	14	2	2023-06-30 14:00:00	Other
29022	3	14	1016	919	57	1257	1158	YX	1753	N228JQ	LGA	SDF	103	659	9	19	2023-03-14 09:00:00	Other
29027	9	28	2344	2045	179	253	17	B6	296	N929JB	JFK	SFO	338	2586	20	45	2023-09-28 20:00:00	Other
29030	7	20	2117	2029	48	52	2357	AS	17	N282AK	JFK	SFO	346	2586	20	29	2023-07-20 20:00:00	Other
29050	6	27	846	828	18	956	959	9E	1481	N915XJ	LGA	BUF	52	292	8	28	2023-06-27 08:00:00	Other
29052	8	10	1821	1755	26	2028	2025	WN	322	N8557Q	LGA	DEN	223	1620	17	55	2023-08-10 17:00:00	Other
29053	2	28	1634	1535	59	1744	1654	B6	409	N318JB	JFK	BOS	44	187	15	35	2023-02-28 15:00:00	BOS
29057	10	19	1356	1259	57	1543	1535	AA	972	N326RP	JFK	PHX	267	2153	12	59	2023-10-19 12:00:00	Other
29062	6	25	1822	1642	100	2211	2017	B6	263	N554JB	JFK	SJC	364	2569	16	42	2023-06-25 16:00:00	Other
29075	1	14	1435	1355	40	1734	1700	B6	635	N206JB	JFK	MCO	129	944	13	55	2023-01-14 13:00:00	MCO
29076	9	8	1802	1503	179	2051	1758	UA	69	N27268	EWR	PBI	134	1023	15	3	2023-09-08 15:00:00	Other
29080	11	3	1011	1000	11	1222	1207	AA	623	N880NN	LGA	CLT	93	544	10	0	2023-11-03 10:00:00	CLT
29083	12	24	2257	2155	62	7	2316	UA	207	N69888	EWR	BTV	49	266	21	55	2023-12-24 21:00:00	Other
29089	7	16	2047	1920	87	27	2235	DL	141	N179DN	JFK	LAX	317	2475	19	20	2023-07-16 19:00:00	LAX
29101	6	16	744	705	39	948	932	UA	459	N27271	EWR	PHX	281	2133	7	5	2023-06-16 07:00:00	Other
29109	8	30	2022	2000	22	2141	2139	B6	739	N354JB	JFK	BUF	51	301	20	0	2023-08-30 20:00:00	Other
29110	7	4	1807	1650	77	1950	1854	YX	990	N417YX	LGA	DSM	137	1031	16	50	2023-07-04 16:00:00	Other
29118	1	22	717	2125	592	844	2247	YX	1783	N245JQ	LGA	ROC	48	254	21	25	2023-01-22 21:00:00	Other
29120	5	7	2232	2135	57	2347	2303	OO	1100	N253SY	JFK	IAD	45	228	21	35	2023-05-07 21:00:00	Other
29127	2	25	1547	1531	16	1733	1713	B6	282	N3008J	JFK	MKE	147	745	15	31	2023-02-25 15:00:00	Other
29129	9	22	646	630	16	929	916	B6	85	N591JB	LGA	MCO	135	950	6	30	2023-09-22 06:00:00	MCO
29135	1	22	2237	2000	157	35	2121	YX	1727	N217JQ	LGA	BOS	42	184	20	0	2023-01-22 20:00:00	BOS
29137	12	10	1731	1705	26	1926	1913	DL	876	N315DN	LGA	DTW	83	502	17	5	2023-12-10 17:00:00	Other
29140	7	26	1940	1830	70	2218	2120	UA	585	N77520	EWR	MCO	124	937	18	30	2023-07-26 18:00:00	MCO
29141	12	23	1555	1508	47	1840	1820	DL	355	N307DX	LGA	PBI	142	1035	15	8	2023-12-23 15:00:00	Other
29142	6	26	2208	1859	189	NA	2105	AA	784	N8030F	JFK	CLT	NA	541	18	59	2023-06-26 18:00:00	CLT
29143	9	15	2011	1948	23	19	2357	UA	570	N37561	EWR	SJU	216	1608	19	48	2023-09-15 19:00:00	Other
29146	12	17	1725	1523	122	2033	1725	YX	1260	N445YX	JFK	RDU	84	427	15	23	2023-12-17 15:00:00	Other
29147	10	18	2042	2030	12	2151	2201	B6	2	N229JB	JFK	BUF	52	301	20	30	2023-10-18 20:00:00	Other
29157	7	26	2039	1900	99	2153	2030	UA	522	N453UA	EWR	BNA	98	748	19	0	2023-07-26 19:00:00	Other
29166	3	30	1837	1825	12	2031	2020	WN	644	N210WN	LGA	STL	143	888	18	25	2023-03-30 18:00:00	Other
29167	6	7	823	810	13	1039	1101	B6	149	N972JT	JFK	LAS	283	2248	8	10	2023-06-07 08:00:00	Other
29170	11	14	1802	1735	27	2048	2041	AS	89	N481AS	EWR	SAN	317	2425	17	35	2023-11-14 17:00:00	Other
29184	7	25	1852	1359	293	2210	1723	B6	575	N521JB	LGA	RSW	166	1080	13	59	2023-07-25 13:00:00	Other
29187	3	5	1541	1530	11	2024	2026	B6	998	N627JB	JFK	SJU	191	1598	15	30	2023-03-05 15:00:00	Other
29194	3	28	1126	927	119	1354	1116	YX	1182	N654RW	EWR	RDU	105	416	9	27	2023-03-28 09:00:00	Other
29195	1	2	626	555	31	747	717	B6	1056	N229JB	JFK	BUF	65	301	5	55	2023-01-02 05:00:00	Other
29201	8	3	1652	1459	113	1835	1708	YX	981	N867RW	JFK	CLE	75	425	14	59	2023-08-03 14:00:00	Other
29220	6	26	2053	1930	83	NA	2257	B6	376	N2039J	JFK	PDX	NA	2454	19	30	2023-06-26 19:00:00	Other
29222	4	15	1611	1520	51	1921	1847	B6	45	N586JB	JFK	RSW	147	1074	15	20	2023-04-15 15:00:00	Other
29223	11	2	1308	1237	31	1418	1346	9E	1620	N912XJ	LGA	BGM	33	147	12	37	2023-11-02 12:00:00	Other
29224	8	4	2057	1955	62	2313	2215	9E	1126	N605LR	LGA	CVG	90	585	19	55	2023-08-04 19:00:00	Other
29225	1	11	1658	1535	83	1945	1857	UA	302	N654UA	EWR	IAH	196	1400	15	35	2023-01-11 15:00:00	Other

Hier sind die Faktorstufen von dest:

flights_train4$dest |> levels()

 [1] "ATL"   "BOS"   "CLT"   "DFW"   "FLL"   "LAX"   "MCO"   "MIA"   "ORD"  
[10] "RDU"   "SFO"   "Other"

Visusalsieren wir die Häufigkeit der Faktorstufen:

flights_train4 %>%
  count(dest) %>%
  ggplot() +
  aes(y = fct_reorder(dest, n), x = n) +
  geom_col()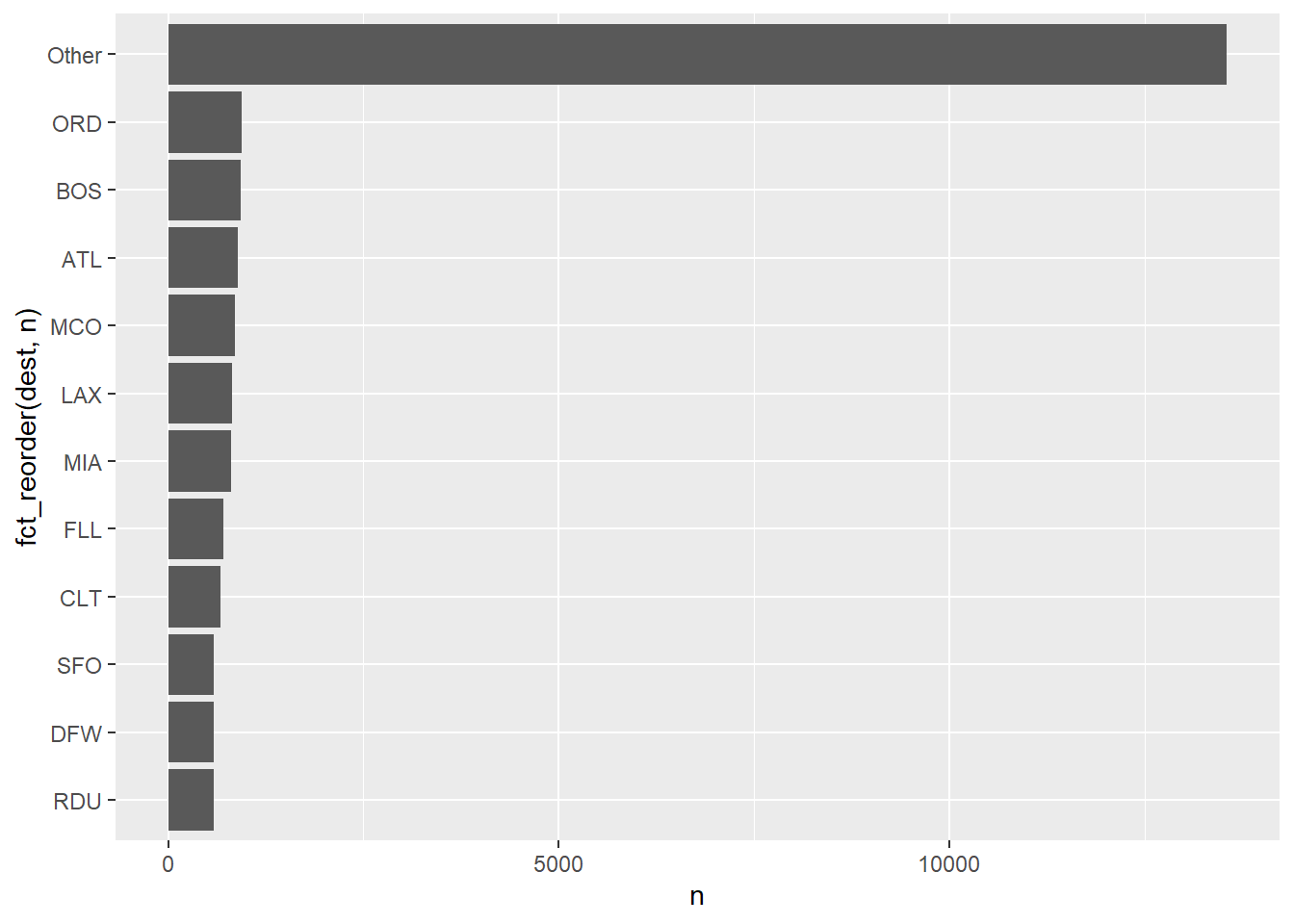

13 flights_test4

Vergessen wir nicht, die Transformation auch auf das Test-Sample anzuwenden:

flights_test4 <-
  flights_test3 %>% 
  mutate(across(
    .cols = where(is.factor),
    .fns = fct_lump_prop, prop = .025
  ))

Wichtig! Im Alle Faktorstufen, die im Test-Set vorkommen, müssen auch im Train-Set vorkommen. Sonst können wir das Regressionsmodell nicht berechnen.

levels(flights_test4$dest) 

 [1] "ATL"   "BOS"   "CLT"   "DFW"   "FLL"   "LAX"   "MCO"   "MIA"   "ORD"  
[10] "Other"

levels(flights_train4$dest)

 [1] "ATL"   "BOS"   "CLT"   "DFW"   "FLL"   "LAX"   "MCO"   "MIA"   "ORD"  
[10] "RDU"   "SFO"   "Other"

Das sieht gut aus: Alle Faktorstufen im Test-Set sind im Train-Set enthalten.

14 lm3: Alle zusammengefassten Faktorvariablen

lm3 <- flights_train4 %>% 
  select(dep_delay, where(is.factor), -tailnum, -id) %>% 
  lm(dep_delay ~ ., data = .)

Achtung! Falls ein Faktor nur über eine einzige Faktorstufe verfügt, wird das Regressionsmodell zusammenbrechen mit einer Fehlermeldung. Adios!

Der Punkt bei dep_delay ~ . meint “nimm alle Variablen im Datensatz (bis auf dep_delay)”.

Der Punkt bei data = . nimm die Tabelle, wie sie dir im letzten Schritt mundgerecht aufbereitet wurde. Man hätte hier auch flights_train4 schreiben können, aber dann hätten wir noch tailnum etc. entfernen müssen.

Eigentlich brauchen wir nicht so viele Dezimalstellen …

options(digits = 2)

model_parameters(lm3)  # Modellkoeffizienten, also die Beta-Gewichte ("estimate")

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	8.87	2.4	0.95	4.1	13.66	3.63	21897	0.00
carrierAA	4.76	1.9	0.95	1.1	8.38	2.57	21897	0.01
carrierB6	15.25	1.5	0.95	12.2	18.25	9.94	21897	0.00
carrierDL	5.90	1.5	0.95	2.9	8.93	3.82	21897	0.00
carrierNK	5.98	2.4	0.95	1.2	10.73	2.47	21897	0.01
carrierUA	8.90	1.7	0.95	5.5	12.25	5.20	21897	0.00
carrierWN	8.89	2.5	0.95	3.9	13.83	3.52	21897	0.00
carrierYX	-4.18	1.4	0.95	-6.9	-1.43	-2.98	21897	0.00
carrierOther	9.39	2.3	0.95	4.9	13.85	4.13	21897	0.00
originJFK	0.42	1.2	0.95	-2.0	2.87	0.34	21897	0.74
originLGA	-1.96	1.1	0.95	-4.2	0.28	-1.71	21897	0.09
destBOS	0.60	2.7	0.95	-4.6	5.83	0.23	21897	0.82
destCLT	1.41	3.0	0.95	-4.5	7.29	0.47	21897	0.64
destDFW	2.07	3.1	0.95	-3.9	8.08	0.68	21897	0.50
destFLL	2.30	2.8	0.95	-3.3	7.86	0.81	21897	0.42
destLAX	-0.77	2.7	0.95	-6.1	4.60	-0.28	21897	0.78
destMCO	6.49	2.7	0.95	1.2	11.75	2.42	21897	0.02
destMIA	-1.99	2.8	0.95	-7.5	3.55	-0.70	21897	0.48
destORD	0.89	2.7	0.95	-4.3	6.13	0.33	21897	0.74
destRDU	2.16	3.0	0.95	-3.8	8.15	0.71	21897	0.48
destSFO	-1.05	3.0	0.95	-7.0	4.85	-0.35	21897	0.73
destOther	-0.07	2.0	0.95	-4.0	3.84	-0.03	21897	0.97

Wie man sieht, wird eine nominalskalierte Variable mit vielen Stufen in entsprechend (viele!) binäre Variablen umgewandelt, die jeweils einen Regressionskoeffizienten ergeben.

r2(lm3)  # R^2

# R2 for Linear Regression
       R2: 0.016
  adj. R2: 0.015

Ein mageres R-Quadrat.

15 lm4: Alle metrischen Variablen

Was sind noch mal unsere metrischen Variablen:

flights_train4 %>% 
  select(where(is.numeric)) %>% 
  names()

 [1] "id"             "month"          "day"            "dep_time"      
 [5] "sched_dep_time" "dep_delay"      "arr_time"       "sched_arr_time"
 [9] "flight"         "air_time"       "distance"       "hour"          
[13] "minute"        

Ok, jetzt eine Regression mit diesen Variablen (ober ohne die ID-Variable):

lm4 <- 
  flights_train4 %>% 
  select(dep_delay, where(is.numeric), -id) %>% 
  lm(dep_delay ~ ., data = .)

r2(lm4)

# R2 for Linear Regression
       R2: 0.061
  adj. R2: 0.061

Tja, das \(R^2\) hat einen nicht gerade um …

16 lm5: Alle metrischen und alle (zusammengefassten) nominalen Variablen

Welche Variablen sind jetzt alle an Bord?

flights_train4 %>% 
  names()

 [1] "id"             "month"          "day"            "dep_time"      
 [5] "sched_dep_time" "dep_delay"      "arr_time"       "sched_arr_time"
 [9] "carrier"        "flight"         "tailnum"        "origin"        
[13] "dest"           "air_time"       "distance"       "hour"          
[17] "minute"         "time_hour"     

time_hour nehmen wir noch einmal raus, da es zum einen redundant ist zu hour etc. und zum anderen noch zusätzlicher Aufbereitung bedarf.

flights_train4 %>% 
  select(minute) %>% 
  describe_distribution()

Variable	Mean	SD	IQR	Min	Max	Skewness	Kurtosis	n	n_Missing
minute	29	20	35	0	59	0.02	-1.2	21919	0

flights_train4 <- 
  flights_train4 %>% 
  select(-time_hour, -tailnum, -id, -minute)    # "minute" machte Probleme, besser rausnehmen
  
lm5 <-lm(dep_delay ~ ., data = flights_train4)

r2(lm5)

# R2 for Linear Regression
       R2: 0.068
  adj. R2: 0.067

Der Vorhersage-Gott ist nicht mit uns. Vielleicht sollten wir zu einem ehrlichen Metier als Schuhverkäufer umsatteln …

17 flights_train5: Fehlenden Werte ersetzen

flights_train4 |> 
  describe_distribution() |> 
  select(Variable, n_Missing)

Variable	n_Missing
month	0
day	0
dep_time	0
sched_dep_time	0
dep_delay	0
arr_time	40
sched_arr_time	0
flight	0
air_time	98
distance	0
hour	0

Glücklicherweise haben wir nicht zu viele fehlende Werte. Bei der Größe der Stichprobe fällt die Anzahl wenig ins Gewicht. Aber zu Übungszwecken ersetzen wir mal die fehlenden Werte.

flights_train5 <-
  flights_train4 |> 
  mutate(air_time = replace_na(air_time, mean(air_time, na.rm = TRUE)))

18 lm6: Wie lm5, aber ohne fehlende Werte

lm6 <-lm(dep_delay ~ ., data = flights_train5)

r2(lm6)

# R2 for Linear Regression
       R2: 0.068
  adj. R2: 0.067

19 flights_train6: Extremwerte entfernen

library(DataExplorer)

flights_train5 |> 
  select(where(is.numeric)) |> 
  plot_density()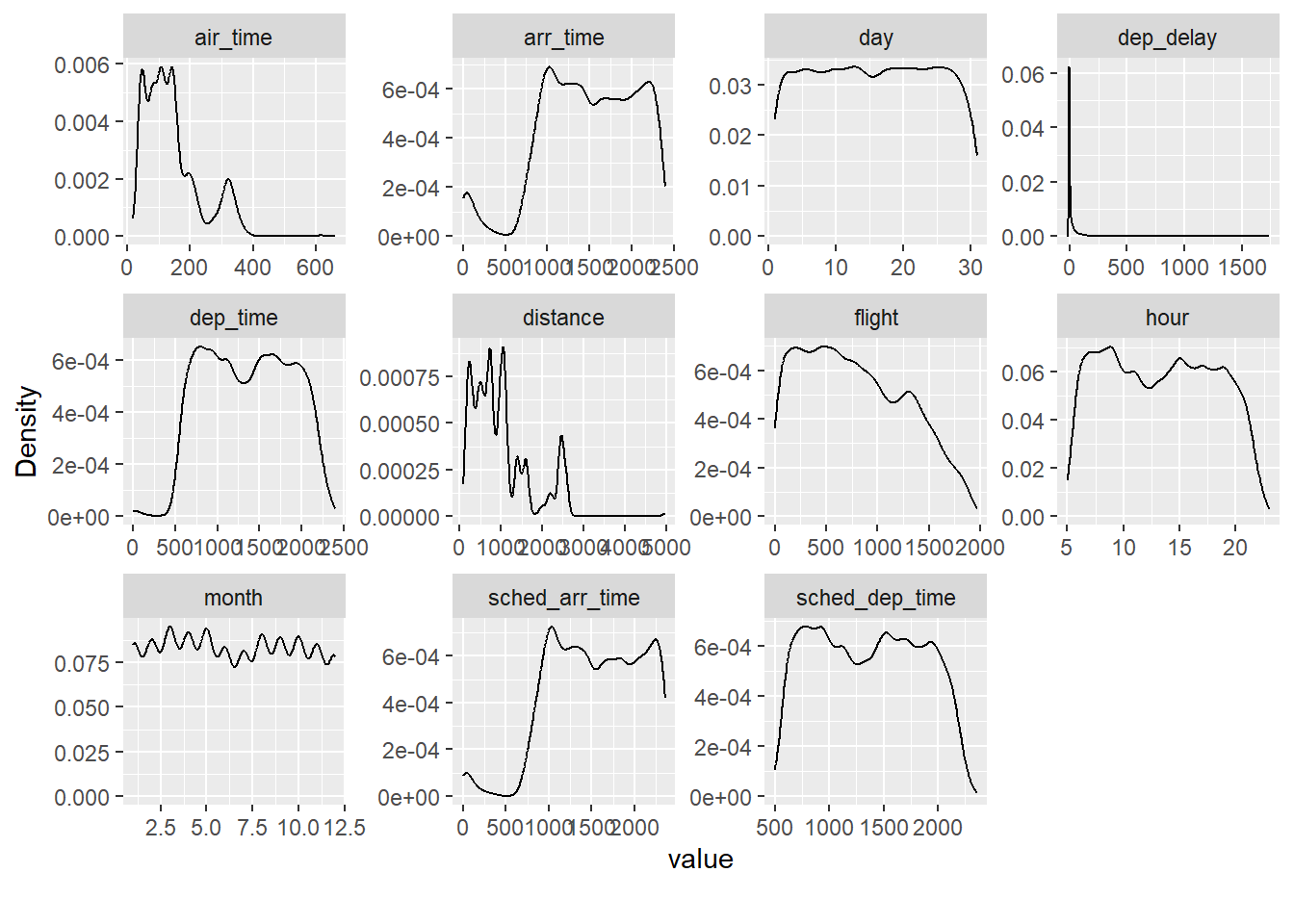

Es sieht so aus, als wäre air_time deutlich rechtsschief mit einigen Ausreißern.

Betrachten wir noch Boxplots, die auch gut Extermwerte visualisieren.

flights_train5 |> 
  select(where(is.numeric), "origin") |> 
  plot_boxplot(by = "origin")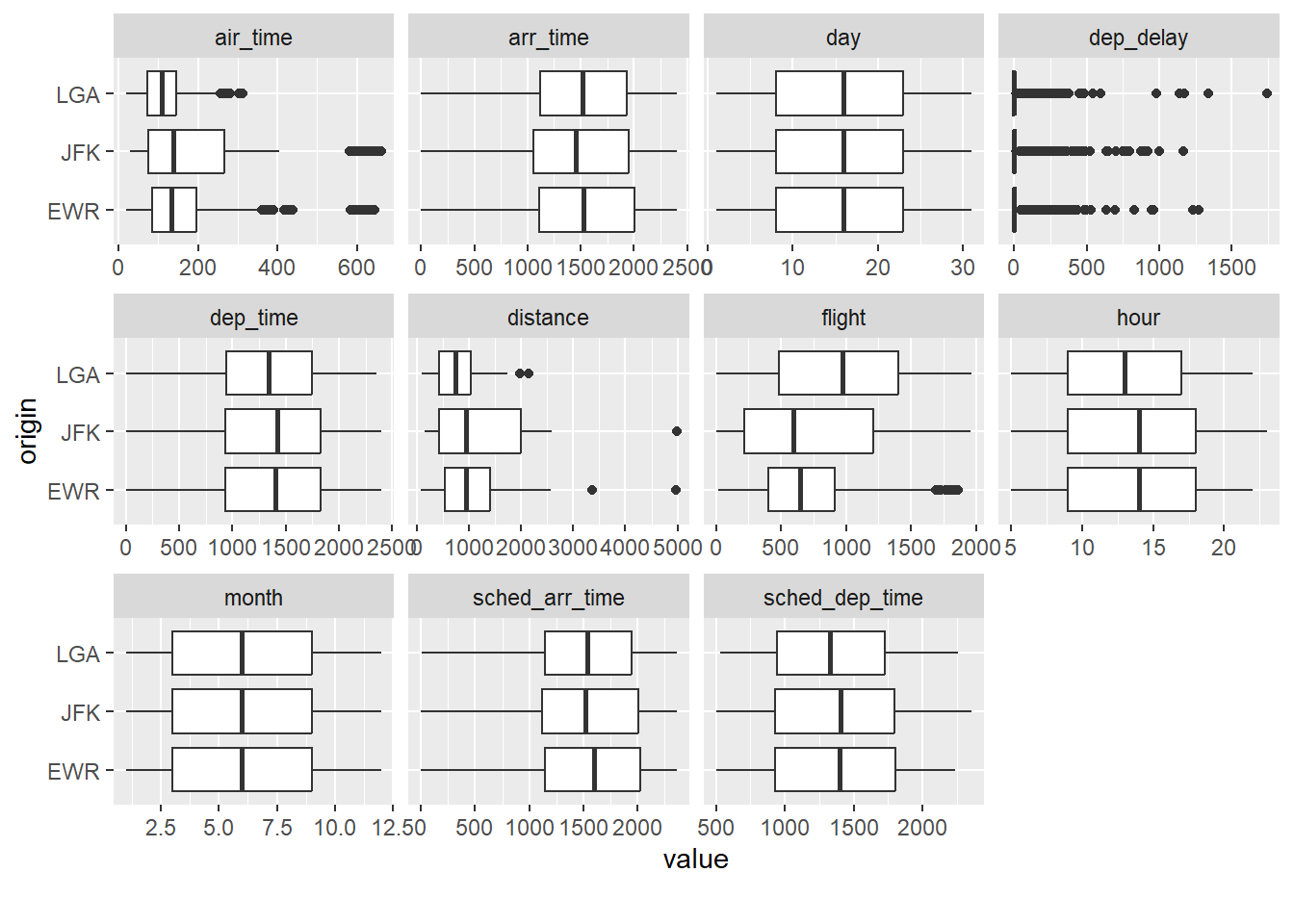

Eine gängige Methode, mit Extermwerten umzugehen, ist, alle Datenpunkte, die im Boxplot als alleinstehende Punkte gezeigt werden, durch den Median zu ersetzen. Achtung: Diese Methode ist nicht perfekt! Es gibt viel sophistiziertere Methoden.

Wir ersetzen dabei alle Werte von air_time, für die gilt, dass sie größer sind als Q3 + 1.5*IQR.

Q3:

flights_train5 |> 
  summarise(iqr_airtime = quantile(air_time, prob = .75))

iqr_airtime
177

IQR:

flights_train5 |> 
  summarise(iqr_airtime = IQR(air_time))

iqr_airtime
99

Der Grenzwert ist also:

(# Q3
  flights_train5 |> 
  summarise(iqr_airtime = quantile(air_time, prob = .75)) 
  ) +
  1.5 * 
 (# IQR
  flights_train5 |> 
  summarise(iqr_airtime = IQR(air_time)) 
 )

iqr_airtime
326

Der Median von air_time beträgt übrigens:

 flights_train5 |> 
  summarise(iqr_airtime = median(air_time)) 

iqr_airtime
122

flights_train6 <-
  flights_train5 |> 
  mutate(air_time = 
           case_when(air_time > 326 ~ 122,
                     TRUE ~ air_time))

Grob auf Deutsch übersetzt:

Wenn ein Flug eine air_time von mehr als 326 Minuten hat, dann sei die airtime gleich 122, ansonsten immer (“TRUE”) ist airtime gleich air_time, bleibt also, wie sie war.

20 lm7: Wie lm5, aber ohne Extremwerte für air_time

lm7 <-lm(dep_delay ~ ., data = flights_train6)

r2(lm7)

# R2 for Linear Regression
       R2: 0.069
  adj. R2: 0.067

Tja….

21 R2 im Testsample

\(R^2\) kann man übrigens auch so berechnen:

Zuerst fügen wir die Vorhersagen zum Datensatz hinzu:

flights_train7_pred <- 
  flights_train6 %>% 
  mutate(lm7_pred = predict(lm7, newdata = flights_train6))  

Dann berechnen wir das R-Quadrat mit der Funktion rsq (wie “r squared”) anhand der beiden relevanten Spalten:

flights_train7_pred %>% 
  rsq(truth = dep_delay,
      estimate = lm7_pred)

.metric	.estimator	.estimate
rsq	standard	0.07

Berechnen wir jetzt die Modellgüte im Testsample.

Fügen wir die Vorhersagewerte dem Testsample dazu:

flights_test4_pred <-
  flights_test4 %>% 
  mutate(pred_lm7 = predict(lm7, newdata = flights_test4))

Check:

flights_test4_pred %>% 
  select(id, dep_delay, pred_lm7) %>%
  head()

id	dep_delay	pred_lm7
1	-5	11.0
2	48	81.1
3	-1	4.3
4	-10	6.3
7	-3	17.9
8	5	27.9

test_rsq <- 
 tibble(model = "lm7") %>% 
  mutate(rsq = rsq_vec(truth = flights_test4_pred$dep_delay,
                       estimate = flights_test4_pred$pred_lm7))

test_rsq

model	rsq
lm7	0.08

Am schwierigsten ist es, bei den ganzen Nummerierungen nicht durcheinander zu kommen. Hier könnte es sich lohnen, ein übersichtlicheres Verfahren einzuführen (mit den Kosten höherer Komplexität).

Prüfen wir noch, wie viele fehlende Werte es bei den vorhergesagten Werten gibt:

flights_test4_pred %>% 
  summarise(pred_isna = sum(is.na(pred_lm7)),
            pred_isna_prop = pred_isna / nrow(flights_test4_pred))  # prop wie "proportion" (Anteil)

pred_isna	pred_isna_prop
29	0

Da fehlende Werte u.U. mit dem Mittelwert (der übrigen prognostizierten Werte) aufgefüllt werden, erledigen wir das gleich, um den Effekt auf \(R^2\) abzuschätzen:

flights_test4_pred2 <- 
flights_test4_pred %>% 
  mutate(pred_lm7 = replace_na(pred_lm7, mean(pred_lm7, na.rm = TRUE)))

flights_test4_pred2 %>% 
  summarise(sum(is.na(pred_lm7)))

sum(is.na(pred_lm7))
0

Keine fehlenden Werte mehr.

Wie sieht \(R^2\) jetzt aus?

flights_test4_pred2 %>% 
  rsq(truth = dep_delay, estimate = pred_lm7)

.metric	.estimator	.estimate
rsq	standard	0.08

Keine (nennenswerte) Veränderung.

22 Einreichen

Das beste Modell im Train-Sample reichen wir ein; in diesem Fall lm7.

submission_df <- 
flights_test4_pred2 |> 
  select(id, pred = pred_lm7)  # gleich umbenennen in "pred"

write_csv(submission_df, file = "Sauer_Sebastian_0123456_Prognose.csv")

23 Was noch?

23.1 Mehr geht immer…

Ein nächster Schritt könnte sein, sich folgende Punkte anzuschauen:

• Interaktionen
• Polynome
• Voraussetzungen

Eine Faustregel zu Interaktionen lautet: Wenn zwei Variablen jeweils einen starken Haupteffekt haben, lohnt es sich u.U., den Interaktionseffekt anzuschauen (vgl. Gelman & Hill, 2007, S. 69).

23.2 Tidymodels

Das ständige Updaten des Test-Datensatzes nervt; mit tidymodels wird es komfortabler und man hat Zugang zu leistungsfähigeren Prognosemodellen. Hier findet sich ein Einstieg und hier eine Fallstudie mit Tutorial.