library(tidyverse)
library(ggpubr)euro-bayes
Exercise
In Information Theory, Inference, and Learning Algorithms, stellt David MacKay folgendes Problem.
“A statistical statement appeared in The Guardian on Friday January 4, 2002:
When spun on edge 250 times, a Belgian one-euro coin came up heads 140 times and tails 110. ‘It looks very suspicious to me,’ said Barry Blight, a statistics lecturer at the London School of Economics. ‘If the coin were unbiased, the chance of getting a result as extreme as that would be less than 7%.’
But do these data give evidence that the coin is biased rather than fair?”
Wie wahrscheinlich ist es, dass die Münze (exakt) fair ist, im Lichte dieser Daten?
Hinweise:
- Untersuchen Sie die Hypothesen \(\pi_0 = 0, \pi_1 = 0.1, \pi_2 = 0.2, ..., \pi_{10} = 1\) für die Trefferwahrscheinlichkeit (Kopf; heads).
- Erstellen Sie ein Bayes-Gitter zur Lösung dieser Aufgabe.
- Gehen Sie davon aus, dass Sie indifferent gegenüber der Hypothesen zu den Parameterwerten der Münze sind.
- Geben Sie Prozentzahlen immer als Anteil an und lassen Sie die führende Null weg (z.B. .42).
Solution
d <-
tibble(
# definiere die Hypothesen (das "Gitter"):
p_Gitter = seq(from = 0, to = 1, by = 0.1),
# bestimme den Priori-Wert:
Priori = 1) %>%
mutate(
# berechne Likelihood für jeden Gitterwert:
Likelihood = dbinom(140, size = 250, prob = p_Gitter),
# berechen unstand. Posteriori-Werte:
unstd_Post = Likelihood * Priori,
# berechne stand. Posteriori-Werte (summiert zu 1):
Post = unstd_Post / sum(unstd_Post)) | p_Gitter | Priori | Likelihood | unstd_Post | Post |
|---|---|---|---|---|
| 0.0 | 1 | 0.00 | 0.00 | 0.00 |
| 0.1 | 1 | 0.00 | 0.00 | 0.00 |
| 0.2 | 1 | 0.00 | 0.00 | 0.00 |
| 0.3 | 1 | 0.00 | 0.00 | 0.00 |
| 0.4 | 1 | 0.00 | 0.00 | 0.00 |
| 0.5 | 1 | 0.01 | 0.01 | 0.27 |
| 0.6 | 1 | 0.02 | 0.02 | 0.73 |
| 0.7 | 1 | 0.00 | 0.00 | 0.00 |
| 0.8 | 1 | 0.00 | 0.00 | 0.00 |
| 0.9 | 1 | 0.00 | 0.00 | 0.00 |
| 1.0 | 1 | 0.00 | 0.00 | 0.00 |
Plotten mit ggplot:
d %>%
ggplot(aes(x=p_Gitter, y = Post)) +
geom_line()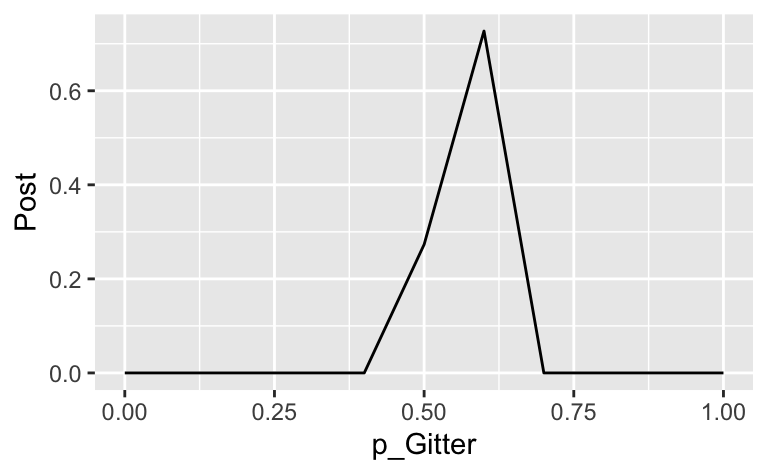
Oder mit ggpubr plotten:
ggline(d, x = "p_Gitter", y = "Post", add = "mean_se",
xlab = "Trefferwahrscheinlichkeit", ylab = "Posteriori-Wahrscheinlichkeit")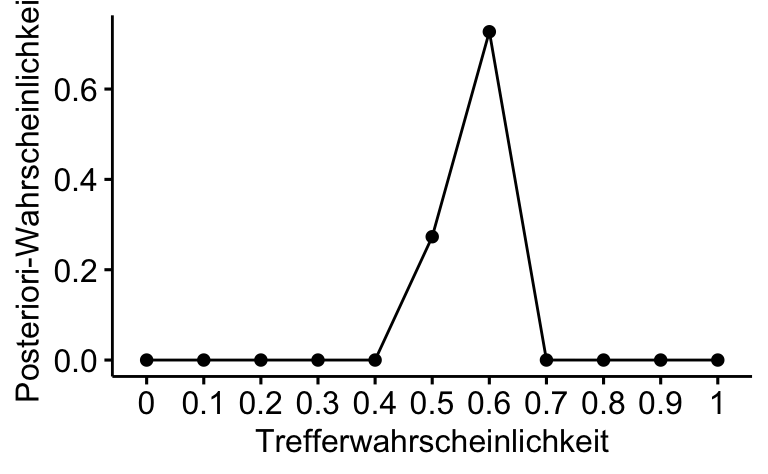
Die Wahrscheinlichkeit \(Pr(\pi = 1/2 \, | \, X=140)\) wenn \(X \sim Bin(250, 1/2)\) beträgt ca. 27% oder .27.
Allerdings würden viele Statistiker:innen nicht (nur) fragen, wie wahrscheinlich 140 Treffer sind. Stattdessen könnte man von folgender Überlegung ausgehen.
Zuerst: Welcher Wert wäre am wahrscheinlichsten, wenn die Münze fair wäre?
dbinom(x = 0:250, size = 250, prob = 1/2) %>% which.max()[1] 126Der 126. Wert in der Liste 0:250 ist der wahrscheinlichste (also 125 Treffer).
Wenn die Münze fair ist, dann wären doch 15 Treffer mehr als 125 genauso so unwahrscheinlich wie 15 Treffer weniger als 125 Treffer. Beide Ereignisse - 110 und 140 Treffer - sind ja gleich weit entfernt von denjenigen Wert, der am wahrscheinlichsten ist, wenn die Münze fair ist.
Eine Statistikerin würde also eher fragen: “Wie wahrscheinlich ist es, dass man ein Ergebnis erhält, dass mind. 15 Treffer entfernt ist von der Trefferzahl, die bei einer fairen Münze zu erwarten ist?”. Aber genug davon für diese Aufgabe :-)
Categories:
- probability
- bayesbox