einsamkeit-modellierung

bayes
regression
fopro
yacsda
Published

June 12, 2025

1 Fallstudie zur Einsamkeitsinduktion

In dieser Fallstudie wird eine studentische Studie vorgestellt, die untersucht, inwieweit Einsamkeit induziert werden kann und welche Effekte die Einsamkeitsinduktion auf das aktuelle Befinden hat.

Das Design ist reichhaltig und lässt viele Analysen zu. Bei diesem Post liegt der Fokus auf der Modellierung der Forschungsfrage.

1.1 Forschungsfrage und Hypothesen

Hat die Induktion (ind) von Einsamkeit einen Effekt auf die wahrgenommenen Einsamkeit (lonely) ?

Insgesamt wird zwei Mal Einsamkeit induziert:

H1: Die Induktion 1 (ind1) verringert die Einsamkeit (Geschichte über Einsamkeit oder neutral)

H2: Die Induktion 2 (ind2) verringert die Einsamkeit (“einsame” Musik oder neutral)

1.2 DAG (Kausalgraph)

Es handelt sich um eine Kausalanalyse, da man am Effekt der Intervention auf die Einsamkeit interessiert ist.

graph LR
  ind1 --> lonely
  ind2 --> lonely
  u --> lonely

1.3 Forschungsdesign

UV1: Einsamkeitsinduktion 1 (Geschichte)

UV2: Einsamkeitsinduktion 2 (Musik)

AV: Einsamkeit

2 Hinweise

Beachten Sie die üblichen Hinweise des Datenwerks.

3 Setup

4 Daten importieren

url <- "https://github.com/sebastiansauer/Datenwerk/raw/refs/heads/main/posts/einsamkeit-modellierung/einsamkeit.csv"
d <- read_csv(url)

Check:

glimpse(d)
Rows: 44
Columns: 21
$ Proband_ID                    <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1…
$ Gruppe                        <dbl> 3, 2, 1, 4, 2, 1, 4, 3, 1, 2, 4, 3, 3, 1…
$ Geschichte                    <chr> "neutrale", "einsame", "neutrale", "eins…
$ Musik                         <chr> "neutrale", "neutrale", "einsame", "eins…
$ SAM_Pleasure_f1               <dbl> 7, 7, 9, 7, 7, 7, 5, 9, 5, 9, 7, 7, 7, 9…
$ SAM_Pleasure_f2               <dbl> 7, 7, 7, 5, 5, 7, 5, 7, 7, 9, 7, 7, 7, 9…
$ SAM_Pleasure_f3               <dbl> 9, 5, 5, 9, 7, 9, 5, 9, 9, 9, 3, 9, 7, 9…
$ SAM_Arousal_f1                <dbl> 3, 1, 3, 7, 5, 3, 3, 5, 5, 7, 3, 5, 1, 3…
$ SAM_Arousal_f2                <dbl> 5, 1, 1, 5, 3, 3, 3, 3, 3, 3, 3, 3, 1, 5…
$ SAM_Arousal_f3                <dbl> 1, 1, 3, 7, 5, 3, 3, 1, 3, 1, 1, 5, 3, 5…
$ SAM_Dominance_f1              <dbl> 5, 5, 9, 7, 7, 7, 5, 7, 3, 7, 3, 5, 7, 5…
$ SAM_Dominance_f2              <dbl> 5, 5, 7, 5, 3, 7, 3, 7, 5, 7, 7, 5, 7, 7…
$ SAM_Dominance_f3              <dbl> 5, 3, 3, 7, 3, 7, 3, 9, 5, 7, 7, 5, 7, 9…
$ Loneliness_mean_f1            <dbl> 1.4, 1.2, 2.2, 1.6, 2.2, 1.4, 2.4, 1.8, …
$ Loneliness_mean_f2            <dbl> 1.2, 1.8, 2.2, 1.6, 2.0, 1.2, 2.4, 1.4, …
$ Loneliness_mean_f3            <dbl> 1.0, 1.8, 2.0, 1.2, 2.0, 1.2, 2.4, 1.4, …
$ Godspeed_Anthropo_mean_f3     <dbl> 2.8, 2.0, 1.0, 2.8, 2.0, 3.8, 1.2, 3.4, …
$ Godspeed_Animacy_mean_f3      <dbl> 3.833333, 2.000000, 2.166667, 3.500000, …
$ Godspeed_Likeability_mean_f3  <dbl> 5.0, 2.8, 2.2, 4.4, 3.0, 4.4, 3.0, 4.8, …
$ Godspeed_Intelligence_mean_f3 <dbl> 3.8, 2.6, 2.6, 3.4, 2.6, 4.4, 2.8, 3.4, …
$ Godspeed_Safety_mean_f3       <dbl> 3.666667, 5.000000, 2.000000, 2.333333, …
d |> 
  describe_distribution() |> 
  kable(digits = 2)
Variable Mean SD IQR Min Max Skewness Kurtosis n n_Missing
Proband_ID 22.50 12.85 22.50 1.0 44.00 0.00 -1.20 44 0
Gruppe 2.50 1.13 2.50 1.0 4.00 0.00 -1.38 44 0
SAM_Pleasure_f1 7.23 1.24 1.50 5.0 9.00 -0.07 -0.29 44 0
SAM_Pleasure_f2 6.59 1.70 2.00 3.0 9.00 -0.53 -0.06 44 0
SAM_Pleasure_f3 7.50 1.56 2.00 3.0 9.00 -0.79 0.11 44 0
SAM_Arousal_f1 3.64 1.92 2.00 1.0 9.00 0.47 0.13 44 0
SAM_Arousal_f2 3.68 2.02 2.00 1.0 9.00 0.53 -0.16 44 0
SAM_Arousal_f3 3.59 1.91 2.00 1.0 9.00 0.54 0.25 44 0
SAM_Dominance_f1 5.68 1.88 2.00 1.0 9.00 -0.22 0.57 44 0
SAM_Dominance_f2 5.27 2.00 2.00 1.0 9.00 -0.29 -0.10 44 0
SAM_Dominance_f3 5.18 1.92 3.50 1.0 9.00 -0.02 -0.13 44 0
Loneliness_mean_f1 1.92 0.34 0.60 1.2 2.60 -0.05 -0.72 44 0
Loneliness_mean_f2 1.95 0.38 0.60 1.2 2.80 0.12 -0.41 44 0
Loneliness_mean_f3 1.92 0.39 0.60 1.0 2.80 0.00 0.18 44 0
Godspeed_Anthropo_mean_f3 2.20 0.79 1.15 1.0 4.00 0.37 -0.46 44 0
Godspeed_Animacy_mean_f3 2.96 0.75 0.96 1.0 4.17 -0.70 0.14 44 0
Godspeed_Likeability_mean_f3 3.83 0.76 1.00 2.0 5.00 -0.44 -0.22 44 0
Godspeed_Intelligence_mean_f3 3.31 0.74 1.20 2.0 5.00 0.42 -0.30 44 0
Godspeed_Safety_mean_f3 3.92 0.77 1.25 2.0 5.00 -0.59 0.09 44 0

5 Ablauf

graph LR
  Start --> Messung_t1 --> Intervention1 --> Messung_t2 --> Intervention2 --> Messung_t3 --> Ende

Die Intervention ist in diesem Fall die Induktion von Einsamkeit.

Es handelt sich um Between-Desing mit Vorher-Nachher-Messung, auch als “Veränderungsmessung” oder Veränderungsdesign bezeichnet.

Die Versuchspersonen durchlaufen nicht die gleichen Bedingungen, sondern verschiedene: einige Probanden sind in der Experimentalgruppe, andere in der Kontrollgruppe.

Schauen wir genauer zur ersten Intervention:

graph LR
  Messung_t1 --> Intervention1 --> Messung_t2

Es gibt zwei Gruppen, die Experimentalgruppe bekommt die Einsamkeit, die Kontrollgruppe die neutrale Bedingung:

graph LR
  Messung_t1 --> G1[Einsamkeits-Induktion] 
  Messung_t1 --> G2[Kontrollgruppe]
  G1 --> Messung_t2 
  G2 --> Messung_t2

6 Berechnung der Deltavariablen

Bei Veränderungsdesigns muss man die Veränderung von einem Messzeitpunkt zum anderen berechnen, pro Person. Dazwischen muss eine Intervention liegen. Dieser Veränderung nennen wir delta, sie misst den kausalen Effekt der Intervention. Je größer das (mittlere) Delta zwischen den Gruppen, desto größer der Effekt.

d_delta <-
  d |> 
  mutate(loneliness_delta1 = Loneliness_mean_f2 - Loneliness_mean_f1,
         loneliness_delta2 = Loneliness_mean_f3 - Loneliness_mean_f2,
         loneliness_delta3 = Loneliness_mean_f3 - Loneliness_mean_f1 )

Visualisierung der Delta-Variablen:

graph LR
  Start --> Messung_t1 --> Intervention1 --> Messung_t2 --> Intervention2 --> Messung_t3
  Messung_t2 -- delta1 --> Messung_t1
  Messung_t3 -- delta2 --> Messung_t2
  Messung_t3 -- delta3 --> Messung_t1

Puh, das ist unübersichtlich. Vielleicht ist die Berechnung der Delta-Variablen so übersichtlicher:

graph LR
  Messung_t2 -- delta1 --> Messung_t1
  Messung_t3 -- delta2 --> Messung_t2
  Messung_t3 -- delta3 --> Messung_t1

7 Modellierung

7.1 Delta 1

7.1.1 Modell

mod_delta1 <- stan_glm(loneliness_delta1 ~ Geschichte, data = d_delta)

Mit lm würde das genau so funktionieren. Nur ohne die Ergebnisse einfach probabilistisch interpretieren zu können.

Ergebnisse:

parameters(mod_delta1) |> 
  print_md()
Parameter Median 95% CI pd Rhat ESS Prior
(Intercept) 0.07 (-0.03, 0.18) 90.53% 1.000 3590.00 Normal (0.02 +- 0.63)
Geschichteneutrale -0.10 (-0.24, 0.05) 90.33% 1.000 3766.00 Normal (0.00 +- 1.25)

Die Nullhypothese kann nicht verworfen werden.

7.1.2 Visualisierung

plot(parameters(mod_delta1))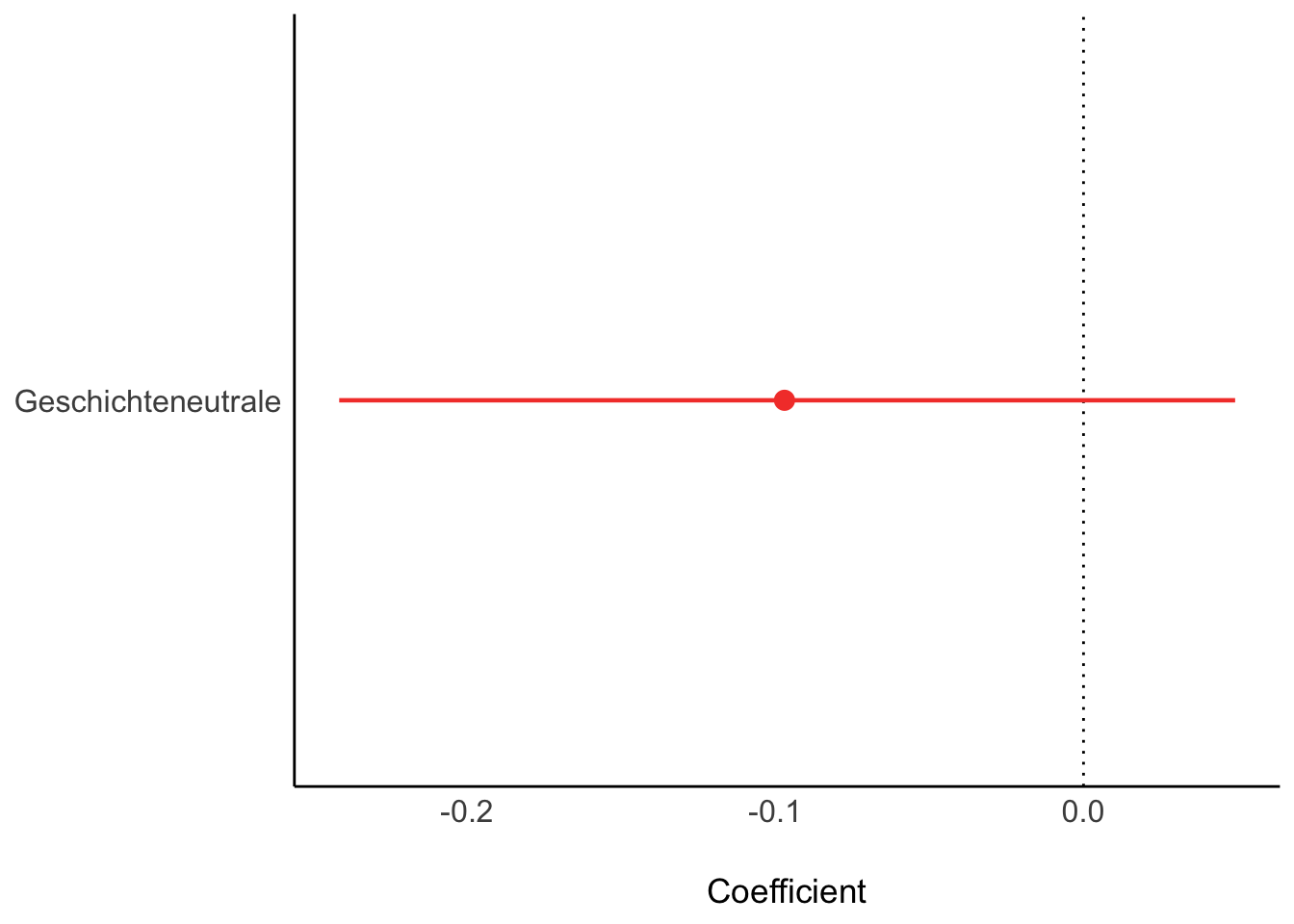

7.1.3 Modellgüte

r2(mod_delta1)
# Bayesian R2 with Compatibility Interval

  Conditional R2: 0.037 (95% CI [8.275e-09, 0.164])

Tja, die Intervention war leider nicht so stark. Aber so ist es nun Mal im harten Forscherleben …

mod_delta1_rope <- rope(mod_delta1)

plot(mod_delta1_rope)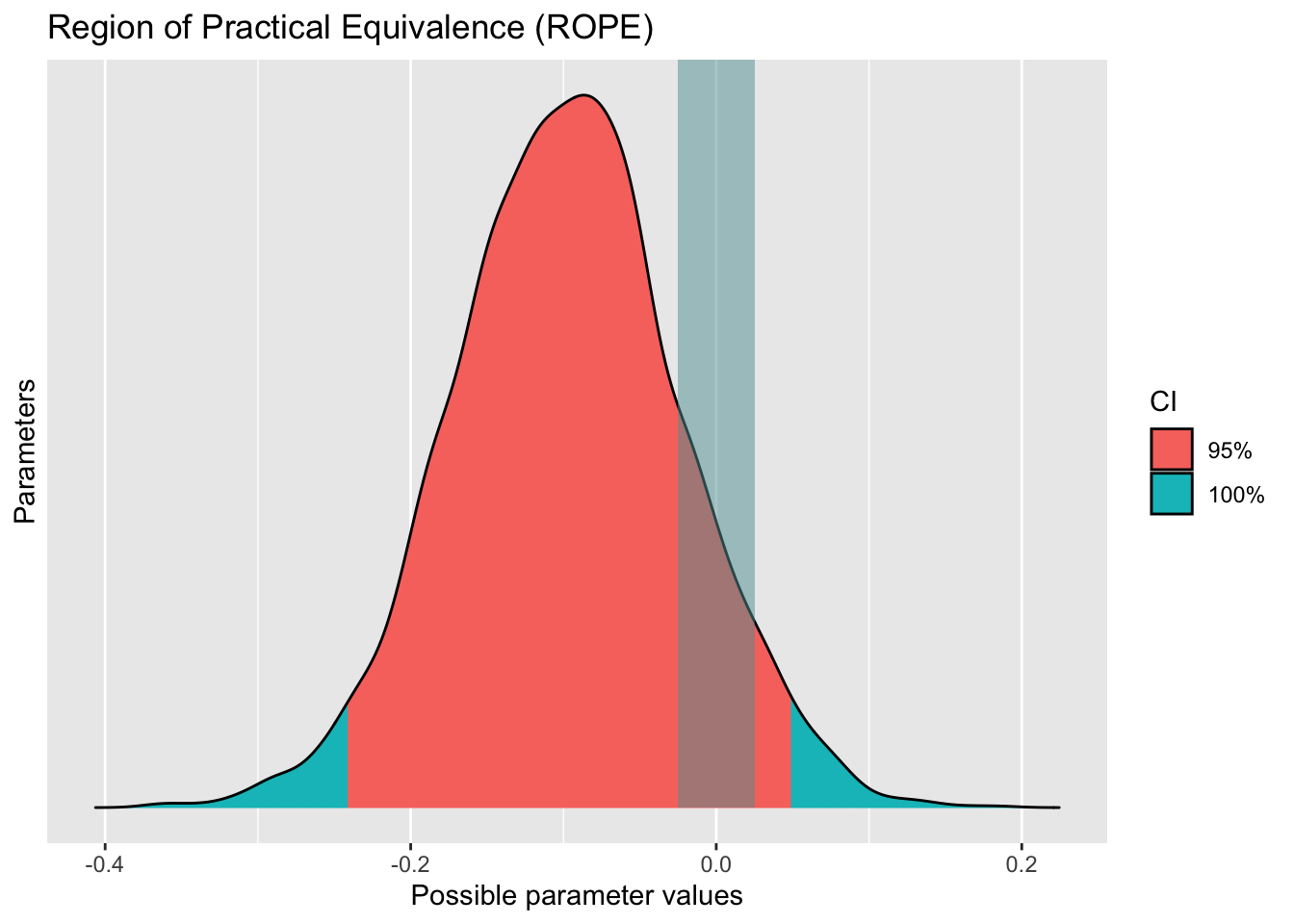

7.2 Delta 2 und 3

… analog

8 Deskriptive Analyse

8.1 Visualisierung

8.1.1 Delta 1

Hier ist die Veränderung der Einsamkeit von Messung t1 zu Messung t2, aufgeteilt nach den beiden Gruppen.

ggboxplot(d_delta, x = "Geschichte", y = "loneliness_delta1",
          add = "jitter")

Tja, leider kein starker Effekt zu erkennen.

d_long <- 
d |> 
  select(Proband_ID, Geschichte, starts_with("Loneliness")) |> 
  pivot_longer(cols = starts_with("Loneliness"),
               names_to = "Messzeitpunkt",
               values_to = "Einsamkeit") |> 
  mutate(t = as.integer(str_extract(Messzeitpunkt, "\\d")))  # Messzeitpunkt als Zahl: 1,2,3
d_long |> 
  head() |> 
  kable(digits = 2)
Proband_ID Geschichte Messzeitpunkt Einsamkeit t
1 neutrale Loneliness_mean_f1 1.4 1
1 neutrale Loneliness_mean_f2 1.2 2
1 neutrale Loneliness_mean_f3 1.0 3
2 einsame Loneliness_mean_f1 1.2 1
2 einsame Loneliness_mean_f2 1.8 2
2 einsame Loneliness_mean_f3 1.8 3 
d_long |>
  ggboxplot(x = "t", y = "Einsamkeit", add = "jitter",
            color = "Geschichte")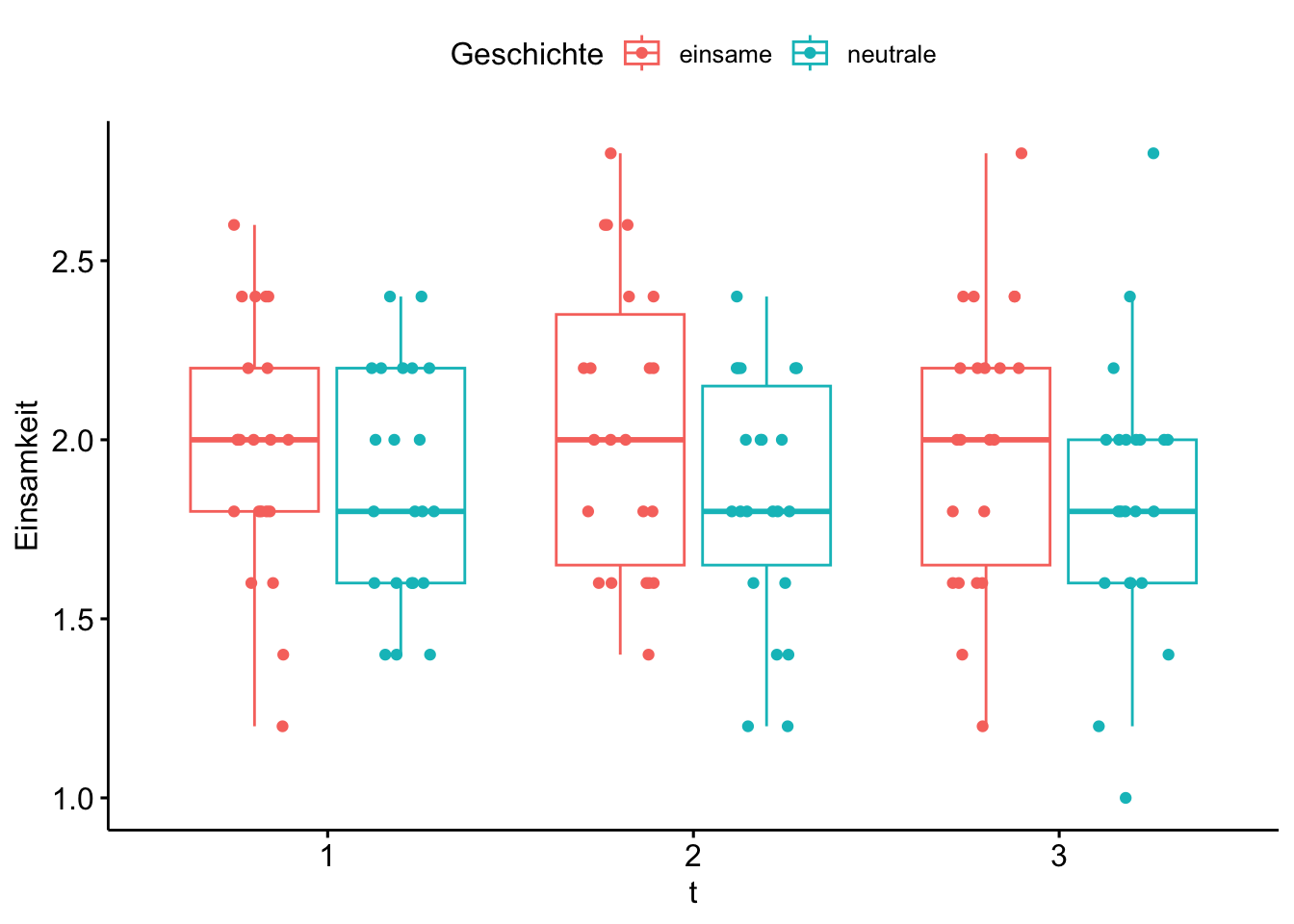

Es ist wenig Effekt zu erkennen. Interessanterweise hat die Gruppe der Einsamkeits-Intervention von vornherein einen höheren Wert in Einsamkeit. Das ist psychologisch interessant und sollte näher untersucht werden.

Andere Visualisierung:

d_long |> 
  ggsummarystats(x = "t",
                 y = "Einsamkeit",
                 ggfunc = ggline,
                 add = "median_iqr",
                 color = "Geschichte",
                 position = position_dodge(width = 0.1),
                 heights  = c(0.6, 0.4),
                 caption = "Error bars show median and IQR")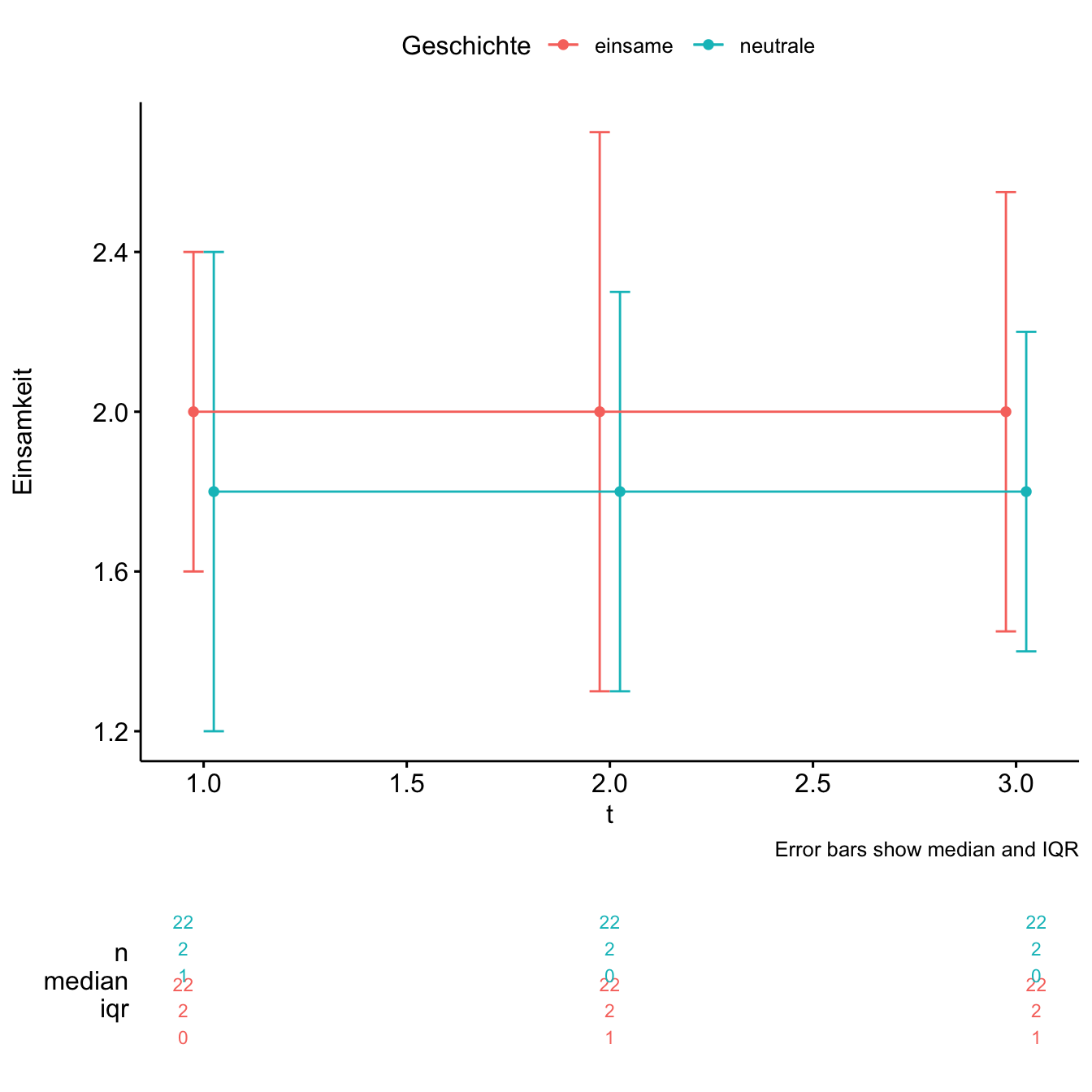

8.1.2 Delta 2 und 3

… analog

8.2 Statistiken pro Gruppe

d_delta |> 
  select(Geschichte, loneliness_delta1) |> 
  group_by(Geschichte) |> 
  summarise(delta1_mean = mean(loneliness_delta1),
            delta1_sd = sd(loneliness_delta1))
Geschichte delta1_mean delta1_sd
einsame 0.0727273 0.2930656
neutrale -0.0272727 0.1980424

9 Fazit

Veränderung-Designs analysiert man im einfachsten Fall mit Hilfe von Delta-Variablen.

In dieser Studie sind zwei UVs hintereinander gelegt. Das macht aber nichts, man kann sie getrennt voneinander analysieren.