November 12, 2024
Ordnen Sie die folgenden Diagrammen von Verteilungen den richtigen Namen (der Verteilung zu).
A
B
C
D
A - Binomialverteilung
B - Normalverteilung
C - Gleichverteilung
D - Expontialverteilung
Bildquelle:
Coded by Rasmus Bååth
rasmus.baath@lucs.lu.se www.sumsar.net
---
# gleich diese Datei in einem Ordner mit Namen der Aufgabe abspeichern!
date: 2024-11-12
draft: false # ACHTUNG DRAFT STEHT AUF TRUE!
title: distros # HIER TITEL DES POSTS EINGEBEN.
execute:
echo: false
eval: true
highlight-style: arrow
cache: true
toc: true
number-sections: true
extype: string
exsolution: ""
exshuffle: no
categories:
- probability # ENTER CATEGORIES HERE
- distributions
- paper
bibliography: "../../library-ses.bib"
knitr:
opts_chunk:
out.width: "75%"
---
# Aufgabe
Ordnen Sie die folgenden Diagrammen von Verteilungen den richtigen Namen (der Verteilung zu).
```{r}
#| echo: false
# Coded by Rasmus Bååth
# rasmus.baath@lucs.lu.se
# www.sumsar.net
# If you modify the code, please keep this header. Thanks!
plot_dist <- function(dist, labels=c(), scale = 1, color="skyblue", plot_dist_name=T) {
old_par <- par(mar = c(0.3, 0, 0, 0), xaxt='n', yaxt='n',ann=FALSE, bty="n", xpd=NA)
x <- dist$x
y <- do.call(dist$ddist, c(list(x=x), dist$ddist_params))
# To always anchor the plot at zero and give some extra top space if neccecary.
plot(c(x[1:2], x), c(0, max(y) / (1- dist$top_space), y), type="l", col="transparent")
# only draw where the distribution is not zero
points_to_NA <- filter(c(0, y, 0), filter=c(1,1, 1)) == 0
points_to_NA <- points_to_NA[-c(1, length(points_to_NA))]
y[points_to_NA] <- NA
if("bar" %in% dist$plot_type) {
lines(x, y, type="h", col=color, lwd=6, lend=1)
# Using legend to draw a white transparent box behind the text
if(plot_dist_name) {
legend(grconvertX(dist$name_pos[1], from="npc"), grconvertY(dist$name_pos[2], from="npc"),
dist$name, cex=1.5 * scale, xjust=0.5, yjust=0.5, bty="o", box.lwd = 0, box.col="transparent",
bg=rgb(1,1, 1,0.5),x.intersp=-1, y.intersp=0 , text.col="transparent")
}
}
if("line" %in% dist$plot_type) {
lines(x, y, type="l", col=color, lwd=3 * scale)
}
lines(grconvertX(c(0.037, (1 - 0.037)), from="npc"), grconvertY(c(-0.02,-0.02), from="npc"), lwd=2 * scale)
if(plot_dist_name) {
text(grconvertX(dist$name_pos[1], from="npc"), grconvertY(dist$name_pos[2], from="npc"), dist$name, cex=1.5 * scale)
}
if(is.character(names(labels))) {
for(label_name in names(labels)) {
xpos <- dist$labels[[label_name]][1]
ypos <- dist$labels[[label_name]][2]
label <- labels[label_name]
text(grconvertX(xpos, from="npc"), grconvertY(ypos, from="npc"), label, cex=2 * scale)
}
} else {
for(i in seq_along(labels)) {
xpos <- dist$labels[[i]][1]
ypos <- dist$labels[[i]][2]
label <- labels[i]
text(grconvertX(xpos, from="npc"), grconvertY(ypos, from="npc"), label, cex=2)
}
}
par(old_par)
}
dists <- list(
normal = list(
# Name of the distribution to be displayed in the plot
name = "???",
# Position of the name in the plot
name_pos = c(0.5, 0.1),
# Plot type, "line" for a line plots and "bar" for bar plots.
plot_type = "line",
# The values of the x-axis.
x = seq(-3.3, 3.3, 0.01),
# If top_space = 0 the distribution extends to the top of the graph, if
# 0 > top_space < 1 then that proportion of space is left at the top.
top_space = 0,
# The function defining the probability density function
ddist = dnorm,
# The arguments given to the probability density function (has to be named)
ddist_params = list(mean=0, sd=1),
# Coordinates and names for the parameter labels
labels = list(mean = c(0.5, 0.3), right_sd = c(0.80, 0.5), left_sd = c(0.20, 0.5))
),
beta = list(
name = "beta",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(0, 1, 0.01),
top_space = 0,
ddist = dbeta,
ddist_params = list(shape1=2, shape2=2),
labels = list(params=c(0.5, 0.4))
),
gamma = list(
name = "gamma",
name_pos = c(0.3, 0.1),
plot_type = "line",
x = seq(0, 2, 0.01),
top_space = 0,
ddist = dgamma,
ddist_params = list(shape=1.3, rate=2.5),
labels = list(params = c(0.60, 0.5))
),
inv_gamma = list(
name = "inv-gamma",
name_pos = c(0.42, 0.1),
plot_type = "line",
x = seq(0, 1.1, 0.01),
top_space = 0,
ddist = function(x, shape, scale) {scale^shape / gamma(shape) * x^(-shape-1)*exp(-scale/x)},
ddist_params = list(shape=3, scale=1),
labels = list(params = c(0.65, 0.5))
),
t = list(
name = "t distrib.",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(-3.0, 3.0, 0.01),
top_space = 0,
ddist = dt,
ddist_params = list(ncp=0, df=3),
labels = list(mean = c(0.5, 0.3), right_scale = c(0.75, 0.65), left_scale = c(0.25, 0.65),
right_df = c(0.90, 0.35), left_df = c(0.10, 0.35))
),
uniform = list(
name = "???",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(0, 1, 0.001),
top_space = 0.6,
ddist = dunif,
ddist_params = list(min=0.15, max=0.85),
labels = list(min=c(0.18,0.55), max=c(0.82,0.55))
),
bernoulli = list(
name = "Bernoulli",
name_pos = c(0.5, 0.1),
plot_type = "bar",
x = round(seq(-0.4, 1.4, 0.1), 1),
top_space = 0.0,
ddist = function(x, p) {ifelse(x == 1, p, ifelse(x==0, 1-p, 0))},
ddist_params = list(p=0.7),
labels = list(p = c(0.5, 0.6))
),
binomial = list(
name = "???",
name_pos = c(0.5, 0.1),
plot_type = "bar",
x = -2:10,
top_space = 0.2,
ddist = dbinom,
ddist_params = list(size=8, prob = 0.45),
labels = list(params = c(0.7, 0.68))
),
folded_t = list(
name = "folded t",
name_pos = c(0.3, 0.1),
plot_type = "line",
x = seq(0.0, 3.0, 0.01),
top_space = 0,
ddist = dt,
ddist_params = list(ncp=0, df=3),
labels = list(mean = c(0.15, 0.5), scale = c(0.43, 0.62), df = c(0.65, 0.4))
),
poisson = list(
name = "Poisson",
name_pos = c(0.3, 0.1),
plot_type = "bar",
x = seq(-1, 10.0, 1),
top_space = 0.0,
ddist = dpois,
ddist_params = list(lambda=2.5),
labels = list(lambda=c(0.60, 0.65))
),
chi_squared = list(
name = "chi-square",
name_pos = c(0.45, 0.1),
plot_type = "line",
x = seq(-1, 8, 0.01),
top_space = 0.0,
ddist = dchisq,
ddist_params = list(df=3),
labels = list(df=c(0.65, 0.60))
),
double_exponential = list(
name = "double exp.",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(-3, 3, 0.01),
top_space = 0,
ddist = function(x, mu, diversity) {diversity * exp(-diversity * abs(x - mu))/2},
ddist_params = list(mu=0, diversity=1),
labels = list(mean = c(0.5, 0.3), right_diversity = c(0.75, 0.5), left_diversity = c(0.25, 0.5))
),
exponential = list(
name = "???",
name_pos = c(0.37, 0.1),
plot_type = "line",
x = seq(0, 1.4, 0.01),
top_space = 0.1,
ddist = dexp,
ddist_params = list(rate=1.5),
labels = list(rate = c(0.55, 0.55))
),
F = list(
name = "F dist.",
name_pos = c(0.3, 0.1),
plot_type = "line",
x = seq(0, 5, 0.01),
top_space = 0,
ddist = df,
ddist_params = list(df1=5, df2=5),
labels = list(params = c(0.60, 0.5))
),
generalized_gamma = list(
name = "gen. gamma",
name_pos = c(0.45, 0.1),
plot_type = "line",
x = seq(0, 5, 0.01),
top_space = 0,
ddist = function(x, r, lambda, b) {(b*lambda^(b*r)*x^(b*r-1) * exp(-(lambda*x)^b ))/gamma(r)},
ddist_params = list(r=3, lambda=1, b=1.4),
labels = list(params = c(0.75, 0.75))
),
logistic = list(
name = "logistic",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(-4.5, 4.5, 0.01),
top_space = 0,
ddist = dlogis,
ddist_params = list(location=0, scale=1),
labels = list(location = c(0.5, 0.3), right_scale = c(0.80, 0.5), left_scale = c(0.20, 0.5))
),
log_normal = list(
name = "log-normal",
name_pos = c(0.48, 0.1),
plot_type = "line",
x = seq(0, 1.7, 0.01),
top_space = 0,
ddist = dlnorm,
ddist_params = list(meanlog=-0.3, sdlog=0.4),
labels = list(meanlog = c(0.43, 0.3), sdlog = c(0.70, 0.5))
),
noncentral_chi_squared = list(
name = "noncentral\nchi-square",
name_pos = c(0.45, 0.2),
plot_type = "line",
x = seq(0, 8, 0.01),
top_space = 0.3,
ddist = dchisq,
ddist_params = list(df=2, ncp=3),
labels = list(params=c(0.70, 0.65))
),
pareto = list(
name = "Pareto",
name_pos = c(0.65, 0.2),
plot_type = "line",
x = seq(0.1, 1, 0.01),
top_space = 0,
ddist = function(x, alpha, c) {alpha*c^alpha*x^-(alpha+1)},
ddist_params = list(alpha=2, c=1),
labels = list(params=c(0.30, 0.65))
),
weibull = list(
name = "Weibull",
name_pos = c(0.35, 0.1),
plot_type = "line",
x = seq(0, 2.5, 0.01),
top_space = 0,
ddist = dweibull,
ddist_params = list(shape=2.1, scale=1),
labels = list(params = c(0.70, 0.60))
),
beta_binomial = list(
name = "beta-binomial",
name_pos = c(0.5, 0.1),
plot_type = "bar",
x = seq(0, 1, 0.1),
top_space = 0,
ddist = dbeta,
ddist_params = list(shape1=2.7, shape2=2.7),
labels = list(params=c(0.5, 0.6))
),
categorical = list(
name = "categorical",
name_pos = c(0.5, 0.1),
plot_type = "bar",
x = 0:5,
top_space = 0.2,
ddist = function(x, p_cat) {
pd <- rep(0, length(x))
pd[x %in% seq_along(p_cat)] <- p_cat[x[x %in% seq_along(p_cat)]]/sum(p_cat)
pd
},
ddist_params = list(p_cat = c(1.5, 3.3, 2, 3)),
labels = list(params=c(0.5, 0.5))
),
noncentral_hypergeometric = list(
name = "noncentral\nhypergeom.",
name_pos = c(0.5, 0.2),
plot_type = "bar",
x = 0:12,
top_space = 0.0,
ddist = dhyper,
ddist_params = list(m=50, n=50, k=12),
labels = list(params=c(0.5, 0.6))
),
negative_binomial = list(
name = "neg. binomial",
name_pos = c(0.5, 0.1),
plot_type = "bar",
x = -2:10,
top_space = 0.1,
ddist = dnbinom,
ddist_params = list(size=25, prob = 0.90),
labels = list(p = c(0.65, 0.65))
),
shifted_exponential = list(
name = "shifted exp.",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(0, 7, 0.01),
top_space = 0.2,
ddist = function(x, rate, shift) {dexp(x - shift, rate)},
ddist_params = list(rate=0.35, shift = 1),
labels = list(params = c(0.6, 0.55))
),
right_censored_normal= list(
name = "r-cens.\nnormal",
name_pos = c(0.5, 0.2),
plot_type = "line",
x = seq(-3.3, 3.3, 0.01),
top_space = 0,
ddist = function(x, mean, sd, right_limit) {ifelse(x < right_limit, dnorm(x, mean, sd), 0)},
ddist_params = list(mean=0, sd=1, right_limit=1.75),
labels = list(mean = c(0.5, 0.45), right_sd = c(0.77, 0.60), right_limit=c(0.83,0.175),
left_sd = c(0.23, 0.60))
),
left_censored_normal= list(
name = "l-cens.\nnormal",
name_pos = c(0.5, 0.2),
plot_type = "line",
x = seq(-3.3, 3.3, 0.01),
top_space = 0,
ddist = function(x, mean, sd, left_limit) {ifelse(x > left_limit, dnorm(x, mean, sd), 0)},
ddist_params = list(mean=0, sd=1, left_limit=-1.75),
labels = list(mean = c(0.5, 0.45), right_sd = c(0.77, 0.60), left_limit=c(0.17,0.175),
left_sd = c(0.23, 0.60))
),
cauchy = list(
name = "Cauchy",
name_pos = c(0.5, 0.1),
plot_type = "line",
x = seq(-3.0, 3.0, 0.01),
top_space = 0,
ddist = dt,
ddist_params = list(ncp=0, df=1),
labels = list(location = c(0.5, 0.3), right_scale = c(0.77, 0.55), left_scale = c(0.23, 0.55))
),
half_t = list(
name = "half-t",
name_pos = c(0.3, 0.1),
plot_type = "line",
x = seq(0.0, 3.0, 0.01),
top_space = 0,
ddist = dt,
ddist_params = list(ncp=0, df=3),
labels = list(scale = c(0.43, 0.62), df = c(0.65, 0.4))
),
half_cauchy = list(
name = "half-Cauchy",
name_pos = c(0.36, 0.1),
plot_type = "line",
x = seq(0.0, 3.0, 0.01),
top_space = 0,
ddist = dt,
ddist_params = list(ncp=0, df=1),
labels = list(scale = c(0.53, 0.5))
),
half_normal = list(
name = "half-normal",
name_pos = c(0.36, 0.1),
plot_type = "line",
x = seq(0.0, 3.0, 0.01),
top_space = 0,
ddist = dnorm,
ddist_params = list(mean=0, sd=1),
labels = list(sd = c(0.53, 0.5))
)
)
plot_dist_svg <- function(dist, labels=c(), fname="", color="skyblue", plot_dist_name=T) {
if(fname == "") {
fname = paste(gsub("\\W", "", gsub("\\s", "_", dist$name)), ".svg", sep="")
}
svg(fname, width=2.25, height=1.688, bg="transparent")
plot_dist(dist, labels, color=color, plot_dist_name=plot_dist_name)
dev.off()
}
plot_dist_png <- function(dist, labels=c(), fname="", color="skyblue", plot_dist_name=T) {
if(fname == "") {
fname = paste(gsub("\\W", "", gsub("\\s", "_", dist$name)), ".png", sep="")
}
png(fname, width=165, height=123, bg="transparent", res=72, )
plot_dist(dist, labels, color=color, plot_dist_name=plot_dist_name)
dev.off()
}
# Function that renders text as an image. Useful for constructing images of equations.
# See ?plotmath for examples and documentation
plot_text_svg <- function(expr, fname) {
svg(fname, bg="transparent")
plot.new()
text(0.5, 0.5, expr)
dev.off()
}
plot_text_png <- function(expr, fname, pointsize=32, width=640, height=480 ) {
png(fname, bg="transparent", width=width, height=height, pointsize=pointsize)
plot.new()
text(0.5, 0.5, expr)
dev.off()
}
```
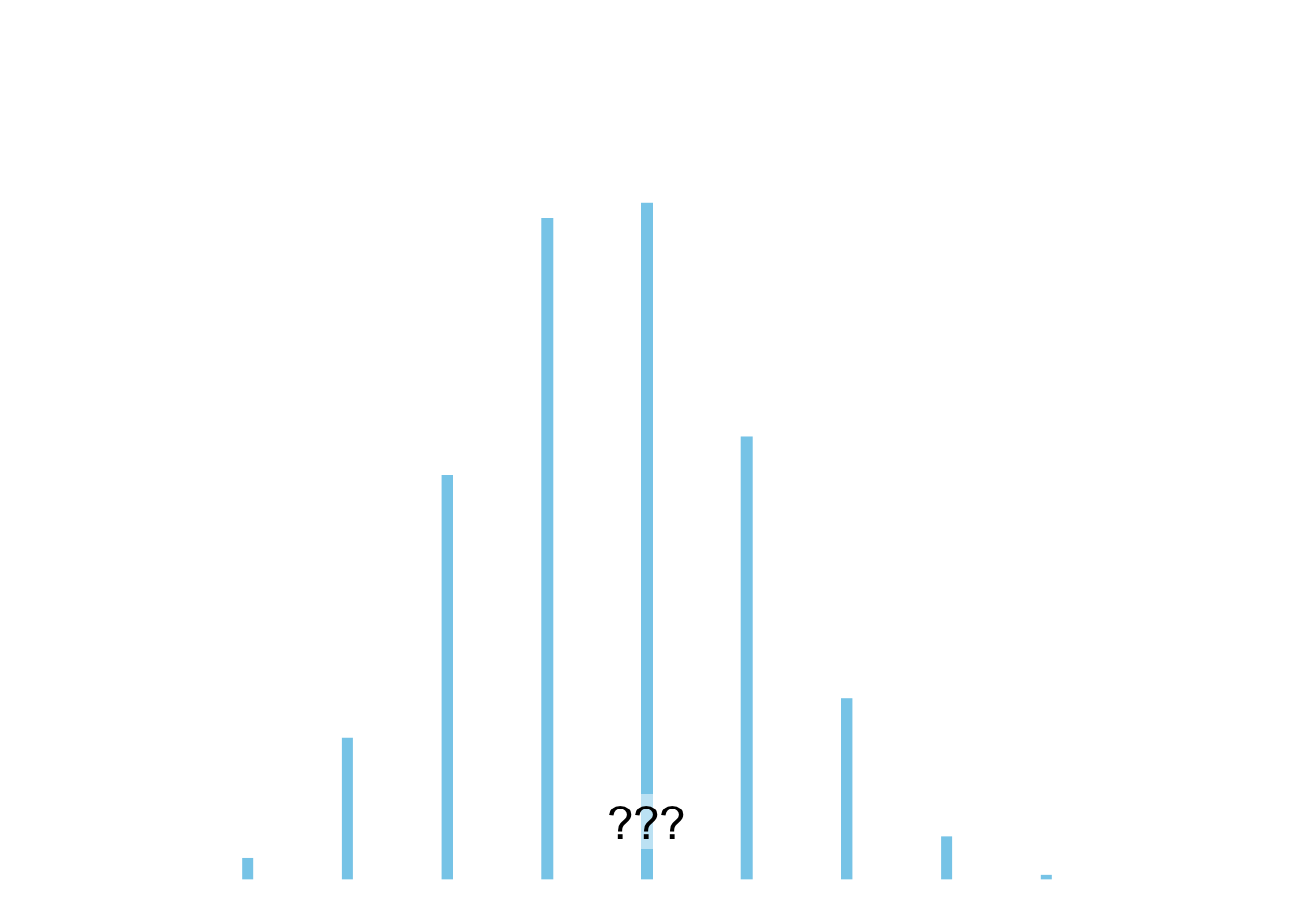
**A**
```{r}
plot_dist(dists$binomial)
```
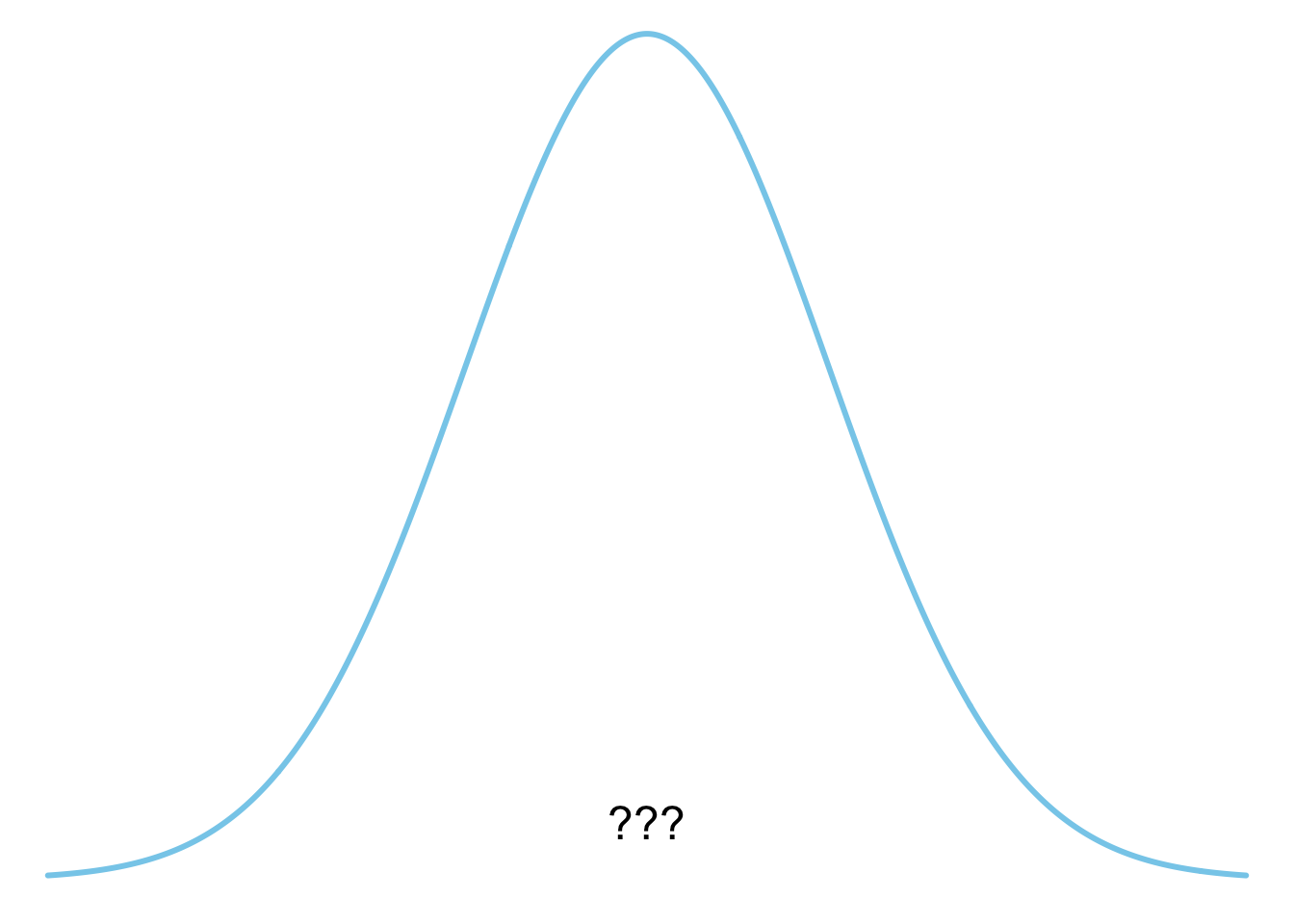
**B**
```{r}
plot_dist(dists$normal)
```
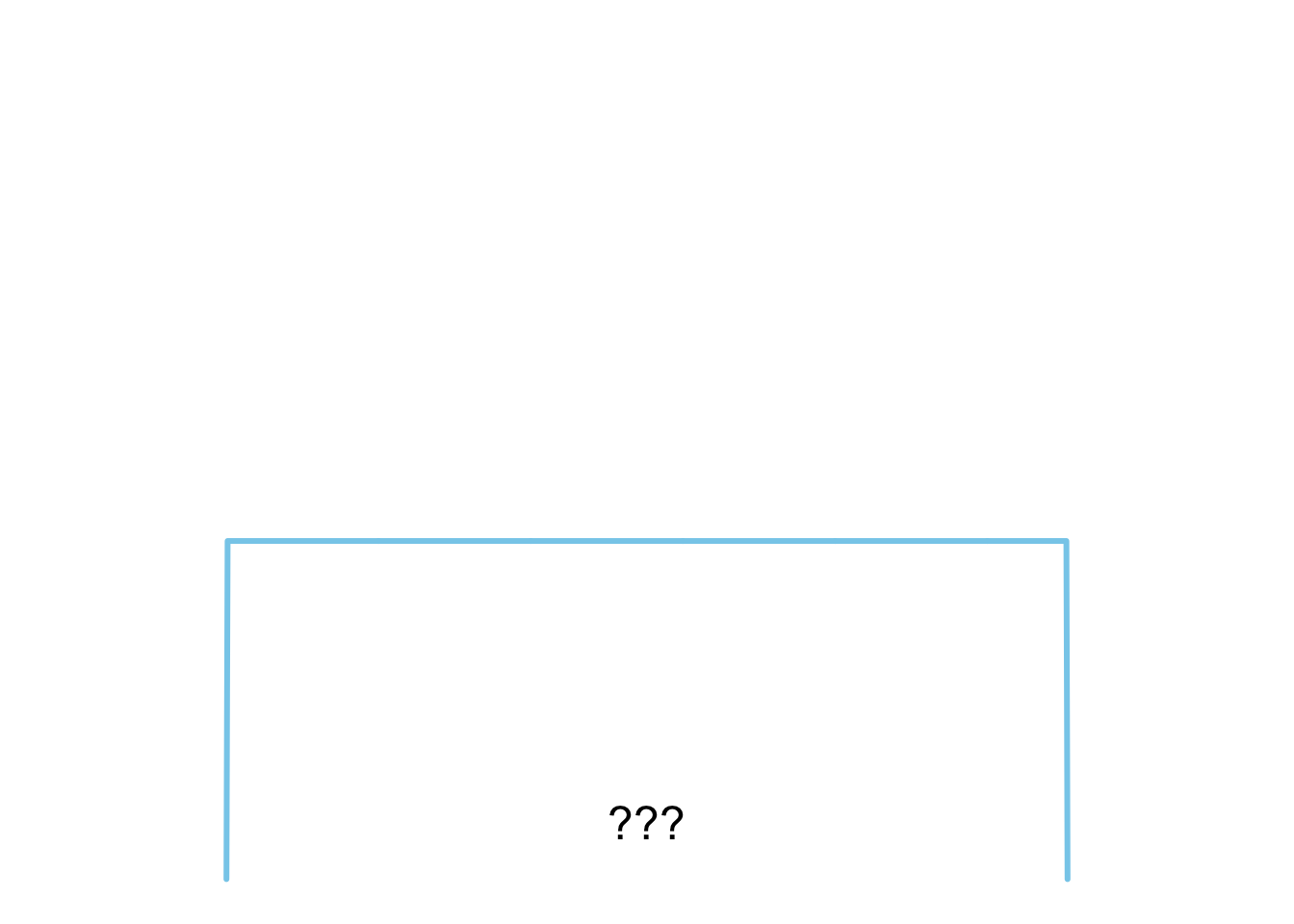
**C**
```{r}
plot_dist(dists$uniform)
```
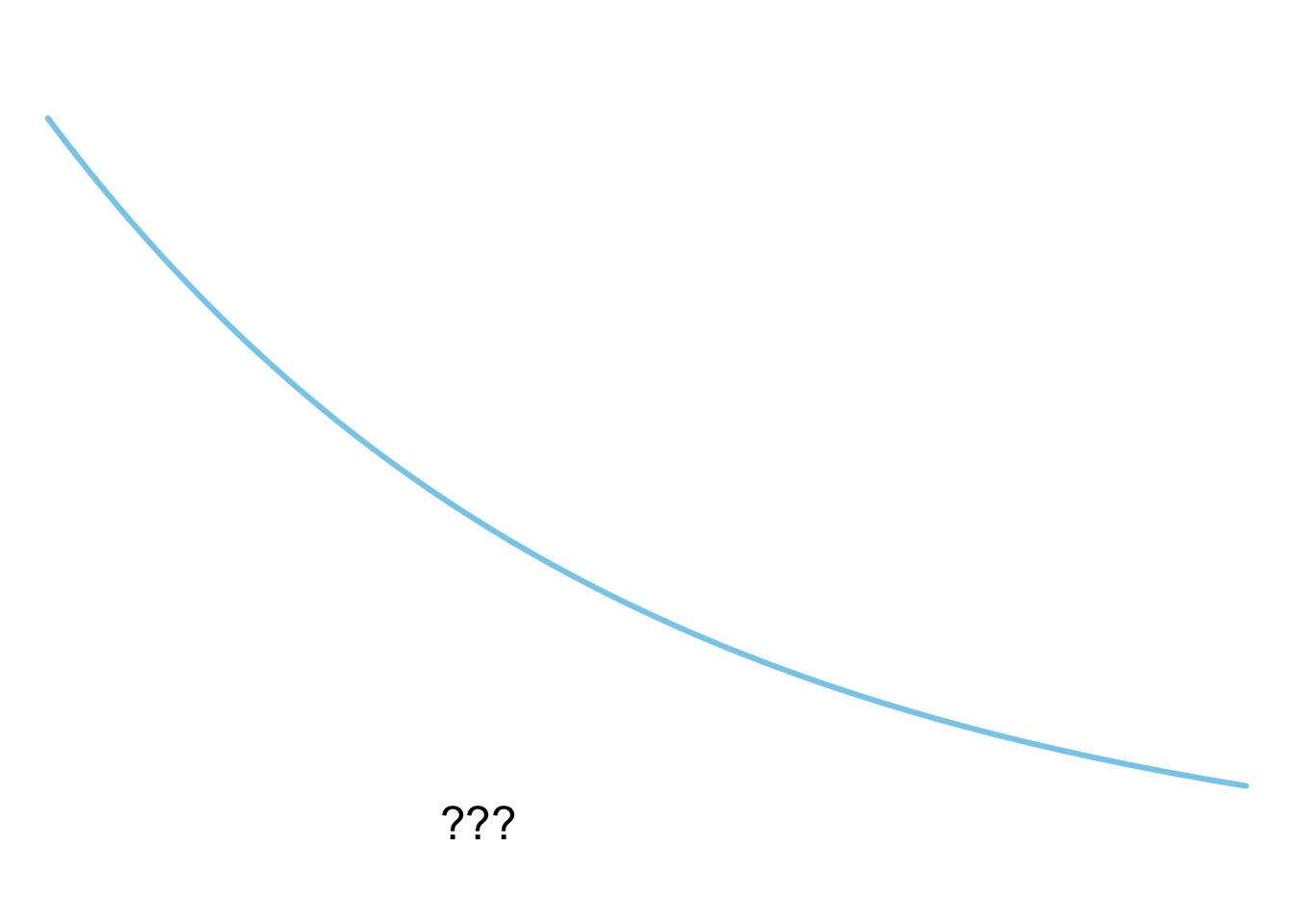
**D**
```{r}
plot_dist(dists$exponential)
```
1. Expontialverteilung
2. Normalverteilung
3. Binomialverteilung
4. Gleichverteilung
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
</br>
# Lösung
**A** - Binomialverteilung
**B** - Normalverteilung
**C** - Gleichverteilung
**D** - Expontialverteilung
Bildquelle:
Coded by Rasmus Bååth
rasmus.baath@lucs.lu.se
www.sumsar.net