bike06

regression

bayes

Published

September 26, 2025

1 Aufgabe

Importieren Sie die Bike-Share-Daten: https://archive.ics.uci.edu/dataset/275/bike+sharing+dataset. Verwenden Sie davon den Datensatz day.

Berechnen Sie das lineare Modell, das die Anzahl der geliehenen Fahrräder auf Basis ob es ein Werktag ist (ja/nein) vorhersagt.

Forschungsfrage:

AV: Anzahl der geliehenen Fahrräder (cnt)
UV: Werktag (ja oder nein) (workingday)

Aufgaben

Was ist der Punktschätzer des Effekts der UV?
Was ist die Modellgüte als Anteil der erklärten Varianz des Modells (durch die UV)?
Ist der Effekt signifikant?
Interpretieren Sie den Effekt inhaltlich!
Kann man die Nullhypothese \(H_0\) verwerfen?

Hinweise:

Beachten Sie die üblichen Hinweise des Datenwerks.

2 Lösung

2.1 Setup

R-Pakete starten:

library(tidyverse)
library(rstanarm)
library(easystats)
library(ggpubr)  # Visualisierung

In dieser Aufgabe geht es un den Bike-Sharing-Datensatz: https://archive.ics.uci.edu/dataset/275/bike+sharing+dataset.

Zuerst Daten von dort herunterladen und in einem geeigneten Ordner speichern.

Dann Daten importieren in RStudio:

library(tidyverse)
day <- read_csv(paste0(here::here(), "/data/bike+sharing+dataset/day.csv"))  # Achtung: Das ist der Pfad auf meinem Computer. Passen Sie ggf. den Pfad an Ihren Computer an.

Lösung

2.2 A) Punktschätzer des Effekts der UV

Regressionsformel: AV ~ UV

m_wday <- stan_glm(cnt ~ workingday, data = day)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 0.000334 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 3.34 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.337 seconds (Warm-up)
Chain 1:                0.095 seconds (Sampling)
Chain 1:                0.432 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1.1e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.11 seconds (Warm-up)
Chain 2:                0.1 seconds (Sampling)
Chain 2:                0.21 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1.1e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.122 seconds (Warm-up)
Chain 3:                0.095 seconds (Sampling)
Chain 3:                0.217 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1.2e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.126 seconds (Warm-up)
Chain 4:                0.095 seconds (Sampling)
Chain 4:                0.221 seconds (Total)
Chain 4:

Parameter des Modells anschauen:

parameters(m_wday)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	4327.5070	0.95	4085.03086	4576.3047	1.00000	0.9997801	4109.836	normal	4504.349	4843.029
workingday	257.7943	0.95	-34.47382	555.8299	0.95375	0.9998838	4052.879	normal	0.000	10409.891

Der Punktschätzer des Effekts der UV ist ca. 250. Der Punktschätzer des IEffekts der UV ist 258.

So bekommt man auch die Regressionskoeffizienten:

coef(m_wday)

(Intercept)  workingday 
  4327.5070    257.7943

2.3 B ) Modellgüte

Die Modellgüte berechnen wir hier mit \(R^2\):

r2(m_wday)

# Bayesian R2 with Compatibility Interval

  Conditional R2: 0.004 (95% CI [8.703e-09, 0.014])

Das Modell erklärt wie viel Prozent der Varianz in der AV durch die UV?

0.4%

Also sehr wenig. Der Werktag-Effekt ist sehr klein.

2.4 C) Signifikant? Nein.

die Null ist im Intervall enthalten, daher ist der Effekt NICHT signifikant.

2.5 D) Interpretation des Effekts

Der Effekt der UV workingday auf die AV cnt ist sehr klein und nicht signifikant.

Das bedeutet, dass es keinen nennenswerten Unterschied in der Anzahl der geliehenen Fahrräder zwischen Werktagen und Nicht-Werktagen gibt.

ggplot(day, aes(x = as.factor(workingday), y = cnt)) +
  geom_boxplot() +
  labs(x = "Werktag (0 = Nein, 1 = Ja)", y = "Anzahl geliehener Fahrräder") +
  theme_minimal()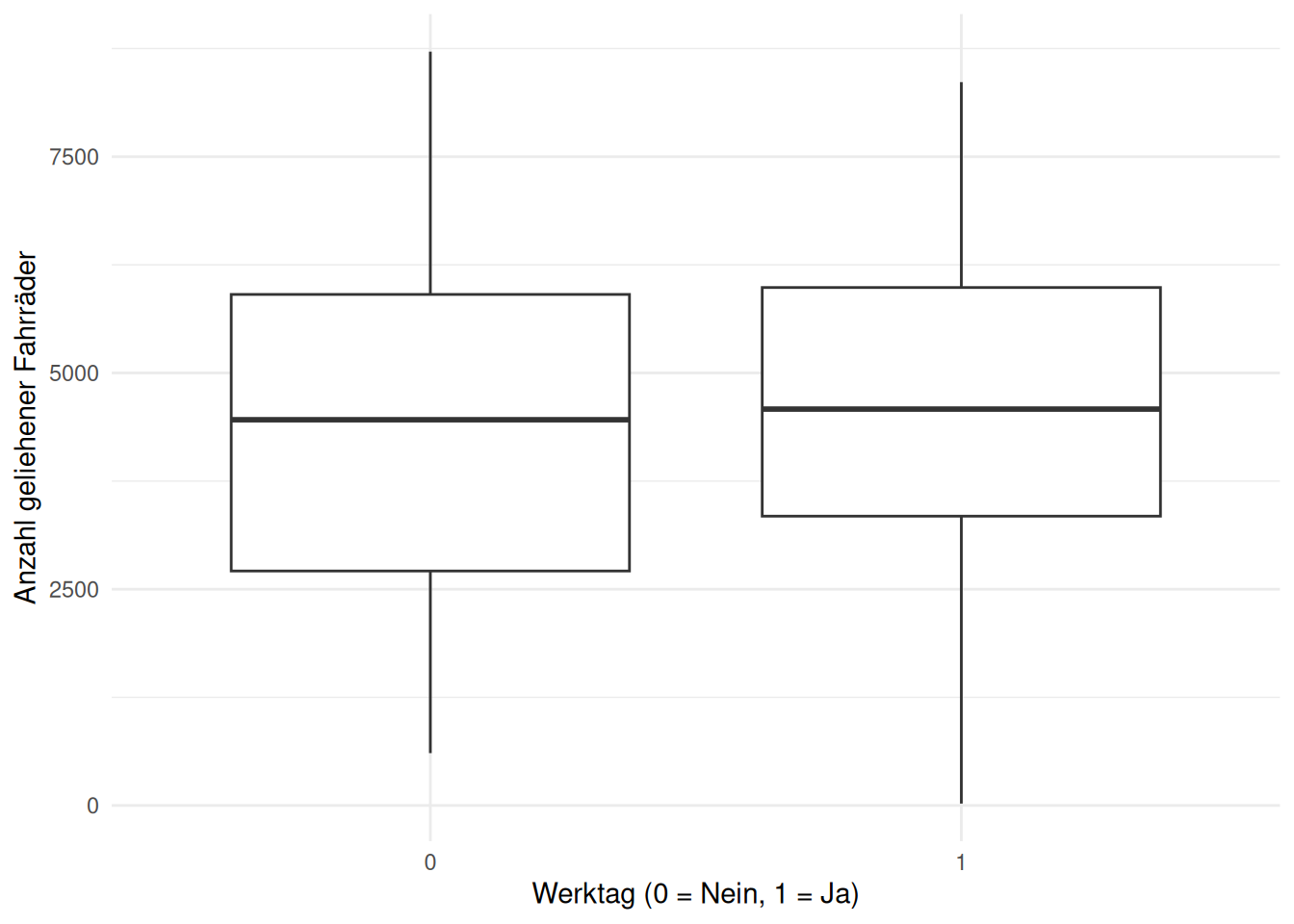

ggboxplot(day, x = "workingday", y = "cnt",
          xlab = "Werktag (0 = Nein, 1 = Ja)",
          ylab = "Anzahl geliehener Fahrräder",
          title = "Anzahl geliehener Fahrräder nach Werktag")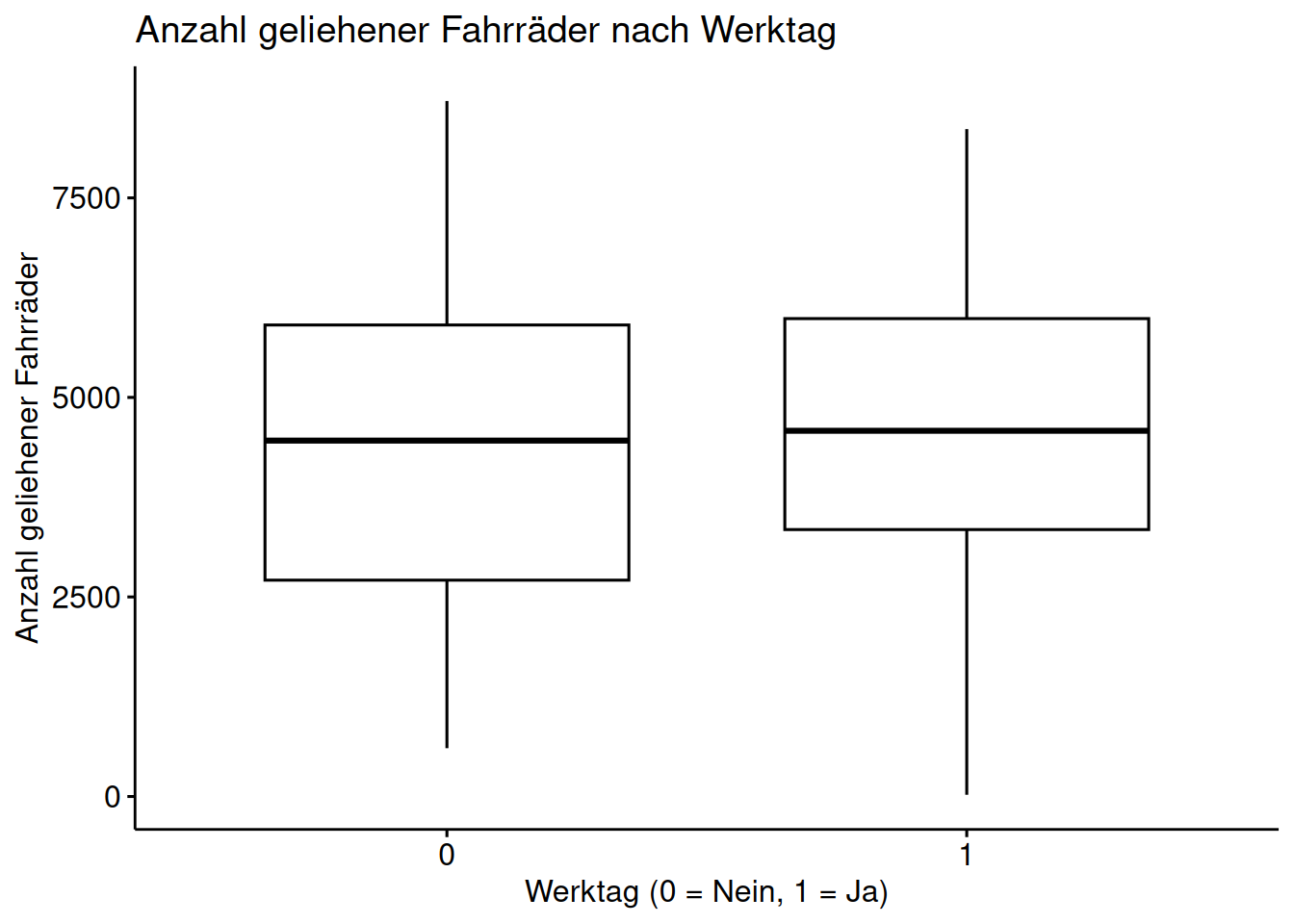

parameters(m_wday) |> plot()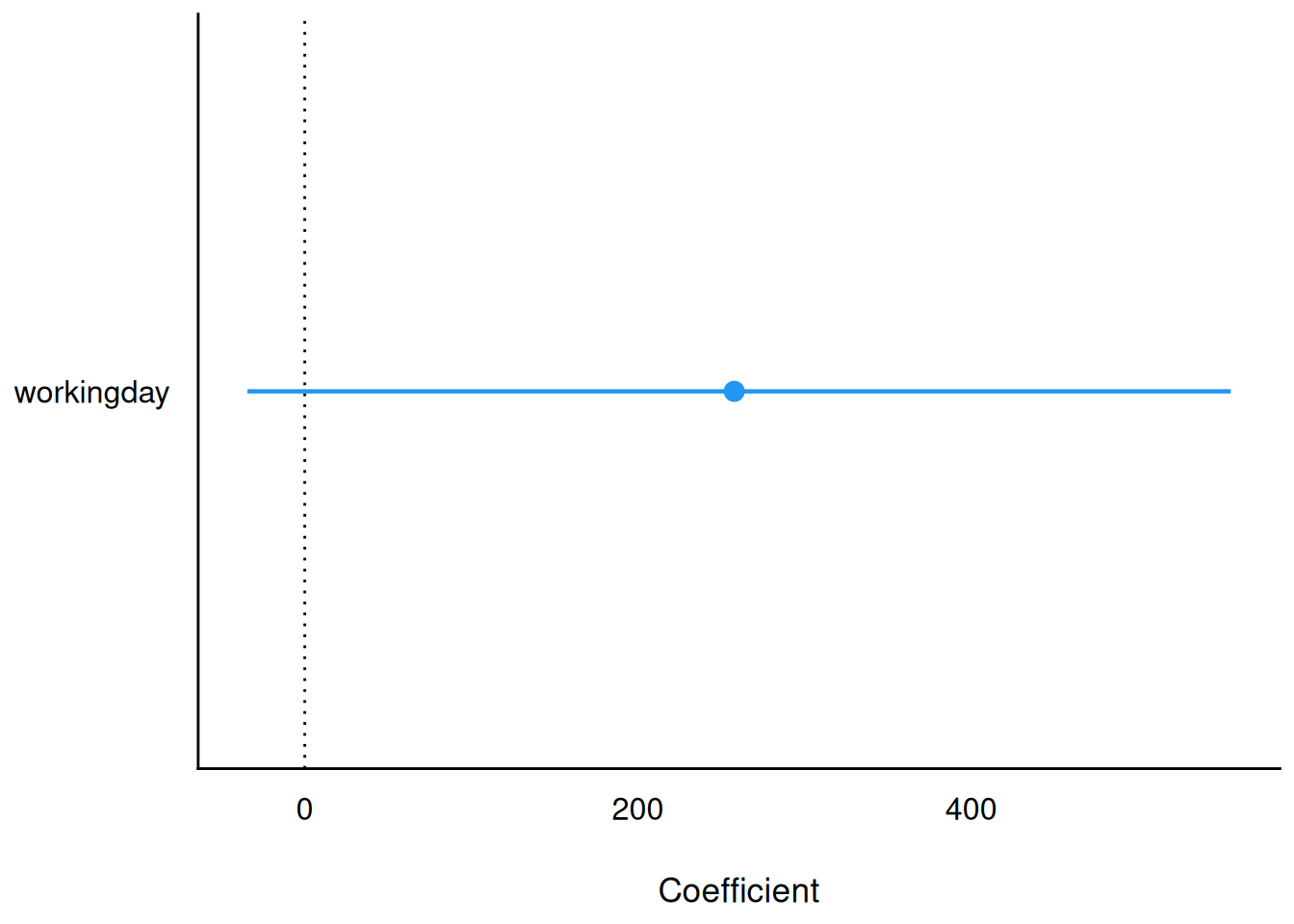

2.6 E) Nullhypothese verwerfen?

Nein, die Nullhypothese kann nicht verworfen werden, da die Null im Bereich plausibler Werte (des Effekts der UV, d.i. das 95% CI) enthalten ist.

3 Aufgabe 2: Effekt von `workingday` und `humidity` auf `cnt`

Berechnen Sie ein multiples Regressionsmodell, das die Anzahl der geliehenen Fahrräder (cnt) auf Basis dob es ein Werktag ist (ja/nein) (workingday) und der Luftfeuchtigkeit (hum) vorhersagt.

Nennen Sie die Regressionsformel
Nennen Sie die Breite des 95%-Konfidenzintervalls des Effekts der UV hum (ETI)
Ist der Effekt von Luftfeuchtigkeit signifikant?
Können wir die Rope-Hypothese verwerfen (± 300 Räder sind sind gerade noch vernachlässigbar).

3.1 A) Regressionsformel

cnt ~ workingday + humidity

Dazu das Modell berechnen:

m_wday_hum <- stan_glm(cnt ~ hum + workingday, data = day, refresh = 0, seed = 42)

3.2 B) Breite des 95%-Konfidenzintervalls des Effekts der UV `humidity` (ETI)

parameters(m_wday_hum)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	5192.2188	0.95	4538.92863	5828.5634	1.00000	0.9998781	5261.804	normal	4504.349	4843.029
hum	-1380.0002	0.95	-2334.85417	-418.7852	0.99800	0.9995747	5455.543	normal	0.000	34003.085
workingday	259.9066	0.95	-18.54882	552.6148	0.96525	1.0002255	4952.819	normal	0.000	10409.891

Die Breite berechnet sich als OG minus UG:

breite <-  -375.38 - -2401.38
breite

[1] 2026

Die Breite des 95%-Konfidenzintervalls des Effekts der UV humidity beträgt 2026.

3.3 C) Ist der Effekt von Luftfeuchtigkeit signifikant?

Hier ist noch mal das 95%-Konfidenzintervall des Effekts der UV hum:

[-2401.38, -375.38]

Wie man sieht, ist die Null NICHT enthalten. Daher ist der Effekt von hum signifikant.

3.4 D) Rope-Hypothese verwerfen?

rope(m_wday_hum, rope = c(-300, 300), parameters = "hum") |> plot()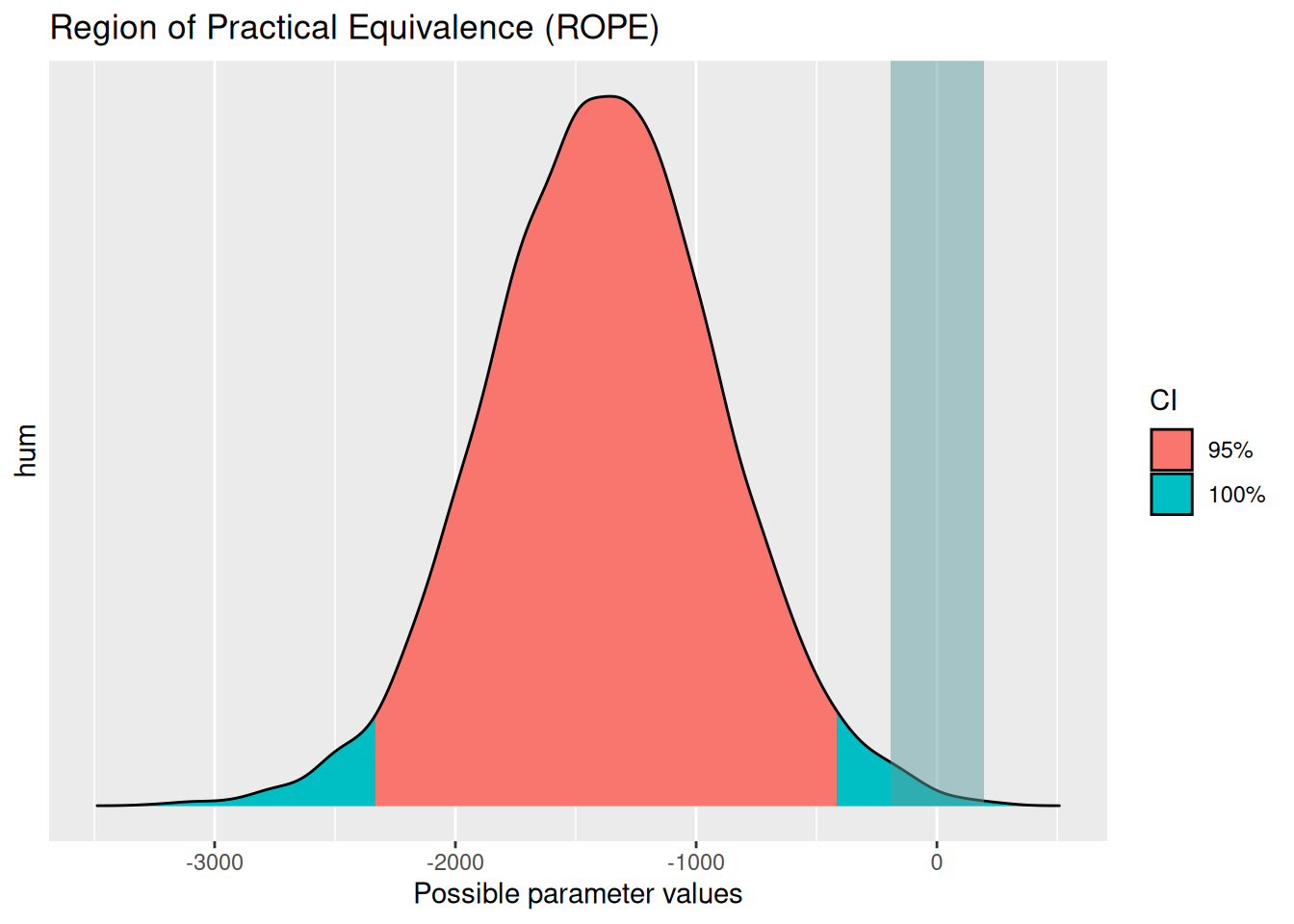

rope(m_wday_hum, rope = c(-300, 300), parameters = "hum")

Parameter	CI	ROPE_low	ROPE_high	ROPE_Percentage	Effects	Component
hum	0.95	-193.7211	193.7211	0	fixed	conditional

JA, die ROPE-Hypothese kann verworfen werden, da das komplette CI (der “rote Bereich der Post-Verteilung”) außerhalb der ROPE liegt.

4 Aufgabe 3: Interaktionseffekt zwischen `workingday` und `humidity` auf `cnt`

Visualisieren Sie das Modell mit den beiden UV workingday und humidity, aber OHNE Interaktionseffekt.

m_wday_hum |> estimate_relation() |> plot() +
  geom_point(data = day, aes(x = hum, y = cnt, color = as.factor(workingday)), alpha = 0.3)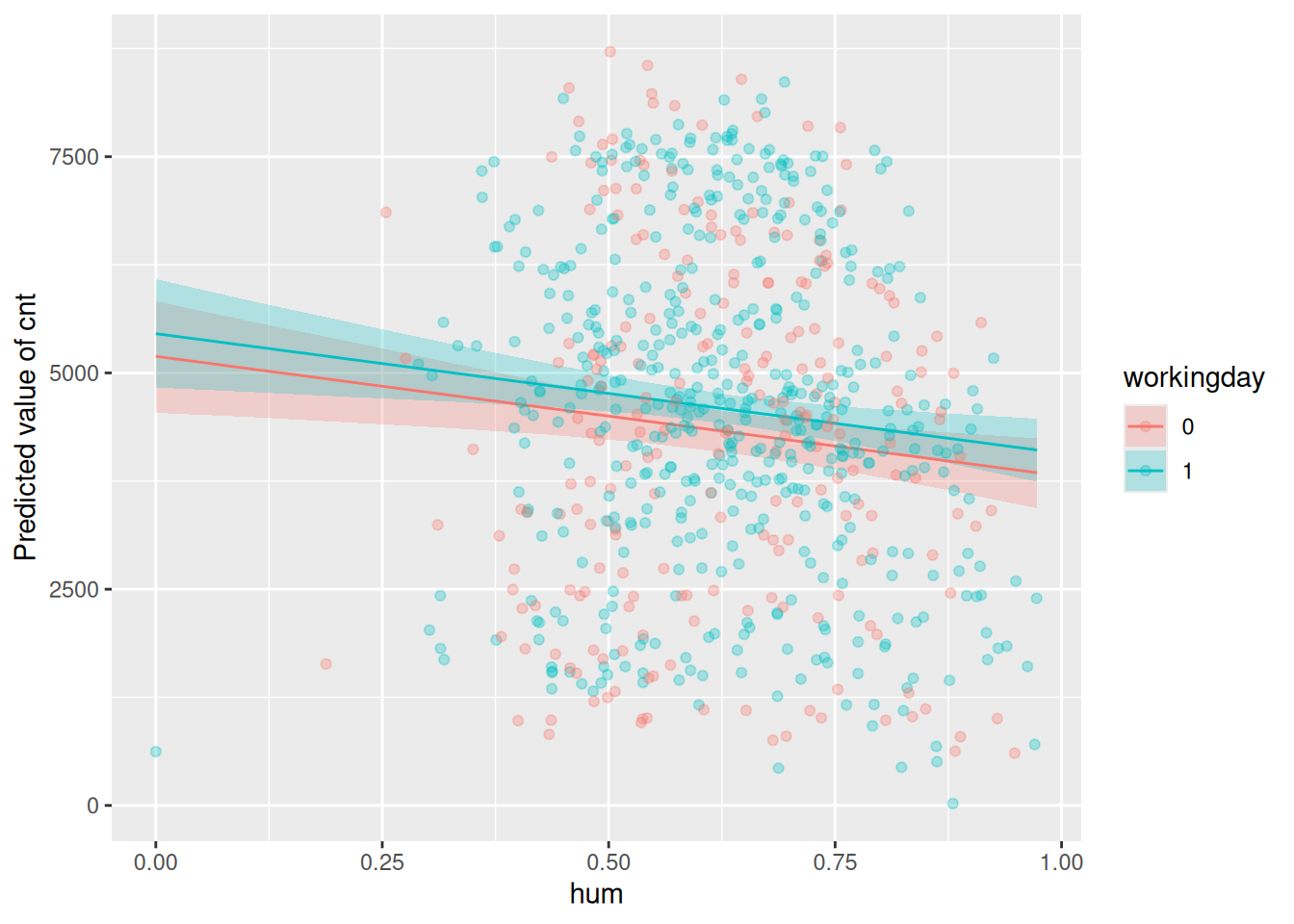

Aufgabe

Berechnen Sie das Modell mit Interaktionseffekt zwischen workingday und humidity. Geben Sie den Punktschätzer des Interaktionseffekts an.
Visualisieren Sie das Modell mit Interaktionseffekt zwischen workingday und humidity.
Interpretieren Sie den Interaktionseffekt inhaltlich.

4.1 A) Berechnen Sie das Modell mit Interaktionseffekt zwischen `workingday` und `humidity`.

Regressionsformel:

cnt ~ hum + workingday + hum:workingday

m_wday_hum_int <- stan_glm(cnt ~ hum + workingday + hum:workingday, data = day, refresh = 0, seed = 42)

Punktschätzer des Interaktionseffekts:

parameters(m_wday_hum_int)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	4468.7297	0.95	3401.66916	5615.8508	1.00000	1.001036	1223.375	normal	4504.349	4843.029
hum	-232.9443	0.95	-2005.44333	1431.7241	0.60025	1.000949	1245.009	normal	0.000	34003.085
workingday	1310.3101	0.95	-21.14374	2711.9522	0.97250	1.000523	1097.217	normal	0.000	10409.891
hum:workingday	-1670.1521	0.95	-3835.65003	406.3614	0.93750	1.000600	1083.852	normal	0.000	15344.292

Antwort: Der Punktschätzer des Interaktionseffekts beträgt -1670.15.

4.2 B) Visualisieren Sie das Modell mit Interaktionseffekt zwischen `workingday` und `humidity`.

ggplot(day, aes(x = hum, y = cnt, color = as.factor(workingday))) +
  geom_point(alpha = 0.5) +
  geom_smooth(method = "lm", se = FALSE) +
  labs(x = "Luftfeuchtigkeit", y = "Anzahl geliehener Fahrräder", color = "Werktag (0 = Nein, 1 = Ja)") +
  theme_minimal()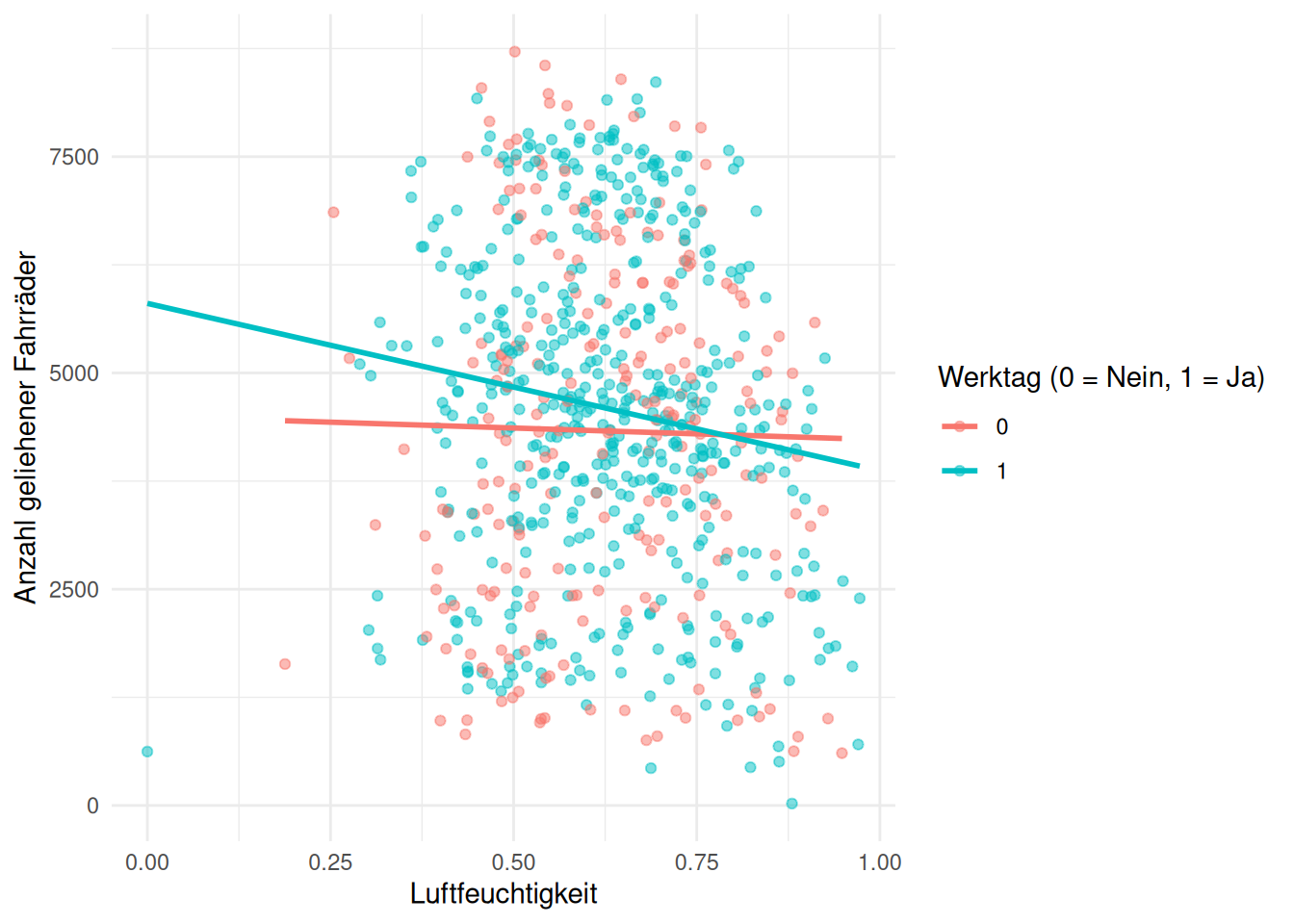

4.3 C) Interpretieren Sie den Interaktionseffekt inhaltlich.

cnt_predicted = 4517 * - 1373 * hum + 1266 * workingday + -1603 * hum*workingday

Das ist der Unterschied in den Steigungen pro Einheit in der UV zwischen den Gruppen.