bike05

probability

Published

December 18, 2025

1 Aufgabe

Laden Sie die Daten day.csv aus dem Bike Sharing Datensatz.

Berechnen Sie folgendes Modell: cnt ~ workingday, data = day.

Nennen Sie dann den Punktschätzer für \(\beta1\).
Interpretieren Sie diesen Wert.
Können wir die \(H_0\) für \(\beta_1\) ablehnen?
Visualisieren Sie den Gruppenunterschied mit einem geeigneten Plot.

Hinweise:

Beachten Sie die üblichen Hinweise des Datenwerks.

2 Lösung

Pakete starten:

library(tidyverse)
library(easystats)
library(rstanarm)

Daten importieren:

Achtung! Die herunter geladenen Daten müssen zuerst entzippt werden.

Bei mir liegen diese Daten hier:

day <- read_csv("C:/Users/sebastian.sauer/Downloads/bike+sharing+dataset/day.csv")

Bei Ihnen liegen die Daten in einem Ordner mit einem anderen Namen.

Falls der Datensatz im gleichen Ordner liegt wie Ihre Quarto-Datei, dann können Sie die Daten ohne Pfadangabe importieren:

day <- read_csv("day.csv")

Das ist auch eine gute Methode, um Daten zu importieren:

day <- read_csv(paste0(here::here(),"/data/bike+sharing+dataset/day.csv"))

3 Modell berechnen

m_cnt_workingday <-
  stan_glm(cnt ~ workingday, data = day)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 2.1e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.21 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.084 seconds (Warm-up)
Chain 1:                0.096 seconds (Sampling)
Chain 1:                0.18 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1.2e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.106 seconds (Warm-up)
Chain 2:                0.093 seconds (Sampling)
Chain 2:                0.199 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1.3e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.282 seconds (Warm-up)
Chain 3:                0.093 seconds (Sampling)
Chain 3:                0.375 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1.1e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.781 seconds (Warm-up)
Chain 4:                0.094 seconds (Sampling)
Chain 4:                0.875 seconds (Total)
Chain 4:

parameters(m_cnt_workingday)

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS	Prior_Distribution	Prior_Location	Prior_Scale
(Intercept)	4328.2613	0.95	4086.25605	4583.6317	1.0000	0.9998315	3906.202	normal	4504.349	4843.029
workingday	256.6653	0.95	-48.15344	562.4876	0.9505	0.9996434	3820.253	normal	0.000	10409.891

coef(m_cnt_workingday)[2]

workingday 
  256.6653

4 Interpretation

Bei mir Werte zwischen 250 und 260 zusätzlich vermietete Fahrräder an Arbeitstagen im Vergleich zu Nicht-Arbeitstagen.

5 Nullhypothese

Wir können die \(H_0\) für \(\beta_1\) NICHT ablehnen: Die Null ist im Konfidenzintervall enthalten.

parameters(m_cnt_workingday) |> plot()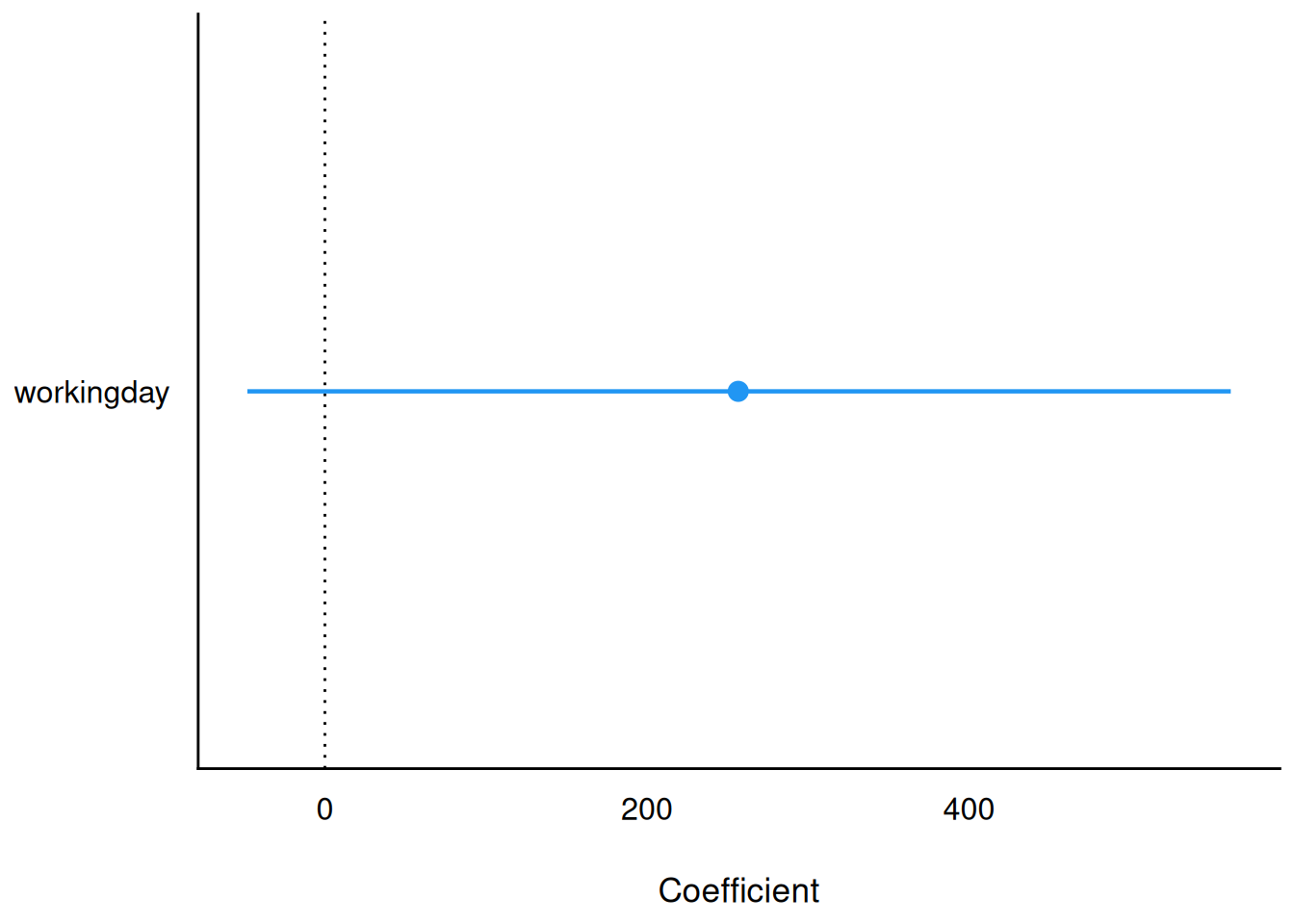

jklöjkjklöök