| z | p |
|---|---|
| -2.0 | 0.02 |
| -1.9 | 0.03 |
| -1.8 | 0.04 |
| -1.7 | 0.04 |
| -1.6 | 0.05 |
| -1.5 | 0.07 |
| -1.4 | 0.08 |
| -1.3 | 0.10 |
| -1.2 | 0.12 |
| -1.1 | 0.14 |
| -1.0 | 0.16 |
| -0.9 | 0.18 |
| -0.8 | 0.21 |
| -0.7 | 0.24 |
| -0.6 | 0.27 |
| -0.5 | 0.31 |
| -0.4 | 0.34 |
| -0.3 | 0.38 |
| -0.2 | 0.42 |
| -0.1 | 0.46 |
| 0.0 | 0.50 |
| 0.1 | 0.54 |
| 0.2 | 0.58 |
| 0.3 | 0.62 |
| 0.4 | 0.66 |
| 0.5 | 0.69 |
| 0.6 | 0.73 |
| 0.7 | 0.76 |
| 0.8 | 0.79 |
| 0.9 | 0.82 |
| 1.0 | 0.84 |
| 1.1 | 0.86 |
| 1.2 | 0.88 |
| 1.3 | 0.90 |
| 1.4 | 0.92 |
| 1.5 | 0.93 |
| 1.6 | 0.95 |
| 1.7 | 0.96 |
| 1.8 | 0.96 |
| 1.9 | 0.97 |
| 2.0 | 0.98 |
bfi10
1 Aufgabe
Auf der Webseite des Leibniz-Instituts für Sozialwissenschaften, GESIS kann man u.a. psychologische Skalen für die Forschung finden. Eine dieser Skalen ist as Big Five Inventory (BFI-10). Autor/in: Rammstedt, B., Kemper, C. J., Klein, M. C., Beierlein, C., & Kovaleva, A. In Tabelle 8 sind “Referenzwerte” für das Merkmal “Extraversion” angegeben. Die Werte sind als Mittelwert und Standardabweichung angegeben:
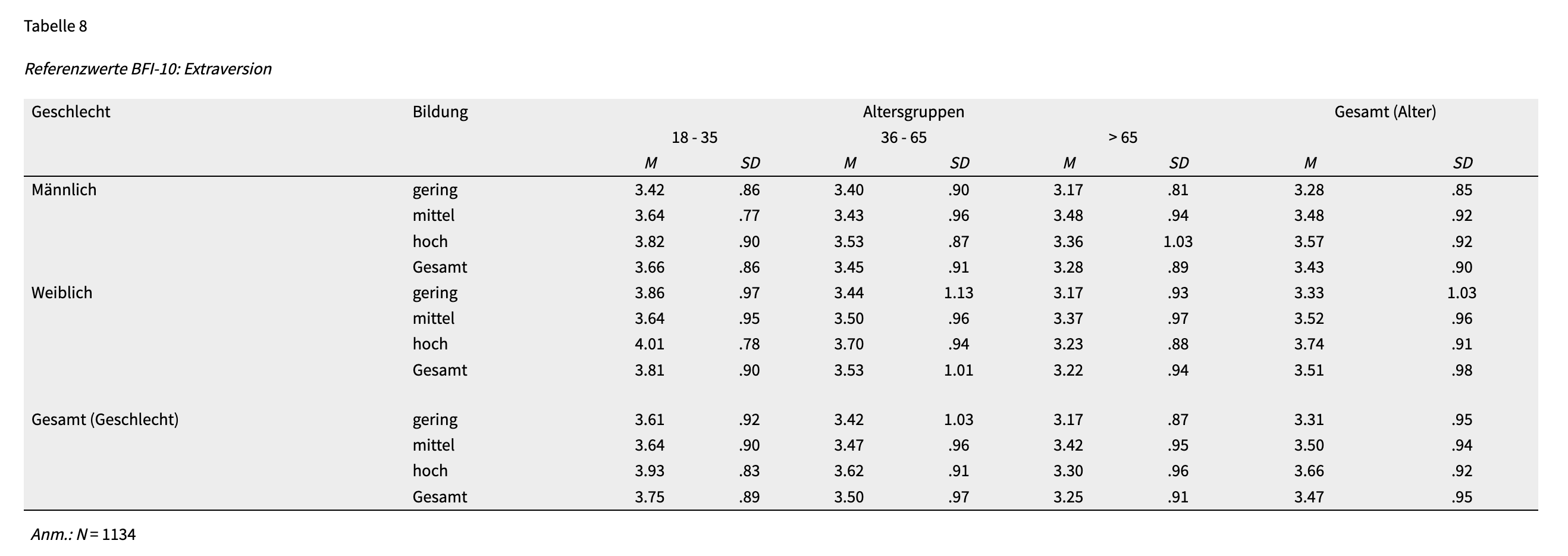
Den Artikel zu dieser Skala findet man hier.
Gehen wir davon aus, dass das Merkmalsverhalten normalverteilt ist. Dann können wir die Verteilungsfunktion der Extraversion berechnen.
Eine Normalverteilungstabelle findet sich z.B. bei Wikipedia oder z.B. hier.
Eine kürzere Tabelle zur Verteilungsfunktion der Standardnormalverteilung ist hier wiedergegeben.
Aufgabe Geben Sie die Wahrscheinlichkeit an, dass ein Mann im Alter von 19 Jahren mit geringer Bildung einen Extraversionsscore von 4.28 oder weniger hat.
2 Lösung
Mit Hilfe des Computers ist es komfortabel. Wir können die Funktion pnorm verwenden, um die Wahrscheinlichkeit zu berechnen, dass ein Mann im Alter von 19 Jahren mit geringer Bildung einen Extraversionsscore von 4.28 oder weniger hat.
pnorm(4.28, mean = 3.42, sd = 0.86)[1] 0.8413447Ansonsten muss man die Standardnormalverteilungstabelle verwenden. Dafür transformiert man den Wert 4.28 in einen z-Wert.
Den Z-wert berechnet man mit der Formel:
\[z = \frac{x - \mu}{\sigma}\]
z <- (4.28 - 3.42) / 0.86
z[1] 1Den Wert der kumulierten Wahrscheinlichkeit kann man in der Tabelle nachschlagen.
Das bedeutet, dass die Wahrscheinlichkeit, dass ein Mann im Alter von 19 Jahren mit geringer Bildung einen Extraversionsscore von 4.28 oder weniger hat, .84 beträgt.
xpnorm(q = 4.28, mean = 3.42, sd = .86)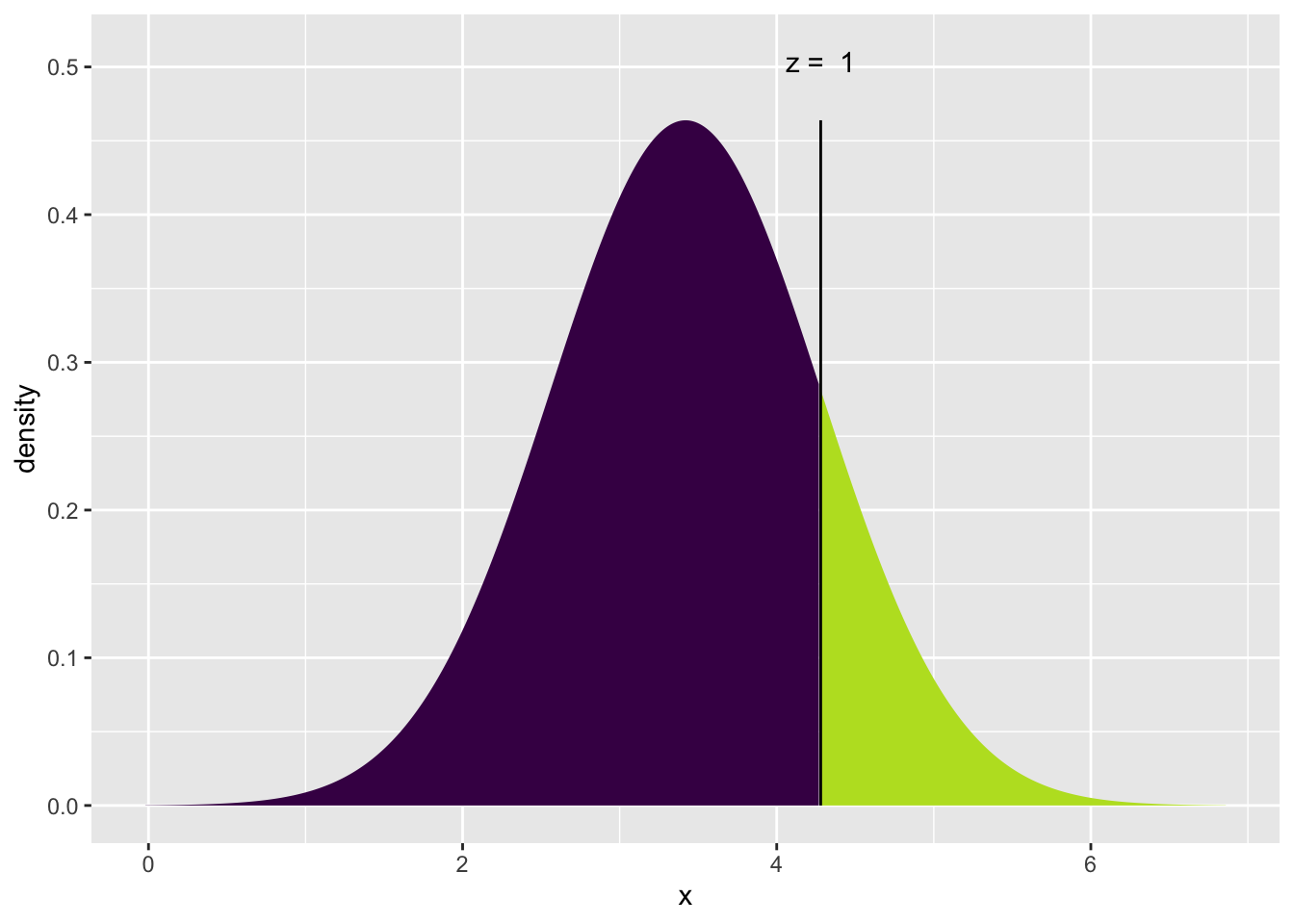
[1] 0.8413447Bonusfrage
Wie hoch ist die Wahrscheinlichkeit, einen jungen Mann mit geringer Bildung (19 Jahre) zu testen, der über einen Extraversionswert von mind. 3.42 verfügt?
Antwort
50%, da 3.42 genau dem Mittelwert der Verteilung entspricht. Da die Verteilung symmetrisch ist, ist die Wahrscheinlichkeit, dass ein Wert größer als der Mittelwert ist, gleich der Wahrscheinlichkeit, dass ein Wert kleiner als der Mittelwert ist.
xpnorm(q = 3.42, mean = 3.42, sd = .86)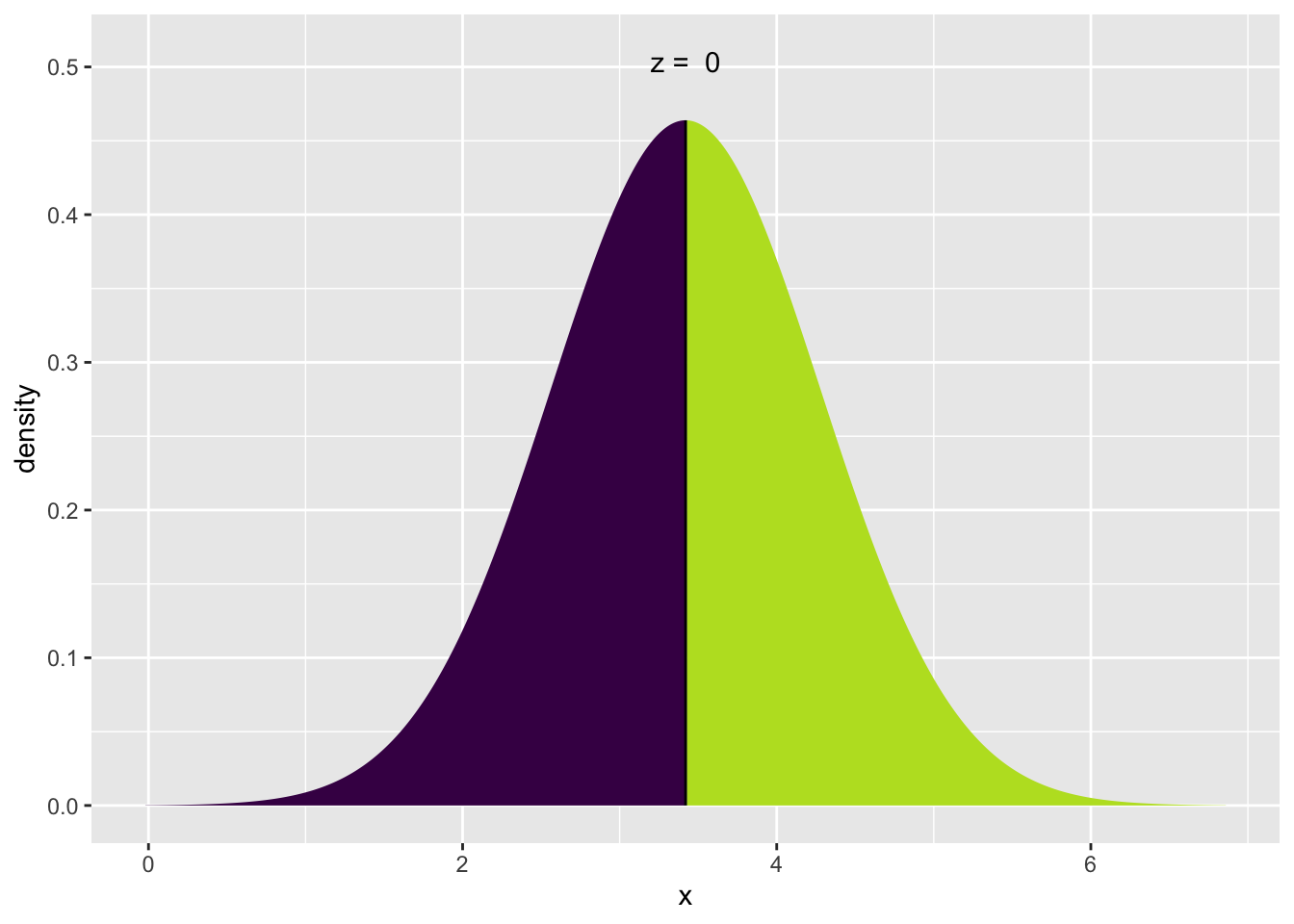
[1] 0.5