d <-
tibble(Lerntyp = c(rep("Weniglerner", times = n_weniglerner),
rep("Viellerner", times = n_viellerner))) %>%
mutate(Lerntyp = factor(Lerntyp)) %>%
mutate(Erfolg_p = case_when(
Lerntyp == "Weniglerner" ~ erfolgsquote_viellerner,
Lerntyp == "Viellerner" ~ erfolgsquote_viellerner,
TRUE ~ NA_real_
)) %>%
mutate(Klausurergebnis = map_chr(.x = Erfolg_p,
.f = ~(sample(Klausurergebnis,
size = 1,
prob = c(.x, 1-.x)))))Bed-Wskt1
Aufgabe
Prof. Bitter-Süß untersucht eine seiner Lieblingsfragen: Wie viel bringt das Lernen auf eine Klausur? Dabei konzentriert er sich auf das Fach Statistik (es gefällt ihm gut). In einer aktuellen Untersuchung hat er \(n=90\) Studierende untersucht (s. Tabelle und Diagramm) und jeweils erfasst, ob die Person die Klausur bestanden (b) hat oder durchgefallen (d) ist. Dabei hat er zwei Gruppen unterschieden: Die “Viel-Lerner” (VL) und die “Wenig-Lerner” (WL).
Berechnen Sie die folgende bedingte Wahrscheinlichkeit: p(Durchfallen|Weniglerner).
Beispiel: Wenn Sie ausrechnen, dass die Wahrscheinlichkeit bei 42 Prozentpunkten liegt, so geben Sie ein: 0,42 bzw. 0.42 (das Dezimalzeichen ist abhängig von Ihren Spracheinstellungen).
Hinweise:
- Geben Sie nur eine Zahl ein (ohne Prozentzeichen o.Ä.), z.B.
0,42. - Andere Angaben können u.U. nicht gewertet werden.
- Runden Sie auf zwei Dezimalstellen.
- Achten Sie darauf, das korrekte Dezimaltrennzeichen einzugeben; auf Geräten mit deutscher Spracheinstellung ist dies oft ein Komma.
ggplot(d) +
aes(x = Lerntyp, fill = factor(Klausurergebnis)) +
geom_bar() +
labs(fill = "")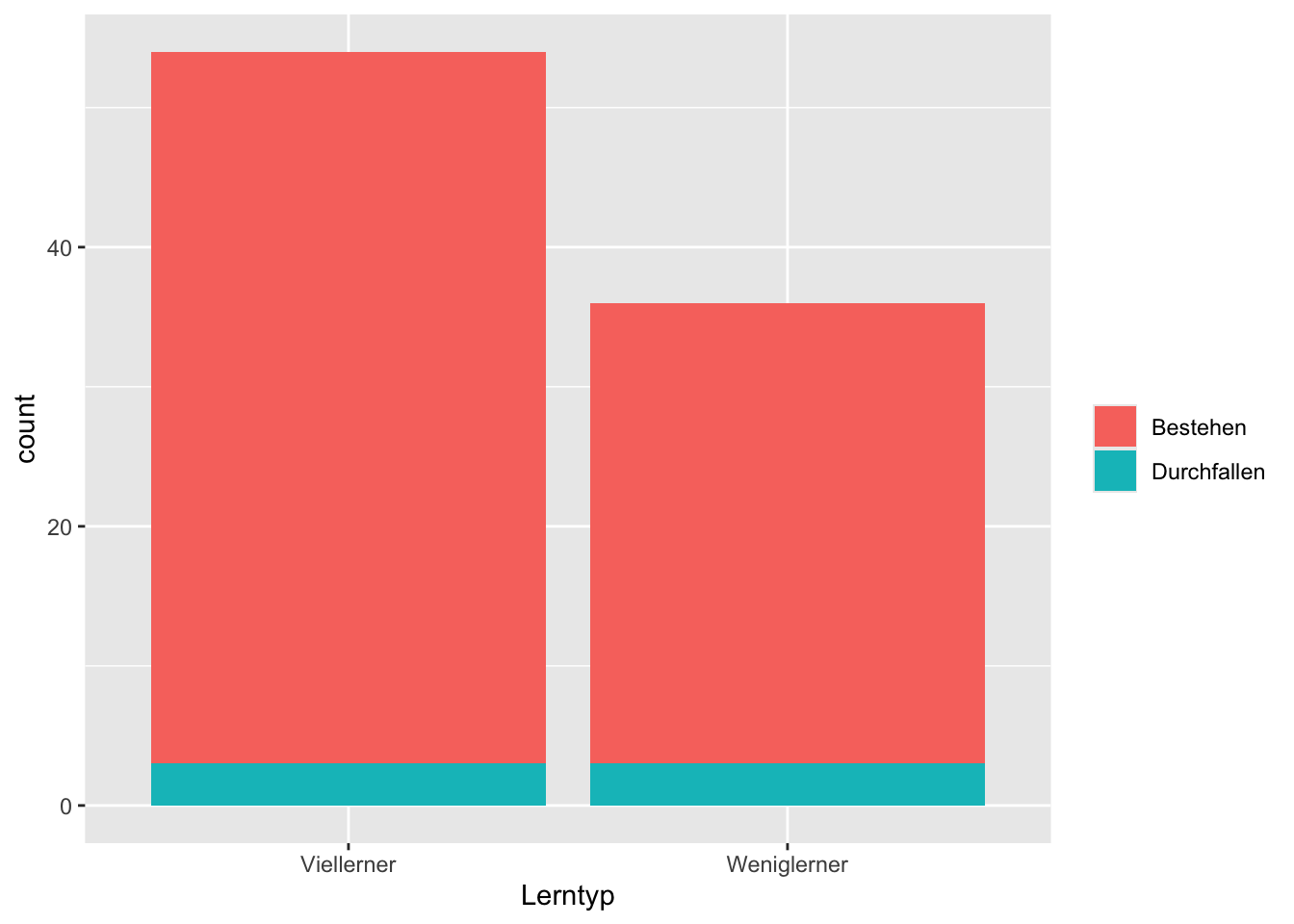
mosaic::tally(Klausurergebnis ~ Lerntyp, data = d) %>%
kbl(caption = "Ergebnisse der Studie") %>%
kable_classic(full_width = F, html_font = "Cambria")| Viellerner | Weniglerner | |
|---|---|---|
| Bestehen | 51 | 33 |
| Durchfallen | 3 | 3 |
Lösung
prob_conditional %>%
filter(Lerntyp == Lerntyp_selected,
Klausurergebnis == Klausurergebnis_selected) %>%
gt()| Lerntyp | Klausurergebnis | n | n_group | prop_conditional_group | N_gesamt |
|---|---|---|---|---|---|
| Weniglerner | Durchfallen | 3 | 36 | 0.08333333 | 90 |
n <-
prob_conditional %>%
filter(Lerntyp == Lerntyp_selected,
Klausurergebnis == Klausurergebnis_selected) |>
pull(n)
n_group <-
prob_conditional %>%
filter(Lerntyp == Lerntyp_selected,
Klausurergebnis == Klausurergebnis_selected) |>
pull(n_group)Antwort: Der gesuchte Wert liegt bei \(3 / 36 = 0.08\).
Categories:
- probability
- bayes
- num